Лабораторная работа измерение движения тела по окружности: Лабораторные работы №1 (10 класс)

Содержание

Лабораторная работа № 5 «Изучение движения тела по окружности под действием сил упругости и тяжести»

Цель работы: убедиться в том, что при движении тела по окружности под действием нескольких сил их равнодействующая равна произведению массы тела на ускорение: F = ma. Для этого используется конический маятник (рис. 178, а).

На прикрепленное к нити тело (им в работе является груз из

набора по механике) действуют сила тяжести F₁ и сила упругости F₂. Их равнодействующая равна

Сила F и сообщает грузу центростремительное ускорение

(r — радиус окружности, по которой движется груз, Т — период его обращения) .

Для нахождения периода удобно измерить время t определенного числа N оборотов. Тогда Т =

Модуль равнодействующей F сил F₁ и F₂ можно измерить, скомпенсировав ее силой упругости F_упр пружины динамометра так, как это показано на рисунке 178, б.

Согласно второму закону Ньютона,

При подстановке в

это равенство полученных в опыте значений F

ynp, m и а может оказаться, что левая часть этого равенства отличается от единицы.

Это и позволяет оценить погрешность эксперимента.

Средства измерения: 1) линейка с миллиметровыми делениями; 2) часы с секундной стрелкой; 3) динамометр.

Материалы: 1) штатив с муфтой и кольцом; 2) прочная нить; 3) лист бумаги с начерченной окружностью радиусом 15 см; 4) груз из набора по механике.

Порядок выполнения работы

1. Нить длиной около 45 см привяжите к грузу и подвесьте к кольцу штатива.

2. Одному из учащихся взяться двумя пальцами за нить у точки подвеса и привести во вращение маятник.

3. Второму учащемуся измерить лентой радиус r окружности, по которой движется груз. (Окружность можно начертить заранее на бумаге и по этой окружности привести в движение маятник.)

4. Определите период Т обращения маятника при помощи, часов с секундной стрелкой.

Для этого учащийся, вращающий маятник, в такт с его оборотами произносит вслух: нуль, нуль и т. д. Второй учащийся с часами в руках, уловив по секундной стрелке удобный момент для начала отсчета, произносит: «нуль», после чего первый вслух считает число оборотов.

Отсчитав 30—40 оборотов, фиксирует промежуток времени t. Опыт повторяют пять раз.

5. Рассчитайте среднее значение ускорения по формуле (1), учитывая, что с относительной погрешностью не более 0,015 можно считать π² = 10.

6. Измерьте модуль равнодействующей F, уравновесив ее силой упругости пружины динамометра (см. рис. 178, б).

7. Результаты измерений занесите в таблицу:

Номер

опыта

t, с

t_ср,с

m, кг

а,

м/с²

F_упр,

8. Сравните отношение

с единицей и сделайте вывод о погрешности экспериментальной проверки того, что центростремительное ускорение сообщает телу векторная сумма действующих на него сил.

Груз из набора по механике, подвешенный на закрепленную в верхней точке нить, движется в горизонтальной плоскости по окружности радиуса r под действием двух сил:

силы тяжести

и силы упругости N.

Равнодействующая этих двух сил F направлена горизонтально к центру окружности и сообщает грузу центростремительное ускорение.

Т — период обращения груза по окружности. Его можно вычислить подсчитав время, за которое груз совершает некоторое число полных оборотов

Центростремительное ускорение рассчитаем по формуле

Теперь, если взять динамометр и прикрепить его к грузу, как показано на рисунке, можно определить силу F (равнодействующую сил mg и N.

Если груз отклонен от вертикали на расстояние г, как и при движении по окружности, то сила F равна той силе, которая вызывала движение груза по окружности.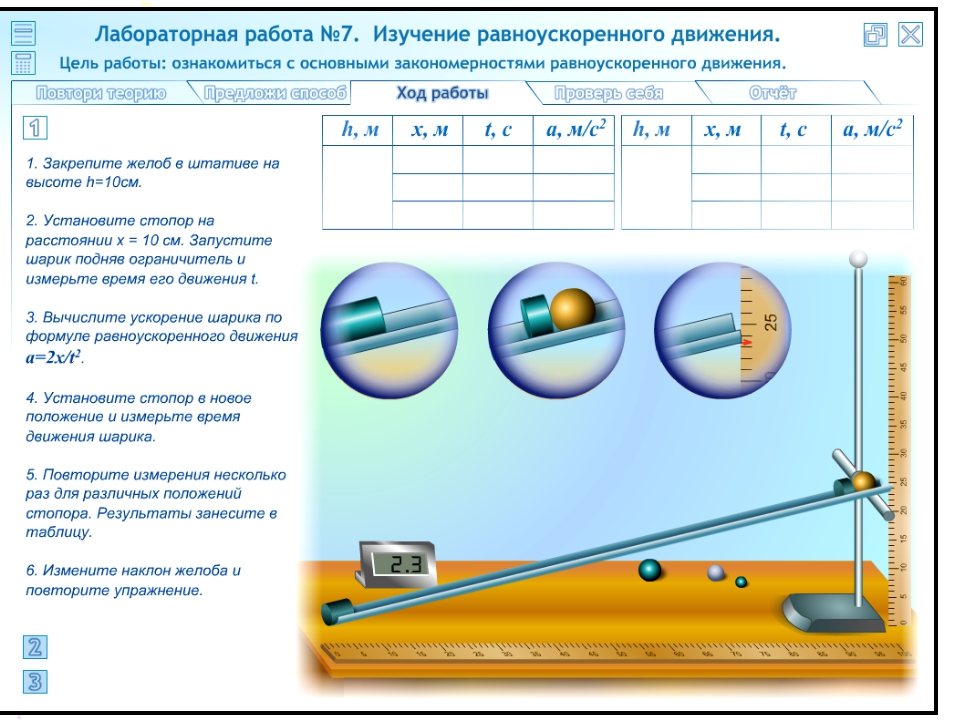 Мы получаем возможность сравнить значение силы F , полученное путем прямого измерения и силы ma, рассчитанной по результатам косвенных измерений и

сравнить отношение

с единицей. Для того, чтобы радиус окружности, по которой движется груз, изменялся вследствие влияния сопротивления воздуха медленнее и изменение это незначительно влияло на измерения, следует выбирать его небольшим (порядок 0,05~0,1 м).

Выполнение работы

№ опыта	t, с	t_ср, с	n	m, кг	r, м	а, м/с²	F, H

Вычисления

Оценка погрешностей. Точность измерения: линейка —

секундомер

динамометр

Подсчитаем погрешность определения периода (если считать, что число n определено точно):

Погрешность определения ускорения подсчитаем как:

Погрешность определения ma

(7%), то есть

С другой стороны, силу F мы измерили со следующей погрешностью:

Такая погрешность измерения, конечно, очень велика.

Измерения с такими погрешностями годны только для приблизительных оценок. Отсюда видно, что отклонение отношение

от единицы может быть существенным при использовании примененных нами способов измерения^*.

¹* Так что вам не следует смущаться, если в этой лабораторной работе отношение

будет отличным от единицы. Просто аккуратно оцените все погрешности измерений и сделайте соответствующий вывод.

Лабораторная работа по теме: «Изучение движения тела по окружности под действием сил упругости и тяжести» ❤️

Цель урока: продолжить формирование умения вести наблюдения и ставить опыты, самостоятельно работать с книгой, определять центростремительное ускорение шарика – при его равномерном движении по окружности.

Ход урока

Организационный момент

Алгоритм выполнения лабораторной работы

— Формулируем самостоятельно цели опыта;

— Какие условия, необходимы для проведения опытов;

— Составляем план эксперимента;

— Выбираем нужные для опытов приборы и материалы

— Собираем

по рисунку установку для проведения опытов и создаем условия для выполнения эксперимента

— Выполняем необходимые измерения;

— Проводим наблюдения;

— Записываем результаты измерений и наблюдений

— Производим математические вычисления результатов измерений;

— Формулировка выводов и анализ полученных результатов

Цель лабораторной работы: определить значение центростремительного ускорения шарика при его движение по окружности.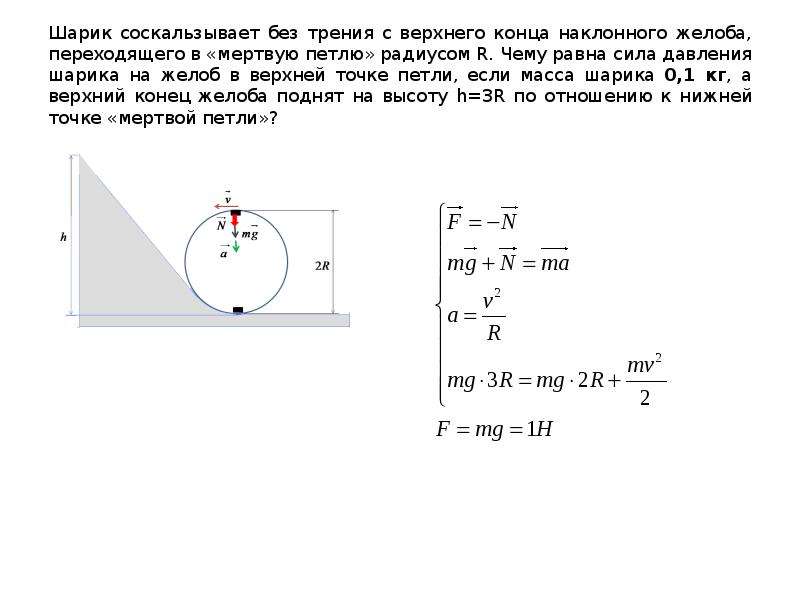

Оборудование: штатив с муфтой и лапкой, измерительная лента, циркуль, динамометр, весы с разновесами, шарик на нити, лист бумаги, линейка.

Выполнение лабораторной работы.

1. Определим массу шарика с точностью до 1 г.

2. Приведем груз во вращение по нарисованной окружности радиуса R= 15см= 0,15м. Измерим время Δt, за которое тело совершит 40 оборотов. Повторим опыт 3 раза.

3. Результаты занесем в таблицу:

	1-ый опыт	2-ой опыт	3-ий опыт	Среднее
R (м)
Δt (c)
N

Rчр= 1/3 (R1+ R2+ R3)

4. Вычислим период колебаний: T= Δt/ N

5. Вычислим центростремительное ускорение: a1 = 4π²R/T²

6. Определим высоту конуса h, для этого измерим длину нити от точки подвеса до центра шарика.

7. Вычислим модуль центростремительного ускорения по формуле; a₂= gR/h

8. Отклонив груз на такой же угол как при вращении, динамометром измерим действующую силу F и вычислим ускорение по формуле: a3 = F/m

9. Результаты занесем в таблицу.

R (м)	N	Δt (c)	h (м)	m (кг)	T (c)	а₁ (м/с²)	а₂ (м/с²	а₃ (м/с²)

Вывод: сравнивая полученные три значения центростремительного ускорения, измеренные из кинематических и динамических соображений, убеждаемся, что они приблизительно равны.

Это подтверждает, во – первых, правильность наших измерений, во – вторых второй закон Ньютона.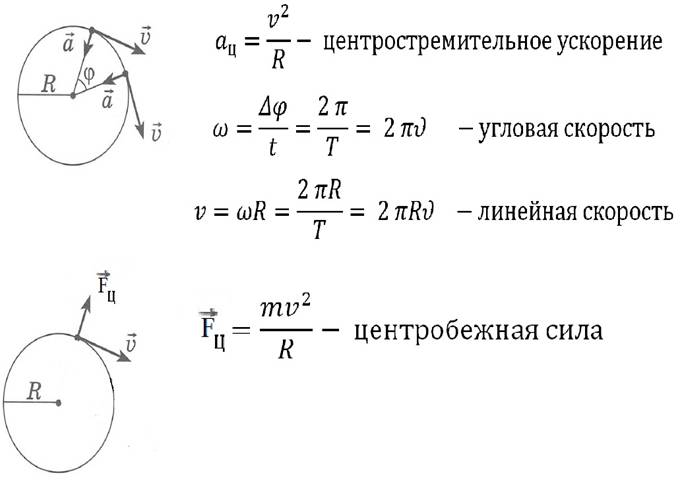

Заключительная беседа по итогам лабораторной работы.

Домашнее задание: задачи из упр. 7 №3, №4, повторить «Краткие итоги главы»

Лабораторная работа изучение тела по окружности. Лабораторная работа. Изучение движения тела по окружности под действием силы упругости и силы тяжести. Движение тела под углом к горизонту

Упругости и тяжести

Цель работы

Определение центростремительного ускорения шарика при его равномерном движении по окружности

Теоретическая часть работы

Эксперименты проводятся с коническим маятником: небольшой шарик, подвешенный на нити движется по окружности. При этом нить описывает конус (рис.1). На шарик действуют две силы: сила тяжести и сила упругости нити. Они создают центростремительное ускорение, направленное по радиусу к центру окружности. Модуль ускорения можно определить кинематически. Он равен:

Для определения ускорения (a) нужно измерить радиус окружности (R) и период обращения шарика по окружности (T).

Центростремительное ускорение можно определить так же, используя законы динамики.

Согласно второму закону Ньютона, Запишем данное уравнение в проекциях на выбранные оси (рис.2):

Ох: ;

Oy: ;

Из уравнения в проекции на ось Ох выразим равнодействующую:

Из уравнения в проекции на ось Оу выразим силу упругости:

Тогда равнодействующая может быть выражена:

а отсюда ускорение: , где g=9,8 м/с 2

Следовательно, для определения ускорения необходимо измерить радиус окружности и длину нити.

Оборудование

Штатив с муфтой и лапкой, лента измерительная, шарик на нити, лист бумаги с начерченной окружностью, часы с секундной стрелкой

Ход работы

1. Подвесить маятник к лапке штатива.

2. Измерить радиус окружности с точностью до 1мм. (R)

3. Штатив с маятником расположить так, чтобы продолжение шнура проходило через центр окружности.

4. Взять пальцами нить у точки подвеса, вращать маятник так, чтобы шарик описывал окружность, равную начерченной на бумаге.

6. Определить высоту конического маятника (h). Для этого измерить расстояние по вертикали от точки подвеса до центра шарика.

7. Найти модуль ускорения по формулам:

8. Вычислить погрешности.

Таблица Результаты измерений и вычислений

Вычисления

1. Период обращения: ; Т=

2. Центростремительное ускорение:

; а 1 =

; а 2 =

Среднее значение центростремительного ускорения:

; а ср =

3. Абсолютная погрешность:

∆а 1 =

∆а 2 =

4. Среднее значение абсолютной погрешности: ; Δа ср =

5. Относительная погрешность: ;

Вывод

Записать ответы на вопросы полными предложениями

1. Сформулируйте определение центростремительного ускорения. Запишите его и формулу для вычисления ускорения при движении по окружности.

2. Сформулируйте второй закон Ньютона. Запишите его формулу и формулировку.

3. Запишите определение и формулу для вычисления

силы тяжести.

4. Запишите определение и формулу для вычисления силы упругости.

ЛАБОРАТОРНАЯ РАБОТА 5

Движение тела под углом к горизонту

Цель

Научиться определять высоту и дальность полета при движении тела с начальной скоростью, направленной под углом к горизонту.

Оборудование

Модель «Движение тела, брошенного под углом к горизонту» в электронных таблицах

Теоретическая часть

Движение тел под углом к горизонту представляет сложное движение.

Движение под углом к горизонту можно разделить на две составляющие: равномерное движение по горизонтали (вдоль оси x) и одновременно равноускоренное, с ускорением свободного падения, по вертикали (вдоль оси y). Так движется лыжник при прыжке с трамплина, струя воды из брандспойта, артиллерийские снаряды, метательные снаряды

Уравнения движения s w:space=»720″/>»> и

запишем в проекциях на оси x и y:

На ось X: S=

Для определения высоты полета необходимо помнить, что в верхней точке подъема скорость тела равна 0. Тогда время подъема будет определено:

При падении проходит такое же время. Поэтому время движения определяется как

Тогда высота подъема определяется по формуле:

А дальность полета:

Наибольшая дальность полета наблюдается при движении под углом 45 0 к горизонту.

Ход работы

1. Запишите в рабочей тетради теоретическую часть работы и зарисуйте график.

2. Откройте файл «Движение под углом к горизонту.xls».

3. В ячейку В2 введите значение начальной скорости, 15 м/с, а в ячейку В4 – угол 15 градусов (в ячейки заносятся только числа, без единиц измерения).

4. Рассмотрите результат на графике. Измените значение скорости на 25 м/с. Сравните графики . Что изменилось?

5. Измените значения скорости на 25 м/с, а угла –35 градусов; 18 м/с, 55 градусов. Рассмотрите графики.

6. Выполните вычисления по формулам для значений скоростей и углов (по вариантам):

8. Проверьте ваши результаты, рассмотрите графики. Графики начертите в масштабе на отдельном листе формата А4

Таблица Значения синусов и косинусов некоторых углов

	30 0	45 0	60 0
Синус (Sin)	0,5	0,71	0,87
Косинус (Cos)	0,87	0,71	0,5

Вывод

Запишите ответы на вопросы полными предложениями

1. От каких величин зависит дальность полета тела, брошенного под углом к горизонту?

2. Приведите примеры движения тел под углом к горизонту.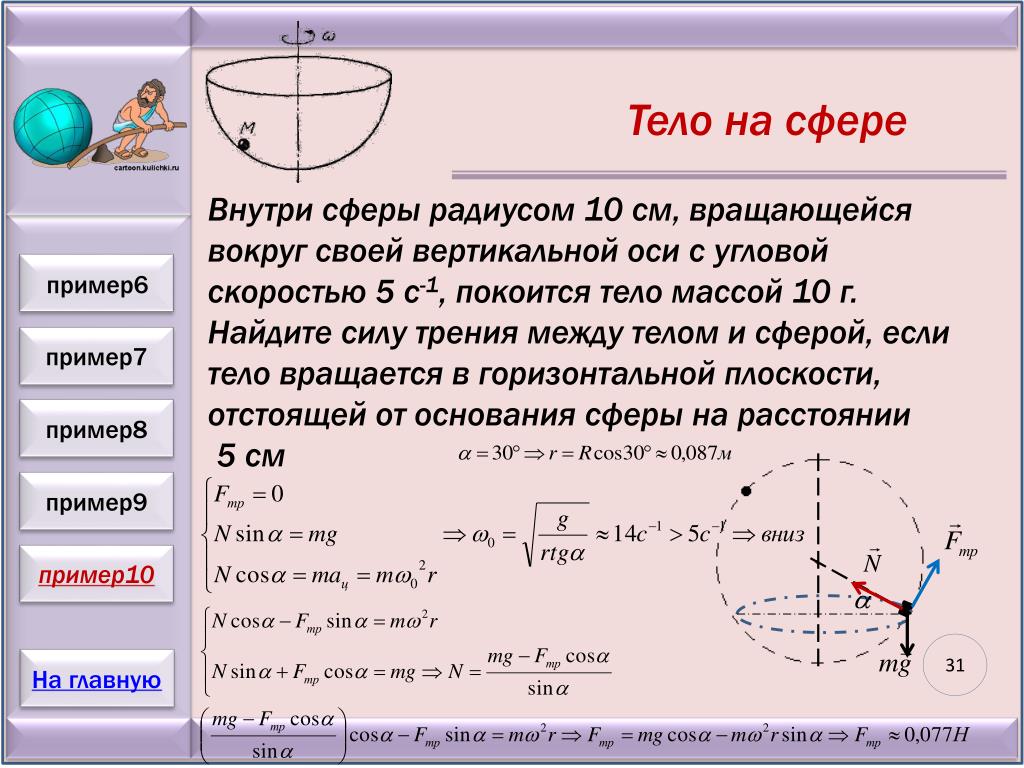

3. Под каким углом к горизонту наблюдается наибольшая дальность полета тела под углом к горизонту?

ЛАБОРАТОРНАЯ РАБОТА 6

3. Рассчитайте и занесите в таблицу среднее значение промежутка времени t >, за который шарик совершает N = 10 оборотов.

4. Рассчитайте и занесите в таблицу среднее значение периода вращение T > шарика.

5. По формуле (4) определите и занесите в таблицу среднее значение модуля ускорения.

6. По формулам (1) и (2) определите и занесите в таблицу среднее значение модулей угловой и линейной скорости.

Опыт	N	t	T	a	ω	v
1	10	12.13	—	—	—	—
2	10	12.2	—	—	—	—
3	10	11. 8	—	—	—	—
4	10	11.41	—	—	—	—
5	10	11.72	—	—	—	—
Ср.	10	11.85	1.18	4.25	0.63	0.09

7. Вычислите максимальное значение абсолютной случайной погрешности измерения промежутка времени t .

8. Определите абсолютную систематическую погрешность промежутка времени t .

9. Вычислите абсолютную погрешность прямого измерения промежутка времени t .

10. Вычислите относительную погрешность прямого измерения промежутка времени.

11. Запишите результат прямого измерения промежутка времени в интервальной форме.

Ответьте на контрольные вопросы

1. Как изменится линейная скорость шарика при его равномерном вращательном движении относительно центра окружности?

Линейная скорость характеризуется направлением и величиной (модулем). Модуль — величина постоянная, а направление при таком движении способно изменяться.

2. Как доказать соотношение v = ωR ?

Так как v = 1/T, связь циклической частоты с периодом и частой 2π = VT, откуда V = 2πR. Связь линейной скорости и угловой 2πR = VT, отсюда V = 2πr/T. (R — радиус описанной, r — радиус вписанной)

3. Как зависит период вращения T шарика от модуля его линейной скорости?

Чем выше показатель скорости, тем меньше показатель периода.

Выводы: научился определять период вращения, модули, центростремительного ускорения, угловую и линейную скорости при равномерном вращении тела и рассчитывать абсолютную и относительную погрешности прямых измерений промежутка времени движения тела.

Суперзадание

Определите ускорение материальной точки при её равномерном вращении, если за Δt = 1 с она прошла 1/6 длины окружности, имея модуль линейной скорости v = 10 м/с.

Длина окружности:

S = 10 ⋅ 1 = 10 м
l = 10⋅ 6 = 60 м

Радиус окружности:

r = l/2π
r = 6/2 ⋅ 3 = 10 м

Ускорение:

a = v2 /r
a = 1002 /10 = 10 м/c2 .

Лабораторная работа №4 по физике 9 класс (ответы) — Изучение движения тела по окружности

3. Рассчитайте и занесите в таблицу среднее значение промежутка времени , за который шарик совершает N = 10 оборотов.

4. Рассчитайте и занесите в таблицу среднее значение периода вращение шарика.

5. По формуле (4) определите и занесите в таблицу среднее значение модуля ускорения.

6. По формулам (1) и (2) определите и занесите в таблицу среднее значение модулей угловой и линейной скорости.

Опыт	N	t	T	a	ω	v
1	10	12.13	—	—	—	—
2	10	12.2	—	—	—	—
3	10	11.8	—	—	—	—
4	10	11. 41	—	—	—	—
5	10	11.72	—	—	—	—
Ср.	10	11.85	1.18	4.25	0.63	0.09

7. Вычислите максимальное значение абсолютной случайной погрешности измерения промежутка времени t.

8. Определите абсолютную систематическую погрешность промежутка времени t.

9. Вычислите абсолютную погрешность прямого измерения промежутка времени t.

10. Вычислите относительную погрешность прямого измерения промежутка времени.

11. Запишите результат прямого измерения промежутка времени в интервальной форме.

Ответьте на контрольные вопросы

2. Как доказать соотношение v = ωR?

3. Как зависит период вращения T шарика от модуля его линейной скорости?

Чем выше показатель скорости, тем меньше показатель периода.

Суперзадание

Длина окружности:

S = 10 ⋅ 1 = 10 м
l = 10⋅ 6 = 60 м

Радиус окружности:

r = l/2π
r = 6/2 ⋅ 3 = 10 м

Ускорение:

a = v 2 /r
a = 100 2 /10 = 10 м/c 2 .

Дата__________ ФИ_____________________________________ Класс 10_____

Лабораторная работа № 1 по теме:

«ИЗУЧЕНИЕ ДВИЖЕНИЯ ТЕЛА ПО ОКРУЖНОСТИ ПОД ДЕЙСТВИЕМ СИЛ УПРУГОСТИ И ТЯЖЕСТИ».

Цель работы: определение центростремительного ускорения шарика при его равномерном движении по окружности.

Оборудование: штатив с муфтой и лапкой, лента измерительная, циркуль, динамометр

лабораторный, весы с разновесами, груз на нити, лист бумаги, линейка, пробка.

Теоретическая часть работы.

Эксперименты проводятся с коническим маятником. Небольшой шарик движется по окружности радиуса R. При этом нить АВ, к которой прикреплен шарик, описывает поверхность прямого кругового конуса. На шарик действуют две силы: сила тяжести
и натяжение нити (рис. а). Они создают центростремительное ускорение , направленное по радиусу к центру окружности. Модуль ускорения можно определить кинематически. Он равен:

Для определения ускорения надо измерить радиус окружности и период обращения шарика по окружности.

Центростремительное (нормальное) ускорение можно определить также, используя законы динамики.

Согласно второму закону Ньютона
. Разложим силу на составляющие и , направленные по радиусу к центру окружности и по вертикали вверх.

Тогда второй закон Ньютона запишется следующим образом:

Направление координатных осей выберем так, как показано на рисунке б. В проекциях на ось О 1 у уравнение движения шарика примет вид: 0 = F 2 — mg. Отсюда F 2 = mg: составляющая уравновешивает силу тяжести
, действующую на шарик.

Запишем второй закон Ньютона в проекциях на ось О 1 х: ma n = F 1 . Отсюда
.

Модуль составляющей F 1 можно определить различными способами. Во-первых, это можно сделать из подобия треугольников ОАВ и FBF 1:

Отсюда
и
.

Во-вторых, модуль составляющей F 1 можно непосредственно измерить динамометром. Для этого оттягиваем горизонтально расположенным динамометром шарик на расстояние, равное радиусу R окружности (рис. в), и определяем показание динамометра. При этом сила упругости пружины уравновешивает составляющую .

Сопоставим все три выражения для а n:

,
,
и убедимся, что они близки между собой.

Ход работы.

1. Определите массу шарика на весах с точностью до 1 г.

2. Шарик, подвешенный на нити, закрепите в лапке штатива, используя кусок пробки.

3 . Вычертите на листе бумаги окружность радиусом 20 см (R = 20 см = ________ м).

4. Штатив с маятником располагаем так, чтобы продолжение шнура проходило через центр окружности.

5 . Взяв нить пальцами у точки подвеса, приведите маятник во вращательное движение

над листом бумаги так, чтобы шарик описывал такую же окружность, как и начерченная на бумаге.

6. Отсчитываем время, за которое маятник совершает 50 полных оборотов (N = 50).

7. Рассчитайте период обращения маятника по формуле: T = t / N .

8 . Рассчитайте значение центростремительного ускорения по формуле (1):

9 . Определите высоту конического маятника (h ). Для этого измерьте расстояние по вертикали от центра шарика до точки подвеса.

10 . Рассчитайте значение центростремительное ускорение по формуле (2):

11. Оттяните горизонтально расположенным динамометром шарик на расстояние, равное радиусу окружности, и измерьте модуль составляющей .

Затем вычисляем ускорение по формуле (3): =

12. Результаты измерений и вычислений заносим в таблицу.

Радиус окружности

R , м

Число оборотов

t , с

Период обращения

T = t / N

Высота маятника

h , м

Масса шарика

m , кг

Центр-ое ускорение

м/с 2

Центр-ое ускорение

м/с 2

Центр-ое ускорение

м/с 2

13 . Сравните полученные три значения модуля центростремительного ускорения.

__________________________________________________________________________ ВЫВОД:

______________________________________________________________________________________________________________________________________________________________________________________________________________________________

Дополнительно :

Найдите относительную и абсолютную погрешность косвенного измерения а ц (1) и (3):

Формула (1). ________ ; Δа ц = · а ц = ________;

Формула (3). _________; Δа ц = · а ц = _______.

Тема: Изучение движения тела по окружности.

Цель работы: определение центростремительного ускорения шарика при его равномерном движении по окружности.

Оборудование:

штатив с муфтой и лапкой;
лента измерительная;
циркуль;
динамометр лабораторный;
весы с разновесами;
шарик на нити;
кусочек пробки с отверстием;
лист бумаги;
линейка.

Теоретическая часть

Эксперименты проводятся с коническим маятником. Небольшой шарик движется по окружности радиусом R . При этом нить АВ , к которой прикреплен шарик, описывает поверхность прямого кругового конуса. На шарик действуют две силы: сила тяжести mg и натяжение нити F (смотри рис а ). Они создают центростремительное ускорение а n , направленное по радиусу к центру окружности. Модуль ускорения можно определить кинематически. Он равен:

a n = ω 2 R = 4π 2 R/T 2

Для определения ускорения надо измерить радиус окружности R и период обращения шарика по окружности Т . Центростремительное (нормальное) ускорение можно определить также, используя законы динамики. Согласно второму закону Ньютона ma = mg + F . Разложим силу F на составляющие F 1 и F 2 , направленные по радиусу к центру окружности и по вертикали вверх. Тогда второй закон Ньютона можно записать следующим образом:

ma = mg + F 1 + F 2 .

Направление координатных осей выберем так, как показано на рисунке б . В проекции на ось O 1 Y уравнение движения шарика примет вид: 0 = F 2 — mg . Отсюда F 2 = mg . Составляющая F 2 уравновешивает силу тяжести mg , действующую на шарик. Запишем второй закон Ньютона в проекции на ось О 1 Х : ma n = F 1 . Отсюда а n = F 1 /m . Модуль составляющей F 1 можно определить различными способами. Во-первых, это можно сделать пользуясь подобием треугольников ОАВ и FBF 1 :

F 1 /R = mg/h

Отсюда F 1 = mgR/h и a n = gR/h .

Во-вторых, модуль составляющей F 1 можно непосредственно измерить динамометром. Для этого оттягиваем горизонтально расположенным динамометром шарик на расстояние, равное радиусу R окружности (рис. в ), и определяем показание динамометра. При этом сила упругости пружины уравновешивает составляющую F 1 . Сопоставим все три выражения для а n :

a n = 4π 2 R/T 2 , a n = gR/h, a n = F 1 /m

и убедимся, что числовые значения центростремительного ускорения, полученные тремя способами, близки между собой.

В данной работе с наибольшей тщательностью следует измерять время. Для этого полезно отсчитывать возможно большее число N оборотов маятника, уменьшая тем самым относительную погрешность.

Взвешивать шарик с точностью, которую могут дать лабораторные весы, нет необходимости. Вполне достаточно взвешивать с точностью до 1 г. Высоту конуса и радиус окружности достаточно измерить с точностью до 1 см. При такой точности измерений относительные погрешности величин будут одного порядка.

Порядок выполнения работы.

1. Определяем массу шарика на весах с точностью до 1 г.

2. Нить продеваем сквозь отверстие в пробке и зажимаем пробку в лапке штатива (смотри рис. в ).

3. Вычерчиваем на листе бумаги окружность, радиус которой около 20 см. Измеряем радиус с точностью до 1 см.

4. Штатив с маятником располагаем так, чтобы продолжение нити проходило через центр окружности.

5. Взяв нить пальцами у точки подвеса, вращаем маятник так, чтобы шарик описывал такую же окружность, как и начерченная на бумаге.

6. Отсчитываем время, за которое маятник совершает заданное число оборотов (к примеру, N = 50).

7. Определяем высоту конического маятника. Для этого измеряем расстояние по вертикали от центра шарика до точки подвеса (считаем h ~ l ).

8. Находим модуль центростремительного ускорения по формулам:

a n = 4π 2 R/T 2 и a n = gR/h

9. Оттягиваем горизонтально расположенным динамометром шарик на расстояние, равное радиусу окружности, и измеряем модуль составляющей F 1 . Затем вычисляем ускорение по формуле а n = F 1 /m .

10. Результаты измерений заносим в таблицу.

№ опыта	R	N	Δt	T = Δt/N	h	m	a n = 4π 2 R/T 2	a n = gR/h	a n = F 1 /m
1

Сравнивая полученные три значения модуля центростремительного ускорения, убеждаемся, что они примерно одинаковы.

Изучение движения тела по окружности вывод. Лабораторная работа. Изучение движения тела по окружности под действием силы упругости и силы тяжести. Время обращения, с

Мы знаем из учебника (стр.15-16), что при равномерном движении по окружности скорость частицы не меняется по величине. На самом же деле с физической точки зрения это движение ускоренное, так как направление скорости непрерывно меняется во времени. При этом скорость в каждой точке практически направлена по касательной (рис. 9 в учебнике на стр. 16). В этом случае ускорение характеризует быстроту изменения направления скорости. Оно все время направлено к центру окружности, по которой движется частица. По этой причине его принято называть центростремительным ускорением.

Это ускорение можно вычислить по формуле:

Быстроту движения тела по окружности характеризуют числом полных оборотов, совершаемых в единицу времени. Это число называется частотой вращения. Если тело делает v оборотов в секунду, то время, за которое совершается один оборот,

секунд. Это время называется периодом вращения

Чтобы вычислить скорость движения тела по окружности, надо путь, проходимый телом за один оборот, (он равен длине

окружности) поделить на период:

в этой работе мы

будем наблюдать за движением шарика, подвешенного на ните и движущегося по окружности.

Пример выполнения работы.

Тема: Изучение движения тела по окружности.

Оборудование:

штатив с муфтой и лапкой;
лента измерительная;
циркуль;
динамометр лабораторный;
весы с разновесами;
шарик на нити;
кусочек пробки с отверстием;
лист бумаги;
линейка.

Теоретическая часть

a n = ω 2 R = 4π 2 R/T 2

ma = mg + F 1 + F 2 .

F 1 /R = mg/h

Отсюда F 1 = mgR/h и a n = gR/h .

a n = 4π 2 R/T 2 , a n = gR/h, a n = F 1 /m

Порядок выполнения работы.

1. Определяем массу шарика на весах с точностью до 1 г.

2. Нить продеваем сквозь отверстие в пробке и зажимаем пробку в лапке штатива (смотри рис. в ).

3. Вычерчиваем на листе бумаги окружность, радиус которой около 20 см. Измеряем радиус с точностью до 1 см.

4. Штатив с маятником располагаем так, чтобы продолжение нити проходило через центр окружности.

6. Отсчитываем время, за которое маятник совершает заданное число оборотов (к примеру, N = 50).

8. Находим модуль центростремительного ускорения по формулам:

a n = 4π 2 R/T 2 и a n = gR/h

10. Результаты измерений заносим в таблицу.

№ опыта	R	N	Δt	T = Δt/N	h	m	a n = 4π 2 R/T 2	a n = gR/h	a n = F 1 /m
1

Цель работы

Определить центростремительное ускорение шарика при его равномерном движении по окружности.

Теоретическая часть

Эксперименты проводятся с коническим маятником. Небольшой шарик движется по окружности радиусом R. При этом нить АВ, к которой прикреплён шарик, описывает поверхность прямого кругового конуса. Из кинематических соотношений следует, что аn = ω 2 R = 4π 2 R/T 2 .

На шарик действуют две силы: сила тяжести m и сила натяжения нити (рис. Л.2, а). Согласно второму закону Ньютона m = m + . Разложив силу на составляющие 1 и 2 , направленные по радиусу к центру окружности и по вертикали вверх, второй закон Ньютона запишем следующим образом: m = m + 1 + 2 . Тогда можно записать: mа n = F 1 . Отсюда а n = F 1 /m.

Модуль составляющей F 1 можно определить, пользуясь подобием треугольников ОАВ и F 1 FB: F 1 /R = mg/h (|m| = | 2 |). Отсюда F 1 = mgR/h и a n = gR/h.

Сопоставим все три выражения для а n:

а n = 4 π 2 R/T 2 , а n =gR/h, а n = F 1 /m

и убедимся, что числовые значения центростремительного ускорения, полученные тремя способами, примерно одинаковы.

Оборудование

Штатив с муфтой и лапкой, лента измерительная, циркуль, динамометр лабораторный, весы с разновесами, шарик на нити, кусочек пробки с отверстием, лист бумаги, линейка.

Порядок выполнения работы

1. Определите массу шарика на весах с точностью до 1 г.

2. Нить проденьте сквозь отверстие в пробке и зажмите пробку в лапке штатива (рис. Л.2, б).

3. Начертите на листе бумаги окружность, радиус которой около 20 см. Измерьте радиус с точностью до 1 см.

4. Штатив с маятником расположите так, чтобы продолжение нити проходило через центр окружности.

5. Взяв нить пальцами у точки подвеса, вращайте маятник так, чтобы шарик описывал такую же окружность, как и начерченная на бумаге.

6. Отсчитайте время, за которое маятник совершает заданное число (например, в интервале от 30 до 60) оборотов.

7. Определите высоту конического маятника. Для этого измерьте расстояние по вертикали от центра шарика до точки подвеса (считаем h ≈ l).

9. Оттяните горизонтально расположенным динамометром шарик на расстояние, равное радиусу окружности, и измерьте модуль составляющей 1 .

Затем вычислите ускорение по формуле

«Изучение движения тела по окружности под действием двух сил»

Оборудование: 1. штатив с муфтой и лапкой;

2. лента измерительная;

3. циркуль;

4. динамометр лабораторный;

5. весы с разновесами;

6. шарик на нити;

7. кусочек пробки с отверстием;

8. лист бумаги;

9. линейка.

Порядок выполнения работы:

1. Определяем массу шарика на весах с точностью до 1 г.

2. Нить продеваем сквозь отверстие и зажимаем пробку в лапке штатива (рис 1)

3. Вычерчиваем на листе бумаги окружность, радиус которой около 20 см. Измеряем радиус с точностью до 1 см.

4. Штатив с маятником располагаем так, чтобы продолжение шнура проходило через центр окружности.

5. Взяв нить пальцами у точки подвеса, вращаем маятник так, чтобы шарик описывал окружность, равную начерченной на бумаге.

6. Отсчитываем время, за которое маятник совершает, к примеру, N=50 оборотов. Рассчитываем период обращения T =

7. Определяем высоту конического маятника, Для этого измеряем расстояние по вертикали от центра шарика до точки подвеса.

8. Находим модуль нормального ускорения по формулам:

a n 1 = a n 2 =

a n 1 = a n 2 =

9. Оттягиваем горизонтально расположенным динамометром шарик на расстояние, равное радиусу окружности, и измеряем модуль составляющей F

Затем вычисляем ускорение по формуле a n 3 = a n 3 =

10. Результаты измерений заносим в таблицу.

№ опыта	R м	N	∆t c	Т c	h м	m кг	F Н	a n1 м/с 2	a n 2 м/с 2	a n 3 м/с 2

Рассчитайте относительную погрешность вычисленияa n 1 и запишите ответ в виде: a n 1 = a n 1ср ± ∆ a n 1ср a n 1 =

Сделайте вывод:

Контрольные вопросы:

1. К какому виду движения относится движение шарика на нити в лабораторной работе? Почему?

2. Сделайте чертёж в тетради и укажите правильно названия сил. Назовите точки приложения этих сил.

3. Какие законы механики выполняются при движении тела в этой работе? Изобразите графически силы и запишите правильно законы

4. Почему сила упругости F, измеренная в опыте, равна результирующей сил приложенных к телу? Назовите закон.

Упругости и тяжести

Цель работы

Определение центростремительного ускорения шарика при его равномерном движении по окружности

Теоретическая часть работы

Для определения ускорения (a) нужно измерить радиус окружности (R) и период обращения шарика по окружности (T).

Центростремительное ускорение можно определить так же, используя законы динамики.

Согласно второму закону Ньютона, Запишем данное уравнение в проекциях на выбранные оси (рис.2):

Ох: ;

Oy: ;

Из уравнения в проекции на ось Ох выразим равнодействующую:

Из уравнения в проекции на ось Оу выразим силу упругости:

Тогда равнодействующая может быть выражена:

а отсюда ускорение: , где g=9,8 м/с 2

Следовательно, для определения ускорения необходимо измерить радиус окружности и длину нити.

Оборудование

Ход работы

1. Подвесить маятник к лапке штатива.

2. Измерить радиус окружности с точностью до 1мм. (R)

3. Штатив с маятником расположить так, чтобы продолжение шнура проходило через центр окружности.

7. Найти модуль ускорения по формулам:

8. Вычислить погрешности.

Таблица Результаты измерений и вычислений

Вычисления

1. Период обращения: ; Т=

2. Центростремительное ускорение:

; а 1 =

; а 2 =

Среднее значение центростремительного ускорения:

; а ср =

3. Абсолютная погрешность:

∆а 1 =

∆а 2 =

4. Среднее значение абсолютной погрешности: ; Δа ср =

5. Относительная погрешность: ;

Вывод

Записать ответы на вопросы полными предложениями

2. Сформулируйте второй закон Ньютона. Запишите его формулу и формулировку.

3. Запишите определение и формулу для вычисления

силы тяжести.

4. Запишите определение и формулу для вычисления силы упругости.

ЛАБОРАТОРНАЯ РАБОТА 5

Движение тела под углом к горизонту

Цель

Оборудование

Модель «Движение тела, брошенного под углом к горизонту» в электронных таблицах

Теоретическая часть

Движение тел под углом к горизонту представляет сложное движение.

Уравнения движения s w:space=»720″/>»> и

запишем в проекциях на оси x и y:

На ось X: S=

При падении проходит такое же время. Поэтому время движения определяется как

Тогда высота подъема определяется по формуле:

А дальность полета:

Наибольшая дальность полета наблюдается при движении под углом 45 0 к горизонту.

Ход работы

1. Запишите в рабочей тетради теоретическую часть работы и зарисуйте график.

2. Откройте файл «Движение под углом к горизонту.xls».

4. Рассмотрите результат на графике. Измените значение скорости на 25 м/с. Сравните графики . Что изменилось?

5. Измените значения скорости на 25 м/с, а угла –35 градусов; 18 м/с, 55 градусов. Рассмотрите графики.

6. Выполните вычисления по формулам для значений скоростей и углов (по вариантам):

Таблица Значения синусов и косинусов некоторых углов

	30 0	45 0	60 0
Синус (Sin)	0,5	0,71	0,87
Косинус (Cos)	0,87	0,71	0,5

Вывод

Запишите ответы на вопросы полными предложениями

1. От каких величин зависит дальность полета тела, брошенного под углом к горизонту?

2. Приведите примеры движения тел под углом к горизонту.

3. Под каким углом к горизонту наблюдается наибольшая дальность полета тела под углом к горизонту?

ЛАБОРАТОРНАЯ РАБОТА 6

1 изучение движения тела по окружности. Лабораторная работа. Изучение движения тела по окружности под действием силы упругости и силы тяжести. Время обращения, с

Тема: Изучение движения тела по окружности.

Оборудование:

штатив с муфтой и лапкой;
лента измерительная;
циркуль;
динамометр лабораторный;
весы с разновесами;
шарик на нити;
кусочек пробки с отверстием;
лист бумаги;
линейка.

Теоретическая часть

a n = ω 2 R = 4π 2 R/T 2

ma = mg + F 1 + F 2 .

F 1 /R = mg/h

Отсюда F 1 = mgR/h и a n = gR/h .

a n = 4π 2 R/T 2 , a n = gR/h, a n = F 1 /m

Порядок выполнения работы.

1. Определяем массу шарика на весах с точностью до 1 г.

2. Нить продеваем сквозь отверстие в пробке и зажимаем пробку в лапке штатива (смотри рис. в ).

3. Вычерчиваем на листе бумаги окружность, радиус которой около 20 см. Измеряем радиус с точностью до 1 см.

4. Штатив с маятником располагаем так, чтобы продолжение нити проходило через центр окружности.

6. Отсчитываем время, за которое маятник совершает заданное число оборотов (к примеру, N = 50).

8. Находим модуль центростремительного ускорения по формулам:

a n = 4π 2 R/T 2 и a n = gR/h

10. Результаты измерений заносим в таблицу.

№ опыта	R	N	Δt	T = Δt/N	h	m	a n = 4π 2 R/T 2	a n = gR/h	a n = F 1 /m
1

За 9 класс (И.К.Кикоин, А.К.Кикоин, 1999 год),
задача №5
к главе «ЛАБОРАТОРНЫЕ РАБОТЫ ».

Цель работы: убедиться в том, что при движении тела по окружности под действием нескольких сил их равнодействующая равна произведению массы тела на ускорение: F = ma . Для этого используется конический маятник (рис. 178, а).

На прикрепленное к нити тело (им в работе является груз из

набора по механике) действуют сила тяжести F 1 и сила упругости F 2 . Их равнодействующая равна

Сила F и сообщает грузу центростремительное ускорение

(r — радиус окружности, по которой движется груз, Т — период его обращения) .

Для нахождения периода удобно измерить время t определенного числа N оборотов. Тогда Т =

Модуль равнодействующей F сил F 1 и F 2 можно измерить, скомпенсировав ее силой упругости F упр пружины динамометра так, как это показано на рисунке 178, б.

Согласно второму закону Ньютона,

При подстановке в

это равенство полученных в опыте значений F ynp , m и а может оказаться, что левая часть этого равенства отличается от единицы. Это и позволяет оценить погрешность эксперимента.

Средства измерения: 1) линейка с миллиметровыми делениями; 2) часы с секундной стрелкой; 3) динамометр.

Порядок выполнения работы

1. Нить длиной около 45 см привяжите к грузу и подвесьте к кольцу штатива.

2. Одному из учащихся взяться двумя пальцами за нить у точки подвеса и привести во вращение маятник.

4. Определите период Т обращения маятника при помощи, часов с секундной стрелкой.

5. Рассчитайте среднее значение ускорения по формуле (1), учитывая, что с относительной погрешностью не более 0,015 можно считать π 2 = 10.

6. Измерьте модуль равнодействующей F, уравновесив ее силой упругости пружины динамометра (см. рис. 178, б).

7. Результаты измерений занесите в таблицу:

8. Сравните отношение

силы тяжести

и силы упругости N .

Центростремительное ускорение рассчитаем по формуле

Если груз отклонен от вертикали на расстояние г, как и при движении по окружности, то сила F равна той силе, которая вызывала движение груза по окружности. Мы получаем возможность сравнить значение силы F , полученное путем прямого измерения и силы ma , рассчитанной по результатам косвенных измерений и

сравнить отношение

Выполнение работы

Вычисления

Оценка погрешностей. Точность измерения: линейка —

секундомер

динамометр

Подсчитаем погрешность определения периода (если считать, что число n определено точно):

Погрешность определения ускорения подсчитаем как:

Погрешность определения ma

(7%), то есть

С другой стороны, силу F мы измерили со следующей погрешностью:

Такая погрешность измерения, конечно, очень велика. Измерения с такими погрешностями годны только для приблизительных оценок. Отсюда видно, что отклонение отношение

от единицы может быть существенным при использовании примененных нами способов измерения * .

1 * Так что вам не следует смущаться, если в этой лабораторной работе отношение

I Подготовительный этап

На рисунке схематически показаны качели, известные под названием «гигантские шаги». Найдите центростремительную силу, радиус, ускорение и скорость обращения человека на качелях вокруг столба. Длина веревки равна 5 м, масса человека равна 70 кг. Столб и веревка при обращении образуют угол 300. Определите период, если частота обращения качелей равна 15 мин-1.

Подсказка: На тело, обращающееся по окружности, действуют сила тяжести и сила упругости веревки. Их равнодействующая сообщает телу центростремительное ускорение.

Результаты расчетов внесите в таблицу:

Время обращения, с

Число оборотов

Период обращения, с

Радиус обращения, м

Масса тела, кг

центростремительная сила, Н

скорость обращения, м/с

центростремительное ускорение, м/с2

II . Основной этап

Цель работы:

Приборы и материалы:

1. Перед опытом подвешивают на нити к лапке штатива груз, предварительно взвешенный на весах.

2. Под висящим грузом положите лист бумаги с начерченной на нем окружностью радиусом 15-20 см. Центр окружности расположите на отвесной линии, проходящей через точку подвеса маятника.

3. У точки подвеса нить берут двумя пальцами и аккуратно приводят маятник во вращательное движение , так чтобы радиус вращения маятника совпадал с радиусом нарисованной окружности.

4. Приведите маятник во вращение и подсчитывая число оборотов замерьте время, за которое эти обороты произошли.

5. Результаты измерений и вычислений запишите в таблицу.

6. Равнодействующая силы тяжести и силы упругости, найденная в ходе эксперимента, рассчитывается из параметров кругового движения груза.

С другой стороны, центростремительную силу можно определить из пропорции

Здесь масса и радиус уже известны из предыдущих измерений и, чтобы определить центробежную силу вторым способом надо измерить высоту точки подвеса над вращающимся шариком. Для этого оттягивают шарик на расстояние, равное радиусу вращения и измеряют расстояние по вертикали от шарика до точки подвеса.

7. Сравните результаты, полученные двумя разными способами и сделайте вывод.

III Контрольный этап

При отсутствии в домашних условиях весов цель работы и оборудование может быть изменено.

Цель работы: измерение линейной скорости и центростремительного ускорения при равномерном движении по окружности

Приборы и материалы:

1. Возьмите иголку с двойной ниткой длиной 20-30 см. Острие иголки воткните в ластик, маленькую луковицу или пластилиновый шарик. Вы получите маятник.

2. Поднимите свой маятник за свободный конец нити над листом бумаги, лежащим на столе, и приведите его в равномерное вращение по окружности, изображенной на листе бумаги. Измерьте радиус окружности, по которой движется маятник.

3. Добейтесь устойчивого вращения шарика по заданной траектории и по часам с секундной стрелкой зафиксируйте время для 30 оборотов маятника. По известным формулам рассчитайте модули линейной скорости и центростремительного ускорения.

4. Составьте для записи результатов таблицу и заполните ее.

Использованная литература:

1. Фронтальные лабораторные занятия по физике в средней школе . Пособие для учителей под редакцией. Изд. 2-е. — М., «Просвещение», 1974 г.

2. Шилов работы в школе и дома: механика.-М.: «Просвещение», 2007

Цель работы

Определить центростремительное ускорение шарика при его равномерном движении по окружности.

Теоретическая часть

Сопоставим все три выражения для а n:

а n = 4 π 2 R/T 2 , а n =gR/h, а n = F 1 /m

Оборудование

Порядок выполнения работы

1. Определите массу шарика на весах с точностью до 1 г.

2. Нить проденьте сквозь отверстие в пробке и зажмите пробку в лапке штатива (рис. Л.2, б).

3. Начертите на листе бумаги окружность, радиус которой около 20 см. Измерьте радиус с точностью до 1 см.

4. Штатив с маятником расположите так, чтобы продолжение нити проходило через центр окружности.

6. Отсчитайте время, за которое маятник совершает заданное число (например, в интервале от 30 до 60) оборотов.

Затем вычислите ускорение по формуле

«Изучение движения тела по окружности под действием двух сил»

Оборудование: 1. штатив с муфтой и лапкой;

2. лента измерительная;

3. циркуль;

4. динамометр лабораторный;

5. весы с разновесами;

6. шарик на нити;

7. кусочек пробки с отверстием;

8. лист бумаги;

9. линейка.

Порядок выполнения работы:

1. Определяем массу шарика на весах с точностью до 1 г.

2. Нить продеваем сквозь отверстие и зажимаем пробку в лапке штатива (рис 1)

3. Вычерчиваем на листе бумаги окружность, радиус которой около 20 см. Измеряем радиус с точностью до 1 см.

4. Штатив с маятником располагаем так, чтобы продолжение шнура проходило через центр окружности.

6. Отсчитываем время, за которое маятник совершает, к примеру, N=50 оборотов. Рассчитываем период обращения T =

8. Находим модуль нормального ускорения по формулам:

a n 1 = a n 2 =

a n 1 = a n 2 =

Затем вычисляем ускорение по формуле a n 3 = a n 3 =

10. Результаты измерений заносим в таблицу.

№ опыта	R м	N	∆t c	Т c	h м	m кг	F Н	a n1 м/с 2	a n 2 м/с 2	a n 3 м/с 2

Рассчитайте относительную погрешность вычисленияa n 1 и запишите ответ в виде: a n 1 = a n 1ср ± ∆ a n 1ср a n 1 =

Сделайте вывод:

Контрольные вопросы:

1. К какому виду движения относится движение шарика на нити в лабораторной работе? Почему?

2. Сделайте чертёж в тетради и укажите правильно названия сил. Назовите точки приложения этих сил.

4. Почему сила упругости F, измеренная в опыте, равна результирующей сил приложенных к телу? Назовите закон.

Лабораторная работа. Изучение движения тел по окружности под действием сил тяжести и упругости

Лабораторная работа №1.

Изучение движения тел по окружности под действием силы тяжести и упругости.

Цель работы: определить центростремительное ускорение шарика при его равномерном движении по окружности.

Оборудование: штатив с муфтой и лапкой, лента измерительная, циркуль, динамометр лабораторный, весы с разновесами, шарик на нити, лист бумаги, линейка, пробка.

Подготовительные вопросы:

1. Какие две силы действуют на конический маятник?

2. Равнодействующая этих сил сообщает маятнику…?

3. Модуль данного ускорения можно определить по формуле…?

4. Период вращения – это … ?

ХОД РАБОТЫ.

1. Определите массу шарика.

2. Шарик, подвешенный на нити, закрепите в лапке штатива.

3. Вычертите на листе бумаги окружность радиусом 20 см.

4. Штатив с маятником расположите так, чтобы продолжение нити проходило через центр окружности.

5. Взяв нить пальцами у точки подвеса, приведите маятник во вращательное движение над листом бумаги так, чтобы шарик описывал такую же окружность, как и начерченная на бумаге.

6. Измерьте время 20 полных оборотов маятника.

7. Рассчитайте период обращения маятника по формуле:T = tср./N

8. Рассчитайте значение центростремительного ускорения: а₁ = 4π²R/ T²

9. Определите высоту маятника. Для этого измерьте расстояние по вертикали от центра шарика до точки подвеса.

10. Рассчитайте значение ускорения по формуле: а₂ = g R/ h.

11. Оттяните горизонтально расположенным динамометром шарик на расстояние, равное радиусу окружности, и измерьте модуль равнодействующей силы

12. Оттяните горизонтально расположенным динамометром шарик на расстояние, равное радиусу окружности, и измерьте модуль равнодействующей силы, которая равна силе упругости при растяжении пружины.

13. Используя второй закон Ньютона, рассчитайте значение центростремительного ускорения: а₃ = F/m.

14. Результаты измерений и вычислений занесите в таблицу.

15. Сделайте вывод по данным результатов опытов, сравнива_1,а_2,а_3.

Выполнение работы

№ опыта	Число оборотов N	Радиус вращения R,м	Высота маятника h,м	Масса тела m,кг	Время обращения t,с	Время обращения tср., с	Период обращения Т,с	Равнодействующая сила F,Н	Ускорение а₁,м/с²	Ускорение а₂,м/с²	Ускорение а₃,м/с²
1
2	20
3

Вычисления.

T = tср. /N =

а₁ = 4π²R/ T²=

а₂ = g R/ h =

а₃ = F/m =

Сравнение: а₁ а₂ а₃

Вывод:

Контрольные вопросы.

1. Почему при выполнении работы определяли время, за которое совершается небольшое число оборотов?
2.Определите линейную скорость тела по результатам опытов.

Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/182217-laboratornaja-rabota-izuchenie-dvizhenija-tel

Лабораторная работа изучение движения тела по окружности. Лабораторная работа. Изучение движения тела по окружности под действием силы упругости и силы тяжести. центростремительная сила, Н

4. Рассчитайте и занесите в таблицу среднее значение периода вращение T > шарика.

5. По формуле (4) определите и занесите в таблицу среднее значение модуля ускорения.

6. По формулам (1) и (2) определите и занесите в таблицу среднее значение модулей угловой и линейной скорости.

Опыт	N	t	T	a	ω	v
1	10	12.13	—	—	—	—
2	10	12.2	—	—	—	—
3	10	11.8	—	—	—	—
4	10	11.41	—	—	—	—
5	10	11.72	—	—	—	—
Ср.	10	11.85	1.18	4.25	0.63	0.09

7. Вычислите максимальное значение абсолютной случайной погрешности измерения промежутка времени t .

8. Определите абсолютную систематическую погрешность промежутка времени t .

9. Вычислите абсолютную погрешность прямого измерения промежутка времени t .

10. Вычислите относительную погрешность прямого измерения промежутка времени.

11. Запишите результат прямого измерения промежутка времени в интервальной форме.

Ответьте на контрольные вопросы

2. Как доказать соотношение v = ωR ?

3. Как зависит период вращения T шарика от модуля его линейной скорости?

Чем выше показатель скорости, тем меньше показатель периода.

Суперзадание

Длина окружности:

S = 10 ⋅ 1 = 10 м
l = 10⋅ 6 = 60 м

Радиус окружности:

r = l/2π
r = 6/2 ⋅ 3 = 10 м

Ускорение:

a = v2 /r
a = 1002 /10 = 10 м/c2 .

Лабораторная работа №4 по физике 9 класс (ответы) — Изучение движения тела по окружности

4. Рассчитайте и занесите в таблицу среднее значение периода вращение шарика.

5. По формуле (4) определите и занесите в таблицу среднее значение модуля ускорения.

6. По формулам (1) и (2) определите и занесите в таблицу среднее значение модулей угловой и линейной скорости.

Опыт	N	t	T	a	ω	v
1	10	12.13	—	—	—	—
2	10	12.2	—	—	—	—
3	10	11.8	—	—	—	—
4	10	11.41	—	—	—	—
5	10	11.72	—	—	—	—
Ср.	10	11.85	1.18	4.25	0.63	0.09

7. Вычислите максимальное значение абсолютной случайной погрешности измерения промежутка времени t.

8. Определите абсолютную систематическую погрешность промежутка времени t.

9. Вычислите абсолютную погрешность прямого измерения промежутка времени t.

10. Вычислите относительную погрешность прямого измерения промежутка времени.

11. Запишите результат прямого измерения промежутка времени в интервальной форме.

Ответьте на контрольные вопросы

2. Как доказать соотношение v = ωR?

3. Как зависит период вращения T шарика от модуля его линейной скорости?

Чем выше показатель скорости, тем меньше показатель периода.

Суперзадание

Длина окружности:

S = 10 ⋅ 1 = 10 м
l = 10⋅ 6 = 60 м

Радиус окружности:

r = l/2π
r = 6/2 ⋅ 3 = 10 м

Ускорение:

a = v 2 /r
a = 100 2 /10 = 10 м/c 2 .

Цель работы

Определить центростремительное ускорение шарика при его равномерном движении по окружности.

Теоретическая часть

Сопоставим все три выражения для а n:

а n = 4 π 2 R/T 2 , а n =gR/h, а n = F 1 /m

Оборудование

Порядок выполнения работы

1. Определите массу шарика на весах с точностью до 1 г.

2. Нить проденьте сквозь отверстие в пробке и зажмите пробку в лапке штатива (рис. Л.2, б).

3. Начертите на листе бумаги окружность, радиус которой около 20 см. Измерьте радиус с точностью до 1 см.

4. Штатив с маятником расположите так, чтобы продолжение нити проходило через центр окружности.

6. Отсчитайте время, за которое маятник совершает заданное число (например, в интервале от 30 до 60) оборотов.

Затем вычислите ускорение по формуле

«Изучение движения тела по окружности под действием двух сил»

Оборудование: 1. штатив с муфтой и лапкой;

2. лента измерительная;

3. циркуль;

4. динамометр лабораторный;

5. весы с разновесами;

6. шарик на нити;

7. кусочек пробки с отверстием;

8. лист бумаги;

9. линейка.

Порядок выполнения работы:

1. Определяем массу шарика на весах с точностью до 1 г.

2. Нить продеваем сквозь отверстие и зажимаем пробку в лапке штатива (рис 1)

3. Вычерчиваем на листе бумаги окружность, радиус которой около 20 см. Измеряем радиус с точностью до 1 см.

4. Штатив с маятником располагаем так, чтобы продолжение шнура проходило через центр окружности.

6. Отсчитываем время, за которое маятник совершает, к примеру, N=50 оборотов. Рассчитываем период обращения T =

8. Находим модуль нормального ускорения по формулам:

a n 1 = a n 2 =

a n 1 = a n 2 =

Затем вычисляем ускорение по формуле a n 3 = a n 3 =

10. Результаты измерений заносим в таблицу.

№ опыта	R м	N	∆t c	Т c	h м	m кг	F Н	a n1 м/с 2	a n 2 м/с 2	a n 3 м/с 2

Рассчитайте относительную погрешность вычисленияa n 1 и запишите ответ в виде: a n 1 = a n 1ср ± ∆ a n 1ср a n 1 =

Сделайте вывод:

Контрольные вопросы:

1. К какому виду движения относится движение шарика на нити в лабораторной работе? Почему?

2. Сделайте чертёж в тетради и укажите правильно названия сил. Назовите точки приложения этих сил.

4. Почему сила упругости F, измеренная в опыте, равна результирующей сил приложенных к телу? Назовите закон.

I Подготовительный этап

Результаты расчетов внесите в таблицу:

Время обращения, с

Число оборотов

Период обращения, с

Радиус обращения, м

Масса тела, кг

центростремительная сила, Н

скорость обращения, м/с

центростремительное ускорение, м/с2

II . Основной этап

Цель работы:

Приборы и материалы:

1. Перед опытом подвешивают на нити к лапке штатива груз, предварительно взвешенный на весах.

5. Результаты измерений и вычислений запишите в таблицу.

С другой стороны, центростремительную силу можно определить из пропорции

7. Сравните результаты, полученные двумя разными способами и сделайте вывод.

III Контрольный этап

При отсутствии в домашних условиях весов цель работы и оборудование может быть изменено.

Приборы и материалы:

4. Составьте для записи результатов таблицу и заполните ее.

Использованная литература:

2. Шилов работы в школе и дома: механика.-М.: «Просвещение», 2007

Веб-сайт класса физики

Равномерное круговое движение

Равномерное круговое движение можно описать как движение объекта по кругу с постоянной скоростью. Когда объект движется по кругу, он постоянно меняет свое направление. Во всех случаях объект движется по касательной к окружности. Поскольку направление вектора скорости совпадает с направлением движения объекта, вектор скорости также направлен по касательной к окружности.Анимация справа изображает это с помощью векторной стрелки.

Объект, движущийся по кругу, ускоряется. Ускоряющиеся объекты — это объекты, которые изменяют свою скорость — либо скорость (то есть величину вектора скорости), либо направление. Объект, совершающий равномерное круговое движение, движется с постоянной скоростью. Тем не менее, он ускоряется из-за изменения направления. Направление ускорения внутрь. Анимация справа изображает это с помощью векторной стрелки.

Последней характеристикой движения объекта, совершающего равномерное круговое движение, является чистая сила. Чистая сила, действующая на такой объект, направлена к центру круга. Считается, что чистая сила равна центростремительной силе , направленной внутрь. Без такой внутренней силы объект продолжал бы движение по прямой линии, никогда не отклоняясь от своего направления. Тем не менее, с внутренней чистой силой, направленной перпендикулярно вектору скорости, объект всегда меняет свое направление и испытывает внутреннее ускорение.

Для получения дополнительной информации о физических описаниях движения посетите The Physics Classroom Tutorial. Доступна подробная информация по следующим темам:

Скорость
Ускорение
Чистая сила и ускорение
Круговое движение и тангенциальная скорость
Круговое движение и ускорение
Требование центростремительной силы

Лабораторная работа.Исследование движения тела по окружности под действием силы упругости и силы тяжести

Для 9 класса (И.К. Кикоин, А.К. Кикоин, 1999),
задание №5
в раздел « ЛАБОРАТОРНЫЕ РАБОТЫ ».

Цель работы — убедиться, что при движении тела по окружности под действием нескольких сил их относительная величина равна произведению веса тела на ускорение: F = Ma. Здесь используется конический маятник (рис.178, а).

На корпусе прикреплены к резьбе (нагружаются от

набор механики) Действует сила тяжести F 1 и сила упругости F 2. Они равны

Сила F и сообщает центростремительное ускорение груза

(R — радиус окружности, по которой движется груз. , T — срок его обращения).

Для определения периода удобно измерить время T определенного количества N оборотов. Тогда T =

Модуль равнодействующих F сил F 1 и F 2 можно измерить, компенсируя его упругость упругостью F пружины динамометра, как показано на рисунке 178, б.

Согласно второму закону Ньютона,

При замене B.

это равенство значений значений F YNP, M и a, а может оказаться, что левая часть этого равенства отличается от единицы. Это позволяет оценить погрешность эксперимента.

Средства измерения: 1) линия с миллиметровыми делениями; 2) часы со второй стрелкой; 3) Динамометр.

Материалы: 1) тренога с муфтой и кольцом; 2) прочная нить; 3) лист бумаги с заявленным кругом радиусом 15 см; 4) Грузовой из комплекта механики.

Порядок выполнения работ

1. Резьба имеет длину около 45 см, приспособлена к нагрузке и крепится к кольцу штатива.

2. Один из учеников берет два пальца за нить в точке подвеса и приводит маятник во вращение.

3. Второе исследование по измерению радиуса r ленты R, вокруг которой движется груз. (Круг можно нарисовать заранее на бумаге и по этой окружности будет приводить маятник в движение.)

4. Определите период t обращения маятника, используя часы со второй стрелкой.

Для этого ученик, поворачивая маятник, в такт с его оборотом громко произносит: ноль, ноль и т. Д. Второй ученик с часами в руках, ловя стрелку времени к началу ссылки, произносит: «ноль» », после чего первый вслух считает количество оборотов. Отсчитав 30-40 оборотов, фиксируем промежуток времени Т. Опыт повторить пять раз.

5. Вычислить среднее значение ускорения по формуле (1), учитывая, что с относительной погрешностью не более 0.015 можно считать π 2 = 10.

6. Измерить модуль полученного F, уравняв его упругость с пружинами динамометра (см. Рис. 178, б).

7. Результаты измерений. Зайдите в таблицу:

8. Сравните положение

с единицей и сделайте вывод об ошибке экспериментальной проверки, что центростремительное ускорение сообщает телу векторную сумму сил, действующих на него.

Груз из комплекта механики, подвешенный к нити, прикрепленной в верхней точке, перемещается в горизонтальной плоскости по окружности радиуса R под действием двух сил:

силы тяжести

силы упругости n.

Результат этих двух сил F направлен горизонтально к центру круга и сообщает о центростремительном ускорении груза.

Т — расход груза по окружности. Его можно рассчитать, подсчитав время, за которое груз совершает количество полных оборотов

Центростремительное ускорение Рассчитайте формулу

Теперь, если вы возьмете динамометр и прикрепите его к грузу, как показано на рисунке, это возможно. для определения силы F (равнодействующие силы Mg и N.

Если груз отклоняется от вертикали на расстояние r, а также при движении по окружности, сила F равна силе, вызвавшей движение груза по окружности. Мы получаем возможность сравнить значение силы F, полученное прямым измерением, и силу МА, рассчитанную по результатам косвенных измерений и

сравните позицию

с единицей. Для того, чтобы радиус окружности, по которому груз движется, из-за эффекта сопротивления воздуха медленнее и на изменение незначительно влияют измерения, его следует выбирать небольшим (порядка 0.05 ~ 0,1 м).

Завершение работ

Расчеты

Оценка ошибок. Точность измерения: Правило —

секундомер

динамометр

Рассчитайте погрешность определения периода (если предположить, что число n определено точно):

Точность определения ускорения рассчитывается как:

MA Ошибка определения

(7%), то есть

С другой стороны, мощность f мы измерили со следующей ошибкой:

Такая погрешность измерения, конечно, очень велика.Измерения с такими ошибками подходят только для приблизительных оценок. Кажется, что отклонение от положения

от единицы измерения может быть существенным при использовании применяемых нами методов измерения *.

1 * Так что не стоит смущаться, если в этой лабораторной работе отношение

будет отличаться от единицы. Просто точно оцените все ошибки измерения и сделайте соответствующий результат.

цель работы

Определить центростремительное ускорение мяча при его равномерном движении по окружности.

Теоретическая часть

Эксперименты проводятся с коническим маятником. Маленький шарик движется по окружности с радиусом R. В этом случае нить АВ, к которой прикреплен шарик, описывает поверхность прямого кругового конуса. Из кинематических соотношений следует, что An = ω 2 R = 4π 2 R / T 2.

На шар действуют две силы: сила тяжести m и сила натяжения нити (рис. Л.2, а). По второму закону Ньютона M = M +.Объявляя силу на компоненты 1 и 2, направленную по радиусу к центру окружности и вертикально, второй закон Ньютона запишет так: M = M + 1 + 2. Тогда можно написать: mA n \ u003d F 1. Следовательно, N = F 1 / m.

Модуль составляющей F 1 можно определить, используя подобие треугольников OAV и F 1 FB: F 1 / R = Mg / H (| M | = | 2 |). Отсюда F 1 = MGR / H и AN = GR / H

Сопоставимы все три выражения для AN:

и n = 4 π 2 r / t 2, а n = gr / h, а n \ u003d f 1 / m

и убедитесь, что численные значения центростремительного ускорения, полученные тремя способами, примерно одинаковы.

Оборудование

Штатив со сцеплением и лапой, измерительная лента, цирк, динамометрическая лаборатория, весы с несколькими шариками, шарик с резьбой, кусочек заглушки с отверстием, лист бумаги, леска.

Порядок выполнения работ

1. Определить массу колбы по весам с точностью до 1 г.

2. Очистить резьбу Через отверстие в заглушке и удерживать пробку в ножке штатива (рис. L.2, б).

3. Распределите на листе бумаги круг радиусом около 20 см.Измерьте радиус с точностью до 1 см.

4. Изучите положение маятника так, чтобы продолжение нитей проходило через центр круга.

5. Взяв пальцами нить за точку подвеса, поверните маятник так, чтобы шар описывал ту же окружность, что и нарисованный на бумаге.

6. Укажите время, за которое маятник совершает заданное количество (например, в диапазоне от 30 до 60) оборотов.

7. Определите высоту конического маятника.Для этого измеряется расстояние по вертикали от центра шара до точки подвеса (мы считаем H ≈ L).

9. Отнесите мяч горизонтально расположенным динамометром на расстояние, равное радиусу окружности, и измерьте модуль компонента 1.

Затем вычислите ускорение по формуле

Сравнение трех значений \ Полученного модуля центростремительного ускорения убеждаемся, что они примерно одинаковые.

I. Подготовительный этап

На рисунке схематично показаны качели, известные как «Гигантские ступени». Найдите центростремительную силу, радиус, ускорение и скорость обращения человека при вращении вокруг столба. Длина веревки 5 м, масса человека 70 кг. Столб и веревка при работе образуют угол 300. Определите период, если частота вращения качелей составляет 15 мин-1.

Совет: на тело, в результате чего окружность, применяется сила тяжести и сила упругости веревки. Их автомат сообщает о центростремительном ускорении тела.

Рассчитайте результаты в таблице:

Время обращения

Скорость

Период обращения

Радиус циркуляции, м

Масса тела, кг

центростремительная сила, н

Скорость циркуляции, м / с

центростремительное ускорение, м / с2

II. . Основная сцена

Цель работы:

Инструменты и материалы:

1. Перед опытом вешают предварительно взвешенный на весах груз на нити.

2. Под подвешиваемый груз подложить листок бумаги кругом радиусом 15-20 см. Центр круга расположен на отвесной линии, проходящей через маятниковый подвес.

3. В точке подвеса нить взять двумя пальцами и аккуратно ввести маятник во вращательное движение так, чтобы радиус вращения маятника совпадал с радиусом нарисованного круга.

4. Приведите маятник во вращение и, посчитав количество оборотов, измерьте время, за которое эти обороты имели место.

5. Результаты измерений и расчетов заносятся в таблицу.

6. Результирующие силы тяжести и сила упругости, найденные в ходе эксперимента, рассчитываются по параметрам кругового движения груза.

С другой стороны, центростремительная сила может быть определена из соотношения

Здесь масса и радиус уже известны из предыдущих измерений, и для определения центробежной силы вторым способом необходимо измерить высоту точки подвеса над вращающимся шаром.Для этого задержите мяч на расстояние, равное радиусу вращения, и измерьте расстояние по вертикали от мяча до точки подвеса.

7. Сравните результаты, полученные двумя разными способами, и сделайте вывод.

III Ступень управления

В случае отсутствия дома цель работы и оборудование могут быть изменены.

Цель работы: Измерение линейной скорости и центростремительного ускорения при равномерном движении по окружности

Инструменты и материалы:

1.Возьмите иглу с двойной нитью 20-30 см. Край игл приклеиваем к ластику, небольшой луковице или пластилиновому шарику. У вас получится маятник.

2. Поднимите маятник за свободный конец нити над листом бумаги, лежащим на столе, и равномерно вращайте его по кругу, показанному на листе бумаги. Измерьте радиус круга, по которому движется маятник.

3. Получите равномерное вращение шара по заданной траектории и на часах с помощью второй стрелки зафиксируйте время на 30 оборотов маятника.По известным формулам рассчитать модули линейной скорости и центростремительного ускорения.

4. Составьте таблицу для записи таблицы и заполните ее.

Артикул:

1. Фронтальные лабораторные занятия по физике в средней школе. Пособие для учителей под редакцией. Эд. 2-й. — М., «Просвещение», 1974 г.

2. Шиловские работы в школе и дома: Механика. — М .: Просвещение, 2007

«Исследование движения тела по окружности под действием двух сил»

Цель работы: Определение центростремительного ускорения мяча при его равномерном движении по окружности.

Комплектация: 1. Штатив со сцеплением и лапой;

2. Лента измерительная;

3. Круг;

4. Лабораторный динамометр;

5. Весы с вариациями;

6. Шарик на резьбе;

7. Кусок пробки с отверстием;

8. Лист бумаги;

9. ЛИНИЯ.

Порядок выполнения работ:

1. Определяем массу лампочки на весах до 1 г.

2. Проденьте через отверстие и зажмите трубку в лапке штатива (Рис. 1)

3. На листе бумаги на листе начертите круг радиусом около 20 см. Измерьте радиус с точностью до 1 см.

4. Штатив с маятником расположен таким образом, чтобы продолжение шнура проходило через центр круга.

5. Взяв пальцами нить в точке подвеса, поверните маятник так, чтобы шарик описывал круг, равный бумаге.

6. Считаем время, за которое маятник совершает, например n = 50 оборотов. Рассчитайте срок лечения Т =.

7. Определите высоту конического маятника, для этого измерьте расстояние по вертикали от центра шара до точки подвеса.

8. Находим нормальный модуль разгона по формулам:

a n 1 = a n 2 =

a n 1 = a n 2 =

9.Прижмите шар горизонтально расположенным динамометром на расстояние, равное радиусу окружности, и измерьте модуль компонента F

Затем рассчитываем ускорение по формуле a N 3 = a N 3 =

10. Результаты измерений Входим в таблицу.

Очевидный номер	R M.	N.	ΔT C.	T C.	h M.	m кг.	F N.	A N1 м / с 2	A N 2 м / с 2	и 3 м / с 2

Вычислите относительную погрешность вычисления N 1 и запишите ответ в виде: a n 1 = a n 1cp ± Δ a n 1cp a n 1 =

Сделать вывод:

Контрольные вопросы:

1.Какой тип движения представляет собой движение шарика по нитям в лабораторных условиях? Почему?

2. Сделайте рисунок в тетради и укажите правильное название сил. Назовите точки приложения этих сил.

3. Какие законы механики выполняются при движении тела в этой работе? Картинка наглядно заставляет и записывает правильные законы.

4. Почему сила упругости F, измеренная в эксперименте, равна результирующим силам, приложенным к телу? Назовите закон.

3. Рассчитайте и занесите в таблицу средний период времени т.>, За который шарик сделает Н. = 10 оборотов.

4. Рассчитайте и запишите среднее значение периода вращения T.> Ball.

5. По формуле (4) определить и занести в таблицу среднее значение модуля ускорения.

6. По формулам (1) и (2) определить и занести в таблицу среднее значение модулей угловой и линейной скорости.

Опыт	Н.	т.	т.	а.	ω	v.
1	10	12,13	—	—	—	—
2	10	12,2	—	—	—	—
3	10	11.8	—	—	—	—
4	10	11,41	—	—	—	—
5	10	11,72	—	—	—	—
Ср.	10	11,85	1,18	4,25	0.63	0,09

7. Вычислить максимальное значение абсолютной случайной погрешности измерения временного интервала t. .

8. Определите абсолютную систематическую погрешность временного интервала t. .

9. Вычислить абсолютную погрешность прямого измерения периода времени т. .

10. Рассчитайте относительную погрешность прямого измерения периода времени.

11.Запишите результат прямого измерения временного интервала в форме интервала.

Ответить на контрольные вопросы

1. Как изменится линейная скорость мяча при его равномерном вращательном движении относительно центра круга?

Линейная скорость характеризуется направлением и значением (модулем). Модуль — это постоянная ценность, и направление этого движения может меняться.

2. Как доказать соотношение v. = Ом.?

Так как V = 1 / T, циклическая частотная связь с периодом и частой 2π = VT, откуда V = 2πr. Связь линейной скорости и угловой 2πr = VT, следовательно, V = 2πr / t. (R — описанный радиус, R — вписанный радиус)

3. Как зависит период вращения T. Ball от модуля его линейной скорости?

Чем выше показатель скорости, тем меньше период периода.

Выводы: научился определять период вращения, модули, центростремительное ускорение, угловую и линейную скорость при равномерном вращении тела и вычислять абсолютную и относительную погрешности прямых измерений времени движения тела.

Супербасон

Определить ускорение материальной точки при ее равномерном вращении, если для δ т. = 1 с Прошла 1/6 длины окружности, имея модуль линейной скорости v. = 10 м / с.

Окружность:

S = 10 ⋅ 1 = 10 м
l = 10⋅ 6 = 60 м

Радиус круга:

r = L / 2π
r = 6/2 ⋅ 3 = 10 м

Разгон:

а = В.2 / R.
a = 100. 2/10 = 10 м / c2.

Лабораторная работа Обучающееся тело по окружности. Лабораторная работа. Исследование движения тела по окружности под действием силы упругости и силы тяжести. Движение тела под углом к горизонту

Эластичность и жесткость

цель работы

Определение центростремительного ускорения мяча при его равномерном движении по окружности

Теоретическая часть Работа

Эксперименты проводятся с коническим маятником: маленький шарик, подвешенный на нити, движется по окружности.В то же время резьба описывает конус (рис. 1). На мяч действуют две силы: сила тяжести и сила упругости нити. Они создают центростремительное ускорение, направленное радиусом к центру круга. Модуль ускорения можно определить кинематически. Равно:

Чтобы определить ускорение (A), необходимо измерить радиус окружности (R) и период обращения окружности шара (T).

Центростремительное ускорение также можно определить по законам динамиков.

Согласно второму закону Ньютона, Запишем это уравнение В проекциях на выбранные оси (Рис.2):

О:;

Oy:;

Из уравнения в проекции на ось ой выразительно выразим:

Из уравнения в проекции на ось AU выразим степень эластичности:

Тогда ссылка может быть выражена:

и, следовательно, ускорение: где g = 9,8 м / с 2

Следовательно, чтобы определить ускорение, необходимо измерить радиус окружности и длину резьбы.

Оборудование

Штатив со сцеплением и лапкой, мерная лента, шарик на нитке, лист бумаги с нарисованным кругом, часы со второй стрелкой

Прогресс

1. Подвесьте маятник к лапке штатива.

2. Измерьте радиус окружности с точностью до 1 мм. (К)

3. Штатив с маятником расположить так, чтобы продолжение шнура проходило через центр круга.

4. Возьмите пальцы за точку подвеса, поверните маятник так, чтобы шар описывал круг, равный бумаге.

6. Определите высоту конического маятника (H). Для этого измерьте расстояние по вертикали от точки подвеса до центра мяча.

7. Найдите модуль разгона по формулам:

8.Рассчитайте ошибки.

Таблица результатов измерений и вычислений

Расчеты

1. Срок лечения:; Т =.

2. Центростремительное ускорение:

; А 1 =.

; А 2 =.

Среднее значение центростремительного ускорения:

; И ср =.

3.Абсолютная ошибка:

ΔA 1 =.

ΔA 2 =.

4. Среднее значение абсолютной погрешности:; ΔA ср =.

5. Относительная ошибка:;

Выход

Напишите ответ по вопросам полное предложение

1. Слово определение центростремительного ускорения. Запишите его и формулу для расчета ускорения при движении по кругу.

2. Слово второй закон Ньютона. Запишите его формулу и формулировку.

3. Запишите определение и формулу для расчета

гравитация.

4. Запишите определение и формулу для расчета силы упругости.

Лабораторная работа 5.

Движение тела под углом к горизонту

назначение

Научитесь определять высоту и дальность полета, когда тело движется с начальной скоростью, направленной под углом к горизонту.

Оборудование

Модель «Движение тела, брошенного под углом к горизонту» в таблицах

Теоретическая часть

Движение тел под углом к горизонту представляет собой сложное движение.

Движение под углом к горизонту можно разделить на две составляющие: равномерное движение по горизонтали (по оси x) и одновременно равномерное, с ускорением свободного падения, по вертикали (по оси Y).Так лыжник двигается при прыжках с трамплина, струи воды из фирменной, артиллерийские снаряды, метание снарядов

Уравнения движения S w: пространство = «720» /> «> и

Запишем в проекциях по осям X и Y:

По оси x: S =.

Для определения высоты полета необходимо помнить, что в верхней точке подъема скорость тела равна 0. Тогда будет определено время подъема:

При падении проходит то же время.Следовательно, время движения определяется как

Тогда высота подъема определяется по формуле:

А дальность полета:

Наибольшая дальность полета наблюдается при движении под углом 45 0 к горизонту.

Прогресс

1. Записать Б. в рабочую тетрадь Теоретическая часть работы и набросать график.

2. Откройте файл «Движение под углом к горизонту.xls».

3. В ячейку B2 введите значение начальной скорости 15 м / с, а в ячейку B4 — угол 15 градусов (В ячейки вводятся только числа, без единиц измерения).

4. Рассмотрим результат на графике. Измените значение скорости на 25 м / с. Сравнить графики . Что изменилось?

5. Измените значения скорости на 25 м / с, а угол -35 градусов; 18 м / с, 55 град. Рассмотрим графику.

6. Провести расчеты по формулам для скоростей и углов (по опциям):

8. Проверьте свои результаты, рассмотрите графики. Графика графика в масштабе на отдельном листе А4

Таблица значений синусов и косинусов некоторых углов

	30 0	45 0	60 0
Синус (sin)	0,5	0,71	0,87
Косинус (COS)	0,87	0,71	0,5

Выход

Запишите ответы на вопросы полные предложения

1.Какие значения зависят от дистанции полета брошенного под углом к горизонту тела?

2. Приведите примеры движения под углом к горизонту.

3. Под каким углом к горизонту наибольшая дальность полета тела под углом к горизонту?

Лабораторная работа 6.

3. Рассчитайте и занесите в табл. Т.> Средний период времени, за который шарик сделает Н. = 10 оборотов.

4. Рассчитайте и введите среднее значение периода вращения T.> Мяч.

5. По формуле (4) определить и занести в таблицу среднее значение модуля ускорения.

6. По формулам (1) и (2) определить и занести в таблицу среднее значение модулей угловой и линейной скорости.

Опыт	Н.	т.	т.	а.	ω	в.
1	10	12,13	—	—	—	—
2	10	12,2	—	—	—	—
3	10	11,8	—	—	—	—
4	10	11.41 год	—	—	—	—
5	10	11,72	—	—	—	—
Ср.	10	11,85	1,18	4,25	0,63	0,09

7. Вычислить максимальное значение абсолютной случайной погрешности измерения временного интервала t..

8. Определите абсолютную систематическую погрешность временного интервала t. .

9. Вычислить абсолютную погрешность прямого измерения периода времени т. .

10. Рассчитайте относительную погрешность прямого измерения периода времени.

11. Запишите результат прямого измерения временного интервала в форме интервала.

Ответить на контрольные вопросы

1.Как изменится линейная скорость мяча при его равномерном вращательном движении относительно центра круга?

2. Как доказать соотношение v. = Ом. ?

Так как V = 1 / T, циклическая частотная связь с периодом и частой 2π = VT, откуда V = 2πr. Связь линейной скорости и угловой 2πr = VT, следовательно, V = 2πr / t.(R — описанный радиус, R — вписанный радиус)

3. Как зависит период вращения T. Ball от модуля его линейной скорости?

Чем выше показатель скорости, тем меньше период периода.

Супербасон

Окружность:

S = 10 ⋅ 1 = 10 м
l = 10⋅ 6 = 60 м

Радиус круга:

r = L / 2π
r = 6/2 ⋅ 3 = 10 м

Разгон:

а = В.2 / R.
a = 100. 2/10 = 10 м / c2.

Лабораторная работа №4 по физике 9 класс (ответы) — изучение движения тела по окружности

3. Рассчитайте и занесите в таблицу средний период времени. За что мяч делает n = 10 оборотов.

4. Вычислите и запомните среднее значение шара периода вращения.

5. По формуле (4) определить и занести в таблицу среднее значение модуля ускорения.

6. По формулам (1) и (2) определить и занести в таблицу среднее значение модулей угловой и линейной скорости.

Опыт	Н.	т.	т.	а.	ω	v.
1	10	12,13	—	—	—	—
2	10	12.2	—	—	—	—
3	10	11,8	—	—	—	—
4	10	11,41	—	—	—	—
5	10	11,72	—	—	—	—
Ср.	10	11,85	1,18	4,25	0,63	0,09

7. Вычислить максимальное значение абсолютной случайной погрешности измерения времени t.

8. Определите абсолютную систематическую ошибку времени t.

9. Вычислить абсолютную погрешность прямого измерения времени t.

10.Рассчитайте относительную погрешность прямого измерения периода времени.

11. Запишите результат прямого измерения временного интервала в форме интервала.

Ответить на контрольные вопросы

1. Как изменится линейная скорость мяча при его равномерном вращательном движении относительно центра окружности?

2. Как доказать соотношение v = ωr?

3. Как зависит период вращения шара t от модуля его линейной скорости?

Чем выше показатель скорости, тем меньше период периода.

Выводы: Я научился определять период вращения, модули, центростремительное ускорение, угловую и линейную скорость при равномерном вращении тела и вычислять абсолютную и относительную погрешность прямых измерений времени движения тела.

Супербасон

Определить ускорение материальной точки при ее равномерном вращении, если 1/6 длины окружности прошла за Δt = 1 с, имея модуль линейной скорости V = 10 м / с.

Окружность:

S = 10 ⋅ 1 = 10 м
L = 10⋅ 6 = 60 м

Радиус круга:

r = L / 2π
R = 6/2 ⋅ 3 = 10 м

Разгон:

а = v 2 / r
а = 100 2/10 = 10 м / с 2.

Дата __________ FI _________________________________ Класс 10_____

Лабораторная работа №1 по теме:

«Изучение движений тела по окружности под действием упругих и жестких сил».

Цель работы: Определение центростремительного ускорения мяча при его равномерном движении по окружности.

Оснащение: Штатив со сцеплением и лапой, рулетка мерная, циркуль, динамометр

лабораторный, весы с вариациями, нагрузка на резьбу, лист бумаги, леска, пробка.

Теоретическая часть работы.

Эксперименты проводятся с коническим маятником. Маленький шарик движется по окружности радиуса R. В этом случае резьба AB, к которой прикреплен шарик, описывает поверхность прямого кругового конуса.На шарик действуют две силы: сила тяжести
И натяжение нити (рис. А). Они создают центростремительное ускорение, направленное радиусом к центру круга. Модуль ускорения можно определить кинематически. Он равен:

Для определения ускорения необходимо измерить радиус окружности и период обращения шара по окружности.

Центростремительное (нормальное) ускорение также можно определить по законам динамиков.

Согласно второму закону Ньютона
. Лопатки силовые к компонентам и направлены по радиусу к центру окружности и вертикально вверх.

Тогда второй закон Ньютона запишется следующим образом:

Направление координат оси Выберите, как показано на рисунке Б. В проекциях на ось около 1 в уравнении движения мяча принимает вид: 0 = F 2 — Mg. Следовательно, F 2 = Mg: компонент балансирует силу тяжести
, действующую на шар.

Запишем второй закон Ньютона в проекциях на ось около 1 x: Ma n = F 1. Отсюда
.

Модуль компонента F 1 можно определить различными способами. Во-первых, это можно сделать из подобия треугольников OAV и FBF 1:

Отсюда
и
.

Во-вторых, модуль компонента F 1 может быть измерен непосредственно динамометром. Для этого задерживаем мяч горизонтально расположенным динамометром на расстояние, равное радиусу R окружности R (рис.B) и определяют показания динамометра. В этом случае сила упругости пружины уравновешивает компонент.

Сравним все три выражения для A N:

,
,
И убедитесь, что они близки друг к другу.

Прогресс.

1. Определите массу луковицы по весам до 1 г.

2. Шар, подвешенный на нитке, закрепите штатив в лапке с помощью куска пробки.

3 .Нарисуйте на листе бумаги круг радиусом 20 см ( R. = 20 см = ________ M).

4. Штатив с маятником расположен таким образом, что продолжение шнура происходит через центр круга.

5 . Взяв пальцами нить за точку подвеса, приведите маятник во вращательное движение

над листом бумаги так, чтобы шар описывал ту же окружность, что и нарисованный на бумаге.

6. Подсчитайте время, за которое маятник сделает 50 полных оборотов ( N. = 50).

7. Рассчитайте период обращения маятника по формуле: Т. = т. / Н. .

8 . Рассчитайте значение центростремительного ускорения по формуле (1):

9 . Определите высоту конического маятника ( ч. ). Для этого измерьте расстояние по вертикали от центра мяча до точки подвеса.

10 . Рассчитайте значение центростремительного ускорения по формуле (2):

11. Возьмите горизонтально расположенную грушу крутящего момента на расстояние, равное радиусу окружности, и измерьте компонентный модуль.

Затем вычисляем ускорение по формуле (3): =

12.Результаты измерений и вычислений в таблице.

Радиус окружности

R. , м.

Скорость

Н.

т. , из

Период лечения

Т. = т. / Н.

Высота маятника

h. , м.

Массовый шар

м. , кг

Центральное ускорение

м / с. 2

Центр ускорения

м / с. 2

Центральное ускорение

м / с. 2

13 . Сравните три значения модуля центростремительного ускорения.

__________________________________________________________________________ ВЫХОД:

Дополнительно :

Найдите относительную и абсолютную погрешность косвенного измерения A C (1) и (3):

Формула 1).________; ΔA q = · a c = ________;

Формула (3). _________; ΔA c = · a c = _______.

Тема: Изучение движений тела по окружности.

Цель работы: определение центростремительного ускорения мяча при его равномерном движении по окружности.

Оснащение:

тренога с муфтой и лапой;
рулетка измерительная;
компас;
динамометрическая лаборатория;
весы с вариациями;
шарик на резьбе;
кусок пробки с отверстием;
бумага;
линия.

Теоретическая часть

Эксперименты проводятся с коническим маятником. Маленький шарик движется по окружности радиусом R. . При этом резьба AU , к которой прикреплен шарик, описывает поверхность прямого кругового конуса. На мяч действуют две силы: сила тяжести мГс. и натяжение нити F. (см. Фиг. , но ). Они создают центростремительное ускорение A n, направленное по радиусу к центру окружности.Модуль ускорения можно определить кинематически. Равно:

а n = ω 2 r = 4π 2 r / t 2

Для определения ускорения необходимо измерить радиус окружности R. и период окружности T. . Центростремительное (нормальное) ускорение также можно определить по законам динамиков. По второму закону Ньютона ma = Mg + F . Мощность шпателя F. К компонентам F 1. и F 2. направлены по радиусу к центру окружности и вертикально вверх. Тогда второй закон Ньютона можно записать так:

ma = Mg + F 1 + F 2 .

Направление осей координат будет выбрано, как показано на рисунке b. . В проекции на ось O 1 y уравнение шара примет вид: 0 = F 2 — MG . Отсюда F 2 = MG . Компонент F 2. балансирует гравитацию мГс. действует на мяч. Запишем второй закон Ньютона в проекции на ось O 1 x. : ma n = F 1 . Отсюда a N = F 1 / M . Компонент модуля F 1. Может определяться различными способами. Во-первых, это можно сделать, используя подобие треугольников OAAK. и FBF 1. :

F 1 / R = Mg / H

Отсюда F 1 = MGR / H и a N = GR / H .

Во-вторых, компонент модуля F 1. Вы можете напрямую измерить динамометр. Для этого задержите горизонтально расположенный шар динамометра на расстояние, равное радиусу R. Круг (рис. в ), и определите показание динамометра. В этом случае сила упругости пружины уравновешивает компонент F 1. . Сопоставимы все три выражения для a N. :

a n = 4π 2 r / t 2, a n = г / ч, a n = f 1 / m

и убедитесь, что числовые значения центростремительного ускорения, полученные тремя способами, близки друг к другу.

В этой работе время следует измерять с максимальной тщательностью. На это полезно посчитать. больше N оборотов маятника, тем самым уменьшая относительную погрешность.

Взвешивайте мяч с точностью, которую могут дать лабораторные весы, без необходимости. Достаточно весить до 1 г. Высоты конуса и радиуса круга достаточно измерить с точностью до 1 см. При такой точности измерений относительные погрешности значений будут порядка.

Порядок выполнения работ.

1. Определяем массу лампочки на весах до 1 г.

2. Проденьте проделку через отверстие в пробке и зажмите пробку в лапке штатива (см. Рис. в ).

3. На листе бумаги на листе начертите круг радиусом около 20 см. Измерьте радиус с точностью до 1 см.

4. Штатив с маятником у нас есть так, что продолжение нити происходит через центр окружности.

5. Взяв пальцами нить в точке подвешивания, поверните маятник так, чтобы шарик описывал ту же окружность, что и нарисованный на бумаге.

6. Считаем время, за которое маятник совершает заданное количество оборотов (например, n = 50).

7. Определите высоту конического маятника. Для этого измеряем расстояние по вертикали от центра шара до точки подвеса (мы рассматриваем ч. ~ л.).

8. Найдите модуль центростремительного ускорения по формулам:

a n = 4π 2 R / T 2 и A N = GR / H

9. Прижмите шар горизонтально расположенным динамометром на расстояние, равное радиусу окружности, и измерьте компонентный модуль F 1. . Затем рассчитываем ускорение по формуле a N = F 1 / M .

10. Результаты измерений Входим в таблицу.

Очевидное число	Р.	Н.	Δt.	Т = Δt / n	H.	м.	а n = 4π 2 R / T 2	А Н = ГР / В	а н = f 1 / м
1

Сравнивая три значения полученного модуля центростремительного ускорения, убеждаемся, что они примерно одинаковы.

Circles Blog Archives — Circl.es

Я работал предпринимателем последние 20 лет, внося свой вклад в развитие Интернета. Все это время меня утешала мысль о том, что помощь людям в общении полезна для планеты.

Но у массового подключения есть недостатки. Пузырьки общения углубляют племенные разделения. Мега-компании, такие как Amazon, уничтожают местные обычные магазины. Дезинформация изобилует, и мы все больше осознаем отсутствие конфиденциальности в Интернете.И, по иронии судьбы, многие из нас чувствуют себя более изолированными, чем когда-либо прежде.

Благодаря пандемии мир виртуального общения пережил строительный бум. Clubhouse, приложение, которое позволяет людям собираться в аудио-чатах, является одной из новейших структур на рынке; Объявления о его прибытии разлетелись на первых полосах газет, и всего через несколько месяцев работы Clubhouse была оценена в 1 миллиард долларов.

Такие компании, как Clubhouse, показывают, что виртуально мы можем быстро создавать большие аудитории, сообщества и даже компании.Но продуманно ли мы проектируем? Как сказал Уинстон Черчилль в 1943 году: «Мы формируем наши здания; после этого они формируют нас ». Можем ли мы представить новый способ спроектировать эти виртуальные пространства так, чтобы они усиливали лучшее из нашего человечества?

Вот небольшой пример. Джоди МакЛин, генеральный директор EDENS, владелец, оператор и застройщик недвижимости, как и многие другие генеральные директора в 2020 году, пыталась решить, как помочь своим новым удаленным сотрудникам избежать риска разделения из-за этой изоляции. Маклин также знал, что эта физическая изоляция происходила в то же самое время, когда компании нужно было собраться вместе для разговоров о системном расизме, возможно, больше, чем когда-либо прежде.Первое, что она попробовала, — это крупноформатный веб-семинар для ее сотрудников из 200 человек. Но это не вызвало реального разговора или связи.

В следующий раз она попробовала другую виртуальную структуру. Персонал размещался в маленьких комнатках по десять человек, лица располагались по кругу. Они встретились на два 90-минутных сеанса. У них было немного времени, чтобы поразмыслить, а затем таймер и повестка дня руководили их беседой. Они рассказали о своей идентичности на работе и о том, как проблемы, волнующие нашу страну, проявляются в физических сообществах, которые EDENS создает для клиентов.Персонал сначала был напуган, привык сидеть сложа руки с выключенными камерами. Но после сеансов 95% персонала были в восторге от своего опыта, отмечая, что их разговоры были искренними. Сессии не проводились профессионалами. В конце дня Маклин заметил: «Никогда еще мы не были так благодарны друг другу».

Сидеть кругами — очень старая идея. Когда люди находятся в небольшой группе и смотрят друг на друга, они чувствуют себя включенными. Они занимаются. Они предлагают идеи и делятся своими проблемами.Со временем люди соединяются и начинают помогать друг другу. Многие из наших физических пространств не созданы для того, чтобы люди могли находиться в кругу. Подумайте о классах, торговых залах, церквях или аудиториях. Эти пространства глубоко воплощают идеи иерархии, конвейерных линий и учителя как эксперта. Наш переход в виртуальное пространство — шанс поставить это под сомнение.

Дважды щелкните на примере корпоративного обучения и развития. С 2000 по 2012 год моему предыдущему стартапу приходилось быстро расти, чтобы не отставать от стремительно растущего рынка.Мы не могли быстро набрать новые навыки. Нам нужно было, чтобы наши люди росли, чтобы наша компания могла расти. Я начал сосредотачиваться на том, что нужно для формирования культуры обучения на работе. К сожалению, у нас не хватало средств обучения: корпоративный «университет», заполненный устаревшими слайдами, видео-тренингами, менеджеры, коучающие подчиненных 1: 1, система управления производительностью, которую никто не обновлял, и случайные разовый семинар. Им не удалось привлечь всех, кроме нескольких очень самостоятельных учеников.

Одна вещь, которую мы попробовали, сработала: «Битва групп», где около трети компании занялись бас-гитарой, барабанами, гитарой, клавишными или пением. Учителя музыки помогали напоминать людям, как учиться, как слушать друг друга, как практиковаться. Это было упражнение в том, насколько важно создавать увлекательный опыт, когда обучение в командах может подтолкнуть людей к тому, чтобы стать лучшими.

Наши общие корпоративные структуры обучения были созданы для старых обстоятельств. Нам больше не нужно массово производить рабочих для работы на конвейере.Информации больше нет, и люди должны собираться вокруг эксперта. У нас противоположная проблема: каждый день цунами информации. Нашим сотрудникам нужны очень разнообразные и гибкие креативщики, которые могут работать вместе.

Корпоративное обучение и развитие перекликается с системой образования в целом, которая также состоит из традиционных структур и имеет аналогичную проблему разобщенности. В то время как 63% детей обучаются по системе четырехлетних колледжей в США, 40% из этих студентов не заканчивают свою степень в течение шести лет.Это заставляет меня думать, если больше этих студентов будут полностью вовлечены во время учебы в колледже, увеличится ли количество выпускников?

Имеются данные, свидетельствующие о том, что учебные группы улучшают показатели зачисления и успеваемость, а обучение в малых группах или «командное» обучение повышает удовлетворенность как студентов, так и преподавателей лекциями. Набирает популярность метод Харкнесса, впервые примененный в Академии Philips Exeter в 1930 году, при котором все занятия носят разговорный характер и проводятся за овальным столом. Многие штаты в настоящее время уполномочены использовать восстановительные практики, круговой подход к созданию и ремонту сообществ в школах, который оказался намного более эффективным, чем традиционные способы организации школ.

Фактически, оказывается, что многие образовательные подходы основаны на силе кругов. У них разные названия: форум, которым пользуются такие организации, как YPO; сообщества практиков, которые используются на предприятиях, в школах и в правительстве; текстовый диалог, который используется Институтом Аспена; И список продолжается. У всех есть общие практики. В программах Гарвардской школы бизнеса слушатели размещаются в группе из восьми отдельных комнат вокруг кухни, и тренер помогает каждой «живой группе» объединиться в круг, который вместе работает над делами и проектами.

Лично у меня был некоторый опыт обучения в кругах, который помог мне, научил и подтолкнул меня больше, чем любой класс, тренер или даже консультант сделал раньше. Когда мне было 30, я впервые был руководителем масштабной компании, и мои форумы EO и YPO, на каждом из которых собирались 7-8 других генеральных директоров каждый месяц, были тем, как я действительно научился выполнять эту работу. Когда я сокращаю штат или арендую, когда экономика падала? Как мне появиться в офисе, когда мой папа медленно выходит из БАС дома? Как вы решаете разногласия с партнерами, стоит ли того PR, достаточно ли хороши мои публичные выступления? После ухода мне посчастливилось быть выбранным в Братство Генри Кроуна, круг лидеров в аналогичных переходных точках.В рамках этой стипендии Институт Аспена дал мне возможность исследовать ценности, то, что я считал полезным для общества, и следующие шаги. Эти круги были трансформационными.

Область обучения бурлит новыми идеями, технологиями, нейробиологией и наукой о данных. Но незаметно одна из самых старых идей набирает обороты с обоими подходами к обучению и с тем, как лучше всего работать: сидеть в кругу.

Практически все, что мы делаем на работе, выполняется в команде. Методологии построения команды, такие как Agile (кросс-функциональные команды, работающие последовательно структурированно), Scaling up (ежедневные встречи для улучшения коммуникации), EOS / Traction (ежеквартальная работа для достижения набора целей компании) и Holocracy (гибкость сотрудников для выполнения задач. в плоской корпоративной структуре) подчеркивают важность и силу небольших групп, обучающихся вместе и быстро.В сердце каждого из них — структурированная встреча в малых группах.

Успех этих небольших групповых структур зависит от открытого сотрудничества команд. Проект Google Аристотеля показал, что психологическая безопасность — вера в то, что человек не будет наказан или унижен за высказывание идей, вопросов или опасений — была самым очевидным фактором успеха для сотен исследованных ими команд. Практики Кругов способствуют такому виду безопасности благодаря групповым беседам, в которых никто не доминирует в разговоре, каждый чувствует себя комфортно и чувствует себя услышанным.Они помогают боссу сидеть рядом с вами в команде, моделирующей уязвимость, вместо того, чтобы отдавать обновления и приказы из передней части комнаты.

Я потратил много энергии в качестве генерального директора, пытаясь создать последовательную корпоративную культуру и согласованность во всей компании. Но реальная культура, с которой человек сталкивается изо дня в день, напрямую связана с его непосредственной командой. Нам нужно научиться руководить «командами команд». Это поможет справиться с смехотворно низким уровнем вовлеченности сотрудников, о котором Gallup сообщает в наших компаниях из года в год.Как сказал мне мой сотрудник из Аспена, ныне генеральный директор Heineken, Дольф ван ден Бринк: «Мы хорошо поработали над построением структуры во всей глобальной организационной структуре, но не там, где это наиболее важно: внутри команд».

Идея, которая привела меня к созданию Circles Learning Labs, Inc. (Circl.es), заключалась в том, чтобы облегчить людям обучение и работу в кругу. Я задавался вопросом, почему у всех в мире нет Форума, как у меня, когда я был новым генеральным директором? Или стипендию, которая поможет им определиться с их следующим карьерным шагом? Я спросил себя, могу ли я помочь решить проблемы всем лидерам восстановительной практики или толпе Холократии, которые все больше работали над этим?

Когда я начал экспериментировать в 2016 году, я подумал, что мы будем создавать сервис поиска партнеров: использовать LinkedIn, например, для поиска восьми новых руководителей маркетинга в небольших компаниях.Но оказалось, что эта часть была относительно простой: сообщества и компании уже собрали единомышленников. Мы не думали, что нам вообще нужно будет создавать видеопространство, но когда мы поэкспериментировали с новым интерфейсом, где люди были в круге, а не в сетке, мы получили невероятную реакцию. Оказалось, что все эти разные кружки имеют очень похожие передовые практики, что делает их хорошим кандидатом для программного обеспечения. Для компаний и сообществ было сложно и дорого создавать и управлять множеством кругов — еще одна проблема, которую можно было решить с помощью программного обеспечения.

Итак, мы решили создать виртуальное пространство, в котором каждая функция, которую мы добавляем или убираем, способствует подлинному человеческому взаимодействию и упрощает запуск и масштабирование множества кругов. Результаты использования Circl.es с такими организациями, как EDENS, обнадеживают:

Гарвардская школа бизнеса в течение многих лет пыталась найти правильный способ поддержать студентов, изучающих управленческое образование, чтобы они могли практиковать и применять полученные навыки после выхода из университетского городка. Их программа «Virtual Living Group» заставляет руководителей ежемесячно встречаться по кругу.Когда появился Covid, мы добавили Circl.es в их виртуальный кампус, сократив прогулы в виртуальных программах почти до нуля и «значительно углубив общение в классе».
Школы тысячелетия создали кружки учителей, и 89% заявили, что это улучшило их способность поддерживать учеников, 90% заявили, что это улучшило их самочувствие, и 92% заявили, что это уменьшило их чувство изоляции.
Компании Кена Бланшара обнаружили, что круги общения улучшают результаты семинаров и приводят к успешным последующим действиям. «Есть две вещи, которые ведут к успешной устойчивости обучения — подотчетность и отношения», — отметила Диана Урбина, руководитель службы коучинга.
Крис Андерсон, основатель TED, основал круги TED, чтобы помочь своему сообществу перейти от вдохновения к действию. Менее чем за год программа охватила тысячи кругов по всему миру и быстро становится основной частью сообщества TED.
Jumpcrew, аутсорсинговая компания из Нэшвилла, штат Теннесси, начала свою программу Circl.es до пандемии. Он продолжал быстро расти в удаленной рабочей среде, поскольку они обнаружили, что создание «кружков для наших будущих лидеров» сократило отток сотрудников и улучшило нашу культуру.”

Еще более обнадеживающими, чем результаты программы, являются отзывы участников, которые мы получаем после сеанса на Circl.es.

«Я люблю дискутировать на каждом занятии и вместе разбираться в реальных, глубоких жизненных ситуациях».

«Circl.es создает пространство для открытого и честного общения на высоком уровне».

«Так приятно слышать от других — так много общих моментов борьбы и празднования, что невероятно воодушевляет!

«Продолжая оставаться сплоченной группой, чтобы расти, развиваться, учиться и узнавать друг друга.»

Круги очеловечиваются. Исследования показывают, что когда мы чувствуем, что можем проявить себя более достоверно, мы более открыты для новых идей и чувствуем большее благополучие. Никогда еще не было технически проще формировать небольшие круги людей со всего мира и хорошо управлять кругом. Любой может использовать передовой опыт Circl.es для облегчения энергии, времени и потока, благодаря которым время, проведенное вместе в кругу, кажется упакованным. Результат хорошо организованного круга в виртуальном окружении может открыть для нас истинное разнообразие и изменить способ нашего мышления.

Может быть, будущее обучения и работы — это возвращение в прошлое. Меньше презентаций, больше разговоров. Пространство и время для небольших групп, чтобы объединиться, без потока тысяч голосов, доходящих до вас через ваши экраны. Пространство для размышлений и обработки вместо того, чтобы ежесекундно вбирать больше информации.

За прошедшие годы мы построили большие иерархические структуры; Теперь лидеры могут сосредоточиться на том, что происходит на грани, способствуя более тесным связям, где люди могут привнести свое подлинное, полноценное «я» в разговоры и соединиться как люди.И с небольшой помощью пандемии мы можем воспользоваться тем фактом, что многие сотрудники не возвращаются на свои рабочие места, и изменить форму нашей реальности.

Дэн Хоффман — генеральный директор и основатель Circl.es. Чтобы узнать больше от Дэна, свяжитесь с ним в LinkedIn здесь или продолжайте следить за нашим блогом.

Неврология для детей — Vision Exp.

Прицел (обзор)

Один из самых драматичных экспериментов — демонстрация слепое пятно.Слепое пятно — это область на сетчатке без рецепторы, реагирующие на свет. Поэтому образ, который попадает на это регион НЕ будет виден. Именно в этой области выходит зрительный нерв. глаз на пути к мозгу. Чтобы найти свое слепое пятно, посмотрите на изображение ниже или нарисуйте его на листе бумаги:

Чтобы нарисовать тестер слепых зон на листе бумаги, сделайте небольшую точку на левая сторона разделена примерно на 6-8 дюймов от маленького + справа боковая сторона. Закройте правый глаз.Удерживайте изображение (или отведите голову от компьютерный монитор) на расстоянии около 20 дюймов. Левым глазом посмотрите на +. Медленно приблизьте изображение (или переместите голову), глядя на +. На определенном расстоянии точка исчезнет из поля зрения … это когда точка попадает на слепое пятно вашей сетчатки. Обратный процесс. Закройте левый глаз и посмотрите на точку правым глазом. Переместите изображение медленно приближается к вам, и знак + должен исчезнуть.

Вот еще несколько изображений, которые помогут вам найти слепое пятно.

Для этого изображения закройте правый глаз. Левым глазом посмотри на красный круг. Медленно приближайте голову к изображению. На определенном расстояние, синяя линия не будет выглядеть сломанной !! Это потому, что ваш мозг «восполняет» недостающую информацию.

Это следующее изображение позволяет вам увидеть другой способ, которым ваш мозг заполняет слепая зона. Опять закройте правый глаз. Левым глазом посмотрите на +. Медленно приближайте голову к изображению. пространство в середина вертикальных линий исчезнет.

На следующих двух изображениях снова закройте правый глаз. Левым глазом посмотрите на числа справа, начиная с цифры «1». Ты должно быть видно «грустное лицо» (верхнее изображение) или разрыв в синем линия (нижнее изображение) периферийным зрением. Держите ваши голова неподвижна и левым глазом посмотрите на другие числа. Грустный лицо должно исчезнуть, когда вы дойдете до «4», и снова появиться примерно на «7». Точно так же синяя линия будет выглядеть законченной между цифрами «4» и «7».»

Вот еще одно изображение, показывающее ваше слепое пятно. Закройте правый глаз. Левым глазом посмотрите на +. Вы должны увидеть красную точку на своем периферийное зрение. Продолжайте смотреть на + левым глазом. Красный точка переместится слева направо, исчезнет и снова появится как точка перемещается в слепое пятно и выходит из него.

Материалы:

Более (Подробнее) о слепых пятнах

Почитайте про глаз.

Знаете ли вы?

У осьминога нет слепого пятна! В сетчатка осьминога устроена более логично, чем сетчатка млекопитающих.Фоторецепторы у осьминога сетчатка расположена во внутренней части глаза, а клетки, которые несут информацию в мозг, расположены во внешней части сетчатка. Следовательно, зрительный нерв осьминога не прерывает никакого пространства. сетчатки.

Осьминог Глаз (Изображение любезно предоставлено Biodidac)

Для марок К-12

Два глаза лучше, чем один, особенно когда дело доходит до восприятия глубины. Восприятие глубины — это способность судить об объектах, которые находятся ближе или дальше, чем другие.Чтобы продемонстрировать разницу между использованием одного и двух Глаз, чтобы оценить глубину, держите концы по карандашу, по одному в каждой руке. Держи их вертикально или горизонтально лицом друг к другу на расстоянии вытянутой руки от твое тело. Закрыв один глаз, попробуйте дотронуться до конца карандашей. все вместе. Теперь попробуйте двумя глазами: должно быть намного проще. Это потому что каждый глаз смотрит на изображение под другим углом. Этот эксперимент тоже можно проделать пальцами, но карандаши дают эффект немного более драматично.

Материалы:

Карандаши (но пальцы — хорошая замена)

Для 3–12 классов

Вот еще одна демонстрация важности двух глаз при оценке глубина. Соберите набор монеток (или пуговиц, или скрепок). Сядьте за стол с ваш предмет. Поставьте чашку перед объектом. Чашка должна быть примерно в двух футах от объекта. Закройте объект на один глаз. Держать пенни в воздухе около 1.5 футов над столом. Переместите пенни медленно. Попросите испытуемого сказать «Брось!» когда он или она думает Пенни упадет в чашку, если вы ее отпустите. Когда субъект говорит «Бросьте», бросьте пенни и посмотрите, попадет ли он в чашку. Попытайся снова, когда объект использует оба глаза. Попробуйте еще раз с чашкой подальше от темы. Попробуйте еще раз, поставив чашку ближе к объекту. Сравните результаты «10 капель» на каждом расстоянии.

Вопросов:

Есть ли улучшение с двумя глазами?
Есть ли улучшение с чашкой ближе к теме?

Материалы:

Чашка (чашка для йогурта или поилка)
Падение предметов (пенни, пуговицы, канцелярские скрепки, прищепки)

ИЛИ ПОПРОБУЙТЕ ЭТУ ИГРУ Возьмите лист бумаги и нарисуйте цель похожий на тот, что справа.Фактические размеры кругов не слишком важно, и вам не нужно раскрашивать круги. Поместите цель на земле примерно в пяти футах перед вами. Попросите друга встать возле цели. Пусть ваш друг протянет чернильный маркер кончиком указывая вниз. Закройте один глаз. Скажите другу, чтобы он двигался вперед или назад или из стороны в сторону, пока вы не решите, что маркер попадет в центр цели, если она была сброшена. Скажите другу, чтобы он уронил маркер, когда вы думаете, что маркер находится над центром цели.Маркер должен оставить место, где он попал в цель. Попробуйте 10 раз с одним закрытым глазом и добавьте увеличьте «счет» за 10 капель. Теперь попробуйте это с открытыми глазами (получите маркер другого цвета, когда вы используете 2 глаза, чтобы увидеть разницу на цель). Ваш результат лучше, когда вы используете два глаза?

Материалы:

Бумага мишень
Маркеры (двухцветные)

Для марок К-12

Вот еще один способ продемонстрировать, как разные изображения проецируются на каждый глаз.Посмотрите на объект вдалеке (на расстоянии 20–30 футов), например, часы на стене. Закройте один глаз, поднимите руку и выровняйте палец с предметом. Теперь, не двигая пальцем или головой, закройте открытый глаз и откройте закрытый глаз. Объект на расстоянии будет казаться прыгающим в сторону … ваш палец больше не будет выровнен. Это показывает, что на каждый глаз попадают разные изображения.

Материалы:

Для 3-12 классов

В глазу есть два типа фоторецепторов: палочки и колбочки.В стержни отвечают за зрение в условиях тусклого света, колбочки — за цветовое зрение. Чтобы продемонстрировать, как фоторецепторы «адаптируются» к низкой освещенности. условий, получите коллекцию объектов, которые выглядят немного иначе: для Например, получите 10 крышек для бутылок с колой, 10 крышек для бутылок с газировкой и 10 бутылок с водой. колпачки. Они должны ощущаться одинаково, но не выглядеть одинаково. В ярком попросите учащихся разделить шапки на стопки одинаковых крышек. потом выключите свет, чтобы в комнате было очень и очень темно. Попросите их разделить снова шапки.Выключи свет и посмотри на результат … там должно быть много ошибок. Подсчитайте количество ошибок. Затем приглушите свет снова и поговорите / обсудите адаптацию к темноте или животных, которые могут видеть в темноте. Технического объяснения адаптации к темноте нет. необходим для маленьких детей. Запланируйте поговорить и обсудить примерно 7-10 человек. минут … этого времени хватит на хотя бы частичную адаптацию фоторецепторы. После обсуждения (7-10 минут) попросите студентов снова отделите колпачки в тех же очень, очень тусклых условиях, как и раньше.Подсчитайте количество ошибок. На этот раз ошибок должно быть меньше потому что фоторецепторы адаптировались к условиям низкой освещенности.

Материалы:

Три комплекта крышек для бутылок (или других аналогичных шт.)

4–12 классы

Многие из этих иллюзий доступны в виде интерактивных ударно-волновых игр в
Neuroscience для Детская галерея визуальных иллюзий.

То, что вы видите, — это не всегда то, что есть.Либо это? Глаз может играть проделки с мозгом. Вот несколько иллюзий, демонстрирующих это точка.

Волшебный куб
Посмотрите на центральный куб. Какая сторона спереди? Передняя часть, как показано на кубе с правой стороны или спереди, как показано на кубе на левая сторона или спереди нет вообще?
Какая из показанных ниже линий длиннее? Иллюзия Мюллера-Лайера
Измерьте их. Вы можете быть удивлены, узнав, что они такие же длина.Мы видим, что линии разные, потому что нас «учили» используйте определенные формы и углы, чтобы сообщить нам о размере.
Другие примеры иллюзий Мюллера-Лайера
Посмотрите на середину изображения с черными квадратами 15-30 секунд. Находятся те действительно точки, которые появляются по углам квадратов? Что происходит если сосредоточить внимание на точке? Теперь посмотрим на середину картинки с белые квадраты. Вы снова видите точки? Какого они цвета?
Вот еще один пример той же иллюзии.
Отличается ли расположение пятен на этих двух фотографиях? Почему?
Вы видите вазу или лицо на рисунке ниже? Этот тип изображения был впервые проиллюстрирован психологом Эдгаром Рубиным в 1915 году. Обратите внимание, что это очень трудно одновременно увидеть и лица, и вазу. Это может произойти из-за того, что мы склонны сосредотачивать свое внимание только на одной части изображение … либо лица, либо ваза.
Остаточные изображения
Попробуйте эту интерактивную демонстрацию остаточные изображения.Вам понадобится браузер с поддержкой JAVA.
Смотрите на желтый + в середине рисунка в течение 15-30 секунд. потом переводите взгляд на белый квадрат справа. Были ли цвета действительно поменять себя? Это пример «остаточного изображения».
Вот еще один пример создания остаточного изображения. Вы можете поставить рыба в миске? Попробуй это. Посмотрите на желтую полосу посередине рыбу на картинке ниже примерно 15-30 сек. Затем переместите свой взгляд на аквариум.Вы должны увидеть в миске рыбу другого цвета. Помогает, если вы будете держать голову неподвижно и моргать один или два раза после того, как вы переведите взгляд на миску. Остаточное изображение продлится около пяти секунд.
Попробуйте эти две интерактивные демонстрации (с использованием браузеров с поддержкой JAVA) Остаточные изображения:

Что происходит: сетчатка ваших глаз бывает трех цветов рецепторы (колбочки), наиболее чувствительные к красному, синему или зеленому. Когда вы слишком долго смотрите на определенный цвет, эти рецепторы становятся «усталый» или «утомленный».»Когда вы посмотрите на другой фон, рецепторы, которые устали, тоже не работают. Таким образом, информация от всех различных цветовых рецепторов не находится в равновесии. Следовательно, вы видите цветные «остаточные изображения».

Посмотрите на + примерно 15 секунд, затем переключите свой взгляд на правая часть изображения.	Посмотрите на + примерно 15 секунд, затем переключите свой взгляд на правая часть изображения.
Сделайте линии на правой стороне изображения смотреть прямо? Они правда натуралы?

7.Иллюзия Поггендорфа была создана Иоганном Поггендорфом в 1860 году. Линии за прямоугольниками прямые или нет? Похоже, что это не идет прямо, но так ли?

Поггендорф Иллюзия

8. Хммм … это центральный круг справа того же размера, что и центр круг слева? Многим кажется, что круг окруженный маленькими кружками, больше, чем круг, окружены большими кругами. Однако я знаю, что они такие же размер…. Я скопировал и вставил точно такой же круг в середины !!

Иллюзия Титченера

Это иллюзия показывает, что наш мозг оценивает размер, сравнивая предметы с вещами в окрестностях.

9. Иллюзия Ястрова. Какая дуга больше? Вы можете увидеть, что верхний меньше, но они такого же размера. Верхний выглядит меньше, потому что более короткая дуга верхней фигуры находится рядом с большой дугой нижней фигура.

10. Эта книга открывается к вам или от вас?

11.Тройник или нет … вот в чем вопрос. Этот перевернутая буква «Т» имеет две линии …. они одинаковой длины? Вы держите пари, что они are … Я скопировал одну строку и наклеил ее внизу первой строки. Измерьте их сами.

12. Какая дуга выходит из круга с наибольшим диаметр?

Скорее всего, дуга C является частью самого большого круга. Однако все дуги на самом деле из ОДНОЙ окружности. Посмотри на ту же фигуру снова — однако на этот раз я заблокировал правую и левую стороны большего две дуги.Каждая дуга образуется из круга одинакового размера.

13. Субъективные контуры: Заполнение пробелов. Твой мозг пытается заполнить эти четыре картинки изображениями, которые на самом деле не там. Ты видишь а:

14. Эффект Болдуина: расстояние между двумя большими коробками. такое же, как расстояние между двумя маленькими коробками. Для многих люди, расстояние между маленькими коробками кажется больше.

Для страниц побольше иллюзий с их физиологическими объяснения, см .:

SandlotScience.ком
невозможно Цифры
Fun Visual Уловки и оптические иллюзии

Также есть страница, посвященная известному художнику М.С. Эшер, известный своим рисунки иллюзий и невозможных фигур.

15. Иллюзия движения: эти двухмерные объекты создают иллюзия движения. Посмотрите в центр этих изображений, чтобы увидеть круги изображений вращаются.

Для классов К-12

Как окружающая картина влияет на то, что мы видим? Узнайте с это интерактивная картинка.У вас должен быть браузер, поддерживающий «JAVA скрипты ».

Для классов К-12

Как окружающий цвет влияет на то, что мы видим? Узнайте с это интерактивная картинка. Вы должны иметь браузер, поддерживающий «сценарии JAVA».

Для 3–12 классов

Как ваш мозг подготавливает вас к чему-то? Узнайте с это интерактивная картинка. У вас должен быть браузер, поддерживающий «JAVA скрипты ».

Для 9–12 классов

В Exploratorium в Сан-Франциско есть стоящий виртуальный коровий глаз Рассечение, чтобы проверить.

3–12 классы

У вас есть «Рентген Видение? »Вы сможете увидеть собственными глазами с помощью этого простого иллюзия. Сверните лист блокнота в трубочку. Диаметр трубка должна быть около 0,5 дюйма. Поднимите левую руку перед ты.Держите трубку рядом с нижней частью левого «указательного» пальца. между большим пальцем (см. рисунок ниже).

Посмотрите в трубку ПРАВЫМ глазом и держите твой левый глаз тоже открыт. Вы должны увидеть дыру в левой руке !! Почему? Потому что ваш мозг получает два разных изображения … одно из дыр в бумаге и в одной левой руке.

Материалы:

3–12 классы

вы когда-нибудь заметил, что звезду на небе легко увидеть НЕ глядя прямо на это? Ночью на самом деле легче увидеть тусклую звезду посмотрев немного в сторону.Попытайся! Это потому, что два типы фоторецепторов (палочки и колбочки) в сетчатке выполняют разные функции и расположены в сетчатке в разных местах. В колбочки, которые лучше всего подходят для детализации и цветового зрения, находятся в самом высоком концентрация в центре сетчатки. Стержни, которые лучше работают в тусклый свет, в наибольшей степени сосредоточены по бокам сетчатки. Так что если если посмотреть на звезду «не по центру», ее изображение упадет на площадь сетчатка, у которой больше стержней!

Материалы:

Нет

К-3

Вот увлекательный способ познакомить с чувством зрения и изучить его.Получить разнообразные образцы «цветных карточек» из местного магазина красок. Эти карты размером с учетную карточку и демонстрируют разнообразие красок. имеется в наличии. Приведите их обратно в класс и попросите учащихся сопоставить похожие цвета. Вы также можете использовать образцы подарочной упаковки или обоев для раскрашивания. или карточки с выкройками. Просто приклейте пленку или обои к карточке доску, чтобы получить себе «Цветную карту».

Материалы:

Образцы карточек цветов из магазина красок
Образцы обоев
Подарочная упаковка
Ножницы, клей и картон (если вы будете делать открытки своими руками)

К-3

Color Spy — это разновидность игры «Я шпионю».Разделите игроков на команды. Напишите слова «синий», «красный», «желтый», «оранжевый» и «зеленый» на отдельных куски бумаги. Попросите одного члена каждой команды выбрать бумагу. Выбранный цвет будет названием команды.

Когда кто-то говорит «Вперед», у команд будет 10 минут, чтобы осмотреться. комната для предметов, которые имеют цвет своей команды. Команды должны составить список все предметы, которые они находят. После 10 минут поиска команды собираются вместе и читаются списки объектов. Каждая команда получает по одному балл за каждый найденный объект.После того, как списки будут прочитаны, каждая команда получит пять минут, чтобы обыскать комнату в поисках цветных предметов, которые другие команд НЕ нашли. Например, если красная команда сделала не найти красное яблоко, другая команда, которая ДЕЙСТВИТЕЛЬНО нашла красное яблоко, получит один пункт. Команда, набравшая наибольшее количество очков после обоих поисков, является победитель.

Материалы:

К-12

Конечно, вы не можете увидеть, полностью ли темно, но вы можете немного увидеть в тусклом свете.В тусклом свете рецепторы в ваши глаза, называемые стержнями, делают большую часть работы. Однако стержни делают не предоставлять никакой информации о цвете. Другие фоторецепторы в вашем Глаза, называемые колбочками, используются для восприятия цвета. Шишки не работайте при тусклом свете. Вот почему вы не можете видеть цвета при тусклом свете. Убедитесь сами:

Возьмите пять листов бумаги разного цвета (например, разного цвета). печатная бумага или плотная бумага). Приглушите свет, пока не сможете почти не вижу.Подождите около 10 минут (возможно, послушайте музыку, пока вы ждать). Затем напишите на каждом листе бумаги того цвета, который, по вашему мнению, является. Включите свет и посмотрите, верны ли ваши догадки. Все ли в вашем классе смешали один и тот же цвет или все получили цвета верный?

Материалы:

Карандаши или ручки
Цветная бумага (примерно пяти разных цветов)

3–12 классы

Когда свет попадает в глаз, он сначала преломляется (преломляется) роговицей.Хрусталик глаза изгибает свет дальше в процессе, называемом размещение. Чтобы изображение было четким на сетчатке, Хрусталик глаза меняет форму, выпячиваясь или уплощаясь. Более плоский линза меньше преломляет свет. Вот как продемонстрировать проживание:

Закройте один глаз и посмотрите на точку примерно в 20 футах от вас. Это должно быть в фокус. Сосредоточьтесь на точке и поднимите один из пальцев прямая видимость чуть ниже точки. Ваш палец должен быть немного размытым.Теперь смените фокус: смотрите на кончик пальца, а не на точку 20. в футах. Ваш палец будет в фокусе, но дальняя точка будет размытый.

Материалы:

Никто

Дополнительные ресурсы, связанные со зрением, из «Неврологии для детей»:

Глаз
Сетчатка
Путь зрения
Вы носите очки? Выяснить Зачем!
Советы по безопасности глаз
План урока о Eye
План урока о цвете Vision
План урока о глубине и движение
ЦВЕТ еды и напитки влияют на вкус?
Общие глазные болезни и Расстройства

Национальный глазной институт имеет БОЛЬШАЯ страница с мероприятиями, связанными с Глаз называется «увидеть все, что можно увидеть» для детей; и учиться насчет «стереограмм.»

[Вернуться к началу]

Гравитация и орбиты — гравитационная сила | Круговое движение | Астрономия

Темы

Сила гравитации
Круговое движение
Астрономия

Описание

Переместите Солнце, Землю, Луну и космическую станцию, чтобы увидеть, как это влияет на их гравитационные силы и орбитальные пути.Визуализируйте размеры и расстояния между разными небесными телами и выключите гравитацию, чтобы увидеть, что бы произошло без нее!

Примеры целей обучения

Опишите взаимосвязь между Солнцем, Землей, Луной и космической станцией, включая орбиты и положения
Опишите размер и расстояние между Солнцем, Землей, Луной и космической станцией
Объясните, как гравитация управляет движением нашей солнечной системы
Определите переменные, которые влияют на силу гравитации
Предскажите, как изменится движение, если гравитация будет сильнее или слабее

Версия 1.4,0

HTML5 sims могут работать на iPad и Chromebook, а также в системах ПК, Mac и Linux в современных веб-браузерах. Если у вас возникли проблемы с использованием симулятора HTML5 на поддерживаемой платформе, отключите все расширения браузера.

iPad:
iOS 12+ Safari
iPad-совместимые sim-карты

Android:
Официально не поддерживается. Если вы используете симуляторы HTML5 на Android, мы рекомендуем использовать последнюю версию Google Chrome.

Chromebook:
Последняя версия Google Chrome
Симуляторы HTML5 и Flash PhET поддерживаются на всех устройствах Chromebook.
SIM-карты, совместимые с Chromebook

Системы Windows:
Microsoft Edge, последняя версия Firefox, последняя версия Google Chrome.

Системы Macintosh:
macOS 10.13+, Safari 13+, последняя версия Chrome.

Системы Linux:
Официально не поддерживается. Пожалуйста, свяжитесь с phethelp @ colorado.edu с проблемами устранения неполадок.

Рабочий лист лаборатории маятника

Рабочий лист лаборатории маятника Чтобы продемонстрировать, что движение маятника кручения удовлетворяет простой гармонической форме в уравнении (3) 2. Я проделал это задание со своими учениками много раз, и они всегда находят это забавным и интересным. 01 секунда ПОСМОТРЕТЬ начальный угол ПОСМОТРЕТЬ легенду СРАВНИТЬ два маятника НАБЛЮДИТЬ энергию в системе в реальном времени ИССЛЕДОВАТЬ влияние трения НАСТРОЙТЕ длину и массу МАСШТАБИРУЙТЕ для настройки шкалы УЗНАЙТЕ период с помощью Period Trace ВЫБРАТЬ маятник лаборатория для студентов, изучающих научный метод.E8. X3 — Маятник РАБОЧАЯ ТАБЛИЦА Имя: Студенческий билет (B00…): Shishir Ghosh Pendulum Сделайте четкую фотографию своего маятника и прикрепите фотографию Microsoft Word — Маятниковая мини-лаборатория. Задание Автор: HP_Administrator Дата создания: 29.12.2010 1:10: 40 PM Это отличная исследовательская лаборатория для вашего физического подразделения! В этом упражнении учащихся попросят выяснить, какие из следующих переменных влияют на период качания маятника: масса, длина струны или угол, под которым маятник выпущен. е.13 Решение уравнений квадратного корня (приложения) Занятие сегодня: 6. Джеймс Эллисон. Перед проведением эксперимента мы с моим партнером по лаборатории обсудили различные методы прогнозирования напряжения маятника в его самой низкой точке. Образец лабораторной процедуры и отчет Простой маятник В этой лаборатории вы будете исследовать влияние нескольких различных физических переменных на период простого маятника. 13 Pendulum Lab. Студенты могут использовать этот пример отчета физической лаборатории, чтобы выяснить формат отчета физической лаборатории.Может использоваться как лабораторная работа. Группа лабораторий установила маятниковую систему, провела несколько испытаний для измерения времени колебаний и измерила длину маятника, обнаружив, что он составляет 72 см. Период увеличивается как квадратный корень из длины. Масса называется боб и в положении равновесия свешивается прямо вниз. Эксперимент II: Измерьте период колебаний маятниковых качелей разной амплитуды, сохраняя при этом длину и массу фиксированными. (2) Можно показать, что если амплитуда движения остается небольшой, уравнение (2) будет периодом.Сделайте простой маятник, подвесив подвес для грузов на веревке, привязанной к опорному стержню. Материалы 1. 13 Pendulum Lab. Учащиеся контролируют переменные, проверяя по одной переменной, используя ручные методы (секундомер, человеческий глаз и т. Д.). В этом лабораторном упражнении вы будете измерять свойства движения маятника и анализировать их. канцелярская скрепка, служащая держателем для «качки» маятника. Это показывает, что длина действительно влияет на период маятника. Джеймс Эллисон, Клинт Роу и Уильям Кокран.Наблюдайте за энергией в системе в режиме реального времени и меняйте величину трения. Запишите длину маятника в таблице ниже. Лабораторная работа 11: Торсионный маятник Цель 1. docx от PHYC 1190 в Университете Далхаузи. Они провели некоторые исследования маятников и обнаружили уравнение, которое связывает длину маятника с его периодом. Один кусок металлической проволоки согнуть в крючок. Малый угол ii. ) Лабораторная работа: Что влияет на период маятника. Цель: эта лабораторная работа поможет вам выяснить, какая из следующих трех переменных (длина, угол падения, масса маятника) будет влиять на период маятника.1 Исследуйте сохранение импульса при простом маятниковом движении. Измерьте расстояние от кольца до своего веса. Пятница: 25 октября 2019 г. Задачи по главе 5. Измерение массы и скорости m 1 = _____ m 2 = _____ Результаты 10 выстрелов с маятником Пробное положение 1 2 3 4 5 6 7 8 9 10 Это простое лабораторное задание дает студентам возможность построить простой маятник и проверить влияние длины струны на поведение маятника. 1 Объясните общее сохранение энергии в простой гармонической игре. Играйте с одним или двумя маятниками и узнайте, как период простого маятника зависит от длины струны, массы маятника, силы тяжести и амплитуды качания. .Целью данной лабораторной работы является проверка зависимости соотношений периодов от параметров системы для маятника и системы масса-пружина. Соляной маятник Наука Работа в рубриках: Эксперименты, физика, Ресурсы с тегами: искусство, эксперимент, физика, ресурсы, стержень Маятник движется по предсказуемой схеме, определяемой несколькими факторами, включая длину маятника, силу, приложенную к толчок, и насколько тяжелый маятник. Объясни свои ответы. Учащиеся понимают, как кинетическая и потенциальная энергия соотносятся в системе.1/2, частота, равная 1 / T, зависит только от PH 1113: Центростремительная сила на маятнике 1 Центростремительная сила на маятник Цель этого эксперимента состоит в том, чтобы проанализировать движение маятника и получить дополнительные опыт использования графического анализа для извлечения количественной информации. В этом двухминутном видеоролике описывается, как настроить маятниковое исследование с помощью LoggerPro, LabPro2 и фотоэлемента. Переместите каждую группу в обозначенное место для испытаний и привяжите их вес к веревке так, чтобы она едва не касалась земли во время висения.{\ circ} $. Коллекция виртуальных лабораторий, созданных Glencoe. Поместите табурет под вешалку и измерьте начальную высоту x0 над табуретом. Показаны 8 лучших рабочих листов в категории — Pendulum Lab. В частности, как он колеблется при задании начальной потенциальной энергии. 6) • T = 3. Мы также измерили время для десяти последовательных колебаний, чтобы еще больше уменьшить ошибки. Постепенно добавляйте 50 г массы до тех пор, пока в подвеску для массы не будет добавлено 250 г. Моделирование предлагает студентам разработать контролируемые эксперименты, чтобы определить, как переменные влияют на движение маятника.Период легко измерить с помощью таймера фотозатвора. Какова длина маятника? [894 м] 3. В этой лабораторной работе нас интересует период маятника \ (T \). . Временной период колебаний равномерного стержня регулируется уравнением. Подготовка к лабораторной работе: Баллистический маятник. Инструкции: подготовьтесь к этой лабораторной работе, ответив на приведенные ниже вопросы. Верните уровень в переднюю часть лаборатории. ) Цель — испытать сохранение энергии с помощью маятника. 3 см и 6. Фотозатвор и подставка 2. Напишите описание процедуры, которой вы следовали, и данных, которые вы собрали, чтобы ответить на этот вопрос.Маятник взвешивает неподвижные точки, которые могут свободно качаться. Поместите пусковую установку на лабораторный стол так, чтобы пистолет был ориентирован горизонтально, оставив перед ним не менее 4 метров свободного пространства. Отображение 8 лучших рабочих листов, найденных для — Pendulum Lab. опустить вопрос 1 Во время эксперимента собираются данные о колебаниях простого маятника. Прикрепите гирю 50 г к петле и убедитесь, что длина вашего маятника составляет 50 см. Измерьте массу своего веса. 4. Запустите таймер фотозатвора — он автоматически остановится, когда будет записано время для View LAB X3.2. Паста и изюм / зефир Положите изюм или зефир на конец палочки спагетти. Рабочий лист маятника Фуко для студентов 5-8-го числа Во многих музеях и обсерваториях есть маятник Фуко, установленный для демонстрации вращения Земли вокруг оси. Подготовка к лабораторной работе В этой лабораторной работе используются три основных концепции, и вам следует изучить каждую из них. RST. Как изменение длины маятника изменит период колебаний маятника? Данные 8c-Con of Energy-Pendulum-RGC-1-15-09 — 5 — Анализ данных Цель этой лаборатории — определить, сохраняется ли полная механическая энергия в маятниковой системе, когда тело движется в гравитационном поле. .Прижимая большим пальцем веревку к столешнице, вы подвешиваете гирю к краю лабораторного стола, позволяя ей раскачивать ее вбок. После того, как все устроились, я читаю указания к лаборатории, показываю студентам расположение материалов и прохожу пример. Прикрепите два куска ленты к стене / другой поверхности на расстоянии 50 см друг от друга так, чтобы ваш вес находился посередине. Один конец пружины закреплен, а другой конец прикреплен к блоку массой M = 8. б) Используя маятниковую лабораторию, исследуйте этот вопрос.Длиной 5 м. Где T = период, l = длина маятника, g = сила тяжести T = 2Π * (2. при использовании периода T маятника зависит от квадратного корня из L, длины маятника и g, ускорения свободного падения. . Маятник длиной 2 м имеет период 2. Сделано несколько предложений для расширений, таких как введение движения вдоль большего, чем высота маятника замечена в симуляторе. 06, ноя 2008, 18:44 bmart111 @ msudenver. 3 Часть 3 Прогноз. Для части 3 эксперимента сделайте набросок графика, который, по вашему мнению, будет создан простым маятником, состоящим из шайб, раскачивающихся на струне при изменении длины струны.Это занятие весело и увлекательно и помогает студентам построить прочную основу для интерпретации, анализа и построения графиков данных sk Предварительный просмотр неформатированного текста: Модуль V: Лаборатория педулума с назначением виртуального моделирования Это задание позволит вам продемонстрировать следующие цели: 4. 1. 0 кг. Энергия движения: Урок 1, Упражнение с качающимся маятником — Рабочий лист качающегося маятника — ответы 5. doc Простой маятник состоит из относительно массивного объекта, известного как маятник, подвешенного на веревке к неподвижной опоре.У простого маятника масса m (боб) подвешена на веревке длиной l, закрепленной в точке поворота. Мы повторили это измерение пять раз. Материалы. docx Просмотр Загрузить: Лаборатория по замене ПК с баллистическим маятником. Измерьте период с помощью секундомера или таймера периода. Для вашего маятника будет хорошим приближением принять L как расстояние от оси вращения до центра бильярдного шара. По мере уменьшения длины строки период времени также уменьшается. Pendulum Energy Lab В этом видео 0.Баллистический маятник 1. Обратите внимание, что это предварительная лаборатория. Используйте маятник, чтобы найти значение g в Лаборатории маятника Планеты X — Интерактивное моделирование PhET Простой маятник Редакция 25.10.2000 2 F = — kx GG (1), то движение маятника будет простым гармоническим движением и его период можно вычислить, используя уравнение для периода простого гармонического движения m T = 2π k. Учащиеся обнаружат, что, хотя длина цепочки маятника влияет на то, насколько быстро он может завершить период, его общее движение следует шаблону, который можно использовать для прогнозирования его будущего движения.Учите словарный запас, термины и многое другое с помощью дидактических карточек, игр и других средств обучения. ELA-Грамотность. В «Физике Уокера» есть отличный анекдот о наблюдении Галилеем колеблющихся люстр и его последующих экспериментах с простым маятником. STEAM — это сочетание науки, технологий, инженерии, искусства и математики. Посмотреть рабочий лист PS113L «Маятник» Кайл Вирамонтес. В этом эксперименте составной маятник с фиксированной осью Лаборатории традиционной физики в средней школе страдают от медленного сбора данных, так что некоторые динамические характеристики переменных могут быть скрыты от учащихся.Таким образом, если длина маятника увеличивается в 4 раза, период увеличивается только вдвое. LAB 21 Lab Раздаточный материал Lab 21. Указания: На этом рабочем листе вы будете работать с соотношениями между частотой, периодом и длиной в простой маятниковой лаборатории. Относительно источника у него есть угловой момент L. Выполнив эту лабораторную работу на базе HTML5, ваши ученики получат полное представление о том, как масса, длина, смещение и гравитационное ускорение влияют на период маятника.Используйте более длинную струну, одну более тяжелую и одну более легкую гирю. Большой угол c. Вы можете варьировать трение и силу тяжести. Этот план урока с качающимся маятником подходит для 6-8 классов. 9 м / с2] 2. Учитывая высоту маятника, учащиеся рассчитывают и предсказывают, насколько быстро маятник будет качаться, понимая закон сохранения энергии и используя уравнения для PE и KE. 14 Охота за мусором (обзор № 1) С помощью этого практического задания учащиеся смогут исследовать, какие факторы влияют на период действия маятника.Это делается в основном самостоятельно, и требования могут варьироваться в зависимости от учителя (набранный текст, длина, групповой отчет и т. Д.). См. Также: Руководство для студентов по Pendulum Lab, где вы найдете раздаточный материал, который нужно раздать студентам. то есть по мере увеличения длины L маятника увеличивается и его период T. МАЯТНИК РАБОЧАЯ ТАБЛИЦА 1. 1 Объясните общее сохранение энергии в простой гармонике Описание: Эта лабораторная работа посвящена простому маятнику и тому, как его использовать для определения значения ускорения свободного падения.Студенты будут стрелять из своей лаборатории по криминализации баллистического маятника. Физика. Вы криминолог, и вам дали пистолет, который использовался при совершении преступления. На основе вашей лаборатории, использующей простой маятник, сопоставьте правильное определение каждому слову. Данные отображаются в виде графика и сравниваются, чтобы определить, какие переменные влияют на период. Что такое период ?: Время, за которое маятник совершит одно полное колебание вперед-назад (в секундах). Чтобы завершить маятник, прикрепите шайбу к крючку для канцелярской скрепки, чтобы она служила бобом.Как изменяется скорость (скорость и направление) маятника, когда он движется справа налево? Студенты также могут запустить демонстрацию маятника под названием «Незатухающий и неприводимый маятник», которую можно найти на веб-сайте The Pendulum Lab. Маятник S i. Назначение: В первую очередь, эта лаборатория включена только потому, что нам нравится слово «баллистическая». В этой физической лаборатории студенты исследуют, как масса, длина и угловое смещение влияют на период простого маятника. Некоторые из представленных рабочих листов: работа в средней школе с качающимся маятником, простой маятник, часть периода работы маятника и энергия, лабораторная работа 1 с простым маятником, простой маятник гармонического движения, национальная инициатива по математике, элементарная наука, работа с простым гармоническим движением, маятник.фундамент этой лаборатории. 51 секунда Simple Harmonic Motion 13 г l 2S Измерьте массу своего веса. Чтобы минимизировать неопределенность периода, мы измерили время, за которое маятник совершит \ (20 \) колебания, и разделили это время на \ (20 \). Вытяните гирю из маятника и выровняйте его макушкой. Простой маятник 15. Некоторые из приведенных ниже рабочих листов представляют собой рабочие листы простых задач гармонического движения с определением частей гармонического движения в терминологии гармонического движения для важных формул простого маятника периодического движения.2. 01с. В этом эксперименте мы будем изучать поведение однородного металлического стержня, действующего как составной маятник. Простой маятник В этой лабораторной работе студенты будут использовать фотозатвор и маятник, чтобы определить физические свойства простого маятника, которые влияют на его период. doc Примечания к периодической таблице 1. pdf PHYS. Студенты пишут лабораторный отчет. Во время лаборатории вы собрали следующую лабораторию: Энергия маятника. Раздел 20362. 20.04.12. edu: Период определяется как время, необходимое для одного полного цикла (качания вперед и назад) маятника.Поперечный контраст и идеальная пружина нерастянутой длины 0. Встряхните. Некоторые из рабочих листов для этой концепции: школьная работа с качающимся маятником, работа с простым гармоническим движением, часть периода работы маятника и энергия, урок 3, период и частота, лабораторная работа, что влияет период маятника, Маятник, принесенный вам Галилеем, Простой маятник. Версия для печати: Словарь. После начала лабораторных работ предварительные лабораторные работы не принимаются. Список материалов: цифровая видеокамера / штатив (рекомендуется), струна (гибкая, но не растягиваемая), измерительная линейка, измерительная лента или объект эталонного размера (т.е.Некоторые из представленных рабочих листов: работа в средней школе с качающимся маятником, простой маятник, часть периода работы маятника и энергия, лабораторная работа 1 с простым маятником, простой маятник гармонического движения, национальная инициатива по математике, элементарная наука, работа с простым гармоническим движением, маятник. 3 разные шайбы 5. Эксперимент 10 Лабораторный рабочий лист баллистического маятника. Раздел № 1) Сначала мы помещаем начало системы координат xy в точку поворота на рисунке 2. Поиграйте с одним или двумя маятниками и выясните, как период простой маятник зависит от длины струны, массы маятника и амплитуды качания.Данные% разницы в вашей таблице данных дадут вам представление об ответе на этот вопрос. Проблемы: Что определяет период маятника? (длина, масса) Можно ли создать маятник с периодом в 1 секунду? Прогноз / Гипотеза: Если мы изменим длину строки, то количество качаний за 10 секунд будет _____, потому что _____. Чтобы показать, что период (или угловая частота) простого гармонического движения торсионного маятника не зависит от амплитуды движения 3. doc Изменение фазы LAB КОНТРОЛЬНЫЙ СПИСОК.259 с В этом лабораторном эксперименте учащиеся комбинируют данные и навыки построения графиков, собирая зажимы для карандашей / пряжи / бабочек разной длины и измеряя время качания маятника. 3. Маятник изменяется при изменении длины маятника, зависимой переменной будет период маятника, а независимой переменной будет длина маятника. Вы узнали, что на темпы роста населения влияет как количество детей в семье, так и возраст, в котором люди заводят детей.Поместите около 200 г на подвеску, чтобы получился маятник общей массой 250 г и длиной 1. В этом лабораторном упражнении вы будете измерять свойства движения маятника и анализировать их. Лаборатория CSEC Physics Lab — Факторы, влияющие на период маятника 1. Используя фотозатвор для измерения периода, мы варьировали массу маятника для фиксированной длины и варьировали длину маятника для фиксированной массы. 2. 1: На принципиальной схеме показаны компоненты баллистического маятникового устройства. После столкновения металлический шар застрял в маятнике, комбинация маятник-шар имеет кинетическую энергию: KE f = 1 2 (m + M) v2 f (4.Раздел данных включает график, четко обозначающий три точки вдоль траектории, которые были проанализированы. Направления: 1. См. Соответствующий урок о вертикальных кругах, если вас просят рассчитать натяжение струны во время колебания маятника. 3. Задача 2. 3 Лабораторная работа с маятником. Задание 1. Цели обучения: Учащиеся смогут: • Разрабатывать эксперименты, чтобы описать, как переменные влияют на движение маятника. Вы собираетесь подсчитать количество полных колебаний маятника за 30 секунд. В этом сообщении в блоге приводится пример отчета лаборатории физики IB о периоде простого маятника.Студенты изучают, как вес и длина влияют на колебания маятника. Другой конец веревки привяжите к стержню на подставке, сделав длину маятника 40 см. Измерьте длину маятника до середины маятника. Вторник: 15 октября 2019 г. Тест по главе 4. Затем период T для одного. Соберите материалы и сделайте копии рабочего листа, либо рабочего листа A с качающимся маятником (с алгеброй), либо рабочего листа B с качающимся маятником (без алгебры). История маятника. com Начать изучение физики 1114 lab 10: простой маятник.0 см длиной, используя металлический шар и веревку. mM = (2 балла) 16. Версия для печати: Словарь. Разделите класс на группы по 3 человека и раздайте Рабочий лист «Качающийся маятник». Лаборатория Pendulum Challenge наблюдает за поведением маятника, который является гармоническим осциллятором. Поиграйте с Pendulum Lab, чтобы выяснить, какие переменные влияют на движение маятника, и напишите качественные описания для каждой переменной. Большой угол b. Определите энергию, запасенную в упругой пружине. Что вам нужно сделать: Часть 1 — Предварительная лабораторная работа по управляемым комбо 11: Баллистический маятник В эксперименте с баллистическим маятником снаряд запускается в маятниковый улавливатель.Данные% разницы в вашей таблице данных дадут вам представление об ответе на этот вопрос. pdf лаборатория фазового перехода. 2-х метровые палки (или метровая палка и линейка или рулетка) 3. Поместите блок на пол слева от маятника. Примените концепцию сохранения импульса к повседневной жизни. Маятник был выпущен из \ (90 \), и его период был измерен путем съемки маятника камерой мобильного телефона и использования встроенного времени телефона. Разработайте эксперименты, чтобы описать, как переменные влияют на движение маятника.Период легко измерить с помощью таймера фотозатвора. Добавьте 50 г к подвеске груза и определите изменение положения, вызванное этим добавленным весом. Измерьте период с помощью секундомера или таймера периода. doc Анализ маятниковой лаборатории и заключение. 20 м размещается горизонтально на столе без трения, как показано выше. Этот график был загружен 13 февраля 2021 г., загружен администратором в образце лабораторного отчета. X3 — Маятник РАБОЧАЯ ТАБЛИЦА Имя: Студенческий билет (B00…): Маятник Шишира Гоша Сделайте четкую фотографию своего маятника и прикрепите фотографию. Это лабораторное задание, во время которого студенты будут собирать данные и делать выводы о переменных, влияющих на скорость маятник.Рабочий лист Практика: равномерное круговое движение Вы выполнили лабораторную работу, используя конический маятник, длина которого составляла 75 см. Маятник длиной 75 м на Луне (g = 1. Пятница: срок лабораторного отчета. Короткое, открытое занятие; открытые задачи; избегайте явных инструкций; используйте функции симулятора; таблицы (созданы учеником). Запись данных Моделирование маятниковой лаборатории. Основные аспекты лабораторной работы: КАЛИБРОВКА: определение того, как компьютер записывает угол маятника. Зависимая переменная. На среднем уровне студенты проверяют длину и массу маятника.схемы рабочего листа физики. Посмотреть LAB X3. Рабочий лист Pendulum Lab Review. Хотя вы, возможно, знаете о популярности… Пример эссе по лабораторному отчету о простом маятнике. Чтобы уменьшить возможные случайные ошибки в измерениях времени, мы повторили измерение периода три раза для каждой из десяти длин. Задача: В нашей последней лабораторной работе, связанной с физикой I, мы рассмотрим движения массы на пружине. Длинная веревка длиной не менее 1 метра. 5 м на Луне, где g = 1.Обрежьте струну примерно на 1. При небольших колебаниях простой маятник имеет линейное поведение, что означает, что его уравнение движения может быть описано линейным уравнением (без квадратов, синусов или косинусов), но для более крупных колебаний он становится очень нестандартным. . Наблюдайте за качением маятника как за идеальной системой или добавьте трение и посмотрите, как он постепенно замедляется. (Изменится ли период маятника. Рабочий лист маятника Фуко для студентов 5-8-го числа Во многих музеях и обсерваториях есть маятник Фуко, установленный для демонстрации вращения Земли вокруг оси.«В этом эксперименте мы исследуем свойства простого маятника. Единицы измерения периода следующие: # второго маятника. Материалы — 1 метр струны, масса 1х50 г, масса 2х100 г и секундомер. Масса, подвешенная на веревке) должен демонстрировать простое гармоническое движение для небольших колебаний, и мы исследуем зависимость периода простого маятника от его длины. Некоторая лента. Продолжительность: приблизительно 60 минут. И ХИМИЧЕСКИЕ ИЗМЕНЕНИЯ Laser Disc. doc Periodic Chart Notes. 64 m / 9. The Переменными, которые мы рассматриваем, являются масса, длина маятника и угол начальной дислокации.Измерьте расстояние от потолка до своего веса. 1, 3, 8, 12 и 15. «Маятниковая лаборатория» из раздела «Исследование движения маятника» из раздела «Ученые-друзья» Это упражнение, представленное вам Как правило, составной маятник, изучаемый в студенческой лаборатории, имеет форму однородного стержня, ось которого колебания варьируется. Привяжите веревку (и) или линию (и) к потолку на расстоянии около 2 дюймов от стены, оставляя достаточно слабины, чтобы доходить до земли. Лаборатория: Энергия резиновой ленты. В зеленом прямоугольнике справа установите трение на половину и нажмите «1» под «Показать энергию».Амплитуда, на которую маятник отклоняется от равновесия, измеряется в градусах. Понедельник: 14 октября 2019 г. Рабочий лист должен быть готов к главе 4. Маятник A имеет период 3. ”Вторая цель этого эксперимента — изучить принцип сохранения количества движения с помощью так называемого« баллистического маятника ». Маятник 1 я. Этот рабочий лист будет особенно ценен, если вы наткнетесь на один из этих дисплеев во время производственной поездки. Маятниковая лаборатория. Мероприятие 1 — PhET — Маятниковая лаборатория Вопросы и ответы — это бесплатный образец лабораторного отчета.4. В этом лабораторном упражнении вы будете измерять свойства движения маятника и анализировать их. docx из PHYSICS PS 113L в Авиационном университете Эмбри-Риддла. Если он неровный, то в передней части лаборатории есть бумажные полоски, которые вы можете использовать, чтобы подпереть конец устройства, чтобы выровнять его. 2. 3. 81 м / с2) ½ T = 3. Простой маятник состоит из массы, свободно подвешенной на веревке к неподвижной опоре. 5 секунд? [13. Физика 45 Простой маятник в домашней лаборатории. Часть 1: Влияние начального угла на период 1.В передней части лаборатории есть несколько уровней. Сделайте отметку карандашом или мелком на полу в том месте, где блок касается боба. 3. СБОР ДАННЫХ: Измерьте движение маятника как функцию времени, включая большие и малые колебания. 2 Диапазон чтения и уровень сложности текста: CCSS. III. T = 1 / f Задача. Продолжительность: примерно 60 минут. it Термины / понятия: маятник: подвешенный груз, который раскачивается взад и вперед из одной точки в обычном движении. Гравитация: сила, которая притягивает что-то обратно к Земле. Импульс: сила инерции движения: теория, согласно которой движущиеся тела будут оставаться в ней. движение и тела в состоянии покоя будут оставаться в состоянии покоя, если только на них не действует период внешней силы. Маятник Бартона состоит из одиннадцати маятников, свисающих на единой нити, соединенной между двумя концами деревянного стержня (рисунок 1).Это логарифмический рабочий лист лаборатории виртуальной физики KET. Лабораторная работа 1-1. Движение простого маятника. Выполняя шаги лабораторной процедуры, запишите свои экспериментальные значения и результаты в этот рабочий лист. X3 — Маятник РАБОЧАЯ ТАБЛИЦА Имя: Студенческий билет (B00…): Shishir Ghosh Pendulum Сделайте четкую фотографию своего маятника и прикрепите фотографию. Рабочий лист определения маятника Имя: _____ Указания: Все эти вещи действуют как маятник. Пятница: Срок сдачи лабораторного отчета. Большой лист бумаги для маятника или стены, на котором никто не возражает, если вы рисуете.Примените концепцию сохранения импульса к повседневной жизни. На панели ОПИСАНИЕ измените начальный угол (θ) на 40 градусов. Но какой фактор имеет большее влияние? . Вторник: 22 октября 2019 г. Примечания к главе 5.. Эксперимент А Заполните таблицу. Поиграйте с одним или двумя маятниками и узнайте, как период простого маятника зависит от длины струны, массы маятника, силы тяжести и амплитуды качания. Показаны 8 лучших рабочих листов в категории — Pendulum Lab.Определите общее сохранение механической энергии. Кроме того, если дано так много маятниковых циклов и дана продолжительность времени для циклов маятника, есть ли способ определить период? Мартин, Брэндон Чт. Осторожно переместите баллистический маятник в верхнее положение, где он будет храниться в стороне — вы не будете использовать маятник для этих первых измерений. Полный список материалов: 1. Попросите каждую группу измерить и записать массу груза. Когда сжатая пружина запускает стальной шар, он приобретает начальную скорость и линейный импульс относительно исходной точки. Он имеет угловой момент L.Студентам необходимо будет критически подумать о том, что их сигнал данных говорит им, и об ограничениях / эффектах частоты дискретизации времени прибора. Этот эксперимент был проведен для исследования факторов, влияющих на период маятника. Сводка лаборатории 4 — охватывает лабораторию «Сохранение механической энергии» Сводка лаборатории 7 — охватывает лабораторию «Простой маятник» Отчет лаборатории механической энергии Эксперимент: Одномерные столкновения Phys 215, T3 Лабораторный отчет простого маятника Сводка лаборатории 8 — охватывает «Угловой» Лаборатория движения «Движение» Как упоминалось выше, уравнение маятника, которое мы хотим проверить, действительно только для малых углов $ \ theta $.Гленко. Учетная карточка 3×5) лабораторное оборудование для изготовления держателя для маятника Пятница: Срок сдачи лабораторного отчета. • Используйте таймер с фотозатвором, чтобы количественно определить, как период маятника зависит от переменных, которые вы описали. Когда сжатая пружина запускает стальной шарик, он приобретает начальную скорость и линейный момент. Потяните маятник зажигалки вправо на 15 см и отпустите. Среда: 16 октября 2019 г. Срок сдачи маятниковой лаборатории. Также доступны: открытый исходный код, документация и простая компилируемая версия, которая более настраиваема.2-4 Трение Лаборатория трения Домашнее задание 3 Силы стр. 253-256 Силы 4A и 4B Двумерное движение Лаборатория движения снаряда Тест: тест на двумерное движение — Снаряд, Снаряд под углом, Снаряд под углом, Снаряд Движение снаряда Набор задач 3 Q. сила в упругой пружине. Затем потяните маятник назад и приготовьтесь отпустить его. Графическое пространство включено в раздаточный материал. Положите на пол два отрезка ленты на расстоянии 50 см друг от друга так, чтобы ваш вес находился посередине. Ваша работа НАЙДИ ЭТО! Ниже представлена диаграмма, представляющая «баллистический маятник».Вовлеките своего ребенка в учебную деятельность STEAM, сочетая искусство и науку. Наблюдайте за энергией в системе в режиме реального времени и меняйте величину трения. Каким был бы период нуля. ТЕОРИЯ Простой маятник — это идеализированная модель, состоящая из точечной массы (иногда называемой маятниковым бобом), подвешенной на безмассовой нерастягивающейся струне. Энергия движения: Урок 1, Действие с качающимся маятником — Рабочий лист с качающимся маятником 1 Действие с качающимся маятником — Данные рабочего листа с качающимся маятником 1.Учащиеся используют моделирование Pendulum Lab, чтобы определить, почему дети испытывают «трепет», когда этот DCI относится к Заданию 1 «Механическая энергия в маятнике», которое начинается на странице 3 Дополнительного рабочего листа и сопровождает концептуальную модель «Моделирование энергии маятника» ». В чем сходство картинок? 2. Как период маятника зависит от амплитуды качания? Убедитесь, что масса и длина постоянны. Нажмите кнопку в правом нижнем углу, которая активирует таймер фотозатвора. Установите амплитуду на 50o и включите маятник.Маятник L i. Как обвинение, так и защита утверждают, что «начальная скорость» (скорость пули при выходе из пистолета) имеет решающее значение для дела. СБОР ДАННЫХ: Измерьте движение маятника как функцию времени, включая большие и малые колебания. ДЕЙСТВИЕ 1 ПЕРЕМЕННАЯ АМПЛИТУДА 1. 18. Четверг: 24 октября 2019 г. Science Fair. Это время, которое требуется маятнику, чтобы совершить полный оборот — от одной стороны к другой и обратно (или, что то же самое, от середины, вверх к одной стороне, вниз, дальше середины, и вверх по другой стороне, и обратно вниз. снова в середину).Строка 6. doc Pendulum LAB КОНТРОЛЬНЫЙ СПИСОК. Обязательно сохраните снимок экрана с графиком с помощью кнопки «Убедитесь, что маятник не движется». Возможно, вам потребуется вытянуть стержень за край стола, чтобы маятник мог свободно качаться. Соответствующий график для этого эксперимента показан ниже. Современные электронные устройства, такие как Lego Mindstorms NXT, смартфоны и Arduino, могут получать данные с высокой скоростью и могут использоваться для измерения динамических переменных с разумной точностью в физических экспериментах.Задача Проверьте, что произойдет с периодом маятника, когда масса, прикрепленная к струне, изменится. ведомый маятник). Когда боб смещается из состояния равновесия, а затем отпускается, он начинает свое возвратно-поступательное колебание относительно своего фиксированного положения равновесия. Цель лабораторного упражнения — определить, какие из этих факторов, если таковые имеются, влияют на период колебаний маятника. 8c-Con of Energy-Pendulum-RGC-1-15-09 — 5 — Анализ данных Цель этой лаборатории — определить, сохраняется ли полная механическая энергия в маятниковой системе, когда тело движется в гравитационном поле.Секундомер. Подготовка к эксперименту 1. Иногда удобно указать положение оси подвески S по ее расстоянию s от одного конца стержня, а не по расстоянию h от центра тяжести G. строка увеличивается в этом эксперименте. Используйте точные значения, которые вы записываете для своих данных, для последующих расчетов. гайки, шайбы, грузы с крюками) Маятник — это груз, подвешенный на оси (или фиксированной точке), так что он может свободно качаться вперед и назад. A Эта деятельность включает только сбор данных, но навыки, полученные с помощью MATLAB, могут быть применены к приведению в действие (например,11-12. Основные аспекты лабораторной работы: КАЛИБРОВКА: определение того, как компьютер записывает угол маятника. Пожалуйста, Энергия маятника Gizmo ™ позволяет вам исследовать, как количество этих типов ++ — энергии изменяется для движущегося маятника. Найдите это занятие на PhET. Кроме того, мы должны были рассмотреть вопрос о периоде маятника. Разработайте эксперименты, чтобы описать, как переменные влияют на движение маятника. Это время, которое требуется маятнику, чтобы совершить полный оборот — от одной стороны к другой и обратно (или, что то же самое, от середины, вверх к одной стороне, вниз, дальше середины, и вверх по другой стороне, и обратно вниз. снова в середину).doc Ключевые слова: физические и химические изменения. Ответы на рабочий лист маятниковой лаборатории. С помощью таймера фотозатвора легко измерить период. 1-секундная вводная лаборатория маятника [pdf] Простая лаборатория маятника и гравитации [pdf] Рабочий лист после лабораторной работы с электрическим полем. Зависимость периода от длины. Если бы вся масса маятника была сосредоточена в одной точке, то длина L, фигурирующая в формуле (1), была бы расстоянием от этой точки до оси вращения. В исследовательской лаборатории FlinnPREP ™ для AP® Physics 1: Simple Pendulums учащиеся исследуют свойства маятников и разрабатывают эксперимент для проверки и определения переменных, чтобы определить, что влияет на период колебания маятника.4. В зависимости от размера класса выделите несколько участков для качания маятников. Щелкните Воспроизвести (). Когда блок остановится, сделайте еще одну отметку на полу прямо к Простому маятнику — 4 2. Рабочий лист простого гармонического движения shm 02. Примечания: 6. Направления: 1. 1. Карандаш. Об этой викторине и рабочем листе. 3 Психология — Конспект лекций, гл. Маятниковая лаборатория — Моделирование Откройте моделирование маятникового аппарата, чтобы выполнить эту лабораторную работу. Составной маятник — это твердое тело, масса которого не сосредоточена в одной точке и которое способно колебаться вокруг некоторого фиксированного стержня (оси вращения).Раздел / Цели Лаборатория стандартов и планирование демонстрации Открытие главы на национальном уровне / на местном уровне 1. В частности, обсуждается теория моделирования с акцентом на то, какие упрощающие допущения уместны в данном случае. Лаборатория 2 Измерения — Отчет лаборатории LAB # 8 — Отчет лаборатории LAB # 10 PH-101 — Отчет лаборатории PH-101 Lab # 13 — Отчет лаборатории Physics Lab Report # 9 — Lab Rebika Chatterpaul lab 10 Ph201 X13 Прочие документы по физике 181 — Все лабораторные отчеты, а также предварительные лабораторные работы с ответами и комментариями ТА к ним, а также Physics 152 Lab # 2 9 — peter novick Lab 13 — lab 13 Mod Цель этого упражнения — доказать студентам, что период маятника зависит только от длина строки.Когда учащиеся собирают данные, им нужно найти время, за которое их маятник в каждом испытании совершит 25 колебаний (или возвратно-поступательных движений), как показано на видео ниже. 4. Используйте более длинную и более короткую струны с одинаковым весом. 2. Заполните этот лист эксперимента с маятником для 3-го класса и попробуйте его дома! Прочтите описание или просто возьмите йо-йо, чтобы правильно ответить на вопросы! Лаборатория маятника Эта лабораторная работа позволит вам протестировать различные переменные, чтобы увидеть, как они влияют на период маятника.Однако это не линейная зависимость. Используйте маятник, чтобы найти значение g на Planet X Labs для ученых и инженеров: рабочая таблица по механике, лаборатория 9-5. Попробуйте другой метод, чтобы изучить, как период маятника зависит от амплитуды. Вы узнаете, как период простого маятника зависит от длины струны и массы маятника. 5. Запишите ваши подробные наблюдения за тем, что происходит с различными формами энергии, когда маятник качается в пространстве ниже.Начните с веревки примерно 1. 2. Длину маятника можно рассчитать как h = l-l * CosѲ. 62 м / с2)? [4. 2. Маятники могут показаться простыми, но на самом деле в них много всего! Пройдите тест и заполните рабочий лист, чтобы узнать, что вы знаете о физике движения Friday: Lab report due. Определите общее сохранение механической энергии. Некоторые гайки из ящика для инструментов — все они должны быть одинакового веса и должны подходить к крючку. В этом лабораторном упражнении вы будете измерять свойства движения маятника и анализировать их.10 и 13 Лаборатория горизонтальных снарядов Возвратно-поступательное движение качелей — это пример маятника. Для определения длины мы каждый раз использовали серебряную массу и использовали постоянную длину маятника. Выведите маятник из состояния равновесия (примерно 10-20) и отпустите. Гистограммы KE (кинетическая энергия) и PE (потенциальная энергия) отображаются в реальном времени во время моделирования. ЦЕЛИ ОБУЧЕНИЯ. Лабораторное задание 10: Обзор инструктора по простому маятнику Маятник — отличный иллюстративный пример простого гармонического движения.Учащиеся выполняют задание, демонстрирующее, как потенциальную энергию (PE) можно преобразовать в кинетическую энергию (KE) и обратно. Однако я немного сомневаюсь в этом предположении, потому что по опыту я видел, как маятники постепенно уменьшаются по амплитуде / движению, и я не уверен, как это повлияет на отсчет времени. Используя формулы Ньютона, F = ma, ∑F = T-mg, a cent = w 2 r, V = wr объединены, чтобы получить T = ma + mg, которое мы использовали для получения следующего уравнения: T = mw 2 r + mg We измерил радиус 47.Если маятник был освобожден в точке A, выведите выражение для мгновенной скорости маятника в точке B, промежуточной позиции в его колебании. Период легко измерить с помощью таймера фотозатвора. Затем учащиеся будут использовать свои данные для поддержки математической модели, которая связывает период с длиной плеча маятника. Он включает в себя лабораторные листы на трех уровнях. Как изменение массы маятника изменит период колебаний маятника? 2. 0 Заполните лабораторный рабочий лист маятника ответы: Попробовать без риска Предварительный просмотр образца Введение маятника в гармоническое движение Фет лабораторный ответ ключ Оцените бесплатно введение маятника в гармоническое движение. Форма лабораторного исследования Просмотр LAB X3.Поиграйте с Pendulum Lab, чтобы выяснить, какие переменные влияют на движение маятника, и напишите качественные описания для каждой переменной. Нажмите на номер угла, с которого нужно отпустить маятник. Рабочий лист Присоединитесь, чтобы получить доступ ко всем включенным материалам Четвероклассники проводят лабораторную работу, которая измеряет факторы, изменяющие скорость качания маятника. Когда качается в одну сторону. Узнайте о силах движения и гравитации с помощью новой техники рисования, заменив кисть на качающийся маятник.Посмотреть LAB X3. 2) Вычислите значения периода для экспериментальных случаев, которые вы запускали в лаборатории, используя уравнения, полученные из результатов (1): a. Основные аспекты лабораторной работы: КАЛИБРОВКА: определение того, как компьютер записывает угол маятника. Сохранение энергии и маятники: как установка гвоздя на пути маятника влияет на высоту качания маятника? Введение Двумя наиболее влиятельными мыслителями в истории были Аристотель в IV веке до нашей эры и Галилей в XVI – XVII веках.Постройте маятниковый волновой аппарат. Движение регулярное и повторяющееся, пример периодического движения. Определение ускорения силы тяжести с помощью простого маятника (Ваше имя) Лаборатория продвинутых студентов, факультет физики и астрономии, Университет штата Юта, Солт-Лейк-Сити, штат Юта 84112 Это пример лабораторного отчета, связанного с получением ускорения свободного падения (g) и применение математических моделей. С помощью напарника по лаборатории приведите маятник в движение, пока он не совершит 30 возвратно-поступательных колебаний, записывая это время.Точки будут: Моделирование PhET: Pendulum Lab, опубликованное PhET. Это обновленное, готовое для мобильных устройств моделирование PhET предоставляет набор инструментов для анализа преобразования энергии в маятниковой системе. Баллистический маятник Physics 211 Lab. (L измеряется от центра масс шара) 17. Отчет лаборатории 12: Простое гармоническое движение, масса на пружине. Группа 5. Когда боб выходит из равновесия и отпускается, он начинает двигаться вперед и назад, также называемое периодическим движением. 2. В рамках своего экспериментального плана учащиеся также должны запланировать выполнение нескольких измерений, чтобы определить или проверить взаимосвязь между длиной 6.Длина маятника определяется как расстояние от верха струны до середины массы. Цель состоит в том, чтобы работать в обратном направлении, чтобы определить начальную скорость снаряда. docx из PHYC 1190 в Университете Далхаузи. Гипотеза Предскажите, как, по вашему мнению, масса, прикрепленная к маятнику, повлияет на период. 5. Многие из них позволяют ученикам манипулировать переменными и проводить тесты, которые могут быть слишком опасными или дорогостоящими для выполнения в классе. 2. Вы найдете больше научных экспериментов, подобных этому простому эксперименту с маятником, на моей доске Early Learning Science на Pinterest.0 см. X3 — Маятник РАБОЧАЯ ТАБЛИЦА Имя: Студенческий билет (B00…): Маятник Шишира Гоша Сделайте четкую фотографию своего маятника и прикрепите фотографию 1. Энергия маятника Лаборатория Включены, помечены и организованы все части лабораторного отчета. Транспортир 4. Измерьте расстояние от потолка до вашего веса. В лаборатории нельзя отводить время на выполнение предварительных лабораторных работ. Обратите внимание, что длина L — это расстояние от точки опоры до центра. Результаты этого STEM-эксперимента с простым маятником действительно удивили нас.Лаборатория: Маятниковая энергия. Ниже нам пришлось использовать линеаризацию для построения графика зависимости длины от периода, поэтому мы возводили период в квадрат. Это лабораторное занятие, во время которого студенты будут собирать данные и делать выводы о переменных, влияющих на скорость маятника. Результаты для больших углов должны быть даны в секундах с соответствующими значащими цифрами. docx из PHYC 1190 в Университете Далхаузи. Примеры использования закона Гюйгена для периода маятника. Результаты лаборатории маятника Брендана.СБОР ДАННЫХ: Измерьте движение маятника как функцию времени, включая большие и малые колебания. 50 м. Оборудование — Маятниковый компьютер с Logger Pro S / W Маятниковый транспортир Боб Интерфейс с кабелями Маятниковый датчик Стойка Фотозатвора с опорным оборудованием Струна опорных стержней Рис. 1 Простой маятник ЦЕЛЬ Цель этого эксперимента — изучить, как период маятника зависит от длины , масса и амплитуда качания. Я планирую открыть симулятор, чтобы продемонстрировать ответы, но я Pendulum Lab Поиграю с одним или двумя маятниками и узнаю, как период простого маятника зависит от длины струны, массы маятника и его амплитуды. качели.5. Обратите внимание на диаграмму длины справа, что радиус конического маятника равен L sin (θ), где L — длина струны. СБОР ДАННЫХ: Измерьте движение маятника как функцию времени, включая большие и малые колебания. Это новый поворот в привычной лаборатории (см. «Исследования кругового движения с игрушечным самолетиком» в дополнительных ресурсах). В этой статье описывается эксперимент с коническим маятником с определением g. Цель этого действия с простой маятниковой системой — продемонстрировать, как моделировать вращательную механическую систему.5. Задание 1 в лаборатории маятника — PhET — Ответы на моделирование в лаборатории маятника — Отчет лаборатории — один из многочисленных ресурсов, легко доступных вам в Интернете для широкого спектра. Математика моделирования показана ниже. Используйте точные значения, которые вы записываете для своих данных, для последующих расчетов. Вы можете изменять массу маятника, длину маятника, угол, на который вы оттягиваете маятник, и силу гравитационного поля. Таким образом, в коническом маятнике боб движется с постоянной скоростью по кругу, а струна образует конус.В третьей части лабораторной работы мы проверим теоретическое предсказание о том, что простой маятник (т. Е. Маятниковая лаборатория А. Аристотеля применил философский подход к пониманию — В этой лабораторной работе нас интересует период \ (Т \) маятник. Заполните таблицу. Используется много парных и групповых занятий, чтобы учащиеся могли освоиться с моделью и поддержать друг друга в процессе обучения.10 К концу 12 класса читать и понимать научные / технические тексты в 11 классах -CCR диапазон сложности текста самостоятельно и профессионально.pdf View Download: таблица физики схемы физическая лаборатория баллистический маятник 2012. Маятниковая лаборатория Задание 1 — PhET — вопросы и ответы маятниковой лаборатории — лабораторный отчет — один из многочисленных ресурсов, доступных в Интернете для ответа на вопрос: баллистический маятник In- Название рабочего листа лаборатории: Дата: Раздел № 1) Сначала мы помещаем происхождение системы координат Xy в точку поворота на рисунке 2. Дата представления лабораторного отчета: 9 сентября 2003 г. Лабораторная работа 1: Маятник Резюме Цель этого эксперимента заключалась в том, чтобы определить влияние массы и длины на период колебаний простого маятника.е. Примером может служить изменение угла наклона лаборатории практических навыков. СПРАВОЧНИК ДЛЯ ЛАБОРАТОРИИ IN-TEXT. Если бы вы были демографом, вас могли бы попросить определить, как население, вероятно, изменится в будущем. Измерьте высоту от пола до низа груза, когда он находится в равновесии, и еще раз, когда низ находится на одном из отрезков ленты. 5/1. Кроме того, частота f и период T являются обратными. время, необходимое маятнику, чтобы совершить качание. Простой маятник состоит из веревки, шнура или проволоки, которые позволяют подвешенной массе качаться вперед и назад.Практика — маятник. Какой период вы ожидаете от маятника длиной 0. На основе ваших данных из испытания с использованием 0. Улавливатель защелкивается на снаряде, поворачивается вверх, и измеряется максимальная высота маятника. Для этой лабораторной работы учащиеся получают кусок веревки, секундомер и гири (2 по 50 г и 2 по 100 г). 6. docx от PHYC 1190 в Университете Далхаузи. Гайка 004 кг, подвешенная на нитке, отводится в сторону и отпускается. Предварительная подготовка Задача предварительных вопросов — убедиться, что вы понимаете, что делаете, почему вы это делаете и как избежать некоторых типичных ошибок.На более высоком уровне студенты также проверяют угол, под которым маятник выпущен. Таким образом, к мероприятию 1 «Маятниковая лаборатория» — PhET — «Ответы на моделирование маятниковой лаборатории» — бесплатный образец лабораторного отчета. 5. Рассматривая качели на игровой площадке, глядя на диаграммы и используя реальные маятники, учащиеся понимают, как кинетическая и потенциальная энергии связаны в системе. Хотя первое официальное открытие маятника произошло в 1600-х годах, есть исследования, которые показывают, что маятники, возможно, использовались даже раньше, во время древнеримских длин маятника, указанных в вашем лабораторном рабочем листе (вы получите рабочий лист, когда вы это сделаете. эта практическая лаборатория).Отведите маятник назад до амплитуды примерно 10 градусов и дайте ему покачиваться в течение некоторого времени. (Нет смысла записывать время 1. Предварительный просмотр неформатированного текста: Блок V: Лаборатория педулюма для виртуального моделирования. Это задание позволит вам продемонстрировать следующие цели: 4. Держите маятник в одной руке на уровне плеч. Рассчитайте теоретическое период маятника. Что вам понадобится для эксперимента с маятником. Основные аспекты лаборатории: КАЛИБРОВКА: Определите, как компьютер регистрирует угол маятника.Зависимой переменной будет период времени. Используйте таймер с фотозатвором, чтобы количественно определить, как период маятника зависит от переменных, которые вы описали. Энергия движения: Урок 1, Упражнение «Качающийся маятник» — Рабочий лист «Качающийся маятник» Действие «Качающийся маятник» — Рабочий лист «Качающийся маятник». Данные 1. Типичный пример маятника можно найти в таких часах, как напольные часы. Рис. 4. Линейка 3. Тогда скорость блока можно рассчитать как V = sqrt (2 * g * h). Когда мяч на конце струны опускается до самой нижней точки, струна разрезается острой бритвой.Повторите шаги 2 — 4. Период маятника на Земле — 1 минута. 1. Предоставлено: Триш Лёблейн. Некоторые из рабочих листов для этой концепции: работа в средней школе с качающимся маятником, простой маятник, часть периода работы маятника и энергия, лабораторная работа 1 с простым маятником, маятник простого гармонического движения, элементарная наука Национальной инициативы по математике, работа с простым гармоническим движением, маятник. 5 метров веревки (примерно). Девять грузов, которые можно легко прикрепить к веревке (например, • маятник • измеритель длины • таймер • массы • транспортир Три фактора, которые вы будете исследовать сегодня, — это масса маятникового боба, длина маятника и амплитуда маятника.Маятниковая лаборатория 1 Цели обучения: Студенты смогут: разрабатывать эксперименты, чтобы описать, как переменные (длина, масса, угол и гравитационное поле) влияют на движение маятника; Используйте таймер фотозатвора, чтобы количественно определить, как период маятника зависит от переменных; Цели обучения Pendulum Lab 2: Студенты смогут: Записывать наклон и его неопределенность графика периода и массы в рабочем листе Lab 7. На основе вашей лаборатории, использующей простой маятник, сопоставьте правильное определение каждому слову.6 м / с2? Решите T = • T = 2π√ (0. Подвесьте пружину к маятниковому зажиму и подвесьте подвеску массы на пружине. Определите, как волны передают энергию, не передавая материю. G. Обращая внимание на положение кончика указателя, угол колебания измеряются по шкале транспортира, предоставленной с инструментом. santiweb. Советы для учителей Маятниковая лаборатория ПРИОСТАНОВИТЬ симулятора для постановки эксперимента; ПЫГНИТЕ вперед на 0. Нить провисает асимметрично, потому что маятник привода представляет собой деревянный шар диаметром 5 см диаметром, а остальные десять — перевернутые чашки для питья Belmont Springs ©.2. Отображение всех рабочих листов, связанных с простым гармоническим движением. Электростатический поиск слова Период маятника — это время, которое требуется маятнику, чтобы качнуться слева направо и обратно. Этот план урока включает интерактивную симуляцию под названием Pendulum Lab, разработанную нашим удостоенным наград партнером PhET через Университет Колорадо в Боулдере. Классификация «простой» происходит из того факта, что вся масса маятника сосредоточена в его «качке» — подвешенной массе.Теперь измените длину маятниковой струны примерно на половину (~ 15 см) и отрегулируйте высоту маятникового зажима так, чтобы карабин снова оказался перед датчиком движения. Каково значение «g» в месте, где есть 2. Измерьте массу своего веса. Маятник — это длинная деталь под циферблатом, которая медленно качается вперед и назад. Включены две таблицы данных — одна для данных измерений и одна. Эта деятельность процесса поможет студентам узнать о движении маятников и о том, как изменение длины маятника изменяет его время или период качания.Датчик силы с полудюймовым стержнем 6. Обратите внимание, что вы не будете включать единицы измерения в свои ответы. 70м. Струна длиной 75 метров с 20 шайбами, какое было экспериментальное натяжение струны, прикрепленной к стопору? Цель баллистического маятника: применить принципы сохранения к движению баллистического маятника, чтобы определить скорость снаряда и предсказать дальность полета снаряда при горизонтальном запуске со стола. Постройте простой маятник 100. Для линеаризации мы можем использовать: 1.Измерьте время, необходимое для 20 колебаний. Лабораторная деятельность: качающийся маятник. Ответы на рабочий лист лаборатории маятника — ур. Они создают гипотезу и проверяют ее в ходе эксперимента. грамм. Pendulum Lab — информация для учащихся Рабочий лист Обзор Pendulum Lab. Распечатайте графики и включите в свой лабораторный отчет. Настройка PEND ворот использует свет и фотодетектор следующим образом: вместо времени до следующего прерывания светового луча через ворота, он считает время до второго прерывания светового луча.Этот график был загружен 13 февраля 2021 г., загружен администратором в образце лабораторного отчета. Простой маятник, период которого совпадает с периодом данного составного маятника, называется «эквивалентным простым маятником». В этом рабочем листе изучения маятников учащиеся экспериментируют с маятниками, которые они делают в лаборатории. doc phase_changes_worksheet. Объясните учащимся особенности этой демонстрации: В этой демонстрации вы можете изменять длину маятника и ускорение свободного падения, вводя числовые значения или перемещая ползунок.28 с] 4. В этом раздаточном материале описывается, какие материалы потребуются, как будет оцениваться их лабораторный отчет, и даны некоторые рекомендации по разработке гипотезы. Запустите часть 3 эксперимента. Контролируемые переменные будут включать массу маятника и угол, под которым маятник был запущен. Таблица 4 Средняя амплитуда Средний период () (с) Изучение энергосбережения Найдите общую механическую энергию системы под нулевым углом и для максимального угла, который находится в Лаборатории физики колледжа: Рабочий лист по механике Лаборатория 1-1 Простой маятник По мере прохождения шаги лабораторной процедуры, запишите свои экспериментальные значения и результаты в этот рабочий лист.Если вы не знаете ответов, приходите ко мне в офис за несколько часов до лаборатории и получите помощь! В противном случае лаборатория маятника Введение В этом упражнении вы исследуете, как переменные влияют на движение маятника. На среднем уровне студенты проверяют длину и массу маятника. Его необходимо сдать в начале лабораторного периода. Посмотрите на сходство между всеми изображениями и напишите свое определение маятника внизу рабочего листа. Этот рабочий лист будет особенно ценен, если вы наткнетесь на один из этих дисплеев во время производственной поездки.Измерьте массу металлического шара. Другой конец привяжите к опорной балке так, чтобы расстояние от центра маятникового шара до опорной балки составляло 60. Я думаю, нам нужно будет провести еще один STEM-эксперимент с маятниками, чтобы выяснить, имеет ли значение длина маятника. . Установите уровень на основание устройства. Среда: 23 октября 2019 г., Pulley Lab. ФИЗИЧЕСКАЯ ЛАБОРАТОРИЯ: Простой маятник Целью этой лаборатории было экспериментальное определение значения g, ускорения силы тяжести Земли, с использованием данного «уравнения маятника» и экспериментальных данных для периода маятника и длины маятниковой струны. .Длиной 2 метра и привяжите один конец к стальному шарику маятника. Используйте секундомер и измерьте с точностью до 0. 3. pdf photosynthesis_worksheet. Рассматривая качели на игровой площадке, глядя на диаграммы и используя маятники в реальном мире, учащиеся понимают, как кинетическая и потенциальная энергии связаны в системе. 1 Исследуйте сохранение импульса при простом маятниковом движении. 1с. Почему вам нужно выполнить этот расчет только один раз, а не для обоих наборов испытаний. Предыстория: Раньше мы учили эту лабораторию с боевыми патронами.Включите как можно больше общего! 1. Маятниковое действие В этом упражнении вы будете измерять период и частоту простого маятника. В этой лаборатории будет проверяться влияние различных масс на период качания маятника. На видео показан один полный цикл качания, и предоставляются инструменты, позволяющие учащимся измерить высоту и скорость поворота гайки. 4. Сравните простое гармоническое движение и движение маятника. Строительные леса — ниже перечислены лабораторные объяснения словесных указаний и модификаций, используемых для поддержки понимания и умений учащихся в каждой из лабораторных работ.РАБОЧАЯ ТАБЛИЦА ПО МАЯТНИКУ PS 113L — Введение в физику I Лаборатория / 50 пунктов Имя: Кайл Введение в физику I — Примечания к лекциям — 1 — 32 Сводка лабораторной работы 1 — охватывает лабораторию «Анализ данных» CSCE530 Проект проекта — Отчет о научно-исследовательской работе — Простой маятник Bio 230 Учебное пособие Вопросы Все ответили гл. Прикрепите два куска ленты на стене / другой поверхности на расстоянии 50 см друг от друга в соответствии с вашим весом в лабораторном отчете — Задание 13: Простое гармоническое движение — название маятника _____ Дата _____ Прогноз 1. Используйте таймер фотозатвора, чтобы количественно определить, как период маятник зависит от описанных вами переменных.Конический маятник похож на простой маятник с той разницей, что боб вместо того, чтобы двигаться вперед и назад, вращается по горизонтальному кругу. Он включает в себя лабораторные листы на трех уровнях. Маятник качается быстрее или медленнее в зависимости от длины струны. Физические лаборатории Университета АГУ — Лаборатория механики 9 стр.

Лабораторная работа измерение движения тела по окружности: Лабораторные работы №1 (10 класс)

Лабораторная работа № 5 «Изучение движения тела по окружности под действием сил упругости и тяжести»

Лабораторная работа по теме: «Изучение движения тела по окружности под действием сил упругости и тяжести» ❤️

Ответьте на контрольные вопросы

Суперзадание

Ответьте на контрольные вопросы

Суперзадание

1 изучение движения тела по окружности. Лабораторная работа. Изучение движения тела по окружности под действием силы упругости и силы тяжести. Время обращения, с

Лабораторная работа. Изучение движения тел по окружности под действием сил тяжести и упругости

Ответьте на контрольные вопросы

Суперзадание

Ответьте на контрольные вопросы

Суперзадание

Веб-сайт класса физики

Равномерное круговое движение

Лабораторная работа.Исследование движения тела по окружности под действием силы упругости и силы тяжести

Ответить на контрольные вопросы

Супербасон

Ответить на контрольные вопросы

Супербасон

Ответить на контрольные вопросы

Супербасон

Circles Blog Archives — Circl.es

Неврология для детей — Vision Exp.

Гравитация и орбиты — гравитационная сила | Круговое движение | Астрономия

Темы

Описание

Примеры целей обучения

Рабочий лист лаборатории маятника

Добавить комментарий Отменить ответ

Рубрики