ГДЗ по алгебре ответы и решения онлайн к учебникам и рабочим тетрадям
Школьная алгебра — одна из тех наук, освоение которой зачастую сопряжено с трудностями у учащихся. Но, учитывая, что существенный блок заданий на обязательном итоговом испытании по математике и в 9-м, и в 11-м классе составляют алгебраические, разобраться в них придется каждому. Для этого школьникам надо заблаговременно подобрать качественные учебные материалы по дисциплине и решебники к ним и:
— заниматься с самого начала введения алгебры — с 7-го класса школы скрупулезно и вдумчиво;
— периодически возвращаться к тому материалу, который вызвал наибольшие сложности, прорабатывать его вновь, устраняя проблемы;
— контролировать достижения, их динамику, при необходимости — корректировать свои планы по изучению алгебры;
— составлять грамотный и эффективный комплект учебной литературы по предмету.
Для решения последней задачи можно привлечь специалистов — экспертов, школьных педагогов, руководителей подготовительных курсов и кружков, репетиторов.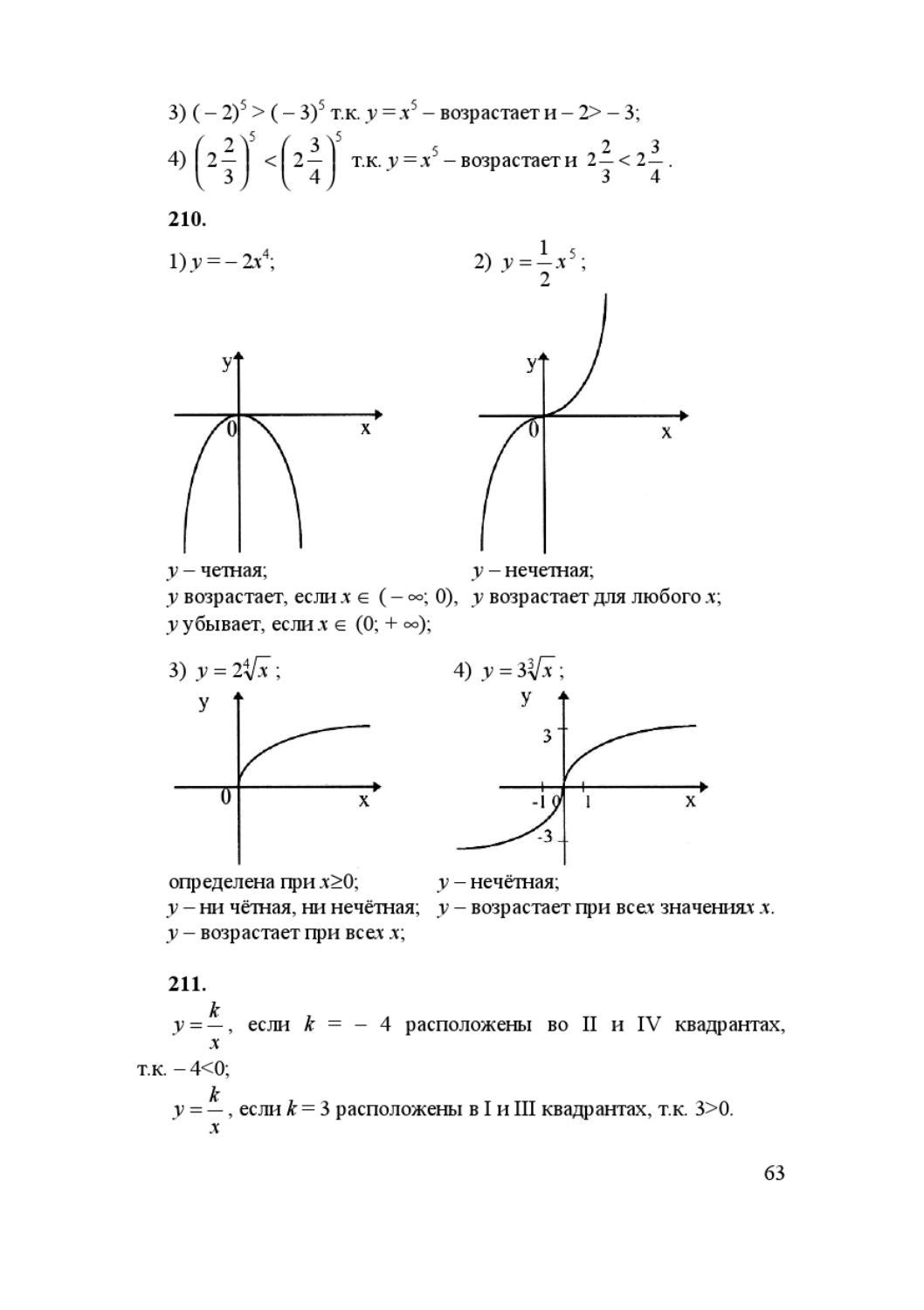
— системно;
— по индивидуальному плану, учитывающему собственный уровень знаний, ответственность, цели и задачи;
— уделяя достаточно количество времени проработки тем и разделов курса.
В числе учебных материалов, которые лежат в основе наиболее популярных УМК по дисциплине, указывают учебники и практикумы по алгебре таких авторов, как:
— Мерзляк, Рабинович, Полонский;
— Мордкович;
— Макарычев;
— Никольский и Потапов;
— Дорофеев;
— Алимов;
— Колмогоров;
— Шестаков;
— Колягин и ряд других.
Помимо базового теоретического учебника по алгебре в комплект следует включить такие практические пособия по предмету, как:
— сборники задач;
— дидактические материалы к курсу;
— рабочие тетради;
— КИМы и т.
 д.
д.Четко следуя установленному плану, регулярно осваивая ту часть курса, которая была запланирована, школьники не только глубоко и полно изучат материал, но и приобретут ценные в школе и после ее окончания навыки самоподготовки, самопроверки и самоконтроля, эффективной и вдумчивой работы с научной и справочной информацией.
ГДЗ по алгебре: особенности, специфика, порядок работы с материалами
Учитывая разнообразие программ и требований, уровня подготовленности учеников и профессионализма педагогов школ и курсов, многие ищут и находят альтернативные формы подготовки. В их числе — актуальные на сегодняшний день решебники к пособиям по предмету. Почему именно гдз по алгебре пользуются такой высокой популярностью у учащихся? Причин этого немало:
— задания по этому предмету составляют основной блок вопросов на ОГЭ и ЕГЭ, которые по математике сдают все без исключения ученики-выпускники 9-х и 11-х классов школ. По этой причине спрос на гдз по алгебре существенно возрастает с переходом ученика в каждый следующий класс;
 Не всегда объяснения учителя достаточно, чтобы понять ту или иную тему. В этой связи решебники позволяют восполнять пробелы, возвращаясь к заданиям еще раз, чтобы разобрать и изучить их в своем темпе, в удобное время;
Не всегда объяснения учителя достаточно, чтобы понять ту или иную тему. В этой связи решебники позволяют восполнять пробелы, возвращаясь к заданиям еще раз, чтобы разобрать и изучить их в своем темпе, в удобное время;— напротив, те, кто всерьез увлечен математикой, применяют гдз по алгебре к задачникам и иным практикумам повышенного уровня. Например, в процессе подготовки к математическим олимпиадам и конкурсам по дисциплине и общематематическим, проводимым на внешкольных и школьных площадках;
— репетиторы, осуществляющие подготовку школьников к экзаменам и конкурсам, не всегда точно знают, каков порядок записи верного ответа. Для них сборники гдз по алгебре — своего рода «шпаргалка», позволяющая изучить такие моменты. Случаи, когда задание верно решено, но результат записан неграмотно, в результате чего сняты баллы или потеряно призовое место — не редкость. Во избежание таких досадных недоразумений стоит внимательно изучать гдз по алгебре и запоминать, как правильно записывать полученный ответ.

Особенности сборников гдз для школьников
Признаками, определяющими грамотность предлагаемых к изучению и работе гдз по алгебре считаются:
1. Наличие на сайте сборников ответов практически ко всем учебникам и пособиям-практикумам по дисциплине в рамках школьных программ и УМК. Дополнительный плюс — решебники к задачникам, содержащим задания повышенной сложности, того уровня, который применяют готовящиеся к математическим олимпиадам.
2. Возможность быстрого поиска нужного гдз по алгебре, а также темы, параграфа, страницы и т. д. Удобство навигации особенно важно для тех, кому надо быстро повторить материал или в условиях сжатых сроков подготовки, дефицита времени на работу.
— порядок записи основных составляющих — дано, формулировки вопроса, решения, ответа;
— алгоритм решения задания;
— логику выбора и записывания результата.
Порядок работы с гдз по алгебре, технологии использования решебников
Просто списать готовое решение из сборника гдз по алгебре — далеко не единственный, и даже не самый популярный способ использования этого полезного ресурса.-reshenie-480.jpg) Хотя время от времени таким образом пользовались ответами почти все школьники. Например, забыв выполнить задание или в условиях ограниченности времени, когда нужно срочно сдать работу педагогу.
Хотя время от времени таким образом пользовались ответами почти все школьники. Например, забыв выполнить задание или в условиях ограниченности времени, когда нужно срочно сдать работу педагогу.
В долгосрочной перспективе гдз по алгебре применяют, чтобы решить гораздо более широкий круг задач. Например, с помощью решебников можно:
2. Самостоятельно изучать ту тему, которая вызвала наибольшее количество вопросов, трудностей при изучении. Например, если школьник болел, был в отъезде и не мог воспользоваться объяснением учителя в классе. В этом случае гдз по алгебре станут материалом для самоподготовки и, одновременно, самопроверки полученных знаний.
3. Учиться дома. Такой способ применения гдз по алгебре широко используют ученики, находящиеся на семейной или дистанционной форме обучения.
 Здесь преимущества от применения сборников тоже очевидны:
Здесь преимущества от применения сборников тоже очевидны:— можно заниматься в удобное для себя время;
— возможность подобрать оптимальный для себя темп работы;
Репетиторы используют сборники решебников для составления интересных заданий, а также наглядного разъяснения порядка их выполнения. Фактически, гдз по алгебре — это готовые полноценные материалы для качественного объяснения даже самых сложных тематик и разделов науки за любой класс. Задания и решения можно сочетать, компоновать, формируя собственную авторскую базу, исходя из целей и задач ученика, его уровня подготовленности, выявляемых проблем и трудностей. Помимо репетиторов, в тех же целях гдз по алгебре могут использовать руководители и педагоги математических кружков и курсов:
Помимо репетиторов, в тех же целях гдз по алгебре могут использовать руководители и педагоги математических кружков и курсов:
— оказывающие услуги по углубленному изучению курса математики, и, в частности — алгебры;
— созданных для помощи неуспевающим. Разбор текущих тем и заданий из итоговых контрольных с помощью сборников гдз по алгебре более эффективный и понятный учащимся средней и старшей школы метод.
Алгоритм работы с гдз по алгебре таков:
1. Определяется тема, раздел или задание, которое необходимо разобрать и выполнить.
2. Ученики самостоятельно решают задачу, пример, уравнение, строят графики функций и т. д., согласно требованиям.
3. Полученный ответ сверяется с эталонным в гдз по алгебре, определяются ошибки непосредственно в логике получения результата, расчетах, порядке записи решения и ответа.
4. Школьник самостоятельно выполняет задание по той же теме из этого же пособия (например, второй вариант) или аналогичное задание из другого пособия.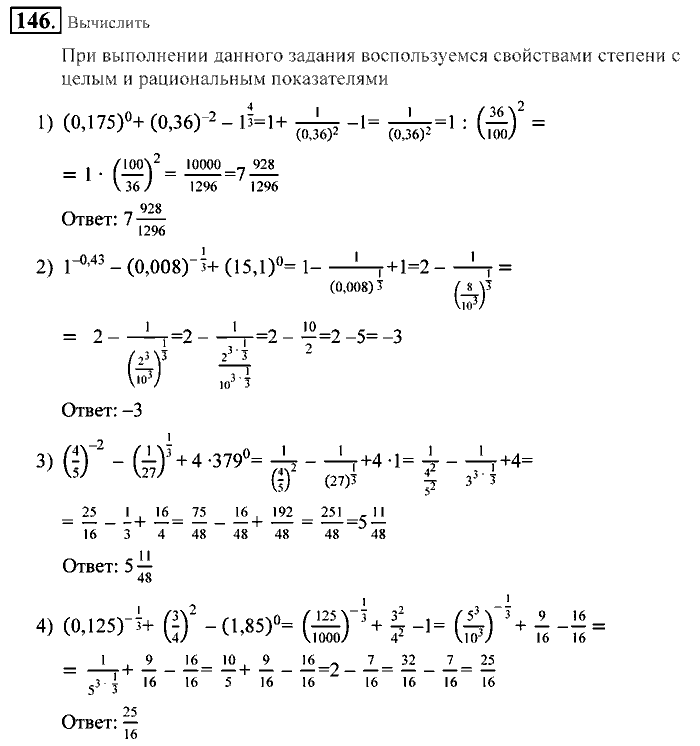
5. Проверяется правильность выполнения путем сопоставления ответа из гдз по алгебре и самостоятельно полученного.
В том случае, если ученик не смог сам выполнить задание, пусть даже и с ошибками, и не знает, как приступить к его выполнению, сразу переходят к этапу разбора гдз по алгебре по изучаемой теме. После того, как задание будет понято, следует перейти к этапу 4 алгоритма использования решебника, решив аналогичное задание по рассматриваемой теме.
Подготовка к итоговым испытаниям с использованием гдз по алгебре проводится примерно по такому же сценарию. Здесь важным отличием является то, что необходимо подобрать нужный комплект теоретической и практической литературы по предмету и гдз по алгебре к ней за ряд лет. Желательно начать такую подготовку совместно с педагогом или репетитором, а также использовать специализированные сборники заданий ОГЭ и ЕГЭ на текущий учебный год. Понадобится:
— составить комплект учебной литературы и найти гдз по алгебре к заданиям, которые вынесены на экзамен;
— осуществлять регулярную систематическую подготовку, периодически контролируя полученные результаты;
— тренировать память, чтобы запомнить, как грамотно записывать результаты полученных решений.
 Постоянное использование в работе гдз по алгебре поможет автоматически вспомнить порядок верного отображения ответа.
Постоянное использование в работе гдз по алгебре поможет автоматически вспомнить порядок верного отображения ответа.Родители и педагоги, а также сами школьники высоко оценивают полезность гдз по алгебре для текущей и итоговой подготовки. Ученики непрофильных школ, в которых математика в целом, и алгебра в частности, является неосновной дисциплиной, тоже активно пользуются сборниками. В их случае, представленные в гдз по алгебре решения позволяют не потерять высокий средний балл, поскольку математика в обязательном порядке изучается во всех школах страны.
Качество знаний — важный совокупный показатель, на формирование которого оказывает влияние множество факторов. Помимо грамотного объяснения, в числе важнейших — системная и регулярная тренировка, отработка заданий и принципов применения четкой математической записи. Электронные сборники гдз по алгебре — оптимальный ресурс, полезность, необходимость и эффективность которого доказана многолетней практикой его применения.
К дополнительным плюсам, определяющим выбор такого ресурса, пользователи относят:
— удобный дружелюбный интерфейс;
— четкость изображений, возможность моментально идентифицировать нужную книгу, задание, без проблем найти верный ответ;
— многочисленные положительные отзывы и рекомендации.
Самые лучшие, крепкие и надежные знания — те, что добыты самостоятельно. И многие преподаватели-предметники сегодня сами рекомендуют своим ученикам в качестве важного и существенного дополнения к школьным объяснениям использовать гдз по алгебре в своей подготовительной практике. Эксперты ОГЭ и ЕГЭ тоже отмечают, что результаты работы тех выпускников, которые активно пользовались такими ресурсами для тренировки математических навыков в течение всего периода подготовки, выше чем у тех, кто предпочел обойтись без них. Более того, есть мнения и данные о том, что в некоторых случаях, такая самоподготовка эффективнее занятий с репетиторами. Ну а приобретенный в ходе использования гдз по алгебре бесценный навык самоподготовки и самопроверки, работы с информацией понадобится не только в школьные годы, но и впоследствии, после её окончания. В том числе — в профессиональной деятельности специалистов различного профиля и сферы.
ГДЗ Алгебра 7 Мордкович (упр. 9.31 — 9.66)
ГДЗ Алгебра 7 класс.-reshenie-203.jpg) Часть 2 Задачник. Мордкович. (Мнемозина, 2019). Глава 2. Линейная функция. § 9. Линейная функция и ее график. Ответы на упражнения 9.31 — 9.66. Вернуться в ОГЛАВЛЕНИЕ.
Часть 2 Задачник. Мордкович. (Мнемозина, 2019). Глава 2. Линейная функция. § 9. Линейная функция и ее график. Ответы на упражнения 9.31 — 9.66. Вернуться в ОГЛАВЛЕНИЕ.
Алгебра 7 Мордкович (упр. 9.31 — 9.66)
§ 9. Линейная функция и ее график
Смотреть Упражнения 9.1 — 9.30 из § 9.
№ 9.31. Постройте график функции у = –0,5х + 2 и прямую у = 4.
а) Найдите координаты точки пересечения прямых.
б) Выделите ту часть графика функции у = –0,5х + 2, которая расположена ниже прямой у = 4. Какие значения у соответствуют выделенной части графика? Какие значения при этом принимает выражение –0,5х + 2?
в) Определите, какие значения х соответствуют выделенной части графика линейной функции.
г) Найдите, при каких значениях х выполняется неравенство –0,5х + 2 > 4.
Смотреть ответы на № 9.31
№ 9.32. Постройте график функции у = –3х + 6.
а) С помощью построенного графика решите уравнение –3х + 6 = 0.
б) Выделите ту часть графика, которая соответствует условию у > 0. Какие значения аргумента соответствуют выделенной части графика?
в) С помощью графика решите неравенство –3х + 6 > 0.
г) Решите неравенство –3х + 6 < 0.
Смотреть ответы на № 9.32
№ 9.33. Постройте график функции у = 2х – 6.
а) С помощью построенного графика решите уравнение 2х – 6 = 0.
б) Выделите ту часть графика, которая соответствует условию у < 0. При каких значениях аргумента функция принимает отрицательные значения?
в) С помощью графика решите неравенство 2х – 6 ≤ 0.
г) Решите неравенство 2х – 6 ≥ 0.
Смотреть ответы на № 9.33
№ 9.34. Постройте график линейной функции у = 3х – 6 и с его помощью решите неравенство:
а) 3х – 6 > 0; б) 3х – 6 ≤ 0; в) 3х – 6 < 0; г) 3х – 6 ≥ 0.
Смотреть ответы на № 9.34
№ 9.35. Постройте график линейной функции у = 4х + 4 и с его помощью решите неравенство:
а) 4х + 4 > 0; б) 4х + 4 < 0; в) 4х + 4 ≤ 0; г) 4х + 4 ≥ 0.
Смотреть ответы на № 9.35
№ 9.36. Постройте график линейной функции у = –х – 2 и с его помощью решите неравенство:
а) –х – 2 > 0; б) –х – 2 < 0; в) –х – 2 < 0; г) –х – 2 > 0.
Смотреть ответы на № 9.36
№ 9.37. Постройте график линейной функции у = –2х + 4 и с его помощью решите неравенство:
а) –2х + 4 > 0; б) –2х + 4 < 0; в) –2х + 4 < 0; г) –2х + 4 > 0.
Смотреть ответы на № 9.37
Смотреть ответы на № 9.38
Смотреть ответы на № 9.39
Смотреть ответы на № 9.40
Смотреть ответы на № 9.41
Смотреть ответы на № 9.42
Смотреть ответы на № 9.43
Смотреть ответы на № 9.44
Смотреть ответы на № 9.45
Линейная функция монотонна, значит, для того чтобы найти наибольшее и наименьшее значения, нужно вычислить значения функции на концах отрезка.
а) –2 + 3 = 1, –1 + 3 = 2. Ответ: 1 — наименьшее; 2 — наибольшее.
б) –(–1) + 5 = б, –4 + 5 = 1. Ответ: 1 — наименьшее: 6 — наибольшее.
в) –3 + 3 = 0, –1 + 3 = 2. Ответ: 0 — наименьшее; 2 — наибольшее.
г) –2 + 5 = 3, –5 + 5 = 0. Ответ: 0 — наименьшее; 3 — наибольшее.
Смотреть ответы на № 9.46
Линейная функция монотонна, значит, для того чтобы найти наибольшее и наименьшее значения, нужно вычислить значения функции на концах отрезка.
а) 4 • (–1) –1 = –5, 4 • 2 – 1 = 7. Ответ: –5 – наименьшее; 7 – наибольшее.
б) –2 • 0 + 5 = 5, –2 • 4 + 5 = –3. Ответ: –3 – наименьшее; 5 – наибольшее.
в) 3 • (–l) –2 = –5, 3 • 1 – 2 = 1. Ответ: –5 – наименьшее; 1 – наибольшее.
г) –5 • 0 + 7 = 7, –5 • 2 + 7 – 3. Ответ: –3 – наименьшее; 7 – наибольшее.
Смотреть ответы на № 9.47
Смотреть ответы на № 9.48
Смотреть ответы на № 9.49
Смотреть ответы на № 9.50
Смотреть ответы на № 9.51
Смотреть ответы на № 9.52
Для того, чтобы выяснить проходит ли график функции через данную точку, нужно подставить значения абсциссы и ординаты точки в уравнение и посмотреть обращается ли уравнение в верное равенство. у = 3,2х – 5:
а) 3,2 • 3 – 5 = 4,6 – верно, значит, проходит;
б) 3,2 • 1,2 – 5 = 0 – неверно, значит, не проходит;
в) 3,2 • 7,5 – 5 = 4 – неверно, значит, не проходит;
г) 3,2 • 2,2 – 5= 2,04 – верно, значит, проходит.
Смотреть ответы на № 9.53
a) ymin = 4.
б) Функция убывает, значит, наибольшее значение в начале промежутка, а наименьшее в конце. Но в конце промежутка стоит знак +∞, следовательно, наименьшего значения не существует. Наибольшее = –0,5 • (–2) + 1 = 2.
в) Функция возрастает, значит, наименьшее значение в начале промежутка, а наибольшее в конце. Наименьшее = 2,5 • 1 – 4 = –1,5. Наибольшее = 2,5 • 2 – 4 = 1.
г) Функция возрастает, значит, наименьшее значение в начале промежутка, а наибольшее в конце. Но в начале промежутка стоит знак –∞, следовательно, наименьшего значения не существует. Наибольшее = 2,5 • 0 – 4 = – 4.
Смотреть ответы на № 9.54
а) Функция возрастает, значит, наименьшее значение в начале промежутка, а наибольшее в конце. Наименьшее =1/4 • (–4) + 2 = 1. Наибольшее = 1/4 • 4 + 2 = 3.
б) Функция возрастает, значит, наименьшее значение в начале промежутка, а наибольшее в конце. Но в конце промежутка стоит знак +∞, следовательно, наибольшего значения не существует. Наименьшее = 1/4 • 0 + 2 = 2.
в) Функция убывает, значит, наибольшее значение в начале промежутка, а наименьшее в конце. Но в начале промежутка стоит знак –∞, следовательно, наибольшего значения не существует. Наименьшее = –1/3 • 6 – 1 = –3.
г) Заданный промежуток является интервалом, следовательно, наибольшего и наименьшего значений не существует.
Смотреть ответы на № 9.55
а) х = 3х – 12; 2х = 12; х = 6. Ответ; (6; 6).
б) x = 5x + 4; 4х = –4; х = – 1. Ответ: (–1; –1).
Смотреть ответы на № 9.56
а) –х = 2х + 9; 3х = –9; х = –3. Ответ: (–3; 3).
б) –х = –3х + 8; 2х = 8; х = 4. Ответ: (4; –4).
Смотреть ответы на № 9.57
а) 2х = х + 15; х = 15;у = 2 • 15 = 30. Ответ: (15; 30).
б) у = 6y – 35; у = 7; х = 3 • 7 = 21. Ответ: (21; 7).
Смотреть ответы на № 9.58
у = –5x + m;
а) –5 • 1 + m = 2; m = 7;
б) –5 • 0,5 + m = 4; m = 6.5;
в) –5 • (–7) + m = 8; m = –27;
г) –5 • 1,2 + m = –3; m = 3.
Смотреть ответы на № 9.59
а) 3k + 4 = 5; k = 1/3;
б) k/2 + 4 = 1; k = –6;
в) –6k + 4 = –8; k = 2;
г) k/3 + 4 = –8. K = –36.
Смотреть ответы на № 9.60
Так как функция у = 2х – 3 возрастает, А = 2 • 2 – 3 = 1.
Так как функция у = 0,5x – 4 возрастает, В = 2 • 0,5 – 4 = –3.
Смотреть ответы на № 9.61
Из того, что функция у = х – 4 возрастает следует, что С = 0 – 4 = –4. Из того что функция у = 4 – х убывает следует, что D = 4 – 1 = 3. Следовательно, D > С.
Смотреть ответы на № 9.62
у = kx + m.
а) Из того, что линейная функция проходит через первый и третий координатные углы следует, что она возрастает, т.с. k > 0. Но еще известно, что функция проходит через второй координатный угол. Откуда следует, что m > 0.
б) Из того, что линейная функция проходит через второй и четвертый координатные углы следует, что она убывает, т.е. k < 0. Но еще известно, что функция проходит через первый координатный угол. Откуда следует, что m > 0.
в) Из того, что линейная функция проходит через первый и третий координатные углы следует, что она возрастает, т.е. k > 0. Но еще известно, что функция проходит через четвертый координатный угол. Откуда следует, что m < 0.
г) Из того, что линейная функция проходит через второй и четвертый координатные углы следует, что она убывает, т.е. k < 0. Но еще известно, что функция проходит через третий координатный угол. Откуда следует, что m < 0.
Смотреть ответы на № 9.63
y = kx + m.
а) Видно, что если мы подставим любое х > 0, то получим, что у > 0, следовательно, график функции проходит через первый координатный угол. Если же мы подставим любое х < 0, то получим, что у < 0, следовательно, график проходит через третий координатный угол. График не проходит через второй и четвертый координатные углы, (не учитывая точку (0; 0)) потому что m = 0. Ответ: график функции проходит через 1 и 3 координатные yглы.
б) Видно, что если мы подставим любое х > 0, то получим, что у < 0, следовательно, график функции проходит через первый координатный угол. Если же мы подставим любое х < 0, то получим, что у > 0, следовательно, график проходит через третий координатный угол. График не проходит через второй и четвертый координатные углы (не учитывая точку (0; 0)) потому, что m = 0. Ответ: график функции проходит через 2 и 4 координатные углы.
в) либо в первой и второй четверти, ибо в третьей и четвертой четверти;
г) совпадает с осью х.
Смотреть ответы на № 9.64
Смотреть ответы на № 9.65
Смотреть ответы на № 9.66
Вернуться в ОГЛАВЛЕНИЕ.
ГДЗ Алгебра 7 класс. Часть 2 Задачник. Мордкович. (Мнемозина, 2019). Глава 2. Линейная функция. § 9. Линейная функция и ее график. Ответы на упражнения 9.31 — 9.66.
Готовые домашние задания для 3–11 класса
Надоело тратить часы на решение задач по алгебре, химии, физике и другим не всегда простым предметам? Снова остался один на один со своей домашней работой? Тогда ты в правильном месте.
У нас собрана уникальная коллекция ГДЗ по всем школьным предметам для 3, 4, 5, 6, 7, 8, 9, 10 или 11 класса. По задачам каждого современного школьного учебника составлены ГДЗ с проставленными номерами заданий и пояснениями к решениям.
| 3 класс | 4 класс | 5 класс | 6 класс | 7 класс | 8 класс | 9 класс | 10 класс | 11 класс | |
| Математика | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Алгебра | |||||||||
| Геометрия | |||||||||
| Русский язык | |||||||||
| Английский язык | |||||||||
| Немецкий язык | |||||||||
| Физика | |||||||||
| Химия |
Новые решебники
ГДЗ по английскому языку 9 класс Афанасьева О. В. и др.
|
ГДЗ по английскому языку 9 класс Афанасьева, Михеева • Авторы: Афанасьева О. В., Михеева И. В. и др. • Год издания: 2002 и выше • Издательство: Просвещение • Формат: PDF; используйте Adobe Reader • Размер: 6,14 МБ Подробней и скачать |
ГДЗ по английскому языку 9 класс Афанасьева О. В. и др.
|
ГДЗ по английскому языку 9 класс Афанасьева, Михеева «Новый курс английского языка для российских школ». 5-й год обучения (9 класс). • Авторы: Афанасьева О. В., Михеева И. В. и др. • Год издания: 2006 и выше, в том числе 2010, 2011 • Издательство: Дрофа • Формат: PDF; используйте Adobe Reader • Размер: 5,24 МБ Подробней и скачать |
ГДЗ по английскому языку 9 класс Кауфман К. И. и др.
|
ГДЗ по английскому языку 9 класс Кауфман • Авторы: Кауфман К. И., Кауфман М. Ю. • Год издания: 2002 и выше, в том числе 2008 • Издательство: Титул • Формат: PDF; используйте Adobe Reader • Размер: 5,47 МБ Подробней и скачать |
ГДЗ по английскому языку 9 класс Кауфман К. И. Рабочая тетрадь.
|
ГДЗ к рабочей тетради по английскому языку 9 класс Кауфман. Часть 1 и 2 • Авторы: Кауфман К. И., Кауфман М. Ю. • Год издания: 2003 и выше, в том числе 2010, 2011 • Издательство: Титул • Формат: PDF; используйте Adobe Reader • Размер: 5,2 МБ Подробней и скачать |
отелей Дубровника рядом с алгеброй — коды GDS и комиссии агентов, отели в центре Дубровника — Поиск отелей по гостиничному индексу и туристическому индексу
Узкие результаты 49 Подходящие отели Очистить фильтры
Сеть гостиниц
Установить радиус поиска Только отели, которые подпадают под Будет показано 2 мили от центра города.Сортировать по
ClassificationNamePrice (High to Low) Price (Low to High) CityCommissionDistance
()
% PDF-1.4 % 1 0 obj > / Метаданные 6 0 R >> эндобдж 7 0 объект > эндобдж 2 0 obj > эндобдж 3 0 obj > эндобдж 4 0 объект > / Doc-Start> /section.1> / уравнение.1.1> /page.2> / уравнение.1.2> /уравнение.1.3> /page.3> / уравнение.1.4> /section.2> / уравнение.2.1> / уравнение.2.2> /page.4> /equation.2.3> /equation.2.4> /equation.2.5> /page.5> / уравнение.2.6> /equation.2.7> /thm.2.1> /page.6> /equation.2.8> /equation.2.9> /equation.2.10> /page.7> /equation.2.11> /equation.2.12> /page.8> / раздел*.1> /cite.Babaoglu04> /cite.Baboglu2_04> /cite.Eden> /page.9> /cite.David85> /cite.David86> / цитировать.Шампанское88> /cite.Olver91> /cite.Hereman96> /cite.Levi88> /cite.Winternitz88> /cite.Grabowski96> /cite.Gungor02-2> >> эндобдж 5 0 obj > / Аннотации [21 0 R 22 0 R] / Содержание 23 0 руб. >> эндобдж 6 0 obj > поток LaTeX с пакетом гиперссылок
Математика
Все классы ЛИЧНО Алгебра IЭто элементарный курс алгебры, в котором упор делается на развитие навыков работы с алгебраической терминологией. Студенты изучают концепции, включая переменные, линейные уравнения, факторинг, построение графиков и вербальные задачи. Аудиторные лекции дополняются домашними заданиями и видеоуроками из электронного учебника.(Также указано для средней школы.)
10: 00–12: 00
$ 1 356,00
* Без занятий Понедельник, 5 июля
Алгебра II
* Осталось 2 местаОбзор и расширение тем из алгебры I, новые темы, изучаемые в алгебре II, включают абсолютные значения, показатели и радикалы, квадратичные и высшие полиномиальные функции и логарифмы. Студенты также получают введение в тригонометрию. Предварительные требования: Алгебра I
21 июня — 30 июля *
10: 00–12: 00
1356 долларов.00
* Без занятий Понедельник, 5 июля
Геометрия
Курс дедуктивной евклидовой геометрии в двух и трех измерениях, студенты изучают логические системы, линии, плоскости, углы, треугольники, конгруэнтность, многоугольники и окружности. Курс также охватывает объем и площадь поверхности трехмерных фигур. Требования: Алгебра I
12: 30–2: 30
$ 1 356,00
* Без занятий Понедельник, 5 июля
Предварительный расчет
Интенсивное развитие элементарных функций одной переменной, студенты узнают о действительных числах, неравенствах, аналитической геометрии плоскости и концепции функции.Подробно изучены полиномиальные, экспоненциальные, логарифмические и тригонометрические функции. Предварительные требования: Алгебра II21 июня — 30 июля *
AM Сессия:
8: 00–10: 00
$ 1 356,00
PM Сессия:
12: 30–2: 30
$ 1 356,00
* Без занятий Понедельник, 5 июля
Введение в математический анализ МИНИ-КУРС
10–12 классы
Цель этого трехнедельного занятия — рассмотреть несколько важных тем из Precalculus for Calculus I или AB осенью.Мы сосредоточимся на различных типах функций, графиках и тригонометрии. Также мы кратко рассмотрим производные и интегралы. Предпосылка: Precalculus
.12 июля — 30 июля
11: 00–12: 00
$ 678
** Репетиторство может быть доступно по любой математической дисциплине. Пожалуйста, свяжитесь с директором летней школы Томом Кэрроллом, чтобы изучить этот вариант.Метод простейших уравнений и его применение для решения нелинейных уравнений NLSE, KGZ, GDS, DS и GZ
Предлагается хорошая идея нахождения точных решений нелинейных эволюционных уравнений.Идея состоит в том, что точные решения уравнений эллиптического типа выводятся с использованием метода простейших уравнений и модифицированного метода простейших уравнений, а затем точные решения класса нелинейных эволюционных уравнений, которые могут быть преобразованы в уравнение эллиптического типа, используя уменьшение бегущей волны. Например, возмущенное нелинейное уравнение Шредингера (НУШ), система Клейна-Гордона-Захарова (КГЗ), с использованием этого метода исследованы обобщенные уравнения Дэви-Стюартсона (GDS), уравнения Дэви-Стюартсона (DS) и обобщенные уравнения Захарова (GZ), и представлены точные решения с использованием этого метода.
1. Введение
Нелинейные явления существуют во всех областях науки и техники, таких как механика жидкости, физика плазмы, оптические волокна, биология, физика твердого тела, химическая кинематика и химическая физика. Хорошо известно, что многие нелинейные уравнения в частных производных (NLPDE) широко используются для описания этих сложных физических явлений. Точное решение дифференциального уравнения дает информацию о построении сложных физических явлений. Поэтому поиск точных решений НЛПД уже давно является одной из центральных тем постоянного интереса математики и физики.С развитием пакетов символьных вычислений, таких как Maple и Mathematica, было предложено множество мощных методов нахождения точных решений, таких как метод однородного баланса [1, 2], метод вспомогательных уравнений [3], метод синус-косинусов [ 4], метод эллиптических функций Якоби [5], метод экспоненциальных функций [6], метод тангенсодержащих функций [7, 8], преобразование Дарбу [9, 10] и метод -расширения [11, 12] ].
Метод простейших уравнений — это очень мощный математический метод нахождения точных решений нелинейных обыкновенных дифференциальных уравнений.Он был разработан Кудряшовым [13, 14] и успешно используется многими авторами для нахождения точных решений ОДУ в математической физике [15–19].
В этой статье мы сначала применяем метод простейшего уравнения и модифицированный метод простейшего уравнения для получения точных решений эллиптического уравнения, а затем точные решения класса нелинейных эволюционных уравнений, которые могут быть преобразованы в эллиптические уравнения. -подобное уравнение с использованием редукции бегущей волны.
2.Описание методов
2.1. Метод простейшего уравнения
Шаг 1. Предположим, что у нас есть нелинейное уравнение в частных производных (PDE) для в форме где — многочлен от своих аргументов.
Шаг 2. Взяв, мы ищем решения бегущей волны уравнения (1) и преобразуем его в обыкновенное дифференциальное уравнение (ОДУ).
Шаг 3. Предположим, что решение (2) можно представить в виде конечного ряда в виде где удовлетворяет уравнению Бернулли или Риккати, является положительным целым числом, которое может быть определено процедурой балансировки, и параметры, которые необходимо определить.
Уравнение Бернулли, которое мы рассматриваем в этой статье, имеет вид где и — константы. Его решения можно записать как где, и — константы.
Для уравнения Риккати где, и — константы, будем использовать решения где .
Шаг 4. Подставляя (3) в (2) на (4) (или (6)), тогда левая часть (2) преобразуется в полином от; приравнивание каждого коэффициента многочлена к нулю дает набор алгебраических уравнений для.Решая алгебраические уравнения с помощью символьных вычислений, мы можем определить эти параметры явно.
Шаг 5. Предполагая, что константы могут быть получены на шаге 4 и подставляя результаты в (3), мы получаем точные решения бегущей волны для (1).
2.2. Метод модифицированного простейшего уравнения
В модифицированной версии анзац для решения составляется как где — произвольные константы, которые необходимо определить, так что и является неопределенной функцией, которая будет определена позже.
Подставляем (8) в (2) и учитываем функцию. В результате такой замены мы получаем многочлен от и его производных. В этом многочлене приравняем коэффициенты той же степени к нулю, где. Эта процедура дает систему уравнений, которую можно решить, чтобы найти, и. Тогда подстановка значений, и в (8) завершает определение точных решений (1).
3. Решения эллиптического уравнения
Теперь выберем следующее уравнение эллиптического типа. где, и — произвольные постоянные.Уравнение (9) является одним из наиболее важных вспомогательных уравнений, поскольку многие нелинейные эволюционные уравнения могут быть преобразованы в (9) с помощью редукции бегущей волны.
3.1. Использование метода простейшего уравнения
3.1.1. Решения (9) Использование уравнения Бернулли в качестве простейшего уравнения
Учитывая однородный баланс между, и, мы получаем, поэтому решение (9) представляет собой форму
Подставляя (10) в (9) и используя уравнение Бернулли (4), а затем приравнивая коэффициенты функций к нулю, мы получаем алгебраическую систему уравнений в терминах, и.Решая эту систему алгебраических уравнений с помощью Maple, получаем
Следовательно, используя решения (5) уравнения (4) и анзац (10), получаем следующее точное решение уравнения (9):
3.1.2. Решения (9) с использованием уравнения Риккати в качестве простейшего уравнения
Предположим, что решения (9) имеют вид
Подставляя (13) в (9) и используя уравнение Риккати (6), а затем приравнивая коэффициенты функций к нулю, мы получаем алгебраическую систему уравнений в терминах, и.Решая эту систему алгебраических уравнений с помощью Maple, одним из возможных наборов значений и является
Следовательно, используя решения (7) уравнения (6) и анзац (13), получаем следующее точное решение уравнения (9):
3.2. Использование модифицированного метода простейшего уравнения
Предположим, что решение (9) имеет вид где и — константы, такие, что, и — неопределенная функция, которую необходимо определить. Несложно подсчитать, что
Подставляя значения, и в (9) и приравнивая коэффициенты, и к нулевому доходу
Решая (18), получаем
И решая (21), получаем
Корпус 1. Когда, мы получаем тривиальное решение; поэтому дело отклоняется.
Случай 2. Когда, (19) и (20) дают Интегрируя (24) по, получаем Используя (25), из (20) получаем
После интегрирования получаем Где и — константы интеграции. Следовательно, точное решение (9) есть
Из (28) получаем точное решение (9), которое имеет вид
Можно произвольно выбирать параметры и.Следовательно, если положить, (29) сводится к
Снова установка, (29) уменьшается до,
Используя тождества гиперболических функций, из (30) и (31) получаем следующие периодические решения
4. Точные решения некоторых классов НЛПД
4.1. Возмущенное нелинейное уравнение Шредингера (НУШ) в форме [20]
Используя где — дисперсия третьего порядка, — нелинейная дисперсия, а также вариант нелинейной дисперсии.Мы предполагаем, что (33) имеет точное решение в виде где, и — произвольные постоянные, подлежащие определению. Подставляя (34) в (33), убирая общий множитель, имеем где, и, и — положительные константы, а штрих означает дифференцирование по. Тогда у нас есть два уравнения:
Интегрируя (36) по одному разу и полагая константу интегрирования равной нулю, имеем
Поскольку (37) и (38) имеют одинаковые решения, мы имеем следующее уравнение: где .
Из (39) можно получить
На основании только что упомянутого вывода мы решаем только (38) или (37) вместо обоих (37) и (38), при условии, что (37) и (36) заменены на (40), соответственно, мы получать
Уравнение (41) идентично (9) и, и определяются как
Тогда решения (33) определяются следующим образом: где, входя в эти решения, задается соотношениями (12), (15) и (28) — (32)., и определены формулами (42).
4.2. Система Клейна-Гордона-Захарова (КГЗ) [21]
Рассмотреть возможность где комплексная неизвестная функция обозначает компонент электрического поля, создаваемого электронами в быстром масштабе времени, а действительная неизвестная функция представляет отклонение плотности ионов. и некоторые реальные параметры.
Мы предполагаем, что
Подставляя (45) в (44), имеем
Интегрируя (47) по двойному разряду и полагая константу интегрирования равной нулю, имеем
Подставляя (48) в (46), имеем
Уравнение (49) идентично (9) и, и определяются как
Тогда решения системы Клейна-Гордона-Захарова (КГЗ) определяются следующим образом: где фигура в этих решениях задается соотношениями (12), (15) и (28) — (32)., и определены формулами (50).
4.3. Класс нелинейных дифференциальных уравнений с частными производными (NPDE)
Мы рассматриваем класс NLPDE с постоянными коэффициентами [22] где — действительные константы и. Уравнения (52) представляют собой класс физически важных уравнений. Фактически, если взять тогда (52) представляют собой уравнения Дэви-Стюартсона (ДС) [23]
Если взять тогда (52) превращаются в обобщенные уравнения Захарова (ГЗ) [24]
Поскольку — комплексная функция, мы предполагаем, что где и — действительные функции, и — константы, которые будут определены позже.Подставляя (57) в (52), получаем ОДУ для и:
Если установить то (58) сводится к
Интегрируя (59) дважды до, получаем где — постоянная интегрирования и Подставляя (62) в (61), получаем
Уравнение (63) идентично (9) и, и определяются как
Тогда решения (52) определяются следующим образом: где фигурирующие в этих решениях задаются соотношениями (12), (15), (28) — (32), а, определяются формулами (64).
Из (54) можно получить, что где — постоянная интегрирования, и тогда (54) сводятся к
Это уравнение также совпадает с (9), где и определяются следующим образом: где, фигурирующие в этих решениях, задаются соотношениями (12), (15), (28) — (32), а, определяются формулами (68).
Из (56) можно получить, что где — постоянная интегрирования, и тогда (56) сводятся к
Это уравнение также совпадает с (9), где и определяются следующим образом: где, фигурирующие в этих решениях, задаются соотношениями (12), (15), (28) — (32), а, определяются формулами (71).
5. Выводы
Метод простейших уравнений — это очень мощный математический метод для нахождения точных решений нелинейных обыкновенных дифференциальных уравнений, а уравнение эллиптического типа является одним из наиболее важных вспомогательных уравнений, поскольку многие нелинейные эволюционные уравнения, такие как возмущенное нелинейное уравнение Шредингера, система Клейна-Гордона-Захарова, обобщенные уравнения Дэви-Стюартсона, уравнения Дэви-Стюартсона, обобщенные уравнения Захарова, уравнение амплитуды Гамильтона, обобщенная связанная система КдФ Хироты-Сацума и обобщенная ZK- Уравнение BBM можно преобразовать в это уравнение с помощью редукции бегущей волны.
В этой статье мы применяем метод простейшего уравнения и модифицированный метод простейшего уравнения для получения точных решений эллиптического уравнения. Получены точные решения возмущенного нелинейного уравнения Шредингера, системы Клейна-Гордона-Захарова, обобщенных уравнений Дэви-Стюартсона, уравнений Дэви-Стюартсона и обобщенных уравнений Захарова. Сравнивая предлагаемый в настоящее время метод с другими методами, такими как метод -расширения, различные расширенные гиперболические методы и метод экспоненциальной функции, мы можем сделать вывод, что некоторые точные решения, которые мы получили, могут быть исследованы с использованием этих методов с помощью программное обеспечение для символьных вычислений, такое как Matlab, Mathematica и Maple, для облегчения сложных алгебраических вычислений.Но с помощью метода простейших уравнений и модифицированного метода простейших уравнений точные решения этих уравнений были получены в этой статье без использования программного обеспечения для символьных вычислений, поскольку вычисления просты. Это исследование показывает, что метод простейшего уравнения и модифицированный метод простейшего уравнения намного проще, чем другие методы, и могут применяться ко многим другим нелинейным эволюционным уравнениям.
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов в отношении публикации данной статьи.
Выражение признательности
Эта работа была поддержана Национальным фондом естественных наук Китая (11161020; 11361023), Фондом естественных наук провинции Юньнань (2011FZ193; 2013FZ117) и Фондом естественных наук комитета образования провинции Юньнань (2012Y452; 2013C079).
Развитие вашего применения технологии GDS
Сегодня наука о графических данных (GDS) обычно применяется в бизнесе с одной или несколькими основными целями: лучших решений, повышение качества прогнозов и создание новых способов внедрения инноваций и обучения.Эти цели все чаще связаны с ощутимыми преимуществами, такими как сокращение финансовых потерь, более быстрое получение результатов, повышение удовлетворенности клиентов и прогнозируемый рост. Возможно, вы пытаетесь улучшить или автоматизировать процесс принятия решений людьми или экспертами в предметной области, которым нужен дополнительный контекст. Или, возможно, ваша цель — повысить точность прогнозов за счет использования взаимосвязей и сетевой структуры в аналитике и машинном обучении (ML).
Графы предоставляют уникальную структуру для обучения, которая помогает развивать методы машинного обучения за счет лучшей абстракции и интерпретируемости.Эти бизнес-цели тесно связаны с тем, как организации интегрируют технологию графов в свои методы работы с данными. На рисунке 3-1 показаны основные этапы типичного путешествия GDS. В этой главе мы рассмотрим каждый из этих этапов. Первые три этапа пути к GDS сегодня наиболее распространены в коммерческом мире, а последние два — это новые этапы на пути к GDS.
Рис. 3-1. Путь к GDS.
Ваша организация может использовать практические шаги для получения немедленной выгоды, а затем применять более сложные методы таким образом, чтобы постоянно увеличивать отдачу от ваших усилий.Графики знаний
Графы знаний являются основой GDS и позволяют оптимизировать рабочие процессы, автоматизировать ответы и масштабировать интеллектуальные решения. На высоком уровне графы знаний представляют собой взаимосвязанные наборы точек данных и описывают сущности, факты или вещи реального мира и их отношения друг с другом в понятной человеку форме. В отличие от простой базы знаний с плоской структурой и статическим содержимым, граф знаний собирает и интегрирует смежную информацию, используя взаимосвязи данных для получения новых знаний.
В качестве первого этапа в GDS графы знаний часто реализуются для объединения разнообразной информации, чтобы помочь экспертам в предметной области находить связанный контент, а также исследовать связи в своих данных. Графы знаний также могут добавлять контекст в приложения, например в системы искусственного интеллекта (ИИ), чтобы они могли принимать более точные и быстрые приближенные решения. Этот подход используется в системах искусственного интеллекта, таких как чат-боты, которые используют граф знаний, например, для лучшей маршрутизации запроса на «летучую мышь на день рождения моего мужа».В этом случае график понимает, что запрос, скорее всего, не относится к летающему млекопитающему, которого кто-то ищет, а к спортивным товарам более высокого качества для особого случая. Чат-бот также может учитывать, что есть на складе, время доставки и специальные продукты, сочетая контекст не только с запросом, но также с поставками и другой логистикой.
Графическая аналитика
После внедрения графа знаний (см. Предыдущий раздел) компании часто начинают использовать аналитику графов, чтобы лучше понимать свои сети и отвечать на конкретные вопросы, основанные на взаимосвязях и топологии.Вы часто пытаетесь понять смысл, основываясь на структуре сети: нахождение кластеров, определение влиятельных узлов, оценка различных путей. Графическая аналитика обычно относится к использованию глобальных запросов и алгоритмов, которые просматривают целые графики для автономного анализа исторических данных. Этот процесс отличается от небольших транзакций в реальном времени и локальных запросов, которые сосредоточены на небольших областях вокруг нескольких узлов.
Графические запросы используются, когда вы точно знаете, что ищете, например, когда задаете вопрос типа «Сколько отношений у Миа?» или «Сколько мошенников или помеченных аккаунтов находятся в четырех переходах?» (Хмель — это уровень или слой отношений.) Подобные вопросы кажутся простыми, потому что мы можем представить, что стоим и смотрим на вещи, которые находятся рядом с нами. Однако решения, которые не хранят взаимосвязи вместе со своими данными, должны выполнять дополнительные процессы для поиска и объединения этой связанной информации. Графики хранят взаимосвязи вместе с данными, поэтому проследить путь взаимосвязей просто и быстро. Базы данных с собственными графами особенно хороши для запросов с несколькими переходами, потому что они позволяют избежать дорогостоящих поисков по индексу и объединения данных за счет хранения и обработки связанной информации рядом и обработки отношений как первоклассных граждан.
Графические алгоритмы — это подмножество алгоритмов науки о данных, которые возникли из науки о сетях, чтобы позволить рассуждать о структуре более неконтролируемым образом. Они используются, когда вы знаете шаблон или индикатор, который ищете, но не совсем то, что найдете. Например, вы можете искать необычно тесные сообщества, в которых узлы имеют больше связей между собой, чем вы ожидаете при случайном или нормальном распределении. Чтобы найти эти сообщества, вы можете использовать алгоритм графа под названием Louvain Modularity , чтобы выявить кластеры с более высокой плотностью взаимодействия внутри, среди членов группы по сравнению с взаимодействиями вне группы.
Графические алгоритмы, наиболее распространенные в коммерческих приложениях, делятся примерно на шесть категорий:
- Поиск пути и поиск: Эти алгоритмы лежат в основе анализа графов и изучения путей между узлами. Они оценивают маршруты для таких целей, как физическая логистика и наименее затратная маршрутизация вызовов или маршрутизации по Интернет-протоколу (IP).
- Центральность (важность): Алгоритмы центральности помогают раскрыть роли отдельных узлов и их влияние.Они идентифицируют влиятельные узлы на основе их положения в сети. Эти алгоритмы определяют динамику группы, такую как надежность, колеблющаяся уязвимость и мосты между группами.
- Обнаружение сообщества: Эти алгоритмы находят сообщества, члены которых имеют более существенное взаимодействие. Эти связи обнаруживают тесные кластеры, изолированные группы и структуры. Эта информация помогает предсказать подобное поведение или предпочтения, оценить устойчивость, найти повторяющиеся объекты или просто подготовить данные для других анализов.
- Сходство: Эти алгоритмы используют сравнение наборов, чтобы определить, насколько похожи отдельные узлы. Свойства и атрибуты узлов используются для оценки сходства между узлами. Этот подход используется в таких приложениях, как персонализированные рекомендации, а также для разработки категориальных иерархий.
- Эвристическое предсказание связи: Эти алгоритмы учитывают близость узлов в сети, а также структурные элементы, такие как возможные треугольники между узлами, для оценки вероятности формирования новых отношений или существования недокументированных соединений.Этот класс алгоритмов имеет множество применений — от перепрофилирования наркотиков до уголовных расследований.
- Встраивание графа: Эти алгоритмы переводят топологию и атрибуты графа в уникальное числовое представление, которое можно использовать для проектирования объектов (см. Следующий раздел «Разработка графических объектов» для получения дополнительной информации), вычислений подобия или визуализаций. В отличие от традиционных алгоритмов графов, которые используют предварительно вычисленные формулы, вложения изучают представление вашего графа на основе моделей нейронных сетей (глубокое обучение) или линейной алгебры.
Разработка графических элементов
Разработка графических элементов — это процесс поиска, объединения и извлечения прогнозных элементов из необработанных данных графа для использования в задачах машинного обучения. Чем больше информации, тем точнее модели машинного обучения, но специалисты по обработке данных редко имеют столько данных, сколько им хотелось бы. Поскольку отношения чрезвычайно предсказывают поведение и по своей сути существуют внутри текущих данных, вы можете использовать разработку графических функций для улучшения прогнозов и повышения точности модели машинного обучения — с данными, которые у вас уже есть.
При проектировании графических объектов используются взаимосвязи и сетевые структуры для создания новых, более значимых объектов. Это следующий шаг к применению того, что вы узнали из графической аналитики, в машинном обучении. Например, вы можете оценивать узлы на основе запроса, который вычисляет, сколько мошенников вышло за четыре перехода, или алгоритма централизации для измерения важности. Вы также можете пометить узлы на основе их идентификатора сообщества. (Идентификатор сообщества присваивается алгоритмом обнаружения сообщества.) Эти оценки и метки затем могут быть извлечены в список или таблицу чисел и идентификаторов (также называемых вектором признаков) для обучения моделей машинного обучения.Функции графа и результирующие метрики машинного обучения часто записываются обратно в базу данных графов для сохранения и использования в будущем.
На рис. 3-2 показано, как использование функций графа для улучшения машинного обучения является частью более крупного рабочего процесса с примерами технологий для иллюстрации.
Для машинного обучения с графическим расширением вы обычно собираете, исследуете и очищаете данные, а затем используете графовые запросы или алгоритмы для проектирования функций. Затем вы подготовите данные для машинного обучения и разделите их на наборы данных для обучения и тестирования.Хотя этот процесс не является полностью линейным, после того, как вы обучили модель и остались довольны результатами, модель можно использовать в производстве. Хотя модель может использовать транзакцию в реальном времени в производственной среде, такую как одобрение кредитных заявок онлайн, проектирование функций графа и машинное обучение выполняются в автономном режиме и периодически обновляются в циклическом процессе. Разработка графических функций предлагает организациям достижимые улучшения модели без необходимости изменять свои конвейеры машинного обучения.
Рис. 3-2. Разработка графических элементов является частью более крупного рабочего процесса машинного обучения.
Встраивание графиков
Встраивание графиков упрощает графы или части графов в вектор признаков или набор векторов, которые имеют более низкоразмерную форму, такую как список чисел. Цель состоит в том, чтобы создать легко потребляемые данные для таких задач, как ML, которые по-прежнему описывают более сложную топологию, возможности подключения или атрибуты узлов. Например, вы можете представить весь граф или путь как вложение, а затем учиться на основе самого графа или путей. Существует три типа вложений графов:
- Вложения узлов описывают связность каждого узла.
- Вложения путей охватывают обходы по графу.
- Вложения графиков кодируют весь граф в один вектор.
Графические сети
Графические сети — это захватывающий новый подход к машинному обучению, который может значительно улучшить результаты с меньшим количеством данных, сделать прогнозы более объяснимыми и привести к новым типам обучения. Графическая сеть и естественное обучение графам — это термины, придуманные Питером Батталья и группой исследователей. Они пришли к выводу, что использование графов для машинного обучения стало следующим крупным достижением самого машинного обучения из-за способности графа абстрагироваться от топологии.Их мышление основано на таком подходе:
- При обучении с использованием собственного графа на входе используется граф, выполняются обучающие вычисления с сохранением переходных состояний, а затем возвращается граф.
- Этот собственный процесс обучения графов позволяет эксперту в предметной области просматривать и проверять траекторию обучения, которая приводит к более объяснимым прогнозам.
- Этот процесс дает более богатые и точные прогнозы, которые используют меньше данных и циклов обучения.
классов, которые нужно учитывать
Какие классы выбрать?
Эти курсы — хорошая отправная точка.Наши предложения предназначены как инструмент для получения идеи и вдохновение перед регистрацией.
Поисковые классы Подать заявку на регистрацию миссий ДЛЯ КЛАССОВ
Нужна помощь при запуске? Попробуйте нашу страницу регистрации Desination и получите информацию о приеме, регистрации и финансовой помощи. У нас также есть регистрационные видеоролики и советы.
Специальные программы
Программа VITA (ACC 053A, ACC 053B и ACC 053C).Предложение начинается зимой 2020 г.
Программа помощи волонтерам по подоходному налогу (VITA) была официально учреждена в 1970-е годы Службой внутренних доходов (IRS) для помощи малоимущим и семьям. при подготовке своих годовых налоговых деклараций.
IRS продолжает эту программу и предлагает бесплатную налоговую помощь людям, которые обычно зарабатывают 56 000 долларов США или меньше, инвалиды, пожилые люди и люди с ограниченным знанием английского языка. умения, которым требуется помощь в составлении собственных налоговых деклараций. Волонтеры, сертифицированные IRS предоставить этим лицам бесплатное оформление базовой налоговой декларации с подачей в электронном виде. После успешного завершения студентом ACC 053A он получит сертификат IRS. волонтеры !!
Помогая налогоплательщикам с низким доходом в районе залива, мы сэкономили им более 18 миллионов долларов в сборы за подготовку налогов в прошлом году. Регистрируясь в этом классе, студенты получают первый шаг к тому, чтобы помочь тем в вашем сообществе, кто в этом больше всего нуждается.
После этого курса студенты получат новые технические навыки, полученные за курс кредит, получить сертификат об окончании налогового управления франчайзинга, иметь ценные опыта, чтобы разместить его в своем резюме!
Программа SAP (курсы ACC и BUS)
Узнай номер в мире.1 вычислительное программное обеспечение — SAP! SAP — крупнейший в мире поставщик корпоративного прикладного программного обеспечения с технологией, поддерживающей управление бизнесом основы для самых сложных требований аналитики. Мы присоединились к SAP Университетские альянсы 3200 учебных заведений в более чем 111 странах для интеграции SAP в наше обучение.
Business Information Professional
(курсы CAP и BUS)Профессиональный курс по бизнес-информации и сертификат предоставят вам технические, коммуникативные и управленческие навыки всего за три семестра для продвижения по карьерной лестнице.
Он предназначен для подготовки студентов к офисной и административной поддержке начального уровня. должности (например, специалисты по офисному администрированию, представители службы поддержки клиентов, информационные клерки и офис-менеджеры) в различных бизнес-средах.
Программа отличия (BIO, CHEM, COM, HIS, HUM, MAT, POL, PSY, SOC)
Программа почестей предоставляет высокомотивированным студентам возможность тесно сотрудничать с преподавателями и другими мотивированными студентами с продвинутым уровнем критического мышления, анализ, исследования, письмо и общение.Студенты проходят курсы высокого уровня в сочетание биологических наук, химии, коммуникативных исследований, истории, гуманитарных наук, математика, политология, психология и социология.
Toastmasters (уточняется в связи с пандемией)
Всемирная организация на территории кампуса Миссионерского колледжа, обслуживающая студентов, желающих присоединиться клуб как внеклассное мероприятие, чтобы помочь укрепить уверенность в себе и отработать навыки в публичных выступлениях.
Курсы для профессионалов бизнеса и переподготовки навыков
Мы гордимся тем, что создаем классы, которые помогут вам преуспеть в практических занятиях. в практических занятиях.Вот некоторые из них, которые следует учитывать, если вы работаете или владеете малым бизнесом или работать в деловом мире.
ACC 033 • Использование Excel для прогнозирования и планированияACC 034 • Финансовое планирование бизнеса с помощью Excel
Наши курсы ACC 033/034 предоставляют реальные сценарии в классе с бухгалтерским учетом. основные курсы повышения квалификации и приложения Excel.Комбинация приводит к более глубокому признанию и навыки, необходимые для работы и бизнеса более высокого уровня / классы аналитики.
ACC 051B • Налогообложение хозяйствующих субъектовПолучите лучшее представление о налоговом законодательстве, связанном с вашим партнерством, корпорацией, имущество или траст.
ACC 060 • QuickbooksПонимать основы бухгалтерского программного обеспечения QuickBooks. Узнайте о бухгалтерских книгах, счетах возвратная задолженность, кредиторская задолженность, настройка заработной платы, создание отчетов и многое другое!
ACC 073 • Бухгалтерские информационные системыУзнай номер в мире.1, которое используется большинством компаний из списка Fortune 1000.
АВТОБУС 028A • Коммерческое право
Какие законы вам нужны, прежде чем открывать собственное дело или повышаться до менеджера? знать, прежде чем приступить к работе на этих новых должностях.
АВТОБУС 054 • Запуск малого бизнеса и управление имХотите начать малый бизнес? Вот твой шанс.Получите советы о том, как исследовать, планировать и начните свой малый бизнес.
АВТОБУС 78B • Деловые коммуникацииСвязь важна. Узнайте, как писать и общаться для бизнеса, в том числе электронная почта, служебные записки, отчеты и письма.
АВТОБУС 118 • Управление человеческими ресурсамиСотрудники — это ваш бизнес. Узнайте, как ими управлять, а также по правилам штата и федеральным правилам. вокруг их трудоустройства, обучения и развития.
Программы ESL
Позвольте нам помочь вашим сотрудникам улучшить свои знания английского языка с помощью уроков по чтению, письму. и грамматика.И для кредита (46 долларов США) за единицу, и без кредита (бесплатно), и для интенсивного ESL классы доступны на esl.missioncollege.edu.
Программа SAP (курсы ACC и BUS)
Изучите компьютерное программное обеспечение №1 в мире — SAP! SAP — крупнейший в мире поставщик корпоративного прикладного программного обеспечения с технологией, поддерживающей управление бизнесом основы для самых сложных требований аналитики.Мы присоединились к SAP Университетские альянсы 3200 учебных заведений в более чем 111 странах для интеграции SAP в наше обучение.
Business Information Professional
(курсы CAP и BUS)Программа Business Information Professional Pathway и сертификат предоставляет вам возможность технические, коммуникативные и управленческие навыки всего за три семестра, чтобы они вы можете быстро начать работать или продвигаться по карьерной лестнице.Он предназначен для подготовки студенты для работы в офисе начального уровня и административных должностей (например, офисные административные специалисты, представители службы поддержки клиентов, информационные клерки и офис-менеджеров) в различных бизнес-средах на рабочем месте.
Пой, танцуй и играй с нами!
Если у вас есть интерес, мы приветствуем ваше участие в следующих мероприятиях, основанных на результатах классы.
Хор миссионерского колледжа
От Питера Гэбриэла, Стинга, классической и поп-музыки, мы поем всего понемногу! Присоединяйтесь к нашей небольшой, но могущественной певческой группе! chorus.missioncollege.edu
Миссия Танцевальная Компания
Mission Dance Company — это некоммерческая организация, управляемая студентами Миссионерского колледжа, предоставление студентам возможности поставить хореографию и исполнить оригинальные произведения искусства и поделитесь ими с более широким сообществом.Танцуй с нами: dance.missioncollege.edu
Симфонический оркестр Миссионерского колледжа
Есть вкус к классической музыке? Хотите выступить в составе нашей симфонии? Присоединиться нас на mcsymphony.com.
Дополнительные курсы по нашему искусству см. Ниже.
Присоединяйтесь к легкоатлетической команде
Вы занимались спортом в старшей школе? Хотите продолжить обучение в колледже? Миссия Saints Athletics всегда ищет студентов-спортсменов для своих команд.И как студент-спортсмен ваше участие — это 3,0 единичный урок по кинезиологии!
Лето 2021 года
Вот некоторые из наших занятий на лето, которые вы могли бы рассмотреть.Ищите здесь самые свежие предложения.
ACC 034 • Финансовое планирование бизнеса с использованием Excel для построения амортизации ссуд, анализа безубыточности, капитального бюджета и ценность времени и денег.
ART 031A • Формальный опыт рисования не требуется. Рисование природных и рукотворных форм с помощью множество средств массовой информации.
ART 033A • 2D Чертеж и элементы двухмерного дизайна.
ART 065 и 067 • Керамика Изготовление гончарных изделий вручную (065) и с помощью гончарного круга (067).
BIO 012 • Новые инфекционные заболевания: узнайте, как инфекционные агенты вызывают болезнь.
BIO 014 • Введение в нейробиологию: узнайте, как нервная система взаимодействует с мозгом и его органами чувств.
CHM 002 • Введение в химию Для студентов, планирующих карьеру в областях, связанных с наукой.
CHM 060 • Обзор по общей, органической и биохимии, предназначенный для студентов, специализирующихся в области здравоохранения, медсестер или физиотерапии.
EGR 010 • Введение в инженерное дело Если вам нравится принимать участие в работе или решать проблемы, это дает вам представление о том, как инженерная сфера.
GDS 041 • Дизайн и разработка мобильных игр Создание мобильных игр с использованием сторонних инструментов разработчика, дизайн, программирование, тестирование и издательское дело.
GDS 074 • Видеопроизводство Научитесь создавать динамические видеоролики и элементы, участвующие в редактировании видеопродукции. и производство.
Курсы гостеприимства
- FDR 050A • Введение в гостиничный менеджмент • Окунитесь в гостиничный бассейн и посмотрите, работает ли ресторан и индустрия гостеприимства предназначен для вас!
- FDR 058 • Контроль затрат в сфере общественного питания • Разберитесь в стоимости еды и ее соотношении с тем, что вы кладете в свое меню.
- FDR 075 • Планирование меню • Планируйте здоровую пищу с ограниченным бюджетом или планируйте большую компанию, мы научим вас что хорошо сочетается с вашей тарелкой.
HIS 020 • История Калифорнии Узнайте, как появилась пятая по величине экономика мира.
KIN 047 • Танцы в стиле хип-хоп От новичков до продвинутых, получайте удовольствие от обучения и исполнения танцевальных движений.
KIN 080 • Оценка танца Изучите функцию танца как искусства, ритуала или социальной деятельности.
MAT 001 • Алгебра колледжа Курс на уровне колледжа включает системы действительных и комплексных чисел, дроби, экспоненты, уравнения и многое другое.
MAT 000D • Тригонометрия Изучите тригонометрические функции, круговые функции, графики, координаты, векторы и комплексные числа.
MAT 010 • Введение в статистику Понимание анализа данных, вероятностей и проверки различных гипотез.
MAT 903 • Элементарная алгебра Действительные и комплексные системы счисления, дроби, показатели, уравнения и многое другое.
MUS 032 • Уроки голоса Любите ли вы петь в душе или петь на сцене, мы научим вас голосу техники, которые заставят вас сиять!
Не знаете, что взять? Спросите у консультанта!
В вашем браузере отключен JavaScript. Пожалуйста, включите его, чтобы использовать полную функциональность веб-сайта
| |||||||||||||||||||||||||||||
