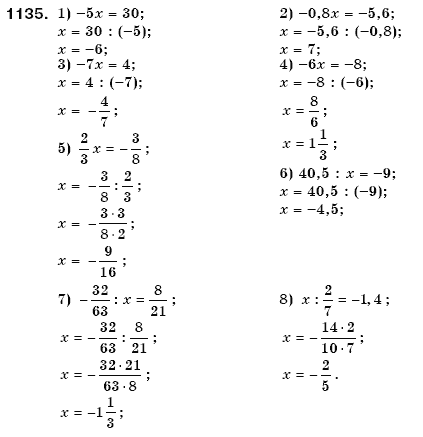Математика 6 класс Мерзляк 2019
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
101 102 103 104 105 106 107 108 109 110
111 112 113 114 115 116 117 118 119 120
121 122 123 124 125 126 127 128 129 130
131 132 133 134 135 136 137 138 139 140
141 142 143 144 145 146 147 148 149 150
151 152 153 154 155 156 157 158 159 160
161 162 163 164 165 166 167 168 169 170
171 172 173 174 175 176 177 178 179 180
181 182 183 184 185 186 187 188 189 190
191 192 193 194 195 196 197 198 199 200
201 202 203 204 205 206 207 208 209 210
211 212 213 214 215 216 217 218 219 220
221 222 223 224 225 226 227 228 229 230
231 232 233 234 235 236 237 238 239 240
241 242 243 244 245 246 247 248 249 250
251 252 253 254 255 256 257 258 259 260
261 262 263 264 265 266 267 268 269 270
271 272 273 274 275 276 277 278 279 280
281 282 283 284 285 286 287 288 289 290
291 292 293 294 295 296 297 298 299 300
301 302 303 304 305 306 307 308 309 310
311 312 313 314 315 316 317 318 319 320
321 322 323 324 325 326 327 328 329 330
331 332 333 334 335 336 337 338 339 340
341 342 343 344 345 346 347 348 349 350
351 352 353 354 355 356 357 358 359 360
361 362 363 364 365 366 367 368 369 370
371 372 373 374 375 376 377 378 379 380
381 382 383 384 385 386 387 388 389 390
391 392 393 394 395 396 397 398 399 400
401 402 403 404 405 406 407 408 409 410
411 412 413 414 415 416 417 418 419 420
421 422 423 424 425 426 427 428 429 430
431 432 433 434 435 436 437 438 439 440
441 442 443 444 445 446 447 448 449 450
451 452 453 454 455 456 457 458 459 460
461 462 463 464 465 466 467 468 469 470
471 472 473 474 475 476 477 478 479 480
481 482 483 484 485 486 487 488 489 490
491 492 493 494 495 496 497 498 499 500
501 502 503 504 505 506 507 508 509 510
511 512 513 514 515 516 517 518 519 520
521 522 523 524 525 526 527 528 529 530
531 532 533 534 535 536 537 538 539 540
541 542 543 544 545 546 547 548 549 550
551 552 553 554 555 556 557 558 559 560
561 562 563 564 565 566 567 568 569 570
571 572 573 574 575 576 577 578 579 580
581 582 583 584 585 586 587 588 589 590
591 592 593 594 595 596 597 598 599 600
601 602 603 604 605 606 607 608 609 610
611 612 613 614 615 616 617 618 619 620
621 622 623 624 625 626 627 628 629 630
631 632 633 634 635 636 637 638 639 640
641 642 643 644 645 646 647 648 649 650
651 652 653 654 655 656 657 658 659 660
661 662 663 664 665 666 667 668 669 670
671 672 673 674 675 676 677 678 679 680
681 682 683 684 685 686 687 688 689 690
691 692 693 694 695 696 697 698 699 700
701 702 703 704 705 706 707 708 709 710
711 712 713 714 715 716 717 718 719 720
721 722 723 724 725 726 727 728 729 730
731 732 733 734 735 736 737 738 739 740
741 742 743 744 745 746 747 748 749 750
751 752 753 754 755 756 757 758 759 760
761 762 763 764 765 766 767 768 769 770
771 772 773 774 775 776 777 778 779 780
781 782 783 784 785 786 787 788 789 790
791 792 793 794 795 796 797 798 799 800
801 802 803 804 805 806 807 808 809 810
811 812 813 814 815 816 817 818 819 820
821 822 823 824 825 826 827 828 829 830
831 832 833 834 835 836 837 838 839 840
841 842 843 844 845 846 847 848 849 850
851 852 853 854 855 856 857 858 859 860
861 862 863 864 865 866 867 868 869 870
871 872 873 874 875 876 877 878 879 880
881 882 883 884 885 886 887 888 889 890
891 892 893 894 895 896 897 898 899 900
901 902 903 904 905 906 907 908 909 910
911 912 913 914 915 916 917 918 919 920
921 922 923 924 925 926 927 928 929 930
931 932 933 934 935 936 937 938 939 940
941 942 943 944 945 946 947 948 949 950
951 952 953 954 955 956 957 958 959 960
961 962 963 964 965 966 967 968 969 970
971 972 973 974 975 976 977 978 979 980
981 982 983 984 985 986 987 988 989 990
991 992 993 994 995 996 997 998 999 1000
1001 1002 1003 1004 1005 1006 1007 1008 1009 1010
1011 1012 1013 1014 1015 1016 1017 1018 1019 1020
1021 1022 1023 1024 1025 1026 1027 1028 1029 1030
1031 1032 1033 1034 1035 1036 1037 1038 1039 1040
1041 1042 1043 1044 1045 1046 1047 1048 1049 1050
1051 1052 1053 1054 1055 1056 1057 1058 1059 1060
1061 1062 1063 1064 1065 1066 1067 1068 1069 1070
1071 1072 1073 1074 1075 1076 1077 1078 1079 1080
1081 1082 1083 1084 1085 1086 1087 1088 1089 1090
1091 1092 1093 1094 1095 1096 1097 1098 1099 1100
1101 1102 1103 1104 1105 1106 1107 1108 1109 1110
1111 1112 1113 1114 1115 1116 1117 1118 1119 1120
1121 1122 1123 1124 1125 1126 1127 1128 1129 1130
1131 1132 1133 1134 1135 1136 1137 1138 1139 1140
1141 1142 1143 1144 1145 1146 1147 1148 1149 1150
1151 1152 1153 1154 1155 1156 1157 1158 1159 1160
1161 1162 1163 1164 1165 1166 1167 1168 1169 1170
1171 1172 1173 1174 1175 1176 1177 1178 1179 1180
1181 1182 1183 1184 1185 1186 1187 1188 1189 1190
1191 1192 1193 1194 1195 1196 1197 1198 1199 1200
1201 1202 1203 1204 1205 1206 1207 1208 1209 1210
1211 1212 1213 1214 1215 1216 1217 1218 1219 1220
1221 1222 1223 1224 1225 1226 1227 1228 1229 1230
1231 1232 1233 1234 1235 1236 1237 1238 1239 1240
1241 1242 1243 1244 1245 1246 1247 1248 1249 1250
1251 1252 1253 1254 1255 1256 1257 1258 1259 1260
1261 1262 1263 1264 1265 1266 1267 1268 1269 1270
1271 1272 1273 1274 1275 1276 1277 1278 1279 1280
1281 1282 1283 1284 1285 1286 1287 1288 1289 1290
1291 1292 1293 1294 1295 1296 1297 1298 1299 1300
1301 1302 1303 1304 1305 1306 1307 1308 1309 1310
1311 1312 1313 1314 1315 1316 1317 1318 1319 1320
1321 1322 1323 1324 1325 1326 1327 1328 1329 1330
1331 1332 1333 1334 1335 1336 1337 1338 1339 1340
1341 1342 1343 1344 1345 1346 1347 1348 1349 1350
1351 1352 1353 1354 1355 1356 1357 1358 1359 1360
1361 1362 1363 1364 1365 1366 1367 1368 1369 1370
1371 1372 1373 1374 1375 1376 1377 1378 1379 1380
1381 1382 1383 1384 1385 1386 1387 1388 1389 1390
1391 1392 1393 1394 1395 1396 1397 1398 1399 1400
1401 1402 1403 1404 1405 1406 1407 1408 1409 1410
1411 1412 1413 1414 1415 1416 1417 1418 1419 1420
1421 1422 1423 1424 1425 1426 1427 1428 1429 1430
1431 1432 1433 1434 1435 1436 1437 1438 1439 1440
1441 1442 1443 1444 1445 1446
ГДЗ по математике 6 класс Мерзляк, Полонский, Якир
6класс
1глава
Делимость натуральных чисел.
(Задачи с 1 по 186)
§1. Делители и кратные
Вопросы после параграфа §1 Решаем устно 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39
§2. Признаки делимости на 10, на 5 и на 2
Вопросы после параграфа §2 Решаем устно 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72
§3. Признаки делимости на 9 и на 3
Вопросы после параграфа §3 Решаем устно 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103
§4. Простые и составные числа
Вопросы после параграфа §4 Решаем устно 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137
§5. Наибольший общий делитель
Вопросы после параграфа §5 Решаем устно 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162
§6. Наименьшее общее кратное
Вопросы после параграфа §6 Решаем устно 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186
2глава
Обыкновенные дроби.
(Задачи с 187 по 575)
§7. Основное свойство дроби
Вопросы после параграфа §7 Решаем устно 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209
§8. Сокращение дробей
Вопросы после параграфа §8 Решаем устно; 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235
§9. Приведение дробей к общему знаменателю. Сравнение дробей
Вопросы после параграфа §9 Решаем устно; 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267
§10. Сложение и вычитание дробей с разными знаменателями
Вопросы после параграфа §10 Решаем устно; 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332
§11. Умножение дробей
Вопросы после параграфа §11 Решаем устно; 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376 377 378 379 380 381 382 383 384 385 386 387 388
§12.
Нахождение дроби от числа
Вопросы после параграфа §12 Решаем устно; 389 390 391 392 393 394 395 396 397 398 399 400 401 402 403 404 405 406 407 408 409 410 411 412 413 414 415 416 417 418 419 420 421 422 423 424 425 426 427 428 429 430 431 432 433
§13. Взаимно обратные числа
Вопросы после параграфа §13 Решаем устно; 434 435 436 437 438 439 440 441 442 443 444 445
§14. Деление дробей
Вопросы после параграфа §14 Решаем устно; 446 447 448 449 450 451 452 453 454 455 456 457 458 459 460 461 462 463 464 465 466 467 468 469 470 471 472 473 474 475 476 477 478 479 480 481 482 483 484 485 486 487 488 489 490 491 492 493 494 495 496
§15. Нахождение числа по заданному значению его дроби
Вопросы после параграфа §15 Решаем устно; 497 498 499 500 501 502 503 504 505 506 507 508 509 510 511 512 513 514 515 516 517 518 519 520 521 522 523 524 525 526 527 528 529 530 531 532 533 534 535 536 537 538 539
§16. Преобразование обыкновенной дроби в десятичную
Решаем устно; 540 541 542 543 544 545 546 547 548 549
§17.
Решаем устно; 550 551 552 553 554 555 556 557 558 559 560
§18. Десятичное приближение обыкновенной дроби
Решаем устно; 561 562 563 564 565 566 567 568 569 570 571 572 573 574 575
3глава
Отношения и пропорции. (Задачи с 576 по 829)
§19. Отношения
Решаем устно; 576 577 578 579 580 581 582 583 584 585 586 587 588 589 590 591 592 593 594 595 596 597 598 599 600 601
§20. Пропорции
Решаем устно; 602 603 604 605 606 607 608 609 610 611 612 613 614 615 616 617 618 619 620 621 622 623 624 625 626 627 628 629 630 631 632
§21. Процентное отношение двух чисел
Решаем устно; 633 634 635 636 637 638 639 640 641 642 643 644 645 646 647 648 649 650 651 652 653 654 655 656 657 658 659 660
§22. Прямая и обратная пропорциональные зависимости
Решаем устно; 661 662 663 664 665 666 667 668 669 670 671 672 673 674 675 676 677 678 679
§23. Деление числа в данном отношении
Решаем устно; 680 681 682 683 684 685 686 687 688 689 690 691 692 693 694 695 696 697 698
§24.
Окружность и круг
Решаем устно; 699 700 701 702 703 704 705 706 707 708 709 710 711 712 713 714 715 716 717 718 719 720 721 722 723 724 725 726 727 728 729 730
§25. Длина окружности. Площадь круга
Решаем устно; 731 732 733 734 735 736 737 738 739 740 741 742 743 744 745 746 747 748 749 750 751 752 753 754 755 756 757 758 759 760 761 762 763 764 765 766
§26. Цилиндр, конус, шар
Решаем устно; 767 768 769 770 771 772 773 774 775 776 777 778 779 780 781 782 783
§27. Диаграммы
Решаем устно; 784 785 786 787 788 789 790 791 792 793 794 795 796 797 798 799 800 801
§28. Случайные события. Вероятность случайного события
Решаем устно; 802 803 804 805 806 807 808 809 810 811 812 813 814 815 816 817 818 819 820 821 822 823 824 825 826 827 828 829
4глава
Рациональные числа и действия над ними. (Задачи с 830 по 1346)
§29. Положительные и отрицательные числа
Решаем устно; 830 831 832 833 834 835 836 837 838 839 840 841 842 843 844 845
§30.
Координатная прямая
Решаем устно; 846 847 848 849 850 851 852 853 854 855 856 857 858 859 860 861 862 863 864 865 866 867 868 869 870
§31. Целые числа. Рациональные числа
Решаем устно; 871 872 873 874 875 876 877 878 879 880 881 882 883 884 885 886 887 888 889 890 891 892 893
§32. Модуль числа
Решаем устно; 894 895 896 897 898 899 900 901 902 903 904 905 906 907 908 909 910 911 912 913 914 915 916 917 918
§33. Сравнение чисел
Решаем устно; 919 920 921 922 923 924 925 926 927 928 929 930 931 932 933 934 935 936 937 938 939 940 941 942 943 944 945 946 947 948 949 950 951
§34. Сложение рациональных чисел
Решаем устно; 952 953 954 955 956 957 958 959 960 961 962 963 964 965 966 967 968 969 970 971 972 973 974 975
§35. Свойства сложения рациональных чисел
Решаем устно; 976 977 978 979 980 981 982 983 984 985 986 987 988 989 990 991 992
§36. Вычитание рациональных чисел
Решаем устно; 993 994 995 996 997 998 999 1000 1001 1002 1003 1004 1005 1006 1007 1008 1009 1010 1011 1012 1013 1014 1015 1016 1017 1018 1019 1020 1021 1022 1023
§37.
Умножение рациональных чисел
Решаем устно; 1024 1025 1026 1027 1028 1029 1030 1031 1032 1033 1034 1035 1036 1037 1038 1039 1040 1041 1042 1043 1044 1045 1046 1047 1048 1049 1050 1051 1052 1053 1054
§38. Переместительное и сочетательное свойства умножения рациональных чисел. Коэффициент
Решаем устно; 1055 1056 1057 1058 1059 1060 1061 1062 1063 1064 1065 1066 1067 1068 1069 1070 1071 1072 1073 1074
§39. Распределительное свойство умножения
Решаем устно; 1075 1076 1077 1078 1079 1080 1081 1082 1083 1084 1085 1086 1087 1088 1089 1090 1091 1092 1093 1094 1095 1096 1097 1098 1099 1100 1101 1102 1103 1104 1105 1106 1107 1108 1109 1110 1111 1112 1113 1114
§40. Деление рациональных чисел
Решаем устно; 1115 1116 1117 1118 1119 1120 1121 1122 1123 1124 1125 1126 1127 1128 1129 1130 1131 1132 1133 1134 1135 1136 1137 1138 1139 1140 1141 1142
§41. Решение уравнений
Решаем устно; 1143 1144 1145 1146 1147 1148 1149 1150 1151 1152 1153 1154 1155 1156 1157 1158 1159 1160 1161 1162 1163 1164 1165 1166 1167 1168 1169 1170 1171 1172
§42. Решение задач с помощью уравнений
Решаем устно; 1173 1174 1175 1176 1177 1178 1179 1180 1181 1182 1183 1184 1185 1186 1187 1188 1189 1190 1191 1192 1193 1194 1195 1196 1197 1198 1199 1200 1201 1202 1203 1204 1205 1206 1207 1208 1209 1210 1211 1212 1213 1214 1215 1216 1217 1218
§43. Перпендикулярные прямые
Решаем устно; 1219 1220 1221 1222 1223 1224 1225 1226 1227 1228 1229 1230 1231 1232 1233 1234 1235 1236 1237 1238 1239 1240 1241 1242 1243
§44. Осевая и центральная симметрии
Решаем устно; 1244 1245 1246 1247 1248 1249 1250 1251 1252 1253 1254 1255 1256 1257 1258 1259 1260 1261 1262 1263 1264 1265 1266 1267 1268 1269 1270 1271 1272 1273 1274 1275 1276 1277 1278 1279
§45. Параллельные прямые
Решаем устно; 1280 1281 1282 1283 1284 1285 1286 1287 1288 1289 1290 1291 1292 1293 1294 1295
§46. Координатная плоскость
Решаем устно; 1296 1297 1298 1299 1300 1301 1302 1303 1304 1305 1306 1307 1308 1309 1310 1311 1312 1313 1314 1315 1316 1317 1318 1319 1320 1321 1322 1323 1324 1325 1326 1327 1328 1329 1330 1331 1332 1333 1334
§47. Графики
Решаем устно; 1335 1336 1337 1338 1339 1340 1341 1342 1343 1344 1345 1346
гдз математика Мерзляк 6 клас
математика
українська мова
українська література
англійська мова
французька мова
німецька мова
біологія
географія
всесвітня історія
інформатика
- Вы здесь:
- Главная
- Математика 6 Мерзляк
Обери свій клас
1
2
3
4
5
6
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
50 51 52 53 54 55 56 57 58 59
60 61 62 63 64 65 66 67 68 69
70 71 72 73 74 75 76 77 78 79
80 81 82 83 84 85 86 87 88 89
90 91 92 93 94 95 96 97 98 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
502
503
504
505
506
507
508
509
510
511
512
513
514
515
516
517
518
519
520
521
522
523
524
525
526
527
528
529
530
531
532
533
534
535
536
537
538
539
540
541
542
543
544
545
546
547
548
549
550
551
552
553
554
555
556
557
558
559
560
561
562
563
564
565
566
567
568
569
570
571
572
573
574
575
576
577
578
579
580
581
582
583
584
585
586
587
588
589
590
591
592
593
594
595
596
597
598
599
600
601
602
603
604
605
606
607
608
609
610
611
612
613
614
615
616
617
618
619
620
621
622
623
624
625
626
627
628
629
630
631
632
633
634
635
636
637
638
639
640
641
642
643
644
645
646
647
648
649
650
651
652
653
654
655
656
657
658
659
660
661
662
663
664
665
666
667
668
669
670
671
672
673
674
675
676
677
678
679
680
681
682
683
684
685
686
687
688
689
690
691
692
693
694
695
696
697
698
699
700
701
702
703
704
705
706
707
708
709
710
711
712
713
714
715
716
717
718
719
720
721
722
723
724
725
726
727
728
729
730
731
732
733
734
735
736
737
738
739
740
741
742
743
744
745
746
747
748
749
750
751
752
753
754
755
756
757
758
759
760
761
762
763
764
765
766
767
768
769
770
771
772
773
774
775
776
777
778
779
780
781
782
783
784
785
786
787
788
789
790
791
792
793
794
795
796
797
798
799
800
801
802
803
804
805
806
807
808
809
810
811
812
813
814
815
816
817
818
819
820
821
822
823
824
825
826
827
828
829
830
831
832
833
834
835
836
837
838
839
840
841
842
843
844
845
846
847
848
849
850
851
852
853
854
855
856
857
858
859
860
861
862
863
864
865
866
867
868
869
870
871
872
873
874
875
876
877
878
879
880
881
882
883
884
885
886
887
888
889
890
891
892
893
894
895
896
897
898
899
900
901
902
903
904
905
906
907
908
909
910
911
912
913
914
915
916
917
918
919
920
921
922
923
924
925
926
927
928
929
930
931
932
933
934
935
936
937
938
939
940
941
942
943
944
945
946
947
948
949
950
951
952
953
954
955
956
957
958
959
960
961
962
963
964
965
966
967
968
969
970
971
972
973
974
975
976
977
978
979
980
981
982
983
984
985
986
987
988
989
990
991
992
993
994
995
996
997
998
999
1000
1001
1002
1003
1004
1005
1006
1007
1008
1009
1010
1011
1012
1013
1014
1015
1016
1017
1018
1019
1020
1021
1022
1023
1024
1025
1026
1027
1028
1029
1030
1031
1032
1033
1034
1035
1036
1037
1038
1039
1040
1041
1042
1043
1044
1045
1046
1047
1048
1049
1050
1051
1052
1053
1054
1055
1056
1057
1058
1059
1060
1061
1062
1063
1064
1065
1066
1067
1068
1069
1070
1071
1072
1073
1074
1075
1076
1077
1078
1079
1080
1081
1082
1083
1084
1085
1086
1087
1088
1089
1090
1091
1092
1093
1094
1095
1096
1097
1098
1099
1100
1101
1102
1103
1104
1105
1106
1107
1108
1109
1110
1111
1112
1113
1114
1115
1116
1117
1118
1119
1120
1121
1122
1123
1124
1125
1126
1127
1128
1129
1130
1131
1132
1133
1134
1135
1136
1137
1138
1139
1140
1141
1142
1143
1144
1145
1146
1147
1148
1149
1150
1151
1152
1153
1154
1155
1156
1157
1158
1159
1160
1161
1162
1163
1164
1165
1166
1167
1168
1169
1170
1171
1172
1173
1174
1175
1176
1177
1178
1179
1180
1181
1182
1183
1184
1185
1186
1187
1188
1189
1190
1191
1192
1193
1194
1195
1196
1197
1198
1199
1200
1201
1202
1203
1204
1205
1206
1207
1208
1209
1210
1211
1212
1213
1214
1215
1216
1217
1218
1219
1220
1221
1222
1223
1224
1225
1226
1227
1228
1229
1230
1231
1232
1233
1234
1235
1236
1237
1238
1239
1240
1241
1242
1243
1244
1245
1246
1247
1248
1249
1250
1251
1252
1253
1254
1255
1256
1257
1258
1259
1260
1261
1262
1263
1264
1265
1266
1267
1268
1269
1270
1271
1272
1273
1274
1275
1276
1277
1278
1279
1280
1281
1282
1283
1284
1285
1286
1287
1288
1289
1290
1291
1292
1293
1294
1295
1296
1297
1298
1299
1300
1301
1302
1303
1304
1305
1306
1307
1308
1309
1310
1311
1312
1313
1314
1315
1316
1317
1318
1319
1320
1321
1322
1323
1324
1325
1326
1327
1328
1329
1330
1331
1332
1333
1334
1335
1336
1337
1338
1339
1340
1341
1342
1343
1344
1345
1346
1347
1348
1349
1350
1351
1352
1353
1354
1355
1356
1357
1358
1359
1360
1361
1362
1363
1364
1365
1366
1367
1368
1369
1370
1371
1372
1373
1374
1375
1376
1377
1378
1379
1380
1381
1382
1383
1384
1385
1386
1387
1388
Любі друзі, будь-ласка, використовуйте ❤️гдз 6 клас математика Мерзляк❤️ Якір Полонський для отримання знань та їх корекції, не обманюйте себе в першу чергу і вчителів.
Якщо ви просто переписали, не розуміючи як розв’язується цей приклад, ви зробили погано лише собі. Запам’ятайте це. Я і вся наша команда дуже надіємося на те, що в нашій країні з кожним роком збільшується кількість батьків, які допомогають своїх дітям розв’язувати математику, а наша праця у вигляді гдз 6 клас математика Мерзляк Якір Полонський буде допомогати вам в цьому.
Где можно делить на 0. Почему нельзя делить на ноль? Примеры, когда нужно передвинуть запятую, а цифр больше нет
В математике число ноль занимает особое место. Дело в том, что оно, по сути, означает «ничего», «пустота», но его значение действительно сложно переоценить. Для этого достаточно вспомнить хотя бы, что именно с нулевой отметки и начинается отсчет координат положения точки в любой системе координат.
Ноль широко используется в десятичных дробях для определения значений «пустых» цифр, как до, так и после запятой. Кроме того, с ним связано одно из фундаментальных правил арифметики, которое гласит, что на ноль делить нельзя.
Его логика, по сути, вытекает из самой сущности этого числа: ведь невозможно представить, чтобы какое-то отличное от него (да и оно само) значение делилось на «ничто».
Примеры расчета
ИЗ ноль выполняются все арифметические операции, а в качестве его «партнеров» могут использоваться целые, обыкновенные и десятичные дроби, причем все они могут иметь как положительные, так и отрицательные значения. Приведем примеры их реализации и некоторые пояснения к ним.
Дополнение
При добавлении нуля к некоторому числу (как целому, так и дробному, как положительному, так и отрицательному) его значение остается абсолютно неизменным.
Пример 1двадцать четыре плюс ноль равно двадцати четырем.
Пример 2Семнадцать целых три восьмых плюс ноль равно семнадцати целых три восьмых.
Умножение
При умножении любого числа (целого, дробного, положительного или отрицательного) на ноль получается ноль .
пятьсот восемьдесят шесть раз ноль равно ноль .
Пример 2Ноль умножить на сто тридцать пять и шесть равняется ноль .
Пример 3Ноль умножить на ноль равно ноль .
Подразделение
Правила деления чисел друг на друга в случаях, когда одно из них равно нулю, различаются в зависимости от того, какую именно роль играет сам ноль: делящегося или делителя?
В тех случаях, когда ноль является делимым, результат всегда равен ему, независимо от значения делителя.
Пример 1Ноль разделить на двести шестьдесят пять равно ноль .
Пример 2Ноль разделить на семнадцать пятьсот девяносто шесть равно ноль .
| 0: | = 0 |
Разделить ноль на ноль по правилам математики невозможно. Это означает, что при выполнении такой процедуры частное неопределенно.
Таким образом, теоретически это может быть абсолютно любое число.
0: 0 = 8, потому что 8 × 0 = 0
В математике такая задача, как разделить ноль на ноль , не имеет никакого смысла, так как ее результатом является бесконечное множество. Это утверждение, однако, верно, если не указаны дополнительные данные, которые могут повлиять на конечный результат.
Те, если они есть, должны быть для указания степени изменения величины как делимого, так и делителя, и даже до момента, когда они превратились в ноль . Если он определен, то выражение типа ноль разделить на ноль , в подавляющем большинстве случаев можно придать какой-то смысл.
В курсе школьной арифметики все математические операции проводятся с действительными числами. Множество этих чисел (или непрерывное упорядоченное поле) обладает рядом свойств (аксиом): коммутативность и ассоциативность умножения и сложения, существование нуля, единицы, противоположных и обратных элементов.
Также аксиомы порядка и непрерывности, используемые для сравнительного анализа, позволяют определить все свойства действительных чисел.
Поскольку деление является обратным умножению, при делении действительных чисел на ноль неизбежно возникают две неразрешимые проблемы. Во-первых, проверка результата деления на ноль с помощью умножения не имеет числового выражения. Каким бы числом ни было частное, если его умножить на ноль, делимое получить нельзя. Во-вторых, в примере 0:0 ответом может служить абсолютно любое число, которое при умножении на делитель всегда превращается в ноль.
Деление на ноль в высшей математике
Перечисленные трудности деления на ноль привели к табу на эту операцию, по крайней мере, в рамках школьного курса. Однако в высшей математике находят способы обойти этот запрет.
Например, путем построения другой алгебраической структуры, отличной от привычной числовой прямой. Примером такой конструкции является колесо. Здесь действуют законы и правила.
В частности, деление не связано с умножением и преобразуется из бинарной операции (с двумя аргументами) в унарную операцию (с одним аргументом), обозначаемую символом /х.
Расширение области действительных чисел происходит за счет введения гипердействительных чисел, которые охватывают бесконечно большие и бесконечно малые величины. Такой подход позволяет рассматривать термин «бесконечность» как определенное число. Более того, это число при расширении числовой линии теряет свой знак, превращаясь в идеализированную точку, соединяющую два конца этой линии. Такой подход можно сравнить со строкой смены даты, когда при перемещении между двумя часовыми поясами UTC+12 и UTC-12 можно оказаться либо в следующем дне, либо в предыдущем. В этом случае утверждение x/0=∞ становится верным для любого x≠0.
Для устранения неопределенности 0/0 для колеса вводится новый элемент ⏊=0/0. В то же время в этой алгебраической структуре есть свои нюансы: 0 x≠0; x-x≠0 в общем случае. Также x·/x≠1, так как деление и умножение больше не считаются обратными операциями.
Но эти особенности колеса хорошо объясняются с помощью тождеств дистрибутивного закона, который действует в такой алгебраической структуре несколько иначе. Более подробные пояснения можно найти в специальной литературе.
Алгебра, к которой все привыкли, на самом деле является частным случаем более сложных систем, например, того же колеса. Как видите, делить на ноль в высшей математике можно. Это требует выхода за границы привычных представлений о числах, алгебраических операциях и законах, которым они подчиняются. Хотя это вполне естественный процесс, сопровождающий любой поиск новых знаний.
Число 0 можно представить как некую границу, отделяющую мир действительных чисел от мнимых или отрицательных. Из-за неоднозначного положения многие операции с этим числовым значением не подчиняются математической логике. Ярким примером этого является невозможность деления на ноль. А разрешенные арифметические операции с нулем можно производить с помощью общепринятых определений.
История нуля
Ноль является точкой отсчета во всех стандартных системах счисления.
Европейцы стали использовать это число относительно недавно, но мудрецы древней Индии использовали ноль в течение тысячи лет, прежде чем пустое число стало регулярно использоваться европейскими математиками. Еще до индейцев ноль был обязательным значением в системе счисления майя. Эти американцы пользовались двенадцатеричной системой и начинали первый день каждого месяца с нуля. Интересно, что у майя знак «ноль» полностью совпадал со знаком «бесконечность». Таким образом, древние майя пришли к выводу, что эти величины идентичны и непознаваемы.
Математические операции с нулем
Стандартные математические операции с нулем можно свести к нескольким правилам.
Дополнение: если к произвольному числу добавить ноль, то оно не изменит своего значения (0+x=x).
Вычитание: при вычитании нуля из любого числа значение вычитаемого остается неизменным (x-0=x).
Умножение: любое число, умноженное на 0, дает 0 в произведении (a*0=0).
Деление: Ноль можно разделить на любое ненулевое число.
В этом случае значение такой дроби будет равно 0. А деление на ноль запрещено.
Возведение в степень. Это действие можно выполнить с любым номером. Произвольное число, возведенное в нулевую степень, даст 1 (x 0 =1).
Нуль в любой степени равен 0 (0 а = 0).
В этом случае сразу возникает противоречие: выражение 0 0 не имеет смысла.
Парадоксы математики
То, что деление на ноль невозможно, многие знают со школы. Но объяснить причину такого запрета почему-то не получается. Действительно, почему формулы деления на ноль не существует, а другие действия с этим числом вполне разумны и возможны? Ответ на этот вопрос дают математики.
Дело в том, что обычные арифметические действия, которые школьники изучают в младших классах, на самом деле далеко не так равнозначны, как мы думаем. Все простые операции с числами можно свести к двум: сложение и умножение. Эти операции составляют сущность самого понятия числа, а остальные операции основаны на использовании этих двух.
Сложение и умножение
Возьмем стандартный пример вычитания: 10-2=8. В школе считается просто: если из десяти предметов отнять два, останется восемь. Но математики смотрят на эту операцию совсем иначе. Ведь для них нет такой операции, как вычитание. Этот пример можно записать иначе: x+2=10. Для математиков неизвестная разница — это просто число, которое нужно прибавить к двум, чтобы получить восемь. И никакого вычитания здесь не требуется, нужно просто найти подходящее числовое значение.
Умножение и деление обрабатываются одинаково. На примере 12:4=3 можно понять, что речь идет о делении восьми предметов на две равные кучки. А на самом деле это просто перевернутая формула записи 3х4=12. Такие примеры на деление можно приводить бесконечно.
Примеры деления на 0
Тут становится немного понятно, почему нельзя делить на ноль. Умножение и деление на ноль имеют свои правила. Все примеры на деление этой величины можно сформулировать как 6:0=x.
А ведь это перевернутое выражение выражения 6*х=0. Но, как известно, любое число, умноженное на 0, дает в произведении только 0. Это свойство заложено в самом понятии нулевого значения.
Получается, что такого числа, которое при умножении на 0 дает какое-либо осязаемое значение, не существует, то есть эта задача не имеет решения. Такого ответа не следует бояться, это естественный ответ для задач такого типа. Просто писать 6:0 не имеет смысла и ничего не может объяснить. Короче говоря, это выражение можно объяснить бессмертным «без деления на ноль».
Есть ли операция 0:0? В самом деле, если операция умножения на 0 допустима, можно ли ноль делить на ноль? Ведь уравнение вида 0x5=0 вполне допустимо. Вместо цифры 5 можно поставить 0, товар от этого не изменится.
Действительно, 0x0=0. Но вы все еще не можете делить на 0. Как было сказано, деление — это просто обратное действие умножения. Таким образом, если в примере 0x5=0, нужно определить второй множитель, то получим 0x0=5.
Или 10. Или бесконечность. Деление бесконечности на ноль — как вам это?
Но если в выражение вписывается любое число, то оно не имеет смысла, мы не можем выбрать одно из бесконечного множества чисел. А раз так, то значит выражение 0:0 не имеет смысла. Оказывается, даже сам ноль нельзя разделить на ноль.
высшая математика
Деление на ноль — головная боль для старшеклассников по математике. Математический анализ, изучаемый в технических вузах, несколько расширяет понятие проблем, не имеющих решения. Например, к уже известному выражению 0:0 добавляются новые, не имеющие решения в школьных курсах математики:
- бесконечность разделить на бесконечность: ∞:∞;
- бесконечность минус бесконечность: ∞−∞;
- единица возведена в бесконечную степень: 1 ∞ ;
- бесконечность умножить на 0: ∞*0;
- некоторые другие.
Решить такие выражения элементарными методами невозможно. Но высшая математика, благодаря дополнительным возможностям для ряда подобных примеров, дает окончательные решения.
Особенно это проявляется при рассмотрении задач теории пределов.
Раскрытие неопределенности
В теории пределов значение 0 заменяется условной бесконечно малой переменной. А выражения, в которых деление на ноль получается при подстановке нужного значения, преобразуются. Ниже приведен стандартный пример предельного расширения с использованием обычных алгебраических преобразований:
Как видно на примере, простое сокращение дроби приводит ее значение к вполне рациональному ответу.
При рассмотрении пределов тригонометрических функций их выражения стремятся свести к первому замечательному пределу. При рассмотрении пределов, в которых знаменатель обращается в 0 при подстановке предела, используется второй замечательный предел.
Метод Лопиталя
В некоторых случаях пределы выражений можно заменить пределами их производных. Гийом Лопиталь — французский математик, основатель французской школы математического анализа. Он доказал, что пределы выражений равны пределам производных от этих выражений.
В математической записи его правило выглядит следующим образом.
Математическое правило деления на ноль обучали всех людей в первом классе общеобразовательной школы. «На ноль делить нельзя», — учили нас всех и запрещали под страхом оплеухи делить на ноль и вообще обсуждать эту тему. Хотя некоторые учителя начальных классов все же пытались объяснить, почему нельзя делить на ноль на простых примерах, эти примеры были настолько нелогичны, что проще было просто запомнить это правило и не задавать лишних вопросов. Но все эти примеры были нелогичны по той причине, что учителя не могли логически объяснить нам это в первом классе, так как в первом классе мы даже не знали, что такое уравнение, а логически это математическое правило можно объяснить только с помощью помощи уравнений.
Всем известно, что при делении любого числа на ноль получится пустота. Почему именно пустота, мы рассмотрим позже.
Вообще в математике независимыми признаются только две процедуры с числами.
Это сложение и умножение. Остальные процедуры считаются производными от этих двух процедур. Давайте посмотрим на это на примере.
Подскажите, сколько будет, например, 11-10? Мы все сразу ответим, что будет 1. И как мы нашли такой ответ? Кто-то скажет, что и так понятно, что будет 1, кто-то скажет, что взял 10 из 11 яблок и подсчитал, что получилось одно яблоко. С точки зрения логики все правильно, но по законам математики эта задача решается иначе. Необходимо помнить, что сложение и умножение считаются основными процедурами, поэтому нужно составить следующее уравнение: х + 10 = 11, и только потом х = 11-10, х = 1. Обратите внимание, что сначала идет сложение , и только потом, исходя из уравнения, мы можем вычесть. Казалось бы, зачем столько процедур? Ведь ответ и так очевиден. Но только такие процедуры могут объяснить невозможность деления на ноль.
Например, мы решаем следующую математическую задачу: мы хотим разделить 20 на ноль. Итак, 20:0=х. Чтобы узнать, сколько это будет, нужно помнить, что процедура деления следует из умножения.
Другими словами, деление есть производная процедура умножения. Следовательно, вам нужно составить уравнение из умножения. Итак, 0*х=20. Вот тупик. Какое бы число мы ни умножали на ноль, оно все равно будет 0, но не 20. Отсюда следует правило: на ноль делить нельзя. Ноль можно делить на любое число, но число на ноль делить нельзя.
Здесь возникает другой вопрос: можно ли делить ноль на ноль? Итак, 0:0=x означает 0*x=0. Это уравнение можно решить. Возьмем, к примеру, x=4, что означает 0*4=0. Оказывается, если ноль поделить на ноль, получится 4. Но и тут не все так просто. Если взять, например, х=12 или х=13, то получится тот же ответ (0*12=0). В общем, какое бы число мы не подставляли, все равно выйдет 0. Поэтому если 0:0, то получится бесконечность. Вот простая математика. К сожалению, бессмысленна и процедура деления нуля на ноль.
Вообще число ноль в математике самое интересное. Например, всем известно, что любое число в нулевой степени дает единицу. Конечно, такого примера в реальной жизни мы не встречаем, а вот с делением на ноль жизненные ситуации попадаются очень часто.
Так что помните, что на ноль делить нельзя.
Линия УМК А. Г. Мерзляк. Математика (5-6)
Математика
Информация о том, что на ноль делить нельзя, известна нам со школьной скамьи. Мы усваиваем это правило раз и навсегда. Однако лишь немногие из нас задаются вопросом, почему на самом деле это невозможно сделать. Но важно знать и понимать причины невозможности этого действия, так как оно раскрывает принципы «работы» и других математических операций.Все математические операции равны, но некоторые более равны, чем другие.
Начнем с того, что четыре арифметических действия — сложение, вычитание, умножение и деление — не равны. И разговор не о том, в каком порядке выполняются действия при решении какого-то примера или уравнения. Нет, это означает само понятие числа. И по его словам, самые важные — это сложение и умножение. И уже из них так или иначе «вытекают» вычитание и деление.
Сложение и вычитание
Например, разберем простую операцию: «3 — 1».
Что это значит? Учащийся легко может объяснить эту задачу: это значит, что предметов было три (например, три апельсина), один вычитается, оставшееся количество предметов и есть правильный ответ. Правильно описал? Верно. Мы бы объяснили себе так же. Но математики видят процесс вычитания иначе.
Операция «3 — 1» рассматривается не с позиции вычитания, а только со стороны сложения. Согласно этому, нет «три минус один», есть «какое-то неизвестное число, которое при прибавлении к единице дает три». Таким образом, простое «три минус один» становится уравнением с одним неизвестным: «х + 1 = 3». Более того, вид уравнения сменил знак — вычитание сменилось сложением. Оставалось только одно задание — найти подходящее число.
Справочник содержит все основные формулы школьного курса математики: алгебры, геометрии и начала анализа. Для удобства пользования справочником составлен предметный указатель. Пособие предназначено для школьников 5-11 классов и абитуриентов.
Умножение и деление
Подобные метаморфозы происходят и с таким действием, как деление.
Математики отказываются воспринимать задачу «6:3» как некие шесть объектов, разделенных на три части. «Шесть разделить на три» — это не что иное, как «неизвестное число, умноженное на три, в результате чего получится шесть»: «х 3».
Разделить на ноль
Уяснив принцип математических действий применительно к задачам на вычитание и деление, рассмотрим наше деление на ноль.
Задача «4:0» превращается в «х 0». Получается, что нам нужно найти такое число, умножение на которое даст нам 4. Известно, что умножение на ноль всегда дает ноль. Это уникальное свойство нуля и, по сути, его суть. Нет такой вещи, как число, умноженное на ноль, которое дает любое число, отличное от нуля. Мы пришли к противоречию, а значит, задача не имеет решения. Следовательно, запись «4:0» не соответствует какому-то конкретному числу, а отсюда вытекает ее бессмысленность. Поэтому, чтобы кратко подчеркнуть непродуктивность такого процесса, как деление на ноль, говорят, что «на ноль делить нельзя».
Еще интересные вещи:
- Типичные ошибки учителей при обучении математике в начальной школе
- Внеклассная работа по математике в начальной школе
- Формирование математической грамотности в начальной школе
Что произойдет, если ноль разделить на ноль?
Представьте себе следующее уравнение: «0 x = 0». С одной стороны, это выглядит вполне справедливо. Представляем ноль вместо неизвестного числа и получаем готовое решение: «0 0 = 0». Отсюда вполне логично сделать вывод, что «0:0 = 0».
Однако теперь подставим любое другое число, например, «х = 7», вместо «х = 0» в то же уравнение с неизвестным. Результирующее выражение теперь выглядит как «0 · 7 = 0». Вроде все правильно. Проделываем обратную операцию и получаем «0:0=7». Но тогда оказывается, что можно взять абсолютно любое число и вывести 0:0=1, 0:0=2… 0:0=145… — и так до бесконечности.
Если для любого числа x справедливо равенство, то мы не имеем права выбрать только одно, исключая остальные.
Это значит, что мы так и не можем ответить, какому числу соответствует выражение «0:0». В очередной раз зайдя в тупик, мы признаем, что и эта операция бессмысленна. Оказывается, ноль нельзя делить даже сам по себе.
Оговоримся, что в математическом анализе иногда встречаются особые условия задачи — так называемое «раскрытие неопределенности». В таких случаях допускается отдавать предпочтение одному из возможных решений уравнения «0 · x = 0». Однако в арифметике таких «допусков» не бывает.
Демо-версия Oge. СЭМ Демонстрации по математике
Оценка
Работа состоит из двух модулей : «Алгебра и геометрия». Всего 26 задач . Модуль «Алгебра» «Геометрия»
3 часа 55 минут (235 минут).
однозначное число
, угольник компас Калькуляторы на экзамене не используется .
паспорт ), пропуск и капилляр или! Разрешается брать с собой воду (в прозрачной бутылке) и в дорогу
Работа состоит из двух модулей : «Алгебра и геометрия».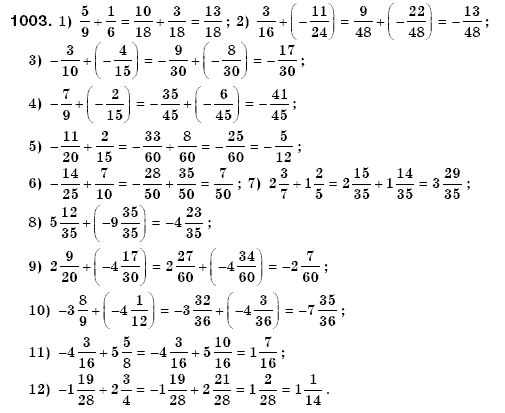
Всего 26 заданий . Модуль «Алгебра» содержит семнадцать заданий: в части 1 — четырнадцать заданий; во 2 части — три задания. Модуль «Геометрия» содержит девять заданий: в части 1 — шесть заданий; во 2 части — три задания.
Для выполнения экзаменационной работы по математике 3 часа 55 минут (235 минут).
Ответы на задания 2, 3, 14 впишите в бланк ответов №1 однозначное число , что соответствует номеру правильного ответа.
Для остальных заданий Части 1 ответом является число или последовательность чисел . Запишите ответ в поле ответа в тексте работы, а затем перенесите его в бланк ответов № 1. Если в ответе получена обыкновенная дробь, переведите ее в десятичную .
При выполнении работы можно воспользоваться основными формулами курса математики, которые выдаются вместе с работой. Разрешается использовать линейку , угольник , другие шаблоны для построения геометрических фигур (циркуль ) Не использовать инструменты с напечатанными на них справочными материалами.
Калькуляторы на экзамене не используются .
На экзамен необходимо иметь при себе документ, удостоверяющий личность ( паспорт ), пропуск и капиллярную ручку или черную гелевую ручку ! Разрешено брать с собой воду (в прозрачной бутылке) и идет (фрукты, шоколад, булочки, бутерброды), но могут попросить выйти в коридор.
Основное общее образование
Линия учебно-методических пособий Мерзляка А.Г. Алгебра (7-9) (базовый)
Математика
Демонстрационный вариант, кодификатор и спецификация ОГЭ 2019 по математике с официального сайта ФИПИ.
Скачать демо ОГЭ 2019 вместе с кодификатором и спецификацией по ссылке ниже:
Следите за информацией о наших вебинарах и трансляциях на канале YouTube, совсем скоро мы обсудим подготовку к ОГЭ по математике.
Издание адресовано учащимся 9 классов для подготовки к ОГЭ по математике. Пособие включает: 850 заданий разного типа, сгруппированных по темам; справочный теоретический материал; ответы на все задания; Подробные решения задач Представлены все учебные темы, знание которых проверяется экзаменом.
Издание поможет учителям в подготовке учащихся к ОГЭ по математике.
Экзаменационная работа (ОГЭ) состоит из двух модулей: «Алгебра» и «Геометрия», которые входят в две части: базовый уровень (часть 1), углубленный и высокий уровень (часть 2). Всего в работе 26 заданий, из них 20 заданий базового уровня, 4 задания высокого уровня и 2 задания высокого уровня. Модуль «Алгебра» содержит 17 заданий: в части 1 – 14 заданий; во 2 части — 3 задания. Модуль Геометрия содержит 9задания: в части 1 — 6 заданий; во 2 части — 3 задания. На экзаменационную работу по математике отводится 3 часа 55 минут (235 минут).
Часть 1
Упражнение 1
Найдите значение выражения
Решение
Ответ: 0,32.
Решение
Поскольку время 5,62 с., норматив девушки на оценку «4» не выполнен, однако это время не превышает 5,9 с. — стандарт для оценки «3». Поэтому его оценка «3».
Ответ: 3.
Решение
Первое число больше 11, поэтому оно не может быть числом A.
Обратите внимание, что точка A находится на второй половине отрезка, а значит, она явно больше 5 (из соображений масштаба координатной линии). Так что это не цифра 3) и не цифра 4). Заметим, что число удовлетворяет неравенству:
Ответ: 2.
Задание 4
Найдите значение выражения
Решение
Свойством арифметического квадратного корня (в A ≥ 0, B ≥ 0), мы имеем:
Ответ: 165.
Решение
. поставленной, достаточно определить цену деления по горизонтальной и вертикальной осям. По горизонтальной оси одна насечка равна 0,5 км., а по вертикальной — 20 мм. с.с. Следовательно, давление равно 620 мм. с.с достиг на высоте 1,5 км.
Ответ: 1,5.
Задача 6
Решите уравнение х 2 + х – 12 = 0.
Если уравнение имеет более одного корня, в ответ запишите больший из них.
Решение
Мы используем формулу корней квадратного уравнения
, где из x 1 = –4, x 2 = 3.
Ответ: 3.
Задача 7
Стоимость проезда в электричке 198 руб. Студентам предоставляется скидка 50%. Сколько рублей будет стоить 4 взрослых и 12 школьников?
Решение
Студенческий билет будет стоить 0,5 · 198 = 99 руб. Таким образом, путешествие для 4 взрослых и 12 студентов обойдется
4198 + 12,99 \ U003D 792 + 1188 \ U003d 1980.
Ответ: 1980.
Решение
Защиты 1) и 2) могут рассматриваться рассматриваются. верно, так как области, соответствующие белкам и углеводам, занимают примерно 36% и 24% от общей части круговой диаграммы. В то же время из диаграммы видно, что жиры занимают менее 16% всей диаграммы, и поэтому утверждение 3) неверно, как неверно и утверждение 4), так как жиры, белки и углеводы составляют большую часть часть схемы.
Ответ: 12 или 21.
Задание 9
На тарелке одинаковые на вид пирожки: 4 с мясом, 8 с капустой и 3 с яблоками. Петя случайным образом выбирает один пирог.
Найти вероятность того, что пирог будет с яблоками.
Решение
Вероятность события в классическом определении есть отношение числа благоприятных исходов к общему числу возможных исходов:
В данном случае число всех возможных исходов равно 4 + 8 + 3 \ u003d 15. Количество благоприятных исходов равно 3. Следовательно,
Ответ: 0,2.
Сопоставьте графики функций с формулами, которые их определяют.
Решение
Первый график, очевидно, соответствует параболе, общее уравнение которой имеет вид:
Следовательно, это формула 1). Второй график соответствует гиперболе, общее уравнение которой имеет вид:
Следовательно, это формула 3). Остается третий график, представляющий собой график прямой пропорциональности:
y = kx .
Это формула 2).
Ответ: 132.
Задача 11
В последовательности чисел первое число равно 6, а каждое последующее на 4 больше предыдущего.
Найдите пятнадцатое число.
Решение
Задача на арифметическую прогрессию с первым членом A 1 \ U003D 6 и разница D \ U003D 4. Общий термин Формула
A N = A 1 + D · ( N — 1) \ U003D 6 + 414 \ U003D 62 62 62
Ответ: 62.
Решение
Вместо того, чтобы сразу подставлять числа в это выражение, сначала упростим его, записав в виде рациональной дроби:
Ответ: 1,25.
Задача 13
Чтобы преобразовать температуру по шкале Цельсия в шкалу Фаренгейта, используйте формулу t F = 1,8 t c + 32, где t c — температура в градусах Цельсия, t F — температура в градусах Фаренгейта. Сколько градусов по шкале Фаренгейта соответствует -25 градусам по шкале Цельсия?
Решение
Подставляем значение –25 в формулу
t F = 1,8 · (–25) + 32 = –13
Ответ: –13.
Укажите решение системы неравенств
Решение
Решив эту систему неравенств, получим:
Следовательно, решением системы неравенств является интервал [–4; –2,6], что соответствует рисунку 2).
Ответ: 2.
Решение
Фигура, изображенная на рисунке, представляет собой прямоугольную трапецию. Средняя опора есть не что иное, как средняя линия трапеции, длина которой рассчитывается по формуле
, где , b — длина оснований. Составим уравнение:
б = 2,5.
Ответ: 2,5.
В равнобедренном треугольнике Abc с основанием AC внешний угол при вершине C равен 123°. Найдите угол ВАС . Дайте ответ в градусах.
Решение
Треугольник ABC равнобедренный, следовательно, угол YOU соответствует углу ICA . А вот угол ICA — прилежащий к углу 123°. Следовательно
∠ ТЫ = ∠ МКА = 180° — 123° = 57°.
Ответ: 57°.
Найдите длину хорды окружности радиусом 13, если расстояние от центра окружности до хорды равно 5.
Решение
Рассмотрим треугольник Aob (см. рисунок).
Он равнобедренный ( AO = OV ) и HE высота в нем (его длина равна условию 5). Значит HE — медиана по свойству равнобедренного треугольника и AN = HB . Найдет из правого треугольника ANO по теореме Pythagorean:
означает AB = 2 AN = 24.
Ответ: 24.
Найдите область \ U200B \ U2003. показано на рисунке.
Решение
Нижнее основание трапеции равно 21. Воспользуемся формулой площади трапеции
Ответ: 168.
Найдите тангенс острого угла, изображенного на рисунке.
Решение
Выберите прямоугольный треугольник (см. рисунок).
Тангенс есть отношение противолежащего катета к прилежащему, отсюда находим
Ответ: 2.
Какие из следующих утверждений верны?
1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
2) Существует треугольник со сторонами 1, 2, 4.
3) В любом параллелограмме есть два равных угла.
Решение
Первое утверждение — это аксиома параллельных прямых. Второе утверждение неверно, так как для отрезков с длинами 1, 2, 4 неравенство треугольника не выполняется (сумма длин любых двух сторон меньше длины третьей стороны)
1 + 2 = 3 > 4.
Верно третье утверждение — в параллелограмме противоположные углы равны.
Ответ: 13 или 31.
Часть 2
Решите уравнение x 4 = (4 x – 5) 2 .
Решение
Используя формулу разности квадратов, исходное уравнение приводится к виду: ) = 0,
Уравнение х 2 – 4 х + 5 = 0 не имеет корней ( D
x 2 + 4 x – 5 = 0
имеет корни −5 и 1.
Ответ: −5; 1.
Рыбак в 5 утра на моторной лодке отплыл от пристани против реки, через некоторое время бросил якорь, 2 часа рыбачил и вернулся обратно в 10 утра того же дня.
Какое расстояние он проплыл от пристани, если скорость течения реки 2 км/ч, а собственная скорость лодки 6 км/ч?
Решение
Пусть рыболов проплывет расстояние, равное с . Время, за которое он проплыл этот путь, равно часам (так как скорость лодки 4 км/ч против течения). Время, которое он потратил на обратный путь, равно одному часу (так как скорость лодки 8 км/ч по течению). Общее время с учетом стоянки – 5 часов. Составим и решим уравнение:
Ответ: 8 километров.
Решение
Область определения рассматриваемой функции содержит все действительные числа, кроме чисел –2 и 3.
Упростим вид аналитической зависимости, разложив числитель дроби на множители :
Таким образом, график этой функции представляет собой параболу
у = х 2 + х – 6,
с двумя «выколотыми» точками, оси абсцисс которых являются 3 Построим этот граф. Координаты вершины параболы
(–0,5; –6,25).
Прямая y = c имеет ровно одну общую точку с графиком, либо когда она проходит через вершину параболы, либо когда она пересекает параболу в двух точках, одна из которых проколота. Координаты «проколотых» точек
(−2; −4) и (3; 6). поэтому с = –6,25, с = –4 или с = 6.
Ответ : с = –6,25; с = –4; c = 6.
В прямоугольном треугольнике ABC прямой угол ИЗ известны катеты: AC = 6, ВС = 8. Найдите медиану SK этого треугольника.
Решение
В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна ее половине. поэтому
Ответ: 5.
В параллелограмме Abcd точка E — середина стороны AB . Известно, что ЕС = ЭД . Докажите, что данный параллелограмм является прямоугольником.
Решение
Рассмотрим треугольники EBC и AED.
Они равны с трех сторон. Действительно, Ae = ЭБ , ЭД = EC (по условию), AD = BC (противоположные стороны параллелограмма). Следовательно, ∠ A = ∠ B , но сумма смежных углов в параллелограмме равна 180°, поэтому ∠ A = 90° и Abcd – это прямоугольник.
Основание AC равнобедренный треугольник ABC равен 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжений сторон треугольника и касается основания AC . Найдите радиус окружности, вписанной в треугольник ABC .
Решение
Пусть O — центр этой окружности, а Q — центр окружности, вписанной в треугольник Абв .
Поскольку точка О равноудалена от сторон угла ∠SVA , до сих пор она лежит на его биссектрисе. При этом на биссектрисе угла ∠SVA лежит точка Q и в силу свойств равнобедренного треугольника эта биссектриса является одновременно медианой и высотой треугольника Abc .
Из этих рассуждений легко сделать вывод, что рассматриваемые окружности касаются в одной точке M точка касания M круги делят AC пополам и Oq перпендикулярно AC .
Нарисуйте лучи Aq и Ao . Легко понять, что Aq и Ao — биссектрисы смежных углов, а значит, угол Oaq прямой. Из прямоугольного треугольника Oaq получаем:
AM 2 = Mq · МО .
Следовательно,
На официальном сайте ФИПИ размещены документы, определяющие структуру и содержание контрольно-измерительных материалов основного государственного экзамена по математике в 2019 году. Они не имеют существенных изменений по сравнению с экзаменом за последний учебный год. Перед вами Демо-версия ОГЭ 2019 по математике с комментариями в удобной для обучения и подготовки форме.
Экзаменационная работа состоит из двух модулей: «Алгебра» и «Геометрия», задания которых разбиты на две части.
В заданиях первой части проверяются только ответы, которые необходимо перенести в специальную форму. Часть вторая требует записи полного решения проблемы. Всего 26 заданий. Модуль «Алгебра» содержит 17 заданий: в части 1 четырнадцать заданий; во 2 части — три задания. Модуль Геометрия содержит 9задания: в части 1 шесть заданий; во 2 части — три задания.
Ранее (в частности, в 2017 году) в демонстрационную версию ЕГЭ по математике входили те же задания, но часть из них выделялась в отдельный раздел, который назывался «Настоящая математика». Как показала практика, для многих детей этот раздел, в общем, дался легче. Возможно, они вам больше понравятся. На всякий случай задачи бывшей «Настоящей математики» по-прежнему отмечены знаком «ПМ», чтобы вы могли проверить себя и оценить свои шансы заработать экзаменационные баллы исходя не только из знаний по математике, но и на основе разумные практические соображения.
Также не забывайте, что содержание базового ЕГЭ за 11 класс существенно пересекается с ОГЭ за девятый класс, ведь за первые 9 лет изучения математики вы узнали больше, чем сможете сделать за оставшиеся два года.
Воспользуйтесь всеми ссылками и комментариями , чтобы найти необходимый материал для подготовки к экзамену.
Внимание: тренажер устроен следующим образом.
1) Синее поле — поле условия задачи. Белая область рядом со словом «Ответить» — это, по сути, кнопка, нажатие на которую показывает правильный ответ. Если вы еще не определились с демо-вариантом, то перед нажатием на кнопку попробуйте сами получить ответ и сравните его с заведомо правильным.
2) Оранжевое поле — поле комментария, ссылки на другие страницы сайта или на экзаменационные задания.
Кнопки работают после полной загрузки страницы.
Часть 1
Модуль алгебры1. Найдите значение выражения
1 _ 4 + 0,07.
Ответ: ______.
2. PM В таблице приведены нормативы бега на 30 метров для учащихся 9-х классов.
Какую оценку получит девушка, пробежавшая это расстояние за 5,62 секунды?
Ответ: ______.
3. Точка A отмечена на линии координат.
Известно, что он соответствует одному из четырех номеров, указанных ниже.
Какое из чисел соответствует точке А?
1) 181 ___ 16 2) √37__ 3) 0,6 4) 4
Ответ: ______.
4. Найдите значение выражения √45 __
√605 ___
.
Ответ: ______.
5. м. На графике представлена зависимость атмосферного давления от высоты над уровнем моря. Горизонтальная ось показывает высоту над уровнем моря в километрах, а вертикальная ось показывает давление в миллиметрах ртутного столба. Определите по графику, на какой высоте атмосферное давление равно 620 миллиметрам ртутного столба. Дайте ответ в километрах.
Ответ: ______.
6. Решите уравнение x 2 + x — 12 = 0 .
Если уравнение имеет более одного корня, в ответ запишите больший из них.
Ответ: ______.
7. PM Стоимость проезда в электричке 198 руб.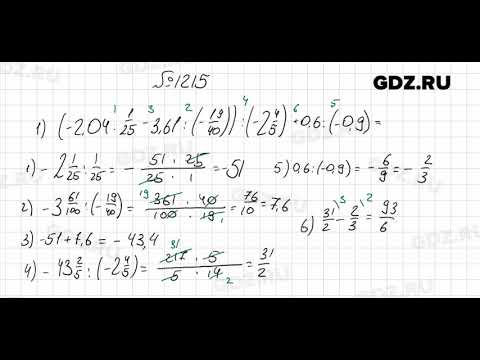
Студентам предоставляется скидка 50%. Сколько рублей будет стоить 4 взрослых и 12 школьников?
Ответ: ______.
8. PM На диаграмме показано содержание питательных веществ в сушеных белых грибах.
* Другие продукты включают воду, витамины и минералы.
1) 1000 г грибов содержат примерно 360 г белка.
2) В 1000 граммах грибов содержится около 1000 граммов углеводов.
3) 1000 г грибов содержат примерно 160 г жира.
4) 1000 г грибов содержат примерно 500 г жиров, белков и углеводов.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Ответ: ______.
9. PM На тарелке одинаковые на вид пирожки: 4 с мясом, 8 с капустой и 3 с яблоками. Петя случайным образом выбирает один пирог. Найти вероятность того, что пирог будет с яблоками.
Ответ: ______.
10. Сопоставьте графики функций с формулами, которые их определяют.
1) у = х 2 2) х = х _ 2 3) у = 2 _ х
В таблице под каждой буквой укажите соответствующий номер.
11. В последовательности чисел первое число равно 6, а каждое последующее на 4 больше предыдущего. Найдите пятнадцатое число.
Ответ: ______.
12. Найдите значение выражения
9 b + 5 а − 9 б 2 ______ б
в a = 9, b = 36 .
Ответ: ______.
13. PM Чтобы преобразовать температуру по Цельсию в градусы Фаренгейта, используйте формулу t F = 1,8 t c + 32, Где t c — температура в градусах Цельсия, t F — температура в градусах Фаренгейта. Сколько градусов по шкале Фаренгейта соответствует -25 градусам по шкале Цельсия?
Ответ: ______.
14. Укажите решение системы неравенств
Ответ: ______.
Геометрический модуль
15. ПМ Односкатная крыша, установленная на трех вертикальных опорах, основания которых расположены на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры 1,7 м, высота средней опоры 2,1 м. Найдите высоту большой опоры. Дайте ответ в метрах.
Ответ: ______.
16. В равнобедренном треугольнике Abc с основанием AC внешний угол при вершине C равен 123º. Найдите угол ВАС . Дайте ответ в градусах.
Ответ: ______.
17. Найдите длину хорды окружности радиусом 13, если расстояние от центра окружности до хорды равно 5.
Ответ: ______.
18. Найдите площадь трапеции, изображенной на рисунке.
Ответ: ______.
19. Найдите тангенс острого угла, изображенного на рисунке.
Ответ: ______.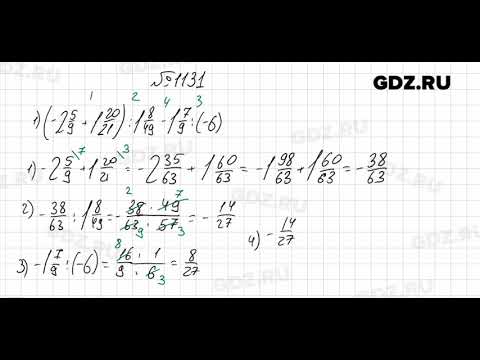
20. Какие из следующих утверждений верны?
1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
2) Существует треугольник со сторонами 1, 2, 4.
3) В любом параллелограмме есть два равных угла.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Ответ: ______.
Часть 2
При выполнении заданий этой части вам потребуется записать полное решение задачи на отдельный лист. И это будет решение, которое будет оцениваться, краткий ответ здесь уже не актуален. Поэтому белое поле после текста задачи — это всего лишь кнопка просмотра решения, рекомендованного авторами варианта. Не спешите ее нажимать, если не пытались решить проблему самостоятельно.
Модуль алгебры
21. Решите уравнение x 4 = (4 x − 5) 2 .
Ответ: ______
Решение.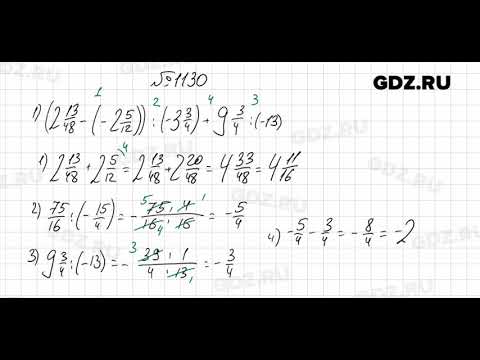
Исходное уравнение приводится к виду: ( x 2 — 4 x + 5)( x 2 + 4 x — 5) = 0.
Уравнение x 2 − 4 x + 5 = 0
не имеет корней.
Уравнение x 2 + 4 x — 5
имеет корни −5 и 1,
Ответ: −5 ; 1.
22. Рыбак в 5 утра на моторной лодке отплыл от причала против реки, через некоторое время стал на якорь, 2 часа рыбачил и вернулся обратно в 10 утра того же дня. На какое расстояние от пристани он отплыл, если скорость течения реки была 2 км/ч, а собственная скорость лодки 6 км/ч?
Ответ: ______.
Решение.
Пусть искомое расстояние будет х км. Скорость лодки при движении против течения 4 км/ч, при движении по течению 8 км/ч. Время, за которое катер будет плыть от места отправления до места назначения и обратно, равно ( х /4 + х /8) часов. Из условий задачи следует, что это время равно 3 часам. Составим уравнение:
х _
4
+ х _
8
= 3.
Решив уравнение, получим х = 8.
Ответ: 8 километров.
23. Функция графика
y = x 4 − 13 x 2 + 36 _____________ . ( x — 3) x + 2)
И определить, при каких значениях из прямая у = с имеет ровно одну общую точку с графиком.
Ответ: ______.
Решение.
Разложите числитель дроби на множители:
x 4 − 13 x 2 + 36 = ( x 2 − 4)( x 2 − 9) = ( x )(020 − 20 27) + 2)( х — 3)( х + 3).
При разрешении x ≠ −2 и x ≠ 3 функция принимает вид: y = ( x — 2)( x + 3) = x 2 + x — 6
, ее график представляет собой параболу, из которой выколоты точки (−2; −4) и (3; 6).
Прямая y = c имеет ровно одну общую точку с графиком либо при прохождении через вершину параболы, либо при пересечении параболы в двух точках, одна из которых проколота.
Вершина параболы имеет координаты (-0,5; -6,25). поэтому с = −6,25, c = −4 или c = 6.
Ответ: c = −6,25 ; с = — 4; c = 6.
ОГЭ по русскому языку в 2019 году будет проходить в два этапа.
Итоговое собеседование (устная часть) является одним из условий допуска обучающихся к письменной части экзамена по русскому языку, проводимой в конце учебного года.
Итоговое собеседование на русском языке проводится для студентов, экстернов во вторую среду февраля по текстам, темам и заданиям, формируемым по часовым поясам Федеральной службой по надзору в сфере образования и науки
Устная часть по русскому языку ОГЭ 2019 (финальное собеседование) — демо версия от ФИПИ
| Демо ОГЭ 2019 устная часть по русскому языку | скачать |
| Спецификация | скачать |
| Критерии оценки | скачать |
Демо-версия ОГЭ по русскому языку 2019 (ГИА 9 класс)
| Демо КИМ ОГЭ по русскому языку | заданий + ответы и критерии оценки |
| Спецификация | скачать |
| Кодификатор | скачать |
Итоговое собеседование на русском языке состоит из двух частей, включающих четыре задания.
Часть 1 состоит из двух задач. Задания 1 и 2 выполняются с использованием одного и того же текста.
Задание 1 — чтение вслух небольшого текста. Время приготовления — 2 минуты.
В задании 2 предлагается пересказать прочитанный текст, дополнив его высказыванием. Время приготовления — 2 минуты. Часть 2 состоит из двух заданий.
Задания 3 и 4 не связаны с текстом, который вы читаете и пересказываете, выполняя задания 1 и 2. Вы должны выбрать одну тему для монолога и диалога.
В задании 3 предлагается выбрать один из трех предложенных вариантов беседы: описание фотографии, повествование на основе жизненного опыта, обсуждение одной из сформулированных проблем. Время приготовления 1 минута.
В задании 4 вам предстоит участвовать в разговоре на тему предыдущего задания. Общее время ответа (включая время на подготовку) – 15 минут.
В течение всего времени отклика ведется запись звука.
Старайтесь полностью выполнять задания, говорите четко и ясно, не уходите от темы.
Так вы сможете набрать наибольшее количество очков.
Итоговое собеседование оценивается по системе зачетно-беззачетно
Экзаменационная работа ОГЭ по русскому языку (письменная часть) состоит из трех частей, включающих 15 заданий.
На экзаменационную работу по русскому языку отводится 3 часа 55 минут (235 минут).
Часть 1 включает одно задание и представляет собой небольшую письменную работу по прослушанному тексту (краткое изложение). Исходный код для краткого изложения прослушивается 2 раза. Это задание выполняется по бланку ответов № 2.
Часть 2 состоит из 13 упражнений (2–14). Задания части 2 выполняются на основе прочитанного текста. Запишите ответ на задания 2 и 3 в бланк ответов №1 одной цифрой, которая соответствует номеру правильного ответа.
Ответами на упражнения 4–14 являются слово (фраза), число или последовательность чисел. написать в поле ответа в тексте работы, а затем перенести в бланк ответов № 1.
Задание части 3 выполняется на основании того же текста, который вы читали при работе над заданиями части 2.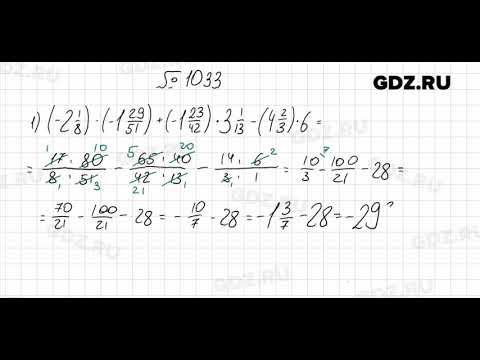
Начиная с части 3 работы, выберите одно из трех предложенных заданий (15.1, 15.2 или 15.3) и дать письменный развернутый аргументированный ответ.
Соотношение количества и количества самостоятельных работ. Отношения величин. Тема урока: «Отношения величин»
Павлова Наталья Валерьевна
учитель математики
меморандум о «Лицее № 6», Voskresensk
Оценка: 6
Тема урока: «Отношения количеств»
Тип урока: «Открытие» из новых знаний.
Основные цели:
Формировать понятие о связи, умение упрощать отношения и находить связи между числами и величинами.
Повторить и закрепить: различие и многократное сравнение чисел и величин; совместные действия с обыкновенными и десятичными дробями; перевод утверждений на математический язык.
Во время занятий
1) Самоопределение к деятельности (организационный момент).
Привет, ребята! Сегодня мы продолжим работу с числами.
Пусть сегодняшний день принесет вам радость общения. Пусть вам поможет ваша смекалка, изобретательность и знания, которые вы уже приобрели.
2) Актуализация знаний и фиксация трудностей в деятельности.
2.1. устная работа.
СЛАЙД2. Мы можем сравнивать числа и величины. Какие знаки сравнения мы используем? ( )
СЛАЙД3. Заменить звездочку знаком сравнения:
Вывод сравнения (не все значения сопоставимы).
2.2 (Работа в группах от 2 человек).
СЛАЙД 4. — Решите задачу: «Кобра живет около 40 лет, а крокодил около 200 лет. Как можно сравнить их срок службы?
СЛАЙД 5. НО ) 200-40=160 (лет). На 160 лет крокодил живет дольше кобры.
B ) 200:40=5 (раз). Кобра живет в 5 раз меньше, чем крокодил.
Продолжительность жизни кобры составляет одну пятую от продолжительности жизни крокодила.
(Поднимите руки, кто решал задачу. Послушайте ребят, решивших разными способами.)
Какие «уточняющие» вопросы можно задать при решении этой задачи? (Какие действия можно использовать для сравнения? Как написать «какая часть жизни кобры от жизни крокодила»?)
Какое сравнение вы использовали? (найти разность или частное).
Существует два способа сравнения значений.
СЛАЙД 6. Первый способ – найти их отличие и отвечает на вопрос «Насколько больше (меньше)?» Это сравнение называется разностью . Второй – найти частное и отвечает на вопрос «Во сколько раз больше (меньше)?» Это сравнение кратно .
2.3 СЛАЙД 7 . Решите задачу-шутку «Кто сильнее: слон или муравей?»
СЛАЙД 8 . «Вес муравья примерно 50 миллиграмм или 0,05 г, слона 5 тонн. При этом муравей способен поднять груз массой 0,5 г, а слон полторы тонны. Так кто из них сильнее?
(Выслушайте решение, направьте ход рассуждений. Дайте установку: узнайте, во сколько раз тяжелее груз, который может поднять муравей, чем он весит сам.
Проделайте то же самое со слоном.)
Решение: Если мы соотнести вес поднятого груза и собственный вес (0,5/0,05=10 и 1,5/5=0,3), получается, что муравей поднимает груз в 10 раз больше, чем весит он сам, а слон — в три десятых его веса. собственный вес. Наверное, недаром в честь трудолюбивого Мураша был назван трехколесный грузовой мотороллер «Муравей».
Итак, какое сравнение помогло нам соотнести силы муравья и слона? (НЕСКОЛЬКО)
3) Постановка учебного задания.
Над каким вопросом мы сегодня работаем?
(Мы будем считать кратным сравнением значений).
Это цель урока.
Для результата множественного сравнения двух величин в математике часто используется термин «отношение».
Теперь сформулируйте тему урока. (соотношения величин).
СЛАЙД 9 .- Молодец! Запишите тему в тетрадях.
(Учитель пишет на доске: Отношения).
4) Строительство проекта выхода из затруднения.
Открытие «новых знаний» детьми.
Как записать соотношение чисел из задачи кобра и крокодил? Какое действие определяет, «сколько раз или какая это часть»? (кто знает, напишите на доске)
СЛАЙД 10 .(составить частное 200 и 40).
Таким образом, отношение находится путем деления.
Откройте 118 страницу учебника и прочитайте рубрику «Говори правильно»
Теперь прочитай это отношение тремя способами.
(1 — отношение числа двести к числу сорок;
2 — отношение числа двести сорок;
3 — отношение двести к сороку).
4.2. -Мы уже знаем, что такое «Определение», и мы можем определить делитель, кратное обратным числам.
СЛАЙД 11 .Вернемся к задаче о кобре и крокодиле. Прочитайте диалоги животных на слайде. Теперь попробуйте дать определение понятию «отношения».
Наводящие вопросы:
Каким действием мы находим отношения? результат деления?
Могут ли числа быть равны нулю?
Что показывает отношение?
А теперь в задаче о кобре и крокодиле обозначим — возраст крокодила, а для б — возраст кобры и составьте определение соотношения чисел к и к .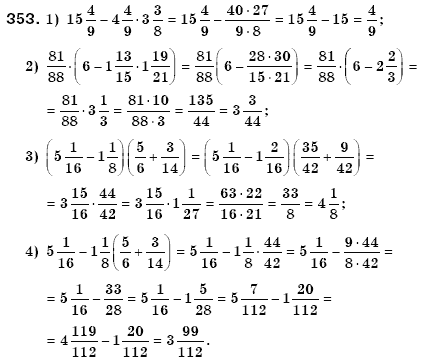
Ожидаемый ответ учащихся на наводящие вопросы учителя:
«Отношение чисел a и b называется:
1. Частное двух чисел a и b;
Имеет ли смысл многократно сравнивать числа, хотя бы одно из которых равно нулю?
2 . числа отличны от нуля;
Какую информацию можно получить из отношений?
(Во сколько раз больше, меньше, какой частью является одно число от другого).
3 .Отношение показывает, во сколько раз первое число больше второго, или какую часть составляет первое число от второго.
-Попробуйте соединить все выводы и сформулируйте определение отношения самостоятельно. (Выслушав формулировку, предложите учащимся прочитать определение на странице 117 учебника).
СЛАЙД 12. 4.3 — На клумбе 6 белых и 12 красных роз. Что показывают отношения?
а) 6:12
б) 12:6
в) 6:18
г) 18:12
а) Белых роз вдвое меньше, чем красных.
б) Количество красных роз в 2 раза больше количества белых роз.
в) Какую часть составляют белые розы от числа всех цветов на клумбе.
г) Во сколько раз количество всех цветов на клумбе больше количества красных роз.
Что такое отношения?
Обратите внимание на случаи а), б). Как называются эти числа?
(Взаимно инверсный).
Что вы заметили при расчете?
(Отношения можно «упростить»; записав их в виде дроби, можно уменьшить эту дробь.)
Соотношение иногда удобно выражать в процентах. Как представить число в %?
(Умножить на 100%). Выразите в процентах, что удобно.
5) Первичное закрепление во внешней речи.
-Выполним упражнение №722 (б, в, г) в тетрадях. (один ученик у доски: пишет, читает, переводит в проценты )
С) 12,3:3=4,1=410%
Д) 9,1:0,07 = 130 = 13000%
2 СЛИД 51539. — Выполнить задание: (в тетради по вариантам и на закрытой доске — 2 ученика по вариантам на карточках) (
см. Приложение ) 1 вариант В классе 10 мальчиков и 15 девочек.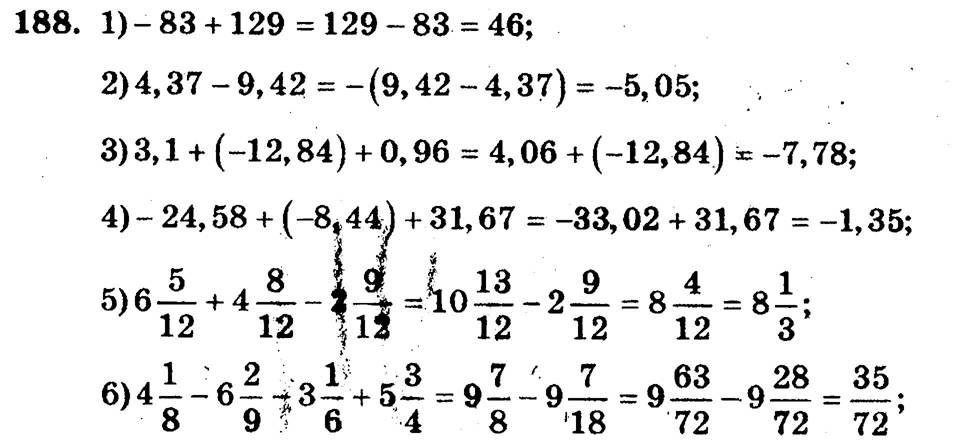
Вариант 2 В тетради 12 листов, 4 из них письменные.
СЛАЙД 14. Решения:
1 вариант
Девочек в классе в 1,5 раза больше, чем мальчиков; девочки на 50% больше.
Мальчики составляют две трети девочек.
Макияж мальчиков из класса.
Макияж девочек из класса.
Вариант 2
Заполняется третья часть тетради.
Листов в тетради всего в 3 раза больше, чем письменных.
Две трети тетради не исписаны.
Листов в тетради всего в полтора раза больше, чем неисписанных.
6) Самостоятельная работа с самопроверкой по эталону на доске. (Для тех, у кого все правильно, поставить 5, для тех, кто не выразил в процентах -4, для остальных — найти ошибки и исправить их)
Найдите отношение, если удобно — выразите в процентах:
7) Отражение деятельности. (Конспект урока).
Чему мы научились сегодня на уроке?
Над чем еще нужно поработать?
Если хотите, отправьте свои тетради на проверку.
МОЛОДЦЫ!
9) Домашнее задание: стр.20, соотв. К вопросам, № 722 (а, д, д), 723, 747
Оборудование:
1.ноутбук;
2.мультимедийный проектор;
4. Раздаточный материал (карточки с заданиями)
1. Виленкин Н.Я. Математика. 6 класс: учебник для общеобразовательных. Учреждения / Н.Я.Виленкин, В.И.Жохов, А.С.Чесноков, С.И.Шварцбурд. — 30-е изд., стер. — М. : Мнемозина, 2013. — 288 с. : больной.;
2. Чесноков А.С., Нешков К.И. Дидактические материалы по математике для 6 класса. М. : Просвещение, 2012.
Приложение.
Опция 2
В тетради 12 листов, 4 из них исписаны.
По этому условию составьте несколько отношений (не менее двух) и объясните их значение. Упростите, если возможно, полученные отношения; если удобно, выразите в процентах.
1 вариант
В классе 10 мальчиков и 15 девочек.
По этому условию составьте несколько отношений (не менее двух) и объясните их значение.
Упростите, если возможно, полученные отношения; если удобно, выразите в процентах.
ОБЯЗАТЕЛЬНАЯ ЧАСТЬ
1 Проверка умение находить соотношение чисел и количеств.
2 Проверка возможность делить число в заданном отношении .
3 Проверяем умение решать уравнения с помощью основного свойства пропорции .
4 Проверка умение решать задачи с прямой и обратной пропорциональностью.
ДОПОЛНИТЕЛЬНАЯ ЧАСТЬ
5 Проверяем умение решать нестандартные задачи с помощью шкалы.
6 Проверяем умение решать нестандартные текстовые задачи.
Контрольная работа № 2. Математика 6 классна тему: «ПРОЦЕНТЫ» (УМК С.М. Никольского)
ОБЯЗАТЕЛЬНАЯ ЧАСТЬ
1 Проверка возможность находить проценты от числа .
2 Проверка возможность найти число по его проценту.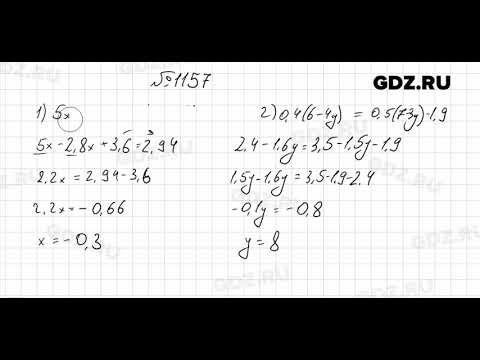
3 Проверка возможность найти процент одного числа от другого .
4 Проверка умение решать текстовую задачу с процентами.
ДОПОЛНИТЕЛЬНАЯ ЧАСТЬ
5 Проверка возможность построить круговую диаграмму .
6 Проверка
ОБЯЗАТЕЛЬНАЯ ЧАСТЬ
1 Проверка умение производить арифметические действия с дробями.
2 Проверка возможность найти часть числа и число по его части.3 .
4 Проверка
5 Проверка умение решать процентные задачи.
6 Проверка – 3 действия .
ДОПОЛНИТЕЛЬНАЯ ЧАСТЬ
7 Проверка способность производить расчеты рациональным способом. .
8 Проверяем умение решать задачи на вероятность события.
Бланк оценок для RBI
учащиеся____ 6-й класс ____________________________
Классзадания
конечный сорт
усл.
знаков
в пунктах
1. Проверка умение производить арифметические действия с дробями
1. Рассчитать
2. Проверка возможность найти часть числа и число по его части
Решить задачу
3. Проверьте свою способность решать уравнения
3. Решить уравнение
4. Проверка умение производить арифметические действия с десятичными дробями.
4. Рассчитать
5 Проверка навыки решения проблем
Решить задачу
6 Проверка умение решать текстовые задачи за 2 – 3 действия .
текстовый
7.
Проверка умения производить рациональные расчеты
Рассчитать наиболее удобным способом
8. Проверка умение решать нестандартные задачи.
задание на
вероятность события
знаю и могу
не знаю
не знаю и не могу
Вариант 2.
Самостоятельная работа на тему: «Взаимоотношения» 6 класс. 2 вариант.
1. В многоэтажном доме 75 квартир. 25 однокомнатных, 30 двухкомнатных, остальные четырехкомнатные. Какую долю всех квартир составляют однокомнатные квартиры. Какой процент всех квартир составляют двухкомнатные квартиры. Во сколько раз меньше четырехкомнатных квартир, чем однокомнатных.
2.
3.
1. В многоэтажном доме 75 квартир. 25 однокомнатных, 30 двухкомнатных, остальные четырехкомнатные. Какую долю всех квартир составляют однокомнатные квартиры. Какой процент всех квартир составляют двухкомнатные квартиры.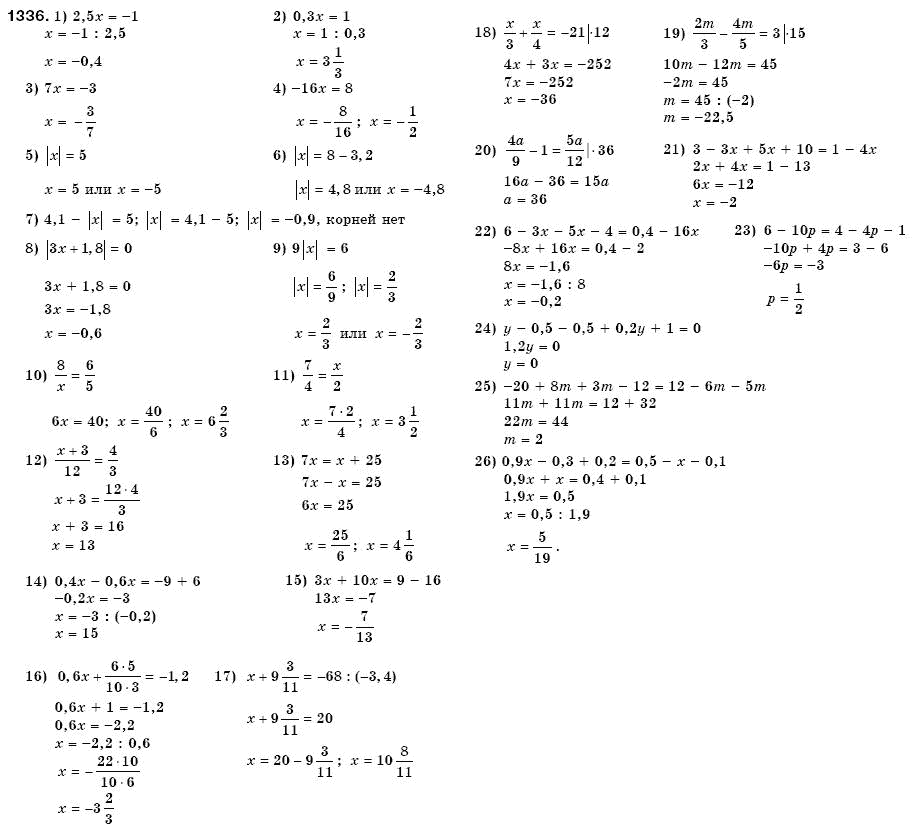
Во сколько раз меньше четырехкомнатных квартир, чем однокомнатных.
2. На сколько процентов увеличилась стоимость товара, если до наценки он стоил 350 руб., а после наценки 420 руб.
3. В классе 25 учеников. Из них контрольная по биологии написана на «отлично» — 4 ученика, 8 учеников написали на «хорошо», 12 учеников на «удовлетворительно», остальные не справились с работой. Какой процент учащихся не справился с работой?
Самостоятельная работа на тему: «Взаимоотношения» 6.9 класс0007
1 вариант.
Самостоятельная работа на тему: «Взаимоотношения» 6 класс. 1 вариант.
1.
2.
3. В классе 24 ученика. Из них 10 ребят занимаются легкой атлетикой, 5 – баскетболом, остальные – плаванием. Какой процент учащихся в классе увлекается плаванием.
1. туристов планировали пройти за три дня
45 км. В первый день прошли 18 км, во второй день 15 км, остаток пути в третий день.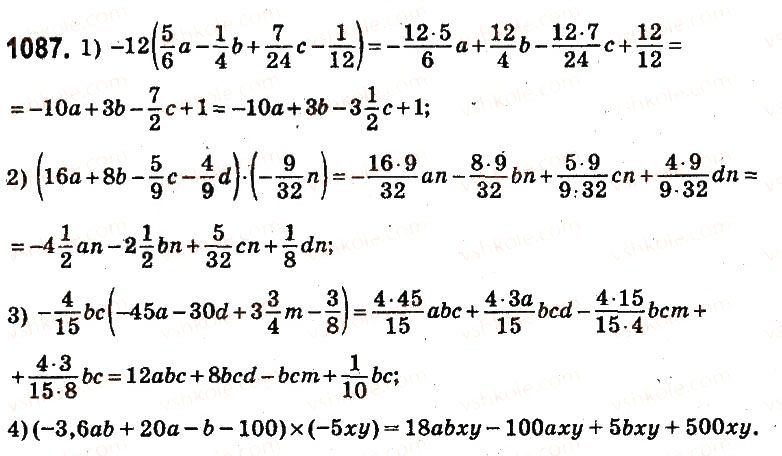
Сколько процентов пути они прошли в первый день. Во сколько раз больше они прошли во второй день, чем в третий. Какую часть пути вы проделали на третий день?
2. Стоимость товара увеличена с 40 руб до 50 руб. На сколько процентов выросла цена?
3. В классе 24 ученика. Из них 10 ребят занимаются легкой атлетикой, 5 – баскетболом, остальные – плаванием. Какой процент учащихся в классе увлекается плаванием.
Самостоятельная работа
Опция
№ 1. Упростить связь: а) ; б)
№ 2. Разделить сумму 560 рублей между тремя людьми в соотношении 1:3:2.
№ 3. Расстояние между двумя деревнями на карте 15 см. Найдите расстояние между этими деревнями на местности, если масштаб карты 1:300000.
№ 4. Ручей длиной 45 м показан на карте отрезком, равным 1 см. Определить масштаб карты
Опция
№ 1. Упростить связь: а) ; б)
№ 2.
Разделить сумму 720 рублей между тремя людьми в соотношении 2:3:4.
№ 3. Расстояние между двумя городами 230 км. Определите расстояние между этими городами по карте масштаба 1:10 000 000.
№ 4. Русло длиной 18 м показано на карте отрезком, равным 5 см. Определите масштаб карты.
Самостоятельная работа на тему «Пропорции. Прямая и обратная пропорциональность»
Опция
№ 1. Из 15 кг помидоров получается 8 кг кетчупа. Сколько помидоров нужно, чтобы получить 12 кг кетчупа?
№ 2. Решить пропорцию:
а): х = 12:25; б)
№ 3. Бригада из 24 человек отремонтировала офис за 5 дней. За сколько дней выполнят ту же работу 15 человек, если они работают с одинаковой производительностью
Опция
№ 1. Из 18 тонн железной руды выплавляется 10 тонн железа. Сколько тонн железа можно выплавить из 36 тонн руды?
№ 2.
Решить пропорцию:
а) 11 : 7 = 10 : X ; б)
№ 3. Для перевозки балки на автомобиле грузоподъемностью 7 тонн необходимо совершить 12 рейсов. Сколько рейсов нужно будет совершить на автомобиле грузоподъемностью 4 т, чтобы перевезти такое же количество леса?
Опция
№ 1. Для изготовления 6 устройств необходимо 14 г металла. Сколько металла потребуется для изготовления 15 одинаковых устройств?
№ 2. Расстояние между двумя городами на земле 720 км. Какое расстояние между ними на карте, если масштаб 1:
00?
№ 3. Решить пропорцию:
а) а : = : ;
№ 4. Для перевозки груза необходимо 20 автомобилей грузоподъемностью 6 тонн. Сколько автомобилей грузоподъемностью 8 т потребуется для перевозки такого же груза?
№ 5. В магазине картофель, свекла и морковь находятся в соотношении 12:6:5. Найдите массу каждого вида овощей, если в магазине 345 кг овощей?
Тест №1 на тему: «Отношения и пропорции»
Опция
№ 1.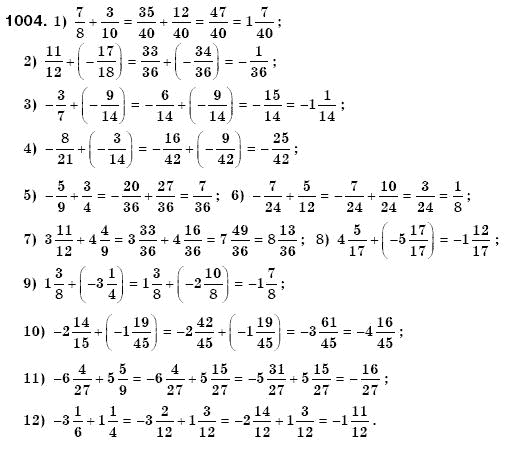
Автомобиль проехал 528 км за 8 часов. Сколько километров он проедет за 10 часов, двигаясь с той же скоростью?
№ 2. Расстояние между двумя точками на карте равно 3 см. Каково расстояние между этими точками на местности, если карта имеет масштаб 1:5 000 000?
№ 3. Решить пропорцию:
а) у: = : ;
№ 4. Бригада из 24 человек отремонтировала квартиру за 5 дней. За сколько дней 15 человек выполнят ту же работу, если они работают с одинаковой производительностью?
№ 5. В детский сад принесли красные, синие и зеленые мячи. Они находятся в соотношении 5:7:6 соответственно. Сколько будет шариков каждого цвета, если в детский сад принесли 540 шариков?
Самостоятельная работа по теме «Задания на интерес»
Опция
№ 1.
№ 2.
№ 3. В первый день Петя прочитал 40 страниц всей книги, во второй — 60 остатка, а в третий — остальные 144 страницы.
Сколько страниц в книге?
Опция
№ 1. В магазин привезли 40 кг сладостей. Из них 60% шоколадные, а остальные карамельные. Сколько килограммов карамели принесли в кафе?
№ 2. Мама собрала 24 боровика, что составляет 60% от всех грибов, которые она собрала. Сколько всего грибов собрала мама?
№ 3. В первый день тракторная бригада вспахала 30 га всего поля, во второй — 75 га, в третий — 42 га. Найдите площадь поля.
Харцызская средняя общеобразовательная школа № 25 «Интеллект» с углубленным изучением отдельных предметов
Наконечная Лариса Петровна
учитель математики
Контрольно-проверочная работа
Математика 6 класс
Тема. Отношения и пропорции
Учебник: Математика. 6 класс: учебник для общеобразовательных учреждений / С.М. Никольский, М.К. Потапов, Н.И. Решетников, А.В. Шевкин. -М.: Просвещение, 2016.
В соответствии с Базовым учебным планом на 2017-2018 учебный год на изучение математики в 6 классе отводится 4 часа в неделю.
На изучение темы «Отношения и пропорции» отводится 12 часов.
Планируемые результаты изучения темы:
Учащиеся научатся использовать понятия соотношения, масштаба, пропорции при решении задач. Приведите примеры использования этих понятий на практике. Решить задачи на пропорциональное деление (в том числе задачи из реальной практики).
Использовать знания о зависимостях (прямых и обратных пропорциях), между величинами (скорость, время, расстояние; работа, производительность, время и др.), при решении текстовых задач: понимать текст задачи, извлекать необходимую информацию, строить логическую цепочку рассуждений, критически оценивать полученный ответ, выполнять несложные практические расчеты.
Результаты освоения содержания темы:
Личный
Формирование коммуникативной компетенции в обучении и сотрудничестве со сверстниками;
Умение точно и грамотно излагать свои мысли при решении задач, понимание смысла задачи, умение аргументировать;
Креативность мышления, инициатива, находчивость, активность в решении арифметических задач;
Формирование способности к эмоциональному восприятию математических объектов, задач, решений, рассуждений.
Метасубъект
Способность самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебно-познавательных задач;
Развитие способности видеть математическую задачу в других дисциплинах, в окружающей жизни;
Понимание сути алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом.
предмет
Владение основным понятийным аппаратом: иметь представление об отношениях, пропорциях, прямой и обратной пропорциональности, масштабе, формирование представлений об закономерностях реального мира;
Умение применять изученные понятия для решения задач на прямую и обратную пропорциональность, деление числа в заданном отношении.
Предлагаемая контрольная работа охватывает материал всей изучаемой темы «Отношения и пропорции» и состоит из 12 заданий, различающихся по уровню сложности и форме изложения, содержание которых соответствует действующей программе по математике для 6 класса общеобразовательной школы.
образовательные учреждения.
Цель работы — проверка уровня усвоения учебного материала по данной теме шестиклассниками с последующей коррекцией знаний и умений.
Первые 9 заданий — это задания на выбор одного правильного ответа. Каждый вопрос имеет четыре возможных ответа, из которых только один правильный. Задание считается выполненным правильно, если учащийся указывает в таблице ответов только одну букву, которая указывает на правильный ответ. Это не требует никаких объяснений. За каждый правильный ответ учащийся получает 1 балл. Максимальное количество баллов — 9
Следующие 3 задания (10 — 12) предполагают установление соответствия между заданиями (1 — 4) и их ответами (А — Г). Для каждого из четырех рядов, обозначенных цифрами, необходимо выбрать один ответ, обозначенный буквой. За каждый правильный ответ учащийся получает 1 балл. Максимальное количество баллов, набранных за 10 — 12 заданий, равно 12. Всего 21 балл
Таблица перевода баллов
балла | знак |
1 — 5 | «один» |
6 — 10 | «2» |
11 — 15 | «3» |
16 — 19 | «четыре» |
20 — 21 | «5» |
45 минут на выполнение задания
Контрольно-испытательные работы
1.
Соотношение 23 и 70 равно:
А) Б) В) 47; Г) 93.
2. Какие из предложенных соотношений равны?
А) 4:7 и 8:28; Б) 30:5 и 65:13; в) 2:1 и 6:3; Г) 3:9 и 13:39.
3. Какое из этих равенств является пропорцией?
А) 40:8 = 4:2; Б) 6:13 = 7:12; В) 7:2 = 21:4; Г) 36:9 = 16:4;
4. Найдите отношение 40 минут к 2 часам
А) 1:3; Б) 20:1; В) 1:20; Г) 3:1.
5. Какие из величин прямо пропорциональны?
а) площадь квадрата и его стороны;
Б) Количество рабочих и время, за которое они выполнят работу;
C) Путь, пройденный пешеходом, и время, в течение которого он находился на дороге;
D) Количество труб, заполняющих бассейн, и время, необходимое для заполнения бассейна.
6. Какая из русских пословиц относится к величинам, обратно пропорциональным?
Б) Шпуля маленькая, но дорогая;
C) Чем выше пень, тем выше тень;
D) Какой привет, это ответ.
7. Какие выражения подходят для вычисления неизвестного члена пропорции : 24 = 3: 7
А).
8. Дана пропорция 13:Х = 17: в. Какое из следующих уравнений не является пропорцией?
А)х:у= 13:17; Б) х:13 = у:17; В)у:х= 17:13; Г)х:у = 17:13.
9. Какое соотношение?
А) 8; Б) ; В) ; ГРАММ).
10. Установите соответствие между отношениями (1 — 4) и величинами (A — D), которыми эти отношения являются.
1. ; А) номер
2. ; Б) цена;
3. ; Б) концентрация;
4. ; Г) скорость;
11. Установите соответствие между данными уравнениями (1 — 4) и корнями каждого из них (A — D)
1. 7 : 8 = Х: 96; А) 2;
2. ; Б) 6
3. т В 1 ;
4. к: Г) 50;
Д) 84.
12. Установите соответствие между заданиями (1 — 4) и числами (А — Г), являющимися ответами на эти задания.
1. В книге Елены Молоховец «Подарок молодым хозяйкам» рецепт черничного пирога. На пирог на 10 человек следует взять полкило чернослива. Сколько граммов чернослива взять на пирог на 3 персоны? Рассмотрим 1 фунт = 400 г. 2. На трех мандариновых деревьях вместе родилось 240 плодов, причем количество плодов на них относилось как 1:3:4. Сколько плодов росло на том дереве, на котором количество плодов не было ни самым большим, ни самым маленьким? 3. Для перевозки груза машиной грузоподъемностью 6 тонн необходимо совершить 10 рейсов. Сколько рейсов нужно сделать, чтобы перевезти этот груз на машине, грузоподъемность которой на 2 т меньше?4. Расстояние между двумя городами на карте 7см. Найдите расстояние в километрах между городами на местности, если масштаб карты 1:200 000. | А) 90; Б) 15; В 12; Г) 120; Г) 14. |
ОТВЕТЫ к заданиям 1 — 9.
ОТВЕТЫ к заданиям 10 — 12
Задание 10
Задание 11
Задание 12
Задание 12
Для исправления характера знаний можно воспользоваться следующей таблицей ошибки
п/п | Символ ошибки | С. Математика, 5 класс М.: 2016 | С.М. Никольского Математика, 6 класс М.: 2016 | ||
теория | практика | теория | практика | ||
Не знаю определения отношений. | пункт 1.1 | №4, №5 | |||
Вы не знаете свойств отношений. | пункт 1.1 | №6, №7, №9 | |||
Вы не умеете находить отношение однородных величин с разными единицами измерения. | пункт 1.1 | №10, №11 | |||
Не знаю, как найти соотношение стоимости разных предметов. | пункт 1. | №12 — №16 №18, №19 | |||
Не знаю определения масштаба | пункт 1.2 | № 21 | |||
Вы не умеете находить расстояние на местности, зная масштаб и расстояние по карте. | пункт 1.2 | №24, №28, №29 | |||
Вы не знаете, как разделить число в заданном отношении. | пункт 1.3 | №36, №37, №39, №40 | |||
Не знаю определения пропорции. | пункт 1.4 | №46 — №48, №50 | |||
Вы не знаете основного свойства пропорции. | пункт 1. | №51, №52 | |||
Не знаю, как найти неизвестный член пропорции. | пункт 1.4 | №53 — №55, №57, №58, №60, №61 | |||
11. | Вы не знаете определения прямо пропорциональных величин. | пункт 1.5 | №72 — №75 | ||
12. | Не знаю определения обратно пропорциональных величин. | пункт 1.5 | №76, №77, №79 | ||
13. | Вы не умеете умножать дроби. | пункт 4.9 | №892 — №900 | ||
14. | Вы не умеете делить дроби. | п.4.11 | №925, №926, №927 | ||
Не могу найти дробь числа | п. | ||||
М. Никольского
1
4