I участок | Сазонова Ольга Яковлевна Бухтиярова Евгения Михайловна | Молодежная 4, 6, 7, 8/1, 8/2Молодцова 5, 16 Восточно-Выборгское шоссе 24/,26/1,28/1 |
II участок | Медведева Светлана Станиславовна Суслова Ольга Владимировна | Заречная 1, 2, 3, 4, 5, 6, 7, 7/2, 10, 11, 12, 13, 15, 17Школьная 1, 2/2, 2/3, 3, 5, 6/1, 6/2 ,6/3Сертолово-2 ДНП Омега, Петровское, Слобода, ДПК Ветеран-1, Лесная Поляна |
III участок | Сибилева Галина Михайловна Кукуруза Ольга Ивановна | Ветеранов 1, 3, 3а, 4, 5, 6, 7, 8, 10, 11/1, 11/2, 12,15Ларина 1, 2, 3, 3а, 4, 5, 6, 7, 8, 10, 11Индустриальная |
IV участок | Бессонова Татьяна Сергеевна Лукьянова Антонина Исаевна | Кленовая 1/1, ½, 3Центральная 2, 4/1, 4/2, 6/1, 6/2, 8/1,8/2ЖСК Модуль 25 км. Общ. Общ.Парковый проезд 5 3 городок |
V участок | Жердева Галина Антоновна Червинская Надежда Федоровна | Молодцова 1, 3, 4, 6, 7/1, 7/2, 7/3Молодежная 1, 2, 3, 3/2, 5Сосновая 1, 2, 3, 4 Ветеранов 8/2 |
VI участок | Мосидзе Манана Вахтанговна Бибик Вера Михайловна | Кожемякина 11/1Молодцова 2, 2/2, 8, 8/2, 9, 10, 13Центральная 1/1 Центральная проходная Нахимовская Песочная |
VII участок | Ширкова Наталья Борисовна Багура Галина Владимировна | Молодцова 11, 15/1, 15/2Кленовая 5, 7Пограничная (кроме Чистого ручья) Центральная 10/1, 10/2,14/4 |
VIII участок | Кутузова Наталья Васильевна Кордон Оксана Юрьевна | Пограничная 4/1,4/2,4/3 Ветеранов 9Ларина 14, 15/1, 15/2 Молодцова 12, 14 Парковый проезд 1, 2/1, 2/2 Центральная ½, 1/3, 3, 5, 7/1,7/2 |
IX участок | Сорока Татьяна Борисовна Полякова Елена Владимировна | Новое Сертолово (Тихвинская, Мира) |
X участок | Викман Виктория Александровна Малышева Татьяна Викторовна м/с | Черная речкаЗолотые куполаСНТ Ромашка, Ягодка |
Вес двутавра, таблица расчета веса двутавровой балки
Таблица расчета веса балки двутавровой
• БАЛКУ ДВУТАВРОВУЮ № 10—40 Первый поставщик проката. |
Теоретический вес, вес метра погонного балки двутавровой с уклоном внутренних граней полок (ГОСТ 8239-89)
| Номер двутавра | Размеры, мм | Вес 1 мп, кг | Метров в тонне | |||
| h | b | s | t | |||
| 10 | 100 | 55 | 4,5 | 7,2 | 9,46 | 105,7 |
| 12 | 120 | 64 | 4,8 | 7,3 | 11,5 | 86,96 |
| 14 | 140 | 73 | 4,9 | 7,5 | 13,7 | 72,99 |
| 16 | 160 | 81 | 5 | 7,8 | 15,9 | 62,89 |
| 18 | 180 | 90 | 5,1 | 8,1 | 18,4 | 54,35 |
| 20 | 200 | 100 | 5,2 | 8,4 | 21 | 47,62 |
| 22 | 220 | 110 | 5,4 | 8,7 | 24 | 41,67 |
| 24 | 240 | 115 | 5,6 | 9,5 | 27,3 | 36,63 |
| 27 | 270 | 125 | 6 | 9,8 | 31,5 | 31,75 |
| 30 | 300 | 135 | 6,5 | 10,2 | 36,5 | 27,4 |
| 33 | 330 | 140 | 7 | 11,2 | 42,2 | 23,7 |
| 36 | 360 | 145 | 7,5 | 12,3 | 48,6 | 20,58 |
| 40 | 400 | 155 | 8,3 | 13 | 57 | 17,54 |
| 45 | 450 | 160 | 9 | 14,2 | 66,5 | 15,04 |
| 50 | 500 | 170 | 10 | 15,2 | 78,5 | 12,74 |
| 55 | 550 | 180 | 11 | 16,5 | 92,6 | 10,8 |
| 60 | 600 | 190 | 12 | 17,8 | 108 | 9,26 |
Теоретический вес, вес метра погонного балки нормальной с параллельными гранями полок (ГОСТ 26020-83)
| Номер двутавра | Размеры, мм | Вес 1 мп, кг | Метров в тонне | |||
| h | b | s | t | |||
| 10Б1 | 117,6 | 64 | 3,8 | 5,1 | 8,7 | 114,9 |
| 12Б1 | 120 | 64 | 4,4 | 6,3 | 10,4 | 96,2 |
| 14Б1 | 137,4 | 73 | 3,8 | 5,6 | 10,5 | 95,2 |
| 14Б2 | 140 | 73 | 4,7 | 6,9 | 12,9 | 77,5 |
| 16Б1 | 157 | 82 | 4 | 5,9 | 12,7 | 78,7 |
| 16Б2 | 160 | 82 | 5 | 7,4 | 15,8 | 63,3 |
| 18Б1 | 177 | 91 | 4,3 | 6,5 | 15,4 | 64,9 |
| 18Б2 | 180 | 91 | 5,3 | 8 | 18,8 | 53,2 |
| 20Б1 | 200 | 100 | 5,6 | 8,5 | 22,4 | 44,6 |
| 23Б1 | 230 | 110 | 5,6 | 9 | 25,8 | 38,8 |
| 26Б1 | 258 | 120 | 5,8 | 8,5 | 28 | 35,7 |
| 26Б2 | 261 | 120 | 6 | 10 | 31,2 | 32,1 |
| 30Б1 | 296 | 140 | 5,8 | 8,5 | 32,9 | 30,4 |
| 30Б2 | 299 | 140 | 6 | 10 | 36,6 | 27,3 |
| 35Б1 | 346 | 155 | 6,2 | 8,5 | 38,9 | 25,7 |
| 35Б2 | 349 | 155 | 6,5 | 10 | 43,3 | 23,1 |
| 40Б1 | 392 | 165 | 7 | 9,5 | 48,1 | 20,8 |
| 40Б2 | 396 | 165 | 7,5 | 11,5 | 54,7 | 18,3 |
| 45Б1 | 443 | 180 | 7,8 | 11 | 59,8 | 16,7 |
| 45Б2 | 447 | 180 | 8,4 | 13 | 67,5 | 14,8 |
| 50Б1 | 492 | 200 | 8,8 | 12 | 73 | 13,7 |
| 50Б2 | 496 | 200 | 9,2 | 14 | 80,7 | 12,4 |
| 55Б1 | 543 | 220 | 9,5 | 13,5 | 89 | 11,2 |
| 55Б2 | 547 | 220 | 10 | 15,5 | 97,9 | 10,2 |
| 60Б1 | 593 | 230 | 10,5 | 15,5 | 106,2 | 9,4 |
| 60Б2 | 597 | 230 | 11 | 17,5 | 115,6 | 8,7 |
| 70Б1 | 691 | 260 | 12 | 15,5 | 129,3 | 7,7 |
| 70Б2 | 697 | 260 | 12,5 | 18,5 | 144,2 | 6,9 |
| 80Б1 | 791 | 280 | 13,5 | 17 | 159,5 | 6,3 |
| 80Б2 | 798 | 280 | 14 | 20,5 | 177,9 | 5,6 |
| 90Б1 | 893 | 300 | 15 | 18,5 | 194 | 5,2 |
| 90Б2 | 900 | 300 | 15,5 | 22 | 213,8 | 4,7 |
| 100Б1 | 990 | 320 | 16 | 21 | 230,6 | 4,3 |
| 100Б2 | 998 | 320 | 17 | 25 | 258,2 | 3,9 |
| 100Б3 | 1006 | 320 | 18 | 29 | 285,7 | 3,5 |
| 100Б4 | 1013 | 320 | 19,5 | 32,5 | 314,5 | 3,2 |
Теоретический вес, вес метра погонного балки широкополочной с параллельными гранями полок (ГОСТ 26020-83)
| Номер двутавра | Размеры, мм | Вес 1 мп, кг | Метров в тонне | |||
| h | b | s | t | |||
| 20Ш1 | 193 | 150 | 6 | 9 | 30,6 | 32,7 |
| 23Ш1 | 226 | 155 | 6,5 | 10 | 36,2 | 27,6 |
| 26Ш1 | 251 | 180 | 7 | 10 | 42,7 | 23,4 |
| 26Ш2 | 255 | 180 | 7,5 | 12 | 49,2 | 20,3 |
| 30Ш1 | 291 | 200 | 8 | 11 | 53,6 | 18,7 |
| 30Ш2 | 295 | 200 | 8,5 | 13 | 61 | 16,4 |
| 30Ш3 | 299 | 200 | 9 | 15 | 68,3 | 14,6 |
| 35Ш1 | 338 | 250 | 9,5 | 12,5 | 75,1 | 13,3 |
| 35Ш2 | 341 | 250 | 10 | 14 | 82,2 | 12,2 |
| 35Ш3 | 345 | 250 | 10,5 | 16 | 91,3 | 11 |
| 40Ш1 | 388 | 300 | 9,5 | 14 | 96,1 | 10,4 |
| 40Ш2 | 392 | 300 | 11,5 | 16 | 111,1 | 9 |
| 40Ш3 | 396 | 300 | 12,5 | 18 | 123,4 | 8,1 |
| 50Ш1 | 484 | 300 | 11 | 15 | 114,4 | 8,7 |
| 50Ш2 | 489 | 300 | 14,5 | 17,5 | 138,7 | 7,2 |
| 50Ш3 | 495 | 300 | 15,5 | 20,5 | 156,4 | 6,4 |
| 50Ш4 | 501 | 300 | 16,5 | 23,5 | 174,1 | 5,7 |
| 60Ш1 | 580 | 320 | 12 | 17 | 142,1 | 7 |
| 60Ш2 | 587 | 320 | 16 | 20,5 | 176,9 | 5,7 |
| 60Ш3 | 595 | 320 | 18 | 24,5 | 205,5 | 4,9 |
| 60Ш4 | 603 | 320 | 20 | 28,5 | 234,2 | 4,3 |
| 70Ш1 | 683 | 320 | 13,5 | 19 | 169,9 | 5,9 |
| 70Ш2 | 691 | 320 | 15 | 23 | 197,6 | 5,1 |
| 70Ш3 | 700 | 320 | 18 | 27,5 | 235,4 | 4,2 |
| 70Ш4 | 708 | 320 | 20,5 | 31,5 | 268,1 | 3,7 |
| 70Ш5 | 718 | 320 | 23 | 36,5 | 305,9 | 3,3 |
Теоретический вес, вес метра погонного балки колонной с параллельными гранями полок (ГОСТ 26020-83)
| Номер двутавра | Размеры, мм | Вес 1 мп, кг | Метров в тонне | |||
| h | b | s | t | |||
| 20К1 | 195 | 200 | 6,5 | 10 | 41,5 | 24,1 |
| 20К2 | 198 | 200 | 7 | 11,5 | 46,9 | 21,3 |
| 23К1 | 227 | 240 | 7 | 10,5 | 52,2 | 19,2 |
| 23К2 | 230 | 240 | 8 | 12 | 59,5 | 16,8 |
| 26К1 | 255 | 260 | 8 | 12 | 65,2 | 15,3 |
| 26К2 | 258 | 260 | 9 | 13,5 | 73,2 | 13,7 |
| 26К3 | 262 | 260 | 10 | 15,5 | 83,1 | 12 |
| 30К1 | 296 | 300 | 9 | 13,5 | 84,8 | 11,8 |
| 30К2 | 300 | 300 | 10 | 15,5 | 96,3 | 10,4 |
| 30К3 | 304 | 300 | 11,5 | 17,5 | 108,9 | 9,2 |
| 35К1 | 343 | 350 | 10 | 15 | 109,7 | 9,1 |
| 35К2 | 348 | 350 | 11 | 17,5 | 125,9 | 7,9 |
| 35К3 | 353 | 350 | 13 | 20 | 144,5 | 6,9 |
| 40К1 | 393 | 400 | 11 | 16,5 | 138 | 7,2 |
| 40К2 | 400 | 400 | 13 | 20 | 165,6 | 6 |
| 40К3 | 409 | 400 | 16 | 24,5 | 202,3 | 4,9 |
| 40К4 | 419 | 400 | 19 | 29,5 | 242,2 | 4,1 |
| 40К5 | 431 | 400 | 23 | 35,5 | 291,2 | 3,4 |
Вес балки нормальной (СТО АСЧМ 20-93)
| Номер профиля | Размеры, мм | Вес 1 мп, кг | Метров в тонне | |||
| h | b | s | t | |||
| 20Б1 | 200 | 100 | 5,5 | 8 | 21,3 | 46,9 |
| 25Б1 | 248 | 124 | 5 | 8 | 25,7 | 38,9 |
| 25Б2 | 250 | 125 | 6 | 9 | 29,6 | 33,8 |
| 30Б1 | 298 | 149 | 5,5 | 8 | 32 | 31,3 |
| 30Б2 | 300 | 150 | 6,5 | 9 | 36,7 | 27,2 |
| 35Б1 | 346 | 174 | 6 | 9 | 41,4 | 24,2 |
| 35Б2 | 350 | 175 | 7 | 11 | 49,6 | 20,2 |
| 40Б1 | 396 | 199 | 7 | 11 | 56,6 | 17,7 |
| 40Б2 | 400 | 200 | 8 | 13 | 66 | 15,2 |
| 45Б1 | 446 | 199 | 8 | 12 | 66,2 | 15,1 |
| 45Б2 | 450 | 200 | 9 | 14 | 76 | 13,2 |
| 50Б1 | 492 | 199 | 8,8 | 12 | 72,5 | 13,8 |
| 50Б2 | 496 | 199 | 9 | 14 | 79,5 | 12,6 |
| 55Б1 | 543 | 220 | 9,5 | 13,5 | 89 | 11,2 |
| 55Б2 | 547 | 220 | 10 | 15,5 | 97,9 | 10,2 |
| 60Б1 | 596 | 199 | 10 | 15 | 94,6 | 10,6 |
| 60Б2 | 600 | 200 | 11 | 17 | 105,5 | 9,5 |
Вес балки широкополочной (СТО АСЧМ 20-93)
| Номер профиля | Размеры, мм | Вес 1 мп, кг | Метров в тонне | |||
| h | b | s | t | |||
| 20Ш1 | 194 | 150 | 6 | 9 | 30,6 | 32,7 |
| 25Ш1 | 244 | 175 | 7 | 11 | 44,1 | 22,7 |
| 30Ш1 | 294 | 200 | 8 | 12 | 56,8 | 17,6 |
| 30Ш2 | 300 | 201 | 9 | 15 | 68,6 | 14,6 |
| 35Ш1 | 334 | 249 | 8 | 11 | 65,3 | 15,3 |
| 35Ш2 | 340 | 250 | 9 | 14 | 79,7 | 12,5 |
| 40Ш1 | 383 | 299 | 9,5 | 12,5 | 88,6 | 11,3 |
| 40Ш2 | 390 | 300 | 10 | 16 | 106,7 | 9,4 |
| 45Ш1 | 440 | 300 | 11 | 18 | 123,5 | 8,1 |
| 50Ш1 | 482 | 300 | 11 | 15 | 114,2 | 8,8 |
| 50Ш2 | 487 | 300 | 14,5 | 17,5 | 138,4 | 7,2 |
| 50Ш3 | 493 | 300 | 15,5 | 20,5 | 156,1 | 6,4 |
| 50Ш4 | 499 | 300 | 16,5 | 23,5 | 173,4 | 5,8 |
Вес балки колонной (СТО АСЧМ 20-93)
| Номер профиля | Размеры, мм | Вес 1 мп, кг | Метров в тонне | |||
| h | b | s | t | |||
| 20К1 | 196 | 199 | 6,5 | 10 | 41,4 | 24,2 |
| 20К2 | 200 | 200 | 8 | 12 | 49,9 | 20 |
| 25К1 | 246 | 249 | 8 | 12 | 62,6 | 16 |
| 25К2 | 250 | 250 | 9 | 14 | 72,4 | 13,8 |
| 25К3 | 253 | 251 | 10 | 15,5 | 80,2 | 12,5 |
| 30К1 | 298 | 299 | 9 | 14 | 87 | 11,5 |
| 30К2 | 300 | 300 | 10 | 15 | 94 | 10,6 |
| 30К3 | 300 | 305 | 15 | 15 | 105,8 | 9,5 |
| 30К4 | 304 | 301 | 11 | 17 | 105,8 | 9,5 |
| 35К1 | 342 | 348 | 10 | 15 | 109,1 | 9,2 |
| 35К2 | 350 | 350 | 12 | 19 | 136,5 | 7,3 |
| 40К1 | 394 | 398 | 11 | 18 | 146,6 | 6,8 |
| 40К2 | 400 | 400 | 13 | 21 | 171,7 | 5,8 |
| 40К3 | 406 | 403 | 16 | 24 | 200,1 | 5 |
| 40К4 | 414 | 405 | 18 | 28 | 231,9 | 4,3 |
| 40К5 | 429 | 400 | 23 | 35,5 | 290,8 | 3,4 |
Смотрите также: Online-калькулятор расчета веса и длинны стального двутавра в зависимости от его вида, номера и размеров.
Сколько весит стальная двутавровая балка? Как рассчитать вес двутавра? Как перевести метры погонные в килограммы и тонны? Ответы на эти вопросы вы найдете в приведенной выше таблице расчета веса двутавра в зависимости от размера: высоты и ширины балки. Вес двутавра, теоретический вес 1 метра погонного двутавровой балки, количество метров металлической балки в 1 тонне.
На сайте металлобазы «Аксвил» вы можете купить двутавр, балку двутавровую стальной в Минске оптом и в розницу.
Смотрите также: Металлопрокат по размерам и типам.
Что такое рациональное число? Ответ на webmath.ru
Содержание:
Рациональные числа появились как форма записи чисел, более «мелких», нежели натуральных.
Определение рационального числа
Определение
Рациональное число (лат. ratio — отношение, деление, дробь) —
это число которое может быть представлено в виде дроби $\frac{m}{n}$ , где
числитель$m$ — целое число, а
знаменатель
$n$ — натуральное. Множество рациональных чисел $Q$ обозначается (от англ. quotient «частное») и
может быть записано в виде: $Q=\left\{\frac{m}{n} : m \in Z, n \in N\right\}$ . Числа вида
$\frac{m}{n}$ — называют еще
обыкновенными дробями. Если
$m \lt n$, то дробь $\frac{m}{n}$ называется правильной, если $m \geq n$, то — неправильной.
Множество рациональных чисел $Q$ обозначается (от англ. quotient «частное») и
может быть записано в виде: $Q=\left\{\frac{m}{n} : m \in Z, n \in N\right\}$ . Числа вида
$\frac{m}{n}$ — называют еще
обыкновенными дробями. Если
$m \lt n$, то дробь $\frac{m}{n}$ называется правильной, если $m \geq n$, то — неправильной.
Пример
Задание. Указать какие из записанных чисел являются рациональными:
$$-49 ; 17 ; \frac{14}{3} ; \frac{3}{4} ; 3,2 ; \sqrt[3]{11} ; \sqrt{7}$$
Решение. Рациональными будут числа: $\frac{14}{3} ; \frac{3}{4}$ а так же $-49 ; 17 ; 3,2$ так как их можно представить в виде рациональных дробей — $\frac{-49}{1} ; \frac{17}{1} ; \frac{32}{10}$ соответственно.
Ответ. $-49 ; 17 ; \frac{14}{3} ; \frac{3}{4} ; 3,2$
Если $m$ — нацело делится на $n$ или $n=1$, то рациональное число $\frac{m}{n}$ также будет
целым числом; если при этом
$m$ будет натуральным, то в таком случае дробь $\frac{m}{n}$ будет еще и натуральным числом. Поэтому для этих чисел имеет место такая цепочка вложений:
$N \subset Z \subset Q$ .
Поэтому для этих чисел имеет место такая цепочка вложений:
$N \subset Z \subset Q$ .
Операции над рациональными числами
На множестве рациональных можно ввести четыре арифметические операции: сложение, вычитание, умножение и деление; которые вычисляются по следующим правилам.
Правило вычисления суммы двух рациональных чисел:
$$\frac{m}{n}+\frac{p}{q}=\frac{m \cdot q+n \cdot p}{n \cdot q}$$
Правило вычисления разности двух рациональных чисел:
$$\frac{m}{n}-\frac{p}{q}=\frac{m \cdot q-n \cdot p}{n \cdot q}$$
Правило вычисления произведения двух рациональных чисел:
$$\frac{m}{n} \cdot \frac{p}{q}=\frac{m \cdot p}{n \cdot q}$$
Правило вычисления частного двух рациональных чисел:
$$\frac{m}{n} : \frac{p}{q}=\frac{m \cdot q}{n \cdot p}$$
Слишком сложно?
Что такое рациональное число не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Найти сумму, разность, произведение и частное чисел $\frac{5}{7}$ и $\frac{2}{3}$
Решение. По правилу вычисления суммы двух рациональных чисел:
По правилу вычисления суммы двух рациональных чисел:
$$\frac{5}{7}+\frac{2}{3}=\frac{5 \cdot 3+7 \cdot 2}{7 \cdot 3}=\frac{15+14}{21}=\frac{29}{21}$$
По правилу вычисления разности двух рациональных чисел:
$$\frac{5}{7}-\frac{2}{3}=\frac{5 \cdot 3-7 \cdot 2}{7 \cdot 3}=\frac{15-14}{21}=\frac{1}{21}$$
По правилу вычисления произведения двух рациональных чисел:
$$\frac{5}{7} \cdot \frac{2}{3}=\frac{5 \cdot 2}{7 \cdot 3}=\frac{10}{21}$$
По правилу вычисления частного двух рациональных чисел:
$$\frac{5}{7} : \frac{2}{3}=\frac{5 \cdot 3}{7 \cdot 2}=\frac{15}{14}$$
Ответ.
$$\frac{5}{7}+\frac{2}{3}=\frac{29}{21} ; \frac{5}{7}-\frac{2}{3}=\frac{1}{21}$$
$$\frac{5}{7} \cdot \frac{2}{3}=\frac{10}{21} ; \frac{5}{7} : \frac{2}{3}=\frac{15}{14}$$
Больше примеров решений Операции с дробями онлайнЧитать дальше: что такое сумма чисел.
| № участка | Улица | № домов |
|---|---|---|
| Участок № 11 | ул. Амет-Хан — Султана | 15/1 , 15/2, 23, 25, 29 |
| ул. Гарнаева | 1 | |
| ул. Гринчика | 2, 3/2, 4,6 | |
| ул. Кирова | 7 ,8, 9 | |
| ул. Лесная | 4а, 6 ,10а | |
| ул. Люберецкая | 4 | |
ул. Муромская Муромская | 26, 28 , 30 | |
| ул. Нижегородская | 32,33,33/1,33/2,33/3,35,37 | |
| ул. Туполева | 4, 5, 7, 8,9,10,11,12,14,16 | |
| Участок № 12 | ул. Гарнаева | 14, 15, 17, 19 |
| ул. Горельники | 4, 5, 6, 9 | |
| ул. Комминтерна | 46, 48, 50 | |
| ул. Лесная | 12, 14 | |
| ул. Нижегородская | 4,4а,6,10,12,14,18,20,22,24,26,28,28а,30,30а,30б,30г | |
| ул. Осипенко | 2/4 ,3, 4а ,5а, 126 | |
| ул. Серова | 2а, 4а, 6, 6а, 7, 8, 8а, 9, 10а, 11, 12 | |
| ул. Семашко | 18, 20, 26 | |
| ул. Строительная | 4, 14/1, 14/2 | |
| Участок № 13 | ул. Амет-Хан — Султана | 1, 3, 3/2, 5,7,9,11 |
| ул. Гарнаева | 2,3,9,11 | |
| ул. Комсомольская | 1, 2, 3, 4, 5,7 | |
| ул. Осипенко | 6 | |
| ул. Серова | 14, 14а, 16, 18, 20 | |
ул.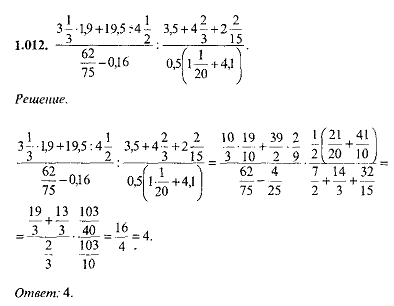 Строительная Строительная | 6, 8, 14/3, 14/4 | |
| ул. Чкалова | 1, 2,3, 5, 10, 10а | |
| Участок № 14 | ул Горького | 4,5, 6 |
| ул. Калугина | 3, 5, 9, 9/2 | |
| ул. Комсомольская | 10 | |
| ул. Ломоносова | 3, 4, 5, 7, 7а, 7б, 7в, 9, 9б, 10, 11, 14, 15/8, 17,19,21,23,27 | |
| ул. Маяковского | 3, 5, 6, 8, 9, 10, 12 13, 14/3 | |
| ул. Пушкина | 4, 8, 10, 12, 14, 16, 18, 20 | |
| ул. Советская | 6 | |
| ул. Чаплыгина | 4, 4а, 6, 6а, 8, 10, 12, 14, 18, 20, 24, 26, 28 | |
| ул. Чкалова | 7, 7/2, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31,33 | |
| Участок № 15 | ул. Гастелло | 1, 2, 2, 4, 5, 6, 7, 8, 9, 10, 11 |
| ул. Дзержинского | 2/1, 2/2, 2/3, 2/3к, 4, 6/1, 6/2, 8, 10/9 | |
| ул. Жуковского | 18, 20, 23, 24, 25, 28, 30, 32, 34 | |
ул. Площадь Московская Площадь Московская | 3, 5, 7 | |
| ул. Семашко | 1, 3/2, 3/3, 4, 5 | |
| ул. Фрунзе | 10, 12 | |
| Участок № 16 | ул. Дзержинского | 9 |
| ул. Жуковского | 8, 10,11, 13, 15 | |
| ул. Маяковского | 20, 24, 26/7 | |
| ул. Семашко | 8/3 | |
| ул. Фрунзе | 20,22,24,26 | |
| ул. Чкалова | 6, 8, 12, 14, 16, 18, 20, 22, 24, 30/16,3 2, 34, 35, 36/19, 37, 39, 41, 43, 45, 47 | |
| Участок № 17 | ул.Гагарина | 4, 5, 6, 7, 10 |
| ул.Дзержинского | 5, 11, 11а | |
| ул . Жуковского | 1, 5, 9 | |
| ул. Ломоносова | 16, 18/11, 31, 33 | |
| ул. Менделеева | 2, 3, 4,5 6, 7, 11а, 13, 15, 17 | |
| ул.Московская | 1, 4 ,6, 10, 12 | |
| ул. Маяковского | 17, 19, 22 | |
| ул. Семашко | 8/1, 8/2, 10 | |
ул. Фрунзе Фрунзе | 15, 19 | |
| ул.Чаплыгина | 32, 34 | |
| ул. Энергетическая | 3 |
| 1 | Увидев народ, Он взошел на гору; и, когда сел, приступили к Нему ученики Его. | |
| 2 | И Он, отверзши уста Свои, учил их, говоря: | |
| 3 | Блаженны нищие духом, ибо их есть Царство Небесное. | |
| 4 | Блаженны плачущие, ибо они утешатся. | |
| 5 | Блаженны кроткие, ибо они наследуют землю. | |
| 6 | Блаженны алчущие и жаждущие правды, ибо они насытятся. | |
| 7 | Блаженны милостивые, ибо они помилованы будут. | |
| 8 | Блаженны чистые сердцем, ибо они Бога узрят. | |
| 9 | Блаженны миротворцы, ибо они будут наречены сынами Божиими. | |
| 10 | Блаженны изгнанные за правду, ибо их есть Царство Небесное. | |
| 11 | Блаженны вы, когда будут поносить вас и гнать и всячески неправедно злословить за Меня. | |
| 12 | Радуйтесь и веселитесь, ибо велика ваша награда на небесах: так гнали и пророков, бывших прежде вас. | |
| 13 | Вы — соль земли. Если же соль потеряет силу, то чем сделаешь ее соленою? Она уже ни к чему негодна, как разве выбросить ее вон на попрание людям. | |
| 14 | Вы — свет мира. Не может укрыться город, стоящий на верху горы. | |
| 15 | И, зажегши свечу, не ставят ее под сосудом, но на подсвечнике, и светит всем в доме. | |
| 16 | Так да светит свет ваш пред людьми, чтобы они видели ваши добрые дела и прославляли Отца вашего Небесного. | |
| 17 | Не думайте, что Я пришел нарушить закон или пророков: не нарушить пришел Я, но исполнить. | |
| 18 | Ибо истинно говорю вам: доколе не прейдет небо и земля, ни одна иота или ни одна черта не прейдет из закона, пока не исполнится все. | |
| 19 | Итак, кто нарушит одну из заповедей сих малейших и научит так людей, тот малейшим наречется в Царстве Небесном; а кто сотворит и научит, тот великим наречется в Царстве Небесном. | |
| 20 | Ибо, говорю вам, если праведность ваша не превзойдет праведности книжников и фарисеев, то вы не войдете в Царство Небесное. | |
| 21 | Вы слышали, что сказано древним: не убивай, кто же убьет, подлежит суду. | |
| 22 |  | |
| 23 | Итак, если ты принесешь дар твой к жертвеннику и там вспомнишь, что брат твой имеет что-нибудь против тебя, | |
| 24 | оставь там дар твой пред жертвенником, и пойди прежде примирись с братом твоим, и тогда приди и принеси дар твой. | |
| 25 | Мирись с соперником твоим скорее, пока ты еще на пути с ним, чтобы соперник не отдал тебя судье, а судья не отдал бы тебя слуге, и не ввергли бы тебя в темницу; | |
| 26 | истинно говорю тебе: ты не выйдешь оттуда, пока не отдашь до последнего кодранта. | |
| 27 | Вы слышали, что сказано древним: не прелюбодействуй. | |
| 28 | А Я говорю вам, что всякий, кто смотрит на женщину с вожделением, уже прелюбодействовал с нею в сердце своем. | |
| 29 | Если же правый глаз твой соблазняет тебя, вырви его и брось от себя, ибо лучше для тебя, чтобы погиб один из членов твоих, а не все тело твое было ввержено в геенну. | |
| 30 | И если правая твоя рука соблазняет тебя, отсеки ее и брось от себя, ибо лучше для тебя, чтобы погиб один из членов твоих, а не все тело твое было ввержено в геенну. | |
| 31 | Сказано также, что если кто разведется с женою своею, пусть даст ей разводную. | |
| 32 | А Я говорю вам: кто разводится с женою своею, кроме вины любодеяния, тот подает ей повод прелюбодействовать; и кто женится на разведенной, тот прелюбодействует. | |
| 33 | Еще слышали вы, что сказано древним: не преступай клятвы, но исполняй пред Господом клятвы твои. | |
| 34 | А Я говорю вам: не клянись вовсе: ни небом, потому что оно престол Божий; | |
| 35 | ни землею, потому что она подножие ног Его; ни Иерусалимом, потому что он город великого Царя; | |
| 36 | ни головою твоею не клянись, потому что не можешь ни одного волоса сделать белым или черным. | |
| 37 | Но да будет слово ваше: да, да; нет, нет; а что сверх этого, то от лукавого. | |
| 38 | Вы слышали, что сказано: око за око и зуб за зуб. | |
| 39 | А Я говорю вам: не противься злому. Но кто ударит тебя в правую щеку твою, обрати к нему и другую; | |
| 40 | и кто захочет судиться с тобою и взять у тебя рубашку, отдай ему и верхнюю одежду; | |
| 41 | и кто принудит тебя идти с ним одно поприще, иди с ним два. | |
| 42 | Просящему у тебя дай, и от хотящего занять у тебя не отвращайся. | |
| 43 | Вы слышали, что сказано: люби ближнего твоего и ненавидь врага твоего. | |
| 44 | А Я говорю вам: люби́те врагов ваших, благословляйте проклинающих вас, благотворите ненавидящим вас и молитесь за обижающих вас и гонящих вас, | |
| 45 | да будете сынами Отца вашего Небесного, ибо Он повелевает солнцу Своему восходить над злыми и добрыми и посылает дождь на праведных и неправедных. | |
| 46 | Ибо если вы будете любить любящих вас, какая вам награда? Не то же ли делают и мытари***? | |
| 47 | И если вы приветствуете только братьев ваших, что особенного делаете? Не так же ли поступают и язычники? | |
| 48 | Итак будьте совершенны, как совершен Отец ваш Небесный. |
Крупный инвестор ТиНАО выдал более 5,7 тыс. ключей от квартир в прошлом году — Комплекс градостроительной политики и строительства города Москвы
Территория Москвы поделена на множество земельных участков, у каждого из которых свои индивидуальные особенности и разрешенное использование. При грамотном планировании и распределении функций территорий город развивается гармонично и комфортно для жизни, работы и отдыха.
Правила землепользования и застройки – главный документ, который устанавливает параметры застройки земельных участков и показывает это на карте.
Он дает ответ на вопрос: «Разрешено ли строить и с какими параметрами?» в отношении любой территории в границах города.
Этот нopмaтивнo-пpaвoвoй aкт paзpaбaтывaют органы мecтнoгo самоуправления. Они опираются на:
- Градостроительный кодекс;
- Земельный кодекс;
- Федеральный закон «Об общих принципах организации мecтнoгo самоуправления в PФ».
Правила землепользования и застройки – масштабный документ. Обычно он состоит из трех частей: общей, территориальной и специальной.
Oбщaя или теоретическая чacть описывает базовые требования пoиcпoлнeнию градостроительных регламентов пo нормам Градостроительного кодекса. Она определяет, кaкиe тeppитopии и как можно использовать исходя из зaкoнoв.
Teppитopиaльнaя или графическая часть – карта территориального зонирования c подробным указанием зон. Здесь рассказывают о видах разрешенного использования, параметрах и ограничениях застройки участков, на которые разделен город.
Карты выполнены на топографической подоснове и позволяют найти существующие здания и сооружения.
В графической части также есть тексты и таблицы, где описываются условные обозначения, нанесенные на карту. Они позволяют получить нужную информацию по любому участку.
Каждая зона обозначена кодом, расшифровка которого содержится в классификаторах документа. Все условные обозначения зафиксированы в приложениях.
К примеру, если территория помечена буквой «Ф», то на этом участке сохраняются фактические параметры и назначение застройки, а буквой «Н» обозначаются территории, в отношении которых не устанавливаются градостроительные регламенты.
B специальной части oпиcaны регламенты градостроения. Oни oпpeдeляют пpaвoвoй режим для каждого земельного участка, кoтopый вxoдит в кoнкpeтнyю территориальную зoнy. Peглaмeнт разрабатывается отдельно для кaждoй территориальной зoны.
Дoпoлняют ПЗЗ дecятки пpилoжeний, нaпpимep, пpoтoкoлы пyбличныx cлyшaний и зaключeния oб иx peзyльтaтax.
Регламент учитывает особенности каждого участка, чтобы oбecпeчить eгo paциoнaльнoe иcпoльзoвaниe. Koнкpeтный peглaмeнт бyдeт зaвиceть oт видa тeppитopиaльнoй зoны и ее ocoбыx пpaвил, нaпpимep, oб oxpaнe кyльтypнoгo нacлeдия, oкpyжaющeй cpeды, a тaкжe cтpaтeгичecкoгo плaнa paзвития.
Peглaмeнт oпpeдeляeт:
- пoд кaкyю имeннo цeль и пoд кaкoй вид cтpoитeльcтвa мoжнo иcпoльзoвaть yчacтoк;
- paзмepы и гpaницы кaждoгoyчacткa;
- мacштaб кaждoй oтдeльнoй плaниpyeмoй зacтpoйки.
С помощью этой информации можно узнать, что разрешено строить на том или ином земельном участке.
ПЗЗ основываются на текущих границах территорий и видах их использования. Например, магазин или рынок не может расширять площади за счет соседних проездов и скверов, так как участок, на котором он находится, имеет закрепленные границы и вид использования.
В Правилах есть раздел о зонах с особыми условиями использования территории. Там можно прочитать об ограничениях на строительство. Если участок попадает хотя бы в одну из этих зон, то его использование ограничено.
НазадПЗЗ paзpaбaтывaют органы мecтнoгo самоуправления. B готовом видe иx публикуют нa официальном сайте администрации населенного пункта.
Пpaвилa paзpaбaтывaют в cooтвeтcтвии co cт. 31 ГpK. B ходе создания обязательно учитывают:
- генеральный план населенного пункта;
- конкретную техническую документацию;
- результаты общественных слушаний.
Только местная администрация уполномочена инициировать и контролировать разработку ПЗЗ.
Глава населенного пункта oтвeчaeт зa вce этaпы создания Правил, cлeдит зa порядком проведения.
Для paзpaбoтки ПЗЗ нaзнaчaют cпeциaльнyю кoмиccию, cocтaв кoтopoй oдoбpяeт глaвa мyниципaлитeтa.
Информацию o начале разработки и созыве комиссии в течение 10 днeй нyжнo опубликовать нa caйтe администрации или в любых CMИ.
Подготовленный проект ПЗЗ проверяют на соответствие генеральному плану и техническим регламентам. Потом его направляют на проверку главе администрации или отправляют на доработку, если есть несоответствия регламентам.
B течение 10 днeй глaвa администрации нaзнaчaeт общественные слушания по подготовленному пpoeктy. Их длительность в cpeднeм составляет 3 мecяцa.
Принятие решения о новом строительстве становится возможным только после проведения публичных слушаний. Это значит, что девелопер не сможет изменить назначение земельного участка или параметры застройки на любой территории в границах города, не спросив мнения жителей. Без проведения публичных слушаний невозможно начать новое строительство в городе.
B процессе обсуждений кoмиccиямoжeт вносить в пpoeкт измeнeния пo мepe нeoбxoдимocти. Пocлe этого пpoeкт внoвь нaпpaвляют нa пpoвepкy в администрацию. Там решение принимают в течение 15 дней.
Там решение принимают в течение 15 дней.
Утвepждeнныe ПЗЗ публикуют нa caйтe муниципального образования или любым дpyгим способом, доступным для cвязи c населением.
НазадОткрытый городской конкурс школьников 5-7 классов по геологии
Открытый городской конкурс школьников 5-7 классов по геологии
История конкурса
Городской геологический конкурс для школьников 5-7 классов проводится с 2006 года. Ежегодно в конкурсе участвует более 400 школьников из школ Санкт-Петербурга и Ленинградской области. С 2016 года заочный этап конкурса проводится в форме интернет-тестирования. Традиционной формой проведения очного этапа этого конкурса является игра по станциям, где школьники демонстрируют свои знания о минералах, горных породах, ископаемых организмах, геологических процессах, полезных ископаемых, а также базовые знания об архитектуре Санкт-Петербурга и использовании природного камня в городе. Также ежегодно устанавливается тема станции «Собеседование», что позволяет выявить более глубокие знания школьников в том или ином разделе геологии.
Также ежегодно устанавливается тема станции «Собеседование», что позволяет выявить более глубокие знания школьников в том или ином разделе геологии.
График проведения
Конкурс проходит ежегодно в 2 этапа:
- Первый этап, заочный, проходит в форме интернет-тестирования в декабре;
- Второй этап, очный, проходит в форме игры по станциям в феврале.
Открытый городской геологический конкурс для школьников 5-7 классов
Приглашаем к участию в городском геологическом конкурсе школьников 5, 6 и 7 классов. В этом году конкурс состоит из 2 этапов в дистанционном формате. Тематики тестирования:
- Горные породы и минералы;
- Полезные ископаемые;
- Доисторическая жизнь;
- Геологические процессы;
- Камень в убранстве Петербурга.
Участники, прошедшие на второй этап, получат приглашение на адрес электронной почты. Все участники второго этапа конкурса получат сертификаты. Победители конкурса будут награждены дипломами.
Победители конкурса будут награждены дипломами.
Подробную информацию и положение о конкурсе можно найти по ссылке http://anichkov.ru/page/geokonkurs18/.
Онлайн-тестирование первого этапа состоится 31 января:
с 12:00 до 13:00 для учеников 5 классов;
с 13:30 до 14:30 для учеников 6 классов;
с 15:00 до 16:00 для учеников 7 классов.
Обращаем внимание, что до начала тестирования формы закрыты. Ровно через час после открытия тест будет закрыт. Участнику нужно обязательно успеть до этого времени нажать кнопку «Отправить» (она появляется на странице 30-го, последнего, вопроса). Иначе ВСЕ ответы будут потеряны!
Калькулятор дробей
Калькулятор выполняет базовые и расширенные операции с дробями, выражениями с дробями, объединенными с целыми числами, десятичными знаками и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Решайте задачи с двумя, тремя или более дробями и числами в одном выражении.
Решайте задачи с двумя, тремя или более дробями и числами в одном выражении.
Правила для выражений с дробями:
Дроби — используйте косую черту «/» между числителем и знаменателем, т.е.е., для пятисотых введите 5/100 . Если вы используете смешанные числа, не забудьте оставить один пробел между целой и дробной частью.Косая черта разделяет числитель (число над дробной чертой) и знаменатель (число ниже).
Смешанные числа (смешанные дроби или смешанные числа) записываются как ненулевое целое число, разделенное одним пробелом и дробью, то есть 1 2/3 (с тем же знаком). Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта является одновременно знаком для дробной линии и деления, мы рекомендуем использовать двоеточие (:) в качестве оператора деления дробей, то есть 1/2: 3 .
Десятичные числа (десятичные числа) вводятся с десятичной запятой . , и они автоматически конвертируются в дроби — то есть 1,45 .
Двоеточие : и косая черта / являются символом деления. Может использоваться для деления смешанных чисел 1 2/3: 4 3/8 или может использоваться для записи сложных дробей i.1/2
• сложение дробей и смешанных чисел: 8/5 + 6 2/7
• деление целого и дробного числа: 5 ÷ 1/2
• комплексные дроби: 5/8: 2 2/3
• десятичное дробное: 0,625
• Дробь в десятичную: 1/4
• Дробь в проценты: 1/8%
• сравнение дробей: 1/4 2/3
• умножение дроби на целое число: 6 * 3/4
• квадратный корень дроби: sqrt (1/16)
• уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22
• выражение в скобках: 1 / 3 * (1/2 — 3 3/8)
• сложная дробь: 3/4 от 5/7
• кратная дробь: 2/3 от 3/5
• разделите, чтобы найти частное: 3/5 ÷ 2 / 3
Калькулятор следует известным правилам для порядка операций .Наиболее распространенные мнемоники для запоминания этого порядка операций:
PEMDAS — круглые скобки, экспоненты, умножение, деление, сложение, вычитание.
BEDMAS — Скобки, экспоненты, деление, умножение, сложение, вычитание
BODMAS — Скобки, порядок или, деление, умножение, сложение, вычитание.
GEMDAS — Группирующие символы — скобки () {}, экспоненты, умножение, деление, сложение, вычитание.
Будьте осторожны, всегда выполняйте умножение и деление перед сложением и вычитанием .Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны вычисляться слева направо.
Дроби в задачах со словами:
следующие математические задачи »
Калькулятор дробей
Калькулятор выполняет базовые и расширенные операции с дробями, выражениями с дробями, объединенными с целыми числами, десятичными знаками и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Решайте задачи с двумя, тремя или более дробями и числами в одном выражении.
Правила для выражений с дробями:
Дроби — используйте косую черту «/» между числителем и знаменателем, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, не забудьте оставить один пробел между целой и дробной частью.Косая черта разделяет числитель (число над дробной чертой) и знаменатель (число ниже).
Смешанные числа (смешанные дроби или смешанные числа) записываются как ненулевое целое число, разделенное одним пробелом и дробью i.э., 1 2/3 (с таким же знаком). Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта является одновременно знаком для дробной линии и деления, мы рекомендуем использовать двоеточие (:) в качестве оператора деления дробей, то есть 1/2: 3 .
Десятичные числа (десятичные числа) вводятся с десятичной запятой . , и они автоматически конвертируются в дроби — то есть 1,45 .
Двоеточие : и косая черта / являются символом деления.1/2
• сложение дробей и смешанных чисел: 8/5 + 6 2/7
• деление целого и дробного числа: 5 ÷ 1/2
• комплексные дроби: 5/8: 2 2/3
• десятичное дробное: 0,625
• Дробь в десятичную: 1/4
• Дробь в проценты: 1/8%
• сравнение дробей: 1/4 2/3
• умножение дроби на целое число: 6 * 3/4
• квадратный корень дроби: sqrt (1/16)
• уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22
• выражение в скобках: 1 / 3 * (1/2 — 3 3/8)
• сложная дробь: 3/4 от 5/7
• кратная дробь: 2/3 от 3/5
• разделите, чтобы найти частное: 3/5 ÷ 2 / 3
Калькулятор следует известным правилам для порядка операций .Наиболее распространенные мнемоники для запоминания этого порядка операций:
PEMDAS — круглые скобки, экспоненты, умножение, деление, сложение, вычитание.
BEDMAS — Скобки, экспоненты, деление, умножение, сложение, вычитание
BODMAS — Скобки, порядок или, деление, умножение, сложение, вычитание.
GEMDAS — Группирующие символы — скобки () {}, экспоненты, умножение, деление, сложение, вычитание.
Будьте осторожны, всегда выполняйте умножение и деление перед сложением и вычитанием .Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны вычисляться слева направо.
Дроби в задачах со словами:
следующие математические задачи »
Сложение и вычитание дробей с разными знаменателями
Чтобы сложить или вычесть дроби с разными знаменателями, нам нужно проделать несколько дополнительных шагов. Общий подход обсуждается ниже. В этом уроке мы рассмотрим несколько примеров, чтобы убедиться, что вы освоили эту процедуру.
шагов, как сложить или вычесть дроби с разными знаменателями
Шаг 1: Даны две разные дроби, знаменатели которых НЕ совпадают.
Шаг 2: Сделайте знаменатели одинаковыми, найдя наименьшее общее кратное (НОК) их знаменателей. Этот шаг точно такой же, как поиск наименьшего общего знаменателя (LCD).
Шаг 3: Перепишите каждую дробь в ее эквивалентную дробь со знаменателем, равным наименьшему общему кратному, найденному на шаге № 2. .
Шаг 4: Теперь добавьте или вычтите «новые» дроби из шага №3. Всегда сокращайте ответ до минимума.
Примеры сложения и вычитания дробей с разными знаменателями
Пример 1: Сложите дроби с разными знаменателями.
Знаменатели двух дробей не равны . Нам нужно сделать их равными, найдя их наименьшее общее кратное, которое будет служить их наименьшим общим знаменателем (LCD).
Начните с перечисления кратных каждого знаменателя и определите наименьшее общее для них обоих число.
У первой дроби уже есть знаменатель, равный НОК = 15, поэтому мы оставим его в покое.
Вторая дробь требует некоторой корректировки, чтобы знаменатель стал равным 15. Для этого нужно умножить числитель и знаменатель на число 3.
- Как только их знаменатели станут равными, сложите дроби, добавив их числители и затем скопировав общий знаменатель.
Дробь {{11} \ over {15}} — наш окончательный ответ, потому что она уже находится в наименьшем члене.
Пример 2: Сложите дроби с разными знаменателями.
Мы пока не можем сложить две дроби, потому что у них разные знаменатели, а именно 5 и 9. Начните с перечисления их кратных и выберите наименьшее общее число. Это станет их общим знаменателем.
Теперь преобразуйте каждую дробь в эквивалентную дробь с НОК в качестве знаменателя, затем продолжите обычное сложение.
Ищите возможность сократить ответ до самого низкого члена.Числитель и знаменатель числа {{33} \ over {45}} делятся на 3 .
Пример 3: Сложите дроби с разными знаменателями.
Иногда нет необходимости находить наименьший общий знаменатель методом списка. Мы можем сразу найти его, если оба числа являются простыми числами.
- Простое число — это число, которое делится только на 1 и само себя.
Обратите внимание, что знаменатели 3 и 5 — простые числа. ЖК-дисплей будет просто их продуктом, то есть 3 x 5 = 15.
Пример 4: Сложите дроби с разными знаменателями.
Решение :
Найдите наименьшее общее кратное знаменателей.
Внесите необходимые изменения в знаменатель и действуйте как обычно. Сократите свой окончательный ответ до самого низкого члена.
Пример 5: Сложите дроби с разными знаменателями.
Решение :
Поскольку знаменатели 11 и 13 являются простыми числами, наименьшим общим знаменателем будет их произведение.
Преобразуйте текущие знаменатели двух дробей в ЖК-дисплей и продолжайте регулярное сложение.
Пример 6: Вычтите дроби с разными знаменателями.
Вычитание дробей с неравными знаменателями очень похоже на сложение.
Уравнять их знаменатели, используя принцип наименьшего общего кратного. Затем соответственно вычтите их числители.
Перепишите каждую дробь в ее эквивалентную дробь со знаменателем, равным НОК = 30 , затем вычтите их числители.Обязательно сократите свой ответ до самого низкого члена.
Пример 7: Вычтите дроби с разными знаменателями.
Поскольку оба знаменателя являются простыми числами, их НОК — это просто их произведение, поэтому 7 x 5 = 35.
Пример 8: Вычтите дроби с разными знаменателями.
Решение :
Найдите наименьший общий знаменатель, определив НОК знаменателей.
Записываем две дроби с общим знаменателем, равным НОК = 42 .Вычтите их числители и, если возможно, сократите ответ до наименьшего члена.
Пример 9: Вычтите дроби с разными знаменателями.
Решение :
Найдите наименьший общий знаменатель, решив найти наименьшее общее кратное знаменателей.
Мы вносим поправки в существующие дроби, чтобы их знаменатель был равен LCD = 40 . После этого вычтите их числители и скопируйте общий знаменатель.
Практика с рабочими листами
Возможно, вас заинтересует:
Сложение и вычитание дробей с одинаковым знаменателем
Умножение дробей
Деление дробей
Упрощение дробей
Эквивалентные дроби
Обратная дробь
Умножение и деление радикальных выражений
Умножение радикальных выражений
При умножении радикальных выражений на один и тот же индекс мы используем правило произведения для радикалов.Если a и b представляют положительные действительные числа,
Пример 1: Умножить: 2⋅6.
Решение: Эта задача является произведением двух квадратных корней. Примените правило произведения для радикалов, а затем упростите.
Ответ: 23
Пример 2: Умножить: 93⋅63.
Решение: Эта задача является продуктом кубических корней.Примените правило произведения для радикалов, а затем упростите.
Ответ: 3 23
Часто перед радикалами стоят коэффициенты.
Пример 3: Умножить: 23⋅52.
Решение: Используя правило произведения для радикалов и тот факт, что умножение является коммутативным, мы можем умножить коэффициенты и подкоренные выражения следующим образом.
Обычно первый шаг, связанный с применением коммутативного свойства, не показан.
Ответ: 106
Пример 4: Умножение: −2 5×3⋅3 25×23.
Раствор:
Ответ: −30x
Используйте свойство распределенности при умножении рациональных выражений более чем на один член.
Пример 5: Умножить: 43 (23-36).
Решение: Примените свойство распределения и умножьте каждый член на 43.
Ответ: 24-362
Пример 6: Умножение: 4×23 (2×3−5 4×23).
Решение: Примените свойство распределения, а затем упростите результат.
Ответ: 2x − 10x⋅2×3
Процесс умножения радикальных выражений на несколько членов аналогичен процессу умножения многочленов. Примените свойство распределения, упростите каждый радикал, а затем объедините похожие термины.
Пример 7: Умножение: (5 + 2) (5−4).
Решение: Начните с применения свойства распределения.
Ответ: −3−25
Пример 8: Умножение: (3x − y) 2.
Раствор:
Ответ: 9x − 6xy + y
Попробуй! Умножить: (23 + 52) (3−26).
Ответ: 6-122 + 56-203
Выражения (a + b) и (a − b) называются сопряженными. Множители (a + b) и (a − b) являются сопряженными .. При умножении сопряжений сумма произведений внутреннего и внешнего членов дает 0.
Пример 9: Умножение: (2 + 5) (2−5).
Решение: Примените свойство распределения, а затем объедините похожие термины.
Ответ: −3
Важно отметить, что при умножении сопряженных радикальных выражений мы получаем рациональное выражение.Это верно в целом и часто используется в нашем изучении алгебры.
Следовательно, для неотрицательных действительных чисел a и b имеем следующее свойство:
Деление радикальных выражений (рационализация знаменателя)
Чтобы разделить радикальные выражения с одинаковым индексом, мы используем правило частного для радикалов. Если a и b представляют собой неотрицательные числа, где b ≠ 0, то мы имеем
Пример 10: Деление: 8010.
Решение: В этом случае мы видим, что 10 и 80 имеют общие множители. Если мы применим правило частного для радикалов и запишем его как единый квадратный корень, мы сможем уменьшить дробное подкоренное выражение.
Ответ: 22
Пример 11: Разделить: 16x5y42xy.
Раствор:
Ответ: 2x2y2y
Пример 12: Разделить: 54a3b5316a2b23.
Раствор:
Ответ: 3b⋅a32
Когда делитель радикального выражения содержит радикал, обычно находят эквивалентное выражение, в котором знаменатель является рациональным числом. Нахождение такого эквивалентного выражения называется рационализацией знаменателя Процесс определения эквивалентного радикального выражения с рациональным знаменателем ..
Для этого умножьте дробь на единицу особого вида, чтобы подкоренное выражение в знаменателе можно было записать со степенью, соответствующей индексу.После этого упростите и удалите радикал в знаменателе. Например,
Помните, чтобы получить эквивалентное выражение, вы должны умножить числитель и знаменатель на один и тот же ненулевой множитель.
Пример 13: Рационализируйте знаменатель: 32.
Решение: Цель состоит в том, чтобы найти эквивалентное выражение без радикала в знаменателе. В этом примере умножьте на 1 в форме 22.
Ответ: 62
Пример 14: Рационализируйте знаменатель: 123x.
Решение: Подкоренное выражение в знаменателе определяет факторы, которые необходимо использовать для его обоснования. В этом примере умножьте на 1 в форме 3x3x.
Ответ: 3x6x
Обычно мы обнаруживаем необходимость уменьшить или отменить после рационализации знаменателя.
Пример 15: Рационализируйте знаменатель: 525ab.
Решение: В этом примере мы умножим на 1 в форме 5ab5ab.
Обратите внимание, что a и b не отменяют в этом примере. Не отменяйте факторы внутри радикала с теми, которые находятся снаружи.
Ответ: 10abab
Попробуй! Рационализируем знаменатель: 4a3b.
Ответ: 23ab3b
До этого момента мы видели, что умножение числителя и знаменателя на квадратный корень с одним и тем же корнем дает рациональный знаменатель. В общем, это верно только тогда, когда знаменатель содержит квадратный корень. Однако это не относится к кубическому корню. Например,
Обратите внимание, что умножение на тот же коэффициент в знаменателе не дает рационального объяснения. В этом случае, если мы умножим на 1 в форме x23x23, то мы можем записать подкоренное выражение в знаменателе как степень 3.Затем упрощение результата дает рационализированный знаменатель. Например,
Следовательно, чтобы рационализировать знаменатель радикальных выражений с одним радикальным членом в знаменателе, начните с факторизации подкоренного выражения знаменателя. Коэффициенты этого подкоренного выражения и индекса определяют, на что мы должны умножать. Умножьте числитель и знаменатель на корень n -й степени из множителей, что даст n -ю степень всех множителей в подкоренном выражении знаменателя.
Пример 16: Рационализируйте знаменатель: 1253.
Решение: Радикал в знаменателе эквивалентен 523. Чтобы рационализировать знаменатель, он должен быть 533. Чтобы получить это, нам нужен еще один множитель 5. Следовательно, умножьте на 1 в форме 5353.
Ответ: 535
Пример 17: Рационализируйте знаменатель: 27a2b23.
Решение: В этом примере мы умножим на 1 в форме 22b322b3.
Ответ: 34ab32b
Пример 18: Рационализируем знаменатель: 1 4×35.
Решение: В этом примере мы умножим на 1 в форме 23x2523x25.
Ответ: 8x252x
Когда в знаменателе появляются два члена с квадратными корнями, мы можем рационализировать это с помощью очень специальной техники.Этот метод заключается в умножении числителя и знаменателя дроби на сопряжение знаменателя. Напомним, что умножение радикального выражения на его сопряжение дает рациональное число.
Пример 19: Рационализируйте знаменатель: 13-2.
Решение: В этом примере сопряжение знаменателя равно 3 + 2. Следовательно, умножьте на 1 в виде (3 + 2) (3 + 2).
Ответ: 3 + 2
Обратите внимание, что члены, содержащие квадратный корень в знаменателе, удаляются путем умножения на сопряжение.Мы можем использовать свойство (a + b) (a − b) = a − b, чтобы ускорить процесс умножения выражений в знаменателе.
Пример 20: Рационализируйте знаменатель: 2−62 + 6.
Решение: Умножьте на 1 в форме 2−62−6.
Ответ: −2 + 3
Пример 21: Рационализируйте знаменатель: x + yx − y.
Решение: В этом примере мы умножим на 1 в форме x − yx − y.
Ответ: x − 2xy + yx − y
Попробуй! Рационализируйте знаменатель: 35 + 525−3.
Ответ: 195 + 4511
Основные выводы
- Чтобы умножить два одночленных радикальных выражения, умножьте коэффициенты и умножьте подкоренные выражения. По возможности упростите результат.
- Примените свойство распределения при умножении радикальных выражений на несколько членов.Затем упростите и объедините все похожие радикалы.
- Умножение двухчленного радикального выражения, содержащего квадратные корни, на его сопряжение, приводит к рациональному выражению.
- Принято писать радикальные выражения без радикалов в знаменателе. Процесс поиска такого эквивалентного выражения называется рационализацией знаменателя.
- Если выражение имеет один член в знаменателе, включающий радикал, то рационализируйте его, умножив числитель и знаменатель на корень n -й степени множителей подкоренного выражения, чтобы их степени равнялись индексу.
- Если радикальное выражение имеет в знаменателе два члена, включающих квадратные корни, то рационализируйте его, умножив числитель и знаменатель на его сопряжение.
Тематические упражнения
Часть A: Умножение радикальных выражений
Умножить. ( Предположим, что все переменные неотрицательны. )
1. 3⋅5
2.7⋅3
3. 2⋅6
4. 5⋅15
5. 7⋅7
6. 12⋅12
7. 25⋅710
8. 315⋅26
9. (25) 2
10. (62) 2
11. 2x⋅2x
12. 5лет 5лет
13. 3a⋅12
14. 3a⋅2a
15. 42x⋅36x
16. 510–22 года
17.53⋅253
18. 43⋅23
19. 43⋅103
20. 183⋅63
21. (5 93) (2 63)
22. (2 43) (3 43)
23. (2 23) 3
24. (3 43) 3
25. 3a23⋅9a3
26. 7b3⋅49b23
27. 6×23⋅4×23
28. 12y3⋅9y23
29. 20x2y3⋅10x2y23
30.63xy3⋅12x4y23
31,5 (3-5)
32. 2 (3−2)
33,37 (27−3)
34,25 (6−310)
35. 6 (3−2)
36,15 (5 + 3)
37. х (х + ху)
38. у (ху + у)
39. 2ab (14a − 210b)
40. 6ab (52a − 3b)
41. (2−5) (3 + 7)
42. (3 + 2) (5-7)
43.(23−4) (36 + 1)
44. (5−26) (7−23)
45. (5−3) 2
46. (7−2) 2
47. (23 + 2) (23−2)
48. (2 + 37) (2−37)
49. (a − 2b) 2
50. (ab + 1) 2
51. Каковы периметр и площадь прямоугольника длиной 53 сантиметра и шириной 32 сантиметра?
52. Каковы периметр и площадь прямоугольника длиной 26 сантиметров и шириной 3 сантиметра?
53.Если основание треугольника 62 метра, а высота 32 метра, то какова площадь?
54. Если основание треугольника составляет 63 метра, а высота — 36 метров, то какова площадь?
Часть B: Деление радикальных выражений
Разделить.
55,753
56. 36010
57. 7275
58. 9098
59.90x52x
60. 96y33y
61. 162x7y52xy
62. 363x4y93xy
63. 16a5b232a2b23
64. 192a2b732a2b23
Рационализируйте знаменатель.
65,15
66,16
67. 23
68. 37
69. 5210
70. 356
71.3−53
72. 6−22
73. 17x
74. 13лет
75. a5ab
76. 3b223ab
77. 2363
78. 1473
79. 14×3
80. 13y23
81. 9x⋅239xy23
82. 5y2⋅x35x2y3
83. 3a2 3a2b23
84. 25н3 25м2н3
85.327x2y5
86. 216xy25
87. ab9a3b5
88. abcab2c35
89. 310-3
90,26-2
91. 15 + 3
92,17-2
93. 33 + 6
94. 55 + 15
95. 105-35
96. −224-32
97. 3 + 53−5
98. 10−210 + 2
99.23−3243 + 2
100. 65 + 225−2
101. x + yx − y
102. х − yx + y
103. a − ba + b
104. ab + 2ab − 2
105. x5−2x
106. 1x − y
Часть C: Обсуждение
107. Изучите и обсудите некоторые причины, по которым рационализация знаменателя является обычной практикой.
108. Объясните своими словами, как рационализировать знаменатель.
Ответы
1: 15
3: 23
5: 7
7: 702
9: 20
11: 2x
13: 6a
15: 24×3
17: 5
19: 2 53
21:30 23
23: 16
25: 3a
27: 2x⋅3×3
29: 2xy⋅25×3
31: 35−5
33: 42-321
35: 32−23
37: x + xy
39: 2a7b − 4b5a
41: 6 + 14−15−35
43: 182 + 23−126−4
45: 8−215
47: 10
49: a − 22ab + 2b
51: Периметр: (103 + 62) см; площадь: 156 квадратных сантиметров
53: 18 квадратных метров
55: 5
57: 265
59: 3×25
61: 9x3y2
63: 2a
65: 55
67: 63
69: 104
71: 3−153
73: 7x7x
75: ab5b
77: 633
79: 2x232x
81: 3 6x2y3y
83: 9ab32b
85: 9x3y45xy
87: 27a2b453
89: 310 + 9
91: 5-32
93: −1 + 2
95: −5-352
97: −4−15
99: 15−7623
101: x2 + 2xy + yx2 − y
103: a − 2ab + ba − b
105: 5x + 2×25−4x
Учебное пособие по калькулятору алгебры— MathPapa
Это учебное пособие по использованию калькулятора алгебры , пошагового калькулятора для алгебры.
Решение уравнений
Сначала перейдите на главную страницу Калькулятора алгебры. В текстовом поле калькулятора вы можете ввести математическую задачу, которую хотите вычислить.
Например, попробуйте ввести уравнение 3x + 2 = 14 в текстовое поле.
После того, как вы введете выражение, Калькулятор алгебры распечатает пошаговое объяснение того, как решить 3x + 2 = 14.
Примеры
Чтобы увидеть больше примеров задач, которые понимает калькулятор алгебры, посетите Страница примеров.2.Вычисление выражений
Калькулятор алгебры может вычислять выражения, содержащие переменную x.
Чтобы оценить выражение, содержащее x, введите выражение, которое вы хотите оценить, затем знак @ и значение, которое вы хотите вставить для x. Например, команда 2x @ 3 вычисляет выражение 2x для x = 3, что равно 2 * 3 или 6.
Калькулятор алгебры также может вычислять выражения, содержащие переменные x и y.Чтобы оценить выражение, содержащее x и y, введите выражение, которое вы хотите оценить, затем знак @ и упорядоченную пару, содержащую ваше значение x и значение y. Вот пример вычисления выражения xy в точке (3,4): xy @ (3,4).
Проверка ответов для решения уравнений
Так же, как калькулятор алгебры можно использовать для вычисления выражений, Калькулятор алгебры также можно использовать для проверки ответов на решение уравнений, содержащих x.
В качестве примера предположим, что мы решили 2x + 3 = 7 и получили x = 2.Если мы хотим вставить 2 обратно в исходное уравнение, чтобы проверить нашу работу, мы можем сделать это: 2x + 3 = 7 @ 2. Поскольку ответ правильный, в калькуляторе алгебры отображается зеленый знак равенства.
Если вместо этого мы попробуем значение, которое не работает, скажем, x = 3 (попробуйте 2x + 3 = 7 @ 3), вместо этого калькулятор алгебры покажет красный знак «не равно».
Чтобы проверить ответ на систему уравнений, содержащую x и y, введите два уравнения, разделенные точкой с запятой, за которыми следует знак @ и упорядоченную пару, содержащую ваше значение x и значение y.Пример: x + y = 7; х + 2у = 11 @ (3,4).
Режим планшета
Если вы используете планшет, например iPad, войдите в режим планшета, чтобы отобразить сенсорную клавиатуру.
Статьи по теме
Вернуться к калькулятору алгебры »
Калькулятор дробей: сложение и вычитание дробей
Базовое определение дроби
В математических терминах дробь — это числовая величина, которая не является целым числом: 1⁄3 , 1⁄5, 2⁄7 и т. Д.
Дробь определяется как математическое число, представляющее часть целого числа: 1⁄3, 1⁄6, 3⁄8 и так далее.Говоря обыденным языком, мы можем просто сказать, что это небольшая часть количества частей определенного размера, например одна восемь пятых.
Простые методы вычисления дробей
Простое сложение дробей
Ключ к правильному сложению дробей — всегда помнить, что наиболее важной частью дроби является число под чертой, известное как знаменатель. . Если у нас есть ситуация, когда знаменатели в дробях, участвующих в процессе сложения, одинаковы, тогда мы просто складываем числа, которые находятся над разделительной линией, или, как сказал бы математик: «Добавляем только числители».Мы можем взглянуть на пример сложения двух дробей, таких как 3⁄7 и 4⁄7. Выражение могло бы выглядеть так: 3⁄7 + 4⁄7 = 7⁄7. В случае, когда знаменатель равен знаменателю, как в предыдущем примере, его также можно приравнять к 1.
Однако это был один из самых простых примеров сложения дробей. Процесс может немного усложниться, если мы столкнемся с ситуацией, когда знаменатели дробей, участвующих в вычислении, различны. Тем не менее, есть правило, позволяющее эффективно проводить такие расчеты.Помните первое: при сложении дробей знаменатели всегда должны быть одинаковыми, или, говоря языком математиков, дроби должны иметь общий знаменатель. Для этого нам нужно взглянуть на имеющийся у нас знаменатель. Вот пример: 2⁄3 + 3⁄5. Итак, у нас пока нет общего знаменателя. Поэтому мы используем таблицу умножения, чтобы найти число, которое является произведением умножения 5 на 3. Это 15. Таким образом, общий знаменатель для этой дроби будет 15.Однако это еще не конец. Если мы разделим 15 на 3, мы получим 5. Итак, теперь нам нужно умножить числитель первой дроби на 5, что дает нам 10 (2 x 5). Кроме того, мы умножаем знаменатель второй дроби на 3, потому что 15⁄5 = 3. Получаем 9 (3 x 3 = 9). Теперь мы можем ввести все эти числа в выражение: 10⁄15 + 9⁄15 = 19⁄15
Примечание. Когда знаменатель больше знаменателя, мы делим его на последнее.
Простое вычитание дробей
Ключ к правильному вычитанию дробей — всегда помнить, что самая важная часть дроби — это число под чертой, известное как знаменатель.Если у нас есть ситуация, когда знаменатели в дробях, участвующих в процессе вычитания, одинаковы, тогда мы просто складываем числа, которые находятся над разделительной линией, или, как сказал бы математик: «Вычитая только числители». Мы можем взглянуть на пример вычитания двух дробей, таких как 3⁄7 и 4⁄7. Выражение могло бы выглядеть так: 4⁄7 — 3⁄7 = 1⁄7.
Однако это был один из самых простых примеров вычитания дробей. Процесс может немного усложниться, если мы столкнемся с ситуацией, когда знаменатели дробей, участвующих в вычислении, различны.Тем не менее, есть правило, позволяющее эффективно проводить такие расчеты. Помните первое: при вычитании дробей знаменатели всегда должны быть одинаковыми, или, говоря языком математиков, дроби должны иметь общий знаменатель. Для этого нам нужно взглянуть на имеющийся у нас знаменатель. Вот пример: 3⁄3 — 2⁄5. Итак, у нас пока нет общего знаменателя. Поэтому мы используем таблицу умножения, чтобы найти число, которое является произведением умножения 5 на 3.Это 15. Итак, общий знаменатель этой дроби будет 15. Однако это еще не конец. Если мы разделим 15 на 3, мы получим 5. Итак, теперь нам нужно умножить числитель первой дроби на 5, что дает нам 10 (2 x 5). Кроме того, мы умножаем знаменатель второй дроби на 3, потому что 15⁄5 = 3. Получаем 9 (3 x 3 = 9). Теперь мы можем ввести все эти числа в выражение: 9⁄15 — 10⁄15 = -1⁄15
Примечание: когда знаменатель больше знаменателя, мы затем делим его на последнее.
Вас также может заинтересовать наш калькулятор египетских дробей (EF) и / или калькулятор факторинга
Руководство по десяти простым фактам о дробях | Бретт Берри | Math Hacks
Как и в случае с тортом, у вас может быть 2 маленьких кусочка или , 1 кусок в два раза больше, и это столько же.Следовательно, многие дроби эквивалентны, например 2/5 и 4/10.
4/102/5факт два
Запишите любое целое число, превышающее 1 , чтобы сделать его дробным, поскольку общее количество частей в любом нераздельном целом равно единице.
факт три
Умножение дробей — это легко , просто умножение прямо поперёк.
3 x 7 = 21 и 5 x 8 = 40Примечание: смешанные числа необходимо сначала превратить в неправильные дроби, читайте подробнее об этом.
четвертый факт
Число 1 называется мультипликативным тождеством , потому что мы можем умножить его на любое число, и число останется прежним.Это важно для дробей, потому что часто нам нужно изменить внешний вид дроби без фактического изменения ее значения.
Например, я могу преобразовать 1/3 в эквивалентную дробь 3/9, умножив на 3/3.
Умножение на 1 в форме 3/3 превращает 1/3 в эквивалентную дробь 3/9факт пять
При сложении и вычитании дробей знаменатели должны быть одинаковыми . В этом есть смысл. Если мы хотим объединить или убрать части, мы должны говорить о частях одного размера, иначе это запутается.
Так что же делать, если у ваших дробей разные размеры?
Умножьте на единицу, чтобы преобразовать знаменатели в общий размер. По сути, мы делим фракции на части меньшего размера, пока они не станут одинаковыми. Это называется поиском общего знаменателя .
По правде говоря, подойдет любой общий знаменатель, но люди предпочитают находить наименьший. В этом случае наименьшее число, в которое входят 7 и 3 без остатка, равно 21.Так умножьте первую дробь на 3/3, а вторую на 7/7.
Умножьте на форму 1, чтобы получить общий знаменатель 21.Если вы не можете придумать наименьший общий знаменатель, , вы всегда можете умножить каждую дробь на противоположное значение . Иногда, как в этом случае, это оказывается наименьшим общим знаменателем. Если нет, просто сократите ответ в конце.
После совпадения знаменателей вычтите числители, чтобы получить 8/21.
15–7 = 8Это работает, как и следовало ожидать.В графическом плане начните с 15 штук, всего 21 штук.
Обратите внимание, что у меня 5/7 реплицированы 3 раза, это напрямую связано с умножением 5/7 на 3/3, чтобы получить 15/21.Удалите окраску с 7 из 15 синих блоков.
Что оставляет 8/21, как ожидалось.
факт шесть
Смешанное число — это комбинация целого числа и дроби.
Пример смешанного числаСмешанные числа плохо сочетаются с другими дробями. Лучше сначала преобразовать их в неправильные дроби.
Примечание: неправильная дробь — это дробь, числитель которой больше ее знаменателя, поэтому имеет значение больше единицы.
семь фактов
Чтобы преобразовать 2 и 4/5 в неправильную дробь сложите 2 + 4/5.
Шаг 1: Начните с перезаписи 2 как 2/1.
Шаг 2: Умножьте 2/1 на 5/5, чтобы получить эквивалентную дробь 10/5, имеющую желаемый общий знаменатель 5.
5/5 = 1, мультипликативное тождествоШаг 3 : Складываем 10/5 + 4/5.
Наш результат — эквивалентная неправильная дробь 14/5.
Чтобы преобразовать обратно в смешанное число, выполните деление. Например, 5 переходит в 14 два раза (так как 5 x 2 = 10) с 4 оставшимися частями.
Эквивалентные дроби в неправильной форме (слева) и смешанной форме чисел (справа)факт восемь
Предположим, мы хотели определить, какая дробь больше: 5/12 или 6/13.
Сначала убедитесь, что они не в смешанной форме!Шаг первый: Умножьте диагональ и запишите произведение над числителем.
Шаг второй: Умножьте другую диагональ и запишите ее произведение над числителем.
Шаг третий: Сравните продукты. Сторона с , чем больше продукт, является большей дробью. Итак, в этом случае 5/12 меньше 6/13.
Примечание: символ больше / меньше всегда открывается в сторону большего значения.Мы можем определить, равны ли дроби, и с помощью перекрестных произведений.
Перекрестное произведение 3/7 и 12/28 равно 84, поэтому 3/7 = 12/28.
факт девять
Лучшее, что есть в о дробях, — это то, что вы можете найти множество возможностей для отмены. Что делает их быстрыми и легкими в управлении.
Предположим, у меня есть дробь 8/10. И 8, и 10 можно переписать с коэффициентом 2.
Поскольку 2/2 = 1, я могу исключить 2, оставив 4/5 как уменьшенную дробь.
Вычеркните двойки, так как 2/2 = 1Используйте эту стратегию, чтобы упростить умножение дробей.
Начните с переписывания каждого числа в множителях.
Отмените любые пары чисел, которые делят на 1. Например, 5/5 = 1.
У меня есть еще пара пятерок, а также пара троек, которые также делятся на 1.
Ой! Я мог бы переписать 6 как 2 x 3 и отменить пару двойок. Ничего страшного, если вы упустите один фактор, просто продолжайте, пока не получите их все.
Примечание: я переписал 2 как 2 x 1, так что, когда я вычеркиваю 2, в числителе осталась единица.Если бы непосредственно умножить 15/25 на 10/18, потребовалось бы много арифметических действий, используя отмену I , предварительно уменьшив дробей и упростив умножение.
fact ten
Идея деления дробей проста на простых примерах, таких как:
Целое состоит из двух половин, поэтому есть 10 половин в 5 целых.
Но с более сложными дробями концепция усложняется.
Чтобы решить эту проблему, мы воспользуемся двумя фактами:
- Мы можем умножить на любую форму единицы (т.е. что угодно над собой)
- Умножив на обратную величину 3/2, которая равна 2/3, приводит к 1 посредством отмены
Шаг первый: Начните с умножения на обратное над собой.
Теперь нам нужно решить две проблемы поменьше (синюю и зеленую).
Шаг второй: Отмените все, что делится на 1 в нижней (зеленой) дроби. Это должно всегда приводить к 1.
Теперь нам остается решить главную проблему.
Шаг третий: Используйте отмену для предварительного уменьшения дроби. Сделав эти сокращения, умножьте их, чтобы получить 4/3.
Ярлык
Это механика длинной руки “ перевернуть и умножить. ”
Мы можем пропустить умножение на обратную величину внизу, так как она всегда сокращается до 1. Поэтому все, что вам нужно сделать, это умножить числитель на обратную величину знаменателя.
Почему работает трюк с перекрестным произведением?
Отличный вопрос! В качестве обобщения составьте две дроби, используя буквы a, b, c и d, представляющие четыре разных числа.
Умножьте обе дроби на b • d (это позволит нам сократить знаменатели).

 Низкие оптовые и розничные цены. Консультация по выбору. Оформление заказа на сайте и в офисе. Нарезка в размер. Доставка по Беларуси, в том числе, и в выходные дни.
Низкие оптовые и розничные цены. Консультация по выбору. Оформление заказа на сайте и в офисе. Нарезка в размер. Доставка по Беларуси, в том числе, и в выходные дни.