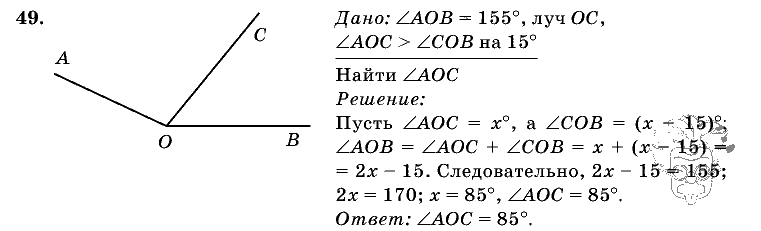ГДЗ по Геометрия 7-9 класс Атанасян
ГДЗ по Геометрия 7-9 класс Атанасян Л.С.
Подробный решебник (ГДЗ) по Геометрии за 7-9 класс
Автор: Атанасян Л.С.
Глава I. Начальные геометрические сведения
§ 1. Прямая и отрезок
1. Точки, прямые, отрезки
2. Провешивание прямой на местности
Практические задания
§ 2. Луч и угол
- 3. Луч
- 4. Угол
- Практические задания
§ 3. Сравнение отрезков и углов
5. Равенство геометрических фигур
6. Сравнение отрезков и углов
Задачи
§ 4. Измерение отрезков
7. Длина отрезка
8. Единицы измерения. Измерительные инструменты
Практические задания
Задачи
§ 5. Измерение углов
9. Градусная мера угла
10. Измерение углов на местности
Практические задания
Задачи
§ 6. Перпендикулярные прямые
Перпендикулярные прямые
11. Смежные и вертикальные углы
12. Перпендикулярные прямые
13. Построение прямых углов на местности
Практические задания
Задачи
Вопросы для повторения к главе I
Дополнительные задачи
Глава II. Треугольники
§ 1. Первый признак равенства треугольников
14. Треугольник
15. Первый признак равенства треугольников
Практические задания
Задачи
§ 2. Медианы, биссектрисы и высоты треугольника
16. Перпендикуляр к прямой
17. Медианы, биссектрисы и высоты треугольника
18. Свойства равнобедренного треугольника
Практические задания
Задачи
§ 3. Второй и третий признаки равенства треугольников
19. Второй признак равенства треугольников
20. Третий признак равенства треугольников
Задачи
§ 4. Задачи на построение
21. Окружность
22. Построения циркулем и линейкой
23. Примеры задач на построение
Примеры задач на построение
Задачи
Вопросы для повторения к главе II
Дополнительные задачи
Глава III. Параллельные прямые
§ 1. Признаки параллельности двух прямых
24. Определение параллельных прямых
25. Признаки параллельности двух прямых
26. Практические способы построения параллельных прямых
Задачи
§ 2. Аксиома параллельных прямых
27. Об аксиомах геометрии
28. Аксиома параллельных прямых
29. Теоремы об углах, образованных двумя параллельными прямыми и секущей
30. Углы с соответственно параллельными или перпендикулярными сторонами
Задачи
Вопросы для повторения к главе III
Дополнительные задачи
Глава IV. Соотношения между сторонами и углами треугольника
§ 1. Сумма углов треугольника
31. Теорема о сумме углов треугольника
32. Остроугольный, прямоугольный и тупоугольный треугольники
Задачи
§ 2. Соотношения между сторонами и углами треугольника
Соотношения между сторонами и углами треугольника
33. Теорема о соотношениях между сторонами и углами треугольника
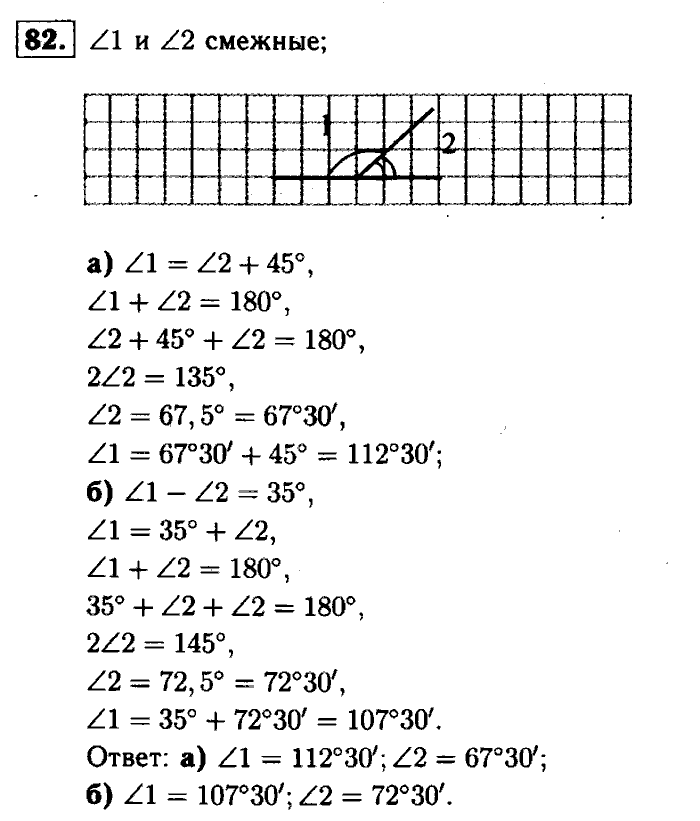
34. Неравенство треугольника
Задачи
§ 3. Прямоугольные треугольники
35. Некоторые свойства прямоугольных треугольников
36. Признаки равенства прямоугольных треугольников
37*. Уголковый отражатель
Задачи
§ 4. Построение треугольника по трём элементам
38. Расстояние от точки до прямой. Расстояние между параллельными прямыми
39. Построение треугольника по трём элементам
Задачи
Вопросы для повторения к главе IV
Дополнительные задачи
Задачи повышенной трудности
Задачи к главе I
Задачи к главе II
Задачи к главам III и IV
Глава V. Четырёхугольники
§ 1. Многоугольники
40. Многоугольник
41. Выпуклый многоугольник
42. Четырёхугольник
Задачи
§ 2. Параллелограмм и трапеция
43. Параллелограмм
Параллелограмм
44. Признаки параллелограмма
45. Трапеция
Задачи
§ 3. Прямоугольник, ромб, квадрат
46. Прямоугольник
47. Ромб и квадрат
48. Осевая и центральная симметрии
Задачи
Вопросы для повторения к главе V
Дополнительные задачи
Глава VI. Площадь
§ 1. Площадь многоугольника
49. Понятие площади многоугольника
50*. Площадь квадрата
51. Площадь прямоугольника
Задачи
§ 2. Площади параллелограмма, треугольника и трапеции
52. Площадь параллелограмма
53. Площадь треугольника
54. Площадь трапеции
Задачи
§ 3. Теорема Пифагора
55. Теорема Пифагора
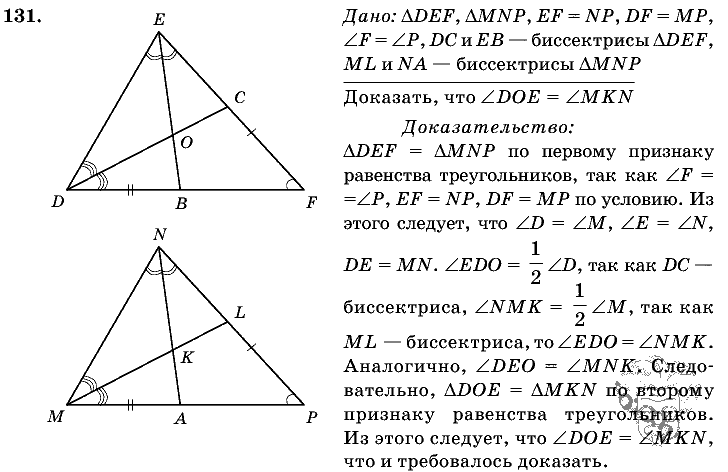
56. Теорема, обратная теореме Пифагора
57. Формула Герона
Задачи
Вопросы для повторения к главе VI
Дополнительные задачи
Глава VII. Подобные треугольники
§ 1. Определение подобных треугольников
58. Пропорциональные отрезки
Пропорциональные отрезки
59. Определение подобных треугольников
60. Отношение площадей подобных треугольников
Задачи
§ 2. Признаки подобия треугольников
61. Первый признак подобия треугольников
62. Второй признак подобия треугольников
63. Третий признак подобия треугольников
Задачи
§ 3. Применение подобия к доказательству теорем и решению задач
64. Средняя линия треугольника
65. Пропорциональные отрезки в прямоугольном треугольнике
66. Практические приложения подобия треугольников
67. О подобии произвольных фигур
Задачи
§ 4. Соотношения между сторонами и углами прямоугольного треугольника
68. Синус, косинус и тангенс острого угла прямоугольного треугольника
69. Значения синуса, косинуса и тангенса для углов 30°, 45° и 60°
Задачи
Вопросы для повторения к главе VI
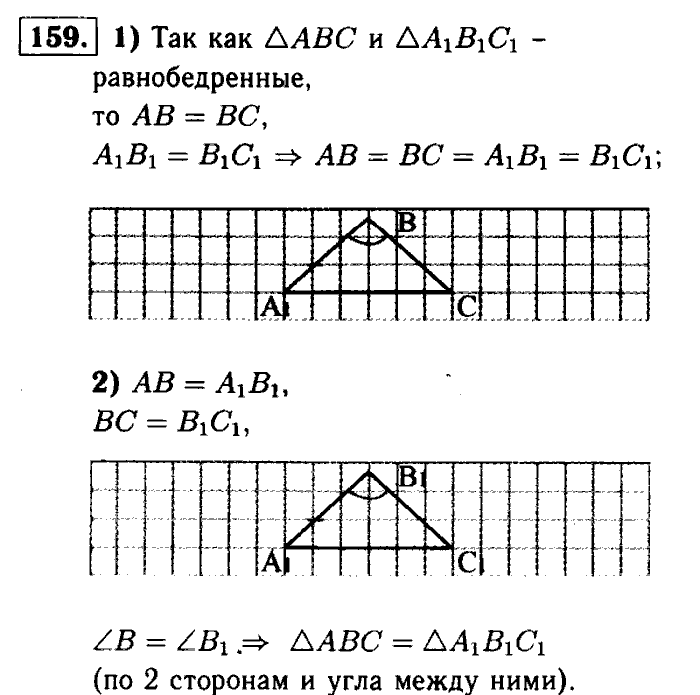
Дополнительные задачи
Глава VIII. Окружность
§ 1. Касательная к окружности
Касательная к окружности
70. Взаимное расположение прямой и окружности
71. Касательная к окружности
Задачи
§ 2. Центральные и вписанные углы
72. Градусная мера дуги окружности
73. Теорема о вписанном угле
Задачи
§ 3. Четыре замечательные точки треугольника
74. Свойства биссектрисы угла
75. Свойства серединного перпендикуляра к отрезку
76. Теорема о пересечении высот треугольника
Задачи
§ 4. Вписанная и описанная окружности
77. Вписанная окружность
78. Описанная окружность
Задачи
Вопросы для повторения к главе VIII
Дополнительные задачи
Глава IX. Векторы
§ 1. Понятие вектора
79. Понятие вектора
80. Равенство векторов
81. Откладывание вектора от данной точки
Практические задания
Задачи
§ 2. Сложение и вычитание векторов
- 82.
 Сумма двух векторов
Сумма двух векторов - 83. Законы сложения векторов. Правило параллелограмма
- 84. Сумма нескольких векторов
- 85. Вычитание векторов
- Практические задания
- Задачи
§ 3. Умножение вектора на число. Применение векторов к решению задач
86. Произведение вектора на число
87. Применение векторов к решению задач
88. Средняя линия трапеции
Практические задания
Задачи
Вопросы для повторения к главе IX
Дополнительные задачи
Задачи повышенной трудности
Задачи к главе V
Задачи к главе VI
Задачи к главе VI
Задачи к главе VIII
Задачи к главе IX
Глава X. Метод координат
§ 1. Координаты вектора
89. Разложение вектора по двум неколлинеарным векторам
90. Координаты вектора
Задачи
§ 2. Простейшие задачи в координатах
91. Связь между координатами вектора и координатами его начала и конца
92. Простейшие задачи в координатах
Простейшие задачи в координатах
Задачи
§ 3. Уравнения окружности и прямой
93. Уравнение линии на плоскости
94. Уравнение окружности
95. Уравнение прямой
96. Взаимное расположение двух окружностей
Задачи
Вопросы для повторения к главе X
Дополнительные задачи
Глава XI. Соотношения между сторонами и углами треугольника. Скалярное произведение векторов
§ 1. Синус, косинус, тангенс, котангенс угла
97. Синус, косинус, тангенс, котангенс
98. Основное тригонометрическое тождество. Формулы приведения
99. Формулы для вычисления координат точки
Задачи
§ 2. Соотношения между сторонами и углами треугольника
100. Теорема о площади треугольника
101. Теорема синусов
102. Теорема косинусов
103. Решение треугольников
104. Измерительные работы
Задачи
§ 3. Скалярное произведение векторов
105. Угол между векторами
Угол между векторами
106. Скалярное произведение векторов
107. Скалярное произведение в координатах
108. Свойства скалярного произведения векторов
Задачи
Вопросы для повторения к главе XI
Дополнительные задачи
Глава XII. Длина окружности и площадь круга
§ 1. Правильные многоугольники
109. Правильный многоугольник
110. Окружность, описанная около правильного многоугольника
111. Окружность, вписанная в правильный многоугольник
112. Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности
113. Построение правильных многоугольников
Задачи
§ 2. Длина окружности и площадь круга
114. Длина окружности
115. Площадь круга
116. Площадь кругового сектора
Задачи
Вопросы для повторения к главе XII
Дополнительные задачи
Глава XIII. Движения
§ 1. Понятие движения
117. Отображение плоскости на себя
Отображение плоскости на себя
118. Понятие движения
119*. Наложения и движения
Задачи
§ 2. Параллельный перенос и поворот
120. Параллельный перенос
121. Поворот
Задачи
Вопросы для повторения к главе XIII
Дополнительные задачи
Глава XIV. Начальные сведения из стереометрии
§ 1. Многогранники
122. Предмет стереометрии
123. Многогранник
124. Призма
125. Параллелепипед
126. Объём тела
127. Свойства прямоугольного параллелепипеда
128. Пирамида
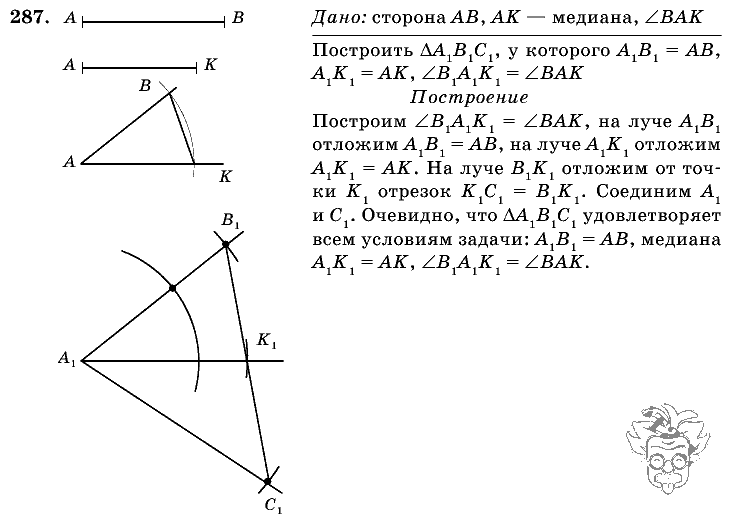
Задачи
§ 2. Тела и поверхности вращения
129. Цилиндр
130. Конус
131. Сфера и шар
Задачи
Вопросы для повторения к главе XIV
Дополнительные задачи
Задачи повышенной трудности
Задачи к главе X
Задачи к главе XI
Задачи к главе XII
Задачи к главе XIII
Задачи к главе XIV
Исследовательские задачи
Темы рефератов
Приложения
1. Об аксиомах планиметрии
Об аксиомах планиметрии
2. Некоторые сведения о развитии геометрии
ГДЗ Геометрия 7-9 класс Погорелов
- Геометрия 7-9 класс
- Тип пособия: Учебник
- Авторы: Погорелов
- Издательство: «Просвещение»
Параграф 1. Основные свойства простейших геометрических фигур. Контрольные вопросы
123456789101112131415161718192021222324252627282930Параграф 1. Основные свойства простейших геометрических фигур. Задачи
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051Параграф 2. Смежные и вертикальные углы. Контрольные вопросы
1234567891011121314Параграф 2. Смежные и вертикальные углы. Задачи
1234567891011121314151617181920212223242526Параграф 3. Признаки равенства треугольников. Контрольные вопросы
12345678910111213Параграф 3. Признаки равенства треугольников. Задачи
12345678910111213141516171819202122232425262728293031323334353637383940Параграф 4.
 Сумма углов треугольника. Контрольные вопросы1234567891011121314151617181920
Сумма углов треугольника. Контрольные вопросы1234567891011121314151617181920Параграф 4. Сумма углов треугольника. Задачи
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051Параграф 5. Геометрические построения. Контрольные вопросы
12345678910111213141516Параграф 5. Геометрические построения. Задачи
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152Параграф 6. Четырёхугольники. Контрольные вопросы
1234567891011121314151617181920212223Параграф 6. Четырёхугольники. Задачи
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677Параграф 7. Теорема Пифагора. Контрольные вопросы
1234567891011121314Параграф 7. Теорема Пифагора. Задачи
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374Параграф 8.
 Декартовы координаты на плоскости. Контрольные вопросы123456789101112131415
Декартовы координаты на плоскости. Контрольные вопросы123456789101112131415Параграф 8. Декартовы координаты на плоскости. Задачи
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162Параграф 9. Движение. Контрольные вопросы
12345678910111213141516171819202122Параграф 9. Движение. Задачи
12345678910111213141516171819202122232425262728293031323334353637383940414243444546Параграф 10. Векторы. Контрольные вопросы
1234567891011121314151617181920212223242526Параграф 10. Векторы. Задачи
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950Параграф 11. Подобие фигур. Контрольные вопросы
123456789101112131415161718192021Параграф 11. Подобие фигур. Задачи
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869Параграф 12.
 Решение треугольников. Контрольные вопросы1234
Решение треугольников. Контрольные вопросы1234Параграф 12. Решение треугольников. Задачи
1234567891011121314151617181920212223242526272829Параграф 13. Многоугольники. Контрольные вопросы
123456789101112131415161718192021Параграф 13. Многоугольники. Задачи
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455Параграф 14. Площади фигур. Контрольные вопросы
12345678910111213Параграф 14. Площади фигур. Задачи
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162Параграф 15. Элементы стереометрии. Задачи
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768Похожие ГДЗ Геометрия 7-9 класс
- Геометрия 7 класс
- Тесты
- Фарков
- Экзамен
Параграф 1.
 Основные свойства простейших геометрических фигур. Контрольные вопросы: 1
Основные свойства простейших геометрических фигур. Контрольные вопросы: 1Условие
Решение
Геометрия – это один из древнейших разделов математики, который изучает формы и пространственные отношения. Ее практическое применение мы видим повсюду. Дома, объекты, вещи — все это имеет геометрическую форму. Знания в этой области профессионально необходимы для многих специальностей, например таких, как архитектор, дизайнер, конструктор, модельер. Без них невозможно спроектировать здание, сшить одежду или разработать какие-либо производственные конструкции. Поэтому каждый должен владеть элементарными знаниями геометрического плана.
Польза геометрии
В системе школьного образования одноименный предмет занимает особо значимое место, поскольку вносит существенный вклад в развитие логического мышления, интуиции и формирует понятие доказательства. Первое знакомство школьника с геометрией начинается достаточно поздно – лишь в седьмом классе. К этому возрасту большинство учеников уже умеет планировать свое учебное время и может работать совершенно самостоятельно с любой вспомогательной литературой. Но изучение геометрии означает не только умение производить расчеты, но еще и пространственное мышление, а также элементарную работу с чертежами.
К этому возрасту большинство учеников уже умеет планировать свое учебное время и может работать совершенно самостоятельно с любой вспомогательной литературой. Но изучение геометрии означает не только умение производить расчеты, но еще и пространственное мышление, а также элементарную работу с чертежами.
Надежный консультант ученика
Вопросов при работе с таким сложным предметом возникают десятки. Но кто поможет школьнику найти на них ответ? Учитель не располагает таким количеством свободного времени, чтобы работать с каждым учеником персонально, а большинство родителей с трудом может вспомнить, что такое синус и косинус. В этом случае на помощь ученику приходит специальная учебная литература – решебник к пособию «Геометрия 7-9 класс Учебник Погорелов Просвещение». Он содержит правильные и максимально понятные ответы абсолютно ко всем номерам упражнений. С его помощью ученик сможет:
- Проверить правильное выполнение работы заданной на дом.
- Тщательно подготовиться к предстоящему уроку.

- Углубить и проработать уже пройденный материал.
- Разобрать особо сложную тему.
Сборник станет прекрасным помощником, который даст возможность понять все тонкости и нюансы предметного материала с легкостью освоить дисциплину.
Что представляет собой решебник
Издание охватывает теоретический и практический учебный материал за три года, рассматривая все основные темы школьной программы по геометрии:
- Планиметрия.
- Стереометрия.
- Векторы.
Пособие поможет ученику и в более старших классах для повторения пройденного материала.
ГДЗ глава 8. задача 716 геометрия 7‐9 класс Атанасян, Бутузов – Telegraph
➡➡➡ ПОДРОБНЕЕ ЖМИТЕ ЗДЕСЬ!
ГДЗ глава 8. задача 716 геометрия 7‐9 класс Атанасян, Бутузов
Подробное решение глава 8 . задача № 716 по геометрии для учащихся 7 ‐9 класса , авторов Атанасян , Бутузов, Кадомцев, Позняк, Юдин . Авторы : Л . С . Атанасян , В .Ф . Бутузов, С .Б . Кадомцев, Э .Г . Позняк, И .И . Юдин . Издательство: Просвещение .
С . Атанасян , В .Ф . Бутузов, С .Б . Кадомцев, Э .Г . Позняк, И .И . Юдин . Издательство: Просвещение .
Вы открыли задание номер 716 из решебника на uchim .org . Другие номера: ГДЗ по геометрии 7 -9 класс Атанасян .
Решение задания из учебника по геометрии для 7 , 8 , 9 класса (Атанасян) http://www .megabotan .ru .
Решебник (ГДЗ ) по Геометрии за 7 ‐9 (седьмой‐девятый ) класс авторы: Атанасян , Бутузов, Кадомцев, Позняк, Юдин издательство Просвещение, 2019 год . Решебник (ГДЗ ) по геометрии за 7 — 9 класс Атанасян , Бутузов . Учебник с ответами ФГОС .
ГДЗ по геометрии 7 -9 класс Атанасян , Бутузов , Кадомцев . Геометрия – наука, требующая от школьника умения эффективно Удобным способом использования решебника по геометрии Атанасяна выступает наш сайт . На нем достаточно кликнуть номер задания на странице . .
ГДЗ решебник и ответы 7 класс , 8 класс , 9 класс , Геометрия , Атанасян Л .С ., Бутузов В .Ф ., Кадомцев С .Б ., Позняк Э .Г Авторы: Атанасян Л . С ., Бутузов В .Ф ., Кадомцев С .Б ., Позняк Э .Г ., Юдина И .И . -2020 год . Вопросы для повторенияк главе VIII (страницы 187-188) .
С ., Бутузов В .Ф ., Кадомцев С .Б ., Позняк Э .Г ., Юдина И .И . -2020 год . Вопросы для повторенияк главе VIII (страницы 187-188) .
ГДЗ по геометрии за 7 , 8 , 9 класс Л .С . Атанасян , В .Ф . Бутузов . Чтобы можно было самостоятельно дома или в школе выполнять задания без посторонней помощи, если возникают какие-то трудности, пользуйтесь готовыми домашними заданиями Атанасяна Левона . .
ГДЗ (домашнее задание ) по геометрии за 7 8 и 9 класс к учебнику Атанасяна , Бутузова, Кадомцева . Конечно же, предоставить посильную помощь ребенку . Именно для этой цели и было создано ГДЗ по геометрии 7 , 8 и 9 класс авторов Атанасян , Бутузова, Кадомцева .
Геометрия 7 -9 класс . Учебник . Атанасян . Просвещение . А если это не получается, то этот процесс облегчит решебник к учебнику «Геометрия 7 -9 класс » Атанасян , Бутузов, Кадомцев, в Кроме того, в ГДЗ по геометрии 7 -9 класс Атанасян включены многочисленные графики и . .
Действительно, ученики 7 , 8 и 9 классов – предельно просто найдут всё по книгам таких авторов, как — Атанасян , Бутузов . Представленные гдз созданы теми, кто отлично знает свое дело и не допускает каких-то промахов и ошибок . Поэтому данный решебник по геометрии рассчитанный . .
Представленные гдз созданы теми, кто отлично знает свое дело и не допускает каких-то промахов и ошибок . Поэтому данный решебник по геометрии рассчитанный . .
ГДЗ Геометрия 7 класс рабочая тетрадь Атанасян можно скачать здесь . ГДЗ к самостоятельным и контрольным работам по геометрии за 7 -9 классы Иченская М .А . можно скачать здесь . ГДЗ к Вопросы для повторения . Глава 1 .
ГДЗ по алгебре 7 -9 класс Атанасян , Бутузов , Кадомцев учебник . Любая математическая наука является довольно интересной и познавательной, но, к сожалению, далеко не все ученики хотят тратить драгоценное время, чтобы найти ответы к сложным задачам .
Сборник задач Атанасян 7 класс 8 класс 9 класс – один из наиболее распространённых учебников по геометрии . Именно этот учебник вызывает наибольшие затруднения у школьников . Поэтому был подготовлен этот сборник ГДЗ Атанасян , который содержит ответы на задачи с . .
ГДЗ (готовые домашние задания ) и решебник по геометрии за 7 ,8 ,9 класс , авторы: Л .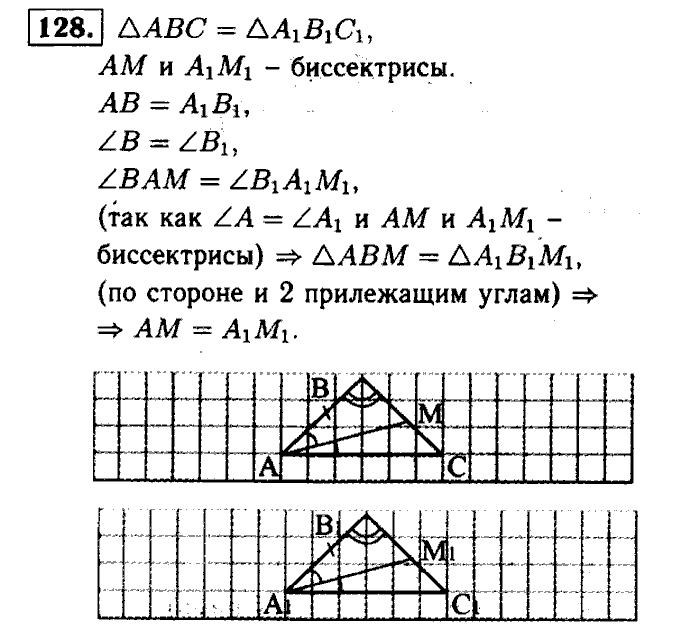 С . Атанасян , В .Ф . Бутузов, С .Б . Кадомцев . Авторский решебник с готовыми домашними заданиями по геометрии автора Атанасяна предлагается для учеников 7 , 8 , 9 класса — он . .
С . Атанасян , В .Ф . Бутузов, С .Б . Кадомцев . Авторский решебник с готовыми домашними заданиями по геометрии автора Атанасяна предлагается для учеников 7 , 8 , 9 класса — он . .
ГДЗ геометрия 7 класс Атанасян Просвещение . Изучение предмета «Геометрия» в системе В итоге учащиеся не могут решить предложенные примеры и задачи в полном объеме . Если вы полагаете, что у вас есть определенные пробелы в знаниях геометрии 7 класса, то вы . .
Подробное решение глава 8 . задача № 716 по геометрии для учащихся 7 ‐9 класса , авторов Атанасян , Бутузов, Кадомцев, Позняк, Юдин . Авторы : Л .С . Атанасян , В .Ф . Бутузов, С .Б . Кадомцев, Э .Г . Позняк, И .И . Юдин . Издательство: Просвещение .
Вы открыли задание номер 716 из решебника на uchim .org . Другие номера: ГДЗ по геометрии 7 -9 класс Атанасян .
Решение задания из учебника по геометрии для 7 , 8 , 9 класса (Атанасян) http://www .megabotan .ru .
Решебник (ГДЗ ) по Геометрии за 7 ‐9 (седьмой‐девятый ) класс авторы: Атанасян , Бутузов, Кадомцев, Позняк, Юдин издательство Просвещение, 2019 год .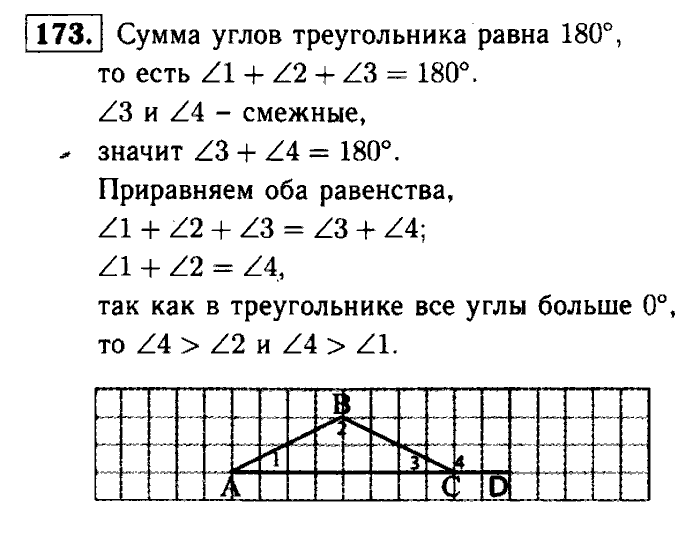 Решебник (ГДЗ ) по геометрии за 7 — 9 класс Атанасян , Бутузов . Учебник с ответами ФГОС .
Решебник (ГДЗ ) по геометрии за 7 — 9 класс Атанасян , Бутузов . Учебник с ответами ФГОС .
ГДЗ по геометрии 7 -9 класс Атанасян , Бутузов , Кадомцев . Геометрия – наука, требующая от школьника умения эффективно Удобным способом использования решебника по геометрии Атанасяна выступает наш сайт . На нем достаточно кликнуть номер задания на странице . .
ГДЗ решебник и ответы 7 класс , 8 класс , 9 класс , Геометрия , Атанасян Л .С ., Бутузов В .Ф ., Кадомцев С .Б ., Позняк Э .Г Авторы: Атанасян Л .С ., Бутузов В .Ф ., Кадомцев С .Б ., Позняк Э .Г ., Юдина И .И . -2020 год . Вопросы для повторенияк главе VIII (страницы 187-188) .
ГДЗ по геометрии за 7 , 8 , 9 класс Л .С . Атанасян , В .Ф . Бутузов . Чтобы можно было самостоятельно дома или в школе выполнять задания без посторонней помощи, если возникают какие-то трудности, пользуйтесь готовыми домашними заданиями Атанасяна Левона . .
ГДЗ (домашнее задание ) по геометрии за 7 8 и 9 класс к учебнику Атанасяна , Бутузова, Кадомцева . Конечно же, предоставить посильную помощь ребенку . Именно для этой цели и было создано ГДЗ по геометрии 7 , 8 и 9 класс авторов Атанасян , Бутузова, Кадомцева .
Конечно же, предоставить посильную помощь ребенку . Именно для этой цели и было создано ГДЗ по геометрии 7 , 8 и 9 класс авторов Атанасян , Бутузова, Кадомцева .
Геометрия 7 -9 класс . Учебник . Атанасян . Просвещение . А если это не получается, то этот процесс облегчит решебник к учебнику «Геометрия 7 -9 класс » Атанасян , Бутузов, Кадомцев, в Кроме того, в ГДЗ по геометрии 7 -9 класс Атанасян включены многочисленные графики и . .
Действительно, ученики 7 , 8 и 9 классов – предельно просто найдут всё по книгам таких авторов, как — Атанасян , Бутузов . Представленные гдз созданы теми, кто отлично знает свое дело и не допускает каких-то промахов и ошибок . Поэтому данный решебник по геометрии рассчитанный . .
ГДЗ Геометрия 7 класс рабочая тетрадь Атанасян можно скачать здесь . ГДЗ к самостоятельным и контрольным работам по геометрии за 7 -9 классы Иченская М .А . можно скачать здесь . ГДЗ к Вопросы для повторения . Глава 1 .
ГДЗ по алгебре 7 -9 класс Атанасян , Бутузов , Кадомцев учебник .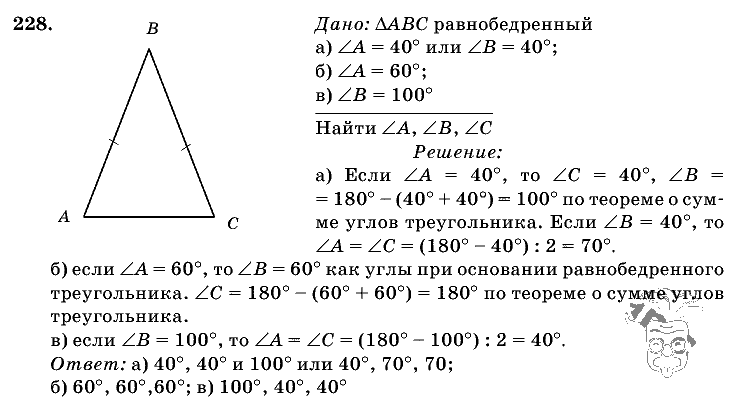 Любая математическая наука является довольно интересной и познавательной, но, к сожалению, далеко не все ученики хотят тратить драгоценное время, чтобы найти ответы к сложным задачам .
Любая математическая наука является довольно интересной и познавательной, но, к сожалению, далеко не все ученики хотят тратить драгоценное время, чтобы найти ответы к сложным задачам .
Сборник задач Атанасян 7 класс 8 класс 9 класс – один из наиболее распространённых учебников по геометрии . Именно этот учебник вызывает наибольшие затруднения у школьников . Поэтому был подготовлен этот сборник ГДЗ Атанасян , который содержит ответы на задачи с . .
ГДЗ (готовые домашние задания ) и решебник по геометрии за 7 ,8 ,9 класс , авторы: Л .С . Атанасян , В .Ф . Бутузов, С .Б . Кадомцев . Авторский решебник с готовыми домашними заданиями по геометрии автора Атанасяна предлагается для учеников 7 , 8 , 9 класса — он . .
ГДЗ геометрия 7 класс Атанасян Просвещение . Изучение предмета «Геометрия» в системе В итоге учащиеся не могут решить предложенные примеры и задачи в полном объеме . Если вы полагаете, что у вас есть определенные пробелы в знаниях геометрии 7 класса, то вы .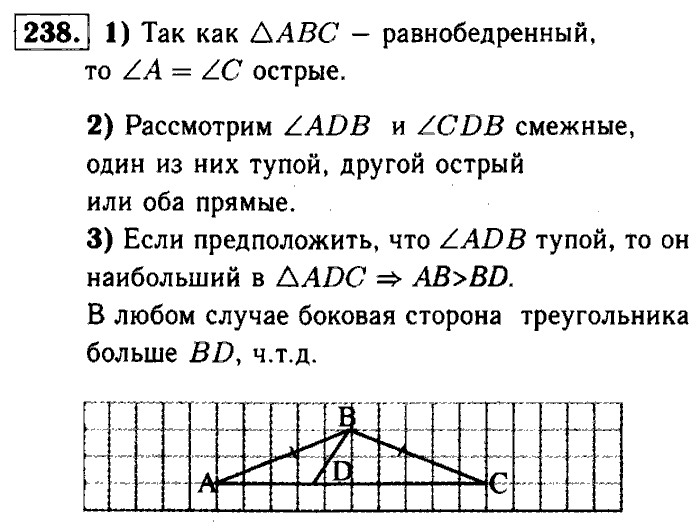 .
.
ГДЗ часть 1 1 история 5 класс рабочая тетрадь Годер
ГДЗ вариант 1 103 математика 5 класс дидактические материалы Мерзляк, Полонский
ГДЗ упражнение 82 русский язык 9 класс Рыбченкова, Александрова
ГДЗ номер 111 информатика 7 класс рабочая тетрадь Босова, Босова
ГДЗ глава 18 / § 18.4 14 химия 9 класс Гузей, Сорокин
ГДЗ упражнение 474 русский язык 4 класс Нечаева, Яковлева
ГДЗ часть 2 (страница) 7 окружающий мир 2 класс Школа 2100 Вахрушев, Бурский
ГДЗ № 807 математика 5 класс Зубарева, Мордкович
ГДЗ контрольная работа / К-1А / вариант 2 2 алгебра 7 класс дидактические материалы Звавич, Кузнецова
ГДЗ номер 586 алгебра 7 класс Макарычев, Миндюк
ГДЗ номер 213 математика 5 класс Мерзляк, Полонский
ГДЗ тематический тест / тематический тест №8. вариант 2 физика 9 класс тесты Слепнева
ГДЗ часть 2. страница 37 математика 4 класс Рудницкая, Юдачева
ГДЗ § 33 33.17 алгебра 8 класс Мерзляк, Поляков
ГДЗ упражнение 266 геометрия 7 класс рабочая тетрадь Мерзляк, Полонский
ГДЗ задание 856 математика 5 класс Никольский, Потапов
ГДЗ тест 9.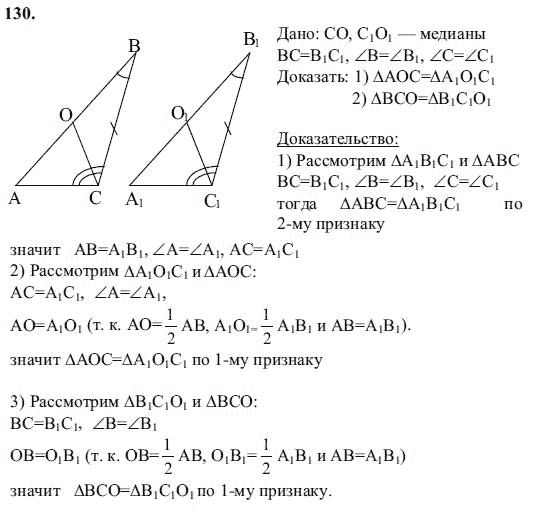 вариант 1 литература 6 класс контрольно-измерительные материалы Королева
вариант 1 литература 6 класс контрольно-измерительные материалы Королева
ГДЗ упражнение 90 русский язык 8 класс Ладыженская, Тростенцова
ГДЗ § 12 4 химия 10 класс Ерёмин, Кузьменко
ГДЗ приложение 65 география 10 класс контрольно-измерительные материалы Жижина
ГДЗ страница 105 английский язык 7 класс Морська, Кучма
ГДЗ тест 7. вариант 1 обществознание 6 класс контрольно-измерительные материалы Поздеев
ГДЗ самостоятельная работа / вариант 1 231 математика 6 класс дидактические материалы Чесноков, Нешков
ГДЗ часть 1 (страница) 57 окружающий мир 4 класс Плешаков, Новицкая
ГДЗ проверь себя стр. 321 алгебра 10 класс Колягин, Ткачева
ГДЗ вопросы в конце параграфа / § 10 1 химия 11 класс Габриелян, Лысова
ГДЗ контрольные работа / К-2 / вариант 4 5 алгебра 8 класс дидактические материалы Потапов
ГДЗ глава 8. задача 716 геометрия 7‐9 класс Атанасян, Бутузов
ГДЗ вопрос / §15 2 география 5‐6 класс Дронов, Савельева
ГДЗ Учебник 2019 / часть 1 404 (404) математика 5 класс Виленкин, Жохов
ГДЗ упражнение 381 русский язык 6 класс Львова, Львов
ГДЗ упражнение 73 геометрия 7 класс рабочая тетрадь Мерзляк, Полонский
ГДЗ параграф 1 история 5 класс Майков
ГДЗ задача 160 геометрия 9 класс рабочая тетрадь Дудницын
ГДЗ § 19 10 алгебра 9 класс Задачник Мордкович
ГДЗ часть 2 / страница 26 3 математика 1 класс Моро, Волкова
ГДЗ учебник 2019 / часть 1. упражнение 637 (632) математика 6 класс Виленкин, Жохов
упражнение 637 (632) математика 6 класс Виленкин, Жохов
ГДЗ страница 5-60 / Стр. 6-20. Wer ist das? 9 немецкий язык 10‐11 класс Воронина, Карелина
ГДЗ номер 1298 алгебра 8 класс Макарычев, Миндюк
ГДЗ задание 430 математика 5 класс Никольский, Потапов
ГДЗ задание 416 физика 9 класс рабочая тетрадь Пурышева, Важеевская
ГДЗ номер 552 алгебра 9 класс Алимов, Колягин
ГДЗ номер 965 математика 6 класс Мерзляк, Полонский
ГДЗ часть 2. страница 21 математика 5 класс рабочая тетрадь к учебнику Зубаревой Ерина
ГДЗ упражнение 486 математика 5 класс Арифметика. Геометрия. Бунимович, Дорофеев
ГДЗ глава 2 / § 6 / вариант 1 50 алгебра 10 класс дидактические материалы Шабунин, Ткачева
ГДЗ упражнение 119 русский язык 7 класс Львова, Львов
ГДЗ номер / § 3 12 алгебра 11 класс Никольский, Потапов
ГДЗ четверть 1 / работа 1. вариант 3 математика 3 класс тетрадь для контрольных работ Рудницкая, Юдачева
ГДЗ 5 глава / §45 8 химия 8 класс Габриелян
ГДЗ номер 825 математика 5 класс Дорофеев, Шарыгин
ГДЗ глава 17 17. 16 химия 8‐11 класс сборник задач и упражнений Хомченко
16 химия 8‐11 класс сборник задач и упражнений Хомченко
ГДЗ часть 1. страница 41 математика 4 класс дидактические материалы Рудницкая, Юдачева
ГДЗ Сборник Упражнений 4 Класс Сахаров
Решебник По Истории 7 Класс Косулин
Обзор экзамена по геометрии, Раздел 7, геометрия, средняя школа, математика, геометрия
НикВагнер
28 февраля 2020 г.
136 просмотров
Привет всем, добро пожаловать в наш обзор модуля 7 о расширении и сходстве. Нажмите напоминание, что наш тест будет в следующую среду, это четвертое, так что, надеюсь, это поможет вам учиться. Хорошо, давайте начнем. В первом вопросе говорится, что отрезок AB имеет концы в отрицательных двух запятых 5 и B двух запятых три, что из следующего является длиной простого числа B, которое является изображением AB после расширения в 6 раз, что является ужасное подчеркивание. Расширение в 6 раз с центром в начале координат. Итак, что мы знаем о расширениях? Мы знаем, что расширение меняет размер, но не меняет реальную форму объекта.

 Итак, я хочу выяснить масштабный коэффициент, необходимый для сопоставления GH с EF. Теперь важен порядок, в котором они это пишут, верно? Мы переходим от GH к EF. Хорошо? Так что мы становимся меньше здесь. Это действительно важно. Используя центральную точку D, хорошо, поэтому масштабный коэффициент, мы знаем, что мы должны делать новое вместо старого. Хорошо? И мы знаем, что он становится меньше, потому что мы переходим от GH к EF. Итак, давайте посмотрим. Если мы сделаем пропорцию GH, деленную на EF, это действительно не поможет, верно? Потому что GH — более длинная сторона. Мы хотим стать меньше. Это не ново. Это на самом деле старо. Над новым. Так что это нехорошо. Хорошо? ДФ над ДХ. Так что это DF такой длины DH. Итак, позвольте мне выделить это. DF — это длина, а DH — это все. Это на самом деле новое по сравнению со старым, верно? Вы начали с DH, потому что опять же, мы начали с GH в качестве линейного сегмента. Это стало ДФ. Хорошо, так что это новое вместо старого. Ваш ответ номер два.
Итак, я хочу выяснить масштабный коэффициент, необходимый для сопоставления GH с EF. Теперь важен порядок, в котором они это пишут, верно? Мы переходим от GH к EF. Хорошо? Так что мы становимся меньше здесь. Это действительно важно. Используя центральную точку D, хорошо, поэтому масштабный коэффициент, мы знаем, что мы должны делать новое вместо старого. Хорошо? И мы знаем, что он становится меньше, потому что мы переходим от GH к EF. Итак, давайте посмотрим. Если мы сделаем пропорцию GH, деленную на EF, это действительно не поможет, верно? Потому что GH — более длинная сторона. Мы хотим стать меньше. Это не ново. Это на самом деле старо. Над новым. Так что это нехорошо. Хорошо? ДФ над ДХ. Так что это DF такой длины DH. Итак, позвольте мне выделить это. DF — это длина, а DH — это все. Это на самом деле новое по сравнению со старым, верно? Вы начали с DH, потому что опять же, мы начали с GH в качестве линейного сегмента. Это стало ДФ. Хорошо, так что это новое вместо старого. Ваш ответ номер два.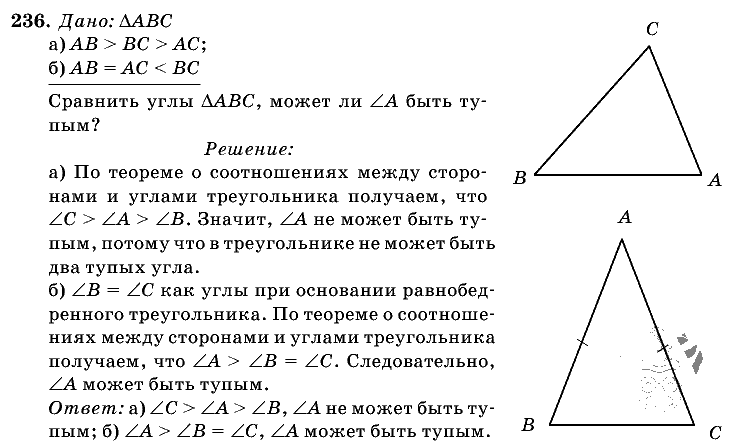
 На самом деле, причина, по которой они говорят нам это, состоит в том, чтобы сказать нам, что эти два треугольника подобны, ясно? Мы видели эту картинку много-много раз в классе, верно? Если эти два параллельны, мы получили соответствующие углы прямо здесь. И здесь достаточно иметь угловой угол. Но я отвлекся. Давайте посмотрим, a, B равно 21. BD равно 7, BC равно 15. Тогда какое из следующих чисел является длиной DE? Итак, это изображение, для которого люди всегда хотят использовать теорему о боковых разделителях, верно? Но мы не можем использовать здесь боковой сплиттер, хорошо, ребята, мы можем использовать размер блиттера только в том случае, если это было 15, а это было X, верно? Есть крест друг от друга. Когда им даны длины или длины, которые мы хотим найти, находятся на параллелях, мы больше не можем использовать боковой разделитель. Это неправильный ответ, так что не записывайте его. Люди хотят это сделать. 21 на 15, потому что эти два вместе равняются чему, 7 на X, но посмотрите, 21 — это длина этого маленького треугольника.
На самом деле, причина, по которой они говорят нам это, состоит в том, чтобы сказать нам, что эти два треугольника подобны, ясно? Мы видели эту картинку много-много раз в классе, верно? Если эти два параллельны, мы получили соответствующие углы прямо здесь. И здесь достаточно иметь угловой угол. Но я отвлекся. Давайте посмотрим, a, B равно 21. BD равно 7, BC равно 15. Тогда какое из следующих чисел является длиной DE? Итак, это изображение, для которого люди всегда хотят использовать теорему о боковых разделителях, верно? Но мы не можем использовать здесь боковой сплиттер, хорошо, ребята, мы можем использовать размер блиттера только в том случае, если это было 15, а это было X, верно? Есть крест друг от друга. Когда им даны длины или длины, которые мы хотим найти, находятся на параллелях, мы больше не можем использовать боковой разделитель. Это неправильный ответ, так что не записывайте его. Люди хотят это сделать. 21 на 15, потому что эти два вместе равняются чему, 7 на X, но посмотрите, 21 — это длина этого маленького треугольника.
 пн до вечера это 12 к 16, если я сделаю это быстро 16 на 12. Если я упрощу это, это просто четыре на три, хорошо? 25 на 15, упрощенно 5 на три. Так что это тоже нехорошо. Так что это должен быть вариант ответа номер четыре. Хорошо, но давай просто убедимся. 9больше 6 — это три тайма. 12 на 8 упрощенно тоже три половинки. Так что они пропорциональны, это правильный ответ. Хорошо, номер 6 и диаграмма ниже. E и F лежат на отрезках DG и DH. Хорошо, опять же, это средние точки. В них нет ничего особенного. Они просто взяли два очка. Какое из следующих утверждений было бы недостаточным для обоснования того, что DEF похож на DG H, хорошо, поэтому, если мы хотим обосновать сходство двух частей, помните, что нам нужно показать. Хорошо? Нам нужно показать либо угол, либо угол, либо сторона, либо сторона, либо сторона, либо сторона. Хорошо, и помните для подобия, что это не конгруэнтные стороны, их стороны пропорциональны. Итак, давайте посмотрим, параллельна ли EF GH, хорошо? Это картина, которую мы видели миллион раз, верно? Это означает, что у нас есть соответствующие углы здесь.
пн до вечера это 12 к 16, если я сделаю это быстро 16 на 12. Если я упрощу это, это просто четыре на три, хорошо? 25 на 15, упрощенно 5 на три. Так что это тоже нехорошо. Так что это должен быть вариант ответа номер четыре. Хорошо, но давай просто убедимся. 9больше 6 — это три тайма. 12 на 8 упрощенно тоже три половинки. Так что они пропорциональны, это правильный ответ. Хорошо, номер 6 и диаграмма ниже. E и F лежат на отрезках DG и DH. Хорошо, опять же, это средние точки. В них нет ничего особенного. Они просто взяли два очка. Какое из следующих утверждений было бы недостаточным для обоснования того, что DEF похож на DG H, хорошо, поэтому, если мы хотим обосновать сходство двух частей, помните, что нам нужно показать. Хорошо? Нам нужно показать либо угол, либо угол, либо сторона, либо сторона, либо сторона, либо сторона. Хорошо, и помните для подобия, что это не конгруэнтные стороны, их стороны пропорциональны. Итак, давайте посмотрим, параллельна ли EF GH, хорошо? Это картина, которую мы видели миллион раз, верно? Это означает, что у нас есть соответствующие углы здесь.
 А это говорит о том, что DE пропорциональна DG. Итак, ДЭ находится в пропорции со всей этой стороной прямо здесь. EF пропорциональна всему дну. Хорошо? Это не доказывает, что эти два треугольника равны. Хорошо, ребята. Это было бы, извините, не конгруэнтное подобное. Это было бы побочным продуктом сходства двух треугольников. Но это не обязательно показывает, что они похожи с самого начала. Хорошо? Так что это ваш ответ за то, что их не оправдывает. Хорошо, переходим к номеру 7. Ладно. На диаграмме прямоугольного треугольника EFG точки H и K расположены на сайтах EG и FG так, что HK перпендикулярны стороне EG, как показано, какое из следующих уравнений должно быть верным на основе этой диаграммы, предполагая, что эти два треугольника конгруэнтны. Ладно, будь осторожен. Эта картинка не такая, как эта, верно? Студент за вещами. Это не высота, потому что она не исходит из противоположной вершины. Так что не путайте эти две вещи, хорошо? Все, что они говорят, это то, что этот большой треугольник EFG подобен маленькому треугольнику.
А это говорит о том, что DE пропорциональна DG. Итак, ДЭ находится в пропорции со всей этой стороной прямо здесь. EF пропорциональна всему дну. Хорошо? Это не доказывает, что эти два треугольника равны. Хорошо, ребята. Это было бы, извините, не конгруэнтное подобное. Это было бы побочным продуктом сходства двух треугольников. Но это не обязательно показывает, что они похожи с самого начала. Хорошо? Так что это ваш ответ за то, что их не оправдывает. Хорошо, переходим к номеру 7. Ладно. На диаграмме прямоугольного треугольника EFG точки H и K расположены на сайтах EG и FG так, что HK перпендикулярны стороне EG, как показано, какое из следующих уравнений должно быть верным на основе этой диаграммы, предполагая, что эти два треугольника конгруэнтны. Ладно, будь осторожен. Эта картинка не такая, как эта, верно? Студент за вещами. Это не высота, потому что она не исходит из противоположной вершины. Так что не путайте эти две вещи, хорошо? Все, что они говорят, это то, что этот большой треугольник EFG подобен маленькому треугольнику.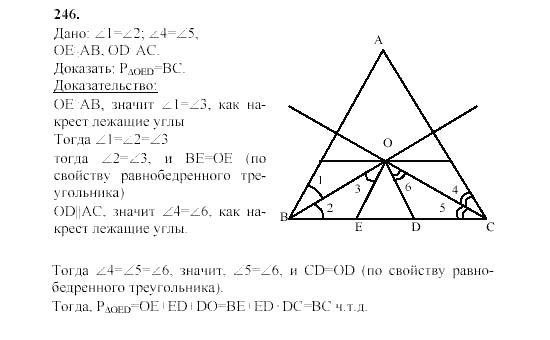 Итак, что я сделал, так это раздвинул эти два треугольника, хорошо? Я взял большой треугольник. Я переписал его. Это E, F, G ладно, не разбирая их, это очень сложно сделать. Хорошо? Теперь я понимаю, почему ты не разорвал их, если думал, что мы занимаемся деревом. То, что мы делаем, хорошо? Но это не деревья, потому что у нас нет высоты. И тогда вы берете свой маленький треугольник. Теперь вы должны быть осторожны, когда берете свой маленький треугольник. Вы должны положить вещи в нужное место. Если ваш правый угол находится внизу слева здесь, вам нужно, чтобы ваш правый угол был внизу слева здесь. И вот где К. Хорошо? Так что в основном просто взять это и перевернуть. Итак, G не двигается, но H собирается подняться сюда. Так что это части, которые соответствуют друг другу. Вы также могли бы просто посмотреть на то, что они написали. E соответствует H, F — K, G — G, что было бы другим способом сделать это. Хорошо? Итак, давайте посмотрим. EG над HG, так что гипотенуза обоих пока так хороша.
Итак, что я сделал, так это раздвинул эти два треугольника, хорошо? Я взял большой треугольник. Я переписал его. Это E, F, G ладно, не разбирая их, это очень сложно сделать. Хорошо? Теперь я понимаю, почему ты не разорвал их, если думал, что мы занимаемся деревом. То, что мы делаем, хорошо? Но это не деревья, потому что у нас нет высоты. И тогда вы берете свой маленький треугольник. Теперь вы должны быть осторожны, когда берете свой маленький треугольник. Вы должны положить вещи в нужное место. Если ваш правый угол находится внизу слева здесь, вам нужно, чтобы ваш правый угол был внизу слева здесь. И вот где К. Хорошо? Так что в основном просто взять это и перевернуть. Итак, G не двигается, но H собирается подняться сюда. Так что это части, которые соответствуют друг другу. Вы также могли бы просто посмотреть на то, что они написали. E соответствует H, F — K, G — G, что было бы другим способом сделать это. Хорошо? Итак, давайте посмотрим. EG над HG, так что гипотенуза обоих пока так хороша. Равняется EF над KG. Это не работает, верно? Потому что EF находится слева от клеток внизу. Это не соответствующие части. Это вне. Ладно, во-вторых, у нас FG пропорционально KG. У нас EF пропорционально HK. Это хорошо, верно? У нас есть сторона, угол, сторона, так что у нас все хорошо. Стороны соответствуют друг другу. Мы готовы к работе. Хорошо, и на самом деле тот факт, что это сторона угла, не имеет значения. Важной частью является то, что они используют соответствующие стороны. Затем отрезок AB имеет конечные точки на трех запятых 7 и B 23 запятая минус три. Хорошо, вот один из этих вопросов о разбиении. Если точка C расположена на AB, так что ваше соотношение таково, что из следующего должно быть координатами C, так что вот что я собираюсь сделать, ребята. Я просто собираюсь сделать формулу. Я знаю, что многие из вас действительно любят рисовать графики, и это здорово. Я тоже люблю его дарить. Просто у меня нет миллиметровки на компе и до 23 дойти сложно. Но помните, мы собираемся снабдить вас миллиметровой бумагой для теста, чтобы у вас было достаточно места, чтобы сделать это, если хотите.
Равняется EF над KG. Это не работает, верно? Потому что EF находится слева от клеток внизу. Это не соответствующие части. Это вне. Ладно, во-вторых, у нас FG пропорционально KG. У нас EF пропорционально HK. Это хорошо, верно? У нас есть сторона, угол, сторона, так что у нас все хорошо. Стороны соответствуют друг другу. Мы готовы к работе. Хорошо, и на самом деле тот факт, что это сторона угла, не имеет значения. Важной частью является то, что они используют соответствующие стороны. Затем отрезок AB имеет конечные точки на трех запятых 7 и B 23 запятая минус три. Хорошо, вот один из этих вопросов о разбиении. Если точка C расположена на AB, так что ваше соотношение таково, что из следующего должно быть координатами C, так что вот что я собираюсь сделать, ребята. Я просто собираюсь сделать формулу. Я знаю, что многие из вас действительно любят рисовать графики, и это здорово. Я тоже люблю его дарить. Просто у меня нет миллиметровки на компе и до 23 дойти сложно. Но помните, мы собираемся снабдить вас миллиметровой бумагой для теста, чтобы у вас было достаточно места, чтобы сделать это, если хотите.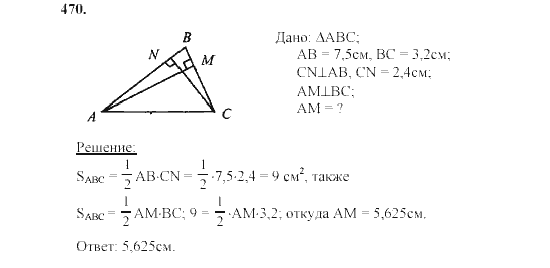 Мы также не будем использовать самые большие числа 23 в тесте. Но давайте попробуем это. Итак, помните формулу, которую я сказал: X равно X один плюс R, где R — это полное отношение. Умножить на Х два минус Х один. Здесь важно то, что, поскольку a стоит первым, нам разрешено использовать только a, так что это мой X один a, это мой X два в B, поэтому подставьте X равно трем плюс теперь ваша скорость или соотношение a соответствует трем здесь. Всего там 5 штук. Так что AC на самом деле составляет три пятых всего этого. Итак, три пятых — это то, что вам нужно. И тогда вы собираетесь сделать минус три минус. Извините, это значение Y, упс. 23. Минус три. Итак, вы получаете Х равно трем плюс три, умноженное на 5, умноженное на 20. Хорошо, вы можете вставить все это в свой калькулятор, и вы получите Х равно 15. Хорошо. Итак, позвольте мне убрать это отсюда. Далее идет Y, Y — это та же формула, только буквально с мудрым вместо X. Таким образом, Y равно Y один плюс R, умноженный на Y два минус Y один.
Мы также не будем использовать самые большие числа 23 в тесте. Но давайте попробуем это. Итак, помните формулу, которую я сказал: X равно X один плюс R, где R — это полное отношение. Умножить на Х два минус Х один. Здесь важно то, что, поскольку a стоит первым, нам разрешено использовать только a, так что это мой X один a, это мой X два в B, поэтому подставьте X равно трем плюс теперь ваша скорость или соотношение a соответствует трем здесь. Всего там 5 штук. Так что AC на самом деле составляет три пятых всего этого. Итак, три пятых — это то, что вам нужно. И тогда вы собираетесь сделать минус три минус. Извините, это значение Y, упс. 23. Минус три. Итак, вы получаете Х равно трем плюс три, умноженное на 5, умноженное на 20. Хорошо, вы можете вставить все это в свой калькулятор, и вы получите Х равно 15. Хорошо. Итак, позвольте мне убрать это отсюда. Далее идет Y, Y — это та же формула, только буквально с мудрым вместо X. Таким образом, Y равно Y один плюс R, умноженный на Y два минус Y один. Опять же, a должно быть Y один B должно быть Y два, потому что это порядок, в котором они это написали. Таким образом, у вас есть Y равно 7 плюс ваша скорость остается той же, что и при погружениях, которые все еще используют a, это наша фокусная точка. Так что ставка по-прежнему три пятых. Это не становится двумя пятыми для значения Y. Раз минус три -7. Хорошо, это 7 плюс три на 5 умноженное на минус десять. Поместите это на свой калькулятор, чтобы Y равнялось единице. Так что ваша точка зрения 15 запятая один. Это выбор. Опять же, если вам нравится отображать это в виде графика, это прекрасно. Мы дадим вам миллиметровку, чтобы сделать это. Где можно добраться до 23. Номер 9, треугольник LMN Шон внизу. Хорошо, у нас есть медианы. Это важно. Под ним проведены точки L и M к точкам P и Q соответственно. Отрезки MQ и LP пересекаются в точках R и Q, вся медиана здесь равна 60. Какова мера MR? Хорошо? Итак, опять же, если у нас есть все медианы парней, мы должны взять это число и разделить его на три, потому что мы собираемся разделить его на трети.
Опять же, a должно быть Y один B должно быть Y два, потому что это порядок, в котором они это написали. Таким образом, у вас есть Y равно 7 плюс ваша скорость остается той же, что и при погружениях, которые все еще используют a, это наша фокусная точка. Так что ставка по-прежнему три пятых. Это не становится двумя пятыми для значения Y. Раз минус три -7. Хорошо, это 7 плюс три на 5 умноженное на минус десять. Поместите это на свой калькулятор, чтобы Y равнялось единице. Так что ваша точка зрения 15 запятая один. Это выбор. Опять же, если вам нравится отображать это в виде графика, это прекрасно. Мы дадим вам миллиметровку, чтобы сделать это. Где можно добраться до 23. Номер 9, треугольник LMN Шон внизу. Хорошо, у нас есть медианы. Это важно. Под ним проведены точки L и M к точкам P и Q соответственно. Отрезки MQ и LP пересекаются в точках R и Q, вся медиана здесь равна 60. Какова мера MR? Хорошо? Итак, опять же, если у нас есть все медианы парней, мы должны взять это число и разделить его на три, потому что мы собираемся разделить его на трети.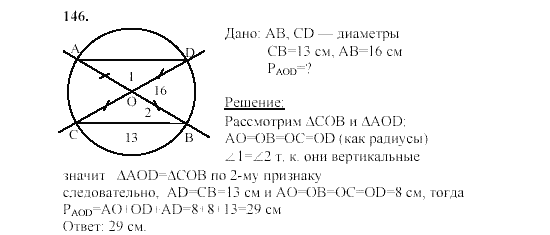 Медианы делят друг друга в отношении два к одному. Таким образом, получается всего три части. Итак, делим на три, получается 20. Помните, если есть три части, то MR — это длинная часть, верно? Так что это два из двух в одном. Таким образом, 20 умножить на два равно 40. Эта часть равна 40, если они просят QR, чего они не сделали. Это будет 20. 20 и 48 до общего числа 60. Итак, 40-е отвечают. Номер десять, только здесь другой цвет. А точки диаграммы E и D являются серединами. Итак, теперь у нас есть средние точки. Это важно здесь. Отрезки AD и BE сторон AC и BC пересекаются в точке F, поэтому BE является медианой. AD — это медиана, верно? Потому что они сказали мне, что E и D являются средними точками. Таким образом, вы должны идентифицировать этот материал. Они не просто расскажут это тебе, ясно? Теперь определяем, что у нас есть. AB — это 28. AD, вся эта длина — 30, и BE, ладно, BE — тоже вся эта длина. Я сойду с ума, чтобы написать это. Я постараюсь сделать это. Я просто собираюсь сделать это действительно большим и обойти все это 24.
Медианы делят друг друга в отношении два к одному. Таким образом, получается всего три части. Итак, делим на три, получается 20. Помните, если есть три части, то MR — это длинная часть, верно? Так что это два из двух в одном. Таким образом, 20 умножить на два равно 40. Эта часть равна 40, если они просят QR, чего они не сделали. Это будет 20. 20 и 48 до общего числа 60. Итак, 40-е отвечают. Номер десять, только здесь другой цвет. А точки диаграммы E и D являются серединами. Итак, теперь у нас есть средние точки. Это важно здесь. Отрезки AD и BE сторон AC и BC пересекаются в точке F, поэтому BE является медианой. AD — это медиана, верно? Потому что они сказали мне, что E и D являются средними точками. Таким образом, вы должны идентифицировать этот материал. Они не просто расскажут это тебе, ясно? Теперь определяем, что у нас есть. AB — это 28. AD, вся эта длина — 30, и BE, ладно, BE — тоже вся эта длина. Я сойду с ума, чтобы написать это. Я постараюсь сделать это. Я просто собираюсь сделать это действительно большим и обойти все это 24. Хорошо? Чему равен периметр треугольника DEF? Итак, этот маленький треугольник посередине. Хорошо. Ну, проще всего найти здесь, вероятно, ED. ED — средний сегмент. Это не медиана. Это средний сегмент, потому что он соединяется со средними точками. Средние сегменты всегда составляют половину стороны, противоположной им. Итак, это 14. Хорошо, нам также нужен FD. Что ж, это часть всего медианного AD, точно так же, как мы решали в прошлой задаче деление на три, что дает вам десять. Хорошо? Итак, этот маленький кусочек равен десяти. Это сделает этот кусок 20, хотя они даже не просили об этом. И FE — это маленькая часть этой медианы, возьмите 24, разделите на три, и вы получите 8. Итак, это 8. Опять же, если бы они хотели эту часть, это было бы 16, просто удвойте 8. А затем сложите их 14 плюс десять. плюс 8, я полагаю, дает вам 32. Значит, там сказано периметр, верно? 14 плюс десять плюс 8 равно 32. Выбор ответа, верно? Теперь я хочу остановиться на этом вопросе еще на минуту. Я хочу кое о чем поговорить.
Хорошо? Чему равен периметр треугольника DEF? Итак, этот маленький треугольник посередине. Хорошо. Ну, проще всего найти здесь, вероятно, ED. ED — средний сегмент. Это не медиана. Это средний сегмент, потому что он соединяется со средними точками. Средние сегменты всегда составляют половину стороны, противоположной им. Итак, это 14. Хорошо, нам также нужен FD. Что ж, это часть всего медианного AD, точно так же, как мы решали в прошлой задаче деление на три, что дает вам десять. Хорошо? Итак, этот маленький кусочек равен десяти. Это сделает этот кусок 20, хотя они даже не просили об этом. И FE — это маленькая часть этой медианы, возьмите 24, разделите на три, и вы получите 8. Итак, это 8. Опять же, если бы они хотели эту часть, это было бы 16, просто удвойте 8. А затем сложите их 14 плюс десять. плюс 8, я полагаю, дает вам 32. Значит, там сказано периметр, верно? 14 плюс десять плюс 8 равно 32. Выбор ответа, верно? Теперь я хочу остановиться на этом вопросе еще на минуту. Я хочу кое о чем поговорить.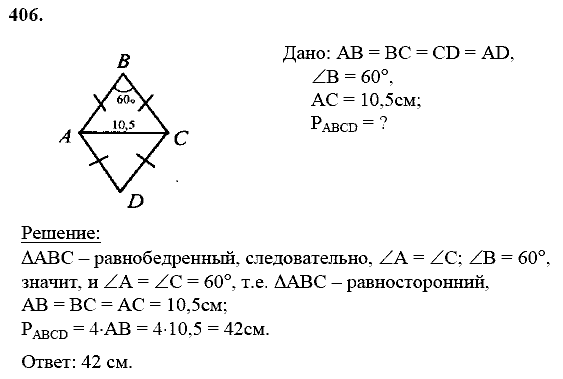 Если бы они попросили вас преобразовать подобия, чтобы преобразовать этот треугольник в треугольник AFB. Преобразование подобия. Вот что вам нужно сделать. Я думаю, все знают, что первым шагом будет поворот на 180° вокруг точки F. У нас не было бы слишком много проблем там. Получил поворот. Теперь второе, помните, это преобразование подобия, вам лучше где-то там сделать расширение. И мы определенно должны сделать FED больше, чтобы соответствовать другому треугольнику. Итак, мы расширили бы, теперь помните, когда вы набираете его, вы должны указать центр расширения. Итак, я хочу сказать с центром, прямо сейчас запомните, если вы повернете это, это будет немного похоже на это. Вот E, вот D, надеюсь, вы видите, что ваш центр расширения должен быть F, потому что вы не хотите, чтобы он двигался, так что его центр находится в F, хорошо? И тогда вам нужен коэффициент масштабирования. И масштабный фактор. Теперь подумайте об этом. Это медианы, да? Это соотношение два к одному. Итак, опять же, если мы хотим, чтобы FD идеально совпадал с AF, мы должны умножить его на два.
Если бы они попросили вас преобразовать подобия, чтобы преобразовать этот треугольник в треугольник AFB. Преобразование подобия. Вот что вам нужно сделать. Я думаю, все знают, что первым шагом будет поворот на 180° вокруг точки F. У нас не было бы слишком много проблем там. Получил поворот. Теперь второе, помните, это преобразование подобия, вам лучше где-то там сделать расширение. И мы определенно должны сделать FED больше, чтобы соответствовать другому треугольнику. Итак, мы расширили бы, теперь помните, когда вы набираете его, вы должны указать центр расширения. Итак, я хочу сказать с центром, прямо сейчас запомните, если вы повернете это, это будет немного похоже на это. Вот E, вот D, надеюсь, вы видите, что ваш центр расширения должен быть F, потому что вы не хотите, чтобы он двигался, так что его центр находится в F, хорошо? И тогда вам нужен коэффициент масштабирования. И масштабный фактор. Теперь подумайте об этом. Это медианы, да? Это соотношение два к одному. Итак, опять же, если мы хотим, чтобы FD идеально совпадал с AF, мы должны умножить его на два.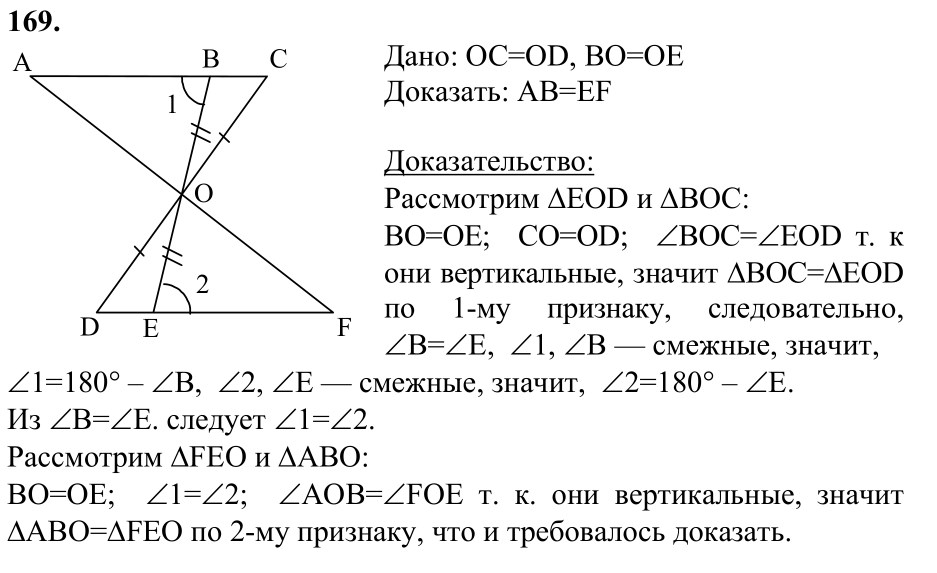 Таким образом, с масштабным коэффициентом два будет нашим ответом здесь. Хорошо? Это может быть полезно знать. Я не знаю, может быть, хороший тестовый вопрос или что-то в этом роде. Хорошо. Число 11, на диаграмме прямоугольный треугольник, QRS, чамбаль, высота. Вот так. Теперь они говорят нам, что это высота, понятно? Это важно. Это должно вызвать лук в наших головах. Проводится от R до гипотенузы QS. Значит, это прямые углы. Итак, вот эта милая картинка, которая нам нравится. Если QT равно 6, TS равно десяти, то какова длина QR? Хорошо, это наш вопрос о дереве, хорошо? Таким образом, вы должны повернуть бумагу так, чтобы QS был внизу. Хорошо? Помните, ребята, есть только три варианта того, какой может быть ваша древовидная цитата без кавычек. Это может быть это, и вы можете быть там, потому что это может быть там. Хорошо? Согласно этому вопросу, меня не интересуют RT или RS, поэтому они не будут моими деревьями. Хорошо, я заметил, что многие из вас хотят сделать высоту деревом каждый раз, когда это не так.
Таким образом, с масштабным коэффициентом два будет нашим ответом здесь. Хорошо? Это может быть полезно знать. Я не знаю, может быть, хороший тестовый вопрос или что-то в этом роде. Хорошо. Число 11, на диаграмме прямоугольный треугольник, QRS, чамбаль, высота. Вот так. Теперь они говорят нам, что это высота, понятно? Это важно. Это должно вызвать лук в наших головах. Проводится от R до гипотенузы QS. Значит, это прямые углы. Итак, вот эта милая картинка, которая нам нравится. Если QT равно 6, TS равно десяти, то какова длина QR? Хорошо, это наш вопрос о дереве, хорошо? Таким образом, вы должны повернуть бумагу так, чтобы QS был внизу. Хорошо? Помните, ребята, есть только три варианта того, какой может быть ваша древовидная цитата без кавычек. Это может быть это, и вы можете быть там, потому что это может быть там. Хорошо? Согласно этому вопросу, меня не интересуют RT или RS, поэтому они не будут моими деревьями. Хорошо, я заметил, что многие из вас хотят сделать высоту деревом каждый раз, когда это не так. Так что я собираюсь использовать свой зеленый маркер здесь, это мое дерево, QR, хорошо? Теперь настройте свою пропорцию. Две дроби равные друг другу. Помните, что верхний левый и нижний правый должны быть так называемым деревом. Хорошо? Или дерево здесь будет QR. Итак, X X идет сюда, X идет туда. Дерево никогда не остается на одном уровне. Они идут по диагонали друг от друга. Теперь дерево может складываться. Вот почему мы используем аналогию с деревом, верно? Может ли дерево упасть на вершину 6? Конечно вы можете. Так что ставьте 6 внизу. В дерево падают сверху десятки, только десятки. Нет. Когда вы срубаете дерево, его корень не проходит через кучу футов и не падает, верно? Просто падает. Однако он может упасть на все это, поэтому все это равно 16. Итак, что мы делаем, перекрестно умножаем и решим, получаем X в квадрате равно квадратному корню из 96. Теперь все ваши ответы даны в простой радикальной форме. Итак, я собираюсь рассказать, как это сделать. Но если вы немного заблудились, вы можете просто все в порядке, чтобы вы могли ввести это в калькулятор и ввести это в калькулятор, она делала то же самое, но давайте упростим это.
Так что я собираюсь использовать свой зеленый маркер здесь, это мое дерево, QR, хорошо? Теперь настройте свою пропорцию. Две дроби равные друг другу. Помните, что верхний левый и нижний правый должны быть так называемым деревом. Хорошо? Или дерево здесь будет QR. Итак, X X идет сюда, X идет туда. Дерево никогда не остается на одном уровне. Они идут по диагонали друг от друга. Теперь дерево может складываться. Вот почему мы используем аналогию с деревом, верно? Может ли дерево упасть на вершину 6? Конечно вы можете. Так что ставьте 6 внизу. В дерево падают сверху десятки, только десятки. Нет. Когда вы срубаете дерево, его корень не проходит через кучу футов и не падает, верно? Просто падает. Однако он может упасть на все это, поэтому все это равно 16. Итак, что мы делаем, перекрестно умножаем и решим, получаем X в квадрате равно квадратному корню из 96. Теперь все ваши ответы даны в простой радикальной форме. Итак, я собираюсь рассказать, как это сделать. Но если вы немного заблудились, вы можете просто все в порядке, чтобы вы могли ввести это в калькулятор и ввести это в калькулятор, она делала то же самое, но давайте упростим это.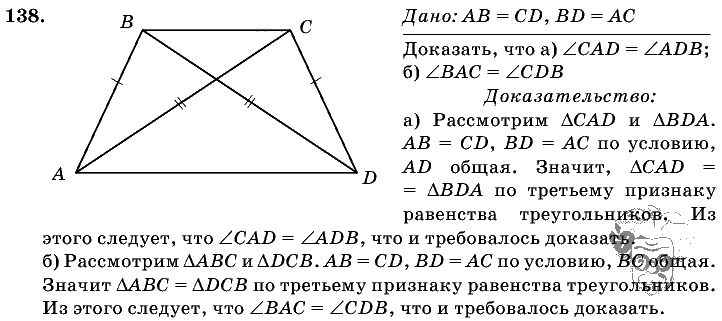 96 делится на 16, ясно? Теперь я знаю это, потому что я сделал это заранее, но ты должен проверить все свои идеальные квадраты, понимаешь? И посмотреть, какой из них работает. 96, деленное на 16, дает вам 6. Итак, давайте разобьем это на радикал 16, радикал 6, квадратный корень из 16 равен четырем. Вы держите рад 6. Вот ваш ответ. Возможно, вам придется протестировать пару, прежде чем вы найдете тот, который работает. Вам 16. Но вы также можете просто бросить это в калькулятор, бросить все это в калькулятор, посмотреть, точно ли это одно и то же. Номер 12 – это наша первая постройка здесь. Таким образом, у нас есть сегмент AB, показанный вместе с точкой C, с использованием только компаса и линейки, расширяющей AB с использованием центра C и масштабного коэффициента, равного трем. Хорошо. Поэтому нам нужен коэффициент масштабирования, равный трем. Позвольте мне достать мой компас. Переместите это вниз. Хорошо. Итак, первое, что мы должны сделать, ребята. Центр находится в точке C, мы хотим расширить AB.
96 делится на 16, ясно? Теперь я знаю это, потому что я сделал это заранее, но ты должен проверить все свои идеальные квадраты, понимаешь? И посмотреть, какой из них работает. 96, деленное на 16, дает вам 6. Итак, давайте разобьем это на радикал 16, радикал 6, квадратный корень из 16 равен четырем. Вы держите рад 6. Вот ваш ответ. Возможно, вам придется протестировать пару, прежде чем вы найдете тот, который работает. Вам 16. Но вы также можете просто бросить это в калькулятор, бросить все это в калькулятор, посмотреть, точно ли это одно и то же. Номер 12 – это наша первая постройка здесь. Таким образом, у нас есть сегмент AB, показанный вместе с точкой C, с использованием только компаса и линейки, расширяющей AB с использованием центра C и масштабного коэффициента, равного трем. Хорошо. Поэтому нам нужен коэффициент масштабирования, равный трем. Позвольте мне достать мой компас. Переместите это вниз. Хорошо. Итак, первое, что мы должны сделать, ребята. Центр находится в точке C, мы хотим расширить AB. Итак, вы возьмете прямой ребро, соедините С с В, они могут составить красивую длинную линию, соедините С с а, получится длинная длинная линия, и это должно быть началом. Хорошо? Это должно начаться таким образом. Вы не хотите подключать B через a и расширять его или что-то в этом роде. Ваш центр — C, вы хотите пойти из C, возьмите свой компас, переместите его в C и найдите расстояние от C до B, по сути, вы просто копируете отрезок три раза. Итак, отметьте этот угол. Если вы не отметите этот угол, я не знаю, что вы сделали, или это расстояние, которое я должен сказать. Теперь поднимитесь к точке B. Отметьте ее снова. Если бы коэффициент масштабирования был равен двум, вы бы закончили, верно? Потому что у вас будет одна, две дуги. Но масштабный коэффициент равен трем. Так что вам просто нужно сделать еще один. Прямо там. Итак, вы закончили с этой частью. Теперь вы просто перемещаете компас вниз к точке C и измеряете его до точки a. Сделай так, чтобы это работало. Опять же, вам нужно три инструмента.
Итак, вы возьмете прямой ребро, соедините С с В, они могут составить красивую длинную линию, соедините С с а, получится длинная длинная линия, и это должно быть началом. Хорошо? Это должно начаться таким образом. Вы не хотите подключать B через a и расширять его или что-то в этом роде. Ваш центр — C, вы хотите пойти из C, возьмите свой компас, переместите его в C и найдите расстояние от C до B, по сути, вы просто копируете отрезок три раза. Итак, отметьте этот угол. Если вы не отметите этот угол, я не знаю, что вы сделали, или это расстояние, которое я должен сказать. Теперь поднимитесь к точке B. Отметьте ее снова. Если бы коэффициент масштабирования был равен двум, вы бы закончили, верно? Потому что у вас будет одна, две дуги. Но масштабный коэффициент равен трем. Так что вам просто нужно сделать еще один. Прямо там. Итак, вы закончили с этой частью. Теперь вы просто перемещаете компас вниз к точке C и измеряете его до точки a. Сделай так, чтобы это работало. Опять же, вам нужно три инструмента. Итак, один, переместите его. Вот два. Положите его еще раз. Есть три. Хорошо? Итак, опять же, если он просит два, вы делаете два. Быстро на три, ты делаешь три. И вы собираетесь соединить эти два, чтобы сделать настоящий отрезок. И тогда вы просто собираетесь обозначить это соответствующим образом. Итак, это было B, теперь это B Prime. Это был прайм. Не забудьте пометить его. Он просит вас пометить его как простое B. Пожалуйста, сделай так. Ладно, дальше. Это мера угла CBA, равная 63°. Итак, вот этот угол, CBA 63, хорошо? Чему равен угол C, B простого числа? Итак, еще раз, если вы не маркировали, вы не знаете, что это такое. Но от C до B простое число прямо здесь. Что это за угол? Ну, надеюсь, вы думаете, что все, что мы делаем, это расширяем что-то, так что угол не изменится. Итак, угол C, B простой, простой равен 63°. Я собираюсь сказать расширения. Сохраняйте угловую меру. Сохраняйте угловую меру. Скажите, что вы расширили в прошлый раз, вы должны все измерить. Что бы вы ни расширяли, вы не измените угол.
Итак, один, переместите его. Вот два. Положите его еще раз. Есть три. Хорошо? Итак, опять же, если он просит два, вы делаете два. Быстро на три, ты делаешь три. И вы собираетесь соединить эти два, чтобы сделать настоящий отрезок. И тогда вы просто собираетесь обозначить это соответствующим образом. Итак, это было B, теперь это B Prime. Это был прайм. Не забудьте пометить его. Он просит вас пометить его как простое B. Пожалуйста, сделай так. Ладно, дальше. Это мера угла CBA, равная 63°. Итак, вот этот угол, CBA 63, хорошо? Чему равен угол C, B простого числа? Итак, еще раз, если вы не маркировали, вы не знаете, что это такое. Но от C до B простое число прямо здесь. Что это за угол? Ну, надеюсь, вы думаете, что все, что мы делаем, это расширяем что-то, так что угол не изменится. Итак, угол C, B простой, простой равен 63°. Я собираюсь сказать расширения. Сохраняйте угловую меру. Сохраняйте угловую меру. Скажите, что вы расширили в прошлый раз, вы должны все измерить. Что бы вы ни расширяли, вы не измените угол.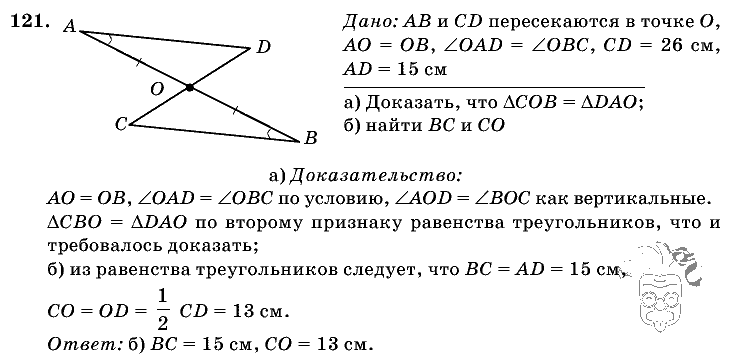 Хорошо, следующий номер 13. У нас есть сегмент RS — это изображение PQ после расширения с центром в неизвестной точке. Используя только линейку, определите центр расширения. Так что подумайте о том, что мы сделали в прошлый раз. Первое, что мы сделали, это соединили центр расширения наружу, хорошо? Теперь, если мы хотим вернуться назад, не могли бы мы просто соединить простое число через а и простое число В через В, и они встретились бы в центре. Так что это именно то, что мы собираемся сделать здесь. Итак, мы собираемся соединить P обратно через R, вот так. И мы собираемся соединить Q обратно через S, где две линии встречаются с тем, что изначально было вашим центром расширения. Он просто делает то, что мы делали в обратном порядке. Так что у меня системный рынок посмотреть. Укажите одно возможное соотношение длин сегментов, которое можно использовать в качестве коэффициента расширения. Опять же, всякий раз, когда мы хотим учитывать факторы, мы хотим, чтобы новое было важнее старого. Хорошо, так что давайте посмотрим.
Хорошо, следующий номер 13. У нас есть сегмент RS — это изображение PQ после расширения с центром в неизвестной точке. Используя только линейку, определите центр расширения. Так что подумайте о том, что мы сделали в прошлый раз. Первое, что мы сделали, это соединили центр расширения наружу, хорошо? Теперь, если мы хотим вернуться назад, не могли бы мы просто соединить простое число через а и простое число В через В, и они встретились бы в центре. Так что это именно то, что мы собираемся сделать здесь. Итак, мы собираемся соединить P обратно через R, вот так. И мы собираемся соединить Q обратно через S, где две линии встречаются с тем, что изначально было вашим центром расширения. Он просто делает то, что мы делали в обратном порядке. Так что у меня системный рынок посмотреть. Укажите одно возможное соотношение длин сегментов, которое можно использовать в качестве коэффициента расширения. Опять же, всякий раз, когда мы хотим учитывать факторы, мы хотим, чтобы новое было важнее старого. Хорошо, так что давайте посмотрим.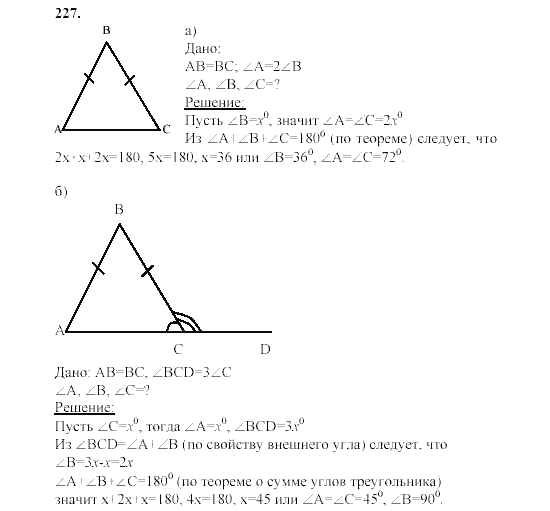 RS — изображение PQ после дилатации. Таким образом, PQ был тем, который расширялся. Хорошо? Таким образом, этот сегмент был расширен прямо здесь. Так что старый был на самом деле от P до C, это был оригинал. Так что это пойдет на нижний ПК. Новинка — RC. Потому что это изображение после расширения. Так что это один из способов сделать это. Хорошо, вы также можете использовать дно, верно? Вы можете сделать SC, это новая часть, вместо QS, которая является старой. Хорошо, следующий интересный вопрос, не тот, который мы действительно задавали раньше, но он действительно подводит нас к важному моменту. Использую составную линейку, так что позвольте мне снова получить свое сейчас. Вот оно. Принесите его вниз. Хорошо. Расширьте AB, используя центр C и масштабный коэффициент 0,5. Итак, мы знаем, что если коэффициент масштабирования равен 0,5, то AB нужно уменьшить. Оставьте все строительные отметки. Так что на самом деле мы не делали ничего подобного, ясно? Но важная часть, которую я собираюсь отметить здесь, заключается в том, что если центральный центр расширения находится на линии, то и сама линия.
RS — изображение PQ после дилатации. Таким образом, PQ был тем, который расширялся. Хорошо? Таким образом, этот сегмент был расширен прямо здесь. Так что старый был на самом деле от P до C, это был оригинал. Так что это пойдет на нижний ПК. Новинка — RC. Потому что это изображение после расширения. Так что это один из способов сделать это. Хорошо, вы также можете использовать дно, верно? Вы можете сделать SC, это новая часть, вместо QS, которая является старой. Хорошо, следующий интересный вопрос, не тот, который мы действительно задавали раньше, но он действительно подводит нас к важному моменту. Использую составную линейку, так что позвольте мне снова получить свое сейчас. Вот оно. Принесите его вниз. Хорошо. Расширьте AB, используя центр C и масштабный коэффициент 0,5. Итак, мы знаем, что если коэффициент масштабирования равен 0,5, то AB нужно уменьшить. Оставьте все строительные отметки. Так что на самом деле мы не делали ничего подобного, ясно? Но важная часть, которую я собираюсь отметить здесь, заключается в том, что если центральный центр расширения находится на линии, то и сама линия. Не двигается. Итак, мы говорили об этом раньше. Например, когда у нас есть линия и на ней есть центр расширения, уравнение этой линии остается точно таким же. Теперь это отрезок линии, поэтому он станет меньше, но применима та же идея. Итак, еще раз, если мы хотим, чтобы это было вдвое меньше, то каким бы ни было расстояние от a до C, мы хотим половину этого во второй раз, каким бы ни было расстояние от C до B, мы хотим половину этого время. Что ж, единственная известная нам конструкция, которая может быть найдена на полпути между двумя точками, — это биссектриса. Итак, что я собираюсь сделать, чтобы начать сегодня идти так долго, как вы хотите, пока это дальше, чем на полпути. Так что я пойду туда, наценю, уценю. Переключитесь на точку С, держите ручку или карандаш в том же круге. Блокировка дуги вверх. Хорошо, тогда все, что вам нужно сделать, это соединить эти два. И где бы они ни проходили через линию, ваша новая точка будет штрихом. Теперь вы должны сделать то же самое здесь с BC.
Не двигается. Итак, мы говорили об этом раньше. Например, когда у нас есть линия и на ней есть центр расширения, уравнение этой линии остается точно таким же. Теперь это отрезок линии, поэтому он станет меньше, но применима та же идея. Итак, еще раз, если мы хотим, чтобы это было вдвое меньше, то каким бы ни было расстояние от a до C, мы хотим половину этого во второй раз, каким бы ни было расстояние от C до B, мы хотим половину этого время. Что ж, единственная известная нам конструкция, которая может быть найдена на полпути между двумя точками, — это биссектриса. Итак, что я собираюсь сделать, чтобы начать сегодня идти так долго, как вы хотите, пока это дальше, чем на полпути. Так что я пойду туда, наценю, уценю. Переключитесь на точку С, держите ручку или карандаш в том же круге. Блокировка дуги вверх. Хорошо, тогда все, что вам нужно сделать, это соединить эти два. И где бы они ни проходили через линию, ваша новая точка будет штрихом. Теперь вы должны сделать то же самое здесь с BC. Так что измеряйте от B в любом месте, если это дальше, чем на полпути. Это выглядит хорошо для меня. Дуга вверх и вниз. Хорошо, перевернитесь к C, сделайте точно такую же дугу вверх и вниз. Хорошо, подключитесь к двум точкам пересечения. Везде, где они пересекают исходную линию, появляется новое простое число B. Итак, вот ваша новая линия от простого до B простого. Опять же, это не очень важно, но верхняя часть такова: если центр расширения находится на линии, то линия не двигается. Она может стать короче, если это сегмент, но сама линия не движется. Далее, на графике, показанном ниже. B prime B prime — это изображение AB после расширения, так что это новое. Это старое. Каково значение масштабного коэффициента дилатации? Итак, нам нужно найти масштабный коэффициент. Итак, опять же, нам нужно сделать новый в целом. Теперь вы можете вычислить расстояние для простого числа B и AB и разделить их, но это какой-то кошмар. Ладно, вот что я бы сделал. Просто возьмите либо вертикальное расстояние, либо горизонтальное расстояние.
Так что измеряйте от B в любом месте, если это дальше, чем на полпути. Это выглядит хорошо для меня. Дуга вверх и вниз. Хорошо, перевернитесь к C, сделайте точно такую же дугу вверх и вниз. Хорошо, подключитесь к двум точкам пересечения. Везде, где они пересекают исходную линию, появляется новое простое число B. Итак, вот ваша новая линия от простого до B простого. Опять же, это не очень важно, но верхняя часть такова: если центр расширения находится на линии, то линия не двигается. Она может стать короче, если это сегмент, но сама линия не движется. Далее, на графике, показанном ниже. B prime B prime — это изображение AB после расширения, так что это новое. Это старое. Каково значение масштабного коэффициента дилатации? Итак, нам нужно найти масштабный коэффициент. Итак, опять же, нам нужно сделать новый в целом. Теперь вы можете вычислить расстояние для простого числа B и AB и разделить их, но это какой-то кошмар. Ладно, вот что я бы сделал. Просто возьмите либо вертикальное расстояние, либо горизонтальное расстояние. Неважно, что ты делаешь. Хорошо? Старое было бы расстоянием от а до начала координат, то есть это расстояние равно одному, двум, трем, четырем, 5, 6, 7, 8. Новое было бы всем этим расстоянием, то есть 8, 9., десять, 11, 12. Хорошо? Таким образом, вы можете просто сделать 12 на 8, что в упрощенном виде равно трем на два. Вот и все. Вы также могли бы сделать горизонтальное расстояние до дна, верно? Внизу раз, два, три, четыре, 5, 6, 7, 8, 9, десять. И 11, 12, 13, 14, 15. Итак, десять и 15, вы могли бы сделать самые новые 15 вместо самых старых десяти и получить 1,5, то есть три больше двух. Не знаю, зачем я написал это 1.5, но то же самое. Если бы вы написали, что 12-часовая ставка равна 1,5, это тоже сработало бы. Хорошо, идем дальше, 16. Выровняйте по уравнению Y равно два X плюс три расширяется с центром расширения в начале координат. Нам нравится видеть, что центр находится в начале, что делает нашу жизнь легкой. Масштабный коэффициент равен 6. Таким образом, он становится в 6 раз больше.
Неважно, что ты делаешь. Хорошо? Старое было бы расстоянием от а до начала координат, то есть это расстояние равно одному, двум, трем, четырем, 5, 6, 7, 8. Новое было бы всем этим расстоянием, то есть 8, 9., десять, 11, 12. Хорошо? Таким образом, вы можете просто сделать 12 на 8, что в упрощенном виде равно трем на два. Вот и все. Вы также могли бы сделать горизонтальное расстояние до дна, верно? Внизу раз, два, три, четыре, 5, 6, 7, 8, 9, десять. И 11, 12, 13, 14, 15. Итак, десять и 15, вы могли бы сделать самые новые 15 вместо самых старых десяти и получить 1,5, то есть три больше двух. Не знаю, зачем я написал это 1.5, но то же самое. Если бы вы написали, что 12-часовая ставка равна 1,5, это тоже сработало бы. Хорошо, идем дальше, 16. Выровняйте по уравнению Y равно два X плюс три расширяется с центром расширения в начале координат. Нам нравится видеть, что центр находится в начале, что делает нашу жизнь легкой. Масштабный коэффициент равен 6. Таким образом, он становится в 6 раз больше.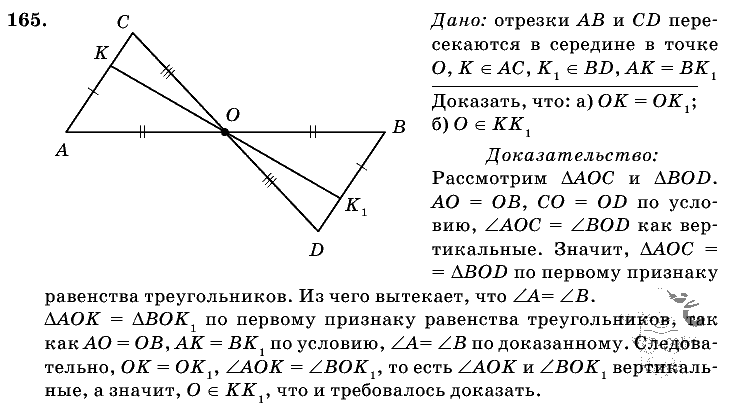 Ава считает, что уравнение будет Y равно 12 X плюс 18, Серена считает, что уравнение два X плюс 18 является одним из них правильным. Если да, то почему? Хорошо? Так что один из них точно правильный. Так что помните, всякий раз, когда мы делаем расширения, я собираюсь сделать еще одно примечание: расширения означают, что наклон не меняется. Хорошо, опять же, точно так же, как не меняются углы, не меняется и наклон линии. Так что Ава не может быть права, она взяла два и умножила наклон на 6, чтобы получить 12. Так нельзя, ясно? Серена сохранила наклон точно таким же, как два, но умножила точку пересечения Y на 6, и это правильно. Хорошо? Так что Серена права. Наклон остается прежним. Наклон остается прежним. Но перехват Y умножается. По шкале. Упс, это ужасно и готово. Масштаб. Хорошо, это все. Идем дальше. Линия, уравнение которой равно Y, равно половине X минус три, расширяется в три раза. Центр на данный момент. Так что это уже не происхождение. Поскольку объясните, почему его уравнение не изменится, хорошо? Ребята, если после расширения уравнение линии не меняется, то причина только одна.
Ава считает, что уравнение будет Y равно 12 X плюс 18, Серена считает, что уравнение два X плюс 18 является одним из них правильным. Если да, то почему? Хорошо? Так что один из них точно правильный. Так что помните, всякий раз, когда мы делаем расширения, я собираюсь сделать еще одно примечание: расширения означают, что наклон не меняется. Хорошо, опять же, точно так же, как не меняются углы, не меняется и наклон линии. Так что Ава не может быть права, она взяла два и умножила наклон на 6, чтобы получить 12. Так нельзя, ясно? Серена сохранила наклон точно таким же, как два, но умножила точку пересечения Y на 6, и это правильно. Хорошо? Так что Серена права. Наклон остается прежним. Наклон остается прежним. Но перехват Y умножается. По шкале. Упс, это ужасно и готово. Масштаб. Хорошо, это все. Идем дальше. Линия, уравнение которой равно Y, равно половине X минус три, расширяется в три раза. Центр на данный момент. Так что это уже не происхождение. Поскольку объясните, почему его уравнение не изменится, хорошо? Ребята, если после расширения уравнение линии не меняется, то причина только одна. Причина, должно быть, в том, что десять запятых два лежат на этой строке. Хорошо, так что я просто собираюсь написать это прямо сейчас. Это единственный жизнеспособный вариант. Десять запятая два лежит на строке. Половина X минус три. Это твой ответ, хорошо? Теперь, если вы хотите показать, почему это работает, давайте подставим десять вместо X и два вместо Y, чтобы получить два, равных половине, умноженной на десять минус три. А это два равно половине, умноженной на десять, равно 5. Минус три и, очевидно, два — это два. Так десять запятая два уже лежит на строчке. Уравнение прямой не изменится. 18 на приведенной ниже диаграмме AE и BD пересекаются в точке C с длинами сегментов, отмеченными, как показано. Опишите преобразование подобия. Это отобразило бы CDE этого треугольника на CBA. Дайте как можно больше подробностей. Итак, во-первых, хорошо, чтобы получить этот треугольник здесь, надеюсь, нам также придется повернуть его. Не отражение, верно? Отражение заставило бы его выглядеть примерно так.
Причина, должно быть, в том, что десять запятых два лежат на этой строке. Хорошо, так что я просто собираюсь написать это прямо сейчас. Это единственный жизнеспособный вариант. Десять запятая два лежит на строке. Половина X минус три. Это твой ответ, хорошо? Теперь, если вы хотите показать, почему это работает, давайте подставим десять вместо X и два вместо Y, чтобы получить два, равных половине, умноженной на десять минус три. А это два равно половине, умноженной на десять, равно 5. Минус три и, очевидно, два — это два. Так десять запятая два уже лежит на строчке. Уравнение прямой не изменится. 18 на приведенной ниже диаграмме AE и BD пересекаются в точке C с длинами сегментов, отмеченными, как показано. Опишите преобразование подобия. Это отобразило бы CDE этого треугольника на CBA. Дайте как можно больше подробностей. Итак, во-первых, хорошо, чтобы получить этот треугольник здесь, надеюсь, нам также придется повернуть его. Не отражение, верно? Отражение заставило бы его выглядеть примерно так. Но мы хотим повернуть его. Итак, я скажу ро Т и помните, что вы должны сказать, сколько градусов, 180°. Если это один 80, вам не нужно говорить по часовой стрелке или против часовой стрелки. Это не имеет значения. И надо сказать по делу. Итак, около или около C хорошо, есть первый шаг. Шаг второй, это снова расширение подобия. Я имею в виду, преобразование подобия, вам лучше расшириться. Итак, вам нужно найти масштабный коэффициент. Так что я собираюсь сказать SF для коэффициента масштабирования. Что ж, новое важнее старого, опять же, новое будет большим треугольником. Так что возьмите одну из больших сторон, это не имеет значения. Скажем, 15. Делим на соответствующую старшую сторону. Ну, его соответствующая старшая сторона — это его 9Прямо здесь. Вы могли бы также разделить десять на 6 и получить то же самое. Это просто новое в целом. Итак, 15 разделить на 9, упростите это. Их обоих можно разделить на три, чтобы получилось 5 на три. Так вот. У нас есть все, что нам нужно. Итак, расширяйтесь, вы должны дать центр.
Но мы хотим повернуть его. Итак, я скажу ро Т и помните, что вы должны сказать, сколько градусов, 180°. Если это один 80, вам не нужно говорить по часовой стрелке или против часовой стрелки. Это не имеет значения. И надо сказать по делу. Итак, около или около C хорошо, есть первый шаг. Шаг второй, это снова расширение подобия. Я имею в виду, преобразование подобия, вам лучше расшириться. Итак, вам нужно найти масштабный коэффициент. Так что я собираюсь сказать SF для коэффициента масштабирования. Что ж, новое важнее старого, опять же, новое будет большим треугольником. Так что возьмите одну из больших сторон, это не имеет значения. Скажем, 15. Делим на соответствующую старшую сторону. Ну, его соответствующая старшая сторона — это его 9Прямо здесь. Вы могли бы также разделить десять на 6 и получить то же самое. Это просто новое в целом. Итак, 15 разделить на 9, упростите это. Их обоих можно разделить на три, чтобы получилось 5 на три. Так вот. У нас есть все, что нам нужно. Итак, расширяйтесь, вы должны дать центр. С центром в 70, надеюсь, мы не хотим, чтобы C двигался, верно? Итак, мы знаем, что это должен быть центр. И масштабный коэффициент, я буду сокращать в интересах времени и масштабного коэффициента 5 вместо трех. Хорошо. Последняя часть здесь, если DE равно 5, найдите длину AB с точностью до десятых. Хорошо, ну, я уже знаю коэффициент масштабирования, верно, ребята? Так что я могу просто взять 5 и умножить на масштабный коэффициент 5 третей, хорошо? Если вы поместите это в калькулятор, вы получите 8,3 повторения. Он просит вас округлить до ближайшей десятой, так что это всего лишь 8,3. Хорошо? Если бы вы не хотели использовать коэффициент масштабирования, вы могли бы установить пропорцию, верно? Вы могли бы установить 15 вместо 9. Эти две стороны соответствуют друг другу, равному X на 5. Тогда вы получите, что, 9 X равно 5 умножить на 15, это что, 75? Разделите их оба на 9. И снова вы получите X, равное 8,3 повторения. Который округляется до 8,3. Так что в любом случае вы получите одно и то же.
С центром в 70, надеюсь, мы не хотим, чтобы C двигался, верно? Итак, мы знаем, что это должен быть центр. И масштабный коэффициент, я буду сокращать в интересах времени и масштабного коэффициента 5 вместо трех. Хорошо. Последняя часть здесь, если DE равно 5, найдите длину AB с точностью до десятых. Хорошо, ну, я уже знаю коэффициент масштабирования, верно, ребята? Так что я могу просто взять 5 и умножить на масштабный коэффициент 5 третей, хорошо? Если вы поместите это в калькулятор, вы получите 8,3 повторения. Он просит вас округлить до ближайшей десятой, так что это всего лишь 8,3. Хорошо? Если бы вы не хотели использовать коэффициент масштабирования, вы могли бы установить пропорцию, верно? Вы могли бы установить 15 вместо 9. Эти две стороны соответствуют друг другу, равному X на 5. Тогда вы получите, что, 9 X равно 5 умножить на 15, это что, 75? Разделите их оба на 9. И снова вы получите X, равное 8,3 повторения. Который округляется до 8,3. Так что в любом случае вы получите одно и то же.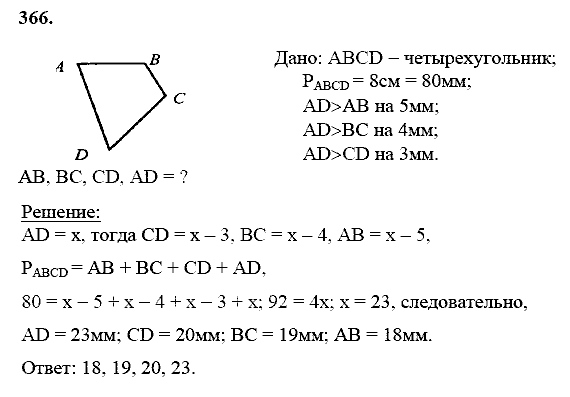 Но если вы уже знаете масштабный коэффициент, ребята, достаточно просто умножить масштабный коэффициент на длину стороны. Ну вот, почти дошло, номер 19. Вот мы и получили на приведенной ниже схеме BD. Он параллелен СЕ. AB равно четырем BC 6 AC равно X плюс три. АС — это Х плюс три. Это буква Д, извините. A D — это X плюс три. Моя группа DE — это два X плюс один, хорошо? С термином значение X все в порядке, так что взгляните, что у нас здесь получилось. Это и есть теорема о размере игрока. Хорошо, нам разрешено использовать для этого боковой сплиттер, что действительно здорово. Это облегчает нашу жизнь. Почему? Вот эти две параллели, поэтому треугольники подобны. У нас есть противоположные стороны. И ни один из них не находится на параллелях. Как у нас было раньше. Итак, сформулируйте свою теорему о размере игрока. Вы можете просто сделать четыре на 6. Равно Х плюс три на два Х плюс один. И есть другие вещи, которые вы можете сделать, хорошо? Вы также можете сделать четыре над Х плюс три равно 6 над двумя Х плюс один, верно? Все эти вещи будут работать.
Но если вы уже знаете масштабный коэффициент, ребята, достаточно просто умножить масштабный коэффициент на длину стороны. Ну вот, почти дошло, номер 19. Вот мы и получили на приведенной ниже схеме BD. Он параллелен СЕ. AB равно четырем BC 6 AC равно X плюс три. АС — это Х плюс три. Это буква Д, извините. A D — это X плюс три. Моя группа DE — это два X плюс один, хорошо? С термином значение X все в порядке, так что взгляните, что у нас здесь получилось. Это и есть теорема о размере игрока. Хорошо, нам разрешено использовать для этого боковой сплиттер, что действительно здорово. Это облегчает нашу жизнь. Почему? Вот эти две параллели, поэтому треугольники подобны. У нас есть противоположные стороны. И ни один из них не находится на параллелях. Как у нас было раньше. Итак, сформулируйте свою теорему о размере игрока. Вы можете просто сделать четыре на 6. Равно Х плюс три на два Х плюс один. И есть другие вещи, которые вы можете сделать, хорошо? Вы также можете сделать четыре над Х плюс три равно 6 над двумя Х плюс один, верно? Все эти вещи будут работать.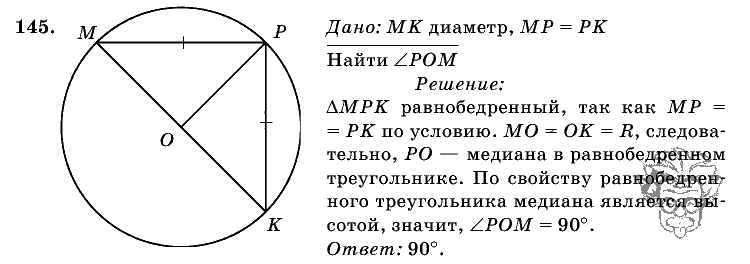 Теперь, когда вы пересекаете умножение, будьте осторожны, вам действительно нужно распределить каждое число. Так что я собираюсь написать это долго, чтобы мы видели это. Это то, что вы действительно делаете. Итак, распределите четыре. Вы получаете 8 X плюс четыре, и вы получаете 6 X плюс 18. Хорошо, переместите 6 X. Идем сюда. У нас получилось два Х плюс четыре. Равно 18. Вычтите четыре из обеих сторон. Вы получаете два X равно 14. И разделите на два, вы получите X равно 7. Итак, вот ваше значение X. Хорошо? Следующая часть CE этих разных цветов равна 30. Мы хотим узнать длину BD. Итак, вот пример, когда вы не можете использовать боковой сплиттер, верно? Потому что мы ищем параллели. Или нам дают параллели. Но можно составить красивую пропорцию. Четыре и X являются частями треугольника ABD. Так что вы можете сделать четыре над X, если хотите. Равно. Теперь 30 является частью большого треугольника ACE. Итак, если вы хотите большой треугольник, вам нужно все HC, что десять на 30. Хорошо, упростите и решите перекрестное умножение, вы получите один 20, равно десяти X, разделите на десять, и вы получите X равно 12 , И это длина.
Теперь, когда вы пересекаете умножение, будьте осторожны, вам действительно нужно распределить каждое число. Так что я собираюсь написать это долго, чтобы мы видели это. Это то, что вы действительно делаете. Итак, распределите четыре. Вы получаете 8 X плюс четыре, и вы получаете 6 X плюс 18. Хорошо, переместите 6 X. Идем сюда. У нас получилось два Х плюс четыре. Равно 18. Вычтите четыре из обеих сторон. Вы получаете два X равно 14. И разделите на два, вы получите X равно 7. Итак, вот ваше значение X. Хорошо? Следующая часть CE этих разных цветов равна 30. Мы хотим узнать длину BD. Итак, вот пример, когда вы не можете использовать боковой сплиттер, верно? Потому что мы ищем параллели. Или нам дают параллели. Но можно составить красивую пропорцию. Четыре и X являются частями треугольника ABD. Так что вы можете сделать четыре над X, если хотите. Равно. Теперь 30 является частью большого треугольника ACE. Итак, если вы хотите большой треугольник, вам нужно все HC, что десять на 30. Хорошо, упростите и решите перекрестное умножение, вы получите один 20, равно десяти X, разделите на десять, и вы получите X равно 12 , И это длина.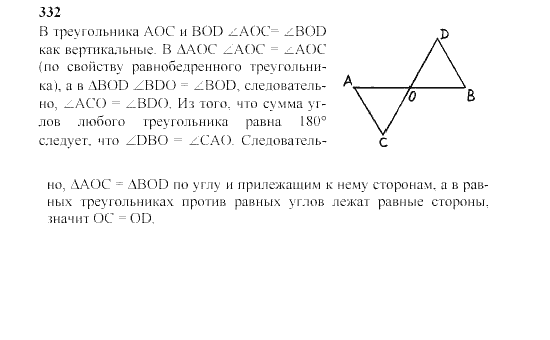 Так что поймите, когда вы можете использовать боковой сплиттер, а когда нет, это будет полезно. Хорошо, поехали. Отрезок a, B имеет концы в минус четыре минус один. Я собираюсь заговорить это. И 8 запятая 7, вот здесь. Хорошо, так вот, вот Б, на этот раз я собираюсь их красиво соединить, чтобы немного облегчить себе жизнь. Хорошо. И посмотрим, чего они хотят. Точка Q лежит где-то на AB, так что мы имеем эту пропорцию. Потрясающий. Итак, мы знаем, как это сделать, чтобы на этот раз получить красивый график. Таким образом, мы можем сделать графически. Итак, создайте свой прямоугольный треугольник. Я собираюсь сделать это. Я буду использовать другой цвет. Я буду продолжать использовать зеленый здесь. Вот вертикаль, вот горизонталь моего прямоугольного треугольника. Хорошо. И теперь нам просто нужно считать коробки, верно? Таким образом, от верха до правого нижнего угла у нас есть один, два, три, четыре, 5, 6, 7, 8, 9., десять, 11, 12 ящиков. И вверх и вниз у нас есть один, два, три, четыре, 5, 6, 7, 8 ящиков.
Так что поймите, когда вы можете использовать боковой сплиттер, а когда нет, это будет полезно. Хорошо, поехали. Отрезок a, B имеет концы в минус четыре минус один. Я собираюсь заговорить это. И 8 запятая 7, вот здесь. Хорошо, так вот, вот Б, на этот раз я собираюсь их красиво соединить, чтобы немного облегчить себе жизнь. Хорошо. И посмотрим, чего они хотят. Точка Q лежит где-то на AB, так что мы имеем эту пропорцию. Потрясающий. Итак, мы знаем, как это сделать, чтобы на этот раз получить красивый график. Таким образом, мы можем сделать графически. Итак, создайте свой прямоугольный треугольник. Я собираюсь сделать это. Я буду использовать другой цвет. Я буду продолжать использовать зеленый здесь. Вот вертикаль, вот горизонталь моего прямоугольного треугольника. Хорошо. И теперь нам просто нужно считать коробки, верно? Таким образом, от верха до правого нижнего угла у нас есть один, два, три, четыре, 5, 6, 7, 8, 9., десять, 11, 12 ящиков. И вверх и вниз у нас есть один, два, три, четыре, 5, 6, 7, 8 ящиков.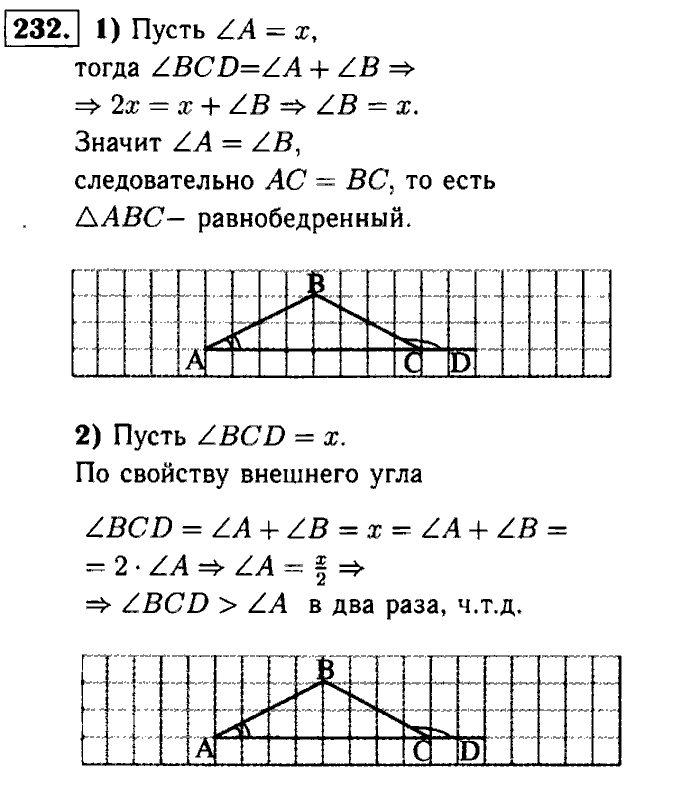 Хорошо? Нам нравится видеть эти числа 12 и 8, верно? Потому что соотношение три к одному говорит нам, что мы разбиваем на четыре части. 12 и 8 делятся на четыре. Это будет легко. Так что, если хотите, можете сказать, что AQ составляет три четверти всего. А БК — это только одна четвертая часть всего этого. И вы можете использовать a или вы можете использовать B, это не имеет значения. Но сначала мы должны разбить его. Итак, если я хочу разбить 12 на четверти, мне нужно пройти каждые три клетки, потому что 12 разделить на четыре равно трем. Итак, я начну раз, два, три, разобью раз, два, три, два, три, раз, два, три, хорошо. И убедитесь, что у вас есть четыре сегмента. Один два три четыре. Хорошо, 8, снова 8 разделить на четыре. Их два, так что я буду ходить через каждые два ящика. Раз, два, два, раз, два, раз, два. Убедитесь, что у вас есть четыре сегмента. Я делаю. Теперь я начну с а, а это три четверти, так что считайте от а один, два, три раздела. Хорошо? Это будет моя вертикальная работа.
Хорошо? Нам нравится видеть эти числа 12 и 8, верно? Потому что соотношение три к одному говорит нам, что мы разбиваем на четыре части. 12 и 8 делятся на четыре. Это будет легко. Так что, если хотите, можете сказать, что AQ составляет три четверти всего. А БК — это только одна четвертая часть всего этого. И вы можете использовать a или вы можете использовать B, это не имеет значения. Но сначала мы должны разбить его. Итак, если я хочу разбить 12 на четверти, мне нужно пройти каждые три клетки, потому что 12 разделить на четыре равно трем. Итак, я начну раз, два, три, разобью раз, два, три, два, три, раз, два, три, хорошо. И убедитесь, что у вас есть четыре сегмента. Один два три четыре. Хорошо, 8, снова 8 разделить на четыре. Их два, так что я буду ходить через каждые два ящика. Раз, два, два, раз, два, раз, два. Убедитесь, что у вас есть четыре сегмента. Я делаю. Теперь я начну с а, а это три четверти, так что считайте от а один, два, три раздела. Хорошо? Это будет моя вертикальная работа.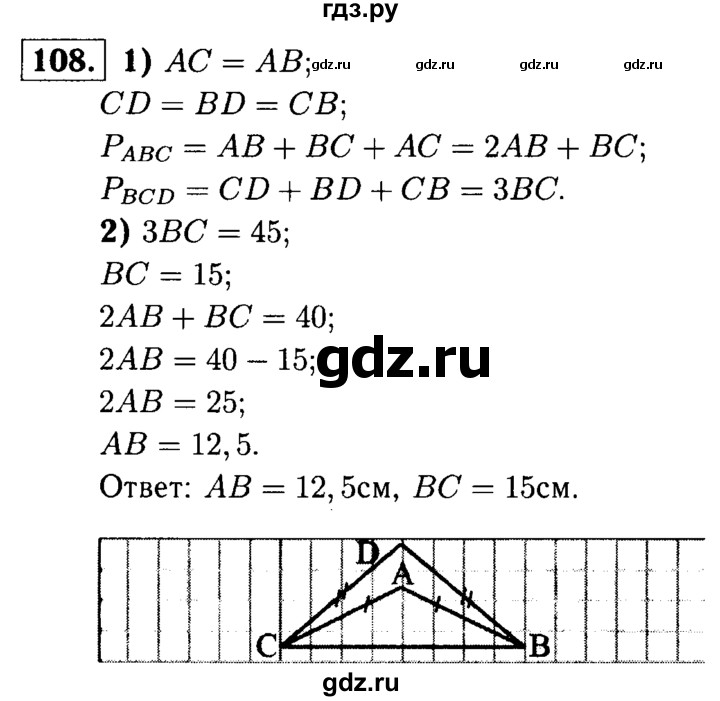 Опять же, я буду продолжать использовать a, так как a находится внизу. Я буду считать снизу один, два, три. Посмотрите, где они соединяются, и это будет моей точкой зрения. В правильно? Итак, Q — это просто 5 запятая 5. Это 5 запятая 5. Вам действительно не нужны равные, но если вы этого хотите. Следующая часть, каково отношение Q к длине AB? Итак, нам нужно соотношение, Q к A, B, ну, подумайте об этом. Мы уже говорили, что AQ составляет три четверти всего этого. Это означает, что AB — это все, или четыре четверти, о чем странно думать, но это работает. Таким образом, 8 Q к AB — это всего лишь соотношение четыре к трем. Если вы хотите, вы можете взять формулу расстояния для AQ и AB и найти отношение оттуда. Но этого достаточно. Просто сделать четыре на три. Ладно, последний вопрос. Деревянная конструкция имеет форму в виде прямоугольного треугольника. Так что посмотрите уже на мою схему. Это уже выглядит как диаграмма, для которой мы можем использовать наши деревья. Или холмы, или дерзость, если вам нравится это использовать.
Опять же, я буду продолжать использовать a, так как a находится внизу. Я буду считать снизу один, два, три. Посмотрите, где они соединяются, и это будет моей точкой зрения. В правильно? Итак, Q — это просто 5 запятая 5. Это 5 запятая 5. Вам действительно не нужны равные, но если вы этого хотите. Следующая часть, каково отношение Q к длине AB? Итак, нам нужно соотношение, Q к A, B, ну, подумайте об этом. Мы уже говорили, что AQ составляет три четверти всего этого. Это означает, что AB — это все, или четыре четверти, о чем странно думать, но это работает. Таким образом, 8 Q к AB — это всего лишь соотношение четыре к трем. Если вы хотите, вы можете взять формулу расстояния для AQ и AB и найти отношение оттуда. Но этого достаточно. Просто сделать четыре на три. Ладно, последний вопрос. Деревянная конструкция имеет форму в виде прямоугольного треугольника. Так что посмотрите уже на мою схему. Это уже выглядит как диаграмма, для которой мы можем использовать наши деревья. Или холмы, или дерзость, если вам нравится это использовать. Поскольку основание 12 футов, а высота 8, он поддерживается проволокой, натянутой от моря до земли. Так что нет никакой опорной проволоки. В этот момент, хорошо? Чтобы провода держались перпендикулярно, это нам уже нарисовали. На каком расстоянии от точки B должна располагаться точка DB. Поэтому я хочу знать это прямо здесь. Опять же, у вас есть только три варианта для вашего дерева. Раз два три. Меня не волнует AC, верно? Меня не волнует CT, но я знаю кое-что о CB, так что это то, что меня волнует. Итак, опять же, это высота, часть посередине. Это не всегда. И еще, мое дерево здесь, вот мое дерево, хорошо? Не будет X, это не всегда X, ребята. Иногда бывает, но не обязательно. Итак, мое дерево снова идет вверху слева, внизу справа, 8 и 8. Если дерево посередине, оно может упасть влево, верно? Это будет 12. Он также может упасть вправо. Это будет X, так что это проще, на самом деле, перекрестное умножение. 8 и 8, 64, равно 12 X, разделите на 12, и вы получите округление до ближайшей десятой.
Поскольку основание 12 футов, а высота 8, он поддерживается проволокой, натянутой от моря до земли. Так что нет никакой опорной проволоки. В этот момент, хорошо? Чтобы провода держались перпендикулярно, это нам уже нарисовали. На каком расстоянии от точки B должна располагаться точка DB. Поэтому я хочу знать это прямо здесь. Опять же, у вас есть только три варианта для вашего дерева. Раз два три. Меня не волнует AC, верно? Меня не волнует CT, но я знаю кое-что о CB, так что это то, что меня волнует. Итак, опять же, это высота, часть посередине. Это не всегда. И еще, мое дерево здесь, вот мое дерево, хорошо? Не будет X, это не всегда X, ребята. Иногда бывает, но не обязательно. Итак, мое дерево снова идет вверху слева, внизу справа, 8 и 8. Если дерево посередине, оно может упасть влево, верно? Это будет 12. Он также может упасть вправо. Это будет X, так что это проще, на самом деле, перекрестное умножение. 8 и 8, 64, равно 12 X, разделите на 12, и вы получите округление до ближайшей десятой. Когда вы округлите его, вы получите X равно 5,3, если вы округлите его правильно. Хорошо, в следующем фрагменте сказано с точностью до десятой доли фута, какой длины ваш поддерживающий трос? Итак, теперь мне нужно новое дерево, верно? Я позвоню в службу поддержки. Я уже использовал X здесь. Итак, я назову его Y, хорошо? Теперь вот дно. Вот нижняя, это X, которую я теперь знаю, я действительно должен переписать это как 5.3. Хорошо? Поддерживающая проволока будет моим деревом. Почему? Потому что теперь я забочусь о проволоке поддержки, верно? Меня не волнует эта линия в середине. Меня волнует только опорный провод. Так что настройте свою пропорцию, хорошо? Для поддержки проволока будет моим деревом. Это означает, что у меня будут Y и Y в левом верхнем углу справа. Теперь может ли опорная проволока упасть на вершину X, которая равна 5,3? Да. Может ли эта опорная проволока складываться поверх 12 только 12? Нет. Он не может внезапно перепрыгнуть сюда, а затем сложить. Это не имеет смысла. Деревья так не делают.
Когда вы округлите его, вы получите X равно 5,3, если вы округлите его правильно. Хорошо, в следующем фрагменте сказано с точностью до десятой доли фута, какой длины ваш поддерживающий трос? Итак, теперь мне нужно новое дерево, верно? Я позвоню в службу поддержки. Я уже использовал X здесь. Итак, я назову его Y, хорошо? Теперь вот дно. Вот нижняя, это X, которую я теперь знаю, я действительно должен переписать это как 5.3. Хорошо? Поддерживающая проволока будет моим деревом. Почему? Потому что теперь я забочусь о проволоке поддержки, верно? Меня не волнует эта линия в середине. Меня волнует только опорный провод. Так что настройте свою пропорцию, хорошо? Для поддержки проволока будет моим деревом. Это означает, что у меня будут Y и Y в левом верхнем углу справа. Теперь может ли опорная проволока упасть на вершину X, которая равна 5,3? Да. Может ли эта опорная проволока складываться поверх 12 только 12? Нет. Он не может внезапно перепрыгнуть сюда, а затем сложить. Это не имеет смысла. Деревья так не делают.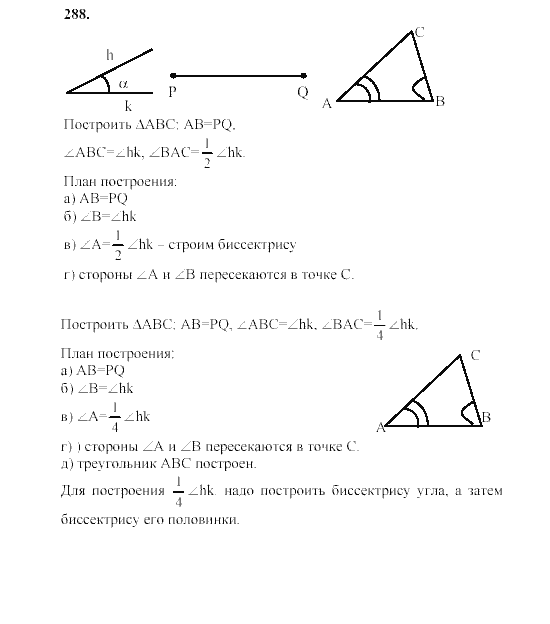 Вот почему мы используем аналогию с деревом. Но это может упасть прямо вниз и упасть на них обоих, верно? Итак, найдите сумму. 12 плюс 5,3 равно 17,3. Так что используйте этот 17.3. Ладно, крест умножь и реши. Y в квадрате равно, вы получите 91.69. Возьмите квадратный корень и помните, что вы округляете до ближайшей десятой, так что вы получите Y равно 9,57, что округляется до 9,6. Ноги. И вот ваш окончательный ответ. Итак, два вопроса с одной и той же диаграммой, но с использованием разных сторон в качестве деревьев без кавычек. Ладно, надеюсь, это было полезно. Хорошо, ребята, изучайте, убедитесь, что вы знаете разные вещи: медианы, высоту, хорошо, отношения, новое по сравнению со старым, хорошо? Масштабное расширение, все такое хорошее. Хорошо, пожалуйста, подойдите к тому, кто является вашим учителем, для дополнительной помощи. И удачи.
Вот почему мы используем аналогию с деревом. Но это может упасть прямо вниз и упасть на них обоих, верно? Итак, найдите сумму. 12 плюс 5,3 равно 17,3. Так что используйте этот 17.3. Ладно, крест умножь и реши. Y в квадрате равно, вы получите 91.69. Возьмите квадратный корень и помните, что вы округляете до ближайшей десятой, так что вы получите Y равно 9,57, что округляется до 9,6. Ноги. И вот ваш окончательный ответ. Итак, два вопроса с одной и той же диаграммой, но с использованием разных сторон в качестве деревьев без кавычек. Ладно, надеюсь, это было полезно. Хорошо, ребята, изучайте, убедитесь, что вы знаете разные вещи: медианы, высоту, хорошо, отношения, новое по сравнению со старым, хорошо? Масштабное расширение, все такое хорошее. Хорошо, пожалуйста, подойдите к тому, кто является вашим учителем, для дополнительной помощи. И удачи.Удалить рекламу
BitsnClicks
BitsnClicks01
Креативный дизайн
Наши услуги по творческому дизайну помогут удовлетворить любые творческие потребности. Оставайтесь уникальными и скажите «нет» бесплатным онлайн-дизайнам или шаблонам.
Оставайтесь уникальными и скажите «нет» бесплатным онлайн-дизайнам или шаблонам.
02
Простые в управлении решения
Мы предоставляем цифровые бизнес-решения, которыми вы можете легко управлять и обслуживать
03
Адаптивный и Pixel Perfect Design
Мы верим в совершенство. Вы получаете именно то, что просили. Наш веб-дизайн идеален для пикселей и совместим с различными устройствами
Наши услуги
Мы повышаем успех бизнеса с помощью технологий
Веб-дизайн
Веб-дизайн указывает на дизайн веб-сайта, который должен отображаться в браузерах.
Электронная коммерция
Мы являемся лидерами в создании вознаграждений с помощью гибкого веб-дизайна и новых технологий UX.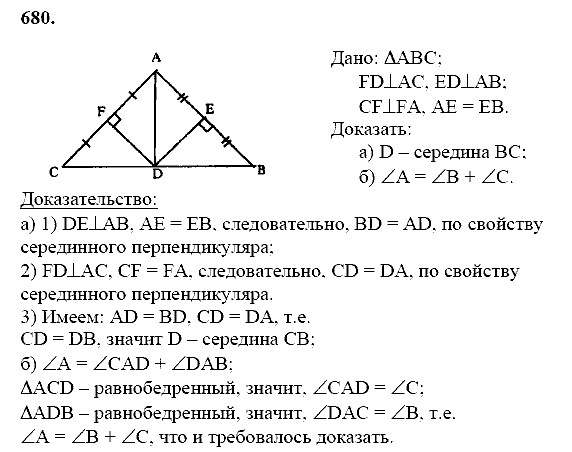
Веб-разработка
Заявите о себе в Интернете, чтобы расширить свой бизнес с помощью бесплатного обслуживания вашего присутствия.
Графический дизайн
У нас есть команда очень творческих графических дизайнеров. Мы используем новейшие технологии и современный дизайн для вашего бренда, который привлекает внимание ваших клиентов.
SEO
Мы оптимизируем веб-сайты с помощью SEO на странице, технического SEO и SEO вне страницы, чтобы ваш сайт отображался в верхней части результатов поиска поисковых систем.
Ибей
Мы предлагаем настройку магазина eBay, индивидуальный дизайн и настройку шаблона, а также оптимизацию ваших объявлений
Цифровой маркетинг
Мы предлагаем Facebook, Instagram и Google Ads, а также кампании PPC
Познакомьтесь с нашей командой
Lorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempor incididunt ut Labore et dolore magna aliqua.
Мухаммад Аднан Джамиль
ОсновательАтта Улла Турк
Бизнес-менеджерАбдул Маннан
Графический дизайнерЗишан Хан
SEO ExecutiveДжамиль Бейг
Разработчик WordPressНавид Ахмад
UI/UX дизайнерСармад Сохаил
Разработчик PhpМухаммад Фейсал
Контроль качества и поддержкаХафиз Акиб
Разработчик Php LaravelНаше портфолио
Мы со страстью и преданностью создаем лучшие веб- и цифровые решения в BitsnClicks
Наш Testomonial
Lorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempor incididunt ut Labore et dolore magna aliqua.
Фрэнк Бернал
— Дизайн логотипа
Мой первый заказ на Fiverr.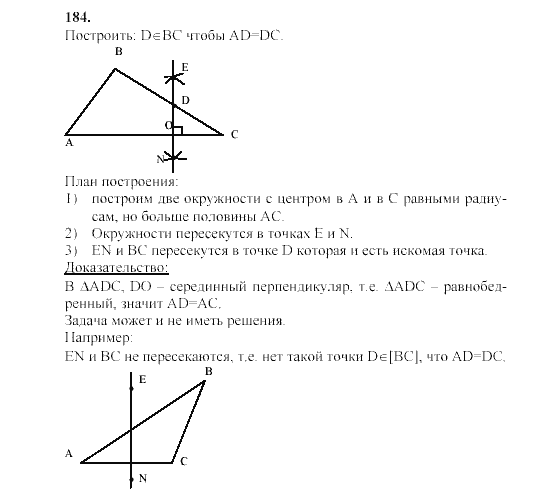 Я не был разочарован. Они сделали все возможное, дав мне именно то, что мне было нужно, и им немного. Я получил больше, чем заплатил, потому что они были достаточно любезны, чтобы дать мне оригинал и исправления. Большое спасибо, я с нетерпением жду возможности поработать с вами в будущем!
Я не был разочарован. Они сделали все возможное, дав мне именно то, что мне было нужно, и им немного. Я получил больше, чем заплатил, потому что они были достаточно любезны, чтобы дать мне оригинал и исправления. Большое спасибо, я с нетерпением жду возможности поработать с вами в будущем!
Трэвис Берг
— Дизайн логотипа
Эти продавцы относились ко мне как к самому ценному покупателю! Они чрезвычайно интуитивны и креативны. Кроме того, я обнаружил, что они очень уважительно относятся к моим идеям и внимательно слушают то, что я описываю. Я буду продолжать полагаться на них для ВСЕХ моих проектов! Уникальный дизайн логотипа Спасибо!!!
Маргаритка9
— Дизайн сайта
Очень профессиональный продавец. Я очень доволен предоставленной услугой. конечный результат был именно таким, как я себе представлял. продавец также сделал все возможное, чтобы убедиться, что я понял, как использовать продукт (html-шаблон), даже включил личную видео-инструкцию. настоятельно рекомендую. Спасибо.
Я очень доволен предоставленной услугой. конечный результат был именно таким, как я себе представлял. продавец также сделал все возможное, чтобы убедиться, что я понял, как использовать продукт (html-шаблон), даже включил личную видео-инструкцию. настоятельно рекомендую. Спасибо.
Антоничжоу
— Дизайн сайта
Аднан сделал работу очень точно. Он имеет опыт создания веб-сайтов и реагирует на различные требования профессиональными решениями.
Джеккартер729
— ебей
Разработал шаблон листинга для своего магазина eBay. Он был невероятно общительным, услужливым и заставил меня почувствовать, что особых проблем не возникло. Мало того, что качество работы было отличным, но он был очень терпелив со мной, так как я новичок в мире аутсорсинга. Его приверженность срокам была превосходной, на самом деле это я не давал ему информацию, которая ему требовалась, быстро, но он был очень понимающим. Буду и обязательно буду рекомендовать! НЕ СТЕСНЯЙТЕСЬ! Еще раз спасибо брат!
Он был невероятно общительным, услужливым и заставил меня почувствовать, что особых проблем не возникло. Мало того, что качество работы было отличным, но он был очень терпелив со мной, так как я новичок в мире аутсорсинга. Его приверженность срокам была превосходной, на самом деле это я не давал ему информацию, которая ему требовалась, быстро, но он был очень понимающим. Буду и обязательно буду рекомендовать! НЕ СТЕСНЯЙТЕСЬ! Еще раз спасибо брат!
550
+
Завершенные проекты
300
+
Счастливые клиенты
6000
+
Отработано часов
4,8/5,0
Средний рейтинг
Свяжитесь с нами
Математика – Quiz Shop
Не можете найти то, что ищете? Дайте нам знать!
Обзор 2D-геометрии (8 класс)
3 вопроса 20 использований
Обзор двухмерной геометрии (8 класс)
- Обычная цена
- $0.
 00
00 - Обычная цена
-
- Цена продажи
- $0.00 Распродажа
- Цена за единицу товара
- / за
- Доступность
- Распроданный
Трехмерные формы и сети
30 вопросов 38 использований
Трехмерные формы и сети
- Обычная цена
- $0.00
- Обычная цена
-
- Цена продажи
- $0.00 Распродажа
- Цена за единицу товара
- /за
- Доступность
- Распроданный
Свойства 3D-формы
4 вопроса 16 использований
Свойства 3D-формы
- Обычная цена
- $0.
 00
00 - Обычная цена
-
- Цена продажи
- $0.00 Распродажа
- Цена за единицу товара
- /за
- Доступность
- Распроданный
Имена и свойства 3D-фигур
4 вопроса 9 использований
Названия и свойства трехмерных фигур
- Обычная цена
- $0.00
- Обычная цена
-
- Цена продажи
- $0.00 Распродажа
- Цена за единицу товара
- /за
- Доступность
- Распроданный
Модульный тест по алгебре для 6-го класса
32 вопроса 0 Использование
Модульный тест по алгебре для 6-го класса
- Обычная цена
- $0.
 00
00 - Обычная цена
-
- Цена продажи
- $0.00 Распродажа
- Цена за единицу товара
- /за
- Доступность
- Распроданный
Модульный тест по алгебре для 6-го класса
28 вопросов 0 Использование
Модульный тест по алгебре для 6-го класса
- Обычная цена
- $0.00
- Обычная цена
-
- Цена продажи
- $0.00 Распродажа
- Цена за единицу товара
- /за
- Доступность
- Распроданный
Повторение геометрии для 6-го класса
6 вопросов 18 использований
Обзор геометрии для 6-го класса
- Обычная цена
- $0.
 00
00 - Обычная цена
-
- Цена продажи
- $0.00 Распродажа
- Цена за единицу товара
- /за
- Доступность
- Распроданный
Математическая разминка для 6-го класса
4 вопроса 2 использования
Разминка по математике для 6-го класса
- Обычная цена
- $0.00
- Обычная цена
-
- Цена продажи
- $0.00 Распродажа
- Цена за единицу товара
- /за
- Доступность
- Распроданный
Математическая разминка для 6-го класса
4 вопроса 1 Использование
Разминка по математике для 6-го класса
- Обычная цена
- $0.


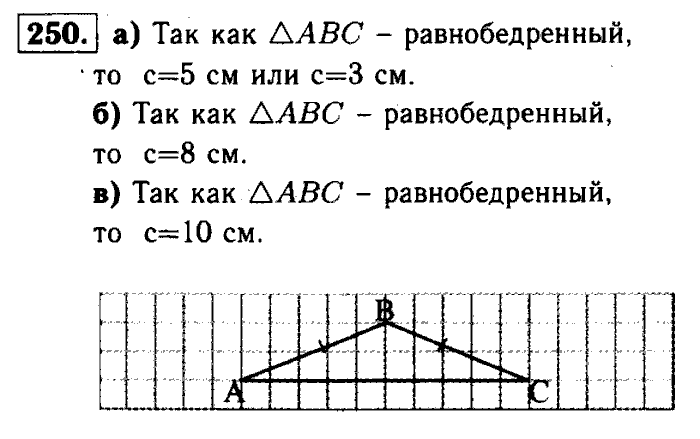 Сумма двух векторов
Сумма двух векторов
 00
00 00
00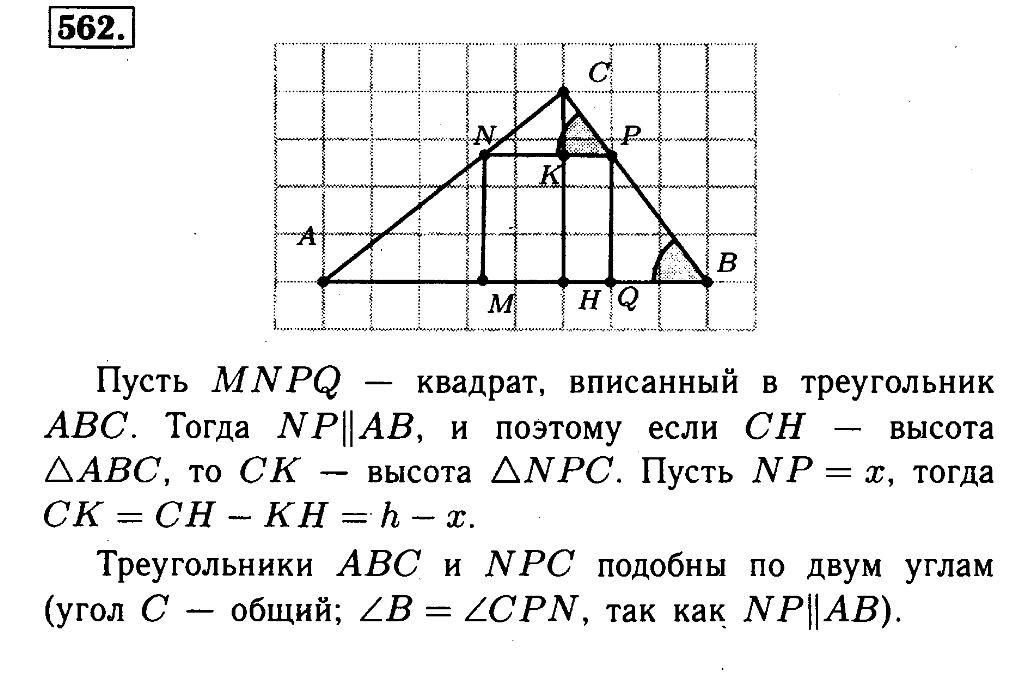 00
00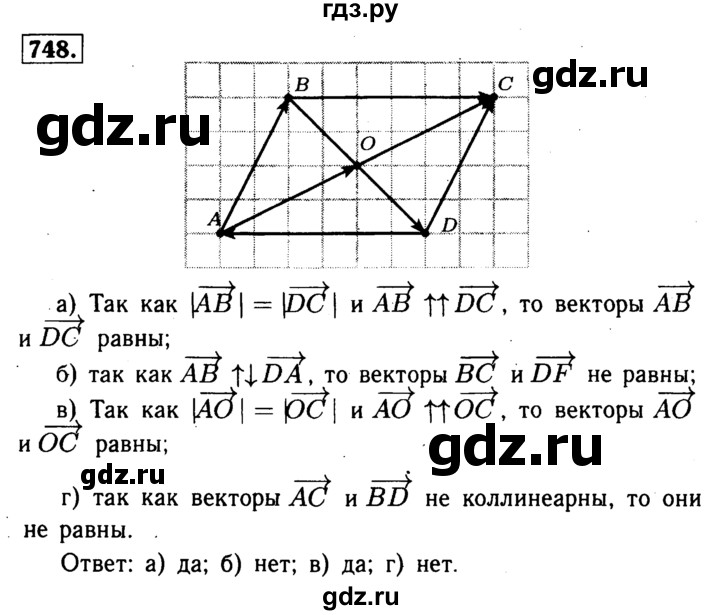 00
00