Слушать УМК Шмелева 9 класс бесплатно
- Стр.11 Глава 1. Упражнение 3. Значения устаревших слов
- Стр.12 Глава 1. Упражнение 4. Значение слова «ночник»
- Стр.

- Стр.19 Глава 1. Упражнение 15. Гласные Е, Ё, Ю, Я, И
- Стр.19 Глава 1. Упражнение 17. В. А. Плунгян. «Почему языки такие разные»
- Стр.
 28
Глава 1. Упражнение 28. Слова для записи
28
Глава 1. Упражнение 28. Слова для записи - Стр.29 Глава 1. Упражнение 30. Е. А. Земская. О словообразовании
- Стр.
 35
Глава 1. Упражнение 37. Этимология слова "атлас"
35
Глава 1. Упражнение 37. Этимология слова "атлас" - Стр.37 Глава 1. Упражнение 39. Употребление фразеологических оборотов
- Стр.40 Глава 1. Упражнение 44. С. И. Ожегов
- Стр.

- Стр.48 Глава 1. Упражнение 53. Заметки в пути на южный берег Крыма
- Стр.50 Глава 1. Упражнение 55. Сочетания слов в предложении
- Стр.
 59
Глава 1. Упражнение 65. В. Башмакова. Как работает мозг
59
Глава 1. Упражнение 65. В. Башмакова. Как работает мозг - Стр.63 Глава 1. Упражнение 69. Мнения о тексте Ю. Коваля
- Стр.67 Глава 1. Упражнение 76. Ю. Коваль. Полёт
- Стр.
 74
Глава 1. Упражнение 84. И. Грекова. Фрагмент рассказа с прямой речью
74
Глава 1. Упражнение 84. И. Грекова. Фрагмент рассказа с прямой речью - Стр.85 Глава 1. Упражнение 99. Фрагмент из книги К. Г. Паустовского
- Стр.91 Глава 1. Упражнение 105. Д. С. Лихачёв. Самое большое
- Стр.

- Стр.100 Глава 1. Упражнение 114. Слова для записи
- Стр.100 Глава 1. Упражнение 115. Слова для записи
- Стр.
 109
Глава 1. Упражнение 142. Д. С. Лихачёв. Любите читать!
109
Глава 1. Упражнение 142. Д. С. Лихачёв. Любите читать! - Стр.115 Глава 2. Упражнение 4. WWW — «всемирная паутина»
- Стр.120 Глава 2. Упражнение 11. Сложные предложения
- Стр.
 124
Глава 2. Упражнение 14. В. Железников. Последний парад (отрывок)
124
Глава 2. Упражнение 14. В. Железников. Последний парад (отрывок) - Стр.129 Глава 2. Упражнение 18. Хрустальный плафон Мраморного зала этнографического музея
- Стр.134 Глава 2. Упражнение 23. Черкасск
- Стр.
 139
Глава 2. Упражнение 29. Нормы общения в разных странах
139
Глава 2. Упражнение 29. Нормы общения в разных странах - Стр.142 Глава 2. Упражнение 33. Пословицы и поговорки
- Стр.144 Глава 2. Упражнение 37. Л. Алексеева, С. Шервинский. Стихотворения
- Стр.
 150
Глава 2. Упражнение 41. А. Герасимова. Первый раз в новый класс
150
Глава 2. Упражнение 41. А. Герасимова. Первый раз в новый класс - Стр.151 Глава 2. Упражнение 42. А. Герасимова. Первый раз в новый класс (Продолжение)
- Стр.157 Глава 2. Упражнение 47. Ивы. Диктант
- Стр.
 161
Глава 2. Упражнение 54. А. П. Бородин
161
Глава 2. Упражнение 54. А. П. Бородин - Стр.167 Глава 2. Упражнение 60. Ф. Искандер. Скорбь
- Стр.167 Глава 2. Упражнение 62. Ростовский Кремль. Диктант
- Стр.
 170
Глава 2. Упражнение 65. Кремль
170
Глава 2. Упражнение 65. Кремль - Стр.183 Глава 2. Упражнение 80. Ответ И. Леенсона
- Стр.184 Глава 2. Упражнение 82. Слова для записи
- Стр.
 184
Глава 2. Упражнение 83. Слова для записи
184
Глава 2. Упражнение 83. Слова для записи - Стр.193 Глава 2. Упражнение 113. Человек и природа
- Стр.198 Глава 3. Упражнение 5. Н. М. Шанский. Воспоминания о Г. О. Винокуре
- Стр.
 204
Глава 3. Упражнение 11. А. В. Драбкина. Волшебные яблоки (отрывок)
204
Глава 3. Упражнение 11. А. В. Драбкина. Волшебные яблоки (отрывок) - Стр.208 Глава 3. Упражнение 14. Союзы и союзные слова
- Стр.216 Глава 3. Упражнение 22. А. Арсирий. Разница между словами "какой" и "который"
- Стр.
 218
Глава 3. Упражнение 24. В. А. Белов. Диктант
218
Глава 3. Упражнение 24. В. А. Белов. Диктант - Стр.222 Глава 3. Упражнение 27. Сложноподчинённые предложения
- Стр.225 Глава 3. Упражнение 30. Предложения для записи_2
- Стр.
 226
Глава 3. Упражнение 32. Дом Пушкина (По Е. Храмову)
226
Глава 3. Упражнение 32. Дом Пушкина (По Е. Храмову) - Стр.232 Глава 3. Упражнение 36. Средства связи частей сложноподчинённых предложений
- Стр.234 Глава 3. Упражнение 39. А. Блок. (По К. Бальмонту)
- Стр.
 240
Глава 3. Упражнение 47. Мнение историка А. Б. Каменского о князе Г. А. Потёмкине
240
Глава 3. Упражнение 47. Мнение историка А. Б. Каменского о князе Г. А. Потёмкине - Стр.246 Глава 3. Упражнение 53. СПП с обстоятельственными придаточными времени
- Стр.252 Глава 3. Упражнение 59. Воробьи. (По Я. Перельману)
- Стр.
 259
Глава 3. Упражнение 66. Самые необычные живые существа (По А. Торгашёву)
259
Глава 3. Упражнение 66. Самые необычные живые существа (По А. Торгашёву) - Стр.260 Глава 3. Упражнение 66. Самые необычные живые существа (По А. Торгашёву)_2
- Стр.263 Глава 3. Упражнение 69. Афганская борзая. (По Е. Коньковой)
- Стр.
 264
Глава 3. Упражнение 71. Ключевской природный парк
264
Глава 3. Упражнение 71. Ключевской природный парк - Стр.269 Глава 3. Упражнение 76. СПП с обстоятельственными придаточными условия
- Стр.275 Глава 3. Упражнение 81. СПП с обстоятельственными придаточными уступки
- Стр.
 279
Глава 3. Упражнение 85. В. Голявкин. Диктант
279
Глава 3. Упражнение 85. В. Голявкин. Диктант - Стр.279 Глава 3. Упражнение 85. В. Голявкин. Отрывок из рассказа
- Стр.284 Глава 3. Упражнение 89. Сложноподчинённые предложения
- Стр.
 287
Глава 3. Упражнение 95. Н. Е. Раковская. Диктант
287
Глава 3. Упражнение 95. Н. Е. Раковская. Диктант - Стр.301 Глава 3. Упражнение 110. Диктант
- Стр.308 Глава 3. Упражнение 117. Изложение
- Стр.
 311
Глава 3. Упражнение 120. Н. С. Валгина. Функционально-смысловые типы речи
311
Глава 3. Упражнение 120. Н. С. Валгина. Функционально-смысловые типы речи - Стр.317 Глава 3. Упражнение 126. Фрагмент радиопередачи «Грамотей»
- Стр.318 Глава 3. Упражнение 127. Высказывание Т. Г. Винокур
- Стр.
 319
Глава 3. Упражнение 128. Интервью с Т. Г. Винокур
319
Глава 3. Упражнение 128. Интервью с Т. Г. Винокур - Стр.324 Глава 3. Упражнение 134. Интервью с Т. Г. Винокур_2
- Стр.324 Глава 3. Упражнение 135. Д. С. Лихачев. Любите читать!
- Стр.
 326
Глава 3. Упражнение 136. Ударение в словах
326
Глава 3. Упражнение 136. Ударение в словах - Стр.326 Глава 3. Упражнение 137. Твёрдые согласные перед буквой "Е"
- Стр.326 Глава 3. Упражнение 138. Словарные слова
- Стр.
 327
Глава 3. Упражнение 143. Предложения с речевыми ошибками
327
Глава 3. Упражнение 143. Предложения с речевыми ошибками - Стр.334 Глава 3. Упражнение 165. О дурных и хороших влияниях. Изложение
- Стр.338 Глава 4. Упражнение 2. Л. В. Щерба. Современный русский литературный язык»
- Стр.
 340
Глава 4. Упражнение 5. Три основных типа интонации
340
Глава 4. Упражнение 5. Три основных типа интонации - Стр.341 Глава 4. Упражнение 5. Восходящая и нисходящая интонация
- Стр.344 Глава 4. Упражнение 7. Сложные предложения
- Стр.
 348
Глава 4. Упражнение 11. М. М. Пришвин. Диктант
348
Глава 4. Упражнение 11. М. М. Пришвин. Диктант - Стр.349 Глава 4. Упражнение 13. А. И. Куприн. Олеся (отрывок)
- Стр.356 Глава 4. Упражнение 20. Сложные предложения
- Стр.
 362
Глава 4. Упражнение 24. Л. Нечаев. Диктант
362
Глава 4. Упражнение 24. Л. Нечаев. Диктант - Стр.368 Глава 4. Упражнение 32. Д. Гранин. Зубр (отрывок)
- Стр.373 Глава 4. Упражнение 38. Точка с запятой
- Стр.
 377
Глава 4. Упражнение 45. Л. Нечаев. Диктант
377
Глава 4. Упражнение 45. Л. Нечаев. Диктант - Стр.380 Глава 4. Упражнение 50. А. М. Пешковский. Биография
- Стр.385 Глава 4. Упражнение 57. Средства выразительности речи
- Стр.
 387
Глава 4. Упражнение 58. Морфемы, участвующие в создании выразительной речи
387
Глава 4. Упражнение 58. Морфемы, участвующие в создании выразительной речи - Стр.389 Глава 4. Упражнение 61. Ударение в словах
- Стр.389 Глава 4. Упражнение 62. Твёрдые согласные перед "E"
- Стр.
 391
Глава 4. Упражнение 71. Предложения с речевыми ошибками
391
Глава 4. Упражнение 71. Предложения с речевыми ошибками - Стр.398 Глава 4. Упражнение 93. В. Железников. «Чучело» (отрывок)
Хотите сохранить материал на будущее? Отправьте себе на почту
в избранноеТолько зарегистрированные пользователи могут добавлять в избранное.
Войдите, пожалуйста.
Назад к аудио
по линии Линия УМК А. Д. Шмелева. Русский язык (5-9)
Д. Шмелева. Русский язык (5-9)
Дополнительные материалы по теме
Учебные издания по теме
Шмелев А.Д.
Русский язык. 9 класс. Учебник (с приложением)
Донскова О.В.
Русский язык. 9 класс. Контрольные и проверочные работы.
Шапиро Н.А.
Русский язык. 9 класс. Рабочая тетрадь
Флоренская Э.А.
Русский язык. 9 класс. Рабочая тетрадь. Правописание, культура речи
Оценка разработки
Для оценки работы вам необходимо авторизоваться на сайте
Войти или зарегистрироваться
Ограничение доступа
Для доступа к материалу требуется регистрация на сайте
Войти или зарегистрироваться
Нужна помощь?
ГДЗ Алгебра 9 класс Макарычев, Миндюк, Нешков, Суворова
Близится выпускной экзамен и степень стресса повышается, а значит многим ученикам пригодится ГДЗ по алгебре для 9 класса Макарычева. Весомый блок задач на ОГЭ составляет именно алгебра. Благодаря правильному решению этих заданий можно получить высокую отметку. Учебник полостью соответствует требованиям ФГОС, поэтому программа затрагивает все темы, которые школьник может встретить на экзамене.
Весомый блок задач на ОГЭ составляет именно алгебра. Благодаря правильному решению этих заданий можно получить высокую отметку. Учебник полостью соответствует требованиям ФГОС, поэтому программа затрагивает все темы, которые школьник может встретить на экзамене.
Хорошая успеваемость, в свою очередь, также играет большую роль под конец девятого года обучения, потому что именно средний балл аттестата влияет на возможность выбора профильного класса или учебного заведения среднего профессионального образования. Если выбор школьника падает на техническую специальность, то учебник по алгебре для 9 класса Макарычева поможет хорошо подготовиться к предстоящему этапу обучения.
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394959697989910010110210310410510610710810911011111211311411511611711811912012112212312412512612712812913013113213313413513613713813914014114214314414514614714814915015115215315415515615715815916016116216316416516616716816917017117217317417517617717817918018118218318418518618718818919019119219319419519619719819920020120220320420520620720820921021121221321421521621721821922022122222322422522622722822923023123223323423523623723823924024124224324424524624724824925025125225325425525625725825926026126226326426526626726826927027127227327427527627727827928028128228328428528628728828929029129229329429529629729829930030130230330430530630730830931031131231331431531631731831932032132232332432532632732832933033133233333433533633733833934034134234334434534634734834935035135235335435535635735835936036136236336436536636736836937037137237337437537637737837938038138238338438538638738838939039139239339439539639739839940040140240340440540640740840941041141241341441541641741841942042142242342442542642742842943043143243343443543643743843944044144244344444544644744844945045145245345445545645745845946046146246346446546646746846947047147247347447547647747847948048148248348448548648748848949049149249349449549649749849950050150250350450550650750850951051151251351451551651751851952052152252352452552652752852953053153253353453553653753853954054154254354454554654754854955055155255355455555655755855956056156256356456556656756856957057157257357457557657757857958058158258358458558658758858959059159259359459559659759859960060160260360460560660760860961061161261361461561661761861962062162262362462562662762862963063163263363463563663763863964064164264364464564664764864965065165265365465565665765865966066166266366466566666766866967067167267367467567667767867968068168268368468568668768868969069169269369469569669769869970070170270370470570670770870971071171271371471571671771871972072172272372472572672772872973073173273373473573673773873974074174274374474574674774874975075175275375475575675775875976076176276376476576676776876977077177277377477577677777877978078178278378478578678778878979079179279379479579679779879980080180280380480580680780880981081181281381481581681781881982082182282382482582682782882983083183283383483583683783883984084184284384484584684784884985085185285385485585685785885986086186286386486586686786886987087187287387487587687787887988088188288388488588688788888989089189289389489589689789889990090190290390490590690790890991091191291391491591691791891992092192292392492592692792892993093193293393493593693793893994094194294394494594694794894995095195295395495595695795895996096196296396496596696796896997097197297397497597697797897998098198298398498598698798898999099199299399499599699799899910001001100210031004100510061007100810091010101110121013101410151016101710181019102010211022102310241025102610271028102910301031103210331034103510361037103810391040104110421043104410451046104710481049105010511052105310541055105610571058105910601061106210631064106510661067106810691070107110721073107410751076107710781079108010811082108310841085108610871088108910901091109210931094109510961097
За год школьникам предстоит изучить важные разделы учебного курса:
- тригонометрия и графики;
- рациональные и иррациональные уравнения;
- системы уравнений и неравенств;
- прогрессия.

Решебник по алгебре авторов Макарычева, Миндюка, Нешкова и Суворова позволит делать работу над ошибками во время выполнения домашней работы. Такая двухэтапная подготовка с использованием ответов поможет школьнику найти свои слабые стороны и самостоятельно их проработать благодаря подробным решениям в ГДЗ. Каждый номер подготавливался опытными педагогами и математиками.
Если какие-то темы были пропущены по причине болезни, их можно будет изучить собственными силами, не прибегая к помощи одноклассников и репетиторов.
Онлайн-формат решебника делает его использование максимально удобным и доступным в любое время. Для того, чтобы сравнить свое решение с готовыми ответами, необходим только смартфон и доступ в интернет. Если раньше все решебники были в формате книг, которые отяжеляли и без того переполненный рюкзак, то теперь такая проблема исчерпана.
Важность и проблематичность Алгебры9 класс крайне важен для любого школьника. Это сложное время подготовки к предстоящим экзаменам и обдумывания своей дальнейшей формы обучения. 9 класс сложен и тем, что, будучи одним из последних классов в школе, сложность изучаемых в нём предметов, соответственно высока. Математика, царица среди всех наук. Её важность и необходимость в современном мире неоценима и бесспорна. Но что алгебра, что геометрия, две основные составляющие математики, обе они крайне сложны в понимании и зачастую, без должного склада ума, понять их крайне проблематично. Алгебра 9 класс – это бесспорно сложный, экзамен, подготовка к которому отнимает большое количество времени и сил. Одним из наиболее известных и проверенных временем и не одним поколением школьников учебников, для изучения предмета является учебное пособие, автором которого является Макарычев.
9 класс сложен и тем, что, будучи одним из последних классов в школе, сложность изучаемых в нём предметов, соответственно высока. Математика, царица среди всех наук. Её важность и необходимость в современном мире неоценима и бесспорна. Но что алгебра, что геометрия, две основные составляющие математики, обе они крайне сложны в понимании и зачастую, без должного склада ума, понять их крайне проблематично. Алгебра 9 класс – это бесспорно сложный, экзамен, подготовка к которому отнимает большое количество времени и сил. Одним из наиболее известных и проверенных временем и не одним поколением школьников учебников, для изучения предмета является учебное пособие, автором которого является Макарычев.
Макарычев 9 класс является одним из популярнейших отечественных изданий предмета, в котором автор вместе со своей командой преподавателей Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова, постарались доступно объяснить все важные темы своего предмета. Но большинству школьников всё равно сложно понять его наполнение и самостоятельно или даже при поддержке учителя разобраться в той или иной теме. Учебник «Алгебра 9 класс Макарывеч» это одобренное множеством экспертов и преподавателей, а также проверенное Министерством образования в соответствии государственным стандартом, учебное пособие, имеющие в своём «арсенале» и дополнительные материалы. Вопреки популярному мнению, «ГДЗ Макарычев 9 класс» это не способ быстро списать определённое упражнение. Это ресурс, где каждый в любое время суток, при этом абсолютно бесплатно может:
Но большинству школьников всё равно сложно понять его наполнение и самостоятельно или даже при поддержке учителя разобраться в той или иной теме. Учебник «Алгебра 9 класс Макарывеч» это одобренное множеством экспертов и преподавателей, а также проверенное Министерством образования в соответствии государственным стандартом, учебное пособие, имеющие в своём «арсенале» и дополнительные материалы. Вопреки популярному мнению, «ГДЗ Макарычев 9 класс» это не способ быстро списать определённое упражнение. Это ресурс, где каждый в любое время суток, при этом абсолютно бесплатно может:
- Дополнительно разобраться в каждой теме и понять правильное решение того или иного примера;
- Запомнить правильность использования той или иной темы;
- Сверить правильность своего решения;
- Выявить при необходимости ошибку в своём решении и определить правильность решения;
- Правильно выполнить домашнее задание.
Соединяя обучение по учебнику «Алгебра Макарычев 9 класс» и его решебник по алгебре 9 класс, можно добиться наилучшего результата в освоении учебного материала.
«ГДЗ по алгебре 9 класс Макарывеч» — это удобный, бесплатный ресурс, представляющий возможность найти верное решение каждой имеющейся в учебнике задачи, выделенной в одноименном разделе. Ресурс разбивает учебник на две структурные части. Кроме раздела «задачи», есть и раздел с контрольными вопросами, относящиеся к каждому, отдельно прономерованному параграфу.
«Решебник по алгебре 9 класс Макарычев» предлагает также:
- Постоянный и неограниченный доступ ко всем заданиям учебного пособия;
- Решение задач разными способами и вариантами в зависимости от программы обучения;
- Комментарии и приложения с объяснениями того или иного решения;
- Наличие таблиц и изображений, для более подробного и наглядного объяснения.
Именно при правильном использовании «решебника по алгебре 9 класс Макарычев», комбинируя его с усидчивым поведением на уроке и домашними занятиями, ученик сможет в полной мере раскрыть его потенциал и подготовиться к предстоящей контрольной или экзамену. К ГДЗ «алгебре 9 класс Макарывеч» прикреплено достаточное количество сопутствующего, учебного материала. Ресурс предназначен не для банального списывания, а именно что для обучения и полного понимания предмета.
К ГДЗ «алгебре 9 класс Макарывеч» прикреплено достаточное количество сопутствующего, учебного материала. Ресурс предназначен не для банального списывания, а именно что для обучения и полного понимания предмета.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Квадратный корень из 128 — Как найти квадратный корень из 128?
LearnPracticeDownload
Квадратный корень из 128 — это число, которое при умножении само на себя дает число 128. Значением квадратного корня может быть десятичное, целое или целое число. Теперь мы рассмотрим, как вычислить квадратный корень из 128, и рассмотрим несколько интересных задач. 128 также представляется как 2 7 . В этом уроке мы будем вычислять квадратный корень из 128 методом деления в большую сторону.
Значением квадратного корня может быть десятичное, целое или целое число. Теперь мы рассмотрим, как вычислить квадратный корень из 128, и рассмотрим несколько интересных задач. 128 также представляется как 2 7 . В этом уроке мы будем вычислять квадратный корень из 128 методом деления в большую сторону.
- Квадратный корень из 128 : √128 = 11,313
- Квадрат 128: 128² = 16 384
| 1. | Что такое квадратный корень из 128? |
| 2. | Является ли квадратный корень из 128 рациональным или иррациональным? |
| 3. | Как найти квадратный корень из 128? |
| 4. | Советы и рекомендации |
| 5. | Часто задаваемые вопросы о квадратном корне из 128 |
| 6. | Важные замечания по квадратному корню из 128 |
Что такое квадратный корень из 128?
Квадратный корень числа — это число, которое при умножении само на себя дает исходное число как произведение. т. е. a × a = n и это 2 = n. Нахождение квадратного корня — это процесс, обратный возведению числа в квадрат. Следовательно, a = √ n
т. е. a × a = n и это 2 = n. Нахождение квадратного корня — это процесс, обратный возведению числа в квадрат. Следовательно, a = √ n
- Радикальная форма: 128 = 2 7 = 2 × 2 × 2 × 2 × 2 × 2 × 2 ⇒ √ 128 = √ ( 2 × 2 × 2 × 2 × 2 × 2 × 2) = × 2) = × 2) = = = × 2). 2 × 2 × 2 × √ 2 = 8 √ 2
- Экспоненциальная форма: 128 ½
- Приблизительное значение: 11,313
Является ли квадратный корень из 128 рациональным или иррациональным?
Рациональное число определяется как число, которое может быть выражено в виде частного или деления двух целых чисел, т. е. p/q, где q не равно 0, √ 128 = 11,31370849898476 некончающееся десятичное число, и, следовательно, доказано, что это иррациональное число.
Как найти квадратный корень из 128?
Квадратный корень из 128 можно вычислить с помощью различных методов, таких как разложение на простые множители, метод длинного деления или метод аппроксимации.
Квадратный корень из 128 методом приближения
- 128 лежит между двумя полными квадратами 121 и 144. 121 < 128 < 144
- √ 121 < √ 128 < √ 144
- 11 < 128 < 12
- Теперь разделите 128 на 11 или 12. Разделим на 11. 128 ÷ 11 = 11,63
- Найдите среднее значение полученного частного с 11. (11,63 + 11) ÷ 2 = 22,63 ÷ 2 = 11,315
- √ 128 ≈ 11,315
Квадратный корень из 128 методом деления в длину
- Шаг 1: Запишите 128 как 128000000. Выберите числа в парах справа. У нас есть 1 слева.
- Разделите 1 на 1 и получите остаток 0. Частное равно 1. Сократите следующую пару, 28. 28 — это новое делимое.
- Шаг 2: Удвойте частное. Имейте 20 на месте нового делителя.
- Найдите число, которое при добавлении к 20 и умножении суммы на то же число дает 28 или меньше.
 1 прибавляется к 2 0 равно 21, а 2 1 × 1 = 21,
1 прибавляется к 2 0 равно 21, а 2 1 × 1 = 21, - Вычтите 21 из 28 и получите в остатке 7. Сложите следующую пару нулей и получите 700 в качестве нового делимого.
- Шаг 3: Теперь частное равно 11. Удвойте его. Получаем 22. Имеем 22 0 на месте нового делителя.
- Определите число, которое при добавлении к 220 и сумме, умноженной на это число, дает произведение 700 или меньше. Ясно, что 22 3 × 3 = 669, .
- Из 700 вычесть 669. Получить остаток 31.
- Теперь повторяйте процесс, пока не приблизите частное к трем знакам после запятой.
Изучите квадратные корни с помощью иллюстраций и интерактивных примеров:
- Квадратный корень из 34
- Квадратный корень из 169
- Квадратный корень из 105
- Квадратный корень из 125
- Квадратный корень из 256
Советы и хитрости
- 128 лежит между двумя полными квадратами √121 и √144 и, следовательно, √128 лежит между 11 и 12.

- Используйте метод усреднения, чтобы аппроксимировать оценку √128.
Важные примечания
- √ 128 в простейшей радикальной форме равно 8 √ 2, а экспоненциальная форма 128 ½
- √ 128 = 11,313
- √128 иррационально.
Пример 1: Оценка: √128 — √32
Решение:
√128 = √(64 × 2) = 8 √2
√32 = √(16 × 2) = 4 √2
√128 — √32 = (8 + 4) √2 90 257 = 12 √2
Следовательно, √128 — √32 = 12√2Пример 2 : Площадь квадратной плитки составляет 12800 квадратных дюймов. Какова длина одной стороны этой плитки с точностью до десятых долей дюйма?
Решение:
Площадь = сторона × сторона, кв. дюйм
12800 = сторона × сторона
Сторона 2 = 12800
Извлекая квадратный корень из обеих сторон, получаем
. (сторона 2 ) ½ = (12800) ½
(сторона 2 ) ½ = (12800) ½
сторона = √128 × √100
Приближая √128 с точностью до десятых, получаем √128 = 11,3
. сторона = 11,3 х 10 = 113 дюймов.
Сторона квадратной плитки = 113 дюймов.
перейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Забронировать бесплатный пробный урок
перейти к слайдуперейти к слайдуперейти к слайду
Часто задаваемые вопросы о квадратном корне из 128
Что такое квадратный корень из 128?
Квадратный корень из 128 равен 11,313.
Почему квадратный корень из 128 упрощен?
Квадратный корень из 128 в упрощенном виде равен 8 √ 2.
Является ли 128 рациональным или иррациональным?
128 является рациональным, поскольку выражается как 128/1 в рациональной форме. Однако квадратный корень из 128 равен 11,3, и это иррационально.
Однако квадратный корень из 128 равен 11,3, и это иррационально.
Между какими двумя целыми числами лежит квадратный корень из 128?
Квадратный корень из 128 лежит между 11 и 12.
Как найти квадратный корень из 128?
Мы используем метод аппроксимации или метод длинного деления, чтобы получить квадратный корень из 128.
Рабочие листы по математике и
визуальные учебные программы
Математика 128A
Математика 128AАбстрактная алгебра I (Математика 128A), осень 2020 г.
Zoom, Пн 9:00-10:15 (Секунда 01, код 48166)
Последнее обновление этой страницы: Пт, 11 дек, 12:20
Текущие полезные ссылки:
- Учебный класс Страница оценок
- Скачать Адоб Скан
- Как сделать видео: Как сделать отправить HW на градоскоп, Как используйте Adobe Scan.
- И вот полное изложение одного эффективного способа использования Gradescope
и Adobe Scan вместе, что должно подойти как для домашней работы, так и для
Экзамены.
 (Пожалуйста, сообщите мне немедленно, если это не сработает для
вам, а я исправлю инструкцию.)
(Пожалуйста, сообщите мне немедленно, если это не сработает для
вам, а я исправлю инструкцию.)- Для начала убедитесь, что вы вошли в Gradescope на ваш телефон.
- Убедитесь, что вы размещаете каждую задачу на отдельной странице (кнопка «Соответствие страниц последовательно»).
- Отсканируйте документ с помощью Adobe Scan и сохраните его в Google Диск («Мой диск»). Убедитесь, что вы используете имя файла, которое вы могу вспомнить.
- Перейдите в Gradescope на своем телефоне и просмотрите отправку. процесс. Когда Gradescope попросит вас выбрать PDF-файл, вы должны получить My Drive в качестве опции, на которой вы можете найти свой PDF используя запоминающееся имя файла. (И как упоминалось выше, когда вы сопоставляете проблемы со страницами, вам нужно сопоставлять страницы последовательно, потому что процесс выбора более неудобен на телефон.)
- Более простая, но медленная альтернатива — отправить PDF-файл себе по электронной почте.
 когда вы создаете его в Adobe Scan, а затем загружаете файл в
ваш ноутбук/настольный компьютер. Как только вы это сделаете, загрузите его в
Gradescope на вашем ноутбуке/настольном компьютере будет относительно
простой. В крайнем случае, вы всегда можете отправить его мне по электронной почте,
а я придумаю что делать.
когда вы создаете его в Adobe Scan, а затем загружаете файл в
ваш ноутбук/настольный компьютер. Как только вы это сделаете, загрузите его в
Gradescope на вашем ноутбуке/настольном компьютере будет относительно
простой. В крайнем случае, вы всегда можете отправить его мне по электронной почте,
а я придумаю что делать. - Класс Пьяцца страница.
Объявления:
- Экзамен 3, понедельник, 23 ноября .
- Учебником для этого класса является « Contemporary» Галлиана.
Абстрактная алгебра , 9-е издание . Делать
обязательно получите 9-е издание (синий пятилистный клевер на черном
фон), потому что в противном случае ваши номера проблем не будут совпадать
мой. Вот несколько хороших способов получить текст менее чем за 100 долларов:
- Ты можно заказать книгу в книжном магазине здесь.
- Ты
можно заказать
книгу напрямую от издателя.
 Это дешевле, но
похоже, что нет политики возврата.
Это дешевле, но
похоже, что нет политики возврата. - Вы может получить книга на амазоне, но они делают эту раздражающую вещь где у них разные цены для разных людей, поэтому я Не могу предсказать, получите ли вы там лучшую или худшую цену. я также понятия не имеют, какова их политика возврата.
- кликните сюда чтобы перейти на нашу страницу Canvas. Вы также можете добраться до нашей площади дискуссионная группа на нашей странице Canvas; нажмите на «Пьяцца» пункт меню слева.
- В качестве альтернативы, чтобы попасть в нашу дискуссионную группу Piazza напрямую, просто нажмите на эту ссылка на сайт.
- Наши еженедельные задачи будут проводиться каждую пятницу, 10 утра-полдень , в Zoom.
- Если вы хотите провести обзор/самостоятельное изучение методов доказательства,
видеть
этот раздаточный материал по написанию доказательств.
 Вы также можете попробовать посмотреть на Чтение,
Написание и проверка Дэппа и Горкина.
Вы также можете попробовать посмотреть на Чтение,
Написание и проверка Дэппа и Горкина.
FUA (часто используемые сокращения):
В поле ниже приведены некоторые аббревиатуры, которые я использую все время, как в классе и при оценивании вашей работы. Вы можете использовать их как Что ж.Административные раздаточные материалы:
Курс зеленый лист, технология ожидания для Math 128A.Примечания к курсу:
Курсовая механика: Домашнее задание по математике 128А, заезды, Письмо доказательства.Выкройки для: D 4 калькуляторов (квадраты), D 5 калькуляторы (пятиугольники), D 6 вычислители (шестиугольники), Платонический твердые вещества.
Кроме того, проверьте Галлиана веб-сайт со ссылками на полезные вещи, такие как онлайн-флэш карточки для определений (печатная копия версия).
Темы для экзаменов:
Экзамен
1, экзамен
2, экзамен
3, финал
экзамен.
Образцы экзаменов:
Экзамен 1, экзамен 2, экзамен 3, финал экзамен.
Онлайн лекций:
Нажмите на ссылку в столбце «Охваченные разделы», чтобы получить копию слайды на день; нажмите на ссылку в «Дополнительных слайдах» для просмотра других вещи, выставленные в тот день; и нажмите на ссылку в разделе «Видео» колонка для просмотра лекции на YouTube или в облачной записи Zoom. Или же просто проверьте из нашего плейлиста класса здесь.
| Дата | Покрываемые разделы | Дополнительные слайды | Видео |
| Ср 19 августа | Ч. 0/обзор | видео | |
| Пн 24 августа | Ч. 1 | видео | |
| Ср 26 августа | Ч. 2 2 | Таблица Кэли D6 | видео |
| Пн 31 августа | Ч. 2-3 | видео | |
| Ср 02 сентября | Ч. 3 | Часть 1, часть 2. | |
| Ср 09 Сен | Ч. 3-4 | видео | |
| Пн 14 сент. | Ч. 4 | видео | |
| Ср 16 сентября | Ч. 4-5 | видео | |
| Образец экзамена 1 | видео | ||
| Ср 23 сентября | Ч. 5 | видео | |
| Пн, 28 сентября | Ч. 5-6 5-6 | видео | |
| Ср 30 сентября | Ч. 6 | видео | |
| Пн, 05 октября | Ч. 6-7 | видео | |
| Ср 07 окт | Ч. 7 | видео | Пн 12 окт | Ч. 7-8 | видео |
| Ср 14 окт | Ч. 8 | видео | |
| Образец экзамена 2 | видео | ||
| Ср 21 окт | Ч. 9 | видео | |
| Пн 26 окт | Ч. 9 | видео | |
| Ср 28 окт | Ч. 9-10 9-10 | видео | |
| Пн 02 ноября | Ч. 10 | видео | |
| Ср Ноя 04 | Ч. 10-11 | видео | |
| Пн 09 ноября | Ч. 11 | видео | |
| Пн 16 ноября | Ч. 12 | видео | |
| Ср 18 ноября | Ч. 12 | видео | |
| Образец экзамена 3 | видео | ||
| Пн 30 ноября | Ч. 14 | видео | |
| Ср 02 декабря | Ч. 14 | видео | |
| Пн, 07 декабря | Обзор семестра | видео | |
| Образец выпускного экзамена | видео |
Наборы задач:
Нажмите на номер или «Просмотреть раздаточный материал» любой выделенной проблемы, установленной для скачать это. (Файлы в формате PDF, которые можно прочитать бесплатно
Adobe
Программа Акробат.)
(Файлы в формате PDF, которые можно прочитать бесплатно
Adobe
Программа Акробат.)| HW | Новые определения | Контур должен | Срок выполнения | Срок последней ревизии | Проблемы |
| PS00 | н/д | н/д | Пн 24 августа | н/д | См. раздаточный материал |
| PS01 | Гл. 1 | Пн 24 августа | Ср 26 августа | Ср 21 октября | См. раздаточный материал |
| PS02 | Гл. 2, 3 | Ср Сентябрь 02 | Ср Сентябрь 09 | Ср 25 ноября | См. раздаточный материал |
| PS03 | Гл. 4 | Ср Сентябрь 09 | Пн, 14 сентября | Ср 25 ноября | См. раздаточный материал (ИСПРАВЛЕНО 9 СЕНТЯБРЯ 2009 г.) раздаточный материал (ИСПРАВЛЕНО 9 СЕНТЯБРЯ 2009 г.) |
| PS04 | Гл. 5 | Ср 23 сентября | Пн, 28 сентября | Ср 25 ноября | См. раздаточный материал |
| PS05 | Гл. 6 | Ср 30 сентября | Пн, 05 октября | Пн, 07 декабря | См. раздаточный материал |
| PS06 | Гл. 7 | Пт 09 окт | Ср 14 окт | Пн, 07 декабря | См. раздаточный материал |
| PS07 | Гл. 8 | Пн, 26 октября | Ср 28 октября | Пн, 07 декабря | См. раздаточный материал |
| PS08 | Гл. 9 | Пн Ноябрь 02 | Ср Ноя 04 | Пн 14 декабря | См. раздаточный материал ( Задача 8 № больше присвоено ) |
| ПС09 | Гл. 10 10 | Пн Ноябрь 09 | Понедельник 16 ноября | Пн 14 декабря | См. раздаточный материал |
| ПС10 | Гл. 11, 12 | Пт 20 ноября | Понедельник 30 ноября | уточняется | См. раздаточный материал |
| ПС11 | Гл. 14 | Ср 02 Дек | Пн, 07 декабря | уточняется | См. раздаточный материал |
Чтение назначено в курсе:
Современная абстрактная алгебра , Галлиан: главы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 14.
Доказательство раздаточный материал: Части I-II, гл. 16, 17, 18.
Другие полезные ссылки:
- Если вам интересна математическая верстка, система, которую я использую для
сделать мои раздаточные материалы называется LaTeX. Если у вас есть ПК с Windows, вы можете
бесплатно загрузите LaTeX с http://www.
 miktex.org; Вы также
нужен хороший текстовый редактор, вроде условно-бесплатной программы WinEdt. PCTeX также делает хорошую рекламу
версия; студенческие цены составляют 150 долларов за версию «Publisher», которую я
рекомендую, если у вас есть деньги, 50 долларов за версию «Писатель», которую я
порекомендуйте, если вы этого не сделаете. Если у вас есть Mac, вы можете загрузить полную
система под названием TeXShop бесплатно.
Если у вас есть компьютер с Linux, у вас уже есть копия этой программы,
поскольку это стандартная программа Unix уже около 20 лет.
miktex.org; Вы также
нужен хороший текстовый редактор, вроде условно-бесплатной программы WinEdt. PCTeX также делает хорошую рекламу
версия; студенческие цены составляют 150 долларов за версию «Publisher», которую я
рекомендую, если у вас есть деньги, 50 долларов за версию «Писатель», которую я
порекомендуйте, если вы этого не сделаете. Если у вас есть Mac, вы можете загрузить полную
система под названием TeXShop бесплатно.
Если у вас есть компьютер с Linux, у вас уже есть копия этой программы,
поскольку это стандартная программа Unix уже около 20 лет.LaTeX стоит изучить, если у вас есть свободное время; это используется для руководств и технических отчетов по всему nerd-dom. За самообучение, настоятельно рекомендую Обучение LaTeX (Griffiths и Higham) для начинающих и Книга LaTeX Лесли Лэмпорт в качестве справочника.
- Бесплатные загрузки: Adobe Acrobat (для чтения файлов .pdf)
- Преподаватель: Тим Хсу.
- Требуемый текст: Современная абстрактная алгебра , Галлиан, 9-е изд.

- Дополнительный текст: Написание доказательств , Хсу, загружаемый здесь
- Домашнее задание: План и окончательная версия должны быть представлены один раз в неделю, кроме экзаменационных недель. Подробнее см. в раздаточном материале по домашнему заданию по математике. 128А.
- Экзамены: Три 50-минутных экзамена в классе плюс выпускной экзамен продолжительностью 2 часа 15 минут. ( Вт, 15 декабря, 7:15–9:30 ).
- Оценка: Итоговые оценки за курс состоят из:
Домашнее задание: 25% Экзамен 1: 14% Экзамены 2 и 3: по 18% Окончательный: 25%
Решения по математике, часть I, для 9 класса, глава 3
Математика, часть I, решения Решения для 9 класса, глава 3, математика Здесь приводятся простые пошаговые объяснения. Эти решения для многочленов чрезвычайно популярны среди учеников 9-го класса.Решения для студентов по математическим полиномам пригодятся для быстрого выполнения домашних заданий и подготовки к экзаменам. Все вопросы и ответы из книги решений по математике, часть I, глава 3 по математике для класса 9, предоставляются здесь для вас бесплатно. Вам также понравится безрекламный опыт решения Mathematics Part I Solutions Solutions от Meritnation. Все решения по математике, часть I Решения для класса 9 по математике подготовлены экспертами и на 100% точны.
Эти решения для многочленов чрезвычайно популярны среди учеников 9-го класса.Решения для студентов по математическим полиномам пригодятся для быстрого выполнения домашних заданий и подготовки к экзаменам. Все вопросы и ответы из книги решений по математике, часть I, глава 3 по математике для класса 9, предоставляются здесь для вас бесплатно. Вам также понравится безрекламный опыт решения Mathematics Part I Solutions Solutions от Meritnation. Все решения по математике, часть I Решения для класса 9 по математике подготовлены экспертами и на 100% точны.
Страница № 39:
Вопрос 1:
Укажите, являются ли данные алгебраические выражения многочленами? Оправдывать.
(i) y + 1y (ii) 2 — 5 x (iii) x2 + 7x + 9 (iv) 2m-2 + 7m — 5 (v) 10
Ответ:
В алгебраическом выражении, если степени переменных — целые числа, тогда алгебраическое выражение — многочлен.
(i)
y+1y=y+y-1
Здесь одна из степеней y равна −1, что не является целым числом. Итак, y + 1y – это , а не – многочлен.
Итак, y + 1y – это , а не – многочлен.
(ii)
2 — 5 x=2–5×12
Здесь степень x равна 12, что не является целым числом. Итак, 2 — 5 x – это , а не – многочлен.
(iii)
x2 + 7x + 9
Здесь степени переменной x равны 2, 1 и 0, то есть целым числам. Итак, x2 + 7x + 9 – многочлен.
(iv)
2m-2 + 7m — 5
Здесь одна из степеней m равна −2, что не является целым числом. Итак, 2 м-2 + 7 м — 5 – это , а не 9.0011 многочлен.
(v)
10 = 10 × 1 = 10 x 0
Здесь степень x равна 0, то есть целому числу. Итак, 10 — это многочлен (или постоянный многочлен).
Страница № 39:
Вопрос 2:
Напишите коэффициент м 3 в каждом из заданных многочленов.
(i) м 3 (ii) -3 2 + m — 3м3 (iii) -23м3 — 5м2 + 7м — 1
Ответ:
(I)
Коэффициент M 3 = 1
(II)
-3 2+M-3M3
Коэффициент M 3 = -3
(III)
-23-3-3 = -3
(III)
-23- 5м2 + 7м — 1
Коэффициент м 3 = -23
Страница № 39:
Вопрос 3:
Используя полученную информацию, запишите многочлен от x 9104.
(i) Одночлен степени 7
(ii) Двухчлен степени 35
(iii) Трехчлен степени 8
Ответ:
(i) Многочлен, имеющий только один член, называется мономом. Кроме того, наибольшая степень переменной в многочлене называется степенью многочлена.
3 x 7 является мономом из x степени 7.
(ii) Многочлен, имеющий только два члена, называется биномом. Кроме того, наибольшая степень переменной в многочлене называется степенью многочлена.
2 х 35 + 1 — это двучлен от x со степенью 35.
(iii) Многочлен, имеющий только три члена, называется трехчленом. Кроме того, наибольшая степень переменной в многочлене называется степенью многочлена.
5 x 8 + 6 x 4 + 7 x является триномиальным в x с степенью 8.
Страница № 40:
Вопрос 4:
. степени заданных многочленов.
степени заданных многочленов.
(i) 5 (ii)x° (iii) x2 (iv) 2 m10 — 7 (v) 2p — 7 + mn
Ответ:
Наибольшая степень переменной в многочлене от одной переменной называется степенью многочлена. Кроме того, наибольшая сумма степеней переменных в каждом члене многочлена более чем от одной переменной является степенью многочлена.
(i)
5=5×1=5×0
Степень многочлена 5 равна 0,
(ii)
Степень полиномиального x 0 равен 0,
(iii)
Степень полиномиального x 2 — 2.
(iv)
многочлен 2m10-7 равен 10.
(v)
Степень многочлена 2p-7 равна 1.
(vi)
Степень многочлена 7y-y3+y5 равна 5.
(vii)
сумма степеней переменных в многочлене xyz+xy-z равна 1 + 1 + 1 = 3 и 1 + 1 = 2,
Степень полинома xyz+xy-z равна 3.
(viii)
Сумма степеней переменных в полиноме m3n7-3m5n+mn равна 3 + 7 = 10, 5 + 1 = 6 и 1 + 1 = 2.
Степень многочлена m3n7-3m5n+mn равна 10.
Страница № 40:
Вопрос 5:
Классифицируйте следующие многочлены как линейные, квадратичные и кубические многочлены.
(i) 2 x 2 + 3 x + 1 (ii) 5p (iii) 2y — 12 (iv) m3 + 7m2 + 52m — 7 (v) a2 (vi) 3r3
Ответ:
(I)
Степень полинома 2 x 2 + 3 x + 1 IS 2.
SO, полиномиальный + 1 — квадратичный многочлен.
(ii)
Степень многочлена 5 p равна 1.
Итак, многочлен 5 p является линейным многочленом.
(iii)
Степень многочлена 2y-12 равна 1.
Итак, многочлен 2y-12 является линейным многочленом.
(iv)
Степень многочлена m3+7m2+52m-7 равна 3.
Итак, многочлен m3+7m2+52m-7 является кубическим многочленом.
(v)
Степень многочлена a 2 равна 2.
Итак, многочлен a 2 является квадратичным многочленом.
(vi)
Степень многочлена 3 r 3 равна 3.
Итак, многочлен 3 r 3 является кубическим многочленом.
Страница № 40:
Вопрос 6:
Запишите следующие многочлены в стандартной форме.
(i) m3 + 3 + 5m (ii) -7y + y5 + 3y3 — 12 + 2y4 — y2
Ответ:
Многочлен, записанный в убывающей или возрастающей степени своей переменной, называется стандартной формой многочлен.
(i)
Данный многочлен равен м 3 + 3 + 5 м .
Стандартная форма многочлена: 3 + 5 м + м 3 или м 3 + 5 м + 3.
(ii)
Данный многочлен есть -7y+y5+2y4-y3-12+.
Стандартная форма полинома – y5+2y4+3y3-y2-7y-12 или -12-7y-y2+3y3+2y4+y5.
Страница № 40:
Вопрос 7:
Запишите следующие многочлены в виде коэффициентов. (iv) -230003
Форма коэффициента многочлена: (1, 0, 0, −2).
(ii)
5 y = 5 y + 0
Форма коэффициента многочлена (5, 0).
(iii)
2m4-3m2+7=2m4+0m3-3m2+0m+7
Форма коэффициентов полинома: (2, 0, −3, 0, 7).
(iv)
Форма коэффициента многочлена -23 равна -23.
Страница № 40:
Вопрос 8:
Запишите многочлены в индексной форме.
(i) (1, 2, 3) (ii) (5, 0, 0, 0, -1) (iii) (-2, 2,-2, 2)
Ответ:
(i)
Форма коэффициента полинома – (1, 2, 3).
Таким образом, форма индекса полинома x 2 + 2 x + 3.
(ii)
Форма коэффициентов полинома (5, 0, 0, 0, −1) .
Таким образом, индекс полинома равен 5 x 4 + 0 x 3 + 0 x 2 + 0 x — 1 или 5 x 4 — 1.
(iii)
Коэффициент коэффициента полиномиала составляет (-2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2. −2, 2).
−2, 2).
Следовательно, индексная форма полинома составляет -2 x 3 + 2 x 2 −2 x + 2.
Страница № 40:
Вопрос 9:
. Впишите соответствующие многочлены в клеточки.
Ответ:
Страница № 43:
Вопрос 1:
Используйте данные буквы, чтобы написать ответ.
(i) В деревне Лат. Если количество деревьев каждый год увеличивается на « b », то сколько деревьев будет через « x » лет?
(ii) Для парада в каждом ряду и учащихся и формируется x таких рядов. Тогда сколько всего студентов собралось на парад?
(iii) Разряд десятков и единиц двузначного числа равен m и n соответственно. Запишите многочлен, представляющий двузначное число.
Ответ:
(i)
Исходное количество деревьев в деревне = a
Увеличение количества деревьев каждый год = b
∴ Количество деревьев в деревне через 1 год x
= Исходное количество деревьев в деревне + Увеличение количества деревьев каждый год × x
= a + bx
Таким образом, количество деревьев через x лет равно a + bx .
(ii)
Количество учеников в каждом ряду = y
Количество рядов = x
∴ Общее количество учеников в параде = Количество учеников в каждом ряду × Количество рядов = 0 y 1 y × x = yx = xy Таким образом, всего xy школьников на парад. (iii) Цифра в разряде единиц = n ∴ Двузначное число = Цифра в разряде десятков × 10 + Цифра в разряде единиц = 1 × 10 + n = 10 m + n Таким образом, многочлен, представляющий двузначное число, равен 10 m + n . Добавить заданные полиномы. (i) x3 – 2×2 – 9 ; 5×3 + 2x + 9 (ii) — 7м4 + 5м3 + 2 ; 5м4 — 3м3 + 2м2 + 3м — 6 (iii) 2у2 + 7у + 5 ; 3 года + 9 ; 3y2 — 4y — 3 Вычесть второй полином из первого. (i) x2 – 9x + 3 ; -19x + 3 + 7×2 (ii) 2ab2 + 3a2b — 4ab ; 3ab -8ab2 + 2a2b Умножьте данные многочлены. (i) 2x ; x2 — 2x — 1 (ii) x5 — 1 ; x3 + 2×2 + 2 (iii) 2y + 1 ; у2 – 2у3 + 3у Разделить первый многочлен на второй многочлен и запишите ответ в виде «Дивиденд = Делитель × Частное + Остаток». (i) Используя метод деления в длину, Дивиденд = Делитель × Частное + Остаток ∴x4-64= x2+4x+16+0 (ii) Используя метод деления в длинную сторону, Дивиденд = Делитель ×Частное + Остаток ∴5×5+4×4-3×3+2×2+2=x2-x×5×3+9×2+6x+8+8x+2 Запишите информацию в форму алгебраического выражения и упростить. Имеется прямоугольная ферма длиной 2a2 + 3b2 метр и шириной (a2 + b2 ) метр. Фермер использовал квадратный участок фермы для постройки дома. Сторона участка составляла ( a2 — b2) метр. Какова площадь оставшейся части фермы? Шего цвета прямоугольной фермы = ( A 2 9000 + 9 9000 + 9 9000 + 9.1040 B
Цифра в разряде десятков = m Страница № 43:
Вопрос 2:
Ответ:
(i)
x3-2×2-9+5×3+2x+9=x3+5×3-2×2+2x-9+9=6×3-2×2+2x
(ii)
-7м4+5м3+2+5м4-3м3+2м2+3м-6=-7м4+5м4+5м3-3м3+2м2+3м+2-6=-2м4+2м3+2м2+3м-6+2
(iii)
2y2+7y+5+3y+9+3y2-4y-3=2y2+3y2+7y+3y-4y+5+9-3=5y2+6y+11 Страница № 43:
Вопрос 3:

Ответ:
(i)
x2-9x+3 —19x+3+7×2=x2-9x+3+19x-3-7×2=x2-7×2-9x+19x+3 -3=-6×2+10x
(ii)
2ab2+3a2b-4ab-3ab-8ab2+2a2b=2ab2+3a2b-4ab-3ab+8ab2-2a2b=2ab2+8ab2+3a2b-2a2b-4ab-3ab=10ab2+ a2b-7ab Страница № 43:
Вопрос 4:
Ответ:
(i)
2xx2 -2x-1=2x×x2+2x×-2x+2x×-1=2×3-4×2-2x
(ii)
x5-1×x3+2×2+2 =x5x3+2×2+2-1×3+2×2+2=x8+2×7+2×5-x3-2×2-2
(iii)
2y+1×y2-2y3+3y=2yy2-2y3+3y+1y2-2y3+3y =2y3-4y4+6y2+y2-2y3+3y=-4y4+2y3-2y3+6y2+y2+3y=-4y4+7y2+3y Страница № 43:
Вопрос 5:
(i) x3 – 64 ; x — 4 (ii) 5×5 + 4×4 – 3×3 + 2×2 + 2 ; х2 — х Ответ:
x3-64=x3+0x2+0x-64
5×5+4×4-3×3+2×2 +2=5×5+4×4-3×3+2×2 +0x+2 Страница № 43:
Вопрос 6:

Ответ:
Lenght прямоугольной фермы = (2 A 2 + 3 B 2 ) M
Сторона квадратного участка = ( A 2 — B 2 ) M
∴ Площадь оставшейся части фермы
= Общая площадь
. ферма − Площадь квадратного участка= Длина прямоугольной фермы × Ширина прямоугольной фермы − (Сторона квадратного участка) 2
= (2 a 2 + 3 b 9 ) × ( a 2 + b 2 ) − ( a 2 − b 2 ) 2
= 2 a 2 ( a 2 + b 2 ) + 3 b 2 ( a 2 + b 2 ) − ( a 4 + b 4 − 2 a 2 b 2 )
= 2 a 4 + 2 a 2 b 2 + 3 a 2 b 2 + 3 b 4 − a 4 − b 4 + 2 A 2 B 2
= 2 A 4 — A 4 + 2 A 2 + 2 A 2 . 3 а 2 b 2 + 2 a 2 b 2 + 3 b 4 − b 4
3 а 2 b 2 + 2 a 2 b 2 + 3 b 4 − b 4
= ( a 4 + 7 a 2 B 2 +2 B 4 ) M 2
Таким образом, площадь оставшейся части фермы составляет ( A 4 +7 A . 2 б 2 + 2 б 4 ) м 2 .
Страница № 46:
Вопрос 1:
Разделите каждый из следующих многочленов методом синтетического деления, а также
методом линейного деления. Напишите частное и остаток.
(i) 2m2-3m+10 ÷ m-5 (ii) x4+2×3+3×2+4x+5 ÷ x+2 (iii) y3-216 ÷ y-6
(iv) 2×4+3×3+4x — 2×2 ÷ x + 3 (v) x4 — 3×2 — 8 ÷ x + 4 (vi) y3 — 3y2 + 5y — 1 ÷ y — 1
Ответ:
(i)
Синтетическое разделение:
Дивиденд = 2M2-3M+10
Divisor = M-5
противоположность −5 = 5
Форма коэффициента из каклат. (2, 7).
(2, 7).
∴ Частное = 2 м + 7 и остаток = 45
Линейный метод:
2м2-3м+10=2мм-5+10м-3м+10=2мм-5+7м-5+35+ 10=m-5×2m+7+45
(ii)
Синтетическое подразделение:
Дивиденд = x4+2×3+3×2+4x+5
Делитель = x+2
Противоположное 2 = −2
Форма коэффициента частного равна (1, 0, 3, −2).
∴ Частное = x 3 + 3 x − 2 и остаток = 9
Линейный метод:
x4+2x3x4+5×2 +4x+5=x3x+2+3xx+2-2x+5=x3x+2+3xx+2-2x+2+4+5=x+2×x3+3x-2+9
(iii)
Синтетический отдел:
Дивиденд = y3-216=y3+0y2+0y-216
Делитель = y-6
Противоположное −6 = 6
Форма коэффициента частного: (1, 6, 36).
∴ Covertient = Y 2 + 6 Y + 36 и остаток = 0
Линейный метод:
Y3-216 = Y2Y-6+ 6Y2-216 = Y2Y-6+ 6YY-6 +36y-216=y2y-6+6yy-6+36y-6+216-216=y2y-6+6yy-6+36y-6=y-6×y2+6y+36
(iv)
Синтетический отдел :
Дивиденд = 2×4+3×3+4x-2×2=2×4+3×3-2×2+4x+0
Делитель = x+3
Противоположно 3 = −3
Форма коэффициента частного равна (2, −3, 7, −17).
∴ Cotent = 2 x 3 -3 x 2 +7 x -17 и оставшаяся часть = 51
Линейный метод:
2×4+3×3-2x 2+4x = 2x3x3x3x3x3x3x3x3x3x3x3x3 x3x3x3x3x3x3x3x3x3x3x3x3x3x3x3x3x3x3x3x3x3x 3x3x3 x 2x. 3-6×3+3×3-2×2+4x=2x3x+3-3x2x+3+9×2-2×2+4x=2x3x+3-3x2x+3+7xx+3-21x+4x=2x3x+3-3x2x+3+7xx+ 3-17x+3+51=x+3×2×3-3×2+7x-17+51
(v)
Синтетическое подразделение:
Дивиденд = x4-3×2-8=x4+0x3-3×2+0x-8
Делитель = x+4
Противоположное 4 = −4
Форма коэффициента частного: (1, −4, 13, −52).
∴ Covertient = x 3 -4 x 2 + 13 x -52 и остаток = 200
Линейный метод:
x4-3×2-8 = x3x+ 4-4-4×3. -3×2-8=x3x+4-4x2x+4+16×2-3×2-8=x3x+4-4x2x+4+13xx+4-52x-8=x3x+4-4x2x+4+13xx+4-52x+4 +208-8=x+4×x3-4×2+13x-52+200
(vi)
Синтетический отдел:
Делимое = y3-3y2+5y-1
Делитель = y-1
Противоположное −1 = 1
Форма коэффициента частного (1, −2, 3).
∴ Коэффициент = Y 2 -2 Y +3 и остаток = 2
Линейный метод:
Y3-3Y2+5Y-1 = Y2Y-1+Y2-3Y2+5Y-1 =y2y-1-2yy-1-2y+5y-1=y2y-1-2yy-1+3y-1+3-1=y-1×y2-2y+3+2
Страница № 48:
Вопрос 1:
Для x = 0 найдите значение многочлена x2 — 5x + 5 .
Ответ:
Пусть px=x2-5x+5.
∴p0=02-5×0+5=0-0+5=5
Следовательно, для x = 0 значение полинома равно 5.
Страница № 48:
Вопрос 2:
Если py = y2 — 32y + 1, то найдите p 32.
Ответ:
py=y2-32y+1
∴p32=322-32×32+1=18-18+1=13
Страница № 48:Вопрос 3:
Если pm = m3 + 2m2 — m + 10, то pa + p-a = ?
Ответ:
pm=m3+2m2-m+10
∴pa=a3+2a2-a+10 …..(1)
Также
p-a=-a3+2-a2—a+10
⇒p-a=-a3+2a2+a+10 …..(2)
Складывая (1) и (2), получаем
pa+p-a=a3+2a2-a+10+-a3+ 2a2+a+10=a3-a3+2a2+2a2-a+a+10+10=4a2+20
∴pa+p-a=4a2+20
Страница № 48:
Вопрос 4:
Если py = 2y3 – 6y2 – 5y + 7, затем найдите p2.
Ответ:
py=2y3-6y2-5y+7
∴p2=2×23-6×22-5×2+7=16-24-10+7=-11
Страница № 53:
Вопрос 1:
Найдите значение многочлена 2x — 2×3 + 7, используя заданные значения для x.
(i) x = 3 (ii) x = -1 (iii) x = 0
Ответ:
Пусть px=2x-2×3+7.
(i)
p3=2×3-2×33+7=6-2×27+7=6-54+7=-41
Таким образом, значение многочлена для x = 3 равно -41 .
(ii)
p-1=2×-1-2×-13+7=-2-2×-1+7=-2+2+7=7
Таким образом, значение многочлена для x = −1 равно 7,
(iii)
p0=2×0-2×03+7=0-0+7=7
Таким образом, значение многочлена для x = 0 равно 7.
Страница № 53:
Вопрос 2:
Для каждого из следующих многочленов найдите p1, p0 и p-2.
(i) px = x3 (ii) py = y2 -2y + 5 (iii) px = x4 -2×2 — x
Ответ:
(i)
px=x3∴p1=13=1p0=03 =0p-2=-23=-8
(ii)
py=y2-2y+5∴p1=12-2×1+5=1-2+5=4p0=02-2×0+5=0 -0+5=5p-2=-22-2×-2+5=4+4+5=13
(iii)
px=x4-2×2-x∴p1=14-2×12-1=1 -2-1=-2p0=04-2×02-0=0-0-0=0p-2=-24-2×-22—2=16-2×4+2=16-8+2 =10
Страница № 53:
Вопрос 3:
Если значение полинома m3 + 2m + a равно 12 при m = 2, то найдите значение a .
Ответ:
Пусть pm=m3+2m+a
Для м = 2, p (2) = 12.
∴23+2×2+a=142⇒ a=12⇒12+a=12⇒a=12-12=0
Таким образом, значение a равно 0.
Страница № 53:
Вопрос 4:
Для многочлена mx2 -2x + 3 если p-1 =7 тогда найдите м.
Ответ:
Пусть px=mx2-2x+3.
∴p-1=7⇒m×-12-2×-1+3=7⇒m+2+3=7⇒m=7-5=2
Таким образом, значение м равно 2.
Страница № 53:
Вопрос 5:
Разделите первый многочлен на второй и найдите остаток, используя факторную теорему.
(i) x2 – 7x +9 ; (x + 1) (ii) 2×3 — 2×2 +ax — a ; ( x — a ) (iii) 54м3 + 18м2 -27м + 5 ; ( m — 3 )
Ответ:
(i)
По синтетическому делению:
Делимое = x2-7x+9
Делитель = x + 1
Противоположное 1 = −1
∴ Частное = x − 8
Остаток = 17
По теореме об остатках:
Пусть px=x2-7x+9.
Делитель = x + 1
По теореме об остатках
Остаток = p (−1) = -12-7×-1+9=1+7+9=19
(ii)
By synthetic division:
Dividend = 2×3-2×2+ax-a
Divisor = x − a
Opposite of − a = a
The coefficient form of the частное равно (2, 2 a — 2, 2 a 2 — a ).
∴ Частное = 2 x 2 + (2 a − 2) x + 2 a 2 4−0 3 91002 Остаток = 2 a 3 − a 2 − a
По теореме об остатках:
Делитель = x − a
По теореме об остатках
Остаток = p ( a ) = 2×a3-2×a2×a2+a3a-a- 2a3-a2-a
(iii)
По синтетическому делению:
Дивиденд = 54м3+18м2-27м+5
Делитель = м — 3
Противоположно -3 = 3
Форма коэффициента частного равна (54, 180, 513).
∴ COTITION = 54 x 2 + 180 x + 513
Остаток = 1544
по теореме оставшегося:
Let PM = 54M3+ 18M2-27M+ 5.
Делитель = м − 3
По теореме об остатках
Остаток = p (3) = 54×33+18×32-27×3+5=54×27+18×9-27× 3+5=1458+162-81+5=1544
Страница № 53:
Вопрос 6:
Если многочлен y3 – 5y2 + 7y + m делится на y + 2 , а остаток равен 50, то найдите значение m.
Ответ:
Пусть py=y3-5y2+7y+m.
Когда многочлен делится на ( y + 2), остаток равен 50. Это означает, что значение многочлена при y = −2 равно 50.
По теореме об остатках,
Остаток = p (−2) = 50
∴-23-5×-22+7×-2+m=50⇒-8-5×4-14+m=50⇒-8-20-14+m= 50⇒-42+м=50⇒м=50+42=92
Таким образом, значение м равно 92.
Страница № 53:
Вопрос 7:
Используйте теорему о множителях, чтобы определить, является ли x + 3 множителем x
5 2 0 90 005
− 3 или нет.
Ответ:
Let P ( x ) = x 2 + 2 x -3.
Divisor = x + 3
й. 2×-3-3=9-6-3=0
Итак, по теореме о факторах ( x + 3) является коэффициентом x 2 + 2 x − 3.
Страница № 53:
Вопрос 8)
x коэффициент — mx2 + 10x — 20 тогда найдите значение m .
Ответ:
Пусть px=x3-mx2+10x-20.
Дано, что ( x — 2) является коэффициентом px=x3-mx2+10x-20.
∴p2=0⇒23-m×22+10×2-20=0⇒8-4m+20-20=0⇒8-4m=0⇒4m=8⇒m=2
Таким образом, значение м равно 2.
Страница № 53:
Вопрос 9:
Используя теорему о множителях в следующих примерах, определите, является ли q ( x ) множителем p ( x 91,041 ) или нет.
(i) px = x3 — x2 — x — 1 , qx = x — 1
(ii) px = 2×3 — x2 -45, qx = x — 3
Ответ:
7Делитель = qx=x-1
∴p1=13-12-1-1=1-1-1-1=-2
Поскольку стр. (1) ≠ 0, поэтому по теореме о множителях qx=x-1 является , а не множителем многочлена px=x3-x2-x-1.
(1) ≠ 0, поэтому по теореме о множителях qx=x-1 является , а не множителем многочлена px=x3-x2-x-1.
(ii)
px=2×3-x2-45
Делитель = qx=x-3
∴p3=2×33-32-45=2×27-9-45=54-54=0
Итак, по теореме о множителях qx=x-3 является множителем многочлена px=2×3-x2-45.
Страница № 53:
Вопрос 10:
Если ( x 31 + 31) разделить на ( x + 1), то найти остаток.
Ответ:
Пусть P ( x ) = x 31 + 31.
Divisor = x + 1
по теореме оставшейся. ) 31 + 31 = -1 + 31 = 30
Таким образом, остаток при делении ( x 31 + 31) на ( x + 1) равен 30.
Вопрос 11:
Покажите, что m -1 является коэффициентом m 21 — 1 и m 22 — 1.
Answer:
Let p ( m ) = m 21 − 1 and q ( m ) = m 22 − 1.
Divisor = M — 1
Теперь,
P (1) = (1) 21 — 1 = 1 — 1 = 0
Следовательно, по теории фактора ( M — 1) является коэффициентом p ( m ) = m 21 − 1,
Кроме того,
q (1) = (1) 22 − 1 = 1 − 1 = 0
Следовательно, по теореме о множителях ( m − 1) есть множитель q 0 ) = м 22 — 1.
Следовательно, ( м — 1) является коэффициентом м 21 — 1 и М 22 — 1.
Страница № 53 53 :
Вопрос 12:
Если x — 2 и x — 12 оба являются факторами многочлена nx 2 — 5 x + M , затем покажите, что M = n = 2
Ответ:
Let P ( x ) = NX 2 — 5 10401. NX 2 — 5 4040404040401) = Н. М. + м .
М. + м .
Учитывая, что ( x − 2) и x-12 являются множителями многочлена p ( x ) = n x 2 1 − 5 1 04 41040 x 910 41,040 x 910
∴ По теореме о факторах p (2) = 0 и p12=0.
p2=0⇒n×22-5×2+m=0⇒4n-10+m=0⇒4n+m=10 …..1
Также
p12=0⇒n122-5×12 +m=0⇒n4+m=52⇒n+4m=10 …..2
Из (1) и (2) имеем
4 n + m = n + 4 m
⇒ 4 n − n = 4 m − m
⇒ 3 n = 3 m
⇒ n = m
Putting n = м в (1) имеем
4 M + M = 10
⇒ 5 M = 10
⇒ M = 2
∴ N = M = 2
PARIE 53:
4102441344134413441344. 41024413441341344.. 13: (i) Если px = 2 + 5x, то p2 + p-2 — p1.
(ii) px = 2×2 — 53x + 5 затем p53.
Ответ:
(i)
px=2+5x∴p2=2+5×2=2+10=12p-2=2+5×-2=2-10=-8p1=2+5 ×1=2+5=7
∴p2+p-2-p1=12+-8-7=12-8-7=12-15=-3
(ii)
px=2×2-53x+5
∴p53=2×532-53×53+5=2×75-25×3+5=150-75+5=80
Страница № 54:
Вопрос 1:
Найдите множители полиномов приведен ниже.
(I) 2 x 2 + x — 1
(II) 2 M 2 + 5 M — 3
(III) 12 x 2
(III) x + 77
(iv) 3 y 2 – 2 y – 1
(v) 3×2+4x+3
(vi) 12×2-12×2-0003
Ответ:
(i)
2×2+x-1=2×2+2x-x-1=2xx+1-1x+1=x+12x-1
(ii)
2m2+5m-3=2m2 +6м-м-3=2мм+3-1м+3=м+32м-1
(iii)
12×2+61x+77=12×2+28x+33x+77=4x3x+7+113x+7=3x+74x +11
(iv)
3y2-2y-1=3y2-3y+y-1=3yy-1+1y-1=y-13y+1
(v)
3×2+4x+3=3×2+3x+x +3=3xx+3+1x+3=x+33x+1
(vi)
12×2-3x+4=12×2-2x-x+4=12xx-4-1x-4=x-412x-1
Страница № 55:
Вопрос 2:
Разложите на множители следующие многочлены.
(я) ( х 2 — x ) 2 — 8 ( x 2 — x ) + 12
(II) ( x — 5) 2 — (5 x — 25 ) — 24
(III) ( x 2 — 6 x ) 2 — 8 ( x 2 — 6 x + 8) — 64
(IV) ( x + 8) — 64
(IV) ( x + 8) — 64
(IV) ( x + 8) — 64
(IV) ( x + 8) 2 – 2 x + 3) ( x 2 – 2 x + 5) – 35
(v) ( y + 2) ( Y — 3) ( Y + 8) ( Y + 3) + 56
(VI) ( Y 2 + 5 Y ) ( Y 2 + 5 y – 2) – 24
(vii) ( x – 3) ( x – 4) 2 ( x – 5) – 6
Ответ:
4)
2 — x ) 2 — 8 ( x 2 — x ) + 12
let x 2 — x = z .
∴x2-x2-8×2-x+12=z2-8z+12=z2-6z-2z+12=zz-6-2z-6=z-6z-2
=x2-x-6×2-x-2 Замените z=x2-x=x2-3x+2x-6×2-2x+x-2=xx-3+2x-3xx-2+1x-2=x-3x+2x-2x+1
(ii)
( x — 5) 2 — (5 x — 25) — 24
= ( x — 5) 2 — 5 ( x — 5) — 24
let x — 5 = z .
∴x-52-5x-5-24=z2-5z-24=z2-8z+3z-24=zz-8+3z-8=z-8z+3
=x-5-8x-5+3 Заменить z=x-5=x-13x-2
(iii)
( x 2 – 6 x ) 2 – 8( x 2 – 6 x + 8) – 64
= ( x 2 – 6 x ) 2 — 8 ( x 2 — 6 x ) — 64 — 64
= ( x 2 — 6 x ) 2 — 8 ( — 6 x ) 2 — 8 (. 2 – 6 x ) – 128
Пусть x 2 – 6 x = z .
∴x2-6×2-8×2-6x-128=z2-8z-128=z2-16z+8z-128=zz-16+8z-16=z-16z+8
=x2-6x-16×2-6x+ 8 Заменить z=x2-6x=x2-8x+2x-16×2-4x-2x+8=xx-8+2x-8xx-4-2x-4=x-8x+2x-4x-2
(iv )
( x 2 – 2 x + 3)( x 2 – 2 x + 5) – 35
Let x 2 – 2 x = z .
∴x2-2x+3×2-2x+5-35=z+3z+5-35=z2+5z+3z+15-35=z2+8z-20=z2+10z-2z-20
=zz+10 -2z+10=z+10z-2=x2-2x+10×2-2x-2 Заменить z=x2-2x
(V)
( Y + 2) ( Y — 3) ( Y + 8) ( Y + 3)+ 56
= ( Y + 2) ( Y + 3 ( Y + 8) ( Y — 3) + 56
= ( Y 2 + 5 Y + 6) ( Y 2 + 5 Y — 24) + 56
Пусть y 2 + 5 y = z .
∴y2+5y+6y2+5y-24+56=z+6z-24+56=z2-18z-144+56=z2-18z-88
=z2-22z+4z-88=zz-22+4z -22=z-22z+4=y2+5y-22y2+5y+4 Заменить z=y2+5y
=y2+5y-22y2+4y+y+4=y2+5y-22yy+4+1y+4=y2+5y-22y+4y+1
(vi)
( y 2 + 5 y )( y 2 + 5 y – 2) – 24
Пусть y 2 + 5 y 91 910 = z 9.1041
∴y2+5yy2+5y-2-24=zz-2-24=z2-2z-24=z2-6z+4z-24=zz-6+4z-6=z-6z+4
=y2+5y -6y2+5y+4 Заменить z=y2+5y=y2+6y-y-6y2+4y+y+4=yy+6-1y+6yy+4+1y+4=y+6y-1y+4y+1
(vii)
( x – 3)( x – 4) 2 ( x — 5) — 6
= ( x — 3) ( x — 5) ( x — 4) 2 — 6
= ( x 2 — 8 x + 15)( x 2 – 8 x + 16) – 6
Пусть x 2 – 8 x 9104.
∴x2-8x+15×2-8x+16-6=z+15z+16-6=z2+31z+240-6=z2+31z+234
=z2+18z+13z+234=zz+18+13z +18=z+18z+13=x2-8x+18×2-8x+13 Заменить z=x2-8x
Страница № 55:
Вопрос 1:
Напишите правильный альтернативный ответ на каждый из следующих вопросов.
(i) Что из следующего является многочленом?
(A) xy (B) x2 — 3x (C) x-2 + 7 (D) 2×2 + 12
(ii) Какова степень многочлена 7?
(A) 12 (B) 5 (C) 2 (D) 0
(iii) Какова степень полинома 0 ?
(A) 0 (B) 1 (C) undefined (D) любое действительное число
(iv) Какова степень многочлена 2 x 2 + 5 x 3 + 7?
(A) 3 (B) 2 (C) 5 (D) 7
(v) Каков вид коэффициента x3 — 1 ?
(A) (1, — 1) (B) (3,-1) (C) (1, 0, 0, -1) (D) (1, 3, — 1)
(vi) p( x) = x2 — 77x + 3, тогда p77 = ?
(A) 3 (B) 77 (C) 42 7 + 3 (D) 497
(vii) Когда x = — 1 , каково значение полинома 2 x 3 + 4 2
(А) 4 (Б) 2 (В) -2 (Г)-4
(viii) Если x-1 , каков множитель полинома 3×2 + mx, тогда найдите значение m .
(A) 2 (B) -2 (C) -3 (D) 3
(ix) Умножить ( x 2 -3) (2 x — 7x 35
4) и напишите степень произведения.
(A) 5 (B) 3 (C) 2 (D) 0
(x) Какой из следующих полиномов является линейным?
(А) x + 5
(Б) x 2 + 5
(c) x 3 + 5
(D) x 4 + 5
Ответ:
(i)
в алгебрие. переменные являются целыми числами, тогда алгебраическое выражение является полиномом.
В выражении 2×2 + 12 степень переменной x равна 2, то есть целому числу. Итак, выражение 2×2 + 12 является многочленом.
Следовательно, правильный ответ — вариант (D).
(ii)
7=7×1=7×0
Степень полинома 7 равна 0.
Следовательно, правильный ответ — вариант (D).
(iii)
Степень полинома 0 не определена.
Следовательно, правильный ответ — вариант (С).
(iv)
Высшая степень переменной в многочлене называется степенью многочлена.
Степень полинома 2 x 2 + 5 x 3 + 7 равно 3.
Следовательно, правильный ответ – вариант (А).
(v)
x3-1=x3+0x2+0x-1
Форма коэффициентов многочлена x3-1 равна (1, 0, 0, −1).
Следовательно, правильный ответ — вариант (С).
(vi)
px= x2-77x+3
∴p77= 772-77×77+3=343-343+3=3
Следовательно, правильный ответ — вариант (A).
(vii)
let p ( x ) = 2 x 3 + 2 x
∴ P (-1) = 2 × (—1) 3 + 2 + 2 (-1) = 2 × (—1) 3 + 2. × (−1) = 2 × (−1) − 2 = −2 − 2 = −4
Таким образом, значение многочлена при x = −1 равно −4.
Следовательно, правильный ответ — вариант (D).
(viii)
Пусть p ( x ) = 3 x 2 + m x .
( x − 1) является коэффициентом p ( x ).
∴ P (1) = 0
⇒ 3 × (1) 2 + M × 1 = 0
⇒ 3+ M = 0
⇒ M = –3
⇒ M = –3 ⇒ M = –3Следовательно, правильный ответ — вариант (С).
(ix)
x2-32x-7×3+4=x22x-7×3+4-32x-7×3+4=2×3-7×5+4×2-6x+21×3-12=-7×5+2×3+21×3+4×2-6x-12 =-7×5+23×3+4×2-6x-12
Таким образом, степень полученного многочлена равна 5.
Следовательно, правильный ответ — вариант (А).
(x)
Многочлен первой степени называется линейным многочленом.
Таким образом, многочлен x + 5 является линейным многочленом.
Следовательно, правильный ответ — вариант (А).
Страница № 56:
Вопрос 2:
Напишите степень полинома для каждого из следующих.
(i) 5 + 3 x 4 (II) 7 (III) AX 7 + BX 9 ( A , B — континт. )
)
.
Наибольшая степень переменной в многочлене от одной переменной называется степенью многочлена.
(i)
Степень многочлена 5 + 3 x 4 равно 4.
(ii)
7 = 7 × 1 = 7 x 0
Степень постоянного многочлена 7 равна 0,9
900 многочлен ax 7 + bx 9 равно 9.
Страница № 56:
Вопрос 3:
Запишите следующие многочлены в стандартной форме.
(i) 4 x 2 + 7 x 4 — x 3 — x +
(II) P + 2 P 3 + 10 P 2 + 5 P 4 -8
9106 + 5 P 4 -8 + 5 P 4 -8.
Многочлен, записанный в убывающей или возрастающей степени своей переменной, называется стандартной формой многочлена.
(i)
Данный многочлен равен 4 x 2 + 7 x 4 − x 3 − x + 9.
. Стандартная форма полиномиала составляет 7 x 4 — x 3 + 4 x 2 — x + 9 или 9 — x + 4 4. x 2 − x 3 + 7 x 4 .
(ii)
. Данный полиномиальный составляет P + 2 P 3 + 10 P 2 + 5 P 4 — 8.
. Стандартная форма из полинома. P 4 +2 P 3 +10 P 2 + P — 8 или −8 + P +10 P 2 +2 P 955 3 . + 5 р 4 .
Страница № 56:
Вопрос 4:
Запишите следующий многочлен в виде коэффициентов.
(i) x 4 + 16 (ii) м 5 + 2 м 2 + 3 м + 15
Ответ:
(i)
x4+16=x4+0x3+0x2+0x+16
Следовательно, данный многочлен в виде коэффициентов равен (1, 0, 0, 0, 16 ).
(ii)
m5+2m2+3m+15=m5+0m4+0m3+2m2+3m+15
Таким образом, данный полином в виде коэффициентов равен (1, 0, 0, 2, 3, 15).
Страница № 56:
Вопрос 5:
Напишите форму индекса полинома, используя переменную x из его формы коэффициента.
(i) (3, -2, 0, 7, 18)
(ii) (6, 1, 0, 7)
(iii) (4, 5, -3, 0)
Ответ:
(i)
Форма коэффициента многочлена: (3, −2, 0, 7, 18).
Therefore, the index form the polynomial is 3 x 4 − 2 x 3 + 0 x 2 + 7 x + 18 or 3 x 4 − 2 x 3 + 7 x + 18.
(ii)
Форма коэффициента полинома (6, 1, 0, 7).
Следовательно, индекс образует полиномиальное составляет 6 x 3 + x 2 + 0 x + 7 или 6 x 3 + x 2 9000+ 7.
(iii)
Форма коэффициента многочлена – (4, 5, −3, 0).
Таким образом, индекс полинома равен 4 x 3 + 5 x 2 − 3 x + 0 или 4 x 3 + 5 x 2 − 3 x .
Страница № 56:
Вопрос 6:
Добавьте следующие многочлены.
(i) 7 x 4 -2 x 3 + x + 10 ; 3 x 4 + 15 x 3 + x 2 -8 x + 2
(II) 3 P 3 Q + 2 P 3 Q + 2 P 3 Q + 2 P 3 Q + 2 P 3 Q + 2 P 3 Q + 2 P 3 2 q + 7 ; 2 p 2 q + 4 pq -2 p 3 q
Answer:
(i)
7×4-2×3+x+10+3×4+15×3+9×2 -8x+2=7×4+3×4-2×3+15×3+9×2+x-8x+10+2=10×4+13×3+9×2-7x+12
(ii)
3p3q+2p2q+7+2p2q+4pq-2p3q=3p3q -2p3q+2p2q+2p2q+4pq+7=p3q+4p2q+4pq+7
Страница № 56:
Вопрос 7:
Вычесть второй полином из первого.
(и) 5 x 2 -2 y + 9 ; 3 x 2 + 5 y -7 (ii) 2 x 2 + 3 x + 5 ; x 2 -2 x + 3
Ответ:
(i)
5×2-2y+9-3×2+5y-7=5×2-2y+9-3x2x5y+7=5×2-2y+9-3x2x5y-7=5×2-2y+9-3×2+5y-7=5×2-2y+9-3×2+5y-7 3×2-2y-5y+9+7=2×2-7y+16
(ii)
2×2+3x+5-x2-2x+3=2×2+3x+5-x2+2x-3=2×2-x2+3x+ 2x+5-3=x2+5x+2
Страница № 56:
Вопрос 8:
Умножьте следующие многочлены.
(I) ( M 3 -2 M + 3) ( M 4 -2 M 2 + 3 M + 2)
575757 (II II ) (5 м 3 -2)( м 2 — м + 3) Ответ:
(i)
м4м3-2м3-2м3 -2м2+3м+2-2мм4-2м2+3м+2+3м4-2м2+3м+2=м7-2м5+3м4+2м3-2м5+4м3-6м2-4м+3м4-6м2+9м+6=м7-2м5 -2м5+3м4+3м4+2м3+4м3-6м2-6м2-4м+9м+6=м7-4м5+6м4+6м3-12м2+5м+6
(ii)
5m3-2m2-m+3=5m3m2-m+3-2m2-m+3=5m5-5m4+15m3-2m2+2m-6
Страница № 56:
Вопрос 9:
Разделить многочлен 3 x 3 — 8 x 2 + x + 7 на x — 3, используя синтетический метод, и запишите частное и остаток.
Ответ:
Делимое = 3×3-8×2+x+7
Делитель = x-3
Противоположное −3 = 3
Форма коэффициента частного: (3, 1, 4).
∴ Covertient = 3 x 2 + x + 4 и оставшаяся часть = 19
Страница № 56:
Вопрос 10:
, для которого значение м , x + 3 — это значение м , x + 3 множитель многочлена x 3 — 2 m x + 21?
Ответ:
Пусть px=x3-2mx+21.
( x + 3) — множитель многочлена px=x3-2mx+21.
∴p-3=0⇒-33-2m×-3+21=0⇒-27+6m+21=0⇒6m-6=0⇒6m=6⇒m=1
Таким образом, значение м равно 1.
Страница № 56:
Вопрос 11:
На конец 2016 года население сел Ковад, Варуд, Чихали составляет 5 x
6 -3
y 2 , 7 y 2 + 2 xy и 9 x 2 + 4 xy соответственно. На начало 2017 года x 2 + xy — y 2 , 5 xy и 3 x 2 + xy человек из каждой из трех деревень соответственно отправились в другую деревню для получения образования, тогда какова оставшаяся общая численность населения этих трех деревень?
На начало 2017 года x 2 + xy — y 2 , 5 xy и 3 x 2 + xy человек из каждой из трех деревень соответственно отправились в другую деревню для получения образования, тогда какова оставшаяся общая численность населения этих трех деревень? Ответ:
Общее население трех деревень
=5×2-3y2+7y2+2xy+9×2+4xy=5×2+9×2-3y2+7y2+2xy+4xy=14×2+4y2+6xy
Общее количество людей, которые уехал в другую деревню учиться
=x2+xy-y2+5xy+3×2+xy=x2+3×2-y2+xy+5xy+xy=4×2-y2+7xy
∴ Оставшееся общее население трех деревень = Общее население трех деревень − Общее количество людей, уехавших в другую деревню для получения образования
= 14×2+4y2+6xy-4×2-y2+7xy=14×2+4y2+6xy-4×2+ y2-7xy=14×2-4×2+4y2+y2+6xy-7xy=10×2+5y2-xy
Таким образом, оставшееся общее население этих трех деревень составляет ху .
Страница № 56:
Вопрос 12:
Многочлены bx 2 + x + 5 и bx 3 -2 x + 5 делятся на многочлен x -3 и остатки m и n соответственно. Если m — n = 0, то найдите значение b .
Если m — n = 0, то найдите значение b .
Ответ:
Пусть px=bx2+x+5 и qx=bx3-2x+5.
Остаток от деления px=bx2+x+5 на ( x − 3) составляет м .
По теореме об остатках
Остаток = p3=m
∴b×32+3+5=m⇒m=9b+8 …..1
Остаток при делении qx=bx3-2x+5 на ( x − 3) равен n .
По теореме об остатках
Остаток = q3=n
∴b×33-2×3+5=n⇒n=27b-6+5⇒n=27b-1 …..2
m-n=0⇒9b+8-27b-1=0 Использование 1 и 2⇒9b-27b+8+1=0⇒-18b+9=0⇒-18b=-9⇒b=-9-18=12
Таким образом, значение b равно 12.
Страница № 56:
Вопрос 13:
Упростить
(8 M 2 + 3 M -6) — (9 M — 7) + (3 M 2 — 2 M + 4)
Ответ:
8м2+3м-6-9м-7+3м2-2м+4=8м2+3м-6-9м+7+3м2-2м+4=8м2+3м2+3м-9м-2м-6+7+4=11м2 -8M + 5
Страница № 56:
Вопрос 14:
, который должен быть вычитан из x 2 + 13 x + 7, чтобы получить полиномиальное 3 x 2 9106 + 5 5. х — 4?
х — 4?
Ответ:
Let P ( x ) быть полиномом, который должен быть вычитается из x 2 + 13 x + 7 до получения полинома 3 x 9 2 2 6 + 2 6 + 2 6 + 2 6 + 2 6 + 2 6 + 2 6 + 2 6. 5 x − 4.
∴ ( x 2 + 13 x + 7) − p ( x ) = 3 x 2 + 5 x − 4
⇒ p ( x ) = ( x 2 + 13 x + 7) — (3 x 2 + 5 x — 4)
⇒ P ( x ) = x 2 + 13 x + 7 a 2 + 13 x + 7 – x 2 − 5 x + 4
⇒ p ( x ) = x 2 − 3 x 2 + 13 x − 5 x + 7 + 4
⇒ p ( x ) = −2 x 2 + 8 x + 11
Таким образом, необходимый полином составляет -2 x 2 +8 x + 11.
Страница № 56:
Вопрос 15:
, что полиномация. 4 m + 2 n + 3, чтобы получить многочлен 6 m + 3 n + 10?
Ответ:
Искомый полином можно получить вычитанием полинома 4 м + 2 n + 3 из 6 м + 3 N + 10.
∴ Требуется полином
= (6 M + 3 N + 10) — (4 M + 2 N + 3)
= 6 M. + 3 n + 10 − 4 m − 2 n − 3
= 6 m − 4 m + 3 n − 2 n + 10 − 3
= 2 m + n + 7
Таким образом, полином 2 m + n + 7 нужно прибавить к 4 м + 2 n + 3 для получения полинома 6 м + 3 n + 10.
21-128 и 15-151, Осенний курс 2020 9
1
Способность логически и ясно рассуждать из набора принятых принципов является фундаментальной не только
в математике, но и в жизни вообще. На этом уроке мы научимся предоставлять
полные объяснения того, почему определенные вещи верны. Мы также определим, как выявлять ложные утверждения
и предоставить убедительные доказательства их ложности.
На этом уроке мы научимся предоставлять
полные объяснения того, почему определенные вещи верны. Мы также определим, как выявлять ложные утверждения
и предоставить убедительные доказательства их ложности. Мы начнем с конкретных объектов, таких как числа, множества и функции, и научимся доказывать
их с помощью элементарной логики. Изучив технику доказательства, известную как индукция, мы рассмотрим
функции и использовать их для классификации размеров бесконечных множеств (да, существуют бесконечные множества разного размера).
наборы).
Далее мы узнаем, как посчитать количество предметов, которые можно получить в результате
определенный процесс. Например, мы можем подсчитать количество различных покерных комбинаций, в которых есть три туза.
и два короля или количество различных пицц с тремя начинками, которые можно приготовить, если десять начинок
доступный. Затем мы решаем элементарные проблемы, связанные с целыми числами, такие как факторизация, делимость
и их возможные применения в криптографии.
Наконец, мы изучим некоторые классические темы из дискретной математики. Элементарная вероятность будет
для того, чтобы выяснить, например, насколько вероятно, что нам сдадут покерную комбинацию, содержащую
три туза и два короля. Мы увидим, что вероятность связана со счетом, и перейдем к изучению
полезные темы в подсчете, известные как принцип сортировки и включение/исключение.
Занятия и лекции: 21-128 встречает MWF с 11:15 до 12:05 в Доэрти 1212.
15-151 встречается с MWF с 1:25 до 2:15 у выхода 4401.
Наши замечательные ассистенты также будут проводить две еженедельные сессии декламации.
Я настоятельно рекомендую вам посещать занятия по чтению, поскольку они являются неотъемлемой частью
курс и может охватывать экзаменационный материал, не затронутый в лекции.
В случае, если в этом семестре ассистенты будут работать онлайн, студенты перейдут на веб-сайт OHQ.
(ОХК)
и при входе найти очередь 21-128/15-151. При добавлении себя в очередь учащиеся должны добавить ссылку в
поле описания к своей личной встрече в масштабе, чтобы ассистенты могли оказать им (и любым соавторам) помощь. Они также могут включать в себя
краткое описание их вопроса (ов). В конце часа ТА войдет в комнату масштабирования, связанную с
календарь для обсуждения общих вопросов. Эта комната будет открыта в течение всего периода ОШ, чтобы студенты могли свободно входить и выходить.
Они также могут включать в себя
краткое описание их вопроса (ов). В конце часа ТА войдет в комнату масштабирования, связанную с
календарь для обсуждения общих вопросов. Эта комната будет открыта в течение всего периода ОШ, чтобы студенты могли свободно входить и выходить.
Офис Макки: Гейтс 4005 Телефон: 268-1204 Электронная почта: [email protected]
Справка: В дополнение к классу, сеансам чтения и офису
часов в университете действуют Центры взаимного обучения.
Индивидуальное обучение и другие варианты помощи также доступны через
Академическое развитие.
Книга: Бесконечный спуск в чистую математику -> https://infiniteescent.xyz/
Бесконечный спуск в чистую математику, по умолчанию, Клайв Ньюстед.
Бесконечный спуск в чистую математику, табличка, Клайв Ньюстед.
Бесконечный спуск в чистую математику, смартфон, Клайв Ньюстед.
Бесконечное нисхождение в чистую математику, печать Клайва Ньюстеда.
Дополнительная (дополнительная) книга: Все, что вы всегда хотели знать о математике, Брендан Салливан,
Дополнительная (дополнительная) Книга: Математическое мышление: решение проблем и доказательства (2-е издание), Д’Анджело и Уэст
Домашнее задание: Домашнее задание является неотъемлемой частью
курс. Трудно понять материал и сделать хорошо на
экзамены, не прорабатывая домашние задания вдумчиво.
Обсуждение домашнего задания со сверстниками приветствуется, но копирование
любая часть домашнего задания другого человека не допускается. Пожалуйста, подумайте о
поставленные проблемы, ваши стратегии и обоснованность вашей логики и
объяснения.
Домашнее задание должно быть отправлено через Gradescope в установленный срок и
время. Домашнее задание, сданное после установленного срока и времени, но до
опубликованы решения, получат половину балла (со звездочкой, чтобы получить полный балл
если оценка за курс пограничная). Каждый набор решений домашнего задания, набранный с использованием
LaTex получит бонус в один балл, начиная со второго домашнего задания.
Если вы решите писать от руки, а затем сканировать домашние задания, то вот полезный ресурс для
сканирование документов в кампусе:
Сканирование документов
Каждый набор решений домашнего задания, набранный с использованием
LaTex получит бонус в один балл, начиная со второго домашнего задания.
Если вы решите писать от руки, а затем сканировать домашние задания, то вот полезный ресурс для
сканирование документов в кампусе:
Сканирование документов
Запросы на изменение домашней работы и экзамена должны быть отправлены в течение одной недели с даты возврата.
Промежуточные экзамены: Будет три промежуточных экзамена и кумулятивный
выпускной экзамен. Даты промежуточных экзаменов следующие:
Промежуточный период 1: Понедельник,
26 сентября
Промежуточный этап 2: Понедельник,
31 октября
Промежуточная 3: Среда,
30 ноября
Оценка : Ваша оценка за курс будет определяться следующим образом:
Каждый из двух высоких промежуточных баллов: 20%
Низкий промежуточный балл: 10%
Домашнее задание: 20%
Итоговый экзамен: 30%
Максимально возможные пороговые значения будут составлять 90 % для A, 80 % для B,
70 % для C и 60 % для D. Эти пороговые значения могут быть немного снижены, но
не будет увеличено.
Эти пороговые значения могут быть немного снижены, но
не будет увеличено.
Калькуляторы : Калькуляторы не будут полезны в этом курсе.
Калькуляторы и другие электронные устройства не допускаются во время экзаменов.
Велнес : Береги себя. Делайте все возможное, чтобы поддерживать здоровый образ жизни в этом семестре, хорошо питаясь, занимаясь спортом, избегая наркотиков и алкоголя,
выспаться и немного отдохнуть. Это поможет вам достичь поставленных целей и справиться со стрессом.
Всем нам нужна поддержка во времена борьбы. Ты не одинок. В кампусе есть много полезных ресурсов, и это важная часть
опыт колледжа учит, как просить о помощи. Просить о поддержке раньше, чем позже, часто бывает полезно.
Если вы или кто-либо из ваших знакомых испытывает академический стресс, трудные жизненные события или такие чувства, как тревога или депрессия, мы настоятельно рекомендуем вам обратиться
поддерживать. Консультационные и психологические службы (CaPS) готовы помочь: позвоните по телефону 412-268-2922 и посетите их веб-сайт http://www. cmu.edu/counseling/. Рассмотреть возможность
обратиться к другу, преподавателю или члену семьи, которому вы доверяете, за помощью в подключении к службе поддержки, которая может помочь.
cmu.edu/counseling/. Рассмотреть возможность
обратиться к другу, преподавателю или члену семьи, которому вы доверяете, за помощью в подключении к службе поддержки, которая может помочь.
Если вы или кто-то из ваших знакомых склонны к суициду или вам грозит членовредительство, немедленно позвоните кому-нибудь днем или ночью:
Телефон: 412-268-2922
Сеть Re:solve Crisis: 888-796-8226
Если ситуация угрожает жизни, позвоните в полицию:
На территории кампуса: CMU Police: 412-268-2323
За пределами кампуса: 911
Если у вас есть вопросы по этой или курсовой работе, дайте мне знать.
Исследование обучения студентов : Марша Ловетт, Клаус Сатнер и я проводим исследование того, как студенты учатся на этом курсе.
Исследование будет включать анализ данных этого курса и 15-051.
Вас не попросят делать что-либо помимо обычных учебных занятий и заданий, являющихся частью этого курса.
Вы можете не участвовать в этом исследовании, и ваше участие не повлияет на вашу оценку за этот курс или вашу академическую карьеру в CMU. Если вы решите не участвовать в исследовании, вы все равно должны выполнить все необходимые курсовые работы, но ваши данные не будут включены в анализ исследования.
Никакой компенсации участники не получат. Данные, собранные в рамках этого исследования, будут включать оценки учащихся. Все анализы данных от участников
Курсовая работа будет проводиться после окончания курса и выставления итоговых оценок. Центр Эберли может оказать поддержку этому исследовательскому проекту в отношении данных.
анализ и интерпретация. Чтобы свести к минимуму риск нарушения конфиденциальности, Eberly Center никогда не будет иметь доступа к данным этого курса, содержащим ваши
персональные идентификаторы. Все данные будут проанализированы в обезличенной форме и представлены в совокупности, без каких-либо личных идентификаторов.
Пожалуйста, свяжитесь с Чадом Хершоком ([email protected]) из Центра Эберли, если у вас есть вопросы или опасения по поводу вашего участия.
Если вы решите не участвовать в исследовании, вы все равно должны выполнить все необходимые курсовые работы, но ваши данные не будут включены в анализ исследования.
Никакой компенсации участники не получат. Данные, собранные в рамках этого исследования, будут включать оценки учащихся. Все анализы данных от участников
Курсовая работа будет проводиться после окончания курса и выставления итоговых оценок. Центр Эберли может оказать поддержку этому исследовательскому проекту в отношении данных.
анализ и интерпретация. Чтобы свести к минимуму риск нарушения конфиденциальности, Eberly Center никогда не будет иметь доступа к данным этого курса, содержащим ваши
персональные идентификаторы. Все данные будут проанализированы в обезличенной форме и представлены в совокупности, без каких-либо личных идентификаторов.
Пожалуйста, свяжитесь с Чадом Хершоком ([email protected]) из Центра Эберли, если у вас есть вопросы или опасения по поводу вашего участия.
Недельное расписание (предварительное) :
Неделя 1 (29 августа — 2 сентября):
- Введение и глава 0
- 1.
 1
1 - 1,2
Неделя 2 (6–9 сентября):
- 1,3
- 2.1
Неделя 3 (12–16 сентября):
- 2.2
- 2.2
- 3.1
Неделя 4 (19-23 сентября):
- 3.2
- 4.1
- Обзор для промежуточного периода
Промежуточный обзор;
Пятница, 23 сентября
Первая среднесрочная;
Понедельник, 26 сентября
Неделя 5 (26–30 сентября):
- Первый промежуточный семестр
- 4.2
- 4.3
Неделя 6 (3–7 октября):
- Индукционный фестиваль 2022
- 5.1
- 5.2
Неделя 7 (10–14 октября):
- 6.1
- 6.2
- 6.2
Неделя 8 (24-27 октября):
- 6.3
- 7.1
Вторая среднесрочная;
Понедельник, 31 октября
Неделя 9 (31 октября — 4 ноября):
- Второй промежуточный срок
- 7.
 1
1 - 7.2
Неделя 10 (7–11 ноября):
- 7.2
- 7.2
- 7.3
Неделя 11 (14–18 ноября):
- 8.1
- 8.1
- 9.1
Неделя 12 (21–22 ноября):
- 9.1
- 10.1
Промежуточный обзор;
Понедельник, 28 ноября
Третий промежуточный;
Среда, 30 ноября
Неделя 13 (28 ноября — 2 декабря):
- Обзор третьего промежуточного срока
- Третий промежуточный срок
- 10.1
Неделя 14 (5–9 декабря):
- 10.1
- 10.2
- 10.2
Заключительный экзамен, назначенный регистратором
Вернуться на страницу приветствия
Tamil Nadu Board Решения Samacheer Kalvi для 9-го класса Ответы на вопросы по математике, глава 3 — Алгебра [Последнее издание] 92 + 3x — 4`
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3. 1 | Вопрос 1. (ii) |
1 | Вопрос 1. (ii) |
Определите, что следующее выражение является полиномиальным. Если не указать причину:
x 2 (x – 1)
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.1 | Вопрос 1. (iii) |
Определите, что следующее выражение является полиномиальным. Если не указать причину:
`1/x(x + 5)`
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.1 | Вопрос 1. (iv) |
Определите, что следующее выражение является полиномиальным. Если не указать причину: 92`
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.1 | Вопрос 3. (iii) | Страница 87
Найдите степень следующего многочлена
x 3 (x 2 + x)
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.1 | Вопрос 3. (iv) | Страница 87
Найдите степень следующего многочлена
3x 4 + 9x 2 + 27x 6
ПОКАЗАТЬ РЕШЕНИЕ
93.102 Упражнение | Вопрос 4. (i) | Страница 87 Перепишите следующий многочлен в стандартной форме 94`
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3. 1 | Вопрос 5. (i) | Страница 87
1 | Вопрос 5. (i) | Страница 87
Сложи следующие многочлены и найди степень полученного многочлена
Упражнение 3.1 | Вопрос 5. (ii) |
Сложите следующие многочлены и найдите степень полученного многочлена
h(x) = 7x 3 – 6x + 1, f(x) = 7x 2 + 17x – 9
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.1 | Вопрос 5. (iii) | Страница 87
Сложи следующие многочлены и найди степень полученного многочлена
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.1 | Вопрос 6. (i) | Страница 87
Вычесть второй многочлен из первого многочлена и найти степень полученного многочлена
p(x) = 7x 2 + 6x – 1, q(x) = 6x – 9
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.1 | Вопрос 6. (ii) | Страница 88
Вычесть из первого многочлена второй многочлен и найти степень полученного многочлена
f(y) = 6y 2 – 7y + 2, g(y) = 7y + y РЕШЕНИЕ
Упражнение 3.1 | Вопрос 6. (iii) | Страница 88
Вычесть второй многочлен из первого многочлена и найти степень полученного многочлена
h(z) = z 5 – 6z 4 + z, f(z) = 6z 2 + 10z – 7
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3. 1 | вопрос 7 |
1 | вопрос 7 |
Что нужно добавить к 2x 3 + 6x 2 – 5x + 8, чтобы получить 3x 3 – 2x 2 + 6x + 15?
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.1 | Вопрос 8 |
Что нужно вычесть из 2x 4 + 4x 2 – 3x + 7, чтобы получить 3x 3 – x 2 + 2x + 1?
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.1 | Вопрос 9. (i) |
Умножьте следующие многочлены и найдите степень полученного многочлена:
p(x) = x 2 – 9, q(x) = 6x 2 + 7x – 2
90 РЕШЕНИЕ 9003 Упражнение 3.1 | Вопрос 9. (ii) |
Умножьте следующие многочлены и найдите степень полученного многочлена:
f(x) = 7x + 2, g(x) = 15x – 9
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.1 | Вопрос 9. (iii) | Страница 88
Умножьте следующие многочлены и найдите степень полученного многочлена:
h(x) = 6x 2 – 7x + 1, f(x) = 5x – 7
ПРОСМОТР РЕШЕНИЯ
Упражнение 3. 1 | Вопрос 10 | Страница 88
1 | Вопрос 10 | Страница 88
Стоимость шоколадки составляет рупий. (x + y) и Амир купили (x + y) шоколадных конфет. Найдите общую сумму, уплаченную им, через x и y. Если x = 10, y = 5, найдите сумму, уплаченную им
ПОКАЗАТЬ РЕШЕНИЕ
Упражнение 3.1 | Вопрос 11 | Страница 88
Длина прямоугольника равна (3x + 2) единицам, а его ширина равна (3x – 2) единицам. Найдите его площадь через х. Какой будет площадь, если x = 20 единиц
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.1 | Вопрос 12 | Page 88
p(x) — многочлен степени 1, а q(x) — многочлен степени 2. Какого рода полиномом является p(x) × q(x)?
ПОСМОТРЕТЬ РЕШЕНИЕ
Tamil Nadu Board Решения Samacheer Kalvi для 9-го класса Математика Ответы Руководство Глава 3 Алгебра Упражнение 3.2 [Страницы 91 — 92]
Упражнение 3.2 | Вопрос 1. (i) | Страница 91
Найдите значение многочлена f(y) = 6y – 3y 2 + 3 при y = 1 92 — 2sqrt(2)x + 1`, найти `»p»(2sqrt(2))`
ПРОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3. 2 | Вопрос 3. (i) | Страница 91
2 | Вопрос 3. (i) | Страница 91
Найдите ноль многочлена следующего:
p(x) = x – 3
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.2 | Вопрос 3. (ii) | Страница 91
Найдите ноль многочлена из следующего:
p(x) = 2x + 5
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.2 | Вопрос 3. (iii) | Страница 91
Найдите ноль многочлена следующего:
q(y) = 2y – 3
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.2 | Вопрос 3. (iv) | Страница 91
Найдите ноль многочлена следующего:
f(z) = 8z
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.2 | Вопрос 3. (iv) |
Найдите нуль многочлена в следующем:
h(x) = ax + b, a ≠ 0, a, b ∈ R
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.2 | Вопрос 3. (д) | Страница 91
Найдите ноль многочлена следующего:
p(x) = ax, когда a ≠ 0
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.2 | Вопрос 4. (i) | Страница 91
Найдите корни полиномиального уравнения
5x – 6 = 0
ПРОСМОТР РЕШЕНИЯ
Упражнение 3. 2 | Вопрос 4. (ii) | Страница 91
2 | Вопрос 4. (ii) | Страница 91
Найдите корни полиномиального уравнения
x + 3 = 0
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.2 | Вопрос 4. (iii) | Страница 91
Найдите корни уравнения полинома
10x + 9 = 0
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.2 | Вопрос 4. (iv) | Страница 91
Найдите корни полиномиального уравнения
9x – 4 = 0
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.2 | Вопрос 5. (i) | Page 91
Проверьте, являются ли нижеприведенные числа нулями полинома, указанного против них, или нет
p(x) = 2x − 1, x = `1/2` Вопрос 5. (ii) | Страница 91
Проверить, являются ли следующие нули полинома, указанного против них, или нет
p(x) = x 3 – 1, x = 1
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.2 | Вопрос 5. (iii) | Страница 91
Проверить, являются ли следующие нули полинома, указанного против них, или нет
p(x) = ax + b, x = `(-«b»)/»a»`
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3. 2 | Вопрос 5. (iv) | Страница 91
2 | Вопрос 5. (iv) | Страница 91
Проверить, являются ли нижеследующие нулями полинома, указанного против них, или нет
p(x) = (x + 3) (x – 4), x = −3, x = 4
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.2 | Вопрос 6. (i) | Страница 92
Найдите количество нулей следующего многочлена, представленного их графиком
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.2 | Вопрос 6. (ii) | Страница 92
Найдите количество нулей следующего многочлена, представленного их графиком
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.2 | Вопрос 6. (iii) | Страница 92
Найдите количество нулей следующего многочлена, представленного их графиком
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.2 | Вопрос 6. (iv) | Страница 92
Найдите количество нулей следующего многочлена, представленного их графиком
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.2 | Вопрос 6. (т) | Страница 92
Найдите количество нулей следующего многочлена, представленного их графиком
ПРОСМОТР РЕШЕНИЯ
Tamil Nadu Board Samacheer Kalvi Solutions for Class 9 Математика Ответы Руководство Глава 3 Алгебра Упражнение 3.
 3 [Страницы 96 — 97]
3 [Страницы 96 — 97] Упражнение 3.3 | Вопрос 1 | Страница 96
Проверить, является ли p(x) кратным g(x) или нет
p(x) = x 3 – 5x 2 + 4x – 3, g(x) = x – 2
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.3 | Вопрос 2. (i) |
По теореме об остатке найдите остаток при делении p(x) на g(x), где p(x) = x 3 – 2x 2 – 4x – 1; g(x) = x + 1
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.3 | Вопрос 2. (ii) | Страница 96
По теореме об остатке найдите остаток при делении p(x) на g(x), где p(x) = 4x 3 – 12x 2 + 14x – 3; g(x) = 2x – 1
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.3 | Вопрос 2. (iii) |
По теореме об остатках найдите остаток при делении p(x) на g(x), где p(x) = x 3 – 3x 2 + 4x + 50; g(x) = x – 3
ПРОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.3 | Вопрос 3 | Страница 96
Найдите остаток при умножении 3x 3 – 4x 2 + 7x – 5 делится на (x + 3)
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3. 3 | Вопрос 4 | Страница 96
3 | Вопрос 4 | Страница 96
Какой остаток при делении x 2018 + 2018 на x – 1
ПРОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.3 | Вопрос 5 |
Для какого значения k полином p(x) = 2x 3 – kx 2 + 3x + 10 делится на (x – 2)
ПОКАЗАТЬ РЕШЕНИЕ
Упражнение 3.3 | Вопрос 6 | Страница 96
Если два полинома 2x 3 + ax 2 + 4x – 12 и x 3 + x 2 – 2x + a оставить тот же остаток при делении на (x – 3), найти значение a и также найти остаток.
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.3 | Вопрос 7. (i) |
Определите, является ли (x – 1) множителем следующих полиномов:
x 3 + 5x 2 – 10x + 4
ПРОСМОТР РЕШЕНИЯ
| Упражнение 3. Вопрос 7. (ii) | Страница 96
Определите, является ли (x – 1) множителем следующих многочленов:
x 4 + 5x 2 – 5x + 1
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3. 3 | Вопрос 8 | Страница 97
3 | Вопрос 8 | Страница 97
Используя факторную теорему, покажите, что (x – 5) является множителем многочлена Вопрос 9 |
Определите значение m, если (x + 3) является коэффициентом x 3 – 3x 2 – mx + 24
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.3 | Вопрос 10 | Страница 97
Если и (x — 2), и `(x — 1/2)` являются множителями ax 2 + 5x + b, то покажите, что a = b
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.3 | Вопрос 11 |
Если (x – 1) делит многочлен kx 3 – 2x 2 + 25x – 26 без остатка, то найдите значение k
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.3 | Вопрос 12 | Страница 97
Проверить, являются ли (x + 2) и (x – 4) сторонами прямоугольника, площадь которого равна x 2 – 2x – 8, используя факторную теорему
ПОСМОТРЕТЬ РЕШЕНИЕ
Tamil Nadu Board Решения Samacheer Kalvi для 9-го класса Математика Ответы Руководство Глава 3 Алгебра Упражнение 3.
 4 [Страницы 101 — 102]
4 [Страницы 101 — 102] Упражнение 3.4 | Вопрос 1. (i) | Страница 101
Разверните следующее:
(2x + 3y + 4z) 2
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.4 | Вопрос 1. (ii) | Страница 101
Разверните следующее:
(−p + 2q + 3r) 2
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.4 | Вопрос 1. (iii) | Страница 101
Разверните следующее:
(2п + 3)(2п – 4)(2п – 5)
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.4 | Вопрос 1. (iv) | Страница 101
Разверните следующее:
(3a + 1)(3a – 2)(3a + 4)
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.4 | Вопрос 2. (i) |
Используя алгебраическое тождество, найдите коэффициенты x 2 , x и постоянный член без фактического расширения
(x + 5)(x + 6)(x + 7)
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.4 | Вопрос 2. (ii) | Страница 101
Используя алгебраическое тождество, найдите коэффициенты x 2 , x и постоянный член без фактического расширения
(2x + 3)(2x – 5)(2x – 6)
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3. 4 | Вопрос 3. (i) | Страница 101
4 | Вопрос 3. (i) | Страница 101
Если (x + a)(x + b)(x + c) = x 3 + 14x 2 + 59x + 70, найдите значение a + b + c
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.4 | Вопрос 3. (ii) | Страница 101
Если (x + a)(x + b)(x + c) = x 3 + 14x 2 + 59x + 70, найдите значение `1/»a» + 1/»b» + 1/»c»`
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.4 | Вопрос 3. (iii) | Страница 101
Если (x + a)(x + b)(x + c) = x 3 + 14x 2 + 59x + 70, найдите значение a 2 + b 2 + c 2
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.4 | Вопрос 3. (iv) | Страница 101
Если (x + a)(x + b)(x + c) = x 3 + 14x 2 + 59x + 70, найдите значение `»a»/»bc» + «b «/»ac» + «c»/»ab»` 93`
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.4 | Вопрос 5. (i) | Страница 101
Оцените следующее, используя тождества:
98 3
ПРОСМОТР РЕШЕНИЯ
Упражнение 3. 4 | Вопрос 5. (ii) | Страница 101
4 | Вопрос 5. (ii) | Страница 101
Оцените следующее, используя тождества:
1001 3
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.4 | Вопрос 6 | Страница 101
Если (x + y + z) = 9 и (xy + yz + zx) = 26, то найти значение x 2 + y 93`
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.4 | Вопрос 12. (ii) | Страница 102
Упрощение: (2a + 3b + 4c) (4a 2 + 9b 2 + 16c 2 – 6ab – 12bc – 8ca)
90 РЕШЕНИЕ 904 | Вопрос 12. (ii) | Страница 102
Упрощение: (x – 2y + 3z) (x 2 + 4y 2 + 9z 2 + 2xy + 6yz – 3xz)
ПРОСМОТР РЕШЕНИЯ 90 0.4 | Вопрос 13. (i) | Страница 102
Используя тождество, оцените следующее:
7 3 – 10 3 + 3 3
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.4 | Вопрос 13. (ii) | Страница 102
Используя тождество, оцените следующее:
`1 + 1/8 — 27/8`
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3. 4 | Вопрос 14 | Страница 102
4 | Вопрос 14 | Страница 102
Если 2x – 3y – 4z = 0, то найти 8x 3 – 27y 3 – 64z 3
ПОСМОТРЕТЬ РЕШЕНИЕ
Решения для Samacher Board Tamilth Mathematics Answers Guide Глава 3 Алгебра Упражнение 3.5 [Страница 105]
Упражнение 3.5 | Вопрос 1. (i) |
Факторизируйте следующее выражение:
2a² + 4a²b + 8a²c
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.5 | Вопрос 1. (ii) |
Факторизируйте следующее выражение:
ab – ac – mb + mc
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.5 | Вопрос 2. (i) | Страница 105
Факторизируйте следующее:
x² + 4x + 4
92 — 18` ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.5 | Вопрос 3. (i) | Page 105
Factorise Следующее:
4x 2 + 9y 2 + 25Z 2 + 12xy+ 30yz+ 20xz
Просмотр решения
Упражнение 3.5 | Вопрос 3. (ii) | Page 105
Factorise Следующее:
25x 2 + 4y 2 + 9Z 2 — 20xy+ 12yz — 30xz
Просмотр решения
Упражнение 3. 5 | Вопрос 4. (i) | Страница 105
5 | Вопрос 4. (i) | Страница 105
Факторизируйте следующее:
8x 3 + 125y 3
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.5 | Вопрос 4. (ii) |
Факторизируйте следующее:
27x 3 – 8y 3
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.5 | Вопрос 4. (iii) | Страница 105
Факторизируйте следующее:
a 6 – 64
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.5 | Вопрос 5. (i) | Страница 105
Факторизируйте следующее:
x 3 + 8y 3 + 6xy – 1
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.5 | Вопрос 5. (ii) | Page 105
Factorise Следующее:
L 3 — 8m 3 — 27N 3 — 18LMN
Просмотр решения
Глава Tamil Nadu Poard 3.6 Страница 107]
Упражнение 3.6 | Вопрос 1. (i) | Страница 107
Факторизируйте следующее:
x² + 10x + 24
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3. 6 | Вопрос 1. (ii) | Страница 107
6 | Вопрос 1. (ii) | Страница 107
Факторизируйте следующее:
z² + 4z – 12
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.6 | Вопрос 1. (iii) | Страница 107
Факторизируйте следующее:
p² – 6p – 16
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.6 | Вопрос 1. (iv) | Страница 107
Факторизируйте следующее:
t² + 72 – 17t
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.6 | Вопрос 1. (д) | Страница 107
Факторизируйте следующее:
y 2 – 16y – 80
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.6 | Вопрос 1. (vi) |
Факторизируйте следующее:
a 2 + 10a – 600
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.6 | Вопрос 2. (i) | Страница 107
Факторизируйте следующее:
2a 2 + 9a + 10
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.6 | Вопрос 2. (ii) | Страница 107
Факторизируйте следующее:
5x 2 – 29xy – 42y 2
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3. 6 | Вопрос 2. (iii) | Страница 107
6 | Вопрос 2. (iii) | Страница 107
Факторизируйте следующее:
9 – 18x + 8x 2
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.6 | Вопрос 2. (iv) |
Факторизируйте следующее:
6x 2 + 16xy + 8y 2
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.6 | Q 2. (v) | Страница 107
Факторизируйте следующее:
12x 2 + 36x 2 y + 27y 2 x 2
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.6 | Вопрос 2. (vi) |
Факторизируйте следующее:
(a + b) 2 + 9(a + b) + 18
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.6 | Вопрос 3. (i) |
Факторизируйте следующее:
(p – q) 2 – 6(p – q) – 16
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.6 | Вопрос 3. (ii) | Страница 107
Факторизируйте следующее: 92 + 2″a» — 3sqrt(5)`
ПРОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.6 | Вопрос 3. (iv) |
Факторизируйте следующее:
a 4 – 3a 2 + 2
ПРОСМОТР РЕШЕНИЯ
Упражнение 3. 2 + 2/(xy)`
2 + 2/(xy)`
ПОСМОТРЕТЬ РЕШЕНИЕ
Tamil Nadu Board Решения Samacheer Kalvi для 9-го класса Математика Ответы Руководство Глава 3 Алгебра Упражнение 3.7 [Страницы 111 — 112]
Упражнение 3.7 | Вопрос 1. (i) | Страница 111
Найдите частное и остаток следующего.
(4x 3 + 6x 2 – 23x + 18) ÷ (x + 3)
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.7 | Вопрос 1. (ii) | Страница 111
Найдите частное и остаток следующего.
(8y 3 – 16y 2 + 16y – 15) ÷ (2y – 1)
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.7 | Вопрос 1. (iii) | Страница 111
Найдите частное и остаток следующего.
(8x 3 – 1) ÷ (2x – 1)
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.7 | Вопрос 1. (iv) | Страница 111
Найдите частное и остаток следующего.
(−18z + 14z 2 + 24z 3 + 18) ÷ (3z + 4)
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3. 7 | вопрос 2 |
7 | вопрос 2 |
Площадь прямоугольника x 2 + 7x + 12. Если его ширина равна (x + 3), то найдите его длину
ПОКАЗАТЬ РЕШЕНИЕ
Упражнение 3.7 | Вопрос 3 | Страница 111
Основание параллелограмма (5x + 4). Найдите его высоту, если площадь равна 25x 2 – 16
ПОКАЗАТЬ РЕШЕНИЕ
Упражнение 3.7 | Вопрос 4 |
Сумма (x + 5) наблюдений равна (x 3 + 125). Найдите среднее значение наблюдений
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.7 | Вопрос 5. (i) | Страница 111
Найдите частное и остаток для следующего с помощью синтетического деления:
(x 3 + x 2 – 7x – 3) ÷ (x – 3)
ПРОСМОТР РЕШЕНИЯ
3.000 | Вопрос 5. (ii) | Страница 111 Найдите частное и остаток для следующего с помощью синтетического деления:
(x 3 + 2x 2 – x – 4) ÷ (x + 2)
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.7 | Вопрос 5. (iii) | Страница 111
Найдите частное и остаток для следующего, используя синтетическое деление:
(3x 3 – 2x 2 + 7x – 5) ÷ (x + 3)
ПРОСМОТР РЕШЕНИЯ 3. 7
7
3
3 | Вопрос 5. (iv) | Страница 111
Найдите частное и остаток для следующего с помощью синтетического деления:
(8x 4 – 2x 2 + 6x + 5) ÷ (4x + 1)
ПРОСМОТР РЕШЕНИЯ 3.
2
2 | Вопрос 6 | Страница 111 Если частное, полученное при делении (8x 4 – 2x 2 + 6x – 7) на (2x + 1), равно (4x 3 + px 2 – qx + 3), то найти p, q, а также остаток
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.7 | вопрос 7 | Страница 112
Если частное, полученное при делении 3x 3 + 11x 2 + 34x + 106 на x – 3, равно 3x 2 + ax + b, то найти a, b, а также остаток
РЕШЕНИЕ Tamil Nadu Board Решения Samacheer Kalvi для класса 9th Mathematics Answers Guide Глава 3 Алгебра Упражнение 3.8 [Страница 114]
Упражнение 3.8 | Вопрос 1. (i) |
Разложите на множители следующие многочлены, используя синтетическое деление:
x 3 – 3x 2 – 10x + 24
ПРОСМОТР РЕШЕНИЯ
Упражнение 3. 8 | Вопрос 1. (ii) | Страница 114
8 | Вопрос 1. (ii) | Страница 114
Разложите на множители следующие многочлены, используя синтетическое деление:
2x 3 – 3x 2 – 3x + 2
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.8 | Вопрос 1. (iii) | Страница 114
Разложите на множители следующие многочлены, используя синтетическое деление:
– 7x + 3 + 4x 3
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.8 | Вопрос 1. (iv) |
Разложите на множители следующие многочлены, используя синтетическое деление:
x 3 + x 2 – 14x – 24
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.8 | Вопрос 1. (д) | Страница 114
Факторизируйте следующие многочлены, используя синтетическое деление:
x 3 – 7x + 6
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.8 | Вопрос 1. (vi) | Страница 114
Разложите на множители следующие полиномы, используя синтетическое деление:
x 3 – 10x 2 – x + 10
ПРОСМОТР РЕШЕНИЯ
Tamil Nadu Board Упражнение 3 Samacheer Kalvithe Solutions for Class.
 [Страница 115]
[Страница 115] Упражнение 3.9 | Вопрос 1. (i) | Страница 115
Найдите НОД для следующего:
P 5 , P 11 , P 9
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.9 | Вопрос 1. (ii) |
Найдите НОД для следующего:
4x 3 , y 3 , z 3
ПРОСМОТР РЕШЕНИЯ
2 | Упражнение 3. Вопрос 1. (iii) | Страница 115 Найдите НОД для следующего:
9a 2 b 2 c 3 , 15a 3 b 0 6 0 90 9005 c 402 ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.9 | Вопрос 1. (iv) | Страница 115
Найдите НОД для следующего:
64x 8 , 240x 6
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.9 | Вопрос 1. (д) | Page 115
Найдите G.C.D для следующего:
AB 2 C 3 , A 2 B 3 C, 3 BC 2
Просмотр решения
Упражнение 3. 9 | Вопрос 1. (vi) | Страница 115
9 | Вопрос 1. (vi) | Страница 115
Найдите НОД для следующего:
35x 5 Y 3 Z 4 , 49x 2 YZ 3 , 14xy 2 Z 2
Просмотр решения
Упражнение 3.9 | Вопрос 1. (vii) |
Найдите НОД для следующего:
25ab 3 c, 100a 2 bc, 125ab
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.9 | Вопрос 1. (viii) | Страница 115
Найдите НОД для следующего:
3abc, 5xyz, 7pqr
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.9 | Вопрос 2. (i) | Страница 115
Найдите НОД следующего числа:
(2x + 5), (5x + 2)
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.9 | Вопрос 2. (ii) | Страница 115
Найдите НОД следующего числа:
a m+1 , a m+2 , a m+3
ПОКАЗАТЬ РЕШЕНИЕ
| Упражнение Вопрос 2. (iii) | Страница 115
Найдите НОД следующего:
2a 2 + a, 4a 2 – 1
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3. 9 | Вопрос 2. (iv) | Страница 115
9 | Вопрос 2. (iv) | Страница 115
Найдите НОД следующего:
3a 2 , 5b 3 , 7c 4
ПРОСМОТР РЕШЕНИЯ
Упражнение | Q 2. (v) |
Найдите НОД следующего числа:
x 4 – 1, x 2 – 1
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.9 | Вопрос 2. (vi) | Страница 115
Найдите НОД следующего:
a 3 – 9ax 2 , (a – 3x) 2
ПОСМОТРЕТЬ РЕШЕНИЕ
Tamil Nadu Board Решения Samacheer Kalvi для 9-го класса Математика Ответы Руководство Глава 3 Алгебра Упражнение 90 100 124 [Страница 0124] Вопрос 1. (i) | Страница 124
Нарисуйте график для следующего
y = 2x
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.10 | Вопрос 1. (ii) | Страница 124
Нарисуйте график для следующего
y = 4x – 1
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.10 | Вопрос 1. (iii) |
Нарисуйте график для следующего
y = `(3/2)x + 3`
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3. 10 | Вопрос 1. (iv) | Страница 124
10 | Вопрос 1. (iv) | Страница 124
Нарисуйте график для следующего
3x + 2y = 14
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.10 | Вопрос 2. (i) | Страница 124
Решить графически
x + y = 7, x – y = 3
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.10 | Вопрос 2. (ii) | Страница 124
Решить графически
3x + 2y = 4, 9x + 6y – 12 = 0
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.10 | Вопрос 2. (iii) |
Решить графически
`x/2 + y/4` = 1, `x/2 + y/4` = 2
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.10 | Вопрос 2. (iv) | Страница 124
Решить графически
x – y = 0, y + 3 = 0
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.10 | Q 2. (v) | Страница 124
Решить графически
y = 2x + 1, y + 3x – 6 = 0
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.10 | Вопрос 2. (vi) | Страница 124
Решить графически
x = −3, y = 3
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3. 10 | Вопрос 3 | Страница 124
10 | Вопрос 3 | Страница 124
Две машины находятся на расстоянии 100 миль друг от друга. Если они едут навстречу друг другу, то встретятся через 1 час. Если они едут в одном направлении, то встретятся через 2 часа. Найдите их скорость графическим методом.
VIEW SOLUTION
Tamil Nadu Board Решения Samacheer Kalvi для класса 9th Mathematics Answers Guide Глава 3 Алгебра Упражнение 3.11 [Страница 126]
Упражнение 3.11 | Вопрос 1. (i) |
Решить методом подстановки
2x – 3y = 7, 5x + y = 9
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.11 | Вопрос 1. (ii) |
Решить методом подстановки
1,5x + 0,1y = 6,2, 3x – 0,4y = 11,2
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.11 | Вопрос 1. (iii) | Страница 126
Решить методом подстановки
10% x + 20% y = 24, 3x – y = 20
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.11 | Вопрос 1. (iv) |
Решить методом подстановки
`sqrt(2)x — sqrt(3)y` = 1, `sqrt(3)x — sqrt(8)y` = 0
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3. 11 | вопрос 2 | Страница 126
11 | вопрос 2 | Страница 126
Возраст Рамана в три раза больше суммы возрастов двух его сыновей. Через 5 лет его возраст будет в два раза больше суммы возрастов двух его сыновей. Найдите возраст Рамана.
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.11 | Вопрос 3 | Страница 126
Средняя цифра числа от 100 до 1000 равна нулю, а сумма другой цифры равна 13. Если цифры поменять местами, то полученное таким образом число превышает исходное число на 495. Найдите число
ПОКАЗАТЬ РЕШЕНИЕ
Tamil Nadu Board Решения Samacheer Kalvi для 9-го класса Математика Ответы Руководство Глава 3 Алгебра Упражнение 3.12 [Страница 128]
Упражнение 3.12 | Вопрос 1. (i) | Страница 128
Решить методом исключения
2x – y = 3, 3x + y = 7
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.12 | Вопрос 1. (ii) |
Решить методом исключения
x – y = 5, 3x + 2y = 25
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.12 | Вопрос 1. (iii) |
Решить методом исключения
`x/10 + y/5` = 14, `x/8 + y/6` = 15
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3. 12 | Вопрос 1. (iv) | Страница 128
12 | Вопрос 1. (iv) | Страница 128
Решить методом исключения
3(2x + y) = 7xy, 3(x + 3y) = 11xy
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.12 | Вопрос 1. (д) |
Решить методом исключения
`4/x + 5y` = 7, `3/x + 4y` = 5
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.12 | Вопрос 1. (vi) |
Решить методом исключения
13x + 11y = 70, 11x + 13y = 74
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.12 | вопрос 2 | Страница 128
Месячные доходы A и B относятся как 3 : 4, а их ежемесячные расходы относятся как 5 : 7. Если каждый из них сберегает 5000 ₹ в месяц, найдите месячный доход каждого
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.12 | Вопрос 3 |
Пять лет назад мужчина был в семь раз старше своего сына, а через пять лет мужчина будет в четыре раза старше своего сына. Найдите их текущий возраст
ПОСМОТРЕТЬ РЕШЕНИЕ
Тамил Наду Доска Samacheer Kalvi решения для 9 класса Математика Ответы Руководство Глава 3 Алгебра Упражнение 3.
 13 [Страница 131]
13 [Страница 131] Упражнение 3.13 | Вопрос 1. (i) | Страница 131
Решить методом перекрестного умножения
8x – 3y = 12, 5x = 2y + 7
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.13 | Вопрос 1. (ii) |
Решить методом перекрестного умножения
6x + 7y – 11 = 0, 5x + 2y = 13
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.13 | Вопрос 1. (iii) |
Решить методом перекрестного умножения
`2/x + 3/y` = 5, `3/x — 1/y + 9` = 0
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.13 | вопрос 2 | Страница 131
У Акшайи в кошельке 2 рупии и 5 рупий. Если всего у нее 80 монет на общую сумму 220 ₹, сколько у нее монет каждого вида.
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.13 | Вопрос 3 | Страница 131
Наполнение бассейна с помощью двух труб занимает 24 часа. Если труба большего диаметра используется в течение 8 часов, а труба меньшего диаметра используется в течение 18 часов. Заполнена только половина бассейна. Сколько времени понадобится каждой трубе, чтобы наполнить бассейн
ПОСМОТРЕТЬ РЕШЕНИЕ
Tamil Nadu Board Решения Samacheer Kalvi для 9-го класса Руководство по математике Глава 3 Упражнение по алгебре 3.
 14 [Страница 133]
14 [Страница 133] Решить любым из способов
Упражнение 3.14 | Вопрос 1 |
Сумма двузначного числа и числа, образованного перестановкой цифр, равна 110. Если из первого числа вычесть 10, новое число будет в 4 раза больше, чем в 5 раз больше суммы цифр первого числа. Найдите первое число.
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.14 | вопрос 2 |
Сумма числителя и знаменателя дроби равна 12. Если знаменатель увеличить на 3, дробь станет `1/2`. Найдите дробь
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.14 | Вопрос 3 |
ABCD — вписанный четырехугольник, такой что ∠A = (4y + 20)°, ∠B = (3y − 5)°, ∠C = (4x)° и ∠D = (7x + 5)°. Найдите четыре угла
ВИД РЕШЕНИЯ
Упражнение 3.14 | Вопрос 4 | Страница 133
При продаже телевизора с прибылью 5% и холодильника с прибылью 10% владелец магазина получает 2000 рупий. 1500 по сделке. Найдите фактическую цену телевизора и холодильника.
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3. 14 | Вопрос 5 | Страница 133
14 | Вопрос 5 | Страница 133
Два числа находятся в отношении 5 : 6. Если из каждого числа вычесть 8, отношение станет 4 : 5. Найдите числа.
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.14 | Вопрос 6 | Страница 133
4 индийца и 4 китайца могут выполнить часть работы за 3 дня. В то время как 2 индийца и 5 китайцев могут закончить его за 4 дня. Сколько времени потребуется 1 индийцу, чтобы сделать это? Сколько времени потребуется 1 китайцу, чтобы сделать это?
ПОСМОТРЕТЬ РЕШЕНИЕ
Tamil Nadu Board Решения Samacheer Kalvi для 9-го класса Руководство по математике Ответы Глава 3 Алгебра Упражнение 3.15 [Страницы 134 — 136]
Вопросы с несколькими вариантами ответов
Упражнение 3.15 | Вопрос 1 |
Если x 3 + 6x 2 + kx + 6 точно делится на (x + 2), то k = ?
−6
−7
−8
11
7 РЕШЕНИЕ0003 Упражнение 3.15 | вопрос 2 | Стр. -2/3`
-2/3`
ПРОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.15 | Вопрос 3 | Страница 134
Тип полинома 4 – 3x 3 is
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.15 | Вопрос 4 | Страница 134
Если x 51 + 51 разделить на x + 1, то в остатке будет
0
1
49
50
Просмотр решения
Упражнение 3.15 | Вопрос 5 | Стр. `
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.15 | Вопрос 6 | Страница 134
Сумма многочленов p(x) = x 3 — x 2 — 2, Q (x) = x 2 — 3x + 1
x 3 — 3x — 1
x 3 + 2x 2 — 1
x 3 — 2x 2 — 3x
x 3 — 2x 2 + 3x — 1
Просмотр раствора
Упражнение 3.15 | вопрос 7 | Страница 134
Степень многочлена (y 3 – 2)(y 3 + 1) равна
9
2
3
6
Просмотр
Упражнение 3. 5`
5`
, затем приказ их степени составляет
A, B, D, C
A, B, C, D
B, D, A
B, A, C, D
ПРОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.15 | Вопрос 9 | Page 134
Если P (a) = 0 Тогда (x — a) — ___________ из P (x)
Divisor
Коэффициент
Остаток
Фактор
Фактор
0003
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.15 | Вопрос 10 | Page 134
нули (2 — 3x) ___________
3
2
`2/3`
`3/2`
. 3.15 | Вопрос 11 | Страница 134 Что из следующего имеет x – 1 в качестве множителя?
2x – 1
3x – 3
4x – 3
3x – 4
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3. 15 | Вопрос 12 | Стр.
15 | Вопрос 12 | Стр.
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.15 | Вопрос 13 |
(x + y)(x 2 – xy + y 2 ) равно
(x + y) 3
(x — y) 3
x 3 + Y 3
x 3 — Y 3
3 — Y 3 9000 2 . 3.15 | Вопрос 14 | Стр. (а + б + в) 2
(a – b – c) 2
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.15 | Вопрос 15 |
Если (x + 5) и (x – 3) являются коэффициентами ax 2 + bx + c, то значения a, b и c равны
1, 2, 3
1, 2, 15
1, 2, −15
1, −2, 15
ПРОСМОТР РЕШЕНИЯ
5 | Упражнение 3. Вопрос 16 | Страница 135 Кубический многочлен может иметь не более ___________ линейных множителей
1
2
3
4
Просмотр
Упражнение 3. 15 | Вопрос 17 | Page 135
15 | Вопрос 17 | Page 135
Степень постоянного полинома — __________
3
2
1
0
Просмотр раствора
. Вопрос 18 |
Найдите значение m из уравнения 2x + 3y = m. Если его единственное решение x = 2 и y = −2
2
— 2
10
0
Просмотр решения
Упражнение 3.15 | Вопрос 19 | Страница 135
Какое из следующих уравнений является линейным?
`x + 1/x` = 2
x (x — 1) = 2
3x + 5 =` 2/3`
x 3 — x = 5
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.15 | Вопрос 20 | Страница 135
Что из следующего является решением уравнения 2x – y = 6?
(2, 4)
(4, 2)
(3, -1)
(0, 6)
. Вопрос 21 |
Если (2, 3) является решением линейного уравнения 2x + 3y = k, то значение k равно0002 13
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3. 15 | Вопрос 22 |
15 | Вопрос 22 |
Какое условие не удовлетворяет линейному уравнению ax + by + c = 0
a ≠ 0, b = 0 = 0, c ≠ 0
a ≠ 0, b ≠ 0
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.15 | Вопрос 23 | Страница 135
Что из следующего не является линейным уравнением с двумя переменными
AX + BY + C = 0
0x + 0y + C = 0
0x + By + C = 0
AX + 0y + C = 0
.
Упражнение 3.15 | Вопрос 24 |
Значение k, для которого пара линейных уравнений 4x + 6y – 1 = 0 и 2x + ky – 7 = 0 представляет параллельные прямые, равно
к = 4
k = − 3
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.15 | Вопрос 25 | Page 135
Пара линейных уравнений не имеет решения. Затем графическое представление составляет
Проседание Раствор
. Вопрос 26 | Страница 136
Вопрос 26 | Страница 136
Если `»a»_1/»a»_2 ≠ «b»_1/»b»_2`, где a 1 x + b 1 y + c 1 = 0 и a 2 x + b 2 Y + C 2 = 0. Затем данная пара линейного уравнения имеет __________ Решение (S)
NO.
бесконечный
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.15 | Вопрос 27 | Страница 136
Если `»a»_1/»a»_2 = «b»_1/»b»_2 ≠ «c»_1/»c»_2`, где a 1 x + b 1 y + c 1 = 0 и а 2 х + b 2 Y + C 2 = 0. Затем данная пара линейного уравнения имеет __________ Решение (S)
NO Solution
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.15 | Вопрос 28 |
НОД любых двух простых чисел равен __________
−1
0
1
2
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.15 | Вопрос 29 | Page 136
G. C.D of x 4 — Y 4 и X 2 — Y 2 IS
C.D of x 4 — Y 4 и X 2 — Y 2 IS
x 4 — Y 4
x 2 ° 2
(x + y) 2
(x + y) 4
Просмотр решения
Реклама Удалить все объявления
.0003
Совет Тамил Наду Решения Samacheer Kalvi для 9-го класса. Ответы на вопросы по математике, глава 3 — Алгебра
Совет Тамил Наду, решения Samacheer Kalvi для 9-го класса. Ответы на вопросы по математике, глава 3 (Алгебра) включают все вопросы с решением и подробным объяснением.
Это избавит студентов от сомнений по любому вопросу и улучшит навыки применения при подготовке к экзаменам. Подробные пошаговые решения помогут вам лучше понять концепции и устранить путаницу, если таковая имеется.
На Shaalaa.com есть Совет по среднему образованию штата Тамил Наду, класс 9.th Mathematics Answers Направляйте решения таким образом, чтобы помочь учащимся лучше и быстрее усвоить основные понятия.
Кроме того, мы в Shaalaa.com предоставляем такие решения, чтобы студенты могли подготовиться к письменным экзаменам. Решения для учебников Tamil Nadu Board Samacheer Kalvi могут стать основной помощью для самостоятельного обучения и идеальным руководством для самопомощи для студентов.
Понятия, изложенные в Руководстве по математике для 9-го класса, глава 3. Алгебра — это алгебраические выражения, многочлены, многочлены от одной переменной, стандартная форма многочлена, степень многочлена, типы многочленов, арифметика многочленов, сложение многочленов, вычитание многочленов, Умножение двух многочленов, Значение многочлена, Корни уравнения полинома, Теорема об остатках, Теорема о факторах, Понятие тождества, Разложение (a + b)2 = a2 + 2ab + b2, Разложение (a — b)2 = a2 — 2ab + b2, Расширение (a + b)(a — b), Расширение (x + a)(x + b), Расширение (a + b + c)2, Расширение (x + a) (x + b)(x + c), Расширение (a + b)3, Расширение (a — b)3, Факторизация с использованием тождеств, Факторизация с использованием тождества a2 + 2ab + b2 = (a + b)2, Факторизация Использование тождества a2 — 2ab + b2 = (a — b)2, Факторизация с использованием тождества a2 — b2 = (a + b)(a — b), Факторизация с использованием тождества a2 + b2 + c2 + 2ab + 2bc + 2ac = (a + b + c)2, Факторизация с использованием Ident a3 + b3 = (a + b)(a2 — ab + b2), факторизация с использованием тождества a3 — b3 = (a — b)(a2 + ab + b2), факторизация с использованием тождества a3 + b3 + c3 — 3abc = ( a + b + c)(a2 + b2 + c2 — ab — bc — ca), Факторизация квадратичного многочлена (трехчлена) типа ax2 + bx + c, a ≠ 0. , Алгоритм деления многочленов, синтетическое деление, наибольшая Общий множитель, общий вид линейного уравнения с двумя переменными, график линейного уравнения с двумя переменными, одновременные линейные уравнения, сравнение отношений коэффициентов линейного уравнения, методы решения одновременных линейных уравнений графическим методом, методы решения одновременных линейных уравнений Уравнения подстановкой, Методы решения одновременных линейных уравнений методом исключения, Методы решения одновременных линейных уравнений методом перекрестного умножения, Совместность и несовместность линейных уравнений с двумя переменными, Нули полинома.
, Алгоритм деления многочленов, синтетическое деление, наибольшая Общий множитель, общий вид линейного уравнения с двумя переменными, график линейного уравнения с двумя переменными, одновременные линейные уравнения, сравнение отношений коэффициентов линейного уравнения, методы решения одновременных линейных уравнений графическим методом, методы решения одновременных линейных уравнений Уравнения подстановкой, Методы решения одновременных линейных уравнений методом исключения, Методы решения одновременных линейных уравнений методом перекрестного умножения, Совместность и несовместность линейных уравнений с двумя переменными, Нули полинома.
Использование Tamil Nadu Board Решения Samacheer Kalvi Class 9th Упражнения по алгебре для учащихся — это простой способ подготовиться к экзаменам, поскольку они включают в себя решения, расположенные по главам и по страницам. Вопросы, связанные с советом Samacheer Kalvi Solutions в Тамил Наду, являются важными вопросами.
которые можно задать на выпускном экзамене. Максимум учащиеся 9-го класса Совета среднего образования штата Тамил Наду предпочитают Samacheer Kalvi Textbook Solutions Совета Тамил Наду, чтобы набрать больше баллов на экзамене.
Максимум учащиеся 9-го класса Совета среднего образования штата Тамил Наду предпочитают Samacheer Kalvi Textbook Solutions Совета Тамил Наду, чтобы набрать больше баллов на экзамене.
Получите бесплатный просмотр дополнительных вопросов главы 3 по алгебре для 9-го класса к Руководству по математике для 9-го класса и можете использовать Shaalaa.com, чтобы держать его под рукой при подготовке к экзамену
Таблицы экспонент и шаблоны
Горячая математика В таблицах степеней целых чисел можно найти много интересных закономерностей.
Полномочия
2
Полномочия
3
Полномочия
4
2
1
знак равно
2 3
1
знак равно
3 4
1
знак равно
4 2
2
знак равно
4 3
2
знак равно
9 4
2
знак равно
16 2
3
знак равно
8 3
3
знак равно
27 4
3
знак равно
64 2
4
знак равно
16 3
4
знак равно
81 4
4
знак равно
256 2
5
знак равно
32 3
5
знак равно
243 4
5
знак равно
1024 2
6
знак равно
64 3
6
знак равно
729 4
6
знак равно
4096 2
7
знак равно
128 3
7
знак равно
2187 4
7
знак равно
16384 2
8
знак равно
256 3
8
знак равно
6561 4
8
знак равно
65536 2
9
знак равно
512 3
9
знак равно
19683 4
9
знак равно
262144 2
10
знак равно
1024 3
10
знак равно
59049 4
10
знак равно
1048576
Одна вещь, которую вы можете заметить, это закономерности в цифрах. В полномочиях
2
таблица, единичные цифры образуют повторяющийся шаблон
2
,
4
,
8
,
6
,
2
,
4
,
8
,
6
,
…
. В полномочиях
3
таблица, единичные цифры образуют повторяющийся шаблон
3
,
9
,
7
,
1
,
3
,
9,
7
,
1
,
…
. Мы оставляем это вам, чтобы выяснить, почему это происходит!
В полномочиях
2
таблица, единичные цифры образуют повторяющийся шаблон
2
,
4
,
8
,
6
,
2
,
4
,
8
,
6
,
…
. В полномочиях
3
таблица, единичные цифры образуют повторяющийся шаблон
3
,
9
,
7
,
1
,
3
,
9,
7
,
1
,
…
. Мы оставляем это вам, чтобы выяснить, почему это происходит!
В полномочиях
4
таблица, чередуются единичные цифры:
4
,
6
,
4
,
6
. На самом деле, вы можете видеть, что силы
4
совпадают с четными степенями
2
:
4
1
знак равно
2
2
4
2
знак равно
2
4
4
3
знак равно
2
6
и т. п.
п.
Такие же отношения существуют между силы
3 и силы
9 :
Полномочия
3
Полномочия
9
3
1
знак равно
3 91
знак равно
9 3
2
знак равно
9 9
2
знак равно
81 3
3
знак равно
27 9
3
знак равно
729 3
4
знак равно
81 9
4
знак равно
6561 3
5
знак равно
243 9
5
знак равно
59 049 3
6
знак равно
729 9
6
знак равно
531 441 3
7
знак равно
2187 9
7
знак равно
4 782 969 3
8
знак равно
6561 9
8
знак равно
43 046 721 3
9
знак равно
19,683 9
9
знак равно
387 420 489 3
10
знак равно
59 049 9
10
знак равно
3 486 784 401
силы
10 легко, потому что мы используем
база
10
: за
10
н
просто напишите »
1
» с
н
нули после него. За
отрицательные силы
10
−
н
, записывать »
0.
» с последующим
н
−
1
нули, а затем
1
. Полномочия
10
широко используются в
научная нотация
, так что это хорошая идея, чтобы освоиться с ними.
За
отрицательные силы
10
−
н
, записывать »
0.
» с последующим
н
−
1
нули, а затем
1
. Полномочия
10
широко используются в
научная нотация
, так что это хорошая идея, чтобы освоиться с ними.
Полномочия
10
10
1
знак равно
10 10
0
знак равно
1 10
2
знак равно
100 10
−
1
знак равно
0,1 10
3
знак равно
1000 10
−
2
знак равно
0,01 10
4
знак равно
10 000 10
−
3
знак равно
0,001 10
5
знак равно
100 000
(сто тысяч)
10
−
4
знак равно
0,0001
(одна десятитысячная)
10
6
знак равно
1 000 000
(один миллион)
10
−
5
знак равно
0,00001
(стотысячный)
10
7
знак равно
10 000 000
(десять миллионов)
10
−
6
знак равно
0,000001
(одна миллионная)
10
8
знак равно
100 000 000
(сто миллионов)
10
−
7
знак равно
0,0000001
(одна десятимиллионная)
10
9
знак равно
1 000 000 000
(один миллиард)
10
−
8
знак равно
0,00000001
(стомиллионный)
10
10
знак равно
10 000 000 000
(десять миллиардов)
10
−
9
знак равно
0,000000001
(одна миллиардная)
Нажмите
здесь
для большего количества имен для
очень большие и очень маленькие числа
.
Многочлен, записанный в убывающей или возрастающей степени своей переменной, называется стандартной формой многочлена.

Данный многочлен равен 4 x 2 + 7 x 4 − x 3 − x + 9.
. Стандартная форма полиномиала составляет 7 x 4 — x 3 + 4 x 2 — x + 9 или 9 — x + 4 4. x 2 − x 3 + 7 x 4 .
. Данный полиномиальный составляет P + 2 P 3 + 10 P 2 + 5 P 4 — 8.
(i)
x4+16=x4+0x3+0x2+0x+16

m5+2m2+3m+15=m5+0m4+0m3+2m2+3m+15
(i)
Форма коэффициента многочлена: (3, −2, 0, 7, 18).
Форма коэффициента полинома (6, 1, 0, 7).

Форма коэффициента многочлена – (4, 5, −3, 0).
(i)
7×4-2×3+x+10+3×4+15×3+9×2 -8x+2=7×4+3×4-2×3+15×3+9×2+x-8x+10+2=10×4+13×3+9×2-7x+12
(ii)
3p3q+2p2q+7+2p2q+4pq-2p3q=3p3q -2p3q+2p2q+2p2q+4pq+7=p3q+4p2q+4pq+7

(i)
5×2-2y+9-3×2+5y-7=5×2-2y+9-3x2x5y+7=5×2-2y+9-3x2x5y-7=5×2-2y+9-3×2+5y-7=5×2-2y+9-3×2+5y-7 3×2-2y-5y+9+7=2×2-7y+16
(ii)
2×2+3x+5-x2-2x+3=2×2+3x+5-x2+2x-3=2×2-x2+3x+ 2x+5-3=x2+5x+2
(i)
м4м3-2м3-2м3 -2м2+3м+2-2мм4-2м2+3м+2+3м4-2м2+3м+2=м7-2м5+3м4+2м3-2м5+4м3-6м2-4м+3м4-6м2+9м+6=м7-2м5 -2м5+3м4+3м4+2м3+4м3-6м2-6м2-4м+9м+6=м7-4м5+6м4+6м3-12м2+5м+6
(ii)
5m3-2m2-m+3=5m3m2-m+3-2m2-m+3=5m5-5m4+15m3-2m2+2m-6

Форма коэффициента частного: (3, 1, 4).
Пусть px=x3-2mx+21.
Таким образом, значение м равно 1.
Общее население трех деревень
=5×2-3y2+7y2+2xy+9×2+4xy=5×2+9×2-3y2+7y2+2xy+4xy=14×2+4y2+6xy
Общее количество людей, которые уехал в другую деревню учиться
=x2+xy-y2+5xy+3×2+xy=x2+3×2-y2+xy+5xy+xy=4×2-y2+7xy
∴ Оставшееся общее население трех деревень = Общее население трех деревень − Общее количество людей, уехавших в другую деревню для получения образования
= 14×2+4y2+6xy-4×2-y2+7xy=14×2+4y2+6xy-4×2+ y2-7xy=14×2-4×2+4y2+y2+6xy-7xy=10×2+5y2-xy
Таким образом, оставшееся общее население этих трех деревень составляет ху .
 Если m — n = 0, то найдите значение b .
Если m — n = 0, то найдите значение b .Пусть px=bx2+x+5 и qx=bx3-2x+5.
Остаток при делении qx=bx3-2x+5 на ( x − 3) равен n .
m-n=0⇒9b+8-27b-1=0 Использование 1 и 2⇒9b-27b+8+1=0⇒-18b+9=0⇒-18b=-9⇒b=-9-18=12
Таким образом, значение b равно 12.
8м2+3м-6-9м-7+3м2-2м+4=8м2+3м-6-9м+7+3м2-2м+4=8м2+3м2+3м-9м-2м-6+7+4=11м2 -8M + 5
 х — 4?
х — 4?Let P ( x ) быть полиномом, который должен быть вычитается из x 2 + 13 x + 7 до получения полинома 3 x 9 2 2 6 + 2 6 + 2 6 + 2 6 + 2 6 + 2 6 + 2 6 + 2 6. 5 x − 4.

Искомый полином можно получить вычитанием полинома 4 м + 2 n + 3 из 6 м + 3 N + 10.
21-128 и 15-151, Осенний курс 2020 9
1
Способность логически и ясно рассуждать из набора принятых принципов является фундаментальной не только
в математике, но и в жизни вообще. На этом уроке мы научимся предоставлять
полные объяснения того, почему определенные вещи верны. Мы также определим, как выявлять ложные утверждения
и предоставить убедительные доказательства их ложности.
На этом уроке мы научимся предоставлять
полные объяснения того, почему определенные вещи верны. Мы также определим, как выявлять ложные утверждения
и предоставить убедительные доказательства их ложности. Мы начнем с конкретных объектов, таких как числа, множества и функции, и научимся доказывать
их с помощью элементарной логики. Изучив технику доказательства, известную как индукция, мы рассмотрим
функции и использовать их для классификации размеров бесконечных множеств (да, существуют бесконечные множества разного размера).
наборы).
Далее мы узнаем, как посчитать количество предметов, которые можно получить в результате
определенный процесс. Например, мы можем подсчитать количество различных покерных комбинаций, в которых есть три туза.
и два короля или количество различных пицц с тремя начинками, которые можно приготовить, если десять начинок
доступный. Затем мы решаем элементарные проблемы, связанные с целыми числами, такие как факторизация, делимость
и их возможные применения в криптографии.
Наконец, мы изучим некоторые классические темы из дискретной математики. Элементарная вероятность будет
для того, чтобы выяснить, например, насколько вероятно, что нам сдадут покерную комбинацию, содержащую
три туза и два короля. Мы увидим, что вероятность связана со счетом, и перейдем к изучению
полезные темы в подсчете, известные как принцип сортировки и включение/исключение.
Занятия и лекции: 21-128 встречает MWF с 11:15 до 12:05 в Доэрти 1212.
15-151 встречается с MWF с 1:25 до 2:15 у выхода 4401.
Наши замечательные ассистенты также будут проводить две еженедельные сессии декламации.
Я настоятельно рекомендую вам посещать занятия по чтению, поскольку они являются неотъемлемой частью
курс и может охватывать экзаменационный материал, не затронутый в лекции.
В случае, если в этом семестре ассистенты будут работать онлайн, студенты перейдут на веб-сайт OHQ.
(ОХК)
и при входе найти очередь 21-128/15-151. При добавлении себя в очередь учащиеся должны добавить ссылку в
поле описания к своей личной встрече в масштабе, чтобы ассистенты могли оказать им (и любым соавторам) помощь. Они также могут включать в себя
краткое описание их вопроса (ов). В конце часа ТА войдет в комнату масштабирования, связанную с
календарь для обсуждения общих вопросов. Эта комната будет открыта в течение всего периода ОШ, чтобы студенты могли свободно входить и выходить.
Они также могут включать в себя
краткое описание их вопроса (ов). В конце часа ТА войдет в комнату масштабирования, связанную с
календарь для обсуждения общих вопросов. Эта комната будет открыта в течение всего периода ОШ, чтобы студенты могли свободно входить и выходить.
Офис Макки: Гейтс 4005 Телефон: 268-1204 Электронная почта: [email protected]
Справка: В дополнение к классу, сеансам чтения и офису
часов в университете действуют Центры взаимного обучения.
Индивидуальное обучение и другие варианты помощи также доступны через
Академическое развитие.
Книга: Бесконечный спуск в чистую математику -> https://infiniteescent.xyz/
Бесконечный спуск в чистую математику, по умолчанию, Клайв Ньюстед.
Бесконечный спуск в чистую математику, табличка, Клайв Ньюстед.
Бесконечный спуск в чистую математику, смартфон, Клайв Ньюстед.
Бесконечное нисхождение в чистую математику, печать Клайва Ньюстеда.
Дополнительная (дополнительная) книга: Все, что вы всегда хотели знать о математике, Брендан Салливан,
Дополнительная (дополнительная) Книга: Математическое мышление: решение проблем и доказательства (2-е издание), Д’Анджело и Уэст
Домашнее задание: Домашнее задание является неотъемлемой частью
курс. Трудно понять материал и сделать хорошо на
экзамены, не прорабатывая домашние задания вдумчиво.
Обсуждение домашнего задания со сверстниками приветствуется, но копирование
любая часть домашнего задания другого человека не допускается. Пожалуйста, подумайте о
поставленные проблемы, ваши стратегии и обоснованность вашей логики и
объяснения.
Домашнее задание должно быть отправлено через Gradescope в установленный срок и
время. Домашнее задание, сданное после установленного срока и времени, но до
опубликованы решения, получат половину балла (со звездочкой, чтобы получить полный балл
если оценка за курс пограничная). Каждый набор решений домашнего задания, набранный с использованием
LaTex получит бонус в один балл, начиная со второго домашнего задания.
Если вы решите писать от руки, а затем сканировать домашние задания, то вот полезный ресурс для
сканирование документов в кампусе:
Сканирование документов
Каждый набор решений домашнего задания, набранный с использованием
LaTex получит бонус в один балл, начиная со второго домашнего задания.
Если вы решите писать от руки, а затем сканировать домашние задания, то вот полезный ресурс для
сканирование документов в кампусе:
Сканирование документов
Запросы на изменение домашней работы и экзамена должны быть отправлены в течение одной недели с даты возврата.
Промежуточные экзамены: Будет три промежуточных экзамена и кумулятивный
выпускной экзамен. Даты промежуточных экзаменов следующие:
Промежуточный период 1: Понедельник,
26 сентября
Промежуточный этап 2: Понедельник,
31 октября
Промежуточная 3: Среда,
30 ноября
Оценка : Ваша оценка за курс будет определяться следующим образом:
Каждый из двух высоких промежуточных баллов: 20%
Низкий промежуточный балл: 10%
Домашнее задание: 20%
Итоговый экзамен: 30%
Максимально возможные пороговые значения будут составлять 90 % для A, 80 % для B,
70 % для C и 60 % для D. Эти пороговые значения могут быть немного снижены, но
не будет увеличено.
Эти пороговые значения могут быть немного снижены, но
не будет увеличено.
Калькуляторы : Калькуляторы не будут полезны в этом курсе.
Калькуляторы и другие электронные устройства не допускаются во время экзаменов.
Велнес : Береги себя. Делайте все возможное, чтобы поддерживать здоровый образ жизни в этом семестре, хорошо питаясь, занимаясь спортом, избегая наркотиков и алкоголя,
выспаться и немного отдохнуть. Это поможет вам достичь поставленных целей и справиться со стрессом.
Всем нам нужна поддержка во времена борьбы. Ты не одинок. В кампусе есть много полезных ресурсов, и это важная часть
опыт колледжа учит, как просить о помощи. Просить о поддержке раньше, чем позже, часто бывает полезно.
Если вы или кто-либо из ваших знакомых испытывает академический стресс, трудные жизненные события или такие чувства, как тревога или депрессия, мы настоятельно рекомендуем вам обратиться
поддерживать. Консультационные и психологические службы (CaPS) готовы помочь: позвоните по телефону 412-268-2922 и посетите их веб-сайт http://www. cmu.edu/counseling/. Рассмотреть возможность
обратиться к другу, преподавателю или члену семьи, которому вы доверяете, за помощью в подключении к службе поддержки, которая может помочь.
cmu.edu/counseling/. Рассмотреть возможность
обратиться к другу, преподавателю или члену семьи, которому вы доверяете, за помощью в подключении к службе поддержки, которая может помочь.
Если вы или кто-то из ваших знакомых склонны к суициду или вам грозит членовредительство, немедленно позвоните кому-нибудь днем или ночью:
Телефон: 412-268-2922
Сеть Re:solve Crisis: 888-796-8226
Если ситуация угрожает жизни, позвоните в полицию:
На территории кампуса: CMU Police: 412-268-2323
За пределами кампуса: 911
Если у вас есть вопросы по этой или курсовой работе, дайте мне знать.
Исследование обучения студентов : Марша Ловетт, Клаус Сатнер и я проводим исследование того, как студенты учатся на этом курсе.
Исследование будет включать анализ данных этого курса и 15-051.
Вас не попросят делать что-либо помимо обычных учебных занятий и заданий, являющихся частью этого курса.
Вы можете не участвовать в этом исследовании, и ваше участие не повлияет на вашу оценку за этот курс или вашу академическую карьеру в CMU. Если вы решите не участвовать в исследовании, вы все равно должны выполнить все необходимые курсовые работы, но ваши данные не будут включены в анализ исследования.
Никакой компенсации участники не получат. Данные, собранные в рамках этого исследования, будут включать оценки учащихся. Все анализы данных от участников
Курсовая работа будет проводиться после окончания курса и выставления итоговых оценок. Центр Эберли может оказать поддержку этому исследовательскому проекту в отношении данных.
анализ и интерпретация. Чтобы свести к минимуму риск нарушения конфиденциальности, Eberly Center никогда не будет иметь доступа к данным этого курса, содержащим ваши
персональные идентификаторы. Все данные будут проанализированы в обезличенной форме и представлены в совокупности, без каких-либо личных идентификаторов.
Пожалуйста, свяжитесь с Чадом Хершоком ([email protected]) из Центра Эберли, если у вас есть вопросы или опасения по поводу вашего участия.
Если вы решите не участвовать в исследовании, вы все равно должны выполнить все необходимые курсовые работы, но ваши данные не будут включены в анализ исследования.
Никакой компенсации участники не получат. Данные, собранные в рамках этого исследования, будут включать оценки учащихся. Все анализы данных от участников
Курсовая работа будет проводиться после окончания курса и выставления итоговых оценок. Центр Эберли может оказать поддержку этому исследовательскому проекту в отношении данных.
анализ и интерпретация. Чтобы свести к минимуму риск нарушения конфиденциальности, Eberly Center никогда не будет иметь доступа к данным этого курса, содержащим ваши
персональные идентификаторы. Все данные будут проанализированы в обезличенной форме и представлены в совокупности, без каких-либо личных идентификаторов.
Пожалуйста, свяжитесь с Чадом Хершоком ([email protected]) из Центра Эберли, если у вас есть вопросы или опасения по поводу вашего участия.
Недельное расписание (предварительное) :
Неделя 1 (29 августа — 2 сентября):
- Введение и глава 0
- 1.
 1
1 - 1,2
Неделя 2 (6–9 сентября):
- 1,3
- 2.1
Неделя 3 (12–16 сентября):
- 2.2
- 2.2
- 3.1
Неделя 4 (19-23 сентября):
- 3.2
- 4.1
- Обзор для промежуточного периода
Промежуточный обзор;
Пятница, 23 сентября
Первая среднесрочная;
Понедельник, 26 сентября
Неделя 5 (26–30 сентября):
- Первый промежуточный семестр
- 4.2
- 4.3
Неделя 6 (3–7 октября):
- Индукционный фестиваль 2022
- 5.1
- 5.2
Неделя 7 (10–14 октября):
- 6.1
- 6.2
- 6.2
Неделя 8 (24-27 октября):
- 6.3
- 7.1
Вторая среднесрочная;
Понедельник, 31 октября
Неделя 9 (31 октября — 4 ноября):
- Второй промежуточный срок
- 7.
 1
1 - 7.2
Неделя 10 (7–11 ноября):
- 7.2
- 7.2
- 7.3
Неделя 11 (14–18 ноября):
- 8.1
- 8.1
- 9.1
Неделя 12 (21–22 ноября):
- 9.1
- 10.1
Промежуточный обзор;
Понедельник, 28 ноября
Третий промежуточный;
Среда, 30 ноября
Неделя 13 (28 ноября — 2 декабря):
- Обзор третьего промежуточного срока
- Третий промежуточный срок
- 10.1
Неделя 14 (5–9 декабря):
- 10.1
- 10.2
- 10.2
Заключительный экзамен, назначенный регистратором
Вернуться на страницу приветствия

 Они также могут включать в себя
краткое описание их вопроса (ов). В конце часа ТА войдет в комнату масштабирования, связанную с
календарь для обсуждения общих вопросов. Эта комната будет открыта в течение всего периода ОШ, чтобы студенты могли свободно входить и выходить.
Они также могут включать в себя
краткое описание их вопроса (ов). В конце часа ТА войдет в комнату масштабирования, связанную с
календарь для обсуждения общих вопросов. Эта комната будет открыта в течение всего периода ОШ, чтобы студенты могли свободно входить и выходить. Книга: Бесконечный спуск в чистую математику -> https://infiniteescent.xyz/
Бесконечный спуск в чистую математику, по умолчанию, Клайв Ньюстед.
Бесконечный спуск в чистую математику, табличка, Клайв Ньюстед.
Бесконечный спуск в чистую математику, смартфон, Клайв Ньюстед.
Бесконечное нисхождение в чистую математику, печать Клайва Ньюстеда.
Дополнительная (дополнительная) книга: Все, что вы всегда хотели знать о математике, Брендан Салливан,
Дополнительная (дополнительная) Книга: Математическое мышление: решение проблем и доказательства (2-е издание), Д’Анджело и Уэст
Домашнее задание: Домашнее задание является неотъемлемой частью курс. Трудно понять материал и сделать хорошо на экзамены, не прорабатывая домашние задания вдумчиво. Обсуждение домашнего задания со сверстниками приветствуется, но копирование любая часть домашнего задания другого человека не допускается. Пожалуйста, подумайте о поставленные проблемы, ваши стратегии и обоснованность вашей логики и объяснения.
Домашнее задание должно быть отправлено через Gradescope в установленный срок и
время. Домашнее задание, сданное после установленного срока и времени, но до
опубликованы решения, получат половину балла (со звездочкой, чтобы получить полный балл
если оценка за курс пограничная). Каждый набор решений домашнего задания, набранный с использованием
LaTex получит бонус в один балл, начиная со второго домашнего задания.
Если вы решите писать от руки, а затем сканировать домашние задания, то вот полезный ресурс для
сканирование документов в кампусе:
Сканирование документов
Каждый набор решений домашнего задания, набранный с использованием
LaTex получит бонус в один балл, начиная со второго домашнего задания.
Если вы решите писать от руки, а затем сканировать домашние задания, то вот полезный ресурс для
сканирование документов в кампусе:
Сканирование документов
Запросы на изменение домашней работы и экзамена должны быть отправлены в течение одной недели с даты возврата.
Промежуточные экзамены: Будет три промежуточных экзамена и кумулятивный выпускной экзамен. Даты промежуточных экзаменов следующие:
Промежуточный период 1: Понедельник, 26 сентября
Промежуточный этап 2: Понедельник, 31 октября
Промежуточная 3: Среда, 30 ноября
Оценка : Ваша оценка за курс будет определяться следующим образом:
Каждый из двух высоких промежуточных баллов: 20%
Низкий промежуточный балл: 10%
Домашнее задание: 20%
Итоговый экзамен: 30%
Максимально возможные пороговые значения будут составлять 90 % для A, 80 % для B,
70 % для C и 60 % для D. Эти пороговые значения могут быть немного снижены, но
не будет увеличено.
Эти пороговые значения могут быть немного снижены, но
не будет увеличено.
Калькуляторы : Калькуляторы не будут полезны в этом курсе. Калькуляторы и другие электронные устройства не допускаются во время экзаменов.
Велнес : Береги себя. Делайте все возможное, чтобы поддерживать здоровый образ жизни в этом семестре, хорошо питаясь, занимаясь спортом, избегая наркотиков и алкоголя, выспаться и немного отдохнуть. Это поможет вам достичь поставленных целей и справиться со стрессом.
Всем нам нужна поддержка во времена борьбы. Ты не одинок. В кампусе есть много полезных ресурсов, и это важная часть опыт колледжа учит, как просить о помощи. Просить о поддержке раньше, чем позже, часто бывает полезно.
Если вы или кто-либо из ваших знакомых испытывает академический стресс, трудные жизненные события или такие чувства, как тревога или депрессия, мы настоятельно рекомендуем вам обратиться
поддерживать. Консультационные и психологические службы (CaPS) готовы помочь: позвоните по телефону 412-268-2922 и посетите их веб-сайт http://www. cmu.edu/counseling/. Рассмотреть возможность
обратиться к другу, преподавателю или члену семьи, которому вы доверяете, за помощью в подключении к службе поддержки, которая может помочь.
cmu.edu/counseling/. Рассмотреть возможность
обратиться к другу, преподавателю или члену семьи, которому вы доверяете, за помощью в подключении к службе поддержки, которая может помочь.
Если вы или кто-то из ваших знакомых склонны к суициду или вам грозит членовредительство, немедленно позвоните кому-нибудь днем или ночью:
Телефон: 412-268-2922
Сеть Re:solve Crisis: 888-796-8226
Если ситуация угрожает жизни, позвоните в полицию:
На территории кампуса: CMU Police: 412-268-2323
За пределами кампуса: 911
Если у вас есть вопросы по этой или курсовой работе, дайте мне знать.
Исследование обучения студентов : Марша Ловетт, Клаус Сатнер и я проводим исследование того, как студенты учатся на этом курсе.
Исследование будет включать анализ данных этого курса и 15-051.
Вас не попросят делать что-либо помимо обычных учебных занятий и заданий, являющихся частью этого курса.
Вы можете не участвовать в этом исследовании, и ваше участие не повлияет на вашу оценку за этот курс или вашу академическую карьеру в CMU. Если вы решите не участвовать в исследовании, вы все равно должны выполнить все необходимые курсовые работы, но ваши данные не будут включены в анализ исследования.
Никакой компенсации участники не получат. Данные, собранные в рамках этого исследования, будут включать оценки учащихся. Все анализы данных от участников
Курсовая работа будет проводиться после окончания курса и выставления итоговых оценок. Центр Эберли может оказать поддержку этому исследовательскому проекту в отношении данных.
анализ и интерпретация. Чтобы свести к минимуму риск нарушения конфиденциальности, Eberly Center никогда не будет иметь доступа к данным этого курса, содержащим ваши
персональные идентификаторы. Все данные будут проанализированы в обезличенной форме и представлены в совокупности, без каких-либо личных идентификаторов.
Пожалуйста, свяжитесь с Чадом Хершоком ([email protected]) из Центра Эберли, если у вас есть вопросы или опасения по поводу вашего участия.
Если вы решите не участвовать в исследовании, вы все равно должны выполнить все необходимые курсовые работы, но ваши данные не будут включены в анализ исследования.
Никакой компенсации участники не получат. Данные, собранные в рамках этого исследования, будут включать оценки учащихся. Все анализы данных от участников
Курсовая работа будет проводиться после окончания курса и выставления итоговых оценок. Центр Эберли может оказать поддержку этому исследовательскому проекту в отношении данных.
анализ и интерпретация. Чтобы свести к минимуму риск нарушения конфиденциальности, Eberly Center никогда не будет иметь доступа к данным этого курса, содержащим ваши
персональные идентификаторы. Все данные будут проанализированы в обезличенной форме и представлены в совокупности, без каких-либо личных идентификаторов.
Пожалуйста, свяжитесь с Чадом Хершоком ([email protected]) из Центра Эберли, если у вас есть вопросы или опасения по поводу вашего участия.
Недельное расписание (предварительное) :
Неделя 1 (29 августа — 2 сентября):
- Введение и глава 0
- 1.
 1
1 - 1,2
Неделя 2 (6–9 сентября):
- 1,3
- 2.1
Неделя 3 (12–16 сентября):
- 2.2
- 2.2
- 3.1
Неделя 4 (19-23 сентября):
- 3.2
- 4.1
- Обзор для промежуточного периода
Промежуточный обзор; Пятница, 23 сентября
Первая среднесрочная; Понедельник, 26 сентября
Неделя 5 (26–30 сентября):
- Первый промежуточный семестр
- 4.2
- 4.3
Неделя 6 (3–7 октября):
- Индукционный фестиваль 2022
- 5.1
- 5.2
Неделя 7 (10–14 октября):
- 6.1
- 6.2
- 6.2
Неделя 8 (24-27 октября):
- 6.3
- 7.1
Вторая среднесрочная; Понедельник, 31 октября
Неделя 9 (31 октября — 4 ноября):
- Второй промежуточный срок
- 7.
 1
1 - 7.2
Неделя 10 (7–11 ноября):
- 7.2
- 7.2
- 7.3
Неделя 11 (14–18 ноября):
- 8.1
- 8.1
- 9.1
Неделя 12 (21–22 ноября):
- 9.1
- 10.1
Промежуточный обзор; Понедельник, 28 ноября
Третий промежуточный; Среда, 30 ноября
Неделя 13 (28 ноября — 2 декабря):
- Обзор третьего промежуточного срока
- Третий промежуточный срок
- 10.1
Неделя 14 (5–9 декабря):
- 10.1
- 10.2
- 10.2
Заключительный экзамен, назначенный регистратором
Вернуться на страницу приветствия
 1 | Вопрос 1. (ii) |
1 | Вопрос 1. (ii) | 1 | Вопрос 5. (i) | Страница 87
1 | Вопрос 5. (i) | Страница 87 1 | вопрос 7 |
1 | вопрос 7 | 1 | Вопрос 10 | Страница 88
1 | Вопрос 10 | Страница 88 2 | Вопрос 3. (i) | Страница 91
2 | Вопрос 3. (i) | Страница 91 2 | Вопрос 4. (ii) | Страница 91
2 | Вопрос 4. (ii) | Страница 91 2 | Вопрос 5. (iv) | Страница 91
2 | Вопрос 5. (iv) | Страница 91 3 | Вопрос 4 | Страница 96
3 | Вопрос 4 | Страница 96 3 | Вопрос 8 | Страница 97
3 | Вопрос 8 | Страница 97 4 | Вопрос 3. (i) | Страница 101
4 | Вопрос 3. (i) | Страница 101 4 | Вопрос 5. (ii) | Страница 101
4 | Вопрос 5. (ii) | Страница 101 4 | Вопрос 14 | Страница 102
4 | Вопрос 14 | Страница 102 5 | Вопрос 4. (i) | Страница 105
5 | Вопрос 4. (i) | Страница 105 6 | Вопрос 1. (ii) | Страница 107
6 | Вопрос 1. (ii) | Страница 107 6 | Вопрос 2. (iii) | Страница 107
6 | Вопрос 2. (iii) | Страница 107 2 + 2/(xy)`
2 + 2/(xy)` 7 | вопрос 2 |
7 | вопрос 2 | 7
7Если частное, полученное при делении (8x 4 – 2x 2 + 6x – 7) на (2x + 1), равно (4x 3 + px 2 – qx + 3), то найти p, q, а также остаток
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.7 | вопрос 7 | Страница 112
Если частное, полученное при делении 3x 3 + 11x 2 + 34x + 106 на x – 3, равно 3x 2 + ax + b, то найти a, b, а также остаток
РЕШЕНИЕTamil Nadu Board Решения Samacheer Kalvi для класса 9th Mathematics Answers Guide Глава 3 Алгебра Упражнение 3.8 [Страница 114]
Упражнение 3.8 | Вопрос 1. (i) |
Разложите на множители следующие многочлены, используя синтетическое деление:
x 3 – 3x 2 – 10x + 24
ПРОСМОТР РЕШЕНИЯ
Упражнение 3. 8 | Вопрос 1. (ii) | Страница 114
8 | Вопрос 1. (ii) | Страница 114
Разложите на множители следующие многочлены, используя синтетическое деление:
2x 3 – 3x 2 – 3x + 2
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.8 | Вопрос 1. (iii) | Страница 114
Разложите на множители следующие многочлены, используя синтетическое деление:
– 7x + 3 + 4x 3
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.8 | Вопрос 1. (iv) |
Разложите на множители следующие многочлены, используя синтетическое деление:
x 3 + x 2 – 14x – 24
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.8 | Вопрос 1. (д) | Страница 114
Факторизируйте следующие многочлены, используя синтетическое деление:
x 3 – 7x + 6
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.8 | Вопрос 1. (vi) | Страница 114
Разложите на множители следующие полиномы, используя синтетическое деление:
x 3 – 10x 2 – x + 10
ПРОСМОТР РЕШЕНИЯ
Tamil Nadu Board Упражнение 3 Samacheer Kalvithe Solutions for Class.
 [Страница 115]
[Страница 115]Упражнение 3.9 | Вопрос 1. (i) | Страница 115
Найдите НОД для следующего:
P 5 , P 11 , P 9
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.9 | Вопрос 1. (ii) |
Найдите НОД для следующего:
4x 3 , y 3 , z 3
ПРОСМОТР РЕШЕНИЯ
2 | Упражнение 3. Вопрос 1. (iii) | Страница 115Найдите НОД для следующего:
9a 2 b 2 c 3 , 15a 3 b 0 6 0 90 9005 c 402 ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.9 | Вопрос 1. (iv) | Страница 115
Найдите НОД для следующего:
64x 8 , 240x 6
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.9 | Вопрос 1. (д) | Page 115
Найдите G.C.D для следующего:
AB 2 C 3 , A 2 B 3 C, 3 BC 2
Просмотр решения
Упражнение 3. 9 | Вопрос 1. (vi) | Страница 115
9 | Вопрос 1. (vi) | Страница 115
Найдите НОД для следующего:
35x 5 Y 3 Z 4 , 49x 2 YZ 3 , 14xy 2 Z 2
Просмотр решения
Упражнение 3.9 | Вопрос 1. (vii) |
Найдите НОД для следующего:
25ab 3 c, 100a 2 bc, 125ab
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.9 | Вопрос 1. (viii) | Страница 115
Найдите НОД для следующего:
3abc, 5xyz, 7pqr
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.9 | Вопрос 2. (i) | Страница 115
Найдите НОД следующего числа:
(2x + 5), (5x + 2)
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.9 | Вопрос 2. (ii) | Страница 115
Найдите НОД следующего числа:
a m+1 , a m+2 , a m+3
ПОКАЗАТЬ РЕШЕНИЕ
| Упражнение Вопрос 2. (iii) | Страница 115
Найдите НОД следующего:
2a 2 + a, 4a 2 – 1
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3. 9 | Вопрос 2. (iv) | Страница 115
9 | Вопрос 2. (iv) | Страница 115
Найдите НОД следующего:
3a 2 , 5b 3 , 7c 4
ПРОСМОТР РЕШЕНИЯ
Упражнение | Q 2. (v) |
Найдите НОД следующего числа:
x 4 – 1, x 2 – 1
ПРОСМОТР РЕШЕНИЯ
Упражнение 3.9 | Вопрос 2. (vi) | Страница 115
Найдите НОД следующего:
a 3 – 9ax 2 , (a – 3x) 2
ПОСМОТРЕТЬ РЕШЕНИЕ
Tamil Nadu Board Решения Samacheer Kalvi для 9-го класса Математика Ответы Руководство Глава 3 Алгебра Упражнение 90 100 124 [Страница 0124] Вопрос 1. (i) | Страница 124
Нарисуйте график для следующего
y = 2x
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.10 | Вопрос 1. (ii) | Страница 124
Нарисуйте график для следующего
y = 4x – 1
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.10 | Вопрос 1. (iii) |
Нарисуйте график для следующего
y = `(3/2)x + 3`
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3. 10 | Вопрос 1. (iv) | Страница 124
10 | Вопрос 1. (iv) | Страница 124
Нарисуйте график для следующего
3x + 2y = 14
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.10 | Вопрос 2. (i) | Страница 124
Решить графически
x + y = 7, x – y = 3
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.10 | Вопрос 2. (ii) | Страница 124
Решить графически
3x + 2y = 4, 9x + 6y – 12 = 0
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.10 | Вопрос 2. (iii) |
Решить графически
`x/2 + y/4` = 1, `x/2 + y/4` = 2
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.10 | Вопрос 2. (iv) | Страница 124
Решить графически
x – y = 0, y + 3 = 0
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.10 | Q 2. (v) | Страница 124
Решить графически
y = 2x + 1, y + 3x – 6 = 0
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.10 | Вопрос 2. (vi) | Страница 124
Решить графически
x = −3, y = 3
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3. 10 | Вопрос 3 | Страница 124
10 | Вопрос 3 | Страница 124
Две машины находятся на расстоянии 100 миль друг от друга. Если они едут навстречу друг другу, то встретятся через 1 час. Если они едут в одном направлении, то встретятся через 2 часа. Найдите их скорость графическим методом.
VIEW SOLUTION
Tamil Nadu Board Решения Samacheer Kalvi для класса 9th Mathematics Answers Guide Глава 3 Алгебра Упражнение 3.11 [Страница 126]
Упражнение 3.11 | Вопрос 1. (i) |
Решить методом подстановки
2x – 3y = 7, 5x + y = 9
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.11 | Вопрос 1. (ii) |
Решить методом подстановки
1,5x + 0,1y = 6,2, 3x – 0,4y = 11,2
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.11 | Вопрос 1. (iii) | Страница 126
Решить методом подстановки
10% x + 20% y = 24, 3x – y = 20
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.11 | Вопрос 1. (iv) |
Решить методом подстановки
`sqrt(2)x — sqrt(3)y` = 1, `sqrt(3)x — sqrt(8)y` = 0
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3. 11 | вопрос 2 | Страница 126
11 | вопрос 2 | Страница 126
Возраст Рамана в три раза больше суммы возрастов двух его сыновей. Через 5 лет его возраст будет в два раза больше суммы возрастов двух его сыновей. Найдите возраст Рамана.
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.11 | Вопрос 3 | Страница 126
Средняя цифра числа от 100 до 1000 равна нулю, а сумма другой цифры равна 13. Если цифры поменять местами, то полученное таким образом число превышает исходное число на 495. Найдите число
ПОКАЗАТЬ РЕШЕНИЕ
Tamil Nadu Board Решения Samacheer Kalvi для 9-го класса Математика Ответы Руководство Глава 3 Алгебра Упражнение 3.12 [Страница 128]
Упражнение 3.12 | Вопрос 1. (i) | Страница 128
Решить методом исключения
2x – y = 3, 3x + y = 7
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.12 | Вопрос 1. (ii) |
Решить методом исключения
x – y = 5, 3x + 2y = 25
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.12 | Вопрос 1. (iii) |
Решить методом исключения
`x/10 + y/5` = 14, `x/8 + y/6` = 15
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3. 12 | Вопрос 1. (iv) | Страница 128
12 | Вопрос 1. (iv) | Страница 128
Решить методом исключения
3(2x + y) = 7xy, 3(x + 3y) = 11xy
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.12 | Вопрос 1. (д) |
Решить методом исключения
`4/x + 5y` = 7, `3/x + 4y` = 5
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.12 | Вопрос 1. (vi) |
Решить методом исключения
13x + 11y = 70, 11x + 13y = 74
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.12 | вопрос 2 | Страница 128
Месячные доходы A и B относятся как 3 : 4, а их ежемесячные расходы относятся как 5 : 7. Если каждый из них сберегает 5000 ₹ в месяц, найдите месячный доход каждого
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.12 | Вопрос 3 |
Пять лет назад мужчина был в семь раз старше своего сына, а через пять лет мужчина будет в четыре раза старше своего сына. Найдите их текущий возраст
ПОСМОТРЕТЬ РЕШЕНИЕ
Тамил Наду Доска Samacheer Kalvi решения для 9 класса Математика Ответы Руководство Глава 3 Алгебра Упражнение 3.
 13 [Страница 131]
13 [Страница 131]Упражнение 3.13 | Вопрос 1. (i) | Страница 131
Решить методом перекрестного умножения
8x – 3y = 12, 5x = 2y + 7
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.13 | Вопрос 1. (ii) |
Решить методом перекрестного умножения
6x + 7y – 11 = 0, 5x + 2y = 13
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.13 | Вопрос 1. (iii) |
Решить методом перекрестного умножения
`2/x + 3/y` = 5, `3/x — 1/y + 9` = 0
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.13 | вопрос 2 | Страница 131
У Акшайи в кошельке 2 рупии и 5 рупий. Если всего у нее 80 монет на общую сумму 220 ₹, сколько у нее монет каждого вида.
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.13 | Вопрос 3 | Страница 131
Наполнение бассейна с помощью двух труб занимает 24 часа. Если труба большего диаметра используется в течение 8 часов, а труба меньшего диаметра используется в течение 18 часов. Заполнена только половина бассейна. Сколько времени понадобится каждой трубе, чтобы наполнить бассейн
ПОСМОТРЕТЬ РЕШЕНИЕ
Tamil Nadu Board Решения Samacheer Kalvi для 9-го класса Руководство по математике Глава 3 Упражнение по алгебре 3.
 14 [Страница 133]
14 [Страница 133]Решить любым из способов
Упражнение 3.14 | Вопрос 1 |
Сумма двузначного числа и числа, образованного перестановкой цифр, равна 110. Если из первого числа вычесть 10, новое число будет в 4 раза больше, чем в 5 раз больше суммы цифр первого числа. Найдите первое число.
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.14 | вопрос 2 |
Сумма числителя и знаменателя дроби равна 12. Если знаменатель увеличить на 3, дробь станет `1/2`. Найдите дробь
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.14 | Вопрос 3 |
ABCD — вписанный четырехугольник, такой что ∠A = (4y + 20)°, ∠B = (3y − 5)°, ∠C = (4x)° и ∠D = (7x + 5)°. Найдите четыре угла
ВИД РЕШЕНИЯ
Упражнение 3.14 | Вопрос 4 | Страница 133
При продаже телевизора с прибылью 5% и холодильника с прибылью 10% владелец магазина получает 2000 рупий. 1500 по сделке. Найдите фактическую цену телевизора и холодильника.
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3. 14 | Вопрос 5 | Страница 133
14 | Вопрос 5 | Страница 133
Два числа находятся в отношении 5 : 6. Если из каждого числа вычесть 8, отношение станет 4 : 5. Найдите числа.
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.14 | Вопрос 6 | Страница 133
4 индийца и 4 китайца могут выполнить часть работы за 3 дня. В то время как 2 индийца и 5 китайцев могут закончить его за 4 дня. Сколько времени потребуется 1 индийцу, чтобы сделать это? Сколько времени потребуется 1 китайцу, чтобы сделать это?
ПОСМОТРЕТЬ РЕШЕНИЕ
Tamil Nadu Board Решения Samacheer Kalvi для 9-го класса Руководство по математике Ответы Глава 3 Алгебра Упражнение 3.15 [Страницы 134 — 136]
Вопросы с несколькими вариантами ответов
Упражнение 3.15 | Вопрос 1 |
Если x 3 + 6x 2 + kx + 6 точно делится на (x + 2), то k = ?
−6
−7
−8
11
 -2/3`
-2/3`0
1
49
50
x 3 — 3x — 1
x 3 + 2x 2 — 1
x 3 — 2x 2 — 3x
x 3 — 2x 2 + 3x — 1
9
2
3
6
 5`
5` A, B, D, C
A, B, C, D
B, D, A
B, A, C, D
Divisor
Коэффициент
Остаток
Фактор
Фактор
0003
3
2
`2/3`
`3/2`
2x – 1
3x – 3
4x – 3
3x – 4
 15 | Вопрос 12 | Стр.
15 | Вопрос 12 | Стр.(x + y) 3
(x — y) 3
x 3 + Y 3
x 3 — Y 3
(a – b – c) 2
1, 2, 3
1, 2, 15
1, 2, −15
1, −2, 15
1
2
3
4
 15 | Вопрос 17 | Page 135
15 | Вопрос 17 | Page 1353
2
1
0
2
— 2
10
0
`x + 1/x` = 2
x (x — 1) = 2
3x + 5 =` 2/3`
x 3 — x = 5
(2, 4)
(4, 2)
(3, -1)
(0, 6)
 15 | Вопрос 22 |
15 | Вопрос 22 |a ≠ 0, b = 0 = 0, c ≠ 0
a ≠ 0, b ≠ 0
AX + BY + C = 0
0x + 0y + C = 0
0x + By + C = 0
AX + 0y + C = 0
к = 4
k = − 3
 Вопрос 26 | Страница 136
Вопрос 26 | Страница 136NO.
бесконечный
NO Solution
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.15 | Вопрос 28 |
НОД любых двух простых чисел равен __________
−1
0
1
2
ПОСМОТРЕТЬ РЕШЕНИЕ
Упражнение 3.15 | Вопрос 29 | Page 136
G. C.D of x 4 — Y 4 и X 2 — Y 2 IS
C.D of x 4 — Y 4 и X 2 — Y 2 IS
x 4 — Y 4
x 2 ° 2
(x + y) 2
(x + y) 4
Просмотр решения
Реклама Удалить все объявления

 , Алгоритм деления многочленов, синтетическое деление, наибольшая Общий множитель, общий вид линейного уравнения с двумя переменными, график линейного уравнения с двумя переменными, одновременные линейные уравнения, сравнение отношений коэффициентов линейного уравнения, методы решения одновременных линейных уравнений графическим методом, методы решения одновременных линейных уравнений Уравнения подстановкой, Методы решения одновременных линейных уравнений методом исключения, Методы решения одновременных линейных уравнений методом перекрестного умножения, Совместность и несовместность линейных уравнений с двумя переменными, Нули полинома.
, Алгоритм деления многочленов, синтетическое деление, наибольшая Общий множитель, общий вид линейного уравнения с двумя переменными, график линейного уравнения с двумя переменными, одновременные линейные уравнения, сравнение отношений коэффициентов линейного уравнения, методы решения одновременных линейных уравнений графическим методом, методы решения одновременных линейных уравнений Уравнения подстановкой, Методы решения одновременных линейных уравнений методом исключения, Методы решения одновременных линейных уравнений методом перекрестного умножения, Совместность и несовместность линейных уравнений с двумя переменными, Нули полинома. Максимум учащиеся 9-го класса Совета среднего образования штата Тамил Наду предпочитают Samacheer Kalvi Textbook Solutions Совета Тамил Наду, чтобы набрать больше баллов на экзамене.
Максимум учащиеся 9-го класса Совета среднего образования штата Тамил Наду предпочитают Samacheer Kalvi Textbook Solutions Совета Тамил Наду, чтобы набрать больше баллов на экзамене.Полномочия 2
Полномочия 3
Полномочия 4
 В полномочиях
2
таблица, единичные цифры образуют повторяющийся шаблон
2
,
4
,
8
,
6
,
2
,
4
,
8
,
6
,
…
. В полномочиях
3
таблица, единичные цифры образуют повторяющийся шаблон
3
,
9
,
7
,
1
,
3
,
9,
7
,
1
,
…
. Мы оставляем это вам, чтобы выяснить, почему это происходит!
В полномочиях
2
таблица, единичные цифры образуют повторяющийся шаблон
2
,
4
,
8
,
6
,
2
,
4
,
8
,
6
,
…
. В полномочиях
3
таблица, единичные цифры образуют повторяющийся шаблон
3
,
9
,
7
,
1
,
3
,
9,
7
,
1
,
…
. Мы оставляем это вам, чтобы выяснить, почему это происходит! п.
п.Полномочия 3
Полномочия 9
 За
отрицательные силы
10
−
н
, записывать »
0.
» с последующим
н
−
1
нули, а затем
1
. Полномочия
10
широко используются в
научная нотация
, так что это хорошая идея, чтобы освоиться с ними.
За
отрицательные силы
10
−
н
, записывать »
0.
» с последующим
н
−
1
нули, а затем
1
. Полномочия
10
широко используются в
научная нотация
, так что это хорошая идея, чтобы освоиться с ними.Полномочия 10
10 5 знак равно 100 000
(сто тысяч)
10 − 4 знак равно 0,0001
(одна десятитысячная)
10 6 знак равно 1 000 000
(один миллион)
10 − 5 знак равно 0,00001
(стотысячный)
10 7 знак равно 10 000 000
(десять миллионов)
10 − 6 знак равно 0,000001
(одна миллионная)
10 8 знак равно 100 000 000
(сто миллионов)
10 − 7 знак равно 0,0000001
(одна десятимиллионная)
10 9 знак равно 1 000 000 000
(один миллиард)
10 − 8 знак равно 0,00000001
(стомиллионный)
10 10 знак равно 10 000 000 000
(десять миллиардов)
10 − 9 знак равно 0,000000001
(одна миллиардная)


 28
Глава 1. Упражнение 28. Слова для записи
28
Глава 1. Упражнение 28. Слова для записи 35
Глава 1. Упражнение 37. Этимология слова "атлас"
35
Глава 1. Упражнение 37. Этимология слова "атлас"
 59
Глава 1. Упражнение 65. В. Башмакова. Как работает мозг
59
Глава 1. Упражнение 65. В. Башмакова. Как работает мозг 74
Глава 1. Упражнение 84. И. Грекова. Фрагмент рассказа с прямой речью
74
Глава 1. Упражнение 84. И. Грекова. Фрагмент рассказа с прямой речью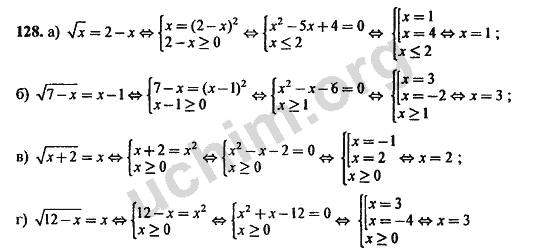
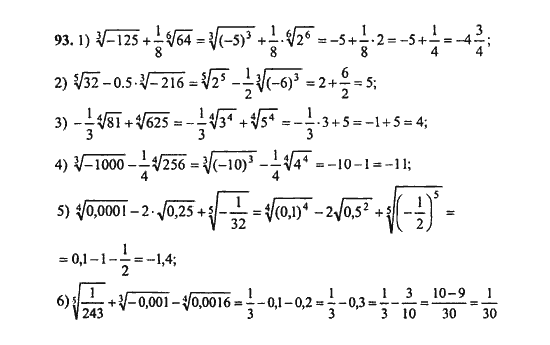 109
Глава 1. Упражнение 142. Д. С. Лихачёв. Любите читать!
109
Глава 1. Упражнение 142. Д. С. Лихачёв. Любите читать! 124
Глава 2. Упражнение 14. В. Железников. Последний парад (отрывок)
124
Глава 2. Упражнение 14. В. Железников. Последний парад (отрывок)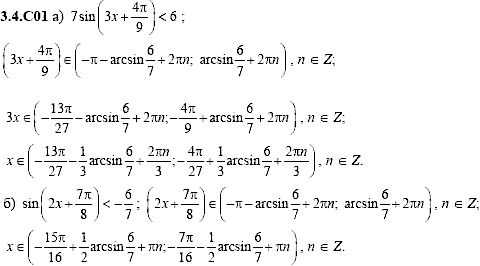 139
Глава 2. Упражнение 29. Нормы общения в разных странах
139
Глава 2. Упражнение 29. Нормы общения в разных странах 150
Глава 2. Упражнение 41. А. Герасимова. Первый раз в новый класс
150
Глава 2. Упражнение 41. А. Герасимова. Первый раз в новый класс 161
Глава 2. Упражнение 54. А. П. Бородин
161
Глава 2. Упражнение 54. А. П. Бородин