Алгебра. 8 класс. Учебник — Макарычев, Миндюк, Нешков, Суворова
Предлагаемый учебник 8 класса Макарычева, Миндюк, Нешкова, Суворовой по алгебре является частью 3-летнего курса для СОШ. Новое издание переработано, дополнено. Его содержание способствует достижению планируемых результатов обучения, гарантируемых ФГОС. В задачный материал вошли новые формы заданий: задания для занятий в парах, задачи-исследования. В заключении учебника приводен список литературы.-Содержание-
ОГЛАВЛЕНИЕ 8
РАЦИОНАЛЬНЫЕ ДРОБИ 04
РАЦИОНАЛЬНЫЕ ДРОБИ. ИХ СВОЙСТВА 6
СУММА — РАЗНОСТЬ ДРОБЕЙ 18
ПРОИЗВЕДЕНИЕ 30
ЧАСТНОЕ ДРОБЕЙ 30
Дополнительные упражнения 54
КВАДРАТНЫЕ КОРНИ 57
ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА 62
АРИФМЕТИЧЕСКИЙ КВАДРАТНЫЙ КОРЕНЬ 75
СВОЙСТВА КВАДРАТНОГО КОРНЯ 90
ПРИМЕНЕНИЕ СВОЙСТВ КВАДРАТНОГО КОРНЯ 98
Дополнительные упражнения110
КВАДРАТНЫЕ УРАВНЕНИЯ 117
КВАДРАТНОЕ УРАВНЕНИЕ.
ДРОБНЫЕ РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ 141
Дополнительные упражнения 152
НЕРАВЕНСТВА 160
ЧИСЛОВЫЕ НЕРАВЕНСТВА. ИХ СВОЙСТВА 161
НЕРАВЕНСТВА ОДНОЙ ПЕРЕМЕННОЙ. ИХ СИСТЕМЫ 179
Дополнительные упражнения 207
СТЕПЕНЬ ЦЕЛЫМ ПОКАЗАТЕЛЕМ. 213
ЭЛЕМЕНТЫ СТАТИСТИКИ 214
СТЕПЕНЬ ЦЕЛЫМ ПОКАЗАТЕЛЕМ. ЕЁ СВОЙСТВА 214
ЭЛЕМЕНТЫ СТАТИСТИКИ 226
Дополнительные упражнения 250
Задачи повышенной трудности 255
Исторические сведения 260
Сведения из курса 266
Список дополнительной литературы 273
Предметный указатель 274
Ответы 275
Скачать
Размер файла: 24 Мб; Формат: pdf/
ИЗДАНИЕ 2007 Г.
Размер файла: 14 Мб; Формат: pdf/zip.
download
Вместе с «Алгебра 8 класс Макарычев» скачивают:
AdminАлгебра 8 Макарычев 2019 (учебник)
Алгебра 8 класс. Учебник УМК Макарычев и другие. Просвещение 2019. Электронная версия (онлайн учебник) для ознакомления при покупке книги: Макарычев, Миндюк, Суворова: Алгебра. 8 класс. Учебник. ФГОС. Цитаты из учебника использованы в учебных целях.
Учебник УМК Макарычев и другие. Просвещение 2019. Электронная версия (онлайн учебник) для ознакомления при покупке книги: Макарычев, Миндюк, Суворова: Алгебра. 8 класс. Учебник. ФГОС. Цитаты из учебника использованы в учебных целях.
Алгебра 8 Макарычев Учебник
ОГЛАВЛЕНИЕ
Глава I. Рациональные дроби
§ 1. Рациональные дроби и их свойства
- Рациональные выражения.
- Основное свойство дроби. Сокращение дробей.
§ 2. Сумма и разность дробей.
- Сложение и вычитание дробей с одинаковыми знаменателями.
- Сложение и вычитание дробей с разными знаменателями.
§ 3. Произведение и частное дробей.
- Умножение дробей. Возведение дроби в степень.
- Деление дробей.
- Преобразование рациональных выражений.
- Функция у = k/x и ее график.
- Представление дроби в виде суммы дробей.
Дополнительные упражнения к главе I
Глава II. Квадратные корни
Квадратные корниДополнительные упражнения к главе II.
Глава III. Квадратные уравненияДополнительные упражнения к главе III
Глава IV. Неравенства§ 10. Числовые неравенства и их свойства.
- Числовые неравенства.
- Свойства числовых неравенств.
- Сложение и умножение числовых неравенств.
- Погрешность и точность приближения
§ 11. Неравенства с одной переменной и их системы.
- Пересечение и объединение множеств
- Числовые промежутки.
- Решение неравенств с одной переменной.
- Решение систем неравенств с одной переменной.
- Доказательство неравенств.
Дополнительные упражнения к главе IV.
Глава V. Степень с целым показателем. Элементы статистики§ 12. Степень с целым показателем и ее свойства
- Определение степени с целым отрицательным показателем.

- Свойства степени с целым показателем
- Стандартный вид числа.
§ 13. Элементы статистики.
- Сбор и группировка статистических данных.
- Наглядное представление статистической информации.
- Функции у = х–1 и у = х–2 и их свойства.
- Дисперсия и средне квадратичное отклонение.
Дополнительные упражнения к главе V.
Задачи повышенной трудности
Алгебра 8 класс. Учебник УМК Макарычев и другие. Просвещение 2019. Электронная версия (онлайн учебник) для ознакомления при покупке книги.
Просмотров: 7 354
8 класс.Дидактические материалы по алгебре — Жохов В.И., Макарычев Ю.Н., Миндюк Н.Г. | 978-5-09-072778-5
Данный товар есть в наличии в следующих магазинах:г. Воронеж, площадь Ленина, д. 4
4
8 (473) 277-16-90
8 (473) 231-87-02
г. Богучар, ул. Дзержинского, д.4
8 (47366) 2-12-90
г. Воронеж, ул. Г. Лизюкова, д. 66 а
8 (473) 247-22-55
г. Поворино, ул.Советская, 87
Поворино, ул.Советская, 878 (47376) 4-28-43
г. Воронеж, ул. Плехановская, д. 33
8 (473) 252-57-43
г. Воронеж, ул. Ленинский проспект д.153
8 (473) 223-17-02
8 (47364) 92-350
г. Воронеж, ул. Хользунова, д. 35
Воронеж, ул. Хользунова, д. 35
8 (473) 246-21-08
г. Россошь, пр. Труда, д. 26А
8 (47396) 5-28-07
г. Лиски, ул. Коммунистическая, д.78 (47391) 2-22-01
г. Белгород, Бульвар Народный, 80б
8 (4722) 42-48-42
г. Курск, пр. Хрущева, д. 5А
Курск, пр. Хрущева, д. 5А
8 (4712) 51-91-15
8 (47241) 7-35-57
г.Воронеж, ул. Жилой массив Олимпийский, д.1
8 (473) 207-10-96
г. Воронеж, ул.Челюскинцев, д 88А
8 (4732) 71-44-70
г.
8 (4725) 23-38-06
г. Воронеж, ул. Ростовская, д,58/24 ТЦ «Южный полюс»
8 (473) 280-22-42
г. Воронеж, ул. Пушкинская, 2
8 (473) 300-41-49
г. Липецк, ул.Стаханова,38 б
8 (4742) 78-68-01
 Курск, ул.Карла Маркса, д.6
Курск, ул.Карла Маркса, д.68 (4712) 54-09-50
г.Старый Оскол, мкр Олимпийский, д. 62
8 (4725) 39-00-10
г. Воронеж, Московский пр-т, д. 129/1
8 (473) 269-55-64
ТРЦ «Московский Проспект», 3-й этаж
г. Курск, ул. Щепкина, д. 4Б
8 (4712) 73-31-39
Макарычев Ю.
 Н., Миндюк Н. Г., Нешков К. И., Суворова С. Б. Алгебра. 8класс / Под ред. С. А. Теляковского
Н., Миндюк Н. Г., Нешков К. И., Суворова С. Б. Алгебра. 8класс / Под ред. С. А. ТеляковскогоПреобразование выражений, содержащих квадратные корни
Алгебра, 8
Дудкина Ирина Константиновна,
МОУ «Лицей» г. Урюпинска
Цели урока:
— развить у учащихся навыки преобразования выражений, содержащих квадратные корни;
— установить уровень овладения учащимися теоретическими знаниями по преобразованию выражений, содержащих квадратные корни.
— повысить интерес к предмету.
Учебник: Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра. 8класс / Под ред. С.А. Теляковского. – М.: Просвещение, 2009
Ход урока
I. Организационный момент
Сообщить
тему урока, сформулировать цели урока.
II. Актуализация знаний учащихся
Проверка домашнего задания. №491.
Слайд 1 (Рис. 1-2) используется для проверки домашнего задания. Правильное решение может быть скрыто от учащихся с использованием инструмента ширмы, т.е. «затемнение экрана». Последовательно убирается затемнение экрана и выполняется проверка.
Рис. 1 Рис. 2
Учащимся предлагается повторить формулы сокращенного умножения, установив соответствие с помощью стрелок разного цвета. Представление такого рода заданий с помощью интерактивной доски позволяет визуализировать процесс рассуждения с одной стороны, и оптимизировать его по времени – с другой стороны. Слайд 2 -3 (рис. 3-4).
Рис. 3 Рис. 4
Теоретический опрос
— Перечислите
свойства арифметического квадратного
корня.
Использование элементов обычной презентации на повторение свойств арифметического квадратного корня. Слайд 4 (рис. 5).
Рис. 5
III. Самостоятельная работа с последующей самопроверкой
Задания для самостоятельного выполнения работы Слайд 5 (рис. 6).
Слайд 6 (рис. 7-8) содержит ответы и подробные пояснения для самопроверки учащихся.
Рис. 6 Рис. 7
Рис. 8
IV. Отработка и закрепление умений и навыков при решении заданий на преобразование выражений, содержащих квадратные корни. Решение этого задания предлагается проверить с помощью раскрытия (увеличения) скрытого текста. Слайд 7 (рис. 9-10).
№1. Разложите
на множители, используя формулу разности
квадратов:
Разложите
на множители, используя формулу разности
квадратов:
a2 — 16 =
a2 — 10 =
3 – 25а2 =
c – 9 =
n – m2 =
n – m =
Рис. 9
Рис. 10
Задание № 1 выполняется с последующей проверкой с помощью скрытого текста, путем переноса овалов. «Сдвинь овал – увидишь ответ». Значения, соответствующие промежуточным действиям, визуально уменьшаются. Проверяя задание, учитель последовательно воспроизводит их соответствующий размер. Слайд 8 (рис. 11-13).
№ 2. Сократите дробь, используя формулу разности квадратов:
Рис. 11 Рис.12
Рис. 13
13
V. Подведение итогов
Домашнее задание и общая оценка работы учащихся. Слайд 9.
Повторить свойства арифметического квадратного корня
№ 426, № 428 (а,б,в)
№ 430, № 441
№ 495(для более подготовленных учащихся)
Рис. 14 Рис. 15
ГДЗ по Алгебре за 8 класс Ю.Н. Макарычев, Н.Г. Миндюк Углубленный уровень
Алгебра 8 класс Ю.Н. Макарычев углубленный уровень
Авторы: Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, И.Е. Феоктистов
С каждым годом количество изучаемых предметов учащихся увеличивается, а школьная программа становится все затруднительнее и насыщеннее. И это уже ни для кого не секрет. Конечно же, все это обусловлено современными условиями, ведь в настоящее время обществу требуются «золотые умы», которые в будущем смогут справиться с любыми задачами. И из-за этого курс школьной программы приходится делать более сложным.
И это уже ни для кого не секрет. Конечно же, все это обусловлено современными условиями, ведь в настоящее время обществу требуются «золотые умы», которые в будущем смогут справиться с любыми задачами. И из-за этого курс школьной программы приходится делать более сложным.
Домашняя работа вызывает огромные затруднения у ученика. В связи с быстрым ритмом жизни школьник не успевает качественно решить все упражнения. Выполнение задания кажется непосильной ношей для ребенка.
Для того чтобы хоть как-то уменьшить учебную нагрузку, восьмиклассникам в изучении алгебры Макарычев создал замечательный решебник, содержащий в себе ответы на вопросы по всем заданиям, который включает учебник по предмету алгебра за 8 класс с углубленным уровнем изучения. Нелегкое упражнение, тяжелое задание, трудный номер — все это больше не проблема, ведь решебник поспособствует в решении любой задачи.
Алгебра — не самый легкий предмет в школе. Она требует к себе особого внимания и усилия. Поэтому ГДЗ к учебнику 8 класса Макарычева охватывает в себе все темы, задания, вопросы к номеру.
Поэтому ГДЗ к учебнику 8 класса Макарычева охватывает в себе все темы, задания, вопросы к номеру.
Решебник поможет родителям контролировать выполнение домашней работы своих детей. Наглядное пособие окажет поддержку на уроках по алгебре. С ГДЗ школьник будет чувствовать себя уверенно, а занятия станут веселыми и интересными.
С использованием такого решебника ученик к концу года будет иметь огромный багаж знаний, который посодействует ему в дальнейшей жизни.
Рабочая программа по алгебре для 8 класса 2017-18 уч. г. (к учебнику Ю.Н. Макарычева) | Рабочая программа по алгебре (8 класс) на тему:
Муниципальное бюджетное общеобразовательное учреждение
Петровская средняя общеобразовательная школа
Согласовано Зам.директора по УР ____________ С.В.Гончарова ______28 .08.2017г. | Утверждаю И.о. директора МБОУ Петровской СОШ ___________Е. Приказ от 28 .08.17 №143 |
Рассмотрено
на заседании методического объединения МБОУ Петровской СОШ
Протокол от 26 .08.17 № 1
Руководитель ШМО _________ /Л.И.Тицкая/
РАБОЧАЯ ПРОГРАММА
по алгебре
для ____8___ класса
на 2017 – 2018 учебный год
Учитель —
Чумакова Людмила Геннадиевна, 1 категория
х. Нижнепетровский
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Рабочая программа по алгебре 8 класса составлена на основе Фундаментального ядра содержания общего образования и Требований к результатам освоения основной общеобразовательной программы основного общего образования, представленных в Федеральном государственном образовательном стандарте общего образования. В ней также учитываются основные идеи и положения Программы развития и формирования универсальных учебных действий для основного общего образования.
В ней также учитываются основные идеи и положения Программы развития и формирования универсальных учебных действий для основного общего образования.
Рабочая программа по алгебре для 8 класса составлена в соответствии с положениями
-Федерального закона № 273 «Об образовании в Российской Федерации» 29.12 2012, ст.12
-Федерального государственного образовательного стандарта основного общего образования второго поколения,
-на основе примерной Программы основного общего образования по математике,
— Программы по алгебре Н.Г. Миндюк 7-9 классы (М.: Просвещение, 2011) к учебнику Ю.Н. Макарычева, Н.Г. Миндюк, К.И. Нешкова и др. (стандарты 2 поколения)
— Учебного плана МБОУ Петровская СОШ на 2017-2018 уч.год,
— Положения о структуре, порядке разработки и утверждения рабочих программ по отдельным учебным предметам, курсам, в том числе внеурочной деятельности
МБОУ Петровской СОШ.
В ходе преподавания алгебры в 8 классе, работы над формированием у обучающихся универсальных учебных действий следует обращать внимание на то, чтобы они овладевали умениями обще учебного характера, разнообразными способами деятельности, приобретали опыт:
- планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов:
- решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;
- исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;
- ясного, точного, грамотного изложения своих мыслей в устной и письменной форме, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;
- проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;
- поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.

Цели обучения
Обучение математике в основной школе направлено на достижение следующих целей:
В направлении личностного развития:
- развитие логического и критического мышления, культуры речи, способности к умственному эксперименту;
- формирование у обучающихся интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;
- воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;
- формирование качеств мышления, необходимых для адаптации в современном информационном обществе;
- развитие интереса к математическому творчеству и математических способностей.
В мета предметном направлении:
- формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;
- развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;
- формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности.

В предметном направлении:
- овладение математическими знаниями и умениями, необходимыми для продолжения обучения в старшей школе или иных общеобразовательных организациях, изучения смежных дисциплин, применения их в повседневной жизни;
- создание фундамента для развития математических способностей, а также механизмов мышления, формируемых математической деятельностью.
Целью изучения курса алгебры 8 класса является развитие вычислительных и формально-оперативных алгебраических умений до уровня, позволяющего уверенно использовать их при решении задач математики и смежных предметов; усвоение аппарата уравнений и неравенств как основного средства математического моделирования прикладных задач; осуществление функциональной подготовки школьников.
На основании требований Федерального государственного образовательного стандарта основного общего образования в содержании предполагается реализовать актуальные в настоящее время компетентностный, личностно ориентированный, деятельностный подходы, которые определяют задачи обучения:
-сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;
-овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;
-изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
-развить логическое мышление и речь- умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
-сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.
Изучение математики в 8 классе направлено на освоение компетенций:
-учебно-познавательной;
-ценностно-ориентационной;
-рефлексивной;
-коммуникативной;
-информационной;
-социально-трудовой.
Общая характеристика учебного предмета
Математическое образование в основной школе складывается из следующих компонентов: арифметика; алгебра; геометрия; элементы комбинаторики, теории вероятностей, статистики и логики.
Арифметика призвана способствовать приобретению практических навыков, необходимых для повседневной жизни. Она служит базой для всего дальнейшего изучения математики, способствует логическому развитию и формированию умения пользоваться алгоритмами.
Алгебра нацелена на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира. Одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов, для формирования у учащихся представлений о роли математики в развитии цивилизации и культуры.
Одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов, для формирования у учащихся представлений о роли математики в развитии цивилизации и культуры.
Геометрия – один из важнейших компонентов математического образования, необходимый для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, для эстетического воспитания учащихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.
Элементы логики, комбинаторики, статистики и теории вероятностей становятся обязательным компонентом школьного образования, усиливающим его прикладное и практическое значение. Этот материал необходим, прежде всего, для формирования функциональной грамотности – умений воспринимать и анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчеты. Изучение основ комбинаторики позволит учащемуся осуществлять рассмотрение случаев, перебор и подсчет числа вариантов, в том числе в простейших прикладных задачах.
Этот материал необходим, прежде всего, для формирования функциональной грамотности – умений воспринимать и анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчеты. Изучение основ комбинаторики позволит учащемуся осуществлять рассмотрение случаев, перебор и подсчет числа вариантов, в том числе в простейших прикладных задачах.
При изучении статистики и теории вероятностей обогащаются представления о современной картине мира и методах его исследования, формируется понимание роли статистики как источника социально значимой информации и закладываются основы вероятностного мышления.
Ценностные ориентиры содержания учебного предмета.
Математическое образование играет важную роль как в практической, так и в духовной жизни общества. Практическая сторона математического образования связана с формированием способов деятельности, духовная- с интеллектуальным развитием человека, формированием характера и общей культуры.
Практическая полезность математики обусловлена тем, что ее предметом являются фундаментальные структуры реального мира: пространственные формы и количественные отношения- от простейших, усваиваемых в непосредственном опыте, до достаточно сложных, необходимых для развития научных и технологических идей. Без конкретных математических знаний затруднено понимание принципов устройства и использования современной техники, восприятие и интерпретация разнообразной социальной, экономической, политической информации, малоэффективна повседневная практическая деятельность. Каждому человеку в своей жизни приходится выполнять достаточно сложные расчеты, находить в справочниках нужные формулы и применять их, владеть практическими приемами геометрических измерений и построений, читать информацию, представленную в виде таблиц, диаграмм, графиков, понимать вероятностный характер событий, составлять несложные алгоритмы и др. Без базовой математической подготовки невозможно стать образованным современным человеком. В школе математика служит опорным предметом для изучения смежных дисциплин. В после школьной жизни реальной необходимостью в наши дни является непрерывное образование, что требует полноценной базовой общеобразовательной подготовки, в том числе и математической.
В школе математика служит опорным предметом для изучения смежных дисциплин. В после школьной жизни реальной необходимостью в наши дни является непрерывное образование, что требует полноценной базовой общеобразовательной подготовки, в том числе и математической.
Обучение математике дает возможность развивать у обучающихся точную, экономную и информативную речь, умение отбирать наиболее подходящие языковые ( в частности, символические, графические) средства.
Изучение математики способствует эстетическому воспитанию человека, пониманию красоты и изящества математических рассуждений, восприятию геометрических форм, усвоению идеи симметрии.
История развития математического знания дает возможность пополнить запас историко-научных знаний школьников, сформировать у них представления о математике как части общечеловеческой культуры.
Планируемые результаты изучения учебного предмета
- Изучение математики в основной школе дает возможность обучающимся достичь следующих результатов:
- В направлении личностного развития:
- умение ясно, точно, грамотно излагать свои мысли в устной и письменной форме, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
- критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;
- представление о математической науке как сфере человеческой деятельности, об этапах ее развития, о ее значимости для развития цивилизации;
- креативность мышления, инициатива, находчивость, активность при решении математических задач
- умение контролировать процесс и результат учебной математической деятельности;
- способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений.

В метапредметном направлении:
- умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
- умение находить в различных источниках информацию, необходимую для решения математических проблем, и представлять ее в понятной форме, принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
- умение понимать и использовать математические средства наглядности (графики, диаграммы, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации;
- умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки;
- умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач;
- понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;
- умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
- умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;
- первоначальные представления об идеях и методах математики как универсальном языке науки и техники, средстве моделирования явлений и процессов.

В предметном направлении:
предметным результатом изучения курса является сформированность следующих умений.
Предметная область «Арифметика»
- переходить от одной формы записи чисел к другой, представлять десятичную дробь в виде обыкновенной и обыкновенную — в виде десятичной, записывать большие и малые числа с использованием целых степеней десятки;
- выполнять арифметические действия с рациональными числами, сравнивать рациональные и действительные числа, находить в несложных случаях значения степеней с целыми показателями, находить значения числовых выражений;
- округлять целые числа и десятичные дроби, находить приближения чисел с недостатком и избытком, выполнять оценку числовых выражений;
- пользоваться основными единицами длины, массы, времени, скорости, площади, объема,
- выражать более крупные единицы через более мелкие и наоборот;
- решать текстовые задачи, включая задачи, связанные с отношением и пропорциональностью величин, с дробями и процентами.

- Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
- решения несложных практических расчетных задач, в том числе с использованием (при необходимости) справочных материалов, калькулятора, компьютера;
- устной прикидки и оценки результата вычислений, проверки результата вычисления с использованием различных приемов;
- интерпретации результатов решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений.
Предметная область «Алгебра»
- составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое, выражать в формулах одну переменную через остальные;
- выполнять: основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; разложение многочленов на множители; тождественные преобразования рациональных выражений;
- решать линейные уравнения, системы двух линейных уравнений с двумя переменными;
- решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений исходя из формулировки задачи;
- изображать числа точками на координатной прямой;
- определять координаты точки плоскости, строить точки с заданными координатами.

- Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
- выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами, нахождения нужной формулы в справочных материалах;
- моделирования практических ситуаций и исследования построенных моделей с использованием аппарата алгебры;
- описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций.
Предметная область «Элементы логики, комбинаторики, статистики и теории вероятностей»
- проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений, использовать
- примеры для иллюстрации и контрпримеры для опровержения утверждений;
- извлекать информацию, представленную в таблицах, на диаграммах, графиках, составлять таблицы, строить диаграммы и графики;
- решать комбинаторные задачи путем систематического перебора возможных вариантов и с использованием правила умножения;
- вычислять средние значения результатов изменений;
- находить частоту события, используя собственные наблюдения и готовые статистические данные;
- находить вероятности случайных событий в простейших случаях.

- Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
- выстраивания аргументации при доказательстве и в диалоге;
- распознавания логически некорректных рассуждений;
- записи математических утверждений, доказательств;
- анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц;
- решения практических задач в повседневной и профессиональной деятельности с использованием действий с числами, процентов, длин, площадей, объемов, времени, скорости;
- решения учебных и практических задач, требующих систематического перебора вариантов;
- сравнения шансов наступления случайных событий, оценки вероятности случайного события в практических ситуациях, сопоставления модели с реальной ситуацией;
- понимания статистических утверждений.
Место предмета в учебном плане
Согласно Федеральному базисному учебному плану на изучение математики в 8 классе отводится в 2017-18 уч. г.173 часа из расчета 5 ч в неделю, при этом разделение часов на изучение алгебры и геометрии следующее:
г.173 часа из расчета 5 ч в неделю, при этом разделение часов на изучение алгебры и геометрии следующее:
3 часа в неделю алгебры, в 2017-18 уч году, итого 103 часа; 2 часа в неделю геометрии, итого 70 часов.
Рабочая программа по алгебре предназначена для обучающихся 8 класса общеобразовательной школы. Базовый уровень.
Последовательность изучения тем следующая:
Рациональные дроби.
Квадратные корни.
Квадратные уравнения
Неравенства.
Степень с целым показателем. Элементы статистики.
Повторение.
Содержание учебного предмета
Рациональные дроби.23ч Рациональная дробь. Основное свойство дроби, сокращение дробей. Тождественные преобразования рациональных выражений. Функция у = k/x и ее график.
Квадратные корни.18ч Понятие об иррациональных числах. Общие сведения о действительных числах. Квадратный корень. Понятие о нахождении приближенного значения квадратного корня. Свойства квадратных корней. Преобразования выражений, содержащих квадратные корни. Функция у = √x, ее свойства и график.
Функция у = √x, ее свойства и график.
Квадратные уравнения.22ч Квадратное уравнение. Формула корней квадратного уравнения. Решение рациональных уравнений. Решение задач, приводящих к квадратным уравнениям и простейшим рациональным уравнениям.
Неравенства.20ч Числовые неравенства и их свойства. Почленное сложение и умножение числовых неравенств. Погрешность и точность приближения. Линейные неравенства с одной переменной и их системы.
Степень с целым показателем. Элементы статистики.11ч Степень с целым показателем и ее свойства. Стандартный вид числа. Приближенные вычисления.
Сбор и группировка статистических данных. Наглядное представление статистической информации.
Повторение.4ч Резерв 2 часа(23.02.18;08.03.18). Итого: 103ч.
Тематическое планирование Алгебра 8 класс
№ п/п | Наименование разделов и тем | Сроки проведения | Всего часов | В том числе на: | ||
Уроки | Контрольные работы | Практические (лабораторные) работы | ||||
1 | Вводное повторение. | 3 | 2 | 1( входная диагностика-тест, 07.09.17) | ||
2 | Рациональные дроби. | 23 | 21 | 2(№1 « Сложение и вычитание рациональных дробей», кр05.10.17;№2 «Умножение и деление рациональных дробей»,кр, 28.10.17) | ||
3 | Квадратные корни | 18 | 16 | 2(№3 «Свойства арифметического квадратного корня»,кр 01.12.17; №4 «Преобразование выражений, содержащих квадратные корни» ,кр,21. | ||
4 | Квадратные уравнения. | 22 | 20 | 2 (№5 «Квадратные уравнения»,кр. 27.01.18; №6 « Дробные рациональные уравнения», кр,22.02.18 ) | ||
5 | Неравенства. | 20 | 18 | 2(№7 «Числовые неравенства и их свойства»,кр,15.03.18; №8 «Решение неравенств и систем неравенств с одной переменной»,кр26.04.18,) | ||
6 | Степень с целым показателем. Элементы статистики. | 11 | 10 | 1(№9 «Степень с целым показателем»,кр,11. | ||
7 | Повторение. | 4 | 3 | 1(итоговая,кр,26.05.18 ) | ||
Резерв | 2 | 23.02.18 08.03.18 | ||||
Итого | 103 | |||||
Календарно-тематическое планирование.
Алгебра 8 класс (УМК Ю. Н.Макарычева)
Н.Макарычева)
№ | Раздел, тема | Кол-во часов | Виды контроля | Дата проведения урока по плану | фактически |
Вводное повторение, 3ч; 1 четверть | |||||
1 | Повторение учебного материала за курс 7 класса | 1 | 01.09 | ||
2 | Повторение учебного материала за курс 7 класса | 1 | 02.09 | ||
3 | Входная контрольная работа | 1 | Контрольная работа (тест) | 07. | |
Рациональные дроби,23ч | |||||
4(1) | Рациональные выражения | 1 | 08.09 | ||
5(2) | Рациональные выражения | 1 | 09.09 | ||
6(3) | Основное свойство дроби | 1 | 14.09 | ||
7(4) | Основное свойство дроби. | 1 | 15.09 | ||
8(5) | Основное свойство дроби. Сокращение дробей. | 1 | 16.09 | ||
9(6) | Сложение дробей с одинаковыми знаменателями. | 1 | 21.09 | ||
10(7) | Вычитание дробей с одинаковыми знаменателями. | 1 | 22.09 | ||
11(8) | Сложение и вычитание дробей с одинаковыми знаменателями. | 1 | 23.09 | ||
12(9) | Сложение дробей с разными знаменателями. | 1 | 28.09 | ||
13(10) | Вычитание дробей с разными знаменателями. | 1 | 29.09 | ||
14(11) | Сложение и вычитание дробей с разными знаменателями. | 1 | Тест. | 30.09 | |
15(12) | Контрольная работа №1 по теме «Сложение и вычитание рациональных дробей» | 1 | Контрольная работа | 05. | |
16(13) | Умножение дробей. Возведение дроби в степень. | 1 | 06.10 | ||
17(14) | Умножение дробей. Возведение дроби в степень. | 1 | 07.10 | ||
18(15) | Деление дробей. | 1 | 12.10 | ||
19(16) | Деление дробей. | 1 | 13. | ||
20(17) | Преобразование рациональных выражений. | 1 | 14.10 | ||
21(18) | Преобразование рациональных выражений. | 1 | 19.10 | ||
22(19) | Преобразование рациональных выражений. | 1 | 20.10 | ||
23(20) | Функция у = k/x и ее график. | 1 | 21. | ||
24(21) | Функция у = k/x и ее график. | 1 | 26.10 | ||
25(22) | Обобщение по теме «Умножение и деление рациональных дробей» | 1 | 27.10 | ||
26(23) | Контрольная работа №2 по теме «Умножение и деление рациональных дробей». | 1 | Контрольная работа. | 28.10 | |
Квадратные корни, 18ч ; 2 четверть | |||||
27(1) | Рациональные числа | 1 | 10. | ||
28(2) | Иррациональные числа | 1 | Тест | 11.11 | |
29(3) | Квадратные корни. Арифметический квадратный корень. | 1 | Тест | 16.11 | |
30(4) | Уравнение | 1 | 17.11 | ||
31(5) | Уравнение | 1 | Тест | 18. | |
32(6) | Нахождение приближенных значений квадратного корня | 1 | 23.11 | ||
33(7) | Функция и ее график | 1 | 24.11 | ||
34(8) | Квадратный корень из произведения, дроби | 1 | 25.11 | ||
35(9) | Квадратный корень из степени | 1 | 30. | ||
36(10) | Контрольная работа № 3 по теме «Свойства арифметического квадратного корня». | 1 | Контрольная работа | 01.12 | |
37(11) | Вынесение множителя из-под знака корня | 1 | 02.12 | ||
38(12) | Внесение множителя под знак корня | 1 | 07.12 | ||
39(13) | Преобразование выражений, содержащих квадратные корни | 1 | 08. | ||
40(14) | Преобразование выражений, содержащих квадратные корни | 1 | 09.12 | ||
41(15) | Преобразование выражений, содержащих квадратные корни | 1 | 14.12 | ||
42(16) | Преобразование выражений, содержащих квадратные корни | 1 | 15.12 | ||
43(17) | Обобщающий урок по теме «Преобразование выражений, содержащих квадратные корни» | 1 | Тест | 16. | |
44(18) | Контрольная работа №4 по теме «Преобразование выражений, содержащих квадратные корни» | 1 | Контрольная работа | 21.12 | |
Квадратные уранения,22ч | |||||
45(1) | Определение квадратного уравнения. Неполные квадратные уравнения. | 1 | 22.12 | ||
46(2) | Определение квадратного уравнения. Неполные квадратные уравнения. | 1 | 23. | ||
47(3) | Решение квадратных уравнений выделением квадрата двучлена. | 1 | Тест | 28.12 | |
48(4) | Решение квадратных уравнений по формуле. | 1 | 3 четв 11.01 | ||
49(5) | Решение квадратных уравнений по формуле. | 1 | 12.01 | ||
50(6) | Решение задач с помощью квадратных уравнений | 1 | 13. | ||
51(7) | Решение задач с помощью квадратных уравнений | 1 | 18.01 | ||
52(8) | Решение задач с помощью квадратных уравнений | 1 | Тест | 19.01 | |
53(9) | Теорема Виета | 1 | 20.01 | ||
54(10) | Теорема Виета | 1 | 25. | ||
55(11) | Обобщающий урок по теме «Квадратные уравнения» | 1 | Тест | 26.01 | |
56(12) | Контрольная работа № 5 по теме «Квадратные уравнения». | 1 | Контрольная работа | 27.01 | |
57(13) | Решение дробных рациональных уравнений | 1 | 01.02 | ||
58(14) | Решение дробных рациональных уравнений | 1 | 02. | ||
59(15) | Решение дробных рациональных уравнений | 1 | Тест | 03.02 | |
60(16) | Решение задач с помощью рациональных уравнений | 1 | 08.02 | ||
61(17) | Решение задач с помощью рациональных уравнений | 1 | 09.02 | ||
62(18) | Решение задач с помощью рациональных уравнений | 1 | 10. | ||
63(19) | Решение задач с помощью рациональных уравнений | 1 | 15.02 | ||
64(20) | Графический способ решения уравнений | 1 | 16.02 | ||
65(21) | Обобщающий урок по теме «Дробные рациональные уравнения». | 1 | 17.02 | ||
66(22) | Контрольная работа № 6 по теме «Дробные рациональные уравнения». | 1 | Контрольная работа | 22.02 | |
Неравенства, 20ч | |||||
67(1) | Числовые неравенства | 1 | 24.02 | ||
68(2) | Свойства числовых неравенств | 1 | Тест | 01.03 | |
69(3) | Сложение и умножение числовых неравенств | 1 | 02. | ||
70(4) | Сложение и умножение числовых неравенств | 1 | 03.03 | ||
71(5) | Погрешность и точность приближения | 1 | 09.03 | ||
72(6) | Обобщающий урок по теме «Свойства числовых неравенств» | 1 | 10.03 | ||
73(7) | Контрольная работа № 7 по теме «Свойства числовых неравенств». | 1 | Контрольная работа | 15.03 | |
74(8) | Пересечение и объединение множеств | 1 | Тест | 16.03 | |
75(9) | Числовые промежутки | 1 | 17.03 | ||
76(10) | Решение неравенств с одной переменной | 1 | 22.03 | ||
77(11) | Решение неравенств с одной переменной | 1 | 4 чтв 05. | ||
78(12) | Решение неравенств с одной переменной | 1 | 06.04 | ||
79(13) | Решение неравенств с одной переменной | 1 | 07.04 | ||
80(14) | Решение систем неравенств с одной переменной | 1 | 12.04 | ||
81(15) | Решение систем неравенств с одной переменной | 1 | 13. | ||
82(16) | Решение систем неравенств с одной переменной | 1 | 14.04 | ||
83(17) | Решение систем неравенств с одной переменной | 1 | Тест | 19.04 | |
84(18) | Доказательство неравенств | 1 | 20.04 | ||
85(19) | Доказательство неравенств | 1 | 21. | ||
86(20) | Контрольная работа №8 «Решение неравенств и систем неравенств с одной переменной» | 1 | Контрольная работа | 26.04 | |
Степень с целым показателем. Элементы статистики.11ч | |||||
87(1) | Определение степени с целым отрицательным показателем | 1 | 27.04 | ||
88(2) | Определение степени с целым отрицательным показателем | 1 | 28. | ||
89(3) | Свойства степени с целым показателем | 1 | 03.05 | ||
90(4) | Свойства степени с целым показателем | 1 | 04.05 | ||
91(5) | Стандартный вид числа | 1 | 05.05 | ||
92(6) | Решение задач | 1 | 10. | ||
93(7) | Контрольная работа № 9 по теме «Степень с целым показателем» | 1 | Контрольная работа | 11.05 | |
94(8) | Сбор и группировка статистических данных | 1 | 12.05 | ||
95(9) | Сбор и группировка статистических данных | 1 | 17.05 | ||
96(10) | Наглядное представление статистической информации. | 1 | 18.05 | ||
97(11) | Наглядное представление статистической информации. | 1 | 19.05 | ||
Повторение,4ч | |||||
98(1) | Повторение. Рациональные дроби. | 1 | 24.05 | ||
99(2) | Повторение. Квадратные корни. Квадратные уравнения. | 1 | 25. | ||
100(3) | Итоговая контрольная работа. | 1 | Контрольная работа | 26.05 | |
101(4) | Повторение. Неравенства | 1 | 31.05 | ||
102 | Резерв | 1 | На | 23.02.18 | |
103 | Резерв | 1 | На | 08. | |
Учебно-методическое и материально-техническое обеспечение образовательного процесса
1. Программы по алгебре Н.Г. Миндюк (М.: Просвещение, 2011) к учебнику Ю.Н. Макарычева, Н.Г. Миндюк, К.И. Нешкова и др. (стандарты 2 поколения)
2. Учебник. «Алгебра 8 класс» Автор Ю.Н. Макарычев и др.. М.; »Просвещение» — 2016 год.
3. Алгебра . 8 класс: поурочные планы по учебнику Ю.Н. Макарычева и др. Авторы-составители Т.М. Ерина,М,Экзамен, 2008
4. Дидактические материалы по алгебре для 8 класса / В.И. Жохов, Ю.Н. Макарычев, Н.Г. Миндюк. – М.: Просвещение, 2006. – 144 с.
5.Рабочая тетрадь по алгебре к учебнику Ю.Н. Макарычева и др «Алгебра. 8 класс», авт. Т.М.Ерина,М, Экзамен, 2013
7.http://school-collection.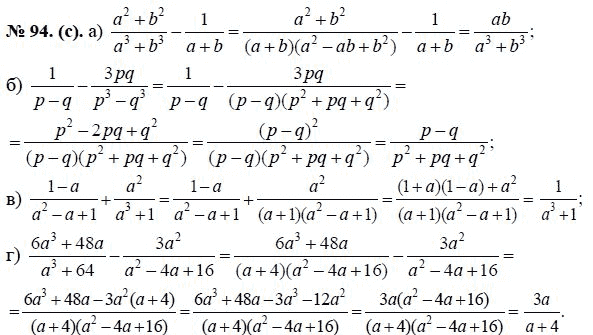 edu.ru/ – единая коллекция цифровых образовательных ресурсов.
edu.ru/ – единая коллекция цифровых образовательных ресурсов.
8. Виртуальная школа Кирилла и Мефодия 7-11 класс
9 Демонстрационные таблицы, портреты математиков, аудиторная доска
10. Технические средства обучения: видеопроектор, компьютер, принтер.
Лист коррекции и внесения изменений
Класс/ предмет | Название раздела, темы | Дата проведения по плану | Причина корректировки | Корректирующие мероприятия | Дата проведения по факту |
Алгебра 8 Макарычев Самостоятельные РАБОТЫ с ОТВЕТАМИ
Самостоятельные работы по алгебре в 8 классе с решениями и ОТВЕТАМИ по учебнику Макарычева. Алгебра 8 Макарычев Самостоятельные — цитаты из пособия для учащихся «Алгебра 8 класс. Дидактические материалы / Жохов, Макарычев, Миндюк — М.: Просвещение». Ознакомительная версия перед покупкой.
Алгебра 8 Макарычев Самостоятельные — цитаты из пособия для учащихся «Алгебра 8 класс. Дидактические материалы / Жохов, Макарычев, Миндюк — М.: Просвещение». Ознакомительная версия перед покупкой.
Представленные работы ориентированы на учебник «Алгебра 8 класс» авторов Ю.Н. Макарычева и др. под редакцией С.А. Теляковского. Ответы на самостоятельные работа по алгебре 8 класс (Макарычев) адресованы учителям и родителям, которые смогут проконтролировать правильность выполнения задания. Цитаты из пособия указаны в учебных целях. При постоянном использовании самостоятельных и контрольных работ по алгебре в 8 классе рекомендуем КУПИТЬ книгу: Алгебра 8 класс. Дидактические материалы/ В.И. Жохов, Ю.Н. Макарычев, Н.Г. Миндюк — М.:Просвещение (переход по ссылке в интернет-магазин «Лабиринт.Ру»)
Самостоятельные работы по алгебре с ответами
(8 класс, УМК Макарычев и др.)
Самостоятельная № 1 С-01 Преобразование целого выражения в многочлен (повторение).
Самостоятельная № 2 С-02 Разложение на множители (повторение).
Самостоятельная № 3 С-03 Целые и дробные выражения.
Самостоятельная № 4 С-04 Основное свойство дроби. Сокращение дробей.
Самостоятельная № 5 С-05 Сокращение дробей (продолжение).
Самостоятельная № 6 С-06 Сложение и вычитание дробей с одинаковыми знаменателями.
Самостоятельная № 7 С-07 Сложение и вычитание дробей с разными знаменателями.
Самостоятельная № 8 С-08 Сложение и вычитание дробей с разными знаменателями (продолжение).
Самостоятельная № 9 С-09. Умножение дробей.
Самостоятельная № 10 С-10. Деление дробей.
Самостоятельная № 11 С-11. Все действия с дробями.
Самостоятельная № 12 С-12. Функция y = k/x и её график.
Самостоятельная № 13 С-13. Рациональные и иррациональные числа.
Самостоятельная № 14 С-14. Арифметический квадратный корень
Самостоятельная № 15 С-15. Решение уравнения вида x2 = a.
Самостоятельная № 16 С-16. Нахождение приближенных значений квадратного корня.
Нахождение приближенных значений квадратного корня.
Самостоятельная № 17 С-17. Функция y = √x.
Самостоятельная № 18 С-18. Квадратный корень из произведения. Произведение корней.
(работы 19 — 44 готовятся к публикации)
Самостоятельная № 45 С-45. Решение неравенств.
Самостоятельная № 46 С-46. Уравнения и неравенства, содержащие переменную под знаком модуля.
Самостоятельная № 47 С-47. Степень с целым показателем.
Самостоятельная № 48 С-48. Преобразование выражений, содержащих степени с целым показателем.
Самостоятельная № 49 С-49. Стандартный вид числа.
Самостоятельная № 50 С-50. Запись приближенных значений
Самостоятельная № 51 С-51. Элементы статистики
Самостоятельная № 52 С-52. Понятие функции. График функции (повторение)
Самостоятельная № 53 С-53 Определение квадратичной функции
Самостоятельная № 54 С-54 Функция y = x2
Самостоятельная № 55 С-55 График функции y = ax2 + bx + c
Самостоятельная № 56 С-56 Решение квадратных неравенств
Самостоятельная № 57 С-57 Метод интервалов
Самостоятельные работы по алгебре в 8 классе с решениями и ОТВЕТАМИ по учебнику Макарычева. Алгебра 8 Макарычев Самостоятельные — цитаты из пособия для учащихся «Алгебра 8 класс. Дидактические материалы / Жохов, Макарычев, Миндюк — М.: Просвещение». Представленные работы ориентированы на учебник «Алгебра 8 класс» авторов Ю.Н. Макарычева и др. под редакцией С.А. Теляковского.
Алгебра 8 Макарычев Самостоятельные — цитаты из пособия для учащихся «Алгебра 8 класс. Дидактические материалы / Жохов, Макарычев, Миндюк — М.: Просвещение». Представленные работы ориентированы на учебник «Алгебра 8 класс» авторов Ю.Н. Макарычева и др. под редакцией С.А. Теляковского.
| Даты | Тема | Преподаватель |
| Неделя 1, пн 31 августа | Введение в линейный Алгоритмы программирования и аппроксимации | Атри Рудра |
| Неделя 1, среда, 02 сентября | Двойственность, дополнительная Вялость, лемма Фаркаша | |
| Неделя 2, пн, сентябрь 07 | Труда день! | Хунг Нго |
| Неделя 2, | An
обзор построения алгоритма аппроксимации через Vertex Cover; маленький
больше о LP и характеристике экстремальных точечных решений. Полуцелость вершинного покрытия. Как сдавать двойную программу. Полуцелость вершинного покрытия. Как сдавать двойную программу. | |
| Неделя 3, пн, 14 сентября | LP / ILP и полная унимодульность. Maxflow / mincut. | |
| Неделя 3, | Всего унимодульность. Эллипсоидный метод, разделение оракул | |
| Неделя 4, пн 21 сентября | Округление и рандомизированное округление. Примеры: вырезать проблемы, покрывающие проблемы, проблемы выполнимости. | |
| Неделя 4, среда 23 сентября | Итеративный округление | |
| Неделя 5, пн, 28 сентября | Йом Кипур! | |
| Неделя 5, | Итеративный округление | |
| Неделя 6, пн 05 октября | Primal-двойной | |
| 6 неделя, | Primal-двойной | |
| Неделя 7, пн 12 октября | Primal-Dual. (Свами
бумага, может быть.) (Свами
бумага, может быть.) | |
| 7 неделя, | Более сложный методы округления. Метрическая врезка | |
| Неделя 8, понедельник 19 октября | Стив
Уутармо:
Анупам Гупта и Кунал Талвар, Approximating Unique Games, SODA
2006. Swapnoneel Рой: Л. Лау, М. Сингх. Приближение минимальных ограниченных степеней остовных деревьев к одному из Оптимально. STOC 2007. | Студент Презентации |
| Неделя 8, | Лей Сюй:
Роберт Д.Карр, Сантош Вемпала: рандомизированное мета-окружение. Случайная структура.
Алгоритмы 20 (3): 343-352 (2002). (также появлялся в STOC’00) Бранислав Стойкович: Джайн и Вазирани, Алгоритмы аппроксимации метрического местоположения объекта и k-медианные задачи с использованием прямо-дуальной схемы и лагранжиана расслабление. ACM 48, 2, 274–296, 2001. | |
| Неделя 9, пн 26 октября | Xi
Ван: Дорит Хохбаум, Н. Мегиддо, Дж. Наор и А. Тамир «Тайт»
Границы и 2-аппроксимационные алгоритмы для целочисленных программ с двумя
Переменные на неравенство, Математическое программирование, 62 (1993) Мегиддо, Дж. Наор и А. Тамир «Тайт»
Границы и 2-аппроксимационные алгоритмы для целочисленных программ с двумя
Переменные на неравенство, Математическое программирование, 62 (1993) | |
| Неделя 9 | Кришна
Рамкумар:
Бансал, Н., Хандекар, Р., и Нагараджан, В. 2008. Добавка
гарантии для направленного проектирования сетей с ограничениями по степени. STOC 2008. Арун Рамачандрамурти: Чунг и Свами, Аппроксимационные алгоритмы для целеустремленных Проблемы максимизации прибыли без зависти при ограниченном предложении, Труды FOCS 2008, страницы 35-44. | |
| Неделя 10, пн, 02 ноября | Thanh-Nhan
Нгуен: Л. Лау, М. Сингх
Аддитивное приближение для ограниченного
Степень выживаемости
Сетевой дизайн. STOC 2008 Натан Рассел: Лави & Swamy, правдивый и почти оптимальный Разработка механизмов посредством линейного программирования, Труды FOCS 2005, страницы 595-604. | |
| неделя 10, ср | Атри Рудра | |
| Неделя 11, пн, ноябрь 09 | ||
| неделя 11, ср | ||
| Неделя 12, пн 16 ноября | ||
| неделя 12, ср | ||
| Неделя 13, пн 23 ноября | Thanh-Nhan
Нгуен: «Первичные двойные алгоритмы для SDP: A
комбинаторный, прямодвойственный подход к решению СДП ». Санджив Арора,
Satyen Kale. Proc. ACM STOC 2007. Санджив Арора,
Satyen Kale. Proc. ACM STOC 2007. Натан Рассел: «Почти оптимальные алгоритмы для уникальных игр», Моисей Чарикар, Константин Макарычев, Юрий Макарычев, STOC 2006 | Студент Презентации |
| Неделя 13, ср | Fall Recess! | |
| Неделя 14, пн 30 ноября | Кришна
Рамкумар: Рагхавендра
Прасад. * Оптимальные алгоритмы и
Результаты неприближаемости
для каждого CSP? * STOC 2008. Arun Рамачандрамурти: Быстрая реализация некоторых алгоритмов на основе SDP: O (\ sqrt {log n}) приближение к SPARSEST CUT за время O (n2).Санджив Арора, Элад Хазан и Сатьен Кале. Proc. Основы компьютерных наук IEEE, 2004. | |
| неделя 14, ср | Си Ван: Евклидово искажение и разреженное сокращение (С. Арора, Дж. Р. Ли и А. Наор) Журнал Американского математического общества, 21 (1): 1-21, 2008. [STOC 2005] | |
| неделя 15, пн, декабрь 07 | Лей Сюй:
«Почти оптимальные алгоритмы для максимального ограничения
Удовлетворение
Проблемы,»
Моисей Чарикар, Константин Макарычев, Юрий Макарычев,
SODA 2007 Бранислав Стойкович: Лука Тревизан Аппроксимационные алгоритмы для уникальных игр Proc.  46-го заседания IEEE FOCS, 2005 г. 46-го заседания IEEE FOCS, 2005 г. | |
| Неделя 15, среда, 9 декабря | Стив
Uutarmo: Уникальные игры по расширению графов ограничений
Легко
Санджив Арора, Субхаш Хот, Александра Колла, Дэвид Стойер, Мадхур
Тулсиани и
Нишит Вишной. Proc. ACM STOC 2008. Swapnoneel Рой: Как обойти любого CSP — Прасад Рагхавендра, Дэйвид Steurer FOCS 2009 |
Возвести указанные числа в степень. Возведение в степень. Резюме раздела и основные формулы
Калькулятор помогает быстро возвести число в степень онлайн.Основанием степени может быть любое число (как целое, так и действительное). Показатель степени также может быть целым или действительным, а также положительным и отрицательным. Следует помнить, что нецелочисленное возведение в степень не определено для отрицательных чисел, и поэтому калькулятор сообщит об ошибке, если вы попытаетесь это сделать.
Калькулятор градусов
Возвести в степень
Экспоненций: 94722
Какова естественная сила числа?
Число p называется n-й степенью числа a, если p равно числу a, умноженному на себя n раз: p = a n = a. .. a
.. a
n — называется степенью , а число a — степенью основания .
Как возвести число в степень?
Чтобы понять, как возвести различные числа в натуральную степень, рассмотрим несколько примеров:
Пример 1 … Возвести число три в четвертую степень. То есть необходимо вычислить 3 4
Решение : как сказано выше, 3 4 = 3 3 3 3 3 = 81.
Ответ : 3 4 = 81.
Пример 2 … Возвести число пять в пятую степень. То есть необходимо вычислить 5 5
Решение : аналогично 5 5 = 5 5 5 5 5 5 = 3125.
Ответ : 5 5 = 3125.
Таким образом, чтобы возвести число в натуральную степень, вам просто нужно умножить его на себя n раз.
Какова отрицательная степень числа?
Отрицательная степень -n числа a равна единице, деленной на степень n: a -n =. В этом случае отрицательная степень существует только для ненулевых чисел, поскольку в противном случае произошло бы деление на ноль.
Как возвести число в степень отрицательного целого?
Чтобы возвести ненулевое число в отрицательную степень, вам нужно вычислить значение этого числа в той же положительной степени и разделить единицу на результат.
Пример 1 … Возводим число два до минус четвертой степени. То есть надо посчитать 2-4
Решение : как сказано выше, 2-4 = = = 0,0625.Ответ : 2-4 = 0,0625.
Формулы мощности используются в процессе сокращения и упрощения сложных выражений, при решении уравнений и неравенств.
Число c — это степень n числа a , когда:
Операции со степенями.
1. Умножая градусы с одинаковым основанием, их показатели складываются:
a m A n = a m + n.
2. При делении степеней с одинаковым основанием вычитаются их показатели:
3. Степень произведения двух или более факторов равна произведению степеней этих факторов:
(abc. ..) n = a n b n c n …
..) n = a n b n c n …
4. Степень дроби равна отношению степеней делимого и делителя:
(а / б) п = а н / б н.
5. Повышая градус до градуса, степень умножается:
(а м) н = а м н.
Каждая из приведенных выше формул верна слева направо и наоборот.
например . (2 · 3 · 5/15) ² = 2² · 3² · 5² / 15² = 900/225 = 4 .
Операции с корнями.
1. Корень произведения нескольких множителей равен произведению корней этих множителей:
2. Корень отношения равен отношению делимого к делителю корней:
3. Возведя корень в степень, достаточно возвести число корня в эту степень:
4. Если вы увеличите степень корня в n один раз и в то же время построите n -ю степень числа корня, значение корня не изменится:
5.Если уменьшить степень корня в n извлечь корень один раз и одновременно n -ю степень радикального числа, то значение корня не изменится:
Градус с отрицательной экспонентой. Степень числа с неположительной (целой) экспонентой определяется как единица, деленная на степень того же числа с показателем, равным абсолютному значению неположительной экспоненты:
Степень числа с неположительной (целой) экспонентой определяется как единица, деленная на степень того же числа с показателем, равным абсолютному значению неположительной экспоненты:
Формула a m : a n = a m — n может использоваться не только для m > n , но и на m n.
например . a 4: a 7 = a 4-7 = a -3 .
Так что формула a m : a n = a m — n стала справедливой при m = n , наличие нулевой степени обязательно.
Нулевая степень. Степень любого ненулевого числа с нулевым показателем степени равна единице.
например . 2 0 = 1, (- 5) 0 = 1, (- 3/5) 0 = 1.
Дробная экспонента. Чтобы возвести действительные числа и до степени m / n , нужно извлечь корень n -й степени m -й степени этого числа и .
можно найти с помощью умножения. Например: 5 + 5 + 5 + 5 + 5 + 5 = 5×6..png) О таком выражении говорят, что сумма равных членов складывается в произведение. И наоборот, если мы прочитаем это равенство справа налево, мы обнаружим, что мы расширили сумму равных членов. Аналогичным образом можно свернуть произведение нескольких равных множителей 5x5x5x5x5x5 = 5 6.
О таком выражении говорят, что сумма равных членов складывается в произведение. И наоборот, если мы прочитаем это равенство справа налево, мы обнаружим, что мы расширили сумму равных членов. Аналогичным образом можно свернуть произведение нескольких равных множителей 5x5x5x5x5x5 = 5 6.
То есть вместо того, чтобы умножать шесть одинаковых множителей 5x5x5x5x5x5, они пишут 5 6 и говорят «пять в шестой степени».
Выражение 5 6 — степень числа, где:
5 — основание степени;
6 — экспонента .
Действия, посредством которых произведение равных множителей складывается в степень, называются возведением в степень .
Обычно степень с основанием «a» и показателем «n» записывается следующим образом:
Возведение числа a в степень n означает нахождение произведения n факторов, каждый из которых равен
Если основание степени «a» равно 1, то значение степени для любого натурального n будет равно 1.Например, 1 5 = 1, 1 256 = 1
Если возвести число «а» до первой степени , то мы получим само число а: а 1 =
Если возвести любое число до ноль градусов , то в результате вычислений мы получим единицу. а 0 = 1
а 0 = 1
Вторая и третья степени числа считаются особенными. Для них были придуманы названия: вторая степень называется квадратным числом , третья — куб этим числом.
Любое число можно возвести в степень: положительную, отрицательную или нулевую. В этом случае не используются следующие правила:
Определение степени положительного числа дает положительное число.
При вычислении нуля в естественной степени мы получаем ноль.
x м x n = x m + n
например: 7 1,7 7 — 0,9 = 7 1,7 + (- 0,9) = 7 1,7 — 0,9 = 7 0,8
Отдо разделить градусы по тем же основаниям базу не меняем, а вычитаем показатели:
x m / x n = x m — n где, m> n,
например: 13 3.8/13 -0,2 = 13 (3,8 -0,2) = 13 3,6
При вычислении возведения в степень мы не меняем основание, а умножаем экспоненты друг на друга.
(для m ) n = y m n
например: (2 3) 2 = 2 3 2 = 2 6
(x y) n = x n · на м. ,
,
например: (2 3) 3 = 2 n 3 м,
При выполнении вычислений по возведению в степень числитель и знаменатель дроби возводятся в эту степень
(x / y) n = x n / y n
например: (2/5) 3 = (2/5) (2/5) (2/5) = 2 3/5 3.
Последовательность выполнения вычислений при работе с выражениями, содержащими степень.
При вычислении выражений без скобок, но содержащих степени, сначала возвести в степень, затем умножить и разделить, и только потом операции сложения и вычитания.
Если необходимо вычислить выражение, содержащее круглые скобки, то сначала в указанном выше порядке мы выполняем вычисления в скобках, а затем остальные действия в том же порядке слева направо.
Очень широко в практических расчетах используются готовые таблицы степеней для упрощения расчетов.
Продолжая разговор о градусе числа, логично разобраться, как найти значение градуса. Этот процесс получил название возведение в степень . .. В этой статье мы просто изучим, как выполняется возведение в степень, затрагивая при этом все возможные показатели — естественные, целые, рациональные и иррациональные. И по традиции подробно рассмотрим решения примеров возведения чисел в разную степень.
.. В этой статье мы просто изучим, как выполняется возведение в степень, затрагивая при этом все возможные показатели — естественные, целые, рациональные и иррациональные. И по традиции подробно рассмотрим решения примеров возведения чисел в разную степень.
Навигация по страницам.
Что означает возведение в степень?
Следует начать с объяснения того, что называется возведением в степень. Вот подходящее определение.
Определение.
Возведение в степень — это нахождение значения степени числа.
Таким образом, найти значение степени числа с показателем r и возвести число a в степень r — это одно и то же. Например, если задача состоит в том, чтобы «вычислить значение степени (0.5) 5 », то его можно переформулировать следующим образом:« Возвести число 0,5 в степень 5 ».
Теперь вы можете перейти непосредственно к правилам, по которым выполняется возведение в степень.
Возведение числа в степень
На практике равенство на основе обычно применяется в форме. То есть при возведении числа a в дробную степень m / n сначала извлекается корень n-й степени числа a, после чего полученный результат возводится в целую степень m.
То есть при возведении числа a в дробную степень m / n сначала извлекается корень n-й степени числа a, после чего полученный результат возводится в целую степень m.
Рассмотрим решения примеров возведения в дробную степень.
Пример.
Рассчитайте значение мощности.
Решение.
Покажем два способа решения.
Первый способ. По определению, дробная экспонента. Под знаком корня вычисляем значение степени, после чего извлекаем кубический корень:.
Второй способ. По определению степени с дробным показателем и исходя из свойств корней, равенства верны … Теперь извлекаем корень окончательно, возводим в целую степень.
Очевидно, что полученные результаты возведения в дробную степень совпадают.
Ответ:
Обратите внимание, что дробная экспонента может быть записана в виде десятичной дроби или смешанного числа, в этих случаях ее следует заменить соответствующей обыкновенной дробью, после чего выполняется возведение в степень.
Пример.
Вычислить (44,89) 2.5.
Решение.
Запишем показатель степени в виде обыкновенной дроби (при необходимости см. Статью):… Теперь выполняем возведение в дробную степень:
Ответ:
(44,89) 2,5 = 13 501,25 · 107 .
Также следует сказать, что возведение чисел в рациональные степени — довольно трудоемкий процесс (особенно когда числитель и знаменатель дробной экспоненты содержат достаточно большие числа), который обычно выполняется с помощью компьютеров.
В заключение остановимся на возведении числа ноль в дробную степень. Мы придали следующий смысл дробной степени нуля формы: для, имеем, а при нуле степень m / n не определена.Итак, ноль в дробной положительной степени равен нулю, например … А ноль в дробно-отрицательной степени не имеет смысла, например, выражения и 0 -4,3 не имеют смысла.
Возведение в иррациональную степень
Иногда возникает необходимость выяснить значение степени числа с иррациональным показателем. В этом случае для практических целей обычно достаточно получить значение градуса с точностью до некоторого знака. Сразу отметим, что на практике это значение рассчитывается с помощью электронно-вычислительной машины, поскольку ручное возведение в иррациональную степень требует большого количества громоздких вычислений.Но все же опишем в общих чертах суть действия.
В этом случае для практических целей обычно достаточно получить значение градуса с точностью до некоторого знака. Сразу отметим, что на практике это значение рассчитывается с помощью электронно-вычислительной машины, поскольку ручное возведение в иррациональную степень требует большого количества громоздких вычислений.Но все же опишем в общих чертах суть действия.
Чтобы получить приблизительное значение степени числа a с иррациональной экспонентой, берется некоторое десятичное приближение показателя степени, и вычисляется значение показателя степени. Это значение является приблизительным значением степени числа a с иррациональным показателем. Чем точнее будет принято десятичное приближение числа изначально, тем более точное значение степени будет получено в итоге.
В качестве примера рассчитаем примерное значение степени 2 1.174367 …. Возьмем следующую десятичную аппроксимацию иррационального показателя :. Теперь возводим 2 в рациональную степень 1,17 (суть этого процесса мы описали в предыдущем абзаце), получаем 2 1,17 ≈2,250116. Таким образом, 2 1,174367 … ≈2 1,17 ≈2,250116 … Если мы возьмем более точное десятичное приближение, например, иррационального показателя, мы получим более точное значение исходного показателя: 2 1,174367 … ≈2 1,1743 ≈2,256833 .
Список использованной литературы.
- Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Учебник математики для 5 класса. образовательные учреждения.
- Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: учебник для 7 класса. Образовательные учреждения.
- Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: учебник для 8 класса общеобразовательных учреждений.
- Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: учебник для 9 класса. образовательные учреждения.
- Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и другие. Алгебра и начало анализа: Учебник для 10-11 классов общеобразовательных учреждений.
- Гусев В.А., Мордкович А.Г. Математика (пособие для поступающих в техникумы).
Разобрались, что такое степень числа в целом. Теперь нам нужно понять, как правильно его вычислить, т.е. возвести числа в степень. В этом материале мы разберем основные правила вычисления степени в случае целого, натурального, дробного, рационального и иррационального показателя.Все определения будут проиллюстрированы примерами.
Концепция возведения в степень
Начнем с формулировки основных определений.
Определение 1
Возведение в степень — это вычисление значения степени некоторого числа.
То есть, слова «вычисление значения степени» и «возведение в степень» означают одно и то же. Итак, если задача — «Возвести число 0, 5 в пятую степень», ее следует понимать как «вычислить значение степени (0, 5) 5».
Теперь мы дадим основные правила, которым нужно следовать при таких расчетах.
Давайте вспомним, какова степень числа с натуральной экспонентой. Для степени с основанием a и показателем n это будет произведение n-го числа множителей, каждый из которых равен a. Это можно записать так:
Чтобы вычислить значение степени, вам необходимо выполнить действие умножения, то есть умножить основания степени указанное количество раз. Само понятие степени с натуральным показателем основано на умении быстро размножаться.Вот несколько примеров.
Пример 1
Условие: возвести — 2 в степень 4.
Решение
Используя определение выше, запишем: (- 2) 4 = (- 2) · (- 2) · (- 2) · (- 2). Далее нам просто нужно выполнить указанные шаги и получить 16.
Возьмем более сложный пример.
Пример 2
Рассчитать значение 3 2 7 2
Решение
Эту запись можно переписать как 3 2 7 · 3 2 7.Ранее мы рассмотрели, как правильно умножить смешанные числа, указанные в условии.
Проделаем эти действия и получим ответ: 3 2 7 3 2 7 = 23 7 23 7 = 529 49 = 10 39 49
Если проблема указывает на необходимость возвести иррациональные числа в естественную степень, нам нужно сначала округлить их основания до цифры, которая позволит нам получить ответ с требуемой точностью. Давайте посмотрим на пример.
Пример 3
Возвести число π в квадрат.
Решение
Сначала округлим до сотых. Тогда π 2 ≈ (3, 14) 2 = 9, 8596. Если π ≈ 3. 14159, то получаем более точный результат: π 2 ≈ (3, 14159) 2 = 9, 8695877281.
Отметим, что необходимость в вычислении степеней иррациональных чисел на практике возникает сравнительно редко. Тогда мы можем записать ответ в виде самой степени (ln 6) 3 или преобразовать, если возможно: 5 7 = 125 5.
Отдельно следует указать, что такое первая степень числа.Здесь вы можете просто запомнить, что любое число в первой степени останется самим собой:
Это ясно из записи.
Не зависит от основания степени.
Пример 4
Итак, (- 9) 1 = — 9, а 7 3, возведенные в первую степень, остается равным 7 3.
Для удобства мы отдельно разберем три случая: если показатель степени является целым положительным числом, если он равен нулю и если это отрицательное целое число.
В первом случае это то же самое, что возведение в натуральную степень: в конце концов, положительные целые числа принадлежат множеству натуральных чисел.Как работать с такими степенями мы уже рассказывали выше.
А теперь посмотрим, как правильно возвести в ноль мощность. С основанием системы счисления, отличным от нуля, это вычисление всегда выводит 1. Мы уже объясняли, что 0-я степень a может быть определена для любого действительного числа, кроме 0, и 0 = 1.
Пример 5
5 0 = 1, (- 2, 56) 0 = 1 2 3 0 = 1
0 0 — не определено.
У нас есть только случай степени с целым отрицательным показателем. Мы уже обсуждали, что такие степени можно записать в виде дроби 1 a z, где a — любое число, а z — целая отрицательная экспонента.Мы видим, что знаменатель этой дроби есть не что иное, как обычная степень с целым положительным показателем степени, и мы уже научились его вычислять. Вот несколько примеров задач.
Пример 6
Возвести 2 в степень — 3.
Решение
Воспользовавшись приведенным выше определением, запишем: 2 — 3 = 1 2 3
Посчитаем знаменатель этой дроби и получим 8: 2 3 = 2 · 2 · 2 = 8.
Тогда ответ: 2 — 3 = 1 2 3 = 1 8
Пример 7
Поднять 1, 43 в степень — 2.
Решение
Переформулируем: 1, 43 — 2 = 1 (1, 43) 2
Вычисляем квадрат в знаменателе: 1,43 · 1,43. Десятичные дроби можно умножить таким образом:
В результате мы получили (1, 43) — 2 = 1 (1, 43) 2 = 1 2, 0449. Нам остается записать этот результат в виде обыкновенной дроби, для которой он необходимо умножить его на 10 тысяч (см. материал по пересчету дробей).
Ответ: (1, 43) — 2 = 10000 20449
Отдельный случай — возведение числа в первую степень минус. Значение этой степени равно обратной величине исходной базовой величины: a — 1 = 1 a 1 = 1 a.
Пример 8
Пример: 3-1 = 1/3
9 13 — 1 = 13 9 6 4 — 1 = 1 6 4.
Как возвести число в дробную степень
Чтобы выполнить такую операцию, нам нужно вспомнить основное определение степени с дробным показателем: a m n = a m n для любого положительного a, целого числа m и натурального n.
Определение 2
Таким образом, вычисление дробной степени должно быть выполнено в два этапа: возведение в целую степень и нахождение корня n-й степени.
Имеем равенство a m n = a m n, которое, учитывая свойства корней, обычно используется для решения задач в виде a m n = a n m. Это означает, что если мы возводим число a в дробную степень m / n, то сначала извлекаем корень n-й степени из a, а затем возводим результат в степень с целым показателем m.
Проиллюстрируем на примере.
Пример 9
Вычислить 8 — 2 3.
Решение
Метод 1. Согласно основному определению, мы можем представить его как: 8 — 2 3 = 8 — 2 3
Теперь посчитаем степень под корнем и извлечем из результата третий корень: 8-2 3 = 1 64 3 = 1 3 3 64 3 = 1 3 3 4 3 3 = 1 4
Способ 2. Преобразуем основное равенство: 8 — 2 3 = 8 — 2 3 = 8 3 — 2
После этого извлеките корень 8 3 — 2 = 2 3 3 — 2 = 2 — 2 и возведите результат в квадрат: 2 — 2 = 1 2 2 = 1 4
Мы видим, что решения идентичны.Вы можете использовать его как хотите.
Бывают случаи, когда степень имеет показатель степени, выраженный как смешанное число или десятичную дробь. Для простоты расчетов лучше заменить ее обыкновенной дробью и считать, как указано выше.
Пример 10
Возвести 44,89 в степень 2,5.
Решение
Преобразуем значение показателя в обыкновенную дробь: 44, 89 2, 5 = 44, 89 5 2.
А теперь выполняем по порядку все указанные выше действия: 44, 89 5 2 = 44, 89 5 = 44, 89 5 = 4489 100 5 = 4489 100 5 = 67 2 10 2 5 = 67 10 5 = = 1350125107 100000 = 13 501, 25107
Ответ: 13 501, 25107.
Если в числителе и знаменателе дробной экспоненты есть большие числа, то вычисление таких степеней с рациональными показателями является довольно сложной задачей. Обычно это требует вычислений.
Остановимся отдельно на степени с нулевым основанием и дробной степени. Выражению вида 0 m n можно придать следующий смысл: если m n> 0, то 0 m n = 0 m n = 0; если m n
Как возвести число в иррациональную степень
Необходимость вычислять значение степени, в экспоненте которой стоит иррациональное число, возникает не так часто.На практике задача обычно ограничивается вычислением приблизительного значения (до определенного количества десятичных знаков). Обычно это рассчитывается на компьютере из-за сложности подобных расчетов, поэтому подробно останавливаться на этом не будем, укажем только основные положения.
Если нам нужно вычислить значение показателя a с иррациональным показателем a, то мы берем десятичное приближение показателя степени и вычисляем его. В результате будет приблизительный ответ.Чем точнее десятичное приближение, тем точнее ответ. Давайте покажем на примере:
Пример 11
Вычислите приблизительное значение 2 до 1,174367 …
Решение
Ограничимся десятичным приближением an = 1, 17. Произведем вычисления с использованием этого числа: 21, 17 ≈ 2, 250116. Если взять, например, приближение an = 1, 1743, то ответ будет немного точнее: 21, 174367…. … ≈ 2 1, 1743 ≈ 2, 256833.
Если вы заметили ошибку в тексте, выделите ее и нажмите Ctrl + Enter
биография Колмогоровская реформа школьного математического образования
Андрей Николаевич Колмогоров (12 (25) апреля, Тамбов — 20 октября, Москва) — выдающийся советский математик.
доктор физико-математических наук, профессор МГУ (), академик АН СССР (), лауреат Сталинской премии, Герой Социалистического Труда.Колмогоров — один из основоположников современной теории вероятностей, он получил фундаментальные результаты в топологии, математической логике, теории турбулентности, теории сложности алгоритмов и ряде других областей математики и ее приложений.
Биография
ранние годы
Мать Колмогорова — Мария Яковлевна Колмогорова (-) умерла при родах. Отец — Николай Матвеевич Катаев, по образованию агроном (окончил Петровскую (Тимирязевскую) академию), погиб в 1919 году во время Деникинского наступления.Мальчика усыновила и растила сестра матери, Вера Яковлевна Колмогорова. Тети Андрея организовали в своем доме школу для разновозрастных детей, которые жили рядом, работали с ними — с десяток детей — по рецептам новейшей педагогики. Для детей издан рукописный журнал «Весенние ласточки». В нем опубликованы творческие работы школьников — рисунки, стихи, рассказы. В нем также появились «научные труды» Андрея — придуманные им арифметические задачи. Здесь мальчик опубликовал свою первую научную работу по математике в возрасте пяти лет.Правда, это была всего лишь известная алгебраическая закономерность, но мальчик сам это заметил, без посторонней помощи!
В возрасте семи лет Колмогоров был переведен в частную гимназию. Он был организован кружком московской прогрессивной интеллигенции и все время находился под угрозой закрытия.
Андрей уже в те годы проявил незаурядные математические способности, но пока рано говорить о том, что его дальнейший путь уже определен. Также было увлечение историей и социологией.Одно время мечтал стать лесником. «В 1920-е годы жизнь в Москве была непростой, , — вспоминал Андрей Николаевич. — В школах серьезно занимались только самые стойкие. В это время мне пришлось уехать на строительство железной дороги Казань-Екатеринбург. Параллельно с работой я продолжал учиться самостоятельно, готовясь к экстернату в средней школе. По возвращении в Москву испытал некоторое разочарование: мне выдали аттестат об окончании школы, даже не удосужившись сдать экзамен.»
Университет
Профессора
А 23 июня 1941 г. состоялось расширенное заседание Президиума АН СССР. Принятое по нему решение закладывает основу для перестройки деятельности научного учреждения … Сейчас главным является военная тема: вся сила, все знания — победа. Советские математики по заданию Главного артиллерийского управления армии проводят комплексные работы в области баллистики и механики.Колмогоров, используя свои исследования теории вероятностей, определяет наиболее выгодный разброс снарядов при стрельбе. После окончания войны Колмогоров возвращается к мирным исследованиям.
Трудно хотя бы вкратце осветить вклад Колмогорова в другие области математики — общую теорию операций над множествами, интегральную теорию, теорию информации, гидродинамику, небесную механику и т. Д., Вплоть до лингвистики. Во всех этих дисциплинах многие методы и теоремы Колмогорова, по общему признанию, являются классическими, и влияние его работы, как и работы его многочисленных учеников, в том числе многих выдающихся математиков, на общий курс развития математики чрезвычайно велико.
Круг жизненных интересов Андрея Николаевича не ограничивался чистой математикой, объединению отдельных разделов которой он посвятил свою жизнь. Его увлекали и философские проблемы (например, он сформулировал новый гносеологический принцип — гносеологический принцип А. Н. Колмогорова), и история науки, и живопись, и литература, и музыка.
Аскетизм Колмогорова, его умение одновременно заниматься практикой — и не без успеха, можно удивить! — много дел одновременно.Это и руководство университетской лаборатории статистических методов исследования, и заботы о физико-математической школе-интернате, инициатором создания которой был Андрей Николаевич, и дела Московского математического общества, и работа в редакциях «Кванта». — журнал для школьников и «Математика в школе» — журнал методический и для учителей, и для научно-педагогической деятельности, и для подготовки статей, брошюр, книг, учебников. Колмогорову никогда не приходилось упрашивать выступить на студенческом диспуте, встретиться со школьниками на вечере.На самом деле его всегда окружала молодежь. Они его очень любили, всегда прислушивались к его мнению. Сыграл роль не только авторитет всемирно известного ученого, но и излучаемые им простота, внимание и душевная щедрость.
Реформа школьного математического образования
К середине 1960-х гг. Руководство Минобразования СССР пришло к выводу, что система преподавания математики в советской средней школе переживает глубокий кризис и нуждается в реформировании.Было признано, что в средней школе преподается только устаревшая математика, а ее новейшие достижения не учитываются. Модернизация системы математического образования была проведена Министерством образования СССР при участии Академии педагогических наук и Академии наук СССР. Руководство Отделения математики АН СССР рекомендовало для проведения модернизации академика А. Н. Колмогорова, сыгравшего ведущую роль в этих реформах.
Результаты этой деятельности академика были оценены неоднозначно и продолжают вызывать множество споров.
Последние годы
Академик Колмогоров — почетный член многих зарубежных академий и научных обществ. В марте 1963 года ученому была присуждена международная премия Бальзана (эта премия была вручена ему вместе с композитором Хиндемитом, биологом Фришем, историком Моррисоном и главой Римско-католической церкви Папой Иоанном XXIII).В том же году Андрею Николаевичу было присвоено звание Героя Социалистического Труда. В 1965 г. ему была присуждена Ленинская премия (совместно с В. И. Арнольдом), в 1980 г. — премия Вольфа. Награжден орденом Н.И. Премия Лобачевского В последние годы Колмогоров возглавлял кафедру математической логики.
| Я принадлежу к тем крайне отчаявшимся кибернетикам, которые не видят принципиальных ограничений в кибернетическом подходе к проблеме жизни и верят, что с помощью методов кибернетики можно анализировать жизнь в целом, включая человеческое сознание.Прогресс в понимании механизма высшей нервной деятельности, в том числе высших проявлений творческих способностей человека, на мой взгляд, ничего не умаляет ценности и красоты творческих достижений человека. А. Н. Колмогоров |
ученик
Когда одного из молодых коллег Колмогорова спросили, какие чувства он испытывает к своему учителю, он ответил: «Паническое уважение … Вы знаете, Андрей Николаевич дает нам столько своих гениальных идей, что их хватило бы на сотни отличных разработок. .«.
Замечательная закономерность: многие ученики Колмогорова, обретя самостоятельность, стали играть ведущую роль в выбранном направлении исследований, среди них — В.И. Арнольд, И.М. Гельфанд, М.Д. Миллионщиков, Ю.В. Прохоров, А.М. Обухов, А. Монин, А. Н. Ширяев, С. М. Никольский, В. А. Успенский. Академик с гордостью подчеркнул, что ему дороже всего те студенты, которые превзошли своих учителей в научных исследованиях.
Литература
Книги, статьи, публикации Колмогорова
- А. Н. Колмогоров, Об операциях над множествами, Матем.Сб, 1928, 35: 3-4
- А. Н. Колмогоров, Общая теория меры и исчисление вероятностей // Известия Коммунистической академии. Математика. — М .: 1929, т. 1.П. 8 — 21.
- А. Н. Колмогоров, Об аналитических методах в теории вероятностей, Успехи матем. Наук, 1938: 5, 5-41 .
- А. Н. Колмогоров, Основные понятия теории вероятностей. Эд. 2, М. Наука, 1974, 120 с.
- А. Н. Колмогоров, Теория информации и теория алгоритмов. — М .: Наука, 1987. — 304 с.
- А.Н. Колмогоров, С. В. Фомин, Элементы теории функций и функционального анализа. 4-е изд. М. Наука. 1976 544 с.
- А. Н. Колмогоров, Теория вероятностей и математическая статистика. М. Наука 1986 534с.
- А. Н. Колмогоров, «О профессии математика». М., Изд-во МГУ, 1988, 32с.
- А. Н. Колмогоров, «Математика — наука и профессия». М .: Наука, 1988.288 с.
- А. Н. Колмогоров, И. Г. Журбенко, А. В. Прохоров, «Введение в теорию вероятностей».М .: Наука, 1982.160 с.
- А.Н. Колмогорова, Grundbegriffe der Wahrscheinlichkeitrechnung, в Ergebnisse der Mathematik, Берлин. 1933.
- А.Н. Колмогоров, Основы теории вероятностей. Chelsea Pub. Co; 2-е издание (1956 г.) 84 стр.
- А.Н. Колмогоров, С.В. Фомин, Элементы теории функций и функционального анализа. Dover Publications (16 февраля 1999 г.), стр. 288. ISBN 978-0486406831
- А.Н. Колмогоров, С.В. Фомин, Вводный реальный анализ (твердый переплет) Р.А. Сильверман (переводчик). Прентис Холл (1 января 2009 г.), 403 стр. ISBN 978-0135022788
О Колмогорове
- 100 великих ученых. Самин Д.К.М .: Вече, 2000. — 592 с. — 100 отлично. ISBN 5-7838-0649-8
см. Также
Ссылки
Некоторые публикации А. Н. Колмогорова
- А. Н. Колмогоров О профессии математика. — М .: Изд-во МГУ, 1988. — 32 с.
- А.Н. Колмогоров Математика — это наука и профессия. — М .: Наука, 1988. — 288 с.
- А. Н. Колмогоров, И. Г. Журбенко, А. В. Прохоров Введение в теорию вероятностей. — М .: Наука, 1982. — 160 с.
- статей Колмогорова в журнале «Квант» (1970–1993).
- А. Н. Колмогоров … — 2-е изд. — Паб Челси. Co, 1956. — 84 с. (Английский)
В Живом Журнале активно обсуждается существенное «упрощение» изложения математики в старшей школе, предложенное министром Фурсенко.
Я крайне скептически отношусь к реформам в современной Российской Федерации в целом. Наше правительство не способно к реформам. Реформа требует политической воли и дальновидности. Реформатор — сильный человек, живущий в другое время. И он твердой рукой из своего «1870 года» воссоздает реальное общество 1830 года. Чтобы его дети не жили в помойке. Мировоззрение современных правителей России — месяц. И у них совсем нет рук. То, что мы называем гордым латинским словом, — это не реформы, а лапа.Мальчик в шортах барахтается, рядом плавает окурок. У него такая ручка была — уф, бяка. А если в РФ случится что-то серьезное, то взрослые дяди на берегу это замышляют. Со свистками и мегафонами. Но, конечно, он дает удар по заднице. Осколок «математики» крутился на поверхности 40 лет и наконец попал в рот малышу. Почему сейчас — да, Браун его знает. И ребенок сказал «тьфу». Не раздумывая, конечно, сказал — машинально. Или, поразмыслив, но все же нет (скорее всего, в сторону вашей любимой латиноамериканской американизации — дешевле, но проще).
Теперь о прикладе. Возьмем учебник геометрии для 9-10 классов моего периода обучения (70-80-е годы). Сначала его написали три человека. Это уже плохой знак. Учебник должен быть написан одним автором, который дает последовательный и последовательный курс знаний и несет ответственность за каждое слово. Сам. Книги соавторства — редкое исключение, часто подозрительное. Само слово «соавторство» — советское, как и знаменитый «массовый героизм».
Но кто эти три гиганта, написавшие учебник для десятков миллионов молодых людей? Никто.«Клопский, Скопец, Ягодовский». Я никогда не встречал Клопски в Интернете. Искал, конечно, не по первой категории, но просидел минут сорок. НУЛЬ. Клопский — новгородский дурак, Христа ради. Был еще Клопский, тоже с прибабахом в 19 веке — Толстовка. Со Скопцом оказалось проще:
Соломон Альтерович Скопец, родился в Прибалтике, получил образование в Риге. Плохо говорил по-русски, всю жизнь проработал в Ярославском педагогическом институте. Видимо мозг тройки — написал какие-то специальные математические работы.Третий — Ягодовский, в 1968 году защитил кандидатскую диссертацию. в области педагогических наук. Из Курского педагогического института.
Этот провинциальный серьезный поставил на уши всю страну. Академик Понтрягин плакал из учебника:
«Мое внимание привлекло определение вектора в школьном учебнике. Вместо общепринятого и наглядного представления его как направленного сегмента (такое определение, например, сохранилось в «Политехническом словаре».М., «Советская энциклопедия», 1976, с. 71) учащиеся вынуждены запоминать следующее:
«Вектор (параллельный перенос), определяемый парой (A, B) несовпадающих точек, представляет собой преобразование пространства, в котором каждая точка M отображается в точку M1 такое, что луч MM1 сонаправлен с лучом AB, а расстояние [MM1] равно расстоянию | AB | » (В. М. Клопский, 3. А. Скопец, М. И. Ягодовский. Геометрия. Учебник для 9 и 10 классов средней школы … 6 изд. М., «Просвещение», 1980, с. 42).
Понять это переплетение слов непросто, а главное, бесполезно, так как его нельзя применить ни в физике, ни в механике, ни в других науках.
Что это? Издевательство? Или бессознательный абсурд? Нет, замена в учебниках многих относительно простых, наглядных формулировок громоздкими, нарочито сложными, оказывается, вызвана желанием … улучшить (!) Преподавание математики. «
Я считаю, что у птицы-тройки было другое стремление.Это желание использовать иностранные и заумные слова среди людей, неуверенных в своей культуре. То есть они культурные, но не уверены в этом. И они постоянно «умничают». Немцы называют это «суперклюге». А на стенку полезли школьники из отъявленных ботаников.
Другой учебник математики — Алгебра и начала анализа — был написан в СССР под редакцией академика Колмогорова. Конечно, опять группа товарищей, но все же это Москва, и это хорошо написано.Только … что бы ни делал дурак, он все делает неправильно. Колмогоров написал учебник не для 30 миллионов 9-10 классов, а для себя. Он придумал, какой учебник ему подойдет, и написал его. Напомню, Колмогоров в 6 лет придумал узор
1 = 1,
1 + 3 = 2 в квадрате,
1 + 3 + 5 = 3 в квадрате,
1 + 3 + 5 + 7 = 4 в квадрате
и т.д.
В 6 лет. Говорят даже на 5.
Учебник не только умный, но и написан «оригинально», то есть во многих случаях не вписывается в основное русло математики.Это учебник всемирной истории, где о Дании написано больше, чем о Франции, Индонезия занимает целый раздел, а Испания — нет. В общем, «почерк гения».
Так что с Колмогоровщины ребята карабкались по стенам еще круче и дальше, чем со Скопца.
Нет сомнений (я писал об этом) школа должна строиться на школьном обучении: неприятных и внешне бессмысленных интеллектуальных процедурах, призванных искусственно накачать интеллект sapiens — умственно не по годам развитого, слабого животного, попавшего в серию с недостатками .
Но эти процедуры должны быть ОБЯЗАТЕЛЬНЫМИ. Каждый может выучить как минимум два иностранных языка. Это больно, неприятно, утомительно, но доступно и гастарбайтеру из горного села. Длинные тексты можно выучить наизусть. И они узнают, даже «Евгений Онегин». Все (все на 80%). Или делать унылые и однообразные вычисления типа 4х (584: 24) + 1826-15х (2346: 345). Поорут и посчитай.
Но нельзя ставить игру на пианино в центр траха.У многих людей НЕТ МУЗЫКАЛЬНОГО СЛУХА. И это не болезнь, не уродство, а генетическая особенность. Не подлежит ликвидации. Ни за что. По методу ударов можно перейти на механические нажатия клавиш, но это будет не музыка, а какофония.
Итак, кого можно вырастить таким образом? Это серийное производство невротиков с заниженной самооценкой и скрытыми комплексами.
Каждый умеет считать. Но дифференциальное и интегральное исчисление НЕ ДОСТУПНО для очень большого числа совершенно нормальных и зачастую умных людей.Уровень учебника Колмогорова доступен 60% детей и 15% девочек. Все. Остальные могут пройти по учебнику только обманом.
Итак, математика была сокращена правильно. Только сомневаюсь, что он будет вырезан правильно и сомневаюсь, что вместо него установят что-то адекватное. Пузырь «Закон Божий» или шахматы.
Напоследок я бы предостерегал людей с высшим математическим образованием от ненужной жестокости. То, что вам кажется естественным, не очень естественно. Это ваша конституциональная генетическая черта.В целом это свидетельствует о более высоком интеллекте человека, но не в каждом отдельном случае, а высокий интеллект заключается, среди прочего, в способности принимать иную точку зрения.
П.С. Небольшой подарок для поклонников Галкова — мои конспекты лекций по математике 🙂
Лидер реформаторов школьного математического образования Алексей Иванович Маркушевич особых заслуг в сфере научной деятельности не проявил, но в псевдонаучном поприще блеснул: отменил гениальный метод Киселева и предстал главным покупатель средневековых европейских рукописей, похищенных из Центрального государственного архива древних актов.Такой полет люди пишут учебники для наших детей с семидесятых годов …
Призывы вернуться к Киселеву раздаются уже тридцать лет. Возмущение началось в конце семидесятых, как только были обнаружены первые результаты реформы. Некоторые связывают это с «ностальгией» …
Академик РАО Ю.М. Колягин, доктор педагогических наук:
« Имя Андрея Петровича Киселева вызывает у учителей старшего поколения чувства, близкие к ностальгии: тоску по старым добрым временам, по делам минувших лет, по их успехам и неудачам в учебе. область образования.Учителя вспоминают то время, когда в школе был только один учебник математики, он работал долго, и поэтому у них была возможность изучить все его достоинства и недостатки.
Даже из тех, кто знает А.П. Киселева не понаслышке, мало кто знает, что его учебные книги охватывали практически все школьные математические дисциплины: арифметику, алгебру, геометрию, начало анализа. Андрей Петрович был не только талантливым педагогом, автором учебников, но и блестящим преподавателем.»
Л.Н. Аверьянова, заместитель директора Государственной научно-педагогической библиотеки им. К.Д. Ушинского:
Андрей Петрович Киселев — эпоха педагогики и преподавания математики в общеобразовательных школах. Его учебники по математике установили рекорд долголетия, оставаясь более 60 лет наиболее стабильные учебники в русской школе и на многие десятилетия определили уровень математической подготовки нескольких поколений граждан нашей страны.
Академик В.И.Арнольд:
«Я бы вернулся к Киселеву …»
Это формальная дань «уважения», по которой вообще невозможно угадать, понимает ли автор первого из этих утверждений, что возвращение учебника «понятно» и дорогой сердцу »со всеми его« недостатками »- это стратегический вопрос выживания страны … Я не преувеличиваю. Сегодня курс математики осваивают не более двадцати процентов школьников. Во время учебы по Киселеву их было восемьдесят процентов.
Взрывной рост и последующий расцвет науки и техники при Сталине были бы просто невозможны при нынешнем уровне овладения математикой в нашей школе. Какого прорыва можно ожидать в России с таким упадком в преподавании математики! А без рывка мы безнадежно будем отставать от конкурентов, и нас просто сожрут.
Несоответствие отсылок к «ностальгии» становится очевидным при внимательном сравнении учебников Киселева с пореформенными.Первым это сделал выдающийся русский математик Лев Семенович Понтрягин. Профессионально проанализировав новые учебники, он на примерах убедительно доказал, что возвращение к учебникам Киселева совершенно необходимо. Потому что все новые учебники ориентированы на естественные науки, точнее на естественные науки , и полностью игнорируют Ученика, психологию его восприятия, которую старые учебники умели учитывать.
Именно «высокий теоретический уровень» современных учебников является первопричиной катастрофического падения качества образования и знаний.Эта причина действует более тридцати лет, не позволяя хоть как-то исправить ситуацию.
Сегодня около 20% студентов осваивают математику в целом. Геометрия — всего 1% … В сороковые годы, сразу после войны, полностью освоили все разделы математики 80% школьников учились по Киселеву … Разве это не аргумент в пользу ее возвращения детям ?!
В восьмидесятые годы призыв академика Понтрягина было проигнорировано Минобразованием под предлогом необходимости усовершенствования учебников.Сегодня мы видим, что сорок лет «совершенствования» плохих учебников не дали хороших. И они не могли родить. Потому что хороший учебник не «пишется» за год-два по заказу министерства или на конкурс. Через десять лет его не «напишут». Его разрабатывает талантливый практикующий преподаватель вместе со студентами на протяжении всей их педагогической жизни, а не профессор математики или академик за письменным столом.
Педагогический талант встречается редко, гораздо реже собственно математика.Хороших математиков — тьма, авторов хороших учебников — единицы. Главное свойство педагогического таланта — умение сочувствовать ученику, что позволяет правильно понимать ход его мысли и причины трудностей. Только при этом субъективном условии могут быть найдены правильные методологические решения. И они еще должны проверяться, исправляться и приводиться к результату многолетним практическим опытом: внимательным, педантичным наблюдением за многочисленными ошибками студентов, их вдумчивым анализом…
Так учитель Воронежского реального училища создавал свои замечательные, уникальные учебники более чем за сорок лет Андрей Петрович Киселев … Его высшей целью было понимание предмета учениками. И он знал, как эта цель достигнута. Вот почему было так легко учиться по его книгам.
Во введении к одному из учебников Андрей Петрович очень кратко изложил свои педагогические принципы: «Автор, прежде всего, поставил перед собой цель добиться трех качеств хорошего учебника: точности формулирования и утверждения концепций, простоты в аргументация и лаконичное изложение ».
Глубокое педагогическое значение этих слов как-то теряется за их простотой. Но эти простые слова стоят тысяч современных тезисов. Давай подумаем! Современные авторы, следуя указаниям Колмогорова, стремятся «к более строгому, с логической точки зрения, построению школьного курса математики». Киселев заботился не о «строгости», а о «точности» формулировок, обеспечивающей их правильное понимание, адекватное науке. Точность — это согласованность со смыслом.Пресловутая формальная «строгость» уводит от смысла и, в конце концов, полностью его разрушает.
Киселев даже не употребляет слова «логика» и говорит не о «логических доказательствах», которые кажутся присущими математике, а о «простых рассуждениях». В них, в этих «рассуждениях», конечно, есть логика, но она занимает подчиненное положение и служит педагогической цели — внятности и убедительности рассуждений для студента, а не для академика.
Наконец, лаконичность.Обратите внимание — не лаконичность, а лаконичность! Как тонко Андрей Петрович чувствовал значение слов! Краткость предполагает сокращение, отбрасывание чего-то, может быть, существенного. Compression — сжатие без потерь. Отсекается только ненужное, отвлекающее, засоряющее, мешающее сосредоточение на значениях. Цель краткости — уменьшить объем. Цель сгущения — чистота сущности! Этот комплимент Киселеву прозвучал на конференции «Математика и общество» в Дубне в 2000 году: «Какая чистота!»
Насколько важен для ребенка правильный подбор слов, — говорит он в одном из своих методических и легендарных в музыкальном мире Галина Степановна Турчанинова, открывшая талант Максима Венгерова.Ее ученики никогда не слышали в классе таких выражений, как «нажать на струну», что у всех ассоциируется с некоторым мышечным усилием, или «отпустить струну», что ассоциируется с вялым или, по крайней мере, неторопливым «отпусканием». Она сказала детям, что палец «падает» на веревку или палец «отскакивает» от веревки.
В сознании ребенка сложился образ некоего мышечного процесса: палец сам падает на струну, и она отскакивает. Падение — отскок, падение — отскок … В результате все ученики Галины Степановны продемонстрировали поразительную свободу и легкость любых движений на перекладине уже на раннем этапе тренировок.
Вот еще один секрет удивительной педагогической силы Киселева! Он не только психологически правильно излагает каждую тему, но и строит свои учебники и выбирает методы объяснения в соответствии с возрастными формами мышления и способностями детей понимать, медленно и всесторонне их развивая. Высочайший уровень педагогического мышления, недоступный современным сертифицированным методистам и коммерчески успешным авторам учебников.
Долго выяснялось, пока меня не осенила мысль обратиться за помощью к Киселеву — вспомнил, что в школе эти вопросы не вызывали никаких затруднений и даже были интересны.Сейчас этот раздел исключен из школьной программы — таким образом Минобразования решило созданную им проблему перегрузки .
Итак, прочитав презентацию Киселева, я был поражен, когда нашел в нем решение конкретной методологической проблемы, с которой долго не мог справиться. Возникла волнующая связь между временами и душами — оказалось, что А.П. Киселев знал о моей проблеме, подумал и решил ее давно!
Решение заключалось в умеренной конкретизации и психологически правильном построении фраз, когда они не только правильно отражают суть, но учитывают ход мысли ученика и направляют его.И пришлось немало вытерпеть в долгосрочном решении методической задачи, чтобы оценить искусство А.П. Киселева. Очень невидимое, очень тонкое и редкое педагогическое искусство. Редкий! Современные ученые-педагоги и авторы коммерческих учебников должны начать изучение учебников учителя гимназии Андрея Петровича Киселева.
A.M. Абрамов, один из реформаторов — он участвовал в написании колмогоровской «Геометрии» — честно признается, что только после многих лет изучения и анализа учебников Киселева он начал немного понимать скрытые педагогические секреты этих книг и глубочайшую педагогическую культуру их автор, , учебники которого являются национальным достоянием России .
Термин «устаревший» — это всего лишь лукавый прием , характерный для модернизаторов всех времен. Техника, влияющая на подсознание. Ничто по-настоящему ценное не устареет , — оно вечно. И не удастся «сбросить его с парохода современности», как не удалось сбросить «устаревшего» Пушкина РАТОП-модернизаторам русской культуры 20-х годов. Киселев никогда не устареет, и Киселев не будет забыт.
Другой аргумент: возврат невозможен из-за изменения программы и слияния тригонометрии с геометрией.Аргумент неубедительный — программу можно снова изменить, а тригонометрию можно отсоединить от геометрии и, что самое главное, от алгебры. Более того, эта «связь» (как и связь алгебры с анализом) — еще одна грубая ошибка реформаторов-70, она нарушает фундаментальное методологическое правило — трудности скорее разделить, чем связать .
Классическое обучение «по Киселеву» тригонометрическим функциям и аппарату их преобразований в виде отдельной дисциплины в X классе, а в конце — применение выученного к решению треугольников и решению стереометрических проблемы.Последние темы были замечательно методично проработаны с использованием последовательности общих задач. Стереометрическая задача «по геометрии с использованием тригонометрии» была обязательным элементом выпускных экзаменов на аттестат зрелости. Студенты хорошо справились с этими заданиями. Сегодня? Абитуриенты МГУ не могут решить простую контурную задачу!
Модернизаторы семидесятых заменили этот принцип антипедагогическим псевдонаучным принципом «строгого» изложения.Именно он разрушил методологию, вызвал непонимание и неприязнь учеников к математике … Я приведу пример педагогических уродств, к которым приводит этот принцип.
Как старый новочеркасский учитель В.К. Совайленко, 25 августа 1977 года состоялось заседание УМС Минобороны СССР, на котором академик А. Колмогоров проанализировал учебники математики для 4-10 классов. Завершая рассмотрение следующего учебника, академик обратился к присутствующим с фразой: « После некоторой настройки это будет отличный учебник, и если вы правильно поняли этот вопрос, то вы одобрит этот учебник. ». Присутствовавший на встрече учитель из Казани с сожалением сказал сидящим рядом:« Это необходимо, гений математики — непрофессионал в педагогике. Он не понимает, что это не учебники, но уроды, а он их хвалит ».
Московский учитель Вейцман говорил в дебатах: « Я прочту из действующего учебника геометрии определение многогранника ». Колмогоров, услышав определение, сказал: « Правильно, верно! ».Учитель ему ответил: « С научной точки зрения все правильно, а с педагогической — вопиющая безграмотность. Это определение выделено жирным шрифтом, поэтому для обязательного запоминания и занимает полстраницы.
Так вот суть школьной математики в том, что миллионы школьников запихнули определения на полстраницы учебника? В то время как у Киселева это определение дано для выпуклого многогранника и занимает менее двух прямых. Это и научно, и педагогически грамотно.
То же самое в своих выступлениях говорили и другие учителя. Подводя итоги, А.Н. Колмогоров сказал: « К сожалению, по-прежнему вместо делового разговора продолжалась ненужная критика. Вы меня не поддержали. договорились с министром Прокофьевым, и он меня полностью поддерживает. ». Этот факт констатировал Б.К. Совайленко в официальном письме в ФЭС от 25 сентября 1994 г.
Еще один интересный пример профанации педагогики специалистами-математиками.Пример, неожиданно открывший одну поистине «тайну» из книг Киселева. Около десяти лет назад я посетил лекцию нашего выдающегося математика. Лекция была посвящена школьной математике. В конце я задал лектору вопрос — как он относится к учебникам Киселева? Ответ: « Учебники хорошие, но уже устаревшие ».
Ответ банальный, но интересное продолжение — для примера лектор нарисовал рисунок Киселевского для знака параллельности двух плоскостей.На этом рисунке плоскости резко изогнуты, чтобы пересекаться. И я подумал: « Действительно, какой абсурдный рисунок! Что не может быть нарисовано! ». И вдруг я отчетливо вспомнил исходный рисунок и даже его положение на странице (внизу слева) в учебнике, который изучал почти сорок лет назад.
И я почувствовал ощущение мышечного напряжения, связанное с рисунком, как будто я пытался насильно соединить две непересекающиеся плоскости. Четкая формулировка возникла из памяти о себе: « Если две пересекающиеся линии одной плоскости параллельны -… », а потом короткое доказательство« от противного ». «Я был шокирован. Оказывается, Киселев навсегда запечатлел в моей памяти этот значимый математический факт.
Наконец, образец непревзойденного искусства Киселева в сравнении с современными авторами. Держу в руках учебник для 9 класса« Алгебра » -9 », изданной в 1990 году. Автор — Ю.Н. Макарычев и К °, и, кстати, это были учебники Макарычева, а также Виленкина, которые привели в пример« некачественно, безграмотно выполненную »Л. .С. Понтрягин. Первые страницы: §1. «Функция. Диапазон определения и диапазон значений функции».
В заголовке сформулирована цель — объяснить студенту три взаимосвязанных математических понятия. Как решается эта педагогическая проблема? Сначала даются формальные определения, потом множество разношерстных абстрактных примеров, потом множество хаотических упражнений, не имеющих рациональной педагогической цели. Перегрузка и абстрактность налицо. Объем презентации — семь страниц.Форма изложения, когда откуда ни возьмись начинают «строгие» определения, а затем «иллюстрируют» их примерами, является стереотипной для современных научных монографий и статей.
Сравним изложение этой же темы А.П. Киселева (Алгебра, ч. 2. М .: Учпедгиз. 1957). Обратная техника … Тема начинается с двух примеров — бытового и геометрического, эти примеры хорошо известны ученику. Примеры представлены таким образом, что они естественным образом ведут к концепциям переменной, аргумента и функции.После этого даются определения и еще 4 примера с очень краткими пояснениями, их цель — проверить понимание ученика, вселить в него уверенность. Последние примеры тоже близки школьнику, они взяты из геометрии и школьной физики.
Презентация состоит из двух страниц. Никакой перегрузки, никакой абстрактности! Пример «психологической презентации» по Ф. Кляйну. Сравнение томов книг показательно. Учебник Макарычева для 9 класса содержит 223 страницы (без исторической справки и ответов).Учебник Киселева содержит 224 страницы, но рассчитан на на три года обучения, на обучение — на 8-10 классы. Громкость увеличилась втрое!
Сегодня очередные реформаторы пытаются уменьшить перегрузку и «очеловечить» образование, якобы заботясь о здоровье школьников. Слова, слова … Фактически, вместо того, чтобы сделать математику понятной, они разрушают ее основное содержание.
Сначала в семидесятые «поднимали теоретический уровень», подрывая психику детей, а теперь «опускают» этот уровень примитивным методом выкидывания «ненужных» участков (логарифмы, геометрия…) и сокращение учебных часов.
« Я счастлив, что дожил до тех дней, когда математика стала достоянием самых широких масс. Можно ли сравнивать скудные тиражи дореволюционного периода с современностью. И это не удивительно. Сейчас вся страна учится. Я рад, что в старости могу быть полезен моей великой Родине », — А.П. Киселев ,
В статье представлены малоизвестные факты, проливающие свет на забытые истоки «Колмогоровской реформы» 1970–1978 годов: ее длительная подготовка, методы, результаты, а также разъясняются ее последствия в современном образовании.Анализируется идеология реформы и доказывается ее антипедагогический характер.
Ключевые слова: реформа-70, Группа-36, Хинчин, Маркушевич, повышение научного уровня, реформа идеи, методы, программы, учебники, методики, Киселев.
А.Н. Колмогоров был назначен руководителем реформы 70 уже на последнем этапе ее подготовки в 1967 году, за три года до ее начала. Его вклад сильно преувеличен — он лишь конкретизировал известные реформистские установки (теоретико-множественное содержание, аксиомы, обобщающие концепции, строгость и т. Д.).) тех лет. Он должен был быть «крайним». Одна из целей статьи — хотя бы частично снять ответственность за результаты реформы-70 с А.Н. Колмогорова.
Забыто, что всю подготовительную работу к реформе более 20 лет вела неформальная группа единомышленников, сформировавшаяся еще в 1930-е, в 1950-1960-е годы. усилены и расширены. Во главе коллектива в 1950-е гг. Академик А.И. Маркушевича, добросовестно, настойчиво и качественно выполнявшего намеченную в 30-е годы программу.математики: Л.Г. Шнирельман, Л.А. Люстерник, Г.М. Фихтенгольц, П.С. Александров, Н.Ф. Четверухин, С.Л. Соболев, А.Я. Хинчин и другие. Будучи очень талантливыми математиками, они совсем не знали школы, не имели опыта обучения детей, не знали детской психологии, поэтому проблема повышения «уровня» математического образования казалась им простой, а методы обучения они предложенные не вызывали сомнений. Кроме того, они были уверены в себе и пренебрегали предупреждениями опытных учителей.
Истоки будущей реформы
Начало будущей реформы можно отсчитать с 1936 года, с декабрьской сессии группы математиков АН СССР. Эта группа, утвержденная Президиумом Академии наук в начале 1936 г., была разделена на две неравные части. В одном — «старые» академики: Н.Н. Лузин (председатель), Д.А. Могила, А. Крылов, С.А.Чаплыгин, Н.Г. Чеботарев, С. Бернштейн, Н.М. Гюнтер. В другом — советская новинка — О.Ю. Шмидт, И.М.Виноградов, С.Л. Соболев, Л. Шнирельман, П. Александров, А. Колмогоров, Н.М.Мусхелишвили, В.Д. Купрадзе, А. Гельфонд, Б. Сигал и другие. Следует отметить, что после июльского «дела Лузина» 1936 года, в котором реформаторы приняли самое активное участие, Лузин был вынужден покинуть группу.
Интересно, что неофициально в нее входило много неакадемиков. Тем не менее они во многом определили ее решения. Они сформировали комиссии, которые готовили материалы для принятия решений.В состав комиссий вошли Г. Фихтенгольц, Л.А. Люстерник, Л.А. Тумаркин, Б.Н. Делоне, Ф. Гантмахер, В.А. Тартаковский, А. Гельфонд и другие. Эта группа (так называемая «Группа-36») и выступила инициатором идей реформы.
В декабре 1936 г. Народный комиссариат просвещения потребовал «радикальной реорганизации организации обучения математике в начальной и средней школе». «Работники университета убеждаются в этом ежедневно», — отметил, в частности, Г.М. Фихтенгольц [Там же.С. 55]. Тем не менее в постановлении, принятом на основании отчетов Г. Фихтенгольц, Л. Шнирельмана обращалось внимание на «неудовлетворительный характер учебных планов и программ, полную неадекватность одних стабильных учебников и многочисленные недостатки остальных» [Там же. С. 78-80].
Вопрос здесь, собственно, один : Вправе ли люди, не работавшие в школе, судить, какие задачи могут и должны решать дети 8-9 лет, не нужен ли устный счет, сколько времени нужно на овладение арифметикой, подходят ли учебники для детей? Очевидно, нет.Но почему молодые советские профессора присвоили себе право категорически судить о том, чего они не знают? Ответ прост: они задумали ввести в школе основы анализа и начали искать, как это можно сделать, что можно выбросить из традиционного образования.
Из постановления декабрьской сессии Группы-36 ясно, что показная идеология реформаторов базировалась на двух безосновательных и нечетко сформулированных постулатах.Во-первых, необходимо поднять «идейный уровень» обучения математике, во-вторых, привести содержание образования «в соответствие с требованиями науки и жизни».
Но что означает «идеологический»? Что означает «уровень»? Что значит «поднять»? И почему «нужно» повышать «требования», которые наука и жизнь «выставляют» к школе, и как они «выставляются»? Эти вопросы не уточнялись и не обсуждались. Но от имени мифического «математического сообщества» агрессивно заявлялось: «это необходимо!»
В 1939 году А.Я. Принял на себя роль общественного идеолога реформы, запланированной «Группой-36». Хинчин. Он опубликовал многочисленные программные статьи в журнале «Математика в школе». Развивая тезис о «неудовлетворительности существующих программ», Хинчин провозглашает их «порочность»: «Программы, — широко объясняет он, -« страдают от изоляции от жизни ». Что значит «непривязанность»? Что «программы должны быть разработаны таким образом, чтобы идеи переменной ценности и функциональной зависимости усваивались учащимися как можно раньше, становясь стержнем всего школьного курса математики.«После этого восстановится ли связь программ с жизнью?»
Следует отметить, что идеи значения и функции переменных тогда присутствовали в школьном курсе. В учебнике Киселева изучались линейные, квадратичные, экспоненциальные и логарифмические функции. Но Хинчин потребовал, чтобы они стали «ядром» и «как можно раньше». Когда это? В начальной школе? Когда дети еще даже не знают чисел? Это означает, что курс школьной математики, сложившийся на протяжении столетия, должен быть уничтожен и заменен курсом, который был изобретен заново.
Аргументы. «Самая категорическая необходимость — ввести в школьные программы основы анализа бесконечно малого». Оценим аргументацию: «Если мы хотим поднять научный и культурный уровень рабочего и колхозника до уровня рабочих инженерно-технического труда, то как можно спокойно смотреть на отсутствие в программах математической школы того, что составляет математическая основа всей современной техники? »Еще один политический аргумент:« школа должна готовить молодежь к работе и защите Советского государства.«А повысится ли готовность советской молодежи к« работе и обороне »после введения в школьную программу основ анализа бесконечно малого»
Основная беда школы Хинчин объявил «недостаточным научным уровнем подавляющего большинства наших учителей». Для искоренения этого «порока» предлагается целая система мер: «создание новых учебников и методических пособий, пропаганда и разъяснение новых программ, переподготовка, методическая и научная переподготовка значительной части учителей, реструктуризация учителей. обучение персонала.«
Опытные учителя, воспитатели и методисты «нововведений» не восприняли. Но реформаторы проигнорировали предупреждения. Хинчин признал, что реформистские идеи массово отвергаются. Но заявили «повторные возражения» лишь «маскировку инерции и рутинности методической среды», «выравнивание с отсталым слоем учителей» [Там же. С. 4].
Учебник атака
Известно «горячее желание наших педагогических масс поднять математическое преподавание в школах до уровня, достойного великих культурных и народнохозяйственных задач третьей сталинской пятилетки.«
«Реформаторы» намеревались провести Реформу-70 еще в 1930-е годы. Первая цель — скинуть сотрудников Наркомата просвещения, которые им мешают. Второй — заменить учебники. Ни одна из целей не была достигнута, потому что нарком просвещения А.С. Бубнов не подпускал к школе «реформаторов».
«В качестве временной меры» обязались исправить «недочеты» А.П. Киселева. В 1938 году Глаголев «переделал» геометрию, в 1940 году Хинчин — арифметику.«Ремиксеры» руководствовались сформулированным Хинчиным «научным» принципом: «Каждый учебник должен быть единым, логически систематизированным целым», т.е. психологическую систематику, ориентированную на понимание, необходимо заменить логической, противоречащей детскому пониманию.
Московское математическое общество рекомендовало «на ближайшее время учебник геометрии А.П. Киселева под редакцией Н.А. Глаголева». Из отзыва учителей: «С первых же дней работы в школе оказалось, что это очень сложно. пользоваться переработанным учебником.«
Обратим внимание на методы и приемы реформаторов 1930-х годов: отсутствие серьезного обоснования своих идей, декларативные цели и нелогичность аргументов, игнорирование аргументов и предупреждений оппонентов, агрессивный тон и унижение инакомыслия, игнорирование результаты практического опыта, использование авторитетных общественных организаций (Академия наук СССР, Московское математическое общество) и т. д. Эти же методы будут использоваться последующими реформаторами-70.
Война немного притормозила активность реформаторов. Но она не остановилась. В 1943 году Академия педагогических наук (АПН) РСФСР и среди ее учредителей (!) Почему-то два математика-реформатора — А.Я. Хинчин, В. Гончаров. Реформаторы взяли под свой контроль методологию и начали готовить кадры «научно проверенных» методистов, необходимых для реформы.
Цели создания АПН были сформулированы в постановлении Правительства РСФСР от 6 октября 1943 года следующим образом: «Научная разработка вопросов общей педагогики, специальной педагогики, истории педагогики, психологии, школьной гигиены, преподавания». методики основных дисциплин в начальной и средней школе, обобщение опыта, оказание научной помощи школам.«Обратим внимание на ключевые термины реформаторов -« повышение научности », а также на идею о необходимости« научного развития методики обучения », выдвинутую в постановлении правительства.
В 1945 году на первых официальных выборах в АПН были приняты еще трое математиков-реформаторов — П.С. Александров, Н.Ф. Четверухин, А. Маркушевич. Все они, ни дня не проработавшие в школе, не знавшие педагогики и пренебрегавшие ею, вдруг стали академиками педагогики.Самый молодой из них, А. Маркушевичу было поручено сделать на заседании АПН1949 г. Вступительное слово. В своем выступлении он поставил перед академией заманчивую задачу «повысить идейно-теоретический уровень преподавания математики в средних школах».
Действия по решению этой проблемы следовали нескольким четко определенным направлениям.
Первая линия — дискредитация учебников А.П. Киселева [Там же. С. 30-32] и «отчисление» их из школы. Цель будет достигнута через 7 лет.
В 1956 году учебники Киселева для неполной средней школы были заменены «пробными», но еще не «реформистскими» (тонкая тактика!). Было предложено написать новые учебники и задачники классическим методистам И. Шевченко, А. Барсуков, Н. Никитин, С.И. Новоселов и другие. Таким образом, было смягчено сопротивление идей реформаторов этими и многими другими опытными учителями и методистами.
Именно с 1956 года, с момента «ссылки» Киселева, качество знаний школьников стало падать.В министерство стали поступать «жалобы из вузов на незнание абитуриентов» [Там же. С. 38]. Этот факт констатировал А.И. Маркушевич, выступавший в ранге заместителя министра на собрании-семинаре учителей в декабре 1961 года. Но, как всегда, исказил суть дела: это были жалобы не на отдельные, по его словам, «недостатки», а на что-то заметное, по сравнению с предыдущими годами, снижение качества знаний.
Вторая линия — повсеместная пропаганда принципов предстоящей реформы и формирование в обществе убеждения в ее неизбежной необходимости.
Это сделал А.И. Маркушевичем и его единомышленниками путем возобновления выпуска журнала в 1930-е гг. «Математическое образование» и через популярный среди учителей журнал «Математика в школе», главным редактором которого в 1958 г. был поставлен «свой человек» Р.С. Черкасов — соавтор реформаторских учебников.
Третья линия — «научное» обоснование направлений будущей реформы и подготовка заинтересованных в этом кадров.
Цель была достигнута путем внедрения реформистских идей в «исследовательскую» деятельность институтов и лабораторий АПН. В частности, была успешно внедрена идея обучения младших школьников перевернутому антипедагогическому принципу «от общего к частному», привязанная к задаче «математического развития».
Задача «математического развития» абстрактно сформулирована Г.М. Фихтенгольца еще в 1936 году. А.И. Маркушевич предложил академикам педагогики способ решения проблемы — «математическое развитие» на основе «обобщающих идей, принципов, концепций», т.е. «От общего к частному» — принцип, по которому он сам перестроил школьную программу и поднял ее «научный уровень». В результате дальнейшего «научного» развития Академия выпустила две инновационные методики обучения — «по системе Занкова» и «по системе Давыдова». По рекомендациям Хинчина расцвел новый высоконаучный метод: учителям, согласившимся использовать этот «метод», повысили зарплату. Академик Российской академии образования Ю.М. Колягин, «обе эти системы не привели к положительным результатам». И они не могли руководить, потому что противоречили законам познания и обучения.
Четвертая линия — замена «устаревших» программ на новые, отвечающие «требованиям жизни».
Цель была поставлена перед APN в том же отчете от 1949 года, и там же было указано, «в каком направлении следует реструктурировать программу». «Направление» заключалось в максимальном усечении традиционного материала, чтобы освободить место для высшей математики.В частности, курс арифметики должен был заканчиваться в 5-м классе (вспомним Г. М. Фихтенгольца), а весь 10-й класс был посвящен аналитической геометрии, анализу и теории вероятностей [Там же. С. 19]. Этой программой (за исключением теории вероятностей) был А.И. Маркушевич сделал это, возглавив в 1965 г. комиссию Академии наук и Академии педагогических наук по определению содержания нового образования.
После провала реформы-70 министерские комиссии и лаборатории APN начали пересматривать содержание предметов и создавать альтернативные программы.Но главный деструктивный принцип, сформулированный А.И. Маркушевич в своем отчете 1949 г. остался без изменений, «несколько вытеснив традиционный и включив в него новый материал» [Там же. С. 20]. В результате вместо целостных учебных предметов появились синтетические конгломераты, состоящие из разнородных «методологических линий» (так сказать, новый научный термин). В начальной школе сжатая арифметика смешивалась с элементами геометрии, алгебры и теории множеств. В 9-10 классах алгебра «интегрировалась» с тригонометрией и анализом.Таким образом, была ликвидирована классическая предметная система обучения, и из школы был вынесен один из основных дидактических принципов — принцип систематического обучения. Это второе принципиальное достижение реформы-70 (первое — «изгнание» Киселева).
Пятая линия — создание новых учебников.
В 1968 г. вышел в свет первый «пробный» учебник Маркушевича «Алгебра и элементарные функции». В разгар реформы «отредактировал» реформаторские учебники алгебры для 6-8 классов (автор Ю.Н. Макарычев и др.). Для старших классов учебники писал А.Н. Колмогорова (также в соавторстве). Создание учебников «авторскими коллективами» — еще одно рационализаторское изобретение реформаторов.
Ложность принципов
А.И. Маркушевич несет не только моральную, но и юридическую ответственность за уничтожение образования.
Помимо «работы» председателем комиссии АПН и Академии наук по определению содержания образования (1965-1970), он «работал» заместителем министра образования РСФСР (1958-1964) и вице-президентом. АПН (1964-1975)… Статус замминистра позволил ему еще в 1950-е годы. сохранить первоначальную пропедевтику реформы, несмотря на сразу проявившиеся негативные результаты и протесты вузов и преподавателей (факт показан выше). Он использовал второй статус вице-президента как раз перед началом реформы, чтобы заблокировать серьезное обсуждение и критику программ и учебников в АПН. Этот факт был признан Президиумом АПН в ответе журналу «Коммунист».Однако, чтобы утверждать, что А. Маркушевич будет не совсем правдой.
Все реформистские идеи Маркушевича можно найти в «отцах-основателях» реформы? 70, задуманный в 1930-х годах. Программа действий для А.И. Маркушевича был составлен в 1939 году А.Я. Хинчин. А.И. Маркушевич был не один, а в сплоченном коллективе, который умело формировался и расширялся. Состав этой команды можно определить по оглавлению журнала «Математическое образование». Это корни двадцатилетней подготовки к реформе.
Проведение реформы 1970-1978 гг. тесно связан с именем академика А.Н. Колмогорова, возглавившего в 1967 г. Научно-методический совет Минобрнауки СССР и сохранявшего эту должность до 1980 г.
Колмогоров взял на себя утверждение собственной программы, детальное уточнение ее руководящих принципов и написание новых учебников. А главное слепо взял на себя ответственность за результат.
Конечную цель реформ с ужасом восприняли в 1978 году, когда первые выпускники «реформированной» молодежи пошли в университеты.По мнению Ю.М. Колягина, «когда были обнародованы результаты вступительных экзаменов, среди ученых АН СССР и преподавателей вузов началась паника. Широко отмечалось, что математические знания выпускников страдают формализмом, вычислительными навыками, элементарными алгебраическими преобразованиями, а решения уравнений практически отсутствуют. Абитуриенты оказались практически неподготовленными к изучению математики в университете »[Там же].
Лучшие математики АН СССР, самые гражданско-ответственные (академики А.Тихонов, Л. Понтрягин, В.С. Владимир и др.) Вступили в открытую и непримиримую борьбу с реформаторами. По их инициативе Бюро Отделения математики АН СССР 10 мая 1978 г. приняло постановление: «Признать существующее положение со школьными программами и учебниками по математике неудовлетворительным, как из-за неприемлемости принципов, лежащих в основе программ, и из-за низкого качества школьных учебников. Примите срочные меры по исправлению положения.Учитывая сложившуюся критическую ситуацию, рассмотреть возможность использования некоторых старых учебников »[Там же. С. 200-201]. Подчеркнем главную, глубоко правильную мысль резолюции — лживость принципов, на которых строились новые программы.
Логическим следствием этого заявления было бы аннулирование всех идей и поступков реформаторов, возврат к старой программе и учебникам Киселева. Это была бы та самая «мера», которая действительно «срочно» исправила бы ситуацию.После этого можно было спокойно думать о реальном совершенствовании действительно хорошего образования, постепенно вводить в него глубоко и всесторонне продуманные изменения, проверенные широкой практикой, понятые и поддерживаемые учителем. Постановление открывало такую возможность: предлагалось вернуться к старым учебникам, а значит, и к старой программе (правда, «в качестве временной меры»). Однако развитие ситуации пошло по другому пути.
5 декабря 1978 г. состоялось общее собрание Отделения математики Академии наук СССР, посвященное итогам реформы.На этой встрече реформаторам удалось выкинуть из решения бюро главное — констатацию порочности принципов реформы. Преобладало среднестатистическое мнение — «жестких решений не надо») … Таким образом, открылась дорога для продолжения реформы через «улучшение» «неудовлетворительных» программ и «некачественных» учебников.
Против педагогического безобразия
Бой продолжился. Статья академика Л.С., опубликованная в 1980 году в журнале «Коммунист», вызвала огромный общественный резонанс.Понтрягина. Академик высокопрофессионально проанализировал идеологию реформаторов и выявил первопричину их неудач: «Современные школьные учебники математики по своей сути несостоятельны, поскольку выхолащивают сущность математического метода». Он назвал программу реформ «намеренно усложненной, вредной по сути» [Там же]. Его окончательное заключение : «Главный недостаток, конечно же, в самом ложном принципе — школа не выиграет от его более совершенного исполнения» [Там же.С. 106].
При поддержке L.S. Понтрягина, вице-президент АН СССР, ректор МГУ, академик-физик А.А. Логунов. В своем выступлении на сессии Верховного Совета СССР в октябре 1980 г. он дал глубокий анализ произошедшего: «Прежняя система преподавания математики формировалась на протяжении многих десятилетий. Он постоянно совершенствовался и, как известно, дал блестящие результаты. Все выдающиеся научно-технические достижения прошлого и настоящего во многом обязаны этой системе преподавания математики.Вместо того, чтобы дальше совершенствовать эту систему с учетом преемственности, внедрять в нее новые научно обоснованные педагогические разработки, Минобразования СССР несколько лет назад, без достаточно глубокого и всестороннего изучения сути дела, резко повернуло в сторону обучение математике. Его представление теперь абстрактно, оторвано от реальных изображений, полностью проникнуто наукой. И отсюда возникли такие «шедевры» — учебники, изучение которых может полностью уничтожить интерес не только к математике, но и к точным наукам в целом.»А.А.Логунов пророчески предсказал то, что мы получили сегодня.
Эту речь услышали все высшие руководители страны. Какой вывод они сделали? Надо поправить, но как, не поняли. Но А.А. Логунов пояснил, что качественное образование развивается «многие десятилетия» и поэтому недопустим «крутой поворот», что реформаторы не понимают «сути дела». Суть их идеологии — «лженаука», и естественным следствием этой идеологии являются вредные учебники и отвращение студентов «к точным наукам в целом».«
А.А. Логунов подтвердил, что нет объективной необходимости ломать идеально работающую систему, которая в прошлом и в настоящем «давала блестящие результаты». По сути, он предлагал те же меры «коррекции», что и Бюро ОМ АН СССР: вернуться к прежней системе обучения (и, конечно, к учебникам) и медленно, осторожно, вдумчиво, по-настоящему научно. оправдано его улучшение. Руководители страны этого не понимали. Через полтора года «Коммунист» опубликовал отзывы и закрыл тему.Даже ему не удалось сломить волю реформаторов. Как это можно объяснить?
Заключение Л.С. Понтрягина, сделанная по свежим следам Реформы-70, подтвердила жизнь. Вывод актуален и по сей день.
Что делать
По этому вопросу академик В.И. Арнольд ответил на аплодисменты участников конференции «Математика и общество» (Дубна, 2000): «Я бы вернулся к Киселеву».
То есть повысить качество обучения и качество знаний школьников можно только за счет возврата к классическому дореформенному образованию и учебникам.Правильность этого была практически доказана в 1930-е годы. советская школа, которая после своего первого реформаторского разрушения в 1920-х гг. возродился через 5-6 лет.
Наши менеджеры в 80-е годы пошли другим путем и не без труда, но преодолели сопротивление ученых с помощью тонкой психологической уловки — они предложили им самим писать учебники. Академики были счастливы попасться на эту приманку. И каков конечный результат их «совершенствования»? То же, что планировалось изначально — «коренное» изменение программ и учебников и «повышение уровня».«
Единственное, чем реформаторы пожертвовали своими «достижениями», — это теоретико-множественное содержание. Но это вовсе не главное. Теоретико-множественный «подход» наиболее ярко высветил педагогическое безобразие реформистских принципов (достаточно вспомнить замену равенства фигур их «конгруэнтностью») и взял на себя всю энергию общественного возмущения. Тем самым отвлекали внимание от всех остальных реформистских пороков. Исключение этой идеи в программах и учебниках создало в педагогических кругах иллюзию «выздоровления нашей школы от теоретико-множественной болезни», избавление от кошмаров реформы и удовлетворения от мнимой победы.
Все основные принципы реформы остались нетронутыми, стали привычными и воплощены в новых учебниках. Этот факт гордо подтверждают сами реформаторы: «Принятие (в 1985 г. — I.K. ) программы 1981 г. всеми сторонами означало: основные идеи А. Колмогорова при построении школьного курса математики. Существующий сегодня (2003 — I.K. ) курс также сохраняет многое из того, что было сделано в 1960-1970 годах, в том числе многие учебники. «
Сопротивление реформаторам, кроме Академии наук, оказало Министерство образования РСФСР.Министр А.И. Данилов возглавил контрреформу под лозунгом «Назад Киселеву». По его поручению были созданы учебники, альтернативные исправительному учреждению. под редакцией академика А.Н. Тихонова. Их авторы старались следовать киселевской традиции. Эти учебники успели попасть в школу, но, к сожалению, в кампании с исправленными реформистскими. Так что проблема учебников, возникшая в результате реформы, тогда не могла быть решена. Это не решено по сей день. Потому что идеологические недостатки этой реформы не устранены.
Наследие реформ
Итак, мы подошли к наследию 70 реформ в сегодняшнем образовании. И здесь надо признать, что все «недостатки» в знаниях школьников, появившиеся в 1978 году, к настоящему времени обострились и стали привычными. Подтвердим этот вывод двумя утверждениями.
1. В 1981 году учителя, методисты и ученые Уральской зоны заявили: «Первокурсники испытывают трудности с операциями с дробями, с выполнением простейших алгебраических преобразований, решением квадратных уравнений, операциями с комплексными числами, построением простейших геометрических фигур и графиков. элементарные функции.Во многом это связано с несовершенством существующих школьных программ и учебников математики. «
19 лет спустя, в 2000 году, на Всероссийской конференции «Математика и общество» те же уральские ученые во главе с академиком Н.Н. Красовский сказал то же самое: «Недооценка арифметики, ограниченное внимание к значимым задачам, ослабление геометрии, по-видимому, является недостаточной подготовкой к логическому мышлению».
2. Надо признать, что все эти и многие другие «недостатки» знаний современных школьников связаны с той далекой реформой-70.Этот вывод, по сути, доказан выше. Подтвердим это еще двумя примерами.
Примеры и выводы
До реформы вычислительные навыки формировались с помощью классического курса твердой арифметики в течение пяти с половиной лет и сохранялись на протяжении всего дальнейшего обучения. Эти навыки были основой успешного изучения алгебры. Реформистское сокращение арифметики и смешение ее с алгеброй и геометрией, продолжающееся и по сей день, разрушило фундамент.Поэтому у современных студентов нет ни вычислительных навыков, ни навыков проведения идентичных алгебраических преобразований на их основе.
«Ограниченное внимание к осмысленным задачам» берет свое начало в диссертации Г.М. Фихтенгольц о «вредности» задач, решаемых в начальной школе. Эту диссертацию подхватил и развил в 1938 г. А.Я. Хинчин, который предложил решать их в старшей школе с помощью уравнений. Эта идея была усилена (начиная с 5 класса) А.И. Маркушевича в 1949 году. В 1961 году А.И. Маркушевич в ранге замминистра потребовал от учителей «критически пересмотреть традиционное отношение к арифметическим методам решения задач и избавиться от пережитков« культа »этих задач в нашей школе».
Отношение «избавиться от» традиционного было введено реформой-70 в школе, она разрушила классическую методику обучения решению систематизированных типовых задач, которая медленно и основательно развивала мышление детей. Это подтвердило международное исследование 1995 года — только 37% восьмиклассников решили задачу: «В классе 28 человек.Соотношение девочек и мальчиков составляет 4/3. Сколько девочек в классе? «… До реформы, в 1949 году, 83,5% пятиклассников решали аналогичные и более сложные задачи.
Сегодня нам предлагают новые объяснения деградации образования, наиболее понятным из которых является отсутствие финансирования. Они переключают наше внимание и нашу деятельность на новые ложные цели — универсальную компьютеризацию и обучение информационным технологиям … Но некоторые научные исследования доказывают, что «обучение» компьютерным технологиям приводит к атрофии способности анализировать информацию, т.е.е. чтобы еще больше одурманивать школьников. Так, в академическом журнале «Физиология человека» отмечаются «грубые функциональные сдвиги, которые были выявлены у детей, обучающихся на компьютере».
Академические часы сокращаются, базовые разделы выбрасываются, при этом строго сохраняются основные «достижения» реформы-70 — «интегрированные» учебные программы вместо целых учебных предметов, суррогат высшей математики в учебных планах, перегрузка , аксиоматика, схоластический формализм и абстрактность изложения в учебниках.Даже учебники реформаторов — А. Колмогоров, А. Маркушевич, Н.Я. Виленкина, А. Погорелова и дополнены учебниками их последователей.
Сегодня многим кажется, что «уровень математической грамотности в стране в целом стал катастрофически падать». Напомним: снижение качества знаний студентов следует отсчитывать с 1956 г., когда вышли учебники А.П. Киселева. Катастрофический коллапс произошел в 1978 году, когда из школы выпустили первую «реформированную» молодежь.Второго катастрофического коллапса не было, но продолжался и продолжается по сей день разложение, вызванное реформой-70, поддерживаемой перманентными «демократическими реформами».
Реформа-70 все отступает и отступает. И мы забываем, что деградация началась именно с этой реформы, а ее идеология является исходной, первопричиной катастрофического падения качества математического образования (как школьного, так и университетского).
Заключение
«Реформа-70» исключила педагогику и методику из учебников, исключила Ученица.Она отвечает за деградацию мышления, а значит и личности учеников. Именно она вызвала у студентов массовое отвращение к учебе. Это породило государственную ложь (так называемую «процентную манию»), которая заблокировала все возможности исправить ситуацию, запустив прогрессирующую коррупцию в секторе образования. По сей день наша школа живет под тяжелым бременем этой реформы.
Один из главных уроков, который следует извлечь из этого исторического анализа, следующий: качество образования тесно связано с сохранением национальной педагогической традиции, его недопустимо прерывать.В математике эта традиция сосредоточена в учебниках А.П. Киселевой. Поэтому необходимым (хотя, возможно, и недостаточным) условием возрождения нашего математического образования является возвращение в школу Киселева А.И. Маркушевич на этом этапе ушел в тень, хотя в том же 1967 году он занял ключевую должность вице-президента Академии педагогических наук СССР, что позволило ему сохранить контроль над ходом реформы. В частности, он заблокировал обсуждение академией учебных программ, учебников и плана реформы.
Журнал «Вокруг света» — один из моих любимых с детства. Его родители всегда выписывали его. Очень хорошо, что я его давно покупаю и читаю, рада, что дочке тоже захотелось прочитать. Последний, апрельский номер, содержит отрывок под названием «Вдохновленная математика» из книги Маши Гессен о Григории Перельмане, которая выходит весной этого года в русском переводе (книга написана на английском). С удивлением обнаружил, что главным героем этого отрывка был Андрей Николаевич Колмогоров!
Чем больше я читал текст, тем яснее становился я о тенденциозности и предвзятости автора, пошедшего по проторенной дорожке обвинений «совка» в непонимании гения, в создании невыносимых трудностей в его жизни и работа, домогательства и даже возможное физическое воздействие на него.Подобным же образом автор не только «отбрасывает тень», но и прямо обвиняет некоторых коллег (Понтрягин Л.С.) Колмогорова в организации политического преследования гения, приписывая коллегам слова, оформленные цитатами, то есть цитируя их.
Из статьи следует, что Колмогорову не доверяли, притесняли, не пускали в атомный проект — из-за его гомосексуальности с 29 лет до конца жизни «делили приют» с топологом имениреком — не скрывая, об этом знали все, а с 1934 года за эти «увлечения» была уголовная статья.
В 1941 году ему была присуждена Сталинская премия I степени, а в 1942 году он женился, брак продлился 45 лет — в статье об этом ни слова.
В 1952 г. появилась еще одна академическая премия, 1962 г. — премия Бальцана, 1963 г. — Герой Социалистического Труда, 1965 г. — Ленинская премия.
С 1963 года (он смог произвести впечатление на Брежнева, «поскольку единственная ценность, которую государство видело в математике и физике, было их военное использование») Колмогоров фактически руководил реформой преподавания математики в школах, имел возможность организовывать математические школы для одаренных дети, в которых работали преподаватели высших учебных заведений — «Эти школы воспитывали вольнодумных снобов.«В одном из них в диссидентский период своей жизни Юлий Ким преподавал историю, обществознание и литературу — этот факт автор отрывка преподносит как прямое противостояние вольнодумного академика и КГБ.
As для «военного применения» — то, что в середине ХХ века математика и физика стали интересны для всех государств мира только из-за их военного использования, никем не оспаривается.
Работа Колмогорова в средней школе закончилась в 1978 г. — по мнению автора, «идеологический конфликт, сделавший невозможными реформы Колмогорова, был очевиден.
А вот мнение академика Понтрягина, который, как следует из статьи, подверг Колмогорова идеологической травле на общем собрании Отделения математики Академии наук: «Руководство Отделения математики Академия наук СССР рекомендовала для модернизационных работ академика А.Н. Колмогорова, сыгравшего ведущую роль в модернизации. Поэтому ответственность за трагические события в вузе во многом лежит на нем.
Математические взгляды Колмогорова, его профессиональные навыки и человеческий характер отрицательно сказались на обучении. Ущерб, нанесенный крахом преподавания математики в советской средней школе, по своему значению можно сравнить с ущербом, который мог быть причинен огромным национальным саботажем …
Введение теоретико-множественной идеологии в школьную математику, несомненно, соответствовали вкусам AN Колмогорова. Но сама эта реализация, я думаю, уже не находилась под его контролем.Его доверили другим лицам, неквалифицированным и недобросовестным. Здесь сказалась черта характера Колмогорова. Охотно взявшись за новое дело, Колмогоров очень быстро охладился и доверил его другим.
При написании новых учебников это вроде бы произошло. Учебники, составленные в описанном стиле, были напечатаны миллионным тиражом и разосланы в школы без проверки со стороны Отделения математики АН СССР. Эта работа выполнялась под руководством Колмогорова методистами Минобразования СССР и Академии педагогических наук.Жалобы школьников и учителей были безжалостно отклонены бюрократическим аппаратом министерства и Академии педагогических наук. Старые опытные учителя в основном разошлись.
Это поражение среднего математического образования длилось более 15 лет, прежде чем его заметили в конце 1977 года ведущие математики Отделения математики Академии наук СССР. Ответственность за случившееся, конечно же, лежит не только на А.Н. Колмогорова, министерства и Академия педагогических наук, а также математический факультет, который, доверив Колмогорову ответственную работу, совершенно не интересовался, как она проводится. … Были рассмотрены конкретные дефекты учебников, и подавляющему большинству присутствующих было совершенно ясно, что так не может оставаться.
Решительными противниками любых действий, направленных на исправление ситуации, были академики С.Л. Соболев и Л.В. Канторович, который сказал, что нужно ждать.Но, несмотря на их сопротивление, было принято решение о вмешательстве в процесс обучения в средних школах.
Главной претензией академических математиков была не идеология. По словам Понтрягина, главный вред от введения множественных теорий Колмогорова в программу средней школы заключался в том, что «основное содержание математики, то есть способность выполнять алгебраические задачи. расчеты и мастерство геометрических рисунков и геометрических изображений отошли на второй план.вне поля зрения учителей и учеников. «
Личное впечатление — я помню школьные учебники по алгебре и геометрии 70-х годов, на первом листе была надпись, объясняющая, что учебник разработан по его программе. Алгебру и геометрию в моей школе преподавали два учителя: один — по Колмогорову, другой (в 9-10 классах) — дополнение сравнений и множеств доколмогоровскими методами и идеями. Я не специалист в топологии и математических теориях, но помню, что доколмогоровские объяснения были намного больше. вменяемый и ближе к реальным проблемам.Это подтвердили в школе — мне действительно хватило школьных и техникумов без колмогоровских нововведений. Но в этой же школе было много всевозможных вероятностных уловок — применительно к тактике, к применению оружия, к оценке точности навигационных измерений — все учителя вздохнули и супер уважительно отзывались о Колмогорове.
В качестве иллюстрации Понтрягин приводит следующий пример: в учебниках Колмогорова «дано следующее определение вектора: вектор — это преобразование пространства, в котором… далее перечисляются свойства, означающие, что это преобразование является переводом пространства. Естественное и необходимое для всех определение вектора как направленного отрезка было отодвинуто на задний план. «Суть претензии ясна и понятна любому человеку с техническим образованием — где тут идеология, которую так настойчиво прописывает Маша Гессен?
» Весной 1979 года входивший в его подъезд Колмогоров получил удар через затылок — предположительно с бронзовой рукоятью, — из-за чего он на время потерял сознание.Однако ему казалось, что за ним кто-то следил », — заключает автор, что покушение было совершено, тем более что, по словам автора,« пресса заклеймила Колмогорова как «агента западного культурного влияния, которым он на самом деле был «
» Якобы … за ним кто-то следил «- ну чушь! В эти годы Сахаров достиг согласия по теории конвергенции — никто не ударил его по голове, Солженицын, прямо сломавший основы советской системы на своем Архипелаге, Шафаревич, напечатавший в самиздате свои безоговорочные антисоветские взгляды — их явные враги, почему их не было ?!
Этот отрывок оставляет печальное впечатление — Маша Гессен не просто находится в плену идеологических установок, она сама создает эти установки, делая оппозиционера из зажиточного советского академика, который с 1921 года совершенно заслуженно не испытывал материальных трудностей (он сам пишет о об этом в его мемуарах), почти открытый враг советского режима, который разрушал его изнутри, создавая математические школы и реформировав преподавание математики в средних школах, что, по-видимому, должно было привести к массовому появлению западноевропейского режима. ориентированная элита «вольнодумных снобов».«
Автор, кстати, учился в Московской математической школе» (и закончил бы ее, если бы моя семья не эмигрировала в США), учителя предупреждали, что никто из нас не сможет поступить на механический факультет и Математика МГУ »- почему? Мой дядя, не будучи снобом и не окончив спецшколу, поступил на механико-математический факультет МГУ, окончил обычную школу в Орехово-Зуеве с золотой медалью. и вошел.
В журнале размещена информация о книгах, которые написала Маша:
— «Снова мертвые: русская интеллигенция после коммунизма»
— «Две бабушки: как мои бабушки пережили гитлеровскую войну и сталинский мир».
Характерные имена.
Резюме — две неприятности. Во-первых — про Перельмана никогда не читал, но интересно! Второе — жаль, что журнал «Вокруг света» начал усердно работать в области десталинизации, публиковать подобные очерки.
Но есть и плюсы — я много узнал о Колмогорове (в основном, не из обсуждаемой статьи — благодаря Википедии), а главное о Льве Семеновиче Понтрягине, слепом с детства, достигшем высших вершин в мире.


 В.Гордиенко
В.Гордиенко







 12.17)
12.17) 05.18 )
05.18 )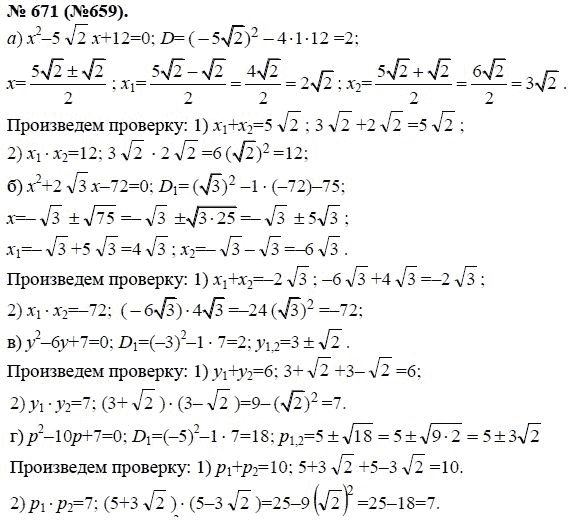 09
09 Сокращение дробей.
Сокращение дробей.
 10
10 10
10 10
10 11
11 11
11 11
11 12
12 12
12 12
12 01
01 01
01 02
02 02
02
 03
03
 04
04 04
04 04
04 04
04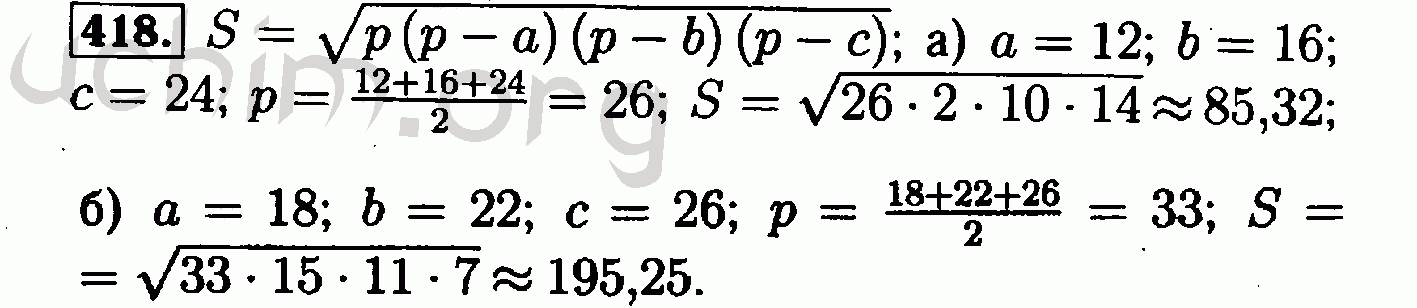 05
05
 05
05 03.18
03.18