Основные определения и теоремы по геометрии. 7 класс — Студопедия
Поделись
- Геометрия – наука, занимающаяся изучением геометрических фигур (в переводе с греческого слово «геометрия» означает «землемерие»).
- В планиметрии изучаются свойства фигур на плоскости. В стереометрии изучаются свойства фигур в пространстве.
- Отрезок — это часть прямой, ограниченная двумя точками. Эти точки называются концами отрезка.
- Угол — это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки. Лучи называются сторонами угла, а точка — вершиной угла.
- Угол называется развёрнутым, если обе его стороны лежат на одной прямой. ( Развёрнутый угол равен 180°).
- Две геометрические фигуры называются равными, если их можно совместить наложением.

- Середина отрезка
- Биссектриса угла — это луч, исходящий из вершины угла и делящий его на два равных угла.
- Угол называется прямым, если он равен 90°.
- Угол называется острым, если он меньше 90° (т.е. меньше прямого угла).
- Угол называется тупым, если он больше 90°, но меньше 180°. (т.е. больше прямого, но меньше развёрнутого).
- Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными. Сумма смежных углов равна 180°.
- Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого. Вертикальные углы равны.
- Две пересекающиеся прямые называются перпендикулярными, если они образуют четыре прямых угла.
- Треугольник — это геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой и трех отрезков, соединяющих эти точки.
 Точки называются вершинами, а отрезки — сторонами треугольника.
Точки называются вершинами, а отрезки — сторонами треугольника. - Если два треугольника равны, то элементы (т.е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника.
- Теорема – утверждение, справедливость которого устанавливается путём рассуждений. Сами рассуждения называются доказательством теоремы.
- (Т. Первый признак равенства треугольников) Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
- (Т. о перпендикуляре к прямой) Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.
- Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
- Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.

- Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.
- (Свойства медианы, биссектрисы и высоты треугольника) В любом треугольнике медианы пересекаются в одной точке; биссектрисы пересекаются в одной точке; высоты или их продолжения также пересекаются в одной точке.
- Треугольник называется равнобедренным, если две его стороны равны. Равные стороны называются боковыми сторонами, а третья сторона — основанием равнобедренного треугольника.
- Треугольник называется равносторонним, если все его стороны равны.
- (Т. о свойстве равнобедренного треугольника) В равнобедренном треугольнике углы при основании равны.
- (Т. о свойстве равнобедренного треугольника) В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
- В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.

- В равнобедренном треугольнике высота, проведенная к основанию, является медианой и биссектрисой.
- (Т. Второй признак равенства треугольников) Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
- (Т. Третий признак равенства треугольников) Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.
- Окружностью называется геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки. Данная точка называется центром окружности.
- Радиус окружности – отрезок, соединяющий центр окружности с какой-либо её точкой.
- Отрезок, соединяющий две точки окружности, называется ее хордой.
- Хорда, проходящая через центр окружности, называется диаметром.

- Круг — это часть плоскости, ограниченная окружностью.
- Две прямые на плоскости называются параллельными , если они не пересекаются.
- При пересечении двух прямых секущей образуется восемь углов: накрест лежащие, односторонние и соответственные.
- (Т. Признак параллельности двух прямых по накрест лежащим углам) Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
- (Т. Признак параллельности двух прямых по соответственным углам) Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
- (Т. Признак параллельности двух прямых по односторонним углам) Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.
- Аксиомы – это утверждения о свойствах геометрических фигур, которые принимаются в качестве исходных положений, на основе которых доказываются теоремы и строится вся геометрия.

- (Аксиома) Через любые две точки проходит прямая, и притом только одна.
- (Аксиома параллельных прямых) Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
- Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
- Если две прямые параллельны третьей прямой, то они параллельны.
- Во всякой теореме две части: условие (то, что дано) и заключение (то, что требуется доказать).
- Теоремой, обратной данной,называется такая теорема, в которой условием является заключение данной теоремы, а заключением – условие данной теоремы.
- (Т. Свойство параллельных прямых) Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
- (Т. Свойство параллельных прямых) Если две параллельные прямые пересечены секущей, то соответственные углы равны.
- (Т. Свойство параллельных прямых) Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°.

- (Т. о сумме углов треугольника) Сумма углов треугольника равна 180°.
- Внешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника.
- Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
- Если все три угла треугольника острые, то треугольник называется остроугольным.
- Если один из углов треугольника тупой, то треугольник называется тупоугольным.
- Если один из углов треугольника прямой, то треугольник называется прямоугольным.
- Сторона прямоугольного треугольника, лежащая против прямого угла, называется
- (Т. о соотношениях между сторонами и углами треугольника) В треугольнике против большей стороны лежит больший угол, и обратно, против большего угла лежит большая сторона.

- В прямоугольном треугольнике гипотенуза больше катета.
- (Признак равнобедр. треугольника) Если два угла треугольника равны, то треугольник равнобедренный.
- (Т. Неравенство треугольника) Каждая сторона треугольника меньше суммы двух других сторон.
- (Свойство прямоугольного треугольника) Сумма двух острых углов прямоугольного треугольника равна 90°.
- (Свойство прямоугольного треугольника) Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.
- (Свойство прямоугольного треугольника ) Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°.
- (Признак равенства прямоугольных треугольников по двум катетам) Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.
- (Признак равенства прямоугольных треугольников по катету и острому углу) Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему острому углу другого, то такие треугольники равны.

- (Т. Признак равенства прямоугольных треугольников по гипотенузе и острому углу) Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.
- (Т. Признак равенства прямоугольных треугольников по гипотенузе и катету
- Расстоянием от точки до прямой называется длина перпендикуляра, проведённого из этой точки к прямой.
- (Т. Свойство параллельных прямых) Все точки каждой из двух параллельных прямых равноудалены от другой прямой.
- Расстоянием между параллельными прямыми называется расстояние от произвольной точки одной из параллельных прямых до другой прямой.
Зачёт по геометрии за 7 класс
6 марта 2021
В закладки
Обсудить
Жалоба
Пробные работы ОГЭ по математике
Вопросы по геометрии. 7 класс
7 класс
1. Сколько прямых можно провести через две точки?
2. Сколько общих точек могут иметь две прямые?
3. Что такое отрезок? Начертить, обозначить и объяснить? Какая точка называется серединой отрезка?
4. Что такое луч? Как обозначаются лучи?
5. Какая фигура называется углом? Объясните, что такое вершина и стороны угла.
6. Какие фигуры называются равными?
7. Как сравнить два угла? Какой луч называется биссектрисой угла?
8. Какой угол называется острым? прямым? тупым?
9. Какие углы называются смежными? Чему равна сумма смежных углов? Уметь их строить.
10. Какие углы называются вертикальными? Каким свойством обладают вертикальные углы? Уметь их строить.
11. Какие прямые называются перпендикулярными? Уметь их строить Объясните, почему две прямые, перпендикулярные к третьей, не пересекаются?
12. Объясните, какая фигура называется треугольником. Начертите треугольник и покажите его стороны, вершины и углы. Что такое периметр треугольника?
13. Какие треугольники называются равными?
Какие треугольники называются равными?
14. Что такое теорема и доказательство теоремы?
15. Сформулируйте первый признак равенства треугольников.
16. Какой отрезок называется медианой треугольника? Сколько медиан имеет треугольник? Уметь их строить.
17. Какой отрезок называется биссектрисой треугольника? Сколько биссектрис имеет треугольник? Уметь их строить.
18. Какой отрезок называется высотой треугольника? Сколько высот имеет треугольник? Уметь их строить.
19. Какой треугольник называется равнобедренным? Уметь его строить. Как называются его стороны?
20. Какой треугольник называется равносторонним? Уметь его строить. Сформулировать основные свойства равнобедренного треугольника.
21. Сформулируйте второй признак равенства треугольников.
22. Сформулируйте третий признак равенства треугольников.
23. Что такое определение? Дайте определение окружности. Что такое центр, радиус, хорда и диаметр окружности?
24. Объясните, как отложить от данного луча в данную плоскость угол, равный данному. (с помощью циркуля и линейки)
(с помощью циркуля и линейки)
25. Объясните как построить биссектрису данного угла.( с помощью циркуля и линейки)
26. Объясните, как построить прямую, проходящую через данную точку, лежащую на данной прямой, и перпендикулярную к этой прямой. .(с помощью циркуля и линейки)
27. Объясните, как построить середину данного отрезка. .(с помощью циркуля и линейки)
28. Дайте определение параллельных прямых. Какие два отрезка называются параллельными?
29. Что такое секущая? Назовите пары углов, которые образуются при пересечении двух прямых секущей. Уметь их построить , показать и обозначить.
30. Сформулируйте признаки параллельности прямых ?
31. Что такое аксиома? Приведите примеры. Сформулируйте аксиому параллельных прямых.
32. Какая теорема называется обратная данной теореме? Приведите примеры теорем, обратных данным.
33. Сформулируйте теоремы об углах, образованных двумя параллельными прямыми и секущей.
34. Сформулируйте теорему о сумме углов треугольника.
35. Какой угол называется внешним углом треугольника? Уметь его строить. Сформулируйте, чему равен внешний угол в треугольнике.
36. Какой треугольник называют остроугольным? Какой треугольник называется тупоугольным? Уметь их строить.
37. Какой треугольник называется прямоугольным? Как называются стороны прямоугольного треугольника?
38. Сформулируйте соотношения между сторонами и углами. Почему в прямоугольном треугольнике гипотенуза больше катета?
39. Сформулируйте теорему о неравенстве треугольника.
40. Сформулируйте некоторые свойства прямоугольных треугольников.
41. Сформулируйте признаки равенства прямоугольных треугольников.
42. Что называется расстоянием от точки до прямой?
43. Что называется расстоянием между двумя параллельными прямыми?
44. Объясните, как построить треугольник по двум сторонам и углу между ними.
45. Объясните, как построить треугольник по стороне и двум прилежащим к ней углам.
46. Объясните, как построить треугольник по трём сторонам. Всегда ли эта задача имеет решение?
Всегда ли эта задача имеет решение?
Задачи к зачету по геометрии. 7 класс
Задача №1. В равнобедренном треугольнике угол при основании в 2 раза меньше, чем угол при вершине. Найдите все углы треугольника.
Задача №2. Высота АD равностороннего треугольника ВАС с основанием ВС равна 10 см, периметр треугольника АDС равен 70 см. Найдите периметр треугольника АВС.
Задача №3. Первый угол треугольника равен 40градусов, а второй больше третьего на 16 градусов. Найдите эти углы треугольника.
Задача №4. В равнобедренном треугольнике периметр равен 150 см, боковая сторона больше основания на 15 см. Найдите все стороны треугольника.
Задача №5. В равнобедренном прямоугольном треугольнике гипотенуза равна 42 см. Найдите высоту проведённую из вершины прямого угла.
Задача №6. В равнобедренном треугольнике внешний угол при вершине равен 40 градусов. Найдите углы этого треугольника.
Задача №7. В равнобедренном треугольнике СDЕ с основанием СЕ проведена биссектриса СF. Найдите угол ЕСF, если угол D равен 54 градуса.
Найдите угол ЕСF, если угол D равен 54 градуса.
Задача №8. Один из углов прямоугольного треугольника равен 60 градусов, а сумма гипотенузы и меньшего катета равна 30 см. Найдите гипотенузу треугольника.
Задача №9. Один из внешних углов равнобедренного треугольника равен 110 градусов. Найдите все углы данного треугольника.
Задача №10. Периметр равнобедренного треугольника равен 65 см, его боковая сторона на 5 см меньше основания. Найдите стороны треугольника.
Задача №11. Периметр равнобедренного тупоугольного треугольника равен 77 см, а одна из его сторон больше другой на 17см. Найдите стороны этого треугольника.
Задача №12. Сумма вертикальных углов АОВ и СОD, образованных при пересечении прямых АD и ВС, равна 108 градусов. Найдите угол ВОD.
Задача №13. В остроугольном треугольнике МNP биссектриса угла М пересекает высоту NК в точке О. причём ОК равно 9 см.
Найдите расстояние от точки О до прямой МN.
Задача №14. Отрезки АВ и СD- диаметры окружности с центром О. Найдите периметр треугольника АОD, если хорда СВ равна 10 см, диаметр АВ равен 12 см.
Найдите периметр треугольника АОD, если хорда СВ равна 10 см, диаметр АВ равен 12 см.
Задача №15. Найдите все неразвёрнутые углы, образованные при пересечении двух прямых, если сумма двух из них равна 296 градусов.
Задача №16. Луч ОС делит угол АОВ на два угла. Найдите угол СОВ, если угол АОВ равен 110 градусов, а угол АОС на 18 градусов меньше угла ВОС.
Задача №17. Углы треугольника относятся как 2: 3: 4. Найдите их градусные меры.
Задача №18. В равнобедренном треугольнике АВС с основанием АС равно 38 см внешний угол при вершине В равен 60 градусов. Найдите расстояние от вершины С до прямой АВ.
Задача №19. Один из углов при пересечении двух параллельных прямых третьей прямой в 2 раза больше другого. Найдите остальные углы.
Задача №20. Один из углов при пересечении двух параллельных прямых третьей прямой на 20 градусов меньше другого. Найдите остальные углы.
Задача №21. В равнобедренном треугольнике АВС с основанием АС равно 42см, внешний угол при вершине С равен 120 градусов. Найдите боковые стороны треугольника АВС.
Найдите боковые стороны треугольника АВС.
geo7.docx
Математика | Сегодня, 18:46
Сборник заданий для подготовки к номеру 15 профильного ЕГЭ.
Образование | Сегодня, 14:17
Министр просвещения России Сергей Кравцов предложил рассмотреть вопрос перехода на специалитет в педагогическом образовании.
Зачёт по геометрии, 7 класс | Методическая разработка по геометрии (7 класс) по теме:
Опубликовано 30.06.2014 — 0:32 — Чернова Анжела Ахмедовна
Основные определения и теоремы для подготовки к зачёту по геометрии, Л.С. Атанасян, 7 класс
Скачать:
Реклама
Подтяните оценки и знания с репетитором Учи.ру
За лето ребенок растерял знания и нахватал плохих оценок? Не беда! Опытные педагоги помогут вспомнить забытое и лучше понять школьную программу. Переходите на сайт и записывайтесь на бесплатный вводный урок с репетитором.
Вводный урок бесплатно, онлайн, 30 минут
Записаться >
Предварительный просмотр:
Зачёт по геометрии (7 класс) __________________________
- Геометрия – наука, занимающаяся изучением геометрических фигур (в переводе с греческого слово «геометрия» означает «землемерие»).

- В планиметрии изучаются свойства фигур на плоскости. В стереометрии изучаются свойства фигур в пространстве.
- Отрезок — это часть прямой, ограниченная двумя точками. Эти точки называются концами отрезка.
- Угол — это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки. Лучи называются сторонами угла, а точка — вершиной угла.
- Угол называется развёрнутым, если обе его стороны лежат на одной прямой. ( Развёрнутый угол равен 180°).
- Две геометрические фигуры называются равными, если их можно совместить наложением.
- Середина отрезка — это точка отрезка, делящая его пополам, т.е. на два равных отрезка.
- Биссектриса угла — это луч, исходящий из вершины угла и делящий его на два равных угла.
- Угол называется прямым, если он равен 90°.
- Угол называется острым, если он меньше 90° (т.е. меньше прямого угла).
- Угол называется тупым, если он больше 90°, но меньше 180°. (т.е. больше прямого, но меньше развёрнутого).

- Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными. Сумма смежных углов равна 180°.
- Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого. Вертикальные углы равны.
- Две пересекающиеся прямые называются перпендикулярными, если они образуют четыре прямых угла.
- Треугольник — это геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой и трех отрезков, соединяющих эти точки. Точки называются вершинами, а отрезки— сторонами треугольника.
- Если два треугольника равны, то элементы (т.е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника.
- Теорема – утверждение, справедливость которого устанавливается путём рассуждений. Сами рассуждения называются доказательством теоремы.
- (Т. Первый признак равенства треугольников) Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

- (Т. о перпендикуляре к прямой) Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.
- Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
- Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.
- Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.
- (Свойства медианы, биссектрисы и высоты треугольника) В любом треугольнике медианы пересекаются в одной точке; биссектрисы пересекаются в одной точке; высоты или их продолжения также пересекаются в одной точке.
- Треугольник называется равнобедренным, если две его стороны равны. Равные стороны называются боковыми сторонами, а третья сторона — основанием равнобедренного треугольника.
- Треугольник называется равносторонним, если все его стороны равны.

- (Т. о свойстве равнобедренного треугольника) В равнобедренном треугольнике углы при основании равны.
- (Т. о свойстве равнобедренного треугольника) В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
- В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
- В равнобедренном треугольнике высота, проведенная к основанию, является медианой и биссектрисой.
- (Т. Второй признак равенства треугольников) Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
- (Т. Третий признак равенства треугольников) Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.
- Окружностью называется геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки.
 Данная точка называется центром окружности.
Данная точка называется центром окружности. - Радиус окружности – отрезок, соединяющий центр окружности с какой-либо её точкой.
- Отрезок, соединяющий две точки окружности, называется ее хордой.
- Хорда, проходящая через центр окружности, называется диаметром.
- Круг — это часть плоскости, ограниченная окружностью.
- Две прямые на плоскости называются параллельными, если они не пересекаются.
- При пересечении двух прямых секущей образуется восемь углов: накрест лежащие, односторонние и соответственные.
- (Т. Признак параллельности двух прямых по накрест лежащим углам) Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
- (Т. Признак параллельности двух прямых по соответственным углам) Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
- (Т. Признак параллельности двух прямых по односторонним углам) Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.

- Аксиомы – это утверждения о свойствах геометрических фигур, которые принимаются в качестве исходных положений, на основе которых доказываются теоремы и строится вся геометрия.
- (Аксиома) Через любые две точки проходит прямая, и притом только одна.
- (Аксиома параллельных прямых) Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
- Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
- Если две прямые параллельны третьей прямой, то они параллельны.
- Во всякой теореме две части: условие (то, что дано) и заключение (то, что требуется доказать).
- Теоремой, обратной данной, называется такая теорема, в которой условием является заключение данной теоремы, а заключением – условие данной теоремы.
- (Т.) Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
- (Т.) Если две параллельные прямые пересечены секущей, то соответственные углы равны.

- (Т.) Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°.
- (Т. о сумме углов треугольника) Сумма углов треугольника равна 180°.
- Внешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника.
- Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
- Если все три угла треугольника острые, то треугольник называется остроугольным.
- Если один из углов треугольника тупой, то треугольник называется тупоугольным.
- Если один из углов треугольника прямой, то треугольник называется прямоугольным.
- Сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой, а две стороны, образующие прямой угол — катетами.
- (Т. о соотношениях между сторонами и углами треугольника) В треугольнике против большей стороны лежит больший угол, и обратно, против большего угла лежит большая сторона.
- В прямоугольном треугольнике гипотенуза больше катета.

- (Признак равнобедр. треугольника) Если два угла треугольника равны, то треугольник равнобедренный.
- (Т. Неравенство треугольника) Каждая сторона треугольника меньше суммы двух других сторон.
- (Свойство прямоугольного треугольника) Сумма двух острых углов прямоугольного треугольника равна 90°.
- (Свойство прямоугольного треугольника) Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.
- (Свойство прямоугольного треугольника) Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°.
- (Признак равенства прямоугольных треугольников по двум катетам) Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.
- (Признак равенства прямоугольных треугольников по катету и острому углу) Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему острому углу другого, то такие треугольники равны.

- (Т. Признак равенства прямоугольных треугольников по гипотенузе и острому углу) Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.
- (Т. Признак равенства прямоугольных треугольников по гипотенузе и катету) Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.
- Расстоянием от точки до прямой называется длина перпендикуляра, проведённого из этой точки к прямой.
- (Т. Свойство параллельных прямых) Все точки каждой из двух параллельных прямых равноудалены от другой прямой.
- Расстоянием между параллельными прямыми называется расстояние от произвольной точки одной из параллельных прямых до другой прямой.
Чертежи ко всем вопросам!!!
По теме: методические разработки, презентации и конспекты
Зачёт по геометрии. Тема:»Метод координат». 9 класс
В данном зачёте учащимся предлагается ответить на 15 вопросов по теме «Метод координат», ответы на которые позволят сделать учителю вывод об уровне усвоения темы. …
…
Зачёт по геометрии. Тема»»Метод координат». 11 класс.
В зачёте учащимся предлагается ответить на вопросы, касающиеся теоретической части темы «Метод координат»….
Зачёт по геометрии «Длина окружности и площадь круга», 9 класс
Для организации зачёта по теме «Длина окружности и площадь круга» приводятся вопросы для подготовки к зачёту и лист для письменного опроса….
Зачёт по геометрии. Тема «Многоугольники». 8 класс
Представленный материал помогает организовать зачёт по теме «Многоугольники. Четырёхугольники» в 8 классе. Здесь вы можете найти вопросы для подготовки к зачёту и листы с двумя видами контроля з…
Билеты к зачёту по геометрии в 8 классе по теме:»Четырёхугольники»
Для проведения зачёта разработанны билеты по геометрии…
Самостоятельная работа к зачёту по геометрии 8 класс
Самостоятельная работа к зачёту по геометрии 8 класс…
материалы для итогового зачёта по геометрии в 7-8 классах
В конце учебного года я во всех классах провожу зачёты по геометрии. Такая форма итоговой аттестации позволяет актуализировать знания за год и выставить объективную годовую оценку.Зачёт проводится в ф…
Такая форма итоговой аттестации позволяет актуализировать знания за год и выставить объективную годовую оценку.Зачёт проводится в ф…
Поделиться:
Математика 7 класс | Геометрия
Учащиеся применяют навыки алгебраического и пропорционального рассуждений для исследования взаимосвязей углов, измерений окружности, уникальности треугольников и решения задач с объемными фигурами.
Раздел 6
7-й класс
Резюме раздела
В Разделе 6 учащиеся седьмого класса изучают широкий спектр тем, от угловых взаимосвязей до окружностей и многоугольников и объемных фигур. Стандарты по геометрии для седьмого класса относятся к категории дополнительных стандартов, однако в этом разделе есть несколько возможностей, когда учащиеся участвуют в основной работе в классе. В начале раздела учащиеся используют и решают уравнения для представления взаимосвязей между углами и находят отсутствующие угловые меры. Исследуя круги, учащиеся обнаруживают пропорциональную связь между длиной окружности и ее диаметром и понимают π как отношение этих двух величин. Студенты также будут использовать свои навыки выражения для написания числовых выражений, которые можно использовать для нахождения площади поверхности и объема трехмерных фигур.
Исследуя круги, учащиеся обнаруживают пропорциональную связь между длиной окружности и ее диаметром и понимают π как отношение этих двух величин. Студенты также будут использовать свои навыки выражения для написания числовых выражений, которые можно использовать для нахождения площади поверхности и объема трехмерных фигур.
На протяжении всего раздела учащиеся сталкиваются с несколькими словарными словами, такими как дополнительные углы, вертикальные углы, радиус и окружность. Многие из этих слов позволяют учащимся быть более точными в общении друг с другом (MP.6). Учащиеся также столкнутся со сложными диаграммами углов и трехмерными фигурами, где им нужно будет понять, какую информацию они могут извлечь из диаграммы, и спланировать путь решения, прежде чем переходить к ней (MP.1). Учащиеся должны иметь доступ к нескольким инструментам, которые они могут использовать на протяжении всего раздела, включая линейки, транспортиры, циркуль и справочные листы (MP.5).
Основополагающие навыки для стандартов в этом блоке получают с четвертого по шестой классы. В четвертом классе учащиеся изучали понятия измерения угла и понимали, что мера угла является аддитивной. В пятом классе учащиеся развили понимание трехмерного объема, которое они получили в шестом классе. Учащиеся шестого класса также начали различать трехмерное пространство, которое занимает объект, и площадь поверхности, которая его покрывает.
В четвертом классе учащиеся изучали понятия измерения угла и понимали, что мера угла является аддитивной. В пятом классе учащиеся развили понимание трехмерного объема, которое они получили в шестом классе. Учащиеся шестого класса также начали различать трехмерное пространство, которое занимает объект, и площадь поверхности, которая его покрывает.
В восьмом классе учащиеся будут увеличивать прямоугольные треугольники и применять теорему Пифагора для определения длин сторон в прямоугольных треугольниках. Они также продолжат решать реальные приложения площади поверхности и объема с добавлением конусов, сфер и цилиндров.
Темп: 23 учебных дня (21 урок, 1 гибкий день, 1 контрольный день)
Fishtank Plus для математики
Разблокируйте функции, чтобы оптимизировать время подготовки, планировать увлекательные уроки и следить за успеваемостью учащихся.
Узнать больше
Оценка
Следующие оценки сопровождают Раздел 6.
Предварительная часть
Предложите учащимся пройти предварительную оценку и самооценку перед началом модуля. Используйте Руководство по анализу предварительной оценки, чтобы определить пробелы в фундаментальном понимании и наметить план ускорения обучения на протяжении всего модуля.
Используйте Руководство по анализу предварительной оценки, чтобы определить пробелы в фундаментальном понимании и наметить план ускорения обучения на протяжении всего модуля.
Промежуточный модуль
Предложите учащимся выполнить оценку промежуточного модуля после урока 11.
Последующий модуль
Используйте приведенные ниже ресурсы для оценки усвоения учащимися содержания модуля и плана действий для будущих модулей.
Постмодальная оценка
Ключ к ответам после модульной оценки
Руководство по анализу послемодульной оценки
92F25A3F-8529-4314-9899-6EE68694E3D0Пост-юнит самооценка
Расширенный пакет оценивания
Используйте данные учащихся для управления планированием с помощью расширенного набора модульных оценок, помогающих оценить способности учащихся с базовыми навыками и понятиями, а также их прогресс в изучении содержания модуля.
Скачать образец
Подготовка блока
Интеллектуальная подготовка
Предложения по подготовке к обучению данного модуля
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Запуск модуля
Подготовьтесь к преподаванию этого модуля, погрузившись в стандарты, большие идеи и связи с предыдущим и будущим содержанием. Запуск модулей включает в себя серию коротких видеороликов, целевую литературу и возможности для планирования действий.
Обновление до Plus
Интернализация стандартов с помощью итоговой оценки
- Пройдите итоговую оценку. Аннотировать для:
- Стандарты, которым соответствует каждый вопрос
- Стратегии и представления, используемые на ежедневных уроках
- Связь с основными понятиями модуля
- Уроки, на которые Оценка указывает
Интернализация траектории отряда
- Прочтите и аннотируйте сводку отряда.
- Обратите внимание на последовательность понятий в модуле с помощью карты урока.

- Выполнить все целевые задачи. Аннотируйте целевые задачи для:
- Основные сведения
- Связь с вопросами послемодульной оценки
- Определите ключевые возможности для вовлечения учащихся в академический дискурс. Прочтите наш Инструмент для учителя на Академический дискурс и ссылайтесь на него на протяжении всего модуля.
Интеллектуальная подготовка для конкретного модуля
- Прочтите Прогресс для общих основных государственных стандартов по математической геометрии, 7–8, старшая школа , чтобы узнать о стандартах, относящихся к этому разделу.
Основные понятия
Основные математические понятия, которые учащиеся должны понять в этом разделе
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950- При пересечении двух прямых образуется пара конгруэнтных вертикальных углов. Это угловое соотношение, наряду с дополнительными и дополнительными угловыми отношениями, можно использовать для определения отсутствующих угловых мер на диаграммах.
 2$$.
2$$. - В любом треугольнике сумма длин любых двух сторон должна быть больше, чем мера третьей стороны. При различных условиях, касающихся мер стороны и угла треугольника, может быть сформирован один уникальный треугольник, может быть сформировано более одного треугольника или не может быть сформирован ни один треугольник.
Материалы
Материалы, иллюстрации и инструменты, которые потребуются преподавателям и учащимся для работы с данным модулем
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950- Транспортир 180° (1 на учащегося)
- Строка (1 на учащегося)
- Компас (1 на учащегося)
- Миллиметровая бумага (2-3 листа на учащегося)
- Чистый лист бумаги (2-3 листа на учащегося)
- Линейка (1 на ученика)
- Раздаточный материал с кружками (по 1 на учащегося)
- AngLegs или подготовленные деревянные шампуры (по 1 на учащегося или небольшую группу) — см. запись в блоге «Треугольные шпажки с неравенством», написанную Элиссой Миллер, чтобы узнать, как приготовить деревянные шампуры.

Чтобы ознакомиться со всеми материалами, необходимыми для этого курса, ознакомьтесь с нашим Обзором материалов курса для 7-го класса.
Запас слов
Terms and notation that students learn or use in the unit
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950adjacent angles
circumference
complementary angles
cross-section
diameter
radius
surface area
дополнительные углы
теорема о неравенстве треугольника
вертикальные углы
объем
Чтобы увидеть весь словарный запас для Раздела 6, просмотрите наш глоссарий лексики для 7-го класса.
Карта урока
Тема A: Соотношение углов
Идентифицировать и определить значения углов в дополнительных и дополнительных отношениях.
7.RUS5
Используйте взаимосвязи вертикальных, дополнительных и дополнительных углов, чтобы найти недостающие углы.
7.RUS5
Используйте уравнения для решения неизвестных углов. (Часть 1)
(Часть 1)
7.RUS5
Используйте уравнения для решения неизвестных углов. (Часть 2)
7.RUS5
Тема Б: Круги
Определите окружность и определите размеры радиуса, диаметра и длины окружности.
7.RUS4
Определите соотношение между длиной окружности и диаметром круга и используйте его для решения задач.
7.RUS4
Решайте реальные и математические задачи, используя соотношение между длиной окружности и ее диаметром.
7.RUS4
Определите соотношение между площадью и радиусом круга и используйте его для решения задач.
7.RUS4
Решайте реальные и математические задачи, используя соотношение между площадью круга и его радиусом.
7.RUS4
Решить задачи на площадь и длину окружности двухмерных фигур (Часть 1).
7.RUS4 7.RUS6
Решение задач на площадь и длину окружности двухмерных фигур (Часть 2).
7.RUS4 7.RUS6
Тема C: Построение многоугольников и треугольников
Рисование двумерных геометрических фигур с помощью линейки, транспортира и циркуля.
7.G.A.2 7.RUS5
Определите, будут ли три длины сторон создавать уникальный треугольник или не создавать треугольник.
7.G.A.2
Найдите уникальные и одинаковые треугольники.
7.G.A.2
Определите, описывают ли условия уникальный треугольник, отсутствие треугольника или более одного треугольника.
7.G.A.2
Тема D: Твердые фигуры
Определите и опишите двухмерные фигуры, полученные в результате разрезания трехмерных фигур.
7.Г.А.3
Найдите площадь поверхности правильной призмы.
7.RUS6
Найти площадь поверхности правильной пирамиды.
7.RUS6
Найдите объем прямых призм и пирамид.
7.RUS6
Решайте реальные и математические задачи, связанные с объемом.
7.RUS6
Различать и решать реальные задачи, связанные с объемом и площадью поверхности.
7.RUS6
Общие основные стандарты
Ключ
Основной кластер
Вспомогательный кластер
Дополнительный кластер
Основные стандарты
Стандарты содержания, рассматриваемые в этом модуле
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Геометрия
7.
 Г.А.2 — Начертить (от руки, с линейкой и транспортиром и с техникой) геометрические фигуры с заданными условиями. Сосредоточьтесь на построении треугольников по трем мерам углов или сторон, отмечая, когда условия определяют уникальный треугольник, более одного треугольника или отсутствие треугольника.
Г.А.2 — Начертить (от руки, с линейкой и транспортиром и с техникой) геометрические фигуры с заданными условиями. Сосредоточьтесь на построении треугольников по трем мерам углов или сторон, отмечая, когда условия определяют уникальный треугольник, более одного треугольника или отсутствие треугольника. 7.Г.А.3 — Опишите двумерные фигуры, которые получаются в результате разрезания трехмерных фигур, например, в плоских сечениях прямоугольных призм и прямоугольных пирамид.
7.GB.4 — знать формулы площади и длины окружности и использовать их для решения задач; дать неформальный вывод отношения между длиной окружности и площадью круга.
7.GB.5 — Используйте факты о дополнительных, дополнительных, вертикальных и смежных углах в многошаговой задаче, чтобы написать и решить простые уравнения для неизвестного угла в фигуре.

7.GB.6 — Решайте реальные и математические задачи, связанные с площадью, объемом и площадью поверхности двух- и трехмерных объектов, состоящих из треугольников, четырехугольников, многоугольников, кубов и прямых призм.
Основополагающие стандарты
Стандарты, рассмотренные в предыдущих разделах или классах, которые являются важными фоновыми для текущего раздела
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Геометрия
5.RUS3
6.Г.А.1
6.Г.А.2
6.Г.А.4
7.Г.А.1
Измерения и данные
4.
 МД.А.3
МД.А.34.MD.C.5
4.MD.C.6
4.MD.C.7
5.MD.C.3
5.MD.C.5
Соотношения и отношения пропорциональности
7.РП.А.2
Будущие стандарты
Стандарты будущих классов или разделов, которые связаны с содержанием данного раздела
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Соответствие
G.CO.B.7
G.CO.B.8
Геометрия
8.Г.А.5
8.
 RUS6
RUS68.RUS7
8.G.C.9
Стандарты математической практики
CCSS.MATH.PRACTICE.MP1 — Разбираться в проблемах и настойчиво решать их.
CCSS.MATH.PRACTICE.MP2 — Рассуждайте абстрактно и количественно.
CCSS.MATH.PRACTICE.MP3 — Придумывайте жизнеспособные аргументы и критикуйте рассуждения других.
CCSS.MATH.PRACTICE.MP4 — Модель с математикой.
CCSS.MATH.PRACTICE.MP5 — Стратегически используйте соответствующие инструменты.
CCSS.MATH.PRACTICE.MP6 — Следите за точностью.
CCSS.MATH.PRACTICE.MP7 — Ищите и используйте структуру.
CCSS.MATH.PRACTICE.MP8 — Ищите и выражайте закономерность в повторяющихся рассуждениях.
Единица измерения 5
Проценты и масштабирование
значок/стрелка/вправо/большой размерЕдиница измерения 7
Статистика
3.
 1 Отрезки, прямые и лучи | Геометрия прямых линий
1 Отрезки, прямые и лучи | Геометрия прямых линийВы, наверное, точно знаете, что такое линия. В этой главе вы узнаете о отрезки и лучи и чем они отличаются от прямых. Вы также узнаете больше о параллельные и перпендикулярные прямые и как мы их обозначаем на диаграмме.
Отрезки, линии и лучи
Отрезки
Измерьте каждую сторону этот четырехугольник. Напишите размеры с каждой стороны.
Каждая сторона четырехугольника является отрезком .
Отрезок линии имеет определенную начальную точку и определенную конечную точку. Мы можем рисовать и измерять отрезки.
Нарисуйте отрезок длиной 12 см.
Мы можем думать о линиях, у которых нет концов, хотя мы не можем нарисовать их полностью. Мы рисуем отрезки для представления линий. Когда мы рисуем отрезок для представления линии, мы можем поставить стрелки на обоих концах, чтобы показать, что он продолжается бесконечно с обеих сторон.
Слово линия используется для обозначения линии, которая идет в обоих направлениях. Мы можем видеть и рисовать только часть линии. Линия не может быть измерена.
Проведите линию АВ.
Вы нарисовали вся линия АВ? Объяснять.
Мы также можем думать о линии, которая имеет определенную начальную точку, но бесконечно продолжается на другом конце. Это называется полулиния или луч .
Мы можем нарисовать начальную точку и часть луча, используя стрелку, чтобы указать, что он продолжается на одном конце.

Ray PQ идет вправо:
Рэй Д.С. идет влево:
Ничья луч ЭФ.
Вы нарисовали весь луч EF? Объяснять.
Соответствуют ли отрезки XY и GH в любом месте?
Соответствуют ли линии KL и NP в любом месте?
Встречаются ли где-нибудь лучи AB и CD?
Встречаются ли где-нибудь лучи FT и MW?
Встречаются ли где-нибудь лучи JK и RS?
Параллельные и перпендикулярные линии
w3.org/1999/xhtml»> Параллельные линииДве линии, находящиеся на постоянном расстоянии друг от друга, называются параллельными линиями . Линии AG и BH ниже параллельны. Символ || используется для обозначения параллельных прямых. Пишем: АГ || БХ.
Мера расстояние между двумя линиями:
в А и Б
в C и D
на E и F
Вот еще несколько параллельных линий:
Нарисуй два параллельные линии.
Нарисовать три линии которые параллельны друг другу.

Будет параллельно линии где-то встречаются?
Считаете ли вы, что прямые PQ и ST параллельны? Как можешь проверить?
Нарисуйте две линии, почти параллельные, но не довольно.
Опишите, что вы сделали для убедитесь, что ваши две линии не параллельны.
Могут ли два отрезка быть параллельно?
Отрезки DK и FS параллельны?
Отрезки MN и AB параллельны?
Что вы можете сделать, чтобы иметь возможность лучше проверить, параллельны ли два вышеупомянутых отрезка прямой или нет?
Может ли линия быть параллельной сама по себе?
Нарисуйте линию, которая параллельно линии XY выше.

Перпендикулярные линии
Линии CD и KL ниже перпендикулярны друг другу. Символ используется для обозначения перпендикулярные линии. Пишем: КД КЛ.
Сколько углы образуются в точке, где пересекаются две вышеуказанные линии?
Две прямые, образующие прямые углы, перпендикулярны друг другу.
Нарисуйте два луча с одинаковыми исходными точками.
Нарисуйте два луча, которые перпендикулярны друг другу и имеют одинаковую начальную точку.
Нарисуйте два луча которые встречаются, но не в своих начальных точках.
Нарисуй два лучи, которые встречаются, но не в своих начальных точках, и которые перпендикулярны друг друга.

Можете ли вы нарисуйте два луча, которые имеют одну и ту же начальную точку и параллельны каждому Другой?
Интерактивные математические навыки в седьмом классе
Геометрия и пространственное чувство — CCSS 6.G.A.1, 7.GB.4, 7.GB.5, 7.GB.6, 8.G.A.1, 8.G.A.1.C, 8.GB.6, 8.GB.7, 8 .G.B.8
Ссылки проверены 09.04.2018
1. Уголки. Щелкните изображение, чтобы увеличить его
Практикуйте свои знания об острых, тупых и параллельных углах. Дополнительные ресурсы находятся на вкладке ученика.  ПОДРОБНЕЕ
2. Окружности и эллипсы. Щелкните изображение, чтобы увеличить его
Разнообразные уроки и занятия по окружностям, дугам и эллипсам.  ПОДРОБНЕЕ
3. Классификация углов. Щелкните изображение, чтобы увеличить его
Пройдите онлайн-викторину с пятью вопросами для самопроверки с несколькими вариантами ответов.  ПОДРОБНЕЕ
4. Конгруэнтность. Щелкните изображение, чтобы увеличить его
Занятия и многочисленные тесты на соответствие треугольников и многоугольников.  ПОДРОБНЕЕ
5. Конструкции. Щелкните изображение, чтобы увеличить его
Построения и преобразования в плоской геометрии. Различные занятия и уроки.  ПОДРОБНЕЕ
6. Определение многоугольников.
Щелкните изображение, чтобы увеличить его
Определить количество сторон и углов многоугольника.  ПОДРОБНЕЕ
7. Измерение углов. Щелкните изображение, чтобы увеличить его
Используйте виртуальный транспортир, чтобы измерить данный угол в вопросе и выбрать правильный вариант ответа.  ПОДРОБНЕЕ
8. Назовите этот многоугольник. Щелкните изображение, чтобы увеличить его
Определите имя заданных компонентов полигона.  ПОДРОБНЕЕ
9. Параллельные линии. Щелкните изображение, чтобы увеличить его
Многочисленные уроки и примеры для практики.  ПОДРОБНЕЕ
10. Точки, линии и плоскости. Щелкните изображение, чтобы увеличить его
Многочисленные уроки, примеры и задания, включая практические задачи.  ПОДРОБНЕЕ
11. Многоугольники. Щелкните изображение, чтобы увеличить его
Многочисленные уроки, примеры и упражнения.  ПОДРОБНЕЕ
12. Пифагорейский исследователь. Щелкните изображение, чтобы увеличить его
Учащиеся находят длину стороны прямоугольного треугольника с помощью теоремы Пифагора, а затем проверяют свои ответы. Дополнительные связанные ресурсы доступны на вкладке учащегося.  ПОДРОБНЕЕ
13. Четырехугольники. Щелкните изображение, чтобы увеличить его
Многочисленные уроки, примеры и упражнения с четырехсторонними фигурами, такими как квадраты, прямоугольники, параллелограммы и т. д.  ПОДРОБНЕЕ
14. Спутниковые орбиты. Щелкните изображение, чтобы увеличить его
Ответьте на пять задач на «три спутника», а затем проверьте свой ответ, чтобы убедиться, что вы правы.  ПОДРОБНЕЕ
15. Объемная геометрия. Щелкните изображение, чтобы увеличить его
Узнайте о различных типах объемной геометрии с помощью этих различных уроков и заданий. Включает в себя кубы, пирамиды, конусы, цилиндры, сферы и т.д.  ПОДРОБНЕЕ
16. Spy Guys Interactive — площадь и периметр. Щелкните изображение, чтобы увеличить его
Смотрите видео и отвечайте в разных местах. Это видео включает в себя разделы, в которых учащимся предлагается ввести ответы.  ПОДРОБНЕЕ
17. Spy Guys Interactive – Объем и перемещение. Щелкните изображение, чтобы увеличить его
Смотрите видео и отвечайте в разных местах. Это видео включает разделы, в которых учащимся предлагается ввести ответы.  ПОДРОБНЕЕ
18. Spy Guys Interactive — работа с углами. Щелкните изображение, чтобы увеличить его
Смотрите видео и отвечайте в разных местах. Это видео включает в себя разделы, в которых учащимся предлагается ввести ответы.  ПОДРОБНЕЕ
19. Квадрат треугольника. Щелкните изображение, чтобы увеличить его
Студенты узнают, как работает теорема Пифагора, изучая стандартное геометрическое доказательство. Параметры: Размеры катетов треугольника. Дополнительные связанные ресурсы на вкладке учащегося.  ПОДРОБНЕЕ
20. Проверьте свои знания угла. 907:50 Щелкните изображение, чтобы увеличить его
Решите, какой угол изображен на каждой диаграмме.  ПОДРОБНЕЕ
21. Проверьте свои знания о треугольниках. Щелкните изображение, чтобы увеличить его
Решите, какой тип треугольника изображен на каждой диаграмме. Вопросы могут включать несколько ответов, поэтому выберите «все подходящие варианты».  ПОДРОБНЕЕ
22. Проблема многих треугольников Щелкните изображение, чтобы увеличить его
Найдите, сколько треугольников есть для каждой задачи.  ПОДРОБНЕЕ
23. Теорема Пифагора. Щелкните изображение, чтобы увеличить его
Онлайн-викторина с пятью вопросами для самопроверки с несколькими вариантами ответов.  ПОДРОБНЕЕ
24. Triangle Explorer. Щелкните изображение, чтобы увеличить его
Учащиеся узнают о площади треугольников и о декартовой системе координат, экспериментируя с треугольниками, нарисованными на сетке. (Дополнительные связанные ресурсы расположены на вкладке учащегося.)  ПОДРОБНЕЕ
25. Идентификация треугольника II. Щелкните изображение, чтобы увеличить его
Определите треугольник: равносторонний, равнобедренный и разносторонний.  ПОДРОБНЕЕ
26. Идентификация треугольника. Щелкните изображение, чтобы увеличить его
Определите треугольник: прямоугольный, остроугольный или тупоугольный.  ПОДРОБНЕЕ
27. Треугольники. Щелкните изображение, чтобы увеличить его
Многочисленные уроки, примеры и задания на треугольники. Включает площадь и периметр треугольников, типы треугольников, конгруэнтные треугольники и т. д.  ПОДРОБНЕЕ
Ключ к ответу для 7 класса Go Math Глава 8 Моделирование геометрических фигур – Ключ к ответу Go Math
Ключ к ответу для 7 класса Go Math 7 класс Глава 8 Моделирование геометрических фигур: Присоединяйтесь к списку лучших учеников с помощью Go Математика 7 класс ответ ключ. Получите доступ к бесплатному файлу «Go Math Class 7 Answer Key Chapter 8 Modeling Geometric Figures». Мы должны подготовить решения таким образом, чтобы все учащиеся могли легко понять концепцию. Быстрое и легкое обучение возможно только в нашем ключе ответов HMH Go Math.
Мы предлагаем учащимся обратиться к главе 8 «Моделирование геометрических фигур» для получения наивысшего балла на экзаменах. Это вызывает у студентов интерес к тому, чтобы стать мастером математики. Изучите понятия геометрических фигур таким образом, чтобы подготовить вопросы самостоятельно. Нажмите на прикрепленные ниже ссылки и получите пошаговое объяснение.
Глава 8 – Моделирование геометрических фигур – Урок: 1
- Практическое руководство – Страница № 240
- Независимая практика — страница № 241
- Страница № 242
Глава 8 – Моделирование геометрических фигур – Урок: 2
- Практическое руководство – Страница № 245
- Независимая практика — страница № 246
Глава 8 – Моделирование геометрических фигур – Урок: 3
- Практическое руководство – Страница № 249
- Страница № 250
Глава 8 – Моделирование геометрических фигур – Урок: 4
- Практика под руководством – Страница № 256
- Независимая практика — страница № 257
- Страница № 258
Глава 8 – Моделирование геометрических фигур
- 8.1 Чертежи подобных форм и масштабов – Страница № 259
- Выбранный ответ — страница № 260
Управляемая практика – страница № 240
Вопрос 1.
Масштаб комнаты на чертеже 3 дюйма : 5 футов. Стена на том же чертеже имеет размер 18 дюймов. Заполните таблицу.
а. Какой длины настоящая стена?
______ футов
Ответ: 30 футов
Объяснение:
Заполним таблицу, используя прямую пропорцию
3 дюйма : 5 футов
Стена на том же чертеже 18 дюймов равна 30 футам.
Вопрос 1.
б. Окно в комнате имеет фактическую ширину 2,5 фута. Найдите ширину окна на чертеже.
______ дюймов
Ответ: 1,5 дюйма
Объяснение:
Определяем количество дюймов, соответствующее 1 футу на фактическом окне
3 дюйма /5 дюймов
Умножить и разделить на 5
(3 дюйма ÷ 5)/(5 футов ÷ 5) = 0,6/1 фут
Таким образом, 1 фут соответствует 0,6 дюйма, поэтому ширина окна в таблице
2,5 × 0,6 = 1,5 дюйма
Вопрос 2.
Масштаб на чертеже 2 дюйма : 4 фута. Каковы длина и ширина реальной комнаты? Найдите площадь реальной комнаты.
Ширина: _________ футов
Длина: _________ футов
Площадь: _________ квадратных футов
Ответ:
Ширина: 28 футов
Длина: 14 футов
Площадь: 392 кв. фута
фута
Пояснение:
Определяем количество футов, соответствующее 1 дюйму на чертеже
2 дюйма/4 дюйма = (2 дюйма ÷ 2)/(4 дюйма ÷ 2) = 1/2
Таким образом, 1 дюйм соответствует 2 футам реальных размеров комнаты.
Определяем фактическую длину комнаты, обозначенную на чертеже 14 дюймов.
14 × 2 = 28 футов
Определяем фактическую ширину комнаты, обозначенную на чертеже как 7 дюймов.
7 × = 14 футов
Вычисляем площадь фактической комнаты:
28 × 14 = 392 квадратных фута.
Вопрос 3.
Масштаб на чертеже 2 см: 5 м. Какова длина и ширина реальной комнаты? Найдите площадь реальной комнаты.
Ширина: _________ м
Длина: _________ м
Площадь: _________ кв.м
Ответ:
Ширина: 25 м
Длина: 15 м
Площадь: 375 кв. 1 сантиметр на чертеже:
2 см/5 см = (2 см ÷ 2)/(5 см ÷ 2) = 1 см/2,5 м
Определяем фактическую длину помещения, обозначенную на чертеже 10 см:
10×2,5 = 25 м
Определяем фактическую ширину помещения, обозначенную на чертеже 6 см:
6×2,5 = 15 м
Мы вычислить площадь комнаты:
25 × 15 = 375 квадратных футов.
Вопрос 4.
Чертеж столовой в масштабе нарисован на бумаге с сантиметровой сеткой, как показано на рисунке. Масштаб 1 см: 4 м.
а. Перерисуйте прямоугольник на бумаге с сантиметровой сеткой, используя масштаб 1 см:6 м.
Введите ниже:
_____________
Ответ:
Вопрос 4.
b. Какова фактическая длина и ширина столовой в исходном масштабе? Каковы фактические размеры столовой в новом масштабе?
Длина: _________ м
Ширина: _________ м
Ответ:
В исходном масштабе размеры на чертеже
l1 = 9 см
w1 = 6 см
Реальную длину определяем, используя исходный масштаб:
9 × 4 = 36
Определяем фактическую ширину, используя исходный масштаб:
6×4 = 24
Во втором масштабе размеры на чертеже
l2 = 6 см
w1 = 4 см ширина с использованием исходного масштаба:
4 × 6 = 24
Таким образом, длина составляет 36 м
Ширина составляет 24 м
Основной вопрос Регистрация
Вопрос 5.
Если у вас есть точный, полный чертеж и масштаб , какие размеры объекта чертежа вы можете найти?
Введите ниже:
_____________
Ответ:
Если у нас есть точный, полный масштабный чертеж и масштаб, мы можем определить все размеры объекта, потому что все они пропорциональны размерам на чертеже, а соотношение является масштабом.
Независимая практика – Страница № 241
Вопрос 6.
Искусство
У Мари есть уменьшенная копия знаменитой картины Рене Магритта «Школьный учитель». Ее копия имеет размеры 2 дюйма на 1,5 дюйма. Масштаб копии 1 дюйм:40 см.
а. Найдите размеры исходной картины.
Длина: _________ см
Ширина: _________ см
Ответ:
Длина: 80 см
Ширина: 60 см
Пояснение:
Нам даны данные
Масштаб: 1 дюйм:40 см
Копия l1 = 2 дюйма
w1 = 1,5 дюйма
Определяем длину l исходной картины
l = 2 × 40 = 80 см
Определяем ширину w исходной картины
w = 1,5 × 40 = 60 см
Вопрос 6.
b. Найдите площадь исходной картины.
_____________ кв. см
Ответ: 4800 кв. см
Пояснение:
Определяем ширину w исходной картины
A = l.w
A = 80 × 60 = 4800 кв. см
Вопрос 6.
c. Поскольку 1 дюйм равен 2,54 сантиметра, найдите размеры исходной картины в дюймах.
Длина: _________ дюймов
Ширина: _________ дюймов
Ответ:
Определяем длину l исходной картины в дюймах:
1 дюйм = 2,54 см
l = 80/2,54 см ≈ 31,5 дюйма
Определяем ширину w исходной картины в дюймах:
w = 60/2,54 ≈ 23,6 дюйма
Вопрос 6.
d. Найдите площадь исходной картины в квадратных дюймах
_____________ кв. дюймов
Ответ: 743,4 квадратных дюйма
Объяснение:
Найдем площадь исходной картины в квадратных дюймах:
l × w = 31,5 × 23,6 = 743,4 кв. дюймов
Таким образом, площадь оригинальной картины составляет 743,4 квадратных дюйма.
Вопрос 7.
В игровой комнате есть пол размером 120 футов на 75 футов. Чертеж пола в масштабе на бумаге с сеткой использует масштаб 1 единица: 5 футов. Каковы размеры чертежа в масштабе?
Чертеж пола в масштабе на бумаге с сеткой использует масштаб 1 единица: 5 футов. Каковы размеры чертежа в масштабе?
Длина: _________ единиц
Ширина: _________ единиц
Ответ:
Длина: 24 единицы
Ширина: 15 единиц
Объяснение:
Нам даны данные: футов, w = 75 футов
Количество единиц на чертеже, соответствующее 1 футу, определяем из реальных размеров.
1 единица/5 футов
(1 единица ÷ 5)/(5 футов ÷ 5) = 0,2 единицы/1 фут
Определяем длину масштабного чертежа:
120 × 0,2 = 24 единицы
Определяем ширину чертежа в масштабе:
75 × 0,2 = 15 единиц
Вопрос 8.
Множественные представления
Длина стола 6 футов. На чертеже в масштабе длина составляет 2 дюйма. Напишите три возможных масштаба рисунка.
Введите ниже:
_____________
Ответ:
l = 6 футов
l1 = 2 дюйма
l = фактическая длина
l1 = длина на чертеже в масштабе
2 дюйма:6 футов
1 дюйм:3 фута
2/ 6×12 = 2/72 = 1/36
1 см: 36 см
Вопрос 9.
Анализ взаимосвязей
Масштаб чертежа в масштабе 10 см:1 мм. Что больше, реальный объект или чертеж в масштабе? Объяснять.
_____________
Ответ:
Нам задан масштаб
10 см: 1 мм
100 мм: 1 м
Это означает, что в реальном размере для 100 мм чертежа соответствует 1 мм, поэтому большему на чертеже соответствует фактическое расстояние меньше, поэтому чертеж в масштабе больше.
Вопрос 10.
Архитектура
Масштабная модель здания высотой 5,4 фута.
а. Если исходное здание имеет высоту 810 метров, в каком масштабе была сделана модель?
______ футов : ______ м
Ответ: 1 фут: 150 м
Объяснение:
Отметим:
h2 = высота на макете
h = фактическая высота
Нам даны данные
h2 = 5,4 фута
h = 810 метров
Определяем масштаб для модели
h2/h = 5,4 фута/810 м = (5,4 фута ÷ 5,4)/(810 ÷ 5,4)
1 фут/150 м
1 фут: 150 м
Вопрос 10.
b. Если модель сделана из крошечных кирпичиков высотой 0,4 дюйма каждый, сколько кирпичиков в высоту у модели?
___________ кирпичей
Ответ: 14 кирпичей
Пояснение:
Определяем масштаб для модели:
h2/0,4 = 5,4/0,4 = 13,5
Количество кирпичей: 14
Номер страницы 245
Вас попросили построить масштабную модель вашей школы из зубочисток.
 Представьте, что ваша школа имеет высоту 30 футов. Ваш масштаб 1 фут:1,26 см.
Представьте, что ваша школа имеет высоту 30 футов. Ваш масштаб 1 фут:1,26 см. а. Если высота зубочистки 6,3 см, сколько зубочисток будет в вашей модели?
______ зубочистки
Ответ: 6
Объяснение:
Учитывая, что
h = 30 футов
1 фут: 1,26 см модель:
h2 = 30 × 1,26 = 37,8 см
h2/6,3 = 37,8/6,3 = 6
Таким образом, количество зубочисток = 6
Вопрос 11.
б. У вашей мамы закончились зубочистки, и она предлагает вместо них использовать ватные палочки. Вы измеряете их, и они 7,6 см в высоту. Сколько ватных палочек будет в высоту у вашей модели?
______ ватных палочек
Ответ: 5
Объяснение:
Находим количество ватных палочек
h2/7,6 = 37,8/7,6 ≈ 5
Таким образом количество ватных палочек = 5
H.O.T.
Сосредоточьтесь на мышлении высшего порядка
Вопрос 12.
Сделайте выводы
Площадь квадратного пола на чертеже в масштабе составляет 100 квадратных сантиметров, а масштаб чертежа составляет 1 см : 2 фута. площадь фактического этажа? Каково отношение площади на чертеже к реальной площади?
площадь фактического этажа? Каково отношение площади на чертеже к реальной площади?
Площадь = ______ кв. футов
Ответ: 400 кв. футов
Пояснение:
A1 = площадь чертежа
A = площадь фактического пола
Нам даны данные:
A1 = 100 см²
1 см: 2 фута
1 см соответствует 2 футам
1 см × 1 см соответствует 2 футам × 2 футам
1 см² соответствует 4 футам²
A = 100. 4 = 400 футов²
Определяем отношение площадей в чертеж к фактической площади:
1 фут = 0,3048 м = 30,48 см
A1/A = 100/400 × 30,48² ≈ 0,0003
Вопрос 13.
Множественные представления
Опишите, как перерисовать чертеж в масштабе с новым масштабом.
Введите ниже:
_____________
Ответ:
Чтобы перерисовать масштабный чертеж в новом масштабе, выполняем 2 шага:
1. Находим во сколько раз новый масштаб больше или меньше старого.
2. Мы умножаем этот масштабный коэффициент на размеры старого чертежа в масштабе, чтобы получить новый чертеж.
Вопрос 14.
Представление реальных проблем
Опишите, как несколько работ или профессий могут использовать чертежи в масштабе на работе.
Введите ниже:
_____________
Ответ:
Чертежи в масштабе чрезвычайно полезны в работах, которые должны представлять большие площади на небольших устройствах, таких как
1. Архитектура/строительство
2. Медицина
3. Сельское хозяйство
4. Туризм
5. Транспорт
Практика под руководством – страница № 245
Укажите, создает ли каждая фигура условия для образования уникального треугольника, нескольких треугольников или отсутствия треугольника.
Вопрос 1.
Введите ниже:
___________
Ответ: Уникальный треугольник
Объяснение:
Даны два угла и сторона, прилежащая к ним, поэтому существует единственный треугольник, поскольку стороны, исходящие из B и A, пересекаются в уникальной точке.
Вопрос 2.
Введите ниже:
_____________
Ответ: Нет треугольника
Объяснение:
Нам даны три стороны треугольника. Проверяем, больше ли сумма любых двух сторон другой.
Проверяем, больше ли сумма любых двух сторон другой.
4 + 11 = 15 > 3
11 + 3 = 14 > 4
3 + 4 = 7 не больше 11.
Поскольку одно неравенство не проверено, треугольник не существует.
Вопрос 3.
Введите ниже:
_____________
Ответ: Уникальный треугольник
Объяснение:
Даны два угла и сторона, прилежащая к ним, поэтому существует единственный треугольник, поскольку стороны, исходящие из B и A, пересекаются в уникальная точка.
Вопрос 4.
Введите ниже:
_______
Ответ: Уникальный треугольник
Пояснение:
Нам даны три стороны треугольника. Проверяем, больше ли сумма любых двух сторон другой.
6 + 12 = 18 > 7
12 + 7 = 19 > 6
6 + 7 = 13 > 12
Поскольку все неравенства проверяются, существует единственный треугольник.
Основной вопрос Проверка
Вопрос 5.
Опишите длины трех отрезков, из которых нельзя составить треугольник.
Введите ниже:
_____________
Ответ:
Найдите длины трех отрезков, не являющихся сторонами треугольника, хотя бы одна сумма двух сторон должна быть меньше другой стороны.
Пусть a, b, c — длины трех отрезков.
a + b не > a + b + k = c
Самостоятельная практика
Вопрос 6.
На отдельном листе бумаги попробуйте нарисовать треугольник со сторонами 3 сантиметра и угол 120°. Определите, образуют ли заданные сегменты и угол уникальный треугольник, более одного треугольника или ни одного треугольника.
Введите ниже:
_____________
Ответ: Уникальный треугольник
Объяснение:
∠A = 120°
AB = 6
AC = 3
Рисуем отрезок AB, угол A и отрезок AC, затем соединяем B и C. В результате получится уникальный треугольник.
Вопрос 7.
Ландшафтный архитектор представил заказчику проект цветника треугольной формы с длинами сторон 21 фут, 37 футов и 15 футов. Объясните, почему архитектора не наняли для создания цветника.
Введите ниже:
_____________
Ответ:
Даны стороны треугольника
21 + 37 = 58 > 15
37 + 15 = 52 > 21
15 + 21 = 36 не > 37
Мы проверили три треугольника неравенства
Таким образом, треугольника не существует, поэтому архитектор не был нанят для создания цветника.
Страница № 246
Вопрос 8.
Сделайте предположение
Углы в реальном треугольном дорожном знаке все имеют меру 60°. Все углы на чертеже знака в масштабе равны 60°. Объясните, как вы можете использовать эту информацию, чтобы решить, можно ли использовать три заданные меры угла для формирования уникального треугольника или более одного треугольника.
Введите ниже:
_____________
Ответ: Три заданные угловые меры, сумма которых равна 180°, могут быть использованы для построения бесконечности треугольников, обладающих тем свойством, что их соответствующие стороны пропорциональны.
Г.О.Т.
Сосредоточьтесь на мышлении высшего порядка
Вопрос 9.
Обмен математическими идеями
На рисунке слева показан отрезок длиной 2 дюйма, образующий угол 45°, с пунктирной линией, длина которой не указана. На рисунке справа показан компас шириной 1 \(\frac{1}{2}\) дюймов с острием на верхнем конце 2-дюймового сегмента. Нарисована дуга, дважды пересекающая пунктирную линию.
Нарисована дуга, дважды пересекающая пунктирную линию.
Объясните, как вы можете использовать этот рисунок, чтобы решить, могут ли две стороны и угол, не включенный между ними, быть использованы для образования уникального треугольника, нескольких треугольников или треугольника вообще не может быть.
Введите ниже:
_____________
Ответ:
Треугольник не существует, потому что одна сторона короче двух других сторон. Окружность пересекает пунктирную линию только один раз, так что один угол равен 45 °, поэтому есть только одно решение. Окружность с центром в B дважды пересекает пунктирную линию, таким образом, образуются два треугольника.
Вопрос 10.
Критическое мышление
Две стороны равнобедренного треугольника имеют длину 6 дюймов и 15 дюймов соответственно. Найдите длину третьей стороны. Объясните свои рассуждения.
_______ дюймов
Ответ: 15 дюймов
Объяснение:
Даны две стороны равнобедренного треугольника
a = 6
b = 15
Есть две возможности, что третья сторона равна a или b. Изучим их оба
Изучим их оба
Случай 1: a = c = 6, b = 15
a + c = 6 + 6 = 12 не более 15 = b
Проверяем три неравенства треугольника
a + b = 6 + 15 = 21 > 15 = c
a + c = 6 + 15 = 21 > 15 = b
b + c = 15 + 15 = 30 > 6 = a
Случай 2: a = 6, b = c = 15.
Таким образом, третья сторона треугольника равна 15.
Вопрос 1.
Введите ниже:
_____________
Ответ: Треугольник/Четырехугольник
Данное поперечное сечение в кубе является треугольником/равносторонним треугольником.
Вопрос 2.
Введите ниже:
_____________
Ответ: Прямоугольник
Данное поперечное сечение в цилиндре является прямоугольником.
Вопрос 3.
Введите ниже:
_____________
Ответ: Треугольник
Пояснение:
Данное поперечное сечение в призме является треугольником.
Вопрос 4.
Введите ниже:
_______
Ответ: Радужная кривая
Данное поперечное сечение в конусе представляет собой радужную кривую.
Основной вопрос Проверка
Вопрос 5.
Каков первый шаг в описании того, какая фигура получается, когда данная плоскость пересекает данную трехмерную фигуру?
Введите ниже:
_____________
Ответ:
Первым шагом в описании того, какая фигура получается, когда данная плоскость пересекает данную трехмерную фигуру, является определение количества сторон, которые имеет поперечное сечение.
Независимая практика
Вопрос 6.
Опишите различные способы пересечения плоскостью цилиндра и полученное поперечное сечение.
Введите ниже:
_____________
Ответ:
Сечение может быть:
1. Окружность
2. Эллипс
3. Прямоугольник
№ страницы 250
2 Вопрос 34. Какие поперечные сечения вы можете увидеть, когда плоскость пересекает конус, и какие вы не увидите, когда плоскость пересекает пирамиду или призму?
Введите ниже:
_____________
Ответ:
Сечение может быть:
1. Окружность
Окружность
2. Эллипс
3. Парабола
4. Гипербола
5. Треугольник
Г.О.Т.
Сосредоточьтесь на мышлении высшего порядка
Вопрос 8.
Критическое мышление
Два рисунка слева внизу показывают, что вы можете составить поперечное сечение куба, который представляет собой пятиугольник. Представьте себе плоскость, разрезающую куб под углом таким образом, чтобы разрезать пять из шести граней куба. Нарисуйте пунктирные линии на третьем кубе, чтобы показать, как сформировать поперечное сечение в виде шестиугольника.
Введите ниже:
_____________
Ответ:
Рисуем плоскость, разрезающую куб так, чтобы сечение было шестиугольником: для этого берем середину 6 смежных сторон:
Вопрос 9.
Анализ отношений
Сфера имеет радиус 12 дюймов. Горизонтальная плоскость проходит через центр сферы.
а. Опишите поперечное сечение, образованное плоскостью и сферой
Введите ниже:
_____________
Ответ: Круг
Объяснение:
Дана сфера и сечение, проходящее через центр сферы:
Сечение, проходящее через центр сферы, представляет собой окружность, радиус которой равен радиусу сферы.
Вопрос 9.
б. Опишите поперечные сечения, образующиеся при пересечении плоскостью внутренней части сферы, но при удалении от центра.
Введите ниже:
_____________
Ответ: Поперечные сечения, образованные плоскостью, пересекающей внутреннюю часть сферы вне центра, представляют собой окружности.
Вопрос 10.
Сообщать математические идеи
Прямоугольная призма пересекается горизонтальной и вертикальной плоскостями. Поперечное сечение, образованное горизонтальной плоскостью и призмой, представляет собой прямоугольник с размерами 8 дюймов и 12 дюймов. Поперечное сечение, образованное вертикальной плоскостью и призмой, представляет собой прямоугольник с размерами 5 дюймов и 8 дюймов. Опишите грани призмы, включая их размеры. Затем найдите его объем.
Введите ниже:
_____________
Ответ: 480 кубических дюймов
Пояснение:
Горизонтальное сечение имеет размеры 8×12, а вертикальное 5×8.
Призма имеет размеры:
5 дюймов, 8 дюймов, 12 дюймов
Находим объем призмы:
5 × 8 × 12 = 480 кубических дюймов
Вопрос 11. мировая ситуация, которая может быть представлена плоскостями, разрезающими трехмерную фигуру, образуя поперечные сечения.
мировая ситуация, которая может быть представлена плоскостями, разрезающими трехмерную фигуру, образуя поперечные сечения.
Введите ниже:
_____________
Ответ:
Примеры реальных ситуаций, которые могут быть представлены плоскостями, разрезающими трехмерные фигуры в поперечные сечения:
– электрические провода
– водопроводные/газовые трубы
– проект дома
– геология
– сейсмология
Практическое руководство – страница № 256
Для 1–2 используйте рисунок.
Вопрос 1.
Словарь
Сумма мер ∠UWV и ∠UWZ равна 90°, поэтому ∠UWV и ∠UWZ составляют _____ углов.
Введите ниже:
_____________
Ответ: Дополнительные углы
Объяснение:
Сумма ∠UWV и ∠UWZ равна 90°, поэтому ∠UWV и ∠UWZ являются дополнительными углами.
Вопрос 2.
Словарь
∠UWV и ∠VWX имеют общую вершину и одну сторону. Они не перекрываются, поэтому ∠UWV и ∠VWX — это _____ углы.
Введите ниже:
_____________
Ответ: Смежные углы
Объяснение:
∠UWV и ∠VWX имеют общую вершину и одну сторону. Они не перекрываются, поэтому ∠UWV и ∠VWX являются смежными углами.
Они не перекрываются, поэтому ∠UWV и ∠VWX являются смежными углами.
Для 3–4 используйте рисунок.
Вопрос 3.
∠AGB и ∠DGE являются _____ углами, поэтому m∠DGE = _____.
Введите ниже:
_____________
Ответ: ∠AGB и ∠DGE — вертикальные углы, поэтому m∠DGE = m∠AGB = 30°
Вопрос 4.
Найдите величину ∠EGF.
_______ °
Ответ: 100°
Объяснение:
m∠CGD + m∠DGE + m∠EGF = 180°
50° + m∠AGB + m∠EGF = 180°
50° + 30° + 2x = 180°
2x = 180° – 80°
2x = 100°
мм∠EGF = 2x = 100°
Вопрос 5.
Найдите значение x и меру ∠MNQ.
х = _______ °
mMNQ = _______ °
Ответ:
∠MNQ + ∠QNP = 90°
3x – 13° + 58° = 90°
3x = 90° + 13° – 58° 3 х 9073 4 °
x = 15°
м∠MNQ = 3x – 13°
= 3×15° – 13°
= 45° – 13°
= 32° Предположим, вы знаете, что ∠T и ∠S являются дополнительными и что m∠T = 3(m∠S). Как найти m∠T?
Введите ниже:
_____________
Ответ:
м∠T + m∠S = 180°
м∠T = 3(m∠S)
м∠S = m∠T/3
Из второго уравнения напишем m ∠S в единицах м∠T
m∠T + m∠T/3 = 3 × 180°
3m∠T + m∠T = 3 × 180°
4m∠T = 540°
м∠T = 540° /4
м∠T = 135°
Независимая практика – № страницы 257
Для 7–11 используйте рисунок.
Вопрос 7.
Назовите пару смежных углов. Объясните, почему они рядом.
Введите ниже:
_____________
Ответ:
Пара смежных углов:
∠SUR и ∠RUN (общая вершина U и одна общая сторона – UR – без перекрытия)
∠NUQ и ∠QUP (общая вершина U и одна общая сторона – UQ – без наложения)
∠PUT и ∠TUS (общая вершина U и одна общая сторона – UT – без наложения)
Вопрос 8.
Назовите пару острых вертикальных углов.
Введите ниже:
_____________
Ответ:
Глядя на рисунок выше, мы можем сказать, что ∠SUR и ∠PUQ — вертикальные углы.
Вопрос 9.
Назовите пару дополнительных углов.
Введите ниже:
_____________
Ответ:
На приведенном выше рисунке показано, что ∠SUR и ∠RUQ являются дополнительными углами.
Вопрос 10.
Обоснование рассуждений
Найти m∠QUR. Обосновать ответ.
_______ °
Ответ:
Мы должны найти m∠QUR.
∠SUR и ∠QURдополнительные углы.
м∠SUR + m∠QUR = 180°
м∠QUR + 41° = 180°
м∠QUR = 180° – 41°
м∠QUR = 139°
Вопрос 11.
Сделайте выводы
Что больше, m∠TUR или m∠RUQ? Объяснять.
Введите ниже:
_____________
Ответ:
m∠QUR = 139°
m∠TUR = m∠TUS + m∠SUR
90° + 41° = 131°
Находим m∠TUR
139° > 139°
m∠QUR > m∠TUR
Для 12–13 используйте рисунок. Велосипедная дорожка пересекает дорогу, как показано на рисунке. Решите для каждой указанной угловой меры или переменной.
Вопрос 12.
х = ?
_______ °
Ответ: х = 21°
Пояснение:
∠KMI и ∠HMG вертикальны, следовательно, конгруэнтны.
Определяем x:
84° = 4x
4x = 84°
x = 84°/4
x = 21°
Вопрос 13.
м∠KMH = ?
_______ °
Ответ: 96°
Объяснение:
∠KMI и ∠KMH являются дополнительными.
Определяем m∠KMH:
m∠KMH + m∠KMI = 180°
m∠KMH + 84° = 180°
m∠KMH = 180° – 84°
m∠KMH = 96°
6 Для
6 –16, используйте рисунок. Решите для каждой указанной угловой меры.
Решите для каждой указанной угловой меры.
Вопрос 14.
м∠CBE = ?
_______ °
Ответ: 118°
Объяснение:
Определяем m∠CBE:
m∠CBE + m∠EBF = 180°
m∠CBE + 62°= 180°
m∠CBE = 180° °
м∠CBE = 118°
Вопрос 15.
м∠ABF = ?
_______ °
Ответ: 28°
Объяснение:
Определяем m∠ABF
m∠ABF + m∠EBF = 90°
m∠ABF + 62° = 90°
m∠ABF = 90° – 62°
м∠ABF = 28°
Вопрос 16.
м∠CBA = ?
_______ °
Ответ: 152°
Объяснение:
Определяем m∠CBA
m∠CBA = m∠DBF = m∠DBE + m∠EBF
90° + 62° = 152°
m∠2CBA = 152°
m∠2CBA °
Вопрос 17.
Размер ∠A на 4° больше размера ∠B. Два угла дополняют друг друга. Найдите величину каждого угла.
мА = __________ °
мБ = __________ °
Ответ:
мА = 47°
мБ = 43°
Пояснение:
Нам даны данные:
м∠А = м∠В + 4°
м∠А + м∠В = 90°
м∠B + 4° + м∠B = 90°
2м∠B = 90° – 4°
2м∠B = 86°
м∠B = 86°/2
м∠B = 43°
m∠A = m∠B + 4°
m∠A = 43° + 4°
m∠A = 47°
Вопрос 18.
Мера ∠D в 5 раз больше меры ∠E. Два угла являются дополнительными. Найдите величину каждого угла.
mD = __________ °
mE = __________ °
Ответ:
mD = 150°
mE = 30°
Пояснение:
Нам даны данные
m∠D = 5(m∠E)
m∠D + м∠Е = 180°
5(m∠E) + m∠E = 180°
6 м∠E = 180°
м∠E = 180°/6
м∠E = 30°
м∠D = 5(m∠E)
m∠D = 5 × 30°
m∠D = 150°
Номер страницы 258
Вопрос 19.
Астрономия
Астрономы иногда используют угловые измерения, разделенные на градусы, минуты и секунды. Один градус равен 60 минутам, а одна минута равна 60 секундам. Предположим, что ∠J и ∠K дополняют друг друга, и что мера ∠J составляет 48 градусов, 26 минут, 8 секунд. Какова мера ∠K?
_______ ° _______ ‘ _______ »
Ответ: 41° 33 ‘ 52″
Пояснение:
Нам даны данные 90° – 48° 26 ‘ 8″
89°60′ – 48° 26 ‘ 8″
89°59’60” – 48° 26 ‘ 8″ = 41° 33 ‘ 52″
Таким образом, мера ∠K равна 41° 33 ’52″
Г. О.Т.
О.Т.
Сосредоточьтесь на мышлении высшего порядка
Вопрос 20.
Представление реальных проблем
Железнодорожные пути встречаются с дорогой, как показано на рисунке. Город разрешит парковку под углом K, если угол K больше 38°. Можно ли построить парковку под углом K? Почему или почему нет?
_______
Ответ:
m∠K = 180° – 50° – 90° = 40°
Поскольку m∠K = 40°> 38°, можно построить парковку.
Вопрос 21.
Обоснуйте рассуждения
Кендра говорит, что она может нарисовать ∠A и ∠B так, что m∠A равно 119°, а ∠A и ∠B являются дополнительными углами. Ты согласен или несогласен? Объясните свои рассуждения.
_______
Ответ:
Нам даны данные
м∠А = 119°
м∠А + м∠В = 90°
м∠В = 90° – м∠А
= 90° – 119° = — 29°
Поскольку m∠B < 0, Кендра ошибается, она не может провести углы.
Вопрос 22.
Сделайте выводы
Если два угла дополнительны, то каждый угол называется дополнением другого. Если два угла являются дополнительными, то каждый угол называется дополнением другого.
Если два угла являются дополнительными, то каждый угол называется дополнением другого.
а. Предположим, что m∠A = 77°. Какова мера дополнения дополнения к ∠A? Объяснять.
_______ °
Ответ: 77°
Объяснение:
90° – (90° – m∠A) = 90° – (90° – 77°)
90° – 77° = 13°
77°
Вопрос 22.
б. Какой вывод можно сделать о дополнении дополнения угла? Объяснять.
Введите ниже:
_____________
Ответ:
Дополнением к углу является сам угол:
90° – (90° – m∠A)
90° – 90° + m∠A
8.1 Аналогично Формы и чертежи в масштабе – страница № 259
Вопрос 1.
Чертеж дома имеет масштаб 1 дюйм : 4 фута. Длина и ширина каждой комнаты в реальном доме показаны в таблице. Заполните таблицу, найдя длину и ширину каждой комнаты на чертеже.
Введите ниже:
_____________
Ответ:
Таким образом, на каждые 4 фута фактического размера приходится 1 дюйм чертежа.
8.2 Геометрические чертежи
Вопрос 2.
Можно ли составить треугольник со сторонами 8 см, 4 см и 12 см?
______
Ответ:
Даны длины сторон
8 + 12 = 20 > 4
4 + 12 = 16 > 8
8 + 4 не > 12
Так как одно из неравенств не проверяется, то три заданные стороны длины не могут образовывать треугольник.
Вопрос 3.
Стороны треугольника равны 11 см и 9 см. Какой может быть величина третьей стороны, 20 см или 15 см?
______
Ответ: 15 см
Объяснение:
Нам известны длины сторон
11, 9
11 + 9 = 20 не > 20 неравенств не проверяется, три заданные длины сторон не могут образовывать треугольник.
11, 9, 15
11 + 9 = 20 > 15
11 + 15 = 26 > 9
15 + 9 = 24 > 11
Проверяем, что неравенства треугольника проверяются, 15 может быть значением третьей стороны.
8.3 Сечения
Вопрос 4.
Назовите одно возможное сечение шара.
Введите ниже:
_____________
Ответ: Окружность
Одним из возможных сечений сферы является окружность.
Вопрос 5.
Назовите не менее двух фигур, являющихся поперечными сечениями цилиндра.
Введите ниже:
_____________
Ответ: Три возможных сечения цилиндра: круг, эллипс и прямоугольник.
Основной вопрос Проверка
Вопрос 5.
Как моделировать геометрические фигуры для решения реальных задач?
Введите ниже:
_____________
Ответ: Вы можете моделировать геометрию для создания зданий и небоскребов, а также магазинов.
8.4 Соотношение углов
Вопрос 6.
∠BGC и ∠FGE являются _____ углами, поэтому m∠FGE = _____
_____ °
Ответ: ∠BGC и ∠FGE — вертикальные углы, поэтому m∠FGE = m∠BGC = 90° – 40° = 50°
Вопрос 7.
Предположим, вы знаете, что ∠S и ∠Y равны комплементарны, и что m∠S = 2(m∠Y) – 30°. Найдите m∠Y.
m?Y = _____ °
Ответ: 40°
Объяснение:
m∠S + m∠Y = 90°
m∠S = 2(m∠Y) – 30°
Заменим выражение m∠ S из второго уравнения в первое можно найти m∠Y
2(m∠Y) – 30° + m∠Y = 90°
3m∠Y = 90° + 30°
3m∠Y = 120°
м∠Y = 120°/3
м∠Y = 40°
Выбранный ответ – Страница № 260
Вопрос 1.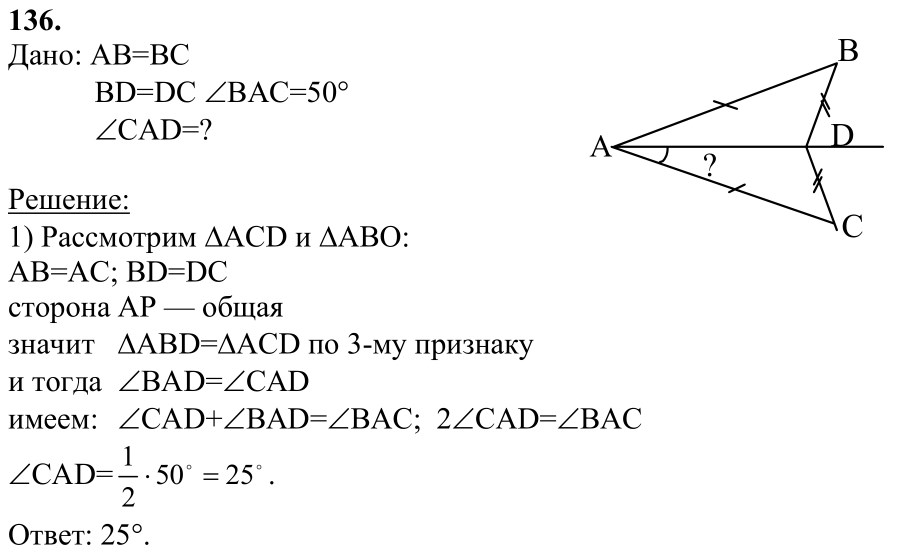
Какое число нужно прибавить к 15, чтобы получить в сумме 0?
Опции:
а. -10
б. -15
г. 0
д. 15
Ответ: -15
Объяснение:
Число, которое мы прибавляем к числу, чтобы получить сумму нуля, является его противоположностью. В противном случае к 15 нужно прибавить -15.
15 + (-15) = 0
Таким образом, правильный ответ — вариант Б.
Вопрос 2.
Учащиеся рисуют декорации к школьному спектаклю. Фон имеет ширину 15 футов и высоту 10 футов. Каждые 16 дюймов на чертеже в масштабе соответствуют 5 футам на фоне. Какова площадь масштабного чертежа?
Опции:
а. 150 в 2
б. 6 в 2
в. 3096
д. 1536 в 2
Ответ: 1536 в 2
Объяснение:
Нам даны размеры l и w фона и масштаб чертежа:
l = 15 футов
w = 10 футов
1 6 дюймов 1 футов
16 дюймов/5 футов = (16 дюймов ÷ 5)/(5 футов ÷ 5) = 3,2 дюйма/1 фут
l1 = 15 × 3,2 = 48 дюймов
w1 = 10 × 32 = 320 дюймов
l1 × w1 = 48 × 32 = 1536 квадратных дюймов
Таким образом, правильный ответ — вариант D.
Вопрос 3.
Две стороны треугольника равны 8 см и 12 см. Что из следующего НЕ МОЖЕТ быть мерой третьей стороны?
Опции:
а. 4
б. 12
г. 8
д. 16
Ответ: 4 см
Пояснение:
Даны две стороны треугольника
а. 4
4 + 8 не > 12
б. 12
12 + 8 > 12
12 + 12 > 8
в. 8
8 + 8 > 12
8 + 12 > 12
d. 16
8 + 12 > 16
8 + 16 > 12
12 + 16 > 8
Таким образом, единственным размером, который не может быть мерой третьей стороны треугольника, является 4 см.
Таким образом, правильный ответ — вариант А.
Вопрос 4.
Сечением называется пересечение трехмерной фигуры и _____ .
Опции:
а. точка
б. самолет
в. строка
д. set
Ответ: Плоскость
Объяснение:
Сечение — это взаимодействие трехмерной фигуры и плоскости.
Таким образом, правильный ответ — вариант Б.
Для 5–6 используйте схему.
Вопрос 5.
Какова мера ∠BFC?
Опции:
а. 18
б. 108
г. 72
д. 144
Ответ: 108°
Объяснение:
∠BFC + ∠BFA = 180°
∠BFC + 72° = 180°
∠BFC = 180° – 72°
∠BFC = 108 ∠BFA являются дополнительными. Определяем ∠BFC.
Таким образом, правильный ответ — вариант B.
Вопрос 6.
Что описывает взаимосвязь между ∠BFA и ∠CFD?
Опции:
а. смежные углы
б. дополнительные углы
c. дополнительные углы
d. вертикальные углы
Ответ: вертикальные углы
Объяснение:
Углы ∠BFA и ∠CFD являются вертикальными углами, поскольку они представляют собой противоположные углы, образованные при пересечении двух прямых.
Таким образом, правильный ответ – вариант D.
Вопрос 7.
На всю одежду скидка 15%. Какое выражение представляет новую розничную цену?
Опции:
а. 0,85x
б. 1,15x
в. 1,85х
д. 0,15x
Ответ: 0,85x
Объяснение:
x = начальная цена
Поскольку цена снизилась на 15%, новая цена будет уменьшена на 15/100 x
x – 0,15x = 0,85x
Таким образом, правильный ответ – вариант А.
Мини-задания
Вопрос 8.
Ира построил модель Великой пирамиды в Египте для школьного проекта. Великая пирамида имеет квадратное основание со сторонами длиной 756 футов. Высота Великой пирамиды составляет 481 фут. Айра построил свою модель пирамиды в масштабе 1 дюйм: 20 футов.
а. Какова длина каждой стороны основания пирамиды Иры?
_____ in
Ответ: 37,8 дюйма
Мы вычисляем количество дюймов, соответствующее 1 футу, исходя из фактических размеров:
1 дюйм/20 футов = (1 дюйм ÷ 20)/(20 футов ÷ 20) = 0,05 дюйма /1 фут.
0,05 дюйма соответствует 1 футу.
Определяем длину основания пирамиды Иры:
756 × 0,05 = 37,8 дюйма
Вопрос 8.
б. Чему равна площадь основания пирамиды Иры?
_____ квадратных дюймов
Ответ: 1428,84 квадратных дюйма
Объяснение:
Определяем площадь основания пирамиды Иры:
37,8 × 37,8 = 1428,84 квадратных дюйма.
Вопрос 8.
c. Какова высота пирамиды Иры?
_____ в
Ответ:
Определяем высоту пирамиды Иры:
481 × 0,05 = 24,05 дюйма
Вопрос 8.
d. Ира построил свою модель, используя поперечные сечения, которые были вырезаны параллельно основанию. Какой формы было каждое поперечное сечение?
Введите ниже:
____________
Ответ: Сечения, параллельные основанию, имеют форму квадрата.
Заключение:
Таким образом, подготовьте своих детей, заставив их попрактиковаться в тесте с помощью Ключа ответов для 7 класса Go Math Глава 8 Моделирование геометрических фигур. Получите решения для всех вопросов с помощью простых приемов для всех глав Go Math Answer Key. Удачи!!!
Цели для 7 класса. Проект «Подключенная математика»
Формы и конструкции: двумерная геометрия
Свойства многоугольников:
Понимание свойств многоугольников, влияющих на их форму.- Узнайте, как многоугольники сортируются в семейства по количеству и длине сторон и величине углов
- Исследуйте закономерности между внутренними и внешними углами многоугольника
- Исследуйте закономерности между длинами сторон многоугольника
- Исследуйте симметрию формы-вращения или отражения
- Определить, какие полигоны подходят друг другу для покрытия плоской поверхности и почему
- Обоснование и решение проблем, связанных с различными полигонами
Отношения между углами:
Понимание особых отношений между углами.
- Исследование методов оценки и измерения углов
- Использование инструментов для рисования углов
- Рассуждение о свойствах углов, образованных параллельными прямыми и секущими
- Использование информации о дополнительных, дополнительных, вертикальных и смежных углах в фигуре для решения неизвестного угла в многошаговой задаче
Построение многоугольников:
Понимание свойств, необходимых для построения многоугольников.- Рисование или набросок многоугольников с заданными условиями с использованием различных инструментов и методов, таких как от руки, использование линейки и транспортира, а также использование технологий
- Определите, какие условия будут создавать уникальный многоугольник, более одного многоугольника или отсутствие многоугольника, особенно треугольники и четырехугольники
- Распознавать особые свойства многоугольников, такие как сумма углов, отношение длины сторон и симметрия, которые делают их полезными в строительстве, дизайне и природе
- Решить задачи, связанные со свойствами фигур
Подчеркните отрицательное: целые числа и рациональные числа
Рациональные числа:
Развивайте понимание рациональных чисел, включая отрицательные рациональные числа.
- Изучение взаимосвязей между положительными и отрицательными числами путем моделирования их на числовой прямой
- Используйте соответствующие обозначения для обозначения положительных и отрицательных чисел
- Сравнивать и упорядочивать положительные и отрицательные рациональные числа (целые числа, дроби, десятичные дроби и ноль) и располагать их на числовой прямой
- Распознавать и использовать взаимосвязь между числом и его противоположностью (аддитивная инверсия) для решения задач
- Соотнести направление и расстояние с числовой прямой
- Использование моделей и рациональных чисел для представления и решения задач
Операции с рациональными числами:
Развивать понимание операций с рациональными числами и их свойств.- Разработка и использование различных моделей (числовой прямой, модели чипа) для представления сложения, вычитания, умножения и деления
- Разработка алгоритмов сложения, вычитания, умножения и деления целых чисел
- Интерпретировать и писать математические предложения, чтобы показать отношения и решить проблемы
- Напишите и используйте связанные семейства фактов для сложения/вычитания и умножения/деления для решения простых уравнений
- Использование скобок и порядка операций в вычислениях
- Понимание и использование переместительного свойства для сложения и умножения
- Применение свойства распределения для упрощения выражений и решения проблем
Растяжение и сжатие: Понимание сходства
Похожие фигуры:
Поймите, что означает сходство фигур.
- Найдите похожие фигуры, сравнив соответствующие стороны и углы
- Используйте масштабные коэффициенты и отношения для описания отношений между длинами сторон, периметрами и площадями подобных фигур
- Обобщить свойства подобных фигур
- Признать роль умножения в отношениях подобия
- Распознать взаимосвязь между масштабным коэффициентом и соотношением в подобных фигурах
- Использование неформальных методов, коэффициентов масштабирования и геометрических инструментов для построения подобных фигур (чертежей в масштабе)
- Сравнение похожих фигур с непохожими фигурами
- Различать алгебраические правила, которые дают похожие фигуры, от тех, которые дают неподобные фигуры
- Используйте алгебраические правила для получения подобных фигур
- Распознавать, когда правило уменьшает или увеличивает цифру
- Исследуйте влияние на изображение фигуры добавления числа к координатам x или y вершин фигуры
Рассуждения с похожими фигурами Разработайте стратегии использования похожих фигур для решения задач.

- Используйте свойства подобия для нахождения расстояний и высот, которые нельзя измерить напрямую
- Предсказать, как растяжение или сжатие фигуры повлияет на длины сторон, меры углов, периметры и площади
- Используйте масштабные коэффициенты или отношения, чтобы найти недостающие длины сторон в паре подобных фигур
- Используйте сходство для решения реальных проблем
Сравнение и масштабирование: соотношения, доли, проценты и доли
Соотношения, доли и проценты:
Понимание соотношений, долей и процентов.- Использование соотношений, ставок, дробей и процентов для записи выражений, сравнивающих две величины в заданной ситуации
- Различать и использовать отношения части к части и части к целому в сравнениях
- Использование процентов для выражения соотношений и пропорций
- Знать, что скорость – это особый коэффициент, с помощью которого сравниваются два измерения в разных единицах
- Анализ сравнительных заявлений, сделанных в отношении количественных данных, на правильность и качество
- Выносить суждения о том, какие утверждения сравнения являются наиболее информативными или лучше всего отражают конкретную точку зрения в конкретной ситуации
Пропорциональность:
Понимание пропорциональности в таблицах, графиках и уравнениях.
- Признать, что постоянный рост в таблице, графике или уравнении связан с пропорциональными ситуациями
- Напишите уравнение для представления закономерности в виде таблицы или графика пропорционально связанных переменных
- Свяжите единичную норму и константу пропорциональности с уравнением, графиком или таблицей, описывающей пропорциональную ситуацию
Рассуждение пропорционально:
Разработайте и используйте стратегии для решения задач, требующих пропорционального мышления.- Распознавать ситуации, в которых пропорциональное рассуждение подходит для решения проблемы
- Масштабируйте соотношение, долю, процент или дробь, чтобы выполнить сравнение или найти эквивалентное представление
- Используйте различные стратегии для нахождения неизвестного в пропорции, включая масштабирование, таблицы ставок, процентные столбцы, удельные ставки и эквивалентные отношения
- Настройка и решение пропорций, возникающих в реальных приложениях, таких как поиск скидок и надбавок и преобразование единиц измерения
Движение прямо вперед: линейные отношения
Линейные отношения:
Распознавание проблемных ситуаций, в которых две или более переменных имеют линейную связь друг с другом.
- Определите и опишите закономерности изменения между независимыми и зависимыми переменными для линейных взаимосвязей, представленных таблицами, графиками, уравнениями или контекстными настройками
- Построение таблиц, графиков и символьных уравнений, представляющих линейные отношения
- Определите скорость изменения между двумя переменными и точками пересечения x и y из графиков, таблиц и уравнений, представляющих линейные отношения
- Преобразование информации о линейных отношениях, представленной в контексте, таблице, графике или уравнении, в одну из других форм
- Напишите уравнения, представляющие линейные отношения с учетом конкретных фрагментов информации, и опишите, какую информацию представляют переменные и числа
- Установите связь между уклоном как отношением расстояния по вертикали к расстоянию по горизонтали между двумя точками на линии и скоростью изменения между двумя переменными, имеющими линейную зависимость
- Признать, что y = m x представляет собой пропорциональную зависимость
- Решать проблемы и принимать решения о линейных отношениях, используя информацию, представленную в таблицах, графиках и уравнениях
Эквивалентность:
Поймите, что знак равенства указывает, что два выражения эквивалентны.
- Знайте, что уравнение y = m x + b представляет собой линейную зависимость и означает, что m x + b является выражением, эквивалентным y
1
- Признайте, что линейные уравнения в одном неизвестном, K = MX + B или Y = M ( T ) + B , где K , T , M , K , T , M , K , T , 21121121, , K , T ,
, , K , T , , . , а b — постоянные числа, частные случаи уравнения г = м х + б - Знайте, что нахождение пропущенного значения одной из переменных в линейной зависимости, y = m x + b , равнозначно нахождению пропущенной координаты точки ( x , y ), которая лежит на графе отношения
- Решение линейных уравнений с одной переменной с использованием символьных методов, таблиц и графиков
- Признать, что линейное неравенство с одним неизвестным связано с линейным уравнением
- Решение линейных неравенств с помощью графиков или алгебраических рассуждений
- Решение линейных неравенств с помощью графиков или алгебраических рассуждений
- Запись и интерпретация эквивалентных выражений
Что вы ожидаете?: Вероятность и ожидаемое значение
Экспериментальные и теоретические вероятности:
Изучение и изучение основных концепций вероятности и понимание того, что вы можете строить модели вероятностей, собирая данные из экспериментов (экспериментальная вероятность) и анализируя возможные равновероятные исходы (теоретическая вероятность).
- Признать, что вероятности полезны для предсказания того, что произойдет в долгосрочной перспективе
- Для события, описанного повседневным языком, определите исходы в выборочном пространстве, которые составляют событие
- Интерпретировать экспериментальные и теоретические вероятности и отношения между ними и признавать, что экспериментальные вероятности являются лучшими оценками теоретических вероятностей, когда они основаны на больших числах
- Различать равновероятные и неравновероятные исходы путем сбора данных и анализа экспериментальных вероятностей
- Поймите, что вероятность простых событий — это доля исходов в выборочном пространстве, для которых происходит событие
- Признать, что вероятность случайного события — это число от 0 до 1, которое выражает вероятность наступления события
- Аппроксимировать вероятность случайного события, собирая данные о случайном процессе, который его производит, и наблюдая его долгосрочную относительную частоту, и предсказывать приблизительную относительную частоту, учитывая вероятность
- Определить честность игры
Рассуждение с вероятностью:
Исследуйте и разрабатывайте вероятностные модели, определяя возможные результаты и анализируя вероятности для решения проблем.
- Разработайте единую вероятностную модель, назначив всем исходам равную вероятность, и используйте эту модель для определения вероятностей событий
- Разработайте вероятностную модель (которая может быть неоднородной) путем наблюдения частот в данных, полученных в результате случайного процесса
- Представление выборочных пространств для простых и составных событий и поиск вероятностей с использованием упорядоченных списков, таблиц, древовидных диаграмм, моделей областей и моделирования
- Поймите, что, как и в случае с простыми событиями, вероятность составного события представляет собой долю исходов в выборочном пространстве, для которого происходит составное событие
- Разработка и использование моделирования для генерации частот для простых и сложных событий
- Анализ ситуаций, включающих два этапа (или два действия)
- Использование моделей областей для анализа теоретических вероятностей двухэтапных исходов
- Анализ ситуаций, связанных с биномиальными исходами
- Использование вероятности для расчета долгосрочного среднего значения азартной игры
- Определить ожидаемое значение вероятностной ситуации
- Использовать вероятность и ожидаемое значение для принятия решения
Наполнение и упаковка: трехмерное измерение
Площадь поверхности и объем многоугольных призм и цилиндров: Понимание площади поверхности и объема призм и цилиндров и того, как они связаны между собой.

- Описывать призмы, используя их вершины, грани и ребра
- Визуализация трехмерных фигур и эффектов разделения этих фигур плоскостями
- Углубить понимание объема и площади поверхности прямоугольных призм
- Оценка и расчет площади поверхности и объема многоугольных призм путем их соотнесения с прямоугольными призмами
- Изучение взаимосвязи между площадью поверхности и объемом призм
- Связь площади поверхности и объема для обычных фигур, особенно оптимизация площади поверхности для фиксированного объема
- Прогнозировать влияние масштабирования размеров на линейные, площадные и объемные меры цилиндров и объемных фигур
- Исследовать взаимосвязь между объемом и площадью поверхности призм и цилиндров
- Использование объема и площади поверхности призм для разработки формул объема и площади поверхности цилиндров
- Обнаружить, что объемы призм и цилиндров можно рассчитать как произведение высоты на площадь основания
- Решать задачи на вопросы о площади поверхности и объеме объемных фигур
Площадь и окружность кругов: Понимание площади и окружности кругов и того, как они связаны.
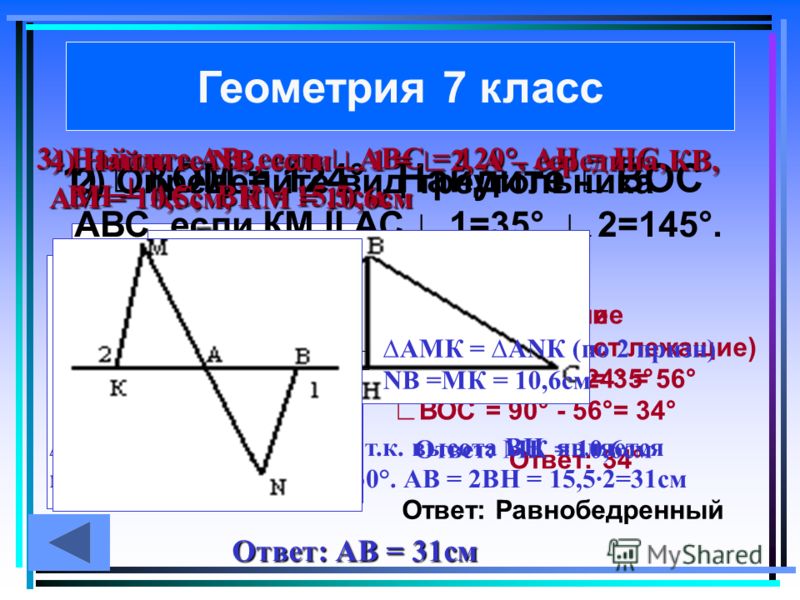
- Отношение площади круга к покрытию фигуры и длины окружности к окружности фигуры
- Оценка и вычисление площади и длины окружности
- Исследуйте взаимосвязь между радиусом (и диаметром) окружности и площадью
- Исследуйте связь числа π с вычислением площади, оценив количество «квадратов радиуса», необходимых для покрытия круга
- Исследуйте взаимосвязь между площадью и длиной окружности
- Решайте задачи на вопросы о площади и длине окружности
Объем сфер, конусов и пирамид: понять взаимосвязь между объемом цилиндров и конусов, сфер и пирамид.
- Отношение объема цилиндров к объему конусов, сфер
- Оценка и расчет объема сфер, конусов и пирамид
- Соотнесите объем конусов с объемом цилиндров и объем пирамид с объемом призм
- Решать задачи, связанные с площадью поверхности и объемом сфер, конусов и пирамид
Выборки и совокупности: сравнение и прогнозирование
Процесс статистического исследования: Понимание и использование процесса статистического исследования.

- Постановка вопросов, сбор и анализ данных и интерпретация ответов на вопросы
- Применение руководства по описанию распределений в качестве инструмента, который следует использовать на этапах анализа и интерпретации процесса статистического исследования
- Создание и использование простых опросов в качестве метода сбора данных
Анализ распределений данных: понимание распределений данных и их анализа.
- Различать данные и типы данных
- Распознавание данных состоит из подсчетов или измерений переменной, которые называются распределением значений данных
- Различать категориальные данные и числовые данные и определять, какие графики и статистические данные можно использовать для представления каждого вида данных
- Использовать несколько представлений
- Организовывать и представлять данные с помощью таблиц, точечных диаграмм, линейных диаграмм, гистограмм значений, гистограмм частот, гистограмм и диаграмм типа «ящик с усами»
- Принимать обоснованные решения о том, какие графики/таблицы используются для отображения анализируемых данных (связь с заданными вопросами, типами данных и т.
 д.)
д.) - Признать, что данные, отображаемые с помощью графика, показывают общую форму распределения и дают общее представление о том, являются ли значения данных симметричными относительно центрального значения или нет ли чего-то необычного в форме
- Признать, что одно число может быть вычислено и использовано для характеристики центра или того, что типично для распределения данных
- Различать и вычислять меры центральной тенденции: среднее значение, медиана или мода данных
- Определите, как медиана и среднее реагируют на изменения количества и величины значений данных в распределении
- Принимать обоснованные решения о том, какие меры центральной тенденции (среднее, медиана или мода) могут использоваться для описания распределения данных
- Признать, что изменчивость возникает всякий раз, когда собираются данные, и описать изменчивость в распределении данного набора данных
- Опишите степень изменчивости в распределении, отметив, являются ли значения данных в значительной степени одинаковыми или сильно разбросанными
- Различать и вычислять показатели разброса: размах, межквартильный размах (IQR) и среднее абсолютное отклонение (MAD)
- Разработка стратегий для анализа и/или сравнения распределений данных
- Определите, какие статистические меры центра и разброса (среднее значение, медиана, мода, диапазон и т.
 д.) наиболее подходят для описания распределения данных
д.) наиболее подходят для описания распределения данных - Использование мер центра и разброса для сравнения распределений данных
Репрезентативные выборки: Поймите, что статистику можно использовать для получения информации о населении путем изучения репрезентативной выборки населения.
- Использовать случайную выборку для отбора репрезентативных выборок и использовать данные из этих выборок, чтобы делать выводы о популяциях
- Изучить влияние размера выборки и процессов отбора выборки на показатели центра и изменчивости, описывающие распределение выборки
- Применение концепций вероятности для выбора случайных выборок из популяций
- Сравнение выборочных распределений с использованием показателей центра (среднее значение, медиана), показателей разброса (диапазон, IQR, MAD) и данных, отображающих эти групповые данные (гистограммы, диаграммы в виде прямоугольников и усов)
Визуализация геометрии: урок математики в 7 классе
Отличные идеи для урока: Визуализация геометрии с Эми Уикер
Уикер: [00:00:08] Меня зовут Эми Уикер. Я преподаю математику в седьмом классе, и сегодня у меня есть отличный урок о визуализации геометрии, которым я хочу поделиться с вами. [00:00:15]
Я преподаю математику в седьмом классе, и сегодня у меня есть отличный урок о визуализации геометрии, которым я хочу поделиться с вами. [00:00:15]
[00:00:15] Итак, ребята, сегодня мы займемся визуализацией геометрии. [00:00:19]
[00:00:19] В моем уроке три разных компонента похожих фигур; трехмерные изображения и виды в поперечном сечении. К концу урока я хочу, чтобы мои ученики смогли установить пропорции и найти недостающие стороны на подобных фигурах. Я хочу, чтобы они также могли брать трехмерную фигуру и иметь возможность перейти к двухмерным представлениям, настроив манипулятивы. Также я хочу, чтобы они могли переходить от трехмерных объектов, таких как цилиндры, призмы и конусы, и создавать виды в поперечном сечении. [00:00:51]
[00:00:53] Сначала мы сделали похожие фигуры. У студентов на парте было несколько фигур, и вместо того, чтобы пытаться визуализировать их мысленное вращение (что иногда срабатывает, иногда нет), мы попросили их взять кальку и обвести фигуры. Затем перемещайте кальку, переворачивайте ее, вращайте, перемещайте ее по столу, а затем сможете выяснить, что с чем совпадает. Мы сделали то же самое на смарт-доске, используя функции переворота и поворота, и попросили их сделать цветовое кодирование, чтобы они могли видеть, что с чем сочетается, и, следовательно, они могли установить свои пропорции намного точнее. [00:01:28]
Затем перемещайте кальку, переворачивайте ее, вращайте, перемещайте ее по столу, а затем сможете выяснить, что с чем совпадает. Мы сделали то же самое на смарт-доске, используя функции переворота и поворота, и попросили их сделать цветовое кодирование, чтобы они могли видеть, что с чем сочетается, и, следовательно, они могли установить свои пропорции намного точнее. [00:01:28]
[00:01:28] Шестнадцать, поехали. [00:01:31]
[00:01:33] Второй этап заключался в двух- и трехмерном представлении вещей. [00:01:37]
[00:01:37] Итак, что я хочу, чтобы вы сделали сейчас с блоками, которые у вас в сумке, я хочу, чтобы вы построили фигуру, которую вы видите на следующих слайдах. [00:01:44]
[00:01:45] Мне нравится использовать манипулятивный метод для геометрии, потому что он дает учащимся что-то практическое и дает им лучшее понимание общих концепций геометрии. [00:01:54]
[00:01:55] Если мы описываем фигуру, это похоже на ступеньки, идущие в двух разных направлениях. [00:02:00]
[00:02:00]
[00:02:00] Я думаю, будет лучше, если ученик на самом деле построит фигуру из настоящих блоков и поместит ее перед собой. [00:02:06]
Ребенок: [00:02:06] Потому что я визуал, и мне нравится видеть вещи и делать что-то своими руками. Вы можете использовать блоки, это облегчает мне задачу, вместо того, чтобы писать или читать их. [00:02:17]
Уикер: [00:02:17] Хорошо, и вы строите оттуда. Сколько будет внутри этого? [00:02:21]
[00:02:22] Еще одна вещь, которую мы сделали, это своего рода вызов, когда им нужно было перейти от двух измерений к трехмерному. [00:02:29]
[00:02:29] Хорошо, это то, что нам нужно сделать сейчас. Если вы посмотрите на следующий слайд, который у вас есть, вы увидите изображение трех разных точек зрения. Вы хотите построить эту трехмерную фигуру на основе этих представлений. [00:02:39]
[00:02:39] Это то, что мы делали на документ-камере, чтобы дети построили фигуру. [00:02:44]
[00:02:44] Можешь сначала построить для нас вид сверху, используя эти блоки? [00:02:47]
[00:02:48] Так что это своего рода вызов для студентов, и, если перед ними нет кубиков, которые они могут использовать, это просто не работает . Затем на третьем этапе были виды в поперечном сечении, которые берут цилиндры, призмы, конусы и пирамиды, разрезают их на разные части, а затем выясняют, как это выглядит, когда мы его открываем. [00:03:08]
Затем на третьем этапе были виды в поперечном сечении, которые берут цилиндры, призмы, конусы и пирамиды, разрезают их на разные части, а затем выясняют, как это выглядит, когда мы его открываем. [00:03:08]
[00:03:08] Мы возьмем этот цилиндр из пластилина Play-Doh, и вы можете видеть, что я его немного подрезал. Мы собираемся разрезать его двумя разными способами. Нам нужно посмотреть, какие формы получатся, когда я разрежу его и открою. Если я разрежу его параллельно основанию, я разрежу его таким образом, поэтому я собираюсь открыть его таким образом. Как мы думаем, какие формы получатся, когда я открою его таким образом? Брэндон, что ты думаешь? [00:03:30]
[00:03:31] Да, если я открою его таким образом, у меня будет два круга. [00:03:35]
[00:03:36] Затем попросили их посмотреть, поняли ли они идею с некоторыми пультами. Так что пульты помогают мне увидеть, о чем они на самом деле думают. [00:03:43]
[00:03:43] Хорошо, похоже, что некоторые выбрали А, большинство выбрали Б.

 Точки называются вершинами, а отрезки — сторонами треугольника.
Точки называются вершинами, а отрезки — сторонами треугольника.










 Данная точка называется центром окружности.
Данная точка называется центром окружности.

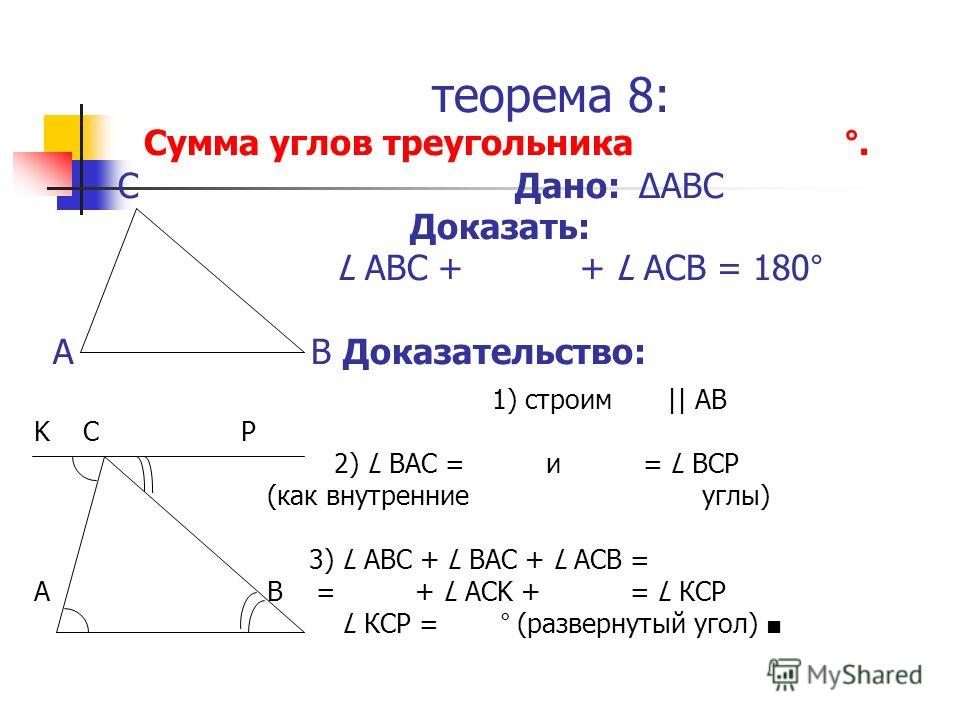


 2$$.
2$$.
 Г.А.2 — Начертить (от руки, с линейкой и транспортиром и с техникой) геометрические фигуры с заданными условиями. Сосредоточьтесь на построении треугольников по трем мерам углов или сторон, отмечая, когда условия определяют уникальный треугольник, более одного треугольника или отсутствие треугольника.
Г.А.2 — Начертить (от руки, с линейкой и транспортиром и с техникой) геометрические фигуры с заданными условиями. Сосредоточьтесь на построении треугольников по трем мерам углов или сторон, отмечая, когда условия определяют уникальный треугольник, более одного треугольника или отсутствие треугольника. 
 МД.А.3
МД.А.3 RUS6
RUS6



  ПОДРОБНЕЕ
 ПОДРОБНЕЕ  Определение многоугольников.
Определение многоугольников.  ПОДРОБНЕЕ
 ПОДРОБНЕЕ   ПОДРОБНЕЕ
 ПОДРОБНЕЕ  Включает в себя кубы, пирамиды, конусы, цилиндры, сферы и т.д.
 ПОДРОБНЕЕ
Включает в себя кубы, пирамиды, конусы, цилиндры, сферы и т.д.
 ПОДРОБНЕЕ  Это видео включает в себя разделы, в которых учащимся предлагается ввести ответы.
 ПОДРОБНЕЕ
Это видео включает в себя разделы, в которых учащимся предлагается ввести ответы.
 ПОДРОБНЕЕ  Вопросы могут включать несколько ответов, поэтому выберите «все подходящие варианты».
 ПОДРОБНЕЕ
Вопросы могут включать несколько ответов, поэтому выберите «все подходящие варианты».
 ПОДРОБНЕЕ  (Дополнительные связанные ресурсы расположены на вкладке учащегося.)
 ПОДРОБНЕЕ
(Дополнительные связанные ресурсы расположены на вкладке учащегося.)
 ПОДРОБНЕЕ  д.
 ПОДРОБНЕЕ
д.
 ПОДРОБНЕЕ  д.)
д.) д.) наиболее подходят для описания распределения данных
д.) наиболее подходят для описания распределения данных