Множество.Элементы множества. Подмножество. Пересечение и объединение множеств. Л.Г.Петерсон — 3 класс
A — множество имен для мальчиков.
B — множество имен для девочек.
Пересекаясь, они образуют новое множество — пересечение A ∩ B. В это множество будут входить имена, которые можно использовать И для мальчиков, И для девочек.
Если мы возьмем вместе все элементы множеств A и B, мы получим новое множество — их объединение. Записывают это так: A∪B. В это множество будут входить имена для мальчиков ИЛИ имена для девочек.
Для того чтобы подсчитать число элементов в объединении двух множеств, нужно посчитать, сколько элементов в первом множестве (в множестве А 8 элементов) и во втором (в множестве B 5 элементов), потом из полученной суммы вычесть число элементов в их пересечении (в пересечении A ∩ B 2 элемента): 5 + 8 — 2 = 11 (эл.) — в объединении этих множеств.
Автор: Рубин Алексей Яковлевич
| Тип | Название материала | Автор | |
|---|---|---|---|
| разное | Множество. Элементы множества. Подмножество. Пересечение и объединение множеств. Л.Г.Петерсон — 3 класс | Рубин Алексей Яковлевич | 30 Мар 2015 |
| документ | Урок информатики в 3 классе на тему «Множество. Подмножество. Пересечение и объединение множеств». | Зайкина Елена Владимировна | 30 Мар 2015 |
| разное | Множество. Подмножество. Пересечение множеств. ( Расселяем множества) | Акбашева Ирина Анатольевна | 30 Мар 2015 |
| презентация | 8 класс. Пересечение и объединение множеств | Кутоманова Евгения Михайловна | 14 Янв 2016 |
| презентация | Презентация для урока по теме «Пересечение и объединение множеств». 8 класс. | Чухарева Елена Александровна | 23 Апр 2015 |
| документ | Пересечение и объединение множеств. | Полиёва Елена Ивановна | 6 Апр 2015 |
| презентация | Пересечение и объединение множеств | Певцова Ольга Викторовна | 4 Апр 2015 |
| презентация | Презентация на тему: «Пересечение и объединение множеств» | Кунделева Оксана Евгеньевна | 5 Апр 2015 |
| презентация | Презентация по теме «Пересечение и объединение множеств».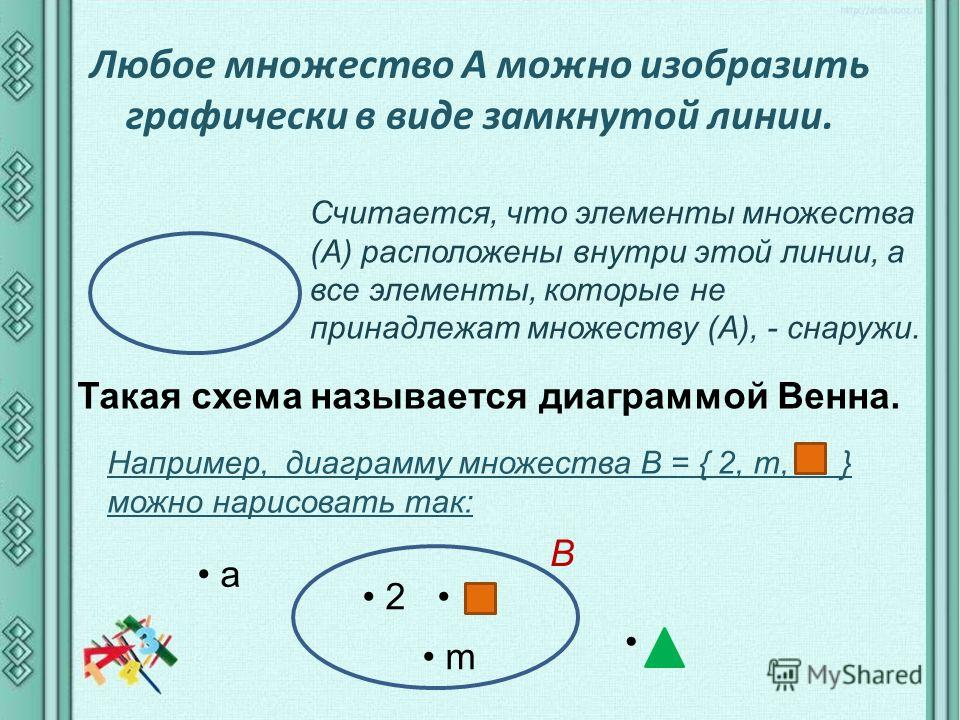 | Ломакина Марина Сергеевна | 4 Апр 2015 |
| документ | Пересечение и объединение множеств | Волкова Любовь Ивановна | 20 Фев 2016 |
| документ | Календарно-тематическое планирование по математике Петерсон С. 13 – 15 Уметь обозначать элементы множеств на диаграмме Эйлера – Венна, находить объединение и пересечение множеств. | Гаммершмидт Инна Александровна | 30 Мар 2015 |
| разное | Пересечение множеств. | Полиёва Елена Ивановна | 15 Апр 2015 |
| документ | План-конспект урока для 3 класса «Элементы, не принадлежащие множеству. | Александр Владимирович | 6 Июн 2015 |
| документ | Урок математики в 3 классе по теме Пересечение множеств | Тимофеева Татьяна Владимировна | 31 Мар 2015 |
| документ | Элементы, не принадлежащие множеству. Пересечение множеств. | Полиёва Елена Ивановна | 6 Апр 2015 |
| презентация, документ | Пересечение множеств | Кохтенко Елена Юрьевна | 30 Мар 2015 |
| документ | Пересечение множеств. | Самохина Эльвира Васильевна | 30 Мар 2015 |
| презентация | Пересечение множеств | Данилова Маргарита Сергеевна | 16 Дек 2015 |
| «Пересечение множеств» | Корякина Ольга Виктровна | 11 Дек 2017 | |
| презентация, документ | Тюкова Лариса Алексеевна | 6 Апр 2015 | |
| презентация | презентация к уроку по информатике «Множества» 3 класс | Киселёва Дарья Олеговна | 21 Мар 2015 |
| разное | Интерактивный учебник по информатике «Изучаем множества» 3 класс | Саликов Денис Александрович | 27 Мая 2015 |
| документ | Урок математики 1 класс по системе Л. В.Занкова с УУД по теме «Объединение множеств. Операция сложения». | Лаврентьева Светлана Фёдоровна | 30 Мар 2015 |
| разное | презентация по математике «Пересечение множеств» | Соболева Наталья Николаевна | 1 Апр 2015 |
| презентация | «Пересечение множеств» | Данилова Маргарита Сергеевна | 16 Дек 2015 |
| Конспект НОД с блоками Дьенеша «Пересечение множеств» | 11 Дек 2017 | ||
Урок информатики. Вложенность (включение) множеств. 3 класс | Шавалиева Алла Борисовна | 30 Мар 2015 | |
| презентация | Урок информатики 3 класс тема: «Множества» | Уманец Кристина Валерьяновна | 30 Мар 2015 |
| документ | Контрольная работа за 1 четверть 3 класс (Л.Г.Петерсон) | Некрасова Елена Михайловна | 30 Мар 2015 |
| разное | КТП по математике Л.Г.Петерсон 3 класс | Петровских Татьяна Ивановна | 30 Мар 2015 |
| документ | Рабочая программа по математике 3 класс (автор Л. Г.Петерсон) | Шестакова Наталья Васильевна | 31 Мар 2015 |
| документ | Контрольная работа за 3 четверть 2 класс Л.Г.Петерсон | YanaKireeva | 17 Сен 2015 |
| документ | РАБОЧАЯ ПРОГРАММА + планирование по математике Л.Г.Петерсон 3 класс | Яшкова Инга Вячеславовна | 24 Янв 2016 |
| документ | Сценарии уроков «День Знаний» для 1, 2, 3, 4 классов. Предложение, суффикс, слово, запятая, правило. Задача, цифра, умножение, уравнение, объединение. Текст, тема, пословица, план, описание. Кодирование, пересечение, множество, алгоритм, г | Кривошеина Ольга Ивановна | 31 Мар 2015 |
| документ | Множество. Элементы множества. 2 класс. | Сарычева Светлана Владимировна | 21 Мар 2015 |
| документ | Конспект урока математики «Объединение множеств. Знак объединения множеств» | Козлова Екатерина Сергеевна | 14 Мая 2015 |
| документ | Урок информатики «Объединение множеств» | Салфетова Анна Александровна | 20 Апр 2015 |
| документ | Проверочная работа по информатике на тему «Множества» (3 класс) | Дегтярева Евгения Валерьевна | 30 Мар 2015 |
| документ | Наглядный материал к теме «МНОЖЕСТВА» информатика 3 класс | Винокурова Ксения Владимировна | 30 Мар 2015 |
| документ | Урок математики, 3 класс.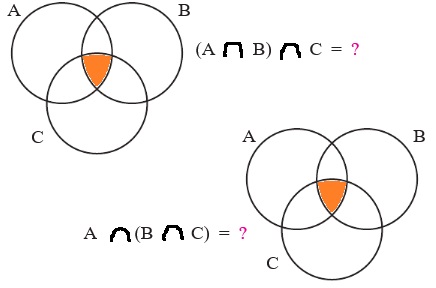 «Классификация. Разбиение множества на части.» | Никишина Светлана Викторовна | 7 Дек 2015 |
Конспект урока по предмету Математика для 3 класса на тему Объединение множеств
Конспект урока по предмету «Математика» (Л.Г. Петерсон)
для 3 класса на тему:
«Объединение множеств. ЗнакU»
Задачи:
Актуализировать знания о множествах.
Познакомить с новой операцией над множествами – объединение.
Создать условия для формирования умения использовать знак U.
Тренировать мыслительные операции: сравнение, анализ, синтез, классификация.
Воспитывать усидчивость, внимательность, терпение.
Ход урока
Организационный момент
— Здравствуйте, ребята! Садитесь!
— Долгожданный дан звонок – начинается урок.
— Все готовы, тогда начинаем, я желаю вам удачи.
— Подготовьте тетради для работы, запишем число классная работа.
II. Актуализация знаний
Какие операции над множествами вы научились выполнять?
Что означают знаки: , , ?
Прочитайте записи:А = {а; 0; Δ; □},В = {б; 0; □; Δ}.
Назовите множество элементов С,которое получается при пересечении данных множеств Аи В.(С = {0; Δ; □}.)
На доске: Прочитайте следующие записи:
а В;А В = В А;
СД;(A B) C = A(B С);
KB;AB = BA.
—Что вызвало затруднение? Почему не смогли прочитать последнюю запись?
III. Постановка темы урока
-На уроке математики учитель задал две очень сложные задачи.
Первую задачу смогли решить только Иван, Михаил и Зоя. А
вторую задачу решили Зоя, Нина и Петр. Покажите это на диаграмме Венна.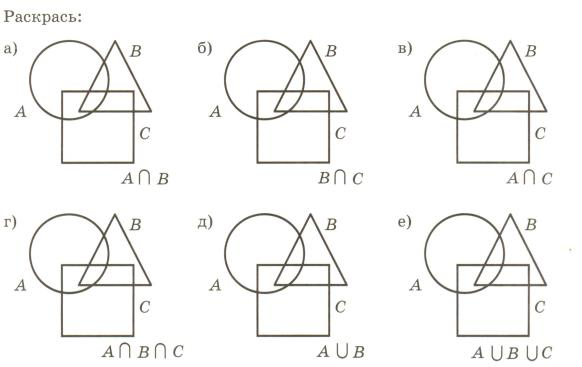
— А как показать множество детей, решивших хотя бы одну задачу? Покажите на нашей диаграмме, обведите это множество.
— Какова тема урока? (Объединение множеств)
Н а доске появляется рисунок: дети, решившие первую задачу
дети, решившие вторую задачу
IV. «Открытие» детьми нового знания
Если слова «объединим» не прозвучит, то это скажет учитель:
Такая операция называется объединением.
Множество детей, решивших первую задачу, назовем множествомА. А множество детей, решивших вторую задачу, назовем множеством В.Как же мы запишем множество всех детей, решивших хотя бы одну задачу? Как на математическом языке записать объединение множеств АиВ?(Дети предлагают свои варианты.)
— В математике существует знак объединения множеств, который можно сравнить с открытой вазой (U), в которую можно сложить все элементы множества.
АUВ={
V.Первичное закрепление
— Откройте учебник на стр.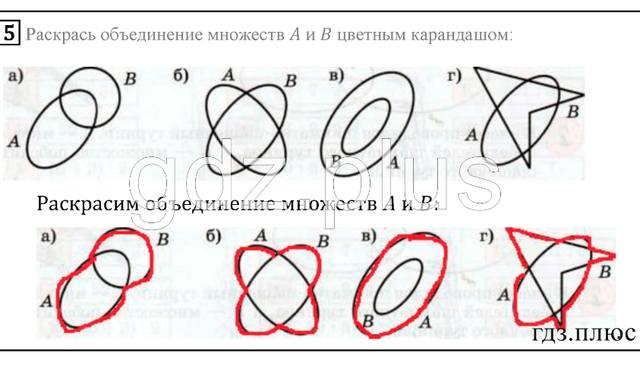
34
№1,2, 3, с. 34 — усвоение нового материала.
№ 4, с. 35 — закрепление с проговариванием вслух.
№ 5, с. 35 — самостоятельная работа с самопроверкой по эталону.
Физкультминутка
VI.Включение в систему знаний
Решение задач. № 9 (а, б), № 10(a).
-К какому виду относятся данные задачи? (Задачи на приведение к единице.)
Задачи можно сразу записать выражением.
№11- решение уравнений с комментированием у доски.
№ 14, 12 (а) — самостоятельная работа.
№ 12 (б) — дополнительное задание.
VII.Итоги урока
С какой новой операцией над множеством вы познакомились? (Объединением)
Что значит «объединить два множества»? (объединить все элементы, принадлежащие этим множествам)
А можно объединить три и более множеств? (да)
Оцените свою работу на уроке.
Домашнее задание
№ 6, с. 35; № 10 (б), с. 36.
Адрес публикации: https://www.
prodlenka.org/metodicheskie-razrabotki/222899-konspekt-uroka-po-predmetu-matematika-dlja-3-
Объединение и пересечение наборов Кардинальный номер набора
Кардинальный номер набора
Число различных элементов или членов в конечном множестве известно как кардинальное число множества. По сути, через кардинальность мы определяем размер множества. Кардинальное число множества A обозначается как n(A), где A — любое множество, а n(A) — количество элементов в множестве A.
Рассмотрим множество A, состоящее из простых чисел меньше 10.
Установите А = {2, 3, 5, 7}.
Поскольку множество A состоит из 4 элементов, поэтому кардинальное число множества A определяется как n(A) = 4.
Свойства, связанные с разностью, объединением и пересечением, а также количественным числом множества
i) Объединение непересекающихся множеств:
Если A и B — два конечных множества и если A ∩ B = ∅, то
n(A ∪ B) = n(A) + n(B)
Простыми словами, если A и B — конечные множества и эти множества не пересекаются, то кардинальное число объединения множеств A и B равно сумме кардинального числа множества A и множества B.
Рисунок 1- Непересекающиеся наборы
Объединение непересекающихся множеств A и B, представленное диаграммой Венна, задается как A ∪ B, и можно видеть, что A ∩ B = ∅, поскольку ни один элемент не является общим для обоих множеств.
ii) Объединение двух комплектов:
Если A и B два конечных множества, то
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
Проще говоря, количество элементов в объединении множеств A и B равно сумме количественных чисел множеств A и B за вычетом их пересечения.
Рисунок 2- Объединение двух комплектов
На приведенном выше рисунке области, заштрихованные по-разному, изображают разные непересекающиеся множества, т. е. A – B, B – A и A ∩ B представляют собой три непересекающихся множества, как показано, и их сумма представляет A ∪ B. Следовательно,
n (A ∪ B) = n (A – B) + n(B – A) + n(A ∩ B)
iii) Объединение трех комплектов
Если A, B и C три конечных множества, то;
n(A ∪ B ∪ C) = n(A) + n(B) + n(C) – n(A ∩ B) – n(B ∩ C) – n(A ∩ C) + n(A ∩ Б ∩ В)
Из диаграммы Венна ясно видно, что объединение трех множеств будет суммой кардинального числа множества A, множества B, множества C и общих элементов трех множеств, исключая общие элементы множеств, взятых попарно.
из двух.
Рисунок 3-Соединение трех наборов
Видео урок
Прикладная концепция – мощность множеств
Решенный пример
Давайте рассмотрим пример, чтобы прояснить нашу точку зрения.
Пример: Всего в XI классе 200 учеников. 120 из них изучают математику, 50 студентов изучают торговлю и 30 студентов изучают как математику, так и торговлю. Найдите количество учеников, которые
i) Изучайте математику, но не коммерцию
ii) Изучайте коммерцию, но не математику
iii) Изучайте математику или коммерцию
Решение: Общее количество студентов представляет кардинальное число универсальный набор. Пусть A обозначает набор студентов, изучающих математику, а набор B представляет студентов, изучающих коммерцию.
Следовательно,
n (U) = 200
n(A) = 120
n(B) = 50
n(A ∩ B) = 30
Диаграмма Венна представляет количество студентов, изучающих математику и коммерцию.
i) Здесь требуется найти разность множеств A и B. n(A ∩ B)
⇒ n (A – B) = 120 – 30 = 90
Количество студентов, изучающих математику, но не коммерцию, равно 90.
комплекты B и A
n (B) = n (B – A) + n (A ∩ B)
⇒ n (B – A) = 50 – 30 = 20
Количество студентов, изучающих торговлю, но не математику, равно 20.
iii) Количество студентов, изучающих математику или торговлю
n (A ∪ B) = n(A) + n(B) – n(A ∩ B)
⇒ n(A ∪ B) = 120 + 50 – 30 = 140
Чтобы лучше учиться и преуспевать во всех сферах жизни, присоединяйтесь к BYJU’S. Приятного обучения!»
Проверьте свое понимание этой концепции, ответив на несколько вопросов MCQ. Нажмите «Начать викторину», чтобы начать!
Выберите правильный ответ и нажмите кнопку «Готово».
Проверьте свои баллы и ответы в конце викторины
Поздравляем!
Посетите BYJU’S, чтобы получить ответы на все вопросы, связанные с математикой, и учебные материалы
Ваш результат, как показано ниже
У жены Петерсона были следы на шее, свидетельство друга0002 ДЖОЛИТ, Иллинойс (Рейтер).
Жена бывшего офицера полиции Чикаго Дрю Петерсона однажды прикрыла следы на шее курткой на молнии и заявила, что ее муж угрожал ей убийством, свидетельствовал одноклассник женщины в четверг в Суд над Петерсоном.Бывший сержант полиции Дрю Петерсон изображен на этой фотографии для бронирования, опубликованной офисом шерифа округа Уилл 8 мая 2009 года. REUTERS/Офис шерифа округа Уилл/Раздаточный материал они были вовлечены в спорный развод в 2004 году и инсценировали ее смерть, чтобы она выглядела как случайное утопление.
Мэри Паркс, дававшая показания ближе к концу второй недели судебного процесса по делу об убийстве Петерсона, сказала, что Савио показал ей следы на ее шее и сказал, что они были вызваны тем, что Петерсон схватил ее и прижал к земле.
Смерть Савио изначально считалась случайностью. Однако подозрения возникли, когда в 2007 году исчезла четвертая жена Петерсона, Стейси Петерсон. Тело Савио было эксгумировано и повторно исследовано, и Петерсону было предъявлено обвинение в убийстве.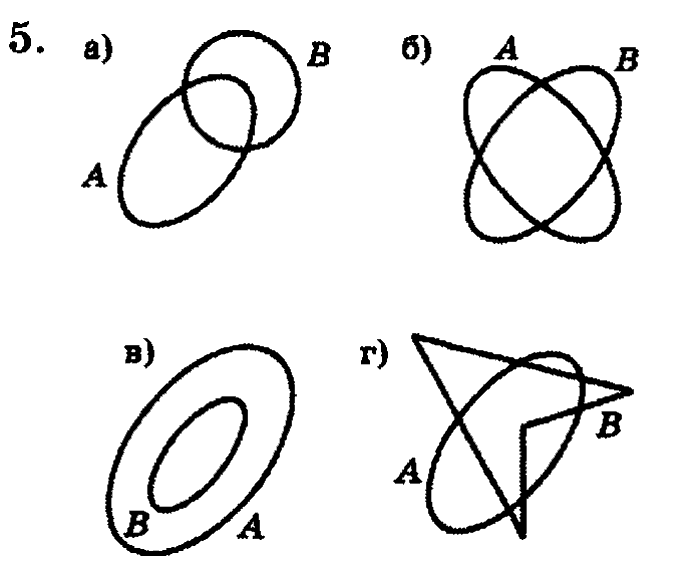
Дело Петерсона привлекло внимание всей страны и стало предметом телевизионного фильма Lifetime «Неприкасаемые» с Робом Лоу в главной роли. Петерсон также является единственным подозреваемым в исчезновении Стейси Петерсон, которую так и не нашли. Его первая и вторая жены повторно вышли замуж.
Паркс, познакомившаяся с Савио, когда они оба учились в медицинском колледже, показала, что Савио сказал ей, что Петерсон угрожал ей во время нападения.
«Кэти сказала мне, что ее муж сказал, и я цитирую: «Почему бы тебе просто не умереть», — сказал Паркс.
Савио считал, что Петерсон мог убить ее и представить это как несчастный случай, свидетельствовала Паркс. «Он мог убить ее и заставить исчезнуть», — сказал ей Паркс, Савио.
Адвокаты защиты попытались выявить несоответствия в показаниях Паркс, указав на допросе, что Паркс сказала, что Савио говорил с ней об угрозах во время занятий осенью 2003 года, но стенограммы показали, что они не посещали занятия в этом семестре.
Затем Паркс сказал, что разговор произошел перед другим классом, который Савио не посещал.
В других случаях адвокат защиты Стив Гринберг пытался охарактеризовать утверждения Савио о Петерсоне как преувеличения разгневанной, ищущей жалости бывшей жены. Паркс отверг эту идею.
«Все, что она мне рассказала, у меня нет оснований полагать, что она лгала», — сказал Паркс. Она добавила, что не присутствовала на поминках и похоронах Савио отчасти потому, что боялась встречи с Петерсоном.
Имея мало вещественных доказательств, связывающих Петерсона со смертью Савио, прокуратура попыталась представить показания о том, что он угрожал ей и пытался нанять киллера.
Адвокаты защиты возражали против показаний как слухов и дважды добивались неправильного судебного разбирательства. Судья Эдвард Бурмила отрицал неправильное судебное разбирательство, но ограничил свидетельские показания, которые могут давать прокуроры.
Ожидается, что суд продолжится в пятницу в округе Уилл.