Решебник по матем 9: Решебник по Алгебре 9 класс (Арефьева) – Решеба

Страница 9 — ГДЗ по Математике 3 класс Моро, Волкова 2 часть

---

• Тип: ГДЗ, Решебник.
• Автор: Моро М. И., Волкова С. И., Бантова М. А.
• Год: 2020.
• Серия: Школа России (ФГОС).
• Издательство: Просвещение.

❤️️Ответ к странице 9. Математика 3 класс учебник 2 часть. Автор: М.И. Моро.

Решебник — страница 9Готовое домашнее задание

Номер 1.

Реши с устным объяснением: 37 ∙ 2, 5 ∙ 19.

Ответ:

37 ∙ 2 = 74 37 ∙ 2 = (30 + 7) ∙ 2 = 60 + 14 = 74 Если 37 представить в виде суммы чисел 30 и 7, то 30 умножить на 2 будет 60, а 7 умножить на 2 будет 14. Сложив полученные числа получим 74.
5 ∙ 19 = 95 5 ∙ 19 = 5 ∙ (10 + 9) = 50 + 45 = 95 Если 19 представить в виде суммы чисел 10 и 9, то 10 умножить на 5 будет 50. А 9 умножить на 5 будет 45. Сложив полученные числа получим 95.

Номер 2.

Ответ:

14 ∙ 6 = (10 + 4) ∙ 6 = 60 + 24 = 84 19 ∙ 4 = (10 + 9) ∙ 4 = 40 + 36 = 76

15 ∙ 6 = (10 + 5) ∙ 6 = 60 + 30 = 90 5 ∙ 20 = 100

Номер 3.

Объясни, почему равны равенства.

Ответ:

8 ∙ 3 + 7 ∙ 3 = (8 + 7) ∙ 3 17 ∙ 5 + 3 ∙ 5 = (17 + 3) ∙ 5 6 ∙ 8 + 4 ∙ 8 = 10 ∙ 8
Все эти равенства верны, поскольку выполнены по правилу умножения суммы на число.

Номер 4.

В конструкторе 54 детали. Из 12 деталей Юра сделал электровоз, а из остальных – вагоны. Сколько получилось вагонов, если на каждый пошло по 7 деталей?

Ответ:

1) 54 – 12 = 42 (д.) – ушло на вагоны. 2) 42 : 7 = 6 (в.) – получилось. Ответ: получилось 6 вагонов.

Номер 5.

Составь по таблице задачу и реши ее.

Ответ:

В магазин привезли 27 кг муки в пакетах по 3 кг в каждой и столько же пакетов с сахаром по 2 кг в каждом пакете. Сколько кг сахара привезли? 1) 27 : 3 = 9 (п.) – муки привезли. 2) 2 ∙ 9 = 18 (кг) Ответ: 18 кг сахара привезли.

Номер 6.

Начерти 3 отрезка: длина первого 12 см, длина второго равна половине длины первого, а длина третьего на 2 см меньше длины второго.

Ответ:

12 : 2 = 6 (см) — длина 2 отрезка. 6 – 2 = 4 (см) — длина 3 отрезка.

Номер 7.

Высота первого дома 15 м, а второго – на ☐ м больше. Вставляй вместо пропуска числа 9, 12, 24 и узнавай каждый раз высоту второго дома.

Ответ:

1) 15 + 9 = 24 м; 2) 15 + 12 = 27 м; 3) 15 + 24 = 39 м. Ответ: 24 м, 27 м, 39 м.

Номер 8.

Реши уравнения.

Ответ:

Номер 9.

Как переложить 3 палочки, чтобы получилось 5 одинаковых треугольников?

Ответ:

Задание внизу страницы

Вычисли.

Ответ:

3 ∙ 26 = 3 ∙ (20 + 6) = 60 + 18 = 78 18 ∙ 2 = (10 + 8) ∙ 2 = 20 + 16 = 36

Рейтинг

Выберите другую страницу

1 часть

Учебник Моро	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63	64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79	80	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95	96	97	98	99	100	101	102	103	104	105	106	107	108	109	110	111

2 часть

4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63	64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79	80	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95	96	97	98	99	100	101	102	103	104	105	106	107	108	109	110	111

Ваше сообщение отправлено!

+

ГДЗ Teme gata pregătite Готовые домашние задания Молдова Математика Акири 9 класс 2016 на MDAGDZ.

COM

Алгебра. Глава 1. Повторение и дополнение

§ 1. Множество действительных чисел

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

§ 2.

Действия над действительными числами 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

§ 3.

Степени и корни 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

Упражнения и задачи для повторения

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

Проверочная работа.

Вариант 1 1 2 3

Проверочная работа. Вариант 2

1 2 3

Глава 2. Функции

§ 1. Понятие функции.Повторение и дополнение

1 2 3 4 6 7 8 9 10 11

§ 2.

Числовые функции. тПовторение и дополнение 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

§ 3.

Функция II степени 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27

§ 4.

9 7

Упражнения и задачи для повторения

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28

Проверочная работа.

1 Вариант 1 2 3

Проверочная работа. 2 Вариант

1 2 3

Глава 3. Многочлены и алгебраические дроби

§ 1. Одночлены. Операции над одночленами

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

§ 2.

Многочлены. Операции над многочленами 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

§ 3.

Деление многочленов 1 2 3 4 5

Bine ați venit pe site-ul unde puteți găsi sarcini gata făcute pentru manualele din Moldova. Ați făcut alegerea corectă!

Programul bogat de formare include multe discipline. Fiecare nouă lecție poartă un flux de termeni, teoreme, exemple. Lecțiile în clasă, temele, orele suplimentare, cursurile elective iau mult timp și energie de la studentul modern. Uneori, informațiile date de profesor sunt dificil de perceput și nu sunt asimilate în patruzeci de minute. Ajuns acasă, elevul nu își poate finaliza cu competența temele, se simte prost și interesul său pentru învățare scade. În astfel de momente, literatura de specialitate pe care echipa noastră a lăsat-o cu atenție vă va fi de folos.

Aici sunt colectate toate soluțiile și răspunsurile corecte în cele mai dificile științe: matematică, algebră și geometrie, fizică și chimie.

Observăm funcțiile utile ale reshebnik-urilor: autoexaminare, analiza muncii lor pentru erori, identificarea lacunelor în cunoștințe în etapa inițială ajuta la îndeplinirea sarcinilor complexe capacitatea părinților de a supraveghea procesul educațional al copilului, precum și de a oferi o explicație a uneia sau altei terminologii creșterea stimei de sine și a încrederii în sine, adaptarea la cursul școlar, manifestarea interesului competitiv. Cunoașterea este putere, fii sigur de ea!

„GDZ” nu se referă la înșelăciune fără minte, este, în primul rând, un instrument pentru creșterea performanței școlare, obținerea maximului beneficiu și plăcere din activitățile de învățare. Manualul este, de asemenea, perfect pentru mame și tati, profesori și tutori.

Samacheer Kalvi 9th Maths Book Answers Solutions Guide — Samacheer Kalvi

11 мая 2023 г. 12 мая 2023 г. / Автор Вир

Опытные преподаватели в SamacheerKalvi.Guru создали Совет штата Тамилнад Samacheer Kalvi 9th Math Book Ответы и Руководство по решениям Pdf Free Download in English Medium и Tamil Medium являются частью Samacheer Kalvi 9th Books Solutions. Здесь мы дали TN State Board New Syllabus Samacheer Kalvi 9th Std Math Guide Pdf of Book Back Вопросы и ответы, важные вопросы по главам, учебные материалы, банк вопросов, примечания, формулы, термины 1, 2, 3.

Учащиеся также могут читать Samacheer Kalvi 9th Science Book Solutions.

Samacheer Kalvi 9th Math Book Back Answers

Tamilnadu State Board Samacheer Kalvi 9th Math Book Answers Solutions Guide Term 1, 2, 3

Samacheer Kalvi 9th Math Book with Answers Chapter 1 Set Language

• Глава 1 Установить язык Ex 1.1
• Настройка языка главы 1 Ex 1. 2
• Настройка языка главы 1 Ex 1.3
• Настройка языка главы 1 Ex 1.4
• Настройка языка главы 1 Ex 1.5
• Настройка языка главы 1 Ex 1.6
• Настройка языка главы 1 Ex 1.7
• Глава 1 Установка дополнительных вопросов языка

Samacheer Kalvi 9th Maths Book Solutions Глава 2 Вещественные числа

• Глава 2 Вещественные числа Ex 2.1
• Глава 2 Реальные числа Пример 2.2
• Глава 2 Реальные числа Ex 2.3
• Глава 2 Реальные числа Ex 2.4
• Глава 2 Реальные числа Ex 2.5
• Глава 2 Реальные числа Ex 2.6
• Глава 2 Реальные числа Ex 2.7
• Глава 2 Реальные числа Ex 2.8
• Глава 2 Реальные числа Ex 2.9
• Глава 2 Реальные числа Дополнительные вопросы

TN 10th Math Guide Samacheer Kalvi Pdf Скачать бесплатно Глава 3 Алгебра

• Глава 3 Алгебра Пример 3.1
• Глава 3 Алгебра Пример 3.2
• Глава 3 Алгебра Пример 3. 3
• Глава 3 Алгебра Пример 3.4
• Глава 3 Алгебра Пример 3.5
• Глава 3 Алгебра Пример 3.6
• Глава 3 Алгебра Пример 3.7
• Глава 3 Алгебра Пример 3.8
• Глава 3 Алгебра Пример 3.9
• Глава 3 Алгебра Пример 3.10
• Глава 3 Алгебра Пример 3.11
• Глава 3 Алгебра Пример 3.12
• Глава 3 Алгебра Пример 3.13
• Глава 3 Алгебра Пример 3.14
• Глава 3 Алгебра Пример 3.15
• Глава 3 Дополнительные вопросы по алгебре

Samacheer Kalvi 9th Math Guide Pdf Free Download Chapter 4 Geometry

• Глава 4 Geometry Ex 4.1
• Глава 4 Геометрия Ex 4.2
• Глава 4 Геометрия Ex 4.3
• Глава 4 Геометрия Ex 4.4
• Глава 4 Геометрия Ex 4.5
• Глава 4 Геометрия Ex 4.6
• Глава 4 Геометрия Ex 4.7
• Глава 4 Дополнительные вопросы по геометрии

Samacheer Kalvi 9th Math Book English Medium Глава 5 Координатная геометрия

• Глава 5 Координатная геометрия Ex 5. 1
• Глава 5 Координатная геометрия Ex 5.2
• Глава 5 Координатная геометрия Ex 5.3
• Глава 5 Координатная геометрия Ex 5.4
• Глава 5 Координатная геометрия Ex 5.5
• Глава 5 Координатная геометрия Ex 5.6
• Глава 5 Координатная геометрия Дополнительные вопросы

9th Standard Samacheer Kalvi Math Guide Free Download Глава 6 Тригонометрия

• Глава 6 Тригонометрия Ex 6.1
• Глава 6 Тригонометрия Ex 6.2
• Глава 6 Тригонометрия Ex 6.3
• Глава 6 Тригонометрия Ex 6.4
• Глава 6 Тригонометрия Ex 6.5
• Глава 6 Дополнительные вопросы по тригонометрии

Samacheer Kalvi 9th Maths Guide Online Глава 7 Измерение

• Глава 7 Измерение Ex 7.1
• Глава 7 Измерение Ex 7.2
• Глава 7 Измерение Ex 7.3
• Глава 7 Измерение Ex 7.4
• Глава 7 Измерение Дополнительные вопросы

Tamilnadu Board Класс 9 Математика Глава 8 Статистика

• Глава 8 Статистика Ex 8. 1
• Глава 8 Статистика Пример 8.2
• Глава 8 Статистика Пример 8.3
• Глава 8 Статистика Пример 8.4
• Глава 8 Статистика Дополнительные вопросы

Совет штата Тамил Наду, 9-я ст. математика Глава 9 Вероятность

• Глава 9 Вероятность Ex 9.1
• Глава 9 Вероятность Ex 9.2
• Глава 9 Вероятность Ex 9.3
• Глава 9 Дополнительные вопросы о вероятности

9-е стандартное руководство по математике на тамильском языке в формате PDF Скачать бесплатно

Samacheer Kalvi 9-е стандартное руководство по математике на тамильском языке в формате PDF скачать бесплатно, 9-е руководство по математике на тамильском языке в формате PDF скачать 2020-2021.

Samacheer Kalvi 9th Maths Book Back Ответы Глава 1 கண மொழி

• Глава 1 கண மொழி Пример 1.1
• Глава 1 கண மொழி Ex 1.2
• Глава 1 கண மொழி Ex 1.3
• Глава 1 கண மொழி Ex 1.4
• Глава 1 கண மொழி Ex 1. 5
• Глава 1 கண மொழி Ex 1.6
• Глава 1 கண மொழி Ex 1.7

Tamilnadu State Board 9th Maths Samacheer Solutions Chapter 2 மெய்யெண்கள்

• Chapter 2 மெய்யெண்கள் Ex 2.1
• Глава 2 மெய்யெண்கள் Ex 2.2
• Глава 2 மெய்யெண்கள் Ex 2.3
• Глава 2 மெய்யெண்கள் Ex 2.4
• Глава 2 மெய்யெண்கள் Ex 2.5
• Глава 2 மெய்யெண்கள் Ex 2.6
• Глава 2 மெய்யெண்கள் Ex 2.7
• Глава 2 மெய்யெண்கள் Ex 2.8
• Глава 2 மெய்யெண்கள் Ex 2.9

Samacheer Kalvi Math Guide For 9th Std Chapter 3 இயற்கணிதம்

• Chapter 3 இயற்கணிதம் Ex 3.1 900 18
• Глава 3 இயற்கணிதம் Ex 3.2
• Глава 3 இயற்கணிதம் Ex 3.3
• Глава 3 இயற்கணிதம் Ex 3.4
• Глава 3 இயற்கணிதம் Ex 3.5
• Глава 3 இயற்கணிதம் Ex 3.6
• Глава 3 இயற்கணிதம் Ex 3.7
• Глава 3 இயற்கணிதம் Ex 3.8
• Глава 3 இயற்கணிதம் Ex 3.9
• Глава 3 இயற்கணிதம் Ex 3.10
• Глава 3 இயற்கணிதம் Ex 3. 11
• Глава 3 இயற்கணிதம் Ex 3.12
• Глава 3 இயற்கணிதம் Ex 3.13
• Глава 3 இயற்கணிதம் Ex 3.14
• Глава 3 இயற்கணிதம் Ex 3.15

9th Standard Maths Answer Key Глава 4 வடிவியல்

• Глава 4 வடிவியல் Пример 4.1
• Глава 4 வடிவியல் Ex 4.2
• Глава 4 வடிவியல் Пример 4.3
• Глава 4 வடிவியல் Пример 4.4
• Глава 4 வடிவியல் Пример 4.5
• Глава 4 வடிவியல் Пример 4.6
• Глава 4 வடிவியல் Пример 4.7

Путеводитель по математике для 9-го класса Государственная программа в формате PDF ை வடிவியல் Ex 5.1

Глава 5 ஆயத்தொலை வடிவியல் Ex 5.2

Глава 5 ஆயத்தொலை வடிவியல் Ex 5.3

Глава 5 ஆயத்தொலை வடிவியல் Ex 5.4

Глава 5 ஆயத்தொலை வடிவியல் Ex 5.5

Глава 5 ஆயத்தொலை வடிவியல் Ex 5.6

9th Samacheer Maths Solution Book Chapter 6 முக்கோணவியல்

• Chapter 6 முக்கோணவியல் Ex 6.1
• Глава 6 முக்கோணவியல் Ex 6. 2
• Глава 6 முக்கோணவியல் Ex 6.3
• Глава 6 முக்கோணவியல் Ex 6.4
• Глава 6 முக்கோணவியல் Ex 6.5

Samacheer 9th Maths Guide Tamil Medium Pdf Free Download Chapter 7 அளவியல்

• Глава 7 அளவியல் Ex 7.1
• Глава 7 அளவியல் Ex 7.2
• Глава 7 அளவியல் Ex 7.3
• Глава 7 அளவியல் Ex 7.4

Samacheer Kalvi Class 9 Math Solutions Chapter 8 புள்ளியியல்

• Chapter 8 புள்ளியியல் Ex 8.1
• Глава 8 புள்ளியியல் Ex 8.2
• Глава 8 புள்ளியியல் Ex 8.3
• Глава 8 புள்ளியியல் Ex 8.4

9th Standard Samacheer Kalvi Math Guide Chapter 9 நிகழ்தகவு

• Глава 9 நிகழ்தகவு Пример 9.1
• Глава 9 நிகழ்தகவு Пример 9.2
• Глава 9 நிகழ்தகவு Пример 9.3

Мы надеемся, что данная книга по математике Samacheer Kalvi Class 9th Math Book Solutions and Answers Pdf Free Download in English Medium and Tamil Medium поможет вам. Если у вас есть какие-либо вопросы относительно нового учебного плана TN State Board Samacheer Kalvi 9th Standard Math Guide Pdf of Book Back Вопросы и ответы, важные вопросы по главам, учебные материалы, банк вопросов, примечания, формулы, термины 1, 2, 3, оставьте комментарий ниже. и мы свяжемся с вами в ближайшее время.

Решения NCERT для математики класса 9, глава 9, области параллелограммов и треугольников

Решения NCERT для математики класса 9, глава 9, области параллелограммов и треугольников Ex 9.1 являются частью решений NCERT для математики класса 9. Здесь мы дали решения NCERT для математики класса 9, глава 9, области параллелограммов и треугольников, пример 9.1.

NCERT Solutions for Class 9 Math Chapter 9 Площади параллелограммов и треугольников Ex 9.1

Ex 9.1 Class 9 Math Question 1
Какие из следующих фигур лежат на одном основании и между одними и теми же параллелями. В таком случае запишите общее основание и две параллели.

Решение:
Фигуры (i), (iii) и (v) лежат на одном основании и между одними и теми же параллелями.

год

	Общая база	Две параллели
Рис. (i)	DC	DC и AB
Рис. (iii)	QR	QR и PS
Рис. (v)	год нашей эры	AD и BQ

Решения NCERT для класса 9 по математике Глава 9 Площадь параллелограммов и треугольников ुजों के क्षेत्रफल) (Hindi Medium) Ex 9.1

NCERT Solutions for Class 9 Math Chapter 9 Areas of Parallelograms и треугольники Упр. 9.2

Упр. 9.2 Класс 9 Математика Вопрос 1.
На рисунке ABCD — параллелограмм, AE ⊥ DC и CF ⊥ AD. Если AB = 16 см, AE = 8 см и CF = 10 см, найдите AD.

Решение:
BSOУ нас есть, AE ⊥ DC и AB = 16 см
∵ AB = CD [Противоположные стороны параллелограмма]
∴ CD = 16 см
Теперь площадь параллелограмма ABCD = CD x AE
= (16 x 8 ) см ² = 128 см ² [∵ AE = 8 см]
Поскольку, CF ⊥ AD
∴ Площадь параллелограмма ABCD = AD x CF
⇒ AD x CF = 128 см
⇒ AD x 10 см = 128 см ² [∵ CF= 10 см]
⇒ AD = \(\frac { 128 }{ 10 }\) см = 12,8 см 10
Таким образом, искомая длина AD равна 12,8 см

Упражнение 9. 2 Математика для 9 класса Вопрос 2.
Если E, F, G и H являются серединами сторон параллелограмма ABCD соответственно, покажите, что ar (EFGH) = \(\frac { 1 }{ 2 } \) ар (ABCD).
Решение:
Объедините GE и HE, где GE || до нашей эры || ДА и ВЧ || АБ || DC
(∵ E, F, G и H — середины сторон || ^gm ABCD).
Если треугольник и параллелограмм лежат в одном основании и между одними и теми же параллелями, то A E U площадь треугольника равна половине площади параллелограмма. 9{ gm }ABCD)\) …(2)
Из (1) и (2) имеем ar(∆APB) = ar(∆BQC).

Пример 9.2 Класс 9 Математика Вопрос 4.
На рисунке P — точка внутри параллелограмма ABCD. Покажите, что

(i) ar (APB) + ar (PCD) = \(\frac { 1 }{ 2 } ar(ABCD)\)
(ii) ar (APD) + ar(PBC) = ar (APB ) + ar (PCD)
Решение:
Имеем параллелограмм ABCD, т. е. AB || КД и БК || ОБЪЯВЛЕНИЕ. Нарисуем EF || АБ и ГГ || AD через P.

(i) ∆APB и || ^gm AEFB находятся на одном основании AB и между одними и теми же параллелями AB и EF. 9{ gm }ABCD)\) …….(6)
Из (3) и (6) имеем
ar(∆APD) + ar(∆PBC) = ar(∆APB) + ar(∆PCD)

Пример 9.2 Класс 9 Математика Вопрос 5.
На рисунке PQRS и ABRS являются параллелограммами, а X – любая точка на стороне BR. Покажите, что
(i) ar (PQRS) = ar (ABRS)
(ii) ar (AXS) = \(\frac { 1 }{ 2 } ar(PQRS)\)

Решение:
(i) Параллелограмм PQRS и параллелограмм ABRS находятся на одном основании RS и между одними и теми же параллелями RS и PB.
∴ ar(PQRS) = ar(ABRS)
(ii) AAXS и || ^гм АБРС находятся на одной базе АС и между теми же параллелями АС и БР. *
∴ ar(AXS) = \(\frac { 1 }{ 2 } ar(ABRS)\) …(1)
Но ar(PQRS) = ar(ABRS) …(2) [Доказано в части (i) ]
Из (1) и (2) получаем
ar(AXS) = \(\frac { 1 }{ 2 } ar(PQRS)\)

Пример 9.2 Математика для 9 класса, вопрос 6.
У фермера было поле в виде параллелограмма PQRS. Она взяла любую точку А на RS и соединила ее с точками P и Q. На сколько частей разбито поле? Каковы формы этих частей? Фермер хочет посеять пшеницу и бобовые на равных участках поля по отдельности. Как она должна это сделать. 9{ gm }PQRS)\) …(2)
Из (1) и (2) имеем
ar(∆PAQ) = ar[(∆APS) + (∆QAR)]
Таким образом, фермер может сеять пшеницу в (∆PAQ) и бобовые в [(∆APS) + (∆QAR)] или пшеницу в [(∆APS) + (∆QAR)] и бобовые в (∆PAQ).

Решения NCERT для математики класса 9 Глава 9 Площади параллелограммов и треугольников Пример 9.3

Пример 9.3 Математика класса 9 Вопрос 1.
На рисунке E — это любая точка на медиане AD ∆ABC. Покажите, что ar (ABE) = ar (ACE).

Решение:
У нас есть ∆ABC такое, что AD является медианой.
∴ ar(∆ABD) = ar(∆ACD) …(1)
[∵ Медиана делит треугольник на два равновеликих треугольника]
Аналогично, в ∆BEC имеем
ar(∆BED) = ar( ∆DEC) …(2)
Вычитая (2) из ​​(1), получаем
ar(∆ABD) – ar(∆BED) = ar(∆ACD) – ar(∆DEC)
⇒ ar(∆ABE) = ар(∆ACE).

Пример 9.3 Математика для 9 класса Вопрос 2.
В треугольнике ABC точка E является серединой медианы AD. Покажите, что ax (BED) = \(\frac { 1 }{ 2 } ar(ABC)\).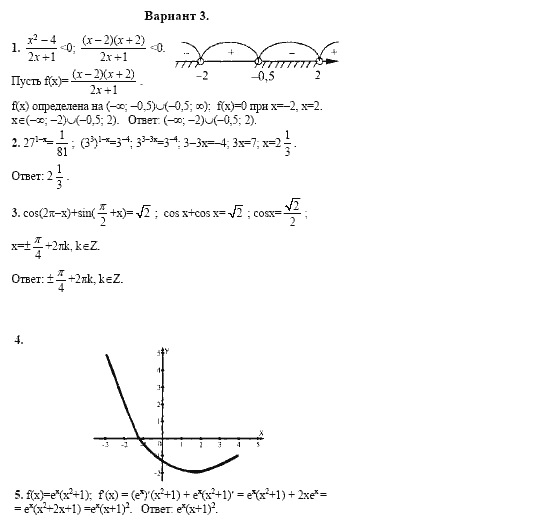
Решение:
У нас есть ∆ABC и его медиана AD.
Соединим B и E.

Так как медиана делит треугольник на два равновеликих треугольника.
ar (∆ABD) = \(\frac { 1 }{ 2 } ar(\Delta ABC)\) …….(1)
Теперь в ∆ABD BE является медианой.
[ ∵ E – середина AD]
∴ ar(∆BED) = \(\frac { 1 }{ 2 } ar(\Delta ABC)\) …(2)
Из (1) и (2) ), имеем
ar(∆BED) = \(\frac { 1 }{ 2 }\) [\(\frac { 1 }{ 2 } ar(\Delta ABC)\) ]
⇒ ar(∆BED) = \(\frac { 1 }{ 4 } ar(\Delta ABC)\)

Упр. 9.3 Класс 9 Математика Вопрос 3.
Покажите, что диагонали параллелограмма делят его на четыре треугольника равной площади.
Решение:
У нас есть параллелограмм ABCD (скажем)
такой, что его диагонали пересекаются в точке O.
∵ Диагонали параллелограмма делят друг друга пополам.
∴ AO = OC и BO = OD
Построим CE ⊥ BD.
Теперь ar(∆BOC) = \(\frac { 1 }{ 2 }\)BO x CE и
ar(∆DOC) = \(\frac { 1 }{ 2 }\)OD x CE

Поскольку , BO = OD
∴ ar(∆BOC) = ar(∆DOC) …(1)
Аналогично, ar(∆AOD) = ar(∆DOC) …(2)
и ar(∆AOB) = ar(∆ BOC) …(3)
Из (1), (2) и (3) имеем
ar(∆AOB) = ar(∆BOC) = ar(∆COD) = ar(∆DOA)
Таким образом, диагонали параллелограмма делят его на четыре равновеликих треугольника.

Упражнение 9.3 Класс 9 Математика Вопрос 4.
На рисунке ABC и ABD представляют собой два треугольника с одним и тем же основанием AB. Если отрезок CD делится пополам отрезком AB в точке O, покажите, что ar(ABC) = ar(ABD)

Решение:
имеем, что ∆ABC и ∆ABD лежат на одном и том же основании AB.
∵ CD делится пополам в точке O. [Дано]
∴ CO = OD
Теперь в ∆ACD AO является медианой
∴ ar(∆OAC) = ar(∆OAD) …(1)
Опять же, в ∆BCD , BO — медиана
∴ ar(∆OBC) = ar(∆ODB) …(2)
Складывая (1) и (2), получаем
ar(∆OAQ + ar(∆OBQ) = ar(∆OAD) + ar(∆ ODB)
⇒ ar(∆ABC) = ar(∆ABD)

Пример 9.3 Класс 9 Математика Вопрос 5.
D, E и F являются соответственно серединами сторон BC, CA и AB ∆ABC. Покажите, что
(i) BDEF является параллелограммом
(ii) ar(DEF) = \(\frac { 1 }{ 4 } ar(ABC)\)
(iii) ar(BDEF) = \(\frac { 1 }{ 4 } ar(ABC)\)

Решение:
У нас есть ∆ABC такое
, что D,E и Fare являются серединами BC, CA и AB соответственно.

(i) В ∆ABC E и F являются серединами AC и B D C AB соответственно.
∴ КВ || BC [Теорема о средней точке]
⇒ EF || BD
Кроме того, EF = \(\frac { 1 }{ 2 } (BC)\)
⇒ EF = BD [D — середина BC]
Поскольку BDEF — четырехугольник, одна пара противоположных сторон которого параллельна и одинаковой длины.
∴ BDEF — параллелограмм.

(ii) Мы доказали, что BDEF является параллелограммом.
Точно так же DCEF является параллелограммом, и DEAF также является параллелограммом.
Теперь параллелограмм BDEF и параллелограмм DCEF находятся на одном основании EF и между одними и теми же параллелями BC и EF.
∴ ar(|| ^гм BDEF) = ar(|| ^гм DCEF)
⇒ \(\frac { 1 }{ 2 }\)ar(|| ^гм BDEF) = \(\frac { 1 }{ 2 }\)ar(|| ^gm DCEF)
⇒ ar(∆BDF) = ar(∆CDE) …(1)
[Диагональ параллелограмма делит его на два равновеликих треугольника]
Аналогично , ar(∆CDE) = ar(∆DEF) …(2)
и ar(∆AEF) = ar(∆DEF) …(3)
Из (1), (2) и (3) имеем
ar(∆AEF) = ar(∆FBD) = ar(∆DEF) = ar(∆CDE)
Таким образом, ar(∆ABC) = ar(∆AEF) + ar(∆FBD) + ar(∆DEF) + ar(∆CDE) = 4 ar(∆DEF)
⇒ ar(∆DEF) = \(\frac { 1 }{ 4 }\)ar(∆ABC)

(iii) Имеем, ar (|| ^гм BDEF) = ar(∆BDF) + ar(∆DEF)
= ar(∆DEF) + ar(∆DEF) [∵ ar(∆DEF) = ar(∆BDF)]
2ar(∆DEF) = 2[\(\frac { 1 }{ 4 }\)ar(∆ABC)]
= \(\frac { 1 }{ 2 }\)ar(∆ABC)
Таким образом, ar (|| ^gm BDEF) = \(\frac { 1 }{ 2 }\)ar(∆ABC)

Упражнение 9. 3 Класс 9 Математика Вопрос 6.
На рисунке диагонали AC и BD четырехугольника ABCD пересекаются в точке 0 так, что OB = OD. Если AB = CD, то покажите, что
(i) ar(DOC) = ar(AOB)
(ii) ar (DCB) = ar (ACB)
(iii) DA || CB или ABCD — параллелограмм

Решение:
Имеем четырехугольник ABCD, диагонали которого AC и BD пересекаются в точке O.
Имеем также, что OB = OD, AB = CD Нарисуем DE ⊥ AC и BF ⊥ AC

(i) В ∆DEO и ∆BFO имеем
DO = BO [Дано]
∠DOE = ∠BOF [Вертикально противоположные углы]
∠DEO = ∠BFO [Каждый 90°]
∴ ∆DEO ≅ ∆BFO [По конгруэнтности A AS]
⇒ DE = BF [По C.P.C.T.]
и ar(∆DEO) = ar(∆BFO) …(1)
Теперь в ∆DEC и ∆BFA имеем
∠DEC = ∠BFA [каждые 90°]
DE = BF [доказано выше]
DC = BA [дано]
∴ ∆DEC ≅ ∆BFA [по RHS-конгруэнтности]
⇒ ar(∆DEC) = ar(∆BFA) …(2)
и ∠1 = ∠2 …(3) [по C.P.C.T.]
Складывая (1) и (2), получаем
ar(∆DEO) + ar(∆DEC) = ar(∆BFO) + ar(∆BFA)
⇒ ar(∆DOC) = ar(∆AOB)

(ii) Поскольку ar(∆DOC) = ar(∆AOB) [ Доказано выше]
Добавляя ar(∆BOC) с обеих сторон, получаем
ar(∆DOC) + ar(∆BOC) = ar(∆AOB) + ar(∆BOC)
⇒ ar(∆DCB) = ar(∆ACB)

(iii) Так как ∆DCS и ∆ACB находятся на одном и том же основании CB и имеют равные площади.
∴ Лежат между одинаковыми параллелями CB и DA.
⇒ КБ || DA
Также ∠1 = ∠2, [по (3)]
, которые являются альтернативными внутренними углами.
Итак, А.Б. || CD
Значит, ABCD — параллелограмм.

Упражнение 9.3 Класс 9 по математике Вопрос 7.
D и E — точки на сторонах AB и AC соответственно ∆ ABC, такие что ar (DBC) = ar (EBC). Докажите, что DE || ДО Н.Э.
Решение:
У нас есть ∆ABC, а точки D и E таковы, что ar(DBC) = ar{EBC)
Так как ∆DBC и ∆EBC лежат на одном основании BC и имеют одинаковую площадь.

∴ Они должны лежать между одними и теми же параллелями DE и BC.
Следовательно, DE || BC

Пример 9.3 Класс 9 Математика Вопрос 8.
XY — это прямая, параллельная стороне BC треугольника ∆ ABC. Если BE ||AC и CF || AB пересекаются с XY в точках E и F соответственно, покажите, что ar (ABE) = ar (ACF)
Решение:
У нас есть ∆ABC такое, что XY || до н.э.,
г. до н.э. || AC и CF || АБ. 9{ gm }BCFX)\) …(2)
Кроме того, параллелограмм BCFX и параллелограмм BCYE находятся на одном основании BC и между одними и теми же параллелями BC и EF.
∴ ar(|| ^гм BCFX) = ar(|| ^гм BCYE) ………(3)
Из (1), (2) и (3) получаем
ar(∆BE) = ar(∆ACF)

Пример 9.3 Класс 9 Математика Вопрос 9.
Сторона AB параллелограмма ABCD проведена в любую точку P. Прямая, проходящая через A и параллельная CP, пересекает CB, полученную в точке Q, и затем завершается параллелограмм PBQR. (см. рисунок). 9{ gm }PBQR)\)
⇒ ar( || ^gm ABCD) = ar(|| ^gm PBQR)

Упражнение 9.3 Класс 9 по математике Вопрос 10.
Диагонали AC и BD трапеции AB CD с АБ | | DC пересекаются в точке O. Докажите, что ar (AOD) = ar (BOC)

Решение:
BBlliWWp имеют трапецию ABCD, имеющую AB || CD и его диагонали AC и BD пересекаются в точке O.
. Так как треугольники на одном основании и между одними и теми же параллелями имеют равные площади.
∆ABD и ∆ABC находятся на одном основании AB и между одними и теми же параллелями AB и DC
∴ ar(∆ABD) = ar(∆ABC)
Вычитая ar(∆AOB) с обеих сторон, получаем

ar(∆ABD) – ar(∆AOB) = ar(∆ABC) – ar(∆AOB) )
⇒ ar(∆AOD) = ar(∆BOC)

Пример 9. 3 Математика для 9 класса Вопрос 11.
На рисунке ABCDE представляет собой пятиугольник. Прямая через B, параллельная AC, пересекает DC, произведенный в F. Покажите, что
(i) ar (ACB) = ar (ACF)
(ii) ar (AEDF) = ar (ABCDE)

Решение:
У нас есть пятиугольник ABCDE, в котором BF || AC и DC получают по F.
(i) Так как треугольники между одними и теми же параллелями и на одном основании равны по площади.
∆ACB и ∆ACF находятся на одном основании AC и между одними и теми же параллелями AC и BF.
∴ ar(∆ACB) = ar(∆ACF)

(ii) Так как ar(∆ACB) = ar(∆ACF) [доказано выше]
Прибавив ar(quad. AEDC) к обеим частям, мы получим
⇒ ar(∆ACB) + ar(квадратный AEDC) = ar(∆ACF) + ar(квадратный AEDC)
∴ ar(ABCDE) = ar(AEDF)

Пример 9.3 Класс 9 Математика Вопрос 12.
Житель деревни У Итваари есть земельный участок в форме четырехугольника. Грам Панчаят из деревни решил занять часть своего участка в одном из углов для строительства Центра здоровья. Итваари соглашается с вышеуказанным предложением при условии, что ему будет предоставлено равное количество земли вместо его земли, примыкающей к его участку, с тем чтобы сформировать треугольный участок. Объясните, как это предложение будет реализовано.
Решение:
У нас есть участок в виде четырехугольника ABCD.
Нарисуем DF || AC и присоединиться к AF и CF.

Теперь ∆DAF и ∆DCF находятся на одном основании DF и между одними и теми же параллелями AC и DF.
∴ ar(ADAF) = ar(ADCF)
Вычитая ar(∆DEF) с обеих сторон, мы получаем
ar(∆DAF) – ar(∆DEF) = ar(∆DCF) – ar(∆DEF)
⇒ ar(∆ADE) = ar(∆CEF)
Часть ∆ADE может быть захвачена Грам Панчаятом путем добавления земли (∆CEF) к его (итваари) земле, чтобы сформировать треугольный участок,
т.е. ∆ABF.
Докажем, что ar(∆ABF) = ar(четв. ABCD), имеем
ar(ACEF) = ar(AADE) [Доказано выше]
Прибавив ar(четв. ABCE) к обеим частям, получим
ar (∆CEF) + ar(четверка ABCE) = ar(∆ADE) + ar (четверка ABCE)
⇒ ar(∆ABF) = ar (четверка ABCD)

Пример 9. 3 Класс 9 Математика Вопрос 13.
ABCD является трапецией с AB || ОКРУГ КОЛУМБИЯ. Прямая, параллельная AC, пересекает AB в точке X и BC в точке Y. Докажите, что ar(ADX) = ar(ACY). [Подсказка Join IX]
Решение:
У нас есть трапеция ABCD такая, что AB || ОКРУГ КОЛУМБИЯ.
XY || AC встречается с AB в X и BC в Y. Соединим CX.

∆ADX и ∆ACX находятся на одном основании AX и между одними и теми же параллелями AX и DC.
∴ ar(∆ADX) = ar(∆ACX) …(1)
∵∆ACX и ∆ACY находятся на одном основании AC и между одними и теми же параллелями AC и XY.
∴ ar(∆ACX) = ar(∆ACY) …(2)
Из (1) и (2) имеем
ar(∆ADX) = ar(∆ACY)

Пример 9.3 Класс 9 Математика Вопрос 14
На рисунке АП || БК || КР. Докажите, что ar(AQC) = ax(PBR).

Решение:
У нас есть, AP || БК || КР
∵ ∆BCQ и ∆BQR находятся на одном основании BQ и между одними и теми же параллелями BQ и CR.
∴ ar(∆BCQ) = ar(∆BQR) …(1)
∵ ∆ABQ и ∆PBQ находятся на одном основании BQ и между одними и теми же параллелями AP и BQ.
∴ ar(∆ABQ) = ar(∆PBQ) …(2)
Складывая (1) и (2), получаем
ar(∆BCQ) + ar(∆ABQ) = ar(∆BQR) + ar( ∆PBQ)
⇒ ar(∆AQC) = ar(∆PBR)

Пример 9.3 Математика 9 класса Вопрос 15.
Диагонали AC и BD четырехугольника ABCD пересекаются в 0 таким образом, что ax(AOD) = ar( БОК). Докажите, что ABCD — трапеция.
Решение:
У нас есть четырехугольник ABCD и его диагонали AC и BD пересекаются в точке O так, что
ar(∆AOD) = ar(∆BOC) [Дано]

Прибавив ar(∆AOB) к обеим сторонам, мы получим
ar(∆AOD) + ar(∆AOB) = ar(∆BOC) + ar(∆AOB)
⇒ ar(∆ABD) = ar(∆ABC)
Кроме того, они находятся на одном и том же основании AB.
Так как треугольники лежат на одном основании и имеют одинаковую площадь.
∴ Они должны лежать между одними и теми же параллелями.
∴ АВ || DC
Итак, ABCD — четырехугольник, у которого пара противоположных сторон параллельна.
Итак, ABCD — трапеция.

Пример 9.3 Класс 9 Математика Вопрос 16.
На рисунке ax(DRC) = ar(DPC) и ai(BDP) = ar(ARC). Докажите, что оба четырехугольника ABCD и DCPR являются трапециями.

Решение:
tfclfiftУ нас есть ar(∆DRC) = ar(∆DPC) [Дано]
И они находятся на одной базе DC.
∴ ∆DRC и ∆DPC должны располагаться между одними и теми же параллелями.
Итак, округ Колумбия || RP, т. е. пара противоположных сторон четырехугольника DCPR параллельна.
∴ Четырехугольник DCPR является трапецией.
Опять у нас
ar(∆BDP) = ar(∆ARC) [Дано] …(1)
Кроме того, ar(∆DPC) = ar(∆DRC) [Дано] …(2)
Вычитая (2) из ​​(1), получаем
ar(∆BDP) – ar(∆DPC) = ar(∆ARQ – ar(∆DRQ
⇒ ar(∆BDC) = ar(∆ADC)
И они находятся на одной базе DC.
∴ ABDC и AADC должны лежать между одними и теми же параллелями
Итак, AB || DC т. е. пара противоположных сторон четырехугольника ABCD параллельна
∴ Четырехугольник ABCD является трапецией

NCERT Решения для математики 9 класса Глава 9 Площади параллелограммов и Треугольники Пр 9.4

Упр. 9.4 Класс 9 Математика Вопрос 1.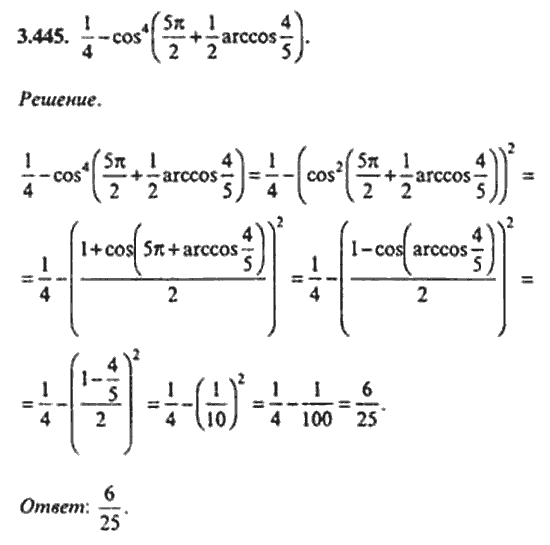
Параллелограмм ABCD и прямоугольник ABEF лежат на одном основании AB и имеют равные площади. Докажите, что периметр параллелограмма больше периметра прямоугольника.
Решение:
Имеются параллелограмм ABCD и прямоугольник ABEF такие, что
ar(||gm ABCD) = ar(прямоугольник ABEF)

AB = CD [Противоположные стороны параллелограмма]
и AB = EF [Противоположные стороны прямоугольник]
⇒ CD = EF
⇒ AB + CD = AB + EF … (1)
BE < BC и AF < AD [В прямоугольном треугольнике гипотенуза — самая длинная сторона] ⇒ (BC + AD) > (BE + АФ) …(2)
Из (1) и (2) имеем
(AB + CD) + (BC+AD) > (AB + EF) + BE + AF)
⇒ (AB + BC + CD + DA) > (AB + BE + EF + FA)
⇒ Периметр параллелограмма ABCD > Периметр прямоугольника ABEF.

Пример 9.4 Математика для 9 класса Вопрос 2.
На рисунке D и E — две точки на BC, такие что BD = DE = EC. Покажите, что ar(ABD) = ar(ADE) = ar(AEC).

Решение:
Проведем AF перпендикулярно BC
так, чтобы AF была высотой ∆ABD, ∆ADE и ∆AEC.

Пример 9.4 Класс 9 Математика Вопрос 3.
На рисунке ABCD, DCFE и ABFE являются параллелограммами. Покажите, что ar(ADE) = ax(BCF).

Решение:
Так как ABCD является параллелограммом [Дано]
∴ Его противоположные стороны параллельны и равны.
т. е. AD = BC …(1)
Теперь ∆ADE и ∆BCF находятся на равных основаниях AD = BC [из (1)] и между одними и теми же параллелями AB и EF.
Итак, ar(∆ADE) = ar(∆BCF).

Упражнение 9.4 Класс 9 Математика Вопрос 4.
На рисунке ABCD представляет собой параллелограмм, а BC приводится в точку Q так, что AD = CQ. Если AQ пересекает DC в точке P, покажите, что ar(BPC) = ax(DPQ).[Подсказка Соедините AC.]

Решение:
У нас есть параллелограмм ABCD и AD = CQ. Присоединяемся к АС.
Мы знаем, что треугольники с одним и тем же основанием и между одними и теми же параллелями равны по площади.
Так как ∆QAC и ∆QDC находятся на одном основании QC и между одними и теми же параллелями AD и BQ.
∴ ar(∆QAC) = ar(∆QDC)
Вычитая ar(∆QPC) с обеих сторон, мы имеем
ar(∆QAQ – ar(∆QPC) = ar(∆QDC) – ar(∆QPC)
⇒ ar(∆PAQ = ar(∆QDP) …(1)
Так как ∆PAC и ∆PBC находятся на одной и той же базовой PC и между одними и теми же параллелями AB и CD.
∴ ar(∆PAC) = ar(∆PBC) …(2)
Из (1) и (2) получаем
ar(∆PBC) = ar(∆QDP)

Пример 9.4 Класс 9 Математика Вопрос 5
На рисунке ABC и BDE — два равносторонних треугольника, среди которых D — середина треугольника BC. Если AE пересекает BC в точке F, покажите, что

[Подсказка Соедините EC и AD. Покажите, что БЫТЬ || AC и DE || AB и др.]
Решение:
Давайте объединим EC и AD. Нарисуйте ЕР ⊥ БК.
Пусть AB = BC = CA = a, тогда
BD = \(\frac { a }{ 2 }\) = DE = BE

(ii) Поскольку треугольники ∆ABC и ∆BED равносторонние.
⇒ ∠ACB = ∠DBE = 60°
⇒ BE || AC
∆BAE и ∆BEC находятся на одной базе BE и между одними и теми же параллелями BE и AC.
ar(∆BAE) = ar(∆BEC)
⇒ ar(∆BAE) = 2 ar(∆BDE) [ DE — медиана ∆EBC. ∴ ар(∆БЭК) = || ar(∆BDE)]
⇒ ar(ABDE) = \(\frac { 1 }{ 2 }\)ar(∆BAE)

(iii) ar(∆ABC) = 4 ar(∆BDE)[Доказано в (i) часть]
ar(∆BEC) = 2 ar(∆BDE)
[ ∵ DE медиана ∆BEC]
⇒ ar(∆ABC) = 2 ar(∆BEC)

(iv) Поскольку, ∆ ABC и ∆BDE — равносторонние треугольники.
⇒ ∠ABC = ∠BDE = 60°
⇒ АБ || DE
∆BED и ∆AED находятся на одном основании ED и между одними и теми же параллелями AB и DE.
∴ ar(∆BED) = ar(∆AED)
Вычитая ar(AEFD) с обеих сторон, получаем
⇒ ar(∆BED) – ar(∆EFD) = ar(∆AED) – ar(∆EFD)
⇒ ar(∆BEE) = ar(∆AFD)

(v) В прямоугольном ∆ABD получаем

Из (1) и (2) получаем
ar(∆AFD) = 2 ar( ∆EFD)
ar(∆AFD) = ar(∆BEF) [Из части (iv)]
⇒ ar(∆BFE) = 2 ar(∆EFD)

(vi) ar(∆AFC) = ar(∆ AFD) + ar(∆ADC)
= ar(∆BFE) + \(\frac { 1 }{ 2 }\) ar(∆ABC) [Из части (iv)]
= ar(∆BFE) + \(\frac { 1 }{ 2 } \) x 4 x ar(∆BDE) [Из части (i)]
= ar(∆BFE) + 2ar(∆BDE)
= 2ar(∆FED) + 2[ar(∆BFE) + ar(∆FED) )]
= 2ar(∆FED) + 2[2ar(∆FED) + ar(∆FED)] [Из части (v)]
= 2ar(∆FED) + 2[3ar(∆FED)]
= 2ar (∆FED) + 6ar(∆FED)
= 8ar(∆FED)
∴ ar(∆FED) = \(\frac { 1 }{ 8 }\) ar(∆AFC)

Ex 9. 4 Class 9 Math Question 6.
диагоналей AC и BD четырехугольника ABCD пересекаются в точке P. Докажите, что
ar(APB) x ar(CPD) = ar(APD) x ar(BPC).
[Подсказка Из A и C проведите перпендикуляры к BD.]
Решение:
У нас есть четырехугольник ABCD, диагонали AC и BD которого пересекаются в точке P.
Проведем AM ⊥ BD и CN ⊥ BD.

Упражнение 9.4 Математика для 9 класса Вопрос 7.
P и Q — середины сторон AB и BC треугольника ABC, а R — середина AP. Покажите, что

Решение:
У нас есть ∆ABC такой, что P — середина AB, а Q — середина BC.
Кроме того, R является средней точкой AP. Давайте присоединимся к AQ, RQ, ПК и ПК.

(i) В ∆APQ R является средней точкой AP. [Дано] B

∴RQ является медианой ∆APQ.
⇒ ar(∆PRQ) = \(\frac { 1 }{ 2 }\)ar(∆APQ) …(1)
В ∆ABQ точка P является серединой AB.
∴ QP является медианой ∆ABQ.
∴ ar(∆APQ) = \(\frac { 1 }{ 2 }\)ar(∆ABQ) …(2)

Пример 9.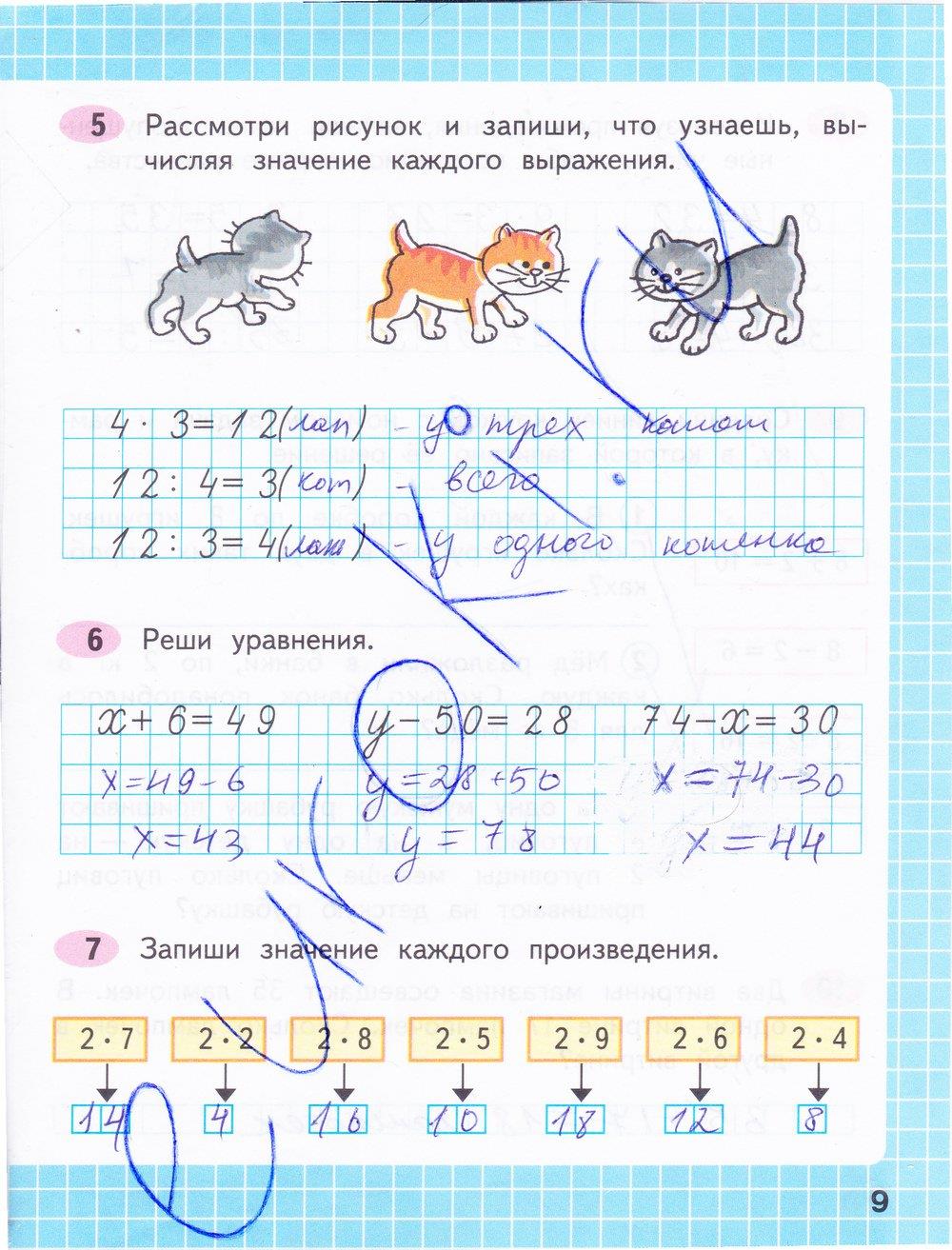 4 Класс 9 Математика Вопрос 8.
На рисунке ABC прямоугольный треугольник с прямым углом в точке A. BCED, ACFG и ABMN — квадраты со сторонами BC, CA и AB соответственно. Отрезок AX ⊥ DE пересекает BC в точке Y. Покажите, что

(i) ∆MBC = ∆ABD
(ii) ar(BYXD) = 2 ar(MBC)
(iii) ar(BYXD) = ax(ABMN)
(iv) ∆FCB ≅ ∆ACE
(v) ar(CYXE) = 2 ar(FCB)
(vi) ar(CYXE) = ax(ACFG)
(vii) ar(BCED) = ar(ABMN) + ar(ACFG)
Решение:
Имеем право ∆ ABC такой, что BCED, ACFG и ABMN являются квадратами со сторонами BC, CA и AB соответственно. Отрезок AX 1 DE также нарисован так, что он пересекает BC в точке Y. обе стороны)
или ∠ABD = ∠MBC
В ∆ABD и ∆MBC имеем
AB = MB [стороны квадрата]
BD = BC
∠ABD = ∠MBC [доказано выше]
∴ ∆ABD = ∆MBC [By конгруэнтность SAS]

(ii) Так как параллелограмм BYXD и ∆ABD лежат на одном основании BD и между одними и теми же параллелями BD и AX.
∴ ar(∆ABD) = \(\frac { 1 }{ 2 }\)ar(|| ^gm BYXD)
Но ∆ABD ≅ ∆MBC [Из части (i)]
Так как конгруэнтные треугольники равны
районов.
∴ ar(∆MBC) = \(\frac { 1 }{ 2 }\)ar(|| ^gm BYXD)
⇒ ar(|| ^gm BYXD) = 2ar(∆MBC)

(iii) Так как ar(|| ^gm BYXD) = 2ar(∆MBC) …(1) [Из (ii ) part]
и or(квадрат ABMN) = 2or(∆MBC) …(2)
[ABMN и AMBC находятся на одном основании MB и между одними и теми же параллелями MB и NC]
Из (1) и (2), у нас есть
ar(BYXD) = ar(ABMN) .

(iv) ∠FCA = ∠BCE (каждый 90°)
или ∠FCA+ ∠ACB = ∠BCE+ ∠ACB
[путем добавления ∠ACB с обеих сторон]
⇒ ∠FCB = ∠ACE
In ∆FCB и ∆ACE , у нас
FC = AC [Стороны квадрата]
CB = CE [Стороны квадрата]
∠FCB = ∠ACE [Доказано выше]
⇒ ∆FCB ≅ ∆ACE [По конгруэнтности SAS]

(v) Поскольку, | | ^gm CYXE и ∆ACE находятся на одном основании CE и между одними и теми же параллелями CE и AX.
∴ ar(|| ^gm CYXE) = 2ar(∆ACE)
Но ∆ACE ≅ ∆FCB [Из (iv) части]
Так как конгруэнтные треугольники равны по площадям.
∴ ar (||< ^gm CYXE) = 2ar(∆FCB)

(vi) Поскольку, ar(|| ^gm CYXE) = 2ar(∆FCB) …(3)
[Из части (v)]
Также (quad.