ГДЗ по Математике за 9 класс Инновационная школа Козлов В.В., Никитин А.А.
ГДЗ от Путина
Математика 9 класс Козлов В.В.
Авторы: Козлов В.В., Никитин А.А., Белоносов В.С., Мальцев А.А.
Математика пришла к нам из древних времён, явилась стимулом к развитию и прогрессу цивилизации и на данный момент на вычислениях основан весь современный высокотехнологичный мир. Эта наука непростая, но очень важная, и досконально разобраться в ней поможет «ГДЗ по Математике 9 класс Инновационная школа Козлов (Русское слово)». Объективно не существует сферы, где не применяются вычисления, расчёты и измерения: так или иначе, но без них попросту невозможно создать ни один предмет из материального мира, от кирпича до суперкомпьютера.
Структура пособия по Математике 9 класс Инновационная школа Козлов
Книга объединяет в себе информацию по нескольким математическим дисциплинам: арифметике, геометрии и алгебре, тригонометрии и основам анализа, изложенным в трёх уровнях сложности. Второй уровень помечен одной, а третий – двумя звёздочками. Вся информация в учебнике разделена на 15 глав, разбитых на параграфы и пункты. Основными темами являются: системы уравнений, формулы преобразования тригонометрических функций, элементы теорий вероятности и математической статистики. К каждому из разделов дополнительно идут задачи, контрольные вопросы, упражнения и тесты.
Второй уровень помечен одной, а третий – двумя звёздочками. Вся информация в учебнике разделена на 15 глав, разбитых на параграфы и пункты. Основными темами являются: системы уравнений, формулы преобразования тригонометрических функций, элементы теорий вероятности и математической статистики. К каждому из разделов дополнительно идут задачи, контрольные вопросы, упражнения и тесты.
Помощь и плюсы онлайн-решебника
В старших классах, особенно касаемо точных наук, родители или бабушка с дедушкой практически никак не могут помочь подростку, ведь выполнение заданного на дом подразумевает использование знаний, полученных на уроке и почерпнутых из учебника, а не самый простой или удобный путь решения. К тому же за годы жизни после школьной скамьи, память перестроилась на решение бытовых и рабочих повседневных проблем.
Нанять репетитора дорого, плюс есть фактор нежелания школьника иметь дополнительного преподавателя в ущерб своему свободному времени. Оптимальным выходом из проблемной ситуации является использование  В., Никитин А.А., Белоносов В.С., Мальцев А.А. (Русское слово)». Оно поможет:
В., Никитин А.А., Белоносов В.С., Мальцев А.А. (Русское слово)». Оно поможет:
- оперативно и самостоятельно справиться с домашним заданием;
- проверить ход своего решения, сравнив свои и верные ответы;
- сэкономить время, которого в старших классах зачастую не хватает.
В онлайн-решебнике содержатся готовые тесты, упражнения и задачи по всем 15 главам за учебный год. Эта наука развивает общий кругозор, формирует культуру мышления и научное мировоззрение. Она предлагает весьма чёткие модели для изучения окружающей действительности. Люди любых профессий так или иначе применяют на практике математические знания: использование персонального компьютера, который теперь присутствует повсеместно, невозможно без них.
Задания
Упс! Какое-то из ваших приложений или расширений браузера ломает код сайта. Пожалуйста, выключите их и перезагрузите страницу. Почините gdz-putina.fun!
Онлайн-ГДЗ по математике для 9 класса, составленное и разработанное Козловым, сумеет вселить любовь к алгебре и геометрии даже самым равнодушным ученикам. Доступное объяснение всех правил – это то, что пригодится не только девятиклассникам, но и всем ребятам, активно изучающим математику. К 9 классу ученики должны уже уверенно представлять себя во всех аспектах предмета. Но даже если в школе у вас было только пару часов математики в неделю, и вы неохотно учили ее дома – выйти на необходимый уровень можно с хорошо подобранной учебно-вспомогательной литературой. ГДЗ гарантированно поможет с такими темами, как:
Доступное объяснение всех правил – это то, что пригодится не только девятиклассникам, но и всем ребятам, активно изучающим математику. К 9 классу ученики должны уже уверенно представлять себя во всех аспектах предмета. Но даже если в школе у вас было только пару часов математики в неделю, и вы неохотно учили ее дома – выйти на необходимый уровень можно с хорошо подобранной учебно-вспомогательной литературой. ГДЗ гарантированно поможет с такими темами, как:
- Возрастание и убывание функции. Квадратный трехчлен. Разложение квадратного трехчлена на множители. Решение задач путем выделения квадрата двучлена из квадратного трехчлена. Функция у=ах2+вх+с, ее свойства и график. Простейшие преобразования графиков функций. Функция у=хn. Определение корня n-й степени. Вычисление корней –й степени.
- Целое уравнение и его корни. Биквадратные уравнения. Дробные рациональные уравнения. Решение неравенств второй степени с одной переменной. Решение неравенств методом интервалов.

- Уравнение с двумя переменными и его график. Графический способ решения систем уравнений. Решение систем, содержащих одно уравнение первой, а другое второй степени. Решение текстовых задач методом составления систем. Неравенства с двумя переменными. Системы неравенств с двумя переменными.
- Последовательности. Арифметическая и геометрическая прогрессии. Формулы n-го члена и суммы n первых членов прогрессии.
- Примеры комбинаторных задач. Перестановки, размещения, сочетания. Относительная частота случайного события. Равновозможные события и их вероятность.
На страницах решебника собраны самые эффективные задания вместе со шкалой оценивания. Процесс самоконтроля теперь станет ещё удобнее и приятнее. Справочник по математике должен иметься у каждого девятиклассника. Ведь даже отличники-трудоголики не всегда успевают попрактиковаться в достаточной мере. А сделать домашнее задание или написать срочное сочинение надо. Для выполнения трудных упражнений советуется следующий алгоритм действий.
Плюсы онлайн-решебника к учебнику по математике за 9 класс Козлова
Учить математику онлайн – не просто модно, но и практично. Особенно когда вы имеете доступ к комплексному пособию под редакцией Козлова, с помощью которого можно за несколько месяцев забыть о каком-то барьере и глупых ошибках. Постоянные самопроверки и углублённое изучение каждой темы даже смогут заменить ученикам девятых классов высококлассных репетиторов. Из всего разнообразия школьных предметов, пожалуй, одним из самых нелюбимых и трудных является математика. А все потому, что она требует большой внимательности, усидчивости, скрупулезности и аккуратности. Едва ли ученик средней школы может похвастаться всеми этими качествами. К тому же, часто случается, что преподаватель плохо вычитал тему, а подросток отсутствовал на уроке и не смог сам освоить весь материал. Для того чтобы избежать плохих оценок, можно использовать пособие, выпущенное издательством «Русское слово», для выполнения каждого задания или в экстренных случаях. Польза этого учебного пособия может казаться неочевидной, но она есть. Некоторые учителя и родители категорически против, чтобы ребёнок пользовался такими инструментами в учебе, но очень часто они становятся единственным способом подготовиться к уроку и не схлопотать двойку. Таким образом, польза от этого ГДЗ выглядит так: помогает проверить свои знания; способствует лучшему освоению материала при самостоятельной работе; основательно объясняет, как правильно решать задания из учебника; с его помощью на урок неподготовленным не пойдёт ни один школьник.
А все потому, что она требует большой внимательности, усидчивости, скрупулезности и аккуратности. Едва ли ученик средней школы может похвастаться всеми этими качествами. К тому же, часто случается, что преподаватель плохо вычитал тему, а подросток отсутствовал на уроке и не смог сам освоить весь материал. Для того чтобы избежать плохих оценок, можно использовать пособие, выпущенное издательством «Русское слово», для выполнения каждого задания или в экстренных случаях. Польза этого учебного пособия может казаться неочевидной, но она есть. Некоторые учителя и родители категорически против, чтобы ребёнок пользовался такими инструментами в учебе, но очень часто они становятся единственным способом подготовиться к уроку и не схлопотать двойку. Таким образом, польза от этого ГДЗ выглядит так: помогает проверить свои знания; способствует лучшему освоению материала при самостоятельной работе; основательно объясняет, как правильно решать задания из учебника; с его помощью на урок неподготовленным не пойдёт ни один школьник. Говорить о пользе таких вспомогательных инструментов можно очень долго, поэтому лучше всего будет взять и на своём опыте попробовать, насколько хорошо и легко с ним решать задачи любой сложности.
Говорить о пользе таких вспомогательных инструментов можно очень долго, поэтому лучше всего будет взять и на своём опыте попробовать, насколько хорошо и легко с ним решать задачи любой сложности.
Преимущества онлайн-решебника по математике для 9 класса к учебнику Козлова В. В., Никитина А. А., Белоносова В. С., Мальцева А. А. (Русское слово)
Каким бы скучным и трудным не казался этот предмет, изучать его необходимо, и домашку делать тоже нужно. Если школьник гуманитарий, у него плохо развито образное мышление и особой аккуратностью он не отличается, то без ответов на задания ему не обойтись. В противном случае, плохие оценки обеспечены, а там и аттестат может быть испорчен. Чтобы максимально хорошо учиться, иногда можно подсмотреть домашку и в решебнике. Ведь у него есть масса преимуществ:
- четкая и понятная структура;
- только верные развернутые ответы;
- полное соответствие учебной программе;
- отличное средство для самоконтроля;
- незаменимый помощник для отстающего ученика.

Обращая внимание только на достоинства этого пособия, в нем можно найти много чего полезного и постепенно выучить даже самые сложные темы. Электронный ресурс становится незаменимым помощником в борьбе за хорошую успеваемость. поможет выиграть время для различных увлечений ребят, которые не связаны с обучением. Дело в том, что пособие направлено на ускорение выполнения второстепенных учебных задач. Так, с его помощью появляется возможность быстро подготавливаться к самостоятельным и тестовым работам. В девятом классе ребята впервые в жизни встанут перед выбором дальнейшего пути обучения. Может быть, они захотят получить специализацию в профессионально-техническом училище или колледже. А, может, перейти в лицей при институте, университете или академии. Или вовсе продолжить получать знания в стенах родной школы. Что бы не выбрал школяр, решебник Козлова всегда поддержит его.
Рекомендуемые ГДЗ
ГДЗ по математике для 9 класса Козлов В.
 В.
В.Глава 1. Решения
Параграф 1
Задачи и упражнения
1 2 3 4 5 6 7 8 9Тесты
1 2Параграф 2
Задачи и упражнения
1 2 3 4 5 6 7 8 9 10 11 12 Тесты
1
2Параграф 3
Задачи и упражнения
1 2 3 4 5 6 7Тесты
1 2 Параграфы»> Контрольные вопросы и задания. Параграфы 1 2 3Глава 2. Решения
Параграф 1
Задачи и упражнения
1 2 3 4 5 6 7 8 9 10 11Тесты
1 2Параграф 2
Задачи и упражнения
1 2 3 4 5 6 7 8Тесты
1 2Параграф 3
Задачи и упражнения
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17Тесты
1 2Параграф 4
Задачи и упражнения
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15Тесты
1 2Параграф 5
Задачи и упражнения
1 2 3 4 5 6Тесты
1 2 Параграфы»> Контрольные вопросы и задания. Параграфы 1 2 3 4 5Глава 3. Решения
Параграф 1
Задачи и упражнения
1 2 3 4 5 6 7 8 9 10Тесты
1 2Параграф 2
Задачи и упражнения
1 2 3 4 5 6Тесты
1 2Параграф 3
Задачи и упражнения
1 2 3 4 5 6 7 8Тесты
1 2Параграф 4
Задачи и упражнения
1 2 3 4 5Тесты
1 2 Параграфы»> Контрольные вопросы и задания. Параграфы 1 2 3 4Глава 4. Решения
Параграф 1
Задачи и упражнения
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18Тесты
1 2Параграф 2
Задачи и упражнения
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15Тесты
1 2 Параграфы»> Контрольные вопросы и задания. Параграфы 1 2Глава 5. Решения
Параграф 1
Задачи и упражнения
1 2 3 4 5 6 7Тесты
1 2Параграф 2
Задачи и упражнения
1 2 3 4 5 6 7 8Тесты
1 2Параграф 3
Задачи и упражнения
1 2 3 4 5Тесты
1 2 Параграфы»> Контрольные вопросы и задания. Параграфы 1 2 3Глава 6. Решения
Параграф 1
Задачи и упражнения
1 2 3 4 5 6Тесты
1 2Параграф 2
Задачи и упражнения
1 2 3 4Тесты
1 2Параграф 3
Задачи и упражнения
1 2 3 4 5 6Тесты
1 2 Параграфы»> Контрольные вопросы и задания. Параграфы 1 2 3Глава 7. Решения
Параграф 1
Задачи и упражнения
1 2 3 4 5 6 7 8 9 10 11Тесты
1 2Параграф 2
Задачи и упражнения
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16Тесты
1 2Параграф 3
Задачи и упражнения
1 2 3 4 5 6Тесты
1 2 Параграфы»> Контрольные вопросы и задания. Параграфы 1 2 3Глава 8. Решения
Параграф 1
Задачи и упражнения
1 2 3 4 5 6Тесты
1 2Параграф 2
Задачи и упражнения
1 2 3Тесты
1 2Параграф 3
Задачи и упражнения
1 2 3Тесты
1 2 Параграфы»> Контрольные вопросы и задания. Параграфы 1 2 3Глава 9. Решения
Параграф 1
Задачи и упражнения
1 2 3 4 5 6 7Тесты
1 2Параграф 2
Задачи и упражнения
1 2 3 4 5 6 7 8 9 10 11 12 13 14Тесты
1 2 Параграфы»> Контрольные вопросы и задания. Параграфы 1 2Глава 10. Решения
Параграф 1
Задачи и упражнения
1 2 3 4 5 6 7 8Тесты
1 2Параграф 2
Задачи и упражнения
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15Тесты
1 2Параграф 3
Задачи и упражнения
1 2 3 4 5 6 7 8 9Тесты
1 2 Параграфы»> Контрольные вопросы и задания. Параграфы 1 2 3Глава 11. Решения
Параграф 1
Задачи и упражнения
1 2 3 4 5 6 7 8 9 10Тесты
1 2Параграф 2
Задачи и упражнения
1 2 3 4 5 6 7 8Тесты
1 2Параграф 3
Задачи и упражнения
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24Тесты
1 2Параграф 4
Задачи и упражнения
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15Тесты
1 2 Параграфы»> Контрольные вопросы и задания. Параграфы 1 2 3 4Глава 12. Решения
Параграф 1
Задачи и упражнения
1 2 3 4 5 6 7 8 9 10Тесты
1 2Параграф 2
Задачи и упражнения
1 2 3 4 5 6 7 8Тесты
1 2Параграф 3
Задачи и упражнения
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24Тесты
1 2 Параграфы»> Контрольные вопросы и задания. Параграфы 1 2 3Глава 13. Решения
Параграф 1
Задачи и упражнения
1 2 3 4 5 6 7 8 9Тесты
1 2Параграф 2
Задачи и упражнения
1 2 3 4 5 6 7 8 9 10Тесты
1 2Параграф 3
Задачи и упражнения
1 2 3 4 5 6 7 8 9Тесты
1 2Параграф 4
Задачи и упражнения
1 2 3 4 5Тесты
1 2 Параграфы»> Контрольные вопросы и задания. Параграфы 1 2 3 4Глава 14. Решения
Параграф 1
Задачи и упражнения
1 2 3 4 5 6 7Тесты
1 2Параграф 2
Задачи и упражнения
1 2 3 4 5 6 7 8 9 10 11 12Тесты
1 2Параграф 3
Задачи и упражнения
1 2 3 4 5 6 7 8 9Тесты
1 2 Параграфы»> Контрольные вопросы и задания. Параграфы 1 2 3Глава 15. Решения
Параграф 1
Задачи и упражнения
1 2 3Тесты
1 2Параграф 2
Задачи и упражнения
1 2 3 4Тесты
1 2Параграф 3
Задачи и упражнения
1 2 3 4 5 6Тесты
1 2Параграф 4
Задачи и упражнения
1 2 3 4 5Тесты
1 2Параграф 5
Задачи и упражнения
1 2 3 4 5Тесты
1 2 Параграфы»> Контрольные вопросы и задания. Параграфы 1 2 3 4 5ГДЗ по математике для 9 класса С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин
Loading
Класс
1 класс
2 класс
- Математика
- Английский язык
3 класс
- Английский язык
- Русский язык
- Математика
4 класс
- Математика
- Русский язык
- Английский язык
5 класс
- Биология
- Английский язык
- Русский язык
- Математика
6 класс
- Математика
- Биология
- Английский язык
- Русский язык
7 класс
- Химия
- Английский язык
- Русский язык
- Физика
- Математика
- Биология
8 класс
- Английский язык
- Биология
- Химия
- Математика
- Физика
- Русский язык
9 класс
- Химия
- Биология
- Английский язык
- Физика
- Русский язык
- Математика
10 класс
- Биология
- Математика
- Физика
- Химия
- Английский язык
11 класс
- Химия
- Английский язык
- Биология
9 КЛАСС
Темы учебника
- Глава 1.
 Неравенства.
Неравенства.- § 1. Линейные неравенства с одним неизвестным
- 1.1 Неравенства первой степени с одним неизвестным
- 1.2. Применение графиков к решению неравенств первой степени с одним неизвестным
- 1.3. Линейные неравенства с одним неизвестным
- 1.4. Системы линейных неравенств с одним неизвестным
- 1.5.* Неравенства, содержащие неизвестное под знаком модуля
- § 2. Неравенства второй степени с одним неизвестным
- 2.1. Понятие неравенства второй степени с одним неизвестным
- 2.2. Неравенства второй степени с положительным дискриминантом
- 2.3. Неравенства второй степени с дискриминантом, равным нулю
- 2.4. Неравенства второй степени с отрицательным дискриминантом
- 2.5. Неравенства, сводящиеся к неравенствам второй степени
- § 3. Рациональные неравенства
- 3.1. Метод интервалов
- 3.2. Решение рациональных неравенств
- 3.3. Системы рациональных неравенств
- 3.
 √x (x>= 0)
√x (x>= 0) - 5.6.* Корень степени n из натурального числа
- 5.7.* Иррациональные уравнения
- Урок 10. Понятие степени с рациональным показателем
- Урок 11. Свойства степени с рациональным показателем
- § 1. Линейные неравенства с одним неизвестным
- Глава 3. Последовательности.
- § 6. Числовые последовательности и их свойства
- 6.1. Понятие числовой последовательности
- 6.2. Свойства числовых последовательностей
- § 7. Арифметическая прогрессия
- 7.1. Понятие арифметической прогрессии
- 7.2. Сумма п первых членов арифметической прогрессии
- § 8. Геометрическая прогрессия
- 8.1. Понятие геометрической прогрессии
- 8.2. Сумма n первых членов геометрической прогрессии
- 8.3.* Бесконечно убывающая геометрическая прогрессия
- Дополнение к главе 3
- Урок 1. Метод математической индукции
- § 6. Числовые последовательности и их свойства
- Глава 4. Тригонометрические формулы.
- § 9.
 Угол и его мера
Угол и его мера- 9.1.* Понятие угла
- 9.2.* Градусная мера угла
- 9.3.* Радианная мера угла
- § 10.* Синус, косинус, тангенс и котангенс угла
- 10.1.* Определение синуса и косинуса угла
- 10.2.* Основные формулы для sinа и cosa
- 10.3.* Тангенс и котангенс угла
- Дополнения к главе 4
- 1. Косинус разности и косинус суммы двух углов
- 2. Формулы для дополнительных углов
- 3. Синус суммы и синус разности двух углов
- 4. Сумма и разность синусов и косинусов
- 5. Формулы для двойных и половинных углов
- 6. Произведение синусов и косинусов
- § 9.
- Глава 5. Элементы приближённых вычислений, статистики, комбинаторики и теории вероятностей
- § 11. Приближения чисел
- 11.1. Абсолютная погрешность приближения
- 11.2. Относительная погрешность приближения
- 11.3.* Приближения суммы и разности
- 11.4.* Приближение произведения и частного
- § 12.
 Описательная статистика
Описательная статистика- 12.1. Способы представления числовых данных
- 12.2. Характеристика числовых данных
- § 13. Комбинаторика
- 13.1. Задачи на перебор всех возможных вариантов
- 13.2. Комбинаторные правила
- 13.3. Перестановки
- 13.4. Размещения
- 13.5. Сочетания
- § 14. Введение в теорию вероятностей
- 14.1. Случайные события
- 14.2. Вероятность случайного события
- 14.3. Сумма, произведение и разность случайных событий
- 14.4. Несовместные события. Независимые события
- 14.5. Частота случайных событий
- Дополнения к главе 5
- § 11. Приближения чисел
ГДЗ Алгебра 9 класс Дорофеев, Суворова
- Алгебра 9 класс
- Тип пособия: Учебник
- Авторы: Дорофеев, Суворова
- Издательство: «Просвещение»
Задания
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325326327328329330331332333334335336337338339340341342343344345346347348349350351352353354355356357358359360361362363364365366367368369370371372373374375376377378379380381382383384385386387388389390391392393394395396397398399400401402403404405406407408409410411412413414415416417418419420421422423424425426427428429430431432433434435436437438439440441442443444445446447448449450451452453454455456457458459460461462463464465466467468469470471472473474475476477478479480481482483484485486487488489490491492493494495496497498499500501502503504505506507508509510511512513514515516517518519520521522523524525526527528529530531532533534535536537538539540541542543544545546547548549550551552553554555556557558559560561562563564565566567568569570571572573574575576577578579580581582583584585586587588589590591592593594595596597598599600601602603604605606607608609610611612613614615616617618619620621622623624625626627628629630631632633634635636637638639640641642643644645646647648649650651652653654655656657658659660661662663664665666667668669670671672673674675676677678679680681682683684685686687688689690691692693694695696697698699700701702703704705706707708709710711712713714715716717718719720721722723724725726727728729730731732733734735736737738739740741742743744745746747748749750751752753754755756757758759760761762763764765766767768769770771772773774775776777778779780781782783784785786787788789790791792793794795796797798799800801Задания: 1
Условие
Решебник №1
Решебник №2
Алгебра в девятом классе – важный предмет
В девятом классе у каждого ученика возникает большая проблема – сдача экзаменов для государственной итоговой аттестации. Как бы печально это не звучало, но одним из самых трудно сдаваемых предметов является как раз алгебра. Ей посвящён целый модуль в экзамене по математике. И именно в нем многие допускают ошибки.
Как бы печально это не звучало, но одним из самых трудно сдаваемых предметов является как раз алгебра. Ей посвящён целый модуль в экзамене по математике. И именно в нем многие допускают ошибки.
Для того чтобы знания по данной дисциплине соответствовали требованиям, школьникам необходимо проводить очень много времени над материалами учебника. Однако не все подростки готовы жертвовать своим личным временем в угоду учебе. Более того, некоторые учащиеся и вовсе норовят уклониться от заучивания сложных правил и формул, рассчитывая на то, что все как-нибудь само утрясется. Естественно, этого не происходит и их успеваемость начинает стремительно падать, так же, как и уровень знаний. Чтобы этого не допустить, специалисты в области образования рекомендуют использовать «ГДЗ по Алгебре 9 класс Учебник Дорофеев, Суворова (Просвещение)», который позволит и время сэкономить и все необходимые навыки получить.
Решебник — лучший помощник
Учебник по алгебре за 9 класс, созданный под редакцией Дорофеева и Суворовой, является лучшим пособием для подготовки к экзаменам и к текущим урокам. Благодаря этому замечательному справочнику вы сможете:
Благодаря этому замечательному справочнику вы сможете:
- Улучшить свои оценки по предмету.
- Понять самые сложные темы.
- Заполнить пробелы в знаниях за прошлые года обучения.
- Плавно подойти к подготовке к Основному Государственному Экзамену по математике.
- Научиться решать разноуровневые задания и номера.
Если же в ходе обучения возникают непреодолимые проблемы, то всегда можно обратиться за помощью к «ГДЗ по Алгебре 9 класс Учебник Дорофеев, Суворова (Просвещение)», в котором подробно расписаны все алгоритмы и пояснения.
Каким образом стоит использовать ГДЗ
Многие школьники начинают злоупотреблять решебниками, поэтому большинство взрослых настроено против них. С другой стороны зачастую ребятам просто не разъясняют, как именно нужно использовать данные справочники, поэтому они идут по самому простому пути — списывают информацию. Конечно, это может принести несколько отличных оценок, но что будет дальше? Без твердых знаний невозможно ни правильно ответить на вопросы учителя, ни написать многочисленные проверочные работы, не говоря уже о сдаче экзаменов.
Так что же предпринять в такой непростой ситуации? Как добиться, чтобы ГДЗ приносили реальную пользу? На самом деле ничего сверхъестественного делать не нужно. Необходимо просто придерживаться нескольких простых правил:
- если не заучивать, то хотя бы читать теоретический материал;
- всегда самостоятельно выполнять все номера;
- только после этого можно воспользоваться решебником;
- в случае обнаружения ошибок, стоит внимательно просмотреть решение, чтобы понять, откуда именно взялась неточность;
- закрепить пройденное, решив еще несколько аналогичных упражнений.
При таком подходе, ученики скоро сами заметят, насколько улучшились их познания и оценки. При этом с каждым разом времени на выполнение домашних заданий и подготовку к контрольным станет уходить все меньше, что несомненно порадует учащихся.
Насколько продуктивны занятия с решебником
Пожалуй из всех школьных предметов именно алгебра отнимает больше всего сил и времени, при этом все так же остается непонятной и сложной. Порой можно хоть целый вечер читать один и тот же параграф, а информация в нем так и остается китайской грамотой. А ведь необходимо не просто ознакомиться с написанным, но и потом успешно применять теорию в действии. Но как это сделать, если учитель толком ничего не показывает, а только требует результата? Вот тут подростки действительно оказываются в тупиковой ситуации.
Порой можно хоть целый вечер читать один и тот же параграф, а информация в нем так и остается китайской грамотой. А ведь необходимо не просто ознакомиться с написанным, но и потом успешно применять теорию в действии. Но как это сделать, если учитель толком ничего не показывает, а только требует результата? Вот тут подростки действительно оказываются в тупиковой ситуации.
Как показывает практика, есть несколько способов разрешения подобных положений:
- Обратиться к репетитору.
- Записаться на дополнительные курсы.
- Просить о помощи родителей.
- Постоянно списывать домашку у одноклассников.
- Заниматься самостоятельно при помощи решебника.
Все эти методы имеют свои плюсы и минусы. Однако большинство из них либо слишком дорогостоящи и отнимают много времени, либо вообще не эффективны. По наблюдениям специалистов в области образования именно занятия с «ГДЗ по Алгебре 9 класс Учебник Дорофеев, Суворова (Просвещение)» приносят больше всего пользы. Почему? Потому, что школьники получают возможность не просто увидеть ответы, но и на наглядных примерах разобрать все необходимые алгебраические нюансы.
Почему? Потому, что школьники получают возможность не просто увидеть ответы, но и на наглядных примерах разобрать все необходимые алгебраические нюансы.
Что можно найти на страницах ГДЗ
Решебники полностью соответствуют ФГОС и имеют ту же структуру, что и учебные пособия, к которым они написаны. Помимо условий заданий, которые приведены ко всем упражнениям, ученики могут ознакомиться с:
- верными ответами к номерам;
- подробными решениями заданий;
- наглядными примерами;
- дополнительными комментариями;
- несколькими вариантами оформления.
Используя «ГДЗ по Алгебре 9 класс Учебник Дорофеев, Суворова (Просвещение)» в качестве подспорья при выполнении домашних заданий, школьники не только получают ценные сведения, но и приобретают необходимые знания. Приведенная информация изложена простым и доступным языком, что позволит запомнить алгоритмы даже сильно отстающим по предмету ребятам. А то, что сборник находится в круглосуточном доступе онлайн, делает его применение еще более удобным, ведь подростки могут работать с ним в любое удобное время где угодно. Таким образом, учебный процесс становится не просто легким, но и начинает приносить определенное удовольствие, ведь какой школьник не захочет продемонстрировать свои познания учителю, заранее будучи уверенным в своих навыках.
А то, что сборник находится в круглосуточном доступе онлайн, делает его применение еще более удобным, ведь подростки могут работать с ним в любое удобное время где угодно. Таким образом, учебный процесс становится не просто легким, но и начинает приносить определенное удовольствие, ведь какой школьник не захочет продемонстрировать свои познания учителю, заранее будучи уверенным в своих навыках.
Систематические занятия с решебником пойдут на пользу не только плохо разбирающимся в дисциплине учащимся, но и круглым отличникам, которые получат шанс быстро перепроверить себя, узнать другие способы решения, сократить до минимума подготовку к проверочным испытаниям.
Макарычев Ю.Н. Решебник по Алгебре 9 класс
- формат exe
- размер 3.11 МБ
- добавлен 30 ноября 2010 г.
Решебник даёт правильные решения по данному предмету. Помогает
ученикам 9-го класса, которые не знают данный предмет.
Помогает
ученикам 9-го класса, которые не знают данный предмет.
Смотрите также
- формат pdf
- размер 42.3 МБ
- добавлен 03 мая 2010 г.
Виленкин Н. Я., Жохов В. И., Чесноков А. С., Шварцбурд С. И. Математика 5 класс, учебник, 2008, 280 с. (+ решебник 2001, 195 с. ) Учебник для общеобразовательных учреждений. Глава 1 — натуральные числа; глава 2 — дробные числа. Решебник составлен для учебника 2000 г., но задачи не изменились, только добавлен ряд новых задач. Например, соответствие номеров учебника и решебника: в учебнике 137 — в решебнике 134, в учебнике 1484 — в решебнике 1457…
- формат djvu, pdf
- размер 4.9 МБ
- добавлен 03 мая 2010 г.
Виленкин Н. Я., Жохов В. И., Чесноков А. С., Шварцбурд С. И. Математика 6 класс, учебник, 1994, 256 с. (+ решебник 2001, 104 с. ) Учебник для 6-го класса средней школы. Глава 1 — обыкновенные дроби; глава 2 — рациональные числа. В архиве с учебником есть решебник.
И., Чесноков А. С., Шварцбурд С. И. Математика 6 класс, учебник, 1994, 256 с. (+ решебник 2001, 104 с. ) Учебник для 6-го класса средней школы. Глава 1 — обыкновенные дроби; глава 2 — рациональные числа. В архиве с учебником есть решебник.
- формат pdf
- размер 8.82 МБ
- добавлен 24 апреля 2011 г.
Домашняя работа (ГДЗ) (решебник) по алгебре за 9 класс к задачнику «Алгебра 9 кл. А. Г. Мордкович и др. М.: «Мнемозина», 2008-2010 годов издания. «
- формат djvu, pdf
- размер 29.88 МБ
- добавлен 24 апреля 2011 г.
Первое издание сборника датировано 1996 годом, и до 2000 года он выходил в 1-й редакции. Впоследствии сборник был переработан и дополнен, и с 2000 года выходит во 2-й редакции. В архиве: 1) Сборник заданий для проведения письменного экзамена по алгебре за курс основной школы, 9 класс. Л. В. Кузнецова, Е. А. Бунимович, Б. П. Пигарев, С. Б. Суворова. — М.: Дрофа, 2008, 2-я редакция, 192 страницы. 2) Сборник заданий для проведения письменного экза…
В архиве: 1) Сборник заданий для проведения письменного экзамена по алгебре за курс основной школы, 9 класс. Л. В. Кузнецова, Е. А. Бунимович, Б. П. Пигарев, С. Б. Суворова. — М.: Дрофа, 2008, 2-я редакция, 192 страницы. 2) Сборник заданий для проведения письменного экза…
- формат djvu
- размер 3.92 МБ
- добавлен 05 января 2011 г.
Наименование: Алгебра. 9 класс: учеб. для учащихся общеобразоват. учреждений Авторы: Макарычев Ю. Н., Миндюк Н. Г., Нешков К. И., Феоктистов И. Е. 7-е издание, исправленное и дополненное Издательство: Мнемозина Дата выпуска: 2008 Листов (страниц): 447 ISBN: 978-5-346-01043-2 Книга представляет собой учебное пособие для школьников, которые обучаются в 9 классе. Настоящее пособие рассчитано на тех, кто углубленно изучает алгебру. Книга является з…
- формат pdf
- размер 1.
 42 МБ
42 МБ - добавлен 08 января 2010 г.
Издательство: Просвещение. Год издания: 2001. Домашняя работа по алгебре за 7 класс к учебнику «Алгебра. Учебник для 7 кл. общеобразовательных учреждений» Ю. Н. Макарычев и др., М.: «Просвещение», 2001 г. «
- формат pdf
- размер 2.49 МБ
- добавлен 25 мая 2010 г.
Издание карманного формата. В пособии решены, и в большинстве случаев подробно разобраны задачи и упражнения из учебника «Алгебра. Учебник для 9 кл. общеобразовательных учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского. — 11 изд. — М.: Просвещение, 2004». Также адресовано родителям, которые смогут проконтролировать правильность решения, а в случае необходимости помочь детям в выполнении домашней. ..
..
- формат exe
- размер 4.42 МБ
- добавлен 30 ноября 2010 г.
Решебник по Алгебре 8 класс Мордкович — даёт правильные решения по данному предмету. Помогает ученикам 7го класса, которые не знаю данный предмет.rn
- формат pdf
- размер 10.64 МБ
- добавлен 31 января 2011 г.
Домашняя работа по алгебре к учебнику ( Алгебра: Учеб. для 7 кл. общеобразоват. учреждений/ Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского — 12-е изд. — М.: Просвещение,2003 г. ) 189 стр.
ГДЗ Teme gata pregătite Готовые домашние задания Молдова Математика Акири 9 класс 2016 на MDAGDZ.COM
Алгебра. Глава 1. Повторение и дополнение
§ 1.
 Множество действительных чисел 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
Множество действительных чисел 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19§ 2.
 Действия над действительными числами 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Действия над действительными числами 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22§ 3.
 Степени и корни 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Степени и корни 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20Упражнения и задачи для повторения
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30Проверочная работа.
 Вариант 1 1
2
3
Вариант 1 1
2
3Проверочная работа. Вариант 2
1 2 3Глава 2. Функции
§ 1. Понятие функции.Повторение и дополнение
1 2 3 4 6 7 8 9 10 11§ 2.
 Числовые функции. тПовторение и дополнение 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Числовые функции. тПовторение и дополнение 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18§ 3.
 Функция II степени 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
Функция II степени 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27§ 4.
 9 7
9 7Упражнения и задачи для повторения
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28Проверочная работа.
 1 Вариант 1
2
3
1 Вариант 1
2
3Проверочная работа. 2 Вариант
1 2 3Глава 3. Многочлены и алгебраические дроби
§ 1. Одночлены. Операции над одночленами
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17§ 2.
 Многочлены. Операции над многочленами 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
Многочлены. Операции над многочленами 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19§ 3.
 Деление многочленов 1
2
3
4
5
Деление многочленов 1
2
3
4
5Bine ați venit pe site-ul unde puteți găsi sarcini gata făcute pentru manualele din Moldova. Ați făcut alegerea corectă!
Programul bogat de formare include multe discipline. Fiecare nouă lecție poartă un flux de termeni, teoreme, exemple. Lecțiile în clasă, temele, orele suplimentare, cursurile elective iau mult timp și energie de la studentul modern. Uneori, informațiile date de profesor sunt dificil de perceput și nu sunt asimilate în patruzeci de minute. Ajuns acasă, elevul nu își poate finaliza cu competența temele, se simte prost și interesul său pentru învățare scade. În astfel de momente, literatura de specialitate pe care echipa noastră a lăsat-o cu atenție vă va fi de folos.
În astfel de momente, literatura de specialitate pe care echipa noastră a lăsat-o cu atenție vă va fi de folos.
Aici sunt colectate toate soluțiile și răspunsurile corecte în cele mai dificile științe: matematică, algebră și geometrie, fizică și chimie.
Observăm funcțiile utile ale reshebnik-urilor: autoexaminare, analiza muncii lor pentru erori, identificarea lacunelor în cunoștințe în etapa inițială ajuta la îndeplinirea sarcinilor complexe capacitatea părinților de a supraveghea procesul educațional al copilului, precum și de a oferi o explicație a uneia sau altei terminologii creșterea stimei de sine și a încrederii în sine, adaptarea la cursul școlar, manifestarea interesului competitiv. Cunoașterea este putere, fii sigur de ea!
„GDZ” nu se referă la înșelăciune fără minte, este, în primul rând, un instrument pentru creșterea performanței școlare, obținerea maximului beneficiu și plăcere din activitățile de învățare. Manualul este, de asemenea, perfect pentru mame și tati, profesori și tutori.
Решения NCERT для математики класса 9 (обновлено для 2021-22)
Если вы ищете Решения NCERT для математики класса 9 , вы попали в нужное место. LearnCBSE.in создал наиболее точные и подробные решения для решений NCERT по математике для класса 9. Решения NCERT по математике для класса 9 включают все вопросы, представленные в соответствии с новой пересмотренной программой в учебнике по математике для класса 9 NCERT. Вы можете скачать PDF-файлы книжных решений NCERT по математике для 9 класса без ВХОДА. Вы также можете попрактиковаться в дополнительных вопросах для класса 9.Математика на сайте LearnCBSE.in
В 9 классе математика состоит из 15 глав. Эти главы закладывают основу для глав, которые будут представлены в 10-м классе. Этот PDF-файл доступен для всех, и они могут использовать этот PDF-файл по своему усмотрению. Здесь ниже мы помогаем вам с обзором каждой главы, появляющейся в учебнике.
Решения NCERT для класса 9 по математике Глава 1
- Класс 9 по математике Системы счисления Упражнение 1.
 1
1 - Класс 9 Математика Системы счисления Упражнение 1.2
- Класс 9 Математика Системы счисления Упражнение 1.3
- Класс 9 Математика Системы счисления Упражнение 1.4
- Класс 9 Математические системы счисления Упражнение 1.5
- Класс 9 Математические системы счисления Упражнение 1.6
- Дополнительные вопросы по системам счисления 9 класса
Решения NCERT для математики класса 9, глава 2
- Математические полиномы класса 9, упражнение 2.1
- Математические многочлены для 9-го класса. Упражнение 2.2
- Класс 9 Математические полиномы Упражнение 2.3
- Математические полиномы для 9 класса. Упражнение 2.4
- Математические полиномы для 9 класса. Упражнение 2.5
- Дополнительные вопросы по полиномам класса 9
Решения NCERT для математики класса 9, глава 3
- Математика, класс 9, координатная геометрия, упражнение 3.1
- Класс 9 Математика Координатная геометрия Упражнение 3.
 2
2 - Класс 9 Математика Координатная геометрия Упражнение 3.3
- Дополнительные вопросы по координатной геометрии, класс 9
Решения NCERT для класса 9Математика Глава 4
- Математика 9 класс Линейные уравнения с двумя переменными Упражнение 4.1
- Математические линейные уравнения с двумя переменными для 9 класса. Упражнение 4.2
- Математические линейные уравнения с двумя переменными для 9 класса. Упражнение 4.3
- Математические линейные уравнения с двумя переменными для 9 класса. Упражнение 4.4
- Линейные уравнения для двух переменных Дополнительные вопросы 9 класса
- Линейные уравнения с двумя переменными Класс 9 Словесные задачи и важные вопросы
Решения NCERT для математики класса 9 Глава 5
- Математика класса 9 Введение в геометрию Евклида Упражнение 5.1
- Глава 5 Введение в геометрию Евклида Упр. 5.2
- Введение в геометрию Евклида, класс 9, дополнительные вопросы
Решения NCERT для класса 9 по математике, глава 6
- Математические линии и углы для класса 9, упражнение 6.
 1
1 - Математические линии и углы, класс 9. Упражнение 6.2
- Класс 9 Математические линии и углы Упражнение 6.3
- Линии и углы Дополнительные вопросы 9 класса
Решения NCERT для класса 9 по математике, глава 7
- Математика, треугольники для класса 9, упражнение 7.1
- Математические треугольники для 9 класса. Упражнение 7.2
- Математические треугольники для 9 класса. Упражнение 7.3
- Математические треугольники для 9 класса. Упражнение 7.4
- Глава 7 Треугольники Ex 7.5
- Треугольники Класс 9 Дополнительные вопросы
Решения NCERT для класса 9 по математике, глава 8
- класс 9Математические четырехугольники. Упражнение 8.1
- Математические четырехугольники для 9 класса. Упражнение 8.2
- Четырехугольники Класс 9 Дополнительные вопросы
- Четырехугольники Класс 9 Математика Важные вопросы
Решения NCERT для 9 класса по математике Глава 9
- Математика для класса 9 Площади параллелограммов и треугольников Упражнение 9.
 1
1 - Класс 9 Математические области параллелограммов и треугольников Упражнение 9.2
- Класс 9 Математика Площади параллелограммов и треугольников Упражнение 9.3
- Глава 9 Площади параллелограммов и треугольников Пример 9.4
- Площади параллелограммов и треугольников Дополнительные вопросы 9 класса
Решения NCERT для класса 9 по математике, глава 10
- Математические кружки для класса 9, упражнение 10.1
- Класс 9 Математические кружки Упражнение 10.2
- Класс 9 Математические кружки Упражнение 10.3
- Класс 9 Математические кружки Упражнение 10.4
- Класс 9 Математические кружки Упражнение 10.5
- Глава 10 Круги Пример 10.6
- Круги Класс 9 Дополнительные вопросы
- Важные вопросы по математике для 9 класса с ответами
Решения NCERT для математики класса 9, глава 11
- Математические построения класса 9, упражнение 11.1
- Класс 9 Математические построения Упражнение 11.
 2
2 - Дополнительные вопросы по конструкции 9 класса
- Класс 9 Математические конструкции Важные вопросы
Решения NCERT для класса 9 по математике, глава 12
- класс 9Математика Формула Герона Упражнение 12.1
- Класс 9 Математика Формула Герона Упражнение 12.2
- Дополнительные вопросы по формуле Герона, класс 9
- . Класс 9. Площади параллелограммов и треугольников. Рабочие листы с решениями .
Решения NCERT для математики класса 9 Глава 13
- Математика класса 9 Площади поверхности и объемы Упражнение 13.1
- Класс 9 Площади поверхностей и объемы по математике Упражнение 13.2
- Класс 9 Математика Площади поверхностей и объемы Упражнение 13.3
- Класс 9 Площади поверхностей и объемы по математике Упражнение 13.4
- Математика класса 9 Площади поверхностей и объемы Упражнение 13.5
- Класс 9 Математика Площади поверхностей и объемы Упражнение 13.
 6
6 - Математика класса 9 Площади поверхностей и объемы Упражнение 13.7
- Математика класса 9 Площади поверхностей и объемы Упражнение 13.8
- Глава 13 Площади поверхности и объемы Ex 13.9
- Площади поверхности и объемы Класс 9 Дополнительные вопросы
- Площади поверхности и объемы Word Проблемы и важные вопросы
Решения NCERT для математики класса 9, глава 14
- Математика, статистика класса 9, упражнение 14.1
- Упражнение по математике и статистике для 9 класса 14.2
- Упражнение по математике и статистике для 9 класса 14.3
- Упражнение по математике и статистике для 9 класса 14.4
- Дополнительные вопросы класса 9 статистики
- Математика Класс 9 Статистика Важные вопросы с решениями
Решения NCERT для математики класса 9, глава 15
- Математическое вероятностное упражнение для класса 9 15.1
- Дополнительные вопросы класса вероятности 9
- Класс 9 Вероятность Важные вопросы
Решения NCERT по математике
В этой статье мы предоставим вам всю необходимую информацию о решениях NCERT по математике для 9-го класса. Решения NCERT для 9-го класса по математике решают опытные учителя, которые обеспечивают вам прочную основу по предмету «Математика». Математика класса 9 NCERT Solutions решается с учетом различных параметров, таких как пошаговые оценки, формулы, распределение оценок и т. Д. Это, в свою очередь, помогает вам не потерять ни одной отметки.
Решения NCERT для 9-го класса по математике решают опытные учителя, которые обеспечивают вам прочную основу по предмету «Математика». Математика класса 9 NCERT Solutions решается с учетом различных параметров, таких как пошаговые оценки, формулы, распределение оценок и т. Д. Это, в свою очередь, помогает вам не потерять ни одной отметки.
Очень важно создать прочную базу по математике. Это один предмет, который будет полезен для каждого студента, независимо от его отрасли. И поэтому мы помогаем вам с решениями NCERT для математики 9 класса. Этот PDF-файл поможет вам найти все решения, данные в учебнике NCERT вместе с упражнением.
Математика играет важную роль в жизни каждого школьника. Работа над решениями NCERT для математических заметок 9-го класса не только поможет вам получить хорошие оценки в 9-м классе, но также поможет вам сдать самые сложные конкурсные экзамены, такие как JEE, NEET, JEE Advanced и т. Д., Кроме того, это 9-й класс.Maths NCERT Solutions также будет полезен для сдачи таких экзаменов, как олимпиада, NTSE, с помощью которых вы можете легко получить стипендию и сделать свое образование без проблем. Читайте дальше, чтобы узнать все о NCERT Solutions Maths Class 9, чтобы получить красочные отметки в 9 классе CBSE.
Читайте дальше, чтобы узнать все о NCERT Solutions Maths Class 9, чтобы получить красочные отметки в 9 классе CBSE.
Решения NCERT для математики для 9-го класса Скачать PDF
Просматривайте все решения NCERT для 9-го класса по математике со своего мобильного или настольного компьютера и получайте больше оценок на экзаменах. Вы также можете просмотреть важные вопросы по математике для 9-го класса по главам, которые помогут вам в дополнительной практике и на экзаменах. Он состоит из вопросов на 1 балл, вопросов на 2 балла, числовых вопросов на 3 балла, вопросов на 4 балла, словесных задач и вопросов предыдущего года (VSAQ, SAQ, LAQ и вопросы на основе значений) из всех глав в классе 9.Математика, разработанная в соответствии с CBSE Class 9 Math Syllabus, изложена в последовательном порядке, что поможет набрать больше баллов на экзаменах Board.
Вы также можете просмотреть важные вопросы по математике для 9-го класса по главам, которые помогут вам в дополнительной практике и на экзаменах. Он состоит из вопросов на 1 балл, вопросов на 2 балла, числовых вопросов на 3 балла, вопросов на 4 балла, словесных задач и вопросов предыдущего года (VSAQ, SAQ, LAQ и вопросы на основе значений) из всех глав в классе 9.Математика, разработанная в соответствии с CBSE Class 9 Math Syllabus, изложена в последовательном порядке, что поможет набрать больше баллов на экзаменах Board.
Класс 9 Математика Глава 1 Системы счисления
Эта глава является продолжением числового ряда, который вы изучали в предыдущих стандартах. В этой главе вы также узнаете, как размещать различные типы чисел на числовой прямой. В общей сложности 6 упражнений в этой главе проведут вас через представление завершающих или не завершающих повторяющихся десятичных знаков на числовой прямой. Наряду с рациональными числами вы также узнаете, куда на числовой прямой помещать квадратные корни из 2 и 3. В этой главе также изучаются законы рациональных показателей и интегральных степеней.
В этой главе также изучаются законы рациональных показателей и интегральных степеней.
Математика для класса 9 Глава 2 Многочлены
В этой главе рассматриваются алгебраические выражения, называемые полиномами, и различные связанные с ними термины. В этой главе можно многое узнать об определении и примерах многочленов, коэффициентов, степеней и членов многочлена. В этой главе изучаются различные типы многочленов, такие как квадратичные многочлены, линейная константа, кубические многочлены, теоремы о факторах, теоремы о факторизации.
Класс 9 Математика Глава 3 Координатная геометрия
В общей сложности 3 упражнения в этой главе помогут вам понять геометрию координат в деталях. Наряду с такими понятиями, как понятия декартовой плоскости, термины и различные термины, связанные с координатной плоскостью, изучаются в этой главе. Вы также узнаете о построении точки на плоскости XY и процессе именования этой точки.
Математика для 9 класса Глава 4 Линейные уравнения с двумя переменными
В этой главе будет представлено новое уравнение ax + by + c = 0 с двумя переменными. Вопросы в этой главе будут связаны с доказательством того, что линейное число имеет бесконечные решения, с использованием барграфа для построения линейного уравнения и обоснованием любой точки на прямой. В общей сложности 4 упражнения для вашей практики и понимания.
Вопросы в этой главе будут связаны с доказательством того, что линейное число имеет бесконечные решения, с использованием барграфа для построения линейного уравнения и обоснованием любой точки на прямой. В общей сложности 4 упражнения для вашей практики и понимания.
Математика для 9 класса Глава 5 Введение в геометрию Евклида
Глава начинается с введения в индийскую геометрию, поскольку она имеет некоторую основу в геометрии Евклида. Введение в геометрию Евклида в этой главе поможет вам в процессе определения геометрических терминов и форм. Всего есть 2 упражнения, в которых вы подробно рассмотрите взаимосвязь между теоремами, постулатами и аксиомами.
Класс 9 Математика Глава 6 Линии и углы
В этой главе учебника NCERT также есть 2 упражнения. В этой главе есть различные теоремы об углах и прямых, которые можно попросить для доказательства. Первая теорема, которую потребуют для доказательства, звучит так: «Если две прямые пересекают друг друга, то образовавшиеся вертикально противоположные углы будут равны».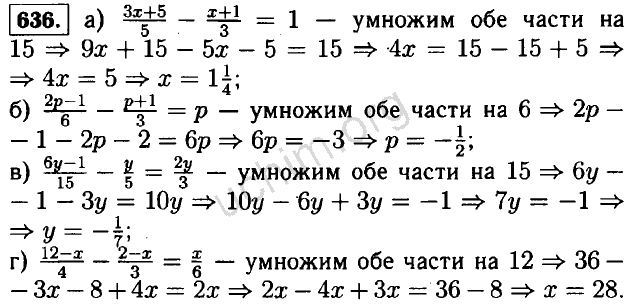 Кроме того, второе доказательство, которое задают, звучит так: «Сумма всех углов, образованных в треугольнике, равна 180°». Приводятся и другие теоремы, но они основаны только на этих двух теоремах.
Кроме того, второе доказательство, которое задают, звучит так: «Сумма всех углов, образованных в треугольнике, равна 180°». Приводятся и другие теоремы, но они основаны только на этих двух теоремах.
Класс 9 Математика Глава 7 Треугольники
Содержание этой главы поможет понять конгруэнтность треугольников, а также правила конгруэнтности. В этой главе также есть две теоремы и в общей сложности 5 упражнений для студентов. Эти две теоремы приведены в качестве доказательства, а другая используется в задачах или приложениях. Кроме того, в этой главе учащимся предстоит изучить множество свойств неравенств и треугольников.
Класс 9 Математика Глава 8 Четырехугольники
Эта глава очень интересна для изучения студентами, и в ней всего 2 упражнения. Вопросы в этой главе связаны со свойствами, относящимися к четырехугольнику и их сочетаниям с треугольниками.
Класс 9 Математика Глава 9 Площади треугольников и параллелограмма
Эта глава важна для понимания значения площади с этим, площади треугольника, параллелограмма и их комбинации задаются в этой главе вместе с их доказательствами.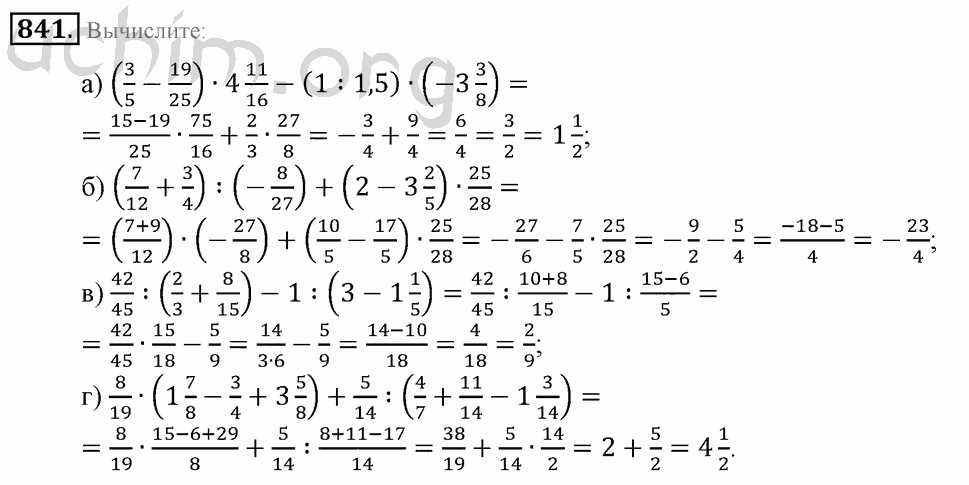 Есть также примеры an, которые используются в качестве доказательства теорем в этой главе.
Есть также примеры an, которые используются в качестве доказательства теорем в этой главе.
Класс 9 Математика Глава 10 Окружности
В этой главе вы познакомитесь с некоторыми интересными темами, такими как равные хорды и их расстояние от центра, хорда точки и стягиваемый ею угол, углы, стягиваемые дугой окружности и вписанных четырехугольников. В этой главе также есть теоремы, которые помогают доказывать вопросы, основанные на четырехугольниках, треугольниках и окружностях.
Класс 9 Математика Глава 11 Конструкции
Эта глава поможет вам изучить две разные категории конструкций. Одним из них является построение треугольника вместе с его основанием, разностью или суммой двух оставшихся сторон и одним углом при основании с углом при основании и параметрами. Другой — построение биссектрис для отрезков и измерение углов, включающих 45/60/9.0 и т. д.
Класс 9 Математика Глава 12 Формула Герона
Эта глава дополняет длинный список глав NCERT, в котором также есть 2 упражнения. В этой главе вы изучите понятия, являющиеся расширением понятий, связанных с площадью треугольника. Кроме того, вы узнаете, как находить площади треугольников, четырехугольников и различных типов многоугольников. Наряду с этим имеется также знание формулы плоских фигур, приведенной в главе.
В этой главе вы изучите понятия, являющиеся расширением понятий, связанных с площадью треугольника. Кроме того, вы узнаете, как находить площади треугольников, четырехугольников и различных типов многоугольников. Наряду с этим имеется также знание формулы плоских фигур, приведенной в главе.
Класс 9 Математика Глава 13 Площади поверхности и объем
Каждый из вас уже изучал измерения в предыдущих стандартах. Таким образом, вы должны знать о поверхностных областях, и эта глава посвящена им. Наряду с этим в этой главе также есть объем кубов, цилиндров, прямоугольных параллелепипедов, конусов, полушарий и сфер. Кроме того, в этой главе вы узнаете о преобразовании одной фигуры в другую и сравнении объемов двух фигур.
Класс 9 Математика Глава 14 Статистика
В этой главе вы получите знания об описательной статистике и сборе данных, основанных на различных аспектах жизни. Это полезно для интерпретации и формулирования выводов из данных. Эта глава дает базовые знания о сборе данных, поскольку данные доступны в необработанном виде. По мере того, как вы продвигаетесь вперед и изучаете 5 упражнений, вы научитесь представлять данные в табличной форме, сохраняя их вместе через равные промежутки времени, рисуя многоугольники, гистограммы или гистограммы. Вы также перейдете к таким темам, как среднее значение, медиана и мода, а также к нахождению центральной тенденции с помощью необработанных данных.
По мере того, как вы продвигаетесь вперед и изучаете 5 упражнений, вы научитесь представлять данные в табличной форме, сохраняя их вместе через равные промежутки времени, рисуя многоугольники, гистограммы или гистограммы. Вы также перейдете к таким темам, как среднее значение, медиана и мода, а также к нахождению центральной тенденции с помощью необработанных данных.
Класс 9 Математика Глава 15 Вероятность
Вероятность в этой книге основана на подходе наблюдения или нахождения частоты. Вопросы в этой главе очень интуитивны, поскольку они основаны на повседневной жизни или повседневных ситуациях. Например, такие инциденты, как бросание игральных костей, подбрасывание монеты, вероятность выпадения колоды карт и простые события. Если вам любопытно, эта глава может быть очень интересной для вас, чтобы выучить и понять.
Несколько раз вам может казаться, что вы застряли и не получаете желаемых решений. Именно здесь мы можем предложить вам решения NCERT для класса 9. математика. Вы можете использовать эту статью в качестве справочника по всем главам книги NCERT.
математика. Вы можете использовать эту статью в качестве справочника по всем главам книги NCERT.
Часто задаваемые вопросы о решениях NCERT для 9-го класса по математике
1. Как подготовиться к 9-му классу CBSE по математике?
Попрактикуйтесь в решениях NCERT по математике для 9 класса и постарайтесь тщательно осветить все темы и вопросы.
2. Как я могу эффективно и быстро выучить математику для 9 класса?
Лучший способ быстро научиться — решить NCERT. NCERT имеет мало вопросов, но имеет большое значение в документах. Если вы можете решить весь NCERT с примерами, вы легко получите хороший результат. Если у вас достаточно времени, попробуйте также обратиться к Р. Д. Шарме, поскольку это лучшая книга.
3. Могу ли я решить математические вопросы для CBSE 9 класса?
Да, вы можете получить решения по математике для экзаменов CBSE 9 класса на нашей странице. Получите доступ к прямым ссылкам, доступным на нашей странице, и загрузите их бесплатно.
4. Какое пособие по математике лучше для 9-го CBSE?
NCERT Solutions for Class 9 Maths поможет вам в подготовке. Получите хорошее представление о предмете, практикуя все больше и больше решений NCERT, преобладающих на нашей странице.
5. Как я могу загрузить книгу решений NCERT для математики класса 9 CBSE?
Претенденты могут загрузить решения NCERT по математике класса 9 CBSE, нажав на доступные прямые ссылки. Заложите более прочную основу концепций, обратившись к решениям NCERT.
6. Как долго ученик 9 класса должен заниматься математикой?
Дело не в ограничении времени. Старайтесь практиковаться как можно больше и пересмотреть полную программу по математике для 9 класса, чтобы экзамены набрали хорошие баллы.
Теперь, когда вам предоставлена вся необходимая информация о решениях NCERT для 9 класса по математике, мы надеемся, что эта подробная статья о решениях NCERT по математике для 9 класса окажется полезной. Если у вас есть какие-либо сомнения относительно этой статьи или решений NCERT по математике для класса 9, оставьте свои комментарии в разделе комментариев ниже, и мы свяжемся с вами как можно скорее.
Если у вас есть какие-либо сомнения относительно этой статьи или решений NCERT по математике для класса 9, оставьте свои комментарии в разделе комментариев ниже, и мы свяжемся с вами как можно скорее.
Решения NCERT для класса 9 по математике Глава 9 Площади параллелограммов и треугольников
Решения NCERT для класса 9Математика Глава 9 Области параллелограммов и треугольников Ex 9.1 являются частью решений NCERT для математики класса 9. Здесь мы дали решения NCERT для математики класса 9, глава 9, области параллелограммов и треугольников, пример 9.1.
Решения NCERT для математики класса 9 Глава 9 Площади параллелограммов и треугольников Упр. 9.1
Упражнение 9.1 Математика класса 9 Вопрос 1
Какие из следующих фигур лежат на одном основании и между одними и теми же параллелями. В таком случае запишите общее основание и две параллели.
Решение:
Фигуры (i), (iii) и (v) лежат на одном основании и между одними и теми же параллелями.
| Общая база | Две параллели | |
Рис. (i) (i) | DC | DC и AB |
| Рис. (iii) | QR | QR и PS |
| Рис. (v) | г. | г. н.э.AD и BQ |
Решения NCERT для класса 9Математическая глава 9 Площадь параллелограммы и треугольников (समान्तर चतुर्भुज और त्ा
NCERT Solutions для математики 9011. 9 Математика Вопрос 1.
На рисунке ABCD — параллелограмм, AE ⊥ DC и CF ⊥ AD. Если AB = 16 см, AE = 8 см и CF = 10 см, найдите AD.
Решение:
BSO Имеем, AE ⊥ DC и AB = 16 см
∵ AB = CD [Противоположные стороны параллелограмма]
∴ CD = 16 см
Теперь площадь параллелограмма ABCD = CD x AE
= (16 x 8) см 2 = 128 см 2 [∵ AE = 8 см]
Поскольку, CF ⊥ AD
∴ Площадь параллелограмма ABCD = AD x CF
⇒ AD x CF = 128 см
⇒ AD x 10 см = 128 см 2 [∵ CF= 10 см]
⇒ AD = \(\frac { 128 }{ 10 }\) см = 12,8 см 10
Таким образом, необходимая длина AD составляет 12,8 см
Упр. { gm }EBCG)\) … (1) 9{ gm }ABCD)\) …(2)
{ gm }EBCG)\) … (1) 9{ gm }ABCD)\) …(2)
Из (1) и (2) имеем ar(∆APB) = ar(∆BQC).
Пример 9.2 Класс 9 Математика Вопрос 4.
На рисунке P — точка внутри параллелограмма ABCD. Покажите, что
(i) ar (APB) + ar (PCD) = \(\frac { 1 }{ 2 } ar(ABCD)\)
(ii) ar (APD) + ar(PBC) = ar (APB ) + ar (PCD)
Решение:
Имеем параллелограмм ABCD, т. е. AB || КД и БК || ОБЪЯВЛЕНИЕ. Нарисуем EF || АБ и ГГ || AD через P.
(i) ∆APB и || gm AEFB находятся на одном основании AB и между теми же параллелями AB и EF. 9{ gm }ABCD)\) …….(6)
Из (3) и (6) имеем
ar(∆APD) + ar(∆PBC) = ar(∆APB) + ar(∆PCD)
Пример 9.2 Класс 9 Математика Вопрос 5.
На рисунке PQRS и ABRS являются параллелограммами, а X – любая точка на стороне BR. Покажите, что
(i) ar (PQRS) = ar (ABRS)
(ii) ar (AXS) = \(\frac { 1 }{ 2 } ar(PQRS)\)
Решение:
(i) Параллелограмм PQRS и параллелограмм ABRS находятся на одном основании RS и между одними и теми же параллелями RS и PB.
∴ ar(PQRS) = ar(ABRS)
(ii) AAXS и || гм АБРС находятся на одной базе АС и между теми же параллелями АС и БР. *
∴ ar(AXS) = \(\frac { 1 }{ 2 } ar(ABRS)\) …(1)
Но ar(PQRS) = ar(ABRS) …(2) [Доказано в части (i) ]
Из (1) и (2) получаем
ar(AXS) = \(\frac { 1 }{ 2 } ar(PQRS)\)
Пример 9.2 Математика для 9 класса, вопрос 6.
У фермера было поле в виде параллелограмма PQRS. Она взяла любую точку А на RS и соединила ее с точками P и Q. На сколько частей разбито поле? Каковы формы этих частей? Фермер хочет посеять пшеницу и бобовые на равных участках поля по отдельности. Как она должна это сделать. 9{ gm }PQRS)\) …(2)
Из (1) и (2) имеем
ar(∆PAQ) = ar[(∆APS) + (∆QAR)]
Таким образом, фермер может сеять пшеницу в (∆PAQ) и бобовые в [(∆APS) + (∆QAR)] или пшеницу в [(∆APS) + (∆QAR)] и бобовые в (∆PAQ).
Решения NCERT для математики класса 9 Глава 9 Площади параллелограммов и треугольников Пример 9.3
Пример 9. 3 Математика класса 9 Вопрос 1.
3 Математика класса 9 Вопрос 1.
На рисунке E — это любая точка на медиане AD ∆ABC. Покажите, что ar (ABE) = ar (ACE).
Решение:
У нас есть ∆ABC такое, что AD является медианой.
∴ ar(∆ABD) = ar(∆ACD) …(1)
[∵ Медиана делит треугольник на два равновеликих треугольника]
Аналогично, в ∆BEC имеем
ar(∆BED) = ar( ∆DEC) …(2)
Вычитая (2) из (1), получаем
ar(∆ABD) – ar(∆BED) = ar(∆ACD) – ar(∆DEC)
⇒ ar(∆ABE) = ар(∆ACE).
Упражнение 9.3 Класс 9 Математика Вопрос 2.
В треугольнике ABC точка E является серединой медианы AD. Покажите, что ax (BED) = \(\frac { 1 }{ 2 } ar(ABC)\).
Решение:
У нас есть ∆ABC и его медиана AD.
Соединим B и E.
Так как медиана делит треугольник на два равновеликих треугольника.
ar (∆ABD) = \(\frac { 1 }{ 2 } ar(\Delta ABC)\) …….(1)
Теперь в ∆ABD BE является медианой.
[ ∵ E – середина AD]
∴ ar(∆BED) = \(\frac { 1 }{ 2 } ar(\Delta ABC)\) …(2)
Из (1) и (2) ), имеем
ar(∆BED) = \(\frac { 1 }{ 2 }\) [\(\frac { 1 }{ 2 } ar(\Delta ABC)\) ]
⇒ ar(∆BED) = \(\frac { 1 }{ 4 } ar(\Delta ABC)\)
Упр. 9.3 Класс 9 Математика Вопрос 3.
9.3 Класс 9 Математика Вопрос 3.
Покажите, что диагонали параллелограмма делят его на четыре треугольника одинаковой площади.
Решение:
У нас есть параллелограмм ABCD (скажем)
такой, что его диагонали пересекаются в точке O.
∵Диагонали параллелограмма делят друг друга пополам.
∴ AO = OC и BO = OD
Построим CE ⊥ BD.
Теперь ar(∆BOC) = \(\frac { 1 }{ 2 }\)BO x CE и
ar(∆DOC) = \(\frac { 1 }{ 2 }\)OD x CE
Поскольку , BO = OD
∴ ar(∆BOC) = ar(∆DOC) …(1)
Аналогично, ar(∆AOD) = ar(∆DOC) …(2)
и ar(∆AOB) = ar(∆ BOC) …(3)
Из (1), (2) и (3) имеем
ar(∆AOB) = ar(∆BOC) = ar(∆COD) = ar(∆DOA)
Таким образом, диагонали параллелограмма делят его на четыре равновеликих треугольника.
Упражнение 9.3 Класс 9 Математика Вопрос 4.
На рисунке ABC и ABD представляют собой два треугольника с одним и тем же основанием AB. Если отрезок CD делится пополам отрезком AB в точке O, покажите, что ar(ABC) = ar(ABD)
Решение:
имеем ∆ABC и ∆ABD на одном и том же основании AB.
∵ CD делится пополам в точке O. [Дано]
∴ CO = OD
Теперь в ∆ACD AO является медианой
∴ ar(∆OAC) = ar(∆OAD) …(1)
Опять же, в ∆BCD , BO — медиана
∴ ar(∆OBC) = ar(∆ODB) …(2)
Складывая (1) и (2), получаем
ar(∆OAQ + ar(∆OBQ) = ar(∆OAD) + ar(∆ ODB)
⇒ ar(∆ABC) = ar(∆ABD)
Пример 9.3 Класс 9 Математика Вопрос 5.
D, E и F являются соответственно серединами сторон BC, CA и AB треугольника ∆ABC. Покажите, что
(i) BDEF является параллелограммом
(ii) ar(DEF) = \(\frac { 1 }{ 4 } ar(ABC)\)
(iii) ar(BDEF) = \(\frac { 1 }{ 4 } ar(ABC)\)
Решение:
У нас есть ∆ABC такое
, что D,E и Fare являются серединами BC, CA и AB соответственно.
(i) В ∆ABC E и F являются серединами AC и B D C AB соответственно.
∴ ЭФ || BC [Теорема о средней точке]
⇒ EF || BD
Кроме того, EF = \(\frac { 1 }{ 2 } (BC)\)
⇒ EF = BD [D — середина BC]
Поскольку BDEF — четырехугольник, одна пара противоположных сторон которого параллельна и одинаковой длины.
∴ BDEF — параллелограмм.
(ii) Мы доказали, что BDEF является параллелограммом.
Точно так же DCEF является параллелограммом, и DEAF также является параллелограммом.
Теперь параллелограмм BDEF и параллелограмм DCEF лежат на одном основании EF и между одними и теми же параллелями BC и EF.
∴ ar(|| гм BDEF) = ar(|| гм DCEF)
⇒ \(\frac { 1 }{ 2 }\)ar(|| гм BDEF) = \(\frac { 1 }{ 2 }\)ar(|| gm DCEF)
⇒ ar(∆BDF) = ar(∆CDE) …(1)
[Диагональ параллелограмма делит его на два равновеликих треугольника]
Аналогично , ar(∆CDE) = ar(∆DEF) …(2)
и ar(∆AEF) = ar(∆DEF) …(3)
Из (1), (2) и (3) имеем
ar(∆AEF) = ar(∆FBD) = ar(∆DEF) = ar(∆CDE)
Таким образом, ar(∆ABC) = ar(∆AEF) + ar(∆FBD) + ar(∆DEF) + ar(∆CDE) = 4 ar(∆DEF)
⇒ ar(∆DEF) = \(\frac { 1 }{ 4 }\)ar(∆ABC)
(iii) Имеем, ar (|| г BDEF) = ar(∆BDF) + ar(∆DEF)
= ar(∆DEF) + ar(∆DEF) [∵ ar(∆DEF) = ar(∆BDF)]
2ar(∆DEF) = 2[\(\frac { 1 }{ 4 }\)ar(∆ABC)]
= \(\frac { 1 }{ 2 }\)ar(∆ABC)
Таким образом, ar (|| gm BDEF) = \(\frac { 1 }{ 2 }\)ar(∆ABC)
Упражнение 9. 3 Класс 9 Математика Вопрос 6.
3 Класс 9 Математика Вопрос 6.
На рисунке диагонали AC и BD четырехугольника ABCD пересекаются в точке 0 так, что OB = OD. Если AB = CD, то покажите, что
(i) ar(DOC) = ar(AOB)
(ii) ar (DCB) = ar (ACB)
(iii) DA || CB или ABCD — параллелограмм
Решение:
Имеем четырехугольник ABCD, диагонали которого AC и BD пересекаются в точке O.
Имеем также, что OB = OD, AB = CD Нарисуем DE ⊥ AC и BF ⊥ AC
(i) В ∆DEO и ∆BFO имеем
DO = BO [Дано]
∠DOE = ∠BOF [Вертикально противоположные углы]
∠DEO = ∠BFO [каждый 90°]
∴ ∆DEO ≅ ∆BFO [по конгруэнтности A AS]
⇒ DE = BF [по C.P.C.T.]
и ar(∆DEO) = ar(∆BFO) …(1)
Теперь в ∆DEC и ∆BFA имеем
∠DEC = ∠BFA [каждые 90°]
DE = BF [доказано выше]
DC = BA [дано]
∴ ∆DEC ≅ ∆BFA [по RHS-конгруэнтности]
⇒ ar(∆DEC) = ar(∆BFA) …(2)
и ∠1 = ∠2 …(3) [по C.P.C.T.]
Складывая (1) и (2), получаем
ar(∆DEO) + ar(∆DEC) = ar(∆BFO) + ar(∆BFA)
⇒ ar(∆DOC) = ar(∆AOB)
(ii) Поскольку ar(∆DOC) = ar(∆AOB) [ Доказано выше]
Добавляя ar(∆BOC) с обеих сторон, мы получаем
ar(∆DOC) + ar(∆BOC) = ar(∆AOB) + ar(∆BOC)
⇒ ar(∆DCB) = ar(∆ACB)
(iii) Так как ∆DCS и ∆ACB находятся на одном и том же основании CB и имеют равные площади.
∴ Лежат между одинаковыми параллелями CB и DA.
⇒ КБ || DA
Также ∠1 = ∠2, [по (3)]
, которые являются альтернативными внутренними углами.
Итак, А.Б. || CD
Значит, ABCD — параллелограмм.
Пример 9.3 Класс 9 Математика Вопрос 7.
D и E — точки на сторонах AB и AC соответственно ∆ ABC, такие что ar (DBC) = ar (EBC). Докажите, что DE || ДО Н.Э.
Решение:
У нас есть ∆ABC, а точки D и E таковы, что ar(DBC) = ar{EBC)
Так как ∆DBC и ∆EBC лежат на одном основании BC и имеют одинаковую площадь.
∴ Они должны лежать между одними и теми же параллелями DE и BC.
Следовательно, DE || BC
Пример 9.3 Класс 9 Математика Вопрос 8.
XY – прямая, параллельная стороне BC треугольника ∆ ABC. Если BE ||AC и CF || AB пересекаются с XY в точках E и F соответственно, покажите, что ar (ABE) = ar (ACF)
Решение:
У нас есть ∆ABC такое, что XY || до н.э.,
г. до н.э. || AC и CF || АБ. 9{ gm }BCFX)\) …(2)
Кроме того, параллелограмм BCFX и параллелограмм BCYE находятся на одном основании BC и между одними и теми же параллелями BC и EF.
∴ ar(|| гм BCFX) = ar(|| гм BCYE) ………(3)
Из (1), (2) и (3) получаем
ar(∆BE) = ar(∆ACF)
Пример 9.3 Класс 9 Математика Вопрос 9.
Сторона AB параллелограмма ABCD приводится в любую точку P. Прямая, проходящая через A и параллельная CP, пересекает CB, полученную в точке Q, и затем завершается параллелограмм PBQR. (см. рисунок). 9{ gm }PBQR)\)
⇒ ar( || gm ABCD) = ar(|| gm PBQR)
Упражнение 9.3 Класс 9 по математике Вопрос 10.
Диагонали AC и BD трапеции ABCD с AB | | DC пересекаются в точке O. Докажите, что ar (AOD) = ar (BOC)
Решение:
BBlliWWp имеют трапецию ABCD, имеющую AB || CD и его диагонали AC и BD пересекаются в точке O.
. Так как треугольники на одном основании и между одними и теми же параллелями имеют равные площади.
∆ABD и ∆ABC находятся на одном основании AB и между одними и теми же параллелями AB и DC
∴ ar(∆ABD) = ar(∆ABC)
Вычитая ar(∆AOB) с обеих сторон, получаем
ar(∆ABD) – ar(∆AOB) = ar(∆ABC) – ar(∆AOB) )
⇒ ar(∆AOD) = ar(∆BOC)
Пример 9. 3 Математика для 9 класса Вопрос 11.
3 Математика для 9 класса Вопрос 11.
На рисунке ABCDE представляет собой пятиугольник. Прямая через B, параллельная AC, пересекает DC, произведенный в F. Покажите, что
(i) ar (ACB) = ar (ACF)
(ii) ar (AEDF) = ar (ABCDE)
Решение:
У нас есть пятиугольник ABCDE, в котором BF || AC и DC получают по F.
(i) Так как треугольники между одними и теми же параллелями и на одном основании равны по площади.
∆ACB и ∆ACF находятся на одном основании AC и между одними и теми же параллелями AC и BF.
∴ ar(∆ACB) = ar(∆ACF)
(ii) Так как ar(∆ACB) = ar(∆ACF) [доказано выше]
Прибавив ar(quad. AEDC) к обеим частям, мы получим
⇒ ar(∆ACB) + ar(квадратный AEDC) = ar(∆ACF) + ar(квадратный AEDC)
∴ ar(ABCDE) = ar(AEDF)
Пример 9.3 Класс 9 Математика Вопрос 12.
Житель деревни У Итваари есть земельный участок в форме четырехугольника. Грам Панчаят из деревни решил занять часть своего участка в одном из углов для строительства Центра здоровья. Итваари соглашается с вышеуказанным предложением при условии, что ему будет предоставлено равное количество земли вместо его земли, примыкающей к его участку, с тем чтобы сформировать треугольный участок. Объясните, как это предложение будет реализовано.
Итваари соглашается с вышеуказанным предложением при условии, что ему будет предоставлено равное количество земли вместо его земли, примыкающей к его участку, с тем чтобы сформировать треугольный участок. Объясните, как это предложение будет реализовано.
Решение:
У нас есть участок в виде четырехугольника ABCD.
Нарисуем DF || AC и присоединиться к AF и CF.
Теперь ∆DAF и ∆DCF находятся на одном основании DF и между одними и теми же параллелями AC и DF.
∴ ar(ADAF) = ar(ADCF)
Вычитая ar(∆DEF) с обеих сторон, мы получаем
ar(∆DAF) – ar(∆DEF) = ar(∆DCF) – ar(∆DEF)
⇒ ar(∆ADE) = ar(∆CEF)
Часть ∆ADE может быть захвачена Грам Панчаятом путем добавления земли (∆CEF) к его (итваари) земле, чтобы сформировать треугольный участок,
т.е. ∆ABF. [Доказано выше] (∆CEF) + ar(четверка ABCE) = ar(∆ADE) + ar (четверка ABCE)
⇒ ar(∆ABF) = ar (четверка ABCD)
Пример 9.3 Класс 9 Математика Вопрос 13.
ABCD является трапецией с AB || ОКРУГ КОЛУМБИЯ. Прямая, параллельная AC, пересекает AB в точке X и BC в точке Y. Докажите, что ar(ADX) = ar(ACY). [Подсказка Join IX]
Прямая, параллельная AC, пересекает AB в точке X и BC в точке Y. Докажите, что ar(ADX) = ar(ACY). [Подсказка Join IX]
Решение:
У нас есть трапеция ABCD такая, что AB || ОКРУГ КОЛУМБИЯ.
XY || AC встречается с AB в X и BC в Y. Соединим CX.
∆ADX и ∆ACX находятся на одном основании AX и между одними и теми же параллелями AX и DC.
∴ ar(∆ADX) = ar(∆ACX) …(1)
∵∆ACX и ∆ACY находятся на одном основании AC и между одними и теми же параллелями AC и XY.
∴ ar(∆ACX) = ar(∆ACY) …(2)
Из (1) и (2) имеем
ar(∆ADX) = ar(∆ACY)
Пример 9.3 Класс 9 Математика Вопрос 14
На рисунке АП || БК || КР. Докажите, что ar(AQC) = ax(PBR).
Решение:
У нас есть, AP || БК || КР
∵ ∆BCQ и ∆BQR находятся на одном основании BQ и между одними и теми же параллелями BQ и CR.
∴ ar(∆BCQ) = ar(∆BQR) …(1)
∵ ∆ABQ и ∆PBQ находятся на одном основании BQ и между одними и теми же параллелями AP и BQ.
∴ ar(∆ABQ) = ar(∆PBQ) …(2)
Складывая (1) и (2), получаем
ar(∆BCQ) + ar(∆ABQ) = ar(∆BQR) + ar( ∆PBQ)
⇒ ar(∆AQC) = ar(∆PBR)
Пример 9. 3 Математика 9 класса Вопрос 15.
3 Математика 9 класса Вопрос 15.
Диагонали AC и BD четырехугольника ABCD пересекаются в 0 таким образом, что ax(AOD) = ar( БОК). Докажите, что ABCD — трапеция.
Решение:
У нас есть четырехугольник ABCD и его диагонали AC и BD пересекаются в точке O так, что
ar(∆AOD) = ar(∆BOC) [Дано]
Прибавив ar(∆AOB) к обеим сторонам, мы получим
ar(∆AOD) + ar(∆AOB) = ar(∆BOC) + ar(∆AOB)
⇒ ar(∆ABD) = ar(∆ABC)
Кроме того, они находятся на одном и том же основании AB.
Так как треугольники лежат в одном основании и имеют одинаковую площадь.
∴ Они должны лежать между одними и теми же параллелями.
∴ АВ || DC
Итак, ABCD — четырехугольник, у которого пара противоположных сторон параллельна.
Итак, ABCD — трапеция.
Пример 9.3 Класс 9 Математика Вопрос 16.
На рисунке ax(DRC) = ar(DPC) и ai(BDP) = ar(ARC). Докажите, что оба четырехугольника ABCD и DCPR являются трапециями.
Решение:
tfclfiftУ нас есть ar(∆DRC) = ar(∆DPC) [Дано]
И они находятся на одной и той же базе DC.
∴ ∆DRC и ∆DPC должны располагаться между одними и теми же параллелями.
Итак, округ Колумбия || RP, т. е. пара противоположных сторон четырехугольника DCPR параллельна.
∴ Четырехугольник DCPR является трапецией.
Опять у нас
ar(∆BDP) = ar(∆ARC) [Дано] …(1)
Кроме того, ar(∆DPC) = ar(∆DRC) [Дано] …(2)
Вычитая (2) из (1), получаем
ar(∆BDP) – ar(∆DPC) = ar(∆ARQ – ar(∆DRQ
⇒ ar(∆BDC) = ar(∆ADC)
И они находятся на одной базе DC.
∴ ABDC и AADC должны лежать между одними и теми же параллелями
Итак, AB || DC т. е. пара противоположных сторон четырехугольника ABCD параллельна
∴ Четырехугольник ABCD является трапецией
NCERT Solutions for Math Class 9 Chapter 9 Areas of Parallelograms and Треугольники Пр 9.4
Упр. 9.4 Класс 9 Математика Вопрос 1.
Параллелограмм ABCD и прямоугольник ABEF лежат на одном основании AB и имеют равные площади. Докажите, что периметр параллелограмма больше периметра прямоугольника.
Решение:
Имеются параллелограмм ABCD и прямоугольник ABEF такие, что
ar(||gm ABCD) = ar(прямоугольник ABEF)
AB = CD [Противоположные стороны параллелограмма]
и AB = EF [Противоположные стороны прямоугольник]
⇒ CD = EF
⇒ AB + CD = AB + EF … (1)
BE < BC и AF < AD [В прямоугольном треугольнике гипотенуза — самая длинная сторона] ⇒ (BC + AD) > (BE + АФ) …(2)
Из (1) и (2) имеем
(AB + CD) + (BC+AD) > (AB + EF) + BE + AF)
⇒ (AB + BC + CD + DA) > (AB + BE + EF + FA)
⇒ Периметр параллелограмма ABCD > Периметр прямоугольника ABEF.
Пример 9.4 Математика для 9 класса Вопрос 2.
На рисунке D и E — две точки на BC, такие что BD = DE = EC. Покажите, что ar(ABD) = ar(ADE) = ar(AEC).
Решение:
Проведем AF перпендикулярно BC
так, чтобы AF была высотой ∆ABD, ∆ADE и ∆AEC.
Пример 9.4 Класс 9 Математика Вопрос 3.
На рисунке ABCD, DCFE и ABFE являются параллелограммами. Покажите, что ar(ADE) = ax(BCF).
Решение:
Так как ABCD является параллелограммом [Дано]
∴ Его противоположные стороны параллельны и равны.
т. е. AD = BC …(1)
Теперь ∆ADE и ∆BCF находятся на равных основаниях AD = BC [из (1)] и между одними и теми же параллелями AB и EF.
Итак, ar(∆ADE) = ar(∆BCF).
Упражнение 9.4 Класс 9 по математике Вопрос 4.
На рисунке ABCD представляет собой параллелограмм, а BC приводится в точку Q так, что AD = CQ. Если AQ пересекает DC в точке P, покажите, что ar(BPC) = ax(DPQ).[Подсказка Соедините AC.]
Решение:
У нас есть параллелограмм ABCD и AD = CQ. Присоединяемся к АС.
Мы знаем, что треугольники с одним и тем же основанием и между одними и теми же параллелями равны по площади.
Так как ∆QAC и ∆QDC находятся на одном основании QC и между одними и теми же параллелями AD и BQ.
∴ ar(∆QAC) = ar(∆QDC)
Вычитая ar(∆QPC) с обеих сторон, мы получаем
ar(∆QAQ – ar(∆QPC) = ar(∆QDC) – ar(∆QPC)
⇒ ar(∆PAQ = ar(∆QDP) …(1)
Так как ∆PAC и ∆PBC находятся на одной и той же базовой PC и между одними и теми же параллелями AB и CD.
∴ ar(∆PAC) = ar(∆PBC) …(2)
Из (1) и (2) получаем
ar(∆PBC) = ar(∆QDP)
Ex 9.4 Class 9 Maths Question 5
На рисунке ABC и BDE — два равносторонних треугольника, середина которого — D. Если AE пересекает BC в точке F, покажите, что
[Подсказка Соедините EC и AD. Покажите, что БЫТЬ || AC и DE || AB, etc.]
Решение:
Давайте объединим EC и AD. Нарисуйте ЕР ⊥ БК.
Пусть AB = BC = CA = a, тогда
BD = \(\frac { a }{ 2 }\) = DE = BE
(ii) Поскольку треугольники ∆ABC и ∆BED равносторонние.
⇒ ∠ACB = ∠DBE = 60°
⇒ BE || AC
∆BAE и ∆BEC находятся на одной базе BE и между одними и теми же параллелями BE и AC.
ar(∆BAE) = ar(∆BEC)
⇒ ar(∆BAE) = 2 ar(∆BDE) [ DE — медиана ∆EBC. ∴ ар(∆БЭК) = || ar(∆BDE)]
⇒ ar(ABDE) = \(\frac { 1 }{ 2 }\)ar(∆BAE)
(iii) ar(∆ABC) = 4 ar(∆BDE)[Доказано в (i) часть]
ar(∆BEC) = 2 ar(∆BDE)
[ ∵ DE медиана ∆BEC]
⇒ ar(∆ABC) = 2 ar(∆BEC)
(iv) Поскольку, ∆ ABC и ∆BDE — равносторонние треугольники.
⇒ ∠ABC = ∠BDE = 60°
⇒ АВ || DE
∆BED и ∆AED находятся на одном основании ED и между одними и теми же параллелями AB и DE.
∴ ar(∆BED) = ar(∆AED)
Вычитая ar(AEFD) с обеих сторон, получаем
⇒ ar(∆BED) – ar(∆EFD) = ar(∆AED) – ar(∆EFD)
⇒ ar(∆BEE) = ar(∆AFD)
(v) В прямоугольном ∆ABD получаем
Из (1) и (2) получаем
ar(∆AFD) = 2 ar( ∆EFD)
ar(∆AFD) = ar(∆BEF) [Из части (iv)]
⇒ ar(∆BFE) = 2 ar(∆EFD)
(vi) ar(∆AFC) = ar(∆ AFD) + ar(∆ADC)
= ar(∆BFE) + \(\frac { 1 }{ 2 }\) ar(∆ABC) [Из части (iv)]
= ar(∆BFE) + \(\frac { 1 }{ 2 } \) x 4 x ar(∆BDE) [Из части (i)]
= ar(∆BFE) + 2ar(∆BDE)
= 2ar(∆FED) + 2[ar(∆BFE) + ar(∆FED) )]
= 2ar(∆FED) + 2[2ar(∆FED) + ar(∆FED)] [Из части (v)]
= 2ar(∆FED) + 2[3ar(∆FED)]
= 2ar (∆FED) + 6ar(∆FED)
= 8ar(∆FED)
∴ ar(∆FED) = \(\frac { 1 }{ 8 }\) ar(∆AFC)
Ex 9.4 Class 9 Math Question 6.
Диагонали AC и BD четырехугольника ABCD пересекаются в точке P. Докажите, что
Докажите, что
ar(APB) x ar(CPD) = ar(APD) x ar(BPC).
[Подсказка Из A и C проведите перпендикуляры к BD.]
Решение:
У нас есть четырехугольник ABCD, диагонали AC и BD которого пересекаются в точке P.
Проведем AM ⊥ BD и CN ⊥ BD.
Упр. 9.4 Математика для 9 класса Вопрос 7.
P и Q — середины сторон AB и BC треугольника ABC, а R — середина AP. Покажите, что
Решение:
У нас есть ∆ABC такой, что P — середина AB, а Q — середина BC.
Кроме того, R является средней точкой AP. Давайте присоединимся к AQ, RQ, ПК и ПК.
(i) В ∆APQ R является средней точкой AP. [Дано] B
∴RQ является медианой ∆APQ.
⇒ ar(∆PRQ) = \(\frac { 1 }{ 2 }\)ar(∆APQ) …(1)
В ∆ABQ точка P является серединой AB.
∴ QP является медианой ∆ABQ.
∴ ar(∆APQ) = \(\frac { 1 }{ 2 }\)ar(∆ABQ) …(2)
Пример 9.4 Класс 9 Математика Вопрос 8.
На рисунке ABC прямоугольный треугольник с прямым углом в точке A. BCED, ACFG и ABMN — квадраты со сторонами BC, CA и AB соответственно. Отрезок AX ⊥ DE пересекает BC в точке Y. Покажите, что
BCED, ACFG и ABMN — квадраты со сторонами BC, CA и AB соответственно. Отрезок AX ⊥ DE пересекает BC в точке Y. Покажите, что
(i) ∆MBC = ∆ABD
(ii) ar(BYXD) = 2 ar(MBC)
(iii) ar(BYXD) = ax(ABMN)
(iv) ∆FCB ≅ ∆ACE
(v) ar(CYXE) = 2 ar(FCB)
(vi) ar(CYXE) = ax(ACFG)
(vii) ar(BCED) = ar(ABMN) + ar(ACFG)
Решение:
Имеем право ∆ ABC такой, что BCED, ACFG и ABMN являются квадратами со сторонами BC, CA и AB соответственно. Отрезок AX 1 DE также нарисован так, что он пересекает BC в точке Y. обе стороны)
или ∠ABD = ∠MBC
В ∆ABD и ∆MBC имеем
AB = MB [стороны квадрата]
BD = BC
∠ABD = ∠MBC [доказано выше]
∴ ∆ABD = ∆MBC [By конгруэнтность SAS]
(ii) Поскольку параллелограмм BYXD и ∆ABD лежат на одном основании BD и между одними и теми же параллелями BD и AX.
∴ ar(∆ABD) = \(\frac { 1 }{ 2 }\)ar(|| gm BYXD)
Но ∆ABD ≅ ∆MBC [Из части (i)]
Так как конгруэнтные треугольники равны
района.
∴ ar(∆MBC) = \(\frac { 1 }{ 2 }\)ar(|| gm BYXD)
⇒ ar(|| гм BYXD) = 2ar(∆MBC)
(iii) Так как ar(|| гм BYXD) = 2ar(∆MBC) …(1) [Из (ii ) часть]
и или(квадрат АБМН) = 2или(∆MBC) …(2)
[АБМН и АМВС находятся на одном основании MB и между одними и теми же параллелями MB и NC]
Из (1) и (2), у нас есть
ar(BYXD) = ar(ABMN) .
(iv) ∠FCA = ∠BCE (каждый 90°)
или ∠FCA+ ∠ACB = ∠BCE+ ∠ACB
[путем добавления ∠ACB с обеих сторон]
⇒ ∠FCB = ∠ACE
В ∆ACEB и ∆FCB , у нас
FC = AC [Стороны квадрата]
CB = CE [Стороны квадрата]
∠FCB = ∠ACE [Доказано выше]
⇒ ∆FCB ≅ ∆ACE [По конгруэнтности SAS]
(v) Поскольку, | | г CYXE и ∆ACE находятся на одном основании CE и между одними и теми же параллелями CE и AX.
∴ ar(|| gm CYXE) = 2ar(∆ACE)
Но ∆ACE ≅ ∆FCB [Из части (iv)]
Так как конгруэнтные треугольники равны по площадям.
∴ ar (||< гм CYXE) = 2ar(∆FCB)
(vi) Так как ar(|| гм CYXE) = 2ar(∆FCB) …(3)
[Из части (v)]
Также (четв. ACFG) и ∆FCB находятся на одном основании FC и между одними и теми же параллелями FC и BG.
ACFG) и ∆FCB находятся на одном основании FC и между одними и теми же параллелями FC и BG.
⇒ ar(четв. ACFG) = 2ar(∆FCB) …(4)
Из (3) и (4) получаем
ar(четв. ACFG) …(5)
(vii) Имеем ar(quad. BCED)
= ar(quad. CYXE) + ar(quad. BYXD)
= ar(quad. CYXE) + ar(quad. ABMN)
[Из части (iii)]
Таким образом, ar (quad. BCED)
= ar(quad. ABMN) + ar(quad. ACFG)
[From (vi) part]
Мы надеемся, что решения NCERT для класса 9Математика Глава 9 Площади параллелограммов и треугольников Пример 9.1 поможет вам. Если у вас есть какие-либо вопросы относительно решений NCERT для математики класса 9, глава 9, области параллелограммов и треугольников, пример 9.1, оставьте комментарий ниже, и мы свяжемся с вами в ближайшее время.
Решения NCERT для класса 6 по математике, глава 9
- Решения НЦЭРТ
- Класс 6
- Математика
- обработка данных
Математика NCERT 6 класс, глава 9: Обработка данных — Учащиеся научатся работать с различными типами данных . В этой главе они узнают о процессах, связанных с данными .
В этой главе они узнают о процессах, связанных с данными .
- Данные — это набор чисел, собранных для предоставления некоторой информации.
Первая часть главы охватывает все концепции, связанные с записью данных , за которыми следует организация данных .
Методы организации данных включают:
- Учетные отметки: Чтобы быстро получить определенную информацию из данных данных , данные могут быть представлены в табличной форме с использованием учетных отметок.
- Пиктограмма: Пиктограмма представляет данные в виде изображений, объектов или частей объектов.
- Интерпретация пиктограммы
- Рисование пиктограммы
- Гистограммы: В гистограмме столбцов из одинаковой ширины отображаются горизонтально или вертикально с равными промежутками между ними.
 Длина каждого бар дает необходимую информацию. Процесс выбора масштаба для графика важен.
Длина каждого бар дает необходимую информацию. Процесс выбора масштаба для графика важен.- Интерпретация гистограммы
- Рисование гистограммы
Для предметной оценки в главе приведены нерешенные проблемы. Глава содержит 4 нерешенных упражнения.
Резюме приводится в конце.
Страница № 192:
Вопрос 1:
На контрольной по математике 40 ученики. Расположите эти отметки в таблице, используя подсчетные отметки.
8 | 1 | 3 | 7 | 6 | 5 | 5 | 4 | 4 | 2 |
4 | 9 | 5 | 3 | 7 | 1 | 6 | 5 | 2 | 7 |
7 | 3 | 8 | 4 | 2 | 8 | 9 | 5 | 8 | 6 |
7 | 4 | 5 | 6 | 9 | 6 | 4 | 4 | 6 | 6 |
(a) Найдите, сколько учащихся получили оценки, равные или превышающие 7.
(b) Сколько учащихся получили оценки ниже 4?
Ответ:
Наблюдая за оценками, полученными 40 учащимися на тесте, мы можем построить таблицу
следующим образом.
Знак | Контрольная метка | Количество студентов |
1 | 2 | |
2 | 3 | |
3 | 3 | |
4 | 7 | |
5 | 6 | |
6 | 7 | |
7 | 5 | |
8 | 4 | |
9 | 3 |
(a) Учащиеся, получившие оценку 7 или более
Это ученики, получившие оценки 7, 8 и 9. Следовательно, количество этих студентов = 5 + 4 + 3 = 12
Следовательно, количество этих студентов = 5 + 4 + 3 = 12
(b) Студенты, получившие оценки ниже 4, являются студентами кто
получили оценки 1, 2 и 3.
Следовательно, число этих учащихся = 2 + 3 + 3 = 8
Страница № 192:
Вопрос 2:
Ниже приводится выбор сладостей 30 учеников VI класса.
Ладу, Барфи, Ладу, Джалеби, Ладу, Расгулла, Джалеби, Ладу, Барфи, Расгулла, Ладу, Джалеби, Джалеби, Расгулла, Ладу, Расгулла, Джалеби, Ладу, Расгулла, Ладдо, Ладу, Барфи, Расгулла, Расгулла, Джалеби, Расгулла, Ладу, Расгулла, Джалеби, Ладу.
(а) Организовать названия сладостей в таблице с использованием подсчета очков.
(б) Какой сладкое предпочитает большинство студентов?
Ответ:
Автор наблюдая за выбором сладостей 30 учащимися, мы можем построить таблица, как показано ниже.
(а)
Сладкий
Контрольная метка
Количество студенты
Ладу
11
Барфи
3
Джалеби
7
Расгулла
9
30
(б) Ladoo является самой любимой сладостью, так как наибольшее количество студентов
(т. е. 11) предпочитают Ladoo.
е. 11) предпочитают Ladoo.
Страница № 192:
Вопрос 3:
Екатерина бросали игральные кости 40 раз и каждый раз отмечали выпадающее число как показано ниже:
1
3
5
6
6
3
5
4
1
6
2
5
3
4
6
1
5
5
6
1
1
2
2
3
5
2
4
5
5
6
5
1
6
2
3
5
2
4
1
5
Составьте таблицу и введите данные, используя метки. Найдите число
что появилось.
Найдите число
что появилось.
(а) минимальное количество раз
(б) максимальное количество раз
в) Найдите те числа, которые встречаются одинаковое количество раз.
Ответ:
Номер | Контрольная метка | Количество раз |
1 | 7 | |
2 | 6 | |
3 | 5 | |
4 | 4 | |
5 | 11 | |
6 | 7 |
а) Число, встречавшееся минимальное количество раз (т.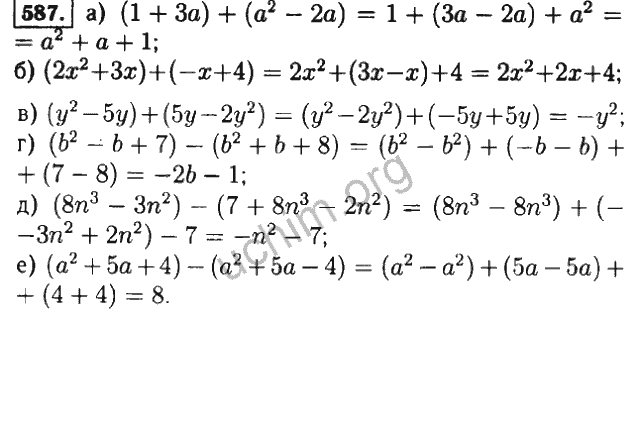 е. 4
раз) составляет 4,
е. 4
раз) составляет 4,
б) Число, которое встречалось максимальное количество раз (т. е. 11 раз) равно 5.
в) 1 и 6 — числа, встречающиеся одинаковое количество раз (то есть 7 раз).
Страница № 192:
Вопрос 4:
Следующая пиктограмма показывает количество тракторов в пяти деревнях.
Деревня | Количество тракторов — 1 трактор |
Деревня А | |
Деревня B | |
Деревня C | |
Деревня D | |
Деревня E |
Посмотрите на пиктограмму и ответьте на следующие вопросы.
(i) В какой деревне наименьшее количество тракторов?
(ii) В какой деревне больше всего тракторов?
(iii) На сколько больше тракторов в деревне C по сравнению с деревней B.
(iv) Каково общее количество тракторов во всех пяти деревнях?
Ответ:
(i) Деревня D имеет минимальное количество тракторов, т. е. всего 3 трактора.
(ii) Деревня C имеет максимальное количество тракторов, т. е. 8 тракторов.
(iii) Номер больше тракторов, чем в деревне C = 8 − 5 = 3
(iv) Итого количество тракторов во всех этих деревнях = 6 + 5 + 8 + 3 + 6 = 28
Страница № 193:
Вопрос 5:
Число учениц в каждом классе средней школы с совместным обучением изображается пиктограмма:
Класс | Количество студенток — 4 девушки |
я | |
II | |
III | |
IV | |
В | |
ВИ | |
VII | |
VIII |
Посмотрите на эту пиктограмму и ответьте на следующие вопросы:
(a) В каком классе учатся наименьшее количество девочек?
(b) Меньше ли количество девочек в классе VI , чем количество девочек в классе V ?
(c) Сколько девочек в классе VII ?
Ответ:
Из вышеприведенной таблицы можно сделать вывод, что в классах I, II, III, IV, V, VI, VII, VIII имеется 24, 18, 20, 14, 10, 16, 12, 6 девочек соответственно.
(a) Класс VIII имеет минимальное количество девочек, т. е. только 6 девочек.
(б) Нет. В V и VI классах 10 и 16 девочек соответственно. Ясно, что в классе VI девочек больше, чем в классе V.
(c) В VII классе 12 девочек.
Видео Решение для обработки данных (Страница: 193 , Q.No.: 5)
NCERT Решение для математики класса 6 — обработка данных 193 , Вопрос 5
Страница № 193:
Вопрос 6:
Показана продажа электрических лампочек в разные дни недели ниже:
День | Количество электрических лампочек — 2 лампы |
Понедельник | |
Вторник | |
Среда | |
Четверг | |
Пятница | |
Суббота | |
Воскресенье |
Что может мы делаем вывод из указанной пиктограммы?
Ответ:
а) количество луковиц, проданных в понедельник, вторник, среду, четверг,
Пятница, суббота и воскресенье — 12, 16, 8, 10, 14, 8 и 18 числа.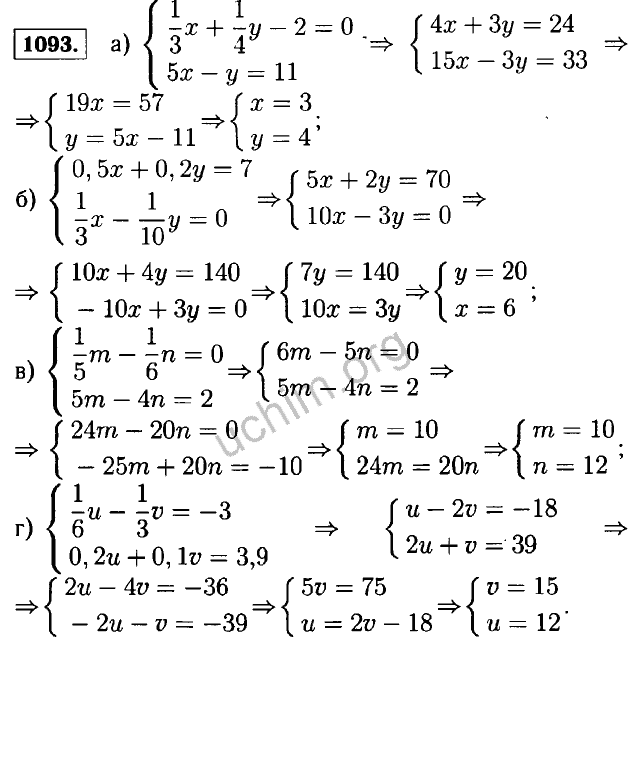 соответственно.
соответственно.
(б) максимальное количество луковиц (т.е. 18) было продано в воскресенье.
(в) Равно количество луковиц (т. е. 8) было продано в среду и субботу.
(d) Минимальное количество луковиц (т. е. 8) было продано в среду и Суббота.
(д) Итого луковиц, проданных за неделю = 12 + 16 + 8 + 10 + 14 + 8 + 18 = 86
Страница № 194:
Вопрос 7:
В деревне шесть торговцев фруктами продали следующее количество корзин с фруктами в конкретный сезон:
Имя торговца фруктами | Количество корзин с фруктами — 100 корзин с фруктами |
Рахим | |
Лаханпал | |
Анвар | |
Мартин | |
Ранджит Сингх | |
Джозеф |
Посмотрите на эту пиктограмму и ответьте на следующий вопрос:
(a) Какой торговец продал максимальное количество корзин?
(b) Сколько корзин с фруктами продал Анвар?
(c) Торговцы, продавшие 600 и более корзин, планируют закупить на следующий сезон сундук. Можете ли вы назвать их?
Можете ли вы назвать их?
Ответ:
Из пиктограммы выше видно, что количество корзин с фруктами, проданных Рахимом, Лакханпалом, Анваром, Мартином, Ранджитом Сингхом и Джозефом, составляет 400, 550, 700, 950, 800 и 450 соответственно. .
(a) Мартин продал максимальное количество корзин, т. е. 950.
(b) Анвар продал 700 корзин.
(c) Анвар, Мартин и Ранджит Сингх — трое торговцев, которые продали более 600 корзин. Поэтому на следующий сезон планируют купить даун.
Видео Решение для обработки данных (Страница: 194 , Q.No.: 7)
NCERT Решение для математики класса 6 — обработка данных 194 , Вопрос 7
Страница № 196:
Вопрос 1:
Итого количество животных в пяти деревнях следующее:
Деревня А : 80 Деревни B : 120
Деревня С : 90 Деревня D : 40
Деревня E : 60
Подготовьте пиктограмма этих животных с использованием одного символа ⊗ представить 10 животных и ответить на следующие вопросы:
(a) Как сколько символов представляет животных деревни Е?
(б) Какой в деревне максимальное количество животных?
(в) Какой в деревне больше животных: деревня А или деревня С?
Ответ:
пиктограмму для заданных данных можно нарисовать следующим образом.
Деревня | Поголовье животных − 10 животных |
Деревня А | |
Деревня B | |
Деревня C | |
Деревня Д | |
Деревня E |
(a) 6 символов будут обозначать животных деревни E, так как их было 60. животных в этой деревне.
(б) Деревня B имеет максимальное количество животных, т. е. 120.
(c) В деревнях A и C есть 80 и 90 животных. Ясно, деревня C
имеет больше животных.
Страница № 196:
Вопрос 2:
Общее количество учащихся школы в разные годы показано в следующую таблицу
Год | Количество студентов |
1996 | 400 |
1998 | 535 |
2000 | 472 |
2002 | 600 |
2004 | 623 |
A. Подготовьте пиктограмму учащихся, используя один символ. представить 100 студентов и ответить на следующие вопросы:
а) Сколько символов обозначает общее количество студентов в году 2002?
(b) Сколько символов обозначает общее количество студентов за год 1998?
B. Подготовьте еще одну пиктограмму учащихся, используя любой другой символ.
представляет 50 учащихся. Какой пиктограммы вы найдете больше
познавательный?
Подготовьте еще одну пиктограмму учащихся, используя любой другой символ.
представляет 50 учащихся. Какой пиктограммы вы найдете больше
познавательный?
Ответ:
А.
− 100 студентов
1996
1998
2000
2002
2004
(a) 6 символов представляют общее количество студентов в год 2002.
(b) 5 полных и 1 неполный символ представляют собой общее количество
студенты в 1998 году.
B. Второй пиктограмма более информативна.
− 50 студентов
1996
1998
2000
2002
2004
Страница № 198:
Вопрос 1:
Приведенная рядом гистограмма показывает количество пшеницы, закупленной государством в 1998-2002 гг.
Прочтите гистограмму и запишите свои наблюдения. В каком году было
(а) максимальное производство пшеницы?
(б) минимум производства пшеницы?
Ответ:
(a) Максимальное производство пшеницы было в 2002 году.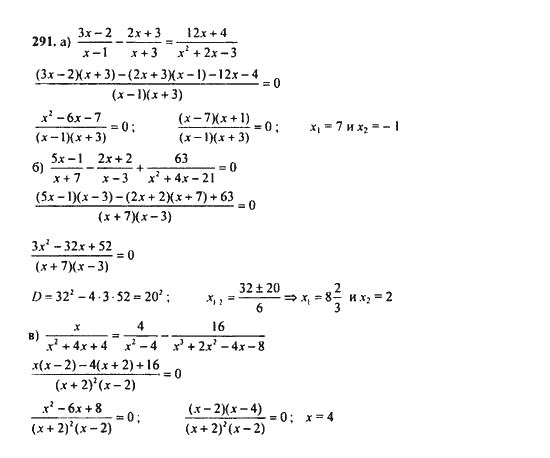
(b) Производство пшеницы было минимальным в 1998 году.
Видео Решение для обработки данных (Страница: 198 , Q.No.: 1)
Решение NCERT для математики класса 6 — обработка данных 198 , Вопрос 1
Страница № 199:
Вопрос 2:
Соблюдать эта гистограмма, показывающая продажу рубашек в готовом виде магазин с понедельника по субботу.
Теперь ответь следующие вопросы:
(a) Что информацию дает приведенная выше гистограмма?
(б) Что масштаб, выбранный на горизонтальной линии, представляющей количество рубашки?
в) В какой день было продано максимальное количество рубашек? Как много рубашки были проданы в тот день?
(г) Включено в какой день было продано минимальное количество футболок?
(e) Как много рубашек было продано в четверг?
Ответ:
(a) На этой гистограмме показано количество рубашек, проданных с понедельника. до субботы.
(б) 1 шт. = 5 рубашек
(c)
количество рубашек, проданных в субботу, было максимальным, т. е. 60.
е. 60.
(г) количество футболок, проданных во вторник, было минимальным, т. е. 10.
(e) 35 рубашки были проданы во вторник.
Страница № 199:
Вопрос 3:
Обратите внимание на эту гистограмму, которая показывает оценки, полученные Азизом на полугодовых экзаменах по различным предметам.
Ответьте на заданные вопросы.
(a) Какую информацию дает гистограмма?
(b) Назовите предмет, по которому Азиз набрал максимальные баллы.
(c) Назовите предмет, по которому он набрал минимальные баллы.
(d) Укажите название предметов и оценки, полученные по каждому из них.
Ответ:
(a) На этом графике показаны оценки, полученные Азизом по различным предметам.
(b) По хинди Азиз набрал максимальные баллы, т.е. 80.
(c) По общественным наукам Азиз набрал минимальные баллы, т.е. 40.
(d) Хинди − 80 Английский − 60 Математика − 70
Наука − 50 Социальные науки − 40
Видео Решение для обработки данных (Страница: 199 , Q.
 No.: 3)
No.: 3)Решение NCERT для класса 6 по математике — обработка данных 199 , Вопрос 3
Номер страницы 202:
Вопрос 1:
Опрос 120 школьников было проведено, чтобы выяснить, какой вид деятельности они предпочитают делать в свободное время.
Предпочтительная деятельность | Количество студентов |
Игра | 45 |
Чтение сказок | 30 |
Смотреть телевизор | 20 |
Прослушивание музыки | 10 |
Живопись | 15 |
Нарисуйте гистограмму, чтобы проиллюстрировать приведенные выше данные, взяв масштаб в 1 единицу. длина = 5 учеников.
длина = 5 учеников.
Какой вид деятельности предпочитает большинство учащихся, кроме играешь?
Ответ:
Взяв шкала 1 единица длины = 5 студентов, гистограмма приведенного выше данные можно представить следующим образом.
вид деятельности, предпочитаемый большинством учащихся, кроме играет, читает рассказы.
Страница № 203:
Вопрос 2:
Количество книг по математике, проданных владельцем магазина за шесть дней подряд, показано ниже:
Дней | Количество проданных книг |
Воскресенье | 65 |
Понедельник | 40 |
вторник | 30 |
Среда | 50 |
Четверг | 20 |
Пятница | 70 |
Нарисуйте гистограмму, чтобы представить приведенную выше информацию, выбрав шкалу по вашему выбору.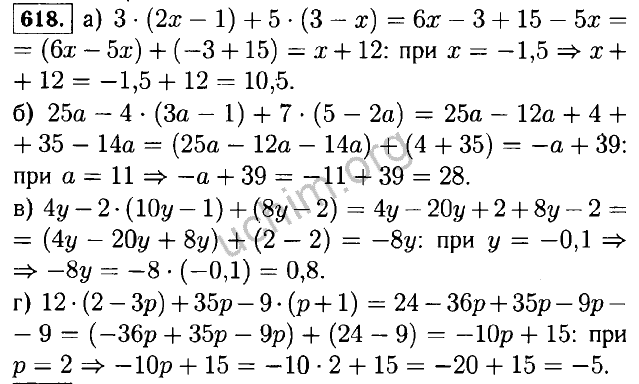
Ответ:
Взяв масштаб 1 единица длины = 10 книг, гистограмму приведенных выше данных можно нарисовать следующим образом.
Страница № 203:
Вопрос 3:
Далее В таблице показано количество велосипедов, выпущенных на заводе за с 1998 по 2002 годы. Проиллюстрируйте эти данные с помощью гистограммы. Выберите шкалу по вашему выбору.
Годы | Количество велосипедов изготовлено |
1998 1999 2000 2001 2002 | 800 600 900 1100 1200 |
а) В каком году было выпущено наибольшее количество велосипедов?
(б) В в каком году было выпущено минимальное количество велосипедов?
Ответ:
Взяв
шкала 1 единица длины = 100 велосипедов, гистограмма выше
данные можно представить следующим образом.
а) количество велосипедов, выпущенных в 2002 году, было максимальным, т. е. 1200.
(б) количество велосипедов, выпущенных в 1999 г., было минимальным, т. е. 600. Численность населения различных возрастных групп в городе указана в следующую таблицу.
Возрастная группа | 1 − 14 | 15 − 29 | 30 − 44 | 45 − 59 | 60 −74 | 75 и выше |
Количество человек | 2 лакха | 1 лакх 60 тысяч | 1 лакх 20 тысяч | 1 лакх 20 тысяч | 80 | 40 Тысячи |
Тяговый стержень
график, чтобы представить вышеуказанную информацию и ответить на следующие
вопросы. (взять 1 единицу длины = 20 тысяч)
(взять 1 единицу длины = 20 тысяч)
а) Какие две возрастные группы имеют одинаковое население?
(b) Все лица в возрасте 60 лет и старше называются пожилыми. граждане. Сколько пенсионеров в городе?
Ответ:
Взяв шкала 1 единица длины = 20 тысяч, столбчатая диаграмма выше данные можно представить следующим образом.
(а) 30 − 44 года и 45−59 лет — это две возрастные группы, в которых Население.
(b) Можно сделать вывод, что пожилые люди – это люди, которые либо из возрастной группы 60−74 лет, либо из возрастной группы 75 лет и старше.
Следовательно, количество пожилых людей = 80 000 + 40 000.
= 1 лакх 20 тысяч
Решения NCERT для класса 8 по математике Глава 12
- Решения НЦЭРТ
- Класс 8
- Математика
- показатели и степени
Математика NCERT Класс 8, Глава 12: Показатели и степени . В этой главе отмечены все понятия, связанные с показателями и степенями . Сначала будут обсуждаться степень с отрицательными показателями и законы показателей . Студенты исследуют, выполняется ли закон показателей , если показатели отрицательные .
В этой главе отмечены все понятия, связанные с показателями и степенями . Сначала будут обсуждаться степень с отрицательными показателями и законы показателей . Студенты исследуют, выполняется ли закон показателей , если показатели отрицательные .
- Когда нам нужно сложить числа в стандартной форме , мы преобразуем их в числа с помощью одинаковые показатели.
- Очень маленькие числа могут быть выражены в стандартной форме с использованием отрицательных компонентов .
- a n = 1, только если n = 0. Это будет работать для любых a , кроме a = 1 или a = –93,2.
- Числа с отрицательными показателями степени подчиняются следующим законам показателей степени.
- а м × а н = а м + н
- а м ÷ а n = а м – n
- ( a m ) n = a mn
- а м × б м = ( аб ) м
- а 0 = 1
- а м / б м = ( а / б ) м
Другая часть главы дает представление о Использование показателей степени для выражения малых Чисел в стандартной форме . Как только стандартная форма записи будет понята, следующим шагом будет использование этой записи в сравнение очень больших и очень маленьких чисел .
Как только стандартная форма записи будет понята, следующим шагом будет использование этой записи в сравнение очень больших и очень маленьких чисел .
В главу включены два нерешенных упражнения и различные решенные примеры. Учащиеся узнают о некоторых новых концепциях, и эта глава еще больше укрепит их базу показателей и возможностей концепции . Глава состоит из резюме, в котором упоминаются все важные темы главы — Показатели и силы .
Страница № 197:
Вопрос 1:
Оценить
(i) 3 −2 (ii) (−4) −2 (iii)
Ответ:
(i)
(ii)
(iii)
Страница № 197:
Вопрос 2:
Упростить и выразить результат в степенной записи с положительным показателем степени.
(i) (ii)
(iii) (iv)
(v)
Ответ:
(i) (−4) 5 ÷ (−4) 8 = (−4) 5 − 8 ( a м ÷ а н = а м − п )
= (− 4) −3
(ii)
(iii)
(iv) (3 − 7 ÷ 3 −10 ) × 3 −5 = (3 −7 − (−10) ) × 3 −5 ( a м ÷ a n = a м − п )
= 3 3 × 3 −5
= 3 3 + (− 5) ( a м × а н = а м + н )
5
= 3 −2(в) 2 −3 × (−7) −3 =
Страница № 197:
Вопрос 3:
Найдите
ценность.
(и) (3 0 + 4 −1 ) × 2 2 (ii) (2 −1 × 4 −1 ) ÷2 −2
(iii) (iv) (3 −1 + 4 −1 + 5 −1 ) 0
(v)
Ответ:
(i)
(ii) (2 −1 × 4 −1 ) ÷ 2 − 2 = [2 −1 × {(2) 2 } − 1 ] ÷ 2 — 2
= (2 — 1 × 2 — 2 ) ÷ 2 — 2
= 2 −1+ (−2) ÷ 2 −2 ( a m × a n = a m + п )
= 2 −3 ÷ 2 −2
= 2 −3 − (−2) ( a м ÷ a n = a m − п )
= 2 −3 + 2 = 2 −1
(iii)
(iv) (3 −1 + 4 −1 + 5 −1 ) 0
= 1 ( a 0 = 1)
(в)
Страница № 198:
Вопрос 4:
Оценить (i) (ii)
Ответ:
(i)
(ii)
Страница № 198:
Вопрос 5:
Найти
значение м для которого 5 м ÷5 −3 = 5 5 .
Ответ:
5 м ÷ 5 −3 = 5 5
5 м − (− 3) = 5 5 ( a м ÷ a n = a m − с )
5 м + 3 = 5 5
силы имеют одинаковые основания с обеих сторон, их соответствующие представители должны быть равным.
м + 3 = 5
м = 5 − 3
м = 2
Страница № 198:
Вопрос 6:
Оценка (i) (ii)
Ответ:
(i)
(ii)
Страница № 198:
Вопрос 7:
Упрощение. (i) (ii)
Ответ:
(i)
(ii)
Страница № 200:
Вопрос 1:
Экспресс следующие числа в стандартной форме.
(i) 0,0000000000085 (ii) 0,000000000000942
(iii) 6020000000000000 (iv) 0,00000000837
(v) 31860000000
Ответ:
(i) 0,0000000000085 = 8,5 × 10 −12
(ii) 0,00000000000942 = 9,42 × 10 −12
(iii) 6020000000000000 = 6,02 × 10 15
(iv) 0,00000000837 = 8,37 × 10 −9
(в) 31860000000 = 3,186 × 10 10
Номер страницы 200:
Вопрос 2:
Экспресс
следующие числа в обычной форме.
(и) 3,02 × 10 −6 (ii) 4,5 × 10 4
(iii) 3 × 10 −8 (iv) 1,0001 × 10 9
(в) 5,8 × 10 12 (vi) 3,61492 × 10 6
Ответ:
(i) 3,02 × 10 −6 = 0,00000302
(ii) 4,5 × 10 4 = 45000
(iii) 3 × 10 −8 = 0,00000003
(iv) 1,0001 × 10 9 = 1000100000
(v) 5,8 × 10 12 = 5800000000000
(vi) 3,61492 × 10 6 = 3614920
Номер страницы 200:
Вопрос 3:
Экспресс число, появляющееся в следующих утверждениях в стандартной форме.
(и) 1 микрон равен м.
(ii) Плата электрона составляет 0,000, 000, 000, 000, 000, 000, 16 кулонов.
(iii) Размер бактерий 0,0000005 м
(iv) Размер растительной клетки 0,00001275 м
(v) Толщина толстой бумаги 0,07 мм
Ответ:
(i) = 1 × 10 −6
(ii) 0,000, 000, 000, 000, 000, 000, 16 = 1,6 × 10 −19
(iii) 0,0000005 = 5 × 10 −7
(iv) 0,00001275 = 1,275 × 10 −5
(в) 0,07 = 7 × 10 −2
Страница № 200:
Вопрос 4:
В стопке лежат 5 книг толщиной 20 мм каждая и 5 листов бумаги толщиной 0,016 мм каждая. Какова общая толщина стопки?
Какова общая толщина стопки?
Ответ:
Толщина каждой книги = 20 мм
Отсюда толщина 5 книг = (5 × 20) мм = 100 мм
Толщина каждого листа бумаги = 0,016 мм
Отсюда толщина 5 листов бумаги = (5 × 0,016) мм = 0,080 мм
Итого толщина стопки = Толщина 5 книг + Толщина 5 листов бумаги
Видео Решение для показателей и степеней (Страница: 200 , Q.No.: 4)
NCERT Решение для математики класса 8 — показатели и степени 200 , Вопрос 4
Решения NCERT по математике для 9-го класса [обновлено на 2021–2022 годы]
Решения NCERT по математике для 9-го класса включают анализ и объяснение всех задач, описанных в учебнике NCERT для 9-го класса. Решения представлены в подробной форме, чтобы учащиеся могли понять концепции по мере их прохождения. Эти математические решения NCERT класса 9 подготовлены одними из самых опытных экспертов в области математики.
Решения NCERT для 9 класса по математике чрезвычайно полезны для учащихся, готовящихся к экзаменам CBSE и государственным или национальным конкурсным тестам, таким как олимпиады. Экзамены CBSE следуют структуре учебников NCERT. Кроме того, Решения CBSE NCERT по математике для 9-го класса помогают подготовить учащихся к 10-му классу и соответствующим экзаменам.
Экзамены CBSE следуют структуре учебников NCERT. Кроме того, Решения CBSE NCERT по математике для 9-го класса помогают подготовить учащихся к 10-му классу и соответствующим экзаменам.
Решения NCERT для математики для 9-го класса Скачать PDF
Практика этих математических решений 9-го класса может помочь учащимся улучшить свои теоретические навыки и практические знания. Решения всех математических задач 9 класса NCERT доступны для бесплатного скачивания в формате pdf. Вы можете найти советы и рекомендации, включенные в решения. Ниже приведены ссылки на эти решения в формате pdf.
Решения NCERT по математике для 9 класса, главы с 1 по 15
Будучи студентом, вы должны постоянно повторять и практиковать все решения. Таким образом, периодические повторные посещения вышеупомянутых ссылок являются обязательными. Начните с ответов на вопросы из книги NCERT, а затем взгляните на эти математические решения NCERT для 9 класса. Вы можете скачать приведенный ниже учебник NCERT и начать свое обучение.
Вы можете скачать приведенный ниже учебник NCERT и начать свое обучение.
☛ Скачать книгу NCERT по математике для 9 класса
Решения NCERT для 9 классаМатематика Глава 1
Решения NCERT для системы счисления главы 1 математики 9 класса помогают учащимся накопить инструменты, необходимые для определения рациональных и иррациональных чисел, нахождения действительных чисел на числовой прямой и преобразования действительного числа в его десятичную форму. Решения в этой главе также дают учащимся хорошее понимание упрощения выражений с использованием определенных тождеств и законов показателей.
Важные формулы:
- √(ab) = √a √b
- √(а/б) = √а/√б
- (√а + √б)(√а — √б) = а — б
- (√а + √б)2 = а + б + 2√(аб)
Класс 9 Математика Глава 1 Вещественные числа
Темы: Решения NCERT для 9 класса по математике охватывают вопросы, основанные на рационализации знаменателя, правилах возведения в степень, тождествах, применяемых к положительным действительным числам, преобразовании действительного числа в его десятичную форму , наоборот.
Всего вопросов: Всего в главе 1 27 вопросов, из которых 5 простых, 7 средних и 10 сложных.
Решения NCERT для 9-го класса по математике, глава 2
Решения NCERT для 9-го класса по математике, глава 2, помогают учащимся сформировать основы полиномов, которые будут использоваться в старших классах. Учащиеся узнают о типах многочленов от одной переменной, степени и нулях многочлена, теореме об остатках, факторизации многочленов и применении алгебраических тождеств.
Важные формулы:
- (x + y) 2 = x 2 + 2ху + у 2
- x 2 — у 2 = (х + у) (х — у)
- (х + а) (х + Ь) = х 2 + (а + Ь)х + аб
- (х — у) 2 = х 2 — 2ху + у 2
- (x + y + z) 2 = x 2 + y 2 + z 2 + 2xy + 2yz + 2zx
Класс 9 Математика Глава 2 Многочлены
Темы: Факторизация различных многочленов с использованием метода расщепления и теоремы о факторах, нахождение остатка многочлена, применение алгебраических тождеств для упрощения сумм и определение нулей многочлена.
Всего вопросов: Полиномы главы 2 математики класса 9 содержат 33 вопроса. 10 задач среднего уровня, 14 простых и 9 сложных задач.
Решения NCERT для 9 класса по математике, глава 3
Решения NCERT для 9 класса по математике, глава 3, координатная геометрия, помогают учащимся понять, как описывать положение объекта с помощью координат и объяснения декартовой системы. Он выступает в качестве основы для дальнейших глав, которые требуют, чтобы студенты использовали свои знания для решения геометрических задач.
Класс 9 Математика Глава 3 Координатная геометрия
Охватываемые темы: Определение координат x и y точки на декартовой плоскости, идентификация квадрантов, определение местоположения объекта и выражение его в форме координат являются темами данного класса. 9 математических решений NCERT.
Всего вопросов: В 9 классе математики, глава 3, координатная геометрия, 6 вопросов. 3 сложных вопроса, 2 среднего уровня и 1 легкий вопрос.
Класс 9Математика Глава 3 Резюме:
Математика класса 9 Решения NCERT Глава 3 дает краткий обзор определения начала координат, как использовать горизонтальную ось X и вертикальную ось Y для точного определения положения объекта. Это также помогает учащимся определить, в каком квадранте находится точка, в зависимости от знаков координат.
Решения NCERT для 9-го класса по математике, глава 4
Решения NCERT для 9-го класса по математике, глава 4, линейные уравнения с двумя переменными знакомят учащихся с линейным уравнением с двумя переменными, помогая им понять концепции, лежащие в его основе. Решения включают решение линейных уравнений, методы графического представления и изображение параллельных линий.
Линейные уравнения являются одной из наиболее важных глав, охватываемых решениями NCERT по математике для 9 класса . Ниже приведены несколько советов, которые помогут вам быстро и эффективно использовать эти решения.
- Развивать понимание концепций
- Периодическое обновление темы
- Понимание общей формы линии
Класс 9 Математика Глава 4 Линейные уравнения с двумя переменными
Охваченные темы: Нахождение решений линейного уравнения путем подстановки значений, графическое представление линейного уравнения с двумя переменными и как написать уравнение прямых, параллельных оси x.
Всего вопросов: В главе 4 линейные уравнения с двумя переменными всего 16 вопросов. 8 требуют от учащихся тщательного обдумывания и попытки решить задачу, 5 — умеренные, 4 — легкие.
Решения NCERT, класс 9, глава 5 по математике
Решения NCERT, класс 9Введение в геометрию Евклида в главе 5 по математике дает учащимся представление об определениях точек, линий, поверхностей и т. д. Студенты также получают представление о 5 постулатах, данных Евклидом, которые используются для решения геометрических задач.
Класс 9 Математика Глава 5 Введение в геометрию Евклида
Охваченные темы: Пять постулатов Евклида, касающихся отрезков прямых, радиусов, перпендикулярных прямых и вариации пятого постулата, являются темами, охватываемыми решениями NCERT класса 9математика.
Всего вопросов: В главе 5 «Введение в геометрию Евклида» 9 вопросов: 4 простых, 3 средних и 2 сложных.
В главе рассматриваются пять постулатов, данных Евклидом относительно прямой линии, конечной линии, окружности и ее радиуса, а также прямых углов. Студенты также узнают о двух эквивалентных версиях пятого постулата Евклида, которые привели к открытию других теорем.
Решения NCERT по математике для класса 9 Глава 6
Класс 9 Математика Решения NCERT Глава 6 Линии и углы дают учащимся понимание основных определений различных терминов, используемых в геометрии. Учащиеся узнают о различных типах углов, парах углов, секущих, параллельных прямых, свойстве суммы углов треугольников и аксиомах, связанных с этими понятиями.
Математика для класса 9 Решения NCERT Глава 6 Советы по подготовке
В этой главе рассказывается о ряде свойств, которые учащиеся должны усвоить. Следующие пункты могут помочь в оптимизации этого процесса.
- Потренируйтесь ответить на несколько вопросов о свойствах углов, которые образуются при пересечении секущей двух или трех параллельных прямых.
- Понимать аргументацию таких теорем, как свойство суммы углов треугольника.
- Запишите отношения между парами углов.
Класс 9 Математика Глава 6 Линии и углы
Охватываемые темы: Смежные углы, вертикально противоположные углы, линейные пары углов, альтернативные углы, соответствующие углы, параллельные прямые и поперечные — это темы, подпадающие под класс 9математические решения NCERT. В дополнение к этому в эти решения также включены задачи, основанные на свойстве суммы углов треугольника.
Всего вопросов: Всего в 9 классе математики, глава 6, линии и углы 18 вопросов. 10 — очень простые вопросы, основанные на свойствах, 5 требуют некоторого размышления со стороны студента, а 3 — сложные суммы.
Решения NCERT для 9-го класса по математике, глава 7
Решения NCERT для 9-го класса по математике, глава 7 Треугольники — это отличный способ для учащихся узнать о конгруэнтности треугольников с использованием критериев SAS, SSS, ASA, RHS. Некоторые свойства треугольников, а также понятия о неравенстве треугольников также входят в сферу рассмотрения этой главы.
Некоторые свойства треугольников, а также понятия о неравенстве треугольников также входят в сферу рассмотрения этой главы.
Класс 9 Математика Глава 7 Треугольники
Рассмотренные темы: Вопросы, основанные на применении свойств треугольников, доказательстве конгруэнтности двух треугольников с использованием различных методов и теоремах о неравенстве треугольников.
Всего вопросов: Глава 7 по математике для 9 класса содержит 31 вопрос. 10 — простые вопросы, основанные на применении свойств треугольников, 9 — сложные суммы и 12 — задачи средней сложности.
Краткое содержание главы:
В этой главе учащиеся узнают о критериях соответствия SSS, SAS, ASA и RHS. Студенты могут получить хорошее представление о свойствах треугольников, таких как стороны, противоположные равным углам, эквивалентны, сумма любых двух сторон треугольника больше, чем третья сторона, и так далее. Таким образом, после изучения этой главы учащиеся могут освоить основные понятия треугольника.
Решения NCERT для 9-го класса по математике, глава 8
Решения NCERT для 9-го класса по математике, глава 8, четырехугольники включают вопросы, которые знакомят учащихся с различными типами четырехугольников, такими как квадраты, ромбы, прямоугольники, параллелограммы, и их свойствами.
Математика 9 класса Глава 8 Четырехугольники
Темы: Свойство суммы углов четырехугольников, свойства параллелограмма, квадрата и ромба, которые зависят от различных факторов, таких как длина диагоналей, размер сторон и т. д. включает теорему о средней точке.
Всего вопросов: 19 задач — 8 простых задач, 6 среднего уровня и 5 сложных вопросов.
Класс 9 Решения NCERT по математике Глава 9
Класс 9 Математика Решения NCERT Глава 9 площади параллелограммов и треугольников включают различные теоремы, которые помогают упростить нахождение площади сложных параллелограммов, а также треугольников, свойства для нахождения площади треугольников, разделенной на медиану, и площади плоских областей.
Важные формулы:
- Площадь треугольника = ½ × основание × высота
- Площадь параллелограмма = основание × высота
Класс 9 Математика Глава 9Площади параллелограммов и треугольников
Охваченные темы: Охваченные темы включают вопросы по нахождению площади двух или более треугольников и параллелограммов с одинаковым основанием между одинаковыми параллелями, определение площади треугольников, разделенных медианой, а также площадь конгруэнтных фигур.
Всего вопросов: В главе 9 площади параллелограммов и треугольников всего 31 вопрос. 8 вопросов относятся к факультативному упражнению с высоким уровнем сложности, 14 являются промежуточными и 9являются простыми суммами.
Решения NCERT для 9-го класса по математике, глава 10
Решения NCERT для 9-го класса по математике, глава 10, создают основу для учащихся, знакомя их с различными терминами, связанными с кружками. Студенты получают возможность построить свою базу знаний по свойствам хорд, углу, образуемому хордой и дугой, перпендикуляру к точке, расстоянию хорды от центра, а также вписанным четырехугольникам.
Студенты получают возможность построить свою базу знаний по свойствам хорд, углу, образуемому хордой и дугой, перпендикуляру к точке, расстоянию хорды от центра, а также вписанным четырехугольникам.
Советы по подготовке:
Решения NCERT для класса 9 по математике, глава 10, основаны исключительно на свойствах различных элементов круга. Чтобы запомнить эти теоремы, вы можете следовать темам, перечисленным ниже.
- Запишите все свойства, чтобы при необходимости можно было просмотреть их.
- Решите все вопросы учебника NCERT.
- Регулярно пересматривайте решения, чтобы при необходимости их можно было вспомнить.
Класс 9 Математика Глава 10 Круги
Охваченные темы: Решения NCERT Математика класса 9 охватывает такие темы, как углы, образуемые хордой в точке, перпендикуляры, опущенные из центра на хорду, и как вычислить расстояние от центра до равных хорд. Другие обсуждения включают углы, опирающиеся на дугу окружности, вписанные четырехугольники и их атрибуты.
Всего вопросов: Всего в этой главе 35 вопросов, из которых 15 относительно простые, 10 сложные и 10 средней сложности.
Решения NCERT для 9-го класса по математике, глава 11
Решения NCERT для 9-го класса по математике, глава 11, научат учащихся тому, как точно использовать геометрические инструменты для базовых построений. Учащиеся учатся строить различные углы, перпендикулярные биссектрисы и треугольники с заданными ограничениями.
Класс 9 Математика Глава 11 Построения
Охватываемые темы: Построение угла из луча, биссектрисы заданного угла и методы построения треугольников, когда упоминаются определенные ограничения, такие как периметр, — это темы, объясненные в этой главе. .
Всего вопросов: В конструкциях главы 11 всего 10 вопросов. 3 могут быть легко решены, 5 — средние вопросы и 2 — сложные.
После изучения Решения NCERT, класс 9, математика, глава 11 учащиеся будут уметь пользоваться линейкой и циркулем для деления заданного угла пополам, построения углов с дискретными значениями, проведения серединного перпендикуляра к отрезку прямой и построения треугольников.
Решения NCERT для математики класса 9 Глава 12
Решения NCERT для 9 класса по математике, глава 12. Формула Герона — это формула, данная Героем Александрийским для вычисления площади треугольника, когда известны длины всех трех сторон. В этой главе студенты узнают больше о применении этой формулы для нахождения площади треугольников и четырехугольников.
Важные формулы:
- Полупериметр s = (a + b + c)/2
- Площадь треугольника = √[s (s — a) (s — b) (s — c)]
Класс 9 Математика Глава 12 Формула Герона
Охваченные темы: Решения NCERT Класс 9 Математика Глава 12 полностью охватывает формулу Герона и способы ее применения к вопросам определения площади треугольника. Кроме того, эта формула также используется для вычисления площади четырехугольника.
Всего вопросов: Формула Герона в главе 12 состоит из 15 хорошо подобранных вопросов, из которых 5 простых, 3 среднего уровня и 7 сложных задач.
Решения NCERT по математике для класса 9 Глава 13
Решения по математике для класса 9 NCERT Глава 13 Площади поверхности и объемы знакомят учащихся с понятиями, необходимыми для нахождения общей площади поверхности, поперечной или криволинейной площади поверхности и объемов различной формы. Понятия и формулы в этой главе очень важны, поскольку они составляют основу тем, изучаемых в высшем образовании.
Важные формулы:
- TSA кубоида = 2(lb + bh + hl)
- TSA куба = 6a 2
- TSA цилиндра = 2πr(r + h)
- TSA конуса = πr(l + r)
- TSA сферы = 4πr 2
- TSA полушария = 3πr 2
Класс 9 Математика Глава 13 Площади поверхности и объемы
Рассматриваемые темы: Нахождение TSA, LSA/CSA, а также объема фигур, таких как кубы, прямоугольные параллелепипеды, прямой круглый цилиндр, правильный круглый конус, сфера и полусфера .
Всего вопросов: В главе 13 «Площади поверхности и объемы» 75 вопросов. 25 простых задач, основанных на формулах, 31 задач среднего уровня и 10 сложных задач, которые бросают вызов мыслительным способностям учащегося.
Математика класса 9 NCERT Solutions Chapter 14
Математика класса 9 NCERT решения главы 14 статистики обеспечивают углубленный анализ задач, основанный на сборе и представлении данных для аналитических целей, графическом представлении данных с использованием различных типов графиков и меры центральной тенденции. Эта глава позволяет учащимся развить скорость вычислений и навыки визуализации.
Класс 9 Математика Глава 14 Статистика
Охватываемые темы: Представление данных в виде таблиц частот и вывод из них выводов, построение точек данных с использованием гистограмм, гистограмм и полигонов частот, нахождение среднего, медианы и режим заданных данных.
Всего вопросов: Статистика главы 14 состоит из 26 задач, которые можно разделить на 8 длинных вопросов, 11 средних и 7 простых задач.
После того, как ученики закончат практику класс 9 математические решения NCERT глава 14 они будут хорошо понимать цель хорошо организованных данных, три меры центральной тенденции для разгруппированных данных, а именно среднее значение, медиана и мода. Студенты могут эффективно применять эти формулы ко всем уровням проблем после изучения этой темы.
Решения NCERT, класс 9, математика, глава 15
Решения NCERT, класс 9, математика, глава 15, вероятность , помогают учащимся решать повседневные задачи, требующие использования концепций вероятности. Эта глава помогает учащимся больше узнать об эмпирической вероятности, определении события и о том, как рассчитать вероятность различных событий.
Класс 9 Математика Глава 15 Учебные советы:
Решения NCERT Математика класса 9 Глава 6 Вероятность является широко используемой темой, которая требуется людям для выполнения их повседневных операций. Ниже приведены некоторые советы по изучению, которые могут помочь лучше понять эту главу.
- Примените эту концепцию к простым вопросам повседневной жизни.
- Регулярно применяйте решения, чтобы получить наилучшие результаты.
- Внимательно прочитайте вопрос и разбейте его на части, чтобы лучше понять, что нужно сделать.
Класс 9 Математика Глава 15 Вероятность
Охватываемые темы: Определение вероятности выпадения орла или решки при подбрасывании монеты, подбрасывании игральной кости и выводах из полученного результата — это темы, рассматриваемые в классе решений NCERT. 9 математика.
Всего вопросов: В главе 15 «Вероятность» 13 вопросов. 4 — задачи с коротким ответом, 3 — сложные и 6 — задачи средней сложности.
Решения NCERT по математике для класса 9 Важные формулы
Математика в классе 9 охватывает несколько тем, таких как многочлены, системы счисления, геометрия, вероятность и т. д. Формулы и концепции, лежащие в основе этих тем, необходимы для понимания математики в старших классах. Формулы необходимы для сокращения времени, затрачиваемого на решение вопросов, и повышения точности. Ниже приводится обзор важных математических формул, содержащихся в решениях NCERT для математики класса 9.
Формулы необходимы для сокращения времени, затрачиваемого на решение вопросов, и повышения точности. Ниже приводится обзор важных математических формул, содержащихся в решениях NCERT для математики класса 9.
Геометрия:
- Площадь треугольника = ½ * b × h
- Периметр треугольника = a + b + c
- Площадь параллелограмма = b × h
- Периметр параллелограмма = 2(a + b)
Площадь поверхности и объем:
- TSA прямоугольного параллелепипеда = 2(lb + bh +lh)
- Объем прямоугольного параллелепипеда = l×b×h
- ТСА куба = 6а 2
- Объем куба = a 3
Алгебра:
- (а + б) 2 = а 2 + б 2 + 2аб
- (а — б) 2 = а 2 + б 2 — 2аб
- (а + b) (а — b) = а 2 — б 2
Важность решений NCERT для математики 9-го класса
Математика 9-го класса Решения NCERT чрезвычайно полезны для учащихся CBSE, поскольку они дают средства для эффективного управления временем и улучшения вспомогательных способностей. Ниже приведены преимущества этих решений.
Ниже приведены преимущества этих решений.
- Практическое применение: Многие суммы, представленные в учебнике NCERT, аналогичны примерам из реальной жизни, особенно когда рассматриваются текстовые задачи. Следуя решениям NCERT по математике в классе 9, учащиеся могут найти точные решения, которые также можно применять к повседневным жизненным задачам.
- Практика: Чтобы решить самые сложные задачи за считанные минуты, вам потребуется должное усердие и регулярная практика. Эти решения NCERT для класса 9математика очень полезна для этой цели, поскольку она дает учащимся подробный обзор того, как решать различные типы сумм. Они также могут помочь учащемуся хорошо завершить учебный план в заданные сроки.
- Обычная редакция: В дни экзаменов у студентов нет времени на решение каждого вопроса. Таким образом, эти решения NCERT по математике для 9-го класса помогают учащимся быстро просмотреть весь учебный план.
 Это также помогает высвободить время, чтобы учащиеся могли сосредоточиться на правильном формировании своих понятий и их точном применении к суммам.
Это также помогает высвободить время, чтобы учащиеся могли сосредоточиться на правильном формировании своих понятий и их точном применении к суммам.
Часто задаваемые вопросы о решениях NCERT для математики класса 9
Почему важны решения NCERT для математики класса 9?
Решения NCERT по математике для 9-го класса жизненно важны для учащихся, поскольку они предоставляют надежные решения, которые учащиеся могут использовать для перепроверки своих ответов. Эти решения NCERT по математике для 9 класса также помогают учащимся явиться на экзамен, чтобы учащиеся могли написать свои ответы, не пропуская ни одного шага, и получить максимально возможный балл.
Где я могу получить решения по главам для математики класса 9 NCERT?
Решения по математике класса 9 NCERT по главам доступны по ссылкам, указанным выше. Кроме того, они разделены на PDF-файлы с упражнениями, которые доступны для бесплатного скачивания. Эти PDF-файлы также совместимы с экранами мобильных устройств и имеют прокручиваемый формат для удобства использования.
Как учащиеся CBSE могут использовать решения NCERT по математике для 9 класса?
Чтобы эффективно использовать решения NCERT по математике в классе 9, учащиеся должны убедиться, что они понимают концепции, используемые для решения задач. Таким образом, когда они начнут обращаться к этим решениям, студенты будут лучше понимать их и смогут более эффективно запоминать то, что они узнали.
Нужно ли делать заметки, ссылаясь на решения NCERT Solutions Class 9 Math?
Заметки служат упрощенным руководством для учащихся, когда они пытаются лучше понять предмет или повторяют этот вопрос. Это хороший способ запомнить и вспомнить концепции, когда это необходимо. Таким образом, очень важно, чтобы учащиеся делали заметки о решениях NCERT для класса 9 по математике , чтобы ускорить процесс обучения.
Каковы наилучшие способы изучения концепций, описанных в решениях NCERT, класс 9й Математика?
Наиболее эффективным способом изучения понятий, описанных в решениях NCERT для 9-го класса математики, является постоянная практика этих решений. Если учащийся находит какую-то концепцию трудной и не может двигаться дальше, пытаясь решить задачу, ему необходимо немедленно прояснить свои сомнения, чтобы не было пробелов в обучении.
Если учащийся находит какую-то концепцию трудной и не может двигаться дальше, пытаясь решить задачу, ему необходимо немедленно прояснить свои сомнения, чтобы не было пробелов в обучении.
Можем ли мы использовать другие методы для решения задач, кроме тех, которые упомянуты в решениях NCERT для математики класса 9?
Возможно, вы не захотите использовать метод, указанный в решениях NCERT для класса 9.математика, однако используемый подход и полученный ответ должны быть общепризнанными. Сказав, что вы не можете использовать приемы, которые полезны при решении задач на конкурсных экзаменах, поскольку они не являются стандартизированными методами.
Почему стоит выбрать Cuemath для решения NCERT по математике для класса 9?
Лучший веб-сайт для решений NCERT по математике для 9 класса — Cuemath. Эти решения готовят специалисты IIT и сертифицированные эксперты по математике. Таким образом, они надежны, точны и дают лучшие методы для решения любой проблемы. Они также включают в себя несколько советов, которые помогут учащимся решать задачи быстро и точно.
Сколько глав в решениях NCERT для математики класса 9?
Решения NCERT по математике для 9 класса состоят из 15 глав. Проблемы, охватываемые ими, фантастически улучшают понимание учащимися различных концепций. Решения NCERT дают глубокий анализ всех проблем с упражнениями.
Нужно ли мне практиковать все вопросы, представленные в NCERT Solutions Class 9 Maths?
Все вопросы, которые включены в домашние экзамены CBSE, основаны на классе 9 NCERT.математика. Таким образом, чтобы получить хорошие оценки, необходимо хорошо разбираться во всех вопросах, охватываемых решениями NCERT по математике для 9 класса, чего можно достичь только путем регулярной практики и должной осмотрительности.
Достаточно ли решений NCERT для математики класса 9 для экзаменов CBSE?
Решения NCERT по математике для 9-го класса достаточно для всех экзаменов CBSE. При наборе работы школьные учителя включают вопросы из учебника NCERT. Язык или значения, указанные в задаче, могут отличаться, однако подход к ее решению более или менее одинаков. Если учащийся хорошо понимает все главы, он может успешно сдать экзамен.
Если учащийся хорошо понимает все главы, он может успешно сдать экзамен.
Какие важные темы рассматриваются в решениях NCERT для математики класса 9?
Все темы, такие как построение, круги, площадь поверхности, объем, статистика и т. д., которые рассматриваются в решениях NCERT для 9 класса по математике, необходимы для 10 класса. Так что пропускать тему не рекомендуется. Кроме того, все темы в рамках математики взаимосвязаны, поэтому необходимо уделять одинаковое внимание, ничего не упуская.
Каковы важные формулы в NCERT Class 9Математические решения?
Вопросы по математике 9 класса решений NCERT в основном основаны на применении теорем и аксиом для доказательства определенной точки зрения. Таким образом, за счет меньшего количества формул не только легко, но и необходимо запомнить их все.
Каковы преимущества решений NCERT по математике для 9 класса для студентов CBSE?
Решения NCERT по математике для 9-го класса помогают учащимся закончить учебный план вовремя, предоставляя им достаточно места для повторения. Они также предоставляют краткий обзор всех задач, которые учащиеся могут использовать в качестве справочного материала при беглом просмотре главы.
Они также предоставляют краткий обзор всех задач, которые учащиеся могут использовать в качестве справочного материала при беглом просмотре главы.
Почему я должен регулярно практиковать решения NCERT для математики класса 9?
Практика решений NCERT для 9 класса по математике поможет ученику достичь цели совершенства. Это помогает учащимся освоиться с рассмотренными понятиями. Таким образом, во время экзамена студенты могут сохранять хладнокровие и спокойно листать бумагу, не нервничая.
Как решения NCERT по математике в классе 9 способствуют решению задач у учащихся?
Решения NCERT по математике для 9-го класса начинаются с объяснения вопросов, а затем разбиваются на части, чтобы объяснить их лучше. Это учит студентов думать о том, почему и как стоит сумма. Эти решения побуждают учащихся использовать аналогичный подход, позволяющий им использовать свои навыки решения проблем и вычислительное мышление.
Решения NCERT для математики класса 4 Продавец мусора Бесплатные видео, тесты MCQ и многое другое.
 Установить сейчас
Установить сейчас
Решения NCERT для математики класса 4 Книжные решения Junk Seller доступны в формате PDF для бесплатной загрузки. Эти мудрые вопросы и ответы, посвященные главам книги, очень полезны для экзамена CBSE. CBSE рекомендует книги NCERT, и большинство вопросов на экзамене CBSE задаются из учебников NCERT. Решение NCERT по математике для класса 4 по математике для книги по математике, все главы можно бесплатно загрузить с нашего веб-сайта и мобильного приложения myCBSEguide.
Решения NCERT для математики 4 класса Скачать в формате PDF
Решения NCERT для математики 4 класса Продавец барахла
Глава 6 Математика класса 4 Продавец барахла
5
Вы также находите математику сложной?Ответ. Я не нахожу математику сложной.
2. Что самое сложное в вашем учебнике по математике?
Ответ. Глава под названием «Как выглядит мир» — самая сложная в учебнике по математике.
Глава под названием «Как выглядит мир» — самая сложная в учебнике по математике.
3. Как вы думаете, какой самый легкий урок?
Ответ. Урок «Поездка в Бхопал» является обязательным.
4. Узнайте: сколько стоит чашка чая?
Спросите людей и узнайте стоимость чашки чая
(а) В чайном киоске
Отв. (a) В чайном киоске стоимость чашки 3 рупии.
(b) В гостинице
Отв. (б) В отеле стоимость чашки составляет 10 рупий.
5. Если человек, который держит чайный киоск, зарабатывает 30 рупий в день, сколько он заработает за 10 дней? А через месяц? Как вы получили ответ? Обсуждать.
Ответ. Заработок владельца чайной лавки в день = 30
рупий Следовательно, заработок владельца чайной палатки за 10 дней =
рупий = 300рупий, а его заработок в месяц = 30 30 рупий = 900 рупий
Я получил ответы умножением.
6. Узнайте: Что такое кредит?
(a) Вы когда-нибудь слышали о том, чтобы кто-то брал кредит? Для чего?
Ответ. (a) Да, я слышал, что кто-то брал кредит. Принято покупать ручную тележку.
(b) Сколько кредита было взято?
Ответ. (б) 300 рупий были взяты в качестве кредита.
(c) Сколько денег было возвращено.
Хария и Бабу пошли покупать ручную тележку за 300 рупий.
Ответ. (c) Hariya: Я взял кредит в размере 300 рупий в банке на шесть месяцев. Я буду ежемесячно платить банку 51 рупию.
Бабу: Но я взял кредит в 300 рупий у Чуннилала. Через шесть месяцев я верну 360 рупий.
(г) Кто должен вернуть больше — Хария или Бабу?
Ответ. (d) В случае Hariya: Деньги, возвращенные банку = Rs. 6 51 = 306 рупий
В случае Бабу: деньги, выплаченные Чуннилалу = 360 рупий
Поскольку 360 рупий больше, чем 300 рупий, значит, Бабу вернул больше денег.
7. (a) Иметь 9 собственных рикш. Я сдаю рикши в аренду, каждая по 20 рупий в день. По воскресеньям я не беру с них денег? Сколько Киран зарабатывает на 9 рикшах в день?
Ответ. (a) За 1 рикшу она получает 20 рупий в день.
Итак, за 9 рикш она заработает 180 рупий.
(b) Как вы это сделали?
Ответ. (б) Я сделал это, перемножив 20 и 9 (20 9=180).
8. Сколько Киран зарабатывает в неделю на одной рикше?
Ответ. Так как по воскресеньям Киран не берет денег за аренду рикши, следовательно, Киран зарабатывает в неделю на одной рикше из расчета 20 рупий в день = 6 20 рупий = 120 рупий.
напишите ответы:
(а) 2 6= __
Отв. (а) 2 6= 12.
(б) 20 6 = __
Отв. (б) 20 6 = 120.
(в) 2 60 = __
Анс. (в) 2 60 = 120.
(в) 2 60 = 120.
(г) 3 42 = __
Анс. (г) 3 42 = 126.
(д) 4 80 = __
Анс. (e) 4 80 = 320.
(f) 4 81 = __
Анс. (е) 4 81 = 324.
(ж) 9 25 = __
Анс. (г) 9 25 = 225.
(ч) 31 9 = __
Анс. (h) 31 9 = 279.
10. 4 81 на 4 больше, чем на 4 80. Я прав?
Ответ. Да.
11. Сколько Киран заплатит за 31 кг газеты?
Ответ. Киран заплатит за 31 кг газеты = рупий (51 30 + 5 1) = 155 рупий.
Ответ. (a) Киран заплатит (42 5) рупий = 210 рупий.
(b) Также найдите стоимость:
(i) 22 кг пластика
Ответ. (b) (i) Стоимость 22 кг пластика = 22 10 рупий = 220 рупий.
(b) (i) Стоимость 22 кг пластика = 22 10 рупий = 220 рупий.
(ii) 23 кг макулатуры
Ответ (b) (ii) Стоимость 23 кг газеты = рупий (23 4) = 92 рупий.
(iii) 12 кг железа.
Ответ. (b) (iii) Стоимость 12 кг железа = (12 12) рупий = 144,9 рупий.0005
13. Вы можете сделать это без письма? Угадайте, сколько Киран заплатит сборщикам барахла. Будет ли: Больше 600? Меньше 600?
Ответ. Менее 600.
14. Киран купила 1 кг пластика за 10 рупий, но продала 1 кг пластика за 12 рупий. Сколько денег она зарабатывает на продаже 1 кг пластика?
Ответ. Прибыль от продажи 1 кг пластика = Цена продажи – Себестоимость = 12 рупий – 10 рупий = 2 9 рупий0005
So, earning on selling 63 kg of plastic = Rs 2 Rs 63
| 60 | 3 |
| 60 2 | 3 2 |
| 120 | 6 |
On adding числа в последней строке = 120 + 6 = 126.
Итак, за 63 кг пластика Киран зарабатывает = 126 рупий.
Математика 4 класса Продавец барахла Железо 32 кг?
Ответ. The rate of 1 kg of iron is Rs 14. So, the cost for 32kg of iron is Rs 14 32.
We write as:
| 30 | 2 | |
| 10 | 30 10 | 2 10 |
| 300 | 20 | |
| 4 | 30 4 | 2 4 |
| 120 | 8 |
So, for 32 kg iron, Dinu will pay Rs 448
16. Киран покупает 1 кг железа за 12 рупий, а продает его за 14 рупий. Сколько она зарабатывает, продавая 32 кг железа?
Ответ. Выручка от продажи 1 кг железа = Цена продажи — Себестоимость = 14 рупий – 12 рупий = 2 рупии
Таким образом, прибыль от продажи 32 кг железа = 2 32 рупий железа = 2 32 рупий
Запишем как:
| 30 | 2 | ||
| 30 2 | 2 2 | ||
| 60 |
| 4 | 100 | 70 |
| 100 4 | 70 4 | |
| 400 | 280 |
So, for 4 kg brass Dinu заплатит Киран 680 рупий.
Математика класса 4 Продавец барахла
19. Сначала угадайте ответ, затем рассчитайте:(a) 37 18
Ответ (a) При угадывании 37 18 может быть = 740,
We write as:
| 30 | 7 | |
| 10 | 30 10 | 7 10 |
| 300 | 70 | |
| 8 | 30 8 | 7 8 |
| 240 | 56 |
Adding the numbers = 300 + 240 + 70 + 56 = 666
So, 37 18 = 666.
Ans. (b) При угадывании 45 24 = 1080
We write as:
| 40 | 7 | |
| 20 | 40 20 | 5 20 |
| 800 | 100 | |
| 4 | 40 4 | 5 4 |
| 160 | 20 |
Добавление чисел = 800 + 160 + 100 + 20 = 1080
SO, 45 24 = 1080
. (c) При угадывании 6952 = 3588
We write as:
| 60 | 9 | |
| 50 | 60 50 | 9 50 |
| 3000 | 450 | |
| 2 | 60 2 | 9 2 |
| 120 | 18 |
Adding the numbers = 3000 + 120 + 450 + 18 = 3588
So, 69 52 = 3588.
(d) 77 55
Ответ (г) On guessing 77 55 = 4235
We write as:
| 70 | 7 | |
| 50 | 70 50 | 7 50 |
| 3500 | 350 | |
| 5 | 70 5 | 7 5 |
| 350 | 35 |
Adding the numbers = 3500 + 350 + 350 + 35 = 4235
So, 77 55 = 4235.
(e) 142 5
Ответ. (e) On guessing 142 5 = 710
We write as:
| 100 | 40 | 2 | |
| 5 | 100 5 | 40 5 | 2 5 |
| 500 | 200 | 10 |
Добавление чисел = 500 + 200 + 10 = 710
SO, 142 5 = 710.
(F) 382 3
. (f) При угадывании 382 3 = 1146
We write as:
| 300 | 80 | 2 | |
| 3 | 300 3 | 80 3 | 2 3 |
| 900 | 240 | 6 |
Сложение чисел = 900 + 240 + 6 = 1146
Итак, 382 3 = 1146
(г) 2 175
Ответ. (g) При угадывании 2 175 = 350
Запишем так:
| 100 | 70 | 5 | |
| 2 | 100 2 | 70 2 | 5 2 |
| 200 | 140 | 10 |
Adding the numbers = 200 + 140 + 10 = 350
Итак, 2 175 = 350.
(h) 4 206
Анс. (h) При угадывании 4 206 = 824
(h) При угадывании 4 206 = 824
Запишем так:
| 200 | 0 | 6 | |
| 4 | 200 4 | 0 4 | 6 4 |
| 800 | 0 | 24 |
Adding the numbers = 800 + 0 + 24 = 824
Итак, 4 206 = 824.
Решения NCERT для математики класса 4 Глава 6 Продавец мусора
Решения NCERT для класса 4 по математике Класс 4 Продавец мусора PDF (скачать) бесплатно в приложении myCBSEguide и на веб-сайте myCBSEguide. Ncert Solution Class 4 Maths включает в себя решения учебников из Class 4 Maths Book. Решения NCERT для математики класса CBSE состоят всего из 14 глав. 4 Решения NCERT по математике в формате PDF для бесплатного скачивания на нашем сайте. Решения Ncert Maths class 4 PDF и Maths ncert class 4 PDF-решения с последними изменениями и в соответствии с последней программой CBSE доступны только в myCBSEguide.
NCERT Solutions for Mathematics Class 3rd to 12th
- NCERT Solutions for Class 12 Mathematics
- NCERT Solutions for Class 11 Mathematics
- NCERT Solutions for Class 10 Mathematics
- NCERT Solutions for Class 9 Mathematics
- NCERT Solutions for Class 8 Математика
- Решения NCERT для математики 7 класса
- Решения NCERT для математики 6 класса
- Решения NCERT для 5 класса математики
- Решения NCERT для математики 4 класса
- Решения NCERT для математики 3 класса
Приложение CBSE для учащихся
Чтобы загрузить решения NCERT для математики 4 класса, EVS Hindi English, Maths Science, проверьте приложение или веб-сайт myCBSEguide. myCBSEguide предоставляет образцы документов с решениями, тестовые документы для практики по главам, решения NCERT, решения NCERT Exemplar, краткие примечания к изменениям для быстрого ознакомления, документы с предположениями CBSE и документы с важными вопросами CBSE.


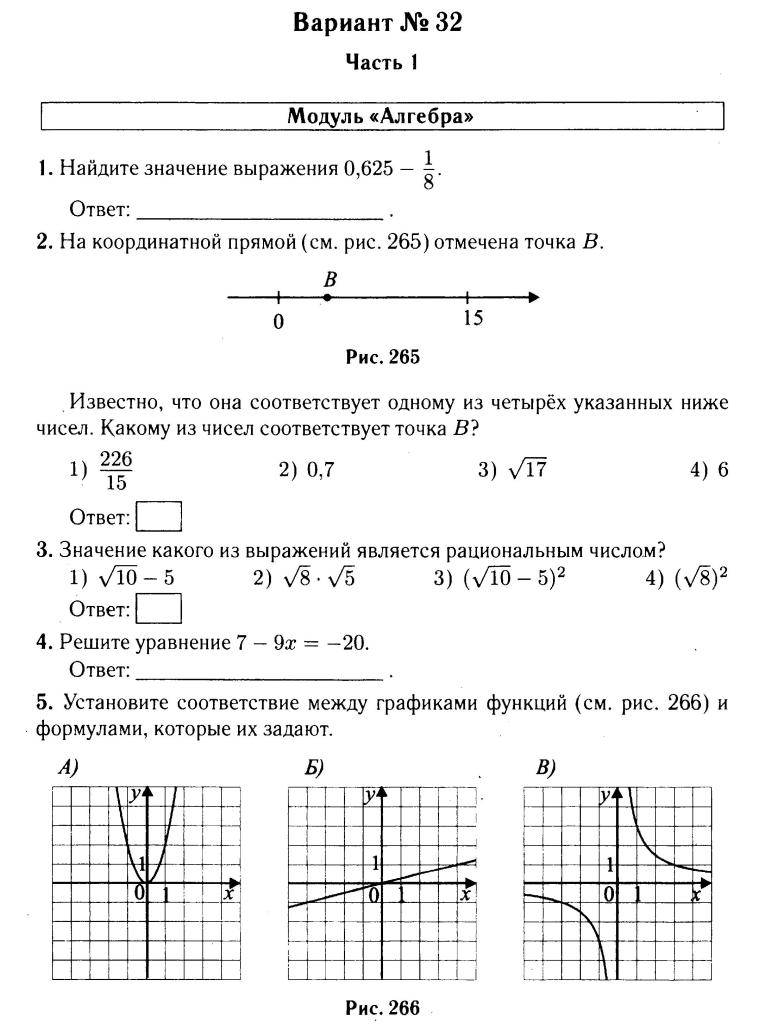
 Неравенства.
Неравенства. √x (x>= 0)
√x (x>= 0) Угол и его мера
Угол и его мера Описательная статистика
Описательная статистика 42 МБ
42 МБ 1
1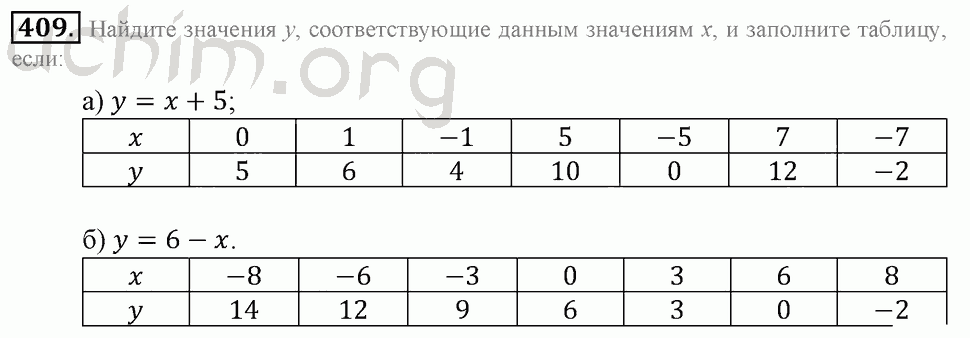 2
2 1
1 1
1 2
2 6
6 Длина каждого бар дает необходимую информацию. Процесс выбора масштаба для графика важен.
Длина каждого бар дает необходимую информацию. Процесс выбора масштаба для графика важен.