Кирсанов М.Н. — Решебник по теоретической механике — DJVU
DJVU-файл из архива «Кирсанов М.Н. — Решебник по теоретической механике», который расположен в категории «». Всё это находится в предмете «теоретическая механика» из раздела «», которые можно найти в файловом архиве МГТУ им. Н.Э.Баумана. Не смотря на прямую связь этого архива с МГТУ им. Н.Э.Баумана, его также можно найти и в других разделах. Архив можно найти в разделе «книги и методические указания», в предмете «теоретическая механика» в общих файлах.
УДК 53Ц075.8) К43 ББК 22.21 Кирсанов М. Н. Решебник. Теоретическая механика / Под ред. А. И. Кириллова. Мл ФИЗМАТЛИТ, 2002. 384 с. 1ЯВМ 5-9221-0281-8. Изложены алгоритмы и примеры решения задач статики, кинематики и динамики из курса теоретической механики, изучаемого в техничЕских вузах. Каждой задаче отведен отдельный раздел, содержащий общую постановку задачи, план ее решения с необходимыми теоретическими пояснениями и пример. Кроме того, в раздел включены десять задач двя самостоятельного решения и ответы к ним, Разобраны характерные ошибки и даны ответы на типичные вопросы, возникающие при решении задач.
Ил. 187. © ФИЗМАТЛИТ, 2002 © М, Н. Кирсанов, 2002 1ЯВг1 5-9221-0281-8 ОГЛАВЛЕНИЕ ПРЕДИСЛОВИЕ СТАТИКА 1.1. Простая стержневая система 1.2. Равновесие цепи 1.3. Теорема о трех силах 14 21 26 31 74 3.1. Трение скольжения 3,2. Трение качения 74 80 86 118 118 122 125 Глава 1. ПЛОСКАЯ СИСТЕМА СХОДЯЩИХСЯ СИЛ Глава 2. ПРОИЗВОЛЬНАЯ ПЛОСКАЯ СИСТЕМА СИЛ 2.1. Равновесие тяжелой рамы 2.2.
Ферма. Аналитические методы расчета . 2.3. Ферма. Графический расчет 2.4. Расчет составной конструкции 2.5. Конструкция с распределенными нагрузками . 2.6. Расчет системы трех тел, соединенных шарниром Глава 3. РАВНОВЕСИЕ ПРИ НАЛИх1ИИ ТРЕНИЯ Глава 4. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ 4.1. Пространственная ферма .
4.2. Момент силы относительно оси………… 4.3. Равновесие вала 4.4. Определение усилий в стержнях, поддерживающих плиту 4. 5. Тело на сферической и стержневых опорах 4.6. Приведение системы сил к простейшему виду Глава 5. ЦЕНТР ТЯ2КЕСТИ 5З. Центр тяжести плоской фигуры ….. 5.2. Пространственнал стержневая система 5.3.
5. Тело на сферической и стержневых опорах 4.6. Приведение системы сил к простейшему виду Глава 5. ЦЕНТР ТЯ2КЕСТИ 5З. Центр тяжести плоской фигуры ….. 5.2. Пространственнал стержневая система 5.3.
Центр тяжести объемного тела 31 37 45 54 61 67 86 91 94 101 106 1П ОГЛАВЛЕНИЕ п. КИНЕМАТИКА 129 131 149 152 Р38 222 222 пп ДИНАМИКА 226 228 228 232 Глава 6. КИНЕМАТИКА ТОх1КИ 6.1. Движение точки в плоскости 6.2. Путь, пройденный точкой 6.3. Движение точки в пространстве 6.4. Естественный способ задания движения точки 6.5. Движение точки в полярных координатах .
Глава 7. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ‘ГЕЛА 7А. Вращательное движение тела 7.2. Передача вращения Глава 8. ПЛОСКОЕ ДВИЖЕНИЕ ТЕЛА 8.1. Скорости точек многозвенного механизма 8.2. Ускорения точек многозвенного механизма 8.3. Уравнение трех угловых скоростей . 8.4. Уравнение трех угловых ускорений …….. 8.5. Кинематические уравнения плоского движения . Глава 9. СЛОяКНОЕ ДВИЖЕНИЕ ‘ГОНКИ 9.1. Сложное движение точки в плоскости 9.
Движение точки по звену механизма . 9.4. Механизм с муфтой Глава 10. СсФЕРИх4ЕСКОЕ ДВИ2КЕНИЕ ТЕЛА 10.1. Скорость и ускорение точки тела . Глава 11. ДИНАМИКА ТОНКИ 11.1. Постоянные силы 11.2. Переменные силы Г л а в а 12. ДИНАМИКА СИСТЕМЫ 12.1. Теорема о движении центра масс 12.2. Кинетическая энергия механической системы 12.3.
Теорема об изменении кинетической энергии…….. 12.4. Теорема о моменте количества движения системы . 12.5. Динамический расчет механизма с неизвестным параметром 131 136 137 140 144 158 170 179 183 188 195 195 202 209 216 236 236 241 247 253 257 ОГЛАВЛЕНИЕ 266 272 279 .. 349 350 350 355 375 377 12.6. Плоское движение системы 12.7. Динамические реакции в подшипниках ротора Глава 13. АНАЛИТИх1ЕСКАЯ МЕХАНИКА 13.1.
Принцип возможных скоростей 13.2. Общее уравнение динамики (одна степень свободы) .. 13.3. Общее уравнение динамики (две степени свободы) 13.4. Уравнение Лагранжа 2-го рода (две степени свободы) 13. 5. Уравнение Лагранжа. Нелинейные уравнения движения 13.6. Уравнение Лагранжа 2-го рода для консервативных систем 13.7.
5. Уравнение Лагранжа. Нелинейные уравнения движения 13.6. Уравнение Лагранжа 2-го рода для консервативных систем 13.7.
Функция Гамильтона 13.8. Уравнения Гамильтона Глава 14. МАЛЫЕ КОЛЕБАНИЯ СИСТЕМЫ 14А. Система с двумя степенями свободы……. 14.2. Колебания узла фермы 1У. РКШКНИЯ В СИСТКМК МАРЬК 17 Глава 15. ПРОГРАММЫ ПО СТАТИКЕ 15.1. Расчет фермы 15.2. Центр тяжести плоской фигуры . Г л аз а 16. ПРОГРАММЫ ПО КИНЕМАТИКЕ 16.1. Кинематика точки 16.2. Механизм с двумя степенями свободы 16.3.
Скорости точек плоского механизма . Г л а в а 17. ПРОГРАММЫ ПО ДИНАМИКЕ 17.1. Принцип возможных скоростей 17.2, Динамика машины с кулисным приводом 17.3. Колебания системы с двумя степенями свободы СПИСОК ЛИТЕРАТУРЫ . ИМЕННОЙ И ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ 279 288 294 300 307 318 324 326 336 336 343 358 358 361 364 368 368 370 373 ПРЕДИСЛОВИЕ Теоретическая механика — одна из важнейших дисциплин в техническом вузе. Решение задач по этой дисциплине всегда представляет определенную трудность для студента.
Вызвано это многообразием тем или обилием уравнений и теорем,множеством методов, уровнем абстракции при решении задач или какими-либо другими причинами — неизвестно. Скорее всего, для студентов младших курсов все эти факторы вместе приводят к тому, что, по общему мнению, теоретическая механика, наряду с математикой и сопротивлением материалов, числится в технических вузах наиболее сложной дисциплиной. При столкновении с трудной задачей лучшим помошником для студента, самостоятельно изучающего науку, является книга. По теоретической механике существует много учебников. Можно рекомендовать, например, изданный большим тиражом краткий курс Тарга С.М.
)19). Очень хорошо подходит для технических вузов учебник 5]. В этих учебниках и во многих других после изложения теории дается несколько примеров решения задач. Ознакомление с готовыми решениями* ) — один из способов обучения, но не самый лучший. Если ставить перед собой цель научиться решать задачи (а не решить вот зту — конкретную задачу), то лучше всего овладеть секретами мастерства; алгоритмами и схемами решений, методами и специальными приемами. РЕШЕБНИК «Теоретическая механика» ставит перед собой именно такую цель. Продолжая традиции РЕШЕБНИКА «Высшая математика» ~10] и РЕШЕБНИКА «Высшая математика. Ы В сети Интернет существуют специальные страницы, где приводятся готовыс решения заданий и задач по теоретической механике.
РЕШЕБНИК «Теоретическая механика» ставит перед собой именно такую цель. Продолжая традиции РЕШЕБНИКА «Высшая математика» ~10] и РЕШЕБНИКА «Высшая математика. Ы В сети Интернет существуют специальные страницы, где приводятся готовыс решения заданий и задач по теоретической механике.
Форма и содержание таких решений часто не удовлетворяют самым скромным запросам, не говоря уже о том, что научить они мало чему смогут. Специальные разделы» 121, в книге даны, во-первых, четкая постановка задачи, во-вторых, конкретный план действий и, наконец, пример решения задачи по этому плану. В качестве примеров взяты задачи из сборника задач Мещерского И.В. 1141 или задачи близкие к ним. В конце каждого параграфа приведены десять задач, которые могут быть решены студентами самостоятельно, а некоторые, наиболее сложные, соответствуют по уровню курсовым работам.
За образец для таких работ взяты задания из сборников Яблонского А.А. «,171 и Новожилова И.В., Зацепина М.Ф. 115~. Ко всем задачам даны не только ответы, но и, как правило, промежуточные результаты.
Даны также предостережения о возможных ошибках в решении задач. В последней части РЕШЕБНИКА приведены примеры решения задач с использованием универсальной математической системы Мар1е У, позволяющей решить задачу в аналитическом виде и изобразить исследуемое явление, например, движение механизма, на экране компьютера. Полные тексты приведенных здесь программ и программы для решения других задач механики с примерами, подробными пояснениями и графическим представлением результатов можно найти на авторской странице Интернет: жч к.асас1еш1аххьтн/во1гегТМ.Ыш1. Ссылка на РЕШЕБНИК «Высшая математика» обозначена как Решебник ВМ с указанием соответствующего параграфа.
В дополнение к этой книге и к программам для Мар1е Ч распространяется пакет программ РЕШЕБНИК.ТМ, представляющий собой электронную версию РЕШЕБНИКА, разработанную на основе пакета АсабепнаХХ1. С помощью пакета программ РЕШЕБНИК.ТМ студент сможет проще решать многие задачи теоретической механики, уделяя больше сил и времени разбору сути задачи и физического явления, лежащего в основе задачи, предоставляя компьютеру рутинную часть работы, связанную с математическими вгякладками и численным счетом. Для преподавателей теоретической механики автор разработал специальную программу-генератор задач, создающую тексты усло- вий и ответов по 50 темам статики, кинематики и динамики.
Тексты задач и рисунки в формате УТЕХ могут быть использованы для очного и дистанционного обучения. Программа содержит сотни тысяч вариантов задач и используется автором в его педагогической работе. По десять задач из почти всех разделов программы-генератора приведены в этой книге в качестве примеров. Подробная информация о пакете РЕШЕБНИК.
Сканави М.И. Решебник задач по математике (полный)
- формат jpeg, jpg, pdf, txt, djvu
- размер 38.42 МБ
- добавлен 10 мая 2010 г.
Книги содержат полный комплекс решений различных уровней сложности задач по математике для поступающих в ВУЗы. 2003 г. В книге собраны задачи различных уровней сложности и их решения.
Смотрите также
- формат jpg
- размер 12.06 МБ
- добавлен 22 января 2010 г.
Методические указания представляют собой практическое пособие к решению задач по элементарной математике. В указаниях рассмотренны основные типы задач, предлагавшихся абитуриентам МГУПП за последние годы. В каждом разделе даны методические рекомендации к решению таких задач. 62 стр. Список литературы: Сборник задач по математике. Сборник конкурсных задач по математике.rn
В указаниях рассмотренны основные типы задач, предлагавшихся абитуриентам МГУПП за последние годы. В каждом разделе даны методические рекомендации к решению таких задач. 62 стр. Список литературы: Сборник задач по математике. Сборник конкурсных задач по математике.rn
- формат djvu
- размер 3.53 МБ
- добавлен 18 марта 2011 г.
— М.; «Обериг», 1994. – 209с. Пособие, написанное известным педагогом, специалистом школьной геометрии, включает как векторные задачи, так и смешанные задачи классической геометрии, решаемые с помощью векторов. В книге решены векторные задачи из сборников задач по математике под редакцией М. И. Сканави разных изданий. Для учащихся школ и техникумов, лицеев и гимназий, классов с углубленным изучением математики, абитуриентов, студентов, учителей и…
- формат djvu
- размер 5.
 99 МБ
99 МБ - добавлен 26 ноября 2010 г.
Сборник задач под ред. Сканави. Содержит задачи по всему курсу алгебры. Позволяет подготовиться к ЕГЭ по математике. Рекомендован для решения в 10-11 классах, в основном в физико-математических классах и (или) для углубленного изучения, подготовки к математическим олимпиадам. Внимание: требует много времени для решения задач, но и результат будет хороший.
- формат pdf
- размер 48.57 МБ
- добавлен 15 января 2010 г.
Сканави М. И, Элементарная математика Сканави М. И. Сборник задач по математике для поступающих во втузы (с решениями) Кн 1 Алгебра Сканави М. И. Сборник задач по математике для поступающих во втузы (с решениями) Кн 2 Геометрия Сканави М. И. Сборник Решений Задач Для Поступающих в ВУЗы Г Сканави М. И. Сборник Решений Задач Для Поступающих в ВУЗы Гру
И. Сборник Решений Задач Для Поступающих в ВУЗы Гру
- формат pdf
- размер 33.97 МБ
- добавлен 02 октября 2010 г.
Под ред. М. И. Сканави. — М. : 000 «Издательство «Мир и Образование»: Мн.: ООО «Харвест», 2003 — 912 с. Впервые в помощь абитуриентам публикуется полный сборник задач с решениями под редакцией М. И. Сканави по всем группам сложности. Книги помогут учащимся научиться решать экзаменационные задачи различного уровня сложности любого вуза, Условия и нумерация всех задач полностью соответствуют изданию «Сборник задач по математике для поступающих в ву…
- формат pdf
- размер 13.18 МБ
- добавлен 04 января 2009 г.
(под ред. Сканави). Группа А. Впервые в помощь абитуриентам публикуется полный сборник задач с решениями под редакцией М. И. Сканави по всем группам сложности. Книги помогут учащимся научиться решать экзаменационные задачи различного уровня сложности любого вуза. Условия и нумерация всех задач полностью соответствуют изданию «Сборник задач по математике для поступающих в вузы» под редакцией М. И. Сканави, 6-е издание (М.: ОНИКС 21 век, Мир и Обра…
И. Сканави по всем группам сложности. Книги помогут учащимся научиться решать экзаменационные задачи различного уровня сложности любого вуза. Условия и нумерация всех задач полностью соответствуют изданию «Сборник задач по математике для поступающих в вузы» под редакцией М. И. Сканави, 6-е издание (М.: ОНИКС 21 век, Мир и Обра…
- формат pdf
- размер 14.88 МБ
- добавлен 17 октября 2009 г.
Описание решения задач по математике из соответствующего сборника задач. Одно из лучших пособий для подготовки по математике.
- формат pdf
- размер 4.09 МБ
- добавлен 02 мая 2009 г.
Решебник Сканави! Впервые в помощь абитуриентам публикуется полный сборник задач с решениями. Всего есть три группы задачников — А, Б, В. Б -средний уровень.
Б -средний уровень.
- формат pdf
- размер 7.6 МБ
- добавлен 02 мая 2009 г.
Решебник Сканави ! Впервые в помощь абитуриентам публикуется полный сборник задач с решениями. Всего есть три группы задачников — А, Б, В. В -самый сложный уровень!
- формат pdf
- размер 41.44 МБ
- добавлен 13 февраля 2009 г.
Книга написана в соответствии с программой для поступающих в Вузы. Задачи объединены по принципу однородности тем типов, методов решения и разбиты на три группы по уровню сложности. Ко многим задачам даны решения подробные. Ну вы и сами знаете учебники под ред. Сканави. Также в данном архиве я поместил решебники к данному учебнику.
Решебник по Математике для 4 класса М.
 И. Моро
И. МороРешеба по математике 4 класс
Онлайн решебник по Математике для 4 класса М. И. Моро, М. А. Бантова, Г. В. Бельтюкова, и ответы к домашнему заданию.
к рабочей тетради по математике за 4 класс Волкова С. И. можно скачать здесь.
к проверочным работам по математике за 4 класс Моро М. И. можно скачать здесь.
к тетради учебных достижений по математике за 4 класс Волкова С. И. можно скачать здесь.
к тестам по математике за 4 класс Волкова С. И. можно скачать здесь.
к конструированию по математике за 4 класс Волкова С. И. можно скачать здесь.
к контрольным работам по математике за 1-4 классы Волкова С. И. можно скачать здесь.
к рабочей тетради по математике за 4 класс Кремнева С. Ю. можно скачать здесь.
к текстовым задачам по математике за 4 класс Давыдкина Л. М. можно скачать здесь.
к тренажёру по математике за 4 класс Яценко И. Ф. можно скачать здесь.
к тестам по математике за 4 класс Быкова Т. П. можно скачать здесь.
к контрольным работам по математике за 4 класс Рудницкая В. Н. можно скачать здесь.
Можно скачать здесь.
Reshebnik. com
08.02.2019 18:10:02
2019-02-08 18:10:02
Источники:
Https://reshebnik. com/gdz/4-class/matematika/reshebnik-moro-m-i-i-dr/
Решебник по математике 4 класс » /> » /> .keyword { color: red; }
Решеба по математике 4 класс
Не смотря на то, что школьная программа еще не слишком усложнилась, многие ученики испытывают трудности в процессе решения уравнений и примеров. Чтобы школьник чувствовал себя уверенно и не боялся сдавать тетрадь с домашним заданием на проверку, лучше всего заранее тщательно готовиться дома. В таком случае помогут Решебники по математике за 4 класс с выполненными заданиями.
В пособиях включены численные ответы, которые укажут на наличие ошибок, которые могли возникнуть в процессе вычисления. Поэтапный разбор заданий позволит лучше понять сам принцип работы с некоторыми типовыми упражнениями.
Решебник за 4 класс по математике.
Resheba. me
28.12.2017 13:12:58
2017-12-28 13:12:58
Источники:
Https://resheba. me/gdz/matematika/4-klass
Решебник () по математике 4 класс Чеботаревская, Николаева » /> » /> .keyword { color: red; }
Решеба по математике 4 класс
В этом учебном году ребенку предстоит повторить весь предыдущий материал предмета и подготовиться к переходу на следующий этап обучения. « по математике для 4 класса Чеботаревская (Начальная школа)» создан специально для того, чтобы каждый ученик смог подтянуть свои слабые стороны и как следует усвоить программу.
Курс для четвероклассников кажется несложным на первый взгляд. Однако не все так однозначно. Ведь далеко не каждый ребенок схватывает материал «на лету». Для того, чтобы справиться с возникающими сложностями, школьнику рекомендуется применять решебник. Он поможет учащемуся не отставать от остального класса и быстро наверстать упущенный материал в комфортной домашней обстановке.
Онлайн-решебник по математике для 4 класса Чеботаревская для младшего школьника
Значительная часть жизни современного человека связана с интернетом. И вот уже школьное образование стремительно переходит в режим онлайн. Чем раньше ребенок научится грамотно пользоваться мировой паутиной, тем больше образовательных возможностей у него появится со временем. Онлайн-решебник отлично способствует этому. Ведь применяя его, школьник учится:
- искать необходимую информацию и применять ее на практике; самостоятельно проверять домашнее задание; своевременно находить и исправлять ошибки; контролировать свою успеваемость.
Пособие содержит правильные ответы на все задания из одноименного учебника, а его интерфейс порадует своим удобством. Поэтому ребенок сможет без труда найти необходимый пример или задачу.
Как помочь ученику раскрыть свой потенциал
Каждый родитель мечтает о том, чтобы его ребенок хорошо учился, был внимательным и ответственным. Применяя « по математике для 4 класса Чеботаревская Т. М., Николаева В. Н. (Начальная школа)» маленький ученик сможет раскрыть свои образовательные способности. Главное — пользоваться решебником с умом и не допускать бездумного списывания. С его помощью, ребенок сможет выполнить домашнее задание, подготовиться к уроку и проверочным работам, разобраться в новом материале и повторить пройденные темы, поднимать руку, чаще выходить к доске и уверенно отвечать перед классом. Задача родителей — научить малыша правильно использовать решебник. Если применять его как дополнение к решебнику, то можно довольно быстро повысить уровень знаний. Это позитивно скажется на успеваемости и мотивации ученика.
М., Николаева В. Н. (Начальная школа)» маленький ученик сможет раскрыть свои образовательные способности. Главное — пользоваться решебником с умом и не допускать бездумного списывания. С его помощью, ребенок сможет выполнить домашнее задание, подготовиться к уроку и проверочным работам, разобраться в новом материале и повторить пройденные темы, поднимать руку, чаще выходить к доске и уверенно отвечать перед классом. Задача родителей — научить малыша правильно использовать решебник. Если применять его как дополнение к решебнику, то можно довольно быстро повысить уровень знаний. Это позитивно скажется на успеваемости и мотивации ученика.
Самостоятельно проверять домашнее задание;.
Megaresheba. ru
06.10.2018 0:10:10
2018-10-06 00:10:10
Источники:
Https://megaresheba. ru/index/b01/0-473
Решебник М.Э.Абрамян APK für Android herunterladen
Startseite » Apps » Bücher & Nachschlagewerke » Решебник М. Э.Абрамян
Э.Абрамян
1.3 for Android
| 0 Reviews | 0 Empfehlungen
24TECH
APK herunterladen
Wie installiert man eine XAPK/APK-Datei
Die Beschreibung von Решебник М.Э.Абрамян
Данная программа помогает студентам которые изучают язык C++ и VB.NET.
В этой версии программы решены задачи из книги М.Э.Абрамян.
Mehr anzeigen
Решебник М.Э.Абрамян 1.3 Aktualisieren
2016-11-23
Добавлено решение на VB.NET
Решебник М.Э.Абрамян Tags
- Bücher & Nachschlagewerke
Add Tags
By adding tag words that describe for Games&Apps, you’re helping to make these Games and Apps be more discoverable by other APKPure users.
Download APK(12.1 MB)
zusätzliche Information
Kategorie:
Gratis Bücher & Nachschlagewerke APP
Aktuelle Version:
1.
 3
3Aktualisiert am:
2016-11-22
Von hochgeladen:
رأفت محمد ابراهيم
Erforderliche Android-Version:
Android 3.0+
Bericht:
Als unangemessen kennzeichnen
Frühere Versionen
Mehr »
V1.3 2.7 MB APK
Решебник М.Э.Абрамян
2016-11-23
V1.2 2.7 MB APK
Решебник М.Э.Абрамян
2016-11-20
V1.1 2.7 MB APK
Решебник М.Э.Абрамян
2016-11-09
Решебник М. Э.Абрамян Alternative
Э.Абрамян Alternative
Mehr »
- ГДЗ: мой решебник
5.4
- Pascal N-IDE
9.5
- English with Lingualeo
7.5
- WordBit Английский язык
10.0
- Learn C#
9.4
- Englisch
9.0
Mehr von 24TECH
Mehr »
- Таджикская клавиатура
10.0
- 2.0.7
- КОНСТИТУТСИЯИ ҶТ (2016)
- 1.5
- Кодексҳои Ҷумҳурии Тоҷикистон
- 1.3
- Толковый словарь Ожегова
- 2.0.1
- Маҷмӯаи иншоҳо
- 1.
 4
4
- Русско — Таджикский разговорни
- 1.0.2
Discover
Mehr »
Google Meet
175.0.473010588.duo.android_20220904.16_p1.s
Google LLC
Spotify
8.7.68.568
Spotify AB
Amazon Kindle
8.66.0.100(1.3.267921.0)
Amazon Mobile LLC
Android für Barrierefreiheit
13.0.0.473912301
Google LLC
Joom. Shopping für jeden Tag.
4.41.0
Joom
Twitter
9.58.2-release.0
Twitter, Inc.
ZEDGE™ Wallpapers & Ringtones
7.46.0
Zedge
Telefon
90.0.475844574
Google LLC
Trip.com
7.62.1
Trip.com
LinkedIn
4.1.735.1
LinkedIn
Beliebte Apps in den letzten 24 Stunden
1
- 2.
 22.21.6
22.21.6 - Kommunikation
2
- Google Maps
- 11.49.0701
- Reisen & Lokales
3
- TikTok
- 26.3.3
- Soziale Netzwerke
4
- Starlink
- 2022.09.1
- Tools
5
- Netflix
- 8.42.0 build 10 50279
- Unterhaltung
6
- 253.0.0.23.114
- Soziale Netzwerke
7
- Google Play Store
- 32.4.15-21 [0] [PR] 474943405
- Tools
8
- Android Auto
- 8.1.626423-release
- Autos & Fahrzeuge
9
- Messenger
- 379.1.0.23.114
- Kommunikation
10
- 385.0.0.32.114
- Soziale Netzwerke
Mehr »
Решебник по Математике за 4 класс М.
 И. Моро, М.А. Бантова, Г.В. Бельтюкова часть 1, 2 на Гитем ми
И. Моро, М.А. Бантова, Г.В. Бельтюкова часть 1, 2 на Гитем миавторы: М.И. Моро, М.А. Бантова, Г.В. Бельтюкова.
Каждый четвероклассник знает, что всего через год ему придется сдавать итоговые тесты по усвоению рабочей программы по ФГОС для перехода из начальной школы в среднюю. Начинать устранение пробелов в знаниях по основным предметам лучше как можно раньше. На четвертом году обучения следует обратить особое внимание на результаты контрольных работ и оценки за решение заданий, заданных на дом – именно они в полной мере отображают ситуацию. Если школьник часто получает тройки, откладывает выполнение упражнений до последнего, учит уроки неохотно до поздней ночи, стоит разобраться, в чем причина. Это могут быть конфликт с учителем-предметником или банальное непонимание какой-то темы.
Любящий, ответственный родитель обязан помочь своему ребенку. Но что делать, если вы не сильны в знаниях по данному предмету, или просто не всегда располагаете временем для совместного освоения рабочей программы со своим учеником? Выход прост – воспользуйтесь современными пособиями для самостоятельного решения заданий – решебниками.
Но что делать, если вы не сильны в знаниях по данному предмету, или просто не всегда располагаете временем для совместного освоения рабочей программы со своим учеником? Выход прост – воспользуйтесь современными пособиями для самостоятельного решения заданий – решебниками.
ГДЗ по математике 4 класс по учебнику М.И. Моро, М.А. Бантова, Г.В. Бельтюкова (Часть 1, 2)
На нашем сайте можно онлайн найти упражнения и посмотреть не только правильный ответ, но и поэтапное выполнение задач с объяснением и ссылкой на теоретический материал. Ознакомьтесь с ним сами или покажите своему школьнику, чтобы он смог разобраться во всем самостоятельно.
Объясните ученику, почему вредно просто списывать верный ответ:
- при вызове к доске учитель поймет, что выполненное на «отлично» домашнее задание сделал не он сам.
- на проверочной работе или тесте решебника не будет.
- дальше темы будут еще сложнее, и лучше выучить правила и вникнуть в них сейчас — потом будет поздно.

На нашем сайте представлена полная версия ГДЗ по математике М.И. Моро в обеих частях бесплатно, без регистрации. Пользуйтесь им совместно с ребенком или предоставьте ему доступ к пособию, разъяснив, как им пользоваться. Вскоре школьник почувствует себя увереннее и начнет справляться с задачами сам, вот увидите!
ГДЗ к рабочей тетради по математике за 4 класс Волкова С.И. можно скачать здесь.
ГДЗ к проверочным работам по математике за 4 класс Моро М.И. можно скачать здесь.
ГДЗ к тетради учебных достижений по математике за 4 класс Волкова С.И. можно скачать здесь.
ГДЗ к тестам по математике за 4 класс Волкова С.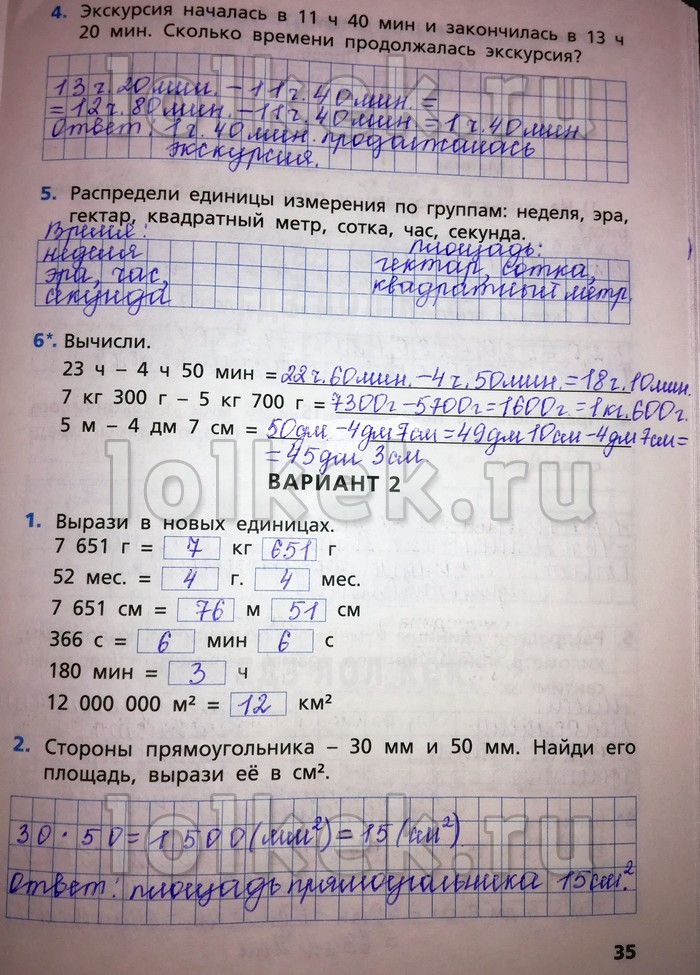 И. можно скачать
здесь.
И. можно скачать
здесь.
ГДЗ к конструированию по математике за 4 класс Волкова С.И. можно скачать здесь.
ГДЗ к рабочей тетради Для тех, кто любит математику за 4 класс Волкова С.И. можно скачать здесь.
ГДЗ к контрольным работам по математике за 1-4 классы Волкова С.И. можно скачать здесь.
ГДЗ к рабочей тетради по математике за 4 класс Кремнева С.Ю. можно скачать здесь.
ГДЗ к текстовым задачам по математике за 4 класс Давыдкина Л.М. можно скачать
здесь.
ГДЗ к тренажёру по математике за 4 класс Яценко И.Ф. можно скачать здесь.
ГДЗ к тестам по математике за 4 класс Быкова Т.П. можно скачать здесь.
ГДЗ к контрольным работам по математике за 4 класс Рудницкая В.Н. можно скачать здесь.
Часть 1
Упражнения
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376 377 378 379 380 381 382 383 384 385 386 387 388 389 390 391 392 393 394 395 396 397 398 399 400 401 402 403 404 405 406 407 408 409 410 411 412 413 414 415 416 417 418 419 420 421 422 423 424 425 426 427 428 429 430 431 432 433 434 435 436 Чему научились»> Что узнали. Чему научилисьЗадания на страницах 18-19
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15Задания на страницах 34-35
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17Задания на страницах 53-54
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28Задания на страницах 69-73
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27Задания на страницах 91-95
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50Вопросы для повторения
Вопросы на странице 19
1 2 3 4Вопросы на странице 35
1 2 3 4 5 6 7Вопросы на странице 55
1 2 3Вопросы на странице 73
1 2 3 4 5 6Вопросы на странице 95
1 2 3 4 5 6 7 8Странички для любознательных
Страница 20
1 2 3 4 5 6 7 8 9 10 11 12Страница 31
1 2 3Страница 70
1 2 3 4Составляй и решай задачи
56-57Проверим себя
Тест на страницах 58-59
Вариант 1
1 2 3 4 5 6 7 8 9 10Вариант 2
1 2 3 4 5 6 7 8 9 10Тест на страницах 74-75
Вариант 1
1 2 3 4 5 6 7 8 9 10Вариант 2
1 2 3 4 5 6 7 8 9 10Тест на страницах 96-97
Вариант 1
1 2 3 4 5 6 7 8 9Вариант 2
1 2 3 4 5 6 7 8 9Тексты для контрольных работ
Задания базового уровня
1 2 3 4 5 6 7 8Задания повышенного уровня
1 2 3 4 5 6 7 8 9Задачи расчёты
Задачи на странице 71
1 2Задания на полях страницы
5 9 10 13 14 15 18 19 22 24 25 26 27 28 30 34 35 36 37 42 43 52 60 62 63 64 66 68 69 72 78 79 82 83 84 85 86 87 88 90 91 94Задания внизу страницы
5 7 8 9 10 11 12 13 14 15 23 24 25 26 27 28 29 37 38 40 42 44 45 46 47 48 49 50 51 60 61 62 63 64 65 67 76 77 78 79 80 81 82 83 84 85 86 87 88 89Часть 2
Упражнения
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322Cтранички для любознательных
Страница 9
1 2 3Страницы 10-11
1 2 3 4Страницы 18-19
1 2 3 4 5 6Страница 24
1 2 3 4 5 6 7 8 9 10 11 12Страницы 52-53
1 2 3 4Страницы 68-69
1 2 3 4 5 6Страницы 78-79
1 2 3 4 5 6 7Страницы 80-81
1 2 3 4 5 6 7 8 9 10 11 12 13 14Страница 103
1 2 3 4 5 6 7 8 9 10 11 12 13 14 Чему научились»> Что узнали. Чему научилисьЗадания на страницах 20-23
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32Задания на страницах 35-37
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28Задания на страницах 54-56
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25Задания на страницах 67-71
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25Задания на страницах 82-85
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37Вопросы для повторения
Вопросы на странице 23
1 2Вопросы на странице 37
1 2Вопросы на странице 56
1 2Проверим себя
Тест на страницах 38-39
Вариант 1
1 2 3 4 5 6 7 8 9 10Вариант 2
1 2 3 4 5 6 7 8 9 10Тексты для контрольных работ
Задания базового уровня
1 2 3 4 5 6 7 8Задания повышенного уровня
1 2 3 4 5 6 7 8 9Наши проекты
Страницы 40-41
1 2 3 4 5Итоговое повторение всего изученного
Нумерация
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29Выражения и уравнения
1 2 3 4 5 6 7 8Сложение и вычитание
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16Умножение и деление
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19Правила о порядке выполнения действий
1 2 3 4 5 6 7Величины
1 2 3 4 5 6Геометрические фигуры
1 2 3 4 5 6 7 8 9 10 11 12Задачи
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39Материал для расширения и углубления знаний
Доли
1 2 3Единицы площади — ар и гектар
1 2 3 4 5 6 7 8 9 10 11 12 13 14Диагонали треугольника
1 2 3 4Куб
1 2Прямоугольный параллелепипед
1 2Пирамида, конус
1 2Цилиндр
1 2Шар
1 2Задания на полях страницы
4 5 12 14 15 16 17 20 23 25 26 27 28 29 31 32 33 34 35 36 37 42 44 46 47 48 49 51 54 55 57 58 59 60 61 62 63 64 65 67 70 72 73 74 75 76 77 82 83 84 86 90 91 92 95 98 99 100 101 102Задания внизу страницы
4 5 6 7 12 13 14 15 16 17 25 26 27 28 29 30 31 32 33 42 43 44 45 46 47 48 49 50 51 57 58 59 60 61 62 63 64 65 72 73 74 75 76 77Решебник по Уравнениям мат физики : Чулан (М)
Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.

| mycoding |
| ||
31/08/09 |
| ||
| |||
| AKM |
| |||||
18/05/09 |
| |||||
| ||||||
| mycoding |
| ||
31/08/09 |
| ||
| |||
| Niclax |
| ||
07/05/08 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 4 ] |
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
Symbolab Math Solver — Пошаговый калькулятор
| \жирный{\mathrm{Basic}} | \жирный {\альфа\бета\гамма} | \bold{\mathrm{AB\Gamma}} | \жирный{\sin\cos} | \жирный{\ge\div\стрелка вправо} | \bold{\overline{x}\space\mathbb{C}\forall} | \bold{\sum\space\int\space\product} | \bold{\begin{pmatrix}\square&\square\\\square&\square\end{pmatrix}} 9{\ квадрат} | \sqrt{\square} | \nthroot[\msquare]{\square} | \frac{\msquare}{\msquare} | \log_{\msquare} | \pi | \ тета | \infty | \внутр | \frac{d}{dx} |
| \ле | \cdot 9{\msquare} | \лим | \сумма | \sin | \cos | \ коричневый | детская кроватка | \csc | мс |
| \альфа | \бета | \гамма | \дельта | \зета | \эта | \ тета | йота | \каппа | \лямбда | \мю |
| \ну | \xi | \pi | \ро | \сигма | \тау | \ипсилон | \фи | \чи | \psi | \омега |
| А | Б | \Гамма | \Дельта | Е | З | Н | \Тета | К | \лямбда | М |
| Н | \Xi | \Пи | Р | \Сигма | Т | \Ипсилон | \фи | Х | \пси | \Омега |
| \sin | \cos | \ коричневый | детская кроватка | мс | \csc | \ш | \кош | \танх | \сеч | |
| \arcsin | Арккос | Арктан | Аркот | \арксек | \arccsc | \arcsinh | Арккош | \arctanh | Арккот | Арксех |
| \begin{case}\square\\\square\end{case} | \begin{cases}\square\\\square\\\square\end{cases} | = | \ne | \дел | \cdot | х | < | > 9{\circ} | \rightarrow | \lпол\квадрат\rпол | \lceil\square\rceil |
| \overline{\square} | \vec{\square} | \в | \для всех | \не | \есть | \mathbb{R} | \mathbb{C} | 9{»} | \frac{\partial}{\partial x} |
| (2\раз2) | (2\раз3) | (3\раз3) | (3\раз2) | (4\раз2) | (4\раз3) | (4\4) | (3\4) | (2\раз4) | (5\х5) | |
| (1\раз2) | (1\раз3) | (1\4) | (1\раз5) | (1×6) | (2\раз1) | (3\раз1) | (4\раз1) | (5\раз1) | (6\раз1) | (7\раз1) |
| \mathrm{Радианы} | \mathrm{Градусы} | \квадрат! | ( | ) | % | \mathrm{очистить} |
| \arcsin | \sin | \sqrt{\square} | 7 | 8 | 9 | \дел |
| \арккос | \cos | \лн | 4 | 5 | 6 | х |
| Арктан | \загар | \лог | 1 | 2 | 3 | — |
| \pi | 9{\ квадрат} | 0 | «> . | \жирный{=} | + |
Word Solver — Составляйте слова легко
Word Solver — это инструмент, который помогает игрокам добиться успеха в играх-головоломках, таких как Scrabble, Words With Friends и ежедневных кроссвордах. Игрок вводит доступные буквы, длину или шаблон, а решатель слов находит множество результатов, которые вписываются в предлагаемые пробелы.
Что такое Word Maker?
Возможно, вы слышали о генераторе слов, а может быть, и нет. Если да, то вы, вероятно, хорошо разбираетесь в том, как это действительно может увеличить ваш счет, когда вы играете в различные словесные игры. Однако, если редактор слов для вас новичок, следите за обновлениями, пока мы объясняем, что это такое и когда это очень удобно.
По сути, это устройство для создания слов из букв, которое создает все возможные варианты из доступных букв. Когда гласные, согласные и даже подстановочные знаки вводятся в генератор слов, инструмент быстро предлагает новые слова из разных комбинаций букв. Это включает в себя создание других слов из букв в существующих словах.
Это включает в себя создание других слов из букв в существующих словах.
Грамматика
- Примеры ассонанса
- Примеры сравнения
- Знаки пунктуации, кавычки
- Образный язык
- Примеры метафор
Количество слов по длине
- Слова из девяти букв
- Слова из восьми букв
- Слова из семи букв
- Слова из шести букв
- Слова из пяти букв
Когда вам нужен Word Solver Tool
Вы начинаете думать о ситуациях, когда использование Word Maker определенно может вам помочь? Например, вы любите играть в настольные игры с друзьями и членами семьи, но ваше умение правильно писать слова часто мешает выиграть? Может быть, вы большой поклонник онлайн-игр в слова и, хотя вы не хотите обманывать, наличие доступа к генераторам слов время от времени будет поддерживать игру в приятном темпе.
Решатель слов может помочь во многих языковых играх. Давайте подробнее рассмотрим некоторые из них, чтобы дать вам еще больше идей.
Составление анаграмм
Если вы действительно увлекаетесь анаграммами, создатель словесных анаграмм поможет вам переставить буквы в существующем слове, фразе или предложении во что-то совершенно новое. Поскольку вы должны использовать все гласные и согласные, присутствующие в исходном слове или более длинном языковом примере, может быть настоящей проблемой придумать что-то другое, содержащее все, что у вас есть. Мало того, вы не хотите тратить весь день на размышления о возможностях — вы хотите быстро найти варианты. Вот где создатель анаграмм является бесценным решателем слов!
Игры в слова
Существует так много уникальных и интересных игр в слова, в которых вам нужно расшифровать набор букв, чтобы заработать очки. Многие из этих игр предназначены как для молодых игроков, так и для взрослых. Например, Scrabble ориентирован на тех, кому от восьми лет и старше, а Words with Friends имеет как детскую, так и взрослую версию.
Если подумать, генератор слов Scrabble или генератор слов Words with Friends могут быть полезны для игроков всех возрастов. Дети, которые все еще расширяют свой словарный запас и понимают, как составлять все больше и больше слов из букв, могут действительно извлечь пользу из использования устройства для поиска слов. Кроме того, участники, которые относительно плохо знакомы с этими играми, получат возможность использовать чит Scrabble или чит Words with Friends. И, если у игрока проблемы с английским, поскольку это не его родной язык, редактор слов может помочь ему в изучении и дать чувство выполненного долга, которое выходит далеко за рамки победы в словесной игре. Конечно, бывалым спортсменам понравится такой тип поддержки, когда они рассматривают плитки, выложенные на их стойке.
Наконец, получив возможность использовать инструмент «Эрудит» или генератор слов в игре «Слова с друзьями», все игроки почувствуют, что у них более равные шансы на победу.
Словари
- Словарь слов с друзьями
- Словарь Эрудита
Поиск слов
- Расшифровать слово Finder
- Дескремблер слов
- Искатель слов Эрудит
- Схватка слов
- Решатель анаграмм
Как использовать веб-сайт Word Solver — 3 простых шага
Веб-сайты, на которых есть инструмент для создания слов из букв, могут быть очень интересными в использовании! Некоторые из них более интуитивно понятны, чем другие, но, как правило, их можно использовать следующим образом:
Шаг № 1: Исследуйте и выбирайте
Прежде чем начать игру, вы должны подготовиться. Сначала попробуйте несколько веб-сайтов для решения слов, чтобы увидеть, как они работают, и остановитесь на том, который вам нравится больше всего. Держите его открытым во время игры.
Сначала попробуйте несколько веб-сайтов для решения слов, чтобы увидеть, как они работают, и остановитесь на том, который вам нравится больше всего. Держите его открытым во время игры.
Шаг № 2: Найдите подходящий инструмент.
Например, если вы пытаетесь решить анаграмму, вы можете нажать на наш Решатель анаграмм.
Шаг №3: Введите буквы
Введите буквы слова, с которым вы работаете.
Скажите, что у вас есть следующее слово ─ ДЕСЕРТ. Как только вы его введете, решатель анаграмм представит это слово ─ STRESSED.
Не забывайте, что вы можете использовать функцию расширенного фильтра. Это поможет вам сосредоточиться на вариантах слов, которые начинаются или заканчиваются определенными буквами или содержат определенные буквы или любые подстановочные знаки.
Блог
Латынь — ее происхождение, влияние и дальнейшее использование
13 пар английских глаголов, посланных, чтобы сбить нас с толку
Последние строки из 19 самых красивых книг, когда-либо написанных
Приложения Wordsolver
Вы также можете загрузить приложение для создания слов на свой мобильный телефон. Там есть очень крутые. По сути, вы просто заходите в магазин приложений на своем телефоне или находите интернет-магазин приложений, просматриваете, что доступно, и загружаете то, которое вам больше всего нравится. Приложения Wordmaker работают аналогично тем, которые вы найдете в Интернете на веб-сайтах.
Там есть очень крутые. По сути, вы просто заходите в магазин приложений на своем телефоне или находите интернет-магазин приложений, просматриваете, что доступно, и загружаете то, которое вам больше всего нравится. Приложения Wordmaker работают аналогично тем, которые вы найдете в Интернете на веб-сайтах.
Составь слова для Scrabble и WWF
Вот еще один пример того, как составлять слова онлайн с помощью генератора случайных слов:
- Шаг 1. Перейдите на веб-сайт, который вы хотите использовать.
- Шаг 2. Найдите программу захвата слов, предназначенную для вашей игры, и нажмите кнопку, чтобы открыть ее на экране.
Например, если вы играете в Scrabble, попробуйте нашу программу поиска слов Scrabble.
- Шаг 3. Введите гласные, согласные и подстановочные знаки, которые у вас есть.
Представим, что у вас есть эти буквы ─ CIUTJSE. Это лишь некоторые из немногих захватывающих комбинаций букв, которые предложит поисковик слов Scrabble ─ СПРАВЕДЛИВОСТЬ, СОКИ, МИЛАШКИ, ИЕСУИТ, СОК, СЮИТА, ШУТКА И СЕКТА.
В приведенном выше примере, в зависимости от того, какие слова вы можете составить из плиток, уже выложенных на доске Scrabble, вы можете получить очень высокий балл!
Инструменты
- Счетчик слов
- Генератор случайных слов
- Генератор случайных имен пользователей
- Генератор случайных паролей
Списки слов
- Слова с буквами
- Слова начинаются с
- Гласные слова
- Согласные слова
- Слова по длине
Генерация слов по длине
Да! Использование генератора комбинаций букв, который преобразует буквы в слова при любых обстоятельствах, может быть абсолютно продуктивным. Продолжайте читать ниже. У нас есть еще больше информации о полезности генератора буквенных слов. Ниже приведены примеры использования генератора расшифровки с разным количеством букв:
3-буквенные примеры слов
UPT становится чашкой или путем
AYW становится Way
NUF становится веселым
4-letter Word Примеры
PEOH становится HOPE
RLUP становится PUR
VELO. Примеры буквенных слов
Примеры буквенных слов
AECGR становится GRACE
IEPDL становится PILED
ENYNP становится PENNY
Примеры 6-буквенных слов
EIDPNN становится PINNED
GAULHS становится LAUGHS
GIHTSL становится LIGHTS
Примеры слов из 7 букв
AERRFMS становится FARMERS
GIOOKNC становится COOKING
YYNMOSN становится SYNONYM
MIT Solve | Решатель в центре внимания | Команды решателей | Социальные предприниматели
Каждый год Solve выбирает самые многообещающие команды Solver®, которые будут способствовать трансформационным изменениям в мире.
arrowСоздано с помощью Sketch.Как сообщества могут подготовиться, обнаружить и отреагировать на возникающие пандемии и угрозы безопасности для здоровья?
Инициатива Памоджи
Культурно адаптированная модель восстановления психического здоровья на базе сообщества
Иреги Мвенджа Руководитель группы
Крауддронинг от GLOBHE
Создавая лучшее будущее с помощью дронов, обнаруживая и прогнозируя стихийные бедствия
Хелена Самсиое Руководитель группы
Компас M’Care
Приложение на базе искусственного интеллекта, которое обнаруживает, диагностирует, лечит и ограничивает распространение болезней и вспышек в условиях ограниченных ресурсов.
Опеолува Ашими Руководитель группы
ANNE One от Sibel
Носимая сенсорная система класса ICU для расширенного удаленного мониторинга состояния пациента
Стив Сюй Руководитель группы
SMILE — интеллектуальная система охлаждения «последней мили»
Ориентированный на пользователя перевозчик последней мили для сведения к минимуму потерь вакцины
Китти С. Ляо Руководитель группы
полосатые
Центральное командование ИИ для реагирования на пандемию
Бенджамин Фелс Руководитель группы
Вула Мобайл
Сеть медицинских работников для общения, выдачи направлений и организации встреч
Уильям Мэпхэм Руководитель группы
Как каждый может получить доступ к цифровой экономике?
Как цветные сообщества могут использовать технологии для продвижения расовой справедливости и доступа к экономическим возможностям, здоровью и безопасности?
finEQUITY
Предоставление бесплатного доступа к кредитам и капиталу для членов сообщества, освобожденных из тюрьмы
Брайан Корниш Руководитель группы
Получить Медиа Л.
 И.Т.
И.Т.Онлайн-платформа с использованием разнообразных супергероев и комиксов для борьбы с расизмом и социально-эмоционального обучения в школах.
Тони Уивер Руководитель группы
Ирт
Рейтинговое приложение для черных и коричневых женщин и рожениц
Кимберли Силс Аллерс Руководитель группы
ПравосудиеТекст
Централизованная инфраструктура для хранения, каталогизации, анализа и обмена видеообнаружениями в системе уголовного правосудия для улучшения результатов дел для обвиняемых с низким доходом
Девши Мехротра Руководитель группы
МЕРА
Платформа для организаций под руководством BIPOC для связи друг с другом и совместной работы
стиля мемов Руководитель группы
Приложение EXHALE
Приложение для эмоционального благополучия, разработанное специально для чернокожих, представителей коренных народов и цветных женщин (BIWOC), чтобы ориентироваться и уменьшать влияние и последствия системного расизма.
Катара Маккарти Руководитель группы
Процветать! Аудит капитала
Разорвать циклы бедности с помощью программного обеспечения для выявления системного расизма в расходах и политике
Омолара Фатиреган Руководитель группы
Как коренные новаторы в США могут использовать традиционные знания и технологии для достижения социальных, экологических и экономических целей своих сообществ?
Вам 24 года и меньше, и вы хотите оказать положительное влияние на свое сообщество и мир? Если ваш ответ «да!», мы хотим услышать о вашем решении.
Cropfix от eAgro
Фермерское хозяйство, ферма вместе с нами
Тафадзва Чикверети Руководитель группы
Этана
Создание гендерно инклюзивной цифровой экономики
Элизабет Ньямванге Руководитель группы
Гидрокво+
Hydroquo+ занимается предоставлением информации о водных ресурсах для повышения безопасности и доступности воды с помощью практических данных.
Захин Разин Руководитель группы
Синхронно
In-Sync — это техническое решение для здоровья, которое обеспечивает оптимальное психическое здоровье людям с психическими заболеваниями и эмоциональными потребностями за счет использования искусственного интеллекта и силы людей.
Опейеми Этиве Руководитель группы
ПравосудиеТекст
Централизованная инфраструктура для хранения, каталогизации, анализа и обмена видеообнаружениями в системе уголовного правосудия для улучшения результатов дел для обвиняемых с низким доходом
Девши Мехротра Руководитель группы
Карполакс
Зеленые нанотехнологии продлевают срок хранения фруктов и овощей на 33 дня
Сандра Намбузо Руководитель группы
КЛАВ Индастриз
KLAW Industries перерабатывает отходы стекла, которые отправляются на свалку, в частичную замену цемента в бетоне под названием Pantheon.
Джейкоб Кумпон Руководитель группы
Спркснг
Sprxng — это многоразовый менструальный продукт, который включает в себя терапию менструальной боли. В Sprxng мы стремимся бороться с менструальной стигмой и менструальной бедностью.
Филлис Мугадза Руководитель группы
Тройной П
Управление пищевыми отходами с использованием технологий насекомых для обеспечения доступных и экологически чистых кормов и удобрений для животных
Глория Чероно Руководитель группы
Винсайт
Предоставление видения, создание понимания
Оларинде Олокунтой Руководитель группы
Как сообщества могут устойчиво защищать, управлять и восстанавливать свои местные экосистемы?
Как мы можем производить и потреблять экологически чистые и питательные продукты с низким содержанием углерода?
Бамбарское молоко
Растительное молоко из арахиса Бамбара; создание возможностей для мелких фермеров, восстановление деградировавших земель и обеспечение доступных питательных веществ для недоедающих групп населения.
Марк Лим Руководитель группы
Бивайз
Обеспечить глобальные запасы продовольствия, спасая пчел с помощью точной робототехники, компьютерного зрения и искусственного интеллекта.
Саар Сафра Руководитель группы
яйцоXYt
Экономия 4 миллиардов цыплят мужского пола, миллиарды долларов, и увеличение мировых поставок на 4 миллиарда яиц.
Иегуда Эльрам Руководитель группы
ИнсектиПро
Использование насекомых в качестве альтернативных источников белка для кормовой промышленности для борьбы с отсутствием продовольственной безопасности и ростом отходов
Талаш Хейберс Руководитель группы
SmartFish Мексика
Модель SmartFish Value Rescue использует рынки для улучшения средств к существованию рыбаков, сохранения морских экосистем и предложения потребителям ответственного выбора.
Сесилия Бласко Руководитель группы
Симброзия
Новая кормовая добавка на основе морских водорослей, которая решает проблему изменения климата, сокращая выбросы метана животноводством более чем в 9 раз.0 процентов
Алексия Акбай Руководитель группы
Весь излишек
Цифровая система управления излишками продуктов питания, в которой приоритет отдается решениям по восстановлению и устойчивости.
Кубра Орак Руководитель группы
Как маргинализированные девочки и молодые женщины могут получить доступ к возможностям качественного обучения, чтобы добиться успеха?
Как каждая женщина, молодая мама и новорожденный могут получить доступ к уходу, необходимому им для выживания и процветания?
Каким образом все молодые учащиеся могут получить доступ к качественной, безопасной и справедливой учебной среде?
Как сообщества во всем мире могут подготовиться, обнаружить и отреагировать на возникающие пандемии и угрозы безопасности для здоровья?
Платформа АХСА
Платформа на основе искусственного интеллекта, которая прогнозирует спрос на основные продукты здравоохранения и обеспечивает их своевременную доставку в системы здравоохранения Африки.
Брамуэль Мвало Руководитель группы
Биометрия для доставки вакцин (Simprints Technology)
Использование бесконтактной биометрии для проверенной доставки вакцин на передовой для минимизации потерь и повышения качества данных
Александра Григоре Руководитель группы
Биоразлагаемые СИЗ на основе джутовой целлюлозы
Средства индивидуальной защиты на основе джутового полимера, пригодные для вторичной переработки, биоразлагаемые, с олигохитозановым покрытием для медицинских работников.
Мехджабин Тишан Махфуз Руководитель группы
КартаДостопримечательности
Система поддержки принятия решений (DSS) с пространственной и временной прогнозной аналитикой для общественного здравоохранения и управления
Адитья Шарма Руководитель группы
Москит (TrakitNow, Inc)
Интегрированная платформа для борьбы с переносчиками и болезнями в режиме реального времени для профилактики и борьбы с болезнями, переносимыми комарами.
Сатиш Черукумалли Руководитель группы
ПЕНСА *660#
Многоканальная и двунаправленная платформа мобильного здравоохранения, предоставляющая бесплатную, одобренную Минздравом медицинскую информацию людям с устаревшими телефонами и ограниченным доступом к медицинским услугам.
Вальтер Кумби Руководитель группы
ПОДД (Opendream)
Платформа эпиднадзора за общественными заболеваниями с участием до распространения болезни
Патипат Сусумпов Руководитель группы
Как маргинализированные слои населения могут получить доступ и создать для себя хорошие рабочие места и возможности для предпринимательской деятельности?
Как мы можем помочь людям предотвращать, выявлять и лечить хронические заболевания, особенно в условиях ограниченных ресурсов?
Как мы можем улучшить результаты обучения беженцев и перемещенных лиц в возрасте до 24 лет?
Как создать более инклюзивное, продуктивное и устойчивое экономическое будущее для всех?
Как отдельные лица и корпорации могут управлять своими выбросами углерода и сокращать их?
Как женщины и девушки любого социально-экономического положения могут использовать технологии для полноценного участия в экономике и ее процветания?
Каким образом коренные новаторы в США могут использовать традиционные знания и технологии для достижения социальных, экологических и экономических результатов в своих сообществах?
EA Эковерсити
Расширение возможностей молодежи и молодых людей из числа коренных жителей Гавайских островов для раскрытия своего максимального потенциала и решения проблем 21 века путем воссоединения со своим родным языком и культурой.
Ку Кахакалау Руководитель группы
Еда из огня
Снизьте пожароопасность и выращивайте продукты питания круглый год с помощью теплиц, отапливаемых биомассой, что способствует устойчивости общин под руководством коренных народов, повышению продовольственной безопасности и адаптации к изменению климата.
Ева Берк Руководитель группы
Коренной округ Колумбия
Мобильное приложение с цифровыми картами, показывающими важные места коренных американцев и их вклад в столицу страны.
Элизабет Рул Руководитель группы
Индийская кухня
Indigikitchen использует цифровые медиа для восстановления знаний, связанных с традиционной кухней коренных народов.
Мэрайя Гладстон Руководитель группы
Международный Вакашанский консорциум искусственного интеллекта
Международные языковые сообщества вакашан объединяются для создания общего голосового ИИ, преодолевая границы и барьеры.
Майкл Бегущий волк Руководитель группы
Защита лекарственных растений
Защищать, сохранять и чтить среду и людей коренных народов.
Ришель Томас Руководитель группы
ShockTalk
ShockTalk — это адаптированная к культурным условиям платформа телементального здоровья с помощью искусственного интеллекта, которая соединяет клиентов из числа коренных народов с терапевтами из числа коренных народов, обученными культурному смирению.
Остин Серио Руководитель группы
Как каждый человек может улучшить здоровье своего мозга и психическую устойчивость?
Как обездоленная молодежь может приобрести навыки, необходимые им для подготовки к работе в будущем и процветанию в 21 веке?
Как городские сообщества могут расширить свой доступ к устойчивым и устойчивым источникам пищи и воды?
CityTaps
Водопровод в каждом городском доме
Грегуар Ландель Руководитель группы
Копия
Сделать пожертвование еды быстро, легко и выгодно
Комал Ахмад Руководитель группы
Свежая прямая Нигерия
Расширение городского сельского хозяйства за счет штабелируемых контейнерных ферм
Ангел Куйе Олуваймика Руководитель группы
Уотериг
Автономные хабы, связанные с блокчейном, производящие чистую воду, еду и электричество
Патрик Суэн Руководитель группы
ЕдаМука
Снабжение городских продовольственных пустынь инновационным источником белка
Габриэль Вимер Руководитель группы
Сторожевая башня робототехника
Находите утечки, экономьте воду, защищайте инфраструктуру
Ю Ву Руководитель группы
Неиспользованный
Расширение доступа к чистой воде за счет устойчивого бизнеса на развивающихся рынках
Дэн Нолан Руководитель группы
Исавьяса
Усовершенствованная система очистки воды с низкими потерями, ориентированная на загрязнение
Венката Чамала Анил Руководитель группы
Как племенные общины могут продвигать возобновляемые источники энергии, продовольствие или доступ к воде и способствовать экономическому процветанию и суверенитету?
Каким образом те, кто больше всего пострадал от технологической трансформации труда, могут создать для себя продуктивные и процветающие средства к существованию?
Как сообщества могут инвестировать в передовых медицинских работников и услуги, чтобы улучшить их доступ к эффективной и доступной помощи?
Как учителя и преподаватели могут обеспечить доступное, персонализированное и творческое обучение для всех?
Как прибрежные сообщества могут смягчить последствия изменения климата и адаптироваться к ним, развиваясь и процветая?
Решения коренных народов, использующие традиционные знания и технологии для создания устойчивых и процветающих средств к существованию для общин коренных народов
Как граждане и сообщества могут создать и улучшить социальную интеграцию и общее процветание?
Как городские жители могут создать среду, способствующую физическому и психическому здоровью, и жить в ней?
Как все дети в возрасте до пяти лет могут развить критическое обучение и когнитивные навыки, необходимые им для полного раскрытия своего потенциала?
Как люди могут создавать и потреблять возобновляемые, ремонтопригодные, многоразовые и перерабатываемые товары?
Назад
наверх
Решатель математических задач и калькулятор
Введите свою задачу ниже, чтобы увидеть
как работает наш решатель уравнений
Введите математическое выражение
Получить математический решатель Чегга
9,95 долларов в месяц (отменить в любое время). См. подробности
См. подробности
Выберите справку по математикеЛьготы | Chegg Math Solver (бесплатно) Попробуйте | Чегг Математический Решатель (9,95 долл. США в месяц) Обновление |
|---|---|---|
| Решение вашей математической задачи | 3 решения в день | Без ограничений |
| Основное объяснение вашей математической задачи | да | да |
| Подробное объяснение с подэтапами | нет | да |
| Без рекламы в приложении | да | да |
| Без рекламы в Интернете | нет | да |
| Графический калькулятор | нет | да |
Никогда больше
не будут превосходить числом вашу домашнюю работу по математике
- Понять как и почему
Узнайте, как решить свои уравнения и почему для их решения следует использовать тот или иной метод, чтобы вам было легче учиться.

- Узнайте из подробных пошаговых объяснений Пройдитесь по каждому шагу решения, чтобы точно знать, какой путь приведет вас к правильному ответу.
- Углубитесь в конкретные шаги Наш решатель делает то, чего не может калькулятор: разбивает ключевые шаги на более мелкие подшаги, чтобы показать вам каждую часть решения.
- Сфотографируйте свою математическую задачу С помощью нашего мобильного приложения вы можете сфотографировать свое уравнение и приступить к работе, стат. Не нужно даже вводить свою математическую задачу.
Получить Chegg Math Solver
9,95 долл. США в месяц (отменить в любое время). Подробнее
- Дробь
- Линейные уравнения 1
- Арифметика
- Отрицательные числа
- Линейные неравенства 1
- Квадратные уравнения
- Линейные уравнения 2
- Системы уравнений 1
- Линейные неравенства 2
- Полиномы и квадратные выражения
- Системы уравнений 2
- Экспоненциальные и логарифмические функции
- Добавление матриц
- Перемножение матриц
- Обратные матрицы и определители
- Фундаментальные производные
- Общие производные
- Рисование кривой
- Основные интегралы
- Общие интегралы
- г.

- Операции с матрицами
- Обратные матрицы
- Детерминанты
- Характеристический полином
- собственных значений
Вариационный решатель собственных значений на фотонном квантовом процессоре
Abstract
Квантовые компьютеры обещают эффективно решать важные задачи, которые невозможно решить на обычном компьютере. Для квантовых систем, где физическое измерение растет экспоненциально, нахождение собственных значений некоторых операторов является одной из таких неразрешимых проблем и остается фундаментальной проблемой. Алгоритм квантовой оценки фазы эффективно находит собственное значение данного собственного вектора, но требует полностью когерентной эволюции. Здесь мы представляем альтернативный подход, который значительно снижает требования когерентной эволюции и комбинирует этот метод с новым подходом к подготовке состояния, основанным на анзаце и классической оптимизации. Мы реализуем алгоритм, комбинируя фотонный квантовый процессор с широкими возможностями реконфигурации и обычный компьютер. Мы экспериментально демонстрируем реализуемость такого подхода на примере из квантовой химии — расчете молекулярной энергии основного состояния для He–H + . Предлагаемый подход резко снижает требования ко времени когерентности, увеличивая потенциал квантовых ресурсов, доступных сегодня и в ближайшем будущем.
Мы реализуем алгоритм, комбинируя фотонный квантовый процессор с широкими возможностями реконфигурации и обычный компьютер. Мы экспериментально демонстрируем реализуемость такого подхода на примере из квантовой химии — расчете молекулярной энергии основного состояния для He–H + . Предлагаемый подход резко снижает требования ко времени когерентности, увеличивая потенциал квантовых ресурсов, доступных сегодня и в ближайшем будущем.
Введение
В химии свойства атомов и молекул можно определить, решив уравнение Шрёдингера. Однако, поскольку размерность задачи растет экспоненциально с размером рассматриваемой физической системы, точная трактовка этих задач остается классически неосуществимой для соединений с более чем 2–3 атомами 1 . Для обработки этих систем было разработано много приближенных методов 2 , но эффективные и точные методы для больших химических задач остаются недоступными для классических компьютеров. Помимо химии, решение больших задач на собственные значения 3 может найти применение в диапазоне от определения результатов поисковых систем в Интернете 4 до разработки новых материалов и лекарств 5 .
Помимо химии, решение больших задач на собственные значения 3 может найти применение в диапазоне от определения результатов поисковых систем в Интернете 4 до разработки новых материалов и лекарств 5 .
Недавние разработки в области квантовых вычислений предлагают путь вперед для определения эффективных решений многих случаев больших задач на собственные значения, которые классически неразрешимы 6,7,8,9,10,11,12 . Квантовые подходы к нахождению собственных значений ранее основывались на алгоритме квантовой оценки фазы (QPE). Алгоритм QPE предлагает экспоненциальное ускорение по сравнению с классическими методами и требует ряда квантовых операций O ( p −1 ) для получения оценки с точностью p (ссылки 13, 14, 15, 16, 17, 18). В стандартной формулировке QPE предполагается, что собственный вектор | ψ › эрмитова оператора, и задача состоит в том, чтобы определить соответствующее собственное значение λ . Время, в течение которого квантовый компьютер должен оставаться когерентным, определяется необходимостью O ( p −1 ) последовательных применений , каждое из которых может потребовать порядка миллионов или миллиардов квантовых вентилей для практических приложений 17 ,19 , по сравнению с десятками и сотнями ворот, достижимыми в краткосрочной перспективе.
Время, в течение которого квантовый компьютер должен оставаться когерентным, определяется необходимостью O ( p −1 ) последовательных применений , каждое из которых может потребовать порядка миллионов или миллиардов квантовых вентилей для практических приложений 17 ,19 , по сравнению с десятками и сотнями ворот, достижимыми в краткосрочной перспективе.
Здесь мы представляем альтернативу QPE, которая значительно снижает требования к согласованной эволюции. Мы разработали реконфигурируемый квантовый процессор (QPU), который эффективно вычисляет среднее значение гамильтониана (), обеспечивая экспоненциальное ускорение по сравнению с точной диагонализацией, единственным известным точным решением проблемы на традиционном компьютере. QPU был экспериментально реализован с использованием технологии интегрированной фотоники со спонтанным параметрическим однофотонным источником с понижающим преобразованием и в сочетании с алгоритмом оптимизации, работающим на классическом процессоре (CPU), который вариативно вычисляет собственные значения и собственные векторы . Используя вариационный алгоритм, этот подход снижает потребность в согласованной эволюции квантового состояния, делая более эффективным использование квантовых ресурсов, и может предложить альтернативный путь к практическим квантовым вычислениям.
Используя вариационный алгоритм, этот подход снижает потребность в согласованной эволюции квантового состояния, делая более эффективным использование квантовых ресурсов, и может предложить альтернативный путь к практическим квантовым вычислениям.
Результаты
Оценка квантового ожидания
Алгоритм оценки квантового ожидания (QEE) вычисляет математическое ожидание данного гамильтониана для входного состояния | ψ ›. Любой гамильтониан может быть записан как
для действительных ч , где римские индексы определяют подсистему, на которую действует оператор, а греческие индексы определяют оператор Паули, например, α = x . Обратите внимание, что для того, чтобы это разложение было верным, не требуется никаких предположений о размерности или структуре эрмитова гамильтониана. Используя линейность квантовых наблюдаемых, следует, что
Мы рассматриваем гамильтонианы, которые могут быть записаны как полиномиальное число членов относительно размера системы. Этот класс гамильтонианов охватывает широкий спектр физических систем, включая гамильтониан электронной структуры квантовой химии, квантовую модель Изинга, модель Гейзенберга 20,21 , матрицы, которые хорошо аппроксимируются как сумма n -кратных тензоров произведения 22,23 и, в более общем случае, любой k -разреженный гамильтониан без очевидной структуры тензорного произведения (подробности см. В Дополнительных методах ). Таким образом, вычисление ‹› сводится к сумме полиномиального числа математических ожиданий простых операторов Паули для квантового состояния | ψ ›, умноженное на некоторые вещественные константы. Квантовое устройство может эффективно оценивать среднее значение тензорного произведения произвольного числа простых операторов Паули 23 . Следовательно, с состоянием n -кубитов мы можем эффективно оценить среднее значение этого 2 n × 2 n гамильтониана.
Этот класс гамильтонианов охватывает широкий спектр физических систем, включая гамильтониан электронной структуры квантовой химии, квантовую модель Изинга, модель Гейзенберга 20,21 , матрицы, которые хорошо аппроксимируются как сумма n -кратных тензоров произведения 22,23 и, в более общем случае, любой k -разреженный гамильтониан без очевидной структуры тензорного произведения (подробности см. В Дополнительных методах ). Таким образом, вычисление ‹› сводится к сумме полиномиального числа математических ожиданий простых операторов Паули для квантового состояния | ψ ›, умноженное на некоторые вещественные константы. Квантовое устройство может эффективно оценивать среднее значение тензорного произведения произвольного числа простых операторов Паули 23 . Следовательно, с состоянием n -кубитов мы можем эффективно оценить среднее значение этого 2 n × 2 n гамильтониана.
Можно попытаться сделать это с помощью классического компьютера, оптимизируя по отдельности все редуцированные состояния, соответствующие желаемым членам гамильтониана, но это будет страдать от N — проблема представимости, которая, как известно, неразрешима как для классических, так и для квантовых компьютеров (находится в квантовом классе сложности QMA-Hard 24 ). Сила нашего подхода проистекает из того факта, что квантовое оборудование может хранить глобальное квантовое состояние с экспоненциально меньшими ресурсами, чем требуется классическому оборудованию, и в результате проблема N -представимости не возникает.
Сила нашего подхода проистекает из того факта, что квантовое оборудование может хранить глобальное квантовое состояние с экспоненциально меньшими ресурсами, чем требуется классическому оборудованию, и в результате проблема N -представимости не возникает.
Среднее значение тензорного произведения произвольного числа операторов Паули можно оценить путем локального измерения каждого кубита 6 . Такие независимые измерения могут выполняться параллельно с постоянными временными затратами. Кроме того, поскольку эти операторы нормированы и конечномерны, их спектры ограничены. В результате каждый может быть оценен с точностью p отдельного элемента с коэффициентом h , который является произвольным элементом из набора констант , стоимостью O (| h max | 2 Mp −2 ) повторений. Здесь M — число слагаемых в разложении гамильтониана, а h max — коэффициент с максимальной нормой в разложении гамильтониана. Преимущество этого подхода в том, что время когерентности для выполнения одного измерения после подготовки состояния составляет O (1). Наоборот, недостатком этого подхода применительно к QPE является масштабирование по общему числу операций, так как функция требуемой точности квадратично хуже ( O ( p −2 ) по сравнению с O ( p −1 )). Кроме того, это масштабирование также будет отражать количество необходимых повторений подготовки состояния, тогда как в QPE количество шагов подготовки состояния является постоянным. По сути, мы резко снижаем требования когерентности по времени, сохраняя при этом экспоненциальное преимущество по сравнению с классическим случаем, добавляя полиномиальное число повторений по отношению к QPE.
Преимущество этого подхода в том, что время когерентности для выполнения одного измерения после подготовки состояния составляет O (1). Наоборот, недостатком этого подхода применительно к QPE является масштабирование по общему числу операций, так как функция требуемой точности квадратично хуже ( O ( p −2 ) по сравнению с O ( p −1 )). Кроме того, это масштабирование также будет отражать количество необходимых повторений подготовки состояния, тогда как в QPE количество шагов подготовки состояния является постоянным. По сути, мы резко снижаем требования когерентности по времени, сохраняя при этом экспоненциальное преимущество по сравнению с классическим случаем, добавляя полиномиальное число повторений по отношению к QPE.
Квантовый вариационный собственный решатель
Описанная выше процедура заменяет длительную когерентную эволюцию, требуемую QPE, множеством коротких когерентных эволюций. Как в QPE, так и в QEE нам требуется хорошее приближение к волновой функции основного состояния для вычисления собственного значения основного состояния, и мы сейчас рассмотрим эту проблему. Предыдущие подходы предлагали готовить основные состояния с помощью адиабатической эволюции 15 или квантового алгоритма Метрополиса 25,26 . К сожалению, оба они требуют длительной последовательной эволюции. Алгоритм квантового вариационного собственного решателя (QVE) представляет собой вариационный метод подготовки собственного состояния и, используя QEE, требует короткой когерентной эволюции. QEE и QVE и их взаимосвязь показаны на рис. 1 и подробно описаны в дополнительных методах.
Предыдущие подходы предлагали готовить основные состояния с помощью адиабатической эволюции 15 или квантового алгоритма Метрополиса 25,26 . К сожалению, оба они требуют длительной последовательной эволюции. Алгоритм квантового вариационного собственного решателя (QVE) представляет собой вариационный метод подготовки собственного состояния и, используя QEE, требует короткой когерентной эволюции. QEE и QVE и их взаимосвязь показаны на рис. 1 и подробно описаны в дополнительных методах.
В QEE предварительно подготовленные квантовые состояния передаются в квантовые модули, которые вычисляют ‹ i ›, где i — любой заданный член в сумме, определяющей . Результаты передаются ЦП, который вычисляет ‹›. В квантовом вариационном собственном решателе классический алгоритм минимизации, работающий на ЦП, принимает ‹› и определяет новые параметры состояния, которые затем возвращаются обратно в QPU.
Изображение полного размера
Хорошо известно, что задача на собственные значения для наблюдаемой, представленной оператором, может быть переформулирована как вариационная задача на фактор Рэлея–Ритца 27,28 , так что собственный вектор | ψ › соответствует наименьшему собственному значению | ψ ›, который минимизирует
Варьируя экспериментальные параметры при приготовлении | ψ › и вычисляя частное Рэлея–Ритца с использованием QEE в качестве подпрограммы в классической минимизации, можно подготовить неизвестные собственные векторы. При завершении работы алгоритма простой рецепт восстановления собственного вектора сохраняется в финальном наборе экспериментальных параметров, определяющих | ψ ›.
Если квантовое состояние характеризуется экспоненциально большим числом параметров, его нельзя подготовить полиномиальным числом операций. Таким образом, множество эффективно подготавливаемых состояний характеризуется полиномиальным числом параметров, и мы выбираем конкретное множество анзац-состояний этого типа. В этих условиях классический алгоритм поиска по экспериментальным параметрам, определяющим | ψ › нужно исследовать только полиномиальное число измерений — требование для эффективности поиска. Одним из примеров квантового состояния, параметризованного полиномиальным числом параметров, для которого не существует известной эффективной классической реализации, является унитарно-связанный кластерный анзац 29
В этих условиях классический алгоритм поиска по экспериментальным параметрам, определяющим | ψ › нужно исследовать только полиномиальное число измерений — требование для эффективности поиска. Одним из примеров квантового состояния, параметризованного полиномиальным числом параметров, для которого не существует известной эффективной классической реализации, является унитарно-связанный кластерный анзац 29
, где |Φ› ref — некоторое эталонное состояние, обычно основное состояние Хартри-Фока, а T — кластерный оператор для электронной системы N , определяемый как
, где
и выше — условия заказа следуют логически. Ясно, что по построению оператор ( T − T † ) является антиэрмитовым, а возведение в степень переводит его в унитарный оператор . Для любого фиксированного уровня возбуждения k сокращенный кластерный оператор записывается как
В целом эффективная реализация этого анзаца для классического компьютера еще не разработана, даже для кластерных операторов низкого порядка, из-за отсутствия усечения серии BCH 29 . Однако это состояние может быть эффективно подготовлено на квантовом устройстве. Приведенный антиэрмитов кластерный оператор ( T ( k ) − T ( k )† ) является суммой полиномиального числа членов, а именно, он содержит ряд членов O ( N k ( M − N ) k ), где M – число одночастичных орбиталей. Путем определения эффективного эрмитова гамильтониана = i ( T ( k ) − T ( k ) † ) и выполнения преобразования Жордана – Вигнера, которое действует на пространственный гамильтониан кубитов, у нас остается гамильтониан, представляющий собой сумму полиномиально многих произведений операторов Паули. Затем проблема сводится к квантовому моделированию этого эффективного гамильтониана , что может быть выполнено за полиномиальное время с использованием процедуры, описанной Ортисом и др. 23 Отметим, что хотя эта процедура подготовки состояния использует инструменты квантового моделирования, полное эффективное время эволюции фиксируется коэффициентами разложения .
Однако это состояние может быть эффективно подготовлено на квантовом устройстве. Приведенный антиэрмитов кластерный оператор ( T ( k ) − T ( k )† ) является суммой полиномиального числа членов, а именно, он содержит ряд членов O ( N k ( M − N ) k ), где M – число одночастичных орбиталей. Путем определения эффективного эрмитова гамильтониана = i ( T ( k ) − T ( k ) † ) и выполнения преобразования Жордана – Вигнера, которое действует на пространственный гамильтониан кубитов, у нас остается гамильтониан, представляющий собой сумму полиномиально многих произведений операторов Паули. Затем проблема сводится к квантовому моделированию этого эффективного гамильтониана , что может быть выполнено за полиномиальное время с использованием процедуры, описанной Ортисом и др. 23 Отметим, что хотя эта процедура подготовки состояния использует инструменты квантового моделирования, полное эффективное время эволюции фиксируется коэффициентами разложения . Это контрастирует с обычными трудностями, возникающими в QPE, где моделирование должно выполняться для времен, которые экспоненциальны в желаемых битах точности.
Это контрастирует с обычными трудностями, возникающими в QPE, где моделирование должно выполняться для времен, которые экспоненциальны в желаемых битах точности.
Хотя в настоящее время не существует известного эффективного классического алгоритма, основанного на этих состояниях анзаца, неунитарно-связанный кластерный анзац иногда называют «золотым стандартом квантовой химии», поскольку он является стандартом точности, которому соответствуют другие методы квантовой химии. часто сравнивают. Считается, что унитарная версия этого анзаца дает результаты, превосходящие даже этот «золотой стандарт» 9.1752 29 .
Демонстрация прототипа
Мы внедрили QPU с использованием интегрированной технологии квантовой фотоники 30 . Наше устройство, схематично показанное на рис. 2, представляет собой реконфигурируемый чип волновода, который может подготавливать и измерять произвольные двухбитовые чистые состояния, используя несколько однокубитных поворотов и один двухкубитный запутывающий вентиль. Состояние кодируется по пути с использованием пар фотонов, генерируемых в процессе спонтанного параметрического преобразования с понижением частоты. Подготовка и измерение состояния в базисе Паули достигается за счет установки 8 фазовращателей, управляемых напряжением, и подсчета событий регистрации фотонов кремниевыми однофотонными детекторами 31 .
Состояние кодируется по пути с использованием пар фотонов, генерируемых в процессе спонтанного параметрического преобразования с понижением частоты. Подготовка и измерение состояния в базисе Паули достигается за счет установки 8 фазовращателей, управляемых напряжением, и подсчета событий регистрации фотонов кремниевыми однофотонными детекторами 31 .
( a ) Подготовка квантовых состояний и измерение математических ожиданий ‹ ψ | σ i ⊗ σ j | ψ › выполняются с использованием квантового фотонного чипа. Пары фотонов, генерируемые с помощью спонтанного параметрического преобразования с понижением частоты, инжектируются в волноводы, кодирующие состояние |00›. государство | ψ ›изготавливается с использованием тепловых фазовращателей φ 1−8 (оранжевые прямоугольники) и один вентиль CNOT и измерено с помощью фотонных детекторов. dc {1–4,9–13} (dc 5–7 ) представляют собой направленные ответвители с коэффициентом отражения 50% (30%). Скорость счета совпадений от детекторов D 1–4 передается в ЦП, выполняющий алгоритм оптимизации. Это вычисляет набор параметров для следующего состояния и записывает их в квантовое устройство. ( b ) Фотография КПУ.
dc {1–4,9–13} (dc 5–7 ) представляют собой направленные ответвители с коэффициентом отражения 50% (30%). Скорость счета совпадений от детекторов D 1–4 передается в ЦП, выполняющий алгоритм оптимизации. Это вычисляет набор параметров для следующего состояния и записывает их в квантовое устройство. ( b ) Фотография КПУ.
Изображение полного размера
Возможность подготовить произвольное двухкубитное разделимое или запутанное состояние позволяет нам исследовать гамильтонианы 4 × 4. Для экспериментальной демонстрации нашего алгоритма выберем задачу из области квантовой химии, а именно определение кривой диссоциации связи молекулы He–H + на минимальной основе. Гамильтониан взаимодействия полной конфигурации для этой системы имеет размерность 4 и может быть компактно записан как
Коэффициенты и были определены с использованием вычислительного пакета PSI3 32 и приведены в таблице 2.
Для расчета диссоциации связи молекулы, мы используем QVE для вычисления ее основного состояния для диапазона значений расстояния между ядрами R . На рис. 3 мы представляем типичный прогон оптимизации для конкретного разделения ядер, демонстрирующий сходимость нашего алгоритма к основному состоянию ( R ) при наличии экспериментального шума. На рис. 3а показана сходимость средней энергии, а на рис. 3б — сходимость перекрытия |‹ ψ j | ψ G ›| текущего состояния | ψ j › с целевым состоянием | ψ G ›. Цвет каждой записи на рис. 3а представляет собой клубок (абсолютное совпадение в квадрате) состояния на этом шаге алгоритма. Известно, что объем сепарабельных состояний вдвойне экспоненциально мал по отношению к остальному пространству состояний 33 . Таким образом, возможность обхода неразделимого пространства состояний увеличивает количество путей, по которым может сходиться алгоритм, и будет требоваться для будущих крупномасштабных реализаций. Более того, ясно, что способность создавать запутанные состояния необходима для точного описания общих квантовых систем, в которых собственные состояния могут быть неразделимыми — например, основное состояние гамильтониана He—H + имеет небольшую, но не незначительная путаница.
На рис. 3 мы представляем типичный прогон оптимизации для конкретного разделения ядер, демонстрирующий сходимость нашего алгоритма к основному состоянию ( R ) при наличии экспериментального шума. На рис. 3а показана сходимость средней энергии, а на рис. 3б — сходимость перекрытия |‹ ψ j | ψ G ›| текущего состояния | ψ j › с целевым состоянием | ψ G ›. Цвет каждой записи на рис. 3а представляет собой клубок (абсолютное совпадение в квадрате) состояния на этом шаге алгоритма. Известно, что объем сепарабельных состояний вдвойне экспоненциально мал по отношению к остальному пространству состояний 33 . Таким образом, возможность обхода неразделимого пространства состояний увеличивает количество путей, по которым может сходиться алгоритм, и будет требоваться для будущих крупномасштабных реализаций. Более того, ясно, что способность создавать запутанные состояния необходима для точного описания общих квантовых систем, в которых собственные состояния могут быть неразделимыми — например, основное состояние гамильтониана He—H + имеет небольшую, но не незначительная путаница.
( a ) Экспериментально рассчитанная энергия ‹› (цветные точки) как функция шага оптимизации j . Цвет представляет запутанность (степень запутанности) физического состояния, оцененную непосредственно из параметров состояния. Красные линии указывают уровни энергии ( R ). Алгоритм оптимизации явно сходится к основному состоянию молекулы, которая имеет небольшой, но ненулевой запутанность. Крестиками показана энергия, рассчитанная на каждом экспериментальном шаге в предположении об идеальном квантовом устройстве. ( b ) Перекрытие |‹ ψ j | ψ G › между экспериментально рассчитанным состоянием | ψ j › на каждом шаге оптимизации j и теоретическое основное состояние , | ψ G ›. Столбики погрешностей меньше, чем точки данных. Более подробная информация представлена в разделе «Методы», «Дополнительная таблица 1» и «Дополнительные методы».
Столбики погрешностей меньше, чем точки данных. Более подробная информация представлена в разделе «Методы», «Дополнительная таблица 1» и «Дополнительные методы».
Полноразмерное изображение
Повторяя эту процедуру для нескольких значений R , мы получаем кривую диссоциации связи, представленную на рис. 4. После поправки вычисленных энергий на экспериментальные ошибки определение равновесной длины связи молекулы было R = 92,3 ± 0,1 пм, с соответствующей электронной энергией основного состояния E = −2,865 ± 0,008 МДж моль −1 . Полная информация о поправке на систематические ошибки и оценке неопределенности на E указаны в дополнительных методах. Соответствующая теоретическая кривая показывает численно точную энергию, полученную из расчета взаимодействия полной конфигурации молекулярной системы на той же основе. Более 96% экспериментальных данных находятся в пределах химической точности по отношению к теоретическим значениям. По завершении оптимизации мы сохраняем полное знание экспериментальных параметров, которые можно использовать для эффективной реконструкции состояния | ψ › если требуются дополнительные физические или химические свойства.
По завершении оптимизации мы сохраняем полное знание экспериментальных параметров, которые можно использовать для эффективной реконструкции состояния | ψ › если требуются дополнительные физические или химические свойства.
Эта кривая получена повторным вычислением энергии основного состояния (как показано на рис. 3) для нескольких значений ( R ). Увеличенный график показывает, что после коррекции измеренной систематической ошибки данные перекрываются с теоретической кривой энергии, и, что важно, мы можем разрешить молекулярное разделение минимальной энергии. Столбики погрешностей показывают стандартное отклонение вычисленной энергии, как описано в разделе «Методы».
Полноразмерное изображение
Обсуждение
QEE использует относительно мало квантовых ресурсов по сравнению с QPE. Вообще говоря, QPE требует последовательного выполнения большого количества n -кубитных квантово-управляемых операций, что предъявляет значительные требования к количеству компонентов и времени когерентности, в то время как присущий нашей схеме параллелизм допускает небольшое количество n операций. -кубитные ворота, которые можно использовать много раз, что резко снижает эти требования. Более того, добавление управления к произвольным унитарным операциям на практике сложно, если вообще возможно, для современных квантовых архитектур (хотя недавно была продемонстрирована предложенная схема добавления управления к произвольным унитарным операциям 9).1752 34 ). Чтобы привести численный пример, схема QPE для гамильтониана 4 × 4, такая как показанная здесь, потребует не менее 12 вентилей CNOT, в то время как наш метод требует только один. Отметим, что экономия ресурсов, обеспечиваемая QEE, требует полиномиальных повторений подготовки состояния по сравнению с единственной копией, требуемой QPE. Во многих случаях (например, в нашей фотонной реализации) повторная подготовка состояния ненамного сложнее, чем подготовка одной копии, требующая лишь полиномиальных накладных расходов по времени без какой-либо модификации устройства.
-кубитные ворота, которые можно использовать много раз, что резко снижает эти требования. Более того, добавление управления к произвольным унитарным операциям на практике сложно, если вообще возможно, для современных квантовых архитектур (хотя недавно была продемонстрирована предложенная схема добавления управления к произвольным унитарным операциям 9).1752 34 ). Чтобы привести численный пример, схема QPE для гамильтониана 4 × 4, такая как показанная здесь, потребует не менее 12 вентилей CNOT, в то время как наш метод требует только один. Отметим, что экономия ресурсов, обеспечиваемая QEE, требует полиномиальных повторений подготовки состояния по сравнению с единственной копией, требуемой QPE. Во многих случаях (например, в нашей фотонной реализации) повторная подготовка состояния ненамного сложнее, чем подготовка одной копии, требующая лишь полиномиальных накладных расходов по времени без какой-либо модификации устройства.
При реализации QVE устройство подготавливает анзац-состояния, которые определяются полиномиальным набором параметров. Этот анзац может быть выбран на основе знаний об интересующей физической системе (как для унитарного связанного кластера и типичного анзаца квантовой химии), таким образом определяя конструкцию устройства. Однако наша архитектура допускает альтернативный и потенциально более многообещающий подход, при котором устройство сначала создается на основе доступных ресурсов, а набор состояний, которые устройство может подготовить, определяется как «анзац устройства». Из-за квантовой природы устройства этот анзац может сильно отличаться от тех, которые используются в традиционной квантовой химии. При этом альтернативном подходе физическая реализация задается известной последовательностью квантовых операций с регулируемыми параметрами, определенными при конструировании устройства, с максимальной глубиной, фиксированной временем когерентности физических кубитов. Этот подход, хотя и приблизительный, обеспечивает вариационно оптимальное решение для заданных квантовых ресурсов и все же может давать качественно правильные решения, как это делают приближенные методы в традиционной квантовой химии (например, Хартри Фока).
Этот анзац может быть выбран на основе знаний об интересующей физической системе (как для унитарного связанного кластера и типичного анзаца квантовой химии), таким образом определяя конструкцию устройства. Однако наша архитектура допускает альтернативный и потенциально более многообещающий подход, при котором устройство сначала создается на основе доступных ресурсов, а набор состояний, которые устройство может подготовить, определяется как «анзац устройства». Из-за квантовой природы устройства этот анзац может сильно отличаться от тех, которые используются в традиционной квантовой химии. При этом альтернативном подходе физическая реализация задается известной последовательностью квантовых операций с регулируемыми параметрами, определенными при конструировании устройства, с максимальной глубиной, фиксированной временем когерентности физических кубитов. Этот подход, хотя и приблизительный, обеспечивает вариационно оптимальное решение для заданных квантовых ресурсов и все же может давать качественно правильные решения, как это делают приближенные методы в традиционной квантовой химии (например, Хартри Фока). Унитарно-связанный кластерный анзац (уравнение (4)) представляет собой конкретный пример, в котором наш подход дает экспоненциальное преимущество перед известными классическими методами. Для этого анзаца, имеющего всего 40–50 кубитов, можно ожидать манипулирования состоянием, которое неэффективно для классического моделирования и может обеспечить решение, превосходящее классический золотой стандарт, неунитарный связанный кластер.
Унитарно-связанный кластерный анзац (уравнение (4)) представляет собой конкретный пример, в котором наш подход дает экспоненциальное преимущество перед известными классическими методами. Для этого анзаца, имеющего всего 40–50 кубитов, можно ожидать манипулирования состоянием, которое неэффективно для классического моделирования и может обеспечить решение, превосходящее классический золотой стандарт, неунитарный связанный кластер.
Мы разработали и экспериментально внедрили новый подход к решению проблемы собственных значений с помощью квантового оборудования. QEE разделяет с QPE необходимость подготовки хорошего приближения к основному состоянию, но заменяет одну длинную когерентную эволюцию рядом более коротких когерентных вычислений, пропорциональных количеству членов в гамильтониане. Хотя влияние ошибок на каждое из этих вычислений такое же, как и в QPE, зависимость от ряда отдельных вычислений делает алгоритм чувствительным к изменениям в подготовке состояния между отдельными квантовыми вычислениями. Этот эффект требует дальнейшего изучения. Наиболее общая локальная гамильтонова задача является QMA-полной 35 . Однако при разумном предположении, что можно подготовить хорошее приближение к состоянию, наш метод и QPE могут эффективно оценивать энергию состояния, и именно в этой настройке мы их сравниваем. В QVE мы экспериментально реализовали процедуру подготовки основного состояния с помощью алгоритма прямого изменения параметров управления квантового оборудования. При желании подготовленное состояние можно использовать либо в QEE 1, либо в QPE. Более крупные расчеты потребуют выбора анзаца, для которого есть две возможности. Можно было бы экспериментально реализовать химически мотивированный анзац, такой как метод унитарных связанных кластеров. В качестве альтернативы можно было бы использовать те анзацы, которые легче всего реализовать экспериментально, — создать новый набор состояний анзаца устройства, которые потребовали бы классификации с точки зрения их перекрытия с химическими основными состояниями.
Этот эффект требует дальнейшего изучения. Наиболее общая локальная гамильтонова задача является QMA-полной 35 . Однако при разумном предположении, что можно подготовить хорошее приближение к состоянию, наш метод и QPE могут эффективно оценивать энергию состояния, и именно в этой настройке мы их сравниваем. В QVE мы экспериментально реализовали процедуру подготовки основного состояния с помощью алгоритма прямого изменения параметров управления квантового оборудования. При желании подготовленное состояние можно использовать либо в QEE 1, либо в QPE. Более крупные расчеты потребуют выбора анзаца, для которого есть две возможности. Можно было бы экспериментально реализовать химически мотивированный анзац, такой как метод унитарных связанных кластеров. В качестве альтернативы можно было бы использовать те анзацы, которые легче всего реализовать экспериментально, — создать новый набор состояний анзаца устройства, которые потребовали бы классификации с точки зрения их перекрытия с химическими основными состояниями. Такая классификация была бы хорошим способом определить ценность данного экспериментального прогресса — для проблем с основным состоянием лучше всего сосредоточить ограниченные экспериментальные ресурсы на тех усилиях, которые в наибольшей степени усилят перекрытие готовых состояний с химическими основными состояниями. В дополнение к вышеупомянутым проблемам, которые мы оставляем для будущей работы, интересным направлением исследований является вопрос о том, можно ли использовать описанный здесь концептуальный подход для решения других трудноразрешимых проблем с квантово-усиленными вычислениями. Примеры, которые можно сопоставить с проблемой основного состояния и где N — проблема репрезентативности не возникает, включая поисковую оптимизацию и распознавание изображений. Следует отметить, что представленный здесь подход не требует никаких управляющих или вспомогательных кубитов, полагаясь только на уже хорошо зарекомендовавшие себя методы измерения. Например, в случае двух кубитов эти измерения идентичны измерениям, выполненным в экспериментах по неравенству Белла.
Такая классификация была бы хорошим способом определить ценность данного экспериментального прогресса — для проблем с основным состоянием лучше всего сосредоточить ограниченные экспериментальные ресурсы на тех усилиях, которые в наибольшей степени усилят перекрытие готовых состояний с химическими основными состояниями. В дополнение к вышеупомянутым проблемам, которые мы оставляем для будущей работы, интересным направлением исследований является вопрос о том, можно ли использовать описанный здесь концептуальный подход для решения других трудноразрешимых проблем с квантово-усиленными вычислениями. Примеры, которые можно сопоставить с проблемой основного состояния и где N — проблема репрезентативности не возникает, включая поисковую оптимизацию и распознавание изображений. Следует отметить, что представленный здесь подход не требует никаких управляющих или вспомогательных кубитов, полагаясь только на уже хорошо зарекомендовавшие себя методы измерения. Например, в случае двух кубитов эти измерения идентичны измерениям, выполненным в экспериментах по неравенству Белла.
Ожидается, что квантовые симуляторы с несколькими десятками кубитов превзойдут возможности обычных компьютеров, не считая открытых вопросов, касающихся отказоустойчивости и ошибок/точности. Наша схема позволила бы реализовать такие устройства с использованием значительно меньших ресурсов, чем наиболее известный в настоящее время подход.
Методы
Классический алгоритм оптимизации
Для классического шага оптимизации нашего интегрированного процессора мы реализовали алгоритм Нелдера-Мида (НМ) 36 , основанный на симплексе метод прямого поиска (DS) для безусловной минимизации целевых функций. Хотя в целом NM может дать сбой из-за ухудшения геометрии симплекса или отсутствия достаточного уменьшения, сходимость этого метода можно значительно улучшить, приняв стратегию перезапуска. Хотя другие методы DS, такие как градиентный спуск, могут работать лучше для гладких функций, они не устойчивы к шуму, что делает целевую функцию негладкой в экспериментальных условиях. NM имеет возможность исследовать соседние долины с лучшими локальными оптимумами, и аналогично эта функция исследования обычно позволяет NM преодолевать негладкости. Мы проверили, что алгоритм минимизации градиентного спуска не может сходиться к основному состоянию нашего гамильтониана в экспериментальных условиях, в основном из-за пуассоновского шума, связанного с нашим источником фотонов, и случайных подсчетов системы обнаружения, в то время как NM сходился к глобальный минимум в большинстве прогонов оптимизации.
NM имеет возможность исследовать соседние долины с лучшими локальными оптимумами, и аналогично эта функция исследования обычно позволяет NM преодолевать негладкости. Мы проверили, что алгоритм минимизации градиентного спуска не может сходиться к основному состоянию нашего гамильтониана в экспериментальных условиях, в основном из-за пуассоновского шума, связанного с нашим источником фотонов, и случайных подсчетов системы обнаружения, в то время как NM сходился к глобальный минимум в большинстве прогонов оптимизации.
Отображение параметров состояния на фазы чипа
Набор фаз { θ i }, который однозначно идентифицирует состояние | ψ ›, не эквивалентен фазам, которые записываются в фотонную схему { φ i }, так как фазы чипа также используются для реализации нужных операторов измерения ⊗ σ β . Поэтому, зная желаемые параметры состояния и оператор измерения, мы вычисляем соответствующие значения фаз чипа на ЦП на каждой итерации алгоритма оптимизации. Алгоритм нахождения параметров состояния { θ i } для произвольного двухкубитного состояния описано в Методах. Эти фазы затем применяются к микросхеме CNOT-MZ с использованием φ 1,2,3,4,7,8 . Здесь φ 7,8 изменены для учета выбора настройки измерения на целевом кубите. (Любое однокубитное проективное измерение можно выполнить с помощью ИМЦ вместе с двумя фазовращателями.) Настройка измерения для управляющего кубита реализована с использованием φ 5,6 .
Алгоритм нахождения параметров состояния { θ i } для произвольного двухкубитного состояния описано в Методах. Эти фазы затем применяются к микросхеме CNOT-MZ с использованием φ 1,2,3,4,7,8 . Здесь φ 7,8 изменены для учета выбора настройки измерения на целевом кубите. (Любое однокубитное проективное измерение можно выполнить с помощью ИМЦ вместе с двумя фазовращателями.) Настройка измерения для управляющего кубита реализована с использованием φ 5,6 .
Оценка ошибки на ‹›
Мы провели измерения статистических и систематических ошибок, которые влияют на наш расчет ‹›.
Статистические ошибки
Статистические ошибки из-за пуассоновского шума, связанного с однофотонной статистикой, присущи оценке математических ожиданий в квантовой механике.
Эти ошибки можно произвольно уменьшить за счет сублинейных затрат времени измерения (то есть эффективно), поскольку величина ошибки пропорциональна квадратному корню из скорости счета. Мы экспериментально измерили стандартное отклонение ожидаемого значения ‹ i › для определенного штата с использованием 50 испытаний. Общая средняя частота совпадений составила ~1500 с −1 . Стандартное отклонение оказалось равным 37 кДж моль −1 , что сравнимо с ошибкой, наблюдаемой при измерении энергии основного состояния, показанной на рис. 4.
Мы экспериментально измерили стандартное отклонение ожидаемого значения ‹ i › для определенного штата с использованием 50 испытаний. Общая средняя частота совпадений составила ~1500 с −1 . Стандартное отклонение оказалось равным 37 кДж моль −1 , что сравнимо с ошибкой, наблюдаемой при измерении энергии основного состояния, показанной на рис. 4.
Минимумы кривой потенциальной энергии определялись обобщенная процедура наименьших квадратов для подгонки квадратичной кривой к точкам экспериментальных данных в области R = (80, 100) pm, как это обычно делается при использовании поиска в области доверия для минимумов 37 , используя обратные экспериментально измеренные отклонения в качестве весов. Ковариации, определенные с помощью обобщенной процедуры наименьших квадратов, использовались в качестве входных данных для процедуры выборки Монте-Карло для определения минимальной энергии и равновесного расстояния связи, а также их неопределенностей с учетом случайной ошибки Гаусса. Представленные неопределенности представляют собой стандартные отклонения. Ошибка выборки в методе Монте-Карло составила 3 × 10 −4 мкм для равновесного расстояния связи и 3 × 10 −8 МДж моль −1 для энергии.
Представленные неопределенности представляют собой стандартные отклонения. Ошибка выборки в методе Монте-Карло составила 3 × 10 −4 мкм для равновесного расстояния связи и 3 × 10 −8 МДж моль −1 для энергии.
На рис. 4 большие отклонения от теоретической линии являются результатом случайного воздействия шума, приводящего к преждевременному прекращению оптимизации. Эти точки можно было бы повторить или исключить, используя предварительное знание гладкости кривой диссоциации. Однако для точного отображения производительности алгоритма точно так, как описано, без вмешательства экспертов, эти точки сохраняются.
Систематические ошибки
Во всех измерениях, описанных выше, мы наблюдали постоянный и воспроизводимый небольшой сдвиг, ε=50 кДж моль −1 , ожидаемого значения по отношению к теоретическому значению энергии. Есть по крайней мере три эффекта, которые способствуют этой систематической ошибке.
Во-первых, источник преобразования с понижением частоты, который мы используем в нашем эксперименте, не создает чистое двухфотонное состояние, необходимое для высокоточной квантовой интерференции. В частности, числа фотонов более высокого порядка и, что более важно, различимость фотонов ухудшают производительность нашего запутывающего вентиля и, следовательно, подготовку состояния | ψ ›. Это приводит к сдвигу измеренной энергии ‹ ψ || ψ ›. Члены более высокого порядка могут быть эффективно устранены за счет использования истинных однофотонных источников (таких как квантовые точки или центры вакансий азота в алмазе), и нет фундаментального ограничения степени неразличимости, которая может быть достигнута за счет улучшенного проектирования состояний.
В частности, числа фотонов более высокого порядка и, что более важно, различимость фотонов ухудшают производительность нашего запутывающего вентиля и, следовательно, подготовку состояния | ψ ›. Это приводит к сдвигу измеренной энергии ‹ ψ || ψ ›. Члены более высокого порядка могут быть эффективно устранены за счет использования истинных однофотонных источников (таких как квантовые точки или центры вакансий азота в алмазе), и нет фундаментального ограничения степени неразличимости, которая может быть достигнута за счет улучшенного проектирования состояний.
Во-вторых, несовершенство реализации фотонной схемы также снижает точность, с которой | ψ › подготовлен и измерен. Небольшие отклонения от расчетных коэффициентов отражения светоделителя и длин пути интерферометра, а также несовершенство калибровки фазовращателей, управляемых напряжением, используемых для управления состоянием, — все это способствует этому эффекту. Однако это технологические ограничения, которые можно значительно улучшить в будущих реализациях.
Наконец, несбалансированная эффективность связи между входом и выходом также приводит к искажению двухфотонной статистики, снова сдвигая измеренное математическое ожидание на ‹›.
Другой систематический эффект, который можно отметить на рис. 4, заключается в том, что величина ошибки экспериментальной оценки энергии основного состояния увеличивается с R . Это связано с тем, что по мере увеличения R первое и второе возбужденные собственные состояния этого гамильтониана становятся вырожденными, что приводит к увеличению сложности классической минимизации, создавая смеси состояний, что увеличивает общую дисперсию оценки.
Точность квантового состояния
В предыдущей работе 31 мы измерили среднюю точность состояний, генерируемых вентилем CNOT, которая оценивалась с помощью томографии квантовых процессов и составила 0,873 ± 0,001. Средняя точность квантового состояния по четырем состояниям Белла составила 0,93. Средняя достоверность для 995 конфигураций (эквивалентная многим таблицам истинности во многих базах) составила 0,990 ± 0,009, при этом 96% конфигураций дают статистику фотонов с f >0,97.
Скорость счета
В нашем эксперименте средняя скорость счета, непосредственно определяющая статистическую погрешность, составляла ~2000–4000 двукратных событий на измерение. Среднее значение данного гамильтониана восстанавливалось в каждой точке из четырех двухкубитных измерений Паули. Для кривой диссоциации связи мы измерили около 100 точек за прогон оптимизации. На полной кривой диссоциации мы нашли основные состояния 79гамильтонианы. Полный эксперимент был проведен примерно за 158 часов.
Подготовка состояния выполняется относительно быстро, требуется несколько миллисекунд для установки фаз на микросхеме. Однако для охлаждения чипа требуется 17 с, что приводит к рабочему циклу ~ 5%. Целью этого является преодоление нестабильности соединения волокна с чипом из-за теплового расширения чипа во время работы. Это не будет проблемой в будущих реализациях, где волокна будут постоянно прикреплены к граням чипа. Более того, используемые здесь тепловые фазовращатели также, вероятно, будут заменены альтернативными технологиями, основанными на электрооптическом эффекте.
Более яркие однофотонные источники значительно сокращают время измерения.
Дополнительная информация
Как цитировать эту статью: Peruzzo, A. et al. Вариационный решатель собственных значений фотонного квантового процессора. Нац. коммун. 5:4213 doi: 10.1038/ncomms5213 (2014).
Ссылки
Тогерсен, Л. и Олсен, Дж. Исследование взаимодействия связанных кластеров и полной конфигурации cn и cn-. Хим. физ. лат. 393 , 36–43 (2004).
КАС ОБЪЯВЛЕНИЯ Статья Google ученый
Helgaker, T., Jorgensen, P. & Olsen, J. Mol. Электронная структура. Теория Wiley, Сассекс (2002).
Саад, Ю. Численные методы решения больших задач на собственные значения Vol. 158 , (SIAM (1992).
Пейдж, Л.
 , Брин, С., Мотвани, Р. и Виноград, Т. Рейтинг цитирования Pagerank: Наведение порядка в Интернете . Технический отчет 1999–66 (Stanford InfoLab, (1999).
, Брин, С., Мотвани, Р. и Виноград, Т. Рейтинг цитирования Pagerank: Наведение порядка в Интернете . Технический отчет 1999–66 (Stanford InfoLab, (1999).Голуб, Г. Х. и ван дер Ворст, Х. А. Вычисление собственных значений в 20 веке. J. Comput. Appl. Math. 123 5, 35–6. (2000)
ОБЪЯВЛЕНИЯ MathSciNet Статья Google ученый
Нильсен, Массачусетс, и Чуанг, И.Л. Квантовые вычисления и квантовая информация Издательство Кембриджского университета (2000).
Китаев А. Квантовые измерения и проблема абелева стабилизатора. Электронный коллоквиум по вычислительной сложности (ECCC) 3 (1996).
Гриффитс, Р. Б. и Ню, К.-С. Квазиклассическое преобразование Фурье для квантовых вычислений. Физ. Преподобный Летт. 76 , 3228–3231 (1996).
КАС ОБЪЯВЛЕНИЯ Статья Google ученый
Невен, Х.
 , Роуз, Г. и Макреди, В. Г. Распознавание изображений с помощью адиабатического квантового компьютера I. Преобразование в квадратичную неограниченную двоичную оптимизацию. Препринт на http://arxiv.org/abs/0804.4457 (2008 г.).
, Роуз, Г. и Макреди, В. Г. Распознавание изображений с помощью адиабатического квантового компьютера I. Преобразование в квадратичную неограниченную двоичную оптимизацию. Препринт на http://arxiv.org/abs/0804.4457 (2008 г.).Харроу А., Хассидим А. и Ллойд С. Квантовый алгоритм для линейных систем уравнений. Физ. Преподобный Летт. 103 , 150502 (2009 г.).
ОБЪЯВЛЕНИЯ MathSciNet Статья Google ученый
Берри, Д. В. Квантовый алгоритм высокого порядка для решения линейных дифференциальных уравнений. J. Phys. А 47 , 105301 (2014).
ОБЪЯВЛЕНИЯ MathSciNet Статья Google ученый
Гарнероне С., Занарди П. и Лидар Д. А. Адиабатический квантовый алгоритм для ранжирования в поисковых системах. Физ. Преподобный Летт. 108 , 230506 (2012).

ОБЪЯВЛЕНИЯ Статья Google ученый
Абрамс Д. С. и Ллойд С. Моделирование ферми-систем многих тел на универсальном квантовом компьютере. Физ. Преподобный Летт. 79 , 2586–2589 (1997).
КАС ОБЪЯВЛЕНИЯ Статья Google ученый
Абрамс, Д. С. и Ллойд, С. Квантовый алгоритм, обеспечивающий экспоненциальное увеличение скорости для нахождения собственных значений и собственных векторов. Физ. Преподобный Летт. 83 , 5162–5165 (1999).
КАС ОБЪЯВЛЕНИЯ Статья Google ученый
Аспуру-Гузик А., Дутой А.Д., Лав П.Дж. и Хед-Гордон М. Моделирование квантовых вычислений молекулярной энергии. Наука 309 , 1704–1707 (2005).
КАС ОБЪЯВЛЕНИЯ Статья Google ученый
Lanyon, B.
 P. et al. К квантовой химии на квантовом компьютере. Нац. хим. 2 , 106–111 (2010).
P. et al. К квантовой химии на квантовом компьютере. Нац. хим. 2 , 106–111 (2010).КАС Статья Google ученый
Уитфилд Дж. Д., Биамонте Дж. и Аспуру-Гузик А. Моделирование гамильтонианов электронной структуры с использованием квантовых компьютеров. Мол. физ. 109 , 735–750 (2011).
КАС ОБЪЯВЛЕНИЯ Статья Google ученый
Аспуру-Гузик, А. и Вальтер, П. Фотонные квантовые симуляторы. Нац. физ. 8 , 285–291 (2012).
КАС Статья Google ученый
Jones, N.C. et al. Более быстрое моделирование квантовой химии на отказоустойчивых квантовых компьютерах. New J. Phys. 14 , 115023 (2012).
Артикул Google ученый
Ллойд С.
 Вычислительная мощность Вселенной. Физ. Преподобный Летт. 88 , 237901 (2002).
Вычислительная мощность Вселенной. Физ. Преподобный Летт. 88 , 237901 (2002).ОБЪЯВЛЕНИЯ Статья Google ученый
Ma, X.-s., Dakic, B., Naylor, W., Zeilinger, A. & Walther, P. Квантовое моделирование волновой функции для исследования фрустрированных спиновых систем Гейзенберга. Нац. физ. 7 , 399–405 (2011).
КАС Статья Google ученый
Оселедец И. Аппроксимация 2 d × 2 d матриц с помощью тензорного разложения. СИАМ Дж. Матричный анал. А 31 , 2130–2145 (2010).
Артикул Google ученый
Ортис Г., Губернатис Дж. Э., Книлл Э. и Лафламм Р. Квантовые алгоритмы для фермионного моделирования. Физ. Ред. A 64 , 022319 (2001 г.
 ).
).ОБЪЯВЛЕНИЯ Статья Google ученый
Лю, Ю.-К., Кристандл, М. и Верстрате, Ф. Квантовая вычислительная сложность n -проблемы представимости: Qma Complete. Физ. Преподобный Летт. 98 , 110503 (2007 г.).
ОБЪЯВЛЕНИЯ Статья Google ученый
Темме, К., Осборн, Т.Дж., Фоллбрехт, К.Г., Пулин, Д. и Верстрате, Ф. Выборка Quantum Metropolis. Природа 471 , 87–90 (2011).
КАС ОБЪЯВЛЕНИЯ Статья Google ученый
Юнг, М.-Х. и Аспуру-Гузик, А. Квантово-квантовый алгоритм Метрополиса. Проц. Натл акад. науч. США 109 , 754–759 (2012).
КАС ОБЪЯВЛЕНИЯ Статья Google ученый
Рэлей, Дж.
 В. В поиске поправки на открытый конец органной трубы. Фил. Транс. 161 , 77 (1870).
В. В поиске поправки на открытый конец органной трубы. Фил. Транс. 161 , 77 (1870).Google ученый
Ritz, W. Über eine neue Methode zur Lösung gewisser Variations probleme der mathematischen physik. Дж. Рейн Ангью. Мат. 135 , 1–61 (1908).
МАТЕМАТИКА Google ученый
Таубе, А. Г. и Бартлетт, Р. Дж. Новые взгляды на теорию унитарных связанных кластеров. Междунар. Дж. Квант. хим. 106 , 3393–3401 (2006).
КАС ОБЪЯВЛЕНИЯ Статья Google ученый
О’Брайен Дж. Л., Фурусава А. и Вукович Дж. Фотонные квантовые технологии. Нац. Фотон. 3 , 687–695 (2009).
КАС ОБЪЯВЛЕНИЯ Статья Google ученый
Шадболт, П.
 и др. Генерация, управление и измерение запутанности и смешения с реконфигурируемой фотонной схемой. Нац. Фотон. 6 , 45–49 (2011).
и др. Генерация, управление и измерение запутанности и смешения с реконфигурируемой фотонной схемой. Нац. Фотон. 6 , 45–49 (2011).ОБЪЯВЛЕНИЯ Статья Google ученый
Кроуфорд, Т. Д. и др. Psi3: пакет электронной структуры ab initio с открытым исходным кодом. Дж. Комп. хим. 28 , 1610–1616 (2007).
КАС Статья Google ученый
Шарек С. Дж. Объем сепарабельных состояний сверхдвукратно экспоненциально мал по количеству кубитов. Физ. Ред. A 72 , 032304 (2005 г.).
ОБЪЯВЛЕНИЯ MathSciNet Статья Google ученый
Чжоу, X.-Q. и другие. Добавление контроля к произвольным неизвестным квантовым операциям. Нац. коммун. 2 , 413 (2011).
Артикул Google ученый
Кемпе Дж.
 , Китаев А. и Регев О. Сложность локальной гамильтоновой проблемы. СИАМ Дж. Вычисл. 35 , 1070–1097 (2006).
, Китаев А. и Регев О. Сложность локальной гамильтоновой проблемы. СИАМ Дж. Вычисл. 35 , 1070–1097 (2006).MathSciNet Статья Google ученый
Нелдер, Дж. А. и Мид, Р. Симплексный метод минимизации функций. Вычисл. J. 7 , 308–313 (1965).
MathSciNet Статья Google ученый
Конн, А. Р., Гулд, Н. И. и Тойнт, П. Л. Методы области доверия Том. 1 ( , Society for Industrial Mathematics (1987).
Ссылки на скачивание
Благодарности
Мы благодарим Скотта Ааронсона, Роберта Чепмена, Сета Ллойда, Тима Ральфа, Терри Рудольфа, Джо Фицсаймонса и Джеймса Уитфилда за обсуждение. финансовая поддержка от EPSRC, ERC, QUANTIP, PHORBITECH, QESSENCE, Nokia, NSQI, Фонда Темплтона и EU DIQIP. поддерживается стипендией DOE Computational Science Graduate Fellowship под номером гранта DE-FG02-9. 7ER25308. М.-Х.Ю. выражает признательность за поддержку со стороны Национальной программы фундаментальных исследований Китая, грантов 2011CBA00300 и 2011CBA00301, грантов Национального фонда естественных наук Китая 61033001 и 61361136003, а также программы «Молодежь 1000 талантов». П.Дж.Л. поддерживается наградой NSF PHY-0955518 и наградой AFOSR №. FA9550-12-1-0046. А.А.-Г. признает поддержку со стороны премии NSF CCI №. CHE-1037992, награда Управления научных исследований ВВС №. FA9550-12-1-0046, Фонд Камиллы и Генри Дрейфус и Фонд Альфреда П. Слоуна. ДЖ.Л.О’Б. отмечает награду Королевского общества Вольфсона за заслуги и кафедру Королевской инженерной академии в области новых технологий.
7ER25308. М.-Х.Ю. выражает признательность за поддержку со стороны Национальной программы фундаментальных исследований Китая, грантов 2011CBA00300 и 2011CBA00301, грантов Национального фонда естественных наук Китая 61033001 и 61361136003, а также программы «Молодежь 1000 талантов». П.Дж.Л. поддерживается наградой NSF PHY-0955518 и наградой AFOSR №. FA9550-12-1-0046. А.А.-Г. признает поддержку со стороны премии NSF CCI №. CHE-1037992, награда Управления научных исследований ВВС №. FA9550-12-1-0046, Фонд Камиллы и Генри Дрейфус и Фонд Альфреда П. Слоуна. ДЖ.Л.О’Б. отмечает награду Королевского общества Вольфсона за заслуги и кафедру Королевской инженерной академии в области новых технологий.
Информация об авторе
Примечания автора
Альберто Перуццо
Текущий адрес: Текущий адрес: Школа физики, Сиднейский университет, Сидней, Новый Южный Уэльс, 2006, Австралия,
Альберто Перуццо и Джаррод МакКлин: эти авторы в равной степени внесли свой вклад в эту работу , БС8 1УБ, Великобритания
Альберто Перуццо, Питер Шадболт, Сяо-Ци Чжоу и Джереми Л.
 О’Брайен
О’БрайенФакультет химии и химической биологии, Гарвардский университет, Кембридж, 02138, Массачусетс, США
Джаррод МакКлин, Ман-Мэн Alán Aspuru-Guzik
Центр квантовой информации, Институт междисциплинарных информационных наук, Университет Цинхуа, Пекин, 100084, КНР
Man-Hong Yung
Факультет физики, Haverford College, Haverford, 19041, Pennsylvania, USA
Peter J. Love
Авторы
- Alberto Peruzzo
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Jarrod McClean
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Peter Shadbolt
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Академия
- Man-Hong Yung
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Xiao-Qi Zhou
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Peter J.
 Love
LoveПросмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Alán Aspuru-Guzik
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Джереми Л. О’Брайен
Просмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Scholar
Contributions
Все авторы внесли большой вклад в работу, представленную в этой статье.
Авторы переписки
Переписка с Альберто Перуццо, Алан Аспуру-Гузик или Джереми Л. О’Брайен.
Заявление об этике
Конкурирующие интересы
Авторы не заявляют о конкурирующих финансовых интересах.
Дополнительная информация
Дополнительная информация
Дополнительные таблицы 1-2, дополнительные методы и дополнительные ссылки (PDF 201 kb) Изображения или другие сторонние материалы в этой статье включены в лицензию Creative Commons на статью, если иное не указано в кредитной строке; если материал не включен в лицензию Creative Commons, пользователям необходимо будет получить разрешение от держателя лицензии на воспроизведение материала. Чтобы просмотреть копию этой лицензии, посетите http://creativecommons.org/licenses/by-nc-nd/4.0/
Чтобы просмотреть копию этой лицензии, посетите http://creativecommons.org/licenses/by-nc-nd/4.0/
Перепечатка и разрешения
Об этой статье
Эта статья цитируется
Метод VQE: краткий обзор и последние разработки
- Федоров Дмитрий Александрович
- Бо Пэн
- Юрий Алексеев
Теория материалов (2022)
Теория сопряженных кластеров: к универсальным многочастичным алгоритмам уменьшения размерности составных квантовых систем в химии и материаловедении
- Николай Петрович Бауман
- Кароль Ковальски
Теория материалов (2022)
Обнаружение и количественная оценка запутанности на ближайших квантовых устройствах
- Кун Ван
- Песня Чжисинь
- Синь Ван
npj Квантовая информация (2022)
Поиск архитектуры квантовой схемы для вариационных квантовых алгоритмов
- Юйсюань Ду
- Тао Хуан
- Дачэн Тао
npj Квантовая информация (2022)
Многокубитная запутанность и алгоритмы квантового компьютера на нейтральном атоме
- Т.
 М. Грэм
М. Грэм - Ю. Сонг
- М. Саффман
Природа (2022)
- Т.
Комментарии
Отправляя комментарий, вы соглашаетесь соблюдать наши Условия и Правила сообщества. Если вы обнаружите что-то оскорбительное или не соответствующее нашим условиям или правилам, отметьте это как неприемлемое.
Anagram Solver: Scrabble, WWF & Crosswords
Anagram Solver — это мощный онлайн-инструмент, который помогает игрокам переставлять буквы и создавать новые шаблоны слов. Просто введите буквы, и Anagram Solver поможет вам улучшить свои навыки в Scrabble, Words With Friends или любой другой словесной игре. Длина и сложность не являются проблемой, Anagram Solver может предоставить все доступные варианты слов.
Анаграммы: примеры и определения
Анаграммы повсюду, возможно, вы слышали о них? Может быть, вы знаете, что такое анаграмма, но просто не можете ее объяснить. С другой стороны, вы можете быть мастером анаграмм и использовать их годами, играя в свои любимые настольные игры и разгадывая кроссворды. Являетесь ли вы новичком или экспертом, это ваш путеводитель по анаграммам.
Что такое анаграмма?
Анаграмма — это фраза или слово, в котором при перестановке букв создается другая фраза или слово. Например, слово СЛУШАЙТЕ можно составить по-разному, чтобы образовать слово МОЛЧАНИЕ , и помните, одно из правил анаграммы состоит в том, что все буквы исходной фразы или слова должны использоваться для создания новой!
Где используются анаграммы?
Со времен древних греков, в средние века и вплоть до современного мира 21-го века анаграммы использовались для кода, псевдонимов, кроссвордов и чаще всего для развлечения! Онлайн-и офлайн-игры используют их уже много лет, и именно тогда Word Finder может стать отличным инструментом, позволяющим вам опередить всех остальных!
20 примеров анаграмм:
Являетесь ли вы новичком или ветераном в мире прыжков гласных, пересечения согласных или скольжения слогов, вот еще несколько примеров анаграмм:
- ТЕПЛО = ЗЕМЛЯ
- ТАР = КРЫСА
- ПАРИЖ = ПАРЫ
- КЛИНТ ИСТВУД = ДЕЙСТВИЯ СТАРОГО ЗАПАДА
- АРК = АВТОМОБИЛЬ
- КОЛЕНО = НИЖЕ
- ПЛОХОЙ КРЕДИТ = ДЕБЕТОВАЯ КАРТА
- СОСТОЯНИЕ = ВКУС
- СИДР = ПЛАЧ
- ПОДТЯЖЕННЫЕ = ДЕСЕРТЫ
- ПЫЛЬНЫЙ = ИССЛЕДОВАНИЕ
- КОД МОРЗЕ = ЗДЕСЬ ТОЧКИ
- ПОХОРОНЫ = НАСТОЯЩЕЕ ВЕСЕЛО
- ВИДЕОИГРА = ДАТЬ ДЕМО
- НОЧЬ = THNG
- ОДИННАДЦАТЬ ПЛЮС ДВА = ДВЕНАДЦАТЬ ПЛЮС ОДИН
- ДЮЙМЫ = ПОДБОРОДЬ
- САН-ДИЕГО = ДИАГНОСТИКА
- ЧЕТВЕРТОЕ ИЮЛЯ = РАДОСТНОЕ ЧЕТВЕРТОЕ
- GAINLY = ПРОКЛАДКА
Решение анаграмм: Scrabble, WWF и кроссворды
Итак, как вам поможет создание анаграммы в вашей игре-головоломке? Простой, он заставляет вас переставлять комбинации букв, которые вы используете, и создает новые возможности для размышлений в вашей голове. Вы начинаете представлять различные сценарии и комбинации, и с правильной анаграммой вы найдете самые прибыльные ходы.
Вы начинаете представлять различные сценарии и комбинации, и с правильной анаграммой вы найдете самые прибыльные ходы.
Решатель анаграмм: 3 шага
Некоторые из них естественны, когда дело доходит до перестановки и создания новых анаграмм. генератор анаграмм — идеальное решение для этого.
Шаг 1: Распознавание некоторых часто используемых префиксов и суффиксовНекоторые распространенные префиксы: AB, AD, DIS, DE, EX, RE, SUB, UN
Некоторые распространенные суффиксы: ED, ER, ING, ISM, LY, MENT , НЕСС, ТИОН
Шаг 2: Выберите их Шаг 3: Измените порядок букв, чтобы создать новые словаПримером этого является слово ХУДОЖНИК . Переместив суффикс в начало, чтобы он стал префиксом, он становится словом ПЕРЕКРАСИТЬ . Буквы также можно переставить так, чтобы получилось слово PERTAIN .
Anagram Maker: Scrabble
Когда вы смотрите на игровое поле с несколькими вариантами ответов, иногда самое длинное слово не приносит прибыли. Опытные игроки в скрэббл знают, что первые несколько ходов в игре самые важные. Тем не менее, застревание в конце игры также является серьезной проблемой. Вот тут-то и появляются генераторы анаграмм. Генератор анаграмм, такой как наш, использует свою огромную базу данных, чтобы дать вам решения с двумя-шестью или более буквами, проверенные в словаре Scrabble. Использование нашего онлайн-инструмента поможет любому игроку в скрэббл набрать эти подстановочные очки и украсть игру, не говоря уже о том, что лучшие игроки в скрэббл будут использовать инструмент анаграммы, чтобы сделать игры более быстрыми и захватывающими.
Опытные игроки в скрэббл знают, что первые несколько ходов в игре самые важные. Тем не менее, застревание в конце игры также является серьезной проблемой. Вот тут-то и появляются генераторы анаграмм. Генератор анаграмм, такой как наш, использует свою огромную базу данных, чтобы дать вам решения с двумя-шестью или более буквами, проверенные в словаре Scrabble. Использование нашего онлайн-инструмента поможет любому игроку в скрэббл набрать эти подстановочные очки и украсть игру, не говоря уже о том, что лучшие игроки в скрэббл будут использовать инструмент анаграммы, чтобы сделать игры более быстрыми и захватывающими.
Искатель анаграмм: Words With Friends
Как и наш Создатель анаграмм, Средство поиска анаграмм может быть столь же бесценным инструментом при игре в другие онлайн-игры-головоломки, такие как Words With Friends. Столкнувшись со строкой символов и более чем 171 000 слов на английском языке, некоторые игроки могут почувствовать необходимость обмана, чтобы не отставать от конкурентов. Для новых игроков сложная задача, заключающаяся в том, чтобы попытаться набрать как можно больше очков, а также играть быстро и уверенно, может стать настоящим испытанием, особенно в хорошо зарекомендовавших себя онлайн-сообществах.
Для новых игроков сложная задача, заключающаяся в том, чтобы попытаться набрать как можно больше очков, а также играть быстро и уверенно, может стать настоящим испытанием, особенно в хорошо зарекомендовавших себя онлайн-сообществах.
Anagram Finder призван уменьшить это беспокойство и помочь новым и старым игрокам участвовать в игре, разгадывать несколько слов и никогда не зацикливаться на словах для игры. Помните, новое расположение слов заставляет ваш разум исследовать новые возможности. Вот где помощь словесной анаграммы может быть незаменимой.
Советы по игре в слова: как решать анаграммы
Вот несколько заключительных советов об удивительном мире задач на анаграммы и словесных задач. Мы надеемся, что вы сможете извлечь полезную информацию из нашей статьи и, возможно, создать небольшую шпаргалку, чтобы опередить конкурентов!
Word Unscrambler
Word Unscrambler, игроки, играющие в слова, могут искать анаграммы, вводя случайные буквы и подстановочные знаки или пустые плитки, которые у них есть. Вы можете использовать базовую панель поиска анаграмм или пойти немного дальше с помощью расширенного фильтра, чтобы найти слова, которые начинаются или заканчиваются определенными буквами или наборами букв.
Вы можете использовать базовую панель поиска анаграмм или пойти немного дальше с помощью расширенного фильтра, чтобы найти слова, которые начинаются или заканчиваются определенными буквами или наборами букв.
Вот несколько примеров:
Рассмотрим исходный термин СЛУШАТЬ . Он содержит буквы E , I , L , N , T , S . Когда плитки вводятся в Word Unscrambler, он быстро находит две долгожданные жемчужины — SILENT и ENLIST .
Точно так же СОХРАНИТЬ , состоящее из букв A, E, S, и V , раскрывает слово ВАЗА в Word Unscrambler.
Phrase Unscrambler
Иногда фразы могут быть немного сложнее для вычисления в нашем мозгу, нам часто бывает трудно извлечь одно слово из двух или трех, и наоборот. Вот почему Phrase Unscrambler может быть лучшим оружием в вашем арсенале, избавляя вас от тяжелой работы по расшифровке анаграмм.

 99 МБ
99 МБ 3
3 4
4 22.21.6
22.21.6



 10.2010, 13:52
10.2010, 13:52  За 4 дня я понял весь семетровый курс и всё сдал.
За 4 дня я понял весь семетровый курс и всё сдал.
