Математика Виленкина Н.Я. и др. для 5-6 классов
|
УМК для 5 класcа УМК для 6 класса |
Учебно-методический комплект (УМК) «Математика» (авторы: Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. и др.) предназначен для 5-6 классов общеобразовательных учреждений. УМК по математике Виленкина и др. используется педагогами уже не одно десятилетие. Он обеспечивает преемственность курсов математики в начальной школе и курсов алгебры в последующих классах для большинства программ, позволяет проводить разноуровневое обучение и качественную подготовку школьников к изучению курсов алгебры и геометрии (в том числе стереометрии) в старших классах, а также смежных дисциплин — физики, химии, географии и др. УМК «Математика» Виленкина Н.Я. и др. для 5-6 классов выпускает издательство «Мнемозина».
Учебники математики Виленкина Н.Я. и др. для 5-6 классов включены в федеральный перечень учебников, рекомендуемых к использованию при реализации имеющих государственную аккредитацию образовательных программ начального общего, основного общего, среднего общего образования (приказ Минпросвещения России от 28.12.2018 N 345).
Учебники, вошедшие в перечень, имеют новое художественное оформление. Содержание учебников соответствует федеральному государственному образовательному стандарту основного общего образования (ФГОС ООО 2010 г.).
Состав УМК «Математика» для 5-6 классов:
— Учебники 5, 6 классы (в двух частях). Авторы: Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И.
— Рабочие тетради 5, 6 классы (в двух частях). Автор Рудницкая В.Н.
— Контрольные работы 5, 6 классы. Авторы: Жохов В.И., Крайнева Л.Б.
— Математические диктанты 5, 6 классы. Авторы: Жохов В.И.
— Математические тренажеры 5, 6 классы. Авторы: Жохов В.И.
— Методическое пособие для учителя. Обучение математике в 5-6 класссах. Автор Жохов В.И.
Учебники по математике Виленкина и др. позволяют вести разноуровневое обучение, обеспечивают качественную подготовку школьников к изучению систематического курса алгебры и геометрии (в том числе стереометрии) в старших классах, а также смежных дисциплин: физики, химии, географии и др.
Учебники напрвлены на решение следующх задач:
— возможность компенсации типичных для начального обучения пробелов в подготовке школьников и недостатков в их математическом образовании, развитии внимания и памяти;
— возможность уровневой дифференциации в ходе обучения — возможность для школы работать по разным учебным планам, использовать учебник и в общеобразовательных классах, и в классах, ориентированных на углубленную подготовку по математике, предоставление необходимой базы для проведения внеклассных занятий по предмету;

Научно-методическая и технологическая составляющие учебников позволяют протянуть линию преемственности в обучении математике практически по любому существующему учебному комплекту для основной школы. Преемственность в обучении обеспечивается сформированными вычислительными навыками, развитым критическим мышлением и читательской компетентностью. А это является залогом успеха в усвоении опорной системы знаний по математике, необходимой для продолжения образования в основной и средней школе.
Рабочие тетради по математике Виленкина и др., используемые в комплекте с учебниками, содержат разнообразные упражнения к каждому параграфу. Среди них: задания, связанные с закреплением изученного материала, задачи повышенной трудности, занимательные и развивающие упражнения. В тетрадях представлены некоторые упражнения из учебника с пояснениями, иллюстрациями, образцами выполнения заданий, помогающими учащимся лучше понять их содержание.
Контрольные работы по математике Виленкина и др. содержат текущие и итоговую контрольные работы, а также диагностические тесты. Для каждой из них указаны пункты учебника, материал которых охватывается соответствующей работой. Все текущие контрольные работы составлены в четырех вариантах и напечатаны на карточках. Итоговая контрольная работа может быть предложена в качестве административной или экзаменационной (при проведении в школе переводного экзамена по математике). В конце пособия даются ответы к четырем заданиям текущих контрольных работ.
содержат текущие и итоговую контрольные работы, а также диагностические тесты. Для каждой из них указаны пункты учебника, материал которых охватывается соответствующей работой. Все текущие контрольные работы составлены в четырех вариантах и напечатаны на карточках. Итоговая контрольная работа может быть предложена в качестве административной или экзаменационной (при проведении в школе переводного экзамена по математике). В конце пособия даются ответы к четырем заданиям текущих контрольных работ.
Математические диктанты — новый вид заданий и по форме, и по содержанию, и по выбору решаемых педагогических задач. Основное их назначение — эффективно тренировать устойчивость внимания детей, оперативную память, умение сосредотачиваться. Пособие позволяет формировать правильную математическую речь учащихся и может быть использовано как при работе с учителем в классе, так и дома — под руководством родителей.
Математические тренажеры могут быть использованы при организации устного счета в 5-6-м классах (в том числе и по другим учебникам) для выработки и совершенствования прочных вычислительных навыков, развития внимания и оперативной памяти — необходимых компонентов успешного овладения школьным курсом математики.
Методические рекомендации содержат указания по работе с учебниками и подробное поурочное планирование учебного материала. Цель пособия — оказать учителю необходимую помощь, освободив его от рутинной, нетворческой работы при подготовке к урокам. В книге охарактеризованы особенности нового варианта учебника.
По материалам сайта: mnemozina.ru
Если материал вам понравился, нажмите кнопку вашей социальной сети:
№ | Тема урока | Домашняя работа | Дата проведения | |||||||
План | Факт. | |||||||||
1 | Повторение. Арифметические действия над натуральными числами | Выполнить работы по индивидуальным карточкам | 2.09 | |||||||
2 | Повторение. Порядок действий в выражениях. Примеры на вычисление. | Выполнить работы по индивидуальным карточкам | 3.09. | |||||||
3 | Повторение. Решение текстовых задач. | Выполнить работы по индивидуальным карточкам | 4.09. | |||||||
4 | Повторение. | Выполнить работы по индивидуальным карточкам | 5.09 | |||||||
5 | Входная контрольная работа | 6.09 | ||||||||
6 | Обозначение натуральных чисел | Выполнить №23,№25,№28 | 9.09 | |||||||
7 | Обозначение натуральных чисел | Выполнить №24,№29 | 10.09 | |||||||
8 | Обозначение натуральных чисел | Выполнить №26,№27,№30 | 11. | |||||||
9 | Отрезок. Длина отрезка. Треугольник. | Выполнить №65,№66,№70,№74(а,б) | 12.09 | |||||||
10 | Отрезок. Длина отрезка. Треугольник. | Выполнить №67,№68,№72,№74(в,г) | 13.09 | |||||||
11 | Отрезок. Длина отрезка. Треугольник. | Выполнить №69,№71,№73 | 16.09 | |||||||
12 | Отрезок. Длина отрезка. Треугольник. | Выполнить ДМ №4 стр. | 17.09 | |||||||
13 | Отрезок. Длина отрезка. Треугольник. | Выполнить ДМ №4,5 (IVв) ,стр. 119 | 18.09 | |||||||
14 | Плоскость. Прямая Луч. | Выполнить №99,№101,№106(а .б) | 19.09 | |||||||
15 | Плоскость. Прямая Луч. | Выполнить №100,№102,№106(в,г) | 20.09 | |||||||
16 | Плоскость. Прямая Луч. | Выполнить №103,№104,№105 | 23. | |||||||
17 | Шкалы и координаты | Выполнить №137,№138,№141 | 24.09 | |||||||
18 | Координатный луч. Определение на шкале единичного отрезка и координат точки. | Выполнить №142,№139,№144 | 25.09 | |||||||
19 | Решение задач по теме «Шкалы и координаты» | Выполнить №140,№141,№143 | 26.09 | |||||||
20 | Меньше или больше | Выполнить №168(а ,б), №169(а ,б),№170 | 27. | |||||||
21 | Меньше или больше | Выполнить №171,№173,№174 | 30.09 | |||||||
22 | Обобщающий урок по теме «Натуральные числа и шкалы». | Выполнить №172,№179,№180 | 1.10 | |||||||
23 | Контрольная работа №1 по теме «Натуральные числа и шкалы» | Выполнить №181 стр.32-33 прочитать | 2.10 | |||||||
24 | Сложение натуральных чисел. | Выполнить №220,№230,№231 | 3. | |||||||
25 | Свойства сложения. Сложение чисел на координатном луче. | Выполнить №235,№239,№240(а-в) | 4.10 | |||||||
26 | Разложение числа по разрядам. | Выполнить №232,№240(а-в),№237 | 7.10 | |||||||
27 | Решение текстовых задач на сложение. | Выполнить №234,№238,№236 | 8.10 | |||||||
28 | Вычитание натуральных чисел. | Выполнить №286,№288,№296(а,б) | 9. | |||||||
29 | Свойства вычитания натуральных чисел. | Выполнить №290,291,№296(в,г) | 10.10 | |||||||
30 | Решение текстовых задач на вычитание. | Выполнить №292,№293 | 14.10 | |||||||
31 | Использование действий сложения и вычитания при решении задач и уравнений. | Выполнить №295,ДМ №74 | 15.10 | |||||||
32 | Обобщающий урок по теме «Сложение и вычитание натуральных чисел». | Выполнить ДМ №76,№78,№79 | 16.10 | |||||||
33 | Контрольная работа № 2 по теме «Сложение и вычитание натуральных чисел» | Повторить правила | 17.10 | |||||||
34 | Числовые выражения. | Выполнить №328,№329,№330 | 18.10 | |||||||
35 | Числовые выражения Буквенные выражения | Выполнить №331,№332,№333 | 21.10 | |||||||
36 | Использование свойств сложения и вычитания для упрощения выражений. | Выполнить №334,№335(а,б) | 22.10 | |||||||
37 | Буквенная запись свойств сложения и вычитания | Выполнить №364,№365,№371(а) | 23.10 | |||||||
38 | Решение текстовых задач на применение буквенной записи. | Выполнить №367,№369,№371(б) | 24.10 | |||||||
39 | Уравнение. | Выполнить №395,397(б),403(а) | 25.10 | |||||||
40 | Уравнение. | Выполнить №396,№397(в),400. | 5.11 | |||||||
41 | Уравнение. | Выполнить №382(устно),№385. | 6.11 | |||||||
42 | Решение задач с помощью уравнений | Выполнить №398,№401,№403(б) | 7.11 | |||||||
43 | Решение задач на составление уравнений. | Выполнить №389, №388 | 8.11 | |||||||
44 | Обобщающий урок по теме «Числовые и буквенные выражения». | Выполнить ДМ К-3, в-3 | 9.11 | |||||||
45 | Контрольная работа № 3 по теме «Числовые и буквенные выражения» | Прочитать стр.65-66. | 12.11 | |||||||
46 | Умножение натуральных чисел | Выполнить №450,№442,№462(а,б) | 13.11 | |||||||
47 | Умножение и натуральных чисел и его свойства. | Выполнить №451,№453,№462(в,г) | 14.11 | |||||||
48 | Выполнение действий, применяя свойства умножения натуральных чисел | Выполнить №455,№454,№461(а) | 15. | |||||||
49 | Решение задач на умножение. | Выполнить №456,№457,№461(б) | 16.11 | |||||||
50 | Деление | Выполнить №517,№516,№519. | 19.11 | |||||||
51 | Деление и его свойства | Выполнить №518,№520,№522 | 20.11 | |||||||
52 | Решение комбинированных задач на применение арифметических действий. | Выполнить №521,№524 | 21. | |||||||
53 | Решение задач на деление. | Выполнить №525,№527 | 22.11 | |||||||
54 | Деление с остатком | Выполнить №550,№551,№555 | 23.11 | |||||||
55 | Решение задач на деление с остатком | Выполнить №553,№556(а) | 26.11 | |||||||
56 | Обобщающий урок по теме «Умножение и деление натуральных чисел» | Выполнить №504,№513 | 27. |
| ||||||
57 | Контрольная работа № 4 по теме «Умножение и деление натуральных чисел» | 28.11 | ||||||||
58 | Упрощение выражений. | Выполнить №612,№609,№616 | 29.11 | |||||||
59 | Применение распределительного свойства умножения. Упрощение выражений | Выполнить №610,№614(а,б) | 30.11 | |||||||
60 | Решение уравнений применяя свойства умножения. | Выполнить №613,№617,№625(а) | 3.12 | |||||||
61 | Решение уравнений на применение распределительного свойства умножения | Выполнить №614(в,г),№625(б) | 4.12 | |||||||
62 | Решение задач на составление уравнений. | Выполнить №619-621,№625(в) | 5.12 | |||||||
63 | Порядок выполнения действий | Выполнить №645,647(а-г) | 6.12 | |||||||
64 | Нахождение значений выражений, используя программу вычислений. | Выполнить №646,№647(д-з) | 7.12 | |||||||
65 | Порядок выполнения действий. Составление схемы вычислений. | Выполнить №648(а,б),№649,№650 | 10.12 | |||||||
66 | Степень числа. Квадрат и куб числа. | Выполнить №666,№670,№672 | 11.12 | |||||||
67 | Решение задач по теме «Квадрат и куб числа». | Выполнить №668(1стол)№670 | 12.12 | |||||||
68 | Обобщающий урок по теме «Упрощение выражений | Выполнить №668(2стол)№671 | 13. | |||||||
69 | Контрольная работа № 5 на тему «Упрощение выражений» | Прочитать стр 102 | 14.12 | |||||||
70 | Формулы. Нахождение значений выражений по формуле. | Выполнить №701,№704,№707(а,б) | 17.12 | |||||||
71 | Формулы. Вычисление по формуле неизвестных. | Выполнить №702,№705,№707(в,г) | 18.12 | |||||||
72 | Площадь. Формула площади прямоугольника | Выполнить №737,738,741 | 19. | |||||||
73 | Формула площади квадрата | Выполнить №740,№742,№744 | 20.12 | |||||||
74 | Единицы измерения площадей | Выполнить №779,№780,№781,№788 | 21.12 | |||||||
75 | Использование единиц измерения площадей при решении задач. | Выполнить №782,№783,№787 | 24.12 | |||||||
76 | Прямоугольный параллелепипед | Выполнить №811,№813,№817(а) | 25. | |||||||
77 | Решение задач на вычисление площади поверхности прямоугольного параллелепипеда. | Выполнить №812, №814, №816 | 26.12 | |||||||
78 | Объем. Объем прямоугольного параллелепипеда | Выполнить №840, №841, №842 | 27.12 | |||||||
79 | Объем куба. Нахождение объёмов параллелепипеда и куба. | Выполнить №843,№844,№846(а,б). | 28.12 | |||||||
80 | Обобщающий урок по теме «Формулы площади и объема» | Выполнить №846(в,г) №847, №848(д,е) | 14. | |||||||
81 | Контрольная работа № 6 на тему «Формулы площади и объема» | Прочитать стр.131-132 | 15.01 | |||||||
82 | . Окружность и круг. | Выполнить №874, №878(а-в),№881 | 16.01 | |||||||
83 | Окружность и круг | Выполнить №875,№878(г-е),№879 | 17.01 | |||||||
84 | Круговые шкалы | Выполнить №880, №881№,882, №883(а,в) | 18. | |||||||
85 | Доли. Обыкновенные дроби. | Выполнить №929,№930, №93№2,934(а) | 21.01 | |||||||
86 | Доли. Обыкновенные дроби. | Выполнить №931, №933, №934(б) | 22.01 | |||||||
87 | Решение задач на нахождение целого по его части и изображение чисел на координатной прямой. | Выполнить №937, №939 | 23.01 | |||||||
88 | Сравнение дробей | Выполнить №965, №967, №969 | 24. | |||||||
89 | Решение упражнений на сравнение дробей. | Выполнить №971, №960, №953 | 25.01 | |||||||
90 | Правильные и неправильные дроби | Выполнить №999, №1000, №1004(а,в) | 28.01 | |||||||
91 | Правильные и неправильные дроби. | Выполнить №1001, №1002, №1004(б,г) | 29.01 | |||||||
92 | Обобщающий урок по теме «Обыкновенные дроби». | Выполнить №996,№,994, №988 | 30. | |||||||
93 | Контрольная работа № 7 «Обыкновенные дроби» | 31.01 | ||||||||
94 | Сложение и вычитание дробей с одинаковыми знаменателями | Выполнить №1039, №1041(а-г),№1043, №1049(а) | 1.02 | |||||||
95 | Решение задач на сложение и вычитание дробей с одинаковыми знаменателями. | Выполнить №1040, №1041(д-з), №1042, №1046 | 4.02 | |||||||
96 | Деление и дроби | Выполнить №1076, №1077, №1078, №1083 | 5. | |||||||
97 | Решение задач на деление и дроби, деление суммы на число. | Выполнить №1079, №1080, №1081, №1082 | 6.02 | |||||||
98 | Смешанные числа | Выполнить №1109, №1110,1№112 | 7.02 | |||||||
99 | Выделение целой части из неправильной дроби. Представление смешанного числа в виде неправильной дроби | Выполнить №1111, №1113, №1114 | 8.02 | |||||||
100 | Сложение и вычитание смешанных чисел | Выполнить №1136(а-г) №1137, №1139 | 11. | |||||||
101 | Выполнение действий со смешанными числами. Вычитание дроби из натурального числа. | Выполнить №1136(д-з), №1138, №1140 | 12.02 | |||||||
102 | Решение задач на сложение и вычитание смешанных чисел. | Выполнить №1141, №1143 | 13.02 | |||||||
103 | Обобщающий урок по теме «Сложение и вычитание смешанных чисел» | Выполнить №1134, №1142 | 14.02 | |||||||
104 | Контрольная работа №8 «Сложение и вычитание смешанных чисел» | 15. | ||||||||
105 | Десятичная запись дробных чисел | Выполнить №1166(а) №1168(а), №1171(а) | 18.02 | |||||||
106 | Перевод обыкновенной дроби со знаменателем 10. 100, 1000 и т.д. в десятичную и наоборот | Выполнить №1166(б) №1168(б), №1171(б) | 19.02 | |||||||
107 | Сравнение десятичных дробей | Выполнить №1167, №1669, №1170, №1201(а-в) | 20.02 | |||||||
108 | Сравнение величин, содержащих десятичные дроби. | Выполнить №1201(г-е) №1203, №1205(а-в) | 21.02 | |||||||
109 | Сложение и вычитание десятичных дробей | Выполнить №1255, №1257 | 22.02 | |||||||
110 | Решение задач на сложение и вычитание десятичных дробей. | Выполнить №1256, №1258 | 25.02 | |||||||
111 | Решение примеров и задач на сложение и вычитание дробей. | Выполнить №1263, №1260, №1262 | 26. | |||||||
112 | Разложение числа по разрядам | Выполнить №1264, №1266 | 27.02 | |||||||
113 | Применение свойств сложения и вычитания при решении примеров. | Выполнить №1265, №1267 | 28.02 | |||||||
114 | Решение уравнений с десятичными дробями | Выполнить №1268, №1269 | 01.03 | |||||||
115 | Приближенное значение чисел. | Выполнить №1297(а) №1301, №1302 | 4.03 | |||||||
116 | Решение примеров и задач на округление чисел. | Выполнить №1297(б) №1303, №1304 | 5.03 | |||||||
117 | Обобщающий урок по теме «Сложение и вычитание десятичных дробей» | Выполнить №1298, №1299(а,в) | 6.03 | |||||||
118 | Контрольная работа № 9 «Сложение и вычитание десятичных дробей» | Прочитать стр 203 | 7. | |||||||
119 | Умножение десятичных дробей на натуральное число | Выполнить №1330, №1331 | 11.03 | |||||||
120 | Умножение десятичных дробей на 10, 100 и т.д. | Выполнить №1333, №1335 | 12.03 | |||||||
121 | Решение задач на применение умножения десятичных дробей на натуральные числа. | Выполнить №1332, №1336 | 13.03 | |||||||
122 | Деление десятичных дробей на натуральное число | Выполнить №1375(а-з),№1378 | 14. | |||||||
123 | Деление десятичных дробей на 10, 100 и т. д. | Выполнить №1375(и-м), №1380(а,б) | 15.03 | |||||||
124 | Задачи на деление. | Выполнить №1383, №1387 | 18.03 | |||||||
125 | Решение уравнений и задач с помощью уравнений. | Выполнить №1379(а-г), №1381, №1384 | 19.03 | |||||||
126 | Обобщающий урок по теме «Умножение и деление десятичных дробей на натуральное число» | Выполнить №1373, №1374, №1389(а,б) | 20. | |||||||
127 | Контрольная работа № 10 «Умножение и деление десятичных дробей на натуральное число» | 21.03 | ||||||||
128 | Умножение десятичных дробей | Выполнить №1431(а),№1432(а-е) | 22.03 | |||||||
129 | Умножение числа на 0,1, 0,01 и т.д. | Выполнить №1431(б,в),№1432(ж-м) | 1.04 | |||||||
130 | Решение задач на упрощение выражений | Выполнить №1439, №1441, №1440 | 2. | |||||||
131 | Решение задач на использование правила умножения. | Выполнить №1433-1436 | 3.04 | |||||||
132 | Деление на десятичную дробь | Выполнить №1483(а-д) №1484 | 4.04 | |||||||
133 | Деление числа на 0,1, 0,01 и т.д. | Выполнить №1483(е-и), №1485 | 5.04 | |||||||
134 | Применение правила деления на десятичную дробь | Выполнить №1486, №1487 | 8. | |||||||
135 | Решение задач на применение правила деления на десятичную дробь | Выполнить №1488,№1492(а,б) | 9.04 | |||||||
136 | Комбинированные задания на умножение и деление десятичных дробей. | Выполнить №1491, №1492(в,г) | 10.04 | |||||||
137 | Решение уравнений и задач с помощью уравнений. | Выполнить №1489, №1490,№1495 | 11.04 | |||||||
138 | Среднее арифметическое | Выполнить №1524(а) №1525, №1535(а) | 12. | |||||||
139 | Средняя скорость. | Выполнить №1526, №1527 | 15.04 | |||||||
140 | Решение задач на нахождение среднего арифметического и средней скорости. | Выполнить №1528-1530 | 16.04 | |||||||
141 | Обобщающий урок по теме «Умножение и деление десятичных дробей» | Выполнить №1531, №1532, №1534(а) | 17.04 | |||||||
142 | Контрольная работа № 11 «Умножение и деление десятичных дробей» | Прочитать стр 231 | 18. | |||||||
143 | Микрокалькулятор. Выполнение действий с помощью микрокалькулятора. | Выполнить №1557, №1558, №1560 | 19.04 | |||||||
144 | Проценты. Чтение, запись и нахождение процентов чисел и величин. | Выполнить №1598, №1599, №1612(а) | 22.04 | |||||||
145 | Решение задач на нахождение числа или величины по заданному проценту. | Выполнить №1600-1603 | 23. | |||||||
146 | Решение задач на нахождение процентов от числа. | Выполнить №1604-1607 | 24.04 | |||||||
147 | Решение задач на сложные проценты. | Выполнить №1608-1609,№1612(б) | 25.04 | |||||||
148 | Комбинированные задачи на проценты. | Выполнить №1611, №1632, №1633 | 26.04 | |||||||
149 | Обобщающий урок по теме «Проценты» | Выполнить №1635,№1637 | 29. | |||||||
150 | Контрольная работа № 12 «Проценты» | Прочитать стр 243 | 30.04 | |||||||
151 | Угол. Обозначение углов. Сравнение углов. | Выполнить №1638, №1639, №1642(а) | 2.05 | |||||||
152 | Прямой и развернутый угол. | Выполнить 1640, №1641, №1642(б) | 3.05 | |||||||
153 | Чертёжный треугольник. | Выполнить №1643, №1646 | 6.05 | |||||||
154 | Построение и обозначение углов. | Выполнить №1644, №1647 | 7.05 | |||||||
155 | Измерение углов. Транспортир | Выполнить №1682, №1689, №1690 | 8.05 | |||||||
156 | Построение углов с помощью транспортира. | Выполнить №1685, №1686 | 10.05 | |||||||
157 | Решение упражнений на построение и измерение углов. | Выполнить №1681, №1688 | 13.05 | |||||||
158 | Круговые диаграммы | Выполнить №1706, №1708, №1701 | 14.05 | |||||||
159 | Построение круговых диаграмм. | Выполнить №1707, №1709, №1702 | 15.05 | |||||||
160 | Решение задач по теме «Углы. Построение углов» | Выполнить №1710, №1704, №1703 | 16.05 | |||||||
161 | Решение задач по теме «Углы. | 17.05 | ||||||||
162 | Повторение. Арифметические действия с натуральными числами. | Выполнить №1814, №1815(а-в) | 20.05 | |||||||
163 | Повторение. Нахождение значения выражения | Выполнить №1815(г-е) | 21.05 | |||||||
164 | Повторение. Решение уравнений | Выполнить №1817, №1820, №1838 | 22.05 | |||||||
165 | Повторение. | Выполнить №1821, №1839, №1840 | 23.05 | |||||||
166 | Повторение. Упрощение выражений. | Выполнить №1836, №1834(в,г) | 24.05 | |||||||
167 | Итоговая контрольная работа. | 27.05 | ||||||||
168 | Решение задач на смекалку | 28.05 | ||||||||
169 | Решение занимательных задач. | 29.05 | ||||||||
170 | Решение занимательных задач. | 30.05 | ||||||||
171 | Итоговый урок. | 31.05 | ||||||||
ГДЗ по математике 5 класс Виленкин, Жохов
Категория: Математика 5 класс
Учебник
Н. Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд.
Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд.
Мнемозина
Здесь вы найдете полные ответы на задания популярного учебника математики Наума Яковлевича Виленкина для учащихся 5 класса. Решебник Виленкина поможет пропустившим уроки школьникам выполнять домашняя работу по ключевому предмету — математике. В свою очередь родители пятиклассников смогут проконтролировать правильность хода решения упражнений из учебника. ГДЗ ЛОЛ КЕК созданы только для проверки!
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495969798991001011021031041051061071081091101111121131141151161171181191201211221231241251261271281291301311321331341351361371381391401411421431441451461471481491501511521531541551561571581591601611621631641651661671681691701711721731741751761771781791801811821831841851861871881891901911921931941951961971981992002012022032042052062072082092102112122132142152162172182192202212222232242252262272282292302312322332342352362372382392402412422432442452462472482492502512522532542552562572582592602612622632642652662672682692702712722732742752762772782792802812822832842852862872882892902912922932942952962972982993003013023033043053063073083093103113123133143153163173183193203213223233243253263273283293303313323333343353363373383393403413423433443453463473483493503513523533543553563573583593603613623633643653663673683693703713723733743753763773783793803813823833843853863873883893903913923933943953963973983994004014024034044054064074084094104114124134144154164174184194204214224234244254264274284294304314324334344354364374384394404414424434444454464474484494504514524534544554564574584594604614624634644654664674684694704714724734744754764774784794804814824834844854864874884894904914924934944954964974984995005015025035045055065075085095105115125135145155165175185195205215225235245255265275285295305315325335345355365375385395405415425435445455465475485495505515525535545555565575585595605615625635645655665675685695705715725735745755765775785795805815825835845855865875885895905915925935945955965975985996006016026036046056066076086096106116126136146156166176186196206216226236246256266276286296306316326336346356366376386396406416426436446456466476486496506516526536546556566576586596606616626636646656666676686696706716726736746756766776786796806816826836846856866876886896906916926936946956966976986997007017027037047057067077087097107117127137147157167177187197207217227237247257267277287297307317327337347357367377387397407417427437447457467477487497507517527537547557567577587597607617627637647657667677687697707717727737747757767777787797807817827837847857867877887897907917927937947957967977987998008018028038048058068078088098108118128138148158168178188198208218228238248258268278288298308318328338348358368378388398408418428438448458468478488498508518528538548558568578588598608618628638648658668678688698708718728738748758768778788798808818828838848858868878888898908918928938948958968978988999009019029039049059069079089099109119129139149159169179189199209219229239249259269279289299309319329339349359369379389399409419429439449459469479489499509519529539549559569579589599609619629639649659669679689699709719729739749759769779789799809819829839849859869879889899909919929939949959969979989991000100110021003100410051006100710081009101010111012101310141015101610171018101910201021102210231024102510261027102810291030103110321033103410351036103710381039104010411042104310441045104610471048104910501051105210531054105510561057105810591060106110621063106410651066106710681069107010711072107310741075107610771078107910801081108210831084108510861087108810891090109110921093109410951096109710981099110011011102110311041105110611071108110911101111111211131114111511161117111811191120112111221123112411251126112711281129113011311132113311341135113611371138113911401141114211431144114511461147114811491150115111521153115411551156115711581159116011611162116311641165116611671168116911701171117211731174117511761177117811791180118111821183118411851186118711881189119011911192119311941195119611971198119912001201120212031204120512061207120812091210121112121213121412151216121712181219122012211222122312241225122612271228122912301231123212331234123512361237123812391240124112421243124412451246124712481249125012511252125312541255125612571258125912601261126212631264126512661267126812691270127112721273127412751276127712781279128012811282128312841285128612871288128912901291129212931294129512961297129812991300130113021303130413051306130713081309131013111312131313141315131613171318131913201321132213231324132513261327132813291330133113321333133413351336133713381339134013411342134313441345134613471348134913501351135213531354135513561357135813591360136113621363136413651366136713681369137013711372137313741375137613771378137913801381138213831384138513861387138813891390139113921393139413951396139713981399140014011402140314041405140614071408140914101411141214131414141514161417141814191420142114221423142414251426142714281429143014311432143314341435143614371438143914401441144214431444144514461447144814491450145114521453145414551456145714581459146014611462146314641465146614671468146914701471147214731474147514761477147814791480148114821483148414851486148714881489149014911492149314941495149614971498149915001501150215031504150515061507150815091510151115121513151415151516151715181519152015211522152315241525152615271528152915301531153215331534153515361537153815391540154115421543154415451546154715481549155015511552155315541555155615571558155915601561156215631564156515661567156815691570157115721573157415751576157715781579158015811582158315841585158615871588158915901591159215931594159515961597159815991600160116021603160416051606160716081609161016111612161316141615161616171618161916201621162216231624162516261627162816291630163116321633163416351636163716381639164016411642164316441645164616471648164916501651165216531654165516561657165816591660166116621663166416651666166716681669167016711672167316741675167616771678167916801681168216831684168516861687168816891690169116921693169416951696169716981699170017011702170317041705170617071708170917101711171217131714171517161717171817191720172117221723172417251726172717281729173017311732173317341735173617371738173917401741174217431744174517461747174817491750175117521753175417551756175717581759176017611762176317641765176617671768176917701771177217731774177517761777177817791780178117821783178417851786178717881789179017911792179317941795179617971798179918001801180218031804180518061807180818091810181118121813181418151816181718181819182018211822182318241825182618271828182918301831183218331834183518361837183818391840184118421843184418451846184718481849
← Предыдущая
1
Следующая →
Сегодня в большинстве школ используется учебник Математика 5 класс Виленкин, как одно из самых качественных изданий по освоению предмета. Предусматривается в первую очередь развитие мышления ребенка, которое закрепляется при применении полученных знаний на примерах. Специальные задания с высоким уровнем сложности помогут определить математический склад ума вашего ребенка.
Предусматривается в первую очередь развитие мышления ребенка, которое закрепляется при применении полученных знаний на примерах. Специальные задания с высоким уровнем сложности помогут определить математический склад ума вашего ребенка.
Ко всем задачам должны быть и ответы, поэтому и к данному учебнику они прилагаются. Решебник поможет детям полностью усвоить материал, разъясняя непонятные моменты, а родителям — не потерять авторитет в глазах ребенка, когда нужно что-то подсказать. Следите, чтобы ребенок не списывал ответы, а путем размышления и анализа сам постепенно приходил к нему.
Прежде всего представленные ответы по математике на 1 и 2 части учебника Виленкина лучше всего использовать родителям. Вам остается только проверить выполнение, что существенно сохранит время, если бы вы решали это сами. К тому же гораздо проще найти ошибку и указать на нее, если ученик затрудняется самостоятельно определить метод решения задачи.
Математика для пятиклассников – один из самых сложных предметов. На 5 год обучения значительно усложняется программа и ученики к этому оказываются не готовы. Поэтому онлайн решебник по математике за 5 класс Виленкина является эффективным способом повысить успеваемость, предлагая правильно выполненные домашние задания бесплатно. Сэкономьте время на домашку и подсмотрите верный ответ на lolkek.ru.
На 5 год обучения значительно усложняется программа и ученики к этому оказываются не готовы. Поэтому онлайн решебник по математике за 5 класс Виленкина является эффективным способом повысить успеваемость, предлагая правильно выполненные домашние задания бесплатно. Сэкономьте время на домашку и подсмотрите верный ответ на lolkek.ru.
Онлайн калькулятор
Отдых от уроков
ГДЗ по математике для 5 класса
ГДЗ по математике для 5 класса — ВиленкинПерейти к содержимому
Решебник предлагает готовые домашние задания к учебнику по математике для 5 класса. Обратившись к ГДЗ, взрослые и школьники забывают о мучительных часах, потраченных на домашнюю работу. Ребята не боятся проверки уроков в классе: с помощью готовых домашних заданий они могут выполнить упражнение любого уровня трудности правильно.
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495969798991001011021031041051061071081091101111121131141151161171181191201211221231241251261271281291301311321331341351361371381391401411421431441451461471481491501511521531541551561571581591601611621631641651661671681691701711721731741751761771781791801811821831841851861871881891901911921931941951961971981992002012022032042052062072082092102112122132142152162172182192202212222232242252262272282292302312322332342352362372382392402412422432442452462472482492502512522532542552562572582592602612622632642652662672682692702712722732742752762772782792802812822832842852862872882892902912922932942952962972982993003013023033043053063073083093103113123133143153163173183193203213223233243253263273283293303313323333343353363373383393403413423433443453463473483493503513523533543553563573583593603613623633643653663673683693703713723733743753763773783793803813823833843853863873883893903913923933943953963973983994004014024034044054064074084094104114124134144154164174184194204214224234244254264274284294304314324334344354364374384394404414424434444454464474484494504514524534544554564574584594604614624634644654664674684694704714724734744754764774784794804814824834844854864874884894904914924934944954964974984995005015025035045055065075085095105115125135145155165175185195205215225235245255265275285295305315325335345355365375385395405415425435445455465475485495505515525535545555565575585595605615625635645655665675685695705715725735745755765775785795805815825835845855865875885895905915925935945955965975985996006016026036046056066076086096106116126136146156166176186196206216226236246256266276286296306316326336346356366376386396406416426436446456466476486496506516526536546556566576586596606616626636646656666676686696706716726736746756766776786796806816826836846856866876886896906916926936946956966976986997007017027037047057067077087097107117127137147157167177187197207217227237247257267277287297307317327337347357367377387397407417427437447457467477487497507517527537547557567577587597607617627637647657667677687697707717727737747757767777787797807817827837847857867877887897907917927937947957967977987998008018028038048058068078088098108118128138148158168178188198208218228238248258268278288298308318328338348358368378388398408418428438448458468478488498508518528538548558568578588598608618628638648658668678688698708718728738748758768778788798808818828838848858868878888898908918928938948958968978988999009019029039049059069079089099109119129139149159169179189199209219229239249259269279289299309319329339349359369379389399409419429439449459469479489499509519529539549559569579589599609619629639649659669679689699709719729739749759769779789799809819829839849859869879889899909919929939949959969979989991000100110021003100410051006100710081009101010111012101310141015101610171018101910201021102210231024102510261027102810291030103110321033103410351036103710381039104010411042104310441045104610471048104910501051105210531054105510561057105810591060106110621063106410651066106710681069107010711072107310741075107610771078107910801081108210831084108510861087108810891090109110921093109410951096109710981099110011011102110311041105110611071108110911101111111211131114111511161117111811191120112111221123112411251126112711281129113011311132113311341135113611371138113911401141114211431144114511461147114811491150115111521153115411551156115711581159116011611162116311641165116611671168116911701171117211731174117511761177117811791180118111821183118411851186118711881189119011911192119311941195119611971198119912001201120212031204120512061207120812091210121112121213121412151216121712181219122012211222122312241225122612271228122912301231123212331234123512361237123812391240124112421243124412451246124712481249125012511252125312541255125612571258125912601261126212631264126512661267126812691270127112721273127412751276127712781279128012811282128312841285128612871288128912901291129212931294129512961297129812991300130113021303130413051306130713081309131013111312131313141315131613171318131913201321132213231324132513261327132813291330133113321333133413351336133713381339134013411342134313441345134613471348134913501351135213531354135513561357135813591360136113621363136413651366136713681369137013711372137313741375137613771378137913801381138213831384138513861387138813891390139113921393139413951396139713981399140014011402140314041405140614071408140914101411141214131414141514161417141814191420142114221423142414251426142714281429143014311432143314341435143614371438143914401441144214431444144514461447144814491450145114521453145414551456145714581459146014611462146314641465146614671468146914701471147214731474147514761477147814791480148114821483148414851486148714881489149014911492149314941495149614971498149915001501150215031504150515061507150815091510151115121513151415151516151715181519152015211522152315241525152615271528152915301531153215331534153515361537153815391540154115421543154415451546154715481549155015511552155315541555155615571558155915601561156215631564156515661567156815691570157115721573157415751576157715781579158015811582158315841585158615871588158915901591159215931594159515961597159815991600160116021603160416051606160716081609161016111612161316141615161616171618161916201621162216231624162516261627162816291630163116321633163416351636163716381639164016411642164316441645164616471648164916501651165216531654165516561657165816591660166116621663166416651666166716681669167016711672167316741675167616771678167916801681168216831684168516861687168816891690169116921693169416951696169716981699170017011702170317041705170617071708170917101711171217131714171517161717171817191720172117221723172417251726172717281729173017311732173317341735173617371738173917401741174217431744174517461747174817491750175117521753175417551756175717581759176017611762176317641765176617671768176917701771177217731774177517761777177817791780178117821783178417851786178717881789179017911792179317941795179617971798179918001801180218031804180518061807180818091810181118121813181418151816181718181819182018211822182318241825182618271828182918301831183218331834183518361837183818391840184118421843184418451846184718481849Психологи предупреждают родителей школьников, перешедших в 5 класс о необходимости быть более внимательными к ребятам, потому что переход из начальной школы в основную — кризисный период. Встретившись с новыми учителями, детям важно сразу показать полученные в начальной школе навыки, справиться с заданием, получить хорошую оценку. Но реальность не всегда совпадает с детскими желаниями. Не всем удается ответить на уроке правильно, еще больше проблем доставляют письменные упражнения и другие задания, особенно математике.
Встретившись с новыми учителями, детям важно сразу показать полученные в начальной школе навыки, справиться с заданием, получить хорошую оценку. Но реальность не всегда совпадает с детскими желаниями. Не всем удается ответить на уроке правильно, еще больше проблем доставляют письменные упражнения и другие задания, особенно математике.
Родителям важно поддерживать психологический комфорт для школьника, не оставлять его наедине с трудными задачами, которые встречаются в учебнике.
2022 gdz-polinkin.ru Все права защищены. Информация взята из открытых источников. По вопросам нарушения авторского права пишите на: [email protected]
Гдз решебник по математике 5 класс Виленкин ответы к учебнику
В ГДЗ по математике за 5 класс Виленкина Н. Я. содержатся готовые пошаговые решения всех заданий из учебника, благодаря которым можно не беспокоиться о плохих оценках за домашнюю работу. За правильность ответов сомневаться также не стоит, ведь авторы решебника – авторитетные ученые-математики. Нумерация упражнений полностью соответствует содержанию учебника. Все задания представлены в соответствии с требованиями средней школы к оформлению работ.
Нумерация упражнений полностью соответствует содержанию учебника. Все задания представлены в соответствии с требованиями средней школы к оформлению работ.
5 класс – переломный момент для школьников и их родителей. Начальная школа уже позади, и теперь детям предстоит углубить свои знания по математике. С каждым годом школьная программа становится все более сложной и объёмной. Это сильно сказывается на успеваемости и самочувствии детей. Готовые домашние задания – это отличный способ быть увереннее в своих оценках и экономить время.
Начальная школа уже позади, и теперь детям предстоит углубить свои знания по математике. С каждым годом школьная программа становится все более сложной и объёмной. Это сильно сказывается на успеваемости и самочувствии детей. Готовые домашние задания – это отличный способ быть увереннее в своих оценках и экономить время.
Наиболее популярным учебным пособием по математике в пятом классе является учебник Виленкина Н. Я., Жохова В. И. и Чеснокова А. С. Учебник был создан в 2013 году и делится на две главы:
- Натуральные числа
- Дробные числа.
Этот учебник зарекомендовал себя как лучший в своем роде, так как был издан популярнейшими учеными России. Авторы понимают, что у школьников и их родителей могут возникнуть проблемы с выполнением домашней работы, поэтому создали эффективную подмогу – решебник по математике за 5 класс по учебнику Виленкина Н. Я. Пошаговые решения будут полезны не только детям, но и их родителям.
В чем преимущества использования ГДЗ?
- Решебники развивают у школьников навык поиска и анализа информации;
- Позволяют детям проводить качественную проверку задания перед сдачей учителю;
- Помогают экономить родителям время на проверке домашней работы детей;
- С их помощью можно потренироваться на аналогичных заданиях, чтобы еще раз закрепить пройденную тему или подготовиться к проверочным работам.

- Пользуясь ГДЗ, родители могут освежить знания в своей голове и помочь ребенку рассуждать в направлении верного решения.
Используя ответы к учебнику по математике 5 класс Виленкина пятиклассники смогут самостоятельно разбираться в пройденных темах и закреплять свои знания, готовиться к проверочным работам или просто оттачивать навык решения похожих заданий. Родители будут тратить намного меньше времени на проверку работы. С помощью решебников можно избежать необходимости услуг репетиторов, ведь родители смогут сами объяснить ребенку любую тему.
Математика 5 класс
SCIRP Открытый доступ
Издательство научных исследований
Журналы от A до Z
Журналы по темам
- Биомедицинские и биологические науки.

- Бизнес и экономика
- Химия и материаловедение.
- Информатика. и общ.
- Науки о Земле и окружающей среде.
- Машиностроение
- Медицина и здравоохранение
- Физика и математика
- Социальные науки. и гуманитарные науки
Журналы по тематике
- Биомедицина и науки о жизни
- Бизнес и экономика
- Химия и материаловедение
- Информатика и связь
- Науки о Земле и окружающей среде
- Машиностроение
- Медицина и здравоохранение
- Физика и математика
- Социальные и гуманитарные науки
Публикация у нас
- Представление статьи
- Информация для авторов
- Ресурсы для экспертной оценки
- Открытые специальные выпуски
- Заявление об открытом доступе
- Часто задаваемые вопросы
Публикуйте у нас
- Представление статьи
- Информация для авторов
- Ресурсы для экспертной оценки
- Открытые специальные выпуски
- Заявление об открытом доступе
- Часто задаваемые вопросы
Подпишитесь на SCIRP
Свяжитесь с нами
клиент@scirp. org org | |
| +86 18163351462 (WhatsApp) | |
| 1655362766 | |
| Публикация бумаги WeChat |
| Недавно опубликованные статьи |
| Недавно опубликованные статьи |
Переломы при болезни Паркинсона ()
Мегана Анагани, Терри Ороси
Здоровье Том 14 № 9, 20 сентября 2022 г.

DOI: 10.4236/здоровье.2022.149070 5 загрузок 24 просмотров
Челюстно-лицевая травма в Дапаонге в Того: около 208 случаев ()
Тамасси Бертран Эссобию, Салиу Адам, Мишель Фабьен Даргани, Солим Узиэль Розелин Боко, Жереми Ананиджин, Александр Палиссам Кехеу, Мохамед Исса, Харефетегена Бисса
Journal of Biosciences and Medicines Vol.10 No.9, 20 сентября 2022 г.
DOI: 10.4236/jbm.2022.109012 3 загрузки 17 просмотров
Дифференциальные эффекты хронического воздействия алкоголя и сигаретного дыма на когнитивно-поведенческую дисфункцию у крыс Long Evans()
Эмине Б.
 Ялчин, Бушра Нур Деликкая, Уильям Пелит, Минг Тонг, Сюзанна М. Де Ла Монте, Шарон Раундс
Ялчин, Бушра Нур Деликкая, Уильям Пелит, Минг Тонг, Сюзанна М. Де Ла Монте, Шарон РаундсЖурнал поведенческих наук и исследований мозга Том 12 № 9, 20 сентября 2022 г.
DOI: 10.4236/jbbs.2022.129024 3 загрузки 20 просмотров
Влияние имбирной муки ( Zingiber officinale ), связанной с Desmodium intortum и/или Stylosanthes guianensis , на показатели роста кролика ( Oryctolagus cuniculus ) в Камеруне ()
Нумедем Фуэгап Джодель Ганди, Мигу Эмиль, Чоффо Эрве, Эбиле Даян Агва, Ямси Седрик, Мучили Мама, Вемо Бертин Нарсисс, Фонтех Флоренс Аньянгве Ангаба
Открытый журнал зоотехники Том 12 № 4, 20 сентября 2022 г.
DOI: 10.
 4236/ojas.2022.124047
3 загрузки 15 просмотров
4236/ojas.2022.124047
3 загрузки 15 просмотровАналитические решения определенных интегралов для комбинаций функций Лежандра, Бесселя и тригонометрических функций, встречающихся в задачах распространения и рассеяния в сферических координатах()
Фархад Азади Намин
Journal of Applied Mathematics and Physics Vol.10 No.9, 20 сентября 2022 г.
DOI: 10.4236/jamp.2022.109179 2 загрузки 15 просмотров
Оценка физической подготовленности больных сахарным диабетом 2 типа: необходимость назначения адаптированной физической активности ()
Венд Пагнанде Абрахам Герман Багбила, Лиевин Энетт, Йемпабу Санья, Уэдраого Пингдевенде Виктор, Кэрол Жильберте Кьелем, Тене Марселин Ямеого, Самдпавинде Макайр Уэдраого, Юссуфу Джозеф Драбо, Седрик Фагур
Открытый журнал внутренних болезней Том 12 № 3, 20 сентября 2022 г.

DOI: 10.4236/ojim.2022.123018 2 загрузки 19 просмотров
Подпишитесь на SCIRP
Свяжитесь с нами
| клиент@scirp.org | |
| +86 18163351462 (WhatsApp) | |
| 1655362766 | |
| Публикация бумаги WeChat |
Бесплатные информационные бюллетени SCIRP
Copyright © 2006-2022 Scientific Research Publishing Inc. Все права защищены.
верхнийДоктор В.
 М. Уэйд — биографические данные Доктор В. М. Уэйд — биографические данные
БИОГРАФИЯ \ РЕЗЮМЕ
М. Уэйд — биографические данные Доктор В. М. Уэйд — биографические данные
БИОГРАФИЯ \ РЕЗЮМЕИМЯ: Уильям Р. Уэйд
ДАТА И МЕСТО РОЖДЕНИЯ: 28 октября 1943 г., Лос-Анджелес, Калифорния
ЗАНЯТОСТЬ:
2012-настоящее время, заведующий кафедрой математики и компьютерных наук, Университет Биола, Ла-Мирада, Калифорния
1978-2011, Профессор Университета
Теннесси
1994–2003 гг., Профессор и доцент
Глава Университета Теннесси
1972-1978, доцент,
Университет Теннесси
1968-1972, доцент,
Университет Теннесси
6/1968-8/1968, компьютерный аналитик, Aerospace Corp. (SBO)
1966–1968, стипендиат NDEA
1965-1966, Выпуск. Ассистент преподавателя, Univ.
Калифорнии (Риверсайд)
КОНСУЛЬТАЦИЯ:
декабрь 1970 г. — август 1976 г., Окриджская национальная лаборатория.
июнь 1969 г. — ноябрь 1970 г., газодиффузионный завод, Ок-Ридж.
ПУБЛИКАЦИИ:
1. Уильям Р. Уэйд, «Теорема единственности для рядов Хаара и Уолша», Транс. амер. Мат. Соц., Том. 141: 187-194, 1969.
2. _____, «Теория единственности суммируемых по Чезаро рядов Хаара», Герцог Математика. Дж., Том. 38: 211-227, 1971.
3. _____, «Суммирование замкнутых U-множеств для рядов Уолша», Proc. амер. Мат. Соц., Том. 29: 123-125, 1971.
4. _____, «Единственность рядов Хаара, которые являются (C, 1) суммируемыми к интегрируемым функциям Данжуа, Trans. Amer. Math. Soc., Vol. 176: 489-498, 1973.
5. _____, «Теорема об ограниченной сходимости», Амер. Мат. Ежемесячно, Том. 81: 387-389, 1974.
6. _____, «Ряды Хаара и Уолша интегрируемых функций Перрона», J. Ind. Math. Соц., Том. 38, 19-35, 1974.
7. _____, «Множества уникальности и -емкости на Группа 2, Trans. Amer. Math. Soc., Vol. 208: 309-315, 1975.
8. _____, «Рост ряда Хаара на двоично-рациональных числах», Proc. амер. Мат. Соц., Том. 50: 198-201, 1975.
амер. Мат. Соц., Том. 50: 198-201, 1975.
9. _____, «Условия роста и уникальность рядов Уолша», Мичиган. Мат. Дж., Том. 24: 153–155, 1977.
10. _____, «Наборы уникальности для рядов Хаара», Acta Math. акад. науч. Венг., Том. 30: 265-281, 1977.
11. ____ и Дэвид С. Харрис, «Множества расхождения на группе 2, Trans. Amer. Soc., Vol. 240: 385-392, 1978.
12. _____, «H(n)-множества для группы целых чисел поле p-серии», Proceedings of Symposia in Pure Mathematics, Vol. 35: 325-327, 1979.
13. _____, «Множества единственности для группы целых чисел р-серии поле», Canadian J. of Math., Vol. 31: 858-866, 1979.
14. _____, и В.А. Скворцов, «Обобщения некоторых результатов относительно рядов Уолша и диадической производной,» Anal. Math., Vol. 5: 249-255, 1979 г.
15. _____, «Ряды Уолша и рост функций на вложенных диадических интервалах», Журнал Ind. Math. Соц., Том. 43: 1-11, 1979.
16. _____, и Г.Е. Липпман, «Псевдофункции и уникальность». о группе целых чисел поля p-серии, Acta. Math. Acad. Sci. Hung.,
Том. 35: 1-12, 1980.
о группе целых чисел поля p-серии, Acta. Math. Acad. Sci. Hung.,
Том. 35: 1-12, 1980.
17. _____, «Единственность рядов Уолша, удовлетворяющих среднему условие роста», SIAM Journal of Mathematical Analysis, Vol. 11: 933-977, 1980.
18. _____ и К.Х. Пауэлл, «Почленная диадическая дифференциация». Канада. Журнал математики, Vol. 33: 247–256, 1981.
19. _____, «Применение уникальности рядов Уолша к выборке теория», 4. Коллоквиум Ахенера, «Теория и приложения обработки сигналов: 64-68, 1981.
20. _____, «Локально постоянные диадические производные», Пер. Мат. Венгрия., Том. 13: 71-74, 1982.
21. _____, и К. Йонеда, «Единственность и квазимеры на группа целых чисел поля p-серии», Proc. Amer. Math. Soc., Vol. 84: 202-206, 1982.
22. _____, «Последние разработки в области теории рядов Уолша», междунар. Дж. Матем. Том. 5, № 4, 625-673, 1982.
23. _____, «Неравенства Lp для рядов Уолша, 0
24. _____, «Коэффициенты Уолша-Фурье и локально постоянные функций», Proc. Amer. Math. Soc., Vol. 87(3): 434-438, 1983.
25. _____, «Распад рядов Уолша и диадическая дифференциация», Транс. амер. Мат. Соц., Том. 277(1): 413-420, 1983.
26. _____, «Оценка роста частичных сумм Чезаро множественные ряды Уолша-Фурье », Colloq. Math. Soc. Janos Bolyai, Vol. 49: 975-991, 1985.
27. _____, «Последние разработки в теории рядов Хаара», Коллоквиум Математикум, Том. 52: 213–238, 1986.
28. _____, «Единый подход к уникальности Уолша Series and Haar Series, Proc. Amer. Math. Soc., Vol. 99: 61-65, 1987.
29. _____, и Ф. Шипп, «Фундаментальная теорема диадического исчисления». для единичной площади », Прикладной анализ, том 34: 203–218, 19.89.
30. _____, Ф. Мориц и Ф. Шипп, «Об интегрируемости
рядов двойного Уолша со специальными коэффициентами», Michigan Math. J. Vol.
37:191-201, 1990.
31. _____, Производная Гиббса и почленная дифференциация из серии Уолша, «Теория и приложения производных Гиббса», П.Л. Батцер и Р. С. Станкович, редакторы, Math. Инст. Белград (1990), 59-72.
32. _____, и С.Х. Пауэлл, Термин за термином Dyadic Дифференциация быстро сходящихся рядов Уолша, J. Approx. Теория и заявл. Том 7: 20-40, 1991.
33. _____, Ф. Шипп и П. Саймон, «Серия Уолша: введение к диадическому гармоническому анализу», A. Hilgar Publishing Ltd. (Институт физики), Бристоль и Нью-Йорк, 1990 [561-страничная исследовательская монография, исчерпывающая масштаб, полный новых идей и лучших методов, чем те, которые были доступны ранее в литература]
34. _____, Ф. Мориц и Ф. Шипп, «Суммируемость по Чезаро двойного Уолша-Фурье Серия», Trans. Amer. Math. Soc., Vol 329: 131–140, 19.92.
35. _____, Обзор «Рядов и преобразований Уолша», Bull. амер. Мат. Соц., Том. 26: 348-359, 1992.
36. _____, (совместно с Ф. Шиппом), «Сходимость по норме и суммируемость Фурье
Ряды по некоторым системам продуктов», Теория приближения,
Том. 138: 437-452, Марсель Деккер, Инк., 1992.
138: 437-452, Марсель Деккер, Инк., 1992.
37. _____, (совместно с Г. Э. Альбертом) «Системы Хаара для компактных геометрий» Акта Математика. Повесили. Том 61: 21–41, 1993.
38. _____, (совместно с К. Пауэллом), «Множества Пэли и термовая диадическая дифференциация из серии Уолша » Acta Math. Hung. Vol 62: 89-96, 1993.
39. _____, Ряды Виленкина-Фурье и приближение, Сб. Мат. соц. Дж. Боляи Том 58: 699-734, 1994.
40. _____, (совместно с С. Фридли), Скорость сходимости и диадическая дифференцируемость серии Уолша, JD Anal. Мат. Том 62: 287-305, 1994.
41. _____, «Введение в анализ», 565 стр., Prentice Hall, 1995.
42. _____, Система Уолша для полярных координат, Computers Math. Прил., Том 30:221-227, 1995.
43. _____, (совместно с Дж. Татеокой), «О сильной аппроксимации и суммируемости» Чезаро Минса о пространствах Бесова над полем 2-й серии, Acta Sci. Math. науч. (Сегед), Том 60: 685-703, 1995.
44. _____, (совместно с Ф. Шиппом), «Преобразования нормированных полей»,
Янус Паннон. ун-т Печ, 1-175, 1995.
Шиппом), «Преобразования нормированных полей»,
Янус Паннон. ун-т Печ, 1-175, 1995.
45. _____, «Гармонический анализ на группах Виленкина», Анализ Фурье и приближение, N.A.I. Опубликовано: 339-370, 1996 г.
46. _____, Диадический гармонический анализ, Contemporary Math., Том 208: 313-350, 1997.
47. _____,Функции Уолша и ряды Уолша, Математическая энциклопедия, Доп. I, Kluwer Publishing Co., с. 484 1997.
48. _____, (совместно с Ф. Шиппом), «Быстрые преобразования Фурье в бинарных полях», прибл. Теория и прил. Том. 14 (1998), 91-100.
49. _____, Рост средних Чезаро двойных рядов Виленкина-Фурье неограниченного типа. Анализ Фурье, Биркхаузер Базель, 41-50, 1999.
50. _____, Оценки суммируемости двойных рядов Виленкина–Фурье, Мат. Паннон. Том 10, 67-75, 1999.
51. _____, (совместно с С. Перрином), Множества единственности для групп Виленкина, Акта. науч. Мат. (Сегед) Том. 66: 631-644, 1999.
52. _____, (совместно с Ф. Шиппом), Преобразования Зака в бинарных полях, Журнал
прибл. Теория Том 101: 182-195, 1999.
Шиппом), Преобразования Зака в бинарных полях, Журнал
прибл. Теория Том 101: 182-195, 1999.
53. _____, Введение в анализ, 2-е изд. Прентис Холл, 2000.
54. _____, (совместно с П.У. Уэйдом), Рекурсии, производящие пифагорейские тройки, математика колледжа. Дж. Том 31: 98-101, 2000.
55. _____, (совместно с Ф. Шиппом), Преобразования Меллина в двоичных полях Применяются и вычислительный гармонический анализ. Том 9: 54-71, 2001.
56. _____, (совместно с Ф. Моричем), Аналог теоремы Ф. Лукача для двойной ряд Уолша, Acta Math. Повесили. Том 95: 323-336, 2002.
57. _____, Множества единственности для мартингальных подпоследовательностей рядов Виленкина, Коллок. Мат. соц. Дж. Боляи: 433-441, 2002.
58. _____, Тауберова теорема для рядов Виленкина, Proc. амер. Мат. соц., Том. 131: 2877-2881, 2003.
59. _____, (совместно с Д. Даниэлем), Уникальность суммируемого по Чезаро двойного ряда Уолша,
Анальный. Мат. Том. 30: 33-46, 2004.
Мат. Том. 30: 33-46, 2004.
60. _____, Введение в анализ, 3-е изд. Прентис Холл, 2004.
61. _____, Единственность почти всюду сходящегося ряда Виленкина, Канада Мат. Бюлл., Том. 47, 475-480, 2004.
62. _____, Обзор «Математического анализа», SIAM Review, Vol. 46, 766-770, 2005
63. ______»Уникальность ряда Уолша, суммируемого с квадратом», Acta. науч. Мат. (Сегед), Том 72: 147-157, 2006.
64. ______ «Диалог между калькулятором и алгеброй», учитель математики. (NCTM), Том 99:391-393, 2006.
65. _____, (совместно с Ф. Моричем), О проблеме единственности констант тригонометрического момента, Acta Math. Венгрия. Vol 111, 313-324, 2007.
66. _____, Введение в анализ, 4-е изд., Prentice Hall, 2009
67. _____, Сходимость фильтрованных рядов Уолша-Фурье, Annales Univ. науч. Будапешт., разд. Комп. Том 33, 365-375, 2010
68. _____, (совместно с К. Пауэллом), «Частичное упорядочение, генерирующее отфильтрованные ряды Уолша», Acta Math. Hung. Том 140, 162-168, 2013.
Hung. Том 140, 162-168, 2013.
69. ____, Почленная диадическая дифференциация рядов Уолша, глава 9, в «Диадическом анализе Уолша с 1924 года», Atlantis Press, Париж, 2015 г., стр. 347–358.
последнее обновление: ноябрь 2015 г.
Фа
CZ — Чешская цифровая математическая библиотека: О средних Нёрлунда ряда Виленкина-Фурье
[1] Благота, И.: О неравенстве по норме относительно виленкиноподобных систем . Акта Математика. Повесили. 89 (2000), 15-27. DOI 10.1023/A:1026769207159 | MR 1
5 | Zbl 0973.42020[2] Благота, И.: Связь между ядрами Дирихле относительно виленкиноподобных систем . Акта акад. Педагог. Агриенсис, Секта. Мат. (NS) 22 (1994), 109-114. Zbl 0882.42017
[3] Благота И., Гат Г.: Суммируемость по норме логарифмических средних Нёрлунда на неограниченных группах Виленкина . Анальный. Теория прил. 24 (2008), 1-17. DOI 10.1007/s10496-008-0001-z | МР 2422455 | Zbl 1164.42022
[4] Благота И. , Тефнадзе Г.: О {$(C,\alpha)$}-средних по системе Уолша . Анальный. Мат. 40 (2014), 161-174. DOI 10.1007/s10476-014-0301-9 | МР 3240221 | Zbl 1313.42083
, Тефнадзе Г.: О {$(C,\alpha)$}-средних по системе Уолша . Анальный. Мат. 40 (2014), 161-174. DOI 10.1007/s10476-014-0301-9 | МР 3240221 | Zbl 1313.42083
[5] Благота И., Тефнадзе Г.: Теорема сильной сходимости для средних Виленкина-Фейера . Опубл. Мат. Дебрецен 85 (2014), 181-196. DOI 10.5486/PMD.2014.5896 | МР 3231514 91$}-функции на обобщенной группе Уолша-Пэли . проц. Являюсь. Мат. соц. 77 (1979), 111-116. MR 0539641
[7] G{á}t, G.: Средние Чезаро интегрируемых функций по неограниченным системам Виленкина . Дж. Прибл. Теория 124 (2003), 25-43. DOI 10.1016/S0021-9045(03)00075-3 | МР 2010779 | Zbl 1032.43003
[8] G{á}t, G.: Исследования некоторых операторов по системе Виленкина . Акта Математика. Повесили. 61 (1993), 131-149. DOI 10.1007/BF01872107 | MR 1200968 | Zbl 0805.42019
[9] Гат Г., Гогинава Ю.: Сходимость почти всюду {$(C,\alpha)$}-средних квадратичных частичных сумм двойных рядов Виленкина-Фурье . Грузинская математика. Журнал 13 (2006), 447-462. МР 2271060 | Zbl 1107.42006
Грузинская математика. Журнал 13 (2006), 447-462. МР 2271060 | Zbl 1107.42006
[10] Гат Г., Гогинава У.: Равномерная и {$L$}-сходимость логарифмических средних рядов Уолша-Фурье . Акта Математика. син., англ. сер. 22 (2006), 497-506. DOI 10.1007/s10114-005-0648-8 | MR 2214371
[11] Гат Г., Надь К.: О логарифмической суммируемости рядов Фурье . Грузинская математика. Журнал 18 (2011), 237-248. MR 2805978 | Zbl 1221.42049
[12] Гогинава, У.: Неравенство слабого типа для максимального оператора средних {$(C,\alpha)$} двумерных рядов Уолша-Фурье . Анальный. Мат. 36 (2010), 1-31. DOI 10.1007/s10476-010-0101-9 | MR 2606574
[13] Гогинава, У.: Максимальные операторы средних Фейера-Уолша . Acta Sci. Мат. 74 (2008), 615-624. MR 2487936 | Збл 1199.42127
[14] Гогинава У.: Максимальный оператор средних Марцинкевича-Фейера {$d$}-мерного ряда Уолша-Фурье . Восток Дж. Прибл. 12 (2006), 295-302. MR 2252557
[15] Гогинава, У. : Максимальный оператор средних {$(C,\alpha)$} ряда Уолша-Фурье . Анна. ун-т науч. Будапешт. Роландо Этвёш, Sect. вычисл. 26 (2006), 127-135. MR 2388683 | Zbl 1121.42020
: Максимальный оператор средних {$(C,\alpha)$} ряда Уолша-Фурье . Анна. ун-т науч. Будапешт. Роландо Этвёш, Sect. вычисл. 26 (2006), 127-135. MR 2388683 | Zbl 1121.42020
[16] Гогинава, У.: Сходимость почти всюду подпоследовательности логарифмических средних рядов Уолша-Фурье . Акта Математика. акад. Педагог. Нихази. (NS) (только в электронном виде) 21 (2005), 169-175. МР 2162613 | Zbl 1093.42018
[17] Гогинава, Ю.: Об аппроксимативных свойствах чезаро-средних отрицательного порядка рядов Уолша-Фурье . Дж. Прибл. Теория 115 (2002), 9-20. DOI 10.1006/jath.2001.3632 | MR 1888974 | Zbl 0998.42018
[18] Moore, CN: Суммируемые ряды и коэффициенты сходимости . Dover Publications, Нью-Йорк (1966). МР 0201863 | Збл 0142.30704
[19] Мориц Ф., Сиддики А.Х.: Аппроксимация средними Нёрлунда ряда Уолша-Фурье . Дж. Прибл. Теория 70 (1992), 375-389. DOI 10.1016/0021-9045(92)
[20] Nagy, K. : Аппроксимация средними Нёрлунда двойных рядов Уолша-Фурье для липшицевых функций . Мат. Неравный. заявл. 15 (2012), 301-322. МР 2962234 | Zbl 1243.42038
: Аппроксимация средними Нёрлунда двойных рядов Уолша-Фурье для липшицевых функций . Мат. Неравный. заявл. 15 (2012), 301-322. МР 2962234 | Zbl 1243.42038
[21] Nagy, K.: Аппроксимация средними Нёрлунда ряда Уолша-Качмарца-Фурье . Грузинская математика. Журнал 18 (2011), 147-162. MR 2787349 | Zbl 1210.42043
[22] Nagy, K.: Аппроксимация средними Чезаро отрицательного порядка ряда Уолша-Качмарца-Фурье . Восток Дж. Прибл. 16 (2010), 297-311. MR 2789336 | Zbl 1216.42006
[23] Nagy, K.: Аппроксимация средними Нёрлунда квадратичных частичных сумм двойных рядов Уолша-Фурье . Анальный. Мат. 36 (2010), 299-319. DOI 10.1007/s10476-010-0404-x | MR 2738323 | Zbl 1240.42133
[24] Пал, Дж., Симон, П.: Об одном обобщении понятия производной . Акта Математика. акад. науч. Повесили. 29 (1977), 155-164. DOI 10.1007/BF01896477 | МР 0450884 | Zbl 0345.42011
[25] Schipp, F.: Перестановки рядов в системе Уолша . Мат. Notes 18 (1976), 701-706 перевод с \kern 3sp Матем. заметки 18 (1975), 193-201. MR 03
Notes 18 (1976), 701-706 перевод с \kern 3sp Матем. заметки 18 (1975), 193-201. MR 03
[26] Simon, P.: Суммируемость по Чезаро относительно двухпараметрических систем Уолша . Монац. Мат. 131 (2000), 321-334. DOI 10.1007/s006050070004 | МР 1813992
[27] Simon, P.: Теорема сильной сходимости для рядов Виленкина-Фурье . Дж. Матем. Анальный. заявл. 245 (2000), 52-68. DOI 10.1006/jmaa.2000.6732 | MR 1756576 | Zbl 0987.42022
[28] Simon, P.: Исследования по системе Виленкина . Анна. ун-т науч. Будапешт. Роландо Этвёш, Sect. Мат. 27 (1984), 87-101. МР 0823096 | Zbl 0586.43001
[29] Simon, P., Weisz, F.: Слабые неравенства для суммирования по Чезаро и Риссу ряда Уолша-Фурье . Дж. Прибл. Теория 151 (2008), 1-19. DOI 10.1016/j.jat.2007.05.004 | MR 2403893 | Zbl 1143.42032
[30] Тефнадзе Г.: О максимальных операторах логарифмических средних Рисса ряда Виленкина-Фурье . Стад. науч. Мат. Повесили. 51 (2014), 105-120. MR 3188506 | Zbl 1299.42098
MR 3188506 | Zbl 1299.42098
[31] Тефнадзе Г.: О частных суммах ряда Виленкина-Фурье . Дж. Контемп. Мат. Анальный. 49 23-32 русский (2014). DOI 10.3103/S1068362314010038 | MR 3237573
[32] Тефнадзе Г.: Сильные теоремы сходимости для средних Уолша-Фейера . Акта Математика. Повесили. 142 (2014), 244-259. DOI 10.1007/s10474-013-0361-5 | MR 3158862 | Zbl 1313.42086
[33] Тефнадзе Г.: О максимальных операторах средних Виленкина-Фейера на пространствах Харди . Мат. Неравный. заявл. 16 (2013), 301-312. MR 3060398 | Zbl 1263.42008
[34] Тефнадзе Г.: О максимальных операторах средних Виленкина-Фейера . Турок. Дж. Матем. 37 (2013), 308-318. MR 3040854 | Збл 1278.42037
[35] Тефнадзе Г.: Замечание о коэффициентах Фурье и частных суммах рядов Виленкина-Фурье . Акта Математика. акад. Педагог. Нихази. (NS) (только в электронном виде) 28 (2012), 167-176. MR 3048092 | Zbl 1289.42084
[36] Тефнадзе Г.: Средства Фейера ряда Виленкина-Фурье . Стад. науч. Мат. Повесили. 49 (2012), 79-90. MR 3059789 | Zbl 1265.42099
Стад. науч. Мат. Повесили. 49 (2012), 79-90. MR 3059789 | Zbl 1265.42099
[37] Тефнадзе Г.: Максимальные операторы логарифмических средних одномерных рядов Виленкина-Фурье . Акта Математика. акад. Педагог. Нихази. (NS) (только в электронном виде) 27 (2011), 245-256. MR 2880697 | Zbl 1265.42100
[38] Виленкин, Н. Дж.: Об одном классе полных ортонормированных систем . Являюсь. Мат. соц. Перевод сер. (2), 28 (1963), 1-35 перевод с \kern 3sp Изв. акад. АН СССР, сер. Мат. 11 (1947), 363-400. МР 0154042 | Zbl 0036.35601
[39] Weisz, F.: $\theta$-суммируемость ряда Фурье . Акта Математика. Повесили. 103 (2004), 139-176. DOI 10.1023/B:AMHU.0000028241.87331.c5 | MR 2047878 | Збл 1060.42021
[40] Weisz, F.: {$(C,\alpha)$} суммируемость рядов Уолша-Фурье . Анальный. Мат. 27 (2001), 141-155. DOI 10.1023/A:1014364010470 | MR 1834858 | Zbl 0992.42016
[41] Weisz, F.: Суммирование по Чезаро одномерных и двумерных рядов Уолша-Фурье . Анальный. Мат. 22 (1996), 229-242. DOI 10.1007/BF02205221 | MR 1627638 | Zbl 0866.42020
Анальный. Мат. 22 (1996), 229-242. DOI 10.1007/BF02205221 | MR 1627638 | Zbl 0866.42020
[42] Weisz, F.: Мартингальные пространства Харди и их приложения в анализе Фурье . Конспект лекций по математике 1568 Springer, Берлин (1994). DOI 10.1007/BFb0073448 | МР 1320508 | Zbl 0796.60049
На средних Нёрлунда ряда Виленкина-Фурье
Иштван Благота; Ларс-Эрик Перссон; Георгий Тефнадзе
Чехословацкий математический журнал (2015)
- Том: 65, выпуск: 4, стр. 983-1002
- ISSN: 0011-4642
Доступ к полной статье
topДоступ к полному тексту
Полный (PDF)
Аннотация
Топ Доказываются и обсуждаются некоторые новые неравенства типа (Hp,Lp) взвешенных максимальных операторов средних Виленкина-Нёрлунда с невозрастающими коэффициентами {qk:k≥0}. Эти результаты являются наилучшими в определенном смысле. В качестве приложений указываются некоторые известные, а также новые результаты теории сильной сходимости таких средних Виленкина-Нёрлунда. Для достижения наших основных целей мы также докажем некоторые новые оценки, представляющие независимый интерес, для ядер этих результатов суммирования. В частных случаях общих средних Нёрлунда tn с невозрастающими коэффициентами аналогичные результаты могут быть получены для средних Фейера и Чезаро путем выбора подходящим образом порождающей последовательности {qk:k≥0}.
Эти результаты являются наилучшими в определенном смысле. В качестве приложений указываются некоторые известные, а также новые результаты теории сильной сходимости таких средних Виленкина-Нёрлунда. Для достижения наших основных целей мы также докажем некоторые новые оценки, представляющие независимый интерес, для ядер этих результатов суммирования. В частных случаях общих средних Нёрлунда tn с невозрастающими коэффициентами аналогичные результаты могут быть получены для средних Фейера и Чезаро путем выбора подходящим образом порождающей последовательности {qk:k≥0}.Как цитировать
топ- MLA
- БибТекс
- РИС
Благота, Иштван, Перссон, Ларс-Эрик и Тефнадзе, Георгий. «О средних Нёрлунда ряда Виленкина-Фурье». Чехословацкий математический журнал 65.4 (2015): 983-1002.
@article{Blahota2015,
abstract = {Мы доказываем и обсуждаем некоторые новые неравенства типа $(H_\{p\},L_\{p\})$ взвешенных максимальных операторов средних Виленкина-Нёрлунда с невозрастающими коэффициенты $\lbrace q_\{k\}\colon k\ge 0\rbrace $. Эти результаты являются наилучшими в определенном смысле. В качестве приложений указываются некоторые известные, а также новые результаты теории сильной сходимости таких средних Виленкина-Нёрлунда. Для достижения наших основных целей мы также докажем некоторые новые оценки, представляющие независимый интерес, для ядер этих результатов суммирования. В частных случаях общих средних Нёрлунда $t_\{n\}$ с невозрастающими коэффициентами аналогичные результаты можно получить для средних Фейера и Чезаро, выбирая порождающую последовательность $\lbrace q_\{k\}\colon k\ge 0\rbrace $ соответствующим образом.},
Эти результаты являются наилучшими в определенном смысле. В качестве приложений указываются некоторые известные, а также новые результаты теории сильной сходимости таких средних Виленкина-Нёрлунда. Для достижения наших основных целей мы также докажем некоторые новые оценки, представляющие независимый интерес, для ядер этих результатов суммирования. В частных случаях общих средних Нёрлунда $t_\{n\}$ с невозрастающими коэффициентами аналогичные результаты можно получить для средних Фейера и Чезаро, выбирая порождающую последовательность $\lbrace q_\{k\}\colon k\ge 0\rbrace $ соответствующим образом.},
автор = {Блахота, Иштван, Перссон, Ларс-Эрик, Тефнадзе, Гиорги},
журнал = {Чехословацкий математический журнал},
ключевые слова = {система Виленкина; группа Виленкина; Норлунд означает; мартингальное пространство Харди; максимальный оператор; ряды Виленкина-Фурье; сильная сходимость; неравенство},
язык = {eng},
номер = {4},
страницы = {983-1002},
издатель = {Институт математики Академии наук Чешской Республики},
title = {О Нерлунде средними рядами Виленкина-Фурье},
url = {http://eudml. org/doc/276158},
org/doc/276158},
volume = {65},
year = {2015},
}
TY — JOUR
AU — Благота, Иштван
AU — Перссон, Ларс -Эрик
AU — Тефнадзе, Георгий
TI — О средних Нёрлунда рядов Виленкина-Фурье
JO — Чехословацкий математический журнал
PY — 2015
PB — Институт математики Академии наук Чехии
VL — 65
IS — 4
SP — 983
EP — 1002
AB — Доказаны и обсуждены некоторые новые неравенства типа $(H_{p},L_{p})$ взвешенных максимальных операторов средних Виленкина-Нёрлунда с невозрастающими коэффициентами $ \lbrace q_{k}\двоеточие k\ge 0\rbrace $. Эти результаты являются наилучшими в определенном смысле. В качестве приложений указываются некоторые известные, а также новые результаты теории сильной сходимости таких средних Виленкина-Нёрлунда. Для достижения наших основных целей мы также докажем некоторые новые оценки, представляющие независимый интерес, для ядер этих результатов суммирования. В частных случаях общих средних Нёрлунда $t_{n}$ с невозрастающими коэффициентами аналогичные результаты можно получить для средних Фейера и Чезаро, выбирая порождающую последовательность $\lbrace q_{k}\colon k\ge 0\rbrace $ соответствующим образом.
LA — eng
KW — система Виленкина; группа Виленкина; Норлунд означает; мартингальное пространство Харди; максимальный оператор; ряды Виленкина-Фурье; сильная сходимость; неравенство
UR — http://eudml.org/doc/276158
ER —
Каталожные номера
наверх- Благота, И., 10.1023/A:1026769207159, Acta Math. Повесили. 89 (2000), 15-27. (2000) Zbl0973.42020MR15DOI10.1023/A:1026769207159
- Блахота, И., Связь между ядрами Дирихле по отношению к системам типа Виленкина, Acta Acad. Педагог. Агриенсис, Секта. Мат. (Н.С.) 22 (1994), 109-114. (1994) Zbl0882.42017
- Благота И., Гат Г., 10.1007/s10496-008-0001-z, Анал. Теория прил. 24 (2008), 1-17. (2008) Zbl1164.42022MR2422455DOI10.1007/s10496-008-0001-z
- Благота И., Тефнадзе Г., 10.1007/с10476-014-0301-9, Анал. Мат. 40 (2014), 161-174. (2014) Zbl1313.42083MR3240221DOI10.
 1007/s10476-014-0301-9
1007/s10476-014-0301-9 - Благота И., Тефнадзе Г., 10.5486/PMD.2014.5896, Опубл. Мат. Дебрецен 85 (2014), 181-196. (2014) MR3231514DOI10.5486/PMD.2014.5896
- Fujii, N., Максимальное неравенство для h2-функций на обобщенной группе Уолша-Пэли, Proc. Являюсь. Мат. соц. 77 (1979), 111-116. (1979) MR0539641
- G{á}t, G., 10.1016/S0021-9045(03)00075-3, J. Прим. Теория 124 (2003), 25-43. (2003) Zbl1032.43003MR2010779DOI10.1016/S0021-9045(03)00075-3
- G{á}t, G., 10.1007/BF01872107, Acta Math. Повесили. 61 (1993), 131-149. (1993) Zbl0805.42019MR1200968DOI10.1007/BF01872107
- Гат, Г., Гогинава, У., Сходимость почти всюду (C,α)-средних квадратичных частичных сумм двойных рядов Виленкина-Фурье, Грузинская математика. Журнал 13 (2006), 447-462. (2006) Zbl1107.42006MR2271060
- Гат Г.
 , Гогинава Ю., 10.1007/s10114-005-0648-8, Acta Math. син., англ. сер. 22 (2006), 497-506. (2006) MR2214371DOI10.1007/s10114-005-0648-8
, Гогинава Ю., 10.1007/s10114-005-0648-8, Acta Math. син., англ. сер. 22 (2006), 497-506. (2006) MR2214371DOI10.1007/s10114-005-0648-8 - Гат, Г., Надь, К., О логарифмической суммируемости рядов Фурье, Georgian Math. Журнал 18 (2011), 237-248. (2011) Zbl1221.42049MR2805978
- Гогинова У., 10.1007/с10476-010-0101-9, Анал. Мат. 36 (2010), 1-31. (2010) MR2606574DOI10.1007/s10476-010-0101-9
- Гогинава У., Максимальные операторы средних Фейера-Уолша, Acta Sci. Мат. 74 (2008), 615-624. (2008) Zbl1199.42127MR2487936
- Гогинава У., Максимальный оператор средних Марцинкевича-Фейера d-мерного ряда Уолша-Фурье, East J. Approx. 12 (2006), 295-302. (2006) MR2252557
- Гогинава Ю., Максимальный оператор (C, α) средних рядов Уолша-Фурье, Ann. ун-т науч. Будапешт. Роландо Этвёш, Sect. вычисл. 26 (2006), 127-135. (2006) Zbl1121.
 42020MR2388683
42020MR2388683 - Гогинава Ю. Сходимость почти всюду подпоследовательности логарифмических средних рядов Уолша-Фурье // Acta Math. акад. Педагог. Нихази. (NS) (только в электронном виде) 21 (2005), 169-175. (2005) Zbl1093.42018MR2162613
- Гогинава, У., 10.1006/jath.2001.3632, Ж. Прибл. Теория 115 (2002), 9-20. (2002) Zbl0998.42018MR1888974DOI10.1006/jath.2001.3632
- Мур, К. Н., Суммируемые ряды и факторы сходимости, Dover Publications, Нью-Йорк (1966). (1966) Zbl0142.30704MR0201863
- Мориц Ф., Сиддики А. Х., 10.1016/0021-9045(92)
- -X, J. Прибл. Теория 70 (1992), 375-389. (1992) Zbl0757.42009MR1178380DOI10.1016/0021-9045(92)
- -X
- Надь, К., Аппроксимация средними Нёрлунда двойных рядов Уолша-Фурье для липшицевых функций, Math. Неравный. заявл. 15 (2012), 301-322. (2012) Zbl1243.
 42038MR2962234
42038MR2962234 - Надь, К., Аппроксимация средними Нёрлунда рядов Уолша-Качмарца-Фурье, Грузинская математика. Журнал 18 (2011), 147-162. (2011) Zbl1210.42043MR2787349
- Надь, К., Аппроксимация средними Чезаро отрицательного порядка рядов Уолша-Качмарца-Фурье, East J. Approx. 16 (2010), 297-311. (2010) Zbl1216.42006MR2789336
- Надь К., 10.1007/с10476-010-0404-х, Анал. Мат. 36 (2010), 299-319. (2010) Zbl1240.42133MR2738323DOI10.1007/s10476-010-0404-x
- Пал, Дж., Саймон, П., 10.1007/BF01896477, Acta Math. акад. науч. Повесили. 29 (1977), 155-164. (1977) Zbl0345.42011MR0450884DOI10.1007/BF01896477
- Шипп, Ф., Перестановки рядов в системе Уолша, Math. Примечания 18 (1976), 701-706 перевод с мат. заметки 18 (1975), 193-201. (1975) MR03
- Симон П., 10.1007/с006050070004, Монац.
 Мат. 131 (2000), 321-334. (2000) MR1813992DOI10.1007/s006050070004
Мат. 131 (2000), 321-334. (2000) MR1813992DOI10.1007/s006050070004 - Simon, P., 10.1006/jmaa.2000.6732, J. Math. Анальный. заявл. 245 (2000), 52-68. (2000) Zbl0987.42022MR1756576DOI10.1006/jmaa.2000.6732
- Саймон, П., Исследования в отношении системы Виленкина, Ann. ун-т науч. Будапешт. Роландо Этвёш, Sect. Мат. 27 (1984), 87-101. (1984) Zbl0586.43001MR0823096
- Саймон П., Вайс Ф., 10.1016/j.jat.2007.05.004, J. Прибл. Теория 151 (2008), 1-19. (2008) Zbl1143.42032MR2403893DOI10.1016/j.jat.2007.05.004
- Тефнадзе Г., О максимальных операторах логарифмических средних Рисса рядов Виленкина-Фурье, Stud. науч. Мат. Повесили. 51 (2014), 105-120. (2014) Zbl1299.42098MR3188506
- Тефнадзе Г., 10.3103/S1068362314010038, J. Contemp. Мат. Анальный. 4923-32 русский (2014). (2014) MR3237573DOI10.3103/S1068362314010038
- Тефнадзе Г.
 , 10.1007/с10474-013-0361-5, Acta Math. Повесили. 142 (2014), 244-259. (2014) Zbl1313.42086MR3158862DOI10.1007/s10474-013-0361-5
, 10.1007/с10474-013-0361-5, Acta Math. Повесили. 142 (2014), 244-259. (2014) Zbl1313.42086MR3158862DOI10.1007/s10474-013-0361-5 - Тефнадзе Г., О максимальных операторах средних Виленкина-Фейера на пространствах Харди, Матем. Неравный. заявл. 16 (2013), 301-312. (2013) Zbl1263.42008MR3060398
- Тефнадзе Г. О максимальных операторах средних Виленкина-Фейера // Тюрк. Дж. Матем. 37 (2013), 308-318. (2013) Zbl1278.42037MR3040854
- Тефнадзе Г., Замечание о коэффициентах Фурье и частных суммах рядов Виленкина-Фурье, Acta Math. акад. Педагог. Нихази. (NS) (только в электронном виде) 28 (2012), 167-176. (2012) Zbl1289.42084MR3048092
- Тефнадзе Г., Средние Фейера ряда Виленкина-Фурье, Stud. науч. Мат. Повесили. 49 (2012), 79-90. (2012) Zbl1265.42099MR3059789
- Тефнадзе Г., Максимальные операторы логарифмических средних одномерных рядов Виленкина-Фурье, Acta Math.
 акад. Педагог. Нихази. (NS) (только в электронном виде) 27 (2011), 245-256. (2011) Zbl1265.42100MR2880697
акад. Педагог. Нихази. (NS) (только в электронном виде) 27 (2011), 245-256. (2011) Zbl1265.42100MR2880697 - Виленкин, Н. Дж., Об одном классе полных ортонормированных систем, Am. Мат. соц. Перевод сер. (2), 28 (1963), 1-35 перевод из Изв. акад. АН СССР, сер. Мат. 11 (1947), 363-400. (1947) Zbl0036.35601MR0154042
- Weisz, F., 10.1023/B:AMHU.0000028241.87331.c5, Acta Math. Повесили. 103 (2004), 139-176. (2004) Zbl1060.42021MR2047878DOI10.1023/B:AMHU.0000028241.87331.c5
- Weisz, F., 10.1023/A:1014364010470, Анал. Мат. 27 (2001), 141-155. (2001) Zbl0992.42016MR1834858DOI10.1023/A:1014364010470
- Weisz, F., 10.1007/BF02205221, Анал. Мат. 22 (1996), 229-242. (1996) Zbl0866.42020MR1627638DOI10.1007/BF02205221
- Weisz, F., 10.1007/BFb0073448, Lecture Notes in Mathematics 1568 Springer, Berlin (1994). (1994) Zbl0796.
 60049MR1320508DOI10.1007/BFb0073448
60049MR1320508DOI10.1007/BFb0073448
Вы должны войти, чтобы оставлять комментарии.
9РЕЗУЛЬТАТЫ МУЛЬТИПЛИКАТОРА НА ЛОКАЛЬНО КОМПАКТНЫХ ГРУППАХ ВИЛЕНКИНА | Ежеквартальный математический журналФильтр поиска панели навигации The Quarterly Journal of MathematicsЭтот выпускPure MathematicsBooksJournalsOxford Academic Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации The Quarterly Journal of MathematicsЭтот выпускPure MathematicsBooksJournalsOxford Academic Термин поиска на микросайте
Расширенный поиск
Журнальная статья
Получить доступ
К. В. ОННЕВЕР,
В. ОННЕВЕР,
К. В. ОННЕВЕР
Ищите другие работы этого автора на:
Оксфордский академический
Google ученый
Т. С. КВЭК
Т. С. Куек
Ищите другие работы этого автора на:
Оксфордский академический
Google ученый
The Quarterly Journal of Mathematics , том 40, выпуск 3, сентябрь 1989 г., страницы 313–323, https://doi.org/10.1093/qmath/40.3.313
Опубликовано:
2 01 сентября 1988 г. История статьи
Получено:
19 декабря 1987 г.
Опубликовано:
01 сентября 1989 г.
Фильтр поиска панели навигации The Quarterly Journal of MathematicsЭтот выпускPure MathematicsBooksJournalsOxford Academic Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации The Quarterly Journal of MathematicsЭтот выпускPure MathematicsBooksJournalsOxford Academic Термин поиска на микросайте
Расширенный поиск
Предварительный просмотр первой страницы статьи PDF
Закрыть
Этот контент доступен только в формате PDF.
© 1989 Oxford University Press
© 1989 Oxford University Press
Раздел выпуска:
Статьи
В настоящее время у вас нет доступа к этой статье.
Скачать все слайды
Войти
Получить помощь с доступом
Получить помощь с доступом
Доступ для учреждений
Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:
Доступ на основе IP
Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.
Войдите через свое учреждение
Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.
- Нажмите Войти через свое учреждение.
- Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
- При посещении сайта учреждения используйте учетные данные, предоставленные вашим учреждением. Не используйте личную учетную запись Oxford Academic.
- После успешного входа вы вернетесь в Oxford Academic.
Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.
Войти с помощью читательского билета
Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.
Если вы не можете войти в систему, обратитесь к своему библиотекарю.
Члены общества
Доступ члена общества к журналу достигается одним из следующих способов:
Войти через сайт сообщества
Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:
- Щелкните Войти через сайт сообщества.
- При посещении сайта общества используйте учетные данные, предоставленные этим обществом. Не используйте личную учетную запись Oxford Academic.
- После успешного входа вы вернетесь в Oxford Academic.
Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.
Вход через личный кабинет
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. Смотри ниже.
Смотри ниже.
Личный кабинет
Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.
Просмотр учетных записей, вошедших в систему
Щелкните значок учетной записи в правом верхнем углу, чтобы:
- Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью.
- Просмотр институциональных учетных записей, предоставляющих доступ.
Выполнен вход, но нет доступа к содержимому
Oxford Academic предлагает широкий ассортимент продукции. Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ. Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю.
Ведение счетов организаций
Для библиотекарей и администраторов ваша личная учетная запись также предоставляет доступ к управлению институциональной учетной записью. Здесь вы найдете параметры для просмотра и активации подписок, управления институциональными настройками и параметрами доступа, доступа к статистике использования и т. д.
Покупка
Стоимость подписки и заказ этого журнала
Варианты покупки книг и журналов в Oxford Academic
Кратковременный доступ
Чтобы приобрести краткосрочный доступ, войдите в свою учетную запись Oxford Academic выше.
У вас еще нет учетной записи Oxford Academic? регистр
H p РЕЗУЛЬТАТЫ МУЛЬТИПЛИКАТОРА НА ЛОКАЛЬНО КОМПАКТНЫХ ГРУППАХ ВИЛЕНКИНА — Доступ 24 часа
ЕВРО €30,00
22 фунта стерлингов
39 долларов США.
Реклама
Цитаты
Альтметрика
Дополнительная информация о метриках
Оповещения по электронной почте
Оповещение об активности статьи
Предварительные уведомления о статьях
Оповещение о новой проблеме
Получайте эксклюзивные предложения и обновления от Oxford Academic
Ссылки на статьи по телефону
Последний
Самые читаемые
Самые цитируемые
Подвыпуклость в неоднородных системах Виноградова
Широкие моменты L-функций II: L-функции Дирихле
Вполне несвязные полугрупповые компактификации топологических групп
Варианты решета Сельберга и почти простых K-кортежей
Регулярность Соболева для функционалов линейного роста, действующих на ℂ-эллиптических операторах
Реклама
Начало Вселенной | Александр Виленкин
Мы живем после великого взрыва — Большого взрыва, который произошел 13,7 миллиарда лет назад. Во время Большого взрыва Вселенная была заполнена огненным шаром, плотной смесью энергетических частиц и излучения. Почти столетие физики изучали, как огненный шар расширялся и охлаждался, как частицы объединялись в атомы и как галактики и звезды постепенно стягивались под действием гравитации. Эта история теперь изучена в мельчайших количественных деталях и подтверждается многочисленными данными наблюдений. 1
Во время Большого взрыва Вселенная была заполнена огненным шаром, плотной смесью энергетических частиц и излучения. Почти столетие физики изучали, как огненный шар расширялся и охлаждался, как частицы объединялись в атомы и как галактики и звезды постепенно стягивались под действием гравитации. Эта история теперь изучена в мельчайших количественных деталях и подтверждается многочисленными данными наблюдений. 1
Однако остается вопрос, действительно ли Большой взрыв был началом Вселенной. Начало в чем? Чем вызвано? И определяется чем или кем? Эти вопросы побудили физиков сделать все возможное, чтобы избежать космического начала.
В этом эссе я расскажу, где мы сейчас находимся.
Теорема Пенроуза о сингулярности
Проблема стоит перед нами с самого начала научной космологии. В 19В 20-х годах русский математик Александр Фридман дал математическое описание расширяющейся Вселенной, решив уравнения общей теории относительности Альберта Эйнштейна. Фридман предположил для простоты, что распределение материи во Вселенной совершенно однородно. Его решения имели загадочную особенность: по мере того, как эволюция Вселенной прослеживается в обратном направлении во времени, плотность материи и кривизна пространства-времени растут безгранично, становясь бесконечными за конечное время назад. 2 Момент бесконечной плотности является космологической сингулярностью. В этот момент математические выражения, входящие в уравнения общей теории относительности, становятся плохо определенными, и эволюция не может продолжаться. Казалось бы, это предполагает, что у Вселенной действительно было начало, но не поддающееся описанию законами физики.
Фридман предположил для простоты, что распределение материи во Вселенной совершенно однородно. Его решения имели загадочную особенность: по мере того, как эволюция Вселенной прослеживается в обратном направлении во времени, плотность материи и кривизна пространства-времени растут безгранично, становясь бесконечными за конечное время назад. 2 Момент бесконечной плотности является космологической сингулярностью. В этот момент математические выражения, входящие в уравнения общей теории относительности, становятся плохо определенными, и эволюция не может продолжаться. Казалось бы, это предполагает, что у Вселенной действительно было начало, но не поддающееся описанию законами физики.
Физики первоначально надеялись, что сингулярность может быть артефактом упрощающего предположения Фридмана об идеальной однородности и что она исчезнет в более реалистичных решениях уравнений Эйнштейна. Роджер Пенроуз закрыл эту лазейку в середине 19-го века.60-х годов, показав, что при очень общем предположении сингулярность неизбежна. 3 При нулевом условии сходимости гравитация всегда заставляет световые лучи сходиться. 4 Это означает, что плотность материи или энергии, измеренная любым наблюдателем, не может быть отрицательной. Вывод справедлив для всех известных форм классической материи.
3 При нулевом условии сходимости гравитация всегда заставляет световые лучи сходиться. 4 Это означает, что плотность материи или энергии, измеренная любым наблюдателем, не может быть отрицательной. Вывод справедлив для всех известных форм классической материи.
Доказательство Пенроуза основано на понятии неполной геодезической. В общей теории относительности траектории материи представлены прямыми линиями в пространстве-времени или геодезическими. Если пространство-время свободно от сингулярностей, все геодезические должны иметь бесконечную протяженность. Геодезическая, встречающая сингулярность, не может быть расширена дальше. Такие геодезические неполны. Пенроуз показал, что пространство-время, удовлетворяющее условию нулевой сходимости (и некоторым дополнительным мягким предположениям), должно содержать неполные геодезические. Сингулярность кажется неизбежной.
Аргумент Пенроуза был не совсем убедительным. Хотя классическая материя удовлетворяет условию нулевой сходимости, квантовые флуктуации могут создавать области с отрицательной плотностью энергии. 5 В экстремальных условиях вблизи Большого взрыва большое значение имеют квантовые флуктуации. Аргумент Пенроуза больше не применим.
5 В экстремальных условиях вблизи Большого взрыва большое значение имеют квантовые флуктуации. Аргумент Пенроуза больше не применим.
Так обстояли дела до начала 1980-х, когда Алан Гут представил идею космической инфляции. 6
Вечная инфляция
Инфляция — это период сверхбыстрого, ускоренного расширения в ранней истории Вселенной. За доли секунды крошечная субатомная область взрывается до размеров, превышающих всю наблюдаемую в настоящее время Вселенную. Расширение происходит за счет ложного вакуума.
Вакуум обычно считают пустым пространством, но, согласно современной физике элементарных частиц, пустое не есть ничто. Вакуум — это физический объект, наделенный плотностью энергии и давлением. Он может находиться в нескольких различных состояниях или вакууме. Свойства и типы элементарных частиц различаются от одного вакуума к другому.
Гравитационная сила, вызванная ложным вакуумом, необычна тем, что она отталкивающая. Чем выше энергия вакуума, тем сильнее отталкивание. Такой вакуум нестабилен. Он распадается на низкоэнергетический вакуум, а избыточная энергия производит огненный шар из частиц и излучения. Ложные вакуумы не были изобретены для целей инфляции. Их существование следует из физики элементарных частиц и общей теории относительности.
Чем выше энергия вакуума, тем сильнее отталкивание. Такой вакуум нестабилен. Он распадается на низкоэнергетический вакуум, а избыточная энергия производит огненный шар из частиц и излучения. Ложные вакуумы не были изобретены для целей инфляции. Их существование следует из физики элементарных частиц и общей теории относительности.
Теория инфляции предполагает, что в какой-то ранний период своей истории Вселенная занимала высокоэнергетический ложный вакуум. Затем отталкивающие гравитационные силы вызвали сверхбыстрое экспоненциальное расширение Вселенной. Существует характерное время, за которое размер Вселенной удваивается. В зависимости от модели время удвоения может составлять всего 10 -37 секунд. Примерно за 330 удвоений Вселенная увеличивается в 10 100 раз. Каким бы ни был ее первоначальный размер, Вселенная очень быстро становится огромной. Поскольку ложный вакуум нестабилен, он в конечном итоге распадается, образуя огненный шар, что означает конец инфляции. Огненный шар продолжает расширяться по инерции и развивается в соответствии со стандартной космологией Большого взрыва.
Огненный шар продолжает расширяться по инерции и развивается в соответствии со стандартной космологией Большого взрыва.
Инфляция объяснила некоторые загадочные особенности Вселенной, вопросы, которые была вынуждена принять космология Большого взрыва. Он объяснил расширение Вселенной, ее высокую температуру и наблюдаемую однородность. Инфляционная теория предсказывала, что евклидова геометрия описывает Вселенную в самых больших масштабах. Он также предсказал почти независимый от масштаба спектр возмущений малой плотности, вызванных квантовыми флуктуациями во время инфляции. Эти прогнозы подтвердились.
Теория инфляции привела к пересмотру нашего взгляда на Вселенную. Инфляция не заканчивается везде сразу. Области, в которых ложный вакуум распадается несколько позже, вознаграждаются большим инфляционным расширением, поэтому области ложного вакуума имеют тенденцию размножаться быстрее, чем они распадаются. В нашем космическом соседстве инфляция закончилась 13,7 миллиарда лет назад; в отдаленных частях вселенной это все еще продолжается. Такие регионы, как наш, постоянно формируются. Этот бесконечный процесс называется вечной инфляцией. Вечная инфляция носит общий характер; и предсказывается большинством моделей.
Такие регионы, как наш, постоянно формируются. Этот бесконечный процесс называется вечной инфляцией. Вечная инфляция носит общий характер; и предсказывается большинством моделей.
Ложное затухание вакуума зависит от модели. В этом эссе я сосредоточусь на моделях, в которых это происходит посредством зарождения пузырьков. Распад вакуума подобен кипению воды. Низкоэнергетические области выглядят как микроскопические пузырьки и сразу же начинают расти со скоростью, быстро приближающейся к скорости света. Затем пузыри разлетаются в результате инфляционного расширения, освобождая место для новых пузырей. Мы живем в одном из таких пузырей, но можем наблюдать лишь небольшую его часть. Как бы быстро мы ни двигались, мы не можем догнать расширяющуюся границу нашей Вселенной.
Наша вселенная — автономная.
Вечная инфляция открывает интригующую возможность. Если инфляция продолжается и продолжается в будущем, могла ли она также продолжаться и продолжаться в прошлом? 7 Вселенная без начала избавит от необходимости спрашивать, как она началась.
Как это часто бывает в физике, непреодолимая сила вот-вот натолкнется на неподвижное препятствие.
Теорема Борде-Гута-Виленкина
Препятствие можно найти в теореме Борде-Гута-Виленкина (БГВ). 8 Грубо говоря, наша теорема утверждает, что если Вселенная в среднем расширяется, то ее история не может бесконечно продолжаться в прошлом. Точнее, если средняя скорость расширения положительна вдоль данной мировой линии или геодезической, то эта геодезическая должна закончиться через конечное время. Разные геодезические, разные времена. Важным моментом является то, что прошлая история Вселенной не может быть полной. Схема доказательства приведена в Приложении.
Теорема BGV допускает некоторые периоды сжатия, но в среднем выигрывает расширение. Объем Вселенной увеличивается со временем. Инфляция не может быть вечной и должна иметь какое-то начало.
Теорема BGV широка в своей общности. Он не делает никаких предположений о гравитации или материи. Гравитация может быть притягивающей или отталкивающей, световые лучи могут сходиться или расходиться, и даже общая теория относительности может прийти в упадок: теорема все равно останется в силе.
Гравитация может быть притягивающей или отталкивающей, световые лучи могут сходиться или расходиться, и даже общая теория относительности может прийти в упадок: теорема все равно останется в силе.
Несколько физиков построили модели вечной вселенной, в которых теорема БГВ больше не актуальна. Джордж Эллис и его сотрудники предположили, что конечная замкнутая Вселенная, в которой пространство замкнуто само на себя, как поверхность сферы, могла существовать вечно в статическом состоянии, а затем взорваться при инфляционном расширении. 9 При усреднении за бесконечное время скорость расширения будет равна нулю, и теорема БГВ не будет применяться. Эллис построил классическую модель стабильной замкнутой Вселенной и представил механизм, вызывающий начало расширения. Эллис не заявлял, что его модель реалистична; это было задумано как доказательство концепции, показывающее, что вечная вселенная возможна. Не так. Статическая Вселенная нестабильна по отношению к квантовому коллапсу. 10 Она может быть стабильной по законам классической физики, но в квантовой физике статическая вселенная может совершить внезапный переход в состояние исчезающего размера и бесконечной плотности. Как бы ни была мала вероятность коллапса, Вселенная не могла существовать бесконечное количество времени до начала инфляции.
10 Она может быть стабильной по законам классической физики, но в квантовой физике статическая вселенная может совершить внезапный переход в состояние исчезающего размера и бесконечной плотности. Как бы ни была мала вероятность коллапса, Вселенная не могла существовать бесконечное количество времени до начала инфляции.
Есть еще один способ, которым вселенная могла быть вечной в прошлом. Он мог пройти через бесконечную последовательность расширений и сжатий. Это понятие на короткое время было популярно в 1930-х годах, но затем от него отказались из-за его явного противоречия второму закону термодинамики. Второй закон требует, чтобы энтропия возрастала в каждом цикле космической эволюции. Если бы Вселенная уже совершила бесконечное число циклов, она достигла бы состояния теплового равновесия и, следовательно, состояния максимальной энтропии. Вся энергия упорядоченного движения обратилась бы в теплоту, во всем царила бы однородная температура.
Мы не находимся в таком состоянии.
Идея циклической Вселенной была недавно возрождена Полом Стейнхардтом и Нилом Туроком. 11 Они предположили, что в каждом цикле расширение больше, чем сжатие, так что объем Вселенной увеличивается. Энтропия Вселенной, которую мы можем сейчас наблюдать, может быть такой же, как энтропия какой-либо подобной области в более раннем цикле; тем не менее, общая энтропия Вселенной увеличилась бы, потому что объем Вселенной теперь больше, чем был раньше. С течением времени и энтропия, и общий объем неограниченно растут, и состояние максимальной энтропии никогда не достигается. Максимальной энтропии нет. 12
Проблема с этим сценарием заключается в том, что в среднем объем Вселенной все еще растет, и поэтому можно применить теорему БГВ. Это сразу же приводит к выводу, что циклическая вселенная не может быть вечной в прошлом.
Божье доказательство
Теологи приветствовали любое свидетельство начала Вселенной как свидетельство существования Бога. «Что касается первопричины Вселенной, — писал британский астрофизик Эдвард Милн, — это остается дополнить читателю, но без Него наша картина будет неполной». 13 Некоторые ученые опасались, что космическое начало невозможно описать научными терминами. «Отрицать бесконечную продолжительность времени, — утверждал Вальтер Нернст, — значило бы предать самые основы науки». 14
«Что касается первопричины Вселенной, — писал британский астрофизик Эдвард Милн, — это остается дополнить читателю, но без Него наша картина будет неполной». 13 Некоторые ученые опасались, что космическое начало невозможно описать научными терминами. «Отрицать бесконечную продолжительность времени, — утверждал Вальтер Нернст, — значило бы предать самые основы науки». 14
Ричард Докинз, Лоуренс Краусс и Виктор Стенгер утверждали, что современная наука не оставляет места для существования Бога. Была организована серия дебатов между наукой и религией, в которых атеисты, такие как Докинз, Дэниел Деннет и Краусс, обсуждали теистов, как Уильям Лейн Крейг. 15 Обе стороны обратились к теореме BGV, обе стороны обратились ко мне — из всех людей! — для лучшего понимания.
Космологический аргумент в пользу существования Бога состоит из двух частей. Первый простой:
- все, что начинает существовать, имеет причину;
- вселенная начала существовать;
- Следовательно, у Вселенной есть причина.
 16
16
Вторая часть утверждает, что причиной должен быть Бог.
Теперь я хотел бы обсудить первую часть аргумента. Современная физика может описать возникновение Вселенной как физический процесс, не требующий причины.
Ничто не может быть создано из ничего, говорит Лукреций, хотя бы потому, что закон сохранения энергии делает невозможным создание ничего из ничего. Для любой изолированной системы энергия пропорциональна массе и должна быть положительной. Любое начальное состояние до создания системы должно иметь ту же энергию, что и состояние после ее создания.
В этом рассуждении есть лазейка. Энергия гравитационного поля отрицательна; 17 возможно, что эта отрицательная энергия могла бы компенсировать положительную энергию материи, делая полную энергию космоса равной нулю. Собственно, именно это и происходит в замкнутой вселенной, в которой пространство замыкается само на себя, подобно поверхности сферы. Из законов общей теории относительности следует, что полная энергия такой Вселенной обязательно равна нулю. Другой сохраняющейся величиной является электрический заряд, и снова оказывается, что полный заряд должен обращаться в нуль в замкнутой Вселенной.
Другой сохраняющейся величиной является электрический заряд, и снова оказывается, что полный заряд должен обращаться в нуль в замкнутой Вселенной.
Я проиллюстрирую эти утверждения для случая электрического заряда, используя двумерную аналогию. Представьте двумерную замкнутую вселенную, которую мы можем представить как поверхность земного шара. Предположим, мы поместили положительный заряд на северный полюс этой вселенной. Тогда линии электрического поля, исходящие от заряда, обернутся вокруг сферы и сойдутся на южном полюсе. Это означает, что там должен присутствовать отрицательный заряд равной величины. Таким образом, мы не можем добавить положительный заряд в замкнутую вселенную, не добавив в то же время равный ему отрицательный заряд. Таким образом, общий заряд замкнутой Вселенной должен быть равен нулю.
Если все сохраняющиеся числа замкнутой вселенной равны нулю, то ничто не препятствует спонтанному созданию такой вселенной из ничего. А согласно квантовой механике с некоторой вероятностью произойдет любой процесс, не запрещенный строго законами сохранения. 18
18
Новорожденная вселенная может иметь множество различных форм и размеров и может быть заполнена различными видами материи. Как обычно в квантовой теории, мы не можем сказать, какая из этих возможностей реализуется на самом деле, но можем рассчитать их вероятности. Это говорит о том, что может существовать множество других вселенных.
Создание квантов похоже на квантовое туннелирование через энергетические барьеры в квантовой механике. Элегантное математическое описание этого процесса можно дать в терминах вращения Вика. Время выражается с помощью мнимых чисел, введенных только для удобства вычислений. Различие между измерениями времени и пространства исчезает. Это описание очень полезно, так как оно обеспечивает удобный способ определения вероятности туннелирования. Наиболее вероятными являются вселенные с наименьшим начальным размером и самой высокой энергией вакуума. Как только Вселенная сформирована, она сразу же начинает расширяться из-за высокой энергии вакуума.
Это начало истории вечной инфляции.
Можно было бы представить, что замкнутые вселенные выскакивают из ничего, как пузыри в бокале шампанского, но эта аналогия не совсем точна. Пузыри лопаются в жидкости, но в случае вселенных нет пространства, из которого они могли бы лопнуть. Зародышевая замкнутая вселенная — это все пространство, которое существует, за исключением несвязанных пространств других закрытых вселенных. За его пределами нет ни пространства, ни времени.
Почему Вселенная возникла из ничего? Причина не нужна. Если у вас есть радиоактивный атом, он распадется, а квантовая механика дает вероятность распада за заданный интервал времени, скажем, за минуту. Нет никакой причины, по которой атом распался именно в этот момент, а не в другой. Процесс совершенно случайный. Для квантового сотворения Вселенной не нужна причина.
Теория квантового сотворения — не более чем спекулятивная гипотеза. Неясно, как и можно ли это проверить наблюдательно. Тем не менее это первая попытка сформулировать проблему космического происхождения и решить ее количественным путем. 19
19
Неразрешимая тайна
Ответ на вопрос «Было ли у Вселенной начало?» то есть: «Вероятно, так и было». У нас нет жизнеспособных моделей вечной вселенной. Теорема БГВ дает нам основания полагать, что такие модели просто невозможно построить.
Когда физики или богословы спрашивают меня о теореме БГВ, я с радостью отвечаю. Но я считаю, что эта теорема ничего не говорит нам о существовании Бога. Остается глубокая тайна. Законы физики, описывающие квантовое создание Вселенной, также описывают ее эволюцию. Это, кажется, предполагает, что они существуют независимо.
Что именно это означает, мы не знаем.
А почему у нас такие законы? Почему не другие законы?
У нас нет возможности приступить к раскрытию этой тайны.
Приложение: математические подробности
В этом приложении я набросал доказательство теоремы БГВ.
Начните с однородной, изотропной и пространственно плоской Вселенной с метрикой:
ds2=dt2-a2tdx→2.
Скорость расширения Хаббла равна H=a˙/a, где точка обозначает производную по времени t. Мы можем представить себе, что Вселенная заполнена сопутствующими частицами, движущимися по времениподобным геодезическим x→=const. Рассмотрим инерциального наблюдателя, мировая линия которого есть xµ(τ), параметризованного собственным временем τ. Для наблюдателя с массой m 4-импульс равен Pμ=m dxμ/dτ, так что dτ=(m/E)dt, где E=P0=p2+m2 обозначает энергию, а p — величину 3 -импульс. Из геодезического уравнения движения следует, что p∝1/a(t), так что pt=a(tf)/a(t)pf, где pf обозначает импульс в некоторый отсчетный момент времени tf.
Таким образом:
∫titfHτdτ=∫a(ti)a(tf)m dam2a2+pf2a2(tf)=Fγf-Fγi≤Fγf,
, где ti Обратите внимание: Fγ=12lnγ+1γ-1, , где γ=1/1-νотн2 — фактор Лоренца, а νотн=p/E — скорость наблюдателя относительно сопутствующей частицы. Для любого несопутствующего наблюдателя γ>1 и Fγ>0. Скорость расширения, усредненная по мировой линии наблюдателя: Hav=1τf-τi∫titfHτdτ. Предположим, что Ср>0, и из первого уравнения следует, что τf-τi≤FγfHav. Отсюда следует, что любая несопутствующая направленная в прошлое времяподобная геодезическая, удовлетворяющая условию Hav>0, должна иметь конечную собственную длину и, следовательно, должна быть неполной в прошлом. Нет апелляции к однородности и изотропности в произвольном пространстве-времени. Представьте, что Вселенная заполнена конгруэнтностью сопутствующих геодезических, представляющих пробные частицы, и рассмотрим несопутствующий геодезический наблюдатель, описываемый мировой линией xµ(τ). 20 Пусть uµ и νµ обозначают 4-скорости пробных частиц и наблюдателя. Тогда фактор Лоренца наблюдателя относительно частиц равен γ=uμνμ. Чтобы охарактеризовать скорость расширения в общем пространстве-времени, достаточно сосредоточиться на геодезических пробных частицах, пересекающих мировую линию наблюдателя. Рассмотрим две такие геодезические, встречающиеся с наблюдателем в моменты времени τ и τ+∆τ. Определите параметр H=lim∆τ→0∆ur∆r, , где ∆ur — относительная скорость частиц в направлении движения наблюдателя, а ∆r — расстояние между частицами. Обе величины вычисляются в системе покоя одной из частиц. Для однородной и изотропной Вселенной это определение сводится к параметру Хаббла. Параметр расширения может быть выражен полной производной, H=ddτFγτ. Интеграл от H вдоль мировой линии наблюдателя по-прежнему определяется разностью F(γ) на ее концах. Выводы об однородных и изотропных вселенных немедленно переносятся на родовые вселенные. Остается нулевой наблюдатель, описанный нулевой геодезической. При этом роль собственного времени τ играет аффинный параметр. BGV показал, что при подходящей нормировке τ скорость расширения составляет H=ddτFγτ, с Fγ=1/γ и γ, определяемым H=lim∆τ→0∆ur∆r.




 Решение уравнений.
Решение уравнений. 09
09 117,119
117,119 09
09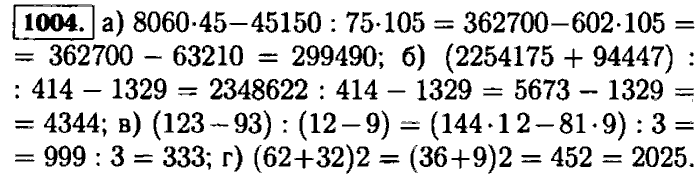 09
09 10
10 10
10



 11
11 11
11 11
11

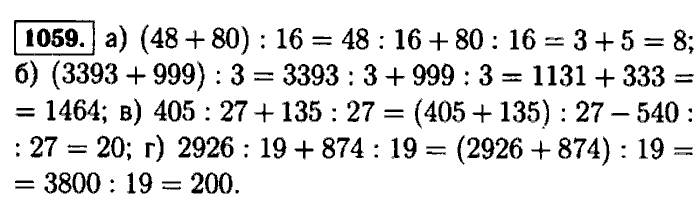 12
12 12
12 12
12 01
01 01
01 01
01 01
01 02
02 02
02 02
02
 02
02 Округление чисел
Округление чисел 03
03 03
03 03
03 04
04 04
04 04
04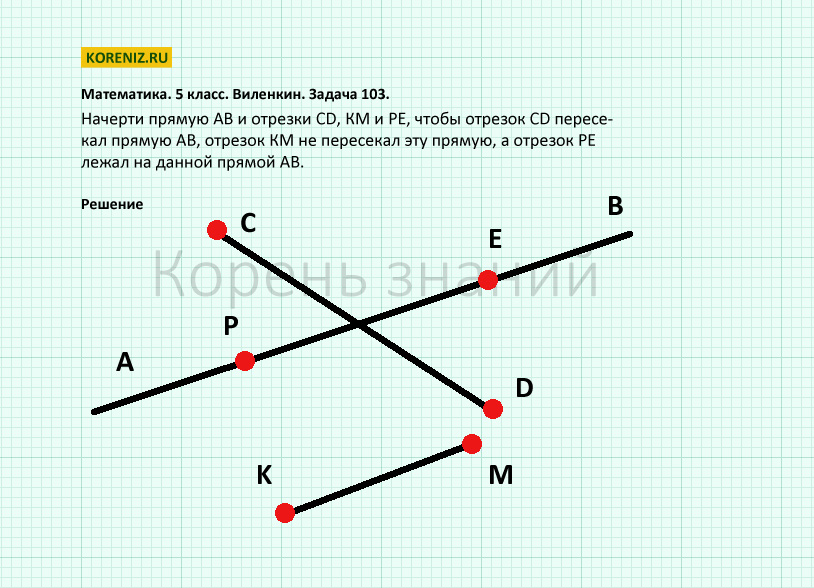 04
04 04
04

 Построение углов»
Построение углов» Решение задач с помощью уравнений.
Решение задач с помощью уравнений.



 Ялчин, Бушра Нур Деликкая, Уильям Пелит, Минг Тонг, Сюзанна М. Де Ла Монте, Шарон Раундс
Ялчин, Бушра Нур Деликкая, Уильям Пелит, Минг Тонг, Сюзанна М. Де Ла Монте, Шарон Раундс 4236/ojas.2022.124047
3 загрузки 15 просмотров
4236/ojas.2022.124047
3 загрузки 15 просмотров