Номер (задание) 848 — гдз по математике 5 класс Виленкин, Жохов, Чесноков
Условие / глава 1 / § 4 / тема 21 / 848
848. Найдите значение выражения: а) 700 700 — 6054 * (47 923 — 47 884) — 65 548; б) 66 509 + 141 400 : (39 839 — 39 739) + 1985; в) (851 + 2331) : 74 — 34; г) (14 084 : 28 — 23) -27 — 12 060; д) (102 + 112 + 122) : 73 + 895; е) 2555 : (132 + 142) + 35.
Решебник №1 / глава 1 / § 4 / тема 21 / 848
youtube.com/embed/TJcw0H-1B4A?start=3746″ frameborder=»0″ allowfullscreen=»»/>
Решебник №2 / глава 1 / § 4 / тема 21 / 848
Решебник №3 / глава 1 / § 4 / тема 21 / 848
Номер (задание) 813 — гдз по математике 5 класс Виленкин, Жохов, Чесноков
Условие / глава 1 / § 4 / тема 20 / 813 813. Найдите площадь поверхности и сумму длин рёбер куба, ребро которого 11 см.
Найдите площадь поверхности и сумму длин рёбер куба, ребро которого 11 см.
Решебник №1 / глава 1 / § 4 / тема 20 / 813
youtube.com/embed/TJcw0H-1B4A?start=878″ frameborder=»0″ allowfullscreen=»»/>
Решебник №2 / глава 1 / § 4 / тема 20 / 813
Решебник №3 / глава 1 / § 4 / тема 20 / 813
Номер (задание) 1100 — гдз по математике 5 класс Виленкин, Жохов, Чесноков
Условие / глава 2 / § 5 / тема 28 / 1100
1100. Какую часть длины отрезка АВ составляет длина каждого отрезка на рисунке 133?
Какую часть длины отрезка АВ составляет длина каждого отрезка на рисунке 133?
youtube.com/embed/KJbHrzZL2KE?start=10226″ frameborder=»0″ allowfullscreen=»»/>
Решебник №2 / глава 2 / § 5 / тема 28 / 1100Решебник №3 / глава 2 / § 5 / тема 28 / 1100
Номер (задание) 1297 — гдз по математике 5 класс Виленкин, Жохов, Чесноков
1297.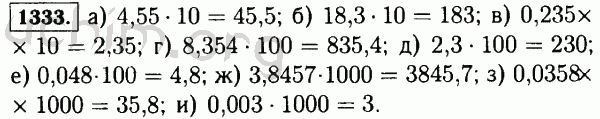 Округлите дроби: а)1,69; 1,198; 37,444; 37,5444; 802,3022 до целых; б)0,3691; 0,8218; 0,9702; 81,3501 до десятых.
Округлите дроби: а)1,69; 1,198; 37,444; 37,5444; 802,3022 до целых; б)0,3691; 0,8218; 0,9702; 81,3501 до десятых.
Решебник №1 / глава 2 / § 6 / тема 33 / 1297
Видеорешение / глава 2 / § 6 / тема 33 / 1297
youtube.com/embed/tkqfBMGQEBY?start=11198″ frameborder=»0″ allowfullscreen=»»/>
Решебник №2 / глава 2 / § 6 / тема 33 / 1297
Решебник №3 / глава 2 / § 6 / тема 33 / 1297
ГДЗ: Математика 5 класс Виленкин, Жохов
Математика 5 класс
Тип: Учебник
Авторы: Виленкин, Жохов
Издательство: Мнемозина
ГДЗ МАТЕМАТИКА 5 КЛАСС — ПОМОЩНИК ДЛЯ ДЕТЕЙ И РОДИТЕЛЕЙ
Математика является достаточно сложным предметом для многих детей. Правильная подача материала, без искаженной или пустой информации поможет детям лучше усваивать новые знания. Преподавание это особое искусство доступное немногим. Кто-то учился этому, а ком-то оно дано от рождения. Однако все это имеет значение в рамках школы. Что же делать если ребенок не усваивает материал и эта работа перекладывается с плечей учителя на плечи родителей? Изучение математики сложно: формулы, законы, теоремы, правила и алгоритмы. Дети путаются в таком количестве материала, делают ошибки. Порой школьники сами стесняются признаться что не понимают материал.
Правильная подача материала, без искаженной или пустой информации поможет детям лучше усваивать новые знания. Преподавание это особое искусство доступное немногим. Кто-то учился этому, а ком-то оно дано от рождения. Однако все это имеет значение в рамках школы. Что же делать если ребенок не усваивает материал и эта работа перекладывается с плечей учителя на плечи родителей? Изучение математики сложно: формулы, законы, теоремы, правила и алгоритмы. Дети путаются в таком количестве материала, делают ошибки. Порой школьники сами стесняются признаться что не понимают материал.
ЧТО ДЕЛАТЬ ЕСЛИ ЧТО-ТО НЕПОНЯТНО
Школа давит на ребенка. Большая часть учеников стесняется признаться что не понимает предмет. Они боятся насмешек сверстников или грубого отношения учителя. Что же делать в таком случае? Есть несколько вариантов:
- Обратиться к родителям или родственникам.
- Обратится к репетитору.
- Воспользоваться онлайн помощником.
Первые два способа не всегда реализуемы. Репетиторы не всем по карману, а родители не всегда могут потратить весь вечер на объяснения давно забытых школьных предметов. Идеальным вариантом становится онлайн-решебник с подробно разобранными заданиями по всем темам. Его преимуществами являются:
Репетиторы не всем по карману, а родители не всегда могут потратить весь вечер на объяснения давно забытых школьных предметов. Идеальным вариантом становится онлайн-решебник с подробно разобранными заданиями по всем темам. Его преимуществами являются:
- Экономия времени.
- Готовые разобранные и обоснованные решения.
- Доступность в любое время.
ЧТО ПРЕДСТАВЛЯЕТ СОБОЙ УЧЕБНИК
Учебник математики 5 класса авторов Виленкина, Жохова, Чеснокова, Шварцбурда тиражирован книгоизданием «Мнемозина». Содержит темы, расположенных по принципу градации уровня сложности, а в конце каждой из них приложены задания на закрепление новой информации. Задачи распределены по блокам, где каждый содержит не более 100 упражнений. Комплектом была разработана специальная рабочая тетрадь, призванная проверять, укреплять навыки.
ЗАЧЕМ НУЖНО ГДЗ
«ГДЗ по Математике 5 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд» выпущен книгоизданием «Мнемозина» с целью контроля получаемых учащимся знаний. Готовые ответы к упражнениям расположены в прямом порядке. Удобство печати позволяет легко найти нужный номер, что поможет полноценно применять решебник для самоконтроля ученику или проверки качества познаний родителями. Можно открыть источник информации онлайн или скачать на компьютер. Не рекомендуется к частому использованию.
Готовые ответы к упражнениям расположены в прямом порядке. Удобство печати позволяет легко найти нужный номер, что поможет полноценно применять решебник для самоконтроля ученику или проверки качества познаний родителями. Можно открыть источник информации онлайн или скачать на компьютер. Не рекомендуется к частому использованию.
ГДЗ по математике 5 класс Виленкин, Жохов
Учебник
Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд.
Мнемозина
Здесь вы найдете полные ответы на задания популярного учебника математики Наума Яковлевича Виленкина для учащихся 5 класса. Решебник Виленкина поможет пропустившим уроки школьникам выполнять домашняя работу по ключевому предмету — математике. В свою очередь родители пятиклассников смогут проконтролировать правильность хода решения упражнений из учебника. ГДЗ ЛОЛ КЕК созданы только для проверки!
Ответы по математике 5 класс Виленкин, Жохов, Чесноков, Шварцбурд:
← Предыдущая
1
Следующая →
Сегодня в большинстве школ используется учебник Математика 5 класс Виленкин, как одно из самых качественных изданий по освоению предмета. Предусматривается в первую очередь развитие мышления ребенка, которое закрепляется при применении полученных знаний на примерах. Специальные задания с высоким уровнем сложности помогут определить математический склад ума вашего ребенка.
Предусматривается в первую очередь развитие мышления ребенка, которое закрепляется при применении полученных знаний на примерах. Специальные задания с высоким уровнем сложности помогут определить математический склад ума вашего ребенка.
Ко всем задачам должны быть и ответы, поэтому и к данному учебнику они прилагаются. Решебник поможет детям полностью усвоить материал, разъясняя непонятные моменты, а родителям — не потерять авторитет в глазах ребенка, когда нужно что-то подсказать. Следите, чтобы ребенок не списывал ответы, а путем размышления и анализа сам постепенно приходил к нему.
Прежде всего представленные ответы по математике на 1 и 2 части учебника Виленкина лучше всего использовать родителям. Вам остается только проверить выполнение, что существенно сохранит время, если бы вы решали это сами. К тому же гораздо проще найти ошибку и указать на нее, если ученик затрудняется самостоятельно определить метод решения задачи.
Математика для пятиклассников – один из самых сложных предметов. На 5 год обучения значительно усложняется программа и ученики к этому оказываются не готовы. Поэтому онлайн решебник по математике за 5 класс Виленкина является эффективным способом повысить успеваемость, предлагая правильно выполненные домашние задания бесплатно. Сэкономьте время на домашку и подсмотрите верный ответ на lolkek.ru.
На 5 год обучения значительно усложняется программа и ученики к этому оказываются не готовы. Поэтому онлайн решебник по математике за 5 класс Виленкина является эффективным способом повысить успеваемость, предлагая правильно выполненные домашние задания бесплатно. Сэкономьте время на домашку и подсмотрите верный ответ на lolkek.ru.
Еще решебники из раздела Математика 5 класс
Математика 5 Виленкин — Жохов
Контрольные работы по математике 5 класс Виленкин (автор — Жохов)
Математика 5 Виленкин — Жохов — это контрольные работы (цитаты) из учебного пособия «Математика. 5 класс. Контрольные работы для учащихся общеобразовательных учреждений / В. И. Жохов, Л. Б. Крайнева. — 5-е изд., стер. — М. : Мнемозина, 2012».
Цитаты из вышеуказанного учебного пособия использованы на сайте в незначительных объемах, исключительно в учебных и информационных целях (пп. 1 п. 1 ст. 1274 ГК РФ): цитаты переработаны в удобный формат (каждая работа на 1-й странице), что дает экономию денежных средств учителю и образовательному учреждению я в использовании бумаги и ксерокопирующего оборудования.
1 п. 1 ст. 1274 ГК РФ): цитаты переработаны в удобный формат (каждая работа на 1-й странице), что дает экономию денежных средств учителю и образовательному учреждению я в использовании бумаги и ксерокопирующего оборудования.
При постоянном использовании контрольных работ по математике в 4 классе рекомендуем купить книгу:
Математика. 5 класс. Контрольные работы для учащихся общеобразовательных учреждений / В. И. Жохов, Л. Б. Крайнева, в которой кроме представленных контрольных работ есть еще 2 варианта КР (итого 4 варианта контрольных работ), а также задания на карточках и проверочные работы. В пособии содержатся карточки для проведения диагностических и проверочных работ по математике в классах, обучающихся по учебнику «Математика 5 класс» Н. Я. Виленкина, В. И. Жохова, А. С. Чеснокова, С. И. Шварцбурда. Соответствует ФГОС основного общего образования.
Для увеличения изображения — нажмите на картинку !
Контрольная работа № 1
Математика 5 класс Виленкин — Жохов. Контрольная работа 1
Контрольная работа 1Контрольная работа № 2
Математика 5 класс Виленкин — Жохов. Контрольная работа 2Контрольная работа № 3
Математика 5 класс Виленкин — Жохов. Контрольная работа 3Контрольная работа № 4
Математика 5 класс Виленкин — Жохов. Контрольная работа 4Контрольная работа № 5
Математика 5 класс Виленкин — Жохов. Контрольная работа 5Контрольная работа № 6
Математика 5 класс Виленкин — Жохов. Контрольная работа 6Контрольная работа № 7
Математика 5 класс Виленкин — Жохов. Контрольная работа 7Контрольная работа № 8
Математика 5 класс Виленкин — Жохов. Контрольная работа 8Контрольная работа № 9
Математика 5 класс Виленкин — Жохов. Контрольная работа 9Контрольная работа № 10
Математика 5 класс Виленкин — Жохов. Контрольная работа 10Контрольная работа № 11
Математика 5 класс Виленкин — Жохов. Контрольная работа 11Контрольная работа № 12
Математика 5 класс Виленкин — Жохов. Контрольная работа 12Контрольная работа № 13
Математика 5 класс Виленкин — Жохов. Контрольная работа 13
Контрольная работа 13Контрольная работа № 14
Математика 5 класс Виленкин — Жохов. Контрольная работа 14Контрольная работа № 15. ИТОГОВАЯ.
Математика 5 класс Виленкин — Жохов. Контрольная работа 15
Вы смотрели Математика 5 Виленкин — Жохов контрольные работы (цитаты) из пособия для учащихся «Математика. 5 класс. Контрольные работы для учащихся общеобразовательных учреждений / В. И. Жохов, Л. Б. Крайнева. — 5-е изд., стер. — М. : Мнемозина, 2012».
Ответов нет !
| Семинар практикующих 2020 Семинар проводится весной 2020 года, вторник и четверг 19:40 — 20:55. Спикер часто не делает копии презентации доступными — для защиты интеллектуальной собственности или соблюдения правил компании. ЭТОТ СЕМИНАР БУДЕТ ПРОВЕДЕН ОНЛАЙН Расписание презентацийЩелкните здесь, чтобы увидеть расписание прошлых презентаций. Прошлые презентации
|
| Семинар практикующих 2017 Семинар проходит весной 2017 года, вторник и четверг 19:40 — 20:55. Место нахождения: Сейчас — Математический корпус 207. Чтобы узнать, как добраться до кампуса, см. Карту кампуса «Морнингсайд».Организатор: Ларс Тайге Нильсен Щелкните здесь, чтобы увидеть расписание презентаций. Щелкните здесь, чтобы увидеть расписание прошлых презентаций. Чтобы подписаться на список рассылки объявлений (или отказаться от подписки на него), отправьте электронное письмо на [email protected] с соответствующего адреса электронной почты, указав «Подписаться» или «Отказаться от подписки» в строке темы или первой строке сообщения. .. Правила
Расписание презентацийСеминар практикующих, весна 2017 г. закрыт.Большое спасибо всем выступающим. Вернемся весной 2018 года. Щелкните здесь, чтобы увидеть расписание прошлых презентаций. Прошлые презентации
|
Ездовые собаки тесно связаны с 9500-летней «древней собакой» — ScienceDaily
Ездовые собаки намного старше и приспособились к арктическим условиям намного раньше, чем считалось ранее. В новом исследовании проекта QIMMEQ исследователи из Копенгагенского университета показывают, что предки современных ездовых собак работали и жили с людьми более 9500 лет.
Собаки играют важную роль в жизни человека во всем мире — будь то член семьи или рабочее животное.Но откуда взялась собака и сколько лет различным группам собак, все еще остается загадкой.
Теперь выяснилось, откуда взялась ездовая собака. В новом исследовании, опубликованном в SCIENCE , исследователи с факультета здравоохранения и медицинских наук Копенгагенского университета показывают, что ездовая собака старше и приспособилась к Арктике намного раньше, чем предполагалось. Исследование проводилось в сотрудничестве с Гренландским университетом и Институтом эволюционной биологии Барселоны.
«Мы выделили ДНК 9 500-летней собаки с сибирского острова Жохов, в честь которой названа собака. На основе этой ДНК мы секвенировали самый старый полный геном собаки на сегодняшний день, и результаты показывают чрезвычайно ранний диверсификация собак по типам ездовых собак », — говорит один из двух первых авторов исследования, докторант Миккель Синдинг из Института глобуса.
До сих пор считалось, что сибирская собака Жохова, которой 9500 лет, была своего рода древней собакой — одной из самых ранних домашних собак и одной из версий общего происхождения всех собак.Но согласно новому исследованию, современные ездовые собаки, такие как сибирский хаски, аляскинский маламут и гренландская ездовая собака, имеют большую часть своего генома с Жоховым.
«Это означает, что современные ездовые собаки и Жохов имели одно и то же общее происхождение в Сибири более 9500 лет назад. До сих пор мы думали, что ездовым собакам было всего 2-3 000 лет», — говорит другой первый автор, доцент Шям Гопалакришнан, Институт глобуса.
Оригинальная ездовая собака
Чтобы узнать больше о происхождении ездовой собаки, исследователи дополнительно секвенировали геномы 33000-летнего сибирского волка и десяти современных гренландских ездовых собак.Они сравнили эти геномы с геномами собак и волков со всего мира.
«Мы видим, что современные ездовые собаки имеют большую часть своих геномов, общих с Жоховым. Таким образом, они более тесно связаны с этой древней собакой, чем с другими собаками и волками. Но не только это — мы видим следы скрещивания с волками, такими как 33000-летний сибирский волк, — но не с современными волками. Это еще раз подчеркивает, что происхождение современной ездовой собаки уходит корнями гораздо дальше, чем мы думали », — говорит Миккель Синдинг.
Современные ездовые собаки имеют большее генетическое совпадение с другими современными породами собак, чем у Жохова, но исследования не показывают нам, где и когда это произошло. Тем не менее, среди современных ездовых собак гренландские ездовые собаки выделяются и меньше всего пересекаются с другими собаками, а это означает, что гренландские ездовые собаки, вероятно, являются самой оригинальной ездовой собакой в мире.
Общие черты инуитов и белых медведей
В дополнение к общему пониманию происхождения ездовых собак, новое исследование также учит исследователей больше узнать о различиях между ездовыми собаками и другими собаками.У ездовых собак нет такой же генетической адаптации к рациону, богатой сахаром и крахмалом, как у других собак. С другой стороны, у них есть адаптация к высокожировой диете с механизмами, аналогичными описанным для белых медведей и арктических людей.
«Это подчеркивает, что ездовые собаки и люди Арктики работали и адаптировались вместе более 9500 лет. Мы также можем видеть, что у них есть адаптации, которые, вероятно, связаны с улучшенным потреблением кислорода, что имеет смысл в отношении катания на санях и дает традиции катания на санях. древние корни », — говорит Шьям Гопалакришнан.
Репозиторий SCOAP3
{
"_oai": {
"обновлено": "2019-04-29T16: 22: 01Z",
"id": "oai: repo.scoap3.org: 42843",
"наборы": [
"PRD"
]
},
"авторы": [
{
"raw_name": "T. \ u2009G. Khunjua",
"affiliations": [
{
"страна": "Россия",
«значение»: «Физический факультет МГУ, 119991, Москва, Россия»
}
],
"фамилия": "Хунджуа",
"given_names": "T. \ u2009G.",
"full_name": "Хунджуа, Т.\ u2009G. "
},
{
"raw_name": "К.Г. Клименко",
"affiliations": [
{
"страна": "Россия",
«значение»: «Институт физики высоких энергий им. Логунова НИЦ« Курчатовский институт », 142281, г. Протвино, Московская область, Россия»
}
],
«фамилия»: «Клименко»,
"given_names": "К. \ u2009G.",
"полное_имя": "Клименко К.Г."
},
{
"raw_name": "Р.Н. Жохов",
"affiliations": [
{
"страна": "Россия",
«значение»: «Институт земного магнетизма, ионосферы и распространения радиоволн им. А.С. Пушкова (ИЗМИРАН), 108840 Троицк, Россия»
}
],
"фамилия": "Жохов",
"given_names": "R.N. ",
"полное_имя": "Жохов Р.Н."
}
],
"названия": [
{
"источник": "АПС",
"title": "Двойственности в плотной кварковой материи с изоспиновым, киральным и киральным изоспиновым дисбалансом в рамках большого - предел модель "
}
],
"dois": [
{
"значение": "10.1103 / PhysRevD.98.054030 "
}
],
"публикации_инфо": [
{
"journal_volume": "98",
"journal_title": "Physical Review D",
"материал": "статья",
"journal_issue": "5",
«год»: 2018
}
],
"$ schema": "http://repo.scoap3.org/schemas/hep.json",
"источник_ приобретения": {
"date": "2019-04-29T15: 48: 59.950087",
"источник": "АПС",
«метод»: «АПС»,
"номер_подачи": "003961306a8511e9a75002163e01809a"
},
"page_nr": [
19
],
"лицензия": [
{
"url": "https: // creativecommons.org / licenses / by / 4.0 / ",
«лицензия»: «CC-BY-4.0»
}
],
"Авторские права": [
{
"statement": "Опубликовано Американским физическим обществом",
«год»: «2018»
}
],
"control_number": "42843",
"record_creation_date": "2018-09-26T16: 30: 15.029947",
"_files": [
{
"контрольная сумма": "md5: dfc787f62afc674d54b7d8067afe43fe",
"filetype": "pdf",
"ведро": "6235802c-d6b0-43ec-87f0-ff4e5fe31069",
"version_id": "256b8b51-ec3c-42ca-b09e-7d56f34445f0",
«ключ»: «10.1103 / PhysRevD.98.054030.pdf »,
"размер": 825621
},
{
«контрольная сумма»: «md5: d5d02683bb2d3ced0200e506430740d8»,
"filetype": "xml",
"ведро": "6235802c-d6b0-43ec-87f0-ff4e5fe31069",
"version_id": "847802a3-0f70-4456-8334-b84ea2587473",
«ключ»: «10.1103 / PhysRevD.98.054030.xml»,
«размер»: 427036
}
],
"коллекции": [
{
"primary": "HEP"
},
{
"primary": "Citeable"
},
{
"primary": "Опубликовано"
}
],
"arxiv_eprints": [
{
"категории": [
"геп-ph",
"hep-th"
],
«значение»: «1804.01014 "
}
],
"аннотации": [
{
"источник": "АПС",
"value": "В этой статье мы исследуем фазовую структуру плотной кварковой материи в присутствии бариона , изоспин , хиральный и хиральный изоспин химические потенциалы в рамках Намбу \ u2013 Модель Йона-Лазинио.Мы показываем, что в большом пределе - ( - количество цветов кварков), в модели существует три двойственных соответствия. Первая двойственность существует между нарушением киральной симметрии и явлениями конденсации заряженных пионов, и есть две новые двойственности, которые справедливы только для явлений нарушения киральной симметрии и явления конденсации заряженных пионов по отдельности.Эти двойственности показывают, что в явлении нарушения киральной симметрии нет разницы между киральным и киральным изоспином < math> \ u03bc I 5 химических потенциалов и заряжен -пионная конденсация не чувствует разницы между изоспином и хиральным химические потенциалы.Мы показываем, что может генерировать конденсацию заряженных пионов, но эта генерация происходит на не столь большом барионе плотности. В случае обоих киральных дисбалансов (хиральный и киральный изоспин химических потенциалов) фазовый портрет довольно богат, и мы показываем, что конденсация заряженных пионов в плотной кварковой материи занимает большую часть фазовой диаграммы.Конденсация заряженных пионов в плотной кварковой материи происходит даже в случае нулевого изоспинового дисбаланса и требует только киральных дисбалансов; этот факт может быть продемонстрирован с использованием одной из новых дуальностей, и это только один пример того, когда эти дуальности очень полезны при исследовании фазовой диаграммы ».
}
],
"отпечатки": [
{
"date": "2018-09-26",
"издатель": "АПС"
}
]
}
В вашем браузере отключен JavaScript.Пожалуйста, включите его, чтобы использовать полную функциональность сайта
| |||||||||||||||||||||||||||||
Науки о Земле | Бесплатный полнотекстовый | Зона устойчивости вечной мерзлоты и газовых гидратов ледниковой части Восточно-Сибирского шельфа
1.Введение
Информация, относящаяся к подводной криолитозоне Восточно-Сибирского арктического шельфа, а именно ее распространение, глубина залегания и мощность мерзлых отложений, необходима для составления прогнозных сценариев потепления климата. Деградирующие подводные замерзшие отложения считаются источником парниковых газов планетарного уровня. Не зная о расширении и структуре криолитозоны, невозможно оценить перспективы эффективного использования Северного морского пути, международной транспортно-логистической системы ближайшего будущего, экологический след от разведки нефтегазовых ресурсов и освоения в Восточной Арктике. полка.
Методы бурения применялись для изучения криолитозоны шельфа морей Лаптевых и Восточно-Сибирского морей только в прибрежной зоне. Максимальное расстояние от скважин до берега — 25 км. Глубина бурения, как правило, не превышает 40–50 м. Скважины глубиной 216 и 203 м (при глубине моря 12 и 14 м соответственно) не вскрыли дно вечной мерзлоты [1]. Пока что скважин на всю толщу вечной мерзлоты не пробурено. Применение сейсмического метода не вышло из стадии разработки.Электроразведка позволила выявить обширную зону талика в Хатангском заливе и заливе Нордвик [2]. Отсутствие возможности получить полную информацию о распространении и мощности вечной мерзлоты с помощью буровых и геофизических методов предопределило широкое использование термоматематического моделирования. Математическое моделирование эволюции и текущего состояния криолитозоны используется с 1970 г. [3] . Обзор подобных исследований на шельфе Восточной Сибири, выполненный в 1970–2000 гг. [4], позволяет авторам не анализировать исследования ХХ века.Разработка методологии и расширение знаний о распространении вечной мерзлоты, ее мощности и глубине залегания были основаны на результатах 10-летних исследований, проведенных Н.Н. Романовский с коллегами [5,6,7,8], а также [9]. В начале 2000-х годов новый подход заключался в использовании гляцио-эвстатических кривых колебаний уровня моря [5] и изотопных палеотемпературных ледниковых данные для создания палеогеографических сценариев, необходимых для математического моделирования [10,11]. Немаловажное значение имела концепция развития озерного термокарста на осушенных частях шельфа [12,13].Это подтверждается широким развитием замкнутых подозерных таликов преимущественно в отрицательных морфоструктурах. Когда их залило бушующее море, они превратились в подводные талики. Кроме того, развитие термокарста вызвало первичное движение моря с севера на юг — по термокарстовым впадинам и речным палеодолинам [14]. Было проведено первое совместное моделирование вечной мерзлоты и зоны стабильности газовых гидратов (ЗГСЗ). Наряду с сходством установлены различия в динамике вечной мерзлоты и GHSZ.Они растут к периферии шельфа [9,15,16]. Позже в исследованиях В.В. Малаховой [17,18,19], разрабатывались подходы, моделировались эволюция и современное состояние вечной мерзлоты и ГГСЗ шельфа Восточной Сибири. Последующие исследования проводились в связи с потеплением климата [20] и экстенсивным развитием. газовых выходов на шельфе Восточной Сибири и других арктических шельфов, образовавшихся в 2003–2010 гг. [20,21,22]. В [23] показано, что с середины 1980 г. по 2009 г. температура воды фактически повысилась на 2 ° C.Однако вечная мерзлота и GHSZ, как было показано ранее [5,8], изменяются в масштабе тысячелетия из-за их большой инерции. Активная эмиссия газа побудила И.П. Семилетов, Н. Шахова, чтобы сформировать гипотезу о дестабилизации метангидрата из-за деградации подводной вечной мерзлоты [24]. Это потребовало внесения корректировок в полученную ранее концепцию непрерывного распространения вечной мерзлоты на исследуемом шельфе [5,9,12]. Моделирование показало возможность образования открытых таликов в местах выхода метана при определенных условиях.Для моделирования последнего авторы использовали в сценарии высокую влажность и соленость отложений до 40 ‰ в грабенах, засоление осадков подводных таликов и температуру придонной воды голоцена по температуре в XX – XXI вв. [25,26,27 ]. Есть некоторые исследователи, придерживающиеся противоположного мнения. В частности, авторы [28] показали, что на шельфе не образовывались открытые талики и не происходили другие процессы, увеличивающие газопроницаемость донных отложений. Геологические причины определили выбросы метана.Другие расчеты [17,29] предсказывают усиление эмиссии метана в случае ускоренной деградации вечной мерзлоты из ее таблицы. Ускорение определяется уменьшением площади морского льда, повышением температуры придонной воды и тепловым потоком рек. Ранее Н.Н. Романовский считал, что прибрежный шельф мог содержать открытые талики из-за разгрузки грунтовых вод с прилегающей суши. Свою точку зрения он обосновал формированием современного талика в более суровых условиях прибрежной суши [30].Обнаруженные области талика в Хатангском заливе и заливе Нордвик подтверждают эту точку зрения [2]. Последняя геокриологическая карта подводной криолитозоны Северного полушария, включающей Восточно-Сибирский шельф, — это карта «Вечная мерзлота в Северном полушарии». опубликовано ГРИД-Арендал [31]. Карта построена на основе результатов численного моделирования, бурения и сейсмических данных [32] .S.O. Разумов и др. [33] исследовали влияние снежно-фирнового покрова толщиной 200 м, предположительно существовавшего в морской изотопной стадии (МИС) 2, на подводную вечную мерзлоту в западной части моря Лаптевых.Авторы пришли к выводу, что за счет этого эффекта мощность мерзлоты уменьшилась не менее чем на 280–360 м. В работе [34] представлены результаты моделирования мощности вечной мерзлоты на севере Западной Сибири (на примере полуострова Ямал) с оценкой уровня Зона устойчивости метаногидратов под влиянием оледенения и последующей морской трансгрессии. Согласно представленным результатам, верхняя граница зоны устойчивости гидратов метана на Ямале могла достигать поверхности земли в периоды ледниковых условий.Этот краткий обзор показывает, что к настоящему времени опубликованы некоторые модели, отражающие современное состояние криолитозоны Восточно-Сибирского сектора в арктических морях. При всех своих достоинствах у них есть и недостатки. Минусы обусловлены недостаточным охватом исследований подводной криолитозоны, геологии шельфа и палеогеографии. Первый недостаток актуален для всех существующих в настоящее время исследований. Имеется в виду гипотетический, схематический, а зачастую и необоснованный характер данных геологических разрезов, на основе которых проводятся расчеты.Второй недостаток — отсутствие тестирования палеогеографического сценария и заданных свойств месторождения. Однако тестирование служит основанием для дальнейшего моделирования, проводимого на его основе. Эти обстоятельства вызывают сомнения в реалистичности полученных результатов. Их часто невозможно проверить из-за отсутствия актуальных данных. Наконец, третий недостаток: все модели основаны на идее отсутствия среднеоплейстоценового оледенения в восточно-сибирском секторе Арктики.Однако информация о ледниковом генезисе подземных льдов на острове Новая Сибирь была опубликована в 2003 г. [35] как предварительная, а в 2006–2008 гг. [36,37] как установленная. Б.Г. Голионко и др. [38] доказали ледниковый характер деформаций в отложениях мела-среднего неоплейстоцена Новой Сибири и Фаддеевских островов.Исходя из вышеизложенного, цель исследования сформулирована следующим образом: оценка эволюции и современного распространения вечной мерзлоты и ГГСЗ, их верхней и нижней границ в ледниковой части Восточно-Сибирского шельфа.Указанная оценка выполнена с использованием термоматематического моделирования и предусматривает сравнение его результатов с параметрами вечной мерзлоты и ГГСЗ в безледниковых условиях. Для достижения поставленной цели в ледниковой зоне и в неледниковых условиях Восточно-Сибирского шельфа решались следующие задачи:
- (1)
Создать сценарий геологического развития исследуемой территории.
- (2)
Для тестирования созданного сценария.
- (3)
Математическое моделирование эволюции и современного распространения вечной мерзлоты и GHSZ, их верхней и нижней границы в пределах ледниковой зоны и в неледниковых условиях.
- (4)
Анализ и проверка полученных результатов.
5. Результаты моделирования
5.1. Тестирование сценария геологического развития
Математическое моделирование на участках, обеспеченных надежными геокриологическими данными, обычно выполняет тестирование.В качестве площади оледенения были взяты участки скважин на острове Новая Сибирь (скважины c-A и c-B) (рис. 1) с геотермическими данными. Бурение и термокаротаж проводились во время государственной геологоразведки в масштабе 1: 200 000 в 1970-х гг. Геологический разрез, необходимый для решения задачи Стефана, в верхних 80 (скважина cB) и 200 м (скважина cA) был установлен результаты бурения, а ниже — по данным геологоразведочных работ, обобщенных в [55,56,72]. По данным геотермальных наблюдений в скважине c-B (расположенной на юго-западной оконечности острова Новая Сибирь) среднегодовая температура составила -11.5 ° С, температура на забое -7,6 ° С. Мощность вечной мерзлоты, рассчитанная по геотермическому градиенту, составляет 250–255 м [71,73]. Палеотемпературная кривая и результаты тестового моделирования показаны на рисунке 7. Корректировка свойств пород позволила получить соответствие между промысловыми и оценочными данными. Мы также провели тестовое моделирование с использованием данных из скважины c-B. Среднегодовая температура грунта в 1970-е годы здесь составляла -13,2 ° C, забойная температура -2 ° C, толщина вечной мерзлоты по данным термокаротажа и геотермального градиента 235–240 м [71].Тестовое моделирование также показало совпадение расчетных данных с промысловыми. Проведенные расчеты позволили сделать вывод, что созданный палеотемпературный сценарий и геологическая модель реалистичны и могут быть использованы для математического моделирования эволюции шельфовой криолитозоны и текущего состояния.5.2. Распределение и толщина вечной мерзлоты
Результаты моделирования внеледниковых и ледниковых условий по сценарию (Рисунок 6) при тепловом потоке 50, 60 и 75 Вт / м 2 показаны на рисунке 8 для площадей 5, 20, и 40-метровые изобаты.На рисунке 8 показана зависимость глубины поверхности (мощности) дна вечной мерзлоты от геотермального потока, глубины моря (изобаты) и истории геологического развития (ледниковые, внеледниковые условия). Плотность геотермального потока определяет скорость промерзания горных пород в течение осушение шельфа и, что особенно важно, скорость деградации вечной мерзлоты при затоплении шельфа. Зависимость толщины вечной мерзлоты от глубины моря — это зависимость от продолжительности периода их нарастания при осушении и деградации при затоплении шельфа.Этот период в пределах ледниковой области намного короче, чем за пределами этой области (Рисунок 9 и Рисунок 10). Согласно вышеизложенному, наибольшая нынешняя мощность вечной мерзлоты должна быть в районе изобат 5 м в внеледниковых условиях, а наименьшая — в области изобат 40 м ледниковой зоны при повышенном тепловом потоке. Действительно, в пределах первого указанного участка он составляет 570 м, внутри второго реликтовая мерзлота полностью деградировала.По этой причине зависимость толщины вечной мерзлоты от величины геотермального потока и глубины моря (изобаты) целесообразно сравнить на примере внеледниковых условий, где эта зависимость четко выражена.В внеледниковых условиях на изобатах 5, 20, 40 м мощность вечной мерзлоты изменяется от 570 до 500 м при тепловом потоке 50 мВт / м 2 , от 430 до 370 м при 60 мВт / м 2 , и от 240 до 220 м при 75 мВт / м 2 .
Зависимость мощности вечной мерзлоты от глубины во внеледниковых условиях намного слабее. Оно постепенно уменьшается по мере увеличения глубины моря от 5 до 20 и далее до 40 м при каждом значении теплового потока 50, 60 и 75 мВт / м 2 .Снижение выражается в значениях от 10 до 20–25 м.
Зависимость толщины вечной мерзлоты от ее расположения в пределах ледниковой зоны или вне ее выражена почти так же четко, как и для теплового потока. Максимальная мощность вечной мерзлоты характерна для площади изобаты 5 м — около 340 м при тепловом потоке 50 мВт / м 2 , что на 220–230 м меньше, чем во внеледниковых условиях. При таком значении теплового потока на изобатах 20 и 40 м толщина вечной мерзлоты уменьшается на 200 м по сравнению с внеледниковыми условиями.При 60 мВт / м 2 такое уменьшение составляет 190 м для изобаты 5 м и 170 м для изобаты 40 м. При 75 мВт / м 2 реликтовые мерзлые отложения обнаруживаются только на изобате 5 м. Их мощность здесь почти 100, что на 130 140 м меньше, чем во внеледниковых условиях. Однако на изобатах 20 и 40 м вечная мерзлота тает. Столь значительная трансформация толщи вечной мерзлоты в пределах ледниковой зоны на изобатах 20 и 40 м при 75 мВт / м 2 обусловлена следующим.
При погружении в море мерзлые отложения представляют собой вечную мерзлоту, скрепленную льдом.По мере разрушения, наряду с повышением температуры грунта, он трансформируется в пласт пластично-мерзлых отложений (ледяная мерзлота), в которой лед содержится в виде включений. На рисунке 8 показаны результаты такой деградации, а именно постепенное уменьшение содержания скрепленной льдом вечной мерзлоты в пластах за счет увеличения объема незамерзшей воды и уменьшения количества льда при тепловом потоке 50 и 60 мВт / м 2 , как для ледниковых, так и для внеледниковых условий.Результаты такой же деградации, вместе с повышением температуры, изменением соотношения незамерзшей воды и льда, отражаются в тепловом потоке 75 мВт / м 2 для 5-метровой изобаты в ледниковых условиях. Иная ситуация на изобатах 20 и 40 м в пределах ледниковой зоны. Резко ускорившаяся деградация свидетельствует о том, что температура в деградационных пластах возрастает до значений, соответствующих точке замерзания – оттаивания поровой воды, что фазовые переходы в ней минимизируются и скорость оттаивания вечной мерзлоты резко возрастает.Скорость роста приводит к полному таянию вечной мерзлоты на изобатах 20–40 м.Таким образом, при тепловом потоке 75 мВт / м 2 в ледниковой зоне может возникать прерывистая или спорадическая реликтовая вечная мерзлота, а в внеледниковых условиях — сплошная реликтовая вечная мерзлота мощностью 200–240 м.
5.3. Эволюция вечной мерзлоты
Результаты моделирования показывают, что наиболее значительное влияние оледенение оказало на эволюцию вечной мерзлоты (Рисунок 9 и Рисунок 10). В внеледниковых условиях вечная мерзлота существовала непрерывно в течение всего расчетного периода (200 тыс. Лет до настоящего времени).В пределах ледниковой зоны, напротив, произошел прорыв. Существование вечной мерзлоты приходилось на интервалы 190–125 и 70–60 тыс. Лет назад. В течение первого интервала они формировались и существовали под ледником, второй — интервал их субаэрального существования. Его начало связано с морской регрессией в МИС-4. Возраст современной вечной мерзлоты составляет 60 000–70 000 лет. Образование и деградация вечной мерзлоты были вызваны колебаниями климата и уровня моря. Следовательно, наблюдаются колебания глубины и мощности дна вечной мерзлоты (Рисунок 9 и Рисунок 10).В этом случае они проявляются в сглаженной форме и с запаздыванием. Наиболее отчетливо гладкость отмечается на изобате 5 м (рис. 9). Запаздывание оптимума MIS-5e (125 000 лет назад) или пессия MIS-2 (20 000 лет назад) (Рисунок 6), например, как во внеледниковых, так и в ледниковых условиях, составляет приблизительно 8 000–9 000 лет. Это хорошо согласуется с результатами других исследований [9,74]. Наибольшая мощность вечной мерзлоты, судя по пессиям МИС-6 и МИС-2, составляет 450 и 380 м соответственно во внеледниковых условиях (рис. 6а, д).В ледниковых условиях (рис. 6б, е), напротив, мощность вечной мерзлоты в МИС-6, образовавшейся под ледником, была меньше (200 м), чем в МИС-2 (360 м). Таким образом, воздействие ледника выразилось в уменьшении толщины вечной мерзлоты на 160 м. В теплые интервалы мощность вечной мерзлоты во внеледниковых условиях была меньше. В ответ на оптимум МИС-5э он составлял 210 м. После самого теплого интервала МИС-3 из-за подъема уровня моря на изобате 40 м он составил 270 м.На изобате 5 м потепление вообще не проявилось, поскольку море достигло только современной изобаты 40 м (рис. 6e).5.4. Текущее состояние зоны стабильности газовых гидратов
GHSZ образовалась вместе с вечной мерзлотой в внеледниковых и ледниковых условиях с тепловым потоком от 50 до 75 мВт / м 2 (Рисунок 9 и Рисунок 10). Положение верхней границы ГГСЗ мало зависит от наличия или отсутствия ледника в прошлом. Он расположен внутри вечной мерзлоты на глубине 130–160 м во внеледниковых условиях и на глубине 140–160 м в ледниковых условиях (рис. 9, рис. 10 и рис. 11).Нижняя граница GHSZ в ледниковых условиях расположена на глубинах около 700 м при 50 мВт / м 2 , на 450–500 м при 60 мВт / м 2 (Рисунок 12). При 75 мВт / м 2 , по нашим расчетам, зона устойчивости гидратов до сих пор не соблюдалась. В внеледниковых условиях его глубины составляют 900–1050 и 770–790 м при 50 и 60 мВт / м 2 соответственно. При 75 мВт / м 2 глубины обычно близки к 400 м. Глубокое положение нижней границы и высокая мощность GHSZ, особенно на изобате 5 м при 50 мВт / м 2 , вызваны большой мощностью вечной мерзлоты.Соответственно, меньшая мощность вечной мерзлоты в ледниковой области определяет более мелководное положение нижней границы и меньшую мощность ГГСЗ по сравнению с внеледниковыми условиями.5.5. Эволюция зоны устойчивости газовых гидратов
Эволюция GHSZ связана с динамикой P-T условий, то есть с динамикой вечной мерзлоты и существованием оледенения. Эволюция проявляется, прежде всего, в периодах существования ВГСЗ, а также в динамике ее нижней и верхней границ и мощности, вызванной колебаниями климата и уровня моря.В внеледниковых условиях время жизни GHSZ превысило расчетный период (Рисунок 9a и Рисунок 10a). В пределах ледниковой зоны периоды GHSZ менялись поочередно с периодами без GHSZ (Рисунок 9b и Рисунок 10b). Периоды существования приходились на интервалы 190–125 и 70–60 тыс. Лет назад с перерывом на интервал 125–70 тыс. Лет назад. Конфигурация нижней и верхней границ ГГСЗ и мощность тесно связаны с климатом, уровнем моря. колебания и существование ледников.В внеледниковых условиях межледниковья (MIS-7, 5e, 1) и кратковременные теплые экстремумы, сопровождавшиеся повышением уровня моря (MIS-5c, 5a, 3), на 40-метровых изобатах выделяются понижениями уровня моря. Кровля ГХС до 100–120 м (рис. 9а). На изобатах 5 м такие впадины характерны только для межледниковья (рис. 10а). Отклик нижней границы ГГСЗ на колебания климата во внеледниковых условиях повторяет рельеф нижней границы вечной мерзлоты (рис. 9а и рис. 10а).Однако он имеет более гладкую форму, чем отклик дна вечной мерзлоты. Задержка имеет ту же последовательность, что и в случае вечной мерзлоты. В пределах ледниковой зоны следует отметить два обстоятельства. Первый — это формирование ЗГСЗ с крышей, совпадающей с ложем ледника (рис. 9б и рис. 10б). Это вызвано ледниковой нагрузкой. Второй — это рельефный отклик кровли, и особенно нижней границы GHSZ, на климат и колебания уровня моря на 40-метровой изобате (рис. 9b).На изобате 5 м это не так. Информация о глубине нижней границы ГГСЗ и толщине при тепловом потоке 60 мВт / м 2 представлена в таблице 1. Следует отметить, что глубина ГГСЗ дно и его мощность во внеледниковых условиях значительно больше, чем в ледниковых условиях. В пределах пессия МИС-6 они составляли 800 и 740 м, в пределах МИС-2–770 и 730 м соответственно.В отличие от результатов численного эксперимента с тепловым потоком 60 мВт / м2, расчет, основанный на потоке 75 мВт / м 2 , показывает, что зона устойчивости газовых гидратов формируется только в периоды океанической регрессии.В то же время в ледниковых условиях ЗГСЗ в последнее время отсутствует. Он был разрушен в голоцене: 4000 лет назад на площади 5-метровых изобат, 5000 лет назад на 20-метровых изобатах и 6000 лет назад на 40-метровых изобатах. Поскольку условия, благоприятные для образования ГГС, нарушены, газовые гидраты, возможно, подвержены деградации, метан накапливается в подмерзлотных горизонтах донных отложений. Последующее разрушение слоя вечной мерзлоты под действием повышенного теплового потока (75 мВт / м 2 и более) в последнее время, вероятно, вызовет увеличение проницаемости донных отложений и притока метана в атмосферу из мелководья. водная полка.
Область высоких выбросов метана к северу от острова Новая Сибирь в исследовании [23] связана с существованием Великой Сибирской Полыньи. Результаты наших исследований указывают на возможную связь этой территории с деградацией вечной мерзлоты и дестабилизацией ГГСЗ в пределах области оледенения среднего неоплейстоцена с повышенным тепловым потоком.6. Обсуждение и выводы
В модели Романовский и др. [9] получили значения толщины вечной мерзлоты и глубины нижней границы ГГСЗ в пределах ледниковой зоны, которые составили 1.В 5 раз больше, чем в нашей модели. Различия объясняются тем, что для исследования авторы использовали не условные, а реальные геологические разрезы. В последнем есть как протяженные интервалы морской седиментации, где нет промерзания пород, так и многочисленные пласты бурого угля с низкой теплопроводностью. В таких исследованиях вызывает озабоченность проверка результатов моделирования. Обеспокоенность возникает из-за отсутствия данных, необходимых для сравнения. Н. Шахова и Д. Никольский предлагают проверку, основанную на местоположении выходов метана [24].Часто сравнивают толщину вечной мерзлоты в прибрежных скважинах [25]. Однако в районе восточной части островов Анжу и архипелага Де Лонг таких скважин, за исключением тех, которые использовались в данном исследовании, нет. Помимо тестирования сценария и геологической модели, авторы использовали процедуру моделирования, чтобы результаты были более реалистичными. Расчеты для береговых площадок скважин и площадок изобат 5, 20 и 40 м выполнены в единой системе. Кроме того, береговые скважины считаются ориентирами.Это геологический ориентир: скважина c-B и результаты обобщения геологического развития региона [55]. Кроме того, геотермальный ориентир в виде результатов измерения температуры для скважины c-B. Таким образом, результаты моделирования постоянно контролировались геокриологическими данными в процессе расчетов, которые рассматривались как проверка окончательной модели.Впервые с помощью математического моделирования изучены распределение и мощность вечной мерзлоты в пределах области оледенения в конце среднего неоплейстоцена на северо-западе Восточно-Сибирского шельфа.
Впервые моделирование основано не на условных схематических разрезах, а на данных бурения отложений, содержащих, перекрывающих и подстилающих пластовый лед острова Новая Сибирь. Мы протестировали палеотемпературный сценарий по результатам геотермальных наблюдений в скважинах. Это обеспечивает реалистичность результатов моделирования.
Результаты моделирования показывают, что в ледниковой зоне мощность многолетнемерзлых пород при тепловых потоках 50 и 60 мВт / м 2 на 150–200 м меньше, чем в внеледниковых.При тепловом потоке 75 мВт / м 2 на изобатах 20–40 м это приводит к образованию прерывистой или спорадической мерзлоты.
В внеледниковых условиях ГГСЗ формировалась при тепловом потоке от 50 до 75 мВт / м 2 . Его нижняя граница в настоящее время расположена на глубине 900–1000 м при 50 мВт / м 2 , на глубине около 400 м при 75 мВт / м 2 .
Вечная мерзлота и пласты GHSZ непрерывно существуют в внеледниковых условиях, по крайней мере, в течение всего оценочного периода (200 тыс. Лет в настоящее время).В пределах ледниковой зоны в течение среднего плейстоцена-голоцена они возникли и деградировали. Современные толщи вечной мерзлоты, а также GHSZ с тепловым потоком 50 и 60 мВт / м 2 существуют со времен MIS-4 (60 000–70 000 лет). При тепловом потоке 75 мВт / м 2 вечная мерзлота сохраняется только в прибрежной зоне и на 5-метровых изобатах, а GHSZ в настоящее время отсутствует.
Обработка итераций без цикла — Настоящий Python
Python map () — это встроенная функция, которая позволяет обрабатывать и преобразовывать все элементы в итерируемом объекте без использования явного цикла for , метод, широко известный как отображение. map () полезен, когда вам нужно применить функцию преобразования к каждому элементу итерации и преобразовать их в новую итерацию. map () — один из инструментов, поддерживающих стиль функционального программирования в Python.
В этом руководстве вы узнаете:
- Как работает карта Python
() - Как преобразовать различных типов итераций Python с помощью
map () - Как объединить
map ()с другими функциональными инструментами для выполнения более сложных преобразований - Какие инструменты вы можете использовать, чтобы заменить
map ()и сделать ваш код более Pythonic
Обладая этими знаниями, вы сможете эффективно использовать map () в своих программах или, альтернативно, использовать составные части списков или выражения генератора, чтобы сделать ваш код более питоническим и читабельным.
Для лучшего понимания map () были бы полезны некоторые предыдущие знания о том, как работать с итерациями, для циклов, функций и лямбда-функций .
Бесплатный бонус: 5 мыслей о Python Mastery, бесплатный курс для разработчиков Python, который показывает вам план развития и образ мышления, который вам понадобится, чтобы вывести свои навыки Python на новый уровень.
Кодирование с функциональным стилем на Python
В функциональном программировании вычисления выполняются путем комбинирования функций, которые принимают аргументы и в результате возвращают конкретное значение (или значения).Эти функции не изменяют свои входные аргументы и не изменяют состояние программы. Они просто предоставляют результат данного вычисления. Такие функции обычно называются чистыми функциями.
Теоретически программы, построенные с использованием функционального стиля, проще:
- Разработка , потому что вы можете кодировать и использовать каждую функцию изолированно
- Отладка и тестирование , потому что вы можете тестировать и отлаживать отдельные функции, не глядя на остальную часть программы
- Понять , потому что вам не нужно иметь дело с изменениями состояния на протяжении всей программы
Функциональное программирование обычно использует списки, массивы и другие итерации для представления данных вместе с набором функций, которые работают с этими данными и преобразуют их.Когда дело доходит до обработки данных в функциональном стиле, обычно используются как минимум три метода:
Отображение состоит из применения функции преобразования к итерируемому объекту для создания нового объекта. Элементы в новой итерации создаются путем вызова функции преобразования для каждого элемента в исходной итерации.
Фильтрация состоит из применения предиката или булевозначной функции к итерируемому объекту для создания нового итерируемого объекта.Элементы в новой итерации создаются путем фильтрации любых элементов в исходной итерации, которые заставляют функцию предиката возвращать false.
Уменьшение состоит из применения функции уменьшения к итерируемому объекту для получения единственного накопленного значения.
По словам Гвидо ван Россума, на Python сильнее влияют императивные языки программирования, чем функциональные языки:
Я никогда не считал, что Python находится под сильным влиянием функциональных языков, независимо от того, что люди говорят или думают.Я был гораздо больше знаком с императивными языками, такими как C и Algol 68, и хотя я сделал функции первоклассными объектами, я не рассматривал Python как язык функционального программирования. (Источник)
Однако еще в 1993 году сообщество Python требовало некоторых функций функционального программирования. Просили:
Эти функциональные возможности были добавлены в язык благодаря участию члена сообщества. В настоящее время map () , filter () и reduce () являются фундаментальными компонентами стиля функционального программирования в Python.
В этом руководстве вы рассмотрите одну из этих функциональных возможностей, встроенную функцию map () . Вы также узнаете, как использовать составные части списков и выражения генератора, чтобы получить те же функциональные возможности, что и map () , в питоническом и удобочитаемом виде.
Начало работы с картой Python
() Иногда вы можете столкнуться с ситуациями, в которых вам нужно выполнить одну и ту же операцию со всеми элементами итерации ввода, чтобы построить новую итерацию.Самый быстрый и распространенный подход к этой проблеме — использовать цикл Python для . Однако вы также можете решить эту проблему без явного цикла, используя map () .
В следующих трех разделах вы узнаете, как работает map () и как вы можете использовать его для обработки и преобразования итераций без цикла.
Понимание карты
() map () перебирает элементы итерируемого ввода (или итераций) и возвращает итератор, который является результатом применения функции преобразования к каждому элементу в исходном итерируемом вводе.
Согласно документации, map () принимает объект функции и итерацию (или несколько итераций) в качестве аргументов и возвращает итератор, который выдает преобразованные элементы по запросу. Сигнатура функции определяется следующим образом:
карта (функция, iterable [, iterable1, iterable2, ..., iterableN])
map () применяет функцию к каждому элементу в итерируемом в цикле и возвращает новый итератор, который выдает преобразованные элементы по запросу. Функция может быть любой функцией Python, которая принимает количество аргументов, равное количеству итераций, которые вы передаете в map () .
Примечание: Первым аргументом функции map () является объект функции , что означает, что вам нужно передать функцию, не вызывая ее. То есть без пары скобок.
Этот первый аргумент map () — это функция преобразования . Другими словами, это функция, которая преобразует каждый исходный элемент в новый (преобразованный) элемент.Несмотря на то, что в документации Python этот аргумент называется функцией , он может быть любым вызываемым Python. Сюда входят встроенные функции, классы, методы, лямбда-функций, функций и пользовательские функции.
Операция, которую выполняет map () , обычно известна как отображение , потому что она отображает каждый элемент во входном итерируемом элементе на новый элемент в результирующем итерируемом. Для этого map () применяет функцию преобразования ко всем элементам во входной итерации.
Чтобы лучше понять map () , предположим, что вам нужно взять список числовых значений и преобразовать его в список, содержащий квадратное значение каждого числа в исходном списке. В этом случае вы можете использовать цикл для и кодировать что-то вроде этого:
>>> числа = [1, 2, 3, 4, 5]
>>> в квадрате = []
>>> для числа в числах:
... squared.append (число ** 2)
...
>>> в квадрате
[1, 4, 9, 16, 25]
Когда вы запускаете этот цикл на числах , вы получаете список квадратных значений.Цикл для выполняет итерацию по числам и применяет операцию мощности к каждому значению. Наконец, он сохраняет полученные значения в квадрате .
Вы можете достичь того же результата без использования явного цикла, используя map () . Взгляните на следующую реализацию приведенного выше примера:
>>> def квадрат (число):
... номер возврата ** 2
...
>>> числа = [1, 2, 3, 4, 5]
>>> в квадрате = карта (квадрат, числа)
>>> список (в квадрате)
[1, 4, 9, 16, 25]
square () — это функция преобразования, которая преобразует число в его квадратное значение.Вызов map () применяет square () ко всем значениям в числах и возвращает итератор, который возвращает квадратные значения. Затем вы вызываете list () на карте map () , чтобы создать объект списка, содержащий квадратные значения.
Поскольку map () написан на C и сильно оптимизирован, его внутренний подразумеваемый цикл может быть более эффективным, чем обычный цикл Python для . Это одно из преимуществ использования map () .
Второе преимущество использования map () связано с потреблением памяти.При использовании цикла для вам необходимо сохранить весь список в памяти вашей системы. С помощью map () вы получаете элементы по запросу, и только один элемент находится в памяти вашей системы в данный момент.
Примечание. В Python 2.x map () возвращает список. Это поведение изменилось в Python 3.x. Теперь map () возвращает объект карты, который является итератором, выдающим элементы по запросу. Вот почему вам нужно вызвать list () , чтобы создать желаемый объект списка.
В качестве другого примера скажем, что вам нужно преобразовать все элементы в списке из строки в целое число. Для этого вы можете использовать map () вместе с int () следующим образом:
>>> str_nums = ["4", "8", "6", "5", "3", "2", "8", "9", "2", "5" ]
>>> int_nums = map (int, str_nums)
>>> int_nums
<объект карты в 0x7fb2c7e34c70>
>>> список (int_nums)
[4, 8, 6, 5, 3, 2, 8, 9, 2, 5]
>>> str_nums
[«4», «8», «6», «5», «3», «2», «8», «9», «2», «5»]
map () применяет int () к каждому значению в str_nums .Поскольку map () возвращает итератор (объект карты), вам потребуется вызвать list () , чтобы вы могли исчерпать итератор и превратить его в объект списка. Обратите внимание, что исходная последовательность не изменяется в процессе.
Использование карты
() с различными видами функций Вы можете использовать любой вид Python, вызываемый с помощью map () . Единственным условием было бы то, что вызываемый объект принимает аргумент и возвращает конкретное и полезное значение. Например, вы можете использовать классы, экземпляры, реализующие специальный метод под названием __call __ () , методы экземпляра, методы класса, статические методы и функции.
Есть несколько встроенных функций, которые можно использовать с map () . Рассмотрим следующие примеры:
>>> числа = [-2, -1, 0, 1, 2]
>>> abs_values = список (карта (абс, числа))
>>> abs_values
[2, 1, 0, 1, 2]
>>> список (карта (с плавающей точкой, числа))
[-2.0, -1.0, 0.0, 1.0, 2.0]
>>> words = ["Добро пожаловать", "в", "Настоящее", "Python"]
>>> список (карта (лен, слова))
[7, 2, 4, 6]
Вы можете использовать любую встроенную функцию с map () при условии, что функция принимает аргумент и возвращает значение.
Обычно при использовании map () используется лямбда-функция в качестве первого аргумента. лямбда-функции удобны, когда вам нужно передать основанную на выражении функцию в map () . Например, вы можете повторно реализовать пример квадратных значений с помощью лямбда-функции следующим образом:
>>> числа = [1, 2, 3, 4, 5]
>>> в квадрате = карта (лямбда-число: число ** 2, числа)
>>> список (в квадрате)
[1, 4, 9, 16, 25]
лямбда-функции весьма полезны при использовании map () .Они могут играть роль первого аргумента для map () . Вы можете использовать лямбда-функции вместе с map () для быстрой обработки и преобразования ваших итераций.
Обработка множественных итераций ввода с помощью карты
() Если вы передаете несколько итераций в map () , то функция преобразования должна принимать столько аргументов, сколько итераций вы передаете. Каждая итерация map () будет передавать одно значение из каждой итерации в качестве аргумента функции .Итерация останавливается в конце самой короткой итерации.
Рассмотрим следующий пример, в котором используется pow () :
>>> first_it = [1, 2, 3]
>>> second_it = [4, 5, 6, 7]
>>> список (карта (pow, first_it, second_it))
[1, 32, 729]
pow () принимает два аргумента, x и y , и возвращает x в степени y . В первой итерации x будет 1 , y будет 4 , а результат будет 1 .Во второй итерации x будет 2 , y будет 5 , и результат будет 32 и так далее. Последняя итерация равна длине самой короткой итерации, которая в данном случае равна first_it .
Этот метод позволяет объединить две или более итерации числовых значений, используя различные виды математических операций. Вот несколько примеров, которые используют лямбда-функции для выполнения различных математических операций с несколькими входными итерациями:
>>> list (map (lambda x, y: x - y, [2, 4, 6], [1, 3, 5]))
[1, 1, 1]
>>> list (map (лямбда x, y, z: x + y + z, [2, 4], [1, 3], [7, 8]))
[10, 15]
В первом примере вы используете операцию вычитания для объединения двух итераций по три элемента в каждом.Во втором примере вы складываете значения трех итераций.
Преобразование итераций строк с помощью карты Python
() Когда вы работаете с итерациями строковых объектов, вам может быть интересно преобразовать все объекты с помощью какой-либо функции преобразования. Карта Python () может быть вашим союзником в этих ситуациях. В следующих разделах вы познакомитесь с некоторыми примерами того, как использовать map () для преобразования итераций строковых объектов.
Методикой
ул. Довольно распространенный подход к манипуляциям со строками заключается в использовании некоторых методов класса str для преобразования заданной строки в новую строку. Если вы имеете дело с итерациями строк и вам нужно применить одно и то же преобразование к каждой строке, вы можете использовать map () вместе с различными строковыми методами:
>>> string_it = ["обработка", "строки", "с", "карта"]
>>> список (карта (ул.заглавные буквы, строка_ит))
["Обработка", "Строки", "С", "Карта"]
>>> список (карта (str.upper, string_it))
["ОБРАБОТКА", "СТРОКИ", "С", "КАРТА"]
>>> список (карта (str.lower, string_it))
['обработка', 'строки', 'с', 'карта']
Есть несколько преобразований, которые вы можете выполнить для каждого элемента в string_it , используя map () и строковые методы. В большинстве случаев вы будете использовать методы, которые не принимают дополнительных аргументов, например str.capitalize () , str.нижний () , str.swapcase () , str.title () и str.upper () .
Вы также можете использовать некоторые методы, которые принимают дополнительные аргументы со значениями по умолчанию, например str.strip () , который принимает необязательный аргумент с именем char , который по умолчанию удаляет пробелы:
>>> with_spaces = ["обработка", "строки", "с", "карта"]
>>> список (карта (str.strip, with_spaces))
['обработка', 'строки', 'с', 'карта']
При использовании ул.strip () , вы полагаетесь на значение по умолчанию char . В этом случае вы используете map () , чтобы удалить все пробелы в элементах with_spaces .
Примечание: Если вам нужно предоставить аргументы, а не полагаться на значение по умолчанию, вы можете использовать лямбда-функцию .
Вот пример, в котором для удаления точек используется str.strip () , а не пробелы по умолчанию:
>>> with_dots = ["обработка.. "," ... строки "," с .... "," ..карта .. "]
>>> список (map (lambda s: s.strip ("."), with_dots))
['обработка', 'строки', 'с', 'карта']
Функция лямбда вызывает .strip () для строкового объекта s и удаляет все начальные и конечные точки.
Этот метод может быть полезен, когда, например, вы обрабатываете текстовые файлы, в которых строки могут иметь завершающие пробелы (или другие символы), и вам необходимо их удалить. Если это так, то вам нужно учитывать, что используя str.strip () без специального символа char также удалит символ новой строки.
Удаление знаков препинания
Когда дело доходит до обработки текста, иногда необходимо удалить знаки препинания, оставшиеся после разделения текста на слова. Чтобы справиться с этой проблемой, вы можете создать настраиваемую функцию, которая удаляет знаки препинания из одного слова, используя регулярное выражение, которое соответствует наиболее распространенным знакам препинания.
Вот возможная реализация этой функции с использованием sub () , которая представляет собой функцию регулярного выражения, которая находится в модуле re в стандартной библиотеке Python:
>>> импорт ре
>>> def remove_punctuation (слово):
... return re.sub (r '[!?.:;, "() -]'," ", word)
>>> remove_punctuation ("... Python!")
'Python'
Внутри remove_punctuation () вы используете шаблон регулярного выражения, который соответствует наиболее распространенным знакам препинания, которые вы найдете в любом тексте, написанном на английском языке. Вызов re.sub () заменяет совпадающие знаки препинания пустой строкой ( "" ) и возвращает очищенное слово .
Имея функцию преобразования, вы можете использовать map () для выполнения преобразования для каждого слова в вашем тексте.Вот как это работает:
>>> text = "" "Некоторые люди, сталкиваясь с проблемой, думают
... «Я знаю, я буду использовать регулярные выражения».
... Теперь у них две проблемы. Джейми Завински "" "
>>> слова = text.split ()
>>> слова
[«Некоторые», «люди», «когда», «столкнулись», «с», «а», «проблема», «думают»
, '"Я', 'знаю,'," Я ", 'использую', 'регулярные', 'выражения.', 'Сейчас', 'они',
'иметь', 'два', 'проблемы.', 'Джейми', 'Завински']
>>> список (карта (remove_punctuation, слова))
[«Некоторые», «люди», «когда», «столкнулись», «с», «а», «проблема», «думают»,
"Я", "знаю", "я", "использую", "регулярные", "выражения", "сейчас", "они", "имеют
',' два ',' проблемы ',' Джейми ',' Завински ']
В этом фрагменте текста некоторые слова содержат знаки препинания.Например, у вас «человек», вместо «человек» , «проблема», « вместо « проблема » и т. Д. Вызов map () применяет remove_punctuation () к каждому слову и удаляет любые знаки препинания. Итак, во втором списке вы очистили слова.
Обратите внимание, что апостроф ( ') отсутствует в вашем регулярном выражении, потому что вы хотите сохранить сокращения вроде , я такими, какие они есть.
Реализация алгоритма шифрования Цезаря
Юлий Цезарь, римский государственный деятель, использовал для защиты сообщений, которые он отправлял своим генералам, зашифровывая их с помощью шифра. Шифр Цезаря сдвигает каждую букву на количество букв. Например, если вы сдвинете букву на на три, вы получите букву d и так далее.
Если сдвиг выходит за пределы конца алфавита, вам просто нужно вернуться к началу алфавита. В случае поворота на три, x превратится в a .Вот как будет выглядеть алфавит после поворота:
- Оригинальный алфавит:
abcdefghijklmnopqrstuvwxyz - Алфавит, повернутый на три:
defghijklmnopqrstuvwxyzabc
Следующий код реализует rotate_chr () , функцию, которая берет символ и поворачивает его на три. rotate_chr () вернет повернутый символ. Вот код:
1def rotate_chr (c):
2 rot_by = 3
3 c = c.ниже()
4 алфавит = "abcdefghijklmnopqrstuvwxyz"
5 # Сохраняйте знаки препинания и пробелы
6, если c не в алфавитном порядке:
7 возврат c
8 rotated_pos = ord (c) + rot_by
9 # Если вращение внутри алфавита
10, если rotated_pos <= ord (алфавит [-1]):
11 вернуть chr (rotated_pos)
12 # Если вращение выходит за рамки алфавита
13 вернуть chr (rotated_pos - len (алфавит))
Внутри rotate_chr () вы сначала проверяете, находится ли символ в алфавите.Если нет, то вы возвращаете тот же символ. Это позволяет сохранить знаки препинания и другие необычные символы. В строке 8 вы вычисляете новую повернутую позицию символа в алфавите. Для этого используется встроенная функция ord () .
ord () принимает символ Юникода и возвращает целое число, которое представляет кодовую точку Юникода входного символа. Например, ord ("a") возвращает 97 , а ord ("b") возвращает 98 :
>>> ord ("а")
97
>>> ord ("б")
98
ord () принимает символ в качестве аргумента и возвращает кодовую точку Unicode входного символа.
Если вы добавите это целое число к целевому числу rot_by , то вы получите повернутую позицию новой буквы в алфавите. В этом примере rot_by - это 3 . Таким образом, буква «a» , повернутая на три, станет буквой в позиции 100 , которая является буквой «d» . Буква "b" , повернутая на три, станет буквой в позиции 101 , то есть буквой "e" и так далее.
Если новая позиция буквы не выходит за пределы позиции последней буквы ( алфавит [-1] ), то вы возвращаете букву в эту новую позицию. Для этого вы используете встроенную функцию chr () .
chr () - это обратное значение ord () . Он принимает целое число, представляющее кодовую точку Unicode символа Unicode, и возвращает символ в этой позиции. Например, chr (97) вернет 'a' , а chr (98) вернет 'b' :
>>> chr (97)
'а'
>>> chr (98)
'b'
chr () принимает целое число, представляющее кодовую точку Unicode символа, и возвращает соответствующий символ.
Наконец, если новая повернутая позиция выходит за пределы позиции последней буквы ( алфавит [-1] ), то вам нужно повернуть обратно к началу алфавита. Для этого вам нужно вычесть длину алфавита из повернутой позиции ( rotated_pos - len (алфавит) ), а затем вернуть букву в этой новой позиции с помощью chr () .
С rotate_chr () в качестве функции преобразования вы можете использовать map () для шифрования любого текста с помощью алгоритма шифрования Цезаря.Вот пример, в котором для объединения строки используется str.join () :
>>> "" .join (map (rotate_chr, "Мое секретное сообщение идет сюда."))
'pb vhfuhw phvvdjh jrhv khuh.'
Строки также являются итерируемыми в Python. Итак, вызов map () применяет rotate_chr () к каждому символу исходной входной строки. В этом случае «M» становится «p» , «y» становится «b» и так далее.Наконец, вызов str.join () объединяет каждый повернутый символ в окончательное зашифрованное сообщение.
Преобразование итераций чисел с помощью карты Python
() map () также имеет большой потенциал, когда дело доходит до обработки и преобразования итераций числовых значений . Вы можете выполнять широкий спектр математических и арифметических операций, преобразовывать строковые значения в числа с плавающей запятой или целые числа и т. Д.
В следующих разделах вы рассмотрите несколько примеров использования map () для обработки и преобразования итераций чисел.
Использование математических операций
Распространенным примером использования математических операций для преобразования итерации числовых значений является использование оператора мощности ( ** ). В следующем примере вы кодируете функцию преобразования, которая принимает число и возвращает число в квадрате и кубе:
>>> def powers (x):
... вернуть x ** 2, x ** 3
...
>>> числа = [1, 2, 3, 4]
>>> список (карта (степени, числа))
[(1, 1), (4, 8), (9, 27), (16, 64)]
powers () принимает число x и возвращает его квадрат и куб.Поскольку Python обрабатывает несколько возвращаемых значений как кортежи, каждый вызов powers () возвращает кортеж с двумя значениями. Когда вы вызываете map () с powers () в качестве аргумента, вы получаете список кортежей, содержащий квадрат и куб каждого числа во входном итеративном элементе.
Есть много математических преобразований, которые можно выполнить с помощью map () . Вы можете добавлять константы и вычитать их из каждого значения. Вы также можете использовать некоторые функции из модуля math , например sqrt () , factorial () , sin () , cos () и т. Д.Вот пример использования factorial () :
>>> импорт математики
>>> числа = [1, 2, 3, 4, 5, 6, 7]
>>> список (карта (math.factorial, numbers))
[1, 2, 6, 24, 120, 720, 5040]
В этом случае вы преобразуете чисел в новый список, содержащий факториал каждого числа в исходном списке.
С помощью функции map () вы можете выполнять широкий спектр математических преобразований для итерации чисел.Насколько далеко вы углубитесь в эту тему, будет зависеть от ваших потребностей и вашего воображения. Подумайте об этом и напишите свои собственные примеры!
Преобразование температур
Другой вариант использования map () - преобразование между единиц измерения . Предположим, у вас есть список температур, измеренных в градусах Цельсия или Фаренгейта, и вам нужно преобразовать их в соответствующие температуры в градусах Фаренгейта или Цельсия.
Для выполнения этой задачи можно закодировать две функции преобразования:
def to_fahrenheit (c):
возврат 9/5 * c + 32
def to_celsius (f):
возврат (ж - 32) * 5/9
to_fahrenheit () измеряет температуру в градусах Цельсия и переводит их в градусы Фаренгейта.Аналогично, to_celsius () принимает температуру в градусах Фаренгейта и преобразует ее в градусы Цельсия.
Эти функции будут вашими функциями преобразования. Вы можете использовать их с map () , чтобы преобразовать повторяющиеся измерения температуры в градусы Фаренгейта и Цельсия соответственно:
>>> celsius_temps = [100, 40, 80]
>>> # Конвертировать в градусы Фаренгейта
>>> список (карта (to_fahrenheit, celsius_temps))
[212,0, 104,0, 176,0]
>>> fahr_temps = [212, 104, 176]
>>> # Конвертировать в градусы Цельсия
>>> список (карта (to_celsius, fahr_temps))
[100.0, 40,0, 80,0]
Если вы позвоните map () с to_fahrenheit () и celsius_temps , то получите список температурных мер в градусах Фаренгейта. Если вы вызовете map () с to_celsius () и fahr_temps , вы получите список измерений температуры в градусах Цельсия.
Чтобы расширить этот пример и охватить любой другой вид преобразования единиц, вам просто нужно закодировать соответствующую функцию преобразования.
Преобразование строк в числа
При работе с числовыми данными вы, вероятно, столкнетесь с ситуациями, когда все ваши данные являются строковыми значениями.Для дальнейших вычислений вам нужно будет преобразовать строковые значения в числовые значения. map () также может помочь в этих ситуациях.
Если вы уверены, что ваши данные чистые и не содержат неправильных значений, вы можете использовать float () или int () в соответствии с вашими потребностями. Вот несколько примеров:
>>> # Преобразовать в числа с плавающей запятой
>>> list (map (float, ["12.3", "3.3", "-15.2"]))
[12,3, 3,3, -15.2]
>>> # Преобразовать в целое число
>>> list (map (int, ["12", "3", "-15"]))
[12, 3, -15]
В первом примере вы используете float () с map () для преобразования всех значений из строковых значений в значения с плавающей запятой. Во втором случае вы используете int () для преобразования строки в целое число. Обратите внимание: если одно из значений не является допустимым числом, вы получите ValueError .
Если вы не уверены, что ваши данные чистые, вы можете использовать более сложную функцию преобразования, например следующую:
>>> >>> def to_float (число):
... пытаться:
... вернуть float (number.replace (",", "."))
... кроме ValueError:
... return float ("nan")
...
>>> list (map (to_float, ["12.3", "3,3", "-15.2", "One"]))
[12,3, 3,3, -15,2, нан]
Внутри to_float () используется оператор try , который перехватывает ValueError , если float () завершается неудачно при преобразовании числа . Если ошибки не возникает, функция возвращает число , преобразованное в допустимое число с плавающей запятой.В противном случае вы получите значение nan (Not a Number), которое представляет собой специальное значение float , которое можно использовать для представления значений, которые не являются допустимыми числами, как и "One" в приведенном выше примере.
Вы можете настроить to_float () в соответствии со своими потребностями. Например, вы можете заменить оператор return float ("nan") на оператор return 0.0 и так далее.
Объединение
map () с другими функциональными инструментами Итак, вы рассмотрели, как использовать map () для выполнения различных задач, связанных с итерациями.Однако, если вы используете map () вместе с другими функциональными инструментами, такими как filter (), и reduce () , вы можете выполнять более сложные преобразования для ваших итераций. Это то, о чем вы собираетесь рассказать в следующих двух разделах.
карта () и фильтр () Иногда вам нужно обработать итерабельность ввода и вернуть другую итерацию, которая является результатом фильтрации нежелательных значений во входной итерации. В этом случае вам может подойти Python filter () . filter () - встроенная функция, которая принимает два позиционных аргумента:
-
функциябудет предикатом или функцией с логическим значением, функцией, которая возвращаетTrueилиFalseв соответствии с входными данными. -
итерациябудет любой итерацией Python.
filter () возвращает элементы входного итеративного , для которых функция возвращает True .Если вы передадите None в функцию , тогда filter () будет использовать функцию идентификации. Это означает, что filter () проверит значение истинности каждого элемента в итеративном и отфильтрует все элементы, которые являются ложными.
Чтобы проиллюстрировать, как можно использовать map () вместе с filter () , скажем, вам нужно вычислить квадратный корень из всех значений в списке. Поскольку ваш список может содержать отрицательные значения, вы получите сообщение об ошибке, потому что квадратный корень не определен для отрицательных чисел:
>>> импорт математики
>>> математика.sqrt (-16)
Отслеживание (последний вызов последний):
Файл "", строка 1, в
math.sqrt (-16)
ValueError: ошибка математического домена
С отрицательным числом в качестве аргумента math.sqrt () вызывает ValueError . Чтобы избежать этой проблемы, вы можете использовать filter () , чтобы отфильтровать все отрицательные значения, а затем найти квадратный корень из оставшихся положительных значений. Посмотрите на следующий пример:
>>> импорт математики
>>> def is_positive (число):
... return num> = 0
...
>>> def sanitized_sqrt (числа):
... cleaned_iter = карта (math.sqrt, фильтр (is_positive, числа))
... вернуть список (cleaned_iter)
...
>>> sanitized_sqrt ([25, 9, 81, -16, 0])
[5,0, 3,0, 9,0, 0,0]
is_positive () - это функция-предикат, которая принимает число в качестве аргумента и возвращает Истина , если число больше или равно нулю. Вы можете передать is_positive () в filter () , чтобы удалить все отрицательные числа из чисел .Таким образом, вызов map () обработает только положительные числа, а math.sqrt () не выдаст ValueError .
карта () и уменьшить () Python reduce () - это функция, которая находится в модуле functools в стандартной библиотеке Python. reduce () - еще один основной функциональный инструмент в Python, который полезен, когда вам нужно применить функцию к итерируемому объекту и уменьшить его до единственного совокупного значения.Этот вид операции обычно известен как уменьшение или складывание . reduce () принимает два обязательных аргумента:
-
функцияможет быть любой вызываемой Python, которая принимает два аргумента и возвращает значение. -
итерацияможет быть любой итерацией Python.
reduce () применит функцию ко всем элементам в итеративном и кумулятивно вычислит окончательное значение.
Вот пример, который объединяет map () и reduce () , чтобы в совокупности вычислить общий размер всех файлов, находящихся в вашем домашнем каталоге:
>>> import functools
>>> оператор импорта
>>> import os
>>> импортировать os.path
>>> files = os.listdir (os.path.expanduser ("~"))
>>> functools.reduce (operator.add, map (os.path.getsize, files))
4377381
В этом примере вы вызываете os.path.expanduser ("~") , чтобы получить путь к вашему домашнему каталогу. Затем вы вызываете os.listdir () по этому пути, чтобы получить список с путями ко всем файлам, которые там находятся.
Вызов map () использует os.path.getsize () для получения размера каждого файла. Наконец, вы используете reduce () с operator.add () , чтобы получить совокупную сумму размера каждого отдельного файла. Конечный результат - это общий размер всех файлов в вашем домашнем каталоге в байтах.
Примечание: Несколько лет назад Google разработал и начал использовать модель программирования, которую они назвали MapReduce. Это был новый стиль обработки данных, предназначенный для управления большими данными с использованием параллельных и распределенных вычислений в кластере.
Эта модель была вдохновлена комбинацией map и сокращения операций , обычно используемых в функциональном программировании.
Модель MapReduce оказала огромное влияние на способность Google обрабатывать огромные объемы данных в разумные сроки.Однако к 2014 году Google больше не использовал MapReduce в качестве основной модели обработки.
В настоящее время можно найти несколько альтернативных реализаций MapReduce, например Apache Hadoop, который представляет собой набор утилит с открытым исходным кодом, использующих модель MapReduce.
Несмотря на то, что вы можете использовать reduce () для решения проблемы, описанной в этом разделе, Python предлагает другие инструменты, которые могут привести к более питоническому и эффективному решению. Например, вы можете использовать встроенную функцию sum () для вычисления общего размера файлов в вашем домашнем каталоге:
>>> импорт ОС
>>> импорт ос.дорожка
>>> files = os.listdir (os.path.expanduser ("~"))
>>> сумма (карта (os.path.getsize, файлы))
4377381
Этот пример намного удобнее и эффективнее, чем предыдущий. Если вы хотите глубже понять, как использовать reduce () и какие альтернативные инструменты вы можете использовать для замены reduce () на Pythonic, тогда ознакомьтесь с Python reduce (): From Functional to Pythonic Style.
Обработка итераций на основе кортежей с помощью
starmap () Python itertools.starmap () создает итератор, который применяет функцию к аргументам, полученным из итерации кортежей, и возвращает результаты. Это полезно, когда вы обрабатываете итерации, которые уже сгруппированы в кортежи.
Основное различие между map () и starmap () заключается в том, что последний вызывает свою функцию преобразования с помощью оператора распаковки ( * ) для распаковки каждого кортежа аргументов в несколько позиционных аргументов. Итак, функция преобразования вызывается как function (* args) вместо function (arg1, arg2 ,... argN) .
В официальной документации для starmap () говорится, что эта функция примерно эквивалентна следующей функции Python:
def starmap (функция, итерация):
для аргументов в итерации:
функция доходности (* аргументы)
Цикл для в этой функции выполняет итерацию по элементам в итеративном и в результате выдает преобразованные элементы. Вызов функции (* args) использует оператор распаковки для распаковки кортежей в несколько позиционных аргументов.Вот несколько примеров того, как работает starmap () :
>>> from itertools import starmap
>>> list (starmap (pow, [(2, 7), (4, 3)]))
[128, 64]
>>> list (starmap (ord, [(2, 7), (4, 3)]))
Отслеживание (последний вызов последний):
Файл "", строка 1, в
список (звездная карта (ord, [(2, 7), (4, 3)]))
TypeError: ord () принимает ровно один аргумент (задано 2)
В первом примере вы используете pow () для вычисления степени первого значения, возведенного во второе значение в каждом кортеже.Кортежи будут иметь вид (основание, показатель степени) .
Если каждый кортеж в вашей итерации имеет два элемента, то функция также должна принимать два аргумента. Если кортежи содержат три элемента, то функция , должна принимать три аргумента и так далее. В противном случае вы получите ошибку TypeError .
Если вы используете map () вместо starmap () , вы получите другой результат, потому что map () берет по одному элементу из каждого кортежа:
>>> list (map (pow, (2, 7), (4, 3)))
[16, 343]
Обратите внимание, что map () принимает два кортежа вместо списка кортежей. map () также принимает одно значение из каждого кортежа на каждой итерации. Чтобы map () возвращал тот же результат, что и starmap () , вам нужно поменять местами значения:
>>> list (map (pow, (2, 4), (7, 3)))
[128, 64]
В этом случае у вас есть два кортежа вместо списка кортежей. Вы также поменяли местами 7 и 4 . Теперь первый кортеж обеспечивает основы, а второй кортеж - показатели.
Кодирование в стиле Pythonic: замена карты
() Инструменты функционального программирования, такие как map () , filter () и reduce () , существуют уже давно.Однако представления списков и выражения генератора стали их естественной заменой почти в каждом случае использования.
Например, функциональные возможности, обеспечиваемые map () , почти всегда лучше выражаются с помощью понимания списка или выражения генератора. В следующих двух разделах вы узнаете, как заменить вызов map () на понимание списка или выражение генератора, чтобы сделать ваш код более читабельным и питоническим.
Использование представлений списков
Существует общий шаблон, который можно использовать для замены вызова map () на понимание списка.Вот как:
# Генерация списка с картой
список (карта (функция, итерация))
# Создание списка с пониманием списка
[функция (x) для x в итерации]
Обратите внимание, что понимание списка почти всегда читается более четко, чем вызов map () . Поскольку составления списков довольно популярны среди разработчиков Python, их можно найти повсюду. Таким образом, замена вызова map () на понимание списка сделает ваш код более знакомым для других разработчиков Python.
Вот пример того, как заменить map () пониманием списка для построения списка квадратных чисел:
>>> # Функция преобразования
>>> def квадрат (число):
... номер возврата ** 2
>>> числа = [1, 2, 3, 4, 5, 6]
>>> # Использование map ()
>>> список (карта (квадрат, числа))
[1, 4, 9, 16, 25, 36]
>>> # Использование понимания списка
>>> [квадрат (x) вместо x в числах]
[1, 4, 9, 16, 25, 36]
Если вы сравните оба решения, то можете сказать, что тот, который использует понимание списка, более читабелен, потому что он читается почти как обычный английский.Кроме того, понимание списков позволяет избежать необходимости явно вызывать list () на карте map () для создания окончательного списка.
Использование выражений генератора
map () возвращает объект карты , который является итератором, выдающим элементы по запросу. Итак, естественной заменой map () является выражение генератора, поскольку выражения генератора возвращают объекты-генераторы, которые также являются итераторами, дающими элементы по запросу.
Python довольно эффективны с точки зрения потребления памяти.По этой причине map () теперь возвращает итератор вместо списка .
Есть небольшая синтаксическая разница между пониманием списка и выражением генератора. В первом используется пара квадратных скобок ( [] ) для ограничения выражения. Во втором используется пара круглых скобок ( () ). Итак, чтобы превратить понимание списка в выражение генератора, вам просто нужно заменить квадратные скобки скобками.
Вы можете использовать выражения генератора для написания кода, который читается более четко, чем код, использующий map () .Посмотрите на следующий пример:
>>> # Функция преобразования
>>> def квадрат (число):
... номер возврата ** 2
>>> числа = [1, 2, 3, 4, 5, 6]
>>> # Использование map ()
>>> map_obj = карта (квадрат, числа)
>>> map_obj
<объект карты в 0x7f254d180a60>
>>> список (map_obj)
[1, 4, 9, 16, 25, 36]
>>> # Использование выражения генератора
>>> gen_exp = (квадрат (x) вместо x в числах)
>>> gen_exp
<объект-генератор в 0x7f254e056890>
>>> список (gen_exp)
[1, 4, 9, 16, 25, 36]
Этот код имеет главное отличие от кода из предыдущего раздела: вы меняете квадратные скобки на пару скобок, чтобы превратить понимание списка в выражение генератора.
Генераторные выражения обычно используются в качестве аргументов в вызовах функций. В этом случае вам не нужно использовать круглые скобки для создания выражения генератора, потому что круглые скобки, которые вы используете для вызова функции, также предоставляют синтаксис для построения генератора. Используя эту идею, вы можете получить тот же результат, что и в приведенном выше примере, вызвав list () следующим образом:
>>> список (квадрат (x) вместо x в числах)
[1, 4, 9, 16, 25, 36]
Если вы используете выражение генератора в качестве аргумента при вызове функции, вам не нужна дополнительная пара круглых скобок.Скобки, которые вы используете для вызова функции, обеспечивают синтаксис для построения генератора.
Выражения генератора столь же эффективны, как map () , с точки зрения потребления памяти, поскольку оба они возвращают итераторы, которые возвращают элементы по запросу. Однако выражения генератора почти всегда улучшают читаемость вашего кода. Они также делают ваш код более Pythonic в глазах других разработчиков Python.
Заключение
Python map () позволяет выполнять операции сопоставления с итерациями.Операция отображения состоит из применения функции преобразования к элементам в итерируемом объекте для создания преобразованного итеративного объекта. В общем случае map () позволит вам обрабатывать и преобразовывать итерации без использования явного цикла.
В этом руководстве вы узнали, как работает map () и как использовать его для обработки итераций. Вы также узнали о некоторых инструментах Pythonic, которые можно использовать для замены map () в своем коде.
Теперь вы знаете, как:
- Работа с картой Python
() - Используйте
map ()- , процесс и преобразуют итераций без использования явного цикла - Объедините
map ()с такими функциями, какfilter ()иreduce ()для выполнения сложных преобразований - Замените
map ()такими инструментами, как анализ списка и выражения генератора
Обладая этими новыми знаниями, вы сможете использовать map () в своем коде и подходить к нему в функциональном стиле программирования.


 Г-н Флейсс начал свою карьеру, управляя исследовательским проектом ИИ, финансируемым Амхерстским колледжем, затем в качестве аналитика и программиста в компании Sloate, Weisman, Murray & Co, которая была приобретена Neuberger Berman.Г-н Флейсс разработал инвестиционные алгоритмы вместе с генеральным директором фирмы Лорой Слоут, которая сейчас является партнером Neuberger Berman и одним из инвесторов, упомянутых в книге Питера Тануса «Инвестиционные гуру». Г-н Флейсс получил степень бакалавра в колледже Амхерст.
Г-н Флейсс начал свою карьеру, управляя исследовательским проектом ИИ, финансируемым Амхерстским колледжем, затем в качестве аналитика и программиста в компании Sloate, Weisman, Murray & Co, которая была приобретена Neuberger Berman.Г-н Флейсс разработал инвестиционные алгоритмы вместе с генеральным директором фирмы Лорой Слоут, которая сейчас является партнером Neuberger Berman и одним из инвесторов, упомянутых в книге Питера Тануса «Инвестиционные гуру». Г-н Флейсс получил степень бакалавра в колледже Амхерст. Д. .A.I. использует свои прогнозы производительности наряду со знанием волатильности и взаимосвязей между акциями для создания портфеля, который уравновешивает риск и ожидаемую доходность. Байесовская статистика служит основой нашего инвестиционного программного обеспечения на основе искусственного интеллекта. Он обеспечивает гибкую структуру, которая позволяет нам автоматически интегрировать новые данные, доступные каждый день, с предыдущими знаниями рынка, чтобы прогнозировать динамику запасов. A.I. анализирует информацию о том, как каждый фактор связан с доходностью акций, чтобы создать оценочное распределение вероятности потенциальной доходности для каждой акции.A.I. анализирует фундаментальные и макро-данные со всего мира, которые ежедневно обновляются и включаются в нашу историческую базу данных.
Д. .A.I. использует свои прогнозы производительности наряду со знанием волатильности и взаимосвязей между акциями для создания портфеля, который уравновешивает риск и ожидаемую доходность. Байесовская статистика служит основой нашего инвестиционного программного обеспечения на основе искусственного интеллекта. Он обеспечивает гибкую структуру, которая позволяет нам автоматически интегрировать новые данные, доступные каждый день, с предыдущими знаниями рынка, чтобы прогнозировать динамику запасов. A.I. анализирует информацию о том, как каждый фактор связан с доходностью акций, чтобы создать оценочное распределение вероятности потенциальной доходности для каждой акции.A.I. анализирует фундаментальные и макро-данные со всего мира, которые ежедневно обновляются и включаются в нашу историческую базу данных. В настоящее время работает в ФСК по ценным бумагам, где специализируется на продуктах дельты 1, таких как свопы и доход / минус.
В настоящее время работает в ФСК по ценным бумагам, где специализируется на продуктах дельты 1, таких как свопы и доход / минус. В настоящее время он также является попечителем Национального музея математики и Университета WorldQuant. До прихода в финансовую индустрию доктор Карр в течение 8 лет был профессором финансов в Корнельском университете, получив докторскую степень. из Калифорнийского университета в Лос-Анджелесе в 1989 году. Он имеет более 85 публикаций в академических и отраслевых журналах и является младшим редактором 8 журналов, связанных с математическими финансами.Он был выбран журналом Risk Magazine в качестве кандидата года в 2003 году и финансовым инженером года по версии IAQF / Sungard в 2010 году. С 2011 по 2014 год доктор Карр входил в список Institutional Investor’s Tech 50, ежегодный список 50 самых влиятельных люди в финансовых технологиях.
В настоящее время он также является попечителем Национального музея математики и Университета WorldQuant. До прихода в финансовую индустрию доктор Карр в течение 8 лет был профессором финансов в Корнельском университете, получив докторскую степень. из Калифорнийского университета в Лос-Анджелесе в 1989 году. Он имеет более 85 публикаций в академических и отраслевых журналах и является младшим редактором 8 журналов, связанных с математическими финансами.Он был выбран журналом Risk Magazine в качестве кандидата года в 2003 году и финансовым инженером года по версии IAQF / Sungard в 2010 году. С 2011 по 2014 год доктор Карр входил в список Institutional Investor’s Tech 50, ежегодный список 50 самых влиятельных люди в финансовых технологиях. Он имеет докторскую степень по физике в Беркли и степень бакалавра физики в Принстоне.Он уроженец Манхэттена, в настоящее время проживает в Бруклине. У него есть сын, который учится на первом курсе в колледже Белойт в Висконсине, сын ученика средней школы, без ума от математики, и приятный кот.
Он имеет докторскую степень по физике в Беркли и степень бакалавра физики в Принстоне.Он уроженец Манхэттена, в настоящее время проживает в Бруклине. У него есть сын, который учится на первом курсе в колледже Белойт в Висконсине, сын ученика средней школы, без ума от математики, и приятный кот.
 До UBS г-н Синь два года работал юристом в Ping An Insurance of China по проектам стратегического планирования. Г-н Синь получает M.S. Имеет степень по прикладной математике Университета Иллинойса в Чикаго и является держателем сертификата CFA.
До UBS г-н Синь два года работал юристом в Ping An Insurance of China по проектам стратегического планирования. Г-н Синь получает M.S. Имеет степень по прикладной математике Университета Иллинойса в Чикаго и является держателем сертификата CFA. Однако практикующие специалисты обычно имеют ограничения по левериджу, часто используют непараметрические модели риска и заботятся о риске хвоста портфеля.В этой статье представлен новый подход к расчету ожидаемой прибыли с ограничениями кредитного плеча. Этот подход достаточно гибкий, чтобы смягчить предположение о нормальном распределении, связать с непараметрическими моделями риска и использовать меры хвостового риска, такие как условный VaR.
Однако практикующие специалисты обычно имеют ограничения по левериджу, часто используют непараметрические модели риска и заботятся о риске хвоста портфеля.В этой статье представлен новый подход к расчету ожидаемой прибыли с ограничениями кредитного плеча. Этот подход достаточно гибкий, чтобы смягчить предположение о нормальном распределении, связать с непараметрическими моделями риска и использовать меры хвостового риска, такие как условный VaR. После Morgan Stanley он руководил небольшим инвестиционным фондом «друзей и семьи», который специализировался на систематической торговле финансовыми фьючерсами. Он был принят на работу в Bloomberg LP для управления наукой о данных в подразделении Bloomberg Global Data и присоединился к JP Morgan в качестве главного специалиста по данным в отделе разработки новых продуктов в 2015 году, став в конечном итоге руководителем отдела исследований в области науки о данных.Он присоединился к новой группе Data Innovation Group («dbDIG») Deutsche Bank в марте 2018 года. В июле 2019 года он создал новое предприятие, чтобы предоставлять клиентам инновационные количественные и первичные исследования.
После Morgan Stanley он руководил небольшим инвестиционным фондом «друзей и семьи», который специализировался на систематической торговле финансовыми фьючерсами. Он был принят на работу в Bloomberg LP для управления наукой о данных в подразделении Bloomberg Global Data и присоединился к JP Morgan в качестве главного специалиста по данным в отделе разработки новых продуктов в 2015 году, став в конечном итоге руководителем отдела исследований в области науки о данных.Он присоединился к новой группе Data Innovation Group («dbDIG») Deutsche Bank в марте 2018 года. В июле 2019 года он создал новое предприятие, чтобы предоставлять клиентам инновационные количественные и первичные исследования.
 С 2009 по 2016 год Леон был директором по управлению рисками группы в RBC Capital Markets, LLC, где он покрывал рыночный риск по секьюритизированным продуктам в областях вторичной торговли, создания и торговли собственностью. У него тридцать два года опыта продаж на рынках с фиксированным доходом, включая позиции трейдера, специалиста по количественной стратегии, разработчика моделей деривативов и аналитика рыночных рисков. (Сведения о продукте: ценные бумаги Казначейства США, ценные бумаги агентств США, процентные деривативы, MBS, ABS и кредитные деривативы.Леон окончил MIT (SB; математика) и был аспирантом по математике в Университете Брауна.
С 2009 по 2016 год Леон был директором по управлению рисками группы в RBC Capital Markets, LLC, где он покрывал рыночный риск по секьюритизированным продуктам в областях вторичной торговли, создания и торговли собственностью. У него тридцать два года опыта продаж на рынках с фиксированным доходом, включая позиции трейдера, специалиста по количественной стратегии, разработчика моделей деривативов и аналитика рыночных рисков. (Сведения о продукте: ценные бумаги Казначейства США, ценные бумаги агентств США, процентные деривативы, MBS, ABS и кредитные деривативы.Леон окончил MIT (SB; математика) и был аспирантом по математике в Университете Брауна. Доступность, структурная гибкость и ценообразование потребительского / коммерческого финансирования и ипотечного финансирования глубоко связаны с принятием решений о риске / вознаграждении спонсорами и инвесторами секьюритизированных продуктов.
Доступность, структурная гибкость и ценообразование потребительского / коммерческого финансирования и ипотечного финансирования глубоко связаны с принятием решений о риске / вознаграждении спонсорами и инвесторами секьюритизированных продуктов. Его команда обеспечивала управление рисками и стратегические консультационные услуги многим крупнейшим банкам и финансовым учреждениям страны.
Его команда обеспечивала управление рисками и стратегические консультационные услуги многим крупнейшим банкам и финансовым учреждениям страны.
 До нынешней должности Илья провел несколько лет в Blackrock и отвечал за управление отношениями с банками и финансовыми учреждениями.Его команда обеспечивала управление рисками и стратегические консультационные услуги многим крупнейшим банкам и финансовым учреждениям страны.
До нынешней должности Илья провел несколько лет в Blackrock и отвечал за управление отношениями с банками и финансовыми учреждениями.Его команда обеспечивала управление рисками и стратегические консультационные услуги многим крупнейшим банкам и финансовым учреждениям страны.
 Темы будут включать практическое применение методов машинного обучения для инвестиционных стратегий FX. Будет предоставлен пример использования, чтобы проиллюстрировать использование обработки естественного языка и таксономий на основе Целей устойчивого развития (ЦУР) для управления рисками и альфа-генерации. Аналитический процесс включает извлечение, обработку, гео-теги и анализ неструктурированных данных из десятков тысяч источников на десятках языков, включая новости, блоги, отчеты компаний и НПО, социальные сети и тенденции Google.Мы обсуждаем проблемы и последствия этого подхода.
Темы будут включать практическое применение методов машинного обучения для инвестиционных стратегий FX. Будет предоставлен пример использования, чтобы проиллюстрировать использование обработки естественного языка и таксономий на основе Целей устойчивого развития (ЦУР) для управления рисками и альфа-генерации. Аналитический процесс включает извлечение, обработку, гео-теги и анализ неструктурированных данных из десятков тысяч источников на десятках языков, включая новости, блоги, отчеты компаний и НПО, социальные сети и тенденции Google.Мы обсуждаем проблемы и последствия этого подхода. Начнем с классических портфелей распределения активов.
Начнем с классических портфелей распределения активов. Борис присоединился к Morgan Stanley в 2003 году и на протяжении многих лет работал над широким спектром проектов, включая исследования производных финансовых инструментов, количественное моделирование, анализ данных и структурирование.На своей нынешней должности Борис занимается количественным анализом фондовых рынков, разработкой альфа-моделей, оценкой альтернативных источников данных и применением количественных методов в традиционных фундаментальных исследованиях. До прихода в исследовательский отдел Morgan Stanley Борис был одним из руководителей группы по структурированию количественных инвестиционных стратегий (QIS) Morgan Stanley в Северной Америке, где он разработал стратегии инвестирования между активами, хеджирования на основе правил и премий за риск для использования в диверсифицированных институциональных портфелях. .Борис имеет степень магистра финансовой математики Колумбийского университета и степень бакалавра финансов и информационных технологий Школы бизнеса Стерна Нью-Йоркского университета.
Борис присоединился к Morgan Stanley в 2003 году и на протяжении многих лет работал над широким спектром проектов, включая исследования производных финансовых инструментов, количественное моделирование, анализ данных и структурирование.На своей нынешней должности Борис занимается количественным анализом фондовых рынков, разработкой альфа-моделей, оценкой альтернативных источников данных и применением количественных методов в традиционных фундаментальных исследованиях. До прихода в исследовательский отдел Morgan Stanley Борис был одним из руководителей группы по структурированию количественных инвестиционных стратегий (QIS) Morgan Stanley в Северной Америке, где он разработал стратегии инвестирования между активами, хеджирования на основе правил и премий за риск для использования в диверсифицированных институциональных портфелях. .Борис имеет степень магистра финансовой математики Колумбийского университета и степень бакалавра финансов и информационных технологий Школы бизнеса Стерна Нью-Йоркского университета.
 Она также является адъюнкт-профессором Корнельского университета. До AbleMarkets Олдридж разрабатывал и запускал стратегии высокочастотной торговли в портфеле активов на 20 миллионов долларов. Еще раньше Олдридж был, наоборот, квантовым торговцем; отвечает за количественную оценку рисков коммерческих кредитов; Руководитель группы по регулированию Базеля; исследователь технологических акций; ведущий системный архитектор в крупных интеграционных проектах, включая веб-безопасность и глобализацию торговых площадок.Олдридж начала свою карьеру в качестве инженера-программиста в сфере финансовых услуг.
Она также является адъюнкт-профессором Корнельского университета. До AbleMarkets Олдридж разрабатывал и запускал стратегии высокочастотной торговли в портфеле активов на 20 миллионов долларов. Еще раньше Олдридж был, наоборот, квантовым торговцем; отвечает за количественную оценку рисков коммерческих кредитов; Руководитель группы по регулированию Базеля; исследователь технологических акций; ведущий системный архитектор в крупных интеграционных проектах, включая веб-безопасность и глобализацию торговых площадок.Олдридж начала свою карьеру в качестве инженера-программиста в сфере финансовых услуг. Ее недавние научные публикации включают «Нейронные сети в финансах: дизайн и эффективность» (совместно с Марко Авельянедой в журнале Financial Data Science, 2019), «Большие данные в управлении портфелем» (Journal of Financial Data Science, 2019), «ETFs, Высокочастотная торговля и мгновенные сбои »(Journal of Portfolio Management, 2016) и« Высокочастотные прогоны и мгновенное предсказание сбоев »(Journal of Portfolio Management, 2014). В настоящее время Олдридж входит в состав Редакционного консультативного совета журнала «Прикладные науки о данных в финансах».
Ее недавние научные публикации включают «Нейронные сети в финансах: дизайн и эффективность» (совместно с Марко Авельянедой в журнале Financial Data Science, 2019), «Большие данные в управлении портфелем» (Journal of Financial Data Science, 2019), «ETFs, Высокочастотная торговля и мгновенные сбои »(Journal of Portfolio Management, 2016) и« Высокочастотные прогоны и мгновенное предсказание сбоев »(Journal of Portfolio Management, 2014). В настоящее время Олдридж входит в состав Редакционного консультативного совета журнала «Прикладные науки о данных в финансах». Как показывает это исследование, полу-контролируемое обучение (SSL) — это метод, который может демократизировать доступ к финансовому анализу.
Как показывает это исследование, полу-контролируемое обучение (SSL) — это метод, который может демократизировать доступ к финансовому анализу. До прихода в JP Morgan в 2011 году Наталья работала менеджером по рыночным рискам в MF Global. Наталья — аналитик и юрист JPM Asset Management Risk в Северной Америке.Она разработала учебную программу и в течение года организовывала глобальные технические тренинги и сетевые мероприятия для аналитиков, сотрудников и стажеров в области управления активами и благосостоянием. Наталья имеет степень магистра финансовой математики Колумбийского университета (2014 г.) и степень бакалавра делового администрирования в области финансов и инвестиций Колледжа Баруха (2009 г.).
До прихода в JP Morgan в 2011 году Наталья работала менеджером по рыночным рискам в MF Global. Наталья — аналитик и юрист JPM Asset Management Risk в Северной Америке.Она разработала учебную программу и в течение года организовывала глобальные технические тренинги и сетевые мероприятия для аналитиков, сотрудников и стажеров в области управления активами и благосостоянием. Наталья имеет степень магистра финансовой математики Колумбийского университета (2014 г.) и степень бакалавра делового администрирования в области финансов и инвестиций Колледжа Баруха (2009 г.).
 Он также является профессором ESADE, где преподает хедж-фонды, большие данные в финансах и финтех. В 2017 году он преподавал первый курс Fintech и больших данных в Лондонской школе бизнеса. В 1993 году он получил степень магистра делового администрирования и степень в области делового администрирования и экономики в ESADE.В 2010 году он получил степень доктора философии в области количественных финансов с отличием Summa Cum Laude (UNED — Мадрид, Испания). В 2012 году он закончил аспирантуру Колумбийской школы бизнеса. Во время работы над докторской степенью он сотрудничал с математическим факультетом Фрибурга. Он также имеет сертификат сертифицированного европейского финансового аналитика (CEFA) 2000 и сертификат ARPM.
Он также является профессором ESADE, где преподает хедж-фонды, большие данные в финансах и финтех. В 2017 году он преподавал первый курс Fintech и больших данных в Лондонской школе бизнеса. В 1993 году он получил степень магистра делового администрирования и степень в области делового администрирования и экономики в ESADE.В 2010 году он получил степень доктора философии в области количественных финансов с отличием Summa Cum Laude (UNED — Мадрид, Испания). В 2012 году он закончил аспирантуру Колумбийской школы бизнеса. Во время работы над докторской степенью он сотрудничал с математическим факультетом Фрибурга. Он также имеет сертификат сертифицированного европейского финансового аналитика (CEFA) 2000 и сертификат ARPM. Финансовые математики должны использовать глубокое обучение при моделировании, чтобы контрастировать с эталонными моделями, иногда заменяя эталонные модели эконометрического / стохастического моделирования, а в некоторых других — использовать параллельные модели с другими свойствами. Мы обсудим достоинства универсальных свойств аппроксимации и стохастического моделирования, а также ограничения интерпретации и потенциального переобучения.
Финансовые математики должны использовать глубокое обучение при моделировании, чтобы контрастировать с эталонными моделями, иногда заменяя эталонные модели эконометрического / стохастического моделирования, а в некоторых других — использовать параллельные модели с другими свойствами. Мы обсудим достоинства универсальных свойств аппроксимации и стохастического моделирования, а также ограничения интерпретации и потенциального переобучения.


 Значительные остатки атрибуции, среднее значение которых не уменьшается до нуля с течением времени, предполагают скрытое воздействие нелинейностей в доходности факторов. Предлагаемая нами корректировка учитывает точку зрения управляющего портфелем при объяснении их воздействия, определяя, какие факторы наклона были наиболее ответственны за необъяснимые результаты.Полученная в результате нелинейная атрибуция лучше согласовывает реализованную прибыль с инвестиционным процессом и поддается проверке на статистическую значимость.
Значительные остатки атрибуции, среднее значение которых не уменьшается до нуля с течением времени, предполагают скрытое воздействие нелинейностей в доходности факторов. Предлагаемая нами корректировка учитывает точку зрения управляющего портфелем при объяснении их воздействия, определяя, какие факторы наклона были наиболее ответственны за необъяснимые результаты.Полученная в результате нелинейная атрибуция лучше согласовывает реализованную прибыль с инвестиционным процессом и поддается проверке на статистическую значимость.
 Она является членом правления CFA Society New York и выпускницей Массачусетского технологического института.
Она является членом правления CFA Society New York и выпускницей Массачусетского технологического института.

 В настоящее время он также является попечителем Национального музея математики и Университета WorldQuant. До прихода в финансовую индустрию доктор Карр в течение 8 лет был профессором финансов в Корнельском университете, получив докторскую степень. из Калифорнийского университета в Лос-Анджелесе в 1989 году. Он имеет более 85 публикаций в академических и отраслевых журналах и является младшим редактором 8 журналов, связанных с математическими финансами. Он был выбран журналом Risk Magazine в качестве специалиста года в 2003 году и финансовым инженером года по версии IAQF / Sungard в 2010 году.С 2011 по 2014 год доктор Карр входил в список Institutional Investor’s Tech 50, ежегодный список 50 самых влиятельных людей в сфере финансовых технологий.
В настоящее время он также является попечителем Национального музея математики и Университета WorldQuant. До прихода в финансовую индустрию доктор Карр в течение 8 лет был профессором финансов в Корнельском университете, получив докторскую степень. из Калифорнийского университета в Лос-Анджелесе в 1989 году. Он имеет более 85 публикаций в академических и отраслевых журналах и является младшим редактором 8 журналов, связанных с математическими финансами. Он был выбран журналом Risk Magazine в качестве специалиста года в 2003 году и финансовым инженером года по версии IAQF / Sungard в 2010 году.С 2011 по 2014 год доктор Карр входил в список Institutional Investor’s Tech 50, ежегодный список 50 самых влиятельных людей в сфере финансовых технологий. В моделях SV справедливая стоимость опциона также зависит от степени ковариации доходности и волатильности. Мы показываем, что парой опционов без денег можно динамически торговать, чтобы получить прибыль в среднем от разницы между этой мгновенной скоростью ковариации и половиной наклона кривой предполагаемой дисперсии BMS. Наконец, в моделях SV справедливая стоимость опциона также зависит от уровня изменчивости. Мы показываем, что тройкой опционов можно динамически торговать, чтобы получить в среднем прибыль от разницы между этой мгновенной скоростью отклонения и показателем выпуклости кривой предполагаемой дисперсии BMS.Наши результаты позволяют получить точную финансовую интерпретацию конкретных показателей уровня, наклона и кривизны кривой предполагаемой дисперсии BMS. Эти интерпретации помогают объяснить стандартные правила котировки, применяемые на внебиржевом рынке для опционов на драгоценные металлы и на иностранную валюту.
В моделях SV справедливая стоимость опциона также зависит от степени ковариации доходности и волатильности. Мы показываем, что парой опционов без денег можно динамически торговать, чтобы получить прибыль в среднем от разницы между этой мгновенной скоростью ковариации и половиной наклона кривой предполагаемой дисперсии BMS. Наконец, в моделях SV справедливая стоимость опциона также зависит от уровня изменчивости. Мы показываем, что тройкой опционов можно динамически торговать, чтобы получить в среднем прибыль от разницы между этой мгновенной скоростью отклонения и показателем выпуклости кривой предполагаемой дисперсии BMS.Наши результаты позволяют получить точную финансовую интерпретацию конкретных показателей уровня, наклона и кривизны кривой предполагаемой дисперсии BMS. Эти интерпретации помогают объяснить стандартные правила котировки, применяемые на внебиржевом рынке для опционов на драгоценные металлы и на иностранную валюту.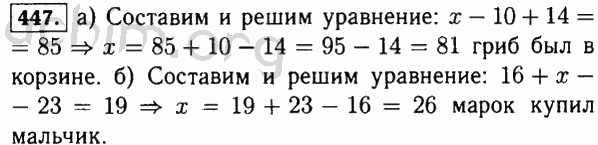 Имеет степень доктора математической статистики Колумбийского университета, где он является профессором Юджина Хиггинса по прикладной теории вероятностей на факультете математики. У него давние связи с исследовательской группой инвестиционной компании INTECH в Принстоне, штат Нью-Джерси.
Имеет степень доктора математической статистики Колумбийского университета, где он является профессором Юджина Хиггинса по прикладной теории вероятностей на факультете математики. У него давние связи с исследовательской группой инвестиционной компании INTECH в Принстоне, штат Нью-Джерси. Это довольно осторожное заявление о так называемом «эффекте размера», которое было задокументировано эмпирически и которому за прошедшие годы было выдвинуто несколько объяснений.Мы рассмотрим анализ этого явления, проведенный Фернхольцем (2001), который показал, что при наличии (надлежащим образом определенной) стабильности для структуры капитала это явление можно полностью отнести к эффектам ребалансировки портфеля и будет происходить независимо от того, будет ли мелкие акции более рискованны, чем их более крупные собратья. Местное время коллизий играет решающую роль в этом анализе, поскольку оно фиксирует текучесть кадров на различных уровнях лестницы капитализации. Мы дадим достаточно полное исследование этого явления в контексте простой модели со стабильным распределением капитала.В качестве следствия мы получим любопытное тождество экспоненциального распределения.
Это довольно осторожное заявление о так называемом «эффекте размера», которое было задокументировано эмпирически и которому за прошедшие годы было выдвинуто несколько объяснений.Мы рассмотрим анализ этого явления, проведенный Фернхольцем (2001), который показал, что при наличии (надлежащим образом определенной) стабильности для структуры капитала это явление можно полностью отнести к эффектам ребалансировки портфеля и будет происходить независимо от того, будет ли мелкие акции более рискованны, чем их более крупные собратья. Местное время коллизий играет решающую роль в этом анализе, поскольку оно фиксирует текучесть кадров на различных уровнях лестницы капитализации. Мы дадим достаточно полное исследование этого явления в контексте простой модели со стабильным распределением капитала.В качестве следствия мы получим любопытное тождество экспоненциального распределения.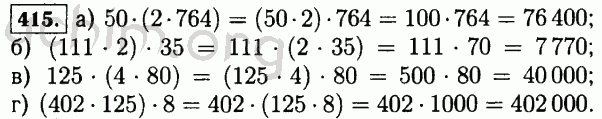 До нынешней должности Илья провел несколько лет в Blackrock и отвечал за управление отношениями с банками и финансовыми учреждениями.Его команда обеспечивала управление рисками и стратегические консультационные услуги многим крупнейшим банкам и финансовым учреждениям страны.
До нынешней должности Илья провел несколько лет в Blackrock и отвечал за управление отношениями с банками и финансовыми учреждениями.Его команда обеспечивала управление рисками и стратегические консультационные услуги многим крупнейшим банкам и финансовым учреждениям страны. , вторник
, вторник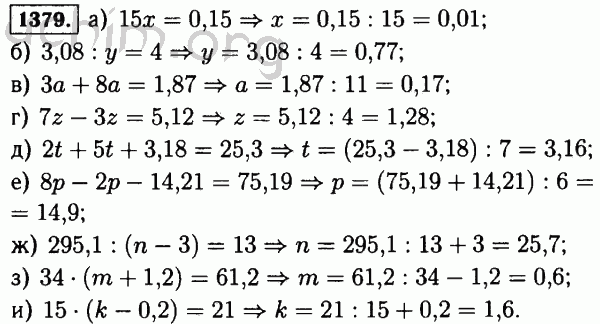 в теории вероятностей и статистике от Ecole des ponts. Он окончил Политехническую школу (Париж), Парижский университет 6 и Ecole des ponts. Большой футбольный фанат, Жюльен также проявляет большой интерес к спортивной аналитике и опубликовал несколько статей о чемпионате мира по футболу, Лиге чемпионов УЕФА и Евро в ведущих газетах, таких как The New York Times, Le Monde. , и El Pais, включая новый, более справедливый метод жеребьевки чемпионата мира по футболу FIFA.
в теории вероятностей и статистике от Ecole des ponts. Он окончил Политехническую школу (Париж), Парижский университет 6 и Ecole des ponts. Большой футбольный фанат, Жюльен также проявляет большой интерес к спортивной аналитике и опубликовал несколько статей о чемпионате мира по футболу, Лиге чемпионов УЕФА и Евро в ведущих газетах, таких как The New York Times, Le Monde. , и El Pais, включая новый, более справедливый метод жеребьевки чемпионата мира по футболу FIFA.