Урок 53. Лабораторная работа 13. Определение длины волны светового излучения с помощью дифракционной решётки
Урок 53. Лабораторная работа 13. Определение длины волны светового излучения с помощью дифракционной решётки
Тема: Определение длины волны светового излучения с помощью дифракционной решётки
Цель: Познакомиться на опыте с явлением многолучевой интерференции световых волн. Используя решётку с известным расстоянием между штрихами измерить длину волны светового излучения.
Оборудование:
- Штатив.
- Дифракционная решётка 100 штрихов на мм.
- Измерительная лента.
Теория
Дифракция волн — огибание волнами различных препятствий (неоднородностей).
Препятствия нарушают прямолинейность распространения фронта волны.
Дифракция волн свойственна всякому волновому движению; проявляется особенно отчетливо в случаях, когда размеры препятствий меньше длины волны или сравнимы с ней, однако проявляется всегда.
Когерентными называются волны, имеющие одинаковую частоту и постоянную разность фаз.
Дифракционная решетка – оптический прибор, представляющий собой большое число параллельных и очень близко расположенных узких щелей, которые пропускают или отражают свет.
Дифракционные решетки с различным числом щелей на 1 мм:
Параллельный пучок света с длиной волны λ, проходя через дифракционную решётку, вследствие дифракции за решёткой, распространяется по всевозможным направлениям и интерферирует. На экране, установленном на пути интерферирующего света, можно наблюдать интерференционную картину:
Максимумы света наблюдаются в точках экрана, для которых выполняется условие максимума:
Условие максимума: на разности хода волн укладывается четное число полуволн (целое число длин волн): Δ=k·λ, (1)
где Δ=АС — разность хода волн; λ — длина световой волны; k — номер максимума.
Центральный максимум (в точке О) называют нулевым; для него Δ=0. Слева и справа от него располагаются максимумы высших порядков.
Условие возникновения максимума можно записать иначе:
d·sinφ=k·λ
где k=0; ± 1; ± 2; ± 3…
Здесь d — период дифракционной решётки в мм, φ — угол, под которым виден световой максимум k-го порядка в точке
Так как углы дифракции малы, то для них можно принять: sinφ ≈ tgφ, а tgφ=a/b.
Поэтому: , и искомая длина световой волны равна (2)
В данной работе формулу (2) используют для вычисления длины световой волны.
Из условия максимума следует sinφ=(k·λ)/d .
Пусть k=1, тогда sinφкр=λкр/d и sinφф=λф/d.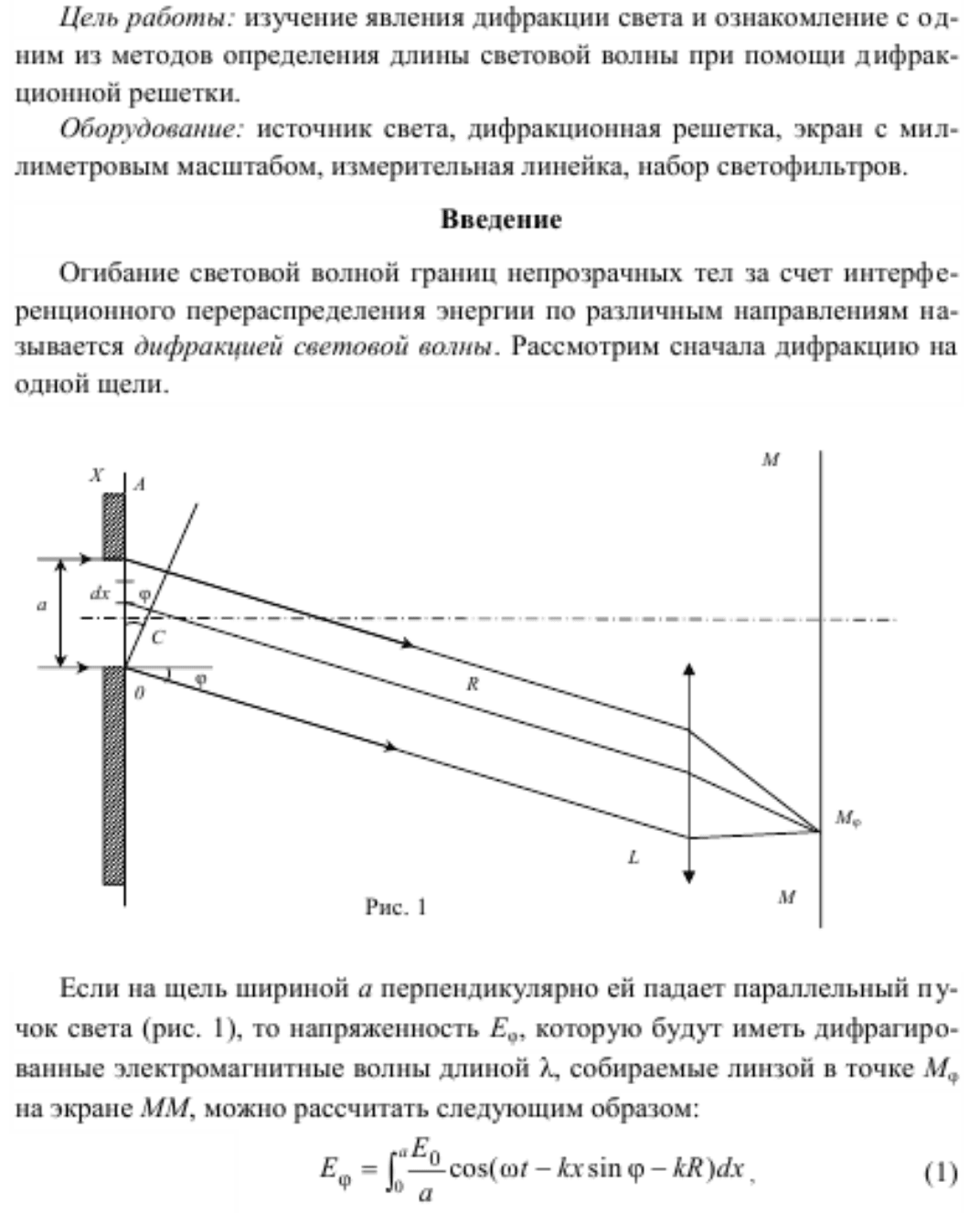
Известно, что λкр>λф , следовательно sinφкр>sinφф. Т.к. y= sinφф — функция возрастающая, то φкр>φф
Поэтому фиолетовый цвет в дифракционном спектре располагается ближе к центру.
Между максимумами расположены минимумы освещенности. Чем больше общее число щелей и чем ближе друг к другу они расположены, тем более широкими промежутками разделены максимумы.
Картина дифракции лазерного излучения красно цвета на решётках с различным числом щелей на 1 мм:
Ход работы
- Перенести рисунок в тетрадь.
- Подготовить таблицу для записи результатов измерений:
|
Порядок спектра, цвет k |
Постоянная d мм |
Расстояние от решётки до экрана, b мм |
Расстояние от нулевого максимума до максимума k-порядка а мм |
Длина волны, нм |
Средняя длина волны нм |
Относительная погрешность δ % |
|
1-ый, красный |
1:100=0,001 |
|||||
|
2-ой, красный |
1:100=0,001 |
|||||
|
1-ый, фиолетовый |
1:100=0,001 |
|||||
|
2-ой, фиолетовый |
1:100=0,001 |
- Укрепить в штативе линейку с экраном и закрепить на направляющей линейки дифракционную решётку.

- Установить расстояние от решётки до экрана 40 см (b).Результат записать в таблицу.
- Смотря через дифракционную решётку, направить прибор на источник света. Пронаблюдать спектр:
Измерить на экране расстояние а между нулевым максимумом и максимумом 1-го порядка для красного света. Результат записать в таблицу.
- Измерить на экране расстояние а между нулевым максимумом и максимумом 2-го порядка для красного света. Результат записать в таблицу.
- Повторить опыт, измерив на экране расстояние а между нулевым максимумом и максимумом 1-го и 2-го порядка для фиолетового света. Результат записать в таблицу.
- По формуле рассчитать длину волны излучения.
- Найти среднее значение длины волны светового излучения для красного λкр ср=( λкр1+λкр2)/2
и фиолетового света . λф ср=( λф1+λф2)/2
λф ср=( λф1+λф2)/2
- Зная истинное значение длины волны лазерного излучения , рассчитать относительную погрешность измерений:
δ=( λкр ср — λкр табл)/λкр табл *100% и δ= ( λф ср — λф табл)/λф табл *100%
Диапазон длин волн, нм
Красный 625—740 нм (λкр табл= 680 нм)
Фиолетовый 380—440 нм (λф табл = 410 нм)
- Записать вывод по результатам выполненной работы.
- Ответить письменно на контрольные вопросы.
Контрольные вопросы
- Какие волны называются когерентными?
- В чём заключается явление дифракции?
- Какие свойства света подтверждает дифракция света?
- При каких условиях наблюдается дифракция света?
- Как образуется дифракционный спектр?
- Почему максимумы располагаются как слева, так и справа от нулевого максимума?
- В чём разница в дифракционных картинах решёток с 50 и 300 штрихами на одном миллиметре?
Отчет по лабораторной работе № 2 определение длины световой волны с использованием бипризмы
Федеральное государственное автономное образовательное учреждение высшего образования «Санкт-Петербургский государственный электротехнический университет «ЛЭТИ»
им. В.И. Ульянова (Ленина)»
В.И. Ульянова (Ленина)»
кафедра физики
Выполнила: Конунников Г. А.
Группа № 0501
Преподаватель: Иманбаева Р. Т.
Вопросы | Задачи ИДЗ | Даты коллоквиума | Итог | |||||||
37 | 42 | |||||||||
Санкт-Петербург, 2021
ЦЕЛЬ
РАБОТЫ: Определение
длины световой волны интерференционным
методом.
ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ:
Источником света служит лампа накаливания. Светофильтр, расположенный перед лампой, пропускает определенную часть спектра излучения лампы, которую и надлежит изучить.
На
оптической скамье, снабженной линейкой
с миллиметровой шкалой, помещены
укрепленные на держателях вертикальная
щель S, бипризма Р и окуляр О. Ширину щели
можно изменять с помощью винта,
находящегося в верхней части его оправы.
Щель и бипризма могут быть повернуты
вокруг горизонтальной оси, а бипризма
также и вокруг вертикальной оси. Для
получения отчетливых интерференционных
полос необходимо, чтобы плоскости щели
и основания бипризмы были параллельны. Это достигается соответствующим
поворотом бипризмы и/или щели. Окуляр
О служит для наблюдения интерференционной
картины. Для измерения расстояния между
полосами он снабжен шкалой, цена малого
деления которой составляет 0.1 мм.
Это достигается соответствующим
поворотом бипризмы и/или щели. Окуляр
О служит для наблюдения интерференционной
картины. Для измерения расстояния между
полосами он снабжен шкалой, цена малого
деления которой составляет 0.1 мм.
ИССЛЕДУЕМЫЕ ЗАКОНОМЕРНОСТИ:
Один из способов наблюдения интерференции световых волн основан на использовании бипризмы Френеля. Бипризма Френеля представляет собой две призмы с очень малым преломляющим углом , сложенные основаниями.
На рисунке 1 схема наблюдения интерференционной картины с помощью бипризмы.
Рисунок 1 – Получение интерференционной картины
с использованием бипризмы Френеля
От
источника света (щели) лучи падают на
обе половины бипризмы Р, преломляются
в ней и за призмой распространяются
так, как если бы исходили из двух мнимых
источников S1 и S2.
Действительно, если смотреть через
верхнюю половину бипризмы, то светящаяся
щель S будет казаться расположенной в
точке S1,
а если смотреть через нижнюю половину
бипризмы, то расположенной в точке S2.
За призмой имеется область пространства, в которой световые волны, преломленные верхней и нижней половинами бипризмы, перекрываются (на рисунке 1 эта область заштрихована). В этой области пространства сводятся воедино две части каждого цуга волн от источника S, прошедшие разные оптические пути, способные при выполнении условия интерферировать, где – разность хода лучей. Длина когерентности определяется как рас- стояние, которое проходит световая волна за время, при котором случайное изменение фазы волны не превышает . При превышении разностью хода длины когерентности волны в точку наблюдения приходят со случайной разностью фаз, и интерференционная картина перестает быть видимой.
Интерференционная
картина, получающаяся от бипризмы,
соответствует интерференции волн,
исходящих из двух когерентных источников,
расположенных в точках S1 и S2.
На экране Э, пересекающем заштрихованную
область, тогда наблюдается ряд светлых
и темных полос, параллельных ребру
бипризмы. Светлые полосы лежат в тех
местах экрана, куда приходят волны от
источников S1 и S2 с разностью хода, равной целому числу
длин волн, темные – в тех местах, куда
приходят волны с разностью хода, равной
нечетному числу полуволн. Расстояние между
светлыми (или темными) полосами
интерференционной картины составляет
Светлые полосы лежат в тех
местах экрана, куда приходят волны от
источников S1 и S2 с разностью хода, равной целому числу
длин волн, темные – в тех местах, куда
приходят волны с разностью хода, равной
нечетному числу полуволн. Расстояние между
светлыми (или темными) полосами
интерференционной картины составляет
(1) |
где a и b – соответственно расстояния от щели до бипризмы и от бипризмы до экрана; d – расстояние между мнимыми источни-ками (см. рисунок 1).
Рисунок 2 – Ход луча через половину бипризмы Френеля
Для определения расстояния d между мнимыми источниками рассмотрим ход луча через одну из половин бипризмы (рисунок 2).
Для точки О в соответствии с законом преломления где – показатель преломления материала призмы;
и – углы падения и преломления. Вследствие
малости углов справедливо .
Аналогично для точки имеем .
Рассматривая треугольники и ,
можно показать, что справедливы
соотношения и .
Из этих соотношений для угла отклонения луча половиной бипризмы
несложно получить .
Вследствие
малости углов справедливо .
Аналогично для точки имеем .
Рассматривая треугольники и ,
можно показать, что справедливы
соотношения и .
Из этих соотношений для угла отклонения луча половиной бипризмы
несложно получить .
Таким образом, в рамках использованных допущений все лучи отклоняются каждой из половин бипризмы на одинаковый угол. Расстояние d как видно из рисунка 1, равно
(2) |
C учетом этого соотношения вместо выражения (1) имеем
(3) |
или
(4) |
Выражения
(3) или (4) устанавливают связь между
длиной световой волны и геометрическими
размерами системы (т. е. источник света
– бипризма Френеля – экран), в которой
реализуется явление интерференции.
Видимость интерференционной картины
зависит от размеров источника света, в
чем нетрудно убедиться, изменяя ширину
щели.
е. источник света
– бипризма Френеля – экран), в которой
реализуется явление интерференции.
Видимость интерференционной картины
зависит от размеров источника света, в
чем нетрудно убедиться, изменяя ширину
щели.
Рисунок 3 – Определение апертуры и угла схождения лучей в опыте с бипризмой Френеля
Для интерференционного эффекта существенны, однако, не сами по себе размеры щели, а угол (рисунок 3) между соответствующими лучами, идущими от S через каждую из двух ветвей интерферометра к точке О. Этот угол, который представляет собой угол раскрытия лучей, называется апертурой интерференции. Ему соответствует в поле интерференции угол схождения лучей , величина которого связана с углом правилами построения изо- бражений. При неизменном расстоянии до экрана тем больше, чем больше .
Из рис. 3 видно, что
(5) |
Подставляя выражение (5) в (1), получаем для расстояния между интерференционными полосами
(6) |
Из рисунка 3 видно также, что
(7) |
и,
кроме того .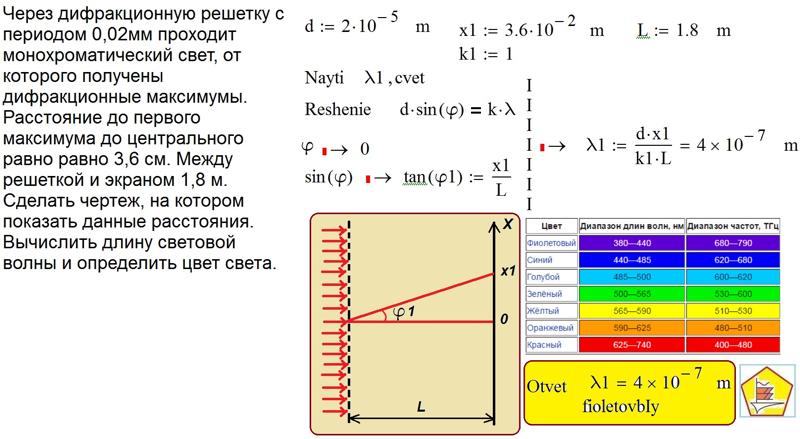 Исключая из двух последних выражений
величину h,
получаем
Исключая из двух последних выражений
величину h,
получаем
(8) |
Из совместного рассмотрения выражений (7) и (8) находим
(9) | |
(10) |
Величина апертуры интерференции тесно связана с допустимыми размерами источника. Теория и опыт показывают, что с увеличением апертуры интерференции уменьшаются допустимые размеры ширины источника, при которых еще имеет место отчетливая интерференционная картина. Условие хорошего наблюдения интерференции от протяженного источника ширины можно записать в виде:
(11) |
В
данной работе монохроматизация света
осуществляется с помощью светофильтра. Нетрудно найти связь между порядком
интерференции m и
шириной спектрального интервала ,
пропускаемого светофильтром. Действительно,
интерференция не будет наблюдаться,
если максимум m-го
порядка для совпадет с максимумом -го порядка для ,
т.е. Для
того чтобы интерференционная картина
при данных значениях
и обладала высокой видимостью, приходится
ограничиваться наблюдением интерференционных
полос, порядок которых много меньше
предельного ,
определяемого условием
Нетрудно найти связь между порядком
интерференции m и
шириной спектрального интервала ,
пропускаемого светофильтром. Действительно,
интерференция не будет наблюдаться,
если максимум m-го
порядка для совпадет с максимумом -го порядка для ,
т.е. Для
того чтобы интерференционная картина
при данных значениях
и обладала высокой видимостью, приходится
ограничиваться наблюдением интерференционных
полос, порядок которых много меньше
предельного ,
определяемого условием
(12) | |
(13) |
Простой метод измерения длины волны света
Том Кунцлеман | Вс, 04.02.2018 — 10:02
Вот уже несколько лет я провожу простой лабораторный эксперимент, который позволяет учащимся рассчитать длину волны различных цветов света. Я использую это задание в начале семестра, когда студенты впервые узнают об измерениях, преобразовании единиц измерения и значащих цифрах. Если вы хотите пропустить чтение деталей, прокрутите немного вниз, и вы найдете видео, демонстрирующее экспериментальные детали и связанный с ними анализ данных.
Я использую это задание в начале семестра, когда студенты впервые узнают об измерениях, преобразовании единиц измерения и значащих цифрах. Если вы хотите пропустить чтение деталей, прокрутите немного вниз, и вы найдете видео, демонстрирующее экспериментальные детали и связанный с ними анализ данных.
Эксперимент основан на дифракции света светодиодов через дифракционную решетку. Я использую радужные очки для дифракционной решетки. Когда свет проходит через дифракционную решетку, часть его «отклоняется» от прямого пути (рис. 1):
дифракционная решетка (радужные очки). Расстояние между источником света и дифракционной решеткой обозначено L.
Обратите внимание, что мы можем направить дифрагированные лучи света обратно к источнику света (рис. 2), так что расстояние y равно расстоянию между источником света и изображением его следующего ближайшего соседа, если смотреть через него. дифракционная решетка:
Это расстояние обозначается y.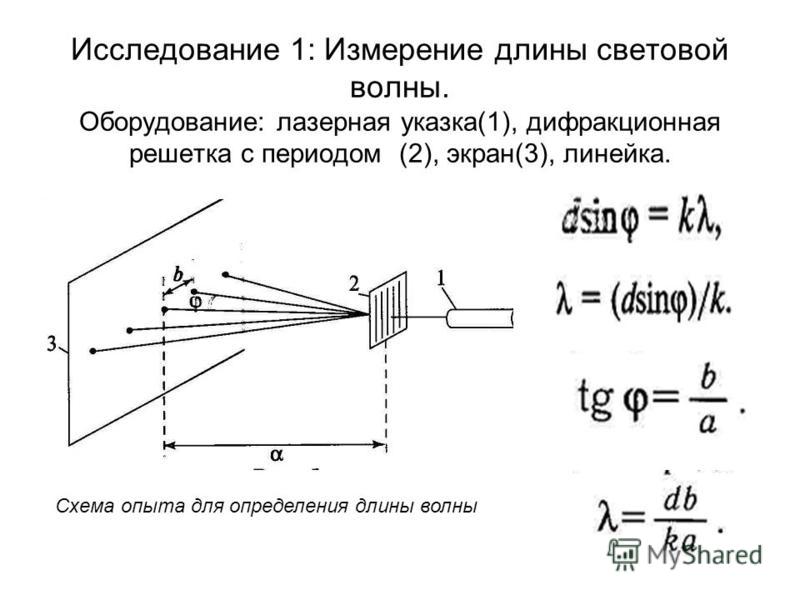
Существует следующая зависимость между длиной волны излучаемого света, l, расстоянием между щелями в дифракционной решетке, d, y и L (см. вывод уравнения 1 в примечании 2):
Обычно этот эксперимент дает хорошие результаты. На самом деле, если учащиеся сообщают о результатах, которые не находятся в пределах 10% от соответствующей длины волны, я знаю, что что-то пошло не так. Иногда виноваты небрежные измерения. Однако чаще всего мешают ошибки в переводе единиц измерения. Я даю студентам значение d = 4,85 x 10 -4 см, а затем пусть они сообщат мне длину волны света в нм. Это необходимо для того, чтобы учащиеся правильно использовали экспоненциальную систему обозначений и преобразование метрических единиц (см в нм) для получения приемлемых результатов. Я также отмечаю, что учащиеся часто измеряют L в метрах, а y в сантиметрах, но не преобразуют их в согласованные единицы при использовании уравнения 1. Это, конечно, приводит к ложным результатам, но дает возможность преподавания важности уделения внимания единицам измерения. И всегда найдется ученик, который измеряет y в дюймах, а L в метрах, но не записывает единицы измерения.
Это, конечно, приводит к ложным результатам, но дает возможность преподавания важности уделения внимания единицам измерения. И всегда найдется ученик, который измеряет y в дюймах, а L в метрах, но не записывает единицы измерения.
Видео ниже демонстрирует, как проводить этот эксперимент и анализировать данные.
Примечания
1. Использование расстояния между щелями (d) в дифракционной решетке, записанное производителем очков, вызвало у меня некоторые затруднения в этом эксперименте. Радужные очки, которые я использую в этом эксперименте, имеют 500 линий на мм, что означает d = 2000 нм (1 мм / 500 линий = 0,002 мм; понимаете, почему это отличная лаборатория для преобразования единиц измерения?). Однако я использовал оптический микроскоп, оснащенный шкалой длины, для измерения d = 4850 нм в очках, которые я использую.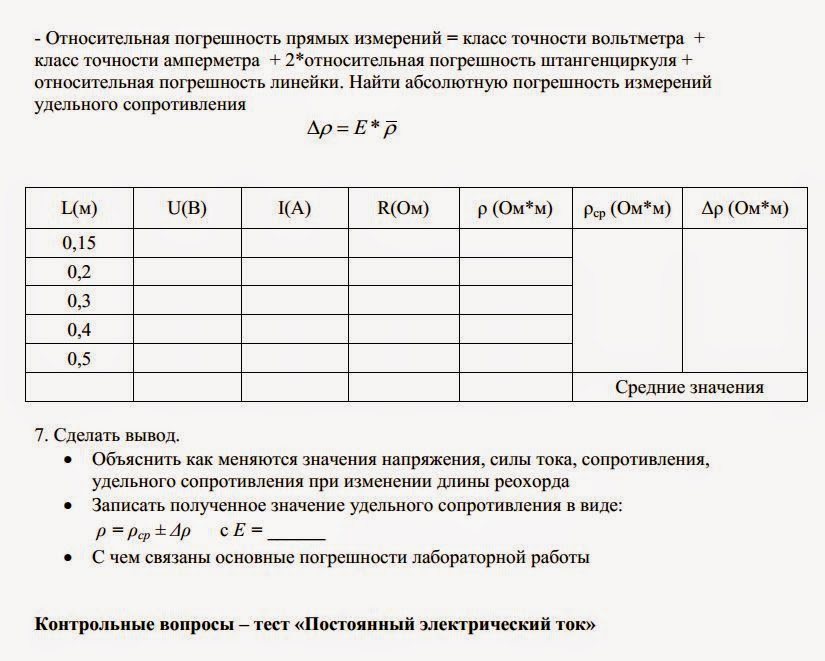 Мораль этой истории такова: если вы заметите, что ваши измеренные длины волн не имеют смысла (например, 200 нм для красного света), то подумайте об измерении d для себя. Если у вас нет оптического микроскопа со шкалой длины, просто проведите этот эксперимент со светом известной длины волны и используйте следующее уравнение для определения d:0003
Мораль этой истории такова: если вы заметите, что ваши измеренные длины волн не имеют смысла (например, 200 нм для красного света), то подумайте об измерении d для себя. Если у вас нет оптического микроскопа со шкалой длины, просто проведите этот эксперимент со светом известной длины волны и используйте следующее уравнение для определения d:0003
2. Преломление или дифракция света на дифракционной решетке определяется по формуле:
Где l — длина волны света, фракционная решетка и q — это угол между прямолинейным лучом света и его следующим ближайшим соседом. Обратите внимание, что мы можем направить дифрагированные лучи света обратно к источнику света (рис. 1). Сделав это, мы получим треугольник с гипотенузой h, а полученные новые углы также будут равны 9.0073 q (рис. 3).
Рисунок 3 — Распространение дифрагированных световых лучей обратно через пространство к источнику света. Угол между прямым лучом и дифрагированными лучами равен q.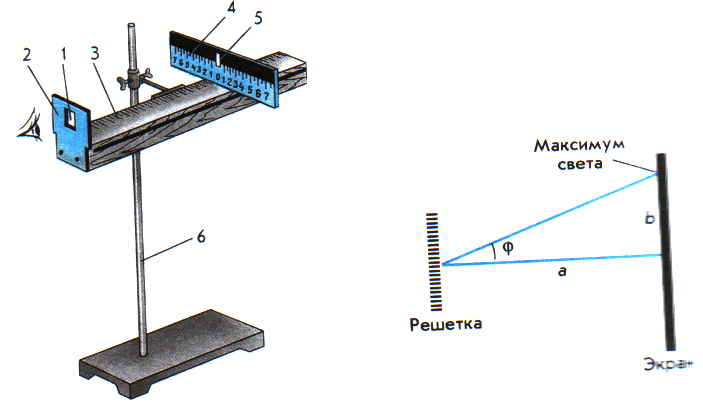 Гипотенуза образовавшегося треугольника обозначается h. Двойная синяя стрелка представляет собой расстояние между источником света и его ближайшим соседом. Это расстояние обозначается y.
Гипотенуза образовавшегося треугольника обозначается h. Двойная синяя стрелка представляет собой расстояние между источником света и его ближайшим соседом. Это расстояние обозначается y.
Можно заменить sin q = y/h в уравнении 2:
Используя h 2 = L 2 + y 2 , мы получаем искомое уравнение:
900 02 Лабораторная ведомость студента включена в вспомогательный информация ниже.Вспомогательная информация:
Коллекция:
Лабораторные оценки и ресурсы
HS-PS4-1: частота, длина волны и скорость волн
Учащиеся, демонстрирующие понимание, могут использовать математические представления для обоснования утверждений о взаимосвязях между частотой, длиной волны и скоростью волн, распространяющихся в различных средах.
*Дополнительную информацию обо всех DCI для HS-PS4 можно найти по адресу https://www.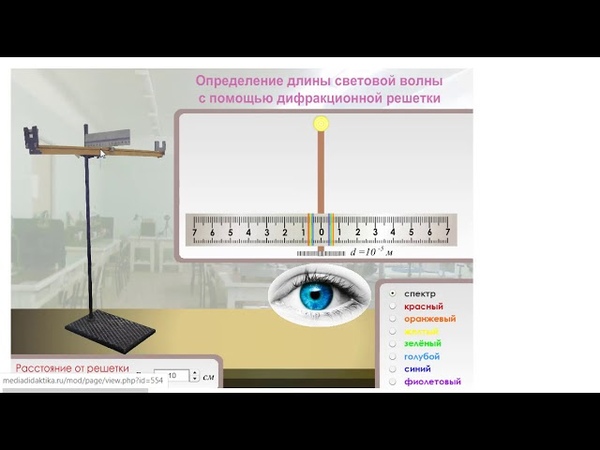 nextgenscience.org/topic-arrangement/hswaves-and-electromagnetic-radiation.
nextgenscience.org/topic-arrangement/hswaves-and-electromagnetic-radiation.
Резюме:
Учащиеся, демонстрирующие понимание, могут использовать математические представления для обоснования утверждений о соотношениях между частотой, длиной волны и скоростью волн, распространяющихся в различных средах.
Граница оценки:
Оценка ограничивается алгебраическими отношениями и качественным описанием этих отношений.
Пояснение:
Примеры данных могут включать электромагнитное излучение, распространяющееся в вакууме и стекле, звуковые волны, распространяющиеся по воздуху и воде, и сейсмические волны, распространяющиеся по Земле.
HS-PS4-3: Волновая и корпускулярная теории электромагнитного излучения
Учащиеся, продемонстрировавшие понимание, могут оценить утверждения, доказательства и аргументы, лежащие в основе идеи о том, что электромагнитное излучение может быть описано либо волновой моделью, либо моделью частиц, и что в некоторых ситуациях одна модель более полезна, чем другая.
*Дополнительную информацию обо всех DCI для HS-PS4 можно найти по адресу https://www.nextgenscience.org/topic-arrangement/hswaves-and-electromagnetic-radiation.
Резюме:
Учащиеся, продемонстрировавшие понимание, могут оценить утверждения, доказательства и аргументы, лежащие в основе идеи о том, что электромагнитное излучение может быть описано либо волновой моделью, либо моделью частиц, и что в некоторых ситуациях одна модель более полезна, чем другая. другой.
Граница оценки:
Оценка не включает использование квантовой теории.
Пояснение:
Акцент делается на том, как экспериментальные данные подтверждают утверждение и как теория обычно модифицируется в свете новых данных. Примеры явления могут включать резонанс, интерференцию, дифракцию и фотоэлектрический эффект.
HS-PS4-4: Частоты электромагнитного излучения
Учащиеся, демонстрирующие понимание, могут оценить обоснованность и достоверность заявлений в опубликованных материалах о влиянии электромагнитного излучения различной частоты при поглощении веществом. *
*
*Более подробную информацию обо всех DCI для HS-PS4 можно найти по адресу https://www.nextgenscience.org/topic-arrangement/hswaves-and-electromagnetic-radiation.
Резюме:
Учащиеся, демонстрирующие понимание, могут оценить обоснованность и достоверность утверждений в опубликованных материалах об эффектах, которые электромагнитное излучение различных частот оказывает при поглощении материей.
Граница оценки:
Оценка ограничена качественными описаниями.
Уточнение:
Акцент сделан на идее о том, что фотоны, связанные с разными частотами света, имеют разную энергию, и от энергии излучения зависит повреждение живых тканей от электромагнитного излучения. Примеры опубликованных материалов могут включать торговые книги, журналы, веб-ресурсы, видео и другие отрывки, которые могут отражать предвзятость.
2.1.5: Спектрофотометрия — Химия LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 1431
Спектрофотометрия — это метод измерения степени поглощения света химическим веществом путем измерения интенсивности света при прохождении луча света через раствор пробы.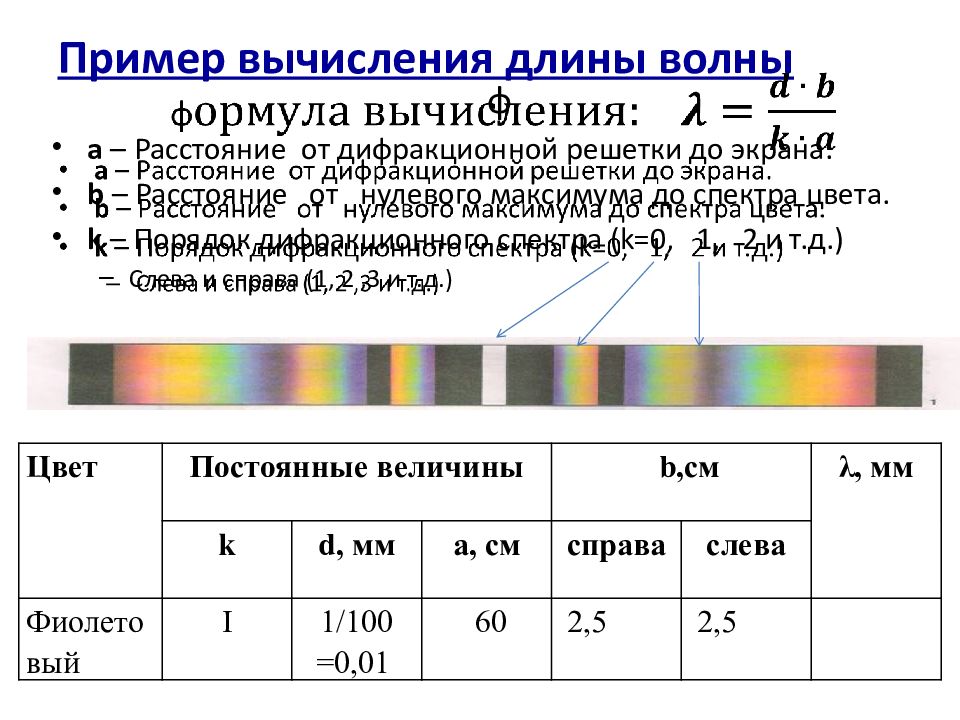 Основной принцип заключается в том, что каждое соединение поглощает или пропускает свет в определенном диапазоне длин волн. Это измерение также можно использовать для измерения количества известного химического вещества. Спектрофотометрия является одним из наиболее полезных методов количественного анализа в различных областях, таких как химия, физика, биохимия, материаловедение и химическая инженерия, а также в клинических применениях.
Основной принцип заключается в том, что каждое соединение поглощает или пропускает свет в определенном диапазоне длин волн. Это измерение также можно использовать для измерения количества известного химического вещества. Спектрофотометрия является одним из наиболее полезных методов количественного анализа в различных областях, таких как химия, физика, биохимия, материаловедение и химическая инженерия, а также в клинических применениях.
Введение
Каждое химическое соединение поглощает, пропускает или отражает свет (электромагнитное излучение) в определенном диапазоне длин волн. Спектрофотометрия — это измерение того, сколько химического вещества поглощает или пропускает. Спектрофотометрия широко используется для количественного анализа в различных областях (например, химия, физика, биология, биохимия, материаловедение и химическая инженерия, клиническое применение, промышленное применение и т. д.). Любое приложение, имеющее дело с химическими веществами или материалами, может использовать этот метод. В биохимии, например, он используется для определения катализируемых ферментами реакций. В клинических применениях он используется для исследования крови или тканей для постановки клинического диагноза. Существует также несколько вариантов спектрофотометрии, таких как атомно-абсорбционная спектрофотометрия и атомно-эмиссионная спектрофотометрия.
В биохимии, например, он используется для определения катализируемых ферментами реакций. В клинических применениях он используется для исследования крови или тканей для постановки клинического диагноза. Существует также несколько вариантов спектрофотометрии, таких как атомно-абсорбционная спектрофотометрия и атомно-эмиссионная спектрофотометрия.
Спектрофотометр — это прибор, который измеряет количество фотонов (интенсивность света), поглощенных после прохождения через раствор образца. С помощью спектрофотометра можно также определить количество известного химического вещества (концентрации) путем измерения интенсивности обнаруженного света. В зависимости от диапазона длины волны источника света его можно разделить на два разных типа:
- УФ-видимый спектрофотометр : использует свет в ультрафиолетовом диапазоне (185–400 нм) и видимом диапазоне (400–700 нм). спектра электромагнитного излучения.
- ИК-спектрофотометр : использует свет в инфракрасном диапазоне (700–15000 нм) спектра электромагнитного излучения.

В видимой спектрофотометрии поглощение или пропускание определенного вещества можно определить по наблюдаемому цвету. Например, образец раствора, который поглощает свет во всех видимых диапазонах (т. е. не пропускает ни одну из видимых длин волн), теоретически кажется черным. С другой стороны, если пропускаются все видимые длины волн (т. Е. Ничего не поглощается), образец раствора кажется белым. Если образец раствора поглощает красный свет (~ 700 нм), он кажется зеленым, потому что зеленый является дополнительным цветом к красному. Спектрофотометры видимого диапазона на практике используют призму для сужения определенного диапазона длин волн (для фильтрации других длин волн), чтобы конкретный луч света проходил через образец раствора.
Устройства и механизм
На рисунке 1 показана основная структура спектрофотометров. Он состоит из источника света, коллиматора, монохроматора, селектора длины волны, кюветы для раствора образца, фотоэлектрического детектора и цифрового дисплея или измерителя.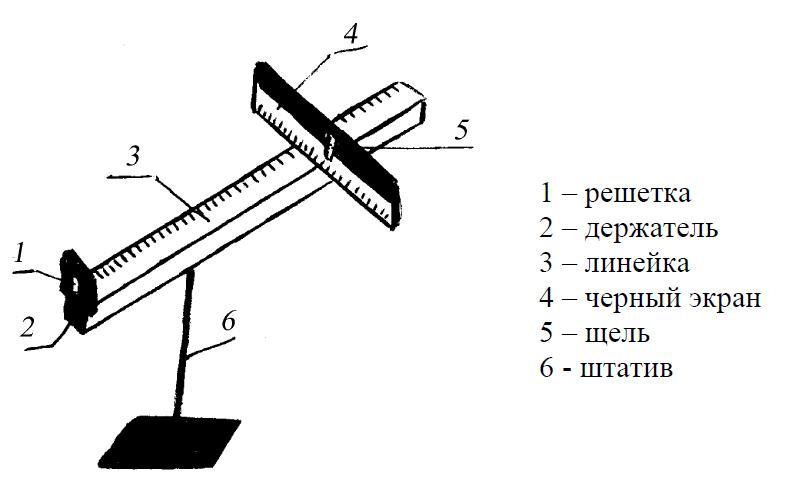 Подробный механизм описан ниже. На рис. 2 показан образец спектрофотометра (модель: Spectronic 20D).
Подробный механизм описан ниже. На рис. 2 показан образец спектрофотометра (модель: Spectronic 20D).
Обычно спектрофотометр состоит из двух устройств; спектрометр и фотометр. Спектрометр — это устройство, которое производит, обычно рассеивает и измеряет свет. Фотометр обозначает фотоэлектрический детектор, который измеряет интенсивность света.
- Спектрометр : Излучает свет в желаемом диапазоне длин волн. Сначала коллиматор (линза) пропускает прямой пучок света (фотоны), который проходит через монохроматор (призму) и разделяет его на несколько составляющих длин волн (спектр). Затем селектор длины волны (щель) передает только нужные длины волн, как показано на рисунке 1.
- Фотометр : после того, как свет с желаемой длиной волны проходит через раствор образца в кювете, фотометр определяет количество поглощенных фотонов и затем посылает сигнал на гальванометр или цифровой дисплей, как показано на рисунке.
 1.
1.
Спектрометр нужен для получения различных длин волн, потому что разные соединения лучше всего поглощают при разных длинах волн. Например, п-нитрофенол (кислотная форма) имеет максимальное поглощение примерно при 320 нм, а п-нитрофенолат (основная форма) лучше всего поглощает при 400 нм, как показано на рисунке 3.
Рисунок 3: Поглощение двух разных соединенийграфик, который измеряет поглощение и длину волны, также можно наблюдать изобестическую точку. изобестическая точка — это длина волны, при которой поглощательная способность двух или более видов одинакова. Появление изобестической точки в реакции свидетельствует о том, что промежуточное соединение НЕ требуется для образования продукта из реагента. На рис. 4 показан пример изобестической точки.
Рисунок 4: Пример изобестической точки (CC BY-4.0; Heesung Shim через LibreTexts) кюветы и концентрации образца. Как только вы узнаете интенсивность света после его прохождения через кювету, вы можете соотнести ее с коэффициентом пропускания (T). Коэффициент пропускания — это доля света, проходящая через образец. Это можно рассчитать с помощью уравнения:
Коэффициент пропускания — это доля света, проходящая через образец. Это можно рассчитать с помощью уравнения:\(Пропускание (T) = \dfrac{I_t}{I_o}\)
Где I t — интенсивность света после прохождения луча света через кювету, а I o — интенсивность света до луч света проходит через кювету. Коэффициент пропускания связан с поглощением выражением:
\(Поглощение (A) = — log(T) = — log(\dfrac{I_t}{I_o})\)
Где поглощение обозначает количество фотонов, которое впитывается. Зная величину поглощения, известную из приведенного выше уравнения, вы можете определить неизвестную концентрацию образца, используя закон Бера-Ламберта. На рис. 5 показан коэффициент пропускания света через образец. Длина \(l\) используется для закона Бера-Ламберта, описанного ниже.
Рисунок 5: Коэффициент пропускания (CC BY-4.0; Heesung Shim через LibreTexts)Закон Бера-Ламберта
Закон Бера-Ламберта (также известный как закон Бера) утверждает, что существует линейная зависимость между поглощением и концентрацией образца . По этой причине закон Бера может применяться только при наличии линейной зависимости. Закон Бера записывается как:
По этой причине закон Бера может применяться только при наличии линейной зависимости. Закон Бера записывается как:
\(A = \epsilon{lc}\)
, где
- \(A\) — мера поглощения (без единиц),
- \(\эпсилон\) — молярный коэффициент экстинкции или молярная абсорбционная способность (или коэффициент поглощения),
- \(l\) — длина пути, а
- \(с\) — концентрация.
Молярный коэффициент экстинкции задается как константа и варьируется для каждой молекулы. Поскольку поглощение не имеет никаких единиц, единицы для \(\эпсилон\) должны компенсировать единицы длины и концентрации. В результате \(\эпсилон\) имеет единицы: л·моль — 1 9{-1}\) и длина пути 1 см. Используя спектрофотометр, вы находите, что \(A_{275}= 0,70\). Какова концентрация гуанозина?
Решение
Чтобы решить эту задачу, вы должны использовать Закон Бера.
\[A = \epsilon lc \nonumber \]
0,70 = (8400 M -1 см -1 )(1 см)(\(c\))
Затем разделите обе стороны на [ (8400 M -1 см -1 )(1 см)]
\(с\) = 8,33×10 -5 моль/л
Пример 2
Вещество в растворе (4 г/л). Длина кюветы 2 см и пропускает только 50% определенного светового пучка. Что такое коэффициент поглощения?
Длина кюветы 2 см и пропускает только 50% определенного светового пучка. Что такое коэффициент поглощения?
Решение
Используя закон Бера-Ламберта, мы можем вычислить коэффициент поглощения. Таким образом,
\(- \log \left(\dfrac{I_t}{I_o} \right) = — \log(\dfrac{0.5}{1.0}) = A = {8} \epsilon\)
Тогда мы получаем, что
\(\эпсилон\) = 0,0376
Пример 3
В приведенном выше примере 2, сколько луча света передается при 8 г/л?
Решение
Поскольку мы знаем \(\эпсилон\), мы можем рассчитать передачу, используя закон Бера-Ламберта. Таким образом,
\(\log(1) — \log(I_t) = 0 — \log(I_t)\) = 0,0376 x 8 x 2 = 0,6016
\(\log(I_t)\) = -0,6016
Следовательно, \(I_t\) = 0,2503 = 25%
Пример 4
Каков в приведенном выше примере 2 молярный коэффициент поглощения, если молекулярная масса равна 100?
Раствор
Его можно просто получить, умножив коэффициент поглощения на молекулярную массу. Таким образом,
Таким образом,
\(\эпсилон\) = 0,0376 x 100 = 3,76 л·моль — 1 ·см — 1
Пример 5
900 02 Коэффициент поглощения гликоген-йодного комплекса составляет 0,20 на свету. 450 нм. Какова концентрация при пропускании 40 % в кювете диаметром 2 см?Решение
Эту задачу также можно решить с помощью закона Бера-Ламберта. Следовательно,
\[- \log(I_t) = — \log(0.4) = 0,20 \times c \times 2 \nonnumber \]
Тогда \(c\) = 0,9948
Ссылки
- Аткинс, Питер и Хулио де Паула. Физическая химия для наук о жизни. Нью-Йорк: Издательство Оксфордского университета, 2006. .
- Чанг, Раймонд. Физическая химия для биологических наук. США: Университетские научные книги, 2005. .
- Гор, Майкл. Спектрофотометрия и спектрофлуориметрия. Нью-Йорк: Издательство Оксфордского университета, 2000. .
- Прайс, Николас и Двек, Рэймонд и Вормолд, Марк. Принципы и проблемы физической химии для биохимиков.



 λф ср=( λф1+λф2)/2
λф ср=( λф1+λф2)/2 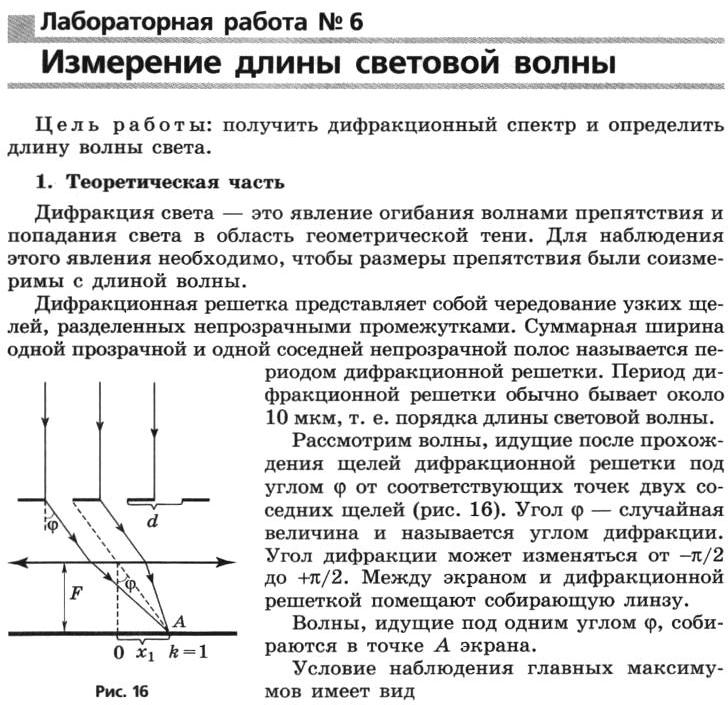
 1.
1.