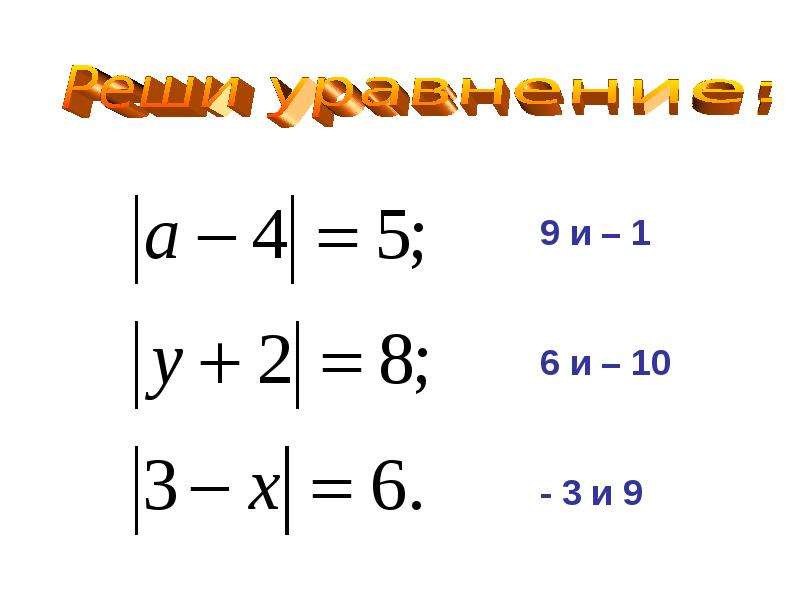Контрольная работа сложение и вычитание рациональных чисел: Контрольная работа «Сложение и вычитание рациональных чисел», 6 класс, Мерзляк А.Г.

Содержание

«Сложение и вычитание рациональных чисел»

Материалы в дополнение к контрольным работам 1 и 2 вариантов из пособия

Мерзляк А.Г. Математика: 6 класс: дидактические материалы: пособие для учащихся общеобразовательных организаций / А.Г. Мерзляк, В.Б. Полонский, Е.М. Рабинович, М.С. Якир. – М. – Вентана-Граф, 2017. – 144 с.

М-6 Демоверсия КР № 8 по теме: «Сложение и вычитание рациональных чисел»

1. Выполните действия:

1) ; 5) ;

2) ; 6) ;

3) ; 7) ;

4) .

2. Решите уравнение:

1) ; 2) .

3. Найдите значение выражения:

1) ;

2) ;

3) .

4. Упростите выражение

и найдите его значение, если .

5. Не выполняя вычислений, сравните:

1) сумму чисел и и их разность;

2) сумму чисел и и сумму чисел и . Ответ обоснуйте.

6. Сколько целых чисел расположено на координатной прямой между числами и ? Чему равна их сумма?

Решите уравнение:

М-6 Ответы к демоверсии КР № 8

М-6 Контрольная работа № 8

Вариант 3

1. Выполните действия:

1) ; 5) ;

2) ; 6) ;

3) ; 7) ;

4) .

2. Решите уравнение:

1) ; 2) .

3. Найдите значение выражения:

1) ;

2) ;

3) .

4. Упростите выражение

и найдите его значение, если .

5. Не выполняя вычислений, сравните:

1) сумму чисел и и их разность;

2) сумму чисел и и сумму чисел и . Ответ обоснуйте.

6. Сколько целых чисел расположено на координатной прямой между числами и ? Чему равна их сумма?

7. Решите уравнение:

М-6 Контрольная работа № 8

Вариант 4

1. Выполните действия:

1) ; 5) ;

2) ; 6) ;

3) ; 7) ;

4) .

2. Решите уравнение:

1) ; 2) .

3. Найдите значение выражения:

1) ;

2) ;

3) .

4. Упростите выражение

и найдите его значение, если .

5. Не выполняя вычислений, сравните:

1) разность чисел и и их сумму;

2) сумму чисел и и сумму чисел и . Ответ обоснуйте.

6. Сколько целых чисел расположено на координатной прямой между числами и ? Чему равна их сумма?

7. Решите уравнение:

М-6 Варианты 1 и 2 из пособия: Мерзляк А.Г. Математика: 6 класс: дидактические материалы: пособие для учащихся общеобразовательных организаций / А.Г. Мерзляк, В.Б. Полонский, Е.М. Рабинович, М.С. Якир. – М. – Вентана-Граф, 2017. – 144 с.

М-6 Контрольная работа № 8

Вариант 1

1. Выполните действия:

1) ; 5) ;

2) ; 6) ;

3) ; 7) ;

4) .

2. Решите уравнение:

1) ; 2) .

3. Найдите значение выражения:

1) ;

2) ;

3) .

4. Упростите выражение

и найдите его значение, если .

5. Не выполняя вычислений, сравните:

1) сумму чисел и и их разность;

2) сумму чисел и и сумму чисел и . Ответ обоснуйте.

6. Сколько целых чисел расположено на координатной прямой между числами и ? Чему равна их сумма?

7. Решите уравнение:

М-6 Контрольная работа № 8

Вариант 2

1. Выполните действия:

1) ; 5) ;

2) ; 6) ;

3) ; 7) ;

4) .

2. Решите уравнение:

1) ; 2) .

3. Найдите значение выражения:

1) ;

2) ;

3) .

4. Упростите выражение

и найдите его значение, если .

5. Не выполняя вычислений, сравните:

1) разность чисел и и их сумму;

2) сумму чисел и и сумму чисел и . Ответ обоснуйте.

6. Сколько целых чисел расположено на координатной прямой между числами и ? Чему равна их сумма?

7. Решите уравнение:

М-6 Ответы на контрольную работу № 8 по теме: «Сложение и вычитание рациональных чисел»

5. 1) сумма чисел меньше их разности, т.к. оба числа – отрицательные;

2) первая сумма больше второй, т.к. одно слагаемое в суммах одинаковое, а другое – больше в первой сумме.

5. 1) разность чисел больше их суммы, т.к. оба числа — отрицательные

2) первая сумма меньше второй, т.к. одно слагаемое в суммах – одинаковое, а другое – меньше в первой сумме.

5. 1) сумма чисел меньше их разности, т.к. оба числа – отрицательные;

2) первая сумма меньше второй, т.к. одно слагаемое в суммах – одинаковое, а другое – меньше в первой сумме.

5. 1) разность чисел больше их суммы, т.к. оба числа — отрицательные

2) первая сумма больше второй, т.к. одно слагаемое в суммах одинаковое, а другое – больше в первой сумме.

Контрольная работа № 7. Рациональные числа. Сравнение рациональных чисел. Математика 6 класс, с ответами

Вариант 1

1. Начертите координатную прямую и отметьте на ней точки А (4), В (–5), С (0,5), D (–0,5). Какие из отмеченных точек имеют противоположные координаты?

Решение:

В D С А
____._____________.___.___.__________.___
-5 -0,5 0 0,5 4
Противоположные: Д и С
Ответ: С (0,5) и D(-0,5)

2. Выберите среди чисел 2; –3; 0; 1/7; –5,6; 9,1; 16 4/13; 28; –23; –1 1/3.
1) натуральные; 2) целые; 3) положительные; 4) целые отрицательные; 5) дробные отрицательные.

Ответы:

1) 2,28
2) 2, -3, 0, 28, -23
3) 2, 1/7, 9, 1, 16_4/13, 28
4) -3, -23
5) -5,6, -1_1/3

3. Сравните числа: 1) –5,8 и 2,4; 2) –3,4 и –3,8.

Решение:

1) -5,8 ˂ 2,4
2) -3,4 ˃ -3,8
Ответ: 1) -5,8 ˂ 2,4; 2) -3,4 ˃ -3,8.

4. Вычислите: 1) |–4,4| + |–3,6| – |–5,64|; 2) |–5/14| : |2 1/7|.

Решение:

1) |-4,4| + |-3,6| — |-5,64| = 4,4 + 3,6 – 5,64 = 8 – 5,64 = 2,36

2) |-5/14| : |2_1/7| = 5/14 : 15/7 = (8 * 7)/(14 * 15) = 1/6
Ответ: 1) 2,36; 2) 1/6.

5. Найдите значение х, если: 1) –х = –16; 2) –(–х) = 9,4.

Решение:

1) –х = — 16
х = 16
2) – (-х) = 9,4
х = 9,4
Ответ: 1) 16; 2) 9,4.

6. Решите уравнение: 1) |x| = 2,8; 2) |x| = –1,6.

Решение:

1) |x| = 2,8
x = ± 2,8
2) |x| = — 1,6 – нет решения
Ответ: 1) 2,8; — 2,8; 2) нет корней.

7. Найдите наибольшее целое значение х, при котором верно неравенство х ≤ –12.

Решение:

х ≤ — 12
х = — 12
Ответ: — 12.

8. Какую цифру можно поставить вместо звёздочки, чтобы получилось верное неравенство (рассмотрите все возможные случаи): –9,6 • 8 > –9,627?

Решение:

– 9,618 > — 9,627
— 9,608 > — 9,627
Ответ: -9,618; -9,608

9. Найдите два числа, каждое из которых больше –3/19, но меньше –2/19.

Решение:

– 3/19 и – 2/19
— 9/57 и – 6/57 => — 8/57 и – 7/57
Ответ: — 8/57 и – 7/57.

Вариант 2

1. Начертите координатную прямую и отметьте на ней точки А (–1), В (4), С (1,5), D (–1,5). Какие из отмеченных точек имеют противоположные координаты?

Решение:

D А С В
___. ___.___.______.____________.__
-1,5 -1 0 1,5 4
Противоположные: Д и С.
Ответ: С (1,5) и D (- 1,5).

2. Выберите среди чисел 9; 1/19; –16; 0; 7,2; –3,8; 4 3/16; –50; –2 6/17; 24:
1) натуральные; 2) целые; 3) положительные; 4) целые отрицательные; 5) дробные отрицательные.

Ответы:

1) 9, 24
2) 9, — 16, — 50, 24
3) 9, 1/19, 7,2, 4_3/16, 24
4) – 16, — 50
5) – 3,8, — 2_6/17

3. Сравните числа: 1) 3,1 и –6,7; 2) –4,2 и –4,6.

Решение:

1) 3,1 > — 6,7
2) – 4,2 > — 4,6
Ответ: 1) 3,1 > — 6,7; 2) – 4,2 > — 4,6.

4. Вычислите: 1) |–7,3| + |–1,8| – |3,45|; 2) |17/90| : |–1 8/9|.

Решение:

1) | — 7,3| + | — 1,8| — |3,45| = 7,3 + 1,8 – 3,45 = 9,1 – 3,45 = 5,65
2) |17/90| : |8/9| = 17/90 : 17/9 = (17 * 9)/(90 * 17) = 1/10 = 0,1
Ответ: 1) 5,65; 2) 0,1.

5. Найдите значение х, если: 1) –х = 25; 2) –(–х) = –4,9.

Решение:

1) – х = 25
х = — 25
2) – (- х) = — 4,9
х = — 4,9
Ответ: 1) – 25; 2) – 4,9.

6. Решите уравнение: 1) |x|= 4,5; 2) |x| = –1,8.

Решение:

1) |x| = 4,5
x = ± 4,5
2) |x| = — 1,8 – нет решений
Ответ: 1) 4,5; — 4,5; 2) нет корней.

7. Найдите наименьшее целое значение х, при котором верно неравенство х > –14.

Решение:

х >14
х > — 13
Ответ: — 13.

8. Какую цифру можно поставить вместо звёздочки, чтобы получилось верное неравенство (рассмотрите все возможные случаи): –5,35* < –5,356?

Решение:

– 5,357 < — 5,356
— 5,358 < — 5,356
— 5,359 < — 5,356
Ответ: — 5,357; — 5,358; — 5,359.

9. Найдите два числа, каждое из которых больше –6/17, но меньше –5/17.

Решение:

– 6/17 и – 5/17
— 18/51 и – 15/51 => — 17/51 и – 16/51
Ответ: — 17/51 и – 16/51.

Самостоятельные и контрольные работы по математике для 6 класса -Ершов

Пособие содержит самостоятельные и контрольные работы по всем важнейшим темам курса математики 6 класса.
Работы состоят из 6 вариантов трех уровней сложности.
Дидактические материалы предназначены для организации дифференцированной самостоятельной работы учащихся.
Скачать бесплатно самостоятельные и контрольные работы по математике для 6 класса. Ершова А.П., Голобородько В.В. 2010 г.

СОДЕРЖАНИЕ
Предисловие
Делимость чисел
С-1. Делители и кратные
С-2. Признаки делимости
С-3. Простые и составные числа. Разложение на простые множители
С-4. Наибольший общий делитель. Наименьшее общее кратное
С-5*. Дополнительные вопросы и задачи о свойствах делимости (домашняя самостоятельная работа)
К-1. Делимость чисел
Сложение и вычитание обыкновенных дробей
С-6. Основное свойство дроби. Сокращение дробей
С-7. Приведение дробей к общему знаменателю. Сравнение дробей
С-8. Сложение и вычитание дробей с разными знаменателями
К-2. Сложение и вычитание дробей
С-9. Сложение и вычитание смешанных чисел
К-3. Сложение и вычитание смешанных чисел
Умножение и деление обыкновенных дробей
С-10. Умножение дробей
С-11. Применение умножения дробей
К-4. Умножение дробей
С-12. Взаимно обратные числа. Деление дробей
С-13. Применение деления дробей
С-14*. Дроби и действия с дробями (домашняя самостоятельная работа)
К-5. Деление дробей

Отношения и пропорции
С-15. Отношения. Понятие пропорции
С-16. Прямая и обратная пропорциональность. Масштаб
С-17. Длина окружности и площадь круга
С-18*. Деление числа в пропорциональном отношении
С-19*. Свойства отношений и пропорций (домашняя самостоятельная работа)
К-6. Отношения и пропорции
К-7. Обыкновенные дроби (итоговая контрольная работа)
Положительные и отрицательные числа
C-20. Координаты на прямой. Противоположные числа
С-21. Модуль числа. Сравнение чисел
С-22*. Свойства отрицательных чисел (домашняя самостоятельная работа)
К-8. Положительные и отрицательные числа
Сложение и вычитание рациональных чисел
С-23. Сложение отрицательных чисел и чисел с разными знаками
С-24. Вычитание отрицательных чисел и чисел с разными знаками
С-25-. Выражения с модулем (домашняя самостоятельная работа)
К-9. Сложение и вычитание положительных и отрицательных чисел
Умножение и деление рациональных чисел
С-26. Умножение и деление положительных и отрицательных чисел
С-27. Рациональные числа и действия с ними
С-28*. Свойства действий с рациональными числами (домашняя самостоятельная работа)
К-10. Умножение и деление рациональных чисел

Решение уравнений
С-29. Раскрытие скобок
С-30. Коэффициент. Приведение подобных слагаемых
К-11. Упрощение выражений
С-31. Уравнения и задачи
С-32*. Анализ и применение уравнений (домашняя самостоятельная работа)
К-12. Решение уравнений
Координаты на плоскости
С-33. Перпендикулярные и параллельные прямые
С-34. Координатная плоскость.
Столбчатые диаграммы
К-13. Координаты на плоскости
К-14. Рациональные числа (итоговая контрольная работа)
Повторение
С-35. Повторение
С-36*. Нестандартные задачи (домашняя самостоятельная работа)
К-15. Годовая контрольная работа
ЛИТЕРАТУРА
ОТВЕТЫ

МОУ «СОШ № 5 х. Восточный»

Подпишитесь на новостную рассылку

Если Вы хотите своевременно получать информацию и быть в курсе событий в школе, то можете подписаться на новостную рассылку.

* Пожалуйста наберите правильно ваш email — [email protected]

Социальные сети и поисковые службы

Информация о школе на сайте ГМУ

Информация о госзакупках СОШ №5

Если Вы хотите узнать на какую сумму были исполнены контракты по государственным закупкам для СОШ №5, Вы можете перейти по этой ссылки на сайт с подобной информацией

Информация о противодействии коррупции в СОШ №5

По этой ссылке Вы перейдете в раздел сайта с информацией о противолействии коррупции в школе

Зачисление в образовательное учреждение

Для зачисления в образовательное учреждение необходимо встать в электронную очередь на сайте. Необходимо зарегистрироваться на нём, и выбрав нашу школу подать заявление на зачисление, приложив предлагаемые документы.

Электронный классный журнал

Для получения информации о текущей успеваемости и посещаемости вашего ребёнка Вы должны перейти по ссылке на https://26gosuslugi.ru/personcab/info_pou?tab=performance. Для входа в систему электронного дневника Вы должны ввести логин и пароль используемый для регистрации на сайте «Госуслуги», и после открытия электронного дневника добавить учащихся, за отметками которых Вы будете следить. Для этого нажмите кнопку «добавить ученика», и во всплывающем окне выбрать район (начтните набирать «сов» и после появления выберите «Советский» после этого начните выберите в следующей строке школу, начните набирать «сош» и выберите «СОШ №5 х. Восточный», и теперь нажмите кнопку «Добаваить». После этого система запомнит ваш выбор и вы сможите получить услугу.

Примите участие!

Уважаемые родители и учащиеся МОУ «СОШ №5 х.Восточный»!

Минпросвещение России совместно с ПАО «Газпром» разработало образовательные программы на основе мероприятий социальной сферы с привлечением отечественных высокотехнологичных компаний, направленных на повышение интереса к инженерному образованию и раннюю профессиональную ориентацию учащейся молодежи школьного возраста, действующих на территории производственной деятельности компании Группы Газпром.

Ознакомиться с ними можно по ссылке

Официальный интернет-портал правовой информации

Посетите официальный портал правовой информации!

На официальном портале правовой информации публикуются нормативные и законодательные акты РФ. Все такие документы перед вступлением в силу должны быть опубликованы на этом портале.

перейти на портал можно по этой ссылке

Сложение и вычитание рациональных чисел

В данном уроке рассматривается сложение и вычитание рациональных чисел. Тема относится к категории сложных. Здесь необходимо использовать весь арсенал полученных ранее знаний.

Правила сложения и вычитания целых чисел справедливы и для рациональных чисел. Напомним, что рациональными называют числа, которые могут быть представлены в виде дроби , где a – это числитель дроби, b – знаменатель дроби. При этом, b не должно быть нулём.

В данном уроке дроби и смешанные числа мы всё чаще будем называть одним общим словосочетанием — рациональные числа.

Пример 1. Найти значение выражения:

Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что плюс который дан в выражении, является знаком операции и не относится к дроби . У этой дроби свой знак плюса, который невидим по причине того, что его не записывают. Но мы запишем его для наглядности:

Это сложение рациональных чисел с разными знаками. Чтобы сложить рациональные числа с разными знаками, нужно из большего модуля вычесть меньший модуль, и перед полученным ответом поставить знак того рационального числа, модуль которого больше. А чтобы понять какой модуль больше, а какой меньше, нужно суметь сравнить модули этих дробей до их вычисления:

Модуль рационального числа больше, чем модуль рационального числа . Поэтому мы из вычли . Получили ответ . Затем сократив эту дробь на 2, получили окончательный ответ .

Некоторые примитивные действия, такие как заключение чисел в скобки и проставление модулей, можно пропустить. Данный пример вполне можно записать покороче:

Пример 2. Найти значение выражения:

Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что минус, стоящий между рациональными числами и является знаком операции и не относится к дроби . У этой дроби свой знак плюса, который невидим по причине того, что его не записывают. Но мы запишем его для наглядности:

Заменим вычитание сложением. Напомним, что для этого нужно к уменьшаемому прибавить число, противоположное вычитаемому:

Получили сложение отрицательных рациональных чисел. Чтобы сложить отрицательные рациональные числа, нужно сложить их модули и перед полученным ответом поставить минус:

Запишем решение данного примера покороче:

Примечание. Заключать в скобки каждое рациональное число вовсе необязательно. Делается это для удобства, чтобы хорошо видеть какие знаки имеют рациональные числа.

Пример 3. Найти значение выражения:

В этом выражении у дробей разные знаменатели. Чтобы облегчить себе задачу, приведём эти дроби к общему знаменателю. Не будем подробно останавливаться на том как это сделать. Если испытываете с этим затруднения, обязательно повторите урок действия с дробями.

После приведения дробей к общему знаменателю выражение примет следующий вид:

Заключим каждое рациональное число в скобки вместе своими знаками:

Это сложение рациональных чисел с разными знаками. Вычитаем из большего модуля меньший модуль, и перед полученным ответом ставим знак того рационального числа, модуль которого больше:

Запишем решение данного примера покороче:

Пример 4. Найти значение выражения

Заключим каждое рациональное число в скобки вместе со своими знаками:

Вычислим данное выражение в следующем порядке: слóжим рациональные числа и , затем из полученного результата вычтем рациональное число .

Первое действие:

Второе действие:

Таким образом, значение выражения равно

Пример 5. Найти значение выражения:

Представим целое число −1 в виде дроби , а смешанное число переведём в неправильную дробь:

Приведём данные дроби к общему знаменателю. После их приведения к общему знаменателю, они примут следующий вид:

Заключим каждое рациональное число в скобки вместе со своими знаками:

Получили сложение рациональных чисел с разными знаками. Вычитаем из большего модуля меньший модуль, и перед полученным ответом ставим знак того рационального числа, модуль которого больше:

Получили ответ .

Есть и второй способ решения. Он заключается в том, чтобы сложить отдельно целые части.

Итак, вернёмся к изначальному выражению:

Заключим каждое число в скобки. Для этого смешанное число временно развернём:

Вычислим целые части:

(−1) + (+2) = 1

В главном выражении вместо (−1) + (+2) запишем полученную единицу:

Полученное выражение свернём. Для этого запишем единицу и дробь вместе:

Запишем решение этим способом покороче:

Пример 6. Найти значение выражения

Переведём смешанное число в неправильную дробь. Остальную часть перепишем без изменения:

Заключим каждое рациональное число в скобки вместе со своими знаками:

Заменим вычитание сложением:

Получили сложение отрицательных рациональных чисел. Слóжим модули этих чисел и перед полученным ответом поставим минус:

Запишем решение данного примера покороче:

Пример 7. Найти значение выражение

Представим целое число −5 в виде дроби , а смешанное число переведём в неправильную дробь:

Заключим каждое рациональное число в скобки вместе со своими знаками:

Заменим вычитание сложением:

Таким образом, значение выражения равно .

Решим данный пример вторым способом. Вернемся к изначальному выражению:

Запишем смешанное число в развёрнутом виде. Остальное перепишем без изменений:

Заключим каждое рациональное число в скобки вместе своими знаками:

Заменим вычитание сложением там, где это можно:

Вычислим целые части:

В главном выражении вместо запишем полученное число −7

Выражение является развёрнутой формой записи смешанного числа . Запишем число −7 и дробь вместе, образуя окончательный ответ:

Запишем это решение покороче:

Пример 8. Найти значение выражения

Переведём смешанные числа в неправильные дроби:

Заключим каждое рациональное число в скобки вместе своими знаками:

Заменим вычитание сложением:

Таким образом, значение выражения равно

Данный пример можно решить и вторым способом. Он заключается в том, чтобы сложить целые и дробные части по отдельности. Вернёмся к изначальному выражению:

Заключим каждое рациональное число в скобки вместе со своими знаками:

Заменим вычитание сложением:

Получили сложение отрицательных рациональных чисел. Слóжим модули этих чисел и перед полученным ответом поставим минус. Но в этот раз слóжим по отдельности целые части (−1 и −2), и дробные и

Запишем это решение покороче:

Пример 9. Найти выражения выражения

Переведём смешанные числа в неправильные дроби:

Заключим рациональное число в скобки вместе своим знаком. Рациональное число в скобки заключать не нужно, поскольку оно уже в скобках:

Приведём данные дроби в общему знаменателю. После их приведения к общему знаменателю, они примут следующий вид:

Таким образом, значение выражения равно

Теперь попробуем решить этот же пример вторым способом, а именно сложением целых и дробных частей по отдельности.

В этот раз, в целях получения короткого решения, попробуем пропустить некоторые действия, такие как: запись смешанного числа в развёрнутом виде и замена вычитания сложением:

Обратите внимание, что дробные части были приведены к общему знаменателю.

Пример 10. Найти значение выражения

Заменим вычитание сложением:

В получившемся выражении нет отрицательных чисел, которые являются основной причиной допущения ошибок. А поскольку нет отрицательных чисел, мы можем убрать плюс перед вычитаемым, а также убрать скобки:

Получилось простейшее выражение, которое вычисляется легко. Вычислим его любым удобным для нас способом:

Пример 11. Найти значение выражения

Это сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший модуль, и перед полученными ответом поставим знак того рационального числа, модуль которого больше:

Пример 12. Найти значение выражения

Выражение состоит из нескольких рациональных чисел. Согласно порядку действий, в первую очередь необходимо выполнить действия в скобках.

Сначала вычислим выражение , затем выражение Полученные результаты слóжим .

Первое действие:

Второе действие:

Третье действие:

Ответ: значение выражения равно

Пример 13. Найти значение выражения

Переведём смешанные числа в неправильные дроби:

Заключим рациональное число в скобки вместе со своим знаком. Рациональное число заключать в скобки не нужно, поскольку оно уже в скобках:

Заменим вычитание сложением:

Получили сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший модуль, и перед полученными ответом поставим знак того рационального числа, модуль которого больше:

Таким образом, значение выражения равно

Рассмотрим сложение и вычитание десятичных дробей, которые тоже относятся к рациональным числам и которые могут быть как положительными, так и отрицательными.

Пример 14. Найти значение выражения −3,2 + 4,3

Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что плюс который дан в выражении, является знаком операции и не относится к десятичной дроби 4,3. У этой десятичной дроби свой знак плюса, который невидим по причине того, что его не записывают. Но мы его запишем для наглядности:

(−3,2) + (+4,3)

(−3,2) + (+4,3) = |+4,3| − |−3,2| = 1,1

Модуль числа 4,3 больше, чем модуль числа −3,2 поэтому мы из 4,3 вычли 3,2. Получили ответ 1,1. Ответ положителен, поскольку перед ответом должен стоять знак того рационального числа, модуль которого больше. А модуль числа 4,3 больше, чем модуль числа −3,2

Таким образом, значение выражения −3,2 + (+4,3) равно 1,1

Этот пример можно записать покороче:

−3,2 + (+4,3) = 1,1

Пример 15. Найти значение выражения 3,5 + (−8,3)

Это сложение рациональных чисел с разными знаками. Как и в прошлом примере из большего модуля вычитаем меньший и перед ответом ставим знак того рационального числа, модуль которого больше:

3,5 + (−8,3) = −(|−8,3| − |3,5|) = −(8,3 − 3,5) = −(4,8) = −4,8

Таким образом, значение выражения 3,5 + (−8,3) равно −4,8

Этот пример можно записать покороче:

3,5 + (−8,3) = −4,8

Пример 16. Найти значение выражения −7,2 + (−3,11)

Это сложение отрицательных рациональных чисел. Чтобы сложить отрицательные рациональные числа, нужно сложить их модули и перед полученным ответом поставить минус.

Запись с модулями можно пропустить, чтобы не загромождать выражение:

−7,2 + (−3,11) = −7,20 + (−3,11) = −(7,20 + 3,11) = −(10,31) = −10,31

Таким образом, значение выражения −7,2 + (−3,11) равно −10,31

Этот пример можно записать покороче:

−7,2 + (−3,11) = −10,31

Пример 17. Найти значение выражения −0,48 + (−2,7)

Это сложение отрицательных рациональных чисел. Слóжим их модули и перед полученным ответом поставим минус. Запись с модулями можно пропустить, чтобы не загромождать выражение:

−0,48 + (−2,7) = (−0,48) + (−2,70) = −(0,48 + 2,70) = −(3,18) = −3,18

Пример 18. Найти значение выражения −4,9 − 5,9

Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что минус который располагается между рациональными числами −4,9 и 5,9 является знаком операции и не относится к числу 5,9. У этого рационального числа свой знак плюса, который невидим по причине того, что он не записывается. Но мы запишем его для наглядности:

(−4,9) − (+5,9)

Заменим вычитание сложением:

(−4,9) + (−5,9)

Получили сложение отрицательных рациональных чисел. Слóжим их модули и перед полученным ответом поставим минус:

(−4,9) + (−5,9) = −(4,9 + 5,9) = −(10,8) = −10,8

Таким образом, значение выражения −4,9 − 5,9 равно −10,8

Запишем решение этого примера покороче:

−4,9 − 5,9 = −10,8

Пример 19. Найти значение выражения 7 − 9,3

Заключим в скобки каждое число вместе со своими знаками

(+7) − (+9,3)

Заменим вычитание сложением

(+7) + (−9,3)

Получили сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший модуль, и перед ответом поставим знак того числа, модуль которого больше:

(+7) + (−9,3) = −(9,3 − 7) = −(2,3) = −2,3

Таким образом, значение выражения 7 − 9,3 равно −2,3

Запишем решение этого примера покороче:

7 − 9,3 = −2,3

Пример 20. Найти значение выражения −0,25 − (−1,2)

Заменим вычитание сложением:

−0,25 + (+1,2)

−0,25 + (+1,2) = 1,2 − 0,25 = 0,95

Запишем решение этого примера покороче:

−0,25 − (−1,2) = 0,95

Пример 21. Найти значение выражения −3,5 + (4,1 − 7,1)

Выполним действия в скобках, затем слóжим полученный ответ с числом −3,5

Первое действие:

4,1 − 7,1 = (+4,1) − (+7,1) = (+4,1) + (−7,1) = −(7,1 − 4,1) = −(3,0) = −3,0

Второе действие:

−3,5 + (−3,0) = −(3,5 + 3,0) = −(6,5) = −6,5

Ответ: значение выражения −3,5 + (4,1 − 7,1) равно −6,5.

Пример 22. Найти значение выражения (3,5 − 2,9) − (3,7 − 9,1)

Выполним действия в скобках. Затем из числа, которое получилось в результате выполнения первых скобок, вычтем число, которое получилось в результате выполнения вторых скобок:

Первое действие:

3,5 − 2,9 = (+3,5) − (+2,9) = (+3,5) + (−2,9) = 3,5 − 2,9 = 0,6

Второе действие:

3,7 − 9,1 = (+3,7) − (+9,1) = (+3,7) + (−9,1) = −(9,1 − 3,7) = −(5,4) = −5,4

Третье действие

0,6 − (−5,4) = (+0,6) + (+5,4) = 0,6 + 5,4 = 6,0 = 6

Ответ: значение выражения (3,5 − 2,9) − (3,7 − 9,1) равно 6.

Пример 23. Найти значение выражения −3,8 + 17,15 − 6,2 − 6,15

Заключим в скобки каждое рациональное число вместе со своими знаками

(−3,8) + (+17,15) − (+6,2) − (+6,15)

Заменим вычитание сложением там, где это можно:

(−3,8) + (+17,15) + (−6,2) + (−6,15)

Выражение состоит из нескольких слагаемых. Согласно сочетательному закону сложения, если выражение состоит из нескольких слагаемых, то сумма не будет зависеть от порядка действий. Это значит, что слагаемые можно складывать в любом порядке.

Не будем изобретать велосипед, а слóжим все слагаемые слева направо в порядке их следования:

Первое действие:

(−3,8) + (+17,15) = 17,15 − 3,80 = 13,35

Второе действие:

13,35 + (−6,2) = 13,35 − −6,20 = 7,15

Третье действие:

7,15 + (−6,15) = 7,15 − 6,15 = 1,00 = 1

Ответ: значение выражения −3,8 + 17,15 − 6,2 − 6,15 равно 1.

Пример 24. Найти значение выражения

Переведём десятичную дробь −1,8 в смешанное число. Остальное перепишем без изменения:

Далее вычисляем данное выражение, применяя ранее изученные правила:

Пример 25. Найти значение выражения

Заменим вычитание сложением. Попутно переведём десятичную дробь (−4,4) в неправильную дробь

В получившемся выражении нет отрицательных чисел. А поскольку нет отрицательных чисел, мы можем убрать плюс перед вторым числом, и убрать скобки. Тогда получим простое выражение на сложение, которое решается легко

Пример 26. Найти значение выражения

Переведём смешанное число в неправильную дробь, а десятичную дробь −0,85 в обыкновенную дробь. Получим следующее выражение:

Пример 27. Найти значение выражения

Переведём обе дроби в неправильные дроби. Чтобы перевести десятичную дробь 2,05 в неправильную дробь, можно перевести ее сначала в смешанное число, а затем в неправильную дробь:

После перевода обеих дробей в неправильные дроби, получим следующее выражение:

Получили сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший модуль и перед полученным ответом поставим знак того числа, модуль которого больше:

Пример 28. Найти значение выражения

Заменим вычитание сложением. Далее переведём десятичную дробь в обыкновенную дробь. Затем вычислим получившееся выражение, применяя ранее изученные правила:

Пример 29. Найти значение выражения

Переведём десятичные дроби −0,25 и −1,25 в обыкновенные дроби, остальное перепишем без изменения. Получим следующее выражение:

Можно сначала заменить вычитание сложением там, где это можно и сложить рациональные числа одно за другим.

Есть и второй вариант: сначала сложить рациональные числа и , а затем из полученного результата вычесть . Этим вариантом и воспользуемся.

Первое действие:

Второе действие:

Ответ: значение выражения равно −2.

Пример 30. Найти значение выражения

Переведём десятичные дроби в обыкновенные. Остальное перепишем без изменения:

Получили сумму из нескольких слагаемых. Если сумма состоит из нескольких слагаемых, то выражение можно вычислять в любом порядке. Это следует из сочетательного закона сложения.

Поэтому мы можем организовать наиболее удобный для нас вариант. В первую очередь можно сложить первое и последнее слагаемое, а именно рациональные числа и . У этих чисел одинаковые знаменатели, а значит это освободит нас от необходимости приводить их к нему.

Первое действие:

Полученное число можно сложить со вторым слагаемым, а именно с рациональным числом . У рациональных чисел и одинаковые знаменатели в дробных частях, что опять же является преимуществом для нас

Второе действие:

Ну и слóжим полученное число −7 с последним слагаемым, а именно с рациональным числом . Удобно то, что при вычислении данного выражения, семёрки исчезнут, поскольку их сумма будет равна нулю:

Третье действие:

Ответ: значение выражения равно

Задания для самостоятельного решения

Задание 1. Найдите значение выражения:

Решение:

Задание 2. Найдите значение выражения:

Решение:

Задание 3. Найдите значение выражения:

Решение:

Задание 4. Найдите значение выражения:

Решение:

Задание 5. Найдите значение выражения:

Решение:

Задание 6. Найдите значение выражения:

Решение:

Задание 7. Найдите значение выражения:

Решение:

Задание 8. Найдите значение выражения:

Решение:

Задание 9. Найдите значение выражения:

Решение:

Задание 10. Найдите значение выражения:

Решение:

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Навигация по записям

Использование рациональных чисел

Как складывать, вычитать, умножать и делить рациональные числа

Рациональное число — это число, которое может быть записано как простая дробь (т.е. как отношение ).

Примеры:

Номер	В виде фракции
5	1/5
1,75	7/4
.001	1/1000
0.111 …	1/9

В целом …

Итак, рациональное число выглядит так:

p q

Но q не может быть нулем, так как оно делится на ноль.

Как сложить, вычесть, умножить и разделить

Если рациональное число представляет собой что-то простое, например 3 или 0,001 , тогда просто используйте мысленную арифметику или калькулятор!

Но как насчет того, чтобы он был в форме p q ?

Здесь мы увидим эти операции в более общем стиле алгебры.

Вы также можете прочитать Дроби в алгебре.

Начнем с умножения, так как это самый простой способ.

Умножение

Чтобы умножить два рациональных числа , умножьте вершины и основания отдельно , например:

Вот пример:

Дивизион

Чтобы разделить два рациональных числа, сначала переверните второе число (сделайте его обратным), а затем произведите умножение, как указано выше:

Вот пример:

Сложение и вычитание

Мы рассмотрим сложение и вычитание за один раз, поскольку это один и тот же метод.

Перед тем, как мы добавим или вычтем, рациональные числа должны иметь то же самое нижнее число (называемое общим знаменателем).

Проще всего это сделать на

Умножьте обе части каждого числа на нижнюю часть другого

Как это (обратите внимание, что точка · означает умножение):

Вот пример сложения:

И пример вычитания (средний шаг пропущен для ускорения):

Простейшая форма

Иногда бывает такое рациональное число:

10 15

Но это не так просто!

Мы можем разделить верх и низ на 5, чтобы получить:

÷ 5

10 15 = 2 3

÷ 5

Теперь он в «простейшей форме», чего хочет большинство людей!

Будьте осторожны со «смешанными дробями»

У нас может возникнуть соблазн написать неправильную дробь (дробь с «тяжелым верхом», т.е.е. где верхнее число больше нижнего) в виде смешанной дроби:

Например, ⁷/₄ = 1 ³/₄, здесь показано:

Но для математики «неправильная» форма (например, ⁷/₄) на самом деле лучше .

Потому что смешанные дроби (например, 1 ³/₄) могут сбивать с толку, когда мы записываем их в формулу, так как это может выглядеть как умножение :

Смешанная фракция:	Что такое:	1 + 2 1 4 ?
	Это:	1 + 2 + 1 4 = 3 1 4 ?
	Или это:	1 + 2 × 1 4 = 1 1 2 ?

Неправильная фракция:	Что такое:	1 + 9 4 ?
	Это:	4 4 + 9 4 = 13 4

Так что попробуйте использовать неправильную дробь при выполнении математических расчетов.

Сложение и вычитание рациональных чисел в числовой строке

Национальная оценка успеваемости выявила тревожный дефицит способности учащихся считать и рассуждать с помощью чисел. Показатели по одному конкретному элементу теста подчеркивают этот недостаток.

«Студентам было предложено оценить ответ на 12/13 + 7/8. Были выбраны 1, 2, 19, 21 и «Я не знаю». Только 24% опрошенных 13-летних выбрали правильный ответ 2.Пятьдесят пять процентов тринадцатилетних выбрали 19 или 21 — они добавили либо числители, либо знаменатели ». (Безук, Крамер 1989)

Этот пример перекликается с моим опытом преподавания математики в средней школе. Самым серьезным препятствием, с которым я сталкиваюсь как учитель, является то, что мои ученики не полностью понимают числа и основные операции. Чтобы справиться с этим недостатком, студенты усвоили уловки и алгоритмы и стали зависимыми от них. Этот модуль просто, но смело направлен на то, чтобы раз и навсегда дать учащимся единый способ осмысления чисел и операций.

Контекст

В следующем году я буду преподавать один раздел математики для седьмого класса и два раздела по математике для восьмого класса в Brentano Math and Science Academy в районе Логан-сквер в Чикаго. Школа имеет право на получение финансирования по титулу 1 и в ней обучаются преимущественно латиноамериканцы. Согласно оценке округа, которая проверяет успеваемость учащихся по стандартам Common Core на уровне своего класса в каждой области, мои поступающие студенты стабильно демонстрируют значительно низкие результаты в области систем счисления.Именно в этой области студенты должны рассуждать и оперировать дробями, десятичными знаками и отрицательными числами. Дефицит моих учеников в этой области очевиден не только на тестах, но и является постоянным препятствием, которое влияет на их повседневную успеваемость в моем классе.

Когда учащихся просят оперировать незнакомыми рациональными числами, они цепляются за ранее изученные алгоритмы, не имея концептуального понимания того, что на самом деле происходит с числами. Их шаткое понимание основных чисел и концепций операций является основным фактором общей нетерпимости и избегания работы над любой задачей, связанной с этими незнакомыми числами.Это создает повторяющиеся проблемы как для каждого индивидуально, так и для класса в целом, поскольку наша учебная программа средней школы предполагает и требует фундаментального и гибкого понимания чисел. Мне никогда не удавалось успешно провести тщательное вмешательство, чтобы исправить эти необходимые фундаментальные концепции. Этот блок будет направлен на формальное и методическое решение фундаментальной проблемы неоднородности и неполноценности числа и умения моих учеников с помощью использования и изучения числовой прямой.

Описание конструкции агрегата

Этот модуль восполнит дефицит, который в настоящее время существует в моей учебной программе, а именно отсутствие связного и полного развития понятий, связанных с арифметикой рациональных чисел. Развитие концепций будет происходить в объединяющем контексте числовой прямой. Как было сказано ранее, моим ученикам не хватает здравого мышления о работе с рациональными числами.

Рисунок 1

Теперь это очень ясно и хорошо организовано.

Как видно на рисунке выше, моя единица измерения, выделенная красным, будет использоваться последовательно с единицей Джеффа Росситера, Размещение рациональных чисел в числовой строке , выделенной синим цветом. Концепции, затронутые в первом разделе, будут сосредоточены на реализации и размещении рациональных чисел на числовой прямой. Предварительным условием будет, чтобы студенты сначала имели единое представление о том, что такое рациональные числа и как они могут быть представлены на числовой прямой, прежде чем переходить к сложению и вычитанию рациональных чисел, что является основной задачей моего модуля.

Для этого модуля поток концепций будет подробно описан в разделе «Концепции модуля» вместе с подробным описанием основных понятий для каждой концепции. Затем в разделах «Подход к обучению» и «Действия» приводится объяснение того, как будет реализована данная единица.

Почему числовая линия

Использование числовой линии является фундаментальным для этого модуля и предназначено для обеспечения контекста привязки, в котором учащиеся могут видеть и представлять числа, а затем понимать операции.Этот модуль будет посвящен только осмыслению сложения и вычитания рациональных чисел и подготовит моих студентов к умножению и делению позже в этом году. Под «осмыслением» я имею в виду понимание и способность ученика визуализировать происходящее при сложении и вычитании рациональных чисел. К седьмому классу у большинства моих учеников появляется множество грубых заблуждений относительно сложения и вычитания. Они полагаются на алгоритмы и калькуляторы, особенно когда дело доходит до работы с целыми числами и дробями.Эти недоразумения подчеркиваются, когда им задают такие вопросы, как «Имеет ли ваш ответ смысл?», «Как вы знаете, что сумма / разница точна?», «Можете ли вы нарисовать представление о своих вычислениях?» Чтобы представить сложение или вычитание целых чисел, учащиеся часто используют ранее изученные приемы, такие как добавление или вычеркивание счетных отметок или счет пальцев. Эти методы подводят их, когда, например, от них требуется сложить дроби с разными знаменателями или вычесть отрицательное из положительного.Студенты редко демонстрируют концептуальное понимание и могут работать только абстрактно, используя алгоритмы. Когда им явно предлагается продемонстрировать такое понимание, они снова полагаются на представления, демонстрирующие ограниченное владение концепциями. Некоторые студенты используют деньги, чтобы рассуждать с помощью десятичных знаков, круговых или мозаичных представлений дробей или разноцветных фишек для чисел со знаком, но в этом и заключается проблема. Учащимся не хватает единого способа думать об этих различных разновидностях чисел, и поэтому они рассматривают сложение и вычитание разных типов как очень разные задачи.Это разрозненное понимание связано с тем, что они не пришли к пониманию того, как работу с этими разными типами чисел следует рассматривать как аналогичные задачи, следующие схожей логике.

Числовая линия в конечном итоге служит цели дать студентам возможность работать с этими различными формами чисел единообразно. В результате изучения предыдущего раздела учащиеся получат единое представление о различных типах чисел с точки зрения расстояния на числовой прямой.Это предварительное условие и основа для развития данного устройства. В следующем разделе я расскажу, как будет преподавать каждое понятие с помощью числовой линии, какой ключевой язык будет использоваться и какие важные моменты необходимо выявить, чтобы ученики достигли полного понимания.

Развитие концепций, рассматриваемых в этом модуле, выглядит следующим образом:

Концепция №1: Сложение и вычитание в контексте измерения длины

Концепция № 2: Сложение и вычитание целых чисел как векторов

Концепция № 3: Сложение и вычитание дробей с одинаковыми знаменателями

Концепция №4: Сложение и вычитание дробей с отличными знаменателями

Концепция №1: Сложение и вычитание в контексте измерения длины

Дополнение

По моему опыту, в средней школе учащиеся хорошо осознают элементарный принцип, согласно которому сложение, по крайней мере, целых чисел, может рассматриваться как процесс соединения вещей.Чтобы все учащиеся твердо усвоили и могли сформулировать эту концепцию в самом общем смысле, я начну этот модуль с использования произвольных столбцов разной длины при отсутствии единиц и номеров. У студентов обычно мало опыта работы с этим типом моделей. Обычно учащиеся полагаются на наборы счетных отметок или счетные предметы, чтобы показать сложение в контексте сложения целых чисел. Студенты будут считать один набор предметов и рассчитывать на второй набор, чтобы найти общую сумму.Следовательно, этот ограниченный опыт заставляет некоторых студентов узко рассматривать сложение как действие, на которое можно положиться. Это устройство не работает, когда учеников затем просят сложить нецелые числа, поскольку их трудно представить и рассчитать с помощью дробей и десятичных знаков. Вместо этого обсуждение сложения с использованием длины столбцов, а не наборов объектов позволяет нам сделать более общий и переносимый момент, что независимо от того, какие количества мы используем, дробные или целые числа, сложение — это вопрос сложения количеств вместе.Кроме того, использование полосок целенаправленно, поскольку позволяет учащимся легче переходить к просмотру чисел с точки зрения линейного измерения на числовой прямой. См. Рисунок 2.

Рисунок 2

Чтобы найти сумму столбцов a и b, мы просто складываем их вместе и берем общую длину. Это геометрическое представление заставляет учащихся рассматривать сложение как «соединение» вещей, а не просто символ, который сигнализирует нам, что нужно рассчитывать. (Хоу, 2016)

Коммутационная собственность

Здесь будет полезно показать коммутативность сложения.См. Рисунок 3.

Рисунок 3

Рисунок 3 предлагает учащимся осознать тот факт, что не имеет значения, какой столбец порядка a соединен со стержнем b , они всегда будут равны одному и тому же, таким образом, приводя геометрический аргумент в пользу коммутативности. Эта простая иллюстрация будет полезна в течение всего года обучения, потому что она обеспечивает приятный и ясный способ просмотра этого свойства, облегчая использование, когда оно нам снова понадобится, в таких темах, как алгебра.

Вычитание

Студенты часто придерживаются узкого взгляда на вычитание как на «отнятие». Студенты также должны понимать, что вычитание во многом связано со сравнением. Чтобы укрепить это понимание в отсутствие чисел, я покажу их вычитание, выровняв две планки и сравнив их длины. См. Рисунок 4 ниже.

Рисунок 4

Если мы сравним стержни a со стержнями b, , мы легко увидим разницу в представленной выступающей части.Учащиеся должны знать, что столбики следует складывать так, чтобы они были равномерно выровнены на одном конце для точного сравнения. Это условие необходимо твердо установить, потому что оно будет использоваться снова, когда мы перейдем к рассмотрению вычитания чисел в числовой строке.

Я не собираюсь потратить более двух или трех занятий на укрепление этих концепций. Мой опыт наводит меня на мысль, что это будет в основном интуитивно понятным и легким для понимания аудиторией средней школы.Несмотря на кажущуюся простоту, эти идеи будут использоваться в качестве основы для рассуждений и способа размышления о сложении и вычитании, не зависящем от символов. Идея объединения и сравнения будет общим языком, используемым в этом модуле. Важно отметить, что у некоторых учащихся будет очень узкое и укоренившееся представление о сложении и вычитании. Учащиеся полагаются на стратегии счета и удаления, которые перестают быть полезными, когда им требуется работать с разными знаменателями, десятичными знаками или числами со знаком.

Когда учащиеся продемонстрируют понимание этого «сложения» и «сравнения разницы» столбцов, я затем предложу им те же рассуждения, но на числовой прямой, присвоив этим столбцам числовое значение в единицах длины. Наконец, я переведу столбчатое представление чисел в векторные представления, подготовив их для следующей концепции.

Концепция № 2: Сложение и вычитание целых чисел как векторов

Сложение целых чисел

Установленный в обязательном модуле Рациональное размещение чисел в числовой строке и снова в Концепции 1 этого модуля, учащиеся уже будут понимать, как представлять положительные и отрицательные числа как величины расстояния с ориентацией.Затем учащиеся должны понять, что сложение и вычитание положительных и отрицательных чисел — это просто вопрос сложения и сравнения этих чисел на числовой строке относительно начала координат. Рассмотрим рисунок 5 как пример сложения двух чисел с одинаковым знаком и двух чисел с разными знаками.

Рисунок 5

Я считаю, что важно использовать осторожный и последовательный язык при обсуждении этих векторных представлений.На рисунке 5a мы перемещаем 4 единицы в положительном направлении вправо, поэтому мы помещаем вектор, начинающийся в начале координат, и расширяем его до 4 в положительном направлении. Знак плюс сигнализирует о сложении следующего числа в его исходной ориентации, которая снова находится в положительном направлении, поскольку это положительное число 3. Теперь мы можем видеть, что комбинированное расстояние, простирающееся от начала до конечной точки второго вектора, равно 7. Язык движения здесь является ключевым. Например: «Мы перемещаем 4 в положительном направлении, а затем еще 3 в положительном направлении.Это объяснение дает дополнительное обоснование векторных представлений. На рисунке 5b положительный вектор 4 соединен с отрицательным 3, который студенты будут знать как вектор длиной 3 единицы, направленный влево. Поскольку мы складываем, мы складываем их вместе, начиная вектор с конца 4. Этот вектор складывается над первым, что позволяет нам видеть оба вектора по отдельности. Расстояние от конечной точки второго вектора до начала координат, 1, является тогда суммой. Эти базовые примеры сложения и вычитания необходимы для точного определения языка.Учащиеся должны легко соглашаться с этими представлениями и сопровождающими их объяснениями. Студенты будут применять эту идею на нескольких примерах, чтобы принять этот новый образ мышления. Это, наконец, обеспечит надежную систему отсчета при работе с положительными и отрицательными числами в абстракции, что традиционно для моих студентов является предметом борьбы.

Вычитание целых чисел

При переходе к вычитанию целых чисел учащиеся должны использовать ту же логику, что и при вычитании столбцов.Мы их выстраиваем и сравниваем. Затем, чтобы основываться на этой логике, нам нужно использовать некоторый дополнительный язык, чтобы объяснить, что происходит в отношении числовой линии.

Рисунок 6

На рисунке 6а мы переносим 4 минус 3 в числовую прямую. Положительный вектор, начинающийся в начале координат, представляет 4, а вектор длиной 3 комбинируется только на этот раз с вычитанием. Перед тем, как объединить тройку, мы меняем ее ориентацию, так как мы ее вычитаем. Вычитание сводится к сложению отрицательного.Теперь мы сравниваем конечную точку второго вектора с исходной точкой для оставшегося расстояния, которое является разницей. Получив достаточный опыт в том, чтобы рассматривать вычитание как изменение ориентации второго числа перед сложением, ученики должны понять, что это то же действие, что и добавление противоположного числа, как показано на рисунке 5a. Это ключевой вывод этого урока.

Вычитание отрицательного числа, как показано на рисунке 6b, следует той же логике. -3 рассматривается как вектор, направленный влево, но затем мы меняем ориентацию на противоположное направление, так как мы вычитаем его.Перевернув -3 на +3, мы привычным способом прибавляем его к +4. Расстояние от конечной точки второго вектора до начала координат будет тогда разницей, 7. И снова суть в том, чтобы не полагаться на другие устройства для понимания этого. Знак вычитания следует рассматривать как изменение ориентации или следующего числа. Если учащиеся полагаются на понимание того, что вычитание — это просто отбрасывание, становится трудно концептуализировать устранение отрицательной величины. Следует отметить, что вычитание не обязательно означает «идти влево по числовой прямой», скорее оно сигнализирует нам о том, что нужно взять противоположное вычитаемому и затем сложить.Если посмотреть на это с этой точки зрения, мы сможем более прочно связать сложение и вычитание. Хорошо! Студенты в конечном итоге придут к выводу, что вычитание — это просто сложение аддитивного обратного, и в этом смысле вычитание поглощается сложением.

Вычитание целых чисел со знаком, по моему опыту, представляет собой сложную концепцию для понимания учащимися и становится еще более сложной, когда используются дроби со знаком. Будет важно, чтобы учащиеся увидели много примеров различных вариантов вычитания целых чисел: вычитание положительного из положительного, положительного из отрицательного, отрицательного из отрицательного и отрицательного из положительного.Учащиеся должны иметь возможность увидеть, как происходит одна и та же задача, и объединить свое понимание вычитания целых чисел, независимо от того, какую комбинацию они представляют. Кроме того, цель состоит в том, чтобы учащиеся понимали, что так же, как сложение и вычитание положительных чисел распространяется на сложение и вычитание положительных рациональных чисел, сложение и вычитание целых чисел распространяется на сложение и вычитание всех знаковых рациональных чисел.

Концепция № 3: Сложение и вычитание дробей с одинаковыми знаменателями

В обязательном модуле учащиеся усвоят представление всех рациональных чисел.В концепциях 1 и 2 этого раздела мы установили основные понятия сложения и вычитания целых чисел на числовой прямой. Поэтому сложение и вычитание дробей с одинаковыми знаменателями должно быть вопросом обращения к одному и тому же пониманию. То же самое, но с меньшим размером. Здесь важно, чтобы учащиеся установили связь, что то, что мы делаем, когда мы работаем с дробями, совпадает с тем, что мы делаем, когда работаем с целыми числами. Это вопрос сложения количеств.Примеры сложения и вычитания см. На рис. 7a и 7b.

Рисунок 7

Концепция №4: Сложение и вычитание дробей с отличными знаменателями

На этом этапе мы рассмотрим сложную концепцию сложения и вычитания дробей. Числовая линия — отличное место для рассмотрения этой концепции, потому что она демонстрирует необходимость найти единообразную единицу. Затем нахождение суммы или разницы сводится к делению единицы таким образом, чтобы интервалы выражали общий знаменатель.Проблема переименования или того, что обычно называется составлением эквивалентных дробей, требует отдельного рассмотрения, прежде чем переходить к сложению и вычитанию, чтобы учащиеся не зависели слепо от методов, которые позволяют им просто находить общие знаменатели, а затем действовать.

Переименование дробей

Существенное понимание, которое необходимо достичь в отношении переименования дробей, состоит в том, что это вопрос переименования количества, выражая его в других единицах. Студенты часто демонстрируют недостаточное понимание эквивалентных дробей из-за их неполного понимания абстрактной концепции эквивалентности.(Hung-Hsi Wu 2013). Обсуждая эту концепцию как переименование, она делает очевидный и правильный вывод, что количество фракции остается неизменным, и мы просто даем ей новое имя, используя другие термины. Студенты обычно знакомы с методом создания эквивалентных дробей путем умножения числителя и знаменателя на один и тот же коэффициент. Однако эта процедура часто выполняется без обоснования того, что физическая величина остается неизменной. Переименование дробей в числовой строке позволяет учащимся создавать эквивалентные дроби, продолжая рассуждать о количестве.Точно так же, как в предварительном модуле, где понимание дробей учащимся было передано от моделей площадей к числовой прямой, мы должны таким же образом руководить переименованием дробей.

Сначала нам нужно развить идею того, что значит быть таким же, потому что для многих студентов это неочевидно. Для этого мы можем начать с представления дроби в модели площади в виде единичного прямоугольника. См. Рис. 8. Вертикальные линии, показывающие сначала четверти, делят прямоугольник. Обращаясь к каждой части, важно использовать язык, который был установлен в первой части.Каждая часть представляет собой 1 предмет, для создания целого которого требуется 4 штуки. (Валовой 2012)

Чтобы переименовать эту фракцию в другие термины, мы можем ввести термин «подразделение». Как видно на рисунке 8, горизонтальная линия показывает, что устройство было разделено пополам, таким образом, каждая четвертая часть была разделена на две равные части. Теперь ученики смогут увидеть, что блок разделен на 8 равных частей. Они восьмые от целого. Наконец, я назову учеников, которые обращают внимание на части 1/4, и приведу их к осознанию того, что мы можем переименовать их в восьмых.Затем визуально подтверждается, что 1/4 — это то же самое, что 2/8. Хотя эта иллюстрация является базовой, она важна для обсуждения переименования дробей как задачи выражения одной и той же величины разными терминами.

Рисунок 8

Когда студенты полностью освоятся с приведенным выше примером моделей деления области, я помогу своим ученикам увидеть, как работает переименование дробей на числовой прямой. См. Рис. 9. Эта модель площади демонстрирует ту же логику, что и на рис. 8, начиная с начальной единицы, разделенной на трети, а затем разделяя каждую часть на четверти, создавая двенадцатые.Опять же, важно подчеркнуть, что все трети четвертей равны. Итак, поскольку 12 из них составляют целое (единичный интервал), они равны двенадцатым. Также можно сделать вывод, что:

Это представление на рисунке 9 — это то, с которым учащиеся не имеют большого опыта, но это важный шаг на пути к тому, чтобы помочь им увидеть эквивалентные дроби на числовой прямой. Когда мы делили с помощью параллельных линий, мы, по сути, делили единицу по длине, что является той же задачей, что и деление единичного интервала на линии.Затем мы можем сжать эти представления площади до числовой линии, сохранив связь переименования доли площади и переименования доли длины в строке.

Рисунок 9

После того, как мы установили идею подразделения для переименования дробей в различные термины и тщательно перенесли эту идею на линию, мы можем применить эту логику к числовой прямой. Вместо того, чтобы разделять области на числовой прямой, нам поручено разделить каждый интервал длины.См. Рисунок 10. Здесь 1/3 можно разделить на каждые 2 равные части, чтобы получить интервалы длиной 1/6. Если вместо этого мы разделим интервал длиной 1/3 на 3 равные части, мы получим отрезки длиной 1/9 и так далее.

Рисунок 10

Как и в случае с моделями площади, числовая линия дает нам удобную иллюстрацию дробей с разными названиями, которые представляют одно и то же количество. Обладая достаточным опытом переименования дробей таким образом, ученики заметят, что, разделив любой заданный интервал на любое число, d, , вы умножаете исходное количество интервалов на это число, d, , получая новый знаменатель.Выделив эквивалентные дроби, мы можем обобщить следующее утверждение, которое мы назовем «Принцип переименования»:

Для любой дроби a / b = ad / bd, для любого целого числа d.

Нахождение общих знаменателей

После того, как студенты получат твердое представление о том, как видеть и создавать эквивалентные дроби на числовой прямой, мы займемся вопросом о дробях с разными знаменателями, чтобы в конечном итоге мы могли складывать и вычитать их. Я начну с создания потребности в общем знаменателе, представив студентам модель числовой линии, такую как рисунок 11a.Здесь мы видим как 1/3, так и 1/2 на одной линии, создающие интервалы разной длины. Учащиеся должны видеть однородность и симметрию интервалов, и в ходе разговора с числами им будет предложено попытаться найти длину этих неопределенных интервалов. После того, как они решат эту проблему, мы в конечном итоге можем прийти к выводу, что для определения этих расстояний нам нужно найти общие знаменатели путем переименования.

Рисунок 11

Было бы полезно обратиться к этой концепции с помощью двух числовых линий с разными дробями, представленными на каждой.См. Рисунок 11b. Разделив интервалы 1/3 на знаменатель 1/2, мы получим общий знаменатель 6. Здесь мы видим, что 3/6 идеально совпадает с 1/2, поэтому 1/2 может быть переименован в 3/6. Это также можно сделать, разделив интервалы 1/2 на 3. Поскольку данная дробь может быть переименована, чтобы иметь знаменатель, равный любому, кратному исходному знаменателю, две дроби могут быть переименованы, чтобы иметь общий знаменатель. В частности, общий знаменатель может быть произведением двух исходных знаменателей.Принцип определяется более кратко:

Для любых 2 дробей a / b + b / d обе могут быть переименованы в дроби с тем же знаменателем. В частности: a / b = ad / bd и c / d = bc / bd .

Чтобы учащиеся лучше познакомились с этой идеей, они будут выполнять несколько задач, где им нужно будет найти общие знаменатели для дробей с разными числами.

Главное здесь то, что при переименовании дробей с разными знаменателями всегда будет общий знаменатель.Это отличается от более типичного подхода к общему знаменателю, не заставляя студентов искать наименьший общий знаменатель. По моему опыту, студенты часто цепляются за идею, что нужно найти наименьший общий знаменатель, чтобы что-то сделать с разными знаменателями. Эти усилия отвлекают от основной идеи — простого поиска общего знаменателя. Наименьший общий знаменатель — это уточнение, которое может быть достигнуто, когда учащиеся полностью поймут концепцию и преимущества переименования дробей в одинаковых терминах.

Я ожидаю, что следующий простой шаг — попросить студентов складывать и вычитать дроби с разными знаменателями. Это только потому, что мы так тщательно продвинулись через прогресс понимания, который заставляет студентов осознать процесс поиска общих знаменателей, всегда думая о количестве в терминах числовой линии. Я надеюсь, что студенты в конечном итоге будут использовать концепции и навыки, рассматриваемые на протяжении всего модуля, для выполнения этой задачи.Сначала им нужно будет найти общий знаменатель, переименовав каждую дробь, разделив интервалы на числовой строке, чтобы они могли правильно разместить обе длины вектора на одной числовой строке, а затем следовать уже известной процедуре сложения и вычитания дробей с одним и тем же знаменателем. . Хотя это утомительно, отчасти это нужно делать на числовой прямой, чтобы обосновать их концептуальное понимание этого процесса звуковым представлением, чтобы они могли лучше рассуждать о абстрактном вычислении дробей.Это должно помочь им понять, что это действительно тот же процесс, что и при сложении целых чисел. Разница только в символическом изображении.

Number Talks

Для этого и предыдущего блока весь контент будет доставлен в виде некоторой разновидности разговора с цифрами. Это рутина, которая длится от пяти до десяти минут в начале урока. Стратегия следует базовому формату: представление подсказки, позволяющее учащимся подумать, поиск решений и, наконец, обсуждение обоснования предлагаемых решений и вынесение всем классом выводов.Следует отметить, что разговоры с числами обычно проводятся с подсказками, которые охватывают общие вычислительные и математические стратегии. Подсказки, приведенные в этом модуле, будут иметь более узкую направленность на представление и интерпретацию сложения и вычитания рациональных чисел через числовую линию. Эти беседы будут служить цели выявления различных способов осмысления числовых концепций, потребуют от студентов обоснования своих идей, используя здравые рассуждения, и помогут друг другу достичь лучшего понимания посредством дискурса под руководством студентов.Эти подсказки будут различаться по своей доставке с точки зрения того, что задают и что спрашивают, но их цель — понять смысл различных представлений о сложении и вычитании рациональных чисел.

Представление подсказок

На протяжении всего раздела я буду показывать своим студентам множество различных подсказок, чтобы вызвать обсуждение желаемого содержания для этого конкретного дня. Большинство подсказок будет проецироваться в передней части комнаты. Студенты ответят на бумаге, где будут пустые числовые строки, чтобы студенты могли ответить на подсказку и объяснить свое мнение.Для определенного количества выступлений я предоставлю параллельные практические подсказки ниже, чтобы студенты могли практиковать и усвоить данную концепцию после обсуждения в группе. Важно предоставить учащимся стандартные числовые линии, чтобы интервалы были точными. Когда учащиеся ознакомятся с характерными структурами числовых линий, я затем посоветую им создать свои собственные числовые линии, чтобы отвечать на подсказки. Их письменные работы будут храниться в портфолио студентов, чтобы студенты могли отслеживать свое обучение и возвращаться к заметкам по всему модулю.

Я ожидаю, что весь блок продлится от 5 до 6 недель в зависимости от того, насколько быстро студенты продемонстрируют владение концепциями. В общей сложности этот блок и предварительный блок должны длиться от 10 до 12 недель. По завершении двух единиц мы рассмотрим более сложные концепции чисел в числовой строке, включая умножение, деление и иррациональные числа.

Подсказки будут отличаться включением или исключением определенной информации в числовой строке и просьбой учащихся выполнить различные задания.Полный набор подсказок и других материалов урока, которые будут использоваться для этого раздела, см. В Приложении 2 для посещения веб-сайта. Ниже приводится описание типов подсказок, которые будут даваться для обучения различным концепциям.

Рисунок 13

Рисунок 13 предлагает студентам что-то «сделать» с векторами, чтобы представить сумму двух величин. Первые ученики должны определить, что представляет собой каждый вектор, используя числовую линию для измерения, уделяя внимание ориентации вектора.Вопрос намеренно расплывчатый, чтобы дать студентам возможность обсудить различные способы восприятия суммы как положительной 1.

Рисунок 14

Рис. 14 является расширением подсказки на рис. 13. Здесь ученики попытаются самостоятельно нарисовать векторы на числовой прямой. Здесь студенты обсудят, как они представляли каждую часть выражения. Это задание требует, чтобы учащиеся взяли каждую часть выражения и визуализировали то, что подразумевается, привнося абстракцию в контекст числовой линии.

Рисунок 15

Рисунок 15 требует от учащихся выполнить обратное задание, представленное на рисунке 14. Важно отметить, что вопрос требует более одного ответа, задавая вопрос: Что это может означать? Учащиеся должны увидеть, что в представлении может отображаться 4 + 3 или 4 — (-3). Этот тип подсказки также следует использовать, чтобы подчеркнуть связь между сложением и вычитанием отрицательного.

Рисунок 16

Рисунок 17

Рисунки 16 и 17 дают студентам задание поэкспериментировать с использованием различных комбинаций чисел для сложения и вычитания.Ценность этой подсказки заключается в том, что она позволяет найти несколько решений и дает учащимся возможность увидеть влияние добавления и вычитания отрицательных или положительных сторон. С помощью множества подсказок этих и подобных типов я буду подталкивать студентов к обобщению и нахождению общего количества возможностей для каждой ситуации.

Рисунок 18

Рисунок 19

На рисунках 18 и 19 учащимся предлагается разобраться с различными концепциями дробей.Чтобы ответить на каждый вопрос, ученики должны будут манипулировать данной числовой линией, добавляя новые отметки интервалов. Чтобы ответить на этот запрос, они должны обратиться к равному подразделению отряда, чтобы определить расстояние.

Рисунок 20

Рисунок 21

Рисунки 20 и 21 заставляют учащихся визуализировать работу с рациональными числами. Рисунок 20 побуждает студентов завершить более формальный процесс переименования дробей, чтобы найти общий знаменатель перед сложением.В то время как рисунок 21 требует от учащихся оценить и использовать свои знания о дробях на числовой прямой, чтобы найти сумму. На рисунке 21 важно побудить студентов объяснить, почему они выбрали свое размещение на числовой строке.

Оценка

Чтобы оценить, насколько хорошо мои ученики усваивают концепции, рассматриваемые в модуле, я проведу предварительный тест. Это будет письменный тест, который будет включать в себя выборку подсказок, которые я буду использовать на протяжении всего модуля. Они потребуют от студентов предоставить письменные ответы.Данные предварительного тестирования позволят мне определить наиболее распространенные заблуждения и диапазон уровней способностей. Эта информация будет важна при планировании дискуссионных групп и количества времени, которое я должен запланировать потратить на каждую концепцию. Такая же оценка будет проводиться в конце раздела, чтобы определить, какие концепции необходимо пересмотреть, чтобы достичь мастерства. Еще раз важно отметить, что прежде чем переходить к этому разделу, необходимо достичь достаточного уровня владения концепциями, рассмотренными в предыдущем разделе.

Чтобы повысить ставки, привлечь студентов к ответственности и оценить их понимание на протяжении всего модуля, я буду проводить еженедельные проверки концепций в качестве формирующей оценки. Это будут короткие проверки, которые потребуют от учащихся продемонстрировать свое понимание концепций недели. Как правило, они просят студентов изобразить предложение сложения или вычитания на числовой прямой или сгенерировать выражение для данной модели числовой линии. Это задание будет сопровождаться подсказкой, требующей от учащихся обоснования своего ответа.По моему опыту, эти проверки концепции необходимы, чтобы убедить студентов в важности ежедневного полноценного участия. Когда студенты знают, что их попросят продемонстрировать свои знания в конце недели, я обнаружил, что они более мотивированы, чтобы предложить свои идеи и попытаться разобраться в том, что говорят другие студенты. Это также важная возможность для студентов отслеживать свои успехи в изучении концепций.

Контекст решения проблем

Сложение и вычитание чисел со знаком — одна из основных задач математической программы средней школы.Чтобы дополнить их работу числовой линией, я также буду предлагать студентам задачи по решению задач, где они могут использовать числовую линию для их решения. Эти проблемы дадут им возможность иметь дело с сложением и вычитанием целых чисел в контекстах, поддерживающих их понимание. Для того, чтобы контексты проблемы были благоприятными, они должны (1) иметь значимое происхождение, (2) включать два различных объекта или движения, которые действуют как положительные и отрицательные целые числа, и (3) приводить к чистой стоимости. Некоторые хорошие контексты включают высоту по сравнению с уровнем моря, движение вперед и назад по городской улице, подъем и падение баланса банковского счета и движение вверх и вниз по футбольному полю.Чтобы подробно описать, как контекст решения проблемы может поддерживать разработку концепции сложения и вычитания целых чисел, я опишу действие, к которому я вернусь на протяжении всего модуля: игра на воздушном шаре.

Игра на воздушном шаре

Одно из полезных упражнений по решению проблем, которое я буду включать в раздел, — это игра в воздушный шар (NCTM 2016). Сюжет игры требует, чтобы ученики представили корзину с прикрепленными к ней воздушными шарами, парящими в воздухе на начальной высоте.Студенты будут понимать эту начальную высоту как начало координат. Чтобы визуализировать это, ученики будут иметь вырезанные из бумаги воздушные шары рядом с вертикальной числовой линией. Игра начинается, как только ученики начинают рисовать карточки, в которых им предлагается добавить или убрать гелиевые шары и мешки с песком. Хотя это и не является научно точным, будет сделано предположение, что на каждый добавленный гелиевый шар корзина поднимется на одну единицу, а при удалении — на одну единицу. Предполагается, что мешки с песком, если они добавлены, вызовут падение высоты корзины на одну единицу, а если их убрать, то корзина поднимется на одну единицу.Партнеры по очереди вытягивают свои карты, на которых написано «плюс» или «минус» заданное количество воздушных шаров или мешков с песком. Затем учащихся заставляют рассуждать о том, что действие в конечном итоге сделает с их корзиной, с точки зрения вертикальной числовой линии. Ценность в этом контексте состоит в том, что он предоставляет конкретный объект для связи с положительными и отрицательными числами. Учащиеся могут видеть положительные числа как воздушные шары, которые вызывают увеличение значения, а отрицательные числа как мешки с песком, которые при добавлении вызывают уменьшение стоимости.Студенты также получат возможность легко прийти к выводу, что если убрать мешки с песком, корзина поднимется. Это поддерживает абстрактную концепцию, согласно которой удаление отрицательных чисел приводит к положительному перемещению числовой прямой.

Следует также отметить, что числовая линия, представленная вертикально, помогает учащимся понять, что значение увеличивается и уменьшается. Обычной причиной путаницы для моих учеников является тот факт, что числа на горизонтальной числовой прямой, по-видимому, увеличиваются вправо от начала координат и влево.По моему опыту, это сбивает студентов с толку в понимании того, что означает «вверх» и «вниз» в определенных задачах со словами. Вертикальная числовая линия лучше поддерживает их понимание «вверх» и «вниз» и предоставит им более простую визуализацию сложения и вычитания целых чисел, которые они затем могут преобразовать в горизонтальную числовую линию.

Этот модуль был написан в соответствии с Общими основными государственными стандартами, принятыми государственными школами Чикаго. В частности, эта единица будет охватывать набор стандартов в рамках ряда систем счисления.

CCSS.MATH.CONTENT.6.NS.C.6

Под рациональным числом понимается точка на числовой прямой. Расширьте числовые линейные диаграммы и оси координат, знакомые по предыдущим классам, для представления точек на прямой и на плоскости с отрицательными числовыми координатами.

CCSS.MATH.CONTENT.6.NS.C.6.A

Распознавать противоположные знаки чисел как указывающие на положения по разные стороны от 0 на числовой прямой; признать, что противоположностью числа является само число, например.g., — (- 3) = 3, и что 0 является своей собственной противоположностью.

CCSS.MATH.CONTENT.6.NS.C.6.C

Найдите и расположите целые числа и другие рациональные числа на горизонтальной или вертикальной числовой линейной диаграмме; найти и расположить пары целых и других рациональных чисел на координатной плоскости.

CCSS.MATH.CONTENT.7.NS.A.1

Применяйте и расширяйте предыдущие представления о сложении и вычитании для сложения и вычитания рациональных чисел; представляют собой сложение и вычитание на горизонтальной или вертикальной числовой линейной диаграмме.

CCSS.MATH.CONTENT.8.NS.A.2

Используйте рациональные приближения иррациональных чисел, чтобы сравнить размер иррациональных чисел, расположить их приблизительно на числовой линейной диаграмме и оценить значение выражений (например, π ²).

Для получения копий всех материалов модуля, которые будут использоваться в этом модуле, посетите веб-сайт www.mrbingea.blogspot.com. На этом веб-сайте есть страница, на которой я буду размещать в моем магазине обновленные подсказки, заметки о том, как представлять определенные числовые выступления, материалы для студентов, примеры студенческих работ и оценки, используемые в рамках модуля.

Безук, Н., и Крамер, К. (1989). Обучение дробям: что, когда и как? В P. Trafton (Ed.), Ежегодник Национального совета учителей математики 1989: Новые направления в математике в начальной школе (стр. 156-167). Рестон, Вирджиния: Национальный совет учителей математики.

Хоу, Роджер и Соломон Фридберг. «Правило знаков в арифметике». (по состоянию на 18 июля 2016 г.).

Хоу, Роджер и Соломон Фридберг.«Трусы на числовой линии». (по состоянию на 18 июля 2016 г.).

Хамфрис, Кэти и Рут Э. Паркер. Делая разговор о числах значимым: развитие математической практики и углубление понимания, 4–10 классы. Издательство Stenhouse, 2015. Печать.

«Переворачивание для целых чисел». NCTM Illuminations. Национальный совет учителей математики, 2016. Интернет. 18 июля 2016 г.

Брутто, травы. «Прилагательное Существительное Математика: Математика как второй язык». Любовная математика .Н.П., 2012. Интернет. Июль-авг. 2016.

У, Хун-Си. «Обучение дробям в соответствии с общими основными стандартами». (2014): п. стр. Беркли . Калифорнийский университет в Беркли, 8 февраля 2014 г. Web. 18 июля 2016 г.

Математика для седьмого класса — сложение и вычитание рациональных чисел

Рациональное число — это любое число, которое может быть выражено как частное или дробь p / q двух целых чисел, числителя p и ненулевого знаменателя q. Прежде чем мы добавим или вычтем, рациональные числа должны иметь одинаковое нижнее число (называемое общим знаменателем).Обучающие видео и приложения дадут вам примеры единиц измерения и помогут узнать о рациональных числах.

Приложения, примеры вопросов, видео и рабочие листы, перечисленные ниже, помогут вам научиться складывать и вычитать рациональные числа

Примеры вопросов по сложению и вычитанию рациональных чисел

Рабочие листы сложения и вычитания рациональных чисел

Образовательные приложения, связанные с номерами Rational

Обучающие видео по рациональным числам

Связанные темы

Как умножать рациональные числа?

Чтобы разделить рациональные числа, вы превращаете задачу деления в задачу умножения, переворачивая второе рациональное число.Затем вы перемножаете вершины и основания вместе, чтобы получить ответ. Если вы можете упростить задачу до умножения, вы можете пойти дальше и сделать ее проще.

Как складывать или вычитать проценты?

Если в вашем калькуляторе нет клавиши процента, и вы хотите добавить процент к числу, умножьте это число на 1 плюс процентную долю. Например, 25000 + 9% = 25000 x 1,09 = 27250. Чтобы вычесть 9 процентов, умножьте число на 1 минус процентную долю.Пример: 25000 — 9% = 25000 x 0,91 = 22750.

Каково определение рационального числа?

Рациональное число — это число, которое можно записать как отношение. Это означает, что его можно записать в виде дроби, в которой числитель (число вверху) и знаменатель (число внизу) являются целыми числами. Число 8 — рациональное число, потому что его можно записать как дробь 8/1.

Что такое рациональные и иррациональные числа?

Все нерациональные числа считаются иррациональными.Иррациональное число можно записать в виде десятичной дроби, но не в виде дроби. Иррациональное число имеет бесконечные неповторяющиеся цифры справа от десятичной точки. Вот несколько иррациональных чисел: π = 3,141592…

онлайн-тест по математике для 7-го класса | Math Practice

Используйте случайную выборку, чтобы делать выводы о совокупности.

MGSE7.SP.1 Поймите, что статистику можно использовать для получения информации о совокупности, исследуя ее выборку; обобщения о совокупности из выборки действительны только в том случае, если выборка является репрезентативной для этой совокупности.Поймите, что случайная выборка имеет тенденцию давать репрезентативные выборки и поддерживать достоверные выводы.

MGSE7.SP.2 Используйте данные из случайной выборки, чтобы сделать выводы о популяции с неизвестной интересующей характеристикой. Создайте несколько выборок (или смоделированных выборок) одинакового размера, чтобы измерить вариации оценок или прогнозов.

Сделайте неформальные сравнительные выводы о двух популяциях.

MGSE7.SP.3 Неформально оцените степень визуального перекрытия двух распределений числовых данных с одинаковой вариабельностью, измеряя разницу между медианами, выражая ее как кратное межквартильному размаху.

MGSE7.SP.4 Используйте меры центра и меры изменчивости для числовых данных из случайных выборок, чтобы сделать неформальные сравнительные выводы о двух популяциях.

Исследуйте случайные процессы, а также разрабатывайте, используйте и оценивайте вероятностные модели.

MGSE7.SP.5 Поймите, что вероятность случайного события — это число от 0 до 1, которое выражает вероятность возникновения события. Большие числа указывают на большую вероятность.Вероятность, близкая к 0, указывает на маловероятное событие, вероятность около ½ указывает на событие, которое не является ни маловероятным, ни вероятным, а вероятность, близкая к 1, указывает на вероятное событие.

MGSE7.SP.6 Оцените вероятность случайного события, собрав данные о случайном процессе, который его порождает, и наблюдая его относительную частоту в долгосрочной перспективе. Предскажите приблизительную относительную частоту с учетом вероятности.

Например, при прокрутке числового куба 600 раз предположите, что число 3 или 6 будет брошено примерно 200 раз, но, вероятно, не точно 200 раз.

MGSE7.SP.7 Разработайте вероятностную модель и используйте ее для определения вероятностей событий. Сравните экспериментальные и теоретические вероятности событий. Если вероятности не близки, объясните возможные источники расхождения.

MGSE7.SP.7a Разработайте единую вероятностную модель, назначив равную вероятность всем исходам, и используйте модель для определения вероятностей событий

MGSE7.SP.7b Разработайте вероятностную модель (которая может быть неоднородной. ), наблюдая за частотами в данных, полученных в результате случайного процесса.

Например, найдите приблизительную вероятность того, что вращающийся пенни упадет орлом вверх или брошенный бумажный стаканчик упадет открытым концом вниз. Являются ли результаты для вращающегося пенни одинаково вероятными на основе наблюдаемых частот?

MGSE7.SP.8 Найдите вероятности сложных событий, используя организованные списки, таблицы, древовидные диаграммы и моделирование.

MGSE7.SP.8a Поймите, что, как и в случае с простыми событиями, вероятность составного события — это доля результатов в пространстве выборки, для которых возникает составное событие.

MGSE7.SP.8b Представьте образцы пространств для составных событий, используя такие методы, как организованные списки, таблицы и древовидные диаграммы. Для события, описываемого повседневным языком (, например, «катящиеся двойные шестерки» ), идентифицируйте результаты в пространстве выборки, которые составляют событие.

MGSE7.SP.8c Объясните способы настройки моделирования и использования моделирования для генерации частот для составных событий.

Например, если 40% доноров имеют кровь типа A, создайте моделирование, чтобы предсказать вероятность того, что потребуется по крайней мере 4 донора, чтобы найти одного с кровью типа A.

Сложение и вычитание рациональных чисел Станции

Описание

Этот набор из 10 математических станций сосредоточен на стандартах 5-го класса для сложения и вычитания рациональных чисел. В 10 различных центрах, где можно практиковаться, ваши ученики мгновенно станут экспертами, играя в эти партнерские математические игры.
Ознакомьтесь с комплектом подготовки к экзамену по математике для 5-го класса.

Здесь вы найдете комплекты для подготовки к экзаменам для третьего и четвертого классов!
Комплект для подготовки к экзамену по математике для 4-го класса
Комплект для подготовки к экзамену по математике для 3-го класса

Этот подготовительный пакет к тесту на сложение и вычитание рациональных чисел для пятого класса представляет собой простой продукт, предназначенный для закрепления знаний учащихся о сложении и вычитании целых, десятичных и дробных чисел для стандартизированного тестирования.Все десять включенных действий были созданы полностью в черно-белом цвете, чтобы сэкономить на цветных чернилах и упростить использование копировального аппарата.

Я использую эти упражнения в классе и в своей группе тестирования после школы.

+++++++++++++++++++++++++++++++++++++++++++++++++ +++
Он был создан с учетом следующих стандартов:
TEKS
5,3k плавное сложение и вычитание положительных рациональных чисел

COMMON CORE
CCSS.MATH.CONTENT.5.NBT.B.7 Сложить, вычесть, умножить и разделить десятичные дроби до сотых, используя конкретные модели или чертежи и стратегии, основанные на значении места, свойствах операций и / или связь между сложением и вычитанием; свяжите стратегию с письменным методом и объясните используемую аргументацию.

++++++++++++++++++++++++++++++++++++++++++++++++ +++
Все включенные упражнения предназначены для заполнения любых пробелов, которые студенты могут понять, как складывать или вычитать рациональные числа.

Каждое задание можно выполнить в различных настройках, чтобы удовлетворить потребности каждого учащегося в вашем классе.
— Независимая оценка
— Партнерская практика
— Математика в малых группах

++++++++++++++++++++++++++++++++++++++++++++++++ +++
Также в этот продукт входит:
При необходимости ключи ответов
Листы записей для привлечения учащихся к ответственности
Словарь содержания для вашей стены слов
Контрольные вопросы

Другие ресурсы Big Ten для 5-го класса:
Сравнение десятичных дробей
Упрощение уравнений
Умножение десятичных дробей
Деление десятичных дробей
Сложение и вычитание рациональных чисел
Деление с использованием единичных дробей
Многоступенчатое решение задач с помощью целых чисел
Построение числовых шаблонов с использованием периметра
, и том
Классификация 2D-фигур
Графики упорядоченных пар
Решение проблем с данными

++++++++++++++++++++++++++++++++++++++++++++++++ ++++
Для получения дополнительной информации о подготовке к экзаменам ознакомьтесь с моей серией Test Smash:
Fourth Grade Test Smash
Пятый класс Test Smash
Third Grade Test Smash

Только зарегистрированные клиенты, которые приобрели этот продукт, могут оставить отзыв.

MAFS.7.NS.1.1 — применять и расширять предыдущие представления о сложении и вычитании для сложения и вычитания рациональных чисел; представляют собой сложение и вычитание на горизонтальной или вертикальной числовой линейной диаграмме. Опишите ситуации, в которых противоположные величины объединяются, чтобы получить 0. Например, атом водорода имеет нулевой заряд, потому что две его составляющие заряжены противоположно. Под p + q понимается число, расположенное на расстоянии | q

MAFS.7.NS.1.1 — Применяет и расширяет предыдущие представления о сложении и вычитании для сложения и вычитания рациональных чисел; представляют собой сложение и вычитание на горизонтальной или вертикальной числовой линейной диаграмме.Опишите ситуации, в которых противоположные величины объединяются, чтобы получить 0. Например, атом водорода имеет нулевой заряд, потому что его две составляющие заряжены противоположно. Под p + q понимается число, расположенное на расстоянии | q | от p, в положительном или отрицательном направлении, в зависимости от того, является ли q положительным или отрицательным. Докажите, что сумма числа и его противоположности равна 0 (аддитивно противоположны). Интерпретируйте суммы рациональных чисел, описывая контексты реального мира. Поймите вычитание рациональных чисел как добавление обратного аддитивного числа, p q = p + (q).Покажите, что расстояние между двумя рациональными числами на числовой прямой является абсолютной величиной их разницы, и примените этот принцип в контексте реального мира. Примените свойства операций как стратегии для сложения и вычитания рациональных чисел.

Веб-сайт несовместим с используемой вами версией браузера. Не все функции могут быть доступны. Пожалуйста, обновите ваш браузер до последней версии.

Опишите ситуации, в которых противоположные количества объединяются, чтобы получить 0. Например, атом водорода имеет нулевой заряд, потому что два его компонента заряжены противоположно.
Под p + q понимается число, расположенное на расстоянии | q | от p, в положительном или отрицательном направлении, в зависимости от того, является ли q положительным или отрицательным. Докажите, что сумма числа и его противоположности равна 0 (аддитивно противоположны). Интерпретируйте суммы рациональных чисел, описывая контексты реального мира.
Под вычитанием рациональных чисел понимается добавление обратного аддитивного числа, p — q = p + (–q).Покажите, что расстояние между двумя рациональными числами на числовой прямой является абсолютной величиной их разницы, и примените этот принцип в контексте реального мира.
Применяйте свойства операций как стратегии для сложения и вычитания рациональных чисел.

Разъяснения

Ожидаемая беглость речи или примеры наиболее эффективных стандартов

Сложение, вычитание, умножение и деление рациональных чисел — это кульминация числовой работы с четырьмя основными операциями.Система счисления продолжит развиваться в 8 классе, расширяясь, чтобы стать действительными числами за счет введения иррациональных чисел, и будет развиваться дальше в старшей школе, расширяясь, чтобы стать комплексными числами с введением мнимых чисел. Поскольку не существует конкретных стандартов для арифметики рациональных чисел в более поздних классах и поскольку очень много другой работы в 7 классе зависит от арифметики рациональных чисел, свободное владение арифметикой рациональных чисел должно быть целью в 7 классе.

Общая информация

Предметная область: Математика

Класс: 7

Домен-Поддомен: Система счисления

Кластер: Уровень 2: Базовое применение навыков и концепций

Дата принятия или пересмотра: 14.02

Дата последней оценки: 14.02

Статус: Утверждено Государственным советом

Оценено: Да

Технические характеристики объекта испытаний

Пределы оценки:
Н / Д
Калькулятор:
Нейтраль
Контекст:
Допустимо

Образцы тестовых заданий (7)

Тестовый элемент №: Образец образца 4
Вопрос:
Показано выражение.
Кендрик использует числовые линии, чтобы найти значение выражения. Его первые два шага показаны.
A. Используйте инструмент «Добавить стрелку», чтобы показать последние два шага.
B. Выберите значение выражения.
Сложность: НЕТ
Тип: GRID: графический элемент ответа

Тестовый элемент №: Образец образца 6
Вопрос:
Сумма a и b составляет c .В числовой строке показаны a и b .
Какие утверждения о c верны?
Сложность: НЕТ
Тип: MS: Multiselect

Связанные точки доступа

Альтернативная версия этого теста для учащихся со значительными когнитивными нарушениями.

Связанные ресурсы

Проверенные ресурсы преподаватели могут использовать для обучения концепциям и навыкам, связанным с этим тестом.

Уроки STEM — Образцовая деятельность по выявлению

Беги, если твоя жизнь тебе дорога!:

На основе ориентированного на учащихся сценария, поощряющего здоровый образ жизни, учащиеся внимательно и внимательно прочитают статью, призывающую к активному и здоровому образу жизни.Во время урока студенты будут анализировать данные из Consumer Reports, сравнивая и сравнивая беговые дорожки и эллиптические тренажеры. Используя собранную информацию, студенты будут собирать данные и убеждать администраторов покупать оборудование, которое будет соответствовать предусмотренному бюджету и поместиться в данном пространстве.

Формирующие оценки MFAS

Изучение обратного аддитивного:

Учащимся предлагается описать пример аддитивного обратного и продемонстрировать концепцию на числовой прямой.

Рациональное управление водными ресурсами:

Учащимся предлагается комбинировать рациональные числа, включая дроби и десятичные дроби, и использовать свойства операций для упрощения вычислений.

Оригинальные уроки по математике для учащихся — 6–8 классы

Удивительные приключения:

Узнайте, как объяснить значение аддитивной инверсии, определить аддитивную инверсию данного рационального числа и обосновать свой ответ числовой прямой в этом оригинальном руководстве.

Ресурсы для учащихся

Проверенные ресурсы учащиеся могут использовать для изучения концепций и навыков, используемых в этом тесте.

Оригинальное учебное пособие для студентов

Удивительные приключения:

Тип: Оригинальное учебное пособие для учащихся

Обучающая игра

Игра с целыми числами:

В этой интерактивной игре есть 4 категории: сложение целых чисел, вычитание целых чисел, умножение целых чисел и деление целых чисел.Студенты могут играть индивидуально или в команде.

Тип: обучающая игра

Образовательное программное обеспечение / инструмент

Арифметическая викторина:

В этом упражнении учащиеся решают арифметические задачи, включающие целые числа, целые числа, сложение, вычитание, умножение и деление.Это упражнение позволяет учащимся отслеживать свой прогресс в обучении арифметике целых и целых чисел. Это упражнение включает в себя дополнительные материалы, в том числе справочную информацию по затронутым темам, описание того, как использовать приложение, и вопросы исследования для использования с java-апплетом.

Тип: Образовательное программное обеспечение / инструмент

Задачи по решению проблем

Расстояния на числовой прямой 2:

Цель этого задания состоит в том, чтобы укрепить понимание учащимися рациональных чисел как точек на числовой прямой и предоставить им наглядный способ понимания того, что сумма числа и его аддитивная обратная величина (обычно называемая его «противоположностью») равно нулю.

Тип: Задача по решению проблем

Сравнение точек замерзания:

В этом задании учащиеся отвечают на вопрос о разнице между двумя отрицательными числами.

Тип: Задача по решению проблем

Операции на числовой линии:

Цель этого задания — помочь учащимся укрепить понимание чисел со знаком как точек на числовой прямой и понять геометрическую интерпретацию сложения и вычитания чисел со знаком.В Стандартах Флориды есть тонкое различие между дробью и рациональным числом. Дроби всегда положительны, и если рассматривать символ ab как дробь, можно интерпретировать его как части равного размера, где b частей составляют одно целое.

Тип: Задача по решению проблем

Учебники

Добавление отрицательных чисел:

Это видео демонстрирует использование числовой прямой и абсолютного значения для сложения отрицательных чисел.

Тип: Учебное пособие

Добавление целых чисел:

Студенты смогут увидеть примеры сложения целых чисел во время просмотра короткого видео и попрактиковаться в сложении целых чисел с помощью онлайн-викторины.

Тип: Учебное пособие

Ресурсы для родителей

Проверенные ресурсы, которые могут использовать воспитатели, чтобы помочь учащимся изучить концепции и навыки, используемые в этом тесте.

Задачи по решению проблем

Расстояния на числовой прямой 2:

Тип: Задача по решению проблем

Сравнение точек замерзания:

В этом задании учащиеся отвечают на вопрос о разнице между двумя отрицательными числами.

Тип: Задача по решению проблем

Операции на числовой линии:

Тип: Задача по решению проблем

Руководство

Добавление целых чисел:

Тип: Учебное пособие

Погрузка….

Сложение и вычитание рациональных выражений с непохожими знаменателями

При сложении или вычитании рациональных выражений с разными знаменателями необходимо выполнить несколько шагов.

Чтобы добавить или вычесть рациональные выражения с непохожими знаменателями, сначала найдите LCM знаменателя. НОК знаменателей доля или рациональные выражения также называют наименьший общий знаменатель , или ЖК-дисплей.

Запишите каждое выражение с помощью ЖК-дисплея. Убедитесь, что знаменателем каждого члена является ЖК-дисплей.

Сложите или вычтите числители.

При необходимости упростите.

Пример 1:

Добавлять 1 3 а + 1 4 б .

Поскольку знаменатели не совпадают, найдите ЖК-дисплей.

С 3 а а также 4 б не имеют общих факторов, LCM — это просто их продукт: 3 а ⋅ 4 б .

То есть ЖКД дробей 12 а б .

Перепишите дроби с помощью ЖК-дисплея.

( 1 3 а ⋅ 4 б 4 б ) + ( 1 4 б ⋅ 3 а 3 а ) знак равно 4 б 12 а б + 3 а 12 а б знак равно 3 а + 4 б 12 а б

Пример 2:

Добавлять 1 4 Икс 2 + 5 6 Икс y 2 .

Поскольку знаменатели не совпадают, найдите ЖК-дисплей.

Здесь GCF из 4 Икс 2 а также 6 Икс y 2 является 2 Икс . Итак, НОК — это произведение, разделенное на 2 Икс :

LCM знак равно 4 Икс 2 ⋅ 6 Икс y 2 2 Икс знак равно 2 ⋅ 2 ⋅ Икс ⋅ Икс ⋅ 6 Икс y 2 2 ⋅ Икс знак равно 12 Икс 2 y 2

Перепишите дроби с помощью ЖК-дисплея.

1 4 Икс 2 ⋅ 3 Икс y 2 3 Икс y 2 + 5 6 Икс y 2 ⋅ 2 Икс 2 Икс знак равно 3 Икс y 2 12 Икс 2 y 2 + 10 Икс 12 Икс 2 y 2 знак равно 3 Икс y 2 + 10 Икс 12 Икс 2 + y 2

Пример 3:

Вычесть 2 а — 3 а — 5 .

Поскольку знаменатели не совпадают, найдите ЖК-дисплей.

LCM а а также а — 5 является а ( а — 5 ) .

То есть ЖКД дробей а ( а — 5 ) .

Перепишите дробь с помощью ЖК-дисплея.

2 а — 3 а — 5 знак равно 2 ( а — 5 ) а ( а — 5 ) — 3 а а ( а — 5 )

Упростите числитель.

знак равно 2 а — 10 а ( а — 5 ) — 3 а а ( а — 5 )

Вычтите числители.

знак равно 2 а — 10 — 3 а а ( а — 5 )

Упрощать.

знак равно — а — 10 а ( а — 5 )

Пример 4:

Добавлять 5 c + 2 + 6 c — 3 .

Поскольку знаменатели не совпадают, найдите ЖК-дисплей.

LCM c + 2 а также c — 3 является ( c + 2 ) ( c — 3 ) .

То есть ЖКД дробей ( c + 2 ) ( c — 3 ) .

Перепишите дробь с помощью ЖК-дисплея.

5 c + 2 + 6 c — 3 знак равно 5 ( c — 3 ) ( c + 2 ) ( c — 3 ) + 6 ( c + 2 ) ( c + 2 ) ( c — 3 )

Упростите каждый числитель.

знак равно 5 c — 15 ( c + 2 ) ( c — 3 ) + 6 c + 12 ( c + 2 ) ( c — 3 )

Сложите числители.

знак равно 5 c — 15 + 6 c + 12 ( c + 2 ) ( c — 3 )

Упрощать.

знак равно 11 c — 3 ( c + 2 ) ( c — 3 )

«Сложение и вычитание рациональных чисел»

Контрольная работа № 7. Рациональные числа. Сравнение рациональных чисел. Математика 6 класс, с ответами

Вариант 1

Вариант 2

Самостоятельные и контрольные работы по математике для 6 класса -Ершов

МОУ «СОШ № 5 х. Восточный»

Информация о школе на сайте ГМУ

Информация о госзакупках СОШ №5

Информация о противодействии коррупции в СОШ №5

Зачисление в образовательное учреждение

Электронный классный журнал

Примите участие!

Уважаемые родители и учащиеся МОУ «СОШ №5 х.Восточный»!

Официальный интернет-портал правовой информации

Посетите официальный портал правовой информации!

Сложение и вычитание рациональных чисел

Задания для самостоятельного решения

Навигация по записям

Использование рациональных чисел

Примеры:

В целом …

Как сложить, вычесть, умножить и разделить

Умножение

Дивизион

Сложение и вычитание

Простейшая форма

Будьте осторожны со «смешанными дробями»

Сложение и вычитание рациональных чисел в числовой строке

Контекст

Описание конструкции агрегата

Почему числовая линия

Концепция №1: Сложение и вычитание в контексте измерения длины

Дополнение

Коммутационная собственность

Вычитание

Концепция № 2: Сложение и вычитание целых чисел как векторов

Сложение целых чисел

Вычитание целых чисел

Концепция № 3: Сложение и вычитание дробей с одинаковыми знаменателями

Концепция №4: Сложение и вычитание дробей с отличными знаменателями

Переименование дробей

Нахождение общих знаменателей

Number Talks

Представление подсказок

Оценка

Контекст решения проблем

Игра на воздушном шаре

Математика для седьмого класса — сложение и вычитание рациональных чисел

Приложения, примеры вопросов, видео и рабочие листы, перечисленные ниже, помогут вам научиться складывать и вычитать рациональные числа

Примеры вопросов по сложению и вычитанию рациональных чисел

Рабочие листы сложения и вычитания рациональных чисел

Образовательные приложения, связанные с номерами Rational

Обучающие видео по рациональным числам

Связанные темы

онлайн-тест по математике для 7-го класса | Math Practice

Сложение и вычитание рациональных чисел Станции

Описание

Веб-сайт несовместим с используемой вами версией браузера. Не все функции могут быть доступны. Пожалуйста, обновите ваш браузер до последней версии.

Разъяснения

Связанные точки доступа

Связанные ресурсы

Уроки STEM — Образцовая деятельность по выявлению

Формирующие оценки MFAS

Оригинальные уроки по математике для учащихся — 6–8 классы

Ресурсы для учащихся

Оригинальное учебное пособие для студентов

Обучающая игра

Образовательное программное обеспечение / инструмент

Задачи по решению проблем

Учебники

Ресурсы для родителей

Задачи по решению проблем

Руководство

Погрузка….

Сложение и вычитание рациональных выражений с непохожими знаменателями

Добавить комментарий Отменить ответ

Рубрики