ГДЗ по геометрии 8 класс дидактические материалы Мерзляк, Полонский Решебник
Вашему вниманию предлагается наш уникальный сайт, где вы найдете самое лучшее подспорье. Одно из направлений царицы наук не каждому по силам – особенно, если были упущены азы. Все дело в том, что именно основные базовые знания закладывают фундамент для того, чтобы последующие более трудные и объемные темы усваивались легче и быстрее. Но если невнимательно слушать педагога на уроках и пропускать это мимо ушей, потом будет только хуже. Однако даже из такой ситуации сможет выручить этот ресурс, о котором мы вам сейчас расскажем поподробнее.
Какую пользу может принести сборник по геометрии за 8 класс дидактические материалы Мерзляк
Объемные домашние работы по всем предметам порой мешают сосредоточиться на геометрической задаче, поэтому этой дисциплине надо уделять особое время. Гдз ответит на все вопросы, сформулированные в оригинальном печатном издании, а именно: сколько общих точек могут иметь две пересекающиеся прямые, в чем состоит кинематический способ получения кривой, как найти площадь четырехугольников, что называется высотой параллелограмма, какие фигуры называются изопериметрическими, что считается площадью круга и так далее. Также онлайн-пособие содержит следующие типы работ: обучающие (для формирования вычислительных навыков), проверочные (для контроля пройденного раздела) и проверь себя (здесь содержатся все тесты для того, чтобы убедиться в усвоении инф-ции). Помимо всего этого, подспорье поможет осознать суть вопроса и разобраться в любой теме, правильно подойти к решению домашнего задания, быть готовым к тому, чтобы выступить у доски или ответить с места с поднятой рукой и сэкономить средства и усилия при поиске необходимых данных, так как все уже есть здесь. Результат не заставит себя долго ждать – вскоре успеваемость ученика резко возрастет, и в дневнике и тетрадках все чаще будут красоваться пятерки. Пособие имеет ряд достоинств:
- онлайн-режим с доступом на любой ПК, IPhone, планшет;
- имеется мгновенный хорошо адаптированный поиск по номерам;
- классификация упражнений по уровню сложности;
- версия сайта обновляется, в соответствии с изменениями в оригинальном издании;
- расписанные комментарии от профессионалов.

Содержание учебно-методического комплекса по геометрии для 8 класса авторы: Мерзляк А. Г., Полонский В. Б., Рабинович Е. М.
Умк включает всю обязательную школьную программу указанного периода образования:
- Параллелограмм, его свойства и признаки.
- Применение подобия к доказательству теорем.
- Взаимное расположение прямой и окружности.
Основные определения и теоремы. Геометрия 8 класс — Студопедия
Основные определения и теоремы. Геометрия 8 класс — Студопедия- Многоугольник — это фигура, составленная из отрезков так, что смежные отрезки не лежат на одной прямой, а несмежные отрезки не имеют общих точек.
- Сумма длин всех сторон многоугольника называется
- Две вершины многоугольника, принадлежащие одной стороне, называются соседними.
- Отрезок, соединяющий любые две несоседние вершины, называется диагональю многоугольника.
- Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.
- Сумма углов выпуклого n-угольника равна (n–2)·180°.
- Четырёхугольник – это многоугольник у которого четыре вершины и четыре стороны.
- Две несмежные стороны четырёхугольника называются противоположными.
- Две вершины, не являющиеся соседними, называются противоположными.
- Сумма углов выпуклого четырехугольника равна 360°.
- Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.
- (Свойства параллелограмма ) В параллелограмме противоположные стороны равны и противоположные углы равны.
 Диагонали параллелограмма точкой пересечения делятся пополам.
Диагонали параллелограмма точкой пересечения делятся пополам. - (Признак параллелограмма) Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник — параллелограмм.
- (Признак параллелограмма) Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
- (Признак параллелограмма) Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
- Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Параллельные стороны трапеции называются ее основаниями, а две другие стороны — боковыми сторонами.
- Трапеция называется
- Трапеция называется прямоугольной, если один из её углов прямой.
- (Т. Фалеса) Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
- Прямоугольником называется параллелограмм, у которого все углы прямые.
- (Особое свойство прямоугольника) Диагонали прямоугольника равны.
- (Признак прямоугольника) Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник.
- Ромбом называется параллелограмм, у которого все стороны равны.
- (Особое свойство ромба) Диагонали ромба взаимно перпендикулярны и делят его углы пополам.
- Квадратом называется прямоугольник, у которого все стороны равны.
- (Основные свойства квадрата) Все углы квадрата прямые. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.
- Две точки А и А1 называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему.

- Две точки А и А1 называются симметричными относительно точкиО, если О – середина отрезка АА1.
- (Основные свойства площадей) Равные многоугольники имеют равные площади.
- Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
- Площадь квадрата равна квадрату его стороны ( S=a2).
- (Т.)Площадь прямоугольника равна произведению его смежных сторон (S=ab).
- (Т.)Площадь параллелограмма равна произведению его основания на высоту (S=ah).
- (Т.)Площадь треугольника равна половине произведения его основания на высоту (S= ah).
- Площадь прямоугольного треугольника равна половине произведения его катетов (S= ab).
- Если высоты двух треугольников равны, то их площади относятся как основания.
- Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
- Площадь трапеции равна произведению полусуммы её оснований на высоту ( S= ·h ).
- (Теорема Пифагора) В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. (с2=a2+b2)
- (Теорема, обратная теореме Пифагора) Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.
- Треугольник со сторонами 3, 4, 5 называют египетским треугольником.
- (Формула Герона) Площадь треугольника со сторонами a, b, c выражается формулой S= , где p = (a+b+c) — полупериметр треугольника.
- Говорят, что отрезки AB и CD пропорциональны отрезкам A1B1 и C1D1 , если = .
- Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.

- Число k, равное отношению сходственных сторон подобных треугольников, называется коэффициентом подобия.
- (Т.)Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
- (Т. Первый признак подобия треугольников) Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
- (Т. Второй признак подобия треугольников) Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
- (Т. Третий признак подобия треугольников) Если три стороны одного треугольника пропорциональны трём сторонам другого, то такие треугольники подобны.
- Средняя линия треугольника — это отрезок, соединяющий середины двух его сторон.
- (Т. о средней линии треугольника) Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
- Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.
- Высота прямоугольного треугольника, проведённая из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.
- Отрезок XY называется средним пропорциональным (или средним геометрическим) для отрезков АВ и CD, если XY=
- Средняя линия трапеции — это отрезок, соединяющий середины ее боковых сторон.
- (Т. о средней линии трапеции) Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме.
- Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
- Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

- Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.
- Тангенс угла равен отношению синуса к косинусу этого угла.
- sin2A+cos2A=1 – основное тригонометрическое тождество.
- Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки.
- Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют одну общую точку.
- Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек.
- Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.
- (Т. о свойстве касательной к окружности) Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.
- (Свойство отрезков касательных, проведённых из одной точки) Отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
- (Т. Признак касательной) Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной
- Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром окружности.
- Угол с вершиной в центре окружности называется её центральным углом.
- Центральный угол измеряется дугой, на которую он опирается.
- Сумма градусных мер двух дуг окружности с общими концами равна 360°.
- Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.
- (Т.) Вписанный угол измеряется половиной дуги, на которую он опирается.

- Вписанные углы, опирающиеся на одну и ту же дугу, равны.
- Вписанный угол, опирающийся на полуокружность – прямой.
- (Теорема о произведении отрезков пересекающихся хорд) Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
- Каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон. Обратно: каждая точка, лежащая внутри угла и равноудалённая от сторон угла, лежит на его биссектрисе.
- Биссектрисы треугольника пересекаются в одной точке.
- Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярная к нему.
- (Теорема о серединном перпендикуляре к отрезку) Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Обратно: каждая точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к нему.
- Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
- Высоты треугольника (или их продолжения) пересекаются в одной точке.
- Четыре точки: точка пересечения медиан, точка пересечения биссектрис, точка пересечения серединных перпендикуляров к сторонам и точка пересечения высот(или их продолжений) называются замечательными точками треугольника.
- Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник – описанным около этой окружности.
- (Теорема об окружности, вписанной в треугольник) В любой треугольник можно вписать окружность.
- В треугольник можно вписать только одну окружность.
- Не во всякий четырёхугольник можно вписать окружность.
- В любом описанном четырёхугольнике суммы противоположных сторон равны.
- Если суммы противоположных сторон выпуклого четырёхугольника равны то в него можно вписать окружность.

- Если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник – вписанным в эту окружность.
- (Теорема об окружности, описанной около треугольника) Около любого треугольника можно описать окружность.
- Около треугольника можно описать только одну окружность.
- Около четырёхугольника не всегда можно описать окружность.
- В любом вписанном четырёхугольнике сумма противоположных углов равна 180°.
- Если сумма противоположных углов четырёхугольника равна 180°, то около него можно описать окружность.
Геометрия. 8 класс. Электронные плакаты и тесты
Наглядно-дидактическое пособие предназначено для использования на уроках геометрии в 8 классе. Оно позволит повысить наглядность изучаемого материала, разнообразить формы учебной деятельности, вовлечь учеников в активный познавательный процесс.
Содержание программы разработано в соответствии с требованиями ФГОС основного общего образования и может использоваться с любой линейкой учебников, входящих в Федеральный перечень.
Пособие включает набор из 17 электронных плакатов, в наглядной и доступной форме представляющих темы:
- Многоугольник;
- Параллелограмм;
- Прямоугольник;
- Ромб и квадрат;
- Трапеция;
- Деление отрезка в данном отношении;
- Площади четырёхугольников;
- Площади треугольников;
- Теорема Пифагора;
- Подобие треугольников;
- Прямоугольный треугольник;
- Соотношения между сторонами и углами прямоугольного треугольника;
- Взаимное расположение прямой и окружности;
- Центральный и вписанный угол;
- Углы, измеряемые дугами;
- Вписанные и описанные треугольники;
- Вписанные и описанные четырёхугольники.

К каждому плакату разработаны интерактивные тестовые задания, которые помогут закрепить и проверить уровень знаний учащихся.
Применение программы
- В кабинете, оснащенном интерактивной доской или другим демонстрационным оборудованием, – организация фронтальной работы с классом при объяснении нового материала, повторении и закреплении знаний;
- В мобильном компьютерном классе – организация индивидуальной и групповой работы учащихся.
Особенности программы
- Реализация требований современных образовательных стандартов
- Возможность применения в аудиториях с демонстрационной техникой (интерактивная доска, проектор и белый экран) и в компьютерном классе
- Специальный режим для увеличения любых фрагментов плакатов
- Инструмент «Чертежник», позволяющий делать подписи и рисунки поверх демонстрируемого материала
- База тестов (85 интерактивных тестовых заданий) с функцией проверки ответов
- Лицензия на образовательное учреждение
Геометрия 8 Мерзляк Контрольная 3 с ответами
Контрольная работа № 3 по геометрии в 8 классе с ответами по УМК Мерзляк и др. Тема контрольной: Теорема Фалеса. Подобие треугольников. Цитаты из пособия «Геометрия: дидактические материалы 8 класс / Мерзляк, Полонский, Рабинович и др. / М.: Вентана-Граф» использованы в учебных целях. Ответы адресованы родителям. Геометрия 8 Мерзляк Контрольная 3 + ответы.
Контрольная работа № 3 по геометрии
8 класс УМК Мерзляк и др.
КР-3. Вариант 1 (транскрипт заданий)
- На рисунке 124 АВ || CD, МА = 12 см, АС = 4 см, BD = б см. Найдите отрезок МВ.
- Треугольники АВС и А1В1С1 подобны, причём сторонам АВ и ВС соответствуют стороны А1В1 и В1С1. Найдите неизвестные стороны этих треугольников, если АВ = 8 см, ВС = 10 см, А1В1 = 4 см, А1С1 = 6 см.

- Отрезок АК — биссектриса треугольника АВС, АВ = 12 см, ВК = 8 см, СК = 18 см. Найдите сторону АС.
- На стороне ВС треугольника АВС отметили точку М так, что ВМ : МС = 2 : 9. Через точку М провели прямую, которая параллельна стороне АС треугольника и пересекает сторону АВ в точке К. Найдите сторону АС, если МК = 18 см.
- В трапеции ABCD с основаниями AD и ВС диагонали пересекаются в точке О, ВС : AD = 3 : 5, BD = 24 см. Найдите отрезки ВО и OD.
- Через точку М, находящуюся на расстоянии 15 см от центра окружности радиусом 17 см, проведена хорда, которая делится точкой М на отрезки, длины которых относятся как 1 : 4. Найдите длину этой хорды.
КР-3. Вариант 2 (транскрипт заданий)
- На рисунке 125 MN || КР, NP = 20 см, РО = 8 см, МК = 15 см. Найдите отрезок КО.
- Треугольники АВС и А1В1С1 подобны, причём сторонам АВ и ВС соответствуют стороны А1В1 и В1С1. Найдите неизвестные стороны этих треугольников, если ВС = 5 см, АВ = б см, В1С1 = 15 см, А1С1 = 21 см.
- Отрезок CD — биссектриса треугольника АВС, АС -= 12 см, ВС = 18 см, AD = 10 см. Найдите отрезок BD.
- На стороне АВ треугольника АВС отметили точку Е так, что АЕ : BE = 3 : 4. Через точку Е провели прямую, которая параллельна стороне АС треугольника и пересекает сторону ВС в точке F. Найдите отрезок ЕF, если АС = 28 см.
- В трапеции ABCD с основаниями AD и ВС диагонали пересекаются в точке О, ВО : OD = 2:3, АС = 25 см. Найдите отрезки АО и ОС.
- Через точку Р, лежащую внутри окружности, проведена хорда, которая делится точкой Р на отрезки, длины которых равны 4 см и 5 см. Найдите расстояние от точки Р до центра окружности, если её радиус равен 6 см.
ОТВЕТЫ на контрольную работу
ОТВЕТЫ НА ВАРИАНТ 1.
№ 1. МВ = 18 см.
№ 2. АС = 12 см; В1С1 = 5 см.
№ 3. АС = 27 см.
№ 4. АС = 22 см.
№ 5. ВО = 9 см; OD = 15 см.
№ 6. АВ = 20 см.
ОТВЕТЫ НА ВАРИАНТ 2.
№ 1. КО = 6 см.
№ 2. АС = 7 см; А1В1 = 18 см.
№ 3. BD = 15 см.
№ 4. EF = 16 см
№ 5. СО = 10 см; АО = 15 см.
№ 6. ОР = 4 см.
Вы смотрели: Контрольная работа № 3 по геометрии в 8 классе с ответами по УМК Мерзляк и др. Тема контрольной: Теорема Фалеса. Подобие треугольников. Цитаты из пособия «Геометрия: дидактические материалы 8 класс / Мерзляк, Полонский, Рабинович и др. / М.: Вентана-Граф» использованы в учебных целях. Ответы адресованы родителям. Геометрия 8 Мерзляк Контрольная 3 + ответы.
Вернуться к списку контрольных работ по геометрии 8 класс (Мерзляк)
| Урок | Цель |
|---|---|
| Треугольники: определение и свойства | Учащиеся изучают термины, относящиеся к треугольникам, такие как смежные, вершины, вершины, сторона, противоположность, основание, вершина и высота. |
| Классификация треугольников по углам и сторонам | На этом уроке учащиеся используют углы и стороны треугольников для определения типа треугольника. |
| Внутренние и внешние углы треугольников: определение и примеры | Инструкторы объясняют, как определить внутренние и внешние углы треугольников. |
| Как определять похожие треугольники | Учащиеся узнают, как определять похожие треугольники. |
| Углы и треугольники: практические задачи | Студенты имеют возможность попрактиковаться в решении углов и треугольников. |
| Построение медианы треугольника | В главе учащиеся проходят этапы построения медианы треугольника. |
| Медиана, высота и биссектриса угла треугольника | Учащиеся изучают значение медианы, биссектрисы высоты и угла, а также способы их обозначения в треугольнике. |
| Построение треугольников: типы геометрического построения | На этом уроке учащиеся учатся строить треугольники, используя различные комбинации заданных сторон и углов. |
| Свойства параллельных линий в треугольнике | Учащиеся изучают некоторые свойства параллельных линий в треугольнике, такие как центроид, высота, биссектриса угла, инцентр и ортоцентр. |
Высшая математика в восьмом классе
Еще в 1990 году изучение алгебры в восьмом классе было уникальным.Ситуация кардинально изменилась за последние годы, и теперь восьмиклассники изучают алгебру больше, чем любой другой математический класс. Зачисление в восьмой класс алгебры — и в другие классы продвинутой математики — зависит от штата. В этом разделе отчета Центра Брауна используется эта вариация для изучения взаимосвязи количества учащихся штатов в продвинутых классах математики и результатов NAEP. Вопрос исследования заключается в том, существует ли взаимосвязь между изменениями в зачислении на продвинутую математику и изменениями в оценках NAEP в 8-м классе. Испытывают ли штаты, которые увеличивают зачисление на более высокий уровень, одновременный рост достижений? Второй анализ использует ту же технику, чтобы посмотреть на вероятность того, что курсы продвинутого уровня «размываются».«Связан ли рост числа учащихся с более низкими средними достижениями в продвинутых классах?
youtube.com/embed/lXLTcYIOw98?version=3&rel=1&showsearch=0&showinfo=1&iv_load_policy=1&fs=1&hl=en-US&autohide=2&wmode=transparent» allowfullscreen=»true» sandbox=»allow-scripts allow-same-origin allow-popups allow-presentation»/>Фон
В 1982 году Роберт Мозес был удостоен стипендии Макартура. Он использовал деньги, чтобы начать проект «Алгебра», общественный проект, направленный на то, чтобы познакомить с алгеброй исторически малообеспеченных учащихся средних школ — в первую очередь, детей из семей с низким доходом и цветных студентов. Моисей назвал алгебру «новым гражданским правом», призывом к справедливости, который пролил свет на курс в новом свете. 32 Администрация Клинтона связала тему справедливости с международной конкурентоспособностью и подтолкнула больше студентов к изучению алгебры перед старшей школой. «Во всем мире средние школьники изучают алгебру и геометрию», — заметил президент Клинтон. «У нас дома только четверть всех учеников изучают алгебру перед старшей школой». 33
Вскоре алгебра стала известна как курс «привратника», класс, стоящий, как часовой, у ворот колледжа. Возьмите его и сдайте, и ваши шансы на поступление в колледж будут хорошими.Возьмите его и проиграйте, и, по крайней мере, вы столкнулись с сложной математикой. Ни в коем случае не принимайте это, и ваши шансы поступить в колледж были близки к нулю. Место алгебры в типичной математической последовательности средней школы повысило ее важность. Предположим, что студенты, поступающие в колледж, должны получить некоторые математические знания в старших классах. В большинстве средних школ ученику, изучающему алгебру I в девятом классе, дается три оставшихся года для изучения алгебры II, геометрии, предварительного расчета / тригонометрии, а затем — исчисления.Это четыре курса. Что-то должно дать. Многие школы меняют порядок курсов, а некоторые смешивают статистику с одним из предложений года, но факт остается фактом: если целью является изучение математики в старших классах средней школы, то изучение алгебры I в девятом классе означает, что существует четыре курса. завершить за три года. Изучение алгебры в восьмом классе открывает дополнительный год для углубленного изучения математики.
завершить за три года. Изучение алгебры в восьмом классе открывает дополнительный год для углубленного изучения математики.
Справедливость, международная конкурентоспособность и практические соображения по поводу последовательностей курсов объединились в середине 2000-х годов, чтобы активизировать кампанию по алгебре для восьмиклассников.Возникло движение «алгебра для всех», которое продвинуло универсальную обязательную алгебру для восьмиклассников. Миннесота ввела новое требование для окончания средней школы, согласно которому, начиная с класса 2015 года, все учащиеся должны сдать зачет по алгебре I к концу восьмого класса. Калифорния использовала свою формулу школьной отчетности для продвижения алгебры в восьмом классе, предлагая на выбор два экзамена по математике для восьмого класса (алгебра и общая математика для восьмого класса), но затем в формуле для расчета индекса академической успеваемости (API) не учитывала успеваемость. уровень учащихся, сдающих общий тест по математике (например, переход к «базовому» учащимся, сдавшим тест и получившим оценку «хорошо»).Этот стимул побудил школы резко увеличить охват восьмиклассников алгеброй, и, хотя правило AYP было позже отменено судами, Калифорния считается лучшим штатом в стране по алгебре и математике в восьмом классе. 34
Данные NAEP о зачислении на углубленный курс математики
Таблица 3-1 иллюстрирует неуклонный рост числа учащихся восьмых классов в США на курсах продвинутой математики. Данные взяты из экзамена NAEP по математике для восьмых классов.Учащимся задают вопрос: «Какой урок математики вы посещаете в этом году?» Категория «Продвинутая математика» объединяет несколько ответов, включая Алгебру I, курсы, которые расширяют содержание Алгебры I за два года (будь то первый или второй год такого курса), и курсы, которые обычно более продвинуты, чем Алгебра I, включая Алгебру II и геометрия. Этот объединенный ответ является зашумленным и обсуждается ниже.
В 1990 году только 16% обучались на курсах алгебры по сравнению с 20% на предварительную алгебру и 61% на математику в 8-м классе.В этой статье последние два курса называются «базовыми».
К 2011 году почти половина (47%) всех восьмиклассников изучали алгебру или более продвинутый курс. Только 48% изучали базовый курс математики, по сравнению с 81% в 1990 году. Процент продвинутой математики может быть занижен в Таблице 3-1 за годы до 2000 года, поскольку это были первые занятия по геометрии, продвинутой алгебре и растяжке. были категориями ответов в анкете NAEP для восьмиклассников. 35 Более того, некоторые студенты — как тогда, так и сейчас — могут ошибочно полагать, что они изучают алгебру или геометрию, хотя на самом деле это не так.Несмотря на эти ограничения данных, число зачисленных на углубленный курс математики значительно выросло с 1990 по 2011 год. 36
Все больше и больше учеников все раньше и раньше берут уроки математики на высшем уровне. Это хорошая идея?
Исследование эффективности алгебры восьмых классов
Национальное лонгитюдное исследование в области образования 1988 года (NELS) предлагает исследователям массу информации, собранной из рандомизированной выборки студентов. В нескольких исследованиях использовались данные NELS, чтобы выяснить, что происходит, когда учащиеся начинают углубленную математику в начале своей академической карьеры, будь то восьмой или девятый класс. 37 Исследователи обнаружили, что учащиеся, изучающие алгебру раньше, а не позже, получают выгоду, в том числе — и это важно для достижения справедливости — учащихся с низкой успеваемостью. Недавний метаанализ исследования по этой теме (Мэри К. Штайн и его коллеги) подтвердил этот положительный результат с оговоркой, что «успехи достигаются в условиях, когда политика сопровождается сильной поддержкой учащихся, испытывающих трудности, особенно большим количеством времени для алгебры. инструкция. У нас нет убедительных доказательств того, что политика универсальной алгебры приводит к успехам без этой сильной поддержки.” 38
инструкция. У нас нет убедительных доказательств того, что политика универсальной алгебры приводит к успехам без этой сильной поддержки.” 38
Более поздние оценки политики, расширяющей набор студентов по алгебре, вызвали тревогу. В Чикаго все девятиклассники должны были пройти то, что считалось подготовительным классом к колледжу, включая алгебру. Оценщики следили за учениками в течение нескольких лет и пришли к выводу: «Хотя больше учеников закончили девятый класс с зачетами по алгебре и английскому языку I, процент отказов увеличился, оценки немного снизились, результаты тестов не улучшились, и у учеников не было больше шансов поступить в колледж. 39 Исследования политики Калифорнии в области алгебры обнаружили компромисс: рост числа учащихся, но также и рост числа неудач. В Северной Каролине исследователи из Дьюка обнаружили отрицательные результаты после изучения инициативы Шарлотты-Мекленбург по расширению алгебры в восьмом классе: более низкие баллы по тесту по алгебре I, а затем более низкие показатели успеваемости по геометрии и алгебре II в последующие годы.
Почему более поздние исследования дали более мрачные результаты, чем предполагалось в более ранней работе? Исследователи Duke считают, что предвзятость отбора исказила более ранние результаты.Более сильные ученики-математики изучают алгебру в восьмом классе, и хотя они действительно могут получить академическую пользу от курса, это не означает, что более слабые ученики также получат пользу от изучения алгебры раньше. «Как только эта предвзятость при отборе будет устранена, оставшийся причинный эффект от ускорения обычного первого курса алгебры до более ранних классов при отсутствии других изменений в учебной программе по математике станет для большинства студентов явно вредным». 40
Stein et al. метаанализ и политические рекомендации команды Duke, хотя и различаются по акцентам, все же имеют небольшую точку соприкосновения.Stein et al. говорят, что без «сильной поддержки» достижений нельзя ожидать. И исследователи Duke предвидят вредные последствия «при отсутствии других изменений в учебной программе по математике». Один условно положительный, другой — отрицательный. Их общая точка зрения — прогнозирование потенциала нейтрального эффекта.
И исследователи Duke предвидят вредные последствия «при отсутствии других изменений в учебной программе по математике». Один условно положительный, другой — отрицательный. Их общая точка зрения — прогнозирование потенциала нейтрального эффекта.
Давайте вернемся к NAEP и посмотрим, что его данные говорят об усилиях государства по поощрению зачисления на курсы продвинутой математики в восьмом классе.
Аналитический метод
Связаны ли зачисления в восьмой класс по продвинутой математике с оценками штата по математике в NAEP? Чтобы ответить на этот вопрос, очевидным первым шагом будет просто изучить список штатов, их баллы по NAEP и процент учащихся каждого штата, изучающих алгебру, геометрию и другие углубленные математические курсы в восьмом классе.Нет четкой взаимосвязи. В 2011 году корреляция между количеством учащихся штатов по математике и успеваемостью NAEP составила 0,07, что неотличимо от 0,00. Штаты с большим количеством восьмиклассников, обучающихся в продвинутых математических классах, не более склонны к получению более высокого балла NAEP по математике, чем штаты с более низким показателем зачисления в эти классы.
Этот вид перекрестного анализа — разумное место для начала, но он ограничивается выявлением корреляций между переменными в определенный момент времени.Это может ввести в заблуждение. Например, исследование, проведенное в отчете Центра Брауна за 2007 год, показало, что количество учебных минут, которые страны посвящают обучению математике, не связано на межсекционной основе с национальными достижениями по математике. В 1995 году корреляция составила 0,05. В 2003 году корреляция составила -0,20. Ни один из статистических показателей существенно не отличается от 0,00. Но когда страны исследуются продольно и данные из двух поперечных сечений моделируются как переменные изменения, исследуемый вопрос переносится на то, связаны ли национальные изменения в учебных протоколах с 1995 по 2003 годы с изменениями в результатах тестов за тот же период времени. .Корреляция для этой связи составляет 0,42, что является статистически значимым. Страны, которые увеличили количество времени, посвященного обучению математике, как правило, испытали повышение оценок по математике TIMSS; в тех странах, которые сократили время, уделяемое обучению математике, как правило, падали свои оценки.
.Корреляция для этой связи составляет 0,42, что является статистически значимым. Страны, которые увеличили количество времени, посвященного обучению математике, как правило, испытали повышение оценок по математике TIMSS; в тех странах, которые сократили время, уделяемое обучению математике, как правило, падали свои оценки.
Почему полезен анализ переменных изменений? Две причины. Во-первых, этот метод помогает контролировать предвзятость, вносимую пропущенными переменными (включая выборку), недостаток которого мешает кросс-секционному анализу достижений.В случае учебных минут, например, школьные системы могут стратегически решить поместить учащихся с низкими показателями в более длинные классы, чтобы помочь им наверстать упущенное. Это может создать впечатление, что большее количество инструкций связано с более низкими достижениями. Если предположить, что систематическая ошибка пропущенной переменной присутствует как в начальной, так и в конечной точках исследуемого временного интервала, а связь с зависимой переменной (интересующий результат) остается неизменной на протяжении всего интервала, такая систематическая ошибка исчезает при вычислении изменения ( см. Gustaffson, 2007, для дальнейших объяснений и приложений к другим образовательным вопросам). 41
Второе преимущество этого подхода состоит в том, что он ставит вопрос первостепенной важности для анализа политики. При рассмотрении вопроса о том, принимать ли политику X, возникает вопрос: если мы примем политику X, каковы ожидаемые изменения в результате Y? Что случится? Поперечный вопрос заключается в следующем: какова связь между политикой X и результатом Y в определенный момент времени? Часто можно услышать перекрестный анализ, показывающий что-то вроде «изменение на одно стандартное отклонение в X приведет к следующему изменению Y», но прогноз является только предполагаемым, поскольку нет никаких наблюдений за изменением (или данных из разные периоды времени) в наборе данных.
Анализ изменений с использованием баллов NAEP
Взаимосвязь между изменением политики и изменением результатов является предметом анализа ниже. Рассматриваемый период времени — с 2005 по 2011 год. Имейте в виду, что, несмотря на улучшение по сравнению с перекрестным анализом, анализ все еще является только корреляционным и, таким образом, ограничивается генерацией правдоподобных гипотез для более строгих исследований. Здесь не утверждается никакой причинности.
Рассматриваемый период времени — с 2005 по 2011 год. Имейте в виду, что, несмотря на улучшение по сравнению с перекрестным анализом, анализ все еще является только корреляционным и, таким образом, ограничивается генерацией правдоподобных гипотез для более строгих исследований. Здесь не утверждается никакой причинности.
В Таблице 3-2 показан конец долгосрочной тенденции, представленной в Таблице 3-1 — рост числа учащихся в продвинутых классах математики и снижение в базовых классах.Медленная, устойчивая национальная тенденция скрывает значительные различия между штатами. В 2005–2011 годах средний прирост числа зачисленных в школу с углубленным изучением математики по штату (по отношению к восьмиклассникам) составил 5,5% со стандартным отклонением 8,4%. В первую четверку штатов, увеличивших число учащихся на продвинутом уровне, вошли Миннесота (35%), Пенсильвания, Вирджиния и Вашингтон (все с 17%). Напротив, два штата, идущие вразрез с общенациональной тенденцией к сокращению числа учащихся с углубленным изучением математики: Невада (-22%) и Джорджия (-17%).
Что касается конкретных курсов, то сорок пять штатов увеличили набор учащихся по алгебре I, в то время как только в трех штатах число учащихся сократилось, а в трех осталось без изменений (при обсуждении оценок NAEP округ Колумбия считается штатом). В 28 штатах количество учащихся по общей математике сократилось, в 20 — увеличилось, а в трех штатах осталось прежним. В общем, записи на курс ведут себя как тюбик с зубной пастой: один конец сдавливается, а другой конец выпячивается. В штатах с растущим набором учащихся продвинутой математики наблюдалось сокращение набора на базовые курсы.И наоборот. Об этом свидетельствуют два штата, в которых наблюдается снижение приема на курсы продвинутой математики. Их зачисление на начальную математику увеличилось. Поступление в Неваду по предалгебре подскочило на 27%. Доля студентов в Грузии, изучающих математику, выросла на 33%.
Есть ли связь между изменением количества зачисленных на курсы штатов и изменением оценок NAEP? Получили ли штаты успехи в программе NAEP одновременно с увеличением числа восьмиклассников, изучающих математику на более высоком уровне? Для исследования этих вопросов был вычислен ряд коэффициентов корреляции (см. Таблицу 3-3).Первая модель исследует взаимосвязь набора учащихся по продвинутой математике и сводных баллов NAEP. Коэффициент корреляции (r = -0,01) статистически неотличим от 0,00.
Таблицу 3-3).Первая модель исследует взаимосвязь набора учащихся по продвинутой математике и сводных баллов NAEP. Коэффициент корреляции (r = -0,01) статистически неотличим от 0,00.
Сводный балл NAEP может оценивать математику слишком широко, чтобы уловить эффект от акцентирования внимания на продвинутой математике, которая в первую очередь включает усиление алгебры. К счастью, NAEP сообщает баллы по конкретным областям содержания, оцененным в рамках теста (так называемым «цепочкам»), включая алгебру и геометрию.Таким образом, вторая модель использует оценку NAEP для цепочки алгебры в качестве переменной достижения, которая должна быть более чувствительной к расширенным знаниям алгебры. Опять же, никаких существенных взаимосвязей не обнаружено.
Третья и четвертая модели используют изменение количества учащихся по алгебре I в качестве переменной курса вместо продвинутой математики на случай, если объединение нескольких курсов в категорию «продвинутый» запутает воду. Изменение составного балла NAEP служит переменной достижения в третьей модели, а изменение балла по шкале алгебры — переменной достижения в четвертой модели.Ни одна из корреляций не достигает статистической значимости.
Пятая и шестая модели повторяют то же самое с геометрией. Изменение курса геометрии в восьмом классе используется в качестве переменной курса — и модели вычисляют, коррелировано ли оно с изменением композита NAEP в модели пять и изменением в балле по геометрии в модели шесть. Ни одна из этих корреляций не является статистически значимой.
В дополнение к корреляциям, указанным здесь, были проведены многомерные регрессии с тремя контролируемыми ковариатами (также переменными, представляющими изменение) — изменение уровней детской бедности в штатах, изучающих английский язык, а также чернокожих и латиноамериканских студентов — демографические характеристики, которые являются известными коррелятами штата. Оценки NAEP.Великая рецессия развернулась в течение исследуемого периода времени, и, например, в некоторых штатах уровень детской бедности рос больше, чем в других штатах. Если в штатах произошли демографические изменения, это могло исказить результаты. Оказалось, что это не так. Ни одна из регрессионных моделей не была статистически значимой.
Если в штатах произошли демографические изменения, это могло исказить результаты. Оказалось, что это не так. Ни одна из регрессионных моделей не была статистически значимой.
В целом, в оценках NAEP не было обнаружено никаких доказательств связи между повышением числа учащихся в штатах на продвинутые курсы математики и повышением успеваемости. В штатах, где процент учащихся, изучающих алгебру или геометрию в восьмом классе, увеличился, вероятность достижения результатов NAEP была не выше, чем в штатах, в которых число учащихся на этих двух курсах сократилось.
Уменьшает ли рост посещаемости курсы продвинутой математики?
Сведены ли курсы продвинутой математики из-за увеличения числа учащихся — важный вопрос. Идея состоит в том, что заполнение продвинутых классов более слабыми в учебе учениками, чем в прошлом, может уменьшить объем знаний, которые могут дать курсы. Это могло бы помочь объяснить нейтральные корреляции, о которых говорилось выше. Это также могло бы помочь объяснить нейтральные или даже отрицательные эффекты, выявленные недавними оценками политики, продвигающей универсальную алгебру в восьмом и девятом классах.Данные NAEP могут лишь ограничиться указанием того, происходит ли снижение уровня выбросов, но они действительно предлагают интересную информацию о том, как смена курса может быть связана с достижениями.
Таблица 3-4 показывает корреляцию между изменением набора учащихся и изменением средней успеваемости студентов, проходящих каждый курс. Отображаются данные четырех курсов. Опять же, процентная доля восьмиклассников штата, проходящих каждый курс, служит переменной зачисления. Курсы расположены иерархически. Геометрия обычно предлагается самым продвинутым ученикам, а общая математика — самым слабым.Статистически значимы три корреляции.
Есть ли признаки полива? Да, но не на всех курсах продвинутого уровня. Начнем с результатов, подтверждающих гипотезу разбавления. Увеличение числа учащихся по алгебре I отрицательно связано с увеличением успеваемости (r = -o. 34, p <.05). Давайте проясним, что это значит. Средний штат зарегистрировал прирост баллов по шкале NAEP на 5,6 среди студентов, изучающих алгебру I. Оценки NAEP для студентов, изучающих алгебру I, не так сильно выросли в штатах, где увеличилось количество учащихся по алгебре I (+5.2) как в штатах, которые либо сохранили набор учащихся на постоянном уровне, либо снизили его (+9,2). Для предалгебры рост числа учащихся также отрицательно связан с результатами тестов (r = -0,34, p <0,05). Обе корреляции согласуются с гипотезой размывания, если студенты, которые в противном случае были бы помещены на более низкие курсы, мигрируют вверх на более высокие курсы. Мы не можем сказать, происходит ли это, используя данные NAEP. И еще раз сделаем важное предупреждение: корреляции не доказывают причинно-следственную связь.
34, p <.05). Давайте проясним, что это значит. Средний штат зарегистрировал прирост баллов по шкале NAEP на 5,6 среди студентов, изучающих алгебру I. Оценки NAEP для студентов, изучающих алгебру I, не так сильно выросли в штатах, где увеличилось количество учащихся по алгебре I (+5.2) как в штатах, которые либо сохранили набор учащихся на постоянном уровне, либо снизили его (+9,2). Для предалгебры рост числа учащихся также отрицательно связан с результатами тестов (r = -0,34, p <0,05). Обе корреляции согласуются с гипотезой размывания, если студенты, которые в противном случае были бы помещены на более низкие курсы, мигрируют вверх на более высокие курсы. Мы не можем сказать, происходит ли это, используя данные NAEP. И еще раз сделаем важное предупреждение: корреляции не доказывают причинно-следственную связь.
Самая сильная корреляция связана с общей математикой (r = 0.47, р <0,01). Положительная связь также согласуется с гипотезой разбавления. Если общая тенденция заключается в переводе учащихся на курсы старшего уровня - а школы избирательны в отношении учащихся, которых они ускоряют, - курсы общей математики, по мере их сокращения, должны все больше преобладать среди учащихся, которые больше всего борются с математикой. Эти курсы, по-видимому, потеряли бы своих лучших учеников. Таким образом, падение количества учащихся будет связано с падением оценок. Классы общей математики, которым удастся удержать учеников, которые проходят ускоренное обучение в другом месте, сравнительно получат более высокие баллы.
Геометрия усложняет дело. Его коэффициент корреляции (0,27) несовместим с историей размывания. Геометрия находится на вершине иерархии курсов. Любое неизбирательное ускорение продвижения студентов вверх (неотъемлемое допущение аргумента о разбавлении) должно в конечном итоге привести к отрицательной связи прироста зачисления и баллов по успеваемости в курсе на вершине. И все же коэффициент корреляции Geometry имеет положительный знак и приближается к статистической значимости. Хотя статистически неотличимо от 0,00 (p = 0,11), это может быть частично связано с уменьшением количества состояний с данными. Только в тридцати шести штатах имеется достаточное количество восьмиклассников-геометров, чтобы получить оценку NAEP.
Хотя статистически неотличимо от 0,00 (p = 0,11), это может быть частично связано с уменьшением количества состояний с данными. Только в тридцати шести штатах имеется достаточное количество восьмиклассников-геометров, чтобы получить оценку NAEP.
Другая возможность связана с зашумленными переменными курса NAEP. Возможно, в 2011 году в категорию курса NAEP по геометрии было включено больше «настоящих» студентов-геометров, чем в 2005 году — другими словами, большая часть тех, кто на самом деле посещает класс геометрии и не ошибается относительно своего курса математики.Как показано в Таблице 3-2 выше, только 5% восьмиклассников были зачислены в Геометрию в 2011 году, по сравнению с 4% в 2005 году. Средний балл NAEP для студентов, изучающих геометрию, составлял 290 в 2005 году и 308 в 2011 году, резкое увеличение на 18 баллов. Прирост на один процентный пункт у студентов, кажется, сильно ударил по баллам NAEP. «Настоящие» ученики-геометры, вероятно, изучали алгебру I в седьмом классе. Как и алгебра для восьмиклассников три или четыре десятилетия назад, геометрия предназначена только для самых лучших школьников-математиков.
Обсуждение
В этом исследовании анализировались вариации в моделях зачисления в школу, чтобы проверить, коррелирует ли рост числа зачисленных на продвинутые курсы математики для восьмых классов с достижениями NAEP. Никаких доказательств того, что они есть, обнаружено не было. В штатах, где процент восьмиклассников, изучающих алгебру I, геометрию и другие продвинутые математические классы, в период с 2005 по 2011 год повысился не больше, чем в штатах, где процент восьмиклассников на этих курсах снизился.
Второй анализ, снова посвященный изменениям в политике и результатах тестов с течением времени, исследовал, связано ли увеличение процента студентов на курсах более высокого уровня со снижением средних баллов этих курсов — предполагая эффект сглаживания. Доказательства согласуются с разбавлением всех курсов, кроме одного. Отрицательные корреляции были обнаружены для алгебры I и предалгебры. На этих курсах средняя успеваемость снижалась по мере увеличения числа учащихся. Успеваемость по курсам общей математики была положительно связана с изменениями в зачислении.Все три корреляции статистически значимы и подтверждают гипотезу размывания.
Отрицательные корреляции были обнаружены для алгебры I и предалгебры. На этих курсах средняя успеваемость снижалась по мере увеличения числа учащихся. Успеваемость по курсам общей математики была положительно связана с изменениями в зачислении.Все три корреляции статистически значимы и подтверждают гипотезу размывания.
Геометрия отличается от других курсов. Была обнаружена положительная связь, которая, хотя статистически неотличима от 0,00, предполагает, по крайней мере, нейтральную взаимосвязь между ростом охвата и изменениями в оценках NAEP. Если бы школы без разбора ускоряли обучение учащихся до восьмого класса геометрии, можно было бы ожидать отрицательной корреляции.
Ни один из этих результатов не может подтвердить или опровергнуть причинно-следственную связь, но они полезны для генерации гипотез для будущего исследования.Они также пролили свет на результаты предыдущих исследований. Например, главный вывод из оценок политики Калифорнии в области алгебры состоит в том, что универсальная алгебра порождает компромиссы. Многие студенты получают пользу от дополнительной задачи. Увеличились показатели набора по алгебре для исторически недоучившихся групп населения (в частности, студентов с низким уровнем SES). Общее количество студентов, сдающих экзамены по окончании курса, также увеличилось. Но обратная сторона заключается в том, что количество студентов, не умеющих изучать алгебру, также увеличивается; и неуспевающие студенты также непропорционально низкие студенты SES. 42 Одно исследование, проведенное в Калифорнии, предполагает, что многим из отстающих студентов было бы лучше потратить дополнительный год на подготовку к алгебре, а не на нее. 43 Эти виды компромиссов, если их агрегировать до уровня штата, могут дать нейтральный чистый эффект.
Анализ того, приводит ли ускорение учащихся в классы продвинутого уровня к снижению достижений до двух разных типов ускорения. Один является выборочным и решается на индивидуальной основе. У каждого студента оцениваются математические навыки и решается, подходит ли ему более продвинутый курс математики. Такое ускорение, по-видимому, происходит в геометрии восьмого класса и, предположительно, в алгебре седьмого класса. Студенты, которым будет полезен более строгий курс, продвигаются по службе. Средние результаты тестов по геометрии в восьмом классе растут или, по крайней мере, остаются прежними, несмотря на рост числа учащихся.
У каждого студента оцениваются математические навыки и решается, подходит ли ему более продвинутый курс математики. Такое ускорение, по-видимому, происходит в геометрии восьмого класса и, предположительно, в алгебре седьмого класса. Студенты, которым будет полезен более строгий курс, продвигаются по службе. Средние результаты тестов по геометрии в восьмом классе растут или, по крайней мере, остаются прежними, несмотря на рост числа учащихся.
Второй тип ускорения — неселективный и групповой. Учащиеся продвигаются вперед на основе характеристик, не зависящих от предыдущих достижений или подготовленности (например,g., уровень обучения или возраст). В будущих исследованиях следует сравнить эти два типа ускорения и выяснить, кто, когда дело доходит до избирательного ускорения, должен ускоряться и когда. При ускорении на основе возраста или класса необходим набор ранних индикаторов (подход универсальной алгебры), которые позволили бы определить учащихся, нуждающихся в поддержке, и тип поддержки, наиболее выгодный для них. Если компромиссы группового ускорения действительно реальны, то цель политики должна заключаться в минимизации негативных эффектов и максимизации выгод.
Последнее замечание по Common Core. Никто не знает, как потребности одаренных студентов будут удовлетворены в эпоху Common Core. Изучение алгебры в восьмом классе стало новой нормой, а изучение алгебры в седьмом классе быстро становится новой нормой для одаренных математиков. В Калифорнии 8,1% семиклассников (почти 38000 студентов) сдали экзамен по алгебре в конце курса в 2012 году. Если Common Core будет означать одинаковую учебную программу для всех, обязательно наступит время, когда отличным ученикам-математикам понадобится необычная учебная программа, подходящая для их.
Часть III Примечания
32. Справочная информация о проекте «Алгебра» доступна на сайте www.algebra.org.
33. Замечания президента Клинтона, Круглый стол по вопросам образования, Средняя школа Спрингбрук, Силвер-Спринг, Мэриленд, 16 марта 1998 г. Доступно по адресу http://www.gpo.gov/fdsys/pkg/WCPD-1998-03-23/pdf /WCPD-1998-03-23.pdf.
Доступно по адресу http://www.gpo.gov/fdsys/pkg/WCPD-1998-03-23/pdf /WCPD-1998-03-23.pdf.
34. Историю политики Калифорнии в области алгебры можно найти в: Политика в области алгебры в Калифорнии: большие надежды и серьезные проблемы, (Окленд: EdSource, май 2009 г.).Также см. Том Лавлесс, Неуместный студент-математик: потерялся в алгебре восьмого класса (Вашингтон, округ Колумбия: Институт Брукингса, 2008).
35. До 2000 г. на категорию «другое» приходилось около 3% ответов, поэтому количество студентов, посещающих более продвинутые классы, вероятно, было очень небольшим.
36. Джилл Уолстон и Джилл Карливати МакКэрролл, Алгебра для восьмых классов: результаты восьмого раунда лонгитюдного исследования в раннем детстве, детский сад 1998–1999 годов (ECLS-K) (Вашингтон, округ Колумбия: Национальный центр Статистика образования, октябрь 2010 г.).
37. См. Дэвид Стивенсон, Кэтрин С. Шиллер и Барбара Шнайдер, «Последовательность возможностей для обучения», Социология образования 67, , вып. 3 (1994): 184–198; Адам Гаморан и Эйлин С. Ханниган, «Алгебра для всех? Преимущества подготовительной математики к колледжу для учащихся с различными способностями в начальной средней школе », Оценка образования и анализ политики 22, вып. 3 (2000): 241-254; Джулия Смит, «Имеет ли значение дополнительный год? Влияние раннего доступа к алгебре на долгосрочные успехи в математике », Оценка образования и анализ политики 18 (1996): 141-153.
38. См. Мэри Штайн, Джулия Кауфман, Милан Шерман и Эми Хиллен, «Алгебра: вызов на стыке политики и практики», Обзор исследований в области образования 81, вып. 4 (2011): 453-492.
39. Элейн Алленсворт, Такако Номи, Николас Монтгомери и Валери Э. Ли, «Подготовительная программа колледжа для всех: академические последствия требования алгебры и английского языка I для девятиклассников в Чикаго», Оценка образования и анализ политики 31, нет. .4 (2009): 367-391.
.4 (2009): 367-391.
40. Чарльз Т. Клотфельтер, Хелен Ф. Лэдд и Джейкоб Л. Вигдор, Последствия ускорения сбора данных по алгебре в рамках инициативы районной политики (Вашингтон, округ Колумбия: Национальный центр анализа продольных данных в исследованиях в области образования, Американские институты для исследований, 2012).
41. Ян-Эрик Густафссон, «Понимание причинных влияний на успеваемость на основе анализа различий во времени внутри стран», в книге Извлеченные уроки: что международные оценки говорят нам об успеваемости по математике , изд.Том Лавлесс (Вашингтон: издательство Brookings Institution Press, 2007).
42. Триш Уильямс, Эдвард Хертел и Майкл У. Кирст, Улучшение успеваемости по математике в средних классах: более пристальный взгляд на политику и практику округа и школы, размещение на курсах и результаты обучения в Калифорнии. Последующий анализ (Маунтин-Вью: EdSource, 2011).
43. Цзянь-Хуа Лян, Пол Хекман и Джамал Абеди, «Что результаты калифорнийских тестов говорят о движении к восьмиклассной алгебре для всех?» Оценка образования и анализ политики 34, no.3 (2012): 328-343.
Геометрия и измерения — Стандарты по математике для восьмого (8-го) класса в I4C
Стандарты по математике для 8-х классов — геометрия и измерения
Чтобы работать над геометрией и эталонами для восьмого класса, нажмите на номера стандартов ниже, чтобы посетить страницы с интернет-ресурсами по каждому из стандартов обучения.
Проверки понимания находятся вверху этой страницы. Прокрутите вниз, чтобы найти интернет-ресурсы, связанные с индикаторами эффективности состояния (SPI).
Проверки понимания (формирующая / итоговая оценка)
0806.4.1 Теорема Пифагора — Модель теоремы Пифагора.
0806.4.2 Обратное по теореме Пифагора — используйте обратное утверждение теоремы Пифагора, чтобы определить, является ли треугольник прямоугольным. 0806.4.3 Измерительный инструмент — выберите или используйте соответствующий измерительный инструмент для определения или создания заданной длины, площади, объема, угла, веса или массы. 0806.4.4 Прецизионность и точность — понимание того, как точность измерения влияет на точность величин, полученных на основе этих измерений. 0806.4.5 Конгруэнтный и дополнительный — Проанализируйте конгруэнтные и дополнительные отношения углов, образованных параллельными линиями и поперечными линиями (например, альтернативный внутренний, альтернативный внешний, соответствующий и смежный). 0806.4.6 Сделать преобразования — Сделайте внутрисистемные и межсистемные преобразования производных величин, включая расстояние, температуру и деньги. 0806.4.7 Трехмерная фигура — Визуализируйте или опишите поперечное сечение, полученное в результате пересечения плоскости с трехмерной фигурой. 0806.4.8 2-х и 3-х мерные фигуры — создавайте, рисуйте и работайте с 2-х и 3-хмерными фигурами с помощью ортогональных видов, проекционных проекций и / или сетей. Показатели государственной деятельности
SPI 0806. 4,1
Используйте теорему Пифагора — Используйте теорему Пифагора для решения контекстных проблем. SPI 0806.4.2 Найти расстояние — примените теорему Пифагора, чтобы найти расстояния между точками на координатной плоскости, чтобы измерить длину и проанализировать многоугольники и многогранники. SPI 0806.4.3 Поперечный разрез — Найдите размеры углов, образованных параллельными линиями, пересеченными поперечным сечением. SPI 0806.4.4 Преобразовать — Преобразование между и в рамках обычной системы США и метрической системы. SPI 0806.4.5 Геометрические фигуры — Определите пересечение двух или более геометрических фигур на плоскости. Геометрия — [классы 6–8] из Национальной библиотеки виртуальных манипуляторов
Measurement — [классы 6–8] из Национальной библиотеки виртуальных манипуляторов
Список понятий по математике для 8-х классов
На уровне восьмого класса есть определенные математические концепции, которые ваши ученики должны усвоить к концу учебного года.Многие математические концепции восьмого класса похожи на седьмой класс.
На уровне средней школы учащиеся обычно проходят всесторонний анализ всех математических навыков. Ожидается овладение концепциями предыдущих классов.
Ожидается овладение концепциями предыдущих классов.
Номера
Никаких реальных новых концепций чисел не вводится, но учащиеся должны уметь вычислять множители, кратные, целые числа и квадратные корни для чисел. К концу восьмого класса ученик должен уметь применять эти числовые концепции при решении задач.
Измерения
Ваши ученики должны уметь правильно использовать термины измерения и уметь измерять различные предметы дома и в школе. Учащиеся должны уметь решать более сложные задачи с оценками измерений и задачи, используя различные формулы.
На этом этапе ваши ученики должны уметь оценивать и рассчитывать площади трапеций, параллелограммов, треугольников, призм и кругов, используя правильные формулы. Точно так же учащиеся должны уметь оценивать и рассчитывать объемы для призм и должны уметь рисовать призмы на основе данных объемов.
Геометрия
Учащиеся должны уметь выдвигать гипотезы, рисовать, определять, сортировать, классифицировать, конструировать, измерять и применять различные геометрические формы и фигуры и задачи. Учитывая размеры, ваши ученики должны уметь рисовать и конструировать различные формы.
Студенты должны уметь создавать и решать различные геометрические задачи. И учащиеся должны уметь анализировать и определять формы, которые были повернуты, отражены, переведены, и описывать конгруэнтные формы.Кроме того, ваши ученики должны уметь определять, будут ли фигуры или фигуры мозаичны на плоскости (мозаика), и уметь анализировать шаблоны мозаики.
Алгебра и моделирование
В восьмом классе ученики будут анализировать и обосновывать объяснения закономерностей и их правил на более сложном уровне. Ваши ученики должны уметь писать алгебраические уравнения и писать утверждения, чтобы понимать простые формулы.
Студенты должны уметь оценивать множество простых линейных алгебраических выражений на начальном уровне, используя одну переменную.Ваши ученики должны уверенно решать и упрощать алгебраические уравнения с помощью четырех операций. И они должны чувствовать себя комфортно, подставляя натуральные числа вместо переменных при решении алгебраических уравнений.
И они должны чувствовать себя комфортно, подставляя натуральные числа вместо переменных при решении алгебраических уравнений.
Вероятность
Вероятность измеряет вероятность того, что событие произойдет. Он использовал его в повседневном принятии решений в науке, медицине, бизнесе, экономике, спорте и инженерии.
Ваши ученики должны уметь разрабатывать опросы, собирать и систематизировать более сложные данные, а также выявлять и объяснять закономерности и тенденции в данных.Учащиеся должны уметь построить множество графиков и соответствующим образом пометить их, а также указать разницу между выбором одного графика над другим. Учащиеся должны уметь описывать собранные данные в терминах среднего, медианного и режима, а также уметь анализировать любую систематическую ошибку.
Цель состоит в том, чтобы учащиеся могли делать более точные прогнозы и понимать важность статистики для принятия решений и в реальных сценариях. Учащиеся должны уметь делать выводы, прогнозы и оценки на основе интерпретации результатов сбора данных.Точно так же ваши ученики должны уметь применять правила вероятности к азартным играм и спорту.
Тестируйте 8-хклассников с этими задачами со словами.
Другие классы
Геометрия для 8-го класса | Что должны знать учащиеся
В 8-м классе учащиеся готовятся к более сложной математической программе старшей школы. Продолжайте читать, чтобы узнать, что будет учить ваш 8-классник и как вы можете помочь ему или ей подготовиться.
Что изучают учащиеся по геометрии для 8-х классов
Переводы, размышления и вращения
В геометрии восьмиклассники переводят, отражают и вращают двухмерные формы.Чтобы перевести фигуру, вы перемещаете фигуру в другое место на координатной плоскости. Чтобы отразил фигуру, вы ее переверните. По сути, формы являются зеркальным отображением друг друга.
Наконец, когда фигура повернута на на , она поворачивается в одном месте, поэтому она указывает в другом направлении, чем исходная форма. Студенты также должны определить, являются ли формы конгруэнтными (идентичными), даже если они переведены, отражены или повернуты.
Студенты также должны определить, являются ли формы конгруэнтными (идентичными), даже если они переведены, отражены или повернуты.
Чтобы практиковать эти навыки дома, нарисуйте на графике фигуру, например треугольник.2, где c представляет собой гипотенузу треугольника, а a и b представляют две его другие стороны. Ваш 8-классник также может использовать теорему Пифагора для вычисления расстояния между двумя точками на координатной плоскости.
Чтобы попрактиковаться в этом дома, восьмиклассник может рассчитать расстояния в реальном мире. Для этого занятия вам нужно будет спланировать воображаемое автомобильное путешествие. Начните с создания прямоугольного треугольника, используя три точки на карте. Измерьте расстояние в милях для двух сторон.2) h, где pi равно 3,14, r — радиус, а h — высота. Итак, для бассейна высотой пять футов и радиусом три (половина шести) объем будет 141,3 кубических фута.
Навыки математики в восьмом классе
Хотите помочь своему восьмикласснику освоить математику? Вот некоторые из навыков, которые ваш ребенок будет изучать в классе.
Числа
Рациональные и иррациональные числа
Разбираются в рациональных и иррациональных числах.Знайте, что рациональное число может быть записано в виде дроби или десятичной дроби (например: ½, 0,5, 2 или -2), но что иррациональное число — например, квадратный корень из 2 или √2 — не может быть записано как дробь. Записанное в десятичной форме иррациональное число не повторяется и не заканчивается.
Выражения и уравнения
Работа с радикалами
Работа с радикалами — математические выражения, включая квадратные корни (символ: √), кубические корни (символ: 3√) и т. Д.
Определите квадратные корни из маленьких идеальных квадратов — например: √49 = 7 (7 x 7 = 49).
Определите кубические корни маленьких идеальных кубиков — например: 3√64 = 4 (4 x 4 x 4 = 64).
Уравнения с показателями степени
Решите простые уравнения с показателями показателей, включая показатели с отрицательным основанием и показатели с основанием десятичной и дробной части.
Научная нотация
Под научной нотацией понимается способ записи слишком больших или слишком маленьких чисел, которые не могут быть легко записаны и прочитаны в десятичной форме — например, преобразовать 7 120 000 000 (стандартное десятичное представление) в 7.9 (научное обозначение). Складывайте, вычитайте, умножайте и делите числа, выраженные в экспоненциальной нотации.
Пропорциональные отношения
Сравните различные пропорциональные отношения, выраженные в различных формах: уравнения, графики, словесные выражения, таблицы и т. Д.
График пропорциональных отношений
График пропорциональных отношений. Интерпретируйте единицу скорости как наклон графика — насколько крутой или пологий будет линия.
Пересечение уклона
Работа с формой отрезка уклона (или отрезка y) линейных уравнений (уравнения, которые образуют прямую линию при построении графика): y = mx + b.
- Поймите, что значения x и y на графике являются решениями уравнения, а м — это наклон линии.
- Под уклоном ( м ) следует понимать изменение y по сравнению с изменением в x (так называемый подъем за пробег): если координата x изменяется на A , координата y изменяется на mx А .
Линейные уравнения
Решите линейные уравнения с одной переменной (как одношаговые, так и двухшаговые).
Одновременные линейные уравнения
Решите совместные линейные уравнения (линейные уравнения с одним и тем же набором переменных). Найдите точку пересечения двух прямых.
Функции
Функции как правила
Под функциями понимаются правила, присваивающие каждому значению x ровно одно значение y (каждому входу — ровно один выход). Используйте функции для описания отношений между числами (количествами) и ситуациями, когда одно количество определяет другое.Например, y = 2x — это способ выразить взаимосвязь между числами 3 и 6, или 4 и 8, или -2 и -4.
Используйте функции для описания отношений между числами (количествами) и ситуациями, когда одно количество определяет другое.Например, y = 2x — это способ выразить взаимосвязь между числами 3 и 6, или 4 и 8, или -2 и -4.
Сравнение свойств функций
Используя таблицы функций, графики, уравнения или описания, сравните свойства двух функций. Поймите, что линейные уравнения — это функции.
Геометрия
Конгруэнтность и подобие
Для двумерных фигур (включая линии и углы) необходимо понимать и определять конгруэнтность (объекты одинакового размера и формы) и сходство (объекты одинаковой формы, но разных размеров).
Теорема Пифагора
Поймите теорему Пифагора, взаимосвязь, уникальную для прямоугольных треугольников. Теорема Пифагора может быть выражена в виде уравнения для определения неизвестной длины сторон прямоугольных треугольников: a² + b² = c². В прямоугольном треугольнике квадрат гипотенузы (самая длинная сторона треугольника, c) равен сумме квадратов двух других сторон (a и b).
Расстояние между двумя точками
Используйте теорему Пифагора, чтобы найти расстояние между двумя точками в системе координат.
Задачи теоремы Пифагора
Используйте теорему Пифагора для решения реальных и математических задач.
Пример:
Библиотека находится в 8 милях к югу от школы. Центр отдыха находится в 15 милях к востоку от библиотеки. Какое расстояние по прямой от школы до рек-центра? Используйте схему, чтобы объяснить свой ответ.
Преобразования
Распознавать и идентифицировать преобразования двумерных фигур
- переводов — скользящее движение фигуры в любом направлении.
- дилатации — уменьшение или расширение фигуры.
- оборотов — поворот фигуры.
- отражений — зеркальное отображение фигуры.
Советы, которые помогут вашему восьмикласснику в классе математики, можно найти на нашей странице с советами по математике для восьмого класса.
Ресурсы Parent Toolkit были разработаны NBC News Learn с помощью профильных экспертов и соответствуют Общим основным государственным стандартам.
Parent Toolkit Staff
Parent Toolkit — это универсальный ресурс для родителей, созданный NBC News Learn.
Словарь по математике для 8-х классов — Математические термины для восьмого класса
VocabularySpellingCity предоставляет эти списки слов по математике для восьмого класса в качестве дополнения к стандартной учебной программе по математике для восьмого класса. Математические термины для 8-го класса собраны в списки математической лексики, используемые в забавных интерактивных и обучающих играх. Просто выберите область математики, выберите список слов и выберите из более чем 35 различных учебных заданий. Предоставленный материал был специально разработан для использования в 8-м классе математики. Узнать большеЧитать меньше
Списки математических слов
Списки математической лексики основаны на Стандартных математических стандартах для восьмых классов.VocabularySpellingCity выбрал академический словарь соответствующего уровня, который относится к ключевым математическим понятиям для учеников восьмого класса. Игры и упражнения позволяют ученикам 8-х классов углубить понимание ключевых понятий во всем, от алгебры до тригонометрии. Учителя восьмого класса могут импортировать эти списки математической лексики в свои учетные записи, а затем редактировать или добавлять к ним.
Математика — один из самых сложных предметов, которые изучает ученик средней школы. Понимание и применение сложной математической лексики средней школы часто является ключом к открытию этого сложного предмета.Учащимся восьмого класса необходимо иметь практические знания математических терминов 8-го класса, прежде чем они смогут применять их к математическим принципам. Использование реальных жизненных связей и примеров, богатых контекстом, позволяет учащимся применить математическую лексику 8-го класса к этим абстрактным математическим понятиям.

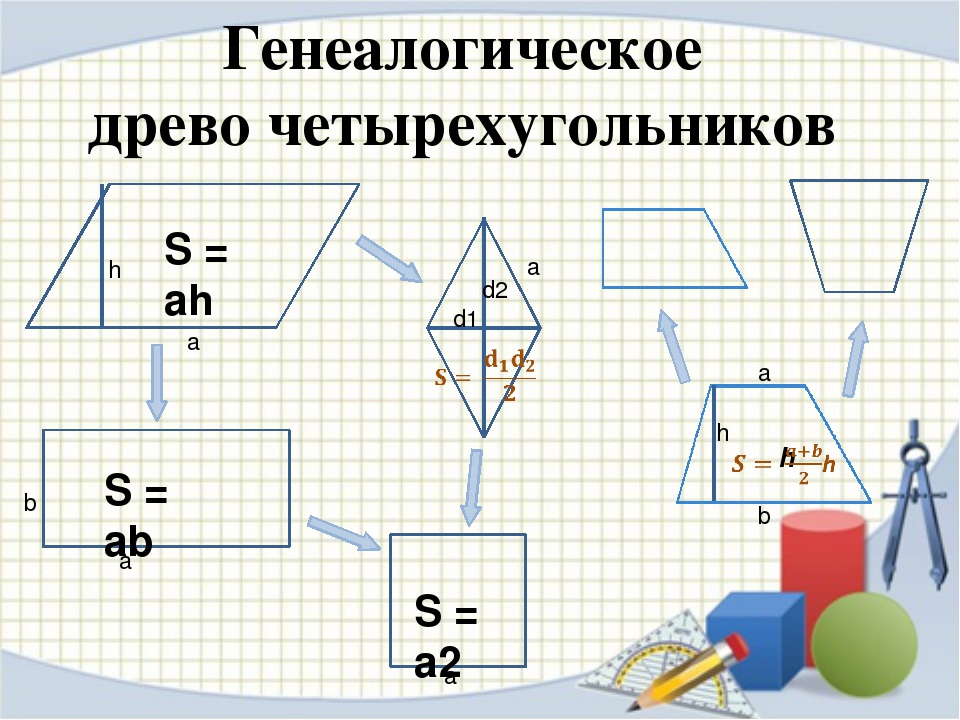
 Диагонали параллелограмма точкой пересечения делятся пополам.
Диагонали параллелограмма точкой пересечения делятся пополам.



 4,1
4,1