Деление числа в данном отношении: Деление числа в данном отношении + задачи с решением

Содержание

Деление числа в данном отношении

Представим себе такую историю…

– Саша, чем ты занимаешься? – поинтересовался у друга Паша.

– Хочу приготовить мороженое, – ответил Саша. – Уже и рецепт нашёл, и подготовил все ингредиенты, но вот только разобраться не могу, сколько чего брать.

– А что в рецепте написано? – уточнил Паша.

– В рецепте сказано, что для приготовления мороженого нужно смешать 3 части молока, 2 части сливок и 1 часть сахара, – прочитал Саша. – А как эти части высчитать, если я хочу приготовить, например, 3 килограмма мороженого?

– И вправду, сложная задача у тебя получается, – задумался Паша. – Как эти части считать, не понятно. Но я знаю, кто нам сможет помочь!

– Ребята, прежде чем я отвечу на ваш вопрос, давайте немного разомнёмся и выполним устные задания, – предложил Мудряш.

– Давайте сверимся! – сказал Мудряш. — Посмотрите, что у вас должно было получиться!

– Ну а теперь вернёмся к вашему вопросу, – начал Мудряш.

– Чтобы ответить на вопрос «Сколько каких ингредиентов нужно взять для приготовления смеси мороженого?», прежде всего нужно научиться выполнять деление числа в данном отношении. Итак, вы хотите приготовить 3 килограмма мороженого. Для удобства давайте переведём килограммы в граммы, всё же так будет легче и привычнее считать.

– Так как 1 килограмм равен 1000 грамм, – стал размышлять Саша, – значит, я хочу приготовить 3000 грамм мороженого.

– Хорошо! – согласился Мудряш. – По рецепту для приготовления мороженого нужно смешать 3 части молока, 2 части сливок и 1 часть сахара. Будем считать, что смесь мороженого состоит из частей, имеющих одинаковые массы. Тогда как посчитать, сколько приходится на 1 часть?

– Нужно 3000 разделить на 6, – ответил Паша.

– Правильно! – сказал Мудряш. – Значит, масса одной части смеси равна 500 граммам. По рецепту молоко в смеси составляет 3 части, сливки – 2 части, а сахар – 1 часть.

Посчитайте, чему же будут равны эти части.

– Тогда масса молока в смеси будет равна и равна 1500 граммам, – принялся считать Саша. – Масса сливок будет равна и равна 1000 грамм, а масса сахара будет равна и равна 500 граммам.

– Получается, что для приготовления 3 килограммов мороженого нужно взять 1500 грамм молока, добавить 1000 грамм сливок, а затем добавить 500 грамм сахара? – решил уточнить Паша.

– Всё верно! – согласился Мудряш. – Из решения вашей задачи следует, что число 3000 можно представить в виде суммы трёх слагаемых – 1500, 1000 и 500, отношение которых равно . В таких случаях говорят, что число 3000 разделили в отношении . Также можно сказать, что число 3000 представили в виде суммы трёх слагаемых, пропорциональных числам 3, 2 и 1.

– И совсем несложная задача оказалась, – заметил Саша. – Теперь я без труда могу приготовить мороженое.

– Эту же задачу можно было решить и другим способом, – продолжил Мудряш. – Пусть масса одной части смеси мороженого составляет х грамм. Тогда массы молока, сливок и сахара составляют соответственно 3х грамм, 2х грамм и х грамм. Поскольку масса всей смеси мороженого равна 3000 грамм, то можем составить уравнение . Решим это уравнение. Получим, что . Отсюда . Тогда массы молока, сливок и сахара равны соответственно грамм, грамм и грамм.

– Сделаем вывод, – сказал Мудряш. – Чтобы разделить число в данном отношении, можно разделить это число на сумму членов отношения, а затем результат умножить на каждый член отношения.

– А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько заданий.

Задание первое: разделите числа в указанных отношениях: а) число в отношении ; б) число в отношении .

Решение: нужно разделить число 12 в отношении 1 к 3. Будем считать, что всё число состоит из частей. Значит, 1 часть равна . Тогда 3 части будут равны . Следовательно, число двенадцать можно разделить в отношении 1 к 3 так: 3 и 9.

В следующем условии нам нужно разделить число 3,5 в отношении 3 к 4. Будем считать, что всё число состоит из частей. Тогда 1 часть равна . Отсюда 3 части числа равны . Следовательно, число 3,5 можно разделить в отношении 3 к 4 так: 1,5 и 2.

Следующее задание:

два числа относятся как 4 к 7. Найдите эти числа, зная, что: их сумма равна 110, их разность равна 12.

Решение: обозначим за х одну часть. Тогда можем записать, что первое число равно 4х, второе – 7х. В первом условии сказано, что сумма этих чисел равна 110. Составим уравнение . Решим его. Получим . Отсюда . Значит, первое число равно , второе – .

Во втором условии сказано, что разность этих чисел равна 12. Составим уравнение . Решим его. Получим . Отсюда . Значит, первое число равно , второе – .

Решим задачу: стороны прямоугольника относятся как 2 к 3. Найдите площадь этого прямоугольника, если его периметр равен 20 сантиметров.

Решение: обозначим за х длины частей, из которых состоят стороны прямоугольника. Так как периметр прямоугольника равен удвоенной сумме длин его соседних сторон, то можем составить уравнение: . Решим уравнение. Получим . Отсюда . Следовательно, одна сторона прямоугольника равна сантиметрам, вторая – сантиметрам. Площадь прямоугольника равна произведению длин соседних сторон. Тогда площадь прямоугольника равна см

2. Запишем ответ.

И решим ещё одну задачу. Для приготовления фарфора смешивают 25 частей белой глины, 2 части песка и 1 часть гипса. Сколько нужно взять каждого материала, чтобы приготовить 504 грамма смеси?

Решение: будем считать, что вся смесь состоит из частей, имеющих одинаковые массы. Тогда 1 часть содержит грамм. Следовательно, чтобы приготовить 504 грамма смеси фарфора, нужно взять: грамм белой глины, грамм песка и грамм гипса.

Не забудем записать ответ.

Онлайн калькулятор деления числа в данном отношении

0
AC		+/-	÷
7	8	9	×
4	5	6	—
1	2	3	+
0	00	,	=

При помощи данного калькулятора вы можете легко разделить число в данном отношении и получить подробное решение

Исходное число

Укажите количество частей в отношении
2345

Укажите значение членов отношения

: : : :

Понятие отношение двух и более чисел подробно описано в данной статье.

Вам могут также быть полезны следующие сервисы

Калькуляторы (Теория чисел)

Калькулятор выражений

Калькулятор со скобками

Калькулятор разложения числа на простые множители

Калькулятор НОД и НОК

Калькулятор НОД и НОК по алгоритму Евклида

Калькулятор НОД и НОК для любого количества чисел

Представление многозначных чисел в виде суммы разрядных слагаемых

Калькулятор деления числа в данном отношении

Калькулятор процентов

Калькулятор перевода числа с Е в десятичное

Калькулятор экспоненциальной записи чисел

Калькулятор нахождения факториала числа

Калькулятор нахождения логарифма числа

Калькулятор квадратных уравнений

Калькулятор остатка от деления

Калькулятор корней с решением

Калькулятор нахождения периода десятичной дроби

Калькулятор больших чисел

Калькулятор округления числа

Калькулятор свойств корней и степеней

Калькулятор комплексных чисел

Калькулятор среднего арифметического

Калькулятор арифметической прогрессии

Калькулятор геометрической прогрессии

Калькулятор модуля числа

Калькулятор абсолютной погрешности приближения

Калькулятор абсолютной погрешности

Калькулятор относительной погрешности

Дроби

Калькулятор интервальных повторений

Учим дроби наглядно

Калькулятор сокращения дробей

Калькулятор преобразования неправильной дроби в смешанную

Калькулятор преобразования смешанной дроби в неправильную

Калькулятор сложения, вычитания, умножения и деления дробей

Калькулятор возведения дроби в степень

Калькулятор перевода десятичной дроби в обыкновенную

Калькулятор перевода обыкновенной дроби в десятичную

Калькулятор сравнения дробей

Калькулятор приведения дробей к общему знаменателю

Калькуляторы (тригонометрия)

Калькулятор синуса угла

Калькулятор косинуса угла

Калькулятор тангенса угла

Калькулятор котангенса угла

Калькулятор секанса угла

Калькулятор косеканса угла

Калькулятор арксинуса угла

Калькулятор арккосинуса угла

Калькулятор арктангенса угла

Калькулятор арккотангенса угла

Калькулятор арксеканса угла

Калькулятор арккосеканса угла

Калькулятор нахождения наименьшего угла

Калькулятор определения вида угла

Калькулятор смежных углов

Калькуляторы систем счисления

Калькулятор перевода чисел из арабских в римские и из римских в арабские

Калькулятор перевода чисел в различные системы счисления

Калькулятор сложения, вычитания, умножения и деления двоичных чисел

Системы счисления теория

N₂ | Двоичная система счисления

N₃ | Троичная система счисления

N₄ | Четырехичная система счисления

N₅ | Пятеричная система счисления

N₆ | Шестеричная система счисления

N₇ | Семеричная система счисления

N₈ | Восьмеричная система счисления

N₉ | Девятеричная система счисления

N₁₁ | Одиннадцатиричная система счисления

N₁₂ | Двенадцатеричная система счисления

N₁₃ | Тринадцатеричная система счисления

N₁₄ | Четырнадцатеричная система счисления

N₁₅ | Пятнадцатеричная система счисления

N₁₆ | Шестнадцатеричная система счисления

N₁₇ | Семнадцатеричная система счисления

N₁₈ | Восемнадцатеричная система счисления

N₁₉ | Девятнадцатеричная система счисления

N₂₀ | Двадцатеричная система счисления

N₂₁ | Двадцатиодноричная система счисления

N₂₂ | Двадцатидвухричная система счисления

N₂₃ | Двадцатитрехричная система счисления

N₂₄ | Двадцатичетырехричная система счисления

N₂₅ | Двадцатипятеричная система счисления

N₂₆ | Двадцатишестеричная система счисления

N₂₇ | Двадцатисемеричная система счисления

N₂₈ | Двадцативосьмеричная система счисления

N₂₉ | Двадцатидевятиричная система счисления

N₃₀ | Тридцатиричная система счисления

N₃₁ | Тридцатиодноричная система счисления

N₃₂ | Тридцатидвухричная система счисления

N₃₃ | Тридцатитрехричная система счисления

N₃₄ | Тридцатичетырехричная система счисления

N₃₅ | Тридцатипятиричная система счисления

N₃₆ | Тридцатишестиричная система счисления

Калькуляторы площади геометрических фигур

Площадь квадрата

Площадь прямоугольника

КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ

Калькуляторы (Комбинаторика)

Калькулятор нахождения числа перестановок из n элементов

Калькулятор нахождения числа сочетаний из n элементов

Калькулятор нахождения числа размещений из n элементов

Калькуляторы линейная алгебра и аналитическая геометрия

Калькулятор сложения и вычитания матриц

Калькулятор умножения матриц

Калькулятор транспонирование матрицы

Калькулятор нахождения определителя (детерминанта) матрицы

Калькулятор нахождения обратной матрицы

Длина отрезка.

Онлайн калькулятор расстояния между точками

Онлайн калькулятор нахождения координат вектора по двум точкам

Калькулятор нахождения модуля (длины) вектора

Калькулятор сложения и вычитания векторов

Калькулятор скалярного произведения векторов через длину и косинус угла между векторами

Калькулятор скалярного произведения векторов через координаты

Калькулятор векторного произведения векторов через координаты

Калькулятор смешанного произведения векторов

Калькулятор умножения вектора на число

Калькулятор нахождения угла между векторами

Калькулятор проверки коллинеарности векторов

Калькулятор проверки компланарности векторов

Генератор Pdf с примерами

Тренажёры решения примеров

Тренажёр таблицы умножения

Тренажер счета для дошкольников

Тренажер счета на внимательность для дошкольников

Тренажер решения примеров на сложение, вычитание, умножение, деление.

Найди правильный ответ.

Тренажер решения примеров с разными действиями

Тренажёры решения столбиком

Тренажёр сложения столбиком

Тренажёр вычитания столбиком

Тренажёр умножения столбиком

Тренажёр деления столбиком с остатком

Калькуляторы решения столбиком

Калькулятор сложения, вычитания, умножения и деления столбиком

Калькулятор деления столбиком с остатком

Конвертеры величин

Конвертер единиц длины

Конвертер единиц скорости

Конвертер единиц ускорения

Цифры в текст

Калькуляторы (физика)

Механика

Калькулятор вычисления скорости, времени и расстояния

Калькулятор вычисления ускорения, скорости и перемещения

Калькулятор вычисления времени движения

Калькулятор времени

Второй закон Ньютона.

Калькулятор вычисления силы, массы и ускорения.

Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния.

Импульс тела. Калькулятор вычисления импульса, массы и скорости

Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы.

Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения

Оптика

Калькулятор отражения и преломления света

Электричество и магнетизм

Калькулятор Закона Ома

Калькулятор Закона Кулона

Калькулятор напряженности E электрического поля

Калькулятор нахождения точечного электрического заряда Q

Калькулятор нахождения силы F действующей на заряд q

Калькулятор вычисления расстояния r от заряда q

Калькулятор вычисления потенциальной энергии W заряда q

Калькулятор вычисления потенциала φ электростатического поля

Калькулятор вычисления электроемкости C проводника и сферы

Конденсаторы

Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе

Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе

Калькулятор вычисления энергии W заряженного конденсатора

Калькулятор вычисления энергии W заряженного конденсатора.

Для плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов

Калькуляторы по астрономии

Вес тела на других планетах

Ускорение свободного падения на планетах Солнечной системы и их спутниках

Генераторы

Генератор примеров по математике

Генератор случайных чисел

Генератор паролей

Ответы Задание 6 1 Часть § 1.3. Деление числа в данном отношении ГДЗ по математике 6 класс рабочая тетрадь Ерина к учебнику Никольского

1 Часть

§ 1.1. Отношения чисел и величин

12345678910111213

§ 1.2. Масштаб

123456789101112

§ 1.3. Деление числа в данном отношении

12345678

§ 1.

4. Пропорции

12345678910111213

§ 1.5. Прямая и обратная пропорциональность

123456789101112

§ 1.6. Понятие о проценте

123456789

§ 1.7. Задачи на проценты

1234567891011121314

§ 1.8.. Круговые диаграммы

1234567

§ 1.8. Дополнение к главе 1

1. Задачи на перебор всех возможных вариантов

12345678910111213141516

2. Вероятность события

12345678910

3. Занимательные задачи

1234567891011

§ 2.1. Отрицательные целые числа

123456789101112

§ 2.2. Противоположные числа. Модуль числа

12345678910111213141516

§ 2.3. Сравнение целых чисел

1234567891011

§ 2.

4. Сложение целых чисел

1234567891011121314151617181920

§ 2.5. Законы сложения целых чисел

1234567

§ 2.6. Разность целых чисел

1234567891011

§ 2.7. Произведение целых чисел

123456789101112

§ 2.8. Частное целых чисел

12345678

§ 2.9. Распределительный закон

123456789101112

§ 2.10. Раскрытие скобок и заключение в скобки

1234567891011

§ 2.11. Действия с суммами нескольких слагаемых

12345678910

§ 2.12.. Представление целых чисел на координатной оси

1234567891011

§ 2.12. Дополнения к главе 2

1. Фигуры на плоскости, симметричные относительно точки

1234567891011

2. Занимательные задачи

1234567

§ 3.1. Отрицательные дроби

12345678910111213141516

§ 3.2. Рациональные числа

1234567891011

§ 3.3. Сравнение рациональных чисел

12345678910

§ 3.4. Сложение и вычитание дробей

1234567891011121314151617181920

§ 3.5. Умножение и деление дробей

123456789101112131415161718

§ 3.6. Законы сложения и умножения

123456789

§ 3.7. Смешанные дроби произвольного знака

1234567891011121314

2 Часть

§ 3.8. Изображение рациональных чисел на координатной оси

1234567891011121314

§ 3.9. Уравнения

1234567891011

§ 3.10.. Решение задач с помощью уравнений

12345678910

§ 3.

10. ДОПОЛНЕНИЯ К ГЛАВЕ 3

1. Буквенные выражения

123456789101112131415161718192021

2. Фигуры на плоскости, симметричные относительно прямой

1234

§ 4.1. Понятие положительной десятичной дроби

23456789

§ 4.2. Сравнение положительных десятичных дробей

1234567891011

§ 4.3. Сложение и вычитание положительных десятичных дробей

123456789

§ 4.4. Перенос запятой в положительной десятичной дроби

123456789101112131415

§ 4.5. Умножение положительных десятичных дробей

12345678910111213

§ 4.6. Деление положительных десятичных дробей

1234567891011121314

§ 4.7. Десятичные дроби и проценты

12345678910

§ 4.

8. Сложные задачи на проценты

12345678910

§ 4.9. Десятичные дроби произвольного знака

123456789

§ 4.10. Приближение десятичных дробей

1234567891011

§ 4.11.. Приближение суммы, разности, произведения и частного двух чисел

123456

§ 4.11. ДОПОЛНЕНИЯ К ГЛАВЕ 4

1. Расчеты с помощью микрокалькулятора

1234

2. Процентные расчеты с помощью калькулятора

1234

3. Фигуры в пространстве, симметричные относительно плоскости

12345

§ 5.1. Разложение положительной обыкновенной дроби в конечную десятичную дробь

1234567891011

§ 5.2. Бесконечные периодические десятичные дроби

1234567

§ 5.3. Периодичность десятичного разложения обыкновенной дроби

12345

§ 5.

4. Непериодические бесконечные десятичные дроби

123456

§ 5.5. Действительные числа

123456789

§ 5.6. Длина отрезка

12345678910

§ 5.7. Длина окружности. Площадь круга

1234567891011121314151617

§ 5.8. Координатная ось

1234567891011121314

§ 5.9. Декартова система координат на плоскости

123456789

§ 5.10. Столбчатые диаграммы и графики

1234567891011121314

Средняя оценка 0 / 5. Количество оценок: 0

Оценок пока нет. Поставьте оценку первым.

Ответы Задание 4 1 Часть § 1.3. Деление числа в данном отношении ГДЗ по математике 6 класс рабочая тетрадь Ерина к учебнику Никольского

1 Часть

§ 1.

1. Отношения чисел и величин

12345678910111213

§ 1.2. Масштаб

123456789101112

§ 1.3. Деление числа в данном отношении

12345678

§ 1.4. Пропорции

12345678910111213

§ 1.5. Прямая и обратная пропорциональность

123456789101112

§ 1.6. Понятие о проценте

123456789

§ 1.7. Задачи на проценты

1234567891011121314

§ 1.8.. Круговые диаграммы

1234567

§ 1.8. Дополнение к главе 1

1. Задачи на перебор всех возможных вариантов

12345678910111213141516

2. Вероятность события

12345678910

3. Занимательные задачи

1234567891011

§ 2.

1. Отрицательные целые числа

123456789101112

§ 2.2. Противоположные числа. Модуль числа

12345678910111213141516

§ 2.3. Сравнение целых чисел

1234567891011

§ 2.4. Сложение целых чисел

1234567891011121314151617181920

§ 2.5. Законы сложения целых чисел

1234567

§ 2.6. Разность целых чисел

1234567891011

§ 2.7. Произведение целых чисел

123456789101112

§ 2.8. Частное целых чисел

12345678

§ 2.9. Распределительный закон

123456789101112

§ 2.10. Раскрытие скобок и заключение в скобки

1234567891011

§ 2.11. Действия с суммами нескольких слагаемых

12345678910

§ 2.

12.. Представление целых чисел на координатной оси

1234567891011

§ 2.12. Дополнения к главе 2

1. Фигуры на плоскости, симметричные относительно точки

1234567891011

2. Занимательные задачи

1234567

§ 3.1. Отрицательные дроби

12345678910111213141516

§ 3.2. Рациональные числа

1234567891011

§ 3.3. Сравнение рациональных чисел

12345678910

§ 3.4. Сложение и вычитание дробей

1234567891011121314151617181920

§ 3.5. Умножение и деление дробей

123456789101112131415161718

§ 3.6. Законы сложения и умножения

123456789

§ 3.7. Смешанные дроби произвольного знака

1234567891011121314

2 Часть

§ 3.

8. Изображение рациональных чисел на координатной оси

1234567891011121314

§ 3.9. Уравнения

1234567891011

§ 3.10.. Решение задач с помощью уравнений

12345678910

§ 3.10. Дополнения к главе 3

1. Буквенные выражения

123456789101112131415161718192021

2. Фигуры на плоскости, симметричные относительно прямой

1234

§ 4.1. Понятие положительной десятичной дроби

23456789

§ 4.2. Сравнение положительных десятичных дробей

1234567891011

§ 4.3. Сложение и вычитание положительных десятичных дробей

123456789

§ 4.4. Перенос запятой в положительной десятичной дроби

123456789101112131415

§ 4.5. Умножение положительных десятичных дробей

12345678910111213

§ 4.

6. Деление положительных десятичных дробей

1234567891011121314

§ 4.7. Десятичные дроби и проценты

12345678910

§ 4.8. Сложные задачи на проценты

12345678910

§ 4.9. Десятичные дроби произвольного знака

123456789

§ 4.10. Приближение десятичных дробей

1234567891011

§ 4.11.. Приближение суммы, разности, произведения и частного двух чисел

123456

§ 4.11. Дополнения к главе 4

1. Расчеты с помощью микрокалькулятора

1234

2. Процентные расчеты с помощью калькулятора

1234

3. Фигуры в пространстве, симметричные относительно плоскости

12345

§ 5.1. Разложение положительной обыкновенной дроби в конечную десятичную дробь

1234567891011

§ 5.

2. Бесконечные периодические десятичные дроби

1234567

§ 5.3. Периодичность десятичного разложения обыкновенной дроби

12345

§ 5.4. Непериодические бесконечные десятичные дроби

123456

§ 5.5. Действительные числа

123456789

§ 5.6. Длина отрезка

12345678910

§ 5.7. Длина окружности. Площадь круга

1234567891011121314151617

§ 5.8. Координатная ось

1234567891011121314

§ 5.9. Декартова система координат на плоскости

123456789

§ 5.10. Столбчатые диаграммы и графики

1234567891011121314

Вам понравился решебник?

Средняя оценка 0 / 5. количество оценок 0

Оценок пока нет. Поставьте оценку первым.

Урок математики в 6-м классе по теме:» Как разделить величину в данном отношении»

Аверченко Галина Алексеевна

Разделы: Математика

Цель: формировать навык деления величин в данном отношении.

ХОД УРОКА

I. Организационный момент

II. Актуализация знаний

Предложить учащимся закончить фразу:

Отношение двух чисел – это …
Отношение 1:5 показывает, что …
Отношение 3:2 показывает, что …
Если отношение двух чисел больше единицы, то это означает, что …
Если первое число в три раза больше второго, то они относятся как …
Если первое число в полтора раза меньше второго, то они относятся как …
Если первое число относится ко второму как 4:7, то второе число относится к первому как …
Отношение 4:12 равно отношению …
Отношение 2:5 можно записать как отношение 6: …

III. Мотивация

Привести примеры, когда необходимо умение делить какую-либо величину в данном отношении.
Учитель: Я предлагаю Вам решить свою задачу:

Задача. В классе 24 ученика. Из них 10 мальчиков и 14 девочек. В каком отношении находится количество мальчики к количеству девочек?

Ученики: 10 : 14, или 5 : 7.
Учитель: Количество мальчиков ко всему количеству ребят в классе.
Ученики: 10 : 24, или 5 : 12
Учитель: Количество девочек ко всему количеству ребят в классе.
Ученики: 14 : 24, или 7 : 12
Учитель: Прекрасно! А как узнать сколько учащихся класса получили за работу «пять» если известно, что таких учеников шестая часть?
Ученики: 24 : 6 = 4 (учащихся)
Учитель: Как узнать, сколько учащихся класса получили «четыре», если известно, что количество таких ребят относится к общему количеству учащихся как 2:6?
Ученики (после обсуждения): Мы не знаем, как разделить величину в данном отношении.

IV. Целеполагание

Учитель: Значит, мы должны научиться делить величину в данном отношении.
Записываем тему урока в тетрадь.

V. Учебные действия

Задача. Отец с сыном собрали 18 кг яблок, причем отец собрал в 2 раза больше яблок, чем сын. Сколько килограммов яблок собрал каждый из них?
Решим задачу.
Поскольку отец собрал в 2 раза больше яблок, то количество собранных отцом и сыном яблок находится в отношении 2 : 1 . Значит, нужно 18 кг разделить на две части, отношение которых равно 2 : 1. Всего имеется 2 + 1 = 3 части, тогда на каждую часть приходится 18 : 3 = 6 (кг) яблок.
Поскольку сын собрал одну часть, то на его долю приходится 6 * 1 = 6 (кг) яблок. Отец собрал 2 части, то есть 6 * 2 = 12 (кг) яблок.
– Скажите, какие действия мы последовательно выполняли, чтобы решить задачу?

Узнали, сколько частей собранных яблок принадлежит отцу, а сколько сыну.
Сложили эти части, получив общее количество частей.
Разделили 18 кг собранных яблок на общее количество частей, получив, сколько килограммов яблок приходится на каждую часть.
Вычислили, сколько яблок собрал отец и сколько сын.

Учитель. Рассмотрим еще один пример.
Разобрать пример из учебника и также выделить последовательность действий, которые необходимо было совершить, чтобы решить задачу.
Учитель. Мы рассмотрели решение двух задач. Что общего в этих задачах
Ученики. Для их решения необходимо было разделить величину в данном отношении.
Учитель. Сравните действия, которые мы выполняли, чтобы разделить величины в данном отношении.
Ученики. Они похожи.
Учитель. Попробуйте вывести алгоритм деления величины в данном отношении

Алгоритм

Чтобы разделить число в отношении а : в, нужно:

Сложить а и в. (Получим общее количество частей.)
Разделить данное число на а + в. (Получим, сколько приходится на каждую часть.)
Умножить результат деления на а. (Получим число, которое содержит а частей данного числа.)
Умножить результат деления на в. (Получим число, которое содержит в частей данного числа.)

– А теперь, работая в группах, придумайте сами задачи, которые решались бы с помощью данного алгоритма.

VI. Контроль

Заполните таблицу.

Число	12	36	45	72	110	144
В каком отношении разделить	1:3	5:1	2:3	4:5	7:3	5:7
Результат	3 и 9

Учитель: Как разделить величину в данном отношении. Необходимо, чтобы учащиеся несколько раз проговорили этот алгоритм (можно своими словами).

VII. Оценка

Самооценка с помощью пятибалльной шкалы.

6.02.2010

Как Разделить Число на Произведение

Основные определения

Давайте для начала вспомним, что такое деление, умножение и, как их правильно записывать.

Умножение — арифметическое действие в виде краткой записи суммы одинаковых слагаемых.

Запись: 2 * 3 = 6, где 2 — множимое, 3 — множитель, 6 — произведение.
2 * 3 = 3 + 3 = 6

В случае, если множимое и множитель поменять ролями, произведение остается одним и тем же.

Например: 3 * 2 = 2 + 2 + 2 = 6.

Поэтому и множитель, и множимое называют сомножителями.

Деление — арифметическое действие обратное умножению.

Запись: 20 : 5 = 4 или 20/5 = 4, где 20 — делимое, 5 — делитель, 4 — частное.

В этом случае произведение делителя 5 и частного 4, в качестве проверки, дает делимое 20.

Если в результате деления, частное является не целым числом, то его можно представить в виде дроби.

Свойства деления в виде формул:

Распределительные свойства

(a + b) : c = a : c + b : c

(a — b) : c = a : c — b : c

(a * b) : c = (a : c) * b = (b : c) * a

a : (b * c) = (a : b) : c = (a : c) : b

Действия с единицей и нулём

a : 1 = a

a : a = 1

0 : a = 0 (a ≠ 0)

на нуль делить нельзя

Практикующий детский психолог Екатерина Мурашова

Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков

Способы деления числа на произведение

Число можно разделить на произведение двумя способами. Сформулируем правило деления числа на произведение для каждого способа и попрактикуемся на примерах.

1 способ

Чтобы разделить число на произведение, нужно сначала выполнить умножение в скобках, а затем разделить число на полученный результат.

Так, например, чтобы найти значение выражения: 666 : (3 * 2), нужно сначала перемножить то, что находится в скобках: 3 * 2 = 6.

Затем и разделить 666 на полученный результат: 666 : 6 = 111. Значит 666 : (3 * 2) = 666 : 6 = 111.

Если число, которое нужно разделить на произведение, делится на каждый сомножитель, из которого состоит данное произведение — можно воспользоваться вторым способом.

2 способ

Чтобы разделить число на произведение, нужно разделить это число на первый сомножитель, а полученный результат разделить на второй сомножитель.

Например, чтобы найти значение выражения: 120 : (5 * 6), нужно сначала разделить 120 на 5: 120 : 5 = 24. Далее, полученное частное 24 разделить на 6: 24 : 6 = 4. А Теперь 120 : (5 * 6) = (120 : 5) : 6 = 24 : 6 = 4.

Так как от перестановки множителей произведение не меняется, то множители можно легко поменять местами: 120 : (6 * 5) и разделить 120 сначала на 6, а затем полученный результат разделить на 5: 120 : (6 * 5) = (120 : 6) : 5 = 20 : 5 = 4.

Проще говоря, не важно на какой множитель первым делить число — результат будет одинаковым. Проверим:

120 : (5 * 6) = (120 : 5) : 6 = 24 : 6 = 4

тоже самое, что и

120 : (6 * 5) = (120 : 6) : 5 = 20 : 5 = 4.

Из этого примера делаем вывод, что значение частного не изменится от порядка выполнения действий.

Эти правила иногда называют свойствами деления числа на произведение. Но, по сути, неважно, как это называть. Главное — как это работает. Далее попрактикуемся на примерах.

Примеры деления числа на произведение

Пример 1. Применить правило деления числа на произведение двух чисел:
24 : ( 3 * 4).

Как рассуждаем:

Чтобы разделить число на произведение, вычислим сначала произведение в скобках: 3 * 4 = 12.

Подставляем полученное число в выражение:

24 : ( 3 * 4) = 24 : 12 = 2.

Вот и ответ. А теперь решим это же выражение другим способом.

Чтобы разделить число на произведение чисел, нужно сначала число 24 разделить на первый множитель 3. А после, разделить полученный на второй множитель 8:

24 : ( 3 * 4) = 24 : 3 : 4 = 8 : 4 = 2.

А как можно еще решить это выражение?

Чтобы число разделить на произведение, нужно сначала число 24 разделить на второй множитель 4. И полученный результат разделить на первый множитель 3:

24 : ( 3 * 4) = 24 : 4 : 3 = 6 : 3 = 2.

Вот, как это работает! Мы нашли значение выражения разными способами, при этом результаты получились одинаковыми.

Пример 2. Вычислить: тысячу разделить на произведение двадцати и пяти.

Ответ:

1000 : (20 * 5) = 1000 : 100 = 100

1000 : (20 * 5) = 1000 : 20 : 5 = 50 : 5 = 10

1000 : (20 * 5) = 1000 : 5 : 2 = 200 : 2 = 10

Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Что такое деление? Определение, формула, шаги, правило, примеры

Допустим, у вас есть 12 пончиков, и вы хотите поровну раздать их трем своим друзьям. Как вы справедливо решаете, сколько получит каждый?

Просто раздели пончики поровну между друзьями! Этот метод распределения группы вещей на равные части называется делением. Это одна из четырех основных арифметических операций, которая дает справедливый результат обмена.

Что такое деление в математике?

Деление противоположно умножению. Если 3 группы по 4 дают при умножении 12, то 12, разделенные на 3 равные группы, дают по 4 в каждой группе при делении.

Основная цель деления состоит в том, чтобы увидеть, сколько равных групп образуется или сколько в каждой группе при справедливом разделении.

В приведенном выше примере, чтобы разделить 12 пончиков на 3 одинаковые группы, вам нужно положить по 4 пончика в каждую группу. Таким образом, 12 разделить на 3 даст результат 4.

Математическая запись деления

Существуют различные признаки, которые можно использовать для обозначения дивизии, таких как

Например:

27 ÷ 3
27/3

6620. Числа в уравнении деления

Каждая часть уравнения деления имеет специальное имя.

Дивиденд: Делимое — это число, которое делится в процессе деления.

Делитель: Число, на которое делится делимое, называется делителем.

Частное: Частное — это результат, полученный в процессе деления.

Остаток : Иногда мы не можем точно разделить вещи. Возможно, остался лишний номер. Это оставшееся число называется остатком.

Отношение между этими четырьмя частями может быть выражено следующим образом:

Дивиденд = Делитель x Частное + Остаток

Это также называется формулой деления для проверки правильности ответа или нет.

Например, давайте разделим 16 на 3. Остаток будет 1.

Здесь делимое = 16, делитель = 3, частное = 5 и остаток = 1

Итак, 16 = 3 × 5 + 1

Свойства деления

Чтобы лучше понять деление, давайте рассмотрим несколько общих правил и свойств деления:

1. Если мы разделим целое число (кроме нуля) само по себе, то в частном или ответе всегда будет 1.

Например:

· 7 ÷ 7 = 1

· 25 ÷ 25 = 1

2. Если разделить целое число на ноль, то ответ будет неопределенным.

Например:

6 ÷ 0 = не определено

325 ÷ 0 = не определено

3. Ноль, разделенный на любое число, даст ответ ноль.

Например:

0 ÷ 5 = 0

0 ÷ 100 = 0

4. Если мы разделим целое число (кроме нуля) на 1, ответом будет само число.

Например:

4 ÷ 1 = 4

11 ÷ 1 = 11

5. Если целое число разделить на другое целое число, частное не обязательно будет целым числом.

Например:

15 ÷ 2 = 7,5

20 ÷ 3 = 6,67

6. В случае точного деления (без остатка) делимым является делитель, умноженный на частное. Это свойство выполняется только в том случае, если все три числа являются целыми числами, отличными от нуля.

Например:

Если 30 ÷ 5 = 6, то 5 × 6 = 30

7. Если есть три ненулевых целых числа a, b и c, и b × c = a, то

a ÷ b = c и a ÷ c = b

Например:

5 × 10 = 50, тогда

· 50 ÷ 5 = 10

· 50÷ 10 = 5

Long Division

7 9000 деление — это математический метод деления больших чисел на более мелкие группы или части. Это помогает разбить проблему на простые и легкие шаги.

Длинные шаги деления

Каждое длинное деление можно решить с помощью пяти шагов, указанных ниже.

Вот пример, который поможет вам понять этапы деления.

Давайте рассмотрим несколько примеров деления, чтобы попрактиковаться в длинных шагах деления. Примеры решения себя)

2. Разделение 6148 на 4.

Решение:

С. С. Так, коэффициент = 1537, остаток = 0

3. Разделите 1579 на 6.

Решение:

. Частное = 263, остаток = 1. , R = 0$

Правильный ответ: Q $ = 344 , R = 3$
Частное (целочисленное деление) $1723/5$ равно 344; остаток («остаток») равен 3. 1723 — это делимое, а 5 — делитель.

Правильный ответ: 73
Здесь остаток равен 1. Таким образом, если кейтеринг расставляет 72 стола, 1 человек не сможет занять место на свадьбе.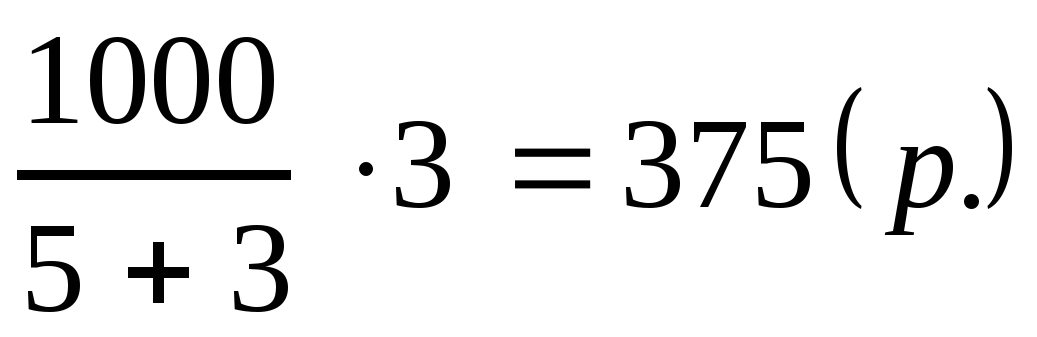 Значит, им предстоит расставить 73 стола.

$\$$2190

$\$$2191

$\$$2192

$\$$2193

Правильный ответ: $\$$2191
Следовательно, каждый получит $\$$2191.

$\$2598

$\$2597

$\$2595

$\$$2594

Правильный ответ: $\$$2594
Следовательно, каждый месяц Гарри зарабатывал $\$$2594.

Часто задаваемые вопросы

Верно ли свойство коммутативности деления?

Коммутативное свойство говорит нам, что если мы можем перемещать или менять местами числа с их позиции при выполнении математических операций, ответ останется прежним.

Это свойство справедливо для умножения и сложения, но не для деления.

Например: 27 × 3 = 3 × 27, но 27 ÷ 3 ≠ 3 ÷ 27

Можно ли разделить путем многократного вычитания?

Да, повторное вычитание — это непрерывное вычитание одного и того же числа из большого числа до тех пор, пока не получится остаток 0 или меньше фактического числа. Разделение — это кратчайший путь к этому процессу.

Есть ли способ проверить частное и остаток в задаче на деление?

Да, вы можете проверить частное и остаток, используя соотношение:

Делимое = Делитель x Частное + Остаток

Обучение соотношению умножения и деления с использованием массивов

Расположение объектов, изображений или чисел в столбцах и строках называется массивом . В этой статье вы узнаете, как использовать массивы, чтобы показать взаимосвязь между умножением и делением.

Ключевой стандарт: Используйте умножение и деление в пределах 100 для решения текстовых задач в ситуациях, связанных с массивами. (3.ОА.А.3)

Учащиеся 3-х классов и старше узнают, что о делении можно думать двумя способами: разделением и измерением. Хотя на этом уровне учащиеся могут не использовать эти названия, вы можете передать значение обоих видов деления, чтобы они могли лучше понять процесс деления. Когда вы делите, чтобы найти количество объектов в каждой группе, это деление называется справедливым разделением или разделением. Например:

Фермер наполняет корзины яблоками. У фермера 24 яблока и 4 корзины. Если она разделит их поровну, сколько яблок она положит в каждую корзину?

Когда вы делите, чтобы найти количество групп, это деление называется измерением или повторным вычитанием. Вы можете продолжать вычитать 4 из 24, пока не достигнете 0. Каждые 4, которые вы вычитаете, представляют собой группу или корзину.

У фермера 24 яблока. Она хочет продать их по цене 4 яблока за 1 доллар. Сколько корзин по 4 штуки она может заполнить?

Array Division

Манипуляции и наглядные пособия важны при обучении умножению и делению. Студенты использовали массивы, чтобы проиллюстрировать процесс умножения. Массивы также могут иллюстрировать деление.

Поскольку деление является обратным или «противоположным» умножению, вы можете использовать массивы, чтобы помочь учащимся понять, как связаны умножение и деление. Если при умножении мы находим произведение двух множителей , то при делении находим недостающий множитель, если известны другой множитель и произведение.

В приведенной ниже модели умножения вы умножаете, чтобы найти общее количество счетчиков. В модели разделения массива вы делите, чтобы найти количество счетчиков в каждой группе. Используются те же три числа. Модель показывает, что деление «отменяет» умножение, а умножение «отменяет» деление. Поэтому при умножении или делении учащиеся могут использовать факт из обратной операции. Например, если учащиеся знают, что 4 × 5 = 20 , они также знают соответствующий факт деления 20 ÷ 4 = 5 или 20 ÷ 5 = 4 . Студенты также могут проверить свою работу, используя обратную операцию.

Связь между умножением и делением

Обратите внимание, что числа в предложениях на умножение и деление имеют специальные названия. При умножении умножаемые числа называются множителями; результат умножения называется произведением. При делении делимое число равно делимое , число которое делит это делитель , а результат деления частное . Обсудите взаимосвязь этих чисел, объясняя, как связаны умножение и деление.

Есть и другие модели, которые учащиеся могут использовать для изучения связи между умножением и делением. Познакомьте учащихся с различными моделями и позвольте учащимся выбрать наиболее полезную модель. Вот пример использования счетчиков для умножения и деления.

Вот пример использования числовой строки.

Еще одна стратегия, которая может оказаться полезной для ваших учеников, — это использование связанного факта умножения для деления. Вот пример.

18 ÷ 6 = ?

Подумайте: 6 × ? = 18 Какое число в шесть раз больше 18?

6 × 3 = 18 , поэтому 18 ÷ 6 = 3 .

Деление на 0 и 1

Когда учащиеся понимают концепцию деления, они могут приступить к изучению правил деления на 0 и 1. Предложите учащимся самостоятельно открыть правила, предложив им использовать счетчики для моделирования деления. Ниже приведены несколько примеров.

Когда любое число (кроме 0) делится само на себя, получается 1 в частном.

Когда любое число делится на 1, в частном получается это число.

Когда 0 делится на любое число (кроме 0), частное равно 0.

Ученикам может быть любопытно, что произойдет, если они разделят на 0. Объясните, что это непростая концепция, и даже профессиональные математики пытаются ее объяснить ! Одна из стратегий, чтобы показать, почему это невозможно, состоит в том, чтобы учащиеся попытались разделить любое число на группы по нулям. Неважно, сколько групп вы создадите, это не сработает.

Деление в реальном мире

Предложите учащимся подумать о взаимосвязи между умножением и делением при решении реальных задач. Например, они могут использовать связанный факт умножения, чтобы найти стоимость единицы товара — например, стоимость одной бейсболки по цене 3 за 18 долларов.

$18 ÷ 3 = ? Подумай: 3 × ? = 18

3 × 6 долларов = 18 долларов, поэтому 18 долларов ÷ 3 = 6 долларов.

Стоимость одной бейсболки составляет 6 долларов.

***

Ищете дополнительную поддержку по вопросу «Как связаны умножение и деление?» Изучите Math 180 , наш революционный подход к математическому вмешательству для 5–12 классов.

Математика 3-5 классы Мероприятия и уроки 1-2 классы Вмешательство

Связанные материалы

Д-р Эми Эндо
Директор по исследованиям в области образования, дополнительный язык и интервенция, язык и грамотность
27 сентября 2022 г.
Ноэль Моррис
Старший директор по взаимодействию с общественностью, HMH; Ведущий HMH Learning Moments: Подкаст учителей в Америке
23 сентября 2022 г.
Кристин Кондон
Shaped Главный редактор
22 сентября 2022 г.

Отдел ÷ | Основы арифметики

На этой странице описаны основы деления (÷) .

См. другие наши арифметические страницы для обсуждения и примеров: сложение ( + ), вычитание (-) и умножение ( × ).

Деление

Обычный письменный символ деления (÷). В электронных таблицах и других компьютерных приложениях используется символ «/» (косая черта).

Деление — это противоположность умножения в математике.

Деление часто считается самой сложной из четырех основных арифметических функций. На этой странице объясняется, как выполнять вычисления деления. Как только мы хорошо разберемся в методе и правилах, мы сможем использовать калькулятор для более сложных вычислений, не делая ошибок.

Разделение позволяет нам разделить или «поделиться» числами, чтобы найти ответ. Например, давайте подумаем, как найти ответ на 10 ÷ 2 (десять разделить на два). Это то же самое, что «делить» 10 конфет между двумя детьми. У обоих детей должно получиться одинаковое количество конфет. В этом примере ответ 5.

Некоторые краткие правила деления:

При делении 0 на другое число ответ всегда будет 0. Например: 0 ÷ 2 = 0. То есть 0 конфет делится поровну между 2 детьми — каждый ребенок получает 0 сладости.
Когда вы делите число на 0, вы вообще не делите (это серьезная проблема в математике). 2 ÷ 0 невозможно. У вас есть 2 конфеты, но нет детей, чтобы разделить их между собой. На 0 делить нельзя.
При делении на 1 ответ совпадает с числом, которое вы делили. 2 ÷ 1 = 2. Две конфеты разделить на одного ребенка.
При делении на 2 число уменьшается пополам. 2 ÷ 2 = 1.
Любое число, деленное на одно и то же число, равно 1. 20 ÷ 20 = 1. Двадцать конфет разделить на двадцать детей — каждый ребенок получает по одной конфете.
Числа должны быть разделены в правильном порядке. 10 ÷ 2 = 5, тогда как 2 ÷ 10 = 0,2. Десять конфет, разделенных на двоих детей, сильно отличаются от 2 конфет, разделенных на 10 детей.
Все дроби, такие как ½, ¼ и ¾, являются суммами деления. ½ равно 1 ÷ 2. Одна конфета делится на двоих детей. См. нашу страницу Фракции для получения дополнительной информации.

Множественные вычитания

Точно так же, как умножение — это быстрый способ вычисления множественных сложений, деление — это быстрый способ выполнения множественных вычитаний.

Например:

Если у Джона в машине 10 галлонов топлива, и он использует 2 галлона в день, сколько дней до того, как у него закончится топливо?

Мы можем решить эту задачу, выполнив серию вычитаний или посчитав в обратном порядке с шагом 2.

В день 1 Джон начинает с 10 галлона и заканчивает 8 галлона. 10 — 2 = 8
В день 2 Джон начинает с 8 галлона и заканчивает 6 галлона. 8 — 2 = 6
В день 3 Джон начинает с 6 галлона и заканчивает 4 галлона. 6 — 2 = 4
В день 4 Джон начинает с 4 галлона и заканчивает 2 галлона. 4 — 2 = 2
В день 5 Джон начинает с 2 галлона и заканчивает 0 галлонов. 2 — 2 = 0

У Джона закончилось топливо на 5-й день.

Более быстрый способ выполнить это вычисление — разделить 10 на 2. То есть, сколько раз 2 делится на 10 или сколько партий по два галлона имеется в десять галлонов? 10 ÷ 2 = 5,

Таблица умножения (см. умножение) может помочь нам найти ответ на простые вычисления деления.

В приведенном выше примере нам нужно было вычислить 10 ÷ 2 . Для этого с помощью таблицы умножения найдите столбец для 2 (красный заштрихованный заголовок). Двигайтесь вниз по столбцу, пока не найдете нужный номер: 10 . Переместитесь по строке влево, чтобы увидеть ответ (красный заштрихованный заголовок) 5 .

Таблица умножения

×	1	2	3	4	5	6	7	8	9	10
1	1	2	3	4	5	6	7	8	9	10
2	2	4	6	8	10	12	14	16	18	20
3	3	6	9	12	15	18	21	24	27	30
4	4	8	12	16	20	24	28	32	36	40
5	5	10	15	20	25	30	35	40	45	50
6	6	12	18	24	30	36	42	48	54	60
7	7	14	21	28	35	42	49	56	63	70
8	8	16	24	32	40	48	56	64	72	80
9	9	18	27	36	45	54	63	72	81	90
10	10	20	30	40	50	60	70	80	90	100

Мы можем выполнить другие простые вычисления деления, используя тот же метод. 56 ÷ 8 = 7 например. Найдите 7 в верхней строке, посмотрите вниз по столбцу, пока не найдете 56 , затем найдите соответствующий номер строки 8 .

Если возможно, вы должны попытаться запомнить приведенную выше таблицу умножения, потому что она значительно ускоряет выполнение простых вычислений умножения и деления.

Деление больших чисел

Вы можете использовать калькулятор для выполнения вычислений с делением, особенно когда вы делите большие числа, которые труднее вычислить в уме. Однако важно понимать, как выполнять вычисления деления вручную. Это полезно, когда у вас нет калькулятора под рукой, но также необходимо, чтобы убедиться, что вы правильно используете калькулятор и не делаете ошибок. Деление может показаться пугающим, но на самом деле, как и в большинстве арифметических операций, оно логично.

Как и в случае со всей математикой, проще всего понять это на примере:

Машине Дэйва нужны новые шины. Ему нужно заменить все четыре шины на машине плюс запаску.

Дэйв получил предложение от местного гаража на 480 фунтов стерлингов, включая шины, установку и утилизацию старых шин. Сколько стоит каждая шина?

Задача, которую нам нужно вычислить, это 480 ÷ 5 . Это то же самое, что сказать, сколько раз 5 будет входить в 480?

Условно запишем так:

Работаем слева направо в логической системе.

Начнем с деления 4 на 5 и сразу наткнемся на проблему. 4 не делится на 5, чтобы получить целое число, так как 5 больше 4.

Язык, который мы используем в математике, может сбивать с толку. Другой способ взглянуть на это — спросить: «Сколько раз 5 входит в 4?».

Мы знаем, что 2 дважды входит в число 4 (4 ÷ 2 = 2), и мы знаем, что 1 входит в число 4 четыре раза (4 ÷ 1 = 4), но 5 не входит в число 4, потому что 5 больше 4.

Число, на которое мы делим (в данном случае 5), должно входить в число, на которое мы делим (в данном случае 4), целое число раз. Как вы увидите, это не обязательно должно быть точное целое число.

Так как 5 не входит в 4, мы ставим 0 в первую колонку (сотни). Для получения справки о столбцах сотен, десятков и единиц см. нашу страницу чисел .

	Сотни	Десятки	Единиц
	0
5	4	8	0

Далее мы двигаемся вправо, чтобы включить столбец десятков. Теперь мы можем увидеть, сколько раз 5 входит в число 48.

5 входит в число 48, поскольку 48 больше 5. Однако нам нужно выяснить, сколько раз оно входит в число 48.

Если мы обратимся к нашей таблице умножения, то увидим, что 9 × 5 = 45 и 10 × 5 = 50 .

48 число, которое мы ищем, находится между этими двумя значениями. Помните, нас интересует целое число раз , которое 5 входит в 48. Десять раз — это слишком много.

Мы видим, что 5 входит в число 48 целое число (9) раз, но не точно, с оставшимися 3.

9 × 5 = 45
48 – 45 = 3

Теперь мы можем сказать, что 5 входит в число 48 девять раз, но с остатком 3. нашли из числа, на которое мы делим: 48 — 45 = 3 .

Таким образом, 5 × 9 = 45, + 3, чтобы получить 48.

Мы можем ввести 9 в столбце десятков в качестве ответа для второй части вычисления и поставить наш остаток перед нашим последним числом в единицах измерения. столбец. Наше последнее число становится 30.

	Сотни	Десятки	Единиц
	0	9
5	4	8	30

Теперь разделим 30 на 5 (или узнаем, сколько раз 5 входит в 30). Используя нашу таблицу умножения, мы видим, что ответ равен ровно 6 без остатка. 5 × 6 = 30. Мы пишем 6 в столбце единиц нашего ответа.

	Сотни	Десятки	Единиц
	0	9	6
5	4	8	30

Поскольку остатка нет, мы закончили расчет и получили ответ 96 .

Новые шины Дейва будут стоить £96 каждая. 480 ÷ 5 = 96 и 96 × 5 = 480 .

Раздел рецептов

Наш последний пример разделения основан на рецепте. Часто при приготовлении пищи рецепты сообщают вам, сколько еды они собираются приготовить, например, достаточно, чтобы накормить 6 человек.

Ингредиенты, указанные ниже, необходимы для приготовления 24 волшебных тортов, однако нам нужно сделать только 8 волшебных тортов. Мы немного изменили ингредиенты для этого примера (оригинальный рецепт: BBC Food).

Первое, что нам нужно установить, это сколько восьмерок в числе 24. Воспользуйтесь приведенной выше таблицей умножения или своей памятью. 3 × 8 = 24 — если мы разделим 24 на 8, мы получим 3. Следовательно, нам нужно разделить каждый ингредиент ниже на 3, чтобы получить нужное количество смеси для приготовления 8 волшебных пирожных.

Ингредиенты

120 г сливочного масла, размягченного при комнатной температуре
120 г сахарной пудры
3 куриных яйца, слегка взбитых
1 чайная ложка ванильного экстракта
120 г самоподнимающейся муки
1-2 столовые ложки молока

Количество масла, сахара и муки одинаковое, 120г. Следовательно, необходимо вычислить 120 ÷ 3 только один раз, так как ответ будет одинаковым для этих трех ингредиентов.

Как и раньше, мы начинаем с левого столбца (сотни) и делим 1 на 3. Однако 3 ÷ 1 не идет, так как 3 больше 1. Далее мы смотрим, сколько раз 3 входит в 12. Используя таблицу умножения, если нужно, мы можем видеть, что 3 входит в 12 ровно 4 раза по без остатка.

	0	4	0
3	1	2	0

120 г ÷ 3, следовательно, 40 г. Теперь мы знаем, что нам понадобится 40 г сливочного масла, сахара и муки.

В исходном рецепте указано 3 яйца, и мы снова делим на 3. Таким образом, 3 ÷ 3 = 1, поэтому необходимо одно яйцо.

Далее по рецепту требуется 1 чайная ложка ванильного экстракта. Нам нужно разделить одну чайную ложку на 3. Мы знаем, что деление можно записать в виде дроби, поэтому 1 ÷ 3 — это то же самое, что ⅓ (одна треть). Вам понадобится ⅓ чайной ложки ванильного экстракта, хотя на самом деле может быть сложно точно отмерить ⅓ чайной ложки!

Оценка может быть полезной, и единицы измерения можно изменить!

Мы можем посмотреть на это по-другому, если мы знаем, что одна чайная ложка равна 5 мл или 5 миллилитрам. (Если вам нужна помощь с единицами измерения, см. нашу страницу Системы измерения .) Если мы хотим быть более точными, мы можем попробовать разделить 5 мл на 3. 3 входит в 5 один раз (3) с 2 в остатке. 2 ÷ 3 равно ⅔, поэтому 5 мл, разделенные на 3, дают нам 1⅔ мл, что в десятичных дробях равно 1,666 мл. Мы можем использовать наши навыки оценки и сказать, что одна чайная ложка, разделенная на три, чуть больше, чем полтора мл. Если у вас на кухне есть несколько таких крошечных мерных ложек, вы можете быть очень точны!

Мы можем оценить ответ, чтобы убедиться, что мы правы. Три партии по 1,5 мл дают нам 4,5 мл. Таким образом, три партии «чуть больше 1,5 мл» дают нам около 5 мл. Рецепты редко являются точной наукой, поэтому небольшая оценка может быть забавой и хорошей практикой для нашей ментальной арифметики.

Далее по рецепту требуется 1–2 ст.л. молока. Это от 1 до 2 столовых ложек молока. У нас нет определенного количества, и то, сколько молока вы добавите, будет зависеть от консистенции вашей смеси.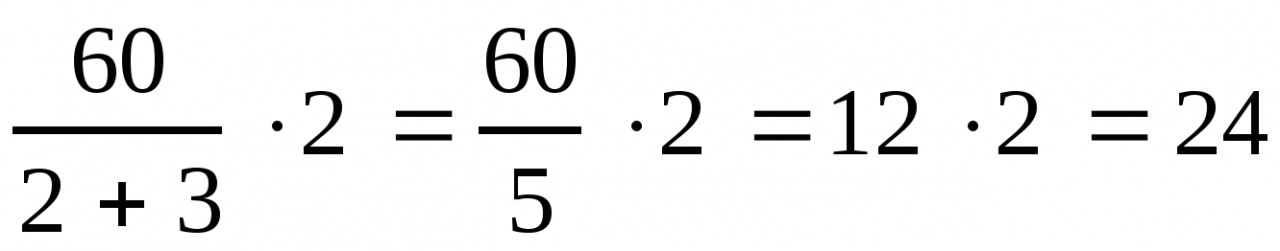

Мы уже знаем, что 1 ÷ 3 равно ⅓, а 2 ÷ 3 равно ⅔. Таким образом, нам понадобится ⅓–⅔ столовой ложки молока, чтобы приготовить восемь волшебных лепешек. Давайте посмотрим на это с другой стороны. Одна столовая ложка равна 15 мл. 15 ÷ 3 = 5, поэтому ⅓–⅔ столовой ложки соответствует 5–10 мл, то есть 1–2 чайным ложкам!

Дополнительная литература по навыкам, которые вам нужны
Основы счета
Часть руководства по навыкам, которые вам необходимы для счета
операции и начать манипулировать числами. Он также включает примеры из реальной жизни, чтобы прояснить, как эти концепции полезны в реальной жизни.
Если вы хотите освежить свои знания или помочь своим детям в обучении, эта книга для вас.
Выкройки в Отделе
Предоставил:
Диего Вт, 15 марта 2022 г., 07:44 UTC
Сюда входит делимость, которая указывает, делится ли число на другое число. Если число без остатка делится на другое число без остатка, то оно делится на это число.
1. 7 класс Математика Раздел 1: Закономерности и отношения
Раздел 1.1 – Шаблоны в разделе
Делимость относится к тому, делится ли число на другое число.
Если число без остатка делится на другое число без остатка, то оно делится на
на это число.
Например, . 36 делится на 4, так как 9 делится без остатка на 36 (нет остатка
).
Делимость на 10
Рассмотрим следующие числа. Обведите числа, которые
делятся на 10.
44 50 62
75 90 38 40
10 88 120
Как узнать, делится ли число на 10?
Правило: ____________________________________________________________________________________________
Делимость на 2
Рассмотрим следующие числа. Обведите числа, которые делятся на 2.
34 99 59
52 78 67 32
52 46 31
Л. Брентон Пейдж | 1
2. Математика для 7 класса. Часть 1: Закономерности и отношения
Как узнать, делится ли число на 2?
Правило: ____________________________________________________________________________________________
Признак кратности 5
Рассмотрим следующие числа. Обведите числа, которые
делятся на 5.
80 49 61
25 40 57 55
78 10 15
Как узнать, делится ли число на 5?
Правило: ____________________________________________________________________________________________
Пример 1:
Обведите числа, которые делятся и на 2, и на 5.
54 20 33
75 40 48 65
22 10 15
Диаграммы Венна — это диаграммы, в которых круги используются для представления групп и для демонстрации отношений между группами.
Л. Брентон Пейдж | 2
3. 7 класс. Математика. Часть 1: Закономерности и отношения
Мы можем использовать диаграмму Венна, чтобы показать числа, которые делятся на 2 и 5.
Делимое Делимое
на 2 на 5
Делится
на 2 И 5
Примечание. Число, которое не делится ни на одно из чисел, помещается снаружи
Делимость на 4 и 8
Попытка выяснить, какие числа делятся на 4 и 8 может быть
немного сложнее. Тем не менее, мы можем разработать правило, которое поможет нам
быстро понять это, не выполняя длинное деление.
На приведенной ниже таблице сотен обведите кружком все числа
, кратные 4.
Л. Брентон Пейдж | 3
4. Математика для 7 класса. Часть 1. Закономерности и взаимосвязи
На приведенной ниже схеме продолжите построение схемы.
Л. Брентон Пейдж | 4
5. 7 класс. Математика. Часть 1. Закономерности и отношения
Что вы заметили? Запишите правило для чисел, делящихся на 4.
Правило: ____________________________________________________________________________________________
Какое из следующих чисел делится на 4? Обосновать ответ.
24 321 436 2048
Пример 2:
Используя цифры 0-9, замените  в каждом числе на все возможности, которые
сделают каждое число делящимся на 4.
a) 13
b) 148
c ) 234
d) 1552
Признак делимости на 8 аналогичен правилу делимости на 4, но вместо
последние две цифры, смотрим на последние три.
Правило: Число делится на 8, если последние три цифры делятся на 8.
Л. Брентон Пейдж | 5
6. 7 класс Математика Раздел 1: Закономерности и отношения
Пример 1:
Объясните, какие из следующих чисел делятся на 8. Покажите, откуда вы знаете.
а) 5872
б) 12 168
в) 3 024
Л. Брентон Страница | 6
7. 7 класс. Математика. Часть 1: Закономерности и отношения
Раздел 1.2. Дополнительные закономерности в делении
Признаки кратности на 3
Заполните приведенную ниже таблицу. Первый сделан для тебя.
Число Делится на 3? Сумма цифр Сумма цифр делится на 3?
30 да 9+0=9 да
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
071 51 51 51 ?
Правило: ____________________________________________________________________________________________
Л. Брентон Пейдж | 7
8. 7 класс Математика.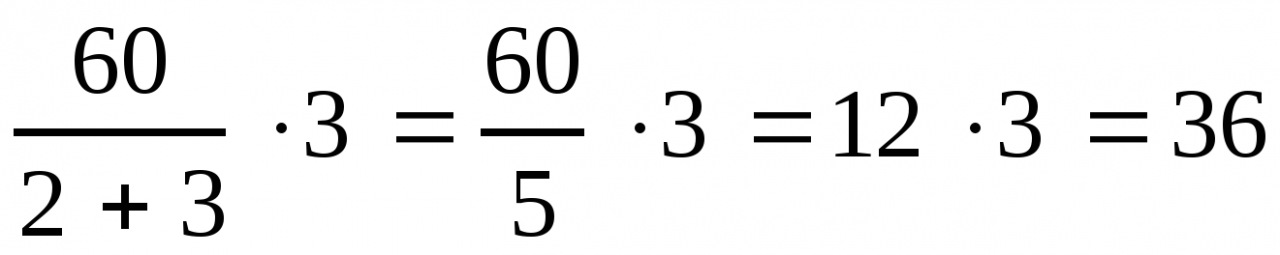 Раздел 1: Закономерности и отношения
Делимость на 9
Заполните таблицу ниже. Первый сделан для вас
Число Делится на 9? Сумма цифр Сумма цифр делится на 9?
18 yes 9+0=9 Yes
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
Что вы заметили?
Правило: ________________________________________________________________________________________________
Л. Брентон Пейдж | 8
9. 7 класс Математика. Часть 1: Закономерности и отношения
Делимость на 6
Отсортируйте следующие числа и поместите их на диаграмму Венна.
12, 21, 36, 42, 56, 61, 74, 88, 93, 135, 246, 453, 728
Делится на 2 Делится на 3 Не делится ни на
Расставим числа на диаграмме Венна!
Что вы заметили в числах в перекрывающихся областях диаграммы?
Запишите правило делимости на 6:
Правило: ____________________________________________________________________________________________
Л. Брентон Пейдж | 9
10. 7 класс Математика Раздел 1: Закономерности и отношения
Мы также можем сортировать числа, используя диаграмму Кэрролла.
Делится на 2 Не делится на 2
Делится на 3
Не делится на 3
Отсортируем эти числа: 1, 11, 15, 20, 24, 35, 47, 98, 100 на 2
Не делится на 2
L. Brenton Page | 10
11. 7 класс Математика Раздел 1: Закономерности и отношения
Раздел 1.3 – Алгебраические выражения
Джо зарабатывает 3 доллара на каждой проданной плитке шоколада. Сколько денег он зарабатывает,
зависит от того, сколько слитков он продает каждую неделю.
Мы можем выразить эту ситуацию как 3b.
 Это означает 3×b (3 умножить на b, так как он получает 3 доллара за плитку шоколада)
 «b» представляет количество плиток шоколада
 «b» называется переменной
3b называется выражением.
В выражении 3b число 3 называется числовым коэффициентом.
Числовой коэффициент: _____________________________________________________________________
Л. Брентон Пейдж | 11
12. 7 класс Математика. Часть 1: Закономерности и отношения
В выражении 3b + 5 число 5 называется константой.
Постоянный член: ____________________________________________________________________________________________
Пример 1:
В каждом выражении определите переменную, числовой коэффициент и постоянный член.
а) 3р+7
Переменная: ____________
Численный коэффициент: ____________
Постоянный член: ____________
b) 4h – 1,3
Переменный: ____________
Численный коэффициент: ____________
Постоянный член: ____________
c) 19 – 6w
Переменный: 7 ____________ ______ 9020 Постоянный член: ____________
d) ½ d+3
Переменный: ____________
Численный коэффициент: ____________
Постоянный член: ____________
Л. Брентон Пейдж | 12
13. 7 класс Математика Раздел 1: Закономерности и отношения
e) 5.4k
Переменная: ____________
Численный коэффициент: ____________
Постоянный член: ____________
f) c – 8
Переменный: ____________
Численный коэффициент: ____________
Пример постоянного члена: ____________
2:
Напишите выражения для следующего:
а) Пять больше, чем число ________________________________________________
б) Число, умноженное на три меньше числа _______________________________________________________
в) число, умноженное на шесть __________________________________________________________
г) число, умноженное на три больше, чем число, умноженное на два _______________________________________________________
д) число, деленное на двадцать _____________________________________________________________
е) сто, разделенное на число ___________________________________________________________
ж) Семь вычесть из четырехкратного числа __________________________________________
h) К пятнадцати прибавляется число двенадцать ______________________________________________
i) Число девять больше, чем утроенное число ________________________________________________________
L. Brenton Page | 13
14. 7 класс. Математика. Раздел 1: Закономерности и отношения
Так же, как мы можем писать выражения для предложений, мы можем писать предложения (слова) для
Пример 3:
а) 13п ____________________________________________________________________________________
б) м + 12 _________________________________________________________________________________
в) п/2 __________________________________________________________________________________________
г) 3к + 6 _______________________________________________________________________________________
д) 16 – н/2 _____________________________________________________________________________
Мы можем вычислить выражение для заданного значения, «подставив» значение туда, где вы видите
переменную.
Пример 4:
Оцените каждое выражение, предполагая, что n = 4.
a) 4n = 4 (4) = 16
b) 12/n =
c) 14 – n =
d) n + 8 =
e) 2n + 7 =
f) 28 – 24/n =
Л. Брентон Пейдж | 14
15. 7 класс Математика Раздел 1: Закономерности и отношения
Рабочий лист
Часть A: Какие слова соответствуют математическим операциям?
Math Symbol Words
+
—
÷
x
Часть B: Напишите английские фразы для следующих математических выражений.
Выражение Предложение
Л. Брентон Пейдж | 15
16. 7 класс Математика Раздел 1: Закономерности и отношения
Часть C: Переведите каждое английское выражение или уравнение в математическую форму.
English Expression
1. Удвоить число
2. Число увеличить на шесть.
3. Число уменьшилось на четыре.
4. Сумма числа и десяти.
5. Семь раз число.
6. На семь меньше числа.
7. Половина числа увеличилась на девять.
8. Число, увеличенное на семь, равно четырнадцати.
9. Трижды число плюс шесть равно двадцати четырем.
10. Одна четверть числа равна восемнадцати.
11. Число, разделенное на пять и затем уменьшенное на
восемь.
12. Семь уменьшилось на число
Вопрос: Какие из перечисленных уравнений являются уравнениями? Откуда вы знаете?
Л. Брентон Пейдж | 16
17. Математика для 7 класса. Часть 1: Закономерности и отношения
. Часть D. Для каждого алгебраического выражения определите числовой коэффициент, переменную
и постоянный член.
Алгебраико-числовой
Постоянный член переменной
Коэффициент выражения
Часть E: Оцените каждое выражение, заменив переменную заданным числом.
Л. Брентон Пейдж | 17
18. 7 класс Математика. Раздел 1: Закономерности и отношения
Раздел 1.4 – Отношения в закономерностях
Рассмотрим шаблон:
1 2 3 4
Мы можем показать это в таблице:
Диаграмма №
1 2 3 4 5
(d)
Количество кругов
(c)
Что вы заметили?
Какую связь вы видите между номером диаграммы и количеством точек?
В Words:
3d — это _________________________________________, потому что переменная _____________ равна
, связанной с количеством кругов, и наоборот.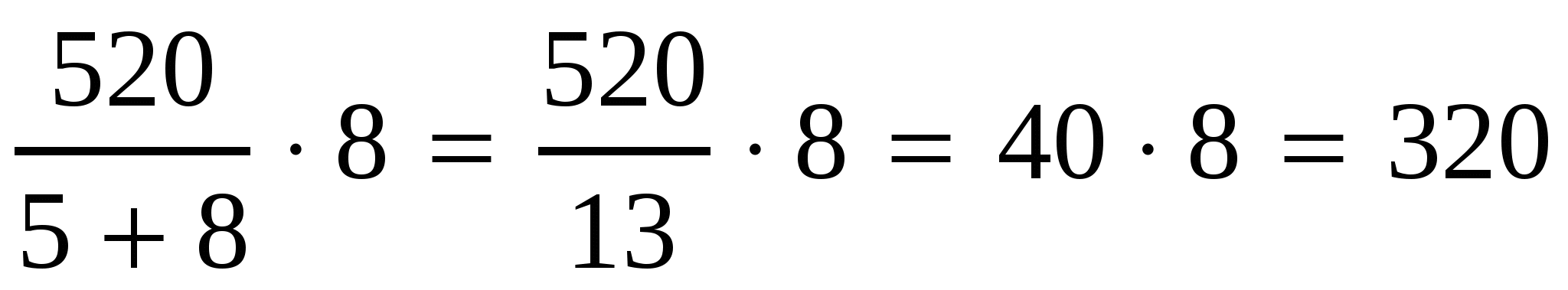
Л. Брентон Пейдж | 18
19. Математика для 7 класса. Часть 1: Закономерности и отношения
Как каждый термин связан с номером термина? Напишите отношение к каждому.
Л. Брентон Пейдж | 19
20. 7 класс Математика Раздел 1: Закономерности и отношения
Раздел 1.5 – Шаблоны и отношения в таблицах
Мы можем представить отношение, используя таблицу ввода/вывода. Мы вводим числа в столбец ввода
, делаем то, что говорит нам отношение, и пишем результат под выводом.
Эти таблицы пригодятся, когда мы хотим построить график наших отношений.
Примеры: Заполните каждую таблицу и объясните, как результат связан с вводом.
Выходное значение в два раза больше входного.
Выход равен двенадцати минус ввод.
Л. Брентон Пейдж | 20
21. 7 класс Математика. Часть 1: Закономерности и отношения
Результат в три раза больше, чем ввод
Мы также можем записать отношение, используя алгебру, когда нам дана таблица.
Примеры: Напишите отношение для каждой таблицы.
Л. Брентон Пейдж | 21
22. 7 класс Математика Раздел 1: Закономерности и отношения
Раздел 1.6 – Графики отношений
Мы можем использовать графики, чтобы показать отношения между двумя величинами.
Рассмотрим пример ниже:
1. Треугольники используются для создания рисунка ниже:
Диаграмма 1 Диаграмма 2 Диаграмма 3
Заполните таблицу и начертите зависимость:
Номер диаграммы Количество заштрихованных
(n) Треугольников (t)
1
2
3
4
5
6
** Помните, ввод идет снизу
(горизонтальная ось) и выход идет на сторону
(вертикальная ось).
Напишите соотношение, показывающее, как
число квадратов связано с числом диаграммы n.
Когда точки на графике падают на прямую линию, отношение называется
L. Brenton Page | 22
23. 7 класс. Математика. Раздел 1. Закономерности и отношения
. Попробуйте следующие примеры:
2. Шейла устроила вечеринку и могла расставить стол и стулья следующим образом:
Заполните таблицу и нарисуйте взаимосвязь.
Число Число
столов (n) человек
1
2
3
4
5
Напишите соотношение, показывающее, как число
квадратов связано с числом на диаграмме, n.
Л. Брентон Пейдж | 23
24. 7 класс Математика Раздел 1: Закономерности и отношения
3. Квадратные плитки используются для создания узора, показанного ниже.
Заполните таблицу и нарисуйте зависимость.
Диаграмма Количество
число(n) квадратов
1
2
3
4
5
Напишите отношение, чтобы показать, как число
квадратов связано с номером диаграммы, n.
Л. Брентон Пейдж | 24
25. 7 класс Математика Раздел 1: Закономерности и отношения
Раздел 1.7 – Чтение и запись уравнений
Давайте будем математическими детективами!!
Пример 1:
Я думаю о числе. Если умножить на 3 и прибавить 4,
получится 13. Что это за число?
(Подсказка: сначала напишите алгебраическое уравнение!)
Что такое алгебраическое уравнение?
Это ________________________________________________________________, описывающее отношение
, используя _______________________________________, между двумя выражениями.
, тогда = __________
, тогда = __________
Пример 2:
Я думаю о числе. Если умножить на 5 и вычесть 4, ответ будет 21.
Что это за число?
Пример 3:
Кейтлин купила 3 компакт-диска. Каждый диск стоил столько же. Общая стоимость составляет 36,00 долларов США.
A) Напишите алгебраическое уравнение
B) Сколько стоит один компакт-диск?
Л. Брентон Пейдж | 25
26. 7 класс Математика Раздел 1: Закономерности и отношения
Пример 4:
Напишите уравнение для каждого предложения:
A) Три больше, чем число, равно 15.
B) Число, вычтенное из 5, равно 1.
C) Восемь, добавленное к трем числам, равно 26.
Пример 5:
Напишите предложение для каждого уравнения:
A)
L. Brenton Страница | 26
27. 7 класс. Математика. Часть 1: закономерности и отношения
B)
C)
L. Brenton Page | 27
28. 7 класс. Математика. Часть 1: Закономерности и отношения
Раздел 1.8. Решение уравнений с использованием алгебраических плиток
Мы можем использовать алгебраические плитки для представления выражения или уравнения.
= +1, называется плиткой единицы.
= x, называется переменной плиткой.
а) может быть представлено как
Какое выражение представлено следующим?
Л. Брентон Пейдж | 28
29. 7 класс Математика Часть 1: Закономерности и отношения
Мы можем решать алгебраические выражения, используя плитки:
Например:
Мы хотим получить переменные плитки (длинные плитки) с одной стороны сами по себе.
Чтобы сделать это, мы убираем 3 плитки с левой стороны… но чтобы сохранить баланс уравнения
, мы должны убрать три плитки с правой стороны
Пример: Используйте плитки для решения каждой:
Л. Брентон Пейдж | 29
30. 7 класс. Математика. Раздел 1: Закономерности и отношения
= = так, =
Л. Брентон Пейдж | 30
31. 7 класс. Математика. Часть 1. Закономерности и отношения
. Если у нас есть , мы хотим .
Итак, нам нужно _______________________________________________________, чтобы составить целое.
Л. Брентон Пейдж | 31
Символы умножения и деления, выражения и отношения
Цель
Этот модуль развивает понимание умножения и деления, включая обратную связь между двумя операциями, а также когда и как их использовать в ситуациях решения задач. Учащиеся изучают правила представления операций умножения и деления в виде уравнений.
Цели достижения
NA3-6: Запишите и интерпретируйте аддитивные и простые мультипликативные стратегии, используя слова, диаграммы и символы, с пониманием равенства.
Разработка АО и другие учебные ресурсы
Конкретные результаты обучения
Читать, писать и понимать символы умножения и деления, знак равенства и язык, связанный с этими символами.
Напишите контекст рассказа для заданных уравнений умножения и деления.
Знайте, что операция умножения коммутативна.
Определите связанные факты умножения и деления («семейства фактов»).
Распознать обратную зависимость операций умножения и деления.
Признать, что деление не является коммутативным.
Используйте слова «фактор» и «продукт» надлежащим образом
Определите коэффициенты заданных сумм.
Описание математики
Эта последовательность уроков устанавливает связь между повторяющимся сложением и умножением. Он вводит деление и исследует взаимосвязь между операциями умножения и деления.
В рамках этих уроков развиваются три основных понимания.
Учащиеся должны понимать отношения между величинами, представленными уравнениями умножения и деления. Например, 4 x 5 = 20 может представлять собой «четыре количества по пять равны 20» или «20 в четыре раза больше, чем 5».

Учащиеся должны выучить словарный запас, связанный с умножением и делением, а также значение этих слов. Важная лексика включает множители (числа умножаются), произведение (ответ на умножение), умножение на (умножение одной величины в х раз), равенство (одинаковость количества).

Умножение также может быть представлено в пространстве. Массивы — это эффективный способ показать структуру и структуру многочисленных групп и, в данном случае, прочно связать умножение и деление с измерением.
При изучении структуры и модели умножения и деления основное внимание уделяется также развитию раннего понимания числовых свойств . На этих уроках формально исследуется коммутативное свойство умножения (то есть порядок, в котором умножаются числа, не меняет ответ). Распределительное свойство, при котором один или оба фактора разделяются для облегчения вычислений (например, 12 x 55 = 10 x 55 + 2 x 55), является основополагающим для стратегий расчета, включая письменные алгоритмы.
При изучении поведения операций умножения и деления важно, чтобы учащиеся делали обобщения, в которых они могли бы указать, «что всегда происходит», когда предпринимаются определенные действия. Например, им следует признать, что, хотя правило «перестановки» (коммутативное) 90 173 всегда верно 90 174 для умножения, оно неверно для деления.
Эта серия уроков посвящена однозначным множителям и делителям. Он признает, что учащиеся должны иметь много возможностей представить умножение и деление. операции для решения текстовых задач. Это подкрепляется глубоким пониманием использования символов и выражений умножения и деления для математического мышления и выражения отношений. Учащиеся также должны уметь создавать контексты, которые может выражать уравнение. Установление связей между языком и символами необходимо для развития правильного понимания математических идей и концепций.
Возможности для адаптации и дифференциации
Возможности обучения в этом модуле можно дифференцировать, предоставляя или удаляя поддержку учащихся и изменяя требования к заданиям.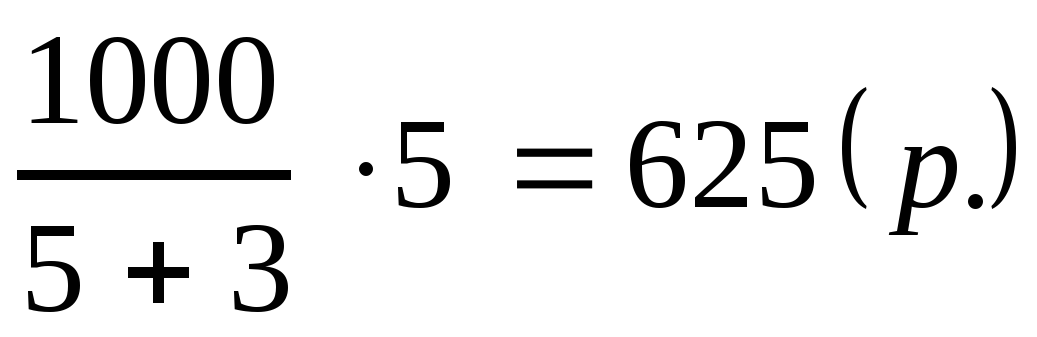 Способы дифференциации включают:
предоставление физических материалов, чтобы учащиеся могли предвидеть действия и обосновывать свои решения. Использование таких материалов, как кубы, квадратные плитки и диаграммы массивов, для моделирования ситуаций и связывания стратегий, используемых учащимися, с представленными величинами.
, соединяющие символы и математический словарь, особенно символы умножения и деления (x, ÷) и равенства (=). Явное моделирование правильного использования уравнений и алгоритмов и обсуждение значения символов в контексте.
изменение сложности используемых чисел. Умножение на такие множители, как два, четыре, пять, десять, и деление на одни и те же делители, как правило, проще, чем на такие множители, как три, шесть, семь, восемь и девять. Подумайте, какие факты умножения ваши ученики будут уверенно применять при решении задач.
побуждает учащихся сотрудничать в малых группах, делиться и обосновывать свои идеи.
с использованием технологий, особенно калькуляторов, в прогнозирующих, основанных на шаблонах способах оценки произведений и частных, например. Если ответ на 4 x 8 = 32, будет ли ответ на 32 ÷ 5 больше или меньше 8? Откуда вы знаете? разрешить использование калькуляторов там, где вы хотите, чтобы учащиеся больше сосредоточились на процессе получения разумного ответа или на выявлении закономерностей, чем на отработке навыков вычисления.
Контекст, используемый для этого модуля, — это стеганые одеяла, тиваевае и ткань тапа. Подумайте, как вы можете использовать знания сообщества в этом контексте. Есть ли члены сообщества, которых вы могли бы пригласить, чтобы поговорить о культурном происхождении тиваев или тапа? В этих контекстах важно обеспечить подлинность, актуальность и цель важных культурных знаний. Вы можете изменить контекст на ситуации, более соответствующие повседневной жизни, интересам или культурной самобытности ваших учащихся. Массивы распространены в разных культурах, и их можно найти в узорах плитки, текстиле, упаковке, стопках домов и игровых досках для игр. Поощряйте учащихся к творчеству, принимая различные стратегии от других и предлагая учащимся создавать свои собственные проблемы, которые должны решать другие, в значимом контексте.
Требуемые ресурсы Материалы
Не менее двух прямоугольных стеганых одеял, тиваева или тапа
Цветные пластиковые квадратные плитки (или маленькие квадратики из картона другого цвета)
Бумага в клетку
Калькуляторы
Кубики Unifix
Игральные карты
PowerPoint 1
PowerPoint 2
Копи-мастер 1
Копи-мастер 2
Копи-мастер 3
Деятельность
Занятие 1
Занятие 1
Покажите учащимся два разных прямоугольных лоскутных одеяла. Это была бы хорошая возможность взглянуть на любую школьную ткань тапа или панели тукутуку. Кроме того, используйте PowerPoint 1, чтобы показать изображения подходящих стеганых одеял или ткани тапа. Например:

Разработайте контекст для обучения этому разделу. Это может включать изготовление одеяла или тапы (даже гипотетически) для детского отделения в местной больнице или хосписе. Подумайте, как вы можете использовать знания своих учеников и их сообщества. Могут ли взрослые принести tivaevae, siapo или сделанные ими одеяла или фотографии вещей?
Вовлеките учащихся в обсуждение лоскутных одеял, установив, как создаются узоры.
Спросите: «Какая математика содержится в этих стеганых одеялах?» (например, лоскутное одеяло 3 x 3)
Запишите идеи учащихся в карточке класса. (Это могут быть числа, геометрия, измерения: например, 3 + 3 + 3 = 9, 3 x 3 = 9, 9 квадратов, один большой квадрат, стороны одинаковой длины, 9 разделить на 3 и т. д.). Сравните количество квадратов в разных примерах.
Выделить операцию и отношения символов (или слов), которые были записаны. Например:
Напишите каждый символ на отдельном листе бумаги формата А4. Попросите пары учащихся взять по одному листу (один символ), и каждый по очереди запишет в заданный период времени (например, за 2 минуты) , используя слова и картинки/диаграммы , и проведите мозговой штурм всего, что они знают об этом символе. (или слово). Попросите учащихся привести пример того, где можно использовать их символ.
Попросите учащихся вернуться на мат, рассаживаясь двумя отдельными группами: группа с операция символа (+ — x ÷) и группа с связью символа (<> =). Попросите выбранные пары учащихся объяснить, почему они сидят на своих местах и какие идеи они записали для своих символов.
В этом обсуждении подчеркните язык , используемый , разработайте понимание того, что такое числовая операция (математический процесс, который изменяет число или сумму), и повторите значение знака равно .
Сохраните листы мозгового штурма для дальнейшего использования.
Мероприятие 2
Подготовьте пакеты по 12, 18, 20, 24 и 30 пластиковых плиток, маленькие цветные квадратики из картона или квадратики из ткани. Сделайте их, карандаши и бумагу, доступными для пар учащихся.

Поставьте задачу. «Покажите, , используя диаграммы и уравнения , сколькими различными способами можно расположить эти лоскуты, чтобы сделать «мини-лоскутное одеяло»?»
Предложите учащимся поработать в парах, чтобы записать свои идеи.
Предложите учащимся поделиться своими идеями с парой, у которой было одинаковое количество плиток, и записать все варианты расположения, о которых они не подумали.
Обменивайтесь идеями в классе, изучайте и записывайте основные понятия в классной таблице. Сохраните эту работу учащихся для занятия 2.
Например: Из пакета с 18 «заплатками» (плитками).

В ходе обсуждения опирайтесь на идеи, которыми поделились в Упражнении 1 (см. выше), выделяя и записывая словами эти идеи:
Аранжировки «патчей» могут быть записаны с использованием различных операций .
Умножение с использованием x символ, может отображать ту же идею как многократное сложение (равных количеств), используя символ + .
Символ для деления или деления на равные группы: ÷ . Он называется символом деления .
Это расположение с одинаковыми строками и столбцами называется массивом .
Встаньте и запишите: «9 + 9 = 6 x 3. Вы согласны или не согласны». Попросите пары студентов обсудить это утверждение и обосновать свою позицию (объяснить, почему они согласны или не согласны и откуда они знают, что они правы).
Запишите обоснование ученика, выделив отношение эквивалентности (оба равны 18, всего 18 патчей в обоих массивах). Выделите мультипликативные представления, такие как «9 равно 3 x 3, поэтому 9 + 9 равно 6 x 3».
Деятельность 3
Напишите два уравнения в таблице классов, одно на умножение и одно на деление.
Например: 6 x 5 = 30 28 ÷ 4 = 7. Прочтите их вместе. Пусть каждый учащийся нарисует схему стеганого одеяла или ткани тапа, представляющую уравнение. Попросите их написать словесное описание того, как стеганое одеяло/ткань представляет собой уравнение.
Упражнение 4
Завершите сеанс просмотром символов операций и взаимосвязей и их значений.
Сессия 2
Занятие 1
Начните с того, что по крайней мере два ученика поделятся своими схемами одеяла/ткани из предыдущего занятия. Попросите других учащихся записать уравнения, представленные на схеме. Подчеркните тот факт, что математику из реальной жизни можно представить с помощью диаграмм, слов и символов.
Проведите мозговой штурм на классной таблице других ситуаций в нашей жизни, где мы видим и используем умножение или деление. Когда учащиеся будут делиться идеями, попросите их назвать конкретные числа. Запишите эти истории, используя диаграммы и слова.
Например: Мы видим умножение, когда:
12 упаковок по 20 мармеладок завернуты вместе в большую упаковку для продажи на школьной ярмарке – четыре упаковки в ряд и три ряда.
Школа покупает три набора хоккейных клюшек по десять штук в каждом.
На мараэ мы сидим в четыре ряда по шесть человек.
Прочтите сказки еще раз вместе. Попросите учащихся использовать символы для записи уравнений для каждой из историй в своих книгах/на доске/бумаге. Те учащиеся, которые закончат быстро, могут придумать больше контекстных историй. Поощряйте учащихся создавать контекстные истории, отражающие их повседневную жизнь (в отличие от выбора «случайных» чисел).
Предложите учащимся в парах поделиться своими уравнениями. Если учащиеся записали, используя многократное сложение, попросите их также записать уравнения умножения.
Упражнение 2
Просмотрите информацию о символах из сеанса 1, выделив символы операций, + — x ÷ , а также символы отношений, равно (=), больше (>) и меньше (<) символы отношений.
Попросите учащихся поработать в парах, используя ситуации из предыдущего задания. Студенты должны обсудить ситуации и посмотреть, сколько уравнений или неравенств они могут написать. Например:
3 x 4 = 4 x 3
3 x 4 < 2 x 10
4 x 6 > 2 x 10 > 4 x 3
Они должны использовать диаграммы, чтобы показать, откуда они знают, что они верны.
Предложите учащимся поделиться своей работой в парах. При этом они должны по очереди читать вслух то, что они написали.
Занятие 3
Вернитесь к стеганым одеялам/тапа-тканям (изображения). Объясните, что некоторым маленьким детям нравятся лоскутные одеяла с алфавитом, в которых на каждой клеточке изображено что-то, начинающееся с другой буквы алфавита. Поговорите о том, что некоторые из них могут быть. Например: A может изображать яблоко, B — бабочку, C — кошку и так далее.

Предоставьте учащимся бумагу, карандаши и фломастеры.
Поставьте задачу: Вы собираетесь сделать лоскутное одеяло/тапа с алфавитом, чтобы подарить кому-нибудь. У вас есть время до конца сегодняшней сессии, чтобы спланировать свой дизайн и то, как вы будете располагать свои «квадратные лоскуты» . Где-то в проблеме может быть вызов. Вы выбираете лучший способ решить эту проблему для вашего дизайна стеганого одеяла.
Сколько букв в алфавите? (26)
Почему изготовление одеяла из 26 квадратов может быть проблемой?
Пусть учащиеся поэкспериментируют с 26 квадратами. Они могут нарисовать возможные варианты использования квадратных плиток или кубов. Цифровые инструменты также можно использовать для упорядочивания плиток и представления работ учащихся.
(26 будет состоять только из массивов 1 x 26 или 2 x 13, что нежелательно для стеганого одеяла такого типа. Учащиеся встретят «остаток» (6 x 4 + 2, 5 x 5 + 1) или найдут некоторые «заплатки» короткие (7 x 4). Примите реалистичные решения для контекста (например, лоскутное одеяло 5 x 5: поместите 2 буквы на одну заплатку, лоскутное одеяло 6 x 4: сделайте его 7 x 4 и включите 2 новых или пустых патчи.)
Предложение: Если мы добавим патчи для каждой из цифр 0-9, сколько тогда будет патчей? (26 + 10 = 36)
Посмотрите, какие одеяла вы могли бы сделать тогда.
Попросите учащихся найти все возможные варианты расположения:
1 x 36 2 x 18 3 x 12 4 x 9 6 x 6 Почему?
Занятие 3
Занятие 1
Предложите учащимся поделиться своими рисунками стеганых одеял с алфавитом для 36 нашивок. Обсудите «оставшуюся проблему» и оцените творческие решения.
Почему нельзя было сделать одеяло с пятью заплатками подряд?
Запишите 36 ÷5 = 7 r 1 и спросите учащихся, что означает r 1 (остаток от 1).
Укажите, что часто задачи на деление решаются неравномерно. Мы называем то, что осталось, , остаток .
Представьте, что у нас есть 26 патчей, и мы пытаемся разместить по шесть патчей в каждом ряду. Один из способов записать эту задачу: 26 ÷ 6 = 4 r2.
На диаграмме классов быстро нарисуйте массивы, которые были разработаны для 26 патчей.
Обсудите «размеры» массива, вводя слова факторы и произведение . Модель с примером:

Попросите каждого учащегося записать под своим дизайном лоскутного одеяла то, что находится в рамке выше, регулируя числа для своего собственного дизайна.
Деятельность 2

Напишите на доске 4 36 9.
Вот еще три числа, которые связаны умножением и делением.
Запишите набор уравнений умножения и деления, используя эти числа.
Предложите учащимся работать в парах, чтобы составить уравнения и создать массив, представляющий все четыре уравнения. Студенты должны быть готовы обосновать свою позицию (объясняя, откуда они знают, что они правы).
4 x 9 = 36 9 x 4 = 36 36 ÷ 4 = 9 36 ÷ 9 = 4 Особое внимание обратите на деление. Например, 36 ÷ 4 = 9дает количество строк, созданных из 36 патчей (площадь), если каждый ряд состоит из четырех патчей.

Подведите итоги на классной таблице. Например:
- Умножение — это операция «переворота». Вы можете изменить порядок факторов без изменения произведения. (Это как сложение.)
  Мы говорим, что умножение (и сложение) равно 9.0041 коммутативный .
  4 х 7 = 7 х 4 = 28
- Деление не является коммутативным, т.е. 36 ÷ 4 = 9, но 4 ÷ 36 = 0,1111… (1/9). Частные деления не совпадают (ответ).
  Мы говорим, что деление (и вычитание) не коммутативно .

Задание 3

Попросите учащихся сыграть в игру Умножение, рисование и запись в парах . Рассмотрите возможность объединения в пары учащихся с одинаковым уровнем знания таблицы умножения, что будет способствовать развитию туакана-тейна и уверенности учащихся в своих навыках.
Им нужны игральные карты (с номерами от 2 до 9), карандаш и бумага.
Победителем становится тот, у кого после десяти раундов будет больше всего пар карточек с одинаковыми продуктами, но изготовленными с использованием разных факторов.
Например: 6 x 4 = 8 x 3 = 24, или 4 x 4 = 2 x 8 = 16
Как играть:
Карты перемешиваются и кладутся лицом вниз в стопку между обоими игроками.
Игроки по очереди переворачивают по три карты из стопки. Это факторы. Игрок возвращает одну карту в низ стопки. Игрок должен написать факт(ы) умножения для двух карт. Они также могут нарисовать массив и записать семейство фактов.
Например:
Учащиеся завершают занятие написанием словесных сценариев для своих наборов уравнений (семейство фактов). Вы можете выбрать работу со студентами, которым нужна дополнительная поддержка, в небольшой группе, в то время как другие студенты будут работать самостоятельно. В конечном счете, все учащиеся должны уметь писать словесные сценарии для наборов уравнений. Они могут быть написаны с использованием цифровых инструментов и могут быть смоделированы с использованием материалов (например, счетчиков). Это не обязательно должны быть сценарии квилтинга.
Например: «Было три мешка по пять яблок в каждом. Пятнадцать поделили на три мешка — это пять. Если эти пятнадцать яблок разложить по пяти мешкам, то в каждом окажется по три. Это будет пять лотов по три.

Занятие 4

Занятие 1

Покажите альтернативный набор стеганых одеял или ткани тапа (PowerPoint 2). Например:

Попросите четырех учащихся записать по одному факту каждого из связанных фактов.
(6 х 5 = 30, 5 х 6 = 30, 30 ÷ 5 = 6, 30 ÷ 6 = 5) и объяснить каждый факт со ссылкой на лоскутное одеяло, включая демонстрацию коммутативного (оборотного) свойства умножения. Поверните одеяло, чтобы продемонстрировать это.

Занятие 2

Раздайте учащимся соединяющие кубики (или цветные фишки). Пусть пары учеников возьмут по 48 кубиков. Спросите, какие множители могут составить 48. Запишите возможности, используя умножение; 1 х 48, 2 х 24, 3 х 16 и т. д.
Попросите одного ученика из каждого ученика смоделировать пару 4 x 12, соединив кубики. Затем пусть его партнер использует те же кубики для моделирования 12 x 4. Обсудите, что получится. (Им нужно было перегруппировать их). Повторите с 6 x 8 и 8 x 6. Подчеркните, что коммутативное свойство включает те же множители и произведение, но требует другого взгляда на массив (т. е. либо строки, либо столбцы образуют одинаковые множества).
Разложите на карточках факты умножения 48 (Переписчик 1). Задержать 5 раз? и 7 х? Соедините пары уравнений, демонстрирующих свойство коммутативности.
Думаете, это все факты умножения на произведение 48? (Вы можете расположить карты в порядке первого множителя.)
Почему нет 5-кратных и 7-кратных фактов? (Используйте карточки. Учащиеся должны понять, что 48 не входит в число кратных 5 и 7. 48 не делится на 5 и 7).
С помощью калькулятора покажите, что 48 ÷ 5 = 9,6 и 48 ÷ 7 = 6,857142857…
Как вы думаете, что показывает десятичная часть произведения? (Остаток, поэтому 48 не делится на 5 и 7)
Попросите учащихся изучить факты умножения с разным количеством кубиков, используя язык тех же множителей и произведений, сосредоточив внимание на перегруппировке. Их исследование может показать, что некоторые числа имеют только два делителя, например 17 и 31. Эти числа являются простыми.

Занятие 3

Запишите одно знакомое уравнение умножения в классную таблицу. Например, 6 x 2 = 12. Пусть один из учеников в каждой паре смоделирует это, составив 6 групп по 2 и , соединив кубики вместе в одну линию из 12.

Запишите 12 ÷ 6 = 2. другой ученик в паре разыгрывает это с кубиками.

Предложите учащимся описать, что произошло, и запишите такие идеи, как: все наоборот, деление вместо умножения, все наоборот, мы вернулись к тому, с чего начали.
Спросите, Всегда ли так? Как мы можем узнать? Принимайте идеи учеников. Они должны включать студентов, изучающих больше примеров.
Сделайте вывод, что невозможно проверить все факты умножения и деления. Скажем, идея «отмены» означает, что умножение и деление являются обратными операциями, как включение и выключение выключателя света. Уничтожение друг друга — это именно то, как ведут себя умножение и деление.
Написать « обратная связь» на диаграмме классов. Обсудите слова, похожие на инверсию, например. перевернуть, отменить, вернуть, вернуть и их значение. Установите связь с обратной зависимостью между сложением и вычитанием. Подчеркните, что в каждой паре операций одна операция или действие отменяет другое.
Вернитесь к одеялу в Упражнении 1 (выше) и к записанным уравнениям:
(6 x 6 = 30, 5 x 6 = 30, 30 ÷ 5 = 6, 30 ÷ 6 = 5)
Попросите учащихся объяснить «отмену» (снова обратная связь со ссылкой на лоскутное одеяло. (Это немного сложнее увидеть, потому что этот массив физически нельзя «отменить». Однако вы можете составить ряды из шести кубиков и показать 5 x 6, расположив пять рядов по вертикали Сколько у меня лоскутов? Что произойдет, если теперь разделить на пять? )
Напишите в таблице класса:
Знание того, что умножение и деление являются обратными операциями, полезно, потому что……. .
Попросите учащихся предложить причины и записать их, в том числе:
Мы можем использовать умножение, чтобы решить задачи на деление.
Мы можем проверить операции деления с помощью умножения. (Как?)

Занятие 4

Раздайте учащимся Copymaster 2 для работы. Подчеркните обратные операции и необходимость для учащихся показать или объяснить , как умножение помогает решать задачи на деление.

Занятие 5

Занятие 1

Повторить основные выводы из Занятия 4. Предложите учащимся поработать в парах, чтобы поделиться своими решениями задач квилтинга из Занятия 4, Занятие 4. Предложите им задавать друг другу вопросы.

Упражнение 2

Покажите несколько примеров стеганых одеял или ткани тапа с помощью PowerPoint 1:
Напишите в таблице классов:
Одно одеяло из шестнадцати заплаток:
Одно одеяло из тридцати заплаток:
Одно одеяло из сорока пяти заплаток:
Если я переставлю заплатки в один ряд, как будет выглядеть одеяло? (Больше похоже на длинный шарф)
Попросите учащихся записать уравнения умножения для каждого из этих утверждений.
Одно одеяло из шестнадцати заплат: 1 x 16 = 16
Одно одеяло из девяти заплат: 1 x 30 = 30
Одно одеяло из тридцати заплат: 1 x 45 = 45
Если ваши уравнения верны, каковы ответы на 16 ÷ 1 = ☐ , 30 ÷ 1 = ☐ , 45 ÷ 1 = ☐?
Попросите учащихся обсудить свои идеи, а затем объяснить и обосновать свое мнение. Связывают ли они деление с вопросом «Сколько столбцов одного патча составляет в общей сложности 16, 30 или 45 патчей?»
Если ваши уравнения верны, каковы ответы на 16 ÷ 16 = ☐ , 30 ÷ 30 = ☐ , 45 ÷ 45 = ☐?
Связывают ли они деление с вопросом «Сколько рядов по 16 нашивок дает в общей сложности 16 накладок и т. д.?»
Приведите другие примеры деления числа на единицу и само на себя. Для проверки ответов можно использовать калькуляторы.

Задание 3

Предложите учащимся работать в группах от 2 до 4 над Это правда? (Переписчик 3 (Цель: различать правильные и неправильные уравнения и выражения умножения и деления и уметь объяснить, почему, обосновывая свое решение)

Учащиеся по очереди выбирают утверждение и объясняют его другим в группе, если и почему утверждение является фактом, или если и почему оно неверно (истинно или ложно)

Попросите учащихся создать свои собственные факты или нефакты, связанные с умножением и делением, т. е. 8 x 9 = 72, поэтому 72 ÷ 18 = 4. Обменяйтесь фактами и не фактами между учащимися.

Занятие 4

Завершите это занятие обзором знаний, полученных за пять занятий.

Домашняя ссылка

Уважаемые родители и whānau,

В алгебре на этой неделе мы изучали числовые операции умножения и деления и взаимосвязь между ними.

Один из способов, с помощью которого учащиеся закрепят изученное, состоит в том, чтобы прочитать верные и ложные утверждения, а также определить и объяснить, какие из них неверны и почему.

Вашему ребенку может понравиться играть в » I s это факт?» игра с тобой. По очереди очень важно, чтобы каждый объяснил, почему утверждение верно или нет.

Надеемся, вам понравится это испытание.

Спасибо.

Попробуйте следующие примеры:

1 x 25 = 25, поэтому 25 ÷ 25 = 1 Верно или неверно

28 ÷ 4 = 7, поэтому 4 ÷ 28 = 7 Верно или неверно

Приложения

Добавить в план

Третий уровень

Дивиденд – определение, формула и важные правила

Дивиденд – это целое число или количество вещей, которые необходимо разделить на определенные равные части. Существует четыре основных операции над числами: сложение, вычитание, умножение и деление. Деление — это процесс деления числа на равные части, оставляющий после себя напоминание, если данное число нельзя разделить на части поровну. Таким образом, деление с остатком или евклидово деление содержит следующее:

Дивиденд — Дивиденд — это число, которое нужно разделить на делитель.
Делитель — Число, на которое нужно разделить делимое, называется делителем.
Частное — Результат деления называется частным.
Остаток — Число, оставшееся после деления, называется остатком.

В этой статье мы обсудим определение и формулу дивидендов. Мы также изучим методы нахождения дивидендов.

Деление без остатка:

Например, у вас есть 20 конфет, и вам нужно разделить их поровну между 4 детьми. Если разделить конфеты поровну, то каждая из них получит по 5 конфет. Рассмотрим в этом случае количество конфет (т. е. 20), которое должно быть разделено между детьми, называется делимым, а количество детей (т. е. 4), между которыми оно должно быть разделено, называется делителем. Помните, что делитель делит делимое или, другими словами, делимое делится на делитель. Результат равного распределения, то есть количество конфет у каждого члена, называется частным.

Дивиденд = 20

Делитель = 4

Частное = 5

Остаток = 0

Деление на остаток:

Рассмотрим тот же вышеупомянутый пример, но с модификацией. Предположим, что на этот раз конфеты нужно раздать трем участникам, то есть 20 конфет нужно раздать трем детям. Разделение показано ниже:

Здесь конфеты поровну распределены между 3 детьми так, что у каждого по 6 конфет, но осталось 2 конфеты, которые нельзя разделить на три целиком. Таким образом, остаток от этого деления называется остатком.

Здесь

Дивиденд = 20

Делитель = 3

Частное = 6

Остаток = 2.

Формула дивиденда:

по следующей формуле дивидендов:

Дивиденд = Делитель x Частное + Остаток.

Это как раз обратный процесс деления. В приведенном выше примере мы сначала разделили делимое на делитель и вычли кратное вместе с делимым. То есть мы сначала разделили, а потом вычли. Таким образом, чтобы найти делимое, нам нужно сделать обратное, то есть сначала нужно умножить вместо деления, а затем сложить вместо вычитания.

Вот примеры делимых для лучшего понимания концепции:

Допустим, нам нужно разделить 11 на 2 равные целые части. Результат будет с остатком 1.

Здесь делимое = 11, делитель = 2, частное = 5 и остаток = 1.

Согласно формуле дивидендов,

Дивиденд = делитель x частное + остаток

11 = (2 x 5) + 1

11 = 10 + 1

11 = 11

Левая сторона = Правая сторона.

Отсюда формула дивиденда

Дивиденд = (делитель x частное) + остаток

Как найти дивиденд?

Мы можем найти дивиденды, используя формулу дивидендов.

Пример: При делении числа на 9 в частном получается 6, а в остатке остается 1. Найдите число.

Решение: Пусть делимое будет x

x = (9 x 6) + 1

= 54 + 1

= 55

Следовательно, значение делимого равно 55.

Важные правила деления:

Правило 1: Всякий раз, когда мы делим 0 на другое число, результат (частное) всегда равен нулю.

Примеры:

(i) 0 ÷ 4 = 0

(ii) 0 ÷ 12 = 0

(iii) 0 ÷ 25 = 0

(iv) 0 ÷ 314 = 0

9207 (v) ÷ 225 = 0

(vi) 0 ÷ 7135 = 0

Правило 2: Всякий раз, когда число делится на единицу, результатом (частным) всегда является само число.

×	1	2	3	4	5	6	7	8	9	10
1	1	2	3	4	5	6	7	8	9	10
2	2	4	6	8	10	12	14	16	18	20
3	3	6	9	12	15	18	21	24	27	30
4	4	8	12	16	20	24	28	32	36	40
5	5	10	15	20	25	30	35	40	45	50
6	6	12	18	24	30	36	42	48	54	60
7	7	14	21	28	35	42	49	56	63	70
8	8	16	24	32	40	48	56	64	72	80
9	9	18	27	36	45	54	63	72	81	90
10	10	20	30	40	50	60	70	80	90	100

×	1	2	3	4	5	6	7	8	9	10
1	1	2	3	4	5	6	7	8	9	10
2	2	4	6	8	10	12	14	16	18	20
3	3	6	9	12	15	18	21	24	27	30
4	4	8	12	16	20	24	28	32	36	40
5	5	10	15	20	25	30	35	40	45	50
6	6	12	18	24	30	36	42	48	54	60
7	7	14	21	28	35	42	49	56	63	70
8	8	16	24	32	40	48	56	64	72	80
9	9	18	27	36	45	54	63	72	81	90
10	10	20	30	40	50	60	70	80	90	100

×	1	2	3	4	5	6	7	8	9	10
1	1	2	3	4	5	6	7	8	9	10
2	2	4	6	8	10	12	14	16	18	20
3	3	6	9	12	15	18	21	24	27	30
4	4	8	12	16	20	24	28	32	36	40
5	5	10	15	20	25	30	35	40	45	50
6	6	12	18	24	30	36	42	48	54	60
7	7	14	21	28	35	42	49	56	63	70
8	8	16	24	32	40	48	56	64	72	80
9	9	18	27	36	45	54	63	72	81	90
10	10	20	30	40	50	60	70	80	90	100