ГДЗ Математика 5 класс Бунимович, Дорофеев, Суворова на Решалка
- Учебники
- 5 класс
- Математика 👍
- Бунимович
ГДЗ Математика 5 класс Бунимович, Дорофеев, Суворова
авторы: Бунимович, Дорофеев, Суворова.
издательство: «Просвещение»
Посмотреть глоссарий
Задачи
- ГЛАВА 1. ЛИНИИ
- 1. Разнообразный мир линий
- Вопросы и задания
- 1
- 2
- 3
- Упражнения
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- Вопросы и задания
- 2.
 Прямая. Части прямой. Ломаная
Прямая. Части прямой. Ломаная- Вопросы и задания
- 1
- 2
- 3
- 4
- Упражнения
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- Вопросы и задания
- 3. Длина линии
- Вопросы и задания
- 1
- 2
- 3
- 4
- 5
- Упражнения
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- Неверно!
- 1
- 37
- 38
- 39
- 40
- Вопросы и задания
- 4.
 Окружность
Окружность- Вопросы и задания
- 1
- 2
- 3
- 4
- 5
- Упражнения
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- Вопросы и задания
- Подведем итоги
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 1. Разнообразный мир линий
- ГЛАВА 2. НАТУРАЛЬНЫЕ ЧИСЛА
- 5. Как записывают и читают числа
- Вопросы и задания
- 1
- 2
- 3
- 4
- Упражнения
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- Неверно!
- 1
- Вопросы и задания
- 6.
 Натуральный ряд. Сравнение натуральных чисел
Натуральный ряд. Сравнение натуральных чисел- Вопросы и задания
- 1
- 2
- 3
- 4
- Упражнения
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- Неверно!
- 1
- Упражнения
- 83
- 84
- 85
- 86
- 87
- Вопросы и задания
- 7. Округление натуральных чисел
- Вопросы и задания
- 1
- 2
- Упражнения
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- Неверно!
- 1
- Вопросы и задания
- 8.
 Комбинаторные задачи
Комбинаторные задачи- Вопросы и задания
- 1
- 2
- Упражнения
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- Вопросы и задания
- Подведем итоги
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 5. Как записывают и читают числа
- ГЛАВА 3. ДЕЙСТВИЯ С НАТУРАЛЬНЫМИ ЧИСЛАМИ
- 9. Сложение и вычитание
- Вопросы и задания
- 1
- 2
- 3
- Упражнения
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- Неверно!
- 1
- Вопросы и задания
- 10.
 Умножение и деление
Умножение и деление- Вопросы и задания
- 1
- 2
- 3
- 4
- Упражнения
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- Неверно!
- 1
- Вопросы и задания
- 11. Порядок действия в вычислениях
- Вопросы и задания
- 1
- 2
- 3
- Упражнения
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- Неверно!
- 1
- Вопросы и задания
- 12.
 Степень числа
Степень числа- Вопросы и задания
- 1
- 2
- 3
- Упражнения
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- Неверно!
- 1
- Вопросы и задания
- 13. Задачи на движения
- Вопросы и задания
- 1
- 2
- Упражнения
- 195
- 196
- 197
- 198
- 199
- 200
- 201
- 202
- 203
- 204
- 205
- 206
- 207
- 208
- 209
- 210
- 211
- 212
- Вопросы и задания
- Подведем итоги
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 9. Сложение и вычитание
- ГЛАВА 4.
 ИСПОЛЬЗОВАНИЕ СВОЙСТВ ДЕЙСТВИЙ В ВЫЧИСЛЕНИЯХ
ИСПОЛЬЗОВАНИЕ СВОЙСТВ ДЕЙСТВИЙ В ВЫЧИСЛЕНИЯХ- 14. Свойства сложения и умножения
- Вопросы и задания
- 1
- 2
- 3
- Упражнения
- 213
- 214
- 215
- 216
- 217
- 218
- 219
- 220
- 221
- 222
- 223
- 224
- 225
- 226
- Вопросы и задания
- 15. Распределительное свойство
- Вопросы и задания
- 1
- 2
- Упражнения
- 227
- 228
- 229
- 230
- 231
- 232
- 233
- Неверно!
- 1
- Упражнения
- 234
- 235
- 236
- 237
- 238
- 239
- 240
- 241
- 242
- 243
- Вопросы и задания
- 16.
 Решение задач
Решение задач- Вопросы и задания
- 1
- 2
- Упражнения
- 244
- 245
- 246
- 247
- 248
- 249
- 250
- 251
- 252
- 253
- 254
- 255
- 256
- 257
- 258
- 259
- 260
- 261
- 262
- Вопросы и задания
- Подведем итоги
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 14. Свойства сложения и умножения
- ГЛАВА 5. УГЛЫ И МНОГОУГОЛЬНИКИ
- 17. Как обозначают и сравнивают углы
- Вопросы и задания
- 1
- 2
- 3
- 4
- Упражнения
- 263
- 264
- 265
- 266
- 267
- 268
- 269
- 270
- 271
- 272
- 273
- 274
- 275
- 276
- Вопросы и задания
- 18.
 Измерение углов
Измерение углов- Вопросы и задания
- 1
- 2
- 3
- 4
- 5
- Упражнения
- 277
- 278
- 279
- 280
- 281
- 282
- 283
- 284
- 285
- 286
- 287
- 288
- 289
- 290
- 291
- 292
- 293
- Вопросы и задания
- 19. Многоугольники
- Вопросы и задания
- 1
- 2
- 3
- 4
- 5
- Упражнения
- 294
- 295
- 296
- 297
- 298
- 299
- 300
- 301
- 302
- 303
- 304
- 305
- 306
- 307
- 308
- Вопросы и задания
- Подведем итоги
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 17. Как обозначают и сравнивают углы
- ГЛАВА 6.
 ДЕЛИМОСТЬ ЧИСЕЛ
ДЕЛИМОСТЬ ЧИСЕЛ- 20. Делители и кратные
- Вопросы и задания
- 1
- 2
- Упражнения
- 309
- 310
- 311
- 312
- 313
- 314
- 315
- 316
- 317
- 318
- 319
- 320
- 321
- 322
- 323
- 324
- 325
- 326
- 327
- 328
- 329
- Вопросы и задания
- 21. Простые числа
- Вопросы и задания
- 1
- 2
- 3
- Упражнения
- 330
- 331
- 332
- 333
- 334
- 335
- 336
- 337
- 338
- 339
- 340
- 341
- 342
- 343
- 344
- 345
- 346
- 347
- 348
- 349
- Вопросы и задания
- 22.
 Делимость суммы и произведения
Делимость суммы и произведения- Вопросы и задания
- 1
- 2
- 3
- Упражнения
- 350
- 351
- 352
- 353
- 354
- 355
- 356
- 357
- 358
- 359
- 360
- 361
- 362
- 363
- 364
- 365
- 366
- 367
- 368
- 369
- 370
- Вопросы и задания
- 23. Признаки делимости
- Вопросы и задания
- 1
- 2
- Упражнения
- 371
- 372
- 373
- 374
- 375
- 376
- 377
- 378
- 379
- 380
- 381
- 382
- 383
- 384
- 385
- 386
- Вопросы и задания
- 24.
 Деление с остатком
Деление с остатком- Вопросы и задания
- 1
- 2
- 3
- Упражнения
- 387
- 388
- 389
- 390
- 391
- 392
- 393
- 394
- Неверно!
- 1
- Упражнения
- 395
- 396
- 397
- 398
- 399
- 400
- 401
- 402
- 403
- Вопросы и задания
- Подведем итоги
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 20. Делители и кратные
- ГЛАВА 7. ТРЕУГОЛЬНИКИ И ЧЕТЫРЕХУГОЛЬНИКИ
- 25. Треугольники и их виды
- Вопросы и задания
- 1
- 2
- 3
- 4
- 5
- Упражнения
- 404
- 405
- 406
- 407
- 408
- 409
- 410
- 411
- 412
- 413
- 414
- 415
- 416
- 417
- 418
- Вопросы и задания
- 26.
 Прямоугольники
Прямоугольники- Вопросы и задания
- 1
- 2
- 3
- 4
- 5
- 6
- Упражнения
- 419
- 420
- 421
- 422
- 423
- 424
- 425
- 426
- 427
- 428
- 429
- 430
- 431
- 432
- Вопросы и задания
- 27. Равенство фигур
- Вопросы и задания
- 1
- 2
- 3
- 4
- Упражнения
- 433
- 434
- 435
- 436
- 437
- 438
- 439
- 440
- 441
- 442
- 443
- 444
- 445
- 446
- Вопросы и задания
- 28.
 Площадь прямоугольника
Площадь прямоугольника- Вопросы и задания
- 1
- 2
- 3
- 4
- 5
- Упражнения
- 447
- 448
- 449
- 450
- 451
- 452
- 453
- 454
- 455
- 456
- 457
- 458
- 459
- 460
- 461
- 462
- Вопросы и задания
- Подведем итоги
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 25. Треугольники и их виды
- ГЛАВА 8. ДРОБИ
- 29. Доли и дроби
- 30. Основное свойство дроби
- 31. Сравнение дробей
- 32.
 Натуральные числа и дроби
Натуральные числа и дроби
- 29. Доли и дроби
- ГЛАВА 9. ДЕЙСТВИЯ С ДРОБЯМИ
- 33. Сложение и вычитание дробей
- 34. Сложение и вычитание смешанных дробей
- 35. Умножение дробей
- 36. Деление дробей
- 37. Нахождение части целого и целого по его части
- 38. Задачи на совместную работу
- 33. Сложение и вычитание дробей
- ГЛАВА 10. МНОГОГРАННИКИ
- 39. Геометрические тела и их изображение
- 40. Параллелепипед и пирамида
- 41. Объем параллелепипеда
- 42. Развертки
- 39. Геометрические тела и их изображение
- ГЛАВА 11. ТАБЛИЦЫ И ДИАГРАММЫ
- 43. Чтение и составление таблиц
- 44. Диаграммы
- 45. Опрос общественного мнения
- 43. Чтение и составление таблиц
Ребенок учится по учебнику Бунимовича/Дорофеева и все чаще возникают сложности с решением домашних заданий? Нужно признать, что программа этого учебника непростая, а наибольшая проблема, с которой сталкиваются школьники и их родители – домашние задания немного другой структуры и алгоритма решения, чем те, которые отведены на рассмотрение в пределах урока. Если учитель дополнительно не объяснит, как решать такие упражнения, то у детей возникают трудности. А если пропустил урок или что-то недослушал – то же самое. Поэтому даже наибольшие противники ГДЗ рано или поздно признают – иногда готовые домашние задания оказываются полезны. И суть не в том, чтобы просто списать ответ. Рассмотрев алгоритм решения, намного проще все понять и в дальнейшем самостоятельно делать аналогичные задачки.
Если учитель дополнительно не объяснит, как решать такие упражнения, то у детей возникают трудности. А если пропустил урок или что-то недослушал – то же самое. Поэтому даже наибольшие противники ГДЗ рано или поздно признают – иногда готовые домашние задания оказываются полезны. И суть не в том, чтобы просто списать ответ. Рассмотрев алгоритм решения, намного проще все понять и в дальнейшем самостоятельно делать аналогичные задачки.
Почему готовые домашние задания должны быть у каждого родителя
Если учесть загруженность школьной программы и родительскую рабочую занятость, то сложно представить, как в таких ритмах выкроить время на выполнение домашних заданий. И это хорошо, если все понятно, и ребенок щелкает задачки, а если случаются какие-то загвоздки, трудно понять суть вопроса? Тогда на мучительную домашку уходят вечера напролет и не факт, что все завершится успехом. В результате подключается вся семье и ответы ищутся коллективно. А что, если родителю просто взять решебник по математике для пятых классов, для себя разобраться в решении, а затем попробовать объяснить все школьнику. Процесс наверняка ускорится. Если у Вас нет времени тщательно проверять самостоятельно сделанные ребенком задания, разбираясь в каждом упражнении, то намного проще будет все сверить с готовыми ответами. Так и Вы, и ребенок будете спокойны, что на следующий день в школе все пройдет без неожиданностей.
Процесс наверняка ускорится. Если у Вас нет времени тщательно проверять самостоятельно сделанные ребенком задания, разбираясь в каждом упражнении, то намного проще будет все сверить с готовыми ответами. Так и Вы, и ребенок будете спокойны, что на следующий день в школе все пройдет без неожиданностей.
На нашем сайте Вы можете в онлайн-режиме воспользоваться ГДЗ по математике за 5 класс к учебнику Дорофеева и немного упростить своей семье насыщенные школьные будни.
Нужны ответы к задачкам Дорофеева, Суворовой и Шарыгина?
У нас Вы найдете решебник к любому учебнику за 5 класс. И главное – в отличие от печатных изданий, мы исключаем возможные опечатки в тексте или тем более неверные решения упражнений. Все проверяется вручную и точность гарантируется. Решалка в 5 классе и тем более последующих старших – настоящая палочка-выручалочка.
Анализ учебного и программно-методического комплекса Е. А. Бунимович Математика 5 класс.
Анализ учебного и программно-методического
комплекса Е. А. Бунимович «Математика 5 класс».
А. Бунимович «Математика 5 класс».
Рабочая программа по математике для 5 класса
учителей, участвующих в эксперименте по введению ФГОС в 5 классе.
(Выступление на заседании городского МО учителей математики)
Учитель математики
МБОУ «СОШ №5»г. Курчатова
Холодова В.В.
2013г.
В концепции развития универсальных учебных действий, изложенных в новых образовательных стандартах второго поколения, обозначена цель общего образования на современном этапе: «Общекультурное, личностное и познавательное развитие учащихся, обеспечивающее такую ключевую компетенцию, как умение учиться». Развитие личности в системе образования обеспечивается, прежде всего, через формирование универсальных учебных действий. В образовательных стандартах второго поколения разработан деятельностный подход к образованию, где преобладает развитие личности учащихся на основе освоения способов деятельности, которые они смогут применять не только в обучении, но и при решении проблем в реальных жизненных ситуациях. Математика – это системообразующий предмет, который формирует общеучебные умения в других предметах школьной программы: химии, физике, биологии. Поэтому, проблема выбора новых УМК стоит перед каждым учителем с каждым новым учебным годом всё острее.
Математика – это системообразующий предмет, который формирует общеучебные умения в других предметах школьной программы: химии, физике, биологии. Поэтому, проблема выбора новых УМК стоит перед каждым учителем с каждым новым учебным годом всё острее.
При переходе на новые УМК возникает проблема преемственности образовательного процесса. Наиболее остро эта проблема стоит в период перехода учащихся из начальной школы в основную.
В УМК «Сферы» «Математика. Арифметика. Геометрия». 5 класс издательства «Просвещение», под редакцией Е.А.Бунимовича и Г.В.Дорофеева, особое внимание обращено на осуществление преемственности с курсом математики начальной школы. При этом основным принципом является принцип открытости. На данный учебник для 5 класса можно переходить после любого учебника начальной школы.
Описание учебно-методического комплекта для 5-6-х классов.
Учебно-методический комплект для 5-6-х классов включает:
учебник;
задачник-тренажер;
тетрадь-тренажер;
тетрадь-экзаменатор;
электронное приложение к учебнику;
методическое пособие для учителя;
поурочное тематическое планирование.

ПРЕДМЕТНАЯ ИНФОРМАЦИОННО-ОБРАЗОВАТЕЛЬНАЯ СРЕДА
«СФЕРЫ». «МАТМАТИКА. АРИФМЕТИКА. ГЕОМЕТРИЯ»
Каждый элемент комплекта дополняет друг друга при изучении и закреплении материала и функционально обеспечивает качество образовательного процесса. Все компоненты УМК имеют современный красочный дизайн, единую навигацию, чёткое функциональное назначение, возможность построения индивидуальной образовательной траектории.
1. Учебник
Учебник – центральное пособие комплекта. Материал учебника продолжает формировать основные математические понятия (число, величина, геометрическая фигура), обеспечивая тем самым преемственность с начальной школой и закладывая базу для дальнейшего обучения предмету, в том числе и при изучении систематических курсов алгебры и геометрии.
Все содержание учебника разбито на главы. Главы подразделяются на пункты. Основной текст разбит на небольшие содержательные блоки, каждый из которых в комплексе с иллюстрациями и сопровождающим его дополнительным материалом является в определенной мере завершенным информационным фрагментом.
Каждый практический разворот содержит набор заданий и упражнений (от базовых до задач-исследований).
Первой темой курса в учебнике является геометрический материал, который не опирается на предварительную математическую подготовку, полученную в начальной школе, что позволяет в начале года параллельно с изучением нового геометрического материала организовать вводное повторение.
Ключевые темы курса раскрываются в учебниках увлекательно и наглядно, язык изложения доступен ученикам, соответствует их возрасту, но при этом сохранена научная достоверность и точность; имеются задания в виде тестов, что усиливает их развивающую роль и готовит обучающихся к будущим экзаменам в форме ЕГЭ.
Практическая направленность учебного материала реализуется в задачах качественного и экспериментального характера. Многие задачи содержат интересные факты из географии, истории, биологии, астрономии, физики, техники. Соседние задания в системе упражнений отличаются по содержанию и по формулировке, что помогает поддерживать интерес к математике и снимает утомление. Достоинством учебника является то, что он содержит небольшой, по сравнению с другими учебниками, объем теоретического материала, адаптированного для данной возрастной группы обучающихся, как по содержанию, так и по объему. Несмотря на то, что учебник адресован ещё достаточно маленьким учащимся, он помогает учителю обеспечить выводы мировоззренческого характера, и, в некоторой степени, уже на уровне 5 класса, раскрывать роль науки в современном мире. Я думаю, что этот учебник способен помочь учителю научить учащихся:
Достоинством учебника является то, что он содержит небольшой, по сравнению с другими учебниками, объем теоретического материала, адаптированного для данной возрастной группы обучающихся, как по содержанию, так и по объему. Несмотря на то, что учебник адресован ещё достаточно маленьким учащимся, он помогает учителю обеспечить выводы мировоззренческого характера, и, в некоторой степени, уже на уровне 5 класса, раскрывать роль науки в современном мире. Я думаю, что этот учебник способен помочь учителю научить учащихся:
самостоятельному, критическому мышлению;
размышлять, опираясь на знание фактов, закономерностей науки, делать обоснованные выводы;
принимать самостоятельные аргументированные решения.
Методической составляющей учебника (и комплекта в целом) авторы уделили достаточное внимание:
тексты и система упражнений тесно взаимосвязаны и способствуют пониманию и осознанности при усвоении материала;
задачный материал представлен на всех уровнях – от репродуктивного до исследовательского;
учебник позволяет реализовать различные формы обучения – от индивидуальной до коллективной;,
материал учебника предоставляет богатые возможности для постановки и решения исследовательских задач, понятных и интересных обучающимся этого возраста.

Ещё одна отличительная особенность учебника (и других компонентов УМК) – это яркая, эмоционально окрашенная подача материала, научный, и в то же время доступный язык текстов, уникальный иллюстративный ряд, что способствует формированию мотивов учения, как социальных, так и познавательных.
Тетрадь-тренажер
Тетрадь-тренажёр является основным инструментом реализации деятельностного подхода в обучении. Материал тетради-тренажёра систематизирован по темам в соответствии с темами учебника, задания сгруппированы по видам деятельности, ранжированы по уровню сложности и служат для формирования универсальных учебных действий средствами предмета. Разнообразие заданий позволяет отрабатывать предметные и надпредметные умения и навыки: решение текстовых задач, отработка начальных геометрических навыков, работа с текстом, развивать творческое мышление. Главное отличие тетради тренажёра от существующих рабочих тетрадей – это функция организатора самостоятельной работы ученика, создателя основы для формирования базовых компетенций.
Основные рубрики «Находим закономерности», «Анализируем и рассуждаем» озаглавлены интересно, необычно, что привлекает внимание учеников и стимулирует интерес к работе.
Завершает каждую главу тест, который ученики могут использовать, например, для самопроверки.
Тетрадь-тренажер — это пособие индивидуального пользования для учеников, задания выполняются непосредственно в нем. Заложенный в структуру тетради-тренажёра этап подведения итогов работы в игровой форме отвечает возрасту обучающихся и помогает учителю ненавязчиво прививать им навыки самоконтроля.
Задачник-тренажер
Неотъемлемой частью комплекта, одним из необходимых дополнений к учебнику является тетрадь-тренажёр как основное средство реализации заявленного авторами системно — деятельностного подхода, он оформлен менее красочно, является дополнением учебника, и содержит различные по уровню сложности группы упражнений.
Задачник-тренажер состоит из двух частей. В первой части содержится система упражнений по всем главам курса (за исключением геометрических), которая дополняет и расширяет содержание практических разворотов учебника. В каждом блоке система упражнений разделена на группы А и Б.. Диапазон сложности заданий, как правило, весьма значителен. Во второй части задачника помещен материал, который можно было бы условно назвать «Для тех, кому интересно».
4.Тетрадь-экзаменатор
Тетрадь-экзаменатор позволяет осуществлять тематический и итоговый контроль. Задания представлены в двух форматах: традиционном и тестовом. Проверочные работы, включенные в пособие, предусматривают проверку достижения всеми учащимися обязательных результатов обучения, а также дают возможность каждому ученику проявить свои знания на более высоком уровне.
5. Методическое пособие и поурочное тематическое планирование.
Большую помощь в работе учителя при подготовке к урокам оказывает методическое пособие и поурочное тематическое планирование. В этих изданиях наиболее полно даны рекомендации по изучению каждой темы, перечислены ЗУН, которыми должны овладеть учащиеся, даже прилагаются планы этапов урока и возможные домашние задания.
В этих изданиях наиболее полно даны рекомендации по изучению каждой темы, перечислены ЗУН, которыми должны овладеть учащиеся, даже прилагаются планы этапов урока и возможные домашние задания.
6. Электронное приложение к учебнику.
Электронное приложение к учебнику включает:
мультимедийные демонстрации;
виртуальные лаборатории;
интерактивные модели;
интерактивные задания;
тренажеры;
тесты;
игры и головоломки;
материалы для математического кружка и организации внеклассной работы;
нужные интернет- ссылки и др.
Электронный учебник — неотъемлемая часть УМК. Основным его достоинством является наличие флеш — презентаций по всем темам курса, интерактивные упражнения, виртуальные лаборатории по всем разделам курса. Возможности электронного приложения делают учебный процесс более привлекательным, личностно ориентированным с высокой степенью индивидуализации обучения.
Таким образом, весь комплект создан в соответствии с современными требованиями дифференцированного подхода в обучении. Это отмечается учителями, участвующими в апробации данного учебника:
В. С. Кулакова: «Наличие материала для работы с обучающимися, проявляющими интерес к математике, и одновременно достаточный запас упражнений для организации учебной деятельности школьников с невысоким уровнем подготовки дают значительную свободу учителю для осуществления дифференцированного подхода к обучающимся, для выстраивания «индивидуальных траекторий» обучения».
Хохлова С.Н.: «С удовольствием воспринимается учениками серия задач рубрики « Задача-исследование», которые помогают развивать творческое мышление.
Т. И. Королёва: «В учебнике и в задачнике удачно определены уровневые задания, выполнение которых придает уверенность как слабому ученику, а также дает возможность глубокой работы заинтересованным детям. Рубрика «Неверно» учит внимательности, умению анализировать задание, проверять свои знания. «Задача-исследование» привлекает заинтересованных учеников, развивает желание постичь науку математику».
«Задача-исследование» привлекает заинтересованных учеников, развивает желание постичь науку математику».
При этом всеми учителями- апробаторами отмечается практико-ориентированная система заданий, которая не только способна обеспечить системное, мотивированное и эффективное овладение содержанием, но и позволяет применять полученные предметные знания и умения в реальной жизни, вся система заданий комплекта может служить средством для формирования универсальных учебных действий средствами предмета.
Учебник «Математика. Арифметика. Геометрия» для 5 класса под ред. Е.А. Бунимовича отличается новым подходом к структурированию теоретического и практического материала. Учителя и учащиеся оценили как достоинства учебника фиксированный в тематических разворотах формат, лаконичность и жесткую структурированность текста, модульность в построении содержания. Набор рубрик «Внимание», «В фокусе», «Читаем и делаем», «Математический блокнот» и их содержание стимулируют активную познавательную деятельность школьников. Рубрики «Записываем решение» и «Кнопка» помогают им научиться оформлять решения математически грамотно, использовать справочный материал.
Рубрики «Записываем решение» и «Кнопка» помогают им научиться оформлять решения математически грамотно, использовать справочный материал.
Большая роль в достижении образовательных результатов при использовании данного учебника отводится иллюстрациям, которые не только очень качественные, но и сами являются источником информации. Многоцветная печать, удобный для чтения шрифт, использование разного шрифта, выделение цветом определений и главных идей содержания, использование «клиповых» вставок как современных форм представления информации, удобная навигация – всё это делает учебник очень привлекательным для школьников. Не случайно 92% всех опрошенных пятиклассников ответили положительно на вопрос о качестве иллюстраций.
При анализе результатов апробации проявилась заинтересованность учителей, которые высоко оценивая весь комплект, указали ошибки и опечатки в нём и его приложениях и предложили авторам свои замечания и пожелания:
УМК под редакцией Е.А. Бунимовича и Г. В. Дорофеева предлагает более совершенную методическую систему обучения математике, учит думать, формирует навыки самостоятельной учебной деятельности, потребность самосовершенствования. УМК способствует развитию познавательной деятельности обучающихся, дает возможность осуществлять личностно-ориентированное обучение, интересен учащимся, содержит много упражнений, развивающих внимание, мышление, логику и воображение учащихся.
В. Дорофеева предлагает более совершенную методическую систему обучения математике, учит думать, формирует навыки самостоятельной учебной деятельности, потребность самосовершенствования. УМК способствует развитию познавательной деятельности обучающихся, дает возможность осуществлять личностно-ориентированное обучение, интересен учащимся, содержит много упражнений, развивающих внимание, мышление, логику и воображение учащихся.
Преимущества данного УМК:
Доступность курса для школьников.
Красочное представление материала.
Материал излагается небольшими порциями и написан простым языком, включены интересные материалы о происхождении математических терминов, что важно для формирования математической культуры.
В учебниках большое количество разнообразных задач практического и познавательного характера, способствующих расширению кругозора.
Пособие формирует самостоятельность мышления учащихся за счёт заданий, в которых необходимо обосновывать ответы, выдвигать гипотезы.

Позволяет развить пространственные представления и воображение за счёт большого количества геометрических задач.
Необычное преподнесение объяснения нового материала.
Помимо учебника к курсу 5-6 классов есть тетрадь-тренажёр, , необходимые для отработки учебного материала, особенно со «слабыми» учениками, для которых большую помощь оказывают пошаговые упражнения, в которых нужно поэтапно заполнять пропуски.
Огромную помощь на первом этапе учителю оказали и авторские разработки уроков, в которых расписаны подробно применяемые на каждом этапе урока составляющие комплекта. Это значительно упрощает работу учителя.
Положено начало изучению новой содержательно-методической линии, включающей комбинаторику, элементы теории вероятностей и статистики.
Расширение информационного поля путем вовлечения в учебный процесс широкого набора медиаресурсов.
Нужно отметить необходимость целостного использования всех дидактических средств, предоставляемых информационно-образовательной средой «Сферы»: электронного учебника, задачников, тетрадей-тренажёров, тетрадей-экзаменаторов.
Новый УМК «Математика. Арифметика. Геометрия. 5 класс» отвечает всем требованиям, предъявляемым к современному образовательному процессу в соответствии с Федеральными государственными образовательными стандартами. Развивает познавательный интерес ученика, повышает мотивацию изучения такого сложного предмета, как математика. Позволяет заложить и сформировать первые геометрические навыки, что вообще отсутствует в других учебниках по математике для 5-6 классов. Помогает развивать у учащихся культуру математической речи, способствует более эффективному обучению применению понятий, правил, определений, формулировок теоретических положений.
Однако, каждый учитель, который планирует использовать данный УМК, должен учитывать дополнительные ежедневные временные затраты, наличие практических навыков работы с компьютером, периферическим оборудованием и интерактивной доской, а так же необходимостью применять указанные технические средства обучения на каждом уроке. Так же, учителю придётся, при подготовке к каждому уроку, делать подборку упражнений из предложенного многообразия заданий, с учётом уровня знаний учеников класса, но я уверена, чем больше времени тратит учитель на подготовку урока, тем меньше времени потребуется ученику для усвоения материала, поэтому эти затраты не напрасны.
Список литературы:
Примерные программы по учебным предметам. Математика. 5-9 классы: проект. – 3-е изд., перераб. – М.: Просвещение, 2011. – 64 с.
Математика. Арифметика. Геометрия. Поурочное тематическое планирование. 5 класс: пособие для учителей общеобразоват. учреждений / [Л.В. Кузнецова, С.С. Минаева, Л.О. Рослова, С.Б. Суворова]; Рос. акад. наук, Рос. акад. образования, изд-во «Просвещение». – М.: Просвещение, 2010. – 96 с.
Математика. Арифметика. Геометрия. 5 класс [Текст]: учебник для учащихся общеобразовательных учреждений / Е.А. Бунимович, Л.В. Кузнецова [и др.]; Рос. акад. наук, Рос. акад. образования. — М.: Просвещение, 2010. — 223 с.
Математика. Арифметика. Геометрия. Задачник-тренажер. 5 класс [Текст]: пособие для учащихся общеобразовательных учреждений / Е.А. Бунимович, Л.В. Кузнецова [и др.]; Рос. акад. наук, Рос. акад. образования. — М.: Просвещение, 2010. — 127 с.

Математика. Арифметика. Геометрия. Тетрадь-тренажер. 5 класс [Текст]: пособие для учащихся общеобразовательных учреждений / Е.А. Бунимович, Л.В. Кузнецова и др.; Рос. акад. наук, Рос. акад. образования. — М.: Просвещение, 2010. — 129 с.
Математика. Арифметика. Геометрия. Электронное приложение к учебнику, 5 класс/ Е.А. Бунимович, Л.В. Кузнецова [и др.]; Рос. акад. наук, Рос. акад. образования. — М.: Просвещение, 2010.
Мухаметзянова Ф.С. Математика. Информационно-образовательная среда как условие реализации ФГОС [Текст]: методические рекомендации. В 3 ч. Часть 2/ Ф.С. Мухаметзянова; под ред. Р.Р. Загидуллина, В.В. Зарубиной, С.Ю. Прохоровой. — Ульяновск: УИПКПРО, 2011. — 52 с.
Петерсон Л.Г., Кубышева М.А., Кудряшова Т.Г. Требование к составлению плана урока по дидактической системе деятельностного метода. – Москва, 2006 г.
Шубина Т.И. Деятельностный метод в школе http://festival.
 1september.ru
1september.ru
Приложение.
1.РАСПРЕДЕЛЕНИЕ УЧЕБНОГО ВРЕМЕНИ
(5 ч в неделю, всего 170 ч) Число уроков
Глава 1. Линии 9
Разнообразный мир линий 2
Прямая. Части прямой. Ломаная 2
Длина линии 2
Окружность 2
Обзорный урок по теме 1
Глава 2. Натуральные числа 12
Как записывают и читают числа 2
Натуральный ряд. Сравнение натуральных чисел … 3
Округление натуральных чисел 2
Перебор возможных вариантов . .’-. 3
Обзорный урок по теме 1
Контроль .’ 1
Глава 3. Действия с натуральными числами 21
9. Сложение и вычитание 3
Умножение и деление 4
Порядок действий в вычислениях 4
Степень числа 3
Задачи на движение 4
Обзорные уроки по теме 2
Контроль 1
Глава 4. Использование свойств действий
Использование свойств действий
при вычислениях 10
Свойства сложения и умножения 2
Распределительное свойство 3
Решение задач 3
Обзорный урок по теме 1
Контроль 1
Глава 5. Углы и многоугольники 9
Как обозначают и сравнивают углы 2
Измерение углов 3
Многоугольники 2
Обзорный урок по теме 1
Контроль 1
Глава 6. Делимость чисел 16
Делители и кратные 3
Простые и составные числа 3
Делимость суммы и произведения 2
Признаки делимости 3
Деление с остатком 3
Обзорный урок по теме 1
Контроль 1
Глава 7. Треугольники и четырехугольники 10
Треугольники и их виды 2
Прямоугольники 2
Равенство фигур 2
Площадь прямоугольника 2
Обзорный урок по теме 1
Контроль 1
Глава 8. Дроби 19
Дроби 19
Доли и дроби 6
Основное свойство дроби 5
Сравнение дробей ‘.’ 4
Натуральные числа и дроби 2
Обзорный урок по теме 1
Контроль 1
Глава 9. Действия с дробями 35
Сложение и вычитание дробей 6
Сложение и вычитание смешанных дробей 6
35.Умножение дробей 5
36.Деление дробей 6
37.Нахождение части целого и целого по его части … 5
38.Задачи на совместную работу 4
Обзорные уроки по теме 2
Контроль 1
Глава 10. Многогранники 11
Геометрические тела и их изображение 2
Параллелепипед и пирамида 3
Объем параллелепипеда 2
Развертки 2
Обзорный урок по теме 1
Контроль 1
Глава 11. Таблицы и диаграммы 9
Чтение и составление таблиц 3
Чтение и построение диаграмм 2
Опрос общественного мнения 2
Обзорный урок по теме 1
Контроль 1
Итоговый контроль 2
Резерв 7
13
Бунимович Е.
 А. `Математика. 5 класс. Учебник (УМК в Мурманске: 113-товаров: бесплатная доставка [перейти]
А. `Математика. 5 класс. Учебник (УМК в Мурманске: 113-товаров: бесплатная доставка [перейти]Партнерская программаПомощь
Мурманск
Каталог
Каталог Товаров
Одежда и обувь
Одежда и обувь
Стройматериалы
Стройматериалы
Здоровье и красота
Здоровье и красота
Текстиль и кожа
Текстиль и кожа
Детские товары
Детские товары
Продукты и напитки
Продукты и напитки
Электротехника
Электротехника
Дом и сад
Дом и сад
Мебель и интерьер
Мебель и интерьер
Промышленность
Промышленность
Сельское хозяйство
Сельское хозяйство
Все категории
ВходИзбранное
Бунимович Е. А. `Математика. 5 класс. Учебник (УМК
А. `Математика. 5 класс. Учебник (УМК
Зак С.М. «Все домашние работы к учебнику и задачнику Бунимовича Е.А. «Математика Арифметика. Геометрия 5 класс». УМК «Сферы». ФГОС»
ПОДРОБНЕЕЕще цены и похожие товары
Примерныерабочиепрограммыфгос Бунимович Е.А.,Кузнецова Л.В.,Минаева С.С. Математика 5-9кл. Сборник (УМК «Сферы»), (Просвещение, 2019), Обл, c.200
ПОДРОБНЕЕЕще цены и похожие товары
295
775
Зак С.М. «ФГОС. Математика к УМК Бунимовича «Сферы»+задачнику. Книга для родителей. 5 класс Зак С.М. | Автор не указан»
ПОДРОБНЕЕЕще цены и похожие товары
Барашкова Е.А. «УМК. Английский язык. 8 класс. Грамматика. Сборник упражнений. Часть 1. К учебнику Ваулиной»
ПОДРОБНЕЕЕще цены и похожие товары
Математика 5 класс. Учебник в 2-х частях. УМК «Учусь учиться». ФГОС | Петерсон Людмила Георгиевна, Дорофеев Георгий Владимирович
Учебник в 2-х частях. УМК «Учусь учиться». ФГОС | Петерсон Людмила Георгиевна, Дорофеев Георгий Владимирович
ПОДРОБНЕЕЕще цены и похожие товары
209
270
Ерина Т.М. «Математика 5 класс. Тесты к учебнику А.Г. Мерзляка и др. УМК Мерзляка. К новому ФПУ. ФГОС | Ерина Татьяна Михайловна»
ПОДРОБНЕЕЕще цены и похожие товары
1 201
1442
Математика 5 класс. Учебник. УМК «Математика Никольского С.М». ФГОС | Никольский Сергей Михайлович
ПОДРОБНЕЕЕще цены и похожие товары
Поурочные разработки по обществознанию. 5 класс : пособие для учителя (к УМК А.И. Кравченко, Е.А. Певцовой)
ПОДРОБНЕЕЕще цены и похожие товары
Изобразительное искусство. Музыка. 3 класс: рабочие программы по учебникам Л. Г. Савенковой, Е. А. Ермолинской и В. О. Усачёвой, Школяр. УМК «Начальная школа XXI века»
А. Ермолинской и В. О. Усачёвой, Школяр. УМК «Начальная школа XXI века»
ПОДРОБНЕЕЕще цены и похожие товары
Ахременкова В. И. «Математика. 5 класс. Рабочая программа. УМК Виленкина. ФГОС.» Предмет:
ПОДРОБНЕЕЕще цены и похожие товары
Технология. 3 класс: рабочая программа и технологические карты уроков по учебнику Е. А. Лутцевой, Т. П. Зуевой. УМК «Школа России»
ПОДРОБНЕЕЕще цены и похожие товары
Барашкова Е.А. «Английский язык 6 класс. Книга для родителей. УМК Афанасьева (к новому ФПУ). ФГОС»
ПОДРОБНЕЕЕще цены и похожие товары
Технология. 4 класс: Рабочая программа и технологические карты уроков по учебнику Е. А. Лутцевой, Т. П. Зуевой. УМК «Школа России»
ПОДРОБНЕЕЕще цены и похожие товары
Ерина Т. М. «УМК. Математика. 5 класс. Рабочая тетрадь. Часть 2. К учебнику Виленкина» Издательство:
М. «УМК. Математика. 5 класс. Рабочая тетрадь. Часть 2. К учебнику Виленкина» Издательство:
ПОДРОБНЕЕЕще цены и похожие товары
Технология. 4 класс: рабочая программа и технологические карты уроков по учебнику Е. А. Лутцевой. УМК «Начальная школа XXI века»
ПОДРОБНЕЕЕще цены и похожие товары
174
306
Павлова О. В. «Технология. 3 класс: рабочая программа и технологические карты уроков по учебнику Е. А. Лутцевой, Т. П. Зуевой. УМК «Школа России»»
ПОДРОБНЕЕЕще цены и похожие товары
172
298
Павлова О. В. «Технология. 1 класс: рабочая программа и технологические карты уроков по учебнику Е. А. Лутцевой, Т. П. Зуевой. УМК «Школа России»»
ПОДРОБНЕЕЕще цены и похожие товары
Биянова Е.Б. «Поурочные разработки по обществознанию 6 класс к УМК А. И.Кравченко,Е.А.Певцовой»
И.Кравченко,Е.А.Певцовой»
ПОДРОБНЕЕЕще цены и похожие товары
266
446
Павлова О. В. «Технология. 3 класс: рабочая программа и технологические карты уроков по учебнику Е. А. Лутцевой. УМК «Начальная школа XXI века»»
ПОДРОБНЕЕЕще цены и похожие товары
1 029
1235
Савенкова Любовь Григорьевна, Ермолинская Елена Александровна «Изобразительное искусство 3 класс. Учебник. ФГОС. УМК «Е.А. Ермолинской» | Ермолинская Елена Александровна, Савенкова Любовь Григорьевна»
ПОДРОБНЕЕЕще цены и похожие товары
Просвещение/Бином. Лаборатория знаний/Дорофеев Г.В.,Петерсон Л.Г. Математика. 5 класс. Учебник. Комплект в 2-х частях. Часть 1
ПОДРОБНЕЕЕще цены и похожие товары
ФГОС Тихомирова Е.М. Тесты по Окружающему миру 4кл (Ч.1/2) (к учеб. Плешакова А. А., Крючковой Е.А. УМК «Школа России» ФПУ-2019), (Экзамен, 2022), Обл, c.64
А., Крючковой Е.А. УМК «Школа России» ФПУ-2019), (Экзамен, 2022), Обл, c.64
ПОДРОБНЕЕЕще цены и похожие товары
Е. Н. Сорокина «Поурочные разработки по обществознанию. 5 класс (к УМК А. И. Кравченко, Е. А. Певцовой)»
ПОДРОБНЕЕЕще цены и похожие товары
Просвещение Рабочая тетрадь. ФГОС. Русский язык к УМК Баранова, Ладыженской, Тростенцовой, новое оформление 7 класс. Ефремова Е. А.
ПОДРОБНЕЕЕще цены и похожие товары
Просвещение / Математика 5 класс. Дидактические материалы к учебнику. УМК «Математика. Дорофеев Г.В. и др. (5-6)», Просвещение
ПОДРОБНЕЕЕще цены и похожие товары
Сорокина Е.Н. «Поурочные разработки по обществознанию. 5 класс : пособие для учителя (к УМК А.И. Кравченко, Е.А. Певцовой)»
ПОДРОБНЕЕЕще цены и похожие товары
Поурочные разработки по обществознанию. 6 класс : пособие для учителя (к УМК А.И. Кравченко, Е.А. Певцовой)
6 класс : пособие для учителя (к УМК А.И. Кравченко, Е.А. Певцовой)
ПОДРОБНЕЕЕще цены и похожие товары
Просвещение / Математика 6 класс. Дидактические материалы к учебнику. УМК «Математика. Дорофеев Г.В. и др. (5-6)», Просвещение
ПОДРОБНЕЕЕще цены и похожие товары
2 страница из 15
Чувствительные нервы препятствуют формированию третичных лимфоидных структур и развитию защитных антимеланомных иммунных реакций
Сохранить цитату в файл
Формат: Резюме (текст)PubMedPMIDAbstract (текст)CSV
Добавить в коллекции
- Создать новую коллекцию
- Добавить в существующую коллекцию
Назовите свою коллекцию:
Имя должно содержать менее 100 символов
Выберите коллекцию:
Не удалось загрузить вашу коллекцию из-за ошибки
Повторите попытку
Добавить в мою библиографию
- Моя библиография
Не удалось загрузить делегатов из-за ошибки
Повторите попытку
Ваш сохраненный поиск
Название сохраненного поиска:
Условия поиска:
Тестовые условия поиска
Эл. адрес:
(изменить)
адрес:
(изменить)
Который день? Первое воскресеньеПервый понедельникПервый вторникПервая средаПервый четвергПервая пятницаПервая субботаПервый деньПервый рабочий день
Который день? ВоскресеньеПонедельникВторникСредаЧетвергПятницаСуббота
Формат отчета: SummarySummary (text)AbstractAbstract (text)PubMed
Отправить максимум: 1 шт. 5 шт. 10 шт. 20 шт. 50 шт. 100 шт. 200 шт.
Отправить, даже если нет новых результатов
Необязательный текст в электронном письме:
Создайте файл для внешнего программного обеспечения для управления цитированием
. 2022 1 сентября; 10 (9): 1141-1154.
doi: 10.1158/2326-6066. CIR-22-0110.
CIR-22-0110.
Кавита Ватс # 1 , Олег Круглов # 1 , Бикрам Саху 2 , Вишал Соман 3 , Цзиин Чжан 1 , Шурин Галина В 4 , Ума Р Чандран 3 , Павел Скумс 2 , Шурин Михаил Р. 4 5 6
Принадлежности
- 1 Кафедра дерматологии Медицинской школы Университета Питтсбурга, Питтсбург, Пенсильвания.

- 2 Департамент компьютерных наук, Университет штата Джорджия, Атланта, Джорджия.
- 3 Кафедра биомедицинской информатики Медицинской школы Университета Питтсбурга, Питтсбург, Пенсильвания.
- 4 Кафедра патологии Медицинской школы Университета Питтсбурга, Питтсбург, Пенсильвания.
- 5 Кафедра иммунологии Медицинской школы Университета Питтсбурга, Питтсбург, Пенсильвания.
- 6 Онкологический центр UPMC Hillman, Питтсбург, Пенсильвания.
# Внесли поровну.
- PMID: 35834791
- DOI:
10.
 1158/2326-6066.CIR-22-0110
1158/2326-6066.CIR-22-0110
Кавита Ватс и др. Рак Иммунол Рез. .
. 2022 сен 1;10(9)):1141-1154.
doi: 10.1158/2326-6066.CIR-22-0110.
Авторы
Кавита Ватс # 1 , Олег Круглов # 1 , Бикрам Саху 2 , Вишал Соман 3 , Цзиин Чжан 1 , Галина В Шурина 4 , Ума Р Чандран 3 , Павел Скумс 2 , Шурин Михаил Р.
Принадлежности
- 1 Кафедра дерматологии Медицинской школы Университета Питтсбурга, Питтсбург, Пенсильвания.
- 2 Департамент компьютерных наук, Университет штата Джорджия, Атланта, Джорджия.
- 3 Кафедра биомедицинской информатики Медицинской школы Университета Питтсбурга, Питтсбург, Пенсильвания.
- 4 Кафедра патологии Медицинской школы Университета Питтсбурга, Питтсбург, Пенсильвания.

- 5 Кафедра иммунологии Медицинской школы Университета Питтсбурга, Питтсбург, Пенсильвания.
- 6 Онкологический центр UPMC Hillman, Питтсбург, Пенсильвания.
# Внесли поровну.
- PMID: 35834791
- DOI: 10.1158/2326-6066.CIR-22-0110
Абстрактный
Периферические нейроны составляют критический компонент микроокружения опухоли (TME). Роль вегетативной иннервации при раке твердо установлена. Однако влияние афферентных (сенсорных) нейронов на прогрессирование опухоли остается неясным. Используя методы хирургической и химической сенсорной денервации кожи, мы показали, что афферентные нейроны поддерживают рост меланомных опухолей in vivo, и продемонстрировали, что сенсорная иннервация ограничивает активацию эффективных противоопухолевых иммунных ответов. В частности, сенсорная абляция приводила к улучшению рекрутирования лейкоцитов в опухоли с уменьшением присутствия лимфоидных и миелоидных иммуносупрессивных клеток и повышенной активацией Т-эффекторных клеток в ТМО. Кожные чувствительные нервы препятствовали созреванию внутриопухолевых венул с высоким эндотелием и ограничивали образование зрелых третичных лимфоидноподобных структур, содержащих организованные скопления CD4+ Т-клеток и В-клеток. Денервация дополнительно увеличивала клональность Т-клеток и расширяла репертуар В-клеток в TME. Важно отметить, что истощение CD8a предотвращало зависимые от денервации противоопухолевые эффекты. Наконец, мы наблюдали, что генные сигнатуры воспаления и содержание транскриптов, связанных с нейронами, обратно коррелировали в первичных меланомах кожи человека, причем последнее представляет собой отрицательный прогностический маркер общей выживаемости пациентов. Наши результаты показывают, что сенсорные нейроны, связанные с опухолью, негативно регулируют развитие защитных противоопухолевых иммунных ответов в пределах TME, тем самым определяя новую цель для терапевтического вмешательства в условиях меланомы.
В частности, сенсорная абляция приводила к улучшению рекрутирования лейкоцитов в опухоли с уменьшением присутствия лимфоидных и миелоидных иммуносупрессивных клеток и повышенной активацией Т-эффекторных клеток в ТМО. Кожные чувствительные нервы препятствовали созреванию внутриопухолевых венул с высоким эндотелием и ограничивали образование зрелых третичных лимфоидноподобных структур, содержащих организованные скопления CD4+ Т-клеток и В-клеток. Денервация дополнительно увеличивала клональность Т-клеток и расширяла репертуар В-клеток в TME. Важно отметить, что истощение CD8a предотвращало зависимые от денервации противоопухолевые эффекты. Наконец, мы наблюдали, что генные сигнатуры воспаления и содержание транскриптов, связанных с нейронами, обратно коррелировали в первичных меланомах кожи человека, причем последнее представляет собой отрицательный прогностический маркер общей выживаемости пациентов. Наши результаты показывают, что сенсорные нейроны, связанные с опухолью, негативно регулируют развитие защитных противоопухолевых иммунных ответов в пределах TME, тем самым определяя новую цель для терапевтического вмешательства в условиях меланомы.
© 2022 Американская ассоциация исследований рака.
Похожие статьи
Терапия на основе агонистов STING способствует нормализации сосудов и формированию третичной лимфоидной структуры в терапевтическом микроокружении меланомы.
Челванамби М., Фечек Р.Дж., Тейлор Дж.Л., Сторкус В.Дж. Челванамби М. и соавт. J Иммунный рак. 2021 фев;9(2):e001906. дои: 10.1136/jitc-2020-001906. J Иммунный рак. 2021. PMID: 33526609 Бесплатная статья ЧВК.
Неоднородность В-клеток третичной лимфоидной структуры коррелирует с выживаемостью пациентов с метастатической меланомой.
Линч К.Т., Янг С.Дж., Менево М.О., Зарплата Н.А., Энгельхард В.Х., Слинглафф С.Л. мл., Молдин И.С. Линч К.Т. и др. J Иммунный рак.

Реакции зародышевого центра в третичных лимфоидных структурах связаны с неоантигенной нагрузкой, гуморальным иммунитетом и длительной выживаемостью при раке поджелудочной железы.
Дж. Гандерсон А., Раджаманикам В., Буй С., Бернард Б., Пуциловска Дж., Баллестерос-Мерино С., Шмидт М., Маккарти К., Филипс М., Пининг Б., Дубей С., Медлер Т., Ньюэлл П., Хансен П., Тран Э., Тан Э., Бифулко С., Криттенден М., Гоф М., Янг К.Х. Дж. Гандерсон А. и соавт. Онкоиммунология. 2021 17 мар;10(1):15. doi: 10.1080/2162402X.2021.15. Онкоиммунология. 2021. PMID: 33796412 Бесплатная статья ЧВК.
Меланома кожи: мутационный статус и потенциальные связи с формированием третичной лимфоидной структуры.

Салем Д., Челванамби М., Сторкус В.Дж., Фечек Р.Дж. Салем Д. и др. Фронт Иммунол. 2021 4 марта; 12:629519. doi: 10.3389/fimmu.2021.629519. Электронная коллекция 2021. Фронт Иммунол. 2021. PMID: 33746966 Бесплатная статья ЧВК. Обзор.
Опухолеинфильтрирующие лимфоциты и их прогностическое значение при меланоме кожи.
Майбах Ф., Садозай Х., Сейед Джафари С.М., Голод Р.Э., Шенк М. Майбах Ф. и соавт. Фронт Иммунол. 2020 10 сентября; 11:21:05. doi: 10.3389/fimmu.2020.02105. Электронная коллекция 2020. Фронт Иммунол. 2020. PMID: 33013886 Бесплатная статья ЧВК. Обзор.
Посмотреть все похожие статьи
термины MeSH
Грантовая поддержка
- P30 CA047904/CA/NCI NIH HHS/США
- RSG-19—088-01-CSM / Грант научного сотрудника
- P01HL114453/Фонд Генри Л.
 Хиллмана
Хиллмана - P30CA047904/Hillman Cancer Genomics Facility and Bioinformatics Services
Полнотекстовые ссылки
Информационные системы Silverchair
Укажите
Формат: ААД АПА МДА НЛМ
Отправить по номеру
Взаимодействие робота и бильярдного стадиона Бунимович
Введение
Хаос — это теория, имеющая разветвления во всей науке 1,2,3 . Работа Лоренца в области метеорологии 4 — это современный краеугольный камень теории хаоса. Влияние теории хаоса распространяется не только на физику и математику, но и на биологию, химию, связь, инженерию, криптографию и робототехнику 5,6,7,8,9,10,11,12,13,14 . Он предоставляет набор концепций и методов для анализа нового поведения, возникающего в широком диапазоне дисциплин 1 . Отличительной чертой хаоса является сверхчувствительность нелинейной системы к своим начальным условиям, что делает классическую динамику непредсказуемой в течение длительных периодов времени 3 .
Отличительной чертой хаоса является сверхчувствительность нелинейной системы к своим начальным условиям, что делает классическую динамику непредсказуемой в течение длительных периодов времени 3 .
Динамика бильярда, пожалуй, самая простая система, в которой возникает хаос 10,15 . Эта система имеет две оси симметрии, которые также можно использовать для увеличения числа траекторий в ней. Движение в бильярде состоит из последовательности прямых полетов, прерываемых зеркальными отражениями. Например, в круговом бильярде стадиона 16 (CSB) эволюция частицы нечувствительна к начальным условиям. В этом случае последовательность прямых полетов и углов отражения дает регулярный временной ряд. Следовательно, частица совершает периодические орбиты, посещая только часть внутренней площади стадиона. Однако, когда граница имеет форму, как на стадионе Бунимовича бильярд 17 (BSB), как показано на рис. 1a, или в бильярде на стадионе Синай 18 (SSB) последовательность прямых полетов и углов представляет собой нетривиальный временной ряд. Это означает, что динамика чувствительна к начальным условиям, является непериодической, и поэтому частица получает доступ ко всем областям стадиона. Таким образом, BSB и SSB являются примерами эргодической динамики 19 , утверждающей, что при определенных условиях среднее время функции вдоль траекторий существует почти всюду и связано со средним по пространству. Помимо эргодических свойств, BSB также является перемешивающей системой со свойством Колмогорова 9.2\). ( b ) Геометрические параметры бильярда стадиона Бунимовича. Красные пунктирные вертикальные линии отделяют полуокружности радиуса r от центрального прямоугольника со стороной 2 a . Общая длина равна \(L=2(r+a)\). ( c ) Робот Arduino, использованный в эксперименте. Размеры робота ( l , w , h ) составляют 14 см, 12,5 см и 16 см соответственно. ( d ) Координаты стадиона в Биркгоф ( p , s ), где \(p\in [-2a-\pi r,+2a+\pi r]\) лежит на границе, а параметр скорости проекции \(s= \sin \theta _{ i}\in [-1,+1]\), где \(\theta _i\) — угол падения.
Это означает, что динамика чувствительна к начальным условиям, является непериодической, и поэтому частица получает доступ ко всем областям стадиона. Таким образом, BSB и SSB являются примерами эргодической динамики 19 , утверждающей, что при определенных условиях среднее время функции вдоль траекторий существует почти всюду и связано со средним по пространству. Помимо эргодических свойств, BSB также является перемешивающей системой со свойством Колмогорова 9.2\). ( b ) Геометрические параметры бильярда стадиона Бунимовича. Красные пунктирные вертикальные линии отделяют полуокружности радиуса r от центрального прямоугольника со стороной 2 a . Общая длина равна \(L=2(r+a)\). ( c ) Робот Arduino, использованный в эксперименте. Размеры робота ( l , w , h ) составляют 14 см, 12,5 см и 16 см соответственно. ( d ) Координаты стадиона в Биркгоф ( p , s ), где \(p\in [-2a-\pi r,+2a+\pi r]\) лежит на границе, а параметр скорости проекции \(s= \sin \theta _{ i}\in [-1,+1]\), где \(\theta _i\) — угол падения.
Увеличенное изображение
Показатель Ляпунова (LE), исторически обозначаемый \(\lambda\), является объективной мерой хаоса. Эта величина связана с линейной устойчивостью траектории. Когда \(\lambda > 0\), существует по крайней мере одно направление в фазовом пространстве, в котором динамика неустойчива, что подразумевает хаотическое поведение. Стандартным методом расчета \(\лямбда\) является так называемый метод касательного пространства, заключающийся в интегрировании уравнения движения системы с его линеаризованными вариантами, рассматриваемыми на последовательных шагах по времени 21 . Исходя из этого и общего начального возмущения, мы надлежащим образом оцениваем наиболее расширяющееся направление отклонений.
В некоторых ситуациях линеаризованная версия уравнений состояния недоступна из-за наличия разрывов. В таких случаях можно использовать метод динамики клонирования 22 . Кроме того, когда имеется только временной ряд наблюдений, алгоритм, предложенный Wolf et al. 23 — альтернатива; их метод основан на методах реконструкции фазового пространства с использованием координат задержки. К сожалению, при использовании методов клона и Вольфа происходит потеря точности, так как получают якобиан приближенными реконструкциями. 92+4ra\), LE равен нулю, когда \(a=0\) и быстро увеличивается с \(\gamma =a/r\), достигая максимального значения \(\lambda \приблизительно 0,43\) при \(\ гамма = 1\). После этого он медленно затухает как \(\gamma \rightarrow \infty\). Обратите внимание, что когда \(\gamma = 0\) бильярд является идеальным CSB, а для \(\gamma \rightarrow \infty\) идеальный BSB ведет себя как совершенная прямоугольная граница, оба случая нехаотичны. Эти результаты были подтверждены численно 10,24 , но нам не известно ни о какой прямой экспериментальной реализации такой идеализированной системы.
23 — альтернатива; их метод основан на методах реконструкции фазового пространства с использованием координат задержки. К сожалению, при использовании методов клона и Вольфа происходит потеря точности, так как получают якобиан приближенными реконструкциями. 92+4ra\), LE равен нулю, когда \(a=0\) и быстро увеличивается с \(\gamma =a/r\), достигая максимального значения \(\lambda \приблизительно 0,43\) при \(\ гамма = 1\). После этого он медленно затухает как \(\gamma \rightarrow \infty\). Обратите внимание, что когда \(\gamma = 0\) бильярд является идеальным CSB, а для \(\gamma \rightarrow \infty\) идеальный BSB ведет себя как совершенная прямоугольная граница, оба случая нехаотичны. Эти результаты были подтверждены численно 10,24 , но нам не известно ни о какой прямой экспериментальной реализации такой идеализированной системы.
Мы можем имитировать классическую динамику частиц в бильярде, используя, например, микроволновые резонаторы 25 , оптические системы 5 и робототехнику 14,26,27 . Оптические системы являются общей темой исследований в фундаментальных науках, тогда как эксперименты с роботами и окружающей средой в основном рассматриваются в прикладных науках и технике 28,29,30 . Здесь мы стремимся показать, что взаимодействие робота и окружающей среды может быть подходящей платформой для изучения фундаментальной науки классической динамики.
Оптические системы являются общей темой исследований в фундаментальных науках, тогда как эксперименты с роботами и окружающей средой в основном рассматриваются в прикладных науках и технике 28,29,30 . Здесь мы стремимся показать, что взаимодействие робота и окружающей среды может быть подходящей платформой для изучения фундаментальной науки классической динамики.
В этой работе мы экспериментально имитируем классическую динамику одиночной частицы в стандартных границах CSB и BSB как взаимодействие робота и окружающей среды. Робот Arduino, использованный в эксперименте, показан на рис. 1в. Наша экспериментальная установка может обеспечить все измерения, необходимые для записи якобиана для идеального BSB. В результате мы получаем LE с использованием метода касательных для шести различных значений \(\gamma\) для BSB, сохраняя его площадь фиксированной в установке длиной 3,38 метра, см. Таблицу 1. Мы сопоставляем наши экспериментальные результаты с прогнозами Benettin и Стрельцин 9 , которые полностью совместимы. В качестве контроля на нашей экспериментальной установке мы определяем поверхность Пуанкаре сечения (SOS) 31,32,33 для стандартных CSB и BSB, используя координаты Биркгофа 34 , как показано на рис. 1d. SOS характеризует все функции системы в фазовом пространстве. Геометрические симметрии бильярда стадиона и динамики частицы внутренне связаны и проявляются как симметрии в SOS Пуанкаре. Симметрия отражения BSB, горизонтальной и вертикальной осей, создает лево-правые симметричные узоры в SOS Пуанкаре, в то время как симметрия обращения времени 35 динамика делает симметричные узоры верх-низ в Ponicaré SOS. Даже неправильные границы с шероховатостью приводят к симметричным рисункам сверху вниз благодаря симметрии обращения времени. Эти симметрии представлены на рис. 3, что будет обсуждаться позже. Несмотря на геометрическую симметрию и симметрию обращения времени, замкнутые траектории ведут себя по-разному. Они производят отдельные точки в SOS Пуанкаре, обычно окруженные пустыми областями.
В качестве контроля на нашей экспериментальной установке мы определяем поверхность Пуанкаре сечения (SOS) 31,32,33 для стандартных CSB и BSB, используя координаты Биркгофа 34 , как показано на рис. 1d. SOS характеризует все функции системы в фазовом пространстве. Геометрические симметрии бильярда стадиона и динамики частицы внутренне связаны и проявляются как симметрии в SOS Пуанкаре. Симметрия отражения BSB, горизонтальной и вертикальной осей, создает лево-правые симметричные узоры в SOS Пуанкаре, в то время как симметрия обращения времени 35 динамика делает симметричные узоры верх-низ в Ponicaré SOS. Даже неправильные границы с шероховатостью приводят к симметричным рисункам сверху вниз благодаря симметрии обращения времени. Эти симметрии представлены на рис. 3, что будет обсуждаться позже. Несмотря на геометрическую симметрию и симметрию обращения времени, замкнутые траектории ведут себя по-разному. Они производят отдельные точки в SOS Пуанкаре, обычно окруженные пустыми областями. Кроме того, чтобы полностью описать динамику бильярда, мы также представляем эволюцию во времени траекторий робота в фазовом пространстве в SOS Пуанкаре для траекторий робота. 94\) столкновения с границей стадиона оказалось достаточно для сходимости ЛЭ. Каждая числовая точка данных соответствует среднему значению ста различных начальных условий. Наши численные результаты согласуются с теми, о которых впервые сообщили Бенеттин и Стрельцин, см. рис. 4 в [1]. 9 .
Кроме того, чтобы полностью описать динамику бильярда, мы также представляем эволюцию во времени траекторий робота в фазовом пространстве в SOS Пуанкаре для траекторий робота. 94\) столкновения с границей стадиона оказалось достаточно для сходимости ЛЭ. Каждая числовая точка данных соответствует среднему значению ста различных начальных условий. Наши численные результаты согласуются с теми, о которых впервые сообщили Бенеттин и Стрельцин, см. рис. 4 в [1]. 9 .
Полная таблица
Рис. 2 Показатель Ляпунова (\(\lambda\)) как функция управляющего параметра \(\gamma =a/r\). Черные открытые кружки — это численные результаты для \(\лямбда\) для идеального BSB. Красные открытые квадраты — это экспериментальные результаты для \(\lambda\) в стандартном BSB. 92\). Как видно из рис. 2, ЛВ идеального и стандартного ОСП в зависимости от \(\gamma\) имеют одинаковое поведение, они быстро возрастают, достигая максимума при \(\gamma =1. 0\) и медленно уменьшаются при \ (\gamma \rightarrow \infty\), что делает этот результат первой экспериментальной реализацией, показывающей правильность теоретического предсказания Бенеттина и Стрельчина 9 . Все интересующие величины, такие как траектория, углы рассеяния и время столкновения, получаются непосредственно из видеозаписи робота и служат входными данными для метода касательных 9.0061 22 , такой же, как и в численной процедуре. Каждое экспериментальное значение, приведенное на рис. 2, представляет собой среднее значение пяти измерений, каждое из которых рассчитано на основе разных временных рядов, записанных в 15-минутном временном окне. Значения LE приведены в таблице 1. Характерные длины BSB приведены на рис. 1b. Как видно из таблицы 1, экспериментальные и численные результаты согласуются.
0\) и медленно уменьшаются при \ (\gamma \rightarrow \infty\), что делает этот результат первой экспериментальной реализацией, показывающей правильность теоретического предсказания Бенеттина и Стрельчина 9 . Все интересующие величины, такие как траектория, углы рассеяния и время столкновения, получаются непосредственно из видеозаписи робота и служат входными данными для метода касательных 9.0061 22 , такой же, как и в численной процедуре. Каждое экспериментальное значение, приведенное на рис. 2, представляет собой среднее значение пяти измерений, каждое из которых рассчитано на основе разных временных рядов, записанных в 15-минутном временном окне. Значения LE приведены в таблице 1. Характерные длины BSB приведены на рис. 1b. Как видно из таблицы 1, экспериментальные и численные результаты согласуются.
 Область определения этих переменных: \(p\in [-2a-\pi r,+2a+\pi r]\) и \(s\in [-1,1]\), геометрические детали см. на рис. 1. . Геометрические параметры, используемые для фиксирования площади: \(r=1,51\) для CSB и \(r=a=1\) для BSB.
Область определения этих переменных: \(p\in [-2a-\pi r,+2a+\pi r]\) и \(s\in [-1,1]\), геометрические детали см. на рис. 1. . Геометрические параметры, используемые для фиксирования площади: \(r=1,51\) для CSB и \(r=a=1\) для BSB.Полноразмерное изображение
Экспериментальные данные на рис. 2 обладают выдающимися характеристиками, на которые следует обратить внимание. Хотя мы знаем, что динамика частиц в идеальном CSB имеет нулевое LE, взаимодействие робота с окружающей средой в стандартном CSB имеет ненулевое LE, \(\lambda = 0,03\), см. Таблицу 1. Это означает, что стандартный CSB используемая в эксперименте, отклоняется от геометрии идеального ЦСБ, что согласуется с основанием теоремы Колмогорова–Арнольда–Мозера 5,36 . Это отклонение проявляется и в максимальном ЛЭ ЧБС, что происходит при \(\gamma=1.0\). Для идеального BSB LE составляет \(\lambda =0,43\), а для взаимодействия робота с окружающей средой в стандартном BSB \(\lambda = 0,47\). Аналогичное отклонение между идеальной и стандартной полугрибовидной полостью также было зарегистрировано в оптическом хаосе 9. 0061 5 . Кроме того, как будет видно, расхождение более заметно в SOS Пуанкаре.
0061 5 . Кроме того, как будет видно, расхождение более заметно в SOS Пуанкаре.
Бильярд, например, BSB, SSB, CSB и эллиптический бильярд, среди прочих, имеет очень богатый SOS Пуанкаре 31,32,33 . Хорошо известно, что SOS Пуанкаре является умной формой для уменьшения размерности динамических систем 37 . Бильярд имеет фазовое пространство с четырьмя измерениями, состоящее из двух пространственных степеней свободы и двух сопряженных импульсов. Кроме того, фазовое пространство этих систем имеет островки устойчивости: орбиты с периодическим, квазипериодическим и хаотическим поведением. Однако из-за сохранения энергии частицы движение фактически происходит по трехмерной поверхности, что может быть достигнуто с помощью SOS Пуанкаре 37 . В этом случае удобно ввести координаты Биркгофа 34 ( p , s ), где \(p\in [-2a-\pi r,+2a+\pi r]\) лежит на границе, и параметр скорости проекции \(s={\hat{v}} \cdot {\hat{n}} = \sin \theta _{i}\in [-1,+1]\), где \(\ theta _i\) – это угол падения, как показано на рис. 1d. SOS представляет собой набор ( p , s ) точки столкновения на границе 37 . Поскольку координаты Биркгофа сохраняют площадь, а соответствующий гамильтониан сохраняет энергию, эффективная размерность фазового пространства для SOS Пуанкаре может быть уменьшена 37,38 . Мы определяем SOS Пуанкаре для стандартных CSB и BSB, чтобы сопоставить совершенный CSB, который не является хаотичным, с BSB, который является хаотичным.
1d. SOS представляет собой набор ( p , s ) точки столкновения на границе 37 . Поскольку координаты Биркгофа сохраняют площадь, а соответствующий гамильтониан сохраняет энергию, эффективная размерность фазового пространства для SOS Пуанкаре может быть уменьшена 37,38 . Мы определяем SOS Пуанкаре для стандартных CSB и BSB, чтобы сопоставить совершенный CSB, который не является хаотичным, с BSB, который является хаотичным.
Кроме того, классическая динамика частицы в бильярде имеет две симметрии: одна связана с симметрией обращения времени, а другая связана с симметрией бильярда стадиона. Первый утверждает, что частица следует по тому же пути, если мы инвертируем течение времени, что приводит к идентичной последовательности длин полетов и времени. С другой стороны, углы падения меняют знак, потому что мы определяем \(\theta _i\) как положительное для вращения по часовой стрелке и отрицательное для против часовой стрелки. Это определение угла падения подразумевает, что для каждой точки ( p , s ) в SOS Пуанкаре есть еще одна точка \((p,-s)\). Последнее является следствием геометрии системы. BSB имеет отражательную симметрию по каждой из двух своих главных осей. Любое начальное состояние во 2-м, 3-м и 4-м квадранте можно сопоставить с 1-м квадрантом и наоборот. Эти две симметрии позволяют преобразовать один временной ряд координат Биркгофа в фактически четыре временных ряда. Следовательно, множество точек столкновения на границе биллиарда x , y можно представить в виде четырех временных рядов: \((p,s)\стрелка вправо (p,-s)\стрелка вправо (-p,s)\стрелка вправо (-p,-s)\). В экспериментах с использованием микроволн 37 и оптических резонаторов 5 количество столкновений очень велико, и нет необходимости использовать симметрию SOS Пуанкаре, поскольку она возникает спонтанно из измеренных данных. В нашем случае стандартный BSB имеет только 200 столкновений, и эти симметрии полезны для заполнения экспериментального ( p , s ) фазовое пространство.
Последнее является следствием геометрии системы. BSB имеет отражательную симметрию по каждой из двух своих главных осей. Любое начальное состояние во 2-м, 3-м и 4-м квадранте можно сопоставить с 1-м квадрантом и наоборот. Эти две симметрии позволяют преобразовать один временной ряд координат Биркгофа в фактически четыре временных ряда. Следовательно, множество точек столкновения на границе биллиарда x , y можно представить в виде четырех временных рядов: \((p,s)\стрелка вправо (p,-s)\стрелка вправо (-p,s)\стрелка вправо (-p,-s)\). В экспериментах с использованием микроволн 37 и оптических резонаторов 5 количество столкновений очень велико, и нет необходимости использовать симметрию SOS Пуанкаре, поскольку она возникает спонтанно из измеренных данных. В нашем случае стандартный BSB имеет только 200 столкновений, и эти симметрии полезны для заполнения экспериментального ( p , s ) фазовое пространство.
 4
4 Динамика КНС Пуанкаре для первых 8 столкновений со стенкой для двух близких начальных условий (красное и черное). Графики ( a ) и ( c ) относятся к CSB, а графики ( b ) и ( d ) к BSB. Красные и черные точки в ( a ) и ( c ) всегда близки друг к другу, тогда как в ( b ) и ( d ) они расходятся. В ( и ) и ( f ) мы показываем SOS Пуанкаре для стандартных CSB и BSB с теми же 8 точками, где мы добавляем стрелки, чтобы указать последовательность столкновений
Полноразмерное изображение
gamma =0\), который имеет регулярный режим, где набор точек ( p , s ) представляет собой горизонтальную линию, как и ожидалось 32 . Это означает, что угол падения при каждом столкновении один и тот же, что дает константу с . Верхняя горизонтальная линия связана с нижней горизонтальной линией, подчиняющейся описанному выше свойству симметрии. На рис. 3b показана SOS Пуанкаре для идеального BSB, \(\gamma =1,0\). {3}\) столкновений.
{3}\) столкновений.
На рис. 3c и d представлены графики SOS Пуанкаре для стандартных CSB (\(\gamma = 0\)) и BSB (\(\gamma = 1\)), соответственно. SOS также рассчитываются из 5 немного разных начальных условий, каждое из которых включает 200 столкновений. На рис. 3с показан нерегулярный режим с множеством точек, распределенных вокруг двух горизонтальных прямых, что контрастирует с регулярным поведением идеального CSB, рис. 3а. Поведение стандартного CSB показывает, что угол падения различен при каждом столкновении, что приводит к плавающему s , что оправдывает ненулевое значение для LE. Однако мы не можем классифицировать это как хаотическую динамику, потому что эти точки не распределены по всей SOS, а значит, робот никогда не будет подчиняться эргодической динамике. Большие различия между SOS Пуанкаре идеального и стандартного КСБ, рис. 3а и в, доказывают, что стандартный биллиард явно отклоняется от геометрии идеального биллиарда, что делает первый более чувствительным к начальным условиям, чем второй, в соответствии с Теорема Колмогорова–Арнольда-Мозера 92\), что составляет примерно \(1\%\) от общей площади A . Хотя эта область мала, она занимает физическую часть стадиона, что имеет определенные последствия. Эта ненулевая область накладывает ограничение в фазовом пространстве. С другой стороны, в идеальном BSB точечная частица имеет свободный доступ ко всему фазовому пространству. Естественно, условие ( p , s )=\((a+ \pi /2 r,1)\) и другие симметричные точки запрещены для стандартного BSB. На рис. 3d мы можем наблюдать четыре малонаселенные области SOS для стандартного BSB около \(p=\pm (1+\pi /2)\) и \(s=\pm 1\). В центре рис. 3d есть еще одна интересная область SOS Пуанкаре. Эта пустая центральная область описывает нехаотическое особое поведение, также известное как периодическое решение, поскольку траектории в этой области являются замкнутыми путями. Островок устойчивости в центре ОНС для идеального и стандартного ЗБС обусловлен решениями с начальными положениями в прямоугольной области рис. 1б со скоростью, направленной вверх, т. е. \({\hat{v}}= {\шляпа{у}}\). Траектории представляют собой прямые с углом падения \(\theta _i=0\).
Хотя эта область мала, она занимает физическую часть стадиона, что имеет определенные последствия. Эта ненулевая область накладывает ограничение в фазовом пространстве. С другой стороны, в идеальном BSB точечная частица имеет свободный доступ ко всему фазовому пространству. Естественно, условие ( p , s )=\((a+ \pi /2 r,1)\) и другие симметричные точки запрещены для стандартного BSB. На рис. 3d мы можем наблюдать четыре малонаселенные области SOS для стандартного BSB около \(p=\pm (1+\pi /2)\) и \(s=\pm 1\). В центре рис. 3d есть еще одна интересная область SOS Пуанкаре. Эта пустая центральная область описывает нехаотическое особое поведение, также известное как периодическое решение, поскольку траектории в этой области являются замкнутыми путями. Островок устойчивости в центре ОНС для идеального и стандартного ЗБС обусловлен решениями с начальными положениями в прямоугольной области рис. 1б со скоростью, направленной вверх, т. е. \({\hat{v}}= {\шляпа{у}}\). Траектории представляют собой прямые с углом падения \(\theta _i=0\). То же самое верно и на экваторе стадиона, что приводит к двум островам в точках \(p=\pm (a+\pi /2r)\) и \(s=0\).
То же самое верно и на экваторе стадиона, что приводит к двум островам в точках \(p=\pm (a+\pi /2r)\) и \(s=0\).
Для системы в регулярном режиме две реализации с бесконечно малыми начальными условиями остаются близкими с течением времени. С другой стороны, если система хаотична, небольшая разница между траекториями быстро расходится. Экспериментальное наблюдение этих утверждений, естественно, затруднено из-за отсутствия контроля в установке. Хотя при наличии набора экспериментальных данных можно извлечь распределение времени возвращения Пуанкаре. Сравнение фазового пространства Пуанкаре SOS с временным фазовым пространством Пуанкаре SOS может выявить эффективные свойства 5 бильярд. Чтобы исследовать такое поведение, мы строим временные ряды двух траекторий с близкими начальными условиями для идеального и стандартного CSB через SOS Пуанкаре на рис. 4a и c соответственно. Каждая точка получается только тогда, когда частица пересекает плоскость сечения в петле фазового пространства, что требует уникального количества столкновений и собственного времени для каждой реализации. По этой причине график соответствует временному ряду SOS Пуанкаре. Однако два временных ряда остаются близкими с течением времени, гарантируя, что CSB не является хаотичным для идеального бильярда, а также для стандартного бильярда. Кроме того, на рис. 4b и d показаны временные ряды с точками разброса для идеального и стандартного BSB, \(\gamma =1\) соответственно. В обоих случаях две траектории вначале почти совпадают, но начинают существенно расходиться, что является явным признаком того, что BSB хаотичен для идеального и стандартного бильярда. Из рис. 4d видно, что всего после 4 столкновений две траектории совершенно разные, что подтверждает высокую чувствительность к начальным условиям стандартного бильярда. Наконец, на рис. 4e и f показано, как две траектории распространяются в фазовом пространстве для стандартных CSB и BSB соответственно. В первом случае p — значения двух траекторий остаются почти постоянными во времени, а значит, они не расходятся друг от друга. В последнем значения p показывают большие изменения во времени, что является типичным поведением хаотической динамики.
По этой причине график соответствует временному ряду SOS Пуанкаре. Однако два временных ряда остаются близкими с течением времени, гарантируя, что CSB не является хаотичным для идеального бильярда, а также для стандартного бильярда. Кроме того, на рис. 4b и d показаны временные ряды с точками разброса для идеального и стандартного BSB, \(\gamma =1\) соответственно. В обоих случаях две траектории вначале почти совпадают, но начинают существенно расходиться, что является явным признаком того, что BSB хаотичен для идеального и стандартного бильярда. Из рис. 4d видно, что всего после 4 столкновений две траектории совершенно разные, что подтверждает высокую чувствительность к начальным условиям стандартного бильярда. Наконец, на рис. 4e и f показано, как две траектории распространяются в фазовом пространстве для стандартных CSB и BSB соответственно. В первом случае p — значения двух траекторий остаются почти постоянными во времени, а значит, они не расходятся друг от друга. В последнем значения p показывают большие изменения во времени, что является типичным поведением хаотической динамики. Рисунок 5 при 30 кадров в секунду. Синим цветом показаны эффективные полукруглые границы, а желтым — центральный прямоугольник со стороной 2 и .
Рисунок 5 при 30 кадров в секунду. Синим цветом показаны эффективные полукруглые границы, а желтым — центральный прямоугольник со стороной 2 и .
Полноразмерное изображение
Экспериментальная установка
Мы провели измерения в шести различных стандартных BSB, записав движение робота в течение пятнадцати минут. Для каждой установки мы провели пять различных видеозаписей с одинаковыми начальными условиями. Длина стадиона колеблется от 1,80 м у ЦСБ до 3,38 м у самого удлиненного БСБ. Геометрические параметры, использованные в экспериментах, описаны в таблице 1 и проиллюстрированы на рис. 1b. Для изготовления стен стадионов мы использовали промышленные деревянные листы МДФ высотой 25 см.
Робот представляет собой плату управления Arduino, питаемую от USB-кабеля и интегрированную с двумя шаговыми двигателями и тремя инфракрасными (ИК) датчиками, рис. 1c. Размеры робота: длина 14 см, ширина 12,5 см, высота 16 см. Видеозаписи были сделаны камерой с разрешением Full HD со скоростью 30 кадров в секунду, расположенной на высоте 2,80 м над центром стадиона. Мы собрали около 27 000 изображений робота за одну запись. Это количество точек траектории робота в ( x , y )-плоскость. Для сбора данных о траектории мы использовали специальный код Matlab с использованием алгоритма отслеживания. На рис. 5 показана черно-белая картина эксперимента для стандартного BSB с траекторией движения робота в плоскости ( x , y ) (красная линия), полученная с помощью алгоритма слежения. Кроме того, мы можем видеть стадион в его реальном размере (деревянная стена) и эффективном размере (синие и желтые линии). Код простой, но с высокой эффективностью, потому что у нас нет окклюзий или нескольких целевых объектов в сценарии. Таким образом, никакие кадры, полученные в экспериментальных кадрах, не теряются, а временной ряд положения робота не имеет пропусков. Средняя скорость робота составила 14,2 см/с, что означает 2 кадра/см, а точнее, пространственную ошибку \(\pm 5\) мм.
Мы собрали около 27 000 изображений робота за одну запись. Это количество точек траектории робота в ( x , y )-плоскость. Для сбора данных о траектории мы использовали специальный код Matlab с использованием алгоритма отслеживания. На рис. 5 показана черно-белая картина эксперимента для стандартного BSB с траекторией движения робота в плоскости ( x , y ) (красная линия), полученная с помощью алгоритма слежения. Кроме того, мы можем видеть стадион в его реальном размере (деревянная стена) и эффективном размере (синие и желтые линии). Код простой, но с высокой эффективностью, потому что у нас нет окклюзий или нескольких целевых объектов в сценарии. Таким образом, никакие кадры, полученные в экспериментальных кадрах, не теряются, а временной ряд положения робота не имеет пропусков. Средняя скорость робота составила 14,2 см/с, что означает 2 кадра/см, а точнее, пространственную ошибку \(\pm 5\) мм.
Между ИК-датчиками и центральным светодиодным пятном имеется зазор, из-за чего алгоритм отслеживания обнаруживает только эффективную зону стадиона. Таким образом, для учета реальных размеров стадиона необходимы определенные корректировки в собранных данных о траектории. На рис. 5 показано изображение стадиона с его фактическими и эффективными размерами. Чтобы принять во внимание эту длину смещения, составляющую примерно 5 см, мы напрямую измерили соотношение между эффективным радиусом r и длиной стороны и от траектории робота. Эта процедура верна только в том случае, если количество столкновений между роботом и границами достаточно велико. Количество столкновений пропорционально времени записи. В нашей процедуре это число всегда больше ста. Мы также заметили, что эффективная \(\gamma _{\mathrm{eff}}\) всегда примерно на \(5\%\) больше, чем построенная \(\gamma\), см. Таблицу 1.
Таким образом, для учета реальных размеров стадиона необходимы определенные корректировки в собранных данных о траектории. На рис. 5 показано изображение стадиона с его фактическими и эффективными размерами. Чтобы принять во внимание эту длину смещения, составляющую примерно 5 см, мы напрямую измерили соотношение между эффективным радиусом r и длиной стороны и от траектории робота. Эта процедура верна только в том случае, если количество столкновений между роботом и границами достаточно велико. Количество столкновений пропорционально времени записи. В нашей процедуре это число всегда больше ста. Мы также заметили, что эффективная \(\gamma _{\mathrm{eff}}\) всегда примерно на \(5\%\) больше, чем построенная \(\gamma\), см. Таблицу 1.
Как показано на На рис. 5 эффективная площадь должна быть наименьшей BSB, охватывающей экспериментальные данные. Расчет эффективного \(\gamma _{\mathrm{eff}}\) зависит от выбора трех свободных параметров. Естественно, у нас есть эффективный радиус r и длину стороны a определить. В эксперименте появляется дополнительный параметр — угол поворота между стадионом и выравниванием камеры. Чтобы найти эти три параметра, мы использовали алгоритмы минимальной ограничивающей рамки 39 . Они могут соединять длины прямоугольника с радиусом и длиной стороны стадиона, что дает \(\gamma _{\mathrm{eff}}\), см. Таблицу 1.
В эксперименте появляется дополнительный параметр — угол поворота между стадионом и выравниванием камеры. Чтобы найти эти три параметра, мы использовали алгоритмы минимальной ограничивающей рамки 39 . Они могут соединять длины прямоугольника с радиусом и длиной стороны стадиона, что дает \(\gamma _{\mathrm{eff}}\), см. Таблицу 1.
Теоретический подход
В этом разделе мы кратко представляем метод касательного пространства, используемый для расчета LE, показанного на рис. 2. LE измеряет степень расхождения между соседними орбитами в пространстве состояний 40 . Рассмотрим \({\mathbf {x}}\equiv (x_1, x_2, \dots , x_\nu )\) как координаты в \(\nu\)-мерном фазовом пространстве. Система развивается в соответствии с автономным дифференциальным уравнением первого порядка, заданным как
$$\begin{align} \frac{d{\mathbf {x}}(t)}{dt} = {\mathbf {F}} ({\mathbf {x}}(t)), \end{align}$$
(1)
, где \({\mathbf {F}}({\mathbf {x}})\) поле скоростей, соответствующее потоку решения уравнения. {(2)}(t) \equiv (\delta x_1, \delta x_2, \dots , \delta x_\nu )\). В бесконечно малом режиме уравнения для этого вектора отклонения являются линейными, определяемыми первым вариационным уравнением
{(2)}(t) \equiv (\delta x_1, \delta x_2, \dots , \delta x_\nu )\). В бесконечно малом режиме уравнения для этого вектора отклонения являются линейными, определяемыми первым вариационным уравнением
$ $ \ begin {align} \ frac {d {\ mathbf {w}} (t)} {dt} = {\ mathbf {J}} ({\ mathbf {x}} (t)) {\ mathbf {w}}(t), \end{aligned}$$
(2)
, где \({\mathbf {J}}\) является \(\nu \times \nu\) матрицей Якоби относительно векторному полю \({\mathbf {F}}({\mathbf {x}}(t))\). Поскольку элементы \({\mathbf {J}}\), предусмотренные (1), являются непрерывной ограниченной функцией от t для \(t\rightarrow \infty\), решения линеаризованного уравнения. (2) расти не более чем по экспоненциальной функции. Для любого начального возмущения \({\mathbf {w}}(0)\) скорость роста
$ $ \ begin {align} \ lambda = {\ displaystyle \ lim _ {t \ rightarrow \ infty} \ ln \ frac {| {\ mathbf {w}} (t) |} {| {\ mathbf {w }}(0)|}} \end{aligned}$$
(3)
определяется как LE. В терминах определения (3) можно охарактеризовать каждое собственное направление системы. Набор всех полученных показателей, называемый спектром Ляпунова, обычно упорядочивается как \(\lambda _1 \ge \lambda _2 \ge \dots \ge \lambda _\nu\) 21 . Обозначаемый \(\lambda _1\), наибольший LE указывает, стабилизируется ли \({\mathbf {x}}(t)\) при существовании предела (3). На наличие расходящихся (сходящихся) траекторий и, следовательно, хаотического (регулярного) режима указывают положительные (отрицательные) показатели. Эта теоретическая основа представляет собой введение в мощный инструмент для обнаружения и количественной оценки хаоса. Аналитически с использованием дифференциально-геометрического подхода имеются исследования, в которых ЛЭ определяется из свойств кривизны риманова многообразия 41,42 . Из долговременного среднего (3) и аргументов эргодичности его также можно получить вычислительным путем путем численного интегрирования отклонений \({\mathbf {w}}(t)\), оцененных вдоль траектории \({ \mathbf {x}}(t)\) 21,43 .
Набор всех полученных показателей, называемый спектром Ляпунова, обычно упорядочивается как \(\lambda _1 \ge \lambda _2 \ge \dots \ge \lambda _\nu\) 21 . Обозначаемый \(\lambda _1\), наибольший LE указывает, стабилизируется ли \({\mathbf {x}}(t)\) при существовании предела (3). На наличие расходящихся (сходящихся) траекторий и, следовательно, хаотического (регулярного) режима указывают положительные (отрицательные) показатели. Эта теоретическая основа представляет собой введение в мощный инструмент для обнаружения и количественной оценки хаоса. Аналитически с использованием дифференциально-геометрического подхода имеются исследования, в которых ЛЭ определяется из свойств кривизны риманова многообразия 41,42 . Из долговременного среднего (3) и аргументов эргодичности его также можно получить вычислительным путем путем численного интегрирования отклонений \({\mathbf {w}}(t)\), оцененных вдоль траектории \({ \mathbf {x}}(t)\) 21,43 .
В контексте экспериментальных данных дискретных измерений методы реконструкции фазового пространства с координатами запаздывания позволяют получить значения ЛЭ, сравнимые со значениями исходного аттрактора 23 . Линеаризованная версия системы не определена для этого экспериментального подхода, в котором отклонения рассчитываются прямым вычитанием между близкими орбитами в восстановленном фазовом пространстве. Таким образом, предполагается, что отклонения достаточно малы, сохраняя свойства величины и направления измерений, генерируемых из касательного пространства.
Линеаризованная версия системы не определена для этого экспериментального подхода, в котором отклонения рассчитываются прямым вычитанием между близкими орбитами в восстановленном фазовом пространстве. Таким образом, предполагается, что отклонения достаточно малы, сохраняя свойства величины и направления измерений, генерируемых из касательного пространства.
В настоящей работе наша экспериментальная установка была сконструирована так, чтобы обеспечить все измерения, требуемые якобианом (2). Как следствие, ЛЭ получается из касательного пространства без необходимости реконструкции фазового пространства, а также без аппроксимаций для определения вектора отклонения. Для робота векторы отклонения эволюционируют согласно двум различным случаям линеаризованных уравнений. Один из них, когда нет столкновений, указанный якобианом:
$$\begin{align} {\mathbf {J}}_0= \begin{bmatrix} &{}1 &{} &{}\tau &{}\\ &{}0 &{} &{} 1&{} \end{bmatrix}, \end{aligned}$$
(4)
, где \(\tau\) представляет время между двумя столкновениями. Другой задает поведение отклонений при столкновениях, в которых имеем
Другой задает поведение отклонений при столкновениях, в которых имеем
$$\begin{aligned} {\mathbf {J}}_c= -\begin{bmatrix} &{}1 &{} &{ } 0 &{}\\ &{}{\displaystyle \frac{2\kappa }{\cos {\varphi }}} &{} &{}1&{} \end{bmatrix}, \end{aligned}$ $
(5)
где \(\каппа\) — кривизна граничной точки, в которой происходит столкновение, а \(\варфи\) — угол падения частицы по отношению к границе. Для стадиона кривизна принимает два разных значения. У нас есть \(\каппа = 0\), когда столкновение происходит в прямоугольной области, а в противном случае \(\каппа = 1/r\), кривизна круглой части. В качестве ограничения наш метод расчета LE из экспериментальных временных рядов требует линеаризованных уравнений, связанных с динамикой, которые имитируют экспериментальную установку.
Выводы
В этой статье мы имитировали динамику частицы в идеальном бильярде на стадионе Бунимовича (BSB) с помощью взаимодействия робота и окружающей среды в стандартном BSB. Было проведено шесть различных экспериментов со стандартными БСП фиксированной площади и определены значения показателя Ляпунова (ЛЭ) методом касательного пространства. LE из наших экспериментальных данных противопоставлены хорошо установленным теоретическим результатам Benettin и Strelcyn 9 с удовлетворительным согласием.
LE из наших экспериментальных данных противопоставлены хорошо установленным теоретическим результатам Benettin и Strelcyn 9 с удовлетворительным согласием.
Мы также определили SOS Пуанкаре бильярда, который указывает на отклонение между геометрией идеальной и стандартной BSB. Наконец, чтобы показать чувствительность к начальным условиям и в качестве экспериментального контроля, мы построили SOS Пуанкаре как функцию времени, рис. 4.
модель путем программирования ответов робота, максимально приближенных к условиям применимости модели. Однако взаимодействие робота с окружающей средой происходит в гораздо более широких сценариях, таких как жестовое общение между человеком и роботом 9.0061 44 , распознавание речевых эмоций 45 , поиск паттернов, скрытых в наборах данных 46,47 , и идентификация пола по речи 48 , и это лишь некоторые из них.
Эта работа прокладывает путь к предложениям идеализированных моделей для этих более сложных ситуаций. Идеализированные модели помогают нам углубить наше понимание сложных реальностей и проливают свет на механизмы, скрытые в основе тонкого поведения.
Идеализированные модели помогают нам углубить наше понимание сложных реальностей и проливают свет на механизмы, скрытые в основе тонкого поведения.
В заключение, наши результаты показывают, что взаимодействие робота и окружающей среды является отличной платформой для экспериментального изучения хаотической динамики, что позволяет проверить другие теоретические предсказания.
Ссылки
Моттер, А. Э. и Кэмпбелл, Д. К. Хаосу пятьдесят. Физ. Сегодня 66 , 27–33. https://doi.org/10.1063/PT.3.1977 (2013 г.).
ОБЪЯВЛЕНИЕ Статья Google ученый
Хикихара Т., Холмс П., Камбе Т. и Рега Г. Введение в основной выпуск: Пятьдесят лет хаоса: прикладное и теоретическое. Хаос 22 , 047501. https://doi.org/10.1063/1.4769035 (2012).
ОБЪЯВЛЕНИЕ Статья пабмед Google ученый
«>Лоренц Э. Н. Детерминированный непериодический поток. Дж Атмос. науч. 20 , 130–141 (1963).
ОБЪЯВЛЕНИЕ MathSciNet Статья Google ученый
Фан, Л., Ян, X., Ванганд, Х. и Ван, Л. В. Наблюдение и контроль оптического хаоса в реальном времени. Науч. Доп. 7 , eabc8448. https://doi.org/10.1126/sciadv.abc8448 (2021 г.).
ОБЪЯВЛЕНИЕ Статья пабмед ПабМед Центральный Google ученый
Иванович А.З., Чупич Ж.Д., Янкович М.М., Колар-Анич Л.З. и Анич С.Р. Хаотические последовательности в реакции Брея-Либхафского в открытом реакторе.
 Физ. хим. хим. физ. 10 , 5848–5858. https://doi.org/10.1039/B804580A (2008 г.).
Физ. хим. хим. физ. 10 , 5848–5858. https://doi.org/10.1039/B804580A (2008 г.).Артикул пабмед Google ученый
Де Леон, Н. и Берн, Б. Динамика реакции в эргодической системе: бильярд на сиамском стадионе. Хим. физ. лат. 93 , 162–168. https://doi.org/10.1016/0009-2614(82)83685-3 (1982).
ОБЪЯВЛЕНИЕ Статья Google ученый
Занг X., Икбал С., Чжу Ю., Лю X. и Чжао Дж. Применение хаотической динамики в робототехнике. Междунар. Дж. Адв. Робот. Сист. 13 , 60. https://doi.org/10.5772/62796 (2016).
Артикул Google ученый
Бенеттин Г. и Стрелкин Дж. М. Численные эксперименты по свободному движению точечной массы, движущейся в плоской выпуклой области: стохастический переход и энтропия.
 Физ. Ред. A 17 , 773–785. https://doi.org/10.1103/PhysRevA.17.773 (1978).
Физ. Ред. A 17 , 773–785. https://doi.org/10.1103/PhysRevA.17.773 (1978).ОБЪЯВЛЕНИЕ Статья Google ученый
Деллаго, К. и Пош, Х. А. Показатели Ляпунова для систем с упругими жесткими столкновениями. Физ. Ред. E 52 , 2401–2406. https://doi.org/10.1103/PhysRevE.52.2401 (1995).
ОБЪЯВЛЕНИЕ MathSciNet КАС Статья Google ученый
Деллаго, К. и Пош, Х. Колмогоров-Синая энтропия и ляпуновские спектры газа твердых сфер. Physica A 240 , 68–83. https://doi.org/10.1016/S0378-4371(97)00131-3 (1997).
ОБЪЯВЛЕНИЕ КАС Статья Google ученый
Канцлер, В., Дункель, Дж., Полин, М. и Гольдштейн, Р. Э. Контактные взаимодействия ресничек преобладают над поверхностным рассеянием плавающих эукариот.
 ПНАС 110 , 1187–1192. https://doi.org/10.1073/pnas.1210548110 (2013 г.).
ПНАС 110 , 1187–1192. https://doi.org/10.1073/pnas.1210548110 (2013 г.).ОБЪЯВЛЕНИЕ Статья пабмед ПабМед Центральный Google ученый
Yu, X. & Zhang, Y. Лучевой хаос в архитектурной акустической системе полустадиона. Хаос 23 , 013107. https://doi.org/10.1063/1.4772969 (2013).
ОБЪЯВЛЕНИЕ MathSciNet Статья пабмед Google ученый
Гараттони, Л. и Бираттари, М. Автономная последовательность задач в рое роботов. Науч. Робот. 3 , eaat0430. https://doi.org/10.1126/scirobotics.aat0430 (2018 г.).
Артикул пабмед Google ученый
Деттманн, С. П. и Джорджиу, О. Вероятность выживания для бильярда на стадионе. Physica D 238 , 2395–2403. https://doi.
 org/10.1016/j.physd.2009.09.019 (2009 г.).
org/10.1016/j.physd.2009.09.019 (2009 г.).ОБЪЯВЛЕНИЕ MathSciNet Статья МАТЕМАТИКА Google ученый
Дрекслер М. и Гандер М. Дж. Круговой бильярд. SIAM Ред. 40 , 315–323. https://doi.org/10.1137/s0036144596310872 (1998 г.).
ОБЪЯВЛЕНИЕ MathSciNet Статья МАТЕМАТИКА Google ученый
Бунимович Л. А. Об эргодических свойствах некоторых бильярдов. Функц. Анальный. заявл. 8 , 254–255. https://doi.org/10.1007/BF01075700 (1974 г.).
MathSciNet Статья МАТЕМАТИКА Google ученый
Синай Ю. Г. Динамические системы с упругими отражениями. Русь. Мат. Surv. 25 , 137–189. https://doi.org/10.1070/rm1970v025n02abeh003794 (1970).
Артикул МАТЕМАТИКА Google ученый
«>Чернов Н. И., Хаскелл К. Неравномерно гиперболические k-системы являются бернуллиевскими. Эргод. Теория Дин. Сист. 16 , 19–44. https://doi.org/10.1017/S0143385700008695 (1996).
MathSciNet Статья МАТЕМАТИКА Google ученый
Пиковский А. и Полити А. Показатели Ляпунова: инструмент для изучения сложной динамики (Cambridge University Press, 2016).
Книга Google ученый
Сориано, округ Колумбия и др. Метод оценки спектра Ляпунова с использованием клонированной динамики и его применение к модели ФитцХью-Нагумо с прерывистым возбуждением.
 Нелинейная динам. 67 , 413–424. https://doi.org/10.1007/s11071-011-9989-2 (2012 г.).
Нелинейная динам. 67 , 413–424. https://doi.org/10.1007/s11071-011-9989-2 (2012 г.).Артикул МАТЕМАТИКА Google ученый
Вольф А., Свифт Дж. Б., Суинни Х. Л. и Вастано Дж. А. Определение показателей Ляпунова по временному ряду. Physica D 16 , 285–317. https://doi.org/10.1016/0167-2789(85)
- -9 (1985).
ОБЪЯВЛЕНИЕ MathSciNet Статья МАТЕМАТИКА Google ученый
Бихам, О. и Квале, М. Нестабильные периодические орбиты в бильярде стадиона. Физ. Ред. A 46 , 6334–6339. https://doi.org/10.1103/PhysRevA.46.6334 (1992).
ОБЪЯВЛЕНИЕ MathSciNet КАС Статья пабмед Google ученый
Штокманн, Х.-Й. & Stein, J. «Квантовый» хаос в бильярде, изученный с помощью микроволнового поглощения.
 Физ. Преподобный Летт. 64 , 2215–2218. https://doi.org/10.1103/physrevlett.64.2215 (1990).
Физ. Преподобный Летт. 64 , 2215–2218. https://doi.org/10.1103/physrevlett.64.2215 (1990).ОБЪЯВЛЕНИЕ Статья пабмед Google ученый
Nehmzow, U. & Walker, K. Количественное описание взаимодействия робота и окружающей среды с использованием теории хаоса. Робот. Автон. Сист. 53 , 177–193. https://doi.org/10.1016/j.robot.2005.09.009 (2005 г.).
Артикул Google ученый
Волос, К., Киприанидис, И. и Стоубулос, И. Генератор хаотического планирования пути для автономных мобильных роботов. Робот. Автон. Сист. 60 , 651–656. https://doi.org/10.1016/j.robot.2012.01.001 (2012 г.).
Артикул Google ученый
Хуан Л. и др. Совместная сетевая обработка изображений: многозадачная семантическая сегментация изображения внутренней сцены на основе CNN.
 Процесс обработки изображений IET. 14 , 3689–3697. https://doi.org/10.1049/iet-ipr.2020.0088 (2020 г.).
Процесс обработки изображений IET. 14 , 3689–3697. https://doi.org/10.1049/iet-ipr.2020.0088 (2020 г.).ОБЪЯВЛЕНИЕ Статья Google ученый
Gao, Q., Liu, J., Ju, Z. & Zhang, X. Обнаружение двух рук для взаимодействия человека и робота с помощью параллельной сети на основе обнаружения рук и оценки позы тела. IEEE Trans. Инд. Электрон. 66 , 9663–9672. https://doi.org/10.1109/tie.2019.2898624 (2019 г.).
Артикул Google ученый
Цзян Д. и др. Семантическая сегментация для многомасштабной цели на основе распознавания объектов с использованием улучшенной модели более быстрой RCNN. Генератор будущего. вычисл. Сист. 123 , 94–104. https://doi.org/10.1016/j.future.2021.04.019 (2021 г.).
Артикул Google ученый
«>Лопац В., Мрконич И., Павин Н. и Радич Д. Хаотическая динамика бильярда эллиптического стадиона в пространстве полных параметров. Физика D 217 , 88–101. https://doi.org/10.1016/j.physd.2006.03.014 (2006 г.).
ОБЪЯВЛЕНИЕ MathSciNet Статья МАТЕМАТИКА Google ученый
Albahaca, J. C. Аналитическое и численное исследование теории Пуанкаре; Карта с приложениями по вычислению периодических орбит . Кандидат наук. диссертация, Уппсальский университет, прикладная математика и статистика (2015).
Биркгоф Г. Д.
 О периодических движениях динамических систем. Акта Мат. 50 , 359–379. https://doi.org/10.1007/bf02421325 (1927 г.).
О периодических движениях динамических систем. Акта Мат. 50 , 359–379. https://doi.org/10.1007/bf02421325 (1927 г.).MathSciNet Статья МАТЕМАТИКА Google ученый
Робертс Дж. Хаос и симметрия обращения времени. Порядок и хаос в обратимых динамических системах. Физ. Представитель 216 , 63–177 (1992).
ОБЪЯВЛЕНИЕ MathSciNet Статья Google ученый
Nöckel, J. U. & Stone, A. D. Лучевой и волновой хаос в асимметричных резонансных оптических резонаторах. Природа 385 , 45–47. https://doi.org/10.1038/385045a0 (1997 г.).
ОБЪЯВЛЕНИЕ Статья Google ученый
Цао, Х. и Вирзиг, Дж. Диэлектрические микрорезонаторы: модельные системы для волнового хаоса и неэрмитовой физики.
 Ред. Мод. физ. 87 , 61–111. https://doi.org/10.1103/revmodphys.87.61 (2015 г.).
Ред. Мод. физ. 87 , 61–111. https://doi.org/10.1103/revmodphys.87.61 (2015 г.).ОБЪЯВЛЕНИЕ MathSciNet Статья Google ученый
Берри М. В. Регулярность и хаос в классической механике на примере трех деформаций круглого «бильярда». евро. Дж. Физ. 2 , 91–102. https://doi.org/10.1088/0143-0807/2/2/006 (1981).
MathSciNet Статья Google ученый
Freeman, H. & Shapira, R. Определение прямоугольника с минимальной площадью для произвольной замкнутой кривой. Комм. АСМ 18 , 409–413. https://doi.org/10.1145/360881.360919 (1975 г.).
MathSciNet Статья МАТЕМАТИКА Google ученый
Вульпиани, А., Чеккони, Ф. и Ченчини, М. Хаос: от простых моделей к сложным системам (World Scientific Publishing Company, 2009).

МАТЕМАТИКА Google ученый
Кайани Л., Казетти Л., Клементи К. и Петтини М. Геометрия динамики, показатели Ляпунова и фазовые переходы. Физ. Преподобный Летт. 79 , 4361–4364. https://doi.org/10.1103/physrevlett.79.4361 (1997).
ОБЪЯВЛЕНИЕ КАС Статья Google ученый
Араужо, Р., Филью, Л.Х.М., Сантос, Ф.А.Н. и Коутиньо-Фильо, М.Д. Геометрия и молекулярная динамика гамильтоновой модели среднего поля в магнитном поле. Физ. Ред. E 103 , 012203. https://doi.org/10.1103/PhysRevE.103.012203 (2021).
ОБЪЯВЛЕНИЕ MathSciNet Статья пабмед Google ученый
Миранда Филью, Л., Амато, М., Элскенс, Ю. и Роча Филью, Т. Вклад отдельных степеней свободы в векторы Ляпунова в системах многих тел. Комм.
 Нелинейная наука. Число. Симул. 74 , 236–247. https://doi.org/10.1016/j.cnsns.2019.03.011 (2019 г.).
Нелинейная наука. Число. Симул. 74 , 236–247. https://doi.org/10.1016/j.cnsns.2019.03.011 (2019 г.).ОБЪЯВЛЕНИЕ MathSciNet Статья МАТЕМАТИКА Google ученый
Цзян Д., Ли Г., Сун Ю., Конг Дж. и Тао Б. Распознавание жестов на основе алгоритма скелетирования и cnn с базой данных asl. Мультимед. Инструменты. заявл. 78 , 29953–29970 (2019).
Артикул Google ученый
Шойынбек А., Кожахмет К., Султанова Н. и Жумалиева Р. Надежные спектральные аудиофункции для распознавания речевых эмоций. Заяв. Мат. Инф. науч. 13 , 867–870. https://doi.org/10.18576/amis/130521 (2019 г.).
Артикул Google ученый
Мохаммед, М. Х. и Абдель-Разек, А. Стеганография на основе ДНК с использованием генетического алгоритма.
 Инф. науч. лат. 9 , 205–210. https://doi.org/10.18576/isl/0 (2020 г.).
Инф. науч. лат. 9 , 205–210. https://doi.org/10.18576/isl/0 (2020 г.).Артикул Google ученый
Шах С. Х., Икбал М. Дж., Бахш М. и Икбал А. Анализ различных алгоритмов кластеризации для извлечения точных знаний из популярных наборов данных. Инф. науч. лат. 9 , 21–31. https://doi.org/10.18576/isl/0 (2020 г.).
Артикул Google ученый
Джаясанкар Т., Виноткумар К. и Виджаясельви А. Автоматическая идентификация пола при распознавании речи с помощью генетического алгоритма. Заяв. Мат. Инф. науч. 11 , 907–913. https://doi.org/10.18576/amis/110331 (2017 г.).
Артикул Google ученый
Сюй, Х.-Ю., Хуанг, Л. и Лай, Ю.-К. Релятивистский квантовый хаос в графене. Физ. Сегодня 74 , 44–49. https://doi.org/10.1063/PT.3.4679 (2021 г.).
КАС Статья Google ученый
Бунимович Л. А. Об эргодических свойствах нигде не расходящихся биллиардов. Комм. Мат. физ. 65 , 295–312. https://doi.org/10.1007/BF01197884 (1979 г.).
ОБЪЯВЛЕНИЕ MathSciNet Статья МАТЕМАТИКА Google ученый
Таннер Г. Насколько хаотичен бильярдный стадион? Полуклассический анализ. J. Phys. А 30 , 2863–2888. https://doi.org/10.1088/0305-4470/30/8/028 (1997 г.).
ОБЪЯВЛЕНИЕ MathSciNet Статья МАТЕМАТИКА Google ученый
Скачать ссылки
Леонид Бунимович — AD Scientific Index 2023
Рейтинг ученых
Технологический институт Джорджии
Естественные науки / Математика
| Редактировать профиль печать Распечатайте свой сертификат | ОЦЕНКИ | РЕЙТИНГ | |||
|---|---|---|---|---|---|
| Технологический институт Джорджии (1757) | В США (270440) | В Северной Америке (302316) | Мир (1083003) | ||
| Всего Н | 40 | #301 | #38701 | #43591 | #100665 |
| Последние 5 лет H | 18 | #700 | #89162 | #100694 | #279128 |
Последние 5 лет / Всего ч | 0,450 | ||||
| Итого i10 | 110 | #219 | № 24946 | № 28301 | #72830 |
| Последние 5 лет i10 | 43 | #440 | #54160 | #61638 | #173326 |
| Последние 5 лет / Всего i10 | 0,391 | ||||
| Всего цитирований | 7380 | #309 | #42257 | № 47038 | #101167 |
| Последние 5 лет Цитаты | 1497 | #698 | # | #101362 | #261436 |
| Последние 5 лет / Всего цитирований | 0,203 | ||||
| Естественные науки * | #52 (223) * | #6615 (35132) * | №7516 (39756) * | #18913 (143892) * | |
| Математика * Нелинейная наука | Математическая физика | Математическая биология | Прикладная математика | Теория сетей | | #8 (42) * | #407 (3849) * | № 461 (4345) * | #1248 (18959) * | |
* 9 октября 2022 г. По данным Total H. БЕТА-ВЕРСИЯ. Рейтинг предметных полей в мире, регионе, стране и университете является бета-версией, поскольку предметное поле «другие» (профиль 482 682 ученых, ветвь которого не может быть определена, еще не отредактирована или определена) исключено, поэтому рейтинг будет меняться по мере редактирования других полей. . Обратите внимание.
Top % 2: Указывает, что ученый входит в число 2 % лучших ученых мира и/или страны в указанном рейтинге. Используйте [email protected], чтобы сообщить о недопустимом профиле, смерти или других обстоятельствах, которые потребуют удаления соответствующего профиля. Нажмите для регистрации и добавления информации.
По данным Total H. БЕТА-ВЕРСИЯ. Рейтинг предметных полей в мире, регионе, стране и университете является бета-версией, поскольку предметное поле «другие» (профиль 482 682 ученых, ветвь которого не может быть определена, еще не отредактирована или определена) исключено, поэтому рейтинг будет меняться по мере редактирования других полей. . Обратите внимание.
Top % 2: Указывает, что ученый входит в число 2 % лучших ученых мира и/или страны в указанном рейтинге. Используйте [email protected], чтобы сообщить о недопустимом профиле, смерти или других обстоятельствах, которые потребуют удаления соответствующего профиля. Нажмите для регистрации и добавления информации.
1-) Об эргодических свойствах нигде не рассеивающихся бильярдов Бунимович Л.А. Сообщения по математической физике 65 (3), 295-312, 19797881979
2-) Статистические свойства газа Лоренца с периодической конфигурацией рассеивателей Бунимович Л.А., Синай Ю.Г. Сообщения по математической физике 78 (4), 479-497, 19815681981
3-) Об эргодических свойствах некоторых биллиардов Бунимович Л. А. Функциональный анализ и его приложения 8 (3), 254-255, 19744391974
А. Функциональный анализ и его приложения 8 (3), 254-255, 19744391974
значок
Академия Google Посетите веб-страницу
значок
Рейтинги университетов Рейтинги Технологического института Джорджии
AD Scientific Index ID 1392352
значок
Идентификатор исследователя Web Of Science
H-Index, проверенные экспертные оценки, цитирующие статьи
ORCID ID
значок
Идентификатор автора Scopus
H-индекс, цитаты, документы
Исследовательский портал
Оценка исследовательского интереса, индекс Хирша
—
emoji_events
Награды и достижения —
Эл. math.gatech.edu
math.gatech.edu
Verified_user
Ссылка на офис, компанию или частный бизнес —
книги
Книги — Электронные книги —
заметка
Конспект лекций —
Люди также ищут математику (#Мировой рейтинг, #Мировой рейтинг за последние 5 лет)
Эрик Ландер
Гарвардский университет
#5, #4
639 Публикации — 586196 Цитаты
Естественные науки / Математика
Stefano Colafrances…
Восточный меннонитский университет.


 Окружность
Окружность Натуральный ряд. Сравнение натуральных чисел
Натуральный ряд. Сравнение натуральных чисел Комбинаторные задачи
Комбинаторные задачи Умножение и деление
Умножение и деление Степень числа
Степень числа ИСПОЛЬЗОВАНИЕ СВОЙСТВ ДЕЙСТВИЙ В ВЫЧИСЛЕНИЯХ
ИСПОЛЬЗОВАНИЕ СВОЙСТВ ДЕЙСТВИЙ В ВЫЧИСЛЕНИЯХ Решение задач
Решение задач Измерение углов
Измерение углов ДЕЛИМОСТЬ ЧИСЕЛ
ДЕЛИМОСТЬ ЧИСЕЛ Делимость суммы и произведения
Делимость суммы и произведения Деление с остатком
Деление с остатком Прямоугольники
Прямоугольники Площадь прямоугольника
Площадь прямоугольника Натуральные числа и дроби
Натуральные числа и дроби


 1september.ru
1september.ru
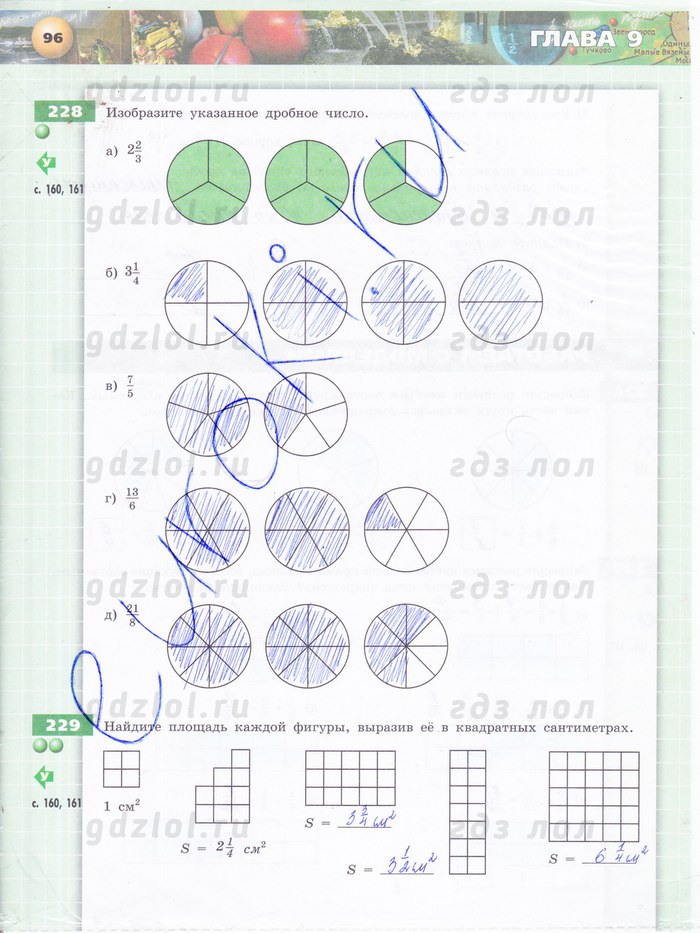 1158/2326-6066.CIR-22-0110
1158/2326-6066.CIR-22-0110


 Хиллмана
Хиллмана Физ. хим. хим. физ. 10 , 5848–5858. https://doi.org/10.1039/B804580A (2008 г.).
Физ. хим. хим. физ. 10 , 5848–5858. https://doi.org/10.1039/B804580A (2008 г.). Физ. Ред. A 17 , 773–785. https://doi.org/10.1103/PhysRevA.17.773 (1978).
Физ. Ред. A 17 , 773–785. https://doi.org/10.1103/PhysRevA.17.773 (1978). ПНАС 110 , 1187–1192. https://doi.org/10.1073/pnas.1210548110 (2013 г.).
ПНАС 110 , 1187–1192. https://doi.org/10.1073/pnas.1210548110 (2013 г.). org/10.1016/j.physd.2009.09.019 (2009 г.).
org/10.1016/j.physd.2009.09.019 (2009 г.). Нелинейная динам. 67 , 413–424. https://doi.org/10.1007/s11071-011-9989-2 (2012 г.).
Нелинейная динам. 67 , 413–424. https://doi.org/10.1007/s11071-011-9989-2 (2012 г.). Физ. Преподобный Летт. 64 , 2215–2218. https://doi.org/10.1103/physrevlett.64.2215 (1990).
Физ. Преподобный Летт. 64 , 2215–2218. https://doi.org/10.1103/physrevlett.64.2215 (1990). Процесс обработки изображений IET. 14 , 3689–3697. https://doi.org/10.1049/iet-ipr.2020.0088 (2020 г.).
Процесс обработки изображений IET. 14 , 3689–3697. https://doi.org/10.1049/iet-ipr.2020.0088 (2020 г.). О периодических движениях динамических систем. Акта Мат. 50 , 359–379. https://doi.org/10.1007/bf02421325 (1927 г.).
О периодических движениях динамических систем. Акта Мат. 50 , 359–379. https://doi.org/10.1007/bf02421325 (1927 г.). Ред. Мод. физ. 87 , 61–111. https://doi.org/10.1103/revmodphys.87.61 (2015 г.).
Ред. Мод. физ. 87 , 61–111. https://doi.org/10.1103/revmodphys.87.61 (2015 г.).
 Нелинейная наука. Число. Симул. 74 , 236–247. https://doi.org/10.1016/j.cnsns.2019.03.011 (2019 г.).
Нелинейная наука. Число. Симул. 74 , 236–247. https://doi.org/10.1016/j.cnsns.2019.03.011 (2019 г.). Инф. науч. лат. 9 , 205–210. https://doi.org/10.18576/isl/0 (2020 г.).
Инф. науч. лат. 9 , 205–210. https://doi.org/10.18576/isl/0 (2020 г.).