gto_norm_03_eng
%PDF-1.5 % 1 0 obj >/OCGs[7 0 R 873 0 R]>>/Pages 3 0 R/Type/Catalog>> endobj 2 0 obj >stream 2018-02-07T10:10:37+03:00Adobe Illustrator CC (Macintosh)2018-02-07T10:11:25+03:002018-02-07T10:11:25+03:00
 01application/pdf
01application/pdf did:ad5746e4-40f4-4df2-a0dd-8ce148479f81uuid:a4c33fb4-763b-c24a-a533-768ad29596d9xmp.did:ea23c21a-bbe9-4f71-ab33-f61c022c02e0proof:pdfuuid:442adba5-f05b-0d48-a507-3ffa9c4db14fxmp.did:d2a3e9b2-404a-4db7-af14-51bdfc7a0cdexmp.did:ea23c21a-bbe9-4f71-ab33-f61c022c02e0proof:pdf
did:ad5746e4-40f4-4df2-a0dd-8ce148479f81uuid:a4c33fb4-763b-c24a-a533-768ad29596d9xmp.did:ea23c21a-bbe9-4f71-ab33-f61c022c02e0proof:pdfuuid:442adba5-f05b-0d48-a507-3ffa9c4db14fxmp.did:d2a3e9b2-404a-4db7-af14-51bdfc7a0cdexmp.did:ea23c21a-bbe9-4f71-ab33-f61c022c02e0proof:pdf 66928 5.66928 303.307 425.197]/Type/Page>>
endobj
10 0 obj
>/Resources>/ExtGState>/ProcSet[/PDF/ImageC]/Properties>/XObject>>>/Thumb 900 0 R/TrimBox[5.66928 5.66928 303.307 425.197]/Type/Page>>
endobj
892 0 obj
>stream
H|n$
z:zd«xKV`2$A_=t5Q:o?~e-3y{q2[:sG-̃OXC
66928 5.66928 303.307 425.197]/Type/Page>>
endobj
10 0 obj
>/Resources>/ExtGState>/ProcSet[/PDF/ImageC]/Properties>/XObject>>>/Thumb 900 0 R/TrimBox[5.66928 5.66928 303.307 425.197]/Type/Page>>
endobj
892 0 obj
>stream
H|n$
z:zd«xKV`2$A_=t5Q:o?~e-3y{q2[:sG-̃OXCТаблица изменения роста и веса ребенка от 1 года до 3 лет
Главная > Календарь развития ребенка > Таблица изменения роста и веса ребенка от 1 года до 3 лет
версия
для печати
Здесь представлены показатели соотношения роста и веса ребенка в разные периоды возраста от 1 до 3 лет. Особое внимание необходимо уделить СООТНОШЕНИЮ роста и веса, которое должно находиться (в таблице) в одном и том же центиле ( в одном столбике таблицы).
Калькулятор роста и веса
Антропометрические (центильные) таблицы
В таблицах роста, веса и окружности головы представлены диапазоны значений по группам. В среднем «голубом» столбце приведен средний показатель для данного возраста. В «зеленых» столбцах справа и слева приведены показатели в пределах нормы, которые чуть ниже или выше среднего показателя. В «желтом» и «красном» столбцах приведены показатели ниже или выше нормальных, требующие особого внимания со стороны родителей и врачей.
В среднем «голубом» столбце приведен средний показатель для данного возраста. В «зеленых» столбцах справа и слева приведены показатели в пределах нормы, которые чуть ниже или выше среднего показателя. В «желтом» и «красном» столбцах приведены показатели ниже или выше нормальных, требующие особого внимания со стороны родителей и врачей.
- Средний рост ребенка должен находится в пределах зеленой и голубой величин (25-75 центилями). Такой рост соответствует среднему росту детей этого возраста.
- Рост, величина которого находится в пределах между желтой и зеленой величинами (10-25 центилями) тоже нормальный, но свидетельствует про тенденцию отставания ребенком в росте.
- Рост, величина которого находится в пределах между голубой и желтой величинами (75-90 центилями) также нормальный, но свидетельствует про тенденцию опережения ребенком в росте.
- Рост, величина которого находится в пределах между красной и желтой величинами — низкий (3-10 центиль), или высокий (90-97 центиль),
что может быть обусловленным как особенностями ребенка, так и заболеванием с нарушением гормонального фона (чаще эндокринологического или наследственного).
 В таких случаях необходимо обратить на это внимание вашего педиатра или семейного врача, который, в случае необходимости, направит к соответствующему специалисту. Обязательно следите за дальнейшим ростом, весом, общим состоянием такого ребенка.
В таких случаях необходимо обратить на это внимание вашего педиатра или семейного врача, который, в случае необходимости, направит к соответствующему специалисту. Обязательно следите за дальнейшим ростом, весом, общим состоянием такого ребенка. - Рост, величина которого находится за красной границей ( менее 3 или более 97 центиля) свидетельствует про патологию роста ребенка. Такие дети обязательно должны быть проконсультированы соответствующими специалистами, прежде всего эндокринологом, которые порекомендуют дальнейшее обследование и назначат соответствующее лечение. Помните, что болезни сопровождающиеся нарушением роста, приводят в дальнейшем к различным нарушениям физического и психического здоровья.
Рост мальчиков от 1 года до 3-х лет (см)
| Возраст | Показатель | ||||||
| очень низкий |
низкий | ниже среднего |
средний | выше среднего |
высокий | очень высокий |
|
| 12 мес | 71,2-72,3 | 72,3-74,0 | 74,0-77,3 | 77,3-79,7 | 79,7-81,7 | >81,7 | |
| 15 мес | 74,8-75,9 | 75,9-77,1 | 77,1-81,0 | 81,0-83,0 | 83,0-85,3 | >85,3 | |
| 18 мес | 76,9-78,4 | 78,4-79,8 | 79,8-83,9 | 83,9-85,9 | 85,9-89,4 | >89,4 | |
| 21 мес | 79,3-80,3 | 80,3-82,3 | 82,3-86,5 | 86,5-88,3 | 88,3-91,2 | >91,2 | |
| 24 мес |
81,3-83,0 | 83,0-84,5 | 84,5-89,0 | 89,0-90,8 | 90,8-94,0 | >94,0 | |
| 27 мес | 83,0-84,9 | 84,9-86,1 | 86,1-91,3 | 91,3-93,9 | 93,9-96,8 | >96,8 | |
| 30 мес | 84,5-87,0 | 87,0-89,0 | 89,0-93,7 | 93,7-95,5 | 95,5-99,0 | >99,0 | |
| 33 мес | 86,3-88,8 | 88,8-91,3 | 91,3-96,0 | 96,0-98,1 | 98,1-101,2 | >101,2 | |
| 3 года | 88,0-90,0 | 90,0-92,3 | 92,3-99,8 | 99,8-102,0 | 102,0-104,5 | >104,5 | |
Вес мальчиков от 1 года до 3-х лет( кг )
| Возраст | Показатель | ||||||
| очень низкий |
низкий | ниже среднего |
средний | выше среднего |
высокий | очень высокий |
|
| 12 мес | 8,5-8,9 | 8,9-9,4 | 9,4-10,9 | 10,9-11,6 | 11,6-12,1 | >12,1 | |
| 15 мес | 9,2-9,6 | 9,6-10,1 | 10,1-11,7 | 11,7-12,4 | 12,4-13,0 | >13,0 | |
| 18 мес | 9,7-10,2 | 10,2-10,7 | 10,7-12,4 | 12,4-13,0 | 13,0-13,7 | >13,7 | |
| 21 мес | 10,2-10,6 | 10,6-11,2 | 11,2-12,9 | 12,9-13,6 | 13,6-14,3 | >14,3 | |
| 24 мес | 10,6-11,0 | 11,0-11,7 | 11,7-13,5 | 13,5-14,2 | 14,2-15,0 | >15,0 | |
| 27 мес | 11,0-11,5 | 11,5-12,2 | 12,2-14,1 | 14,1-14,8 | 14,8-15,6 | >15,6 | |
| 30 мес | 11,4-11,9 | 11,9-12,6 | 12,6-14,6 | 14,6-15,4 | 15,4-16,1 | >16,1 | |
| 33 мес | 11,6-12,3 | 12,3-13,1 | 13,1-15,2 | 15,2-16,0 | 16,0-16,8 | >16,8 | |
| 3 года | 12,1-12,8 | 12,8-13,8 | 13,8-16,0 | 16,0-16,9 | 16,9-17,7 | >17,7 | |
Окружность головы мальчиков,(см)
| Возраст | Показатель | ||||||
| очень низкий |
низкий | ниже среднего |
средний | выше среднего |
высокий | очень высокий |
|
| 12 мес | 44,6-45,3 | 45,3-46,2 | 46,2-49,1 | 49,1-49,8 | 49,8-50,7 | >50,7 | |
| 15 мес | 45,3-46,0 | 46,0-46,7 | 46,7-49,5 | 49,5-50,3 | 50,3-51,3 | >51,3 | |
| 18 мес | 46,0-46,6 | 46,6-47,3 | 47,3-49,9 | 49,9-50,7 | 50,7-51,6 | >51,6 | |
| 21 мес | 46,5-47,2 | 47,2-47,7 | 47,7-50,3 | 50,3-51,0 | 51,0-52,0 | >52,0 | |
| 24 мес | 47,0-47,6 | 47,6-48,1 | 48,1-50,5 | 50,5-51,3 | 51,3-52,3 | >52,3 | |
| 27 мес | 47,3-47,9 | 47,9-48,5 | 48,5-50,8 | 50,8-51,7 | 51,7-52,7 | >52,7 | |
| 30 мес | 47,5-48,2 | 48,2-48,8 | 48,8-51,1 | 51,1-52,0 | 52,0-53,0 | >53,0 | |
| 33 мес | 47,8-48,4 | 48,4-49,2 | 49,2-51,3 | 51,3-52,3 | 52,3-53,3 | >53,3 | |
| 3 года | 48,0-48,6 | 48,6-49,5 | 49,5-51,5 | 51,5-52,6 | 52,6-53,5 | >53,5 | |
Рост девочек от 1 года до 3-х лет (см)
| Возраст | Показатель | ||||||
| очень низкий |
низкий | ниже среднего |
средний | выше среднего |
высокий | очень высокий |
|
| 12 мес | 70,1-71,4 | 71,4-72,8 | 72,8-75,8 | 75,8-78,0 | 78,0-79,6 | >79,6 | |
| 15 мес | 72,9-74,5 | 74,5-76,0 | 76,0-79,1 | 79,1-81,5 | 81,5-83,4 | >83,4 | |
| 18 мес | 75,8-77,1 | 77,1-78,9 | 78,9-82,1 | 82,1-84,5 | 84,5-86,8 | >86,8 | |
| 21 мес | 78,0-79,5 | 79,5-81,2 | 81,2-84,5 | 84,5-87,5 | 87,5-89,5 | >89,5 | |
| 24 мес | 80,1-81,7 | 81,7-83,3 | 83,3-87,5 | 87,5-90,1 | 90,1-92,5 | >92,5 | |
| 27 мес | 82,0-83,5 | 83,5-85,4 | 85,4-90,1 | 90,1-92,4 | 92,4-95,0 | >95,0 | |
| 30 мес | 83,8-85,7 | 85,7-87,7 | 87,7-92,3 | 92,3-95,0 | 95,0-97,3 | >97,3 | |
| 33 мес | 85,8-87,6 | 87,6-89,8 | 89,8-94,8 | 94,8-97,0 | 97,0-99,7 | >99,7 | |
| 3 года | 89,0-90,8 | 90,8-93,0 | 93,0-98,1 | 98,1-100,7 | 100,7-103,1 | >103,1 | |
Вес девочек от 1 года до 3-х лет (кг)
| Возраст | Показатель | ||||||
| очень низкий |
низкий | ниже среднего |
средний | выше среднего |
высокий | очень высокий |
|
| 12 мес | 8,0-8,5 | 8,5-9,0 | 9,0-10,2 | 10,2-10,8 | 10,8-11,3 | >11,3 | |
| 15 мес | 8,6-9,2 | 9,2-9,7 | 9,7-10,9 | 10,9-11,5 | 11,5-12,1 | >12,1 | |
| 18 мес | 9,0-9,8 | 9,8-10,3 | 10,3-11,5 | 11,5-12,2 | 12,2-12,8 | >12,8 | |
| 21 мес | 9,7-10,3 | 10,3-10,6 | 10,6-12,2 | 12,2-12,8 | 12,8-13,4 | >13,4 | |
| 2 года | 10,2-10,8 | 10,8-11,3 | 11,3-12,8 | 12,8-13,5 | 13,5-14,1 | >14,1 | |
| 27 мес | 10,6-11,2 | 11,2-11,7 | 11,7-13,3 | 13,3-14,2 | 14,2-14,8 | >14,8 | |
| 30 мес | 11,0-11,6 | 11,6-12,3 | 12,3-13,9 | 13,9-14,8 | 14,8-15,5 | >15,5 | |
| 33 мес | 11,5-12,1 | 12,1-12,7 | 12,7-14,5 | 14,5-15,4 | 15,4-16,3 | >16,3 | |
| 3 года | 11,7-12,5 | 12,5-13,3 | 13,3-15,5 | 15,5-16,5 | 16,5-17,6 | >17,6 | |
Окружность головы девочек, (см)
| Возраст | Показатель | ||||||
| очень низкий |
низкий | ниже среднего |
средний | выше среднего |
высокий | очень высокий |
|
| 12 мес | 43,5-44,2 | 44,2-45,0 | 45,0-48,2 | 48,2-49,2 | 49,2-50,1 | >50,1 | |
| 15 мес | 44,2-45,1 | 45,1-45,9 | 45,9-48,7 | 48,7-49,6 | 49,6-50,5 | >50,5 | |
| 18 мес | 44,9-45,7 | 45,7-46,4 | 46,4-49,0 | 49,0-49,9 | 49,9-50,9 | >50,9 | |
| 21 мес | 45,4-46,1 | 46,1-46,9 | 46,9-49,4 | 49,4-50,2 | 50,2-51,2 | >51,2 | |
| 24 мес | 46,0-46,6 | 46,6-47,3 | 47,3-49,7 | 49,7-50,5 | 50,5-51,5 | >51,5 | |
| 27 мес | 46,5-47,0 | 47,0-47,8 | 47,8-50,0 | 50,0-50,7 | 50,7-51,8 | >51,8 | |
| 30 мес | 47,0-47,5 | 47,5-48,0 | 48,0-50,4 | 50,4-51,0 | 51,0-52,0 | >52,0 | |
| 33 мес | 47,3-47,9 | 47,9-48,4 | 48,4-50,6 | 50,6-51,4 | 51,4-52,4 | >52,4 | |
| 3 года | 47,6-48,1 | 48,1-48,6 | 48,6-51,0 | 51,0-51,7 | 51,7-52,7 | >52,7 | |
Читайте также: Нанизм (низкорослость) .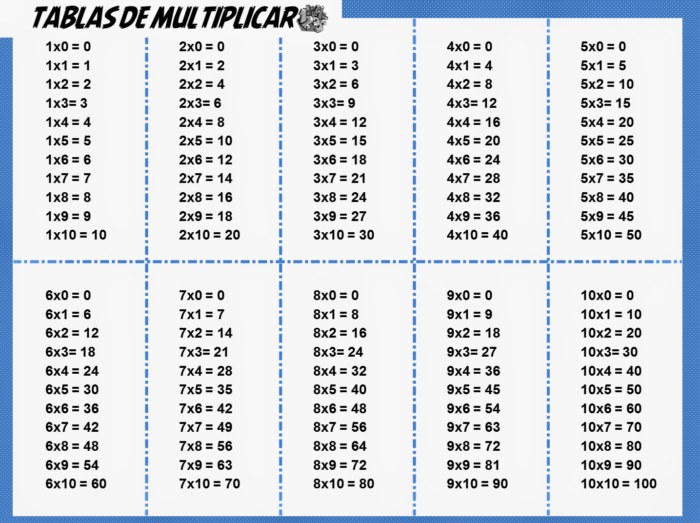
Гормоны роста человека ( СТГ и ИФР ) — нормы у детей, лабораторная диагностика, измерение, лечение.
Тэги : центильные таблицы соотношение роста и веса изменение роста и веса рост и вес ребенка от 1 года
- Календарь развития ребёнка от рождения и до года
- Календарь развития ребёнка от года до 6 лет
- Физическое развитие детей до года
- Таблица изменения роста и веса ребенка от 0 до года.
- Таблица изменения роста и веса ребенка от 1 года до 3 лет
- Таблица изменения роста и веса ребенка от 3 до 7 лет
- Таблица изменения роста и веса ребенка от 7 до 17 лет
- Норма роста и веса для подростков
- Гормоны роста человека (СТГ и ИФР)
- Тяжелая кость : сколько на самом деле весил скелет человека
- Ожирение у детей
Калькулятор дробей
Этот калькулятор дробей выполняет базовые и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила выражения с дробями:
Дроби — используйте косую черту для деления числителя на знаменатель, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта является одновременно знаком дробной части и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т.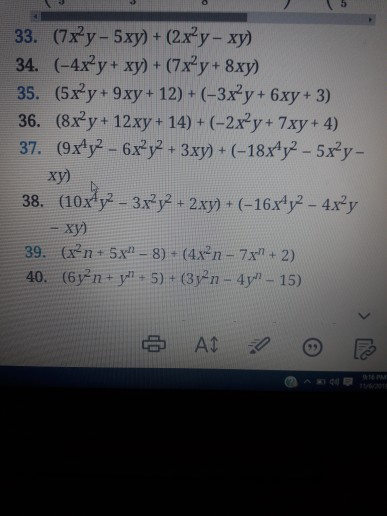 е. 1,45 .
е. 1,45 .
Math Symbols
| Symbol | Symbol name | Symbol Meaning | Example | |
|---|---|---|---|---|
| + | plus sign | addition | 1/2 + 1/3 | |
| — | знак минус | вычитание | 1 1/2 — 2/3 | |
| * | asterisk | multiplication | 2/3 * 3/4 | |
| × | times sign | multiplication | 2 /3 × 5/6 | |
| : | division sign | division | 1/2 : 3 | |
| / | division slash | division | 1/3 / 5 1/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 • квадратный корень дроби: sqrt(1/16) • уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций .
more math problems »
| |
| 9 | Оценить | квадратный корень из 12 | ||
| 10 | Оценить | квадратный корень из 20 | ||
| 11 | Оценить | квадратный корень из 50 | 94 | |
| 18 | Оценить | квадратный корень из 45 | ||
| 19 | Оценить | квадратный корень из 32 | ||
| 20 | Оценить | квадратный корень из 18 | 92 |
Уравнения и неравенства
Принцип сложения
Изучив этот раздел, вы сможете:
1. Решать уравнения вида x + b = c, используя принцип сложения.
Решать уравнения вида x + b = c, используя принцип сложения.
2. Использование принципа сложения
Когда мы используем знак равенства (=), мы указываем, что два выражения равны по значению. Это называется уравнением . Например, x + 5 = 23 — это уравнение. Выбирая определенные процедуры, можно шаг за шагом перейти от заданного уравнения к уравнению x = некоторому числу. Число является решением уравнения.
Одна из первых процедур, используемых при решении уравнений, нашла применение в нашем повседневном мире. Предположим, мы поместили 10-килограммовый ящик с одной стороны качелей и 10-килограммовый камень с другой стороны. Если центр ящика находится на таком же расстоянии от точки баланса, как и центр камня, мы ожидаем, что качели будут балансировать. Коробка и камень не выглядят одинаково, но имеют одинаковую ценность по весу. Если мы добавим 2-килограммовый свинцовый груз к центру веса каждого объекта одновременно, качели все равно должны балансировать. Результаты равны.
Результаты равны.
Похожий принцип есть и в математике. Мы можем выразить это такими словами.
Принцип сложения
Если к обеим частям уравнения прибавить одно и то же число, результаты каждой стороны будут равны по значению.
Мы можем переформулировать это в символах таким образом.
Для действительных чисел a, b, c, если a=b thenat+tc=b+ec
Вот пример.
Если 3=6/2, то 3+5=6/2+5
Поскольку мы добавили одинаковое количество 5 к обеим сторонам, каждая сторона имеет одинаковую ценность.
3+5=6/2+5
8 =6/2+10/2
8 = 16/2
8=8
Мы можем использовать принцип сложения для решения уравнения.
ПРИМЕР 1 Найдите x. x + 16 = 20
x + 16 + (-16) = 20 + (-16) Используйте принцип сложения, чтобы добавить -16 к обеим частям.
x+0=4 Упростить.
x=4 Значение x равно 4.
Мы только что нашли решение уравнения. Решение — это значение переменной, которая делает уравнение верным. Затем мы говорим, что значение 4 в нашем примере удовлетворяет уравнению. Мы можем легко проверить, что 4 является решением, подставив это значение в исходное уравнение. Этот шаг называется проверка решения.
Затем мы говорим, что значение 4 в нашем примере удовлетворяет уравнению. Мы можем легко проверить, что 4 является решением, подставив это значение в исходное уравнение. Этот шаг называется проверка решения.
Чек . x + 16 = 20
4 + 16 ≟ 20
20 = 20 ✔
Когда одно и то же значение появляется с обеих сторон знака равных, мы называем уравнение Identity . Поскольку две части уравнения в нашей проверке имеют одинаковое значение, мы знаем, что исходное уравнение было решено правильно. Мы нашли решение.
Когда вы пытаетесь решить эти типы уравнений, вы замечаете, что вы должны добавить определенное число к обеим частям уравнения. Какой номер выбрать? Посмотрите на число, которое находится на той же стороне уравнения, что и х, то есть на число, прибавленное к х. Затем подумайте о числе, которое равно напротив знака . Это называется добавкой , обратной числа. Аддитивное значение, обратное 16, равно -16. Аддитивное обратное значение -3 равно 3. Число, которое нужно добавить к обеим частям уравнения, и есть это аддитивное обратное.
Аддитивное обратное значение -3 равно 3. Число, которое нужно добавить к обеим частям уравнения, и есть это аддитивное обратное.
Неважно, какая часть уравнения содержит переменную. Термин x может быть справа или слева. В следующем примере член x будет справа.
ПРИМЕР 2 Найдите x. 14 =x- 3
14+3=x-3 +3 Добавьте 3 к обеим частям, так как 3 является аддитивной инверсией к -3. Это устранит -3 справа и изолирует x.
17 =x+0 Упростить.
17=x Значение x равно 17.
Чек . 14 = x-3
14 ≟ 17-3 Замените x на 17.
14 =14 ✔ Упрощение. Это проверяет. Решение x = 17.
Прежде чем прибавлять число к обеим частям, всегда следует упростить уравнение. В следующем примере показано, как объединение чисел путем сложения по отдельности в обеих частях уравнения упрощает уравнение.
ПРИМЕР 3 Найдите х. 15 +2=3+x+2
17=x+5 Упростите, добавив.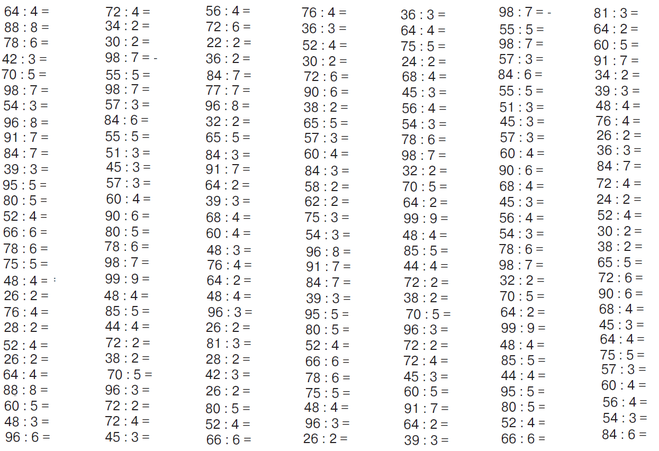
17+ (-5) =x+5+(-5) Добавьте значение -5 к обеим сторонам, так как -5 является аддитивной величиной, обратной 5.
12=x Упростите. Значение x равно 12.
Чек . 15+2 = 3+x+2
15+2 ≟ 3+12+2 Замените x на 12 в исходном уравнении.
17=17 ✔ Проверено.
В примере 3 мы добавили -5 к каждой стороне. Вы можете вычесть по 5 с каждой стороны и получить тот же результат. В предыдущем уроке мы обсуждали, что вычитание 5 равносильно прибавлению минус 5. Понимаете, почему?
Мы можем определить, является ли значение решением уравнения, выполнив те же шаги, что и для проверки ответа. Подставьте проверяемое значение переменной в исходное уравнение. Мы получим тождество, если значение является решением.
ПРИМЕР 4 Является ли x = 10 решением уравнения -15 + 2 = x-3? Если это не так, найдите решение.
Подставим x в уравнение на 10 и посмотрим, получится ли тождество.
-15+2=х-3
-15+2=10-3
-13 ≠ 7 Это неправда. Это не личность.
Таким образом, x = 10 не является решением. Теперь возьмем исходное уравнение и решим, чтобы найти решение.
-15+2=x-3
-13=x-3 Упростите, добавив.
-13+3=x-3+3 Прибавьте 3 к обеим сторонам. 3 является аддитивной инверсией -3.
-10=x
Проверить, является ли решение x = -10. Значение x = 10 было неверным из-за ошибки знака. Мы должны быть особенно внимательны, чтобы писать правильный знак для каждого числа при решении уравнений.
ПРИМЕР 5 Найдите значение x, удовлетворяющее уравнению 1/5+x = −1/10+1/2
Чтобы объединить дроби, дроби должны иметь общие знаменатели. Наименьший общий знаменатель (LCD) дробей равен 10.
(1*2)/(5*2)+x = −1/10+(1*5)/(2*5) Замените каждую дробь на эквивалентная дробь со знаменателем 10.
2/10 + x = −1/10+5/10 Это эквивалентное уравнение.
2/10+x = 4/10 Упростите, добавив.
2/10+(-2/10)+x = 4/10+(-2/10) Добавить добавку, обратную 2/10, к каждой стороне
x=2/10 Сложите дроби.
x= 1/5 Упростите ответ.
Чек . Подставим 1/5 вместо x в исходное уравнение и посмотрим, получим ли мы тождество.
1/5+x = −1/10+1/2
1/5+1/5 ≟ −1/10+1/2 Подставьте 1/5 вместо x
2/5 ≟ −1/10 +1/2
2/5 = 4/10
2/5 = 2/5 ✔ Проверено.
Принцип умножения
Изучив этот раздел, вы сможете:
1. Решать уравнения вида 1/ax=b.
2. Решить уравнения вида ax = b.
Решение уравнений вида 1/ax=b
Принцип сложения позволяет нам добавлять одно и то же число к обеим частям уравнения. Что произойдет, если мы умножим каждую часть уравнения на одно и то же число? Например, что произойдет, если мы умножим каждую часть уравнения на 3?
Чтобы ответить на этот вопрос, вернемся к нашему простому примеру с коробкой и камнем на сбалансированных качелях. Если мы утроим количество грузов с каждой стороны (мы умножаем каждую сторону на 3), качели все равно должны балансировать. «Значение веса» каждой стороны остается равным.
Если мы утроим количество грузов с каждой стороны (мы умножаем каждую сторону на 3), качели все равно должны балансировать. «Значение веса» каждой стороны остается равным.
На словах мы можем выразить этот принцип так.
Принцип умножения
Если обе части уравнения умножить на одно и то же число, результаты на каждой стороне
равны по значению.
В символах мы можем переформулировать принцип умножения таким образом.
|
Для вещественных чисел a,b,c с #0 ifa@=b thenca=cb |
Давайте посмотрим на уравнение, в котором было бы полезно умножить каждую часть уравнения на 3.
ПРИМЕР 1 Найдите х. 1/3x=-15
Мы знаем, что (3)(1/3) = 1. Мы умножим каждую часть уравнения на 3, потому что мы хотим изолировать переменную x.
(3)(1/3x)=3(-15) Умножьте каждую часть уравнения на 3, так как (3)(1/3) = 1.
(3/1)(1/3)(x )=-45
1x=-45 Упрощение.
x= -45
Проверить . 1/3(-45) ≟ -15 Замените x на -45 в исходном уравнении.
1/3(-45) ≟ -15 Замените x на -45 в исходном уравнении.
-15=-15 ✔ Проверяет.
Обратите внимание, что 1/5x можно записать как x/5. Чтобы решить уравнение x/5=3, мы могли бы умножить каждую часть уравнения на 5. Попробуйте. Затем проверьте свое решение.
Решение уравнений вида ax = b
Мы можем видеть, что использование принципа умножения для умножения каждой стороны уравнения на 1/2 равносильно делению каждой стороны уравнения на 2. Таким образом, было бы кажется, что принцип умножения позволил бы нам разделить каждую часть уравнения на любое ненулевое действительное число. Есть ли реальный пример этой идеи?
Вернемся к нашему простому примеру с коробкой и камнем на сбалансированных качелях. Предположим, что мы должны были разрезать два объекта пополам (так, чтобы количество веса каждого было разделено на 2). Затем мы возвращаем предметы на те же места на качелях. Качели все равно будут балансировать. «Значение веса» каждой стороны остается равным.
На словах мы можем сформулировать этот принцип так:
Принцип деления
Если обе части уравнения разделить на одно и то же ненулевое число, результаты
с каждой стороны равны по значению.
Примечание : Мы накладываем ограничение на число, на которое мы делим. Мы не можем разделить на ноль. Мы говорим, что такие выражения, как 2/0, не определены. Таким образом, мы ограничиваем наш делитель ненулевыми числами. Мы можем переформулировать принцип деления таким образом.
a b
Для действительных чисел a, b, c, где c ~ 0, если a=b, то — = —
coc
ПРИМЕР 2 Найдите x. 5x = 125
(5x)/5=125/5 Поделите обе части на 5.
x = 25 Упростите. Решение 25.
Чек . 5x = 125
5(25) ≟ 125 Замените x на 25.
125 = 125 ✔ Это проверяет.
Для уравнений вида ax = b (число, умноженное на x, равно другому числу), мы решаем уравнение, разделив обе части на определенное число. Какой номер выбрать? Смотрим на ту часть уравнения, которая содержит х. Мы замечаем число, которое умножается на х. Делим на это число. Принцип деления говорит нам, что у нас все еще может быть истинное уравнение, если мы разделим на это число 9.1424 с обеих сторон уравнения.
Какой номер выбрать? Смотрим на ту часть уравнения, которая содержит х. Мы замечаем число, которое умножается на х. Делим на это число. Принцип деления говорит нам, что у нас все еще может быть истинное уравнение, если мы разделим на это число 9.1424 с обеих сторон уравнения.
Решением уравнения может быть правильная или неправильная дробь.
ПРИМЕР 3 Найдите x. 4x = 38
(4x)/4= 38/4 Поделите обе части на 4.
x=19/2 Упростите. Решение 19/2.
Если оставить решение в виде дроби, будет легче проверить это решение в исходном уравнении.
Проверить : 4x = 38 Заменить x на 19/2.
4(19/2) ≟ 38
38 = 38 ✔ Проверяет.
В примерах 2 и 3 мы делили на число, умноженное на х (коэффициент при х). Эта процедура выполняется независимо от того, положительный или отрицательный знак этого числа.
ПРИМЕР 4 Найдите x. -3x = 48
(-3x)/-3=48/-3 Поделите обе части на -3.
x=-16 Решение равно -16.
Коэффициент x может быть 1 или -1. Возможно, вам придется переписать уравнение так, чтобы коэффициент 1 или -1 был очевиден. С практикой вы сможете «увидеть» коэффициент, фактически не переписывая уравнение.
ПРИМЕР 5 Найдите x. -x = -24
-1x = -24 Перепишите уравнение. -1x совпадает с -x. Теперь коэффициент -1 очевиден.
(-1x)/-1=-24/-1 Поделите обе части на -1
x= 24 Решение равно 24.
Используйте вместе принципы сложения и умножения
умеет:
1. Решать уравнения вида ax + b =c.
2. Решите уравнения, в которых переменная присутствует в обеих частях уравнения.
3. Решите уравнения со скобками.
Решение уравнений вида ax +b=c
Для решения многих уравнений мы должны использовать как принцип сложения, так и принцип умножения.
ПРИМЕР 1 Найдите x и проверьте свое решение. 5x +3 = 18
5x + 3 + (-3)= 18+ (-3) Добавьте -3 к обеим частям, используя принцип сложения.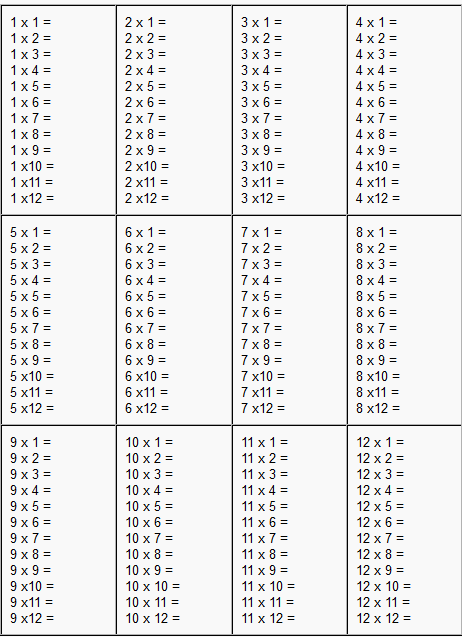
5x = 15 Упростить.
(5x)/5=15/5 Поделите обе части на 5, используя принцип деления.
x=3 Решение 3.
Проверить . 5(3)+3 ≟ 18
Чек . 15+3 ≟ 18
Чек . 18=18 ✔ Проверил.
Переменная в обеих частях уравнения
В некоторых случаях переменная появляется в обеих частях уравнения. Мы хотели бы переписать уравнение так, чтобы все члены, содержащие переменную, оказались с одной стороны. Для этого применим принцип сложения к переменному члену.
ПРИМЕР 2 Найдите x. 9x = 6x + 15
9x + (-6x) = 6x + (-6x) + 15 Добавьте -6x к обеим сторонам. Обратите внимание, что 6x + (-6x) исключает переменную с правой стороны.
3x = 15 Соберите одинаковые термины.
(3x)/3=15/3 Поделите обе части на 3.
x=5 Решение равно 5.
Многие задачи имеют переменные и постоянные члены в обеих частях уравнения.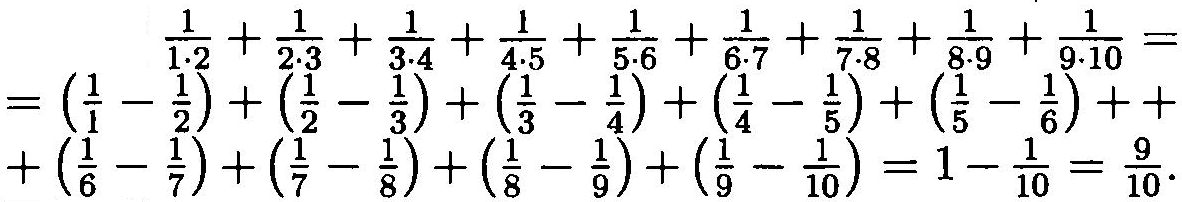 Вы захотите получить все переменные члены с одной стороны и все постоянные члены с другой стороны.
Вы захотите получить все переменные члены с одной стороны и все постоянные члены с другой стороны.
ПРИМЕР 3 Найдите x и проверьте свое решение. 9х + 3 = 7х -2.
9x + (-7x) + 3 = 7x + (-7x) — 2 Добавьте -7x к обеим частям уравнения.
2x+3=-2 Объедините одинаковые термины.
2x + 3+ (-3) = -2 + (-3) Добавьте -3 к обеим сторонам.
2x = -5 Упростить.
(2x)/2=-5/2 Поделите обе части на 2.
x = -5/2 Решение равно −5/2.
Чек . 9x + 3 = 7x -2
Чек . 9(-5/2)+3 ≟ 7(-5/2)-2 Замените x на −5/2.
Чек . −45/2+3 ≟ −35/2-2 Упростить.
Чек . −45/2+6/2 ≟ −35/2-4/2 Переведите в эквивалентные дроби с общим знаменателем.
Чек . −39/2 = −39/2 ✔ Это проверка. x = −5/2 является решением.
В следующем примере мы изучим уравнения, которые необходимо упростить, прежде чем предпринимать какие-либо другие шаги. 2, попытайтесь собрать их на одной стороне уравнения. Если квадратный член выпадает, вы можете решить его как уравнение первой степени, используя методы, обсуждаемые в этом разделе. 92 = 0.
2, попытайтесь собрать их на одной стороне уравнения. Если квадратный член выпадает, вы можете решить его как уравнение первой степени, используя методы, обсуждаемые в этом разделе. 92 = 0.
6y+y-2=-y+y+12 Добавьте y к каждой стороне.
7y-2= 12 Упростить.
7y-2+2=12+2 Добавьте по 2 с каждой стороны.
7y=14 Упрощение.
(7y)/7 = 14/7 Разделите каждую сторону на 7.
y=2 Упростите. Решение 2.
Решение уравнений со скобками
Уравнения, которые вы только что решили, представляют собой более простые версии уравнений, которые мы сейчас обсудим. Эти уравнения содержат круглые скобки. Если скобки сначала удалить, проблемы становятся такими же, как те, с которыми мы сталкивались ранее. Мы используем распределительное свойство, чтобы удалить круглые скобки.
ПРИМЕР 6 Найдите x и проверьте свое решение. 4(x + 1)- 3(x-3) = 25
4(x + 1)- 3(x-3) = 25
4x +4-3x+9 = 25 Умножьте на 4 и -3, чтобы убрать скобки. Будьте осторожны со знаками. Помните, что (-3)(-3) = 9.
Будьте осторожны со знаками. Помните, что (-3)(-3) = 9.
После удаления скобок важно собрать одинаковые члены с каждой стороны уравнения. Сделайте это, прежде чем переходить к изоляции переменной.
x + 13 = 25 Соберите одинаковые термины.
x+ 13-13 = 25-13 Добавьте -13 к обеим сторонам, чтобы изолировать переменную.
x = 12 Решение 12.
Проверить . 4(12+1)-3(12-3) ≟ 25 Замените x на 12.
4(13)-3(9) ≟ 25 Объедините числа в скобках.
52-27 ≟ 25 Умножить.
25=25 ✔ Упрощение. Это проверяет.
В задачах с десятичными дробями следует проявлять большую осторожность. На некоторых шагах вы будете умножать десятичные числа, а на других шагах вы будете их складывать.
ПРИМЕР 7 Найдите x. 0,3(1,2x-3,6) = 4,2x-16,44
0,36x-1,08 = 4,2x -16,44 Удалите скобки.
0,36x-0,36x-1,08 = 4,2x-0,36x-16,44 Вычтите 0,36x с обеих сторон.
-1,08 = 3,84x -16,44 Соберите одинаковые термины.
-1,08 + 16,44 = 3,84x-16,44 + 16,44 Прибавьте 16,44 к обеим сторонам.
15,36 = 3,84x Упростить.
15,36/3,84=(3,84x)/3,84 Поделите обе стороны на 3,84.
4=x Решение x = 4.
ПРИМЕР 8 Найдите z и проверьте. 2(3z-5) + 2 = 4z -3(2z + 8)
6z-10 + 2 = 4z-6z-24 Удалите скобки.
6z- 8 = -2z-24 Соберите одинаковые термины.
6z-8 + 2z = -2z + 2z-24 Добавьте по 2z с каждой стороны.
8z-8 = -24 Упростить.
8z-8 +8 = -24+ 8 Добавьте 8 с каждой стороны.
8z =-16 Упрощение.
(8z)/8=-16/8 Разделите каждую сторону на 8.
z=-2 Упростите. Решение -2.
Чек . 2[3(-2)-5] +2 ≟ 4(-2)-3[2(-2) + 8] Замените z на -2.
2[-6-5] +2 ≟ -8 -3[-4 + 8] Умножить.
2[-11] +2 ≟ -8 -3[4] Упростить.
-22 +2 ≟ -8 -12
-20 = -20 ✔ Проверяет.
Уравнения с дробями
Изучив этот раздел, вы сможете:
1. Решать уравнения с дробями.
Решение уравнений с дробями
Уравнения с дробями решить довольно сложно. Эта трудность просто из-за особой осторожности, которую мы обычно должны проявлять при вычислениях с дробями. Фактические процедуры решения уравнений одинаковы, с дробями или без них. Чтобы избежать лишней работы, преобразуем данное уравнение с дробями в эквивалентное уравнение, не содержащее дробей. как нам это сделать? Умножаем каждую часть уравнения на наименьший общий знаменатель всех дробей, содержащихся в уравнении. Затем мы используем распределительное свойство, так что LCD умножается на каждый член уравнения.
ПРИМЕР 1 Найдите x. 1/4x-2/3=5/12x
Сначала находим, что LCD = 12.
12(1/4x-2/3)=12(5/12x) Умножаем каждую сторону на 12
(12 /1)(1/4)(x)-(12/1)(2/3)=(12/1)(5/12)(x) Используйте распределительное свойство.
3x-8 = 5x Упростить.
3x + (-3x)-8 = 5x + (-3x) Добавьте -3x к каждой стороне.
-8 = 2x Упростить.
-8/2=(2x)/2 Поделить каждую сторону на 2.
-4= x Упростить.
Проверка . 1/4(-4)-2/3 ≟ 5/12(-4)
-1-2/3 ≟ −5/3
-3/3-2/3 ≟ −5/3
− 5/3 = -5/3 ✔ Проверяет.В примере 1 мы умножили каждую часть уравнения на LCD. Обычной практикой является немедленно перейти ко второму шагу и умножить каждое слагаемое на LCD, а не
ПРИМЕР 2 Найти x. (x+5)/7=x/4+1/2
x/7+5/7=x/4+1/2 Сначала запишем отдельными дробями
(28)(x/7)+( 28)(5/7)=(28)(x/4)+(28)(1/2) Мы видим, что LCD равно 28, поэтому мы умножаем каждое слагаемое на 28.
4x + 20 = 7x + 14 Упрощение.
4x-4x + 20 = 7x-4x + 14 Добавьте -4x к обеим сторонам.
20 = 3x + 14 Соберите одинаковые члены.
20-14=3x + 14- 14 Добавьте -14 к обеим сторонам.
6 = 3x Соберите одинаковые термины.
6/3=(3x)/3 Разделите обе части на 3.
2=x Решение: x = 2.
Если в задаче есть и скобки, и дроби, лучше сначала убрать скобки. Многие студенты считают полезным иметь письменную процедуру решения этих более сложных уравнений.
Процедура решения линейных уравнений
1. Удалите все скобки.
2. Если существуют дроби, умножьте все члены с обеих сторон на наименьший общий знаменатель всех дробей.
3. Соберите одинаковые термины, если это возможно. Если возможно, упростите числовую работу.
4. Добавьте или вычтите члены с обеих сторон уравнения, чтобы получить все члены с переменной на одной стороне уравнения.
5. Добавьте или вычтите значение в обеих частях уравнения, чтобы получить все члены, не содержащие переменную в другой части уравнения.
6. Разделите обе части уравнения на коэффициент при переменной.
7. Упростите решение (если возможно).
8. Проверьте свое решение.
Давайте используем каждый шаг в решении этого примера.
ПРИМЕР 3 Найдите x и проверьте свое решение. 1/3(x-2)= 1/5(x+4)+2
Шаг 1 x/3-2/3=x/5+4/5+2 Удалите скобки.
Шаг 2 15(x/3)-15(2/3) = 15(x/5) +15(4/5) +15(2) Умножить на ЖК-дисплей, 15.
Шаг 3 5x-10 = 3x + 12 + 30 Упрощение.
5x-10 = 3x + 42 Упростить.
Шаг 4 5x-3x-10 = 3x-3x + 42 Добавьте -3x к обеим сторонам.
2x-10 = 42 Упростить.
Шаг 5 2x-10+ 10 = 42+ 10 Прибавьте 10 к обеим сторонам.
2x = 52 Упростить.
Шаг 6 (2x)/2=52/2 Разделите обе части на 2.
Шаг 7 x = 26 Упростите решение.
Шаг 8 Проверка . 1/3(26-2) ≟ 1/5(26 +4)+2 Замените x на 26.
1/3(24) ≟ 1/5(30)+2 Объедините значения в скобках.
8 ≟ 6+2 Упростить.
8 = 8 ✔ x=26 — это решение.
Следует помнить, что не каждый шаг будет необходим в каждой задаче. Вы также можете комбинировать некоторые шаги, если вы постоянно получаете правильное решение. Тем не менее, вам рекомендуется записывать каждый шаг, чтобы избежать ошибок по невнимательности.
Важно помнить, что когда мы пишем десятичные дроби, эти числа на самом деле представляют собой дроби, записанные особым образом. Таким образом, 0,3 = 7 и 0,07 = 745. Можно взять линейное уравнение, содержащее десятичные дроби, и умножить каждый член на соответствующее значение, чтобы получить целые коэффициенты.
Формулы
Изучив этот раздел, вы сможете:
1. Решать формулы для заданной переменной.
Решение указанной переменной в формуле
Формулы — это уравнения с одной или несколькими переменными, которые используются для описания реальных ситуаций. Формула описывает отношения, существующие между переменными. Например, в формуле d = rt расстояние (d) связано с показателем скорости (r) и временем (t). Мы можем использовать эту формулу, чтобы найти расстояние, если мы знаем скорость и время. Иногда, однако, нам дают расстояние и скорость, и нас просят найти время.
Например, в формуле d = rt расстояние (d) связано с показателем скорости (r) и временем (t). Мы можем использовать эту формулу, чтобы найти расстояние, если мы знаем скорость и время. Иногда, однако, нам дают расстояние и скорость, и нас просят найти время.
ПРИМЕР 1 Джозеф проехал 156 миль со средней скоростью 52 мили в час. Сколько времени понадобилось Иосифу, чтобы совершить путешествие?
d= rt Используйте формулу расстояния.
156 = 52t Подставьте известные значения переменных.
156/52=52/52t Поделите обе части уравнения на 52, чтобы найти t.
3=t Мы нашли t.
Джозефу потребовалось 3 часа, чтобы проехать 156 миль со скоростью 52 мили в час.
Если у нас есть много задач, требующих нахождения времени по расстоянию и скорости, может оказаться целесообразным переписать формулу с точки зрения времени.
ПРИМЕР 2 Решите для t. d=rt
d/r=(rt)/r Мы хотим изолировать t. Поэтому мы делим обе части уравнения на коэффициент при t, который равен r.
d/r=t Вы решили для указанной переменной.
Простое уравнение первой степени с двумя переменными можно рассматривать как уравнение прямой. Часто полезно найти у, чтобы упростить построение графика.
ПРИМЕР 3 Решите для y. 3x-2y = 6
-2y = 6-3x Мы хотим изолировать член, содержащий y, поэтому мы вычитаем 3x с обеих сторон.
(-2y)/(-2)= (6-3x)/(-2) Поделите обе части на коэффициент y.
y=6/-2+(-3x)/-2 Перепишите дробь.
y= 3/2x-3 Упростите и перегруппируйте.
Это известно как форма уравнения линии с пересечением наклона.
Наша процедура решения уравнения первой степени может быть переписана так, чтобы получить процедуру решения формулы для заданной переменной.
Процедура решения формулы для указанной переменной
1. Удалите все скобки.
2. Если существуют дроби, умножьте все члены с обеих сторон на ЖКИ всех дробей.
3. Соберите одинаковые термины или упростите, если возможно.
4. Добавьте или вычтите члены с обеих сторон уравнения, чтобы получить все члены с нужной переменной на одной стороне уравнения.
5. Прибавьте или вычтите соответствующую величину, чтобы получить все члены, в которых нет нужной переменной на другой стороне уравнения.
6. Разделите обе части уравнения на коэффициент при нужной переменной.
7. Если возможно, упростите.
ПРИМЕР 4 Трапеция – четырехгранная фигура с двумя параллельными сторонами. Если параллельные стороны равны a и b, а высота равна h, площадь определяется как
A=h/2(a+b)
Решите это уравнение для a.
A=h/2(a+b)
A=(ha)/2+(hb)/2 Удалите скобки.
2(A) = 2((га)/2)+2((hb)/2) Умножьте все слагаемые на LCD на 2.
2A = га + hb Упростите.
2A-hb = ha Мы хотим выделить термин, содержащий a. Поэтому мы вычитаем hb с обеих сторон.
(2A-hb)/h= (га)/h Поделите обе части на h (коэффициент при а).
(2A-hb)/h=a Решение получено.
Примечание : Хотя решение представлено в простой форме, его можно записать другим способом. Поскольку
(2A-hb)/h=(2A)/h-(hb)/h=(2A)/h-b
, мы могли бы иметь (2A)/h-b = a в качестве альтернативного способа записи ответа.
Запись и графическое отображение неравенств
Изучив этот раздел, вы сможете:
1. Интерпретировать утверждение о неравенстве.
2. Нарисуйте неравенство на числовой прямой.
Заявления о неравенстве
Мы часто говорим, что одно значение больше или меньше другого значения. Мы говорим, что «5 меньше 7» или «9 больше 4». Эти соотношения называются неравенствами . Мы можем записать неравенства в математике, используя символы. Мы используем символ < для представления слов «меньше чем». Мы используем символ > для представления слов «больше чем».
Заявление в словах в алгебре
5 меньше 7. 5 <7
9 больше 4. 9> 4
Примечание . «5 меньше 7» и «7 больше 5» имеют одинаковый смысл. Точно так же 5 < 7 и 7 > 5 имеют одинаковый смысл. Они представляют собой два эквивалентных способа описания одной и той же связи между двумя числами 5 и 7.
«5 меньше 7» и «7 больше 5» имеют одинаковый смысл. Точно так же 5 < 7 и 7 > 5 имеют одинаковый смысл. Они представляют собой два эквивалентных способа описания одной и той же связи между двумя числами 5 и 7.
Мы можем проиллюстрировать концепцию неравенства графически, если рассмотрим числовую прямую.
+++ +—_ +++ +_+_+—_—_+_¢_ _ +>
-5 -4 -3 -—2 -] 0 I 2 3 4 5 6 7 8
Мы говорим, что одно число больше другого, если оно находится справа от другого на числовой прямой. Таким образом, 7 > 5, так как 7 правее 5.
А как насчет отрицательных чисел? Мы можем сказать: «-1 больше, чем -3» и записать это символами -1 > -3, потому что мы знаем, что -1 лежит справа от -3 на числовой прямой.
ПРИМЕР 1 Замените вопросительный знак символом < или > в каждом утверждении.
(а) 3 ? -1 (б) -2 ? 1 (в) -3 ? -4 (г) 0 ? 3
(a) 3>-1 Используйте >, так как 3 справа от -1.
(b) -2< 1 Use <, поскольку -2 находится слева от 1. (Или, что то же самое, мы могли бы сказать, что 1 находится справа от -2.)
(Или, что то же самое, мы могли бы сказать, что 1 находится справа от -2.)
(c) -3 > -4 Так как -3 справа от -4.
(d) 0<3
Построение графика неравенства на числовой прямой
Иногда мы будем использовать неравенство, чтобы выразить связь между переменной и числом. x > 3 означает, что x может иметь значение любого числа больше 3. Это можно изобразить на числовой прямой на графике следующим образом:
-5 -4 -3 -2 -1 0 l 2 3 4 5
Обратите внимание, что незаштрихованный кружок на цифре 3 означает, что мы не включаем точку для числа 3.
-2 следующим образом:
$$ —} fj —_ + —_;_+_+_+_ + > x
-5 -4 -3 -2 -l 0 I 2 3 #4 = =# §
Иногда переменная может быть больше или равна определенному числу. В утверждении «x больше или равно 3» мы подразумеваем, что x может иметь значение 3 или любое число больше 3. Мы запишем это как x >= 3. Мы представим это графически следующим образом:
—+—. >! 4H_{_AH_ ee ee et
—2 -1 0 l 2 3 4 5 6 7
Обратите внимание, что замкнутый кружок на цифре 3 указывает на то, что мы делаем включаем точку для числа 3.
x <= -2 следующим образом:
—— t+. et Ht HH HH
-5 -4 -3 -2 -1 0 1 2 3 4 5
ПРИМЕР 2 Назовите каждое математическое соотношение словами, а затем проиллюстрируйте его графически.
(а) x< -2 (б) -3 (a) Мы утверждаем, что «x меньше -2». x<-20 ——+-+—O—_1+—_+—_+—_++— (б) Мы можем утверждать, что -3 меньше x» или, эквивалентное утверждение, »x больше -3». Убедитесь, что вы видите, что -3 < x эквивалентно x > -3. Хотя оба способа верны, мы обычно записываем сначала переменную в простом линейном неравенстве, содержащем переменную и числовое значение. (c) Мы утверждаем, что «х меньше или равно -6». _-—od—_tH¥!_t—_t*—_+—_ +t + Есть много повседневных ситуаций с участием неизвестного значение и неравенство. Мы можем перевести эти ситуации в алгебраические утверждения. Это первый шаг в решении текстовых задач с использованием неравенств. ПРИМЕР 3 Переведите каждое английское выражение в алгебраическое выражение. (a) Прибывшая на место полиция сообщила, что автомобиль двигался со скоростью более 80 миль в час (используйте переменную s для скорости). (b) Владелец автотранспортной компании сказал, что полезная нагрузка грузовика никогда не должна превышать 4500 фунтов (используйте переменную p для полезной нагрузки). (a) Поскольку скорость должна быть больше 80, мы имеем s > 80. (b) Если полезная нагрузка грузовика никогда не может превышать 4500 фунтов, то полезная нагрузка всегда должна быть меньше или равна 4500 фунтов. Таким образом, мы пишем p <= 4500. Изучив этот раздел, вы сможете: 1. Решить неравенство. Решение неравенств Возможные значения, которые делают неравенство верным, называются его решениями . Таким образом, когда мы решим неравенство , мы найдем все значений, которые делают его верным. Сначала мы рассмотрим закономерность, возникающую при выполнении данной операции с обеих сторон неравенства. Пример 1 Оригинальное неравенство Новое неравенство (a) 3 <5 → Умножение обеих сторон на 2 → 6 <10 (b) -2 <-1 → Добавить -3 к обеим сторонам на 2 → стороны. → -5<-4 (c) 0>-4 → Поделить обе части на 2. → 0>-2 (d) 8 >4 → Вычтите 6 с обеих сторон. → 2>-2 Обратите внимание, что мы избегали умножения или деления на отрицательное число ! Теперь давайте посмотрим, что произойдет, если мы умножим или разделим на отрицательное число. Оригинальное неравенство Новое неравенство 3 <5 → Умножение на -2. → 6 ? -10 Какой правильный знак неравенства? Поскольку -6 находится справа от -10, мы знаем, что новое неравенство должно быть -6 > -10, если мы хотим, чтобы утверждение оставалось верным. Обратите внимание, как мы меняем направление неравенства с < (меньше) на > (больше). Таким образом, мы получили бы новое неравенство -6 > -10. Таким образом, 3<5 → Умножить на -2. → -6>-10 Знак <, с которого мы начали (3 < 5), меняется на > (-6 > -10). Аналогичное обращение имеет место в следующем примере. Пример 2 Оригинальное неравенство Новое неравенство (a) -2 <-1 → Умножение на -3. → 6>3 (b) 0>-4 → Поделите обе части на -2. → 0<2 (c) 8 >4 → Поделите обе части на -4. Обратите внимание, что мы выполняем арифметические действия с числами со знаком так же, как всегда. Но новое неравенство имеет обратный знак неравенства (по сравнению с исходным неравенством). Всякий раз, когда обе части неравенства умножаются или делятся на отрицательное число, направление неравенства меняется на противоположное. Порядок решения неравенств ПРИМЕР 3 Решите и начертите 3x + 7 >= 13. 3x +7-7>=13-7 Вычтите 7 с обеих сторон. 3x>= 6 Упрощение. (3x)/3>=6/3 Обе части разделить на 3. x>=2 Упростить. Обратите внимание, что направление неравенства не изменилось, так как мы разделили на положительное число. Графическое представление en ee ПРИМЕР 4 Решите и начертите 5-3x > 7. 5-5-3x>7-5 Вычтите 5 с обеих сторон. -3x>2 Упрощение. (-3x)/-3<2/-3 Разделите на -3 и измените неравенство, так как обе части делятся на минус 3. x< -2/3 Обратите внимание на направление неравенства. Графическое представление Ht Ht Как и уравнения, некоторые неравенства содержат круглые скобки и дроби. Начальные шаги для решения этих неравенств будут такими же, как и для решения уравнений со скобками и дробями. Когда переменная появляется в обеих частях неравенства, целесообразно собрать члены x в левой части символа неравенства. ПРИМЕР 5 Решить и построить график −(13x)/2<=x/2-15/8 (8)((-13x)/2)<=(8)(x/2)-(8 )(15/8) Умножить все члены на LCD = 8. Мы делаем , а не , меняем направление символа неравенства, поскольку мы умножаем на положительное число, 8. -52x <= 4x-5 Упростить. -52x-4x <= 4x-15-4x Добавьте -4x к обеим сторонам. -56x <= -15 Объедините одинаковые термины. (-56x)/56>= -15/-56 Поделите обе части на -56. Мы реверс направление неравенства, когда мы делим обе части на отрицательное число. x>=15/56 Графическое представление: 0 15 28 l Наиболее распространенная ошибка, которую учащиеся допускают при решении неравенств, заключается в том, что они забывают поменять направление символа неравенства на противоположное при умножении или делении на отрицательное число.
-4 -3 -2 -!1 0 ] 2
-7 -6 -5 -4 -3 -2 -1 0 л 2
Решать неравенства
 Чтобы решить неравенство, мы упрощаем его до такой степени, что можем ясно видеть возможные значения переменной. Мы решали уравнения путем сложения, вычитания, умножения и деления определенного значения в обеих частях уравнения. Здесь мы проделываем аналогичные операции с неравенствами, за одним важным исключением. Мы покажем несколько примеров, чтобы вы могли увидеть операции, которые мы можем выполнять с неравенствами так же, как и с уравнениями.
Чтобы решить неравенство, мы упрощаем его до такой степени, что можем ясно видеть возможные значения переменной. Мы решали уравнения путем сложения, вычитания, умножения и деления определенного значения в обеих частях уравнения. Здесь мы проделываем аналогичные операции с неравенствами, за одним важным исключением. Мы покажем несколько примеров, чтобы вы могли увидеть операции, которые мы можем выполнять с неравенствами так же, как и с уравнениями. Начнем с исходного, истинного неравенства. Мы хотим получить новое, тоже истинное неравенство.
Начнем с исходного, истинного неравенства. Мы хотим получить новое, тоже истинное неравенство.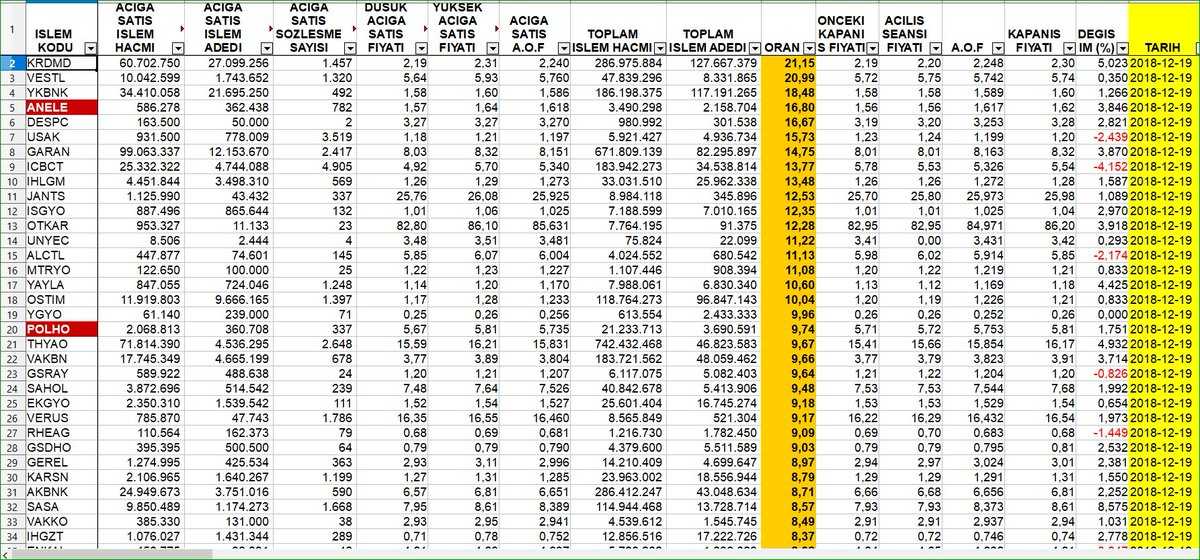 → -2<-1
→ -2<-1
| Вы можете использовать те же процедуры для решения неравенств, что и для решения уравнений, за исключением того, что направление неравенства меняется на противоположное, если вы умножаете или делите
обе части на отрицательное число.
—2 -Il 0 I 2 3 4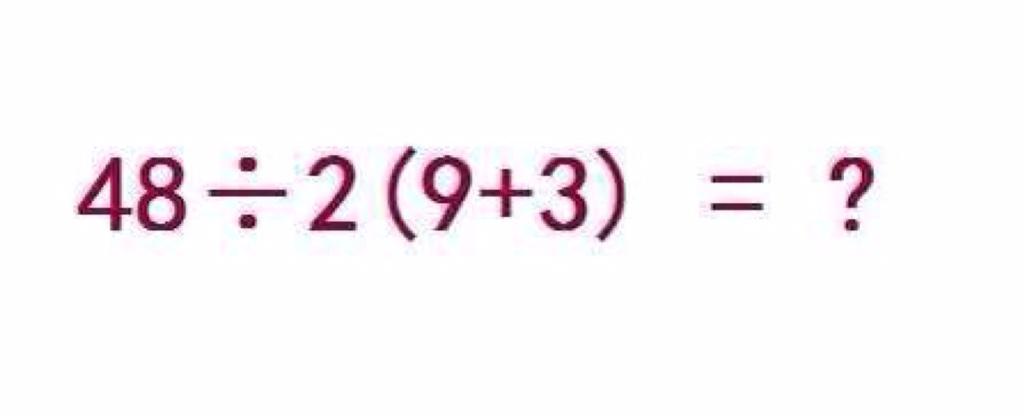
-1_2_1 0 l
3 3
56 56
. ] Эквивалентные дроби для 5/12
Калькулятор эквивалентных дробей
| Числитель: |
| Знаменатель: |
| Эквивалентные дроби для 12.05: |
Важно: 512 выглядит как дробь, но на самом деле это неправильная дробь. Существует бесконечное количество эквивалентных дробей до 512. Чтобы найти эквивалентную дробь до 512, или любой другой дроби, нужно просто умножить (или разделить, если дробь еще не уменьшена) оба числителя а знаменатель данной дроби на любое ненулевое натуральное число. Умножая исходную дробь на 2, получаем: 5 × 2 12 × 2 = 1024 Вот полный список дробей, эквивалентных 512. 512, 1024, 1536, 2048, 2560, 3072, 3584, 4096, 45108, 50120, 55132, 60144, 65156, 70168, 75180, 80192, 85204, Подробнее о том, как найти эквивалентные дроби для 5/12 или любой другой дроби , ниже на этой странице. Упрощенный список для копирования и вставки: 5/12, 24.10, 15/36, 20/48, 25/60, 30/72, 35/84, 40/96, 45/108, 50/120, 55/132, 60/144, 65/156, 70/168, 75/180, 80/192, 85/204, 90/216, 95/228, 100/240… |
Вот ответ на вопросы типа: 5/12 или Какие числа эквивалентны 5/12?
Этот калькулятор эквивалентных дробей шаг за шагом покажет вам эквивалентные дроби для любой введенной вами дроби.
См. ниже пошаговое решение, как найти эквивалентные дроби.
Как найти равные дроби?
Две дроби эквивалентны, если они обе равны при записи в наименьшем выражении. Дробь 1024 равна 512 при сокращении до наименьших членов. Чтобы найти равнозначные дроби, нужно просто умножить числитель и знаменатель той сокращенной дроби (512) на одно и то же натуральное число, т. е. умножить на 2, 3, 4, 5, 6…
Дробь 1024 равна 512 при сокращении до наименьших членов. Чтобы найти равнозначные дроби, нужно просто умножить числитель и знаменатель той сокращенной дроби (512) на одно и то же натуральное число, т. е. умножить на 2, 3, 4, 5, 6…
Важно: 512 выглядит как дробь, но на самом деле это неправильная дробь.
- 1024 эквивалентен 512, потому что 5 × 212 × 2 = 1024
- 1536 эквивалентен 512, потому что 5 × 312 × 3 = 1536
- 2048 — Equivent, Equivent, Equivent, 512, 512, 512, 512, 512, 512, 512, 512, 512. = 2048
- 2560 эквивалентно 512, потому что 5 × 512 × 5 = 2560
- и так далее…
получить одно и то же значение, показывающее, что они эквивалентны. Если данная дробь не приводится к наименьшему члену, вы можете найти другие эквивалентные дроби, разделив числитель и знаменатель на одно и то же число.
Что такое эквивалентная дробь? Как узнать, равны ли две дроби?
Нахождение эквивалентных дробей может быть легким, если вы используете это правило:
Определение эквивалентных дробей: две дроби ab и cd эквивалентны, только если произведение (умножение) числителя (a) первой дроби и знаменателя (d ) другой дроби равно произведению знаменателя (b) первой дроби на числитель (c) другой дроби.
Другими словами, если вы перемножите (ab и cd) равенство останется, т. е. a.d = b.c. Итак, вот несколько примеров:
- 1024 эквивалентно 512, потому что 10 × 12 = 24 × 5 = 120
- 1536 эквивалентно 512, потому что 15 × 12 4 1 1 3 0 9 0 1 8 0 9 0 = 36 8 5 = 2 880 90 эквивалентно 512, потому что 20 × 12 = 48 × 5 = 240
Таблица/таблица эквивалентных дробей
Эта таблица/таблица эквивалентных дробей содержит общепринятые практические дроби. Вы можете легко конвертировать дроби в десятичные, а также из долей дюймов в миллиметры.
| 1 / 64 | 1 / 32 | 1 / 16 | 1 / 8 | 1 / 4 | 1 / 2 | Десятичный | мм | |
|---|---|---|---|---|---|---|---|---|
| 1 / 64 | 0,015625 | 0,397 | ||||||
| 2 / 64 | 1 / 32 | 0,03125 | 0,794 | |||||
| 3 / 64 | 0,046875 | 1. 191 191 | ||||||
| 4 / 64 | 2 / 32 | 1 / 16 | 0,0625 | 1,588 | ||||
| 5 / 64 | 0,078125 | 1,984 | ||||||
| 6 / 64 | 3 / 32 | 0,09375 | 2,381 | |||||
| 7 / 64 | 0,109375 | 2,778 | ||||||
| 8 / 64 | 4 / 32 | 2 / 16 | 1 / 8 | 0,125 | 3,175 | |||
| 9 / 64 | 0,140625 | 3,572 | ||||||
| 10 / 64 | 5 / 32 | 0,15625 | 3,969 | |||||
| 11 / 64 | 0,171875 | 4,366 | ||||||
| 12 / 64 | 6 / 32 | 3 / 16 | 0,1875 | 4,763 | ||||
| 13 / 64 | 0,203125 | 5,159 | ||||||
| 14 / 64 | 7 / 32 | 0,21875 | 5,556 | |||||
| 15 / 64 | 0,234375 | 5,953 | ||||||
| 16 / 64 | 8 / 32 | 4 / 16 | 2 / 8 | 1 / 4 | 0,25 | 6,35 | ||
| 17 / 64 | 0,265625 | 6,747 | ||||||
| 18 / 64 | 9 / 32 | 0,28125 | 7.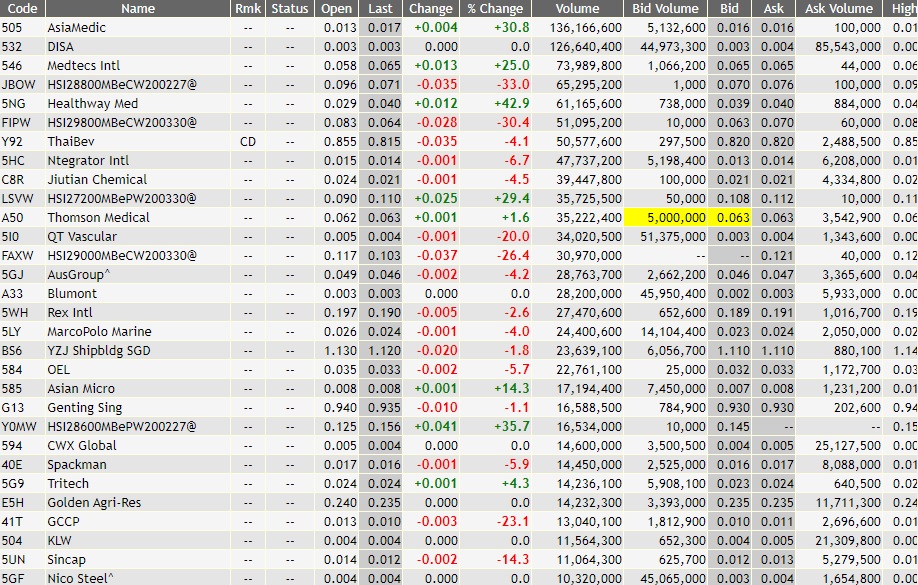 144 144 | |||||
| 19 / 64 | 0,296875 | 7,541 | ||||||
| 20 / 64 | 10 / 32 | 5 / 16 | 0,3125 | 7,938 | ||||
| 21 / 64 | 0,328125 | 8.334 | ||||||
| 22 / 64 | 11 / 32 | 0,34375 | 8.731 | |||||
| 23 / 64 | 0,359375 | 9.128 | ||||||
| 24 / 64 | 12 / 32 | 6 / 16 | 3 / 8 | 0,375 | 9,525 | |||
| 25 / 64 | 0,3 | 9,922 | ||||||
| 26 / 64 | 13 / 32 | 0,40625 | 10. 319 319 | |||||
| 27 / 64 | 0,421875 | 10,716 | ||||||
| 28 / 64 | 14 / 32 | 7 / 16 | 0,4375 | 11.113 | ||||
| 29 / 64 | 0,453125 | 11.509 | ||||||
| 30 / 64 | 15 / 32 | 0,46875 | 11.906 | |||||
| 31 / 64 | 0,484375 | 12.303 | ||||||
| 32 / 64 | 16 / 32 | 8 / 16 | 4 / 8 | 2 / 4 | 1 / 2 | 0,5 | 12,7 | |
| 33 / 64 | 0,515625 | 13. 097 097 | ||||||
| 34 / 64 | 17 / 32 | 0,53125 | 13.494 | |||||
| 35 / 64 | 0,546875 | 13.891 | ||||||
| 36 / 64 | 18 / 32 | 9 / 16 | 0,5625 | 14.288 | ||||
| 37 / 64 | 0,578125 | 14.684 | ||||||
| 38 / 64 | 19 / 32 | 0,59375 | 15.081 | |||||
| 39 / 64 | 0,609375 | 15.478 | ||||||
| 40 / 64 | 20 / 32 | 10 / 16 | 5 / 8 | 0,625 | 15. 875 875 | |||
| 41 / 64 | 0,640625 | 16.272 | ||||||
| 42 / 64 | 21 / 32 | 0,65625 | 16,669 | |||||
| 43 / 64 | 0,671875 | 17.066 | ||||||
| 44 / 64 | 22 / 32 | 11 / 16 | 0,6875 | 17.463 | ||||
| 45 / 64 | 0,703125 | 17.859 | ||||||
| 46 / 64 | 23 / 32 | 0,71875 | 18.256 | |||||
| 47 / 64 | 0,734375 | 18. 653 653 | ||||||
| 48 / 64 | 24 / 32 | 12 / 16 | 6 / 8 | 3 / 4 | 0,75 | 19.05 | ||
| 49 / 64 | 0,765625 | 19.447 | ||||||
| 50 / 64 | 25 / 32 | 0,78125 | 19.844 | |||||
| 51 / 64 | 0,796875 | 20.241 | ||||||
| 52 / 64 | 26 / 32 | 13 / 16 | 0,8125 | 20,638 | ||||
| 53 / 64 | 0,828125 | 21. 034 034 | ||||||
| 54 / 64 | 27 / 32 | 0,84375 | 21.431 | |||||
| 55 / 64 | 0,859375 | 21.828 | ||||||
| 56 / 64 | 28 / 32 | 14 / 16 | 7 / 8 | 0,875 | 22.225 | |||
| 57 / 64 | 0,8 | 22.622 | ||||||
| 58 / 64 | 29 / 32 | 0, | 23.019 | |||||
| 59 / 64 | 0, 5 | 23.416 | ||||||
| 60 / 64 | 30 / 32 | 15 / 16 | 0,9375 | 23. 813 813 | ||||
| 61 / 64 | 0,953125 | 24.209 | ||||||
| 62 / 64 | 31 / 32 | 0,96875 | 24.606 | |||||
| 63 / 64 | 0,984375 | 25.003 | ||||||
| 64 / 64 | 32 / 32 | 16 / 16 | 8 / 8 | 4 / 4 | 2 / 2 | 1 | 25,4 |
Ссылка:
- [1] Как найти эквивалентные дроби
эквивалентные фракции — образцы
- Эквивалентные фракции 21/95
- Эквивалентные фракции 13/24
- эквивалентные фракции 36/69
- эквивалентные фракции из 18/43 90868
- 908 0208 Equivent Fractions 908066068 Equivent 908
- 8
- 8.

- 7
- 7
- 7
- 7
- Эквивалентные дроби числа 28/43
- Эквивалентные дроби числа 30/60
- Эквивалентные дроби числа 27/79
- Эквивалентные дроби числа 30/47
- Эквивалентные дроби числа 29/21
- Equivalent fractions of 23/27
- Equivalent fractions of 30/62
- Equivalent fractions of 4/57
- Equivalent fractions of 44/48
- Equivalent fractions of 35/51
Disclaimer
While every прилагаются усилия для обеспечения точности информации, представленной на этом веб-сайте, ни этот веб-сайт, ни его авторы не несут ответственности за какие-либо ошибки или упущения. Поэтому содержимое этого сайта не подходит для любого использования, связанного с риском для здоровья, финансов или имущества.
Калькулятор эквивалентных дробей
Создано Wojciech Sas, PhD кандидатом
Отредактировано Bogna Szyk и Jack Bowater
Последнее обновление: 29 ноября 2021 г.
- Что такое эквивалентная дробь?
- Как найти эквивалентные дроби?
- Как пользоваться калькулятором эквивалентных дробей?
- Что такое эквивалентные дроби…
Калькулятор эквивалентных дробей — отличный инструмент, который поможет вам найти эквивалентные дроби для любой дроби по вашему желанию. Это подходящее место для обучения что такое эквивалентная дробь x , или как найти эквивалентные дроби . Хотите знать, равны ли две дроби? Вы также можете получить ответ на этот вопрос!
Что такое эквивалентная дробь?
Дробь представляет собой отношение двух чисел, числителя , A и знаменателя , B . Как вы уже знаете из калькулятора коэффициентов, коэффициент равен некоторому конкретному значению, x , где х = А / В .
Определение эквивалентной дроби говорит нам, что любые две дроби A / B и C / D эквивалентны, если они равны одному и тому же значению. Мы можем определить, эквивалентны ли две дроби, проверив одно из следующих условий:
Мы можем определить, эквивалентны ли две дроби, проверив одно из следующих условий:
-
A = CиB = D -
А * Г = В * С -
С = к * АиD = k * B, для любого числаk
Преобразование двух эквивалентных дробей в проценты даст нам точно такое же число.
Как найти равные дроби?
Для любой дроби существует бесконечно много эквивалентных дробей. Такие значения удобно представлять в виде отношения двух целых чисел. Вот как мы делим вещи в повседневной жизни, например, разрезаем пиццу на кусочки (и берем несколько штук).
В качестве примера проверим, как найти эквивалентные дроби 4 / 6 . Мы можем выполнить следующие шаги:
Убедитесь, что и числитель, и знаменатель являются целыми числами. Если нет, начните умножать оба числа на 10, пока не останется десятичных цифр.
 В нашем случае и 4, и 6 уже являются целыми числами.
В нашем случае и 4, и 6 уже являются целыми числами.Найдем дробь в простейшем виде. Для этого вычислите наибольший общий делитель числителя и знаменателя. Здесь GCF 4 и 6 равен 2, поэтому
4 / 6является эквивалентной дробью2 / 3, а последнее представляет собой простейшую форму этого соотношения. Поэтому2 / 3— наша база.Умножить основание на последовательные натуральные числа:
-
2·2 / 2·3 = 4 / 6 -
3·2 / 3·3 = 6 / 9 -
4·2 / 4·3 = 8 / 12 - и т.д…
- Все значения являются эквивалентными дробями
2 / 3, а также эквивалентны4 / 6, с которого мы начали.
Процедура проста, но что, если вы хотите найти 20 или 30 эквивалентных дробей? Ну, это занимает довольно много времени. Однако, если вы используете наш калькулятор эквивалентных дробей, мы можем избавить вас от всех этих хлопот.
Вы всегда можете преобразовать любую десятичную дробь в дробь, а затем вычислить из нее эквивалентные дроби.
Как пользоваться калькулятором эквивалентных дробей?
Вы можете выбрать один из двух разных режимов. Первый поможет вам найти столько дробей, которые эквивалентны вашему числу, сколько вы хотите. Ознакомьтесь с предыдущим разделом, чтобы узнать, как работают эти расчеты.
Второй вариант помогает определить, эквивалентны ли две дроби. Например, это 13 / 16 дробь, эквивалентная 3 / 4 ? Давайте проверим одно из условий, например. умножьте числитель и знаменатель из противоположных дробей:
-
13 * 4 = 52 -
16 * 3 = 48
Исходы разные, поэтому дроби 13 / 16 и 3 / 4 НЕ эквивалентны. Как насчет
Как насчет 12 / 16 и 3 / 4 ?
-
12 * 4 = 48 -
16 * 3 = 48
На этот раз оба числа совпадают, поэтому 12 / 16 эквивалентно 3 / 4 . Используя этот калькулятор эквивалентных дробей, вы также можете увидеть, как получить одну дробь из другой!
Что такое эквивалентные доли…
Вот список некоторых дробей и их эквивалентов:
Equivalent fractions of
1 / 1:2 / 2,3 / 3,4 / 4,5 / 5Эквивалентные дроби
1 / 2:2 / 4,3 / 6,4 / 8,0 5 53256 . 
Equivalent fractions of
1 / 3:2 / 6,3 / 9,4 / 12,5 / 15Equivalent fractions of
2 / 3:4 / 6,6 / 9,8 / 12,10 / 15эквивалентные фракции
1 / 4:2 / 8,3 / 12.123232323232323232323232323232323232323232323232323232328444132328423843884238423884413823844413884444138н.2324/ 16,5 / 20Equivalent fractions of
3 / 4:6 / 8,9 / 12,12 / 16,15 / 20Эквивалентные дроби
1 / 5:2 / 10,3 / 15,4 / 20,5 / 25Equivalent fractions of
2 / 5:4 / 10,6 / 15,8 / 20,10 / 25Equivalent fractions of
3 / 5:6 / 10,9 / 15,12 / 20,15 / 25Equivalent fractions of
4 / 5:8 / 10,12 / 15,16 / 20,20 / 25Equivalent fractions of
1 / 6:2 / 12,3 / 18,4 / 24,5 / 30Эквивалентные дроби
5 / 6:10 / 12,15 / 18,20 / 24,25 / 30Wojciech SAS, кандидат PhD
Выберите, что вы хотите увидеть
Фракция в
Числовере (n₁)
DENIMATATE0004
Сложение дробейСравнение дробейДесятичная дробь… Еще 14
Римлянам, ГЛАВА 12 | USCCB
ГЛАВА 12
Жертвоприношение тела и разума.
 1 * Итак умоляю вас, братия, милосердием Божиим принести тела ваши в жертву живую, святую и богоугодную, вашему духовному поклонению. и 2 Не сообразуйтесь с веком сим, но преобразуйтесь обновлением ума вашего, дабы вы могли познавать, что есть воля Божия, что есть добро, угождение и совершенство. б
1 * Итак умоляю вас, братия, милосердием Божиим принести тела ваши в жертву живую, святую и богоугодную, вашему духовному поклонению. и 2 Не сообразуйтесь с веком сим, но преобразуйтесь обновлением ума вашего, дабы вы могли познавать, что есть воля Божия, что есть добро, угождение и совершенство. б Множество деталей в одном корпусе. 3 c Ибо по данной мне благодати говорю каждому из вас не думать о себе больше, чем должно думать, но мыслить трезво, каждому по мере веры, какую определил Бог. 4 d Ибо, как в одном теле у нас много частей, и не все части имеют одну и ту же функцию, 5 так мы, хотя нас и много, составляем одно тело во Христе * , а по отдельности части друг друга. 6 e Поскольку у нас есть дары, которые различаются в зависимости от данной нам благодати, давайте использовать их: * если пророчество, пропорционально вере; 7если служение, в служении; если кто-то учитель, в обучении; 8если кто увещевает, в увещании; если кто-то вносит свой вклад, из щедрости; если один над другими, * с усердием; если кто делает дела милосердия, с радостью.

Взаимная любовь. 9Пусть любовь будет искренней; ненавидь зло, держись добра; ф 10любите друг друга взаимной любовью; предвосхищать друг друга в оказании чести. г 11 В усердии не ослабевайте, духом пламенейте, Господу служите. ч 12Радуйтесь в надежде, терпите в скорби, будьте настойчивы в молитве. и 13 Содействуйте нуждам святых, j проявляйте гостеприимство. 14 * Благословляйте тех, кто преследует [вас], k благословляйте, а не проклинайте их. л 15 Радуйтесь с радующимися, плачьте с плачущими. м 16 Уважайте друг друга одинаково; не превозносись, но общайся с униженными; не будь мудр в своих собственных оценках. н 17 Не воздавайте никому злом за зло; заботьтесь о том, что благородно в глазах всех. или 18Если возможно, живите со всеми в мире. р 19 Возлюбленный, не жди мести, но оставляй место для гнева; ибо написано: «Мне отмщение, Я воздам, говорит Господь».
 к 20 Скорее, «если враг твой голоден, накорми его; если он хочет пить, дайте ему что-нибудь попить; ибо, поступая так, ты соберешь ему на голову горящие угли». р 21 Не будь побежден злом, но побеждай зло добром.
к 20 Скорее, «если враг твой голоден, накорми его; если он хочет пить, дайте ему что-нибудь попить; ибо, поступая так, ты соберешь ему на голову горящие угли». р 21 Не будь побежден злом, но побеждай зло добром.* [12:1–13:14] Поскольку Христос отмечает прекращение действия Моисеева закона как основного источника руководства для народа Божьего (Рим. 10:4), апостол объясняет, как христиане могут действовать в свете дар оправдания через веру, в их отношении друг к другу и к государству.
* [12:1–8] Кодекс Моисея включал подробные указания о жертвоприношениях и других культовых обрядах. Однако Евангелие призывает верующих принести свои тела в жертву живую (Рим. 12:1). Вместо того, чтобы быть ограниченными конкретными юридическими максимами, христиане освобождаются для осуществления здравого суждения, когда они сталкиваются со многими и разнообразными решениями, необходимыми в ходе повседневной жизни. Чтобы помочь им, Бог раздает верующим различные дары, в том числе пророчества, учения и увещевания (Рим.
 12:6–8). Пророки помогают сообществу понять волю Божью применительно к нынешней ситуации (Рим. 12:6). Учителя помогают людям понять себя и свои обязанности по отношению к другим (Рим. 12:7). Тот, кто увещевает, ободряет общину проявлять свою веру в совершении всего, что угодно Богу (Рим. 12:8). Действительно, именно этот раздел, начиная с Рим. 12:1, является образцом собственного стиля увещевания Павла.
12:6–8). Пророки помогают сообществу понять волю Божью применительно к нынешней ситуации (Рим. 12:6). Учителя помогают людям понять себя и свои обязанности по отношению к другим (Рим. 12:7). Тот, кто увещевает, ободряет общину проявлять свою веру в совершении всего, что угодно Богу (Рим. 12:8). Действительно, именно этот раздел, начиная с Рим. 12:1, является образцом собственного стиля увещевания Павла.* [12:5] Одно тело во Христе: о церкви как теле Христовом см. 1 Кор. 12:12–27.
* [12:6] У каждого есть дар, который можно использовать на благо общества. Когда наставление об оправдании верой будет правильно понято, обладатель дара поймет, что это не орудие самовозвеличивания. Обладание даром не является показателем качества веры. Скорее, дар является вызовом для верного использования.
* [12:8] Над другими: обычно означает «власть над», но, возможно, «служить покровителем». Более состоятельных членов греко-римских общин часто просили помочь в проектах общественных услуг.
 Ввиду упоминаний о щедрости и милосердии Павел может иметь в виду таких людей, как Феба (Рим. 16:1–2), которую называют благодетельницей (или «покровительницей») из-за услуг, которые она оказала многие христиане, включая Павла.
Ввиду упоминаний о щедрости и милосердии Павел может иметь в виду таких людей, как Феба (Рим. 16:1–2), которую называют благодетельницей (или «покровительницей») из-за услуг, которые она оказала многие христиане, включая Павла.* [12:14–21] Поскольку Бог оправдал верующих, им нет необходимости брать правосудие в свои руки и мстить. В конце концов, Бог будет справедливо обращаться со всеми, включая тех, кто причиняет вред верующим. Этот вопрос о личных правах как о справедливости подготавливает почву для более подробного рассмотрения государства как арбитра.
а. [12:1] 2 Кор 1:3 / 6:13; 1 Пет 2:5.
б. [12:2] Эф 4:17, 22–23; 1 Пт 1:14 / Еф 5:10, 17; Фил 1:10.
в. [12:3] 15:15 / Фил. 2:3 / 1 Кор. 12:11; Еф 4:7.
д. [12:4–5] 1 Коринфянам 12:12, 27; Еф 4:25.
эл. [12:6–8] 1 Кор. 12:4–11, 28–31; Еф 4:7–12; 1 Пт 4:10–11 / 2 Кор 9:7.
ф. [12:9] 2 Кор. 6:6; 1 Тм 1:5; 1 Пт 1:22 / Ам 5:15.
г. [12:10] Ин 13:34; 1 Фесс. 4:9; 1 Пт 2:17; 2 Пт 1:7 / Флп 2:3.


 В таких случаях необходимо обратить на это внимание вашего педиатра или семейного врача, который, в случае необходимости, направит к соответствующему специалисту. Обязательно следите за дальнейшим ростом, весом, общим состоянием такого ребенка.
В таких случаях необходимо обратить на это внимание вашего педиатра или семейного врача, который, в случае необходимости, направит к соответствующему специалисту. Обязательно следите за дальнейшим ростом, весом, общим состоянием такого ребенка. Наиболее распространенные мнемоники для запоминания этого порядка операций:
Наиболее распространенные мнемоники для запоминания этого порядка операций:  Есть четыре курицы. Какую часть животных составляют куры? Выразите ответ дробью в простейшей форме.
Есть четыре курицы. Какую часть животных составляют куры? Выразите ответ дробью в простейшей форме. Какую часть составляют девочки?
Какую часть составляют девочки? Например:
Например:
 В нашем случае и 4, и 6 уже являются целыми числами.
В нашем случае и 4, и 6 уже являются целыми числами.

 1 * Итак умоляю вас, братия, милосердием Божиим принести тела ваши в жертву живую, святую и богоугодную, вашему духовному поклонению. и 2 Не сообразуйтесь с веком сим, но преобразуйтесь обновлением ума вашего, дабы вы могли познавать, что есть воля Божия, что есть добро, угождение и совершенство. б
1 * Итак умоляю вас, братия, милосердием Божиим принести тела ваши в жертву живую, святую и богоугодную, вашему духовному поклонению. и 2 Не сообразуйтесь с веком сим, но преобразуйтесь обновлением ума вашего, дабы вы могли познавать, что есть воля Божия, что есть добро, угождение и совершенство. б 
 к 20 Скорее, «если враг твой голоден, накорми его; если он хочет пить, дайте ему что-нибудь попить; ибо, поступая так, ты соберешь ему на голову горящие угли». р 21 Не будь побежден злом, но побеждай зло добром.
к 20 Скорее, «если враг твой голоден, накорми его; если он хочет пить, дайте ему что-нибудь попить; ибо, поступая так, ты соберешь ему на голову горящие угли». р 21 Не будь побежден злом, но побеждай зло добром. 12:6–8). Пророки помогают сообществу понять волю Божью применительно к нынешней ситуации (Рим. 12:6). Учителя помогают людям понять себя и свои обязанности по отношению к другим (Рим. 12:7). Тот, кто увещевает, ободряет общину проявлять свою веру в совершении всего, что угодно Богу (Рим. 12:8). Действительно, именно этот раздел, начиная с Рим. 12:1, является образцом собственного стиля увещевания Павла.
12:6–8). Пророки помогают сообществу понять волю Божью применительно к нынешней ситуации (Рим. 12:6). Учителя помогают людям понять себя и свои обязанности по отношению к другим (Рим. 12:7). Тот, кто увещевает, ободряет общину проявлять свою веру в совершении всего, что угодно Богу (Рим. 12:8). Действительно, именно этот раздел, начиная с Рим. 12:1, является образцом собственного стиля увещевания Павла. Ввиду упоминаний о щедрости и милосердии Павел может иметь в виду таких людей, как Феба (Рим. 16:1–2), которую называют благодетельницей (или «покровительницей») из-за услуг, которые она оказала многие христиане, включая Павла.
Ввиду упоминаний о щедрости и милосердии Павел может иметь в виду таких людей, как Феба (Рим. 16:1–2), которую называют благодетельницей (или «покровительницей») из-за услуг, которые она оказала многие христиане, включая Павла.