Номер №449 — ГДЗ по Математике 6 класс: Мерзляк А.Г.
войтирегистрация
- Ответкин
- Решебники
- 6 класс
- Математика
- Мерзляк
- Номер №449
НАЗАД К СОДЕРЖАНИЮ
2014г.ВыбранВыбрать ГДЗ (готовое домашние задание из решебника) на Номер №449 по учебнику Математика. 6 класс. Учебник для учащихся общеобразовательных организаций / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. Вентана-Граф. 2014г.
2019г.ВыбранВыбрать
ГДЗ (готовое домашние задание из решебника) на Номер №449 по учебнику Математика. 6 класс. Учебник / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир, под редакцией В.Е. Подольского. Вентана-Граф. 4 издание, дополненное.
2019г.
Условие 20142019г.
Cменить на 2014 г.
Cменить на 2019 г.
Найдите частное:
1) 6: 7/9 ;
2) 16: 4/11 ;
3) 13: 26/29 ;
4) 7/9:5 ;
5) 9/16:6 ;
6) 1 5/9:1 8/27 ;
7) 2 10/13:3 3/26 ;
8) 2 4/7:1 1/35.
Найдите частное:
1) 6: 7/9 ;
2) 16: 4/11 ;
3) 13: 26/29 ;
4) 7/9:5 ;
5) 9/16:6 ;
6) 1 5/9:1 8/27 ;
7) 2 10/13:3 3/26 ;
8) 2 4/7:1 1/35.
Решение 1
Решение 2
Решение 1
Решение 3
Решение 2
Решение 4
Решение 3
ГДЗ по Математике 6 класс: Виленкин Н.Я.
Издатель: Виленкин Н.Я. Жохов В.И. Чесноков А.С. Шварцбурд С.И. 2013/2019г.
ГДЗ по Математике 6 класс: Мерзляк А.
Г.
Издатель: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. 2014г. / 2019г.
ГДЗ по Математике 6 класс: Никольский С.М.
Издатель: С.М. Никольский, М.К, Потапов, Н.Н. Решетников, А.В. Шевкин. 2015-2018
ГДЗ по Математике 6 класс: Зубарева, Мордкович
Издатель: И.И. Зубарева, А.Г. Мордкович. 2014-2019г.
ГДЗ по Математике 6 класс: Дорофеев Г.В.
Издатель: Г.В. Дорофеев, И.Ф. Шарыгин, С.Б. Суворова. 2016-2019г.
Сообщить об ошибке
Выберите тип ошибки:
Решено неверно
Опечатка
Плохое качество картинки
Опишите подробнее
в каком месте ошибка
Ваше сообщение отправлено
и скоро будет рассмотрено
ОК, СПАСИБО
[email protected]
© OTVETKIN.INFO
Классы
Предметы
| 1 | Множитель | x^2-4 | |
| 2 | Множитель | 4x^2+20x+16 | |
| 3 | График | y=-x^2 | |
| 4 | Вычислить | 2+2 | |
| 5 | Множитель | x^2-25 | |
| 6 | Множитель | x^2+5x+6 | |
| 7 | Множитель | x^2-9 | |
| 8 | Множитель | x^3-8 | |
| 9 | Вычислить | квадратный корень из 12 | |
| 10 | Вычислить | квадратный корень из 20 | |
| 11 | Вычислить | квадратный корень из 50 | |
| 12 | Множитель | x^2-16 | |
| 13 | Вычислить | квадратный корень из 75 | |
| 14 | Множитель | x^2-1 | |
| 15 | Множитель | x^3+8 | |
| 16 | Вычислить | -2^2 | |
| 17 | Вычислить | квадратный корень из (-3)^4 | |
| 18 | Вычислить | квадратный корень из 45 | |
| 19 | Вычислить | квадратный корень из 32 | |
| 20 | Вычислить | квадратный корень из 18 | |
| 21 | Множитель | x^4-16 | |
| 22 | Вычислить | квадратный корень из 48 | |
| 23 | Вычислить | квадратный корень из 72 | |
| 24 | Вычислить | квадратный корень из (-2)^4 | |
| 25 | Множитель | x^3-27 | |
| 26 | Вычислить | -3^2 | |
| 27 | Множитель | x^4-1 | |
| 28 | Множитель | x^2+x-6 | |
| 29 | Множитель | x^3+27 | |
| 30 | Множитель | x^2-5x+6 | |
| 31 | Вычислить | квадратный корень из 24 | |
| 32 | Множитель | x^2-36 | |
| 33 | Множитель | x^2-4x+4 | |
| 34 | Вычислить | -4^2 | |
| 35 | Множитель | x^2-x-6 | |
| 36 | Множитель | x^4-81 | |
| 37 | Множитель | x^3-64 | |
| 38 | Вычислить | 4^3 | |
| 39 | Множитель | x^3-1 | |
| 40 | График | y=x^2 | |
| 41 | Вычислить | 2^3 | |
| 42 | Вычислить | (-12+ квадратный корень из -18)/60 | |
| 43 | Множитель | x^2-6x+9 | |
| 44 | Множитель | x^2-64 | |
| 45 | График | y=2x | |
| 46 | Множитель | x^3+64 | |
| 47 | Вычислить | (-8+ квадратный корень из -12)/40 | |
| 48 | Множитель | x^2-8x+16 | |
| 49 | Вычислить | 3^4 | |
| 50 | Вычислить | -5^2 | |
| 51 | Множитель | x^2-49 | |
| 52 | Вычислить | (-20+ квадратный корень из -75)/40 | |
| 53 | Множитель | x^2+6x+9 | |
| 54 | Множитель | 4x^2-25 | |
| 55 | Вычислить | квадратный корень из 28 | |
| 56 | Множитель | x^2-81 | |
| 57 | Вычислить | 2^5 | |
| 58 | Вычислить | -8^2 | |
| 59 | Вычислить | 2^4 | |
| 60 | Множитель | 4x^2-9 | |
| 61 | Вычислить | (-20+ квадратный корень из -50)/60 | |
| 62 | Вычислить | (-8+ квадратный корень из -20)/24 | |
| 63 | Множитель | x^2+4x+4 | |
| 64 | Множитель | x^2-10x+25 | |
| 65 | Вычислить | квадратный корень из -16 | |
| 66 | Множитель | x^2-2x+1 | |
| 67 | Вычислить | -7^2 | |
| 68 | График | f(x)=2^x | |
| 69 | Вычислить | 2^-2 | |
| 70 | Вычислить | квадратный корень из 27 | |
| 71 | Вычислить | квадратный корень из 80 | |
| 72 | Множитель | x^3+125 | |
| 73 | Вычислить | -9^2 | |
| 74 | Множитель | 2x^2-5x-3 | |
| 75 | Вычислить | квадратный корень из 40 | |
| 76 | Множитель | x^2+2x+1 | |
| 77 | Множитель | x^2+8x+16 | |
| 78 | График | y=3x | |
| 79 | Множитель | x^2+10x+25 | |
| 80 | Вычислить | 3^3 | |
| 81 | Вычислить | 5^-2 | |
| 82 | График | f(x)=x^2 | |
| 83 | Вычислить | квадратный корень из 54 | |
| 84 | Вычислить | (-12+ квадратный корень из -45)/24 | |
| 85 | Множитель | x^2+x-2 | |
| 86 | Вычислить | (-3)^3 | |
| 87 | Множитель | x^2-12x+36 | |
| 88 | Множитель | x^2+4 | |
| 89 | Вычислить | квадратный корень из (-8)^2 | |
| 90 | Множитель | x^2+7x+12 | |
| 91 | Вычислить | квадратный корень из -25 | |
| 92 | Множитель | x^2-x-20 | |
| 93 | Вычислить | 5^3 | |
| 94 | Множитель | x^2+8x+15 | |
| 95 | Множитель | x^2+7x+10 | |
| 96 | Множитель | 2x^2+5x-3 | |
| 97 | Вычислить квадратный корень | квадратный корень из 116 | |
| 98 | Множитель | x^2-x-12 | |
| 99 | Множитель | x^2-x-2 | |
| 100 | Вычислить | 2^2 |
Удивительные закономерности в квадратных числах (1, 4, 9, 16…) – BetterExplained
Небольшая загадка для вас — посмотрите на первые несколько квадратных чисел:
1, 4, 9, 16, 25, 36 , 49…
А теперь найдите разницу между последовательными квадратами:
1 к 4 = 3 от 4 до 9 = 5 от 9 до 16 = 7 от 16 до 25 = 9 от 25 до 36 = 11 …
А? Нечетные числа зажаты между квадратами?
Странно, но факт.
Потратьте некоторое время, чтобы выяснить, почему — еще лучше, найдите причину, которая подействовала бы на девятилетнего ребенка. Иди, я буду здесь.
Изучение закономерностей
Мы можем объяснить эту закономерность несколькими способами. Но цель состоит в том, чтобы найти убедительное объяснение, где мы ударяем себя по форхендам «а, вот почему!». Давайте перейдем к трем объяснениям, начиная с наиболее интуитивных, и посмотрим, как они помогут объяснить остальные.
Восторг геометра
Легко забыть, что квадратные числа, ну… квадратные! Попробуйте нарисовать их камешками
Ничего не заметили? Как перейти от одного квадратного числа к другому? Ну и вытаскиваем каждую сторону (правую и нижнюю) и заправляем уголок:
В то время как на 4 (2×2) мы можем перейти к 9 (3×3) с расширением: мы добавляем 2 (справа) + 2 (снизу) + 1 (угол) = 5. И да, 2 ×2 + 5 = 3×3. И когда мы на 3, мы переходим к следующему квадрату, вытягивая стороны и заполняя угол: Действительно, 3 × 3 + 3 + 3 + 1 = 16.
Каждый раз изменение на 2 больше, чем раньше, так как у нас есть еще одна сторона в каждом направлении (правая и нижняя).
Еще одно интересное свойство: переход к следующей клетке всегда нечетный, поскольку мы меняем на «2n + 1» (2n должно быть четным, поэтому 2n + 1 нечетное). Поскольку изменение нечетное, это означает, что квадраты должны циклически повторяться: четное, нечетное, четное, нечетное…
И подождите! Это имеет смысл, потому что сами целые числа циклически повторяют четное, нечетное, четно-нечетное… в конце концов, квадрат сохраняет «четность» корня числа (четное * четное = четное, нечетное * нечетное = нечетное).
Забавно, сколько понимания скрывается в простом узоре. (Я называю эту технику «геометрией», но, наверное, это неправильно — это просто визуализация чисел).
Прозрение алгебраиста
Рисовать квадраты камешками? Что это, древняя Греция? Нет, современный студент мог бы возразить:
- У нас есть два последовательных числа, n и (n+1)
- Их квадраты равны n 2 и (n+1) 2
- Разница равна (n+1) 2 – n 2 = (n 2 + 2n + 1) – n 2 = 2n + 1
Например, если n=2, то n 2 =4.
Таким образом, разница до следующего квадрата равна (2n + 1) = 5.
Действительно, мы нашли ту же самую геометрическую формулу. Но удовлетворяет ли алгебраическая манипуляция? Для меня это немного стерильно и не имеет того самого «ага!» хлопнуть по лбу. Но это другой инструмент, и когда мы комбинируем его с геометрией, понимание становится глубже. 92 получаем:
Близко, но не совсем! Где недостающий +1?
Давайте отступим. Исчисление исследует плавные, непрерывные изменения, а не «прыгающую» последовательность, которую мы взяли от 2 2 до 3 2 (как мы перескочили от 2 к 3, не посетив сначала 2,5 или 2,00001?).
Но не теряйте надежды. Исчисление имеет алгебраические корни, а +1 скрыто. Давайте стряхнем пыль с определения производной:
Забудьте пока о границах — сосредоточьтесь на том, что это значит (чувство, любовь, связь!). Производная говорит нам: «Сравни до и после и раздели на внесенное изменение». Если мы сравним «до и после» для f(x) = x^2 и назовем наше изменение «dx», мы получим:
Теперь мы кое-что получили.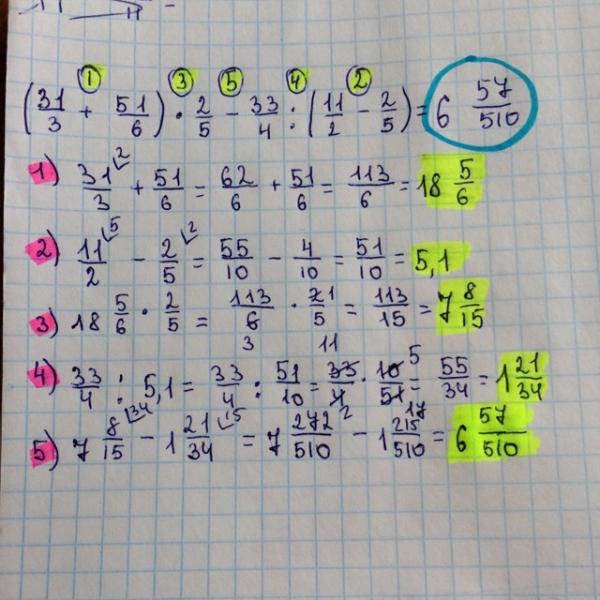
Производная глубокая, но сосредоточьтесь на общей картине — она говорит нам «отдачу от доллара», когда мы меняем нашу позицию с «x» на «x + dx». На каждую единицу «dx», которую мы идем, наш результат изменится на 2x + dx.
Например, если мы выбираем «dx» равным 1 (например, переходим от 3 к 4), производная говорит: «Хорошо, на каждую единицу, которую вы переходите, выход изменяется на 2x + dx (2x + 1, в данном случае ), где x — ваша первоначальная начальная позиция, а dx — общее количество перемещений». Давайте попробуем:
Переход от 3 2 к 4 2 будет означать:
- x = 3, dx = 1
- изменение на единицу ввода: 2x + dx = 6 + 1 = 7
- сумма сдачи: dx = 1
- ожидаемое изменение: 7 * 1 = 7
- фактическое изменение: 4 2 – 3 2 = 16 – 9 = 7
Мы предсказали сдачу 7, а получили сдачу 7 — сработало! И мы можем менять «dx» сколько угодно. Давайте перепрыгнем с 3 2 на 5 2 :
- х = 3, дх = 2
- изменение на единицу ввода: 2x + dx = 6 + 2 = 8
- количество изменений: dx = 2
- общее ожидаемое изменение: 8 * 2 = 16
- фактическое изменение: 5 2 – 3 2 = 25 – 9 = 16
Ого! Уравнение сработало (я тоже был удивлен).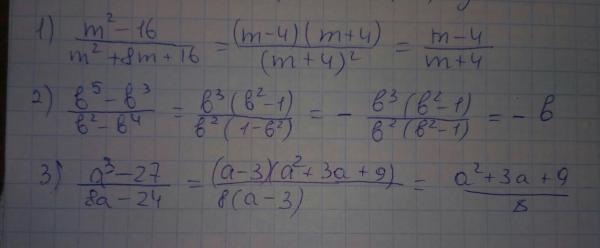
Мы можем не только перепрыгнуть через скучный «+1» с 3 2 на 4 2 , мы могли бы даже перейти с 3 2 на 10 2 , если бы захотели!
Конечно, мы мог бы вычислить это с помощью алгебры, но с нашей шляпой исчисления мы начали думать о произвольных количествах изменений, а не только +1. Мы взяли нашу скорость и масштабировали ее, точно так же, как расстояние = скорость * время (скорость 50 миль в час не означает, что вы можете путешествовать только в течение 1 часа, верно? Почему 2x + dx должны применяться только для одного интервала?).
Мой педантометр гудит, так что помните гигантское предостережение: исчисление касается микромасштаба. Производная «хочет», чтобы мы исследовали изменения, которые происходят через крошечные интервалы (мы перешли от 3 к 4, не посещая сначала 3,000000001!). Но не обижайтесь — нам пришла в голову идея исследовать произвольный интервал «dx», и, черт возьми, мы с ней справились. Мы сохраним крошечные приращения на другой день.
Извлеченные уроки
Изучение квадратов дало мне несколько идей:
- Казалось бы, простые шаблоны (1, 4, 9, 16…) можно исследовать с помощью нескольких инструментов, чтобы получить новое понимание для каждого. Я совершенно забыл, что идеи исчисления (от x к x + dx) могут помочь исследовать дискретные последовательности.
- Слишком легко помещать в песочницу математический инструмент, такой как геометрия, и думать, что он не может пролить свет на более высокие уровни (геометрические изображения действительно помогают алгебре, особенно +1, поп). Даже с исчислением мы привыкли сводить его к крошечным изменениям — почему бы не оставить dx большим? 909:50
- Аналогии работают на нескольких уровнях. Понятно, что квадраты и коэффициенты переплетены — начиная с одного сета, можно разобраться и в другом. Исчисление расширяет эту связь, позволяя нам переключаться между интегралом и производной.
Изучая новые техники, не забывайте применять их к урокам старых.