ГДЗ По Алгебре 9 Мордкович Задачник – Telegraph
>>> ПОДРОБНЕЕ ЖМИТЕ ЗДЕСЬ <<<
ГДЗ По Алгебре 9 Мордкович Задачник
ГДЗ : готовые ответы по алгебре Задачник за 9 класс, решебник Мордкович, Базовый уровень ФГОС, часть 2 онлайн решения на GDZ .RU . Очень часто даже отличники начинают путаться и сомневаться в правильности полученного ответа . Издание «Решебник по Алгебре 9 класс» . .
Решебник (ГДЗ ) по Алгебре за 9 (девятый ) класс Задачник авторы: Мордкович, Александрова, Мишустина издательство Мнемозина, 2019 год Авторы: Мордкович А .Г ., Александрова Л .А ., Мишустина Т .Н . Издательство: Мнемозина 2019 год . Тип: Задачник, Базовый уровень .
ГДЗ по алгебре 9 класс — задачник от Мордковича , Мишустиной, Тульчинской и Александровой . В году издательство «Мнемозина» в 12 раз выпустило известный учебник по алгебре для девятиклассников, написанного под редакцией Мордоковича А .Г . Учебное пособие состоит из . .
.
ГДЗ по алгебре за 9 класс Мордкович включает в себя 21 параграф . Далее следуют решения пяти контрольных работ с двумя вариантами ответов . ГДЗ к задачнику по алгебре 9 класс Мордкович, (углубленный уровень) можно посмотреть здесь .
Мордкович , Александрова . «Просвещение» . год . ГДЗ по алгебре 9 класс Мордкович , Александрова, Мишустина, Тульчинская ответы к 2 части задачника .
Краткая информация по решебнику: Алгебра 9 класс Мордкович , Мишустина, Тульчинская . В 9 классе у школьников наступает нелёгкая пора . В заключении хочется добавить, что теперь появилась достойная альтернатива списыванию — гдз по алгебре 9 класс Мордкович .
ГДЗ (ответы онлайн) к задачнику ФГОС по алгебре автора А .Г . Мордкович для учащихся 9 класса . Перед вами решения всех упражнений из задачника по алгебре за 9 класс по Мордковичу . Этот решебник по ФГОС поможет школьникам овладеть программой по алгебре . .
ГДЗ по алгебре 9 класс Мордкович , Мишустина, Тульчинская ч2 задачник 2000 г онлайн . Мордкович, Мишустина, Тульчинская .
Мордкович, Мишустина, Тульчинская .
Алгебра является серьезным предметом, который является обязательным экзаменом для всех учащихся . Каждый ученик должен ответственно отнестись к изучению математики, чтобы получить на экзамене высокий балл . В связи с тяжелыми школьными нагрузками, ученик не . .
В решебнике решены примеры и задания , даны ответы к задачнику по алгебре за 9 класс от авторов Мордкович А .Г, Александрова Л .А ГДЗ по алгебре адресованы родителям, которые смогут проверить правильность решения, а также ученикам для проверки выполнения . .
Спрос на ГДЗ по алгебре 9 класс Мордкович увеличивается в геометрической прогрессии . Это связано с важными функциями данного Внутри лучшего пособия . Решебник за девятый класс станет основой отличной успеваемости по алгебре . Причина этого кроется в его эффективном . .
Готовая домашняя работа по алгебре за 9 класс . «Алгебра . Задачник » . Мордкович А .Г . Издание года . Ответы к задачам . Решение контрольных и самостоятельных работ по алгебре за 9 класс к пособию «Алгебра .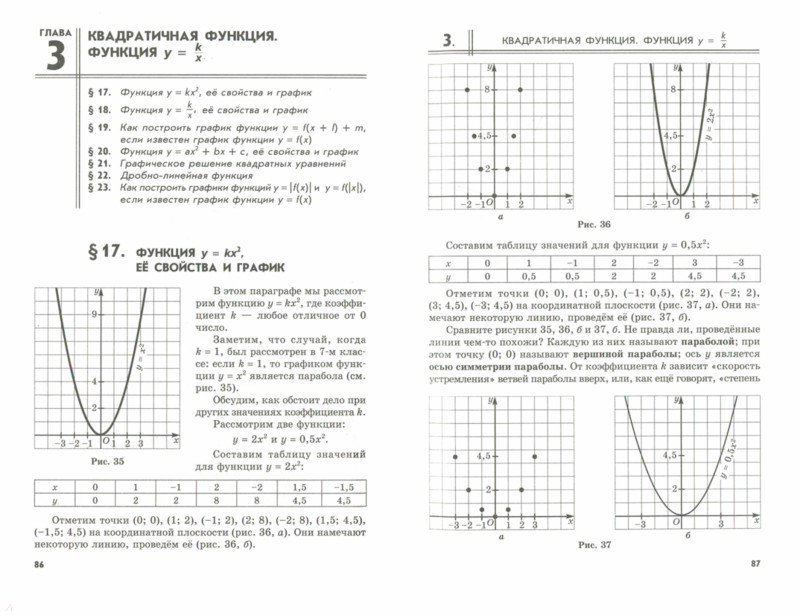 Дидактические материалы .
Дидактические материалы .
Посмотрите у нас гдз от Путина по алгебре 9 класс, у нас сможете списать с ответов к Заключительная часть решебника и сборника ГДЗ по математике 9 класса, который имеет, наверное, наиболее объемный и полный перечень задач, которые окажутся крайне полезными . .
ГДЗ :Алгебра . Автор:Мордкович А .Г . Класс:9 класс . Год издания: . Список решебников по алгебре за 9 класс .
Готовые Домашние Задания по Алгебре 9 класс . Мордкович Школьная программа по алгебре за 9 класс посвящена закреплению материала, пройденного за предыдущие годы . | У нас все ГДЗ . Заходи и Спиши!
ГДЗ : готовые ответы по алгебре Задачник за 9 класс, решебник Мордкович, Базовый уровень ФГОС, часть 2 онлайн решения на GDZ .RU . Очень часто даже отличники начинают путаться и сомневаться в правильности полученного ответа . Издание «Решебник по Алгебре 9 класс» . .
Решебник (ГДЗ ) по Алгебре за 9 (девятый ) класс Задачник авторы: Мордкович, Александрова, Мишустина издательство Мнемозина, 2019 год Авторы: Мордкович А . Г ., Александрова Л .А ., Мишустина Т .Н . Издательство: Мнемозина 2019 год . Тип: Задачник, Базовый уровень .
Г ., Александрова Л .А ., Мишустина Т .Н . Издательство: Мнемозина 2019 год . Тип: Задачник, Базовый уровень .
ГДЗ по алгебре 9 класс — задачник от Мордковича , Мишустиной, Тульчинской и Александровой . В году издательство «Мнемозина» в 12 раз выпустило известный учебник по алгебре для девятиклассников, написанного под редакцией Мордоковича А .Г . Учебное пособие состоит из . .
ГДЗ по алгебре за 9 класс Мордкович включает в себя 21 параграф . Далее следуют решения пяти контрольных работ с двумя вариантами ответов . ГДЗ к задачнику по алгебре 9 класс Мордкович, (углубленный уровень) можно посмотреть здесь .
Мордкович , Александрова . «Просвещение» . год . ГДЗ по алгебре 9 класс Мордкович , Александрова, Мишустина, Тульчинская ответы к 2 части задачника .
Краткая информация по решебнику: Алгебра 9 класс Мордкович , Мишустина, Тульчинская . В 9 классе у школьников наступает нелёгкая пора . В заключении хочется добавить, что теперь появилась достойная альтернатива списыванию — гдз по алгебре 9 класс Мордкович .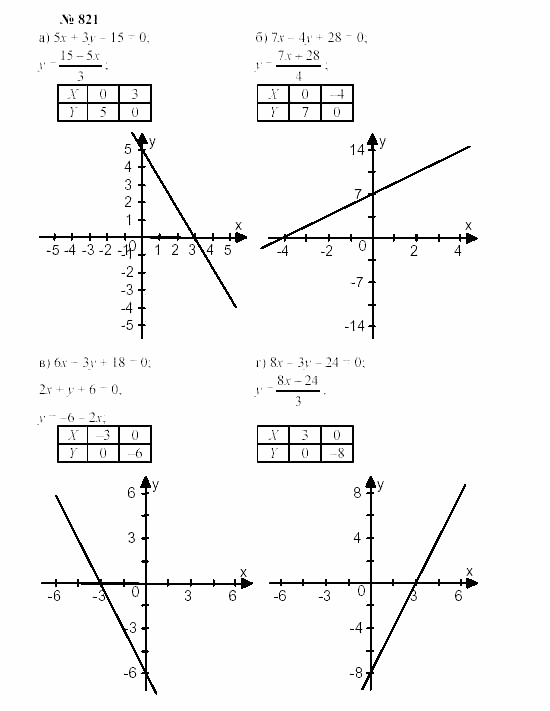
ГДЗ (ответы онлайн) к задачнику ФГОС по алгебре автора А .Г . Мордкович для учащихся 9 класса . Перед вами решения всех упражнений из задачника по алгебре за 9 класс по Мордковичу . Этот решебник по ФГОС поможет школьникам овладеть программой по алгебре . .
ГДЗ по алгебре 9 класс Мордкович , Мишустина, Тульчинская ч2 задачник 2000 г онлайн . Мордкович, Мишустина, Тульчинская .
Алгебра является серьезным предметом, который является обязательным экзаменом для всех учащихся . Каждый ученик должен ответственно отнестись к изучению математики, чтобы получить на экзамене высокий балл . В связи с тяжелыми школьными нагрузками, ученик не . .
В решебнике решены примеры и задания , даны ответы к задачнику по алгебре за 9 класс от авторов Мордкович А .Г, Александрова Л .А ГДЗ по алгебре адресованы родителям, которые смогут проверить правильность решения, а также ученикам для проверки выполнения . .
Спрос на ГДЗ по алгебре 9 класс Мордкович увеличивается в геометрической прогрессии . Это связано с важными функциями данного Внутри лучшего пособия . Решебник за девятый класс станет основой отличной успеваемости по алгебре . Причина этого кроется в его эффективном . .
Это связано с важными функциями данного Внутри лучшего пособия . Решебник за девятый класс станет основой отличной успеваемости по алгебре . Причина этого кроется в его эффективном . .
Готовая домашняя работа по алгебре за 9 класс . «Алгебра . Задачник » . Мордкович А .Г . Издание года . Ответы к задачам . Решение контрольных и самостоятельных работ по алгебре за 9 класс к пособию «Алгебра . Дидактические материалы .
Посмотрите у нас гдз от Путина по алгебре 9 класс, у нас сможете списать с ответов к Заключительная часть решебника и сборника ГДЗ по математике 9 класса, который имеет, наверное, наиболее объемный и полный перечень задач, которые окажутся крайне полезными . .
ГДЗ :Алгебра . Автор:Мордкович А .Г . Класс:9 класс . Год издания: . Список решебников по алгебре за 9 класс .
Готовые Домашние Задания по Алгебре 9 класс . Мордкович Школьная программа по алгебре за 9 класс посвящена закреплению материала, пройденного за предыдущие годы . | У нас все ГДЗ . Заходи и Спиши!
Заходи и Спиши!
Русский Язык 4 Решебник ГДЗ Канакина
ГДЗ По Английскому Языку Упражнение 3
ГДЗ Английский Язык Вербицкой Часть Первая
ГДЗ Алгебра 7 Углубленный Уровень
Математика 4 ГДЗ 2 Часть Автор
Истомина 2 Класс 1 Часть Решебник
ГДЗ По Немецкому Языку Седьмой Класс Бим
ГДЗ По Русскому Языку Гармония Четвертый Класс
ГДЗ По Литературе 6 Часть
ГДЗ По Математике Учебник Дорофеев Миракова
ГДЗ По Ино 9 Класс Вербицкая Учебник
ГДЗ По Русскому 8 Класс Бахрудинов
ГДЗ По Матем Муравин Муравина
Решебник По Математике Л П Стойлова
ГДЗ Английский Михеева Седьмой Класс
ГДЗ По Русскому Тетрадь Богданова 8
Решебник По Ан 6 Класс Английский Язык
ГДЗ По Английскому 5 Класс Юлия Евгеньевна
История 5 Класс Тетрадь Решебник
Решебник 4 Класс Русский Язык Иванов Кузнецова
ГДЗ По Математике Виноградовой 4 Класс
ГДЗ Русский Ладыженский 7
ГДЗ Алгебра 8 Класс Мордкович Николаев
ГДЗ Английский Язык 6 Класс Ваулин
ГДЗ 7 И 8 Класс
Решебник По Математике Виленкин Чесноков Шварцбурд
ГДЗ По Задачнику 7 9 Класс
Решебник 10 Класс Геометрия Погорелова
ГДЗ По Математике 6 Класс Дорофеев
ГДЗ По Географии 7 Класс Липкина Учебник
ГДЗ Русский Язык 8 Класс Номер 12
ГДЗ По Географии 11 Класс Кузнецов Учебник
ГДЗ Русский Язык Быстрова 2 Часть
ГДЗ По Английскому Языку Раунд Ап 3
ГДЗ Алгебра Алимов 10 11 Скачать
ГДЗ По Математике 9 Мерзляк Алгебра
Габриелян 10 Класс Базовый Уровень ГДЗ
ГДЗ Тетрадь Бененсон 2 Класс
ГДЗ По Окружающему Трофимов 3 Класс
Сонин 7 Класс Учебник ГДЗ
Решебник Дидактический Материал 10 Класс Алгебра
ГДЗ По Литературе Шестой Класс Курдюмова
ГДЗ По Матем 4 Класс Истомина Учебник
ГДЗ Истории России 6 Класс Симонова
ГДЗ 4 Класс Литература Рабочая Кубасова
ГДЗ Путина Географии 5 Класс
ГДЗ По Родному Русскому Языку 7 Класс
ГДЗ По Английскому Старлайт 7 Учебник
Решебники Для 3 Класса По Всем Предметам
ГДЗ По Родной Литературе
Решебник По Русскому 10 Класс
Гдз По Русскому Восьмого Класса
Русский Язык 8 Класс Бунеев Бунеева ГДЗ
ГДЗ По Математике 3 Класс Козлова
Гдз По Русскому Базовый Уровень
ГДЗ по алгебре 9 класс Учебник, Задачник А.
 Г. Мордкович, Н.П. Николаев, П.В. Семенов, Л.И. Звавич, А.Р. Рязановский, Л.А. Александрова Углубленный уровень
Г. Мордкович, Н.П. Николаев, П.В. Семенов, Л.И. Звавич, А.Р. Рязановский, Л.А. Александрова Углубленный уровень- 7
- 8
- 9
- 10
- 11
- ГДЗ
- 9 класс
- углубленное изучение Мордкович
Авторы: А.Г. Мордкович, Н.П. Николаев, П.В. Семенов, Л.И. Звавич, А.Р. Рязановский, Л.А. Александрова.
В средней школе ребенок уже освоился и научился самостоятельно справляться с возникающими трудностями, но в 9 классе нагрузка увеличивается. Особенно по предметам, которые являются обязательными для сдачи на основном государственном экзамене. Для подготовки лучше всего обращаться к ГДЗ по алгебре 9 класс Мордкович, Николаев, Семенов, поскольку он был составлен авторами, максимально тщательно подбиравшими материалы, которые в итоге вошли в сборник.
А именно развернутые ответы на вопросы для самопроверки к 28 параграфам, пошаговый разбор решения каждого задания, имеющегося на 429 страницах учебного пособия, дополнительная информация по темам, которая может понадобиться для выполнения. Решебник удобно разделен на номера каждого параграфа, а также часть с итоговым повторением. Используя его, девятиклассники легко смогут проработать свои слабые места, так как сразу увидят ошибку в решении и разберут непонятный момент. Это будет полезно и родителям, так как не придется нанимать репетитора или заниматься поиском специальных курсов. Школьники недолюбливают математику чаще всего из-за неправильного подхода учителя к процессу обучения и большого объема информации, которую он рассказывает за один урок. Домашние задания по алгебре вызывают не менее противоречивых чувств из-за их количества и трудности. Тем не менее, изучать ее необходимо для развития логического и аналитического мышления, поэтому важно постоянно заниматься и тренироваться в выполнении задач на все изученные темы.
Тяжелая наука древности
Алгебра – предмет требовательный. Тут банальной зубрёжкой не отделаться. И отсидеться на задней парте не удастся. Целесообразно овладеть необходимыми навыками, которые ученик получит только в том случае, если будет слушать педагога и выполнять проверочные задания. Чуть облегчить процесс познания можно с «ГДЗ по алгебре 9 класс Задачник Мордкович, Звавич Углубленный уровень».
При освоении этой дисциплины важно понять механизм решения той или иной задачи. Это возможно при внимательном прослушивании учителя. Изложим содержание и рассмотрим «подводные камни» образовательной деятельности. На этом этапе часть часов отдано повторению, но многое даётся впервые. Тут ребенка и поджидают трудности восприятия. Перечислим параграфы, к которым следует подойти особенно тщательно:
На этом этапе часть часов отдано повторению, но многое даётся впервые. Тут ребенка и поджидают трудности восприятия. Перечислим параграфы, к которым следует подойти особенно тщательно:
- элементы теории нескольких тригонометрических функций;
- расчет вероятностей;
- комбинаторика;
- различные степенные вариации графиков и их свойства;
- системы уравнений на движение и работу;
- квадратные интервалы и метод их нахождения.
Восполнить пробелы в знаниях и не попасть в список отстающих поможет «ГДЗ по алгебре 9 класс Задачник А.Г. Мордкович, Звавич Углубленный уровень».
Онлайн-решебник по алгебре за 9 класс от Мордковича придёт на выручку
Решебник не просто содержит результаты упражнения, также он даёт подробные пояснения по всем пунктам. Прочие преимущества обучения с данным помощником:
- доступ с любого устройства, имеющего выход в интернет;
- подготовки к контрольным работам и ОГЭ;
- самостоятельного изучения материала наперед;
- номера ответов полностью соответствуют вопросам в справочнике;
- освобождается существенное количество времени;
- проверки домашних заданий.

- положительные оценки;
- повышение лояльности со стороны преподавателя, видящего старания своего подопечного.
Залог хорошей успеваемости кроется в множестве факторов, но, бесспорно, одним из таковых является использование решебника в качестве дополнительного издания. Школьник станет более самостоятельным и уверенным в своих знаниях, перестанет с неохотой садиться за уроки, начнет более качественно и исполнительно относиться к учебе в целом. Родителям останется только радоваться успехам и больше не тратить время на выполнение домашних заданий за своих детей.
ГДЗ по алгебре 9 класс Мордкович А.Г., Николаев Л.П., Семенов П.В. используется в качестве дополнительного учебника, предоставляя множество полезной информации, за что регулярно получает положительные отзывы от пользователей.
- ГДЗ контрольным работам по алгебре за 7-9 классы Мордкович А.Г. (углубленный уровень)
- ГДЗ к самостоятельным работам по алгебре за 9 классы Александрова Л.

- ГДЗ к учебнику по алгебре за 9 класс Мордкович А.Г. (Просвещение)
- ГДЗ к задачнику по алгебре за 9 класс Мордкович А.Г. (базовый уровень)
- ГДЗ к контрольным работам по алгебре за 9 класс Александрова Л.А. (базовый уровень)
- ГДЗ к самостоятельным работам по алгебре за 9 класс Александрова Л.А (базовый уровень)
- ГДЗ к контрольным и самостоятельным работам по алгебре за 9 класс Попов М.
 А.
А.
Некоторые ребята теряются без контроля и поддержки со стороны учителя. Чтобы не растеряться при работе над домашними заданиями, можно обратится к полезному пособию — «ГДЗ по алгебре 9 класс Мордкович, Николаев Углубленный уровень (Мнемозина)». Ребята в этом учебном году делятся на два лагеря. Часть учащихся планирует покинуть в этом году стены родной школы. Они вступают во взрослую жизнь сразу, либо продолжают получать знания в техникумах и колледжах. Большая же часть нацелена на поступление в высшие учебные заведения, эти ребята остаются до одиннадцатого класса, чтобы сдать ЕГЭ. Но и тем, и другим предстоит ещё один серьезный экзамен, который проводится именно в этом году – ОГЭ. Математика является обязательной для сдачи как в 9, так и в 11 классе. Это дополнительные нервы и нагрузка. В эти моменты важно собраться и все свои усилия направить на подготовку.
Программа и подводные камни
Ряд сложных тем девятиклассника может напугать, особенно, если это углубленный уровень. С одной стороны, более подробное и дотошное прохождение материала скажется положительно на багаже знаний, с другой стороны, столь серьезная загруженность может привести к стрессам. Перечислим наиболее сложные темы:
С одной стороны, более подробное и дотошное прохождение материала скажется положительно на багаже знаний, с другой стороны, столь серьезная загруженность может привести к стрессам. Перечислим наиболее сложные темы:
- система из линейных и квадратных неравенств;
- методы алгебраического сложения;
- исследование функций на четность;
- характеристическое свойство арифметической прогрессии;
- комбинаторика и теория вероятностей;
- тригонометрические формулы, теории и элементы.
Расставить все по полочкам поможет «ГДЗ по алгебре 9 класс А.Г. Мордкович, Николаев Углубленный уровень (Мнемозина)».
Онлайн-решебник по алгебре за 9 класс от Мордковича — ключ к пониманию дисциплины
С алгеброй трудно разобраться без помощи извне. Очевидные плюсы при подготовке вместе с этим изданием:
- удобство онлайн-использования;
- возможность самопроверки на месте;
- комфортный поиск номеров верных ответов;
- подробные пояснения и объяснения условий;
- экономия времени;
- появление стрессоустойчивости.

С ГДЗ учебник становится ближе и понятнее для любознательного школьника. А папы и мамы начнут радоваться успехам детей, обретут спокойствие и уверенность за судьбу своего чада.
Системы линейных неравенств. Системы неравенств
Урок и презентация на тему: «Системы неравенств. Примеры решений»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Учебные пособия и тренажеры в интернет-магазине Интеграл для 9 класса
Интерактивный учебник для 9 класса «Правила и упражнения по геометрии»
Электронное учебное пособие «Понятная геометрия» для 7-9 классов
Система неравенств
Ребята, вы изучили линейные и квадратные неравенства, научились решать задачи по этим темам. Теперь перейдем к новому понятию в математике — системе неравенств. Система неравенств аналогична системе уравнений. Вы помните системы уравнений? Вы изучали системы уравнений в седьмом классе, попробуйте вспомнить, как вы их решали.
Вы помните системы уравнений? Вы изучали системы уравнений в седьмом классе, попробуйте вспомнить, как вы их решали.
Введем определение системы неравенств.
Несколько неравенств с некоторой переменной x образуют систему неравенств, если нужно найти все значения x, при которых каждое из неравенств образует правильное числовое выражение.
Любое значение x, которое делает каждое неравенство допустимым числовым выражением, является решением неравенства. Его также можно назвать частным решением.
Что такое конкретное решение? Например, в ответ мы получили выражение х > 7. Тогда х = 8, или х = 123, или какое-то другое число больше семи — это частное решение, а выражение х > 7 — общее решение… Общее решение состоит из многих частных решений.
Как мы объединили систему уравнений? Правильно, с фигурной скобкой, так и с неравенствами делают то же самое. Рассмотрим пример системы неравенств: $\begin(cases)x+7>5\x-3
Если система неравенств состоит из тех же выражений, например, $\begin(cases)x+7 > 5\x + 7
Так что же значит найти решение системы неравенств?
Решением неравенства называется множество частных решений неравенства, удовлетворяющих сразу обоим неравенствам системы.
Общий вид системы неравенств запишем в виде $\begin(cases)f(x)>0\g(x)>0\end(cases)$
общее решение неравенства f(x)>0.
$X_2$ — общее решение неравенства g(x)>0.
$X_1$ и $X_2$ — множество частных решений.
Решением системы неравенств будут числа, принадлежащие как $X_1$, так и $X_2$.
Вспомним операции над множествами. Как найти элементы множества, принадлежащие сразу обоим множествам? Правильно, для этого есть операция пересечения. Итак, решением нашего неравенства будет множество $A = X_1∩X_2$.
Примеры решения систем неравенств
Рассмотрим примеры решения систем неравенств.
Решите систему неравенств.
а) $\begin (случаи) 3x-1>2\5x-10 б) $\begin (случаи) 2x-4≤6 \ — x-4
Решение.
а) Решите каждое неравенство отдельно.
$ 3х-1>2; \; 3х > 3; \; х > 1 $.
$ 5x-10
Отметим наши интервалы на одной координатной линии.
Решением системы будет отрезок пересечения наших интервалов. Неравенство строгое, тогда отрезок будет открытым.
Неравенство строгое, тогда отрезок будет открытым.
Ответ: (1; 3).
Б) Также решаем каждое неравенство отдельно.
$ 2x-4≤6; 2x≤ 10; х ≤ 5 $.
$-x-4-5$.
Решением системы будет отрезок пересечения наших интервалов. Второе неравенство строгое, тогда отрезок будет открытым влево.
Ответ: (-5; 5].
Подытожим полученные знания.
Допустим, необходимо решить систему неравенств: $\begin(cases)f_1(x)>f_2(x)\g_1(x )> g_2(x)\end(случаи)$.
Тогда интервал ($ x_1; x_2 $) является решением первого неравенства.
Интервал ($y_1;y_2$) является решением второго неравенства.
Решением системы неравенств является пересечение решений каждого неравенства.
Системы неравенств могут состоять из неравенств не только первого порядка, но и любых других видов неравенств.
Важные правила решения систем неравенств.
Если одно из неравенств системы не имеет решений, то и вся система не имеет решений. 92 + 4x + 4 > 0 \ end (случаи) $.
Раствор.
а) Первое неравенство имеет решение x > 1.
Найдем дискриминант второго неравенства.
$Д=16-4*2*4=-16$. $ D Вспомните правило, когда одно из неравенств не имеет решений, то и вся система не имеет решений.
Ответ: Решений нет.
B) Первое неравенство имеет решение x > 1.
Второе неравенство больше нуля при всех x. Тогда решение системы совпадает с решением первого неравенства. 92 + 36
Неравенства и системы неравенств — одна из тем, изучаемых в средней школе по алгебре. По сложности он не самый сложный, так как имеет простые правила (о них чуть позже). Как правило, решение систем неравенств школьники усваивают достаточно легко. Это связано еще и с тем, что преподаватели просто «тренируют» своих учеников по этой теме. И не могут этого не делать, потому что она изучается в дальнейшем с использованием других математических величин, а также проверяется на ОГЭ и ЕГЭ. В школьных учебниках очень подробно раскрыта тема неравенств и систем неравенств, поэтому если вы собираетесь ее изучать, то лучше всего прибегнуть к ним. Данная статья является лишь пересказом большого материала, и могут быть некоторые пропуски.
Данная статья является лишь пересказом большого материала, и могут быть некоторые пропуски.
Понятие системы неравенств
Если обратиться к научному языку, то можно дать определение понятию «система неравенств». Именно такая математическая модель представлена несколькими неравенствами. От этой модели, конечно, требуется решение, и ее емкость будет общим ответом на все неравенства системы, предложенной в задаче (обычно в ней написано, например: «Решить систему неравенств 4 х + 1 > 2 и 30 — х > 6…»). Однако, прежде чем перейти к видам и способам растворения, нужно понять еще кое-что.
Системы неравенств и системы уравнений
В процессе изучения новой темы очень часто возникают недоразумения. С одной стороны все понятно и я бы скорее приступил к решению задач, но с другой стороны некоторые моменты остаются в «тени», они не очень хорошо осмыслены. Также некоторые элементы уже полученных знаний могут переплетаться с новыми. Ошибки часто возникают в результате этого наложения.
Поэтому, прежде чем приступить к разбору нашей темы, следует вспомнить отличия уравнений и неравенств, их системы. Для этого нужно еще раз уточнить, что это за математические понятия. Уравнение — это всегда равенство, и оно всегда чему-то равно (в математике это слово обозначается знаком «=»). Неравенство — это модель, в которой одна величина либо больше, либо меньше другой, либо содержит утверждение, что они не совпадают. Таким образом, в первом случае уместно говорить о равенстве, а во втором, как бы очевидно это ни звучало из самого названия, о неравенстве исходных данных. Системы уравнений и неравенств практически не отличаются друг от друга и методы их решения одинаковы. Разница лишь в том, что в первом используются равенства, а во втором — неравенства.
Виды неравенств
Неравенства бывают двух видов: числовые и с неизвестной переменной. Первый тип представляет собой предоставленные значения (числа), неравные друг другу, например, 8 > 10. Второй — неравенства, содержащие неизвестную переменную (обозначается любой буквой латинского алфавита, чаще всего X). Эту переменную нужно найти. В зависимости от того, сколько их, математическая модель различает неравенства с одной (составляют систему неравенств с одной переменной) или с несколькими переменными (составляют систему неравенств с несколькими переменными).
Эту переменную нужно найти. В зависимости от того, сколько их, математическая модель различает неравенства с одной (составляют систему неравенств с одной переменной) или с несколькими переменными (составляют систему неравенств с несколькими переменными).
Последние два вида по степени их построения и уровню сложности решения делятся на простые и сложные. Простые еще называют линейными неравенствами. Они, в свою очередь, делятся на строгие и нестрогие. Строгие специально «говорят», что одна величина обязательно должна быть либо меньше, либо больше, поэтому это неравенство в чистом виде. Можно привести несколько примеров: 8 х + 9 > 2, 100 — 3 х > 5 и т. д. К нестрогим относится и равенство. То есть одна величина может быть больше или равна другой величине (знак «≥») или меньше или равна другой величине (знак «≤»). Даже в линейных неравенствах переменная не стоит в корне, в квадрате, ни на что не делится, поэтому они и называются «простыми». Сложные переменные включают неизвестные переменные, для поиска которых требуется больше математических операций. Они часто встречаются в квадрате, кубе или под корнем, могут быть модульными, логарифмическими, дробными и т. д. Но так как наша задача разобраться в решении систем неравенств, то будем говорить о системе линейных неравенств. Однако перед этим следует сказать несколько слов об их свойствах.
Они часто встречаются в квадрате, кубе или под корнем, могут быть модульными, логарифмическими, дробными и т. д. Но так как наша задача разобраться в решении систем неравенств, то будем говорить о системе линейных неравенств. Однако перед этим следует сказать несколько слов об их свойствах.
Свойства неравенств
К свойствам неравенств относятся следующие положения: 2 ≥ т 1).

Теперь, изучив основные положения теории, связанные с неравенствами, мы можем перейти непосредственно к рассмотрению правил решения их систем.
Решение систем неравенств. Основная информация. Решения
Как было сказано выше, решением являются значения переменной, удовлетворяющие всем неравенствам заданной системы. Решение систем неравенств — это выполнение математических действий, которые в конечном итоге приводят к решению всей системы или доказывают, что она не имеет решений. В этом случае говорят, что переменная относится к пустому числовому набору (записывается так: переменная буква ∈ (знак «принадлежит») ø (знак «пустое множество»), например, x ∈ ø (читается так: «Переменная «x» принадлежит пустому множеству»). Существует несколько способов решения систем неравенств: графический, алгебраический, метод подстановки. Стоит отметить, что они относятся к тем математическим моделям, которые имеют несколько неизвестных переменных. В том случае, когда он только один, сработает метод разноса.
Существует несколько способов решения систем неравенств: графический, алгебраический, метод подстановки. Стоит отметить, что они относятся к тем математическим моделям, которые имеют несколько неизвестных переменных. В том случае, когда он только один, сработает метод разноса.
Графический способ
Позволяет решить систему неравенств с несколькими неизвестными (из двух и более). Благодаря этому методу система линейных неравенств решается довольно легко и быстро, поэтому он является наиболее распространенным методом. Это связано с тем, что построение графика уменьшает количество написания математических операций. Особенно приятно немного отвлечься от пера, взять в руки карандаш с линейкой и приступить к дальнейшим действиям с их помощью, когда работы проделано много и хочется немного разнообразия. Однако некоторым этот способ не нравится из-за того, что приходится отрываться от задачи и переключать мыслительную деятельность на рисование. Однако это очень мощный способ.
Для решения системы неравенств графическим методом необходимо все члены каждого неравенства перевести в их левую часть. Знаки поменяются местами, справа нужно написать ноль, затем каждое неравенство нужно написать отдельно. В результате из неравенств будут получены функции. После этого можно достать карандаш и линейку: теперь нужно нарисовать график каждой полученной функции. Весь набор чисел, который окажется в интервале их пересечения, и будет решением системы неравенств.
Знаки поменяются местами, справа нужно написать ноль, затем каждое неравенство нужно написать отдельно. В результате из неравенств будут получены функции. После этого можно достать карандаш и линейку: теперь нужно нарисовать график каждой полученной функции. Весь набор чисел, который окажется в интервале их пересечения, и будет решением системы неравенств.
Алгебраический способ
Позволяет решить систему неравенств с двумя неизвестными. Также неравенства должны иметь одинаковый знак неравенства (т. е. содержать либо только знак «больше», либо только знак «меньше» и т. д.). Несмотря на свои ограничения, этот способ также более сложен. Применяется в два этапа.
Первый включает в себя действия по избавлению от одной из неизвестных переменных. Сначала нужно ее выделить, затем проверить наличие цифр перед этой переменной. Если их нет (тогда переменная будет иметь вид одной буквы), то ничего не меняем, если есть (тип переменной будет например такой — 5у или 12у), то надо чтобы в каждом неравенстве число перед выбранной переменной было одинаковым. Для этого нужно каждый член неравенств умножить на общий множитель, например, если первое неравенство содержит 3у, а второе 5у, то нужно все члены первого неравенства умножить на 5, а второй на 3. Вы получаете 15y и 15y соответственно.
Для этого нужно каждый член неравенств умножить на общий множитель, например, если первое неравенство содержит 3у, а второе 5у, то нужно все члены первого неравенства умножить на 5, а второй на 3. Вы получаете 15y и 15y соответственно.
Второй этап решения. Необходимо левую часть каждого неравенства перенести в их правую часть с изменением знака каждого члена на противоположный, справа записать ноль. Дальше начинается самое интересное: избавление от выбранной переменной (по-другому это называется «редукция») при сложении неравенств. В результате получается неравенство с одной переменной, которое необходимо решить. После этого следует проделать то же самое, только с другой неизвестной переменной. Полученные результаты и будут решением системы.
Метод подстановки
Позволяет решить систему неравенств, когда можно ввести новую переменную. Обычно этим методом пользуются, когда неизвестную переменную в одном члене неравенства возводят в четвертую степень, а в другом возводят в квадрат. Таким образом, этот метод направлен на снижение степени неравенства в системе. Неравенство выборки x 4 — x 2 — 1 ≤ 0 таким образом решается следующим образом. Вводится новая переменная, например t. Пишут: «Пусть t = x 2», тогда модель переписывается в новом виде. В нашем случае получаем t 2 — t — 1 ≤0. Это неравенство нужно решить методом интервалов (о нем чуть позже), затем вернуться к переменной X, затем проделать то же самое с другим неравенством. Полученные ответы и будут решением системы.
Таким образом, этот метод направлен на снижение степени неравенства в системе. Неравенство выборки x 4 — x 2 — 1 ≤ 0 таким образом решается следующим образом. Вводится новая переменная, например t. Пишут: «Пусть t = x 2», тогда модель переписывается в новом виде. В нашем случае получаем t 2 — t — 1 ≤0. Это неравенство нужно решить методом интервалов (о нем чуть позже), затем вернуться к переменной X, затем проделать то же самое с другим неравенством. Полученные ответы и будут решением системы.
Метод интервалов
Это самый простой способ решения систем неравенств, и в то же время он универсальный и распространенный. Его используют в старших классах и даже старшей школе. Суть его заключается в том, что учащийся ищет промежутки неравенства на числовой прямой, которая начерчена в тетради (это не график, а просто обычная линия с цифрами). Там, где интервалы неравенств пересекаются, находится решение системы. Чтобы использовать метод интервала, вам необходимо выполнить следующие шаги:
- Все члены каждого неравенства переносятся в левую часть с изменением знака на противоположный (ноль пишется справа).

- Неравенства выписываются отдельно, определяется решение каждого из них.
- Найдите точки пересечения неравенств на числовой прямой. Все числа, расположенные на этих перекрестках, будут решением.
Какой способ использовать?
Очевидно, тот, который кажется самым простым и удобным, но бывают случаи, когда задачи требуют определенного метода. Чаще всего в них написано, что решать нужно либо по графику, либо интервальным методом. Алгебраический метод и подстановка используются крайне редко или не используются вовсе, так как они достаточно сложны и запутаны, к тому же они больше применяются для решения систем уравнений, а не неравенств, поэтому следует прибегать к рисованию графиков и интервалов. Они вносят наглядность, что не может не способствовать эффективному и быстрому выполнению математических операций.
Если что-то не получается
При изучении той или иной темы по алгебре, естественно, могут возникнуть проблемы с ее пониманием. И это нормально, потому что наш мозг устроен таким образом, что не способен схватывать сложный материал за один раз. Часто вам нужно перечитать абзац, воспользоваться помощью учителя или потренироваться в решении типовых задач. В нашем случае они выглядят, например, так: «Решить систему неравенств 3 х + 1 ≥ 0 и 2 х — 1 > 3». Таким образом, личная приверженность, помощь со стороны и практика помогают в понимании любой сложной темы.
И это нормально, потому что наш мозг устроен таким образом, что не способен схватывать сложный материал за один раз. Часто вам нужно перечитать абзац, воспользоваться помощью учителя или потренироваться в решении типовых задач. В нашем случае они выглядят, например, так: «Решить систему неравенств 3 х + 1 ≥ 0 и 2 х — 1 > 3». Таким образом, личная приверженность, помощь со стороны и практика помогают в понимании любой сложной темы.
Решебник?
И решебник тоже очень хорошо подходит, только не для списывания домашних заданий, а для самопомощи. В них можно найти системы неравенств с решением, посмотреть на них (как на шаблоны), попытаться понять, как именно автор решения справился с задачей, а затем попытаться сделать это в самостоятельном порядке.
выводы
Алгебра — один из самых сложных предметов в школе. Ну, что вы можете с этим поделать? С математикой всегда было так: кому-то дается легко, а кому-то трудно. Но в любом случае следует помнить, что общеобразовательная программа построена таким образом, что с ней справится любой школьник. Кроме того, надо иметь в виду огромное количество помощников. Некоторые из них были упомянуты выше.
Кроме того, надо иметь в виду огромное количество помощников. Некоторые из них были упомянуты выше.
В этом уроке мы начнем изучать системы неравенств. Сначала рассмотрим системы линейных неравенств. В начале урока рассмотрим, где и почему возникают системы неравенств. Далее мы изучим, что значит решить систему, и вспомним объединение и пересечение множеств. В конце решим конкретные примеры для систем линейных неравенств.
Тема : Диета Реальные неравенства и их системы
Урок: Основные понятия, решение систем линейных неравенств
До сих пор мы решали отдельные неравенства и применяли к ним метод интервалов, это может быть линейных неравенств6, а 900 и рациональный. Теперь перейдем к решению систем неравенств — сначала линейных систем … Рассмотрим пример, откуда возникает необходимость рассматривать системы неравенств.
Найти область определения функции
Найти область определения функции
Функция существует, когда существуют оба квадратных корня, т. е.
е.
Как решить такую систему? Необходимо найти все x, удовлетворяющие как первому, так и второму неравенству.
На оси быка отобразить множество решений первого и второго неравенств.
Интервал пересечения двух лучей и есть наше решение.
Этот метод изображения решения системы неравенств иногда называют методом крыши.
Решением системы является пересечение двух множеств.
Изобразим это графически. У нас есть множество A произвольной природы и множество B произвольной природы, которые пересекаются.
Определение: Пересечением двух множеств А и В является третье множество, состоящее из всех элементов, входящих как в А, так и в В.
Рассмотрим на конкретных примерах решения линейных систем неравенств, как найти пересечения множеств решений отдельных неравенств, входящих в систему.
Решите систему неравенств:
Ответ: (7; 10].
4. Решите систему
Откуда второе неравенство системы? Например, из неравенства
Обозначим графически решения каждого неравенства и найдем интервал их пересечения
Таким образом, если мы имеем систему, в которой одно из неравенств удовлетворяет любому значению x, то его можно исключить.
Ответ: система несовместима.
Мы рассмотрели типовые опорные задачи, к которым сводится решение любой линейной системы неравенств.
Рассмотрим следующую систему.
7.
Иногда линейная система задается двойным неравенством; рассмотреть этот случай.
8.
Мы рассмотрели системы линейных неравенств, поняли откуда они берутся, рассмотрели типовые системы, к которым относятся все линейные системы, и решили некоторые из них.
1. Мордкович А.Г. и др. Алгебра 9 класс: Учебник. Для общего образования. Учреждения. — 4-е изд. — М.: Мнемосина, 2002. — 192 с.: ил.
2. Мордкович А.Г. и др. Алгебра 9 класс: Задача для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемосина, 2002. — 143 с.: ил.
3. Макарычев Ю.В. Н. Алгебра. 9 класс: учеб. для учащихся общеобразовательных школ. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К.И. Нешков, И.Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемосина, 2008.
Г. Миндюк, К.И. Нешков, И.Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемосина, 2008.
4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. – М., 2011. – 287 с.
5. Мордкович А.Г. Алгебра. 9 класс. В 14 ч. Часть 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. – М.: 2010. – 224 с.: ил.
6. Алгебра. 9 класс. В 14 ч. Ч. 2. Сборник задач для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Эд. А. Г. Мордкович. — 12-е изд., испр. — М.: 2010. — 223 с.: ил.
1. Портал естественных наук ().
2. Электронный учебно-методический комплекс для подготовки 10-11 классов к вступительным экзаменам по информатике, математике, русскому языку ().
4. Образовательный центр «Технология обучения» ().
5. Раздел College.ru по математике ().
1. Мордкович А.Г. и др. Алгебра 9 класс: Задача для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. – М.: Мнемозина, 2002. – 143 с.: ил. № 53; 54; 56; 57.
Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. – М.: Мнемозина, 2002. – 143 с.: ил. № 53; 54; 56; 57.
В статье рассмотрим решение неравенства … Расскажем в доступной форме про как построить решение неравенства, с наглядными примерами!
Прежде чем рассматривать решение неравенств на примерах, давайте разберемся с основными понятиями.
Общие сведения о неравенствах
Неравенством называют выражение, в котором функции связаны знаками отношения >,. Неравенства бывают как числовые, так и буквенные.
Неравенства с двумя знаками связи называются двойными, с тремя — тройными и т. д. Например:
а (х) > b (х),
а (х) а (х) b (х),
а ( х) б (х).
а (х) Неравенства, содержащие знак > или или, не являются строгими.
Решение неравенства — любое значение изменения, при котором это неравенство верно.
« Решить неравенство » означает, что необходимо найти множество всех его решений. Существуют различные способов решения неравенств .



 А.
А.