ГДЗ (решебник) к учебнику Мерзляк А.Г. и др. Алгебра 9 класс (углубленное изучение) ФГОС ОНЛАЙН
Решебники (ГДЗ) для школьников
Домашняя работа по алгебре за 9 класс к учебнику авторов А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. «Алгебра 7 класс : учебник для учащихся общеобразовательных организаций (углубленное изучение)».
В пособии решены и в большинстве случаев подробно разобраны задачи и упражнения из учебника «Мерзляк А.Г. Алгебра : 9 класс : учебник для учащихся общеобразовательных организаций / А.Г. Мерапяк, В.М. Поляков. — М., 2018. — 368 с.».
Пособие адресовано родителям, которые смогут проконтролировать правильность решения, а в случае необходимости помочь детям в выполнении домашней работы по алгебре.
Учебник находится здесь: https://edu-lib.com/matematika-2/dlya-shkolnikov/merzlyak-algebra-uchebnik-dlya-9-klassa-uglublennoe-izuchenie
Оглавление
Глава 1.
Квадратичная функция
§ 1. Функция
§ 2. Возрастание и убывание функции. Наибольшее и наименьшее значения функции
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16§ 3. Чётные и нечётные функции
§ 4. Построение графиков функций у = kf(x), у = f(kx)
§ 5. Построение графиков функций у = f(x) + b и у = f(x + а)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16§ 6. Построение графиков функций у = f(|x|) и у = |f(x)|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16§ 7. Квадратичная функция, ее график и свойства
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25§ 8. Решение квадратных неравенств
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31§ 9. Решение неравенств методом интервалов
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47§ 10. Расположение нулей квадратичной функции относительно данной точки
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20Глава 2.
Уравнения с двумя переменными и их системы
§ 11. Уравнение с двумя переменными и его график
§ 12. Графические методы решения систем уравнений с двумя переменными
1 2 3 4 5 6 7 8 9 10 11 12§ 13. Решение систем уравнений с двумя переменными методом подстановки и методами сложения и умножения
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29§ 14. Метод замены переменных и другие способы решения систем уравнений с двумя переменными
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45Глава 3. Неравенства с двумя переменными и им системы. Доказательство неравенств
§ 15. Неравенства с двумя переменными
§ 16. Системы неравенств с двумя переменными
1 2 3 4 5 6 7 8 9 10 11 12 13§ 17. Основные методы доказательства неравенств
§ 18.
Неравенства между средними величинами. Неравенство Коши — Буняковского
Эффективные приемы доказательства неравенств
Глава 4. Элементы прикладной математики
§ 19. Математическое моделирование
§ 20. Процентные расчеты
§ 21. Абсолютная и относительная погрешности
Глава 5. Элементы комбинаторики и теории вероятностей
§ 22. Метод математической индукции
Различные схемы применения метода математической индукции
§ 23. Основные правила комбинаторики. Перестановки
§ 24. Размещения
§ 25. Сочетания
§ 26. Частота и вероятность случайного события
§ 27. Классическое определение вероятности
§ 28. Вычисление вероятностей с помощью правил комбинаторики
Глава 6.
Числовые последовательности
§ 29. Числовые последовательности
О кроликах, подсолнухах, сосновых шишках и золотом сечении
§ 30. Арифметическая прогрессия
§ 31. Сумма н первых членов арифметической прогрессии
§ 32. Геометрическая прогрессия
§ 33. Сумма n первых членов геометрической прогрессии
§ 34. Представление о пределе последовательности. Сумма бесконечной геометрической прогрессии, у которой модуль знаменателя меньше единицы
§ 35. Суммирование
ГДЗ по алгебре 9 класс Мерзляк, Полонский, Якир
ГДЗ по алгебре 9 класс Мерзляк, Полонский, Якиргдз-дома.
ру
- Класс: ГДЗ 9 класс
- Автор:А.Г. Мерзляк, В.Б. Полонский, М.С. Якир.
- Описание: Высокий уровень знаний по математике дает школьный учебник Алгебра за 9 класс. С его помощью будущие выпускники школы освоят весь набор тем, предусмотренный стандартом образования по алгебре. Структура учебника авторов Мерзляк, Полонский подразумевает сначала изучение теоретической базы, разбор примеров и индивидуальное решение упражнений. Проверить ответ к каждому из них помогут готовые домашние задания по алгебре для 9 класса. Решебник способствует качественному изучению школьного материала и помогает результативно готовиться к предстоящим выпускным экзаменам.
Номера
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394959697989910010110210310410510610710810911011111211311411511611711811912012112212312412512612712812913013113213313413513613713813914014114214314414514614714814915015115215315415515615715815916016116216316416516616716816917017117217317417517617717817918018118218318418518618718818919019119219319419519619719819920020120220320420520620720820921021121221321421521621721821922022122222322422522622722822923023123223323423523623723823924024124224324424524624724824925025125225325425525625725825926026126226326426526626726826927027127227327427527627727827928028128228328428528628728828929029129229329429529629729829930030130230330430530630730830931031131231331431531631731831932032132232332432532632732832933033133233333433533633733833934034134234334434534634734834935035135235335435535635735835936036136236336436536636736836937037137237337437537637737837938038138238338438538638738838939039139239339439539639739839940040140240340440540640740840941041141241341441541641741841942042142242342442542642742842943043143243343443543643743843944044144244344444544644744844945045145245345445545645745845946046146246346446546646746846947047147247347447547647747847948048148248348448548648748848949049149249349449549649749849950050150250350450550650750850951051151251351451551651751851952052152252352452552652752852953053153253353453553653753853954054154254354454554654754854955055155255355455555655755855956056156256356456556656756856957057157257357457557657757857958058158258358458558658758858959059159259359459559659759859960060160260360460560660760860961061161261361461561661761861962062162262362462562662762862963063163263363463563663763863964064164264364464564664764864965065165265365465565665765865966066166266366466566666766866967067167267367467567667767867968068168268368468568668768868969069169269369469569669769869970070170270370470570670770870971071171271371471571671771871972072172272372472572672772872973073173273373473573673773873974074174274374474574674774874975075175275375475575675775875976076176276376476576676776876977077177277377477577677777877978078178278378478578678778878979079179279379479579679779879980080180280380480580680780880981081181281381481581681781881982082182282382482582682782882983083183283383483583683783883984084184284384484584684784884985085185285385485585685785885986086186286386486586686786886987087187287387487587687787887988088188288388488588688788888989089189289389489589689789889990090190290390490590690790890991091191291391491591691791891992092192292392492592692792892993093193293393493593693793893994094194294394494594694794894995095195295395495595695795895996096196296396496596696796896997097197297397497597697797897998098198298398498598698798898999099199299399499599699799899910001001100210031004100510061007100810091010101110121013101410151016101710181019102010211022102310241025102610271028102910301031103210331034103510361037103810391040104110421043
Работа и время — Алгебра среднего уровня
Глава 9.
Радикалы Если Фелиции нужно 4 часа, чтобы покрасить комнату, а ее дочери Кэти — 12 часов, чтобы покрасить ту же комнату, то, работая вместе, они могли бы покрасить комнату за 3 часа. Уравнение, используемое для решения задач этого типа, является одним из обратных уравнений. Выводится следующим образом:
[латекс]\текст{скорость}\раз\текст{время}=\текст{выполненная работа}[/латекс]
Для этой задачи:
[латекс]\begin{array}{rrrl} \text{Скорость Фелиции: }&F_{\text{скорость}}\times 4 \text{h}&=&1\text{room} \\ \\ \text{ Скорость Кэти: }&K_{\text{rate}}\times 12 \text{h}&=&1\text{room} \\ \\ \text{Изолирование их ставок: }&F&=&\dfrac{1}{ 4}\text{h и }K = \dfrac{1}{12}\text{h} \end{массив}[/latex]
Чтобы превратить это уравнение в решаемое уравнение, найдите общее время [латекс](Т)[/латекс], необходимое Фелиции и Кэти, чтобы покрасить комнату. На этот раз это сумма ставок Фелиции и Кати, или:
[латекс]\begin{array}{rcrl} \text{Общее время: } &T \left(\dfrac{1}{4}\text{h}+\dfrac{1}{12}\text{h} \right)&=&1\text{ room} \\ \\ \text{Это также можно записать как: }&\dfrac{1}{4}\text{ h}+\dfrac{1}{12}\ text{ h}&=&\dfrac{1 \text{ room}}{T} \\ \\ \text{Решение этого дает:}&0.
25+0.083&=&\dfrac{1 \text{room}} {T} \\ \\ &0,333&=&\dfrac{1 \text{room}}{T} \\ \\ &t&=&\dfrac{1}{0,333}\text{ или }\dfrac{3\ текст{ч}}{\текст{комната}} \end{массив}[/латекс]
Карл может убрать комнату за 3 часа. Если его младшая сестра Кира поможет, они смогут убрать его за 2,4 часа. Сколько времени Кире понадобится, чтобы сделать эту работу в одиночку?
Уравнение для решения:
[латекс]\begin{array}{rrrrl} \dfrac{1}{3}\text{ h}&+&\dfrac{1}{K}&=&\dfrac {1}{2.4}\text{h} \\ \\ &&\dfrac{1}{K}&=&\dfrac{1}{2.4}\text{h}-\dfrac{1}{3}\ text{h}\\ \\ &&\dfrac{1}{K}&=&0.0833\text{ или }K=12\text{h} \end{массив}[/latex]
Дугу требуется в два раза больше времени, чем Бекки, чтобы закончить проект. Вместе они могут завершить проект за 10 часов. Сколько времени потребуется каждому из них, чтобы завершить проект в одиночку?
Уравнение, которое необходимо решить:
[латекс]\begin{array}{rrl} \dfrac{1}{R}+\dfrac{1}{2R}&=&\dfrac{1}{10}\ text{ h,} \\ \text{где ставка Дага (} \dfrac{1}{D}\text{)}& =& \dfrac{1}{2}\times \text{ Бекки (}\dfrac{ 1}{R}\text{) скорость.
} \\ \\ \text{Суммируйте скорости: }\dfrac{1}{R}+\dfrac{1}{2R}&=&\dfrac{2}{ 2R} + \dfrac{1}{2R} = \dfrac{3}{2R} \\ \\ \text{Найти R: }\dfrac{3}{2R}&=&\dfrac{1}{10 }\text{ h} \\ \text{что означает }\dfrac{1}{R}&=&\dfrac{1}{10}\times\dfrac{2}{3}\text{h} \\ \text{so }\dfrac{1}{R}& =& \dfrac{2}{30} \\ \text{ или }R &= &\dfrac{30}{2} \end{array}[/ латекс]
Поскольку Дугу требуется в два раза больше времени, чем Бекки, время Дуга составляет [latex]30\text{ ч}[/latex].
Джоуи может построить большой сарай на 10 дней меньше, чем Космо. Если бы они построили его вместе, это заняло бы у них 12 дней. Сколько времени потребуется каждому из них, работающему в одиночку?
[латекс]\begin{array}{rl} \text{Решаемое уравнение:}& \dfrac{1}{(C-10)}+\dfrac{1}{C}=\dfrac{1} {12}, \text{ где }J=C-10 \\ \\ \text{Умножьте каждый член на ЖК-дисплей:}&(C-10)(C)(12) \\ \\ \text{Это оставляет }&12C+12(C-10)=C(C-10) \\ \\ \text{Умножая это:}&12C+12C-120=C^2-10C \\ \\ \text{Что упрощает до} &C^2-34C+120=0 \\ \\ \text{Который будет учитывать}& (C-30)(C-4) = 0 \end{массив}[/latex]
Космо может построить большой сарай за 30 или 4 дня.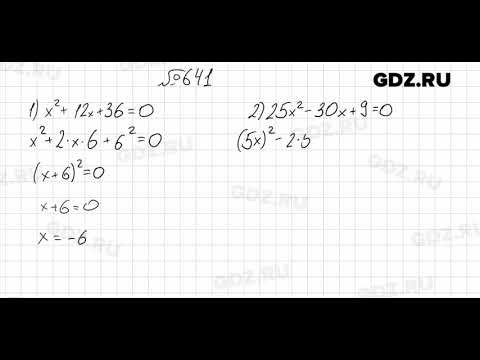
2-17A +6=0 \\ \\ \text{Это приведет к } & (5A-2)(A-3)=0 \end{массив}[/latex]
Ученик может выполнить работу либо за [latex]\dfrac{2}{5}[/latex] ч (отказ), либо за 3 ч. Кларк занимает 2 часа.
Раковину можно наполнить через трубу за 5 минут, но чтобы осушить полную раковину, нужно 7 минут. Если и труба, и слив открыты, сколько времени потребуется, чтобы наполнить раковину?
7 минут на слив будут вычтены.
[латекс]\begin{array}{rl} \text{Уравнение для решения} & \dfrac{1}{5}-\dfrac{1}{7}=\dfrac{1}{X} \ \ \\ \begin{array}{r} \text{Чтобы удалить дроби} \\ \text{умножьте каждый член на ЖК-дисплей}\end{array} & (5)(7)(X)\\ \ \ \text{Выходит} & (7)(X)-(5)(X)=(5)(7)\\ \\ \text{Умножение дает} & 7X-5X=35\\ \\ \text{Что упрощает до} & 2X=35\text{ или }X=\dfrac{35}{2}\text{ или }17,5 \end{array}[/latex]
17,5 мин или 17 мин 30 сек — решение
Для вопросов с 1 по 8 напишите формулу, определяющую отношение. Не решить!!
- Отец Билла может покрасить комнату на 2 часа меньше, чем потребовалось бы Биллу, чтобы покрасить ее.
Работая вместе, они могут выполнить работу за 2 часа 24 минуты. Сколько времени потребовалось бы каждому для работы в одиночку? - Из двух подводящих труб меньшей трубе требуется на четыре часа больше времени, чем большей, чтобы наполнить бассейн. Когда обе трубы открыты, бассейн наполняется за три часа сорок пять минут. Если открыта только большая труба, сколько часов потребуется, чтобы наполнить бассейн?
- Джек может помыть и отполировать семейную машину на час меньше, чем Боб. Двое работающих вместе могут выполнить работу за 1,2 часа. Сколько времени потребовалось бы каждому, если бы они работали в одиночку?
- Если Юсеф может выполнить часть работы в одиночку за 6 дней, а Бриджит может сделать это в одиночку за 4 дня, сколько времени потребуется им двоим, чтобы выполнить работу, работая вместе?
- Работая в одиночку, Джон работает на 8 часов дольше, чем Карлос. Работая вместе, они могут выполнить работу за 3 часа. Сколько времени потребуется каждому, чтобы выполнить работу в одиночку?
- Работая в одиночку, Марьям может выполнить часть работы за 3 дня, которую Нур может сделать за 4 дня, а Элана — за 5 дней. Сколько времени им потребуется, чтобы сделать это, работая вместе?
- Радж может выполнить работу за 4 дня, а Руби — за половину времени. Сколько времени им потребуется, чтобы выполнить работу вместе?
- Цистерну можно наполнить по одной трубе за 20 минут, по другой за 30 минут. За какое время обе трубы вместе наполнят бак?
Работая вместе, они могут выполнить работу за 2 часа 24 минуты. Сколько времени потребовалось бы каждому для работы в одиночку?Для вопросов 9до 20, найдите и решите уравнение, описывающее взаимосвязь.
- Если ученик может выполнить часть работы за 24 дня, а ученик и инструктор вместе могут сделать это за 6 дней, сколько времени потребуется инструктору, чтобы выполнить эту работу в одиночку?
- Плотник и его помощник могут выполнить часть работы за 3,75 дня. Если бы плотник сам мог выполнить работу один за 5 дней, то сколько времени потребовалось бы помощнику, чтобы выполнить эту работу в одиночку?
- Если Сэм может выполнить определенную работу за 3 дня, а Фреду потребуется 6 дней, чтобы выполнить ту же работу, сколько времени потребуется им, работая вместе, чтобы выполнить эту работу?
- Тим может закончить определенную работу за 10 часов. Его жене Джоанне требуется всего 8 часов, чтобы выполнить ту же работу. Если они будут работать вместе, сколько времени им потребуется, чтобы выполнить работу?
- Два человека, работающие вместе, могут выполнить работу за 6 часов. Если один из них работает в два раза быстрее другого, сколько времени потребуется более медленному человеку, работающему в одиночку, чтобы выполнить эту работу?
- Если два человека, работая вместе, могут выполнить работу за 3 часа, сколько времени потребуется более быстрому человеку, чтобы выполнить ту же работу, если один из них в 3 раза быстрее другого?
- Резервуар для воды можно наполнить через впускную трубу за 8 часов. Выходная труба опорожняет резервуар в два раза дольше. За какое время наполнится бак, если обе трубы будут открыты?
- Раковину можно наполнить из крана за 5 минут. Опорожнение раковины при открытом сливе занимает всего 3 минуты. Если раковина полная, а кран и слив открыты, сколько времени потребуется, чтобы опорожнить раковину?
- Наполнение бассейна с помощью впускной трубы занимает 10 часов.