Физика 9 класс упражнение 21: Упражнение 21 №1, Параграф 21

(iii) Радиус = 14 см

Площадь поверхности = 4×22/7×(14) ²

= 2464

Площадь поверхности 2464 см ²

Вопрос 2: Найдите площадь поверхности сферы диаметром:

(i) 14 см (ii) 21 см (iii) 3,5 см

Решение:

Площадь поверхности сферы = 4πr ²

Где r = радиус сферы

(i) Диаметр = 14 см

Итак, радиус = диаметр/2 = 14/2 см = 7 см

Площадь поверхности = 4×22/7×(7) ²

= 616

Площадь поверхности 616 см ²

(ii) Диаметр = 21 см

Итак, радиус = диаметр/2 = 21/2 см = 10,5 см

Площадь поверхности= 4×22/7×(10,5) ²

= 1386

Площадь поверхности 1386 см ²

(iii) Диаметр = 3,5 см

Итак, радиус = диаметр/2 = 3,5/2 см = 1,75 см

Площадь поверхности = 4×22/7×(1,75) ²

= 38,5

Площадь поверхности 38,5 см ²

Вопрос 3: Найдите общую площадь поверхности полусферы и сплошной полусферы радиусом 10 см каждая. (π=3,14)

Решение:

Радиус полусферы = Радиус сплошной полусферы = 10 см (Дано)

Площадь поверхности полушария = 2πr ²

= 2×3,14×(10) ² см ²

= 628 см ²

А, площадь поверхности твердого полушария = 3πr ²

= 3×3,14×(10) ² см ²

= 942 см ²

Вопрос 4: Площадь поверхности шара 5544 см ² , найдите его диаметр.

Решение:

Площадь поверхности сферы = 4πr ²

Итак, 4πr ² = 5544

4×22/7×(r) ² = 5544

г ² = (5544 × 7)/88

г ² = 441

или r = 21см

Теперь диаметр = 2 (радиус) = 2 (21) = 42 см

Вопрос 5: Полусферическая чаша из латуни имеет внутренний диаметр 10,5 см. Найти стоимость лужения его изнутри из расчета 4 рубля за 100 см ² .

Решение:

Внутренний диаметр полусферической чаши = 10,5 см

Итак, радиус = диаметр/2 = 10,5/2 см = 5,25 см

Теперь площадь поверхности полусферической чаши = 2πr ²

= 2 × 3,14 × (5,25) ²

= 173,25

Значит, площадь поверхности полусферической чаши 173,25 см

Узнать стоимость:

Стоимость лужения 100 см ² площадь = 4 рупии (данная)

Стоимость лужения 173,25см ² площадь = рупий. 4×173,25100 = рупий. 6,93

Следовательно, стоимость лужения внутренней стороны полусферической чаши составляет рупий. 6.93.

Вопрос 6: Купол здания имеет форму полусферы. Его радиус составляет 63 дм. Найдите стоимость его покраски из расчета 500 руб. 2 на кв.м.

Решение:

Радиус полусферического купола = 63 дм или 6,3 м

Площадь внутренней поверхности купола = 2πr ²

=2×3,14×(6,3) ²

= 249,48

Итак, площадь внутренней поверхности купола 249,48 м ²

Теперь найдем стоимость:

Стоимость покраски 1 м ² = 2 рупии (данные)

Следовательно, стоимость покраски 249,48 м ² = руб.

Упражнение 21.2 Номер страницы: 21.19

Вопрос 1: Найдите объем сферы, радиус которой:

(i) 2 см (ii) 3,5 см (iii) 10,5 см.

Решение:

Объем сферы = 4/3πr ³ Кубические единицы

Где r = радиус сферы

(i) Радиус = 2 см

Объем = 4/3 × 22/7 × (2) ³

= 33,52

Объем = 33,52 см ³

(ii) Радиус = 3,5 см

Следовательно, объем = 4/3×22/7×(3,5) ³

= 179,666

Объем = 179,666 см ³

(iii) Радиус = 10,5 см

Объем = 4/3×22/7×(10,5) ³

= 4851

Объем = 4851 см ³

Вопрос 2: Найдите объем сферы, диаметр которой:

Решение:

Объем сферы = 4/3πr ³ Кубические единицы

Где r = радиус сферы

(i) диаметр =14 см

Итак, радиус = диаметр/2 = 14/2 = 7 см

Объем = 4/3×22/7×(7) ³

= 1437,33

Объем = 1437,33 см ³

(ii) диаметр = 3,5 дм

Итак, радиус = диаметр/2 = 3,5/2 = 1,75 дм

Объем = 4/3×22/7×(1,75) ³

= 22,46

Объем = 22,46 дм ³

(iii) диаметр = 2,1 м

Итак, радиус = диаметр/2 = 2,1/2 = 1,05 м

Объем = 4/3×22/7×(1,05) ³

= 4,851

Объем = 4,851 м ³

Вопрос 3: Полусферический резервуар имеет внутренний радиус 2,8 м. Найдите его вместимость в литрах.

Решение:

Радиус полусферического резервуара = 2,8 м

Емкость полусферического бака = 2/3 πr ³

=2/3×22/7×(2,8) ³ м ³

= 45,997 м ³

Следовательно, вместимость в литрах = 45997 литров

Вопрос 4: Чаша полусферической формы изготовлена ​​из стали толщиной 0,25 см. Внутренний радиус чаши 5 см. Найдите объем стали, израсходованной на изготовление чаши.

Решение:

Внутренний радиус полусферической чаши = 5 см

Внешний радиус полусферической чаши = 5 см + 0,25 см = 5,25 см

Используемый объем стали = Внешний объем – Внутренний объем

= 2/3×π×((5,25) ³ − (5) ³ )

= 2/3×22/7×((5,25) ³ − (5) ³ )

= 41,282

Объем используемой стали 41,282 см ³

Вопрос 5. Сколько пуль можно сделать из свинцового куба со стороной 22 см и диаметром каждой пули 2 см?

Решение:

Ребро куба = 22 см

Диаметр пули = 2 см

Итак, радиус пули (r) = 1 см

Объем куба = (сторона) ³ = (22) ³ см ³ = 10648 см ³

А,

Объем каждой пули, которая будет иметь сферическую форму = 4/3πr ³

= 4/3 × 22/7 × (1) ³ см ³

= 4/3 × 22/7 см ³

= 88/21 см ³

Количество пуль = (Объем куба) / (Объем пули)

= 10648/88/21

= 2541

Следовательно, можно сделать 2541 пулю.

Вопрос 6: У лавочника есть ладду радиусом 5 см. Сколько ладду радиусом 2,5 см можно сделать из одного и того же материала?

Решение:

Объем ладду радиусом 5 см (V1) = 4/3×22/7×(5) ³

= 11000/21 см ³

Кроме того, объем ладду с радиусом 2,5 см (V2) = 4/3πr ³

= 4/3×22/7×(2,5) ³ см ³

= 1375/21 см ³

Следовательно,

Количество ладду радиусом 2,5 см, которое можно изготовить = V1/V2 = 11000/1375 = 8

Вопрос 7: Шар из свинца диаметром 3 см расплавляют и переплавляют в три сферических шара. Если диаметры двух шаров равны 3/2 см и 2 см, найдите диаметр третьего шара.

Решение:

Объем свинцового шара радиусом 3/2 см = 4/3πr ³

= 4/3×π×(3/2) ³

Пусть диаметр первого шара (d1) = 3/2см

Радиус первого шара (r1) = 3/4 см

Диаметр второго шара (d2) = 2 см

Радиус второго шарика (r2) = 2/2 см = 1 см

Диаметр третьего шара (d3) = d

Радиус третьего шара (r3) = d/2 см

Сейчас,

Итак, диаметр третьего шарика 2,5см.

Вопрос 8: Шар радиусом 5 см погружен в воду, наполненную в цилиндре, и уровень воды поднялся на 5/3 см. Найдите радиус цилиндра.

Решение:

Радиус сферы = 5 см (Дано)

Пусть r будет радиусом цилиндра.

Мы знаем, объем шара = 4/3πr ³

Подставляя значения, получаем

= 4/3×π×(5) ³

Высота (h) подъема воды 5/3 см (Дано)

Объем подъема воды в цилиндре = πr ² ч

Следовательно, объем подъема воды в цилиндре = Объем шара

Итак, πr ² h = 4/3πr ³

π r ² × 5/3 = 4/3 × π × (5) ³

или г ² = 100

или r = 10

Следовательно, радиус цилиндра равен 10 см.

Вопрос 9: Если радиус сферы увеличить вдвое, каково отношение объема первой сферы к объему второй сферы?

Решение:

Пусть r — радиус первой сферы, тогда 2r — радиус второй сферы.

Сейчас,

Отношение объема первой сферы ко второй сфере 1:8.

Вопрос 10: Конус и полусфера имеют одинаковые основания и равные объемы. Найдите отношение их высот.

Решение:

Объем конуса = Объем полушария (Дано)

1/3πr ² h = 2/3 πr ³

(с использованием соответствующих формул)

г ² ч = 2р ³

или h = 2r

Поскольку конус и полусфера имеют одинаковые основания, это означает, что они имеют одинаковый радиус.

ч/об = 2

или ч : г = 2 : 1

Следовательно, отношение их высот 2:1

Вопрос 11: Сосуд в виде полусферической чаши наполнен водой. Его содержимое выливается в правильный круговой цилиндр. Внутренние радиусы чаши и цилиндра равны 3,5 см и 7 см соответственно. Найдите высоту, на которую поднимется вода в цилиндре.

Решение:

Объем воды в полусферической чаше = Объем воды в цилиндре… (Дано)

Внутренний радиус чаши ( r ₁ ) = 3,5см

Внутренний радиус цилиндра (r ₂ ) = 7см

Объем воды в полусферической чаше = Объем воды в цилиндре

2/3πr ₁ ³ = πr ₂ ² ч

Где h – высота, на которую поднимается вода в цилиндре.

2/3π(3,5) ³ = π(7) ² ч

или ч = 7/12

Следовательно, 7/12 см — это высота, на которую поднимается вода в цилиндре.

Вопрос 12: Цилиндр, высота которого составляет две трети его диаметра, имеет тот же объем, что и сфера радиусом 4 см. Вычислите радиус основания цилиндра.

Решение:

Радиус сферы (R)= 4 см (Дано)

Высота цилиндра = 2/3 диаметра (данные)

Мы знаем, Диаметр = 2(Радиус)

Пусть h будет высотой, а r будет радиусом основания цилиндра, тогда

ч = 2/3× (2р) = 4р/3

Объем цилиндра = Объем сферы

πr ² h = 4/3πR ³

π × r ² × (4r/3) = 4/3 π (4) ³

(г) ³ = (4) ³

или г = 4

Следовательно, радиус основания цилиндра равен 4 см.

Вопрос 13: Сосуд в виде полусферической чаши наполнен водой. Содержимое выливается в цилиндр. Внутренние радиусы чаши и цилиндра соответственно 6 см и 4 см. Найдите высоту воды в цилиндре.

Решение:

Радиус чаши (R)= 6 см (Дано)

Радиус цилиндра (r) = 4 см (данные)

Пусть h высота цилиндра.

Сейчас,

Объем воды в полусферической чаше = Объем цилиндра

2/3 π R ³ = πr ² ч

2/3 π (6) ³ = π(4) ² ч

или ч = 9

Следовательно, высота воды в цилиндре равна 9см.

Вопрос 14: Цилиндрическая ванна радиусом 16 см содержит воду на глубину 30 см. В ванну опустили шаровидный железный шар, в результате чего уровень воды поднялся на 9 см. Каков радиус мяча?

Решение:

Пусть r — радиус железного шара.

Радиус цилиндра (R) = 16 см (Дано)

В цилиндр брошен сферический железный шар, в результате чего уровень воды повысится на 9см. Итак, высота (h) = 9 см

Из заявления,

Объем железного шара = Объем воды, поднятой в ступице

4/3πr ³ = πR ² ч

4/3 r ³ = (16) ² × 9

или г ³ = 1728

или г = 12

Следовательно, радиус шара = 12см.

Упражнения VSAQ Страница №: 21.25

Вопрос 1: Найдите площадь поверхности сферы радиусом 14 см.

Решение:

Радиус сферы (r) = 14 см

Площадь поверхности сферы = 4πr ²

= 4 × (22/7) × 14 ² см ²

= 2464 см ²

Вопрос 2: Найдите площадь полной поверхности полушария радиусом 10 см.

Решение:

Радиус полусферы (r) = 10 см

Полная площадь поверхности полушария = 3πr ²

= 3 × (22/7) × 10 ² см ²

= 942 см ²

Вопрос 3: Найдите радиус сферы, площадь поверхности которой 154 см ² .

Решение:

Площадь поверхности сферы = 154 см ²

Мы знаем, площадь поверхности сферы = 4πr ²

Итак, 4πr ² = 154

4 x 22/7 x r ² = 154

г ² = 49/4

или r = 7/2 = 3,5

Радиус сферы 3,5 см.

Вопрос 4: Полая сфера, в которой цирковой мотоциклист выполняет свои трюки, имеет диаметр 7 м. Найдите участок, доступный мотоциклисту для езды.

Решение:

Диаметр полой сферы = 7 м

Итак, радиус полой сферы = 7/2 м = 3,5 см

Сейчас,

Площадь, доступная мотоциклисту для езды = Площадь поверхности сферы = 4πr ²

= 4 × (22/7) × 3,5 ² м ²

= 154 м ²

Вопрос 5. Найдите объем шара, площадь поверхности которого равна 154 см ² .

Решение:

Площадь поверхности сферы = 154 см ²

Мы знаем, площадь поверхности сферы = 4πr ²

Итак, 4πr ² = 154

4 x 22/7 x r ² = 154

или г ² = 49/4

или r = 7/2 = 3,5

Радиус (r) = 3,5 см

Сейчас,

Объем сферы = 4/3 π r ³

= (4/3) π × 3,5 ³

= 179,66

Следовательно, объем сферы равен 179,66 см ³ .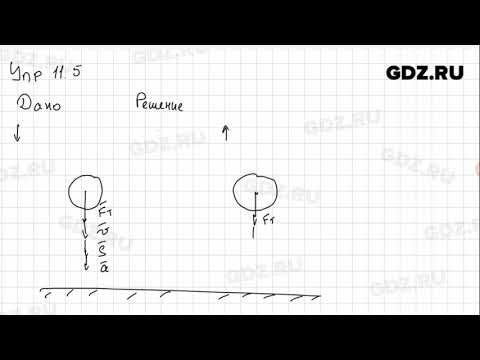

RD Sharma Solutions for Class 9 Math Chapter 21 Площадь поверхности и объем сферы

В главе 21 класса 9 RD Sharma Solutions учащиеся изучат важные концепции, перечисленные ниже:

• Введение сферы
• Разрез сферы плоскостью
• Площадь поверхности сферы, полусферы и сферической оболочки
• Объем сферы, полусферы и сферической оболочки

Часто задаваемые вопросы о решениях RD Sharma для математики 9-го класса, глава 21

Q1

Каковы ключевые особенности решений RD Sharma для математики 9-го класса, глава 21?

RD Sharma Решения по математике для 9-го класса В главе 21 представлены решения для всех вопросов упражнений, точно основанные на уровне интеллекта учащихся. Решения предлагают различные способы решения каверзных вопросов без особых усилий и немедленного устранения сомнений, возникающих при решении задач. Решение этих вопросов позволяет учащимся проанализировать уровень своей подготовки и поработать над областями, требующими большей практики.

Q2

Чем RD Sharma Solutions for Class 9 Maths Chapter 21 полезен с точки зрения экзамена?

RD Sharma Solutions for Class 9 Math Chapter 21 — самый популярный учебный материал, используемый учащимися для подготовки к ежегодным экзаменам. Усердное применение этих решений поможет учащимся мгновенно избавиться от сомнений и получить хорошие оценки на выпускных экзаменах. Эти решения RD Sharma для математики класса 9 подготовлены на основе самой последней программы Совета CBSE, охватывающей все важнейшие темы соответствующего предмета.

Q3

Что означает объем Sphere согласно RD Sharma Solutions for Class 9 Maths Chapter 21?

Согласно RD Sharma Solutions for Class 9 Maths Chapter 21, объем сферы — это ее емкость. Форма шара круглая и объемная. Он имеет три оси, а именно ось x, ось y и ось z, которые определяют его форму. Такие вещи, как футбол и баскетбол, являются примерами сфер, которые имеют объем. Объем здесь зависит от диаметра или радиуса сферы, так как если взять поперечное сечение сферы, то это круг. Площадь поверхности сферы – это площадь или область ее внешней поверхности.

widgets-close-button

Загрузить PDF-файл RD Sharma Solutions for Class 9 Math Chapter 21 Площадь поверхности и объем сферы Упражнение 211 Решения RD Sharma для математики 9 класса, глава 21 Площадь поверхности и объем сферы, упражнение 211

Решения RD Sharma для математики 9 класса, глава 21, площадь поверхности и объем сферы, упражнение 21.1 , представлены здесь. Этот учебный материал является неоценимой помощью для студентов, когда им нужна помощь в выполнении домашних заданий и при подготовке к экзаменам. Здесь все вопросы из учебника RD Sharma Solutions Class 9объясняются в подробном и пошаговом формате, чтобы помочь учащимся понять концепции простым способом. Нажмите на ссылки ниже, чтобы получить решения в формате PDF прямо сейчас.

Access Answers to RD Sharma Solutions for Class 9 Math Chapter 21 Площадь поверхности и объем сферы Упражнение 21.

Вопрос 1: Найдите площадь поверхности сферы радиусом:

(i) 10,5 см (ii) 5,6 см (iii) 14 см

Решение:

Площадь поверхности сферы = 4πr ²

Где r = радиус сферы

(i) Радиус = 10,5 см

Площадь поверхности = 4 x 22/7 x (10,5) ²

= 1386

Площадь поверхности 1386 см ²

(ii) Радиус = 5,6 см

Площадь поверхности = 4×22/7×(5,6) ²

= 394,24

Площадь поверхности 394,24 см ²

(iii) Радиус = 14 см

Площадь поверхности = 4×22/7×(14) ²

= 2464

Площадь поверхности 2464 см ²

Вопрос 2: Найдите площадь поверхности сферы диаметром:

(i) 14 см (ii) 21 см (iii) 3,5 см

Решение:

Площадь поверхности сферы = 4πr ²

Где r = радиус сферы

(i) Диаметр = 14 см

Итак, радиус = диаметр/2 = 14/2 см = 7 см

Площадь поверхности = 4×22/7×(7) ²

= 616

Площадь поверхности 616 см ²

(ii) Диаметр = 21 см

Итак, радиус = диаметр/2 = 21/2 см = 10,5 см

Площадь поверхности= 4×22/7×(10,5) ²

= 1386

Площадь поверхности 1386 см ²

(iii) Диаметр = 3,5 см

Итак, радиус = диаметр/2 = 3,5/2 см = 1,75 см

Площадь поверхности = 4×22/7×(1,75) ²

= 38,5

Площадь поверхности 38,5 см ²

Вопрос 3: Найдите общую площадь поверхности полусферы и сплошной полусферы радиусом 10 см каждая. (π=3,14)

Решение:

Радиус полусферы = Радиус сплошной полусферы = 10 см (Дано)

Площадь поверхности полушария = 2πr ²

= 2×3,14×(10) ² см ²

= 628 см ²

А, площадь поверхности твердого полушария = 3πr ²

= 3×3,14×(10) ² см ²

= 942 см ²

Вопрос 4: Площадь поверхности шара 5544 см ² , найдите его диаметр.

Решение:

Площадь поверхности шара 5544 см ²

Площадь поверхности сферы = 4πr ²

Итак, 4πr ² = 5544

4×22/7×(r) ² = 5544

г ² = (5544 × 7)/88

г ² = 441

или r = 21см

Теперь диаметр = 2 (радиус) = 2 (21) = 42 см

Вопрос 5: Полусферическая чаша из латуни имеет внутренний диаметр 10,5 см. Найти стоимость лужения его изнутри из расчета 4 рубля за 100 см ² .

Решение:

Внутренний диаметр полусферической чаши = 10,5 см

Итак, радиус = диаметр/2 = 10,5/2 см = 5,25 см

Теперь площадь поверхности полусферической чаши = 2πr ²

= 2 × 3,14 × (5,25) ²

= 173,25

Значит, площадь поверхности полусферической чаши 173,25 см ²

Узнать стоимость:

Стоимость лужения 100 см ² площадь = 4 рупии (данные)

Стоимость лужения 173.25см ² площадь = рупий. 4×173,25100 = рупий. 6,93

Таким образом, стоимость лужения внутренней стороны полусферической чаши составляет 6,93 рупий.

Вопрос 6: Купол здания имеет форму полусферы. Его радиус составляет 63 дм. Найдите стоимость его покраски из расчета 500 руб. 2 на кв.м.

Решение:

Радиус полусферического купола = 63 дм или 6,3 м

Площадь внутренней поверхности купола = 2πr ²

=2×3,14×(6,3) ²

= 249,48

Итак, площадь внутренней поверхности купола 249,48 м ²

Теперь найдем стоимость:

Стоимость покраски 1 м ² = 2 рупии (данные)

Следовательно, стоимость покраски 249,48 м ² = руб.