Тесты по геометрии для 8 класса онлайн
Окружность
-
ВПР математика 8 класс
04.05.2020 5112 0
Назначение ВПР по математике — оценить уровень общеобразовательной подготовки обучающихся 8 класса. В работе 19 заданий. 14 заданий курса алгебре и 5 заданий курса геометрии. Максимальное количество баллов 25.
-
Тест_по_теме_»Средняя линия треугольника»
02.11.2022 690 0
Тест по геометрии для 8 класса на закрепление понятия средней линии треугольника
Теорема Пифагора
29.
 12.2022
1238
12.2022
1238
Тест для обучающихся 8 — го класса по геометрии. Тема: «Теорема Пифагора»
-
Теорема Пифагора (домашнее задание №1)
22.11.2021 2572
Домашнее задание в тестовой форме. В тесте 5 вопросов. Система оценивания: «5» — 5 верно выполненных заданий (95%) «4» — 4 верно выполненных заданий (75%) «3» — 3 верно выполненных заданий (55%) «2» — 2 и менее верно выполненных заданий (меньше 55%)
-
Площадь. 8 класс
14.12.2019 15050
Тест предназначен для повторения темы «Площадь».
 Базовый уровень сложности. 5 заданий. Время выполнения 15 минут.
Базовый уровень сложности. 5 заданий. Время выполнения 15 минут. -
СООТНОШЕНИЯ В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ. ТЕОРЕМА ПИФАГОРА
16.04.2020 4216 0
Тест по темам: «Соотношения в прямоугольном треугольника. Теорема Пифагора» для обучающихся в 8 классе.
-
Теорема Пифагора
04.12.2021 2340
Тест содержит 7 вопросов по геометрии,тема теорема Пифагора, предназначен для учеников 8 класса. В тесте 2 задания с выбором ответа и 5 заданий с вводом числового ответа. Тест содержит простые задачи на умение находить гипотенузу и катет прямоугольного треугольника,по известным 2 сторонам.
 В нем есть более сложные задачи с использованием теоремы Пифагора и других формул и теорем геометрии, например, формул площадей и периметра геометрических фигур. В заданиях кроме прямоугольного треугольника надо знать и уметь применять свойства равнобедренного треугольника, прямоугольника, ромба. Вычислять площадь прямоугольника, прямоугольного треугольника, ромба. Уметь вычислять площадь ромба через диагонали.
В нем есть более сложные задачи с использованием теоремы Пифагора и других формул и теорем геометрии, например, формул площадей и периметра геометрических фигур. В заданиях кроме прямоугольного треугольника надо знать и уметь применять свойства равнобедренного треугольника, прямоугольника, ромба. Вычислять площадь прямоугольника, прямоугольного треугольника, ромба. Уметь вычислять площадь ромба через диагонали. -
Площади четырёхугольников. 8 класс.
07.11.2020 4372 0
Тест предназначен для проверки теоретических знаний по теме » Площади четырёхугольников», 8 класс.Тест ориентирован на учебник «Геометрия 7-9 классы » Л.С.Атанасян и др. В тесте 27 вопросов. Для ответа случайным образом выбирается 15 вопросов. Может быть использован для подготовки к ОГЭ по математике.

-
Итоговый тест по геометрии, тема: «Решение треугольника, подобные треугольники»
27.04.2020 469 0
Проверочный тест к теме «Решение треугольников и подобные треугольники»
-
Определение подобных треугольников. 8 класс
20.01.2020 10299
Самостоятельная работа в форме теста по теме: «Определение подобных треугольников»
-
Признаки подобия треугольников. 8 класс
07.
 02.2022
5004
02.2022
5004
Тест «Признаки подобия треугольников» состоит из трех вопросов (задач), выпадающих случайным образом из общего списка.
-
Тест по теме «Соотношения между сторонами и углами прямоугольного треугольника»
02.02.2022 1635 0
Данный тест проверяет знания по теме «Соотношения между сторонами и углами прямоугольного треугольника», геометрия, 8 класс
-
Площадь треугольника
06.02.2023 81 0
Тест по теме «Площадь треугольника» проверяет усвоение формул для вычисления площади треугольника.

-
Геометрия 8 класс
20.02.2023 127 0
Данный тест состоит из 30 вопросов. большая часть из которых состоит из вопросов теоретического характера. На некоторых заданиях указаны количества баллов,это вопросы наиболее сложные. Остальные опросы на 1 балл-они очень простые, на знание формул. Желаю удачи!
-
Площадь многоугольника.
20.02.2021 202 0
Проверочная работа по теме «Площадь многоугольника» предназначена для проверки знаний по указанной теме. Работа составлена на основе прототипов заданий ОГЭ по математике.
-
Векторы на плоскости Основные понятия.

31.10.2021 1384 0
Тест содержит вопросы на основные определения, связанные с векторами, а также на действия с векторами на плоскости.
-
Вписанные и центральные углы. 8 класс. урок 2. Повторение.
13.04.2020 155 0
Тетс составлен к теме «Вписанные и описанные углы» по учебнику Л.С.Атаносяна геометрия 8 класс.
-
8 класс Глава 7 Подобные треугольники ТЕОРИЯ
09.05.2021
Тест содержит 20 заданий. Задания в тест выбираются случайным образом из общей базы заданий.
 Критерии: «3» 50-69%, «4» 70-90%, «5» 91-100%. Оценка выставляется сразу после прохождения теста.
Критерии: «3» 50-69%, «4» 70-90%, «5» 91-100%. Оценка выставляется сразу после прохождения теста. -
Тест для внесения ответов по практической задаче
13.02.2023 9 0
Тест предназначен для внесения ответов к практическим задачам по геометрии
-
Входной тест Геометрия 8
23.07.2020 278 0
Входной тест по геометрии, нацеленный на проверку остаточных знаний по геометрии в начале учебного года, проверяет программу по геометрии 7 класса.
-
ВПР-2020.
 8 класс. Математика. Тест 2
8 класс. Математика. Тест 2
13.02.2020 395 0
Тест 2 — подготовка к Всероссийской проверочной работе по математике. 8 класс.
-
Пропорциональные отрезки. Подобные треугольники.
07.02.2021 371 0
Тест составлен по вопросам к учебнику А.Г. Мерзляк, В.Б Полонский. В тесте содержатся вопросы о свойстве биссектрисы треугольника, свойстве касательной и секущей, свойстве отрезков пересекающихся хорд.
-
ГЕОМЕТРИЯ выбор верных утверждений 8 класс
12.04.2021 4699 0
Тест содержит 30 заданий.
 Задания в тест выбираются случайным образом из общей базы заданий. Критерии: «3» 50-69%, «4» 70-90%, «5» 91-100%. Оценка выставляется сразу после прохождения теста. Время ОГРАНИЧЕНО 20 минут.
Задания в тест выбираются случайным образом из общей базы заданий. Критерии: «3» 50-69%, «4» 70-90%, «5» 91-100%. Оценка выставляется сразу после прохождения теста. Время ОГРАНИЧЕНО 20 минут. -
8 класс. Геометрия. Соотношения в прямоугольном треугольнике
04.04.2015 8949
Тест предназначен для учащихся 8 классов при отработке навыков решения задач по теме «Соотношения в прямоугольном треугольнике».
-
ОГЭ 8 класс математика
29.04.2020 717 0
Вариант ОГЭ математика 2020 год. Содержит 25 демонстрационных вариантов из сборника подготовки к ОГЭ, адаптированных к программе 8 класса.

-
8 класс Глава 8 Окружность ТЕОРИЯ
08.05.2021 821 0
Тест содержит 20 заданий. Задания в тест выбираются случайным образом из общей базы заданий. Критерии: «3» 50-69%, «4» 70-90%, «5» 91-100%. Оценка выставляется сразу после прохождения теста.
-
Центральный и вписанный углы
11.05.2020 66 0
Тест предназначен для самостоятельной работы с учебником. Задания составлены так, чтобы каждый участник мог в должной мере оценить знания по предмету, причем участвовать можно как группой, так и индивидуально.
-
Центральные и вписанные углы
24.
 11.2020
146
0
11.2020
146
0
Тест составлен на основе учебника по геометрии за 8 класс авторы Мерзляк А.Г., Полонский В. Б., Якир М. С. Параграф девять. Глава один
-
Теорема Фалеса и пропорциональные отрезки
10.02.2023 8 0
Данный тест состоит из 11 вопросов различной вариативности, от теоретических вопросов до решения задач и уровня сложности от простого до сложного!
-
8 класс Геометрия
15.03.2019 29343
Данный тест предназначен для определения знания предмета «Геометрия» за курс 8 класса.

-
Центральные и вписанные углы
29.04.2020 6115 0
Тест позволяет закрепить тему «Центральные и вписанные углы». Тест содержит две задачи из кзаменационных материалов ОГЭ.
-
Итоговый тест 8 класс геометрия ТЕОРИЯ
08.05.2021 3492 0
Тест содержит 30 заданий. Задания в тест выбираются случайным образом из общей базы заданий. Критерии: «3» 50-69%, «4» 70-90%, «5» 91-100%. Оценка выставляется сразу после прохождения теста.
-
Практические задачи на тему: «Подобие треугольников».

03.02.2022 956 0
Тестовые задания, проверяющие умение применять подобие треугольников для решения практических задач.
-
8 класс. Геометрия. Центральные и вписанные углы.
25.07.2017 20377
Тест предназначен для учащихся 8 классов при отработке навыков решения задач по теме «Центральные и вписанные углы».
-
Викторина о тригонометрии
21.02.2022 471 0
Викторина о разделе математики, изучающем функции угла: синус, косинус и т.
 п. В рамках школьной программы.
п. В рамках школьной программы. -
ВПР-2020. 8 класс. Математика. Тест 1
07.02.2020 6102 0
Тест 1 — подготовка к Всероссийской проверочной работе по математике. 8 класс.
-
Вариант 2 Свойства биссектрисы угла и серединного перпендикуляра к отрезку
24.04.2020 646 0
Тест ориентирован на учебник Л.С. Атанасяна и др. «Геометрия. 7 — 9 классы». Направлен на первичный контроль текущего усвоения материала. Задания проверяют понимание новой терминологии, распознавание видов фигур и их свойств.
-
Итоговая контрольная работа по математике за курс 8 класса.
 8Б класс
8Б класс
08.05.2020 286 0
Итоговая работа соответствует матералам 8 класса, изучаемым по учебникам Алгебра 8 клаас (Колягин) и Геометрия 8 класс (Ататнасян). Работа содержит 10 заданий (6 по алгебре и 4 по геометрии). На выполнение работы отводится 1час 30 минут. Количество прохождений: 1.
-
Неравенство треугольника
17.12.2020 74 0
Тест предназначен для учащихся средней школы для проверки уровня знаний по теме «Неравенство треугольника».
-
8 класс Глава 6 Площадь ТЕОРИЯ
09.
 05.2021
304
0
05.2021
304
0
Тест содержит 20 заданий. Критерии: «3» 50-69%, «4» 70-90%, «5» 91-100%. Оценка выставляется сразу после прохождения теста.
-
Итоговый тест 8 класс геометрия ЗАДАЧИ
09.05.2021 2182 0
Тест содержит 20 заданий. Критерии: «3» 50-69%, «4» 70-90%, «5» 91-100%. Оценка выставляется сразу после прохождения теста.
-
Прямоугольник. 8 класс
07.10.2021 3162
Тест для контроля знаний учащихся по теме «Прямоугольник». Геометрия 8 класс.
-
Центральная и осевая симметрия 8 класс 14.
 10.2021
10.2021
11.10.2021 438 0
Тест для контроля по теме «Центральная и осевая симметрия» для учащихся 8 класса
-
Формула Пика. Задачи на клетчатой бумаге.
24.11.2021 189 0
Данный тест будет полезен педагогу для проверки знаний по теме «Площади многоугольников» и ребятам для закрепления материала.
-
Г8_Тест 1_Многоугольники. Площади фигур
26.12.2022 94 0
Тест по темам «Многоугольники» и «Площадь многоугольника».
 Учебник: Геометрия 7-9 класс. Автор: Атаносян Л.С., Бутузов В.Ф.
Учебник: Геометрия 7-9 класс. Автор: Атаносян Л.С., Бутузов В.Ф. -
Теорема Пифагора
29.12.2022 6 0
Тест для обучающихся 8 класса Теорема Пифагора____________________
-
Тест по заданию №17 (ОГЭ-2020 по математике) по теме: Решение геометрических задач по теме «Окружность и круг».
16.02.2020 907 0
Тест содержит десять тестовых заданий по основным прототипам задания №17 (ОГЭ 2020). К каждому номеру ответом является число (без единиц измерения).
-
свойство хорд и углов, образованных касательными и хордами
14.
 04.2020
223
0
04.2020
223
0
Тест предназначен ддля первичного закрепления на уроке по теме «Свойство хорд окружности». Все задачи решаются устно с последующей самопроверкой
-
8 класс. Центральные и вписанные углы
20.04.2020 683 0
Для успешного прохождения теста повторите, что такое центральные и вписанные углы, свойства биссектрисы угла. Время прохождения теста — 30 минут. Удачи!
-
Геометрия 8 класс. Окружность.
22.04.2020 300
Тест по теме: «Окружность». Теоретические вопросы по данной теме.

-
МД «Свойство биссектрисы угла»
23.04.2020 750 0
Решение задач по готовым чертежам по теме «Биссектриса угла» геометрия 8 класс по учебнику Атоносяна. Проводится в начале урока «Серединный перпендикуляр»
-
Площадь многоугольника.
24.04.2020 187 0
Тест предназначен для проверки знаний по геометрии по теме «Площадь».
-
Промежуточная аттестация
11.05.2020 179 0
Данный тест предназначен для определения знания предмета «Геометрия» за курс 8 класса.

-
окружность_ геометрия_8класс
21.05.2020 542 0
Геометрия 8 класс. Тема Окружность. Учебник Атанасяна Л.С. и др. Итоговый тест
-
Четырехугольники и их свойства. 8 класс.
06.11.2020 5738 0
Тест предназначен для проверки теоретических знаний по теме » Четырёхугольники и их свойства.» 8 класс.Тест ориентирован на учебник «Геометрия 7-9 классы » Л.С.Атанасян и др. В тесте 44 вопроса. Для ответа случайным образом выбирается 20 вопросов.
-
Контрольная работа за І семестр по геометрии 8 класс
11.
 12.2020
190
0
12.2020
190
0
Контрольная работа за I семестр по геометрии состоит из 10 заданий. с 1 по 6 — тестовые задания (от 1 до 3 правильных), с 7 по 8 — установить соответствие, 9 — расположить в правильной последовательности, 10 — указать только ответ (число).
-
Углы, образованные хордами, секущими и касательными
14.03.2021 318 0
Тренировочный тест предназначен для учащихся 8-ых классов при отработке навыков решения задач по теме «Углы, образованные хордами, секущими и касательными».
-
Окружность (итоговый тест)
14.03.2021 1874 0
Тренировочный тест предназначен для учащихся 8-ых классов при отработке навыков решения задач по теме «Окружность».

-
8 класс Глава 5 Четырёхугольники ТЕОРИЯ
09.05.2021 2957 0
Тест содержит 20 заданий. Задания в тест выбираются случайным образом из общей базы заданий. Критерии: «3» 50-69%, «4» 70-90%, «5» 91-100%. Оценка выставляется сразу после прохождения теста.
-
геометрия к ОГЭ
09.08.2021 119 0
Данный тест составлен на основе вопросов ОГЭ по теме «Углы» по курсу геометрии 8 класса. Он поможет проверит основные знания.
-
Теорема Пифагора
10.
 11.2021
226
0
11.2021
226
0
Тест по геометрии по теме «Теорема Пифагора» 8 класс по учебнику Погорелова
-
теорема Пифагора
10.11.2021 511 0
Тест по геометрии 8 класс по учебнику Погорелов по закреплению теорема Пифагора
-
Теорема Пифагора
10.11.2021 1559
тест по геометрии 8 класс , учебник Погорелов , по теме : Теорема Пифагора
-
Тест по теме «Четырехугольники» 8 класс
25.
 11.2021
502
11.2021
502
Тест предназначен для учащихся 8 класса для проверки и закрепления знаний по теме «Четырехугольники»
-
Тест № 1. Тема «Окружность»
10.09.2022 8 0
Тест представляет собой теоретические вопросы по теме: «Окружность». Тест предназначен для определения предметных результатов учащихся 8 класса по теме.
-
Тест № 2 по теме «Окружность»
10.09.2022 15 0
Тест содержит пятнадцать практических заданий по теме «Окружность» и предназначен для определения предметных результатов учащихся 8 класса.

-
Теорема Пифагора
29.12.2022 4 0
Тест для обучающихся 8 класса по геометрии. Тема: «Теорема Пифагора»
-
тема урока: «Теорема Пифагора»
07.01.2023 6 0
Данный тест состоит из 15 вопросов различной вариативности, от теоретических вопросов до решения задач и уровня сложности от простого до сложного, некоторые вопросы включены из сборника ОГЭ!
-
8 класс. Геометрия. Площади многоугольников.
07.
 02.2023
87
0
02.2023
87
0
Тест на проверку знаний по теме «Площади многоугольников». Содержит вопросы теоритического характера, задачи устного характера, а также задачи с применением теоремы Пифагора.
Урок по геометрии “Решение задач по теме «Теорема Пифагора»” 8 класс | План-конспект урока по геометрии (8 класс):
МБОУ «Апраксинская СОШ»
Урок по геометрии, 8 класс
“Решение задач по теме
«Теорема Пифагора»”
Подготовила и провела: Алякина Е.И.
Декабрь 2020
Решение задач по теме: «Терема Пифагора»
Цель урока:
Применение теоремы Пифагора при решении задач.
Задачи:
- Обобщить и систематизировать знания учащихся по теме.
- Развивать внимание учащихся, логическое мышление, математическую речь.
- Прививать интерес к предмету геометрия.
Тип урока: урок обобщения и закрепления полученных знаний.
Формы работы на уроке: фронтальная, индивидуальная, самостоятельная.
Оборудование: компьютер; мультимедийный проектор; презентация к уроку.
Ход урока
1. Мотивационно-организационный этап.
Приветствие, проверка готовности к уроку (рабочих тетрадей, учебников, письменных принадлежностей).
— Ребята, мы продолжаем изучать одну из самых известных теорем, теорему Пифагора. Значение теоремы Пифагора состоит в том, что с её помощью можно доказать многие другие теоремы и решить множество задач.
Ещё в 17 веке немецкий астроном и математик И. Кеплер сказал, что геометрия обладает двумя великими сокровищами. Первое – это теорема Пифагора, которую можно сравнить с мерой золота. А второе – деление отрезка в крайнем и среднем отношении, которое напоминает драгоценный камень.
Древнегреческий философ и математик (VI в до н.э.) Пифагор – едва ли не самый популярный за всю историю человечества. Вокруг его личности образовалось множество легенд. Одни его называли математиком, пророком, философом, другие шарлатаном. Пифагор много путешествовал. Пифагор основал школу «Пифагорийский союз», в школу принимались молодые представители аристократии, с большими церемониями, после долгих испытаний. Каждый вступающий отрекался от своего имущества и давал клятву хранить в тайне учения основателя. Пифогорийцы занимались математикой, философией, естественными науками, сделали много важных открытий в арифметике и геометрии. Но в школе существовал Декрет, по которому авторство всех математических работ приписывалось Пифагору.
Пифагор много путешествовал. Пифагор основал школу «Пифагорийский союз», в школу принимались молодые представители аристократии, с большими церемониями, после долгих испытаний. Каждый вступающий отрекался от своего имущества и давал клятву хранить в тайне учения основателя. Пифогорийцы занимались математикой, философией, естественными науками, сделали много важных открытий в арифметике и геометрии. Но в школе существовал Декрет, по которому авторство всех математических работ приписывалось Пифагору.
Напомните, пожалуйста. формулировку теоремы Пифагора.
(В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов)
А обратная теорема?
Доказательство теоремы называли «мостом ослов», т.к. слабые ученики, заучивающие теоремы наизусть, без понимания, и прозванные поэтому «ослами», были не в состоянии преодолеть теорему Пифагора, служащую для них вроде непреодолимого моста. Или «бегство убогих», т.к. некоторые «убогие» ученики, не имевшие серьезной математической подготовки, бежали от геометрии. Саму теорему называли «ветряной мельницей», «теоремой – бабочкой» или «теоремой невесты». Известно около 150, а по некоторым источникам около 500 различных доказательств теоремы Пифагора, поэтому она занесена в книгу рекордов Гиннеса.
Саму теорему называли «ветряной мельницей», «теоремой – бабочкой» или «теоремой невесты». Известно около 150, а по некоторым источникам около 500 различных доказательств теоремы Пифагора, поэтому она занесена в книгу рекордов Гиннеса.
Однако эту теорему знали за много лет до Пифагора. Так, за 1500 лет до Пифагора древние египтяне знали о том, что треугольник со сторонами 3, 4и 5 является прямоугольным и применяли этот способ для строительства пирамид.В самом древнем индийском геометрическом сборнике «Сульвасутра» («Правила веревки, 600 год до н.э.) даются правила построения прямых углов при помощи веревки с узлами, расстояния между которыми равны 15, з6 и з9 падас (мера длины). В Древнем Китае уже около 2200г. до н.э. для треуголдьника со стороной 3, 4, 5 было найдено правило «гоу-гоу», с помощью которого можно было по известной гипотенузе и одному из катетов находить другой неизвестный катет, а так же гипотенузу, если известны оба катета.
2. Устный опрос
- Какой треугольник называется прямоугольным? (если есть прямой угол)
- Чему равна сумма углов прямоугольного треугольника? (1800)
- Чему равна сумма острых углов в прямоугольном треугольнике? (900)
- Сформулируйте свойство катета, лежащего против угла в 30 градусов.

(Катет прямоугольного треугольника, лежащий против угла в 30° равен половине гипотенузы)
- Сформулируйте теорему Пифагора.
(В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов)
- Как называется сторона противолежащая прямому углу? (Гипотенуза)
- Как называется сторона прилежащая к прямому углу? (Катет)
3. Решение задач (устно)
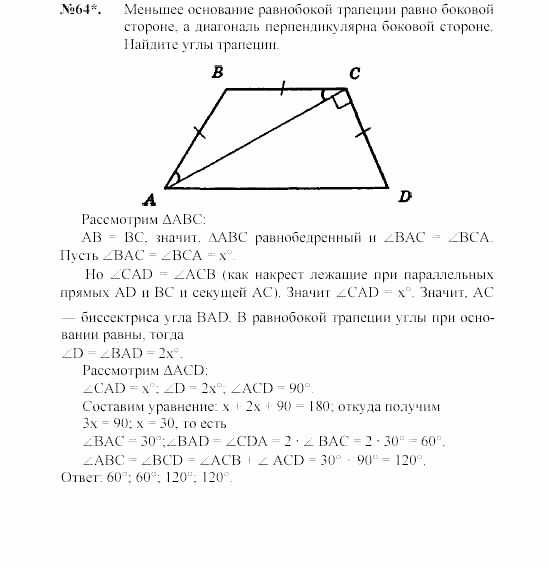
4. Решение задач
Найти: ВС.
№ 2.
На какое расстояние следует отодвинуть от стены дома нижний конец лестницы, длина которой 13 м, чтобы верхний ее конец оказался на высоте 12 м?
№3.
Дано: ∆АВС равнобедренный, АВ = 13 см,
ВД – высота, ВД=12 см
Найти: АС
№ 4.
Дано: ABCD – ромб, АС, ВД – диагонали, АС = 12 см, BD = 16 см.
Найти: PABCD
№ 5.
Угол С=900, а угол B=300. Гипотенуза АВ = 6. Найдите сторону BC.
5. Физкультпауза
6. Тест
1. Теорему какого учёного мы применяли сегодня на уроке?
а) Демокрита; б) Магницкого; в) Пифагора; г) Ломоносова.
2. Что открыл этот математик?
а) теорему; б) рукопись; в) древний храм; г) задачу.
3. Как называется большая сторона в прямоугольном треугольнике?
а) медиана; б) катет; в) биссектриса; г) гипотенуза.
4. Почему теорему назвали «теоремой невесты»
а)потому, что она была написана для невесты;
б) потому, что она была написана невестой;
в) потому, что чертеж похож на «бабочку», а «бабочка» переводится как «нимфа» или» невеста»;
г) потому, что это загадочная теорема.
5. Почему теорему назвали «мостиком ослов»
а) она применялась для дрессировки осликов;
б) только умный и упрямый мог преодолеть этот мостик и доказать эту теорему;
в) написали ее «ослики»;
г) очень сложное доказательство теоремы.
6. В теореме Пифагора квадрат гипотенузы равен
а) сумме длин сторон треугольника; б) сумме квадратов катетов;
в) площади треугольника; г) площади квадрата.
7. Чему равны стороны египетского треугольника?
а) 1, 2, 3; б) 3,4,5; в)2,3,4; г) 6,7,8.
7. Дифференцированная самостоятельная работа.
Обучающимся предлагается выбрать для решения любые 2-4 задания. Проверка при наличии времени по готовым ответам на уроке, либо работы сдают на проверку.
Ответы
№ задачи | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Ответ | 10 | 5 | 2V2 | 16 | 16 | V2 | V3 |
8. Итог урока, выставление оценок.
Итог урока, выставление оценок.
Домашнее задание — № 491, № 492, № 493.
Р е ф л е к с и я
«Я повторил…» «Я узнал…»
«Я закрепил…» «Я научился решать…»
«Мне понравилось…»
Самостоятельная работа
Сведения об общеобразовательной организации
Сведения об общеобразовательной организацииЦвет:C C C
Изображения Вкл. Выкл.
Обычная версия сайта
- Телефон доверия: 8 800 200-01-22
Ошибка 404
К сожалению запрашиваемая страница не найдена.
Но вы можете воспользоваться поиском или картой сайта ниже
|
|
Как решать задачи по геометрии.
 Часть 1
Часть 1Геометрия… Страшное слово для бесчисленного множества учеников. Они знают свойства фигур и выучили определения и теоремы, но задачи по геометрии все равно остаются какой-то китайской грамотой.
Это про тебя? Тогда ты попал туда, куда нужно!
Проблема подавляющего большинства учеников в том, что они не умеют обдумывать задачу по геометрии. Их этому не научили (ну, или они не захотели научиться, когда была возможность). Именно в этой статье, я объясню саму технологию обдумывания и, в конечном счете, нахождения решения ПРАКТИЧЕСКИ ЛЮБОЙ задачи по геометрии.
Сразу оговорюсь — без знания теории в геометрии никак. В смысле, вообще никак, от слова «совсем». Чтоб тебе было полегче при чтении этой статьи, я буду внутри решений задач в скобках курсивом указывать используемые свойства и теоремы. Но помни: если вдруг в знании теории у тебя пробел – закрытие его за тобой! Бери учебник и читай. Причем главные вещи – заучивай (или понимай). Знать теорию – обязательно!
Знать теорию – обязательно!
Ладно, к делу.
Ты играл когда-нибудь в квесты? Неважно в реальной жизни или в компьютере. Во всех квестах принцип один – у тебя есть что-то (вещи, знания, навыки) и есть цель (раскрыть какую-нибудь тайну, найти некий предмет, «спасти принцессу» и т.д.). При этом путь к цели – неизвестен. И зачем нужны эти самые имеющиеся у тебя «вещи, знания, навыки» – тоже непонятно. Что делать? Как достичь цели?
Известно как: использовать то, что есть, и искать, куда это применить, чтоб продвинуться к цели. То есть, делать шаги от своего текущего местонахождения – к цели. При этом понятно, что некоторые шаги будут вести нас не туда, куда надо, а совсем даже в тупик. А иногда мы будем находить вещи или информацию, вроде бы напрямую к цели не ведущие, но как выяснится в дальнейшем – необходимую.
Более того, порой можно логически двигаться и наоборот – от цели к твоей текущей позиции. Например, если нужно «спасти принцессу из замка», то понятно, что, скорее всего, надо будет как-то попасть в замок. А для этого надо оказаться на острове, где этот замок стоит. Как попасть? Может быть на лодке. Или найти телепорт. Или использовать магию. Но на остров – надо. Начинаем искать пути на остров. Это уже логические шаги от цели к текущей позиции.
А для этого надо оказаться на острове, где этот замок стоит. Как попасть? Может быть на лодке. Или найти телепорт. Или использовать магию. Но на остров – надо. Начинаем искать пути на остров. Это уже логические шаги от цели к текущей позиции.
К чему весь этот разговор? Решение задачи по геометрии это точно такой же «квест», только математический . Вдумайся: у нас всегда есть некоторые исходные данные и есть то, что нужно найти (или доказать – разницы на самом деле практически нет). И наша задача – построить логическую цепочку от исходных данных к цели. Строительным материалом при этом у нас будут данные (исходные и полученные при рассуждениях), а также теоремы и свойства.
Ладно, давай уже конкретный пример разберем.
Задача. В треугольнике \(ABC\) из точки \(B\) проведена высота \(BH\). Найти длину отрезка \(AH\), если известно, что сторона \(AC\; =\; 14\) см и угол \(A\) равен углу \(C\).
Так. С чего начинается решение геометрической задачи? Ну, а с чего начинается решение квеста? Правильно, осматриваемся по сторонам, изучаем, что у нас есть и куда нас жизнь закинула.
С чего начинается решение геометрической задачи? Ну, а с чего начинается решение квеста? Правильно, осматриваемся по сторонам, изучаем, что у нас есть и куда нас жизнь закинула.
В геометрии это означает:
- построить чертежа выделить из условия задачи исходные данные, то есть, выяснить, что нам дано.
- выделить из условия задачи исходные данные, то есть, выяснить, что нам дано.
Хорошо. Значит, текущая ситуация у нас такова:
Давайте потихоньку развеивать туман. Нам известно, что углы \(А\) и \(С\) равны, а это значит, что треугольник \(АВС\) – равнобедренный с основанием АС (теория – «признак равнобедренного треугольника: равенство углов при одной из сторон. Она и является основанием»). Это новая информация, новые данные, изначально неизвестные. Делаем шаг.
Отлично. Теперь смотрим, что у нас есть еще? Еще у нас есть информация, что \(BH\) – высота.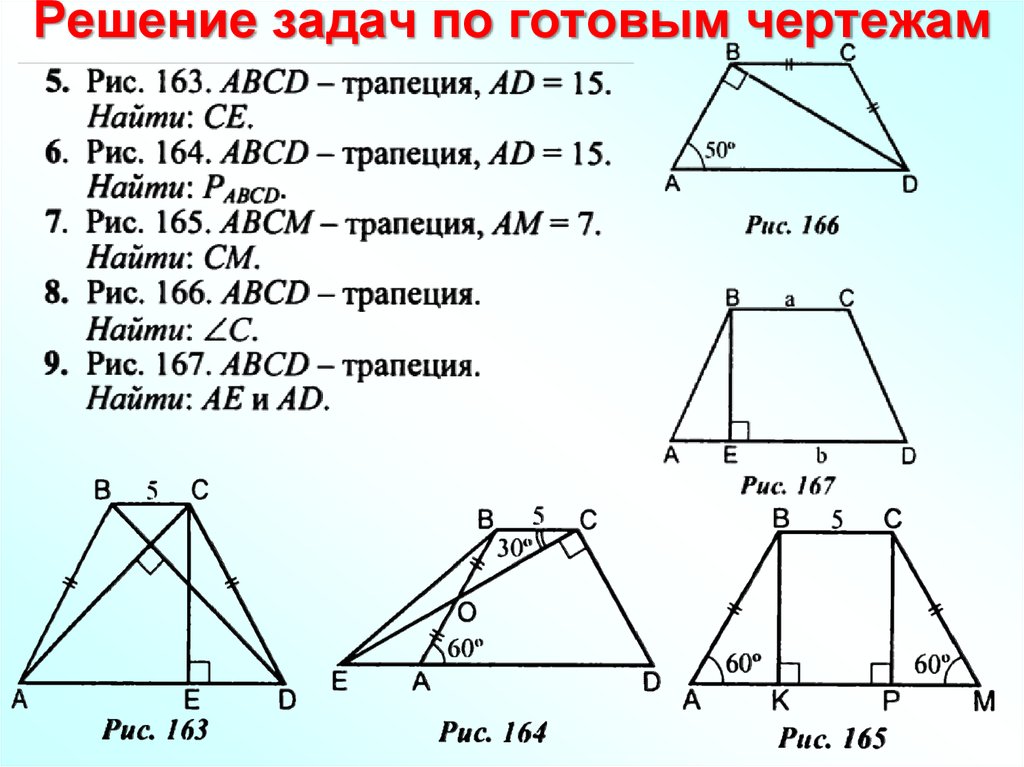 А раз треугольник \(ABC\) – равнобедренный, то значит \(BH\) еще и медиана (теорема о высоте в равнобедренном треугольнике: высота, проведенная к основанию равнобедренного треугольника является медианой и биссектрисой). То есть, мы, используя новые, полученные на предыдущем шаге данные, а также исходные данные и знание теории, делаем еще один шаг и опять получаем новую информацию.
А раз треугольник \(ABC\) – равнобедренный, то значит \(BH\) еще и медиана (теорема о высоте в равнобедренном треугольнике: высота, проведенная к основанию равнобедренного треугольника является медианой и биссектрисой). То есть, мы, используя новые, полученные на предыдущем шаге данные, а также исходные данные и знание теории, делаем еще один шаг и опять получаем новую информацию.
А что мы знаем про медиану? Она делит противоположную сторону на две равные части (определение медианы: отрезок, соединяющий вершину треугольника с серединой противоположной стороны). Но тогда получается, что точка \(H\) делит сторону \(AC\) пополам. То есть \(AH = HC\).
Стоп. Так у нас же есть длина стороны \(AC\)! И если мы знаем, что точка \(H\) делит сторону \(AC\) пополам, значит, \(AH\) равен половине \(AC\)! Таким образом, получаем, что \(AH = AC/2 = 14/2=7\) см.
Готово. Ответ получен.
Естественно, такие конструкции с «пятном тумана» рисовать каждый раз не нужно, эта схема показывает логическую цепочку решения у нас в голове.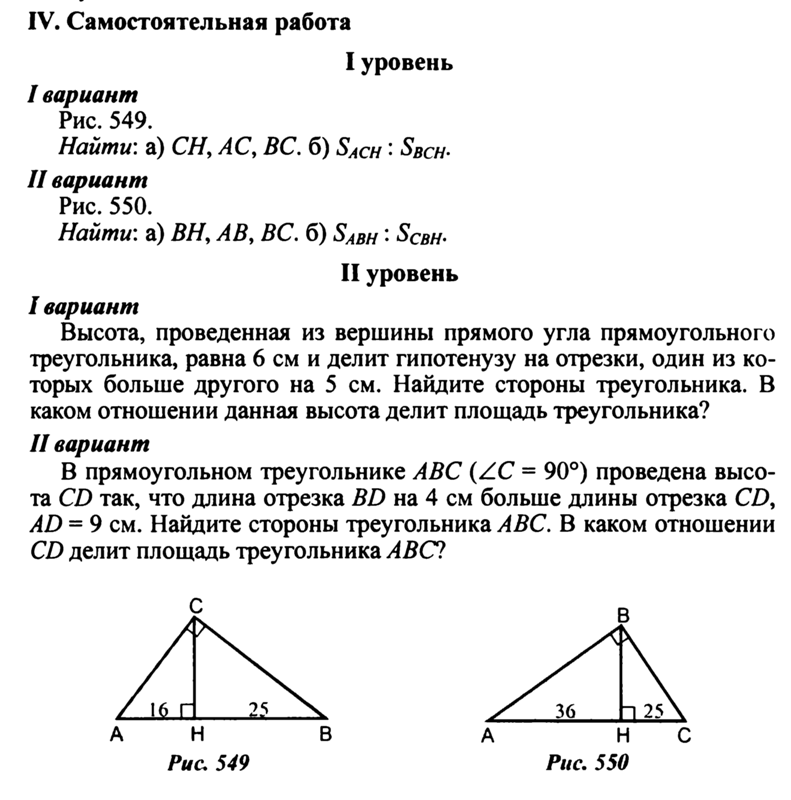 А записывается примерно так:
А записывается примерно так:
Технологическая карта урока геометрии 8 класс по теме Определение подобных треугольников. Отношение площадей подобных треугольников. Решение задач
Технологическая карта урока:
«Определение подобных треугольников. Решение задач».
Учитель:Хертек Надежда Чолаачыевна.
Предмет:геометрия.
Класс:8 «б».
Тема урока: «Определение подобных треугольников. Решение задач».
Типурока: урок обобщения знаний.
Цель урока: формирование у обучающихся деятельных способностей и способностей к структурированию и систематизации знаний по теме «Определение подобных треугольников. Решение задач».
Задачи урока:
Образовательные: отработатьумение применять определение подобных треугольников и отношение площадей подобных треугольников при решении задач.
Развивающие:
развивать умение выражать свои мысли;
развивать умения ставить цель, планировать деятельность, оценивать результаты деятельности.
Воспитательные: воспитывать интерес к предмету, учебной деятельности, доброжелательное отношение к товарищам.
Универсальные учебные действия:
Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений.
Регулятивные: целеполагание, планирование деятельности, оценка.
Коммуникативные: умеют работать в сотрудничестве с учителем, аргументировать и отстаивать свою точку зрения.
Результаты:
Предметные: Знать: определение подобных треугольников и отношение площадей подобных треугольников.
Уметь: применять теоретические знания на практике.
Личностные: развивается мотивация к учебной деятельности, рефлексивная самооценка, умение делать анализ.
Метапредметные:
1) обучающиеся овладевают способностями:
принимать и сохранять цели и задачи учебной деятельности, находить средства и способы ее осуществления, решать творческую задачу, способностьюслушать;
2) обучающиеся овладевают умениями: планировать, контролировать, оценивать учебную деятельность, использовать речевые средства для решения коммуникативных задач, использование различных способов поиска информации.
Основные понятия: пропорциональные отрезки, определение подобных треугольников, отношение площадей подобных треугольников.
Формы работы: фронтальная, групповая, индивидуальная.
Технология урока: здоровьесберегающие, информационно — коммуникационные, технология использование в обучении игровых методов, обучение в сотрудничестве.
Оборудование: мультимедийный проектор, экран , презентация, раздаточные карточки с заданиями, учебник «Геометрия 7-9 кл.» авт.Атанасян Л.С. и др, «Задачи на готовых чертежах для 7-9 классов», Э.Н. Балаяна.
Этапы урока | Задачи этапа | Деятельность учителя | Деятельность учащихся | УУД |
1.Организационный момент и мотивация к учебной деятельности. | Создать благоприятный психологический настрой на работу, ознакомление с правилом игры. Мотивирует учащихся, подводит их к формулировке темы и целей урока, акцентирует внимание на значимость темы. | Приветствие, проверка подготовленности к учебному занятию, организация внимания учащихся. (Слайд №2, 3) Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи – решайте их!» Дьёрдь Пойа — Наш сегодняшний урок мы начинаем с высказывания великоговенгерского математика Дьёрдь Пойа. Скажите, что мы будем делать на уроке? — Правильно. Сегодня на этом уроке мы будем решать задачи? -А какие будем решать задачи, вы ответите, посмотрев следующие слайды. — Правильно. Мы будем решать геометрические задачи на подобие. -Для того чтобы решать задачи, что мы должны знать? -Правильно! Мы должны знать определение подобных треугольников, отношение площадей подобных треугольников. Учащиеся разделены на 3 группы. Группам даются вопросы. Отвечает один ученик из группы. Каждая группа отвечает на вопрос, выбирает правильный ответ и поднимает карточку с буквой, затем комментирует, доказывает выбор ответа. Задания для теоретиков: Повторяют теорию по учебнику. Решают задачи в тетради вместе со всеми, получая «ордена». Зелёная дорожка вы имеете право на две ошибки Желтая дорожка – одна ошибка Красная – ни одной ошибки | Включаются в деловой ритм урока. Учащиеся отвечают на вопросы, высказывают свои мнения и мысли. Учащиеся знакомится с правилом интеллектуальной игры «Умники и умницы» | Коммуникативные: слушать и понимать речь учителя, соседа по парте, соблюдать нормы речевого этикета. Регулятивные: умение организовать рабочее место. Личностные: осознавать неполноту знаний, проявлять интерес к новому содержанию. Коммуникативные: формулировать, аргументировать, отстаивать свое мнение. Регулятивные: определять учебную задачу на основе соотнесения того, что известно и того, что неизвестно. Познавательные: учатся извлекать информацию из иллюстраций, умение формулировать проблему.. |
2.Актуализация опорных знаний. | Актуализация опорных знаний и устный опрос по изученной теории. | Первый уровень: Теоретический. (Слайд №4,5,6) 1.Какие треугольники называются подобными? а) стороны пропорциональны. б) соответствующие углы равны. в) сходственные стороны пропорциональны. г) нет правильного ответа. (Ответ: б,в) 2.Какие стороны треугольников называются сходственными? а) Равные стороны. б) Пропорциональные стороны. в) Стороны, лежащие напротив равных углов. г) Нет правильного ответа. (Ответ: в) 3. Что такое коэффициент подобия? а) Отношение сторон. б) Отношение сходственных сторон. в) Отношение соответственных сторон. г) Все ответы правильные. (Ответ: б) 4. Чему равно отношение площадей подобных треугольников? а) Коэффициенту подобия. б) Отношению сходственных сторон. в) Отношение соответственных сторон. г) Квадрату коэффициента подобия. (Ответ: г) 5. Чему равно отношение периметров подобных треугольников? а) Коэффициенту подобия. б) Отношению сходственных сторон. в) Отношение соответственных сторон. г) Квадрату коэффициента подобия. (Ответ: а) | Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого. Сходственные стороны подобных треугольников — стороны, лежащие напротив равных углов. Числоk, равное отношению сходственных сторон подобных треугольников , называется коэффициентом подобия. Отношение площадей подобных треугольников равно квадрату коэффициента подобия. Отношение периметров равно коэффициенту подобия. | Личностные: самооценка на основе успешности учебной деятельности. Коммуникативные: взаимодействовать с учителем во время опроса. Уметь точно и грамотно выражать свои мысли. Регулятивные: оценка и самоконтроль знаний. Познавательные: извлекать и актуализировать необходимую информацию для дальнейшей работы на уроке. |
3.Решение задач по готовым чертежам. | На простых задачах проверить уровень усвоения определения подобных треугольников и отношение площадей подобных треугольников. | Второй уровень. Базовый.(Слайд №7) Решение задач на готовых чертежах. 1.∆ABC~∆A1B1C1.Найтиx, y. а) 6 и 8 б) 1,5 и 8в) 1,5 и 2г) 6 и 2 2. .∆ABC~∆A1B1C1.Найти:x, y, z. а) 2,14,16 б) 12, 16, 18в) 3,4,5 г) 14, 16, 18 3.∆ABC~∆A1B1C1.Найти:x а ) 600 б) 200 в) 400 г) 800 4.∆MNT~∆M1N1T1;S ∆MNT =75; S ∆M1N1T1 = 225. Найти: x а) 6 б) 3 в) 4,5 г) 7 | Учащиеся решают задачи и устно дают ответы с комментированием. (Ответ: г) (Ответ: а) (Ответ: а) (Ответ: б) | Коммуникативные: уметь слушать вступать в диалог. Владеть грамотной математической речью. Регулятивные: планировать деятельность при решении поставленной задачи, самоконтроль, коррекция. Познавательные: уметь осуществлять анализ объектов с выделением существенных и несущественных признаков. |
4. Минутка релаксации | Предупреждение утомляемости учащихся. | Показ видеоролика для релаксации. | Смотрят видеоролик «Самые красивые места на Земле» | Предупреждение утомляемости учащихся на уроке. |
5.Применение знаний и умений в новой ситуации | Решение практических задач. | Третий уровень. Практический. (Слайд №8,9) Геометрия – это не просто наука о свойствах треугольников, параллелограммов, окружностей. Геометрия – это целый мир, который окружает нас с самого рождения. Геометрия учит внимательно смотреть вокруг и видеть красоту обычных вещей, смотреть и думать, думать и делать выводы. Однажды подобие прямоугольных треугольников помогло одному древнегреческому учёному Фалесу Милетскому измерить высоту Египетской пирамиды. В один из солнечных дней он вместе с главным жрецом храма Изиды проходил мимо пирамиды Хеопса. — Знает ли кто-либо, какова её высота? – спросил мудрец. — Нет, сын мой, — ответил жрец – Древние папирусы не сохранили нам этого, а наши знания не дают возможности судить о ней даже приблизительно. — Но ведь это можно сказать совсем точно и даже сейчас. Вот смотри, мой рост 3 царских вавилонских локтя (1 локоть = 462 мм=46 см 2 мм). А вот моя тень. Её длина такая же. И какой бы ты предмет ни взял именно в это время, тень от него, если ты поставишь его вертикально, точно равна длине предмета. Этот предмет и его тень образуют прямоугольный треугольник; знай же, что такие треугольники подобны. Учёный привёл в удивление жрецов, измерив высоту пирамиды без всяких приборов по отбрасываемой ею тени. Задача. Человек ростом 1,7 м стоит на расстоянии 9 метров от столба, на котором висит фонарь. Человек отбрасывает тень длиной 3 м. Найдите высоту столба. | Слушают речь учителя, задают вопросы, решают задачу с комментированием и доказательством. | Коммуникативные: взаимодействуют с другими членами группы, учитывают позицию собеседника, осуществляют сотрудничество и кооперацию с учителем и одноклассником. Регулятивные: оценивают предложенные варианты, выбирают наиболее точный. Происходит восприятие, осмысление, запоминания материала. Познавательные: развитие и углубление потребностей и мотивов учебно-познавательной деятельности. |
6. Рефлексия Подведение итогов урока. | Дать качественную оценку работы каждой группы и отдельных учеников | -Что изучили сегодня на уроке? Сформулируйте возможный алгоритм решения задач на подобие треугольников. -Оцените свою работу в группе. Ответственный в группе, оценивает работу каждого члена группы, выставляет оценки. Идущие по красной дорожки получают оценку «5», желтая дорожка «4», зеленая дорожка «3». Также выставляется оценки «теоретикам». -Какие затруднения возникли? Оценить отдельных учащихся (Слайд №10) Домашнее задание: повторить п.58, выучить формулировку отношения площадей подобных треугольников, решать задачу №549. Дополнительная задача для сильных учащихся. Н а сколько метров поднимется прикреплённый к колодезному журавлю конец верёвки, если человек опустил короткий конец журавля на 80 см? Плечи журавля составляют 2 м и 6 м. | Отвечают на вопросы. А) Находим пару предполагаемо подобных треугольников. Б) Доказываем, что эти треугольники подобны, используя признак подобия треугольников. В) Определяем сходственные стороны треугольников и составляем соответствующую пропорцию. С) Находим неизвестные члены этой пропорции. | Личностные: устанавливают связь между целью деятельности и ее результатом. Коммуникативные: формулируют и аргументируют свое мнение. Регулятивные: оценивают личные достижения, осознают качество и уровень усвоения материала. |
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/296068-tehnologicheskaja-karta-uroka-geometrii-8-kla
Решение задач на построение – УчМет
Хомицкая Эльвира Станиславовна
г. Североморск, Мурманская область
Североморск, Мурманская область
МБОУСОШ №1
Геометрия
Геометрия 7-9 Атанасян Л.С.
Решение задач на построение
8 класс
45 мин
Microsoft Word, Paint
Тема: Решение задач на построение
Урок – исследовательская работа
Цель: построить квадрат, равновеликий данному кругу, и оценить точность построения
Задачи:
1) Совершенствовать навык решения простых задач на построение;
Показать пример комплексного применения знаний;
Развивать внимание, логическое мышление учащихся, наблюдательность, способность видеть различные варианты решения задач, способность сравнивать, самостоятельно проводить анализ, делать выводы.
Оборудование:
Линейка, простой карандаш, циркуль,
калькулятор.
Этапы урока: 1) организационный;
2) актуализация;
3) проблемный вопрос;
4) усвоение образца комплексного
применения знаний;
5) самостоятельное применение
знаний, умений и навыков в
новых условиях;
6) контроль и самоконтроль
результатов;
7) итог урока:
8) домашнее задание.
Организационный момент: проверка готовности необходимого оборудования и материалов; объявление темы и общей цели урока (найти способ построения квадрата, равновеликого данному кругу, и оценить его точность).
Актуализация необходимых знаний:
У доски (вызвать 3 уч.) – задания по карточкам.
Фронтальный опрос (устно)
3,1416≈ ….
 . (π)
. (π)
Чему должно равняться отношение площадей, чтобы фигуры были равны?
Проблемный вопрос (формирование познавательного мотива): Как построить квадрат, равновеликий кругу?
Новый материал: параллельный показ презентации
а) смысл выражения «квадратура круга»;
б) невозможность точного решения этой задачи с помощью построений (выступление «теоретика» у доски):
SO=π r2 и S=а2, если SO= S, то π r2=а2, следовательно а=√ π r2 .
Для решения задачи необходимо построить отрезок а= r√ π
г) существование способов приблизительного решения этой задачи
Поиск способа построения квадратуры круга:
а) построить круг с d=9клеток
б) сосчитать, чему равна площадь круга в клетках (для простоты взять 1/4 круга)
Ответ: SO ≈64 клетки
в) S=64
клетки. Чему равна сторона квадрата?
Ответ:8 клеток
Чему равна сторона квадрата?
Ответ:8 клеток
г)Установите взаимосвязь между стороной квадрата и диаметром круга. Ответ а=
Оценим точность данного построения: (выступление «теоретика» у доски)
SO=π r2= π (0,5d)2=0,25 πd2≈0,7854 d2
S=а2=(8/9d)2≈0,7901d2
S больше SO. Во сколько раз? S/SO≈1,006 раз («эталонная точность»).
Применение полученных знаний (проведение лабораторной работы):
Оборудование: линейка без делений, циркуль, калькулятор, бланк для проведения работы на нелинованной бумаге.
Бланк: Лабораторная работа по теме «Квадратура круга»
Ученика ______ класса___________________________________________(фамилия, имя)
Цель________________________________________________________________________
Этапы: — найти и начертить диаметр круга;
— с помощью циркуля и линейки без делений разделить диаметр на 9 равных частей;
-построить на бланке прямой угол;
-на сторонах угла отложить отрезки, равные 8/9 диаметра, достроить фигуру до квадрата;
-измерить радиус круга, вычислить его площадь по формуле SO=π r2;
-измерить сторону квадрата, вычислить его площадь по формуле S=а2;
-ответить на вопрос: какая площадь больше, во сколько раз?
-сделать вывод: построил_______________________________________________________
погрешность моего построения_____________________________________
разность между моей и «эталонной» погрешностью равна______________
причины возникшей разности______________________________________
Итог
урока: обсудить итоги лабораторной
работы, причины возникших трудностей.
Дмашнее задание: разобрать еще один способ «решения» задачи о квадратуре круга и оценить погрешность построения.
SO= π r2= π 32≈28,27см2
Sбольш> SO
Sмал< SO
Sсред≈ SO
Указание:
Sбольш найти по рисунку;
Sмал найти с применением теоремы Пифагора
Sсред найти как среднее арифметическое Sбольш и Sмал
Найти отношение Sсред/ SO, сделать вывод.
8 класс | Математика | Iowa Department of Education
В 8-м классе учебное время должно быть сосредоточено на трех важнейших областях: (1) формулировка и обоснование выражений и уравнений, включая моделирование ассоциации двумерных данных с линейным уравнением, а также решение линейных уравнений и систем линейных уравнений. уравнения; (2) понимание концепции функции и использование функций для описания количественных отношений; (3) анализ двух- и трехмерного пространства и фигур с использованием расстояния, угла, подобия и конгруэнтности, а также понимание и применение теоремы Пифагора.
уравнения; (2) понимание концепции функции и использование функций для описания количественных отношений; (3) анализ двух- и трехмерного пространства и фигур с использованием расстояния, угла, подобия и конгруэнтности, а также понимание и применение теоремы Пифагора.
- Учащиеся используют линейные уравнения и системы линейных уравнений для представления, анализа и решения различных задач. Учащиеся узнают уравнения для пропорций (y/x = m или y = mx) как специальные линейные уравнения (y = mx + b), понимая, что константа пропорциональности (m) — это наклон, а графики — это линии, проходящие через начало координат. Они понимают, что наклон (m) линии представляет собой постоянную скорость изменения, так что если входные данные или координата x изменяются на величину A, выходные данные или координата y изменяются на величину m·A. Учащиеся также используют линейное уравнение для описания связи между двумя величинами в двумерных данных (например, между размахом рук и ростом учащихся в классе).
 На этом уровне подгонка модели и оценка ее соответствия данным выполняются неформально. Интерпретация модели в контексте данных требует, чтобы учащиеся выражали взаимосвязь между двумя рассматриваемыми величинами и интерпретировали компоненты взаимосвязи (такие как наклон и пересечение оси Y) с точки зрения ситуации.
На этом уровне подгонка модели и оценка ее соответствия данным выполняются неформально. Интерпретация модели в контексте данных требует, чтобы учащиеся выражали взаимосвязь между двумя рассматриваемыми величинами и интерпретировали компоненты взаимосвязи (такие как наклон и пересечение оси Y) с точки зрения ситуации.Учащиеся стратегически выбирают и эффективно реализуют процедуры для решения линейных уравнений с одной переменной, понимая, что при использовании свойств равенства и концепции логической эквивалентности они сохраняют решения исходного уравнения. Учащиеся решают системы двух линейных уравнений с двумя переменными и связывают системы с парами прямых на плоскости; они пересекаются, параллельны или являются одной и той же линией. Учащиеся используют линейные уравнения, системы линейных уравнений, линейные функции и свое понимание наклона линии для анализа ситуаций и решения проблем.
- Учащиеся усваивают понятие функции как правила, которое назначает каждому входу ровно один выход.
 Они понимают, что функции описывают ситуации, когда одна величина определяет другую. Они могут переводиться между представлениями и частичными представлениями функций (отмечая, что табличные и графические представления могут быть частичными представлениями), и они описывают, как аспекты функции отражаются в различных представлениях.
Они понимают, что функции описывают ситуации, когда одна величина определяет другую. Они могут переводиться между представлениями и частичными представлениями функций (отмечая, что табличные и графические представления могут быть частичными представлениями), и они описывают, как аспекты функции отражаются в различных представлениях. - Учащиеся используют идеи о расстоянии и углах, их поведении при перемещении, вращении, отражении и расширении, а также идеи о конгруэнтности и сходстве для описания и анализа двухмерных фигур и решения задач. Учащиеся показывают, что сумма углов в треугольнике есть угол, образованный прямой линией, и что различные конфигурации линий порождают подобные треугольники из-за углов, образующихся при пересечении параллельных прямых секущей. Учащиеся понимают формулировку теоремы Пифагора и ее обратной формы, а также могут объяснить, почему теорема Пифагора верна, например, путем разложения квадрата двумя разными способами. Они применяют теорему Пифагора для нахождения расстояний между точками на координатной плоскости, для нахождения длин и для анализа многоугольников.
 Учащиеся завершают свою работу над объемом, решая задачи, связанные с конусами, цилиндрами и сферами.
Учащиеся завершают свою работу над объемом, решая задачи, связанные с конусами, цилиндрами и сферами.
Система счисления (8.NS)
Знайте, что есть нерациональные числа, и аппроксимируйте их рациональными числами. (8.NS.A)
- Знайте, что числа, не являющиеся рациональными, называются иррациональными. Неформально поймите, что каждое число имеет десятичное расширение; для рациональных чисел показать, что десятичное расширение в конечном итоге повторяется, и преобразовать десятичное расширение, которое в конечном итоге повторяется, в рациональное число. (8.NS.A.1) (ДОК 1)
- Используйте рациональные приближения иррациональных чисел, чтобы сравнить размер иррациональных чисел, расположить их приблизительно на диаграмме числовых линий и оценить значение выражений (например, π2). Например, усекая десятичное разложение √2, покажите, что √2 находится между 1 и 2, затем между 1,4 и 1,5, и объясните, как продолжить, чтобы получить более точные приближения.
 (8.НС.А.2) (ДОК 1,2)
(8.НС.А.2) (ДОК 1,2)
Выражения и уравнения (8.EE)
Работа с радикалами и целыми показателями. (8.EE.A)
- Знать и применять свойства целочисленных показателей степени для создания эквивалентных числовых выражений. Например, 32 × 3–5 = 3–3 = 1/33 = 1/27. (8.EE.A.1) (DOK 1)
- Используйте символы квадратного корня и кубического корня для представления решений уравнений вида x2 = p и x3 = p, где p — положительное рациональное число. Вычислите квадратные корни из маленьких совершенных квадратов и кубические корни из маленьких совершенных кубов. Знайте, что √2 иррационально. (8.EE.A.2) (ДОК 1)
- Используйте числа, выраженные в виде одной цифры, умноженной на целую степень числа 10, для оценки очень больших или очень малых величин и для выражения того, во сколько раз одно больше другого. Например, оцените население Соединенных Штатов как 3 × 108, а население мира как 7 × 109 и определите, что население мира более чем в 20 раз больше. (8.
 EE.A.3) (DOK 1,2)
EE.A.3) (DOK 1,2) - Выполнение операций с числами, выраженными в экспоненциальном представлении, включая задачи, в которых используется как десятичное, так и экспоненциальное представление. Используйте научные обозначения и выбирайте единицы соответствующего размера для измерения очень больших или очень малых величин (например, используйте миллиметры в год для распространения по морскому дну). Интерпретировать научную нотацию, созданную технологией. (8.EE.A.4) (ДОК 1,2)
Понимать связи между пропорциональными отношениями, линиями и линейными уравнениями. (8.EE.B)
- График пропорциональных соотношений, интерпретируя удельную скорость как наклон графика. Сравните два разных пропорциональных отношения, представленных по-разному. Например, сравните график «расстояние-время» с уравнением «расстояние-время», чтобы определить, какой из двух движущихся объектов имеет большую скорость. (8.EE.B.5) (ДОК 1,2,3)
- Используйте подобные треугольники, чтобы объяснить, почему наклон m одинаков между любыми двумя различными точками на невертикальной линии в координатной плоскости; выведите уравнение y = mx для прямой, проходящей через начало координат, и уравнение y = mx + b для прямой, пересекающей вертикальную ось в точке b.
 (8.EE.B.6) (ДОК 1,2,3)
(8.EE.B.6) (ДОК 1,2,3)
Анализ и решение линейных уравнений и пар одновременных линейных уравнений. (8.EE.C)
- Решение линейных уравнений с одной переменной.
- Приведите примеры линейных уравнений с одной переменной с одним решением, бесконечным числом решений или без решений. Покажите, какая из этих возможностей имеет место, последовательно преобразовывая данное уравнение в более простые формы, пока не получится эквивалентное уравнение вида x = a, a = a или a = b (где a и b — разные числа).
- Решите линейные уравнения с коэффициентами рациональных чисел, включая уравнения, решения которых требуют расширения выражений с использованием свойства дистрибутивности и сбора подобных членов. (8.EE.C.7) (DOK 1,2)
- Анализ и решение пар одновременных линейных уравнений.
- Поймите, что решения системы двух линейных уравнений с двумя переменными соответствуют точкам пересечения их графиков, потому что точки пересечения удовлетворяют обоим уравнениям одновременно.

- Решите системы двух линейных уравнений с двумя переменными алгебраически и оцените решения, построив уравнения в виде графика. Решите простые случаи путем проверки. Например, 3x + 2y = 5 и 3x + 2y = 6 не имеют решения, потому что 3x + 2y не может быть одновременно 5 и 6.
- Решите реальные и математические задачи, ведущие к двум линейным уравнениям с двумя переменными. Например, зная координаты двух пар точек, определите, пересекает ли линия, проходящая через первую пару точек, линию, проходящую через вторую пару. (8.EE.C.8) (ДОК 1,2,3)
Функции (8.F)
Определение, оценка и сравнение функций. (8.F.A)
- Поймите, что функция — это правило, которое назначает каждому входу ровно один выход. График функции представляет собой набор упорядоченных пар, состоящих из входа и соответствующего выхода. (8.Ф.А.1) (ДОК 1,2)
- Сравните свойства двух функций, каждая из которых представлена по-разному (алгебраически, графически, численно в таблицах или словесными описаниями).
 Например, если дана линейная функция, представленная таблицей значений, и линейная функция, представленная алгебраическим выражением, определите, какая функция имеет большую скорость изменения. (8.Ф.А.2) (ДОК 1,2)
Например, если дана линейная функция, представленная таблицей значений, и линейная функция, представленная алгебраическим выражением, определите, какая функция имеет большую скорость изменения. (8.Ф.А.2) (ДОК 1,2) - Интерпретировать уравнение y = mx + b как определяющее линейную функцию, график которой представляет собой прямую линию; приведите примеры функций, которые не являются линейными. Например, функция A = s2, задающая площадь квадрата как функцию длины его стороны, не является линейной, поскольку ее график содержит точки (1,1), (2,4) и (3,9), которые равны не по прямой. (8.F.A.3) (ДОК 1,2)
Используйте функции для моделирования отношений между величинами. (8.F.B)
- Построить функцию для моделирования линейной зависимости между двумя величинами. Определить скорость изменения и начальное значение функции по описанию зависимости или по двум значениям (x, y), в том числе прочитать их из таблицы или из графика. Интерпретируйте скорость изменения и начальное значение линейной функции с точки зрения ситуации, которую она моделирует, и с точки зрения ее графика или таблицы значений.
 (8.Ф.Б.4) (ДОК 1,2,3)
(8.Ф.Б.4) (ДОК 1,2,3) - Качественно описать функциональную связь между двумя величинами, анализируя график (например, где функция возрастает или убывает, линейна или нелинейна). Нарисуйте график, демонстрирующий качественные характеристики функции, описанной словесно. (8.Ф.Б.5) (ДОК 1,2,3)
Геометрия (8.G)
Понимание конгруэнтности и подобия с помощью физических моделей, прозрачных пленок или программного обеспечения для геометрии. (8.G.A)
- Проверить экспериментально свойства вращения, отражения и перемещения:
- Линии превращаются в прямые, а отрезки прямых в отрезки одинаковой длины.
- Углы принимают за углы одной и той же меры.
- Параллельные линии превращаются в параллельные. (8.G.A.1) (ДОК 2)
- Понять, что двумерная фигура конгруэнтна другой, если вторая может быть получена из первой последовательностью поворотов, отражений и перемещений; Даны две конгруэнтные фигуры, опишите последовательность, демонстрирующую их конгруэнтность.
 (8.Г.А.2) (ДОК 1,2)
(8.Г.А.2) (ДОК 1,2) - Описать эффект расширения, перемещения, поворота и отражения двухмерных фигур с использованием координат. (8.Г.А.3) (ДОК 1,2)
- Понять, что двумерная фигура подобна другой, если вторая может быть получена из первой последовательностью поворотов, отражений, перемещений и расширений; Имея две подобные двумерные фигуры, опишите последовательность, демонстрирующую сходство между ними. (8.Г.А.4) (ДОК 1,2)
- Используйте неформальные аргументы, чтобы установить факты о сумме углов и внешнем угле треугольников, об углах, образующихся при пересечении параллельных прямых секущей, и критерий угла-угла для подобия треугольников. Например, расположите три копии одного и того же треугольника так, чтобы сумма трех углов представляла собой линию, и приведите аргумент в терминах секущей, почему это так. (8.Г.А.5) (ДОК 1,2,3)
Понять и применить теорему Пифагора. (8.G.B)
 (8.G.B.6) (ДОК 2,3)
(8.G.B.6) (ДОК 2,3)Решайте реальные и математические задачи на объем цилиндров, конусов и сфер. (8.G.C)
Статистика и вероятность (8.SP)
Исследовать закономерности связи в двумерных данных. (8.СП.А)
- Построение и интерпретация точечных диаграмм для данных двумерных измерений для исследования закономерностей связи между двумя величинами. Опишите шаблоны, такие как кластеризация, выбросы, положительная или отрицательная связь, линейная связь и нелинейная связь. (8.СП.А.1) (ДОК 1,2,3)
- Знайте, что прямые линии широко используются для моделирования отношений между двумя количественными переменными.
 Для точечных диаграмм, которые предполагают линейную связь, неформально аппроксимируют прямую линию и неформально оценивают соответствие модели, оценивая близость точек данных к линии. (8.СП.А.2) (ДОК 1,2)
Для точечных диаграмм, которые предполагают линейную связь, неформально аппроксимируют прямую линию и неформально оценивают соответствие модели, оценивая близость точек данных к линии. (8.СП.А.2) (ДОК 1,2) - Используйте уравнение линейной модели для решения задач в контексте данных двумерных измерений, интерпретируя наклон и точку пересечения. Например, в линейной модели для биологического эксперимента интерпретируйте наклон 1,5 см/ч как означающий, что дополнительный час солнечного света каждый день связан с дополнительными 1,5 см высоты взрослого растения. (8.СП.А.3) (ДОК 1,2)
- Поймите, что закономерности ассоциации также можно увидеть в двумерных категориальных данных, отображая частоты и относительные частоты в двусторонней таблице. Постройте и интерпретируйте двустороннюю таблицу, обобщающую данные по двум категориальным переменным, собранным у одних и тех же субъектов. Используйте относительные частоты, рассчитанные для строк или столбцов, чтобы описать возможную связь между двумя переменными.
 Например, соберите данные от учеников вашего класса о том, соблюдается ли у них комендантский час по вечерам в школе и есть ли у них работа по дому. Есть ли доказательства того, что те, у кого комендантский час, также, как правило, занимаются домашними делами? (8.СП.А.4) (ДОК 1,2,3)
Например, соберите данные от учеников вашего класса о том, соблюдается ли у них комендантский час по вечерам в школе и есть ли у них работа по дому. Есть ли доказательства того, что те, у кого комендантский час, также, как правило, занимаются домашними делами? (8.СП.А.4) (ДОК 1,2,3)
рабочих листов | TPT
by
Kaitlynn Albani
Внутри вы найдете 6 забавных и уникальных шрифтов в ZIP-файле! Большинство акцентных символов включены во все шрифты. Пожалуйста, проверьте предварительный просмотр, чтобы увидеть все шрифты, включенные в этот набор! Примечания. Включено 5 шрифтов + 1 шрифт для каракулей. Все шрифты с заглавными буквами Elementary. Проверьте предварительный просмотр, чтобы увидеть все шрифты в действии! $ СЭКОНОМЬТЕ ДЕНЬГИ $ БОЛЕЕ 400 ШРИФТОВ + КАЖДЫЙ НОВЫЙ ШРИФТ БЕСПЛАТНО! ПРОВЕРЬТЕ РАСШИРЯЮЩИЙСЯ НАБОР ШРИФТОВ ЗДЕСЬУсловия использования * Шрифты
Предметы:
Для всех предметов, Товары для продавцов ТРТ, Специальность
Классы:
PreK — 12th, Высшее образование, Обучение взрослых, Штат by
Учитель по соседству
18,00 $
14,25 $
Bundle
Ищете способ сделать обучение написанию абзацев намного проще? Хотите помочь своим ученикам писать хорошо продуманные абзацы? Этот полный набор для написания абзацев как в печатном, так и в цифровом виде поможет вам научить каждую часть абзаца напрямую! Он сочетает в себе четыре моих очень популярных набора стратегий письма: цветовое кодирование и выделение абзацев, тематические предложения, переходы в письме и заключительные предложения. Здесь есть все, что вам нужно, чтобы помочь вашим ученикам по-настоящему понять, как создавать
Здесь есть все, что вам нужно, чтобы помочь вашим ученикам по-настоящему понять, как создавать
Предметы:
Английская словесность, информационный текст, письменное объяснение
Классы:
3-8
Типы:
Графические органайзеры, плакаты
CCSS:
2, W.3.3003, W.30003 .5.2, W.5.2a, W.5.2b…
by
My Teaching Pal
22,00 $
15,00 $
Bundle
Этот комплект содержит ОГРОМНЫЕ 263 математических листа для первых классов! Рабочие листы охватывают сложение и вычитание, числа и разрядность, 2D и 3D фигуры, данные и графики, дроби и разбиение на части и время. Эти веселые рабочие листы отлично подходят для использования в течение всего года, они идеально подходят для занятий в классе, математических станций, быстрых финишеров, домашних заданий и повторения. Этот комплект состоит из следующих пакетов: Рабочие листы для сложения и вычитания для первого классаРабочие листы для первого класса 2D и 3D
Субъекты:
Основные операции, математика, номера
Оценки:
Типы:
печатные изделия, рабочие книги, рабочие листы
по
Lucky Little Cemancers
$ 34. 00
00
$ 23.00
. или Phonics Mats, являются идеальным ресурсом без подготовки, распечатайте и идите, чтобы помочь учащимся превратить отдельные фонетические навыки в чтение текста! Учащиеся практикуют изолированные фонетические навыки, декодирование, беглость речи и понимание в одном ресурсе. *** НОВОЕ ОБНОВЛЕНИЕ *** Этот ресурс обновлен новой версией 2022 года! В новых ковриках для фонетики есть декодируемые отрывки, вопросы на понимание, практика написания слов и страница для разминки для каждого навыка. Обязательно загрузите превью
Предметы:
Акустика, чтение, письмо
Классы:
Типы:
Печатные формы, рабочие листы
CCSS:
RF.2.3, RF.2.3c, RF.2.2.2 .2.3d…
по
Путь 2 Успех
14,00 $
Используйте эти уроки, чтобы развить у детей навыки самоконтроля! Действия сосредоточены на понимании самоконтроля, импульсивного контроля, остановке и обдумывании, чтобы принять решение, ожидании своей очереди, соблюдении правил и указаний, сохранении мотивации, выполнении нашей работы наилучшим образом, управлении эмоциями, использовании стратегий преодоления и практике самоконтроля для укрепления. навыки со временем. Также рассматриваются другие навыки, влияющие на самоконтроль, включая планирование, управление временем и настойчивость. Цифровая версия обновлена до 9.0003
навыки со временем. Также рассматриваются другие навыки, влияющие на самоконтроль, включая планирование, управление временем и настойчивость. Цифровая версия обновлена до 9.0003
Предметы:
Школьное консультирование, социальное эмоциональное обучение, специальное образование
Оценки:
4 -й — 8 -е
Типы:
Урок, печатные изготовления
на
Ничего, кроме класса
$ 15.75
Это новое исследование для номана. «Отверстия» Луиса Сашара содержит 124 страницы ресурсов, включая понимание и словарный запас по главам, действия по чтению ответов, оценки и многое другое. Стандарты фокусировки включают образный язык, тему, анализ персонажей, сюжет и написание мнений. Не требующее подготовки, предсказуемое и чрезвычайно удобное для пользователя, это руководство по литературе идеально подходит для всего класса, небольшой группы или самостоятельного изучения. ♥Вы можете использовать печатную или цифровую версию; ОБА входят в комплект поставки Pur 9. 0003
0003
субъекты:
Английский язык искусства, литература, чтение
Оценки:
3 -й — 6th
Типы:
Литературные круги, печатные изготовления
CCS:
RL.3.2, RL.3.3, RL. RL.3.6, RL.3.7…
Также включено в: Holes and The Lion, the Witch, and the Платяной шкаф | Novel Study Bundle
by
Patricia Pat Resources
$10.00
Трудно ли вашим ученикам писать полные предложения или строить предложения? Если это так, вам понравится, как эти рабочие листы для написания предложений помогут вам научить строить и писать полные предложения. ✏️ Многие задания в этом пакете помогут вашим ученикам ЯСНО ПОНЯТЬ структуру предложения и создать уверенную и прочную основу для письма. ✏️ Это ресурс без предварительной подготовки, который понравится даже неохотным писателям, плюс вы сэкономите много времени с Дифференциациями и Scaffoldi 9.0003
Предметы:
EFL — ESL — ELD, английский язык, специальное образование
Классы:
K — 3-й
Типы:
Центры, распечатки, рабочие листы
CC0SS3 1. 1a, W.K.2, W.2.3, SL.1.5…
1a, W.K.2, W.2.3, SL.1.5…
Также включено в: Центр написания предложений | Полные предложения | Структура предложения | Малые группы
по
Джоанн Миллер
Вы хотите познакомить своих учеников с новыми жанрами или новым выбором книг? Проведите ДЕГУСТАЦИЯ КНИГ в своем классе! Это мероприятие мотивирует и вдохновляет ваших учеников на чтение! Проводите это мероприятие 2-3 раза в год в своем классе и/или сделайте его вечерним, чтобы родители могли «попробовать» новые книги со своими детьми. Ресурс включает в себя: книжное дегустационное меню салфетки для рефлектора закладки предварительный просмотр книги знаки жанров с определениями жанровые закладки с определениями семь признаков событий, таблица
субъекты:
Английский языковой искусство, чтение
Оценки:
3 -е — 8 -е
Типы:
Действия, для родителей
на
Джоан Миллер
УВЕЛИЧА примечания. Эти игровые доски можно использовать с любым предметом или уроком. Они идеально подходят для обзора или подготовки к тесту. Учащиеся могут работать как команды, партнеры или весь класс. Используйте свой уже распечатанный рабочий лист или рабочую тетрадь и добавьте эти игровые доски, чтобы заинтересовать и мотивировать своих учеников! Это идеальный способ оживить повторный урок или использовать его для подготовки к экзаменам. ***Включены версии PowerPoint и PDF. *Эти игровые доски были дези
Эти игровые доски можно использовать с любым предметом или уроком. Они идеально подходят для обзора или подготовки к тесту. Учащиеся могут работать как команды, партнеры или весь класс. Используйте свой уже распечатанный рабочий лист или рабочую тетрадь и добавьте эти игровые доски, чтобы заинтересовать и мотивировать своих учеников! Это идеальный способ оживить повторный урок или использовать его для подготовки к экзаменам. ***Включены версии PowerPoint и PDF. *Эти игровые доски были дези
Предметы:
Английский язык, для всех предметов, математика
Классы:
2–6
Типы:
Задания, игры, презентации PowerPoint
Также включены в: Интерактивный набор игр Вовлечение учащихся
by
Кейтлин Олбани
Этот ресурс представляет собой более продвинутую версию моих отрывков для чтения в детском саду, предназначенную для первого класса / начала второго класса. Пожалуйста, посмотрите на изображения для предварительного просмотра, чтобы определить, соответствует ли этот набор потребностям ваших учеников. Этот пакет состоит из двух разделов, сложность которых постепенно увеличивается. 20 отрывков = заголовок, отрывок для чтения, картинка, 4 вопроса с несколькими вариантами ответов 20 отрывков = заголовок, отрывок для чтения, картинка, 4 вопроса для записи. Вы можете найти набор для чтения для начинающих, похожий на этот по кл
Этот пакет состоит из двух разделов, сложность которых постепенно увеличивается. 20 отрывков = заголовок, отрывок для чтения, картинка, 4 вопроса с несколькими вариантами ответов 20 отрывков = заголовок, отрывок для чтения, картинка, 4 вопроса для записи. Вы можете найти набор для чтения для начинающих, похожий на этот по кл
субъекты:
Английский язык искусства, чтение, стратегии чтения
Оценки:
1 -й — 2 -й
Типы:
Центры, печатные изготовления, рабочие листы
по
Девушки Moffatt
. концепция для многих видов, но этот пакет NO PREP наполнен практическими здесь, увлекательными и забавными ресурсами, чтобы помочь детям освоить эту концепцию. час⭐️ Время с шагом в десять минут⭐️ Время с шагом в пять минут⭐️ Время с шагом в 1 минутуЛУЧШЕЕ в этом пакете то, что НЕТ ПОДГОТОВКИ! БЕЗ ламинирования, БЕЗ дорогостоящих цветных чернил, БЕЗ резки… просто ПЕЧАТАЙТЕ и УЧИТЕСЬ!
Предметы:
Классы:
1-3
Типы:
Центры, Печатные формы, Рабочие листы
by
Кейтлин Олбани
3 900 проходов внутри детского сада 600023 900 проходов! Эти отрывки отлично подходят для детей младшего возраста, а также подойдут для первоклассников или первоклассников, в зависимости от того, как вы их используете. В комплекте много разнообразия. Пожалуйста, проверьте изображения и просмотрите, чтобы увидеть, подойдут ли эти отрывки для ваших учеников. Отрывки разбиты на три категории… Первые 20 отрывков: Основная история с 3 вопросами. Студентам дается два ответа на выбор на каждый вопрос. Вторые 20 отрывков: Базовый
В комплекте много разнообразия. Пожалуйста, проверьте изображения и просмотрите, чтобы увидеть, подойдут ли эти отрывки для ваших учеников. Отрывки разбиты на три категории… Первые 20 отрывков: Основная история с 3 вопросами. Студентам дается два ответа на выбор на каждый вопрос. Вторые 20 отрывков: Базовый
Предметы:
Английский язык искусства, чтение, стратегии чтения
Оценки:
K — 1st
Типы:
Центры, печатные изготовления, рабочие листы
на
ваши ученики практикуют почерк, в котором они нуждаются, в увлекательной форме. Они будут развивать выносливость при письме, повторять построение букв и цифр и практиковаться в словах, изучая новые шутки и забавные факты! и почерк, который не является «детским»? Глупые шутки и забавные факты привлекут ваших учеников, пока они
субъекты:
Сбалансированная грамотность, почерк, написание
. НАПОЛНЕН увлекательными заданиями, которые помогут учащимся освоить простые дроби! УДОВОЛЬСТВИЕ, практический и интерактивный подход позволяет преподавателям учить несколькими способами! ЛУЧШЕЕ в этом пакете то, что НЕТ ПОДГОТОВКИ! БЕЗ ламинирования, БЕЗ дорогостоящих цветных чернил, БЕЗ резки… просто ПЕЧАТАЙТЕ и УЧИТЕСЬ!0003
Subjects:
Fractions, Math, Word Problems
Grades:
1st — 3rd
Types:
Centers, Printables, Worksheets
by
My Nerdy Teacher by Alina V
$100. 00
00
$19.00
⭐⭐⭐ СРОЧНАЯ РАСПРОДАЖА ⭐⭐⭐Получите Mega Bundle The Decodable Readers Passages всего за 19 долларов! Спешите, время истекает! Ваши ученики могут практиковаться в чтении в увлекательной игровой форме, используя эти декодируемые тексты. Наука чтения AlignedLow Требуется подготовка. Просто распечатайте и идите. Эти декодируемые отрывки помогут вашим ученикам практиковать фонетические модели, которым вы их учите. Идеально подходит для центров, домашних заданий, утренней работы и многого другого. Печатные и цифровые (Google Slides™) Идеально подходит для дошкольного детского сада, 1-й класс
Предметы:
Акустика, Чтение, Письмо
Классы:
К — 2-й
Виды:
Занятия, Центры, Печатные формы
CCSS, RF.K.3.K. .K.3c, RF.1.2c, RF.1.2d…
по
Универсальный центр для учителей
14,99 $
9,99 $
Ваши учащиеся испытывают трудности при написании хорошо структурированных абзацев? Paragraph of the Week, еженедельная система практики написания абзацев, предоставит вашим ученикам МНОГО возможностей для практики в написании хорошо организованных абзацев в увлекательной и увлекательной форме. Получите задания по написанию абзацев и письменные подсказки на весь год! ЦИФРОВАЯ версия также включена! Студенты могут печатать прямо на страницах. Создано с помощью Google Slides. Идеально подходит для Google Classroom или любой онлайн-платформы обучения. САВ
Получите задания по написанию абзацев и письменные подсказки на весь год! ЦИФРОВАЯ версия также включена! Студенты могут печатать прямо на страницах. Создано с помощью Google Slides. Идеально подходит для Google Classroom или любой онлайн-платформы обучения. САВ
Предметы:
Английский язык искусства, письменное письмо, письменное экспозиция
Оценки:
3 -е — 6 -е
Типы:
Центры, домашнее задание
также включены в: чтение и письменный пакет ресурсов
на
Брокек. Reagan
Visual Classroom Schedules *** Этот продукт был обновлен в декабре 2022 г.: Включает в себя больше вариантов шаблонов расписаний, больше карточек с расписаниями и больше редактируемых параметров! Никаких предварительных распечаток и редактируемых вариантов визуальных расписаний для учащихся. В визуальном расписании используются изображения, чтобы сообщать о предстоящих мероприятиях и задачах для учащихся. Многие учащиеся могут извлечь пользу из использования визуального расписания, поскольку оно обеспечивает структуру. Эти визуальные расписания легко редактировать и модифицировать в соответствии с вашими потребностями. Полезно wi
Эти визуальные расписания легко редактировать и модифицировать в соответствии с вашими потребностями. Полезно wi
субъекты:
Управление в классе, для всех предметов, специальное образование
. способ научить предварительным навыкам письма, основам почерка и укрепить мелкую моторику мышц. В дневнике так много упражнений на мелкую моторику! Это похоже на мини-портфолио всех их мелкой моторики, все организовано и собрано в одном месте, что позволяет легко визуально увидеть рост ученика. Вот некоторые действия, которые можно выполнять в дневниках мелкой моторики: написание типов строк/букв (также известный как забавный почерк), действия с именами, действия с буквами, действия с числами, печать ac
Субъекты:
Английский язык искусства
Оценки:
Prek — K
Типы:
Действия
Также включены в: Preschool, Pre -K и Cindergarten Complete Curric Bundle
на
Deedee
33333333333333333333333333333333333333333333333333333333333333н.
$10.00
Практика письма и обучение здесь! Умение свободно писать буквы приводит к большим успехам в чтении. Исследования мозга подтверждают необходимость четкого почерка и инструкций по движению и связывают правильный почерк с лучшими письменными результатами учащихся! Быстро, лаконично, легко реализовать! Моя своеобразная инструкция по письму. УРОКИ ПОЧЕРКОПИСАНИЯ — ЭТО НЕ ТОЛЬКО ЕЩЕ ОДНА ВЕЩЬ! Когда вы обучаете учащихся письму во время обучения фонетике, у учащихся развивается кинестетическая мышечная память на все
Субъекты:
Сбалансированная грамотность, английский язык искусства, почерк
Оценки:
Prek — 1st
Типы:
, печатные изготовления
CCS:
L.K.1A
.
25,00 $
Полный комплект учебников для детского сада, игр, раскрашивания по коду и многого другого для более чем 200 высокочастотных слов! ЛУЧШИЙ ПРОДАВЕЦ на TpT с более чем 7000 отзывов учителей! Оцените эту невероятную стоимость всего, что вам нужно для практики словесного зрения! Ваша практика словесного зрения стала намного лучше благодаря этому огромному файлу печатных форм, занятий, центров и многого другого. Каждое включенное прицельное слово имеет отдельный файл с 67 страницами действий! Идеально подходит для детского сада, первого класса
Каждое включенное прицельное слово имеет отдельный файл с 67 страницами действий! Идеально подходит для детского сада, первого класса
Предметы:
Английский язык, чтение
Классы:
PreK — 1st
Типы:
Занятия, распечатки, рабочие листы
CCSS, RF.3.9002. .K.3c
by
WFO Creative
Шаблоны резюме учителей разработаны специально для преподавателей. Все шаблоны загружены образовательной терминологией, образцами текста и советами. Преподавателям больше не нужно переформатировать шаблоны в соответствии с потребностями, связанными с образованием.страницы загружены информацией о написании резюме, связанном с образованием и обучением. Качественные и проверенные шаблоны резюме с чистым и современным дизайном. Идеальный способ произвести наилучшее впечатление. Легко E
Субъекты:
занятость
Оценки:
Не специфические оценки
Типы:
Профессиональные документы
на
Эми Гроусбек
Сохранить 25% и покупка выбора Ag в растущем пучке! Пакет включает в себя 8 шрифтов истинного типа с испанским, французским и норвежским акцентами: AG Можете ли вы не AG Можете ли вы не светиться AG Можете ли вы не жирный AG Couch PotatoAG Как вы выживаете AG Нет вопросов сегодня AG Тако вторник AG Это нет от меня Посмотрите предварительный просмотр, чтобы увидеть, что именно вы получите! Хотите больше шрифтов? Проверьте: AG Fonts Volume OneAG Fonts Volume TwoAG Fonts Volume ThreeAG Fonts Volume FiveAG Fonts Volume SixAG Fonts Volume SevenAG Fonts
Предметы:
Другие (специальные), продукты для продавцов TpT
Классы:
Не зависят от класса
Типы:
Bundle
by
Amy Groesbeck
Сэкономьте 25% и приобретите шрифты AG Select в РАСТУЩЕМ НАБОРЕ! BundayAG Нет, не сегодняAG Опоздание — это мое кардиоAG Извините, не извиняйтесьAG Третий — это WordВсе шрифты включают испанский, французский, норвежский и немецкий акценты, а также макронизированные гласные. **ОБНОВЛЕНО: 17.02.22** Заглавные буквы добавлены ко всем шрифтам Вам нужен сон, а третий — слово. Посмотрите предварительный просмотр, чтобы узнать, что именно вы получите!W
**ОБНОВЛЕНО: 17.02.22** Заглавные буквы добавлены ко всем шрифтам Вам нужен сон, а третий — слово. Посмотрите предварительный просмотр, чтобы узнать, что именно вы получите!W
Субъекты:
Продукты для продавцов TPT
Оценки:
Не специфические оценки
Типы:
Продавцы TPT для продавцов TPT, Fonts
также включены в: Amy Groesbeck Fonts: растущий пучок
на
.Rachel Lynette
Префиксы, суффиксы и корни необходимы для расширения словарного запаса, и эти рабочие листы идеально подходят для того, чтобы учащиеся отрабатывали проблемы с префиксами, суффиксами и корнями. » Слайды GoogleПрефиксы и суффиксы для самостоятельной оценки Быстрые викторины (формы Google)Упражнения в мольбертеВАРИАНТЫ РАЗЛИЧИЯ:Цифровой или печатный Самопроверка или краткий ответМного разных уровней заданийОтлично подходит для 3-го, 4-го, 5-го или 6-го класса! ПОСМОТРЕТЬ ПРЕДВАРИТЕЛЬНУЮ
Субъекты:
EFL — ESL — ELD, ELA TEST PREP, Словарь
Оценки:
3 -е — 6th
Типы:
Независимый рабочий пакет, рабочие листы
CCSS:
L. 4B, L. 4.4b, L.5.4b, CCRA.L.4
4B, L. 4.4b, L.5.4b, CCRA.L.4
Также включено в: ELA Review No Prep Bundle, Grammar and Vocabulary Printed and Digital Versions
CMP2 Grade 8 — Connected Mathematics Project
Thinking with Mathematical Models
Main Идеи | Примеры домашних заданий
В разделе «Мышление с помощью математических моделей» учащиеся будут изучать, сравнивать и обобщать две очень разные схемы, связанные с двумя переменными. В частности, они узнают, как:
- Распознавать линейные и нелинейные закономерности в таблицах и графиках и описывать эти закономерности с помощью слов и символьных выражений;
- Напишите уравнения для выражения линейных закономерностей, появляющихся в таблицах, графиках и задачах «историй»;
- Решение линейных уравнений;
- Модели ситуаций с неравенствами;
- Напишите уравнения, описывающие обратную вариацию;
- Используйте линейные и обратные уравнения для решения задач, прогнозирования и принятия решений.

В поисках Пифагора
Основные идеи | Примеры проработанной домашней работы
В поисках Пифагора учащиеся изучают важное соотношение прямоугольных треугольников, которое связывает алгебру и геометрию, называемое теоремой Пифагора. Они учатся:
- Соотносить площадь квадрата с длиной стороны квадрата;
- Оценка квадратных корней;
- Разработка стратегий нахождения расстояния между двумя точками на координатной сетке;
- Понять и применить теорему Пифагора;
- Используйте теорему Пифагора для решения множества задач.
Рост, рост, рост
Основные идеи | Worked Homework Examples
Growing, Growing, Growing был создан, чтобы помочь учащимся разобраться в экспоненциальных отношениях. В этом блоке студенты научатся:
- Распознавать ситуации, когда одна переменная является экспоненциальной функцией другой переменной;
- Распознавать связи между экспоненциальными уравнениями и закономерностями роста в таблицах и графиках этих отношений;
- Построение уравнений для выражения экспоненциальных закономерностей, которые появляются в таблицах данных, графиках и условиях задачи;
- Понимать и применять правила работы с числовыми выражениями с показателями степени;
- Решать задачи об экспоненциальном росте и убывании в различных ситуациях, таких как наука или бизнес;
- Сравните экспоненциальные и линейные зависимости.

Лягушки, блохи и нарисованные кубики
Основные идеи | Примеры выполненных домашних заданий
В «Лягушках, блохах и раскрашенных кубиках» учащиеся изучают важный тип нелинейных отношений — квадратичные функции. Модуль должен помочь учащимся:
- Распознать закономерности изменения квадратичных отношений в таблице, графике, уравнении и проблемной ситуации;
- Построение уравнений для выражения квадратичных отношений, которые появляются в таблицах, графиках и проблемных ситуациях;
- Распознавать связи между квадратными уравнениями и шаблонами в таблицах и графиках этих отношений;
- Используйте квадратичные таблицы, графики и уравнения для определения максимального и минимального значений зависимой переменной, точек пересечения x и y и других важных характеристик парабол, графиков квадратичных зависимостей;
- Распознавать эквивалентные символьные выражения для зависимой переменной в квадратичных соотношениях;
- Используйте распределительное свойство для записи эквивалентных квадратных выражений в факторизованной или расширенной форме;
- Использование таблиц, графиков и уравнений квадратичных отношений для решения задач в различных ситуациях из геометрии, естественных наук и бизнеса;
- Сравните свойства квадратичных, линейных и экспоненциальных зависимостей.

Калейдоскопы, колпаки и зеркала
Основные идеи | Примеры выполненных домашних заданий
В разделе «Колпаки, калейдоскопы и зеркала» учащиеся исследуют симметрию и преобразования. Этот модуль поможет им:
- Понять важные свойства симметрии;
- Распознавать и описывать симметрию фигур;
- Используйте инструменты для изучения симметрий и преобразований;
- Создание фигур с заданной симметрией;
- Определить основные элементы дизайна, которые можно использовать для воспроизведения данного дизайна;
- Выполнять преобразования симметрии фигур, включая отражения, переводы и повороты;
- Изучить и описать симметрию рисунка, созданного из фигуры и ее изображений при преобразовании симметрии;
- Дайте точные математические указания для выполнения отражений, вращений и перемещений;
- Делать выводы о фигуре, такие как размеры сторон и углов, длины диагоналей или точки пересечения диагоналей, на основе того, какой симметрией или симметриями обладает фигура;
- Поймите, что фигуры одинаковой формы и размера конгруэнтны;
- Используйте преобразования симметрии, чтобы выяснить, конгруэнтны ли две фигуры;
- Приведите примеры минимальных наборов мер углов и сторон, гарантирующих конгруэнтность двух треугольников;
- Используйте конгруэнтность треугольников, чтобы исследовать конгруэнтность двух четырехугольников;
- Использовать симметрию и конгруэнтность для вывода свойств фигур;
- Написать правила координат для задания изображения общей точки (x, y) при определенных преобразованиях;
- Научитесь ценить силу трансформационной геометрии для описания движений, узоров, конструкций и свойств форм в реальном мире
Скажи это символами
Основные идеи | Примеры домашних заданий
Say It With Symbols был создан, чтобы помочь учащимся разобраться в символических представлениях. В этом разделе студенты учатся:
В этом разделе студенты учатся:
- Моделировать ситуации с помощью символических выражений;
- Напишите эквивалентные выражения;
- Определить, являются ли математически эквивалентными различные символьные выражения;
- Интерпретировать информационные эквивалентные выражения, представленные в данном контексте;
- Определите, какое эквивалентное выражение использовать для ответа на определенные вопросы;
- Решение линейных уравнений с использованием скобок;
- Решать квадратные уравнения факторингом;
- Используйте уравнения, чтобы делать прогнозы и принимать решения;
- Просканируйте уравнение, чтобы оценить закономерности, которые появятся в табличном или графическом представлении;
- Понимать, как и когда следует использовать символы для отображения отношений, обобщений и доказательств.
Формы алгебры
Основные идеи | Примеры домашних заданий
The Shapes of Algebra был разработан, чтобы помочь учащимся извлечь выгоду из тесных связей между алгеброй и геометрией, чтобы расширить понимание и навыки учащихся в нескольких важных аспектах этих двух ключевых направлений в учебной программе средних классов:
- Создание и использование уравнений кругов
- Определите, являются ли линии параллельными или перпендикулярными, просматривая закономерности на их графиках, координатах вершин и уравнениях
- Найдите середины отрезков и используйте отношения средних точек, чтобы вывести дополнительные свойства треугольников и четырехугольников
- Напишите неравенства, удовлетворяющие заданным ситуациям
- Находить решения неравенств по заданному графику или уравнению
- Решать линейные системы и находить пересечения линий и уравнений с помощью графиков, комбинаций и замещений
- Стратегически выберите из трех изученных алгебраических методов тот, который следует использовать для конкретной системы линейных уравнений
- Напишите линейные неравенства с двумя переменными для сопоставления ограничений в условиях задачи
- Графики линейных неравенств с двумя переменными и системами таких условий и использование результатов для решения задач
Выборки и совокупности
Основные идеи | Примеры выполненных домашних заданий
В разделе «Выборки и совокупности» учащиеся собирают, систематизируют и анализируют данные. Они учатся:
Они учатся:
- Использовать процесс статистического исследования для изучения проблем;
- Выберите соответствующие выборки из популяций и используйте информацию из выборок, чтобы сделать выводы о популяциях;
- Изучить влияние размера выборки и процессов отбора выборки при попытке получить выборку, которая может быть предиктивной в отношении генеральной совокупности
- Применение концепций вероятности для выбора случайных выборок из совокупности
- Сравнение выборочных распределений с использованием показателей центра (среднее значение, медиана), показателей разброса (диапазон, от наименьшего до наибольшего значения данных, процентили) и данных, отображающих эти групповые данные (гистограммы, диаграммы в виде коробочек и усов)
- Изучение отношений между парными значениями числовых атрибутов
Умный счет (CMP1)
Основные идеи | Примеры выполненных домашних заданий
Модуль «Умный счет» был разработан, чтобы помочь учащимся:
- Узнавать, какие приемы счета применяются;
- Создавайте упорядоченные списки результатов для сложных процессов и выявляйте закономерности, помогающие подсчитывать результаты этих процессов
- Используйте диаграммы, таблицы и символические выражения для организации примеров в задачах перечисления и подсчета;
- Анализ полезности деревьев подсчета и использование деревьев подсчета;
- Используйте арифметику в уме, чтобы делать оценки в вычислениях умножения и деления;
- Изобретать стратегии для решения задач, связанных со счетом;
- Анализ задач на счет, связанных с выбором в различных контекстах;
- Различать ситуации, в которых порядок имеет и не имеет значения, в которых повторы допускаются и не допускаются;
- Анализ количества путей в сети;
- Сравните структуру сетей с задачами на комбинации;
- Создание сетей, удовлетворяющих заданным ограничениям;
- Применить навыки мышления и рассуждения в ситуации с открытым исходом, в которой необходимо сделать предположения, и создать убедительный аргумент в поддержку предположения;
Standards Toolkit » Common Core Standards по математике для 8-го класса
K123
4567
89-12
Grade 8 PDF
Launch Search
В 8-м классе следует сосредоточиться на трех важных областях обучения и сосредоточиться на трех важных областях обучения: рассуждения о выражениях и уравнениях, включая моделирование ассоциации двумерных данных с линейным уравнением и решение линейных уравнений и систем линейных уравнений; (2) понимание концепции функции и использование функций для описания количественных отношений; (3) анализ двух- и трехмерного пространства и фигур с использованием расстояния, угла, подобия и конгруэнтности, а также понимание и применение теоремы Пифагора.
1. Учащиеся используют линейные уравнения и системы линейных уравнений для представления, анализа и решения различных задач. Учащиеся узнают уравнения для пропорций (y/x = m или y = mx) как специальные линейные уравнения (y = mx + b), понимая, что константа пропорциональности (m) — это наклон, а графики — это линии, проходящие через начало координат. Они понимают, что наклон (m) линии представляет собой постоянную скорость изменения, так что если входные данные или координата x изменяются на величину A, выходные данные или координата y изменяются на величину m·A. Учащиеся также используют линейное уравнение для описания связи между двумя величинами в двумерных данных (например, между размахом рук и ростом учащихся в классе). На этом уровне подгонка модели и оценка ее соответствия данным выполняются неформально. Интерпретация модели в контексте данных требует, чтобы учащиеся выражали взаимосвязь между двумя рассматриваемыми величинами и интерпретировали компоненты взаимосвязи (такие как наклон и пересечение оси Y) с точки зрения ситуации.
Учащиеся стратегически выбирают и эффективно применяют процедуры для решения линейных уравнений с одной переменной, понимая, что при использовании свойств равенства и концепции логической эквивалентности они сохраняют решения исходного уравнения. Учащиеся решают системы двух линейных уравнений с двумя переменными и связывают системы с парами прямых на плоскости; они пересекаются, параллельны или являются одной и той же линией. Учащиеся используют линейные уравнения, системы линейных уравнений, линейные функции и свое понимание наклона линии для анализа ситуаций и решения проблем.
2. Учащиеся усвоили понятие функции как правила, которое назначает каждому входу ровно один выход. Они понимают, что функции описывают ситуации, когда одна величина определяет другую. Они могут переводиться между представлениями и частичными представлениями функций (отмечая, что табличные и графические представления могут быть частичными представлениями), и они описывают, как аспекты функции отражаются в различных представлениях.
3. Учащиеся используют идеи о расстоянии и углах, их поведении при перемещении, вращении, отражении и расширении, а также идеи о конгруэнтности и сходстве для описания и анализа двумерных фигур и решения задач. Учащиеся показывают, что сумма углов в треугольнике есть угол, образованный прямой линией, и что различные конфигурации линий порождают подобные треугольники из-за углов, образующихся при пересечении параллельных прямых секущей. Учащиеся понимают формулировку теоремы Пифагора и ее обратной формы, а также могут объяснить, почему теорема Пифагора верна, например, путем разложения квадрата двумя разными способами. Они применяют теорему Пифагора для нахождения расстояний между точками на координатной плоскости, для нахождения длин и для анализа многоугольников. Учащиеся завершают свою работу над объемом, решая задачи, связанные с конусами, цилиндрами и сферами.
| Домен | Кластер | Код | Единый государственный стандарт |
|---|---|---|---|
| Система счисления | Знай, что есть нерациональные числа, и аппроксимируй их рациональными числами. | 8.НС.1 | Неформально понимать, что каждое число имеет десятичное расширение; рациональные числа имеют десятичные расширения, которые заканчиваются нулями или в конечном итоге повторяются, и наоборот. |
| 8.НС.2 99, и определить, что население мира более чем в 20 раз больше. | |||
| 8.EE.4 | Выполнение операций с числами, выраженными в экспоненциальном представлении, включая задачи, в которых используется как десятичное, так и экспоненциальное представление. Используйте научные обозначения и выбирайте единицы соответствующего размера для измерения очень больших или очень малых величин (например, используйте миллиметры в год для распространения по морскому дну). Интерпретировать научную нотацию, созданную технологией. | ||
| Понимание связей между пропорциональными отношениями, линиями и линейными уравнениями. | 8.EE.5 | График пропорциональных отношений с интерпретацией удельной скорости как наклона графика. Сравните два разных пропорциональных отношения, представленных по-разному. Например, сравните график «расстояние-время» с уравнением «расстояние-время», чтобы определить, какой из двух движущихся объектов имеет большую скорость. Сравните два разных пропорциональных отношения, представленных по-разному. Например, сравните график «расстояние-время» с уравнением «расстояние-время», чтобы определить, какой из двух движущихся объектов имеет большую скорость. | |
| 8.EE.6 | Используйте подобные треугольники, чтобы объяснить, почему наклон m одинаков между любыми двумя различными точками на невертикальной линии в координатной плоскости; выведите уравнение y = mx для линии, проходящей через начало координат, и уравнение y = mx + b для линии, пересекающей вертикальную ось в точке b. | ||
| Анализ и решение линейных уравнений и пар одновременных линейных уравнений. | 8.EE.7 | Решите линейные уравнения с одной переменной. а. Приведите примеры линейных уравнений от одной переменной с одним решением, бесконечным числом решений или отсутствием решений. Покажите, какая из этих возможностей соответствует случаю , последовательно преобразовывая данное уравнение в более простые формы, пока эквивалентное уравнение вида x = a, a = a или a = b не даст (где a и b — разные числа).  б. Решите линейные уравнения с коэффициентами рациональных чисел, включая уравнения, решения которых требуют расширения выражений с использованием дистрибутивного свойства и сбора подобных членов | |
| 8.EE.8 | Анализ и решение пар одновременных линейных уравнений. а. Поймите, что решения системы двух линейных уравнений с двумя переменными соответствуют точкам пересечения их графиков, , потому что точки пересечения удовлетворяют обоим уравнениям одновременно. б. Решите системы двух линейных уравнений с двумя переменными алгебраически и оцените решения, построив уравнения в виде графика. Решите простые случаи путем проверки. Например, 3x + 2y = 5 и 3x + 2y = 6 не имеют решения, потому что 3x + 2y не может одновременно быть 5 и 6. c. Решайте реальные и математические задачи, приводящие к двум линейным уравнениям с двумя переменными. Например, зная координаты двух пар точек, определите, пересекается ли линия, проходящая через первую пару точек, с линией, проходящей через вторую пару.  | ||
| Функции | Определение, оценка и сравнение функций. | 8.F.1 | Поймите, что функция — это правило, которое назначает каждому входу ровно один выход. График функции представляет собой набор упорядоченных пар, состоящих из входа и соответствующего выхода. (Обозначение функции не требуется в 8 классе.) |
| 8.F.2 | Сравните свойства двух функций, каждая из которых представлена по-разному (алгебраически, графически, численно в таблицах или словесными описаниями). Например, если дана линейная функция, представленная таблицей значений, и линейная функция, представленная алгебраическим выражением, определите, какая функция имеет большую скорость изменения. 92, дающая площадь квадрата как функцию длины его стороны, нелинейна, потому что ее график содержит точки (1,1), (2,4) и (3,9), которые не лежат на прямой. | ||
Используйте функции для моделирования отношений между величинами. | 8.F.4 | Создайте функцию для моделирования линейной зависимости между двумя величинами. Определить скорость изменения и начальное значение функции по описанию зависимости или по двум значениям (x, y), в том числе прочитать их из таблицы или из графика. Интерпретируйте скорость изменения и начальное значение линейной функции с точки зрения ситуации, которую она моделирует, и с точки зрения ее графика или таблицы значений. | |
| 8.F.5 | Качественно описать функциональную связь между двумя величинами, анализируя график (например, где функция возрастает или убывает, линейна или нелинейна). Нарисуйте график, демонстрирующий качественные характеристики функции, описанной словесно. | ||
| Геометрия | Понимание конгруэнтности и сходства с использованием физических моделей, прозрачных пленок или программного обеспечения для геометрии. | 8.Г.1 | Экспериментально проверьте свойства вращения, отражения и переноса: а.  Линии превращаются в прямые, а отрезки прямых в отрезки прямой одинаковой длины. Линии превращаются в прямые, а отрезки прямых в отрезки прямой одинаковой длины. б. Углы принимаются равными углам. с. Параллельные прямые переводятся в параллельные прямые. |
| 8.G.2 | Поймите, что двумерная фигура конгруэнтна другой, если вторая может быть получена из первой последовательностью поворотов, отражений и перемещений; Даны две конгруэнтные фигуры, опишите последовательность, демонстрирующую их конгруэнтность. | ||
| 8.G.3 | Опишите эффект расширения, перемещения, поворота и отражения двухмерных фигур с использованием координат. | ||
| 8.G.4 | Поймите, что двумерная фигура подобна другой, если вторая может быть получена из первой последовательностью поворотов, отражений, перемещений и расширений; Имея две подобные двумерные фигуры, опишите последовательность, демонстрирующую сходство между ними. | ||
| 8.G.5 | Используйте неформальные аргументы, чтобы установить факты о сумме углов и внешнем угле треугольников, об углах, образующихся при пересечении параллельных прямых секущей, и критерий угла-угла для подобия треугольников. Например, расположите три копии одного и того же треугольника так, чтобы казалось, что три угла образуют линию, и приведите аргумент в терминах секущей, почему это так. Например, расположите три копии одного и того же треугольника так, чтобы казалось, что три угла образуют линию, и приведите аргумент в терминах секущей, почему это так. | ||
| Понять и применить теорему Пифагора. | 8.Г.6 | Объясните доказательство теоремы Пифагора и ее обращения. | |
| 8.G.7 | Примените теорему Пифагора для определения неизвестных длин сторон в прямоугольных треугольниках в реальных и математических задачах в двух и трех измерениях. | ||
| 8.G.8 | Примените теорему Пифагора, чтобы найти расстояние между двумя точками в системе координат. | ||
| Решайте реальные и математические задачи, связанные с объемом цилиндров, конусов и сфер. | 8.G.9 | Знать формулы объема конусов, цилиндров и сфер и использовать их для решения реальных и математических задач. | |
| Статистика и вероятность | Исследование закономерностей связи в двумерных данных. | 8.СП.1 | Построение и интерпретация диаграмм рассеяния для данных двумерных измерений для исследования закономерностей связи между двумя величинами. Опишите шаблоны, такие как кластеризация, выбросы, положительная или отрицательная связь, линейная связь и нелинейная связь. |
| 8.СП.2 | Знайте, что прямые линии широко используются для моделирования отношений между двумя количественными переменными. Для точечных диаграмм, которые предполагают линейную связь, неформально аппроксимируют прямую линию и неформально оценивают соответствие модели, оценивая близость точек данных к линии. | ||
| 8.СП.3 | Используйте уравнение линейной модели для решения задач в контексте данных двумерных измерений, интерпретации наклона и точки пересечения. Например, в линейной модели для биологического эксперимента интерпретируйте наклон 1,5 см/ч как означающий, что дополнительный час солнечного света каждый день связан с дополнительными 1,5 см высоты взрослого растения. | ||
| 8.СП.4 | Поймите, что закономерности связи также можно увидеть в двумерных категориальных данных, отображая частоты и относительные частоты в двусторонней таблице. Постройте и интерпретируйте двустороннюю таблицу, обобщающую данные по двум категориальным переменным, собранным у одних и тех же субъектов. Используйте относительные частоты, рассчитанные для строк или столбцов, чтобы описать возможную связь между двумя переменными. Например, соберите данные от учеников вашего класса о том, соблюдается ли у них комендантский час по вечерам в школе и есть ли у них работа по дому. Есть ли доказательства того, что те, у кого комендантский час, также, как правило, занимаются домашними делами? |
Математика 8 класса. Национальные стандарты STEM. Национальные стандарты STEM.
Теоретическая вероятность и счет. Теоретическая вероятность — это вероятность того, что определенный результат произойдет на основе всех возможных результатов. Иногда количество способов, которыми может произойти событие, зависит от порядка. Перестановка — это расположение объектов, в котором порядок имеет значение. Комбинация — это набор объектов, порядок в которых не имеет значения. Вероятность также основана на том, являются ли события зависимыми или независимыми друг от друга. Подробнее… iWorksheets: 3Study Guides: 1
Иногда количество способов, которыми может произойти событие, зависит от порядка. Перестановка — это расположение объектов, в котором порядок имеет значение. Комбинация — это набор объектов, порядок в которых не имеет значения. Вероятность также основана на том, являются ли события зависимыми или независимыми друг от друга. Подробнее… iWorksheets: 3Study Guides: 1
Вещественные числа Вещественные числа представляют собой множество рациональных и иррациональных чисел. Множество рациональных чисел включает целые числа, целые числа и натуральные числа. Рациональное число — это число, которое можно превратить в дробь. Десятичные числа, которые повторяются или заканчиваются, рациональны, потому что их можно превратить в дроби. Иррациональное число – это число, которое нельзя превратить в дробь. Десятичные числа, которые не повторяются и не заканчиваются, являются иррациональными числами. Подробнее… iWorksheets: 4Study Guides: 1
ШТОК.М. МАТЕМАТИКА: Национальный совет учителей математики (NCTM)
NCTM.
 1. Номер и операции
1. Номер и операции1.1. Понимать числа, способы представления чисел, отношения между числами и системы счисления.
1.1.1. Гибко работайте с дробями, десятичными знаками и процентами для решения задач.
Десятичные операции Десятичные операции относятся к математическим операциям, которые можно выполнять с десятичными дробями: сложение, вычитание, умножение и деление. Для получения правильного ответа необходимо соблюдать процесс сложения, вычитания, умножения и деления десятичных дробей. Подробнее… iWorksheets :3Учебные пособия :1
Знакомство с процентами Что такое проценты? Процент — это термин, который описывает десятичную дробь с точки зрения ста. Процент означает на сотню. Проценты, дроби и десятичные дроби могут быть равны друг другу, например, 10%, 0,1 и 1/10. Проценты могут быть больше 100% или меньше 1%. Наценка от стоимости изготовления изделия до фактической цены продажи обычно превышает 100%. Комиссия продавца может составлять 1/2% в зависимости от проданного товара. Подробнее… iWorksheets :4Учебные пособия :1
Подробнее… iWorksheets :4Учебные пособия :1
Применение процентов Применение процентов — это термин, обозначающий различные способы использования процентов. Процент изменения относится к проценту увеличения или уменьшения суммы в зависимости от предыдущих сумм или чисел. Применение процентов также означает вычисление простых процентов с использованием уравнения процентов I = P · r · t, где P – основная сумма долга; r — скорость, t — время. Подробнее… iWorksheets:3Учебные пособия:1
Рациональные числа и операции Рациональное число — это число, которое можно превратить в дробь. Десятичные числа, которые повторяются или заканчиваются, рациональны, потому что их можно превратить в дроби. Квадратный корень из числа — это число, которое при умножении само на себя дает исходное число. Квадратный корень из 4 равен 2, потому что 2 · 2 = 4. Подробнее… iWorksheets :3Study Guides :1
Числа и проценты Числа и проценты относятся к отношениям между дробями, десятичными знаками и процентами. Процент — это термин, который описывает десятичную дробь с точки зрения ста. Процент означает на сотню. Проценты, дроби и десятичные дроби могут быть равны друг другу, например, 10%, 0,1 и 1/10. Дроби и десятичные числа можно легко преобразовать в проценты. Есть три случая процента. Подробнее… iWorksheets :3Учебные пособия :1
Процент — это термин, который описывает десятичную дробь с точки зрения ста. Процент означает на сотню. Проценты, дроби и десятичные дроби могут быть равны друг другу, например, 10%, 0,1 и 1/10. Дроби и десятичные числа можно легко преобразовать в проценты. Есть три случая процента. Подробнее… iWorksheets :3Учебные пособия :1
Применение процентов Процент увеличения или уменьшения можно найти по формуле: процент изменения = фактическое изменение/исходная сумма. Изменение является либо увеличением, если суммы увеличились, либо уменьшением, если суммы уменьшились. Если число изменится с 33 на 89, процент увеличения будет следующим: Процент увеличения = (89 -33) ÷ 33 = 56 ÷ 33 ≈ 1,6969 ≈ 170% Подробнее… iWorksheets :4Study Guides :1
1.1 .2. Эффективно сравнивайте и упорядочивайте дроби, десятичные числа и проценты и находите их приблизительное расположение на числовой прямой.
Экспоненты, множители и дроби БесплатноВ математическом выражении, в котором одно и то же число умножается много раз, часто полезно записать число как основание с показателем степени. Экспоненты также используются для оценки чисел. Любое число в нулевой степени равно 1, а любое число в отрицательной степени является числом меньше 1. В экспоненте экспоненты используются для облегчения записи очень больших или очень маленьких чисел. Подробнее… iWorksheets:8Учебные пособия:1
Экспоненты также используются для оценки чисел. Любое число в нулевой степени равно 1, а любое число в отрицательной степени является числом меньше 1. В экспоненте экспоненты используются для облегчения записи очень больших или очень маленьких чисел. Подробнее… iWorksheets:8Учебные пособия:1
1.1.3. Разработайте значение для процентов больше 100 и меньше 1.
Знакомство с процентами Что такое проценты? Процент — это термин, который описывает десятичную дробь с точки зрения ста. Процент означает на сотню. Проценты, дроби и десятичные дроби могут быть равны друг другу, например, 10%, 0,1 и 1/10. Проценты могут быть больше 100% или меньше 1%. Наценка от стоимости изготовления изделия до фактической цены продажи обычно превышает 100%. Комиссия продавца может составлять 1/2% в зависимости от проданного товара. Подробнее… iWorksheets :4Учебные пособия :1
1.1.4. Понимать и использовать отношения и пропорции для представления количественных отношений.

Числовые пропорции Числовые пропорции сравнивают два числа. Числа могут иметь одни и те же единицы измерения, такие как отношение, или числа могут иметь разные единицы измерения, такие как ставки. Пропорция обычно имеет форму a:b или a/b. Соотношения используются для сравнения объектов, выигрышей и проигрышей, сторон фигуры с ее площадью и многого другого. Ставки используются для сравнения миль в час, слов в минуту и многих других. Единица измерения – это когда знаменатель пропорции равен единице. Подробнее… iWorksheets :4Учебные пособия :1
Соотношения, пропорции и проценты Числовые пропорции сравнивают два числа. Пропорция обычно имеет форму a:b или a/b. В пропорции 4 части, и ее можно решить, если известны 3 из 4 частей. Пропорции можно решить с помощью свойства перекрестного произведения, которое утверждает, что перекрестные произведения пропорции равны. Подробнее… iWorksheets :4Study Guides :1
Сходство и масштаб Сходство относится к подобным фигурам и способности сравнивать их, используя пропорции. Подобные фигуры имеют равные соответствующие углы и соответствующие стороны, которые пропорциональны. Уравнение пропорции можно использовать, чтобы доказать, что две фигуры подобны. Если две фигуры похожи, уравнение пропорции можно использовать, чтобы найти недостающую сторону одной из фигур. Подробнее… iWorksheets :7Учебные пособия :1
Подобные фигуры имеют равные соответствующие углы и соответствующие стороны, которые пропорциональны. Уравнение пропорции можно использовать, чтобы доказать, что две фигуры подобны. Если две фигуры похожи, уравнение пропорции можно использовать, чтобы найти недостающую сторону одной из фигур. Подробнее… iWorksheets :7Учебные пособия :1
Числа и проценты Числа и проценты относятся к отношениям между дробями, десятичными знаками и процентами. Процент — это термин, который описывает десятичную дробь с точки зрения ста. Процент означает на сотню. Проценты, дроби и десятичные дроби могут быть равны друг другу, например, 10%, 0,1 и 1/10. Дроби и десятичные числа можно легко преобразовать в проценты. Есть три случая процента. Подробнее… iWorksheets:3Учебные пособия:1
1.1.5. Развивайте понимание больших чисел, а также распознавайте и правильно используйте экспоненциальную, научную и калькуляторную нотацию.
Экспоненты, множители и дроби БесплатноВ математическом выражении, в котором одно и то же число умножается много раз, часто полезно записать число как основание с показателем степени. Экспоненты также используются для оценки чисел. Любое число в нулевой степени равно 1, а любое число в отрицательной степени является числом меньше 1. В экспоненте экспоненты используются для облегчения записи очень больших или очень маленьких чисел. Подробнее… iWorksheets:8Учебные пособия:1
Экспоненты также используются для оценки чисел. Любое число в нулевой степени равно 1, а любое число в отрицательной степени является числом меньше 1. В экспоненте экспоненты используются для облегчения записи очень больших или очень маленьких чисел. Подробнее… iWorksheets:8Учебные пособия:1
Полиномы и экспоненты FreeМногочлен — это выражение в форме axn, где a — любое действительное число, а n — целое число. Если многочлен имеет только один член, он называется мономом. Если в нем два члена, то это двучлен, а если три члена, то это трехчлен. Стандартная форма многочлена — это когда степени переменных уменьшаются слева направо. Подробнее… iWorksheets:6Учебные пособия:1
1.1.6. Используйте множители, кратные, разложение на простые множители и относительно простые числа для решения задач.
Экспоненты, множители и дроби БесплатноВ математическом выражении, в котором одно и то же число умножается много раз, часто полезно записать число как основание с показателем степени. Экспоненты также используются для оценки чисел. Любое число в нулевой степени равно 1, а любое число в отрицательной степени является числом меньше 1. В экспоненте экспоненты используются для облегчения записи очень больших или очень маленьких чисел. Подробнее… iWorksheets:8Учебные пособия:1
Экспоненты также используются для оценки чисел. Любое число в нулевой степени равно 1, а любое число в отрицательной степени является числом меньше 1. В экспоненте экспоненты используются для облегчения записи очень больших или очень маленьких чисел. Подробнее… iWorksheets:8Учебные пособия:1
1.1.7. Разработайте значение целых чисел, а также представьте и сравните с ними величины.
Использование целых чисел Целые числа — это отрицательные числа, нуль и положительные числа. Для сравнения целых чисел можно использовать числовую прямую. На числовой прямой отрицательные целые числа находятся слева от нуля, причем чем больше отрицательное число, тем оно левее. Положительный целые числа находятся справа от нуля на числовой прямой. Если число находится слева от другого числа, говорят, что оно меньше этого числа. В координатной плоскости ось x представляет собой горизонтальную линию с отрицательными числами, нулями и положительными числами. Подробнее… iWorksheets :4Учебные пособия :1
Десятичные операции Десятичные операции относятся к математическим операциям, которые можно выполнять с десятичными числами: сложение, вычитание, умножение и деление. Для получения правильного ответа необходимо соблюдать процесс сложения, вычитания, умножения и деления десятичных дробей. Подробнее… iWorksheets :3Study Guides :1
Для получения правильного ответа необходимо соблюдать процесс сложения, вычитания, умножения и деления десятичных дробей. Подробнее… iWorksheets :3Study Guides :1
Операции с целыми числами Операции с целыми числами — это математические операции с целыми числами. Целые числа — это отрицательные числа, ноль и положительные числа. Сложение и вычитание целых чисел полезно в повседневной жизни, потому что во многих ситуациях используются отрицательные числа, например, при вычислении уровня моря или температуры. Уравнения с целыми числами решаются с помощью обратных операций. Сложение и вычитание — операции, обратные друг другу, а умножение и деление — операции, обратные друг другу. Подробнее… iWorksheets :4Учебные пособия :1
1.2. Понимать значения операций и то, как они связаны друг с другом.
1.2.1. Понимать значение и эффекты арифметических операций с дробями, десятичными и целыми числами.
Десятичные операции Десятичные операции относятся к математическим операциям, которые можно выполнять с десятичными дробями: сложение, вычитание, умножение и деление. Для получения правильного ответа необходимо соблюдать процесс сложения, вычитания, умножения и деления десятичных дробей. Подробнее… iWorksheets :3Учебные пособия :1
Для получения правильного ответа необходимо соблюдать процесс сложения, вычитания, умножения и деления десятичных дробей. Подробнее… iWorksheets :3Учебные пособия :1
Операции с целыми числами Операции с целыми числами — это математические операции с целыми числами. Целые числа — это отрицательные числа, ноль и положительные числа. Сложение и вычитание целых чисел полезно в повседневной жизни, потому что во многих ситуациях используются отрицательные числа, например, при вычислении уровня моря или температуры. Уравнения с целыми числами решаются с помощью обратных операций. Сложение и вычитание — операции, обратные друг другу, а умножение и деление — операции, обратные друг другу. Подробнее… iWorksheets :4Учебные пособия :1
Рациональные числа и операции Рациональное число — это число, которое можно превратить в дробь. Десятичные числа, которые повторяются или заканчиваются, рациональны, потому что их можно превратить в дроби. Квадратный корень из числа — это число, которое при умножении само на себя дает исходное число. Квадратный корень из 4 равен 2, потому что 2 · 2 = 4. Подробнее… iWorksheets :3Study Guides :1
Квадратный корень из 4 равен 2, потому что 2 · 2 = 4. Подробнее… iWorksheets :3Study Guides :1
1.2.2. Используйте ассоциативные и коммутативные свойства сложения и умножения, а также распределительное свойство умножения над сложением, чтобы упростить вычисления с целыми числами, дробями и десятичными дробями.
Использование целых чисел Целые числа — это отрицательные числа, нуль и положительные числа. Для сравнения целых чисел можно использовать числовую прямую. На числовой прямой отрицательные целые числа находятся слева от нуля, причем чем больше отрицательное число, тем оно левее. Положительный целые числа находятся справа от нуля на числовой прямой. Если число находится слева от другого числа, говорят, что оно меньше этого числа. В координатной плоскости ось x представляет собой горизонтальную линию с отрицательными числами, нулями и положительными числами. Подробнее… iWorksheets :4Учебные пособия :1
1.3. Свободно считайте и делайте разумные оценки.

1.3.1. Выберите подходящие методы и инструменты для вычислений с дробями и десятичными знаками из числа вычислений в уме, оценки, калькуляторов или компьютеров, бумаги и карандаша, в зависимости от ситуации, и примените выбранные методы.
Десятичные операции Десятичные операции относятся к математическим операциям, которые можно выполнять с десятичными дробями: сложение, вычитание, умножение и деление. Для получения правильного ответа необходимо соблюдать процесс сложения, вычитания, умножения и деления десятичных дробей. Подробнее… iWorksheets :3Учебные пособия :1
Рациональные числа и операции Рациональное число — это число, которое можно превратить в дробь. Десятичные числа, которые повторяются или заканчиваются, рациональны, потому что их можно превратить в дроби. Квадратный корень из числа — это число, которое при умножении само на себя дает исходное число. Квадратный корень из 4 равен 2, потому что 2 · 2 = 4. Подробнее. .. iWorksheets :3Study Guides :1
.. iWorksheets :3Study Guides :1
1.3.2. Разрабатывайте и анализируйте алгоритмы вычислений с дробями, десятичными и целыми числами и развивайте беглость в их использовании.
Использование целых чисел Целые числа — это отрицательные числа, нуль и положительные числа. Для сравнения целых чисел можно использовать числовую прямую. На числовой прямой отрицательные целые числа находятся слева от нуля, причем чем больше отрицательное число, тем оно левее. Положительный целые числа находятся справа от нуля на числовой прямой. Если число находится слева от другого числа, говорят, что оно меньше этого числа. В координатной плоскости ось x представляет собой горизонтальную линию с отрицательными числами, нулями и положительными числами. Подробнее… iWorksheets :4Учебные пособия :1
Десятичные операции Десятичные операции относятся к математическим операциям, которые можно выполнять с десятичными числами: сложение, вычитание, умножение и деление. Для получения правильного ответа необходимо соблюдать процесс сложения, вычитания, умножения и деления десятичных дробей. Подробнее… iWorksheets :3Study Guides :1
Для получения правильного ответа необходимо соблюдать процесс сложения, вычитания, умножения и деления десятичных дробей. Подробнее… iWorksheets :3Study Guides :1
Операции с дробями Операции с дробями — это процессы сложения, вычитания, умножения и деления дробей и смешанных чисел. Смешанное число – это дробь с целым числом. Добавление дробей распространено во многих повседневных событиях, таких как создание рецепта и измерение древесины. Чтобы складывать и вычитать дроби, дроби должны иметь одинаковый знаменатель. Подробнее… iWorksheets :3Учебные пособия :1
Операции с целыми числами Операции с целыми числами — это математические операции с целыми числами. Целые числа — это отрицательные числа, ноль и положительные числа. Сложение и вычитание целых чисел полезно в повседневной жизни, потому что во многих ситуациях используются отрицательные числа, например, при вычислении уровня моря или температуры. Уравнения с целыми числами решаются с помощью обратных операций. Сложение и вычитание — операции, обратные друг другу, а умножение и деление — операции, обратные друг другу. Подробнее… iWorksheets :4Учебные пособия :1
Сложение и вычитание — операции, обратные друг другу, а умножение и деление — операции, обратные друг другу. Подробнее… iWorksheets :4Учебные пособия :1
Рациональные числа и операции Рациональное число — это число, которое можно превратить в дробь. Десятичные числа, которые повторяются или заканчиваются, рациональны, потому что их можно превратить в дроби. Квадратный корень из числа — это число, которое при умножении само на себя дает исходное число. Квадратный корень из 4 равен 2, потому что 2 · 2 = 4. Подробнее… iWorksheets :3Учебные пособия :1
1.3.4. Разработайте, проанализируйте и объясните методы решения задач, связанных с пропорциями, таких как масштабирование и нахождение эквивалентных соотношений.
Числовые пропорции Числовые пропорции сравнивают два числа. Числа могут иметь одни и те же единицы измерения, такие как отношение, или числа могут иметь разные единицы измерения, такие как ставки. Пропорция обычно имеет форму a:b или a/b. Соотношения используются для сравнения объектов, выигрышей и проигрышей, сторон фигуры с ее площадью и многого другого. Ставки используются для сравнения миль в час, слов в минуту и многих других. Единица измерения – это когда знаменатель пропорции равен единице. Подробнее… iWorksheets :4Учебные пособия :1
Соотношения используются для сравнения объектов, выигрышей и проигрышей, сторон фигуры с ее площадью и многого другого. Ставки используются для сравнения миль в час, слов в минуту и многих других. Единица измерения – это когда знаменатель пропорции равен единице. Подробнее… iWorksheets :4Учебные пособия :1
Геометрические пропорции Геометрические пропорции сравнивают два подобных многоугольника. Подобные многоугольники имеют равные соответствующие углы и соответствующие стороны, которые пропорциональны. Уравнение пропорции можно использовать, чтобы доказать, что две фигуры подобны. Если две фигуры похожи, уравнение пропорции можно использовать, чтобы найти недостающую сторону одной из фигур. Подробнее… iWorksheets:4Учебные пособия:1
Соотношения, пропорции и проценты Числовые пропорции сравнивают два числа. Пропорция обычно имеет форму a:b или a/b. В пропорции 4 части, и ее можно решить, если известны 3 из 4 частей. Пропорции можно решить с помощью свойства перекрестного произведения, которое утверждает, что перекрестные произведения пропорции равны. Подробнее… iWorksheets :4Учебные пособия :1
Подробнее… iWorksheets :4Учебные пособия :1
Сходство и масштаб Сходство означает сходство фигур и возможность их сравнения с использованием пропорций. Подобные фигуры имеют равные соответствующие углы и соответствующие стороны, которые пропорциональны. Уравнение пропорции можно использовать, чтобы доказать, что две фигуры подобны. Если две фигуры похожи, уравнение пропорции можно использовать, чтобы найти недостающую сторону одной из фигур. Подробнее… iWorksheets :7Study Guides :1
Числа и проценты Числа и проценты относятся к отношениям между дробями, десятичными знаками и процентами. Процент — это термин, который описывает десятичную дробь с точки зрения ста. Процент означает на сотню. Проценты, дроби и десятичные дроби могут быть равны друг другу, например, 10%, 0,1 и 1/10. Дроби и десятичные числа можно легко преобразовать в проценты. Есть три случая процента. Подробнее… iWorksheets :3Учебные пособия :1
NCTM.2. Алгебра
2.
 1. Понимать закономерности, отношения и функции.
1. Понимать закономерности, отношения и функции.2.1.1. Представляйте, анализируйте и обобщайте различные шаблоны с помощью таблиц, графиков, слов и, по возможности, символических правил.
Введение в функции Функция — это правило, которое применяется к числу, называемому входом, для получения результата, называемого выходом. Правило состоит из одной или нескольких математических операций, которые выполняются над входными данными. Примером функции является y = 2x + 3, где x — вход, а y — выход. Операции умножения и сложения выполняются на входе x, чтобы получить выход y. Подставляя число вместо x, можно определить выход. Подробнее… iWorksheets :6Учебные пособия :1
Последовательности Последовательность — это упорядоченный список чисел. Последовательности являются результатом шаблона или правила. Образцом или правилом может быть любое другое число или некоторая формула, например y = 2x + 3. Когда задан образец или правило, можно найти последовательность. Когда задана последовательность, можно найти шаблон или правило. Подробнее… iWorksheets:5Учебные пособия:1
Когда задана последовательность, можно найти шаблон или правило. Подробнее… iWorksheets:5Учебные пособия:1
2.2. Представляйте и анализируйте математические ситуации и структуры, используя алгебраические символы.
2.2.1. Разработайте начальное концептуальное понимание различных способов использования переменных.
Введение в алгебру Алгебра — это практика использования выражений с буквами или переменными, представляющими числа. Слова можно преобразовать в математическое выражение, используя слова плюс, превышает, уменьшает, меньше, умножает, произведение, делит, частное и многие другие. Алгебра использует переменные для представления значения, которое еще не известно. Подробнее… iWorksheets :4Study Guides :1
Решение уравнений и неравенств Алгебраические уравнения — это математические уравнения, которые содержат букву или переменную, представляющую число. Для решения алгебраического уравнения используются обратные операции. Алгебраические неравенства — это математические уравнения, которые сравнивают две величины, используя больше чем, >; больше или равно, ≥; меньше, <; и меньше или равно ≤. Когда происходит умножение или деление на отрицательное число, знак неравенства меняется на противоположный по сравнению с исходным знаком неравенства, чтобы неравенство было правильным. Подробнее... iWorksheets :3Учебные пособия :1
Алгебраические неравенства — это математические уравнения, которые сравнивают две величины, используя больше чем, >; больше или равно, ≥; меньше, <; и меньше или равно ≤. Когда происходит умножение или деление на отрицательное число, знак неравенства меняется на противоположный по сравнению с исходным знаком неравенства, чтобы неравенство было правильным. Подробнее... iWorksheets :3Учебные пособия :1
2.2.2. Исследуйте отношения между символическими выражениями и графиками линий, уделяя особое внимание значению пересечения и наклона.
Введение в функции Функция — это правило, которое применяется к числу, называемому входом, для получения результата, называемого выходом. Правило состоит из одной или нескольких математических операций, которые выполняются над входными данными. Примером функции является y = 2x + 3, где x — вход, а y — выход. Операции умножения и сложения выполняются на входе x, чтобы получить выход y. Подставляя число вместо x, можно определить выход. Подробнее… iWorksheets :6Учебные пособия :1
Подробнее… iWorksheets :6Учебные пособия :1
Нелинейные функции и теория множеств Функция может быть представлена в виде y = mx + b. Это уравнение прямой, поэтому говорят, что это линейная функция. Нелинейные функции — это функции, не являющиеся прямыми линиями. Некоторыми примерами нелинейных функций являются экспоненциальные функции. и параболические функции. Экспоненциальная функция y = aˆx представляет собой кривую линию, которая приближается к оси x, но не касается ее. Параболическая функция y = ax² + bx +c представляет собой U-образную линию, которая может быть обращена либо вверх, либо вниз. Подробнее… iWorksheets :5Учебные пособия :1
Линейные уравнения Линейные уравнения — это уравнения с двумя переменными, которые на графике представляют собой прямую линию. Линейное уравнение может быть построено на основе их наклона и y-пересечения. Стандартное уравнение для прямой: y = mx + b, где m — наклон, а b — точка пересечения с осью y. Наклон можно найти по формуле m = (y2 — y1)/(x2 — x1), которая представляет собой изменение y по сравнению с изменением x. Подробнее… iWorksheets:6Учебные пособия:1
Наклон можно найти по формуле m = (y2 — y1)/(x2 — x1), которая представляет собой изменение y по сравнению с изменением x. Подробнее… iWorksheets:6Учебные пособия:1
2.2.3. Используйте символическую алгебру для представления ситуаций и решения проблем, особенно тех, которые связаны с линейными отношениями.
Введение в алгебру Алгебра — это практика использования выражений с буквами или переменными, представляющими числа. Слова можно преобразовать в математическое выражение, используя слова плюс, превышает, уменьшает, меньше, умножает, произведение, делит, частное и многие другие. Алгебра использует переменные для представления значения, которое еще не известно. Подробнее… iWorksheets:4Study Guides:1
Уравнения и неравенства Алгебраические уравнения — это математические уравнения, которые содержат букву или переменную, представляющую число. Для решения алгебраического уравнения используются обратные операции. Обратная операция сложения — вычитание, обратная операция вычитания — сложение. Неравенства — это математические уравнения, которые сравнивают две величины, используя больше, >; больше или равно ≥; меньше, <; и меньше или равно ≤. Подробнее... iWorksheets :6Учебные пособия :1
Неравенства — это математические уравнения, которые сравнивают две величины, используя больше, >; больше или равно ≥; меньше, <; и меньше или равно ≤. Подробнее... iWorksheets :6Учебные пособия :1
Алгебраические неравенства FreeАлгебраические неравенства — это математические уравнения, сравнивающие две величины по следующим критериям: больше, меньше, меньше или равно, больше или равно. Единственное правило неравенств, которое необходимо помнить, состоит в том, что при умножении или делении переменной на отрицательное число знак меняется на противоположный. Подробнее… iWorksheets :3Study Guides :1
Уравнения и неравенства Уравнение – это математическое утверждение, которое показывает, что два выражения равны друг другу. Выражения, используемые в уравнении, могут содержать переменные или числа. Неравенства — это математические уравнения, которые сравнивают две величины, используя больше, >; больше или равно ≥; меньше, <; и меньше или равно ≤. Неравенства также решаются с помощью обратных операций. Подробнее… iWorksheets :3Учебные пособия :1
Неравенства также решаются с помощью обратных операций. Подробнее… iWorksheets :3Учебные пособия :1
Решение линейных уравнений На графике линейное уравнение представляет собой прямую линию. Хотя стандартное уравнение для прямой имеет вид y = mx + b, где m — наклон, а b — точка пересечения с осью y, в линейных уравнениях часто обе переменные находятся по одну сторону от знака равенства. Линейные уравнения могут быть решены для одной переменной, когда задана другая переменная. Подробнее… iWorksheets:5Учебные пособия:1
2.2.4. Распознавать и генерировать эквивалентные формы для простых алгебраических выражений и решать линейные уравнения
Введение в алгебру Алгебра — это практика использования выражений с буквами или переменными, представляющими числа. Слова можно преобразовать в математическое выражение, используя слова плюс, превышает, уменьшает, меньше, умножает, произведение, делит, частное и многие другие. Алгебра использует переменные для представления значения, которое еще не известно. Подробнее… iWorksheets:4Study Guides:1
Подробнее… iWorksheets:4Study Guides:1
Уравнения и неравенства Алгебраические уравнения — это математические уравнения, которые содержат букву или переменную, представляющую число. Для решения алгебраического уравнения используются обратные операции. Обратная операция сложения — вычитание, обратная операция вычитания — сложение. Неравенства — это математические уравнения, которые сравнивают две величины, используя больше, >; больше или равно ≥; меньше, <; и меньше или равно ≤. Подробнее... iWorksheets :6Учебные пособия :1
Уравнения и неравенства Уравнение — это математическое выражение, показывающее, что два выражения равны друг другу. Выражения, используемые в уравнении, могут содержать переменные или числа. Неравенства — это математические уравнения, которые сравнивают две величины, используя больше, >; больше или равно ≥; меньше, <; и меньше или равно ≤. Неравенства также решаются с помощью обратных операций. Подробнее... iWorksheets :3Учебные пособия :1
Операции с целыми числами Операции с целыми числами — это математические операции с целыми числами. Целые числа — это отрицательные числа, ноль и положительные числа. Сложение и вычитание целых чисел полезно в повседневной жизни, потому что во многих ситуациях используются отрицательные числа, например, при вычислении уровня моря или температуры. Уравнения с целыми числами решаются с помощью обратных операций. Сложение и вычитание — операции, обратные друг другу, а умножение и деление — операции, обратные друг другу. Подробнее… iWorksheets :4Учебные пособия :1
Целые числа — это отрицательные числа, ноль и положительные числа. Сложение и вычитание целых чисел полезно в повседневной жизни, потому что во многих ситуациях используются отрицательные числа, например, при вычислении уровня моря или температуры. Уравнения с целыми числами решаются с помощью обратных операций. Сложение и вычитание — операции, обратные друг другу, а умножение и деление — операции, обратные друг другу. Подробнее… iWorksheets :4Учебные пособия :1
2.3. Используйте математические модели для представления и понимания количественных отношений.
2.3.1. Моделируйте и решайте контекстуализированные задачи, используя различные представления, такие как графики, таблицы и уравнения.
Алгебраические уравнения Что такое алгебраические уравнения? Алгебраические уравнения — это математические уравнения, содержащие букву или переменную, представляющую число. Когда алгебраические уравнения записываются словами, слова должны быть заменены соответствующими числами и переменными для решения. Подробнее… iWorksheets :5Учебные пособия :1
Подробнее… iWorksheets :5Учебные пособия :1
2.4. Проанализируйте изменения в различных контекстах.
2.4.1. Используйте графики для анализа характера изменения величин в линейных зависимостях.
Нелинейные функции и теория множеств Функция может быть представлена в виде y = mx + b. Это уравнение прямой, поэтому говорят, что это линейная функция. Нелинейные функции — это функции, не являющиеся прямыми линиями. Некоторыми примерами нелинейных функций являются экспоненциальные функции. и параболические функции. Экспоненциальная функция y = aˆx представляет собой кривую линию, которая приближается к оси x, но не касается ее. Параболическая функция y = ax² + bx +c представляет собой U-образную линию, которая может быть обращена либо вверх, либо вниз. Подробнее… iWorksheets :5Учебные пособия :1
NCTM.3. Геометрия
3.1. Анализировать характеристики и свойства двух- и трехмерных геометрических фигур и разрабатывать математические аргументы в отношении геометрических взаимосвязей.

3.1.1. Точно описывать, классифицировать и понимать отношения между типами двух- и трехмерных объектов, используя их определяющие свойства.
Плоские фигуры: линии и углы Плоские фигуры в отношении линий и углов относятся к координатной плоскости и различным линиям и углам внутри координатной плоскости. Линии на координатной плоскости могут быть параллельными или перпендикулярными. Углы в координатной плоскости могут быть острыми, тупыми, прямыми и прямыми. Смежными углами называются два угла, имеющие общую вершину и общую сторону, но не пересекающиеся. Подробнее… iWorksheets :3Учебные пособия :1
Плоские фигуры: отношения замкнутых фигур Плоские фигуры в отношении отношений замкнутых фигур относятся к координатной плоскости и конгруэнтным фигурам, окружностям, круговым диаграммам, преобразованиям и симметрии. Конгруэнтные фигуры имеют одинаковый размер и форму. Преобразования состоят из переводов, поворотов и отражений. Перевод фигуры сохраняет размер и форму фигуры, но перемещает ее в другое место. Вращение поворачивает фигуру вокруг точки на фигуре. Отражение фигуры производит зеркальное отражение фигуры, когда оно отражается в данной линии. Подробнее… iWorksheets :3Учебные пособия :1
Перевод фигуры сохраняет размер и форму фигуры, но перемещает ее в другое место. Вращение поворачивает фигуру вокруг точки на фигуре. Отражение фигуры производит зеркальное отражение фигуры, когда оно отражается в данной линии. Подробнее… iWorksheets :3Учебные пособия :1
Исследование площади и площади поверхности Площадь — это площадь поверхности, которую покрывает фигура. Площадь измеряется в квадратных единицах, будь то дюймы, футы, метры или сантиметры. Формула площади треугольника: A = 1/2 · b · h, где b — основание, а h — высота. Формула площади круга: A = π · r², где π обычно равно 3,14, а r – радиус круга. Формула площади параллелограмма: A = b · h, где b – площадь основание и h высота. Подробнее… iWorksheets :4Учебные пособия :1
Объем в поисках Объем измеряет количество, которое может удерживать твердая фигура. Объем измеряется в кубических единицах и может быть измерен в дюймах, футах, метрах, сантиметрах и миллиметрах. Формула объема прямоугольной призмы: V = l · w · h, где l — длина, w — ширина, h — высота. Подробнее… iWorksheets :4Study Guides :1
Формула объема прямоугольной призмы: V = l · w · h, где l — длина, w — ширина, h — высота. Подробнее… iWorksheets :4Study Guides :1
Фигуры на плоскости Фигуры на плоскости относятся к точкам, линиям, углам и плоскостям в координатной плоскости. Линии могут быть параллельными или перпендикулярными. Углы можно разделить на острые, тупые и прямые. Углы также могут быть дополнительными или дополнительными в зависимости от того, сколько градусов они составляют в сумме. Плоские фигуры также могут относиться к фигурам на координатной плоскости. Треугольники, четырехугольники и другие многоугольники могут отображаться в координатной плоскости. Подробнее… iWorksheets :4Учебные пособия :1
Периметр и площадь Что такое периметр и площадь? Периметр – это измерение расстояния вокруг фигуры. Он измеряется в единицах и может измеряться в дюймах, футах, блоках, метрах, сантиметрах или миллиметрах. Чтобы найти периметр любой фигуры, просто сложите стороны фигуры. Площадь — это количество поверхности, которую покрывает фигура. Площадь измеряется в квадратных единицах, будь то дюймы, футы, метры или сантиметры. Формула площади параллелограмма: A = b · h, где b — основание, а h — высота. Подробнее… iWorksheets :4Учебные пособия :1
Площадь — это количество поверхности, которую покрывает фигура. Площадь измеряется в квадратных единицах, будь то дюймы, футы, метры или сантиметры. Формула площади параллелограмма: A = b · h, где b — основание, а h — высота. Подробнее… iWorksheets :4Учебные пособия :1
Трехмерная геометрия/измерения Трехмерная геометрия/измерения относятся к трехмерным (3D) формам и измерению их форм относительно объема и площади поверхности. Фигуры призм, цилиндров, пирамид, конусов и сфер — все это трехмерные фигуры. Объем измеряет количество, которое может вместить твердая фигура. Объем измеряется в единицах³ и может измеряться в дюймах, футах, метрах, сантиметрах и миллиметрах. Подробнее… iWorksheets:11Учебные пособия:1
3.1.2. Понимать отношения между углами, длинами сторон, периметрами, площадями и объемами подобных объектов.
Геометрические пропорции Геометрические пропорции сравнивают два подобных многоугольника. Подобные многоугольники имеют равные соответствующие углы и соответствующие стороны, которые пропорциональны. Уравнение пропорции можно использовать, чтобы доказать, что две фигуры подобны. Если две фигуры похожи, уравнение пропорции можно использовать, чтобы найти недостающую сторону одной из фигур. Подробнее… iWorksheets :4Учебные пособия :1
Уравнение пропорции можно использовать, чтобы доказать, что две фигуры подобны. Если две фигуры похожи, уравнение пропорции можно использовать, чтобы найти недостающую сторону одной из фигур. Подробнее… iWorksheets :4Учебные пособия :1
Соотношения, пропорции и проценты Числовые пропорции сравнивают два числа. Пропорция обычно имеет форму a:b или a/b. В пропорции 4 части, и ее можно решить, если известны 3 из 4 частей. Пропорции можно решить с помощью свойства перекрестного произведения, которое утверждает, что перекрестные произведения пропорции равны. Подробнее… iWorksheets :4Study Guides :1
Сходство и масштаб Сходство относится к подобным фигурам и способности сравнивать их, используя пропорции. Подобные фигуры имеют равные соответствующие углы и соответствующие стороны, которые пропорциональны. Уравнение пропорции можно использовать, чтобы доказать, что две фигуры подобны. Если две фигуры похожи, уравнение пропорции можно использовать, чтобы найти недостающую сторону одной из фигур. Подробнее… iWorksheets :7Учебные пособия :1
Подробнее… iWorksheets :7Учебные пособия :1
3.1.3. Создавайте и критикуйте индуктивные и дедуктивные аргументы, касающиеся геометрических идей и отношений, таких как конгруэнтность, подобие и пифагорейские отношения.
Геометрические пропорции Геометрические пропорции сравнивают два подобных многоугольника. Подобные многоугольники имеют равные соответствующие углы и соответствующие стороны, которые пропорциональны. Уравнение пропорции можно использовать, чтобы доказать, что две фигуры подобны. Если две фигуры похожи, уравнение пропорции можно использовать, чтобы найти недостающую сторону одной из фигур. Подробнее… iWorksheets :4Учебные пособия :1
Плоские фигуры: линии и углы Плоские фигуры в отношении линий и углов относятся к координатной плоскости и различным линиям и углам внутри координатной плоскости. Линии на координатной плоскости могут быть параллельными или перпендикулярными. Углы в координатной плоскости могут быть острыми, тупыми, прямыми и прямыми. Смежными углами называются два угла, имеющие общую вершину и общую сторону, но не пересекающиеся. Подробнее… iWorksheets :3Учебные пособия :1
Смежными углами называются два угла, имеющие общую вершину и общую сторону, но не пересекающиеся. Подробнее… iWorksheets :3Учебные пособия :1
Плоские фигуры: отношения замкнутых фигур Плоские фигуры в отношении отношений замкнутых фигур относятся к координатной плоскости и конгруэнтным фигурам, окружностям, круговым диаграммам, преобразованиям и симметрии. Конгруэнтные фигуры имеют одинаковый размер и форму. Преобразования состоят из переводов, поворотов и отражений. Перевод фигуры сохраняет размер и форму фигуры, но перемещает ее в другое место. Вращение поворачивает фигуру вокруг точки на фигуре. Отражение фигуры производит зеркальное отражение фигуры, когда оно отражается в данной линии. Подробнее… iWorksheets :3Учебные пособия :1
Теорема Пифагора Теорема Пифагора — это фундаментальное соотношение в евклидовой геометрии. Он гласит, что сумма квадратов катетов прямоугольного треугольника равна квадрату длины
гипотенузы. Определить расстояние между двумя точками по теореме Пифагора. Подробнее… iWorksheets:10Учебные пособия:2
Подробнее… iWorksheets:10Учебные пособия:2
Образцы в геометрии Образцы в геометрии относятся к формам и их размерам. Формы могут быть конгруэнтны друг другу. Формы также можно манипулировать, чтобы сформировать похожие формы. Типы преобразований: отражение, вращение, расширение и перемещение. При отражении фигура отражается или переворачивается на линии так, что новая фигура является зеркальным отражением на другой стороне линии. Вращение вращает или поворачивает форму, чтобы создать новую фигуру. Расширение уменьшает или увеличивает фигуру. Перевод сдвигает фигуру на новую позицию. Подробнее… iWorksheets :3Учебные пособия :1
Соотношения, пропорции и проценты Числовые пропорции сравнивают два числа. Пропорция обычно имеет форму a:b или a/b. В пропорции 4 части, и ее можно решить, если известны 3 из 4 частей. Пропорции можно решить с помощью свойства перекрестного произведения, которое утверждает, что перекрестные произведения пропорции равны. Подробнее… iWorksheets :4Study Guides :1
Подробнее… iWorksheets :4Study Guides :1
Сходство и масштаб Сходство относится к подобным фигурам и способности сравнивать их, используя пропорции. Подобные фигуры имеют равные соответствующие углы и соответствующие стороны, которые пропорциональны. Уравнение пропорции можно использовать, чтобы доказать, что две фигуры подобны. Если две фигуры похожи, уравнение пропорции можно использовать, чтобы найти недостающую сторону одной из фигур. Подробнее… iWorksheets :7Учебные пособия :1
3.2. Укажите местоположения и опишите пространственные отношения, используя координатную геометрию и другие системы представления.
3.2.1. Используйте координатную геометрию для представления и изучения свойств геометрических фигур.
Плоские фигуры Плоские фигуры относятся к точкам, линиям, углам и плоскостям на координатной плоскости. Линии могут быть параллельными или перпендикулярными. Углы можно разделить на острые, тупые и прямые. Углы также могут быть дополнительными или дополнительными в зависимости от того, сколько градусов они составляют в сумме. Плоские фигуры также могут относиться к фигурам на координатной плоскости. Треугольники, четырехугольники и другие многоугольники могут отображаться в координатной плоскости. Подробнее… iWorksheets :4Учебные пособия :1
Углы также могут быть дополнительными или дополнительными в зависимости от того, сколько градусов они составляют в сумме. Плоские фигуры также могут относиться к фигурам на координатной плоскости. Треугольники, четырехугольники и другие многоугольники могут отображаться в координатной плоскости. Подробнее… iWorksheets :4Учебные пособия :1
3.2.2. Используйте координатную геометрию для изучения специальных геометрических фигур, таких как правильные многоугольники или многоугольники с парами параллельных или перпендикулярных сторон.
Плоские фигуры Плоские фигуры относятся к точкам, линиям, углам и плоскостям на координатной плоскости. Линии могут быть параллельными или перпендикулярными. Углы можно разделить на острые, тупые и прямые. Углы также могут быть дополнительными или дополнительными в зависимости от того, сколько градусов они составляют в сумме. Плоские фигуры также могут относиться к фигурам на координатной плоскости. Треугольники, четырехугольники и другие многоугольники могут отображаться в координатной плоскости. Подробнее… iWorksheets :4Учебные пособия :1
Подробнее… iWorksheets :4Учебные пособия :1
3.3. Применяйте преобразования и используйте симметрию для анализа математических ситуаций.
3.3.1. Опишите размеры, положение и ориентацию фигур при неформальных преобразованиях, таких как перевороты, повороты, слайды и масштабирование.
Образцы в геометрии Образцы в геометрии относятся к формам и их размерам. Формы могут быть конгруэнтны друг другу. Формы также можно манипулировать, чтобы сформировать похожие формы. Типы преобразований: отражение, вращение, расширение и перемещение. При отражении фигура отражается или переворачивается на линии так, что новая фигура является зеркальным отражением на другой стороне линии. Вращение вращает или поворачивает форму, чтобы создать новую фигуру. Расширение уменьшает или увеличивает фигуру. Перевод сдвигает фигуру на новую позицию. Подробнее… iWorksheets :3Учебные пособия :1
Сходство и масштаб Сходство означает сходство фигур и возможность их сравнения с использованием пропорций. Подобные фигуры имеют равные соответствующие углы и соответствующие стороны, которые пропорциональны. Уравнение пропорции можно использовать, чтобы доказать, что две фигуры подобны. Если две фигуры похожи, уравнение пропорции можно использовать, чтобы найти недостающую сторону одной из фигур. Подробнее… iWorksheets :7Учебные пособия :1
Подобные фигуры имеют равные соответствующие углы и соответствующие стороны, которые пропорциональны. Уравнение пропорции можно использовать, чтобы доказать, что две фигуры подобны. Если две фигуры похожи, уравнение пропорции можно использовать, чтобы найти недостающую сторону одной из фигур. Подробнее… iWorksheets :7Учебные пособия :1
3.3.2. Исследуйте конгруэнтность, сходство и линейную или вращательную симметрию объектов с помощью преобразований.
Образцы в геометрии Образцы в геометрии относятся к формам и их размерам. Формы могут быть конгруэнтны друг другу. Формы также можно манипулировать, чтобы сформировать похожие формы. Типы преобразований: отражение, вращение, расширение и перемещение. При отражении фигура отражается или переворачивается на линии так, что новая фигура является зеркальным отражением на другой стороне линии. Вращение вращает или поворачивает форму, чтобы создать новую фигуру. Расширение уменьшает или увеличивает фигуру. Перевод сдвигает фигуру на новую позицию. Подробнее… iWorksheets :3Учебные пособия :1
Подробнее… iWorksheets :3Учебные пособия :1
3.4. Используйте визуализацию, пространственные рассуждения и геометрическое моделирование для решения задач.
3.4.4. Используйте геометрические модели для представления и объяснения числовых и алгебраических взаимосвязей.
Измерение, периметр и окружность Для измерения объектов используются две системы: обычная система США и метрическая система. Традиционная система США измеряет длину в дюймах, футах, ярдах и милях. Метрическая система представляет собой систему с основанием десять и измеряет длину в километрах, метрах и миллиметрах. Периметр – это измерение расстояния вокруг фигуры. Он измеряется в единицах и может измеряться в дюймах, футах, блоках, метрах, сантиметрах или миллиметрах. Чтобы получить периметр любой фигуры, просто сложите стороны фигуры. Подробнее… iWorksheets :3Учебные пособия :1
Исследование площади и площади поверхности Площадь — это площадь поверхности, которую покрывает фигура. Площадь измеряется в квадратных единицах, будь то дюймы, футы, метры или сантиметры. Формула площади треугольника: A = 1/2 · b · h, где b — основание, а h — высота. Формула площади круга: A = π · r², где π обычно равно 3,14, а r – радиус круга. Формула площади параллелограмма: A = b · h, где b – площадь
основание и h высота. Подробнее… iWorksheets :4Учебные пособия :1
Площадь измеряется в квадратных единицах, будь то дюймы, футы, метры или сантиметры. Формула площади треугольника: A = 1/2 · b · h, где b — основание, а h — высота. Формула площади круга: A = π · r², где π обычно равно 3,14, а r – радиус круга. Формула площади параллелограмма: A = b · h, где b – площадь
основание и h высота. Подробнее… iWorksheets :4Учебные пособия :1
Объем в поисках Объем измеряет количество, которое может удерживать твердая фигура. Объем измеряется в кубических единицах и может быть измерен в дюймах, футах, метрах, сантиметрах и миллиметрах. Формула объема прямоугольной призмы: V = l · w · h, где l — длина, w — ширина, h — высота. Подробнее… iWorksheets:4Учебные пособия:1
Периметр и площадь Что такое периметр и площадь? Периметр – это измерение расстояния вокруг фигуры. Он измеряется в единицах и может измеряться в дюймах, футах, блоках, метрах, сантиметрах или миллиметрах. Чтобы найти периметр любой фигуры, просто сложите стороны фигуры. Площадь — это количество поверхности, которую покрывает фигура. Площадь измеряется в квадратных единицах, будь то дюймы, футы, метры или сантиметры. Формула площади параллелограмма: A = b · h, где b — основание, а h — высота. Подробнее… iWorksheets :4Учебные пособия :1
Площадь — это количество поверхности, которую покрывает фигура. Площадь измеряется в квадратных единицах, будь то дюймы, футы, метры или сантиметры. Формула площади параллелограмма: A = b · h, где b — основание, а h — высота. Подробнее… iWorksheets :4Учебные пособия :1
Трехмерная геометрия/измерения Трехмерная геометрия/измерения относятся к трехмерным (3D) формам и измерению их форм относительно объема и площади поверхности. Фигуры призм, цилиндров, пирамид, конусов и сфер — все это трехмерные фигуры. Объем измеряет количество, которое может вместить твердая фигура. Объем измеряется в единицах³ и может измеряться в дюймах, футах, метрах, сантиметрах и миллиметрах. Подробнее… iWorksheets:11Учебные пособия:1
NCTM.4. Измерение
4.1. Понимать измеримые атрибуты объектов и единиц, систем и процессов измерения.
4.1.3. Понимать, выбирать и использовать единицы соответствующего размера и типа для измерения углов, периметра, площади, площади поверхности и объема.

Плоские фигуры: линии и углы Плоские фигуры в отношении линий и углов относятся к координатной плоскости и различным линиям и углам внутри координатной плоскости. Линии на координатной плоскости могут быть параллельными или перпендикулярными. Углы в координатной плоскости могут быть острыми, тупыми, прямыми и прямыми. Смежными углами называются два угла, имеющие общую вершину и общую сторону, но не пересекающиеся. Подробнее… iWorksheets :3Учебные пособия :1
4.2. Применяйте соответствующие методы, инструменты и формулы для определения измерений.
4.2.2. Выбирайте и применяйте методы и инструменты для точного нахождения мер длины, площади, объема и угла с соответствующим уровнем точности.
Плоские фигуры: линии и углы Плоские фигуры в отношении линий и углов относятся к координатной плоскости и различным линиям и углам внутри координатной плоскости. Линии на координатной плоскости могут быть параллельными или перпендикулярными. Углы в координатной плоскости могут быть острыми, тупыми, прямыми и прямыми. Смежными углами называются два угла, имеющие общую вершину и общую сторону, но не пересекающиеся. Подробнее… iWorksheets :3Учебные пособия :1
Углы в координатной плоскости могут быть острыми, тупыми, прямыми и прямыми. Смежными углами называются два угла, имеющие общую вершину и общую сторону, но не пересекающиеся. Подробнее… iWorksheets :3Учебные пособия :1
Измерение, периметр и окружность Для измерения объектов используются две системы: обычная система США и метрическая система. Традиционная система США измеряет длину в дюймах, футах, ярдах и милях. Метрическая система представляет собой систему с основанием десять и измеряет длину в километрах, метрах и миллиметрах. Периметр – это измерение расстояния вокруг фигуры. Он измеряется в единицах и может измеряться в дюймах, футах, блоках, метрах, сантиметрах или миллиметрах. Чтобы получить периметр любой фигуры, просто сложите стороны фигуры. Подробнее… iWorksheets :3Учебные пособия :1
Исследование площади и площади поверхности Площадь — это площадь поверхности, которую покрывает фигура. Площадь измеряется в квадратных единицах, будь то дюймы, футы, метры или сантиметры. Формула площади треугольника: A = 1/2 · b · h, где b — основание, а h — высота. Формула площади круга: A = π · r², где π обычно равно 3,14, а r – радиус круга. Формула площади параллелограмма: A = b · h, где b – площадь
основание и h высота. Подробнее… iWorksheets :4Учебные пособия :1
Формула площади треугольника: A = 1/2 · b · h, где b — основание, а h — высота. Формула площади круга: A = π · r², где π обычно равно 3,14, а r – радиус круга. Формула площади параллелограмма: A = b · h, где b – площадь
основание и h высота. Подробнее… iWorksheets :4Учебные пособия :1
Объем в поисках Объем измеряет количество, которое может удерживать твердая фигура. Объем измеряется в кубических единицах и может быть измерен в дюймах, футах, метрах, сантиметрах и миллиметрах. Формула объема прямоугольной призмы: V = l · w · h, где l — длина, w — ширина, h — высота. Подробнее… iWorksheets:4Учебные пособия:1
Периметр и площадь Что такое периметр и площадь? Периметр – это измерение расстояния вокруг фигуры. Он измеряется в единицах и может измеряться в дюймах, футах, блоках, метрах, сантиметрах или миллиметрах. Чтобы найти периметр любой фигуры, просто сложите стороны фигуры. Площадь — это количество поверхности, которую покрывает фигура. Площадь измеряется в квадратных единицах, будь то дюймы, футы, метры или сантиметры. Формула площади параллелограмма: A = b · h, где b — основание, а h — высота. Подробнее… iWorksheets :4Учебные пособия :1
Площадь измеряется в квадратных единицах, будь то дюймы, футы, метры или сантиметры. Формула площади параллелограмма: A = b · h, где b — основание, а h — высота. Подробнее… iWorksheets :4Учебные пособия :1
Трехмерная геометрия/измерения Трехмерная геометрия/измерения относятся к трехмерным (3D) формам и измерению их форм относительно объема и площади поверхности. Фигуры призм, цилиндров, пирамид, конусов и сфер — все это трехмерные фигуры. Объем измеряет количество, которое может вместить твердая фигура. Объем измеряется в единицах³ и может измеряться в дюймах, футах, метрах, сантиметрах и миллиметрах. Подробнее… iWorksheets:11Учебные пособия:1
4.2.3. Разрабатывайте и используйте формулы для определения длины окружности и площади треугольников, параллелограммов, трапеций и окружностей, а также разрабатывайте стратегии для нахождения площади более сложных фигур.
Измерение, периметр и окружность Для измерения объектов используются две системы: обычная система США и метрическая система. Традиционная система США измеряет длину в дюймах, футах, ярдах и милях. Метрическая система представляет собой систему с основанием десять и измеряет длину в километрах, метрах и миллиметрах. Периметр – это измерение расстояния вокруг фигуры. Он измеряется в единицах и может измеряться в дюймах, футах, блоках, метрах, сантиметрах или миллиметрах. Чтобы получить периметр любой фигуры, просто сложите стороны фигуры. Подробнее… iWorksheets :3Учебные пособия :1
Традиционная система США измеряет длину в дюймах, футах, ярдах и милях. Метрическая система представляет собой систему с основанием десять и измеряет длину в километрах, метрах и миллиметрах. Периметр – это измерение расстояния вокруг фигуры. Он измеряется в единицах и может измеряться в дюймах, футах, блоках, метрах, сантиметрах или миллиметрах. Чтобы получить периметр любой фигуры, просто сложите стороны фигуры. Подробнее… iWorksheets :3Учебные пособия :1
Исследование площади и площади поверхности Площадь — это площадь поверхности, которую покрывает фигура. Площадь измеряется в квадратных единицах, будь то дюймы, футы, метры или сантиметры. Формула площади треугольника: A = 1/2 · b · h, где b — основание, а h — высота. Формула площади круга: A = π · r², где π обычно равно 3,14, а r – радиус круга. Формула площади параллелограмма: A = b · h, где b – площадь основание и h высота. Подробнее… iWorksheets :4Учебные пособия :1
Периметр и площадь Что такое периметр и площадь? Периметр – это измерение расстояния вокруг фигуры. Он измеряется в единицах и может измеряться в дюймах, футах, блоках, метрах, сантиметрах или миллиметрах. Чтобы найти периметр любой фигуры, просто сложите стороны фигуры. Площадь — это количество поверхности, которую покрывает фигура. Площадь измеряется в квадратных единицах, будь то дюймы, футы, метры или сантиметры. Формула площади параллелограмма: A = b · h, где b — основание, а h — высота. Подробнее… iWorksheets :4Учебные пособия :1
Он измеряется в единицах и может измеряться в дюймах, футах, блоках, метрах, сантиметрах или миллиметрах. Чтобы найти периметр любой фигуры, просто сложите стороны фигуры. Площадь — это количество поверхности, которую покрывает фигура. Площадь измеряется в квадратных единицах, будь то дюймы, футы, метры или сантиметры. Формула площади параллелограмма: A = b · h, где b — основание, а h — высота. Подробнее… iWorksheets :4Учебные пособия :1
4.2.4. Разработайте стратегии для определения площади поверхности и объема выбранных призм, пирамид и цилиндров.
Исследование площади и площади поверхности Площадь — это площадь поверхности, которую покрывает фигура. Площадь измеряется в квадратных единицах, будь то дюймы, футы, метры или сантиметры. Формула площади треугольника: A = 1/2 · b · h, где b — основание, а h — высота. Формула площади круга: A = π · r², где π обычно равно 3,14, а r – радиус круга. Формула площади параллелограмма: A = b · h, где b – площадь
основание и h высота. Подробнее… iWorksheets :4Учебные пособия :1
Подробнее… iWorksheets :4Учебные пособия :1
Объем в поисках Объем измеряет количество, которое может удерживать твердая фигура. Объем измеряется в кубических единицах и может быть измерен в дюймах, футах, метрах, сантиметрах и миллиметрах. Формула объема прямоугольной призмы: V = l · w · h, где l — длина, w — ширина, h — высота. Подробнее… iWorksheets:4Study Guides:1
Трехмерная геометрия/измерения Трехмерная геометрия/измерения относятся к трехмерным (3D) формам и измерению их форм относительно объема и площади поверхности. Фигуры призм, цилиндров, пирамид, конусов и сфер — все это трехмерные фигуры. Объем измеряет количество, которое может вместить твердая фигура. Объем измеряется в единицах³ и может измеряться в дюймах, футах, метрах, сантиметрах и миллиметрах. Подробнее… iWorksheets:11Учебные пособия:1
4.2.5. Решайте задачи, связанные с масштабными факторами, используя соотношение и пропорцию.
Геометрические пропорции Геометрические пропорции сравнивают два подобных многоугольника. Подобные многоугольники имеют равные соответствующие углы и соответствующие стороны, которые пропорциональны. Уравнение пропорции можно использовать, чтобы доказать, что две фигуры подобны. Если две фигуры похожи, уравнение пропорции можно использовать, чтобы найти недостающую сторону одной из фигур. Подробнее… iWorksheets :4Учебные пособия :1
Подобные многоугольники имеют равные соответствующие углы и соответствующие стороны, которые пропорциональны. Уравнение пропорции можно использовать, чтобы доказать, что две фигуры подобны. Если две фигуры похожи, уравнение пропорции можно использовать, чтобы найти недостающую сторону одной из фигур. Подробнее… iWorksheets :4Учебные пособия :1
Соотношения, пропорции и проценты Числовые пропорции сравнивают два числа. Пропорция обычно имеет форму a:b или a/b. В пропорции 4 части, и ее можно решить, если известны 3 из 4 частей. Пропорции можно решить с помощью свойства перекрестного произведения, которое утверждает, что перекрестные произведения пропорции равны. Подробнее… iWorksheets :4Study Guides :1
Сходство и масштаб Сходство относится к подобным фигурам и способности сравнивать их, используя пропорции. Подобные фигуры имеют равные соответствующие углы и соответствующие стороны, которые пропорциональны. Уравнение пропорции можно использовать, чтобы доказать, что две фигуры подобны. Если две фигуры похожи, уравнение пропорции можно использовать, чтобы найти недостающую сторону одной из фигур. Подробнее… iWorksheets :7Учебные пособия :1
Если две фигуры похожи, уравнение пропорции можно использовать, чтобы найти недостающую сторону одной из фигур. Подробнее… iWorksheets :7Учебные пособия :1
4.2.6. Решите простые задачи, связанные с расходами и производными измерениями таких атрибутов, как скорость и плотность.
Числовые пропорции Числовые пропорции сравнивают два числа. Числа могут иметь одни и те же единицы измерения, такие как отношение, или числа могут иметь разные единицы измерения, такие как ставки. Пропорция обычно имеет форму a:b или a/b. Соотношения используются для сравнения объектов, выигрышей и проигрышей, сторон фигуры с ее площадью и многого другого. Ставки используются для сравнения миль в час, слов в минуту и многих других. Единица измерения – это когда знаменатель пропорции равен единице. Подробнее… iWorksheets :4Учебные пособия :1
Соотношения, пропорции и проценты Числовые пропорции сравнивают два числа. Пропорция обычно имеет форму a:b или a/b. В пропорции 4 части, и ее можно решить, если известны 3 из 4 частей. Пропорции можно решить с помощью свойства перекрестного произведения, которое утверждает, что перекрестные произведения пропорции равны. Подробнее… iWorksheets:4Учебные пособия:1
В пропорции 4 части, и ее можно решить, если известны 3 из 4 частей. Пропорции можно решить с помощью свойства перекрестного произведения, которое утверждает, что перекрестные произведения пропорции равны. Подробнее… iWorksheets:4Учебные пособия:1
NCTM.5. Анализ данных и вероятность
5.1. Сформулируйте вопросы, на которые можно ответить с помощью данных, и соберите, систематизируйте и отобразите соответствующие данные, чтобы ответить на них.
5.1.1. Сформулируйте вопросы, спланируйте исследования и соберите данные о характеристике, общей для двух популяций, или о разных характеристиках в одной популяции.
Сбор и описание данных Сбор и описание данных относятся к различным способам сбора данных и различным способам организации данных, независимо от того, представлены ли они в виде таблицы, графика или круговой диаграммы. Данные могут быть собраны либо путем выборки населения, либо путем проведения опроса. При описании данных рассматриваются данные после того, как они были организованы, и делаются выводы о данных. Подробнее… iWorksheets :3Учебные пособия :1
Подробнее… iWorksheets :3Учебные пособия :1
Вероятность эксперимента FreeЭкспериментальная вероятность — это вероятность того, что наступит определенный результат, основанный на многократном проведении эксперимента. Рабочие листы с вероятностными задачами. Подробнее… iWorksheets:3Учебные пособия:1
5.1.2. Выбирайте, создавайте и используйте подходящие графические представления данных, включая гистограммы, ящичные диаграммы и диаграммы рассеяния.
Анализ, построение графиков и отображение данных Существует много типов графиков, таких как гистограммы, гистограммы и линейные графики. Гистограмма сравнивает данные по категориям и использует столбцы, вертикальные или горизонтальные. Гистограмма похожа на гистограмму, но в гистограммах столбцы соприкасаются друг с другом, тогда как в гистограммах столбцы не касаются друг друга. Линейный график полезен для отображения того, как данные изменяются с течением времени. На линейном графике данные отображаются в виде точек, а линии рисуются для соединения точек, чтобы показать, как изменяются данные. Подробнее… iWorksheets :6Учебные пособия :1
Подробнее… iWorksheets :6Учебные пособия :1
Использование графиков для анализа данных Существуют различные типы графиков и способы анализа данных с помощью графиков. Графики основаны на координатной плоскости. Данные — это точки на плоскости. Если собирать данные о возрасте людей, живущих на одной улице, то это все возрасты. Затем данные могут быть организованы в группы и оценены. Среднее значение, мода и медиана — это разные способы оценки данных. Подробнее… iWorksheets :7Учебные пособия :1
Отображение данных Отображение данных относится ко многим способам отображения данных, будь то гистограмма, линейный график, круговая диаграмма, пиктограмма, линейный график, точечная диаграмма или другой способ. Определенные данные лучше отображаются с помощью разных графиков, а не других графиков. Например. если нужно отобразить данные о стоимости фильма за последние 5 лет, лучше всего будет линейный график. Круговая диаграмма не подходит для использования, потому что круговая диаграмма представляет данные, которые в сумме могут составлять 1 или 100 %. Подробнее… iWorksheets :4Учебные пособия :1
Подробнее… iWorksheets :4Учебные пособия :1
5.2. Выберите и используйте соответствующие статистические методы для анализа данных.
5.2.1. Найдите, используйте и интерпретируйте показатели центра и разброса, включая среднее значение и межквартильный диапазон.
Организация данных Данные можно группировать и анализировать. Среднее значение, мода, медиана и диапазон — это разные способы оценки данных. Среднее значение — это среднее значение данных. Мода относится к числу, которое чаще всего встречается в данных. Медиана — это среднее число, когда данные расположены в порядке от наименьшего к наибольшему. Диапазон — это разница в числах, когда наименьшее число вычитается из наибольшего числа. Данные могут быть организованы в виде таблицы, например таблицы частот. Подробнее… iWorksheets :3Учебные пособия :1
Использование графиков для анализа данных Существуют различные типы графиков и способы анализа данных с помощью графиков. Графики основаны на координатной плоскости. Данные — это точки на плоскости. Если собирать данные о возрасте людей, живущих на одной улице, то это все возрасты. Затем данные могут быть организованы в группы и оценены. Среднее значение, мода и медиана — это разные способы оценки данных. Подробнее… iWorksheets:7Учебные пособия:1
Графики основаны на координатной плоскости. Данные — это точки на плоскости. Если собирать данные о возрасте людей, живущих на одной улице, то это все возрасты. Затем данные могут быть организованы в группы и оценены. Среднее значение, мода и медиана — это разные способы оценки данных. Подробнее… iWorksheets:7Учебные пособия:1
Сбор и описание данных Под сбором и описанием данных понимаются различные способы сбора данных и различные способы организации данных, независимо от того, представлены ли они в виде таблицы, графика или круговой диаграммы. Данные могут быть собраны либо путем выборки населения, либо путем проведения опроса. При описании данных рассматриваются данные после того, как они были организованы, и делаются выводы о данных. Подробнее… iWorksheets:3Учебные пособия:1
5.2.2. Обсудите и поймите соответствие между наборами данных и их графическими представлениями, особенно гистограммами, диаграммами «стебли и листья», ящичковыми диаграммами и диаграммами рассеяния.

Анализ, построение графиков и отображение данных Существует множество типов графиков, таких как гистограммы, гистограммы и линейные графики. Гистограмма сравнивает данные по категориям и использует столбцы, вертикальные или горизонтальные. Гистограмма похожа на гистограмму, но в гистограммах столбцы соприкасаются друг с другом, тогда как в гистограммах столбцы не касаются друг друга. Линейный график полезен для отображения того, как данные изменяются с течением времени. На линейном графике данные отображаются в виде точек, а линии рисуются для соединения точек, чтобы показать, как изменяются данные. Подробнее… iWorksheets :6Учебные пособия :1
Использование графиков для анализа данных Существуют различные типы графиков и способы анализа данных с помощью графиков. Графики основаны на координатной плоскости. Данные — это точки на плоскости. Если собирать данные о возрасте людей, живущих на одной улице, то это все возрасты. Затем данные могут быть организованы в группы и оценены. Среднее значение, мода и медиана — это разные способы оценки данных. Подробнее… iWorksheets :7Учебные пособия :1
Среднее значение, мода и медиана — это разные способы оценки данных. Подробнее… iWorksheets :7Учебные пособия :1
Отображение данных Отображение данных относится ко многим способам отображения данных, будь то гистограмма, линейный график, круговая диаграмма, пиктограмма, линейный график, точечная диаграмма или другой способ. Определенные данные лучше отображаются с помощью разных графиков, а не других графиков. Например. если нужно отобразить данные о стоимости фильма за последние 5 лет, лучше всего будет линейный график. Круговая диаграмма не подходит для использования, потому что круговая диаграмма представляет данные, которые в сумме могут составлять 1 или 100 %. Подробнее… iWorksheets :4Учебные пособия :1
5.3. Разрабатывайте и оценивайте выводы и прогнозы, основанные на данных.
5.3.2. Сделайте предположения о возможных отношениях между двумя характеристиками выборки на основе диаграмм рассеяния данных и приблизительных линий соответствия.

Анализ, построение графиков и отображение данных Существует много типов графиков, таких как гистограммы, гистограммы и линейные графики. Гистограмма сравнивает данные по категориям и использует столбцы, вертикальные или горизонтальные. Гистограмма похожа на гистограмму, но в гистограммах столбцы соприкасаются друг с другом, тогда как в гистограммах столбцы не касаются друг друга. Линейный график полезен для отображения того, как данные изменяются с течением времени. На линейном графике данные отображаются в виде точек, а линии рисуются для соединения точек, чтобы показать, как изменяются данные. Подробнее… iWorksheets :6Учебные пособия :1
Использование графиков для анализа данных Существуют различные типы графиков и способы анализа данных с помощью графиков. Графики основаны на координатной плоскости. Данные — это точки на плоскости. Если собирать данные о возрасте людей, живущих на одной улице, то это все возрасты. Затем данные могут быть организованы в группы и оценены. Среднее значение, мода и медиана — это разные способы оценки данных. Подробнее… iWorksheets :7Учебные пособия :1
Среднее значение, мода и медиана — это разные способы оценки данных. Подробнее… iWorksheets :7Учебные пособия :1
Отображение данных Отображение данных относится ко многим способам отображения данных, будь то гистограмма, линейный график, круговая диаграмма, пиктограмма, линейный график, точечная диаграмма или другой способ. Определенные данные лучше отображаются с помощью разных графиков, а не других графиков. Например. если нужно отобразить данные о стоимости фильма за последние 5 лет, лучше всего будет линейный график. Круговая диаграмма не подходит для использования, потому что круговая диаграмма представляет данные, которые в сумме могут составлять 1 или 100 %. Подробнее… iWorksheets :4Учебные пособия :1
Линейные отношения Линейные отношения относятся к двум величинам, которые связаны линейным уравнением. Поскольку линейное уравнение представляет собой линию, линейная связь относится к двум величинам на линии и их отношению друг к другу. Эта зависимость может быть прямой или обратной. Если y изменяется прямо как x, это означает, что если y удваивается, то x удваивается. Формула прямой вариации: y = kx, где k — постоянная вариации. Подробнее… iWorksheets :3Учебные пособия :1
Эта зависимость может быть прямой или обратной. Если y изменяется прямо как x, это означает, что если y удваивается, то x удваивается. Формула прямой вариации: y = kx, где k — постоянная вариации. Подробнее… iWorksheets :3Учебные пособия :1
5.3.3. Используйте предположения, чтобы сформулировать новые вопросы и спланировать новые исследования, чтобы ответить на них.
Сбор и описание данных Сбор и описание данных относятся к различным способам сбора данных и различным способам организации данных, независимо от того, представлены ли они в виде таблицы, графика или круговой диаграммы. Данные могут быть собраны либо путем выборки населения, либо путем проведения опроса. При описании данных рассматриваются данные после того, как они были организованы, и делаются выводы о данных. Подробнее… iWorksheets :3Учебные пособия :1
Вероятность эксперимента FreeЭкспериментальная вероятность — это вероятность того, что наступит определенный результат, основанный на многократном проведении эксперимента. Рабочие листы с вероятностными задачами. Подробнее… iWorksheets:3Учебные пособия:1
Рабочие листы с вероятностными задачами. Подробнее… iWorksheets:3Учебные пособия:1
5.4. Понимать и применять основные понятия вероятности
5.4.2. Используйте пропорциональность и базовое понимание вероятности, чтобы делать и проверять предположения о результатах экспериментов и моделирования.
Введение в теорию вероятности Вероятность — это возможность того, что определенное событие произойдет. Событие, которое обязательно произойдет, имеет вероятность 1. Событие, которое не может произойти, имеет вероятность 0. Следовательно, вероятность того, что событие произойдет, всегда находится между 0 и 1. Рабочие листы задач на определение вероятностей. Подробнее… iWorksheets :4Study Guides :1
Вероятность эксперимента FreeЭкспериментальная вероятность — это вероятность того, что будет получен определенный результат, основанный на многократном проведении эксперимента. Рабочие листы с вероятностными задачами. Подробнее. .. iWorksheets :3Учебные пособия :1
.. iWorksheets :3Учебные пособия :1
5.4.3. Вычисляйте вероятности простых составных событий, используя такие методы, как организованные списки, древовидные диаграммы и модели областей.
Использование вероятности Вероятность — это возможность того, что определенное событие произойдет. Вероятность – это вероятность события, деленная на общее количество возможных исходов. Вероятность основана на том, являются ли события зависимыми или независимыми друг от друга. Независимое событие относится к исходу одного события, не влияющему на исход другого события. Зависимое событие — это когда результат одного события влияет на результат другого события. Вероятностные словесные задачи. Подробнее… iWorksheets :3Учебные пособия :1
NCTM.6. Решение проблем
6.1. Создавайте новые математические знания, решая задачи.
Математические процессы Математические процессы относятся к навыкам и стратегиям, необходимым для решения математических задач. Если одна стратегия не помогает найти решение проблемы, использование другой стратегии может помочь решить ее. Навыки решения проблем относятся к математическим методам, которые необходимо использовать для решения проблемы. Если бы задача заключалась в определении периметра квадрата, необходимым навыком было бы знание того, что означает периметр, и умение складывать числа. Подробнее… iWorksheets :3Учебные пособия :1
Если одна стратегия не помогает найти решение проблемы, использование другой стратегии может помочь решить ее. Навыки решения проблем относятся к математическим методам, которые необходимо использовать для решения проблемы. Если бы задача заключалась в определении периметра квадрата, необходимым навыком было бы знание того, что означает периметр, и умение складывать числа. Подробнее… iWorksheets :3Учебные пособия :1
6.2. Решайте задачи, возникающие в математике и в других контекстах.
Математические процессы Математические процессы относятся к навыкам и стратегиям, необходимым для решения математических задач. Если одна стратегия не помогает найти решение проблемы, использование другой стратегии может помочь решить ее. Навыки решения проблем относятся к математическим методам, которые необходимо использовать для решения проблемы. Если бы задача заключалась в определении периметра квадрата, необходимым навыком было бы знание того, что означает периметр, и умение складывать числа. Подробнее… iWorksheets :3Учебные пособия :1
Подробнее… iWorksheets :3Учебные пособия :1
6.3. Применяйте и адаптируйте различные подходящие стратегии для решения проблем.
Математические процессы Математические процессы относятся к навыкам и стратегиям, необходимым для решения математических задач. Если одна стратегия не помогает найти решение проблемы, использование другой стратегии может помочь решить ее. Навыки решения проблем относятся к математическим методам, которые необходимо использовать для решения проблемы. Если бы задача заключалась в определении периметра квадрата, необходимым навыком было бы знание того, что означает периметр, и умение складывать числа. Подробнее… iWorksheets :3Учебные пособия :1
NCTM.7. Рассуждение и доказательство
7.1. Признать рассуждение и доказательство фундаментальными аспектами математики.
Математические процессы Математические процессы относятся к навыкам и стратегиям, необходимым для решения математических задач. Если одна стратегия не помогает найти решение проблемы, использование другой стратегии может помочь решить ее. Навыки решения проблем относятся к математическим методам, которые необходимо использовать для решения проблемы. Если бы задача заключалась в определении периметра квадрата, необходимым навыком было бы знание того, что означает периметр, и умение складывать числа. Подробнее… iWorksheets :3Учебные пособия :1
Если одна стратегия не помогает найти решение проблемы, использование другой стратегии может помочь решить ее. Навыки решения проблем относятся к математическим методам, которые необходимо использовать для решения проблемы. Если бы задача заключалась в определении периметра квадрата, необходимым навыком было бы знание того, что означает периметр, и умение складывать числа. Подробнее… iWorksheets :3Учебные пособия :1
7.2. Делайте и исследуйте математические предположения.
Математические процессы Математические процессы относятся к навыкам и стратегиям, необходимым для решения математических задач. Если одна стратегия не помогает найти решение проблемы, использование другой стратегии может помочь решить ее. Навыки решения проблем относятся к математическим методам, которые необходимо использовать для решения проблемы. Если бы задача заключалась в определении периметра квадрата, необходимым навыком было бы знание того, что означает периметр, и умение складывать числа. Подробнее… iWorksheets :3Учебные пособия :1
Подробнее… iWorksheets :3Учебные пособия :1
7.3. Разрабатывайте и оценивайте математические аргументы и доказательства.
Математические процессы Математические процессы относятся к навыкам и стратегиям, необходимым для решения математических задач. Если одна стратегия не помогает найти решение проблемы, использование другой стратегии может помочь решить ее. Навыки решения проблем относятся к математическим методам, которые необходимо использовать для решения проблемы. Если бы задача заключалась в определении периметра квадрата, необходимым навыком было бы знание того, что означает периметр, и умение складывать числа. Подробнее… iWorksheets :3Учебные пособия :1
7.4. Выбирать и использовать различные типы рассуждений и способов доказательства.
Математические процессы Математические процессы относятся к навыкам и стратегиям, необходимым для решения математических задач. Если одна стратегия не помогает найти решение проблемы, использование другой стратегии может помочь решить ее. Навыки решения проблем относятся к математическим методам, которые необходимо использовать для решения проблемы. Если бы задача заключалась в определении периметра квадрата, необходимым навыком было бы знание того, что означает периметр, и умение складывать числа. Подробнее… iWorksheets :3Учебные пособия :1
Навыки решения проблем относятся к математическим методам, которые необходимо использовать для решения проблемы. Если бы задача заключалась в определении периметра квадрата, необходимым навыком было бы знание того, что означает периметр, и умение складывать числа. Подробнее… iWorksheets :3Учебные пособия :1
NCTM.9. Соединения
9.2. Поймите, как математические идеи соединяются и строятся друг на друге, создавая связное целое.
Математические процессы Математические процессы относятся к навыкам и стратегиям, необходимым для решения математических задач. Если одна стратегия не помогает найти решение проблемы, использование другой стратегии может помочь решить ее. Навыки решения проблем относятся к математическим методам, которые необходимо использовать для решения проблемы. Если бы задача заключалась в определении периметра квадрата, необходимым навыком было бы знание того, что означает периметр, и умение складывать числа. Подробнее… iWorksheets :3Учебные пособия :1
NCTM.
 11. Координаторы учебной программы 8 класса
11. Координаторы учебной программы 8 класса11.1. Алгебра: анализ и представление линейных функций, решение линейных уравнений и систем линейных уравнений
11.1.1. Учащиеся используют линейные функции, линейные уравнения и системы линейных уравнений для представления, анализа и решения различных задач. Они признают пропорцию (y/x = k или y = kx) как частный случай линейного уравнения формы y = mx + b, понимая, что константа пропорциональности (k) — это наклон, а результирующий график линия через начало координат. Учащиеся понимают, что наклон (m) линии представляет собой постоянную скорость изменения, поэтому, если входные данные или координата x изменяются на определенную величину, a, выходные данные или координата y изменяются на величину ma. Учащиеся переводят между словесными, табличными, графическими и алгебраическими представлениями функций (признавая, что табличные и графические представления обычно являются лишь частичными представлениями), и они описывают, как такие аспекты функции, как наклон и точка пересечения по оси y, проявляются в различных представлениях.
 Учащиеся решают системы двух линейных уравнений с двумя переменными и связывают системы с парами прямых, которые пересекаются, параллельны или представляют собой одну и ту же прямую на плоскости. Учащиеся используют линейные уравнения, системы линейных уравнений, линейные функции и свое понимание наклона линии для анализа ситуаций и решения проблем.
Учащиеся решают системы двух линейных уравнений с двумя переменными и связывают системы с парами прямых, которые пересекаются, параллельны или представляют собой одну и ту же прямую на плоскости. Учащиеся используют линейные уравнения, системы линейных уравнений, линейные функции и свое понимание наклона линии для анализа ситуаций и решения проблем.Введение в функции Функция — это правило, которое применяется к числу, называемому входом, для получения результата, называемого выходом. Правило состоит из одной или нескольких математических операций, которые выполняются над входными данными. Примером функции является y = 2x + 3, где x — вход, а y — выход. Операции умножения и сложения выполняются на входе x, чтобы получить выход y. Подставляя число вместо x, можно определить выход. Подробнее… iWorksheets :6Учебные пособия :1
Линейные уравнения Линейные уравнения — это уравнения с двумя переменными, которые на графике представляют собой прямую линию. Линейное уравнение может быть построено на основе их наклона и y-пересечения. Стандартное уравнение для прямой: y = mx + b, где m — наклон, а b — точка пересечения с осью y. Наклон можно найти по формуле m = (y2 — y1)/(x2 — x1), которая представляет собой изменение y по сравнению с изменением x. Подробнее… iWorksheets :6Study Guides :1
Линейное уравнение может быть построено на основе их наклона и y-пересечения. Стандартное уравнение для прямой: y = mx + b, где m — наклон, а b — точка пересечения с осью y. Наклон можно найти по формуле m = (y2 — y1)/(x2 — x1), которая представляет собой изменение y по сравнению с изменением x. Подробнее… iWorksheets :6Study Guides :1
Линейные отношения Линейные отношения относятся к двум величинам, которые связаны линейным уравнением. Поскольку линейное уравнение представляет собой линию, линейная связь относится к двум величинам на линии и их отношению друг к другу. Эта зависимость может быть прямой или обратной. Если y изменяется прямо как x, это означает, что если y удваивается, то x удваивается. Формула прямой вариации: y = kx, где k — постоянная вариации. Подробнее… iWorksheets :3Учебные пособия :1
Функции FreeФункция — это правило, которое применяется к числу, называемому входом, для получения результата, называемого выходом. Правило состоит из одной или нескольких математических операций, которые выполняются над входными данными. Примером функции является y = 2x + 3, где x — вход, а y — выход. Операции умножения и сложения выполняются на входе x, чтобы получить выход y. Подставляя число вместо x, можно определить выход. Подробнее… iWorksheets :5Учебные пособия :1
Правило состоит из одной или нескольких математических операций, которые выполняются над входными данными. Примером функции является y = 2x + 3, где x — вход, а y — выход. Операции умножения и сложения выполняются на входе x, чтобы получить выход y. Подставляя число вместо x, можно определить выход. Подробнее… iWorksheets :5Учебные пособия :1
11.2. Геометрия и измерение: анализ двух- и трехмерного пространства и фигур с использованием расстояния и угла
11.2.1. Учащиеся используют фундаментальные факты о расстоянии и углах для описания и анализа фигур и ситуаций в двух- и трехмерном пространстве, а также для решения задач, в том числе многошаговых. Они доказывают, что определенные конфигурации линий порождают подобные треугольники из-за конгруэнтных углов, возникающих при пересечении параллельных прямых секущей. Учащиеся применяют это рассуждение о подобных треугольниках для решения множества задач, в том числе и тех, которые требуют нахождения высот и расстояний.
 Они используют факты об углах, которые образуются, когда секущая пересекает параллельные прямые, чтобы объяснить, почему сумма мер углов в треугольнике равна 180 градусам, и они применяют этот факт о треугольниках, чтобы найти неизвестные меры углов. Учащиеся объясняют, почему теорема Пифагора верна, используя различные методы, например, разлагая квадрат двумя разными способами. Они применяют теорему Пифагора для нахождения расстояний между точками в декартовой координатной плоскости для измерения длин и анализа многоугольников и многогранников.
Они используют факты об углах, которые образуются, когда секущая пересекает параллельные прямые, чтобы объяснить, почему сумма мер углов в треугольнике равна 180 градусам, и они применяют этот факт о треугольниках, чтобы найти неизвестные меры углов. Учащиеся объясняют, почему теорема Пифагора верна, используя различные методы, например, разлагая квадрат двумя разными способами. Они применяют теорему Пифагора для нахождения расстояний между точками в декартовой координатной плоскости для измерения длин и анализа многоугольников и многогранников.Теорема Пифагора Теорема Пифагора — это фундаментальное соотношение в евклидовой геометрии. Он гласит, что сумма квадратов катетов прямоугольного треугольника равна квадрату длины гипотенузы. Определить расстояние между двумя точками по теореме Пифагора. Подробнее… iWorksheets:10Учебные пособия:2
Соотношения, пропорции и проценты Числовые пропорции сравнивают два числа. Пропорция обычно имеет форму a:b или a/b. В пропорции 4 части, и ее можно решить, если известны 3 из 4 частей. Пропорции можно решить с помощью свойства перекрестного произведения, которое утверждает, что перекрестные произведения пропорции равны. Подробнее… iWorksheets :4Учебные пособия :1
В пропорции 4 части, и ее можно решить, если известны 3 из 4 частей. Пропорции можно решить с помощью свойства перекрестного произведения, которое утверждает, что перекрестные произведения пропорции равны. Подробнее… iWorksheets :4Учебные пособия :1
Сходство и масштаб Сходство означает сходство фигур и возможность их сравнения с использованием пропорций. Подобные фигуры имеют равные соответствующие углы и соответствующие стороны, которые пропорциональны. Уравнение пропорции можно использовать, чтобы доказать, что две фигуры подобны. Если две фигуры похожи, уравнение пропорции можно использовать, чтобы найти недостающую сторону одной из фигур. Подробнее… iWorksheets :7Учебные пособия :1
11.3. Анализ данных, числа, операции и алгебра: анализ и обобщение наборов данных
11.3.1. Учащиеся используют описательную статистику, включая среднее значение, медиану и диапазон, для суммирования и сравнения наборов данных, а также систематизируют и отображают данные, чтобы ставить вопросы и отвечать на них.
 Они сравнивают информацию, предоставленную средним значением и медианой, и исследуют различные эффекты, которые изменения значений данных оказывают на эти меры центра. Они понимают, что мера центра сама по себе не полностью описывает набор данных, потому что очень разные наборы данных могут иметь одну и ту же меру центра. Учащиеся выбирают среднее значение или медиану в качестве подходящей меры центра для данной цели.
Они сравнивают информацию, предоставленную средним значением и медианой, и исследуют различные эффекты, которые изменения значений данных оказывают на эти меры центра. Они понимают, что мера центра сама по себе не полностью описывает набор данных, потому что очень разные наборы данных могут иметь одну и ту же меру центра. Учащиеся выбирают среднее значение или медиану в качестве подходящей меры центра для данной цели.Организация данных Данные можно группировать и анализировать. Среднее значение, мода, медиана и диапазон — это разные способы оценки данных. Среднее значение — это среднее значение данных. Мода относится к числу, которое чаще всего встречается в данных. Медиана — это среднее число, когда данные расположены в порядке от наименьшего к наибольшему. Диапазон — это разница в числах, когда наименьшее число вычитается из наибольшего числа. Данные могут быть организованы в виде таблицы, например таблицы частот. Подробнее… iWorksheets :3Учебные пособия :1
Использование графиков для анализа данных Существуют различные типы графиков и способы анализа данных с помощью графиков. Графики основаны на координатной плоскости. Данные — это точки на плоскости. Если собирать данные о возрасте людей, живущих на одной улице, то это все возрасты. Затем данные могут быть организованы в группы и оценены. Среднее значение, мода и медиана — это разные способы оценки данных. Подробнее… iWorksheets:7Учебные пособия:1
Графики основаны на координатной плоскости. Данные — это точки на плоскости. Если собирать данные о возрасте людей, живущих на одной улице, то это все возрасты. Затем данные могут быть организованы в группы и оценены. Среднее значение, мода и медиана — это разные способы оценки данных. Подробнее… iWorksheets:7Учебные пособия:1
Сбор и описание данных Под сбором и описанием данных понимаются различные способы сбора данных и различные способы организации данных, независимо от того, представлены ли они в виде таблицы, графика или круговой диаграммы. Данные могут быть собраны либо путем выборки населения, либо путем проведения опроса. При описании данных рассматриваются данные после того, как они были организованы, и делаются выводы о данных. Подробнее… iWorksheets :3Study Guides :1
Отображение данных Отображение данных относится ко многим способам отображения данных, будь то гистограмма, линейный график, круговая диаграмма, пиктограмма, линейный график, точечная диаграмма или другим способом. Определенные данные лучше отображаются с помощью разных графиков, а не других графиков. Например. если нужно отобразить данные о стоимости фильма за последние 5 лет, лучше всего будет линейный график. Круговая диаграмма не подходит для использования, потому что круговая диаграмма представляет данные, которые в сумме могут составлять 1 или 100 %. Подробнее… iWorksheets :4Учебные пособия :1
Определенные данные лучше отображаются с помощью разных графиков, а не других графиков. Например. если нужно отобразить данные о стоимости фильма за последние 5 лет, лучше всего будет линейный график. Круговая диаграмма не подходит для использования, потому что круговая диаграмма представляет данные, которые в сумме могут составлять 1 или 100 %. Подробнее… iWorksheets :4Учебные пособия :1
NCTM.12. Связь с координаторами 8-го уровня
12.1. Алгебра: учащиеся сталкиваются с некоторыми нелинейными функциями (например, с обратными пропорциями, которые они изучали в 7 классе, а также с основными квадратичными и экспоненциальными функциями), скорость изменения которых отличается от постоянной скорости изменения линейных функций. Они рассматривают арифметические последовательности, в том числе возникающие из шаблонов или проблем, как линейные функции, входными данными которых являются числа. Они применяют идеи о линейных функциях для решения задач, связанных с такими скоростями, как движение с постоянной скоростью.

Нелинейные функции и теория множеств Функция может быть представлена в виде y = mx + b. Это уравнение прямой, поэтому говорят, что это линейная функция. Нелинейные функции — это функции, не являющиеся прямыми линиями. Некоторыми примерами нелинейных функций являются экспоненциальные функции. и параболические функции. Экспоненциальная функция y = aˆx представляет собой кривую линию, которая приближается к оси x, но не касается ее. Параболическая функция y = ax² + bx +c представляет собой U-образную линию, которая может быть обращена либо вверх, либо вниз. Подробнее… iWorksheets :5Учебные пособия :1
Последовательности Последовательность — это упорядоченный список чисел. Последовательности являются результатом шаблона или правила. Образцом или правилом может быть любое другое число или некоторая формула, например y = 2x + 3. Когда задан образец или правило, можно найти последовательность. Когда задана последовательность, можно найти шаблон или правило. Подробнее… iWorksheets :5Учебные пособия :1
Подробнее… iWorksheets :5Учебные пособия :1
Функции FreeФункция — это правило, которое выполняется над числом, называемым входом, для получения результата, называемого выходом. Правило состоит из одной или нескольких математических операций, которые выполняются над входными данными. Примером функции является y = 2x + 3, где x — вход, а y — выход. Операции умножения и сложения выполняются на входе x, чтобы получить выход y. Подставляя число вместо x, можно определить выход. Подробнее… iWorksheets :5Учебные пособия :1
12.2. Геометрия: Имея линию на координатной плоскости, учащиеся понимают, что все «треугольники наклона» — треугольники, созданные отрезком вертикальной «подъемной» линии (показывающим изменение y), горизонтальным отрезком «бегущей» линии. (показывая изменение x), и отрезок самой прямой — подобны. Они также понимают отношение этих подобных треугольников к постоянному наклону линии.
Введение в функции Функция — это правило, которое применяется к числу, называемому входом, для получения результата, называемого выходом. Правило состоит из одной или нескольких математических операций, которые выполняются над входными данными. Примером функции является y = 2x + 3, где x — вход, а y — выход. Операции умножения и сложения выполняются на входе x, чтобы получить выход y. Подставляя число вместо x, можно определить выход. Подробнее… iWorksheets :6Учебные пособия :1
Правило состоит из одной или нескольких математических операций, которые выполняются над входными данными. Примером функции является y = 2x + 3, где x — вход, а y — выход. Операции умножения и сложения выполняются на входе x, чтобы получить выход y. Подставляя число вместо x, можно определить выход. Подробнее… iWorksheets :6Учебные пособия :1
Линейные уравнения Линейные уравнения — это уравнения с двумя переменными, которые на графике представляют собой прямую линию. Линейное уравнение может быть построено на основе их наклона и y-пересечения. Стандартное уравнение для прямой: y = mx + b, где m — наклон, а b — точка пересечения с осью y. Наклон можно найти по формуле m = (y2 — y1)/(x2 — x1), которая представляет собой изменение y по сравнению с изменением x. Подробнее… iWorksheets:6Учебные пособия:1
12.3. Анализ данных. Основываясь на своей работе в предыдущих классах по организации и отображению данных для постановки вопросов и ответов на них, учащиеся теперь видят числовые данные в виде совокупности, которую они часто могут суммировать с помощью одного или нескольких чисел.
 В дополнение к медиане учащиеся определяют 25-й и 75-й процентили (1-й и 3-й квартили) для получения информации о разбросе данных. Для передачи этой информации они могут использовать графики типа «ящик с усами». Учащиеся строят диаграммы рассеяния для отображения двумерных данных и неформально оценивают линии, наиболее подходящие для выдвижения и проверки предположений.
В дополнение к медиане учащиеся определяют 25-й и 75-й процентили (1-й и 3-й квартили) для получения информации о разбросе данных. Для передачи этой информации они могут использовать графики типа «ящик с усами». Учащиеся строят диаграммы рассеяния для отображения двумерных данных и неформально оценивают линии, наиболее подходящие для выдвижения и проверки предположений.Организация данных Данные можно группировать и анализировать. Среднее значение, мода, медиана и диапазон — это разные способы оценки данных. Среднее значение — это среднее значение данных. Мода относится к числу, которое чаще всего встречается в данных. Медиана — это среднее число, когда данные расположены в порядке от наименьшего к наибольшему. Диапазон — это разница в числах, когда наименьшее число вычитается из наибольшего числа. Данные могут быть организованы в виде таблицы, например таблицы частот. Подробнее… iWorksheets :3Учебные пособия :1
Анализ, построение графиков и отображение данных Существует много типов графиков, таких как гистограммы, гистограммы и линейные графики. Гистограмма сравнивает данные по категориям и использует столбцы, вертикальные или горизонтальные. Гистограмма похожа на гистограмму, но в гистограммах столбцы соприкасаются друг с другом, тогда как в гистограммах столбцы не касаются друг друга. Линейный график полезен для отображения того, как данные изменяются с течением времени. На линейном графике данные отображаются в виде точек, а линии рисуются для соединения точек, чтобы показать, как изменяются данные. Подробнее… iWorksheets :6Учебные пособия :1
Гистограмма сравнивает данные по категориям и использует столбцы, вертикальные или горизонтальные. Гистограмма похожа на гистограмму, но в гистограммах столбцы соприкасаются друг с другом, тогда как в гистограммах столбцы не касаются друг друга. Линейный график полезен для отображения того, как данные изменяются с течением времени. На линейном графике данные отображаются в виде точек, а линии рисуются для соединения точек, чтобы показать, как изменяются данные. Подробнее… iWorksheets :6Учебные пособия :1
Использование графиков для анализа данных Существуют различные типы графиков и способы анализа данных с помощью графиков. Графики основаны на координатной плоскости. Данные — это точки на плоскости. Если собирать данные о возрасте людей, живущих на одной улице, то это все возрасты. Затем данные могут быть организованы в группы и оценены. Среднее значение, мода и медиана — это разные способы оценки данных. Подробнее… iWorksheets:7Учебные пособия:1
Сбор и описание данных Под сбором и описанием данных понимаются различные способы сбора данных и различные способы организации данных, независимо от того, представлены ли они в виде таблицы, графика или круговой диаграммы. Данные могут быть собраны либо путем выборки населения, либо путем проведения опроса. При описании данных рассматриваются данные после того, как они были организованы, и делаются выводы о данных. Подробнее… iWorksheets :3Study Guides :1
Данные могут быть собраны либо путем выборки населения, либо путем проведения опроса. При описании данных рассматриваются данные после того, как они были организованы, и делаются выводы о данных. Подробнее… iWorksheets :3Study Guides :1
Отображение данных Отображение данных относится ко многим способам отображения данных, будь то гистограмма, линейный график, круговая диаграмма, пиктограмма, линейный график, точечная диаграмма или другим способом. Определенные данные лучше отображаются с помощью разных графиков, а не других графиков. Например. если нужно отобразить данные о стоимости фильма за последние 5 лет, лучше всего будет линейный график. Круговая диаграмма не подходит для использования, потому что круговая диаграмма представляет данные, которые в сумме могут составлять 1 или 100 %. Подробнее… iWorksheets :4Учебные пособия :1
Линейные отношения Линейные отношения относятся к двум величинам, которые связаны линейным уравнением. Поскольку линейное уравнение представляет собой линию, линейная связь относится к двум величинам на линии и их отношению друг к другу. Эта зависимость может быть прямой или обратной. Если y изменяется прямо как x, это означает, что если y удваивается, то x удваивается. Формула прямой вариации: y = kx, где k — постоянная вариации. Подробнее… iWorksheets :3Учебные пособия :1
Поскольку линейное уравнение представляет собой линию, линейная связь относится к двум величинам на линии и их отношению друг к другу. Эта зависимость может быть прямой или обратной. Если y изменяется прямо как x, это означает, что если y удваивается, то x удваивается. Формула прямой вариации: y = kx, где k — постоянная вариации. Подробнее… iWorksheets :3Учебные пособия :1
12.4. Числа и операции: учащиеся используют показатели степени и научную запись для описания очень больших и очень маленьких чисел. Они используют квадратные корни, когда применяют теорему Пифагора.
Экспоненты, множители и дроби БесплатноВ математическом выражении, в котором одно и то же число умножается много раз, часто полезно записать число как основание с показателем степени. Экспоненты также используются для оценки чисел. Любое число в нулевой степени равно 1, а любое число в отрицательной степени является числом меньше 1. В экспоненте экспоненты используются для облегчения записи очень больших или очень маленьких чисел. Подробнее… iWorksheets :8Учебные пособия :1
Подробнее… iWorksheets :8Учебные пособия :1
Теорема Пифагора Теорема Пифагора — это фундаментальное соотношение в евклидовой геометрии. Он гласит, что сумма квадратов катетов прямоугольного треугольника равна квадрату длины гипотенузы. Определить расстояние между двумя точками по теореме Пифагора. Подробнее… iWorksheets :10Study Guides :2
Полиномы и экспоненты FreeМногочлен — это выражение в форме axn, где a — любое действительное число, а n — целое. число. Если многочлен имеет только один член, он называется мономом. Если в нем два члена, то это двучлен, а если три члена, то это трехчлен. Стандартная форма многочлена — это когда степени переменных уменьшаются слева направо. Подробнее… iWorksheets :6Учебные пособия :1
Переход из 8 класса в среднюю школу по математике
Подарите образование, которое изменит вашу жизнь! Пожертвовать сейчас!
Обзор курса
Математика для 8 класса Обзор курса
Математика для 8 класса свяжет концепции десятичных дробей, соотношений, ставок, процентов, показателей степени в сочетании с простыми интересами для решения реальных жизненных задач и принятия обоснованных финансовых решений. Учащиеся будут готовиться к старшей школе, так как некоторые расширенные алгебраические навыки будут частью нашего внимания. Они освоят работу с очень большими или маленькими числами, используя экспоненциальную запись.
Учащиеся будут готовиться к старшей школе, так как некоторые расширенные алгебраические навыки будут частью нашего внимания. Они освоят работу с очень большими или маленькими числами, используя экспоненциальную запись.
Справочные видеоролики предоставляются для базовой поддержки. За инструкциями обращайтесь к Анилу Кумару.
Социальные и эмоциональные навыки: Творческое вовлечение ума — это наш подход к поддержке изучения математических понятий, чтобы быть готовым к будущему с позитивным настроем. Это неотъемлемая часть каждого передаваемого навыка, который может помочь учащимся укрепить уверенность и преодолеть тревогу.
Числа : Вещественные числа (и рациональные, и иррациональные числа)
- Понимание системы счисления и разницы между рациональными и иррациональными числами
- Использовать научную нотацию для представления очень больших или очень маленьких чисел
- Оценка и вычисление квадратного корня без калькулятора
- Применение законов экспоненты для мысленных вычислений с большими числами
- Решите задачи, связанные с комбинацией прямоугольных треугольников, используя теорему Пифагора
- Используйте свойства порядка операций для упрощения выражений, включающих десятичные дроби, отношения, показатели степени и квадратный корень.

- Умножайте и делите дроби на дроби и упрощайте, используя несколько шагов.
- Применять пропорциональные рассуждения для решения проблем во многих приложениях.
Алгебра: Операции с полиномами
- Демонстрировать четкое понимание переменных, выражений, уравнений и неравенств и применять это в решении реальных жизненных ситуаций
- Выполнение операций сложения, вычитания и умножения одночленов и двучленов
- Решение многошаговых уравнений с дробями
- Решение неравенств с целыми числами
- Определить явные правила шаблона для поиска отсутствующих и/или неизвестных терминов
- Моделирование ситуаций и применение полученных навыков для поиска стратегических решений словесных задач, связанных с расстоянием, скоростью, временем, возрастом и смесью
- Демонстрация навыков применения унитарного метода для решения задач
- Подход UMCL к решению проблем является эффективной техникой для практики на этом уровне
Данные: Управление, анализ и использование данных для эффективной коммуникации
- Определите ситуации с одной переменной и ситуации с двумя переменными и объясните, когда необходим каждый тип данных.

- Работа с непрерывными и дискретными данными и выбор типа графика, наиболее подходящего для представления полученной информации
- Создайте инфографику о наборе данных, представляя данные соответствующим образом, включая таблицу, линейный график, круговой график и гистограмму, чтобы объяснить сценарий.
- Используйте математический язык, включая термины «сильный», «слабый», «нет», «положительный», «отрицательный», для описания взаимосвязи между двумя переменными для различных наборов данных с выбросами и без них.
- Понять влияние добавления или удаления данных из набора данных на показатель центральной тенденции и описать, как эти изменения влияют на форму и распределение презентации.
- Проанализируйте вводящие в заблуждение графики и представьте убедительные аргументы, чтобы устранить вводящие в заблуждение предвзятые представления и убедительно завершить интерпретацию.
Вероятность: Концепция множеств, диаграмм Венна и древовидных диаграмм
- Опишите разницу между независимыми и зависимыми событиями, приводя пример
- Анализ теоретической и экспериментальной вероятности независимых событий
- Делать прогнозы на основе вероятности одного или нескольких событий
- Опишите вероятность события и используйте эту информацию для прогнозирования
- Прогнозируйте возможность событий, используя такие инструменты, как диаграмма Венна, древовидная диаграмма и таблицы решений.

Пространственное чувство: геометрическое мышление:
- Определение геометрических свойств мозаичных форм и определение преобразований, происходящих в мозаиках
- Создание чертежей в масштабе для расчета фактической длины и площади
- Создавайте объектные модели в соответствующем масштабе, показывая виды сверху, спереди и сбоку.
- Описать и классифицировать цилиндры, конусы, призмы, пирамиды в соответствии с их геометрическими свойствами.
- Построение углов, параллельных/перпендикулярных линий, треугольников и четырехугольников
Пространственное чувство: Движение:
- Выполнить расширение и описать сходство между объектом и изображением
- Выполнение перемещений, отражений и вращения в декартовой плоскости
Пространственное чувство: Измерения:
- Представление очень больших (мега, гига, тера) и очень малых значений (микро, нано, пико) метрических единиц с использованием моделей, отношений с основанием десяти и экспоненциальной записи.

- Решение параллельных и поперечных линий со свойствами угла
- Опишите разницу и сходство между объемом и емкостью
- Найти площадь и периметр двумерных составных фигур
- Расчет площади поверхности и объема составных объектов
Финансовая грамотность
Ценить деньги и применять математические концепции для критического осмысления их
- Определять и сравнивать обменные курсы и конвертировать иностранные валюты
- Опишите некоторые преимущества и недостатки различных способов оплаты, которые можно использовать при работе с несколькими валютами
- Объясните, как изменение процентной ставки может повлиять на сбережения или кредиты в нашей обычной жизни.
Проект и оценка: Применение приобретенных навыков для демонстрации критического мышления и решения проблем
- Создание, отслеживание и корректировка типовых бюджетов, предназначенных для достижения долгосрочных целей
- Исследования по интересующей теме и представление информации, демонстрирующей применение полученных навыков
Цели
Привлечь учащихся к построению фундамента по математике, чтобы быть готовыми к будущему и добиться успеха.
Предпосылки
- Понимать порядок операций и работу с дробями
- Пройдите тест ССЫЛКА: СРЕДНЯЯ ШКОЛА ТЕСТ
Цены
- Стоимость курса указана за месяц для индивидуальных индивидуальных занятий. В месяц будет 4 занятия. Гибкий график обсуждается отдельно.
- Иногда предлагаются групповые занятия. Вы можете проверить веб-сайт популярных групповых математических программ .
- Программа Fast Track доступна по запросу. Мы можем подготовить студентов к экзамену в ограниченное время. Вы можете заполнить Регистрационная форма и обсудить возможности.
Часто задаваемые вопросы
Политика возврата регистрационных взносов.
Учащиеся могут прийти в первые 30 минут занятия и получить полную компенсацию. Затем урок начнется после 5-минутного перерыва в течение следующих 30 минут. Деньги за курс не возвращаются, если студент продолжает посещать первое занятие после перерыва.
Как мы учим и стоит ли проходить курс?
Вы лучший человек, чтобы ответить на этот вопрос. Интернет полон знаний, и для вас открыто множество вариантов. Исследуйте, а потом решайте. Мы предоставили ссылки на несколько видеороликов, связанных с этим курсом. Они могут помочь вам принять решение в нашу пользу.
Пример группы Класс:
Часто задаваемые вопросы
Политика возврата регистрационных взносов.
Учащиеся могут прийти в первые 30 минут занятия и получить полную компенсацию. Затем урок начнется после 5-минутного перерыва в течение следующих 30 минут. Деньги за курс не возвращаются, если студент продолжает посещать первое занятие после перерыва.
Как мы учим и стоит ли проходить курс?
Вы лучший человек, чтобы ответить на этот вопрос. Интернет полон знаний, и для вас открыто множество вариантов. Исследуйте, а потом решайте. Мы предоставили ссылки на несколько видеороликов, связанных с этим курсом. Они могут помочь вам принять решение в нашу пользу.
Просмотрите список примеров справочных видео, чтобы получить представление о наших занятиях
Содержание курса
Примеры видео
SKILLS
Curriculum Overview
PREREQUISITE
NUMBERS and APPLICATION
Surds and Radicals
Fractions
Integers
Algebra
Ratio, Proportions and Rate
Percent, Decimals and Fractions
Data Management
Spatial Чувство: Преобразования
Чувство Пространства: Измерения
Чувство Пространства: Визуализация и трехмерное представление
Вероятность
Геометрия и построение
Extended: Inequalities
Extended Applications
Extended: Series and Sequences
Financial Applications
Polynomials
Challenge Questions
Pythagorean Theorem
Problem Solving Strategies
PROJECT and ASSIGNMENT
International Competitions
GCSE 2017
Проблемы с Word
Часто задаваемые вопросы
Политика возврата регистрационных взносов.

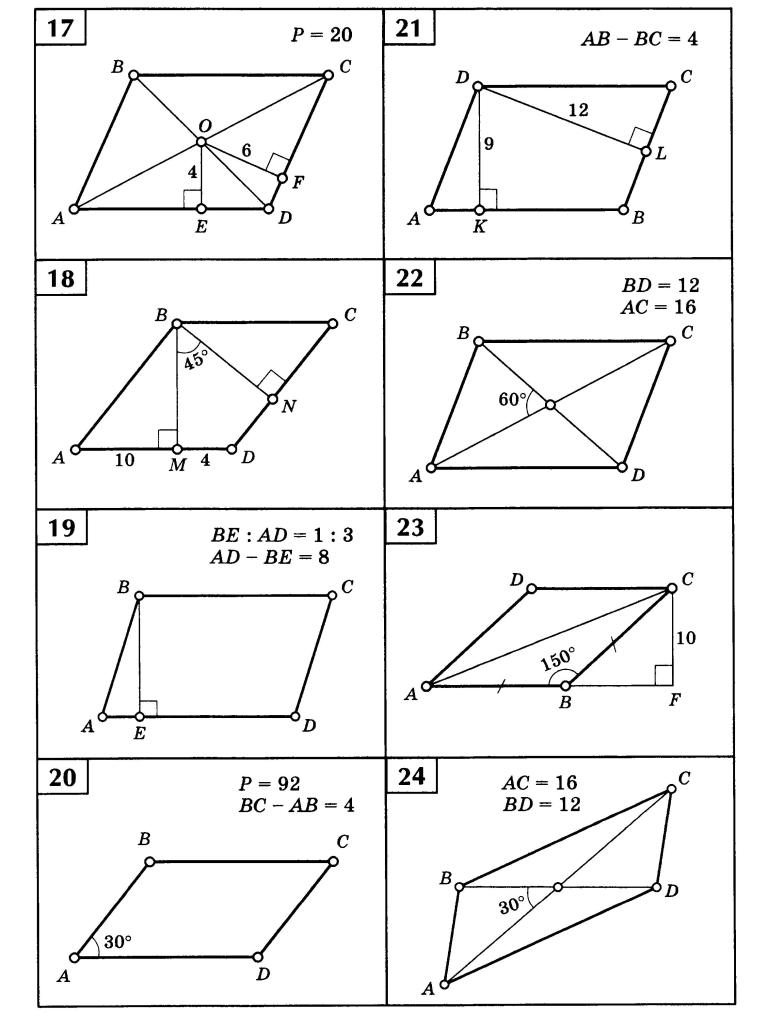 Базовый уровень сложности. 5 заданий. Время выполнения 15 минут.
Базовый уровень сложности. 5 заданий. Время выполнения 15 минут.  В нем есть более сложные задачи с использованием теоремы Пифагора и других формул и теорем геометрии, например, формул площадей и периметра геометрических фигур. В заданиях кроме прямоугольного треугольника надо знать и уметь применять свойства равнобедренного треугольника, прямоугольника, ромба. Вычислять площадь прямоугольника, прямоугольного треугольника, ромба. Уметь вычислять площадь ромба через диагонали.
В нем есть более сложные задачи с использованием теоремы Пифагора и других формул и теорем геометрии, например, формул площадей и периметра геометрических фигур. В заданиях кроме прямоугольного треугольника надо знать и уметь применять свойства равнобедренного треугольника, прямоугольника, ромба. Вычислять площадь прямоугольника, прямоугольного треугольника, ромба. Уметь вычислять площадь ромба через диагонали.
 02.2022
5004
02.2022
5004
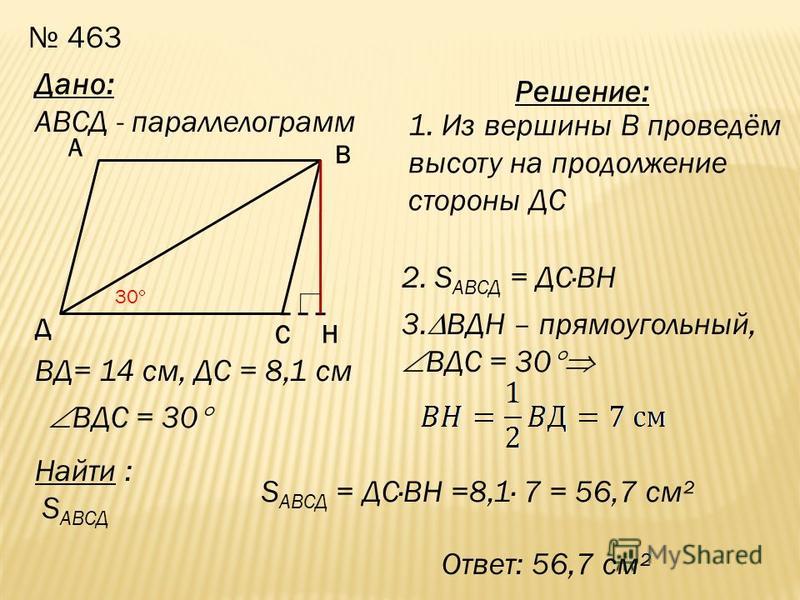

 Критерии: «3» 50-69%, «4» 70-90%, «5» 91-100%. Оценка выставляется сразу после прохождения теста.
Критерии: «3» 50-69%, «4» 70-90%, «5» 91-100%. Оценка выставляется сразу после прохождения теста.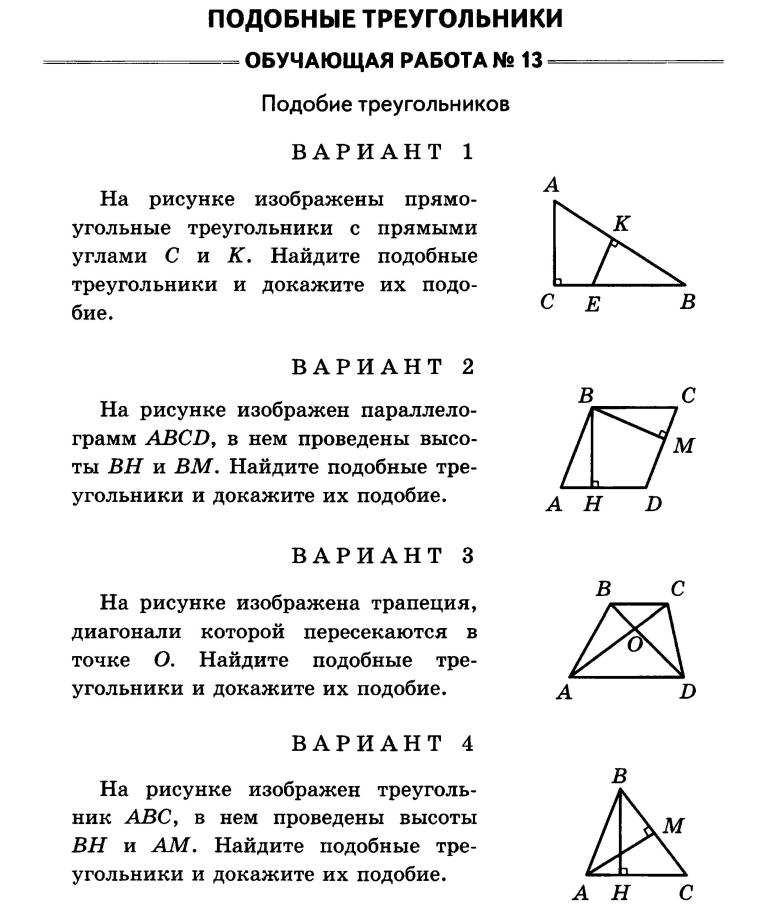 8 класс. Математика. Тест 2
8 класс. Математика. Тест 2
 Задания в тест выбираются случайным образом из общей базы заданий. Критерии: «3» 50-69%, «4» 70-90%, «5» 91-100%. Оценка выставляется сразу после прохождения теста. Время ОГРАНИЧЕНО 20 минут.
Задания в тест выбираются случайным образом из общей базы заданий. Критерии: «3» 50-69%, «4» 70-90%, «5» 91-100%. Оценка выставляется сразу после прохождения теста. Время ОГРАНИЧЕНО 20 минут.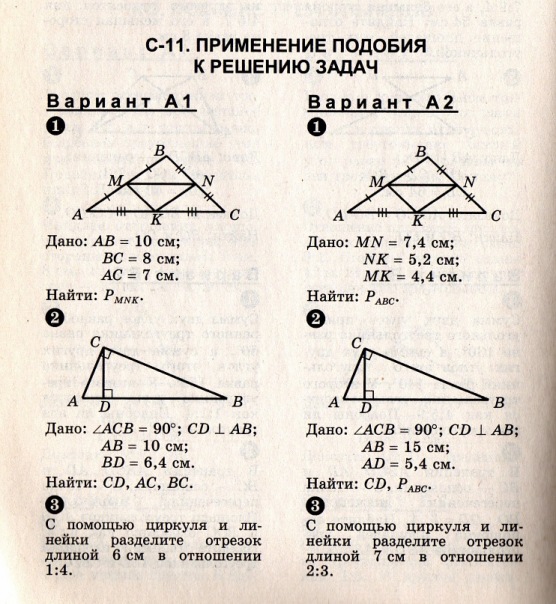
 11.2020
146
0
11.2020
146
0


 п. В рамках школьной программы.
п. В рамках школьной программы. 8Б класс
8Б класс
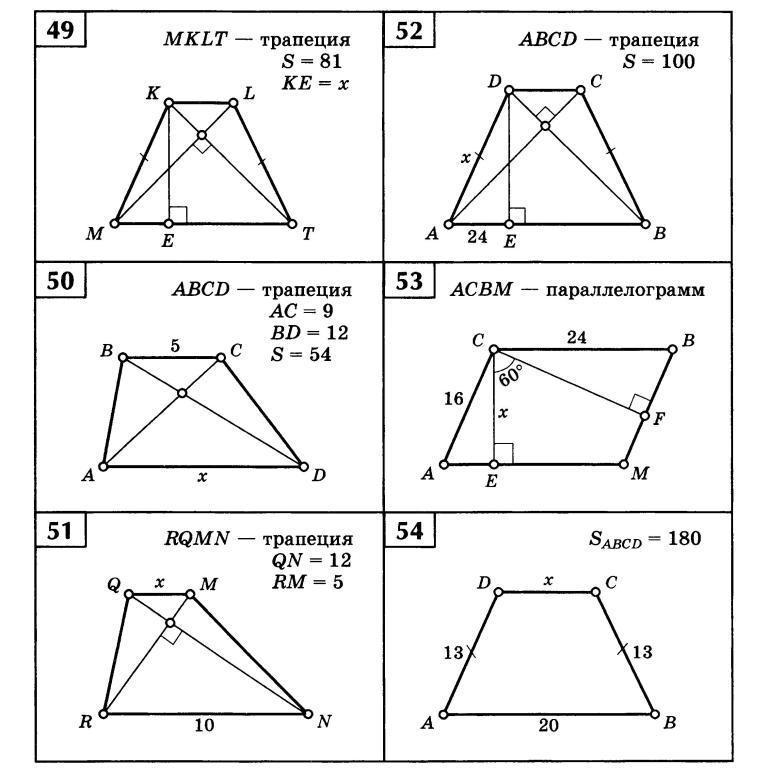 05.2021
304
0
05.2021
304
0
 10.2021
10.2021
 Учебник: Геометрия 7-9 класс. Автор: Атаносян Л.С., Бутузов В.Ф.
Учебник: Геометрия 7-9 класс. Автор: Атаносян Л.С., Бутузов В.Ф. 04.2020
223
0
04.2020
223
0
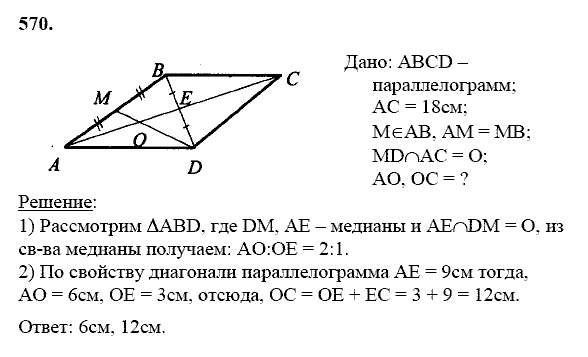

 12.2020
190
0
12.2020
190
0

 11.2021
226
0
11.2021
226
0
 11.2021
502
11.2021
502
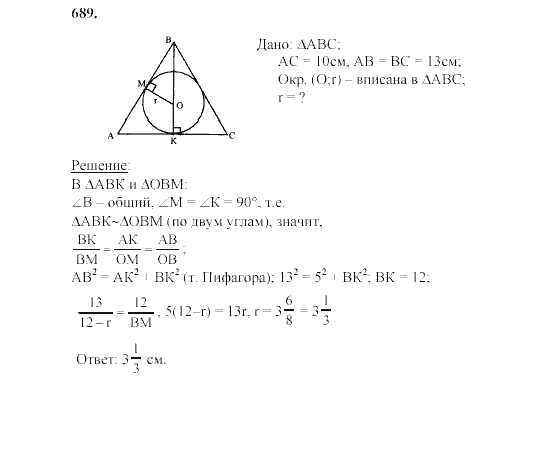
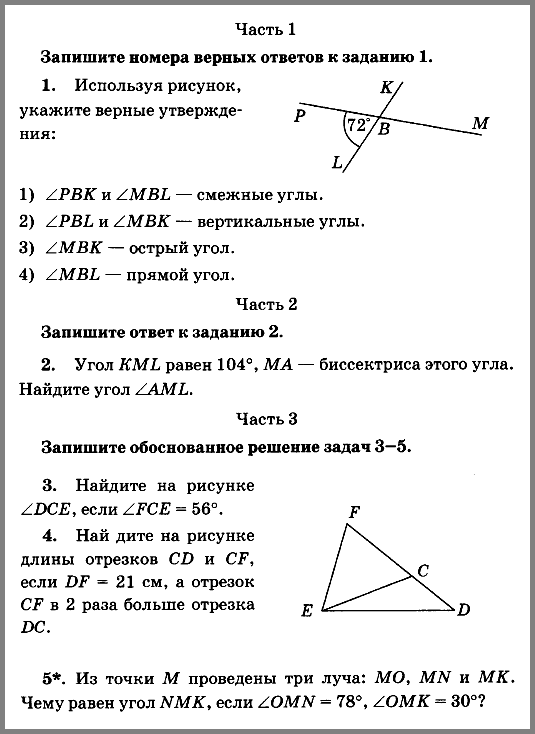 02.2023
87
0
02.2023
87
0

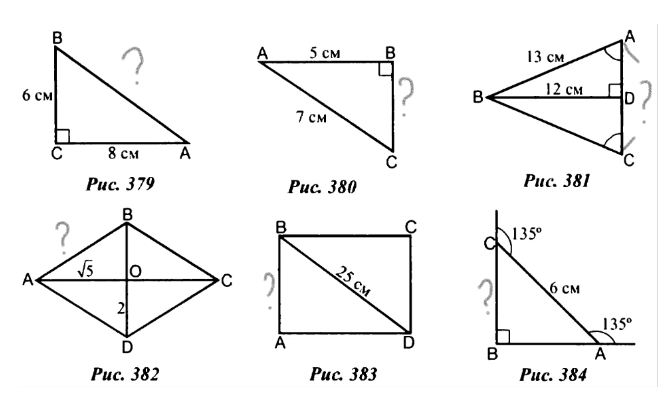 Педагогический (научно-педагогический) состав
Педагогический (научно-педагогический) состав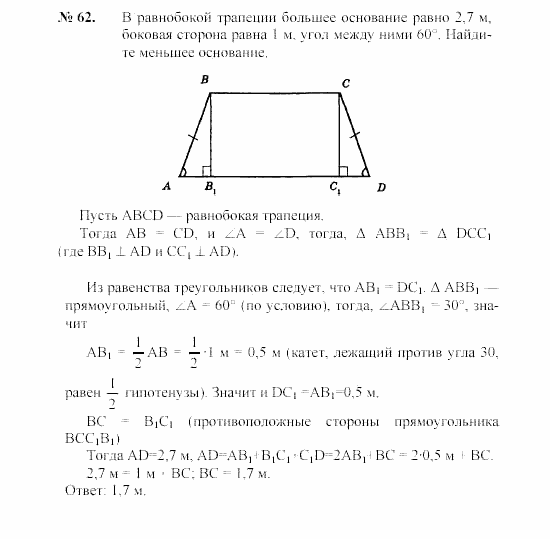 Курсы/ Кружки/ Факультативы
Курсы/ Кружки/ Факультативы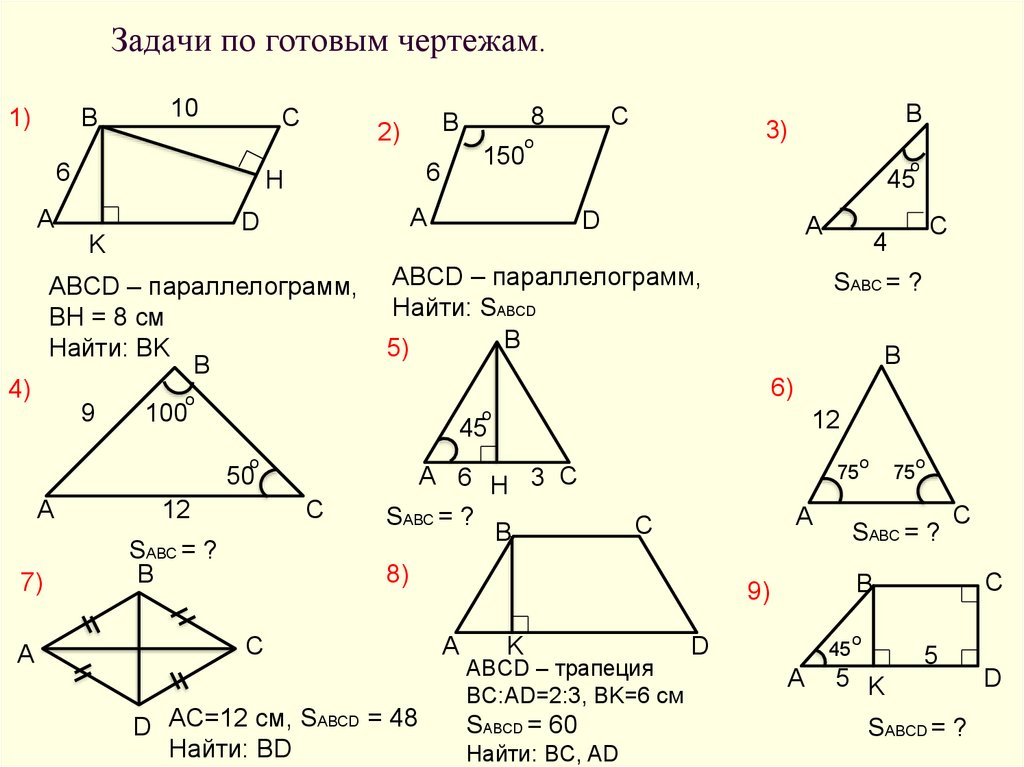
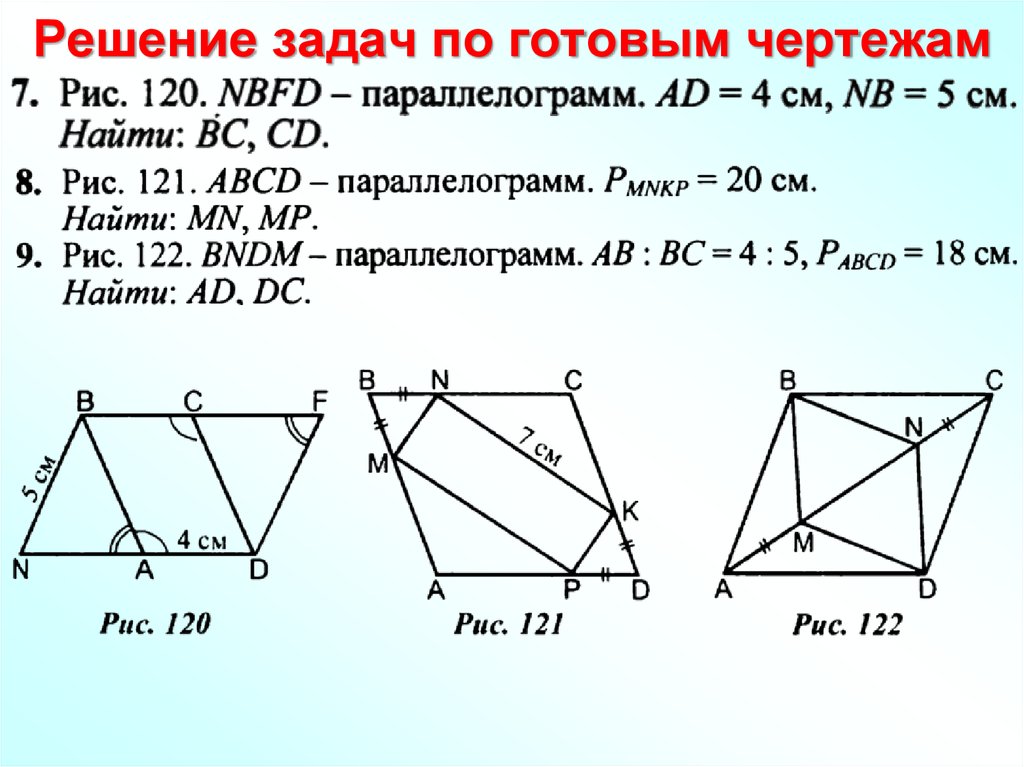 В начале игры все группы получают зелёные карточки, что соответствует тому, что они идут по зелёной дорожке. Если ответ неправильный, то данная группа получает жёлтую карточку, что соответствует жёлтой дорожке и предупреждает: быть внимательными, после второй ошибки группа получает красную карточку-предупреждение, что ошибаться больше нельзя. После третьей ошибки группа учащихся выходят из игры, но продолжает работу, становясь теоретиками.
В начале игры все группы получают зелёные карточки, что соответствует тому, что они идут по зелёной дорожке. Если ответ неправильный, то данная группа получает жёлтую карточку, что соответствует жёлтой дорожке и предупреждает: быть внимательными, после второй ошибки группа получает красную карточку-предупреждение, что ошибаться больше нельзя. После третьей ошибки группа учащихся выходят из игры, но продолжает работу, становясь теоретиками.