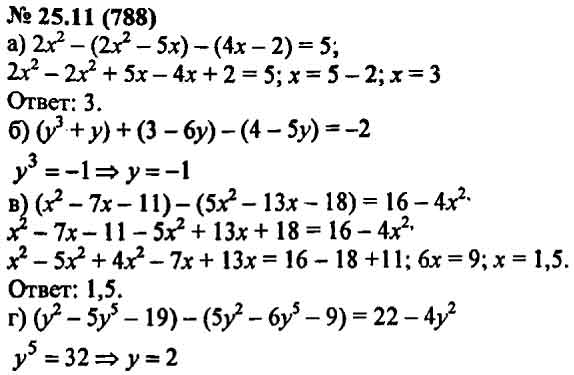-
Школьный помощник
- математика 5 класс
- математика 6 класс
- алгебра 8 класс
- геометрия 7 класс
- русский язык 5 класс
- русский язык 6 класс
- русский язык 7 класс
- математика
- алгебра
- геометрия
- русский язык
«»
следующая предыдущая вернуться на предыдущую страницуТакой страницы нет !!!
- Популярные запросы
- Обстоятельство
- Дополнение
- Определение
- Деление дробей
- Русский язык 6 класс
- Алгебра 8 класс
- Русский язык 7 класс
- Математика 6 класс
- Алгебра 7 класс
- Русский язык 5 класс
- Математика 5 класс
- Наименьшее общее кратное
- Буквы о и а в корнях -кос- / -кас-; -гор- / — гар-; -клан- / -клон-; -зар- / -зор-
- Наибольший общий делитель.
 Взаимно простые числа
Взаимно простые числа - Квадратный корень из неотрицательного числа
- Доли. Обыкновенные дроби
- Деление и дроби
- Буквы о и а в корнях -кос- / -кас-; -гор- / — гар-; -клан- / -клон-; -зар- / -зор-
- Окружность и круг
- Антонимы. Синонимы
- Десятичная запись дробных чисел
- Буквы о – а в корнях -лаг- / -лож-, -рос- / -раст- (-ращ-)
Урок 29. решение задач с помощью квадратных уравнений — Алгебра — 8 класс
Тема: Решение задач с помощью квадратных уравнений.
Содержание модуля (краткое изложение модуля):
Задача №1.
Иван Иванович приехал в магазин покупать изгородь для своего дачного участка, имеющего прямоугольную форму, но забыл его размеры. Какой длины изгородь надо купить Ивану Ивановичу, если единственное, что он помнит, это площадь участка – 750 м2, и то, что длина участка на 5 метров больше ширины?
 Чаще всего удобнее брать за х меньшую из неизвестных величин. Тогда длина участка составит х + 5.
Чаще всего удобнее брать за х меньшую из неизвестных величин. Тогда длина участка составит х + 5. Площадь прямоугольника S = х • (x + 5)
x • (x + 5) = 750,
x2 + 5x — 750 = 0.
Найдем дискриминант этого уравнения и его корни.
a = 1, b = 5, c = -750
D = b2 — 4ac
D = 52 — 4 • 1 • (-750) = 25 + 3000 = 3025 = 552
x1,2 = (-5 ± √3025)/(2 • 1), x1 = (-5 — 55)/2 или x2 = (-5 + 55)/2.
x1 = -30 или x2 = 25
Первый из найденных корней является посторонним по смыслу задачи, значит, ширина участка будет равна 25 м. Следовательно, длина окажется равной 25 + 5 = 30 м.
Теперь Иван Иванович может рассчитать периметр своего участка.
Необходимо купить 110 м изгороди.
Задача №2.

Известно, что в прямоугольном треугольнике один из катетов на 4 сантиметра меньше гипотенузы, а другой – на 2 сантиметра меньше гипотенузы. Найдем длину гипотенузы.
Пусть гипотенуза треугольника будет равна х см. Тогда бОльший катет будет равен х – 2 см, а меньший х – 4 см.
По теореме Пифагора
x2 = (x — 2)2 + (x — 4)2
Упростим полученное уравнение, используя формулу квадрат разности.
x2 = x2 — 4x + 4 + x2 — 8x + 16
x2 = 2x2 — 12x + 20
x2 — 12x + 20 = 0
Решив полученное квадратное уравнение, найдем два корня.
x1
2 является посторонним корнем по смыслу задачи, т. к. в этом случае один из катетов получится равным 0, а второй будет отрицательным. Значит, гипотенуза треугольника равна 10 см, а его катеты 8 см и 6 см.

Алгебра. 8 класс: учеб. для общеобразоват. организаций / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. – 6-е изд. – М.: Просвещение, 2017.
Алгебра 8 класс — Math
Решение уравнений, приводящихся к квадратным. Биквадратные уравнения. Замена переменной в уравнениях. Какое уравнение является биквадратным. Определение биквадратного уравнения. Как решать биквадратное уравнение. Как найти корни биквадратного уравнения. Уравнения, приводящиеся к квадратным путем замены переменной. Квадратные уравнения. Алгебра 8 класс. Примеры с решением.
- Подробности
- Автор: Math
- Категория: Алгебра 8 класс.
Квадратные уравнения. Теорема Виета. Решение квадратных уравнений по теореме Виета. Решение квадратных уравнений методом подбора. Какое квадратное уравнение называется приведенным? Как решить квадратное уравнение без дискриминанта. Как решить квадратное уравнение методом подбора. Как записать теорему Виета. Как решить квадратное уравнение по теореме Виета. Примеры с решением и объяснением. Видеоуроки по математике. Устранение пробелов в знаниях. Подготовка к ЗНО ( ВНО ) по математике. Подготовка к ЕГЭ, ДПА ( ГИА ), ОГЭ по математике.
Как решить квадратное уравнение методом подбора. Как записать теорему Виета. Как решить квадратное уравнение по теореме Виета. Примеры с решением и объяснением. Видеоуроки по математике. Устранение пробелов в знаниях. Подготовка к ЗНО ( ВНО ) по математике. Подготовка к ЕГЭ, ДПА ( ГИА ), ОГЭ по математике.
- Подробности
- Автор: Math
- Категория: Алгебра 8 класс.
Квадратные уравнения. Какое квадратное уравнение называется полным? Формула дискриминанта и корней полного квадратного уравнения. Уравнения с дробями. Как избавиться от всех знаменателей сразу. Алгебра 8 класс. Примеры с решением и объяснением. Видеоуроки по математике. Устранение пробелов в знаниях. Подготовка к ЗНО ( ВНО ) по математике. Подготовка к ЕГЭ, ДПА ( ГИА ), ОГЭ по математике.
- Подробности
- Автор: Math
- Категория: Алгебра 8 класс.

Материал доступен только для зарегистрированных пользователей.
Здравствуйте:-). Искренне надеюсь, что видео уроки просмотрены, теория записана, задания сделаны и пришло время сверять ответы:-).
- #91 Урок 1. Арифметический квадратный корень. Понятие и основные свойства корня. Алгебра 8 класс.
- #92 Урок 2. Уравнения, содержащие знак корня. Иррациональные уравнения. Алгебра 8 класс.
- #93 Урок 3. Неполные квадратные уравнения. х2=а. Алгебра 8 класс.
- #94 Урок 4. Преобразование выражений с квадратным корнем. Корень из а в квадрате. Алгебра 8 класс.
- #95 Урок 5. Квадратный корень. Решение уравнений и построение графиков с преобразованием квадратного корня. Алгебра 8 класс.
- #96 Урок 6. Вынесение множителя из под знака корня.Алгебра 8 класс.
- Подробности
- Автор: Math
- Категория: Алгебра 8 класс.
Преобразование выражений с корнем. Приведение дробей с квадратным корнем к общему знаменателю. Иррациональные дроби. Арифметический квадратный корень. Упростить выражение с квадратным корнем. Деление дробей с корнем. Сокращение дробей с корнем. Умножение выражений с квадратным корнем. Разложение на множители выражений с корнем. Разложение на множители выражений с иррациональностью. Алгебра 8 класс. Примеры с решением. Задания с объяснением. Иррациональные выражения. Выражения с иррациональностью. Математика. Образование.
Приведение дробей с квадратным корнем к общему знаменателю. Иррациональные дроби. Арифметический квадратный корень. Упростить выражение с квадратным корнем. Деление дробей с корнем. Сокращение дробей с корнем. Умножение выражений с квадратным корнем. Разложение на множители выражений с корнем. Разложение на множители выражений с иррациональностью. Алгебра 8 класс. Примеры с решением. Задания с объяснением. Иррациональные выражения. Выражения с иррациональностью. Математика. Образование.
- Подробности
- Автор: Math
- Категория: Алгебра 8 класс.
Арифметический квадратный корень. Упростить выражение, вынеся множитель из-под знака корня и преобразовав подкоренное выражение. Алгебра 8 класс. Математика, образование. Вынести множитель. Вынести множитель в выражении с переменными. Примеры с решением.
- Подробности org/Person»> Автор: Math
- Категория: Алгебра 8 класс.
Как вынести множитель из-под знака корня? Вынесение множителя из-под корня. Алгебра 8 класс. Примеры с решением. Математика. Образование. Пример 1: Вынести множитель из-под знака корня.
- Подробности
- Автор: Math
- Категория: Алгебра 8 класс.
Урок 1. Арифметический квадратный корень. Определение арифметического квадратного корня. Основные понятия. Базовые свойства. Как извлечь арифметический квадратный корень. Свойства корня. Математика. Алгебра 8 класс. Образование. Примеры с решением.
- Пример 1: Найдите значение арифметического квадратного корня.
- Пример 2: Имеет ли смысл выражение.
- Пример 3-4: Найдите значение выражения.
- Пример 5: Найдите значение корня.
- Подробности
- Автор: Math
- Категория: Алгебра 8 класс.

Материал доступен только для зарегистрированных пользователей.
Тест сделан и можно сверять ответы:-). Искренне надеюсь, что у Вас все правильно. Если это так, то Вы молодцы и можете смело приступать к изучению программы 9 класса. Но если вдруг случилось ток, что % правильных ответов меньше 80, то пробелы в знаниях есть, причем существенные. И, возможно, есть смысл обратится к профессиональному преподавателю или репетитору для их устранения. Если такой возможности, по каким-либо причинам нет, то предлагаем пройти курс дистанционный курс «Алгебра 8 класс».
- Подробности
- Автор: Math
- Категория: Алгебра 8 класс.
Прежде, чем проходить тест АЛГЕБРА 8 КЛАСС, очень рекомендуем пройти тесты на знание базовых тем по программам математики 5, 6 классов и алгебры 7 класса.
Математика 5 класс. Тест.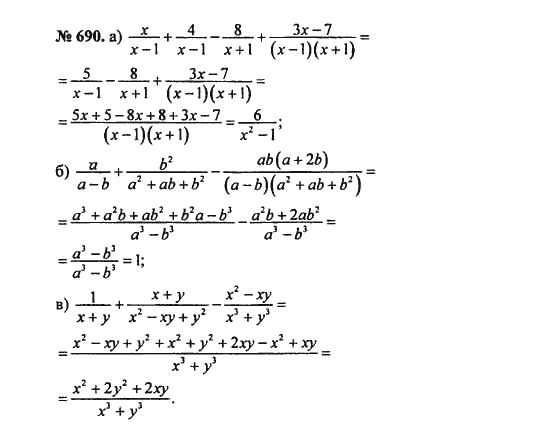
Математика 6 класс. Тест.
Алгебра 7 класс. Тест.
Почему это важно? Дело в том, что если есть «пробелы» в знаниях по программе 5, 6 или 7 классов, то с освоением программы алгебры 8 класса могут возникнуть определенные трудности.
Дело в том, что математика ( алгебра, геометрия ), в отличие от, например, географии, преподается «линейно-прогрессивно». Географию можно представить в виде огромной игры — сложение паззлов, в которой вы должны подобрать друг к другу все кусочки. Если вдруг вы не можете найти соответствующего кусочка (то есть не понимаете чего-то), это не так уж страшно — вы можете отложить это занятие и подобрать нужный элемент после.
- Подробности
- Автор: Math
- Категория: Алгебра 8 класс.
Конспект открытого урока по алгебре 8 класс по теме «Решение квадратных уравнений»
Конспект открытого урока по алгебре в 8 классе по теме «Решение квадратных уравнений»
Учебник: Алгебра. 8 класс: учеб. для общеобразоват. организаций / Ю.М. Колягин, М.В. Ткачёва, Н.Е. Фёдорова, М.И., М.И.Шабунин –4-е изд. – М. : Просвещение, 2016. – 336 с.
8 класс: учеб. для общеобразоват. организаций / Ю.М. Колягин, М.В. Ткачёва, Н.Е. Фёдорова, М.И., М.И.Шабунин –4-е изд. – М. : Просвещение, 2016. – 336 с.
Цель: закрепить знание формулы корней квадратного уравнения, знание количества корней в зависимости от значения дискриминанта, умение находить корни квадратного уравнения с помощью формулы корней квадратного уравнения,
Задачи:
1) Предметные: закрепить знание формулы корней квадратного уравнения, знание количества корней в зависимости от значения дискриминанта, умение находить корни квадратного уравнения по формуле корней.
2) личностные: выступать перед публикой (классом), умение представлять задачу, коммуникабельность, умение работать в коллективе, умение оценивать свою деятельность и деятельность коллектива, умение правильно вести себя на уроке.
2) метапредметные: развивать умения самостоятельно определять цели обучения, оценивать правильность выполнения задачи, умение осуществлять контроль и оценку результатов своей деятельности, умения владеть основами самоконтроля, самооценки,
принятия решений.
Используемые материалы: раздаточный материал, презентация.
Ход урока
1. Определение темы урока(2 мин).
Учитель: Здравствуйте дети и гости. Садитесь, пожалуйста. Хотелось бы начать урок с такого стихотворения:
Чтобы «х» нам узнать, надо дробь написать.
«b» в числителе поставить, знак при этом изменить.
И советуем плюс, минус перед корнем не забыть.
А под корнем «b» квадрат, минус, только не спешить,
«a» на «с» умножить нужно, а потом учетверить.
Вот числитель весь, друзья. В знаменателе «2а».
Как выдумаете, о чем это стихотворение? (Ответ: формула корней квадратного уравнения)
Совершенно верно и тема сегодняшнего занятия «Решение квадратных уравнений»
(Учащиеся записывают число, классная работа, «Решение квадратных уравнений», так же на доске записаны номера(№436(1,3), 437(1,3)), которые нужно выполнить в классе (на левой доске) и домашнее задание(на правой доске))
2. Актуализация изученной на предыдущем занятии темы (1 мин).
Актуализация изученной на предыдущем занятии темы (1 мин).
Учитель вызывает одного из учащихся, который на доске записывает вид квадратного уравнения, формулу корней, и зависимость количества корней от значения дискриминанта)
, ,
если D>0, то ,
если D=0, то ,
если D<0, то корней нет.
3. Устная работа по теме урока(5-6 мин).
Учитель: Решим следующие задания. (Презентация «Решение квадратных корней», слайд 2,3)
1. Ученики устно исправляют ошибки и называют количество корней в зависимости от дискриминанта.
2. Ученики называют пропущенные числа.
(После ответа ученика, учитель просит поднять руки всем кто согласен с ответом)
3. Закрепление изученного материала (работа с учебником)(12-15мин).
Решение у доски №435(1), № 436(1), 437(3).
Учитель вызывает к доске 3 учеников (центральная доска пополам), один работает вслух с пояснениями, остальные молча. Когда садится первый, вызывает еще одного. Затем оставшиеся ученики также объясняют решение примеров. Суть задания в том чтобы посмотреть различные результаты при решении квадратных уравнений и сделать выводы о трех возможных результатах в зависимости от D.
Когда садится первый, вызывает еще одного. Затем оставшиеся ученики также объясняют решение примеров. Суть задания в том чтобы посмотреть различные результаты при решении квадратных уравнений и сделать выводы о трех возможных результатах в зависимости от D.
Если остается время решить еще № 435(5,7), №440(1).
4. Физминутка (минутка расслабления и отдыха). (1 мин)
Учитель предлагает детям расслабиться, закрыть глаза и представить себе берег моря, представить, как они отдыхают на берегу моря. Учитель включает музыку «Шум моря». (слайд 4)
5. Обучающая самостоятельная работа.
На столах учащихся раздаточный материал. Ученики решают самостоятельно уравнения. Затем на слайде 5 учитель выводит верные ответы, ученики меняются работами и проводят рефлексию.
Учитель: проверьте работу соседа по слайду 5, если выполнены все примеры верно – оценка «5», если 2 — «4», если один – «3».
6. Выступление ученика (учеников) с докладом по применению квадратных уравнений к решению задач из других наук.
Выступление ученика (учеников) с докладом по применению квадратных уравнений к решению задач из других наук.
Учитель: Давайте теперь посмотрим, как применяется решение квадратных уравнений для решения задач в других наук. Ученик вашего класса (ИФ называет) представит вам решение физической задачи.
Ученик выходит к доске и представляет на слайде 6 решение задачи №5 стр. 221 учебника. (Подготовить выступление заранее)
Если останется время представить химическую задачу №491 стр. 198, тоже заранее подготовленную (слайд 7).
Ученики делают вывод, что квадратные уравнения используются при решении задач из других наук и учебных курсов.
7. Домашнее задание.
Записать д/з с доски № 435(6,8), 436(2,4), 437(2,4).
8. Рефлексия учебной деятельности.
Фамилия и Имя | Какой основной термин сегодняшнего занятия вы можете назвать? | Как вы думаете, что нужно сделать, чтобы научиться решать квадратные уравнения и хорошо усвоить тему урока? | Оцените свою работу на уроке по пятибалльной шкале. | Оцените урок по пятибалльной шкале. |
Учитель: Какой основной термин сегодняшнего занятия вы можете назвать?
Ученики: Квадратное уравнение.
Учитель: Как вы думаете, что нужно сделать, чтобы решать квадратные уравнения и хорошо усвоить тему урока?
Ученики: Выучить формулу корней квадратного уравнения и уметь подставлять а, в и с в формулу.
Учитель: Оцените себя и урок по пятибалльной шкале.
Учитель выставляет оценки и благодарит учеников за урок.
Учебники по алгебре за 8 класс в электронном виде
Показано 1 — 13 из 13
Пособие содержит таблицы по всем наиболее важным разделам школьного курса арифметики, алгебры, начал анализа. В таблицах кратко изложена теория по каждой теме, приведены основные формулы, графики, примеры решений типовых задач. В конце книги помещен …
В конце книги помещен …
Пособие содержит контрольные работы для 8-11 классов, задания выпускных экзаменов по математике в 9 и 11 классах с углубленным и профильным изучением математики, а также практикум для поступающих в вузы. Ко всем заданиям даны ответы. Книга может испо
Данное пособие предусматривает занятия с учащимися, проявляющими интерес и способности к математике. Целью работы в соответствующих классах является формирование у школьников устойчивого интереса к предмету, дальнейшее развитие их математических спос …
Задачник полностью соответствует учебнику. В каждом параграфе содержится система упражнений, тщательно выстроенная по степени нарастания трудности и достаточная для занятий в классе, выполнения домашних заданий и самостоятельных работ. ОГЛАВЛЕНИЕ …
Учебник для 8 класса с углубленным изучением математики под редакцией Н.Я. Виленкина: — Полностью соответствует современным образовательным стандартам; — Содержит весь необходимый текстовый и иллюстрированный материал для изучения курса по основным и . ..
..
Учебник по алгебре для 8 классов общеобразовательных учреждений. Ш. А. Алимов, Ю. М. Колягин, Ю. В. Сидоров и др. ОГЛАВЛЕНИЕ Глава I. Неравенства § 1. Положительные и отрицательные числа 3 § 2. Числовые неравенства 10 § 3. Основные свойства ч …
Учебник соответствует федеральным компонентам Государственного стандарта общего образования. Учебно-методический комплект по алгебре для 8 класса под редакцией Г. В. Дорофеева включает учебник, рабочую тетрадь, тематические тесты, дидактические матер …
Алгебра. 8 класс. Учебник. Макарычев Ю.Н. и др. ОГЛАВЛЕНИЕ ГЛАВА I. РАЦИОНАЛЬНЫЕ ДРОБИ § 1. РАЦИОНАЛЬНЫЕ ДРОБИ И ИХ СВОЙСТВА 3 1. Рациональные выражения — 2. Основное свойство дроби. Сокращение дробей 7 § 2. СУММА И РАЗНОСТЬ ДРОБЕЙ 15 3. Сл
Данный учебник предназначен для углубленного изучения алгебры в 8 классе и входит в комплект из трех книг: «Алгебра-7», «Алгебра-8» и «Алгебра-9». Его содержание полностью соответствует современным образовательным стандартам, а особенностями являются …
Его содержание полностью соответствует современным образовательным стандартам, а особенностями являются …
Учебник написан в соответствии с действующими программами для общеобразовательной школы. Материалы учебника изложены подробно и обстоятельно, что позволяет использовать их для самостоятельного изучения. Приоритетной содержательно-методической основой …
Это — учебник для классов с повышенным уровнем математической подготовки в общеобразовательных школах. Он написан в русле той концепции, которая использована в соответствующем учебнике А. Г. Мордковича для 8-го класса общеобразовательных учреждений, …
Учебник представляет собой новый тип учебника, который содержит материал, как для общеобразовательных классов, так и для классов с углубленным изучением Математики. Учащиеся могут переходить с одной Программы обучения на другую, не меняя книги. Глав …
Книга представляет собой сборник задач по курсу алгебры, предназначенный для учащихся 8-9 классов с углубленным изучением математики. В пособии содержатся задачи, способствующие систематическому углублению изучаемого материала и развитию навыков реше …
В пособии содержатся задачи, способствующие систематическому углублению изучаемого материала и развитию навыков реше …
Показано 1 — 13 из 13
Тесты по алгебре Корни (8 класс) онлайн
Сложность: знаток.Последний раз тест пройден 5 часов назад.
Материал подготовлен совместно с учителем высшей категории
Опыт работы учителем математики — более 33 лет.
Вопрос 1 из 10
Вычислитe
- Правильный ответ
- Неправильный ответ
- Вы и еще 78% ответили правильно
- 78% ответили правильно на этот вопрос
В вопросе ошибка?
Следующий вопросОтветитьВопрос 2 из 10
Вычислитe
- Правильный ответ
- Неправильный ответ
- Вы и еще 73% ответили правильно
- 73% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 3 из 10
Выберите число, которое может принимать а в выражении
- Правильный ответ
- Неправильный ответ
- Вы и еще 71% ответили правильно
- 71% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 4 из 10
Вычислитe
- Правильный ответ
- Неправильный ответ
- Вы и еще 65% ответили правильно
- 65% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 5 из 10
Упростите выражение
- Правильный ответ
- Неправильный ответ
- Вы ответили лучше 77% участников
- 23% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 6 из 10
Вычислите
- Правильный ответ
- Неправильный ответ
- Вы и еще 70% ответили правильно
- 70% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 7 из 10
Вычислитe
- Правильный ответ
- Неправильный ответ
- Вы и еще 65% ответили правильно
- 65% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 8 из 10
Вычислитe
- Правильный ответ
- Неправильный ответ
- Вы ответили лучше 57% участников
- 43% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 9 из 10
Упростите выражение
- Правильный ответ
- Неправильный ответ
- Вы ответили лучше 64% участников
- 36% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 10 из 10
Вычислитe
- Правильный ответ
- Неправильный ответ
- Вы и еще 72% ответили правильно
- 72% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Доска почёта
Чтобы попасть сюда — пройдите тест.
-
Евгений Кочкин
7/10
Галина Кропотина
10/10
Александр Александровский
9/10
Александр Чернов
10/10
Давид Смык
10/10
Аида Крутая
8/10
Олеся Вьюшкова
6/10
Татьяна Федотова
8/10
Михаил Сапрыкин
8/10
Анастасия Михлик
6/10
Нет сомнения, что тема «Квадратные корни» является одной из достаточно трудных, но при этом и очень важной, а потому тест «Корни» (8 класс) будет, безусловно, полезен всем школьникам, стремящимся хорошо знать алгебру. Решение заданий теста потребует от школьника как знания теоретического материала, так и владения навыками вычисления корней.
Тест по алгебре «Квадратные корни» представляет собой десять заданий разного уровня сложности, которые надо сначала выполнить, а затем среди предложенных найти правильный ответ. Задания помогают подготовиться к итоговому или тематическому контролю в школе, а также могут быть полезны старшеклассникам, готовящимся к сдаче ЕГЭ.
Тест онлайн вы найдете на нашем сайте.
Рейтинг теста
Средняя оценка: 3.5. Всего получено оценок: 2152.
А какую оценку получите вы? Чтобы узнать — пройдите тест.
8 класс
Иррациональные уравнения
07:26
03:41
08:16
открытых учебников | Сиявула
Математика
Наука
- Читать онлайн
Учебники
Английский
класс 7A
Марка 7Б
Класс 7 (вместе A и B)
Африкаанс
Граад 7А
Граад 7Б
Граад 7 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
класс 8A
марка 8Б
Оценка 8 (вместе A и B)
Африкаанс
Граад 8А
Граад 8Б
Граад 8 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 9А
Марка 9Б
Оценка 9 (комбинированные A и B)
Африкаанс
Граад 9А
Граад 9Б
Граад 9 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
класс 4A
класс 4Б
Класс 4 (вместе A и B)
Африкаанс
Граад 4А
Граад 4Б
Граад 4 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 5А
Марка 5Б
Оценка 5 (комбинированные A и B)
Африкаанс
Граад 5А
Граад 5Б
Граад 5 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
класс 6А
класс 6Б
Класс 6 (вместе A и B)
Африкаанс
Граад 6А
Граад 6Б
Граад 6 (A en B saam)
Пособия для учителя
Наша книга лицензионная
Эти книги не просто бесплатные, они также имеют открытую лицензию! Один и тот же контент, но разные версии (брендированные или нет) имеют разные лицензии, как объяснено:
CC-BY-ND (фирменные версии)
Вам разрешается и поощряется свободное копирование этих версий.Вы можете делать ксерокопии, распечатывать и распространять их сколько угодно раз. Вы можете скачать их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете адаптировать или изменять эти версии учебников, их содержание или обложки каким-либо образом, поскольку они содержат соответствующие бренды Siyavula, спонсорские логотипы и одобрены Департаментом базового образования. Для получения дополнительной информации посетите Creative Commons Attribution-NoDerivs 3.0 Непортированный.
Узнайте больше о спонсорстве и партнерстве с другими, которые сделали возможным выпуск каждого из открытых учебников.
CC-BY (версии без марочного знака)
Эти небрендированные версии одного и того же контента доступны для вас, чтобы вы могли делиться ими, адаптировать, трансформировать, модифицировать или дополнять их любым способом, с единственным требованием — дать соответствующую оценку Siyavula. Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Рабочие листы с заданиями по математике для 8-х классов
Решение математических задач может напугать восьмиклассников.Не должно. Объясните учащимся, что вы можете использовать основы алгебры и простые геометрические формулы для решения, казалось бы, неразрешимых задач. Ключ состоит в том, чтобы использовать предоставленную вам информацию, а затем изолировать переменную для алгебраических задач или знать, когда использовать формулы для геометрических задач. Напомните учащимся, что всякий раз, когда они решают задачу, что бы они ни делали с одной стороной уравнения, они должны делать с другой. Итак, если они вычтут пять из одной части уравнения, им нужно будет вычесть пять из другой.
Бесплатные распечатываемые рабочие листы, представленные ниже, дадут учащимся возможность решить задачи и заполнить свои ответы в отведенных для этого пустых местах. После того, как учащиеся завершат работу, используйте рабочие листы для быстрой формирующей оценки для всего класса математики.
Рабочий лист № 1
Деб Рассел
Распечатать PDF : Рабочий лист № 1
В этом PDF-файле ваши ученики будут решать такие задачи, как:
«5 хоккейных шайб и три клюшки стоят 23 доллара.5 хоккейных шайб и 1 клюшка стоят 20 долларов. Сколько стоит 1 хоккейная шайба? »
Объясните ученикам, что им нужно будет учитывать то, что они действительно знают, например, общую стоимость пяти хоккейных шайб и трех хоккейных клюшек (23 доллара США), а также общую стоимость пяти хоккейных шайб и одной клюшки (20 долларов США). Укажите студентам, что они начнут с двух уравнений, каждое из которых дает общую цену, а каждое включает пять хоккейных клюшек.
Рабочий лист № 1 Решения
Деб Рассел
Распечатать PDF : Рабочий лист №1 Решения
Чтобы решить первую проблему на листе, настройте ее следующим образом:
Пусть «P» представляет переменную для «шайбы».
Пусть «S» представляет переменную для «палки».
Итак, 5P + 3S = 23 доллара, а 5P + 1S = 20 долларов.
Затем вычтите одно уравнение из другого (поскольку вы знаете сумму в долларах):
5P + 3S — (5P + S) = 23 — 20 долларов.
Таким образом:
5P + 3S — 5P — S = 3 доллара. Вычтем 5P из каждой части уравнения, что даст: 2S = 3 доллара.Разделите каждую часть уравнения на 2, и получится, что S = 1,50 доллара.
Затем подставьте 1,50 доллара США вместо S в первом уравнении:
5P + 3 (1,50 доллара) = 23 доллара, что дает 5P + 4,50 доллара = 23 доллара. Затем вы вычитаете 4,50 доллара из каждой части уравнения, получая: 5P = 18,50 доллара.
Разделите каждую часть уравнения на 5, чтобы получить:
P = 3,70 долл. США
Обратите внимание, что ответ на первый вопрос на листе ответов неверен. Это должно быть 3,70 доллара. Остальные ответы на листе решения верны.
Рабочий лист № 2
Деб Рассел
Распечатать PDF : Рабочий лист № 2
Чтобы решить первое уравнение на листе, учащимся необходимо знать уравнение для прямоугольной призмы (V = lwh, где «V» означает объем, «l» означает длину, «w» означает ширину, а «h». равна высоте). Проблема заключается в следующем:
«На вашем заднем дворе ведутся земляные работы для бассейна. Его размеры 42F x 29F x 8F. Грязь будет вывезена на грузовике, вмещающем 4 человека.53 кубических фута Сколько грузовиков с землей увезут? »
Рабочий лист № 2 Решения
Деб Рассел
Распечатать PDF : Рабочий лист № 2 Решения
Чтобы решить проблему, сначала рассчитайте общий объем бассейна. Используя формулу для объема прямоугольной призмы (V = lwh), вы получите:
V = 42F x 29F x 8F = 9744 кубических футов
Затем разделите 9744 на 4,53, или:
9744 кубических футов ÷ 4.53 кубических фута (на грузовик) = 2151 грузовик
Вы даже можете облегчить атмосферу своего класса, воскликнув: «Вам придется потратить немало грузовиков, чтобы построить этот пул».
Обратите внимание, что ответ на листе решения этой проблемы неверен. Это должно быть 2151 кубический фут. Остальные ответы на листе решения верны.
Оценка: 8 — Алгебра и функции 1
Особенности специального образования
Рекомендации по специальному образованию, написанные учителями специального образования штата Индиана, предназначены для повышения вовлеченности и поддержки роста учащихся в рамках специального образования.Это не исчерпывающий список стратегий, но эта поддержка поможет вам сделать обучение математике более доступным для учащихся. Педагоги должны адаптировать стратегии к потребностям ваших учеников и убедиться, что вы создаете возможности для всех учеников, чтобы они могли взаимодействовать с строгим содержанием.
| Универсальные стратегии для математиков, испытывающих трудности | |
|---|---|
Стратегии | Примеры |
Вовлечение в стратегии исполнительного функционирования |
|
Примеры |
|
Поощрение и моделирование математической беседы |
|
Проверить понимание при использовании «математических правил»; объясните почему |
|
Обучение математике: ключевые слова |
|
Используйте сокращения, чтобы помочь учащимся запомнить шаги / процессы |
|
(PDF) Алгебраическое мышление учащихся 8 класса при решении текстовых задач с помощью электронной таблицы
РЕШЕНИЕ ПРОБЛЕМ И ИЗУЧЕНИЕ АЛГЕБРЫ
Контекстное решение задач — важный тип задач, ведущих к алгебраической деятельности.
Согласно Кирану (2004) работу по алгебре можно разделить на три области:
поколенческие, трансформационные и глобальные / метауровневые действия. Деятельность поколения
соответствует построению и интерпретации алгебраических объектов.
Действия по преобразованию включают в себя упрощение алгебраических выражений, решение
уравнений и неравенств и манипулирование выражениями. Наконец, глобальные / метауровневые действия
включают решение проблем и математическое моделирование, включая обобщение шаблона
и анализ вариаций.
Характер алгебраических рассуждений зависит от возраста и математического опыта
учащихся. Студенты более продвинутого уровня могут естественно использовать символические выражения и уравнения
вместо чисел и операций. Но для студентов, которые
еще не выучили алгебраические обозначения, более общие способы мышления о числах
, операциях и обозначениях могут эффективно считаться алгебраическими (Kieran,
2007).Контексты, которые включают числа, функциональные отношения, закономерности и другие свойства
, являются важной основой для понимания алгебраических структур
. Например, при написании символьных числовых отношений можно использовать
букв. Однако использование технологических инструментов позволяет другие представления для таких отношений
, а также новые формы исследования, которые могут рассматриваться как аналогичные
деятельности поколений и преобразований в алгебре.Таким образом, кажется уместным
, что такие новые представления и связанное с ними математическое мышление
включены в область алгебры (Kieran, 1996). Более того, Lins & Kaput (2004)
утверждают, что алгебру можно рассматривать из арифметического поля, поскольку существует множество
свойств, структур и взаимосвязей, общих для этих двух областей.
Следовательно, арифметика и алгебра могут развиваться как единая область знаний
.В этом исследовании мы принимаем эту точку зрения, рассматривая алгебраическое мышление как
как широкий образ мышления, не ограниченный формальными процедурами алгебры.
влечет за собой отделение алгебраического мышления от алгебраического символизма (Zazkis & Liljedhal,
2002).
ТАБЛИЦЫ В РАЗВИТИИ АЛГЕБРАИЧЕСКОГО МЫШЛЕНИЯ
Электронная таблица поддерживает связь между различными регистрами (числовыми,
реляционными и графическими).Одна особенность, которая выделяется в этом инструменте, — это возможность
перетаскивать маркер ячейки, содержащей формулу, вдоль столбца. Это действие
,генерирует «столбец переменной». Использование этого инструмента для решения проблем подчеркивает необходимость
идентифицировать релевантные переменные и поощряет поиск отношений
зависимости между переменными. Определение промежуточных отношений между переменными
, то есть разрыв сложных отношений зависимости в последовательных более простых отношениях
, представляет собой процесс, предоставляемый этим инструментом, с решающими последствиями в процессе решения проблем
(Carreira, 1992; Haspekian , 2005).Как отмечает
Haspekian (2005), электронная таблица также позволяет алгебраическую организацию, по-видимому,
M / J Pre-Algebra для 8 классов — 1205070
Дом на дереве Хейли: похожие треугольники и склон:Узнайте, как похожие прямоугольные треугольники могут показать, насколько одинаковый уклон между любыми двумя разными точками на не вертикальной линии, когда вы помогаете Хейли построить лестницу к ее дому на дереве в этом интерактивном руководстве.
Тип: Оригинальное учебное пособие для учащихся
Математические модели и социальное дистанцирование:Узнайте, как математические модели могут показать, почему социальное дистанцирование во время эпидемии или пандемии важно, в этом интерактивном руководстве.
Тип: Оригинальное учебное пособие для учащихся
Создание функций с двух точек зрения:В этом интерактивном руководстве научитесь создавать функцию для моделирования линейной зависимости между двумя величинами и определять наклон и точку пересечения по оси Y с учетом двух точек, которые представляют функцию.
Тип: Оригинальное учебное пособие для учащихся
Многоступенчатые уравнения: часть 5 Сколько решений ?:Узнайте, как уравнения могут иметь одно решение, без решения или бесконечно много решений в этом интерактивном руководстве.
Это пятая из пяти серии статей, посвященных решению многоступенчатых уравнений.
- Нажмите , чтобы открыть Часть 1: Объединение одинаковых терминов
- Нажмите ЗДЕСЬ , чтобы открыть Часть 2: Распределительное свойство
- Нажмите ЗДЕСЬ , чтобы открыть Часть 3: Переменные на обеих сторонах
- Нажмите ЗДЕСЬ , чтобы открыть Часть 4: Собираем все вместе
- [ТЕКУЩИЙ РУКОВОДСТВО] Часть 5: Сколько решений?
Тип: Оригинальное учебное пособие для учащихся
Многоступенчатые уравнения: часть 4 Собираем все вместе:Изучите альтернативные методы решения многошаговых уравнений в этом интерактивном руководстве.
Это пятая из пяти серии статей, посвященных решению многоступенчатых уравнений.
- Нажмите , чтобы открыть Часть 1: Объединение одинаковых терминов
- Нажмите ЗДЕСЬ , чтобы открыть Часть 2: Распределительное свойство
- Нажмите ЗДЕСЬ , чтобы открыть Часть 3: Переменные на обеих сторонах
- [ТЕКУЩЕЕ РУКОВОДСТВО] Часть 4: Собираем все вместе
- Нажмите ЗДЕСЬ , чтобы открыть Часть 5: Сколько решений?
Тип: Оригинальное учебное пособие для учащихся
Объем сферического пузырькового чая:Узнайте, как рассчитать объем сфер, узнав, как они делают Bubble Tea, в этом интерактивном руководстве.
Тип: Оригинальное учебное пособие для учащихся
Многоступенчатые уравнения: Часть 3 Переменные с обеих сторон:Узнайте, как решать многоступенчатые уравнения, которые содержат переменные с обеих сторон уравнения, в этом интерактивном руководстве.
Это пятая из пяти серии статей, посвященных решению многоступенчатых уравнений.
- Нажмите , чтобы открыть Часть 1: Объединение одинаковых терминов
- Нажмите ЗДЕСЬ , чтобы открыть Часть 2: Распределительное свойство
- [ТЕКУЩЕЕ РУКОВОДСТВО] Часть 3: Переменные на обеих сторонах
- Нажмите ЗДЕСЬ , чтобы открыть Часть 4: Собираем все вместе
- Нажмите ЗДЕСЬ , чтобы открыть Часть 5: Сколько решений?
Тип: Оригинальное учебное пособие для учащихся
Многоступенчатые уравнения: Часть 2 Распределительное свойство:Узнайте, как решать многоступенчатые уравнения с помощью свойства распределения в этом интерактивном руководстве.
Это вторая часть из пяти из серии, посвященной решению многоступенчатых уравнений.
- Нажмите , чтобы открыть Часть 1: Объединение одинаковых терминов
- [ТЕКУЩЕЕ РУКОВОДСТВО] Часть 2: Распределительная собственность
- Нажмите ЗДЕСЬ , чтобы открыть Часть 3: Переменные на обеих сторонах
- Нажмите ЗДЕСЬ , чтобы открыть Часть 4: Собираем все вместе
- Нажмите ЗДЕСЬ , чтобы открыть Часть 5: Сколько решений?
Тип: Оригинальное учебное пособие для учащихся
Круиз по функциям:Путешествуйте вместе, узнавая, как качественно описывать функции в этом интерактивном руководстве.
Тип: Оригинальное учебное пособие для учащихся
Многоступенчатые уравнения: Часть 1 Объединение одинаковых терминов:Узнайте, как решать многоступенчатые уравнения, содержащие похожие термины, в этом интерактивном руководстве.
Это первая часть из пяти в серии, посвященной решению многоступенчатых уравнений.
- [ТЕКУЩЕЕ РУКОВОДСТВО] Часть 1. Объединение одинаковых терминов
- Щелкните , чтобы открыть Часть 2: Распределительное свойство
- Нажмите ЗДЕСЬ , чтобы открыть Часть 3: Переменные на обеих сторонах
- Нажмите ЗДЕСЬ , чтобы открыть Часть 4: Собираем все вместе
- Нажмите ЗДЕСЬ , чтобы открыть Часть 5: Сколько решений?
Тип: Оригинальное учебное пособие для учащихся
Функции, сладкие функции:Посмотрите, как приятно определять наклон линейных функций и сравнивать их в этом интерактивном руководстве.Определите и сравните наклон или скорость изменения, используя словесные описания, таблицы значений, уравнения и графические формы.
Тип: Оригинальное учебное пособие для учащихся
Лето развлечений:Развлекайтесь с функциями! Узнайте, как определять линейные и нелинейные функции в этом интерактивном руководстве.
Тип: Оригинальное учебное пособие для учащихся
Управляется функциями:Узнайте, как определить, является ли связь функцией, в этом интерактивном руководстве, которое показывает вам входные и выходные данные, уравнения, графики и словесные описания.
Тип: Оригинальное учебное пособие для учащихся
Понятие движения, часть 3 — Средняя скорость:Опишите среднюю скорость багги для дюн, используя кинематику в этом интерактивном руководстве.Вы рассчитаете смещение и среднюю скорость, создадите и проанализируете график рассеяния скорости в зависимости от времени и свяжете среднюю скорость с наклоном графика рассеяния положения и времени.
Это часть 3 из 3 из серии, которая отражает практические занятия, основанные на запросах, из наших популярных семинаров.
- Щелкните, чтобы открыть «Понятие движения», часть 1 — Измерения времени
- Щелкните ЗДЕСЬ, чтобы открыть «Понятие движения», часть 2 — Позиция и время
Тип: Оригинальное учебное пособие для учащихся
Понятие движения, часть 2 — Положение против времени:Продолжить изучение кинематики для описания линейного движения, сосредоточив внимание на измерениях положения и времени из испытания движения в части 1.В этом интерактивном руководстве вы определите измерения местоположения с помощью искровой ленты, проанализируете диаграмму рассеяния данных местоположения-времени, вычислите и интерпретируете наклон на графике местоположения-времени и сделаете выводы о средней скорости багги-багги
Тип: Оригинальное учебное пособие для учащихся
Диаграммы рассеяния. Часть 6: Использование линейных моделей:Узнайте, как использовать уравнение линейной линии тренда для интерполяции и экстраполяции двумерных данных, построенных на диаграмме рассеяния.В этом онлайн-руководстве вы увидите полезность линий тренда и то, как они используются.
Тип: Оригинальное учебное пособие для учащихся
Диаграммы рассеяния, часть 3: Линии тренда:Изучите неформальную подгонку линии тренда к данным, изображенным на диаграмме рассеяния, в этом интерактивном онлайн-руководстве.
Это часть 3 из 6 серий. Щелкните ниже, чтобы открыть другие руководства из этой серии.
Тип: Оригинальное учебное пособие для учащихся
Преобразования дома:Научитесь описывать последовательность преобразований, в результате которых получаются похожие фигуры.Это интерактивное руководство позволит вам попрактиковаться в поворотах, переводах, отражениях и растяжениях.
Тип: Оригинальное учебное пособие для учащихся
Изменить возраст вождения ?:Узнайте, как оценить обоснованность аргументов нескольких выступающих, когда они обсуждают, следует ли повышать возраст вождения с 16 до 18 или даже выше, с помощью этого интерактивного руководства.
Тип: Оригинальное учебное пособие для учащихся
Куда делись все скраб-сойки ?:Изучите ограничивающие факторы экосистемы Флориды и опишите, как эти ограничивающие факторы влияют на одно коренное население — Флоридскую скраб-сойку — с помощью этого интерактивного учебного пособия.
Тип: Оригинальное учебное пособие для учащихся
По горячим следам:Изучите, как температура влияет на скорость химических реакций, в этом интерактивном руководстве.
Тип: Оригинальное учебное пособие для учащихся
Да или нет ГМО ?:Узнайте, что такое генная инженерия и некоторые применения этой технологии.В этом интерактивном руководстве вы получите представление о некоторых преимуществах и потенциальных недостатках генной инженерии. В конечном итоге вы сможете критически относиться к генной инженерии и написать аргумент, описывающий вашу собственную точку зрения на ее влияние.
Тип: Оригинальное учебное пособие для учащихся
Построение линейных функций из таблиц:Научитесь создавать линейные функции из таблиц, содержащих наборы данных, которые связаны друг с другом особым образом, по мере того, как вы завершите это интерактивное руководство.
Тип: Оригинальное учебное пособие для учащихся
Образцы плитки I: восьмиугольники и квадраты:В этом задании ученикам дается узор плитки, состоящий из равных правильных восьмиугольников и квадратов.Их просят определить внутренний угол восьмиугольника и проверить атрибуты квадрата.
Тип: Задача по решению проблем
Разбиение шестиугольника:Цель этого задания — помочь учащимся найти способ разложить правильный шестиугольник на конгруэнтные фигуры.Это задумано как учебное задание, которое дает студентам возможность попрактиковаться в работе с преобразованиями.
Тип: Задача по решению проблем
Пенни в рай:Цель этого задания — дать учащимся контекст для исследования больших чисел и измерений.Студенты должны плавно переводить единицы с очень большими числами, чтобы успешно выполнить эту задачу. Общее количество монет, отчеканенных за один год или за последнее столетие, феноменально велико, и его трудно понять. Один из способов оценить, насколько велико это число, — это рассмотреть, насколько далеко все эти гроши достигли бы, если бы мы могли сложить их один на другой: это еще одно феноменально большое число, но то, насколько оно велико, может стать неожиданностью. .
Тип: Задача по решению проблем
Прибыль DVD, Вариант 1:В этом задании учащихся просят определить цену за единицу продукта при двух различных обстоятельствах.Их также просят обобщить стоимость производства x единиц в каждом случае.
Тип: Задача по решению проблем
Очки:В этом материале учащиеся определят объем трех стаканов для питья разной формы.Им потребуются предварительные знания формул объема для цилиндров, конусов и сфер, а также опыт решения уравнений, упрощения квадратных корней и применения теоремы Пифагора.
Тип: Задача по решению проблем
Как погода?:Это задание можно использовать в качестве быстрой оценки, чтобы увидеть, могут ли учащиеся разобраться в графике в контексте реальной ситуации.Студенты также должны обратить внимание на шкалу на вертикальной оси, чтобы найти правильное соответствие. Первый и третий графики на первый взгляд выглядят очень похожими, но значения функций сильно различаются, поскольку шкалы на вертикальных осях сильно различаются. Задачу также можно использовать для группового обсуждения интерпретации функций, заданных графами.
Тип: Задача по решению проблем
Интерпретация графика:Цель этого задания — помочь студентам научиться читать информацию о функции из ее графика, попросив их показать часть графика, которая демонстрирует определенное свойство функции.Задача может быть использована для дальнейшего обучения пониманию функций или в качестве инструмента оценки, с оговоркой, что это требует некоторого творческого подхода, чтобы решить, как лучше всего проиллюстрировать некоторые из утверждений.
Тип: Задача по решению проблем
Купон или скидка:В этом задании студентам предлагается реальная проблема, связанная с ценой продаваемого товара.Чтобы ответить на вопрос, учащиеся должны представить проблему, указав переменную и связанные с ней величины, а затем написать и решить уравнение.
Тип: Задача по решению проблем
Паста из киноа 1:В этом задании учащимся предлагается найти количество двух ингредиентов в смеси для макарон.Задача предоставляет всю информацию, необходимую для решения проблемы путем постановки двух линейных уравнений с двумя неизвестными. Эта последовательность задач помогает различать ожидания 8-го класса и старшей школы, связанные с системами линейных уравнений.
Тип: Задача по решению проблем
Решение уравнений:В этом упражнении студента просят решить множество уравнений (одно решение, бесконечное количество решений, нет решения) традиционным алгебраическим способом и использовать изображения балансировочных весов, чтобы показать процесс решения.
Тип: Задача по решению проблем
Тарифы на сотовый телефон:Это задание представляет собой реальную задачу, требующую от студентов написать линейные уравнения для моделирования различных планов сотового телефона. Рассмотрение графиков линий в контексте планов сотовых телефонов позволяет студентам связать значения точек пересечения двух линий с одновременным решением двух линейных уравнений.Студенты должны найти решение алгебраически для выполнения задачи.
Тип: Задача по решению проблем
Знак решений:Можно многое сказать о решении уравнения, не решая его на самом деле, просто глядя на структуру и операции, составляющие уравнение.Это упражнение переключает внимание с знакомой проблемы «поиска решения» на размышления о том, что на самом деле означает, что число является решением уравнения.
Тип: Задача по решению проблем
Две строки:В этой задаче нам дается график из двух линий, включая координаты точки пересечения и координаты двух вертикальных пересечений, и запрашиваются соответствующие уравнения линий.Это очень простая задача, которая соединяет графики, уравнения, решения и точки пересечения.
Тип: Задача по решению проблем
У кого лучшая работа ?:В этом задании студенту предлагается построить график и сравнить два пропорциональных отношения и интерпретировать удельную ставку как наклон графика.
Тип: Задача по решению проблем
Кофе за фунт:В этом примере учащиеся ответят на вопросы о цене за единицу кофе, построят график информации и объяснят значение наклона в данном контексте.
Тип: Задача по решению проблем
Велосипедная гонка:Цель этого задания состоит в том, чтобы учащиеся интерпретировали два графика «расстояние-время» в контексте велогонки. Здесь есть два основных математических аспекта: интерпретация того, что означает конкретная точка на графике с точки зрения контекста, и понимание того, что «крутизна» графика что-то говорит нам о том, насколько быстро движутся велосипедисты.
Тип: Задача по решению проблем
Лисы и кролики:Эта задача подчеркивает важность предложения «каждый вход имеет ровно один выход» в определении функции, которое нарушается в таблице значений двух совокупностей.Примечательно, что, поскольку данные представляют собой набор пар ввода-вывода, словесного описания функции не дается, поэтому часть задачи заключается в обработке того, как будет выглядеть «форма правила» предлагаемых функций.
Тип: Задача по решению проблем
Правила функции:Эту задачу можно выполнять как игру, в которой учащиеся должны угадать правило, а инструктор дает все больше и больше входных выходных пар.Указания только трех пар вход-выход может быть недостаточно, чтобы прояснить правило. Преподаватели могут рассмотреть возможность изменения входных данных, например, во второй таблице, чтобы обеспечить нецелочисленные записи. Хороший вариант игры — попросить учеников, которые думают, что они нашли правило, поставляют пары вход-выход, а учителя подтверждают или отрицают их правоту. Вербализация правила требует точности языка. Эту задачу можно использовать, чтобы представить идею функции как правила, которое назначает уникальный выход каждому входу.
Тип: Задача по решению проблем
Введение в линейные функции:Это задание позволяет учащимся изучить различия между линейными и нелинейными функциями. В отличие от двух, он усиливает свойства линейных функций.
Тип: Задача по решению проблем
Моделирование с помощью линейной функции:Основная цель этого задания — выявить распространенные заблуждения, которые возникают, когда учащиеся пытаются моделировать ситуации с помощью линейных функций.Эта задача, будучи множественным выбором, также может служить быстрой оценкой, чтобы оценить понимание класса моделирования с линейными функциями.
Тип: Задача по решению проблем
Приливы:Это простая задача по интерпретации графика функции с точки зрения взаимосвязи между величинами, которые он представляет.
Тип: Задача по решению проблем
Катание по библиотеке:В этом задании учащиеся рисуют графики двух функций из словесных описаний. Обе функции описывают одну и ту же ситуацию, но изменение точки зрения наблюдателя меняется, когда функция имеет нулевое выходное значение.Этот небольшой поворот заставляет студентов тщательно обдумать интерпретацию зависимой переменной. Эту задачу можно использовать по-разному: Для создания обсуждения в классе графиков. В качестве быстрой оценки построения графиков, например, во время разминки в классе. Чтобы вовлечь студентов в обсуждение в малых группах.
Тип: Задача по решению проблем
Вычисление квадратного корня из 2:Это задание предназначено для учебных целей, чтобы учащиеся могли научиться и уверенно пользоваться калькулятором и понять, что он может, а что не может.Эта задача дает возможность поработать над понятием разряда (в частях [b] и [c]), а также понять часть аргумента, почему квадратный корень из 2 не является рациональным числом.
Тип: Задача по решению проблем
Сравнение снежных конусов:Учащиеся будут просто узнавать о сходстве в этом классе, поэтому они могут не осознавать, что это необходимо в данном контексте.Учителя должны быть готовы оказать поддержку учащимся, которые борются с этой частью задания. Чтобы упростить задачу, учитель может просто сказать ученикам, что, исходя из наклона чашки с усеченным конусом, весь конус будет иметь высоту 14 дюймов, а отрезанная часть — 10 дюймов. (См. Объяснение в решении.) Стоит обсудить части (c) и (e). Для снежных шишек процентное увеличение меньше, чем для соков. Снежные конусы имеют объем, равный объему сока, плюс объем купола, который одинаков в обоих случаях.Добавление одного и того же числа к двум числам в соотношении всегда будет приближать их отношение к единице, что в данном случае означает, что соотношение — и, следовательно, процентное увеличение — будет меньше.
Тип: Задача по решению проблем
Конгруэнтные сегменты:Первый опыт трансформации учащихся, скорее всего, будет связан с определенными формами, такими как треугольники, четырехугольники, круги и фигуры с симметрией.Демонстрация последовательности преобразований, которая показывает, что два общих линейных сегмента одинаковой длины совпадают, — это хороший способ для учащихся начать думать о преобразованиях в более широком смысле.
Тип: Задача по решению проблем
Конгруэнтные треугольники:Это задание преследует две цели: во-первых, научить учащихся понимать жесткие движения в контексте демонстрации конгруэнтности.Во-вторых, знания учащихся об размышлениях уточняются за счет рассмотрения понятия ориентации в части (b). Каждый раз, когда плоскость отражается относительно линии, это меняет на противоположные понятия «по часовой стрелке» и «против часовой стрелки».
Тип: Задача по решению проблем
Отражая отражения:В этом материале учащиеся экспериментируют с последовательными отражениями треугольника в координатной плоскости.
Тип: Задача по решению проблем
Оценка квадратного корня:По определению, квадратный корень из числа n — это число, возведенное в квадрат, чтобы получить n . Цель этого задания — научить учащихся использовать значение квадратного корня, чтобы найти десятичное приближение квадратного корня из неквадратного целого числа.Учащимся может потребоваться руководство, чтобы понять, как подойти к задаче.
Тип: Задача по решению проблем
Отражение точки:Цель этого задания — применить отражение к одной точке. Стандарт просит студентов применять жесткие движения к линиям, отрезкам и углам.Хотя в этой задаче отражение применяется только к одной точке, она имеет высокий когнитивный спрос, если учащихся просят представить картинку. Это потому, что координаты точки (1000,2012) очень большие. Если ученики попытаются нанести эту точку и линию отражения на обычную координатную сетку xy, то либо график будет слишком большим, либо точка будет лежать так близко к линии отражения, что неясно, лежит она или нет. в этой строке. Хорошая картинка требует тщательного выбора подходящего участка плоскости и соответствующих надписей.Более того, отражения линий, сегментов линий и углов обнаруживаются путем отражения отдельных точек.
Тип: Задача по решению проблем
Отражение прямоугольника по диагонали:Задача предназначена для учебных целей и предполагает, что учащиеся знают свойства жестких преобразований, описанных в.Обратите внимание, что вершины рассматриваемых прямоугольников не попадают точно в точки пересечения горизонтальных и вертикальных линий сетки. Это означает, что учащимся необходимо приблизиться, и это создает дополнительную проблему. Проблема также в том, что сетки нарисованы так, что они выровнены по диагонали прямоугольников, а не по вертикали и горизонтали страницы. Однако такой выбор сетки также упрощает рассуждение об отражениях, если они понимают описания жестких движений, указанные в MAFS.8.G.1.3.
Тип: Задача по решению проблем
Скоростной спуск:Эта задача особенно хорошо подходит для учебных целей. Учащимся будет полезно обсудить в классе наклон, точку пересечения по оси y, точку пересечения по оси x и значение ограниченной области для более точной интерпретации того, что моделирует уравнение.
Тип: Задача по решению проблем
Найдите угол:Используйте неформальные аргументы, чтобы установить факты о сумме углов и внешнем угле треугольников, об углах, образованных, когда параллельные прямые пересекаются трансверсалью, и о критерии подобия треугольников угол-угол.
Тип: Задача по решению проблем
Найдите недостающий угол:Эта задача дает нам возможность увидеть, как со временем созревают математические идеи, заложенные в стандарты и кластеры. Задание «Использует факты о дополнительных, дополнительных, вертикальных и смежных углах в многоэтапной задаче для написания и решения простых уравнений для неизвестного угла на фигуре ()», за исключением того, что оно требует, чтобы учащиеся знали, кроме того, кое-что о параллельные линии, которые ученики не увидят до 8-го класса.В результате эта задача особенно хорошо иллюстрирует связи между соответствующими стандартами на разных уровнях обучения.
Тип: Задача по решению проблем
Вазы для цветов:Цель этого задания — дать студентам возможность попрактиковаться в работе с формулами объема цилиндров, конусов и сфер в увлекательном контексте, который дает возможность придать смысл ответам.
Тип: Задача по решению проблем
Это прямоугольник ?:Цель этого задания — предоставить студентам возможность применить широкий спектр идей из геометрии и алгебры, чтобы показать, что данный четырехугольник является прямоугольником.Здесь очень важен творческий подход, поскольку единственная информация — это декартовы координаты вершин четырехугольника. Использование этой информации для демонстрации того, что четыре угла являются прямыми углами, потребует некоторых вспомогательных построений. Студентам потребуется достаточно времени, а по некоторым из методов, описанных ниже, — руководство. Награда за тщательное выполнение этой задачи должна оправдывать усилия, потому что она дает студентам возможность увидеть несколько геометрических и алгебраических построений, объединенных для достижения общей цели.Учитель может пожелать, чтобы учащиеся сначала провели мозговой штурм по методам демонстрации того, что четырехугольник является прямоугольником (перед тем, как представить им явные координаты прямоугольника для этой задачи): в идеале они могут затем разделиться на группы и сразу же приступить к работе после того, как представят координаты четырехугольника для этой задачи.
Тип: Задача по решению проблем
Определение рациональных чисел:Задание предполагает, что учащиеся могут выразить данную повторяющуюся десятичную дробь в виде дроби.Учителя, которым нужно заполнить эти базовые знания, могут рассмотреть связанную задачу «8.NS Преобразование десятичных представлений рациональных чисел в дробные представления».
Тип: Задача по решению проблем
Иррациональные числа на числовой прямой:Когда учащиеся наносят иррациональные числа на числовую линию, это помогает укрепить идею о том, что они вписываются в систему счисления, которая включает более знакомые целые и рациональные числа.Сейчас хорошее время для учителей, чтобы начать использовать термин «реальная числовая линия», чтобы подчеркнуть тот факт, что числовая система, представленная числовой линией, является действительными числами. Когда ученики начинают изучать комплексные числа в старшей школе, они сталкиваются с числами, которые не находятся на прямой числовой прямой (а фактически находятся на «числовой плоскости»). Эту задачу можно использовать для оценивания или, если немного доработать, можно использовать в учебной обстановке.
Тип: Задача по решению проблем
Доставка овсяных хлопьев:Студенты должны подумать о различных способах размещения цилиндрических контейнеров в прямоугольной коробке.В процессе обучения учащиеся должны понимать, что, хотя некоторые настройки могут показаться разными, в результате получается коробка с одинаковым объемом. Кроме того, учащиеся должны прийти к осознанию (путем обсуждения и / или вопросов), что толщина картонной коробки очень мала и не окажет существенного влияния на расчеты.
Тип: Задача по решению проблем
Образцы плитки II: шестиугольники:Это задание идеально подходит для учебных целей, когда студенты могут не торопиться и разработать несколько стандартов математической практики, поскольку математическое содержание напрямую связано с содержанием стандарта по суммам углов в треугольниках, но несколько превосходит его.Тщательный анализ углов требует от учащихся построения обоснованных аргументов (MAFS.K12.MP.3.1) с использованием абстрактных и количественных рассуждений (MAFS.K12.MP.2.1). Создание изображения в части (c) помогает учащимся определить общий математический аргумент, повторяющийся несколько раз (MAFS.K12.MP.8.1). Если учащиеся используют блоки шаблонов, чтобы развить интуицию при разложении шестиугольника на треугольники, то это также пример MAFS.K12.MP.5.1.
Тип: Задача по решению проблем
Соответствие треугольника координатам:В этом материале учащиеся решат, как использовать преобразования в координатной плоскости, чтобы перевести треугольник в конгруэнтный треугольник.Включены исследовательские примеры, чтобы стимулировать аналитическое мышление.
Тип: Задача по решению проблем
Сравнение рациональных и иррациональных чисел:Студентам дается пара цифр. Их просят определить, что больше, а затем обосновать свой ответ.Используемые числа — это рациональные числа и обычные иррациональные числа, такие как p и квадратные корни. Эту задачу можно использовать для построения или оценки начального понимания рациональных приближений иррациональных чисел.
Тип: Задача по решению проблем
Музыка и спорт:В этом задании учащемуся предлагается собрать данные о том, играют ли одноклассники на каком-либо инструменте и / или участвуют ли они в каком-либо виде спорта, суммировать данные в таблице и решить, существует ли связь между занятиями спортом и игрой на музыкальном инструменте.Наконец, студента просят создать график, чтобы отобразить любую связь между переменными.
Тип: Задача по решению проблем
Какой твой любимый урок?:Учащимся предлагается изучить данные, представленные в формате таблицы, а затем вычислить процентное соотношение строк или столбцов и сформулировать вывод о значении данных.Любой расчет подходит для решения, поскольку нет четкой взаимосвязи между переменными. Видит ли учащийся сильную ассоциацию или нет, менее важно, чем то, правильно ли использует его или ее ответ данные и демонстрирует понимание того, что ассоциация означает, что распределение любимого предмета различно для учеников 7 и 8 классов.
Тип: Задача по решению проблем
Текстовые сообщения и оценки I:Студентам предлагается изучить диаграмму рассеяния, а затем интерпретировать ее значение.Учащиеся должны определить форму взаимосвязи (линейная, изогнутая и т. Д.), Направление или корреляция (положительная или отрицательная), любые конкретные выбросы, силу взаимосвязи между двумя переменными и любые другие соответствующие наблюдения.
Тип: Задача по решению проблем
Аэропорты США:В этом ресурсе двумерные данные реального мира отображаются в виде точечной диаграммы.Предоставляется уравнение линейной функции, моделирующей взаимосвязь между двумя переменными, и оно изображено на диаграмме рассеяния. Студентов просят использовать модель для интерпретации данных и делать прогнозы.
Тип: Задача по решению проблем
Сравнение скоростей в графиках и уравнениях:Это задание дает учащимся возможность рассуждать о графиках, наклонах и показателях, не имея шкалы на осях или уравнения для представления графиков.Студенты, которые предпочитают работать с конкретными числами, могут писать шкалы на осях, чтобы помочь им начать работу.
Тип: Задача по решению проблем
Скорость в зависимости от расстояния:В этом задании учащиеся интерпретируют два графика, которые выглядят одинаково, но показывают очень разные величины.Первый график дает информацию о том, насколько быстро движется автомобиль, а второй график дает информацию о положении автомобиля. Эта задача хорошо подходит для проведения обсуждения в классе или небольшой группе. Учащиеся узнают, что графики рассказывают истории и что их нужно интерпретировать, тщательно обдумывая отображаемые величины.
Тип: Задача по решению проблем
Мусор США, версия 1:В этой задаче правило функции более концептуально.Мы присваиваем году (входу) общее количество мусора, произведенного в этом году (соответствующий выход). Даже если бы мы не знали точное количество мусора за год, ясно, что в одном году не будет производиться два разных количества мусора. Таким образом, это имеет смысл как «правило», даже несмотря на то, что не существует алгоритмического способа определения выхода для данного входа, кроме поиска его в таблице.
Тип: Задача по решению проблем
Продажа мазута в убыток:Задача представляет собой задачу моделирования, которая связана с финансовыми решениями, с которыми постоянно сталкиваются предприятия, а именно с балансом между поддержанием запасов и привлечением краткосрочного капитала для инвестиций или реинвестирования в развитие бизнеса.
Тип: Задача по решению проблем
Курица и стейк, Вариант 1:В этом задании по решению задач студентам предлагается применить свое понимание линейных отношений для определения количества курицы и стейка, необходимого для барбекю, что будет включать в себя создание уравнения, построение графика и интерпретацию того и другого.Этот ресурс также включает комментарии по согласованию стандартов и аннотированные решения.
Тип: Задача по решению проблем
Кими и Джордан:Студентам предлагается составить линейные уравнения и построить график для сравнения сбережений двух человек.Назначение таблицы в (а) — помочь студентам заполнить (б), заметив регулярность в повторяющихся рассуждениях, необходимых для заполнения таблицы (Стандарт для математической практики).
Тип: Задача по решению проблем
Персики и сливы:В этом задании учащимся предлагается поразмышлять об относительных затратах на фунт двух фруктов, не зная, каковы на самом деле затраты.Студенты, которым это сложно, могут добавить шкалу к графику и рассуждать о значениях упорядоченных пар. Сравнение двух подходов в ходе обсуждения в классе может быть полезным способом помочь учащимся разобраться в уклоне.
Тип: Задача по решению проблем
Видео трансляция:Создайте функцию для моделирования линейной зависимости между двумя величинами.Определите скорость изменения и начальное значение функции по описанию взаимосвязи или по двум (x, y) значениям, включая чтение их из таблицы или графика. Интерпретируйте скорость изменения и начальное значение линейной функции в терминах моделируемой ситуации, а также в терминах ее графика или таблицы значений.
Тип: Задача по решению проблем
Бег по футбольному полю:Студентам необходимо подумать о том, как они могут использовать теорему Пифагора для определения расстояний, пройденных Беном Ватсоном и Чемпом Бейли.Здесь следует сосредоточиться не на том, кто пробежал большее расстояние, а на том, чтобы увидеть, как построить прямоугольные треугольники, чтобы применить теорему Пифагора к этой проблеме. Студенты должны использовать свои навыки измерения и делать разумные оценки, чтобы строить треугольники и правильно применять теорему.
Тип: Задача по решению проблем
Курица и стейк, Вариант 2:В этом задании по решению задач студентам предлагается применить свое понимание линейных отношений для определения количества курицы и стейка, необходимого для барбекю, что будет включать в себя создание уравнения, построение графика и интерпретацию того и другого.Этот ресурс также включает комментарии по согласованию стандартов и аннотированные решения.
Тип: Задача по решению проблем
Расстояние по каналу:В этой задаче по решению проблем учащимся предлагается найти линейную функцию, которая моделирует что-то в реальном мире.После нахождения уравнения линейной зависимости между глубиной воды и расстоянием через канал, учащиеся должны озвучить значение уклона и пересечения линии в контексте этой ситуации. Также включены комментарии по согласованию стандартов и иллюстрированные решения.
Тип: Задача по решению проблем
Уравнения линий:Это задание просит учащегося понять взаимосвязь между наклоном и изменениями значений x и y линейной функции.
Тип: Задача по решению проблем
Найдите изменение:Это задание побуждает учащихся распознать взаимосвязь между наклоном и разницей в значениях x- и y- линейной функции.Помогите учащимся укрепить свое понимание линейных функций и подтолкнуть их к более свободным рассуждениям о наклонах и пересечениях по оси Y. Эта задача также дала разумную отправную точку для обсуждения формы линейного уравнения с точкой наклона.
Тип: Задача по решению проблем
Ремонт печи:Студентам предлагается написать уравнения для моделирования затрат на ремонт трех разных компаний и определить условия, при которых каждая компания будет наименее затратной.Это задание можно использовать как для оценки понимания учащимися систем линейных уравнений, так и для стимулирования обсуждения и размышления учащихся, которые позволят более прочно закрепить эти концепции. Решение может быть найдено несколькими способами, включая графический или алгебраический подход.
Тип: Задача по решению проблем
Гигантбургеры:Студента просят выполнить операции с числами, выраженными в научных обозначениях, чтобы решить, действительно ли 7% американцев действительно едят в Giantburger каждый день.
Тип: Задача по решению проблем
Расширение определений экспонент, вариант 1:Это учебное задание, предназначенное для обсуждения значения отрицательных целочисленных показателей. Хотя некоторым ученикам это может быть незнакомо, для них полезно усвоить условное обозначение, что отрицательным временем считается любое время до t = 0.
Тип: Задача по решению проблем
Сколько решений ?:Студенту дается уравнение 5x-2y = 3 и просят, если возможно, написать второе линейное уравнение, создающее системы, приводящие к одному, двум, бесконечным и никаким решениям.
Тип: Задача по решению проблем
Идет дождь!!! (Сравните площади протертых лобовых стекол):В этом задании по решению проблем ученикам предлагается определить, позволяют ли дворники на автомобиле или на грузовике лучше видеть водителю большую площадь.Чтобы решить эту проблему, учащиеся должны применить теорему Пифагора и свою способность находить области кругов и параллелограммов, чтобы найти ответ. Обязательно нажимайте ссылки на оранжевой полосе вверху страницы, чтобы получить дополнительную информацию о задаче. Из рисунка NCTM: Это! Математические задачи для семей.
Тип: Задача по решению проблем
Доказательство совпадающих углов:В этом учебном пособии учащихся просят доказать, что два угла совпадают, когда им предоставляется ограниченная информация.Перед просмотром этого видео учащиеся должны иметь основу из параллельных линий, поперечных линий и треугольников.
Тип: Учебное пособие
Объем конуса:В этом видеоролике объясняется формула объема конуса и применяется формула для решения проблемы.
Тип: Учебное пособие
Формула расстояния и теорема Пифагора:Из этого туториала Вы узнаете, как найти расстояние между линиями с помощью теоремы Пифагора.В этом видео показана связь между формулой расстояния и теоремой Пифагора.
Тип: Учебное пособие
Сумма мер доказательства треугольников:Это видео демонстрирует сумму углов в треугольнике.Это видео полезно как для студентов, изучающих алгебру и геометрию.
Тип: Учебное пособие
Метод замены:В этом видео показано, как решить систему уравнений с помощью метода подстановки.
Тип: Учебное пособие
Распознавание линейных функций:В этом видео вы определите, является ли ситуация линейной или нелинейной, путем определения скорости изменения между координатами.Вы сможете проверить свою работу, нанеся на график данные координаты.
Тип: Учебное пособие
Сравнение линейных функций на графике:В этом руководстве студенты будут сравнивать линейные функции на графике. Студенты должны понимать наклон и скорость изменения, прежде чем просматривать это руководство.
Тип: Учебное пособие
Сравните линейные функции из таблицы и графика:В этом руководстве показано, как сравнить линейные функции, представленные как в таблице, так и на графике. Перед просмотром этого видео учащиеся должны иметь представление о скорости изменений.
Тип: Учебное пособие
Сравнение линейных функций:Студенты сравнят линейные функции, представленные на графике и в таблице. Перед просмотром этого учебного пособия учащиеся должны хорошо понимать скорость изменений.
Тип: Учебное пособие
Линейная функция: трата денег:В этом руководстве вы попрактикуетесь в использовании уравнения в форме пересечения наклона для нахождения координат, а затем нанесете на график координаты, чтобы предсказать ответ на проблему.
Тип: Учебное пособие
Интерпретация линейных графиков:В этом руководстве вы рассмотрите несколько реальных примеров линейных графиков и интерпретируете взаимосвязь между двумя переменными.
Тип: Учебное пособие
Построение линейного уравнения с помощью таблицы:Студенты узнают, как построить линейное уравнение с помощью таблицы.Студентам не нужно будет строить графики из формы с пересечением наклона, хотя они будут преобразовывать уравнение из стандартной формы в форму с пересечением наклона перед созданием таблицы.
Тип: Учебное пособие
Использование формы наклона-пересечения линии:В этом видео вы попрактикуетесь в написании уравнений линий в форме пересечения наклона из графиков.Затем вы попрактикуетесь в построении линий из уравнений в форме пересечения наклона.
Тип: Учебное пособие
Нахождение наклона из двух упорядоченных пар:В этом руководстве показан пример определения наклона между двумя упорядоченными парами.Наклон представлен как подъем / спуск, изменение y, деленное на изменение x, а также как m.
Тип: Учебное пособие
Как приблизительно вычислить квадратные корни:В этом видео вы попрактикуетесь в приближении квадратных корней из чисел, не являющихся точными квадратами.Вы найдете идеальный квадрат внизу и вверху, чтобы приблизительно определить значение квадратного корня между двумя целыми числами.
Тип: Учебное пособие
Классифицирующие числа:В этом уроке вы попрактикуетесь в классификации чисел как целых, целых, рациональных и иррациональных чисел.
Тип: Учебное пособие
Отрицательные показатели:Этот учебник показывает студентам правило отрицательных показателей.Учащиеся увидят, используя переменные, закономерность для отрицательных показателей.
Тип: Учебное пособие
Отрицательные показатели:В этом руководстве студенты узнают об отрицательных показателях степени.Упор делается на умножение на обратную величину.
Тип: Учебное пособие
Нахождение кубических корней:Узнайте, как найти кубический корень из -512 с помощью разложения на простые множители.
Тип: Учебное пособие
Введение в кубические корни:Студенты узнают значение кубических корней и узнают, как их найти. Студенты также узнают, как найти кубический корень отрицательного числа.
Тип: Учебное пособие
Введение в квадратные корни:Учащиеся узнают о символе квадратного корня (главный корень) и о том, что значит найти квадратный корень.Студенты также узнают, как решать простые уравнения с квадратным корнем.
Тип: Учебное пособие
Экспоненты с отрицательным основанием:В этом руководстве вы примените все, что вы знаете об умножении отрицательных чисел, чтобы определить, как влияют отрицательные основания с показателями и какие паттерны развиваются.
Тип: Учебное пособие
Проблема слова линейного уравнения:Узнайте, как решить проблему со словами, написав уравнение для моделирования ситуации. В этом видео мы используем линейное уравнение 210 (t-5) = 41790.
Тип: Учебное пособие
Решение уравнений: проблема со словом:В этом уроке показана задача со словами, в которой учащиеся найдут размеры сада, учитывая только его периметр.Учащиеся создадут уравнение для решения.
Тип: Учебное пособие
Двухступенчатые уравнения:Студенты будут практиковать двухшаговые уравнения, некоторые из которых требуют объединения одинаковых терминов и использования свойства распределения.
Тип: Учебное пособие
Решение двухэтапных уравнений:В этом видео показано, как решить двухэтапное уравнение.Он начинается с концепции равенства: то, что делается с одной стороной уравнения, должно быть сделано с другой стороной уравнения.
Тип: Учебное пособие
Линейные уравнения:Этот учебник поможет вам изучить наклоны линий и увидеть, как наклон представлен на осях x-y.
Тип: Учебное пособие
Показатели и степени:В этом руководстве рассматривается концепция степеней и степеней и рассказывается, как оценивать степени с отрицательными знаками.
Тип: Учебное пособие
Мощность энергетического имущества:В этом руководстве показано, как использовать мощность степенного свойства как с числами, так и с переменными.
Тип: Учебное пособие
Линейные уравнения:Уравнения вида y = mx описывают прямые в декартовой плоскости, которые проходят через начало координат. Тот факт, что многие функции линейны при рассмотрении в мелком масштабе, важен в таких областях математики, как исчисление.
Тип: Учебное пособие
Решение многоступенчатых уравнений:В этом коротком видеоролике объясняется, как решать многоступенчатые уравнения с переменными с обеих сторон и почему необходимо выполнять одни и те же шаги с обеих сторон уравнения.
Тип: Учебное пособие
Возведение экспоненциальных выражений в степень:Если термин, возведенный в степень, заключен в круглые скобки, а затем возведен в другую степень, это выражение можно упростить, используя правила умножения показателей.
Тип: Учебное пособие
Повышение качества продуктов и удельного веса:Любое выражение, состоящее из членов умножения и деления, можно заключить в круглые скобки и возвести в степень. Затем это можно упростить, используя правила умножения показателей.
Тип: Учебное пособие
Диаграммы разброса:Диаграммы рассеяния используются для визуализации взаимосвязи между двумя количественными переменными в бинарном отношении. Например, тенденции во взаимосвязи между ростом и весом группы людей можно изобразить и проанализировать с помощью диаграммы рассеяния.
Тип: Учебное пособие
Решение несовместимых или зависимых систем:Решая систему линейных уравнений относительно x и y с одним решением, мы получаем уникальную пару значений для x и y. Но что происходит, когда вы пытаетесь решить систему без решений или с бесконечным количеством решений?
Тип: Учебное пособие
Форма пересечения склона:Линейные уравнения вида y = mx + b могут описывать любую невертикальную линию в декартовой плоскости.Константа m определяет наклон линии, а константа b определяет точку пересечения y и, следовательно, вертикальное положение линии.
Тип: Учебное пособие
Научная нотация:Научная нотация используется для удобной записи чисел, для представления которых требуется много цифр.В этом руководстве объясняется, как преобразовать стандартную нотацию в научную.
Тип: Учебное пособие
Линейные уравнения с одной переменной:Этот урок знакомит учащихся с линейными уравнениями с одной переменной, показывает, как их решать, используя свойства равенств сложения, вычитания, умножения и деления, и позволяет учащимся определить, является ли значение решением, существует ли бесконечно много решений или вообще нет решения.Сайт содержит объяснение уравнений и линейных уравнений, как решать уравнения в целом, а также стратегию решения линейных уравнений. Урок также объясняет противоречие (уравнение без решения) и тождество (уравнение с бесконечными решениями). В конце есть пять практических задач, чтобы студенты могли проверить свои знания со ссылками на ответы и объяснениями, как эти ответы были найдены. Также указаны дополнительные ресурсы.
Тип: Учебное пособие
Основные аддитивные цвета:Этот ресурс помогает пользователю изучить три основных цвета, которые имеют фундаментальное значение для человеческого зрения, изучить различные цвета в видимом спектре, увидеть цвета, получаемые при добавлении двух цветов, и узнать, что такое белый свет.Комбинация текста и виртуального манипулятора позволяет пользователю исследовать эти концепции множеством способов.
Тип: Учебное пособие
Основные субтрактивные цвета:Пользователь изучит три основных субтрактивных цвета в видимом спектре, исследует результирующие цвета, когда два субтрактивных цвета взаимодействуют друг с другом, и изучит формирование черного цвета.
Тип: Учебное пособие
Преобразование единиц скорости:На этом уроке учащиеся будут просматривать видеоролик Khan Academy, в котором будет показано, как преобразовывать коэффициенты с использованием единиц скорости.
Тип: Учебное пособие
Ползунок наклона:В этом упражнении учащиеся настраивают ползунки, которые регулируют коэффициенты и константы линейной функции, и исследуют, как их изменения влияют на график.Уравнение линии может иметь форму пересечения уклона или стандартную форму. Это задание позволяет учащимся изучить линейные уравнения, уклоны и точки пересечения по оси Y, а также их визуальное представление на графике. Это упражнение включает в себя дополнительные материалы, в том числе справочную информацию по затронутым темам, описание того, как использовать приложение, и вопросы исследования для использования с java-апплетом.
Тип: виртуальный манипулятор
Линейная функциональная машина:В этом упражнении учащиеся подставляют значения в независимую переменную, чтобы увидеть, каковы выходные данные для этой функции.Затем на основе этой информации они должны определить коэффициент (наклон) и константу (пересечение оси y) для линейной функции. Это упражнение позволяет студентам изучить линейные функции и то, какие входные значения полезны при определении правила линейной функции. Это упражнение включает в себя дополнительные материалы, в том числе справочную информацию по затронутым темам, описание того, как использовать приложение, и вопросы исследования для использования с апплетом Java.
Тип: виртуальный манипулятор
Графические линии:Позволяет учащимся получить доступ к декартовой системе координат, в которой можно построить график линейных уравнений и наблюдать за деталями линии и наклона.
Тип: виртуальный манипулятор
Информационный флаер:С помощью этого виртуального манипулятора учащиеся могут изобразить функцию и набор упорядоченных пар на одной и той же координатной плоскости. Константы, коэффициенты и показатели можно регулировать с помощью ползунков, чтобы учащийся мог исследовать влияние на график при изменении параметров функции.Студенты также могут проверить отклонение данных от функции. Это упражнение включает в себя дополнительные материалы, в том числе справочную информацию по затронутым темам, описание того, как использовать приложение, и вопросы исследования для использования с java-апплетом.
Тип: виртуальный манипулятор
Функциональный флаер:В этом онлайн-инструменте учащиеся вводят функцию для создания графика, на котором константы, коэффициенты и показатели можно регулировать с помощью ползунков.Этот инструмент позволяет учащимся изучать графики функций и то, как изменение чисел в функции влияет на график. Используя вкладки в верхней части страницы, вы также можете получить доступ к дополнительным материалам, включая справочную информацию о затронутых темах, описание того, как использовать приложение, и вопросы исследования для использования с java-апплетом.
Тип: виртуальный манипулятор
Advanced Data Grapher:Это онлайн-утилита для построения графиков, которую можно использовать для создания ящичных диаграмм, пузырьковых диаграмм, диаграмм рассеяния, гистограмм и диаграмм типа «стержень-лист».
Тип: виртуальный манипулятор
Number Cruncher:В этом упражнении учащиеся вводят вводимые данные в функциональную машину. Затем, исследуя выходные данные, они должны определить, какую функцию выполняет машина.Это упражнение позволяет студентам изучить функции и то, какие входные данные наиболее полезны для определения правила функции. Это упражнение включает в себя дополнительные материалы, в том числе справочную информацию по затронутым темам, описание того, как использовать приложение, и вопросы исследования для использования с java-апплетом.
Тип: виртуальный манипулятор
Подгонка кривой:С помощью мыши учащиеся будут перетаскивать точки данных (со своими планками ошибок) и мгновенно наблюдать за формой наиболее подходящей полиномиальной кривой.Студенты могут выбрать тип соответствия: линейный, квадратичный, кубический или квартичный. Может отображаться наилучшая или регулируемая посадка.
Тип: виртуальный манипулятор
График уравнений:Это интерактивное моделирование исследует построение графиков линейных и квадратных уравнений.Пользователям предоставляется возможность определять и изменять коэффициенты и константы, чтобы наблюдать результирующие изменения на графике (ах).
Тип: виртуальный манипулятор
Линия Best Fit:Эта манипуляция позволяет пользователю ввести несколько координат на сетке, оценить линию наилучшего соответствия, а затем определить уравнение для линии наилучшего соответствия.
Тип: виртуальный манипулятор
Вращение точки:Этот виртуальный манипулятор представляет собой интерактивное визуальное представление вращения точки вокруг начала системы координат. Исходную точку можно перетаскивать в разные положения, а угол поворота можно изменять с шагом 90 °.
Тип: виртуальный манипулятор
Задачи по математике для 8-х классов с ответами
ЗАДАЧИ ПО МАТЕМАТИЧЕСКИМ КЛАССАМ С ОТВЕТАМИВопрос 1:
На какое наименьшее число можно разделить 256, чтобы частное получилось точным кубом?
(A) 2 (B) 3 (C) 4
Решение:
Чтобы найти число, необходимое для деления 256, чтобы частное получилось идеальным кубом, мы должны разложить 256 на простые множители.
= ∛256 = ∛ (2⋅2⋅2⋅2⋅2⋅2⋅2⋅2) Когда мы группируем простые множители внутри кубического корня как тройки, мы оставляем 2⋅2. 4. Следовательно, 4 — это наименьшее число, необходимое для деления 256, чтобы частное получилось идеальным кубом. |
Вопрос 2:
Сколько цифр в квадратном корне из 4456321?
(A) 2 цифры (B) 4 цифры (C) 3 цифры
Решение:
Квадратный корень из 1 цифры, а 2-значное число содержит 1 цифру.
Квадратный корень из 3- и 4-значного числа состоит из 2-х цифр.
Квадратный корень из 5- и 6-значного числа состоит из 3-х цифр.
Квадратный корень из 7 и 8-значного числа состоит из 4-х цифр.
Итак, квадратный корень данного числа состоит из 4 цифр.
Вопрос 3:
Найдите значение 3x 3 — 4x 2 + x — 5, когда x = -3
(A) -54 (B) -71 (C) -32
Решение:
Пусть f (x) = 3x 3 — 4x 2 + x — 5
x = — 3
f (-3) = 3 (-3) 3 — 4 (-3) 2 + (-3) — 5
= 3 (9) — 4 (9) — 3 — 5
= 27 — 36 — 3 — 5
= 27-44
= -17
Вопрос 4:
Периметр прямоугольника 52 см.Если его ширина на 2 см больше одной трети его длины, найдите размеры прямоугольника.
(A) 12 см x 4 см (B) 18 см x 8 см (C) 15 см x 9 см
Решение:
Периметр прямоугольника = 52 см
2 (длина + ширина) = 52 ==> l + w = 26
Пусть x будет длиной
шириной = (x / 3) + 2
x + (x / 3) + 2 = 26
[(3x + x) / 3 ] + 2 = 26
4x / 3 = 24
4x = 24 (3)
x = 6 (3) ==> 18 см
Ширина = (18/3) + 2
= 6 + 2 = 8 см
Итак, требуемый размер 18 см х 8 см.
Вопрос 5:
Что нужно прибавить к числителю и знаменателю дроби 7/11, чтобы получилось 3/4
(A) 9 (B) 5 (C) 12
Решение:
Пусть x будет числом, которое нужно добавить к числителю и знаменателю дроби.
(7 + x) / (11 + x) = 3/4
4 (7 + x) = 3 (11 + x)
28 + 4x = 33 + 3x
4x — 3x = 33 — 28
x = 5
Итак, 5 — необходимое число, которое нужно добавить, чтобы сделать дробь 7/11 как 3/4.
Вопрос 6:
Линия, которая пересекает две или более линий в разных точках, называется ____________
(A) параллельной (B) пересекающейся (C) поперечной
Решение:
Линия, которая пересекает две или более линии в разных точках, называется параллельной.
Вопрос 7:
Противоположные углы циклического четырехугольника равны _______________
(A) Дополнительный (B) Дополнительный (C) Ни один из этих
Решение:
Сумма противоположных углов циклического четырехугольник 180 градусов.
Итак, ответ дополнительный.
Вопрос 8:
В треугольник ABC вписана окружность с центром O, а BC — диаметр, если угол BAC равен 50 °, найдите угол ABC.
(A) 50 ° (B) 40 ° (C) 48 °
Раствор:
В прямоугольном треугольнике ABC

 Взаимно простые числа
Взаимно простые числа