ГДЗ Алгебра 8 класс Дорофеев, Суворова
- Алгебра 8 класс
- Тип пособия: Учебник
- Авторы: Дорофеев, Суворова
- Издательство: «Просвещение»
Задания
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325326327328329330331332333334335336337338339340341342343344345346347348349350351352353354355356357358359360361362363364365366367368369370371372373374375376377378379380381382383384385386387388389390391392393394395396397398399400401402403404405406407408409410411412413414415416417418419420421422423424425426427428429430431432433434435436437438439440441442443444445446447448449450451452453454455456457458459460461462463464465466467468469470471472473474475476477478479480481482483484485486487488489490491492493494495496497498499500501502503504505506507508509510511512513514515516517518519520521522523524525526527528529530531532533534535536537538539540541542543544545546547548549550551552553554555556557558559560561562563564565566567568569570571572573574575576577578579580581582583584585586587588589590591592593594595596597598599600601602603604605606607608609610611612613614615616617618619620621622623624625626627628629630631632633634635636637638639640641642643644645646647648649650651652653654655656657658659660661662663664665666667668669670671672673674675676677678679680681682683684685686687688689690691692693694695696697698699700701702703704705706707708709710711712713714715716717718719720721722723724725726727728729730731732733734735736737738739740741742743744745746747748749750751752753754755756757758759760761762763764765766767768769770771772773774775776777778779780781782783784785786787788789790791792793794795796797798799800801802803804805806807808809810811812813814815816817818819820821822823824825826827828829830831832833834835836837838839840841842843844845846847848849850851852853854855856857858859860861862863864865866867868869870871872873874875876877878879880881882883884885886887888889890891892893894895896897898899900901902903904905906907908909910Это надо уметь.
 Глава 1123456789101112131415161718
Глава 1123456789101112131415161718Это надо знать. Глава 1
1234567891011Провер себя. Глава 1
12345678910111213141516Это надо уметь. Глава 2
12345678910111213141516171819Это надо знать. Глава 2
123456789Провер себя. Глава 2
1234567891011121314151617181920Это надо уметь. Глава 3
12345678Это надо знать. Глава 3
123456789Провер себя. Глава 3
123456789101112131415161718Это надо уметь. Глава 4
1234567891011Это надо знать. Глава 4
1234567891011Это надо уметь. Глава 5
12345678910Это надо знать. Глава 5
1234567891011Провер себя. Глава 5
123456789101112131415Это надо уметь. Глава 6
1234Это надо знать. Глава 6
123Провер себя. Глава 6
Задания : 1
Условие
Решебник №1
Решебник №2
Одним из разделов математики является алгебра. Она изучает свойства и действия над различными величинами, а также методы решения уравнений. В отличие от арифметики в алгебре используются буквенные обозначения, что позволяет записывать свойства действий в краткой форме. Основы предмета школьники начинают изучать в пятом классе, и далее вплоть до выпуска совершенствуют свои навыки и умения. Довольно часто при изучении дисциплины возникают определенные трудности, разрешить которые поможет подросткам «ГДЗ по Алгебре 8 класс Учебник Дорофеев, Суворова (Просвещение)».
Она изучает свойства и действия над различными величинами, а также методы решения уравнений. В отличие от арифметики в алгебре используются буквенные обозначения, что позволяет записывать свойства действий в краткой форме. Основы предмета школьники начинают изучать в пятом классе, и далее вплоть до выпуска совершенствуют свои навыки и умения. Довольно часто при изучении дисциплины возникают определенные трудности, разрешить которые поможет подросткам «ГДЗ по Алгебре 8 класс Учебник Дорофеев, Суворова (Просвещение)».
Для чего нужно знать алгебру
Ученики, осваивая учебную программу восьмого класса, смогут познакомиться с рациональными дробями, их свойствами и действиями с ними. Кроме этого, они рассмотрят такое понятие как арифметический корень и изучат его применение при решении задач. Далее ученики освоят числовые неравенства и степени с целым показателем. Восьмиклассники научатся:
- Решать задачи с помощью квадратных уравнений.

- Умножать, делить и сокращать дроби.
- Сравнивать и упорядочивать рациональные числа.
- Понимать и применять алгебраические термины и символы.
- Строить графики квадратичной функции.
Уроки дисциплины учат ясно и точно излагать свои мысли, понимать смысл поставленных задач, а также анализировать, сопоставлять и делать выводы. С помощью решебника учащиеся легко справятся со всеми проблемными моментами, которые рано или поздно встают перед каждым ребенком.
Чем поможет решебник
Дисциплина, однако даётся не всем легко. Это довольно сложный предмет, который не терпит произвола и условностей. Многие ученики не понимают учебный материал, и это не лучшим образом отражается на знаниях и оценках. Хорошим подспорьем в такой ситуации станет «ГДЗ по Алгебре 8 класс Учебник Дорофеев, Суворова (Просвещение)». Страницы онлайн-решебника содержат правильные и предельно понятные ответы, которые школьник с лёгкостью сможет отыскать по номеру упражнения. Они помогут:
Они помогут:
- проверить правильное выполнение домашней работы;
- проработать допущенные ошибки и понять основную суть;
- тщательно подготовиться к предстоящему уроку;
- сэкономить время и силы на поиск нужной информации.
Постоянное использование ГДЗ только положительно скажется на результатах учёбы. Кроме этого, ученик сможет разобраться и понять все нюансы дисциплины самостоятельно, не прибегая к услугам репетиторов. Заниматься с данным пособием легко, ведь оно доступно онлайн круглосуточно, а это значит, что дети смогут выполнять уроки в удобном для себя темпе.
Эффективность учебника и ГДЗ
Прекрасным базовым пособием по мнению экспертов является учебник по алгебре за 7 класс авторы Дорофеев, Суворова. Весь материал прописан понятным и доступным языком, важные формулы и определения выделены в рамки и имеют отдельный шрифт, что способствует лучшему запоминанию, наличие дополнительной информации упрощает процесс обучения. Пособие поможет школьникам приобрести навыки и умения алгебраического характера в том объёме, который предусмотрен учебными стандартами.
Пособие поможет школьникам приобрести навыки и умения алгебраического характера в том объёме, который предусмотрен учебными стандартами.
- верные ответы на все номера;
- подробные образцы решений;
- дополнительные комментарии.
Эти сведения позволят учащимся легко ориентироваться в учебной программе, планомерно готовиться к многочисленным проверочным работам, разбирать и грамотно исправлять ошибки, улучшить качество своих знаний, и т.д. С решебником восьмиклассники смогут самостоятельно освоить даже самые сложные формулы и алгоритмы, не обращаясь за помощью к родителям или непроверенным источникам.
Решебник нужно использовать правильно
Школьников обычно не волнует, как именно они получат желаемый результат, главное, чтобы учитель поставил в итоге хорошую оценку, поэтому чаще всего прибегают к списыванию.
- Ухудшение успеваемости.
- Упущение важных сведений.
- Плохие оценки по контрольным.
Необходимо планомерно проработать все недочеты, пока ситуация не ухудшилась до крайности. Многим школьникам требуется помощь для преодоления затруднений, так как сами они справиться не в состоянии. Родители в этот период времени, как правило, стараются нанять своим детям репетиторов, считая, что это единственный выход. Но на самом деле это не так. Есть намного более эффективный метод привить учащимся полное понимание данного предмета.
«ГДЗ по Алгебре 8 класс Учебник Дорофеев, Суворова (Просвещение)» позволит ученикам с разным уровнем знаний стабилизировать свои навыки, не затрачивая на это много сил и времени. Однако не стоит относиться к этому сборнику, как к обычной шпаргалке, иначе ничего не поменяется.
Иногда подросткам не хочется тратить лишнее время на штудирование материала. Именно в этом и состоит их ошибка. Стоит упустить что-то на начальном этапе, как потом придется потратить не одну неделю на восполнение пробелов. При этом основная программа продолжает стремительно двигаться вперед, так что об отдыхе речи вообще не будет. Так зачем усложнять себе обучение? Лучше с самого начала воспользоваться решебником, и не переживать о том, что что-то останется недопонятым. С ГДЗ учебный процесс станет приносить только положительные эмоции.
ГДЗ по алгебре 8 класс дидактические материалы Мерзляк А.
 Г., Полонский В.Б., Рабинович М.С., Якир М.С.
Г., Полонский В.Б., Рабинович М.С., Якир М.С.- 7
- 8
- 9
- 10
- 11
- ГДЗ
- 8 класс
- дидактические материалы Мерзляк
Авторы: Мерзляк А.Г., Полонский В.Б., Рабинович М.С., Якир М.С..
Данную математическую дисциплину освоить придётся каждому школьнику, так как это одна из главных наук, не сбиться на этом пути поможет ГДЗ по алгебре за 8 класс дидактические материалы Мерзляк
.Алгебра берет своё начало в океане математики, которая делится на две дисциплины в седьмом классе. Вторая несёт название геометрии, изучает взаимодействие тел в пространстве. Там присутствует много различных теорем, построений и теоретических знаний. Алгебра же более конкретная вещь, обобщает и углубляется в арифметические операции. Для учащихся важно понять каждую тему, не допуская пропусков, забыв предыдущие параграфы, дальше далеко не уйдешь. Очень много заданий из этой науки встречается в тестах единого государственного экзамена, а также в более близком ОГЭ по математике, с которым предстоит встретиться уже на девятом году обучения.
Алгебра же более конкретная вещь, обобщает и углубляется в арифметические операции. Для учащихся важно понять каждую тему, не допуская пропусков, забыв предыдущие параграфы, дальше далеко не уйдешь. Очень много заданий из этой науки встречается в тестах единого государственного экзамена, а также в более близком ОГЭ по математике, с которым предстоит встретиться уже на девятом году обучения.
Как поможет онлайн-помощник по алгебре за 8 класс дидактические материалы Мерзляка
Часов на алгебру отведено немало, 4-5 в неделю, немного меняется количество в зависимости от четверти. Предмет серьёзный, требовательный, отнестись к нему целесообразно со всей ответственностью. Пройдемся по основным тезисам программы, чтобы понять, с чем столкнуться учащиеся в этом году:
- алгебраические дроби и действия с ними, сложение и вычитание;
- видоизменение рациональных выражений для их упрощения;
- арифметический квадратный корень из неотрицательного числа;
- различные функции и их графики;
- графическое нахождение ответов уравнений квадратного вида;
- решение неравенств повышенной сложности.

Скомпоновать всё полезное у себя в голове возможно вместе с пособием по алгебре за 8 класс дидактические материалы Мерзляка. Решебник призван дать ответы на любые возникающие вопросы у учеников, имеет развёрнутые пояснения для более детального анализа. Сборник обладает рядом преимуществ, например, домашние задания выполняются быстро и без ошибок, самопроверка воспитывает инициативность и контроль над собой, круглосуточный доступ.
Желаем успехов с этой капризной наукой и пятерок в аттестате. Всё получится, если много трудиться над получением знаний и иногда прибегать к решебнику по математике.
- ГДЗ к учебнику по алгебре за 8 класс Мерзляк А.Г.
- ГДЗ к рабочей тетради по алгебре за 8 класс Мерзляк А.Г.
- ГДЗ к методическому пособию по алгебре за 8 класс Буцко Е.
 В.
В.
Вариант 1
- 1
- 2
- 3
- 4
- 5
- 6
- 7
Вариант 2
- 1
- 2
- 3
- 4
- 5
- 6
- 7
ГДЗ по Алгебре 8 класс Мерзляк, Полонский, Якир — учебник
Номера упражнений
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- 195
- 196
- 197
- 198
- 199
- 200
- 201
- 202
- 203
- 204
- 205
- 206
- 207
- 208
- 209
- 210
- 211
- 212
- 213
- 214
- 215
- 216
- 217
- 218
- 219
- 220
- 221
- 222
- 223
- 224
- 225
- 226
- 227
- 228
- 229
- 230
- 231
- 232
- 233
- 234
- 235
- 236
- 237
- 238
- 239
- 240
- 241
- 242
- 243
- 244
- 245
- 246
- 247
- 248
- 249
- 250
- 251
- 252
- 253
- 254
- 255
- 256
- 257
- 258
- 259
- 260
- 261
- 262
- 263
- 264
- 265
- 266
- 267
- 268
- 269
- 270
- 271
- 272
- 273
- 274
- 275
- 276
- 277
- 278
- 279
- 280
- 281
- 282
- 283
- 284
- 285
- 286
- 287
- 288
- 289
- 290
- 291
- 292
- 293
- 294
- 295
- 296
- 297
- 298
- 299
- 300
- 301
- 302
- 303
- 304
- 305
- 306
- 307
- 308
- 309
- 310
- 311
- 312
- 313
- 314
- 315
- 316
- 317
- 318
- 319
- 320
- 321
- 322
- 323
- 324
- 325
- 326
- 327
- 328
- 329
- 330
- 331
- 332
- 333
- 334
- 335
- 336
- 337
- 338
- 339
- 340
- 341
- 342
- 343
- 344
- 345
- 346
- 347
- 348
- 349
- 350
- 351
- 352
- 353
- 354
- 355
- 356
- 357
- 358
- 359
- 360
- 361
- 362
- 363
- 364
- 365
- 366
- 367
- 368
- 369
- 370
- 371
- 372
- 373
- 374
- 375
- 376
- 377
- 378
- 379
- 380
- 381
- 382
- 383
- 384
- 385
- 386
- 387
- 388
- 389
- 390
- 391
- 392
- 393
- 394
- 395
- 396
- 397
- 398
- 399
- 400
- 401
- 402
- 403
- 404
- 405
- 406
- 407
- 408
- 409
- 410
- 411
- 412
- 413
- 414
- 415
- 416
- 417
- 418
- 419
- 420
- 421
- 422
- 423
- 424
- 425
- 426
- 427
- 428
- 429
- 430
- 431
- 432
- 433
- 434
- 435
- 436
- 437
- 438
- 439
- 440
- 441
- 442
- 443
- 444
- 445
- 446
- 447
- 448
- 449
- 450
- 451
- 452
- 453
- 454
- 455
- 456
- 457
- 458
- 459
- 460
- 461
- 462
- 463
- 464
- 465
- 466
- 467
- 468
- 469
- 470
- 471
- 472
- 473
- 474
- 475
- 476
- 477
- 478
- 479
- 480
- 481
- 482
- 483
- 484
- 485
- 486
- 487
- 488
- 489
- 490
- 491
- 492
- 493
- 494
- 495
- 496
- 497
- 498
- 499
- 500
- 501
- 502
- 503
- 504
- 505
- 506
- 507
- 508
- 509
- 510
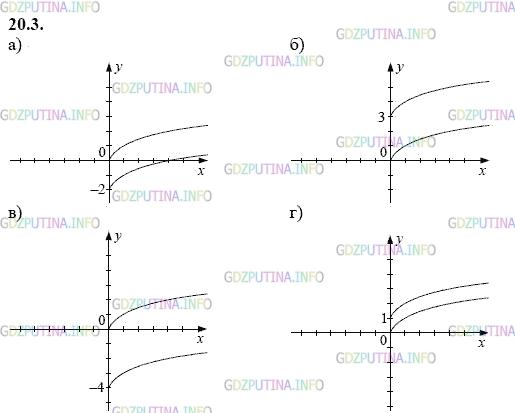
- 511
- 512
- 513
- 514
- 515
- 516
- 517
- 518
- 519
- 520
- 521
- 522
- 523
- 524
- 525
- 526
- 527
- 528
- 529
- 530
- 531
- 532
- 533
- 534
- 535
- 536
- 537
- 538
- 539
- 540
- 541
- 542
- 543
- 544
- 545
- 546
- 547
- 548
- 549
- 550
- 551
- 552
- 553
- 554
- 555
- 556
- 557
- 558
- 559
- 560
- 561
- 562
- 563
- 564
- 565
- 566
- 567
- 568
- 569
- 570
- 571
- 572
- 573
- 574
- 575
- 576
- 577
- 578
- 579
- 580
- 581
- 582
- 583
- 584
- 585
- 586
- 587
- 588
- 589
- 590
- 591
- 592
- 593
- 594
- 595
- 596
- 597
- 598
- 599
- 600
- 601
- 602
- 603
- 604
- 605
- 606
- 607
- 608
- 609
- 610
- 611
- 612
- 613
- 614
- 615
- 616
- 617
- 618
- 619
- 620
- 621
- 622
- 623
- 624
- 625
- 626
- 627
- 628
- 629
- 630
- 631
- 632
- 633
- 634
- 635
- 636
- 637
- 638
- 639
- 640
- 641
- 642
- 643
- 644
- 645
- 646
- 647
- 648
- 649
- 650
- 651
- 652
- 653
- 654
- 655
- 656
- 657
- 658
- 659
- 660
- 661
- 662
- 663
- 664
- 665
- 666
- 667
- 668
- 669
- 670
- 671
- 672
- 673
- 674
- 675
- 676
- 677
- 678
- 679
- 680
- 681
- 682
- 683
- 684
- 685
- 686
- 687
- 688
- 689
- 690
- 691
- 692
- 693
- 694
- 695
- 696
- 697
- 698
- 699
- 700
- 701
- 702
- 703
- 704
- 705
- 706
- 707
- 708
- 709
- 710
- 711
- 712
- 713
- 714
- 715
- 716
- 717
- 718
- 719
- 720
- 721
- 722
- 723
- 724
- 725
- 726
- 727
- 728
- 729
- 730
- 731
- 732
- 733
- 734
- 735
- 736
- 737
- 738
- 739
- 740
- 741
- 742
- 743
- 744
- 745
- 746
- 747
- 748
- 749
- 750
- 751
- 752
- 753
- 754
- 755
- 756
- 757
- 758
- 759
- 760
- 761
- 762
- 763
- 764
- 765
- 766
- 767
- 768
- 769
- 770
- 771
- 772
- 773
- 774
- 775
- 776
- 777
- 778
- 779
- 780
- 781
- 782
- 783
- 784
- 785
- 786
- 787
- 788
- 789
- 790
- 791
- 792
- 793
- 794
- 795
- 796
- 797
- 798
- 799
- 800
- 801
- 802
- 803
- 804
- 805
- 806
- 807
- 808
- 809
- 810
- 811
- 812
- 813
- 814
- 815
- 816
- 817
- 818
- 819
- 820
- 821
- 822
- 823
- 824
- 825
- 826
- 827
- 828
- 829
- 830
- 831
- 832
- 833
- 834
- 835
- 836
- 837
- 838
- 839
- 840
- 841
- 842
- 843
- 844
- 845
- 846
- 847
- 848
- 849
- 850
- 851
- 852
- 853
- 854
- 855
- 856
- 857
- 858
- 859
- 860
- 861
- 862
- 863
- 864
- 865
- 866
- 867
- 868
- 869
- 870
- 871
- 872
- 873
- 874
- 875
- 876
- 877
- 878
- 879
- 880
- 881
- 882
- 883
- 884
- 885
- 886
- 887
- 888
- 889
- 890
- 891
- 892
- 893
- 894
- 895
- 896
- 897
- 898
- 899
- 900
- 901
- 902
- 903
- 904
- 905
- 906
- 907
- 908
- 909
- 910
- 911
- 912
- 913
- 914
- 915
- 916
- 917
- 918
- 919
- 920
- 921
- 922
- 923
- 924
- 925
- 926
- 927
- 928
- 929
- 930
- 931
- 932
- 933
- 934
- 935
- 936
- 937
- 938
Проверь себя
- 1
- 2
- 3
- 4
- 5
- 6
Ответы на вопросы к параграфу
- 1
- 2
- 3
- 4
- 5
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 18
- 19
- 20
- 21
- 22
Когда сделаны уроки — страница 126
- 1
- 2
Когда сделаны уроки — страница 194
- 1
- 2
- 3
- 4
- 5
- 6
- 7
Описание
ГДЗ по алгебре для 8 класса соответствует учебнику авторского коллектива А. Г. Мерзляк, В.Б. Полонский, М.С. Якир.
Г. Мерзляк, В.Б. Полонский, М.С. Якир.
Упражнения следуют по порядку, друг за другом, единым блоком. Их 938. Отсканированные страницы школьной тетради, заполненные вручную, представлены в хорошем качестве. Почерк чёткий, разборчивый, необходимые краткие записи с пояснениями имеются.
Решения соответствуют темам и разделам: «Квадратные уравнения», «Рациональные дроби», «Числовые множества», «Равносильные уравнения» и др. Материал учебника разбит на три главы, каждая из которых завершается рубрикой «Учимся делать нестандартные шаги». Предусмотрена уровневая дифференциация. Решебник предполагает работу на базовом уровне.
Комментарии
Ваше сообщение отправлено!
+
Продвинутая математика в восьмом классе
Еще в 1990 году изучение алгебры в восьмом классе было уникальным. В последние годы ситуация резко изменилась, и сейчас больше восьмиклассников изучают алгебру, чем любой другой математический предмет. Зачисление в восьмой класс по алгебре и другим продвинутым математическим дисциплинам зависит от штата. В этом разделе отчета Центра Брауна этот вариант используется для изучения взаимосвязи между числом зачисленных в штаты на курсы высшей математики и баллами по NAEP. Исследовательский вопрос заключается в том, существует ли связь между изменениями в количестве зачисленных по продвинутой математике и изменениями в баллах NAEP в 8-м классе. Наблюдается ли одновременный рост успеваемости в штатах, повышающих число зачисленных на более высокий уровень? Второй анализ использует тот же метод, чтобы посмотреть на потенциал «разбавления» продвинутых курсов. Связан ли рост числа учащихся с более низкой средней успеваемостью в продвинутых классах?
В этом разделе отчета Центра Брауна этот вариант используется для изучения взаимосвязи между числом зачисленных в штаты на курсы высшей математики и баллами по NAEP. Исследовательский вопрос заключается в том, существует ли связь между изменениями в количестве зачисленных по продвинутой математике и изменениями в баллах NAEP в 8-м классе. Наблюдается ли одновременный рост успеваемости в штатах, повышающих число зачисленных на более высокий уровень? Второй анализ использует тот же метод, чтобы посмотреть на потенциал «разбавления» продвинутых курсов. Связан ли рост числа учащихся с более низкой средней успеваемостью в продвинутых классах?
История вопроса
В 1982 году Роберт Мозес получил стипендию Макартура. Он использовал деньги, чтобы начать проект «Алгебра», общественную попытку донести алгебру до исторически малообеспеченных учащихся средних школ, в первую очередь детей из семей с низким доходом и цветных учащихся. Мозес назвал алгебру «новым гражданским правом», взыванием к справедливости, которое проливает новый свет на курс. 32 Администрация Клинтона связала тему справедливости с международной конкурентоспособностью и настаивала на том, чтобы больше учащихся изучали алгебру до окончания средней школы. «Во всем мире учащиеся средних классов изучают алгебру и геометрию, — заметил президент Клинтон. «Здесь дома только четверть всех учеников сдают алгебру до школы». 33
Он использовал деньги, чтобы начать проект «Алгебра», общественную попытку донести алгебру до исторически малообеспеченных учащихся средних школ, в первую очередь детей из семей с низким доходом и цветных учащихся. Мозес назвал алгебру «новым гражданским правом», взыванием к справедливости, которое проливает новый свет на курс. 32 Администрация Клинтона связала тему справедливости с международной конкурентоспособностью и настаивала на том, чтобы больше учащихся изучали алгебру до окончания средней школы. «Во всем мире учащиеся средних классов изучают алгебру и геометрию, — заметил президент Клинтон. «Здесь дома только четверть всех учеников сдают алгебру до школы». 33
Алгебра вскоре стала известна как курс «привратник», курс, стоящий как часовой у ворот колледжа. Возьмите его и сдайте, и ваши шансы поступить в колледж будут хорошими. Возьмите его и провалите его, и, по крайней мере, вы столкнулись со сложной математикой. Не принимайте это вообще, и ваши шансы поступить в колледж были близки к нулю. Место алгебры в типичной школьной математической последовательности повысило ее важность. Предположим, что учащиеся, поступающие в колледж, должны получить некоторые математические знания на последнем курсе. В большинстве средних школ у учащегося, изучающего алгебру I в девятом классе, есть три оставшихся года для изучения алгебры II, геометрии, предварительной математики/тригонометрии, а затем исчисления. Это четыре курса. Что-то должно дать. Многие школы меняют порядок курсов, а некоторые смешивают статистику с одним из предложений года, но факт остается фактом: если целью является изучение математического анализа в старших классах средней школы, то изучение алгебры I в девятом классе означает наличие четырех курсов. завершить за три года. Изучение алгебры в восьмом классе открывает дополнительный год для углубленной математики.
Место алгебры в типичной школьной математической последовательности повысило ее важность. Предположим, что учащиеся, поступающие в колледж, должны получить некоторые математические знания на последнем курсе. В большинстве средних школ у учащегося, изучающего алгебру I в девятом классе, есть три оставшихся года для изучения алгебры II, геометрии, предварительной математики/тригонометрии, а затем исчисления. Это четыре курса. Что-то должно дать. Многие школы меняют порядок курсов, а некоторые смешивают статистику с одним из предложений года, но факт остается фактом: если целью является изучение математического анализа в старших классах средней школы, то изучение алгебры I в девятом классе означает наличие четырех курсов. завершить за три года. Изучение алгебры в восьмом классе открывает дополнительный год для углубленной математики.
Справедливость, международная конкурентоспособность и практическая озабоченность по поводу последовательности курсов объединились в середине 2000-х годов, чтобы активизировать кампанию по алгебре для восьмого класса. Возникло движение «алгебра для всех», которое продвигало универсальную обязательную алгебру в восьмом классе. Миннесота ввела новое требование об окончании средней школы, согласно которому, начиная с класса 2015 года, все учащиеся должны получить кредит по алгебре I к концу восьмого класса. Калифорния использовала свою формулу подотчетности школ для продвижения алгебры в восьмом классе, предлагая на выбор две оценки по математике в восьмом классе (алгебра и общая математика в восьмом классе), но затем, в формуле для расчета индекса академической успеваемости (API), сбрасывая со счетов успеваемость уровень учащихся, сдающих тест по общей математике (например, понижение до «базового» уровня тех учащихся, которые прошли тест и получили «уровень знаний»). Этот стимул побудил школы резко увеличить набор учащихся по алгебре в восьмом классе, и хотя позже суды отменили правило AYP, Калифорния считается лучшим штатом в стране по набору учащихся в восьмой класс по алгебре и высшей математике. 34
Возникло движение «алгебра для всех», которое продвигало универсальную обязательную алгебру в восьмом классе. Миннесота ввела новое требование об окончании средней школы, согласно которому, начиная с класса 2015 года, все учащиеся должны получить кредит по алгебре I к концу восьмого класса. Калифорния использовала свою формулу подотчетности школ для продвижения алгебры в восьмом классе, предлагая на выбор две оценки по математике в восьмом классе (алгебра и общая математика в восьмом классе), но затем, в формуле для расчета индекса академической успеваемости (API), сбрасывая со счетов успеваемость уровень учащихся, сдающих тест по общей математике (например, понижение до «базового» уровня тех учащихся, которые прошли тест и получили «уровень знаний»). Этот стимул побудил школы резко увеличить набор учащихся по алгебре в восьмом классе, и хотя позже суды отменили правило AYP, Калифорния считается лучшим штатом в стране по набору учащихся в восьмой класс по алгебре и высшей математике. 34
Данные NAEP о зачислении на курсы высшей математики
Данные взяты из теста по математике NAEP для восьмого класса. Студентов спрашивают: «Какой урок математики вы посещаете в этом году?» Категория «продвинутая математика» объединяет несколько ответов, в том числе «Алгебра I», курсы, которые растягивают содержание «Алгебры I» на два года (будь то первый или второй год такого курса), и курсы, которые обычно более продвинуты, чем «Алгебра I», включая «Алгебру». II и геометрия. Этот объединенный ответ является зашумленным и более подробно обсуждается ниже.
Студентов спрашивают: «Какой урок математики вы посещаете в этом году?» Категория «продвинутая математика» объединяет несколько ответов, в том числе «Алгебра I», курсы, которые растягивают содержание «Алгебры I» на два года (будь то первый или второй год такого курса), и курсы, которые обычно более продвинуты, чем «Алгебра I», включая «Алгебру». II и геометрия. Этот объединенный ответ является зашумленным и более подробно обсуждается ниже.
Связанные книги
В 1990 г. только 16 % посещали курс алгебры, по сравнению с 20 % в подготовительной алгебре и 61 % в 8-м классе математики. В этой статье последние два курса называются «базовыми».
К 2011 году почти половина (47%) всех восьмиклассников изучала алгебру или более сложные курсы. Только 48% посещали базовый курс математики, по сравнению с 81% в 1990 году. Процент продвинутой математики может быть занижен в таблице 3-1 за годы до 2000 года, поскольку это были первые уроки геометрии, продвинутой алгебры и алгебры. были категориями ответов в анкете NAEP для восьмиклассников. 35 Более того, некоторые ученики — и тогда, и сейчас — могут ошибочно полагать, что они учатся на уроках алгебры или геометрии, хотя на самом деле это не так. Несмотря на эти ограничения данных, число учащихся, обучающихся по математике с углубленным изучением математики, значительно выросло с 1990 по 2011 год. Это хорошая идея?
были категориями ответов в анкете NAEP для восьмиклассников. 35 Более того, некоторые ученики — и тогда, и сейчас — могут ошибочно полагать, что они учатся на уроках алгебры или геометрии, хотя на самом деле это не так. Несмотря на эти ограничения данных, число учащихся, обучающихся по математике с углубленным изучением математики, значительно выросло с 1990 по 2011 год. Это хорошая идея?
Исследование эффективности алгебры в восьмом классе
Национальное лонгитюдное исследование образования 1988 (NELS) предлагает исследователям кладезь информации, собранной из рандомизированной выборки студентов. В нескольких исследованиях использовались данные NELS для изучения того, что происходит, когда учащиеся изучают высшую математику в начале академической карьеры, будь то в восьмом или девятом классе. 37 Исследователи обнаружили преимущества для учащихся, изучающих алгебру раньше, чем позже, включая — и это важно для достижения справедливости — учащихся с низкой успеваемостью. Недавний метаанализ исследований по этой теме (проведенный Мэри К. Стейн и ее коллегами) подтвердил этот позитивный вывод, с оговоркой, что «прирост успеваемости происходил в условиях, когда политика сопровождалась сильной поддержкой отстающих учащихся, особенно больше времени для изучения алгебры». инструкция. У нас нет убедительных доказательств того, что универсальная алгебраическая политика приводит к повышению успеваемости за вычетом этой сильной поддержки». 38
Недавний метаанализ исследований по этой теме (проведенный Мэри К. Стейн и ее коллегами) подтвердил этот позитивный вывод, с оговоркой, что «прирост успеваемости происходил в условиях, когда политика сопровождалась сильной поддержкой отстающих учащихся, особенно больше времени для изучения алгебры». инструкция. У нас нет убедительных доказательств того, что универсальная алгебраическая политика приводит к повышению успеваемости за вычетом этой сильной поддержки». 38
Более поздние оценки политик, расширяющих охват алгеброй, вызывают предостережения. Чикаго обязал всех девятиклассников пройти то, что считалось подготовительными к колледжу, включая алгебру. Оценщики следили за учащимися в течение нескольких лет и пришли к выводу: «Хотя больше учащихся закончили девятый класс с зачетными баллами по алгебре и английскому языку I, процент неуспеваемости увеличился, оценки немного снизились, результаты тестов не улучшились, и у учеников больше не было шансов поступить в колледж». 39 Исследования калифорнийской политики в области алгебры выявили компромисс: рост количества учащихся, но также и рост числа неудачников. В Северной Каролине исследователи из Дьюка обнаружили отрицательные результаты после изучения инициативы Шарлотты-Мекленбург по расширению алгебры в восьмом классе: более низкие баллы по алгебре I, а затем более низкие показатели по геометрии и алгебре II в последующие годы.
39 Исследования калифорнийской политики в области алгебры выявили компромисс: рост количества учащихся, но также и рост числа неудачников. В Северной Каролине исследователи из Дьюка обнаружили отрицательные результаты после изучения инициативы Шарлотты-Мекленбург по расширению алгебры в восьмом классе: более низкие баллы по алгебре I, а затем более низкие показатели по геометрии и алгебре II в последующие годы.
Почему более поздние исследования дали более мрачные результаты, чем предполагалось в более ранней работе? Исследователи из Университета Дьюка считают, что систематическая ошибка отбора исказила предыдущие выводы. Более сильные учащиеся-математики изучают алгебру в восьмом классе, и хотя они действительно могут получить пользу от курса в учебе, это не означает, что более слабые учащиеся также получат пользу от изучения алгебры раньше. «Как только эта предвзятость выбора устранена, оставшийся причинный эффект ускорения обычного первого курса алгебры до более ранних классов, при отсутствии других изменений в учебной программе по математике, определенно вреден для большинства учащихся». 40
40
The Stein et al. мета-анализ и политические рекомендации команды Дьюка, хотя и различаются по акценту, имеют небольшой участок точки соприкосновения. Штейн и др. говорят, что без «сильной поддержки» нельзя ожидать достижений. И исследователи Дьюка предвидят вредные последствия «в отсутствие других изменений в учебной программе по математике». Один условно положительный, другой условно отрицательный. Общая основа, которую они разделяют, заключается в прогнозировании потенциала нейтрального эффекта.
Давайте вернемся к NAEP и посмотрим, что его данные говорят об усилиях государства по поощрению зачисления на углубленные математические курсы в восьмом классе.
Аналитический метод
Связано ли зачисление в восьмой класс по углубленной математике с оценками штата по математике в NAEP? Чтобы ответить на этот вопрос, очевидным первым шагом будет просто изучить список штатов, их баллы по NAEP и процентную долю учащихся каждого штата, изучающих алгебру, геометрию и другие углубленные математические курсы в восьмом классе. Нет четкой взаимосвязи. В 2011 г. корреляция между числом зачисленных в высшие учебные заведения по математике в штатах и достижениями в программе NAEP составляет 0,07, что неотличимо от 0,00. В штатах, где больше восьмиклассников посещают уроки математики с углубленным изучением математики, вероятность того, что они зарегистрируют более высокий балл NAEP по математике, не выше, чем в штатах с более низким уровнем зачисления в эти классы.
Нет четкой взаимосвязи. В 2011 г. корреляция между числом зачисленных в высшие учебные заведения по математике в штатах и достижениями в программе NAEP составляет 0,07, что неотличимо от 0,00. В штатах, где больше восьмиклассников посещают уроки математики с углубленным изучением математики, вероятность того, что они зарегистрируют более высокий балл NAEP по математике, не выше, чем в штатах с более низким уровнем зачисления в эти классы.
Этот вид поперечного анализа является разумным началом, но он ограничен выявлением корреляций между переменными в один момент времени. Это может ввести в заблуждение. Например, исследование, опубликованное в отчете Центра Брауна за 2007 год, показало, что количество учебных минут, которые страны посвящают обучению математике, не связано, на перекрестной основе, с национальными достижениями в области математики. В 1995 г. корреляция составляла 0,05. В 2003 г. корреляция составила -0,20. Ни один из показателей существенно не отличается от 0,00. Но когда страны исследуются лонгитюдно, а данные из двух поперечных срезов моделируются как переменные изменения, вопрос, находящийся под пристальным вниманием, смещается в сторону того, изменяются ли национальные учебные минуты с 19с 95 по 2003 год связаны с изменениями результатов тестов за тот же период времени. Корреляция для этой связи составляет 0,42, что является статистически значимым. В странах, которые увеличили количество времени, отводимого на обучение математике, как правило, наблюдался рост математических баллов TIMSS; те страны, которые сократили время, отводимое на обучение математике, имели тенденцию к снижению своих результатов.
Но когда страны исследуются лонгитюдно, а данные из двух поперечных срезов моделируются как переменные изменения, вопрос, находящийся под пристальным вниманием, смещается в сторону того, изменяются ли национальные учебные минуты с 19с 95 по 2003 год связаны с изменениями результатов тестов за тот же период времени. Корреляция для этой связи составляет 0,42, что является статистически значимым. В странах, которые увеличили количество времени, отводимого на обучение математике, как правило, наблюдался рост математических баллов TIMSS; те страны, которые сократили время, отводимое на обучение математике, имели тенденцию к снижению своих результатов.
Почему полезен анализ переменных изменений? Две причины. Во-первых, этот метод помогает контролировать систематическую ошибку, вызванную пропущенными переменными (включая выборку), недостатком, мешающим перекрестному анализу достижений. В случае с учебными минутами, например, школьная система может принять стратегическое решение о размещении учащихся с низкими достижениями в более длительных классах, чтобы помочь им наверстать упущенное. Это могло бы создать впечатление, что большее количество инструкций связано с более низкими достижениями. Предполагая, что систематическая ошибка пропущенной переменной присутствует как в начальной, так и в конечной точках исследуемого временного интервала, а связь с зависимой переменной (исследуемый результат) остается неизменной на протяжении всего интервала, такая систематическая ошибка исчезает при расчете изменения ( см. Gustaffson, 2007, для дальнейшего объяснения и приложений к другим образовательным вопросам). 41
Это могло бы создать впечатление, что большее количество инструкций связано с более низкими достижениями. Предполагая, что систематическая ошибка пропущенной переменной присутствует как в начальной, так и в конечной точках исследуемого временного интервала, а связь с зависимой переменной (исследуемый результат) остается неизменной на протяжении всего интервала, такая систематическая ошибка исчезает при расчете изменения ( см. Gustaffson, 2007, для дальнейшего объяснения и приложений к другим образовательным вопросам). 41
Второе преимущество этого подхода заключается в том, что он ставит вопрос, имеющий первостепенное значение для анализа политики. Рассмотрение вопроса о том, следует ли принять политику X, приводит к вопросу: если мы примем политику X, каково ожидаемое изменение результата Y? Что случится? Общий вопрос заключается в следующем: какова связь между политикой X и результатом Y в определенный момент времени? Часто можно услышать об анализе поперечных сечений, показывающем что-то вроде «изменение X на одно стандартное отклонение приведет к следующему изменению Y», но прогноз делается только на основе вывода, а наблюдений за изменениями (или данных из различные периоды времени) в наборе данных.
Анализ изменений с использованием баллов NAEP
Взаимосвязь между изменением политики и изменением результатов является предметом приведенного ниже анализа. Рассматриваемый период времени — с 2005 по 2011 год. Имейте в виду, что, несмотря на улучшение по сравнению с перекрестным анализом, анализ по-прежнему является только корреляционным и, таким образом, ограничивается созданием правдоподобных гипотез для более строгих планов исследования. Здесь не утверждается причинно-следственная связь.
Таблица 3-2 показывает окончание долгосрочной тенденции, представленной в Таблице 3-1, — увеличение числа учащихся в математических классах с углубленным изучением и снижение в базовых классах. За медленной, устойчивой национальной тенденцией скрываются значительные различия между штатами. В 2005–2011 годах средний прирост числа учащихся по математике с углубленным изучением математики (в процентном отношении к восьмиклассникам) по штату составил 5,5% при стандартном отклонении 8,4%. В первые четыре штата, в которых увеличилось количество зачисленных в старшие классы, вошли Миннесота (35%), а также Пенсильвания, Вирджиния и Вашингтон (все с 17%). Напротив, два штата выделяются тем, что идут вразрез с общенациональной тенденцией сокращения количества учащихся, обучающихся по высшей математике: Невада (-22%) и Джорджия (-17%).
В первые четыре штата, в которых увеличилось количество зачисленных в старшие классы, вошли Миннесота (35%), а также Пенсильвания, Вирджиния и Вашингтон (все с 17%). Напротив, два штата выделяются тем, что идут вразрез с общенациональной тенденцией сокращения количества учащихся, обучающихся по высшей математике: Невада (-22%) и Джорджия (-17%).
Что касается конкретных курсов, то в 45 штатах число учащихся по алгебре I увеличилось, в то время как только в трех штатах число учащихся сократилось, а в трех осталось на прежнем уровне (в этом обсуждении оценок NAEP округ Колумбия считается штатом). Двадцать восемь штатов сократили набор по общей математике, двадцать увеличили, а три остались прежними. В общем, зачисленные на курс ведут себя как тюбик зубной пасты — один конец сжимается, а другой выпячивается. В штатах с растущим числом учащихся, обучающихся по продвинутой математике, число учащихся на базовых курсах сократилось. Наоборот. Два штата, в которых наблюдается снижение числа учащихся на курсах продвинутой математики, иллюстрируют эту мысль. Количество учащихся по базовой математике выросло. В Неваде число учащихся, изучающих алгебру, подскочило на 27%. Доля учащихся в общей математике в Грузии выросла на 33%.
Количество учащихся по базовой математике выросло. В Неваде число учащихся, изучающих алгебру, подскочило на 27%. Доля учащихся в общей математике в Грузии выросла на 33%.
Есть ли связь между изменениями количества зачисленных на курсы в штатах и изменениями баллов NAEP? Наблюдались ли в штатах успехи в NAEP одновременно с увеличением числа восьмиклассников, изучающих высшую математику? Для исследования этих вопросов был рассчитан ряд коэффициентов корреляции (см. Таблицу 3-3). Первая модель исследует взаимосвязь числа зачисленных по продвинутой математике и сводных баллов NAEP. Коэффициент корреляции (r = -0,01) статистически неотличим от 0,00.
Совокупный балл NAEP может слишком широко оценивать математику, чтобы уловить влияние акцента на продвинутой математике, которая в первую очередь включает повышение уровня алгебры. К счастью, NAEP сообщает о баллах по конкретным областям содержания, оцениваемым в рамках теста (называемым «нитями»), включая алгебру и геометрию. Таким образом, вторая модель использует подсчет NAEP для раздела алгебры в качестве переменной успеваемости, которая должна быть более чувствительной к расширению знаний по алгебре. Опять же, никакой существенной связи не обнаружено.
Таким образом, вторая модель использует подсчет NAEP для раздела алгебры в качестве переменной успеваемости, которая должна быть более чувствительной к расширению знаний по алгебре. Опять же, никакой существенной связи не обнаружено.
В третьей и четвертой моделях в качестве переменной курса используется изменение числа зачисленных по алгебре I вместо продвинутой математики на тот случай, если объединение нескольких курсов в категорию «продвинутый» запутало ситуацию. Изменение общего балла NAEP служит в качестве переменной достижения в третьей модели, а изменение балла по алгебраической нити — в качестве переменной достижения в четвертой модели. Ни одна из корреляций не достигает статистической значимости.
Модели пять и шесть повторяют одинаковую обработку геометрии. Изменение курса геометрии в восьмом классе используется в качестве переменной курса, и модели рассчитывают, коррелирует ли оно с изменением сводного показателя NAEP в пятой модели и изменением балла по геометрии в шестой модели. Ни одна из корреляций не является статистически значимой.
Ни одна из корреляций не является статистически значимой.
В дополнение к описанным здесь корреляциям были проведены многомерные регрессии с тремя контролируемыми ковариантами (также переменными, представляющими изменения) — изменением уровня детской бедности в штатах, изучающих английский язык и чернокожих и латиноамериканских учащихся — демографическими характеристиками, которые являются известными коррелятами государственные баллы NAEP. Великая рецессия развернулась в течение изучаемого периода времени, и в некоторых штатах, например, уровень детской бедности рос больше, чем в других штатах. Если в штатах произошли демографические изменения, это могло исказить результаты. Оказалось, что это не так. Ни одна из регрессионных моделей не была статистически значимой.
Таким образом, в баллах NAEP не было обнаружено никаких доказательств взаимосвязи между штатами, повышающими зачисление на продвинутые курсы математики, и повышением успеваемости. Штаты, которые увеличили процент учащихся, изучающих алгебру или геометрию в восьмом классе, имели не больше шансов заявить о приросте NAEP, чем штаты с меньшим количеством зачисленных на эти два курса.
Снижает ли количество учащихся курсы продвинутой математики?
Важный вопрос, будут ли продвинутые математические курсы разбавлены из-за увеличения числа учащихся. Идея состоит в том, что заполнение продвинутых классов академически более слабыми учениками, чем в прошлом, может уменьшить объем обучения, который могут дать курсы. Это может помочь объяснить нейтральные корреляции, о которых сообщалось выше. Это также могло бы помочь объяснить нейтральные или даже негативные эффекты, выявленные недавними оценками политики, продвигающей всеобщую алгебру в восьмом и девятом классах. Данные NAEP могут лишь показать, имеет ли место размывание, но они предлагают интересные идеи о том, как могут быть связаны изменение курса и достижения.
В таблице 3-4 представлены корреляции между изменением количества учащихся и изменением средней успеваемости учащихся, изучающих каждый курс. Отображаются данные четырех курсов. Опять же, процент восьмиклассников штата, изучающих каждый курс, служит переменной зачисления. Курсы расположены иерархически. Геометрия обычно предлагается для самых продвинутых учеников, а общая математика — для самых слабых. Три корреляции являются статистически значимыми.
Курсы расположены иерархически. Геометрия обычно предлагается для самых продвинутых учеников, а общая математика — для самых слабых. Три корреляции являются статистически значимыми.
Есть ли признаки разбавления? Да, но не на всех курсах повышения квалификации. Начнем с результатов, подтверждающих гипотезу размывания. Увеличение числа учащихся по алгебре I отрицательно связано с ростом успеваемости (r = -0,34, p < 0,05). Давайте проясним, что это значит. В среднем штате было зарегистрировано увеличение баллов по шкале NAEP на 5,6 среди учащихся по алгебре I. Показатели NAEP для учащихся классов алгебры I выросли не так сильно в штатах, в которых увеличилось количество учащихся по алгебре I (+5,2), как в штатах, где количество учащихся либо осталось постоянным, либо уменьшилось (+9)..2). Для Pre-Algebra рост числа учащихся также отрицательно связан с результатами тестов (r = -0,34, p < 0,05). Обе корреляции согласуются с гипотезой ослабления, если студенты, которые в противном случае были бы помещены на более низкие курсы, переходят на более высокие курсы. Мы не можем сказать, происходит ли это, используя данные NAEP. И, чтобы еще раз сделать важное предупреждение, корреляции не доказывают причинно-следственную связь.
Мы не можем сказать, происходит ли это, используя данные NAEP. И, чтобы еще раз сделать важное предупреждение, корреляции не доказывают причинно-следственную связь.
Самая сильная корреляция связана с общей математикой (r = 0,47, p < 0,01). Положительная связь также согласуется с гипотезой ослабления. Если общая тенденция состоит в том, чтобы переводить учащихся на курсы более высокого уровня — а школы избирательны в отношении учеников, которых они ускоряют, — курсы общей математики, по мере их сокращения, должны все в большей степени доминировать среди учащихся, которые испытывают наибольшие затруднения в математике. Эти курсы, по-видимому, потеряли бы своих лучших студентов. Таким образом, падение числа учащихся будет связано с падением показателей. Занятия по общей математике, которым удается удержать учащихся, которые проходят ускоренное обучение в другом месте, в сравнении с этим получат более высокие баллы.
Геометрия усложняет дело. Его коэффициент корреляции (0,27) не согласуется с разбавленной историей. Геометрия находится на вершине иерархии курсов. Любое неизбирательное ускорение студентов вверх (неотъемлемое предположение аргумента о размывании) должно в конечном итоге привести к отрицательной связи прироста зачисления и оценок успеваемости по курсу на вершине. И все же коэффициент корреляции Geometry имеет положительный знак и приближается к статистической значимости. Хотя статистически это неотличимо от 0,00 (p = 0,11), это может быть частично связано с меньшим количеством штатов с данными. Только в тридцати шести штатах есть достаточное количество учащихся восьмого класса по геометрии, чтобы получить балл NAEP.
Геометрия находится на вершине иерархии курсов. Любое неизбирательное ускорение студентов вверх (неотъемлемое предположение аргумента о размывании) должно в конечном итоге привести к отрицательной связи прироста зачисления и оценок успеваемости по курсу на вершине. И все же коэффициент корреляции Geometry имеет положительный знак и приближается к статистической значимости. Хотя статистически это неотличимо от 0,00 (p = 0,11), это может быть частично связано с меньшим количеством штатов с данными. Только в тридцати шести штатах есть достаточное количество учащихся восьмого класса по геометрии, чтобы получить балл NAEP.
Другая возможность связана с зашумленными переменными курса NAEP. Возможно, в 2011 г. в категорию курсов NAEP по геометрии было включено больше «настоящих» студентов-геометриков, чем в 2005 г., другими словами, большая доля тех, кто действительно посещает уроки геометрии и не ошибается в своем курсе математики. Как показано в Таблице 3-2 выше, только 5% восьмиклассников были зачислены на геометрию в 2011 г. , по сравнению с 4% в 2005 г. Средний балл NAEP для учащихся-геометриков составил 290 в 2005 г. 18 баллов. Прирост студентов на один процентный пункт, похоже, стал ударом с точки зрения результатов NAEP. «Настоящие» учащиеся геометрии, вероятно, изучали алгебру I в седьмом классе. Как и алгебра для восьмиклассников три или четыре десятилетия назад, геометрия предназначена для самых лучших студентов-математиков сегодня.
, по сравнению с 4% в 2005 г. Средний балл NAEP для учащихся-геометриков составил 290 в 2005 г. 18 баллов. Прирост студентов на один процентный пункт, похоже, стал ударом с точки зрения результатов NAEP. «Настоящие» учащиеся геометрии, вероятно, изучали алгебру I в седьмом классе. Как и алгебра для восьмиклассников три или четыре десятилетия назад, геометрия предназначена для самых лучших студентов-математиков сегодня.
Обсуждение
В этом исследовании были проанализированы различия в структуре зачисления в штате, чтобы проверить, коррелирует ли рост числа зачислений на математические курсы в восьмом классе с повышением успеваемости по NAEP. Доказательств того, что они есть, не обнаружено. Штаты с растущим процентом восьмиклассников, изучающих алгебру I, геометрию и другие математические предметы продвинутого уровня, не более склонны повышать свои баллы NAEP в период с 2005 по 2011 год, чем штаты со снижающимся процентом восьмиклассников на этих курсах.
Второй анализ, в котором снова рассматривались изменения в политике и результатах тестов с течением времени, исследовал, связано ли увеличение процента студентов на курсах более высокого уровня со снижением средних баллов по этим курсам, что предполагает эффект ослабления. Доказательства согласуются с разбавлением во всех курсах, кроме одного. Отрицательные корреляции были обнаружены для алгебры I и предварительной алгебры. На этих курсах средний прирост успеваемости снижался по мере увеличения количества зачисленных. Рост успеваемости по общим математическим курсам был положительно связан с изменениями в наборе учащихся. Все три из этих корреляций являются статистически значимыми и поддерживают гипотезу ослабления.
Геометрия отличается от других курсов. Была обнаружена положительная связь, которая, хотя статистически неотличима от 0,00, предполагает, по крайней мере, нейтральную связь между ростом числа учащихся и изменениями показателей NAEP. Если бы школы без разбора переводили учеников в восьмой класс по геометрии, можно было бы ожидать отрицательной корреляции.
Ни один из этих выводов не может подтвердить или опровергнуть причинно-следственную связь, но они полезны для выработки гипотез для будущих исследований. Они также проливают свет на результаты предыдущих исследований. Например, ключевой вывод из оценок политики Калифорнии в отношении алгебры заключается в том, что универсальная алгебра приводит к компромиссам. Многим учащимся выгодна дополнительная задача. Показатели охвата алгеброй для исторически недостаточно зачисленных групп населения (в частности, учащихся с низким уровнем SES) увеличились. Также увеличилось количество студентов, успешно сдавших выпускные экзамены. Но недостатком является то, что число студентов, не сдавших алгебру, также растет; и неуспевающие учащиеся тоже имеют непропорционально низкий уровень SES. 42 Одно исследование, проведенное в Калифорнии, предполагает, что многим неуспевающим ученикам было бы лучше потратить дополнительный год на подготовку к алгебре, чем сдавать ее. 43 Такого рода компромиссы, если их агрегировать на уровне штатов, могут дать нейтральный чистый эффект.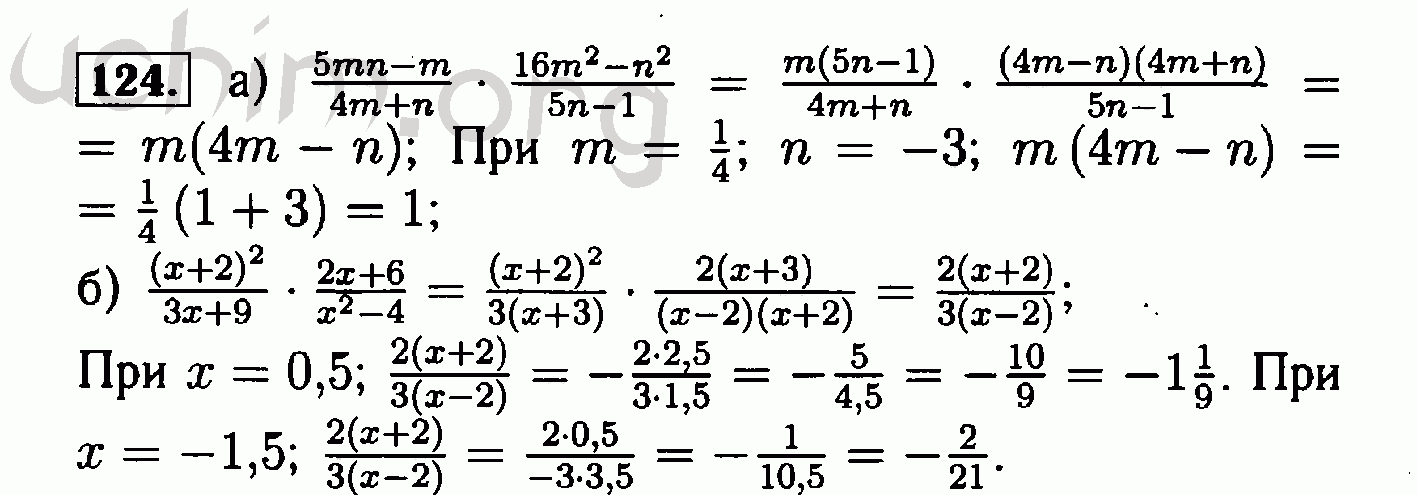
Анализ того, снижает ли перевод учащихся в продвинутые классы успеваемость, указывает на два разных типа ускорения. Один выборочный и решается на индивидуальной основе. Оцениваются математические навыки каждого учащегося и принимается решение о том, подходит ли более продвинутый курс математики или нет. Похоже, такое ускорение происходит в восьмом классе геометрии и, предположительно, в седьмом классе алгебры. Студенты, которым был бы полезен более строгий курс, продвигаются по службе. Средние результаты тестов по геометрии в восьмом классе растут или, по крайней мере, остаются прежними, несмотря на рост числа учащихся.
Второй тип ускорения неселективный и групповой. Учащиеся продвигаются вперед на основе характеристик, не зависящих от предыдущих достижений или подготовленности (например, уровня обучения или возраста). Будущие исследования должны сравнить эти два типа ускорения и выяснить, кто, когда речь идет об избирательном ускорении, должен быть ускорен и когда. При ускорении на основе возраста или класса необходим набор ранних индикаторов (универсальный алгебраический подход), которые определяли бы учащихся, нуждающихся в поддержке, и тип поддержки, наиболее полезный для них. Если компромиссы группового ускорения действительно реальны, то цель политики должна состоять в том, чтобы свести к минимуму негативные последствия и максимизировать выгоды.
Если компромиссы группового ускорения действительно реальны, то цель политики должна состоять в том, чтобы свести к минимуму негативные последствия и максимизировать выгоды.
Последнее замечание по Common Core. Никто не знает, как будут удовлетворены потребности одаренных студентов в эпоху Common Core. Изучение алгебры в восьмом классе — это новая норма, а изучение алгебры в седьмом классе быстро становится новой нормой для одаренных учащихся-математиков. В Калифорнии 8,1% семиклассников (почти 38 000 учащихся) сдавали экзамен по алгебре в конце курса в 2012 году. Если Common Core означает одинаковую учебную программу для всех, обязательно придет время, когда выдающимся математикам понадобится необычная учебная программа, подходящая для их.
| « Часть II: Возрождение способности и постоянство отслеживания |
Примечания к части III
32. Справочная информация о проекте «Алгебра» доступна на сайте www.алгебра.org.
Справочная информация о проекте «Алгебра» доступна на сайте www.алгебра.org.
33. Замечания президента Клинтона, Круглый стол по вопросам образования, Средняя школа Спрингбрука, Силвер-Спринг, Мэриленд, 16 марта 1998 г. Доступно на http://www.gpo.gov/fdsys/pkg/WCPD-1998-03-23/ pdf/WCPD-1998-03-23.pdf.
34. Историю политики Калифорнии в отношении алгебры можно найти в: Политика в области алгебры в Калифорнии: большие надежды и серьезные проблемы (Окленд: EdSource, май 2009 г.). См. также Том Лавлесс, Потерянный студент-математик: заблудился в алгебре для восьмого класса (Вашингтон, округ Колумбия: Институт Брукингса, 2008).
35. По категории «другое» до 2000 г. доля ответивших составляла около 3%, поэтому число учащихся, посещающих более сложные курсы, вероятно, было очень небольшим.
36. Джилл Уолстон и Джилл Карливати Маккэрролл, Алгебра для восьмого класса: результаты лонгитюдного исследования в раннем детстве для восьмого класса, класс детского сада 1998–1999 гг. (ECLS-K) (Вашингтон, округ Колумбия: Национальный центр Статистика образования, октябрь 2010 г.).
(ECLS-K) (Вашингтон, округ Колумбия: Национальный центр Статистика образования, октябрь 2010 г.).
37. См. Дэвид Стивенсон, Кэтрин С. Шиллер и Барбара Шнайдер, «Последовательности возможностей для обучения», Sociology of Education 67 , no. 3 (1994): 184-198; Адам Гаморан и Эйлин С. Ханниган, «Алгебра для всех? Преимущества подготовки к колледжу по математике для учащихся с разными способностями в младших классах средней школы», Оценка образования и анализ политики 22, вып. 3 (2000): 241-254; Джулия Смит, «Имеет ли значение лишний год? Влияние раннего доступа к алгебре на долгосрочные достижения в области математики», Educational Evaluation and Policy Analysis 18 (1996): 141-153.
38. См. Мэри Стейн, Джулия Кауфман, Милан Шерман и Эми Хиллен, «Алгебра: вызов на перекрестке политики и практики», Review of Educational Research 81, no. 4 (2011): 453-492.
39. Элейн Алленсворт, Такако Номи, Николас Монтгомери и Валери Э. Ли, «Подготовительная программа колледжа для всех: академические последствия требования алгебры и английского языка I для девятиклассников в Чикаго», Educational Evaluation and Policy Analysis 31, нет. 4 (2009): 367-391.
Ли, «Подготовительная программа колледжа для всех: академические последствия требования алгебры и английского языка I для девятиклассников в Чикаго», Educational Evaluation and Policy Analysis 31, нет. 4 (2009): 367-391.
40. Charles T. Clotfelter, Helen F. Ladd, and Jacob L. Vigdor, The Aftermath of Accelerating Algebra Evidence from the District Policy Initiative (Washington, DC: National Center for Analysis of Longitudinal Data in Education Research, American Институты исследований, 2012).
41. Ян-Эрик Густафссон, «Понимание причинно-следственного влияния на образовательные достижения посредством анализа различий во времени в странах», в извлеченных уроках: что международные оценки говорят нам о математических достижениях , изд. Том Лавлесс (Вашингтон: Brookings Institution Press, 2007).
42. Триш Уильямс, Эдвард Хэртел и Майкл В. Кирст, Улучшение успеваемости по математике в средних классах: более пристальный взгляд на политику и практику округа и школы, зачисление на курсы и результаты учащихся в Калифорнии. Последующий анализ (Маунтин-Вью: EdSource, 2011).
Последующий анализ (Маунтин-Вью: EdSource, 2011).
43. Цзянь-Хуа Лян, Пол Хекман и Джамал Абеди, «Что говорят результаты испытаний стандартов Калифорнии о движении к восьмому классу алгебры для всех?» Оценка образования и анализ политики 34, вып. 3 (2012): 328-343.
Математика / Математика 8-го класса
Математика 8-го класса
Средняя школа Скарсдейла имеет три уровня математики в восьмом классе. Различия между уровнями заключаются в продолжительности, интенсивности, темпе и подходе. Каждый ученик помещается в курс на основе его или ее рекомендации учителя седьмого класса. В зависимости от индивидуальных потребностей и успеваемости учащимся может потребоваться изменить уровень как вверх, так и вниз. Ниже приведены описания каждого уровня и типа студента, выбранного для каждого курса.
Математика 8-1 (один раздел):
Большинство учащихся, прошедших курс математики 7-1, будут рекомендованы для прохождения этого курса. Математика 8-1 завершает учебную программу восьмого класса и включает несколько тем девятого класса. Студентам будут предложены интегрированные темы по алгебре и геометрии, и в то же время у них будет возможность закрепить навыки, изученные на предыдущих математических курсах.
Математика 8-1 завершает учебную программу восьмого класса и включает несколько тем девятого класса. Студентам будут предложены интегрированные темы по алгебре и геометрии, и в то же время у них будет возможность закрепить навыки, изученные на предыдущих математических курсах.
Математика 8-1 Учебное пособие
Политика выставления оценок для 8-1:
Оценка на конец года состоит из 90 % баллов за четыре контрольных периода (по 22,5 % за каждый), а остальные 10 % — из итогового экзаменационного балла.
Математика 8-2 (Математика 412) (два раздела) и Математика 8-3 (Математика 413) (один раздел): Основная учебная программа, а также некоторые дополнительные темы. Кульминацией является экзамен Риджентс по алгебре I штата Нью-Йорк в июне. Студенческая класс на конец года станет частью стенограммы учащегося средней школы.
Математика 8-2: Студенты, успешно завершившие курс Математика 7-2, будут рекомендованы для прохождения этого курса. Этот курс для восьмого класса является продолжением курса Math 7-2, но учащиеся заметят повышение точности из-за сложного характера изучаемых тем. Этот курс предназначен для студентов, которые продемонстрировали сильные способности в математике.
Этот курс для восьмого класса является продолжением курса Math 7-2, но учащиеся заметят повышение точности из-за сложного характера изучаемых тем. Этот курс предназначен для студентов, которые продемонстрировали сильные способности в математике.
Математика 8-3: Этот курс предназначен для учащихся, которые продемонстрировали исключительные способности в математике и могут извлечь выгоду из сложной задачи, выходящей за рамки традиционной продвинутой программы. В дополнение к темам, затронутым в курсе Math 8-2, этот класс знакомит учащихся с абстрактными идеями, более высокими уровнями интеграции и применения и продвигается в быстром темпе. Темы представлены более подробно, чтобы бросить вызов даже нашим самым успешным студентам-математикам. Ожидается, что студенты будут анализировать сложные проблемы с небольшим обзором или помощью наставника. Часто некоторая часть экзаменов будет содержать вопросы, с которыми учащиеся ранее не сталкивались в классе или домашнем задании.
Руководство по учебной программе по математике 8-2 и 8-3
Политика выставления оценок по 8-2 и 8-3:
В аттестат учащегося заносится только итоговая оценка на конец года. . Оценка состоит из 90 % баллов за четыре контрольных периода (по 22,5 % каждый), а последние 10 % — из результатов экзамена Риджентс.
. Оценка состоит из 90 % баллов за четыре контрольных периода (по 22,5 % каждый), а последние 10 % — из результатов экзамена Риджентс.
Процесс зачисления:
Учащиеся были зачислены на курс математики восьмого класса по рекомендации учителя седьмого класса. Учащиеся седьмого класса, которые были помещены в математику 8-2, но хотят быть помещены в математику 8-3, могут запросить вступительный тест при условии, что они имеют средний балл A- или выше за год и набрали 9 баллов.0% или выше на выпускном экзамене. Чтобы попасть на 8-3 балла, необходимо набрать 85% или выше на вступительном экзамене. Экзамен будет сдан в августе заведующим отделением средней школы. Пожалуйста, свяжитесь с учителем математики, чтобы обсудить этот вариант. Форма запроса на вступительный экзамен должна быть получена до 15 июля.
В восьмом классе учащиеся могут переходить как на более высокий, так и на более низкий уровень. Как правило, переход с одного уровня курса на другой уровень курса должен происходить не позднее, чем через неделю после выдачи второго табель успеваемости. Изменения уровня могут быть одобрены только школьным советником и заведующим кафедрой математики после консультации с учеником, учителем и родителями. Изменения уровня в течение третьей четверти возможны только в том случае, если учащийся, родитель, школьный советник, учитель и заведующий кафедрой математики посовещались до начала третьей четверти и подписали продление. Советник факультета должен хранить подписанное письменное соглашение в официальном деле студента. Никакие изменения уровня не возможны в четвертом квартале без письменного одобрения Принципала.
Изменения уровня могут быть одобрены только школьным советником и заведующим кафедрой математики после консультации с учеником, учителем и родителями. Изменения уровня в течение третьей четверти возможны только в том случае, если учащийся, родитель, школьный советник, учитель и заведующий кафедрой математики посовещались до начала третьей четверти и подписали продление. Советник факультета должен хранить подписанное письменное соглашение в официальном деле студента. Никакие изменения уровня не возможны в четвертом квартале без письменного одобрения Принципала.
Если учащийся меняет уровень, применяется следующая политика выставления оценок:
- В течение контрольного периода 1 — только курсовая работа, выполненная в новом курсе, будет использоваться для подсчета оценки за 1-й контрольный период. Все четыре контрольных периода и итоговый экзамен/экзамен Риджентс будут использоваться для подсчета оценки учащегося на конец года.
- В конце отчетного периода 1 – оценка за первую четверть будет исключена из расчета на конец года.
 Периоды оценки 2, 3 и 4 будут учитываться по 30% каждый, а итоговый экзамен/экзамен Риджентс — 10%.
Периоды оценки 2, 3 и 4 будут учитываться по 30% каждый, а итоговый экзамен/экзамен Риджентс — 10%. - Любой балл во время второго периода оценивания. Учитель, школьный консультант и родитель должны обсудить и согласовать политику оценивания. Примечание: на самом деле не должно быть большого движения во время или после второго периода маркировки.
Зачисление в девятый класс проводится учителем восьмого класса и обсуждается на школьной конференции весной 8-го класса. Все места размещения пересматриваются в июне.
Математика 8-1. После успешного завершения этого курса учащиеся получат право на поступление на курс алгебры 1 уровня Риджентс в девятом классе (математика 412).
Математика 8-2: После успешного завершения этого курса учащимся, как правило, рекомендуется сдать математику 422 или 423 (продвинутый уровень математики в десятом классе). Из-за особых обстоятельств учащийся может быть помещен в математику 424 (математика с отличием десятого класса), но этот ученик, скорее всего, был переведен в математику 8-3 в течение 8-го класса.
Математика 8-3: После успешного завершения этого курса учащимся будет рекомендовано изучение математики 423 (продвинутый уровень математики в десятом классе) или математики 424 (математика с отличием в десятом классе).
Рекомендуется посетить каталог курсов средней школы, чтобы найти описания математических курсов. Политика старшей школы допускает переопределение с 422 по 423, однако переопределения в 4-уровневые курсы (424) нет. Учащийся может запросить вступительный экзамен для прохождения теста в 424, заполнив требуемую форму, которую можно получить у школьного советника до 1 июня. Это жесткий крайний срок, и требуется рекомендация учителя восьмого класса. Кроме того, учащиеся должны иметь средний балл A- или выше, чтобы сделать этот запрос.
**Сплошными линиями обозначен типичный путь. Пунктирные линии указывают возможные пути, которые обычно возникают при выполнении промежуточных шагов.
Математика 8 класс Математика | GreatSchools.
 org
orgМатематика для восьмого класса может показаться отдельным языком или, по крайней мере, параллельной вселенной определений. Когда ваш ребенок говорит о радикальных, иррациональных и изменчивых вещах, скорее всего, он имеет в виду уроки математики, а не размышляет о жизни.
Ключевые математические навыки 8-го класса, которые ваш ребенок должен освоить к концу года:
- Понимание иррациональных чисел и сравнение их с рациональными числами.
- Использование линейных уравнений, линейных функций и систем линейных уравнений для объяснения отношений между двумя переменными или значениями.
- Создание графиков и других диаграмм для иллюстрации этих взаимосвязей.
- Понимание концепции функции как изменение одной величины или значения другой величины или значения.
- Вычисление квадратных корней и их противоположностей, показателей степени.
- Определение идентичности фигур путем их поворота, отражения и перемещения на графике.

- Применение теоремы Пифагора для нахождения неизвестных длин в прямоугольных треугольниках и объяснение, почему она работает.
- Найдите объем трехмерных фигур, включая конусы, сферы и цилиндры.
Иллюстрация взаимосвязей между двумя наборами данных на диаграммах и объяснение закономерностей.
Это так иррационально
Рациональные числа включают положительные и отрицательные целые числа, простые дроби и десятичные дроби (включая те, которые имеют повторяющиеся шаблоны, такие как .2323…). Иррациональные числа — это десятичные числа, которые продолжаются бесконечно, не повторяя последовательность чисел. Пи – π – самое известное иррациональное число. Он был рассчитан более чем на квадриллион знаков после запятой, но закономерности до сих пор нет! Неудивительно, что у него есть свой собственный день.
Выражения и уравнения
Большая часть математики в восьмом классе посвящена линейным уравнениям, линейным функциям и системам линейных уравнений, которые используются для демонстрации взаимосвязи между двумя переменными.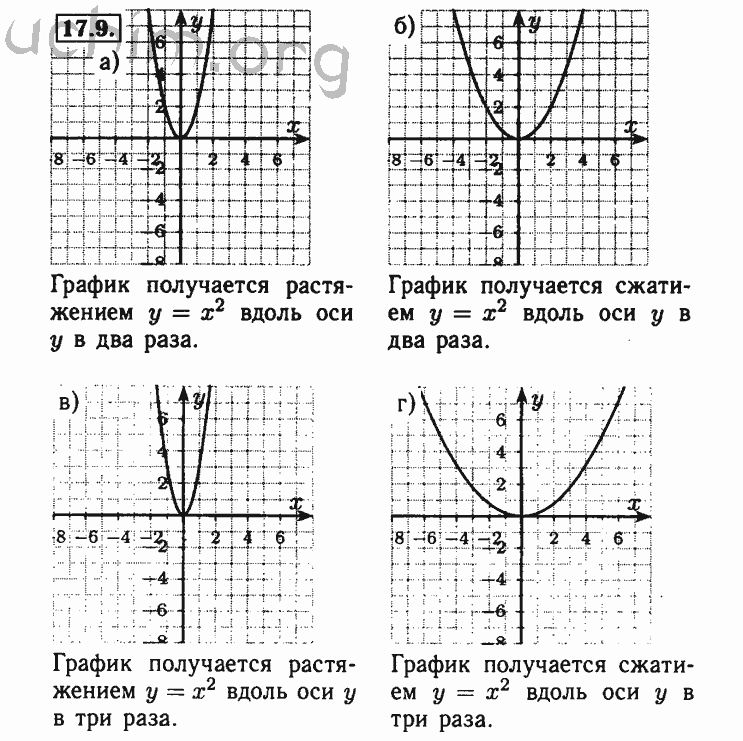 Идея их может показаться пугающей, но вы используете их все время, не задумываясь об этом. Посмотрите это видео GreatSchools, чтобы увидеть реальный пример.
Идея их может показаться пугающей, но вы используете их все время, не задумываясь об этом. Посмотрите это видео GreatSchools, чтобы увидеть реальный пример.
Advertisement
«Это самая важная и сложная концепция для изучения в восьмом классе», — сказал Райан Редд, учитель математики в средней школе Roland-Grise в Уилмингтоне, Северная Каролина. «Это важнейший базовый навык для математики в средней школе».
Восьмиклассники научатся отображать эти отношения на графиках; создание наклонов, которые облегчают сравнение пропорциональных отношений и выглядят так.
Входы и выходы
Как это ни звучит, функция описывает отношения, в которых одно влияет на другое. Например, результат теста вашего ребенка зависит от того, сколько он учился.
Математически функция — это когда одно число, называемое входом, изменяет следующее число, известное как выход.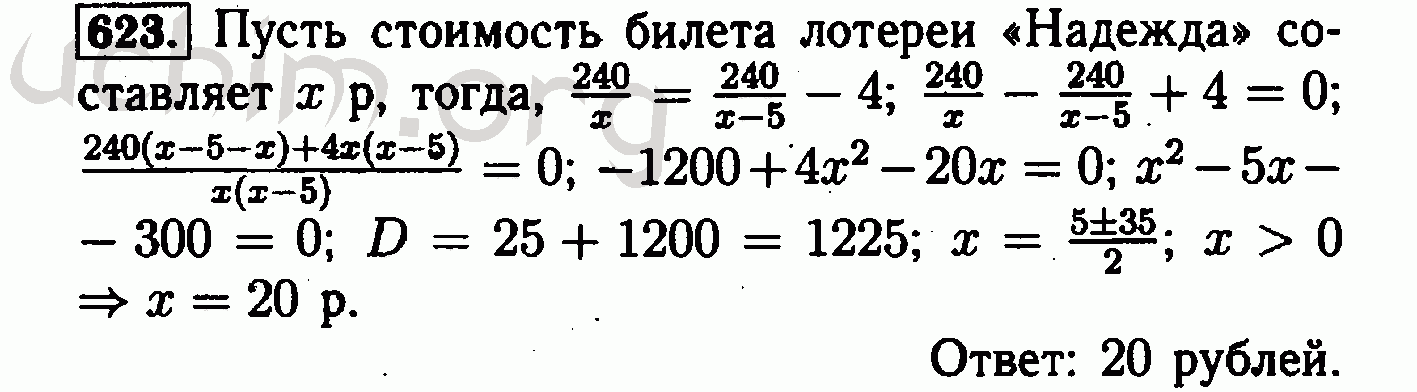 Для каждого входа есть только один выход.
Для каждого входа есть только один выход.
Пример: Какая связь между быстрой ездой и пробегом? Подсчитайте, насколько расход топлива уменьшается на каждую милю, превышающую установленную вами скорость.
Функции бывают либо линейными (т. е. они образуют прямую линию при нанесении на график), либо нелинейными (т. е. не образуют прямой).
Подкоренные корни
Ваш восьмиклассник также узнает о корнях , известных как подкоренных чисел , и показателях степени. Квадратные корни являются наиболее распространенными радикалами. Символ выглядит как галочка, √. Когда после знака квадратного корня стоит число, например √49, ученикам предлагается найти число, которое при умножении само на себя равно 49. Квадратный корень из 49 равен 7.
Оборотная сторона корней — это степени . Они указывают, сколько раз нужно умножить число само на себя. Показатель степени записывается так: 67. Здесь 7, которая как бы сидит на плече у 6, является показателем степени.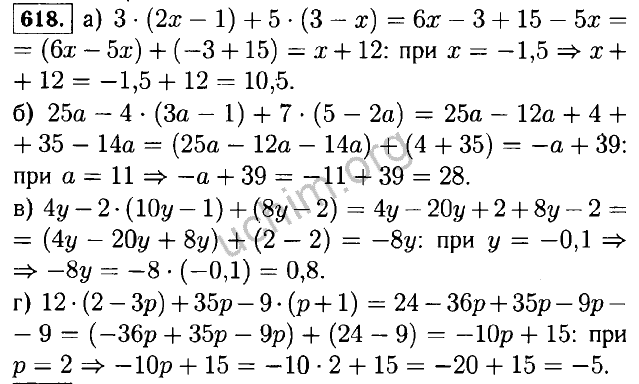 Его также можно записать так: 6 х 6 х 6 х 6 х 6 х 6 х 6. Ваш ребенок также будет работать с отрицательными показателями в восьмом классе.
Его также можно записать так: 6 х 6 х 6 х 6 х 6 х 6 х 6. Ваш ребенок также будет работать с отрицательными показателями в восьмом классе.
Форма вселенной
Ваш восьмиклассник много лет играет с фигурами в классе и за его пределами. Если она занимается полевыми видами спорта, она уже свободно мыслит треугольниками (три игрока, каждый из которых держит точку), меняет их ориентацию, вращает их и перемещает по плоскости (например, к цели) — три ключевых навыка, которые она освоит. нужно сделать на уроке математики в этом году.
Ваш ребенок также познакомится с магией теоремы Пифагора. Забыли этот древний алгоритм? В прямоугольном треугольнике, если а — длина одного из катетов, а b — длина другого катета, то длину третьей стороны, противоположной прямому углу (гипотенузе), можно найти по следующей формуле: a2 + b2 = с2 и с — длина гипотенузы. Ожидается, что ваш ребенок не только воспользуется удобной формулой Пифгаориана, но и объяснит, почему она работает.
Наконец, ожидается, что ваш ребенок расширит свое мастерство владения объемом: найдет внутреннее пространство более сложных трехмерных форм, таких как конусы, сферы и цилиндры. Вот краткое обновление этих формул.
Вот краткое обновление этих формул.
С точки зрения статистики
Если ваш восьмиклассник жалуется, что сложная математика, которую он начинает учить, не имеет отношения к его повседневной жизни, вы можете аргументировать это одним простым словом: статистика.
Понимание статистики поможет вашему ребенку сделать важный жизненный выбор, например, какую машину купить, какие продукты есть, на какую фэнтези-футбольную команду делать крупные ставки. В восьмом классе ученики только начинают сравнивать разные наборы данных и узнают, какие выводы они могут сделать из них.
Восьмиклассники должны уметь анализировать данные с помощью диаграмм и графиков и объяснять закономерности в данных. Например, детей могут попросить собрать данные о том, с какими учениками разрешено встречаться, а от каких ожидается выполнение работы по дому, а затем составить график этих результатов, чтобы увидеть, есть ли корреляция. Дети, которые встречаются, чаще или реже занимаются домашними делами?
Математика в восьмом классе очень важна для того, чтобы в старшей школе появилась большая кахуна-математика.

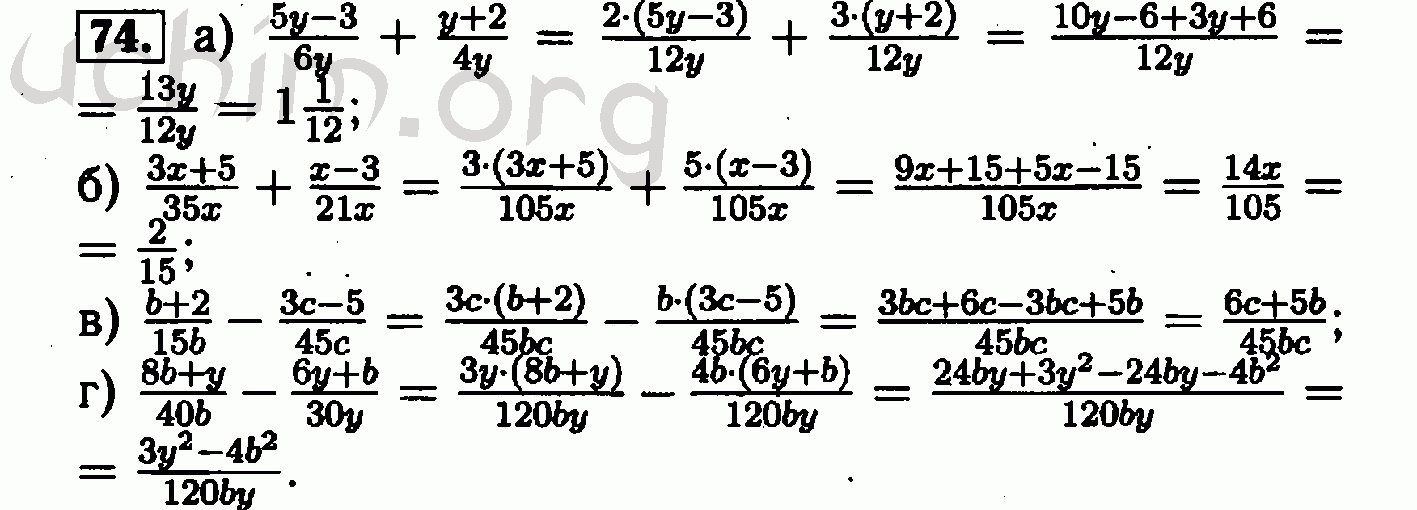
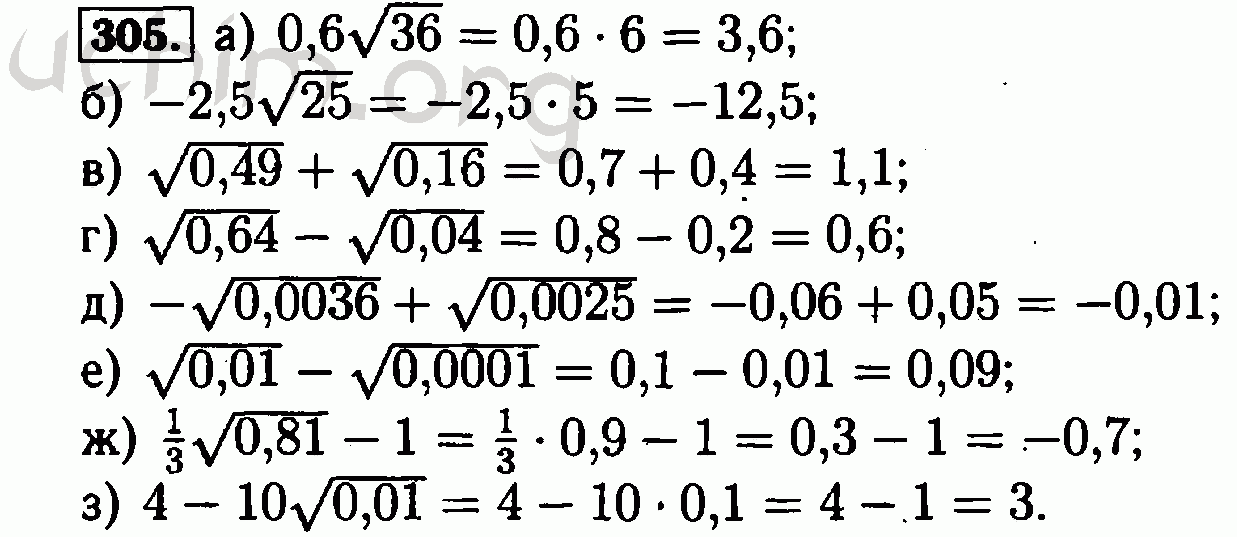
 В.
В. Периоды оценки 2, 3 и 4 будут учитываться по 30% каждый, а итоговый экзамен/экзамен Риджентс — 10%.
Периоды оценки 2, 3 и 4 будут учитываться по 30% каждый, а итоговый экзамен/экзамен Риджентс — 10%. 