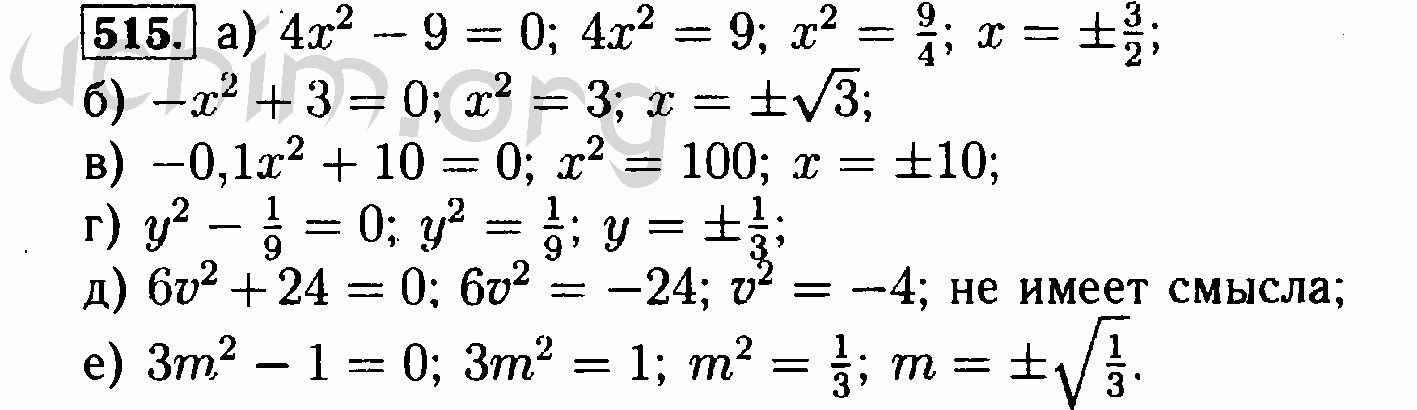ГДЗ Решебник Алгебра 8 класс Учебник (Углубленный уровень) Алгоритм успеха «Вентана-Граф» Мерзляк, Поляков.
ГДЗ Решебник Алгебра 8 класс Учебник (Углубленный уровень) Алгоритм успеха «Вентана-Граф» Мерзляк, Поляков.Алгебра 8 классУчебник (Углубленный уровень)Алгоритм успехаМерзляк, Поляков«Вентана-Граф»
Зачастую обучение в школе проходит не так гладко, как хотелось бы большинству родителей. Да это и не удивительно, учитывая сложность учебной программы. Поэтому учащимся может весьма пригодится решебник к учебнику «Алгебра 8 класс Учебник (Углубленный уровень), авторы: Мерзляк, Поляков» от издательства Вентана-Граф, которое входит в серии УМК «Алгоритм успеха». В сборнике подробно приводятся решения всех заданий, которые так же сопровождаются условиями.
ГДЗ «Алгебра 8 класс Учебник (Углубленный уровень), авторы: Мерзляк, Поляков» поможет преодолеть множество трудностей в ходе обучения:
- дополнить и углубить свои познания;
- разобраться в мельчайших аспектах предмета Алгебра;
- исправить допущенные ошибки;
- повысить успеваемость.
Делитесь решением с друзьями, оставляйте комментарии — они помогают нам становится лучше!
Параграф 1
123456789101112131415161718192021222324252627282930313233Параграф 2
1234567891011121314151617181920212223Параграф 3
12345678910111213141516171819202122232425262728Параграф 4
1234567891011121314151617181920Параграф 5
123456789101112131415Параграф 6
12345678910111213141516171819202122232425262728293031323334353637383940Параграф 7
12345678910111213141516171819202122232425262728293031Параграф 8
12345678910111213141516171819202122232425262728293031323334353637383940414243444546Параграф 9
123456789101112131415161718192021222324252627282930313233343536Параграф 10
123456789101112131415161718192021222324252627282930Параграф 11
12345678910111213141516171819202122Параграф 12
1234567891011121314Параграф 13
12345678910111213141516171819202122232425262728293031323334353637383940Параграф 14
1234567891011121314151617181920212223242526272829303132333435Параграф 15
1234567891011121314151617181920212223242526272829303132333435363738394041424344Параграф 16
12345678910111213141516171819202122232425262728293031323334353637383940Параграф 17
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152Параграф 18
123456789101112131415161718192021222324252627Параграф 19
12345678910111213141516171819202122232425262728293031323334Параграф 20
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748Параграф 21
123456789101112131415161718192021222324252627282930313233Параграф 22
12345678910111213141516171819202122Параграф 23
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647Параграф 24
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647Параграф 25
1234567891011121314151617181920212223242526272829303132333435Параграф 26
1234567891011121314151617181920212223242526Параграф 27
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152Параграф 28
1234567891011121314151617181920212223242526272829303132Параграф 29
1234567891011121314151617181920212223242526272829303132333435363738394041424344Параграф 30
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657Параграф 31
123456789101112131415161718192021222324Параграф 32
1234567891011121314151617181920212223242526272829303132Параграф 33
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152Параграф 34
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647Параграф 35
1234567891011121314151617181920212223242526272829Параграф 36
123456789101112131415161718192021Параграф 37
1234567891011121314151617181920212223242526272829303132Параграф 38
123456789101112131415161718192021222324252627282930313233Параграф 39
123456789101112Параграф 40
123456789101112131415161718192021Параграф 41
12345678Похожие ГДЗ Алгебра 8 класс
Алгебра 8 классУчебникМерзляк, Полонский, Якир«Вентана-Граф»
Алгебра 8 классДидактические материалыМерзляк, Полонский, Рабинович, Якир«Вентана-Граф»
Алгебра 8 классСамостоятельные и контрольные работы Алгоритм успехаМерзляк, Полонский, Рабинович«Вентана-Граф»
Алгебра 8 классРабочая тетрадьАлгоритм успеха1, 2Мерзляк, Полонский, Якир«Вентана-Граф»
Параграф 1: 1
Предыдущее
Следующее
Решение
Предыдущее
Следующее
закрытьГДЗ и решебники
ГДЗ 8 Класс Алгебра Мордкович Углубленный Уровень – Telegraph
>>> ПОДРОБНЕЕ ЖМИТЕ ЗДЕСЬ <<<
ГДЗ 8 Класс Алгебра Мордкович Углубленный Уровень
Задачник 8 класс (углубленный уровень )» Мордкович, Звавич, Рязановский, в котором приведены самые полные данные .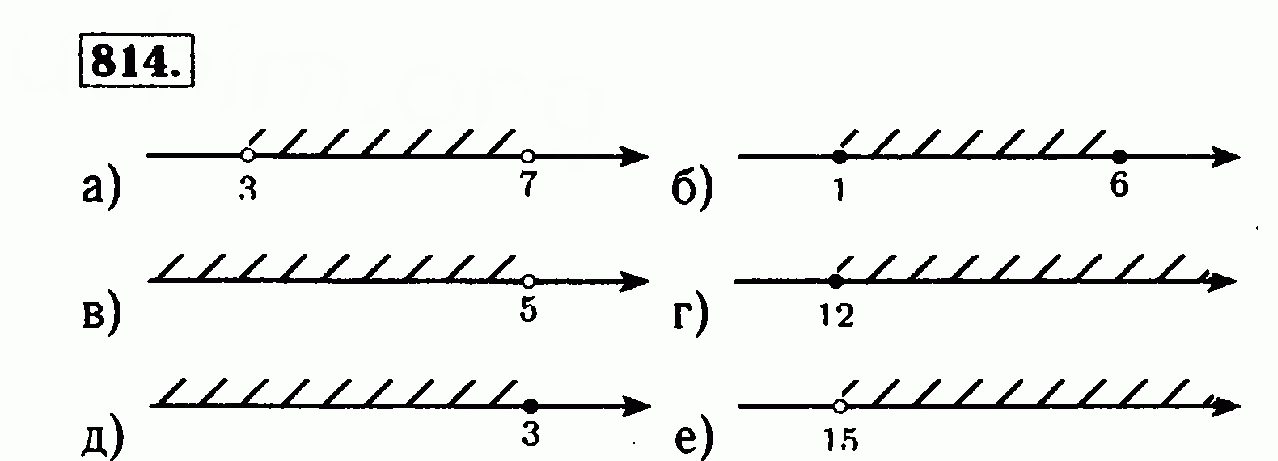
Помимо этого в издание вошли комбинированные задачи и задания для итогового повторения . ГДЗ по алгебре 8 класс Мордкович помогает осознать . .
Для этого мы разместили на нашем портале гдз Алгебра 8 класс А .Г . Мордкович, Л .И . Звавич Часть 2 . Проверяйте выполненные самостоятельно Запомните, что бездумное переписывание решений не повысить уровень ваших знаний . Ответственно относитесь к своему образованию . .
Готовые домашние задания по алгебре для 8 класса – решебник Мордокович А .Г . и др ., ответы в один клик, круглосуточно, бесплатно и ГДЗ по алгебре за 7 класс Мордокович – это электронный сборник решений по учебнику Мордоковича А .Г ., Александровой Л .А ., Мишустиной . .
Решебник (ГДЗ ) по Алгебре за 8 (восьмой ) класс задачник авторы: Мордкович, Александрова, Мишустина издательство Мнемозина, 2019 год Как использовать онлайн-решебник по алгебре за 8 класс от Мордковича . Важно понимать, что простое списывание не исправит пробелы в . .
авторы: Мордкович А .
Г ., Александрова Л .А ., Мишустина Т .Н . Математика и восьмиклассник . Помочь ребенку в освоении одного из сложных математических навлений призван «ГДЗ по алгебре 8 класс задачник Мордкович, Александрова (Мнемозина)» .
Готовое домашние задание (гдз , решебник) по алгебре . 8 класс . Часть 2 . Задачник для учащихся общеобразовательных Решебник от Путина по алгебре 8 класс Мордкович с полным решением . В 8 классе учебная программа алгебры комплексна и содержательна .
Учебник по алгебре Мордковича 8 класс часто вызывает много сложностей у школьников, особенно после 7 класса , когда уроки алгебры только начались, а опыта решения сложных уравнений и задач недостаточно . В таком случае, на помощь приходит решебник и гдз . .
Видеоуроки, тесты и тренажёры по предмету Алгебра за 8 класс по учебнику Мордкович А .Г .
Алгебра . 8 класс . В 2 ч . Ч . 2 . Задачник / под ред . А . Г . Мордковича ; А . Г . Мордкович . Преподавание алгебры в 8 —9 классах по учебникам А .
Г . Мордковича , Н . П . Николаева . Методическое пособие для учителя; А . Г . Мордкович . Алгебра . 7—9 классы .
Другие решебники по алгебре для 8 классa . А .Г . Мордкович , Т .Н . Мишустина, Е .Е . Тульчинская 2009 А .Г . Мордкович, Т .Н . Мишустина, Е .Е .Тульчинская .
Алгебра (углубленное изучение) . 8 класс . Задачник . Вторая часть УМК Алгебра углубленная подготовка 8 класс под ред . Мордкович А .Г . УМК для классов с повышенным уровнем математической подготовки в общеобразовательных школах .
Для скачивания предлагается учебник 8 класса по алгебре с повышенным уровнем математической подготовки в СОШ . Написан учебник по той же концепции, что использована в соответствующем учебнике для обычных школ Мордковича, с соблюдением той же структуры . .
ГДЗ по алгебре 8 класс Мордкович, Мишустина, Тульчинская задачник 2002 г онлайн — Примеры .
ГДЗ Алгебра 8 класс Мордкович . Часть 2 (задачник) А .Г . Мордкович , Л .А . Александрова, Т .Н . Мишустина, Е .
Е . Тульчинская Мнемозина . Ниже вы найдете решенные упражнения из задачника по алгебре автора Мордкович А .Г . за 8 класс основной школы .
Тут можно абсолютно бесплатно использовать решебник (ГДЗ ) для учебника по алгебре Мордкович за 8 -й класс . Пособие предназначено для родителей . Всегда помните, что нужно не бездумно списывать, это не прибавляет знаний . .
Задачник 8 класс (углубленный уровень )» Мордкович, Звавич, Рязановский, в котором приведены самые полные данные . Помимо этого в издание вошли комбинированные задачи и задания для итогового повторения . ГДЗ по алгебре 8 класс Мордкович помогает осознать . .
Для этого мы разместили на нашем портале гдз Алгебра 8 класс А .Г . Мордкович, Л .И . Звавич Часть 2 . Проверяйте выполненные самостоятельно Запомните, что бездумное переписывание решений не повысить уровень ваших знаний . Ответственно относитесь к своему образованию . .
Готовые домашние задания по алгебре для 8 класса – решебник Мордокович А .Г .
и др ., ответы в один клик, круглосуточно, бесплатно и ГДЗ по алгебре за 7 класс Мордокович – это электронный сборник решений по учебнику Мордоковича А .Г ., Александровой Л .А ., Мишустиной . .
Решебник (ГДЗ ) по Алгебре за 8 (восьмой ) класс задачник авторы: Мордкович, Александрова, Мишустина издательство Мнемозина, 2019 год Как использовать онлайн-решебник по алгебре за 8 класс от Мордковича . Важно понимать, что простое списывание не исправит пробелы в . .
авторы: Мордкович А .Г ., Александрова Л .А ., Мишустина Т .Н . Математика и восьмиклассник . Помочь ребенку в освоении одного из сложных математических навлений призван «ГДЗ по алгебре 8 класс задачник Мордкович, Александрова (Мнемозина)» .
Готовое домашние задание (гдз , решебник) по алгебре . 8 класс . Часть 2 . Задачник для учащихся общеобразовательных Решебник от Путина по алгебре 8 класс Мордкович с полным решением . В 8 классе учебная программа алгебры комплексна и содержательна .
Учебник по алгебре Мордковича 8 класс часто вызывает много сложностей у школьников, особенно после 7 класса , когда уроки алгебры только начались, а опыта решения сложных уравнений и задач недостаточно .
В таком случае, на помощь приходит решебник и гдз . .
Видеоуроки, тесты и тренажёры по предмету Алгебра за 8 класс по учебнику Мордкович А .Г .
Алгебра . 8 класс . В 2 ч . Ч . 2 . Задачник / под ред . А . Г . Мордковича ; А . Г . Мордкович . Преподавание алгебры в 8 —9 классах по учебникам А . Г . Мордковича , Н . П . Николаева . Методическое пособие для учителя; А . Г . Мордкович . Алгебра . 7—9 классы .
Другие решебники по алгебре для 8 классa . А .Г . Мордкович , Т .Н . Мишустина, Е .Е . Тульчинская 2009 А .Г . Мордкович, Т .Н . Мишустина, Е .Е .Тульчинская .
Алгебра (углубленное изучение) . 8 класс . Задачник . Вторая часть УМК Алгебра углубленная подготовка 8 класс под ред . Мордкович А .Г . УМК для классов с повышенным уровнем математической подготовки в общеобразовательных школах .
Для скачивания предлагается учебник 8 класса по алгебре с повышенным уровнем математической подготовки в СОШ . Написан учебник по той же концепции, что использована в соответствующем учебнике для обычных школ Мордковича, с соблюдением той же структуры .
.
ГДЗ по алгебре 8 класс Мордкович, Мишустина, Тульчинская задачник 2002 г онлайн — Примеры .
ГДЗ Алгебра 8 класс Мордкович . Часть 2 (задачник) А .Г . Мордкович , Л .А . Александрова, Т .Н . Мишустина, Е .Е . Тульчинская Мнемозина . Ниже вы найдете решенные упражнения из задачника по алгебре автора Мордкович А .Г . за 8 класс основной школы .
Тут можно абсолютно бесплатно использовать решебник (ГДЗ ) для учебника по алгебре Мордкович за 8 -й класс . Пособие предназначено для родителей . Всегда помните, что нужно не бездумно списывать, это не прибавляет знаний . .
ГДЗ Окружающий Мир 1 Класс Школа России
ГДЗ По Чтению 3 Класс Часть 1
ГДЗ По Алгебре 8 Класс Ткачева Учебник
ГДЗ По Английскому Ваулина Тренировочные Упражнения
Проверочные Работы 6 Класс Барашков ГДЗ
ГДЗ Английский 3 Класс Верещагина Грамматика
ГДЗ По Афанасьева Учебник 4
Решебник Физика 10 Задачник
ГДЗ По Геометрии 7 9 Атасян
ГДЗ По Литературе 2 Класс 1 Часть
Михайлова 2 Класс Решебник
ГДЗ 1 Класс Бунеев Бунеева
ГДЗ Алгебра 7 Класс Номер 5
ГДЗ Русск Яз 5 Ладыженская
Решебник 5 Класса Мерзляков
ГДЗ По Алгебре 9 Якир
ГДЗ Решебник По Алгебре 7 Класс Мерзляк
Русский Язык 2 Часть Баранов Решебник
ГДЗ По Алгебре 7 Класс Звавич
Решебник Евдокимова 3 Класс
ГДЗ От Путина По Алгебре 10
Решебник По Алгебре 6 Класс Никольский
Математика 8 Класс Макарычев ГДЗ 274
ГДЗ По Английскому 5 Класс Грамматика
Решебник По Белорусскому Языку 7 2020
ГДЗ Нач Школа 21 Века 4 Класс
ГДЗ По Литературе 3 Бунеева
Рудницкая 4 Класс Математика Решебник ГДЗ Учебник
Решебник По Немецкому Языку 7 Класс Аверин
ГДЗ По Английскому 6 Класс Энджой Инглиш
Химия 11 Класс Габриелян ГДЗ Углубленный Уровень
ГДЗ Афанасьева 5 Класс 1 Часть Учебник
ГДЗ По Окружающему Федотова 2 Часть
ГДЗ По Алгебре Мерзляков
Решебник По Литературному Чтению В Тетради
ГДЗ Решебник По Алгебре 10 11
ГДЗ 3 Класс Страница 18
ГДЗ По Р 4 Класс Русский
Решебник По Алгебре 7 Алимов
Решебник Rainbow 11
ГДЗ 3 Г Класс Русский Язык
Spotlight 4 Класс ГДЗ С Переводом
Spotlight 11 Учебник ГДЗ С Переводом
ГДЗ По Русскому Языку 3 Учебник
Решебник По Белорусскому Языку 3 1 Часть
Решебник По Русскому Языку 1 Иванов
ГДЗ По Английскому Языку 6 Класс Грамматика
ГДЗ По Занимательному Русскому Языку 2
Решебник Русскому Языку 1 Класс Канакин
ГДЗ Азбука 1 Класс Школа России
ГДЗ Русский Язык 6 Львова Учебник
ГДЗ Таможняя 8 Класс
Решебник 1 Класс Рабочая Тетрадь
Гдз По Русскому Языку Пименова
ГДЗ По Алгебре 8 Класс Суворова
35 оценка значения выражения.
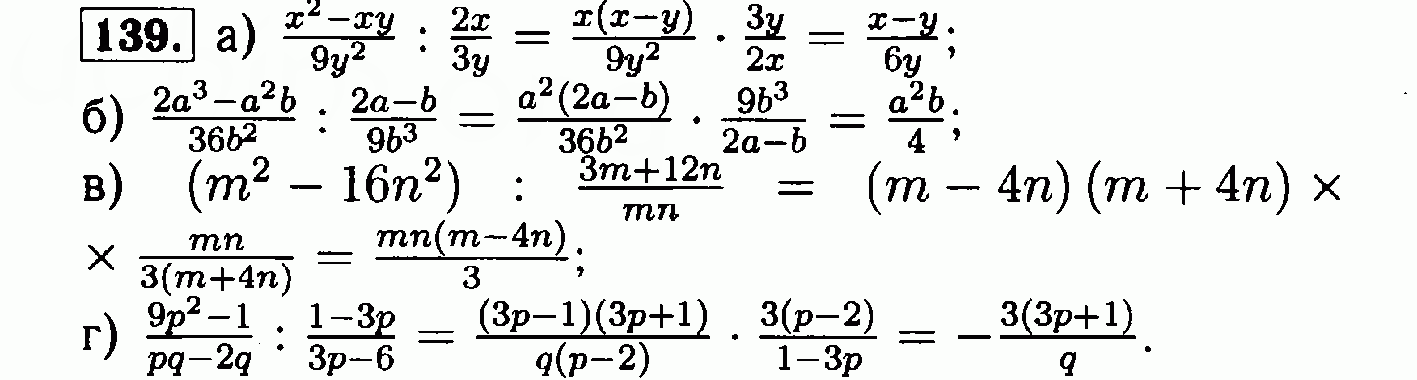Как вы оцениваете значение выражения? Методы получения оценок, примерыконспекты других презентаций
«Сложение и вычитание алгебраических дробей» — Алгебраические дроби. 4а? B. Изучение новой темы. Задачи: Помните! Кравченко Г.М. Примеры:
«Степени с целым показателем» — Феоктистов Илья Евгеньевич Москва. 3. Градус с целым показателем (5 часов) стр.43. Преподавание алгебры в 8 классе с углубленным изучением математики. Отсроченное введение степени с целым отрицательным показателем… Знать определение степени с целым отрицательным показателем. 2.
«Типы квадратных уравнений» — Неполные квадратные уравнения. Вопросы… Полные квадратные уравнения. Квадратные уравнения. Определение квадратного уравнения Виды квадратных уравнений Решение квадратных уравнений. Методы решения квадратных уравнений. Группа «Дискриминант»: Миронов А., Мигунов Д., Зайцев Д., Сидоров Е., Иванов Н., Петров Г. Редуцированное квадратное уравнение. Выполнено: учащиеся 8 класса.
Метод полноквадратичного отбора. Типы квадратных уравнений. Пусть будет. Графический способ.
«Численные неравенства 8 класса» — A-c>0. Неравенства. A = «Больше или равно». б> в. Напишите a > b или a 0. B-c > 0. Числовые неравенства. Лакс. Свойства числовых неравенств. Примеры: Если а
«Решение квадратных уравнений Теорема Виета» — Один из корней уравнения равен 5. Задание №1. МОУ «Кисловская СОШ». Научный руководитель: учитель математики Баранникова Е.А. Кисловка — 2008 (Презентация к уроку алгебры в 8 классе). Найдите x2 и k. Работу выполнил: учащийся 8 класса Слинько В. Решение квадратных уравнений с использованием теоремы Виета.
М.: 2014 — 288с. М.: 2012 — 256с.
«Решебник» содержит ответы на все задания и упражнения из «Дидактических материалов по алгебре 8 класс»; подробно анализируются методы и методы их решения. «Решебник» адресован исключительно родителям учеников, для проверки домашних заданий и помощи в решении задач.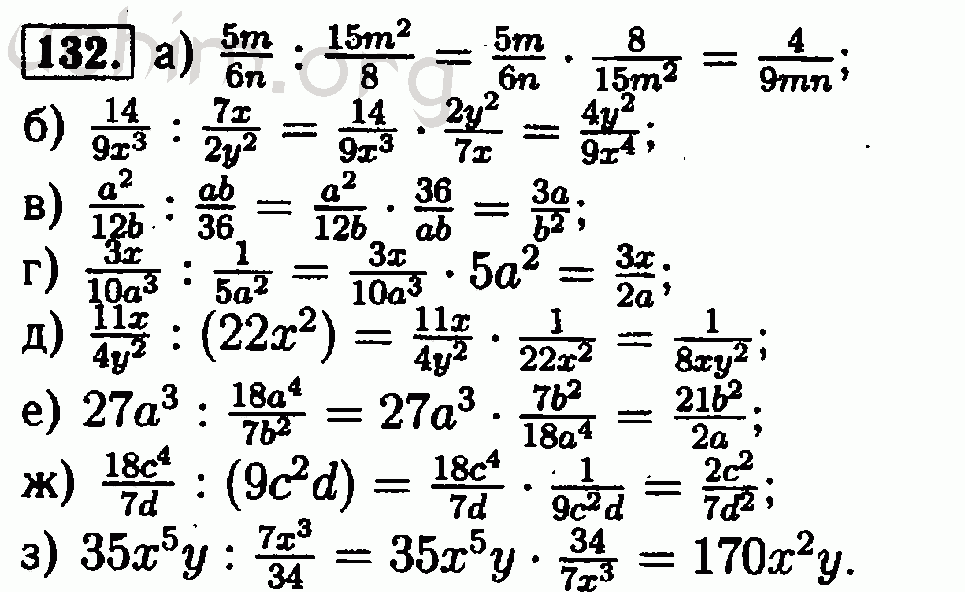
За короткое время родители могут стать весьма эффективными домашними воспитателями.
Формат: pdf ( 201 4 , 28 8с., Ерин В.К.)
Размер: 3,5 Мб
Смотреть, скачать: диск.гугл
Формат: pdf ( 2012 , 256 стр., Морозов А.В.)
Размер: 2.1 МБ
Смотреть, скачать: ссылки удалены (см. примечание!!)
Формат: pdf( 2005 , 224с., Федоскина Н.С.)
Размер: 1.7 МБ
Смотреть, скачать: диск.гугл
Содержание
Самостоятельная работа 4
Вариант 1 4
к полиному (повторение) 4
С-2. Факторинг (повторение) 5
C-3. Целочисленные и дробные выражения 6
C-4. Основное свойство дроби. Редукционные фракции 7
С-5. Сокращающие дроби (продолжение) 9
с одинаковыми знаменателями 10
с разными знаменателями 12
знаменатели (продолжение) 14
C-9.
С-10. Разделение фракций 17
С-11. Все действия с дробью 18
S-12. Функция 19
S-13. Рациональные и иррациональные числа 22
S-14. Арифметический квадратный корень из 23
S-15. Решение уравнений вида x2 = 27
квадратный корень из 29
S-17. Функция y = \ / x 30
Произведение корней 31
Частные корни 33
S-20. Квадратный корень из степени 34
Разложение под знаком корня 37
, содержащее квадратный корень 39
С-23. Уравнения и их корни 42
Неполные квадратные уравнения 43
S-25. Решение квадратных уравнений 45
(продолжение) 47
S-27. Теорема Виета 49
квадратные уравнения 50
множители. Биквадратные уравнения 51
S-30. Дробные рациональные уравнения 53
рациональные уравнения 58
S-32. Сравнение номеров (повторение) 59
S-33. Свойства числовых неравенств 60
S-34. Сложение и умножение неравенств 62
S-36.
Оценка значения выражения 65 S-37. Оценка погрешности аппроксимации 66
S-38. Округление числа 67
С-39. Относительная ошибка 68
S-40. Пересечение и объединение комплектов 68
С-41. Количество пролетов 69
С-42. Решение неравенств 74
S-43. Решение неравенств (продолжение) 76
S-44. Решение систем неравенств 78
S-45. Решение неравенств 81
переменная под знаком модуля 83
С-47. Целое число градусов 87
градусов с целым числом 88
S-49. Стандартный номер 91
S-50. Запись приблизительных значений 92
S-51. Элементы статистики 93
(повтор) 95
С-53. Определение квадратичной функции 99
S-54. Функция y = ax2 100
S-55. График функции y = ax2 + bzh + c 101
S-56. Решение квадратных неравенств 102
S-57. Интервальный метод 105
C-1. Преобразование целочисленного выражения
в полином (повторение) 108
C-2. Факторинг (повтор) 109
C-3.
Целочисленные и дробные программные выражения C-4. Основное свойство дроби.
Восстанавливающие фракции 111
С-5. Восстанавливающие фракции (продолжение) 112
C-6. Сложение и вычитание дробей
с одинаковыми знаменателями 114
C-7. Сложение и вычитание дробей
с разными знаменателями 116
C-8. Сложение и вычитание дробей с разными знаменателями
(продолжение) 117
С-9. Умножение дробей 118
S-10. Разделение фракций 119
С-11. Все действия с дробью 120
S-12. Функция 121
S-13. Рациональные и иррациональные числа 123
S-14. Арифметический квадратный корень из 124
S-15. Решение уравнений вида x2 = a 127
S-16. Нахождение приблизительных значений
квадратного корня из 129
S-17. Функция y = Vx 130
S-18. Квадратный корень из произведения.
Продукт корней 131
S-19. Квадратный корень из дроби.
Частные корни 133
S-20. Корень квадратный из степени 134
S-21. Удаление множителя из знака корня
Введение множителя под знаком корня 137
S-22.
Преобразование выражений, , содержащих квадратные корни 138
S-23. Уравнения и их корни 141
S-24. Определение квадратного уравнения.
Неполные квадратные уравнения 142
S-25. Решение квадратных уравнений 144
S-26. Решение квадратных уравнений
(продолжение) 146
С-27. Теорема Виета 148
S-28. Решение задач с
квадратными уравнениями 149
S-29. Разложение квадратного трехчлена на
множителей. Биквадратные уравнения 150
S-31. Решение задач с
рациональными уравнениями 157
S-32. Сравнение номеров (повторение) 158
S-33. Свойства числовых неравенств 160
С-34. Сложение и умножение неравенств 161
S-35. Доказательство неравенств 162
С-36. Оценка значения выражения 163
S-37. Оценка погрешности аппроксимации 165
S-38. Округление номера 165
С-39. Относительная ошибка 166
S-40. Пересечение и объединение комплектов 166
С-41.
Номер пролета 167 С-42. Решение неравенств 172
S-43. Решение неравенств (продолжение) 174
S-44. Решение систем неравенств 176
S-45. Решение неравенств 179
S-46. Уравнения и неравенства, содержащие
переменных под знаком модуля 181
С-47. Целое число Степень 185
S-48. Преобразование выражений, содержащих
градусов, в целое число 187
S-49. Стандартный номер 189
S-50. Запись приблизительных значений 190
S-51. Статистика Предметов 192
S-52. Концепция функции. График функций
(повтор) 193
S-53. Определение квадратичной функции 197
S-54. Функция y = ax2 199
S-55. График функции y = ax2 + txr + c 200
S-56. Решение квадратных неравенств 201
S-57. Интервальный метод 203
Работы по обследованию 206
Вариант 1 206
Садовая мебель-1 206
Садовая мебель-2 208
Садовая мебель-3 212
Садовая мебель-4 215
Садовая мебель-5 218
Садовая мебель-6 621 900 7 223
Дачная мебель-8 226
Дачная мебель-9 229
К-10 (окончательная) 232
Вариант 2 236
К-1А 236
К-2А 238
К-ЗА 9006 К-ЗА 906 242
К-А -5А 246
К-6А 249
К-7А 252
К-8А 255
К-9А (заключительный) 257
Заключительное повторение по теме 263
Осенняя Олимпиада 274
Весенняя Олимпиада 275
35 соединяет знаки чисел 3 и 5.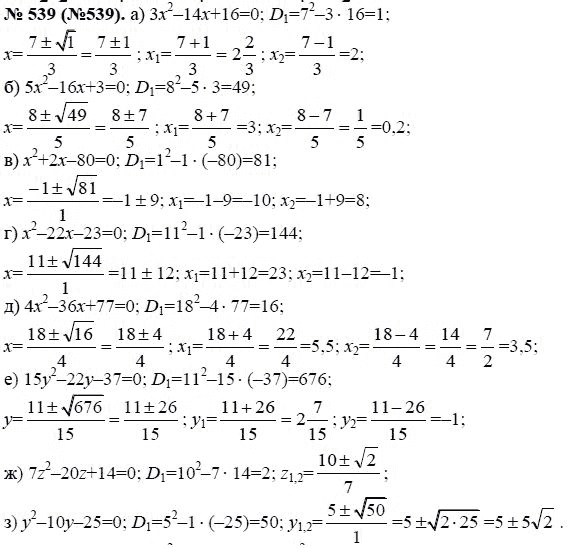
Тройка резонирует с вибрациями вдохновения и радости, энтузиазма и самовыражение. Это триединство прошлого, настоящего и будущего; тело, ум и дух. Человек под знаком тройки энергичен, талантлив, честен, горд и независим.
Пятерка добавляет в копилку общей вибрации долю эмоциональности и свободного выбора. Среди минусов — излишняя обидчивость и частые перепады настроения, негативное влияние которых компенсируется оптимизмом тройки. 35 в общих чертах олицетворяет творческую энергию, возможности, желание поменяться местами.
Соединение числа с символом
Что означает число 35 в судьбе человека, если оно определяется датой рождения? Это придает ему особую харизму, привлекающую к нему друзей и последователей. Такие люди всегда окружены поклонниками, которые выбирают их на роль общественного деятеля или неформального лидера.
Отрицательная сторона этого сочетания чисел в том, что человек использует свой авторитет для личного обогащения. У представителей 35 лет слабо развита духовная сфера.
Зараженные прагматизмом и тщеславием, они способны, независимо от лица, «идти по головам» к намеченной цели.
Магические свойства
Мистическое значение числа 35 связано с тем, что оно предсказывает встречу со смертельным искушением. Единственный способ избежать грубых ошибок такого испытания — сохранять спокойствие и рассудительность.
Сакральные сопоставления числа можно найти в Библии, где оно упоминается 5 раз. На тридцать пятый день поста в пустыне Люцифер подошел к Иисусу, чтобы искушать его.
Что означает число 35, если оно часто встречается
Если ангелы-хранители постоянно заставляют вас видеть цифру 35, они показывают, что вы не достигаете своих целей. Вы честны и старательны, но удача обходит вас стороной.
Вы сталкиваетесь с бесчисленными препятствиями и не уверены в своем будущем. Управитель числа 35, планета Сатурн, имеет такое влияние на вашу жизнь. Его скрытое действие проявляется через число 8, которое получается при сложении 3 и 5.
Возможно, вы отклоняетесь от своей цели и играете чужую роль. Чтобы найти свое истинное призвание, прислушайтесь к тому, что просит ваша душа, и следуйте ее невысказанному зову.
Наш «Решебник» содержит ответы на все задания и упражнения из «Дидактических материалов по алгебре 8 класс»; подробно анализируются методы и методы их решения. «Решебник» адресован исключительно родителям учеников, для проверки домашних заданий и помощи в решении задач.
За короткое время родители могут стать весьма эффективными домашними репетиторами.
Вариант 1 4
до полинома (повторение) 4
С-2. Факторинг (повторение) 5
С-3. Целочисленные и дробные выражения 6
С-4. Основное свойство дроби. Сокращение дробей. 7
С-5; Сокращение дробей (продолжение) 9
с одинаковыми знаменателями 10
с разными знаменателями 12
знаменатели (продолжение) 14
C-9. Умножение дробей 16
S-10. Разделение фракций 17
С-11.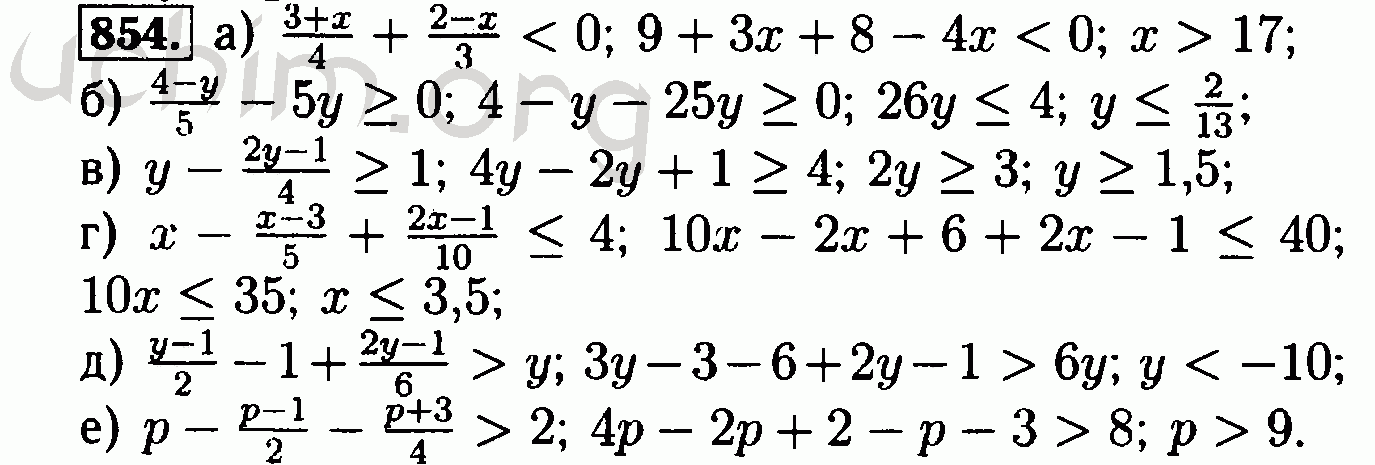
Все действия с дробями 18
С-12. Функция 19
S-13. Рациональные и иррациональные числа 22
S-14. Арифметический квадратный корень из 23
С-15. Решение уравнений вида x2 = a 27
S-16. Нахождение приблизительных значений
квадратный корень из 29
S-17. Функция y = d/x 30
Произведение корней 31
Частные корни 33
S-20. Корень квадратный из степени 34
S-21. Вычитание множителя из знака корня Вставка множителя из знака корня 37
S-23. Уравнения и их корни 42
Неполные квадратные уравнения 43
С-25. Решение квадратных уравнений 45
(продолжение) 47
S-27. Теорема Виета 49
S-28. Решение задач с
квадратными уравнениями 50
множителей. Биквадратные уравнения 51
S-30. Дробные рациональные уравнения 53
S-31. Решение задач с
рациональными уравнениями 58
S-32. Сравнение номеров (повтор) 59
С-33. Свойства числовых неравенств 60
С-34.
Сложение и умножение неравенств 62
С-35. Доказательство неравенств 63
S-36. Оценка значения выражения 65
S-37. Оценка погрешности аппроксимации 66
С-38. Округление цифр 67
С-39. Относительная ошибка 68
С-40. Пересечение и объединение комплектов 68
С-41. Количество пролетов 69
С-42. Решение неравенств 74
С-43. Решение неравенств (продолжение) 76
С-44. Решение систем неравенств 78
С-45. Решение неравенств 81
переменная под знаком модуля 83
S-47. Целое число градусов 87
градусов с целым числом 88
S-49. Стандартный номер 91
S-50. Запись приблизительных значений 92
S-51. Элементы статистики 93
(повтор) 95
С-53. Определение квадратичной функции 99
S-54. Функция y = ax2 100
S-55. График функции у = ах2 + бж + с 101
S-56. Решение квадратных неравенств 102
С-57. Интервальный метод 105
Вариант 2 108
C-1.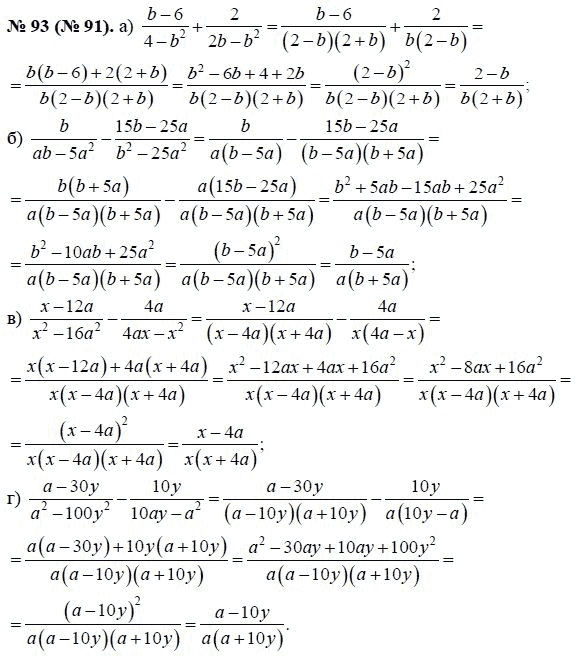
Преобразование целочисленного выражения
в полиномиальное (повторение) 108
C-2. Факторинг (повторение) 109
С-3. Целочисленные и дробные выражения 110
C-4. Основное свойство дроби.
Восстанавливающие фракции 111
С-5. Восстанавливающие фракции (продолжение) 112
C-6. Сложение и вычитание дробей
с одинаковыми знаменателями 114
С-7. Сложение и вычитание дробей
e разные знаменатели 116
C-8. Сложение и вычитание дробей с разными
знаменателями (продолжение) 117
C-9. Умножение дробей, 118
С-10. Разделение фракций 119
С-11. Все действия с дробями 120
С-12. Функция 121
S-13. Рациональные и иррациональные числа 123
S-14. Арифметический квадратный корень из 124
S-15. Решение уравнений вида x2 — a 127
С-16. Нахождение приблизительных значений квадратного корня из 129
S-17. Функция y=\/x»130
S-18. Корень квадратный из произведения.
Произведение корней 131
S-19. Корень квадратный из дроби.
Частные корни 133
S-20. Квадратный корень из степени 134
S-21.Выведение множителя из знака корня
Введение множителя под знаком корня 137
S-22.Преобразование выражений,
С-23. Уравнения и их корни 141
S-24. Определение квадратного уравнения.
Неполные квадратные уравнения 142
S-25. Решение квадратных уравнений 144
S-26. Решение квадратных уравнений
(продолжение) 146
С-27. Теорема Виета 148
S-28. Решение задач с
квадратными уравнениями 149
S-29. Разложение квадратного трехчлена на
множителей. Биквадратные уравнения 150
С-30. Дробные рациональные уравнения 152
S-31. Решение задач с
рациональными уравнениями 157
S-32. Сравнение номеров (повтор) 158
S-33. Свойства числовых неравенств 160
С-34. Сложение и умножение неравенств 161
С-35.
Доказательство неравенств 162
S-36. Оценка значения выражения 163
S-37. Оценка погрешности аппроксимации 165
С-38. Округление чисел 165
С-39. Относительная ошибка 166
С-40. Пересечение и объединение комплектов 166
С-41. Номер пролета 167
С-42. Решение неравенств 172
S-43. Решение неравенств (продолжение) 174
С-44. Решение систем неравенств 176
С-45. Решение неравенств 179
S-46. Уравнения и неравенства, содержащие
переменных под знаком модуля 181
S-47. Целое число Степень 185
S-48. Преобразование выражений, содержащих
градуса с целым числом 187
S-49. Стандартный номер 189
S-50. Запись приблизительных значений 190
S-51. Статистические данные 192
S-52. Концепция функции. График функций
(повтор) 193
S-53. Определение квадратичной функции 197
S-54. Функция y = ax2 199
S-55. График функции у = ах24-бж + с 200
С-56.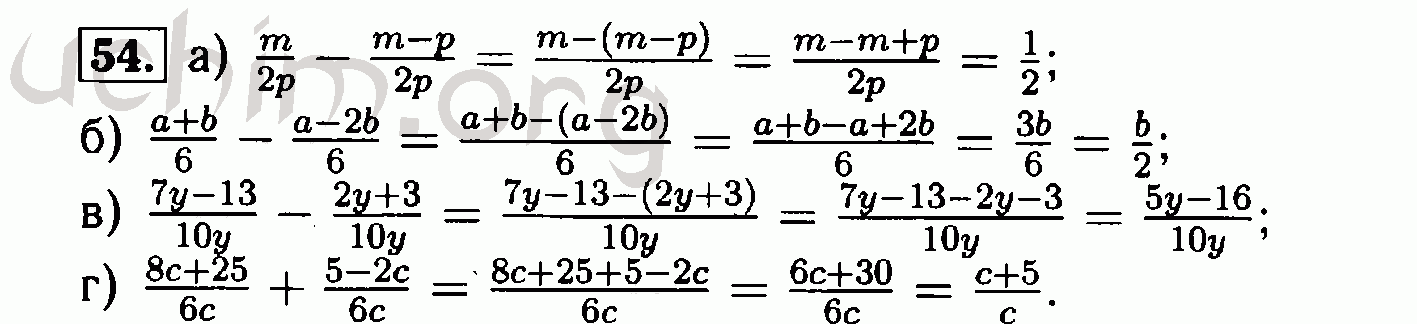
Решение квадратных неравенств 201
S-57. Интервальный метод 203
Экзамены. 263
Осенняя олимпиада 274
Весенняя олимпиада 275
УРОК №5 Тема. Почленное сложение и умножение неравенств. Применение свойств числовых неравенств для оценки значений выражений Цель занятия: добиться усвоения учащимися содержания понятия «сложить неравенства почленно» и «перемножить неравенства почленно», а также содержания свойств числовых неравенств, выраженных теоремы о почленном сложении и почленном умножении числовых неравенств и следствия из них. Развивать умение воспроизводить названные свойства числовых неравенств и использовать эти свойства для оценки значений выражений, а также продолжать работу по развитию навыков доказывания неравенств, сравнения выражений с использованием определения и свойств числовых неравенств Тип урока: закрепление знаний, развитие начальных навыков. Обзорность и оборудование: реферат № 5. Во время занятий I. Организационный этап Учитель проверяет готовность учащихся к уроку, настраивает их на работу. II. Проверка домашнего задания Учащиеся выполняют тестовые задания с последующей проверкой. III. Формулировка цели и задач урока. Для сознательного участия учащихся в постановке цели урока можно предложить им практические задачи геометрического содержания (например, на оценку периметра и площади прямоугольника, длин смежных сторон которые оцениваются в виде двойных неравенств). В ходе беседы учитель должен направить мысли учащихся на то, что хотя задачи и аналогичны тем, которые решались на предыдущем уроке (см. урок № 4, оценить значение выражений), однако, в отличие от названных, они не может быть решена теми же средствами, так как необходимо вычислять значения выражений, содержащих две (а в дальнейшем и больше) буквы. Результатом проделанной работы является формулировка цели урока: изучить вопрос о таких свойствах неравенств, которые можно применять в случаях, аналогичных описанным в предложенной задаче для учащихся; для чего необходимо четко сформулировать математическим языком и в словесной форме, а затем привести соответствующие свойства числовых неравенств и научиться использовать их в сочетании с ранее изученными свойствами числовых неравенств для решения типовых задач. IV. Обновление базовых знаний и навыков учащихся устные упражнения 1. Сравните числа a и b, если: 1) а — б = -0,2; 2) а — б = 0,002; 3) а = б — 3; 4) а — б = м 2 ; 5) а = б — м 2 . 3. Сравните значения выражений а+b и abif a=3, b=2. Обоснуйте свой ответ. Полученное соотношение будет выполнено, если: 1) а = -3, б = -2; 2) а = -3, б = 2? V. План изучения нового материала 1. Свойство почленного сложения числовых неравенств (с тонкой настройкой). 2. Свойство почленного умножения числовых неравенств (с тонкой настройкой). 3. Последствия. Свойство почленного умножения числовых неравенств (с тонкой настройкой). 4. Примеры применения проверенных свойств. Справочная записка № 5
Методический комментарий Для осознанного восприятия нового материала преподаватель может на этапе актуализации основных знаний и умений учащихся предложить решения устных упражнений с воспроизведением соответственно определения сравнения чисел и свойств числовых неравенств, изученных на предыдущих уроки (см. выше), а также рассмотрение соответствующих свойств числовых неравенств. Обычно студенты хорошо усваивают содержание теорем о почленном сложении и умножении числовых неравенств, однако опыт работы свидетельствует о склонности студентов к некоторым ложным обобщениям. Сознательное применение свойств числовых неравенств невозможно без умения записывать эти свойства как на математическом языке, так и в словесной форме; · теоремы почленного сложения и умножения числовых неравенств выполняются только для неправильностей одного знака; Свойство почленного сложения числовых неравенств выполняется при определенном условии (см. выше) для любых чисел, а теорема о почленном умножении (в форме, изложенной в справочном реферате № 5) только для положительных чисел; теоремы о почленном вычитании и почленном делении числовых неравенств не изучены, поэтому в тех случаях, когда необходимо оценить разность или пропорцию выражений, эти выражения представляют в виде суммы или произведения, соответственно, а затем при определенных условиях использовать свойства почленного сложения и умножения числовых неравенств. VI. Формирование навыков устные упражнения 1. Сложить почленные неравенства: 1) а > 2, б > 3; 2) с-2, д 4. Или одни и те же неравенства можно почленно умножать? Обоснуйте ответ. 2. Умножить неравенства почленно: 1) а > 2, б > 0,3; 2) в > 2, г > 4. Или можно такие же неровности добавить? Обоснуйте ответ. 3. Определите и обоснуйте, верно ли утверждение, что если 2 а 3, 1 б 2, то: 1) 3 а + б 5; 2) 2 аб 6; 3) 2 — 1 а — б 3 — 2; Письменные упражнения Для достижения дидактической цели урока следует решить упражнения следующего содержания: 1) сложить и умножить почленно эти числовые неравенства; 2) оценивает значение суммы, разности, произведения и частного двух выражений по заданным оценкам каждого из этих чисел; 3) оценивают значение выражений, содержащих эти буквы, по оценкам каждой из этих букв; 4) доказывает неравенство, используя теоремы почленного сложения и умножения для числовых неравенств и используя классические неравенства; 5) повторить изученные на предыдущих уроках свойства числовых неравенств. Методический комментарий Письменные упражнения, которые предлагаются для решения на данном этапе урока, должны способствовать выработке устойчивых навыков почленного сложения и умножения неравенств в простых случаях. (При этом очень важный момент: проверка соответствия записи неравенств в условии теоремы и правильности записи суммы и произведения левой и правой частей неравенств. Подготовительная работа проводится в ходе выполнение устных упражнений.) Для лучшего усвоения материала необходимо требовать от учащихся воспроизведения изученных теорем при комментировании действий. После того, как учащиеся успешно проработают теоремы в простых случаях, они могут постепенно переходить к более сложным случаям (для вычисления разности и частного двух выражений и более сложных выражений). На этом этапе работы учитель должен внимательно следить за тем, чтобы учащиеся не допускали типичных ошибок, пробуя разницу и оценивая долю за собственными ложными правилами. Также на уроке (разумеется, если позволяет время и уровень усвоения содержания материала учащимися) следует уделить внимание упражнениям по применению изученных теорем для доказательства более сложных неравенств. VII. Краткое содержание урока Известно, что 4 на 5; 6 б 8. Найдите неверные неравенства и исправьте ошибки. Обоснуйте ответ. 1) 10 а + б 13; 2) -4 а — б -1; 3) 24 аб 13; 4) ; 5) ; 7) 100 а2 + Ь 2 169? VIII. Домашнее задание 1. Изучить теоремы о почленном сложении и умножении числовых неравенств (с уточнением). 2. Выполнять упражнения репродуктивного характера, аналогичные тем, что выполняются на уроках. 3. Для повторения: упражнения на применение определения сравнения чисел (на приведение неправильностей и на сравнение выражений). | ||||||
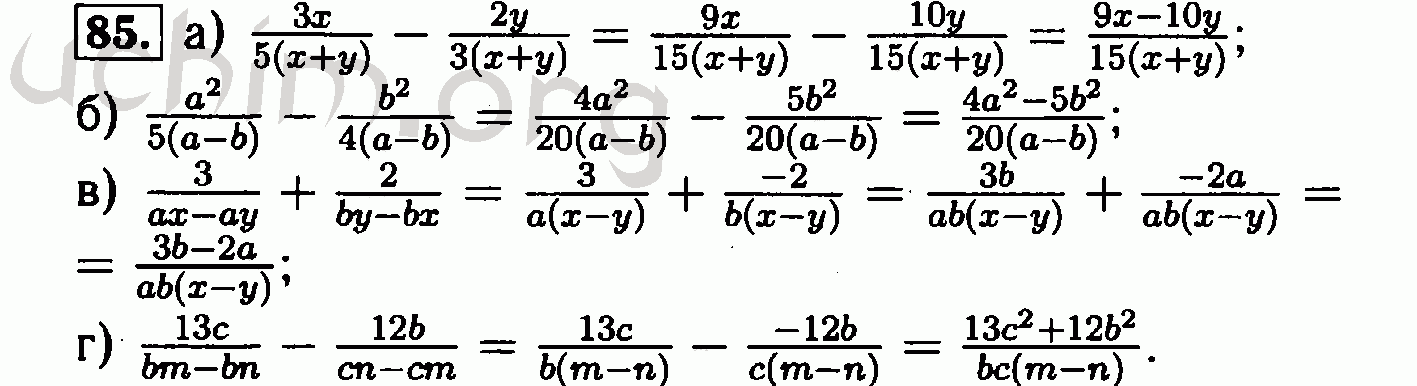Таким образом, учащиеся осознают наличие противоречия между полученными ими к этому моменту знаниями и необходимостью решения определенной задачи.
Формирование знаний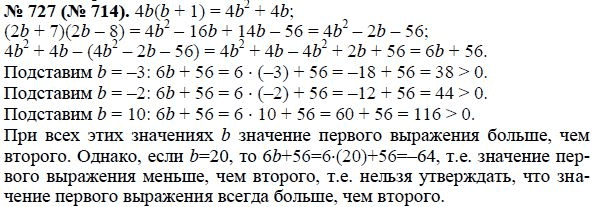
Если 0 a b , то an bn , где n — натуральное число.
(2)
Поэтому, чтобы не допустить ошибок в формировании знаний учащихся по данному вопросу путем демонстрации примеров и контрпримеров, учителю следует акцентировать внимание на следующих моментах: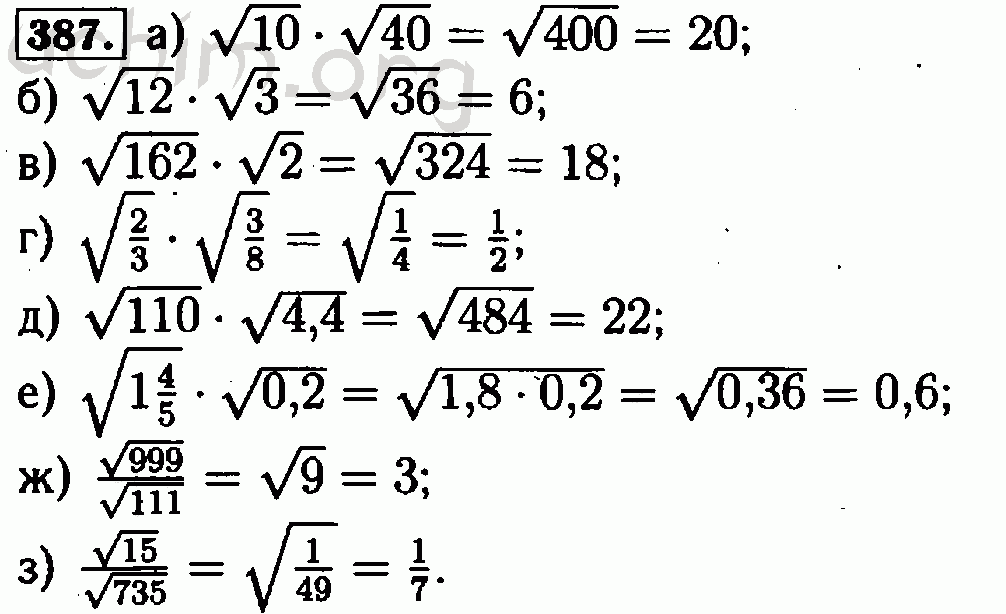
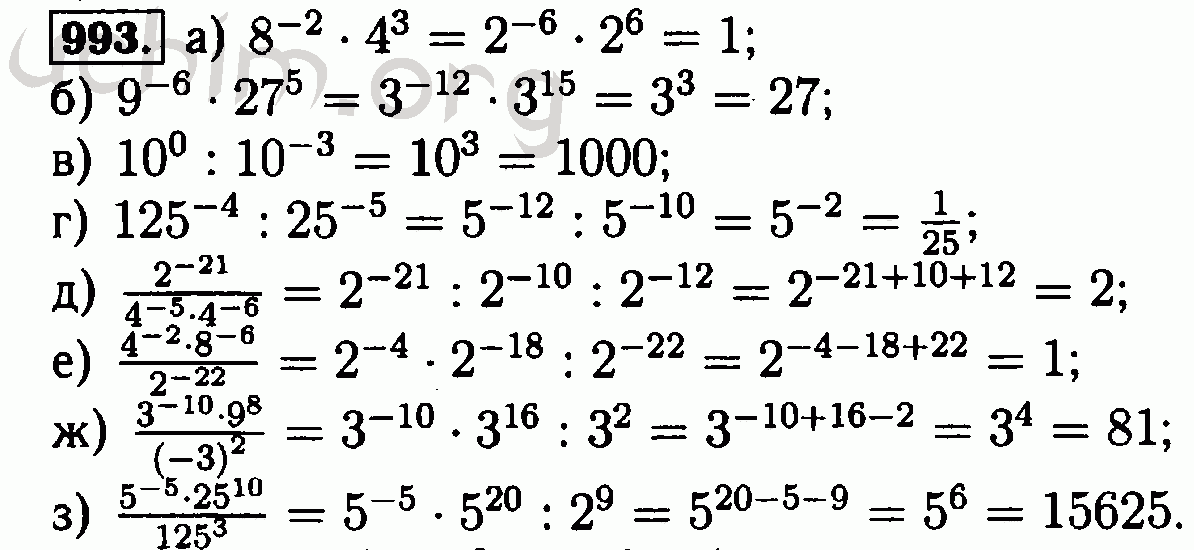
Среди минусов — излишняя обидчивость и частые перепады настроения, негативное влияние которых компенсируется оптимизмом тройки. 35 в общих чертах олицетворяет творческую энергию, благоприятные возможности, стремление перемениться местами.
Цели: Помните! Кравченко Г. М. Примеры:
B-c>0. Числовые неравенства. Нестрогий. Свойства числовых неравенств. Примеры: Если a b, то a-5>b-5. A>0 означает, что a — положительное число;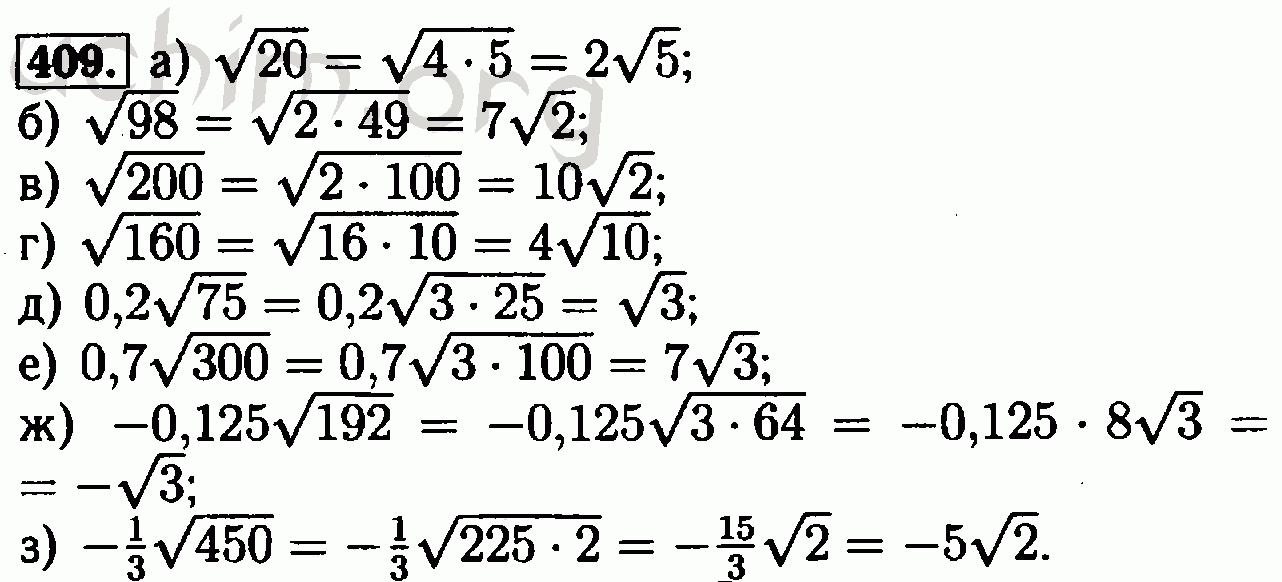 
Основное свойство дроби. Сокращение фракции. 7
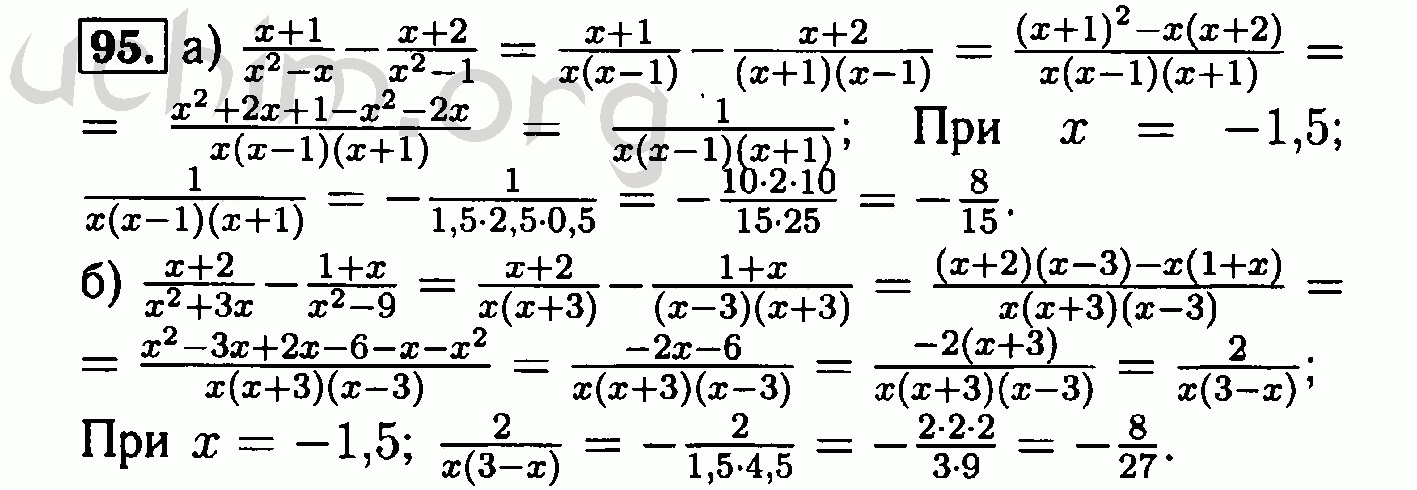Биквадратные уравнения 51
Определение квадратичной функции 99
Решение уравнений вида х2-а 127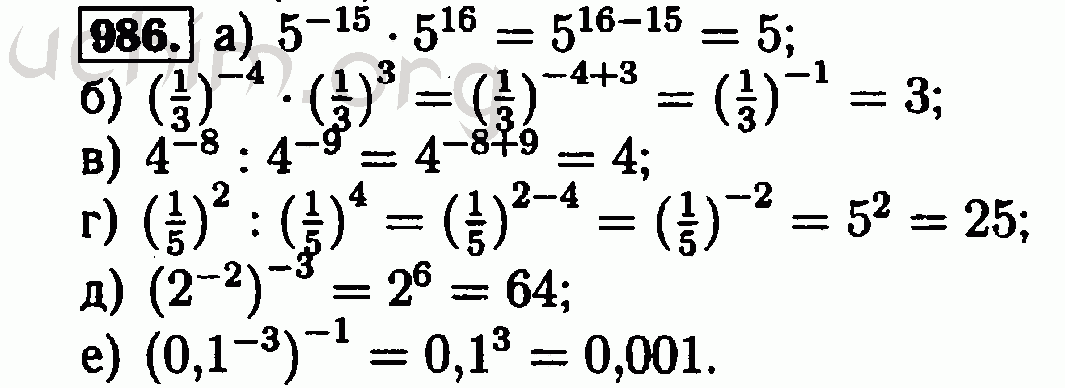
Сравнение номеров (обзор) 158