Решебник по алгебре за 8 класс, ответы онлайн
- ГДЗ
- 8 класс
- Алгебра
Алгебра 8 класс Учебник, Задачник
Авторы: Мордкович А.Г. Александрова Л.А.
Алгебра 8 класс рабочая тетрадь
Авторы: Колягин Ю. М. Ткачева М.
 В.
В.Алгебра 8 класс дидактические материалы
Авторы: Жохов В.И. Макарычев Ю.Н.
Алгебра 8 класс
Авторы: Ю.Н. Макарычев Н.Г. Миндюк
Алгебра 8 класс самостоятельные и контрольные работы, геометрия
Авторы: А.П. Ершова В.В. Голобородько
Алгебра 8 класс
Авторы: Г.В. Дорофеев С.Б. Суворова
Алгебра 8 класс
Авторы: С.
 М. Никольский М.К. Потапов
М. Никольский М.К. ПотаповАлгебра 8 класс
Авторы: Ш.А. Алимов Ю.М. Колягин
Алгебра 8 класс
Авторы: Е.П. Кузнецова Г.Л. Муравьева
Алгебра 8 класс
Авторы: А.Г. Мерзляк В.Б. Полонский
Алгебра 8 класс
Авторы: Г.К. Муравин К.С. Муравин
Алгебра 8 класс
Автор: Истер О.С.

Алгебра 8 класс
Авторы: Бевз Г.П. Бевз В.Г.
Алгебра 8 класс
Авторы: Мерзляк А.Г. Полонский В.Б.
Алгебра 8 класс сборник задач и контрольных работ
Авторы: А.Г. Мерзляк В.Б. Полонський
Алгебра 8 класс
Авторы: Біляніна О.Я. Кінащук Н.Л.
Алгебра 8 класс сборник задач
Авторы: Кузнецова Е.
 П. Муравьева Г.Л.
П. Муравьева Г.Л.Алгебра 8 класс итоговые контрольные работы
Авторы: Мерзляк А.Г. Полонский В.Б
Алгебра 8 класс
Авторы: Ю.Н. Макарычев Н.Г. Миндюк
Алгебра 8-9 класс задачник
Авторы: Галицкий М.Л. Гольдман А.М.
Алгебра 8 класс дидактические материалы
Авторы: Мерзляк А.Г. Полонский В.
 Б.
Б.Алгебра 8 класс задачник
Авторы: А.Г. Мордкович Л.И. Звавич
-
Алгебра 8 класс
Авторы: Мерзляк А.Г. Поляков В.М.
Алгебра 8 класс
Авторы: Петерсон Л.Г. Агаханов Н.Х.
Алгебра 7-9 класс контрольные работы
Автор: Мордкович А.Г.
Алгебра 8 класс дидактические материалы
Автор: Попов М.
 А.
А.Авторы: Звавич Л.И. Дьяконова Н.В.
Алгебра 8 класс дидактические материалы
Авторы: Ткачева М.В. Федорова Н.Е.
Алгебра 8 класс
Авторы: Колягин Ю.М. Ткачева М.В.
Алгебра 8 класс контрольно-измерительные материалы
Автор: Черноруцкий В.В.
Алгебра 8 класс контрольные работы
Авторы: Кузнецова Л.
 В. Минаева С.С.
В. Минаева С.С.Алгебра 8 класс контрольные работы
Автор: Александрова Л.А.
Алгебра 8 класс самостоятельные работы
Автор: Александрова Л.А.
Алгебра 8 класс самостоятельные работы
Автор: Александрова Л.А.
Авторы: Арефьева И.Г. Пирютко О.Н.
Алгебра 8 класс тематические тесты
Авторы: Чулков П.
 В. Струков Т.С.
В. Струков Т.С.
Алгебра 8 класс дидактические материалы
Автор: Потапов М.К.
Алгебра 8 класс самостоятельные и контрольные работы
Авторы: Мерзляк А.Г. Полонский В.В.
Алгебра 8 класс тематические тесты ОГЭ
Авторы: Дудницын Ю.П. Кронгауз В.Л.
Алгебра 8 класс дидактические материалы
Авторы: Евстафьева Л.
 П. Карп А.П.
П. Карп А.П.Алгебра 8 класс тематические тесты ОГЭ
Авторы: Кузнецова Л.В. Минаева С.С.
Алгебра 7-9 класс тесты
Авторы: Мордкович А.Г. Тульчинская Е.Е.
Алгебра 8 класс тематические тесты ОГЭ
Автор: Ткачева М.В.
Алгебра 8 класс рабочая тетрадь
Авторы: Миндюк Н.Г. Шлыкова И.С.
Алгебра 8 класс рабочая тетрадь
Авторы: Минаева С.
 С. Рослова Л.О.
С. Рослова Л.О.Алгебра 8 класс рабочая тетрадь
Авторы: Мерзляк А.Г. Полонский В.Б.
Алгебра 8 класс рабочая тетрадь
Авторы: Муравин Г.К. Муравина О.В.
Алгебра 8 класс рабочая тетрадь
Авторы: Зубарева И.И. Мильштейн М.С.
Алгебра 8 класс
Авторы: Тарасенкова Н.А. Богатырева И.М.
Алгебра 8 класс
Авторы: Кравчук В.
 Р. Пидручна М.В.
Р. Пидручна М.В.Алгебра 8 класс тестовый контроль знаний
Автор: Гальперина А.Р.
Алгебра 8 класс дидактические материалы
Автор: Феоктистов И.Е.
Алгебра 8 класс
Авторы: Бунимович Е.А. Кузнецова Л.В.
Алгебра 8 класс
Авторы: Абылкасымова А.Е. Кучер Т.П.
Алгебра 8 класс
Авторы: Шыныбеков А.
 Н. Шыныбеков Д.А.
Н. Шыныбеков Д.А.Алгебра 8 класс
Авторы: Мордкович А.Г. Семенов П.В.
Алгебра 8 класс рабочая тетрадь
Авторы: М.К. Потапов А.В. Шевкин
Алгебра 8 класс контрольные работы
Автор: Шуркова М.В.
Алгебра 8 класс задачник-тренажёр
Авторы: Е.А. Бунимович Л.В. Кузнецова
Алгебра 8 класс рабочая тетрадь
Автор: Шуркова М.
 В.
В.
Алгебра 8 класс Тетрадь контрольных тестовых работ
Автор: В.И. Стокоз
Алгебра 8 класс тесты
Авторы: С.Г. Журавлев В.В. Ермаков
Алгебра 8 класс тесты
Авторы: Е.М. Ключникова И.В. Комиссарова
Алгебра 8 класс тесты
Авторы: Ю.А. Глазков М.Я. Гаиашвили
Алгебра 8 класс контрольные работы
Авторы: Ю.
 П. Дудницын B.Л. Кронгауз
П. Дудницын B.Л. КронгаузАлгебра 8 класс рабочая тетрадь
Автор: Т.М. Ерина
Алгебра 8 класс практикум
Автор: Левитас Г.Г.
Алгебра 8 класс
Авторы: Солтан Г.Н. Солтан А.Е.
Алгебра 8 класс рабочая тетрадь
Авторы: Журавлев С.Г. Перепелкина Ю.В.
Алгебра 8 класс контрольные и самостоятельные работы
Автор: Попов М.
 А.
А.Алгебра 8 класс дидактические материалы
Авторы: Зив Б.Г. Гольдич В.А.
Алгебра 8 класс рабочая тетрадь
Авторы: Ключникова Е.М. Комиссарова И.В.
Алгебра 8 класс Контрольные измерительные материалы
Авторы: Ю. А. Глазков М. Я. Гаиашвили
Алгебра 8 класс самостоятельные и контрольные работы
Авторы: Глазков Ю.
 А. Гаиашвили М.Я.
А. Гаиашвили М.Я.Алгебра 8 класс Контрольные работы (из Методического пособия)
Авторы: Буцко Е.В. Мерзляк А.Г.
Алгебра 8 класс Математические диктанты, Контрольные работы (из Методического пособия)
Авторы: Буцко Е.В. Мерзляк А.Г.
Алгебра 8 класс Поурочные разработки (контрольные работы)
Автор: Рурукин А.Н.
Алгебра 8 класс тематические проверочные работы
Автор: Александрова Л.
 А.
А.
Алгебра Алимов 8 класс 2019 Упражнение 573 Решебники, ГДЗ TUV
Повторение курса Алгебры 7 класса
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28ГЛАВА I.
 АЛГЕБРАИЧЕСКИЕ ДРОБИ И ДЕЙСТВИЯ НАД НИМИ
АЛГЕБРАИЧЕСКИЕ ДРОБИ И ДЕЙСТВИЯ НАД НИМИ§1. Алгебраические выражения
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16§2.
 Алгебраическая дробь. Сокращение дробей 21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
Алгебраическая дробь. Сокращение дробей 21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45§3.
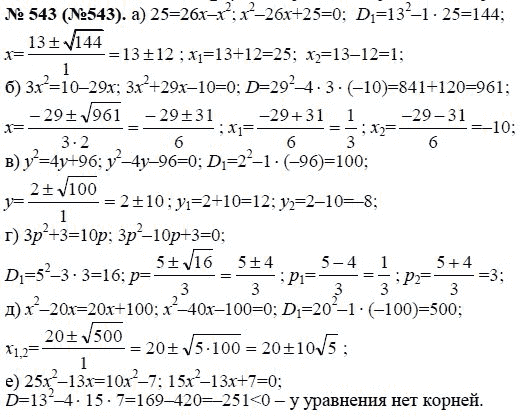 Приведение дробей к общему знаменателю 46
47
48
49
50
51
52
53
Приведение дробей к общему знаменателю 46
47
48
49
50
51
52
53§4.
 Сложение и вычитание алгебраических дробей 54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
Сложение и вычитание алгебраических дробей 54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73§5.
 Умножение и деление алгебраических дробей 74
75
76
77
78
79
80
81
82
83
84
85
86
Умножение и деление алгебраических дробей 74
75
76
77
78
79
80
81
82
83
84
85
86§6.
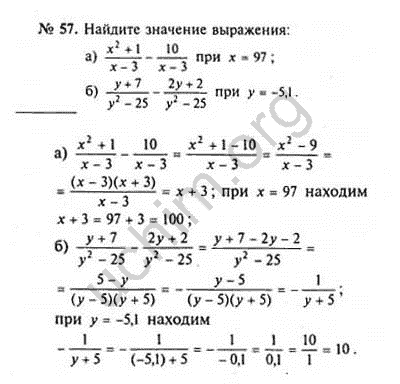 Замена дробно-рациональных выражений тождественными 87
88
89
90
91
92
93
94
95
96
Замена дробно-рациональных выражений тождественными 87
88
89
90
91
92
93
94
95
96§7.
 Функция У = k/x . Ее свойства и график 97
98
99
100
101
102
103
104
Функция У = k/x . Ее свойства и график 97
98
99
100
101
102
103
104§8.
 Арифмерический корень натуральной степени и его свойства…. 106
107
108
109
110
111
112
113
114
Арифмерический корень натуральной степени и его свойства…. 106
107
108
109
110
111
112
113
114§9.
 Степень с рациональным показателем и его свойства 117
118
119
120
121
122
123
124
125
126
127
128
129
Степень с рациональным показателем и его свойства 117
118
119
120
121
122
123
124
125
126
127
128
129§10.
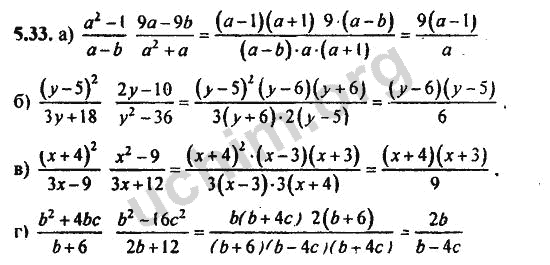 Упрощение алгебраических выражений, содержащих степень с рациональным показателем 130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
Упрощение алгебраических выражений, содержащих степень с рациональным показателем 130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145Упражнения к главе I
147 148 149 150 151 152 153 154 155 156 157 158 159Проверь себя
1 2 3 4 5 6Тестовые задания к главе I.
 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22ГЛАВА II НЕРАВЕНСТВА
§11.
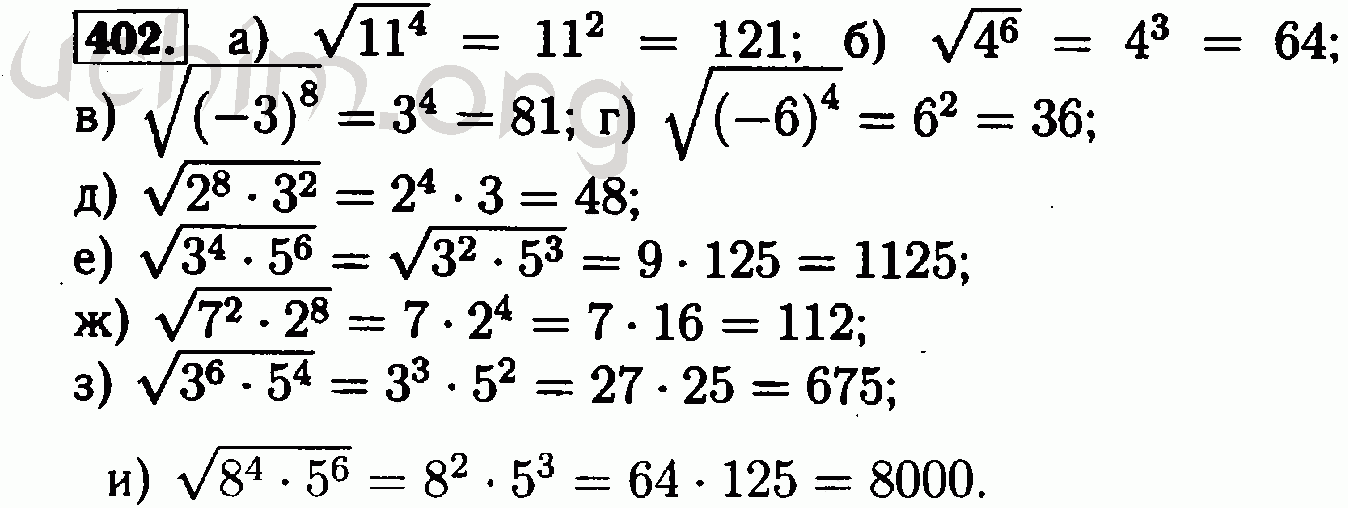 Числовые неравенства 178
179
180
181
182
183
Числовые неравенства 178
179
180
181
182
183§12. Основые свойства числовых неравенств
184 185 186 187 188 189 190 191 192 193 194§13.
 Сложение и умножение неравенств 196
197
199
200
201
202
204
205
206
207
208
209
Сложение и умножение неравенств 196
197
199
200
201
202
204
205
206
207
208
209§14.
 Возведение числовых неравенств в степень 211
212
213
214
215
216
217
218
Возведение числовых неравенств в степень 211
212
213
214
215
216
217
218§15.
 Неравенство с одним неизвестным 219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
Неравенство с одним неизвестным 219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240§16.
 Системы неравенств с одним неизвестным. Числовые промежутки..94 241
Системы неравенств с одним неизвестным. Числовые промежутки..94 241§16. Системы неравенств с одним неизвестным. Числовые промежутки..95
242§16. Системы неравенств с одним неизвестным. Числовые промежутки..96
243§16. Системы неравенств с одним неизвестным. Числовые промежутки..97
244§16.
 Системы неравенств с одним неизвестным. Числовые промежутки..98 245
Системы неравенств с одним неизвестным. Числовые промежутки..98 245§16. Системы неравенств с одним неизвестным. Числовые промежутки..99
246§16. Системы неравенств с одним неизвестным. Числовые промежутки..100
247§16. Системы неравенств с одним неизвестным. Числовые промежутки..101
248§16.
 Системы неравенств с одним неизвестным. Числовые промежутки..102 249
Системы неравенств с одним неизвестным. Числовые промежутки..102 249§16. Системы неравенств с одним неизвестным. Числовые промежутки..103
250§16. Системы неравенств с одним неизвестным. Числовые промежутки..104
251§16. Системы неравенств с одним неизвестным. Числовые промежутки..105
252§16.
 Системы неравенств с одним неизвестным. Числовые промежутки..106 253
Системы неравенств с одним неизвестным. Числовые промежутки..106 253§16. Системы неравенств с одним неизвестным. Числовые промежутки..107
254§16. Системы неравенств с одним неизвестным. Числовые промежутки..108
255§16. Системы неравенств с одним неизвестным. Числовые промежутки..109
256§16.
 Системы неравенств с одним неизвестным. Числовые промежутки..110 257
Системы неравенств с одним неизвестным. Числовые промежутки..110 257§16. Системы неравенств с одним неизвестным. Числовые промежутки..111
258§16. Системы неравенств с одним неизвестным. Числовые промежутки..112
259§16. Системы неравенств с одним неизвестным. Числовые промежутки..113
260§16.
 Системы неравенств с одним неизвестным. Числовые промежутки..114 261
Системы неравенств с одним неизвестным. Числовые промежутки..114 261§16. Системы неравенств с одним неизвестным. Числовые промежутки..115
262§16. Системы неравенств с одним неизвестным. Числовые промежутки..116
263§16. Системы неравенств с одним неизвестным. Числовые промежутки..117
264§16.
 Системы неравенств с одним неизвестным. Числовые промежутки..118 265
Системы неравенств с одним неизвестным. Числовые промежутки..118 265§17. Модуль числа. Уравнения и неравенства, содержащие модуль
267 268 269 270 271 272 273 274 275 276 277 278 279§18.
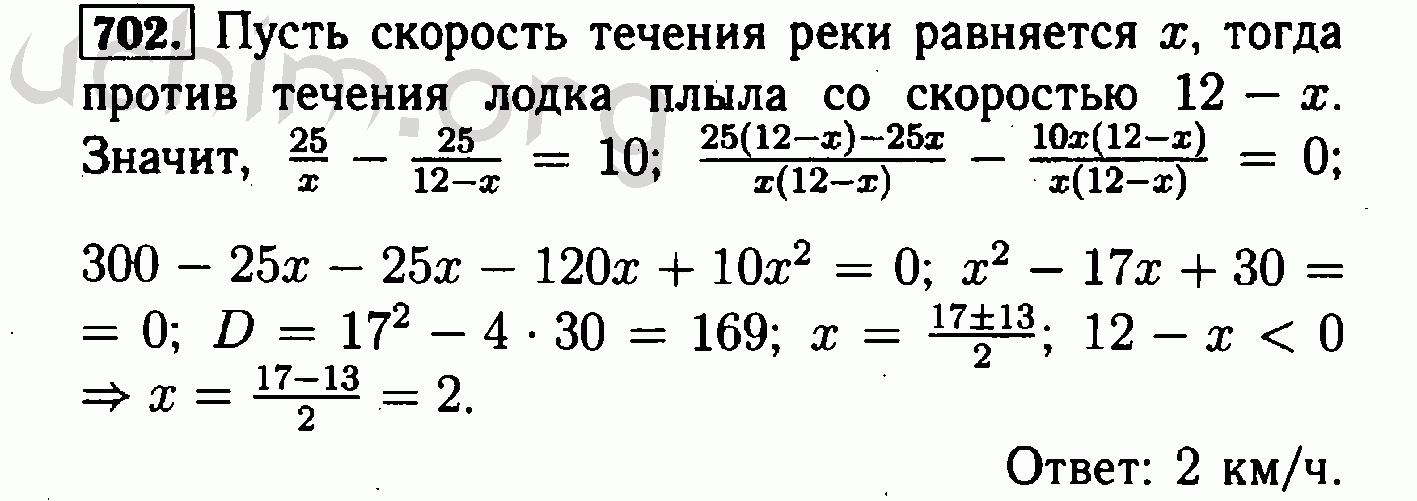 Приближенные вычисления, приближенные значения величин. Погрешность приближения §19. Оценка погрешностей, 282
283
284
285
286
287
Приближенные вычисления, приближенные значения величин. Погрешность приближения §19. Оценка погрешностей, 282
283
284
285
286
287§20.
 Округление чисел 288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
Округление чисел 288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304§21.
 Относительная погрешность 305
306
307
308
309
310
311
Относительная погрешность 305
306
307
308
309
310
311Упражнения к главе II.
 312
313
314
315
316
317
318
319
320
321
322
323
324
325
327
328
329
312
313
314
315
316
317
318
319
320
321
322
323
324
325
327
328
329Проверь себя
1 2 3Тестовые задания к главе II
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25ГЛАВА III КВАДРАТНЫЕ УРАВНЕНИЯ
§22.
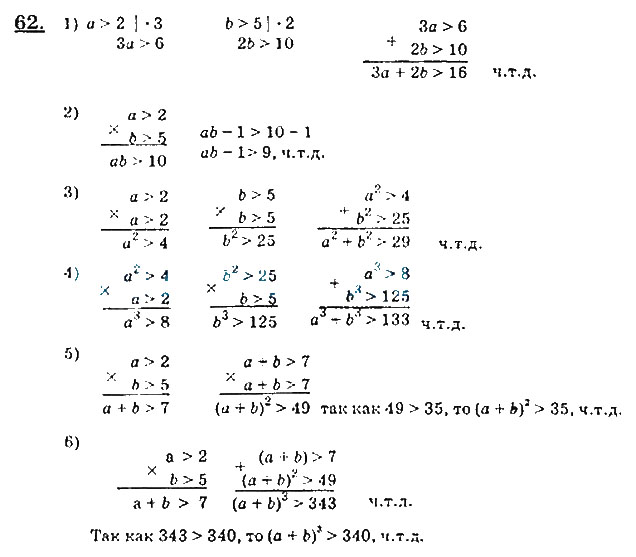 Квадратные уравнения и их корни 345
346
347
350
352
Квадратные уравнения и их корни 345
346
347
350
352§23. Неполные квадратные уравнения и их решение
353 354 355 356 357 358§24.
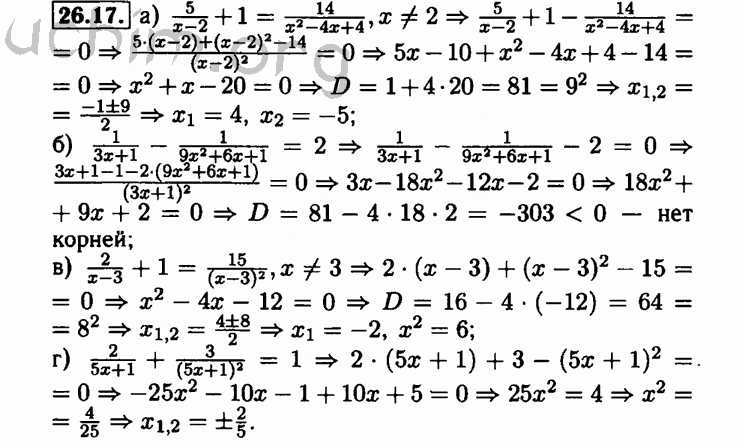 Формулы нахождения корней квадратного уравнения. 359
360
361
362
363
364
365
367
368
369
370
371
372
373
374
375
376
Формулы нахождения корней квадратного уравнения. 359
360
361
362
363
364
365
367
368
369
370
371
372
373
374
375
376§25.
 Теорема Виета. Разложение квадратного трехчлена на линейные множители 381
382
383
384
385
386
387
388
Теорема Виета. Разложение квадратного трехчлена на линейные множители 381
382
383
384
385
386
387
388§26.
 Биквадратные уравнения. Уравнения, сводящиеся к квадратным. 389
390
391
392
393
394
395
396
397
398
399
400
401
Биквадратные уравнения. Уравнения, сводящиеся к квадратным. 389
390
391
392
393
394
395
396
397
398
399
400
401§27.
 Решение задач с помощью квадратных уравнений 402
403
404
405
406
407
408
409
410
411
412
Решение задач с помощью квадратных уравнений 402
403
404
405
406
407
408
409
410
411
412Упражнения к главе III
413 414 415 416 417 418 419 420 421 422 423 424 425 426 427 428 429 430 431 432Проверь себя
1 2 3Тестовые задания к главе III
1 2 3 4 5 6 7 8 9 10 11 12 13 14Исторические задачи
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31Практические и межпредметные задачи
433 439 440 441 442 444 445 452 453 455 456 457 458 459 460 461 462 463 464 465 466ГЛАВА IV АНАЛИЗ ДАННЫХ
§28.
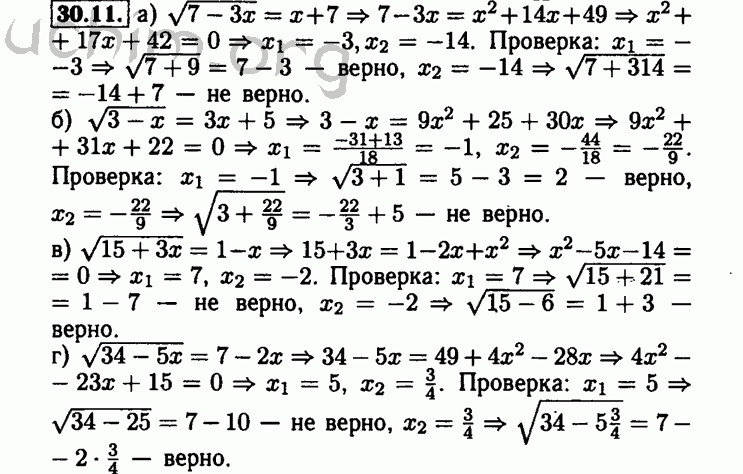 Анализ данных. Представление данных 467
468
469
470
471
472
Анализ данных. Представление данных 467
468
469
470
471
472§29. Среднее значение. Мода. Медиана
475 476 477 478 479 480 481§30.
 Решение комбинаторных задач методом перебора 482
483
484
485
486
487
488
489
490
491
Решение комбинаторных задач методом перебора 482
483
484
485
486
487
488
489
490
491§31.
 Основной закон комбинаторики и его применение при решении задач 492
493
494
495
496
497
498
499
500
501
503
504
505
506
507
508
509
510
511
512
513
514
515
Основной закон комбинаторики и его применение при решении задач 492
493
494
495
496
497
498
499
500
501
503
504
505
506
507
508
509
510
511
512
513
514
515Упражнения к главе IV
516 517 518 519 520 521 522 523 524 525 527 528 529 530Тестовые задания к главе IV
1 2 3 4 5 6 7 8 9 10 11 12 13 14Практические и межпредметные задачи
531 532 535 537 538 540 541 542 543Упражнения для повторения курса „Алгебры“ 8 класса
544 545 546 547 548 549 550 551 552 553 556 557 558 559 560 561 562 563 564 565 566 567 568 569 570 571 572 573 574 575 576 577 578 579 580 581 582 583 584 585 586 587 588 589 590 591 592ГДЗ Решебник Алгебра 8 класс Учебник «Просвещение» Макарычев, Миндюк, Нешков.
 ГДЗ Решебник Алгебра 8 класс Учебник «Просвещение» Макарычев, Миндюк, Нешков.
ГДЗ Решебник Алгебра 8 класс Учебник «Просвещение» Макарычев, Миндюк, Нешков.Алгебра 8 классУчебникМакарычев, Миндюк, Нешков«Просвещение»
Зачастую обучение в школе проходит не так гладко, как хотелось бы большинству родителей. Да это и не удивительно, учитывая сложность учебной программы. Поэтому учащимся может весьма пригодится решебник к учебнику «Алгебра 8 класс Учебник, авторы: Макарычев, Миндюк, Нешков» от издательства Просвещение, которое входит в серии УМК «». В сборнике подробно приводятся решения всех заданий, которые так же сопровождаются условиями.
ГДЗ «Алгебра 8 класс Учебник, авторы: Макарычев, Миндюк, Нешков» поможет преодолеть множество трудностей в ходе обучения:
- дополнить и углубить свои познания;
- разобраться в мельчайших аспектах предмета Алгебра;
- исправить допущенные ошибки;
- повысить успеваемость.
Делитесь решением с друзьями, оставляйте комментарии — они помогают нам становится лучше!
Контрольные вопросы и задания
стр. 17стр. 28стр. 49стр. 73стр. 88стр. 96стр. 105стр. 139стр. 148стр. 178стр. 202стр. 225стр. 241
17стр. 28стр. 49стр. 73стр. 88стр. 96стр. 105стр. 139стр. 148стр. 178стр. 202стр. 225стр. 241Упражнения
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495969798991001011021031041051061071081091101111121131141151161171181191201211221231241251261271281291301311321331341351361371381391401411421431441451461471481491501511521531541551561571581591601611621631641651661671681691701711721731741751761771781791801811821831841851861871881891901911921931941951961971981992002012022032042052062072082092102112122132142152162172182192202212222232242252262272282292302312322332342352362372382392402412422432442452462472482492502512522532542552562572582592602612622632642652662672682692702712722732742752762772782792802812822832842852862872882892902912922932942952962972982993003013023033043053063073083093103113123133143153163173183193203213223233243253263273283293303313323333343353363373383393403413423433443453463473483493503513523533543553563573583593603613623633643653663673683693703713723733743753763773783793803813823833843853863873883893903913923933943953963973983994004014024034044054064074084094104114124134144154164174184194204214224234244254264274284294304314324334344354364374384394404414424434444454464474484494504514524534544554564574584594604614624634644654664674684694704714724734744754764774784794804814824834844854864874884894904914924934944954964974984995005015025035045055065075085095105115125135145155165175185195205215225235245255265275285295305315325335345355365375385395405415425435445455465475485495505515525535545555565575585595605615625635645655665675685695705715725735745755765775785795805815825835845855865875885895905915925935945955965975985996006016026036046056066076086096106116126136146156166176186196206216226236246256266276286296306316326336346356366376386396406416426436446456466476486496506516526536546556566576586596606616626636646656666676686696706716726736746756766776786796806816826836846856866876886896906916926936946956966976986997007017027037047057067077087097107117127137147157167177187197207217227237247257267277287297307317327337347357367377387397407417427437447457467477487497507517527537547557567577587597607617627637647657667677687697707717727737747757767777787797807817827837847857867877887897907917927937947957967977987998008018028038048058068078088098108118128138148158168178188198208218228238248258268278288298308318328338348358368378388398408418428438448458468478488498508518528538548558568578588598608618628638648658668678688698708718728738748758768778788798808818828838848858868878888898908918928938948958968978988999009019029039049059069079089099109119129139149159169179189199209219229239249259269279289299309319329339349359369379389399409419429439449459469479489499509519529539549559569579589599609619629639649659669679689699709719729739749759769779789799809819829839849859869879889899909919929939949959969979989991000100110021003100410051006100710081009101010111012101310141015101610171018101910201021102210231024102510261027102810291030103110321033103410351036103710381039104010411042104310441045104610471048104910501051105210531054105510561057105810591060106110621063106410651066106710681069107010711072107310741075107610771078107910801081108210831084108510861087108810891090109110921093109410951096109710981099110011011102110311041105110611071108110911101111111211131114111511161117111811191120112111221123112411251126112711281129113011311132113311341135113611371138113911401141114211431144114511461147114811491150115111521153Похожие ГДЗ Алгебра 8 класс
Алгебра 8 классДидактические материалыЖохов, Макарычев, Миндюк«Просвещение»
Алгебра 8 классУчебник (Углубленный уровень)Макарычев, Миндюк, Нешков, Феоктистов«Мнемозина»
Алгебра 8 классУчебник (Углубленный уровень)Макарычев, Миндюк, Нешков«Просвещение»
Контрольные вопросы и задания: стр.
 17
17Предыдущее
Следующее
Условие
Решебник №1
Решебник №2
Решебник №3
Решебник №4
Решебник №5
Предыдущее
Следующее
закрытьГДЗ и решебники
ГДЗ по алгебре для 8 класса от Спиши фан
Решебник по алгебре 8 класс Ш.А. Алимов
Авторы: Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров
Рабочая Тетрадь по алгебре 8 класс Муравин Г.К.
Авторы: Муравин Г.К., Муравина О.В.
Решебник по алгебре 8 класс Г.
 К. Муравин
К. МуравинАвторы: Г.К. Муравин, К.С. Муравин, О.В. Муравина
Рабочая Тетрадь по алгебре 8 класс Минаева С.С.
Авторы: Минаева С.С., Рослова Л.О.
Сборник Задач по алгебре 8 класс Кузнецова Е.П.
Авторы: Кузнецова Е.П., Муравьева Г.Л., Шнеперман Л.Б.
Решебник по алгебре 8 класс Ю.Н. Макарычев, Углубленный уровень
Авторы: Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, И.Е. Феоктистов
org/Book»>Рабочая Тетрадь по алгебре 8 класс Колягин Ю. М.
Авторы: Колягин Ю. М., Ткачева М. В., Федорова Н.Е.
Контрольные Работы по алгебре 8 класс Мерзляк А.Г.
Авторы: Мерзляк А.Г., Полонский В.Б, Прокопенко Н.С., Якир М.С.
Решебник по алгебре 8 класс Г.В. Дорофеев
Авторы: Г.В. Дорофеев, С.Б. Суворова, Е.А. Бунимович, Л.В. Кузнецова, С.С. Минаева, Л.О. Рослова
Решебник по алгебре 8 класс Мерзляк А.Г.
Авторы: Мерзляк А.Г., Полонский В.
 Б., Якир М.С.
Б., Якир М.С.Задачник по алгебре 8 класс Мордкович А.Г., Базовый уровень
Авторы: Мордкович А.Г., Александрова Л.А., Тульчинская Е.Е., Мишустина Т.Н.
Решебник по алгебре 8 класс А.Г. Мерзляк
Авторы: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир
Решебник по алгебре 8 класс Біляніна О.Я.
Авторы: Біляніна О.Я., Кінащук Н.Л., Черевко І.М.
Решебник по алгебре 8 класс Истер О.
 С.
С.Автор: Истер О.С.
Решебник по алгебре 8 класс Е.П. Кузнецова
Авторы: Е.П. Кузнецова, Г.Л. Муравьева, Л.Б. Шнеперман, Б.Ю. Ящин
Решебник по алгебре 8 класс С.М. Никольский
Авторы: С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин
Решебник по алгебре 8 класс Бевз Г.П.
Авторы: Бевз Г.П., Бевз В.Г.
Сборник Задач по алгебре 8 класс А.
 Г. Мерзляк
Г. МерзлякАвторы: А.Г. Мерзляк, В.Б. Полонський, Ю.М. Рабінович, М.С. Якір
Решебник по алгебре 8 класс Ю.Н. Макарычев
Авторы: Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова
Дидактические Материалы по алгебре 8 класс Жохов В.И.
Авторы: Жохов В.И., Макарычев Ю.Н., Миндюк Н.Г.
Самостоятельные И Контрольные Работы по алгебре 8 класс А.П. Ершова
Авторы: А.П. Ершова, В.В. Голобородько, А.С. Ершова
org/Book»>Дидактические Материалы по алгебре 8 класс Мерзляк А.Г.
Авторы: Мерзляк А.Г., Полонский В.Б., Рабинович М.С., Якир М.С.
Задачник по алгебре 8 класс А.Г. Мордкович, Углубленный уровень
Авторы: А.Г. Мордкович, Л.И. Звавич, А.Р. Рязановский, Л.А. Александрова
Сборник Задач по алгебре 8 класс Галицкий М.Л.
Авторы: Галицкий М.Л., Гольдман А.М., Звавич Л.И.
Решебник по алгебре 8 класс Мерзляк А.Г., Углубленный уровень
Авторы: Мерзляк А.
 Г., Поляков В.М.
Г., Поляков В.М.Решебник по алгебре 8 класс Петерсон Л.Г.
Авторы: Петерсон Л.Г., Агаханов Н.Х., Петрович А.Ю.
Контрольные Работы по алгебре 8 класс Мордкович А.Г., Углубленный уровень
Автор: Мордкович А.Г.
Дидактические Материалы по алгебре 8 класс Попов М.А.
Автор: Попов М.А.
Дидактические Материалы по алгебре 8 класс Звавич Л.
 И.
И.Авторы: Звавич Л.И., Дьяконова Н.В.
Дидактические Материалы по алгебре 8 класс Ткачева М.В.
Авторы: Ткачева М.В., Федорова Н.Е., Шабунин М.И.
Решебник по алгебре 8 класс Колягин Ю.М.
Авторы: Колягин Ю.М., Ткачева М.В., Федорова Н.Е.
Контрольно-Измерительные Материалы (Ким) по алгебре 8 класс Черноруцкий В.В.
Автор: Черноруцкий В.В.
- org/Book»>
Контрольные Работы по алгебре 8 класс Александрова Л.А., Базовый уровень
Автор: Александрова Л.А.
Самостоятельные Работы по алгебре 8 класс Александрова Л.А., Базовый уровень
Автор: Александрова Л.А.
Самостоятельные Работы по алгебре 8 класс Александрова Л.А., Углубленный уровень
Автор: Александрова Л.А.
Контрольные Работы по алгебре 8 класс Кузнецова Л.В.
Авторы: Кузнецова Л.В., Минаева С.С., Рослова Л.О.
- org/Book»>
Тематические Тесты по алгебре 8 класс Чулков П.В.
Авторы: Чулков П.В., Струков Т.С.
Дидактические Материалы по алгебре 8 класс Потапов М.К.
Автор: Потапов М.К.
Самостоятельные И Контрольные Работы по алгебре 8 класс Мерзляк А.Г., Углубленный уровень
Авторы: Мерзляк А.Г., Полонский В.В., Рабинович Е.М.
Решебник по алгебре 8 класс Арефьева И.Г.
Авторы: Арефьева И.Г., Пирютко О.Н.
- org/Book»>
Дидактические Материалы по алгебре 8 класс Евстафьева Л.П.
Авторы: Евстафьева Л.П., Карп А.П.
Тематические Тесты по алгебре 8 класс Кузнецова Л.В.
Авторы: Кузнецова Л.В., Минаева С.С., Рослова Л.О.
Тесты по алгебре 8 класс Мордкович А.Г., Базовый уровень
Авторы: Мордкович А.Г., Тульчинская Е.Е.
Тематические Тесты по алгебре 8 класс Дудницын Ю.П.
Авторы: Дудницын Ю.П., Кронгауз В.Л.
- org/Book»>
Рабочая Тетрадь по алгебре 8 класс Миндюк Н.Г.
Авторы: Миндюк Н.Г., Шлыкова И.С.
Рабочая Тетрадь по алгебре 8 класс Мерзляк А.Г.
Авторы: Мерзляк А.Г., Полонский В.Б., Якир М.С.
Рабочая Тетрадь по алгебре 8 класс Зубарева И.И.
Авторы: Зубарева И.И., Мильштейн М.С.
Тематические Тесты по алгебре 8 класс Ткачева М.В.
Автор: Ткачева М.В.
- org/Book»>
Решебник по алгебре 8 класс Кравчук В.Р.
Авторы: Кравчук В.Р., Пидручна М.В., Янченко Г. М.
Тестовый Контроль Знаний по алгебре 8 класс Гальперина А.Р.
Автор: Гальперина А.Р.
Дидактические Материалы по алгебре 8 класс Феоктистов И.Е., Углубленный уровень
Автор: Феоктистов И.Е.
Решебник по алгебре 8 класс Тарасенкова Н.А.
Авторы: Тарасенкова Н.А., Богатырева И.М., Коломиец О.М., Сердюк З.О.
- org/Book»>
Решебник по алгебре 8 класс Абылкасымова А.Е.
Авторы: Абылкасымова А.Е., Кучер Т.П., Корчевский В.Е. ., Жумагулова З.А.
Решебник по алгебре 8 класс Шыныбеков А.Н.
Авторы: Шыныбеков А.Н., Шыныбеков Д.А., Жумабаев Р.Н.
Решебник по алгебре 8 класс Мордкович А.Г.
Авторы: Мордкович А.Г., Семенов П.В., Александрова Л.
 А., Мардахаева Е.Л.
А., Мардахаева Е.Л.
Решебник по алгебре 8 класс Бунимович Е.А.
Авторы: Бунимович Е.А., Кузнецова Л.В., Минаева С.С., Рослова Л.О.
Рабочая Тетрадь по алгебре 8 класс М.К. Потапов
Авторы: М.К. Потапов, А.В. Шевкин
Контрольные Работы по алгебре 8 класс Шуркова М.В.
Автор: Шуркова М.В.
Задачник-Тренажёр по алгебре 8 класс Е.А. Бунимович
Авторы: Е.А. Бунимович, Л.В. Кузнецова, С.С. Минаева, Л.О. Рослова
Рабочая Тетрадь по алгебре 8 класс Шуркова М.
 В.
В.Автор: Шуркова М.В.
Тетрадь Контрольных Тестовых Работ по алгебре 8 класс В.И. Стокоз
Автор: В.И. Стокоз
Тесты по алгебре 8 класс С.Г. Журавлев
Авторы: С.Г. Журавлев, В.В. Ермаков, Ю.В. Перепелкина, В.А. Свентковский
Тесты по алгебре 8 класс Е.М. Ключникова
Авторы: Е.М. Ключникова, И.В. Комиссарова
Тесты по алгебре 8 класс Ю.
 А. Глазков
А. ГлазковАвторы: Ю.А. Глазков, М.Я. Гаиашвили
Контрольные Работы по алгебре 8 класс Ю.П. Дудницын
Авторы: Ю.П. Дудницын, B.Л. Кронгауз
Рабочая Тетрадь по алгебре 8 класс Т.М. Ерина
Автор: Т.М. Ерина
Практикум по алгебре 8 класс Левитас Г.Г., Базовый уровень
Автор: Левитас Г.Г.
Решебник по алгебре 8 класс Солтан Г.
 Н.
Н.Авторы: Солтан Г.Н., Солтан А.Е., Жумадилова А.Ж.
Рабочая Тетрадь по алгебре 8 класс Журавлев С.Г.
Авторы: Журавлев С.Г., Перепелкина Ю.В.
Контрольные И Самостоятельные Работы по алгебре 8 класс Попов М.А.
Автор: Попов М.А.
Дидактические Материалы по алгебре 8 класс Зив Б.Г.
Авторы: Зив Б.Г., Гольдич В.А.
Рабочая Тетрадь по алгебре 8 класс Ключникова Е.
 М.
М.Авторы: Ключникова Е.М., Комиссарова И.В.
Контрольно-Измерительные Материалы (Ким) по алгебре 8 класс Ю. А. Глазков
Авторы: Ю. А. Глазков, М. Я. Гаиашвили, В. И. Ахременкова
Самостоятельные И Контрольные Работы по алгебре 8 класс Глазков Ю.А.
Авторы: Глазков Ю.А., Гаиашвили М.Я.
Контрольные Работы (Методическое Пособие) по алгебре 8 класс Буцко Е.В., Углубленный уровень
Авторы: Буцко Е.В., Мерзляк А.Г., Полонский В.Б., Якир М.С.
org/Book»>
Математические Диктанты, Контрольные Работы (Методическое Пособие) по алгебре 8 класс Буцко Е.В.
Авторы: Буцко Е.В., Мерзляк А.Г., Полонский В.Б., Якир М.С.
Поурочные Разработки по алгебре 8 класс Рурукин А.Н.
Автор: Рурукин А.Н.
Тематические Проверочные Работы по алгебре 8 класс Александрова Л.А.
Автор: Александрова Л.А.
Самостоятельные И Контрольные Работы по алгебре 8 класс Петерсон Л.Г.
Авторы: Петерсон Л.Г., Баханова О.
 В.
В.
Алгебра 8 класс, ответы на экзаменационные вопросы
- Файлы
- Абитуриентам и школьникам
- Математика
- Подготовка к экзамену по математике
Математика
6 класс
Алгебра
Геометрия
Для внеклассного чтения
Домашняя работа по математике
Задачники по математике для школьников
Математика в начальной школе
Подготовка к экзамену по математике
Школьные математические олимпиады
- формат doc
- размер 410 КБ
- добавлен
18 мая 2010 г.

Какую дробь называют рациональной? Приведите пример. Напишите формулу корней квадратного уравнения.
Дайте определение тождества. Приведите пример. Что называют дискриминантом квадратного уравнения? Сколько корней может иметь квадратное уравнение?
Сформулируйте и запишите основное свойство дроби. Что называется степенью с целым отрицательным показателем?
Сформулируйте правило об изменении знака перед дробью, приведите пример. Какую запись числа называют его стандартным видом?
Сформулируйте правило сложения дробей с одинаковыми знаменателями. Покажите на примере, как представить число в стандартном виде.
Сформулируйте правило вычитания дробей с одинаковыми знаменателями. Что означает запись икс равно а плюс минус эйч.
Как выполняют сложение и вычитание дробей с разными знаменателями?
Напишите формулу корней квадратного уравнения, в котором второй
коэффициент является четным числом.
Сформулируйте правило умножения рациональных дробей. Приведите пример целого уравнения и пример дробного рационального уравнения.
Сформулируйте правило возведения рациональной дроби в степень. Что называется решением неравенства? Что значит решить неравенство?
Сформулируйте правило деления рациональных дробей. Что называется решением системы неравенств? Что значит решить систему неравенств?
Какая функция называется обратной пропорциональностью? В каких координатных четвертях расположен ее график при ка больше нуля, при ка меньше нуля. Какое уравнение называют неполным квадратным уравнением? Приведите примеры неполных квадратных уравнений различных видов, сколько корней имеет уравнение каждого вида?
Какие числа образуют множество рациональных, иррациональных, действительных чисел? Сформулируйте теоремы, выражающие основные свойства числовых неравенств.
Сформулируйте определение арифметического квадратного корня. Как
решают дробное рациональное уравнение? Сформулируйте теоремы о
почленном сложении и о почленном умножении неравенств. Какова
область определения функции игрек равен корень квадратный из игрек?
Как расположен график этой функции в координатной плоскости?
Какова
область определения функции игрек равен корень квадратный из игрек?
Как расположен график этой функции в координатной плоскости?
Какое уравнение называют приведенным квадратным уравнением? Приведите примеры и расскажите как внести множитель под знак корня как вынести множитель из-под знака корня?
Покажите, как можно освободиться от иррациональности в знаменателе дроби Как округляют результат при сложении и вычитании приближенных значении
Сформулируйте определение квадратного уравнения. Как округляют результат при умножении и делении приближенных значений
Читать онлайн
Смотрите также
- формат pdf
- размер 3.14 МБ
- добавлен 08 января 2010 г.
Тип: Справочник. Издательство: Просвещение. Год издания: 2001. Домашняя работа по алгебре за 10 класс к учебнику «Алгебра и начала анализа 10-11 класс» Алимов Ш. А. и др., М.: «Просвещение», 2001 г.
Издательство: Просвещение. Год издания: 2001. Домашняя работа по алгебре за 10 класс к учебнику «Алгебра и начала анализа 10-11 класс» Алимов Ш. А. и др., М.: «Просвещение», 2001 г.
- формат djvu
- размер 3.92 МБ
- добавлен 05 января 2011 г.
Наименование: Алгебра. 9 класс: учеб. для учащихся общеобразоват. учреждений Авторы: Макарычев Ю. Н., Миндюк Н. Г., Нешков К. И., Феоктистов И. Е. 7-е издание, исправленное и дополненное Издательство: Мнемозина Дата выпуска: 2008 Листов (страниц): 447 ISBN: 978-5-346-01043-2 Книга представляет собой учебное пособие для школьников, которые обучаются в 9 классе. Настоящее пособие рассчитано на тех, кто углубленно изучает алгебру. Книга является з…
- формат djvu
- размер 3.17 МБ
- добавлен
11 февраля 2011 г.

10-е изд., испр. — М.: Мнемозина, 2010. — 384 с. Данный учебник предназначен для углубленного изучения алгебры в 8 классе и входит в комплект из трех книг: «Алгебра-7», «Алгебра-8» и «Алгебра-9». Его содержание полностью соответствует современным образовательным стандартам, а особенностями являются расширение и углубление традиционных учебных тем за счет теоретико-множественной, вероятностно-статистической и историко-культурной линий. В учебнике…
- формат djvu
- размер 3.08 МБ
- добавлен 30 марта 2010 г.
Книга: Алгебра и начала анализа. 10-11 класс. Учебник Автор: Мордкович А. Г. Издательство: Мнемозина Страниц: 335 Формат: DJVU Размер: 3.08 MB Качество: Отличное Язык: Русский Год издания: 2001
- формат djvu
- размер 2.21 МБ
- добавлен
23 ноября 2010 г.

Мордкович А. Г. Алгебра. 8 класс: учеб. для учащихся общеобразоват. учреждений. Издательство: Мнемозина. Год: 2008. Страниц: 240. ISBN: 978-5-346-01011-1. Это — учебник для классов с повышенным уровнем математической подготовки в общеобразовательных школах. Он написан в русле той концепции, которая использована в соответствующем учебнике А. Г. Мордковича для 8-го класса общеобразовательных учреждений, с соблюдением практически того же порядка сле…
- формат pdf
- размер 1.62 МБ
- добавлен 08 января 2010 г.
Учебно-практическое пособие. Страниц ч.1. 247 и ч.2. 45. к задачнику «Алгебра. 7 класс: Задачник для общеобразоват. учреждений. — 3-е изд., доработ. » А. Г. Мордкович и др. VI.: «Мнемозина», 2000 г. Часть I и 2.
- формат djvu
- размер 2.
 08 МБ
08 МБ - добавлен 06 июля 2010 г.
Мордкович А. Г., Николаев Н. П. Алгебра. 7 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений Издательство: Мнемозина Год: 2009 Страниц: 207 Это — вторая часть комплекта для изучения алгебры-7 для классов с повышенным уровнем математической подготовки в общеобразовательных школах (первая часть — учебник). Данный комплект адресован не специализированным математическим школам или классам с собственными авторскими программами…
- формат pdf
- размер 1.94 МБ
- добавлен 23 января 2010 г.
Ответы на все домашние контрольные работы и на все номера в задачнике 2000 года издания.
- формат djvu
- размер 2.17 МБ
- добавлен
15 июня 2011 г.

Алгебра: 9 класс: Дидактические материалы; Контрольные и самостоятельные работы; Краткие решения; Ответы Школа XXI в. 2004 г Пособие содержит тематические зачеты, контрольные и самостоятельные работы, а также дополнительные задачи по всем разделам курса алгебры 9 класса общеобразовательной школы.
ГДЗ,Алгебра,8 класс,Алимов Ш.А. – Рамблер/класс
621 вопрос
624 ответа
Помогите найти погрешность. Алгебра. 8 класс. Пар.№11. Упр.№202. Учебник Алимов Ш.А.
Здравствуйте! Известно, что сумма внутренних углов четырехугольника равна 360°. При нахождении суммы внутренних углов четырехугольника (Подробнее…)
ГДЗ8 классАлгебраАлимов Ш.А.
С задачкой поможете? Алгебра. 8 класс. Пар.№7. Упр.№108. Учебник Алимов Ш.А.
Здравствуйте! Сколько железнодорожных платформ потребуется для перевозки 183 контейнеров, если на одной платформе можно разместить не (Подробнее. 2 ≤ (Подробнее…)
2 ≤ (Подробнее…)
ГДЗ8 классАлгебраАлимов Ш.А.
Помогите вычислить. Алгебра. 8 класс. Пар.№23. Упр.№345. Учебник Алимов Ш.А.
Здравствуйте! Помогите вычислить: (Подробнее…)
ГДЗ8 классАлгебраАлимов Ш.А.
Помогите вычислить кинетическую энергию. Алгебра. 8 класс. Гл.№2. Упр.№300. Учебник Алимов Ш.А.
Здравствуйте! Помогите: (Подробнее…)
ГДЗ8 классАлгебраАлимов Ш.А.
Помогите с точными значениями величин. Алгебра. 8 класс. Гл.№1. Упр.№197. Учебник Алимов Ш.А.
Здравствуйте! Помогите высказать предположение, какие из приведенных в приме-
рах чисел являются точными значениями величин, а (Подробнее…)
ГДЗ8 классАлгебраАлимов Ш.А.
Помогите найти произведение . Алгебра. 8 класс. Пар.№16. Упр.№250. Учебник Алимов Ш.А.
Здравствуйте! Помогите найти произведение с точностью до 0,01:
1) 4,31 ∙ 28,37; 2) 56,78 ∙ 2,3404;
3) 507,63 (Подробнее. 2 возрастает:
2 возрастает:
1) на отрезке [1; 4]; 2) на интервале (2; (Подробнее…)
ГДЗ8 классАлгебраАлимов Ш.А.
Помогите пожалуйста, доказать неравенство. Алгебра 8 класс. Параграф№2. Упражнение№32. Учебник Алимов Ш.А.
Здравствуйте! Выручайте). 32) Доказать, что при любых значениях а (Подробнее…)
ГДЗ8 классАлгебраАлимов Ш.А.
Решим выражения? Алгебра. 8 класс.Пар.№7. Упр№95. Учебник Алимов Ш.А.
Всем привет помогите выяснить, при каких значениях у выражение принимает отрицательные значения:
(Подробнее…)
ГДЗ8 классАлгебраАлимов Ш.А.
Свести к квадратным следующие неравенства. Упр. 650, Алгебра, 8 класс, Алимов Ш.А.
Привет. А вот это уже кто-о сделал или нет?!
Свести к квадратным следующие неравенства:
1) х2 < 3х + 4; (Подробнее…)
ГДЗАлгебраАлимов Ш. А.8 класс
А.8 класс
Решим неравенства? Алгебра. 8 класс. Гл.№1. Упр.№183. Учебник Алимов Ш.А.
Здравствуйте! Помогите решить неравенство:
1) | х — 1 | ≤ 3,4; 2) | х — 1 | ≥ 3,4; 3) | х — 1 | < 3,4;
1) | 2х + 1 (Подробнее…)
ГДЗ8 классАлгебраАлимов Ш.А.
Помогите решить задачу. Алгебра. 8 класс. Пар.№14. Упр.№232. Учебник Алимов Ш.А.
Здравствуйте! Двое учащихся, выполняя практическую работу на измерение длин отрезков, в результате получили (203 ± 1) мм и (120 ± 1) (Подробнее…)
ГДЗ8 классАлгебраАлимов Ш.А.
Записать уравнение параболы…. Упр. 620, Алгебра, 8 класс, Алимов Ш.А.
Мне снова нужна ваша помощь. Поможете?
Записать уравнение параболы, пересекающей ось абсцисс в точках х = -1 и х = 3, а ось (Подробнее…)
ГДЗАлгебраАлимов Ш.А.8 класс
Помогите с квадратными уравнениями. Алгебра. 8 класс. Гл.№4. Упр.№565. Учебник Алимов Ш.А.
Гл.№4. Упр.№565. Учебник Алимов Ш.А.
Здравствуйте! Помогите: (Подробнее…)
ГДЗ8 классАлгебраАлимов Ш.А.
Помогите решить уравнения. Алгебра. 8 класс. Гл.№4. Упр.№547. Учебник Алимов Ш.А.
Здравствуйте! Помогите решить уравнение: (Подробнее…)
ГДЗ8 классАлгебраАлимов Ш.А.
Помогите с погрешностью. Алгебра. 8 класс. Пар.№11. Упр.№204. Учебник Алимов Ш.А.
Здравствуйте! (Подробнее…)
ГДЗ8 классАлгебраАлимов Ш.А.
Помогите с дробями. Алгебра. 8 класс. Пар.№26. Упр.№422. Учебник Алимов Ш.А.
Здравствуйте! При каких значениях «х» значения данных дробей равны: (Подробнее…)
ГДЗ8 классАлгебраАлимов Ш.А.
похожие темы
Экскурсии
Мякишев Г.Я.
Досуг
Химия
Go Math, 8 класс, ответ, глава 8, Решение систем линейных уравнений – Go Math, ответ
Go Math, 8 класс, ответ, глава, 8, решение систем линейных уравнений для лучшей практики математики. Все ответы и объяснения объясняются лучшими специалистами по математике. Все студенты могут быстро открыть наш сайт и начать практиковать прямо сейчас. Если у вас нет подключения к Интернету, загрузите бесплатный pdf-файл Go Math Grade 8 Chapter 8 Solving Systems of Linear Equations Answer Key и начните практиковаться в автономном режиме. Плата за получение ключа для ответов Go Math Grade 8 не требуется.
Все ответы и объяснения объясняются лучшими специалистами по математике. Все студенты могут быстро открыть наш сайт и начать практиковать прямо сейчас. Если у вас нет подключения к Интернету, загрузите бесплатный pdf-файл Go Math Grade 8 Chapter 8 Solving Systems of Linear Equations Answer Key и начните практиковаться в автономном режиме. Плата за получение ключа для ответов Go Math Grade 8 не требуется.
Иногда очень сложно выбрать лучший математический ключ, чтобы узнать правильные ответы. Надежный гид поможет вам в совершенстве учиться и улучшить свои математические навыки. Одним из таких лучших онлайн-руководств является Go Math Grade 8 Answer Key Chapter 8 Solving Systems of Linear Equations. Обратитесь к ключу решения Go Math Grade 8, чтобы узнать, как легко заниматься математикой.
Урок 1: Решение систем линейных уравнений с помощью графиков
- Решение систем линейных уравнений с помощью графиков – Страница № 232
- Решение систем линейных уравнений с помощью графиков — Страница № 233
- Решение систем линейных уравнений с помощью графического урока Проверка — Страница № 234
Урок 2: Решение систем с помощью замены
- Решение систем с помощью замены – страница № 240
- Решающие системы путем подстановки — Страница № 241
- Решение систем с помощью проверки урока подстановки — страница № 242
Урок 3: Решение систем методом исключения
- Системы решения методом исключения – стр.
 № 248
№ 248 - Решающие системы методом исключения — Страница № 249
- Системы решения с помощью проверки урока на выбывание — страница № 250
Урок 4: Решение систем методом исключения с умножением
- Решение систем методом исключения с умножением – Страница № 256
- Системы решения методом исключения с умножением — Страница № 257
- Решение систем методом исключения с проверкой урока умножения — страница № 258
Урок 5: Решение специальных систем
- Решение специальных систем – Страница № 262
- Решение для специальных систем — страница № 263
- Решаем специальные системы, проверка урока — стр. № 264
Опрос по моделям
- Опрос по моделям — Страница № 265
Обзор
- Смешанный обзор – Страница № 266
Учебное пособие – Решение систем линейных уравнений с помощью графика – Страница № 232
Решите каждую систему с помощью графика.
Вопрос 1.
\(\left\{\begin{array}{l}y=3 x-4 \\y=x+2\end{array}\right.\)
Введите ниже:
______________
Ответ:
Объяснение:
y = 3x – 4
y = x + 2
Решением этой линейной системы уравнений является точка пересечения двух уравнений.
(3, 5) — решение системы уравнений.
Если x = 3, y = 3(3) – 4 = 9 – 4 = 5; у = 3 + 2 = 5
5 = 5; True
Вопрос 2.
\(\left\{\begin{array}{l}x-3 y=2 \\-3x+9y=-6\end{array}\right.\)
Введите ниже :
______________
Ответ:
Бесконечное множество решений
Объяснение:
x – 3y = 2
-3x + 9y = -6
x – 3y – x = -x + 2
-3y = -x + 2 9008 у = 1/3. х – 2/3
-3х + 9у + 3х = 3х – 6
9у = 3х – 6
у = 3/9 . х – 6/9
у = 1/3 . x – 2/3
Решением линейной системы уравнений является пересечение двух уравнений.
Бесконечное множество решений
Вопрос 3.
Миссис Моралес написала тест с 15 вопросами, касающимися орфографии и словарного запаса. Вопросы по орфографии (x) оцениваются в 5 баллов, а вопросы по лексике (y) — в 10 баллов. Максимально возможное количество баллов за тест – 100.
Вопросы по орфографии (x) оцениваются в 5 баллов, а вопросы по лексике (y) — в 10 баллов. Максимально возможное количество баллов за тест – 100.
a. Напишите уравнение в форме пересечения наклона, чтобы представить количество вопросов в тесте.
Введите ниже:
______________
Ответ:
y = -x + 15
Объяснение:
Миссис Моралес написала тест с 15 вопросами, касающимися орфографии и словарного запаса. Вопросы по орфографии (x) оцениваются в 5 баллов, а вопросы по лексике (y) — в 10 баллов.
х + у = 15
х + у – х = -х + 15
у = -х + 15
Вопрос 3.
б. Напишите уравнение в форме пересечения наклона, чтобы представить общее количество баллов в тесте.
Введите ниже:
______________
Ответ:
y = -1/2 . x + 10
Объяснение:
Общее количество баллов за тест 100
5x + 10y = 100
5x + 10y – 5x = -5x + 100
10y = -5x + 100
y = -5/10 . х + 100/10
у = -1/2. х + 10
Вопрос 3.
c. Изобразите решения обоих уравнений.
Введите ниже:
______________
Ответ:
Вопрос 3.
d. Используйте свой график, чтобы определить, сколько вопросов каждого типа есть в тесте.
_________ вопросов по правописанию
_________ вопросов по лексике
Ответ:
10 вопросов по правописанию
5 вопросов по лексике
ОСНОВНОЙ ВОПРОС РЕГИСТРАЦИЯ
Вопрос 4.
Когда вы рисуете систему линейных уравнений, почему пересечение двух линий представляет собой решение системы?
Введите ниже:
______________
Ответ:
Решить систему линейных уравнений означает найти решения, удовлетворяющие всем уравнениям этой системы. Когда мы рисуем систему линейных уравнений, точка пересечения лежит на линии каждого уравнения, что означает, что она удовлетворяет всем уравнениям. Поэтому он считается решением этой системы.
Решение систем линейных уравнений с помощью графиков — стр. № 233
Вопрос 5.
Словарь
A_________________ представляет собой набор уравнений с одними и теми же переменными.
______________
Ответ:
система уравнений
Объяснение:
Система уравнений – это набор уравнений с одинаковыми переменными.
Вопрос 6.
Восемь друзей начали свой бизнес. Во время работы они будут носить либо бейсболку, либо рубашку с их логотипом. Они хотят потратить ровно 36 долларов на рубашки и кепки. Рубашки стоят 6 долларов каждая, а кепки — 3 доллара.
а. Напишите систему уравнений, описывающую ситуацию. Пусть x обозначает количество футболок, а y обозначает количество кепок.
______________
Ответ:
6x + 3y = 36
Объяснение:
Сумма кепок и рубашек равна 8. Общая стоимость кепок и рубашек составляет 36 долларов.
х + у = 8
6х + 3у = 36
Вопрос 6.
б. Нарисуйте систему. Что такое решение и что оно представляет?
Введите ниже:
______________
Ответ:
Решение (4, 4)
Объяснение:
x + y – x = -x + 8
y = -x + 8
6x + 3y – 6x = -6x + 36
3y = -6x + 36
г = -6/2. х + 36/3
х + 36/3
у = -2х + 12
(4, 4). Они должны заказать 4 рубашки и 4 кепки.
Вопрос 7.
Мультишаг В таблице указана стоимость игры в боулинг в двух кегельбанах.
а. Напишите систему уравнений, где одно уравнение описывает стоимость игры в Bowl-o-Rama, а другое — стоимость игры в Bowling Pinz. Для каждого уравнения пусть x представляет количество сыгранных игр, а y представляет общую стоимость.
Введите ниже:
______________
Ответ:
y = 2,5x + 2
y = 2x + 4
Объяснение:
Стоимость в Bowl-o-Rama => y = 2,5x + 2
Стоимость в Bowling Pinz => у = 2х + 4
Вопрос 7.
б. Нарисуйте систему. Что такое решение и что оно представляет?
Введите ниже:
______________
Ответ:
Объяснение:
Решением линейной системы уравнений является пересечение двух уравнений.
(4, 12)
При игре в 4 игры общая стоимость составляет 12 долларов.
Решение систем линейных уравнений с помощью графиков — страница № 234
Вопрос 8.
Многошаговый Джереми пробегает 7 миль в неделю и каждую неделю увеличивает дистанцию на 1 милю. Тони пробегает 3 мили в неделю и каждую неделю увеличивает дистанцию на 2 мили. Через сколько недель Джереми и Тони пробегут одинаковую дистанцию? Каким будет это расстояние?
Введите ниже:
______________
Ответ:
Через 4 недели Джереми и Тони будут бежать одинаковое расстояние, и это расстояние составит 11 миль.
Пояснение:
Многошаговый Джереми пробегает 7 миль в неделю и каждую неделю увеличивает дистанцию на 1 милю.
y = x + 7
Тони пробегает 3 мили в неделю и каждую неделю увеличивает дистанцию на 2 мили.
y = 2x + 3
Решение системы линейных уравнений (4, 11) означает, что через 4 недели Джереми и Тони пробегут одинаковое расстояние, и это расстояние составит 11 миль.
Вопрос 9.
Критическое мышление Напишите реальную ситуацию, которую можно представить системой уравнений, показанной ниже.
\(\left\{\begin{array}{l}y=4 x+10 \\y=3x+15\end{array}\right. \)
\)
Введите ниже:
______________
Ответ:
Плата за вход в первый спортзал составляет 10 долларов, и за каждый час, который вы там проводите, вы платите дополнительно 4 доллара. Если мы обозначим через x количество часов, которые кто-то проводит в тренажерном зале, а через y общая стоимость составит
y = 4x + 10
Плата за вход во второй тренажерный зал составляет 15 долларов, и за каждый час, проведенный в нем, вы платите дополнительные 3 доллара. Если мы обозначим через x количество часов, которые кто-то проводит в спортзале, а через y общая стоимость составит
y = 3x + 15
y = 4x + 10
y = 3x + 15
ФОКУС НА МЫШЛЕНИИ ВЫСШЕГО ПОРЯДКА
Вопрос 10.
Многошаговый В таблице показаны два варианта, предоставляемые провайдером высокоскоростного Интернета.
а. Через сколько месяцев общая стоимость обоих вариантов будет одинаковой? Какова будет эта стоимость?
________ месяцев
$ ________
Ответ:
5 месяцев
$ 200
Объяснение:
Пусть y будет общей стоимостью после x месяца
y = 30x + 50
Пусть y будет общей стоимостью через x месяцев
y = 40x
Замените y = 40x на y = 30x + 50
40x = 30x + 50
40x – 30x = 50
10x = 50
x = 50/10 x 9008 5
Общая стоимость обоих вариантов будет одинаковой через 5 месяцев. Общая стоимость составит y = 40(5) = 200 долларов.
Общая стоимость составит y = 40(5) = 200 долларов.
Вопрос 10.
б. Если вы планируете отказаться от интернет-услуги через 9 месяцев, какой вариант будет дешевле? Объяснять.
______________
Ответ:
Когда x = 9 месяцев
y = 30(9) + 50 = $320
y = 40(9) = $360
$320 < $360
Вариант 1 дешевле, так как общая стоимость меньше варианта 1
Вопрос 11.
Сделайте выводы Сколько решений имеет система, образованная x − y = 3 и ay − ax + 3a = 0 имеют для ненулевого числа a? Объяснять.
Введите ниже:
______________
Ответ:
x – y = 3
ay – ax + 3a =0
ay – ax + 3a – 3a = 0 – 3a
ay – ax = – 3a
a(y – x) = -3a
y – x = -3
x – y = 3
Оба уравнения одинаковы. Система линейных уравнений имеет бесконечно много решений.
Практическое руководство – Решение систем с помощью подстановки – Страница № 240
Решите каждую систему линейных уравнений с помощью подстановки.
Вопрос 1.
\(\left\{\begin{array}{l}3x-2y=9 \\y=2x-7\end{массив}\right.\)
x = ________
y = ________
Ответ:
x = 5
y = 3
Объяснение:
\(\left\{\begin{array}{l}3x-2y=9 \\y=2x-7\end{array}\ справа.\)
Подставить 2x – 7 в 3x – 2y = 9
3x – 2(2x – 7) = 9
3x – 4x + 14 = 9
-x + 14 = 9
-x + 14 – 14 = 9 – 14
-x = -5
x = -5/-1 = 5
y = 2(5) – 7 = 3
Решение (5 , 3)
Вопрос 2.
\(\left\{\begin{array}{l}y=x-4 \\2x+y=5\end{array}\right.\)
x = ________
y = ________
Ответ:
x = 3
y = -1
Объяснение:
\(\left\{\begin{array}{l}y=x-4 \\2x+y=5\end{ array}\right.\)
2x + x – 4 = 5
3x – 4 = 5
3x – 4 + 4 = 5 + 4
3x = 9
x = 9/3 = 3
y = 3 – 4 = -1
Решение (3, -1)
Вопрос 3.
\(\left\{\begin{array}{l}x+4y=6 \\y=-x+3\end{array}\right .\)
x = ________
y = ________
Ответ:
x = 2
y = 1
Объяснение:
\(\left\{\begin{array}{l}x+4y=6 \\y =-x+3\end{массив}\right. \)
\)
Подставить y = -x + 3 в x + 4y = 6
x + 4(-x + 3) = 6
x – 4x + 12 = 6
-3x + 12 = 6
-3x + 12 – 12 = 6 – 12
-3x = -6
x = -6/-3 = 2
y = -2 + 3 = 1
Решение (2, 1 )
Вопрос 4.
\(\left\{\begin{array}{l}x+2y=6 \\xy=3\end{array}\right.\)
x = ________
y = ________
Ответ:
x = 4
y = 1
Объяснение:
\(\left\{\begin{array}{l}x+2y=6 \\xy=3\end{array}\right.\)
y = x – 3
Замена y = x – 3 в x + 2y = 6
x + 2(x – 3) = 6
x + 2x – 6 = 6
3x = 12
x = 12/3
x = 4
4 – y = 3
-y = 3 – 4
-y = -1
y = 1
Решение (4, 1)
Решить каждую систему. Сначала оцените решение.
Вопрос 5.
\(\left\{\begin{array}{l}6x+y=4 \\x-4y=19\end{array}\right.\)
Оценка ______________
Решение ______________
Введите ниже:
______________
Ответ:
Оценка (2, -5)
Решение (1.4, -4. 4)
4)
Объяснение:
\(\left\{\begin{array}{l}6x+y=4 \ \x-4y=19\end{array}\right.\)
Найдем оценку, построив уравнения на графике
Оценка: (2, -5)
x = 4y + 19
6(4y + 19) + y = 4
24y + 114 + y = 4
25y + 114 = 4
25y = 4 – 114
25y = -110
y2 = -110/110/110/114
y = -4,4
x + 4(-4,4) = 19
x + 17,6 = 19
x = 19 – 17,6
x = 1,4
Решение (1,4, -4,4)
Вопрос 6.
\(\ left\{\begin{array}{l}x+2y=8 \\3x+2y=6\end{array}\right.\)
Оценка ______________
Решение ______________
Введите ниже:
______________
Ответ:
Оценка (-1, 5)
Решение (-1, 4.5)
Объяснение:
\(\left\{\begin{array}{l}x+2y=8 \\3x+2y=6\end{array}\right.\)
Найдем оценку, построив графически уравнения
Оценка: (-1, 5)
x = -2y + 8
Подставим уравнение x = -2y + 8 в 3x + 2y = 6
3(-2y + 8) + 2y = 6
-6y + 24 + 2y = 6
-4y = 6 – 24
-4y = -18
y = -18/-4
y = 4,5
x + 2(4,5) = 8
x + 9 = 8
x = 8 – 9
x = -1
Решение: (-1, 4,5)
Вопрос 7.
\(\left\{\begin{array}{l}3x+y=4 \\5x-y=22\end{array}\right.\)
Оценка ______________
Решение ______________
Введите ниже :
______________
Ответ:
Оценка (3, -6)
Решение (3,25, -5,75)
Объяснение:
\(\left\{\begin{array}{l}3x+y=4 \\5x -y=22\end{массив}\right.\)
Найдите оценку, используя графические уравнения.
Оценка: (3, -6)
y = -3x + 4
Замена y = -3x + 4 в 5x – y = 22
5x – (-3x + 4) = 22
5x + 3x -4 = 22
8x = 26
x = 26/8
x = 3,25
3(3,25) + y = 4
9,75 + y = 4
y = 4 – 9,75
y = -5,75
Решение (3,25, -5,75)
Вопрос 8.
\(\left\{\begin{array}{l}2x+7y=2 \\x+y= -1\end{массив}\right.\)
Оценка ______________
Решение ______________
Введите ниже:
______________
Ответ:
Оценка (-2, 1)
Решение (-1,8, 0,8)
Объяснение:
\ (\left\{\begin{массив}}{l}2x+7y=2 \\x+y=-1\end{массив}\right.\)
Найдите оценку, построив уравнения в виде графика.
Оценка: (-2, 1)
y = -x -1
Замена y = -x – 1 в 2x + 7y = 2
2x + 7(-x – 1) = 2
2x – 7x -7 = 2
-5x = 2 + 7
-5x = 9
x = -9/5
x = -1,8
-1,8 + y = -1
y = -1 + 1,8
y = 0,8
Решение (- 1.8, 0.8)
Вопрос 9.
Билеты для взрослых в парк развлечений Space City стоят x долларов. Детские билеты стоят y долларов. Семья Хенсон купила 3 взрослых и 1 детский билет за 163 доллара. Семья Гарсия купила 2 взрослых и 3 детских билета за 174 доллара.
а. Напишите уравнения, представляющие стоимость Хенсона и стоимость Гарсиаса.
Стоимость Хенсона: ________________
Стоимость Гарсиаса:__________________
Введите ниже:
______________
Ответ:
Стоимость Хенсона: 3x + y = 163
Стоимость Гарсии: 2x + 3y = 174
Стоимость Henson’s 9008 3x + y = 163
Стоимость Гарсии
2x + 3y = 174
Вопрос 9.
b. Решите систему.
стоимость билета для взрослого: $ _________
стоимость Гарсиаса: $ _________
Ответ:
цена билета для взрослых: 45 долларов
стоимость Гарсиаса: 28 долларов
Объяснение:
y = -3x + 163
Замена y = -3x + 163 в 2x + 3y = 174
2x + 3(-3x + 163) = 174
2x -9x + 489 = 174
-7x = -315
x = -315/-7 = 45
3(45) + y = 163
135 + y = 163
y = 163 – 135
y = 28
цена билета для взрослых: 45 долларов
стоимость Гарсиаса: 28 долларов
ОСНОВНОЙ ВОПРОС ПРОВЕРКА
Вопрос 10.
Как решить, какую переменную решать в первую очередь при решении линейной системы по замене?
Введите ниже:
______________
Ответ:
При решении линейной системы подстановкой первой следует решить переменную с единичным коэффициентом.
8.2 Независимая практика – Решение систем путем подстановки – Страница № 241
Вопрос 11.
Проверка разумности Зак решает систему
\(\left\{\begin{array}{l}x+y=-3 \ \x-y=1\end{массив}\right.\)
и находит решение (1, -2). Используйте график, чтобы объяснить, разумно ли решение Зака.
Введите ниже:
______________
Ответ:
Объяснение:
\(\left\{\begin{array}{l}x+y=-3 \\x-y=1\end{array}\right. \)
Координата x решения отрицательна, поэтому решение Зака не является разумным.
Представление реальных проблем Анджело купил яблоки и бананы в фруктовом киоске. Он купил 20 фруктов и потратил 11,50 долларов. Яблоки стоят 0,50 доллара, а бананы — 0,75 доллара за штуку.
а. Напишите систему уравнений для моделирования задачи. (Подсказка: одно уравнение будет представлять количество кусочков фруктов. Второе уравнение будет представлять деньги, потраченные на фрукты.)
Введите ниже:
______________
Ответ:
x + y = 20
0,5x + 0,75y = 11,5
Объяснение:
x + y = 20
0,5x + 0,75y =
0,5x + 0,75y = 11,9 Яблоки и y — это количество бананов.
Вопрос 12.
б. Решить систему алгебраически. Скажи, сколько яблок и бананов купил Анджело.
________ яблок
________ бананов
Ответ:
14 яблок
6 бананов
Объяснение:
y = -x + 20
Замена y = -x + 20 в 0,5x + 0,75y = 11,5
0,5x + 0,75(-x + 20) = 11,5
0,5x – 0,75x + 15 = 11,5
-0,25x + 15 = 11,5
-0,25 x = 11,5 – 15
-0,25x = -3,5
x = -3,5/-0,25
x = 14
14 + y = 20
y = 6
Анджело купил 14 яблок и 6 бананов.
Вопрос 13.
Репрезентация реальных задач В банке находится n пятицентовых монет и d десятицентовых монет. Всего в банке 200 монет. Стоимость монет составляет 14 долларов США. Сколько пятицентовиков и сколько десятицентовиков в банке?
Всего в банке 200 монет. Стоимость монет составляет 14 долларов США. Сколько пятицентовиков и сколько десятицентовиков в банке?
________ пятицентовых монет
________ пятицентовых монет
Ответ:
120 пятицентовых монет
80 десятицентовых монет
Пояснение:
В банке находится n пятицентовых монет и d десятицентовых монет. Всего в банке 200 монет. Стоимость монет составляет 14 долларов США.
14 долларов = 1400 центов
n + d = 200
5n + 10d = 1400
d = -n + 200
5n + 10(-n + 200) = 1400
n = -600/-5
n = 120
120 + d = 200
d = 200 – 120
d = 80
В банке 120 пятаков и 80 десятицентовиков.
Вопрос 14.
Многошаговый На графике показан треугольник, образованный осью x, линией 3x−2y=0 и линией x+2y=10. Выполните следующие действия, чтобы найти площадь треугольника.
а. Найдите координаты точки A, решив систему
\(\left\{\begin{array}{l}3x-2y=0 \\x-2y=10\end{array}\right.\)
Точка A : ____________________
Введите ниже:
______________
Ответ:
Точка A: (2. 5, 3.75)Координата точки A (2.5, 3.75)
5, 3.75)Координата точки A (2.5, 3.75)
Объяснение:
\(\left\{\begin{array}{l}3x-2y=0 \\x-2y=10\end{array}\right.\)
x = -2y + 10
Замените x = -2y + 10 в 3x – 2y = 0
3(-2y + 10) -2y = 0
-6y + 30 – 2y = 0
-8y = -30
y = -30/-8 = 3,75
x + 2( 3,75) = 10
х + 7,5 = 10
х = 10 – 7,5
х = 2,5
Координата точки А равна (2,5, 3,75)
Вопрос 14.
b. Используя координаты точки А, найдите высоту треугольника.
высота:__________________
высота: \(\frac{□}{□}\) единиц
Ответ:
высота: 3,75
высота: \(\frac{15}{4}\) единиц
Объяснение:
Высота треугольника — координата y точки A . Чему равна длина основания треугольника?
основание:________________
основание: ______ единиц
Ответ:
основание: 10 единиц
Объяснение:
Длина основания = 10
Вопрос 14.
d. Чему равна площадь треугольника?
A = ______ \(\frac{□}{□}\) квадратных единиц
Ответ:
A = 18,75 квадратных единиц
A = 18 \(\frac{3}{4}\) квадратных единиц
Объяснение:
Площадь треугольника = 1/2 . Высота . База
Высота . База
Площадь = 1/2 . 3,75 . 10 = 18,75
Решение систем методом подстановки – страница № 242
Вопрос 15.
Джед рисует конструкцию воздушного змея на координатной сетке. Четыре вершины воздушного змея находятся в A(−\(\frac{4}{3}\), \(\frac{2}{3}\)), B(\(\frac{14}{3} \), −\(\frac{4}{3}\)), C(\(\frac{14}{3}\), −\(\frac{16}{3}\)) и D (\(\frac{2}{3}\), −\(\frac{16}{3}\)). Одна распорка воздушного змея соединит точки A и C. Другая соединит точки B и D. Найдите точку пересечения распорок.
Введите ниже:
______________
Ответ:
Стойки пересекаются как (8/3, 10/3)
Объяснение:
1. Из AC
Наклон = (y2 – y1)/(x2 – x1) = [ (-16/3)-(2/3)] ÷ [(14/3) – (-4/3)] = (-18/3) ÷ (18/3) = -1
y = mx + b
2/3 = -1(-4/3) + b
2/3 = 4/3 + b
1. Из BD
Наклон = (y2 – y1)/(x2 – x1) = [(-16/ 3)-(-4/3)] ÷ [(2/3) – (144/3)] = (-12/3) ÷ (-12/3) = 1
y = mx + b
-4/ 3 = 1(14/3) + b
-4/3 = 14/3 + b
-18/3 = b
-6 = b
y = mx + b
y = x -6
3.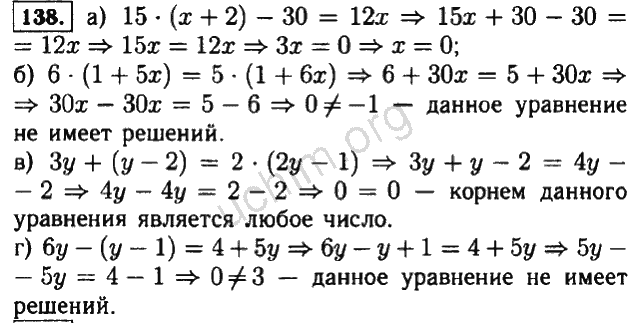 y = -x -2/3
y = -x -2/3
y = x – 6
4. y = -x – 2/3
x – 6 = — х – 2/3
х = -х – 2/3 + 6
х = – х + 16/3
2х = 16/3
х = 16/6
х = 8/3
тогда у = х – 6
y = 8/3 – 18/3
y = -10/3
Распорки пересекаются как (8/3, 10/3)
Фокус на мышлении высшего порядка система
\(\left\{\begin{array}{l}6x-3y=15 \\x+3y=-8\end{массив}\right.\)
Опишите три различных метода подстановки, которые можно использовать для решения этой системы. Затем решить систему.
Введите ниже:
______________
Ответ:
(1, -3) — ответ.
Объяснение:
Так как существует три различных метода подстановки, мы можем написать
Найти y в первом уравнении, а затем подставить это значение во второе уравнение.
Найдите x во втором уравнении, затем подставьте это значение в первое уравнение.
Решите любое уравнение для 3y, затем подставьте это значение в другое уравнение.
Из второго метода
x + 3y = -8
x = -3y – 8
6x – 3y = 15
6 (-3y – 8) -3y = 15
-18y – 48 -3y = 15
-21y – 48 = 15
-21y = 63
y = -3
x + 3y = -8
x + 3(-3) = -8
x – 9 = -8
x = 1
(1, -3) это ответ.
Вопрос 17.
Сообщать математические идеи Объясните преимущества, если таковые имеются, решения системы линейных уравнений методом подстановки по сравнению с решением той же системы с помощью графика.
Введите ниже:
______________
Ответ:
Преимущество решения системы линейных уравнений с помощью графика заключается в том, что это относительно легко сделать и требует очень мало алгебры.
Вопрос 18.
Упорство в решении проблем Создайте систему уравнений вида
\(\left\{\begin{array}{l}Ax+By=C \\Dx+Ey=F\end{array} \right.\)
, решением которого является (7, −2). Объясните, как вы нашли систему.
Введите ниже:
______________
Ответ:
x + y = 5
x – y = 9
решает в:
x = (5+9)/2 = 7
y = 5-9)/2 = -2
A=1, B=2, C= 5
D=1 , E= -1, F=9
x = 7
y = -2
ЕСТЬ система (даже если она тривиальна) уравнений, поэтому такой ответ будет приемлемым.
Целью системы является найти ее НАБОР РЕШЕНИЙ, а не заключать с x=a и y=b
Управляемая практика – Решение систем методом исключения – Страница № 248
Вопрос 1.
Решить систему
\( \left\{\begin{массив}{l}4x+3y=1 \\x-3y=-11\end{массив}\right.\)
, добавив.
Введите ниже:
______________
Ответ:
4x + 3y = 1
x – 3y = -11
Сложите два приведенных выше уравнения
4x + 3y = 1
+(x – 3y = -11)
Сложите, чтобы исключить переменная y
5x + 0y = -10
Упростите и решите x
5x = -10
Разделите обе стороны на 5
x = -10/5 = -2
Подставьте в одно из исходных уравнений и решите y.
4(-2) + 3y = 1
-8 + 3y = 1
3y = 9
y = 9/3 = 3
Таким образом, (-2, 3) является решением системы.
Решите каждую систему уравнений путем сложения или вычитания.
Вопрос 2.
\(\left\{\begin{array}{l}x+2y=-2 \\-3x+2y=-10\end{array}\right.\)
x = ________
y = ________
Ответ:
x = 2
y = -2
Объяснение:
\(\left\{\begin{array}{l}x+2y=-2 \\-3x+2y=- 10\end{массив}\right.\)
Вычесть уравнения
x + 2y = -2
-(-3x + 2y = -10)
y исключается, так как имеет обратные коэффициенты. Решите для х
Решите для х
x + 2y + 3x – 2y = -2 + 10
4x = 8
x = 8/4 = 2
Подставив x в любое из уравнений, чтобы найти y
2 + 2y = -2
2 + 2y -2 = -2 -2
2y = -4
y = -4/2 = -2
(2, -2) является ответом.
Вопрос 3.
\(\left\{\begin{array}{l}3x+y=23 \\3x-2y=8\end{array}\right.\)
(________ , ________)
Ответ:
(6, 5)
Объяснение:
\(\left\{\begin{array}{l}3x+y=23 \\3x-2y=8\end{array}\right.\)
Вычтите уравнения
3x + y = 23
-(3x – 2y = 8)
x исключается, так как имеет обратные коэффициенты. Найдите y
3x + y – 3x + 2y = 23 – 8
3y = 15
y = 15/3 = 5
Подставив y в любое из уравнений, чтобы найти x
3x + 5 = 23
3x + 5 – 5 = 23 – 5
3x = 18
x = 18/3 = 6
Решение: (6, 5)
Вопрос 4.
\(\left\{\begin{array}{l}-4x-5y=7 \\3x+5y=-14\end{массив}\right.\)
(________ , ________)
Ответ:
(7, -7)
Объяснение:
\(\left\{\begin{array}{l}-4x-5y=7 \\3x+5y=-14\end{array}\right. \)
\)
Сложите уравнения
-4x – 5y = 7
+(3x + 5y = -14)
y исключается, так как имеет обратные коэффициенты. Найдите x
-4x -5y +3x + 5y = 7 -14
-x = -7
x = -7/-1 = 7
Подставив x в любое из уравнений, чтобы найти y
3(7) + 5y = -14
21 + 5y -21 = -14 -21
5y = -35
y = -35/5 = -7
Ответ: (7, -7)
Вопрос 5.
\(\left\ {\ begin {массив} {l} x-2y = -19\\5x+2y=1\end{массив}\right.\)
(________ , ________)
Ответ:
(-3, 8)
Объяснение:
\(\left\{\begin{array} {l}x-2y=-19 \\5x+2y=1\end{массив}\right.\)
Складываем уравнения
x – 2y = -19
+(5x + 2y = 1)
y исключается так как он имеет обратные коэффициенты. Найдите x
x – 2y + 5x + 2y = -19 + 1
6x = -18
x = -18/6 = -3
Подставив x в любое из уравнений, найдите y
-3 -2y = -19
-3 -2у + 3 = -19 + 3
-2у = -16
y = -16/-2 = 8
Ответ: (-3, 8)
Вопрос 6.
\(\left\{\begin{array}{l}3x+4y=18 \\-2x+ 4y=8\end{массив}\right. \)
\)
(________ , ________)
Ответ:
(2, 3)
Объяснение:
\(\left\{\begin{array}{l}3x+ 4y=18 \\-2x+4y=8\end{массив}\right.\)
Вычесть уравнения
3x + 4y = 18
-(-2x + 4y = 8)
y исключается, так как имеет обратные коэффициенты . Решите для x
3x + 4y + 2x – 4y = 18 – 8
5x = 10
x = 10/5 = 2
Подставив x в любое из уравнений, чтобы найти y
3(2) + 4y = 18
6 + 4y – 6 = 18 – 6
4y = 12
y = 12/4 =3
Решение (2, 3)
Вопрос 7.
\(\left\{\begin{array}{l}-5x+7y=11 \\-5x+3y=19\end{array}\right.\)
(________ , ________)
Ответ:
(-5, -2)
Объяснение:
\(\left\{\begin{array}{l}-5x+7y=11 \\-5x+3y=19\end{array} \right.\)
Вычтите уравнения
-5x + 7y = 11
-(-5x + 3y = 19)
x исключается, так как имеет обратные коэффициенты. Решите для у
-5x + 7y + 5x – 3y = 11 – 19
4y = -8
y = -8/4 = -2
Подставив y в любое из уравнений, чтобы найти x
-5x + 7(-2) = 11
-5x -14 + 14 = 11 + 14
-5x = 25
x = 25/-5 = -5
Решение: (-5, -2)
Вопрос 8.
Автострада Грин-Ривер имеет минимум и ограничение максимальной скорости. Тони проехал 2 часа на минимальной скорости и 3,5 часа на максимальной, проехав 355 миль. Рэй проехал 2 часа на минимальной скорости и 3 часа на максимальной, проехав 320 миль. Какие два ограничения скорости?
а. Напишите уравнения, представляющие расстояние Тони и расстояние Рэй.
Введите ниже:
______________
Ответ:
Расстояние Тони: 2x + 3,5y = 355
Расстояние Рэя: 2x + 3y = 320
, где x — минимальная скорость, а y — максимальная скорость.
Вопрос 8.
б. Решите систему.
ограничение минимальной скорости:______________
ограничение максимальной скорости______________
ограничение минимальной скорости: ________ миль/ч
ограничение максимальной скорости: ________ миль/ч
Ответ:
ограничение минимальной скорости:55
ограничение максимальной скорости70
ограничение минимальной скорости: 55 миль/ч
ограничение максимальной скорости: 70 миль/ч
Объяснение:
Вычесть уравнения
2x + 3,5y = 355
-(2x + 3y = 320)
x исключается, так как имеет обратные коэффициенты. Найдите y
Найдите y
2x + 3,5y – 2x – 3y = 355 – 320
0,5y = 35
y = 35/0,5 = 70
Подставив y в любое из уравнений, чтобы найти x
2x + 3(70) = 320
2х + 210 – 210 = 320 – 210
2х = 110
х = 110/2 = 55
Ограничение минимальной скорости: 55 миль в час
Ограничение максимальной скорости: 70 миль в час
ОСНОВНОЙ ВОПРОС ПРОВЕРКА
Вопрос 9.
Можете ли вы использовать сложение или вычитание для решения любой системы? Объяснять.
________
Ответ:
Нет. Одна из переменных должна иметь одинаковый коэффициент, чтобы складывать или вычитать систему.
8.3 Независимая практика – Решение систем путем исключения – Страница № 249
Вопрос 10.
Репрезентация реальных проблем Марта купила новых рыбок для своего домашнего аквариума. Она купила 3 гуппи и 2 пеги на общую сумму 13,9 долларов.5. Хэнк также купил гуппи и пецилий для своего аквариума. Он купил 3 гуппи и 4 пецилии на общую сумму 18,33 доллара. Найдите цену гуппи и цену пецилии.
Найдите цену гуппи и цену пецилии.
Guppy: $ ________
Platy: $ ________
Ответ:
Гуппи: 3,19 долл. и y цена за единицу плиты
Вычтите уравнения
3x + 2y = 13,95
-(3x + 4y = 18,33)
x исключается, так как имеет обратные коэффициенты. Найдите y
3x + 2y – 3x – 4y = 13,95 – 18,33
-2y = -4,38
y = -4,38/-2 = 2,19
Подставив y в любое из уравнений, чтобы найти x
3x + 2(2,19) = 13,95
3x + 4,38 – 4,38 = 13,95 – 4,38
3x = 9,57
x = 9,57/3 = 3,19
Цена гуппи – 3,19 доллара, а цена пецилии – 2,19 доллара. Правило количества рыб в домашнем аквариуме: 1 галлон воды на каждый дюйм длины рыбы. Аквариум Марты вмещает 13 галлонов, а аквариум Хэнка — 17 галлонов. Основываясь на количестве рыб, купленных в упражнении 10, определите длину гуппи и пецилии?
Длина гуппи = ________ дюймов
Длина пеленки = ________ дюймов
Ответ:
Длина гуппи = 3 дюйма
Длина пеленки = 2 дюйма
Объяснение:
3x + 2y = 13
, где x — длина гуппи, а y — длина пеструшки
Вычтите уравнения
3x + 2y = 13
-(3x + 4y = 17)
x исключается, так как имеет обратные коэффициенты.
 Решите для y
Решите для y 3x + 2y – 3x – 4y = 13 – 17
-2y = -4
y = -4/-2 = 2
Подставив y в любое из уравнений, чтобы найти x
3x + 2(2) = 13
3x + 4 – 4 = 13 – 4
3x = 9
x = 9/3 = 3
Длина гуппи равна 3 дюймов, а цена тарелки 2 дюйма
Вопрос 12.
Прямая m проходит через точки (6, 1) и (2, -3). Прямая n проходит через точки (2, 3) и (5, -6). Найдите точку пересечения этих прямых.
Введите ниже:
________________
Ответ:
Пересечение этих линий (3,5, -1,5)
Объяснение:
Найдите наклон линии m = (y2 – y1)/(x2 – x1), где (x2, y2) = (2, -3) и (x1, y1) = (6, 1)
Наклон = (-3 -1)/(2 – 6) = -4/-4 = 1
Подставить значение m и любую из заданной упорядоченной пары (x, y) в точечно-наклонную форму уравнения: y – y1 = m(x – x1)
y – 1 = 1(x – 6)
y – 1 = x – 6
y = x – 6 + 1
x – y = 5
Найдите наклон прямой n = (y2 – y1)/(x2 – x1), где (x2, y2) = (5, -6) и (x1, y1) = (2, 3)
Наклон = (-6 -3)/(5 – 2) = -9/3 = -3
Подставьте значение m и любую из данной упорядоченной пары (x, y) в форму уравнения с наклоном точки: y – y1 = m(x – x1)
y – 3 = -3(x – 2)
y – 3 = -3x + 6
y = -3x + 6 + 3
3x + y = 9
Складываем уравнения
x – y = 5
+(3x + y = 9)
y исключается так как он имеет обратные коэффициенты.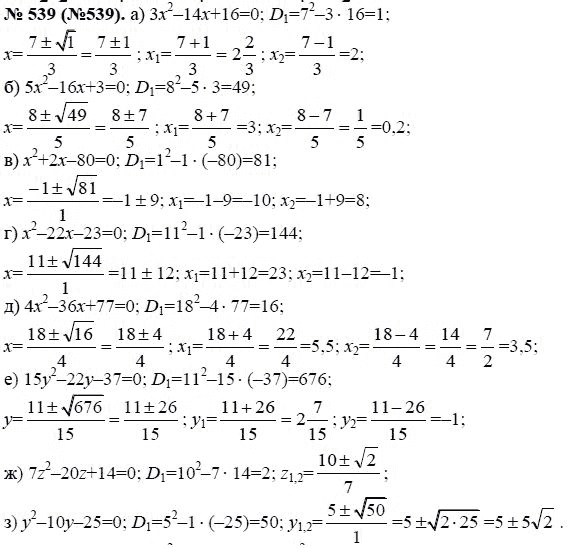 Найдите x
Найдите x
x – y + 3x + y = 5 + 9
4x = 14
x = 14/4 = 3,5
Подставив x в любое из уравнений, найдите y
3,5 – y = 5
3,5 – y – 3,5 = 5 – 3,5
-y = 1,5
y = -1,5
Пересечение этих линий равно (3,5, -1,5)
Вопрос 13.
Реальные проблемы Две машины меняли масло в одной и той же автомастерской. Магазин взимает с клиентов плату за каждую кварту масла плюс фиксированную плату за работу. Замена масла для одной машины требовала 5 литров масла и стоила 22,45 доллара. Замена масла в другом автомобиле потребовала 7 литров масла и стоила 25,45 долларов. Сколько стоит оплата труда и сколько стоит литр масла?
Оплата труда: $ ________
Кварта масла: $ ________
Ответ:
Оплата труда: $ 14,95
Кварта масла: $ 1,5
Объяснение:
5x + y = 22,45
7x + y = 25,45 кварт
где x — стоимость единицы нефть, а y — фиксированная плата за труд.
Вычтем уравнения
5x + y = 22,45
-(7x + y = 25,45)
y исключается, так как имеет обратные коэффициенты. Найдите x
Найдите x
5x + y – 7x – y = 22,45 – 25,45
-2x = -3
x = -3/-2 = 1,5
Подставив x в любое из уравнений, чтобы найти y
5(1,5) + y = 22,45
7,5 + y – 7,5 = 22,45 – 7,5
y = 14,95
Оплата труда составляет 14,95 долл. США, а себестоимость кварты масла – 1,5 долл. США
Вопрос 14.
Реальные задачи A менеджер заметил, что количество проданных единиц футболок двух стилей, стиля А и стиля В, было одинаковым в июне и июле. В июне общий объем продаж двух стилей составил 2779 долларов, при этом A продавался по 15,95 доллара за рубашку, а B — по 22,95 доллара за рубашку. В июле общий объем продаж двух стилей составил 2385,10 долларов США, при этом A продавался по той же цене, а B продавался со скидкой в 22% от июньской цены. Сколько футболок каждого фасона было продано в июне и июле вместе взятых?
________ Футболки фасона А и фасона Б были проданы в июне и июле.
Ответ:
15,95x + 22,95y = 2779
15,95x + 17,9y = 2385,10
где x — номер рубашки стиля A, а y — номер рубашки стиля B
В июле цена рубашки стиля B составляет 22 % от цены рубашки фасона B в июне, следовательно, 0,78(22,95) = 17,90
Вычтем уравнения
15,95x + 22,95y = 2779
-(15,95x + 17,9y = 2385,10)
x исключается, так как имеет обратные коэффициенты .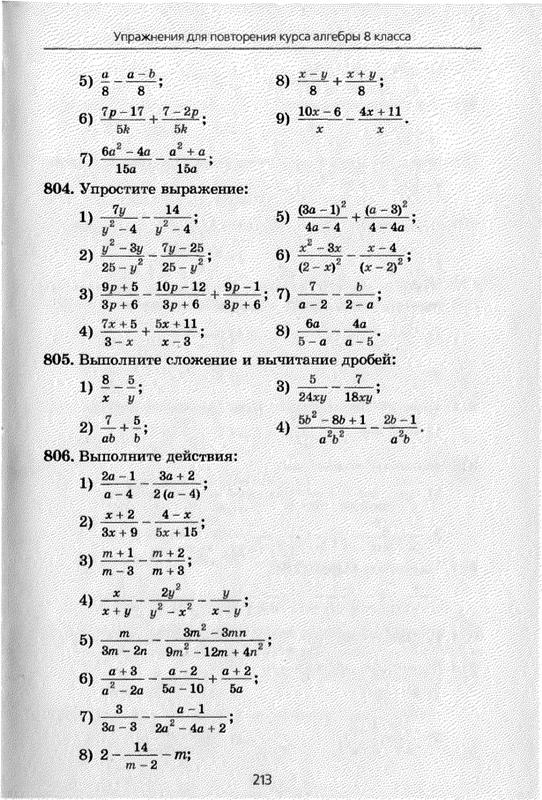 Решите для у
Решите для у
15,95x + 22,95 – 15,95x – 17,9y = 2779 – 2385,10
5,05y = 393,9
y = 393,9/5,05 = 78
Подставив y в любое из уравнений, чтобы найти x
15,95×792 15,95x + 1790,1 – 1790,1 = 2779 – 1790,1
15,95x = 988,9
x = 988,9/15,95 = 62
Количество футболок стиля А, проданных в июне, равно 62.
то же самое, общее количество = 2,62 = 124,
Количество футболок стиля B, проданных в июне, равно 78,
Поскольку количество футболок, проданных под обоими номерами, одинаково, общее число = 2,78 = 156,
Вопрос 15.
Репрезентация реальных проблем Билеты для взрослых на баскетбольный матч стоят 5 долларов. Студенческие билеты стоят 1 доллар. Всего при продаже 1246 билетов было собрано 2874 доллара. Сколько билетов каждого типа было продано?
img 14
________ взрослый билет
________ студенческий билет
Ответ:
407 взрослый билет
839 студенческий билет
Объяснение:
x + y = 1246
5x + y = 2874
где x — количество проданных билетов для взрослых, а y — количество проданных билетов для учащихся.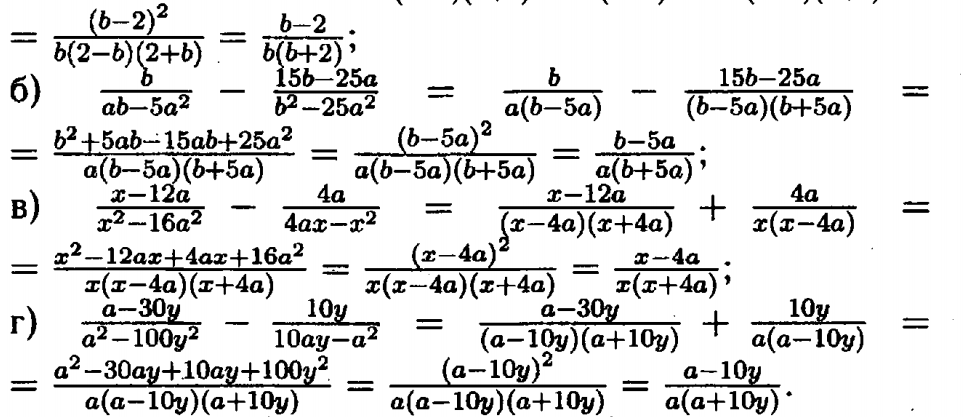
Вычтем уравнения
x + y = 1246
-(5x + y = 2874)
y исключается, так как имеет обратные коэффициенты. Найдите x
x + y – 5x – y = 1246 – 2874
-4x = -1628
x = -1628/-4 = 407
Подставив x в любое из уравнений, чтобы найти y
407 + y = 1246
407 + y – 407 = 1246 – 407
y = 839
Продано 407 билетов для взрослых и 839 билетов для студентов..
ФОКУС НА МЫШЛЕНИИ ВЫСШЕГО ПОРЯДКА – Решение систем методом исключения – Страница № 250
Вопрос 16.
Обмен математическими идеями Можно ли решить систему
\(\left\{\begin{array}{l}3x- 2y=10 \\x+2y=6\end{массив}\right.\)
с помощью подстановки? Если да, то объясните как. Какой метод, замена или удаление, более эффективен? Почему?
________
Ответ:
Система может быть решена подстановкой, поскольку x в уравнении 2 может быть изолирован.
3x – 2y = 10
x + 2y = 6
Решите уравнение относительно x в уравнении.
x = -2y + 6
Подставьте выражение для x в другое уравнение и решите.
3(-2y + 6) -2y = 10
-6y + 18 – 2y = 10
-8y + 18 = 10
-8y = -8
y = -8/-8 = 1
Подставить значения y в одно из уравнений и решить для другой переменной х.
x + 2(1) = 6
x = 4
Решение (4, 1)
Поскольку коэффициент, если переменная y противоположна, он будет исключен и решен для x за меньшее количество шагов.
Устранение будет более эффективным.
Вопрос 17.
Дженни использовала замену для решения системы
\(\left\{\begin{array}{l}2x+y=8 \\x-y=1\end{array}\right.\). Ее решение показано ниже.
Шаг 1: y = -2x + 8 Решите первое уравнение относительно y.
Шаг 2: 2x + (-2x + 8) = 8 Подставьте значение y в исходное уравнение.
Шаг 3: 2x – 2x + 8 = 8 Используйте свойство Distribution.
Шаг 4: 8 = 8 Упрощение.
а. Объясните ошибку Объясните ошибку, которую допустила Дженни. Напишите как исправить.
Введите ниже:
______________
Ответ:
2x + y = 8
x – y = 1
Переписанное уравнение следует заменить другим исходным уравнением
Ошибка в том, что Дженни решила для y в первом уравнении и подставила его в исходное уравнение.
х – (-2х + 8) = 1
3х – 8 = 1
3х = 9
х = 9/3 = 3
х = 3
Вопрос 17.
б. Обмен математическими идеями Было бы добавление уравнений лучшим методом для решения системы? Если да, объясните почему.
________
Ответ:
Да
Объяснение:
В качестве коэффициента, если переменная y является противоположной, он будет исключен и решен для x за меньшее количество шагов.
Практическое руководство – Решение систем методом исключения с умножением – Страница № 256
Вопрос 1.
Решите систему
\(\left\{\begin{array}{l}3x-y=8 \\-2x+ 4y=-12\end{массив}\right.\)
путем умножения и сложения.
Введите ниже:
______________
Ответ:
\(\left\{\begin{array}{l}3x-y=8 \\-2x+4y=-12\end{array}\right.\)
Умножьте каждое слагаемое в первом уравнении на 4, чтобы получить получить противоположные коэффициенты для y-членов.
4(3x – y = 8)
12x – 4y = 32
Добавить второе уравнение в новое уравнение
12x – 4y = 32
+(-2x + 4y = -12)
Добавить, чтобы исключить переменную y = 20
Разделите обе части на 10
x = 20/10 = 2
Подставьте в одно из исходных уравнений и найдите y
y = 3(2) – 8 = -1
S0, (2, -2) — решение системы.
Решите каждую систему уравнений путем умножения.
Вопрос 2.
\(\left\{\begin{array}{l}x+4y=2 \\2x+5y=7\end{array}\right.\)
(________ , ________ )
Ответ:
(6, -1)
Объяснение:
x + 4y = 2
2x + 5y = 7
Чтобы исключить члены x, умножьте второе уравнение на 2
2(x + 4y = 2)
2x + 8y = 4
Вычесть уравнения
2x + 8y = 4
-(2x + 5y = 7)
x исключается, так как имеет обратные коэффициенты. Найдите y
2x + 8y – 2x – 5y = 4 – 7
3y = -3
y = -3/3 = -1
Подставив y в любое из уравнений, чтобы найти x
x + 4(-1) = 2
x – 4 + 4 = 2 + 4
x = 6
Решение: (6, -1)
Вопрос 3.
\(\left\{\begin{array}{l}3x+y=-1 \\2x+3y=18\end{массив}\right.\)
(________ , ________ )
Ответ:
(-3, 8)
Объяснение:
\(\left\{\begin{array} {l}3x+y=-1 \\2x+3y=18\end{массив}\right.\)
Чтобы исключить члены y, умножьте первое уравнение на 3
3(3x + y = -1)
9x + 3y = -3
Вычтите уравнения
9x + 3y = -3
-(2x + 3y = 18)
y исключается, так как имеет обратные коэффициенты.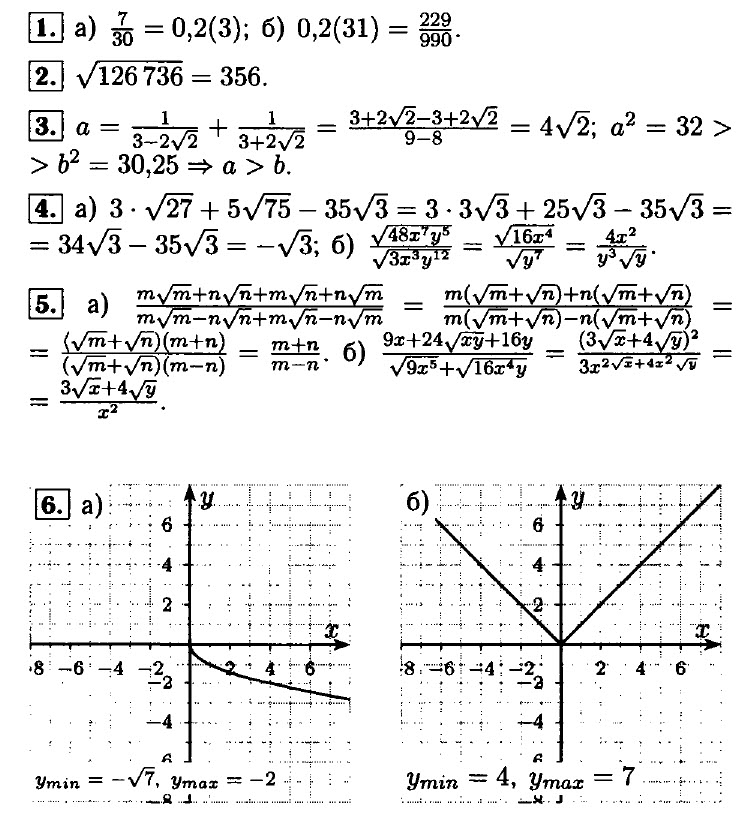 Найдите x
Найдите x
9x + 3y – 2x – 3y = -3 -18
7x = -21
x = -21/7
x = -3
Подставив x в любое из уравнений, чтобы найти y
3(-3) + y = -1
-9 + y + 9 = -1 + 9
y = 8
Решение: (-3, 8)
Вопрос 4.
\(\left\{\begin{array}{l} 2x+8y=21 \\6x-4y=14\end{массив}\right.\)
Введите ниже:
______________
Ответ:
Суть (3.5, 1.75)
Объяснение:
\(\left\{\begin{array}{l}2x+8y=21 \\6x-4y=14 \end{массив}\right.\)
Чтобы исключить члены y, умножьте второе уравнение на 2
2(6x – 4y = 14)
2x + 8y = 21
Сложите уравнения
2x + 8y = 21
+( 12x – 8y = 28)
y исключается, у него обратные коэффициенты. Найдите x
2x + 8y + 12x – 8y = 21 + 28
14x = 49
x = 49/14 = 3,5
Подставив x в любое из уравнений, найдите y
6(3.5) – 4y = 14
21 – 4y – 21 = 14 – 21
-4y = -7
y = -7/-4 = 1.75
Сущность (3.5, 1.75)
Вопрос 5.
\(\left\{\begin{array}{l}2x+y=3 \\-x+3y=-12\end{массив}\right.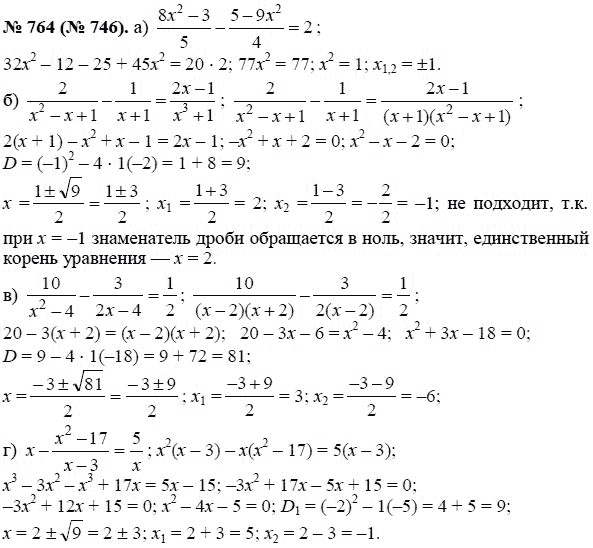 \)
\)
(________ , ________ )
Ответ:
Объяснение:
\(\left\{\begin{array}{l}2x+y=3 \\-x+3y=-12\end{array}\right.\)
Чтобы исключить x членов, умножьте 2-й уравнение на 2
2(-x + 3y = -12)
-2x + 6y = -24
Сложите уравнения
2x + y = 3
+(-2x + 6y = -24)
x исключается, коэффициенты меняются местами. Найдите y
2x + y – 2x + 6y = 3 – 24
7y = -21
y = -21/7 = -3
Подставив y в любое из уравнений, чтобы найти x
-x + 3(-3) = -12
-x -9 + 9 = -12 + 9
-x = -3
x = 3
Суть (3, -3)
Вопрос 6.
\(\left\{\begin{ array}{l}6x+5y=19 \\2x+3y=5\end{массив}\right.\)
(________ , ________ )
Ответ:
Суть (4, -1)
Объяснение :
\(\left\{\begin{array}{l}6x+5y=19 \\2x+3y=5\end{array}\right.\)
Чтобы исключить x членов, умножьте второе уравнение на 3
3(2x + 3y = 5)
6x + 9y = 15
Вычесть уравнения
6x + 5y = 19
-(6x + 9y = 15)
x исключается, имеет обратные коэффициенты. Найдите y
Найдите y
6x + 5y – 6x – 9y = 19 – 15
-4y = 4
y = 4/-4 = -1
Подставив y в любое из уравнений, чтобы найти x
2x + 3(-1) = 5
2x – 3 + 3 = 5 + 3
2x = 8
x = 8/2 = 4
Суть (4, -1)
Вопрос 7.
\(\left\{\begin{array}{l}2x+5y=16 \\-4x+3y=20\end{array}\right .\)
(________ , ________ )
Ответ:
Суть (-2, 4)
Объяснение:
\(\left\{\begin{array}{l}2x+5y=16 \\- 4x+3y=20\end{массив}\right.\)
Чтобы исключить x членов, умножьте первое уравнение на 2
2(2x + 5y = 16)
4x + 10y = 32
Сложите уравнения
4x + 10y = 32
+(-4x + 3y = 20)
x исключается, коэффициенты меняются местами. Решите для у
10y + 3y = 32 + 20
13y = 52
y = 52/13 = 4
Подставив y в любое из уравнений, чтобы найти x
2x + 5(4) = 16
2x + 20 – 20 = 16 – 20
2x = -4
x = -4/2 = -2
Мысль (-2, 4)
Вопрос 8.
Брайс потратил 5,26 доллара на несколько яблок по цене 0,64 доллара за штуку и несколько груш по цене 0,45 доллара за штуку. В другом магазине он мог бы купить такое же количество яблок по 0,32 доллара за штуку и такое же количество груш по 0,39 доллара за штуку на общую сумму 3,62 доллара. Сколько яблок и сколько груш купил Брайс?
В другом магазине он мог бы купить такое же количество яблок по 0,32 доллара за штуку и такое же количество груш по 0,39 доллара за штуку на общую сумму 3,62 доллара. Сколько яблок и сколько груш купил Брайс?
а. Напишите уравнения, представляющие расходы Брайса в каждом магазине
Первый магазин: _____________
Второй магазин: _____________
Введите ниже:
_____________
Ответ:
Первый магазин: 0,64x + 0,45y = 5,26
Второй магазин: 0,32x + 0,39y = 3,62
Объяснение:
Первый магазин = 0,64x + 0,45y = 5,26
Второй магазин = 0,32x + 0,39y = 3,62
, где x — количество яблок, а y — количество груш.
Вопрос 8.
б. Решите систему.
Количество яблок: _______
Количество груш: _______
Ответ:
Количество яблок: 4
Количество груш: 6
Объяснение:
Первый магазин = 0,64x + 0,45y = 5,269 Второй магазин = 0,26 0,39y = 3,62
Умножьте на 100
64x + 45y = 526
32x + 39y = 362
уравнения
64x + 45y = 526
-(64x + 78y = 724)
x исключается, имеет обратные коэффициенты.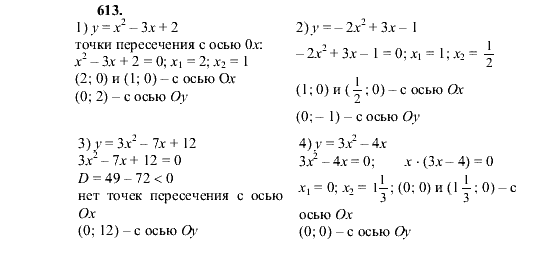 Решите для у
Решите для у
64x + 45y – 64x – 78y = 526 – 724
-33y = -198
y = -198/-33 = 6
Подставив y в любое из уравнений, чтобы найти x
32x + 39(6) = 362
32x + 234 – 234 = 362 – 234
32x = 128
x = 128/32 = 4
Он купил 4 яблока и 6 груш.
ОСНОВНОЙ ВОПРОС ПРОВЕРКА
Вопрос 9.
Решая систему путем умножения, а затем сложения или вычитания, как вы решаете, следует ли складывать или вычитать?
Введите ниже:
_____________
Ответ:
Если переменная с одинаковым коэффициентом, но с обратным знаком, мы складываем, а если они имеют одинаковый знак, мы вычитаем.
Решение систем методом исключения с умножением — страница № 257
Вопрос 10.
Объясните ошибку Гвен использовала исключение с умножением для решения системы
\(\left\{\begin{array}{l}2x+6y= 3 \\x-3y=-1\end{массив}\right.\)
Показана ее работа по поиску x. Объясните ее ошибку. Затем решить систему.
2(х — 3у) = -1
2x − 6y = -1
+2x + 6y = 3
_____________
4x + 0y = 2
x = \(\frac{1}{2}\)
Введите ниже:
____________
Ответ:
2x + 6y = 3
x – 3y = -1
Чтобы исключить члены x, умножьте второе уравнение на 2
2(x – 3y = -1)
2x – 6y = -2
Ошибка заключается в том, что Gnew не умножил все выражение на 2.
Складываем уравнения
2x + 6y = 3
+(2x – 6y = -2)
y исключается, имеет обратные коэффициенты. Решите для x
2x + 6y + 2x – 6y = 3 – 2
4x = 1
x = 1/4
Подставив x в любое из уравнений, чтобы найти y
x – 3y = -1
1/4 – 3y – 1/4 = -1 -1/4
-3y = — 5/4
y = -5/4(-3) = 5/12
Вопрос 11.
Представляют проблемы реального мира В Raging River Sports спальные мешки с полиэстеровым наполнителем продаются по цене 79 долларов. Спальные мешки с пуховым наполнителем продаются за 149 долларов. За одну неделю магазин продал 14 спальных мешков за 1456 долларов.
а. Пусть x представляет количество проданных мешков с полиэфирным наполнителем, а y представляет количество проданных мешков с пуховым наполнителем. Напишите систему уравнений, которую вы можете решить, чтобы найти количество проданных автомобилей каждого типа.
Введите ниже:
____________
Ответ:
x + y = 14
79x + 149y = 1456
где x – полиэфирные мешки, а y – количество пуховых мешков
Вопрос 11.
b. Объясните, как вы можете решить систему для y, умножая и вычитая.
Введите ниже:
____________
Ответ:
x + y = 14
79x + 149y = 1456
Умножьте второе уравнение на 79. Вычтите новое уравнение из первого уравнения и решите полученное уравнение относительно y.
Вопрос 11.
c. Объясните, как можно решить систему для y с помощью подстановки.
Введите ниже:
____________
Ответ:
Решите второе уравнение для x. Подставьте выражение для x в первое уравнение и решите полученное уравнение относительно y.
Вопрос 11.
d. Сколько сумок каждого типа было продано?
_______ полиэстер-наполнитель
_______ наполнитель-наполнитель
Ответ:
9 наполнитель-полиэстер
5 наполнитель-наполнитель
Объяснение:
x + y = 14
79x + 149y = 1456
Чтобы исключить члены x, умножьте второе уравнение на 2
79(x + y = 14)
79x + 149y = 1456
Вычтите уравнения
79x + 79y = 11096 -(79x + 149y = 1456)
x исключается, коэффициенты меняются местами.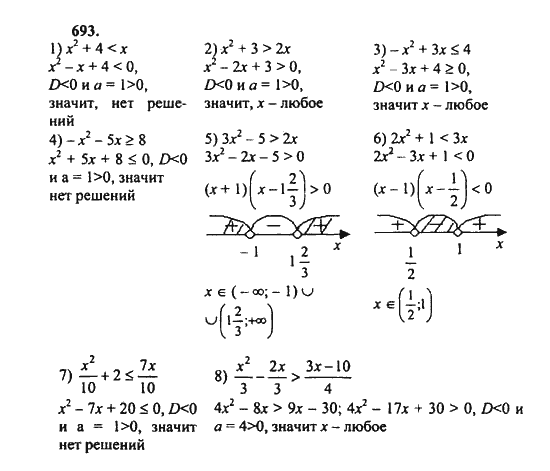 Найдите y
Найдите y
79x + 79y – 79x – 149y = 1106 – 1456
-70y = -350
y = -350/-70 = 5
Подставив y в любое из уравнений, чтобы найти x
x + 5 = 14
x = 14 – 5
x = 9
Было продано 9 мешков с полиэфирным наполнителем и 5 мешков с пуховым наполнением.
Вопрос 12.
Дважды число плюс дважды второе число равно 310. Разница между числами равна 55. Найдите числа, написав и решив систему уравнений. Объясните, как вы решили систему.
x = _______
y = _______
Ответ:
x = 105
y = 50
Объяснение:
2x + 2y = 310
x – y = 55
(x – y = 55)
2x – 2y = 110
Сложите уравнения
2x + 2y = 310
+ (2x – 2y = 110)
y исключается, у него обратные коэффициенты. Найдите x
2x + 2y + 2x – 2y = 310 + 110
4x = 420
x = 420/4 = 105
Подставив x в любое из уравнений, найдите y
105 – y = 55
y = 105 – 55
y = 50
Решение: (105, 50)
Решение систем методом исключения с умножением – страница № 258
Вопрос 13.
Репрезентация задач реального мира На прилавке фермы продаются яблочные пироги и банки яблочного пюре. В таблице указано количество яблок, необходимое для приготовления пирога и баночки яблочного пюре. Вчера ферма собрала 169Яблоки Гренни Смит и 95 яблок Red Delicious. Сколько пирогов и банок яблочного пюре может приготовить ферма, если использовать каждое яблоко?
_______ пирогов
_______ банок яблочного пюре
Ответ:
21 пирог
16 банок яблочного пюре
Объяснение:
5x + 4y = 169
3x + 2y = 169
3x + 2y = число яблока 9090 это количество яблок в банке яблочного пюре
Чтобы исключить члены y, умножьте второе уравнение на 2
2(3x + 2y = 95)
6x + 4y = 190
Вычесть уравнения
5x + 4y = 169
– (6x + 4y = 190)
y исключается, у него обратные коэффициенты. Найдите x
5x + 4y – 6x – 4y = 169 – 190
-x = -21
x = -21/-1 = 21
Подставив x в любое из уравнений, чтобы найти y
5(21) + 4y = 169
105 + 4y – 105 = 169 – 105
4y = 64
y = 64/4 = 16
Количество яблок, необходимых для пирога, равно 21, а количество яблок для банки яблочного пюре равно 16.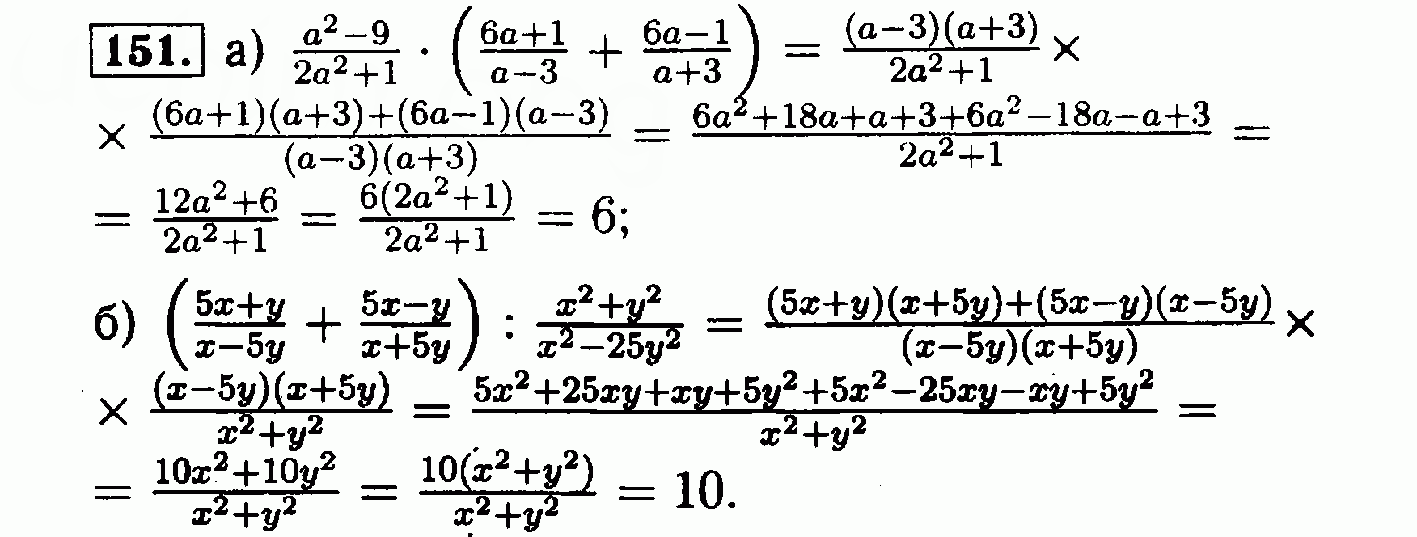
ФОКУС НА МЫШЛЕНИЕ ВЫСШЕГО ПОРЯДКА
Вопрос 14.
Сделать предположение Лена попыталась решить систему линейных уравнений алгебраически и в процессе нашла уравнение 5 = 9. Лена подумала, что что-то не так, поэтому нарисовала уравнения и обнаружила, что они представляют собой параллельные линии. Объясните, что могут означать график и уравнение Лены.
Введите ниже:
____________
Ответ:
График Лены представляет собой параллельную прямую, что означает, что графики не пересекаются друг с другом, следовательно, у них нет решений. Уравнение 5 = 9означает, что переменные исключены, и это утверждение неверно. Эта линейная система не имеет решений.
Вопрос 15.
Рассмотрим систему
\(\left\{\begin{array}{l}2x+3y=6 \\3x+7y=-1\end{array}\right.\)
a. Сообщите математические идеи Опишите, как решить систему, умножая первое уравнение на константу и вычитая. Почему этот метод не идеален?
Введите ниже:
____________
Ответ:
Умножение первого уравнения на константу и вычитание
2x + 3y = 6
3x + 7y = -1
Умножьте первое уравнение на 1,5 и вычтите. Это было бы далеко не идеально, потому что вы вводили бы десятичные дроби в процесс решения.
Это было бы далеко не идеально, потому что вы вводили бы десятичные дроби в процесс решения.
Вопрос 15.
б. Сделайте выводы Можно ли решить систему, умножая оба уравнения на целые константы? Если да, то объясните как.
Введите ниже:
____________
Ответ:
Да
Объяснение:
Умножьте первое уравнение на 3, а второе уравнение на 2. Оба коэффициента x-члена будут равны 6. Решите, исключив x-члены с помощью вычитания.
Вопрос 15.
c. Используйте свой ответ из части b, чтобы решить систему.
(_______ , _______)
Ответ:
(9, -4)
Объяснение:
2x + 3y = 6
3x + 7y = -1
Умножьте первое уравнение на 3, а второе уравнение на 2.
3 (2x + 3y = 6)
2(3x + 7y = -1)
Вычесть уравнения
6x + 9y = 18
-(6x + 14y = -2)
x исключается, имеет обратные коэффициенты. Решите для y
6x + 9y – 6x – 14y = 18 + 2
-5y = 20
y = 20/-5 = -4
Подставив y в любое из уравнений, чтобы найти x
2x + 3(-4) = 6
2x = 18
x = 18/2 = 9
Решение (9, -4)
Управляемая практика – Решение специальных систем – Страница № 262
Используйте график для решения каждой системы линейных уравнений
Вопрос 1.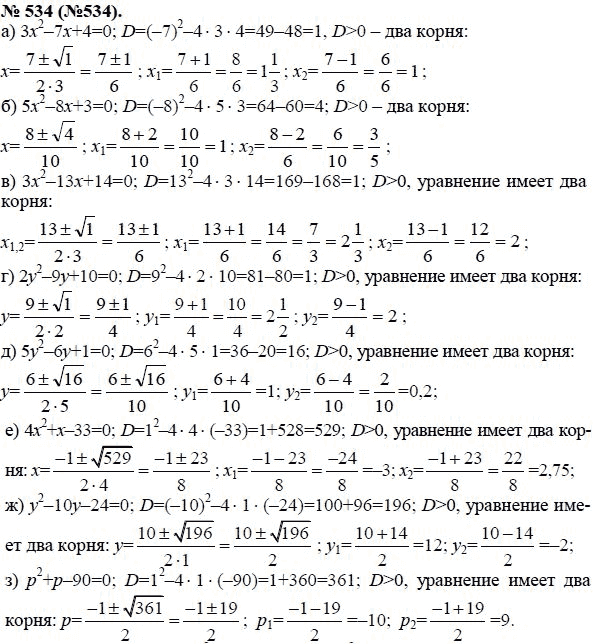
A. \(\left\{\begin{array} {l}4x-2y=-6 \\2x-y=4\end{массив}\right.\)
B. \(\left\{\begin{array}{l}4x-2y=-6 \ \x+y=6\end{массив}\right.\)
C. \(\left\{\begin{array}{l}2x-y=4 \\6x-3y=-12\end{массив }\право.\)
ШАГ 1 Решите, пересекаются ли графики уравнений в каждой системе, параллельны или представляют собой одну прямую.
Система A: графики __________
Система B: графики __________
Система C: графики __________
Ответ:
Система A: графики параллельны
Система B: графики пересекаются
Система C: графики представляют собой та же строка
Объяснение:
Система A: 4x – 2y = -6
2x – y = 4
Система B: 4x – 2y = -6
x + y = 6
Система C: 2x – y = 4
6x – 3y = 12
Вопрос 1.
ШАГ 2 Определите, сколько точек общего на графиках.
а. Пересекающиеся прямые имеют _______________ общих точек.
б. Параллельные прямые имеют _______________ общих точек.
с. Одни и те же прямые имеют ___________ общих точек.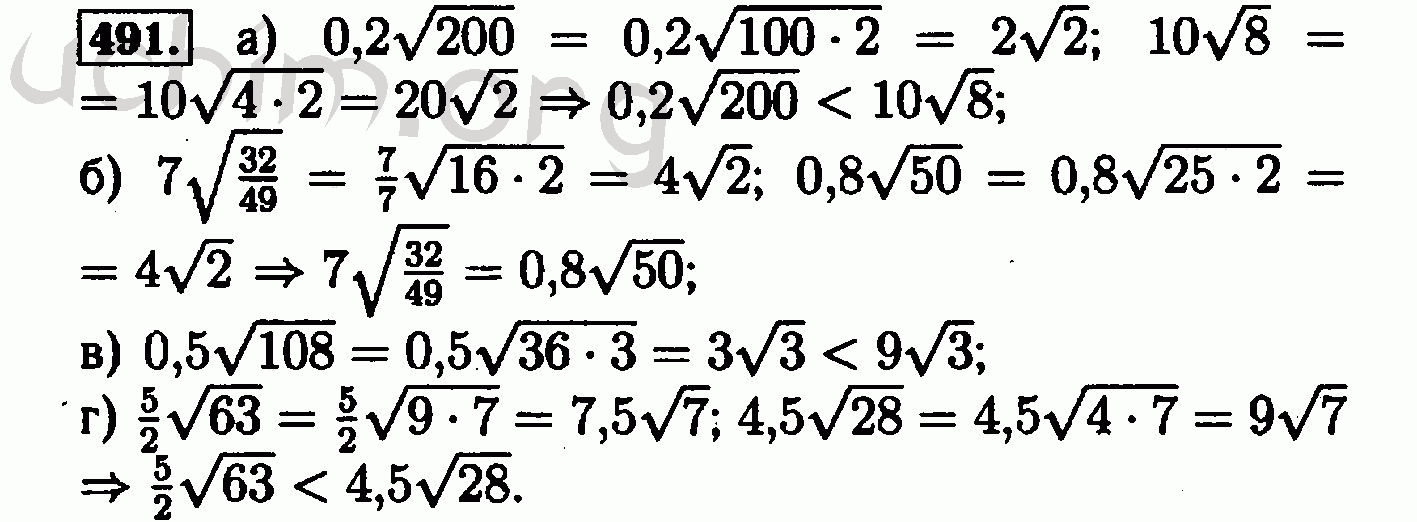
а. __________
б. __________
г. __________
Ответ:
а. Пересекающиеся прямые имеют одну общую точку.
б. Параллельные прямые не имеют общих точек.
с. Одни и те же прямые имеют бесконечно много общих точек (точек).
Объяснение:
Из графиков:
Пересекающиеся прямые имеют одну общую точку (точки)
Параллельные прямые не имеют общей точки (точек)
Одинаковые прямые имеют бесконечно много общих точек
Вопрос 1.
ШАГ 3 Решите каждую систему.
Система А имеет __________ общих точек, поэтому она имеет __________ решение.
Система B имеет __________ общей точки. Эта точка является решением, __________.
Система C имеет __________ общих точек. ________ упорядоченные пары в строке сделают оба уравнения верными.
Введите ниже:
___________
Ответ:
Система A не имеет общих точек, поэтому у нее нет решения. Система B имеет одну общую точку. Эта точка является решением (1,5). Система C имеет бесконечное число общих точек. Все упорядоченные пары на линии сделают оба уравнения верными.
Все упорядоченные пары на линии сделают оба уравнения верными.
Объяснение:
Количество решений для каждой системы
Система А не имеет общих точек, поэтому у нее нет решения. Система B имеет одну общую точку. Эта точка является решением (1,5). Система C имеет бесконечное число общих точек. Все упорядоченные пары на линии сделают оба уравнения верными.
Решить каждую систему. Укажите, сколько решений имеет каждая система.
Вопрос 2.
\(\left\{\begin{array}{l}x-3y=4 \\-5x+15y=-20\end{array}\right.\)
___________
Ответ :
бесконечно много решений
Объяснение:
x – 3y = 4
-5x + 15y = -20
Чтобы исключить члены y, умножьте первое уравнение на 5
5(x – 3y = 4)
5x – 15y = 20
Сложите уравнения
5x – 15y = 20
+(-5x + 15y = -20)
x и y исключаются, так как коэффициенты у них меняются местами.
5x – 15y – 5x + 15y = 20 – 20
0 = 0
Утверждение верно, следовательно, решение имеет бесконечно много решений.
Вопрос 3.
\(\left\{\begin{array}{l}6x+2y=-4 \\3x+y=4\end{array}\right.\)
___________
Ответ:
нет решения
Объяснение:
6x + 2y = -4
3x + y = 4
Чтобы исключить члены y, умножьте второе уравнение на 5
2(3x + y = 4)
6x + 2y = 8
Вычтите уравнения
6х + 2у = -4
-(6х + 2у = 8)
x и y исключается, так как имеет обратные коэффициенты.
6x + 2y – 6x – 2y = -4 -8
0 = -12
Утверждение неверно, следовательно, решение не имеет решения.
Вопрос 4.
\(\left\{\begin{array}{l}6x-2y=-10 \\3x+4y=-25\end{array}\right.\)
___________
Ответ:
одно решение
Объяснение:
6x – 2y = -10
3x + 4y = -25
Чтобы исключить члены y, умножьте первое уравнение на 2
2(6x – 2y = -10)
12x – 4y = -20
Сложите уравнения
12x – 4y = -20
+(3x + 4y = -25)
y исключается, так как имеет обратные коэффициенты. Решите для х.
12x – 4y + 3x + 4y = -20 – 25
15x = -45
x = -45/15 = -3
Подставьте x в любое из исходных уравнений и найдите y
3(-3) + 4y = -25
-9 + 4y + 9 = -25 + 9
4y = -16
y = -16/4
y = -4
Существует одно решение, (-3, -4)
ОСНОВНОЙ ВОПРОС CHECK-IN
Вопрос 5.
Когда вы решаете систему уравнений алгебраически, как вы можете определить, имеет ли система ноль, единицу или бесконечное число решений?
Введите ниже:
___________
Ответ:
Когда x и y исключены и утверждение верно, система имеет бесконечно много решений.
Когда x и y исключены, а утверждение ложно, система не имеет решений.
Когда система имеет одно решение путем решения, система имеет одно решение.
8.5 Самостоятельная практика – Решение специальных систем – № страницы 263
Решите каждую систему с помощью графика. Проверьте свой ответ алгебраически.
Вопрос 6.
\(\left\{\begin{array}{l}-2x+6y=12 \\x-3y=3\end{array}\right.\)
Решение: ______________
___________
Ответ:
\(\left\{\begin{array}{l}-2x+6y=12 \\x-3y=3\end{array}\right.\)
Нарисуйте уравнения по той же координате плоскость
Нет решения, так как уравнения параллельны
Чтобы исключить члены y, умножьте второе уравнение на 2
2(x – 3y = 3)
2x – 6y = 6
Сложите уравнения
-2x + 6y = 12
2x – 6у = 6
x и y исключается, так как имеет обратные коэффициенты.
-2x + 6y + 2x – 6y = 12 + 6
0 = 18
Утверждение неверно, следовательно, система не имеет решения.
Вопрос 7.
\(\left\{\begin{array}{l}15x+5y=5 \\3x+y=1\end{array}\right.\)
Решение: ______________
___________
Ответ:
\(\left\{\begin{array}{l}15x+5y=5 \\3x+y=1\end{array}\right.\)
Начертите уравнения на той же координатной плоскости
Бесконечное множество решений, так как уравнения перекрываются
Чтобы исключить члены y, умножьте второе уравнение на 5
5(3x + y = 1)
15x + 5y = 5
Вычтите уравнения
15x + 5y = 5
-(15x + 5y = 5)
x и y исключается, так как имеет обратные коэффициенты.
15x + 5y -15x – 5y = 5 – 5
0 = 0
Утверждение верно, следовательно, система имеет бесконечно много решений.
Для Exs. 8–
14, укажите количество решений каждой системы линейных уравнений
Вопрос 8.
система, графики которой имеют одинаковый наклон, но разные точки пересечения у но разные наклоны
___________
Ответ:
Одно решение
Объяснение:
Уравнения пересекаются
Одно решение
Вопрос 10.
система, графики которой имеют одинаковые точки пересечения y и одинаковые наклоны
___________
Ответ:
бесконечно много решений
Объяснение:
Уравнения перекрываются
бесконечно много решений
Вопрос 11.
Система, графики которой имеют разные y-intercepts и разные склоны
___________
.
Объяснение:
Уравнения пересекаются
Одно решение
Вопрос 12.
система
\(\left\{\begin{array}{l}y=2 \\y=-3\end{array}\right. \)
___________
Ответ:
Нет решений
Объяснение:
Уравнения параллельны
Нет решений
Вопрос 13.
система
\(\left\{\begin{array}{l}y=2 \\y= -3\end{массив}\right.\)
___________
Ответ:
Одно решение
Объяснение:
Уравнения пересекаются
Одно решение
Вопрос 14.
система, графики которой были построены с использованием следующих таблиц значений:
___________
Ответ:
Нет решений
Объяснение:
Уравнения параллельны Наклон обоих уравнений одинаков, но точка пересечения с осью Y различна.
Нет решений
Вопрос 15.
Сделать выводы График линейной системы приведен в учебнике. Вы можете видеть, что линии на графике не пересекаются, но и не кажутся параллельными. Можно ли сделать вывод, что система не имеет решений? Объяснять.
___________
Ответ:
Нет; хотя линии не пересекаются на графике, они пересекаются в точке, которой нет на графике. Чтобы доказать, что система не имеет решений, вы должны сделать это алгебраически
Решение специальных систем – страница № 264
Вопрос 16.
Репрезентация реальных задач Две школьные группы идут на каток для катания на роликах. Одна группа платит 243 доллара за 36 входных билетов и 21 прокат коньков. Другая группа платит 81 доллар за 12 входных билетов и 7 прокатов коньков. Пусть x представляет стоимость входного билета, а y представляет стоимость проката коньков. Достаточно ли информации, чтобы найти значения x и y? Объяснять.
___________
Ответ:
36x + 21y = 243
12x + 7y = 81
где x — стоимость входного билета, а y — стоимость аренды доли.
Хотя информацию можно использовать для разработки системы линейных уравнений, где каждое уравнение имеет две переменные, при решении системы количество решений бесконечно, Mee значения x и y не могут быть определены.
№
Вопрос 17.
Представляют реальные проблемы Хуан и Тори тренируются перед соревнованиями по легкой атлетике. Они начинают свои тренировочные заезды в один и тот же момент, но Тори начинает через 1 минуту после Хуана. Оба бегут со скоростью 704 фута в минуту. Догонит ли Тори Хуана? Объяснять.
___________
Ответ:
Нет; И Хуан, и Тори бегут с одинаковой скоростью, поэтому линии, представляющие расстояния, которые пробежал каждый, параллельны. Система не имеет решения
Сфокусируйтесь на мышлении высшего порядка
Вопрос 18.
Обоснование рассуждений Линейная система без решения состоит из уравнения y = 4x − 3 и второго уравнения вида y = mx + б. Что вы можете сказать о значениях m и b? Объясните свои рассуждения.
Введите ниже:
___________
Ответ:
y = 4x – 3
y = mx + b
Поскольку система не имеет решений, два уравнения параллельны. Значение наклона m будет таким же, т.е. 4. Значение точки пересечения по оси y b может быть любым числом, кроме -3, поскольку b отличается для параллельных линий.
Вопрос 19.
Обоснование рассуждений Линейная система с бесконечным числом решений состоит из уравнения 3x + 5 = 8 и второго уравнения вида Ax + By = C. Что вы можете сказать о значениях A, B и С? Объясните свои рассуждения.
Введите ниже:
___________
Ответ:
3x + 5 = 8
Ax + By = C
Поскольку система имеет бесконечно много решений, значения A, B и C должны быть кратны 3, 5 и 8 соответственно. Два уравнения представляют собой одну прямую, поэтому коэффициенты и константы одного уравнения должны быть кратны другим.
Вопрос 20.
Сделайте выводы Обе точки (2, -2) и (4, -4) являются решениями системы линейных уравнений.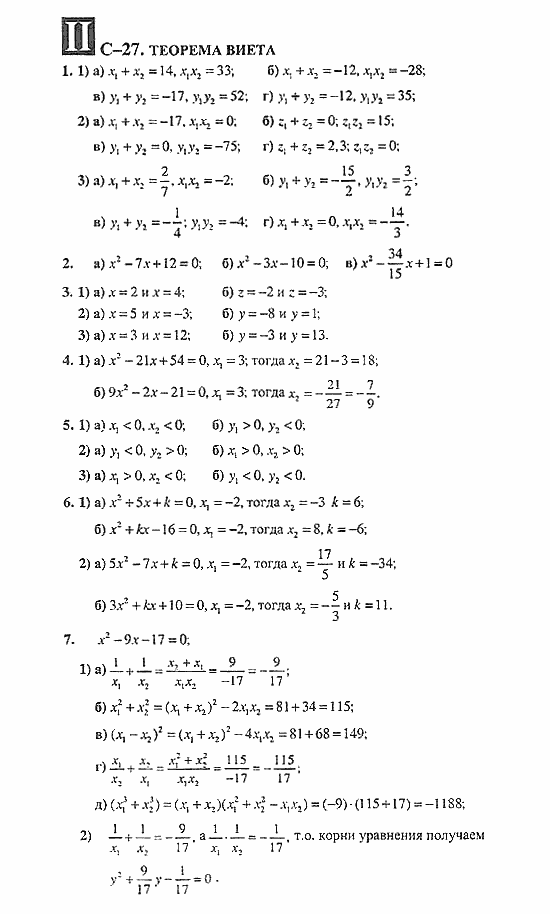 Какие выводы вы можете сделать об уравнениях и их графиках?
Какие выводы вы можете сделать об уравнениях и их графиках?
Введите ниже:
___________
Ответ:
Если система имеет более одного решения, уравнения представляют собой одну и ту же прямую и имеют бесконечно много решений.
Готовы продолжить? – Викторина по модели – Страница № 265
8.1 Решение систем линейных уравнений с помощью графика
Решите каждую систему с помощью графика.
Вопрос 1.
\(\left\{\begin{array}{l}y=x-1 \\y=2x-3\end{array}\right.\)
(________, ________)
Ответ:
(2, 1)
Объяснение:
y = x – 1
y = 2x – 3
Начертить уравнения на одной координатной плоскости
Решением системы является точка пересечения
Решением является (2, 1)
Вопрос 2.
\(\left\{\begin{array}{l}x+2y=1 \\-x+y=2\end{array}\right.\)
(________ , ________)
Ответ:
(-1, 1)
Объяснение:
x + 2y = 1
-x + y = 2
Нарисуйте уравнения на той же координатной плоскости
Решением системы является точка пересечения
Решением является (-1, 1)
8. 2 Решение систем подстановкой
2 Решение систем подстановкой
Решите каждую систему уравнений подстановкой.
Вопрос 3.
\(\left\{\begin{array}{l}y=2x \\x+y=-9\end{array}\right.\)
(________ , ________)
Ответ:
(-3, -6)
Объяснение:
y = 2x
x + y = -9
Подставьте y из уравнения 1 в другое уравнение.
x + 2x = -9
3x = -9
x = -9/3
x = -3
Тогда y = 2(-3) = -6
Решение: (-3, -6)
Вопрос 4.
\(\left\{\begin{array}{l}3x-2y=11 \\x+2y=9\end{array}\right.\)
(________ , ________)
Ответ:
(5, 2)
Объяснение:
3x – 2y = 11
x + 2y = 9
Найдите x в уравнении 2
x = – 2y + 9
Подставьте x из уравнения 2 в другое уравнение
3(- 2у + 9) – 2у = 11
-6у + 27 -2у = 11
-8у = -16
y = -16/-8 = 2
Подставьте y в любое из уравнений, чтобы найти x
x + 2(2) = 9
x + 4 – 4 = 9 – 4
x = 5
Решение (5 , 2)
8. 3 Решение систем методом исключения
3 Решение систем методом исключения
Решите каждую систему уравнений путем сложения или вычитания.
Вопрос 5.
\(\left\{\begin{array}{l}3x+y=9 \\2x+y=5\end{array}\right.\)
(________ , ________)
Ответ:
(4, -3)
Объяснение:
\(\left\{\begin{array}{l}3x+y=9\\2x+y=5\end{массив}\right.\)
Вычесть уравнения
3x + y = 9
-(2x + y = 5)
y исключается, так как имеет обратные коэффициенты. Найдите x
3x + y – 2x – y = 9 – 5
x = 4
Подставьте x в любое из уравнений, чтобы найти y
2(4) + y = 5
8 + y – 8 = 5 – 8
y = -3
Решение: (4, -3)
Вопрос 6.
\(\left\{\begin{array}{l}-x-2y=4 \\3x+2y=4\end{ массив}\право.\)
(________ , ________)
Ответ:
(4, -4)
Объяснение:
\(\left\{\begin{array}{l}-x-2y=4 \\3x+2y=4\end{array}\right.\)
Сложите уравнения
-x – 2y = 4
+(3x + 2y = 4)
y исключается, так как имеет обратные коэффициенты.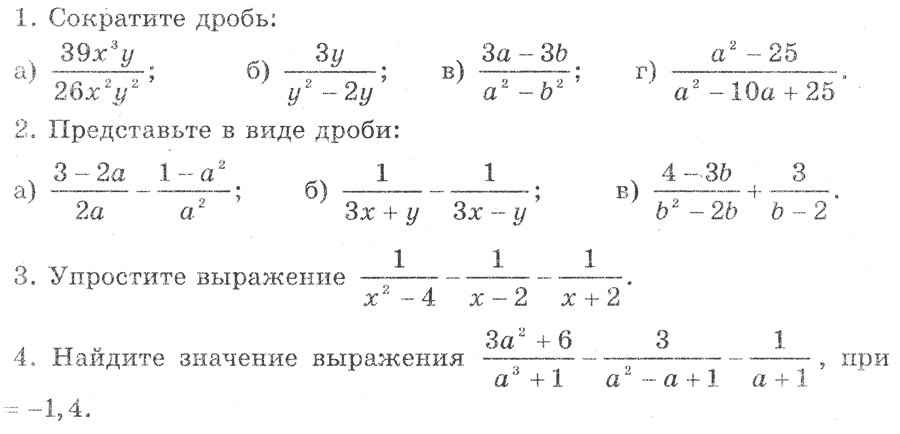 Найдите x
Найдите x
-x – 2y + 3x + 2y = 4 + 4
2x = 8
x = 8/2 = 4
Подставьте x в любое из уравнений, чтобы найти y
3(4) + 2y = 4
12 + 2y – 12 = 4 – 12
2y = -8
y = -8/2 = -4
Решение (4, -4)
8.4 Решение систем методом исключения с умножением
Решите каждую систему уравнений путем умножения.
Вопрос 7.
\(\left\{\begin{array}{l}x+3y=-2 \\3x+4y=-1\end{array}\right.\)
(________ , ________ )
Ответ:
(1, -1)
Объяснение:
\(\left\{\begin{array}{l}x+3y=-2 \\3x+4y=-1\end{array} \right.\)
Вычесть уравнения
3x + 9y = -6
-(3x + 4y = -1)
x исключается, так как имеет обратные коэффициенты. Решите для y
3x + 9y – 3x – 4y = -6 + 1
5y = -5
y = -5/5
y = -1
Подставив y в любое из уравнений, чтобы найти x
x + 3(-1) = -2
x – 3 = -2
x = — 2 + 3
x = 1
Решение: (1, -1)
Вопрос 8.
\(\left\{\begin{array}{l}2x+8y=22 \\3x-2y=5\ end{массив}\right.\)
(________ , ________)
Ответ:
(3, 2)
Объяснение:
\(\left\{\begin{array}{l}2x+8y=22 \ \3x-2y=5\end{массив}\right.\)
Умножить уравнение 2 на 4, чтобы можно было исключить y
4(3x – 2y = 5)
12x – 8y = 20
Сложите уравнения
2x + 8y = 22
+(12x – 8y = 20)
y исключается, так как имеет обратные коэффициенты. Найдите x
2x + 8y + 12x – 8y = 22 + 20
14x = 42
x = 42/14
x = 3
Подставив y в любое из уравнений, чтобы найти x
2(3) + 8y = 22
6 + 8y = 22
8y = 22 – 6
8y = 16
y = 16/8
y = 2
Решение (3, 2)
8.5 Решение специальных систем
Решить каждую систему. Укажите, сколько решений имеет каждая система.
Вопрос 9.
\(\left\{\begin{array}{l}-2x+8y=5 \\x-4y=-3\end{array}\right.\)
_____________
Ответ :
нет решения
Объяснение:
\(\left\{\begin{array}{l}-2x+8y=5 \\x-4y=-3\end{array}\right. \)
\)
Умножение уравнения 2 на 2, чтобы можно было исключить y
2(x – 4y = -3)
2x – 8y = -6
Сложить уравнения
-2x + 8y = 5
+(2x – 8y = -6)
x и у исключается
-2x + 8y + 2x – 8y = 5 – 6
0 = -1
Утверждение неверно. Следовательно, система не имеет решений.
Вопрос 10.
\(\left\{\begin{array}{l}6x+18y=-12 \\x+3y=-2\end{array}\right.\)
_____________
Ответ:
бесконечно много решений
Объяснение:
\(\left\{\begin{array}{l}6x+18y=-12 \\x+3y=-2\end{массив}\right.\)
Уравнение умножения 2 на 6, чтобы x можно было исключить
6(x + 3y = -2)
6x + 18y = -12
Вычесть уравнения
6x + 18y = -12
-(6x + 18y = -12)
x и y исключаются
6x + 18y -6x -18y = -12 + 12
0 = 0
Утверждение верно. Следовательно, система имеет бесконечно много решений.
ОСНОВНОЙ ВОПРОС
Вопрос 11.
Каковы возможные решения системы линейных уравнений и что они изображают графически?
Введите ниже:
___________
Ответ:
Система линейных уравнений не может иметь решения, представленного параллельными прямыми; одно решение, которое изображается пересекающимися линиями; и бесконечно много решений, которые представлены перекрывающимися линиями.
Выбранный ответ – Смешанный обзор – № страницы 266
Вопрос 1.
График какого уравнения показан?
Варианты:
A. y = −2x + 2
B. y = −x + 2
C. y = 2x + 2
D. y = 2x + 1
Ответ:
C. y = 2x + 2
Объяснение:
Варианты A и B исключены, так как наклон графика равен 2.
Вариант D исключен, так как точка пересечения с осью y должна быть равна 2.
Вариант C представляет собой уравнение графика
Вопрос 2
Что лучше всего описывает решения системы
\(\left\{\begin{array}{l}x+y=-4 \\-2x-2y=0\end{array}\right.\)
Опции :
A. одно решение
B. нет решений
C. бесконечно много
D. (0, 0)
Ответ:
B. нет решений
Объяснение:
\(\left\{\begin{array}{ l}x+y=-4 \\-2x-2y=0\end{массив}\right.\)
Умножить уравнение 1 на 2, чтобы x можно было исключить
2(x + y = -4)
2x + 2y = -8
Сложите уравнения
2x + 2y = -8
-2x – 2y = 0
x и y исключаются
2x + 2y – 2x -2y = -8 + 0
0 = -8
Утверждение неверно.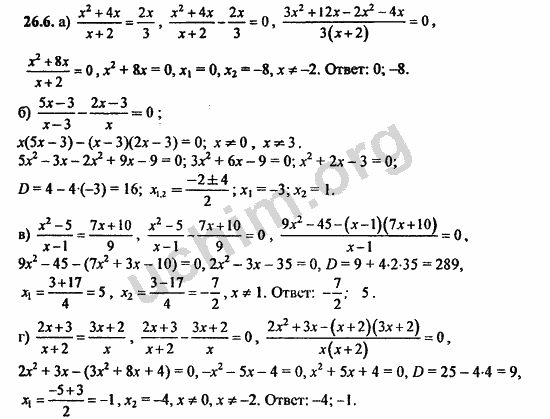 Следовательно, система не имеет решений.
Следовательно, система не имеет решений.
Вопрос 3.
Что из следующего представляет 0,000056023, записанное в экспоненциальном представлении?
Варианты:
A. 5.6023 × 10 5
B. 5,6023 × 10 4
C. 5,6023 × 10 -4
D. 5.6023 × 10 -5
D. 5.6023 × 10 -5
D. 5.6023 × 10 -5
D. 5.6023 × 10 -5
D. 10 -5
Объяснение:
Переместите запятую на 5 знаков вправо, чтобы получить уравнение.
D. 5,6023 × 10 -5
Вопрос 4.
Какое решение
\(\left\{\begin{array}{l}2x-y=1 \\4x+y=11\end {массив}\право.\)
Варианты:
А. (2, 3)
Б. (3, 2)
В. (-2, 3)
Г. (3, -2)
Ответ:
A. (2, 3)
Объяснение:
\(\left\{\begin{array}{l}2x-y=1 \\4x+y=11\end{array}\right.\)
Добавить уравнение
2x – y = 1
4x + y = 11
y исключается, поскольку имеет обратные коэффициенты. Решите для х.
Решите для х.
2x – y + 4x + y = 1 + 11
6x = 12
x = 12/6 = 2
Подставив x в любое из уравнений, чтобы найти y
4(2) + y = 11
8 + y = 11
y = 11 – 8
y = 3
Решение (2, 3)
Вопрос 5.
Какое выражение можно подставить в указанное уравнение, чтобы решить
\(\left\{\begin{array}{l }3x-y=5 \\x+2y=4\end{массив}\right.\)
Опции:
A. 2y – 4 вместо x в 3x – y = 5
B. 4 – x вместо y в 3x – y = 5
C. 3x – 5 вместо y в 3x – y = 5
D. 3x – 5 вместо y в x + 2y = 4
Ответ:
D. 3x – 5 вместо y в x + 2y = 4
Объяснение:
\(\left\{\begin{array}{l }3x-y=5 \\x+2y=4\end{массив}\right.\)
Найдите y в уравнении 1
y = 3x – 5
Подставьте в другое уравнение x + 2y = 4
Вопрос 6
Какое решение системы линейных уравнений изображено на графике?
Варианты:
А. -1
Б. -2
В. (-1, -2)
Г. (-2, -1)
Ответ:
В. (-1, -2)
Объяснение:
Точка пересечения (-1, -2), которая является решением системы
Вопрос 7.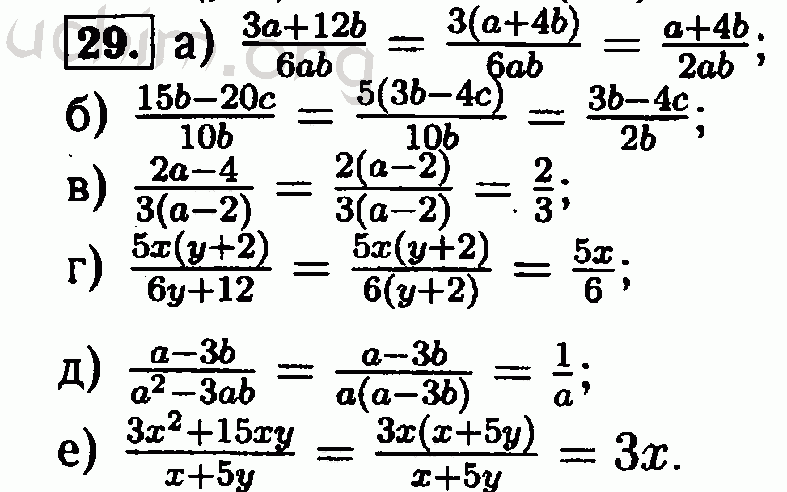
С какого шага вы могли бы начать решение
\(\left\{\begin{array }{l}x-6y=8 \\2x-5y=3\end{массив}\right.\)
Опции:
A. Добавить 2x – 5y = 3 к x – 6y = 8.
B. Умножить x – 6y = 8 на 2 и прибавьте к 2x – 5y = 3.
C. Умножьте x – 6y = 8 на 2 и вычтите из 2x – 5y = 3.
D. Подставьте x = 6y – 8 вместо x в 2x – 5y = 3.
Ответ:
C. Умножьте x – 6y = 8 на 2 и вычтите из 2x – 5y = 3.
Объяснение:
x – 6y = 8
2x – 5y = 3
Умножьте 1-е уравнение на 2 так, чтобы коэффициент переменной x одинаков в обоих уравнениях
Вычтите уравнения, так как x имеет один и тот же знак.
Мини-задание
Вопрос 8.
Воздушный шар начинает подниматься от земли со скоростью 4 метра в секунду, в то же время парашютист раскрывается на высоте 200 метров. Парашютист спускается со скоростью 6 метров в секунду.
а. Определите переменные и напишите систему, которая представляет ситуацию.
Введите ниже:
_____________
Ответ:
y представляет расстояние от земли, а x представляет время в секундах
y = 4x
y = -6x + 200
Вопрос 8.
b. Найти решение. Что это значит?
Введите ниже:
_____________
Ответ:
Подставьте y из уравнения 1 в уравнение 2
4x = -6x + 200
4x + 6x = -6x + 200 + 6x
10x = 200
x = 200/10 = 20
Подставьте x в любое из уравнений и найдите x
y = 4(20) = 80
Решение: (20, 80)
Воздушный шар и парашют встречаются через 20 секунд на высоте 80 м от земли.
Заключение:
Перейти к математике 8 класс Ключ к ответу Глава 8 Решение систем линейных уравнений PDF для всех учащихся, которые хотят изучать математику. См. вопросы главы 8 для 8 класса вместе с ответами и пояснениями. Немедленно приступайте к практике прямо сейчас.
Восьмой класс (8 класс) Алгебраические выражения Вопросы для тестов и рабочих листов
Выбрать все вопросы Оцените алгебраическое выражение для x = 5 и y = -2.| х + у |
- 4
- 7
- 3
- -3
В отличие от уравнений, алгебраические выражения не обязательно должны иметь знаки равенства.
- Истинный 92[/математика]
- 30
- 17
- 45
- 25
93/х[/математика].
- 1/4
- 37/4
- 5
- 4
одинаковые переменные возведены в одинаковые степени.

- Абсолютные значения
- Переменные
- Коэффициенты
- Нравятся условия
Символ (обычно буква), представляющий одно или несколько чисел.
- коэффициент
- база
- переменная
- экспонента
Ниже приведен пример алгебраического выражения:
[math]7x + 3 -4y[/math]- Истинный
- ЛОЖЬ
Если x = 4, найдите значение [math]-3x (-5x + 10)[/math].

- 360
- -120
- 75
- 120
Лучшее определение для переменной
- термины, использующие одну и ту же переменную с одним и тем же показателем степени.
- значение, представленное буквой.
- число перед переменной.

- комбинация чисел и/или переменных.
Постоянный мультипликативный коэффициент терма.
- одночлен
- коэффициент
- абсолютная величина
92[/математика].
- 895
- 775
- 825
- 695
92-9xy+6x.
 [/математика]
[/математика]- Истинный
- ЛОЖЬ
Лучшее определение для подобных терминов
- комбинация чисел и/или переменных.
- термины, использующие одну и ту же переменную с одним и тем же показателем степени.
- значение, представленное буквой.
- часть уравнения, составленного с членами.
 92р[/математика]
92р[/математика]Полностью факторизовать следующее алгебраическое выражение.
[математика]6m + 9n[/математика]Математика для 8 класса Ответы на основные темы Страницы 1-50 — Flip PDF Download
Главная Исследуйте Ответы на основные вопросы по математике для 8 класса
Нравится эта книга? Вы можете бесплатно опубликовать свою книгу в Интернете всего за несколько минут! Создайте свой собственный флипбук
Просмотр в полноэкранном режиме
Опубликовано Институтом образования Маврикия, 2019-04-11 18:08:46
Описание: Основные ответы по математике для 8 классаПрочитать текстовую версию
Без текстового содержания!
- 1 — 50
- 51 — 100
- 101 — 119
Страницы:
1)(5 − 2) (h) (7 − )( − 2) Глава 9.
 НОК алгебраических членов и алгебраических дробей Упражнение 9.1 1. (a) 24 (b) 20 (c) 48 (d) 60 (д) 56 (е) 70 (ж) 72 (з) 42 (и) 30 (к) 100 (л) 108 (м) 120
Упражнение 9.2 (б) 9(в) 12 (г) (д)10 (е) 24 (з) 48 (и)28 (к)22 (л)3 (л) 40г 1. (а) 2 (о) 4 (о)26 ( р) (ж) 21 (м) 45 2. (а) 2 (б) 622 (в) 22 (г) 22 (д) 622 (е) 222 (и) 633 (л) 282 (ж) 732 (з) ) 303y3 (o)6c43 (к) 16023 (л) 2442 (м)11232 (н) 18 3. (а) 24 (б) 12 (в) 4022 (г) 242б (д)322 (е)122 (ж) ) р23р (к) 16222 (л) 1534 (л)33223 (м) 33 (з) 33 (и) 423 (н) 123223 (о) 3432 Упражнение 9.3 (б)6 (в) 3 (г) 2 (д) 1 1. (а) 7 7 7 3 4 (е) 1 (ж) 2 (з) 15 9 3 4 2. (а) 4 ( б) 2 (в) 72 (г) 3 (д) 5 3 5 7 722 (е) 11ℎ3 (ж) 182 (з) 172 21 3 Упражнение 9.4 (б) 5 (в) 23 (г) 7 (д) 191. (а) 17 30 18 24 2 (е) 43 (ж) 50 (з) 35 (и) 29 (к) 1 1 36 63 48 75 6 (л) 17 (м) 43 20 40
НОК алгебраических членов и алгебраических дробей Упражнение 9.1 1. (a) 24 (b) 20 (c) 48 (d) 60 (д) 56 (е) 70 (ж) 72 (з) 42 (и) 30 (к) 100 (л) 108 (м) 120
Упражнение 9.2 (б) 9(в) 12 (г) (д)10 (е) 24 (з) 48 (и)28 (к)22 (л)3 (л) 40г 1. (а) 2 (о) 4 (о)26 ( р) (ж) 21 (м) 45 2. (а) 2 (б) 622 (в) 22 (г) 22 (д) 622 (е) 222 (и) 633 (л) 282 (ж) 732 (з) ) 303y3 (o)6c43 (к) 16023 (л) 2442 (м)11232 (н) 18 3. (а) 24 (б) 12 (в) 4022 (г) 242б (д)322 (е)122 (ж) ) р23р (к) 16222 (л) 1534 (л)33223 (м) 33 (з) 33 (и) 423 (н) 123223 (о) 3432 Упражнение 9.3 (б)6 (в) 3 (г) 2 (д) 1 1. (а) 7 7 7 3 4 (е) 1 (ж) 2 (з) 15 9 3 4 2. (а) 4 ( б) 2 (в) 72 (г) 3 (д) 5 3 5 7 722 (е) 11ℎ3 (ж) 182 (з) 172 21 3 Упражнение 9.4 (б) 5 (в) 23 (г) 7 (д) 191. (а) 17 30 18 24 2 (е) 43 (ж) 50 (з) 35 (и) 29 (к) 1 1 36 63 48 75 6 (л) 17 (м) 43 20 40- 1 — 50
- 51 — 100
- 101 — 119
Страницы:
Автор
Популярный поиск
бизнес дизайн мода Музыка здоровье жизнь спортивный маркетинг
8-й класс — вмешательство уровня 3
T3 1–5.
 OA.1 (Оцените числовые выражения с помощью круглых скобок)
OA.1 (Оцените числовые выражения с помощью круглых скобок)Пособия для учителей и мастер-копии
T3 1–1 -5. Оценка числовых выражений с помощью круглых скобок)
T3 1 — 5.OA.1 — Копия для учащихся (оценка числовых выражений с использованием круглых скобок)
T3 1 — 5.OA.1 — Карточки для моделирования и практических занятий
Видео
8T3 1 — 5.OA.1 — Сборка
T3 1 — 5.OA.1 — Нарисовать
T3 1 — 5.OA.1 — Написать
Вариант виртуального манипулирования для управляемой практики
Занятие 2: Мы делаем/Вы делаете вместе
T3 2 – 5.NBT.5 (Умножение многозначных чисел)
Пособия для учителей и мастер-классы
— Копия учителя (умножение многозначных чисел)
T3 2 — 5.NBT.5 — Копия ученика (умножение многозначных чисел)
T3 2 — 5.NBT.5 — Карточки для моделирования и пошаговой практики
T3 2 — 5.
 NBT.5 — Карточки с расстановкой значений
NBT.5 — Карточки с расстановкой значенийКоврики для умножения и деления
Видео
NBT.5 — Build
T3 2 — 5.NBT.5 — Draw
T3 2 — 5.NBT.5 — Write
Virtual Manipulative Option For Guided Practice
91:007 We Do Session Session Задачи 1–4
Занятие 1. Вы делаете вместе Задачи 5–8
Занятие 2. Мы делаем вместе, задачи 1–4
Занятие 2. Вы делаете вместе, задачи 5–8
Пособия для учителей и мастер-копииT3 3 — 5.NBT.6 — Копия для учителя (разделение четырехзначных чисел)
T3 3 — 5.NBT.6 — Копия для учащихся (разделение четырехзначных чисел)
T3 3 — 5.NBT.6 — Карточки моделирования и практики
T3 3 — 5.NBT.6 — Карточки значений места
Маты умножения и деления
Видео
T3 3 — 5.
 NBT.6 — Сборка
NBT.6 — СборкаT3 3 — 5.NBT.6 — Рисование
T3 0.6 — 3N 0.6 — 3N 3 3
Опция виртуальной манипуляции для управляемой практики
Сессия 1: Мы делаем вместе проблемы 1-4
Сессия 1: Вы делаете проблемы 5-8
Сессия 2: Мы делаем вместе. Проблемы 1 1. -4
Занятие 2: Вы делаете вместе Задачи 5–8
T3 4–5.NF.1 (Сложение и вычитание смешанных чисел с разными знаменателями)
Пособия для учителей и мастер-классы
T3 4–5.NF.1 .NF.1 — Копия для учителя (сложение и вычитание смешанных чисел с разными знаменателями)
T3 4 — 5.NF.1 — Копия для учащихся (сложение и вычитание смешанных чисел с разными знаменателями)
T3 4 — 5.NF.1 — полоски фракций (4 комплекта)
Видео
T3 4 — 5.NF.1 — Построить
T3 4 — 5.NF.1 — Нарисовать
T3 4 — 5.
 NF.1 — Записать
NF.1 — ЗаписатьПрактика
Занятие 1: Мы делаем/Вы делаете вместе
Занятие 2: Мы делаем/Вы делаете вместе
T3 5 — 5.NF.4b (Умножение дробей)
8Copy Masters
T3 5 – 5.NF.4b — Учительское копирование (умножение дробей)
T3 5 – 5.NF.4b – Ученический экземпляр (умножение дробей)
T3 5 – 5.NF.4b – Пособия по рисованию дробей (9 пособий) (2 набора)
Видео
T3 5 — 5.NF.4b — Сборка
T3 5 — 5.NF.4b — Нарисовать
T3 5 — 0 0 3 90 90
Вариант виртуального манипулирования для управляемой практики
Сессия 1: Мы делаем/вы делаете вместе
Занятие 2: Мы делаем/Вы делаете вместе
T3 6 – 5.NF.7a (Деление дробной части на целое число)
Пособия для учителей и мастер-классы
2 — 5 T . NF.7a — Копия учителя (деление дробной части на целое число)
NF.7a — Копия учителя (деление дробной части на целое число)T3 6 — 5.NF.7a — Копия учащегося (деление дробной единицы на целое число)
T3 6 — 5.NF.7a — Направляющие для деления дробей
T3 6 — 5.NF.7a — Квадраты для деления дробей
Видео
T3 6 — 5.nf.7a — Build
T3 6 — 5.nf.7a — Draw
T3 6 — 5.nf.7a — Напишите
Виртуальная манипуляция Вариант для пошаговой практики
Занятие 1. Мы делаем/вы делаете вместе
Занятие 2. Мы делаем/вы делаете вместе
T3 7 — 5.NF.7b (Деление целого числа на единицу) дробь)
Пособия для учителей и копии мастеров
T3 7 – 5.NF.7b – Копия для учителя (Деление целого числа на дробную часть)
T3 7 – 5.NF.7b – Копия для учащегося (Деление целого числа на дробную часть)
T3 7 — 5.NF.7b — Руководство по делению дробей
T3 7 — 5.
 NF.7b — Целые числа для деления
NF.7b — Целые числа для деленияВидео
T3 7 — 5.NF.7b — 3 T3
— 5.NF.7b — Нарисовать
T3 7 — 5.NF.7b — Написать
Вариант виртуального манипулирования для управляемой практики
Занятие 1: Мы делаем/вы делаете вместе
Занятие 2: Мы делаем/вы делаете вместе
T3 8–6.NS.1 (Умножение и деление дробей)
3 Учителя
3 и Copy Masters
T3 8 — 6.NS.1 — Копирование для учителя (умножение и деление дробей)
T3 8 — 6.NS.1 — Копирование для учащихся (умножение и деление дробей)
T3 8 — 6.NS .1 — Руководства по рисованию дробей
Видеоролики
T3 8 — 6.NS.1 — Build
T3 8 — 6.NS.1 — Draw
T3 8 — 6.NS.1 — Write
Virtual Manipulative Option For Guided Practice 03 9000
Занятие 1. Мы делаем/вы делаете вместе
Занятие 2.
 Мы делаем/вы делаете вместе
Мы делаем/вы делаете вместе T3 9 — 6.NS.6c (Найти упорядоченную пару на координатной плоскости)
Учитель Направляющие и мастера копирования
T3 9 — 6.NS.6c — Копия учителя (Найти упорядоченную пару на координатной плоскости)
T3 9 – 6.NS.6c – Студенческая копия (Найти упорядоченную пару на координатной плоскости) .6c — Build
T3 9 — 6.NS.6c — Draw
T3 9 — 6.NS.6c — Write
Virtual Manipulative Option For Guided Practice
Dostitute Session for Westitute Session Вы делаете вместеСессия 2 Заменяет We Do/You Do Together
T3 10 — 6.EE.2a (Перевод алгебраических выражений между словами и символами)
Пособия для учителей и мастер-копии
T3 10 — 6.EE.2a — Перевод алгебраических выражений между словами и символы)
T3 10 — 6.EE.2a — Копия для учащихся (перевод алгебраических выражений между словами и символами)
T3 10 — 6.
 EE.2a — Карточки для моделирования и практических занятий
EE.2a — Карточки для моделирования и практических занятийT3 10 — 6.EE. 2a — Плитки положительной алгебры
Видео
T3 10 — 6.EE.2a — Build
T3 10 — 6.EE.2a — Draw
T3 10 — 6.EE.2a — напишите
Виртуальная манипуляция Вариант для управляемой практики
Занятие 1 Замените We Do/You Do Together
Занятие 2 Замените We Do/You Do Together
T3 11 — 6.EE.2c (оцените алгебраические выражения8)
Пособия для учителей и копии мастеров
T3 11 – 6.EE.2c – Копия для учителя (оценка алгебраических выражений) Карточки с пошаговыми инструкциями
T3 11 – 6.EE.2c – Положительные алгебраические плитки
Видеоролики
T3 11 – 6.EE.2c – Построение
900 — 03T3 12 – 11 T3 11 — 6.EE.2c — Запись
Вариант виртуального манипулирования для практического применения
Занятие 1 Заменяет We Do/You Do Together
Занятие 2 Заменяет We Do/You Do Together
T3 12 — 6.


 В.
В.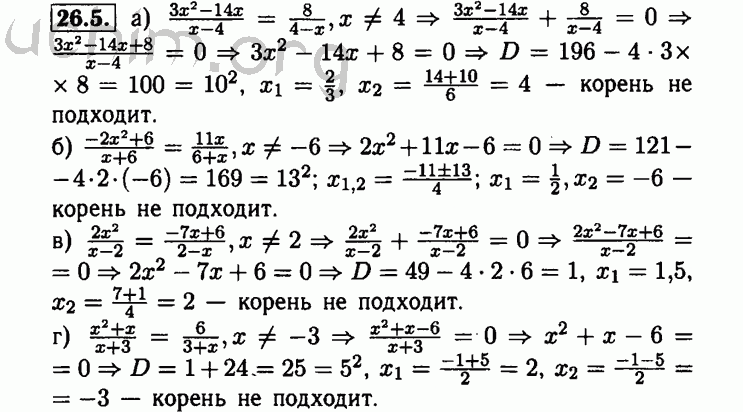 М. Никольский М.К. Потапов
М. Никольский М.К. Потапов
 П. Муравьева Г.Л.
П. Муравьева Г.Л.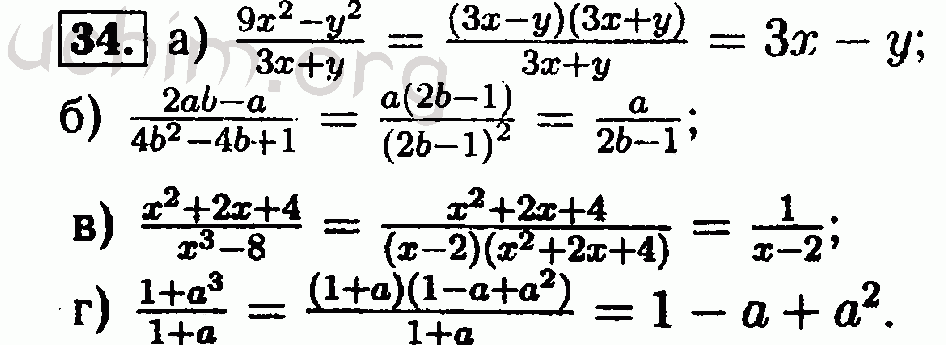 Б.
Б.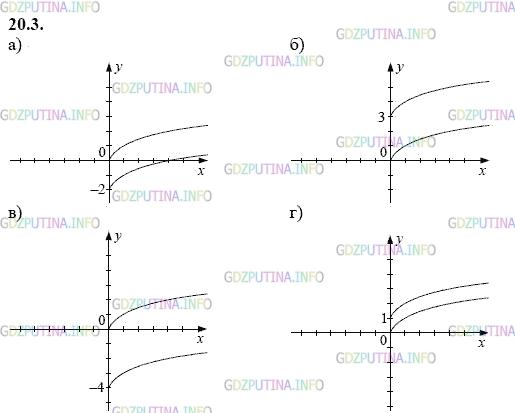 А.
А. В. Минаева С.С.
В. Минаева С.С. В. Струков Т.С.
В. Струков Т.С.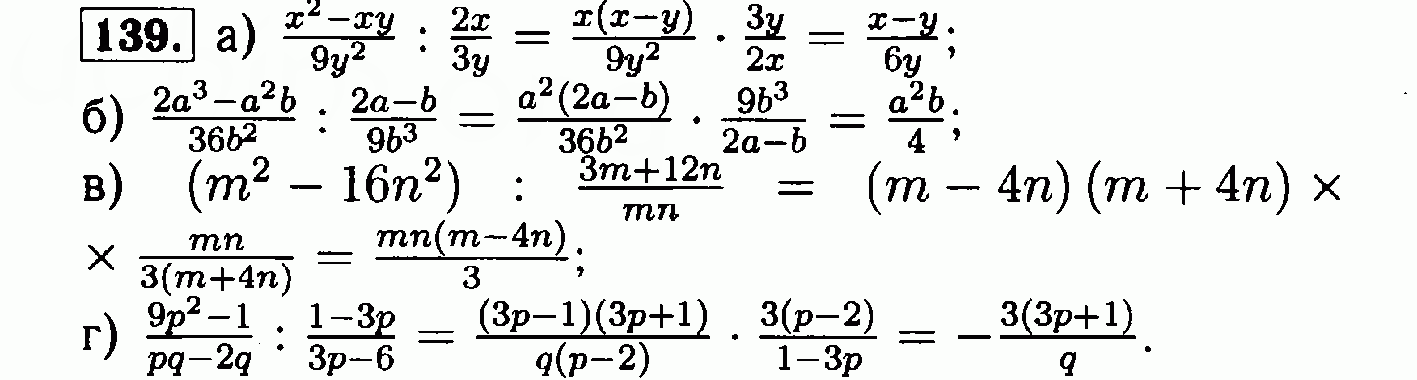 П. Карп А.П.
П. Карп А.П. С. Рослова Л.О.
С. Рослова Л.О. Р. Пидручна М.В.
Р. Пидручна М.В. Н. Шыныбеков Д.А.
Н. Шыныбеков Д.А. В.
В. П. Дудницын B.Л. Кронгауз
П. Дудницын B.Л. Кронгауз А.
А.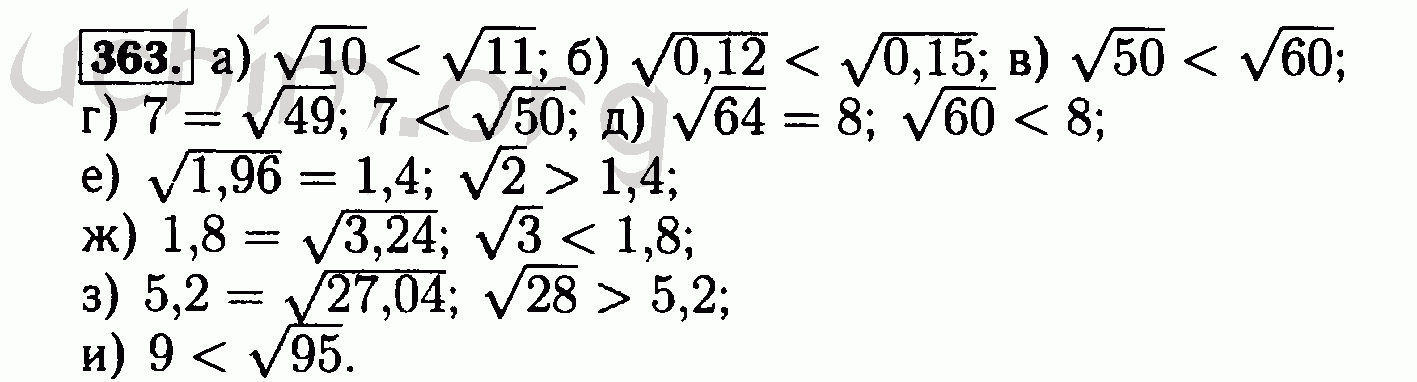 А. Гаиашвили М.Я.
А. Гаиашвили М.Я. А.
А.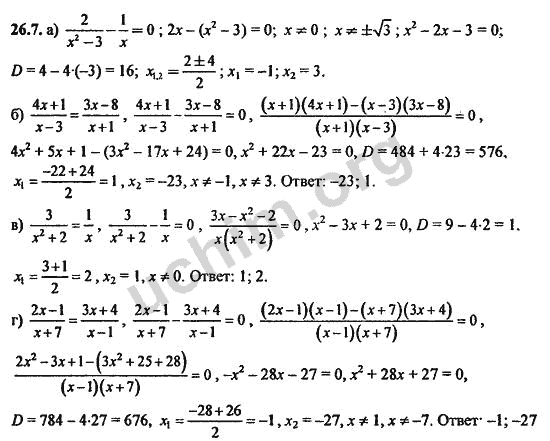 К. Муравин
К. Муравин Б., Якир М.С.
Б., Якир М.С. С.
С. Г. Мерзляк
Г. Мерзляк Г., Поляков В.М.
Г., Поляков В.М. И.
И. А., Мардахаева Е.Л.
А., Мардахаева Е.Л. В.
В. А. Глазков
А. Глазков Н.
Н. М.
М. В.
В.


 08 МБ
08 МБ
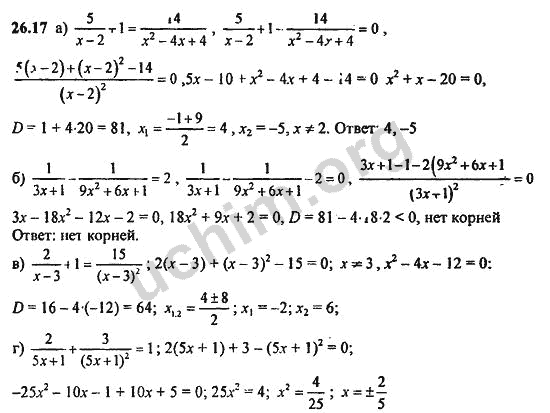 № 248
№ 248


 [/математика]
[/математика] 92р[/математика]
92р[/математика] НОК алгебраических членов и алгебраических дробей Упражнение 9.1 1. (a) 24 (b) 20 (c) 48 (d) 60 (д) 56 (е) 70 (ж) 72 (з) 42 (и) 30 (к) 100 (л) 108 (м) 120
Упражнение 9.2 (б) 9(в) 12 (г) (д)10 (е) 24 (з) 48 (и)28 (к)22 (л)3 (л) 40г 1. (а) 2 (о) 4 (о)26 ( р) (ж) 21 (м) 45 2. (а) 2 (б) 622 (в) 22 (г) 22 (д) 622 (е) 222 (и) 633 (л) 282 (ж) 732 (з) ) 303y3 (o)6c43 (к) 16023 (л) 2442 (м)11232 (н) 18 3. (а) 24 (б) 12 (в) 4022 (г) 242б (д)322 (е)122 (ж) ) р23р (к) 16222 (л) 1534 (л)33223 (м) 33 (з) 33 (и) 423 (н) 123223 (о) 3432 Упражнение 9.3 (б)6 (в) 3 (г) 2 (д) 1 1. (а) 7 7 7 3 4 (е) 1 (ж) 2 (з) 15 9 3 4 2. (а) 4 ( б) 2 (в) 72 (г) 3 (д) 5 3 5 7 722 (е) 11ℎ3 (ж) 182 (з) 172 21 3 Упражнение 9.4 (б) 5 (в) 23 (г) 7 (д) 191. (а) 17 30 18 24 2 (е) 43 (ж) 50 (з) 35 (и) 29 (к) 1 1 36 63 48 75 6 (л) 17 (м) 43 20 40
НОК алгебраических членов и алгебраических дробей Упражнение 9.1 1. (a) 24 (b) 20 (c) 48 (d) 60 (д) 56 (е) 70 (ж) 72 (з) 42 (и) 30 (к) 100 (л) 108 (м) 120
Упражнение 9.2 (б) 9(в) 12 (г) (д)10 (е) 24 (з) 48 (и)28 (к)22 (л)3 (л) 40г 1. (а) 2 (о) 4 (о)26 ( р) (ж) 21 (м) 45 2. (а) 2 (б) 622 (в) 22 (г) 22 (д) 622 (е) 222 (и) 633 (л) 282 (ж) 732 (з) ) 303y3 (o)6c43 (к) 16023 (л) 2442 (м)11232 (н) 18 3. (а) 24 (б) 12 (в) 4022 (г) 242б (д)322 (е)122 (ж) ) р23р (к) 16222 (л) 1534 (л)33223 (м) 33 (з) 33 (и) 423 (н) 123223 (о) 3432 Упражнение 9.3 (б)6 (в) 3 (г) 2 (д) 1 1. (а) 7 7 7 3 4 (е) 1 (ж) 2 (з) 15 9 3 4 2. (а) 4 ( б) 2 (в) 72 (г) 3 (д) 5 3 5 7 722 (е) 11ℎ3 (ж) 182 (з) 172 21 3 Упражнение 9.4 (б) 5 (в) 23 (г) 7 (д) 191. (а) 17 30 18 24 2 (е) 43 (ж) 50 (з) 35 (и) 29 (к) 1 1 36 63 48 75 6 (л) 17 (м) 43 20 40 OA.1 (Оцените числовые выражения с помощью круглых скобок)
OA.1 (Оцените числовые выражения с помощью круглых скобок) NBT.5 — Карточки с расстановкой значений
NBT.5 — Карточки с расстановкой значений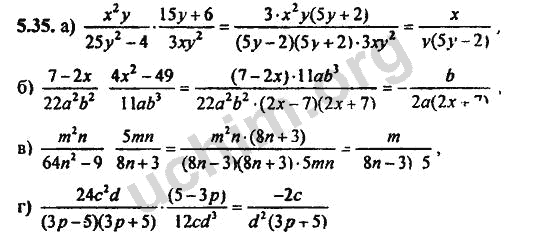 NBT.6 — Сборка
NBT.6 — Сборка NF.1 — Записать
NF.1 — Записать NF.7a — Копия учителя (деление дробной части на целое число)
NF.7a — Копия учителя (деление дробной части на целое число)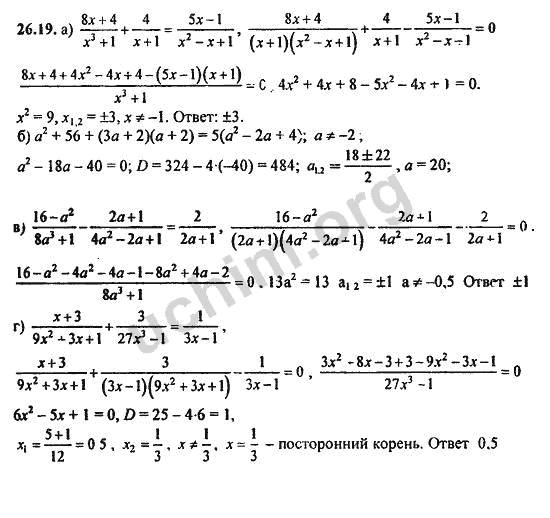 NF.7b — Целые числа для деления
NF.7b — Целые числа для деления Мы делаем/вы делаете вместе
Мы делаем/вы делаете вместе 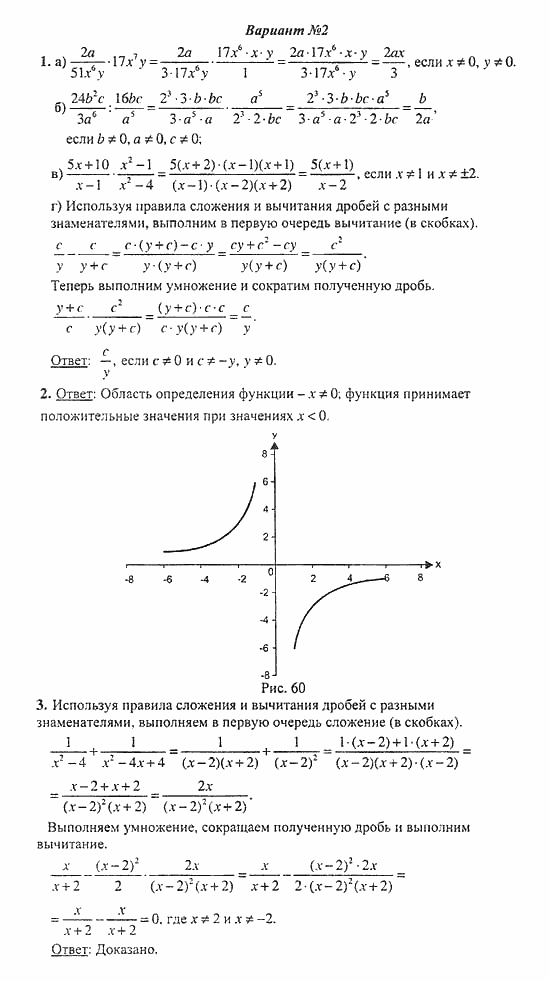 EE.2a — Карточки для моделирования и практических занятий
EE.2a — Карточки для моделирования и практических занятий