Самостоятельная работа по теме «Линейные уравнения с одной переменной» (40 вариантов)
ВАРИАНТ 1 | ВАРИАНТ 2 | ВАРИАНТ 3 | ВАРИАНТ 4 | ВАРИАНТ 5 |
1. 7 – 2х = 9 – 3х 2. 11х = 6 + 5(2х – 1) 3. 6(2х – 3) – 3х = 2х – 4 4. 4(3х + 5) – 5(4х – 3) = 3 5. 5х – 3(4х – 1) = 7 – 2(7х + 2) 6. –5,6(x – 3) + 2,lx = –3,5x + 10 | 1. 7х + 10 = 5х + 2 2. 4(3х – 2) + 5 = 9 3. 2х – 5 = 7(3х + 4) + 5 4. 28 – 4(3х + 2) = 5(2х – 7) 5. 6. 7(x – 4) + 3 = 3(2x – 7) + x – 8 | 1. 5 – 6х = –10х – 3 2. 6(2х + 5) – 8х = 2 3. 3 + 4(5х – 3) = 4х + 7 4. 3(5х – 7) – 7(4х + 5) = х 5. 2(6х – 5) – 7(3х – 5) = 4х – 1 6. –12x + 4(x – 3) = – 8x – 12 | 1. 17 – 2х = 5 – 6х 2. 2(4х – 5) = 2х + 8 3. 3х – 10 = 5х + 2(4х + 5) 4. 6х – 6(2х + 5) = 4(5х – 1) 5. 11 – 4(3х – 1) – 5(4х – 3) = 3х 6. 8(x – 3) + 1 = 5(2x + 3) – 2х | 1. 9х + 13= 7х + 5 2. 3(2х + 5) + 6 = 3 3. 5х + 18 = 7х + 6(3х – 7) 4. 5. 13 – 3(5х + 1) – 6(4х – 3) = 5х 6. 4(x + 2) – 0,7 = 2(2x + 4) + 0,3 |
ВАРИАНТ 6 | ВАРИАНТ 7 | ВАРИАНТ 8 | ВАРИАНТ 9 | ВАРИАНТ 10 |
1. –5х – 9 = –6х – 10 2. 4х = 7 + 3(4х + 3) 3. 5(3х + 1) + 2х = 4х + 5 4. 3(7х – 1) – 6(5х + 2) = 3 5. 3х – 5(2х + 3) = 15 – 4(6х – 1) 6. 1,9x + 0,3(7 – x) = 2,1 – 0,2х | 1. 12х – 5 = 7х + 10 2. 4(3х + 5) – 6х = 2 3. 4. 17 – 2(6х – 5) = 4(7х – 2) 5. 6х – 3(5х + 4) – 2(7х – 3) = –6 6. –2(x + 21) – 3(x – 14) = –5x | 1. 6х – 11 = х + 14 2. 5(6х – 1) = 3х – 5 3. 5 + 3(7х + 4) = 6х – 13 4. 5(3х + 4) – 6(3х – 7) = 23х 5. 4(5х – 3) – 5(3х + 7) = 6х – 23 6. 2(x + 21) + 3(x – 4) = 5(x + 6) | 1. 10х + 15 = 7х + 6 2. 3(4х – 1) + 5х = 14 3. 4х + 8 = 6х + 4(5х + 2) 4. 7(2х – 5) – 5(4х + 3) = 4х 5. 8 – 7(2 – 5х) – 4(2х + 3) = 3х 6. 2,1(x – 0,3) + 0,7x = 2,8x + 0,7 | 1. 2. 4(5х + 2) = 7х – 5 3. 7(2х – 1) – 3х = х – 17 4. 5х – 5(4х + 3) = 6(5х – 1) 5. 4х – 7(3х – 5) = 4 – 3(4х – 7) 6. 2,4(x – 0,1) – 0,26 = 2,4x – 0,4 |
ВАРИАНТ 11 | ВАРИАНТ 12 | ВАРИАНТ 13 | ВАРИАНТ 14 | ВАРИАНТ 15 |
1. –4х – 21 = –7х – 3 2. 7(3х – 4) – 5 = 9 3. 5х + 4 = 3(6х + 5) + 2 4. 6(2х + 3) – 2(7х – 4) = 23 5. 7х – 5(4х – 5) – 2(6х + 7) = 1 6. –11(x – 2) + (2x – 3) = –9x + 19 | 1. 2. 7х = 5 + 2(6х – 5) 3. 9 + 5(4х – 3) = 7х – 6 4. 25 – 4(3х + 5) = 7(4х + 3) 5. 6(2х + 7) – 2(6х – 5) = 3х – 2 6. 11(x – 2) – (2x – 3) = 9(x + 2) | 1. –3х – 10 = –12 – 5х 2. 16х = 7(3х – 1) + 2 3. 4 + 6(3х + 1) = 5х + 10 4. 7(3х – 4) – 4(6х + 5) = –55 5. 18 – 6(3х + 7) – 2(4х – 1) = 7х 6. –1,7(x + 2) – 0,3x = 2(2 – x) | 1. 5 – 4х = 7 – 5х 2. 6(2х – 3) + 4 = 10 3. 7х – 4 = 4(2х – 7) + 2х 4. 2 – 5(4х – 7) = 3(6х + 5) 5. 3х – 6(5х + 2) = 4 – 5(3х + 4) 6. | 1. 13 – 4х = 1 – 8х 2. 5(3х + 4) – 2х = 7 3. 3х – 10 = 4х + 3(5х + 2) 4. 6(4х + 7) – 3(8х – 3) = 17х 5. 4х – 3(6х – 1) – 7(4х – 3) = 10 6. 2(x – 23) + 3(15 – x) = –(x + 1) |
ВАРИАНТ 16 | ВАРИАНТ 17 | ВАРИАНТ 18 | ВАРИАНТ 19 | ВАРИАНТ 20 |
1. –6х – 23 = –9х – 5 2. 2(4х – 3) = 5х + 3 3. 6х + 7 = 5(4х – 1) – 16 4. 15х – 4(3х + 5) = 7(2х + 5) 5. 6. 2(x – 23) + 3(15 – x) = –x + 1 | 1. 7х + 10 = 5х + 12 2. 3(2х – 5) + 5х = 7 3. 5х – 3 = 6(2х + 5) + 2 4. 17х – 3(5х – 4) = 8(3х – 4) 5. 7(4х + 5) – 4(2 + 3х) = 6х – 3 6. 2,1(2 – x) + 1,4(1,5x – 3) = 0 | 1. 9х + 13= 6х + 4 2. 9х = 3 + 4(5х + 2) 3. 6 + 7(4х – 3) = 3х – 65 4. 5(4х + 3) – 7(4х – 7) = 24 5. 1 – 5(2х – 5) – 3(2 – 3х) = 4х 6. 2,1(2 – x) + 1,4(1,5x – 3) = 2 | 1. 9х – 7 = 4х + 18 2. 7(3х + 1) = 4х – 10 3. 6х + 14 = 4х + 5(3х + 8) 4. 5. 2х – 4(5х – 3) = 21 – 7(3х + 2) 6. 2,1(2x – 1) = 1,4(3x – 4) + 0,3 | 1. 13х – 2 = 8х + 13 2. 5(4х + 7) – 3 = 12 3. 4(3х – 2) – 2х = 5х + 12 4. 2(8х – 3) – 4(6х + 5) = 6х 5. 5х – 2(7х + 2) – 3(4х + 5) = 2 6. 21(x – 3) + 20 = 7(3x – 2) |
ВАРИАНТ 21 | ВАРИАНТ 22 | ВАРИАНТ 23 | ВАРИАНТ 24 | ВАРИАНТ 25 |
1. 11х – 3= 6х + 12 2. 3. 6х – 1 = 3х + 5(4х – 7) 4. 4(6х + 5) – 5(7х – 4) = х 5. 4х – 6(3х + 8) – 5(2х – 7) = 35 6. 7(2x – 3) + 1 = 2(7x – 10) | 1. 7х – 8 = 2х + 17 2. 2х = 3(2х + 1) + 5 3. 7(2х + 3) + х = 4х – 12 4. 7х – 3(4х – 3) = 7(3х + 5) 5. 5(2 – 5х) – 7(4х – 1) = 6х – 42 6. 2(8x – 1) – 8(2x – 3) = 13 | 1. 7х + 11 = 4х + 2 2. 4(5х – 1) = 3х + 13 3. 7х + 3 = 4(3х – 2) + 1 4. 5(3х – 2) – 3(6х + 5) = –1 5. 3 – 4(5х + 2) – 3(6х – 5) = 2х 6. 8(2x – 1) – 2(8x – 3) = 2 | 1. 2. 2(4х + 3) – 5х = 3 3. 9 + 2(7х + 6) = 5х + 12 4. 16 – 3(4х + 5) = 7(2х – 3) 5. 6х – 2(5х + 4) = 1 – 7(4х + 3) 6. 8(2x – 1) – 2(8x – 3) = –2 | 1. 6 – 5х = –9х – 2 2. 2(5х – 1) + 8 = 6 3. 4 + 5(3х – 4) = 7х – 8 4. 6(3х + 4) – 5(4х – 3) = 29 5. 2х – 4(7х – 3) = 10 – 5(3х – 7) 6. 11(2x – 3) = 5(4x – 6) + 2x |
ВАРИАНТ 26 | ВАРИАНТ 27 | ВАРИАНТ 28 | ВАРИАНТ 29 | ВАРИАНТ 30 |
1. 2. 7(4х – 3) – 2х = 5 3. 4х + 5 = 2х + 3(5х + 6) 4. 25 – 4(4х – 3) = 3(5х + 2) 5. 7х – 2(5х – 3) – 4(2 – 3х) = 1 6. 9(2x – 1) + 2 = 2(9x – 3) – 1 | 1. 7х + 5 = 5х + 7 2. 4х = 4 + 2(3х + 5) 3. 4(2х – 5) – х = 3х + 8 4. 7(3х – 2) – 6(4х + 7) = 18х 5. 2(6х – 5) – 5(3х + 4) = 7х – 10 6. 9(2x – 1) + 2 = 2(8x – 3) + 2х | 1. 9 – 3х = 11 – 4х 2. 3(7х – 2) = 4х – 6 3. 5х – 6 = 6(3х + 4) – 4 4. 3х – 5(3х – 2) = 4(6х – 5) 5. 3 – 3(2 – 7х) – 6(3 + 4х) = 4х 6. | 1. 15 – 3х = 3 – 7х 2. 9х = 7 + 4(3х – 1) 3. 6х – 5 = 3(7х – 4) + 7 4. 29 – 6(3х – 4) = 5(4х + 3) 5. 5х – 4(6 – 7х) – 3(4х + 3) = 2 6. –4,3(x – 3) + 0,8x = –3,5x + 10 | 1. 3 – 4х = –8х – 5 2. 4(3х + 4) – 5 = –1 3. 5 + 4(3х + 5) = 2х – 5 4. 6(2х + 3) – 7(3х – 4) = 14х 5. 4(3х + 7) – 6(2х + 5) = 5х – 1 6. 6(x – 4) + 2,3 = 3(2x – 7) – 8 |
ВАРИАНТ 31 | ВАРИАНТ 32 | ВАРИАНТ 33 | ВАРИАНТ 34 | ВАРИАНТ 35 |
1. 2. 5(2х – 1) + х = 6 3. 3х + 11 = 5х + 7(3х – 5) 4. 3х – 4(5х + 2) = 3(7х – 2) 5. 17 – 2(3х – 5) – 5(4х – 1) = 6х 6. –11x + 3(x – 3) = – 8x – 9 | 1. 6х + 7 = 4х – 1 2. 6(4х + 3) = 5х – 1 3. 6(2х + 1) + 2х = 5х – 12 4. 3(5х – 2) – 7(3х + 4) = –24 5. 7х – 7(4х – 1) = 1 – 3(5х – 2) 6. 4,8(x – 3) + 1 = 2,4(2x + 3) | 1. 8х – 9 = 3х + 16 2. 6(3х – 4) – 4х = 4 3. 5х – 6 = 7х + 4(3х + 2) 4. 2х – 6(2х – 5) = 5(4х – 3) 5. 3(5х – 2) – 4(3х – 5) = 7х – 2 6. | 1. 15х – 4 = 10х + 11 2. 5(6х – 1) = 2х + 23 3. 5(2х – 3) – 3х = 4х – 9 4. 4(5х + 3) – 6(4х – 7) = 36 5. 4 – 7(3х – 4) – 4(2х + 5) = 3х 6. 3,2x + 0,3(7 – x) = 2,1 + 1,1х | 1. 7х + 11 = 5х + 3 2. 4х = 6 + 2(4х – 1) 3. 4х – 7 = 7(3х + 2) + 13 4. 17 – 5(2х + 7) = 4(5х – 3) 5. 3х – 5(6х – 7) = 5 – 6(2х + 5) 6. –3(x + 12) – 2(x – 18) = –5x |
ВАРИАНТ 36 | ВАРИАНТ 37 | ВАРИАНТ 38 | ВАРИАНТ 39 | ВАРИАНТ 40 |
1. 2. 3(2х + 1) + 7 = 4 3. 6 + 3(5х – 7) = 4х + 7 4. 3(7х – 4) – 4(6х + 5) = х 5. 3х – 5(2х + 3) – 6(5х – 4) = –28 6. 3(x + 21) + 2(x – 4) = 5(x + 11) | 1. –3х – 25 = –6х – 7 2. 5(3х – 1) – 6 = 4 3. 9х + 2 = 4(5х – 3) – 8 4. 4 – 2(6х – 5) = 6(4х + 3) 5. 6(3х – 4) – 7(2х + 5) = 2х – 1 6. 2,3(x – 0,3) + 0,5x = 2,8x | 1. 14 – 5х = 2 – 9х 2. 4(5х – 2) – 3х = 9 3. 5 + 6(4х + 5) = 3х – 7 4. 5(4х + 7) – 3(8х – 3) = 7х 5. 32 – 3(6х – 1) – 5(4х + 7) = 5х 6. | 1. 4 – 5х = 6 – 6х 2. 2(4х + 5) = 7х – 1 3. 7х – 12 = 4х + 9(2х – 3) 4. 47х – 7(4х – 3) = 4(5х – 2) 5. 7х – 3(3х + 5) = 1 – 4(4х – 3) 6. 8(x – 2) + (3x – 3) = 11x – 19 | 1. –6х – 13 = –7х – 14 2. 5х = 8 + 3(2х + 3) 3. 3(4х + 1) + 3х = 2х – 23 4. 7(2х – 5) – 4(5х + 3) = –33 5. 6х – 7(3х – 5) – 2(4х – 7) = 3 6. 12(x – 2) – (4x – 3) = 8(x + 3) |
вариант 1 | вариант 2 | вариант 3 | вариант 4 | вариант 5 |
1. | 1. –4 | 1. –2 | 1. –3 | 1. –4 |
2. 1 | 2. 1 | 2. –7 | 2. 3 | 2. –3 |
3. 2 | 3. –2 | 3. 1 | 3. –2 | 3. 3 |
4. 4 | 4. | 4. –4 | 4. –1 | 4. |
5. 0 | 5. | 5. 2 | 5. | 5. |
6. | 6. | 6. R | 6. | 6. |
вариант 6 | вариант 7 | вариант 8 | вариант 9 | вариант 10 |
1. | 1. 3 | 1. 5 | 1. –3 | 1. 1 |
2. –2 | 2. –3 | 2. 0 | 2. 1 | 2. –1 |
3. 0 | 3. 2 | 3. –2 | 3. 0 | 3. –1 |
4. –2 | 4. | 4. | 4. –5 | 4. – |
5. 2 | 5. 0 | 5. –24 | 5. | 5. 2 |
6. R | 6. R | 6. R | 6. | 6. |
вариант 11 | вариант 12 | вариант 13 | вариант 14 | вариант 15 |
1. | 1. –2 | 1. –1 | 1. 2 | 1. –3 |
2. 2 | 2. 1 | 2. 1 | 2. 2 | 2. –1 |
3. –1 | 3. 0 | 3. 0 | 3. 8 | 3. –1 |
4. | 4. – | 4. | 4. | 4. 3 |
5. | 5. 18 | 5. – | 5. | 5. |
6. R | 6. | 6. | 6. | 6. R |
вариант 16 | вариант 17 | вариант 18 | вариант 19 | вариант 20 |
1. | 1. 1 | 1. –3 | 1. 5 | 1. 3 |
2. 3 | 2. 2 | 2. –1 | 2. –1 | 2. –1 |
3. 2 | 3. –5 | 3. –2 | 3. –2 | 3. 4 |
4. –5 | 4. 2 | 4. 5 | 4. 1 | 4. – |
5. 1 | 5. –3 | 5. 4 | 5. – | 5. –1 |
6. | 6. R | 6. | 6. | 6. |
вариант 21 | вариант 22 | вариант 23 | вариант 24 | вариант 25 |
1. | 1. 5 | 1. –3 | 1. 1 | 1. –2 |
2. 3 | 2. –2 | 2. 1 | 2. –1 | 2. 0 |
3. 2 | 3. –3 | 3. 2 | 3. –1 | 3. 1 |
4. | 4. –1 | 4. –8 | 4. | 4. 5 |
5. –2 | 5. 1 | 5. | 5. – | 5. –3 |
6. R | 6. | 6. | 6. R | 6. |
вариант 26 | вариант 27 | вариант 28 | вариант 29 | вариант 30 |
1. | 1. 1 | 1. 2 | 1. –3 | 1. –2 |
2. 1 | 2. –7 | 2. 0 | 2. –1 | 2. –1 |
3. –1 | 3. 7 | 3. –2 | 3. 0 | 3. –3 |
4. 1 | 4. – | 4. | 4. 1 | 4. 2 |
5. | 5. –2 | 5. –3 | 5. | 5. – |
6. R | 6. | 6. | 6. | 6. |
вариант 31 | вариант 32 | вариант 33 | вариант 34 | вариант 35 |
1. | 1. –4 | 1. 5 | 1. 3 | 1. –4 |
2. 1 | 2. –1 | 2. 2 | 2. 1 | 2. –1 |
3. 2 | 3. –2 | 3. –1 | 3. 2 | 3. –2 |
4. – | 4. – | 4. | 4. | 4. – |
5. 1 | 5. 0 | 5. 4 | 5. | 5. 4 |
6. R | 6. | 6. | 6. R | 6. R |
вариант 36 | вариант 37 | вариант 38 | вариант 39 | вариант 40 |
1. | 1. 6 | 1. –3 | 1. 2 | 1. –1 |
2. –1 | 2. 1 | 2. 1 | 2. –11 | 2. –17 |
3. 2 | 3. 2 | 3. –2 | 3. 1 | 3. –2 |
4. –8 | 4. – | 4. 4 | 4. 29 | 4. – |
5. 1 | 5. 29 | 5. 0 | 5. 2 | 5. 2 |
6. R | 6. | 6. | 6. R | 6. |
7 класс, алгебра, обучающая самостоятельная работа по алгебре по теме: «Решение уравнений и задач на составление уравнений»
Главная / Старшие классы / Алгебра
Скачать
31. 5 КБ, 508030.doc Автор: Козлова Наталья Павловна, 21 Мар 2015
5 КБ, 508030.doc Автор: Козлова Наталья Павловна, 21 Мар 2015
В самостоятельной работе даётся образец типичного уравнения с пошаговым его решением. Далее предлагается решить четыре уравнения, постепенно, усложняя их.
Так же разобран пример решения типичной задачи на составление уравнений, содержащей проценты. Самостоятельно предлагается решить три задачи разного уровня.
Самостоятельная работа расчитана на урок, предпологается дифференцация учащихся, в зависимости от сложности решаемых уравнений и задач.
Автор: Козлова Наталья Павловна
Похожие материалы
| Тип | Автор | Опубликован | |
|---|---|---|---|
| документ | 7 класс, алгебра, обучающая самостоятельная работа по алгебре по теме: «Решение уравнений и задач на составление уравнений» | Козлова Наталья Павловна | 21 Мар 2015 |
| документ | Самостоятельная работа по алгебре 7 класс по теме «Решение задач с помощью системы двух линейных уравнений с двумя переменными » | Ольга Михайловна Щербакова | 6 Дек 2015 |
| документ | Самостоятельная работа по алгебре по теме:Решение уравнений 7 класс | Терехина Надежда Викторовна | 4 Апр 2015 |
| документ | Самостоятельная работа по алгебре «Системы уравнений» | Тюрина Екатерина Михайловна | 15 Ноя 2015 |
| разное | 5 класс. Математика.Проект урока и презентация к уроку по теме: решение уравнений и несложных задач на составление уравнений, урок в коррекционном классе 7-го вида Математика.Проект урока и презентация к уроку по теме: решение уравнений и несложных задач на составление уравнений, урок в коррекционном классе 7-го вида | Козлова Наталья Павловна | 20 Мар 2015 |
| разное | Козлова Наталья Павловна | 20 Мар 2015 | |
| разное | 5 класс. Математика.Проект урока и презентация к уроку по теме: решение уравнений и несложных задач на составление уравнений, урок в коррекционном классе 7-го вида | Козлова Наталья Павловна | 20 Мар 2015 |
| документ | интегрированный урок по алгебре 7 класс по теме «Решение задач с помощью уравнений» | Рыбина Татьяна Викторовна | 1 Апр 2015 |
| презентация, документ | Открытый урок по алгебре в 8 классе на тему «Решение задач с помощью дробных рациональных уравнений» | Логинова Алевтина Владимировна | 7 Апр 2015 |
| презентация, документ | Разработка урока по теме: Решение задач на составление уравнений 6 класс | Тагильцева Елена Юрьевна | 31 Мар 2015 |
| документ | План-конспект урока по алгебре 7 класс по теме:Решение задач с помощью систем уравнений | Краснова Лидия Егоровна | 15 Окт 2015 |
| контрольная работа по алгебре 8 класс на тему: «Система уравнений» | Воробьева Юлия Викторовна | 14 Ноя 2015 | |
| презентация, документ | Урок по теме «Уравнения. Решение задач на составление уравнений» Решение задач на составление уравнений» | Гуреева Ирина Львовна | 1 Апр 2015 |
| документ | Самостоятельная работа по алгебре по теме: «Числовые и буквенные выражения», 7 класс | МАРИЧ ОЛЬГА ИВАНОВНА | 31 Мар 2015 |
| презентация | Презентация к уроку математики в классе — комплекте (5,6 класс) по теме «Решение уравнений и задач при помощи уравнений» | Лобанова Елена Васильевна | 1 Апр 2015 |
| разное | Урок по математике «Решение уравнений и задач с помощью уравнений», 6 класс. | Королева Татьяна Вячеславовна | 1 Апр 2015 |
| документ | урок по алгебре «решение задач с помощью уравнений» | Курдина Оксана Вадимовна | 7 Июл 2015 |
| документ | Контрольная работа №9 по алгебре для 7 класса по теме «Системы линейных уравнений» | Баринова Елена Валерьевна | 8 Фев 2016 |
| презентация | Презентация по алгебре 7 класс по теме: «Системы линейных уравнений с двумя переменными» | Полякова Ольга Васильевна | 15 Дек 2015 |
| документ | Итоговый урок по теме:Решение задач на составление систем уравнений второй степени в форме защиты проектов. | Музюкова Надежда Николаевна | 9 Авг 2015 |
| документ | Методическая разработка для 7 класса по алгебре на тему «Решение линейных уравнений» | Файзуллина Марьям Талгатовна | 15 Окт 2015 |
| презентация | презентация урока по алгебре и началам анализа в 10 классе по теме «Решение простейших тригонометрических уравнений» | Панина Елена Юрьевна | 7 Апр 2016 |
| документ | Самостоятельная работа по алгебре в 7 класс по теме»Линейная функция» | Чебырова Людмила Ивановна | 14 Ноя 2015 |
| документ | урок по алгебре 8 класс «Решение неполных квадратных уравнений» | Миронова Любовь Васильевна | 7 Апр 2016 |
| разное | Урок по алгебре «Системы показательных уравнений и неравенств» | Лошкарёва Галина Александровна | 7 Мая 2015 |
| документ | Самостоятельная работа по алгебре и началам анализа 10 класс по теме «Тригонометрические уравнения» | Лапатин Алексей Леонидович | 21 Мар 2015 |
| документ | Самостоятельная работа по алгебре по теме «Рациональные и иррациональные числа»,8 класс | Саблина Татьяна Алексеевна | 21 Мар 2015 |
| документ | РАЗРАБОТКА УРОКА ПО МАТЕМАТИКЕ В 5 КЛАССЕ НА ТЕМУ «РЕШЕНИЕ УРАВНЕНИЙ И ЗАДАЧ С ПОМОЩЬЮ УРАВНЕНИЙ» | Бадыкова Светлана Геннадьевна | 31 Мар 2015 |
| документ | Самоанализ урока по алгебре » Решение задач с помощью дробных рациональных уравнений» | Логинова Алевтина Владимировна | 21 Мар 2015 |
| документ | Конспект урока по математике на тему:»Закрепление изученного. | Пономаренко Людмила Николаевна | 30 Мар 2015 |
| разное | Конспект урока «Уравнения. Решение задач с помощью уравнений» Урок-сказка по теме: «Уравнение. Решение задач с помощью уравнений», 5 класс | Свечкарева Ирина Михайловна | 1 Апр 2015 |
| документ | Алгоритм решения задач на составление уравнений в 5 классе | Смирнова Нина Ивановна | 21 Мар 2015 |
| презентация, документ | Решение задач на составление уравнений | Фоменко Марина Вячеславовна | 1 Апр 2015 |
| разное | Решение задач на составление уравнений | Подгорбунская Ирина Викторовна | 5 Сен 2015 |
| документ | Контрольная работа по теме: Решение уравнений 7 класс | Терехина Надежда Викторовна | 4 Апр 2015 |
| презентация | Интегрированный урок по алгебре и истории математики в 7 классе по теме: «Решение линейных систем уравнений с двумя переменными». систем систем | Степушкина Наталья Юрьевна | 1 Апр 2015 |
| документ | Индивидуальные задания по математике для 5 класса на тему «Задачи на составление уравнений» | Козлова Светлана Львовна | 6 Дек 2015 |
| документ | Конспект урока по алгебре для 7 класса по теме «Решение уравнений» | Захарова Валентина Владимировна | 1 Апр 2015 |
| документ | План-конспект урока по алгебре в 7 классе по теме: «Решение систем линейных уравнений» | Болдинова Людмила Игнатьевна | 19 Мар 2016 |
| разное | Методическая разработка урока по алгебре для 7 класса по теме «Решение линейных уравнений» | Фадеева Елена Анатольевна | 8 Фев 2016 |
ГДЗ: Алгебра 7 класс Звавич, Кузнецова
Вариант I.
 С-1.Вычисление значения числового выражения1 2 3 4 5 6
С-1.Вычисление значения числового выражения1 2 3 4 5 6Вариант I. С-2.Вычисление значения числового выражения
1 2 3 4Вариант I. С-3. Решение задач на проценты
1 2 3 4 5 6 7 8 9Вариант I. С-4. Нахождение значений буквенных выражений
1 2 3 4 5 6 7 8Вариант I. С-5. Сравнение значений выражений
1 2 3 4 5 6 7 8Вариант I. С-6. Применение свойств действий над числами к вычислениям
1 2 3 4 5Вариант I. С-7. Приведение подобных слагаемых и раскрытие скобок
1 2 3 4 5 6 7Вариант I. С-8. Решение линейных уравнений
1 2 3 4 5Вариант I. С-9. Решение уравнений, сводящихся к линейным
1 2 3 4 5Вариант I. С-10. Решение задач с помощью уравнений
1 2 3 4 5 6 7 8Вариант I. С-11. Построение точек в координатной плоскости
1 2 3 4 5 6Вариант I. С-12. Нахождение значений функции по формуле. Статистические характеристики
1 2 3 4 5 6 7Вариант I. С-13. Построение графика функции вида у = кх + y
1 2 3 4 5 6 7Вариант I.
 С-14. Построение графика функции вида у = кх1 2 3 4 5 6 7
С-14. Построение графика функции вида у = кх1 2 3 4 5 6 7Вариант I. С-15. Чтение графика линейной функции
1 2 3 4Вариант I. С-16. Взаимное расположение графиков на координатной плоскости
1 2 3 4 5 6 7Вариант I. С-17. Построение и чтение графиков линейных функций (практические задания)
1 2Вариант I. С-18. Вычисление значения числового выражения, содержащего степень
1 2 3 4 5 6 7 8 9Вариант I. С-19. Вычисление значения буквенного выражения, содержащего степень
1 2 3 4 5Вариант I. С-20. Умножение и деление степеней с одинаковыми основаниями
1 2 3 4 5 6 7 8 9 10Вариант I. С-21. Возведение в степень произведения и степени
1 2 3 4 5 6 7 8 9Вариант I. С-22. Различные преобразования выражений, содержащих степени
1 2 3 4 5Вариант I. С-23. Вычисление значения одночлена
1 2 3 4Вариант I. С-24. Умножение многочленов и возведение одночлена в степень
1 2 3 4 5 6 7 8Вариант I. С-25. Приведение многочленов к стандартному виду
1 2 3 4 5 6 7 8Вариант I.
 С-26. Сложение и вычитание многочленов1 2 3 4 5 6
С-26. Сложение и вычитание многочленов1 2 3 4 5 6Вариант I. С-27. Заключение многочленов в скобки
1 2 3 4Вариант I. С-28. Умножение одночлена на многочлен
1 2 3 4 5Вариант I. С-29. Решение уравнений
1 2 3 4Вариант I. С-30. Решение уравнений
1 2Вариант I. С-31. Решение задач
1 2Вариант I. С-32. Вынесение общего множителя за скобки
1 2 3 4 5Вариант I. С-33. Умножение многочленов
1 2 3 4Вариант I. С-34. Умножение многочленов
1 2 3 4 5Вариант I. С-35. Разложение многочленов на множители способом группировки
1 2 3 4Вариант I. С-36. Чтение и запись алгебраических выражений
1 2 3 4Вариант I. С-37. Возведение в квадрат по формулам
1 2 3 4Вариант I. С-38. Преобразование выражений с применением формул квадрата суммы и квадрата разности
1 2 3 4Вариант I. С-39. Разложение на множители с помощью формул квадрата суммы и квадрата разности
1 2 3Вариант I. С-40. Умножение многочленов с использованием формулы (a-fe)(a + 6) = a2-fe2
1 2 3Вариант I.
 С-41. Применение формул к преобразованию выражений1 2 3 4 5
С-41. Применение формул к преобразованию выражений1 2 3 4 5Вариант I. С-42. Разложение на множители по формуле
1 2 3Вариант I. С-43. Преобразование целых выражений
1 2 3 4 5Вариант I. С-44. Разложение многочленов на множители с использованием нескольких способов
1 2 3 4 5Вариант I. С-45. Графическое решение систем линейных уравнений
1 2 3 4 5Вариант I. С-46. Решение систем линейных уравнений способом подстановки
1 2 3 4Вариант I. С-47. Решение систем линейных уравнений способом сложения
1 2 3 4Вариант I. С-48. Решение систем линейных уравнений
1 2 3 4Вариант I. С-49. Составление системы уравнений по условию задачи
1 2 3Вариант I. С-50. Решение задач с помощью составления системы уравнений
1 2 3 4 5 6 7Вариант I. С-51. Нахождение значения алгебраической дроби. Нахождение допустимых значений букв, входящих в дробь
1 2 3 4Вариант I. С-52. Сокращение алгебраических дробей
1 2 3Вариант I.
 С-53. Сложение и вычитание алгебраических дробей с одинаковыми знаменателями1 2 3
С-53. Сложение и вычитание алгебраических дробей с одинаковыми знаменателями1 2 3Вариант I. С-54. Сложение и вычитание алгебраических дробей с разными знаменателями
1 2 3 4Вариант I. С-55. Умножение и деление алгебраических дробей
1 2 3Вариант I. С-56. Умножение и деление алгебраических дробей
1 2 3Вариант II. С-1. Вычисление значения числового выражения
1 2 3 4 5 6 7Вариант II. С-2. Вычисление значения числового выражения
1 2 3 4Вариант II. С-3. Решение задач на проценты
1 2 3 4 5 6 7 8 9Вариант II. С-4. Нахождение значений буквенных выражений
1 2 3 4 5 6 7 8Вариант II. С-5. Сравнение значений выражений
1 2 3 4 5 6 7 8Вариант II. С-6. Применение свойств действий над числами к вычислениям
1 2 3 4 5Вариант II. С-6. Применение свойств действий над числами к вычислениям
1 2 3 4 5 6 7Вариант II. С-9. Решение уравнений, сводящихся к линейным
1 2 3 4 5Вариант II. С-9. Решение уравнений, сводящихся к линейным
1 2 3 4 5Вариант II.
 С-10. Решение задач с помощью уравнений1 2 3 4 5 6 7 8
С-10. Решение задач с помощью уравнений1 2 3 4 5 6 7 8Вариант II. С-11. Построение точек в координатной плоскости:
1 2 3 4 5 6Вариант II. С-12. Нахождение значений функции по формуле. Статистические характеристики
1 2 3 4 5 6 7Вариант II. С-13. Построение графика функции вида у = кх + y
1 2 3 4 5 6 7Вариант II. С-14. Построение графика функции вида у = кх
1 2 3 4 5 6 7Вариант II. С-15. Чтение графика линейной функции
1 2 3 4Вариант II. С-16. Взаимное расположение графиков на координатной плоскости
1 2 3 4 5 6 7Вариант II. С-17. Построение и чтение графиков линейных функций (практические задания)
1 2Вариант II. С-18. Вычисление значения числового выражения, содержащего степень:
1 2 3 4 5 6 7 8 9Вариант II. С-19. Вычисление значения буквенного выражения, содержащего степень
1 2 3 4 5Вариант II. С-20. Умножение и деление степеней с одинаковыми основаниями
1 2 3 4 5 6 7 8 9 10Вариант II. С-21.
 Возведение в степень произведения и степени1 2 3 4 5 6 7 8 9
Возведение в степень произведения и степени1 2 3 4 5 6 7 8 9Вариант II. С-22. Различные преобразования выражении, содержащих степени
1 2 3 4 5Вариант II. С-23. Вычисление значения одночлена
1 2 3 4Вариант II. С-24. Умножение многочленов и возведение одночлена в степень
1 2 3 4 5 6 7 8Вариант II. С-25. Приведение многочленов к стандартному виду
1 2 3 4 5 6 7 8Вариант II. С-26. Сложение и вычитание многочленов
1 2 3 4 5 6Вариант II. С-27. Заключение многочленов в скобки
1 2 3 4Вариант II. С-28. Умножение одночлена на многочлен
1 2 3 4 5Вариант II. С-29. Решение уравнений
1 2 3 4Вариант II. С-30. Решение уравнений
1 2Вариант II. С-31. Решение задач
1 2Вариант II. С-32. Вынесение общего множителя за скобки
1 2 3 4 5Вариант II. С-33. Умножение многочленов
1 2 3 4Вариант II. С-34. Умножение многочленов
1 2 3 4 5Вариант II. С-35. Разложение многочленов на множители способом группировки
1 2 3 4Вариант II.
 С-36. Чтение и запись алгебраических выражений1 2 3 4
С-36. Чтение и запись алгебраических выражений1 2 3 4Вариант II. С-37. Возведение в квадрат по формулам
1 2 3 4Вариант II. С-38. Преобразование выражений с применением формул квадрата суммы и квадрата разности
1 2 3 4Вариант II. С-39. Разложение на множители с помощью формул квадрата суммы и квадрата разности
1 2 3Вариант II. С-40. Умножение многочленов с использованием формулы
1 2 3Вариант II. С-41. Применение формул к преобразованию выражений
1 2 3 4 5Вариант II. С-42. Разложение на множители по формуле
1 2 3Вариант II. С-43. Преобразование целых выражений
1 2 3 4Вариант II. С-44. Разложение многочленов на множители с использованием нескольких способов
1 2 3 4 5Вариант II. С-45. Графическое решение систем линейных уравнений
1 2 3 4 5Вариант II. С-46. Решение систем линейных уравнений способом подстановки
1 2 3 4Вариант II. С-47. Решение систем линейных уравнений способом сложения
1 2 3 4Вариант II.
 С-48. Решение систем линейных уравнений1 2 3 4
С-48. Решение систем линейных уравнений1 2 3 4Вариант II. С-49. Составление системы уравнений по условию задачи
1 2 3Вариант II. С-50. Решение задач с помощью составления системы уравнений
1 2 3 4 5 6 7Вариант II. С-51. Нахождение значения алгебраической дроби. Нахождение допустимых значений букв, входящих в дробь
1 2 3 4Вариант II. С-52. Сокращение алгебраических дробей
1 2 3Вариант II. С-53. Сложение и вычитание алгебраических дробей с одинаковыми знаменателями
1 2 3Вариант II. С-54. Сложение и вычитание алгебраических дробей с разными знаменателями
1 2 3 4Вариант II. С-55. Умножение и деление алгебраических дробей
1 2 3Вариант II. С-56. Умножение и деление алгебраических дробей
1 2 3Контрольная работа 1
Вариант 1 Вариант 2 Вариант 3 Вариант 4Контрольная работа 1A
Вариант 1 Вариант 2 Вариант 3 Вариант 4Контрольная работа 2
Вариант 1 Вариант 2 Вариант 3 Вариант 4Контрольная работа 2a
Вариант 1 Вариант 2 Вариант 3 Вариант 4Контрольная работа 3
Вариант 1 Вариант 2 Вариант 3 Вариант 4Контрольная работа 3a
Вариант 1 Вариант 2 Вариант 3 Вариант 4Контрольная работа 4
Вариант 1 Вариант 2 Вариант 3 Вариант 4Контрольная работа 4a
Вариант 1 Вариант 2 Вариант 3 Вариант 4Контрольная работа 5
Вариант 1 Вариант 2 Вариант 3 Вариант 4Контрольная работа 5a
Вариант 1 Вариант 2 Вариант 3 Вариант 4Контрольная работа 6
Вариант 1 Вариант 2 Вариант 3 Вариант 4Контрольная работа 6a
Вариант 1 Вариант 2 Вариант 3 Вариант 4Контрольная работа 7
Вариант 1 Вариант 2 Вариант 3 Вариант 4Контрольная работа 7a
Вариант 1 Вариант 2 Вариант 3 Вариант 4Контрольная работа 8
Вариант 1 Вариант 2 Вариант 3 Вариант 4Контрольная работа 8a
Вариант 1 Вариант 2 Вариант 3 Вариант 4Контрольная работа 9
Вариант 1 Вариант 2 Вариант 3 Вариант 4Контрольная работа 9a
Вариант 1 Вариант 2 Вариант 3 Вариант 4Итоговая контрольная работа 1
Вариант 1 Вариант 2 Вариант 3 Вариант 4Итоговая контрольная работа 2
Вариант 1 Вариант 2 Вариант 3 Вариант 4Итоговая контрольная работа 3
Вариант 1 Вариант 2 Вариант 3 Вариант 4Задания для школьных олимпиад.
 Осенняя олимпиадаВариант 1 Вариант 2
Осенняя олимпиадаВариант 1 Вариант 2Задания для школьных олимпиад. Новогодняя олимпиада
Вариант 1 Вариант 2Задания для школьных олимпиад. Весенняя олимпиада
Вариант 1 Вариант 2Нулевые решения: у знак равно − 2 Икс + 4 у знак равно − 2 Икс − 3 | |
Одно решение: у знак равно 0,5 Икс + 2 у знак равно − 2 Икс − 3 | |
Бесконечное множество решений: у знак равно − 2 Икс − 4 у + 4 знак равно − 2 Икс | Существует несколько различных методов решения систем линейных уравнений:
См. второй график выше. Решение находится там, где две линии пересекаются, точка ( − 2 , 1 ) . Пример 1: Решите систему { 3 Икс + 2 у знак равно 16 7 Икс + у знак равно 19 Решите второе уравнение для у . у знак равно 19 − 7 Икс Заменять
19
−
7
Икс
за
у
в первом уравнении и решить
Икс
. 3 Икс + 2 ( 19 − 7 Икс ) знак равно 16 3 Икс + 38 − 14 Икс знак равно 16 − 11 Икс знак равно − 22 Икс знак равно 2 Заменять
2
за
Икс
в
у
знак равно
19
−
7
Икс
и решить для
у
. у знак равно 19− 7 ( 2 ) у знак равно 5 Решение ( 2 , 5 ) .Пример 2: Решите систему { 4 Икс + 3 у знак равно − 2 8 Икс − 2 у знак равно 12 Умножьте первое уравнение на
−
2
и добавьте результат ко второму уравнению. − 8 Икс − 6 у знак равно 4 8 Икс − 2 у знак равно 12 _ − 8 у знак равно 16 Решить для
у
. у знак равно − 2 Замена для у в любом из исходных уравнений и решить для Икс . 4 Икс + 3 ( − 2 ) знак равно − 2 4 Икс − 6 знак равно − 2 4 Икс знак равно 4 Икс знак равно 1 Решение
(
1
,
−
2
)
. |
Системы линейных уравнений
Линейное уравнение представляет собой уравнение для линии .
Линейное уравнение не всегда имеет вид y = 3,5 − 0,5x ,
Оно также может иметь вид y = 0,5(7 − x)
Или как y + 0,5x = 3,96
Или как у + 0,5х — 3,5 = 0 и другие.
(Примечание: это все одно и то же линейное уравнение!)
Система линейных уравнений — это когда у нас есть два или более линейных уравнения , работающих вместе.
Пример: Вот два линейных уравнения:
| 2x | + | и | = | 5 |
| −x | + | и | = | 2 |
Вместе они представляют собой систему линейных уравнений.
Можете ли вы сами определить значения x и y ? (Просто попробуйте, поиграйте с ними немного.)
Давайте попробуем построить и решить пример из реального мира:
Пример: Вы против Лошади
Это гонка!
Вы можете пробежать 0,2 км каждую минуту.
Лошадь может пробежать 0,5 км каждую минуту. Но чтобы оседлать лошадь, нужно 6 минут.
Как далеко ты уедешь, прежде чем тебя догонит лошадь?
Мы можем составить из двух уравнений ( d = расстояние в км, t = время в минутах)
Итак, у нас есть система уравнений ( линейных ):
- д = 0,2т
- d = 0,5(t−6)
Решим на графике:
Видите, как лошадь стартует через 6 минут, а потом бежит быстрее?
Кажется, тебя поймали через 10 минут. .. ты проехал всего 2 км.
.. ты проехал всего 2 км.
В следующий раз беги быстрее.
Итак, теперь вы знаете, что такое система линейных уравнений.
Давайте продолжим узнавать о них больше ….
Решение
Способов решения линейных уравнений может быть много!
Давайте посмотрим на другой пример:
Пример: Решите эти два уравнения:
- x + y = 6
- -3х + у = 2
На этом графике показаны два уравнения:
Наша задача — найти место пересечения двух линий.
Ну, мы можем видеть, где они пересекаются, так что это уже решено графически.
А теперь давайте решим ее с помощью алгебры!
Хммм… как это решить? Способов может быть много! В этом случае в обоих уравнениях есть «y», поэтому давайте попробуем вычесть все второе уравнение из первого:
x + y − (−3x + y) = 6 − 2
Теперь давайте упростим его:
x + y + 3x — y = 6 — 2
4x = 4
x = 1
Итак, теперь мы знаем, что линии пересекаются в точке x=1 .
И мы можем найти соответствующее значение y , используя любое из двух исходных уравнений (потому что мы знаем, что они имеют одно и то же значение при x=1). Используем первый (второй можете попробовать сами):
x + y = 6
1 + y = 6
y = 5
Решение:
x = 1 и y = 5
График показывает, что мы правы!
Линейные уравнения
В линейных уравнениях допускаются только простые переменные. no x 2 , Y 3 , √x и т. Д. :
Линейный против нелинейного
аспекты
A
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 3х – 7(3х – 4) = 5(2х – 7)
3х – 7(3х – 4) = 5(2х – 7) 3х – 7 = 4(2х – 3) – 5
3х – 7 = 4(2х – 3) – 5 8х + 11 = 6х + 13
8х + 11 = 6х + 13 4 – 3х = –7х – 4
4 – 3х = –7х – 4 –11(x – 2) + 2(3 – 2x) + 15x = 0
–11(x – 2) + 2(3 – 2x) + 15x = 0 5(3х – 8) – 3(2 – 5х) = 4х – 20
5(3х – 8) – 3(2 – 5х) = 4х – 20 9 – 6(3х – 4) = 5(4х – 1)
9 – 6(3х – 4) = 5(4х – 1) 6(2х – 5) – 4 = 2
6(2х – 5) – 4 = 2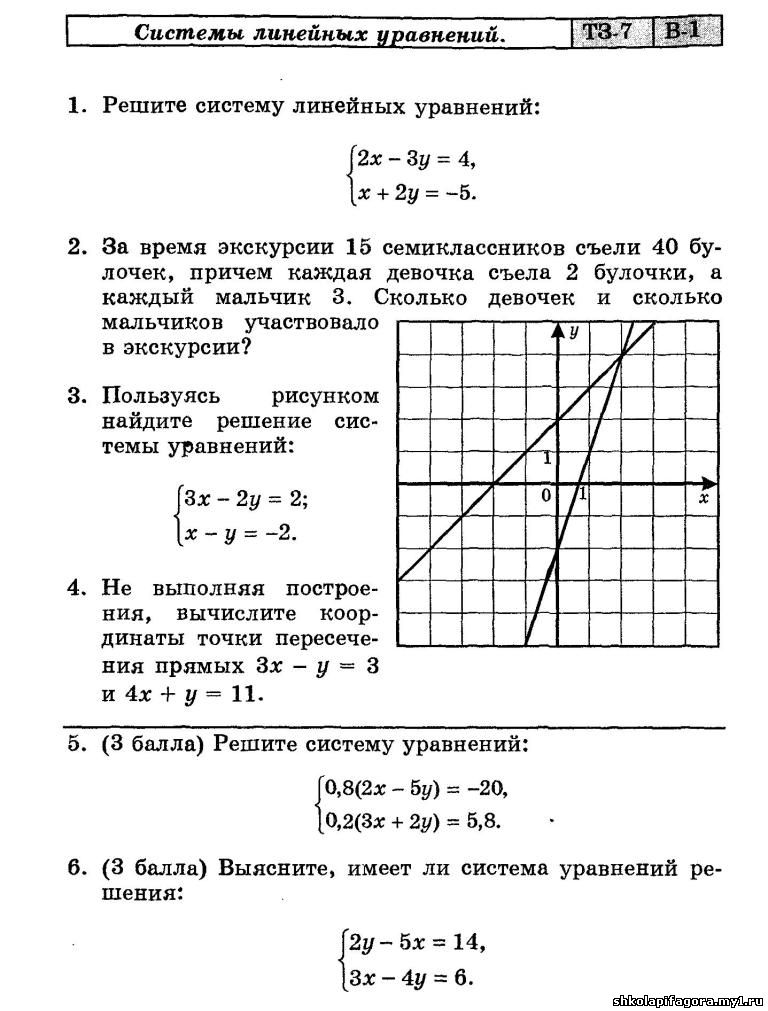 9х + 10 = 7х + 12
9х + 10 = 7х + 12 –5х – 22 = –8х – 4
–5х – 22 = –8х – 4 3(x + 2) = 2(1,5x + 4) – 2,4
3(x + 2) = 2(1,5x + 4) – 2,4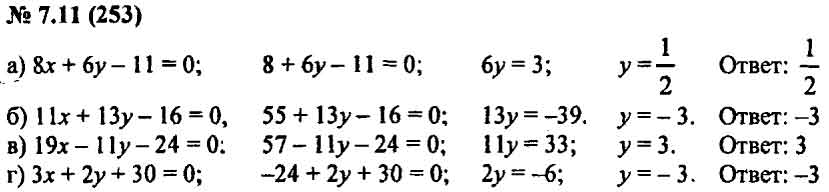 –4х – 11 = –5х – 12
–4х – 11 = –5х – 12 6(x + 2) – 0,7 = 3(2x + 4) + 1,3
6(x + 2) – 0,7 = 3(2x + 4) + 1,3 8х + 12 = 5х + 3
8х + 12 = 5х + 3 1,2(2x – 0,1) = 2,4x + 0,08
1,2(2x – 0,1) = 2,4x + 0,08 2
2 –1
–1 6
6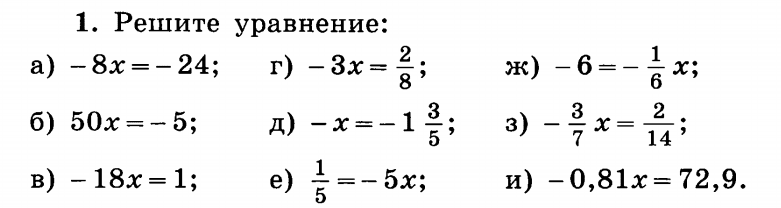 6
6 3
3 6
6 –1
–1 –3
–3 Это полезно, когда вам просто нужен грубый ответ, или вы уверены, что пересечение происходит в целочисленных координатах. Просто нарисуйте две линии и посмотрите, где они пересекаются!
Это полезно, когда вам просто нужен грубый ответ, или вы уверены, что пересечение происходит в целочисленных координатах. Просто нарисуйте две линии и посмотрите, где они пересекаются! (Если это проще, вы можете начать с решения уравнения для
Икс
с точки зрения
у
, тоже – такая же разница!)
(Если это проще, вы можете начать с решения уравнения для
Икс
с точки зрения
у
, тоже – такая же разница!)

 Затем решите для
Икс
(или же
у
, в зависимости от того, что осталось) и подставьте обратно, чтобы получить другую координату.
Затем решите для
Икс
(или же
у
, в зависимости от того, что осталось) и подставьте обратно, чтобы получить другую координату.


 .. или в 3-х измерениях …
.. или в 3-х измерениях …  д.
д.

 Вот…
Вот… Потому что есть A Решение. Уравнения «Последователи»
Потому что есть A Решение. Уравнения «Последователи»  Давайте используем первое уравнение и переменную «x».
Давайте используем первое уравнение и переменную «x». Мы добились некоторого прогресса, но еще не все.
Мы добились некоторого прогресса, но еще не все.

 д., если это поможет.
д., если это поможет. е. разделите на 2):
е. разделите на 2): Это и есть ответ.
Это и есть ответ.
 ..
.. 

 :
:
 Производитель отслеживает свои затраты, которые представляют собой сумму, которую он тратит на производство плат, и свой доход, который представляет собой сумму, которую он зарабатывает на продаже своих плат. Как компания может определить, получает ли она прибыль от своей новой линии? Сколько скейтбордов нужно произвести и продать, чтобы можно было получить прибыль? В этом разделе мы рассмотрим линейные уравнения с двумя переменными, чтобы ответить на эти и подобные вопросы.
Производитель отслеживает свои затраты, которые представляют собой сумму, которую он тратит на производство плат, и свой доход, который представляет собой сумму, которую он зарабатывает на продаже своих плат. Как компания может определить, получает ли она прибыль от своей новой линии? Сколько скейтбордов нужно произвести и продать, чтобы можно было получить прибыль? В этом разделе мы рассмотрим линейные уравнения с двумя переменными, чтобы ответить на эти и подобные вопросы. Некоторые линейные системы могут не иметь решения, а другие могут иметь бесконечное число решений. Чтобы линейная система имела единственное решение, в ней должно быть не меньше уравнений, чем переменных. Тем не менее, это не гарантирует уникальности решения.
Некоторые линейные системы могут не иметь решения, а другие могут иметь бесконечное число решений. Чтобы линейная система имела единственное решение, в ней должно быть не меньше уравнений, чем переменных. Тем не менее, это не гарантирует уникальности решения.
 Линии имеют одинаковый наклон и разные г- перехватов. Нет общих точек для обеих прямых; следовательно, система не имеет решений.
Линии имеют одинаковый наклон и разные г- перехватов. Нет общих точек для обеих прямых; следовательно, система не имеет решений.

 Классифицируйте каждое решение как последовательное или непоследовательное. Если система непротиворечива, определите, зависима она или независима. Возможно, вам будет проще построить каждую систему по отдельности, а затем очистить свои записи, прежде чем строить следующую.
Классифицируйте каждое решение как последовательное или непоследовательное. Если система непротиворечива, определите, зависима она или независима. Возможно, вам будет проще построить каждую систему по отдельности, а затем очистить свои записи, прежде чем строить следующую.  Напомним, что мы можем решать только для одной переменной за раз, поэтому метод подстановки ценен и практичен.
Напомним, что мы можем решать только для одной переменной за раз, поэтому метод подстановки ценен и практичен.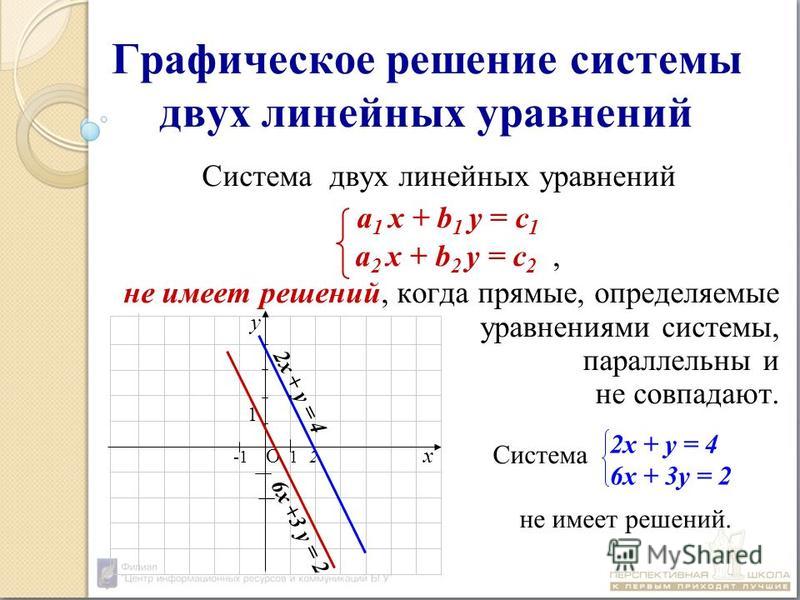



 Они никогда не пересекутся. При поиске решения для несогласованной системы мы придем к ложному утверждению, например [латекс]12=0[/латекс].
Они никогда не пересекутся. При поиске решения для несогласованной системы мы придем к ложному утверждению, например [латекс]12=0[/латекс].
 В этом случае, в зависимости от того, что вы положили на x , y будет определено через x как [латекс]-\frac{1}{3}x+\frac{2}{3}[/latex].
В этом случае, в зависимости от того, что вы положили на x , y будет определено через x как [латекс]-\frac{1}{3}x+\frac{2}{3}[/latex]. Функция дохода показана оранжевым цветом на графике ниже.
Функция дохода показана оранжевым цветом на графике ниже. Функция прибыли представляет собой функцию дохода минус функция затрат, записанную как [латекс]Р\влево(х\вправо)=R\влево(х\вправо)-С\влево(х\вправо)[/латекс]. Очевидно, что знание количества, при котором затраты равны выручке, имеет большое значение для бизнеса.
Функция прибыли представляет собой функцию дохода минус функция затрат, записанную как [латекс]Р\влево(х\вправо)=R\влево(х\вправо)-С\влево(х\вправо)[/латекс]. Очевидно, что знание количества, при котором затраты равны выручке, имеет большое значение для бизнеса.
 Если было куплено 1650 талонов на питание на общую сумму 14 200 долларов, сколько детей и сколько взрослых купили талоны на питание?
Если было куплено 1650 талонов на питание на общую сумму 14 200 долларов, сколько детей и сколько взрослых купили талоны на питание?
 В этом методе мы находим одну переменную в одном уравнении и подставляем результат во второе уравнение.
В этом методе мы находим одну переменную в одном уравнении и подставляем результат во второе уравнение.