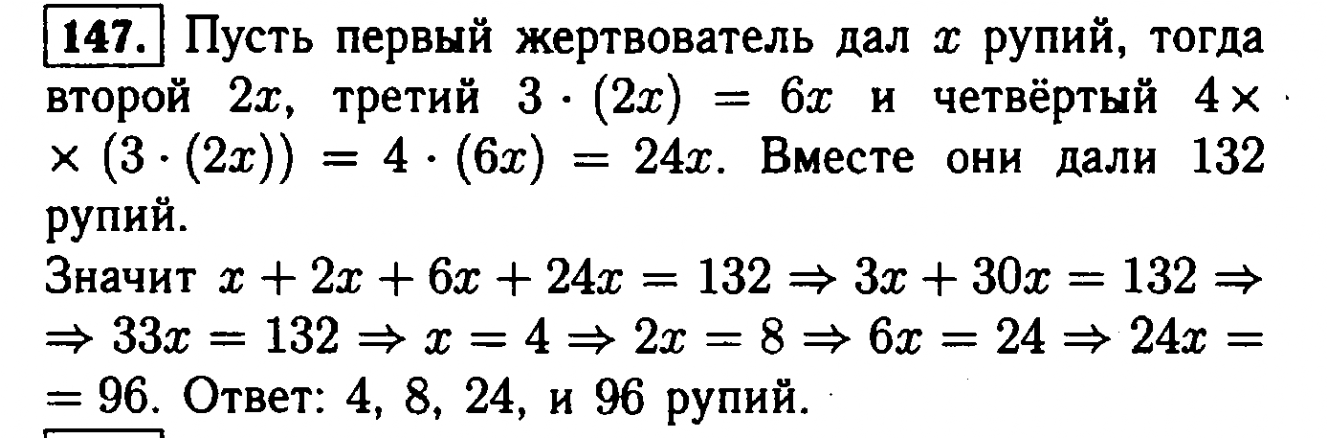ГДЗ по алгебре 7 класс Дорофеев Суворова Бунимович Минаева Рослова
ГДЗ готовые домашние задания учебника по алгебре (математике) 7 класс Дорофеев Суворова Бунимович Минаева Рослова ФГОС от Путина. Решебник (ответы на вопросы и задания) учебников и рабочих тетрадей необходим для проверки правильности домашних заданий без скачивания онлайн
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 Это надо уметь Проверьте себя (тест) 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 Это надо уметь Проверьте себя (тест) 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 Это надо уметь Проверьте себя (тест) 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376 377 378 379 380 381 382 383 384 385 386 387 388 389 390 391 392 393 394 395 396 397 398 399 400 401 402 403 404 405 406 407 408 409 410 411 412 413 414 415 416 417 418 419 420 421 422 423 424 425 426 427 428 429 430 431 432 433 434 435 Это надо уметь Проверьте себя (тест) 436 437 438 439 440 441 442 443 444 445 446 447 448 449 450 451 452 453 454 455 456 457 458 459 460 461 462 463 464 465 466 467 468 469 470 471 472 473 474 475 476 477 478 479 480 481 482 483 484 485 486 487 488 489 490 491 492 493 494 495 496 497 498 499 500 501 502 503 504 505 506 507 508 509 510 511 512 513 514 515 516 517 518 519 520 521 522 523 Это надо уметь Проверьте себя (тест) 524 525 526 527 528 529 530 531 532 533 534 535 536 537 538 539 540 541 542 543 544 545 546 547 548 549 550 551 552 553 554 555 556 557 558 559 560 561 562 563 564 565 566 567 568 569 570 571 572 573 574 575 576 577 578 579 580 581 582 583 584 585 586 587 588 589 590 591 592 593 594 595 596 597 598 599 600 601 602 603 604 605 606 607 608 609 610 611 612 613 614 615 616 617 618 619 620 621 622 623 624 625 626 627 628 629 630 631 632 633 Это надо уметь Проверьте себя (тест) 634 635 636 637 638 639 640 641 642 643 644 645 646 647 648 649 650 651 652 653 654 655 656 657 658 659 660 661 662 663 664 665 666 667 668 669 670 671 672 673 674 675 676 677 678 679 680 681 682 683 684 685 686 687 688 689 690 691 692 693 694 695 696 697 698 699 700 701 702 703 704 705 706 707 708 709 710 711 712 713 714 715 716 717 718 719 720 721 722 723 724 725 726 727 728 729 730 731 732 733 734 735 736 737 738 739 740 741 742 743 744 745 746 747 748 749 750 751 752 753 754 755 756 757 758 759 760 761 762 763 764 765 766 767 768 769 770 771 772 773 774 775 776 777 778 779 780 781 782 783 784 785 786 787 788 789 790 791 792 793 794 795 796 797 798 799 800 801 802 803 804 805 806 807 808 809 810 Это надо уметь Проверьте себя (тест) 811 812 813 814 815 816 817 818 819 820 821 822 823 824 825 826 827 828 829 830 831 832 833 834 835 836 837 838 839 840 841 842 843 844 845 846 847 848 849 850 851 852 853 854 855 856 857 858 859 860 861 862 863 864 865 866 867 868 869 870 871 872 873 874 875 876 877 878 879 880 881 882 883 884 885 886 887 888 889 890 891 892 893 894 895 896 897 898 899 900 901 902 903 904 905 906 907 908 909 910 911 912 913 914 915 916 917 918 919 920 921 922 923 924 925 926 927 928 929 930 931 932 933 934 935 936 937 Это надо уметь Проверьте себя (тест) 938 939 940 941 942 943 944 945 946 947 948 949 950 951 952 953 954 955 956 957 958 959 960 961 962 963 964 965 966 967 968 969 970 971 972 973 974 975 976 977 978 979 980 981 982 983 984 985 986 987 988 989 Это надо уметь Проверьте себя (тест)
Страница не найдена
Новости
21 фев
В Барнауле оперативные службы проводят проверку в связи с поступлением сообщений о минировании ряда школ.
Министр образования Подмосковья Ирина Каклюгина отметила, что итоговое собеседование по русскому языку успешно прошли 99,5% девятиклассников Подмосковья. В регионе уже опубликовали результаты.
19 фев
Из-за сильных морозов в школах некоторых городов и посёлков Мурманской области отменены школьные занятия.
19 фев
Министр образования Подмосковья Ирина Каклюгина рассказала, что регион присоединился к всероссийской акции «100 баллов для Победы».
18 фев
Во всех возрастных группах жителей Москвы наблюдается спад заболеваемости коронавирусной инфекцией. Об этом сообщила заместитель столичного мэра по вопросам социального развития Анастасия Ракова.
18 фев
17 фев
В Московской области стартовала всероссийская акция «Единый день сдачи ЕГЭ родителями», она продолжится в марте и апреле.
Итоговая контрольная работа по алгебре 7 класс
Итоговая контрольная работа
по алгебре
за 2019-2020 учебный год
ученика(цы) 7 класса
ФИ в родительном падеже
Вариант 5.
А1. Найдите значение функции y=3,5х–8 при х=-1,2
1) -3,8 2) -12,2 3) 34 4) -7,58
А2. Функция задана формулой y=-5х-14. Выберите значение аргумента, при котором y=31
Функция задана формулой y=-5х-14. Выберите значение аргумента, при котором y=31
1) -3,4 2) 9 3) 10
А3. Какая из точек принадлежит графику функции ?
1) М(15;6) 2) Т(-25;-8) 3) N(-10;5) 4)K(35;10)
А4. Найдите значение выражения:
1) 6 2) 36 3) 216 4) 1296
А5. Упростите выражение:
1) 2) 3) 4)
А6. Представьте в виде одночлена стандартного вида:
Представьте в виде одночлена стандартного вида:
1) 2) 3) 4)
А7. Упростите выражение:
1) 2) 3) 4)
А8. Найдите корень уравнения:
1) -2 2) 15 3) 2 4) — 15
А9. Выполните умножение:
1) 2) 3) 4)
А10. Выполните умножение:
1) 2) 3) 4)
А11. Решите уравнение: .
Ответ: ____________
Часть В.
В1. Решите уравнение: (6х+1)2 – (6х – 2)(2+6х)=17.
В2. Найдите координаты точки пересечения прямых:
у = 3x-1 и у = 5х-15
В3. Докажите, что значение выражения
0,6х(2y—x) – 0,3y( 4х – 5 )+(0,6x2 -1,5y+13) не зависит от значения переменных .
Рособрнадзор опубликовал график проведения всероссийских проверочных работ
Федеральная служба по надзору в сфере образования и науки утвердила расписание проведения всероссийских проверочных работ (ВПР) в 2021 году.
Проверочные работы пройдут для учеников 4-8 классов в штатном режиме, для выпускников 11 классов – по решению школы.
Конкретные даты каждая школа будет определять самостоятельно.
Выпускники сдадут проверочные работы по истории, биологии, географии, физике, химии и иностранным языкам (английскому, немецкому или французскому) в период с 1 по 26 марта.
ВПР по географии школы могут провести для учеников 11 или 10 классов в зависимости от своего учебного плана.
С 15 марта по 21 мая пройдут ВПР для 4 классов (по русскому языку, математике и окружающему миру), 5 классов (русский язык, математика, история, биология), 6 и 8 классов (русский язык и математика), 7 классов (русский язык, математика, история, биология, география, обществознание, физика). Эти проверочные работы пройдут для всех классов в параллели.
Также семиклассники напишут с 1 апреля по 21 мая ВПР по иностранному языку (английскому, немецкому или французскому).
Ученики 6 и 8 классов с 15 марта по 21 мая напишут ВПР еще по двум предметам на основе случайного выбора. Шестиклассникам могут встретиться ВПР по истории, биологии, географии или обществознанию, восьмиклассникам – по истории, биологии, географии, обществознанию, химии или физике. Информация о распределении предметов по классам в каждой параллели будет направлена школам через их личные кабинеты в Федеральной информационной системе оценки качества образования.
«ВПР рекомендуется проводить на 2-4 уроках. Время, отведенное на написание проверочной работы по разным предметам и классам, будет указано в инструкции по их выполнению», — отметили в пресс-службе ведомства.
РешенияNCERT для математики класса 7 (обновлено для 2020 г.
Если вы ищете решения NCERT для математики класса 7, то вы попали в нужное место. Опытные преподаватели LearnCBSE.in создали подробные учебники математики CBSE для 7-го класса. Мы предлагаем точные и абсолютно безошибочные решения. Решения по математике NCERT класса 7 включают в себя все вопросы, представленные в соответствии с новой пересмотренной программой в учебнике по математике NCERT класса 7. Решения NCERT по математике класса 7 в формате pdf можно загрузить одним щелчком мыши без ВХОДА .Вы также можете попрактиковаться в дополнительных вопросах для класса 7 по математике на LearnCBSE.in
Решения по математике NCERT класса 7 включают в себя все вопросы, представленные в соответствии с новой пересмотренной программой в учебнике по математике NCERT класса 7. Решения NCERT по математике класса 7 в формате pdf можно загрузить одним щелчком мыши без ВХОДА .Вы также можете попрактиковаться в дополнительных вопросах для класса 7 по математике на LearnCBSE.in
Решения NCERT для математики класса 7
Подробные решения NCERT для математики класса 7 приведены ниже.
Вы также можете бесплатно скачать NCERT Solutions for Class 7 Maths All Chapters PDF или сохранить изображения решений и распечатать их, чтобы они были всегда под рукой при подготовке к экзаменам.
Решения NCERT для математики класса 7 Глава 1 Целые числа
Решения NCERT для математики класса 7 Глава 2 Дроби и десятичные дроби
Решения NCERT для математики класса 7 Глава 3 Обработка данных
Решения NCERT для математики класса 7 Глава 4 Простые уравнения
Решения NCERT для математики класса 7 Глава 5 Линии и углы
Решения NCERT для математики класса 7 Глава 6 Треугольники и их свойства
Решения NCERT для математики класса 7 Глава 7 Конгруэнтность треугольников
Решения NCERT для математики класса 7 Глава 8 Сравнение количеств
Решения NCERT для математики класса 7 Глава 9 Рациональные числа
Решения NCERT для математики класса 7 Глава 10 Практическая геометрия
Решения NCERT для математики класса 7 Глава 11 Периметр и площадь
Решения NCERT для математики класса 7 Глава 12 Алгебраические выражения
Решения NCERT для математики класса 7 Глава 13 Показатели и степени
Решения NCERT для математики класса 7 Глава 14 Симметрия
Решения NCERT для математики класса 7 Глава 15 Визуализация твердых форм
Решения NCERT для математики класса 7 (Загрузить PDF)
Решения NCERT по математике
Математические формулы для класса 7
Основные характеристики Математика класса 7 Решения NCERT:
- Математика класса 7 Решения NCERT были подготовлены профильными экспертами.

- Пошаговые решения для лучшего понимания проблем.
- Подробное объяснение решения проблем и формулы упоминаются между шагами для эффективного обучения.
- Решения по математике класса 7 также доступны для легкого доступа.
- Вы можете загрузить NCERT Solutions for Class 7 Maths PDF или сохранить изображения решений и распечатать их, чтобы они были всегда под рукой при подготовке к экзаменам.
Мы стремимся помогать студентам всеми возможными способами, в том числе предлагать решения по каждому предмету.Учебники NCERT считаются лучшими учебниками для школьного образования, и мы предлагаем решения, подходящие для книг.
Математика является довольно ужасным предметом для большинства школьников, и мы считаем, что небольшая практика может решить эту проблему. Поэтому наши решения сосредоточены на построении концепций, основанных на фундаментальных принципах, а также на изучении альтернативных методов решения конкретной проблемы. .
Просмотрите все решения Class 7 Maths NCERT со своего планшета, настольного компьютера или мобильного устройства и получите больше баллов на выпускных экзаменах.Вы также можете пройти через решения RD Sharma Class 7 и RS Aggarwal Class 7, которые помогут вам в дополнительной практике и экзаменах.
Вот список основных тем из учебника NCERT по математике для класса 7:
Математика класса 7 Глава 1 Целые числа
После введения в целые числа в классе 6 в этой главе рассматриваются целые числа, как положительные, так и отрицательные, чтобы дать учащимся возможность почувствовать действительные числа. Эта глава дает студентам новый взгляд на свойства и важность целых чисел.Упражнения предназначены для того, чтобы учащиеся полностью усвоили всю концепцию.
- 1.1 Введение
- 1.2 Отзыв
- 1.3 Свойства сложения и вычитания целых чисел
- 1.4 Умножение целых чисел
- 1.5 Свойства умножения целых чисел
- 1.
 6 Деление целых чисел
6 Деление целых чисел - 1.7 Свойства деления целых чисел
Математика класса 7 Глава 2 Дроби и десятичные дроби
Это не совсем новая концепция, а, скорее, дальнейшее исследование старых концепций.В этой главе рассматриваются свойства дробей и десятичных знаков, а также операции над ними. Они также имеют дело с изображением дробей и десятичных знаков на числовой прямой, а также их разложением и вычитанием.
- 2.1 Введение
- 2.2 Насколько хорошо вы узнали о дробях?
- 2.3 Умножение дробей
- 2.4 Деление на дроби
- 2.5 Насколько хорошо вы знаете десятичные числа
- 2.6 Умножение десятичных чисел
- 2.7 деление десятичных чисел
Математика класса 7 Глава 3 Обработка данных
Эту главу можно рассматривать как первый шаг к статистике, так как она касается сбора данных, интерпретации данных и построения графиков, не отставая от реальных примеров. В главах также рассказывается, как сделать несколько выводов из накопленных данных. Упражнения очень близки к примерам из реальной жизни, и, таким образом, их выполнение дает лучшее ощущение того же.
Упражнения очень близки к примерам из реальной жизни, и, таким образом, их выполнение дает лучшее ощущение того же.
- 3.1 Введение
- 3.2 Сбор данных
- 3.3 Организация данных
- 3.4 Репрезентативные значения
- 3,5 Среднее арифметическое
- 3.6 Режим
- 3,7 Медиана
- 3.8 Использование гистограмм с другой целью
- 3.9 Шанс и вероятность
Математика для класса 7 Глава 4 Простые уравнения
Как следует из названия, эта глава посвящена формулировке и применению простых уравнений. В этой главе подробно рассматривается теория уравнений, от создания простых уравнений до их решения.Проблемы подробно обсуждались в решениях.
- 4.1 Игра для чтения мыслей!
- 4.2 Установка уравнения.
- 4.3 Обзор того, что нам известно.
- 4.4 Что такое уравнение?
- 4.5 Другие уравнения.
- 4.6 От решения к уравнению.
- 4.7 Приложения простых уравнений к практическим ситуациям.

Математика класса 7 Глава 5 Линии и углы
Первая глава геометрии в классе 7, линии и углы, начинается с фундаментальных определений линии и угла.В этой главе будут рассмотрены концепции параллельных линий и связанных с ними углов, таких как альтернативные внутренние углы, соответствующие углы, вертикально противоположные углы. Эта довольно простая глава становится еще интереснее с помощью упражнений, и решения эффективно подтверждают то же самое.
- 5.1 Введение.
- 5.2 Связанные углы.
- 5.3 Пары линий.
- 5.4 Проверка параллельных линий.
Класс 7 по математике Глава 6 Треугольник и его свойства
Вторая глава геометрии посвящена треугольникам и их свойствам.В этой главе рассказывается о типах треугольников, свойстве суммы углов, медианах и высотах, а также о теореме Пифагора. Студенты получат представление о том, что такое треугольники в целом, и о конкретных приложениях теоремы Пифагора в этой главе.
- 6.1 Введение.
- 6.2 Медианы треугольника.
- 6.3 Высота треугольника.
- 6.4 Внешний угол треугольника и его свойство.
- 6.5 Сумма углов треугольника.
- 6.6 Два особых треугольника: равносторонний и равнобедренный.
- 6.7 Сумма длин двух сторон треугольника.
- 6.8 Прямоугольные треугольники и свойство Пифагора.
Математика 7 класс Глава 7 Конгруэнтность треугольников
После общего введения треугольников в главе 6, седьмая глава посвящена специфическому свойству конгруэнтности треугольников. В этой главе рассматриваются все критерии конгруэнтности и рассматриваются различные виды проблем.В решениях подробно обсуждаются критерии конгруэнтности, по возможности с использованием альтернативного подхода.
- 7.1 Введение.
- 7.2 Соответствие плоских фигур.
- 7.3 Соответствие линейных сегментов.
- 7.4 Конгруэнтность углов.
- 7.5 Конгруэнтность треугольников.

- 7.6 Критерии конгруэнтности треугольников.
- 7.7 Конгруэнтность прямоугольных треугольников.
Математика класса 7 Глава 8 Сравнение количеств
Эту главу можно смело считать одной из наиболее ориентированных на прикладные задачи глав во всей программе математики 7 класса.Как следует из названия, в этой главе представлен инструмент для измерения и сравнения количеств. Инструменты — это в первую очередь проценты, коэффициенты, прибыль и убыток и проценты. Эта глава пригодится во всех сферах жизни, поскольку полученные здесь вычисления чаще всего используются в реальном мире.
- 8.1 Введение.
- 8.2 Эквивалентные соотношения.
- 8.3 Процент — еще один способ сравнения количеств.
- 8.4 Использование процентов.
- 8.5 Цены, связанные с предметом или покупкой и продажей.
- 8.6 Комиссия за заемные деньги или простой процент.
Математика класса 7 Глава 9 Рациональные числа
После подробного обсуждения целых чисел в первой главе эта глава возвращается к числам, а именно к рациональным числам. В этой главе рассматриваются определения и свойства рациональных чисел.
В этой главе рассматриваются определения и свойства рациональных чисел.
- 9.1 Введение
- 9.2 Потребность в рациональных числах.
- 9.3 Что такое рациональные числа?
- 9.4 Положительные и отрицательные рациональные числа.
- 9.5 Рациональные числа на числовой прямой.
- 9.6 Рациональные числа в стандартной форме.
- 9.7 Сравнение рациональных чисел.
- 9.8 Рациональные числа между двумя рациональными числами.
- 9.9 Операции с рациональными числами.
Класс 7 по математике Глава 10 Практическая геометрия
В этой главе рассматривается изображение геометрии на бумаге с точки зрения построения линий и углов. Это довольно простая глава, которая требует выполнения только установленной процедуры при построении конструкции.
- 10.1 Введение
- 10.2 Построение прямой, параллельной заданной, через точку не на прямой.
- 10.3 Построение треугольников.
- 10.
 4 Построение треугольника, когда известны длины трех его сторон (критерий SSS)
4 Построение треугольника, когда известны длины трех его сторон (критерий SSS) - 10.5 Построение треугольника, когда известны длины двух сторон и величина угла между ними. (Критерий SAS)
- 10.6 Построение треугольника, если заданы размеры двух его углов и длина стороны, лежащей между ними.(Критерий ASA)
- 10.7 Построение прямоугольного треугольника при заданной длине одной ножки и ее гипотенузе (критерий RHS).
Математика 7 класса Глава 11 Периметр и площадь
Эта глава вводит часть учебного плана по измерению. Он имеет дело с областями и периметрами всех важных фигур в математике. Глава очень простая, без введения каких-либо сложных форм.
- 11.1 Введение.
- 11.2 квадрата и прямоугольника.
- 11.3 Площадь параллелограмма.
- 11.4 Площадь треугольника.
- 11,5 Круги.
- 11.6 Пересчет единиц.
- 11.7 Приложения.
Математика 7 класса Глава 12 Алгебраические уравнения
В этой главе рассматривается преобразование простых математических утверждений в алгебраические уравнения и их использование для решения определенных задач с использованием принципов алгебры. Математические утверждения тесно связаны с некоторыми примерами из реальной жизни, где алгебра действительно может быть использована.Упражнения делают это вдвойне веселее.
Математические утверждения тесно связаны с некоторыми примерами из реальной жизни, где алгебра действительно может быть использована.Упражнения делают это вдвойне веселее.
- 12.1 Введение.
- 12.2 Как формируются выражения?
- 12.3 Термины выражения.
- 12.4. Термины, похожие и отличные.
- 12.5 Мономы, биномы, трехчлены и многочлены.
- 12.6 Сложение и вычитание алгебраических выражений.
- 12.7 Определение значения выражения.
- 12.8 Использование алгебраических выражений — формул и правил.
Математика класса 7 Глава 13 Показатели и степени
В этой главе рассматривается введение в показатели степени, правила умножения и деления показателей, степень степени, десятичную систему и выражение очень больших чисел в стандартной форме или научной нотации.
- 13.1 Введение.
- 13,2 Экспоненты.
- 13.3 Законы экспонент.
- 13.4 Разные примеры, использующие законы экспонент.

- 13.5 Десятичная система счисления.
- 13.6. Выражение больших чисел в стандартной форме.
Математика класса 7 Глава 14 Симметрия
Эта глава дает учащимся представление о симметричных формах. Симметрия широко используется мастерами и дизайнерами для разработки сложных шаблонов дизайна.Эта глава о симметрии призвана дать учащимся общее представление о симметрии в мире.
- 14.1 Введение: симметрия
- 14.2 Линии симметрии правильных многоугольников.
- 14.3 Вращательная симметрия.
- 14.4 Симметрия линий и вращательная симметрия.
Математика для класса 7 Глава 15 Визуализация твердых форм
В этой главе рассматриваются визуальные элементы геометрии, объясняются различные геометрические формы, которые используются при проектировании окружающих нас повседневных предметов.В этой главе рассматриваются как плоские, так и твердые фигуры.
- 15.1 Введение. Плоские фигуры и твердые фигуры.

- 15.2 Грани, края и вершины.
- 15.3 Сети для построения трехмерных фигур.
- 15.4 Рисование твердых тел на плоской поверхности.
- 15.5 Просмотр различных частей твердого тела.
Часто задаваемые вопросы о решениях NCERT для математики класса 7
1. Как я могу получить хорошие отметки по математике в 7 классе?
Тщательно ознакомьтесь с концепциями и подготовьтесь в соответствии с темами, используя решения NCERT.Убедитесь, что вы разработали правильную стратегию подготовки, чтобы легко сдать экзамен 7 класса.
2. Какой лучший справочник по математике для 7 класса?
По основам учебников NCERT, предписанных Советом CBSE, более чем достаточно для получения более высоких оценок на экзамене по математике в 7 классе.
3. Почему решения NCERT для математики 7 класса важны?
Математика класса 7 Решения NCERT подготовлены экспертами и предоставляют пошаговые решения, позволяющие лучше понять проблемы. Они могут быть весьма кстати во время приготовления.
Они могут быть весьма кстати во время приготовления.
4. Как бесплатно скачать NCERT Solutions for Class 7?
Кандидатымогут бесплатно загрузить решения NCERT для класса 7 с нашего сайта. Используйте их в качестве справочника и помощи в подготовке.
5. Какие главы содержатся в решениях NCERT для математики класса 7?
Вы можете просмотреть список глав математических решений NCERT Class 7, перейдя на нашу страницу.Обратитесь к темам в каждой главе и соответствующим образом спланируйте свою подготовку.
6. Где я могу получить решения NCERT для математики седьмого класса?
Вы можете получить NCERT Solutions for Class 7th Maths, перейдя на нашу страницу. Получите доступ к прямым ссылкам, чтобы просмотреть или загрузить и использовать их в качестве справочника во время подготовки.
Мы надеемся, что у вас будет большой опыт использования этих решений. Вы можете скачать решения, перейдя по ссылкам выше в описании.
Математические неравенства в 7-м классе
Пятый класс Шестой класс, седьмой класс, восьмой класс, девятый класс, десятый класс, одиннадцатый класс, двенадцатый класс Понимание идеальных квадратов и квадратного корня. Математика в 8 классе »Раздел: Показатели и радикалы. Цель: учащиеся научатся решать неравенства и отображать их в виде графика на числовой прямой. Чтобы решить неравенство с помощью калькулятора неравенства, введите неравенство, например x + 7> 9. Затем решатель неравенства покажет вам шаги, которые помогут вам узнать, как решить эту проблему самостоятельно.
Математика в 7-м классе: домой Знакомьтесь, ваши учителя Еженедельные информационные бюллетени … Неравенство, бюджетирование и Chromebook. Геометрия, масштаб, чертежи. Обзор модуля 7 • 1 класс 7 • Модуль 1 Соотношения и пропорциональные отношения ОБЗОР В Модуле 1 учащиеся основываются на своих рассуждениях 6-го класса о соотношениях, оценках и оценках единиц (6.RP.A.1, 6.RP.A.2 , 6.RP.A.3), чтобы формально определить пропорциональные отношения и константу пропорциональности (7. RP.A.2). В теме A студенты изучают …
RP.A.2). В теме A студенты изучают …
Обзор модуля 7 • 1 класс 7 • Модуль 1 Соотношения и пропорциональные отношения ОБЗОР В модуле 1 учащиеся основываются на своих рассуждениях 6-го класса о соотношениях, ставках и оценках единиц (6.RP.A.1, 6.RP.A .2, 6.RP.A.3), чтобы формально определить пропорциональные отношения и константу пропорциональности (7.RP.A.2). В теме A учащиеся изучают … Этот рабочий лист по математике для седьмого класса — отличный способ для учащихся попрактиковаться в базовой алгебре. Семиклассники должны решить 8 уравнений, вычислив правильные значения переменных.Вот две версии этого бесплатного рабочего листа по математике для седьмого класса: Рабочий лист решения уравнений для седьмого класса в формате PDF — Скачать, Лучшее качество для 7-го класса. Элементарно. Числовые диаграммы. Линейные неравенства. Математические игры и веселые сайты. Интерактивные учебные пособия по математике.7.EE.B.4.A — Решайте задачи со словами, приводящие к уравнениям вида px + q = r и p (x + q) = r, где p, q и r — конкретные рациональные числа. Бегло решать уравнения этих форм. Эта БЕСПЛАТНАЯ математическая игра «Я МОГУ» фокусируется на решении и построении графиков неравенств с задачами со словами в 7-м классе! ALL I Can Math Games можно использовать для самостоятельных занятий, занятий в небольших группах, обзора всей группы или для отслеживания прогресса.Возможности безграничны! Если вам понравился этот БЕСПЛАТНЫЙ образец, ch
Бегло решать уравнения этих форм. Эта БЕСПЛАТНАЯ математическая игра «Я МОГУ» фокусируется на решении и построении графиков неравенств с задачами со словами в 7-м классе! ALL I Can Math Games можно использовать для самостоятельных занятий, занятий в небольших группах, обзора всей группы или для отслеживания прогресса.Возможности безграничны! Если вам понравился этот БЕСПЛАТНЫЙ образец, ch
14 июля 2012 г. · Занятия по математике для детей в 7-м классе. На этой странице есть множество математических ресурсов для семиклассников, таких как рабочие листы по математике, забавные математические игры, карточные игры, настольные игры, игры PowerPoint, викторины, головоломки, тесты и многое другое, которое скоро появится. Математические игры I CAN — отличный способ развлечься математикой! Эта математическая игра для 7-х классов нацелена на решение и построение графиков неравенств с помощью задач со словами и предоставляет учащимся возможность попрактиковаться в форме вопросов с множественным выбором или коротких ответов.
Привет, ребята, я действительно застрял на балансировке химических уравнений в 7-м классе и наверняка кое-что поможет мне начать с расстояния до точек, гипербол и расстояния до точек. Скоро сдаются мои анализы. Я даже думал о найме репетитора по алгебре, но это так дорого.
Глава 2: математика iLEAP, 7 класс. В этом разделе описывается общий дизайн теста iLEAP Math, который будет проводиться для учащихся 7-го класса. Технические требования к тесту, образцы вопросов теста и критерии выставления оценок предоставлены, чтобы учителя могли согласовать практику в классе с оценкой штата.Структура теста Бесплатная распечатка 7.SP.C.7. Рабочий лист для учащихся 7-х классов, позволяющий овладеть навыками решения задач со словами линейного неравенства. Задачи по математике для 8-го класса Г-жа Алкала и ее ученики-математики седьмого класса изучают решение проблем неравенства. Г-жа Алькала начинает свой урок с того, что учащиеся наносят решения в виде графиков, чтобы они развили концептуальное понимание, прежде чем переходить к обозначениям. Она говорит, что этот метод помогает учащимся использовать предыдущие знания, чтобы понять новую концепцию, а не изучать уловки для устранения неравенства.Глава 2: математика iLEAP, 7 класс. В этом разделе описывается общий дизайн теста iLEAP Math, который будет проводиться для учащихся 7-го класса. Технические требования к тесту, образцы вопросов теста и критерии выставления оценок предоставлены, чтобы учителя могли согласовать практику в классе с оценкой штата. Структура теста. Если вы хотите получить полный доступ ко всем нашим праздничным урокам математики и полной программе по математике для 6-го класса, математике для 7-го класса и 8-го класса, тогда присоединяйтесь к сообществу тренеров по математике! Не забудьте прикрепить эти раскраски по математике на День Благодарения! 6.1 Решение одноступенчатых линейных неравенств 6.2 Решение многоступенчатых линейных неравенств 6.3 Решение сложных неравенств 6.4 Решение абсолютных уравнений и неравенств 6.5 Графическое отображение линейных неравенств в двух переменных 6.
Она говорит, что этот метод помогает учащимся использовать предыдущие знания, чтобы понять новую концепцию, а не изучать уловки для устранения неравенства.Глава 2: математика iLEAP, 7 класс. В этом разделе описывается общий дизайн теста iLEAP Math, который будет проводиться для учащихся 7-го класса. Технические требования к тесту, образцы вопросов теста и критерии выставления оценок предоставлены, чтобы учителя могли согласовать практику в классе с оценкой штата. Структура теста. Если вы хотите получить полный доступ ко всем нашим праздничным урокам математики и полной программе по математике для 6-го класса, математике для 7-го класса и 8-го класса, тогда присоединяйтесь к сообществу тренеров по математике! Не забудьте прикрепить эти раскраски по математике на День Благодарения! 6.1 Решение одноступенчатых линейных неравенств 6.2 Решение многоступенчатых линейных неравенств 6.3 Решение сложных неравенств 6.4 Решение абсолютных уравнений и неравенств 6.5 Графическое отображение линейных неравенств в двух переменных 6. 6 Стволовые и листовые графики и среднее значение, медиана и мода 6.7 Вставка. and-Whisker Plots
6 Стволовые и листовые графики и среднее значение, медиана и мода 6.7 Вставка. and-Whisker Plots
В седьмом классе ученики возвращаются, чтобы вспомнить эти концепции и навыки, чтобы решить одно- и двухэтапные уравнения и неравенства с рациональными числами, включая отрицательные. В восьмом классе ученики изучают сложные многоступенчатые уравнения; однако они обнаружат, что эти многоступенчатые уравнения можно упростить в формы, знакомые с тем, что они видели в седьмом классе.
Глава 111. Подраздел B
Глава 111. Техас. Основные знания и навыки для математики
Подраздел B. Средняя школа
Законодательные органы: Положения данного Подглавы B выпущен в соответствии с Кодексом образования Техаса, 7.102 (c) (4), 28.002, 28.0021 (a) (1), и 28.008, если не указано иное.
111,25. Выполнение Техасских основных знаний и навыков для математики, средняя школа, принята 2012 г.
(а) Положения пунктов 111.26-111.28 настоящего подраздела
реализуются школьными округами.
(б) Не позднее 31 августа 2013 г., уполномоченный образование должно определить, было ли финансирование учебных материалов предоставлены в государственные школы Техаса для материалов, которые охватывают основные знания и навыки по математике, принятые в пунктах 111.26-111.28 настоящего подраздел.
(c) Если комиссар принимает решение, что инструктивный финансирование материалов было предоставлено в соответствии с подразделом (b) этого раздела, 111.26-111.28 настоящего подраздела вводить в действие, начиная с 2014-2015 учебный год и распространяется на 2014-2015 и последующие учебные годы.
(d) Если комиссар не принимает решение
финансирование учебных материалов доступно в подразделе
(b) данного раздела комиссар не позднее августа определяет
31 каждого последующего учебного года ли финансирование учебных материалов
был доступен.Если комиссар определит, что инструкция
выделено финансирование материалов, уполномоченный должен уведомить
Государственное управление образования и школьных округов, 111. 26-111.28 г.
подраздел вводится в действие на следующий учебный год.
26-111.28 г.
подраздел вводится в действие на следующий учебный год.
Источник: Положения настоящего стандарта 111.25 приняты для вступления в силу. 10 сентября 2012 г., 37 TexReg 7109; внесены изменения, вступающие в силу 31 декабря 2014 г., 39 TexReg 10470.
111.26. 6 класс, принято 2012.
(а) Введение.
(1) Стремление к совершенству в образовании является движущей силой основных знаний и навыков Техаса по математике, руководствуясь стандартами готовности к колледжу и карьере. Встраивая статистику, вероятность и финансы, уделяя особое внимание вычислительному мышлению, математическому свободное владение языком и твердое понимание, Техас будет лидером в области математического образования и подготовить всех студентов Техаса к испытаниям, с которыми они столкнутся в 21-м век.
(2) Стандарты процессов описывают способы, которыми
Ожидается, что студенты будут вовлечены в содержание. Размещение процесса
стандарты в начале знаний и навыков, указанные для каждого класса
и конечно намеренно. Стандарты процессов объединяют другие знания
и навыки вместе, чтобы учащиеся могли успешно решать проблемы и
эффективно и результативно использовать математику в повседневной жизни. Стандарты процесса
интегрированы в каждый класс и курс.По возможности студенты будут
применять математику к проблемам, возникающим в повседневной жизни, в обществе и на рабочем месте.
Студенты будут использовать модель решения проблем, которая включает анализ заданных
информация, формулирование плана или стратегии, определение решения, обоснование
решение, а также оценка процесса решения проблем и разумности
решения. Студенты выберут соответствующие инструменты, такие как реальные объекты,
манипуляторы, алгоритмы, бумага и карандаш, а также технологии и методы
такие как мысленная математика, оценка, чувство чисел, а также обобщение и абстракция
решить проблемы.
Размещение процесса
стандарты в начале знаний и навыков, указанные для каждого класса
и конечно намеренно. Стандарты процессов объединяют другие знания
и навыки вместе, чтобы учащиеся могли успешно решать проблемы и
эффективно и результативно использовать математику в повседневной жизни. Стандарты процесса
интегрированы в каждый класс и курс.По возможности студенты будут
применять математику к проблемам, возникающим в повседневной жизни, в обществе и на рабочем месте.
Студенты будут использовать модель решения проблем, которая включает анализ заданных
информация, формулирование плана или стратегии, определение решения, обоснование
решение, а также оценка процесса решения проблем и разумности
решения. Студенты выберут соответствующие инструменты, такие как реальные объекты,
манипуляторы, алгоритмы, бумага и карандаш, а также технологии и методы
такие как мысленная математика, оценка, чувство чисел, а также обобщение и абстракция
решить проблемы. Студенты будут эффективно передавать математические идеи,
рассуждения и их последствия с использованием нескольких представлений, таких как символы,
диаграммы, графики, компьютерные программы и язык. Студенты будут использовать математические
отношения для выработки решений, установления связей и прогнозов.
Студенты будут анализировать математические отношения, чтобы общаться и общаться
математические идеи. Студенты будут отображать, объяснять или обосновывать математические
идеи и аргументы с использованием точного математического языка в письменной или устной форме
коммуникация.
Студенты будут эффективно передавать математические идеи,
рассуждения и их последствия с использованием нескольких представлений, таких как символы,
диаграммы, графики, компьютерные программы и язык. Студенты будут использовать математические
отношения для выработки решений, установления связей и прогнозов.
Студенты будут анализировать математические отношения, чтобы общаться и общаться
математические идеи. Студенты будут отображать, объяснять или обосновывать математические
идеи и аргументы с использованием точного математического языка в письменной или устной форме
коммуникация.
(3) Основное внимание в 6 классе уделяется количеству
и операции; соразмерность; выражения, уравнения и отношения;
и измерения и данные. Студенты используют концепции, алгоритмы и свойства
рациональных чисел, чтобы исследовать математические отношения и описывать
все более сложные ситуации. Студенты используют понятия соразмерности
исследовать, развивать и сообщать математические отношения. Студенты
использовать алгебраическое мышление, чтобы описать, как изменение одной величины в отношениях
приводит к изменению другого.Студенты соединяют словесные, числовые, графические,
и символические представления отношений, включая уравнения и неравенства.
Студенты используют геометрические свойства и отношения, а также пространственные рассуждения,
моделировать и анализировать ситуации и решать проблемы. Студенты передают информацию
о геометрических фигурах или ситуациях путем количественной оценки атрибутов, обобщить
процедуры, основанные на опыте измерений, и использовать эти процедуры для решения проблем.Студенты используют соответствующую статистику, представления данных и рассуждения.
делать выводы, оценивать аргументы и давать рекомендации. В то время как
важно использование всех видов техники, упор на готовность к алгебре
навыки требуют внедрения графической технологии.
Студенты
использовать алгебраическое мышление, чтобы описать, как изменение одной величины в отношениях
приводит к изменению другого.Студенты соединяют словесные, числовые, графические,
и символические представления отношений, включая уравнения и неравенства.
Студенты используют геометрические свойства и отношения, а также пространственные рассуждения,
моделировать и анализировать ситуации и решать проблемы. Студенты передают информацию
о геометрических фигурах или ситуациях путем количественной оценки атрибутов, обобщить
процедуры, основанные на опыте измерений, и использовать эти процедуры для решения проблем.Студенты используют соответствующую статистику, представления данных и рассуждения.
делать выводы, оценивать аргументы и давать рекомендации. В то время как
важно использование всех видов техники, упор на готовность к алгебре
навыки требуют внедрения графической технологии.
(4) Заявления, содержащие слово «включая»
справочный контент, который необходимо освоить, а те, которые содержат фразу
«такие как» предназначены в качестве возможных иллюстративных примеров.
(b) Знания и навыки.
(1) Стандарты математических процессов. Студент использует математические процессы для получения и демонстрации математического понимания. Ожидается:
(A) применять математику к возникающим проблемам в повседневной жизни, в обществе и на рабочем месте;
(B) использовать модель решения проблем, которая включает анализ данной информации, формулирование плана или стратегии, определение решение, обоснование решения и оценка процесса решения проблемы и разумности решения;
(C) выберите инструменты, включая реальные объекты, манипуляторы, бумагу и карандаш, и технология и методы, включая мысленную математику, оценку, и чувство числа, если необходимо, чтобы решить проблемы;
(D) передает математические идеи, рассуждения и их последствия, используя несколько представлений, включая символы, диаграммы, графики и соответствующий язык;
(E) создавать и использовать представления для организации, записывать и передавать математические идеи;
(F) анализировать математические отношения к соединять и передавать математические идеи; и
(G) отображать, объяснять и обосновывать математические идеи и аргументы, используя точные
математический язык в письменном или устном общении.
(2) Число и операции. Студент подает заявку стандарты математического процесса для представления и использования рациональных чисел в разнообразие форм. Ожидается:
(A) классифицирует целые числа, целые числа и рациональные числа с использованием визуального представления, такого как диаграмма Венна, для описания отношения между наборами чисел;
(B) идентифицирует число, его противоположность и его абсолютная величина;
(C) найти, сравнить, и порядок целых и рациональных чисел с помощью числовой строки;
(D) порядок набора рациональных чисел, возникающих из математического и реального контекстов; и
(E) расширить представления для разделения на включить дробное обозначение, например, a / b представляет то же число как a b , где b ≠ 0.
(3) Число и операции. Студент подает заявку
стандарты математического процесса для представления сложения, вычитания, умножения,
и разделение при решении проблем и обосновании решений. Студент
ожидается:
Студент
ожидается:
(A) признать, что деление на рациональное число и умножение на обратный результат в эквивалентных значениях;
(B) определяет, с расчетом и без него, увеличивается или уменьшается количество при умножении на дробь, включая значения больше или меньше единицы;
(C) представляют собой целочисленные операции с конкретными моделирует и связывает действия с моделями со стандартизованными алгоритмами;
(D) складывать, вычитать, умножать и делить целые числа бегло; и
(E) умножить и разделить положительное рациональное числа бегло.
(4) Пропорциональность. Студент применяет математические стандарты процесса для развития понимания пропорциональных отношений в проблемных ситуациях. Ожидается:
(A) сравнить два правила словесно, численно, графически и символически в форма y = ax или y = x + a , чтобы различать между аддитивными и мультипликативными отношениями;
(B) применять качественные и количественные рассуждения для решения задач прогнозирования и сравнения реальных проблем с использованием соотношений и ставки;
(C) приведены примеры соотношений как мультипликативных сравнения двух величин, описывающих один и тот же атрибут;
(D) приведены примеры ставок для сравнения путем деления двух величин с разными атрибутами, включая ставки как частные;
(E) представляют собой отношения и проценты с бетоном модели, дроби и десятичные дроби;
(F) представляют собой контрольные доли и проценты, такие как 1%, 10%, 25%, 33 1/3%, и кратные этих значений с использованием сеток 10 на 10, ленточных диаграмм, числовых линий и чисел;
(G) генерировать эквивалент формы дробей, десятичных знаков и процентов с использованием реальных задач, в том числе проблемы, связанные с деньгами; и
(H) преобразовать единицы измерения
система, включая использование пропорций и удельных ставок.
(5) Пропорциональность. Студент применяет математические стандарты процесса для решения проблем, связанных с пропорциональными отношениями. Ожидается:
(A) представляет математический и реальный мир проблемы, связанные с соотношениями и коэффициентами с использованием масштабных коэффициентов, таблиц, графиков и пропорции;
(B) решать реальные проблемы для найти целое с учетом части и процентов, чтобы найти часть с учетом целого и проценты, и найти проценты для части и целого, включая использование конкретных и графических моделей; и
(C) использовать эквивалентные дроби, десятичные дроби, и проценты, чтобы показать равные части одного и того же целого.
(6) Выражения, уравнения и отношения. Студент применяет стандарты математического процесса для использования нескольких представлений для описания алгебраических отношений. Ожидается:
(A) определяет независимые и зависимые количества из таблиц и графики;
(B) напишите уравнение, которое представляет взаимосвязь между независимыми и зависимыми величинами из стол; и
(C) представляют
данный
ситуации с использованием словесных описаний, таблиц, графиков и
уравнения в виде y = kx или y = x + b .
(7) Выражения, уравнения и отношения. Студент применяет стандарты математического процесса для разработки концепций выражения и уравнения. Ожидается:
(A) генерировать эквивалентные числовые выражения, использующие порядок операций, включая целочисленные показатели и разложение на простые множители;
(B) различать выражения и уравнения словесно, численно и алгебраически;
(C) определить, если два выражения эквивалентны с использованием конкретных моделей, графических моделей и алгебраических представлений; и
(D) генерировать эквивалентные выражения используя свойства операций: обратная, тождественная, коммутативная, ассоциативные и распределительные свойства.
(8) Выражения, уравнения и отношения. Студент применяет стандарты математического процесса, чтобы использовать геометрию для представления отношения и решать проблемы. Ожидается:
(A) расширить предыдущие знания о треугольниках и их свойства, чтобы включать сумму углов треугольника, отношение между длинами сторон и размерами углов в треугольнике, и определение когда три длины образуют треугольник;
(B) модель формулы площади для параллелограммов, трапеций, и треугольники, разложив и переставив части этих фигур;
(C) написать уравнения которые представляют собой проблемы, связанные с областью прямоугольники, параллелограммы, трапеции, треугольники и объем справа прямоугольные призмы с положительными рациональными размерами числа; и
(D) определить
решения проблем, связанных с областью
прямоугольники, параллелограммы, трапеции, треугольники и объем справа
прямоугольные призмы с положительными рациональными размерами
числа.
(9) Выражения, уравнения и отношения. Студент применяет стандарты математического процесса для использования уравнений и неравенств. представлять ситуации. Ожидается:
(A) написать уравнения с одной переменной и одним шагом и неравенства для обозначения ограничений или условий в рамках проблем;
(B) представляют решения для одной переменной, одношаговые уравнения и неравенства на числовых прямых; и
(C) напишите соответствующие реальные проблемы с учетом уравнений или неравенств с одной переменной, одношаговых.
(10) Выражения, уравнения и отношения. Студент применяет стандарты математического процесса для использования уравнений и неравенств. решить проблемы. Ожидается:
(A) и решите одну переменную, одношаговое уравнения и неравенства, представляющие проблемы, включая геометрические понятия; и
(B) определить, соответствует ли данное значение (я)
Однопеременные, одношаговые уравнения или неравенства верны.
(11) Измерения и данные. Студент подает заявку стандарты математического процесса для использования координатной геометрии для определения местоположений на плоскости. Ожидается, что ученик наберет точки во всех четырех квадрантах. с помощью упорядоченные пары рациональных чисел.
(12) Измерения и данные. Студент подает заявку стандарты математических процессов для использования числовых или графических представлений анализировать проблемы. Ожидается:
(A) представляют числовые данные графически, включая точечные диаграммы, диаграммы стеблей и листьев, гистограммы и ящичковые диаграммы;
(B) использовать графическое представление числовых данные для описания центра, распространения и формы распределения данных;
(C) суммирует числовые данные с числовые сводки, включая среднее и медианное значение (меры центра), а также размах и межквартильный размах (IQR) (меры распространения), и используйте эти сводки для описания центра, распространения, и форма распределения данных; и
(D) суммирует категориальные данные с числовыми
и графические сводки, включая режим, процент значений в каждом
категории (таблица относительной частоты) и гистограммы процентов, и используйте их
резюме для описания распределения данных.
(13) Измерения и данные. Студент подает заявку стандарты математических процессов для использования числовых или графических представлений решить проблемы. Ожидается:
(A) интерпретация числовых данных, представленных в виде точечных диаграмм, стебель и лист графики, гистограммы и коробчатые диаграммы; и
(B) различать ситуации дающие данные с вариабельностью и без нее.
(14) Личная финансовая грамотность. Студент применяет стандарты математического процесса для развития экономического мышления и решение проблем, полезных в жизни знающего потребителя и инвестора.Ожидается:
(A) сравните характеристики и стоимость проверки счет и дебетовая карта, предлагаемые различными местными финансовыми учреждениями;
(B) различают дебетовые и кредитные карты открытки;
(C) балансировать регистр чеков, который включает депозиты, снятие средств и переводы;
(D) объясните, почему важно установить положительная кредитная история;
(E) описать информацию в кредитном отчете и как долго он сохраняется;
(F) описывает ценность кредитных отчетов для заемщикам и кредиторам;
(G) объясняет различные методы оплаты обучения в колледже, в том числе через сбережения, гранты, стипендии, студенческие ссуды и работу-учебу; и
(H) сравнить годовую зарплату нескольких профессий
требующие различных уровней послесреднего образования или профессионального обучения
и рассчитать влияние различных годовых зарплат на пожизненный доход.
Источник: Положения настоящего стандарта 111.26 приняты для вступления в силу. 10 сентября 2012 г., 37 TexReg 7109.
111,27. 7 класс, принято 2012.
(а) Введение.
(1) Стремление к совершенству в образовании является движущей силой основных знаний и навыков Техаса по математике, руководствуясь стандартами готовности к колледжу и карьере. Встраивая статистику, вероятность и финансы, уделяя особое внимание вычислительному мышлению, математическому свободное владение языком и твердое понимание, Техас будет лидером в области математического образования и подготовить всех студентов Техаса к испытаниям, с которыми они столкнутся в 21-м век.
(2) Стандарты процессов описывают способы, которыми
Ожидается, что студенты будут вовлечены в содержание. Размещение процесса
стандарты в начале знаний и навыков, указанные для каждого класса
и конечно намеренно. Стандарты процессов объединяют другие знания
и навыки вместе, чтобы учащиеся могли успешно решать проблемы и
эффективно и результативно использовать математику в повседневной жизни. Стандарты процесса
интегрированы в каждый класс и курс.По возможности студенты будут
применять математику к проблемам, возникающим в повседневной жизни, в обществе и на рабочем месте.
Студенты будут использовать модель решения проблем, которая включает анализ заданных
информация, формулирование плана или стратегии, определение решения, обоснование
решение, а также оценка процесса решения проблем и разумности
решения. Студенты выберут соответствующие инструменты, такие как реальные объекты,
манипуляторы, алгоритмы, бумага и карандаш, а также технологии и методы
такие как мысленная математика, оценка, чувство чисел, а также обобщение и абстракция
решить проблемы.Студенты будут эффективно передавать математические идеи,
рассуждения и их последствия с использованием нескольких представлений, таких как символы,
диаграммы, графики, компьютерные программы и язык. Студенты будут использовать математические
отношения для выработки решений, установления связей и прогнозов.
Стандарты процесса
интегрированы в каждый класс и курс.По возможности студенты будут
применять математику к проблемам, возникающим в повседневной жизни, в обществе и на рабочем месте.
Студенты будут использовать модель решения проблем, которая включает анализ заданных
информация, формулирование плана или стратегии, определение решения, обоснование
решение, а также оценка процесса решения проблем и разумности
решения. Студенты выберут соответствующие инструменты, такие как реальные объекты,
манипуляторы, алгоритмы, бумага и карандаш, а также технологии и методы
такие как мысленная математика, оценка, чувство чисел, а также обобщение и абстракция
решить проблемы.Студенты будут эффективно передавать математические идеи,
рассуждения и их последствия с использованием нескольких представлений, таких как символы,
диаграммы, графики, компьютерные программы и язык. Студенты будут использовать математические
отношения для выработки решений, установления связей и прогнозов. Студенты будут анализировать математические отношения, чтобы общаться и общаться
математические идеи. Студенты будут отображать, объяснять или обосновывать математические
идеи и аргументы с использованием точного математического языка в письменной или устной форме
коммуникация.
Студенты будут анализировать математические отношения, чтобы общаться и общаться
математические идеи. Студенты будут отображать, объяснять или обосновывать математические
идеи и аргументы с использованием точного математического языка в письменной или устной форме
коммуникация.
(3) Основное внимание в 7 классе уделяется количеству
и операции; соразмерность; выражения, уравнения и отношения;
и измерения и данные. Студенты используют концепции, алгоритмы и свойства
рациональных чисел, чтобы исследовать математические отношения и описывать
все более сложные ситуации. Студенты используют понятия соразмерности
для изучения, развития и передачи математических взаимосвязей, в том числе
число, геометрия и измерение, статистика и вероятность.Студенты
использовать алгебраическое мышление, чтобы описать, как изменение одной величины в отношениях
приводит к изменению другого. Студенты соединяют словесные, числовые, графические,
и символические представления отношений, включая уравнения и неравенства. Студенты используют геометрические свойства и отношения, а также пространственные рассуждения,
моделировать и анализировать ситуации и решать проблемы. Студенты передают информацию
о геометрических фигурах или ситуациях путем количественной оценки атрибутов, обобщить
процедуры, основанные на опыте измерений, и использовать эти процедуры для решения проблем.Студенты используют соответствующую статистику, представления данных и рассуждения.
делать выводы, оценивать аргументы и давать рекомендации. В то время как
важно использование всех видов техники, упор на готовность к алгебре
навыки требуют внедрения графической технологии.
Студенты используют геометрические свойства и отношения, а также пространственные рассуждения,
моделировать и анализировать ситуации и решать проблемы. Студенты передают информацию
о геометрических фигурах или ситуациях путем количественной оценки атрибутов, обобщить
процедуры, основанные на опыте измерений, и использовать эти процедуры для решения проблем.Студенты используют соответствующую статистику, представления данных и рассуждения.
делать выводы, оценивать аргументы и давать рекомендации. В то время как
важно использование всех видов техники, упор на готовность к алгебре
навыки требуют внедрения графической технологии.
(4) Заявления, содержащие слово «включая» справочный контент, который необходимо освоить, а те, которые содержат фразу «такие как» предназначены в качестве возможных иллюстративных примеров.
(b) Знания и навыки.
(1) Стандарты математических процессов. Студент
использует математические процессы для получения и демонстрации математического понимания. Ожидается:
Ожидается:
(A) применять математику к возникающим проблемам в повседневной жизни, в обществе и на рабочем месте;
(B) использовать модель решения проблем, которая включает анализ данной информации, формулирование плана или стратегии, определение решение, обоснование решения и оценка процесса решения проблемы и разумности решения;
(C) выберите инструменты, включая реальные объекты, манипуляторы, бумагу и карандаш, и технология и методы, включая мысленную математику, оценку, и чувство числа, если необходимо, чтобы решить проблемы;
(D) передает математические идеи, рассуждения и их последствия, используя несколько представлений, включая символы, диаграммы, графики и соответствующий язык;
(E) создавать и использовать представления для организации, записывать и передавать математические идеи;
(F) анализировать математические отношения к соединять и передавать математические идеи; и
(G) отображать, объяснять и обосновывать математические идеи и аргументы, используя точные
математический язык в письменном или устном общении.
(2) Число и операции. Студент подает заявку стандарты математического процесса для представления и использования рациональных чисел в разнообразие форм. Ожидается, что студент расширит предыдущие знания наборы и подмножества с использованием визуального представления для описания отношений между наборы рациональных чисел.
(3) Число и операции. Студент подает заявку стандарты математического процесса для сложения, вычитания, умножения и деления решение проблем и обоснование решений.Ожидается:
(A) сложение, вычитание, умножение и деление рациональных чисел числа бегло; и
(B) применять и расширять предыдущие договоренности операций для решения задач с использованием сложения, вычитания, умножения, и деление рациональных чисел.
(4) Пропорциональность. Студент применяет математические стандарты процессов для представления и решения проблем, связанных с пропорциональными отношениями. Ожидается:
(A) представляют постоянную скорость изменения в математических и реальных задачах, заданных графическими, табличными, словесными, числовые, графические и алгебраические представления, в том числе d = rt ;
(B) рассчитать удельные расценки по ставкам в математической и проблемы реального мира;
(C) определить коэффициент пропорциональности ( k = y / x ) в рамках математических и реальных задач;
(D) решать проблемы, связанные с соотношения, ставки и проценты, включая многоэтапные задачи с процентами рост и снижение процента, и проблемы с финансовой грамотностью; и
(E) преобразование между системами измерения, включая использование
пропорций и использования единичных ставок.
(5) Пропорциональность. Студент применяет математические стандарты процессов для использования геометрии для описания или решения проблем, связанных с пропорциональные отношения. Ожидается:
(A) обобщить критические атрибуты сходство, включая соотношения внутри и между подобными формами;
(B) описывает π как отношение длины окружности к ее диаметру; и
(C) решить математическую и реальные проблемы, связанные с чертежами аналогичной формы и масштаба.
(6) Пропорциональность. Студент применяет математические стандарты процессов для использования вероятности и статистики для описания или решения проблем вовлекающие пропорциональные отношения. Ожидается:
(A) представляют собой пробелы для простых и составные события с использованием списков и древовидных диаграмм;
(B) выберите и используйте различные модели для представляют простые и сложные события с технологиями и без них;
(C) делать прогнозы и определять решения использование экспериментальных данных для простых и сложных событий;
(D) делать прогнозы и определять решения использование теоретической вероятности для простых и сложных событий;
(E) найти вероятности простого событие и его дополнение и описывают отношения между ними;
(F) использовать данные из случайной выборки для делать выводы о населении;
(G) решить проблемы с использованием данных, представленных в виде гистограмм, точечных диаграмм и круговых диаграмм, включая частичные сравнения и эквиваленты;
(H) решать проблемы с помощью качественные и количественные прогнозы и сравнения из простых экспериментов; и
(I) определяют экспериментальные и теоретические
вероятности, связанные с простыми и сложными событиями, с использованием данных и выборки
пробелы.
(7) Выражения, уравнения и отношения. Студент применяет стандарты математического процесса для представления линейных отношений. с использованием нескольких представлений. Ожидается, что ученик будет представлять линейные отношения с помощью словесных описаний, таблиц, графиков, и уравнения, которые упрощаются до формы y = mx + b .
(8) Выражения, уравнения и отношения. Студент применяет стандарты математического процесса для построения геометрических соотношений. с объемом.Ожидается:
(A) моделирование отношений между объемом прямоугольной призмы и прямоугольной пирамиды, имеющей оба совпадающих основания и высоты и соединяются это отношение к формулам;
(B) объяснять словесно и символически соотношение между объемом треугольной призмы и треугольной пирамида, имеющая одинаковое основание и высоту и соединяющая это отношение к формулам; и
(C) использовать модели для определения приблизительных формул
для окружности и площади круга и соедините модели с актуальными
формулы.
(9) Выражения, уравнения и отношения. Студент применяет стандарты математического процесса для решения геометрических задач. Ожидается:
(A) решить проблемы объемные прямоугольные призмы, треугольные призмы, прямоугольные пирамиды и треугольные пирамиды;
(B) определить окружность и площадь круги;
(C) определить площадь составных фигур содержащий комбинации прямоугольников, квадратов, параллелограммов, трапеций, треугольники, полукруги и четверти окружности; и
(D) решить проблемы, связанные с боковой и общая площадь поверхности прямоугольной призмы, прямоугольной пирамиды, треугольная призма и треугольная пирамида путем определения площадь сетки фигуры.
(10) Выражения, уравнения и отношения. Студент применяет стандарты математического процесса для использования уравнений с одной переменной и неравенство для представления ситуаций. Ожидается:
(A) запись с одной переменной, двухступенчатая уравнения и неравенства для представления ограничения или условия в рамках проблем;
(B) представляют решения для одной переменной, двухступенчатой уравнения и неравенства на числовых линиях; и
(C) напишите соответствующую реальную проблему
учитывая двухступенчатое уравнение с одной переменной или
неравенство.
(11) Выражения, уравнения и отношения. Студент применяет стандарты математического процесса для решения уравнений с одной переменной. и неравенство. Ожидается:
(A) моделирование и решение двухэтапных уравнений и неравенств с одной переменной;
(B) определить, значение (я) составляют двухступенчатые уравнения с одной переменной и неравенство истинный; и
(C) писать и решать уравнения, используя геометрию концепции, включая сумму углов в треугольнике и угловые отношения.
(12) Измерения и данные. Студент подает заявку стандарты математических процессов для использования статистических представлений для анализа данные. Ожидается:
(A) сравнить две группы числовых данных, используя сравнительные точечные или коробчатые диаграммы путем сравнения их форм, центров и спреды;
(B) использовать данные из случайная выборка, чтобы сделать выводы о совокупности; и
(C) сравнить две популяции на основе данных
в случайных выборках из этих популяций, включая неформальные сравнительные выводы
о различиях между двумя популяциями.
(13) Личная финансовая грамотность. Студент применяет стандарты математического процесса для развития экономического мышления и решение проблем, полезных в жизни знающего потребителя и инвестора. Ожидается:
(A) рассчитать налог с продаж для данной покупки и рассчитать подоходный налог с заработной платы;
(B) идентифицируют компоненты личного бюджет, включая доходы; запланированные сбережения на колледж, пенсию и чрезвычайные ситуации; налоги; постоянные и переменные расходы, и посчитайте, какой процент каждый категория состоит из общего бюджета;
(C) создание и организация финансовых активов и обязательства записывают и составляют отчет о чистой стоимости активов;
(D) используйте оценщик семейного бюджета для определения минимальный семейный бюджет и средняя почасовая оплата, необходимая семье для удовлетворить свои базовые потребности в студенческом городе или другом крупном городе поблизости;
(E) рассчитать и сравнить простые проценты и доход от сложных процентов; и
(F) анализировать и сравнивать денежные стимулы,
включая продажи, скидки и купоны.
Источник: Положения настоящего стандарта 111.27 приняты для вступления в силу. 10 сентября 2012 г., 37 TexReg 7109.
111,28. 8 класс, принято 2012.
(а) Введение.
(1) Стремление к совершенству в образовании является движущей силой основных знаний и навыков Техаса по математике, руководствуясь стандартами готовности к колледжу и карьере. Встраивая статистику, вероятность и финансы, уделяя особое внимание вычислительному мышлению, математическому свободное владение языком и твердое понимание, Техас будет лидером в области математического образования и подготовить всех студентов Техаса к испытаниям, с которыми они столкнутся в 21-м век.
(2) Стандарты процессов описывают способы, которыми
Ожидается, что студенты будут вовлечены в содержание. Размещение процесса
стандарты в начале знаний и навыков, указанные для каждого класса
и конечно намеренно. Стандарты процессов объединяют другие знания
и навыки вместе, чтобы учащиеся могли успешно решать проблемы и
эффективно и результативно использовать математику в повседневной жизни. Стандарты процесса
интегрированы в каждый класс и курс.По возможности студенты будут
применять математику к проблемам, возникающим в повседневной жизни, в обществе и на рабочем месте.
Студенты будут использовать модель решения проблем, которая включает анализ заданных
информация, формулирование плана или стратегии, определение решения, обоснование
решение, а также оценка процесса решения проблем и разумности
решения. Студенты выберут соответствующие инструменты, такие как реальные объекты,
манипуляторы, алгоритмы, бумага и карандаш, а также технологии и методы
такие как мысленная математика, оценка, чувство чисел, а также обобщение и абстракция
решить проблемы.Студенты будут эффективно передавать математические идеи,
рассуждения и их последствия с использованием нескольких представлений, таких как символы,
диаграммы, графики, компьютерные программы и язык. Студенты будут использовать математические
отношения для выработки решений, установления связей и прогнозов.
Стандарты процесса
интегрированы в каждый класс и курс.По возможности студенты будут
применять математику к проблемам, возникающим в повседневной жизни, в обществе и на рабочем месте.
Студенты будут использовать модель решения проблем, которая включает анализ заданных
информация, формулирование плана или стратегии, определение решения, обоснование
решение, а также оценка процесса решения проблем и разумности
решения. Студенты выберут соответствующие инструменты, такие как реальные объекты,
манипуляторы, алгоритмы, бумага и карандаш, а также технологии и методы
такие как мысленная математика, оценка, чувство чисел, а также обобщение и абстракция
решить проблемы.Студенты будут эффективно передавать математические идеи,
рассуждения и их последствия с использованием нескольких представлений, таких как символы,
диаграммы, графики, компьютерные программы и язык. Студенты будут использовать математические
отношения для выработки решений, установления связей и прогнозов.-reshenie-137.jpg) Студенты будут анализировать математические отношения, чтобы общаться и общаться
математические идеи. Студенты будут отображать, объяснять или обосновывать математические
идеи и аргументы с использованием точного математического языка в письменной или устной форме
коммуникация.
Студенты будут анализировать математические отношения, чтобы общаться и общаться
математические идеи. Студенты будут отображать, объяснять или обосновывать математические
идеи и аргументы с использованием точного математического языка в письменной или устной форме
коммуникация.
(3) Основные направления в 8-м классе — пропорциональность;
выражения, уравнения, отношения и основы функций; и измерения
и данные. Студенты используют концепции, алгоритмы и свойства действительных чисел
исследовать математические отношения и описывать все более сложные
ситуации. Студенты используют концепции соразмерности для изучения, развития,
и сообщать математические отношения. Студенты используют алгебраическое мышление
чтобы описать, как изменение одной величины в отношениях приводит к изменению
в другом.Студенты соединяют словесные, числовые, графические и символические представления
соотношений, включая уравнения и неравенства. Студенты начинают
развить понимание функциональных отношений. Студенты используют геометрические
свойства и отношения, а также пространственные рассуждения для моделирования и анализа
ситуации и решать проблемы. Студенты сообщают информацию о геометрических
цифры или ситуации путем количественной оценки атрибутов, обобщить процедуры из
измерения и использовать процедуры для решения проблем.Студенты
использовать соответствующую статистику, представления данных и рассуждения для рисования
выводы, оценивать аргументы и давать рекомендации. Хотя использование
важны все виды техники, упор на навыки алгебры
требует внедрения графической технологии.
Студенты используют геометрические
свойства и отношения, а также пространственные рассуждения для моделирования и анализа
ситуации и решать проблемы. Студенты сообщают информацию о геометрических
цифры или ситуации путем количественной оценки атрибутов, обобщить процедуры из
измерения и использовать процедуры для решения проблем.Студенты
использовать соответствующую статистику, представления данных и рассуждения для рисования
выводы, оценивать аргументы и давать рекомендации. Хотя использование
важны все виды техники, упор на навыки алгебры
требует внедрения графической технологии.
(4) Заявления, содержащие слово «включая» справочный контент, который необходимо освоить, а те, которые содержат фразу «такие как» предназначены в качестве возможных иллюстративных примеров.
(b) Знания и навыки.
(1) Стандарты математических процессов. Студент
использует математические процессы для получения и демонстрации математического понимания. Ожидается:
Ожидается:
(A) применять математику к возникающим проблемам в повседневной жизни, в обществе и на рабочем месте;
(B) использовать модель решения проблем, которая включает анализ данной информации, формулирование плана или стратегии, определение решение, обоснование решения и оценка процесса решения проблемы и разумности решения;
(C) выберите инструменты, включая реальные объекты, манипуляторы, бумагу и карандаш, и технология и методы, включая мысленную математику, оценку, и чувство числа, если необходимо, чтобы решить проблемы;
(D) передает математические идеи, рассуждения и их последствия, используя несколько представлений, включая символы, диаграммы, графики и соответствующий язык;
(E) создавать и использовать представления для организации, записывать и передавать математические идеи;
(F) анализировать математические отношения к соединять и передавать математические идеи; и
(G) отображать, объяснять и обосновывать математические идеи и аргументы, используя точные
математический язык в письменном или устном общении.
(2) Число и операции. Студент подает заявку стандарты математического процесса для представления и использования действительных чисел в различных форм. Ожидается:
(A) расширить предыдущие знания о множествах и подмножества с использованием визуального представления для описания отношений между наборами действительных чисел;
(B) приблизительное значение иррационального числа, включая π и квадрат корни чисел меньше 225 и расположите это приближение рационального числа на числовой прямой;
(C) преобразование между стандартным десятичным представлением и научное обозначение; и
(D) заказать набор настоящих числа, возникающие из математических и контексты реального мира.
(3) Пропорциональность. Студент применяет математические стандарты процесса для использования пропорциональных соотношений для описания расширений. Ожидается:
(A) обобщают, что отношение соответствующих стороны одинаковых форм пропорциональны, включая форму и ее расширение;
(B) сравнить и сопоставить атрибуты формы и ее расширения (ов) на координатной плоскости; и
(C) использовать алгебраическое представление для объяснения влияния данного положительного рационального масштабного коэффициента, применяемого к двумерным фигурам, на координату
плоскость с центром в центре расширения.
(4) Пропорциональность. Студент применяет математические стандарты процесса для объяснения пропорциональных и непропорциональных отношений с уклоном. Ожидается:
(A) используйте аналогичные прямоугольные треугольники для построения понимание этого уклона, м, , заданного как скорость, сравнивающего изменение значений и на изменение x -значения, (y 2 — y 1 ) / (x 2 — x 1 ), то же самое для любых двух точек (x 1 , y 1 ) и (x 2 , y 2 ) в той же строке;
(B) график пропорциональных отношений, интерпретация единичная ставка как наклон линии, моделирующей взаимосвязь; и
(C) использовать данные из таблицы или графика для определения скорость изменения или наклона и y — перехват в математическом и реальном мире проблемы.
(5) Пропорциональность. Студент применяет математические
стандарты процесса использовать пропорциональные и непропорциональные отношения
разработать основные концепции функций. Ожидается:
Ожидается:
(A) представляют линейно-пропорциональный ситуации с таблицами, графиками и уравнениями в виде y = kx ;
(B) представляют линейные непропорциональные ситуации с таблицами, графики и уравнения в виде y = mx + b , где b ≠ 0;
(C) сопоставьте двумерные наборы данных, которые предполагают линейная связь с двумерными наборами данных, которые не предполагайте линейную зависимость от графического представления;
(D) используйте линию тренда, которая приближается к линейной взаимосвязь между двумерными наборами данных для прогнозирования;
(E) решать проблемы, связанные с прямая вариация;
(F) различают пропорциональные и непропорциональные ситуаций с использованием таблиц, графиков и уравнений в форма y = kx или y = mx + b , где b ≠ 0;
(G) идентифицирует функции с помощью наборов упорядоченных пары, таблицы, отображения и графики;
(H) определяет примеры пропорциональных и непропорциональных функций, которые возникают из математических и проблемы реального мира; и
(I) напишите уравнение в форме y = mx + b для моделирования линейной зависимости
между двумя величинами с помощью словесного,
числовые, табличные и графические представления.
(6) Выражения, уравнения и отношения. Студент применяет стандарты математического процесса для разработки математических отношения и устанавливать связи с геометрическими формулами. Ожидается студент к:
(A) описывает формулу объема В = Bh цилиндра по площади основания и высоте;
(B) моделирование отношений между объемом цилиндра и конусом, имеющим равные основания и высоту, и соединяют это отношение к формулам; и
(C) используйте модели и диаграммы для объясните теорему Пифагора.
(7) Выражения, уравнения и отношения. Студент применяет стандарты математического процесса, чтобы использовать геометрию для решения проблемы. Ожидается:
(А) решить задачи, связанные с объемом цилиндров, конусов, и сферы;
(B) использовать предыдущие знания площади поверхности чтобы сделать связи с формулами для боковой и общей площади поверхности и определять решения проблем с прямоугольными призмами, треугольными призмы и цилиндры;
(C) использовать теорему Пифагора и ее обратное решить проблемы; и
(D) определить расстояние между двумя точками
на координатной плоскости с помощью теоремы Пифагора.
(8) Выражения, уравнения и отношения. Студент применяет стандарты математического процесса для использования уравнений с одной переменной или неравенство в проблемных ситуациях. Ожидается:
(A) запишите уравнения или неравенства с одной переменной с обеих сторон переменных, которые представляют проблемы, используя коэффициенты и константы рациональных чисел;
(B) напишите соответствующую реальную проблему когда задано уравнение с одной переменной или неравенство с переменными с обеих сторон знака равенства с использованием рационального числа коэффициенты и константы;
(C) и решите одну переменную уравнения с переменными по обе стороны от знака равенства, представляющие математические и реальные проблемы с использованием коэффициенты и константы рациональных чисел; и
(D) использовать неформальные аргументы для установления фактов
о сумме углов и внешнем угле треугольников, углы, созданные при
параллельные линии отсекаются трансверсалью, а угловой критерий для
подобие треугольников.
(9) Выражения, уравнения и отношения. Студент применяет стандарты математического процесса для использования нескольких представлений разработать основные концепции одновременных линейных уравнений. Студент ожидается определение и проверка значений x и y , которые одновременно удовлетворяют двум линейным уравнениям вида y = mx + b из пересечения графических уравнений.
(10) Двумерные формы.Студент подает заявку стандарты математического процесса для разработки концепций трансформационной геометрии. Ожидается:
(A) обобщают свойства ориентации и согласованность вращений, отражений, переводов и растяжения двумерных фигур по координате самолет;
(B) различать преобразования сохраняющие конгруэнтность и несоответствующие;
(C) объяснить эффект переводов, отражений по оси x или y , а вращение ограничено до 90, 180, 270 и 360 в зависимости от ситуации к двумерным фигурам на координатной плоскости с помощью алгебраической представление; и
(D) моделирует влияние на линейные и площадные измерения
расширенных двумерных форм.
(11) Измерения и данные. Студент подает заявку стандарты математических процессов для использования статистических процедур для описания данных. Ожидается:
(A) построить диаграмму рассеяния и описать наблюдаемые данные для решения таких вопросов ассоциации, как линейные, нелинейные и нет связи между двумерными данными;
(B) определить среднее абсолютное отклонение и используйте эту величину как меру данные о среднем расстоянии взяты от среднего с использованием набора данных не более 10 данных точки; и
(C) моделировать генерацию случайных выборок того же размера из популяции с известными характеристиками для развития понятие случайной выборки, репрезентативной для населения, из которого он был выбран.
(12) Личная финансовая грамотность. Студент
применяет стандарты математического процесса для развития экономического мышления
и решение проблем, полезных в жизни знающего потребителя и инвестора. Ожидается:
Ожидается:
(A) решать реальные проблемы, сравнивая процентная ставка и срок кредита влияют на стоимость кредита;
(B) рассчитать общую стоимость погашения ссуды, включая кредитные карты и легкодоступные ссуды, по различным ставкам проценты и за разные периоды с помощью онлайн-калькулятора;
(C) объясните, как вложены небольшие суммы денег регулярно, включая деньги, откладываемые на учебу и пенсию, со временем растут;
(D) рассчитать и сравнить простые проценты и доход от сложных процентов;
(E) определить и объяснить преимущества и недостатки разных способов оплаты;
(F) анализирует ситуации, чтобы определить, представлять финансово ответственные решения и определять преимущества финансовых ответственность и издержки финансовой безответственности; и
(G) оценка стоимости двухлетнего и четырехлетнего
высшее образование, включая семейный вклад, и периодически сберегать
план по накоплению денег, необходимых для вклада в общую стоимость
посещаемость не менее первого года обучения в колледже.
Источник: Положения настоящего стандарта 111.28 приняты для вступления в силу. 10 сентября 2012 г., 37 TexReg 7109.
Для дополнительная информация, электронная почта [email protected].
Центр отчетов
Рейтинги соответствия и удобства использования присваиваются на основе оценки материалов по ряду критериев и индикаторы с рецензентами, предоставляющими подтверждающие доказательства для определения и обоснования каждого присужденного балла.
Для
ELA и математика, рейтинги совмещения представляют собой степень соответствия материалов ожиданиям, частично соответствия
ожиданиям или не соответствуют ожиданиям в отношении соответствия стандартам подготовки к колледжу и карьере, включая все
стандарты присутствуют и рассматриваются с должной глубиной, чтобы помочь студентам в освоении навыков и
знания, необходимые для подготовки к поступлению в колледж и карьере.
Для науки рейтинги соответствия представляют собой степень соответствия материалов ожиданиям или частичного соответствия ожиданиям или не соответствуют ожиданиям в отношении соответствия научным стандартам нового поколения, включая все стандарты присутствуют и рассматриваются с должной глубиной, чтобы помочь студентам в освоении навыков и знания, необходимые для подготовки к поступлению в колледж и карьере.
Для всех областей содержимого рейтинги юзабилити представляют собой степень соответствия материалов ожиданиям, частичного соответствия ожиданиям или не соответствуют ожиданиям в отношении эффективных практик (как указано в инструменте оценки) для использования и дизайн, планирование и обучение учителей, оценка, дифференцированное обучение и эффективное использование технологий.
Математика K-8- Фокус и согласованность — 14 возможных точек
12–14 баллов: соответствует ожиданиям
8–11 баллов: частично соответствует ожиданиям
Ниже 8 баллов: не оправдывает ожиданий
- Строгость и математическая практика — 18 возможных баллов
16–18 баллов: соответствует ожиданиям
11-15 баллов: частично соответствует ожиданиям
Ниже 11 баллов: не оправдывает ожиданий
- Поддержка инструкций и удобство использования — 38 возможных баллов
31–38 баллов: соответствует ожиданиям
23–30 баллов: частично соответствует ожиданиям
Ниже 23: не оправдывает ожиданий
- F ocus и Coherence — 18 возможных точек
14-18 баллов: оправдывает ожидания
10-13 баллов: частично соответствует ожиданиям
Ниже 10 баллов: не оправдывает ожиданий
- Строгость и математическая практика — 16 возможных баллов
14–16 баллов: соответствует ожиданиям
10-13 баллов: частично соответствует ожиданиям
Ниже 10 баллов: не оправдывает ожиданий
- Поддержка с инструкциями и удобство использования — 36 возможных баллов
30-36 баллов: соответствует ожиданиям
22-29 баллов: частично соответствует ожиданиям
Ниже 22: не оправдывает ожиданий
- Сложность и качество текста — 58 возможных баллов
52-58 баллов: соответствует ожиданиям
28-51 баллов: частично соответствует ожиданиям
Ниже 28 баллов: не оправдывает ожиданий
- Формирование знаний с помощью текстов, словарного запаса и задач — 32 возможных балла
28-32 балла: оправдать ожидания
16–27 баллов: частично соответствует ожиданиям
Ниже 16 баллов: не оправдывает ожиданий
- Поддержка с инструкциями и удобство использования — 34 возможных балла
30-34 балла: соответствует ожиданиям
24-29 баллов: частично соответствует ожиданиям
Ниже 24 баллов: не оправдывает ожиданий
- Сложность и качество текста — 42 возможных балла
37-42 балла: соответствует ожиданиям
21-36 баллов: частично соответствует ожиданиям
Ниже 21 балла: не оправдывает ожиданий
- Формирование знаний с помощью текстов, словарного запаса и задач — 32 возможных балла
28-32 балла: оправдать ожидания
16–27 баллов: частично соответствует ожиданиям
Ниже 16 баллов: не оправдывает ожиданий
- Поддержка с инструкциями и удобство использования — 34 возможных балла
30-34 балла: соответствует ожиданиям
24-29 баллов: частично соответствует ожиданиям
Ниже 24 баллов: не оправдывает ожиданий
- Сложность и качество текста — 36 возможных баллов
32-36 баллов: соответствует ожиданиям
18–31 балл: частично соответствует ожиданиям
Ниже 18 баллов: не оправдывает ожиданий
- Формирование знаний с помощью текстов, словарного запаса и задач — 32 возможных балла
28-32 балла: оправдать ожидания
16–27 баллов: частично соответствует ожиданиям
Ниже 16 баллов: не оправдывает ожиданий
- Поддержка с инструкциями и удобство использования — 34 возможных балла
30-34 балла: соответствует ожиданиям
24-29 баллов: частично соответствует ожиданиям
Ниже 24 баллов: не оправдывает ожиданий
Средняя школа ELA
- Сложность и качество текста — 32 возможных балла
28-32 балла: соответствует ожиданиям
16–27 баллов: частично соответствует ожиданиям
Ниже 16 баллов: не оправдывает ожиданий
- Формирование знаний с помощью текстов, словарного запаса и задач — 32 возможных балла
28-32 балла: оправдать ожидания
16–27 баллов: частично соответствует ожиданиям
Ниже 16 баллов: не оправдывает ожиданий
- Поддержка с инструкциями и удобство использования — 34 возможных балла
30-34 балла: соответствует ожиданиям
24-29 баллов: частично соответствует ожиданиям
Ниже 24 баллов: не оправдывает ожиданий
- Разработано для NGSS — 26 возможных точек
22-26 баллов: соответствует ожиданиям
13–21 балл: частично соответствует ожиданиям
Ниже 13 баллов: не оправдывает ожиданий
- Согласованность и область действия — 56 возможных точек
48-56 баллов: соответствует ожиданиям
30–47 баллов: частично соответствует ожиданиям
Ниже 30 баллов: не оправдывает ожиданий
- Поддержка с инструкциями и удобство использования — 54 возможных балла
46-54 балла: соответствует ожиданиям
29–45 баллов: частично соответствует ожиданиям
Ниже 29 баллов: не оправдывает ожиданий
Математические приложения для 7-х классов для iPad, iPhone, Android, Windows 8
iTooch 7 класс MathApp Store 4. 7
7
Откройте для себя наше математическое приложение для семиклассников
Седьмой класс — это год, который расширяет возможности обучения концепциям, которые включают порядок операций, операции с целыми числами и различные арифметические свойства. Выявление и решение уравнений и неравенств представлены как общие базовые стандарты. Студентам предоставляются возможности расширения в процентах за счет расчета скидки и наценки, открывая для себя их применение в реальных ситуациях. Умножение и деление одночленов представлены и служат фундаментальной базой в алгебре.Знания правил экспоненты исследуются и расширяются в их применении к концепциям алгебры. Стандарты, представленные в приложении для седьмого класса, связаны с общими основными стандартами по математике и предназначены для того, чтобы дать учащимся возможность укрепить навыки применения стандартов по математике.
Загруженные тысячами вопросов, приложения охватывают официальные образовательные программы и соответствуют Общим основным государственным стандартам. Это приложение создает отличную динамику игры и стимулы, так что пользователь всегда хочет развиваться дальше в приложении. Приложения включают в себя доску и калькулятор, чтобы студенты могли писать и вычислять прямо на экране, не выходя из приложения. К каждой главе прилагается краткое содержание урока, чтобы подчеркнуть основные концепции, которые студенты должны знать, чтобы отвечать на вопросы. Мгновенно переходите от одного экрана к другому. Перестаньте ждать загрузки информации с сервера: пропускная способность больше не является проблемой. Приложения автоматически синхронизируются в фоновом режиме, чтобы загружать новые действия при наличии подключения к Интернету. Вы представитель школы и хотели бы купить iTooch 7th Grade Math для всей организации? Хорошие новости! iTooch 7th Grade Math имеет право на участие в программе Apple Volume Purchase Program (VPP) для образовательных учреждений. iTooch, автор 7-го класса математики, Райан Миллер, имеет степень бакалавра делового администрирования Калифорнийского университета в Риверсайде и степень магистра начального образования Клермонтского университета.До того, как стать классным учителем, он пять лет проработал репетитором математики для учеников младших и старших классов. В 2006 году он начал обучать школьников начальной школы математике и естественным наукам. В течение следующих пяти лет он работал учителем 5-го, 6-го и 7-го классов в Объединенном школьном округе Hesperia. Наоми Холл, редактор 7-го класса по математике iTooch, имеет степень бакалавра наук. в комплексном естественнонаучном образовании и степень доктора медицины в математике и технологическом образовании. За последние девять лет она преподавала различные курсы естествознания, математики и технологий. Наоми увлечена образованием и любит видеть, как ученики преуспевают и преуспевают в ее уроках. Наоми выросла в Нью-Гэмпшире и прожила там всю свою жизнь. Она любит все времена года, но осень — ее любимое время. Ей нравится проводить время со своей семьей и играть со своими племянницами и племянниками.В свободное время Наоми любит бегать, рисовать, шить и играть на фортепиано и кларнете. 7 класс / Искусство английского языка / Средняя школа 7 класс / 8 класс / Музыка Номера и операции
 С. Обычное (1)
С. Обычное (1) Алгебраические структуры
Статистика
Функции
Геометрия
Характеристики
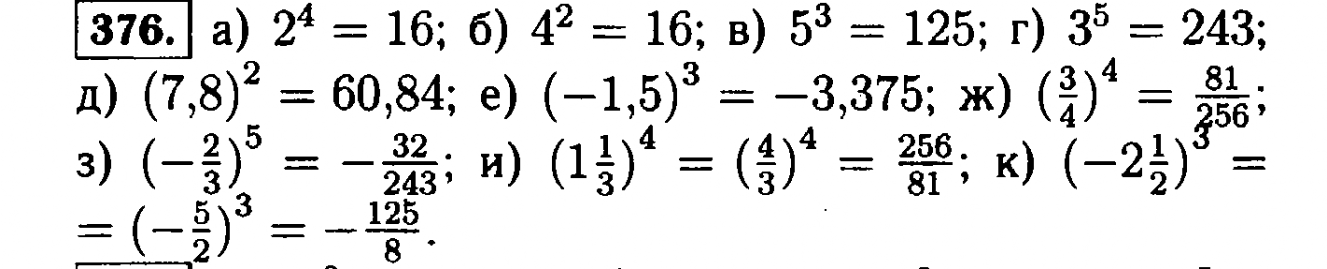
Право на участие в программе оптовых закупок Apple
(только для iOS) -reshenie-327.jpg) Мы предложим вам специальные цены при покупке 20 и более приложений.Чтобы воспользоваться этим предложением, вы можете купить наше приложение iTooch для 7-го класса по математике вместо того, чтобы покупать контент в качестве покупки в нашем приложении для средней школы iTooch. Дополнительную информацию о программе оптовых закупок можно найти на веб-сайте Apple. Есть вопросы? Не стесняйтесь связаться с нами.
Мы предложим вам специальные цены при покупке 20 и более приложений.Чтобы воспользоваться этим предложением, вы можете купить наше приложение iTooch для 7-го класса по математике вместо того, чтобы покупать контент в качестве покупки в нашем приложении для средней школы iTooch. Дополнительную информацию о программе оптовых закупок можно найти на веб-сайте Apple. Есть вопросы? Не стесняйтесь связаться с нами. Познакомьтесь с командой математиков 7-го класса:
Райан Миллер
 В настоящее время он преподает математику и естественные науки в 7 классе в средней школе Hesperia. Он получает диплом по школьному консультированию. Сейчас Райан живет с женой, сыном и дочерью в Викторвилле, Калифорния.
В настоящее время он преподает математику и естественные науки в 7 классе в средней школе Hesperia. Он получает диплом по школьному консультированию. Сейчас Райан живет с женой, сыном и дочерью в Викторвилле, Калифорния. Наоми Холл
Вам также могут понравиться эти другие приложения для 7-го класса:
Сайт г-на Миллера по математике / 7-й класс Common Core
Экзаменационные вопросы, отсортированные по стандарту
общих вопросов основного экзамена, отсортированных по стандарту (набирается в WORD и редактируется)
Старые экзаменационные вопросы (до общего ядра), отсортированные по темам
Старые экзамены (до общего ядра)
Модули 7-го класса
Модуль 1 Модуль 2 Модуль 3 Модуль 4 Модуль 5 Модуль 6
Полезные ресурсы для улучшения понимания стандартов, изучаемых в классе
Академия Хана
https: // www. khanacademy.org/math/engageny/on-grade-engageny/7th-engage-ny Видео и практические задачи
khanacademy.org/math/engageny/on-grade-engageny/7th-engage-ny Видео и практические задачи
Видеоуроки Common Core и флип-чарты NYS
https://embarc.online/Дополнительные тренировочные листы
https: //www.mathgames.ru / standard / grade7 — вопросы по стандартам https://www.mathgames.com/worksheets/grade7 — листы по темам http://www.kutasoftware.com/ http://www.commoncoresheets.com/ http://www.onlinemathlearning.com/common-core-grade7.html Сортировано по стандарту математики 7-го класса, содержит: уроки, рабочие листы и игры по каждому стандарту http: //www.onlinemathlearning.com / common-core-math-worksheets-grade7.html рабочие листы
https://www.mathopolis.com/questions/skills.php?year=7 вопросов о навыках
https://www. mathopolis.com/questions/course.php?year=7 курс
mathopolis.com/questions/course.php?year=7 курс
http://www.mathsisfun.com/links/core-grade-7.html Учебные пособия по стандарту
http://www.mathworksheetsland.com/7/ Дополнительная практика, отсортированная по стандартам, с управляемыми уроками
http: // www.mathworksheetsland.com/7/posters.html Плакаты, обобщающие основные темы по стандарту. Выберите бесплатный, который разблокирован
http://www.mathworksheets4kids.com/activities/7th-grade.php (некоторые бесплатно, если вы хотите больше, это 19,95 долларов в год)
Интерактивные занятия и короткие видеоролики по математике
http://www.learnalberta.ca/content/mejhm/index.html?l=0
Emoji math
https: // www.решитьmoji.com/Математические игры
http://www. math-play.com/7th-grade-math-games.html Игры для каждого стандарта https://www.hoodamath.com/ https://www.mathgames.com/standards/ https://www.mathgames.com/math-games.html — бесплатные игры (со звездочками нужно подписаться) Практика по стандартам www.commoncoresheets.com НЕОБХОДИМО использовать GOOGLE CHROME
math-play.com/7th-grade-math-games.html Игры для каждого стандарта https://www.hoodamath.com/ https://www.mathgames.com/standards/ https://www.mathgames.com/math-games.html — бесплатные игры (со звездочками нужно подписаться) Практика по стандартам www.commoncoresheets.com НЕОБХОДИМО использовать GOOGLE CHROME Система счисления
7.NS.1a Стандартные целые числа сложения и вычитания
7.NS.1a Сложение и вычитание целых чисел с числовой строкой
7.NS.1a Сложить и вычесть до нуля
7.NS.A.1b Найдите положительные и отрицательные суммы на числовой прямой
7.NS.1b Игра сложения и вычитания целых чисел (Прогулка по доске)
7.NS.1d Применение свойств операций для сложения и вычитания рациональных чисел
7. NS.2a Умножение и деление целых чисел
NS.2a Умножение и деление целых чисел
7.NS.2b Тест на деление целых чисел
7.NS.2 Игра на умножение и деление целых чисел
7.NS.1 и 7. NS.2. Операции с целыми числами. Игра «Опасность»
Соотношение и пропорциональные отношения
7.RP.1 Использование удельных расценок с дробями
7.RP.1 Определение доли эквивалентной единицы с дробями
7.RP.1 Общие сведения о ставке
7.RP.1 Общие сведения о расценке единицы с дробями
7.RP.2b Константа пропорциональности (графики)
7.RP.2b Константа пропорциональности (таблицы)
7.RP.3 Определение сумм с пропорциональным соотношением
7.RP.3 Сложение и вычитание процентов от количества
Геометрия
7.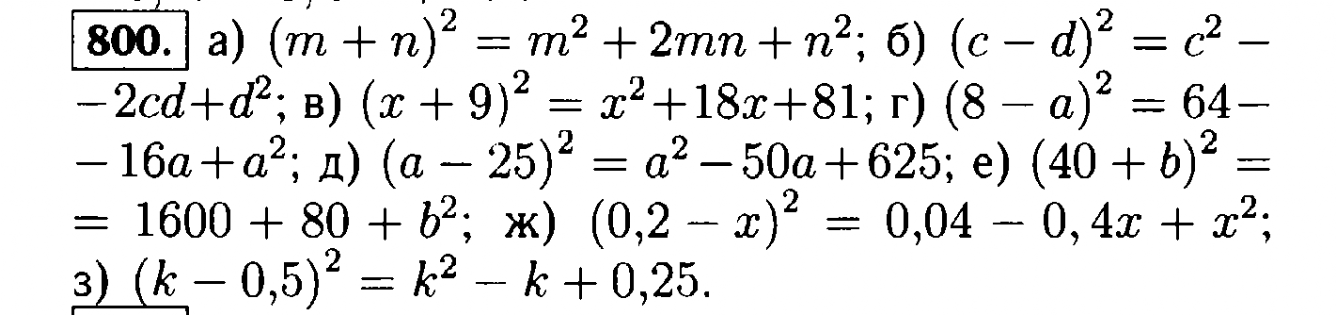 G.1 Определение высоты, ширины и площади прямоугольников шкалы
G.1 Определение высоты, ширины и площади прямоугольников шкалы
7.G.4 Площадь круга
7.G.4 Окружность круга
7.G.4 Нахождение площади и окружности кругов
Выражения и уравнения
7.EE.1 без викторины, только листы
7.EE.2 без листов или викторины
7.EE.3 Сложение и вычитание процентов и десятичных знаков
7.EE.3 Нахождение процента от десятичной дроби
7.EE.4a Нет листов или викторины
7.EE.4b без листов или викторины
Вероятность и статистика
6.SP.4 Среднее значение двух чисел
6.SP.4 Поиск квартилей
6.SP.4 Создание коробчатых диаграмм
7.


 6 Деление целых чисел
6 Деление целых чисел
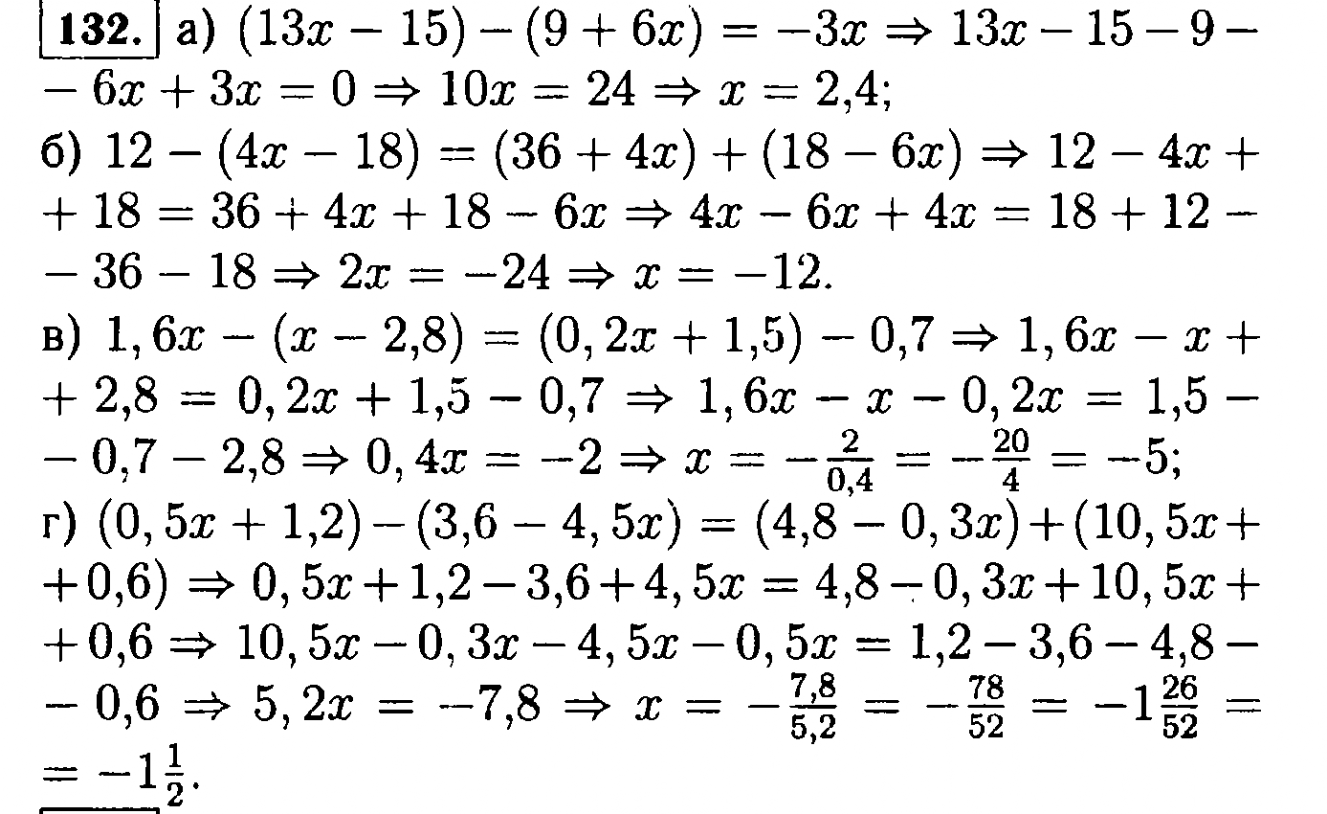
 4 Построение треугольника, когда известны длины трех его сторон (критерий SSS)
4 Построение треугольника, когда известны длины трех его сторон (критерий SSS)