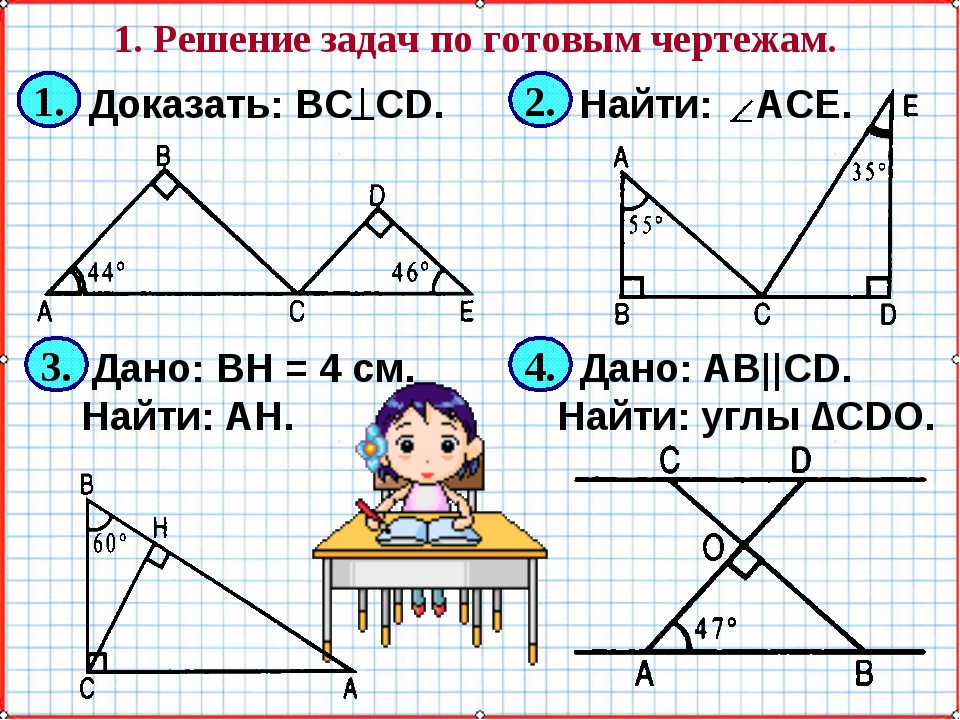
Зачёт по геометрии за 7 класс
Вопросы по геометрии. 7 класс1. Сколько прямых можно провести через две точки?
2. Сколько общих точек могут иметь две прямые?
3. Что такое отрезок? Начертить, обозначить и объяснить? Какая точка называется серединой отрезка?
4. Что такое луч? Как обозначаются лучи?
5. Какая фигура называется углом? Объясните, что такое вершина и стороны угла.
6. Какие фигуры называются равными?
7. Как сравнить два угла? Какой луч называется биссектрисой угла?
8. Какой угол называется острым? прямым? тупым?
9. Какие углы называются смежными? Чему равна сумма смежных углов? Уметь их строить.
10. Какие углы называются вертикальными? Каким свойством обладают вертикальные углы? Уметь их строить.
11. Какие прямые называются перпендикулярными? Уметь их строить Объясните, почему две прямые, перпендикулярные к третьей, не пересекаются?
12. Объясните, какая фигура называется треугольником. Начертите треугольник и покажите его стороны, вершины и углы.
Что такое периметр треугольника?
13. Какие треугольники называются равными?
14. Что такое теорема и доказательство теоремы?
15. Сформулируйте первый признак равенства треугольников.
16. Какой отрезок называется медианой треугольника? Сколько медиан имеет треугольник? Уметь их строить.
17. Какой отрезок называется биссектрисой треугольника? Сколько биссектрис имеет треугольник? Уметь их строить.
18. Какой отрезок называется высотой треугольника? Сколько высот имеет треугольник? Уметь их строить.
19. Какой треугольник называется равнобедренным? Уметь его строить. Как называются его стороны?
20. Какой треугольник называется равносторонним? Уметь его строить. Сформулировать основные свойства равнобедренного треугольника.
21. Сформулируйте второй признак равенства треугольников.
22. Сформулируйте третий признак равенства треугольников.
23. Что такое определение? Дайте определение окружности. Что такое центр, радиус, хорда и диаметр окружности?
24.
Объясните, как отложить от данного луча в данную плоскость угол, равный данному.(с помощью циркуля и линейки)
25. Объясните как построить биссектрису данного угла.( с помощью циркуля и линейки)
26. Объясните, как построить прямую, проходящую через данную точку, лежащую на данной прямой, и перпендикулярную к этой прямой. .(с помощью циркуля и линейки)
27. Объясните, как построить середину данного отрезка. .(с помощью циркуля и линейки)
28. Дайте определение параллельных прямых. Какие два отрезка называются параллельными?
29. Что такое секущая? Назовите пары углов, которые образуются при пересечении двух прямых секущей. Уметь их построить , показать и обозначить.
30. Сформулируйте признаки параллельности прямых ?
31. Что такое аксиома? Приведите примеры. Сформулируйте аксиому параллельных прямых.
32. Какая теорема называется обратная данной теореме? Приведите примеры теорем, обратных данным.
33. Сформулируйте теоремы об углах, образованных двумя параллельными прямыми и секущей.
34. Сформулируйте теорему о сумме углов треугольника.
35. Какой угол называется внешним углом треугольника? Уметь его строить. Сформулируйте, чему равен внешний угол в треугольнике.
36. Какой треугольник называют остроугольным? Какой треугольник называется тупоугольным? Уметь их строить.
37. Какой треугольник называется прямоугольным? Как называются стороны прямоугольного треугольника?
38. Сформулируйте соотношения между сторонами и углами. Почему в прямоугольном треугольнике гипотенуза больше катета?
39. Сформулируйте теорему о неравенстве треугольника.
40. Сформулируйте некоторые свойства прямоугольных треугольников.
41. Сформулируйте признаки равенства прямоугольных треугольников.
42. Что называется расстоянием от точки до прямой?
43. Что называется расстоянием между двумя параллельными прямыми?
44. Объясните, как построить треугольник по двум сторонам и углу между ними.
45. Объясните, как построить треугольник по стороне и двум прилежащим к ней углам.
46. Объясните, как построить треугольник по трём сторонам. Всегда ли эта задача имеет решение?
Задачи к зачету по геометрии. 7 класс
Задача №1. В равнобедренном треугольнике угол при основании в 2 раза меньше, чем угол при вершине. Найдите все углы треугольника.
Задача №2. Высота АD равностороннего треугольника ВАС с основанием ВС равна 10 см, периметр треугольника АDС равен 70 см. Найдите периметр треугольника АВС.
Задача №3. Первый угол треугольника равен 40градусов, а второй больше третьего на 16 градусов. Найдите эти углы треугольника.
Задача №4. В равнобедренном треугольнике периметр равен 150 см, боковая сторона больше основания на 15 см. Найдите все стороны треугольника.
Задача №5. В равнобедренном прямоугольном треугольнике гипотенуза равна 42 см. Найдите высоту проведённую из вершины прямого угла.
Задача №6. В равнобедренном треугольнике внешний угол при вершине равен 40 градусов. Найдите углы этого треугольника.
Задача №7. В равнобедренном треугольнике СDЕ с основанием СЕ проведена биссектриса СF. Найдите угол ЕСF, если угол D равен 54 градуса.
Задача №8. Один из углов прямоугольного треугольника равен 60 градусов, а сумма гипотенузы и меньшего катета равна 30 см. Найдите гипотенузу треугольника.
Задача №9. Один из внешних углов равнобедренного треугольника равен 110 градусов. Найдите все углы данного треугольника.
Задача №10. Периметр равнобедренного треугольника равен 65 см, его боковая сторона на 5 см меньше основания. Найдите стороны треугольника.
Задача №11. Периметр равнобедренного тупоугольного треугольника равен 77 см, а одна из его сторон больше другой на 17см. Найдите стороны этого треугольника.
Задача №12. Сумма вертикальных углов АОВ и СОD, образованных при пересечении прямых АD и ВС, равна 108 градусов. Найдите угол ВОD.
Задача №13. В остроугольном треугольнике МNP биссектриса угла М пересекает высоту NК в точке О. причём ОК равно 9 см.
Найдите расстояние от точки О до прямой МN.
Задача №14. Отрезки АВ и СD- диаметры окружности с центром О. Найдите периметр треугольника АОD, если хорда СВ равна 10 см, диаметр АВ равен 12 см.
Задача №15. Найдите все неразвёрнутые углы, образованные при пересечении двух прямых, если сумма двух из них равна 296 градусов.
Задача №16. Луч ОС делит угол АОВ на два угла. Найдите угол СОВ, если угол АОВ равен 110 градусов, а угол АОС на 18 градусов меньше угла ВОС.
Задача №17. Углы треугольника относятся как 2: 3: 4. Найдите их градусные меры.
Задача №18. В равнобедренном треугольнике АВС с основанием АС равно 38 см внешний угол при вершине В равен 60 градусов. Найдите расстояние от вершины С до прямой АВ.
Задача №19. Один из углов при пересечении двух параллельных прямых третьей прямой в 2 раза больше другого. Найдите остальные углы.
Задача №20. Один из углов при пересечении двух параллельных прямых третьей прямой на 20 градусов меньше другого.
Найдите остальные углы.
Задача №21. В равнобедренном треугольнике АВС с основанием АС равно 42см, внешний угол при вершине С равен 120 градусов. Найдите боковые стороны треугольника АВС.
geo7.docx
Геометрия 7 Атанасян Задачи 1-23
Практические задания и задачи №№ 1 — 23 из учебника геометрии (УМК Атанасян) для 7 класса с ОТВЕТАМИ и решениями к Главе 1 «Начальные геометрические сведения». Геометрия Атанасян Задачи 1-23 к:
- § 1. Прямая и отрезок (1. Точки, прямые, отрезки. 2. Провешивание прямой на местности)
- § 2. Луч и угол. (3. Луч. 4. Угол)
- § 3. Сравнение отрезков и углов. (5. Равенство геометрических фигур. 6. Сравнение отрезков и углов)
Вернуться в ОГЛАВЛЕНИЕ Смотреть задачи 24-40
Ознакомительная версия перед покупкой книги. Цитаты из учебника представлены в учебных целях.
Практические задания №№ 1-7
Практические задания №№ 8-17
Задачи №№ 18-23
Геометрия 7 класс (УМК Атанасян)
к § 1.
«Измерение отрезков»:
№ 1. Проведите прямую, обозначьте её буквой а и отметьте точки А и В, лежащие на этой прямой, и точки Р, Q и R, не лежащие на ней. Опишите взаимное расположение точек А, В, Р, Q, R и прямой а, используя символы ∈ и ∉.
Смотреть РЕШЕНИЕ упражнения 1 в тетради
№ 2. □ Отметьте три точки А, В и С, не лежащие на одной прямой, и проведите прямые АВ, ВС и СА.
Смотреть РЕШЕНИЕ упражнения 2 в тетради
№ 3. Проведите три прямые так, чтобы каждые две из них пересекались. Обозначьте все точки пересечения этих прямых. Сколько получилось точек? Рассмотрите все возможные случаи.
Смотреть РЕШЕНИЕ упражнения 3 в тетради
№ 4. Отметьте точки А, В, С, D так, чтобы точки А, В, С лежали на одной прямой, а точка D не лежала на ней. Через каждые две точки проведите прямую. Сколько получилось прямых?
Смотреть РЕШЕНИЕ упражнения 4 в тетради
№ 5.
Проведите прямую а и отметьте на ней точки А и В. Отметьте: а) точки М и N, лежащие на отрезке АВ; б) точки Р и Q, лежащие на прямой а, но не лежащие на отрезке АВ; в) точки R и S, не лежащие на прямой а.
Смотреть РЕШЕНИЕ упражнения 5 в тетради
№ 6. Проведите прямую и отметьте на ней три точки. Сколько отрезков получилось на прямой?
Смотреть РЕШЕНИЕ упражнения 6 в тетради
№ 7. □ На рисунке 10 изображена прямая, на ней отмечены точки А, В, С и D. Назовите все отрезки: а) на которых лежит точка С; б) на которых не лежит точка В.
Смотреть РЕШЕНИЕ упражнения 7 в тетради
к § 2 «Луч и угол»
Практические задания №№ 8-17№ 8. Проведите прямую, отметьте на ней точки А и В и на отрезке АВ отметьте точку С. а) Среди лучей АВ, ВС, СА, АС и ВА назовите совпадающие лучи; б) назовите луч, который является продолжением луча СА.
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
№ 9. Начертите три неразвёрнутых угла и обозначьте их так: ∠AOB, ∠hk, ∠M.
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
№ 10. Начертите два развёрнутых угла и обозначьте их буквами.
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
№ 11. Начертите три луча h, k и I с общим началом. Назовите все углы, образованные данными лучами.
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
№ 12. Начертите неразвёрнутый угол hk. Отметьте две точки внутри этого угла, две точки вне этого угла и две точки на сторонах угла.
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
№ 13. Начертите неразвёрнутый угол. Отметьте точки А, В, М и N так, чтобы все точки отрезка АВ лежали внутри угла, а все точки отрезка MN лежали вне угла.
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
№ 14. Начертите неразвёрнутый угол АОВ и проведите: а) луч ОС, который делит угол АОВ на два угла; б) луч OD, который не делит угол АОС на два угла.
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
№ 15. □ Сколько неразвёрнутых углов образуется при пересечении двух прямых?
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
№ 16. □ Какие из точек, изображённых на рисунке № 17, лежат внутри угла hk, а какие — вне этого угла?
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
№ 17. Какие из лучей, изображённых на рисунке № 18, делят угол АОВ на два угла?
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
к § 3 «Сравнение отрезков и углов»
Задачи №№ 18-23№ 18. На луче с началом О отмечены точки А, В и С так, что точка В лежит между точками О и А, а точка А — между точками О и С. Сравните отрезки ОВ и ОА, ОС и О А, ОВ и ОС.
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
№ 19. Точка О является серединой отрезка АВ. Можно ли совместить наложением отрезки: а) ОА и ОВ; б) ОА и АВ?
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
№ 20.
□ На рисунке 25 отрезки АВ, ВС, CD и DE равны. Укажите: а) середины отрезков АС, АЕ и СЕ; б) отрезок, серединой которого является точка D; в) отрезки, серединой которых является точка С.
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
№ 21. Луч ОС делит угол АОВ на два угла. Сравните углы АОВ и АОС.
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
№ 22. □ Луч l — биссектриса угла hk. Можно ли наложением совместить углы: a) hl и lk; б) hl и hk?
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
№ 23. □ На рисунке 26 углы, обозначенные цифрами, равны. Укажите: а) биссектрису каждого из углов АОС, BOF, АОЕ; б) все углы, биссектрисой которых является луч ОС.
Нажмите на этот спойлер, чтобы увидеть ОТВЕТ
Вы смотрели: Практические задания и задачи №№ 1 — 23 из учебника геометрии (УМК Атанасян) для 7 класса с ОТВЕТАМИ и решениями к Главе 1 «Начальные геометрические сведения»: § 1.
Прямая и отрезок; § 2. Луч и угол; § 3. Сравнение отрезков и углов. Геометрия Атанасян Задачи к Главе 1 задачи 1-23.
Вернуться в ОГЛАВЛЕНИЕ учебника Смотреть задачи 24-40
Решения NCERT для математики класса 7. Глава 10 «Практическая геометрия» скачать бесплатно PDF
*Согласно последнему учебному плану CBSE 2023-24, эта глава была удалена.
Решения NCERT для математики класса 7 Глава 10 Практическая геометрия скачать PDF приведены ниже. Главная цель — помочь учащимся понять и решить эти проблемы. Мы в BYJU’S подготовили решения NCERT для математики класса 7 и решили их шаг за шагом с полным описанием.
В главе 10 «Практическая геометрия решений NCERT для математики 7 класса» представлены 5 упражнений. Понятия, рассматриваемые в этой главе, включают
- Построение линии, параллельной заданной линии, через точку, не лежащую на линии
- Построение треугольника
- Построение треугольника по известным длинам его трех сторон (критерий SSS)
- Построение треугольника по известным длинам двух сторон и величине угла между ними (критерий SAS)
- Построение треугольника по заданным величинам двух его углов и длине стороны, проходящей между ними (критерий ASA)
- Построение прямоугольного треугольника по заданным длине катета и его гипотенузе (критерий RHS)
Скачать PDF
карусельExampleControls112
Предыдущий
Следующий
Упражнения доступа к решениям NCERT для математики класса 7 Глава 10 Практическая геометрия
Упражнение 10.
1 Решения
Упражнение 10.2 Решения
Упражнение 10.3 Решения
Упражнение 10.4 Решения
Упражнение 10.5 Решения
Доступ к ответам на математику 7 класса NCERT, глава 10 — Практическая геометрия
Упражнение 10.1 Страница: 196
1. Проведите линию, скажем, АВ, возьмем за нее точку С. Через С проведите линию, параллельную АВ, используя только линейку и циркуль.
Решение:-
Ступени для строительства
1. Проведите линию АВ.
2. Возьмите любую точку Q на AB и точку P вне AB и соедините PQ.
3. Используя Q в качестве центра и любой радиус, нарисуйте дугу, чтобы разрезать AB в точке E и PQ в точке F.
4. Используя P в качестве центра и того же радиуса, нарисуйте дугу IJ, чтобы разрезать QP в точке G.
5. Поместите острый конец циркуля в точку E и отрегулируйте отверстие так, чтобы кончик карандаша находился в точке F.
6.
С тем же отверстием, что и в шаге 5, и с G в центре, нарисуйте дугу, пересекающую дугу IJ в точке H.
7. Теперь присоединяйтесь к PH, чтобы нарисовать линию CD.
2. Проведите прямую L. Проведите перпендикуляр к L в любой точке на L. На этом перпендикуляре выберите точку X, отстоящую от l на 4 см. Через X проведите линию m, параллельную L.
Решение:-
Ступени для строительства
1. Нарисуйте линию L.
2. Возьмем любую точку P на прямой L.
3. В точке P провести перпендикуляр N.
4. Поместите острие циркуля в точку Р и отрегулируйте циркуль до длины 4 см, проведите дугу, чтобы пересечь этот перпендикуляр в точке Х.
5. В точке Х снова провести перпендикулярную линию М.
3. Пусть L — прямая, а P — точка не на L. Через P проведите прямую m, параллельную L. Теперь соедините P с любой точкой Q на L. Выберите любую другую точку R на m.
Через R проведите линию, параллельную PQ. Пусть это встретится с буквой L в точке S. Какую форму образуют два набора параллельных линий?
Решение:-
Ступени для строительства
1. Нарисуйте линию L.
2. Возьмите любую точку Q на L и точку P вне L и соедините PQ.
3. Убедиться, что углы в точке P и точке Q равны, т.е. ∠Q = ∠P
4. В точке P продлите линию, чтобы получить линию M, параллельную L.
5. Затем взять любую точку R на прямой M.
6. В точке R начертите такой угол, что ∠P = ∠R.
7. В точке R продлите линию, пересекающую линию L в точке S, и нарисуйте линию RS.
Упражнение 10.2 Страница: 199
1. Постройте ΔXYZ, где XY = 4,5 см, YZ = 5 см и ZX = 6 см.
Решение:-
Ступени строительства
1. Нарисуйте отрезок YZ = 5 см.
2. Используя Z в качестве центра и радиус 6 см, нарисуйте дугу.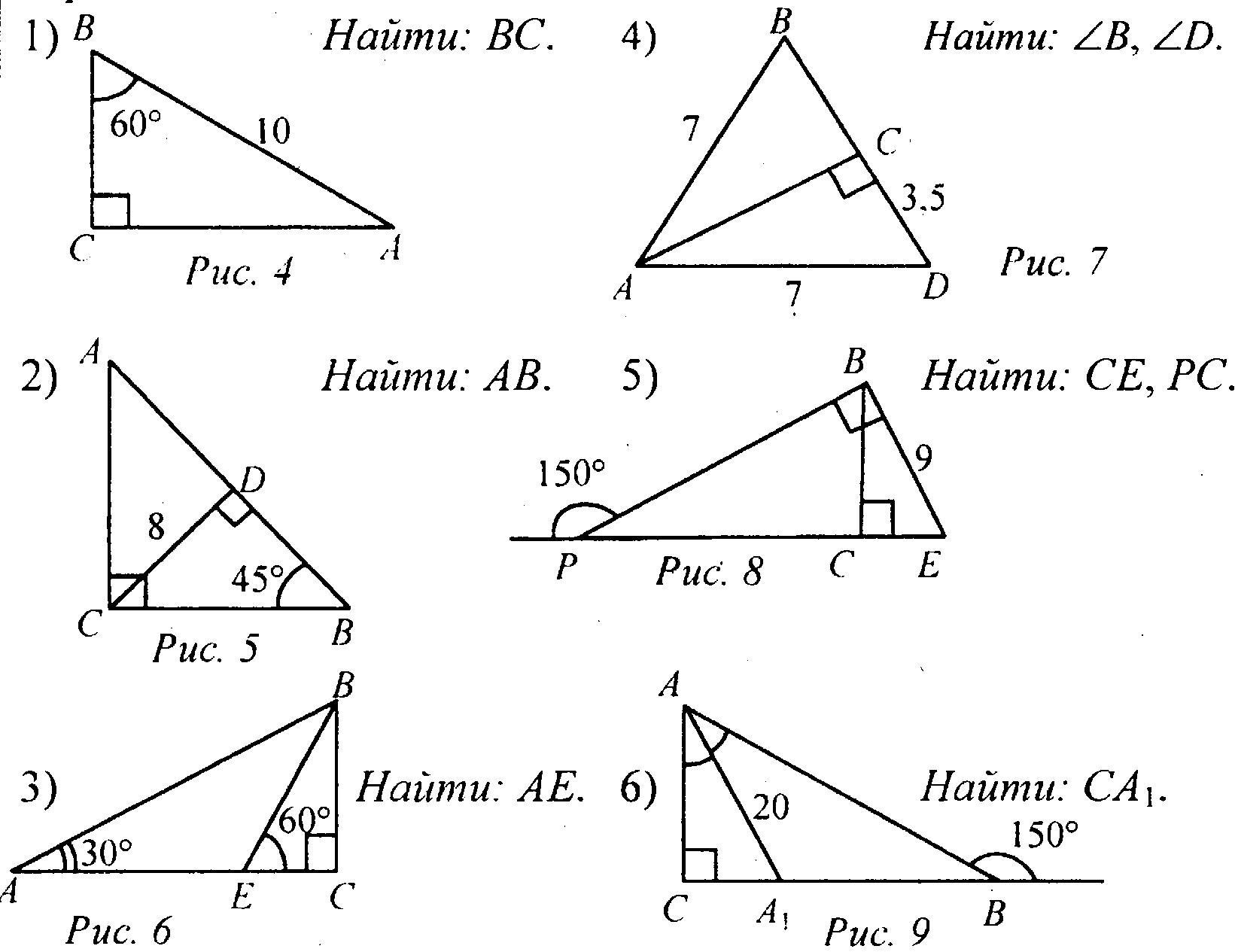
3. Используя Y в качестве центра и радиус 4,5 см, нарисуйте еще одну дугу, разрезая предыдущую дугу в точке X.
4. Соедините XY и XZ.
Тогда ΔXYZ искомый треугольник.
2. Постройте равносторонний треугольник со стороной 5,5 см.
Решение:-
Ступени строительства
1. Нарисуйте отрезок АВ = 5,5 см.
2. С центром в точке А и радиусом 5,5 см нарисуйте дугу.
3. С центром В и радиусом 5,5 см нарисуйте еще одну дугу, разрезая предыдущую дугу в точке С.
4. Присоединяйтесь к CA и CB.
Тогда ΔABC искомый равносторонний треугольник.
3. Нарисуйте ΔPQR, где PQ = 4 см, QR = 3,5 см и PR = 4 см. Какой это тип треугольника?
Решение:-
Ступени строительства
1. Нарисуйте отрезок QR = 3,5 см.
2. Используя Q в качестве центра и радиус 4 см, нарисуйте дугу.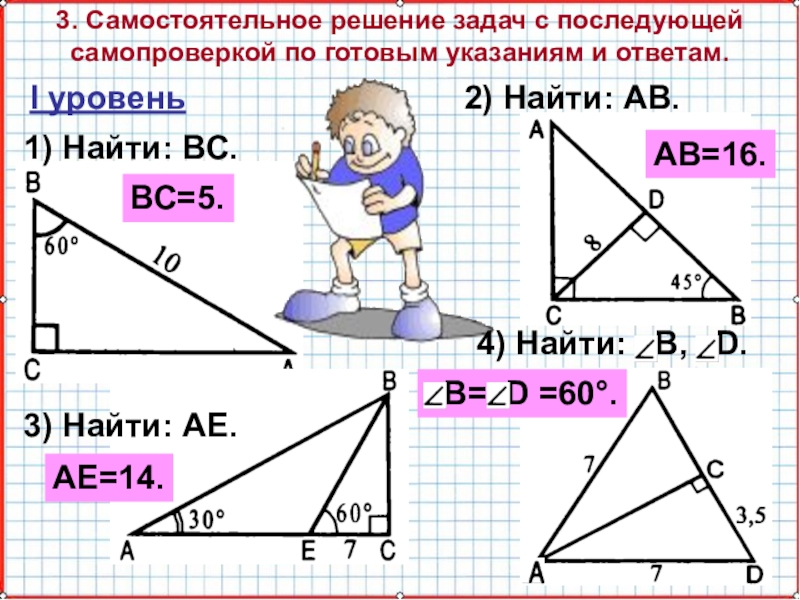
3. Используя R в качестве центра и радиус 4 см, нарисуйте еще одну дугу, разрезая предыдущую дугу в точке P.
4. Присоединяйтесь к PQ и PR.
Тогда ΔPQR — искомый равнобедренный треугольник.
4. Постройте ΔABC так, чтобы AB = 2,5 см, BC = 6 см и AC = 6,5 см. Измерьте ∠B.
Решение:-
1. Нарисуйте отрезок ВС = 6 см.
2. С центром В и радиусом 2,5 см нарисуйте дугу.
3. С центром С и радиусом 6,5 см нарисуйте еще одну дугу, разрезая предыдущую дугу в точке А.
4. Соедините AB и AC.
Тогда ΔABC искомый треугольник.
5. Когда мы измерим угол B треугольника транспортиром, угол будет равен ∠B = 90 o
Упражнение 10.3 Страница: 200
1. Постройте ΔDEF так, чтобы DE = 5 см, DF = 3 см и m∠EDF = 90 o .
Решение:-
Ступени строительства
1.
2. В точке D провести луч DX до угла 90 o, , т. е. ∠XDF = 90 o .
3. По DX отступ DE = 5см.
4. Присоединяйтесь к EF.
Тогда ΔEDF — искомый прямоугольный треугольник.
2. Постройте равнобедренный треугольник, у которого длины каждой из равных сторон равны 6,5 см, а угол между ними равен 110 o .
Решение:-
Ступени строительства
1. Нарисуйте отрезок АВ = 6,5 см.
2. В точке А провести луч AX до угла 110 o , т. е. ∠XAB = 110 o .
3. По оси АХ отступ АС = 6,5см.
4. Вступить в СВ.
Тогда ΔABC искомый равнобедренный треугольник.
3. Построить ΔABC, где BC = 7,5 см, AC = 5 см и m∠C = 60°.
Решение:-
Ступени строительства
1. Нарисуйте отрезок ВС = 7,5 см.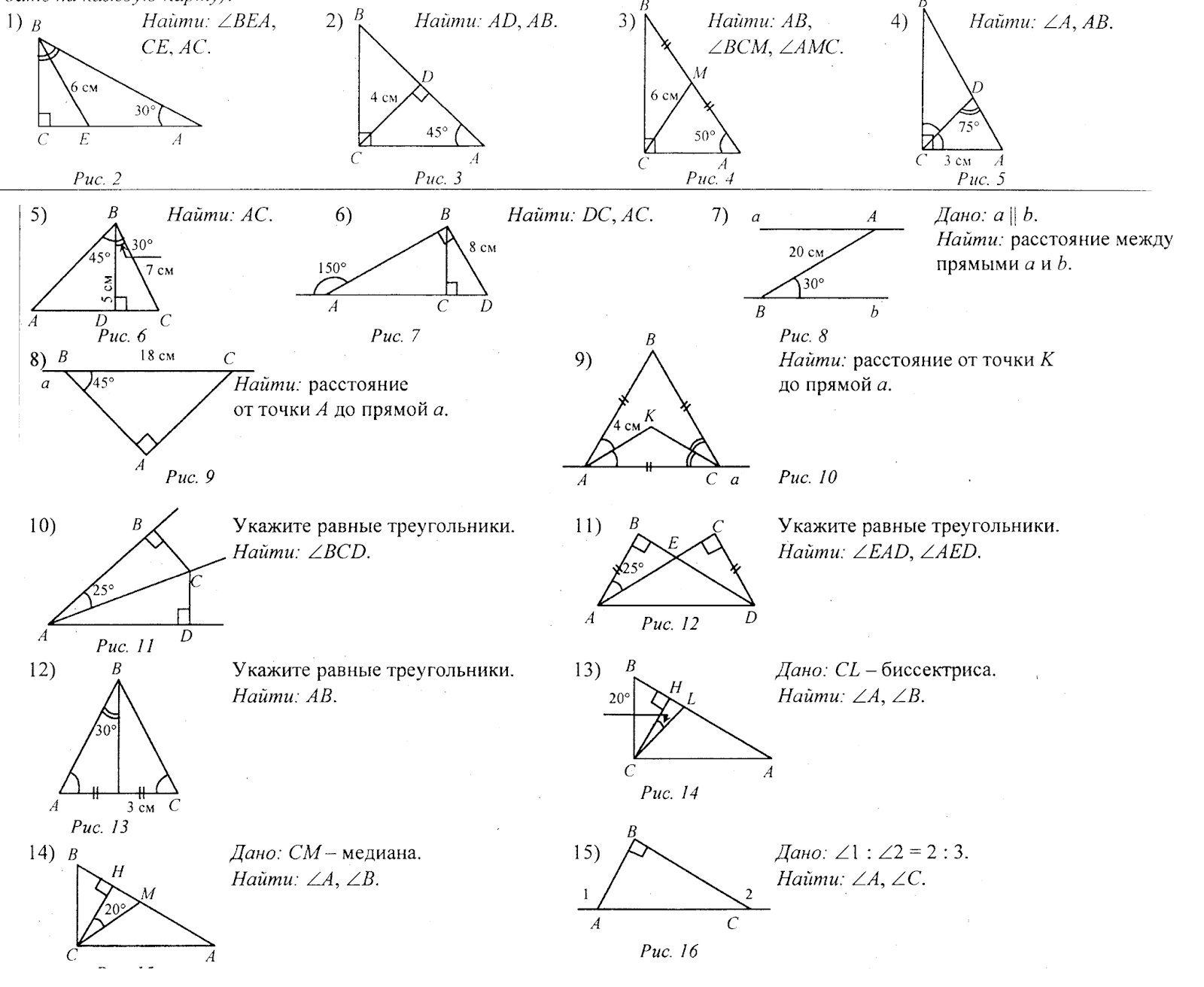
2. В точке C провести луч CX до угла 60 o , т. е. ∠XCB = 60 o .
3. По СХ отступ АС = 5см.
4. Присоединяйтесь к АВ.
Тогда ΔABC искомый треугольник.
Упражнение 10.4 Страница: 202
1. Построить ΔABC, учитывая m ∠A =60 o , m ∠B = 30 o и AB = 5,8 см.
Решение:-
Ступени строительства:
1. Нарисуйте отрезок АВ = 5,8 см.
2. В точке A провести луч P под углом 60 o , т. е. ∠PAB = 60 o .
3. В точке B провести луч Q под углом 30 o , т. е. ∠QBA = 30 o .
4. Теперь два луча – AP и BQ – пересекаются в точке C.
Тогда ΔABC искомый треугольник.
2. Построить ΔPQR, если PQ = 5 см, m∠PQR = 105 o и m∠QRP = 40 o .
(Подсказка: вспомните свойство суммы углов треугольника).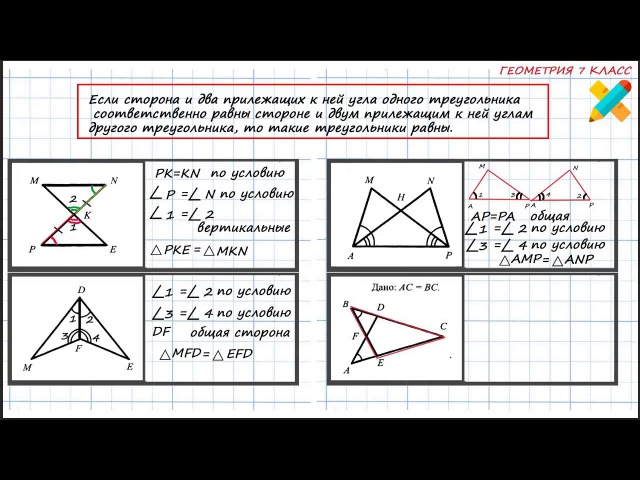
Решение:-
Мы знаем, что сумма углов треугольника равна 180 o .
∴ ∠PQR + ∠QRP + ∠RPQ = 180 или
= 105 o + 40 o + ∠RPQ = 180 o
= 145 o + ∠RPQ = 180 o
= ∠RPQ = 180 o – 145 0
= ∠RPQ = 35 или
Следовательно, размер ∠RPQ равен 35 o .
Ступени строительства
1. Нарисуйте отрезок PQ = 5 см.
2. В точке P провести луч L под углом 105 9 .0224 o , т. е. ∠LPQ = 35 o .
3. В точке Q провести луч M под углом 40 o , т. е. ∠MQP = 105 o .
4. Теперь два луча – PL и QM – пересекаются в точке R.
Тогда ΔPQR искомый треугольник.
3. Проверьте, можете ли вы построить ΔDEF так, чтобы EF = 7,2 см, м∠E = 110° и м∠F = 80°.
Обосновать ответ.
Решение:-
Из вопроса дано, что
EF = 7,2 см
∠E = 110 или
∠F = 80 или
Теперь нужно проверить, можно ли построить ΔDEF по заданным значениям.
Мы знаем, что сумма углов треугольника равна 180 o .
Затем
∠D + ∠E + ∠F = 180 или
∠D + 110 o + 80 o = 180 o
∠D + 190 о = 180 о
∠D = 180 или – 190 0
∠D = -10 или
Мы можем заметить, что сумма двух углов 190 o больше, чем 180 o . Следовательно, построить треугольник невозможно.
Упражнение 10.5 Страница: 203
1. Постройте прямоугольную ΔPQR, где m∠Q = 90°, QR = 8 см и PR = 10 см.
Решение:-
Этапы строительства
1.
Нарисуйте отрезок QR = 8 см.
2. В точке Q провести луч QY под углом 90 o , т. е. ∠YQR = 90 o .
3. Используя R в качестве центра и радиус 10 см, нарисуйте дугу, которая пересекает луч QY в точке P.
4. Присоединяйтесь к PR.
Тогда ΔPQR — искомый прямоугольный треугольник.
2. Построить прямоугольный треугольник, длина гипотенузы которого 6 см, а длина одного из катетов 4 см
Решение:-
Предположим, что ΔABC является прямоугольным треугольником при ∠B = 90 o
Затем
AC — гипотенуза = 6 см… [Дано в вопросе]
ВС = 4 см
Теперь нам нужно построить прямоугольный треугольник, используя приведенные выше значения.
Ступени строительства
1. Нарисуйте отрезок ВС = 4 см.
2. В точке B провести луч BX до угла 90 o , т. е. ∠XBC = 90 o .
3. С центром С и радиусом 6 см нарисуйте дугу, пересекающую луч ВХ в точке А.
4. Присоединиться к AC.
Тогда ΔABC искомый прямоугольный треугольник.
3. Постройте равнобедренный прямоугольный треугольник ABC, где m∠ACB = 90° и AC = 6 см.
Решение:-
Ступени строительства
1. Нарисуйте отрезок ВС = 6 см.
2. В точке C провести луч CX с углом 90 o , т. е. ∠XCB = 90 o .
3. С центром С и радиусом 6 см начертите дугу, пересекающую луч СХ в точке А.
4. Присоединяйтесь к АВ.
Тогда ΔABC искомый прямоугольный треугольник.
Отказ от ответственности:
Удаленные темы- 10.1 Введение, 10.2 Построение прямой, параллельной заданной прямой, через точку, не лежащую на прямой, 10.3 Построение треугольников, 10.4 Построение треугольника по известным длинам трех его сторон (критерий SSS), 10.5 Построение треугольника, когда известны длины двух сторон и мера угла между ними (критерий SAS), 10.
6 Построение треугольника, когда известны меры двух его углов и длина стороны, заключенной между ними (ASA критерий),
10.7 Построение прямоугольного треугольника по длине катета и его гипотенузе (критерий RHS).
Часто задаваемые вопросы о решениях NCERT для математики класса 7, глава 10
Q1
В чем важность изучения решений NCERT для математики класса 7, глава 10?
Решения NCERT Class 7 Maths Chapter 10 помогают учащимся понять сводку шаблона вопросника, включая различные вопросы, повторяющиеся вопросы, вопросы с кратким и длинным ответом, вопросы с несколькими вариантами ответов, оценки и т. д. Чем больше типы вопросов, которые решают учащиеся, тем больше баллов они набирают.
Q2
Упомяните концепции, которые важны с точки зрения экзамена в NCERT Solutions for Class 7 Maths Chapter 10.
Важными концепциями с точки зрения экзамена в NCERT Solutions for Class 7 Maths Chapter 10 заданной прямой, через точку, не лежащую на прямой, построение треугольника, построение треугольника, когда известны длины его трех сторон (критерий SSS), построение треугольника, когда длины двух сторон и мера угла между ними равны известный (критерий SAS), построение треугольника, когда заданы меры двух его углов и длина стороны, наклоненной между ними (критерий ASA), и построение прямоугольного треугольника, когда даны длина одного катета и его гипотенуза.
(критерий RHS).
Q3
Сколько упражнений содержится в NCERT Solutions for Class 7 Math Chapter 10?
В NCERT Solutions for Class 7 Maths Chapter 10 есть 5 упражнений. В первом упражнении 3 вопроса, во втором упражнении 4 вопроса, в третьем упражнении 2 вопроса со множеством подвопросов, в четвертом упражнении 3 вопроса и Последнее и последнее упражнение состоит из 3 вопросов, основанных на построении прямоугольного треугольника по заданным длине катета и его гипотенузе (критерий RHS).
Репетиторство по математике для экспертов в Великобритании
Нас окружают фигуры, и мы знаем об этих формах в деталях благодаря геометрии. На предыдущих занятиях учащиеся должны были узнать об этих формах или фигурах, которые они видят повсюду. Решения NCERT для математики класса 7, глава 10 «Практическая геометрия», даст представление о построении геометрических фигур и компонентов, таких как параллельные линии, различные виды треугольников и т. Д.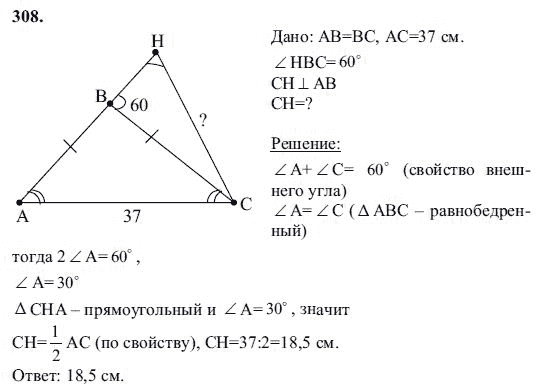
, При условии, что учащиеся имеют базовые знания об отрезках, углах, биссектрисе угла. и т. д., так как это наиболее распространенные основы, когда вы начинаете с геометрии.
Учащиеся, изучая эту главу 10 математики класса 7 NCERT, узнают, каковы важные критерии для построения треугольников, а также, иногда, какие измерения не могут составить треугольник. PDF-файл математических решений NCERT для класса 7, глава 10 «Практическая геометрия», приведен ниже, а некоторые из них также можно найти в упражнениях, приведенных ниже.
- Решения NCERT, класс 7, математика, глава 10, пример 10.1
- NCERT Solutions Class 7 Math Chapter 10 Ex 10.2
- NCERT Solutions Class 7 Math Chapter 10 Ex 10.3
- NCERT Solutions Class 7 Math Chapter 10 Ex 10.4
- NCERT Solutions Class 7 Math Chapter 10 Ex 10.5
NCERT Solutions for Class 7 Math Chapter 10 PDF
Треугольники — очень простая структура в геометрии. Они составляют основу для рисования многих других геометрических фигур, поэтому полезно лучше их понимать.
Классификацию упражнений в решениях NCERT Класс 7 по математике Глава 10 Практическая геометрия можно найти ниже:
NCERT Класс 7 по математике Глава 10
Решения NCERT для класса 7 по математике Глава 10 Практическая геометрия
90 002 В этой главе есть хорошо составленные упражнения, основанные на стратегическом подходе, включая по одному критерию в каждом из них, чтобы учащиеся не запутались. Разделение количества вопросов в NCERT Solutions Class 7 Maths Chapter 10 Practical Geometry приведено ниже.- Класс 7 Математика Глава 10 Пример 10.1 — 3 вопроса
- Класс 7 Математика Глава 10 Упражнение 10.2 — 4 вопроса
- Класс 7 Математика Глава 10 Упражнение 10.3 — 3 вопроса
- Класс 7 Математика Глава 10 Упражнение 10.4 — 3 вопроса
- Класс 7 Математика Глава 10 Упражнение 10.5 — 11 вопросов
☛ Загрузить Книгу NCERT по математике для 7 класса, главу 10
Охваченные темы: Математика для 7 класса, решения NCERT Глава 10 включает в себя хорошо объясненные процессы построения параллельной линии в точке за пределами линии, построения различных видов треугольников на основе критерия конгруэнтности Сторона-Сторона-Сторона, Сторона-Угол-Сторона, Угол-Сторона-Угол, а также критериев RHS для прямоугольных треугольников.
Всего вопросов: Математика для 7 класса Глава 10 Практическая геометрия Глава 10 состоит из 24 вопросов, из которых 12 простых, а 10 относятся к разным типам, где учащиеся потребуют некоторого размышления о том, можно ли рисовать треугольник с заданными измерениями или нет, с указанием соответствующих причин.
Список формул в NCERT Solutions Class 7 Math Chapter 10
NCERT Solutions Class 7 Math Chapter 10 посвящен построению треугольников, поэтому учащимся важно помнить все основные факты о треугольниках. Важно то, что сумма его углов равна 180 градусам. А также, что внешний угол треугольника равен сумме внутренних противоположных углов треугольника. Эти важные факты, обобщенные в Решениях NCERT для математики класса 7, Глава 10, следующие:
- Сумма углов треугольника: A + B + C = 180 градусов, где A, B и C — углы треугольника
- Внешний угол треугольника = Сумма внутренних противоположных углов треугольника
Важные вопросы по математике для класса 7.
Решения NCERT Глава 10 Видео по математике Глава 10| Видеоматериалы NCERT по математике для класса 7 по главе 10 | |
|---|---|
| Видеорешения для математического упражнения 7 класса 10.1 | |
| Упражнение 10.1 Вопрос 1 | Упражнение 10.1 Вопрос 3 |
| Упражнение 10.1 Вопрос 2 | |
| Видеорешения для математического упражнения 7 класса 10.2 | |
| Упражнение 10.2 Вопрос 1 | Упражнение 10.2 Вопрос 3 |
| Упражнение 10.2 Вопрос 2 | Упражнение 10.2 Вопрос 4 |
| Видеорешения для математического упражнения 7 класса 10.3 | |
| Упражнение 10.3 Вопрос 1 | Упражнение 10.3 Вопрос 3 |
| Упражнение 10.3 Вопрос 2 | |
Видеорешения для математического упражнения 7 класса 10. 4 | |
| Упражнение 10.4 Вопрос 1 | Упражнение 10.4 Вопрос 3 |
| Упражнение 10.4 Вопрос 2 | |
| Видеорешения для математического упражнения 7 класса 10.5 | |
| Упражнение 10.5 Вопрос 1 | Упражнение 10.5 Вопрос 3 |
| Упражнение 10.5 Вопрос 2 | |
Часто задаваемые вопросы о решениях NCERT, класс 7, математика, глава 10
Нужно ли мне практиковать все вопросы, представленные в решениях NCERT, класс 7 по математике, практическая геометрия?
Учащимся определенно будет полезно, если они будут практиковать все вопросы, составленные экспертами NCERT, поскольку эти вопросы были тщательно подобраны, чтобы получить более глубокое понимание каждого аспекта построения треугольников и параллельных линий. Учащиеся должны сначала попрактиковаться в примерах и упражнениях, чтобы получить лучшее представление о соответствующих темах.
Почему решения NCERT Solutions Class 7 Math Chapter 10 важны?
NCERT — признанная и заслуживающая доверия государственная организация, отвечающая за качественное образование и его исследования. Это означает, что есть ученые-эксперты, которые после долгих исследований пришли к знаниям о построении треугольника и разработали действия, примеры и проблемы вокруг него. CBSE также рекомендует учащимся обращаться к книгам NCERT, что делает главу 10 по математике класса 7 решений NCERT важным ресурсом для изучения.
Как учащиеся CBSE могут эффективно использовать NCERT Solutions Class 7 Math Chapter 10?
Учащиеся найдут множество простых заданий и примеров в Главе 10 по математике для 7 класса NCERT Solutions. Они должны регулярно выполнять каждое из них, чтобы расширить свою базу знаний. Это также поможет им с легкостью и уверенностью подходить к вопросам упражнений, тем самым заставляя их эффективно использовать содержание, собранное в главе.
Какие важные темы рассматриваются в математической главе 7 класса NCERT Solutions Chapter 10?
Учащиеся найдут NCERT Solutions Class 7 Math Chapter 10, начиная с основ рисования параллельных линий и заканчивая объяснением различных критериев построения треугольника, таких как Side-Side-Side, Side-Angle-Side, Angle-Side-Angle.