Решебник по алгебре за 7 класс, ответы онлайн
- ГДЗ
- 7 класс
- Алгебра
Алгебра 7 класс дидактические материалы
Авторы: Л.И. Звавич Л.В. Кузнецова
Алгебра 7 класс
Авторы: Е.П. Кузнецова Г.Л. Муравьева
Авторы: С.
 М. Никольский М.К. Потапов
М. Никольский М.К. ПотаповАлгебра 7 класс
Авторы: Ю.Н. Макарычев Н.Г. Миндюк
Алгебра 7 класс Учебник, Задачник
Авторы: А.Г. Мордкович Л.А. Александрова
Алгебра 7 класс
Авторы: Г.В. Дорофеев С.Б. Суворова
Алгебра 7 класс
Авторы:
Ю.Н. Макарычев Н.Г. МиндюкАлгебра 7 класс
Авторы: Ш.
 А. Алимов Ю.М. Колягин
А. Алимов Ю.М. КолягинАлгебра 7 класс самостоятельные и контрольные работы
Авторы: А.П. Ершова В.В. Голобородько
Алгебра 7 класс
Авторы: А. Г. Мерзляк В. Б. Полонский
Алгебра 7 класс
Авторы: А. Г. Рубин П. В. Чулков
Алгебра 7 класс
Авторы: Г. К. Муравин К. С. Муравин
Алгебра 7 класс
Авторы: Бевз Г.
 П. Бевз В.Г.
П. Бевз В.Г.Алгебра 7 класс
Автор: Истер О.С.
Алгебра 7 класс
Авторы: Кравчук В.Р. Янченко Г.М.
Алгебра 7 класс рабочая тетрадь
Авторы: Кузнецова Е.П. Муравьева Г.Л.
Алгебра 7 класс сборник задач
Авторы: А. Г. Мерзляк В. Б. Полонський
Алгебра 7 класс
Авторы: Мерзляк А.
 Г. Полонський В.Б.
Г. Полонський В.Б.
Алгебра 7 класс
Автор: Гальперина А.Р.
Алгебра 7 класс дидактические материалы
Автор: Феоктистов И.Е.
Алгебра 7 класс рабочая тетрадь
Авторы: С.Г. Журавлев Ю.В. Перепелкина
Алгебра 7 класс
Авторы: Мерзляк А.Г. Поляков В.М.
Алгебра 7 класс дидактические материалы, к учебнику Мордкович
Автор: Попов М.
А.
Алгебра 7-9 класс контрольные работы
Автор: Мордкович А.Г.
Алгебра 7 класс дидактические материалы
Авторы: Мерзляк А.Г. Полонский В.Б.
Алгебра 7 класс
Авторы: Арефьева И.Г. Пирютко О.Н.
Алгебра 7 класс дидактические материалы
Авторы: Потапов М.К. Шевкин А.В.
Алгебра 7 класс рабочая тетрадь
Автор: Ерина Т.
 М.
М.Алгебра 7 класс дидактические материалы
Авторы: Ткачева М.В. Федорова Н.Е.
Алгебра 7 класс контрольно-измерительные материалы
Автор: Мартышова Л.И.
Алгебра 7 класс контрольные работы
Авторы: Кузнецова Л.В. Минаева С.С.
Алгебра 7 класс тематические тесты
Автор: Чулков П.В.
Алгебра 7 класс контрольные работы
Автор: Александрова Л.
 А.
А.Алгебра 7 класс самостоятельные работы
Автор: Александрова Л.А.
Алгебра 7 класс учебник, задачник
Алгебра 7 класс самостоятельные и контрольные работы
Авторы: Мерзляк А.Г. Полонский В.В.
Алгебра 7 класс самостоятельные работы
Автор: Александрова Л.А.
Алгебра 7 класс тематические тесты ГИА
Авторы: Кузнецова Л.
 В. Минаева С.С.
В. Минаева С.С.- Алгебра 7 класс
дидактические материалы
Авторы: Евстафьева Л.П., Карп А.П.
Алгебра 7 класс тематические тесты
Авторы: Дудницын Ю.П. Кронгауз В.Л.
Алгебра 7-9 класс тесты
Авторы: Мордкович А.Г. Тульчинская Е.Е.
Алгебра 7 класс дидактические материалы к учебнику Макарычева
Авторы: Звавич Л.

Алгебра 7 класс рабочая тетрадь
Авторы: Ключникова Е.М. Комиссарова И.В.
Алгебра 7 класс рабочая тетрадь
Авторы: Миндюк Н.Г. Шлыкова И.С.
Алгебра 7 класс тематические тесты ОГЭ
Автор: Ткачева М.В.
Алгебра 7 класс рабочая тетрадь
Авторы: Муравин Г.К. Муравина О.
 В.
В.Алгебра 7 класс рабочая тетрадь
Авторы: Колягин Ю.М. Ткачева М.В.
Алгебра 7 класс рабочая тетрадь
Авторы: Потапов М.К. Шевкин А.В.
Алгебра 7 класс
Авторы: Колягин Ю.М. Ткачева М.В.
Алгебра 7 класс рабочая тетрадь
Авторы: Минаева С.С. Рослова Л.О.
Алгебра 7 класс
Автор: Цейтлiн О.
 I.
I.Алгебра 7 класс рабочая тетрадь
Авторы: Мерзляк А.Г. Полонский В.В.
Алгебра 7 класс
Авторы: Тарасенкова Н.А. Богатырева И.М.
Алгебра 7 класс
Авторы: Бунимович Е.А. Кузнецова Л.В.
Алгебра 7 класс
Авторы: Шыныбеков А.Н. Шыныбеков Д.А
Алгебра 7 класс
Авторы: Абылкасымова А.
 Е. Кучер Т.П.
Е. Кучер Т.П.Алгебра 7 класс
Авторы: Мордкович А.Г. Семенов П.В.
Алгебра 7 класс рабочая тетрадь
Авторы: Лебединцева Е. А. Беленкова Е. Ю.
Алгебра 7 класс рабочая тетрадь
Авторы: Зубарева И.И. Мильштейн М.С.
Алгебра 7 класс сборник задач
Авторы: Рурукин А.Н. Гусева Н.Н.
Алгебра 7 класс задачник-тренажёр
Авторы: Бунимович Е.
 А. Кузнецова Л.В.
А. Кузнецова Л.В.Алгебра 7 класс контрольные работы
Автор: М.В. Шуркова
Алгебра 7 класс тесты
Авторы: Глазков Ю. А. Гаиашвили М. Я.
Алгебра 7 класс тематические проверочные работы
Автор: Александрова Л.А.
Алгебра 7 класс тесты
Авторы: Журавлев С.Г. Ермаков В.В.
Алгебра 7 класс тесты
Авторы: Ключникова Е.
 М. Комиссарова И.В.
М. Комиссарова И.В.
Алгебра 7 класс рабочая тетрадь
Автор: Шуркова М.В.
Алгебра 7 класс Тетрадь контрольных тестовых работ
Автор: О.Н. Парфентьева
Алгебра 7 класс контрольные и самостоятельные работы
Автор: Попов М.А.
Алгебра 7 класс практикум
Автор: Красс Э.Ю.
Алгебра 7 класс контрольные измерительные материалы
Авторы: Глазков Ю.
 А. Гаиашвили М.Я.
А. Гаиашвили М.Я.Алгебра 7 класс самостоятельные и контрольные работы
Авторы: Глазков Ю.А. Гаиашвили М.Я.
Алгебра 7 класс дидактические материалы
Авторы: Б.Г. Зив В.А. Гольдич
Алгебра 7 класс Контрольные работы (из Методического пособия)
Авторы: Буцко Е.В. Мерзляк А.Г.
Алгебра 7 класс Математические диктанты, Контрольные работы (из Методического пособия)
Авторы: Буцко Е.
 В. Мерзляк А.Г.
В. Мерзляк А.Г.
ГДЗ решебник по алгебре 7 класс Александрова самостоятельные работы Мнемозина
Алгебра 7 класс
Тип пособия: Самостоятельные работы
Авторы: Александрова
Издательство: «Мнемозина»
Навыки владения алгебраической наукой имеют большое значение в жизни человека. Расчетные действия и операции мы встречаем повсеместно. Наука необходима для понимания принципов работы различных устройств, восприятия научно-технических идей, а также для моделирования и изучения явлений и процессов, которые происходят в природе.
Необходимость знаний по алгебре
Постигая учебный курс седьмого класса школьники познакомятся с такими понятиями как многочлен и функция, подробно изучат степени с натуральным показателем и линейные уравнения. В результате они должны научиться:
- знаниям и умениям для продолжения обучения;
- пользоваться математическими формулами;
- решать задачи и системы уравнений;
- грамотно работать и анализировать математический текст и извлекать из него нужную информацию и др.

Изучение науки в рамках школьной программы направлено на развитие логики и практического мышления.
Полезность решебника
Освоение предметного материала сложный и трудоемкий процесс, который требует к себе серьёзнейшего подхода. К сожалению, многие ученики с огромным трудом справляются с дисциплиной. Проблемы непонимания и неудовлетворительные оценки негативно влияют на успеваемость. На помощь в такой ситуации придёт «ГДЗ по Алгебре 7 класс Самостоятельные работы Александрова (Мнемозина)».
Сборник с готовыми и досконально расписанными онлайн-ответами поможет семикласснику понять алгоритм решения задач и примеров, а также:
- Без ошибок выполнить домашнюю работу;
- Разобрать сложную тему и поработать над ней;
- Заранее подготовиться к любой поверки знаний на уроке.
Структура решебника позволяет быстро и легко найти необходимую информацию по номеру упражнения, это значительно экономит время и силы, что немаловажно для ученика, а цифровой формат приложения обеспечивает доступность и удобство использования. Применяя регулярно ГДЗ в процессе обучения качество знаний заметно улучшится и успеваемость будет на высоте.
Применяя регулярно ГДЗ в процессе обучения качество знаний заметно улучшится и успеваемость будет на высоте.
Краткое описание учебника
Контроль предметных навыков и умений поможет выявить уровень усвояемости учебного материала. Для этой цели прекрасно подойдут самостоятельные работы по алгебре за 7 класс автор Александрова. Задания и упражнения имеются по всем основным темам. Они помогут провести как текущую, так и итоговую проверку. По результатам выполненных работ учитель сможет отследить где и в какой области у школьника пробелы и недочёты и своевременно их исправить.
Самостоятельная работа 1. Числовые выражения
Вариант 1Вариант 2Вариант 3Вариант 4Самостоятельная работа 2. Алгебраические выражения
Вариант 1Вариант 2Вариант 3Вариант 4Самостоятельная работа 3. Что такое математический язык
Вариант 1Вариант 2Вариант 3Вариант 4Самостоятельная работа 4. Что такое математическая модель
Вариант 1Вариант 2Вариант 3Вариант 4Самостоятельная работа 5.
 Линейное уравнение с одной переменнойВариант 1Вариант 2Вариант 3Вариант 4
Линейное уравнение с одной переменнойВариант 1Вариант 2Вариант 3Вариант 4Самостоятельная работа 6. Координатная прямая
Вариант 1Вариант 2Вариант 3Вариант 4Самостоятельная работа 7. Данные и ряды данных
Вариант 1Вариант 2Вариант 3Вариант 4Самостоятельная работа 8. Координатная плоскость
Вариант 1Вариант 2Вариант 3Вариант 4Самостоятельная работа 9. Линейное уравнение с двумя переменными и его график
Вариант 1Вариант 2Вариант 3Вариант 4Самостоятельная работа 10. Линейная функция и её график
Вариант 1Вариант 2Вариант 3Вариант 4Самостоятельная работа 11. Линейная функция и её график
Вариант 1Вариант 2Вариант 3Вариант 4Самостоятельная работа 12. Линейная функция y=kx
Вариант 1Вариант 2Вариант 3Вариант 4Самостоятельная работа 13. Основные понятия
Вариант 1Вариант 2Вариант 3Вариант 4Самостоятельная работа 14. Метод подстановки
Вариант 1Вариант 2Вариант 3Вариант 4Самостоятельная работа 15.
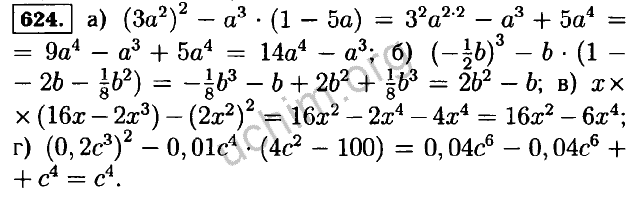 Метод подстановкиВариант 1Вариант 2Вариант 3Вариант 4
Метод подстановкиВариант 1Вариант 2Вариант 3Вариант 4Самостоятельная работа 16. Метод алгебраического сложения
Вариант 1Вариант 2Вариант 3Вариант 4Самостоятельная работа 17. Метод алгебраического сложения
Вариант 1Вариант 2Вариант 3Вариант 4Самостоятельная работа 18. Системы двух линейных уравнений как математические модели реальных ситуаций
Вариант 1Вариант 2Вариант 3Вариант 4Самостоятельная работа 19. Определение степени с натуральным показателем
Вариант 1Вариант 2Вариант 3Вариант 4Самостоятельная работа 20. Таблица основных степеней
Вариант 1Вариант 2Вариант 3Вариант 4Самостоятельная работа 21. Свойства степени с натуральным показателем
Вариант 1Вариант 2Вариант 3Вариант 4Самостоятельная работа 22. Умножение и деление степеней с одинаковыми показателями. Степень с нулевым показателем
Вариант 1Вариант 2Вариант 3Вариант 4Самостоятельная работа 23. Таблицы распределения
Вариант 1Вариант 2Вариант 3Вариант 4Самостоятельная работа 24.
 Стандартный вид одночлена. Сложение и вычитание одночленовВариант 1Вариант 2Вариант 3Вариант 4
Стандартный вид одночлена. Сложение и вычитание одночленовВариант 1Вариант 2Вариант 3Вариант 4Самостоятельная работа 25. Сложение и вычитание одночленов
Вариант 1Вариант 2Вариант 3Вариант 4Самостоятельная работа 26. Умножение одночленов. Возведение одночлена в натуральную степень
Вариант 1Вариант 2Вариант 3Вариант 4Самостоятельная работа 27. Деление одночлена на одночлен
Вариант 1Вариант 2Вариант 3Вариант 4Самостоятельная работа 28. Основные понятия
Вариант 1Вариант 2Вариант 3Вариант 4Самостоятельная работа 29. Сложение и вычитание многочленов
Вариант 1Вариант 2Вариант 3Вариант 4Самостоятельная работа 30. Умножение многочлена на одночлен
Вариант 1Вариант 2Вариант 3Вариант 4Самостоятельная работа 31. Умножение многочлена на одночлен
Вариант 1Вариант 2Вариант 3Вариант 4Самостоятельная работа 32. Умножение многочлена на многочлен
Вариант 1Вариант 2Вариант 3Вариант 4Самостоятельная работа 33.
 Формулы сокращённого умножения. Квадрат двучленаВариант 1Вариант 2Вариант 3Вариант 4
Формулы сокращённого умножения. Квадрат двучленаВариант 1Вариант 2Вариант 3Вариант 4Самостоятельная работа 34. Формулы сокращённого умножения. Разность квадратов
Вариант 1Вариант 2Вариант 3Вариант 4Самостоятельная работа 35. Формулы сокращённого умножения. Сумма и разность кубов. Комбинации различных формул
Вариант 1Вариант 2Вариант 3Вариант 4Самостоятельная работа 36. Процентные частоты
Вариант 1Вариант 2Вариант 3Вариант 4Самостоятельная работа 37. Вынесение общего множителя за скобки
Вариант 1Вариант 2Вариант 3Вариант 4Самостоятельная работа 38. Способ группировки
Вариант 1Вариант 2Вариант 3Вариант 4Самостоятельная работа 39. Разложение многочленов на множители с помощью формул сокращённого умножения. Разность квадратов
Вариант 1Вариант 2Вариант 3Вариант 4Самостоятельная работа 40. Разложение многочленов на множители с помощью формул сокращённого умножения. Сумма и разность кубов
Вариант 1Вариант 2Вариант 3Вариант 4Самостоятельная работа 41.
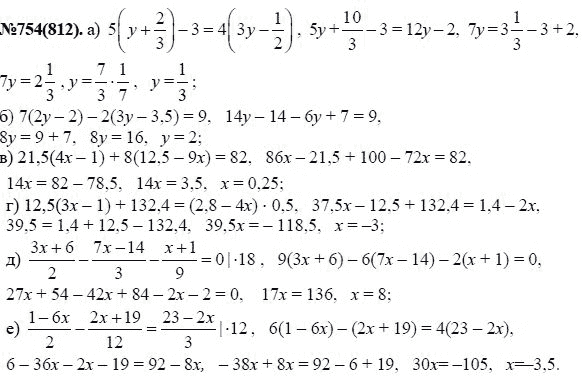 Разложение многочленов на множители с помощью формул сокращённого умножения. Квадрат двучленаВариант 1Вариант 2Вариант 3Вариант 4
Разложение многочленов на множители с помощью формул сокращённого умножения. Квадрат двучленаВариант 1Вариант 2Вариант 3Вариант 4Самостоятельная работа 42. Разложение многочленов на множители с помощью комбинации различных приёмов
Вариант 1Вариант 2Вариант 3Вариант 4Самостоятельная работа 43. Сокращение алгебраических дробей
Вариант 1Вариант 2Вариант 3Вариант 4Самостоятельная работа 44. Среднее значение
Вариант 1Вариант 2Вариант 3Вариант 4Похожие ГДЗ Алгебра 7 класс
Алгебра 7 класс
Контрольные работы
Александрова
«Мнемозина»
Алгебра 7 класс
Учебник
Мордкович, Александрова, Мишустина
«Мнемозина»
Алгебра 7 класс
Тетрадь для п/р
Александрова
«Мнемозина»
Самостоятельная работа 1. Числовые выражения: Вариант 1
ГДЗ Алгебра 7 класс Никольский, Потапов, Решетников, Шевкин на Решалка
ГДЗ Алгебра 7 класс Никольский, Потапов, Решетников, Шевкин
авторы: Никольский, Потапов, Решетников, Шевкин.
издательство: Просвещение
Задачи
- ГЛАВА 1. Действительные числа
- §1. Натуральные числа
- 1.1. Натуральные числа и действия с ними
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 1.
 2. Степень числа
2. Степень числа- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 1.3. Простые и составные числа
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 1.4. Разложение натуральных чисел на множители
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 1.1. Натуральные числа и действия с ними
- §2.
 Рациональные числа
Рациональные числа- 2.1. Обыкновенные дроби. Конечные десятичные дроби.
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 2.2. Разложение обыкновенной дроби в конечную десятичную дробь
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 2.3. Периодические десятичные дроби
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 2.4. Периодичность десятичного разложения обыкновенной дроби
- 88
- 89
- 90
- 91
- 92
- 93
- 2.
 5. Десятичное разложение рациональных чисел
5. Десятичное разложение рациональных чисел- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 2.1. Обыкновенные дроби. Конечные десятичные дроби.
- §3. Действительные числа
- 3.1. Иррациональные числа
- 106
- 107
- 108
- 109
- 110
- 3.2. Понятие действительного числа
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 3.3. Сравнение действительных чисел
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 3.
 4. Основные свойства действительных чисел
4. Основные свойства действительных чисел- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 3.5. Приближения чисел
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 3.6. Длина отрезка
- 163
- 164
- 165
- 166
- 167
- 168
- 3.
 7. Координатная ось
7. Координатная ось- 169
- 170
- 171
- 172
- 3.1. Иррациональные числа
- Дополнение к главе 1
- 1. Делимость чисел
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 2. Исторические сведения
- 181
- 1. Делимость чисел
- §1. Натуральные числа
- ГЛАВА 2. Алгебраические выражения
- §4. Одночлены
- 4.1. Числовые выражения
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 4.2. Буквенные выражения
- 191
- 192
- 193
- 194
- 195
- 196
- 197
- 198
- 199
- 200
- 4.
 3. Понятие одночлена
3. Понятие одночлена- 201
- 202
- 203
- 204
- 205
- 206
- 4.4. Произведение одночленов
- 207
- 208
- 209
- 210
- 211
- 212
- 213
- 214
- 215
- 216
- 217
- 218
- 219
- 220
- 221
- 222
- 223
- 224
- 4.5. Стандартный вид одночлена
- 225
- 226
- 227
- 228
- 229
- 230
- 4.6. Подобные одночлены
- 231
- 232
- 233
- 234
- 235
- 236
- 237
- 238
- 239
- 240
- 4.1. Числовые выражения
- §5.
 Многочлены
Многочлены- 5.1. Понятие многочлена
- 241
- 242
- 243
- 244
- 245
- 246
- 247
- 5.2. Свойства многочленов
- 248
- 249
- 250
- 251
- 252
- 253
- 5.3. Многочлены стандартного вида
- 254
- 255
- 256
- 257
- 258
- 259
- 5.4. Сумма и разность многочленов
- 260
- 261
- 262
- 263
- 264
- 265
- 266
- 267
- 268
- 269
- 270
- 271
- 272
- 273
- 274
- 275
- 5.
 5. Произведение одночлена и многочлена
5. Произведение одночлена и многочлена- 276
- 277
- 278
- 279
- 280
- 281
- 282
- 283
- 284
- 285
- 286
- 287
- 288
- 289
- 290
- 5.6. Произведение многочленов
- 291
- 292
- 293
- 294
- 295
- 296
- 297
- 298
- 299
- 300
- 301
- 302
- 303
- 304
- 305
- 306
- 307
- 308
- 309
- 310
- 311
- 5.
 7. Целые выражения
7. Целые выражения- 312
- 313
- 314
- 315
- 316
- 317
- 318
- 5.8. Числовое значение целого выражения
- 319
- 320
- 321
- 322
- 323
- 324
- 325
- 326
- 327
- 328
- 329
- 330
- 331
- 332
- 5.9. Тождественное равенство целых выражений
- 333
- 334
- 335
- 336
- 337
- 5.1. Понятие многочлена
- §6. Формулы сокращенного умножения
- 6.1. Квадрат суммы
- 338
- 339
- 340
- 341
- 342
- 343
- 344
- 345
- 346
- 347
- 348
- 349
- 350
- 6.
 2. Квадрат разности
2. Квадрат разности- 351
- 352
- 353
- 354
- 355
- 356
- 357
- 358
- 359
- 360
- 361
- 362
- 363
- 6.3. Выделение полного квадрата
- 364
- 365
- 366
- 367
- 368
- 369
- 370
- 371
- 372
- 373
- 6.4. Разность квадратов
- 374
- 375
- 376
- 377
- 378
- 379
- 380
- 381
- 382
- 383
- 384
- 385
- 386
- 387
- 388
- 389
- 6.
 5. Сумма кубов
5. Сумма кубов- 390
- 391
- 392
- 393
- 394
- 395
- 396
- 397
- 398
- 399
- 400
- 401
- 6.6. Разность кубов
- 402
- 403
- 404
- 405
- 406
- 407
- 408
- 409
- 410
- 411
- 412
- 6.7. Куб суммы
- 413
- 414
- 415
- 416
- 417
- 418
- 419
- 420
- 6.8. Куб разности
- 421
- 422
- 423
- 424
- 425
- 426
- 427
- 428
- 429
- 6.
 9. Применение формул сокращенного умножения
9. Применение формул сокращенного умножения- 430
- 431
- 432
- 433
- 434
- 435
- 436
- 437
- 438
- 439
- 440
- 441
- 442
- 443
- 444
- 445
- 446
- 447
- 448
- 449
- 6.10. Разложение многочлена на множители
- 450
- 451
- 452
- 453
- 454
- 455
- 456
- 457
- 458
- 459
- 460
- 461
- 462
- 463
- 464
- 465
- 466
- 467
- 468
- 469
- 470
- 471
- 472
- 473
- 474
- 475
- 476
- 477
- 478
- 479
- 6.1. Квадрат суммы
- §7.
 Алгебраические дроби
Алгебраические дроби- 7.1. Алгебраические дроби и их свойства
- 480
- 481
- 482
- 483
- 484
- 485
- 486
- 487
- 488
- 489
- 490
- 491
- 492
- 493
- 494
- 495
- 7.2. Приведение алгебраических дробей к общему знаменателю
- 496
- 497
- 498
- 499
- 500
- 501
- 502
- 7.3. Алгебраические действия с алгебраическими дробями
- 503
- 504
- 505
- 506
- 507
- 508
- 509
- 510
- 511
- 512
- 513
- 514
- 515
- 516
- 517
- 518
- 519
- 520
- 521
- 522
- 523
- 524
- 525
- 526
- 527
- 528
- 529
- 530
- 531
- 532
- 7.
 4. Рациональные выражения
4. Рациональные выражения- 533
- 534
- 535
- 536
- 537
- 538
- 539
- 540
- 7.5. Числовое значение рационального выражения
- 541
- 542
- 543
- 544
- 545
- 546
- 547
- 548
- 549
- 550
- 551
- 552
- 553
- 554
- 555
- 556
- 557
- 558
- 559
- 560
- 561
- 7.6. Тождественное равенство рациональных выражений
- 562
- 563
- 564
- 565
- 566
- 567
- 568
- 569
- 7.1. Алгебраические дроби и их свойства
- §8.
 Степень с целым показателем
Степень с целым показателем- 8.1. Понятие степени с целым показателем
- 570
- 571
- 572
- 573
- 574
- 575
- 576
- 577
- 578
- 579
- 580
- 581
- 582
- 583
- 584
- 8.2. Свойства степени с целым показателем
- 585
- 586
- 587
- 588
- 589
- 590
- 591
- 592
- 593
- 594
- 595
- 596
- 597
- 598
- 599
- 600
- 601
- 8.3. Стандартный вид числа
- 602
- 603
- 604
- 605
- 606
- 607
- 608
- 609
- 610
- 611
- 8.
 4. Преобразование рациональных выражений
4. Преобразование рациональных выражений- 612
- 613
- 614
- 615
- 616
- 617
- 618
- 619
- 620
- 621
- 8.1. Понятие степени с целым показателем
- Дополнения к главе 2
- 1. Делимость многочленов
- 622
- 623
- 624
- 625
- 626
- 627
- 628
- 629
- 630
- 2. Исторические сведения
- 631
- 632
- 1. Делимость многочленов
- §4. Одночлены
- ГЛАВА 3. Линейные уравнения
- §9. Линейные уравнения с одним неизвестным
- 9.1. Уравнения первой степени с одним неизвестным
- 633
- 634
- 635
- 636
- 637
- 638
- 639
- 640
- 641
- 9.
 2. Линейные уравнения с одним неизвестным
2. Линейные уравнения с одним неизвестным - 9.3. Решение линейных уравнений с одним неизвестным
- 9.4. Решение задач с помощь линейных уравнений
- 9.1. Уравнения первой степени с одним неизвестным
- §10. Системы линейных уравнений
- 10.1. Уравнения первой степени с двумя неизвестными
- 10.2. Системы двух уравнений первой степени с двумя неизвестными
- 10.3. Способ подстановки
- 10.4. Способ уравнивания коэффицентов
- 10.5. Равносильность уравнений и систем уравнений
- 10.6. Решение систем двух линейных уравнений с двумя неизвестными
- 10.7. О количестве решений системы двух уравнений первой степени с двумя неизвестными
- 10.8. Системы уравнений первой степени с тремя неизвестными
- 10.9. Решение задач при помощи систем уравнений первой степени
- 10.1. Уравнения первой степени с двумя неизвестными
- Дополнения к главе 3
- 1. Линейные диофантовы уравнения
- 2.
 Метод Гаусса
Метод Гаусса - 3. Исторические сведения
- 1. Линейные диофантовы уравнения
- §9. Линейные уравнения с одним неизвестным
- Задания для повторения
- Натуральные числа
- Целые числа
- Обыкновенные дроби
- Рациональные числа
- Десятичные дроби
- Совместные действия с обыкновенными и десятичными дробями
- Действительные числа
- Координатная ось и координатная плоскость
- Буквенные выражения
- Линейные уравнения
- Системы линейных уравнений
- Текстовые задачи
- Натуральные числа
- Задания на исследование
- Задания для самоконтроля
Семиклассникам, часто пропускающим уроки, например, из-за болезни или поездки на спортивные сборы, творческие конкурсы или находящимся на дистанционном обучении, в качестве эффективного и интересного пособия подойдет ГДЗ по алгебре за 7 класс Никольского.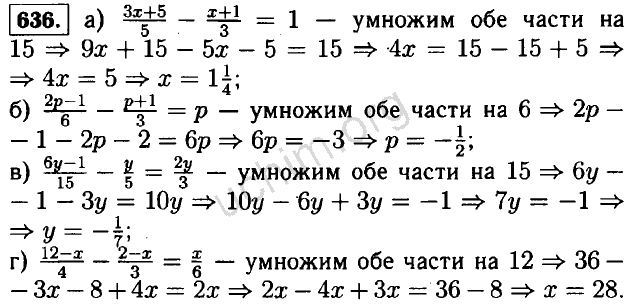 Такой решебник поможет отслеживать алгоритмы решения даже самых сложных заданий в рамках курса дисциплины. Ученик сможет разобраться в логике вопросов и примеров ответов, научится правильно отображать результаты.
Такой решебник поможет отслеживать алгоритмы решения даже самых сложных заданий в рамках курса дисциплины. Ученик сможет разобраться в логике вопросов и примеров ответов, научится правильно отображать результаты.
Кому будет полезен решебник Никольский, Потапов, Решетников, Шевкин?
Далеко не только школьники могут использовать ГДЗ по алгебре за 7 класс. Это непростой учебник с заданиями разной сложности, а поэтому готовые ответы пригодятся родителям семиклассников. Они смогут быстрее проверить домашку и не сомневаться в результате, оценить уровень знаний своих детей, их подготовку к проверочной, самостоятельной или контрольной работе. Также сами педагоги-предметники, репетиторы для ускорения проверки правильности выполнения задания учениками нередко используют онлайн-ГДЗ за 7 класс. Применение таких справочников позволяет технологически правильно организовать преподавание дисциплины согласно действующим образовательным стандартам.
Решебник по алгебре от авторского коллектива Никольский, Потапов, Решетников, Шевкин способствует развитию навыков работать самостоятельно, улучшению успеваемости.
Готовые ответы для учебников седьмого класса
Преимущество онлайн-сервисов в их доступности, наглядности и возможности применения в любое удобное время. «Решалка» предлагает понятную платформу с организованным поиском нужных решений максимально быстро в условиях ограниченного времени. Готовые домашние задания отлично помогут «подтянуть» упущенный материал и получать регулярно только хорошие отметки. Пособие станет настоящей палочкой-выручалочкой, ведь его удобно использовать онлайн, а значит можно проверить задание везде, где есть доступ к Интернету с любого гаджета.
Математика 7 класс | Уравнения и неравенства
Учащиеся решают уравнения и неравенства с рациональными числами и сталкиваются с реальными ситуациями, которые можно смоделировать и решить с помощью уравнений и неравенств.
Раздел 4
7-й класс
Fishtank Plus для математики
Разблокируйте функции, чтобы оптимизировать время подготовки, планировать увлекательные уроки и следить за успеваемостью учащихся.
Подробнее
Оценка
Следующие оценки сопровождают Модуль 4.
Предварительная часть
Предложите учащимся пройти Предварительную оценку и Предварительную самооценку учащихся перед началом занятия. Используйте Руководство по анализу предварительной оценки, чтобы определить пробелы в фундаментальном понимании и наметить план ускорения обучения на протяжении всего модуля.
Промежуточный модуль
После урока 4 учащиеся должны пройти промежуточную оценку.
Постмодальная оценка
Ключ к ответам после модульной оценки
Руководство по анализу послемодульной оценки
92F25A3F-8529-4314-9899-6EE68694E3D0Самооценка студентов после окончания обучения
Расширенный пакет оценивания
Используйте данные учащихся для управления планированием с помощью расширенного набора модульных оценок, помогающих оценить уровень владения учащимися базовыми навыками и понятиями, а также их прогресс в изучении содержания модуля.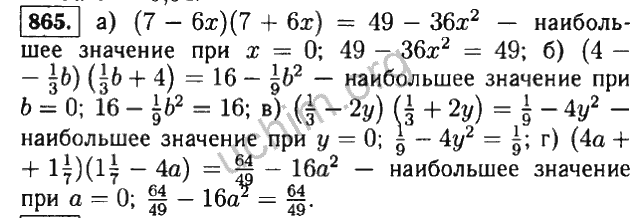
Скачать образец
Подготовка блока
Интеллектуальная подготовка
Рекомендации по подготовке к изучению этого модуля
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Запуск модуля
Подготовьтесь к преподаванию этого модуля, погрузившись в стандарты, большие идеи и связи с предыдущим и будущим содержанием. Запуск модулей включает в себя серию коротких видеороликов, целевую литературу и возможности для планирования действий.
Обновление до Плюс
Интернализация стандартов через итоговую оценку
- Пройдите итоговую оценку. Аннотировать для:
- Стандарты, которым соответствует каждый вопрос
- Стратегии и представления, используемые на ежедневных уроках
- Связь с основными понятиями модуля
- Уроки, на которые Оценка указывает
Интернализация траектории отряда
- Прочтите и аннотируйте сводку отряда.
- Обратите внимание на продвижение понятий по блоку, используя карту урока.

- Выполнить все целевые задачи. Аннотируйте целевые задачи для:
- Основные понятия
- Связь с вопросами послемодульной оценки
- Определите ключевые возможности для вовлечения учащихся в академический дискурс. Прочтите наш Инструмент для учителя на Академический дискурс и ссылайтесь на него на протяжении всего модуля.
Интеллектуальная подготовка для конкретного подразделения
- Прочтите разделы 6–8 «Выражения и уравнения» для соответствующих стандартов в этой области «Выражения и уравнения».
- Прочтите следующую таблицу, в которой указаны модели, используемые во всем устройстве.
| Модель | Пример |
| Диаграмма ленты и уравнения | $$3(x+4)=45$$ $$3x+4=45$$ |
Основные понятия
Основные математические понятия, которые учащиеся поймут в этом модуле
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950- Уравнения и неравенства — это мощные инструменты, которые можно использовать для моделирования и решения реальных ситуаций с неизвестными величинами.

- Уравнения можно решить, рассуждая об арифметике, необходимой для раскрытия значения неизвестного. Уравнения также можно решать алгебраически, используя свойства операций и равенства.
- Неравенства имеют бесконечные решения, которые можно изобразить графически на числовой прямой. В контексте эти решения иногда ограничены тем, что имеет смысл в данной ситуации; например, при поиске максимального количества людей, которые могут поместиться в лодке, набор решений будет ограничен положительными целыми числами.
Запас слов
Термины и обозначения, которые учащиеся изучают или используют на уроке
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950уравнение
неравенство
решение
замена
ленточная диаграмма
Чтобы увидеть весь словарный запас для модуля 4, просмотрите наш глоссарий лексики для 7-го класса.
Карта урока
Тема A: Решение и моделирование с помощью уравнений
Решите одношаговые уравнения с рациональными числами.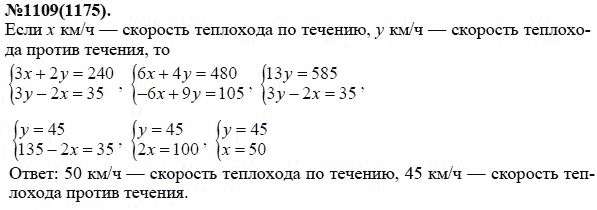
7.EE.B.4.A
Представляйте уравнения в формах $${px+q=r}$$ и $${p(x+q)=r}$$, используя ленточные диаграммы.
7.EE.B.4.A
Решите уравнения в формах $${px+q=r}$$ и $${p(x+q)=r}$$ , используя ленточные диаграммы.
7.EE.B.3 7.EE.B.4.A
Решите уравнения в формах $${px+q=r }$$ и $${p(x+q)=r}$$ алгебраически.
7.EE.B.4.A
Решите текстовые задачи, ведущие к уравнениям в формах $${px+q=r}$$ и $${p(x+q)=r}$$ (Часть 1).
7.EE.B.3 7.EE.B.4.A
Решите текстовые задачи, ведущие к уравнениям в формах $${px+q=r}$$ и $${p(x+q)=r }$$ (Часть 2).
7.EE.B.3 7.EE.B.4.A
Модель с уравнениями вида $${px+q=r}$$ и $${p(x+q)=r}$$.
7.EE.B.3 7.EE.B.4.A
Тема B: Решение и моделирование с помощью неравенств
Решить одношаговое неравенство и построить график.
7.EE.B.4.B
Напишите и решите неравенства в формах $${px+q>r}$$ или $${px+q
7.EE.B.4.B
Решите неравенства с отрицательными коэффициентами.
7.EE.B.4.B
Решите текстовые задачи, ведущие к неравенствам в формах $${px+q>r}$$ или $${px+q 7.EE.B.4.B Модель с неравенствами. 7.EE.B.3
7.EE.B.4.B Ключ Основной кластер Вспомогательный кластер Дополнительный кластер Общие базовые стандарты
Основные стандарты
Стандарты контента, рассматриваемые в этом разделе
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Выражения и уравнения
7.EE.B.3 — Решайте многоэтапные задачи из реальной жизни и математические задачи, связанные с положительными и отрицательными рациональными числами в любой форме (целые числа, дроби и десятичные дроби), стратегически используя инструменты. Применять свойства операций для вычисления с числами в любой форме; конвертировать между формами по мере необходимости; и оценить обоснованность ответов, используя умственные вычисления и стратегии оценки.
 Например: если женщина, зарабатывающая 25 долларов в час, получает надбавку на 10 %, она будет получать дополнительно 1/10 своей зарплаты в час, или 2,50 доллара, за новую зарплату в 27,50 долларов. Если вы хотите разместить перекладину для полотенец длиной 9 3/4 дюйма в центре двери шириной 27 1/2 дюйма, вам нужно будет разместить перекладину примерно в 9 дюймах от каждого края; эту оценку можно использовать в качестве проверки точного вычисления.
Например: если женщина, зарабатывающая 25 долларов в час, получает надбавку на 10 %, она будет получать дополнительно 1/10 своей зарплаты в час, или 2,50 доллара, за новую зарплату в 27,50 долларов. Если вы хотите разместить перекладину для полотенец длиной 9 3/4 дюйма в центре двери шириной 27 1/2 дюйма, вам нужно будет разместить перекладину примерно в 9 дюймах от каждого края; эту оценку можно использовать в качестве проверки точного вычисления. 7.EE.B.4 — Используйте переменные для представления величин в реальной или математической задаче и создавайте простые уравнения и неравенства для решения задач, рассуждая о величинах.
7.EE.B.4.A — Решите текстовые задачи, ведущие к уравнениям вида px + q = r и p(x + q) = r, где p, q и r — конкретные рациональные числа. Решите уравнения этих форм бегло. Сравните алгебраическое решение с арифметическим, указав последовательность операций, используемых в каждом подходе.
 Например, периметр прямоугольника равен 54 см. Его длина составляет 6 см. Какова его ширина?
Например, периметр прямоугольника равен 54 см. Его длина составляет 6 см. Какова его ширина? 7.EE.B.4.B — Решите текстовые задачи, ведущие к неравенствам вида px + q > r или px + q. Например: как продавец, вам платят 50 долларов в неделю плюс 3 доллара за продажу. На этой неделе вы хотите, чтобы ваша зарплата была не менее 100 долларов. Напишите неравенство для количества продаж, которое вам нужно сделать, и опишите решения.
Основополагающие стандарты
Стандарты, описанные в предыдущих модулях или классах, которые являются важной основой для текущего модуля
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Выражения и уравнения
6.EE.B.5
6.EE.B.7
6.EE.B.8
Будущие стандарты
Стандарты будущих классов или разделов, которые связаны с содержанием данного раздела
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Выражения и уравнения
8.
 EE.C.7
EE.C.78.EE.C.8
Стандарты математической практики
CCSS.MATH.PRACTICE.MP1 — Разбираться в проблемах и настойчиво решать их.
CCSS.MATH.PRACTICE.MP2 — Рассуждайте абстрактно и количественно.
CCSS.MATH.PRACTICE.MP3 — Придумывайте жизнеспособные аргументы и критикуйте рассуждения других.
CCSS.MATH.PRACTICE.MP4 — Модель с математикой.
CCSS.MATH.PRACTICE.MP5 — Стратегически используйте соответствующие инструменты.
CCSS.MATH.PRACTICE.MP6 — Следите за точностью.
CCSS.MATH.PRACTICE.MP7 — Ищите и используйте структуру.
CCSS.MATH.PRACTICE.MP8 — Ищите и выражайте закономерность в повторяющихся рассуждениях.
Модуль 3
Числовые и алгебраические выражения
значок/стрелка/вправо/большойМодуль 5
Проценты и масштабирование
Математика, 7 класс, алгебраическое рассуждение
CCSS. Math.Content.7.EE.A.1
7 класс, выражения и уравнения
Math.Content.7.EE.A.1
7 класс, выражения и уравнения
Кластер: использование свойств операций для создания эквивалентных выражений
Стандарт: применение свойств операций в качестве стратегий для сложения, вычитания, факторизации и расширения линейных выражений с рациональными коэффициентами.
CCSS.Math.Content.7.EE.A.2 7 класс, выражения и уравнения
Кластер: использование свойств операций для создания эквивалентных выражений
Стандарт: понимание того, что переписывание выражения в различных формах в контексте задачи может пролить свет на проблему и на то, как связаны величины в ней. Например, a + 0,05a = 1,05a означает, что «увеличение на 5%» равнозначно «умножению на 1,05».
CCSS.Math.Content.7.EE.B.3 7 класс, выражения и уравнения
Кластер: решение реальных и математических задач с использованием числовых и алгебраических выражений и уравнений
Стандарт: решение многоэтапных реальных и математических задач, поставленных с положительными и отрицательными числа, дроби и десятичные дроби), используя инструменты стратегически. Применяйте свойства операций как стратегии для расчетов с числами в любой форме; конвертировать между формами по мере необходимости; и оценить обоснованность ответов, используя умственные вычисления и стратегии оценки. Например: если женщина, зарабатывающая 25 долларов в час, получает надбавку на 10%, она будет получать дополнительную 1/10 своей зарплаты в час, или 2,50 доллара, за новую зарплату в 27,50 долларов. Если вы хотите разместить полотенцесушитель 93/4 дюйма длиной в центре двери шириной 27 1/2 дюйма, вам нужно будет разместить планку примерно в 9 дюймах от каждого края; эту оценку можно использовать в качестве проверки точного вычисления.
Применяйте свойства операций как стратегии для расчетов с числами в любой форме; конвертировать между формами по мере необходимости; и оценить обоснованность ответов, используя умственные вычисления и стратегии оценки. Например: если женщина, зарабатывающая 25 долларов в час, получает надбавку на 10%, она будет получать дополнительную 1/10 своей зарплаты в час, или 2,50 доллара, за новую зарплату в 27,50 долларов. Если вы хотите разместить полотенцесушитель 93/4 дюйма длиной в центре двери шириной 27 1/2 дюйма, вам нужно будет разместить планку примерно в 9 дюймах от каждого края; эту оценку можно использовать в качестве проверки точного вычисления.
CCSS.Math.Content.7.EE.B.4 7 класс, выражения и уравнения
Кластер: решение реальных и математических задач с использованием числовых и алгебраических выражений и уравнений
Стандарт: использование переменных для представления величин в реальной или математической задаче и построение простых уравнений и неравенств для решения проблемы, рассуждая о количествах.
CCSS.Math.Content.7.EE.B.4a 7 класс, выражения и уравнения
Кластер: решение реальных и математических задач с использованием числовых и алгебраических выражений и уравнений
Стандарт: решение текстовых задач, приводящих к уравнениям вида px + q = r и p(x + q) = r, где p, q и r — конкретные рациональные числа. Решите уравнения этих форм бегло. Сравните алгебраическое решение с арифметическим, указав последовательность операций, используемых в каждом подходе. Например, периметр прямоугольника равен 54 см. Его длина составляет 6 см. Какова его ширина?
CCSS.Math.Content.7.EE.B.4b 7 класс, выражения и уравнения
Кластер: решение реальных и математических задач с использованием числовых и алгебраических выражений и уравнений
Стандарт: решение текстовых задач, приводящих к неравенствам вида px + q > r или px + q < r, где p, q и r — конкретные рациональные числа. Нарисуйте график множества решений неравенства и интерпретируйте его в контексте проблемы. Например, как продавец, вам платят 50 долларов в неделю плюс 3 доллара за продажу. На этой неделе вы хотите, чтобы ваша зарплата была не менее 100 долларов. Напишите неравенство для количества продаж, которое вам нужно сделать, и опишите решения.
Например, как продавец, вам платят 50 долларов в неделю плюс 3 доллара за продажу. На этой неделе вы хотите, чтобы ваша зарплата была не менее 100 долларов. Напишите неравенство для количества продаж, которое вам нужно сделать, и опишите решения.
CCSS.Math.Practice.MP.1 Математические практики
Кластер: Математические практики
Стандарт: Разбираться в проблемах и настойчиво решать их. Подкованные в математике учащиеся начинают с того, что объясняют себе смысл задачи и ищут пути ее решения. Они анализируют данные, ограничения, отношения и цели. Они строят предположения о форме и значении решения и планируют путь решения, а не просто пытаются найти решение. Они рассматривают аналогичные проблемы и пробуют частные случаи и более простые формы исходной задачи, чтобы получить представление о ее решении. Они контролируют и оценивают свой прогресс и при необходимости меняют курс. Учащиеся постарше могут, в зависимости от контекста задачи, преобразовывать алгебраические выражения или менять окно просмотра на своем графическом калькуляторе, чтобы получить необходимую им информацию.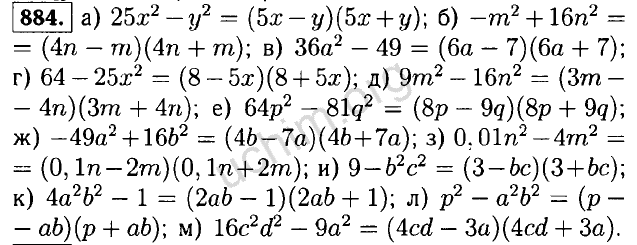 Подкованные в математике учащиеся могут объяснять соответствия между уравнениями, словесными описаниями, таблицами и графиками или рисовать диаграммы важных функций и взаимосвязей, графически отображать данные и искать закономерности или тенденции. Младшие школьники могут полагаться на использование конкретных объектов или изображений, чтобы помочь осмыслить и решить проблему. Математически подкованные учащиеся проверяют свои ответы на задачи, используя другой метод, и они постоянно спрашивают себя: «Имеет ли это смысл?» Они могут понять подходы других к решению сложных проблем и определить соответствие между различными подходами.
Подкованные в математике учащиеся могут объяснять соответствия между уравнениями, словесными описаниями, таблицами и графиками или рисовать диаграммы важных функций и взаимосвязей, графически отображать данные и искать закономерности или тенденции. Младшие школьники могут полагаться на использование конкретных объектов или изображений, чтобы помочь осмыслить и решить проблему. Математически подкованные учащиеся проверяют свои ответы на задачи, используя другой метод, и они постоянно спрашивают себя: «Имеет ли это смысл?» Они могут понять подходы других к решению сложных проблем и определить соответствие между различными подходами.
CCSS.Math.Practice.MP.2 Математические практики
Кластер: Математические практики
Стандарт: Рассуждать абстрактно и количественно. Учащиеся, обладающие математическими способностями, понимают величины и их отношения в проблемных ситуациях. Студенты привносят две взаимодополняющие способности в решение проблем, связанных с количественными отношениями: способность деконтекстуализировать — абстрагировать данную ситуацию и представлять ее символически и манипулировать репрезентирующими символами, как если бы они жили собственной жизнью, не обязательно обращая внимание на их референты — и способность контекстуализировать, делать паузы по мере необходимости в процессе манипулирования, чтобы исследовать референты для задействованных символов.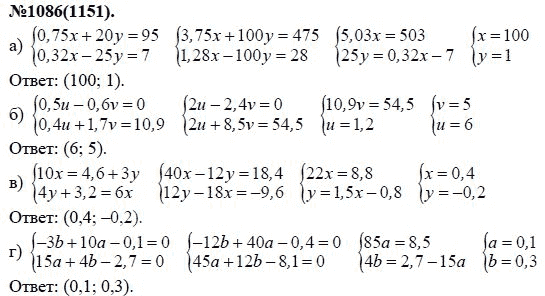 Количественное рассуждение влечет за собой привычки создавать последовательное представление проблемы; рассмотрение задействованных единиц; обращать внимание на значение величин, а не только на то, как их вычислять; знание и гибкое использование различных свойств операций и объектов.
Количественное рассуждение влечет за собой привычки создавать последовательное представление проблемы; рассмотрение задействованных единиц; обращать внимание на значение величин, а не только на то, как их вычислять; знание и гибкое использование различных свойств операций и объектов.
CCSS.Math.Practice.MP.3 Математические практики
Кластер: Математические практики
Стандарт: Придумывать жизнеспособные аргументы и критиковать рассуждения других. Подкованные в математике учащиеся понимают и используют заявленные предположения, определения и ранее установленные результаты при построении аргументов. Они строят предположения и выстраивают логическую последовательность утверждений, чтобы исследовать истинность своих предположений. Они способны анализировать ситуации, разбивая их на случаи, а также могут распознавать и использовать контрпримеры. Они обосновывают свои выводы, сообщают их другим и отвечают на аргументы других. Они индуктивно рассуждают о данных, выдвигая правдоподобные аргументы, учитывающие контекст, из которого эти данные возникли. Подкованные в математике учащиеся также способны сравнивать эффективность двух правдоподобных аргументов, отличать правильную логику или рассуждения от ошибочных и, если в аргументе есть изъян, объяснять, в чем он заключается. Учащиеся начальной школы могут создавать аргументы, используя конкретные референты, такие как объекты, рисунки, диаграммы и действия. Такие аргументы могут иметь смысл и быть правильными, даже если они не обобщаются и не становятся формальными до более поздних классов. Позже учащиеся учатся определять области, к которым применяется аргумент. Учащиеся всех классов могут слушать или читать аргументы других, решать, имеют ли они смысл, и задавать полезные вопросы, чтобы прояснить или улучшить аргументы.
Подкованные в математике учащиеся также способны сравнивать эффективность двух правдоподобных аргументов, отличать правильную логику или рассуждения от ошибочных и, если в аргументе есть изъян, объяснять, в чем он заключается. Учащиеся начальной школы могут создавать аргументы, используя конкретные референты, такие как объекты, рисунки, диаграммы и действия. Такие аргументы могут иметь смысл и быть правильными, даже если они не обобщаются и не становятся формальными до более поздних классов. Позже учащиеся учатся определять области, к которым применяется аргумент. Учащиеся всех классов могут слушать или читать аргументы других, решать, имеют ли они смысл, и задавать полезные вопросы, чтобы прояснить или улучшить аргументы.
CCSS.Math.Practice.MP.4 Математические практики
Кластер: Математические практики
Стандарт: Модель с математикой. Учащиеся, хорошо разбирающиеся в математике, могут применять математику, которую они знают, для решения проблем, возникающих в повседневной жизни, обществе и на рабочем месте. В младших классах это может быть так же просто, как написать уравнение сложения для описания ситуации. В средних классах учащийся может применять пропорциональные рассуждения, чтобы спланировать школьное мероприятие или проанализировать проблему в сообществе. К старшей школе учащийся может использовать геометрию для решения задачи проектирования или использовать функцию для описания того, как одна интересующая величина зависит от другой. Подкованные в математике учащиеся, которые могут применять то, что они знают, спокойно делают предположения и приближения, чтобы упростить сложную ситуацию, понимая, что позже они могут потребовать пересмотра. Они способны определять важные величины в практической ситуации и отображать их отношения, используя такие инструменты, как диаграммы, двусторонние таблицы, графики, блок-схемы и формулы. Они могут математически анализировать эти отношения, чтобы делать выводы. Они обычно интерпретируют свои математические результаты в контексте ситуации и размышляют о том, имеют ли результаты смысл, возможно, улучшая модель, если она не достигла своей цели.
В младших классах это может быть так же просто, как написать уравнение сложения для описания ситуации. В средних классах учащийся может применять пропорциональные рассуждения, чтобы спланировать школьное мероприятие или проанализировать проблему в сообществе. К старшей школе учащийся может использовать геометрию для решения задачи проектирования или использовать функцию для описания того, как одна интересующая величина зависит от другой. Подкованные в математике учащиеся, которые могут применять то, что они знают, спокойно делают предположения и приближения, чтобы упростить сложную ситуацию, понимая, что позже они могут потребовать пересмотра. Они способны определять важные величины в практической ситуации и отображать их отношения, используя такие инструменты, как диаграммы, двусторонние таблицы, графики, блок-схемы и формулы. Они могут математически анализировать эти отношения, чтобы делать выводы. Они обычно интерпретируют свои математические результаты в контексте ситуации и размышляют о том, имеют ли результаты смысл, возможно, улучшая модель, если она не достигла своей цели.
CCSS.Math.Practice.MP.5 Математические практики
Кластер: Математические практики
Стандарт: Стратегическое использование соответствующих инструментов. Подкованные в математике учащиеся рассматривают доступные инструменты при решении математической задачи. Эти инструменты могут включать карандаш и бумагу, конкретные модели, линейку, транспортир, калькулятор, электронную таблицу, систему компьютерной алгебры, статистический пакет или программное обеспечение для динамической геометрии. Профессиональные учащиеся достаточно хорошо знакомы с инструментами, соответствующими их классу или курсу, чтобы принимать обоснованные решения о том, когда каждый из этих инструментов может быть полезен, признавая как получаемое понимание, так и их ограничения. Например, математически подкованные старшеклассники анализируют графики функций и решений, построенные с помощью графического калькулятора. Они обнаруживают возможные ошибки, стратегически используя оценку и другие математические знания.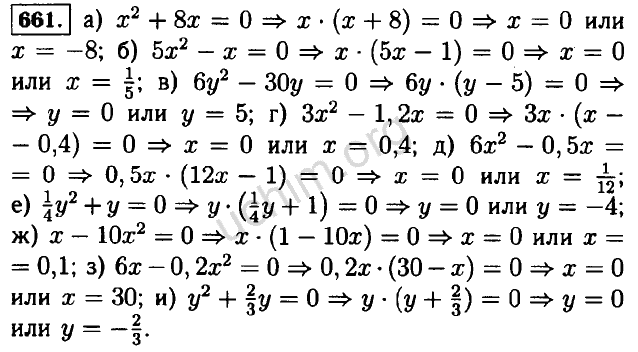 Создавая математические модели, они знают, что технологии позволяют визуализировать результаты различных предположений, исследовать последствия и сравнивать прогнозы с данными. Подкованные в математике учащиеся разных классов способны идентифицировать соответствующие внешние математические ресурсы, такие как цифровой контент, размещенный на веб-сайте, и использовать их для постановки или решения задач. Они могут использовать технологические инструменты для изучения и углубления своего понимания концепций.
Создавая математические модели, они знают, что технологии позволяют визуализировать результаты различных предположений, исследовать последствия и сравнивать прогнозы с данными. Подкованные в математике учащиеся разных классов способны идентифицировать соответствующие внешние математические ресурсы, такие как цифровой контент, размещенный на веб-сайте, и использовать их для постановки или решения задач. Они могут использовать технологические инструменты для изучения и углубления своего понимания концепций.
CCSS.Math.Practice.MP.6 Математические практики
Кластер: Математические практики
Стандарт: внимание к точности. Математически подкованные ученики стараются точно общаться с другими. Они стараются использовать четкие определения в обсуждениях с другими и в собственных рассуждениях. Они заявляют о значении выбранных ими символов, включая последовательное и уместное использование знака равенства. Они внимательно относятся к указанию единиц измерения и маркировке осей, чтобы прояснить соответствие с количествами в задаче. 2 + x + 1) может привести их к общей формуле суммы геометрического ряда. Работая над решением задачи, математически подкованные ученики контролируют процесс, уделяя внимание деталям. Они постоянно оценивают обоснованность своих промежуточных результатов.
2 + x + 1) может привести их к общей формуле суммы геометрического ряда. Работая над решением задачи, математически подкованные ученики контролируют процесс, уделяя внимание деталям. Они постоянно оценивают обоснованность своих промежуточных результатов.
MCCRS.Math.Content.7.EE.A.1 7 класс
Область обучения: выражения и уравнения
Стандарт: использование свойств операций для создания эквивалентных выражений
Индикатор: применение свойств операций в качестве стратегий для сложения, вычитания, факторизации и расширения линейных выражений с рациональными коэффициентами.
MCCRS.Math.Content.7.EE.A.2 7 класс
Область обучения: выражения и уравнения
Стандарт: использование свойств операций для создания эквивалентных выражений
Индикатор: понимание того, что переписывание выражения в различных формах в контексте задачи может пролить свет на проблему и на то, как связаны в ней количества.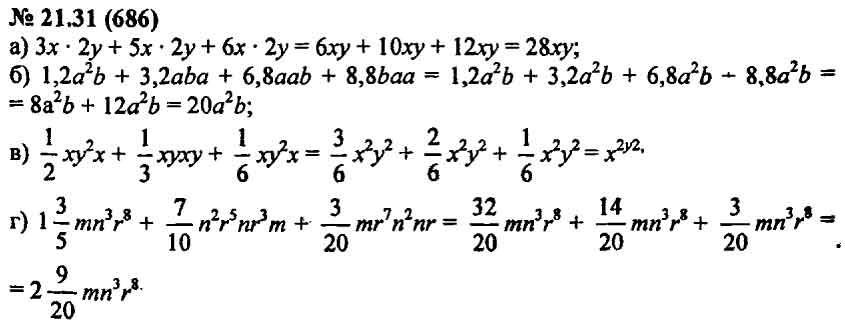 Например, a + 0,05a = 1,05a означает, что «увеличение на 5%» — это то же самое, что «умножение на 1,05». —
Например, a + 0,05a = 1,05a означает, что «увеличение на 5%» — это то же самое, что «умножение на 1,05». —
MCCRS.Math.Content.7.EE.B.3 7 класс
Область обучения: выражения и уравнения
Стандарт: решение реальных и математических задач с использованием числовых и алгебраических выражений и уравнений
Индикатор: решение многоэтапных реальных и математических задач, связанных с положительными и отрицательными рациональными числами в любой форме (целые числа, дроби и десятичные дроби) , используя инструменты стратегически. Применяйте свойства операций как стратегии для расчетов с числами в любой форме; конвертировать между формами по мере необходимости; и оценить обоснованность ответов, используя умственные вычисления и стратегии оценки. Например: если женщина, зарабатывающая 25 долларов в час, получает надбавку на 10%, она будет получать дополнительную 1/10 своей зарплаты в час, или 2,50 доллара, за новую зарплату в 27,50 долларов. Если вы хотите разместить полотенцесушитель 93/4 дюйма длиной в центре двери шириной 27 1/2 дюйма, вам нужно будет разместить планку примерно в 9 дюймах от каждого края; эту оценку можно использовать в качестве проверки точного вычисления.
Если вы хотите разместить полотенцесушитель 93/4 дюйма длиной в центре двери шириной 27 1/2 дюйма, вам нужно будет разместить планку примерно в 9 дюймах от каждого края; эту оценку можно использовать в качестве проверки точного вычисления.
MCCRS.Math.Content.7.EE.B.4 7 класс
Область обучения: выражения и уравнения
Стандарт: решение реальных и математических задач с использованием числовых и алгебраических выражений и уравнений
Индикатор: использование переменных для представления величин в реальной или математической задаче и построение простых уравнений и неравенства для решения проблем, рассуждая о количествах.
MCCRS.Math.Content.7.EE.B.4a 7 класс
Область обучения: выражения и уравнения
Стандарт: решение реальных и математических задач с использованием числовых и алгебраических выражений и уравнений
Индикатор: решение текстовых задач, приводящих к уравнениям вида px + q = r и p(x + q) = r, где p, q и r — конкретные рациональные числа.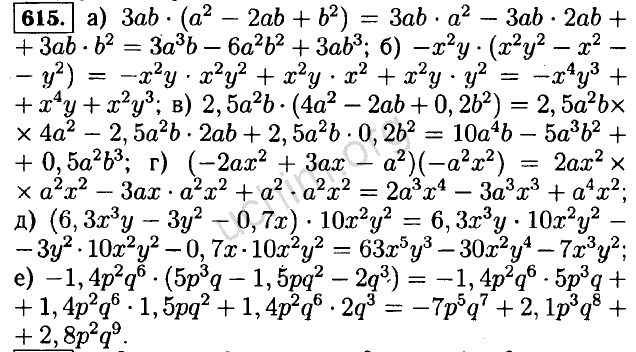 Решите уравнения этих форм бегло. Сравните алгебраическое решение с арифметическим, указав последовательность операций, используемых в каждом подходе. Например, периметр прямоугольника равен 54 см. Его длина составляет 6 см. Какова его ширина?
Решите уравнения этих форм бегло. Сравните алгебраическое решение с арифметическим, указав последовательность операций, используемых в каждом подходе. Например, периметр прямоугольника равен 54 см. Его длина составляет 6 см. Какова его ширина?
MCCRS.Math.Content.7.EE.B.4b 7 класс
Область обучения: выражения и уравнения
Стандарт: решение реальных и математических задач с использованием числовых и алгебраических выражений и уравнений
Индикатор: решение текстовых задач, приводящих к неравенствам вида px + q > r или px + q < r, где p, q и r — конкретные рациональные числа. Нарисуйте график множества решений неравенства и интерпретируйте его в контексте проблемы. Например, как продавец, вам платят 50 долларов в неделю плюс 3 доллара за продажу. На этой неделе вы хотите, чтобы ваша зарплата была не менее 100 долларов. Напишите неравенство для количества продаж, которое вам нужно сделать, и опишите решения.
MCCRS.Math.Practice. MP.1
Классы K-12
MP.1
Классы K-12
Область обучения: Математические практики
Стандарт: Математические практики
Показатель: Разбираться в задачах и настойчиво решать их. Подкованные в математике учащиеся начинают с того, что объясняют себе смысл задачи и ищут пути ее решения. Они анализируют данные, ограничения, отношения и цели. Они строят предположения о форме и значении решения и планируют путь решения, а не просто пытаются найти решение. Они рассматривают аналогичные проблемы и пробуют частные случаи и более простые формы исходной задачи, чтобы получить представление о ее решении. Они контролируют и оценивают свой прогресс и при необходимости меняют курс. Учащиеся постарше могут, в зависимости от контекста задачи, преобразовывать алгебраические выражения или менять окно просмотра на своем графическом калькуляторе, чтобы получить необходимую им информацию. Подкованные в математике учащиеся могут объяснять соответствия между уравнениями, словесными описаниями, таблицами и графиками или рисовать диаграммы важных функций и взаимосвязей, графически отображать данные и искать закономерности или тенденции. Младшие школьники могут полагаться на использование конкретных объектов или изображений, чтобы помочь осмыслить и решить проблему. Подкованные в математике учащиеся проверяют свои ответы на задачи, используя другой метод, и они постоянно спрашивают себя: «Имеет ли это смысл?». Они могут понять подходы других к решению сложных задач и определить соответствие между различными подходами.
Младшие школьники могут полагаться на использование конкретных объектов или изображений, чтобы помочь осмыслить и решить проблему. Подкованные в математике учащиеся проверяют свои ответы на задачи, используя другой метод, и они постоянно спрашивают себя: «Имеет ли это смысл?». Они могут понять подходы других к решению сложных задач и определить соответствие между различными подходами.
MCCRS.Math.Practice.MP.2 Классы K-12
Область обучения: Математические практики
Стандарт: Математические практики
Индикатор: Рассуждать абстрактно и количественно. Учащиеся, обладающие математическими способностями, понимают величины и их отношения в проблемных ситуациях. Студенты привносят две взаимодополняющие способности в решение проблем, связанных с количественными отношениями: способность деконтекстуализировать — абстрагировать данную ситуацию и представлять ее символически и манипулировать репрезентирующими символами, как если бы они жили своей собственной жизнью, не обязательно обращая внимание на свои референты — и способность контекстуализировать, делать паузы по мере необходимости в процессе манипулирования, чтобы исследовать референты для задействованных символов. Количественное рассуждение влечет за собой привычки создавать последовательное представление проблемы; рассмотрение задействованных единиц; обращать внимание на значение величин, а не только на то, как их вычислять; знание и гибкое использование различных свойств операций и объектов.
Количественное рассуждение влечет за собой привычки создавать последовательное представление проблемы; рассмотрение задействованных единиц; обращать внимание на значение величин, а не только на то, как их вычислять; знание и гибкое использование различных свойств операций и объектов.
MCCRS.Math.Practice.MP.3 Классы K-12
Область обучения: Математические практики
Стандарт: Математические практики
Показатель: Придумывать обоснованные аргументы и критиковать рассуждения других. Подкованные в математике учащиеся понимают и используют заявленные предположения, определения и ранее установленные результаты при построении аргументов. Они строят предположения и выстраивают логическую последовательность утверждений, чтобы исследовать истинность своих предположений. Они способны анализировать ситуации, разбивая их на случаи, а также могут распознавать и использовать контрпримеры. Они обосновывают свои выводы, сообщают их другим и отвечают на аргументы других.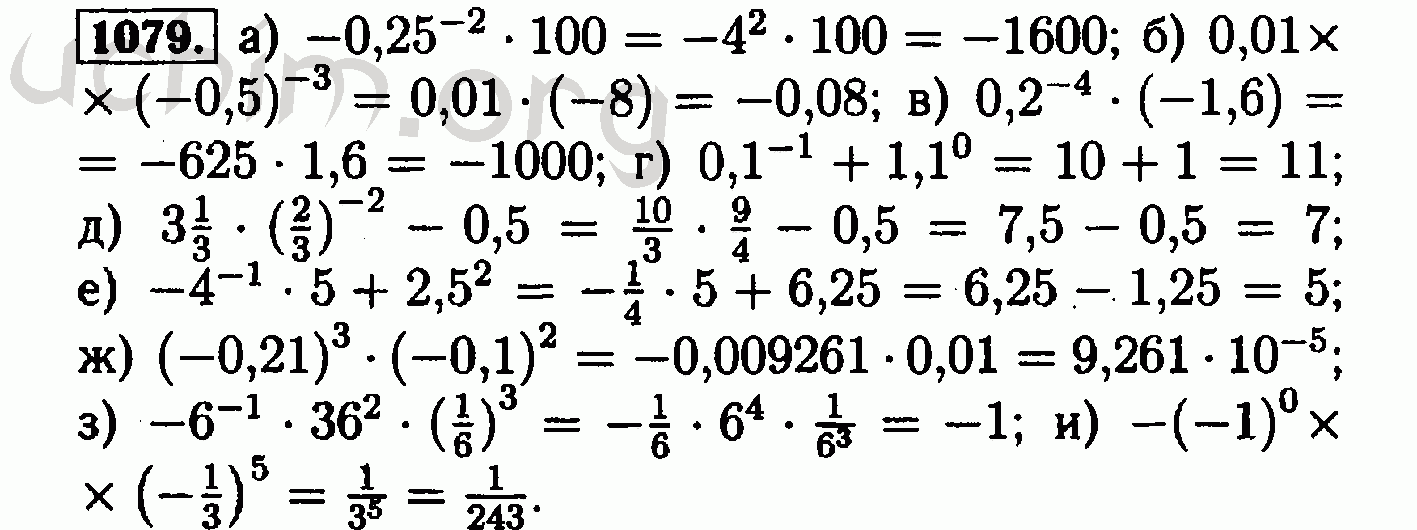 Они индуктивно рассуждают о данных, выдвигая правдоподобные аргументы, учитывающие контекст, из которого эти данные возникли. Подкованные в математике учащиеся также способны сравнивать эффективность двух правдоподобных аргументов, отличать правильную логику или рассуждения от ошибочных и «если в аргументе есть изъян» объяснять, в чем он заключается. Учащиеся начальной школы могут создавать аргументы, используя конкретные референты, такие как объекты, рисунки, диаграммы и действия. Такие аргументы могут иметь смысл и быть правильными, даже если они не обобщаются и не становятся формальными до более поздних классов. Позже учащиеся учатся определять области, к которым применяется аргумент. Учащиеся всех классов могут слушать или читать аргументы других, решать, имеют ли они смысл, и задавать полезные вопросы, чтобы прояснить или улучшить аргументы.
Они индуктивно рассуждают о данных, выдвигая правдоподобные аргументы, учитывающие контекст, из которого эти данные возникли. Подкованные в математике учащиеся также способны сравнивать эффективность двух правдоподобных аргументов, отличать правильную логику или рассуждения от ошибочных и «если в аргументе есть изъян» объяснять, в чем он заключается. Учащиеся начальной школы могут создавать аргументы, используя конкретные референты, такие как объекты, рисунки, диаграммы и действия. Такие аргументы могут иметь смысл и быть правильными, даже если они не обобщаются и не становятся формальными до более поздних классов. Позже учащиеся учатся определять области, к которым применяется аргумент. Учащиеся всех классов могут слушать или читать аргументы других, решать, имеют ли они смысл, и задавать полезные вопросы, чтобы прояснить или улучшить аргументы.
MCCRS.Math.Practice.MP.4 Классы K-12
Область обучения: Математические практики
Стандарт: Математические практики
Индикатор: Модель с математикой. Учащиеся, хорошо разбирающиеся в математике, могут применять математику, которую они знают, для решения проблем, возникающих в повседневной жизни, обществе и на рабочем месте. В младших классах это может быть так же просто, как написать уравнение сложения для описания ситуации. В средних классах учащийся может применять пропорциональные рассуждения, чтобы спланировать школьное мероприятие или проанализировать проблему в сообществе. К старшей школе учащийся может использовать геометрию для решения задачи проектирования или использовать функцию для описания того, как одна интересующая величина зависит от другой. Подкованные в математике учащиеся, которые могут применять то, что они знают, спокойно делают предположения и приближения, чтобы упростить сложную ситуацию, понимая, что позже они могут потребовать пересмотра. Они способны определять важные величины в практической ситуации и отображать их отношения, используя такие инструменты, как диаграммы, двусторонние таблицы, графики, блок-схемы и формулы.
Учащиеся, хорошо разбирающиеся в математике, могут применять математику, которую они знают, для решения проблем, возникающих в повседневной жизни, обществе и на рабочем месте. В младших классах это может быть так же просто, как написать уравнение сложения для описания ситуации. В средних классах учащийся может применять пропорциональные рассуждения, чтобы спланировать школьное мероприятие или проанализировать проблему в сообществе. К старшей школе учащийся может использовать геометрию для решения задачи проектирования или использовать функцию для описания того, как одна интересующая величина зависит от другой. Подкованные в математике учащиеся, которые могут применять то, что они знают, спокойно делают предположения и приближения, чтобы упростить сложную ситуацию, понимая, что позже они могут потребовать пересмотра. Они способны определять важные величины в практической ситуации и отображать их отношения, используя такие инструменты, как диаграммы, двусторонние таблицы, графики, блок-схемы и формулы. Они могут математически анализировать эти отношения, чтобы делать выводы. Они обычно интерпретируют свои математические результаты в контексте ситуации и размышляют о том, имеют ли результаты смысл, возможно, улучшая модель, если она не достигла своей цели.
Они могут математически анализировать эти отношения, чтобы делать выводы. Они обычно интерпретируют свои математические результаты в контексте ситуации и размышляют о том, имеют ли результаты смысл, возможно, улучшая модель, если она не достигла своей цели.
MCCRS.Math.Practice.MP.5 Классы K-12
Область обучения: Математические практики
Стандарт: Математические практики
Индикатор: Стратегически используйте соответствующие инструменты. Подкованные в математике учащиеся рассматривают доступные инструменты при решении математической задачи. Эти инструменты могут включать карандаш и бумагу, конкретные модели, линейку, транспортир, калькулятор, электронную таблицу, систему компьютерной алгебры, статистический пакет или программное обеспечение для динамической геометрии. Профессиональные учащиеся достаточно хорошо знакомы с инструментами, соответствующими их классу или курсу, чтобы принимать обоснованные решения о том, когда каждый из этих инструментов может быть полезен, признавая как получаемое понимание, так и их ограничения. Например, математически подкованные старшеклассники анализируют графики функций и решений, построенные с помощью графического калькулятора. Они обнаруживают возможные ошибки, стратегически используя оценку и другие математические знания. Создавая математические модели, они знают, что технологии позволяют визуализировать результаты различных предположений, исследовать последствия и сравнивать прогнозы с данными. Подкованные в математике учащиеся разных классов способны идентифицировать соответствующие внешние математические ресурсы, такие как цифровой контент, размещенный на веб-сайте, и использовать их для постановки или решения задач. Они могут использовать технологические инструменты для изучения и углубления своего понимания концепций.
Например, математически подкованные старшеклассники анализируют графики функций и решений, построенные с помощью графического калькулятора. Они обнаруживают возможные ошибки, стратегически используя оценку и другие математические знания. Создавая математические модели, они знают, что технологии позволяют визуализировать результаты различных предположений, исследовать последствия и сравнивать прогнозы с данными. Подкованные в математике учащиеся разных классов способны идентифицировать соответствующие внешние математические ресурсы, такие как цифровой контент, размещенный на веб-сайте, и использовать их для постановки или решения задач. Они могут использовать технологические инструменты для изучения и углубления своего понимания концепций.
MCCRS.Math.Practice.MP.6 Классы K-12
Область обучения: математические практики
Стандарт: математические практики
Показатель: внимание к точности. Математически подкованные ученики стараются точно общаться с другими. Они стараются использовать четкие определения в обсуждениях с другими и в собственных рассуждениях. Они заявляют о значении выбранных ими символов, включая последовательное и уместное использование знака равенства. Они внимательно относятся к указанию единиц измерения и маркировке осей, чтобы прояснить соответствие с количествами в задаче. Они рассчитывают точно и эффективно, выражают числовые ответы с точностью, соответствующей контексту задачи. В начальных классах учащиеся дают тщательно сформулированные объяснения друг другу. К тому времени, когда они переходят в старшие классы, они уже научились анализировать утверждения и явно использовать определения.
Они стараются использовать четкие определения в обсуждениях с другими и в собственных рассуждениях. Они заявляют о значении выбранных ими символов, включая последовательное и уместное использование знака равенства. Они внимательно относятся к указанию единиц измерения и маркировке осей, чтобы прояснить соответствие с количествами в задаче. Они рассчитывают точно и эффективно, выражают числовые ответы с точностью, соответствующей контексту задачи. В начальных классах учащиеся дают тщательно сформулированные объяснения друг другу. К тому времени, когда они переходят в старшие классы, они уже научились анализировать утверждения и явно использовать определения.
MCCRS.Math.Practice.MP.7 Классы K-12
Область обучения: Математические практики
Стандарт: Математические практики
Индикатор: Ищите и используйте структуру. Математически подкованные учащиеся внимательно смотрят, чтобы различить закономерность или структуру. Например, учащиеся младшего возраста могут заметить, что три и еще семь — это то же самое, что семь и еще три, или они могут отсортировать набор фигур по количеству сторон у фигур.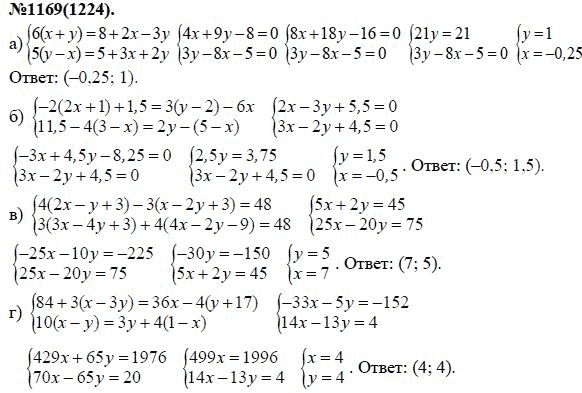 2 + 92 как 5 минус положительное число, умноженное на квадрат, и используйте это, чтобы понять, что его значение не может быть больше 5 для любых действительных чисел x и y.
2 + 92 как 5 минус положительное число, умноженное на квадрат, и используйте это, чтобы понять, что его значение не может быть больше 5 для любых действительных чисел x и y.
MCCRS.Math.Practice.MP.8 Классы K-12
Область обучения: Математические практики
Стандарт: Математические практики
Показатель: Ищите и выражайте регулярность в повторяющихся рассуждениях. Подкованные в математике учащиеся замечают, повторяются ли вычисления, и ищут как общие методы, так и упрощения. Учащиеся старших классов могут заметить, что при делении 25 на 11 они повторяют одни и те же вычисления снова и снова, и прийти к выводу, что у них есть повторяющаяся десятичная дробь. Уделяя внимание вычислению наклона, постоянно проверяя, находятся ли точки на прямой, проходящей через (1, 2) с наклоном 3, учащиеся средней школы могут абстрагироваться от уравнения (y — 2)/(x -1) = 3. Заметив регулярность в том, как члены сокращаются при расширении (x — 1) (x + 1), (x — 1) (x ^ 2 + x + 1) и (x — 1) (x ^ 3 + x ^ 2 + x + 1) может привести их к общей формуле суммы геометрического ряда.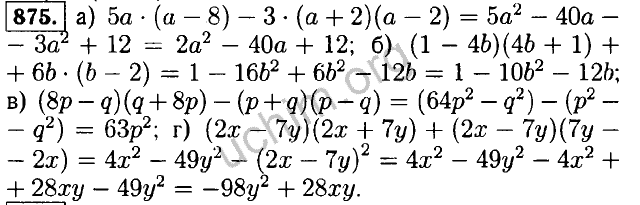 Работая над решением задачи, математически подкованные ученики контролируют процесс, уделяя внимание деталям. Они постоянно оценивают обоснованность своих промежуточных результатов.
Работая над решением задачи, математически подкованные ученики контролируют процесс, уделяя внимание деталям. Они постоянно оценивают обоснованность своих промежуточных результатов.
M/J Ускоренный курс математики, 7 класс — 1205050
Теорема Пифагора. Часть 3:
Используйте теорему Пифагора, чтобы найти стороны прямоугольного треугольника в математическом и реальном контексте в этом интерактивном учебном пособии.
Это третья часть из трех частей. Щелкните ниже, чтобы ознакомиться с другими руководствами из этой серии.
- Теорема Пифагора. Часть 1
- Теорема Пифагора. Часть 2
Тип: оригинальное учебное пособие для учащихся
Теорема Пифагора. Часть 2:
Используйте теорему Пифагора, чтобы найти гипотенузу прямоугольного треугольника в математическом и реальном контекстах в этом интерактивном руководстве.
Это вторая часть из трех частей. Щелкните ниже, чтобы ознакомиться с другими руководствами из этой серии.
Щелкните ниже, чтобы ознакомиться с другими руководствами из этой серии.
- Теорема Пифагора. Часть 1
- Теорема Пифагора. Часть 3
Тип: оригинальное учебное пособие для учащихся
Как текстовые разделы передают цель автора:
Изучите выдержки из необычной автобиографии Повествование о жизни Фредерика Дугласа , исследуя цель написания автора и использование им структуры текста задачи и решения. К концу этого урока вы должны быть в состоянии объяснить, как Дуглас использует структуру текста задачи и решения в этих отрывках, чтобы передать цель своего письма.
Тип: Оригинальное учебное пособие для учащихся
Теорема Пифагора. Часть 1:
В этом интерактивном учебном пособии вы узнаете, что означают теорема Пифагора и ее обращение, а также что такое пифагорейские тройки.
Это первая часть из трех частей. Щелкните ниже, чтобы ознакомиться с другими руководствами из этой серии.
- Теорема Пифагора. Часть 2
- Теорема Пифагора. Часть 3
Тип: Оригинальное учебное пособие для студентов
Рискованные ставки: анализ универсальной темы (часть третья):
Погрузитесь глубже в знаменитый рассказ Антона Чехова «Пари» и изучите влияние пятнадцатилетнего пари, заключенного между юрист и банкир.
В третьей части вы узнаете об универсальных темах и объясните, как конкретная универсальная тема развивается в «Ставке».
Обязательно завершите первые две части серии до начала третьей части . Нажмите ЗДЕСЬ , чтобы просмотреть первую часть. Нажмите ЗДЕСЬ , чтобы просмотреть вторую часть.
Тип: оригинальное учебное пособие для учащихся
Анализ использования автором сопоставления в «Джейн Эйр» (часть вторая):
Во второй части этой серии из двух частей вы продолжите изучение отрывков из романтического романа Джейн Эйр Шарлотта Бронте. В этом уроке вы изучите использование автором сопоставления, которое представляет собой метод размещения двух или более элементов рядом, чтобы вызвать сравнение или противопоставление. К концу этого руководства вы должны быть в состоянии объяснить, как автор использует сопоставление в отрывках из первых двух глав Джейн Эйр определяет точку зрения Джейн на обращение с ней в семье Ридов.
В этом уроке вы изучите использование автором сопоставления, которое представляет собой метод размещения двух или более элементов рядом, чтобы вызвать сравнение или противопоставление. К концу этого руководства вы должны быть в состоянии объяснить, как автор использует сопоставление в отрывках из первых двух глав Джейн Эйр определяет точку зрения Джейн на обращение с ней в семье Ридов.
Обязательно завершите первую часть, прежде чем начинать вторую. Нажмите ЗДЕСЬ , чтобы просмотреть первую часть.
Тип: Оригинальное учебное пособие для учащихся
Выявление риторических обращений в «Похвальной речи о собаке» (Часть вторая):
Продолжайте изучать речь Джорджа Веста «Похвальная речь о собаке» и его использование риторических обращений. Во второй части этой серии из двух частей вы узнаете, как он использует этос и пафос на протяжении всей своей речи.
Обязательно завершите первую часть до начала второй части .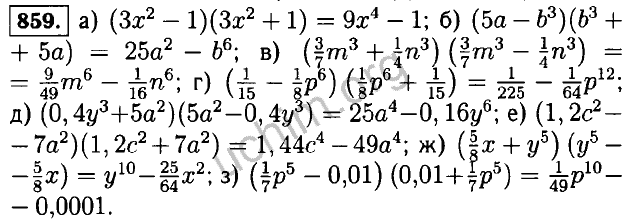 Нажмите ЗДЕСЬ , чтобы запустить первую часть.
Нажмите ЗДЕСЬ , чтобы запустить первую часть.
Тип: Оригинальное учебное пособие для учащихся
Определение риторических призывов в «Похвальной речи о собаке» (часть первая):
Прочитайте речь Джорджа Веста «Похвальная речь о собаке» в этом интерактивном учебном пособии, состоящем из двух частей. В этой серии вы узнаете и исследуете использование Вестом этоса, пафоса и логоса в его речи. В первой части вы узнаете, как Вест использовал логотипы в первой части своей речи. Во второй части вы узнаете, как он использует этос и пафос в своей речи.
Обязательно выполните обе части этой серии! Нажмите ЗДЕСЬ , чтобы запустить вторую часть.
Тип: Оригинальное учебное пособие для учащихся
Квадратный корень, часть 3. Упрощение радикалов:
В этом интерактивном учебном пособии вы узнаете, как упростить радикалы.
Тип: оригинальное учебное пособие для учащихся
Квадратный корень, часть 2: несовершенные квадраты:
Узнайте, что такое несовершенные квадраты, и найдите десятичную аппроксимацию их квадратных корней в этом интерактивном учебном пособии.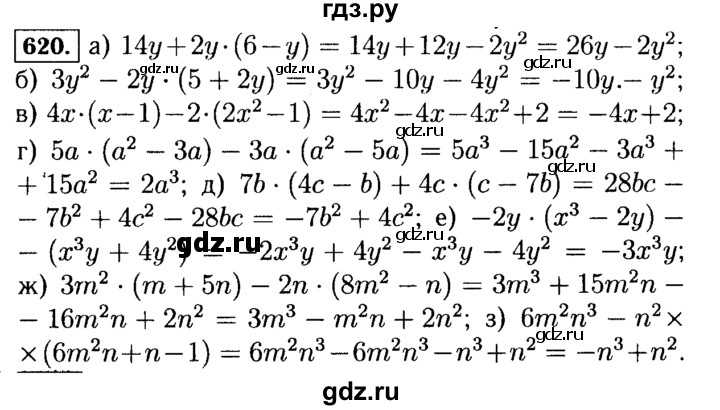
Тип: Оригинальное учебное пособие для учащихся
Это так эпично: как эпические сравнения влияют на настроение (часть вторая):
Продолжайте изучать эпические сравнения в отрывках из «Илиада» во второй части этой серии из двух частей. Во второй части вы узнаете о настроении и о том, как язык эпического сравнения создает определенное настроение в отрывках из «Илиады» .
Обязательно завершите первую часть, прежде чем начинать вторую. Нажмите ЗДЕСЬ , чтобы просмотреть «Это так эпично: как эпические сравнения влияют на настроение (часть первая)».
Тип: оригинальное учебное пособие для учащихся
Это так эпично: как эпические сравнения влияют на настроение (часть первая):
Узнайте о том, как эпические сравнения создают настроение в тексте, особенно в отрывках из Илиады , в этом двух- часть серии.
В первой части вы определите эпическое сравнение, определите эпическое сравнение на основе определенных характеристик и объясните сравнение, созданное в эпическом сравнении.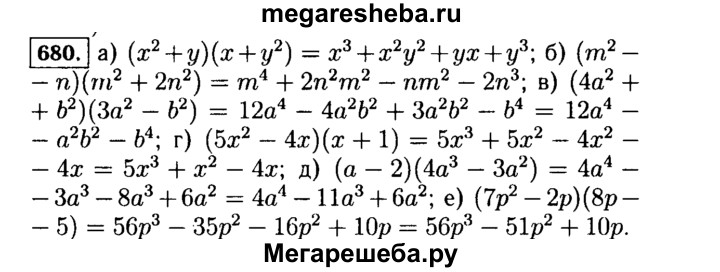
Во второй части вы узнаете о настроении и о том, как язык эпического сравнения создает определенное настроение в отрывках из Илиада . Обязательно выполните обе части!
Нажмите ЗДЕСЬ , чтобы просмотреть «Это так эпично: как эпические сравнения влияют на настроение (часть вторая)».
Тип: Оригинальное учебное пособие для учащихся
Квадратный корень Часть 1: Совершенные квадраты:
Узнайте, что такое идеальные квадраты, и найдите их квадратные корни в этом интерактивном учебном пособии.
Тип: оригинальное учебное пособие для учащихся
Рискованные ставки: текстовые доказательства и выводы (часть вторая):
Тип: оригинальное учебное пособие для учащихся
Рискованные ставки: текстовые доказательства и выводы (часть первая):
Прочтите знаменитый рассказ Антона Чехова «Пари» и узнайте о влиянии пятнадцатилетнего пари, заключенного между юристом и банкиром, в этой трехчастной книге. обучающая серия.
обучающая серия.
В первой части вы будете цитировать текстовые свидетельства, подтверждающие анализ того, что в тексте говорится явно или прямо, а также делать выводы и подтверждать их текстовыми свидетельствами. К концу первой части вы должны быть в состоянии сделать три вывода о том, как пари изменило адвоката к середине истории, и подкрепить свои выводы текстовыми свидетельствами.
Обязательно выполните все три части!
Нажмите ЗДЕСЬ , чтобы запустить «Рискованные ставки: текстовые доказательства и выводы (часть вторая)».
Нажмите ЗДЕСЬ , чтобы запустить «Рискованные ставки: анализ универсальной темы (часть третья)».
Тип: оригинальное учебное пособие для учащихся
Анализ звука в стихотворении По «Ворон»:
Определите рифму, аллитерацию и повторение в произведении Эдгара Аллана По «Ворон» и проанализируйте, как использовались эти звуковые приемы для воздействия на стихотворение в этом интерактивном руководство.
Тип: Оригинальное учебное пособие для учащихся
Экспоненциальное представление: Выражение больших величин:
В этом интерактивном учебном пособии вы узнаете, как выразить большие количества с помощью экспоненциального представления.
Тип: оригинальное учебное пособие для учащихся
На водительском сиденье: взаимодействие персонажей в «Маленьких женщинах»:
Изучите отрывки из классического американского романа « Маленькие женщины » Луизы Мэй Олкотт в этом интерактивном учебном пособии по английскому языку. Используя выдержки из восьмой главы Маленькие женщины, вы узнаете ключевых персонажей и их действия. Вы также объясните, как взаимодействие между персонажами способствует развитию сюжета.
Тип: Оригинальное учебное пособие для учащихся
Что значит подарить подарок: как аллюзии влияют на смысл книги «Дар волхвов»:
Изучите, как аллюзии влияют на смысл отрывков из классического американского рассказа О. Генри « Дар волхвов». В этом интерактивном учебном пособии вы определите, как аллюзии в тексте лучше раскрывают ключевые сюжетные элементы сеттинга, персонажей и конфликта, а также объясните, как аллюзия на волхвов способствует основной идее истории о том, что это значит подарить
Генри « Дар волхвов». В этом интерактивном учебном пособии вы определите, как аллюзии в тексте лучше раскрывают ключевые сюжетные элементы сеттинга, персонажей и конфликта, а также объясните, как аллюзия на волхвов способствует основной идее истории о том, что это значит подарить
Тип: оригинальное учебное пособие для учащихся
Анализ образов в «Сонете 18» Шекспира:
Научитесь определять образы в «Сонете 18» Уильяма Шекспира и объясните, как эти образы влияют на смысл стихотворения, с помощью этого интерактивного руководства.
Тип: Оригинальное учебное пособие для учащихся
Сравнение универсальных тем в «Сонете 18» Шекспира:
Изучите «Сонет 18» Уильяма Шекспира, чтобы определить и сравнить две универсальные темы и то, как они развиваются на протяжении всего сонета.
Тип: оригинальное учебное пособие для учащихся
Как форма влияет на значение «Сонета 18» Шекспира:
Изучите форму и значение «Сонета 18» Уильяма Шекспира. В этом интерактивном руководстве вы изучите, как определенные слова и фразы влияют на значение сонета, выберете особенности шекспировского сонета в стихотворении, определите решение проблемы и объясните, как форма шекспировского сонета способствует значение «Сонета 18».
В этом интерактивном руководстве вы изучите, как определенные слова и фразы влияют на значение сонета, выберете особенности шекспировского сонета в стихотворении, определите решение проблемы и объясните, как форма шекспировского сонета способствует значение «Сонета 18».
Тип: Оригинальное учебное пособие для учащихся
Анализ универсальных тем в «Даре волхвов»:
Проанализируйте, как О. Генри использует детали для рассмотрения тем ценности, жертвенности и любви в своем знаменитом рассказе «Дар» волхвов». В этом интерактивном уроке вы также определите две универсальные темы истории.
Тип: оригинальное учебное пособие для учащихся
Взаимодействие элементов повествования в «Даре волхвов» — часть вторая:
Исследуйте ключевые элементы повествования в других отрывках из классического американского рассказа «Дар волхвов» О. Генри
Во второй части этой серии, состоящей из двух частей, вы проанализируете, как важная информация о двух главных героях раскрывается в контексте сюжета и сюжетных событий.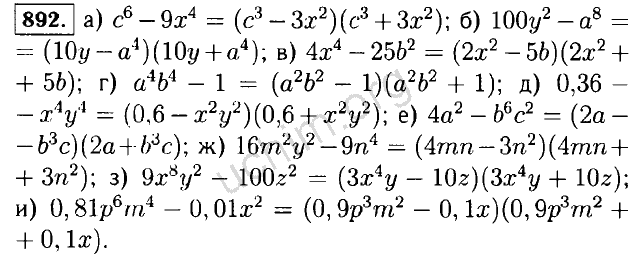 К концу этого урока вы должны быть в состоянии объяснить, как развитие персонажа, сеттинг и сюжет взаимодействуют в «Даре волхвов».
К концу этого урока вы должны быть в состоянии объяснить, как развитие персонажа, сеттинг и сюжет взаимодействуют в «Даре волхвов».
Обязательно завершите первую часть, прежде чем начинать вторую. Нажмите ЗДЕСЬ, чтобы запустить первую часть.
Тип: Оригинальное учебное пособие для учащихся
Взаимодействие элементов истории в «Даре волхвов» — часть первая:
Изучите ключевые элементы классической американской новеллы «Дар волхвов» О. Генри. В этом руководстве, состоящем из двух частей, вы проанализируете, как важная информация о двух главных героях раскрывается в контексте сюжета и сюжетных событий. К концу этой серии руководств вы должны быть в состоянии объяснить, как развитие персонажа, сеттинг и сюжет взаимодействуют в отрывках из этого короткого рассказа.
Обязательно заполните обе части! Нажмите ЗДЕСЬ, чтобы просмотреть «Как взаимодействуют элементы истории в «Даре волхвов» — часть вторая».
Тип: оригинальное учебное пособие для учащихся
Архетипы. Часть вторая: Изучение архетипов в «Принцессе и гоблине»:
Часть вторая: Изучение архетипов в «Принцессе и гоблине»:
Узнайте больше из фантастического романа Джорджа Макдональда « Принцесса и гоблин » во второй части этой серии из трех частей. . К концу этого урока вы сможете сравнить и сопоставить архетипы двух персонажей романа.
Обязательно заполните все три части этой серии, чтобы сравнить и сопоставить использование архетипов в двух текстах. 9.
Нажмите ЗДЕСЬ , чтобы просмотреть «Архетипы. Часть третья: сравнение и противопоставление архетипов в двух фэнтезийных историях».
Тип: оригинальное учебное пособие для учащихся
Архетипы. Часть первая: Изучение архетипа в «Принцессе и гоблине»:
Научитесь определять важные черты главной героини по имени Принцесса Ирэн в отрывках из фантастического романа Принцесса и гоблин Джорджа Макдональда. В этом интерактивном руководстве вы также определите ее архетип и объясните, как текстовые подробности о ее характере поддерживают ее архетип.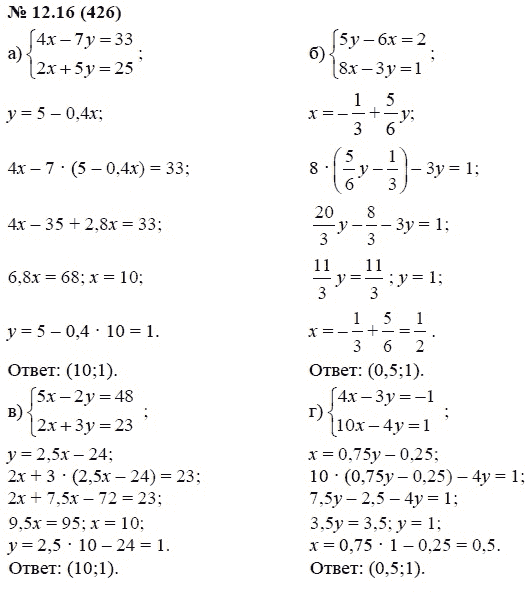
Обязательно заполните все три части этой серии, чтобы сравнить и сопоставить использование архетипов в двух текстах.
Нажмите ЗДЕСЬ , чтобы просмотреть «Архетипы. Часть вторая: изучение архетипов в Принцессе и гоблине». »
Нажмите ЗДЕСЬ для просмотра «Архетипы. Часть третья: сравнение и противопоставление архетипов в двух фэнтезийных историях».
Тип: Оригинальное учебное пособие для учащихся
Способность исцелять или наносить ущерб: важность настройки в «Желтых обоях» — часть первая:
Обои», леденящий душу рассказ Шарлотты Перкинс Гилман, в котором исследуется влияние на рассказчика того, что он ограничен в основном одной комнатой. Вы также определите, как описания рассказчиком обстановки рассказа лучше раскрывают ее эмоциональное и психическое состояние. Этот интерактивный учебник является первой частью серии из двух частей. К концу второй части вы должны быть в состоянии объяснить, как рассказчик меняется благодаря своему взаимодействию с обстановкой.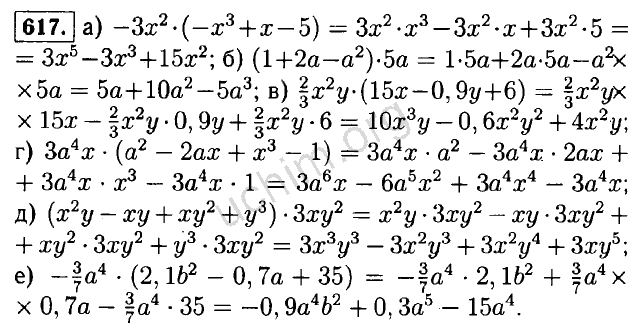 Нажмите ниже, чтобы запустить вторую часть.
Нажмите ниже, чтобы запустить вторую часть.
Способность исцелять или наносить ущерб: важность настройки в «Желтых обоях» — часть вторая
Тип: оригинальное учебное пособие для учащихся
Способность лечить или наносить ущерб: важность настройки в «Желтых обоях» » — Часть вторая:
Продолжайте изучать несколько отрывков из леденящего душу рассказа Шарлотты Перкинс Гилман «Желтые обои», в котором исследуется влияние на рассказчика того, что он заперт в основном в одной комнате. Во второй части этой серии руководств вы определите, как описания рассказчиком места действия рассказа показывают его влияние на ее эмоциональное и психическое состояние. К концу этого урока вы должны быть в состоянии объяснить, как рассказчик меняется при взаимодействии с окружением.
Обязательно выполните первую часть до , начало второй части. Нажмите ЗДЕСЬ , чтобы запустить «Сила лечения или ухудшения: важность настройки в «Желтых обоях» – часть первая».
Тип: оригинальное учебное пособие для учащихся
Тайна прошлого: как форма вилланеллы влияет на смысл «Дома на холме»:
Исследуйте загадочную поэму Эдвина Арлингтона Робинсона «Дом на холме» в этом интерактивном уроке. Исследуя послание стихотворения о прошлом, вы определите черты вилланеллы в стихотворении. К концу этого урока вы должны быть в состоянии объяснить, как форма вилланеллы влияет на смысл стихотворения.
Тип: Оригинальное учебное пособие для учащихся
Углы игровой площадки, часть 1:
Вместе с Джейкобом исследуйте взаимодополняющие и дополнительные углы игровой площадки в этом интерактивном учебном пособии.
Это первая часть из двух частей. Нажмите ЗДЕСЬ, чтобы открыть Углы игровой площадки: часть 2.
Тип: оригинальное учебное пособие для учащихся
Углы игровой площадки: часть 2:
Помогите Джейкобу написать и решить уравнения, чтобы найти отсутствующие угловые меры на основе взаимосвязи между углами, сумма которых равна 90 градусов и 180 градусов в этом интерактивном учебном пособии на тему игровой площадки.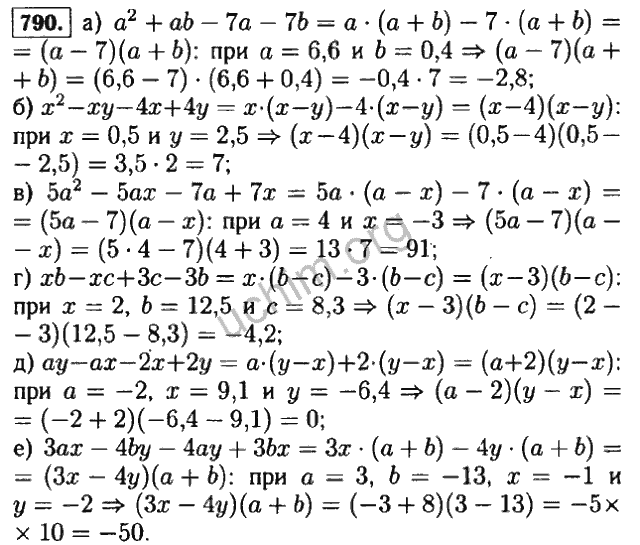
Это вторая часть серии из двух частей. Нажмите ЗДЕСЬ , чтобы открыть Playground Angles: Часть 1.
Тип: Оригинальное учебное пособие для учащихся
Гигант размера и силы. Часть вторая: Как форма сонета влияет на смысл в «Новом колоссе»:
Продолжить изучить значение знаменитой поэмы «Новый Колосс» Эммы Лазарус, строки из которой выгравированы на постаменте Статуи Свободы.
Во второй части этой серии из двух частей вы узнаете особенности сонета в поэме «Новый Колосс». К концу этого урока вы должны быть в состоянии объяснить, как форма сонета влияет на смысл стихотворения.
Обязательно завершите первую часть до начала второй части .
Нажмите ЗДЕСЬ , чтобы запустить «Гигант размера и мощи. Часть первая: изучение значения «Нового колосса»».
Тип: оригинальное учебное пособие для учащихся
Анализ начала «Красного зонта» — часть вторая: как сеттинг влияет на персонажей:
Продолжайте изучать, как сеттинг влияет на персонажей в отрывках из «Красный зонт» Кристины Диас Гонсалес с помощью этого интерактивного руководства.
Это вторая часть серии из двух частей. Обязательно сначала выполните первую часть. Нажмите ЗДЕСЬ , чтобы запустить «Анализ начала Красный зонтик — Часть первая: как обстановка влияет на события».
Тип: Оригинальное учебное пособие для учащихся
Гигант размера и мощи — Часть первая: Изучение значения «Нового колосса»:
В первой части исследуйте значение знаменитого стихотворения «Новый колосс» Эммы Лазаря, линии которого выгравированы на постаменте Статуи Свободы.
Это известное стихотворение тоже написано в форме сонета. Во второй части этой серии из двух частей вы определите черты сонета в стихотворении. К концу этой серии руководств вы должны быть в состоянии объяснить, как форма сонета влияет на смысл стихотворения. Обязательно выполните обе части!
Нажмите ЗДЕСЬ, , чтобы запустить «Гигант размера и силы. Часть вторая: как форма сонета влияет на смысл в «Новом колоссе». Красный зонт – часть первая: как обстановка влияет на события:
Красный зонт – часть первая: как обстановка влияет на события:
В этой серии из двух частей изучите отрывки из начала исторического фантастического романа Кристины Диас Гонсалес « Красный зонт ». В первой части вы изучите, как сеттинг влияет на события. Во второй части вы исследуете, как сеттинг влияет на персонажей.
Обязательно заполните обе части! Нажмите ЗДЕСЬ , чтобы запустить вторую часть.
Тип: Оригинальное учебное пособие для учащихся
Функции, повсюду функции: Часть 1:
Что такое функция? Где мы видим функции в реальной жизни? Изучите эти и другие вопросы, используя различные контексты, в этом интерактивном руководстве.
Это первая часть из двух статей о функциях. Нажмите ЗДЕСЬ, чтобы открыть часть 2.
Тип: Оригинальное учебное пособие для учащихся
Физические науки Раздел: Водные пляжные каникулы, урок 17 Видео:
Это видео SaM-1 предлагает учащимся дополнительный «изюминку» для Урока 17 и задания по выявлению модели (MEA), над которым они работали в 3-м классе раздела «Физические науки: Каникулы на воде и пляже».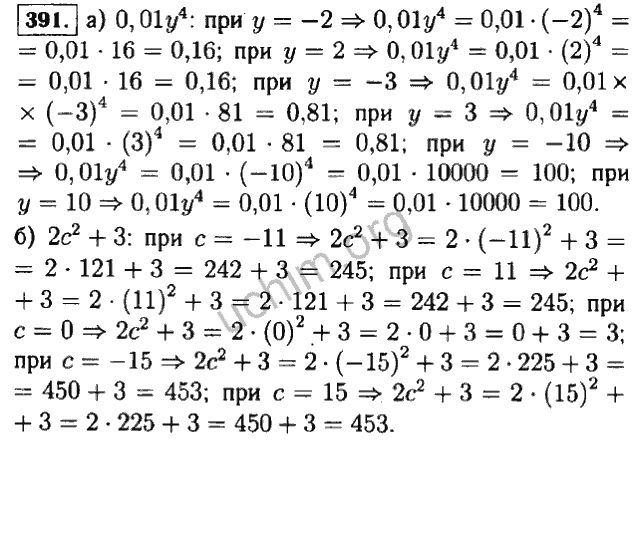
Чтобы просмотреть все уроки этого модуля, посетите https://www.cpalms.org/page818.aspx.
Тип: оригинальное учебное пособие для учащихся
Физические науки Раздел: отпуск на воде, пляж, урок 14 Видео:
Изменения, которым подвергается вода, когда она меняет свое состояние. Этот MEA предоставляет учащимся возможность разработать на основе фактических данных процедуру выбора наиболее эффективного охладителя.
Это видео SaM-1 должно быть использовано с уроком 14 в разделе физико-математических наук 3 класса: Каникулы на воде и пляже. Чтобы просмотреть все уроки этого модуля, посетите https://www.cpalms.org/page818.aspx.
Тип: оригинальное учебное пособие для учащихся
Дом на дереве Хейли: похожие треугольники и наклон:
Узнайте, как похожие прямоугольные треугольники могут показать, что наклон между любыми двумя различными точками на невертикальной линии одинаков, помогая Хейли строить лестницы ее дом на дереве в этом интерактивном руководстве.
Тип: оригинальное учебное пособие для учащихся
Математические модели и социальное дистанцирование:
Узнайте, как математические модели могут показать, почему социальное дистанцирование во время эпидемии или пандемии важно, из этого интерактивного учебного пособия.
Тип: оригинальное учебное пособие для учащихся
Построение функций по двум точкам:
С помощью этого интерактивного учебного пособия вы научитесь строить функцию для моделирования линейной зависимости между двумя величинами и определять наклон и точку пересечения по оси Y для двух точек, представляющих функцию.
Тип: оригинальное учебное пособие для учащихся
Многошаговые уравнения: часть 5. Сколько решений?:
Из этого интерактивного руководства вы узнаете, как уравнения могут иметь 1 решение, не иметь решения или иметь бесконечно много решений.
Это пятая из пяти статей серии о решении многошаговых уравнений.
- Нажмите ЗДЕСЬ , чтобы открыть Часть 1: Объединение похожих терминов
- Нажмите ЗДЕСЬ , чтобы открыть Часть 2: Распространяемое свойство
- Нажмите ЗДЕСЬ , чтобы открыть часть 3: переменные на обеих сторонах
- Нажмите ЗДЕСЬ , чтобы открыть Часть 4: Собираем все вместе
- [ТЕКУЩЕЕ РУКОВОДСТВО] Часть 5. Сколько решений?
Тип: оригинальное учебное пособие для учащихся
Многошаговые уравнения: часть 4 Собираем все вместе:
Изучите альтернативные методы решения многошаговых уравнений в этом интерактивном учебном пособии.
Это пятая из пяти статей серии о решении многошаговых уравнений.
- Нажмите ЗДЕСЬ , чтобы открыть Часть 1: Объединение похожих терминов
- Нажмите ЗДЕСЬ , чтобы открыть Часть 2: Распространяемое свойство
- Нажмите ЗДЕСЬ , чтобы открыть Часть 3: Переменные на обеих сторонах
- [ТЕКУЩЕЕ РУКОВОДСТВО] Часть 4.
 Собираем все вместе
Собираем все вместе - Нажмите ЗДЕСЬ , чтобы открыть Часть 5: Сколько решений?
Тип: оригинальное учебное пособие для учащихся
Многошаговые уравнения: часть 3 Переменные с обеих сторон:
В этом интерактивном учебном пособии вы узнаете, как решать многошаговые уравнения, содержащие переменные в обеих частях уравнения.
Это пятая из пяти статей серии о решении многошаговых уравнений.
- Нажмите ЗДЕСЬ , чтобы открыть Часть 1: Объединение похожих терминов
- Нажмите ЗДЕСЬ , чтобы открыть Часть 2: Распространяемое свойство
- [ТЕКУЩЕЕ РУКОВОДСТВО] Часть 3. Переменные на обеих сторонах
- Нажмите ЗДЕСЬ , чтобы открыть Часть 4. Собираем все вместе
- Нажмите ЗДЕСЬ , чтобы открыть Часть 5: Сколько решений?
Тип: оригинальное учебное пособие для учащихся
Многошаговые уравнения: часть 2 Распределительное свойство:
В этом интерактивном учебном пособии вы узнаете, как решать многошаговые уравнения с использованием распределительного свойства.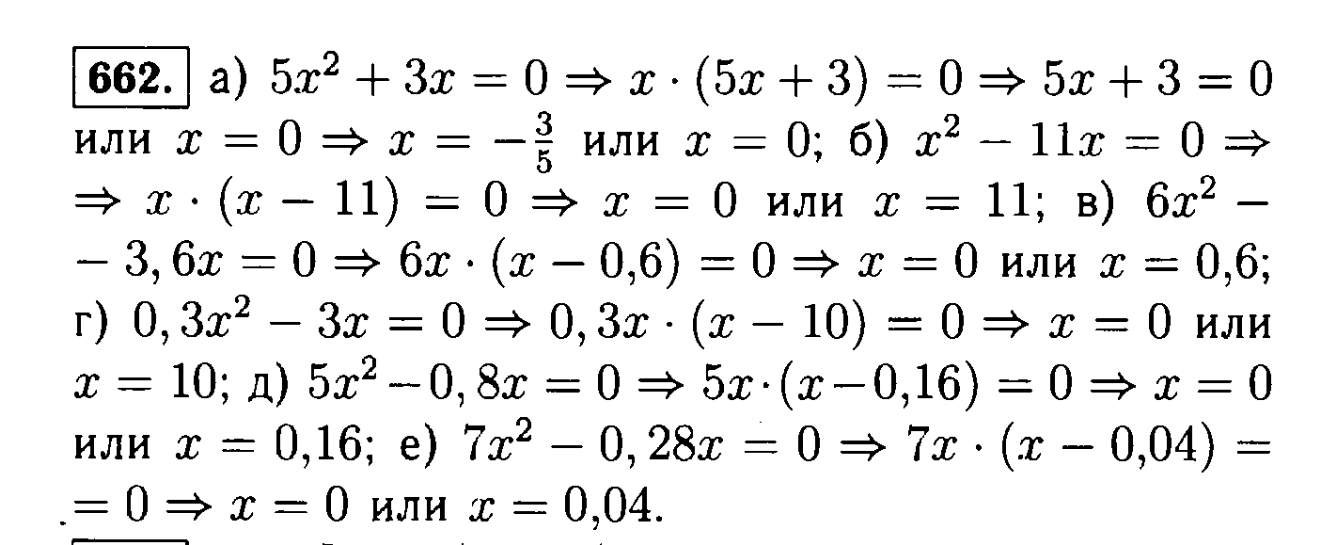
Это вторая из пяти частей серии о решении многошаговых уравнений.
- Нажмите ЗДЕСЬ , чтобы открыть Часть 1: Объединение похожих терминов
- [ТЕКУЩЕЕ РУКОВОДСТВО] Часть 2: Распространяемое свойство
- Нажмите ЗДЕСЬ , чтобы открыть Часть 3: Переменные на обеих сторонах
- Нажмите ЗДЕСЬ , чтобы открыть Часть 4: Собираем все вместе
- Нажмите ЗДЕСЬ , чтобы открыть Часть 5: Сколько решений?
Тип: Оригинальное учебное пособие для учащихся
Путешествие по функциям:
Путешествуйте, узнавая, как качественно описать функции в этом интерактивном учебном пособии.
Тип: оригинальное учебное пособие для учащихся
Многошаговые уравнения: часть 1. Объединение одинаковых членов:
В этом интерактивном учебнике вы узнаете, как решать многошаговые уравнения, содержащие одинаковые члены.
Это первая из пяти статей серии о решении многошаговых уравнений.
- [ТЕКУЩЕЕ РУКОВОДСТВО] Часть 1: Объединение похожих терминов
- Нажмите ЗДЕСЬ , чтобы открыть Часть 2: Распространяемое свойство
- Нажмите ЗДЕСЬ , чтобы открыть часть 3: переменные на обеих сторонах
- Нажмите ЗДЕСЬ , чтобы открыть Часть 4: Собираем все вместе
- Нажмите ЗДЕСЬ , чтобы открыть Часть 5: Сколько решений?
Тип: Оригинальное учебное пособие для учащихся
Чтение слов с несколькими значениями:
Исследуйте стихотворение Роберта Фроста «Восстановление стены» и исследуйте слова, фразы и строки с несколькими значениями. В этом интерактивном руководстве вы проанализируете, как эти множественные значения могут повлиять на интерпретацию стихотворения читателем.
Тип: Оригинальное учебное пособие для учащихся
Профессор Э.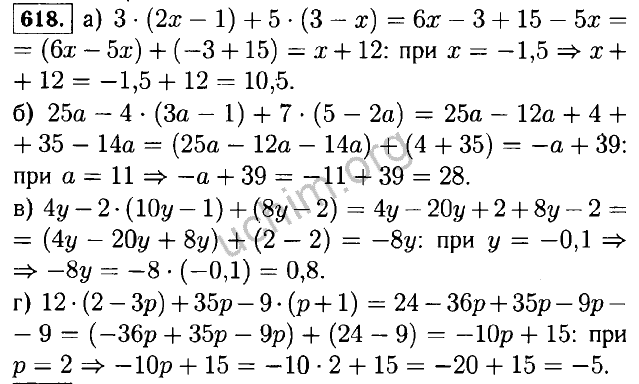 Квал. Часть 2. Двухшаговые уравнения и рациональные числа:
Квал. Часть 2. Двухшаговые уравнения и рациональные числа:
Попрактикуйтесь в решении и проверке двухэтапных уравнений с рациональными числами в этом интерактивном учебном пособии.
Это вторая часть серии статей о двухшаговых уравнениях, состоящей из двух частей. Нажмите ЗДЕСЬ, чтобы открыть Часть 1.
Тип: Оригинальное учебное пособие для учащихся
Профессор Э. Квал. Часть 1: 2-этапные уравнения:
Профессор Э. Квал научит вас решать и проверять двухэтапные уравнения в этом интерактивном руководство.
Это первая часть серии из двух частей о решении двухшаговых уравнений. Нажмите ЗДЕСЬ, чтобы открыть Часть 2.
Тип: Оригинальное учебное пособие для учащихся «Пигмалион» Овидия и рассказ «Родинка» Натаниэля Готорна. К концу этой серии интерактивных руководств, состоящей из двух частей, вы должны быть в состоянии объяснить, как рассказ опирается на исходный материал из оригинального мифа и преобразует его.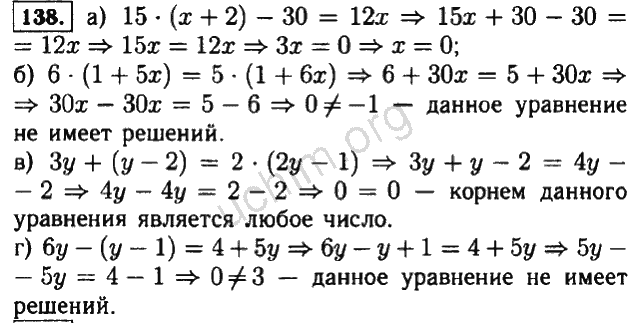
Этот учебник является вторым в серии из двух частей. Нажмите ЗДЕСЬ, чтобы запустить первую часть.
Тип: оригинальное учебное пособие для учащихся
От мифа к рассказу: опираясь на исходный материал — часть первая:
Изучите темы трансформации и совершенства, читая отрывки из «Мифа о Пигмалионе» Овидия и рассказа «Родинка» Натаниэля Хоторна. К концу этой серии интерактивных руководств, состоящей из двух частей, вы должны быть в состоянии объяснить, как рассказ опирается на исходный материал из оригинального мифа и преобразует его.
Это руководство является первым в серии из двух частей. Нажмите ЗДЕСЬ, чтобы запустить вторую часть.
Тип: Оригинальное учебное пособие для учащихся
Функции, удобные функции:
Посмотрите, как приятно определять наклон линейных функций и сравнивать их в этом интерактивном учебном пособии. Определите и сравните наклоны или скорости изменения, используя словесные описания, таблицы значений, уравнения и графические формы.
Тип: оригинальное учебное пособие для учащихся
Балансировка машины:
Используйте модели для решения проблем балансировки на космической станции в этом интерактивном учебном пособии по математике и естественным наукам.
Тип: Оригинальный учебник для учащихся
Лето FUNctions:
Развлекайтесь с FUNctions! Узнайте, как идентифицировать линейные и нелинейные функции в этом интерактивном руководстве.
Тип: Оригинальное учебное пособие для учащихся
Не занимайтесь плагиатом: ссылайтесь на свои источники!:
Узнайте больше об этом страшном слове— плагиат — в этом интерактивном руководстве речь пойдет о цитировании ваших источников, создании страницы с цитированием работ и предотвращении академической нечестности!
Тип: Оригинальное учебное пособие для учащихся
Управляемые функциями:
Узнайте, как определить, является ли отношение функцией, из этого интерактивного учебного пособия, которое показывает входные данные, выходные данные, уравнения, графики и словесные описания.
Тип: Оригинальный учебник для учащихся
Избегайте плагиата и цитирования источников:
Узнайте больше об этом страшном слове — плагиат — в этом интерактивном руководстве, посвященном цитированию ваших источников и избеганию академической нечестности!
Тип: оригинальное учебное пособие для учащихся
Анализ выбора слов в книге Эмерсона «Уверенность в себе»: Часть 2:
Изучите отрывки из эссе Ральфа Уолдо Эмерсона «Уверенность в себе» в этой серии из двух частей. Это руководство является второй частью. В этом руководстве вы продолжите изучение отрывков из эссе Эмерсона, посвященных теме путешествий. Вы изучите значения слов и определите коннотации конкретных слов. Вы также проанализируете влияние выбора конкретных слов на значение этой части эссе.
Обязательно сначала выполните первую часть. Нажмите ЗДЕСЬ , чтобы запустить первую часть.
Тип: оригинальное учебное пособие для учащихся
Это скользкий склон!:
Узнайте, что такое уклон в математике и как рассчитать его на графике и с помощью формулы уклона, в этом интерактивном руководстве.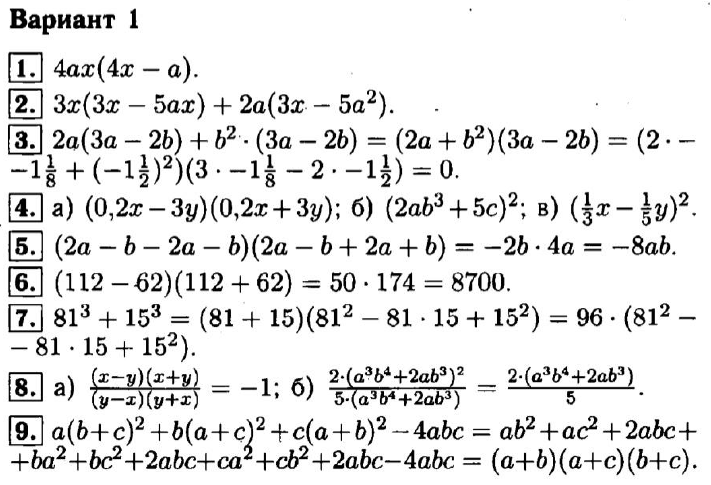
Тип: оригинальное учебное пособие для учащихся
Анализ выбора слов в книге Эмерсона «Уверенность в себе»: часть 1:
Изучите отрывки из эссе Ральфа Уолдо Эмерсона «Уверенность в себе» в этой серии интерактивных учебных пособий, состоящей из двух частей. Вы изучите значения слов, изучите тонкие различия между словами с похожими значениями и подумайте об эмоциях или ассоциациях, связанных с конкретными словами. Наконец, вы проанализируете влияние выбора конкретных слов на значение этих отрывков.
Обязательно заполните обе части! Нажмите ЗДЕСЬ , чтобы запустить вторую часть.
Тип: оригинальное учебное пособие для учащихся
Анализ образного значения в книге Эмерсона «Уверенность в себе»: часть 2:
Изучите отрывки из эссе Ральфа Уолдо Эмерсона «Уверенность в себе» в этом интерактивном учебном пособии, состоящем из двух частей. Это руководство является второй частью. В этой серии из двух частей вы научитесь расширять свои впечатления от эссе Эмерсона, анализируя использование им слова «гений». Вы проанализируете переносное значение слова «гений» у Эмерсона и то, как он развивает и уточняет значение этого слова в ходе эссе.
В этой серии из двух частей вы научитесь расширять свои впечатления от эссе Эмерсона, анализируя использование им слова «гений». Вы проанализируете переносное значение слова «гений» у Эмерсона и то, как он развивает и уточняет значение этого слова в ходе эссе.
Обязательно завершите первую часть, прежде чем начинать вторую. Нажмите ЗДЕСЬ , чтобы просмотреть первую часть.
Тип: оригинальное учебное пособие для учащихся
Анализ образного значения в книге Эмерсона «Уверенность в себе»: часть 1:
Изучите выдержки из эссе Ральфа Уолдо Эмерсона «Уверенность в себе» в этом интерактивном учебном пособии, состоящем из двух частей. В первой части вы научитесь улучшать свое восприятие текста, анализируя использование переносного значения слова. В частности, вы изучите образное значение Эмерсона ключевого термина «гений». Во второй части вы узнаете, как отслеживать развитие переносного значения слова по ходу текста.
Обязательно выполните обе части обучения! Нажмите ЗДЕСЬ , чтобы запустить вторую часть.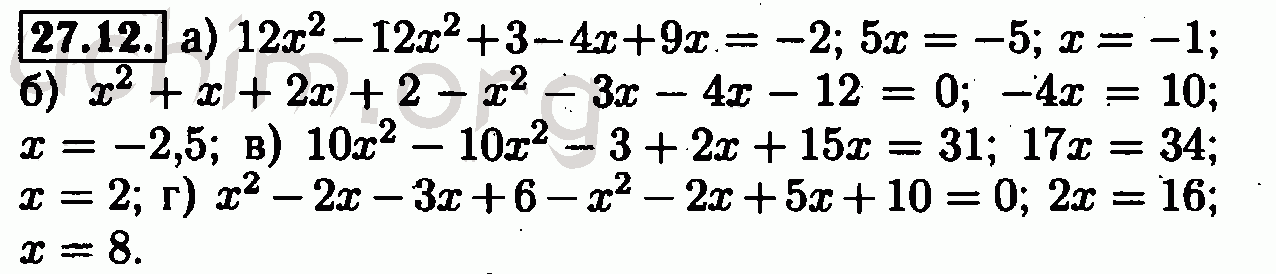
Тип: оригинальное учебное пособие для учащихся
Анализ выбора слов в «Вороне» По — Часть вторая:
Практика анализа выбора слов в «Вороне» Эдгара Аллана По, включая значения слов, тонкие различия между словами с похожими значениями , и эмоции, связанные с конкретными словами. В этом интерактивном уроке вы также проанализируете влияние выбора конкретных слов на смысл стихотворения.
Это вторая часть серии из двух частей. Первая часть должна быть завершена до начала второй части. Нажмите ЗДЕСЬ , чтобы открыть первую часть.
Тип: Оригинальное учебное пособие для учащихся
Анализ выбора слов в «Вороне» По — часть первая:
Попрактикуйтесь в анализе выбора слов в «Вороне» Эдгара Аллана По в этом интерактивном учебном пособии. В этом уроке вы изучите значения слов, исследуете тонкие различия между словами с похожими значениями и подумаете об эмоциях, связанных с конкретными словами. Вы также проанализируете влияние выбора конкретных слов на смысл стихотворения.
Вы также проанализируете влияние выбора конкретных слов на смысл стихотворения.
Это руководство является первой частью серии из двух частей, посвященной роману По «Ворон». Нажмите ЗДЕСЬ, чтобы открыть вторую часть.
Тип: Оригинальное учебное пособие для учащихся
Пицца Пи: Окружность:
Исследуйте происхождение числа Пи как отношение длины окружности к диаметру круга. В этом интерактивном руководстве вы будете работать с формулой длины окружности, чтобы определить длину окружности, и работать в обратном порядке, чтобы определить диаметр и радиус окружности.
Тип: оригинальное учебное пособие для учащихся
Поэма на 2 голоса: Джекил и Хайд:
Узнайте, как создать поэму на 2 голоса, из этого интерактивного руководства. Этот учебник является третьей частью серии из трех частей. В этом уроке вы узнаете, как создать стихотворение в 2 голоса, используя доказательства, взятые из литературного текста: Странная история доктора Джекила и мистера Хайда Роберта Луи Стивенсона.
Прежде чем приступить к третьей части, вы должны пройти первую и вторую части этой серии.
Нажмите ЗДЕСЬ для запуска первой части. Нажмите ЗДЕСЬ , чтобы запустить вторую часть.
Тип: оригинальное учебное пособие для учащихся
Голоса Джекила и Хайда, часть вторая:
Приготовьтесь отправиться в прошлое, в Лондон, Англию, в викторианскую эпоху, в этом интерактивном учебном пособии, в котором используются отрывки из текста Странная история Доктор Джекил и мистер Хайд . Этот учебник является второй частью серии из трех частей. Перед тем, как приступить к этому руководству, вы должны пройти первую часть. Во второй части вы прочтете отрывки из последней половины рассказа и попрактикуетесь в цитировании доказательств в поддержку анализа художественного текста. В третьем уроке этой серии вы узнаете, как создать поэму на два голоса, используя факты из этой истории.
Обязательно выполните все три части! Нажмите, чтобы ЗДЕСЬ запустить первую часть. Нажмите ЗДЕСЬ , чтобы запустить третью часть.
Нажмите ЗДЕСЬ , чтобы запустить третью часть.
Тип: Оригинальное учебное пособие для учащихся
Все о настроении: «Нулевой час» Брэдбери:
Узнайте, как авторы создают настроение в рассказе с помощью этого интерактивного учебного пособия. Вы прочтете научно-фантастический рассказ автора Рэя Брэдбери и проанализируете, как он использует изображения, звук, диалоги, обстановку и действия персонажей для создания различных настроений. Это руководство является первой частью серии из двух частей. Во второй части вы будете использовать историю Брэдбери, чтобы создать «Найденную поэму», которая передает различные настроения.
После завершения первой части нажмите ЗДЕСЬ , чтобы запустить вторую часть.
Тип: Оригинальное учебное пособие для учащихся
Написание пояснения: Глаза в небе (часть 4 из 4):
Попрактикуйтесь в написании различных аспектов пояснительного эссе об ученых, использующих дроны для исследования ледников в Перу. Этот интерактивный учебник является четвертой частью серии из четырех частей. В этом заключительном уроке вы узнаете об элементах основного абзаца. Вы также создадите основной абзац с подтверждающими доказательствами. Наконец, вы узнаете об элементах заключения и попрактикуетесь в создании «подарка».
Этот интерактивный учебник является четвертой частью серии из четырех частей. В этом заключительном уроке вы узнаете об элементах основного абзаца. Вы также создадите основной абзац с подтверждающими доказательствами. Наконец, вы узнаете об элементах заключения и попрактикуетесь в создании «подарка».
Это руководство является четвертой частью серии из четырех частей. Нажмите ниже, чтобы открыть другие руководства из этой серии.
- Дроны и ледники: глаза в небе (часть 1)
- Дроны и ледники: глаза в небе (часть 2)
- Письмо-объяснение: Глаза в небе (часть 3)
- Письмо-объяснение: Глаза в небе (Часть 4)
Тип: оригинальное учебное пособие для учащихся
Голоса Джекила и Хайда, часть первая:
Попрактикуйтесь в цитировании доказательств в поддержку анализа художественного текста, когда вы читаете отрывки из одного из самых известных произведений литературы ужасов всех времен, Странная история доктора Джекила и мистера Хайда.
Это руководство является первой частью руководства, состоящего из трех частей. Во второй части вы продолжите анализ текста. В третьей части вы узнаете, как создать стихотворение на два голоса, используя факты из этой истории. Обязательно выполните все три части!
Нажмите ЗДЕСЬ , чтобы запустить вторую часть. Нажмите ЗДЕСЬ , чтобы запустить третью часть.
Тип: Оригинальное учебное пособие для учащихся
Написание пояснений: Глаза в небе (часть 3 из 4):
Из этого интерактивного руководства вы узнаете, как написать введение для описательного эссе. Этот учебник является третьей частью серии из четырех частей. В предыдущих уроках этой серии учащиеся проанализировали информационный текст и видео об ученых, использующих дроны для исследования ледников в Перу. Студенты также определили центральную идею и важные детали текста и написали эффективное резюме. В третьей части вы узнаете, как написать введение для описательного эссе об исследованиях ученых.
Это руководство является третьей частью серии из четырех частей. Нажмите ниже, чтобы открыть другие руководства из этой серии.
- Дроны и ледники: глаза в небе (часть 1)
- Дроны и ледники: глаза в небе (часть 2)
- Письмо-объяснение: Глаза в небе (часть 3)
- Письмо-объяснение: Глаза в небе (Часть 4)
Тип: оригинальное учебное пособие для учащихся
Понятие движения, часть 2. Положение и время:
Продолжить изучение кинематики для описания линейного движения, сосредоточив внимание на измерениях положения-времени из испытания движения в части 1. В этом интерактивном руководстве вы определите измерения положения по искровой ленте, проанализируете диаграмму рассеяния данных положения-времени. , вычислить и интерпретировать наклон на графике положение-время и сделать выводы о средней скорости багги для дюн
Тип: оригинальное учебное пособие для учащихся
Дроны и ледники: глаза в небе (часть 2 из 4):
Узнайте, как определить центральную идею и важные детали текста, а также как написать эффективное резюме в этом интерактивном руководстве. Этот учебник является вторым в серии из четырех частей, в которой рассматривается, как ученые используют дроны для исследования ледников в Перу.
Этот учебник является вторым в серии из четырех частей, в которой рассматривается, как ученые используют дроны для исследования ледников в Перу.
Это руководство является второй частью серии из четырех частей. Нажмите ниже, чтобы открыть другие руководства из этой серии.
- Дроны и ледники: глаза в небе (часть 1)
- Дроны и ледники: глаза в небе (часть 2)
- Письмо-объяснение: Глаза в небе (часть 3)
- Письмо-объяснение: Глаза в небе (Часть 4)
Тип: оригинальное учебное пособие для учащихся
Дроны и ледники: глаза в небе (часть 1 из 4):
Узнайте, как исследователи используют дроны, также называемые беспилотными летательными аппаратами или БПЛА, для изучения ледников в Перу. В этом интерактивном руководстве вы потренируетесь цитировать текстовые доказательства, отвечая на вопросы по тексту.
Это руководство является первой частью серии из четырех частей. Нажмите ниже, чтобы открыть другие руководства из этой серии.
- Дроны и ледники: глаза в небе (часть 1)
- Дроны и ледники: глаза в небе (часть 2)
- Письмо-объяснение: Глаза в небе (часть 3)
- Письмо-объяснение: Глаза в небе (Часть 4)
Тип: Оригинальное учебное пособие для учащихся
Предотвращение плагиата: это не чудо:
Узнайте, как избежать плагиата в этом интерактивном учебном пособии. Вы также узнаете, как следовать стандартному формату цитирования и как оформлять исследовательскую работу в стиле MLA. По пути вы также узнаете о мастере фокусника Гарри Гудини. Этот учебник является второй частью серии из двух частей, посвященных написанию исследований.
Обязательно сначала выполните первую часть. Нажмите, чтобы просмотреть первую часть.
Тип: Оригинальное учебное пособие для учащихся
Алиса в стране математики:
Помогите Алисе узнать, что сложные вероятности могут быть определены с помощью вычислений или рисования древовидных диаграмм в этом интерактивном учебном пособии.
Тип: Оригинальное учебное пособие для студентов
Написание научных исследований: это не чудо:
Узнайте о перефразировании и использовании прямых кавычек в этом интерактивном учебном пособии по написанию научных исследований. По пути вы также узнаете о мастере-фокуснике Гарри Гудини. Этот учебник является первой частью серии из двух частей, поэтому обязательно выполните обе части.
Ознакомьтесь со второй частью — Избегайте плагиата: это не магия здесь.
Тип: Оригинальное учебное пособие для учащихся
Пицца Пи: Площадь:
В этом интерактивном учебном пособии вы узнаете, как вычислить площадь круга в единицах числа Пи и с приближениями числа Пи. Вы также столкнетесь с ситуациями с нестандартными площадями, которые требуют использования формулы площади круга.
Тип: Оригинальное учебное пособие для учащихся
Все дело в настроении: Создание найденного стихотворения:
В этом интерактивном уроке вы узнаете, как создать стихотворение «Найденная книга» с изменяющимся настроением.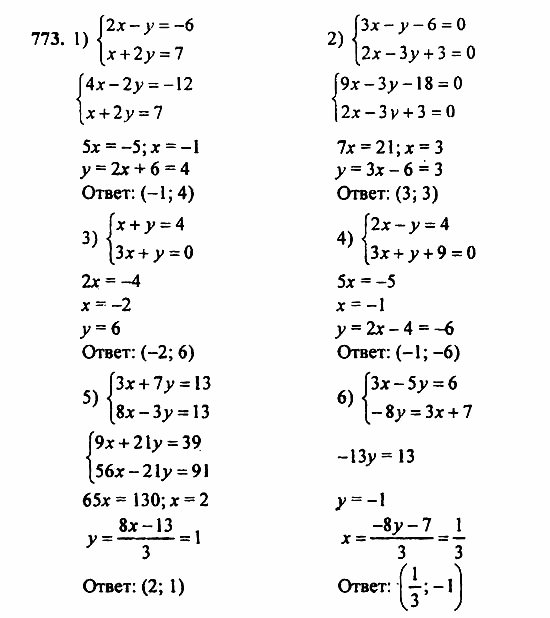 Этот учебник является второй частью серии из двух частей. В первой части учащиеся прочитали «Нулевой час», научно-фантастический рассказ автора Рэя Брэдбери, и рассмотрели, как он использовал различные литературные приемы для создания меняющегося настроения. Во второй части учащиеся будут использовать слова и фразы из «Нулевого часа», чтобы создать «Найденное стихотворение» с двумя одинаковыми настроениями из рассказа Брэдбери.
Этот учебник является второй частью серии из двух частей. В первой части учащиеся прочитали «Нулевой час», научно-фантастический рассказ автора Рэя Брэдбери, и рассмотрели, как он использовал различные литературные приемы для создания меняющегося настроения. Во второй части учащиеся будут использовать слова и фразы из «Нулевого часа», чтобы создать «Найденное стихотворение» с двумя одинаковыми настроениями из рассказа Брэдбери.
Нажмите ЗДЕСЬ , чтобы запустить первую часть.
Тип: Оригинальный учебник для учащихся
Счастливого Хэллоуина! Текстовые свидетельства и выводы:
Приведите текстовые свидетельства и сделайте выводы о «настоящей» истории Хэллоуина в этом жутком интерактивном руководстве.
Тип: Оригинальный учебник для учащихся
Плагиат: что это такое? Как этого избежать?:
Узнайте больше об этом страшном слове — плагиат — в этом интерактивном руководстве, посвященном цитированию ваших источников и избеганию академической нечестности!
Тип: Оригинальный учебник для учащихся
Кибервойна! Ссылаясь на доказательства и делая выводы:
Узнайте, как ссылаться на доказательства и делать выводы в этом интерактивном руководстве. Используя информационный текст о кибератаках, вы потренируетесь находить текстовые доказательства и делать выводы на основе текста.
Используя информационный текст о кибератаках, вы потренируетесь находить текстовые доказательства и делать выводы на основе текста.
Тип: Оригинальное учебное пособие для учащихся
Вперед за золотом: написание утверждений и использование доказательств:
Узнайте, как определять и идентифицировать утверждения, сделанные в тексте. Этот учебник также покажет вам, как можно эффективно использовать доказательства для поддержки сделанного заявления. Наконец, этот учебник поможет вам написать сильные, убедительные собственные заявления.
Тип: Оригинальное учебное пособие для учащихся
Западное направление: изучение доказательств и выводов:
Научитесь находить явные текстовые доказательства и делать выводы на основе текста. В этом интерактивном руководстве вы улучшите свои аналитические навыки, читая о знаменитых американских исследователях Льюисе и Кларке и их надежном спутнике Сакагавее. Вы будете практиковаться в анализе явных текстовых свидетельств в тексте, а также будете делать собственные выводы на основе имеющихся свидетельств.
Вы будете практиковаться в анализе явных текстовых свидетельств в тексте, а также будете делать собственные выводы на основе имеющихся свидетельств.
Тип: Оригинальное учебное пособие для учащихся
Прогнозирование результатов на карнавале:
В этом интерактивном руководстве вы узнаете, как использовать вероятность для прогнозирования ожидаемых результатов на карнавале.
Тип: Оригинальное учебное пособие для учащихся
Дикие слова: анализ расширенной метафоры в «Украденном ребенке»:
Научитесь определять и анализировать расширенные метафоры с помощью W.B. Стихотворение Йейтса «Украденный ребенок». В этом интерактивном уроке мы рассмотрим, как Йейтс использует образный язык для выражения расширенной метафоры в этом стихотворении. Мы сосредоточимся на использовании им этих семи типов образов: визуальных, слуховых, вкусовых, обонятельных, тактильных, кинестетических и органических. Наконец, мы проанализируем, как расширенная метафора стихотворения передает более глубокий смысл в тексте.
Тип: Оригинальное учебное пособие для учащихся
Готовьтесь: Анализ центральной идеи:
Научитесь определять и анализировать центральную идею информационного текста. В этом интерактивном руководстве вы прочтете несколько информационных отрывков из истории пиратов. Во-первых, вы изучите четырехэтапный процесс определения центральной идеи. Затем вы проанализируете каждый отрывок, чтобы увидеть, как центральная идея развивается по всему тексту.
Тип: оригинальное учебное пособие для учащихся
Обоснованные шаги:
Узнайте, как объяснить шаги, используемые для решения многошаговых линейных уравнений, и аргументируйте эти шаги с помощью этого интерактивного руководства.
Тип: Оригинальное учебное пособие для учащихся
Плавание по кругу:
В этом интерактивном учебном пособии вы научитесь решать задачи на окружность и площадь круглых бассейнов.
Тип: оригинальное учебное пособие для учащихся
«Последний лист» — выводы:
Узнайте, как делать выводы на основе информации, содержащейся в тексте этого интерактивного руководства. Используя рассказ О. Генри «Последний лист», вы потренируетесь определять в рассказе как явную, так и неявную информацию. Вы будете применять свои собственные рассуждения, чтобы делать выводы на основе того, что указано в тексте как явно, так и неявно.
Тип: Оригинальный учебник для учащихся
«Медвежонок» Подробности:
Присоединяйтесь к Медвежонку , чтобы ответить на вопросы о ключевых деталях его любимых историй с помощью этого интерактивного руководства. Узнайте о персонажах, обстановке и событиях, отвечая на вопросы кто, где и какие.
Тип: оригинальное учебное пособие для учащихся
Построение линейных функций из таблиц:
Изучив этот интерактивный учебник, вы научитесь строить линейные функции из таблиц, содержащих наборы данных, которые особым образом связаны друг с другом.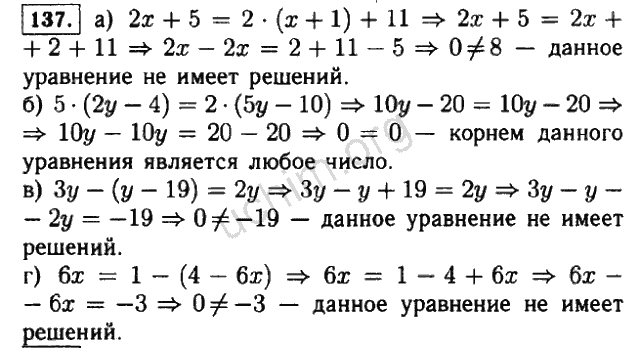
Тип: Оригинальное учебное пособие для учащихся
Округление масштаба:
В этом интерактивном учебном пособии вы научитесь использовать архитектурные чертежи в масштабе для строительства новой конной арены и решите задачи, связанные с чертежами в масштабе. К концу вы должны быть в состоянии вычислить фактическую длину, используя масштаб и пропорции.
Тип: Оригинальное учебное пособие для учащихся
Выживание в экстремальных условиях:
В этом учебном пособии вы потренируетесь находить соответствующие улики в тексте, читая отрывки из рассказа Джека Лондона «Развести огонь». Затем вы будете практиковать свои навыки письма, составляя краткий ответ, используя примеры соответствующих фактов из истории.
Тип: оригинальное учебное пособие для учащихся
Изучение текстов:
Научитесь делать выводы, используя роман Угу в этом интерактивном уроке.

 М. Никольский М.К. Потапов
М. Никольский М.К. Потапов А. Алимов Ю.М. Колягин
А. Алимов Ю.М. Колягин П. Бевз В.Г.
П. Бевз В.Г. Г. Полонський В.Б.
Г. Полонський В.Б.
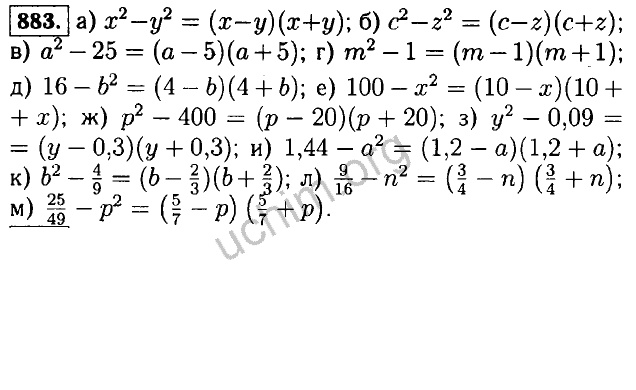 М.
М. А.
А.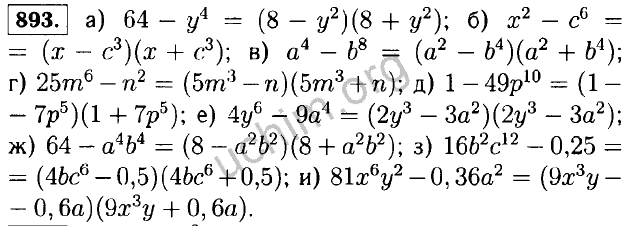 В. Минаева С.С.
В. Минаева С.С.
 В.
В. I.
I. Е. Кучер Т.П.
Е. Кучер Т.П.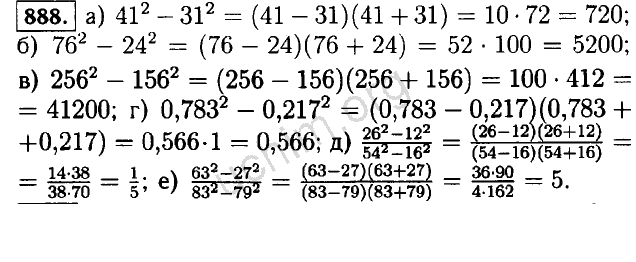 А. Кузнецова Л.В.
А. Кузнецова Л.В.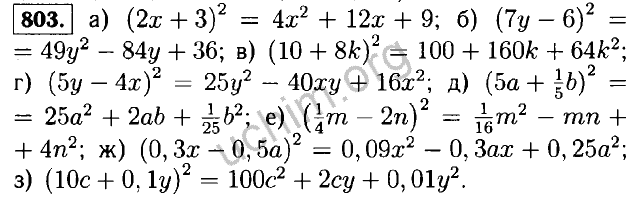 М. Комиссарова И.В.
М. Комиссарова И.В.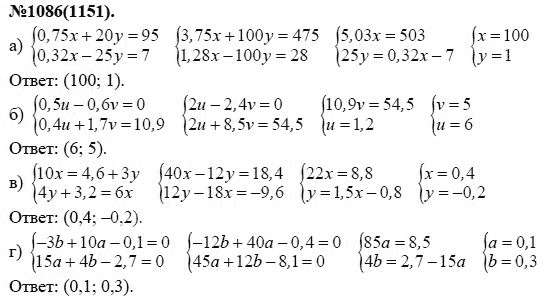 А. Гаиашвили М.Я.
А. Гаиашвили М.Я.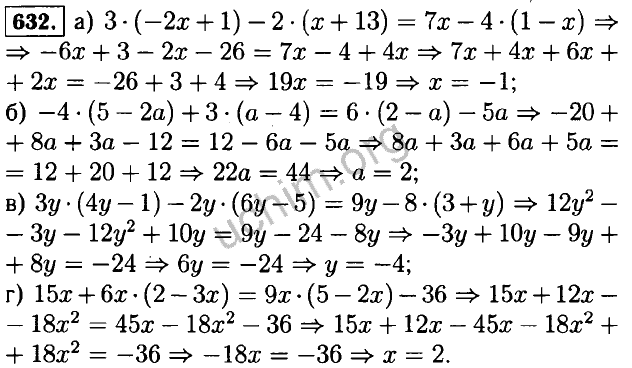 В. Мерзляк А.Г.
В. Мерзляк А.Г.
 2. Степень числа
2. Степень числа Рациональные числа
Рациональные числа 5. Десятичное разложение рациональных чисел
5. Десятичное разложение рациональных чисел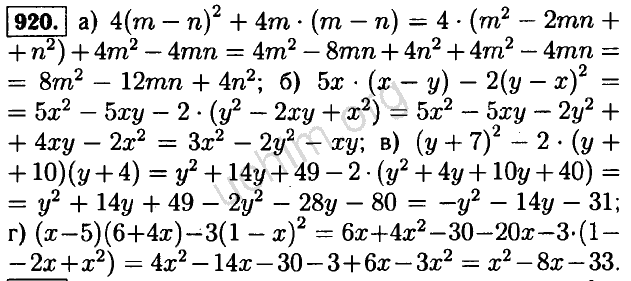 4. Основные свойства действительных чисел
4. Основные свойства действительных чисел 7. Координатная ось
7. Координатная ось 3. Понятие одночлена
3. Понятие одночлена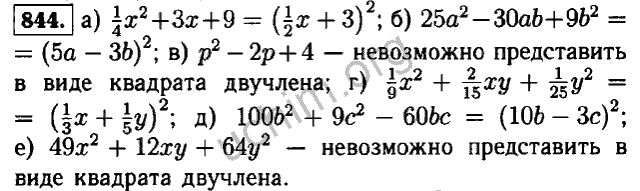 Многочлены
Многочлены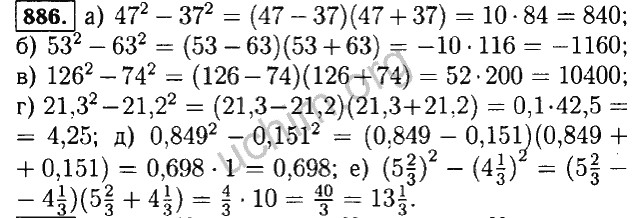 5. Произведение одночлена и многочлена
5. Произведение одночлена и многочлена 7. Целые выражения
7. Целые выражения 2. Квадрат разности
2. Квадрат разности 5. Сумма кубов
5. Сумма кубов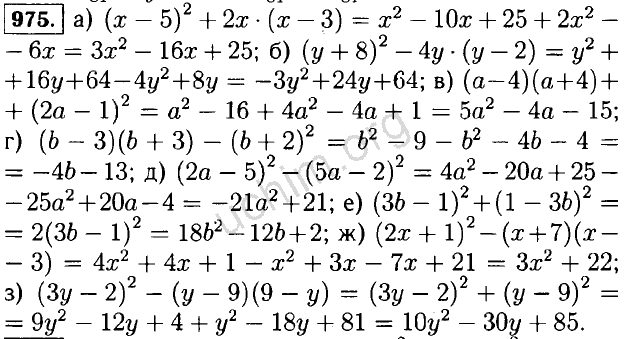 9. Применение формул сокращенного умножения
9. Применение формул сокращенного умножения Алгебраические дроби
Алгебраические дроби 4. Рациональные выражения
4. Рациональные выражения Степень с целым показателем
Степень с целым показателем 4. Преобразование рациональных выражений
4. Преобразование рациональных выражений 2. Линейные уравнения с одним неизвестным
2. Линейные уравнения с одним неизвестным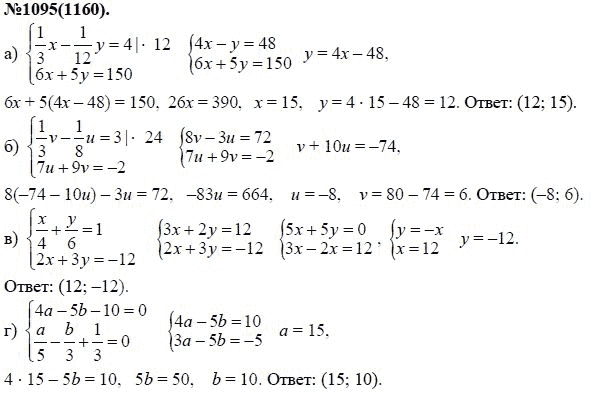 Метод Гаусса
Метод Гаусса
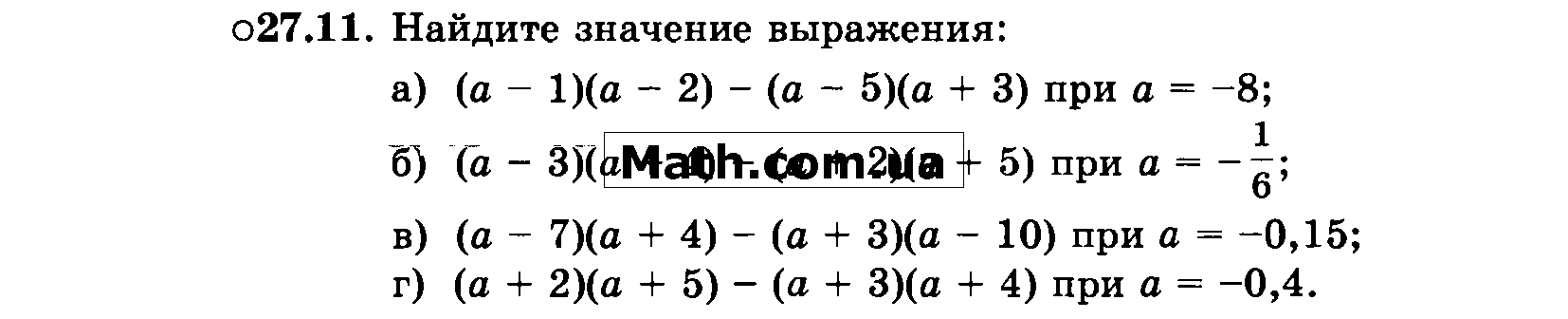
 Например: если женщина, зарабатывающая 25 долларов в час, получает надбавку на 10 %, она будет получать дополнительно 1/10 своей зарплаты в час, или 2,50 доллара, за новую зарплату в 27,50 долларов. Если вы хотите разместить перекладину для полотенец длиной 9 3/4 дюйма в центре двери шириной 27 1/2 дюйма, вам нужно будет разместить перекладину примерно в 9 дюймах от каждого края; эту оценку можно использовать в качестве проверки точного вычисления.
Например: если женщина, зарабатывающая 25 долларов в час, получает надбавку на 10 %, она будет получать дополнительно 1/10 своей зарплаты в час, или 2,50 доллара, за новую зарплату в 27,50 долларов. Если вы хотите разместить перекладину для полотенец длиной 9 3/4 дюйма в центре двери шириной 27 1/2 дюйма, вам нужно будет разместить перекладину примерно в 9 дюймах от каждого края; эту оценку можно использовать в качестве проверки точного вычисления.  Например, периметр прямоугольника равен 54 см. Его длина составляет 6 см. Какова его ширина?
Например, периметр прямоугольника равен 54 см. Его длина составляет 6 см. Какова его ширина?  EE.C.7
EE.C.7 Собираем все вместе
Собираем все вместе