ГДЗ за 7 класс, решебники в седьмом классе, ответы
ГДЗ за 7 класс – это многочисленные решебники, составленные на базе основных учебников по предметам, используемых общеобразовательными школами России. Они служат опорой школьников в деле выполнения домашних работ, а также помощниками, родителей, желающих отследить успеваемость своих детей.
Как семикласснику проверить свою домашнюю работу по решебнику 7 класса?
Когда домашние задачки по алгебре и геометрии решены, тесты по физике сделаны, а упражнение по русскому языку выполнено, приходит время проверки заданий. Для этих целей школьникам удобнее всего использовать решебники для 7 класса. Эти практические пособия содержат готовые ответы, а также структуру оформления задач и примеров.
На основе сборников готовых домашних заданий можно также:
- детально разобраться в сложных примерах и упражнениях;
- устранить допущенные ошибки;
- подготовиться к итоговым контрольным и экзаменам.
Важную роль играют ГДЗ и в деле проверки успеваемости школьников родителями: теперь они смогут качественно оценить результат, процесс выполнения задания и его оформление. К тому же отпадет необходимость в найме репетитора – на базе готовых упражнений ученики смогут разобраться в сложных упражнениях.
К тому же отпадет необходимость в найме репетитора – на базе готовых упражнений ученики смогут разобраться в сложных упражнениях.
В чем выгоды использования сайта готовых домашних заданий (гдз) в седьмом классе?
Для того чтобы качественно и быстро сделать домашние задания по многочисленным предметам школьного курса – алгебре, геометрии, физике, географии, языкам, семикласснику стоит воспользоваться онлайн-решебниками, представленными на нашем сайте.
Практические пособия предназначены отнюдь не для бездумного списывания. Они выступают основой для проверки выполненных задач и упражнений; на их базе можно разобраться с запутанными и сложными заданиями и подготовиться к итоговому контролю.
Наш ресурс предоставляет пользователям уникальные выгоды:
- все материалы доступны в бесплатном режиме и без регистрации;
- найти нужный ответ можно через поисковую строку – в ней нужно прописать номер задачки или часть ее условия;
- регулярно обновляемые сборники ГДЗ обеспечивают совпадение номеров заданий и готовых решений.

Такие условия позволяют найти готовое упражнение всего за пару секунд. К тому же корректность оформления готовых заданий не может быть подвергнута сомнению.
ГДЗ Алгебра 7 класс. Ответы и решения по Алгебре для 7 го класса на VipGDZ.ru
На протяжении многих столетий одной из основных частей процесса школьного обучения являются домашние задания. Их главная роль состоит в закреплении новых тем детьми. Особенно много упражнений ученики 7 класса получают во время изучения алгебры. Конечно, что самостоятельно справится с данным объемом работы достаточно тяжело, поэтому школьники все чаще стали прибегать к новому методу в обучении – ГДЗ. Такие вспомогательные книги как решебники, хоть и появились совсем недавно, но уже стали неотъемлемой частью жизни подростков.
Кроме того, ГДЗ по алгебре за 7 класс являются верными напарниками и родителей, которые используют учебники такого формата для осуществления проверки заданий своих детей. Но папы и мамы не являются единственными представителями взрослых пользователей решебников. Эти книги считаются настоящим кладезем идей для педагогов, которые черпают из них методы доступного объяснения детям нового материала.
Эти книги считаются настоящим кладезем идей для педагогов, которые черпают из них методы доступного объяснения детям нового материала.
Плюсы, которые приносят ответы по алгебре
Отметим, что и родители, и учителя только поддерживают использование детьми таких книг, как правильные ответы. Это происходит благодаря положительному влиянию данных справочников на семиклассников.
Большинство ГДЗ за седьмой класс нацелены не только на то, чтобы дать школьникам решения заданий, но и лучше закрепить новые темы. Это оказывает огромное положительное влияние и на самих школьников, и на их учебный процесс. Пользуясь книгами такого формата, ученики укрепляют свою самостоятельность, ведь они теперь могут без вмешательства взрослых выполнять даже самые сложные задания и осуществлять их проверку.
Такие действия приводят к тому, что ученик 7 класса становится увереннее в себе и может без волнений отстаивать свое мнение. Все это мотивирует его получать новые знания и достигать высоких результатов.
VIPGDZ.ru — хранилище качественных ГДЗ
Если говорить о лучшем месте, где нужно искать надежные решебники по алгебре, то им, по праву, считается наш сайт VIPGDZ.ru, проверенный временем и пользователями. На наших страницах расположились только качественные ГДЗ для учеников 7 класса, которые полностью соответствуют школьным учебникам. Почему же стоит остановить своей выбор на нашем сайте? Ответ на данный вопрос кроется во всех его преимуществах. Любого пользователя порадует то, что все информационные материалы на VIPGDZ.ru поданы совершенно бесплатно. Для того чтобы просматривать книги, не нужно даже прохождения регистрации. Также, отличной нашей инновацией считается наличие мобильной версии портала, с которой просматривать нужные ГДЗ можно будет независимо от того, дома вы находитесь или нет.
Хочется добавить, что сотрудничать со всеми материалами на нашем портале в режиме онлайн достаточно просто, благодаря его удобному интерфейсу. Вы всегда можете добавить страницу нашего интернет ресурса в закладки браузера для быстрого поиска нужных книг.С ГДЗ на нашем сайте VIPGDZ.ru семиклассники обязательно полюбят алгебру и будут легко выполнять различные упражнения по данной дисциплине!
Каждое задание указывает на определенное место в районе проведения второго этапа. Адрес места может быть задан явно в виде названия улицы и номера дома, а может быть зашифрован в виде загадки, фотографии, частичного адреса (например, может быть дано только название улицы). Некоторые названия улиц даны по старой карте. Каждое задание могло принести команде определенное количество баллов (от 1 до 4). Участникам надо было прийти по данному адресу и выполнить задание. При этом не нужно было посещать все КП (посетить все точки было невозможно!). Карта, выданная участникам на старте Задания первой части (до Промежуточного финиша)Для раскрытия ответов нажмите на задание. Старт: Сад Эрмитаж (Каретный ряд, дом 3).
Задания второй части (от Промежуточного финиша до финиша)
|
7 класс | Олимпиадные задания
Содержание Part 1 — Listening (time – 15 minutes , 15 points) Task 1 Task 2 Part 2 — Reading (time-15 minutes, 7 points) Part 3 — Use of English (time – 30 minutes, 33 points) Task 1 Task 2 Task 3 Критерии оценивания Part 1 — Listening (time – 15 minutes , 15 points) […]
1447 21.12.2020
Содержание Part 1 «Listening» Part 2 «Reading» Task 1 Task 2 Part 3 «Use of English» Task 1 Task 2 Task 3 Audioscript (Part 1 «Listening») Keys Part 1 «Listening» Part 2 «Reading» Part 3 «Use of English» Part 1 «Listening» Time: 10 minutes Maximum points – 7 How do British people recognize a Russian […]
22426
06. 10.2020
10.2020
Содержание Part 1 Listening (15 minutes) Part 2 Reading (15 minutes) Part 3 Use of English (30 minutes) Task 1 Task 2 Task 3 Audioscript KEYS Part 1 Listening Part 2 Reading Part 3 Use of English Part 1 Listening (15 minutes) Maximum points – 5 You will hear a conversation between a boy, Leon, […]
14390 18.09.2020
Содержание Задача 1 Задача 2 Задача 3 Задача 4 Задача 5 Задача 6 Задача 7 Задача 8 Задача 9 Задача 10 Задача 1 Что изображено на фотографии? чёрная дыра (первое изображение!) гора Олимп тёмное образование в атмосфере Юпитера солнечное пятно Ответ: 4 (2 балла) Задача 2 Изображение участка какого созвездия приведено на фотографии? Большая Медведица […]
7631 18.12.2019
Содержание Part 1 «Listening» Task 1 Task 2 Part 2 «Reading» Task 1 Task 2 Task 3 Part 3 «Use of English» Task 1 Task 2 Task 3 Part 4 «Writing» KEYS Part 1 (Listening) Part 2 (Reading) Part 3 (Use of English) Подсчёт баллов за все конкурсы Критерии оценивания конкурса письменной речи (writing) Script […]
35350
11. 12.2019
12.2019
Содержание Part 1 «Listening» Part 2 «Reading» Task 1 Task 2 Part 3 «Use of English» Task 1 Task 2 Task 3 Part 4 «Writing» Keys Part 1 «Listening» (5 points) Part 2 «Reading» Part 3 «Use of English» Подсчёт баллов за все конкурсы Script (Part 1. Listening ) Part 1 «Listening» Time: 15 minutes […]
54342 10.12.2019
Содержание Задание 1 (10 баллов) Задание 2 (20 баллов) Критерии оценки аргументации Задание 3 (30 баллов) КРИТЕРИИ ОЦЕНКИ ПИСЬМЕННОГО РАССУЖДЕНИЯ ПОЯСНЕНИЕ К ШКАЛЕ ОЦЕНОК Уважаемый участник! При выполнении заданий Вам предстоит определённая работа, которую лучше организовывать так: внимательно прочитайте задание и посмотрите на предложенные Вам источники; для выполнения заданий, содержащих иллюстрации, у Вас должны […]
1438 27.11.2019
Содержание Задание 1. [35 баллов] ПЕРЕВОД С РУССКОГО НА РУССКИЙ Задание 2. [40 баллов] РАБОТА С ТЕКСТОМ Вариант 1. Прозаический текст Вариант 2. Поэтический текст Задание 1. [35 баллов] ПЕРЕВОД С РУССКОГО НА РУССКИЙ. Текст одного из известных русских стихотворений был переведён компьютером последовательно на несколько языков, а затем обратно на русский. Перед вами отредактированный […]
[35 баллов] ПЕРЕВОД С РУССКОГО НА РУССКИЙ Задание 2. [40 баллов] РАБОТА С ТЕКСТОМ Вариант 1. Прозаический текст Вариант 2. Поэтический текст Задание 1. [35 баллов] ПЕРЕВОД С РУССКОГО НА РУССКИЙ. Текст одного из известных русских стихотворений был переведён компьютером последовательно на несколько языков, а затем обратно на русский. Перед вами отредактированный […]
6625 18.11.2019
Содержание Задание 1 Задание 2 Задание 3 Задание 4 Задание 5 Задание 6 Задание 7 Задание 8 Задание 9 Задание 1 Установите истинность или ложность суждений. Обозначьте «да» истинные суждения, «нет» – ложные. Ответы внесите в таблицу. 1.1. Первые государства возникли примерно в третьем тысячелетии до н.э. 1.2. Религия – оциальный институт, характерный в первую […]
7073 07.11.2019
Содержание Задача 1. Турнир Задача 2. Дорожка в парке Задача 3. Расстановка знаков Задача 4. Решение задач Задания по программированию Задача 1. Турнир В турнире по круговой системе участвуют пять команд. Каждая команда должна сыграть один матч со всеми остальными командами. Турнир проводится в несколько туров, в каждом туре может быть сыгран один или несколько […]
Расстановка знаков Задача 4. Решение задач Задания по программированию Задача 1. Турнир В турнире по круговой системе участвуют пять команд. Каждая команда должна сыграть один матч со всеми остальными командами. Турнир проводится в несколько туров, в каждом туре может быть сыгран один или несколько […]
8707 06.11.2019
Содержание Задание 1 Ответы и критерии оценивания к заданию 1 Задание 2 Ответы и критерии оценивания к заданию 2 Задание 3 Ответы и критерии оценивания к заданию 3 Задание 4 Ответы и критерии оценивания к заданию 4 Задание 1 Пользуясь знаниями по географии, полученными в предыдущие годы, а также картами атласа, определите ошибку в логических […]
5066 31.10.2019
Содержание Часть 1 Часть 2 Часть 3 Часть 4 Ответы Часть 1 Часть 2 Часть 3 Часть 4 Система оценивания Часть 1 На каждый вопрос даны четыре варианта ответов. Выберите только один правильный и внесите его в матрицу (часть 1). Живыми клетками проводящей ткани растений являются: а) клетки сосудов; б) ситовидные клетки; в) клетки трахеид; […]
Выберите только один правильный и внесите его в матрицу (часть 1). Живыми клетками проводящей ткани растений являются: а) клетки сосудов; б) ситовидные клетки; в) клетки трахеид; […]
9417 25.10.2019
Содержание Задача 1 Возможное решение 1 Возможное решение 2 Задача 2 Возможное решение Задача 3 Возможное решение Задача 1 Карлсон съедает 30 конфет каждый раз, когда летит от своего домика на крыше до квартиры Малыша. Однажды мотор Карлсона заглох в полёте, поэтому оставшиеся две трети пути до дома Малыша Карлсону пришлось идти пешком. Известно, что […]
6532 18.10.2019
Содержание Part 1 Listening Part 2 Reading Part 3 Use of English Task 1 Task 2 Task 3 Part 4 Writing Текст для аудирования KEYS Part 1. Listening Part 2 Reading Part 3 Use of English Подсчёт баллов за все конкурсы Дополнительные материалы для скачивания Part 1 Listening Time: 10 minutes (5 points) Task 1 […]
27054
17. 10.2019
10.2019
Содержание Задача 1 Задача 2 Задача 3 Задача 4 Задача 5 Задача 1 Какие из перечисленных планет могут наблюдаться с Земли в противостоянии: Юпитер, Уран, Нептун, Марс, Сатурн? Ответ: все перечисленные планеты могут наблюдаться в противостоянии. Критерии оценивания: Указание всех планет оценивается в 8 баллов. Если указано 4 планеты из 5, оценка составляет 4 балла, […]
1746 17.10.2019
Поиск Поиск-
Школьный помощник
- математика 5 класс
- математика 6 класс
- алгебра 7 класс
- алгебра 8 класс
- геометрия 7 класс
- русский язык 5 класс
- русский язык 6 класс
- русский язык 7 класс
- математика
- алгебра
- геометрия
- русский язык
«»
следующая предыдущая вернуться на предыдущую страницуТакой страницы нет !!!
- Популярные запросы
- Обстоятельство
- Дополнение
- Определение
- Деление дробей
- Математика 6 класс
- Русский язык 6 класс
- Русский язык 7 класс
- Алгебра 7 класс
- Русский язык 5 класс
- Наименьшее общее кратное
- Математика 5 класс
- Буквы о и а в корнях -кос- / -кас-; -гор- / — гар-; -клан- / -клон-; -зар- / -зор-
- Буквы о и а в корнях -кос- / -кас-; -гор- / — гар-; -клан- / -клон-; -зар- / -зор-
- Наибольший общий делитель.
 Взаимно простые числа
Взаимно простые числа - Алгебра 8 класс
- Квадратный корень из неотрицательного числа
- Деление и дроби
- Доли. Обыкновенные дроби
- Окружность и круг
- Антонимы. Синонимы
- Десятичная запись дробных чисел
- Буквы о – а в корнях -лаг- / -лож-, -рос- / -раст- (-ращ-)
Электронное приложение к учебнику «Информатика» для 7 класса (УМК Босова Л.Л. и др. 5-9 кл.)
- Главная
- >
- Методист
- >
- Авторские мастерские
- >
- Информатика
- >
- Босова Л. Л.
Введение
Презентация «Введение в курс информатики»
Презентация «Введение в курс информатики» (Open Document Format)
Техника безопасности
Ссылки на ресурсы ЕК ЦОР
- клавиатурный тренажер «Руки солиста» (N 128669)
- демонстрация к лекции «Место информатики в системе наук» (N 119015)
- демонстрация к лекции «ИКТ в современном мире» (N 118942)
- демонстрация к лекции «Цели и задачи изучения предмета «Информатика и ИКТ»» (N 118498)
- демонстрация к лекции «Техника безопасности и санитарные нормы» (N 119260)
Глава 1. Информация и информационные процессы
Информация и информационные процессы
§ 1.1. Информация и её свойства
Презентация «Информация и её свойства»
Презентация «Информация и её свойства» (Open Document Format)
Интерактивные тесты
- Онлайн тест «Информация и ее свойства». Вариант 1
- Онлайн тест «Информация и ее свойства». Вариант 2
Ссылки на ресурсы ЕК ЦОР
- анимация «Субъективный подход к определению понятия «информация»» (N 134931)
- анимация «Пример отличия информации от материальных объектов» (N 134860)
- демонстрация к лекции «Восприятие информации» (N 119295)
- анимация «Кто как видит» (N 135131)
- виртуальная лаборатория «Оптические иллюзии» (N 134876)
- анимация «Классификация информации по способу ее восприятия» (N 134872)
- тест по теме «Восприятие информации» «Система тестов и заданий N4» (N 134948)
- опорная схема «Свойства информации» (N 135118)
- анимация «Актуальность (своевременность) информации» (N 134946)
- анимация «Достоверность информации» (N 135076)
- анимация «Объективность информации» (N 134992)
- анимация «Полнота информации» (N 134891)
- анимация «Понятность информации» (N 134896)
- анимация «Ценность информации» (N 134963)
- анимация «Синергетический эффект» (N 135116)
- тест по теме «Свойства информации» «Система тестов и заданий N6» (N 134994)
§ 1. 2. Информационные процессы
2. Информационные процессы
Презентация «Информационные процессы»
Презентация «Информационные процессы» (Open Document Format)
Интерактивные тесты
- Онлайн тест «Информационные процессы». Вариант 1
- Онлайн тест «Информационные процессы». Вариант 2
Ссылки на ресурсы ЕК ЦОР
- анимация «Виды информационных процессов» (N 118499)
- анимация «Информационные процессы для человека и компьютера» (N 134831)
- анимация «Создание информации» (N 135069)
- анимация «Обработка информации» (N 119294)
- анимация «Хранение информации. Память» (N 135156)
- анимация «Информация и ее носитель» (N 134874)
- анимация «Документы» (N 134981)
- анимация «История средств хранения информации» (N 125863)
- анимация «Потеря информации» (N 135081)
- анимация «Источник и приемник информации» (N 135155)
- анимация «Помехи при передаче информации» (N 134850)
- анимация «Информация в человеческом обществе – новостная информация» (N 134836)
- анимация «Информация в человеческом обществе» (N 135083)
- анимация «Информация в технике» (N 134950)
- анимация «Информация в живой природе» (N 134839)
- анимация «Информация в неживой природе» (N 135142)
- тест по темам «Источник и приемник информации», «Информация и ее носитель» – «Система тестов и заданий N8» (N 134927)
§ 1. 3. Всемирная паутина
3. Всемирная паутина
Презентация «Всемирная паутина»
Презентация «Всемирная паутина» (Open Document Format)
Интерактивные тесты
- Онлайн тест «Всемирная паутина». Вариант 1
- Онлайн тест «Всемирная паутина». Вариант 2
Ссылки на ресурсы ЕК ЦОР
- демонстрационный имитатор «Работа поисковой системы в Интернете» (N 119393)
§ 1.4. Представление информации
Презентация «Представление информации»
Презентация «Представление информации» (Open Document Format)
Интерактивные тесты
- Онлайн тест «Представление информации». Вариант 1
- Онлайн тест «Представление информации». Вариант 2
Ссылки на ресурсы ЕК ЦОР
- анимация «Виды знаков по способу восприятия» (N 135070)
- анимация «Классификация знаков по способу восприятия. Сигналы» (N 135152)
- анимация «Классификация знаков по способу восприятия.
 Пиктограммы» (N 135159)
Пиктограммы» (N 135159) - анимация «Классификация знаков по способу восприятия. Символы» (N 135002)
- анимация «Один и тот же символ может обозначать разную информацию» (N 135132)
- анимация «Использование символов для технических устройств» (N 134848)
- анимация «Использование символов для живых существ» (N 134916)
- тест по теме «Знаки» – «Система тестов и заданий N9» (N 135130)
- демонстрация к лекции «Информация и письменность» (N 119187)
- демонстрация к лекции «Языки естественные и формальные» (N 119246)
§ 1.5. Двоичное кодирование
Презентация «Двоичное кодирование»
Презентация «Двоичное кодирование» (Open Document Format)
Интерактивные тесты
- Онлайн тест «Двоичное кодирование». Вариант 1
- Онлайн тест «Двоичное кодирование». Вариант 2
Ссылки на ресурсы ЕК ЦОР
- анимация «Определение понятия «кодирование информации»» (N 135044)
- анимация «Понятие «код»» (N 134945)
- анимация «Примеры кодов» (N 135115)
- анимация «Определение понятия «перекодирование информации»» (N 135147)
- тест по теме «Кодирование информации» – «Система тестов и заданий N10» (N 134851)
- виртуальная лаборатория «Цифровые весы» (N 135009)
§ 1. 6. Измерение информации
6. Измерение информации
Презентация «Измерение информации»
Презентация «Измерение информации» (Open Document Format)
Интерактивные тесты
- Онлайн тест «Измерение информации». Вариант 1
- Онлайн тест «Измерение информации». Вариант 2
Ссылки на ресурсы ЕК ЦОР
- анимация «Вычисление количества информации: алфавитный подход» (N 134881)
- тренажер «Интерактивный задачник. Раздел «Измерение информации»» (N 119252)
Интерактивный тест по теме «Информация и информационные процессы»
Тест 1
Глава 2. Компьютер как универсальное устройство для работы с информацией
§ 2.1. Основные компоненты компьютера и их функции
Презентация «Основные компоненты компьютера и их функции»
Презентация «Основные компоненты компьютера и их функции» (Open Document Format)
Интерактивные тесты
- Онлайн тест «Основные компоненты компьютера и их функции».
 Вариант 1
Вариант 1 - Онлайн тест «Основные компоненты компьютера и их функции». Вариант 2
Ссылки на ресурсы ЕК ЦОР
- анимация «Компьютер и его назначение» (N 134879)
- анимация «Внутренняя память ЭВМ: видеопамять» (N 135057)
- анимация «Внутренняя память ЭВМ: емкость памяти» (N 134929)
- анимация «Внутренняя память ЭВМ: кэш-память» (N 134947)
- анимация «Внутренняя память ЭВМ: оперативная память» (N 135117)
- анимация «Внутренняя память ЭВМ: ПЗУ BIOS» (N 135033)
- анимация «Внутренняя память ЭВМ: постоянная память» (N 135086)
- анимация «Внутренняя память ЭВМ: энергонезависимая оперативная память (CMOS RAM)» (N 135042)
- анимация «Структура цифровой ЭВМ» (N 135052)
- анимация «Структура цифровой ЭВМ – магистраль (шина)» (N 135096)
- программа-тренажер «Устройство компьютера-1» (N 119293)
§ 2.2. Персональный компьютер
Презентация «Персональный компьютер»
Презентация «Персональный компьютер» (Open Document Format)
Интерактивные тесты
- Онлайн тест «Персональный компьютер».
 Вариант 1
Вариант 1 - Онлайн тест «Персональный компьютер». Вариант 2
Ссылки на ресурсы ЕК ЦОР
- анимация «Составляющие системного блока» (N 134863)
- анимация «Системный блок (вид сзади)» (N 135112)
- анимация «Системный блок ПЭВМ» (N 134890)
- анимация «Накопитель на жестких магнитных дисках (НЖМД)» (N 135012)
- анимация «Открытая архитектура ЭВМ» (N 135123)
- программа-тренажер «Устройство компьютера — 2» (N 119274)
- анимация «Мышь: механическая» (N 135006)
- анимация «Мышь: оптико-механическая» (N 134877)
- анимация «Мышь: оптическая» (N 135140)
- анимация «Мышь: современная оптическая» (N 134828)
- анимация «Клавиатура ПЭВМ: принципы работы устройство клавиши» (N 134923)
- анимация «Клавиатура ПЭВМ: принципы работы сканирование клавиш» (N 135019)
Ссылки на ресурсы ФЦИОР:
- информационный модуль по теме «Конфигурация компьютера.
 Выбор конфигурации в зависимости от решаемых задач»
Выбор конфигурации в зависимости от решаемых задач» - практический модуль теме «Конфигурация компьютера. Выбор конфигурации в зависимости от решаемых задач»
- контрольный модуль по теме «Конфигурация компьютера. Выбор конфигурации в зависимости от решаемых задач»
§ 2.3. Программное обеспечение компьютера
Презентация «Программное обеспечение компьютера»
Презентация «Программное обеспечение компьютера» (Open Document Format)
Интерактивные тесты
- Онлайн тест «Программное обеспечение компьютера». Вариант 1
- Онлайн тест «Программное обеспечение компьютера». Вариант 2
Ссылки на ресурсы ЕК ЦОР
- демонстрация к лекции «Структура программного обеспечения ПК» (N 119268)
- демонстрация к лекции «Системное программное обеспечение» (N 119016)
- демонстрация к лекции «Операционная система» (N 119104)
- демонстрация к лекции «Системы программирования» (N 119289)
- демонстрация к лекции «Прикладное программное обеспечение» (N 119242)
- тест по теме «Компьютер как средство автоматизации информационных процессов» – «Система тестов и заданий №13» (N 134951)
Ссылки на ресурсы ФЦИОР:
- информационный модуль по теме «Компьютерные вирусы и антивирусные программы»
- практический модуль теме «Компьютерные вирусы и антивирусные программы»
- контрольный модуль по теме «Компьютерные вирусы и антивирусные программы»
- информационный модуль по теме «Программы архивирования данных»
- практический модуль теме «Программы архивирования данных»
- контрольный модуль по теме «Программы архивирования данных»
§ 2. 4. Файлы и файловые структуры
4. Файлы и файловые структуры
Презентация «Файлы и файловые структуры»
Презентация «Файлы и файловые структуры» (Open Document Format)
Интерактивные тесты
- Онлайн тест «Файлы и файловые структуры». Вариант 1
- Онлайн тест «Файлы и файловые структуры». Вариант 2
Ссылки на ресурсы ЕК ЦОР
- демонстрация к лекции «Файлы и файловые структуры» (N 119112)
- демонстрация к лекции «Файловая структура диска» (N 119256
- демонстрация к лекции «Имя файла. Путь к файлу» (N 119114)
- анимация «Файлы и папки» (N 196624)
§ 2.5. Пользовательский интерфейс
Презентация «Пользовательский интерфейс»
Презентация «Пользовательский интерфейс» (Open Document Format)
Интерактивные тесты
- Онлайн тест «Пользовательский интерфейс». Вариант 1
- Онлайн тест «Пользовательский интерфейс». Вариант 2
Ссылки на ресурсы ФЦИОР:
- информационный модуль по теме «Основные элементы интерфейса и управления»
- практический модуль теме «Основные элементы интерфейса и управления»
- контрольный модуль по теме «Основные элементы интерфейса и управления»
Интерактивный тест по теме «Компьютер как универсальное устройство для работы с информацией»
Тест 2
Глава 3. Обработка графической информации
Обработка графической информации
§ 3.1. Формирование изображения на экране монитора
Презентация «Формирование изображения на экране монитора»
Презентация «Формирование изображения на экране монитора» (Open Document Format)
Интерактивные тесты
- Онлайн тест «Формирование изображения на экране монитора». Вариант 1
- Онлайн тест «Формирование изображения на экране монитора». Вариант 2
Ссылки на ресурсы ЕК ЦОР
- анимация «Цветовая модель RGB» (N 179672)
- анимация «Цветовая модель CMYK» (N 179601)
- тренажер «Интерактивный задачник: раздел «Представление графической информации»» (N 125772)
§ 3.2. Компьютерная графика
Презентация «Компьютерная графика»
Презентация «Компьютерная графика» (Open Document Format)
Интерактивные тесты
- Онлайн тест «Компьютерная графика». Вариант 1
- Онлайн тест «Компьютерная графика».
 Вариант 2
Вариант 2
Ссылки на ресурсы ЕК ЦОР
- анимация «Изображения на компьютере» (N 196610)
§ 3.3. Создание графических изображений
Презентация «Создание графических изображений»
Презентация «Создание графических изображений» (Open Document Format)
Интерактивные тесты
- Онлайн тест «Создание графических файлов». Вариант 1
- Онлайн тест «Создание графических файлов». Вариант 2
Ссылки на ресурсы ЕК ЦОР
- анимация «Цветовая модель HSB» (N 179727)
Ссылки на ресурсы ФЦИОР:
- практический модуль теме «Векторный редактор»
- контрольный модуль по теме «Векторный редактор»
- практический модуль теме «Растровый редактор»
- контрольный модуль по теме «Растровый редактор»
- практический модуль теме «Растровая и векторная графика»
- контрольный модуль по теме «Растровая и векторная графика»
Задания для практических работ
Задание 3. 2.
2.
- Устройства.jpeg
Задание 3.3.
- Сказка.jpeg
Задание 3.4.
- Стрекоза.jpeg
Задание 3.6.
- Панель.jpeg
Оперативная память.jpeg
Винчестер.jpeg
Диск.jpeg
Дискета.jpeg
Флэшка.jpeg
Схема.jpeg
Задание 3.10.
- Акробат.bmp
Задание 3.11.
- Мамонт.jpeg
Интерактивный тест по теме «Обработка графической информации»
Тест 3
Глава 4. Обработка текстовой информации
§ 4.1. Текстовые документы и технологии их создания
Презентация «Текстовые документы и технологии их создания»
Презентация «Текстовые документы и технологии их создания» (Open Document Format)
Интерактивные тесты
- Онлайн тест «Текстовые документы и технология их создания». Вариант 1
- Онлайн тест «Текстовые документы и технология их создания». Вариант 2
Ссылки на ресурсы ЕК ЦОР
- тренажер «Руки солиста» (N 128669)
§ 4. 2. Создание текстовых документов на компьютере
2. Создание текстовых документов на компьютере
Презентация «Создание текстовых документов на компьютере»
Презентация «Создание текстовых документов на компьютере» (Open Document Format)
Интерактивные тесты
- Онлайн тест «Создание текстовых документов на компьютере». Вариант 1
- Онлайн тест «Создание текстовых документов на компьютере». Вариант 2
§ 4.3. Форматирование текста
Презентация «Форматирование текста»
Презентация «Форматирование текста» (Open Document Format)
Интерактивные тесты
- Онлайн тест «Форматирование текста». Вариант 1
- Онлайн тест «Форматирование текста». Вариант 2
§ 4.4. Визуализация информации в текстовых документах
Презентация «Визуализация информации в текстовых документах»
Презентация «Визуализация информации в текстовых документах» (Open Document Format)
Интерактивные тесты
- Онлайн тест «Визуализация информации в текстовых документах».
 Вариант 1
Вариант 1 - Онлайн тест «Визуализация информации в текстовых документах». Вариант 2
§ 4.5. Инструменты распознавания текстов и компьютерного перевода
Презентация «Инструменты распознавания текстов и компьютерного перевода»
Презентация «Инструменты распознавания текстов и компьютерного перевода» (Open Document Format)
Интерактивные тесты
- Онлайн тест «Инструменты распознавания текстов и компьютерного перевода». Вариант 1
- Онлайн тест «Инструменты распознавания текстов и компьютерного перевода». Вариант 2
Ссылки на ресурсы ФЦИОР
- контрольный модуль «Программы-переводчики»
§ 4.6. Оценка количественных параметров текстовых документов
Презентация «Оценка количественных параметров текстовых документов»
Презентация «Оценка количественных параметров текстовых документов» (Open Document Format)
Интерактивные тесты
- Онлайн тест «Оценка количественных параметров текстовых документов».
 Вариант 1
Вариант 1 - Онлайн тест «Оценка количественных параметров текстовых документов». Вариант 2
Ссылки на ресурсы ЕК ЦОР
- тренажер «Интерактивный задачник. Раздел «Представление символьной информации»» (N 119265)
Ссылки на ресурсы ФЦИОР
- информационный модуль по теме «Представление текста в различных кодировках»
- практический модуль теме «Представление текста в различных кодировках»
- контрольный модуль по теме «Представление текста в различных кодировках»
Задания для практических работ
Задание 4.3.
- Вставка.rtf
Задание 4.4.
- Замена.rtf
Задание 4.5.
- Поиск_и_замена.rtf
Задание 4.6.
- Удаление.rtf
Задание 4.7.
- Перемещение.rtf
Задание 4.9.
- Строки.rtf
Задание 4.10.
- Цвет.rtf
Задание 4.12.
- Эффекты.
 rtf
rtf
Задание 4.20.
- Мышь.jpeg
Итоговая работа. Введение.rtf
Начало эпохи ЭВМ.rtf
Первое поколение ЭВМ.rtf
Второе поколение ЭВМ.rtf
Третье поколение ЭВМ.rtf
Четвёртое поколение ЭВМ.rtf
Заключение.rtf
Интерактивный тест по теме «Обработка текстовой информации»
Тест 4
Глава 5. Мультимедиа
§ 5.1. Технология мультимедиа
Презентация «Технология мультимедиа»
Интерактивные тесты
- Онлайн тест «Технология мультимедиа». Вариант 1
- Онлайн тест «Технология мультимедиа». Вариант 2
Ссылки на ресурсы ЕК ЦОР
- анимация «Представление звука в компьютере» (N 196609)
- анимация «Аналого-цифровое и цифро-аналоговое преобразование» (N 135035)
- анимация «Эффект движения» (N 179677)
- анимация «Покадровая анимация» (N 179530)
- анимация «Анимация спрайтами» (N 179768)
§ 5. 2. Компьютерные презентации
2. Компьютерные презентации
Презентация «Компьютерные презентации»
Интерактивные тесты
- Онлайн тест «Компьютерные презентации». Вариант 1
- Онлайн тест «Компьютерные презентации». Вариант 2
Сложные загадки на логику — логические задачи с ответами
Логическая загадка любой сложности заставит вас подумать о давно забытых предметах, вспомнить содержание детских сказок и смириться с тем, что ваш ребенок находит ответы быстрее вас. Хотите проверить? Мы подготовили специальную подборку сложных логических загадок!
Зачем решать логические загадки?
При решении логических задачек и поиске «отгадки» у человека начинают работать оба полушария мозга. Левое полушарие отвечает за логику и стремится разобраться в причинных связях. Правое несет ответственность за интуицию, учится строить целостную картину и формировать образное мышление.
У современных людей левое полушарие включается в работу не так часто — «загуглили» и отправились по делам. И, конечно, свою “логическую мышцу” можно и нужно тренировать — тут нам и пригодятся загадки на логику – они помогают держать мозг в тонусе даже в самые «ленивые» дни.
И, конечно, свою “логическую мышцу” можно и нужно тренировать — тут нам и пригодятся загадки на логику – они помогают держать мозг в тонусе даже в самые «ленивые» дни.
Эффект от «логических тренировок» даст о себе знать уже после первых занятий — натренированный мозг быстрее соображает, позволяя решать не только математические задачи, но и находить выход из жизненных ситуаций.
Зачем детям развивать логику?
Развитое логическое мышление поможет вашему ребенку легко справляться с математическими задачами не только в начальной, но и в старшей школе.
Умение анализировать выручит его на литературе, а способность нестандартно мыслить пригодится в творческих кружках и школьных активах. И, конечно, он всегда сможет дать аргументированный ответ на поставленный учителем каверзный вопрос, а еще переспорит одноклассников и точно завоюет авторитет в школе!
Боитесь, что ваш ребенок не справится, потому что «гуманитарий»? В Умназии вы найдете сотни загадок на логику, которые адаптированы для детей разных классов и возрастов, которые позволяют развивать Логику постепенно.
Не отказывайтесь от «мозговых тренировок» — начните мыслить не так, как все!
Сложные загадки на логику
Давайте попробуем разгадать 5 загадок на логику. Дети и взрослые могут размышлять над ответом вместе.
Загадка №1
Каких камней не бывает в речке?
Показать ответ
Ответ: В речке вы никогда не найдете сухих камней. А вот драгоценные попасться могут 🙂
Загадка №2
На столе лежат две монеты, в сумме они дают 3 рубля. Одна из них — не 1 рубль. Какие это монеты?
Показать ответ
Ответ: На столе лежат 2 рубля и 1 рубль. В условии сказано, что только одна из монет – не рубль.
Загадка №3
Что не вместится даже в самую большую кастрюлю?
Показать ответ
Ответ: Крышка этой кастрюли 🙂 Не ходите на кухню и не проверяйте – точно застрянет!
Загадка №4
Что может в одно и то же время стоять и ходить, висеть и стоять, ходить и лежать?
Показать ответ
Загадка №5
Завязать можно, а развязать нельзя. Что это такое?
Что это такое?
Показать ответ
Ответ: Нет, не шнурки от старых кроссовок. Правильный ответ — разговор.
Справились? Если да – вы молодцы. А если что-то не получилось – приходите в Умназию и тренируйте ум с умом!
Умназия – образовательная онлайн-платформа для учеников начальной школы. На платформе ребенок сможет:
Развить логику и внимание на тренажере навыков, прокачать память и стать финансово грамотным!
У нас ребенку не будет скучно: умные алгоритмы подготовят для него индивидуальную программу, а в онлайн-тренажере он будет раскрывать тайны, получать достижения и становиться героем Умназии.
А для самых умных и мотивированных ребят у нас проводятся олимпиады по 4 предметам, которые готовят детей к будущим олимпиадам в школах. Приходите и развивайтесь вместе с нами!
Теперь приступим к более сложным заданиям. Включайте логику и начинайте!
Загадка №6
Я – вода, и по воде плаваю. Кто я такая?
Показать ответ
Ответ: Льдина.
Загадка №7
Ползут 3 черепахи.1-я черепаха говорит: за мной ползут две черепахи.
2-я черепаха говорит: за мной ползёт одна черепаха и передо мной ползёт одна черепаха. А 3-я черепаха: передо мной ползут две черепахи, и за мной ползёт одна черепаха.
Как такое может быть?
Показать ответ
Ответ: Черепахи ползут по кругу!
Загадка №8
На ферме было 2 коня, 1 кролик, 1 щенок, 1 кошка, свинья и поросенок, корова и теленок, индюк и гусь.
Пришел хозяин с собакой. Сколько на ферме стало ног?
Показать ответ
Ответ: 24. Почему? Потому что ноги только у человека, лошадей, свиней и коров. У остальных животных — лапы.
Загадка №9
Где впервые был обнаружен картофель?
Показать ответ
Ответ: Отгадка предельно простая – в земле.
Загадка №10
Странный дождь порой идет: сотней струй он кверху бьет.
Показать ответ
Ответ: Фонтан.
Почему логические загадки полезны для детей? Они развивают смекалку, учат работать с информацией, «прокачивают» логико-математический интеллект и делают ребенка более самостоятельным.
Помимо успехов в школе, о которых мы уже говорили, развитое логическое мышление способствует формированию уверенности в себе в процессе повседневной жизни.
>25 тысяч учеников уже решают авторские задачи в Умназии!
А теперь продолжим тренироваться, ведь долго без логики не протянешь!
Загадка №11
Скажешь «не приходи!» — всё равно приходит. Скажешь «не уходи!» — всё равно уходит. Что это такое?
Показать ответ
Загадка №12
Вы сидите в самолете, впереди вас лошадь, сзади автомобиль. Где вы находитесь?
Показать ответ
Ответ: Вы катаетесь на карусели.
Загадка №13
Чем больше из нее берешь, тем больше она становится. Что это?
Показать ответ
Загадка №14
Что принадлежит вам, однако другие этим пользуются чаще, чем вы сами?
Показать ответ
Ответ: Ваше имя.
Загадка №15
Сколько яиц можно съесть натощак?
Показать ответ
Ответ: нет, размер вашего аппетита тут не при чем. Натощак можно съестьскушать только 1 яйцо, потому что все следующие будут съедены уже не на пустой желудок.
На сегодня это все — мы с вами славно потрудились.
Не хотите останавливаться на достигнутом? Регистрируйтесь в на нашей платформе и решайте тысячи задач в онлайн-режиме. Создавайте индивидуальный учебный план для вашего ребенка и развивайте пять навыков в удобное время.
Начните заниматься с ребенком уже сегодня!
Развитие логики у детей 7-10 лет
Развиваем критическое нестандартное мышление, учим работать с информацией и принимать верные решения
узнать подробнееЧитайте также:
математиков средней школы (6, 7, 8, 9 классы)
6, 7, 8 и 9 классы представлены вопросы и задачи по математике для проверки глубокого понимания математических концепций и вычислительных процедур учащихся. Ответы на вопросы приведены в конце каждой страницы.
Ответы на вопросы приведены в конце каждой страницы.
Дроби Вопросы и проблемы с решениями
6 класс
Алгебра Вопросы и задачи с подробными решениями и объяснениями.Примеры и вопросы по терминам в алгебраических выражениях с подробными решениями и пояснениями.
Прямоугольные системы координат
Найдите множители и кратные целых чисел; примеры и вопросы с подробными решениями и пояснениями.
простая факторизация; примеры и вопросы с подробными решениями и пояснениями.
Расчет площадей квадратов, прямоугольников, треугольников, параллелограммов и трапеций, решения и пояснения к вопросам о том, как рассчитывать площади основных форм.
«Расчет площадей составных фигур», вопросы с подробными решениями и пояснениями для расчета площадей составных фигур.
Алгебраические выражения, подробные решения и объяснения вопросов по алгебраическим выражениям.

Упростите алгебраические выражения. Используйте похожие термины, вопросы с подробным объяснением того, как упростить алгебраические выражения.
Использование распределительного свойства в алгебре; вопросы для расширения и факторизации алгебраических выражений с подробными решениями и объяснениями.
Уравнения в одной переменной, вопросы, в том числе задачи со словами, с подробными решениями и пояснениями к алгебраическим выражениям.
Задачи по математике для 6 класса с подробными решениями и полными объяснениями.
Дроби и смешанные числа — 6 класс. Также включены подробные решения и полные объяснения.
дробей по математике, объясните дроби на нескольких примерах с подробными решениями.
Калькулятор дробей, который поможет вам развить навыки уменьшения, сложения и умножения дробей.
интерактивное руководство по эквивалентным дробям. Исследуйте эквивалентные дроби в интерактивном режиме с помощью апплета.
% — вопросы и проблемы 6-го класса. Также включены подробные решения и полные объяснения.

Interactive Tutorial on Percentage Интерактивное руководство по процентам с использованием апплета.
Преобразование процентов, дробей и десятичных знаков Учебное пособие по преобразованию процентов, дробей и десятичных знаков. Представлены вопросы с подробными решениями, а также упражнения с ответами.
7 класс
Вопросы и задачи по алгебре с подробными решениями и объяснениями.Умножение и упрощение мономов
Графические функции
Что такое экспоненты в математике? ; примеры и вопросы с подробными решениями включены.
Что такое радикалы в математике? ; включены примеры и вопросы с подробными решениями.
Простые и составные числа; примеры и вопросы с подробными решениями включены.
простая факторизация; примеры и вопросы с подробными решениями включены.
Калькулятор общих факторов. Онлайн-калькулятор, вычисляющий общие множители и GCF двух или более положительных целых чисел.

наибольший общий коэффициент (GCF); примеры и вопросы с подробными решениями включены.
наименьшее общее кратное (LCM); примеры и вопросы с подробными решениями включены.
Как уменьшить дроби; примеры и вопросы с подробными решениями включены.
Как перекрестное умножение используется для решения уравнений? ; примеры и вопросы с подробными решениями включены.
Как решить проблемы скорости? ; Включены вопросы 7-й степени с подробными решениями.
Найдите соотношение в математике; Включены вопросы 7-й степени с подробными решениями.
Найти скорость по математике; Включены вопросы 7-й степени с подробными решениями.
Решить математические пропорции; Вопросы 7 степени с подробными решениями включены.
7 класс Математические задачи с ответами. Также включены Решения и объяснения.
Дроби и смешанные числа — вопросы по математике для 7 класса и задачи с ответами. Также включены решения и объяснения.
7 класс Вопросы по теории множеств с ответами.
 Также включены решения и объяснения.
Также включены решения и объяснения. Подобных терминов в алгебре — 7 класс Вопросы по математике и задачи с ответами
Сложение и вычитание многочленов — 7 класс Вопросы и задачи с ответами
8 класс
Приложения линейных уравнений — задачи с ответами для 8 класса с решениями и объяснениямиВопросы о дробях и задачи с решениями
Вопросы для 8-го класса по упрощению выражений с отрицательными показателями с решениями и объяснениями включены онлайн-калькуляторы и решатели тригонометрии
задач по квадратичным уравнениям для 8-го класса с решениями и объяснениями включены
вопросов по алгебре с ответами и решениями для 8-го класса
and Simplify Monomials
8 класс Математика слово Задачи с ответами Также включены решения и объяснения.
8 класс Задачи по геометрии и вопросы с ответами. Также включены решения и объяснения.
Задачи и вопросы о треугольниках для 8 класса с ответами. Также включены решения и объяснения.
Вопросы для 8 класса с ответами на углы в треугольниках. Также включены решения с пояснениями.
Задачи 8 класса и вопросы о кругах с ответами. Также включены решения и объяснения.
Упростите калькулятор квадратного корня
Что такое радикалы в математике? ; включены примеры и вопросы с подробными решениями.
9 класс
Экспоненты Вопросы с ответами для 9 класса; Также включены Решения и подробные объяснения.Что такое радикалы в математике? ; включены примеры и вопросы с подробными решениями.
Примеры одночленов и вопросы с решениями для 9 класса
Сложение и вычитание многочленов — 9 класс, примеры и вопросы с подробными решениями
Решение уравнений — 9 класс, примеры и вопросы с подробными решениями
Вопросы о дробях и задачи с решениями
Умножение многочленов — оценка 9 и решения умноженных многочленов.
Задачи по математике со словами с ответами — 9 класс; Также включены Решения и подробные объяснения.
вопросов по алгебре с ответами для 9 класса. Также включены Решения и подробные объяснения.
Задачи по геометрии и вопросы с ответами для 9 класса. Также включены Решения и подробные объяснения.
Соотношение задач со словами и ответами — 9 класс. Также включены Решения и подробные объяснения.
Умножение и упрощение мономов
Онлайн-калькуляторы для практики и понимания концепций
Калькулятор решения линейных уравненийКалькулятор проверки делимости.Онлайн-калькулятор, проверяющий видимость целых чисел с помощью 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 и 13. Калькулятор наименьшего общего кратного (lcm)
. Вычислите наименьшее общее кратное двух натуральных чисел.
Калькулятор наибольшего общего коэффициента (gcf). Вычислите наибольший общий делитель двух натуральных чисел.
Калькулятор основных факторов. Разложите положительное целое число на простые множители.
Упростите калькулятор квадратного корня
Калькулятор сложения дробей. Добавьте 2 или 3 дроби и уменьшите окончательный ответ.Калькулятор дробей
, который поможет вам еще больше развить навыки уменьшения, сложения и умножения дробей.
Калькулятор умножения дробей. Умножьте 2 дроби и уменьшите ответ.
Калькулятор деления дробей. Разделите 2 дроби и уменьшите ответ.
Калькулятор дробей. Перепишите дроби в уменьшенном виде. Больше начальной математики (4 и 5 классы) с бесплатными вопросами и задачами с ответами
Больше математики средней школы (10, 11 и 12 классы) — Бесплатные вопросы и задачи с ответами Домашняя страница сообщить об этом объявлении
Перейти по математике 7 класс Ключ к ответу Глава 6 Алгебраические выражения — ответ на вопросы математики
Получите подробные решения для учеников 7-х классов в HMH Go Math Answer Key Глава 6 Алгебраические выражения. Мы советуем студентам, желающим набрать наивысшие оценки на экзаменах, пройти курс математики для 7-го класса. Ответы на вопросы главы 6 «Алгебраические выражения». Изучите концепции мысленных вычислений из нашей ключевой главы 6 «Алгебраические выражения» по математике для 7-го класса.
Мы советуем студентам, желающим набрать наивысшие оценки на экзаменах, пройти курс математики для 7-го класса. Ответы на вопросы главы 6 «Алгебраические выражения». Изучите концепции мысленных вычислений из нашей ключевой главы 6 «Алгебраические выражения» по математике для 7-го класса.
Перейти к математике 7 класс Ответы на ключевые слова Глава 6 Алгебраические выражения
Получите ответы на свои вопросы, загрузив ключ к ответам по математике для 7 класса, глава 6, Алгебраические выражения, pdf. Мы предоставили пошаговое объяснение по теме.Итак, проверьте темы, прежде чем начинать подготовку. После подготовки у вас есть возможность проверить свои математические навыки, решив вопросы, приведенные в конце главы.
Глава 6 Алгебраические выражения — Урок: 1
Глава 6 Алгебраические выражения — Урок: 2
Глава 6 Алгебраические выражения — Урок: 3
Глава 6 Алгебраические выражения — Урок: 4
Глава 6 Алгебраические выражения
Управляемая практика — стр.
 176
176 Вопрос 1.
У менеджера летнего лагеря 14 бейсбольных и 23 теннисных мяча. Менеджер покупает несколько коробок с бейсбольными мячами по 12 мячей в коробке и такое же количество коробок с теннисными мячами с 16 теннисными мячами в коробке. Напишите выражение, представляющее общее количество шаров.
______ + ______ №
Ответ: 37 + 28n
Пояснение:
При этом,
У менеджера летнего лагеря 14 бейсбольных и 23 теннисных мяча.
Менеджер покупает несколько коробок бейсбольных мячей по 12 мячей в коробке и такое же количество коробок теннисных мячей с 16 теннисными мячами в коробке.
Пусть n будет количеством коробок каждого типа
Бейсбольные мячи: 14 + 12n
Теннисные мячи: 23 + 16n
Теперь добавьте одинаковые термины
14 + 12n + 23 + 16n
(14 + 23) + (12 + 16) n
37 + 28n
Таким образом, общее количество шаров выражается как 37 + 28n
Вопрос 2.
Используйте выражение, которое вы нашли выше, чтобы найти общее количество бейсбольных и теннисных мячей, если менеджер купил 9 коробок каждого типа.
Ответ: 289
Объяснение:
Выражение, которое мы нашли в приведенном выше вопросе, это 37 + 28n
n = 9 прямоугольников
Подставьте значение n в выражение
37 + 28 (9) = 37 + 252 = 289
Таким образом, общее количество шаров = 289
Используйте свойство распределения, чтобы развернуть каждое выражение.
Вопрос 3.
0,5 (12 м — 22 н)
______ м — ______ н
Ответ: 6м — 11н
Explanation:
Мы используем свойство распределения, чтобы расширить выражение.
0,5 (12m — 22n) = 0,5 (12m) — 0,5 (22n)
= 16m — 11n
Таким образом, расширение 0,5 (12m — 22n) составляет 16m — 11n
Вопрос 4.
\ (\ frac {2} {3} \) (18x + 6z)
______ x + ______ z
Ответ: 12x + 4z
Explanation:
Мы используем свойство распределения, чтобы расширить выражение.
\ (\ frac {2} {3} \) (18x + 6z) = \ (\ frac {2} {3} \) (18x) + \ (\ frac {2} {3} \) (6z)
= \ (\ frac {36} {3} \) + \ (\ frac {12} {3} \)
= 12x + 4z
Таким образом, расширение \ (\ frac {2} {3} \) ( 18x + 6z) равно 12x + 4z
Разложите на множители каждое выражение.
Вопрос 5.
2x + 12
Введите ниже:
_____________
Ответ: 2 (x + 6)
Объяснение:
Общий множитель равен 2. Фактор выражения:
2x + 12 = 2 (x + 6)
Вопрос 6.
12x + 24
Введите ниже:
_____________
Ответ: 12 (x + 2)
Пояснение:
Общий множитель 12.Разложим выражение на множители
12x + 24 = 12 (x + 2)
Вопрос 7.
7x + 35
Введите ниже:
_____________
Ответ: 7 (x + 5)
Объяснение:
Общий множитель равен 7. Фактор выражения:
7x + 35 = 7 (x + 5)
Регистрация основных вопросов
Вопрос 8.
Какая связь между умножением и факторингом?
Ответ:
Разложение числа на множители означает запись его в виде произведения — списка чисел, которые при умножении дают вам исходное число, таким образом, факторинг подразумевает умножение.
С другой стороны, мы можем интерпретировать взаимосвязь между факторизацией и умножением как одно противостояние, потому что разложение выражения на множители означает деление каждого члена выражения на одно и то же число / коэффициент.
Независимая практика — стр. № 177
Напишите и упростите выражение для каждой ситуации.
Вопрос 9.
Компания сдает в аренду 15 продовольственных киосков и 20 игровых киосков на окружной ярмарке. Плата за продуктовый киоск составляет 100 долларов плюс 5 долларов в день.Плата за игровую будку составляет 50 долларов плюс 7 долларов в день. Ярмарка длится d дней, а все киоски сданы в аренду на все время. Напишите и упростите выражение для суммы в долларах, которую платят компании.
______ + ______ д
Ответ: 2500 + 215d
Пояснение:
Учитывая это,
Компания сдает в аренду 15 киосков с едой и 20 киосков с дичью на окружной ярмарке.
Стоимость киоска с едой составляет 100 долларов плюс 5 долларов в день.
Плата за игровую будку составляет 50 долларов плюс 7 долларов в день.
Пусть d будет количество дней, на которые сдаются в аренду будки.
Нам нужно написать выражение для суммы денег для продуктовых будок
15 (100 + 5d)
Мы должны написать выражение для суммы денег для игровых будок
20 (50 + 7d)
Мы должны напишите выражение для суммы денег для всех будок
15 (100 + 5d) + 20 (50 + 7d)
1500 + 75d + 1000 + 140d
Объедините одинаковые термины
2500 + 215d
Таким образом, выражение для суммы в долларах, которые платят компании 2500 + 215d
Вопрос 10.
Ковровщик использует узор, который представляет собой прямоугольник длиной 96 дюймов и шириной 60 дюймов. Производитель ковров хочет увеличить каждое измерение на разную величину. Пусть l и w будут увеличиваться в дюймах длины и ширины. Напишите и упростите выражение для периметра нового узора.
______ + ______ l + ______ w
Ответ:
Ковровщик использует узор, который представляет собой прямоугольник длиной 96 дюймов и шириной 60 дюймов. Изготовитель ковров хочет увеличить каждое измерение на разную величину.
Формула для периметра прямоугольника: 2 Длина + 2 Ширина
2 × (96 + l + 60 + w)
= 2 × (156 + l + w)
= (312 + 2l + 2w) дюймов
В 11–12 определите два фактора, которые были умножены вместе, чтобы сформировать массив плиток. Затем определите произведение двух факторов.
Вопрос 11.
______ x + ______
Ответ: 3x + 6
Объяснение:
Два множителя:
Ширина = 3
Длина = x + 2
Площадь является произведением двух чисел:
3 (x + 2) = 3 (x) + 3 (2)
3x + 6
Вопрос 12.
______ х — ______
Ответ: 8x — 4
Объяснение:
Два множителя:
Ширина = 4
Длина = 2x — 1
Площадь является произведением двух чисел:
4 (2x — 1) = 4 (2x) + 4 (-1) = 8x — 4
Вопрос 13.
Объясните, как на рисунке показано, что 6 (9) = 6 (5) + 6 (4).
Тип ниже:
___________
Ответ:
Обратите внимание, что левая часть рисунка имеет 6 единиц сверху вниз и 5 единиц слева направо, что составляет 6 × 5.С другой стороны, правая часть также имеет 6 единиц сверху вниз, но 4 единицы слева направо, что составляет 6 × 4. Сложение двух выражений даст (6 × 5) + (6 × 4).
В 14–15 указан периметр рисунка. Найдите длину указанной стороны.
Вопрос 14.
Введите ниже:
_____________
Ответ: 3x — 7
Пояснение:
Мы знаем, что периметр фигуры — это сумма всех сторон. Следовательно, мы можем определить длину другой стороны, представив ее переменной s
сторона + сторона + сторона = периметр
s + (x + 3) + (2x +4) = 6x
s + 3x + 7 = 6x
s = 6x — 3x — 7
Объедините похожие термины
s = 3x — 7
Вопрос 15.
Тип ниже:
_____________
Ответ: 2x + 6
Пояснение:
Мы знаем, что периметр фигуры — это сумма всех сторон. Следовательно, мы можем определить длину другой стороны, представив ее переменной s
2side + 2side = периметр
2s + 2 (3x — 3) = 10x + 6
2s + 6x — 6 = 10x + 6
2s = 10x + 6-6x + 6
2s = 4x + 12
2s = 2 (2x + 6)
s = 2x + 6
Стр. № 178
Вопрос 16.
Настойчиво решать проблемы
На рисунках показаны размеры теннисного корта и баскетбольной площадки, выраженные в ширине x в футах теннисного корта.
а. Напишите выражение для периметра каждого корта.
Тип ниже:
_____________
Ответ:
Поскольку корты прямоугольные, мы можем сложить все стороны корта, используя следующие выражения:
Теннис:
x + x + (2x + 6) + (2x + 6)
= 2x + 4x + 12
= 6x + 12
Баскетбол:
(1/2 x + 32) + (1/2 x + 32) + (3x — 14) + (3x — 14)
x + 64 + 6x — 28
Теперь объедините похожие условия
7х + 36
Вопрос 16.
б. Напишите выражение, описывающее, насколько периметр баскетбольной площадки больше, чем периметр теннисного корта.
Введите ниже:
_____________
Ответ: x + 24
Пояснение:
Поскольку периметр баскетбольной площадки больше, мы вычитаем из этого периметр теннисного корта.
Следовательно, выражение (7x + 36) — (6x + 12)
= 7x + 36 — 6x — 12 = x + 24
Вопрос 16.
c. Предположим, теннисный корт имеет ширину 36 футов. Найдите все размеры двух кортов.
Ширина теннисного корта: _________ футов
Длина теннисного корта: _________ футов
Ширина баскетбольной площадки: _________ футов
Длина баскетбольной площадки: _________ футов
Ответ:
Чтобы найти все размеры, подставляем 36 в x теннисного корта и решаем длину.
Для теннисного корта:
Ширина: x = 36 футов
Длина: 2x + 6 = 2 (36) + 6 = 72 + 6 = 78 футов
Для баскетбольной площадки:
Ширина: 1/2 x + 32 = 1 / 21 (36) + 32 = 18 + 32 = 50 футов
Длина: 3x — 14 = 3 (36) — 14 = 108-14 = 94 футов
Вопрос 17.
Выводы нарисуйте
Используйте цифру, чтобы найти произведение (x + 3) (x + 2). (Подсказка: найдите площадь каждого маленького квадрата или прямоугольника, затем сложите.)
Введите ниже:
_____________
Ответ: x² + 5x + 6
Пояснение:
Мы можем сложить площади меньших квадратов, чтобы найти площадь всей фигуры.
Обратите внимание, что есть один xx = x²
Есть 3 (x.1) = 3x
Есть 2 (x.1) = 2x
Есть 6 (1.1) = 6
Сложив их вместе, мы получим x² + 3x + 2x + 6 = x² + 5x + 6
Вопрос 18.
Сообщайте математические идеи
Десмонд утверждает, что продукт, показанный справа, иллюстрирует свойство распределения. Ты согласен? Объясните, почему да или почему нет.
________
Ответ: Да
Пояснение:
Умножение можно записать:
58 × 23 = 58 (20 + 3)
58 (20) + 58 (3)
1160 + 174
Мы замечаем, что произведения 174 и 1160 были получены с использованием свойства распределения. .
.
Вопрос 19.
Обоснуйте рассуждение
Опишите два различных способа найти произведение 8 × 997, используя математические вычисления. Найдите продукт и объясните, почему ваши методы работают.
Введите ниже:
_____________
Ответ:
Нам дается произведение
8 × 997
Для мысленного вычисления мы используем тот факт, что 997 близко к 1000
8 × 997 = 8. (1000 — 3)
8 × 1000 — 8 × 3
8000 — 24
7976
Другой метод:
8 × 997 = 8. (900 + 90 + 7)
8 (900) + 8 (90) + 8 (7)
7200 + 720 + 56
7976
Управляемая практика — стр.182
В таблице показана средняя температура в Барроу, Аляска, за три месяца в течение одного года.
Вопрос 1.
На сколько градусов выше средняя температура в ноябре, чем в январе?
________ ° F
Ответ: 11,7 ° F
Пояснение:
Пусть x представляет собой количество градусов, на которое температура в ноябре теплее, чем в январе.
x + (-13,4) = -1,7
x — 13,4 + 13,4 = -1,7 + 3,4
x = 11,7
Таким образом, средняя температура в ноябре составляет 11.На 7 ° F теплее.
Вопрос 2.
Предположим, что в течение одного периода сильного холода средняя дневная температура снижалась на 1 \ (\ frac {1} {2} \) ° F каждый день. За сколько дней температура снизилась на 9 ° F?
________ дней
Ответ: 6 дней
Пояснение:
Пусть x будет количеством дней, которое потребовалось для понижения температуры на 9 ° F
(-1 1/2) x = -9
-3 / 2x = -9
-3x = -18
x = 6
Понижение температуры на 9 ° F заняло 6 дней.
Используйте обратные операции для решения каждого уравнения.
Вопрос 3.
−2x = 34
________
Ответ: -17
Объяснение:
Нам дано уравнение:
−2x = 34
x = -17
Вопрос 4.
г — 3,5 = −2,1
________
Ответ: 1,4
Пояснение:
Дано уравнение:
y — 3,5 = −2,1
y = -2,1 + 3,5
y = 1,4
Вопрос 5.
\ (\ frac {2} {3} \) z = −6
________
Ответ: -9
Пояснение:
Нам дано уравнение:
\ (\ frac {2} {3} \) z = −6
z = -6 × \ (\ frac {3} {2} \)
z = -9
Регистрация основных вопросов
Вопрос 6.
Как написание уравнения помогает решить проблему?
Введите ниже:
_____________
Ответ:
Написание уравнения помогает нам смоделировать проблему. После того, как уравнение написано, мы можем применить математические правила для определения неизвестного в уравнении.
Независимая практика — стр. № 183
В таблице указаны высоты в футах на пиках нескольких гор. Используйте таблицу для 7–9.
Вопрос 7.
Mt. Эверест — 8707.37 футов выше, чем Mt. Мак-Кинли. Какая высота Mt. Эверест?
________ футов
Ответ: 29 087,87
Пояснение:
Учитывая это,
Mt. Эверест на 8707,37 футов выше, чем гора. Мак-Кинли.
Добавьте 8707,37 к высоте горы. МакКинли, чтобы найти высоту горы. Эверест.
МакКинли, чтобы найти высоту горы. Эверест.
20 321,5 + 8 707,37 = 29 028,87
Таким образом, высота горы. Высота Эвереста составляет 29 087,87 футов
Вопрос 8.
Лиам спустился с вершины К2 на высоту 23 201.06 футов. На сколько футов спустился Лиам? Каково было его изменение высоты?
________ футов
Ответ: 5050,25 футов
Пояснение:
Дано,
Лиам спустился с вершины К2 на высоту 23 201,06 фута.
Вычтите высоту горы К2 и ее высоту после спуска, чтобы найти количество футов, на которые он спустился. Поскольку он спустился с горы, изменение высоты является отрицательной величиной для количества футов, на которые он спустился.
спуск: 28 251.31 — 23 201,06 = 5050,25 футов
Изменение высоты: -5050,25 футов
Вопрос 9.
K2 на 11 194,21 футов выше, чем Mt. Кения. Напишите и решите уравнение, чтобы найти высоту горы. Кения.
________ футов
Ответ: 17 057,1
Пояснение:
Пусть h будет высотой Mt. Кения.
Кения.
Напишите уравнение, используя предоставленную информацию, что K2 с высотой 28 251,31 футов на 11 194,21 футов выше, чем Mt. Кения.
ч + 11,194,21 = 28,251,31
ч = 17057.1 фут
Вопрос 10.
Воздушный шар начинает спуск со скоростью 22 \ (\ frac {1} {2} \) футов в минуту. За какое время высота воздушного шара изменится на -315 футов?
________ минут
Ответ: 14 минут
Пояснение:
Воздушный шар начинает снижаться со скоростью 22 \ (\ frac {1} {2} \) футов в минуту.
315/22 \ (\ frac {1} {2} \) = 315 / \ (\ frac {45} {2} \)
= 315 × \ (\ frac {2} {45} \) = 14 минут
Вопрос 11.
Во время другой части полета воздушный шар из Упражнения 10 изменил высоту на -901 фут за 34 минуты.Какова была скорость его спуска?
________ \ (\ frac {□} {□} \) футов в минуту
Ответ:
Разделите количество футов на количество минут
\ (\ frac {901} {34} \) = 26,5 футов в минуту
(Или)
\ (\ frac {901} {10} \) = 90,1 футов на минута
В таблице показаны средние температуры в нескольких штатах с января по март. Используйте таблицу для 12–14.
Используйте таблицу для 12–14.
Вопрос 12.
Напишите и решите уравнение, чтобы определить, насколько средняя трехмесячная температура в Монтане выше, чем в Миннесоте.
________ ° С
Ответ: 1,8 ° C
Пояснение:
Напишите уравнение, где t — количество градусов выше, чем температура в Монтане по сравнению с температурой Миннесоты
-2,5 + t = -0,7
t = -0,7 + 2,5
t = 1,8 ° C
Вопрос 13.
Насколько теплее средняя трехмесячная температура во Флориде, чем в Монтане?
________ ° С
Ответ: 18,8 ° C
Пояснение:
Вычтем температуры Флориды и Монтаны
18,1 — (-0,7) = 18.1 + 0,7 = 18,8 ° С
Вопрос 14.
Как должна измениться средняя температура в Техасе, чтобы соответствовать средней температуре во Флориде?
________ ° С
Ответ: увеличить на 5,6 ° C
Пояснение:
Вычтем температуры Флориды и Техаса
18,1–12,5 = 5,6 ° C
Вопрос 15.
У футбольной команды чистый ярд -26 \ (\ frac {1} {3} \) ярдов в серии игр. Команде нужно чистое расстояние в 10 ярдов, чтобы получить первый удар. Сколько ярдов им нужно пройти в следующем розыгрыше, чтобы получить первый даун?
________ \ (\ frac {□} {□} \) ярдов
Ответ: 36 \ (\ frac {1} {3} \) ярдов
Пояснение:
Вычтите окончательный чистый ярд и текущий чистый метр, чтобы определить, сколько еще ярдов им нужно
10 — (−26 \ (\ frac {1} {3} \)) = 10 + 26 \ (\ frac { 1} {3} \)
= 36 \ (\ frac {1} {3} \)
Им нужно набрать 36 \ (\ frac {1} {3} \) ярдов в следующей игре, чтобы получить первый даун. .
Стр. № 184
Вопрос 16.
Дайвер начинает на уровне моря и спускается вертикально со скоростью 2 \ (\ frac {1} {2} \) футов в секунду. Сколько времени требуется дайверу, чтобы достичь высоты -15,6 футов?
________ секунд
Ответ: 6,24 секунды
Пояснение:
Разделите количество футов, на которое спускается дайвер, на скорость спуска.
время = расстояние / скорость
\ (\ frac {-15.6} {- 2.5} \)
= 6,24 секунды
Вопрос 17.
Анализ взаимосвязей
В упражнении 16, какова связь между скоростью, с которой дайвер спускается, высотой, которую он достигает, и временем, которое требуется, чтобы достичь этой отметки?
Введите ниже:
_____________
Ответ: Высота, которую он достигает (y), прямо пропорциональна времени, необходимому для достижения этой высоты (x), а скорость снижения (k) — константа пропорциональности.
Вопрос 18.
Проверка на разумность
Джейн снимала деньги со своего сберегательного счета каждые 5 месяцев. Средняя сумма, которую она снимала в месяц, составляла 45,50 долларов. Сколько всего она сняла за 5 месяцев? Покажите, что ваш ответ разумный.
$ ________
Ответ: 227,50 $
Пояснение:
Умножьте сумму, которую она снимала в месяц, на количество месяцев.
45,50 × 5 = 227,50
Поскольку 45,50 ≈ 50 и 50 × 5 = 250, что близко к 227. 50, ответ разумный.
50, ответ разумный.
Вопрос 19.
Обоснование рассуждений
Рассмотрим две проблемы, указанные ниже. Какие значения в задачах представлены отрицательными числами? Объяснить, почему.
(1) Дайвер ниже уровня моря поднимается на 25 футов к рифу на глубине -35,5 футов. Какая высота была у дайвера до того, как она поднялась на риф?
(2) Самолет снижается на 1,5 мили до высоты 3,75 мили. Какой была высота самолета перед спуском?
Введите ниже:
_____________
Ответ:
Высота -35.5 и высота после подъема представлены отрицательными числами. Изменение высоты обозначается отрицательным числом, поскольку плоскость спускается.
Вопрос 20.
Анализ взаимосвязей
Чем решение -4x = -4,8 отличается от решения — \ (\ frac {1} {4} \) x = -4,8? Как связаны решения?
Введите ниже:
_____________
Ответ:
Когда вы решаете -4x = -4,8, вы делите обе части на -4, чтобы найти x.
Когда вы решаете — \ (\ frac {1} {4} \) x = -4. 8, вы умножаете обе части на -4, чтобы найти x.
8, вы умножаете обе части на -4, чтобы найти x.
Тогда ответы на второе уравнение будут в 16 раз больше, чем на первую задачу, поскольку 4 × 4 = 16
Вопрос 21.
Сообщайте математические идеи
Флинн открывает сберегательный счет. За один трехмесячный период он делает депозиты в размере 75,50 и 55,25 долларов. Он снимает 25,15 и 18,65 долларов. Его баланс на конец трехмесячного периода составляет 210,85 доллара. Объясните, как узнать сумму его первоначального депозита.
$ ________
Ответ: 123 $.90
Пояснение:
Пусть x будет его начальным депозитом. Напишите уравнение его баланса после внесения дополнительных депозитов и снятия средств.
x + 75,50 + 55,25 — 25,15 — 18,65 = 210,58
x + 86,95 = 210,85
Упростим левую часть уравнения
x = 123,90
Таким образом, начальная сумма депозита составляет 123,90 доллара США
Управляемая практика — стр. № 188
Нарисуйте плитки алгебры для моделирования данного двухшагового уравнения.
Вопрос 1.
2x + 5 = 7
Введите ниже:
_____________
Ответ: 1
Explanation:
Сначала нарисуйте два положительных прямоугольника слева, чтобы обозначить 2x, и пять положительных квадратов, чтобы представить 5.На правой стороне нарисуйте 7 положительных квадратов, чтобы представить 7.
Вопрос 2.
−3 = 5 — 4x
Введите ниже:
_____________
Ответ: 2
Пояснение:
Нарисуйте 3 отрицательных квадрата с левой стороны, чтобы обозначить -3. С правой стороны нарисуйте 5 положительных квадратов, представляющих 5, и 4 отрицательных прямоугольника, представляющих -4x.
Вопрос 3.
Группа взрослых и один ребенок посещают фильм в Cineplex 15. Билеты стоят 9 долларов для взрослых и 6 долларов для детей.Общая стоимость фильма — 78 долларов. Напишите уравнение, чтобы найти количество взрослых в группе.
________ взрослых
Ответ: 8 взрослых
Пояснение:
Дано,
Группа взрослых и один ребенок посещают фильм в Cineplex 15.
Билеты стоят 9 долларов для взрослых и 6 долларов для детей.
Общая стоимость фильма 78 долларов.
Напишите уравнение для общей стоимости, пусть a будет количеством взрослых.
9a + 6 = 78
9a = 72
a = 8
Следовательно, в группе 8 взрослых.
Вопрос 4.
Разбейте уравнение 2x + 10 = 16, чтобы проанализировать каждую часть.
Введите ниже:
_____________
Ответ:
Поскольку x — это значение, которое мы пытаемся найти, x — это решение. Это означает, что 2x — это количество, которое мы ищем, умноженное на 2. 10 прибавляется к 2x = 16, что означает, что результат равен 16.
Вопрос 5.
Напишите соответствующую реальную проблему для представления 2x — 125 = 400.
Введите ниже:
_____________
Ответ:
Реальная проблема может заключаться в следующем: однажды летом вы продаете лимонад.Вы заплатили 125 долларов за все необходимые вам принадлежности. Если вы взимаете с клиентов 2 доллара за чашку лимонада, сколько чашек лимонада вам нужно продать, чтобы получить прибыль в 400 долларов?
Регистрация основных вопросов
Вопрос 6.
Опишите шаги, которые вы должны выполнить, чтобы написать двухэтапное уравнение, которое можно использовать для решения реальной проблемы.
Введите ниже:
_____________
Ответ:
Сначала вы должны определить, что вы ищете, с помощью переменной.В реальной задаче я написал задачу 5, где переменная x представляет количество проданных чашек. Затем решите, как остающаяся информация связана с переменной. Так как x — это количество проданных чашек, а 2 доллара — цена за чашку, тогда в уравнении должно быть 2x.
Поскольку прибыль = доход — стоимость расходных материалов, стоимость 125 долларов необходимо вычесть из 2x и уравнение должно равняться прибыли в 400 долларов. Это даст уравнение 2x — 125 = 400.
Независимая практика — стр.189
Вопрос 7.
Опишите, как смоделировать -3x + 7 = 28 с помощью плиток алгебры.
Введите ниже:
_____________
Ответ:
На левой стороне нарисуйте 3 отрицательных прямоугольника, чтобы представить -3x, и 7 положительных квадратов, чтобы представить 7. С правой стороны нарисуйте 28 положительных квадратов, чтобы представить 28.
С правой стороны нарисуйте 28 положительных квадратов, чтобы представить 28.
Вопрос 8.
Вэл арендовала велосипед, пока была в отпуске. Она платила фиксированную арендную плату в размере 55 долларов плюс 8,50 долларов каждый день. Общая стоимость составила 123 доллара. Напишите уравнение, которое вы сможете использовать, чтобы определить количество дней, на которые она арендовала велосипед.
________ дней
Ответ: 8 дней
Пояснение:
Пусть x будет количеством дней, тогда ежедневная комиссия составит 8,50x.
Поскольку существует фиксированная комиссия в размере 55 долларов, общая сумма комиссии составляет 8,50x + 55
8,50x + 55 = 123
8,50x = 123-55
8,50x = 68
x = 68 / 8,50
x = 8
Таким образом, она арендовал велосипед на 8 дней.
Вопрос 9.
Ресторан продает кружку для наполнения кофе за 6,75 доллара. Стоимость каждого пополнения составляет 1,25 доллара США. В прошлом месяце Кейт потратил 31,75 доллара на кружку и заправку. Напишите уравнение, которое вы можете использовать, чтобы найти количество добавок, которые купил Кейт.
Напишите уравнение, которое вы можете использовать, чтобы найти количество добавок, которые купил Кейт.
________ заправки
Ответ: 20 заправок
Пояснение:
Учитывая это,
Ресторан продает кружку для наполнения кофе за 6,75 доллара.
Стоимость каждого пополнения составляет 1,25 доллара США. В прошлом месяце Кейт потратил 31,75 доллара на кружку и заправку.
Пусть x представляет количество заправок, тогда общее количество заправок будет 1,25x.
Поскольку стоимость кружки составляла 6,75 доллара, общая стоимость составляет 6,75 + 1,25x
6,75 + 1,25x = 31,75
1.25x = 31,75 — 6,75
1,25x = 25
x = 25 / 1,25
x = 20
Таким образом, Кейт купил 20 картриджей.
Вопрос 10.
В тренажерном зале проводится одно 60-минутное занятие по субботам и несколько 45-минутных занятий в течение недели. На прошлой неделе все занятия длились 285 минут. Напишите уравнение, которое вы можете использовать, чтобы найти количество уроков в будние дни.
________ классы
Ответ: 5 классов
Пояснение:
Given,
В тренажерном зале проводится одно 60-минутное занятие по субботам и несколько 45-минутных занятий в течение недели.
На прошлой неделе все занятия продолжались 285 минут.
Пусть x будет количеством 45-минутных занятий, тогда общее время 45-минутных занятий, если 45x общее время всех классов будет тогда 60 + 45x = 285
45x = 285-60
45x = 225
x = 225/45
x = 5
Таким образом, количество занятий в будний день равно 5.
Вопрос 11.
Множественные представления
В зоопарке Спрингдейла обитают 172 южноамериканских животного. Это на 45 больше половины числа африканских животных в зоопарке.Напишите уравнение, которое вы могли бы использовать, чтобы найти n — количество африканских животных в зоопарке.
________ животные
Ответ: 254 животных
Пояснение:
В зоопарке Спрингдейла обитают 172 южноамериканских животного. Это на 45 больше половины числа африканских животных в зоопарке.
n / 2 + 45 = 172
n / 2 = 172 — 45
n / 2 = 127
n = 127 × 2
n = 254 животных
Таким образом, количество африканских животных в зоопарке составляет 254.
Вопрос 12.
Школа купила баскетбольное оборудование и форму на 548 долларов на сумму 29 долларов.50 каждый. Общая стоимость составила 2023 доллара. Напишите уравнение, которое вы сможете использовать, чтобы найти количество школьной формы, купленной в школе.
________ форменная
Ответ: 50 униформ
Пояснение:
Общая стоимость равна стоимости баскетбольного инвентаря плюс стоимость формы.
Пусть x представляет количество униформы. Поскольку каждая униформа стоит 29,50 долларов, то стоимость x униформы составляет 29,50 долларов.
Стоимость баскетбольного инвентаря 548 долларов, итого 548 + 29.50x
Предполагается, что общая стоимость составляет 2023 доллара, поэтому, если установить это значение равным полученному нами выражению для общей стоимости, получится уравнение 548 + 29,50x = 2023
29,50x = 2023 — 548
29,50x = 1475
x = 1475 / 29,50
x = 50
Таким образом, школа купила 50 единиц формы.
Вопрос 13.
Финансовая грамотность
У Хизер на сберегательном счете 500 долларов. Она снимает 20 долларов в неделю за бензин. Напишите уравнение, которое Хизер может использовать, чтобы узнать, сколько недель ей понадобится, чтобы иметь баланс в 220 долларов.
________ недель
Ответ: 14 недель
Пояснение:
Учитывая,
Хизер имеет 500 долларов на ее сберегательном счете. Она снимает 20 долларов в неделю за бензин.
Пусть x будет количеством недель. Поскольку она снимает 20 долларов каждую неделю, то через x недель ее счет изменится на -20 долларов.
Ее первоначальный баланс составлял 500 долларов, поэтому через x недель ее конечный баланс составляет 500–20 долларов.
Предполагается, что ее конечный баланс составляет 220 долларов, поэтому уравнение:
500 — 20x = 220
-20x = 220-500
-20x = -280
x = 280/20
x = 14
Потребуется 14 недель, чтобы иметь баланс 220 долларов.
Вопрос 14.
Critique Reasoning
Для 9x + 25 = 88 Дина написала ситуацию: «Я купила в магазине несколько рубашек по 9 долларов за штуку и получила скидку в 25 долларов. Мой общий счет составил 88 долларов. Сколько рубашек я купил? »
Мой общий счет составил 88 долларов. Сколько рубашек я купил? »
а. Какую ошибку допустила Дина?
Введите ниже:
_____________
Ответ: Ее ошибка заключалась в том, что скидка уменьшила бы сумму, которую она заплатила, поэтому в ее уравнении нужно было вычесть 25, а не прибавить.
Вопрос 14.
б. Перепишите уравнение, чтобы оно соответствовало ситуации Дины.
Введите ниже:
_____________
Ответ: Замена сложения в 9x + 25 = 88 на вычитание дает 9x — 25 = 88
Вопрос 14.
c. Как бы вы могли переписать ситуацию, чтобы она соответствовала уравнению?
Введите ниже:
_____________
Ответ: Вместо скидки ситуацию можно переписать так, чтобы она покупала другой товар, например брюки или свитер, по цене 25 долларов.
Стр. № 190
Вопрос 15.
Multistep
Сэнди взимает с каждой семьи, где она нянчится, фиксированную плату в размере 10 долларов за ночь и дополнительно 5 долларов за ребенка. Кимми берет 25 долларов за ночь, независимо от того, сколько детей в семье.
Кимми берет 25 долларов за ночь, независимо от того, сколько детей в семье.
а. Напишите двухэтапное уравнение, чтобы сравнить, сколько берут две девушки, и определить, когда их гонорары одинаковы.
Введите ниже:
_____________
Ответ: 10 + 5x = 25
Объяснение:
Пусть x будет количеством детей.
Сэнди взимает с каждой семьи, где она нянчится, фиксированную плату в размере 10 долларов за ночь и дополнительно 5 долларов за ребенка. Кимми берет 25 долларов за ночь, независимо от того, сколько детей в семье.
Это означает, что она заряжает в сумме 10 + 5x за ночь.
Kimmi взимает только фиксированную плату в размере 25 долларов за ночь.
Так как вам нужно сравнить их сборы, установите эти выражения равными друг другу.
Сэнди: 10 + 5x
Кимми: 25
Уравнение: 10 + 5x = 25
Вопрос 15.
б. Сколько детей должно быть в семье, чтобы Сэнди и Кимми взимали одинаковую сумму?
________ дети
Ответ: 3 детей
Объяснение:
Вычтите 10 с обеих сторон, а затем разделите обе стороны на 5, чтобы найти x.
10 + 5x = 25
5x = 25-10
5x = 15
x = 3 ребенка
Вопрос 15.
c. В семье Сандерсонов пятеро детей. Какую няню им выбрать, если они хотят сэкономить на присмотре за детьми и почему?
_____________
Ответ: Кимми, экономит им $ 10
Explanation:
Подставьте x = 5 в уравнение выше для Sandy.
10 + 5 (5) = 10 + 25 = 35
Это на 10 долларов больше, чем 25 долларов, которые взимает Кимми, поэтому им следует выбрать Kimmi, потому что это сэкономит им 10 долларов.
H.O.T.
Сосредоточьтесь на мышлении высшего порядка
Вопрос 16.
Анализ взаимосвязей
Каждый ученик написал двухэтапное уравнение. Питер написал уравнение 4x — 2 = 10, а Андрес — уравнение 16x — 8 = 40. Учитель посмотрел на их уравнения и попросил их сравнить их. Опишите один способ, в котором уравнения похожи.
Введите ниже:
_____________
Ответ:
Каждый ученик написал двухступенчатое уравнение. Питер написал уравнение 4x — 2 = 10, а Андрес написал уравнение 16x — 8 = 40.
Питер написал уравнение 4x — 2 = 10, а Андрес написал уравнение 16x — 8 = 40.
4x — 2 = 10
4x = 10 + 2
4x = 12
x = 3
16x — 8 = 40
16x = 40 + 8
16x = 48
x = 48/16
x = 3
Они также похожи, потому что если вы умножите обе части 4x — 2 = 10 на 4, вы получите 16x — 8 = 40
Вопрос 17.
Что за ошибка?
У Дэймона в кармане 5 центов и несколько пятак на общую сумму 1,20 доллара. Чтобы найти количество пятаков, которое есть у Деймона, студент написал уравнение 5n + 50 = 1.20. Найдите ошибку в уравнении ученика.
Введите ниже:
_____________
Ответ:
Ошибка в том, что он написал сумму денег в левой части уравнения в центах, а сумму денег в левой части уравнения написал в долларах. Ему нужно записать уравнение как 5n + 50 = 120. или 0,05n + 0,50 = 1,20
Вопрос 18.
Представьте реальные проблемы
Напишите реальную проблему, на которую вы могли бы ответить, решив уравнение -8x + 60 = 28.
Введите ниже:
_____________
Ответ:
Возможная реальная проблема: у вас есть 60 долларов, которые можно потратить на одежду. Вы хотите купить футболки по 8 долларов каждая. После того, как вы пошли за покупками, у вас осталось 28 долларов. Сколько футболок ты купил?
Управляемая практика — стр. № 194
Уравнение 2x + 1 = 9 смоделировано ниже
Вопрос 1.
Чтобы решить уравнение с элементами алгебры, сначала удалите _____
Затем разделите каждую сторону на _____
Введите ниже:
_____________
Ответ:
Первый шаг — удалить по одному положительному квадрату с каждой стороны.Затем разделите каждую сторону на 2 равные группы.
Вопрос 2.
Решение: x = _____
x = ______
Ответ: x = 4
Пояснение:
Решение: x = 4, поскольку удаление одного квадрата с каждой стороны дает 2x = 8, а затем деление каждой стороны на две равные группы дает x = 4.
Решите каждую проблему, написав и решив уравнение.
Вопрос 3.
Прямоугольная рамка для фотографий имеет периметр 58 дюймов. Высота рамы 18 дюймов.Какая ширина рамки?
______ дюймов
Ответ: 11 дюймов
Пояснение:
Прямоугольная рамка для картины имеет периметр 58 дюймов. Высота рамы 18 дюймов.
Периметр прямоугольника равен P = 2w + 2h.
Принято, что периметр прямоугольной рамки P = 58 дюймов, а высота h = 18 дюймов.
P = 2w + 2h
58 = 2w + 2 (18)
2w = 58 — 36
2w = 22
w = 11 дюймов
Таким образом, ширина рамки составляет 11 дюймов.
Вопрос 4.
Школьный магазин имеет на складе 1200 карандашей и продает в среднем 24 карандаша в день. Менеджер повторно заказывает, когда количество карандашей на складе составляет 500. Через сколько дней менеджеру придется делать повторный заказ?
______ дней
Ответ: 30 дней
Пояснение:
Школьный магазин имеет на складе 1200 карандашей и продает в среднем 24 карандаша в день.
Менеджер меняет заказ, когда количество карандашей на складе составляет 500.
Пусть x будет количеством дней
1200 — 24x = 500
-24x = -700
x ≈ 30
Таким образом, менеджер должен переупорядочить 30 дней.
Регистрация основных вопросов
Вопрос 5.
Как решить, какие операции использовать для решения двухэтапного уравнения?
Введите ниже:
_____________
Ответ:
При решении двухэтапного уравнения необходимо использовать обратные операции. Вы удаляете сложение, вычитая обратную операцию вычитания. Вы избавитесь от умножения, используя обратную операцию деления.
Стр. № 195
Вопрос 6.
9s + 3 = 57
______
Ответ: 6
Пояснение:
Нам дано уравнение
9s + 3 = 57
9s = 57 — 3
9s = 54
s = 54/9
s = 6
Вопрос 7.
4д + 6 = 42
______
Ответ: 9
Пояснение:
Дано уравнение
4d + 6 = 42
4d = 42 — 6
4d = 36
d = 36/4
d = 9
Вопрос 8.
−3y + 12 = −48
______
Ответ: 20
Пояснение:
Нам дано уравнение
−3y + 12 = −48
-3y = -48-12
-3y = -60
3y = 60
y = 20
Вопрос 9.
\ (\ frac {k} {2} \) + 9 = 30
______
Ответ: 42
Пояснение:
Нам дано уравнение
\ (\ frac {k} {2} \) + 9 = 30
\ (\ frac {k} {2} \) = 30 — 9
k / 2 = 21
к = 42
Вопрос 10.
\ (\ frac {g} {3} \) — 7 = 15
______
Ответ: 66
Пояснение:
Нам дано уравнение
\ (\ frac {g} {3} \) — 7 = 15
\ (\ frac {g} {3} \) = 15 + 7
г / 3 = 22
г = 22 × 3
г = 66
Вопрос 11.
\ (\ frac {z} {5} \) + 3 = −35
______
Ответ: -190
Пояснение:
У нас есть уравнение
\ (\ frac {z} {5} \) + 3 = −35
\ (\ frac {z} {5} \) = −35 — 3
z / 5 = -38
z = -38 × 5
z = -190
Вопрос 12.
−9ч — 15 = 93
______
Ответ: -12
Объяснение:
Дано уравнение
−9h — 15 = 93
-9h = 93 + 15
-9h = 108
-h = 108/9
h = -12
Вопрос 13.
−3 (n + 5) = 12
______
Ответ: -9
Пояснение:
Нам дано уравнение
−3 (n + 5) = 12
-3n — 15 = 12
-3n = 12 + 15
-3n = 27
-n = 27/3
n = -9
Вопрос 14.
−17 + \ (\ frac {b} {8} \) = 13
______
Ответ: 240
Пояснение:
Нам дано уравнение
−17 + \ (\ frac {b} {8} \) = 13
b / 8 = 13 + 17
b / 8 = 30
b = 30 × 8
b = 240
Вопрос 15.
7 (с — 12) = −21
______
Ответ: 9
Пояснение:
Нам дано уравнение
7 (c — 12) = −21
7c — 84 = -21
7c = -21 + 84
7c = 63
c = 63/7
c = 9
Вопрос 16.
−3 + \ (\ frac {p} {7} \) = −5
______
Ответ: -14
Пояснение:
Нам дано уравнение
−3 + \ (\ frac {p} {7} \) = −5
\ (\ frac {p} {7} \) = -5 + 3
\ (\ frac {p} {7} \) = -2
p = -2 × 7
p = -14
Вопрос 17.
46 = −6 т — 8
______
Ответ: -9
Пояснение:
Нам дано уравнение
46 = −6t — 8
-6t — 8 = 46
-6t = 46 + 8
-6t = 54
-t = 54/6
t = -9
Вопрос 18.
После внесения депозита на сберегательном счету Пуджи было 264 доллара. Она заметила, что если она прибавит 26 долларов к сумме, изначально находящейся на счете, и удвоит сумму, она получит новую сумму. Сколько у нее изначально было на счету?
$ ______
Ответ: 106 $
Пояснение:
Пусть x будет исходной суммой.Добавление 26 долларов к исходной сумме дает сумму x + 26.
Затем удвоение суммы дает 2 (x + 26), поэтому новая сумма составляет 2 (x + 26) доллара.
Принято, что новая сумма составляет 264 доллара, поэтому 2 (x + 26) = 264
2 (x + 26) = 264
x + 26 = 264/2
x + 26 = 132
x = 132 — 26
x = 106
Таким образом, у нее изначально на счету 106 долларов.
Вопрос 19.
Текущая температура в Смоллтауне 20 ° F. Это на 6 градусов меньше, чем в два раза выше, чем шесть часов назад.Какой была температура в Смоллтауне шесть часов назад?
______ ° F
Ответ: 13 ° F
Пояснение:
Текущая температура в Смоллтауне 20 ° F. Это на 6 градусов меньше, чем в два раза выше, чем шесть часов назад.
Это на 6 градусов меньше, чем в два раза выше, чем шесть часов назад.
Пусть x будет температурой шесть часов назад
2x — 6 = 20
2x = 20 + 6
2x = 26
x = 13
Таким образом, шесть часов назад температура в Смоллтауне была 13 ° F.
Вопрос 20.
Одно измерение на арктической исследовательской станции показало, что температура была -35 ° C.Что это за температура в градусах Фаренгейта?
______ ° F
Ответ: -31 ° F
Пояснение:
Одно измерение на арктической исследовательской станции показало, что температура была -35 ° C.
Замените C = -35 в формулу для преобразования температур по Цельсию и Фаренгейту
C = 5/9 (F — 32)
-35 = \ (\ frac {5} {9} \) (F — 32)
-35 × \ (\ frac {9} {5} \) = F — 32
-7 × 9 = F — 32
-63 = F — 32
F = -63 + 32
F = -31 ° F
Таким образом, температура в градусах по Фаренгейту составляет -31 ° F
Вопрос 21.
Арто заметил, что если он возьмёт противоположность своего возраста и прибавит 40, он получит число 28. Сколько лет Арто?
Сколько лет Арто?
______ лет
Ответ: 12 лет
Объяснение:
Арто заметил, что если он возьмёт противоположность своего возраста и прибавит 40, то получит число 28.
Пусть x будет его возрастом
-x + 40 = 28
x = 40 — 28
x = 12
Таким образом Арто 12 лет.
Вопрос 22.
У Свена 11 клиентов более чем в два раза больше, чем когда он начал продавать газеты.Сейчас у него 73 клиента. Сколько у него было, когда он начал?
______ клиентов
Ответ: 31 покупатель
Пояснение:
Пусть x будет количеством клиентов, с которыми он начал
11 + 2x = 73
2x = 73 — 11
2x = 62
x = 62/2
x = 31
Таким образом, у Свена было 31 покупатель, когда он начал.
Вопрос 23.
Паула купила лыжную куртку на распродаже за 6 долларов меньше половины ее первоначальной цены. За куртку она заплатила 88 долларов. Какая была первоначальная цена?
$ ______
Ответ: 188 $
Пояснение:
Учитывая это,
Паула купила лыжную куртку на распродаже за 6 долларов меньше половины ее первоначальной цены. За куртку она заплатила 88 долларов.
За куртку она заплатила 88 долларов.
Пусть x будет исходной ценой
1/2 x — 6 = 88
1/2 x = 88 + 6
1/2 x = 94
x = 94 × 2
x = 188
Таким образом, исходная цена составляет 188 долларов.
Вопрос 24.
Семья Макинтош пошла собирать яблоки. Всего было собрано 115 яблок. Семья съедала в общей сложности 8 яблок каждый день. Через сколько дней у них осталось 19 яблок?
______ дней
Ответ: 12 дней
Пояснение:
Семья Макинтош пошла собирать яблоки.Всего было собрано 115 яблок. Семья съедала в общей сложности 8 яблок каждый день
Пусть x будет количеством дней.
115 — 8x = 19
115-19 = 8x
8x = 96
x = 96/8
x = 12
Таким образом, ответ на вышеуказанный вопрос составляет 12 дней.
Используйте калькулятор для решения каждого уравнения.
Вопрос 25.
−5,5x + 0,56 = −1,64
______
Ответ: 0,4
Объяснение:
Дано уравнение
−5,5x + 0,56 = −1,64
Вычесть 0. 56 с обеих сторон
56 с обеих сторон
-5,5x = -2,2
Разделите обе стороны на -5,5
x = 0,4
Вопрос 26.
−4,2x + 31,5 = −65,1
______
Ответ: 23
Объяснение:
Дано уравнение
−4,2x + 31,5 = −65,1
Вычтем 31,5 с обеих сторон
-4,2x = -96,6
4,2x = 96,6
x = 96,6 / 4,2
x = 23
Вопрос 27.
\ (\ frac {k} {5.2} \) + 81,9 = 47,2
______
Ответ: -180,44
Пояснение:
Нам дано уравнение
\ (\ frac {k} {5.2} \) + 81,9 = 47,2
k / 5,2 = 47,2 — 81,9
k / 5,2 = -34,7
k = -180,44
Стр. № 196
Вопрос 28.
Напишите двухэтапное уравнение, которое включает умножение и вычитание, включает отрицательный коэффициент и имеет решение x = 7.
Введите ниже:
____________
Ответ:
Возможное двухэтапное уравнение, которое включает умножение и вычитание, включает отрицательный коэффициент и имеет решение x = 7: -2x — 7 = -21
-2x = -21 + 7
-2x = -14
2x = 14
x = 14/2
x = 7
Вопрос 29.
Напишите двухэтапное уравнение, включающее деление и сложение, которое имеет решение x = -25
Введите ниже:
____________
Ответ: \ (\ frac {x} {5} \) + 20 = 15
Пояснение:
Возможное двухэтапное уравнение, которое включает деление и сложение и имеет решение x = -25: \ (\ frac {x} {5} \) + 20 = 15
\ (\ frac {x} { 5} \) = 15 — 20
\ (\ frac {x} {5} \) = -5
x = -25
Вопрос 30.
Объясните ошибку
Показано решение учащегося уравнения 3x + 2 = 15.Опишите и исправьте ошибку, допущенную учеником.
3x + 2 = 15 Разделим обе стороны на 3.
x + 2 = 5 Вычтем 2 с обеих сторон.
x = 3
\ (\ frac {□} {□} \)
Ответ:
Ее ошибка заключалась в том, что она разделила обе стороны на 3.
Она не делила 2 на 3. Она должна была получить x + \ (\ frac {2} {3} \) = 5 после разделения обеих сторон. на 3.
Ее первым шагом должно было быть вычитание обеих сторон на 2 вместо деления обеих сторон на 3.
3x + 2 = 15
3x = 15 — 2
3x = 13
x = 13/2
Вопрос 31.
Множественные представления
Объясните, как можно использовать обратную стратегию решения задач для решения уравнения \ (\ frac {x} {4} \) — 6 = 2.
______
Ответ: Работать в обратном направлении означало бы назвать результат 2 и прибавить к нему 6, чтобы получить 8. Затем умножив это на 4, чтобы получить 32.
H.O.T.
Сосредоточьтесь на мышлении высшего порядка
Вопрос 32.
Reason Abstractly
Формула F = 1.8C + 32 позволяет вам найти температуру по Фаренгейту (F) для данной температуры по Цельсию (C).Решите уравнение для C, чтобы получить формулу для определения температуры по Цельсию для заданной температуры по Фаренгейту.
Тип ниже:
____________
Ответ:
F = 1,8C + 32
F — 32 = 1,8C
1,8C = F — 32
C = (F — 32) / 1,8
Вопрос 33.
Reason Abstractly
Уравнение P = 2 (l + w) может быть использовано для определения периметра P прямоугольника длиной l и шириной w. Решите уравнение для w, чтобы получить формулу для определения ширины прямоугольника с учетом его периметра и длины.
Решите уравнение для w, чтобы получить формулу для определения ширины прямоугольника с учетом его периметра и длины.
Тип ниже:
____________
Ответ:
P = 2 (l + w)
P / 2 = l + w
P / 2 — l = w
w = P / 2 — l
Вопрос 34.
Причина абстрактно
Решите уравнение ax + b = c относительно x.
Тип ниже:
____________
Ответ:
Вычтем обе части на b
ax = c — b
x = (c — b) / a
6.1 Алгебраические выражения — Стр. № 197
Вопрос 1.
Научный клуб совершил двухдневную экскурсию. В первый день участники заплатили 60 долларов за проезд плюс 15 долларов за билет в планетарий.На второй день они заплатили 95 долларов за проезд плюс 12 долларов за билет в геологический музей. Напишите выражение, представляющее общую стоимость двух дней для n членов клуба.
Тип ниже:
____________
Ответ: 155 + 27n
Пояснение:
Пусть n будет количеством элементов. Тогда n также представляет количество билетов.
В первый день билеты стоят 15 долларов каждый, поэтому для n участников стоимость билета составляет 15 миллионов долларов. Участники также должны заплатить 60 долларов за транспорт, поэтому общая стоимость первого дня составит 60 + 15 долларов.
На второй день билеты стоят 12 долларов каждый, поэтому для n участников стоимость билета составляет 12n долларов. Члены также должны заплатить 95 долларов за транспорт, поэтому общая стоимость первого дня составит 95 + 12 долларов.
Общая стоимость двух дней составит (60 + 15n) + (95 + 12n).
Объедините похожие термины.
27н + 155
6.2 Одношаговые уравнения с рациональными коэффициентами
Решить.
Вопрос 2.
ч + 9,7 = −9,7
______
Ответ: h = -19.4
Пояснение:
Нам дано уравнение
h + 9,7 = -9,7
h = -9,7 — 9,7
h = -19,4
Вопрос 3.
\ (- \ frac {3} {4} + p = \ frac {1} {2} \)
\ (\ frac {□} {□} \)
Ответ: p = 1 \ (\ frac {1} {4} \)
Объяснение:
Нам дано уравнение
\ (- \ frac {3} {4} + p = \ frac {1} {2} \)
-3/4 + p = 1/2
p = 1 / 2 + 3/4
p = 1 \ (\ frac {1} {4} \)
Вопрос 4.
−15 = −0,2k
______
Ответ: k = 75
Пояснение:
Дано уравнение
−15 = −0.2k
0,2k = 15
k = 15 / 0,2
k = 150/2
k = 75
Вопрос 5.
\ (\ frac {y} {- 3} = \ frac {1} {6} \)
\ (\ frac {□} {□} \)
Ответ: y = — \ (\ frac {1} {2} \)
Пояснение:
Нам дано уравнение
\ (\ frac {y} {- 3} = \ frac {1} {6} \)
y = -3/6
y = -1/2
Вопрос 6.
— \ (\ frac {2} {3} \) m = −12
______
Ответ: m = 18
Пояснение:
Нам дано уравнение
— \ (\ frac {2} {3} \) m = −12
\ (\ frac {2} {3} \) m = 12
m = 12 × 3 / 2
м = 6 × 3
м = 18
Вопрос 7.
2,4 = — \ (\ frac {t} {4.5} \)
______
Ответ: t = -10,8
Пояснение:
Нам дано уравнение
2,4 = — \ (\ frac {t} {4.5} \)
-t = 2,4 × 4,5
t = -10,8
6.3 Написание двухшаговых уравнений
Вопрос 8.
Джерри начал делать приседания каждый день. В первый день он сделал 15 приседаний. Каждый день после этого он делал на 2 приседания больше, чем накануне. Сегодня Джерри сделал 33 приседания. Напишите уравнение, которое можно решить, чтобы определить количество дней, в течение которых Джерри приседал, не считая первого дня.
В первый день он сделал 15 приседаний. Каждый день после этого он делал на 2 приседания больше, чем накануне. Сегодня Джерри сделал 33 приседания. Напишите уравнение, которое можно решить, чтобы определить количество дней, в течение которых Джерри приседал, не считая первого дня.
______ дней
Ответ: 2x + 15 = 33
Пояснение:
Пусть x будет количеством дней, тогда количество дополнительных приседаний равно 2x, так как он делает еще 2 приседания в каждый день, не считая первого дня.
Поскольку он начал делать 15 приседаний в первый день, общее количество приседаний после x будет 2x +15
2x + 15 = 33
6.4 Решение двухэтапных уравнений
Решить.
Вопрос 9.
5n + 8 = 43
______
Ответ: n = 7
Пояснение:
Нам дано уравнение
5n + 8 = 43
5n = 43-8
5n = 35
n = 35/5
n = 7
Вопрос 10.
\ (\ frac {y} {6} \) — 7 = 4
______
Ответ: y = 66
Пояснение:
Нам дано уравнение
\ (\ frac {y} {6} \) — 7 = 4
\ (\ frac {y} {6} \) = 4 + 7
\ (\ frac {y } {6} \) = 11
y = 11 × 6
y = 66
Вопрос 11.
8н — 15 = 57
______
Ответ: w = 9
Пояснение:
Нам дано уравнение
8w — 15 = 57
8w = 57 + 15
8w = 72
w = 72/8
w = 9
Вопрос 12.
\ (\ frac {g} {3} \) + 11 = 25
______
Ответ: g = 42
Пояснение:
Нам дано уравнение
\ (\ frac {g} {3} \) + 11 = 25
\ (\ frac {g} {3} \) = 25 — 11
\ (\ frac {g } {3} \) = 14
г = 14 × 3
г = 42
Вопрос 13.
\ (\ frac {f} {5} \) — 22 = −25
______
Ответ: f = -15
Пояснение:
Нам дано уравнение
\ (\ frac {f} {5} \) — 22 = −25
\ (\ frac {f} {5} \) = -25 + 22
\ (\ frac {f} {5} \) = -3
f = -3 × 5
f = -15
Вопрос 14.
−4p + 19 = 11
______
Ответ: p = 2
Пояснение:
Нам дано уравнение
−4p + 19 = 11
-4p = 11-19
-4p = -8
p = 2
Основной вопрос
Вопрос 15.
Как можно использовать двухэтапные уравнения для представления и решения реальных проблем?
Введите ниже:
___________
Ответ:
Для представления и решения реальных проблем можно использовать пошаговые двухэтапные уравнения, переведя слова в алгебраическое уравнение, решив уравнение и затем интерпретируя решение уравнения.
Выбранный ответ — Страница № 198
Вопрос 1.
Такси стоит 1,50 доллара за первую милю и 0,75 доллара за каждую дополнительную милю.Какое уравнение можно решить, чтобы определить, сколько миль вы можете проехать в такси за 10 долларов, учитывая, что x — это количество дополнительных миль?
Опции:
а. 1,5x + 0,75 = 10
б. 0,75x + 1,5 = 10
в. 1,5х — 0,75 = 10
д. 0,75x — 1,5 = 10
Ответ: 0,75x + 1,5 = 10
Объяснение:
Пусть x будет количеством дополнительных миль, тогда плата за дополнительные мили составит 0,75x, тогда общая стоимость будет 1,50 + 0,75x = 10
Таким образом, правильный ответ — вариант B.
Вопрос 2.
Какое решение является \ (\ frac {t} {2.5} \) = −5,2?
Опции:
а. -13
г. -2.08
с. 2.08
г. 13
Ответ: -13
Объяснение:
t / 2,5 = -5,2
t = -5,2 × 2,5
t = -13
Таким образом, правильный ответ — вариант A.
Вопрос 3.
Какое выражение эквивалентно 5x — 30?
Опции:
а. 5 (х — 30)
г. 5 (х — 6)
с. 5x (x — 6)
г. х (5–30)
Ответ: 5 (x — 6)
Пояснение:
Выносим за скобки 5 из каждого члена.
5x — 30 = 5 (x — 6)
Таким образом, правильный ответ — вариант B.
Вопрос 4.
В научном эксперименте температура вещества изменяется с 42 ° F до -54 ° F со средней скоростью -12 градусов в час. Через сколько часов происходит смена?
Опции:
а. -8 часов
б. 18 часов
c. 1 час
д. 8 часов
Ответ: 8 часов
Пояснение:
В научном эксперименте температура вещества изменяется с 42 ° F до -54 ° F со средней скоростью -12 градусов в час.
Пусть x будет количеством часов.
42 — 12x = -54
-12x = -54 — 42
-12x = -96
12x = 96
x = 96/12
x = 8 часов
Таким образом, правильный ответ — вариант D.
Вопрос 5.
Какое утверждение наилучшим образом представляет расстояние на числовой прямой между -14 и -5?
Опции:
а. −14 — (−5)
−14 — (−5)
б. −14 + (−5)
с. −5 — (−14)
д. -5 + (-14)
Ответ: −5 — (−14)
Пояснение:
Расстояние — это разница между наибольшим числом и наименьшим числом, поэтому расстояние между -5 и -14 равно -5 — (-14), поскольку -5 больше, чем -14.
Таким образом, правильный ответ — вариант C.
Вопрос 6.
Какая крупа стоит больше всего за унцию?
Опции:
а. 4,92 доллара за 12 унций
b. 4,25 доллара за 10 унций
c. 5,04 доллара за 14 унций
d. 3,92 доллара за 8 унций
Ответ: 3,92 доллара за 8 унций
Пояснение:
Найдите стоимость единицы для каждого варианта ответа, разделив стоимость на количество унций и округлив до двух десятичных знаков, если это необходимо.
а. 4,92 доллара за 12 унций
4,92 / 12 = 0 долларов.41 за унцию
б. 4,25 доллара за 10 унций
4,25 / 10 ≈ 0,43 за унцию
c. 5,04 доллара за 14 унций
5,04 / 14 = 0,36 за унцию
d. 3,92 доллара за 8 унций
3,92 / 8 = 0,49 за унцию
Таким образом, правильный ответ — вариант D.
Мини-задание
Вопрос 7.
Кейси купил 9 билетов на концерт. Общая стоимость составила 104 доллара, включая 5 долларов за обслуживание.
а. Напишите уравнение, которое вы можете решить, чтобы найти c, стоимость одного билета.
Введите ниже:
_____________
Ответ: 9c + 5 = 104
Пояснение:
Пусть c будет стоимость каждого билета, общая стоимость 9 билетов до платы за обслуживание составит 9 центов, прибавив плату за обслуживание, мы получим общую сумму 9 центов + 5
Вопрос 7.
г. Объясните, как вы можете оценить решение своего уравнения.
Введите ниже:
_____________
Ответ:
104 — это примерно 105. вычитание 5 из этого дает 100. 9 — это примерно 10, а 100, деленное на 10, дает 10, поэтому цена билета составляет около 10 долларов.
Вопрос 7.
c. Решите уравнение. Сколько стоил каждый билет?
$ ______
Ответ:
9c = 99
c = 99/9
c = 11
Заключение:
Понятие алгебры полезно для студентов в реальной жизни. Таким образом, ученикам 7-го стандарта очень важно выучить уловки и использовать их в реальном времени. Добавьте в закладки наш ключ с ответами по математике, чтобы получить краткое объяснение всех глав. Всего наилучшего!!!!
Таким образом, ученикам 7-го стандарта очень важно выучить уловки и использовать их в реальном времени. Добавьте в закладки наш ключ с ответами по математике, чтобы получить краткое объяснение всех глав. Всего наилучшего!!!!
Урок для 7-го класса — Католическая церковь Святого Альберта Великого
Урок для 7-го класса — Католическая церковь Святого Альберта Великого — Сан-Прери, Висконсин- Дом
- О компании
- Информация о приходе
- Членство
- Участие прихода
- Приходская жизнь
- Приходские события
- Литургия и Таинства
- Масса
- Литургические служения
- Таинства
- Похороны
- Формирование веры
- Обучение взрослых
- Информация о программе религиозного образования
- Уроки религиозного образования
- Евангелизация
- Министерства
- Молодежное служение
- Продовольственная помощь
- Местное информирование
- Приходская программа Twinning
Письмо для 7-го класса — Sirius Education Solutions
Новый ТЕКС!
Написание 7-го класса
Подготовка и практика по STAAR
Написание 7 классов содержит 18 отрывков для редактирования и редактирования и 5 подсказок для сочинения. 18 интерактивных уроков по навыкам содержат пошаговые инструкции, а также самостоятельную и управляемую практику. В программе также:
18 интерактивных уроков по навыкам содержат пошаговые инструкции, а также самостоятельную и управляемую практику. В программе также:
- Revision Skills: 5 интерактивных уроков по навыкам с подробными инструкциями и практическими рекомендациями по ответам на вопросы теста STAAR.
- Навыки редактирования: 6 интерактивных уроков по точной грамматике, пунктуации и использованию навыков из выпущенных тестов STAAR
- Практика STAAR: 12 отрывков редактирования и редактирования предлагают аутентичную практику STAAR в случайном порядке — точно так же, как STAAR тест.
- Навыки и практика композиции: 7 интерактивных уроков по навыкам, основанных на оценках и подсказках5 с графическими органайзерами и контрольными списками.
- Трехэтапный подход: Дополнительный подход для определения приоритетов и индивидуализации исправлений при мониторинге прогресса.
- Teacher’s Edition: Color TE включает полные пояснения к выбору ответов, чтобы помочь учителю дать учащимся полезную обратную связь о том, почему один вариант ответа лучше.

Письмо для учителей 7 класса
Эта полноцветная спиральная TE дает подробные ответы на каждый вопрос, поэтому учителя или репетиторы могут дать студентам конкретные отзывы о том, почему один ответ лучше.Образцы ответов учащихся предоставляются для каждого запроса на практику, а также ресурсы, которые помогут учителям точно оценивать сочинения учащихся.
Также доступны…
Сочинение 7-го класса: ответы на наиболее часто проверяемые вопросы STAAR
Zingers помогает всем учащимся научиться решать наиболее часто проверяемые вопросы на экзамене STAAR. Zinger легко внедряется в различных условиях и обеспечивает комплексное обучение и практику, а также позволяет студентам правильно отвечать на большее количество вопросов.Используйте Zinger для разминки, разминки и интенсивной подготовки непосредственно перед тестом STAAR.
Практические тесты по письму по STAAR для 7-го класса Предоставляет два отдельных полноразмерных буклета с тестами — Форма A и Форма B, которые соответствуют плану и опубликованным тестам STAAR. Также включены листы с ответами учащихся (пузырьковые листы) и версия для учителя, в которой представлены полные объяснения ответов, чтобы учителя могли дать учащимся содержательные отзывы.
Также включены листы с ответами учащихся (пузырьковые листы) и версия для учителя, в которой представлены полные объяснения ответов, чтобы учителя могли дать учащимся содержательные отзывы.
SE: G7WSE, 180 стр .; TE: G7WTE, 124 стр .; Практические тесты: G7WPT; Зингер: G7WZ
Сопутствующие товары
% PDF-1.7
%
975 0 объект
>
endobj
xref
975 159
0000000016 00000 н.
0000004691 00000 н.
0000004929 00000 н.
0000004965 00000 н.
0000005503 00000 н.
0000005540 00000 н.
0000005654 00000 н.
0000007560 00000 н.
0000009340 00000 п.
0000011073 00000 п.
0000012886 00000 п.
0000014808 00000 п.
0000016963 00000 п.
0000017145 00000 п.
0000017532 00000 п.
0000018010 00000 п.
0000018192 00000 п.
0000018304 00000 п.
0000018561 00000 п.
0000019122 00000 п.
0000021579 00000 п.
0000025294 00000 п.
0000027943 00000 н.
0000043127 00000 п.
0000061554 00000 п.
0000061812 00000 п.
0000061928 00000 п.
0000092990 00000 п. 0000093261 00000 п.
0000093517 00000 п.
0000093794 00000 п.
0000096946 00000 п.
0000097285 00000 п.
0000097673 00000 п.
0000103036 00000 н.
0000103305 00000 н.
0000103612 00000 н.
0000112102 00000 п.
0000112143 00000 н.
0000112179 00000 н.
0000112258 00000 н.
0000144247 00000 н.
0000144577 00000 н.
0000144646 00000 н.
0000144764 00000 н.
0000144788 00000 н.
0000144867 00000 н.
0000156597 00000 н.
0000157712 00000 н.
0000157781 00000 н.
0000157899 00000 н.
0000157935 00000 п.
0000158014 00000 н.
0000166585 00000 н.
0000166918 00000 н.
0000166987 00000 н.
0000167105 00000 н.
0000167129 00000 н.
0000167208 00000 н.
0000169816 00000 н.
0000170231 00000 п.
0000170300 00000 п
0000170418 00000 н.
0000170454 00000 н.
0000170533 00000 п.
0000185983 00000 н.
0000186316 00000 н.
0000186385 00000 н.
0000186503 00000 н.
0000186527 00000 н.
0000186606 00000 н.
0000197658 00000 н.
0000198219 00000 н.
0000198288 00000 н.
0000198406 00000 н.
0000198442 00000 н.
0000093261 00000 п.
0000093517 00000 п.
0000093794 00000 п.
0000096946 00000 п.
0000097285 00000 п.
0000097673 00000 п.
0000103036 00000 н.
0000103305 00000 н.
0000103612 00000 н.
0000112102 00000 п.
0000112143 00000 н.
0000112179 00000 н.
0000112258 00000 н.
0000144247 00000 н.
0000144577 00000 н.
0000144646 00000 н.
0000144764 00000 н.
0000144788 00000 н.
0000144867 00000 н.
0000156597 00000 н.
0000157712 00000 н.
0000157781 00000 н.
0000157899 00000 н.
0000157935 00000 п.
0000158014 00000 н.
0000166585 00000 н.
0000166918 00000 н.
0000166987 00000 н.
0000167105 00000 н.
0000167129 00000 н.
0000167208 00000 н.
0000169816 00000 н.
0000170231 00000 п.
0000170300 00000 п
0000170418 00000 н.
0000170454 00000 н.
0000170533 00000 п.
0000185983 00000 н.
0000186316 00000 н.
0000186385 00000 н.
0000186503 00000 н.
0000186527 00000 н.
0000186606 00000 н.
0000197658 00000 н.
0000198219 00000 н.
0000198288 00000 н.
0000198406 00000 н.
0000198442 00000 н. 0000198521 00000 н.
0000203909 00000 н.
0000204241 00000 н.
0000204310 00000 н.
0000204428 00000 н.
0000204516 00000 н.
0000205547 00000 н.
0000205849 00000 н.
0000206153 00000 н.
0000206333 00000 н.
0000206423 00000 н.
0000206749 00000 н.
0000206941 00000 н.
0000207266 00000 н.
0000207590 00000 н.
0000207938 00000 п.
0000208305 00000 н.
0000208611 00000 н.
0000208794 00000 н.
0000209107 00000 н.
0000209324 00000 н.
0000212051 00000 н.
0000212092 00000 н.
0000212168 00000 н.
0000212294 00000 н.
0000212593 00000 н.
0000212669 00000 н.
0000213468 00000 н.
0000213518 00000 н.
0000213554 00000 н.
0000213633 00000 н.
0000233902 00000 н.
0000234263 00000 п.
0000234332 00000 н.
0000234460 00000 н.
0000234496 00000 п.
0000234575 00000 н.
0000234688 00000 н.
0000261904 00000 н.
0000262266 00000 н.
0000262335 00000 н.
0000262463 00000 н.
0000427246 00000 н.
0000428495 00000 н.
0000428571 00000 н.
0000428873 00000 н.
0000428949 00000 н.
0000428985 00000 п.
0000198521 00000 н.
0000203909 00000 н.
0000204241 00000 н.
0000204310 00000 н.
0000204428 00000 н.
0000204516 00000 н.
0000205547 00000 н.
0000205849 00000 н.
0000206153 00000 н.
0000206333 00000 н.
0000206423 00000 н.
0000206749 00000 н.
0000206941 00000 н.
0000207266 00000 н.
0000207590 00000 н.
0000207938 00000 п.
0000208305 00000 н.
0000208611 00000 н.
0000208794 00000 н.
0000209107 00000 н.
0000209324 00000 н.
0000212051 00000 н.
0000212092 00000 н.
0000212168 00000 н.
0000212294 00000 н.
0000212593 00000 н.
0000212669 00000 н.
0000213468 00000 н.
0000213518 00000 н.
0000213554 00000 н.
0000213633 00000 н.
0000233902 00000 н.
0000234263 00000 п.
0000234332 00000 н.
0000234460 00000 н.
0000234496 00000 п.
0000234575 00000 н.
0000234688 00000 н.
0000261904 00000 н.
0000262266 00000 н.
0000262335 00000 н.
0000262463 00000 н.
0000427246 00000 н.
0000428495 00000 н.
0000428571 00000 н.
0000428873 00000 н.
0000428949 00000 н.
0000428985 00000 п.


 Нужно было проложить маршрут, оптимальный по интересности, длине, количеству баллов за задания и т.п.
Нужно было проложить маршрут, оптимальный по интересности, длине, количеству баллов за задания и т.п.
 дом просто переезжает на 50 метров вглубь квартала.Сегодня этот памятник полностью скрыт сталинскими домами и новым зданием МХАТа по Камергерскому переулку.
дом просто переезжает на 50 метров вглубь квартала.Сегодня этот памятник полностью скрыт сталинскими домами и новым зданием МХАТа по Камергерскому переулку. В песне поется про изготовление пушек и кузницу, а какое оружие ещё могли изготовлять в этом районе? Посмотрите внимательно на карту и найдите переулок, название которого подскажет ответ. Пройдите вдоль переулка и перечислите все театры, выходящие на него. Обратите внимание на красивые фонари на этом переулке (считать их не надо). (2 балла)
В песне поется про изготовление пушек и кузницу, а какое оружие ещё могли изготовлять в этом районе? Посмотрите внимательно на карту и найдите переулок, название которого подскажет ответ. Пройдите вдоль переулка и перечислите все театры, выходящие на него. Обратите внимание на красивые фонари на этом переулке (считать их не надо). (2 балла) Сергея Эйзенштейна (улица Каретный Ряд, дом 5/10). Перепишите номер билета в одной из витрин библиотеки. (1 балл)
Сергея Эйзенштейна (улица Каретный Ряд, дом 5/10). Перепишите номер билета в одной из витрин библиотеки. (1 балл) Посчитайте квадратные изразцы на здании театра. (2 балла)
Посчитайте квадратные изразцы на здании театра. (2 балла)
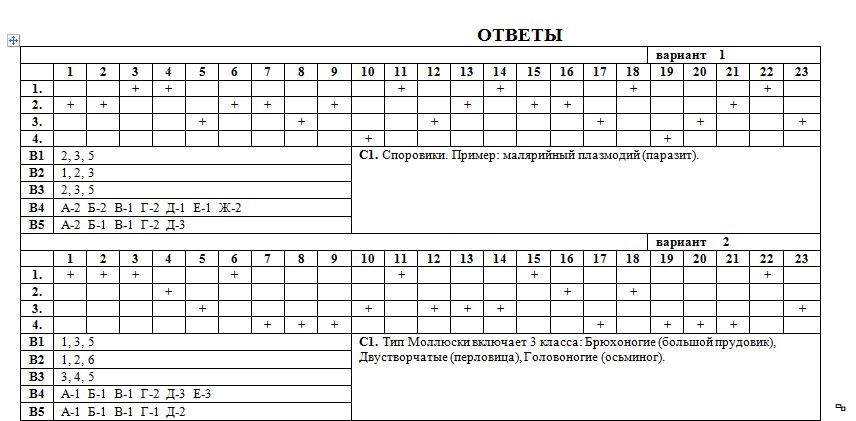 Двигайтесь прямо, пока не увидите сквер с левой стороны. Кто нарисован на граффити (ответ №2)? Продолжайте движение прямо, пока надпись по правую руку не напомнит о том, что дает корова. После этого кафе поверните направо во двор и напишите номер дома, в который вы упретесь, войдя во двор (ответ №3). Вернитесь обратно на улицу и идите до первого поворота направо. Поверните на пешеходную улицу. Двигайтесь прямо до четвёртого двойного фонарного столба, после которого справа вы увидите фреску — название кафе (к сожалению, закрытого). Как оно называлось (ответ №4)? (4 балла)
Двигайтесь прямо, пока не увидите сквер с левой стороны. Кто нарисован на граффити (ответ №2)? Продолжайте движение прямо, пока надпись по правую руку не напомнит о том, что дает корова. После этого кафе поверните направо во двор и напишите номер дома, в который вы упретесь, войдя во двор (ответ №3). Вернитесь обратно на улицу и идите до первого поворота направо. Поверните на пешеходную улицу. Двигайтесь прямо до четвёртого двойного фонарного столба, после которого справа вы увидите фреску — название кафе (к сожалению, закрытого). Как оно называлось (ответ №4)? (4 балла) После этого кафе поверните направо во двор и напишите номер дома, в который вы упретесь, войдя во двор (ответ №3 – 7/5 стр.4) Вернитесь обратно на улицу и идите до первого поворота направо. Поверните на пешеходную улицу (вы повернули в Камергерский переулок). Двигайтесь прямо до четвёртого двойного фонарного столба, после которого справа вы увидите фреску — название кафе (к сожалению, закрытого). Как оно называлось (ответ №4 – Кафе-кондитерская «Счастье»)?
После этого кафе поверните направо во двор и напишите номер дома, в который вы упретесь, войдя во двор (ответ №3 – 7/5 стр.4) Вернитесь обратно на улицу и идите до первого поворота направо. Поверните на пешеходную улицу (вы повернули в Камергерский переулок). Двигайтесь прямо до четвёртого двойного фонарного столба, после которого справа вы увидите фреску — название кафе (к сожалению, закрытого). Как оно называлось (ответ №4 – Кафе-кондитерская «Счастье»)? Сколько струн на его гитаре?(1 балл)
Сколько струн на его гитаре?(1 балл) В период с 1817 по 1819 годы трёхкилометровый участок реки заключили в трубу, которая представляла собой кирпичный свод.
В период с 1817 по 1819 годы трёхкилометровый участок реки заключили в трубу, которая представляла собой кирпичный свод.  Под крышей этого здания насчитывается 30 скульптур (8+8+10+4).
Под крышей этого здания насчитывается 30 скульптур (8+8+10+4). (1 балл)
(1 балл)
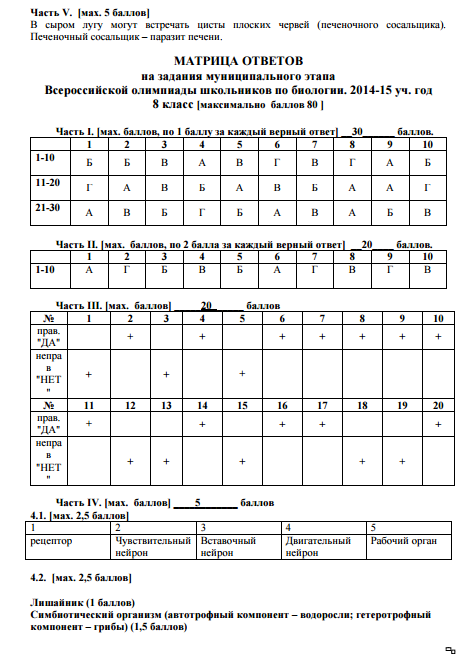

 Перепишите даты с памятника. (1 балл)
Перепишите даты с памятника. (1 балл) О.Топорков, М.Н.Кедров, А.К.Тарасова, С.В.Образцов, С.И.Юткевич
О.Топорков, М.Н.Кедров, А.К.Тарасова, С.В.Образцов, С.И.Юткевич
 Сейчас в этом здании они же и располагаются. Последнее слово на барельефе – CCCР.
Сейчас в этом здании они же и располагаются. Последнее слово на барельефе – CCCР.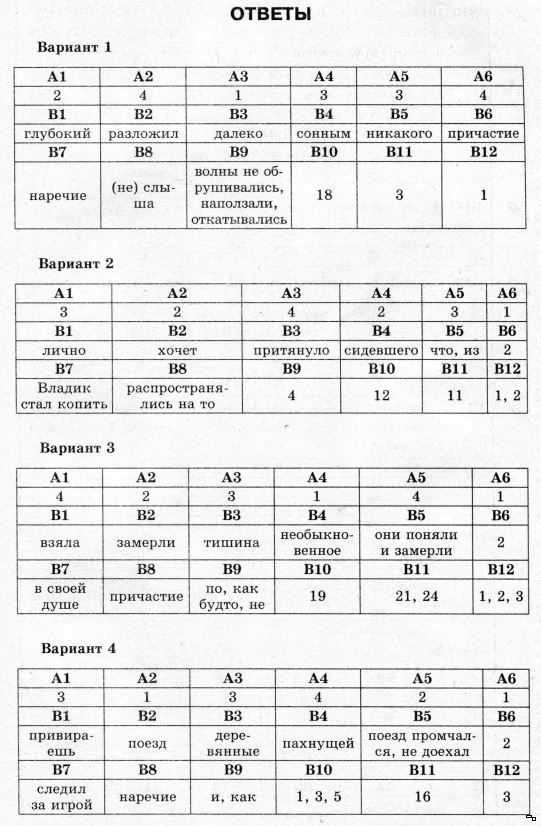 Прочтите и перепишите латинскую надпись на фасаде особняка. (1 балл)
Прочтите и перепишите латинскую надпись на фасаде особняка. (1 балл)  Взаимно простые числа
Взаимно простые числа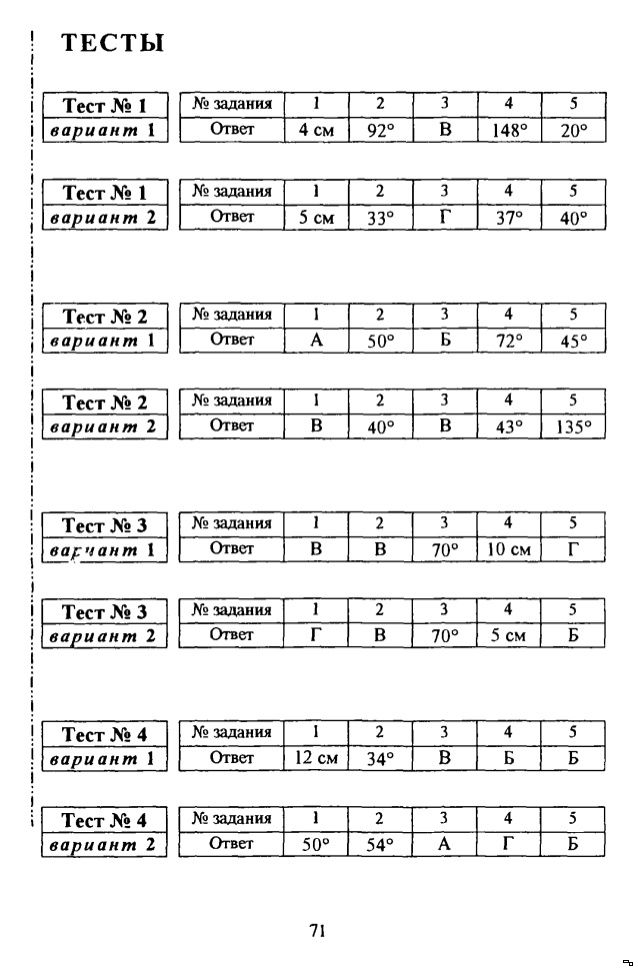 Пиктограммы» (N 135159)
Пиктограммы» (N 135159) Вариант 1
Вариант 1 Вариант 1
Вариант 1 Выбор конфигурации в зависимости от решаемых задач»
Выбор конфигурации в зависимости от решаемых задач» Вариант 2
Вариант 2 Вариант 1
Вариант 1 Вариант 1
Вариант 1 rtf
rtf