Урок » Графический способ решения систем уравнений», 7 класс
Урок «Графический способ решения систем уравнений»
Для учащихся 7 класса.
Урок усвоения новых знаний.
Цели урока:
Образовательные
. Обучить соответствующим навыкам
. Вывести необходимые формулы
. Закрепить полученные знания в ходе решения задач
. Повторение и актуализация опорных знаний
Развивающие
. Развитие умения анализировать, обобщать и систематизировать знания
. Формирование у учащихся самостоятельности мышления.
. Развивать творческие способности путем решения задач
. Развитие речи, умение лаконично излагать свои мысли, анализировать и делать выводы
Воспитательные
.Побуждать учащихся к самоконтролю и взаимоконтролю своей деятельности
. Воспитание взаимопомощи и взаимовыручки
Методы организации урока:
. Наглядность (использование ИКТ, построение графиков с помощью «Живой математики»)
. Фронтальный и индивидуальный опросы
. нарастающая сложность решаемой проблемы
Этапы урока
1. Организационная
2. постановка задачи в ее развитии
3. Домашняя работа
1. Вспомним понятие линейной функции и построим графики функций:
1.
2.
3.
(трое учащихся строят графики на доске)
2. 1.Решим системы уравнений и построим графики уравнений, входящих в системы:
1.
2.
( Выполняем задания самостоятельно в тетрадях)
Сравним решение систем уравнений с координатами точек пересечения графиков.
Вывод: Решение систем уравнений совпадают с координатами точек пересечения графиков.
2. Всегда ли система уравнений имеет решение? Нет.
Решим систему уравнений и построим графики уравнений:
Имеет ли эта система решение? Как расположены графики уравнений?
Вывод: Если система уравнений не имеет решения, то графики уравнений параллельны.
3. Может ли система уравнений иметь бесконечное множество решений? Да.
Решим систему уравнений и построим графики уравнений:
Сколько решений имеет эта система? Как расположены графики?
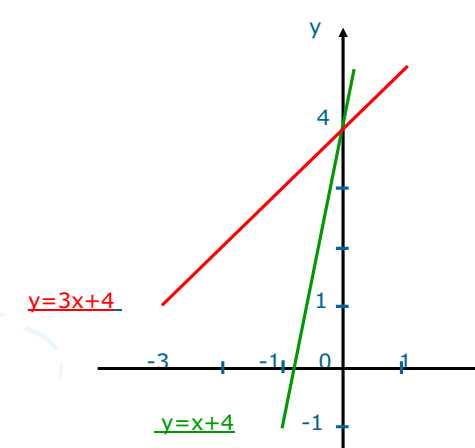
Вывод: Если система уравнений имеет бесконечное множество решений,
то графики уравнений совпадают.
4. Закрепление.
Решаем задания из учебника № 644(2), 647(2), 648(2)
3. Домашнее задание № 644(2), 647(1), 648(1), 642(4)
infourok.ru
«Решение систем линейных уравнений с двумя переменными графическим способом». 7-й класс
Разделы: Математика
Маршрутный лист №1 по теме:
“Решение систем линейных уравнений с двумя переменными графическим способом”
Ученика 7 класса____________________________
| Шаг 1. | Запишите систему линейных уравнений с двумя переменными | |
| Шаг 2. | Что значит: “Решить систему уравнений?” | Решить систему уравнений – значит найти все её решения или доказать, что решений нет. |
| Шаг 3 | Из первого уравнения выразите у через х | У=2х-1 |
| Шаг 4 | Из второго уравнения выразите у через х | У=х-1 |
| Шаг 5 | Графиками линейных уравнений
являются прямые. Запишите это утверждение в тетрадь. |
Графиками линейных уравнений У=2х-1 и У=х-1, являются прямые. |
| Шаг 6 | В одной и той же координатной плоскости постройте графики уравнений | |
| Шаг 7 | Найдите координаты точки пересечения графиков. Запишите ответ. | Т. М(0;-1) точка пересечения
графиков Ответ: (0;-1) |
| Шаг 8 | Решите систему линейных уравнений с двумя переменными графическим способом: | |
| Шаг 9 | Сделайте вывод о взаимном расположении прямых и решении системы уравнений. | |
Маршрутный лист №2 по теме:
“Решение систем линейных уравнений с двумя переменными графическим способом”
Ученика 7 класса____________________________
| Шаг 1. | Запишите систему линейных уравнений с двумя переменными | |
| Шаг 2. | Что значит: “Решить систему уравнений?” | Решить систему уравнений – значит найти все её решения или доказать, что решений нет. |
| Шаг 3 | Из первого уравнения выразите у через х | У=-2х+4 |
| Шаг 4 | Из второго уравнения выразите у через х | У=-2х-2 |
| Шаг 5 | Графиками линейных уравнений являются прямые. | |
| Шаг 6 | В одной и той же координатной плоскости постройте графики уравнений | |
| Шаг 7 | Прямые, являющиеся графиками линейных функций параллельны. Данная система уравнений не имеет решения. Запишите ответ. | Ответ: система не имеет решения. |
| Шаг 8 | Решите систему линейных уравнений с двумя переменными графическим способом: | |
| Шаг 9 | Сделайте вывод о взаимном расположении прямых и решении системы уравнений. | |
8.04.2015
Поделиться страницей:urok.1sept.ru
Презентация урока для интерактивной доски по алгебре (7 класс) на тему: Презентация «Системы линейных уравнений с двумя переменными. Графический способ решения.» 7 класс
Слайд 1
МОБУ СОШ № 24 г. Сочи Собина Н.Н. Системы линейных уравнений с двумя переменными . Графический способ решения.Слайд 2
1. На рисунке изображен график функции y = х – 1: Проверить истинность утверждения: 2. Значение функции y = 2x – 1 в точке x = 3 равно 5. 3. Значение функции у = 0,5 x – 4 равно -5 при х = 2. 4. Уравнение вида ax + by = c называют линейным уравнением с тремя переменными.
Слайд 7
Система имеет множество решений Система решений не имеет
Слайд 8
Используя блок-схему, найдите количество решений систем уравнений: Система имеет единственное решение Система имеет множество решений Система решений не имеет
Слайд 9
Выразить переменную у через х , т.е. представить уравнения в виде линейной функции y = kx + b . 2. Составить расчётные таблицы для каждой функции. 3. Строим графики функций в одной координатной плоскости. 4. Определяем число решений: Если прямые пересекаются, то одно решение пара чисел ( х ; у) – координаты точки пересечения. Если прямые параллельны, то нет решений. Если прямые совпадают, то бесконечно много решений. 5. Записываем ответ. Алгоритм решения системы линейных уравнений с двумя переменными графическим способом.
Слайд 10
Решить систему графическим способом: Решение: Построим график первого уравнения: x 1 0 y -1 1 Построим график второго уравнения: x 1 0 y -1 -4 Ответ: (1; -1)
Слайд 11
Решить системы уравнений графическим способом: (2; 4) Множество решений Нет решений
Слайд 12
Рефлексия : ЗНАЮ УМЕЮ Определение линейного уравнения с двумя переменными Приводить примеры линейных уравнений с двумя переменными Что является решением системы линейных уравнений с двумя переменными Строить график линейного уравнения с двумя переменными Сколько решений может иметь система уравнений с двумя переменными Выяснять, сколько решений имеет система уравнений с двумя переменными Алгоритм графического способа решения систем уравнений с двумя переменными Находить решения системы уравнений
Слайд 13
СПАСИБО ЗА УРОК!
nsportal.ru
Основные понятия. Графический метод (С.М.Слупко). Видеоурок. Алгебра 7 Класс
На этом уроке мы познакомимся с системами линейных уравнений и научимся их решать графическим методом.
Мы начинаем разговор о системах линейных уравнений. Этот урок будет разделен на две части:
Обсуждение того, что такое система. Решение систем.
Начнем с первого вопроса – что такое система.
Пример:
Если сыщик знает про одного преступника, что тот высокий (см. Рис. 1), а про второго, что тот блондин (см. Рис. 2), то эти два условия не объединены в систему, они относятся к разным неизвестным, к разным преступникам.
Рис. 1. Высокие преступники
Рис. 2. Преступники-блондины
Если это информация про одного и того же преступника, то это – система. Оба условия выполняются одновременно. Одну информацию можно использовать для уточнения другой. Преступник – высокий блондин. (См. Рис. 3.)
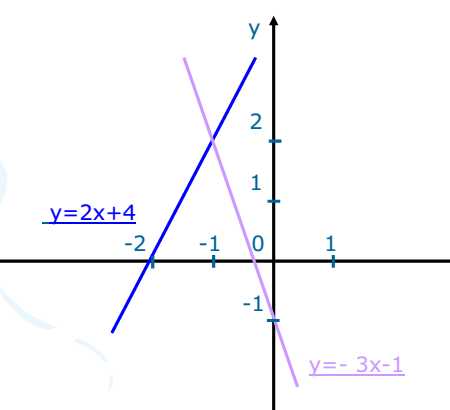
Рис. 3. Преступник – высокий блондин
Пример:
Пусть нам известно, что дом находится на ул. Гоголя. Вариантов, где точно расположен дом, много – целая улица. (См. Рис. 4.)
Рис. 4. Улица Гоголя
Дом находится на проспекте Мира. То же самое – вариантов много. (См. Рис. 5.)
Рис. 5. Проспект Мира
Но если эта информация относится к одному и тому же дому, то сразу понятно, что дом находится на перекрестке. (См. Рис. 6.) Два условия объединены в систему.
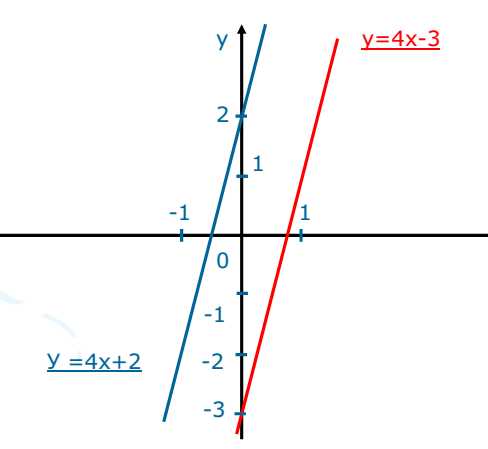
Рис. 6. Дом находится на перекрестке
Итак, система – это объединение нескольких условий так, чтобы они выполнялись одновременно.
Решим такую задачу. Два человека вскопали огород площадью . Сколько вскопал каждый? (См. Рис. 7.)
Рис. 7. Иллюстрация к задаче
Решение
Запишем условие уравнением: , где – площадь, которую вскопал первый человек, – площадь, которую вскопал второй человек.
Решение такого уравнения – пара чисел. Их бесконечно много. Например, один вскопал , другой – . (См. Рис. 8.) Или один вскопал все , другой – ничего. (См. Рис. 9.)
Рис. 8. Один вскопал , другой –
Рис. 9. Один вскопал все , другой – ничего
Можно изобразить каждое такое решение в виде точки на координатной плоскости. Все решения выстроятся в одну прямую. (См. Рис. 10.) Эту прямую называют графиком уравнения.
Презентация к уроку по алгебре (7 класс) на тему: Графический метод решения систем уравнений
Орг момент. Здравствуйте! Садитесь! Меня зовут Васильев Николай Ильич, и я буду вести у вас урок алгебры.
Все готовы к уроку?
Повторение Для начала давайте повторим пройденные нами темы.
Что такое линейное уравнение
Что представляет собой график линейного уравнения
Что такое система уравнений
Какие методы решения систем линейных уравнений вы знаете? Молодцы!
Изуч новых знаний Давайте решим систему линейных уравнений любым методом которое вы умеете. У=2х у=-2х+2.Решаем. (а я тем временем решу своим методом которое я умею) Что у вас получилось?(1;2) Молодцы у всех получилось? (Вне зависимости от решения)
Попробуем нарисовать графики этих линейных уравнений в одной координатной плоскости?
Что сначала нам требуется для того чтобы нарисовать графики этих уравнений?
Правильно составить расчетную таблицу. Так как график любого линейного уравнения является прямой, нам достаточно двух точек. Затем по двум точкам мы проводим прямые и получаем графики наших уравнений. Рисуем. Что у вас получилось? Где пересеклись ваши графики? Каким будет наш ответ?
Вы уже догадались о теме нашего урока?
Как можно назвать наш метод?
Мы использовали графики наших линейных уравнений.
Основная часть. Записываем тему нашего урока Графический метод решения систем линейных уравнений.
Запишем алгоритм решения нашим графическим методом
1 Составляем расчетные таблицы наших уравнений
2 Рисуем графики на одной координатной плоскости
3 находим точку пересечения этих графиков
4 записываем ответ
Давайте разделимся на три группы. Каждой группе я дам задания с разными заданиями и каждая группа покажет свое решение.
1 У=4+2х у=2х-3 2 У=3х+3 у=3+3х 3 У=6х у=-3х+1
1 группа Какое решение у вас получилось при решении первой системы. Пусть выйдет один и покажет свое решение.
2 группа При решении второй системы
3 группа При решении третей системы
Запишем новые правила
Какому выводу пришла 1 группа
Если графики уравнений параллельны, то система уравнений не имеет решений
2 группа
Если графики уравнений совпадают, то система уравнений имеет бесконечное множество решений.
3 группа
Не все системы линейных уравнений удобно решать графическим методом.
Физминутка. Давайте немного отлучимся от работы. Встанем. И немного помечтаем. Закрываем глаза. Представим что мы проснулись, светлым, теплым солнечным утром. Яркие солнечные лучи попадая в наши глаза, заставляют нас щурится. Медленно не спеша мы встаем с кровати. Разводим руки в стороны. Потягиваемся. С приподнятым настроением мы выходим на улицу и видим прекрасный вид. Перед нами алас с широким озером в центре. Где волны поблескивают на свете утренней зари. И над аласом веселый, легкий ветерок играет макушками деревьев. И птички радостно поют, встречая новый день. И мы стоим умиляясь и наслаждаясь звуками и видом данными нам матушкой природой. Открываем глаза. Садитесь. Давайте таким же воодушевленным настроением продолжим наш урок.
Закрепление нового изученного. Дополнительная работа по карточкам
Взаимопроверка. Давайте обменяемся работами с соседями по парте. Проверка. Обмен обратно.
Итог. Подведем итоги нашего урока.
Перед вами таблица с вашими именами. Каждый учащийся ставит точку на уровень, которого он достиг по своему мнению.
Как мы видим у нас получился не равномерный график уровня. В идеале у нас должно получится прямолинейный график на высшем уровне. Давайте на каждом уроке все попытаемся достичь прямолинейного графика на высшем уровне.
Домашнее задание узнать какие еще существуют методы решения систем линейных уравнений?
Всем спасибо! Мне было очень приятно работать с вами. До свидания!
nsportal.ru
«Решение системы линейных уравнений с двумя переменными графическим способом»
Функция. График функции(17 ч)
Название школы
Дата
ФИО учителя
7 «Б»
Присутствуют
Отсутствуют
Цель обучения
7.4.2.4 решать системы линейных уравнений графическим способом;
38. Тема урока
Решение системы линейных уравнений с двумя переменными графическим способом
Цели урока
Закрепление знаний, умений и навыков по теме; приобретение учащимися функционального навыка исследования как универсального способа получения новых прочных знаний, развитие способности к исследовательскому типу мышления, активизации личностной позиции учащегося в образовательном процессе; продолжить формирование графических навыков; тренировка способности применять знания на практике, развитие умения анализировать, сопоставлять, сравнивать, выделять главное, устанавливать причинно-следственные связи; приводить примеры, формировать умения работы с графиками.
Критерии успеха
Должны знать, что называется решением системы линейных уравнений с двумя неизвестными; уметь проверять, является ли данная пара чисел решением системы; знают алгоритм решения системы уравнений графическим способом. Решают систему линейных уравнений графическим способом, умеют читать графики.
Языковые цели
Используют термины: «алгоритм, график, уравнения, пересечения, нет решения, бесконечное множество решений…»
Привитие ценностей
уважение к себе и другим, уважение разнообразию мнений; умение учиться, добывать самостоятельно информацию, анализировать ситуацию, работать в команде, отвечать за качество своей работы; способность видеть и понимать проблемы окружающих, другие точки зрения; умение правильно реагировать на критику;
Межпред-метные связи
Данная тема необходима при моделировании реальных зависимостей между величинами в курсе физики, а так же является основой для решения различных уравнений графическим способом.
Предвари-тельные знания
Знание понятий прямая и обратная пропорциональные зависимости, умение строить график прямо пропорциональной зависимости. Умение выполнять преобразования выражений с переменными. Умение работать с формулами.
Ход урока
Этапы урока
Планируемая работа
Ресурсы
Начало урока
Организация начала урока. Приветствие. Отметка отсутствующих. Проверка готовности учащихся к уроку. Чтобы работать более оперативно и качественно, давайте разобьемся на группы.
Класс делится на 3 группы.
Повторение и закрепление по вопросам: Математический диктант. Повторение:
1. Являются ли данные уравнения линейными?
3x-y=17; х2-2y=5; 13x+6y=0; xy+2x=9
2. Является ли пара чисел (4;1) решением уравнения 5x-4y=16?
3. Из линейного уравнения 4x-2y=16 выразите переменную y.
4. Что является графиком линейного уравнения ax+by+c=0?
5. Как могут располагаться графики линейных функций на координатной плоскости?
Взаимопроверка по кругу. Правильный ответ 1 балл.
Ответы:
да, нет, да, нет
да
у=2х-8
прямая
пересекаться, быть парал., совпадать
фишки: зелёные – хорошо; жёлтые – внимание; красные – тревога
Середина урока
У каждой группы в конвертах лежат задания. Решите систему уравнений графическим способом. Данная работа будет оцениваться по критериям. Учащиеся предлагают свои критерии. Затем учитель открывает свои и смотрят совпадения.
1 группа: если угловые коэффициенты различны, то система имеет единственное решение.
2 группа: если угловые коэффициенты одинаковы, то система не имеет решений.
3 группа: если и угловые коэффициенты и свободные члены одинаковы, то система имеет бесконечное множество решений. Самооценка.
Проверим, какие результаты у вас получились, сделаем выводы
Конец урока
Применение полученных знаний на практике. В осенне-весенний период многие из нас начинают болеть. Посмотрим на эту проблему с точки зрения математики.
Количество болезнетворных микробов в организме описывается по формуле y-50000=5000t. Человек начинает принимать лекарство. Количество микробов, уничтожаемых лекарством, y=15000t. t – время в сутках. Какое время человек должен принимать лекарство?
Некоторые сюжетные задачи по графику.
Ответы: 5, 2000,3,-10,-7,13,11,39,13400,
Рефлексия
Рефлексия; «Дерево успеха»
1. Что нового узнали на уроке?
2. Чему научились?
3. Какие испытывали затруднения?
Рефлексия по уроку
Были ли цели урока/цели обучения реалистичными?
Все ли учащиеся достигли ЦО?
Если нет, то почему?
Правильно ли проведена дифференциация на уроке?
Выдержаны ли были временные этапы урока?
Какие отступления были от плана урока и почему?
infourok.ru
Графический метод решения систем линейных уравнений
План урока математики в 7 классе
Тема урока: «Графический метод решения систем уравнений с двумя
переменными»
Предмет: алгебра
Класс: 7
Базовый учебник: А.Г. Мордкович «Алгебра. 7класс»
Тип урока: Урок — введение нового материала с использованием презентации и практической работы по графическому решению систем двух линейных уравнений с двумя переменными.
Цели урока: 1. Сформировать у учащихся понятие о
системе двух линейных уравнений с двумя переменными.
2. Объяснить, что значит решить систему двух уравнений.
3. Продолжить формирование графических навыков.
Способствовать формированию у учащихся
навыков построения графиков линейных функций и
нахождения решений систем уравнений.
4.Обратить внимание учащихся на частные случаи решения
систем:
когда система не имеет решений (т. е несовместна), и
когда система имеет бесконечное множество решений (т. е. неопределенна)
5. Развивать самостоятельность мышления, воспитывать
у учащихся чувство ответственного отношения к учёбе.
Методы обучения: объяснение нового материала в сочетании с
индивидуальной работой учащихся в тетрадях
и самопроверкой в программе «Математический
конструктор»
Оборудование: проектор, компьютер учителя, компьютеры учеников,
задачники «Алгебра 7» Ч.II, и тетради.
Программы и файлы:
Презентация «Графический метод решения систем линейных уравнений»
Программа «Математический конструктор» с приготовленной заранее системой координат
Файл с записью физкультминутки
План урока: I. Организационная часть
II. Изучение нового материала в ходе фронтальной работы
с использованием презентации
III. Физкультминутка
IV. Актуализация знаний. Закрепление изученного в ходе
выполнения задания по графическому решению систем
в тетрадях и самопроверке в программе
«Математический конструктор»
V . Подведение итогов.
VI . Домашнее задание.
Ход урока.
I.Организационный момент
1) Приветствие учителя. Создание доброжелательной атмосферы в классе.
2) Отметить отсутствующих.
3) Проверка подготовки учащихся к уроку.
4) Сообщение темы, целей и задач урока.
II. Изучение нового материала в ходе работы с презентацией
Постановка обучающих целей урока.
Познакомиться с понятием системы двух линейных уравнений с двумя переменными и её графическим решением.
Научиться графически решать системы, состоящие из двух линейных уравнений с двумя переменными.
Научиться, по виду графиков, определять имеет ли система единственное решение, или она не имеет решений, или имеет бесконечное множество решений
Работа с презентацией
Слайд 2.
После введения понятия общего решения двух линейных уравнений с двумя переменными
На доске проецируется третий слайд презентации.

Графический метод решения систем двух линейных уравнений с двумя
переменными.
Объяснение материала с использованием слайда 4.

Фронтальная работа с классом. Все объекты слайда последовательно появляются после ответов учащихся и иллюстрируют их.
3. Частные случаи решения систем:
На доске переходим к слайду 5.
Все объекты на слайде появляются последовательно по щелчку в ходе фронтального обсуждения хода построения графиков.
Цель – подвести учащихся к самостоятельному выводу о том, что система не имеет решений.
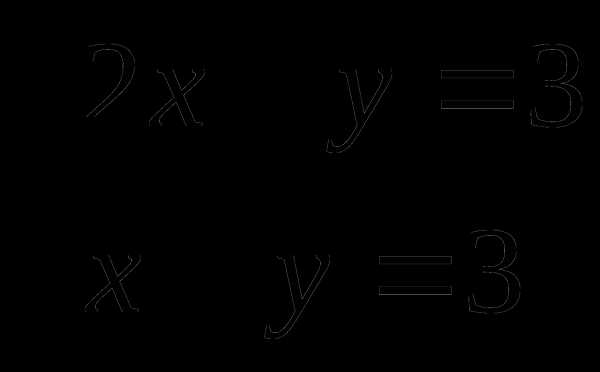
Обращаем внимание учащихся на то, как записываются ответ.
Случай 2.
(т. е. неопределенна)
Слайд 7.
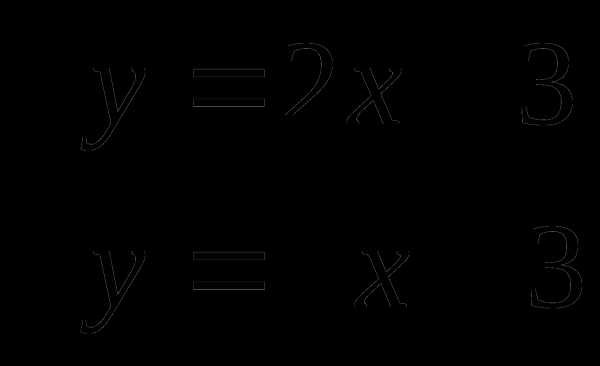
Физкультминутка
IV. Формирование навыков графического решения систем
Слайд 8.

1.Учащиеся выполняют работу в тетрадях и после решения задания большинством учащихся на экран выводится решение для проведения самоконтроля.
Работа в тетрадях по графическому решению систем уравнений.
На доске переходим к слайду 9.
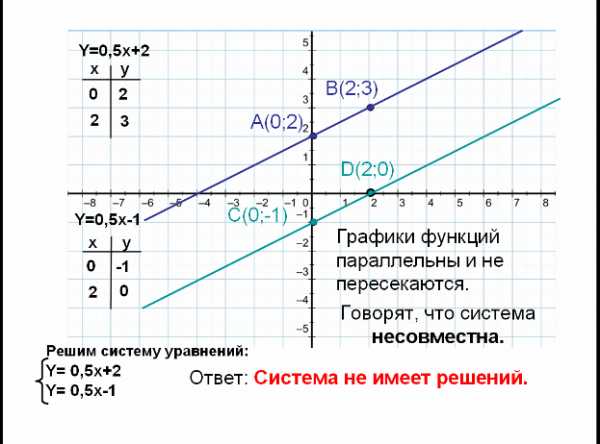
Индивидуальная работа учащихся в тетрадях.
Учащиеся выполняют задание №11.10(б)
Задание №11.10(в) выполнят те, кто быстро справился с первым заданием.
Самопроверка после выполнения задания производится путём
сравнения с решением системы в «Математическом конструкторе».
Один из учащихся, вводит вид функций на компьютере учителя и используя инструмент «Построить график» выполняет построение и находит координаты точки пересечения графиков.
V. Подведение итогов урока.
После выполнения работы и самопроверки перед учащимися ставится вопрос:
« Что нового вы узнали сегодня на уроке?»
«Чему научились?».
Учитель подводит итоги работы учащихся и ставит оценки за работу на уроке.
Домашнее задание . Слайд 9.

kopilkaurokov.ru
