7 класс. Геометрия. Атанасян. Учебник. Ответы к стр. 24
Начальные геометрические сведения
Перпендикулярные прямые
Смежные и вертикальные углы. Перпендикулярные прямые. Построение прямых углов на местности
Ответы к стр. 24
Практические задания
54. Начертите острый угол АОВ и на продолжении луча ОВ отметьте точку D. Сравните углы АОВ и AOD.
Углы АОВ и АОD — смежные, ∠АОВ — острый, ∠АОD — тупой ⇒ ∠АОВ < ∠АОD.
55. Начертите три угла: острый, прямой и тупой. Для каждого из них начертите смежный угол.
∠АОВ — острый, смежный угол ВОС (тупой).
∠DOE — прямой, смежный угол EOF (прямой).
∠KОL — тупой, смежный угол LOM (острый).
56. Начертите неразвернутый угол hk. Постройте угол h1k1 так, чтобы углы hk и h1k1 были вертикальными.
Углы hk и h1k1 — вертикальные (∠hk = ∠h1k1).
57. Начертите неразвернутый угол MON и отметьте точку Р внутри угла и точку Q — вне его. С помощью чертежного угольника и линейки через точки Р и Q проведите прямые, перпендикулярные к прямым ОМ и ON.
α ⊥ ОN, b ⊥ OM, c ⊥ ON, d ⊥ OM.
Задачи
58. Найдите угол, смежный с углом ABC, если: a) ∠ABC = 111°; б) ∠ABC = 90°; в) ∠ABC = 15°.
Р е ш е н и е
Сумма смежных углов равна 180°.
а) 180° — 111° = 69°;
б) 180° — 90° = 90°;
в) 180° — 15° = 165°.
О т в е т. а) 69°, б) 90°, в) 165°.
59. Один из смежных углов прямой. Каким (острым, прямым, тупым) является другой угол?
Р е ш е н и е
Сумма смежных углов равна 180°.
180° — 90° = 90° — прямой смежный угол.
О т в е т. Прямой.
60. Верно ли утверждение: если смежные углы равны, то они прямые?
Р е ш е н и е
Сумма смежных углов равна 180°.
180° : 2 = 90° — два смежных угла по 90° каждый.
О т в е т. Верно.
61. Найдите смежные углы hk и kl, если:
a) ∠hk меньше ∠kl на 40°;
б) ∠hk больше ∠kl на 120°;
в) ∠hk больше ∠kl на 47°18′;
г) ∠hk = 3∠kl;
д) ∠hk : ∠kl = 5 : 4.
Р е ш е н и е
Сумма смежных углов равна 180°.
а) ∠hk + ∠kl = 180°, ∠hk = ∠kl — 40°, тогда:
(∠kl — 40°) + ∠kl = 180°,
2∠kl = 180° + 40°,
∠kl = 220° : 2,
∠kl = 110°
∠hk = ∠kl — 40° = 110° — 40° = 70°
б) ∠hk + ∠kl = 180°, ∠hk = ∠kl + 120°, тогда:
(∠kl + 120°) + ∠kl = 180°,
2∠kl = 180° — 120°,
∠kl = 60° : 2,
∠kl = 30°
∠hk = ∠kl + 120° = 30° + 120° = 150°
в) ∠hk + ∠kl = 180°, ∠hk = ∠kl + 47°18′, тогда:
(∠kl + 47°18′) + ∠kl = 180°,
2∠kl = 180° — 47°18′,
∠kl = 132°42′ : 2,
∠kl = 66°21′
∠hk = ∠kl + 47°18′ = 66°21′ + 47°18′ = 113°39′
г) ∠hk + ∠kl = 180°, ∠hk = 3∠kl, тогда:
3∠kl + ∠kl = 180°,
4∠kl = 180°,
∠kl = 180° : 4,
∠kl = 45°
∠hk = 3∠kl = 3 • 45° = 135°
д) ∠hk + ∠kl = 180°, ∠hk : ∠kl = 5 : 4 или ∠hk : ∠kl = 5/4 ⇒ ∠hk = 5/4 • ∠kl, тогда:
5/4 ∠kl + ∠kl = 180°,
9/4 ∠kl = 180°,
∠kl = 180° : 9/4,
∠kl = 180° • 4/9,
∠kl = 80°
∠hk = 5/4 ∠kl = 5/4 • 80° = 100°
О т в е т.
а) ∠kl = 110°, ∠hk = 70°;
б) ∠kl = 30°, ∠hk = 150°;
в) ∠kl = 66°21′, ∠hk = 113°39′;
г) ∠kl = 45°, ∠hk = 135°;
д) ∠kl = 80°, ∠hk = 100°.
62. На рисунке 46 углы BOD и COD равны. Найдите угол AOD, если ∠COB = 148°.
Р е ш е н и е
∠AOD = ∠AOC + ∠COD
Углы AOC и COB — смежные, тогда:
∠AOC + ∠COB = 180° ⇒ ∠АОС = 180° — ∠СОВ = 180° — 148° = 32°.
∠СОВ = ∠СОD + ∠DOB = 148°, ∠СОD = ∠DOB ⇒ ∠СОD = 148° : 2 = 74°.
∠AOD = 32° + 74° = 106°.
О т в е т. ∠AOD = 106°.
63. Даны два равных угла. Равны ли смежные с ними углы?
Р е ш е н и е
∠1 = ∠2
∠1 + ∠3 = 180° ⇒ ∠3 = 180° — ∠1
∠2 + ∠4 = 180° ⇒ ∠4 = 180° — ∠2
Так как ∠1 = ∠2, то ∠3 = 180° — ∠1 = 180° — ∠2 = ∠4 или
∠4 = 180° — ∠2 = 180° — ∠1 = ∠3
О т в е т.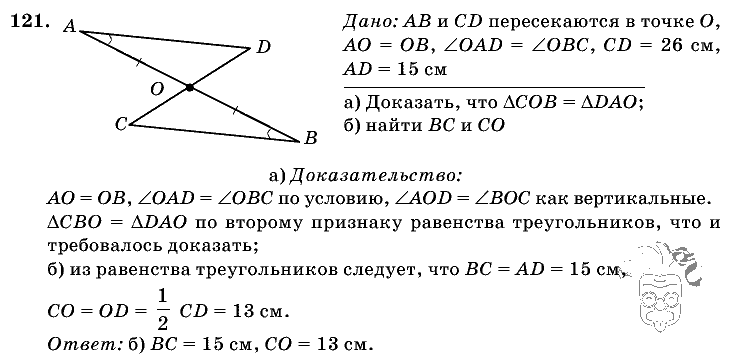
Равны.
64. Найдите изображенные на рисунке 41 углы:
а) 1, 3, 4, если ∠2 = 117°;
б) 1, 2, 4, если ∠3 = 43°27′.
Р е ш е н и е
а) Углы 2 и 4 — вертикальные, тогда ∠2 = ∠4 = 117°
Углы 1 и 2 — смежные, тогда ∠1 + ∠2 = 180° ⇒ ∠1 = 180° — ∠2 = 180° — 117° = 63°
Углы 1 и 3 — вертикальные, тогда ∠1 = ∠3 = 63°
б) Углы 1 и 3 — вертикальные, тогда ∠1 = ∠3 = 43°27′
Углы 1 и 2 — смежные, тогда ∠1 + ∠2 = 180° ⇒ ∠2 = 180° — ∠1 = 180° — 43°27′ = 136°33′
Углы 2 и 4 — вертикальные, тогда ∠2 = ∠4 = 136°33′
О т в е т. а) ∠1 = ∠3 = 63°, ∠4 = 117°; б) ∠1 = 43°27′, ∠2 = ∠4 = 136°33′.
ГДЗ. Ответы по геометрии. 7 класс. Учебник. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И.
Геометрия. 7 класс
ГДЗ Дидактические материалы по Геометрии 7 класс Мерзляк Алгоритм успеха
Все ГДЗ по Геометрии 7 класс Алгоритм успеха
Семиклассники на занятиях математического раздела добьются впечатляющих результатов своими силами, лишь изредка пользуясь содержательными консультациями интернет-самоучителя – «ГДЗ Геометрия Дидактические материалы 7 класс Мерзляк (Вентана-граф)».
Решебник составлен специально для дидактического дополнения к учебнику (в наличии достоверные ответы на любые вопросы и номера практических упражнений). Над содержанием поработали опытные преподаватели, специализирующиеся на разделе математики.
Совместно выполненная с ГДЗ работа удовлетворит даже самого строгого и придирчивого наставника. Учитель не заподозрит своего подопечного в списывании, так как повествовательный стиль решебника похож на грамотные размышления самих подростков.
Геометрия является важным элементом общеобразовательного обучения. Наука появляется в расписании в седьмом классе, после окончания основного курса математики. Наравне с алгеброй, геометрия является узконаправленной дисциплиной. Она рассматривает объекты на плоскости, а также их свойства и составные элементы. Подобный вид познания развивает умственные способности. Появляется абстрактное виденье мира, умение устанавливать причинно-следственные связи, делать выводы. Совершенствуется логика. Если выразиться проще – дети начинают лучше соображать.
Характеристика процесса изучения геометрии в седьмом классе
Ученики в этом году изучают наиболее элементарные геометрические фигуры, знакомятся с новыми теоремами и аксиомами. Для более подробного анализа учебной программы перечислим несколько тем из теоретической части учебно-методического комплекта:
- перпендикулярные прямые;
- виды треугольников;
- уголковый отражатель.
«ГДЗ Геометрия Дидактические материалы 7 класс Мерзляк А.Г., Полонский В.Б. (Вентана-граф)» поможет пользователю на практике по геометрии. Ребята смогут справиться с контрольными или самостоятельными работами успешно, исключительно на пятёрки и четвёрки. Главное заранее запомнить конкретные верные ответы из ГДЗ.
Достоинства решебника Геометрия Дидактические материалы 7 класс Мерзляк
ГДЗ присутствует в онлайн-пространстве, поэтому актуален для современного учащегося. Другие плюсы ГДЗ: быстрая постраничная навигация, верные ответы есть на все номера вопросов и домашние задания выполняются в кратчайшие сроки.
Ребёнок будет доволен обновленным образовательным процессом в команде с решебником.
Ответы из решебника
Упражнения
Вариант 1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174
Вариант 2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 85 86 87 88 89 90 91 92 93 94 95 96 97 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 161 163 164 165 166 167 168 169 170 171 172 173 174
Контрольные работы
Вариант 1
КР-1 КР-2 КР-3 КР-4 КР-5
Вариант 2
КР-1 КР-2 КР-3 КР-4 КР-5
Образование | Лицей №64
Информация для выпускников лицея о возможности подачи документов для зачисления на обучение в государственные образовательные организации высшего образования посредством суперсервиса «Поступление в вузы онлайн».
Доступно по ссылке.
Организация образовательного процесса
БОУ г. Омска «Лицей № 64» реализует основные общеобразовательные программы на государственном языке Российской Федерации (русском) по уровням образования:
1. начального общего образования (1-4 класс) — 4 года, 1 — 3 классы по программе «Школа России», 4 классы по программе «Перспектива»;
2. основного общего образования (5-9 класс) — 5 лет;
3. среднего общего образования (10-11 класс) — 2 года.
В соответствии со ст.17 п. 2 Федерального закона «Об образовании в Российской Федерации» от 29 декабря 2012 г. № 273-ФЗ образование в БОУ города Омска «Лицей № 64» может быть получено в следующих формах получения образования:
— очной;
— очно-заочной;
— заочной.
учреждением создаются условия для прохождения промежуточной и государственной итоговой аттестации для обучающихся, получающих общее образование в форме семейного образования и самообразования.
Основной формой реализации общеобразовательных программ начального общего, основного общего и среднего общего образования в БОУ города Омска «Лицей № 64» является очная форма обучения.
В лицее допускается сочетание различных форм получения образования и различных форм обучения, а также может быть предоставлено обучение по индивидуальному учебному плану с правом последующего прохождения промежуточной и государственной итоговой аттестации.
Для всех форм получения образования в пределах конкретной основной общеобразовательной программы действует единый федеральный государственный образовательный стандарт соответствующего уровня общего образования.
При реализации образовательных программ в лицее могут быть использованы электронное обучение и дистанционные образовательные технологии.
Количество обучающихся в 2022-2023 учебном году (на 1 августа 2022 года, по предварительному комплектованию):
1 — 4 кл. — 524 человек,
5 — 9 кл.
— 602 человек,
10 — 11 кл. — 220 человек,
Всего 1346 человек.
Лицеем не заключены договоры по вопросам образования с иностранными и (или) международными организациями.
Аккредитация и лицензирование
Лицензия на образовательную деятельность
Лицензия на образовательную деятельность (Приложение)
Свидетельство о государственной аккредитации
Свидетельство о государственной аккредитации (приложение)
Срок действия государственной аккредитации до 4 июня 2026 г.
Документы:
Программа развития БОУ города Омска «Лицей № 64» «Самоопределение обучающихся в образовательной среде лицея»
Управленческий проект «Инженерно-политехническое образование в условиях общеобразовательного лицея № 64»
Презентация управленческого проекта «Инженерно-политехническое образование в условиях общеобразовательного лицея»
Основная образовательная программа начального общего образования БОУ города Омска «Лицей № 64»
Рабочие программы по учебным предметам для 1 класса начального общего образования
«Музыка»
«Технология»
«Математика»
«Русский язык»
«Окружающий мир»
«Физическая культура»
«Литературное чтение»
«Изобразительное искусство»
Рабочие программы по учебным предметам для 2 класса основного общего образования
«Музыка»
«Технология»
«Математика»
«Русский язык»
«Английский язык»
«Окружающий мир»
«Физическая культура»
«Литературное чтение»
«Изобразительное искусство»
Рабочие программы по учебным предметам для 3 класса основного общего образования
«Музыка»
«Технология»
«Математика»
«Русский язык»
«Английский язык»
«Окружающий мир»
«Физическая культура»
«Литературное чтение»
«Родной язык (русский)»
«Изобразительное искусство»
«Литературное чтение на родном (русском) языке»
Рабочие программы по учебным предметам для 4 класса основного общего образования
«Музыка»
«Математика»
«Русский язык»
«Английский язык»
«Окружающий мир»
«Физическая культура»
«Родной язык (русский)»
«Изобразительное искусство»
«Основы религиозных культур и светской этики»
«Литературное чтение на родном (русском) языке»
Приказ от 30.
08.2022 года № 372 «О внесении изменений в основные образовательные программы основного общего и среднего общего образования БОУ города Омска «Лицей № 64»
Основная образовательная программа основного общего образования БОУ города Омска «Лицей № 64» с изменениями от 23 августа 2022 года
Описание основной образовательной программы основного общего образования
Рабочие программы по учебным предметам для 5 класса основного общего образования
«Музыка»
«История»
«Биология»
«География»
«Технология»
«Литература»
«Математика»
«Русский язык»
«Физическая культура»
«Введение в информатику»
«Иностранный язык (английский)»
Рабочие программы по учебным предметам для 6 класса основного общего образования
«Музыка»
«История»
«Биология»
«География»
«Технология»
«Литература»
«Математика»
«Русский язык»
«Обществознание»
«Физическая культура»
«Введение в информатику»
«Иностранный язык (английский)»
Рабочие программы по учебным предметам для 7 класса основного общего образования
«Музыка»
«Алгебра»
«История»
«Биология»
«Геометрия»
«География»
«Технология»
«Литература»
«Русский язык»
«Информатика»
«Обществознание»
«Физическая культура»
«Вероятность и статистика»
«Иностранный язык (английский)»
«Геометрия (углубленный уровень)»
Рабочие программы по учебным предметам для 8 класса основного общего образования
«Химия»
«Физика»
«Музыка»
«Алгебра»
«История»
«Биология»
«Геометрия»
«География»
«Технология»
«Литература»
«Русский язык»
«Информатика»
«Обществознание»
«Физическая культура»
«Вероятность и статистика»
«Иностранный язык (английский)»
«Алгебра (углубленный уровень)»
«Геометрия (углубленный уровень)»
«Основы безопасности жизнедеятельности»
«Вероятность и статистика (углубленный уровень)»
Рабочие программы по учебным предметам для 9 класса основного общего образования
«Химия»
«Физика»
«Алгебра»
«История»
«Биология»
«Черчение»
«География»
«Геометрия»
«Экономика»
«Литература»
«Русский язык»
«Обществознание»
«Информатика 7-9»
«Родной язык (русский)»
«Родная литература (русская)»
«Физическая культура»
«Английский язык_New Millenium»
«Второй иностранный язык (немецкий)»
«Основы безопасности жизнедеятельности»
Описание основной образовательной программы среднего общего образования
Основная образовательная программа среднего общего образования
Рабочие программы (приложения к основной образовательной программе среднего общего образования):
Право (углубленный уровень)
Химия (базовый уровень)
Химия(углубленный уровень)
Физика (базовый уровень)
Физика (углубленный уровень)
История
Биология
География
Литература
Астрономия
Экономика (базовый уровень)
Экономика (углубленный уровень)
Математика (углубленный уровень)
Информатика (базовый уровень)
Информатика (углубленный уровень)
Русский язык
Родной язык (русский)
Английский язык
Обществознание
Физическая культура
Основы безопасности жизнедеятельности
Рабочая программа воспитания БОУ города Омска «Лицей № 64 » (проект)
Описание адаптированной основной образовательной программы начального общего образования
Адаптированная образовательная программа начального общего образованияобучающихся с нарушениями опорно-двигательного аппарата (вариант 6.
1)
Обучение детей-инвалидов в соответствии с ИПРА организовано по основным образовательным программам начального общего, основного общего и среднего общего образования.
Перечень программ, учебников и учебных пособий к учебному плану на 2022/2023 год (электронный вариант Excel)
Годовой календарный учебный график и режим работы БОУ города Омска «Лицей № 64» на 2022-2023 учебный год
Приказ от 23.08.2022 года № 368 «О внесении изменений в годовой календарный учебный график и режим работы БОУ города Омска «Лицей № 64″ на 2022 — 2023 учебный год»
Приказ от 14.09.2020 года № 312 «О реализации образовательных программ с применением электронного обучения и дистанционных образовательных технологий в случае закрытия класса на карантин»
Приказ от 12.08.2022 года № 364 «О соблюдении санитарно-эпидемиологических правил в лицее в условиях распространения новой коронавирусной инфекции (COVID-19)
Приказ от 22.
08.2022 года № 367 «О соблюдении санитарно-эпидемиологических правил в лицее в условиях распространения энтеровирусной инфекции
Приказ от 24.08.2022 года № 369 «О соблюдении санитарно-эпидемиологических правил в лицее в условиях распространения новой коронавирусной инфекции (COVID-19)
Приказ от 30.08.2022 г. № 385 «О мероприятиях по профилактике гриппа и острых респираторных вирусных инфекций в эпидсезоне 2022 — 2023 годов в Омской области
Приказ от 24.09.2022г. № 430 «О проведении противоэпидемических мероприятий в лицее»
Учебный план БОУ города Омска «Лицей № 64» на 2022 — 2023 учебный год для обучающихся, находящихся на длительном лечении в Областной детской клинической больнице
Учебный план на 2022-2023 учебный год. Сетки часов 1-11 классов
Учебный план на 2022-2023 учебный год (обучение на дому). Сетки часов 1-11 классов
Аннотации к учебным программам
Аннотации к рабочим программам учебных дисциплин в 5-9 классах
Дополнительные образовательные программы
В мире искусства (1-8 классы)
Умелые руки (2 класс)
Детям о праве (3 — 4 классы)
Краеведение для младших школьников (3 — 4 классы)
Игротека (5 класс)
Мой город (5 класс)
Культура общения (6 — 8 классы)
Школа вожатого (7 — 9 классы)
Математика для всех (9 классы)
Театр песни (9 — 11 класс)
Творческая мастерская (5 — 11 классы)
Развитие ресурсов творческой личности через проектную деятельность (5 — 11 классы)
Методические и иные документы, разработанные для обеспечения образовательного процесса
Полезные ресурсы
NCERT Solutions for Class 8 Math Chapter 4
- Решения НЦЭРТ
- Класс 8
- Математика
- практическая геометрия
Математика NCERT 8 класс, Глава 4: Практическая геометрия — Глава начинается с небольшого задания.
В первой части главы учащиеся узнают, как построить уникальный четырехугольник .
- Пять измерений могут однозначно определить четырехугольник .
Перечислены различные случаи, и каждый случай объяснен должным образом. Случаи конструкции , которые объясняются в этой главе, следующие:
- При наличии четырех сторон и одной диагонали .
- Когда даны две диагонали и три стороны .
- Когда даны две смежные стороны и три угла .
- Когда даны три стороны и два включенных угла .
- Когда известны другие особые свойства .
Решаемые примеры приведены для справки.
После обсуждения того, как выполнить построение из перечисленных выше случаев, также рассматриваются некоторые частные случаи.
Приведены некоторые примеры для изучения особых случаев, когда четырехугольник рисуется с использованием специальных свойств.
Студенты найдут вопросы, в которых им будет предложено построить ромб , прямоугольник , параллелограмм и т. д. с некоторыми заданными размерами.
Вопросы этой главы могут занять много времени. Таким образом, учащиеся должны практиковать достаточное количество вопросов, чтобы улучшить свою скорость и избежать ошибок. Эта глава содержит в общей сложности 5 нерешенных упражнений, а в конце также приводится краткое изложение главы.
Страница № 60:
Вопрос 1:
Постройте следующие четырехугольники.
(I) Квадратный ABCD
AB = 4,5 см
до н.э. = 5,5 см
CD = 4 см
AD = 6 см
AC = 7 см
(II) QUADRILARAT
UM = 4 см
MP = 5 см
PJ = 4,5 см
УЕ = 6,5 см
(iii) Параллелограмм MORE
OR = 6 см
см 9RE0019
EO = 7,5 см
(iv) Ромб BEST
BE = 4,5 см
ET = 6 см
Ответ:
(i) Во-первых, грубый набросок этого четырехугольника можно нарисовать следующим образом.
(1) ΔABC можно построить, используя данные измерения следующим образом.
(2) Вершина D находится на расстоянии 6 см от вершины А. Поэтому, взяв А за центр, начертите дугу радиусом 6 см.
(3) Взяв С за центр, нарисуйте дугу радиусом 4 см, пересекая предыдущую дугу в точке D. Соедините D с А и С.
ABCD — искомый четырехугольник.
(ii) Во-первых, грубый набросок этого четырехугольника можно нарисовать следующим образом.
(1) Δ JUP можно построить, используя данные измерения следующим образом.
(2) Вершина M находится на расстоянии 5 см от вершины P и 4 см от вершины U. Взяв P и U за центры, начертите дуги радиусами 5 см и 4 см соответственно. Пусть точкой пересечения будет M.
(3) Соедините M с P и U.
JUMP — искомый четырехугольник.
(iii) Мы знаем, что противоположные стороны параллелограмма равны по длине, а также параллельны друг другу.
Следовательно, ME = OR, MO = ER
Грубый набросок этого параллелограмма можно нарисовать следующим образом.
(1) Δ EOR можно построить с использованием данных измерений следующим образом.
(2) Вершина M находится на расстоянии 4,5 см от вершины O и 6 см от вершины E. Поэтому, взяв за центры O и E, начертите дуги радиусом 4,5 см и радиусом 6 см соответственно. Они пересекутся друг с другом в точке М.
(3) Соединить M с O и E.
MORE — искомый параллелограмм. |
(iv) Мы знаем, что все стороны ромба имеют одинаковую меру.
Следовательно, BE = ES = ST = TB
Грубый набросок этого ромба можно нарисовать следующим образом.
(1) Δ BET можно построить, используя данные измерения следующим образом.
(2) Вершина S находится на расстоянии 4,5 см от вершины E, а также от вершины T.
Поэтому, взяв E и T за центры, начертите дуги радиусом 4,5 см, которые будут пересекаться в точке S.
(3) Соединить S с E и T.
BEST — искомый ромб. |
Видео Решение для практической геометрии (Страница: 60 , Q.№: 1)
NCERT Решение для 8 класса математика — практическая геометрия 60 , Вопрос 1
Страница № 62:
Вопрос 1:
Постройте следующие четырехугольники.
(I) Квадратный подъем
LI = 4 см
IF = 3 см
TL = 2,5 см
LF = 4,5 см
IT = 4 см
(II) QUADLATERAL GOLD
9004 CM
(II).
GL = 6 см
GD = 6 см
LD = 5 см
OD = 10 см
(iii) Ромб ИЗГИБ
BN = 5,6 см
DE = 6,5 см
Ответ:
(i) Грубый набросок этого четырехугольника можно нарисовать следующим образом.
(1) Δ ITL можно построить, используя данные измерения следующим образом.
(2) Вершина F находится на расстоянии 4,5 см от вершины L и 3 см от вершины I. Поэтому, взяв L и I за центры, начертите дуги радиусом 4,5 см и радиусом 3 см соответственно, которые будут пересекаться друг друга в точке F.
(3) Соедините F с T и F с I.
ПОДЪЕМ — искомый четырехугольник. |
(ii) Грубый набросок этого четырехугольника можно нарисовать следующим образом.
(1) Δ GDL можно построить, используя данные измерения следующим образом.
(2) Вершина O находится на расстоянии 10 см от вершины D и 7,5 см от вершины L. Поэтому, взяв D и L за центры, начертите дуги радиусом 10 см и радиусом 7,5 см соответственно. Они пересекутся друг с другом в точке O.
(3) Соединить O с G и L.
ЗОЛОТО — искомый четырехугольник. |
(iii) Мы знаем, что диагонали ромба всегда делят друг друга пополам под углом 90º. Предположим, что они пересекаются друг с другом в точке О этого ромба.
Отсюда EO = OD = 3,25 см
Грубый набросок этого ромба можно нарисовать следующим образом.
(1) Нарисуйте отрезок BN длиной 5,6 см, а также начертите его биссектрису. Пусть он пересекает отрезок BN в точке O.
(2) Приняв O за центр, проведите дуги радиусом 3,25 см, чтобы пересечь серединный перпендикуляр в точках D и E.
(3) Соединить точки D и E к точкам B и N.
ИЗГИБ — искомый четырехугольник. |
Видео Решение по практической геометрии (Страница: 62 , Q.
No.: 1)NCERT Решение по математике для 8 класса — Практическая геометрия 62 , Вопрос 1
Страница № 64:
Вопрос 1:
8
8 Постройте следующие четырехугольники.
(I) Квадратный наборочный больше
MO = 6 см
или = 4,5 см
♂ = 60 °
♂ = 105 °
T = 105 °
(II) КВАРТАТОРНЫЙ ПЛАН. = 4 см
LA = 6,5 см
↑P = 90 °
♂ = 110 °
тнаг = 85 °
(III) Параллелограмма Слушайте
HE = 5 CM
44. 6 CM = 6 CM = 6 CM = 6 CM = 6 CM = 6 CM = 6 CM = 6 CM = 6 CM = 6 CM = 6 CM = 6 CM = 6 CM = 6 CM = 6 CM = 6 CM = 6 CM = 6 CM.
. = 85°
(iv) Прямоугольник OKAY
OK = 7 см
KA = 5 см
Ответ:
(i)
(1)Грубый набросок этого четырехугольника можно нарисовать следующим образом.
(2) Нарисуйте отрезок MO длиной 6 см и углом 105º в точке O.
Так как вершина R находится на расстоянии 4,5 см от вершины O, отрежьте от этого луча отрезок OR длиной 4,5 см.
(3) Снова начертите угол 105º в точке R.
(4) Нарисуйте угол 60º в точке M. Пусть этот луч встретится с ранее проведенным лучом из R в точке E.
БОЛЬШЕ — искомый четырехугольник.
(ii)
(1) Сумма углов четырехугольника равна 360°.
В четырехугольнике в плане, ∠P + ∠L + ∠A + ∠N = 360°
90° + ∠L + 110° + 85° = 360°
285° + ∠L = 360°
∠L 9006 = 360° − 285° = 75°(2)Грубый набросок этого четырехугольника выглядит следующим образом.
(3) Нарисуйте отрезок PL длиной 4 см и начертите угол 75º в точке L. Поскольку вершина A находится на расстоянии 6,5 см от вершины L, отрежьте от этого луча отрезок LA длиной 6,5 см.
(4) Снова начертите угол 110º в точке A.
(5) Начертите угол 90º в точке P. Этот луч встретится с ранее проведенным лучом из A в точке N.
ПЛАН — искомый четырехугольник.
(iii)
(1) Во-первых, грубый набросок этого четырехугольника выглядит следующим образом.
(2) Нарисуйте отрезок HE длиной 5 см и углом 85º в точке E. Поскольку вершина A находится на расстоянии 6 см от вершины E, отрежьте от этого луча отрезок EA длиной 6 см.
(3) Вершина R находится на расстоянии 6 см и 5 см от вершин H и A соответственно. Приняв радиус за 6 см и 5 см, проведите дуги из точек Н и А соответственно. Они будут пересекаться друг с другом в точке R.
Соединить R с H и A.
HEAR – искомый четырехугольник.
(iv)
(1)Грубый набросок этого четырехугольника рисуется следующим образом.
(2) Нарисуйте отрезок OK длиной 7 см и углом 90º в точке K.
Так как вершина A находится на расстоянии 5 см от вершины K, отрежьте от этого луча отрезок KA длиной 5 см.
(3) Вершина Y находится на расстоянии 5 см и 7 см от вершины О и А соответственно. Приняв радиус за 5 см и 7 см, проведите дуги из точек О и А соответственно. Они будут пересекаться друг с другом в точке Y.
(4) Соедините Y с A и O.
OKAY — это искомый четырехугольник.
Видео Решение для практической геометрии (Страница: 64 , Q.No.: 1)
NCERT Решение для 8 класса математика — практическая геометрия 64 , Вопрос 1
Страница № 67:
Вопрос 1:
Постройте следующие четырехугольники,
(i) Четырехугольник DEAR
DE = 49 см 90 4 см 5 cm
AR = 4.5 cm
∠E = 60°
∠A = 90°
(ii) Quadrilateral TRUE
TR = 3.5 cm
RU = 3 cm
UE = 4 cm
∠ R = 75°
∠U = 120°
Ответ:
(i)
(1)Грубый набросок этого четырехугольника можно нарисовать следующим образом.
(2) Нарисуйте отрезок DE длиной 4 см и угол 60º в точке E. Поскольку вершина A находится на расстоянии 5 см от вершины E, отрежьте от этого луча отрезок EA длиной 5 см.
(3) Снова начертите угол 90º в точке A. Поскольку вершина R находится на расстоянии 4,5 см от вершины A
, отрежьте от этого луча отрезок RA длиной 4,5 см.
(4) Соедините D с R.
ДОРОГОЙ — искомый четырехугольник.
(ii)
(1)Грубый набросок этого четырехугольника можно нарисовать следующим образом.
(2) Проведите отрезок RU длиной 3 см и углом 120º в точке U. Поскольку вершина E находится на расстоянии 4 см от вершины U, отрежьте от этого луча отрезок UE длиной 4 см
.
(3) Затем в точке R начертите угол 75º. Так как вершина T находится на расстоянии 3,5 см от вершины R, отрежьте от этого луча отрезок RT длиной 3,5 см.
(4) Соедините T с E.
ИСТИНА — искомый четырехугольник.
Видео Решение по практической геометрии (Страница: 67 , Q.No.: 1)
NCERT Решение по математике для 8 класса — Практическая геометрия 67 , Вопрос 1
Страница № 68:
Вопрос 1:
Нарисуйте следующие:
Площадь ПРОЧИТАЙТЕ с RE = 5,1 см
Ответ:
Все стороны квадрата имеют одинаковую меру, а также все внутренние углы квадрата равны 90º мера. Таким образом, данный квадрат READ можно нарисовать следующим образом.
(1)А Набросок этого квадрата READ можно нарисовать следующим образом.
(2) Начертите отрезок RE длиной 5,1 см и углом 90º при точки R и E.
(3) Поскольку вершины A и D находятся на расстоянии 5,1 см от вершин E и R соответственно, отрежьте отрезки EA и RD, каждый по 5,1 см от этих лучи.
(4) Соедините D с A.
READ — это необходимый квадрат.
Страница № 68:
Вопрос 2:
Нарисуйте следующий:
Ромб
диагонали которого равны 5,2 см и 6,4 см.
Ответ:
В ромба, диагонали которого пересекаются под углом 90°. Следовательно заданный ромб ABCD можно нарисовать следующим образом.
(1)А Набросок этого ромба ABCD выглядит следующим образом.
(2) Нарисуйте отрезок AC длиной 5,2 см и проведите к нему перпендикуляр. биссектриса. Пусть он пересекает отрезок AC в точке O.
(3) Нарисуйте дуги на обе стороны от этого серединного перпендикуляра. Пусть дуги пересекают Биссектриса в точках B и D.
(4) Соедините точки B и D с точками A и C.
ABCD — искомый ромб.
Страница № 68:
Вопрос 3:
Нарисуйте следующий:
А прямоугольник со смежными сторонами 5 см и 4 см.
Ответ:
Напротив стороны прямоугольника имеют одинаковые длины, а также все внутренние углы прямоугольника равны 90º мера. данный прямоугольник ABCD можно нарисовать следующим образом.
(1)А
Набросок этого прямоугольника ABCD можно нарисовать следующим образом.
(2) Нарисуйте отрезок AB длиной 5 см и углом 90º в точке А и Б.
(3) Поскольку вершины C и D находятся на расстоянии 4 см от вершин B и A соответственно, Отрежьте от этих лучей отрезки AD и BC по 4 см каждый.
(4) Соедините D с C.
ABCD — искомый прямоугольник.
Страница № 68:
Вопрос 4:
Нарисуйте следующее:
Параллелограмм OKAY, где OK = 5,5 см и KA = 4,2 см.
Ответ:
Противоположные стороны параллелограмма равны и параллельны друг другу. Данный параллелограмм OKAY можно нарисовать следующим образом.
(1)Грубый набросок этого параллелограмма OKAY нарисован следующим образом.
(2) Нарисуйте отрезок OK длиной 5,5 см и луч в точке K под удобным углом.
(3) Проведите в точке O луч, параллельный лучу в K. Поскольку вершины A и Y находятся на расстоянии 4,2 см от вершин K и O соответственно, отрежьте отрезки KA и OY по 4,2 см, от этих лучей.
(4) Соедините Y с A.
OKAY — искомый параллелограмм.
Геометрия — математика для старших классов
Все ресурсы по математике для старших классов
8 Диагностические тесты 613 практических тестов Вопрос дня Карточки Учитесь по концепции
← Предыдущая 1 2 … 20 21 22 23 24 25 26 27 28 … 69 70 Следующая →
Справка по математике для средней школы » Геометрия
Эрин готовится посадить свой сад тюльпанов. Она хочет посадить два тюльпана на квадратный метр сада. Если ее прямоугольный сад огорожен забором длиной 24 фута, а длина забора в два раза больше его ширины, сколько тюльпанов посадит Эрин?
Возможные ответы:
64
24
16
48
32
Правильный ответ:
64
Объяснение:
Мы знаем, что следующая формула представляет собой формулу для периметра прямоугольника:
В данном конкретном случае нам говорят, что длина забора в два раза больше ширины.
Мы можем записать это как следующее выражение:
Используйте эту информацию, чтобы заменить переменную для длины, которая соответствует переменной для ширины в нашем уравнении периметра.
Мы также знаем, что длина в два раза больше ширины; поэтому мы можем написать следующее:
Площадь прямоугольника находится по этой формуле:
Площадь сада составляет 32 квадратных фута. Эрин посадит два тюльпана на квадратный фут; таким образом, она посадит 64 тюльпана.
Сообщить об ошибке
Какова длина диагонали квадрата с длиной стороны? Округлите до десятых.
Возможные ответы:
Правильный ответ:
Пояснение:
Квадрат состоит из двух прямоугольных треугольников 45-45-90. Гипотенуза прямоугольного треугольника 45-45-90 следует следующему правилу, где — длина сторон.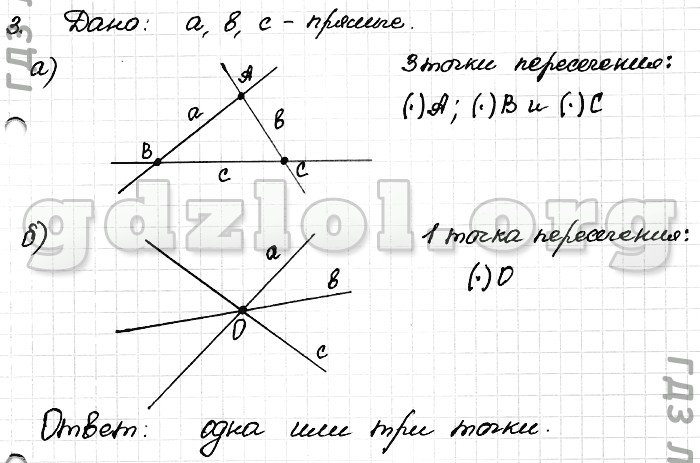
В данном случае равно 6.
Сообщить об ошибке
Сторона квадрата равна . Какова длина диагонали этого квадрата?
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы найти диагональ квадрата, мы эффективно разрезаем квадрат на два треугольника.
Выкройка сторон а.
Поскольку две стороны равны , этот треугольник будет иметь стороны .
Таким образом, диагональ (гипотенуза) будет иметь длину .
Сообщить об ошибке
Стороны квадрата равны . Какова длина диагонали этого квадрата?
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы найти диагональ квадрата, мы эффективно разрезаем квадрат на два треугольника.
Выкройка сторон а.
Поскольку две стороны равны , этот треугольник будет иметь стороны .
Таким образом, диагональ (гипотенуза) будет иметь длину .
Сообщить об ошибке
Какова длина диагонали квадрата со стороной ?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти диагональ квадрата, мы должны использовать длину стороны, чтобы создать треугольник с углами 90 градусов, длины сторон которого равны , , а гипотенуза равна диагонали.
Теорема Пифагора утверждает , где a и b — катеты, а c — гипотенуза.
Возьмите и и подставьте их в уравнение для и :
После возведения чисел в квадрат сложите их вместе:
Получив сумму, извлеките квадратный корень из обеих частей:
Упростите, чтобы найти ответ: , или .
Сообщить об ошибке
Какова длина диагонали квадрата 7 на 7? (Округлите до десятых.)
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти диагональ квадрата, мы должны использовать длины сторон, чтобы создать 90-градусный треугольник с длинами сторон 7 и гипотенузой, равной диагонали.
Мы можем использовать теорему Пифагора здесь, чтобы найти гипотенузу прямоугольного треугольника.
Теорема Пифагора утверждает , где a и b — длины сторон, а c — гипотенуза.
Подставьте длины сторон в уравнение как и :
Возведите числа в квадрат:
Сложите члены в левой части уравнения вместе:
Извлеките квадратный корень из обеих частей:
Следовательно, длина диагонали равна 9,9.
Сообщить об ошибке
Периметр квадрата равен 48. Какова длина его диагонали?
Возможные ответы:
Правильный ответ:
Объяснение:
Периметр = сторона * 4
48 = сторона * 4
Сторона = 12
Квадрат можно разбить на два равных прямоугольных треугольника. Тогда диагональ квадрата является гипотенузой этих двух треугольников.
Следовательно, мы можем использовать теорему Пифагоре, чтобы решить для диагонала:
Ошибка ABC. 3 TASE ABS 3 TASE ABS 3 TAME ABS 3 TASE ABS 3 TASE ABS 3 TASE ABSTHGH. из ЕФГХ. Если площадь EFGH равна 25, какова площадь ABCD?
Возможные ответы:
15
25
5
75
225
Правильный ответ:
225
Объяснение:
Назначьте переменные таким образом, чтобы
Одна сторона ABCD = a
и одна сторона EFGH = e
Обратите внимание, что в квадрате все стороны одинаковы.
Так как периметр есть сумма всех сторон, согласно вопросу:
4а = 3 х 4е = 12е или а = 3е
Из этой области EFGH 25,
e x e = 25, поэтому e = 5
Подставьте вместо a = 3e, чтобы a = 15
Мы еще не закончили. Поскольку нас спросили о площади ABCD, это равно a x a = 225.
Сообщить об ошибке
Квадрат имеет площадь 36. Если все стороны удвоить, какова новая площадь?
Возможные ответы:
144
48
108
132
72
1 Правильный ответ: 900019 144 Пояснение: Пусть S будет исходной длиной стороны. S * S будет представлять исходную область. Удвоение длины стороны даст вам 2S*2S, упрощение до 4*(S*S), даст новую площадь в 4 раза больше исходной или 144. Сообщить об ошибке Если периметр квадрата равен удвоенному его площадь, какова длина одной из его сторон? Возможные ответы: Правильный ответ: Объяснение: Площадь квадрата по каждой из его сторон: Площадь = S x S Периметр квадрата: Периметр = 4S Итак, если «периметр квадрата равен удвоенному площадь’: 2 x Площадь = Периметр 2 x [S x S] = [4S]; разделить на 2: S x S = 2S; разделить на S: S = 2 Сообщить об ошибке ← Предыдущий 1 2 … 20 21 22 23 24 25 26 27 28 … 6970 Далее → Уведомление об авторских правах 8 Диагностические тесты
613 практических тестов
Вопрос дня
Карточки
Learn by Concept 9 Диагностические тесты
164 практических теста
Вопрос дня
Карточки
Учитесь по концепции ← Предыдущая 1 2 3 Следующая → Справка по базовой геометрии »
Плоская геометрия »
Треугольники »
Прямоугольные треугольники »
How to find an angle in a right triangle Find angle C. Possible Answers: C=53 None of these C=70 C=65 C=72 Правильный ответ: C=65 Пояснение: Во-первых, знайте, что сумма всех углов треугольника равна 180 градусам. У каждого треугольника 3 угла. Таким образом, у нас есть сумма трех углов, как показано на рисунке: , где у нас есть углы A, B и C. В нашем прямоугольном треугольнике один угол равен 25 градусам, и мы назовем этот угол A. Другой известный угол равен 90 градусов, и мы назовем этот угол B. Таким образом, у нас есть Упростите и решите для C. Сообщить об ошибке Что из следующего может быть двумя мерами угла прямоугольного треугольника ? Возможные ответы: Правильный ответ: Пояснение: В прямоугольном треугольнике не может быть тупого угла; это исключает выбор между 100 и 10. Сумма острых углов прямоугольного треугольника должна составлять 90 градусов. По этому критерию можно исключить три варианта: Оставшийся вариант правильный: Сообщить об ошибке Угол прямоугольного треугольника в 15 раз больше, чем у другого. Чему равен меньший угол? Возможные ответы: Правильный ответ: Объяснение: Сумма углов треугольника равна 180. В прямоугольном треугольнике один угол равен 90. Таким образом, сумма двух других углов будет равна 90. Пусть = первый угол и = второй угол Итак уравнение для решения принимает вид или Таким образом, первый угол равен , а второй угол равен . Таким образом, меньший угол равен Сообщить об ошибке Угол в показанном ниже треугольнике (не в масштабе) равен 35 градусам. Возможные ответы: градусов градусов градусов градусов Правильный ответ: градусов Все ресурсы по математике для старших классов
Как найти угол в прямоугольном треугольнике
Все ресурсы по базовой геометрии
Что такое угол?
Сумма внутренних углов треугольника всегда равна 180 градусам. Нам дан угол и, поскольку указано, что это прямоугольный треугольник, мы знаем, что угол равен 90 градусов. Таким образом, мы знаем 2 из 3 и можем определить третий угол.
Угол равен 55 градусам.
Сообщить об ошибке
Что из следующего не может быть верным для прямоугольного треугольника?
Возможные ответы:
Катет может быть длиннее гипотенузы.
Прямоугольный треугольник может иметь тупой угол.
Прямоугольный треугольник может быть равносторонним.
Ни одно из других утверждений не может быть верным для прямоугольного треугольника.
Меры углов прямоугольного треугольника могут суммироваться.
Правильный ответ:
Ни одно из других утверждений не может быть верным для прямоугольного треугольника.
Объяснение:
Все из этих утверждений ложны.
Прямоугольный треугольник может быть равносторонним.
Неверно: Равносторонний треугольник должен иметь три угла, каждый из которых измеряется.
Один катет может быть длиннее гипотенузы.
Ложь: Каждый катет в раз короче гипотенузы.
Прямоугольный треугольник может иметь тупой угол.
Ложь: Оба угла прямоугольного треугольника, которые не являются прямыми , должны быть острыми.
Меры углов прямоугольного треугольника могут суммироваться.
Ложь: Меры любой суммы треугольников .
Сообщить об ошибке
Какова мера угла треугольника?
Возможные ответы:
Правильный ответ:
Объяснение:
Формула для нахождения всех углов треугольника:
Чтобы найти меру угла , мы подставляем значения и . Поскольку угол прямой, мы знаем, что мера будет равна .
Сообщить об ошибке
Найдите градусную меру недостающего угла.
Возможные ответы:
Правильный ответ:
Пояснение:
Сумма всех углов треугольника равна 180º.
Чтобы найти значение остаточного угла, вычтите известные углы из 180º:
Следовательно, третий угол равен 43º.
Сообщить об ошибке
Прямоугольный треугольник имеет два равных угла, какова их мера?
Возможные ответы:
Правильный ответ:
Пояснение:
Внутренние углы треугольника всегда составляют в сумме 180 градусов, и было дано, что треугольник прямоугольный, а это означает, что один из углов равен 90 градусам.
Это оставляет 90 градусов, чтобы равномерно разделить два оставшихся угла, как было показано в вопросе.
Следовательно, каждый из двух равных углов имеет размер 45 градусов.
Сообщить об ошибке
Какого угла не хватает в этом прямоугольном треугольнике?
Возможные ответы:
Правильный ответ:
Пояснение:
Сумма всех углов треугольника равна .