Категории: 6 класс.

Виленкин 6 класс 479: Номер №479 — ГДЗ по Математике 6 класс: Виленкин Н.Я.

 Комментировать

Номер 479 — ГДЗ по Математике 6 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2020. Часть 1 (решебник)

Номер 479 — ГДЗ по Математике 6 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2020. Часть 1 (решебник) — GDZwow

Перейти к содержанию

Search for:

Авторы: Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И.

Издательство: Мнемозина

Тип: Учебник

Новая версия

Старая версия

ЧАСТЬ 1
Выберите номер упражнения

123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325326327328329330331332333334335336337338339340341342343344345346347348349350351352353354355356357358359360361362363364365366367368369370371372373374375376377378379380381382383384385386387388389390391392393394395396397398399400401402403404405406407408409410411412413414415416417418419420421422423424425426427428429430431432433434435436437438439440441442443444445446447448449450451452453454455456457458459460461462463464465467468469470471472473474475476477478479480481482483484485486487488489490491492493494495496497498499500501502503504505506507508509510511512513514515516517518519520521522523524525526527528529530531532533534535536537538539540541542543544545546547548549550551552553554555556557558559560561562563564565566567568569570571572573574575576577578579580581582583584585586587588589590591592593594595596597598599600601602603604605606607608609610611612613614615616617618619620621622623624625626627628629630631632633634635636637638639640641642643644645646647648649650651652653654655656657658659660661662663664665666667668669670671672673674675676677678679680681682683684685686687688689690691692693694695696697698699700701702703704705706707708709710711712713714715716717718719720721722723724725726727728729730731732733734735736737738739740741742743744745746747748749750751753754755756757758759760761762763764765766767768769770771772773774775776777778779780781782783784785786787788789790791792793794795796797798799800801802803804805806807809810811812813814815816817818819820821822823824825826827828829830831832833834835836837838839840841842843844845846847848849850851852853854855856857858859860861862863864865866867868869870871872873874875876877878879880881882883884885886887888889890891892893894895896897

ЧАСТЬ 2
Выберите номер упражнения

1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495969798991001011021031041051061071081091101111121131141151161171181191201211221231241251261271281291301311321331341351361371381391401411421431441451461471481491501511521531541551561571581591601611621631641651661671681691701711721731741751761771781791801811821831841851861871881891901911921931941951961971981992002012022032042052062072082092102112122132142152162172182192202212222232242252262272282292302312322332342352362372382392402412422432442452462472482492502512522532542552562572582592602612622632642652662672682692702712722732742752762772782792802812822832842852862872882892902912922932942952962972982993003013023033043053063073083093103113123133143153163173183193203213223233243253263273283293303313323333343353363373383393403413423433443453463473483493503513523533543553563573583593603613623633643653663673683693703713723733743753763773783793803813823833843853863873883893903913923933943953963973983994004014024034044054064074084094104114124134144154164174184194204214224234244254264274284294304314324334344354364374384394404414424434444454464474484494504514524534544554564574584594604614624634644654664674684694704714724734744754764774784794804814824834844854864874884894904914924934944954964974984995005015025035045055065075085095105115125135145155165175185195205215225235245255265275285295305315325335345355365375385395405415425435445455465475485495505515525535545555565575585595605615625635645655665675685695705715725735745755765775785795805815825835845855865875885895905915925935945955965975985996006016026036046056066076086096106116126136146156166176186196206216226236246256266276286296306316326336346356366376386396406416426436446456466476486496506516526536546556566576586596606616626636646656666676686696706716726736746756766776786796806816826836846856866876886896906916926936946956966976986997007017027037047057068928938948958968978988999009019029039049059069079089099109119129139149159169179189199209219229239249259269279289299309319329339349359369379389399409419429439449459469479489499509519529539549559569579589599609619629639649659669679689699709719729739749759769779789799809819829839849859869879889899909919929939949959969979989991000100110021003100410051006100710081009101010111012101310141015101610171018101910201021102210231024102510261027102810291030103110321033103410351036103710381039104010411042104310441045104610471048104910501051105210531054105510561057105810591060106110621063106410651066106710681069107010711072107310741075107610771078107910801081108210831084108510861087108810891090109110921093109410951096109710981099110011011102110311041105110611071108110911101111111211131114111511161117111811191120112111221123112411251126112711281129113011311132113311341135113611371138113911401141114211431144114511461147114811491150115111521153115411551156115711581159116011611162116311641165116611671168116911701171117211731174117511761177117811791180118111821183118411851186118711881189119011911192119311941195119611971198119912011202120312041205120612071208120912101211121212131214121512161217121812191220122112221223122412251226122712281229123012311232123312341235123612371238123912401241124212431244124512461247124812491250125112521253125412551256125712581259126012611262126312641265126612671268126912701271127212731274127512761277127812791280128112821283128412851286128712881289129012911292129312941295129612971298129913001301130213031304130513061307130813091310131113121313131413151316131713181319132013211322132313241325132613271328132913301331133213331334133513361337133813391340134113421343134413451346134713481349135013511352135313541355135613571358135913601361136213631364136513661367136813691370137113721373137413751376137713781379138013811382138313841385138613871388138913901391139213931394139513961397139813991400140114021403140414051406140714081409141014111412141314141415141614171418141914201421142214231424142514261427142814291430143114321433143414351436143714381439144014411442144314441445144614481449145014511452145314541455145614571458145914601461146214631464146514681469147014711472147314741475147614771478147914801481148214831484148514861487148814891490149114921493149414951496149714981499150015011502150315041505150615071508150915101511151215131514151515161517151815191520152115221523152415251526152715281529153015311532153315341535153615371538153915401541154215431544154515461547154815491550155115521553155415551556155715581559156015611562156315641565156615671568156915701571157215731574157515761577157815791580158115821583158415851586158715881589159015911592159315941595

Adblock
detector

Ответы Задание 479 .

ГДЗ по математике 6 класс Виленкин Жохов Чесноков Шварцбурд учебник


12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394959697989910010110210310410510610710810911011111211311411511611711811912012112212312412512612712812913013113213313413513613713813914014114214314414514614714814915015115215315415515615715815916016116216316416516616716816917017117217317417517617717817918018118218318418518618718818919019119219319419519619719819920020120220320420520620720820921021121221321421521621721821922022122222322422522622722822923023123223323423523623723823924024124224324424524624724824925025125225325425525625725825926026126226326426526626726826927027127227327427527627727827928028128228328428528628728828929029129229329429529629729829930030130230330430530630730830931031131231331431531631731831932032132232332432532632732832933033133233333433533633733833934034134234334434534634734834935035135235335435535635735835936036136236336436536636736836937037137237337437537637737837938038138238338438538638738838939039139239339439539639739839940040140240340440540640740840941041141241341441541641741841942042142242342442542642742842943043143243343443543643743843944044144244344444544644744844945045145245345445545645745845946046146246346446546646746846947047147247347447547647747847948048148248348448548648748848949049149249349449549649749849950050150250350450550650750850951051151251351451551651751851952052152252352452552652752852953053153253353453553653753853954054154254354454554654754854955055155255355455555655755855956056156256356456556656756856957057157257357457557657757857958058158258358458558658758858959059159259359459559659759859960060160260360460560660760860961061161261361461561661761861962062162262362462562662762862963063163263363463563663763863964064164264364464564664764864965065165265365465565665765865966066166266366466566666766866967067167267367467567667767867968068168268368468568668768868969069169269369469569669769869970070170270370470570670770870971071171271371471571671771871972072172272372472572672772872973073173273373473573673773873974074174274374474574674774874975075175275375475575675775875976076176276376476576676776876977077177277377477577677777877978078178278378478578678778878979079179279379479579679779879980080180280380480580680780880981081181281381481581681781881982082182282382482582682782882983083183283383483583683783883984084184284384484584684784884985085185285385485585685785885986086186286386486586686786886987087187287387487587687787887988088188288388488588688788888989089189289389489589689789889990090190290390490590690790890991091191291391491591691791891992092192292392492592692792892993093193293393493593693793893994094194294394494594694794894995095195295395495595695795895996096196296396496596696796896997097197297397497597697797897998098198298398498598698798898999099199299399499599699799899910001001100210031004100510061007100810091010101110121013101410151016101710181019102010211022102310241025102610271028102910301031103210331034103510361037103810391040104110421043104410451046104710481049105010511052105310541055105610571058105910601061106210631064106510661067106810691070107110721073107410751076107710781079108010811082108310841085108610871088108910901091109210931094109510961097109810991100110111021103110411051106110711081109111011111112111311141115111611171118111911201121112211231124112511261127112811291130113111321133113411351136113711381139114011411142114311441145114611471148114911501151115211531154115511561157115811591160116111621163116411651166116711681169117011711172117311741175117611771178117911801181118211831184118511861187118811891190119111921193119411951196119711981199120012011202120312041205120612071208120912101211121212131214121512161217121812191220122112221223122412251226122712281229123012311232123312341235123612371238123912401241124212431244124512461247124812491250125112521253125412551256125712581259126012611262126312641265126612671268126912701271127212731274127512761277127812791280128112821283128412851286128712881289129012911292129312941295129612971298129913001301130213031304130513061307130813091310131113121313131413151316131713181319132013211322132313241325132613271328132913301331133213331334133513361337133813391340134113421343134413451346134713481349135013511352135313541355135613571358135913601361136213631364136513661367136813691370137113721373137413751376137713781379138013811382138313841385138613871388138913901391139213931394139513961397139813991400140114021403140414051406140714081409141014111412141314141415141614171418141914201421142214231424142514261427142814291430143114321433143414351436143714381439144014411442144314441445144614471448144914501451145214531454145514561457145814591460146114621463146414651466146714681469147014711472147314741475147614771478147914801481148214831484148514861487148814891490149114921493149414951496149714981499150015011502150315041505150615071508150915101511151215131514151515161517151815191520152115221523152415251526152715281529153015311532153315341535153615371538153915401541154215431544154515461547154815491550155115521553155415551556155715581559156015611562156315641565156615671568156915701571157215731574157515761577157815791580158115821583158415851586158715881589159015911592159315941595




great-math-books.

dvi

%PDF-1.7 % 1 0 объект > эндообъект 4 0 объект >поток 2014-03-12T17:34:12-04:002014-03-12T17:34:05-04:002014-03-12T17:34:12-04:00dvips(k) 5.98 Copyright 2009 Radical Eye Softwareapplication/pdf

  • отлично -math-books.dvi
  • БрайанБ
    • uuid:421ab7c4-cc4f-4027-a443-5771ed864d9auuid:827cb267-7a03-4cd0-9ac6-40ab3694983aAcrobat Distiller 8.1.0 (Windows) конечный поток эндообъект 9wɼK2l/ed2`ش`JX4>
    FʀUɴlcHf(9ڏ

    Чистая квантовая Вселенная как альтернатива инфляции

    Abstract

    Предложена модель расширения Вселенной, основанная на предположении, что Вселенная находится на ранних стадиях находился не в горячем состоянии, а в чистом, метастабильном квантовом состоянии.

    Это предположение позволяет с единых позиций и в рамках стандартной модели решить основные парадоксы стандартной космологии, а именно проблему горизонта, проблему плоскостности Вселенной, проблема отсутствия монополей и проблема преобладания материи над антиматерией 9.0007

    Ключевые слова: Плоскостность Вселенной; запутанность; Горизонт; декогеренция; бариогенез; Сверхсветовая связь.

    Введение

    В настоящее время ранние этапы эволюции Вселенной моделируются как в рамках инфляционных моделей, так и с использованием других подходов. Одной из основ для понимания механизмов расширения Вселенной являются такие ее свойства, как однородность, плоскостность и другие. Для решения этих проблем была предложена инфляционная парадигма (см., например, [1-5]), в рамках которой можно решить некоторые важные проблемы расширяющейся Вселенной.

    Проблема однородности (проблема горизонта) заключается в том, что температура микроволнового излучения отличается всего на несколько сотен тысячных в разных направлениях. Однако размеры Вселенной слишком велики для этой однородности, так как удаленные части Вселенной не могли быть связаны друг с другом даже со скоростью света, а термализация быстрее скорости света считается невозможной. Во-вторых, проблема плоского мира. В настоящее время геометрия Вселенной лишь немного отличается от евклидовой модели. Это накладывает очень сильные ограничения на кривизну Вселенной на ранних стадиях ее эволюции. Такие ограничения трудно объяснить в рамках стандартной космологической модели. Третья проблема – отсутствие монополий. Согласно стандартной модели, при энергии 1016 ГэВ симметрия нарушается и должны появиться монополи. Если бы их нельзя было аннигилировать, то их отношение к числу фотонов оставалось бы постоянным. Тогда на один нуклон в настоящее время должен приходиться один монополь, что не соответствует экспериментальным данным.

    Перечисленные проблемы можно решить, если предположить, что на ранних этапах эволюции Вселенная экспоненциально расширялась, в результате чего стала практически плоской. Однако сама инфляционная парадигма выходит за рамки стандартной модели, и обосновать ее с первых принципов до настоящего времени не удалось. Другим недостатком является то, что он предполагает существование структур, которые на много порядков больше, чем наша Вселенная. Такое предсказание трудно проверить экспериментально.

    В целом можно отметить, что как инфляционная модель, так и альтернативные модели (см., например, [6,7]) содержат большое количество настраиваемых параметров, что можно отнести к недостаткам обоих подходов.

    С другой стороны, остается еще ряд важных нерешенных космологических проблем, среди которых можно отметить проблему преобладания материи над антиматерией. Согласно современным наблюдениям, антиматерия в нашей Вселенной практически отсутствует. В настоящее время предложен ряд сценариев этого явления (см., например, [8]), однако его механизм во многом остается неясным. Обратите внимание, что большинство сценариев нарушения симметрии также требуют выхода за рамки стандартной модели.

    Цель этой статьи — показать, что перечисленные проблемы можно решить, просто предположив, что Вселенная на ранних стадиях находилась не в горячем, а в чистом квантовом состоянии.

    Расширение Вселенной: уравнение Фридмана или волновая функция?

    В настоящее время считается, что Вселенная возникла из горячего сверхплотного состояния. Дальнейшая эволюция Вселенной обычно описывается на основе уравнений Фридмана, являющихся следствием общей теории относительности для случая изотропной жидкости [8-10]. Такие уравнения (содержащие термодинамические параметры, такие как, например, давление) могут быть применены к случаю локального равновесия во Вселенной. Наличие такого равновесия постулируется.

    Альтернативой является моделирование расширения Вселенной с помощью волновой функции. В работах Хартла Дж.Б. и Виленкина А. [11,12] расширение Вселенной моделировалось на основе уравнения Уилера-де Витта, которое имеет вид [13]:

    Ĥ WdW ·Ψ= 0

    где Ĥ WdW — гамильтониан Уилера-де Витта, а Ψ — волновая функция Вселенной. При этом предлагается ряд сценариев возникновения Вселенной «из ничего», когда полная энергия системы (равная сумме гравитационной энергии и энергии частиц) равна нулю. Уравнение Уилера-де Витта считается хорошим первым приближением для описания квантовой эволюции Вселенной.

    Эти два подхода являются альтернативами друг друга, так как в первом случае в системе постулируется термодинамическое равновесие (т.е. система находится в смешанном состоянии), а во втором случае термодинамические параметры в системе отсутствуют. система, а сама она находится в чистом состоянии.

    Во втором случае чистого состояния Вселенной возникает проблема самовоздействия, так как Вселенная при расширении действует «на себя». Если система находится в локальном термодинамическом равновесии, то такой проблемы не возникает, так как одни части системы могут воздействовать на другие ее части. Однако для чистого состояния в системе невозможно выделить ее «части» — система описывается одной волновой функцией. Может ли система в чистом виде создавать искривление пространства, определяя тем самым собственную динамику?

    Понятие «Квантовая Вселенная» часто подразумевает квантовую гравитацию [14]. В то же время необходимо отметить, что возможна ситуация, когда частицы ведут себя существенно квантово, а поля — нет. Например, при расчете энергетических уровней в атоме квантованием полей можно в значительной степени пренебречь, основываясь только на квантовом поведении электронов (хотя сам переход частицы на более низкий уровень тесно связан с квантованием полей). Предполагается, что квантование гравитации важно при плотностях порядка планковской, но при дальнейшем расширении Вселенной эффекты квантования гравитации можно считать малыми. Также существует большое количество подходов к квантованию пространства-времени [14], которые не будут рассматриваться в данной статье.

    Модель чисто квантового состояния Вселенной

    Для решения проблем плоскостности, однородности Вселенной и других проблем, перечисленных выше, мы предполагаем, что Вселенная в начале расширения находилась в чисто квантовом состоянии.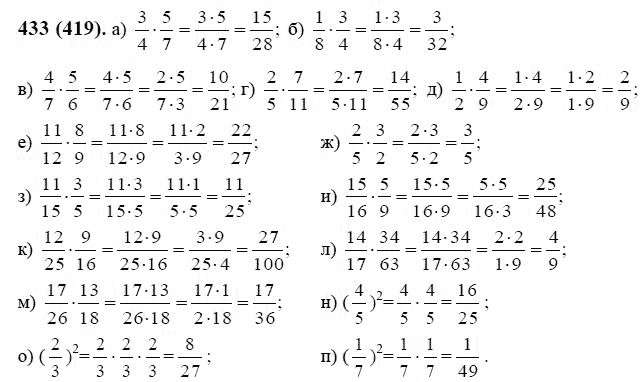 Такое утверждение относительно Вселенной также требует некоторых вспомогательных (но естественных) предположений:

    1. Вселенная родилась «из ничего», то есть ее полная энергия, включая гравитационную энергию и энергию частиц, была равна нулю. То есть в «начальный» момент времени Вселенная, по сути, была свободной частицей.

    2. В процессе расширения, пока состояние Вселенной чистое, действие Вселенной на себя отсутствует. Кривизна пространства-времени строго равна нулю. То есть Вселенная расширяется в плоском пространстве, представляя собой сферическую волну

    3. Чистое состояние Вселенной метастабильно. В результате взаимодействия с флуктуациями вакуума через определенное время τ чисто Вселенная переходит в смешанное состояние.

    4. В чистом виде Вселенная представляет собой конденсат, описываемый одной волновой функцией, несмотря на то, что может состоять из большого числа частиц. Такой конденсат можно рассматривать как набор из запутались частиц.

    5. После перехода Вселенной из чистого состояния в смешанное в результате множества последующих рождений и аннигиляций частиц формируется локальное термодинамическое равновесие, т.е. Вселенная термализуется и нагревается (рис. 1).

    Поскольку Вселенная находится в чистом состоянии, то до декогеренции (перехода в смешанное состояние) нельзя говорить о какой-то определенной кривизне пространства-времени, так как в уравнениях ОТО используются только классические (неквантовые) параметры (ср. , например, нельзя говорить об определенном положении квантовой частицы перед измерением). Следовательно, уравнения Фридмана на данном этапе расширения Вселенной неприменимы.

    Такой процесс расширения во многом аналогичен эксперименту ЭПР, когда пара частиц изначально находится в синглетном чистом состоянии и постепенно удаляется друг от друга. В этом случае такая пара частиц описывается одной волновой функцией. В результате измерения параметров одной из частиц вторая частица также мгновенно переходит в смешанное состояние.

    Показано, что на основе предложенной модели могут быть решены основные проблемы начальных стадий расширения Вселенной.

    Запутанность, сверхсветовая связь и проблема горизонта

    Сначала рассмотрим основные свойства запутанных частиц и законы распада запутанности. Существует несколько определений термина «запутанность», см., например, [15]. Одно определение следующее:

    ‘ Запутанность подразумевает, что вся система не может быть представлена ​​как продукт подсистем ’.

    Это свойство означает, что до измерения запутанные частицы ведут себя как одна частица, поведение которой описывается одной волновой функцией.

    Как будет показано ниже, проблема однородности температур дальних регионов Вселенной может быть решена на основе сверхсветовой связи. Проблема сверхсветовой связи рассматривалась неоднократно и имеет различные аспекты.

    С одной стороны, существуют теоремы об отсутствии связи. Эти теоремы ограничивают скорость передачи информации в произвольной квантовой системе (см. , например, [16]). Квантовая запутанность может создать впечатление, что информация может передаваться быстрее скорости света. Однако, согласно теореме об отсутствии связи, эти явления не допускают истинной коммуникации, они позволяют только двум наблюдателям в разных местах одновременно видеть одну и ту же систему, без какого-либо контроля над тем, что они видят.

    С другой стороны, в экспериментах с запутанными частицами [17] было обнаружено, что сигнал об измерении состояния одной частицы из запутанной пары распространяется со скоростью, намного превышающей скорость света. Одним из аргументов против распространения информации быстрее скорости света является также возможное нарушение второго начала термодинамики [18]. По мнению автора, если между двумя запутанными частицами нет взаимодействия (например, в эксперименте ЭПР), однако при измерении одной частицы изменяется и состояние второй, что соответствует дополнительному уменьшению энтропии изолированной системы. Поскольку подобные процессы запрещены вторым законом термодинамики, именно это и рассматривается рядом авторов как запрет на сверхсветовую связь. Однако из этого рассуждения имплицитно следует, что в системе имеются термодинамические параметры, такие как энтропия, температура и т. д. Однако для системы, находящейся в чистом состоянии, нет оснований вводить какие-либо термодинамические параметры, так как система не в равновесии.

    Еще одно проявление сверхсветовой связи — эксперименты Уилера с задержкой. Мысленный эксперимент Уилера [19] представляет собой вариант эксперимента с двумя щелями, в котором одна из щелей может закрыться после того, как фотон прошел через обе щели, но еще не достиг экрана. То есть фактически выбор структуры системы, с которой взаимодействует фотон, откладывается. В настоящее время этот эксперимент реализуется, хотя и в несколько ином виде (см., например, [20-25]).

    Таким образом, по проблеме сверхсветовой связи можно сделать следующие выводы:

    — Запутанные частицы могут быть связаны с произвольной скоростью (по крайней мере, насколько это позволяют проверить современные приборы),

    — С какой скоростью информация может передаваться из одной точки системы в другую — это другое дело. Ответ на него во многом зависит от определения информации. Однако скорость передачи информации не имеет ничего общего со скоростью декогеренции и термализации. При декогеренции информационный канал не формируется, так как передача взаимодействия происходит только в одном направлении.

    Различные сценарии декогеренции кубитов в зависимости от их корреляционной длины рассматриваются в исследовании Breuer HP et al. [26]. В частности, для случая, когда корреляционная длина велика, коллективное взаимодействие кубитов может привести к значительному усилению декогеренции.

    Таким образом, если движущиеся частицы Вселенной были запутаны друг с другом, то эти частицы одновременно перейдут в свое основное состояние (распад), как бы далеко они ни находились друг от друга. Это означает, что их дальнейшая термализация (связанная с рождением и аннигиляцией других частиц) будет зависеть от степени запутанности начального состояния, а не от размера системы.

    Таким образом, на начальном чистом этапе эволюции Вселенной термодинамические параметры отсутствуют, и размер Вселенной изменяется по закону:

    R=ct

    основное состояние существенно зависит от перехода других, это явление можно трактовать как фазовый переход.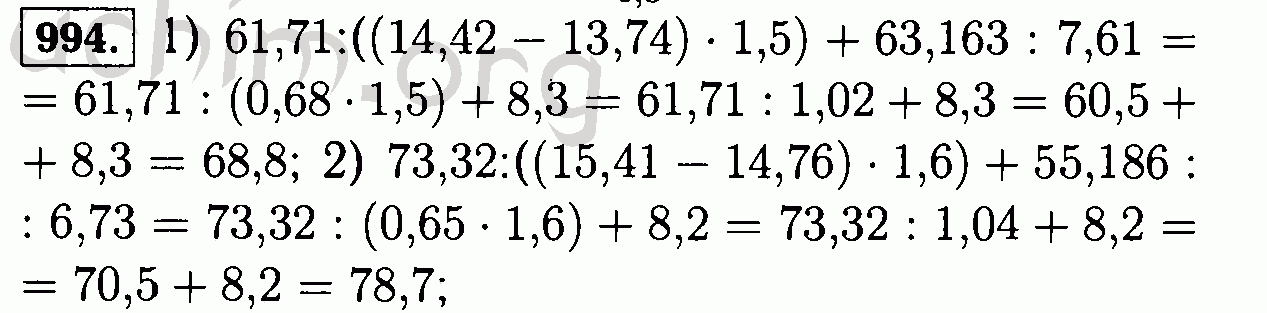

    Позднее, после установления термодинамического равновесия, согласно современным моделям (см., например, [8]), масштабный фактор изменился на эпоху рекомбинации как

    А после эпохи рекомбинации до настоящего времени как

    Таким образом, проблема горизонта решается тем, что запутанные частицы термализуются, какое бы расстояние между ними ни было, даже если это расстояние превышает значение ct .

    Проблема плоской Вселенной

    Так как в чистой фазе (в моменты времени t< τ чисто ) расширения Вселенной на себя не действует, то, как уже отмечалось выше, кривизна Вселенная остается нулем на протяжении всей этой фазы. В классической механике самовоздействие частиц связано с излучением ими электромагнитных волн (см., например, [27]). Переход чистого состояния системы в смешанное вызывается именно излучением частиц. Поэтому, пока частицы (любые) не излучаются, а система остается в чистом состоянии, самовоздействия нет. Тогда в процессе расширения Вселенной в чистой фазе должно выполняться следующее условие:

    Ω-1=0

    , где Ω=ρ/ρ c характеризует отличие средней плотности ρ от критической ρ c . Это условие, являющееся следствием чистоты квантового состояния, автоматически решает проблему тонкой настройки Вселенной на ранних стадиях. Проблема тонкой настройки состоит в том, что экстраполяция известных законов расширения Вселенной в рамках стандартной космологической модели (без инфляции) на планковские времена tP требует такой тонкой настройки параметра Ω, что (см., например, [28] ):

    0 ≤ Ω-1=10 -60

    Это означало бы, что кинетическая составляющая при tP должна была отличаться от гравитационной примерно на одну 1060-ю часть. С другой стороны, кинетическая и гравитационная составляющие теперь сопоставимо.

    Таким образом, в начале следующего этапа, когда разрушается чистое состояние и устанавливается термодинамическое равновесие, средняя плотность Вселенной в точности равна критической.

    Проблема монополей

    Модели элементарных частиц предполагают, что при энергии больше 1016 ГэВ симметрия нарушается. Это приводит к неизбежному возникновению монополий [8]. Если бы они не смогли аннигилировать, то их отношение к числу фотонов останется примерно постоянным. В то время теперь на нуклон должен приходиться один монополь, что совершенно не согласуется с экспериментальными данными.

    Монополи на самом деле были топологическими дефектами. Инфляционная парадигма предполагает, что из-за экспоненциального расширения Вселенной, даже если монополи существовали на ее ранних стадиях, после инфляции их плотность оказалась настолько малой, что обнаружить их в нашей части Вселенной не представляется возможным. Однако если Вселенная была в чистом состоянии, то отсутствие дефектов вполне естественно. Это отсутствие можно считать одним из определений чистого состояния. Таким образом, в процессе расширения Вселенной в чистом квантовом состоянии монополи не могли существовать. Если после декогеренции чистого состояния температура Вселенной оказалась недостаточной (менее 1015 ГэВ), то монополи и на этой стадии не могли сформироваться на сколько-нибудь значительном уровне.

    Проблема преобладания материи над антиматерией

    Поскольку в настоящее время материя преобладает над антиматерией, этот факт необходимо обосновать. После работы Сахарова [29] был предложен ряд механизмов бариогенеза (см., например, [30-32]), большинство из которых выходят за рамки стандартной модели и также требуют дополнительных предположений. Основные условия бариогенеза следующие [8]:

    1. Должен существовать физический процесс, нарушающий закон сохранения барионного числа.
    2. Должно быть нарушение инвариантности C и CP.
    3. Должно быть нарушение состояния теплового равновесия.

    Относительно этих условий можно отметить, что они не имеют прямого отношения к инфляционной парадигме и требуют дополнительных допущений. Нарушение C- и CP-инвариантности обнаружено экспериментально, однако насколько велико это влияние? Слабое нарушение закона сохранения барионного заряда предсказывают несколько теорий, выходящих за рамки стандартной модели (см. также [33-36]). Может ли такое слабое нарушение играть решающую роль в нуклеосинтезе? Существует также ряд моделей нарушения симметрии и теплового равновесия [8].

    Мы показываем, что эта задача также может быть решена на основе запутанности расширяющейся квантовой системы. Предположим, что летящие частицы (конденсат) с равной вероятностью могут распадаться на частицы и античастицы. При отсутствии какой-либо асимметрии рождение частицы или античастицы в этом случае является случайным процессом (рис. 2). Однако, поскольку частицы (из которых впоследствии рождаются барионы) запутываются друг с другом, такое нарушение будет происходить сразу во всей системе, а не в отдельных ее областях. То есть результирующая флуктуация будет значительно усилена за счет запутанности и охватит всю систему. Тогда в системе будет либо материя, либо антиматерия. Если запутывание между исходными частицами не полное, то преобладание материи над антиматерией (или наоборот) тоже будет неполным, но достаточным для образования барионов. В результате после аннигиляции части материи и антиматерии будет избыток того или другого.

    После коллапса чистого состояния Вселенной температура сначала сильно возрастает из-за декогеренции, а затем наступает эпоха доминирования излучения, во время которой температура начинает снижаться. Дальнейшую эволюцию Вселенной можно описать известными моделями, согласно которым в дальнейшем (см., например, [8]) электрослабое взаимодействие отделяется от сильного, затем образуются кварки и известные элементы.

    Другие следствия модели чистой Вселенной

    Поскольку после декогеренции почти мгновенно «включается» гравитация, ускорение также становится существенно переменным. Поскольку гравитационные волны вызваны переменным ускорением, это должно было привести к существованию первичных гравитационных волн. Эти волны должны сопровождать процесс декогеренции чистой вселенной. Открытие таких волн в настоящее время является одной из важных задач экспериментальной космологии.

    Как уже отмечалось выше, декогеренцию большого числа запутанных частиц можно трактовать как фазовый переход. Важнейшее свойство такого фазового перехода состоит в том, что он происходит одновременно во всей системе и не связан с наличием критического зародыша. Это свойство характерно для фазовых переходов второго рода. В таких системах, как и в широком классе систем, связанных с самоорганизованной критичностью, спектр возмущений является масштабно-инвариантным ввиду отсутствия в системе характерного размера. Как известно, именно такой спектр наблюдается при распределении вещества в галактиках (см., например, [37]).

    С другой стороны, спектр мощности возмущений может не быть напрямую связан с инфляцией или любыми другими начальными условиями. Известно, что системы с доминирующей гравитацией (а именно Вселенная на довольно поздней стадии) не являются локально равновесными, а представляют собой существенно хаотические нелинейные системы с дальнодействующим взаимодействием . При этом спектр мощности характерен для широкого класса систем с гравитацией (см., например, [38-40]) и слабо зависит от типа начальных возмущений, а значит, и от состояния Вселенной в ранние стадии.

    Заключение

    Таким образом, чистое состояние расширяющейся Вселенной на ранних стадиях позволяет без дополнительных допущений (в рамках стандартной модели) объяснить плоскостность и однородность Вселенной с единой точки зрения, а также как преобладание материи над антиматерией и отсутствие монополей. Такой механизм можно рассматривать как альтернативу инфляционной парадигме.

    Литература

    1. Старобинский А.А. Новый тип изотропных космологических моделей без сингулярности. Phys Letter B . 1980 г.; 91(1): 99-102. doi: 10.1016/0370-2693(80)90670-X