Номер 301 — ГДЗ по Математике для 6 класса Учебник Виленкин, Жохов, Чесноков, Шварцбурд Часть 2.
Номер 301 — ГДЗ по Математике для 6 класса Учебник Виленкин, Жохов, Чесноков, Шварцбурд Часть 2. — ГДЗ РЕДПерейти к содержанию
Search for:
Авторы: Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И.
Издательство: Мнемозина
Тип: Учебник
Новая версия
ЧАСТЬ 1
Выберите номер упражнения
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325326327328329330331332333334335336337338339340341342343344345346347348349350351352353354355356357358359360361362363364365366367368369370371372373374375376377378379380381382383384385386387388389390391392393394395396397398399400401402403404405406407408409410411412413414415416417418419420421422423424425426427428429430431432433434435436437438439440441442443444445446447448449450451452453454455456457458459460461462463464465467468469470471472473474475476477478479480481482483484485486487488489490491492493494495496497498499500501502503504505506507508509510511512513514515516517518519520521522523524525526527528529530531532533534535536537538539540541542543544545546547548549550551552553554555556557558559560561562563564565566567568569570571572573574575576577578579580581582583584585586587588589590591592593594595596597598599600601602603604605606607608609610611612613614615616617618619620621622623624625626627628629630631632633634635636637638639640641642643644645646647648649650651652653654655656657658659660661662663664665666667668669670671672673674675676677678679680681682683684685686687688689690691692693694695696697698699700701702703704705706707708709710711712713714715716717718719720721722723724725726727728729730731732733734735736737738739740741742743744745746747748749750751753754755756757758759760761762763764765766767768769770771772773774775776777778779780781782783784785786787788789790791792793794795796797798799800801802803804805806807809810811812813814815816817818819820821822823824825826827828829830831832833834835836837838839840841842843844845846847848849850851852853854855856857858859860861862863864865866867868869870871872873874875876877878879880881882883884885886887888889890891892893894895896897
ЧАСТЬ 2
Выберите номер упражнения
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495969798991001011021031041051061071081091101111121131141151161171181191201211221231241251261271281291301311321331341351361371381391401411421431441451461471481491501511521531541551561571581591601611621631641651661671681691701711721731741751761771781791801811821831841851861871881891901911921931941951961971981992002012022032042052062072082092102112122132142152162172182192202212222232242252262272282292302312322332342352362372382392402412422432442452462472482492502512522532542552562572582592602612622632642652662672682692702712722732742752762772782792802812822832842852862872882892902912922932942952962972982993003013023033043053063073083093103113123133143153163173183193203213223233243253263273283293303313323333343353363373383393403413423433443453463473483493503513523533543553563573583593603613623633643653663673683693703713723733743753763773783793803813823833843853863873883893903913923933943953963973983994004014024034044054064074084094104114124134144154164174184194204214224234244254264274284294304314324334344354364374384394404414424434444454464474484494504514524534544554564574584594604614624634644654664674684694704714724734744754764774784794804814824834844854864874884894904914924934944954964974984995005015025035045055065075085095105115125135145155165175185195205215225235245255265275285295305315325335345355365375385395405415425435445455465475485495505515525535545555565575585595605615625635645655665675685695705715725735745755765775785795805815825835845855865875885895905915925935945955965975985996006016026036046056066076086096106116126136146156166176186196206216226236246256266276286296306316326336346356366376386396406416426436446456466476486496506516526536546556566576586596606616626636646656666676686696706716726736746756766776786796806816826836846856866876886896906916926936946956966976986997007017027037047057068928938948958968978988999009019029039049059069079089099109119129139149159169179189199209219229239249259269279289299309319329339349359369379389399409419429439449459469479489499509519529539549559569579589599609619629639649659669679689699709719729739749759769779789799809819829839849859869879889899909919929939949959969979989991000100110021003100410051006100710081009101010111012101310141015101610171018101910201021102210231024102510261027102810291030103110321033103410351036103710381039104010411042104310441045104610471048104910501051105210531054105510561057105810591060106110621063106410651066106710681069107010711072107310741075107610771078107910801081108210831084108510861087108810891090109110921093109410951096109710981099110011011102110311041105110611071108110911101111111211131114111511161117111811191120112111221123112411251126112711281129113011311132113311341135113611371138113911401141114211431144114511461147114811491150115111521153115411551156115711581159116011611162116311641165116611671168116911701171117211731174117511761177117811791180118111821183118411851186118711881189119011911192119311941195119611971198119912011202120312041205120612071208120912101211121212131214121512161217121812191220122112221223122412251226122712281229123012311232123312341235123612371238123912401241124212431244124512461247124812491250125112521253125412551256125712581259126012611262126312641265126612671268126912701271127212731274127512761277127812791280128112821283128412851286128712881289129012911292129312941295129612971298129913001301130213031304130513061307130813091310131113121313131413151316131713181319132013211322132313241325132613271328132913301331133213331334133513361337133813391340134113421343134413451346134713481349135013511352135313541355135613571358135913601361136213631364136513661367136813691370137113721373137413751376137713781379138013811382138313841385138613871388138913901391139213931394139513961397139813991400140114021403140414051406140714081409141014111412141314141415141614171418141914201421142214231424142514261427142814291430143114321433143414351436143714381439144014411442144314441445144614481449145014511452145314541455145614571458145914601461146214631464146514681469147014711472147314741475147614771478147914801481148214831484148514861487148814891490149114921493149414951496149714981499150015011502150315041505150615071508150915101511151215131514151515161517151815191520152115221523152415251526152715281529153015311532153315341535153615371538153915401541154215431544154515461547154815491550155115521553155415551556155715581559156015611562156315641565156615671568156915701571157215731574157515761577157815791580158115821583158415851586158715881589159015911592159315941595
Adblockdetector
Номер 301 — ГДЗ по Математике 6 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2020.
 Часть 2 (решебник)Номер 301 — ГДЗ по Математике 6 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2020. Часть 2 (решебник) — GDZwow
Часть 2 (решебник)Номер 301 — ГДЗ по Математике 6 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2020. Часть 2 (решебник) — GDZwowПерейти к содержанию
Search for:
Авторы: Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И.
Издательство: Мнемозина
Тип: Учебник
Новая версия
ЧАСТЬ 1
Выберите номер упражнения
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325326327328329330331332333334335336337338339340341342343344345346347348349350351352353354355356357358359360361362363364365366367368369370371372373374375376377378379380381382383384385386387388389390391392393394395396397398399400401402403404405406407408409410411412413414415416417418419420421422423424425426427428429430431432433434435436437438439440441442443444445446447448449450451452453454455456457458459460461462463464465467468469470471472473474475476477478479480481482483484485486487488489490491492493494495496497498499500501502503504505506507508509510511512513514515516517518519520521522523524525526527528529530531532533534535536537538539540541542543544545546547548549550551552553554555556557558559560561562563564565566567568569570571572573574575576577578579580581582583584585586587588589590591592593594595596597598599600601602603604605606607608609610611612613614615616617618619620621622623624625626627628629630631632633634635636637638639640641642643644645646647648649650651652653654655656657658659660661662663664665666667668669670671672673674675676677678679680681682683684685686687688689690691692693694695696697698699700701702703704705706707708709710711712713714715716717718719720721722723724725726727728729730731732733734735736737738739740741742743744745746747748749750751753754755756757758759760761762763764765766767768769770771772773774775776777778779780781782783784785786787788789790791792793794795796797798799800801802803804805806807809810811812813814815816817818819820821822823824825826827828829830831832833834835836837838839840841842843844845846847848849850851852853854855856857858859860861862863864865866867868869870871872873874875876877878879880881882883884885886887888889890891892893894895896897
ЧАСТЬ 2
Выберите номер упражнения
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495969798991001011021031041051061071081091101111121131141151161171181191201211221231241251261271281291301311321331341351361371381391401411421431441451461471481491501511521531541551561571581591601611621631641651661671681691701711721731741751761771781791801811821831841851861871881891901911921931941951961971981992002012022032042052062072082092102112122132142152162172182192202212222232242252262272282292302312322332342352362372382392402412422432442452462472482492502512522532542552562572582592602612622632642652662672682692702712722732742752762772782792802812822832842852862872882892902912922932942952962972982993003013023033043053063073083093103113123133143153163173183193203213223233243253263273283293303313323333343353363373383393403413423433443453463473483493503513523533543553563573583593603613623633643653663673683693703713723733743753763773783793803813823833843853863873883893903913923933943953963973983994004014024034044054064074084094104114124134144154164174184194204214224234244254264274284294304314324334344354364374384394404414424434444454464474484494504514524534544554564574584594604614624634644654664674684694704714724734744754764774784794804814824834844854864874884894904914924934944954964974984995005015025035045055065075085095105115125135145155165175185195205215225235245255265275285295305315325335345355365375385395405415425435445455465475485495505515525535545555565575585595605615625635645655665675685695705715725735745755765775785795805815825835845855865875885895905915925935945955965975985996006016026036046056066076086096106116126136146156166176186196206216226236246256266276286296306316326336346356366376386396406416426436446456466476486496506516526536546556566576586596606616626636646656666676686696706716726736746756766776786796806816826836846856866876886896906916926936946956966976986997007017027037047057068928938948958968978988999009019029039049059069079089099109119129139149159169179189199209219229239249259269279289299309319329339349359369379389399409419429439449459469479489499509519529539549559569579589599609619629639649659669679689699709719729739749759769779789799809819829839849859869879889899909919929939949959969979989991000100110021003100410051006100710081009101010111012101310141015101610171018101910201021102210231024102510261027102810291030103110321033103410351036103710381039104010411042104310441045104610471048104910501051105210531054105510561057105810591060106110621063106410651066106710681069107010711072107310741075107610771078107910801081108210831084108510861087108810891090109110921093109410951096109710981099110011011102110311041105110611071108110911101111111211131114111511161117111811191120112111221123112411251126112711281129113011311132113311341135113611371138113911401141114211431144114511461147114811491150115111521153115411551156115711581159116011611162116311641165116611671168116911701171117211731174117511761177117811791180118111821183118411851186118711881189119011911192119311941195119611971198119912011202120312041205120612071208120912101211121212131214121512161217121812191220122112221223122412251226122712281229123012311232123312341235123612371238123912401241124212431244124512461247124812491250125112521253125412551256125712581259126012611262126312641265126612671268126912701271127212731274127512761277127812791280128112821283128412851286128712881289129012911292129312941295129612971298129913001301130213031304130513061307130813091310131113121313131413151316131713181319132013211322132313241325132613271328132913301331133213331334133513361337133813391340134113421343134413451346134713481349135013511352135313541355135613571358135913601361136213631364136513661367136813691370137113721373137413751376137713781379138013811382138313841385138613871388138913901391139213931394139513961397139813991400140114021403140414051406140714081409141014111412141314141415141614171418141914201421142214231424142514261427142814291430143114321433143414351436143714381439144014411442144314441445144614481449145014511452145314541455145614571458145914601461146214631464146514681469147014711472147314741475147614771478147914801481148214831484148514861487148814891490149114921493149414951496149714981499150015011502150315041505150615071508150915101511151215131514151515161517151815191520152115221523152415251526152715281529153015311532153315341535153615371538153915401541154215431544154515461547154815491550155115521553155415551556155715581559156015611562156315641565156615671568156915701571157215731574157515761577157815791580158115821583158415851586158715881589159015911592159315941595
Adblockdetector
ГДЗ задание 301 математика 5 класс Никольский, Потапов – Telegraph
>>> ПОДРОБНЕЕ ЖМИТЕ ЗДЕСЬ <<<
ГДЗ задание 301 математика 5 класс Никольский, Потапов
ГДЗ (готовое домашние задание из решебника) на Номер №301 по учебнику Математика . 5 класс . Учебник для общеобразовательных организаций / С .М . Никольский , М .К, Потапов, Н .Н . Решетников, А .В . Шевкин . — 14 издание . Просвещение .
5 класс . Учебник для общеобразовательных организаций / С .М . Никольский , М .К, Потапов, Н .Н . Решетников, А .В . Шевкин . — 14 издание . Просвещение .
Задача №301 , ГДЗ по математике за 5 класс к учебнику Никольского . Бесплатные ответы . Никольский , Потапов, Решетников . Натуральные числа и нуль . § 1 .17 . Задачи на нахождение двух чисел по их сумме и разности . Номер №301 .
ГДЗ по математике за 5 класс Никольский, это сборник ответов, разделённый на четыре главы . Все упражнения соответствуют принятым стандартам и расположены так же ГДЗ к задачам на смекалку по математике за 5-6 классы Шарыгин И .Ф . можно посмотреть здесь . Номера задач .
Современные учебники по математике за 5 класс отличаются изложением материала в разной интерпретации . В этом поможет дополнительное пособие в формате ГДЗ по математике 5 класс авторов: Никольский С .М . Потапов М .К . Решетников Н .Н . Шевкин А .В . 299 . 300 . 301 .
ГДЗ (решебник) по математике за 5 класс Никольский , Потапов , Решетников, Шевкин — ответы онлайн . Чтобы ГДЗ по математике 5 класс Никольский и повысили оценки, и подтянули знания, работать с ними нужно с умом: При нехватке времени ученику достаточно списать задания . .
Чтобы ГДЗ по математике 5 класс Никольский и повысили оценки, и подтянули знания, работать с ними нужно с умом: При нехватке времени ученику достаточно списать задания . .
Никольский , Потапов , Решетников . Просвещение . год . ГДЗ (решебник) по математике 5 класс Никольский , Потапов, Решетников, Шевкин . Школьники невероятно загружены . Приходится по 7-8 часов быть в школе, затем посещать кружки и факультативы .
Гдз по математике за 5 класс Никольский , Потапов ответ на номер № 301 . Авторы: С .М . Никольский , М .К . Потапов , Н .Н . Решетников, А .В . Шевкин . Издательство: Просвещение . Тип: Учебник, МГУ — школе . Подробный решебник (ГДЗ ) по Математике за 5 (пятый ) класс . .
Математика 5 класс . Учебник . Никольский , Потапов, Решетников . Просвещение . В сборник вошли ответы по всем заданиям . Одна тысяча двести пятнадцать упражнений разбиты по «ГДЗ по Математике 5 класс Никольский» доступен онлайн, поэтому пользоваться им очень . .
Убедись в правильности решения задачи вместе с ГДЗ по Математике за 5 класс С . М . Никольский , М .К . Потапов, Н .Н . Решетников, А .В Забота об успешном освоении ребенком школьной программы может проявляться не только в том, чтобы учиться и выполнять задания . .
М . Никольский , М .К . Потапов, Н .Н . Решетников, А .В Забота об успешном освоении ребенком школьной программы может проявляться не только в том, чтобы учиться и выполнять задания . .
Категория: ГДЗ Математика учебник 5 класс Никольский , Потапов , Решетников . Задание № 301 . Первый магический квадрат был составлен в Китае в V−IV веке до н .э . Другой магический квадрат был составлен в Индии в I веке н .э . Сравните суммы чисел в строчках, столбцах и . .
На помощь придет онлайн-ГДЗ по Математике 5 класс автора Никольский С .М .,М .К . Потапов,Н .Н . Решетников, А .В . Шевкин ! Не нужно покупать книгу в магазине, тратить деньги на репетиторов или просить списать у одноклассников . Найдите номер упражнения и посмотрите . .
Учебное пособие «Математика 5 класс Учебник Никольский , Потапов, Решетников, Шевкин Просвещение» Проверку исполняемых заданий можно возложить на решебники . Что представляет собой решебник . Сборник «ГДЗ по Математике 5 класс Никольского . .
ГДЗ по математике 5 класс Никольский .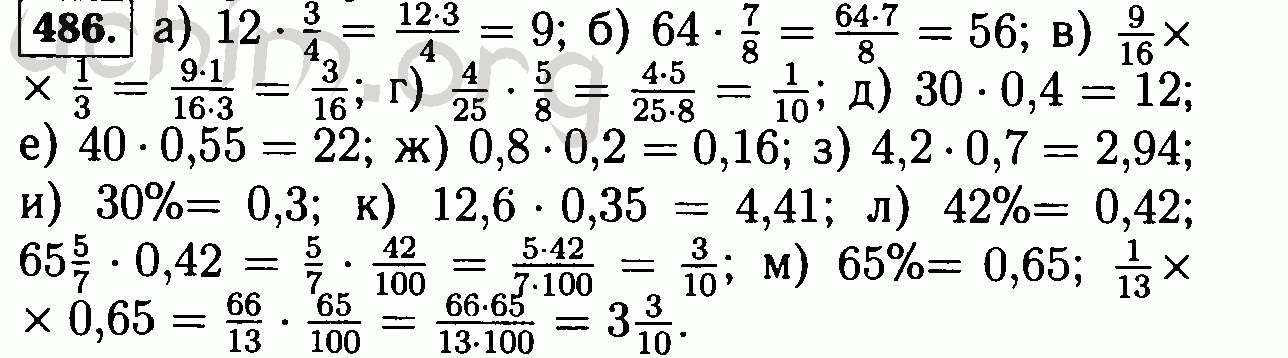 авторы: Никольский С .М ., М .К . Потапов, Н .Н . Решетников . ГДЗ — Готовые Домашние Задания . support@reshalka .
авторы: Никольский С .М ., М .К . Потапов, Н .Н . Решетников . ГДЗ — Готовые Домашние Задания . support@reshalka .
Математика 5 класс . Учебник . Никольский , Потапов, Решетникова . Просвещение . Все примеры соответствуют тем, что есть в учебном пособии . Тщательно выверенные ответы в ГДЗ по математике 5 класс помогут точно понять что и как именно нужно делать .
Разбор задач из учебника по математике за 5 класс Никольского С .М ., Потапова М .К . Решетникова Н .Н . Шевкина А .В . Все выполненные задания проверены учителями Понимание предмета становится эффективнее с ГДЗ по математике для 5 класса к учебнику Никольского .
ГДЗ (готовое домашние задание из решебника) на Номер №301 по учебнику Математика . 5 класс . Учебник для общеобразовательных организаций / С .М . Никольский , М .К, Потапов, Н .Н . Решетников, А .В . Шевкин . — 14 издание . Просвещение .
Задача №301 , ГДЗ по математике за 5 класс к учебнику Никольского . Бесплатные ответы . Никольский , Потапов, Решетников .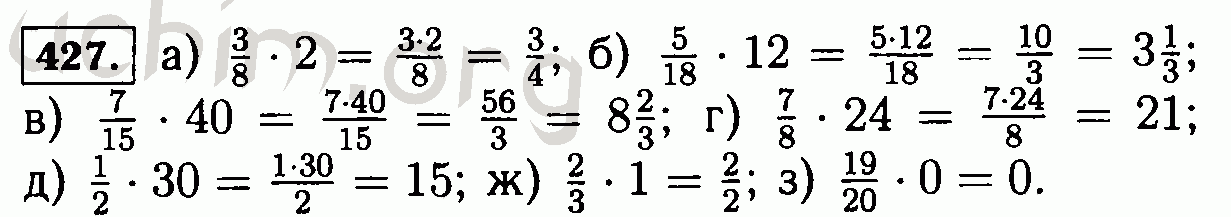 Натуральные числа и нуль . § 1 .17 . Задачи на нахождение двух чисел по их сумме и разности . Номер №301 .
Натуральные числа и нуль . § 1 .17 . Задачи на нахождение двух чисел по их сумме и разности . Номер №301 .
ГДЗ по математике за 5 класс Никольский, это сборник ответов, разделённый на четыре главы . Все упражнения соответствуют принятым стандартам и расположены так же ГДЗ к задачам на смекалку по математике за 5-6 классы Шарыгин И .Ф . можно посмотреть здесь . Номера задач .
Современные учебники по математике за 5 класс отличаются изложением материала в разной интерпретации . В этом поможет дополнительное пособие в формате ГДЗ по математике 5 класс авторов: Никольский С .М . Потапов М .К . Решетников Н .Н . Шевкин А .В . 299 . 300 . 301 .
ГДЗ (решебник) по математике за 5 класс Никольский , Потапов , Решетников, Шевкин — ответы онлайн . Чтобы ГДЗ по математике 5 класс Никольский и повысили оценки, и подтянули знания, работать с ними нужно с умом: При нехватке времени ученику достаточно списать задания . .
Никольский , Потапов , Решетников . Просвещение . год . ГДЗ (решебник) по математике 5 класс Никольский , Потапов, Решетников, Шевкин . Школьники невероятно загружены . Приходится по 7-8 часов быть в школе, затем посещать кружки и факультативы .
год . ГДЗ (решебник) по математике 5 класс Никольский , Потапов, Решетников, Шевкин . Школьники невероятно загружены . Приходится по 7-8 часов быть в школе, затем посещать кружки и факультативы .
Гдз по математике за 5 класс Никольский , Потапов ответ на номер № 301 . Авторы: С .М . Никольский , М .К . Потапов , Н .Н . Решетников, А .В . Шевкин . Издательство: Просвещение . Тип: Учебник, МГУ — школе . Подробный решебник (ГДЗ ) по Математике за 5 (пятый ) класс . .
Математика 5 класс . Учебник . Никольский , Потапов, Решетников . Просвещение . В сборник вошли ответы по всем заданиям . Одна тысяча двести пятнадцать упражнений разбиты по «ГДЗ по Математике 5 класс Никольский» доступен онлайн, поэтому пользоваться им очень . .
Убедись в правильности решения задачи вместе с ГДЗ по Математике за 5 класс С .М . Никольский , М .К . Потапов, Н .Н . Решетников, А .В Забота об успешном освоении ребенком школьной программы может проявляться не только в том, чтобы учиться и выполнять задания . .
.
Категория: ГДЗ Математика учебник 5 класс Никольский , Потапов , Решетников . Задание № 301 . Первый магический квадрат был составлен в Китае в V−IV веке до н .э . Другой магический квадрат был составлен в Индии в I веке н .э . Сравните суммы чисел в строчках, столбцах и . .
На помощь придет онлайн-ГДЗ по Математике 5 класс автора Никольский С .М .,М .К . Потапов,Н .Н . Решетников, А .В . Шевкин ! Не нужно покупать книгу в магазине, тратить деньги на репетиторов или просить списать у одноклассников . Найдите номер упражнения и посмотрите . .
Учебное пособие «Математика 5 класс Учебник Никольский , Потапов, Решетников, Шевкин Просвещение» Проверку исполняемых заданий можно возложить на решебники . Что представляет собой решебник . Сборник «ГДЗ по Математике 5 класс Никольского . .
ГДЗ по математике 5 класс Никольский . авторы: Никольский С .М ., М .К . Потапов, Н .Н . Решетников . ГДЗ — Готовые Домашние Задания . support@reshalka .
Математика 5 класс .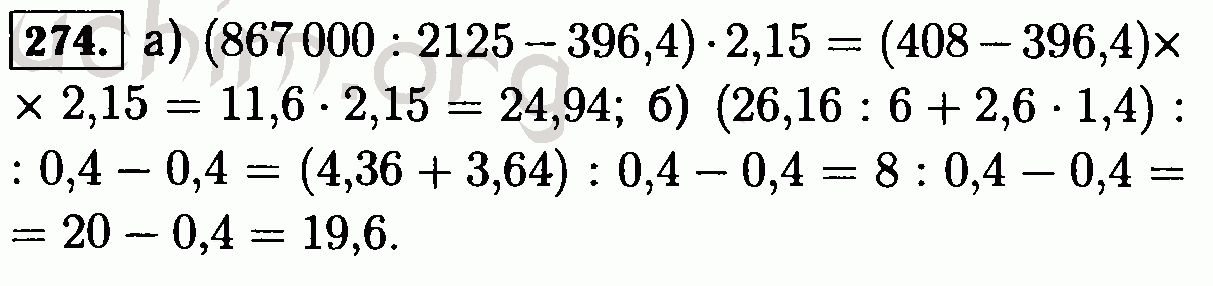 Учебник . Никольский , Потапов, Решетникова . Просвещение . Все примеры соответствуют тем, что есть в учебном пособии . Тщательно выверенные ответы в ГДЗ по математике 5 класс помогут точно понять что и как именно нужно делать .
Учебник . Никольский , Потапов, Решетникова . Просвещение . Все примеры соответствуют тем, что есть в учебном пособии . Тщательно выверенные ответы в ГДЗ по математике 5 класс помогут точно понять что и как именно нужно делать .
Разбор задач из учебника по математике за 5 класс Никольского С .М ., Потапова М .К . Решетникова Н .Н . Шевкина А .В . Все выполненные задания проверены учителями Понимание предмета становится эффективнее с ГДЗ по математике для 5 класса к учебнику Никольского .
ГДЗ упражнения 484 алгебра 9 класс Макарычев, Миндюк
ГДЗ учебник 2009 / вопрос §39 физика 9 класс Перышкин, Гутник
ГДЗ страница 8 обществознание 7 класс рабочая тетрадь Соболева
ГДЗ часть 2. местоимение 17 русский язык 4 класс Зеленина, Хохлова
ГДЗ номер 183 алгебра 8 класс Макарычев, Миндюк
ГДЗ глава 11 / параграф 1 / упражнение 2 математика 5 класс Козлов, Никитин
ГДЗ контрольная работа / Виленкин / К-3 В2 математика 6 класс дидактические материалы Чесноков, Нешков
ГДЗ вправа 1526 математика 5 класс Истер
ГДЗ глава 5 / КР-5 / вариант 2 1 алгебра 10 класс дидактические материалы Шабунин, Ткачева
ГДЗ упражнение 116 русский язык 10‐11 класс Гольцова, Шамшин
ГДЗ упражнение 188 алгебра 7 класс рабочая тетрадь Минаева, Рослова
ГДЗ глава 16 28 физика 9 класс Задачник Генденштейн, Кирик
ГДЗ номер 1618 физика 7‐9 класс сборник задач Лукашик, Иванова
ГДЗ страница 79 алгебра 9 класс рабочая тетрадь Колягин, Сидоров
ГДЗ по математике 6 класс тематические тесты Кузнецова, Минаева Решебник
ГДЗ § 18 18. 46 физика 7 класс задачник Генденштейн, Кирик
46 физика 7 класс задачник Генденштейн, Кирик
ГДЗ контрольная работа / контрольная работа 3 В2 химия 8 класс задачник Кузнецова, Левкин
ГДЗ страница 97 английский язык 4 класс Карпюк
ГДЗ параграф 22 10 алгебра 7 класс рабочая тетрадь Мерзляк, Полонский
ГДЗ упражнение Понаблюдайте стр.212 русский язык 5 класс Разумовская, Львова
ГДЗ задание 285 математика 5 класс Никольский, Потапов
ГДЗ вопросы и задания / часть 1. страница 147 (164) русский язык 5 класс Ладыженская, Баранов
ГДЗ страница 56 английский язык 9 класс рабочая тетрадь rainbow Афанасьева, Михеева
ГДЗ глава 8. задача 701 геометрия 7‐9 класс Атанасян, Бутузов
ГДЗ страница 106 физика 9 класс тетрадь-тренажёр Артеменков, Белага
ГДЗ часть 2 165 математика 4 класс ИстоминаБ
ГДЗ учебник 2009 / упражнения / упражнение 11 2 физика 9 класс Перышкин, Гутник
ГДЗ номер 116 математика 5 класс рабочая тетрадь Мерзляк, Полонский
ГДЗ номер 79 биология 5 класс рабочая тетрадь Пасечник
ГДЗ номер 1440 физика 7‐9 класс Сборник задач Перышкин
ГДЗ вопросы к § 13 геометрия 7 класс Мерзляк, Полонский
ГДЗ тетрадь №3. упражнение 51 русский язык 2 класс рабочая тетрадь Яковлева
упражнение 51 русский язык 2 класс рабочая тетрадь Яковлева
ГДЗ упражнение 404 русский язык 6 класс Бунеев, Бунеева
ГДЗ страница 28 математика 2 класс контрольно-измерительные материалы Глаголева, Волковская
ГДЗ Учебник 2019 / часть 1 603 (604) математика 5 класс Виленкин, Жохов
ГДЗ номер 710 физика 7‐9 класс Сборник задач Перышкин
ГДЗ упражнение 89 русский язык 6 класс рабочая тетрадь Ларионова
ГДЗ по русскому языку за 10 класс, решебник и ответы онлайн
ГДЗ § 7. Строение клетки / Вопросы 3 биология 5 класс Пасечник
ГДЗ вправа 519 алгебра 8 класс Тарасенкова, Богатырева
ГДЗ вариант 2 50 математика 5 класс дидактические материалы Мерзляк, Полонский
ГДЗ часть №2 150 математика 6 класс Петерсон, Дорофеев
ГДЗ страница 75 немецкий язык 8 класс рабочая тетрадь Horizonte Аверин, Джин
ГДЗ часть 1. страница 42 математика 4 класс дидактические материалы Рудницкая, Юдачева
ГДЗ обучающие работы / О-39 4 математика 5 класс дидактические материалы Кузнецова, Минаева
ГДЗ упражнение 174 русский язык 7 класс Баранов, Ладыженская
ГДЗ самостоятельные работы / СР-43. вариант 1 физика 8 класс самостоятельные и контрольные работы Марон, Марон
вариант 1 физика 8 класс самостоятельные и контрольные работы Марон, Марон
ГДЗ часть 1. страница 73 математика 6 класс Козлова, Рубин
ГДЗ Царство Животные. Подцарство Одноклеточные 1 биология 7 класс Захаров, Сонин
ГДЗ часть 2. страница 56 русский язык 2 класс рабочая тетрадь к учебнику Канакиной Тихомирова
ГДЗ По Алгебре 7 Класс Номер 1027
Решебник 2 Класс Рабочая
Окружающий Мир Рабочая Тетрадь 1 Класс ГДЗ
ГДЗ Проверочная Тетрадь 3 Класс Волкова
ГДЗ Математика 6 Класс Виленкин Жуков
ГДЗ по математике 5 класс Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
Авторы: Виленкин Н.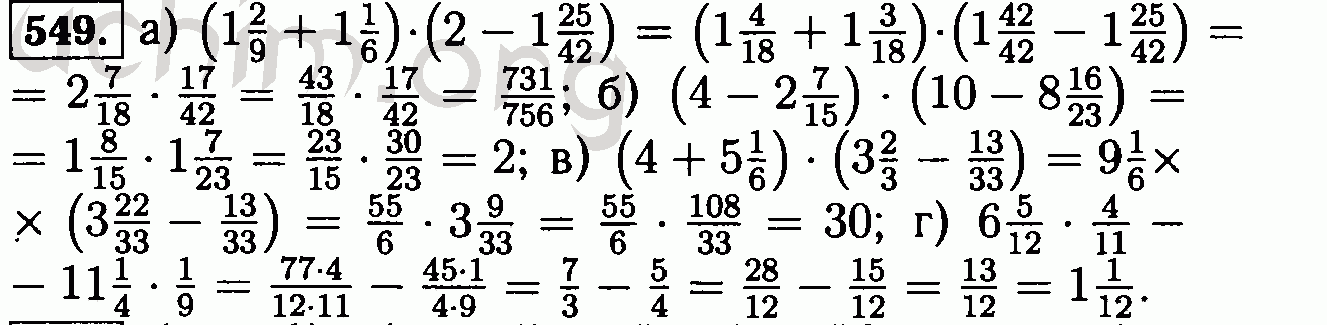 Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И..
Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И..
Обучение в школе бывает разным, кто-то «схватывает» любую тему моментально, а кому-то требуются дополнительные объяснения. Не является секретом, что учителя зачастую ориентируются именно на тех, кто быстро осваивает информацию и дает полную отдачу на уроке. Но что же делать детям, которым не обойтись без дополнительной помощи? К сожалению, реальность такова, что далеко не каждый преподаватель захочет тратить свое время на такого ученика и в итоге школьник совсем забросит предмет, и потеряет энтузиазм в обучении. Но на помощь всегда готов прийти решебник.
ГДЗ по математике для 5 класса от Виленкин Н.Я.,Жохов В.И., Чесноков А.С.,Шварцбурд С.И. — это настоящее спасение, для тех кто плохо разбирается в этой трудной науке и незаменимый помощник для отличников, которые всегда хотят оставаться на высоком уровне.
Да, решебник предназначен не только для двоечников, как считают многие, на самом деле он способен принести пользу пятиклассникам любого уровня знаний, ведь в нем:
- представлены исключительно правильные, составленные по нормам ФГОС ответы, по которым можно сверять уже выполненные ребенком задания;
- содержатся подробные объяснения решений с объяснениями, позволяющие разобраться даже в самых запутанных примерах;
- удобная навигация, позволяющая быстро сориентироваться и разобраться в использовании.

Такая умная книга позволит школьнику перевести свои знания и занятия на новый уровень. Теперь у ребенка под рукой всегда будут ответы на все вопросы из учебника. Неважно, насколько запутанное задание вам попалось, теперь вы сможете распутать любой пример и даже объяснить его одноклассникам.
Родители тоже должны понимать всю пользу пособия и в следующий раз, когда застанут школьника за использованием этой книги, нужно не отбирать ее, а просто объяснить, насколько важно обучение математикой и что ГДЗ предназначено именно для помощи, а не списывания. Небольшой разговор поможет поставить детей на истинную тропу и успокоить заботливых взрослых. Решебник по математике по редакцией Виленкина Н.Я. находится в онлайн-доступе, а значит, пользоваться им можно в любое время и в любом месте.
- ГДЗ к учебнику по математике за 5 класс Виленкин Н.Я. (синий)
- ГДЗ к учебнику по математике за 5 класс Виленкин 1, 2 часть (Просвещение 2021)
- ГДЗ к тестам по математике за 5 класс Рудницкая В.

- ГДЗ к рабочей тетради по математике за 5 класс Рудницкая В.Н.
- ГДЗ к дидактическим материалам по математике за 5 класс Попов М.А.
- ГДЗ к дидактическим материалам по математике за 5 класс Чесноков А.С.
- ГДЗ к рабочей тетради по математике за 5 класс Ерина Т.М.
- ГДЗ к рабочей тетради Универсальные учебные действия по математике за 5 класс Ерина Т.М.
- ГДЗ к контрольным работам по математике за 5 класс Жохов В.
 И.
И. - ГДЗ к математическому тренажёру за 5 класс Жохов В.И.
- ГДЗ к рабочей тетради по математике за 5 класс Лебединцева Е.А.
Гдз математика 6 класс Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд ответы к номерам
Предмет: Математика
Авторы: Виленкин, Жохов, Чесноков, Шварцбурд
Класс: 6 класс
Автор решений: Бакулина Полина
 Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд это книга универсальный помощник для ученика, в которой имеются все необходимые примеры решения тех, или иных задач. В учебнике содержатся сотни готовых примеров решения домашнего задания, построены таким образом, что после первого знакомства с изложенным материалом школьник начинает понимать суть наглядно показанного примера. Логически выстроенная цепочка даёт глубокое осмысление задачи перед школьником, поэтому работая с Гдз по математике 6 класс авторы Виленкин школьник начинает усваивать пройденный материал в течении кратчайшего времени, что положительно сказывается на общей успеваемости по всем предметам в школе.
Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд это книга универсальный помощник для ученика, в которой имеются все необходимые примеры решения тех, или иных задач. В учебнике содержатся сотни готовых примеров решения домашнего задания, построены таким образом, что после первого знакомства с изложенным материалом школьник начинает понимать суть наглядно показанного примера. Логически выстроенная цепочка даёт глубокое осмысление задачи перед школьником, поэтому работая с Гдз по математике 6 класс авторы Виленкин школьник начинает усваивать пройденный материал в течении кратчайшего времени, что положительно сказывается на общей успеваемости по всем предметам в школе.Гдз по математике 6 класс авторы Виленкин это большой сборник решения задач для школьника дома, книга сочетает в себе несколько функций одновременно, это функция настольного помощника, учителя, и незаменимого источника важной информации по решению математических задач для школьника. Гдз по математике 6 класс авторы Виленкин пользуется спросом у многих школ, имеет рекомендации учителей, и непосредственных классных руководителей. После детального ознакомления с изложенным материалом, у школьника вырабатываются определенные навыки, базовые знания закрепляются на подсознательном уровне, этого авторы смогли добиться благодаря простому языку изложения книги, в которой на доступном для школьника языке описаны фундаментальные представления о материале, и работе с ним. Гдз по математике 6 класс авторы Виленкин будет отличным помощником для тех, то всерьёз задумывается о зарабатывании хороших оценок, и углубить свои познания в области точных наук, и в математике особенно.
После детального ознакомления с изложенным материалом, у школьника вырабатываются определенные навыки, базовые знания закрепляются на подсознательном уровне, этого авторы смогли добиться благодаря простому языку изложения книги, в которой на доступном для школьника языке описаны фундаментальные представления о материале, и работе с ним. Гдз по математике 6 класс авторы Виленкин будет отличным помощником для тех, то всерьёз задумывается о зарабатывании хороших оценок, и углубить свои познания в области точных наук, и в математике особенно.
Множество готовых, и легких примеров делают Решебник по математике 6 класс авторы Виленкин незаменимым помощником для современного ученика. Сложность школьных программ, которая с каждым годом становится все труднее, и труднее это доказывает. А практика использования книг серии Ответы по математике 6 класс авторы Виленкин показывает, что ученики работающие по материалу изложенному в книге уже за первое полугодие успевают подтянуться буквально за несколько месяцев. При максимально усиленном занятии, школьник может без особого труда перекрыть все плохие оценки к концу учебного года, и переломить ситуацию в обучении коренным образом.
При максимально усиленном занятии, школьник может без особого труда перекрыть все плохие оценки к концу учебного года, и переломить ситуацию в обучении коренным образом.
Математика 6 класс
Точные неравенства типа H p $H_{p}$ — L p $L_{p}$ взвешенных максимальных операторов средних Виленкина-Нёрлунда и их приложения | Журнал неравенств и приложений
- Исследования
- Открытый доступ
- Опубликовано:
- Лаша Барамидзе 1 ,
- Ларс-Эрик Перссон 2,3 ,
- Георгий Тефнадзе 1,2 и
- …
- Питер Уолл 2
Журнал неравенств и приложений том 2016 , Номер статьи: 242 (2016) Процитировать эту статью
990 доступов
13 цитирований
Сведения о показателях
Abstract
Доказываются и обсуждаются некоторые новые неравенства типа \(H_{p}\)-\(L_{p}\) взвешенных максимальных операторов средних Виленкина-Нёрлунда с монотонными коэффициентами. Доказано также, что эти неравенства являются наилучшими в специальном смысле. Мы также применяем эти результаты для доказательства сильной суммируемости таких средних значений Виленкина-Нёрлунда. В качестве приложений указываются как некоторые известные, так и новые результаты. 9{\infty}\) в n th Среднее Чезаро дано точно.
Доказано также, что эти неравенства являются наилучшими в специальном смысле. Мы также применяем эти результаты для доказательства сильной суммируемости таких средних значений Виленкина-Нёрлунда. В качестве приложений указываются как некоторые известные, так и новые результаты. 9{\infty}\) в n th Среднее Чезаро дано точно.
Хорошо известно, что системы Виленкина не образуют базисов в пространстве \(L_{1} ( G_{m} ) \). Кроме того, в пространстве Харди есть функция \(H_{1} ( G_{m} ) \), такая, что частичные суммы f не ограничены в \(L_{1}\)-норме. Саймон [15] (для неограниченных систем Виленкина в случае \(p=1\) см. [16] и для \(0 . Мориц и Сиддики [21] исследовали аппроксимационные свойства некоторого специального среднего Нёрлунда функции \(L_{p}\) в норме. Дополнительную информацию о средних Нёрлунда см. В [27] для \(p=1/(1+\alpha)\) и в [28] для \(0 (6) В [29] доказано, что в граничном случае \(p=1/(1+\alpha) \) оба условия (3) и (4) точны в специальном смысле . В работе исследуется случай, когда \(0< p< 1/ ( 1+\alpha )\) и доказываются неравенства (5) и (6) для \(f\in H_{p} \) и Виленкина -средние Нёрлунда с невозрастающими коэффициентами, но с более слабыми условиями, чем (3) и (4), что дает возможность доказать аналогичные результаты для более широкого класса средних Виленкина-Нёрлунда, когда \(0< p< 1/ ( 1+ \альфа)\). В качестве приложений указываются как некоторые известные, так и новые результаты. Эта статья организована следующим образом: Чтобы не мешать нашим обсуждениям в дальнейшем, некоторые определения и обозначения приведены в разделе 2. Основные результаты можно найти в разделе 3. Для доказательства основных результатов нам понадобятся некоторые леммы, как хорошо известные, так и некоторые новые, представляющие самостоятельный интерес. Эти результаты представлены в разделе 4. Подробные доказательства приведены в разделе 5. Некоторые известные и новые следствия наших основных результатов представлены в разделе 6. Обозначим через \(\mathbb{N} _{+}\) множество натуральных чисел, \(\mathbb{N} :=\mathbb{N} _{+}\cup\{0\}\ ). Пусть \(m:=(m_{0},m_{1},\ldots)\) — последовательность натуральных чисел не меньше 2. Обозначим через $$ Z_{m_{k}}:=\ {0,1,\ldots,m_{k}-1\} $$ аддитивная группа целых чисел по модулю \(m_{k}\). Определим группу \(G_{m}\) как полное прямое произведение групп \(Z_{m_{i}}\) на произведение дискретных топологий \(Z_{m_{j}} \). Прямое произведение µ мер $$ \mu_{k} \bigl( \{j\} \bigr) :=1/m_{k}\quad (j\in Z_{m_{k} }) $$ — мера Хаара на \(G_{m}\) с \(\mu ( G_{m} ) =1\). В этой статье мы обсуждаем ограниченные группы Виленкина, т. е. случай, когда \(\sup_{n}m_{n}<\infty\). Элементы \(G_{m}\) представлены последовательностями $$ x:= ( x_{0},x_{1},\ldots,x_{j},\ldots)\quad ( x_{j}\in Z_{m_{j}} ) . $$ Легко дать базу для окрестности \(G_{m}\): $$ I_{0} ( x ) :=G_{m}, \quad\quad I_{n}(x) :=\{y \in G_{m}\mid y_{0}=x_{0},\ldots,y_{n-1}=x_{n-1} \}, $$ , где \(x \in G_{m}\), \(n\in \mathbb{N} \). Обозначим \(I_{n}:=I_{n} ( 0 ) \) для \(n\in \mathbb{N} _{+}\) и \(\overline{I_{n}}: =G_{m}\обратная косая черта I_{n}\). $$ \overline{I_{N}}= \Bigl( \overset{N-2}{\underset{k=0}{\bigcup}}\overset{m_{k}-1}{ \underset{ s_{k}=1}{\bigcup}}\overset{N-1}{\underset{l=k+1}{ \bigcup}}\overset{m_{l}-1}{ \underset{s_{ l}=1}{\bigcup}}I_{l+1}(s_{k}e_{k}+s_{l}e_{l}) \Bigr) \cup \biggl( \underset{k=1} {\ bigcup ^ {N-1}} \ overset {m_ {k} -1} {\ underset {s_ {k} = 1} {\ bigcup }} I_ {N} (s_ {k} e_ {k}) \biggr). (13) Мы всегда предполагаем, что \(q_{0}>0\) и \(\lim_{n\rightarrow\infty }Q_{n}=\infty\). В этом случае хорошо известно, что метод суммирования, порожденный \(\{q_{k}:k\geq0\}\), является регулярным тогда и только тогда, когда $$ \lim_{n\rightarrow\infty}\frac {q_{n-1}}{Q_{n}}=0. $$ По поводу этого факта и связанных с ним основных результатов отсылаем к [32]. Если \(q_{n}\equiv1\), то мы получаем n -е среднее Фейера и ядро Фейера 9{n}D_{k}, $$ соответственно. Пусть \(t,n\in\mathbb{N}\). Хорошо известно, что (см. [33]) $$ K_{M_{n}} ( x ) =\left \{ \textstyle\begin{array}{l@{\quad }l} 0, & \ text{if }x-x_{t}e_{t}\notin I_{n}, x\in I_{t}\backslash I_{t+1}, \\ \frac{M_{t}}{1- r_{t} ( x ) }, & \text{if }x-x_{t}e_{t}\in I_{n}, x\in I_{t}\обратная косая черта I_{t+1}, \\ ( M_{n}+1 )/2, & \text{if }x\in I_{n}. (14) \(( C,\alpha ) \)-средние рядов Виленкина-Фурье определяются равенством 9{-1/p},\quad \quad \operatorname {supp}( a ) \subset I. $$ Наш острый \(H_{p}\)-\(L_{p} \ ) неравенство имеет следующий вид. Пусть \(f\in H_{p}\), , где \(0 (15) Пусть \(0 (16) Тогда неравенство (15) является точным в том смысле, что существует среднее Нёрлунда с не — возрастающей последовательностью \(\{q_{k}:k\in\mathbb{N}\}\) , удовлетворяющий условиям (11) и (12) и мартингейлу \(е\в H_{P} \) такое, что $$ \sup_{k\in\mathbb{N}}\frac{\Vert \frac {t_{M_{2n_{k}}+1}f_{k}}{\Phi _{M_{2n_{ k}}+1}}\Vert _{\mathrm{weak}\text{-}L_{p}}}{\Vert f_{k}\Vert _{H_{p}}}=\infty. Наш новый результат о сильной суммируемости средних Нёрлунда с невозрастающими последовательностями выглядит следующим образом. Пусть \(f\in H_{p}\), , где \(0<\alpha<1\), \(0< p<1/ ( 1+\alpha) \), и пусть \(\{q_{n}:n\geq0\}\) — последовательность не — возрастающих чисел , , удовлетворяющих условиям (11), и (12). Тогда существует абсолютная константа 9{р} $$ содержит . Нам понадобится следующая известная лемма Вейса [34]. Предположим, что оператор Т это σ — линейные и для некоторых \(0< р\leq1\)
и 9{p}\,d\mu\leq c_{p}< \infty, $$ за каждые р — атом и , , где я обозначает носитель атома . $$ \Vert Tf\Vert _{p}\leq c_{p}\Vert f\Vert _{H_{p}}. $$ Следующие результаты принадлежат Блахоте, Перссону и Тефнадзе [27]. Пусть \(s_{n}M_{n}< r\leq ( s_{n}+1 ) M_{n}\), , где \(1\leq s_{n}\leq m_{n}-1\). Тогда для каждого среднего Nörlund , без каких-либо ограничений на порождающую последовательность \(\{q_{k}:k\in\mathbb{N}\}\) имеем следующее равенство : $$\begin{aligned} Q_{r}F_{r} =&Q_{r}D_{s_{n}M_{n}}-\psi _{s_{n} M_{n}-1}\overset{s_{n}M_{n}-2}{\underset{l=1}{\sum}} ( q_{r-s_{n}M_{n}+l} -q_{r-s_{n}M_{n}+l+1} ) l\overline{K_{l}} \\ &{}-\psi_{s_{n}M_{n}-1} ( s_ {n}M_{n}-1 ) q_{r-1} \overline{K_{s_{n}M_{n}-1}}+\psi_{s_{n}M_{n}}Q_{r- s_{n}M_{n}}F_{r-s_{n}M_{n}}. \end{выровнено}$$ Нам также понадобятся следующие новые леммы, представляющие самостоятельный интерес. (17) Пусть \(0<\альфа\leq1\)
и \(\{q_{n}:n\geq0\}\) — последовательность не — возрастающих чисел , , удовлетворяющих условиям (11), и (12). Если \(r\geq M_{N}\), 9{1+\alpha}},\quad x\in I_{l+1} ( s_{k}e_{k}+s_{l}e_{l} ), $$ где $$ 1\leq s_{k}\leq m_{k}-1, \quad\quad 1\leq s_{l}\leq m_{l}-1\quad (k=0,\dots,N -2, l=k+1,\dots,N-1) $$ и $$ \int_{I_{N}} \bigl\vert F_{r} ( x-t ) \bigr\vert \,d\mu( t ) \leq\frac{c_{\alpha}M_{k}} {M_{N}},\quad x\in I_{N} ( s_{k}e_{k} ), $$ 9{\alpha-2}\phi _{j}\delta_{j}, $$ для всех \(j\in\mathbb{N} \), где \(\delta_{j}\) — любая функция , такое что $$ \underset{j\rightarrow\infty}{\overline{\lim}}\delta_{j}=\infty . $$ (21) При условии (19) существует возрастающая последовательность \(\{ \alpha_{k}:k\geq0 \} \), такая, что \(\alpha_{k+1}\geq2 \alpha_{k}\) и $$ \delta_{\alpha_{k}}\uparrow\infty. Доказательство завершается объединением приведенных выше оценок. □ Пусть \(x\in I_{l+1} ( s_{k}e_{k}+s_{l}e_{l} )\), \(1\leq s_{k}\leq m_{k }-1\), \(1\leq s_{l}\leq m_{l}-1\). Тогда, применяя (14), имеем $$ K_{M_{n}} ( x ) =0,\quad \text{когда }n>l>k. $$ Предположим, что \(k< n\leq l\). Более того, используя (14), получаем $$ \bigl\vert K_{M_{n}} ( x ) \bigr\vert \leq cM_{k}. $$ 9{\ альфа} M_ {N}}. $$ (28) Пусть \(x\in I_{N} ( s_{k}e_{k} ) \), \(k=0,\dots,N-1\). Тогда, применяя (8) и (9), мы имеем $$\begin{aligned} \int_{I_{N}} \bigl\vert F_{r} ( x-t ) \bigr\vert \,d\mu ( t ) \leq& \frac{1}{Q_{n}}\overset{n}{\underset{m=1}{\sum }}q_{nm} \int_{I_{N}} \bigl\vert D_{m} ( xt ) \bigr\vert \,d\mu( t ) \\ \leq& \frac{1}{Q_{n}}\overset{n}{\underset{m=1}{\sum }}q_{nm}\frac{cM_{k}}{M_{N}}\leq\frac{cM_{k}}{M_{N}}. Установить $$ f_{k}:=D_{M_{2n_{k}+1}}-D_{M_{2n_{k}}}. $$ Затем $$ \widehat{f}_{k} ( i ) =\left \{ \textstyle\begin{array}{l@{\quad }l} 1, & i=M_{2n_ {k}},\ldots,M_{2n_{k}+1}-1, \\ 0, & \text{иначе},\end{массив}\displaystyle \right . $$ (32) и $$ S_{i}f_{k}=\left \{ \textstyle\begin{array}{l@{\quad }l} D_{i}-D_{ M_{2n_{k}}}, & i=M_{2n_{k}}+1,\ldots,M_{2n_{k}+1}-1, \\ f_{k}, & i\geq M_{ 2n_{k}+1}, \\ 0 и \text{иначе}.\end{массив}\displaystyle \right . $$ 9{1-1/p}, $$ (34) , где \(\lambda=\sup_{n}m_{n}\). Используя (33), мы получаем $$\begin{aligned} \frac{\vert t_{M_{2n_{k}}+1}f_{k}\vert}{\Phi_{M_{2n_{ k}}+1}} =& \frac{q_{0}\vert S_{M_{2n_{k}}+1}\vert }{Q_{M_{2n_{k}}+1}\Phi _{ M_{2n_{k}}+1}} \\ =&\frac{q_{0}\vert D_{M_{2n_{k}}+1}-D_{M_{2n_{k}}}\vert } {Q_{M_{2n_{k}}+1}\Phi_{M_{2n_{k}}+1}}=\frac{q_{0}\vert \psi _{M_{2n_{k}}}\ vert }{Q_{M_{2n_{k}}+1}\Phi_{M_{2n_{k}}+1}}\geq\frac{c_{\alpha}}{M_{2n_{k}}^{ \alpha}\Phi_{M_{2n_{k}}+1}\varphi_{M_{2n_{k}}+1}}. , что завершает доказательство. □ Заметим, что при условиях (3) и (4) мы видим, что условия (11) и (12) также выполняются. Пусть \(0<\alpha\leq1\). Мы можем написать $$ \vert Q_{n} \vert =\Bigl\vert \overset{n-2}{\underset{j=1}{ \sum }}( q_{j}-q_{j+ 1} ) j+q_{n-1}(n-1)+q_{0}\Bigr\vert . $$ 9{1+\varepsilon}} \rightarrow0,\quad \text{as }n \rightarrow\infty, $$ для любого \(\varepsilon>0\). Поскольку случай \(q_{0}n/Q_{n}=O ( 1 ) \), как \(n\rightarrow\infty\), уже был рассмотрен, его можно исключить. Отсюда можно считать, что \(\{q_{k}:k\geq0\}\) удовлетворяет условиям (3) и (4) и, кроме того, удовлетворяет следующему условию: $$ \frac{Q_{ n}}{q_{0}n}=o(1) ,\quad \text{as }n\стрелка вправо\infty. $$ Отсюда следует, что $$\begin{aligned}& q_{n}=q_{0}\frac{q_{n}n}{q_{0}n}\leq q_{0} \frac {Q_{n}}{q_{0}n}=o(1), \quad \text{as}n\rightarrow\infty, \\& q_{n}=\overset{\infty}{\underset{ l=n}{\sum}} (q_{l}-q_{l+1}) \leq\overset{\infty}{\underset{l=n}{\sum}}\frac{1}{l ^{2-\alpha}}\leq\frac{c}{n^{1-\alpha}}, \end{aligned}$$ 9{\альфа}. □ Из замечания 1 сразу видно, что верно следующее. Условия (3) и (4) обеспечивают более широкий класс средних значений Нёрлунда с не — повышающими коэффициентами, чем условия (11), и (12). Из доказательства замечания 1 для \(\alpha=1 \) сразу получаем следующее. Пусть \(\alpha=1\) и \(\{q_{k}:k\in\mathbb{N}\}\) — последовательность невозрастающих чисел. Тогда автоматически выполняется условие (12), 9{1+\varepsilon}}\rightarrow0,\quad \text{as }n\rightarrow \infty, $$ для любого \(\varepsilon>0\). Применяя замечание 2 и теорему 1, получаем следующее. Пусть \(f\in H_{p}\), , где \(0 <р<1/2\)
9{1/p-2} \bigr) \Bigr\Vert _{p}\leq c_{\alpha,p} \Vert f\Vert _{H_{p}} $$ (36) содержит . Пусть \(\{ \Phi_{n}:n\in\mathbb{N}_{+} \} \)
9{1/p-2}}{\Phi_{n}}=\infty. $$ Тогда неравенство (36) является точным в том смысле, что существует среднее Нёрлунда с не — возрастающей последовательностью \(\{q_{k}:k\in\mathbb{N}\}\) , удовлетворяющее условию (11) такое, что $$ \sup_{k\in\mathbb{N}}\frac{\Vert \frac {t_{M_{2n_{k}}+1}f_{k}}{\Phi _{M_{2n_{ k}}+1}}\Vert _{\mathrm{weak}\text{-}L_{p}}}{\Vert f_{k}\Vert _{H_{p}}}=\infty. $$ Применяя замечание 2 и теорему 2, получаем следующее. Пусть \(f\in H_{p}\), , где \(0<р<1/2\)
и \(\{q_{n}:n\geq 0\}\) — последовательность не — возрастающих чисел , , удовлетворяющая условию (11). ограничено мартингальным пространством Харди \(Н_{р}\) в пространство Лебега \(L_{p}\). Пусть 9{1/p-2}}{\Phi _{n}}=\infty. $$ Затем $$ \sup_{k\in\mathbb{N}}\frac{\Vert \frac{\sigma _{M_{2n_{k}}+1}f_{k}}{\Phi_{M_{2n_ {k}}+1}}\Vert _{\mathrm{weak}\text{-}L_{p}}}{\Vert f_{k}\Vert _{H_{p}}}=\infty. $$ Кроме того, из теоремы 4 вытекает следующий результат Тефнадзе [18]. Пусть \(f\in H_{p}\), , где \(0<р<1/2\). Тогда существует абсолютная константа \(c_{p}\), зависит только от p , такое, что $$ \overset{\infty}{\underset{k=1}{\sum}}\frac{\Vert \sigma _{k}f\Vert _{p}^{p}}{k^{ 2-2p}}\leq c_{p}\Vert f\Vert _{H_{p}}^{p}. Далее отметим, что из теоремы 1 и замечания 1 вытекают следующие результаты Блахоты, Тефнадзе [13] для \(0<\alpha<1\). Пусть \(f\in H_{p}\), , где \(0<р<1/(1+\альфа)\)
9{1/p-1-\alpha}} $$ ограничено мартингальным пространством Харди \(Н_{р}\) в пространство Лебега \(L_{p}\). 9{\alpha}_{M_{2n_{k}}+1}f_{k}}{\Phi_{M_{2n_{k}}+1}}\Vert _{\mathrm{weak}\text{-} L_{p}}}{\Vert f_{k}\Vert _{H_{p}}}=\infty. $$ Аналогично, из теоремы 2 и замечания 1 сразу следует следующий результат Блахоты, Тефнадзе [13] для \(0<\alpha<1\). Наконец, мы также отмечаем некоторые новые следствия наших результатов. Прежде всего отметим, что из теоремы 1 и замечания 1 сразу следует следующий новый результат. Пусть \(f\in H_{p}\), 9{1/p-1-\alpha}} $$ ограничено мартингальным пространством Харди \(Н_{р}\) в пространство Лебега \(L_{p}\). 9{\alpha,\beta}_{M_{2n_{k}}+1}f_{k}}{\Phi_{M_{2n_{k}}+1}}\Vert _{\mathrm{weak}\text {-}L_{p}}}{\Vert f_{k}\Vert _{H_{p}}}=\infty. $$ Аналогичным образом мы видим, что теорема 2 и замечание 1 немедленно порождают следующий новый результат. Шипп, Ф.: Некоторые перестановки рядов в системе Уолша. Мат. заметки 18 (2), 193-201 (1975) (на русском языке) MathSciNet
Google ученый Пал, Дж., Саймон, П.: Об обобщении понятия производной. Акта Математика. акад. науч. Повесили. 29 (1-2), 155-164 (1977) MathSciNet
Статья
МАТЕМАТИКА
Google ученый
9{1}\)-функции на обобщенной группе Уолша-Пэли. проц. Являюсь. Мат. соц. 77 (1), 111-116 (1979) MathSciNet
МАТЕМАТИКА
Google ученый Саймон, П.: Исследования в отношении системы Виленкина. Анна. ун-т науч. бп. Роландо Этвёш Nomin., Sect. Мат. 27 , 87-101 (1985) MathSciNet
МАТЕМАТИКА
Google ученый Вайс, Ф.: Суммируемость по Чезаро одномерных и двумерных рядов Уолша-Фурье. Анальный. Мат. 22 (3), 229-242 (1996) MathSciNet
Статья
МАТЕМАТИКА
Google ученый Саймон, П.: Суммируемость по Чезаро по отношению к двухпараметрическим системам Уолша. Монатшефте Матем. 131 (4), 321-334 (2000) Артикул
МАТЕМАТИКА
Google ученый Гогинава, Ю.: Максимальный оператор средних Марцинкевича-Фейера d -мерных рядов Уолша-Фурье. Восток Дж. Прибл. 12 (3), 295-302 (2006) MathSciNet
Google ученый Тефнадзе, Г.: Средние Фейера рядов Виленкина-Фурье. Студия наук. Мат. Повесили. 49 (1), 79-90 (2012) MathSciNet
МАТЕМАТИКА
Google ученый Вайс, Ф.: Q-суммируемость рядов Фурье. Акта Математика. Повесили. 103 (1-2), 139-175 (2004) MathSciNet
Статья
МАТЕМАТИКА
Google ученый Weisz, F: \(( C,\alpha ) \) суммируемость рядов Уолша-Фурье. Анальный. Мат. 27 (2), 141-156 (2001) MathSciNet
Статья
МАТЕМАТИКА
Google ученый Гогинава Ю.: Максимальный оператор средних \((C,\alpha)\) рядов Уолша-Фурье. Анна. ун-т науч. бп. Роландо Этвёш Nomin., Sect. вычисл. 26 , 127-135 (2006) MathSciNet
МАТЕМАТИКА
Google ученый Саймон, П., Вайс, Ф.: Слабые неравенства для суммирования по Чезаро и Риссу рядов Уолша-Фурье. Дж. Прибл. Теория 151 (1), 1-19 (2008) MathSciNet
Статья
МАТЕМАТИКА
Google ученый Благота И., Тефнадзе Г. О \((С,\альфа)\)-средних по системе Уолша. Анальный. Мат. 40 , 161-174 (2014) MathSciNet
Статья
МАТЕМАТИКА
Google ученый Блахота И., Тефнадзе Г., Толедо Р. Теорема о сильной сходимости средних Чезаро по системе Уолша. Математика Тохоку. J. 67 (4), 573-584 (2015) MathSciNet
Статья
МАТЕМАТИКА
Google ученый Саймон, П. Теорема о сильной сходимости для рядов Виленкина-Фурье. Дж. Матем. Анальный. заявл. 245 , 52-68 (2000) MathSciNet
Статья
МАТЕМАТИКА
Google ученый Гат, Г.: Исследования некоторых операторов по системе Виленкина. Акта Математика. Повесили. 61 , 131-149 (1993) MathSciNet
Статья
МАТЕМАТИКА
Google ученый Тефнадзе, Г. О частных суммах рядов Виленкина-Фурье. Дж. Контемп. Мат. Анальный. 49 (1), 23-32 (2014) MathSciNet
Статья
МАТЕМАТИКА
Google ученый Тефнадзе, Г. Теоремы сильной сходимости средних Уолша-Фейера. Акта Математика. Повесили. 142 (1), 244-259 (2014) MathSciNet
Статья
МАТЕМАТИКА
Google ученый Тефнадзе, Г.: Примечание о коэффициентах Фурье и частных суммах рядов Виленкина-Фурье. Акта Математика. акад. Педагог. Нихази. 28 , 167-176 (2012) MathSciNet
МАТЕМАТИКА
Google ученый Благота И., Тефнадзе Г. Теорема сильной сходимости для средних Виленкина-Фейера. Опубл. Мат. (дебр.) 85 (1-2), 181-196 (2014) MathSciNet
Статья
МАТЕМАТИКА
Google ученый Мориц, Ф., Сиддики, А.: Аппроксимация средними Нёрлунда рядов Уолша-Фурье. Дж. Прибл. Теория 70 (3), 375-389 (1992) MathSciNet
Статья
МАТЕМАТИКА
Google ученый Блахота, И., Гат, Г.: Суммируемость по норме логарифмических средних Нёрлунда на неограниченных группах Виленкина. Анальный. Теория прил. 24 (1), 1-17 (2008) MathSciNet
Статья
МАТЕМАТИКА
Google ученый Надь, К.: Приближение средними Нёрлунда квадратичных частичных сумм двойных рядов Уолша-Фурье. Анальный. Мат. 36 (4), 299-319 (2010) MathSciNet
Статья
МАТЕМАТИКА
Google ученый Надь, К.: Аппроксимация средними Нёрлунда двойных рядов Уолша-Фурье для липшицевых функций. Мат. Неравный. заявл. 15 (2), 301-322 (2012) MathSciNet
МАТЕМАТИКА
Google ученый Надь, К.: Аппроксимация средними Нёрлунда рядов Уолша-Качмарца-Фурье. Грузинская математика. J. 18 (1), 147-162 (2011) MathSciNet
МАТЕМАТИКА
Google ученый Надь, К.: Аппроксимация средними Чезаро отрицательного порядка рядов Уолша-Качмарца-Фурье. Восток Дж. Прибл. 16 (3), 297-311 (2010) MathSciNet
МАТЕМАТИКА
Google ученый Благота И., Перссон Л.Е., Тефнадзе Г. О средних Нёрлунда рядов Виленкина-Фурье. Чехослов. Мат. Журнал 65 (4), 983-1002 (2015) MathSciNet
Статья
МАТЕМАТИКА
Google ученый Благота И., Тефнадзе Г.: Замечание о максимальных операторах средних Виленкина-Нёрлунда. Акта Математика. акад. Педагог. Нихази. 32 , 203-213 (2016) Google ученый Мемич, Н., Перссон, Л.Е., Тефнадзе, Г.: Замечание о максимальных операторах средних Виленкина-Нёрлунда с невозрастающими коэффициентами. Студия наук. Мат. Повесили. дои: 10.1556/012.2016.1342 Виленкин, Н.Ю.: Об одном классе полных ортонормированных систем. Перевод Являюсь. Мат. соц. 28 (2), 1-35 (1963) MathSciNet
Статья
МАТЕМАТИКА
Google ученый Вайс, Ф.: Мартингальные пространства Харди и их приложения в анализе Фурье. Конспект лекций по математике, том. 1568. Спрингер, Берлин (1994). МАТЕМАТИКА
Google ученый Мур, К.Н.: Суммируемые ряды и факторы сходимости. Довер, Нью-Йорк (1966) МАТЕМАТИКА
Google ученый Гат, Г. Чезаровские средние интегрируемых функций по неограниченным системам Виленкина. MathSciNet
Статья
МАТЕМАТИКА
Google ученый Вайс, Ф.: Пространства Харди и средние Чезаро двумерных рядов Фурье. Бойяи Соц. Мат. Стад. 5 , 353-367 (1996) MathSciNet
МАТЕМАТИКА
Google ученый Тефнадзе, Г. О максимальных операторах средних Виленкина-Фейера на пространствах Харди. Мат. Неравный. заявл. 16 (2), 301-312 (2013) MathSciNet
МАТЕМАТИКА
Google ученый Скачать ссылки Исследование выполнено при поддержке Национального научного фонда им. Шота Руставели, грант №. DO/24/5-100/14 и YS15-2.1.1-47, стипендия Шведского института №. 10374-2015 и по гранту целевых научно-исследовательских программ для студентов факультета точных и естественных наук. Кафедра математики, Факультет точных и естественных наук, Тбилисский государственный университет имени Иване Джавахишвили, ул. 1, Тбилиси, 0128, Грузия Лаша Барамидзе и Георге Тефнадзе Факультет инженерных наук и математики, Технологический университет Лулео, Лулео, 971 87, Швеция Ларс-Эрик Валл&9 Джордж Тефна0037 UiT, Арктический университет Норвегии, P.O. Box 385, Narvik, 8505, Норвегия Ларс-Эрик Перссон Авторы Просмотр публикаций автора Вы также можете искать этого автора в
PubMed Google Scholar Просмотр публикаций автора Вы также можете искать этого автора в
PubMed Google Scholar Просмотр публикаций автора Вы также можете искать этого автора в
PubMed Google Scholar Ларс-Эрик Перссон. Авторы заявляют об отсутствии конкурирующих интересов. Все авторы внесли одинаковый и значительный вклад в написание этой статьи. Все авторы прочитали и одобрили окончательный вариант рукописи. Открытый доступ Эта статья распространяется в соответствии с условиями международной лицензии Creative Commons Attribution 4.0 (http://creativecommons.org/licenses/by/4.0/), которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии вы должным образом указываете автора (авторов) и источник, предоставляете ссылку на лицензию Creative Commons и указываете, были ли внесены изменения. Перепечатки и разрешения Приложение, к которому вы пытаетесь получить доступ, в настоящее время недоступно. Если проблемы с доступом сохраняются, обратитесь за помощью в наш отдел технической поддержки по телефону 1-800-877-4253. Еще раз спасибо, что выбрали Gale, обучающую компанию Cengage. org.springframework.remoting.RemoteAccessException: невозможно получить доступ к удаленной службе [authorizationService@theBLISAuthorizationService]; вложенным исключением является com.zeroc.Ice.UnknownException
unknown = «java.lang.IndexOutOfBoundsException: индекс 0 выходит за границы для длины 0
в java.base/jdk.internal.util.Preconditions.outOfBounds(Preconditions.java:64)
в java.base/jdk.internal.util.Preconditions.outOfBoundsCheckIndex(Preconditions.java:70)
в java.base/jdk.internal.util.Preconditions.checkIndex(Preconditions.java:248)
в java.base/java.util.Objects.checkIndex(Objects.java:372)
в java.base/java.util. Том 34, номер 2 Предыдущий выпуск
Next Issue Некоторые оценки преобразования Фурье на симметричных пространствах ранга 1 М. Эль Хамма, Р. Дахер и А. Ахлидж 10.4208/ata.2018.v34.n2.1 Анал. Прикладная теория, 34 (2018), стр. 103-111. Предварительный просмотр
Купить PDF 1128 16834Abstract Коэффициентные неравенства для $p$-валентных функций T. 10.4208/ata.7 Anal 9018.v20.n2 Прикладная теория, 34 (2018), стр. 112-126. Предварительный просмотр 9+)$ в $B(E, F)$ Чжаофэн Ма 10.4208/ata.2018.v34.n2.3 Анал. Прикладная теория, 34 (2018), стр. 127-134. Предварительный просмотр
Купить PDF в статье Блахоты и Гата [22] и Надя [23] (см. также [24, 25] и [26]).
в статье Блахоты и Гата [22] и Надя [23] (см. также [24, 25] и [26]).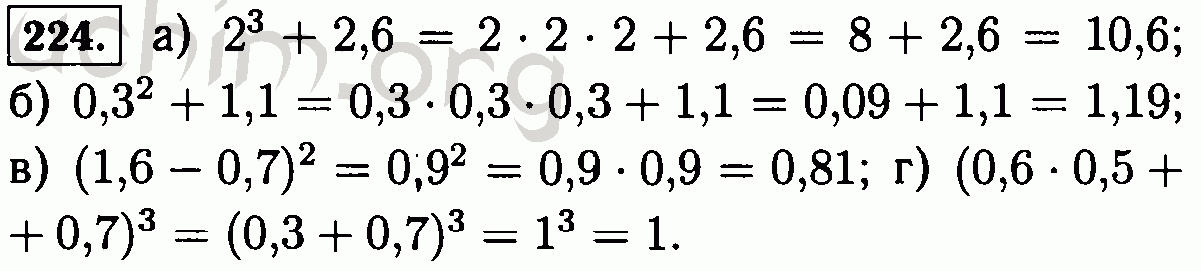
Определения и обозначения

 {n-1}\psi_{k} \quad (n\in \mathbb{N}_{+}), \end{aligned}$$ 9{\varepsilon}}=0, \text{для каждого} \varepsilon>0. $$
{n-1}\psi_{k} \quad (n\in \mathbb{N}_{+}), \end{aligned}$$ 9{\varepsilon}}=0, \text{для каждого} \varepsilon>0. $$ \end{массив}\displaystyle \right . $$
\end{массив}\displaystyle \right . $$ Основные результаты
Теорема 1
 $$
$$ Теорема 2
Леммы
Лемма 1
 Если Т ограничено \ (L _ {\ infty} \)
9от 0065 до \(L_{\infty}\), , затем
Если Т ограничено \ (L _ {\ infty} \)
9от 0065 до \(L_{\infty}\), , затем Лемма 2
 { \alpha} \varphi_{j}\vert K_{M_{j}}\vert \Biggr\} , $$ 9{\varepsilon}}=0,\quad \textit{для каждого} \varepsilon>0. $$
{ \alpha} \varphi_{j}\vert K_{M_{j}}\vert \Biggr\} , $$ 9{\varepsilon}}=0,\quad \textit{для каждого} \varepsilon>0. $$ Лемма 4
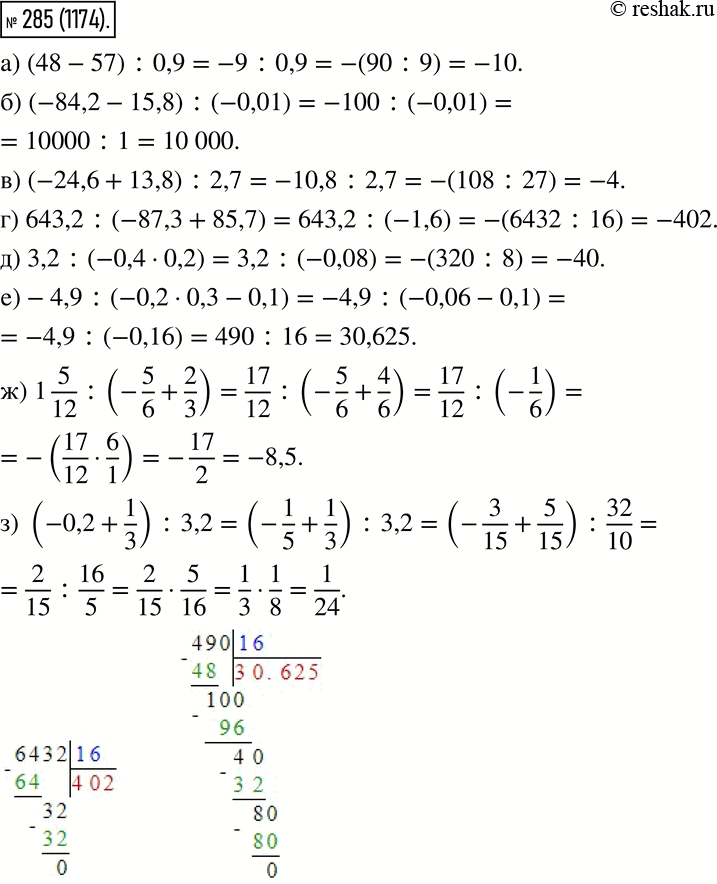 {\альфа}. \end{выровнено}$$ 9{\alpha} \vert K_{M_{j}}\vert . \end{aligned}$$
{\альфа}. \end{выровнено}$$ 9{\alpha} \vert K_{M_{j}}\vert . \end{aligned}$$ Доказательство леммы 4
 \end{выровнено}$$
\end{выровнено}$$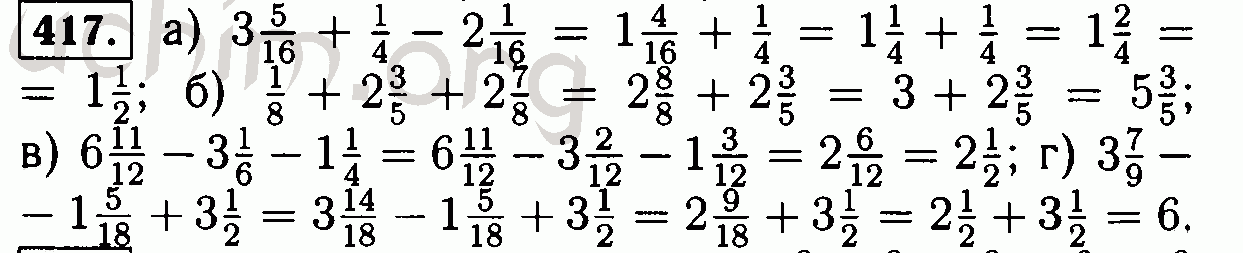 \end{выровнено}$$ 9{2- ( 1+\alpha ) p}}\leq c_{\alpha,p}< \infty, \end{aligned}$$
\end{выровнено}$$ 9{2- ( 1+\alpha ) p}}\leq c_{\alpha,p}< \infty, \end{aligned}$$ Приложения и заключительные замечания
Замечание 1
Доказательство
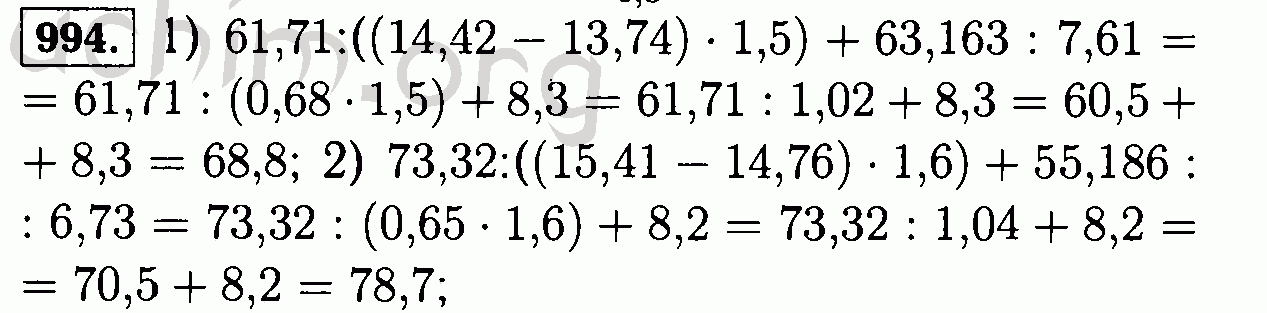 $$
$$ Следствие 1
Замечание 2
Теорема 3

Теорема 4
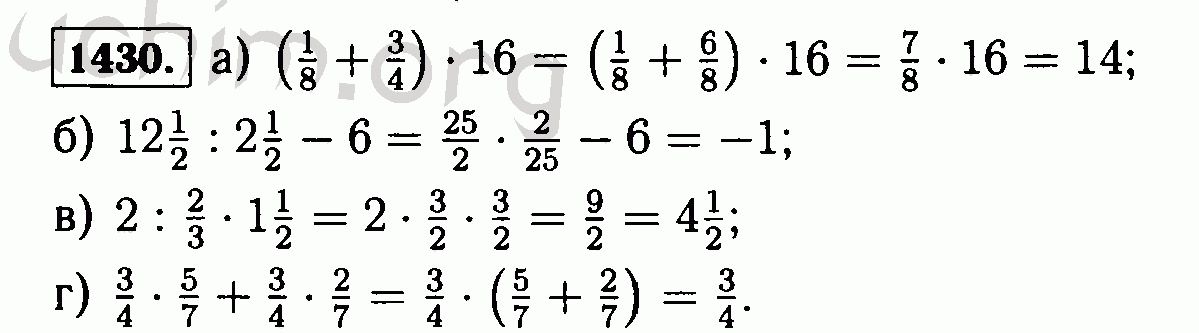 {1/p-2}} $$
{1/p-2}} $$ Следствие 3
 $$
$$ Следствие 4
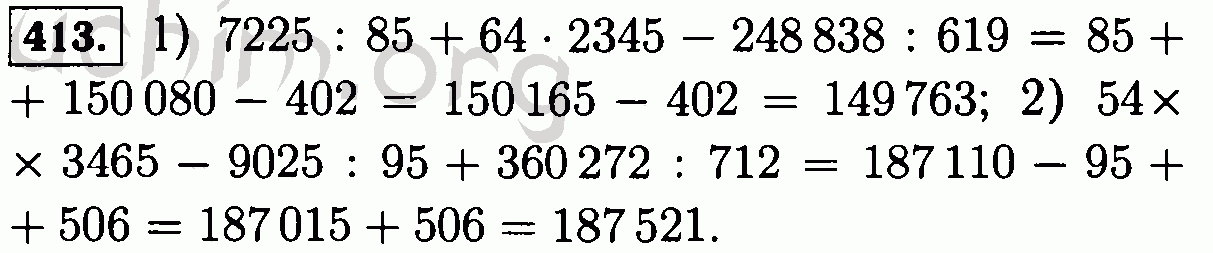 {p}. $$ 9{\alpha,\beta} \) удовлетворяет условиям (11) и (12), но не удовлетворяет (3) и (4).
{p}. $$ 9{\alpha,\beta} \) удовлетворяет условиям (11) и (12), но не удовлетворяет (3) и (4). Следствие 6
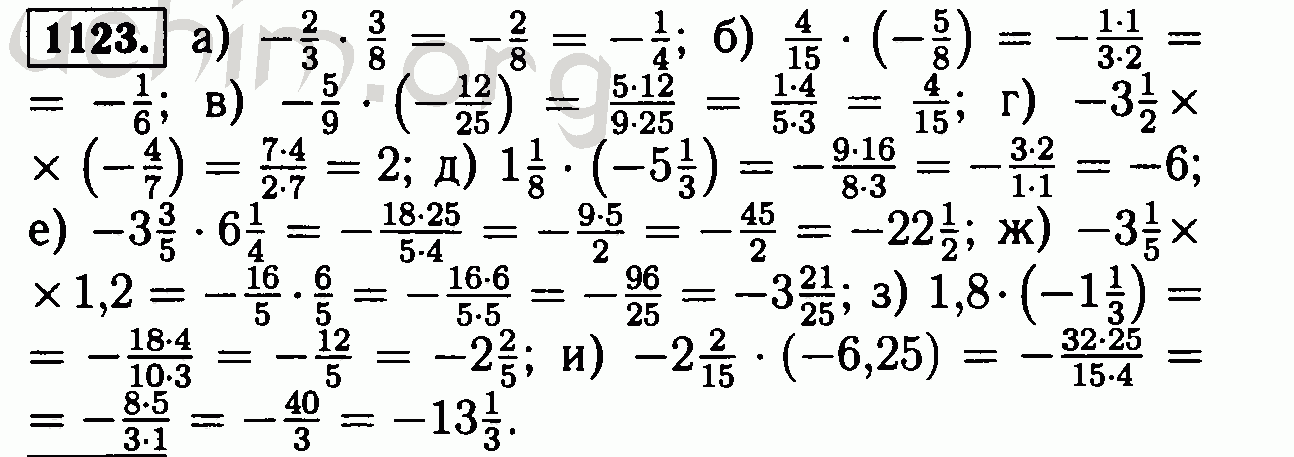 {p}. $$
{p}. $$ Каталожные номера
 Дж. Прибл. Теория 124 (1), 25-43 (2003)
Дж. Прибл. Теория 124 (1), 25-43 (2003) Благодарности
 Авторы хотели бы поблагодарить рецензентов за полезные предложения.
Авторы хотели бы поблагодарить рецензентов за полезные предложения. Информация об авторе
Авторы и организации
Автор, ответственный за корреспонденцию

Дополнительная информация
Конкурирующие интересы
Вклад авторов
Права и разрешения
Об этой статье
Приложения Gale — Технические трудности
 Приносим свои извинения за доставленные неудобства. Повторите попытку через несколько секунд.
Приносим свои извинения за доставленные неудобства. Повторите попытку через несколько секунд. ArrayList.get(ArrayList.java:458)
в com.gale.blis.data.subscription.dao.LazyUserSessionDataLoaderStoredProcedure.populateSessionProperties(LazyUserSessionDataLoaderStoredProcedure.java:60)
в com.gale.blis.data.subscription.dao.LazyUserSessionDataLoaderStoredProcedure.reQuery(LazyUserSessionDataLoaderStoredProcedure.java:53)
в com.gale.blis.data.model.session.UserGroupEntitlementsManager.reinitializeUserGroupEntitlements(UserGroupEntitlementsManager.java:30)
в com.gale.blis.data.model.session.UserGroupSessionManager.getUserGroupEntitlements(UserGroupSessionManager.java:17)
в com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getProductSubscriptionCriteria(CrossSearchProductContentModuleFetcher.java:244)
на com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getSubscribedCrossSearchProductsForUser(CrossSearchProductContentModuleFetcher.
ArrayList.get(ArrayList.java:458)
в com.gale.blis.data.subscription.dao.LazyUserSessionDataLoaderStoredProcedure.populateSessionProperties(LazyUserSessionDataLoaderStoredProcedure.java:60)
в com.gale.blis.data.subscription.dao.LazyUserSessionDataLoaderStoredProcedure.reQuery(LazyUserSessionDataLoaderStoredProcedure.java:53)
в com.gale.blis.data.model.session.UserGroupEntitlementsManager.reinitializeUserGroupEntitlements(UserGroupEntitlementsManager.java:30)
в com.gale.blis.data.model.session.UserGroupSessionManager.getUserGroupEntitlements(UserGroupSessionManager.java:17)
в com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getProductSubscriptionCriteria(CrossSearchProductContentModuleFetcher.java:244)
на com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getSubscribedCrossSearchProductsForUser(CrossSearchProductContentModuleFetcher. java:71)
на com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getAvailableContentModulesForProduct(CrossSearchProductContentModuleFetcher.java:52)
на com.gale.blis.api.authorize.strategy.productentry.strategy.AbstractProductEntryAuthorizer.getContentModules(AbstractProductEntryAuthorizer.java:130)
на com.gale.blis.api.authorize.strategy.productentry.strategy.CrossSearchProductEntryAuthorizer.isAuthorized(CrossSearchProductEntryAuthorizer.java:82)
на com.gale.blis.api.authorize.strategy.productentry.strategy.CrossSearchProductEntryAuthorizer.authorizeProductEntry(CrossSearchProductEntryAuthorizer.java:44)
на com.gale.blis.api.authorize.strategy.ProductEntryAuthorizer.authorize(ProductEntryAuthorizer.java:31)
в com.gale.blis.api.BLISAuthorizationServiceImpl.authorize_aroundBody0(BLISAuthorizationServiceImpl.java:57)
на com.gale.blis.api.BLISAuthorizationServiceImpl.
java:71)
на com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getAvailableContentModulesForProduct(CrossSearchProductContentModuleFetcher.java:52)
на com.gale.blis.api.authorize.strategy.productentry.strategy.AbstractProductEntryAuthorizer.getContentModules(AbstractProductEntryAuthorizer.java:130)
на com.gale.blis.api.authorize.strategy.productentry.strategy.CrossSearchProductEntryAuthorizer.isAuthorized(CrossSearchProductEntryAuthorizer.java:82)
на com.gale.blis.api.authorize.strategy.productentry.strategy.CrossSearchProductEntryAuthorizer.authorizeProductEntry(CrossSearchProductEntryAuthorizer.java:44)
на com.gale.blis.api.authorize.strategy.ProductEntryAuthorizer.authorize(ProductEntryAuthorizer.java:31)
в com.gale.blis.api.BLISAuthorizationServiceImpl.authorize_aroundBody0(BLISAuthorizationServiceImpl.java:57)
на com.gale.blis.api.BLISAuthorizationServiceImpl. authorize_aroundBody1$advice(BLISAuthorizationServiceImpl.java:61)
на com.gale.blis.api.BLISAuthorizationServiceImpl.authorize(BLISAuthorizationServiceImpl.java:1)
в com.gale.blis.auth.AuthorizationService._iceD_authorize(AuthorizationService.java:97)
в com.gale.blis.auth.AuthorizationService._iceDispatch(AuthorizationService.java:406)
в com.zeroc.IceInternal.Incoming.invoke(Incoming.java:221)
в com.zeroc.Ice.ConnectionI.invokeAll(ConnectionI.java:2706)
на com.zeroc.Ice.ConnectionI.dispatch(ConnectionI.java:1292)
в com.zeroc.Ice.ConnectionI.message(ConnectionI.java:1203)
в com.zeroc.IceInternal.ThreadPool.run(ThreadPool.java:412)
в com.zeroc.IceInternal.ThreadPool.access$500(ThreadPool.java:7)
в com.zeroc.IceInternal.ThreadPool$EventHandlerThread.run(ThreadPool.java:781)
в java.base/java.lang.Thread.run(Thread.java:834)
»
org.
authorize_aroundBody1$advice(BLISAuthorizationServiceImpl.java:61)
на com.gale.blis.api.BLISAuthorizationServiceImpl.authorize(BLISAuthorizationServiceImpl.java:1)
в com.gale.blis.auth.AuthorizationService._iceD_authorize(AuthorizationService.java:97)
в com.gale.blis.auth.AuthorizationService._iceDispatch(AuthorizationService.java:406)
в com.zeroc.IceInternal.Incoming.invoke(Incoming.java:221)
в com.zeroc.Ice.ConnectionI.invokeAll(ConnectionI.java:2706)
на com.zeroc.Ice.ConnectionI.dispatch(ConnectionI.java:1292)
в com.zeroc.Ice.ConnectionI.message(ConnectionI.java:1203)
в com.zeroc.IceInternal.ThreadPool.run(ThreadPool.java:412)
в com.zeroc.IceInternal.ThreadPool.access$500(ThreadPool.java:7)
в com.zeroc.IceInternal.ThreadPool$EventHandlerThread.run(ThreadPool.java:781)
в java.base/java.lang.Thread.run(Thread.java:834)
»
org. springframework.remoting.ice.IceClientInterceptor.convertIceAccessException(IceClientInterceptor.java:348)
org.springframework.remoting.ice.IceClientInterceptor.invoke(IceClientInterceptor.java:310)
org.springframework.remoting.ice.MonitoringIceProxyFactoryBean.invoke(MonitoringIceProxyFactoryBean.java:71)
org.springframework.aop.framework.ReflectiveMethodInvocation.proceed(ReflectiveMethodInvocation.java:186)
org.springframework.aop.framework.JdkDynamicAopProxy.invoke(JdkDynamicAopProxy.java:215)
com.sun.proxy.$Proxy151.authorize(Неизвестный источник)
com.
springframework.remoting.ice.IceClientInterceptor.convertIceAccessException(IceClientInterceptor.java:348)
org.springframework.remoting.ice.IceClientInterceptor.invoke(IceClientInterceptor.java:310)
org.springframework.remoting.ice.MonitoringIceProxyFactoryBean.invoke(MonitoringIceProxyFactoryBean.java:71)
org.springframework.aop.framework.ReflectiveMethodInvocation.proceed(ReflectiveMethodInvocation.java:186)
org.springframework.aop.framework.JdkDynamicAopProxy.invoke(JdkDynamicAopProxy.java:215)
com.sun.proxy.$Proxy151.authorize(Неизвестный источник)
com. gale.auth.service.BlisService.getAuthorizationResponse(BlisService.java:61)
com.gale.apps.service.impl.MetadataResolverService.resolveMetadata(MetadataResolverService.java:65)
com.gale.apps.controllers.DiscoveryController.resolveDocument(DiscoveryController.java:57)
com.gale.apps.controllers.DocumentController.redirectToDocument(DocumentController.java:22)
jdk.internal.reflect.GeneratedMethodAccessor246.invoke (неизвестный источник)
java.base/jdk.internal.reflect.DelegatingMethodAccessorImpl.invoke(DelegatingMethodAccessorImpl.java:43)
java.
gale.auth.service.BlisService.getAuthorizationResponse(BlisService.java:61)
com.gale.apps.service.impl.MetadataResolverService.resolveMetadata(MetadataResolverService.java:65)
com.gale.apps.controllers.DiscoveryController.resolveDocument(DiscoveryController.java:57)
com.gale.apps.controllers.DocumentController.redirectToDocument(DocumentController.java:22)
jdk.internal.reflect.GeneratedMethodAccessor246.invoke (неизвестный источник)
java.base/jdk.internal.reflect.DelegatingMethodAccessorImpl.invoke(DelegatingMethodAccessorImpl.java:43)
java. base/java.lang.reflect.Method.invoke(Method.java:566)
org.springframework.web.method.support.InvocableHandlerMethod.doInvoke(InvocableHandlerMethod.java:205)
org.springframework.web.method.support.InvocableHandlerMethod.invokeForRequest(InvocableHandlerMethod.java:150)
org.springframework.web.servlet.mvc.method.annotation.ServletInvocableHandlerMethod.invokeAndHandle(ServletInvocableHandlerMethod.java:117)
org.springframework.web.servlet.mvc.method.annotation.RequestMappingHandlerAdapter.invokeHandlerMethod (RequestMappingHandlerAdapter.java:895)
org.springframework.web.
base/java.lang.reflect.Method.invoke(Method.java:566)
org.springframework.web.method.support.InvocableHandlerMethod.doInvoke(InvocableHandlerMethod.java:205)
org.springframework.web.method.support.InvocableHandlerMethod.invokeForRequest(InvocableHandlerMethod.java:150)
org.springframework.web.servlet.mvc.method.annotation.ServletInvocableHandlerMethod.invokeAndHandle(ServletInvocableHandlerMethod.java:117)
org.springframework.web.servlet.mvc.method.annotation.RequestMappingHandlerAdapter.invokeHandlerMethod (RequestMappingHandlerAdapter.java:895)
org.springframework.web. servlet.mvc.method.annotation.RequestMappingHandlerAdapter.handleInternal (RequestMappingHandlerAdapter.java:808)
org.springframework.web.servlet.mvc.method.AbstractHandlerMethodAdapter.handle(AbstractHandlerMethodAdapter.java:87)
org.springframework.web.servlet.DispatcherServlet.doDispatch(DispatcherServlet.java:1067)
org.springframework.web.servlet.DispatcherServlet.doService(DispatcherServlet.java:963)
org.springframework.web.servlet.FrameworkServlet.processRequest(FrameworkServlet.java:1006)
org.springframework.web.servlet.FrameworkServlet.doGet(FrameworkServlet.java:898)
javax.
servlet.mvc.method.annotation.RequestMappingHandlerAdapter.handleInternal (RequestMappingHandlerAdapter.java:808)
org.springframework.web.servlet.mvc.method.AbstractHandlerMethodAdapter.handle(AbstractHandlerMethodAdapter.java:87)
org.springframework.web.servlet.DispatcherServlet.doDispatch(DispatcherServlet.java:1067)
org.springframework.web.servlet.DispatcherServlet.doService(DispatcherServlet.java:963)
org.springframework.web.servlet.FrameworkServlet.processRequest(FrameworkServlet.java:1006)
org.springframework.web.servlet.FrameworkServlet.doGet(FrameworkServlet.java:898)
javax. servlet.http.HttpServlet.service(HttpServlet.java:626)
org.springframework.web.servlet.FrameworkServlet.service(FrameworkServlet.java:883)
javax.servlet.http.HttpServlet.service(HttpServlet.java:733)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:227)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.apache.tomcat.websocket.server.WsFilter.doFilter(WsFilter.java:53)
org.apache.catalina.core.ApplicationFilterChain.
servlet.http.HttpServlet.service(HttpServlet.java:626)
org.springframework.web.servlet.FrameworkServlet.service(FrameworkServlet.java:883)
javax.servlet.http.HttpServlet.service(HttpServlet.java:733)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:227)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.apache.tomcat.websocket.server.WsFilter.doFilter(WsFilter.java:53)
org.apache.catalina.core.ApplicationFilterChain. internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.apache.catalina.filters.HttpHeaderSecurityFilter.doFilter(HttpHeaderSecurityFilter.java:126)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.servlet.resource.ResourceUrlEncodingFilter.doFilter(ResourceUrlEncodingFilter.java:67)
org.
internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.apache.catalina.filters.HttpHeaderSecurityFilter.doFilter(HttpHeaderSecurityFilter.java:126)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.servlet.resource.ResourceUrlEncodingFilter.doFilter(ResourceUrlEncodingFilter.java:67)
org. apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.RequestContextFilter.doFilterInternal (RequestContextFilter.java:100)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.
apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.RequestContextFilter.doFilterInternal (RequestContextFilter.java:100)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org. springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:102)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
com.gale.common.http.filter.SecurityHeaderFilter.doFilterInternal(SecurityHeaderFilter.java:29)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.
springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:102)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
com.gale.common.http.filter.SecurityHeaderFilter.doFilterInternal(SecurityHeaderFilter.java:29)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org. apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:102)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.owasp.validation.GaleParameterValidationFilter.doFilterInternal(GaleParameterValidationFilter.java:97)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.
apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:102)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.owasp.validation.GaleParameterValidationFilter.doFilterInternal(GaleParameterValidationFilter.java:97)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org. apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.boot.web.servlet.support.ErrorPageFilter.doFilter(ErrorPageFilter.java:126)
org.springframework.boot.web.servlet.support.ErrorPageFilter.access$000(ErrorPageFilter.java:64)
org.springframework.boot.web.servlet.support.ErrorPageFilter$1.doFilterInternal(ErrorPageFilter.java:101)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.
apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.boot.web.servlet.support.ErrorPageFilter.doFilter(ErrorPageFilter.java:126)
org.springframework.boot.web.servlet.support.ErrorPageFilter.access$000(ErrorPageFilter.java:64)
org.springframework.boot.web.servlet.support.ErrorPageFilter$1.doFilterInternal(ErrorPageFilter.java:101)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org. springframework.boot.web.servlet.support.ErrorPageFilter.doFilter(ErrorPageFilter.java:119)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.FormContentFilter.doFilterInternal (FormContentFilter.java:93)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.
springframework.boot.web.servlet.support.ErrorPageFilter.doFilter(ErrorPageFilter.java:119)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.FormContentFilter.doFilterInternal (FormContentFilter.java:93)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org. apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.boot.actuate.metrics.web.servlet.WebMvcMetricsFilter.doFilterInternal (WebMvcMetricsFilter.java:96)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.CharacterEncodingFilter.doFilterInternal (CharacterEncodingFilter.
apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.boot.actuate.metrics.web.servlet.WebMvcMetricsFilter.doFilterInternal (WebMvcMetricsFilter.java:96)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.CharacterEncodingFilter.doFilterInternal (CharacterEncodingFilter.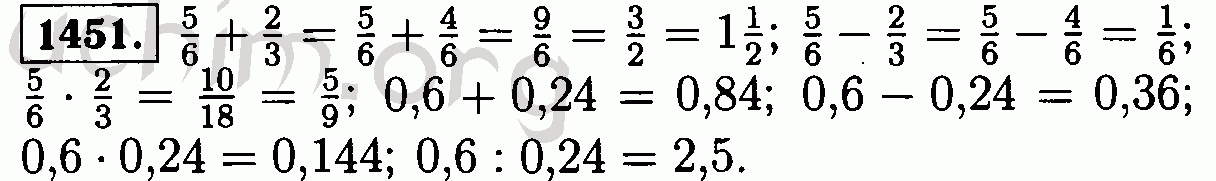 java:201)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.apache.catalina.core.StandardWrapperValve.invoke(StandardWrapperValve.java:202)
org.apache.catalina.core.StandardContextValve.invoke(StandardContextValve.java:97)
org.apache.catalina.authenticator.
java:201)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.apache.catalina.core.StandardWrapperValve.invoke(StandardWrapperValve.java:202)
org.apache.catalina.core.StandardContextValve.invoke(StandardContextValve.java:97)
org.apache.catalina.authenticator.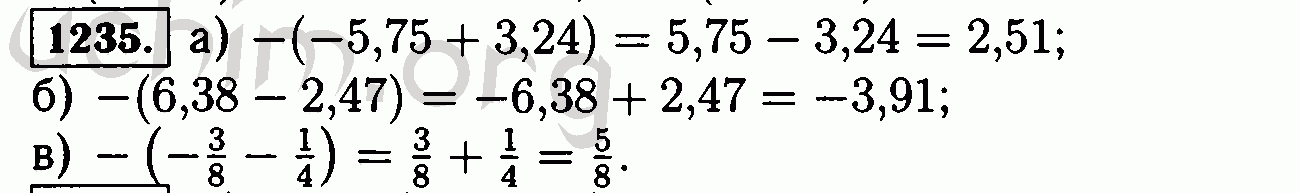 AuthenticatorBase.invoke(AuthenticatorBase.java:542)
org.apache.catalina.core.StandardHostValve.invoke(StandardHostValve.java:143)
org.apache.catalina.valves.ErrorReportValve.invoke(ErrorReportValve.java:92)
org.apache.catalina.valves.AbstractAccessLogValve.invoke(AbstractAccessLogValve.java:687)
org.apache.catalina.core.StandardEngineValve.invoke(StandardEngineValve.java:78)
org.apache.catalina.connector.CoyoteAdapter.service(CoyoteAdapter.java:357)
org.apache.coyote.http11.Http11Processor.
AuthenticatorBase.invoke(AuthenticatorBase.java:542)
org.apache.catalina.core.StandardHostValve.invoke(StandardHostValve.java:143)
org.apache.catalina.valves.ErrorReportValve.invoke(ErrorReportValve.java:92)
org.apache.catalina.valves.AbstractAccessLogValve.invoke(AbstractAccessLogValve.java:687)
org.apache.catalina.core.StandardEngineValve.invoke(StandardEngineValve.java:78)
org.apache.catalina.connector.CoyoteAdapter.service(CoyoteAdapter.java:357)
org.apache.coyote.http11.Http11Processor. service(Http11Processor.java:374)
org.apache.coyote.AbstractProcessorLight.process(AbstractProcessorLight.java:65)
org.apache.coyote.AbstractProtocol$ConnectionHandler.process(AbstractProtocol.java:893)
org.apache.tomcat.util.net.NioEndpoint$SocketProcessor.doRun(NioEndpoint.java:1707)
org.apache.tomcat.util.net.SocketProcessorBase.run(SocketProcessorBase.java:49)
java.base/java.util.concurrent.ThreadPoolExecutor.runWorker(ThreadPoolExecutor.java:1128)
java.base/java.util.concurrent.ThreadPoolExecutor$Worker.
service(Http11Processor.java:374)
org.apache.coyote.AbstractProcessorLight.process(AbstractProcessorLight.java:65)
org.apache.coyote.AbstractProtocol$ConnectionHandler.process(AbstractProtocol.java:893)
org.apache.tomcat.util.net.NioEndpoint$SocketProcessor.doRun(NioEndpoint.java:1707)
org.apache.tomcat.util.net.SocketProcessorBase.run(SocketProcessorBase.java:49)
java.base/java.util.concurrent.ThreadPoolExecutor.runWorker(ThreadPoolExecutor.java:1128)
java.base/java.util.concurrent.ThreadPoolExecutor$Worker.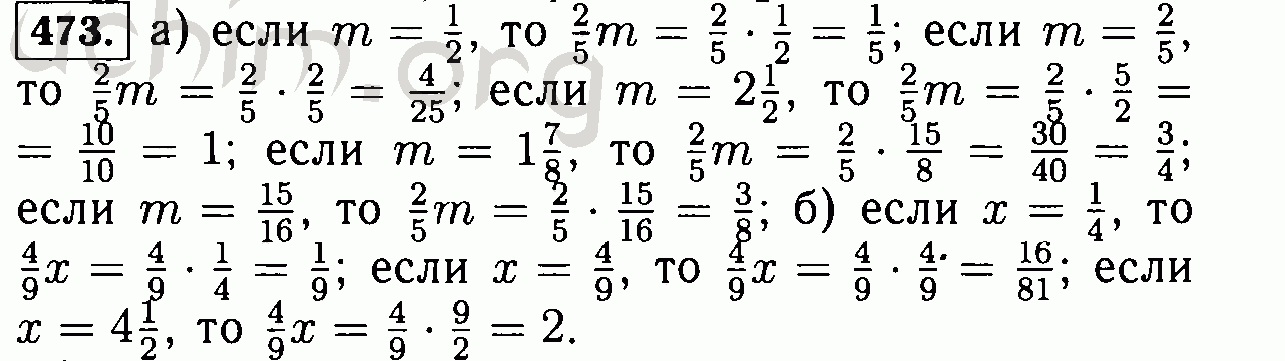 run(ThreadPoolExecutor.java:628)
org.apache.tomcat.util.threads.TaskThread$WrappingRunnable.run(TaskThread.java:61)
java.base/java.lang.Thread.run(Thread.java:834)
run(ThreadPoolExecutor.java:628)
org.apache.tomcat.util.threads.TaskThread$WrappingRunnable.run(TaskThread.java:61)
java.base/java.lang.Thread.run(Thread.java:834) Анализ в теории и приложениях ATA Том 34, номер 2
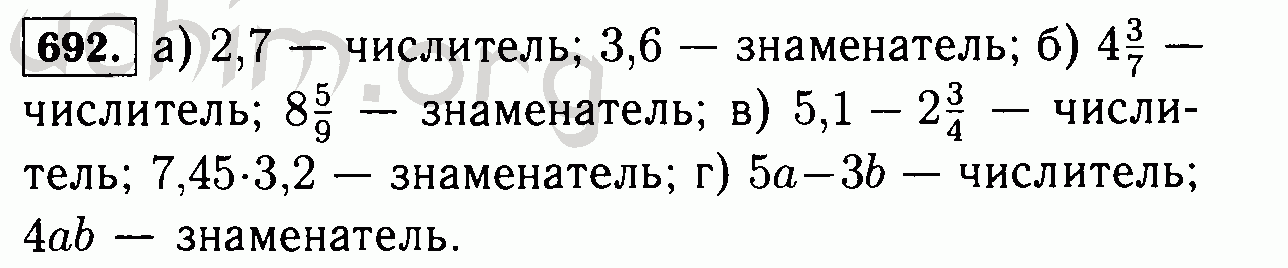 Panigrahi & R. N. Mohapatra
Panigrahi & R. N. Mohapatra
Овайс Ахмад и Неяз А. Шейх Прикладная теория, 34 (2018), стр. 135-146.
Предварительный просмотр Купить PDF
1025 16942Abstract
Некоторые результаты для многочленов смешанного типа Петерса с двумя переменными и связанных с ними полиномов
Газала Ясмин
10. 4208/ata.2018.v3. Прикладная теория, 34 (2018), стр. 147-164.
4208/ata.2018.v3. Прикладная теория, 34 (2018), стр. 147-164.
Предварительный просмотр Купить PDF
935 15845Abstract
Certain Integral Transforms of Generalized $k$-Bessel Function
Kottakkaran Sooppy Nisar, Waseem Ahmad Khan & Mohd Ghayasuddin
10.4208/ata.2018.v34.n2.6
Anal. Прикладная теория, 34 (2018), стр. 165-174.
Предварительный просмотр Купить PDF
965 16206Аннотация
Неравенства о максимальном модуле полиномов
Б. А. Заргар, А. В. Манзур и Шайста Башир
А. Заргар, А. В. Манзур и Шайста Башир
10.4208/ata.2018.v34.n2.7
Анал. Прикладная теория, 34 (2018), стр. 175-186.
Предварительный просмотр Купить PDF
960 16149Аннотация
О потенциально графических последовательностях $G−E(H)$
Билал А. Чат и С. Пирзада
10.4208/ata.3 Прикладная теория, 34 (2018), стр. 187-198.
Предварительный просмотр Купить PDF
940 15891Abstract
Требуется авторизация
Этот сервер не смог проверить, что вы авторизованы для доступа к документу
просил. Либо
вы указали неправильные учетные данные (например, неверный пароль), или ваш браузер не
понять
как предоставить необходимые учетные данные.
Либо
вы указали неправильные учетные данные (например, неверный пароль), или ваш браузер не
понять
как предоставить необходимые учетные данные.
Сервер Apache/2.2.15 (CentOS) на www.global-sci.org Порт 80
Университет Джорджии
Георгий Тефнадзе
Исследователь
Доктор
Институт математики
Школа науки и технологий
Образование
— — Бакалавр — 07. 09.2007 — 25.07.2011
09.2007 — 25.07.2011
— — Мастер — 07.09.2011 — 24.07.2013
— — Доктор — 09/10/2013 — 22/07/2016
Технологический университет Лулео — кафедра инженерных наук и математики — Доктор — 10.09.2017 — 10.09.2017
Публикации
Google ученый — https://scholar.google.com/citations?hl=ru&user=CGjcCXcAAAAJ
г. Г. Тефнадзе, Максимальные операторы логарифмических средних одномерных рядов Виленкина-Фурье, Acta Math.
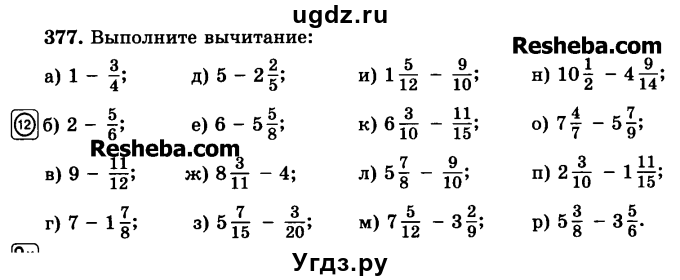 акад. Паед. Ньирег., 27 (2011), 245-256. — 2011
акад. Паед. Ньирег., 27 (2011), 245-256. — 2011Г. Тефнадзе, Замечание о коэффициентах Фурье и частных суммах рядов Виленкина-Фурье, Acta Math. акад. Паед. Ньирег., 28 (2012), 167-176. — 2012
г. — 2012
Г. Тефнадзе, О максимальных операторах средних Виленкина-Фейера, Тюрк. J. Math., 37, (2013), 308-318. — 2013
Г. Тефнадзе, О максимальных операторах средних Виленкина-Фейера на пространствах Харди, Матем. Неравный.
 Приложение, 16, 2 (2013), 301-312. — 2013
Приложение, 16, 2 (2013), 301-312. — 2013г. Г. Тефнадзе, Сильная сходимость двумерных рядов Уолша-Фурье, Укр. Мат. Ж., 65, 6 (2013), 822-834. — 2013
Г. Тефнадзе, О коэффициентах Виленкина-Фурье, Грузинский матем. Ж., 20, 1 (2013), 169–177. — 2013
Г. Тефнадзе, О максимальных операторах средних Уолша-Качмарца-Фейера, Период. Мат. Венгрия, 67, 1 (2013), 33-45. — 2013
Г. Тефнадзе, Замечание о сильной сходимости двумерных рядов Уолша-Фурье, Proc.
 Размадзе мат. ин-т, 162 (2013), 93-97. — 2013
Размадзе мат. ин-т, 162 (2013), 93-97. — 2013Тефнадзе Г., О частных суммах рядов Виленкина-Фурье, J. Contemp. Мат. Анал., 49, 1 (2014), 23-32. — 2014
Г. Тефнадзе, Сильные теоремы сходимости средних Уолша-Фейера, Acta Math. Венгрия, 142, 1 (2014), 244–259.. — 2014
Г. Тефнадзе, О максимальных операторах логарифмических средних Рейса рядов Виленкина-Фурье, Stud. науч. Мат. Венгрия, 51, 1 (2014), 105-120. — 2014
Г.
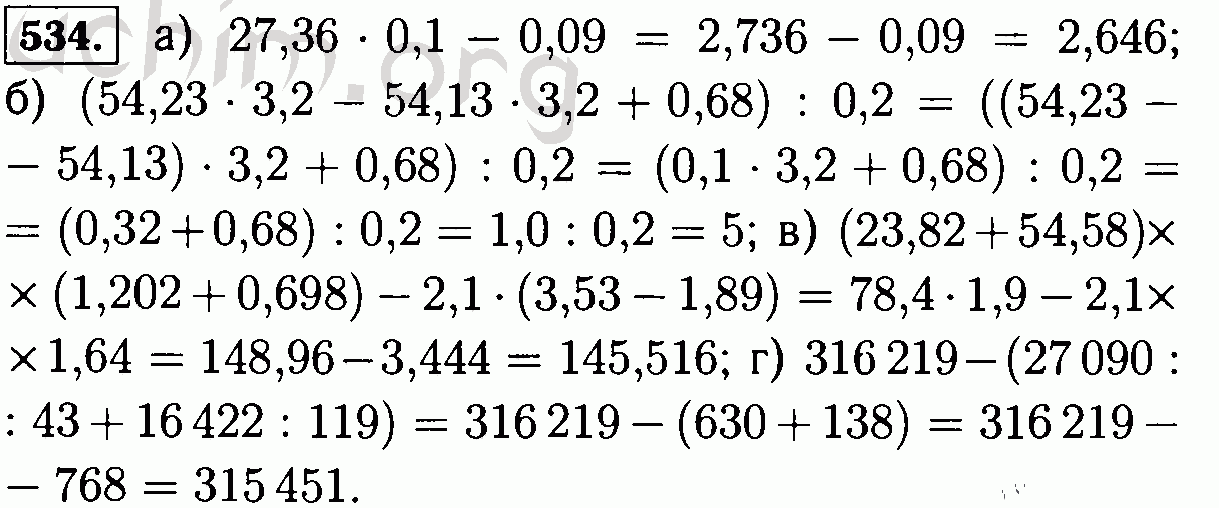 Тефнадзе, Аппроксимация средними Уолша-Качмарца-Фейера на пространстве Харди, Acta Math. наук, 34, 5 (2014), 1593-1602. — 2014
Тефнадзе, Аппроксимация средними Уолша-Качмарца-Фейера на пространстве Харди, Acta Math. наук, 34, 5 (2014), 1593-1602. — 2014Г. Тефнадзе, Замечание о сходимости по норме средними Виленкина-Фейера, Грузинская математика. Ж., 21, 4 (2014), 511-517. — 2014
К. Надь, Г. Тефнадзе, Аппроксимация средними Уолша-Марцинкевича на пространстве Харди, Kyoto J. Math., 54, 3 (2014), 641-652. — 2014
г. К. Надь, Г. Тефнадзе, О средних Уолша-Марцинкевича на пространстве Харди, Cent. Евро. J. Math., 12, 8 (2014), 1214-1228. — 2014
И.
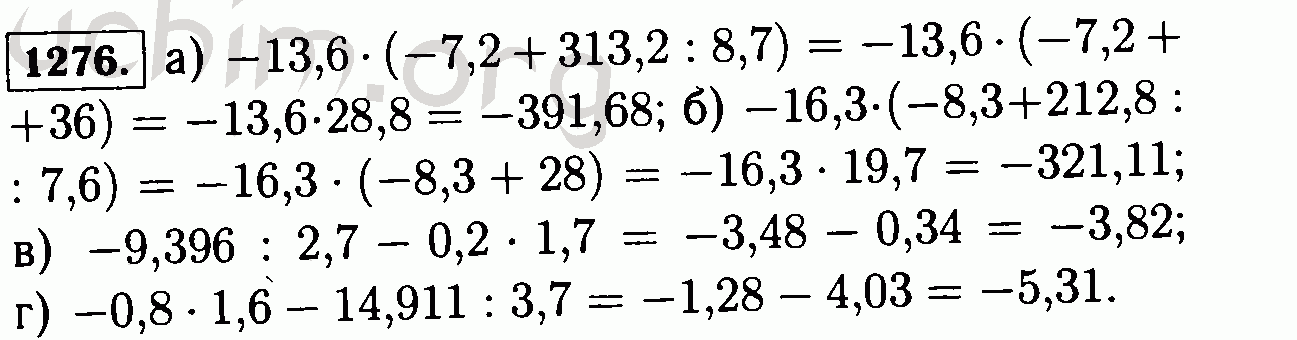 Блахота, Г. Тефнадзе, Сильная теорема сходимости для средних Виленкина-Фейера, Опубл. Мат. Дебрецен, 85 (1–2) (2014), 181–19.6. — 2014
Блахота, Г. Тефнадзе, Сильная теорема сходимости для средних Виленкина-Фейера, Опубл. Мат. Дебрецен, 85 (1–2) (2014), 181–19.6. — 2014И. Блахота, Г. Тефнадзе, О (C,α)-средних по системе Уолша, Анал. Матем., 40 (2014), 161-174. — 2014
К. Надь, Г. Тефнадзе, Аппроксимация средними Уолша-Качмарца-Марцинкевича на пространстве Харди H_{2/3}, Бюллетень ТИКМИ, 18, 1 (2014), 110–121. — 2014
г. Л.Э. Перссон, Г. Тефнадзе, Заметка о средних Виленкина-Фейера на мартингальных пространствах Харди Бюллетень ТИКМИ, 18, 1 (2014), 55–64. — 2014
А.
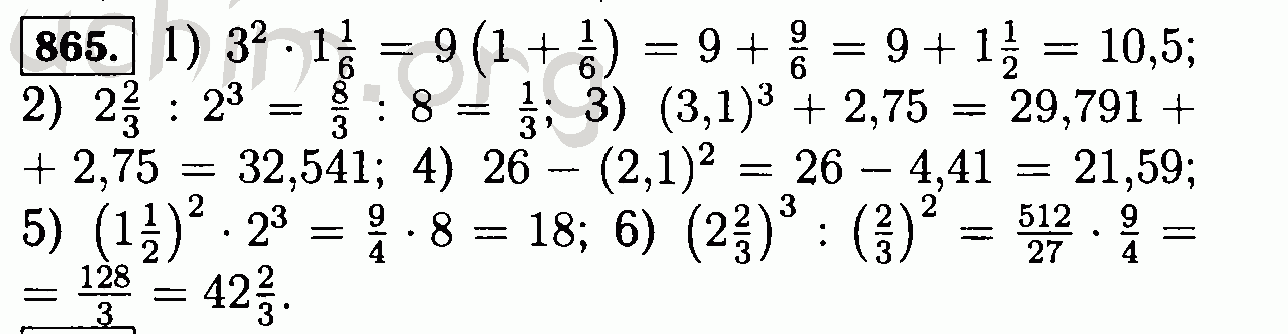 Гогатишвили, У. Гогинава, Г. Тефнадзе, Отношения между и классами функций, Польская академия наук, Институт математики. Публикации Банахового центра, 102, (2014), 89-98. — 2014
Гогатишвили, У. Гогинава, Г. Тефнадзе, Отношения между и классами функций, Польская академия наук, Институт математики. Публикации Банахового центра, 102, (2014), 89-98. — 2014Л. Э. Перссон, Г. Тефнадзе, П. Уолл, О максимальных операторах средних Виленкина-Нёрлунда, J. Fourier Anal. Приложение, 21, 1 (2015), 76-94. — 2015
Р. Дудучава, Э. Шаргородский, Г. Тефнадзе, Расширение единичного нормального векторного поля с гиперповерхности, Грузин. матем. Ж., 22, 3 (2015), 355-359. — 2015
Л. Э. Перссон, Г. Тефнадзе, П. Уолл, Некоторые новые неравенства типа (H_{p},L_{p}) максимальных операторов средних Виленкина-Нёрлунда с неубывающими коэффициентами, J.
 Math. Неравный, 9, 4 (2015), 1055-1069. — 2015
Math. Неравный, 9, 4 (2015), 1055-1069. — 2015Г. Тефнадзе, О частных суммах рядов Уолша-Фурье, Colloq. Матем., 141, 2 (2015), 227-242. — 2015
г. И. Благота, Л.Е. Перссон, Г. Тефнадзе, О средних Нёрлунда рядов Виленкина-Фурье, Чеш. Math J., 65, 4 (2015), 983-1002. — 2015
Г. Тефнадзе, О максимальных операторах средних Качмарца-Нёрлунда, Acta Math. акад. Паед. Ньирег., 31 (2015), 259–271. — 2015
И. Блахота, Г. Тефнадзе, Р.
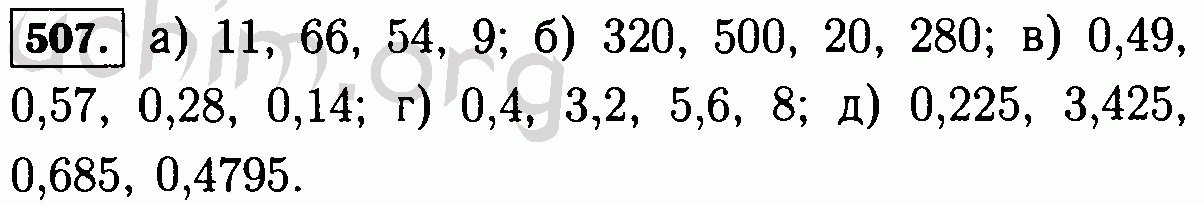 Толедо, Теорема о сильной сходимости (C,α)-средних по системе Уолша, Tohoku Math. Ж., 67, 4 (2015), 573-584. — 2015
Толедо, Теорема о сильной сходимости (C,α)-средних по системе Уолша, Tohoku Math. Ж., 67, 4 (2015), 573-584. — 2015Г. Тефнадзе, О сходимости средних Фейера рядов Уолша-Фурье в пространстве H_{p}, J. Contemp. Мат. Анал., 51, 2 (2016), 51-63. — 2016
г. Н. Мемич, И. Симон, Г. Тефнадзе, Сильная сходимость двумерных рядов Виленкина-Фурье, Матем. нахр., 289, 4 (2016) 485–500. — 2016
К. Надь, Г. Тефнадзе, Теорема о сильной сходимости для средних Уолша-Марцинкевича, Math. Неравный. Прил., 19, 1 (2016), 185–195. — 2016
Л.
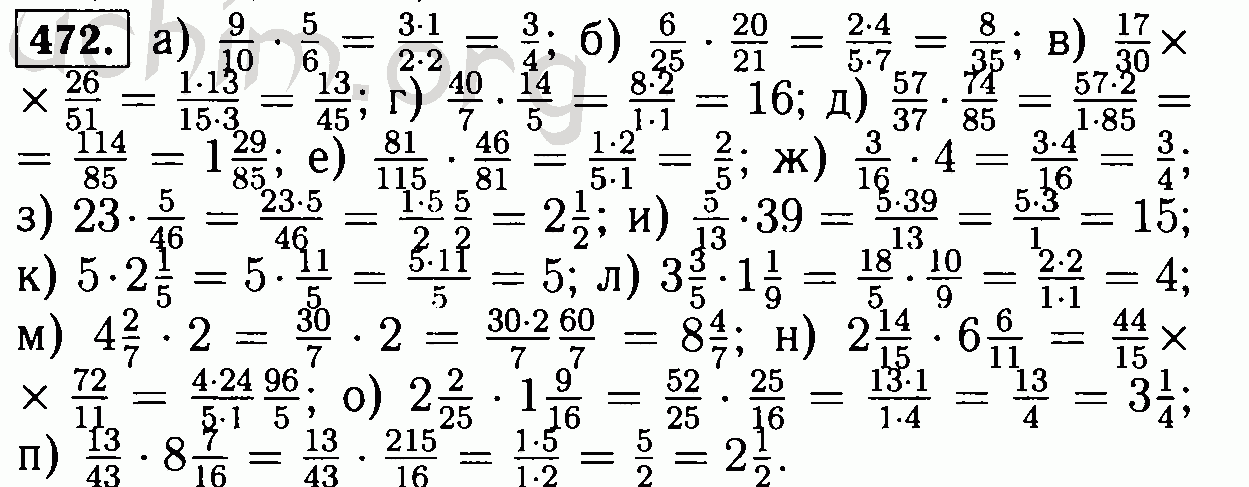 Э. Перссон, Г. Тефнадзе, Результат о точной ограниченности некоторых максимальных операторов средних Виленкина-Фейера, Mediterr. J. Math., 13, 4 (2016) 1841-1853. — 2016
Э. Перссон, Г. Тефнадзе, Результат о точной ограниченности некоторых максимальных операторов средних Виленкина-Фейера, Mediterr. J. Math., 13, 4 (2016) 1841-1853. — 2016К. Надь, Г. Тефнадзе, Средние Качмарца-Марцинкевича и пространства Харди, Acta math. Венгрия, 149, 2 (2016), 346-374. — 2016
И. Блахота, Г. Тефнадзе, Замечание о максимальных операторах средних Виленкина-Нёрлунда, Acta Math. акад. Паед. Ньирег., 32 (2016), 203–213. — 2016
Н. Мемич, Л. Э. Перссон, Г. Тефнадзе, Замечание о максимальных операторах средних Виленкина-Нёрлунда с невозрастающими коэффициентами, Stud.
 науч. Мат. Венгрия, 53, 4 (2016) 545-556. — 2016
науч. Мат. Венгрия, 53, 4 (2016) 545-556. — 2016г. Т. Бучукури, Р. Дудучава, Г. Тефнадзе, Уравнение Лапласа-Бельтрами на гиперповерхностях и $\Gamma$-сходимость, Труды Математического института им. А. Размадзе, 170, 3 (2016) 300–307. — 2016
Л. Барамидзе, Л. Э. Перссон, Г. Тефнадзе и П. Уолл, Суммируемость по Шртонгу и ограниченность максимальных операторов средних Виленкина-Нёрлунда с невозрастающими коэффициентами, J. Inequal. заявл., 2016. DOI: 10.1186/s13660-016-1182-1. — 2016
г. Т. Бучукури, Р. Дудучава, Г. Тефнадзе, Уравнение Лапласа-Бельтрами на гиперповерхностях и $\Gamma$-сходимость, Матем.
 Мет. Приложение. наук, 40, 13 (2017) 4637-4657. — 2017
Мет. Приложение. наук, 40, 13 (2017) 4637-4657. — 2017И. Блахота, Л. Э. Перссон, Г. Тефнадзе, Двусторонние оценки констант Лебега относительно систем Виленкина и приложений, Glasgow Math. Ж., 60 (2018) 17–34. — 2018
г. Г. Тефнадзе, О сходимости частичных сумм по системе Виленкина на мартингальных пространствах Харди, J. Contemp. Мат. Анал., 53, 5, (2018) 294–306. — 2018
Л. Э. Перссон, Г. Тефнадзе, П. Уолл, Об аппроксимации двумерных рядов Уолша-Фурье в мартингальных пространствах Харди, Ann. Функц. Анал., 9, 1 (2018), 137-150. — 2018
Л.
 Э. Перссон, Г. Тефнадзе, П. Уолл, О логарифмических средних Нёрлунда по системе Виленкина в мартингальном пространстве Харди $H_{1}$, Acta math. Венгрия, 154, 2 (2018) 289-301. — 2018
Э. Перссон, Г. Тефнадзе, П. Уолл, О логарифмических средних Нёрлунда по системе Виленкина в мартингальном пространстве Харди $H_{1}$, Acta math. Венгрия, 154, 2 (2018) 289-301. — 2018И. Блахота, К. Надь, Л. Э. Перссон, Г. Тефнадзе, Результат о точной ограниченности максимальных операторов рядов Виленкина-Фурье на мартингальных пространствах Харди, Грузинская математика, Ж., 26, 3 (2019), 351–360. — 2019
И. Блахота, К. Надь, Г. Тефнадзе, Аппроксимация $\Theta$-средними Марцинкевича двойных рядов Уолша-Фурье, Матем. Неравный. Приложение, 22, 3 (2019) 837-853. — 2019
Г.
 Тефнадзе, Сходимость и сильная суммируемость двумерного ряда Виленкина-Фурье, Нелинейные исследования, 26, 4, (2019) 973-989. — 2019
Тефнадзе, Сходимость и сильная суммируемость двумерного ряда Виленкина-Фурье, Нелинейные исследования, 26, 4, (2019) 973-989. — 2019Л. Э. Перссон, Г. Тефнадзе, Г. Тутберидзе, Об ограниченности подпоследовательностей средних Виленкина-Фейера на мартингальных пространствах Харди, операторы и матрицы, 14, 1 (2020), 283–294. — 2020
Д. Луккассен, Л. Э. Перссон, Г. Тефнадзе, Г. Тутберидзе, Некоторые неравенства, связанные с сильной сходимостью логарифмических средних Рисса рядов Виленкина-Фурье, J. Inequal. Appl., 2020, DOI: https://doi.org/10.1186/s13660-020-02342-8. — 2020
г. Г.
 Тефнадзе, Г. Тутберидзе, Замечание о максимальных операторах логарифмических средних Нёрлунда рядов Виленкина-Фурье, Тр. А. Размадзе Матем. ин-т, 174, 1 (2020), 107–112. — 2020
Тефнадзе, Г. Тутберидзе, Замечание о максимальных операторах логарифмических средних Нёрлунда рядов Виленкина-Фурье, Тр. А. Размадзе Матем. ин-т, 174, 1 (2020), 107–112. — 2020Г. Тефнадзе, Заметка о сильной суммируемости двумерных рядов Уолша-Фурье, Грузинская математика, Ж., 2021, 28 (3), 477–482. — 2021
г. Л. Э. Перссон, Г. Тефнадзе, Г. Тутберидзе, П. Уолл, Результат сильной суммируемости средних Виленкина-Фейера на ограниченных группах Виленкина, Укр. Мат. Ж., 73 (4), (2021), 544-555. — 2021
Н. Гоголашвили, К. Надь, Г. Тефнадзе, Теорема сильной сходимости для Уолша-Качмарца-Фея\'er означает, Mediterr.
 J. Math., 2021, 18 (2), 37. — 2021
J. Math., 2021, 18 (2), 37. — 2021Н. Гоголашвили, Г. Тефнадзе, О максимальных операторах $T$ средних по системе Уолша-Качмарца, Stud. науч. Мат. Венгрия, 2021, 58 (1), 119–135. — 2021
Н. Гоголашвили, Г. Тефнадзе, Максимальные операторы средних $T$ по системе Уолша-Качмажа, Матем. Неравный. Appl., 24, 3 (2021) 737–750. — 2021
г. Д. Барамидзе, Л.-Э. Перссон, Х. Сингх, Г. Тефнадзе, Некоторые новые результаты и неравенства для подпоследовательностей логарифмических средних Нёрлунда рядов Уолша-Фурье, J. Inequal. Appl., 2022, DOI: https://doi.org/10.1186/s13660-022-02765-5.
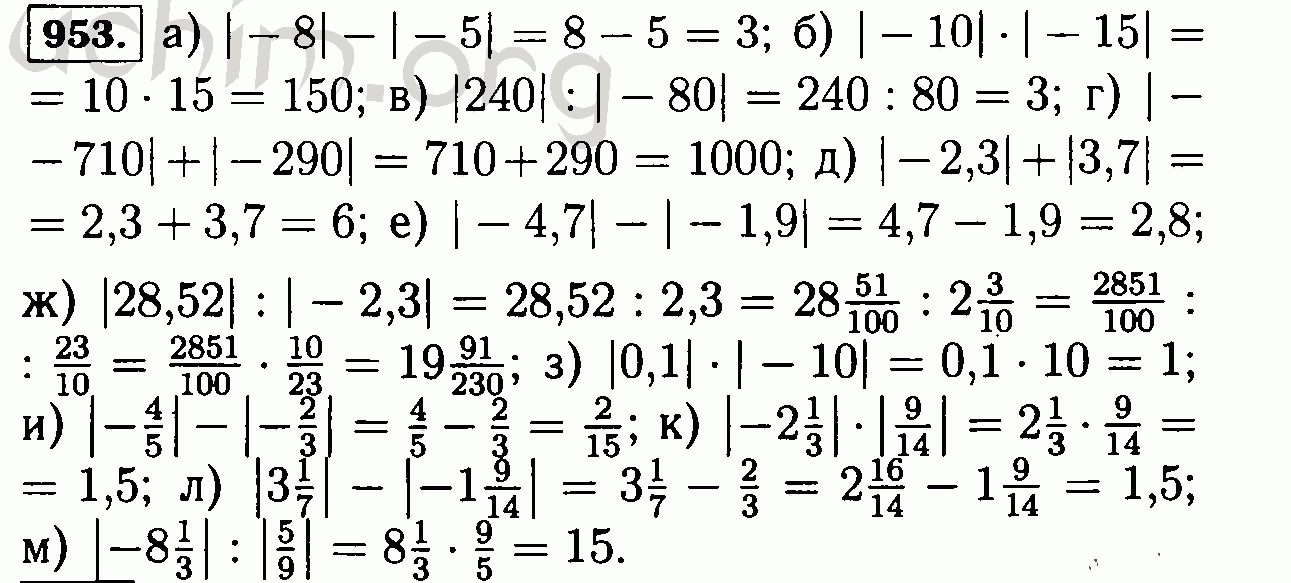 — 2022
— 2022Л.-Э. Перссон, Ф. Шипп, Г. Тефнадзе и Ф. Вайс, Аналогия теоремы Карлесона-Ханта относительно систем Виленкина, J. Fourier Anal. заявл., 28, 48 (2022), 1-29. — 2022
Н. Надирашвили, Г. Тефнадзе и Г. Тутберидзе, Почти всюду и сходимость по норме приближенного тождества и средних Фейера тригонометрических и виленкинских систем, Тр. А. Размадзе Матем. Инст. (в печати), 2022. — 2022
Д. Барамидзе, Н. Надирашвили, Л.-Э. Перссон и Г. Тефнадзе, Некоторые неравенства слабого типа и почти всюду сходимость средних Виленкина-Нёрлунда, J. Inequal. Appl., 2022 (в печати).
 — 2022
— 2022г. 5. Н. Надирашвили, Л.-Э. Перссон, Г. Тефнадзе, Ф. Вайс, точки Виленкина-Лебега и почти всюду сходимость средних и приложений Виленкина-Фейера, Mediterr. J. Math., (представлено). — 2022
Л. Э. Перссон, Г. Тефнадзе и Ф. Вайс, Мартингальные пространства Харди и суммируемость рядов Виленкина-Фурье, рукопись книги, Биркхойзер, 2022 г. (будет опубликовано). — 2022
г. Г. Тефнадзе, Одномерные мартингальные пространства Харди, частные суммы и средние значения Фейера по системе Уолша, Мемуары по дифференциальным уравнениям и математической физике, 2022 г.
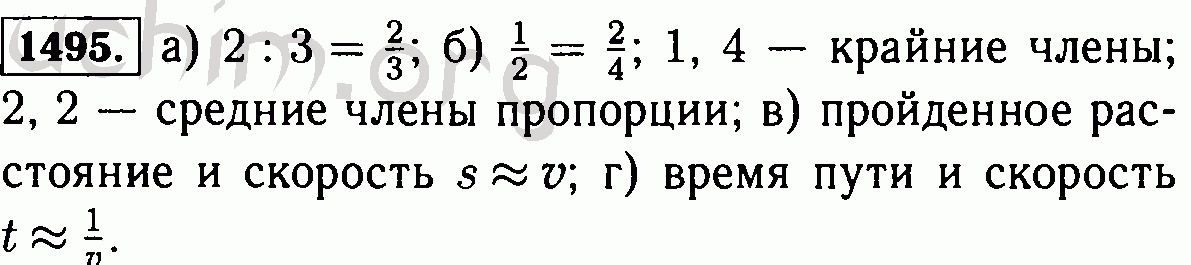 (будет опубликовано). — 2022
(будет опубликовано). — 2022Конференции
математика — 03.08.2010
г. Механика сплошных сред и смежные проблемы анализа — 05-05-2011
III международная конференция ГМУ — 09-05-2012
— 18-11-2012
г. IV международная конференция ГМУ — 03-09-2013
Анализ Фурье и теория приближений — 09.
 08.2013
08.2013Диадический анализ и смежные области с приложениями — 13-03-2014
г. — 18-04-2014
V международная конференция ГМУ — 09-02-2014
Кавказская математическая конференция I — 09.05.2014
— 10.08.2014
г. — 03.10.2015
— 24-05-2015
— 09.
 10.2015
10.2015— 11.10.2015
г. — 09.03.2016
— 12.06.2016
Числа уравнений в частных производных — 05.08.2017
Семинар для аспирантов по математике — 22-06-2017
г. Серия международных конференций Silkroad Mathematics Center по уравнениям в частных производных — 16-07-2017
математика — 09.
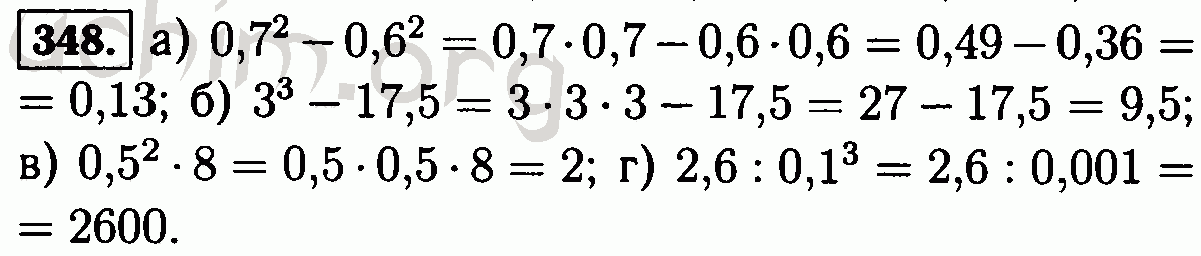 04.2017
04.2017Семинар по гармоническому анализу и аппроксимации — 16-10-2017
г. Семинар для аспирантов по математике — 10-12-2017
Практикум по реальному анализу — 17-01-2018
Практикум по уравнениям в частных производных — 29-06-2018
Семинар для аспирантов по математике — 07.09.2018
IX международная конференция Математического союза Грузии — 03-09-2018
Числа уравнений в частных производных — 29-03-2019
Семинар для аспирантов и молодых исследователей по математике — 05.
 01.2019
01.2019Международный семинар по теории операторов и ее приложениям (IWOTA) 2019 — 22-07-2019
Международная конференция-«Кавказская математическая конференция III», — 26-08-2019
Семинар по реальному анализу и смежным областям II — 16-12-2019
Практикум по реальному анализу — 17-09-2020
Онлайн-конференция «13-й Конгресс ISAAC» — 08.02.2021
г. Онлайн-конференция — «XI международная конференция Математического Союза Грузии» — 23-08-2021
Семинар по реальному анализу и смежным областям — 09.
 07.2021
07.2021Семинар в Техническом университете Берлина – 16 декабря 2021 г.
г. Международный двухнедельный онлайн-семинар — «Тбилиси Анализ & Семинар PDE — 28 февраля 2022 г.
Еженедельный онлайн-семинар для школьников «Увлекательный мир математики» — 16-04-2022
Еженедельный онлайн-семинар для школьников «Увлекательный мир математики» — 30-04-2022
г. Международная конференция-«XII международная конференция Математического Союза Грузии» — 29-08-2022
Международный семинар по теории и приложениям операторов, IWOTA — 09.
 06.2022
06.2022Научные проекты
Геометрия функциональных пространств, интерполяция и теоремы вложения — 2012-2014
г. Асимптотическая модель тонкой оболочки — 2013-2015
Ограниченные операторы на мартингальных пространствах Харди — 2014
Ограниченные операторы на мартингальных пространствах Харди — 2014-2016
г. Функциональные пространства, весовые неравенства для интегральных операторов и проблемы суммирования рядов Фурье — 2014-2016
О частных суммах и средних Марцинкевича-Фейера на одномерном и двумерном однопараметрических пространствах Харди — 2015-2016
г.
 Сходимость и суммируемость одномерного и двумерного рядов Виленкина-Фурье на мартингальных пространствах Харди — 2015-2017
Сходимость и суммируемость одномерного и двумерного рядов Виленкина-Фурье на мартингальных пространствах Харди — 2015-2017Новое развитие d-мерных рядов Уолша-Фурье на мартингальных пространствах Харди — 2016-2017
г. Сходимость и суммируемость двумерных рядов Уолша-Фурье на мартингальных пространствах Харди — 2017-2018
Сходимость и суммируемость рядов Уолша-Фурье на мартингальных пространствах Харди — 2018-2020
— 2020-2023
г.
 Увлекательный мир математики — 2021-2022
Увлекательный мир математики — 2021-2022Увлекательный мир математики — 2022-2023
Многолетняя динамика эллиптических и параболических систем с учетом аномальной диффузии и необратимости — 2022-2023 гг.
г. Подвижные коллекторы — 2022-2025
Курсы
Исследование-STEM0001 ( 2021/2022; 2022/2023; )
г.
 Комплексный анализ-MATh4121 (
2018/2019;
)
Комплексный анализ-MATh4121 (
2018/2019;
)Теория функций комплексных переменных-MATH5126 ( 2020/2021; )
г. Теория функций комплексных переменных-MATH5014 ( 2020/2021; )
Теория функций комплексных переменных-MATH5032 ( 2021/2022; )
г.
 Математика для экономистов и бизнеса II-MATh2216 (
2017/2018;
2018/2019;
2019/2020;
2020/2021;
)
Математика для экономистов и бизнеса II-MATh2216 (
2017/2018;
2018/2019;
2019/2020;
2020/2021;
)г. Математика для экономистов и бизнеса I-MATh2122 ( 2016/2017; 2017/2018; 2018/2019; 2019/2020; 2020/2021; )
г.
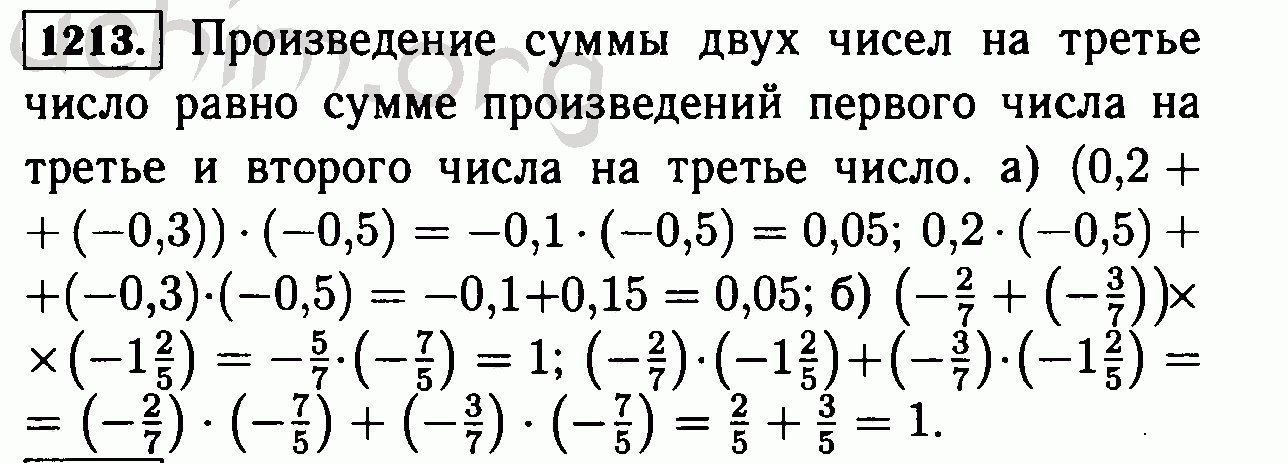 Математика для экономистов II-MATh2211E (
2018/2019;
)
Математика для экономистов II-MATh2211E (
2018/2019;
)Математика для экономистов I-MATh2111E ( 2016/2017; 2017/2018; )
г. Математический анализ III-MATH 2114 ( 2018/2019; 2019/2020; 2021/2022; )
Математический анализ II-MATh2212 ( 2017/2018; 2018/2019; 2020/2021; )
Математический анализ I-MATh2112 ( 2018/2019; )
Математическая статистика-MATH5007 ( 2021/2022; )
г.
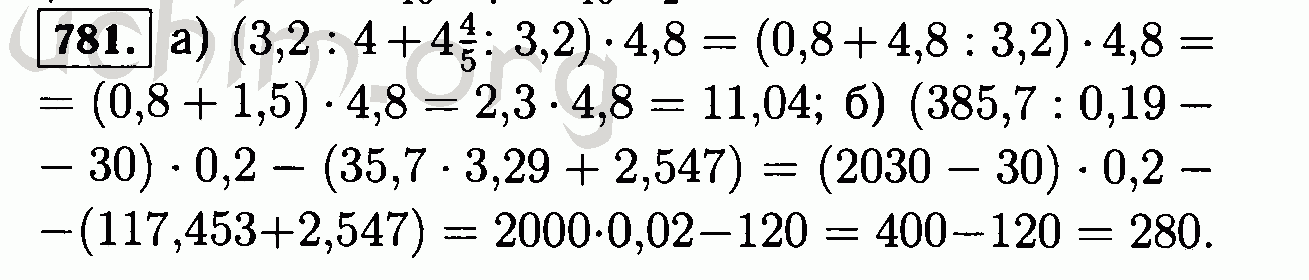 Мартингалы и их приложения к математическому анализу-MATH5017 (
2021/2022;
)
Мартингалы и их приложения к математическому анализу-MATH5017 (
2021/2022;
)Реальный и комплексный анализ-MATH7007 ( 2020/2021; 2021/2022; )
г. Реальный анализ II-MATh4225 ( 2019/2020; )
Реальный анализ I-MATh4124 ( 2017/2018; 2019/2020; )
Теория функций действительного переменного-MATH5015( 2020/2021; )
Теория функций действительной переменной-MATH5030 ( 2021/2022; 2022/2023; )
г.
 Теория функций действительных переменных-MATH51225 (
2019/2020;
)
Теория функций действительных переменных-MATH51225 (
2019/2020;
)Анализ Фурье-MATH5021 ( 2020/2021; 2022/2023; )
г. Гармонический анализ-MATH5010 ( 2021/2022; )
Расписание
Исследования-STEM0001
Теория функций комплексных переменных-MATH5032
г.


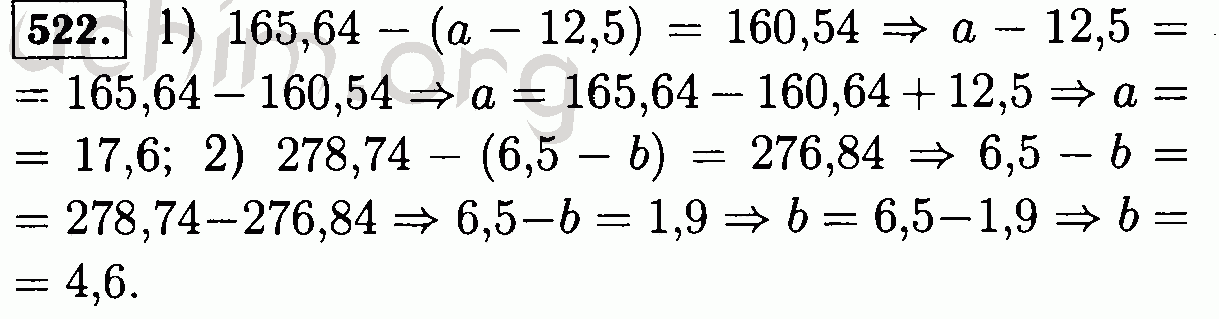

 И.
И.