ГДЗ по Математике 6 класс Ткачева
Автор: Ткачева М.В..
Изучение предмета математики долгий процесс. Он начинается с первых классов и тянется на протяжении всего обучения. Знания, полученные за время учебы, позволяют не только легко приспособится к жизни в обществе, но и обучают основам логического мышления и адаптируют к решению сложных повседневных задач. С каждым классом проверка домашнего задания ребенка все более серьезная задача. Времени самостоятельно вспоминать школьную программу и решать задачи школьного курса у взрослых нет. Именно в такой ситуации на помощь приходят ГДЗ по математике 6 класс Ткачева. Они содержат решения всех уравнений и задач с подробным описанием. Однако предназначено не только для родителей. Шестиклассники уже достаточно самостоятельны, чтобы перепроверять самих себя, а также совершенствовать свои знания вперед школьной программы. Пособие также поможет при составлении планов уроков или подборе заданий для проверочных работ.
Учеба с ГДЗ по математике за 6 класс Ткачевой
Хорошие знания математики – это большие возможности для школьников при дальнейшем обучении. Математика один из основных предметов и средний балл влияет на:
- выбор учебного заведения;
- выбор профессии;
- выбор высокооплачиваемого рабочего места.
Чем выше успеваемость, тем больше шансов выбрать более качественное образование. Об этом необходимо задумываться задолго до выпускного, чтобы не допустить критических пробелов в знаниях.
Шестой класс – это переход к более сложным математическим понятиям. Программа шестого класса включает следующие темы:
- координаты и понятие пространства;
- делимость;
- основы геометрии;
- модуль;
- целые числа;
- дробные числа.

Эти темы могут вызвать множество сложностей у учеников при изучении, поэтому необходимо использовать только качественный решебник по математике для 6 класса (автор: Ткачева М. В.).
Репетитору по математике для работы в 5-6 классе — Колпаков Александр Николаевич
Предлагаю вашему вниманию страницу, на которой размещаются тематические ссылки на описания моих методик преподавания. Здесь вы найдете информацию о частных приемах, используемых репетитором математики в работе с детьми 5 — 6 классов самого разного уровня знаний и способностей: от участников математических олимпиад до сильно запущенных отстающих учеников.
Методические статьи:
Репетитор по математике о цветовой поддержке темы «вычитание»
Простой и полезный прием, помогающий удержать внимания слабого ученика на структуре алгоритма вычитания отрицательных чисел.
 Об использовании цвета для выделений знаков арифметических действий в длинных примерах на вычисление.
Об использовании цвета для выделений знаков арифметических действий в длинных примерах на вычисление.Методика повторов в условиях задач
Описание приема, которым репетитор по математике регулярно пользуется на занятиях с остающими учениками 5 — 6 классов по теме задачи на дроби. Использование одинаковых сюжетов в текстовых задачах. Один из методов улучшения концентрации внимания учащихся.
О работе репетитора по математике с признаками делимости.
Приемы, облегчающие учащимся выполнение некоторых упражнений на признаки и усвоение их доказательств (для сильных школьников). Оценка уровня сложности преподавания темы. Связь со следующим материалом. Актуальность темы. Характерные особенности заданий. Виды заданий репетитора. Математика 5 класс по Петерсону и 6 класс по Виленкину.
Рациональная дробь на уроке у репетитора по математике
Как отбиться от вопросов любознательных учеников о причинах введения того или иного определения или понятия. Мастеркласс репетитора по математике для ведения урока на тему «Рациональная дробь» (6 класс, Виленкин). Начинающему преподавателю на земетку.
Мастеркласс репетитора по математике для ведения урока на тему «Рациональная дробь» (6 класс, Виленкин). Начинающему преподавателю на земетку.
Поиск наименьшего общего кратного (6 класс)
На странице рассказывается о том, почему репетитор по математике отказывается от формулировки правила находения НОКа, предложенного учебником (5 класс по Петерсону или 6 класс по Виленкину). Методы объяснений, особенности подбора слов для текстов правил. Опорные фразы репетитора, многократно повторяемые на уроках для запоминания алгоритма.
Cложение рациональных чисел с репетитором по математике О том, в каком ключе лучше провести урок на сложение отрицательных и положительных чисел со слабым учеником в 6 классе. Эффективный прием объяснения через практическую задачу о сумме денег на телефоне.
Репетитор по математике о работе с правилом вычитания отрицательных чисел. Об особенностях работы с правилом a-b=a+(-b) и приемы подачи темы отстающему ученику. Советы по оформлению решений и адаптации правила перевода вычитания в сложение. Cпособы объяснения материала и характер заданий репетитора. 6 класс.
Советы по оформлению решений и адаптации правила перевода вычитания в сложение. Cпособы объяснения материала и характер заданий репетитора. 6 класс.
Подготовка в Курчатовскую школу
О том, как происходит подготовка способных детей к ежегодной вступительной олимпиаде по математике (4 — 5 класс), проходящей в стенах Курчатовской школы. Особенности подготовки в соответствии с уровнем ученика. Этапы подготовки. Приемы, используемые в олимпиадной репетиторской практике.
Прием репетитора по математике в работе с задачами на движение. 5 класс.. Оформление схемок для визуального представления данных условий задач. Использование методики пропусков на уроках математики в 5 классе. Для оптимизации поиска решений задач на движение и снижения количества ошибок от невнимательности. Для работы репетитора со слабым учеником.
Как репетитор по математике оптимизирует задания на дроби
Описание особенностей изучения с репетитором одной из самых сложных тем школьного курса за 5-6 класс — текстовые задачи на части (на дроби). Методика оптимизации и сортировки информации в текстах и оформления кратких записей, важные моменты в объяснениях, обсуждение проблем преподавания. Правила, которые использует репетитор по математике в условиях занятий с учеником низких способностей.
Методика оптимизации и сортировки информации в текстах и оформления кратких записей, важные моменты в объяснениях, обсуждение проблем преподавания. Правила, которые использует репетитор по математике в условиях занятий с учеником низких способностей.
Устный счет с репетитором по математике
Обсуждение проблем проведения устной работы с учащимися. Советы репетиторам и школьным учителям, примеры отдельных упражнений, обоснование эффективности использования устной формы работы для формирования вычислительных и мыслительных навыков. Методика организации работы на занятиях с высокой периодичностью их проведения
Репетитор по математике о задачах на дроби
Общие вопросы методики изучения текстовых задач на части и доли. Стратигия подбора подготовительных задач и приемы работы репетитора с текстами. Цветовые выделения, особенности оформление кратких записей. Спецприемы и фишечки для репетиторов. Терминология для записи правил в теоретическоую тетрадь. Типы базовых задач на дроби.
Типы базовых задач на дроби.
Решение уравнений в 5 — 6 классах
Методика обучения подбору действий при решении простейших типовых уравнений по программе 5 и 6 класса. Работа ученика с уменьшаемым, вычитаемым и разностью; делимым, делителем и частным; множителями и произведением, слагаемыми и суммой. Типичные проблемы слабых учеников и пути выхода репетитора из тупиковых ситуаций. Сложные случаи.
Метод умножения на 9 на пальцах
Почему я объединяю возраста? Хороший частный репетитор по математике записывает на занятия учащихся разных учебных программ. А они, как известно, отличаются порядком расположения тем. По одному пособию обыкновенные дроби умножают в 5 классе, а по другому только в 6-ом. Делить страницы по отдельным классам, во-первых технически неудобно, а во-вторых это бы сузило репетитору математики — посетителю сайта диапазон приемов для ознакомления. Почему? Большинство моих подходов имеют обобщенный и в чем то даже универсальный стержень.
Поэтому минимальная интеграция классов необходима. Однако, есть темы «интернациональные», которые репетиторы математики дают в одном и том же возрасте. Например, в 7 классе это формулы сокращенного умножения, в восьмом — корни. Для их методик будут сделаны узкоспециализированные страницы. Но это в перспективе. Пока ссылки классифицированы так: математика 5-6 класс, 7-8 класс, 8-9 класс, 10-11 класс, высшая математика и подготовка к ЕГЭ.
Изучайте и пользуйтесь на здоровье!
Репетитор по математике Колпаков А.Н.
Игра по математике 6 класс «Счастливый случай»
Игра по математике 6 класс «Счастливый случай»
«Счастливый случай « Элизбарян Р. Г.
Участники игры: 6б класс, 6в класс
Цели внеклассного мероприятия: повторить пройденный материал за весь пятый класс; развивать в детях дух коллективизма; развивать смекалку, логику и внимательность; воспитывать в детях уверенность в себе и умение быстро сосредотачиваться на главном; развивать в детях интерес к математике.
Ход мероприятия
1. Организационный момент (3 мин)
На перемене расставить столы и стулья для двух команд и распределить детей. На мероприятии рассадить детей по командам.
Учитель: Сегодня у нас будет проводиться игра «Счастливый случай». Но хотя игра носит такое название, выиграет та команда, которая лучше училась в течение года. Все задания и вопросы будут по пройденному материалу за 5-ый класс. Поэтому проще выиграть будет тем, кто учил все правила, выполнял, все домашние работы и внимательно слушал на уроках. Но, конечно, победа зависит и от вашей удачи. Напомню, что многое зависит и от вашего поведения. Поэтому у команды, которая не умеет себя вести, будут сниматься баллы. Для начала выбирается, капитан команды и мы приступаем непосредственно к игре.
Но хотя игра носит такое название, выиграет та команда, которая лучше училась в течение года. Все задания и вопросы будут по пройденному материалу за 5-ый класс. Поэтому проще выиграть будет тем, кто учил все правила, выполнял, все домашние работы и внимательно слушал на уроках. Но, конечно, победа зависит и от вашей удачи. Напомню, что многое зависит и от вашего поведения. Поэтому у команды, которая не умеет себя вести, будут сниматься баллы. Для начала выбирается, капитан команды и мы приступаем непосредственно к игре.
2. Гейм «Разминка»(10 мин)
Учитель: Первый гейм — это разминка. Каждой команде предлагается по 15 вопросов. За каждый правильный ответ присуждается 1 балл. Вопросы читаются сначала одной команде, затем другой. Когда вопрос прочитан, тот, кто знает правильный ответ, поднимает руку, а капитан называет имя того, кто имеет право ответить. На вопрос можно ответить только один раз. Отвечает только один участник. Если на вопрос дают ответ двое, то ответ не засчитывается. Надо учесть, что один и тот же человек может в гейме отвечать только на два вопроса. В том числе и капитан, он отвечает только на два вопроса.
Надо учесть, что один и тот же человек может в гейме отвечать только на два вопроса. В том числе и капитан, он отвечает только на два вопроса.
Вопросы первой команде:
1. Дать определение отрезку. (Часть прямой, ограниченная с двух сторон точками)
2. Как найти неизвестный делитель? (Надо делимое разделить на частное)
3. а * 0 = … (0)
4. 1 м2 = ? дм2 (100)
5. Найти объем куба с ребром 3 см (27 см3)
6. Как найти площадь прямоугольника? (Надо длину умножить на ширину)
7. 4 х = 20, Х = ? (х = 5)
8. Сколько ребер у параллелепипеда? (12)
9. Назвать наибольшее двузначное число. (99)
10. Велосипедист едет со скоростью 20 км/ч. За какое время он проедет 60 км? (3 ч)
11. 92 = ? (81)
12. Выразить в килограммах 3 кг 13 г. (3,013 кг)
13. Что больше: 5,1 или 5,01? (5,1)
14. Найти среднее арифметическое для чисел 15, 10 и 35. (20)
(20)
15. Перевести в про центы 0,4. (40%)
Вопросы второй команде:
1. Что меньше: 0,12 или 1,012? (0,12)
2. 0 + а = ? (а)
3. 42 = ? (16)
4. Как найти периметр квадрата? (Надо длину стороны умножить на 4)
5. 1 м2= ? см2
6. Перевести в десятичную дробь 0,02 (2%)
7. 5 + у = 30, у =? (25)
8. Измерения параллелепипеда l см, 2 см и 5 см. Найти объем. (10 см3)
9. Найти среднее арифметическое чисел 54 и 66. (55)
10. Сколько граней у куба? (6)
11. Назвать наименьшее двузначное число. (10)
12. Дать определение лучу. (Часть прямой, ограниченная с одной стороны точкой.)
13. Как найти неизвестное уменьшаемое? (Надо к вычитаемому прибавить разность.)
14. Пешеход идет 2 ч. со скоростью 4 км/ч. Сколько километров он прошел? (8 км)
15. Выразить в метрах 6 см (0,06 м)
16. После ответов обеих команд подсчитываются баллы.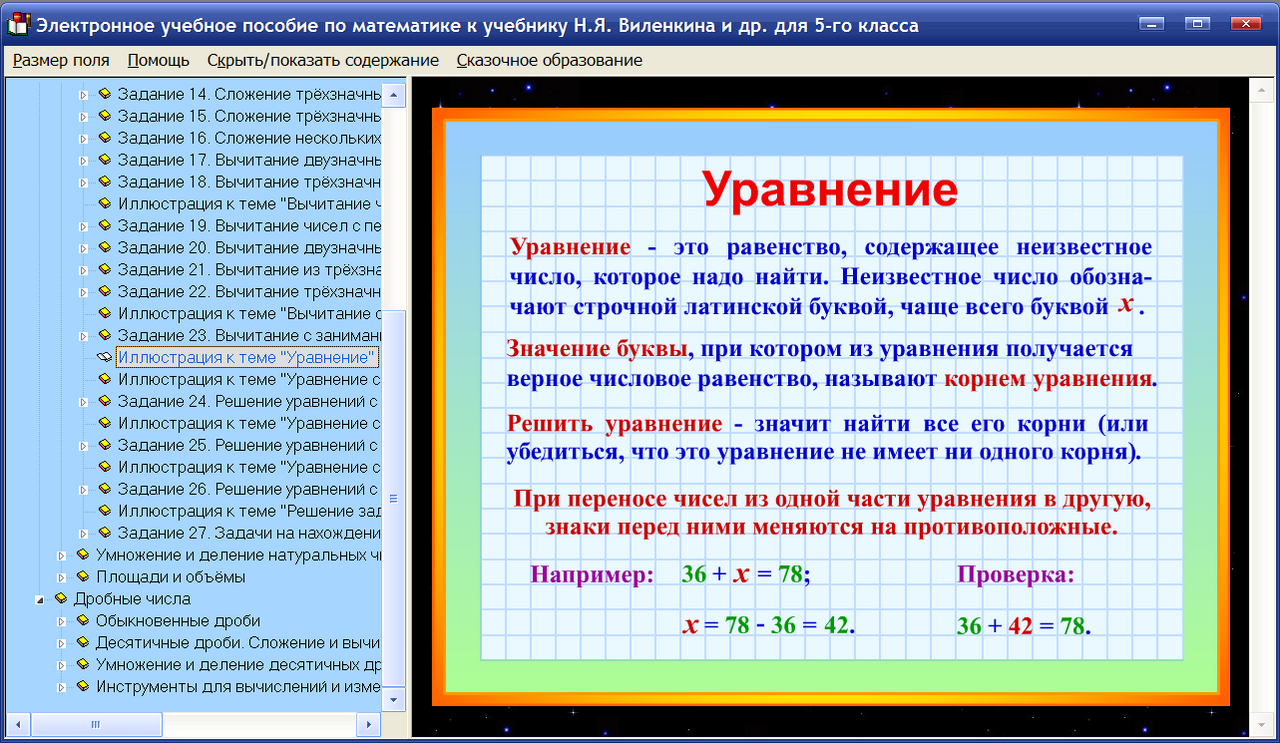
3. Гейм «3аморочки из бочки» (10 мин)
Учитель: Переходим к следующему гейму. Вот в нем вам может помочь удача. В мешочке находятся 9 бочонков. Каждый из 8 номеров соответствует номеру задачи, которую вам нужно будет решить. Вытаскивать «заморочки» начинает команда, которая проигрывает. После прочтения задачи у команды есть 1 минута на совещание, после этого она дает ответ. Если ответили верно, то прибавляется 2 балла. Если же ответ неверный, то ответить могут соперники, но они за правильный ответ получают только 1 балл. Но наша игра — «Счастливый случай», поэтому в мешочке под 9-ым номером прячется 2 балла. То есть, если вы вытащите «заморочку» под 9 номером, то без решения задачи получаете 2 балла.
Задачки-«заморочки»:
1. Кирпич весит 2 кг и еще полкирпича. Сколько весит кирпич? (3 кг)
2. Пара лошадей пробежала 40 км. Сколько километров пробежала каждая лошадь? (40 км)
3. Сейчас 6 часов вечера. Какая часть суток прошла? (3/4)
4. Пять лет назад брату и сестре вместе было 8 лет. Сколько лет им будет вместе через 5 лет? (13)
Пять лет назад брату и сестре вместе было 8 лет. Сколько лет им будет вместе через 5 лет? (13)
5. На столе лежали конфеты в кучке. Две матери, две дочери да бабушка с внучкой взяли конфет по одной штучке, и не стало этой кучки. Сколько было конфет в кучке? (3)
6. Зайцы пилят бревно. Они сделали 12 распилов. Сколько получилось чурбаков? (13)
7. К Айболиту на прием пришли звери. Все, кроме двух, собаки. Все, кроме двух, кошки. Все, кроме двух, зайцы. Сколько животных пришло к Айболиту? (3)
8. У семи братьев по одной сестре. Сколько всего детей? (8)
После проведения гейма подсчитываются общие баллы.
4. Гейм «Темная лошадка» (7 мин)
Учитель: Следующий гейм называется «Темная лошадка». Его проведет преподаватель, который в течение всего учебного года заботился о вас, помогал вам, часто виделся с вашими родителями, и многие праздники вы проводили вместе с ним.
— Приглашается классный руководитель. Тем, кто угадал, кого пригласили, прибавляется 1 балл. Затем классный руководитель 6в класса Петросян Елена Карленовна задает по два вопроса каждой команде. За правильный ответ прибавляется еще по 2 балла.
Затем классный руководитель 6в класса Петросян Елена Карленовна задает по два вопроса каждой команде. За правильный ответ прибавляется еще по 2 балла.
Подсчитываются баллы за проведенные конкурсы.
5. Гейм «Ты — мне, я — тебе» (6 мин)
Учитель: А теперь пришла пора показать себя капитанам команд.
Каждый из них может задать сопернику по два вопроса. Отвечать могут только капитаны. Если на вопрос ответили правильно, то получаете 2 балла. Если же ответ неверный, то 1 балл зарабатывает капитан, который задавал вопрос, но только после того, как сам дает правильный ответ.
Подсчитываются баллы.
6. Гейм «Гонка за лидером» (6 мин)
Учитель: Ну, а теперь заключительный гейм: «Гонка за лидером».
Начнет его команда, которая проигрывает по очкам. У нее есть возможность вырваться вперед. В течение 1минуты будут задаваться вопросы. За это время команда должна ответить на как можно большее количество вопросов. Правила первого гейма переносятся на этот. Отвечает тот, на кого показывает капитан. Каждый участник отвечает не более, чем на 2 вопроса. Верный ответ — это 1 балл.
Правила первого гейма переносятся на этот. Отвечает тот, на кого показывает капитан. Каждый участник отвечает не более, чем на 2 вопроса. Верный ответ — это 1 балл.
Вопросы первой команде:
1. Сколько сантиметров в 1 дециметре? (10)
2. Чему равна площадь квадрата со стороной 5 см (25 см2)
3. Какое название имеет 1/2 дробь? (Половина)
4. Сколько процентов составляет 2 от 200? (1 %)
5. Округлить 5,7 до единиц. (6)
6. Имеет ли длину отрезок? (Да)
7. В чем измеряются углы? (В градусах)
8. Умножение, на какое число дает все время само число? (На 1)
9. Найти два пятых от 30. (12)
Вопросы второй команде:
1. Сколько метров в одном километре? (1000)
2. Чему равен периметр квадрата со стороной 2см? (8см)
3. Какое название имеет1/4 дробь — ? (Четверть)
4. Сколько процентов составляет 100 от 200? (50%)
5. Округлить 12,3 до единиц. (12)
(12)
6. Имеет ли длину луч? (Нет)
7. В чем измеряются отрезки? (В см)
8. Деление, на какое число дает 1? (На само себя)
9. Найти две третьих от 90. (60)
Подсчитываются баллы. Разбираются вопросы, на которые были даны неправильные ответы.
7. Подведение итогов (3 мин)
Подсчитать баллы и похвалить выигравшую команду. Разобрать темы, на которые были ошибки, и дать по этим темам задание на дом. Похвалить детей за активность и дружбу между собой. Поздравить победителей.
Урок- викторина 6 класс
Урок- викторина 6 класс
Автор: edu1
Методическая копилка — Математика
Урок- викторина 6 класс.
Цели урока:
- Образовательная: закрепить и обобщить основной и дополнительный материал к учебнику математики 6 класса в форме викторины.

- Развивающая: развивать умения самостоятельно воспринимать и осознавать пройденный материал.
- Воспитательная: воспитывать интерес к предмету в целом, вкус к успеху и способности к творчеству.
Ход урока.
1. Организационный момент.
Друзья мои, я очень рада
Войти в приветливый наш класс.
И для меня уже награда
Внимание ваших умных глаз.
Я знаю, каждый в классе гений,
Но без труда талант не впрок.
Возьмём же ручки и мелок
И вместе сочиним урок.
2. Мотивация урока.
— Здравствуйте, ребята! Садитесь! Сегодня у нас с вами необычный урок, сегодня у нас викторина, по результатам которой получим лучшего ученика класса по математике, самого эрудированного, смекалистого, про которого можно будет сказать: «У него острый глаз, цепкий ум, твёрдая рука и много других полезностей».
Итак, НАЧИНАЕМ!!!
3. Актуализация опорных знаний.
Конкурс “Веселый счет”. От каждой команды представить по одному участнику. Команда, участник которой затратит меньше времени, получат жетон. (Необходимо найти все числа от 1 до 24.)
Конкурс Марафон:
|
Вопрос |
Ответ |
|
Площадь прямоугольника со сторонами 15 и 5 см? |
75 см |
|
Наименьшее число, кратное 11? |
11 |
|
Число, которое составляет 1/9 от 153? |
17 |
|
Среднее арифметическое чисел 16, 27, 98? |
47 |
|
Площадь квадрата, периметр которого 36 см? |
81 см |
|
Самое маленькое четырехзначное число, в записи которого цифры различны? |
1023 |
|
3/5 часа, выраженные в минутах? |
36 минут |
|
Участок, площадью 1 ар? |
Сотка |
|
Точка, равноудаленная от всех точек окружности? |
Центр |
|
Отрезок ломаной? |
Звено |
|
Математический знак, используемый для записи чисел? |
Запятая |
|
Совокупность делений на линейках различных форм? |
Шкала |
|
Расстояние, измеряемое между концами отрезка? |
Длина |
|
Запись, состоящая из одной или нескольких цифр? |
Число |
|
Значение буквы, при котором уравнение превращается в верное числовое равенство? |
Корень |
|
Число, которое не может быть делителем? |
Ноль |
|
Угол, образованный двумя дополнительными лучами? |
Развернутый |
|
Выражение, показывающее соотношение между величинами? |
Пропорция |
|
Место, занимаемое цифрой в записи числа? |
Разряд |
|
Равенство, устанавливающее связь между независимой искомой величиной и известными величинами? |
Уравнение |
|
Замена числа его приближенным значением? |
Округление |
|
Величина, измеряемая в кубических единицах? |
Объем |
|
Выражение, представляющее произведение одинаковых множителей? |
Степень |
|
Квадрат наименьшего простого числа |
4 |
|
Отношение длины окружности к длине ее диаметра? |
Число |
|
Слагаемые, имеющие одинаковую буквенную часть? |
Подобные |
|
Дробь, числитель которой меньше ее знаменателя? |
Правильная |
|
Прямоугольный параллелепипед, все измерения которого равны? |
Куб |
|
Все целые и дробные числа? |
Рациональные |
|
60 часть градуса? |
Минута |
|
1/180 часть развернутого угла? |
Градус |
|
10000 м |
гектар |
|
Часть, которую составляет 20%от числа? |
1/5 |
|
Множество точек угла, равноудаленных от его сторон? |
Биссектриса |
|
Число, показывающее, сколько квадратных единиц содержится в плоской фигуре? |
Площадь |
|
Дробное выражение, числитель и знаменатель которого не имеют общих делителей, кроме1? |
Несократимая дробь |
Конкурс «Шарады».
Необходимо отгадать четыре шарады. Кто быстрее отгадает – получает жетон.
*Предлогом стоит в моем начале,
В конце же — загородный дом.
А целое мы все решали
И у доски, и за столом.
(За + Дача = Задача)
* Игра — в ней лошади нужны,
К игре проступок пристегни.
И называй, дружочек, смело
То, что давно уже не цело.
(Поло + Вина = Половина)
* Первый можно завязать,
Если галстук папин взять.
А второй, словарь листая, —
Мера скорости морская.
(Узел)
* Две ноты — два слога,
А слово — одно,
И меру длины
Означает оно.
(Ми + Ля = Миля)
Практический конкурс:
№1. Имеется два сосуда: один на 3 литра, а другой на 2 литра.
Как с помощью этих сосудов отмерить 4 литра воды из водопроводного крана?
№2. На складе имеются гвозди в ящиках по 16 кг , 17кг , 40 кг.
Может ли кладовщик отпустить 50 кг гвоздей, не вскрывая ящик?
№3. Корзина с 3 яблоками.
Надо поделить между 3 друзьями, чтобы одно яблоко осталось в корзине?
(За каждое задание по 2 баллов).
Конкурс «Дальше… дальше»
Время зря ты не теряй,
на вопросы отвечай!
Вопросы:
1. Предмет для демонстрации симметрии. (Зеркало)
2. Цифровой знак, обозначающий отсутствие величины. (0)
3. Чему равен вес соли, которую надо съесть, чтобы хорошо узнать человека? (Пуд)
4. Третья степень числа. (Куб)
5. Французский миллиард. (Биллион)
6. Приплюснутый круг (овал).
7. Английская мера длины, давшая имя героине известной сказки. (Дюйм)
8. Заменитель числа 1 при счёте. (Раз)
9. Шесть квадратов на двенадцати рёбрах. (Куб)
10. Между плюсом и минусом. (Ноль)
11. Единица измерения углов. (Градус)
12. Дуэт в кубе. (Восемь)
13. Этим математическим способом размножаются простейшие организмы. (Деление)
(Деление)
14. Нахождение неизвестного. (Решение)
15. Единица со свитой из шести нулей. (Миллион)
16. Эту неотъемлемую часть геометрической фигуры можно превратить в полезное ископаемое при помощи мягкого знака. (Угол)
17. Что такое жидкий килограмм? (Литр)
18. Вопрос для решения. (Задача)
19. Какую скорость развивает во время полёта птица Эму? (Страусы не летают)
20. Сколько граней у шестигранного карандаша? (8)
21. Какую часть от часа составляет 5 минут? (5/60 или 1/12)
Конкурс «Ребусы»
Кроссворд.
Ваша задача – как можно быстрее разгадать кроссворд.
Вопросы:
1. Числа, употребляемые при счете предметов. (Натуральные)
2. Четырехугольник с прямыми углами. (Прямоугольник)
3. Цифры 0, 1, 2, 3… (Арабские)
4. Наглядное представление разных числовых данных. (Диаграмма)
5. Результат от деления. (Частное)
(Частное)
6. Число, показывающее, на сколько равных частей разделено целое. (Знаменатель)
7. Сумма одинаковых слагаемых. (Произведение)
8. Закон сложения. (Переместительный)
9. Площадь квадрата со стороной 100м. (Гектар)
10. Отрезок, длина которого равна 1. (Единичный)
11. Угол меньше прямого. (Острый)
Ключевое слово: Лобачевский.
Подведение итогов
Команда победителей определяет лучшего игрока, которому присваивается звание «Лучшего математика класса».
Давайте, ребята, давайте считать:
Делить, прибавлять, умножать, вычитать.
Смекалку свою проявите:
Считайте, рисуйте, чертите!
Вы все молодцы! Вы все удальцы!
И пусть на года любимой всегда
Для вас математика будет!
скачать документ
ГДЗ по математике 6 класс контрольно-измерительные материалы Попова Решебник
Автор: Попова Л. П.
П.Издательство: ВАКО 2017
Тип книги: Контрольно-измерительные материалы (КИМ)
Если вам тяжело дается учеба, то можно заглянуть на наш замечательный сервис и отыскать там ГДЗ контрольно-измерительные материалы по математике 6 класс Попова . Конечно, все знают, что самые большие трудности и проблемы у всех возникают с царицей наук. И дело тут не в том, что она неинтересная, скучная или ненужная. Просто для того, чтобы быть успешным, надо учить массу формул, законов, теорем, аксиом, постулатов. Также важно научиться применять эту пройденную теорию на практике, а для этого, в первую очередь, нужно ее понимать, вникать в это. К сожалению, не всегда у учителя получается за 40-45 минут разъяснить обширную и сложную тему всем. Разумеется, некоторые ребята остаются неподготовленными и не знают, как делать работу на дом. В таких ситуациях на помощь и приходит подспорье, доступ к которому открыт круглосуточно!
Также важно научиться применять эту пройденную теорию на практике, а для этого, в первую очередь, нужно ее понимать, вникать в это. К сожалению, не всегда у учителя получается за 40-45 минут разъяснить обширную и сложную тему всем. Разумеется, некоторые ребята остаются неподготовленными и не знают, как делать работу на дом. В таких ситуациях на помощь и приходит подспорье, доступ к которому открыт круглосуточно!
Какую пользу можно извлечь из учебно-методического комплекса с кимами по математике за шестой класс от Поповой
Предложенный решебник был выпущен знаменитым издательством «Мнемозина» в 2011 году. А его созданием занимались квалифицированные и известные специалисты. Они много лет жизни посвятили преподаванию в школах, гимназиях, лицеях, а некоторые – даже в высших учебных заведениях. Благодаря этому опыту у них есть точное и ясное представление о том, как нужно подавать материал детям, даже самым отстающим. Ведь любого ребенка можно научить и превратить в отличника, главное – желание и старания. Список преимуществ онлайн-решебника по математике контр-измер. матер. за шестой класс от Поповой:
Список преимуществ онлайн-решебника по математике контр-измер. матер. за шестой класс от Поповой:
- помогает развить метапредметные, предметные и личностные универсальные учебные действия;
- полное соответствие с оригинальным печатным учебником и с его структурой;
- экономия времени на проверку д/з, что позволит уделять больше внимания другим не менее важным занятиям и секциям;
- на сайте представлены пояснения, рассортированные по категориям. Это позволяет без проблем найти нужные ответы и справиться с задачей.
Тест 1. Варианты
Тест 2.
 Варианты
ВариантыТест 3. Варианты
Тест 4. Варианты
Тест 5. Варианты
Тест 6. Варианты
Тест 7. Варианты
Тест 8. Варианты
Тест 9. Варианты
Тест 10. Варианты
Тест 11. Варианты
Тест 12.
 Варианты
ВариантыТест 13. Варианты
Тест 14. Варианты
Тест 15. Варианты
Тест 16. Варианты
Тест 17. Варианты
Тест 18. Варианты
Тест 19. Варианты
Тест 20. Варианты
Тест 21. Варианты
Тест 22.
 Варианты
ВариантыТест 23. Варианты
Тест 24. Варианты
Тест 25. Варианты
Тест 26. Варианты
Тест 27. Варианты
Тест 28. Варианты
Тест 29. Варианты
Тест 30. Варианты
Тест 31. Варианты
Тест 32.
 Варианты
ВариантыТест 33. Варианты
Тест 34. Варианты
Контрольные работы
КР-1. Варианты
КР-2. Варианты
КР-3. Варианты
КР-4. Варианты
КР-5. Варианты
КР-6. Варианты
КР-7. Варианты
КР-8.
 Варианты
ВариантыКР-9. Варианты
КР-10. Варианты
КР-11. Варианты
КР-12. Варианты
КР-13. Варианты
КР-14. Варианты
Итоговая контрольная работа. Варианты
На любой ступени обучения школьнику требуется помощь по учёбе. Но иногда ребёнок не хочет получать её от взрослых, желает разобраться самостоятельно. Такое возникает чаще всего в среднем звене ввиду подросткового возраста. Конечно, мамы и папы переживают, некоторые даже нанимают репетиторов. Но ведь далеко не каждая семья может позволить себе такую роскошь. Поэтому мы и предлагаем вам абсолютно бесплатный ресурс, который в любой ситуации сможет помочь.
Такое возникает чаще всего в среднем звене ввиду подросткового возраста. Конечно, мамы и папы переживают, некоторые даже нанимают репетиторов. Но ведь далеко не каждая семья может позволить себе такую роскошь. Поэтому мы и предлагаем вам абсолютно бесплатный ресурс, который в любой ситуации сможет помочь.
Почему всем так нравится сборник по математике КИМ за 6 класс от Поповой
Чтобы найти ключ, выполняя домашнее задание, достаточно указать страницу, соответствующую школьному изданию. При выполнении д/з школьнику понадобится оригинальная тетрадь и онлайн-книга, которую можно открыть на телефоне. При выборе номера ученик получит подробное письменное решение и верные ответы. Любой пользователь легко разберется в представленном материале. Наглядные схемы, яркие рисунки помогут донести информацию в более понятной форме. К тому же, навигация у сайта удобна и понятна, в ней сможет разобраться даже младшеклассник. В связи со всем вышеперечисленным процесс обучения станет приятным и веселым, а не скучным и однообразным. Ведь с помощью этого учебно-методического комплекса учитель-предметник сможет составлять интересные и увлекательные задания, а не просто давать упражнения из оригинального печатного учебника. В итоге даже те дети, которые далеко не в восторге от царицы наук, начнут включаться в учебный процесс и познавать все тайны и хитрости. Ведь лучшая награда для преподавателя – это успешные и положительные результаты его учащихся. Также мамы и папы будут радоваться, подписывая каждую неделю дневник своему чаду. Не думайте, что ребята будут просто бездумно переписывать всю инф-цию, объясните им правила работы с онлайн-гдз, и успех не заставит долго ждать! А теперь давайте обратимся к преимуществам, о которых мы еще не успели сказать:
Ведь с помощью этого учебно-методического комплекса учитель-предметник сможет составлять интересные и увлекательные задания, а не просто давать упражнения из оригинального печатного учебника. В итоге даже те дети, которые далеко не в восторге от царицы наук, начнут включаться в учебный процесс и познавать все тайны и хитрости. Ведь лучшая награда для преподавателя – это успешные и положительные результаты его учащихся. Также мамы и папы будут радоваться, подписывая каждую неделю дневник своему чаду. Не думайте, что ребята будут просто бездумно переписывать всю инф-цию, объясните им правила работы с онлайн-гдз, и успех не заставит долго ждать! А теперь давайте обратимся к преимуществам, о которых мы еще не успели сказать:
- выполнение внеклассных задач проходит качественнее и быстрее, освобождается время для хобби, посещений кружков или просто для активного отдыха;
- при самостоятельной подготовке домашнего задания учащийся может проверить свои знания и восполнить пробелы в памяти;
- возможность использование ресурса с любого электронного устройства с выходом в интернет.

Содержание пособия по математике для шестого класса авторы: Попова Л. П.
Книга включает главы и параграфы, обязательные для усвоения:
- Простые и составные числа.
- Приведение дробей к общему знаменателю.
- Прямая и обратная пропорциональные зависимости.
Обзор 6 класса по Математике
Новый уровень уже появился на нашей платформе, поэтому будем знакомиться. Наш традиционный обзор курса расскажет родителям и ученикам, что будет их ждать во время нового этапа обучения. Поэтому, если хотите узнать больше о самых интересных задания уровня, — продолжайте читать!
Почему курс стоит внимания?
Для школы 6 класс по математике — это особенно важный этап. Ученик отходит от понятия математики и становится ближе к алгебре и геометрии. Хотя наша платформа не планирует в будущем делить эти два понятия, уровень с 6 класса нацелен на активную подготовку ученика к этому этапу. Курс состоит и из алгебраических аспектов, и из геометрических.
Курс состоит и из алгебраических аспектов, и из геометрических.
Платформа learning.ua — это не альтернатива школе, а ее поддержка, прогресс и постоянное развитие. Поэтому необходимо понимать, что наш курс — это прогрессивный метод закрепления и совершенствования знаний и навыков.
Именно этот уровень целесообразно изучать ученикам от 11 до 12 лет. В случае необходимости, возрастные рамки можно менять. Однако, ни в коем случае не стоит спешить или давить на ребенка.
Мы не меняем общие стандарты: яркие персонажи, задания для углубленного изучения, бонусы за правильно выполненные упражнения и решения к задачам (за неправильные ответы) — все это традиционно ждет учеников нашего портала. Общее количество заданий на уровне — 333. Для того, чтобы более подробно рассмотреть, какие задачи появились на уровне, мы подготовили обзор нескольких из них. Давайте исследовать:
Н.11 Растворы
Это упражнение стоит первым в обзоре не случайно. Оно относится к разделу «Процентов» и отражает то, что мы закладывали в весь курс. Это задание не просто учит ребенка ориентироваться в процентах, оно является практическим и прикладным. Тема растворов расскажет ученику о том, как может меняться консистенция смеси в зависимости от того, сколько процентов того или иного ингредиента добавили. С этим сталкивается и мама, когда готовит пищу, и папа, когда строит дом, и врач, когда дает рецепт лекарства. Поэтому прикладная часть действительно важна. В этом же задании ребенок более подробно рассмотрит проценты и изучит аспекты их применения.
Оно относится к разделу «Процентов» и отражает то, что мы закладывали в весь курс. Это задание не просто учит ребенка ориентироваться в процентах, оно является практическим и прикладным. Тема растворов расскажет ученику о том, как может меняться консистенция смеси в зависимости от того, сколько процентов того или иного ингредиента добавили. С этим сталкивается и мама, когда готовит пищу, и папа, когда строит дом, и врач, когда дает рецепт лекарства. Поэтому прикладная часть действительно важна. В этом же задании ребенок более подробно рассмотрит проценты и изучит аспекты их применения.
В.3 Выбираем степени, значения которых являются отрицательными (положительными)
Ученик 6 класса уже знаком с рациональными числами. Теперь он знает, что существуют не только положительные числа и ноль, но и отрицательные. Это понятие позволяет усвоить числовая прямая, которая показывает, что положительные и отрицательные числа расположены по обе стороны от нуля. Каждое положительное число имеет соответствующее отрицательное. Как известно, возведение в степень — это действие умножения. Ребенок должен знать, каким образом выполнять действия с положительными и отрицательными числами. Это упражнение тренирует ученика сразу видеть и понимать, каким будет число в финале (даже без выполнения действий). Особенно это касается знака числа. Ребенку достаточно выбрать из таблицы те выражения, которые в результате останутся отрицательными.
Каждое положительное число имеет соответствующее отрицательное. Как известно, возведение в степень — это действие умножения. Ребенок должен знать, каким образом выполнять действия с положительными и отрицательными числами. Это упражнение тренирует ученика сразу видеть и понимать, каким будет число в финале (даже без выполнения действий). Особенно это касается знака числа. Ребенку достаточно выбрать из таблицы те выражения, которые в результате останутся отрицательными.
П. 4 Древние единицы измерения веса
Единицы измерения — достаточно важный аспект в математике. Более того, они нужны для легкого ориентирования в повседневной жизни. Сколько сантиметров ткани нужно отрезать, с какой скоростью ехать машине и сколько килограммов помидоров необходимо взвесить. Однако, все эти единицы формировались в течение многих веков и претерпевали изменения. Этим упражнением мы хотим погрузить ребенка в прошлое, в историю народа. Перед учеником является таблица, которая с одной стороны содержит Злотник (старинные русские единицы измерения массы, 1 Злотник — 4,27 г), а с другой — граммы. Задача ученика — распределить между собой категории таблицы так, чтобы масса злотников соответствовала количеству граммов. Для того, чтобы 6-классник не растерялся — над таблицей есть знак (подсказка, которая поможет в решении задачи).
Задача ученика — распределить между собой категории таблицы так, чтобы масса злотников соответствовала количеству граммов. Для того, чтобы 6-классник не растерялся — над таблицей есть знак (подсказка, которая поможет в решении задачи).
Р.1 Временные промежутки
Время — это одно из важнейших понятий в жизни человека. Кроме того, чтобы понимать единицы его измерения, нужно уметь рассчитывать промежутки времени так, чтобы планировать свой день. Никто не любит опозданий, поэтому это упражнение может удачно помочь ученику и в личном тайм-менеджменте.
На картинке ребенок видит девушку (Лесю). Задача состоит в том, чтобы помочь Лесе выбрать время начала физических упражнений. При этом, необходимо посчитать, сколько девушка потратит на все упражнения в целом, а затем выбрать целесообразное время начала активности. Учитывая, что успеть Леся должна до 14:15.
С 3 Работа по прайс-листу
В нашем мире технологий словарный запас человека должен постоянно пополняться новыми и современными словами. Наша платформа хочет, чтобы дети были готовы к взрослой жизни и работе, поэтому мы готовы толковать ученику, что такое прайс-лист. Благодаря этой задаче у ребенка формируется общее видение понятия прайс-листа. Он поймет, что у каждого товара есть своя цена, которая должна ему соответствовать. К тому же, упражнение исключительно прикладное. 6-классник больше никогда не растеряется в магазине или на рынке.
Наша платформа хочет, чтобы дети были готовы к взрослой жизни и работе, поэтому мы готовы толковать ученику, что такое прайс-лист. Благодаря этой задаче у ребенка формируется общее видение понятия прайс-листа. Он поймет, что у каждого товара есть своя цена, которая должна ему соответствовать. К тому же, упражнение исключительно прикладное. 6-классник больше никогда не растеряется в магазине или на рынке.
С.4 Математика в профессиях
Важно понимать, что школа — это не просто место, которое научит ребенка теоретическим основам и принципам. Это этап жизни, который должен научить ребенка понимать, как двигаться дальше. Ориентироваться в деньгах, работе, разобраться в том, сколько можно зарабатывать и что за этим стоит. То есть ученик должен иметь полную базу для взрослой и осознанной жизни. С этой целью мы создали задание, которое покажет ребенку, каким образом можно рассчитать собственную заработную плату. Примером для этого станет водитель, который будет работать 2. 5 ч.
5 ч.
Ф.4 Свойства сложения и умножения для функций
Функции — это, пожалуй, одни из самых главных тренажеров математики. Они не всегда требуют числового решения, однако, они требуют широких знаний в математике. Это касается всех аспектов: умножение, деление, сложение и вычитание, а также их свойств. Ученик должен вспоминать все понятия и приемы, которые изучал в течение многих лет. Конкретно это упражнение показывает ребенку два выражения: одно сложное, а второе уже упрощенное. Задача ученика — проанализировать приведенные выражения и указать, благодаря каким свойствам образовалось второе выражение.
Ц.4 Геометрия в жизни
Математика — достаточно важная наука. Некоторые разделы, которые изучает ребенок, действительно пригодятся в жизни, они развивают мыслительные процессы и умственную деятельность. Однако, большинство тем все-таки прикладные. Особенно геометрия. Простая задача — выбрать скатерть для стола площадью 5 м2. А сделать это можно только понимая законы геометрии! На экране перед учеником содержится геометрическая фигура — новая для каждого следующего этапа. Некоторые ее стороны указаны, некоторые — нет. Ученику нужно проанализировать приведенные данные и, учитывая их, ответить на поставленный вопрос.
А сделать это можно только понимая законы геометрии! На экране перед учеником содержится геометрическая фигура — новая для каждого следующего этапа. Некоторые ее стороны указаны, некоторые — нет. Ученику нужно проанализировать приведенные данные и, учитывая их, ответить на поставленный вопрос.
Д.2 Графическое изображение десятичной дроби
Раздел «Дроби» снова говорит ученику о том, что существуют не только целые числа, но и дробные. Причем, это могут быть обычные дроби, неправильные, смешанные и десятичные. Эта задача будет касаться последних. Ученик видит перед собой десятичную дробь, и его задача состоит в том, чтобы распределить все её составляющие на разряды. Понятие разрядности ребенок изучает ещё с первого класса. Такая задача научит ученика легко и быстро записывать подобные числа, ориентироваться в том, как они читаются.
Я.5 Решаем задачи на вероятность
Вероятности — это еще одна довольно важная тема по математике. Она позволяет рассчитать, сколько шансов существует у того или иного события, чтобы произойти. Это можно использовать и в жизни. Иногда вероятности могут давать погрешность, но на то они и вероятности, что рассчитывают приблизительные шансы. В этом упражнении перед учеником стоит задача вычислить определенную вероятность. Например, в коробке есть 7 шариков, и нужно понять, какой будет вероятность получить один определенного цвета. Для этого необходимо создать дробь, в знаменателе которого — общее количество шариков в коробке, а в числителе — количество всех шаров определенного цвета. Стоит помнить о том, что дроби могут сокращаться.
Она позволяет рассчитать, сколько шансов существует у того или иного события, чтобы произойти. Это можно использовать и в жизни. Иногда вероятности могут давать погрешность, но на то они и вероятности, что рассчитывают приблизительные шансы. В этом упражнении перед учеником стоит задача вычислить определенную вероятность. Например, в коробке есть 7 шариков, и нужно понять, какой будет вероятность получить один определенного цвета. Для этого необходимо создать дробь, в знаменателе которого — общее количество шариков в коробке, а в числителе — количество всех шаров определенного цвета. Стоит помнить о том, что дроби могут сокращаться.
В этом обзоре лишь 10 из 333 упражнений нашего уровня. Но, как видите, они уже обещают огромное количество интересностей. Поэтому скорее присоединяйтесь к нам!
Темы исследовательских проектов по математике в 6 классе
На страничке представлены темы проектов по математике для 6 класса школы, по которым учащимися предлагается проведение исследований, связанных с делимостью чисел, наибольшим общим делителем и наименьшим общим кратным, сложением и вычитанием обыкновенных дробей с разными знаменателями, умножением и делением обыкновенных дробей.
Представленные темы проектов по математике для 6 класса позволяют в процессе исследовательской работы более углубленно изучить основные арифметические действия с отрицательными числами, линейные уравнения с одной неизвестной, прорешать более сложные задачи.
Руководитель проекта поможет подстроить представленные темы исследовательских работ по математике для 6 класса школьникам под специфику работы, учитывая индивидуальные особенности автора проекта.
Темы исследовательских работ по математике для 6 класса
Примерные темы исследовательских работ по математике для учащихся 6 класса:
Авторские задачи для учащихся 6-го класса по теме «Проценты».
Алгебра в арифметике.
Арифметика Магницкого
Астрология на координатной плоскости
Влияние математических действий на аликвоты
Веселые математические задачки
Геометрия в национальном костюме народов России.
Действительные числа.
Делимость чисел
Делимость чисел и метод подобия.
Делимость чисел. Принцип Дирихле.
Десятичные дроби
Десятичные дроби и действия над десятичными дробями.
Дроби и единицы измерения.
Дроби и проценты
Дроби. Сравнение дробей.
Египетские дроби
Его величество процент.
Загадочный мир пропорций!
Задачи на делимость чисел.
Задачи на десятичную запись числа.
Задачи на переливание жидкости
Задачи о четных и нечетных числах.
Занимательная математика.
Занимательные задачи по математике для учащихся 6-х классов.
Золотая пропорция
Золотое сечение — высшее совершенство.
Золотое сечение в математике.
Знаменитые задачи древности. Трисекция угла.
Из истории возникновения математических знаков и символов.
Иллюстрации и решения занимательных задач по математике для учеников 6-го класса.
Исследование признаков делимости чисел
История календаря.
История модуля
История Москвы в задачах.
Как люди научились считать?
Как с помощью НОК и НОД решаются разнообразные и интересные задачи.

Координатная плоскость и знаки зодиака
Координатная плоскость и шахматы
Координатная плоскость в рисунках.
Кратные числа
Леонид Филиппович Магницкий.
Летопись открытий в мире чисел и фигур.
Магический квадрат — магия или наука
Магия чисел и знаков.
Магические числа
Масштаб и его применение.
Масштаб. Работа с компасом, GPS-навигация
Математика на клетчатой бумаге
Математическая модель вышивания на окружности.
Математические головоломки.
Меры времени.
Метрическая система мер.
Многоугольники.
Модуль и его свойства
Модуль числа.
«Модуль» – пособие в помощь ученику.
Наименьшее общее кратное взаимно простых чисел.
Начальные понятия теории чисел для шестиклассников.
Начальные сведения о модуле.
НОД и НОК и их практическое применение.
НОД и НОК при решении задач.
Темы проектов по математике для 6 класса
Примерные темы проектов по математике для учащихся 6 класса:
Орнаментальное и геометрическое искусство М.
 Эшера.
Эшера.Откуда возникла геометрия?
Отрицательные и положительные числа.
По жизни с дробями
Положительные и отрицательные числа вокруг нас.
Приемы быстрого счета.
Приемы удобного счета.
Признаки делимости многозначных чисел на однозначное число.
Признаки делимости натуральных чисел на числа от 2 до 25 и на 50.
Признаки делимости натуральных чисел.
Признаки делимости чисел.
Применение признаков делимости при решении задач.
Принцип Дирихле.
Про любовь к математике и отрицательные числа.
Пропорции.
Пропорция в жизни человека.
Пропорция в работах великого Леонардо да Винчи.
Пропорция и золотое сечение.
Простые и составные числа.
Решето Эратосфена.
Связь НОК и НОД.
Секрет происхождения арабских цифр
Системы счисления.
Системы счисления разных цивилизаций
Сложение дробей с разными знаменателями.
Сокращение дробей
Сравнение, сложение и вычитание дробей с разными знаменателями.

Сравнения как метод исследования делимости натуральных чисел.
Старинные задачи на дроби
Старинные задачи на составление уравнений.
Старинные задачи.
Старинные математические задачи
Теория вероятностей в задачах.
Теория делимости
Треугольные числа.
Трудные задачи на движение.
Трудные задачи на на работу.
Удивительный мир периодических дробей.
Уравнения с одной переменной.
Числа знакомые и незнакомые.
Числа и их делимость.
Эти «непростые» простые числа.
Перейти к разделу:Если страница Вам понравилась, поделитесь в социальных сетях:
Исследовательские проекты по математике
Темы проектов по математике по фгос
Учебная программа по математике для 6-х классов — Общие основные уроки и тесты
Что такое математика в шестом классе?
В шестом классе ученики изучают ключевые понятия по мере продвижения к алгебре в средней школе. Соотношения и пропорции возникают как новая область обучения, где студенты исследуют и рассуждают с помощью соотношений и оценок для решения задач. Шестиклассники также впервые исследуют отрицательные числа и завершат свое изучение рациональной системы счисления, прежде чем оперировать всеми рациональными числами в седьмом классе.Работа с числовыми выражениями распространяется на алгебраические выражения, которые заставляют студентов решать одношаговые уравнения и неравенства. Студенты также продолжат изучение площади и объема геометрических фигур и узнают, как статистику можно использовать для лучшего понимания данных о нашем мире.
Шестиклассники также впервые исследуют отрицательные числа и завершат свое изучение рациональной системы счисления, прежде чем оперировать всеми рациональными числами в седьмом классе.Работа с числовыми выражениями распространяется на алгебраические выражения, которые заставляют студентов решать одношаговые уравнения и неравенства. Студенты также продолжат изучение площади и объема геометрических фигур и узнают, как статистику можно использовать для лучшего понимания данных о нашем мире.
Как мы заказывали блоки?
Шестиклассники начинают свой год с раздела по коэффициентам. В блоке 1 «Понимание и представление соотношений » учащиеся имеют возможность изучить совершенно новую для них концепцию, опираясь при этом на навыки рассуждений на основе мультипликативных сравнений, полученные в предыдущих классах.Студенты изучают как конкретные, так и абстрактные представления, включая двойные числовые линии и таблицы, которые они смогут использовать в течение года.
В Блок 2, Единичные ставки и процент студенты продолжают изучение соотношений, расширяя концепцию до ставок и процентов. Учащиеся используют представления, которые они выучили в Блоке 1, для решения более сложных задач, связанных с соотношением, оценкой и процентом. Позже в Модуле 6 студенты вернутся к решению процентных задач при изучении решения уравнений.
В курсах , блок 3, многозначное и дробное вычисление , и , блок 4, рациональные числа , учащиеся сосредотачиваются на системе счисления, оттачивая навыки, которые они развивали в предыдущих классах, с беглостью, применяя понимание к новым вычислениям с дробями. и расширяют свое понимание мира чисел за счет включения минусов. Включение этих единиц в этот момент в году дает возможность исправить любые связанные с предыдущим уровнем навыков и концепции на ранней стадии, а также дает время для наращивания и интеграции этих навыков в будущие единицы.
Раздел 5, Числовые и алгебраические выражения и Раздел 6, Уравнения и неравенства , готовит учащихся к будущей работе с более сложными уравнениями в седьмом и восьмом классах. Студенты опираются на свою работу с системой счисления из блока 3, чтобы поддерживать свою работу с числовыми выражениями и решением уравнений. В Модуле 6 учащиеся пересматривают концепции соотношений из первых двух модулей, представляя отношения в координатной плоскости и с помощью уравнений. Учащиеся также применяют свои навыки уравнения к задачам на процентное соотношение в качестве еще одного метода решения задач.
Студенты опираются на свою работу с системой счисления из блока 3, чтобы поддерживать свою работу с числовыми выражениями и решением уравнений. В Модуле 6 учащиеся пересматривают концепции соотношений из первых двух модулей, представляя отношения в координатной плоскости и с помощью уравнений. Учащиеся также применяют свои навыки уравнения к задачам на процентное соотношение в качестве еще одного метода решения задач.
В блоке 7 , Геометрия учащиеся узнают, как составление и разложение незнакомых форм на знакомые может расширить их способность находить площадь и объем. Учащиеся опираются на знания и навыки из основной работы класса, охваченной в предыдущих разделах года, чтобы определять измерения, понимать формулы и представлять двумерные формы в координатной плоскости. В Блок 8, Статистика , последний блок года, студенты знакомятся с изучением статистики.Они узнают, как представлять наборы данных и как использовать различные измерения набора данных для анализа информации и ответа на статистический вопрос. Изучая числа в статистическом контексте, студенты могут расширить и укрепить свое понимание системы счисления.
Изучая числа в статистическом контексте, студенты могут расширить и укрепить свое понимание системы счисления.
Обратите внимание, что этот курс соответствует рамкам учебной программы штата Массачусетс 2017 года, которые включают Общие основные стандарты по математике.
Прочитайте больше… Читать меньше …
Математика 6-го класса — Учебная программа, Вопросы по математике 6-го класса
Учебная программа по математике 6-го класса
Математика 6-го класса, несомненно, является шагом вперед по сравнению с тем, что дети изучали в 5-м классе.Но не волнуйтесь, репетиторы Cuemath здесь, чтобы помочь и убедиться, что у вашего ребенка не возникнет проблем с выполнением учебной программы с онлайн-уроками. Многие дети сталкиваются с лежачими полицейскими разного размера на пути к математике. Это особенно верно в 6-м классе, когда со всех сторон появляется множество новых, часто сложных математических теорий и моделей. Но репетиторы Cuemath могут помочь преодолеть этот страх в вашем ребенке и изменить его обучение.
Почему вашему ребенку в 6 классе нужно дополнительное обучение?
Учащиеся 6-го класса начинают узнавать много нового и выполнять операции над алгебраическими выражениями.Репетиторы Cuemath позаботятся о том, чтобы ваш ребенок легко перешел из 5-го в 6-й класс, и каждое онлайн-обучение позволит ему узнать что-то новое, будь то периметр, площадь поверхности и объем. Наши онлайн-занятия по математике помогут облегчить процесс обучения ваших детей в 6-м классе. Чего вы ждете, подпишитесь на бесплатное занятие по математике с одним из наших опытных учителей, а частные уроки ноу-хау могут повысить ценность вашего малыш в 6-м классе.
Онлайн-обучение математике для вашего чемпиона в 6-м классе.
Из соотношения, пропорции, унитарного метода и процентного соотношения нет конца количеству способов, которыми ваш ребенок в 6-м классе может улучшить свои математические навыки.Увлекательные занятия, а не скучные рабочие листы увлекут детей новым опытом обучения, и Cuemath Tutors гарантирует, что сильный акцент делается на концептуальном понимании, а не на повторяющихся упражнениях. Каждое онлайн-обучение вашего ребенка в 6-м классе будет охватывать новую концепцию, и вскоре вы начнете замечать значительные улучшения в их успеваемости.
Каждое онлайн-обучение вашего ребенка в 6-м классе будет охватывать новую концепцию, и вскоре вы начнете замечать значительные улучшения в их успеваемости.
>> Визуализируйте математику с помощью интерактивных заданий по математике для 6-го класса
Найти репетитора для детей 6-го класса стало еще проще!
Будь то линии, углы, треугольники, четырехугольники или круги, репетиторы Cuemath помогут вам и вашему ребенку открыть для себя лучшее из математики 6-го класса.Большинству детей непросто понять все сложности математики в 6-м классе, но онлайн-обучение в Cuemath может помочь облегчить процесс обучения. Живые и персонализированные репетиторы Cuemath помогают раскрыть лучшее в вашем ребенке.
Чего вы ждете? Помогите своему шестикласснику влюбиться в математику вместо того, чтобы бояться этого предмета. Обучайте его онлайн с Cuemath!
Cuemath позволяет детям творить с помощью кода! Узнайте больше о том, как учащиеся могут научить детей программировать в Интернете и создать что-нибудь для себя.
Что вы изучаете математику в шестом классе?
Математические концепции шестого класса связаны с очень широким диапазоном математики темы. Тем не менее, это математические концепции, которые студенты должны понимать к концу шестого класса на основе Национального совета учителей математики стандартов.
Что касается концепций Numbers and Operations , то это концепции, которые изучают ученики шестого класса. Студенты изучают дроби, десятичные дроби и проценты.Они используют эти концепции для решения проблем, проблемы со словами и уметь правильно разместить их на числовой строке. Они учатся применять и использовать проценты, превышающие 100 и меньше 1. Понимание дробей имеет решающее значение для их способность изучать математику более высокого уровня в старших классах средней школы.
Другая область чисел и операций, которую они изучают, — это использование факторов,
кратные, простые числа для решения задач и задач со словами. Они
продолжить свою подготовку по элементарной алгебре, используя и применяя
распределительное свойство и коммутативное свойство в дополнение и
умножение. Затем они дополнительно применяют свойство ассоциативности.
и умножение. Их исследования продолжаются в области квадратных корней.
чисел, поскольку они применяются к обратным отношениям сложения
и вычитание.
Затем они дополнительно применяют свойство ассоциативности.
и умножение. Их исследования продолжаются в области квадратных корней.
чисел, поскольку они применяются к обратным отношениям сложения
и вычитание.
В области Геометрия концепции учащиеся шестого класса развивают понимание двух и трехмерных объектов, таких как: квадраты, прямоугольники, конусы, сферы, цилиндры и т. д. Они также изучают многоугольники поскольку они относятся к линиям, которые параллельны и перпендикулярны.Дополнительный области геометрии и форм — в центре внимания трансформации и симметрия форм при их переворачивании, повороте и повороте.
Студенты также узнают, как определять площадь и объем предметов, используя математические формулы. К ним относятся квадраты, призмы, прямоугольники, конусы, круги, сферы, цилиндры и т. д. Они также тратят время на изучение как применять геометрические фигуры в реальных приложениях, а также подключения к тематическим областям контента.
Область концепции Измерение ориентирована на использование стандарта
и нестандартные единицы измерения для определения взаимосвязей
между разными объектами. Это также связано с геометрией как
они учатся измерять площадь, объем и массу различных
геометрические фигуры. Они учатся измерять все аспекты кругов,
призмы и пирамиды.
Это также связано с геометрией как
они учатся измерять площадь, объем и массу различных
геометрические фигуры. Они учатся измерять все аспекты кругов,
призмы и пирамиды.
В области концепций Анализ данных и вероятность , студенты используйте соответствующий язык для объяснения результатов экспериментов и моделирования. Они учатся составлять вопросы, которые помогут им найти различия. между выборками буксировки в популяции.
Когда дело доходит до решения задач , учащиеся разрабатывают задачу стратегии решения, чтобы помочь им развить фундаментальное понимание математики.Учащиеся используют задачи со словами и другие симуляции реального мира. в проблемных ситуациях.
В концепции Представление , студенты учатся собирать
и систематизировать данные. Затем используйте данные для решения проблем. Ответы
представлены в виде физических и социальных моделей. Они используют данные
рисовать графики, диаграммы, таблицы и другие формы, чтобы объяснить, как они
решил проблему.
Для Connection концепций учащиеся учатся устанавливать связи к реальным приложениям и другим предметным областям контента.Это включает в себя установление связей с другими понятиями в математике.
Студенты учатся Сообщать свои математические идеи в форма предложений, рисунков, плакатов и мультимедийных приложений. Это используется для определения уровня их понимания, когда они объясняют математические концепции другим студентам и учителям.
Студенты используют логическое Рассуждение и доказательство , чтобы объяснить свои математические выводы и методы решения проблем. Эта концепция также используется как метод для студентов, чтобы защитить ответы, которые они получите во время расчетов.Эта концепция используется для улучшения умственных способностей. математические навыки и связи с другими математическими концепциями.
Все эти математические концепции используются для разработки всестороннего
базовые знания математических идей и языка по мере успеваемости студентов
к более высоким уровням математики.
Математика / Задачи изучения математики в шестом классе
Математика для шестого класса
Смысл номера и операции
- Представьте положительные и отрицательные числа в числовой строке
- Определить абсолютное значение числа
- Применение операций с положительными дробями и десятичными знаками
- Понимание взаимосвязи между дробями, десятичными знаками и процентами
Коэффициенты и пропорциональные отношения
- Рассчитать удельные ставки
- Используйте ставки, чтобы понять связь между скоростью, расстоянием и временем
- Найдите эквивалентные соотношения и используйте двойные числовые линии для решения пропорциональных вопросов
- Рассчитать проценты
- Процент количества, процент изменения, налог, чаевые, скидки, вычислить проценты по строке с двойным числом
Выражения, уравнения и неравенства
- Упростите выражения, комбинируя похожие термины и используя свойство распределения
- Решите одно- и двухэтапные уравнения с переменными на одной стороне уравнения
- Напишите и изобразите неравенства, отражающие реальные жизненные ситуации
Геометрия и измерения
- Построение положительных и отрицательных точек на числовых прямых и координатных плоскостях (во всех 4-х квадрантах)
- Понимание и применение формул площади и объема к реальным проблемам
- Сетки твердых тел
- Площадь окружностей, окружность окружностей, площадь треугольников, параллелограммов и трапеций
- Площадь поверхности кубов, прямоугольных призм, треугольных призм и трапециевидных призм
- Объем призм
Анализ данных, статистика и вероятность
- Интерпретация, описание и отображение данных
- Темы: Среднее значение, медиана, режим, среднее абсолютное отклонение, отображение данных в таблице частот, линейный график, счетные диаграммы, `гистограмма и диаграмма прямоугольников и усов
Помощник по математике для 6-го класса | Thinkwell
Для учащихся, уже посещающих курс математики 6 классов , это идеальное учебное пособие с тысячами автоматически оцениваемых заданий для 6-х классов, распечатываемыми рабочими листами по каждой теме и подразделам, интерактивными интерактивными анимациями и многим другим. В основе курса — увлекательные и эффективные видеоуроки, которые любят использовать студенты. Он охватывает те же темы, что и в любом учебнике математики для 6 классов -го класса , поэтому за ним легко следить, он доступен круглосуточно и без выходных и стоит гораздо дешевле, чем репетитор.
В основе курса — увлекательные и эффективные видеоуроки, которые любят использовать студенты. Он охватывает те же темы, что и в любом учебнике математики для 6 классов -го класса , поэтому за ним легко следить, он доступен круглосуточно и без выходных и стоит гораздо дешевле, чем репетитор.
Эдвард Бургер — отмеченный наградами математик и профессор, увлеченный преподаванием математики. Он делает математику в шестом классе увлекательной и полезной для всех учеников.
Если вы ищете курс домашнего обучения под ключ, см. Thinkwellhomeschool.com.
Наш полный пакет «Помощник по математике для 6-х классов» включает:
- 12-месячная онлайн-подписка на наш полный курс математики для 6-х классов с видео-уроками, автоматически оцениваемыми упражнениями и многим другим.
Математика 6-го класса
Companion МатериалыОнлайн-подписка,
Доступ на 12 месяцевДоступ к полному онлайн-пакету, который включает в себя все необходимое:
- Высококачественные видеоуроки объясняют все концепции математики в шестом классе
- Упражнения с автоматической оценкой и немедленной обратной связью позволяют отслеживать свой прогресс
- Подписки начинаются, когда вы будете готовы.
 Купите сейчас и активируйте свой курс в любое удобное время. Подождите до одного года, чтобы активировать подписку; ваша 12-месячная подписка не начнется, пока вы об этом не скажете!
Купите сейчас и активируйте свой курс в любое удобное время. Подождите до одного года, чтобы активировать подписку; ваша 12-месячная подписка не начнется, пока вы об этом не скажете!
6-й класс по математике
Товарищ Подробности Программа Thinkwell’s 6th Grade Math Companionвключает в себя все следующие функции для вашего ученика:
- Соответствует национальным математическим стандартам 6-го класса
- Более 100 тем с 250+ видеоуроками
- Более 1000 интерактивных упражнений с мгновенной обратной связью позволяют отслеживать свой прогресс
- Более 60 интерактивных функций со звуком
- Автоматически оцениваемые тесты по математике для 6-го класса, включая тесты по 13 главам, а также практические тесты, промежуточный и заключительный экзамены.
- Примеры реальных приложений в лекциях и упражнениях
- Глоссарий, содержащий более 200 математических терминов
- Скрытые субтитры для всех видеоуроков (большинство также доступно на испанском языке)
- Совершенно новый контент, который поможет студентам улучшить свои математические знания:
- операции с целыми числами, дробями, десятичными знаками, а также положительными и отрицательными числами (целыми числами)
- гистограммы, гистограммы и линейные графики
- решение уравнений и неравенств
- ставки, соотношения, проценты и пропорции
- линий, углов и многоугольников
- преобразования и симметрия
- условных и метрических единиц
- периметр и площадь полигонов
- окружность и площадь окружностей
- объем и площадь поверхности трехмерных фигур
- взаимосвязанные таблицы и графики
- графические функции и наклон
- экспериментальная и теоретическая вероятность
Содержание
1.
 Целые числа и узоры
Целые числа и узоры- 1.1 Целые числа и экспоненты
- 1.1.1 Сравнение и заказ целых чисел
- 1.1.2 Оценка целыми числами
- 1.2 Использование целых чисел
- 1.2.1 Порядок действий
- 1.2.2 Свойства и методы рассуждений
- 1.2.3 Выбор метода расчета
- 1.2.4 Паттерны и последовательности
2.Введение в алгебру
- 2.1 Переменные и выражения
- 2.1.1 Переменные и выражения
- 2.1.2 Перевод между словами и математикой
- 2.1.3 Преобразование таблиц и выражений
- 2.2 Введение в уравнения
- 2.2.1 Уравнения и их решения
- 2.2.3 Уравнения вычитания
- 2.2.4 Уравнения умножения
3.Десятичные числа
- 3.1 Введение в десятичные дроби
- 3.
 1.1 Представление, сравнение и порядок десятичных знаков
1.1 Представление, сравнение и порядок десятичных знаков
- 3.1.2 Округление и оценка десятичных знаков
- 3.1.3 Сложение и вычитание десятичных знаков
- 3.
- 3.2 Умножение и деление десятичных знаков
- 3.2.1 Умножение десятичных знаков
- 3.2.2 Применение экспонентов: научная нотация
- 3.2.3 Деление десятичных знаков на целые числа
- 3.2.4 Деление на десятичные дроби
- 3.2.5 Решение десятичных уравнений
4. Теория чисел и дроби
- 4.1 Теория чисел
- 4.1.2 Факторы и простое факторизация
- 4.1.3 Наибольший общий коэффициент
- 4.2 Представление дробей
- 4.2.1 Десятичные и дроби
- 4.2.2 Эквивалентные доли
- 4.2.3 Смешанные числа и неправильные дроби
- 4.
 3 Введение в операции с дробями
3 Введение в операции с дробями- 4.3.1 Сравнение и заказ дробей
- 4.3.2 Сложение и вычитание с одинаковыми знаменателями
- 4.3.3 Оценка сумм и разностей дробей
5. Операции с дробями
- 5.1 Сложение и вычитание дробей
- 5.1.1 Наименьшее общее кратное
- 5.1.2 Сложение и вычитание с отличными знаменателями
- 5.1.3 Сложение и вычитание смешанных чисел
- 5.1.4 Перегруппировка для вычитания смешанных чисел
- 5.1.5 Решение уравнений дроби: сложение и вычитание
- 5.2 Умножение и деление дробей
- 5.2.1 Умножение дробей на целые числа
- 5.2.2 Умножение дробей
- 5.2.3 Умножение смешанных чисел
- 5.2.4 Деление дробей и смешанных чисел
- 5.2.5 Решение уравнений дроби: умножение и деление
6.
 Дисплеи данных
Дисплеи данных- 6.1 Организация и отображение данных
- 6.1.1 Меры центральной тенденции
- 6.1.2 Таблицы частот, графики стеблей и листьев и линейные графики
- 6.1.3 Гистограммы и гистограммы
- 6.2 линейных графика и оценочные дисплеи
- 6.2.3 Выбор подходящего дисплея
7. Пропорциональные отношения
- 7.1 Соотношения и пропорции
- 7.1.2 Применение ставок и коэффициентов
- 7.2 Применение пропорций
- 7.2.2 Косвенное измерение
- 7.2.3 Чертежи и карты в масштабе
- 7,3%
- 7.3.2 Проценты, десятичные дроби и дроби
8.Геометрические отношения
- 8.1 Линии и углы
- 8.1.1 Точки, линии и плоскости
- 8.1.2 Измерение и классификация углов
- 8.
 1.3 Угловые отношения
1.3 Угловые отношения
- 8.3 Отношения многоугольников
9. Измерение
- 9.1 Обычные и метрические измерения
- 9.1.1 Общие сведения об обычных единицах измерения
- 9.1.2 Метрические единицы измерения
- 9.1.3 Преобразование обычных единиц
- 9.1.4 Преобразование метрических единиц
- 9.1.5 Время и температура
- 9.2 Измерение геометрических фигур
- 9.2.1 Определение угловых мер в многоугольниках
- 9.2.3 Окружность и окружность
10. Площадь и объем
- 10,1 Площадь
- 10.1.1 Площадь прямоугольников и параллелограммов
- 10.1.2 Площадь треугольников и трапеций
- 10.1.3 Площадь составных фигур
- 10.1.4 Изменение размеров
- 10.2 Объем и площадь поверхности
- 10.
 2.1 Трехмерные фигуры
2.1 Трехмерные фигуры
- 10.2.3 Объем цилиндров
- 10.
11. Целые числа и координатная плоскость
- 11.1 Введение в целые числа
- 11.1.1 Целые числа в реальных ситуациях
- 11.1.2 Сравнение и порядок целых чисел
- 11.1.3 Координатная плоскость
- 11.1.4 Преобразования в координатной плоскости
- 11.2 Операции с целыми числами
- 11.2.2 Вычитание целых чисел
- 11.2.3 Умножение целых чисел
- 11.2.5 Решение целочисленных уравнений
12. Функции, уравнения и неравенства
- 12.1 Функции
- 12.1.1 Таблицы и функции
- 12.1.2 Графические функции
- 12.1.3 Наклон и скорость изменения
- 12.2 Решение уравнений и неравенств
- 12.2.1 Решение двухшаговых уравнений
- 12.
 2.2 Устранение неравенств
2.2 Устранение неравенств
- 12.2.3 Решение двухэтапных неравенств
13. Вероятность
- 13.1 Понимание вероятности
- 13.1.1 Введение в вероятность
- 13.1.2 Экспериментальная вероятность
- 13.1.3 Методы подсчета и пробелы
- 13.2 Определение вероятностей
- 13.2.1 Теоретическая вероятность
- 13.2.3 Прогнозирование
Об авторе
Эдвард Бургер
Эдвард Бургер — отмеченный наградами профессор, увлеченный преподаванием математики.
С 2013 года Эдвард Бургер является президентом Юго-Западного университета, ведущего гуманитарного колледжа в Джорджтауне, штат Техас. Ранее он был профессором математики в колледже Уильямс. Доктор Бургер получил докторскую степень. в Техасском университете в Остине, получив диплом с отличием по математике в Коннектикутском колледже.
Уникальное чувство юмора профессора Бургера и его педагогический опыт делают его идеальным ведущим развлекательных и информативных видеолекций Thinkwell.
Математика для 6-го класса: чего ожидать
Кажется, вчера вы считали с первоклассником пенни, листья и золотые звезды. Сейчас она изучает математику в шестом классе. Это шок для многих родителей — и детей тоже.
Хорошая новость: академические стандарты разработаны таким образом, чтобы дети постепенно готовились к обучению от одного класса к другому. Если ваш ребенок стабильно учился в начальной школе, математика в шестом классе будет всего лишь еще одним управляемым шагом.Фактически, исследования показывают, что, когда математику преподают хорошо, дети этого возраста просто обожают ее — в конце концов, это способ обнаружить смысл и закономерности в мире и почувствовать себя чертовски умными в процессе.
Так чего же вам ожидать? Поскольку штатам разрешено выбирать свои собственные стандарты в разделе «Ни одного отстающего ребенка», могут быть некоторые различия. Для получения более подробной информации не забудьте ознакомиться с академическими стандартами вашего штата на веб-сайте министерства образования. Также разумно попросить свою школу показать вам свои рамки и тексты, чтобы вы могли точно увидеть, как стандарты будут соблюдаться в течение года.
Для получения более подробной информации не забудьте ознакомиться с академическими стандартами вашего штата на веб-сайте министерства образования. Также разумно попросить свою школу показать вам свои рамки и тексты, чтобы вы могли точно увидеть, как стандарты будут соблюдаться в течение года.
В целом, однако, вы можете ожидать эти темы по математике в шестом классе:
Что мой ребенок уже должен знать?
Как правило, учителя надеются, что к концу пятого класса ученики будут иметь очень твердые практические знания обо всех четырех «операциях» — сложении, вычитании, умножении и делении, — а также о дробях, простых процентах, десятичных дробях и базовых принципах. построение графиков. Как минимум, они также должны знать основные формулы для периметра, площади и геометрических форм.
Чему мой ребенок должен учиться в этом классе?
Чувство числа: оно основано непосредственно на базовых навыках начальной школы — сложении, вычитании, умножении, делении, дробях и десятичных дробях — но теперь более сложное. Поговорите об этих вычислениях со своим ребенком: Как переводит дробь в десятичные числа? Почему мы называем умножение и деление «обратными операциями»? Это также время, когда многие учителя начинают вводить отрицательные числа, что может быть непросто.Вы можете помочь в реальных жизненных ситуациях, например: «Да, вы можете одолжить у меня 10 долларов, чтобы позволить себе эту игрушку, но это означает, что ваш счет упадет до отрицательных 10 долларов».
Поговорите об этих вычислениях со своим ребенком: Как переводит дробь в десятичные числа? Почему мы называем умножение и деление «обратными операциями»? Это также время, когда многие учителя начинают вводить отрицательные числа, что может быть непросто.Вы можете помочь в реальных жизненных ситуациях, например: «Да, вы можете одолжить у меня 10 долларов, чтобы позволить себе эту игрушку, но это означает, что ваш счет упадет до отрицательных 10 долларов».
Алгебра: Давным-давно эту тему изучали в девятом классе. В настоящее время все больше и больше штатов призывают школы преподавать алгебру для начинающих всех восьмиклассников, чтобы в старших классах оставалось больше времени для изучения продвинутых тем. Так что не удивляйтесь: в шестом классе во многих школах детям преподают основы алгебры. Попробуйте поговорить с ребенком в реальной жизни.Например: «Мы ходим в магазин за пять миль за той крутой обувью, которую вы хотите. Мы будем путешествовать со скоростью пятнадцать миль в час. Как быстро мы туда доберемся? » Ум вашего ребенка может быть сосредоточен на обуви, но процесс мышления носит алгебраический характер.
Как быстро мы туда доберемся? » Ум вашего ребенка может быть сосредоточен на обуви, но процесс мышления носит алгебраический характер.
Геометрия: углы, четырехугольники, объем? Давай. Не удивляйтесь, если ваш шестиклассник обнаружит область трехмерной формы. Для многих детей геометрическое мышление является изюминкой математики в средней школе. Эта часть учебной программы легко поддается практическому изучению и прекрасно сочетается с искусством.
Статистика и вероятность: На этом этапе дети увидят простые проблемы с подбрасыванием монеты, бросанием кубика и т.д.
Рассуждение, решение проблем и связи. Для учителей математики это действительно высшие цели математического образования. Важно ли получить «правильный» ответ на проблему? Конечно. Но, как говорят учителя математики, еще более важно знать, что вы можете придумать свой путь к этому ответу — иногда двумя или тремя разными способами — снова и снова.
Звучит сложно? Учителя математики надеются на это . .. но они также много работают, чтобы сделать это достижимым. Окружающий мир наполнен математикой, будь то расчет налогов, составление бюджетов или определение расходов. Это идеальное время для вашего молодого гражданина, чтобы собрать эти уроки воедино. Благодаря вашей постоянной поддержке вы можете быть поражены тем, на что готов взяться ваш ребенок.
.. но они также много работают, чтобы сделать это достижимым. Окружающий мир наполнен математикой, будь то расчет налогов, составление бюджетов или определение расходов. Это идеальное время для вашего молодого гражданина, чтобы собрать эти уроки воедино. Благодаря вашей постоянной поддержке вы можете быть поражены тем, на что готов взяться ваш ребенок.
Цели и задачи для шестиклассников по математике
Шестиклассники осваивают основные операции, такие как умножение и деление рациональных чисел, дробей и десятичных знаков.Они должны понимать концепции предалгебры, такие как решение для отдельных переменных, и знать, как использовать отношения и скорости для сравнения данных. Цели сосредоточены на способности учащихся решать уравнения, вычислять вероятность, оценивать, измерять двух- и трехмерные фигуры и понимать отношения между числами.
Вычисления и операции
Шестиклассники выполняют вычисления, которые включают сложение, вычитание, деление и умножение целых чисел, смешанных чисел, отрицательных чисел, дробей, десятичных дробей и процентилей, согласно данным Чикагского университета. Учащиеся должны хорошо понимать числовые значения, расширенные обозначения, наибольший общий множитель, наименьший общий множитель и эквиваленты. Они учатся делать разумные оценки и использовать соотношения и пропорции для решения проблем. Основная цель шестиклассников — уметь выполнять сложные математические операции с калькуляторами и без них.
Учащиеся должны хорошо понимать числовые значения, расширенные обозначения, наибольший общий множитель, наименьший общий множитель и эквиваленты. Они учатся делать разумные оценки и использовать соотношения и пропорции для решения проблем. Основная цель шестиклассников — уметь выполнять сложные математические операции с калькуляторами и без них.
Анализ данных и вероятность
Студенты должны научиться оценивать и систематизировать математические данные, чтобы делать прогнозы и делать выводы, часто включая интерпретацию графиков и диаграмм.Шестиклассники должны уметь распознавать группы, кластеры, вершины и симметрию в соответствии с Инициативой Common Core State Standards Initiative. Расчет среднего, медианного и модового значений, а также способность понимать изменчивость необходимы для эффективного анализа данных. Цель состоит в том, чтобы учащиеся могли принимать обоснованные решения на основе статистического анализа и факторов вероятности.
Геометрия и измерение
Шестиклассники учатся сортировать, классифицировать и измерять двух- и трехмерные фигуры, такие как треугольники, четырехугольники, кубы, призмы и пирамиды, по данным Министерства образования Вирджинии.Они учатся вычислять расстояние, площадь и объем и сообщать свои ответы, используя точные термины, такие как мили, квадратные мили или кубические футы. Освоение геометрии в шестом классе включает в себя измерение углов, определение конгруэнтных фигур и рисование примеров отражений, перемещений и вращений. Цель состоит в том, чтобы учащиеся углубили свои знания о геометрических измерениях и визуально представили эти измерения с помощью рисунков и графиков.
Базовая алгебра, шаблоны и функции
Ученики средней школы получают первую серьезную дозу алгебры в шестом классе.Они создают и интерпретируют числовые шаблоны, решают линейные уравнения и понимают алгебраические обозначения, такие как использование букв для представления неизвестных переменных.

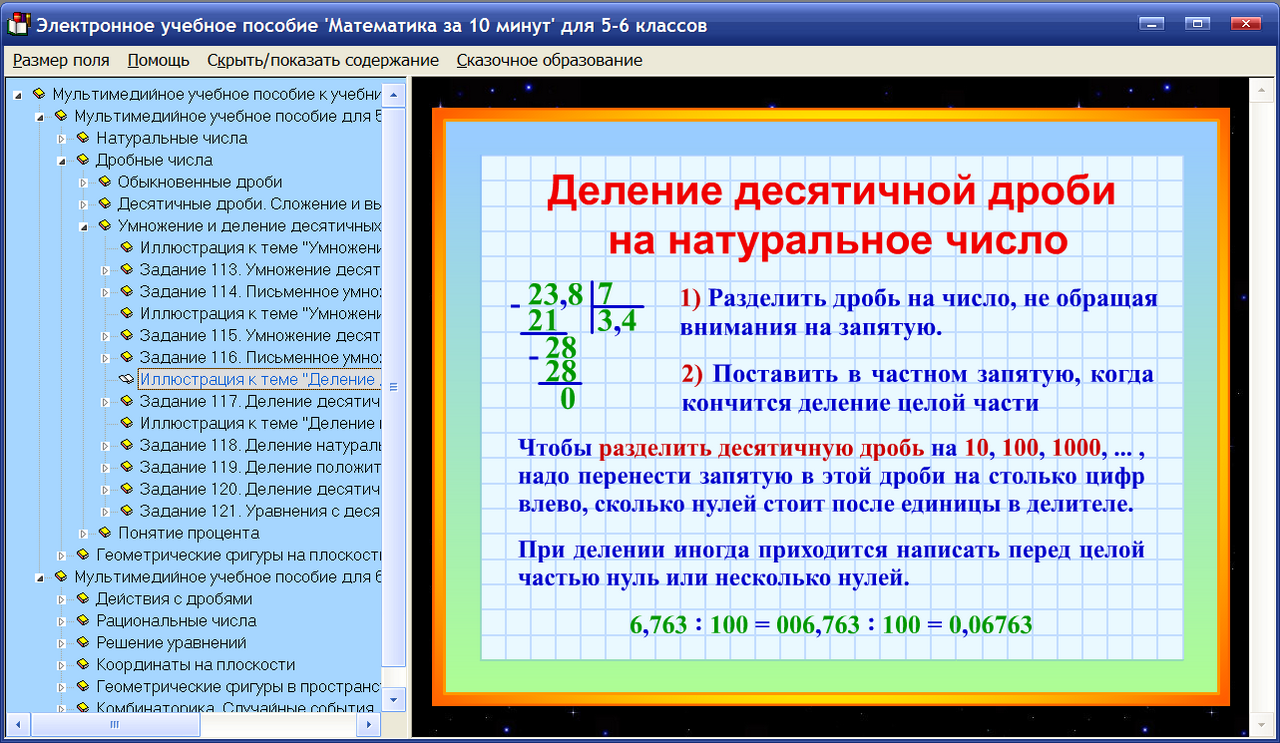

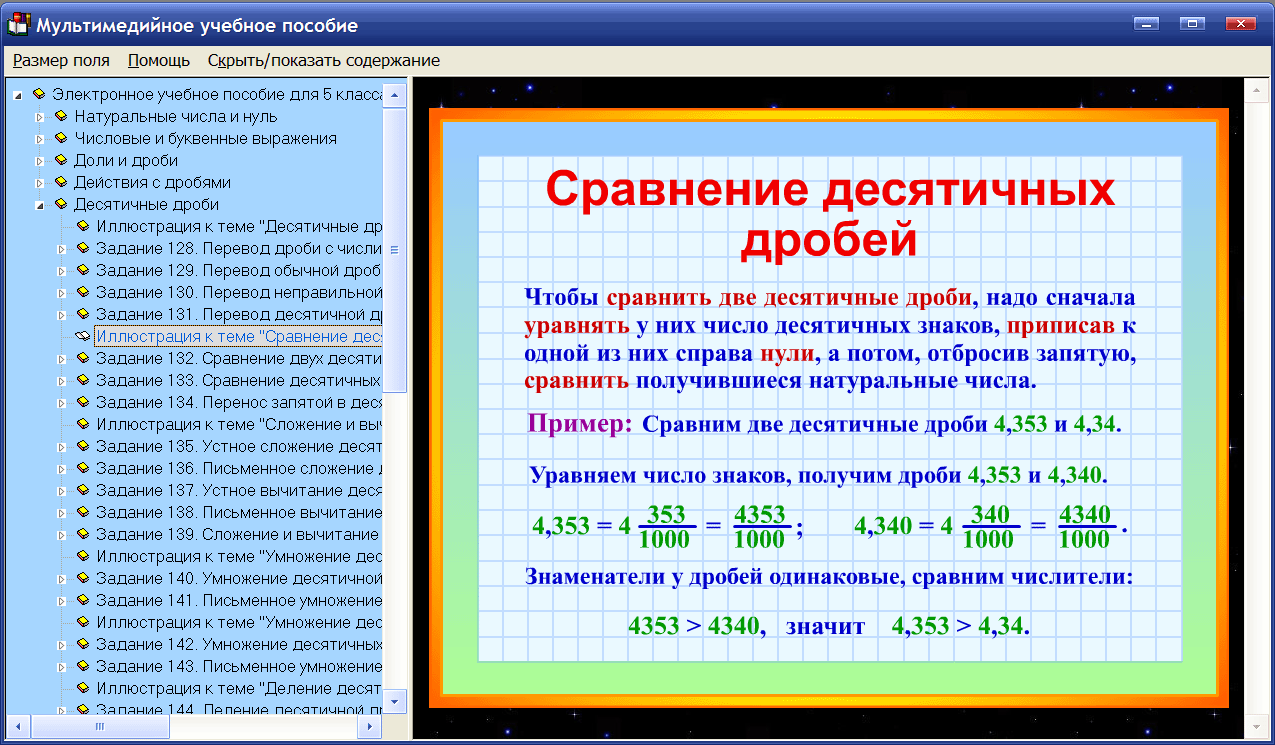
 Купите сейчас и активируйте свой курс в любое удобное время. Подождите до одного года, чтобы активировать подписку; ваша 12-месячная подписка не начнется, пока вы об этом не скажете!
Купите сейчас и активируйте свой курс в любое удобное время. Подождите до одного года, чтобы активировать подписку; ваша 12-месячная подписка не начнется, пока вы об этом не скажете! 1.1 Представление, сравнение и порядок десятичных знаков
1.1 Представление, сравнение и порядок десятичных знаков 3 Введение в операции с дробями
3 Введение в операции с дробями 1.3 Угловые отношения
1.3 Угловые отношения 2.1 Трехмерные фигуры
2.1 Трехмерные фигуры 2.2 Устранение неравенств
2.2 Устранение неравенств