Решебник по матем 6 класс мерзляк: Мерзляк. Решебник с подробными ответами

Содержание

ГДЗ по Математике 6 класс Мерзляк, Полонский Учебник

ГДЗ по Математике за 6 класс Мерзляка, Полонского созданы для школьников, которые хотят не только правильно выполнять задания, но и повысить свои оценки. Это сложный предмет, особенно если ученик гуманитарий или с творческим складом ума. Но с этим материалом — математические науки станут доступны каждому ребенку.

Решебник по математике позволит каждому стать отличником. Данное пособие станет полезным и для родителей. Они в удобное время могут проверить выполненные задания или проверить уже пройденный материал в школе. Наш сайт содержит правильные и полные ответы ко всем заданиям из учебника издательства Вентана-Граф. Это позволит вспомнить предыдущий материал и быть подготовленным к новой теме.

Выберите номер

12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394959697989910010110210310410510610710810911011111211311411511611711811912012112212312412512612712812913013113213313413513613713813914014114214314414514614714814915015115215315415515615715815916016116216316416516616716816917017117217317417517617717817918018118218318418518618718818919019119219319419519619719819920020120220320420520620720820921021121221321421521621721821922022122222322422522622722822923023123223323423523623723823924024124224324424524624724824925025125225325425525625725825926026126226326426526626726826927027127227327427527627727827928028128228328428528628728828929029129229329429529629729829930030130230330430530630730830931031131231331431531631731831932032132232332432532632732832933033133233333433533633733833934034134234334434534634734834935035135235335435535635735835936036136236336436536636736836937037137237337437537637737837938038138238338438538638738838939039139239339439539639739839940040140240340440540640740840941041141241341441541641741841942042142242342442542642742842943043143243343443543643743843944044144244344444544644744844945045145245345445545645745845946046146246346446546646746846947047147247347447547647747847948048148248348448548648748848949049149249349449549649749849950050150250350450550650750850951051151251351451551651751851952052152252352452552652752852953053153253353453553653753853954054154254354454554654754854955055155255355455555655755855956056156256356456556656756856957057157257357457557657757857958058158258358458558658758858959059159259359459559659759859960060160260360460560660760860961061161261361461561661761861962062162262362462562662762862963063163263363463563663763863964064164264364464564664764864965065165265365465565665765865966066166266366466566666766866967067167267367467567667767867968068168268368468568668768868969069169269369469569669769869970070170270370470570670770870971071171271371471571671771871972072172272372472572672772872973073173273373473573673773873974074174274374474574674774874975075175275375475575675775875976076176276376476576676776876977077177277377477577677777877978078178278378478578678778878979079179279379479579679779879980080180280380480580680780880981081181281381481581681781881982082182282382482582682782882983083183283383483583683783883984084184284384484584684784884985085185285385485585685785885986086186286386486586686786886987087187287387487587687787887988088188288388488588688788888989089189289389489589689789889990090190290390490590690790890991091191291391491591691791891992092192292392492592692792892993093193293393493593693793893994094194294394494594694794894995095195295395495595695795895996096196296396496596696796896997097197297397497597697797897998098198298398498598698798898999099199299399499599699799899910001001100210031004100510061007100810091010101110121013101410151016101710181019102010211022102310241025102610271028102910301031103210331034103510361037103810391040104110421043104410451046104710481049105010511052105310541055105610571058105910601061106210631064106510661067106810691070107110721073107410751076107710781079108010811082108310841085108610871088108910901091109210931094109510961097109810991100110111021103110411051106110711081109111011111112111311141115111611171118111911201121112211231124112511261127112811291130113111321133113411351136113711381139114011411142114311441145114611471148114911501151115211531154115511561157115811591160116111621163116411651166116711681169117011711172117311741175117611771178117911801181118211831184118511861187118811891190119111921193119411951196119711981199120012011202120312041205120612071208120912101211121212131214121512161217121812191220122112221223122412251226122712281229123012311232123312341235123612371238123912401241124212431244124512461247124812491250125112521253125412551256125712581259126012611262126312641265126612671268126912701271127212731274127512761277127812791280128112821283128412851286128712881289129012911292129312941295129612971298129913001301130213031304130513061307130813091310131113121313131413151316131713181319132013211322132313241325132613271328132913301331133213331334133513361337133813391340134113421343134413451346

Выберите параграф

1234567891011121314151718192021222425262728293031323334363739404143444546

Решаем устно

стр. 5стр.11стр.15стр.22стр.29-30стр.34стр.42стр.46стр.51стр.56-57стр.66-67стр.75стр.81стр.85стр.92стр.99стр.102стр.104-105стр.113стр.119стр.125стр.134стр.138стр.143-144стр.149стр.158стр.162стр.172стр.179стр.183стр.188стр.194стр.198стр.205стр.209стр.212стр.218стр.225стр.229стр.235стр.241стр.245стр.253стр.259стр.268стр.274стр.282

Выберите страницу учебника

5678910111213141516171822232425293031333435364243444647484951525354565758596061626364666768697071727375767778798182838586878889909192939495969799100102103104105106113114115116118119120121122123124125126127128133134135136137138139140143144145146147149150151152153154157158159162163164165166167168169172173174175179180181182183184185186188189190194195196197198199200201202204205206207208209210211212213214215216218219220221222225226227229230231232233234235236237238239241242243244245246247248249250252253254255259260261262263264265267268269270273274275276277278282283284285286287

Учебник Мерзляка для шестого класса может показаться сложным для школьников. Детям за один год предстоит изучить несколько тем, для понимания которых требуется внимательность и хороший учитель:

Делимость натуральных чисел.
Обыкновенные дроби.
Отношения и пропорции.
Рациональные числа и действия над ними.

Поэтому если ребенок испытывает проблемы с предметом, правильным решением будет обращение за помощью к ГДЗ. Выберите нужную страницу учебника, и вы получите ответы на все упражнения. Каждый номер имеет детальное пояснение, которое способствует быстрому усвоению материала.

В решебнике автора Мерзляка можно найти всю необходимую для учебы информацию. Несмотря на то, что в конце учебника даны ответы почти на все задания, это не заменяет ГДЗ, поскольку решение там не написано. А это значит, что если ученик не понял, как решать, ему нужно посмотреть ход решения и разобраться с ним, а не просто списать ответ.

А если по какой-то причине вы не успели сделать домашнюю работу, то можно просто списать решение перед уроком. Но мы рекомендуем не злоупотреблять списыванием, а обращаться к решебнику только чтобы проверить ход своих мыслей и ответы. Тогда у вас возникнет меньше трудностей при изучении математики в старших классах. Не забывайте, что важную роль в обеспечении контроля при выполнении домашних заданий играют родители и учитель.

ГДЗ Решебник Математика 6 класс Учебник Алгоритм успеха «Вентана-Граф» Мерзляк, Полонский, Якир.

Математика 6 классУчебникАлгоритм успехаМерзляк, Полонский, Якир«Вентана-Граф»

У каждого ученика есть любимые уроки, которым они готовы уделять на изучение больше времени. У многих школьников таким уроком является математика. Предмет требует времени, сил и внимания, чтобы понимать его и владеть в совершенстве. В шестом классе программа по математике более углубленная и появляются новые понятия, правила и задачи. Поэтому педагоги рекомендуют заниматься по решебнику к учебнику «Математика 6 класс Учебник Мерзляк, Полонский, Якир Вентана-Граф Алгоритм успеха» для лучшего усвоения темы.

Что включает в себя решебник

Пособие разделено на четыре больших темы, каждая из которых соответствует программе шестого класса. Также в нем содержатся задачи для устного решения. Ученики отдают свое предпочтение данному решебнику так как в нем:

хорошая подача информации;
подробные примеры решений;
разнообразные задания.

Школьник может заниматься по учебнику как в школе с учителем, так и самостоятельно и проверять правильность решения задач с помощью ответов.

Какие преимущества решебника

ГДЗ позволяет ученикам изучить и разобраться в теме досконально, отработать пройденный материал, подготовится к проверочным работам и олимпиадам, повысить успеваемость по предмету.

Упражнения

Вопросы к параграфам

§1§2§3§4§5§6§7§8§9§10§11§12§13§14§15§16§17§18§19§20§21§22§24§25§26§27§28§29§30§31§32§33§34§36§37§39§40§41§43§44§45§46

Решаем устно

§1§2§3§4§5§6§7§8§9§10§11§12§13§14§15§16§17§18§19§20§21§22§23§24§25§26§27§28§29§30§31§32§33§34§35§36§37§38§39§40§41§42§43§44§45§46§47

Упражнения: 1

Предыдущее

Следующее

Условие

Решебник №1

Решебник №2

Предыдущее

Следующее

закрыть

ГДЗ и решебники

ГДЗ решебник по математике 6 класс Мерзляк, Полонский, Якир

В 6 классе ученики начинают проходить довольно сложную часть математики. Именно тогда к цифрам добавляются буквы, что может запутать школьника. Для того, чтобы этого не произошло, было составлено ГДЗ по книге, написанной авторами Мерзляк, Полонский и Якир. Теперь ребенку будет намного проще делать домашнюю работу. ГДЗ позволит повысить успеваемость школьника и сделать его отличником. Пособие может быть использовано в любое время. ГДЗ можно носить как с собой, так и открывать его только дома.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376 377 378 379 380 381 382 383 384 385 386 387 388 389 390 391 392 393 394 395 396 397 398 399 400 401 402 403 404 405 406 407 408 409 410 411 412 413 414 415 416 417 418 419 420 421 422 423 424 425 426 427 428 429 430 431 432 433 434 435 436 437 438 440 441 443 444 445 446 447 448 449 450 451 452 453 454 455 456 457 458 459 460 461 462 463 464 465 466 467 468 469 470 471 472 473 474 475 476 477 478 479 480 481 482 483 484 485 486 488 489 490 491 492 493 494 495 496 497 498 499 500 501 502 503 504 505 506 507 508 509 510 511 512 513 514 515 516 517 518 519 520 521 522 523 524 525 526 527 528 529 530 531 532 533 534 535 536 537 538 539 540 541 542 543 544 545 546 547 548 549 550 551 552 553 554 555 556 557 558 559 560 561 562 563 564 565 566 567 568 569 571 572 573 574 575 576 577 578 579 580 581 582 583 584 585 586 587 588 589 590 591 592 593 594 595 596 597 598 599 600 601 602 603 604 605 606 607 608 609 610 611 612 613 614 615 616 617 618 619 620 621 622 623 624 625 626 627 628 629 630 631 632 633 634 635 636 637 638 639 640 641 642 643 644 645 646 647 648 649 650 651 652 653 654 655 656 657 658 659 660 661 662 663 664 665 666 667 668 669 670 671 672 673 674 675 676 677 678 679 680 681 682 683 684 685 686 687 688 689 690 691 692 693 694 695 696 697 698 699 700 701 702 703 704 705 706 707 708 709 710 711 712 713 714 715 716 717 718 719 720 721 722 723 724 725 726 727 728 729 730 731 732 733 734 736 737 738 739 740 741 742 743 744 745 746 747 748 749 750 751 752 753 754 755 756 757 758 759 760 761 762 763 764 765 766 767 768 769 770 771 772 773 774 775 776 777 778 779 781 782 783 784 785 786 787 788 789 790 791 792 793 794 795 796 797 798 799 800 801 802 803 804 805 806 807 808 809 810 811 812 813 814 815 816 817 818 819 820 821 822 823 824 825 826 827 828 829 830 831 832 833 834 835 836 837 838 839 840 841 842 843 844 845 846 847 848 849 850 851 852 853 854 855 856 857 858 859 860 861 862 863 864 865 866 867 868 869 870 871 872 873 874 875 876 877 878 879 880 881 882 883 884 885 886 887 888 889 890 891 892 893 894 895 896 897 898 899 900 901 902 903 904 905 906 907 908 909 910 911 912 913 914 915 916 917 918 919 920 921 922 923 924 925 926 927 928 929 930 931 932 933 934 935 936 937 938 939 940 941 942 943 944 945 946 947 948 949 950 951 952 953 954 955 956 957 958 959 960 961 962 963 964 965 966 967 968 969 970 971 972 973 974 975 976 977 978 979 980 981 982 983 984 985 986 987 988 989 990 991 992 993 994 995 996 997 998 999 1000 1001 1002 1003 1004 1005 1006 1007 1008 1009 1010 1011 1012 1013 1014 1015 1016 1017 1018 1019 1020 1021 1022 1023 1024 1025 1026 1027 1028 1029 1030 1031 1032 1033 1034 1035 1036 1037 1038 1039 1040 1041 1042 1043 1044 1045 1046 1047 1048 1049 1050 1051 1052 1053 1054 1055 1056 1057 1058 1059 1060 1061 1062 1063 1064 1065 1066 1067 1068 1069 1070 1071 1072 1073 1074 1075 1076 1077 1078 1079 1080 1081 1082 1083 1084 1085 1086 1087 1088 1089 1090 1091 1092 1093 1094 1095 1096 1097 1098 1099 1100 1101 1102 1103 1104 1105 1106 1107 1108 1109 1110 1111 1112 1113 1114 1115 1116 1117 1118 1119 1120 1121 1122 1123 1124 1125 1126 1127 1128 1129 1130 1131 1132 1133 1134 1135 1136 1137 1138 1139 1140 1141 1142 1143 1144 1145 1146 1147 1148 1149 1150 1151 1152 1153 1154 1155 1156 1158 1159 1160 1161 1162 1163 1164 1165 1166 1167 1168 1169 1170 1171 1172 1173 1174 1175 1176 1177 1178 1179 1180 1181 1182 1183 1184 1185 1186 1187 1188 1189 1190 1191 1192 1193 1194 1195 1196 1197 1198 1199 1200 1201 1202 1203 1204 1205 1206 1207 1208 1209 1210 1211 1212 1213 1214 1215 1216 1217 1218 1219 1220 1221 1222 1223 1224 1225 1226 1227 1228 1229 1230 1231 1232 1233 1234 1235 1236 1237 1238 1239 1240 1241 1242 1243 1244 1245 1246 1247 1248 1249 1250 1251 1252 1253 1254 1255 1256 1257 1258 1259 1260 1261 1262 1263 1264 1265 1266 1267 1268 1269 1270 1271 1272 1273 1274 1275 1276 1277 1278 1279 1280 1281 1282 1283 1284 1285 1286 1287 1288 1289 1290 1291 1292 1293 1294 1295 1296 1297 1298 1299 1300 1301 1302 1303 1304 1305 1306 1307 1308 1309 1310 1311 1312 1313 1314 1315 1316 1317 1318 1319 1320 1321 1322 1323 1324 1325 1326 1327 1328 1329 1330 1331 1332 1333 1334 1335 1336 1337 1338 1339 1340 1341 1342 1343 1344 1345 1346 1347 1348 1349 1350 1351 1352 1353 1354 1355 1356 1357 1358 1359 1360 1361 1362 1363 1364 1365 1366 1367 1368 1369 1370 1371 1372 1373 1374 1375 1376 1377 1378 1379 1380 1381 1382 1383 1384 1385 1386 1387 1389 1390 1391 1392 1393 1394 1395 1396 1397 1398 1399 1400 1401 1402 1403 1404 1405 1406 1407 1408 1409 1410 1411 1412 1413 1414 1415 1416 1417 1418 1419 1420 1421 1422

Оценить:

2 / 5. Оценок: 14

ГДЗ решебник по математике 6 класс Мерзляк, Полонский, Рабинович дидактические материалы Вентана-Граф

Математика 6 класс

Серия: Алгоритм успеха.

Тип пособия: Дидактические материалы

Авторы: Мерзляк, Полонский, Рабинович

Издательство: «Вентана-Граф»

ГДЗ – твердая поддержка шестиклассников

«ГДЗ по математике 6 класс дидактические материалы Мерзляк (Вентана-Граф)» окажет твердую поддержку шестиклассникам в освоении «царицы наук». Учебное пособие разработано в соответствии с требованиями Федерального государственного образовательного стандарта признанными авторами в данной области. Решебник включает верные ответы на все номера заданий основного издания.

В шестом классе программа по математике значительно усложняется, и включает элементы геометрии. Поэтому без хорошего подспорья в учебном процессе ученикам не обойтись. Данное учебно-методическое пособие, в котором собраны самые подробные решения всех номеров, позволит ребятам правильно выполнить домашние упражнения и потренироваться в решении примеров и задач перед контрольной работой.

Подготовка с решебником – ключ к фундаментальным познаниям в математике

«ГДЗ по математике 6 класс дидактические материалы Мерзляк А. Г., Полонский В. Б. (Вентана-Граф)» находится в круглосуточном онлайн-доступе. Простая навигация моментально отправляет к нужному номеру учебника. Нумерация ресурса полностью совпадает с оригинальным изданием.

Планомерная подготовка с онлайн-сборником способствует лучшему усвоению разделов курса. По мнению методистов, основное внимание следует уделить темам:

практическое применение переместительного свойства умножения;
способы сложения и вычитания с помощью координатной прямой;
свойства действий с рациональными числами.

Используя решебник, учащиеся получают хорошие оценки в дневник и заслуженное одобрение преподавателя.

Продуктивное использование ГДЗ

Правильное использование онлайн-ресурса подразумевает работу с ним по схеме:

выполнить упражнения самостоятельно;
проверить себя по ресурсу;
проанализировать ошибки и выявить темы, требующие более глубокого рассмотрения по учебнику;
проштудировать проблемные вопросы еще раз.

С таким внимательным отношением к интернет-помощнику молодым людям гарантировано успешное овладение математикой. Применяя онлайн-сборник в учёбе, школьники смогут сэкономить время на приготовлении домашних заданий, разобрать сложные номера, наверстать пропущенные уроки.

А приятным бонусом станут уверенные эрудированные ответы на уроках и положительные эмоции от результатов своего совместного труда с решебником.

Желаем успешного овладения точной наукой!

КР-1. Делимость натуральных чисел

В-1В-2

КР-2. Сравнение, сложение и вычитание дробей

В-1В-2

КР-3. Умножение дробей

В-1В-2

КР-4. Деление дробей

В-1В-2

КР-5. Отношения и пропорции. Процентное отношение двух чисел

В-1В-2

КР-6. Прямая и обратная пропорциональные зависимости. Окружность и круг

В-1В-2

КР-7. Рациональные числа. Сравнение рациональных чисел

В-1В-2

КР-8. Сложение и вычитание рациональных чисел

В-1В-2

КР-9.

Умножение и деление рациональных чиселВ-1В-2

КР-10. Решение уравнений и задач с помощью уравнений

В-1В-2

КР-11. Перпендикулярные и параллельные прямые. Координатная плоскость

В-1В-2

КР-12. Итоговая

В-1В-2

Упражнения. В-1

Упражнения. В-2

1234510111213141516171819202122232425262728293031323334353637383940414243444546474849100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229

Упражнения.

В-3123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229

Упражнения. В-4

КР-1.

Делимость натуральных чисел: В-1

ГДЗ по математике 6 класс Мерзляк Полонский Якир

ГДЗ / Решебники / 6 класс / Математика 👍 / Мерзляк Полонский Якир

Авторы: Мерзляк А.Г., Полонский В.Б., Якир М.С.
Издательство: Дрофа

Онлайн решебник к учебнику по математике за 6 класс авторов Мерзляк А.Г., Полонский В.Б., Якир М.С.. Содержит решения к 1422 заданиям.

Быстрый поиск

7137147157167177187197207217227237247257267277287297307317327337347367377387397407417427437447457467477487497507517527537547557567577587597607617627637647657667677687697707717727737747757767777787797817827837847857867877887897907917927937947957967977987998008018028038048058068078088098108118128138148158168178188198208218228238248258268278288298308318328338348358368378388398408418428438448458468478488498508518528538548558568578588598608618628638648658668678688698708718728738748758768778788798808818828838848858868878888898908918928938948958968978988999009019029039049059069079089099109119129139149159169179189199209219229239249259269279289299309319329339349359369379389399409419429439449459469479489499509519529539549559569579589599609619629639649659669679689699709719729739749759769779789799809819829839849859869879889899909919929939949959969979989991000100110021003100410051006100710081009101010111012101310141015101610171018101910201021102210231024102510261027102810291030103110321033103410351036103710381039104010411042104310441045104610471048104910501051105210531054105510561057105810591060106110621063106410651066106710681069107010711072107310741075107610771078107910801081108210831084108510861087108810891090109110921093109410951096109710981099110011011102110311041105110611071108110911101111111211131114111511161117111811191120112111221123112411251126112711281129113011311132113311341135113611371138113911401141114211431144114511461147114811491150115111521153115411551156115811591160116111621163116411651166116711681169117011711172117311741175117611771178117911801181118211831184118511861187118811891190119111921193119411951196119711981199120012011202120312041205120612071208120912101211121212131214121512161217121812191220122112221223122412251226122712281229123012311232123312341235123612371238123912401241124212431244124512461247124812491250125112521253125412551256125712581259126012611262126312641265126612671268126912701271127212731274127512761277127812791280128112821283128412851286128712881289129012911292129312941295129612971298129913001301130213031304130513061307130813091310131113121313131413151316131713181319132013211322132313241325132613271328132913301331133213331334133513361337133813391340134113421343134413451346134713481349135013511352135313541355135613571358135913601361136213631364136513661367136813691370137113721373137413751376137713781379138013811382138313841385138613871389139013911392139313941395139613971398139914001401140214031404140514061407140814091410141114121413141414151416141714181419142014211422

Оцените решебник:

Загрузка. ..

ГДЗ решебник по математике 6 класс Мерзляк Полонский Якир

Здесь представлены ответы к учебнику по математике 6 класс Мерзляк Полонский Якир. Вы можете смотреть и читать гдз онлайн (без скачивания) с компьютера и мобильных устройств.

Выберите номер задания учебника

Задание:

Быстрый поиск

Решите пример, раскрыв скобки.

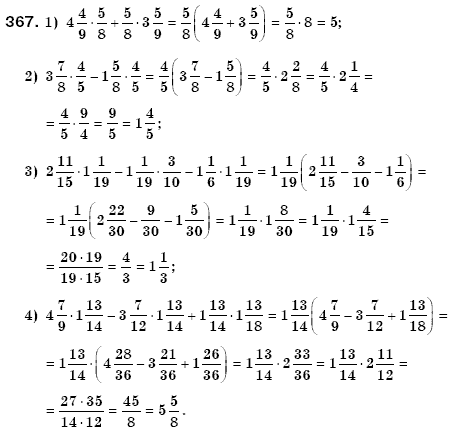Раскрывающие скобки

для образования возможности раскрытия скобок с учетом знака перед скобками;

разработка:

развивать логическое мышление, внимание, математическую речь, умение анализировать, сравнивать, обобщать, делать выводы; воспитателей:
формирование ответственности, познавательного интереса к предмету

На занятиях

I. Организационный момент.

Зацени, приятель
Ты готов к уроку?
Все ли на месте? Всё хорошо?
Ручка, книга и блокнот.
Все ли сидят правильно?
Все внимательно смотрят?

Хочу начать урок с вопроса к вам:

Как вы думаете, что самое ценное на земле? (Ответы детей.)

Этот вопрос волнует человечество уже тысячи лет. Вот ответ, который дал известный ученый Аль-Бируни: «Знание — самое превосходное владение. Все к этому стремятся, но это не приходит само собой».

Пусть эти слова станут девизом нашего урока.

II. Актуализация ранее полученных знаний, умений, навыков:

Счет словесный:

1.1. Какое сегодня число?

2. Что вы знаете о числе 20?

3. А где находится этот номер на координатной линии?

4. Назовите номер своего реверса.

5. Назовите число напротив него.

6. Как называется число — 20?

7. Какие числа называются противоположными?

8. Какие числа называются отрицательными?

9. Чему равен модуль числа 20? — 20?

10. Чему равна сумма противоположных чисел?

2. Объясните следующие записи:

а) Гениальный древний математик Архимед родился в 0 287 г. до н.э.

б) Гениальный русский математик Н.И. Лобачевский родился в 1792 году.

в) Первые Олимпийские игры состоялись в Греции в 776 году.

г) Первые Международные Олимпийские игры состоялись в 189 году6.

д) XXII зимние Олимпийские игры состоялись в 2014 году.

3. Узнать, какие числа крутятся на «математической карусели» (все действия выполняются устно).

II. Формирование новых знаний, умений и навыков.

Вы научились выполнять различные операции с целыми числами. Что мы будем делать дальше? Как мы будем решать примеры и уравнения?

Найдем смысл этих выражений

7 + (3 + 4) = -7 + 7 = 0
-7 + 3 + 4 = 0

Какова процедура в 1 примере? Сколько в скобках? Порядок действий во втором примере? Результат первого действия? Что можно сказать об этих выражениях?

Разумеется, результаты первого и второго выражений совпадают, поэтому между ними можно поставить знак равенства: -7 + (3 + 4) = -7 + 3 + 4

Что мы сделали с скобки? (Потеряно.)

Как вы думаете, что мы будем делать сегодня на уроке? (Дети формулируют тему урока.) В нашем примере какой знак стоит перед скобками. (Плюс.)

И так мы приходим к следующему правилу:

Если перед скобками стоит знак +, то скобки и этот знак + можно опустить, сохранив знаки термов в скобках. Если первое слагаемое в скобках пишется без знака, то его нужно писать со знаком +.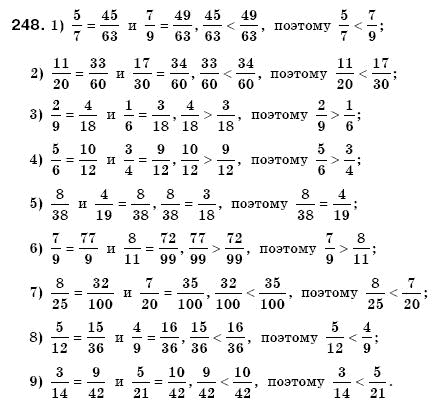

А если перед скобками стоит знак минус?

В этом случае нужно рассуждать так же, как и при вычитании: нужно прибавить число, противоположное вычитаемому:

7 – (3 + 4) = -7 + (-7) = -7 + (-3) + (-4) = -7 – 3 – 4 = -14

— Итак, мы раскрыли скобки, когда перед ними стоял знак минус.

Правило раскрытия скобок при наличии перед скобками знака «-».

Чтобы раскрыть скобки, перед которыми стоит знак -, нужно заменить этот знак на +, поменяв знаки всех терминов в скобках на противоположные, а затем раскрыть скобки.

Послушаем правила раскрытия скобок в стихах:

Перед скобкой стоит плюс.
Он говорит об этом
Что ты опускаешь скобки
Выпусти все знаки!
Перед скобкой минус строгий
Преградит нам путь
Убрать скобки
Нам нужно поменять знаки!

Да, ребята, знак минус очень коварный, это «сторож» у ворот (скобки), он выпускает числа и переменные только тогда, когда они меняют «паспорта», то есть свои знаки.

Зачем вообще нужно открывать скобки? (Когда есть скобки, есть момент какого-то элемента незавершенности, какой-то тайны. Это как закрытая дверь, за которой находится что-то интересное.) Сегодня мы пережили эту тайну.

Небольшой экскурс в историю:

Фигурные скобки появляются в трудах Виета (1593 г.). Скобки получили широкое распространение только в первой половине 18 века, благодаря Лейбницу и тем более Эйлеру.

Физкультминутка.

III. Закрепление новых знаний, навыков и умений.

Учебная работа:

№1234 (открытые скобки) — устно.

№ 1236 (открытые скобки) — устно.

№1235 (найти смысл выражения) — письменно.

№1238 (упростите выражения) — работайте в парах.

IV. Подведение итогов урока.

1. Объявлены результаты.

2. Дом. упражнение. 39 № 1254 (а, б, в), 1255 (а, б, в), 1259.

3. Что мы узнали сегодня?

Чему ты научился?

А закончить урок хочу пожеланиями для каждого из вас:

«Прояви способности к математике,
Не ленись, а развивайся ежедневно.
Умножать, делить, трудиться, думать,
Не забывать дружить с математикой.

Скобки используются для обозначения порядка выполнения действий в числовых и буквенных выражениях, а также в выражениях с переменными. От выражения со скобками удобно перейти к тождественно равному выражению без скобок. Этот метод называется раскрытием скобок.

Раскрыть скобки означает избавить выражение от этих скобок.

Отдельного внимания заслуживает еще один момент, который касается особенностей написания растворов при раскрытии скобок. Мы можем записать исходное выражение со скобками и результат, полученный после раскрытия скобок, как равенство. Например, после раскрытия скобок вместо выражения
3−(5−7) мы получим выражение 3−5+7. Мы можем записать оба этих выражения в виде равенства 3−(5−7)=3−5+7.

И еще один важный момент. В математике для сокращения записей принято не писать плюсик, если он стоит первым в выражении или в скобках. Например, если мы сложим два положительных числа, например, семь и три, то напишем не +7+3, а просто 7+3, несмотря на то, что семь тоже положительное число. Точно так же, если вы видите, например, выражение (5+x) — знайте, что перед скобкой стоит плюс, который не пишется, а перед скобкой стоит плюс + (+5+x). пять.

Правило расширения скобки для добавления

При раскрытии скобок, если перед скобками стоит плюс, то этот плюс опускается вместе со скобками.

Пример. Раскрыть скобки в выражении 2+(7+3) Перед скобками плюс, далее символы перед цифрами в скобках не меняются.

2 + (7 + 3) = 2 + 7 + 3

Правило раскрытия скобок при вычитании

Если перед скобками стоит минус, то этот минус вместе со скобками опускается, но слагаемые, которые были в скобках, меняют знак на противоположный. Отсутствие знака перед первым членом в круглых скобках означает наличие знака +.

Пример. Открытые скобки в выражении 2 − (7 + 3)

Перед скобками стоит минус, поэтому нужно поменять знаки перед цифрами из скобок. Знака в скобках перед цифрой 7 нет, значит, семерка положительная, считается, что перед ней стоит знак +.

2 − (7 + 3) = 2 − (+ 7 + 3)

При раскрытии скобок убираем из примера минус, который был перед скобками, а сами скобки 2 − (+ 7 + 3 ), и меняем знаки, которые были в скобках, на противоположные.

2 − (+ 7 + 3) = 2 − 7 − 3

Раскрывающие скобки при умножении

Если перед скобками стоит знак умножения, то каждое число внутри скобок умножается на множитель перед скобками. При этом умножение минуса на минус дает плюс, а умножение минуса на плюс, как и умножение плюса на минус, дает минус.

Таким образом, скобки в произведениях раскрываются в соответствии с распределительным свойством умножения.

Пример. 2 (9 — 7) = 2 9 — 2 7

При умножении скобок на скобки каждый член первой скобки умножается на каждый член второй скобки.

(2 + 3) (4 + 5) = 2 4 + 2 5 + 3 4 + 3 5

На самом деле нет необходимости запоминать все правила, достаточно запомнить только одно, вот это: c(a−b)=ca−cb. Почему? Потому что, если мы подставим единицу вместо c, мы получим правило (a−b)=a−b. А если мы подставим минус один, то получим правило −(a−b)=−a+b. Ну а если вместо с подставить другую скобку, то можно получить последнее правило.

Раскрывать скобки при делении

Если после скобок стоит знак деления, то каждое число внутри скобок делится на делитель после скобок, и наоборот.

Пример. (9 + 6) : 3=9: 3 + 6: 3

Как раскрыть вложенные скобки

Если выражение содержит вложенные скобки, то они раскрываются по порядку, начиная с внешних или внутренних.

При этом, открывая одну из скобок, важно не трогать другие скобки, просто переписав их как есть.

Пример. 12 — (а + (6 — b) — 3) = 12 — а — (6 — b) + 3 = 12 — а — 6 + b + 3 = 9 — а + b

В данной статье мы рассмотрим подробно изложены основные правила такой важной темы курса математики, как раскрытие скобок. Нужно знать правила раскрытия скобок, чтобы правильно решать уравнения, в которых они используются.

Как правильно открывать скобки при сложении

Раскрыть скобки перед знаком «+»

Это самый простой случай, т.к. если перед скобками стоит знак сложения, то при раскрытии скобок знаки внутри них не меняются. Пример:

(9 + 3) + (1 — 6 + 9) = 9 + 3 + 1 — 6 + 9 = 16.

Как открыть скобки перед знаком «-»

В этом случае нужно перепишите все члены без скобок, но при этом поменяйте внутри них все знаки на противоположные. Знаки меняются только у терминов из тех скобок, перед которыми стоял знак «-». Пример:

(9 + 3) — (1 — 6 + 9) = 9 + 3 — 1 + 6 — 9 = 8.

Как открывать скобки при умножении

Перед скобками стоит множитель

В этом случае нужно каждое слагаемое умножить на коэффициент и раскрыть скобки, не меняя знаки. Если множитель стоит со знаком «-», то при умножении знаки слагаемых меняются местами. Пример:

3 * (1 — 6 + 9) = 3 * 1 — 3 * 6 + 3 * 9 = 3 — 18 + 27 = 12.

Как открыть две скобки со знаком умножения между ними

В В этом случае вам нужно умножить каждое слагаемое из первых скобок на каждое слагаемое из вторых скобок, а затем сложить результаты. Пример: 92) * 12 = 1728.

Как раскрыть 3 скобки

Существуют уравнения, в которых умножаются сразу 3 скобки. В этом случае необходимо сначала умножить члены первых двух скобок между собой, а затем умножить сумму этого умножения на члены третьей скобки. Пример:

(1 + 2) * (3 + 4) * (5 — 6) = (3 + 4 + 6 + 8) * (5 — 6) = — 21.

Эти правила раскрытия скобок в равной степени применяются к как линейные, так и тригонометрические уравнения.

На этом уроке вы узнаете, как преобразовать выражение, содержащее скобки, в выражение, не содержащее скобок. Вы узнаете, как открывать скобки, перед которыми стоит знак плюс и минус. Вспомним, как открывать скобки, используя распределительный закон умножения. Рассмотренные примеры позволят связать новый и ранее изученный материал в единое целое.

Тема: Решение уравнений

Урок: Раскрытие скобок

Как открыть скобки, перед которыми стоит знак «+». Использование ассоциативного закона сложения.

Если вам нужно прибавить к числу сумму двух чисел, то к этому числу можно прибавить первое слагаемое, а затем второе.

Слева от знака равенства находится выражение со скобками, а справа — выражение без скобок. Это означает, что при переходе от левой части равенства к правой скобки были раскрыты.

Рассмотрим примеры.

Пример 1

Раскрыв скобки, мы изменили порядок операций. Считать стало удобнее.

Пример 2

Пример 3

Обратите внимание, что во всех трех примерах мы просто удалили скобки. Сформулируем правило:

Комментарий.

Если первое слагаемое в скобках беззнаковое, то оно должно быть записано со знаком плюс.

Вы можете следовать пошаговому примеру. Во-первых, добавьте 445 к 889.. Это умственное действие можно выполнить, но это не очень легко. Раскроем скобки и увидим, что измененный порядок операций значительно упростит расчеты.

Если следовать указанному порядку действий, то из 512 нужно сначала вычесть 345, а затем к результату прибавить 1345. Раскрыв скобки, мы изменим порядок действий и значительно упростим расчеты.

Наглядный пример и правило.

Рассмотрим пример: . Вы можете найти значение выражения, сложив 2 и 5, а затем взяв полученное число с обратным знаком. Получаем -7.

С другой стороны, тот же результат можно получить, сложив противоположные числа.

Сформулируем правило:

Пример 1

Пример 2

Правило не меняется, если в скобках не два, а три и более условия.

Пример 3

Комментарий. Знаки меняются местами только перед терминами.

Чтобы раскрыть скобки в данном случае, нужно вспомнить о распределительном свойстве.

Сначала умножьте первую скобку на 2, а вторую на 3.

Перед первой скобкой стоит знак «+», что означает, что знаки нужно оставить без изменений. Второму предшествует знак «-», поэтому все знаки нужно поменять местами

Библиография

Виленкин Н. Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика: 6. — Математика. Мнемозина, 2012.
Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. — Гимназия, 2006.
Депман И.Я., Виленкин Н.Я. За страницами учебника математики. — Просвещение, 1989.
Рурукин А.Н., Чайковский И.В. Задания по курсу математики 5-6 класс — ЗШ МИФИ, 2011.
Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5-6. Пособие для учащихся 6 классов заочной школы МИФИ. — ЗШ МИФИ, 2011.
Шеврин Л.Н., Гейн А.Г., Коряков И.О., Волков М.В. Математика: Учебник-собеседник для 5-6 классов средней школы. Библиотека учителя математики. — Просвещения, 1989.

Онлайн тесты по математике ().
Вы можете скачать указанные в п.1.2. книги ().

Домашнее задание

Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. — М.: Мнемозина, 2012. (см. ссылку 1.2)
Домашнее задание: №1254, №1255, №1256(б,г)
Прочие присвоения: № 1258(с), № 1248

Егэ решить.

Подготовка к ЕГЭ по математике (профильный уровень): задачи, решения и пояснения

Среднее общеобразовательное

Строка УМК Г.К. Муравина. Алгебра и начала математический анализ(10-11)(углубленный)

Линия УМК Мерзляк. Алгебра и начало анализа (10-11) (У)

Математика

Разбираем задачи и решаем примеры с учителем

Экзаменационная работа профильного уровня длится 3 часа 55 минут (235 минут).

Минимальный порог — 27 баллов.

Экзаменационная работа состоит из двух частей, различающихся по содержанию, сложности и количеству заданий.

Отличительной чертой каждой части работы является форма заданий:

часть 1 содержит 8 заданий (задания 1-8) с кратким ответом в виде целого числа или конечной десятичной дроби;
часть 2 содержит 4 задания (задания 9-12) с кратким ответом в виде целой или конечной десятичной дроби и 7 заданий (задания 13-19) с развернутым ответом (полная запись решения с обоснованием выполняемые действия).

Панова Светлана Анатольевна , учитель математики высшей категории школы, стаж работы 20 лет:

«Для получения школьного аттестата выпускник должен сдать два обязательных экзамена по форме ЕГЭ, один из которых по математике. В соответствии с Концепцией развития математического образования в Российской Федерации ЕГЭ по математике делится на два уровня: базовый и специализированный. Сегодня мы рассмотрим варианты профильного уровня.

Задание №1 — проверяет у участников ЕГЭ умение применять навыки, полученные на курсе 5-9занятия по элементарной математике в практической деятельности. Участник должен иметь вычислительные навыки, уметь работать с рациональными числами, уметь округлять десятичные дроби, уметь переводить одни единицы измерения в другие.

Пример 1 В квартире, где проживает Петр, установлен счетчик (счетчик) холодной воды. Первого мая счетчик показывал расход 172 куб. м воды, а на первое июня — 177 куб. м. Какую сумму должен заплатить Петр за холодную воду за май, если цена 1 куб. м холодной воды 34 рубля 17 копеек? Дайте ответ в рублях.

Решение:

1) Найдите количество израсходованной воды в месяц:

177 — 172 = 5 (куб. м)

2) Найдите, сколько денег будет выплачено за израсходованную воду:

34,17 5 = 170,85 (руб.)

Ответ: 170,85.

Задание №2 — это одно из самых простых заданий ЕГЭ. С ней успешно справляется большинство выпускников, что свидетельствует о владении определением понятия функции. Тип задания № 2 по кодификатору требований – это задание на использование полученных знаний и умений в практической деятельности и повседневной жизни. Задание № 2 состоит в описании с помощью функций различных реальных отношений между величинами и интерпретации их графиков. Задание №2 проверяет умение извлекать информацию, представленную в таблицах, схемах, графиках. Выпускники должны уметь определять значение функции по значению аргумента при различных способах задания функции и описывать поведение и свойства функции по ее графику. Также необходимо уметь находить максимальное или наименьшее значение и строить графики исследуемых функций. Допущенные ошибки носят случайный характер при чтении условий задачи, чтении схемы.

#ADVERTISING_INSERT#

Пример 2 На рисунке показано изменение курсовой стоимости одной акции горнодобывающей компании в первой половине апреля 2017 года. 7 апреля бизнесмен приобрел 1000 акций этой компании. 10 апреля он продал три четверти купленных акций, а 13 апреля продал все оставшиеся. Сколько бизнесмен потерял в результате этих операций?

Решение:

2) 1000 3/4 = 750 (акций) — составляют 3/4 всех купленных акций.

6) 247500 + 77500 = 325000 (рублей) — получил бизнесмен после продажи 1000 акций.

7) 340 000 — 325 000 = 15 000 (рублей) — бизнесмен потерял в результате всех операций.

Оценка

две части , в том числе 19 задач . Часть 1 Часть 2

3 часа 55 минут (235 минут).

Ответы

Но можно сделать компас Калькуляторы на экзамене не используется .

паспорт ), проход и капиллярный или! Разрешено брать с собой воду (в прозрачной бутылке) и продукты питания

Экзаменационный лист состоит из двух частей , в том числе 19 заданий . Часть 1 содержит 8 заданий базового уровня сложности с краткими ответами. Часть 2 содержит 4 задания повышенного уровня сложности с кратким ответом и 7 заданий повышенного уровня сложности с развернутым ответом.

На выполнение экзаменационной работы по математике дается 3 часа 55 минут (235 минут).

Ответы на задания 1–12 записываются как целое или десятичное число в конце . Запишите цифры в полях ответов в тексте работы, а затем перенесите их в бланк ответов №1, выдаваемый на экзамене!

При выполнении работы можно использовать выданные вместе с работой. Можно использовать только линейку , но можно сделать циркуль своими руками. Запрещается использовать инструменты со справочными материалами. Калькуляторы на экзамене не используются .

На экзамен необходимо иметь при себе документ, удостоверяющий личность. паспорт ), пропуск и ручка капиллярная или гелевая с черными чернилами ! Разрешено взять с собой вода (в прозрачной бутылке) и еда (фрукты, шоколад, булочки, бутерброды), но могут попросить оставить в коридоре.

Программа экзамена, как и в предыдущие годы, составлена из материалов основных математических дисциплин. Билеты будут включать в себя математические, геометрические и алгебраические задачи.

В КИМ ЕГЭ 2020 по математике на профильном уровне изменений нет.

Особенности заданий ЕГЭ по математике-2020

При подготовке к ЕГЭ по математике (профильному) обратите внимание на основные требования экзаменационной программы. Он предназначен для проверки знаний углубленной программы: векторные и математические модели, функции и логарифмы, алгебраические уравнения и неравенства.
Отдельно потренируйтесь решать задачи на.
Важно проявить нестандартное мышление.

Структура ЕГЭ

Задания ЕГЭ по профильной математике разделен на два блока.

Часть — краткие ответы , включает 8 заданий, проверяющих базовую математическую подготовку и умение применять знания по математике в повседневной жизни.
Часть — кратких и подробных ответов . Он состоит из 11 заданий, 4 из которых требуют краткого ответа, а 7 — развернутого с аргументацией выполняемых действий.

Повышенной сложности — задания 9-17 второй части КИМ.
Высокий уровень сложности — задания 18-19 –. В этой части экзаменационных заданий проверяется не только уровень математических знаний, но и наличие или отсутствие творческого подхода к решению сухих «цифровых» задач, а также эффективность умения использовать знания и навыки в качестве профессионального инструмента.

Важно! Поэтому при подготовке к экзамену всегда подкрепляйте теорию по математике решением практических задач.

Как будут распределяться баллы?

Задания первой части КИМ по математике близки к базовым ЕГЭ, поэтому высокий балл получить за них невозможно.

Баллы за каждое задание по математике на профильном уровне распределились следующим образом:

за правильные ответы на задания №1-12 — по 1 баллу;
№13-15 — по 2 шт.;
№16-17 — по 3 шт.;
№18-19 — по 4 штуки.

Продолжительность экзамена и правила поведения на экзамене

Для сдачи экзамена -2020 студенту назначено 3 часа 55 минут (235 минут).

В это время учащийся не должен:

шуметь;
пользоваться гаджетами и другими техническими средствами;
списание;
попробуй помочь другим или попроси помощи для себя.

За такие действия экзаменатор может быть исключен из аудитории.

На Госэкзамен по математике допускается сдача с собой только линейка, остальные материалы вам выдадут непосредственно перед экзаменом. выдается на месте.

Эффективная подготовка — решение онлайн-тестов по математике 2020. Выбирайте и получайте высший балл!

USE 2017 Пробная версия

Уровень профиля
Условия задачи с

Экзаменационная работа состоит из двух частей, включающих 19 заданий. На выполнение экзаменационной работы по математике отводится 3 часа 55 минут. Ответы на задания 1-12 записываются в виде целого числа или конечной десятичной дроби. При выполнении заданий 13–19, вам нужно записать полное решение.

Часть 1

Ответ на задания 1- 12 является целым числом или конечным десятичным числом. Ответ следует записать в бланк ответов №1 справа от номера соответствующего задания, начиная с первой ячейки. Запишите каждую цифру, знак минус и десятичную точку в в отдельной ячейке в соответствии с образцами, приведенными в форме. Единицы измерения не требуются.

1 . На заправке литр бензина стоит 33 рубля. 20 коп. Водитель залил в бак 10 литров бензина и купил бутылку воды за 41 рубль. Сколько рублей сдачи он получит из 1000 рублей?

2 . На рисунке представлен график осадков в Калининграде с 4 по 10 февраля 1974 г. По оси абсцисс отложены дни, по оси ординат — количество осадков в мм. Определите по рисунку, за сколько дней из этого периода выпало от 2 до 8 мм осадков.

3 . На клетчатой бумаге два круга. Площадь внутреннего круга равна 2. Найдите площадь заштрихованной фигуры.

4 . Вероятность того, что студент Петя правильно решит более 8 задач на контрольной по истории, равна 0,76. Вероятность того, что Петя правильно решит более 7 задач, равна 0,88. Найти вероятность того, что Петя правильно решит ровно 8 задач.

5 . Решите уравнение. Если уравнение имеет более одного корня, в ответе укажите меньший из них.

6 . Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из сторон на два отрезка, длины которых равны 10 и 1, считая от вершины, противоположной основанию. Найдите периметр треугольника.

7 . На рисунке показан график производной функции , определено на интервале (–8; 9). Найдите количество точек минимума функции , , принадлежащих отрезку [–4; восемь].

8 . Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен , а высота равна .

9 . Найти значение выражения

10 . Расстояние от наблюдателя, находящегося на высоте ч м над землей, выраженное в километрах, до линии горизонта, которую он видит, рассчитывается по формуле, где R = 6400 км — радиус Земли. Человек, стоящий на берегу, видит горизонт на расстоянии 4,8 километра. К пляжу ведет лестница, каждая ступенька которой имеет высоту 10 см. Какое наименьшее количество ступеней нужно пройти человеку, чтобы он мог видеть горизонт на расстоянии не менее 6,4 километра?

11 . Два человека выходят из одного дома на прогулку на опушку леса, расположенную в 1,1 км от дома. Один идет со скоростью 2,5 км/ч, а другой – со скоростью 3 км/ч. Дойдя до края, второй возвращается с той же скоростью. На каком расстоянии от точки старта они встретятся? Дайте ответ в километрах.

12 . Найдите точку минимума функции, принадлежащую интервалу .

Для записи решений и ответов на задания 13- 19 используйте лист ответов № 2. Сначала запишите номер выполняемого задания, а затем полное мотивированное решение и ответ.

13 . а) Решите уравнение. б) Определите, какие из его корней принадлежат отрезку.

14 . В параллелепипеде ABCDA 1 B 1 C 1 D 1 точка M среднее ребро C 1 D 1 и точка K делит ребро AA 1 против AK:KA= 1:3. Через точки K и M проведена плоскость α, параллельная прямой BD и пересекающая диагональ A 1 C в точке O .
а) Докажите, что плоскость α делит диагональ A 1 C в соотношении A 1 O: OC = 3:5.
б) Найдите угол между плоскостью α и плоскостью ( ABC ), если известно, что ABCDA 1 B 1 C 1 D 1 — куб.

15 . Решите неравенство.

16 . Параллелограмм ABCD и окружность расположены так, что сторона AB касается окружности CD и является хордой, а стороны D A и BC пересекают окружность в точках P и Q соответственно. .
а) Докажите, что около четырехугольника ABQP можно описать окружность.
б) Найдите длину отрезка DQ , если известно, что AP = a , BC = b , BQ = c .

17 . Вася взял кредит в банке на сумму 270 200 руб. Схема погашения кредита такова: в конце каждого года банк увеличивает оставшуюся сумму долга на 10%, а затем Вася перечисляет банку свой очередной платеж. Известно, что Вася погасил кредит за три года, и каждый его последующий платеж был ровно в три раза больше предыдущего. Сколько Вася заплатил в первый раз? Дайте ответ в рублях.

18 . Найти все такие значения параметра , для каждого из которых уравнение имеет решения на отрезке ..

Многих абитуриентов волнует вопрос, как самостоятельно приобрести знания, необходимые для успешной сдачи испытаний перед поступлением. В 2017 году они часто обращаются к Интернету, чтобы найти решение. Решений много, действительно стоящие стоит искать очень долго. К счастью, есть известные и проверенные системы. Один из них Решу ЕГЭ Дмитрий Гущин.

Система обучения Дмитрия Гущина под названием «Решу ЕГЭ» подразумевает комплексную подготовку к предстоящему экзамену. Дмитрий Гущин создавал и старался бесплатно давать необходимые знания, чтобы будущее поколение могло успешно сдать экзамены. Система предназначена для самостоятельного изучения предметов. Я решаю ЕГЭ на основе единой подачи информации, которая последовательно, тема за темой, укладывается в мозг ученика.

ЕГЭ-2017 по математике базовый уровень

Дмитрий Гущин берется помочь с такими экзаменами, как ОГЭ и ЕГЭ, по очень распространенной методике. Он заключается в том, что все новые знания излагаются и систематизируются по темам. Студент может легко выбрать, что ему нужно повторить для окончательного закрепления материала.

Задания доступны на базовом и профильном уровнях. Математика — яркий пример таких задач. Основной (базовый) уровень охватывает общешкольную совокупность знаний. Здесь необходимы знания, которые каждый школьник получает в 11 лет. Профильный уровень рассчитан на выпускников профильных школ с уклоном в конкретный предмет.

Интересной особенностью системы является ее сходство с реальным экзаменом. В случае задания итогового контроля они сдаются в формате ЕГЭ. Студент также может узнать свой итоговый балл после прохождения теста. Это помогает мотивировать человека на достижение новых целей и изучение нового материала. Осознание своих реальных шансов на экзамене помогает собраться с мыслями и понять, что именно вам нужно выучить.

Самые популярные предметы в «Я решу ЕГЭ» представлены наряду с другими. Русский язык Дмитрия Гущина включает в себя правила грамматики, пунктуации и синтаксиса, а также лексику. Химия содержит примеры решения конкретных задач, специальные формулы. Раздел химии также включает в себя различные соединения и понятия о химических веществах. Раздел биологии охватывает жизнедеятельность всех царств живых организмов. Он содержит важную теорию, которая в конечном итоге поможет вам успешно сдать экзамен.

Следующая особенность заключается в том, что ваш прогресс записывается, и вы можете отслеживать свой прогресс. Такой подход поможет вам мотивировать себя, даже когда вам больше не хочется учиться. Ваш собственный результат всегда заставляет вас делать больше.

В системе также есть критерии оценки работ. Они сделают подготовку к экзамену плановой и продуманной. Будущий студент всегда сможет прочитать их и понять, на что экзаменатор обратит внимание. Это важно для того, чтобы обратить внимание на некоторые важные аспекты работы. В целом студент полностью осознает важность своего выбора и помнит критерии оценивания.

Когда ставить скобки в предложении. Как использовать простые скобки

Эта часть уравнения представляет собой выражение в скобках. Чтобы открыть скобки, посмотрите на знак перед скобками. Если стоит плюсик, то при раскрытии скобок в записи выражения ничего не изменится: достаточно убрать скобки. Если стоит знак минус, то при раскрытии скобок необходимо поменять все знаки, которые изначально стоят в скобках, на противоположные. Например, -(2x-3)=-2x+3.

Умножение двух скобок.
Если в уравнении есть произведение двух скобок, раскладывание скобок по стандартному правилу. Каждый член первой скобки умножается на каждый член второй скобки. Полученные числа суммируются. 2-17x-4. 93
Формулы для возведения выражения больше трех можно составить с помощью треугольника Паскаля.

Источники:

формула раскрытия скобок

Математические операции, заключенные в скобки, могут содержать переменные и выражения различной степени сложности. Для умножения таких выражений придется искать решение в общем виде, раскрывая скобки и упрощая результат. Если в скобках указаны операции без переменных, только с числовыми значениями, то раскрывать скобки не нужно, так как при наличии компьютера его пользователю доступны весьма значительные вычислительные ресурсы — их проще использовать, чем упрощать выражение.

Инструкция

Умножьте последовательно каждое (или уменьшенное из него), содержащееся в одной скобке, на содержимое всех остальных скобок, если вы хотите получить общий результат. Например, пусть исходное выражение будет записано так: (5+x)∗(6-x)∗(x+2). Тогда последовательное умножение (то есть раскрытие скобок) даст следующий результат: (5+x)∗(6-x)∗(x+2) = (5∗6-5∗x)∗(5∗x+ 5*2) + (6*х-х*х)*(х*х+2*х) = (5*6*5*х+5*6*5*2) — (5*х*5*х+ 5* х*5*2) + (6*х*х*х+6*х*2*х) — (х*х*х*х+х*х*2*х) = 5*6*5 *х + 5*6*5*2 — 5*х*5*х — 5*х*5*2 + 6*х*х*х + 6*х*2*х — х*х*х*х*х — х * х * 2 * х = 150 * х + 300 — 25 * х² — 50 * х + 6 * х³ + 12 * х² — х * х³ — 2 * х³.

Упрощать после результата, сокращая выражения. Например, выражение, полученное на предыдущем шаге, можно упростить следующим образом: 150*x + 300 — 25*x² — 50*x + 6*x³ + 12*x² — x*x³ — 2*x³ = 100*x + 300 — 13* х² — 8* х³ — х* х³.

Используйте калькулятор, если вам нужно умножить, содержащие только числовые значения без неизвестных переменных. Встроенное ПО

Основная функция скобок – изменение порядка действий при вычислении значений. Например , в числовом выражении \(5 3+7\) сначала будет вычисляться умножение, а затем сложение: \(5 3+7 =15+7=22\). Но в выражении \(5·(3+7)\) сначала будет вычисляться сложение в скобках, а только потом умножение: \(5·(3+7)=5·10=50\).

Пример. Раскройте скобку: \(-(4m+3)\).
Решение : \(-(4m+3)=-4m-3\).

Пример. Раскройте скобку и дайте подобные термины \(5-(3x+2)+(2+3x)\).
Решение : \(5-(3x+2)+(2+3x)=5-3x-2+2+3x=5\).

Пример. Раскройте скобки \(5(3-x)\).
Решение : У нас есть \(3\) и \(-x\) в скобках и пять перед скобкой. Это означает, что каждый член скобки умножается на \(5\) — напомню, что знак умножения между числом и скобкой в математике не пишется для уменьшения размера записи .

Пример. Раскройте скобки \(-2(-3x+5)\).
Решение : Как и в предыдущем примере, скобки \(-3x\) и \(5\) умножаются на \(-2\).

Пример. Упростите выражение: \(5(x+y)-2(x-y)\).
Решение : \(5(х+у)-2(х-у)=5х+5у-2х+2у=3х+7у\).

Осталось рассмотреть последнюю ситуацию.

При умножении скобок на скобки каждый член первой скобки умножается на каждый член второй:

\((c+d)(a-b)=c (a-b)+d (a-b)=ca-cb+da-db\)

Пример. Раскройте скобки \((2-x)(3x-1)\).
Решение : У нас есть произведение из скобок, и его можно сразу открыть по приведенной выше формуле. Но чтобы не запутаться, давайте делать все пошагово.
Шаг 1. Удалите первую скобку — каждый из ее членов умножается на вторую скобку:

Шаг 2. Разложите произведения скобки на множитель, как описано выше:
— первый сначала…

Потом второй.

Шаг 3. Теперь умножаем и приводим подобные члены:

Не обязательно подробно расписывать все преобразования, можно сразу умножать. Но если вы только учитесь открывать скобки — пишите подробно, меньше шансов ошибиться.

Примечание ко всему разделу. На самом деле вам не нужно запоминать все четыре правила, достаточно запомнить только одно, вот это: \(c(a-b)=ca-cb\) . Почему? Потому что, если мы подставим единицу вместо c, мы получим правило \((a-b)=a-b\) . А если мы подставим минус один, то получим правило \(-(a-b)=-a+b\) . Ну а если вместо с подставить другую скобку, то можно получить последнее правило.

скобки внутри скобок

Иногда на практике возникают проблемы со скобками, вложенными в другие скобки. Вот пример такой задачи: упростить выражение \(7x+2(5-(3x+y))\).

Для успешного решения этих задач необходимо:
— внимательно разбираться во вложении скобок — какая в какую;
— открывать скобки последовательно, начиная, например, с самой внутренней.

Важно при открытии одной из скоб не трогайте остальную часть выражения , просто перепишите его как есть.
Возьмем в качестве примера приведенную выше задачу.

Пример. Раскройте скобки и дайте подобные термины \(7x+2(5-(3x+y))\).
Решение:

Пример. Раскройте скобки и дайте аналогичные термины \(-(x+3(2x-1+(x-5)))\).
Решение :

\(-(х+3(2х-1\)\(+(х-5)\) \())\)

Это тройное вложение скобок. Начнем с самого внутреннего (выделено зеленым). Перед скобкой стоит плюс, поэтому ее просто убирают.

\(-(х+3(2х-1\)\(+х-5\) \())\)

Теперь нужно открыть вторую скобу, промежуточную. Но перед этим мы упростим выражение, замаскировав похожие термины во второй скобке.

\(=-(х\)\(+3(3х-6)\) \()=\)

Теперь открываем вторую скобку (выделено синим цветом). Перед скобками стоит множитель, поэтому каждое слагаемое в скобках умножается на него.

\(=-(х\)\(+9x-18\) \()=\)

И откройте последнюю скобку. Перед скобкой минус — значит все знаки меняются местами. 93 + 5x + 1 \)

Сумма нескольких полиномов может быть преобразована (упрощена) в полином стандартной формы.

Иногда члены полинома необходимо разделить на группы, заключив каждую группу в круглые скобки. Так как круглые скобки противоположны скобкам, то легко сформулировать правила раскрытия круглых скобок:

Если перед скобками ставится знак +, то термины, заключенные в скобки, записываются теми же знаками. 93 \)

Произведение одночлена на многочлен тождественно равно сумме произведений этого одночлена и каждого из членов многочлена.

Этот результат формулируется как правило.

Чтобы умножить одночлен на многочлен, нужно умножить этот одночлен на каждый член многочлена.

Мы неоднократно использовали это правило для умножения на сумму.

Произведение многочленов. Преобразование (упрощение) произведения двух многочленов

В общем случае произведение двух многочленов тождественно равно сумме произведений каждого члена одного многочлена и каждого члена другого.

Обычно используют следующее правило.

Чтобы умножить многочлен на многочлен, нужно умножить каждый член одного многочлена на каждый член другого и сложить полученные произведения.

Формулы сокращенного умножения. Сумма, разность и квадраты разности

С некоторыми выражениями в алгебраических преобразованиях приходится иметь дело чаще, чем с другими. Возможно, наиболее распространенными выражениями являются \((a + b)^2, \; (a — b)^2 \) и \(a^2 — b^2 \), то есть квадрат суммы, квадрат разности и квадрат разности. 2 \) — это, конечно, не просто квадрат суммы, а квадрат суммы а и б. Однако квадрат суммы а и b встречается не так часто, как правило, вместо букв а и Ь в нем содержатся различные, иногда довольно сложные выражения. 92 = (a — b)(a + b) \) — разность квадратов равна произведению разности на сумму.

Эти три тождества позволяют при преобразованиях заменять их левые части на правые и наоборот — правые части на левые. Самое сложное в этом случае — увидеть соответствующие выражения и понять, какие в них заменяются переменные a и b. Давайте рассмотрим несколько примеров использования формул сокращенного умножения.

Тема: Решение уравнений

Урок: Раскрытие скобок

Как открыть скобки, перед которыми стоит знак «+». Использование ассоциативного закона сложения.

Рассмотрим примеры.

Пример 1

Раскрыв скобки, мы изменили порядок операций. Считать стало удобнее.

Пример 2

Пример 3

Обратите внимание, что во всех трех примерах мы просто удалили скобки. Сформулируем правило:

Комментарий.

Если первое слагаемое в скобках беззнаковое, то оно должно быть записано со знаком плюс.

Вы можете следовать пошаговому примеру. Во-первых, прибавьте 445 к 889. Это мысленное действие можно выполнить, но это не очень легко. Раскроем скобки и увидим, что измененный порядок операций значительно упростит расчеты.

Наглядный пример и правило.

С другой стороны, тот же результат можно получить, сложив противоположные числа.

Сформулируем правило:

Пример 1

Пример 2

Правило не меняется, если в скобках не два, а три и более условия.

Пример 3

Комментарий. Знаки меняются местами только перед терминами.

Чтобы раскрыть круглые скобки, в этом случае помните о распределительном свойстве.

Сначала умножьте первую скобку на 2, а вторую на 3.

Библиография

Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. — М.: Мнемозина, 2012.
Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. — Гимназия, 2006.
Депман И.Я., Виленкин Н.Я. За страницами учебника математики. — Просвещение, 1989.
Рурукин А.Н., Чайковский И.В. Задания по курсу математики 5-6 класс — ЗШ МИФИ, 2011.
Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5-6. Пособие для учащихся 6 классов заочной школы МИФИ. — ЗШ МИФИ, 2011.
Шеврин Л.Н., Гейн А.Г., Коряков И.О., Волков М.В. Математика: Учебник-собеседник для 5-6 классов средней школы. Библиотека учителя математики. — Просвещение, 1989.

Онлайн тесты по математике ().
Вы можете скачать указанные в п.1.2. книги ().

Домашнее задание

Виленкин Н. Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. — М.: Мнемозина, 2012. (см. ссылку 1.2)
Домашнее задание: №1254, №1255, №1256(б,г)
Прочие присвоения: № 1258(с), № 1248

В этой статье мы подробно рассмотрим основные правила такой важной темы курса математики, как открывающие скобки. Нужно знать правила раскрытия скобок, чтобы правильно решать уравнения, в которых они используются.

Как правильно открывать скобки при сложении

Раскрыть скобки перед знаком «+»

(9 + 3) + (1 — 6 + 9) = 9 + 3 + 1 — 6 + 9 = 16.

Как открыть скобки перед знаком «-»

В этом случае вы нужно переписать все термины без скобок, но при этом поменять все знаки внутри них на противоположные. Знаки меняются только у терминов из тех скобок, перед которыми стоял знак «-». Пример:

(9 + 3) — (1 — 6 + 9) = 9 + 3 — 1 + 6 — 9 = 8.

Как открывать скобки при умножении

Скобкам предшествует множитель

В этом случае , нужно каждое слагаемое умножить на множитель и раскрыть скобки, не меняя знаки. Если множитель стоит со знаком «-», то при умножении знаки слагаемых меняются местами. Пример:

3 * (1 — 6 + 9) = 3 * 1 — 3 * 6 + 3 * 9 = 3 — 18 + 27 = 12.

Как открыть две скобки со знаком умножения между ними 92) * 12 = 1728.

Как раскрыть 3 скобки

(1 + 2) * (3 + 4) * (5 — 6) = (3 + 4 + 6 + 8) * (5 — 6) = — 21.

Открывающие скобки — Гипермаркет знаний. Открытие скобок: правила и примеры (7 класс)

Тема: Решение уравнений

Урок: Раскрытие скобок

Как открыть скобки, перед которыми стоит знак «+». Использование ассоциативного закона сложения.

Рассмотрим примеры.

Пример 1

Раскрыв скобки, мы изменили порядок операций. Считать стало удобнее.

Пример 2

Пример 3

Обратите внимание, что во всех трех примерах мы просто удалили скобки. Сформулируем правило:

Комментарий.

Если первое слагаемое в скобках беззнаковое, то оно должно быть записано со знаком плюс.

Наглядный пример и правило.

С другой стороны, тот же результат можно получить, сложив противоположные числа.

Сформулируем правило:

Пример 1

Пример 2

Правило не меняется, если в скобках не два, а три и более условия.

Пример 3

Комментарий. Знаки меняются местами только перед терминами.

Чтобы раскрыть скобки в данном случае, нужно вспомнить о распределительном свойстве.

Сначала умножьте первую скобку на 2, а вторую на 3.

Библиография

Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. — М.: Мнемозина, 2012.
Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. — Гимназия, 2006.
Депман И.Я., Виленкин Н.Я. За страницами учебника математики. — Просвещение, 1989.
Рурукин А.Н., Чайковский И.В. Задания по курсу математики 5-6 класс — ЗШ МИФИ, 2011.
Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5-6. Пособие для учащихся 6 классов заочной школы МИФИ. — ЗШ МИФИ, 2011.
Шеврин Л.Н., Гейн А.Г., Коряков И.О., Волков М.В. Математика: Учебник-собеседник для 5-6 классов средней школы. Библиотека учителя математики. — Просвещение, 1989.

Онлайн тесты по математике ().
Вы можете скачать указанные в п.1.2. книги ().

Домашнее задание

Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. — М.: Мнемозина, 2012. (см. ссылку 1.2)
Домашнее задание: №1254, №1255, №1256(б,г)
Прочие присвоения: № 1258(с), № 1248

6 класс. Частью урока является объяснение нового материала.

Отверстие кронштейна.

Сначала расшифруем этот термин. Что значит «раскрыть скобки»? Это означает, что выражение, в котором есть скобки, должно быть представлено как равное ему выражение, но без скобок. На самом деле это занятие для вас не новое. Вы уже изучили ассоциативный закон сложения, из которого узнали, что

(a + c) + c = a + (b + c) = a + c + c

Три числа можно добавлять в любом порядке. Раскрываем скобки, и добавляем цифры так, как нам удобно.

Например,

(980 + 275) + 20

понятно, что гораздо проще сначала сложить 980 и 20, а потом прибавить 275 к 1000, поэтому мы раскроем скобки и выполним сложение так, как нам проще.

(980 + 275) + 20 = 980 + 20 + 275 = 1000 + 275 = 1275

Мы можем назвать эти привычные вам действия раскрытием скобок. Было выражение со скобками, стало без них.

Кроме того, вы знаете распределительный закон умножения, в котором также раскрываются скобки

a × (b + c) = ab + ac.

То же самое касается вычитания.

a × (b — c) = ab — ac

В левой части уравнения скобки стоят, а в правой скобок нет — скобки открыты.

Кстати, если поменять местами правую и левую части равенств, то эту формулу можно назвать «правилом заключения общего множителя в квадратные скобки»

ср + ас = а × (б + с)

ср — ас = а × (б — с)

Что нового мы узнаем о раскрытии скобок в этом 6 классе? В этом году мы познакомились с отрицательными числами, научились их складывать, умножать и делить. Мы сейчас часто встречаем выражения, в которых много-много скобок. И нужно выяснить универсальное правило раскрытия этих скобок.

Это правило звучит просто:

Если перед скобками стоит знак +, то скобки и этот + можно опустить и знаки слагаемых в скобках не изменятся. Вы помните, что отсутствие знака перед числом (или скобками) мы понимаем как знак +.

+ (а + б — в) = а + б — в

(а — б + в) = а — б + в

(- а + б + в) = — а + б + в

Если стоит знак — перед скобками, то скобки и эту — можно опустить и знаки слагаемых в скобках поменяются на противоположные.

— (а + Ь — с) = — а — с + с

— (а — с + с) = — а + с — с

— (- а + Ь + с) = а — c — c

Итак, плюс не меняет знаки членов в скобках, минус меняет. И еще отмечу, что речь идет только о смене знаков + и -. Никакие другие символы не меняются.

Пример:

3 + (-5) – (-7)

Здесь мы видим две пары скобок, которые мы будем раскрывать. + перед первой скобкой, минус перед второй.

3 + (-5) – (-7) = -3 — 5 +7 = -8 + 7 = -1

4,74 — (2а + 3,74)‏ = 4,74 — 2а — 3,74 = 1 — 2а

А теперь давайте подумаем, как мы будем действовать, если нам нужно раскрыть скобки в таком выражении:

2 × (-5 + а)

По распределительному закону умножения нам нужно по очереди умножить два с каждым слагаемым в скобках и записать в ответ сумму полученных результатов.

2 × (-5 + a) = 2 × (-5) + 2 × a = -10 + 2a

Знак умножения между числом и буквой можно опустить.

В этом случае множитель перед скобками был положительным.

3 × (-5 + 2у) = 15 — 6у

42 × (2в — 11) = -84в + 462

Подведем итог: мы выяснили, что значит «раскрывать скобки», и научились выполнить это действие в примерах, где есть отрицательные числа.

Основная функция скобок — изменить порядок действий при вычислении значений. Например, , в числовом выражении \(5 3+7\) сначала будет вычисляться умножение, а затем сложение: \(5 3+7 =15+7=22\). Но в выражении \(5·(3+7)\) сначала будет вычисляться сложение в скобках, а только потом умножение: \(5·(3+7)=5·10=50\).

Пример. Раскройте скобку: \(-(4m+3)\).
Решение : \(-(4m+3)=-4m-3\).

Пример. Раскройте скобку и дайте подобные термины \(5-(3x+2)+(2+3x)\).
Решение : \(5-(3x+2)+(2+3x)=5-3x-2+2+3x=5\).

Пример. Раскройте скобки \(-2(-3x+5)\).
Решение : Как и в предыдущем примере, скобки \(-3x\) и \(5\) умножаются на \(-2\).

Пример. Упростите выражение: \(5(x+y)-2(x-y)\).
Решение : \(5(х+у)-2(х-у)=5х+5у-2х+2у=3х+7у\).

Осталось рассмотреть последнюю ситуацию.

При умножении скобок на скобки каждый член первой скобки умножается на каждый член второй:

\((c+d)(a-b)=c (a-b)+d (a-b)=ca-cb+da-db\)

Шаг 2. Разложите произведения скобки на множитель, как описано выше:
— первый сначала…

Потом второй.

Шаг 3. Теперь умножаем и приводим подобные члены:

скобки внутри скобок

Пример. Раскройте скобки и дайте подобные термины \(7x+2(5-(3x+y))\).
Решение:

Пример. Раскройте скобки и дайте аналогичные термины \(-(x+3(2x-1+(x-5)))\).
Решение :

\(-(х+3(2х-1\)\(+(х-5)\) \())\)		Это тройное вложение скобок. Начнем с самого внутреннего (выделено зеленым). Перед скобкой стоит плюс, поэтому ее просто убирают.
\(-(х+3(2х-1\)\(+х-5\) \())\)		Теперь нужно открыть вторую скобу, промежуточную. Но перед этим мы упростим выражение, замаскировав похожие термины во второй скобке.
\(=-(х\)\(+3(3х-6)\) \()=\)		Теперь открываем вторую скобку (выделено синим цветом). Перед скобками стоит множитель, поэтому каждое слагаемое в скобках умножается на него.
\(=-(х\)\(+9x-18\) \()=\)
		И откройте последнюю скобку. Перед скобкой минус — значит все знаки меняются местами.

Открытие скобок — это базовый математический навык. Без этого навыка невозможно иметь оценку выше тройки в 8 и 9 классах. Поэтому рекомендую хорошо разбираться в этой теме.

Расширение скобок — это тип преобразования выражения. В этом разделе мы опишем правила раскрытия скобок, а также рассмотрим наиболее распространенные примеры заданий.

Яндекс.РТБ R-A-339285-1

Что такое раскрытие скобок?

Скобки используются для указания порядка выполнения действий в числовых и буквенных выражениях, а также в выражениях с переменными. От выражения со скобками удобно перейти к тождественно равному выражению без скобок. Например, замените выражение 2 (3 + 4) выражением вида 2 3 + 2 4 без скобок. Этот метод называется раскрытием скобок.

Определение 1

Под раскрытием скобок понимаются способы избавления от скобок и обычно рассматриваются применительно к выражениям, которые могут содержать:

знаки «+» или «-» перед скобками, содержащие суммы или разности;
произведение числа, буквы или нескольких букв на сумму или разность, которые заключаются в скобки.

Так мы рассматривали процесс раскрытия скобок в курсе школьной программы. Впрочем, никто не мешает нам взглянуть на это действие шире. Мы можем назвать расширение скобок переходом от выражения, которое содержит отрицательные числа в скобках, к выражению, которое не имеет скобок. Например, мы можем перейти от 5 + (− 3) − (− 7) к 5 − 3 + 7. По сути, это тоже раскрытие скобок.

Таким же образом можно заменить произведение выражений в скобках вида (a + b) · (c + d) суммой a · c + a · d + b · c + b · d . Этот прием также не противоречит смыслу раскрытия скобок.

Вот еще один пример. Можно предположить, что в выражениях вместо чисел и переменных могут использоваться любые выражения. Например, выражению x 2 1 a — x + sin (b) будет соответствовать выражение без скобок вида x 2 1 a — x 2 x + x 2 sin (b) .

Особого внимания заслуживает еще один момент, который касается особенностей написания растворов при раскрытии скобок. Мы можем записать исходное выражение со скобками и результат, полученный после раскрытия скобок, как равенство. Например, после раскрытия скобок вместо выражения 3 − (5 − 7) получаем выражение 3 − 5 + 7 . Мы можем записать оба этих выражения в виде равенства 3 − (5 − 7) = 3 − 5 + 7 .

Выполнение действий с громоздкими выражениями может потребовать записи промежуточных результатов. Тогда решение будет иметь вид цепочки равенств. Например, 5 — (3 — (2 — 1)) = 5 — (3 — 2 + 1) = 5 — 3 + 2 — 1 или 5 — (3 — (2 — 1)) = 5 — 3 + (2 — 1) = 5 — 3 + 2 — 1 .

Правила раскрытия скобок, примеры

Начнем с правил раскрытия скобок.

Одиночные числа в скобках

В выражениях часто встречаются отрицательные числа в скобках. Например, (− 4) и 3 + (− 4) . Положительные числа в скобках также имеют место.

Сформулируем правило раскрытия скобок, содержащих одиночные положительные числа. Предположим, что а — любое положительное число. Тогда мы можем заменить (а) на а, + (а) на + а, — (а) на — а. Если вместо а взять конкретное число, то по правилу: число (5) запишется как 5 , выражение 3 + (5) без скобок примет вид 3 + 5 , так как + (5) заменяется на + 5 , а выражение 3 + (− 5) эквивалентно выражению 3 − 5 , потому что + (− 5) заменен на — 5 .

Положительные числа обычно записываются без скобок, так как скобки в этом случае избыточны.

Теперь рассмотрим правило раскрытия скобок, содержащих одно отрицательное число. + (−a) заменяем на − a , − (−a) заменяем на + a . Если выражение начинается с отрицательного числа (-a) , которое записывается в скобках, то скобки опускаются и вместо (-a) остается − a .

Вот несколько примеров: (- 5) можно записать как — 5 , (- 3) + 0 , 5 становится — 3 + 0 , 5 , 4 + (- 3) становится 4 — 3 , а − (− 4) − (− 3) после раскрытия скобок принимает вид 4 + 3 , так как − (− 4) и − (− 3) заменен на + 4 и + 3 .

Следует понимать, что выражение 3 · (− 5) не может быть записано как 3 · − 5. Это будет обсуждаться в следующих параграфах.

Давайте посмотрим, на чем основаны правила раскрытия скобок.

По правилу разность a − b равна a + (− b) . Исходя из свойств действий с числами, мы можем составить цепочку равенств (a + (− b)) + b = a + ((− b) + b) = a + 0 = a , что будет справедливо. Эта цепочка равенств в силу смысла вычитания доказывает, что выражение a + (− b) есть разность а-б .

Основываясь на свойствах противоположных чисел и правилах вычитания отрицательных чисел, мы можем утверждать, что − (− a) = a , a − (− b) = a + b .

Существуют выражения, состоящие из числа, знака минус и нескольких пар скобок. Использование приведенных выше правил позволяет последовательно избавляться от скобок, переходя от внутренних скобок к внешним или наоборот. Примером такого выражения может быть — (- ((- (5)))) . Раскроем скобки, двигаясь изнутри наружу: — (- ((- (5)))) = — (- ((- 5))) = — (- (- 5)) = — (5) = — 5 . Этот пример также можно разобрать в обратном порядке: − (− ((− (5)))) = ((− (5))) = (− (5)) = − (5) = − 5 .

Под a и b могут пониматься не только как числа, но и как произвольные числовые или буквенные выражения со знаком «+» впереди, которые не являются суммами или разностями. Во всех этих случаях вы можете применять правила так же, как мы это делали с одиночными числами в скобках.

Например, после раскрытия скобок выражение — (- 2 x) — (x 2) + (- 1 x) — (2 x y 2: z) принимает вид 2 x — x 2 — 1 x — 2 x y 2: z . Как мы это сделали? Мы знаем, что − (− 2 x) равно + 2 x , а поскольку это выражение стоит первым, то + 2 x можно записать как 2 x , — (x 2) = — x 2 , + (− 1 x) знак равно — 1 х и — (2 х у 2: г) знак равно — 2 х у 2: г .

В произведениях двух чисел

Начнем с правила раскрытия скобок в произведении двух чисел.

Давайте представим, что a и b — два положительных числа. В этом случае произведение двух отрицательных чисел − a и − b вида (− a) (− b) можно заменить на (ab) , а произведения двух чисел с противоположными знаками вида (− a) b и a (− b) можно заменить на (− a b) . Умножение минуса на минус дает плюс, а умножение минуса на плюс, как и умножение плюса на минус, дает минус.

Правильность первой части написанного правила подтверждается правилом умножения отрицательных чисел. Чтобы подтвердить вторую часть правила, мы можем использовать правила умножения чисел с разными знаками.

Давайте рассмотрим несколько примеров.

Пример 1

Рассмотрим алгоритм раскрытия скобок в произведении двух отрицательных чисел — 4 3 5 и — 2 вида (- 2) · — 4 3 5 . Для этого заменим исходное выражение на 2 · 4 3 5 . Раскроем скобки и получим 2 · 4 3 5 .

А если взять частное отрицательных чисел (− 4) : (− 2) , то запись после раскрытия скобок будет иметь вид 4:2

Вместо отрицательных чисел — a и — b могут быть любыми выражениями с ведущим знаком минус, которые не являются суммами или разностями. Например, это могут быть произведения, дроби, степени, корни, логарифмы, тригонометрические функции и т. д.

Раскроем скобки в выражении — 3 · x x 2 + 1 · x · (- ln 5) . Согласно правилу, мы можем сделать следующие преобразования: — 3 x x 2 + 1 x (- ln 5) = — 3 x x 2 + 1 x ln 5 = 3 x x 2 + 1 x ln 5 .

Выражение (− 3) 2 можно преобразовать в выражение (− 3 2) . После этого можно раскрыть скобки: − 3 2 .

2 3 — 4 5 = — 2 3 4 5 = — 2 3 4 5

Для деления чисел с разными знаками также может потребоваться предварительное раскрытие скобок: (- 5) : 2 = (- 5 : 2) = − 5:2 и 2 3 4: (- 3 , 5) = — 2 3 4 : 3 , 5 = — 2 3 4 : 3 , 5 .

Правило можно использовать для выполнения умножения и деления выражений с разными знаками. Приведем два примера.

1 х + 1: х — 3 = — 1 х + 1: х — 3 = — 1 х + 1: х — 3

sin(x) (- x 2) = (- sin(x) x 2) = — sin(x)x 2

В произведениях трех и более чисел

Перейдем к произведениям и частным, которые содержат большее количество чисел. Для раскрывающихся скобок здесь будет применяться следующее правило. При четном числе отрицательных чисел скобки можно опустить, заменив числа их противоположностями. После этого нужно заключить полученное выражение в новые скобки. Для нечетного числа отрицательных чисел, опуская скобки, замените числа их противоположностями. После этого полученное выражение необходимо взять в новые скобки и поставить перед ним знак минус.

Пример 2

Например, возьмем выражение 5 · (− 3) · (− 2) , которое является произведением трех чисел. Есть два отрицательных числа, поэтому мы можем записать выражение как . (5 3 2) и, наконец, раскроем скобки, получив выражение 5 3 2 .

В произведении (− 2 , 5) (− 3) : (− 2) 4: (− 1 , 25) : (− 1) пять чисел отрицательные. поэтому (− 2 , 5) (− 3) : (− 2) 4: (− 1 , 25) : (− 1) = (− 2 , 5 3: 2 4: 1 , 25: 1) . Окончательно раскрывая скобки, получаем −2,5 3:2 4:1,25:1 .

Приведенное выше правило можно обосновать следующим образом. Во-первых, мы можем переписать такие выражения в виде произведения, заменив деление умножением на обратное. Мы представляем каждое отрицательное число как произведение множителя и заменяем — 1 или — 1 на 90 591 (- 1) на 90 594 .

Используя свойство перестановочности умножения, мы поменяем местами множители и перенесем все множители равные − 1 , в начало выражения. Произведение четного числа минус единицы равно 1, а нечетное число равно – 1 , что позволяет нам использовать знак минус.

Если бы мы не использовали правило, то цепочка действий по раскрытию скобок в выражении — 2 3: (- 2) 4: — 6 7 выглядела бы так:

2 3: (- 2) 4: — 6 7 = — 2 3 — 1 2 4 — 7 6 = = (- 1) 2 3 (- 1) 1 2 4 (- 1 ) 7 6 = = (- 1) (- 1) (- 1) 2 3 1 2 4 7 6 = (- 1) 2 3 1 2 4 7 6 = = — 2 3 1 2 4 7 6

Приведенное выше правило можно использовать при раскрытии скобок в выражениях, являющихся произведениями и частными со знаком минус которые не являются суммами или разностями. Возьмем, к примеру, выражение

х 2 (- х) : (- 1 х) х — 3: 2 .

Можно сократить до выражения без скобок x 2 · x: 1 x · x — 3: 2 .

Открывающие круглые скобки, которым предшествует знак +

Рассмотрим правило, которое можно применить для раскрытия квадратных скобок, которым предшествует знак плюс, и «содержимое» этих скобок не умножается и не делится ни на какое число или выражение.

Согласно правилу, скобки вместе со знаком перед ними опускаются, а знаки всех терминов в скобках сохраняются. Если перед первым слагаемым в скобках знака нет, то нужно поставить знак плюс.

Пример 3

Например, мы даем выражение (12 — 3 , 5) — 7 . Опуская скобки, мы сохраняем знаки слагаемых в скобках и ставим знак плюс перед первым слагаемым. Запись будет иметь вид (12 − 3, 5) − 7 = + 12 − 3, 5 − 7. В приведенном примере перед первым слагаемым ставить знак не нужно, так как + 12 — 3, 5 — 7 = 12 — 3, 5 — 7.

Пример 4

Рассмотрим еще один пример. Возьмем выражение х + 2 а — 3 х 2 + 1 — х 2 — 4 + 1 х и проделаем с ним действия х + 2 а — 3 х 2 + 1 — х 2 — 4 + 1 х = = х + 2 а — 3 х 2 + 1 — х 2 — 4 + 1 х

Вот еще один пример раскрывающихся скобок:

Пример 5

2 + x 2 + 1 x — x y z + 2 x — 1 + (- 1 + x — x 2) = = 2 + x 2 + 1 x — x y z + 2 x — 1 — 1 + x + x2

Как раскрыть скобки, перед которыми стоит знак минус

Рассмотрим случаи, когда перед скобками стоит знак минус, и которые не умножаются (или не делятся) ни на какие число или выражение. Согласно правилу раскрытия скобок, которым предшествует знак «-», скобки со знаком «-» опускаются, а знаки всех членов внутри скобок меняются местами.

Пример 6

Например:

1 2 = 1 2, — 1 х + 1 = — 1 х + 1, — (- х 2) = х 2

Переменные выражения можно преобразовать с помощью оператора то же правило:

Х + х 3 — 3 — — 2 х 2 + 3 х 3 х + 1 х — 1 — х + 2,

получаем х — х 3 — 3 + 2 х 2 — 3 х 3 х + 1 х — 1 — х + 2 .

Открытие скобок при умножении числа на скобку, выражения на скобку

Здесь мы рассмотрим случаи, когда необходимо раскрыть скобки, которые умножаются или делятся на какое-либо число или выражение. Здесь формулы вида (a 1 ± a 2 ± … ± a n) b = (a 1 b ± a 2 b ± … ± a n b) или b (a 1 ± a 2 ± … ± a n) = (b a 1 ± b a 2 ± … ± b a n) , где a 1 , a 2 , … , a n и b — некоторые числа или выражения.

Пример 7

Например, раскроем скобки в выражении (3 − 7) 2 . Согласно правилу, мы можем сделать следующие преобразования: (3 − 7) 2 = (3 2 − 7 2) . Получаем 3 · 2 − 7 · 2 .

Раскрывая скобки в выражении 3 х 2 1 — х + 1 х + 2, получаем 3 х 2 1 — 3 х 2 х + 3 х 2 1 х + 2.

Умножение скобки на скобку

Рассмотрим произведение двух скобок вида (a 1 + a 2) · (b 1 + b 2) . Это поможет нам получить правило раскрытия скобок при умножении скобки на скобку.

Чтобы решить приведенный выше пример, мы обозначаем выражение (b 1 + b 2) как b. Это позволит нам использовать правило умножения выражения в скобках. Получаем (a 1 + a 2) (b 1 + b 2) = (a 1 + a 2) b = (a 1 b + a 2 b) = a 1 b + a 2 b . Делая обратную замену b на (b 1 + b 2), снова применим правило умножения выражения на скобку: a 1 b + a 2 b = = a 1 (b 1 + b 2) + a 2 (b 1 + b 2) = = (a 1 b 1 + a 1 b 2) + (a 2 b 1 + a 2 b 2) = = a 1 b 1 + a 1 b 2 + a 2 b 1 + a 2 b 2

Благодаря ряду простых приемов мы можем прийти к сумме произведений каждого из слагаемых из первой скобки и каждого из слагаемых из второй скобки. Правило можно распространить на любое количество терминов в скобках.

Сформулируем правила умножения скобки на скобку: чтобы умножить две суммы между собой, необходимо каждое из слагаемых первой суммы умножить на каждое из слагаемых второй суммы и сложить результаты .

Формула будет иметь вид:

(a 1 + a 2 + . . . + a m) (b 1 + b 2 + . . . . + b n) = = a 1 b 1 + a 1 b 2 + . . . + а 1 б п + + а 2 б 1 + а 2 б 2 + . . . + а 2 б п + + . . . + + а м б 1 + а м б 1 + . . . a m b n

Раскроем скобки в выражении (1 + x) · (x 2 + x + 6) Это произведение двух сумм. Запишем решение: (1 + х) (х 2 + х + 6) = = (1 х 2 + 1 х + 1 6 + х х 2 + х х + х 6) = = 1 х 2 + 1 х + 1 6 + x x 2 + x x + x 6

Отдельно стоит остановиться на тех случаях, когда в скобках наряду со знаками плюс стоит знак минус. Например, возьмем выражение (1 − x) · (3 · x · y − 2 · x · y 3) .

Сначала представим выражения в скобках в виде сумм: (1 + (− x)) (3 x y + (− 2 x y 3)) . Теперь мы можем применить правило: (1 + (- x)) (3 x y + (- 2 x y 3)) = = (1 3 x y + 1 (- 2 x y 3) + (- x) 3 x y + (- x) (− 2 x y 3))

Раскроем скобки: 1 3 x y − 1 2 x y 3 − x 3 x y + x 2 x y 3 .

Раскрытие скобок в произведениях нескольких скобок и выражений

При наличии в выражении трех и более выражений в скобках необходимо последовательно раскрывать скобки. Начать преобразование нужно с того, что в скобки взяты первые два множителя. Внутри этих скобок мы можем выполнять преобразования по описанным выше правилам. Например, скобки в выражении (2 + 4) 3 (5 + 7 8) .

Выражение содержит сразу три множителя (2 + 4) , 3 и (5 + 7 8) . Раскроем скобки последовательно. Заключим первые два множителя еще в одну скобку, которую для наглядности сделаем красной: (2 + 4) 3 (5 + 7 8) = ((2 + 4) 3) (5 + 7 8) .

В соответствии с правилом умножения скобки на число можно выполнить следующие действия: ((2 + 4) 3) (5 + 7 8) = (2 3 + 4 3) (5 + 7 8 ).

Умножить скобку на скобку: (2 3 + 4 3) (5 + 7 8) = 2 3 5 + 2 3 7 8 + 4 3 5 + 4 3 7 8 .

Скобки в натуре

Степени, основаниями которых являются некоторые выражения, записанные в скобках, с натуральными показателями можно рассматривать как произведение нескольких скобок. Причем, по правилам из двух предыдущих пунктов, их можно писать и без этих скобок.

Рассмотрим процесс преобразования выражения (а + б + в) 2 . Его можно записать как произведение двух скобок (a + b + c) (a + b + c) . Умножаем скобку на скобку и получаем a a + a b + a c + b a + b b + b c + c a + c b + c c .

Возьмем другой пример:

Пример 8

1 x + 2 3 = 1 x + 2 1 x + 2 1 x + 2 = = 1 x 1 x + 1 x 2 + 2 1 x + 2 2 1 x + 2 = = 1 x 1 x 1 x + 1 x 2 1 x + 2 1 x 1 x + 2 2 1 x + 1 x 1 x 2 + + 1 x 2 2 + 2 1 x 2 + 2 2 2

Деление скобки на число и скобки на скобку

Деление скобки на число предполагает, что вы должны разделить на число все термины, заключенные в скобки. Например, (х 2 — х) : 4 = х 2: 4 — х: 4 .

Деление можно предварительно заменить умножением, после чего можно использовать соответствующее правило раскрытия скобок в произведении. То же правило применяется при делении скобки на скобку.

Например, нам нужно раскрыть скобки в выражении (x + 2) : 2 3 . Для этого сначала замените деление умножением на обратную величину (x + 2) : 2 3 = (x + 2) · 2 3 . Умножьте скобку на число (x + 2) 2 3 = x 2 3 + 2 2 3 .

Вот еще один пример деления скобками:

Пример 9

1 х + х + 1: (х + 2) .

Заменим деление умножением: 1 x + x + 1 1 x + 2 .

Выполним умножение: 1 х + х + 1 1 х + 2 = 1 х 1 х + 2 + х 1 х + 2 + 1 1 х + 2 .

Порядок раскрытия скобок

Теперь рассмотрим порядок применения рассмотренных выше правил в общих выражениях, т.е. в выражениях, содержащих суммы с разностями, произведения с частными, скобки в натуральном выражении.

Порядок действий:

первый шаг — возведение скобок в натуральную степень;
на втором этапе открываются скобки в произведениях и приватах;
последний шаг — открыть скобки в суммах и разностях.

Рассмотрим порядок действий на примере выражения (− 5) + 3 · (− 2) : (− 4) − 6 · (− 7) . Преобразуем из выражений 3 (− 2) : (− 4) и 6 (− 7) , которые должны принять вид (3 2:4) и (− 6 7) . Подставив полученные результаты в исходное выражение, получим: (− 5) + 3 (− 2) : (− 4) − 6 (− 7) = (− 5) + (3 2 : 4) − (− 6 7 ). Раскройте скобки: − 5 + 3 2 : 4 + 6 7 .

При работе с выражениями, содержащими скобки внутри скобок, удобно выполнять преобразования изнутри наружу.

Если вы заметили ошибку в тексте, выделите ее и нажмите Ctrl+Enter

«Раскрывающие скобки» — Учебник по математике 6 класс (Виленкин)

Краткое описание:

В этом разделе вы научитесь правильно раскройте скобки в примерах. Для чего это? Все для того же, что и раньше — чтобы вам было все легче и легче считать, чтобы было меньше ошибок, а в идеале (мечта вашей учительницы математики) чтобы решить все вообще без ошибок.
Вы уже знаете, что скобки в математической записи ставятся, если два математических знака идут подряд, если мы хотим показать объединение чисел, их перестановку. Раскрыть скобки означает избавиться от лишних символов. Например: (-15)+3=-15+3=-12, 18+(-16)=18-16=2. Вы помните распределительное свойство умножения по отношению к сложению? Ведь в том примере мы тоже избавились от скобок для упрощения вычислений. Названное свойство умножения можно применить и к четырем, трем, пяти и более терминам. Например: 15*(3+8+9+6)=15*3+15*8+15*9+15*6=390. Вы замечали, что при раскрытии скобок числа в них не меняют знак, если число перед скобками положительное? Ведь пятнадцать — положительное число. А если решить этот пример: -15*(3+8+9+6)=-15*3+(-15)*8+(-15)*9+(-15)*6=-45+( — 120)+(-135)+(-90)=-45-120-135-90=-390. Перед скобками у нас стояло отрицательное число минус пятнадцать, когда мы раскрывали скобки все числа начинали менять свой знак на другой — противоположный — с плюса на минус.
На основании приведенных примеров можно озвучить два основных правила раскрытия скобок:
1. Если у вас перед скобками стоит положительное число, то после раскрытия скобок все знаки чисел в скобках не меняются, но остаются точно такими же, как и были.
2. Если у вас перед скобками стоит отрицательное число, то после раскрытия скобок знак минус уже не пишется, а знаки всех абсолютных чисел в скобках резко меняются местами.

ГДЗ по Математике 6 класс Мерзляк, Полонский Учебник

ГДЗ Решебник Математика 6 класс Учебник Алгоритм успеха «Вентана-Граф» Мерзляк, Полонский, Якир.

Что включает в себя решебник

Какие преимущества решебника

Упражнения

Вопросы к параграфам

Решаем устно

Похожие ГДЗ Математика 6 класс

Упражнения: 1

Условие

Решебник №1

Решебник №2

ГДЗ и решебники

ГДЗ решебник по математике 6 класс Мерзляк, Полонский, Якир

ГДЗ решебник по математике 6 класс Мерзляк, Полонский, Рабинович дидактические материалы Вентана-Граф

ГДЗ – твердая поддержка шестиклассников

Подготовка с решебником – ключ к фундаментальным познаниям в математике

Продуктивное использование ГДЗ

КР-1. Делимость натуральных чисел

КР-2. Сравнение, сложение и вычитание дробей

КР-3. Умножение дробей

КР-4. Деление дробей

КР-5. Отношения и пропорции. Процентное отношение двух чисел

КР-6. Прямая и обратная пропорциональные зависимости. Окружность и круг

КР-7. Рациональные числа. Сравнение рациональных чисел

КР-8. Сложение и вычитание рациональных чисел

КР-9.

КР-10. Решение уравнений и задач с помощью уравнений

КР-11. Перпендикулярные и параллельные прямые. Координатная плоскость

КР-12. Итоговая

Упражнения. В-1

Упражнения. В-2

Упражнения.

Упражнения. В-4

Похожие ГДЗ Математика 6 класс

КР-1.

ГДЗ по математике 6 класс Мерзляк Полонский Якир

ГДЗ решебник по математике 6 класс Мерзляк Полонский Якир

Решите пример, раскрыв скобки.

Правило расширения скобки для добавления

Правило раскрытия скобок при вычитании

Раскрывающие скобки при умножении

Раскрывать скобки при делении

Как раскрыть вложенные скобки

Как правильно открывать скобки при сложении

Раскрыть скобки перед знаком «+»

Как открыть скобки перед знаком «-»

Как открывать скобки при умножении

Перед скобками стоит множитель

Как открыть две скобки со знаком умножения между ними

Как раскрыть 3 скобки

Егэ решить.

Оценка

ЕГЭ-2017 по математике базовый уровень

Когда ставить скобки в предложении. Как использовать простые скобки

При умножении скобок на скобки каждый член первой скобки умножается на каждый член второй:

скобки внутри скобок

Произведение многочленов. Преобразование (упрощение) произведения двух многочленов

Формулы сокращенного умножения. Сумма, разность и квадраты разности

Как правильно открывать скобки при сложении

Раскрыть скобки перед знаком «+»

Как открыть скобки перед знаком «-»

Как открывать скобки при умножении

Скобкам предшествует множитель

Как открыть две скобки со знаком умножения между ними 92) * 12 = 1728.

Как раскрыть 3 скобки

Открывающие скобки — Гипермаркет знаний. Открытие скобок: правила и примеры (7 класс)

При умножении скобок на скобки каждый член первой скобки умножается на каждый член второй:

скобки внутри скобок

Что такое раскрытие скобок?

Правила раскрытия скобок, примеры

Одиночные числа в скобках

В произведениях двух чисел

В произведениях трех и более чисел

Открывающие круглые скобки, которым предшествует знак +

Как раскрыть скобки, перед которыми стоит знак минус

Открытие скобок при умножении числа на скобку, выражения на скобку

Умножение скобки на скобку

Раскрытие скобок в произведениях нескольких скобок и выражений

Скобки в натуре