Решебник по Математике за 6 класс А.Г. Мерзляк, В.Б. Полонский, М.С. Якир на Гитем ми
Рабочая программа по математике за 6 класс автора А. Г. Мерзляк полностью соответствует ФГОС, поэтому используется многими учителями обычных и профильных математических школ. Правильные ответы по указанному учебнику школьники найдут на этом сайте.
Онлайн-ГДЗ по математике для 6 класса (авторы: Мерзляк А.Г., Полонский В.Б. Якир М.С.) предназначается для учеников, их родителей, педагогов–предметников, студентов, проходящих педагогическую практику. Его регулярное использование в учебной деятельности оказывает положительное влияние на все стороны образовательного процесса. Улучшается успеваемость, у детей появляется устойчивая мотивация быть в числе лидеров среди одноклассников. Обучающиеся учатся ответственности, самоконтролю, самоподготовке, становятся более уверенными в своих силах.
Наблюдения показывают, что сокращение времени на приготовлении уроков за счет проверки задач на сайте ГДЗ благотворно отражается на здоровье и развитии подрастающего поколения.
Преимущества проверочных работ
Открывая онлайн решебник, шестиклассники повторяют изученный материал, разбирают пройденное, учатся решать сложные задачи по аналогии, развивают мышление, логику и аналитический склад ума. Это поможет им сдать математические тесты, написать контрольные работы на хорошие оценки, занять призовые места в олимпиадах, исправить двойки и стать отличниками.
Плюсы ресурса:
- массовая доступность;
- приятный дизайн, простое использование и быстрый поиск по страницам и номерам;
- подробное решение заданий;
- адаптированность под мобильные устройства;
- только верные ответы с понятным описанием;
- качественная подготовка к урокам;
- повторение и закрепление упражнений, которые были решены в классе;
- возможность домашнего обучения;
- конфиденциальность.

Решебник по математике А.Г. Мерзляка можно использовать без ограничений, ежедневно, под контролем взрослых или без него. Результатом регулярной самопроверки станет улучшение качественных показателей по изучаемому предмету.
Решение задач онлайн
Решение Ваших математических задач в онлайн режиме. Бесплатная версия программы предоставляет Вам только ответы. Если вы хотите увидеть полное решение, Вы должны зарегистрироваться для бесплатной полной пробной версии.
Другие программы
Основы математики
Онлайн программа решения математических задач предлагает Вам решение в режиме онлайн задач с дробями, корнями, метрическими преобразованиями.
Вы можете упростить, найти значение, объединять и умножать выражения.
Онлайн программа решения задач курса предварительной алгебры (геометрии)
Вы можете решать все задачи с основного раздела математики а также координатных задач, простых уравнений, неравенств, упрощать выражения.
Вы можете подсчитывать выражения, объединить выражения и умножать / делить выражения.
Онлайн программа решения задач по алгебре
Мы рекомендуем Вам зарегистрироваться для этой онлайн программы.Решите Ваши задачи (уравнения, неравенства, радикалы, построение графиков, решение полиномов) в онлайн режиме.
Если Ваша домашняя работа включает в себя математические уравнения, неравенства, функции, многочлены, матрицы, значит регистрация для тестовой версии — это правильный выбор.
Онлайн программа решения задач по тригонометрии
Находит значения всех типов выражений (синус, косинус, тангенс, котангенс, секанс, косеканс), уравнений, неравенств.Строит графики тригонометрических функций.
Тригонометрия прямоугольного треугольника.
Онлайн программа решения задач курса предварительной алгебры
Включает в себя все вышеперечисленное функции плюс нахождение пределов (LIM), сумм, матриц.
Онлайн программа решения задач курса высшей математики
Решение задач c определенными, неопределенными интегралами.
Онлайн программа решения статистических задач
Решайте задач с нахождением вероятности, комбинаторные задачи.
Статистические задачи — найти среднее (арифметическое, геометрическое, квадратическое) значение, распределение, нормальное распределение, т-распределение.
Онлайн программа успешно проводит тестирование статистических гипотез
Решебник По Математике 6 Класс Виленкин – Telegraph
>>> ПОДРОБНЕЕ ЖМИТЕ ЗДЕСЬ <<<
Решебник По Математике 6 Класс Виленкин
Готовые Домашние Задания Окружающий Мир 4 Класс
Решебник Макарычев 7 Класс
Математика 5 Класс Готовые Домашние Задания Мерзляк
Готовые Домашние Задания По Русскому 3
Готовые Домашние Задания По Математике Юдачева
Гдз По Русскому Языку 4 21 Век
Мякишев 10 Класс Физика Электродинамика Гдз
Гдз По Обществознанию Класс Иванова Хотеенкова
Гдз По Русскому 7 Класс Ладыженская Ответы
Решебник Английский Третий Класс Рабочая
Французский Рабочая Тетрадь 5 Класс Гдз
Гдз По Ли Литературе 7 Класс Коровина
Решебник По Химии 10 Класс Новошинский
Решебник По Немецкому Языку 7 Класс Будько
Решебник По Алгебре 7 Класс Мерзляк Углубленное
Решебник Учебник Макарычев Миндюк
Гдз По Русскому Максимов
Решебник Дидактические Алгебра 10 Класс Шабунин
Гдз По Окружающему Рабочая Тетрадь Ответы
Гдз По Литературе 9 Зинин 1 Часть
Решебник Enjoy English 10 Класс
Геометрия Гдз Атанасян 79
Гдз По Математике Виленкина Пятый
М М Разумовская 6 Класс Гдз
Кострикин Сборник Задач По Алгебре Решебник
Гдз Биология 5 Класс Пономарева Учебник Ответы
Гдз По Физике 7 Артеменков
Решебник По Обществознанию 10 Класс Боголюбова Учебник
Немецкий Язык 11 Класс Карелина Гдз
Гдз По Русскому Языку Авторы Кузнецова
Гдз 6 Шварцбурд
Гдз 3 Класс Россия
Гдз По Р Языку 2 Класс
Гдз По Геометрии 1
Решебник По Английскому 11 Класс Дули
Гдз Синица 6 Класс Рабочая Тетрадь
Решебник По Математике 9 Класс Алгебра Макарычев
Гдз По Алгебре 7 Класс Ким
Гдз Дидактические Математика 6 Виленкин
Гдз По Информатике 8 Класс 2
Гдз По Физике 9 Минькова
Решебник По Английскому 3 Класс Учебник Starlight
Гдз По Русскому Языку 5 Львова Львов
Гдз По Русскому 4 Класса 2 Часть
Русский Язык 3 Бунеев Гдз Ответы
Английский Язык Гдз Reader 3 Класс
Гдз По Английскому Языку Класс Forward
Гдз По Русскому Р Т 3
Гдз По Русскому Языку Разумовская Номер
Гдз По Алгебре 8 Класс Ткачев
Гдз По Математике 6 Класс 60
Решебник Алгебра 8 Миндюк
Гдз По Английскому Класс Учебник Афанасьева
Русский Язык 7 Класс Купалова Гдз Учебник
Гдз По Английскому Печатная Тетрадь
ГДЗ по математике для 6 класса . 6 класс – это переходной этап от изучения основ арифметики до основных математических дисциплин — алгебры, посвященной изучению сложных уравнений, и геометрии – науке о формах предмета и их пространственного соотношения .
6 класс – это переходной этап от изучения основ арифметики до основных математических дисциплин — алгебры, посвященной изучению сложных уравнений, и геометрии – науке о формах предмета и их пространственного соотношения .
Достоинства ГДЗ по математике для 6 класса Виленкина . Решебник по математике за 6 класс (авторы: Н . Я . Виленкин, В . И . Жохов, А . С . Чесноков, С . И . Шварцбурд) поможет учащимся чувствовать себя увереннее на уроке, так что вопросы учителя теперь не страшны .
Решебник для учебника по математике 6 класса от Виленкина . ГДЗ по математике для 6 класса позволяет ученикам проверять правильность выполнения домашних заданий . С его помощью им удается понять алгоритм решения сложных задач самостоятельно .
6 класс . ГДЗ по математике за 6 класс Виленкин . Решение, ответы и решебник к учебнику . Виленкин, Жохов, Чесноков . Мнемозина, .
Н .Я . Виленкин , В .И . Жохов, А .С . Чесноков . Решебник (ГДЗ) по Математике за 6 (шестой ) класс авторы: Виленкин, Жохов, Чесноков, Шварцбурд издательство Мнемозина, год .
В гдз по математике 6 класса Виленкина больше полторы тысячи заданий . Каждое из них шестиклассник должен решить, полностью в них разобраться и суметь понять похожие задания . .
Достаточно просто использовать решебник к пособию «Математика 6 класс Учебник Виленкин, Жохов, Чесноков Мнемозина» . Чтобы применение решебника к пособию «Математика 6 класс Учебник Виленкин» было более продуктивно, следует сначала самостоятельно решить . .
Всего их в ГДЗ по математике 6 класс Виленкин насчитывается более полутора тысяч упражнений . Они распределены по тематическим главам, так что школьники могут при надобности повторить любую из них . Поможет ли решебник в учебе .
Математика в 6 классе включает в себя большой объем знаний . Решебник по математике Виленкина помогает ученику расставить все по полочкам . Большое количество материала, не всегда хорошо усваивается учениками в школе .
ГДЗ по математике 6 класс , авторы: , Виленкин Н .Я ., Жохов В .И ., Чесноков А .С ., Шварцбурд С . И ., Мнемозина 2020-2021 год .
И ., Мнемозина 2020-2021 год .
Онлайн решебник (гдз) по математике 6 класс Виленкин , Жохов без скачивания — Решатор! Часто ГДЗ по математике за 6 класс Виленкина , Жохова, Чеснокова пользуются не только ученики, но и их родители . Использование решебника дает возможность
На этой странице 1595 решенных примеров из учебника Н .Я Виленкин , В .И . Жохов, А .С . Чесноков, С .И . Шварцбург «Математика 6 класс . .
ГДЗ решебник и ответы 6 класс , Математика , Виленкин Н .Я ., Жохов В .И ., Чесноков А .С ., Шварцбург С .И ., Учебник, год, 2019 год, 2019 год, 2019 год, 2020 год, 2020 год . Готовые домашние задания с подробными ответами .
Популярный учебник по математике для 6 класса авторов Н .Я . Виленкин, В .И . Жохов, А .С . Чесноков, С .И . Шварцбурд представляет собой Не все из них с лёгкостью будут решены большинством учащихся, поэтому методисты снабдили книгу подробным решебником со . .
Специально для вас (учащиеся шестых классов и их родители) мы подготовили подробные видео уроки, в каждом видео уроке объясняется как решается та или иная задача из учебника по математике Виленкина . На нашем сайте вы найдете как сами задания из учебника по . .
На нашем сайте вы найдете как сами задания из учебника по . .
Смотрите любимые видео, слушайте любимые песни, загружайте собственные ролики и делитесь ими с друзьями, близкими и целым миром .
Убедись в правильности решения задачи вместе с ГДЗ по Математике за 6 класс Виленкин Н .Я ., Жохов В .И ., Чесноков А .С ., Шварцбурд С .И . часть 1, 2 . Ответы сделаны к книге 2019 года от Мнемозина ФГОС .
ГДЗ по математике 6 класс Виленкин Н . Я . Авторы: Н . Я . Виленкин, В . И . Жохов, А . С . Чесноков, С . И . Шварцбурд . В решебнике две главы . В первой изучаются дроби, пропорции и делимость чисел, во второй рациональные числа, ряд заданий на вычитание и сложение .
Категория: Решебник (ГДЗ) по математике для 6 класса к учебнику «Математика . 6 класс » Виленкин Н .Я . — год .
В шестом классе происходит процесс разделения предмета математики на алгебру и геометрию . Однако не каждый школьник сможет освоить такой материал самостоятельно, и тут на помощь придет решебник , созданный автором Н .-reshenie-25.16.jpg) Я . Виленкин .
Я . Виленкин .
ГДЗ по математике для 6 класса . 6 класс – это переходной этап от изучения основ арифметики до основных математических дисциплин — алгебры, посвященной изучению сложных уравнений, и геометрии – науке о формах предмета и их пространственного соотношения .
Достоинства ГДЗ по математике для 6 класса Виленкина . Решебник по математике за 6 класс (авторы: Н . Я . Виленкин, В . И . Жохов, А . С . Чесноков, С . И . Шварцбурд) поможет учащимся чувствовать себя увереннее на уроке, так что вопросы учителя теперь не страшны .
Решебник для учебника по математике 6 класса от Виленкина . ГДЗ по математике для 6 класса позволяет ученикам проверять правильность выполнения домашних заданий . С его помощью им удается понять алгоритм решения сложных задач самостоятельно .
6 класс . ГДЗ по математике за 6 класс Виленкин . Решение, ответы и решебник к учебнику . Виленкин, Жохов, Чесноков . Мнемозина, .
Н .Я . Виленкин , В .И . Жохов, А .С . Чесноков . Решебник (ГДЗ) по Математике за 6 (шестой ) класс авторы: Виленкин, Жохов, Чесноков, Шварцбурд издательство Мнемозина, год .
Решебник (ГДЗ) по Математике за 6 (шестой ) класс авторы: Виленкин, Жохов, Чесноков, Шварцбурд издательство Мнемозина, год .
В гдз по математике 6 класса Виленкина больше полторы тысячи заданий . Каждое из них шестиклассник должен решить, полностью в них разобраться и суметь понять похожие задания . .
Достаточно просто использовать решебник к пособию «Математика 6 класс Учебник Виленкин, Жохов, Чесноков Мнемозина» . Чтобы применение решебника к пособию «Математика 6 класс Учебник Виленкин» было более продуктивно, следует сначала самостоятельно решить . .
Всего их в ГДЗ по математике 6 класс Виленкин насчитывается более полутора тысяч упражнений . Они распределены по тематическим главам, так что школьники могут при надобности повторить любую из них . Поможет ли решебник в учебе .
Математика в 6 классе включает в себя большой объем знаний . Решебник по математике Виленкина помогает ученику расставить все по полочкам . Большое количество материала, не всегда хорошо усваивается учениками в школе .
ГДЗ по математике 6 класс , авторы: , Виленкин Н .Я ., Жохов В .И ., Чесноков А .С ., Шварцбурд С .И ., Мнемозина 2020-2021 год .
Онлайн решебник (гдз) по математике 6 класс Виленкин , Жохов без скачивания — Решатор! Часто ГДЗ по математике за 6 класс Виленкина , Жохова, Чеснокова пользуются не только ученики, но и их родители . Использование решебника дает возможность
На этой странице 1595 решенных примеров из учебника Н .Я Виленкин , В .И . Жохов, А .С . Чесноков, С .И . Шварцбург «Математика 6 класс . .
ГДЗ решебник и ответы 6 класс , Математика , Виленкин Н .Я ., Жохов В .И ., Чесноков А .С ., Шварцбург С .И ., Учебник, год, 2019 год, 2019 год, 2019 год, 2020 год, 2020 год . Готовые домашние задания с подробными ответами .
Популярный учебник по математике для 6 класса авторов Н .Я . Виленкин, В .И . Жохов, А .С . Чесноков, С .И . Шварцбурд представляет собой Не все из них с лёгкостью будут решены большинством учащихся, поэтому методисты снабдили книгу подробным решебником со . .
.
Специально для вас (учащиеся шестых классов и их родители) мы подготовили подробные видео уроки, в каждом видео уроке объясняется как решается та или иная задача из учебника по математике Виленкина . На нашем сайте вы найдете как сами задания из учебника по . .
Смотрите любимые видео, слушайте любимые песни, загружайте собственные ролики и делитесь ими с друзьями, близкими и целым миром .
Убедись в правильности решения задачи вместе с ГДЗ по Математике за 6 класс Виленкин Н .Я ., Жохов В .И ., Чесноков А .С ., Шварцбурд С .И . часть 1, 2 . Ответы сделаны к книге 2019 года от Мнемозина ФГОС .
ГДЗ по математике 6 класс Виленкин Н . Я . Авторы: Н . Я . Виленкин, В . И . Жохов, А . С . Чесноков, С . И . Шварцбурд . В решебнике две главы . В первой изучаются дроби, пропорции и делимость чисел, во второй рациональные числа, ряд заданий на вычитание и сложение .
Категория: Решебник (ГДЗ) по математике для 6 класса к учебнику «Математика . 6 класс » Виленкин Н . Я . — год .
Я . — год .
В шестом классе происходит процесс разделения предмета математики на алгебру и геометрию . Однако не каждый школьник сможет освоить такой материал самостоятельно, и тут на помощь придет решебник , созданный автором Н .Я . Виленкин .
вопросов и задач по алгебре для 6 класса
Задачи и вопросы по алгебре 6 класса представлены с подробными решениями. Включены вопросы по расширению и упрощению выражений, решению линейных уравнений, факторингу выражений и т. Д.
-
Перечислите все похожие термины, включенные в каждое из приведенных ниже выражений.
A) 6 x + 5 + 12 x — 6
B) 2 x 2 — 4 + 9 x 2 + 9
C) x / 5 + x / 7 + 7
D) 0,2 x + 1,2 x + x / 2 + 5
E) 5 x — 8 + 7 x — 2 x 2 -4 + 9 x 2 + 4 x 3
F) 5 a + 8-7 ab
G) 5 a b + 8 + 6 ba — a + 3 b -
Вычислите каждое из выражений для заданного значения (значений) переменной (переменных).
A) 6 x + 5 для x = 2
B) 12 x 2 + 5 x — 2 для x = 1
C) 2 (x + 7) + x для x = 0
D) 2 a + 3b — 7 для a = 2 и b = 4 -
Разверните (при необходимости) и упростите каждое из приведенных ниже выражений.
A) 3 x + 5 x
B) 2 (x + 7) + x
C) 2 (x + 3) + 3 (x + 5) + 3
D) 2 (a + 1) + 5b + 3 (a + b) + 3 -
Разложите на множители каждое из приведенных ниже выражений.
A) 3 x + 3
B) 8 x + 4
C) ax + 3 a
D) (x +1) y + 4 (x + 1)
E) x + 2 + bx + 2 b -
Решите каждое из приведенных ниже уравнений и проверьте свой ответ.
A) x + 5 = 8
B) 2 x = 4
C) x / 3 = 2
D) 0,2 x = 1
D) 3 x + 6 = 12
E) 3 (x + 2) + 2 = 8 -
В большой сумке n коробок и m игрушек в каждой. Сколько всего игрушек в сумке? -
Перепишите выражения a a a — b b, используя экспоненту. -
Длина прямоугольника равна x + 2, а его ширина равна 3. Дайте упрощенное выражение площади этого прямоугольника. -
Две трети учащихся в классе изучают математику, а остальные восемь учащихся не изучают математику. Какое общее количество учеников в этом классе?
Какое общее количество учеников в этом классе? -
Автомобиль преодолевает 60 километров за час. При этом какое расстояние преодолеет эта машина за y час? -
Оцените выражения.
A) 2 3 + 3 2
B) 0,1 3
C) 6 (2/3) -
Сумка содержит три красных шарика; пять синих шариков и семь зеленых шариков. Каково отношение синих шариков к общему количеству шариков?
Каково отношение синих шариков к общему количеству шариков? -
Решите пропорцию: a / 3 = 5/18 -
Какая из следующих упорядоченных пар является решением уравнения 2 x + 3 y = 8?
A) (0, 0)
B) (4, 0)
C) (1, 2) -
Перечислите все множители следующих чисел.
A) 4
B) 12
C) 50 -
Найдите наибольший общий делитель для каждой пары данных чисел.
A) 6 и 3
B) 18 и 24
C) 50 и 60 -
Запишите число «Шестьсот семьдесят два миллиона двести пятьдесят девять», используя цифры.
-
Какие из следующих выражений эквивалентны?
A) 2 (x + 3) — 2
B) 2x + 4
C) 3 (x + 3) — x — 5 -
Найдите наименьшее общее кратное для каждой пары данных чисел.
A) 2 и 3
B) 7 и 14
C) 25 и 15 -
Сложить и / или вычесть и упростить
A) 1/3 + 2/3
B) 2/5 — 1/7 -
Что такое 2/3 из 21? -
Что составляет 40% от 1/4? -
Что такое 20% от 50%? -
Сколько секунд в одном часе? -
Сколько минут в январе? -
Каково расположение каждой из точек: (-2, 0), (0, 3) и (-2, — 3) в координатной плоскости? -
Порядок 7/5, 12/10, 21/20 и 111% от наименьшего к наибольшему.
Больше математики в средней школе (10, 11 и 12 классы) — бесплатные вопросы и проблемы с ответами
Больше начальной математики (4 классы и 5) с бесплатными вопросами и задачами с ответами
Домашняя страница
Алгебра Класс 6 Дополнительные вопросы Математика Глава 11
Алгебра Класс 6 Дополнительные вопросы Математика Глава 11
Дополнительные вопросы для 6 класса по математике Глава 11 Алгебра
Дополнительные вопросы по алгебре 6 класс Очень короткий ответ Тип
Вопрос 1.
Шесть меньше числа равно двум. Какой номер?
Пусть число будет «x».
По условию имеем x — 6 = 2
По проверкам имеем 8-6 = 2
∴ x = 8
Таким образом, необходимое число — 8.
Вопрос 2.
Напишите алгебраическое выражение для каждого из следующих значений:
(a) 3, вычтенное из числа y.
(b) 5 прибавляется к троекратному числу x.
Решение:
(a) Требуемое выражение — y — 3
(b) Требуемое выражение — 5 + 3x
Вопрос 3.
Напишите алгебраическое выражение для следующих выражений:
(a) Сумма чисел x и 4 удваивается.
(b) Одна четвертая числа x прибавляется к одной трети того же числа.
Решение:
(a) Требуемое выражение — 2 x (x + 4)
(b) Требуемое выражение — \ (\ frac {1} {4} \) x + \ (\ frac {1} {3} \) х
Вопрос 4.
Придумайте число x. Умножьте его на 3 и прибавьте к произведению 5, а затем вычтите y. Найдите получившееся число.
Требуемое число (3x + 5)
Теперь мы должны вычесть y из результата i.э., 3х + 5 — у
Вопрос 5.
Вот образец домиков со спичками:
Напишите общее правило для этого образца.
Решение:
Один домик состоит из 6 спичек, т. Е. 6 x 1
Два домика состоят из 12 спичек, т. Е. 6 x 2
Три домика состоят из 18 спичек, т. Е. 6 x 3
Е. 6 x 3
∴ Правило 6n, где n представляет количество дома.
Вопрос 6.
Если сторона равностороннего треугольника равна x, найдите его периметр.
Решение:
Мы знаем, что три стороны равностороннего треугольника равны.
∴ х + х + х = 3х.
Таким образом, требуемый периметр = 3x единицы.
Вопрос 7.
Если x = 3, найдите значение следующего:
(i) x + 5
(ii) 2x — 3
(iii) x — 7
(iv) \ (\ frac {x} { 3} \) — 1
Учитывая, что x = 3
(i) x + 5 = 3 + 5 = 8
(ii) 2x — 3 = 2 x 3 — 3 = 6 — 3 = 3
(iii ) x — 7 = 3-7 = -4
(iv) \ (\ frac {x} {3} \) — 1 = \ (\ frac {3} {3} \) -1 = 1 — 1 = 0
Вопрос 8.
Если x = 2, y = 3 и 2 = 5, найдите значение;
(a) 2x + y + z
(b) 4x -y + z
(c) x — y + z
Решение:
(a) Учитывая, что: x — 2, y = 3 и z = 5
∴ 2x + y + 2 = 2 x 2 + 3 + 5
= 4 + 3 + 5 = 12
(б) 4x — y + z = 4 x 2 — 3 + 5
= 8 — 3 + 5 = 5 + 5 = 10
(c) x — y + z = 2-3 + 5 = -1 + 5 = 4
Вопрос 9.
Укажите, какие из следующих уравнений являются уравнениями с переменной?
(a) 12 = x — 5
(b) 2x> 7
(c) \ (\ frac {x} {2} \) = 5
(d) 5 + 7 = 3 + 9
(e) 7 = (11 x 5) — (12 x 4)
Решение:
(a) 12 = x — 5 — уравнение с переменной x.
(b) 2x> 7 не является уравнением, потому что у него нет знака «=».
(d) 5 + 7 = 3 + 9 не является уравнением, потому что у него нет переменной.
(e) 7 = (11 x 5) — (12 x 4) не является уравнением, поскольку не имеет переменной.
Вопрос 10.
Придумайте число, прибавьте к нему 2, а затем умножьте сумму на 6, получится 42.
Решение:
Пусть число будет x.
∴ Сумма x и 2 = x + 2
Теперь, умножив сумму на 6, мы получим
6 × (x + 2) = 42
⇒ 6 × x + 6 × 2 = 42
⇒ 6x + 12 = 42
По осмотру получаем
6 × 5 + 12 = 42
⇒ 30 + 12 = 42
∴ 42 = 42
Итак, необходимое число = 5
Дополнительные вопросы по алгебре 6 класс Краткий ответ типа
Вопрос 11.
Сторона правильного шестиугольника s см. Найдите его периметр.
Решение:
Каждая сторона правильного шестиугольника = s
∴ его периметр = s + s + s + s + s + s = 6s cm
Вопрос 12.
Если a = 3, b = \ (\ frac {1 } {2} \) и c = \ (\ frac {1} {4} \), найдите значение
Решение:
Вопрос 13.
Заполните таблицу и найдите решение уравнения 19 — x = 13
Решение:
По осмотру имеем
Таким образом, необходимое решение — 6.
Вопрос 14.
Если x = — \ (\ frac {1} {2} \), y = \ (\ frac {1} {4} \) и z = 0, найдите значение заданных выражений
( a) 8z + 2x -y
(b) z — y + 3x
Решение:
Вопрос 15.
Заполните пропуски:
(a) 5 прибавлено к -5 = ……….
(b) Если x = 3, то 3x — 5 = ……….
(c) Если x = 1 и y = 2, то 2x + 3y = ……….
(d) Если 10x — 6 = 14, то x = ……….
(e) 4 меньше числа x = ……….
Решение:
(a) 0
(b) 4
(c) 8
(d) 2
(e) x — 4
Дополнительные вопросы по алгебре 6 класса Навыки мышления высшего порядка (HOTS)
Вопрос 16.
A выезжает на машине из Дели в 6.00 утра в Амритсар. Равномерная скорость его машины составляет x км / ч. В 12.00 он обнаруживает, что все еще находится в 50 км от Амритсара. Найдите расстояние между Дели и Амритсаром.
Решение:
Время, затраченное А. на то, чтобы добраться до Амритсара = 12.00 — 6.00 = 6 часов.
Равномерная скорость автомобиля = x км / час
∴ Общее расстояние, пройденное A = Время x скорость = 6x км.
∴ Расстояние между Дели и Амритсаром = (6x + 50) км.
Вопрос 17.
Оценка Аншики по естествознанию на 15 больше, чем две трети ее оценки по санскриту.Если она набрала x баллов по санскриту, найдите ее оценку по естествознанию.
Решение:
Оценка Аншики по санскриту = x
∴ Ее оценки по науке = \ (\ frac {2} {3} \) x +15
∴ Таким образом, оценка Аншики по науке = \ (\ frac {2} {3 } \) х + 15
Дополнительные вопросы по математике 6 класса
Решения NCERT для математики 6 класса
Примечания по алгебре, класс 6, математика, глава 11
CBSE, класс 6, математические заметки, глава 11, алгебра,
Раздел математики, в котором мы изучаем числа, называется арифметикой.
В алгебре мы используем буквы. Использование букв помогает нам во многих отношениях:
- Используя буквы, мы можем писать правила и формулы в общем виде.
- Используя буквы, мы можем говорить о любом числе, а не только о конкретном числе.
- Буквы могут означать неизвестное количество. Обучаясь методам определения неизвестных, мы разрабатываем мощные инструменты для решения головоломок и многих повседневных проблем.
- Поскольку буквы обозначают числа, над ними можно выполнять операции как над числами. Это приводит к изучению алгебраических выражений и их свойств.
Выкройки из спичек
С помощью спичек мы можем делать буквы и другие формы. Мы можем записать общее соотношение между количеством спичек, необходимых для повторения данной формы. Количество повторений данной формы варьируется; принимает значения 1, 2, 3,…. Это переменная, обозначаемая некоторой буквой n.
Это переменная, обозначаемая некоторой буквой n.
Идея переменной
Переменная означает нечто, что может изменяться (или меняться). Значение переменной не фиксировано. Может принимать разные значения. Длина квадрата может иметь любое значение. Это переменная. Но количество углов треугольника имеет фиксированное значение 3. Это не переменная. Мы можем использовать любую букву n, l, m, p, x, y, z и т.д., чтобы показать переменную.
Больше выкройки из спичек
Из спичек можно сделать много букв алфавита и других форм. Например, U, V, треугольник, квадрат и т. Д.В шаблонах спичек мы используем переменную n, чтобы дать нам общее правило для количества спичек, необходимых для создания шаблона. Это важное использование переменных в математике.
Дополнительные примеры переменных
Чтобы показать переменную, мы можем использовать любую букву в качестве n, m, l, p, x, y, z и т. Д. Напомним, что переменная — это число, которое не имеет фиксированного значения. Может принимать разные значения. Например, число 10, число 100 или любое другое заданное число не являются переменной. У них есть фиксированные значения.Аналогично фиксируется количество углов четырехугольника (4); это также не переменная.
Может принимать разные значения. Например, число 10, число 100 или любое другое заданное число не являются переменной. У них есть фиксированные значения.Аналогично фиксируется количество углов четырехугольника (4); это также не переменная.
Использование переменных в общих правилах
Правила из геометрии
Периметр квадрата (p) = 4l, где l — длина стороны квадрата
Периметр прямоугольника (p) = 2l + 2b, где l — длина стороны квадрата. длина, а b ширина прямоугольника.
Правила арифметики
Коммутативность сложения
Пусть a и b — две переменные, которые могут принимать любое числовое значение.
Тогда a + b = b + a
Коммутативность умножения
Пусть a и b — две переменные.
Тогда a × b = b × a
Дистрибутивность умножения над сложением
Пусть a, b и c — три переменные.
Тогда a × (b + c) = a × b + a × c
Ассоциативность сложения
Пусть a, b и c — три переменные.
Тогда (a + b) + c = a + (b + c).
Выражения с переменными
Мы знаем, что переменные могут принимать разные значения; у них нет фиксированной стоимости.Но это числа. Вот почему, как и в случае с числами, над ними могут выполняться операции сложения, вычитания, умножения и деления. Используя различные операции, мы можем формировать выражения с такими переменными, как x — 2, x + 1, 3n, 2m, \ (\ frac {p} {4} \), 2y + 5, 3l — 7 и т. Д.
Примечание. Ряд выражений можно вычислить немедленно.
Например: 3 × 4 + 6 = 12 + 6 = 18
Но выражение, содержащее переменную x, не может быть вычислено, пока x не будет присвоено такое же значение.
Например,
Когда x = 1, 4x + 3 = 4 × 1 + 3 = 4 + 3 = 7.
Практическое использование выражений
Многие операторы, описанные на обычном языке, можно преобразовать в операторы, использующие выражения с переменными.
Что такое уравнение?
Уравнение — это условие переменной. Это выражается в том, что выражение с переменной равно фиксированному числу.
Например, x — 3 = 2.
Уравнение имеет две стороны, левую и правую, а между ними — знак равенства (=).
Уравнение утверждает, что значение левой части (LHS) равно значению правой части (RHS).
Если LHS не равно RHS, мы не получаем уравнения.
Например, выражение 2n> 10 или 2n <10 не является уравнением.
Примечание. Уравнение, подобное 10 — 1 = 9, называется числовым уравнением, поскольку ни одна из его двух сторон не содержит переменной. Обычно слово уравнение используется только для уравнений, включающих одну или несколько переменных.
Решение уравнения
Значение переменной в уравнении, для которого левая часть уравнения становится равной правой части уравнения, считается удовлетворяющим уравнению и само называется решением уравнения.Например, n = 2 является решением уравнения 2n = 4, где n = 3 не является решением уравнения 3n = 13.
Получение решения уравнения
Одним из методов получения решения уравнения является метод проб и ошибок. В этом методе мы присваиваем переменной некоторое значение и проверяем, удовлетворяет ли она уравнению. Таким образом мы продолжаем присваивать переменной разные значения, пока не найдем правильное значение, которое удовлетворяет уравнению.
В этом методе мы присваиваем переменной некоторое значение и проверяем, удовлетворяет ли она уравнению. Таким образом мы продолжаем присваивать переменной разные значения, пока не найдем правильное значение, которое удовлетворяет уравнению.
Но это не прямой и практический способ найти решение.Нам нужен более систематический способ получения решения уравнения, чем метод проб и ошибок. В случае очень простых уравнений переменная заменяется заполнителем I, и ее значение определяется обычными методами. Таким образом, полученное значение переменной является решением уравнения.
Использование уравнения
Первоначально нам дано уравнение для переменной, значение которой нам неизвестно. Решить уравнение — значит найти неизвестное значение. Таким образом, переменная в уравнении рассматривается как неизвестная, и, начиная с неизвестного, мы можем увидеть уравнение.Таким образом, решение уравнения — это метод поиска неизвестного. Следовательно, это мощный метод решения головоломок и проблем.
Заметки по математике для класса 6
Примечания к редакции по математике Глава 11 — Алгебра (6-й класс)
Введение в алгебруЕсть так много разделов математики —
Изучение чисел называется Арифметика .
Изучение форм называется Геометрия .
Учебное пособие по использованию букв и символов в математике называется Алгебра .
Алгебра — это часть математики, в которой буквы и символы используются для представления чисел в уравнениях. Это помогает нам изучать неизвестные величины.
Образцы спичек
Количество спичек, использованных для изготовления 1 st квадрат = 4
№спичек, из которых получилось 2 и квадратных = 7
Количество спичек, использованных для изготовления 3 квадрат = 10
Итак, паттерн, который мы здесь наблюдаем, это 3n + 1
С помощью этого шаблона мы можем легко найти необходимое количество спичек в любом количестве квадратов.
Пример
Сколько спичек будет использовано в цифре 50 -й ?
Решение
3н + 1
3 × 50 + 1
= 151 спичка
Идея переменнойПеременная относится к неизвестным величинам, которые могут меняться или изменяться и представлены строчными буквами английского алфавита.
Одним из таких примеров является правило, которое мы использовали в шаблоне спички
.3н + 1
Здесь значение n неизвестно и может время от времени меняться.
Дополнительные примеры переменныхМы можем использовать в качестве переменной любую букву, но только строчные английские алфавиты.
Числа нельзя использовать для переменной, так как они имеют фиксированное значение.
Они также могут помочь в решении некоторых других проблем.
Пример: 1
Каран хотел купить книги рассказов в книжном киоске. Она хотела купить 3 книги для себя, 2 для брата и 4 для 2 своих друзей. Каждая книга стоит 15 рупий. Сколько денег она должна заплатить продавцу?
Она хотела купить 3 книги для себя, 2 для брата и 4 для 2 своих друзей. Каждая книга стоит 15 рупий. Сколько денег она должна заплатить продавцу?
Решение: 1
Стоимость 1 книги = 15 рупий
Нам нужно найти стоимость 9 книг.
| Кол-во ноутбуков | 1 | 2 | 3 | 4 | ……. | a | … ….. |
| Итого | 15 | 30 | 45 | 60 | ……. | 15 а | ……. |
В текущей ситуации a (это переменная) означает 9
Следовательно,
Стоимость 9 книг = 15 × 9
= 135
Следовательно, Каран должен заплатить рупий.135 владельцу книжного киоска.
Переменная и константа не только умножаются друг на друга, но также могут складываться или вычитаться в зависимости от ситуации.
Пример: 2
У Ману на 2 ластика больше, чем у Тану. Сформируйте выражение для утверждения.
Решение: 2.1
Ластики, которые есть у Тану, можно представить с помощью переменной (x)
Ластики, которые есть у Ману = резинки, которые есть у Тану + 2
Ластик с Manu = x + 2
Решение: 2.2
Ластики, которые есть у Ману, можно представить с помощью переменной (y)
Ластики, которые есть у Тану = Ластики, которые есть у Ману — 2
Ластик с Tanu = y — 2
Использование переменных в общих правилах (геометрия)1. Периметр квадрата
Периметр квадрата = Сумма всех сторон
= 4 × сторона
= 4 с
Таким образом, p = 4s
Здесь s переменная, поэтому периметр изменяется при изменении значения стороны.
2. Периметр прямоугольника
Периметр прямоугольника = 2 (длина + ширина)
= 2 (l + b) или 2l + 2b
Таким образом, p + 2 × (l + b) или 2l + 2b
Где, l и b являются переменными, а значение периметра изменяется с изменением l и b.
1. Коммутативность сложения
5 + 4 = 9
4 + 5 = 9
Таким образом, 5 + 4 = 4 + 5
Это коммутативное свойство сложения чисел, при котором результат остается неизменным, даже если мы поменяем числа местами.
а + Ь = Ь + а
Здесь a и b — разные переменные.
Пример
а = 16 и б = 20
По коммутативному свойству
16 + 20 = 20 + 16
36 = 36
2. Коммутативность умножения
8 × 2 = 16
2 × 8 = 16
Таким образом, 8 × 2 = 2 × 8
Это коммутативное свойство умножения, при котором результат остается неизменным, даже если мы поменяем числа местами.
а × б = б × а
Здесь a и b — разные переменные.
Пример
18 × 12 = 216, 12 × 18 = 216
Таким образом, 18 × 12 = 12 × 18
3. Распределенность номеров
Распределенность номеров
6 × 32
Это сложная сумма, но есть простой способ ее решить. Он известен как распределенность умножения на сложение чисел .
6 × (30 + 2)
= 180 + 12
= 192
Таким образом, 6 × 32 = 192
A × (b + c) = a × b + a × c
Здесь a, b и c — разные переменные.
4. Ассоциативность сложения
Это свойство указывает, что результат добавления чисел останется неизменным независимо от их группировки.
(a + b) + c = a + (b + c)
Пример
(4 + 2) + 7 = 4 + (2 + 7)
6 + 7 = 4 + 9
13 = 13
ВыраженияВ арифметических выражениях могут использоваться числа и все операции, такие как сложение, вычитание, умножение и деление
Пример
2 + (9 — 3), (4 × 6) — 8 и т. Д.…
(4 × 6) — 8 = 24 — 8
= 16
Выражения с переменной
Мы можем создавать выражения, используя такие переменные, как
2м, 5 + т и т. д…..
д…..
Выражение, содержащее переменную / ы, нельзя проанализировать, пока не будет указано его значение.
Пример
Найдите 3x — 12, если x = 6
Решение
(3 × 6) — 12
= 18–12
= 5
Таким образом,
3x — 12 = 5
Формирование выражений| Заявление | Выражение |
у вычтено из 12 | 12 — й |
x умноженное на 6 | 6x |
t Умножить на 4, а затем вычесть 5 из произведения. | 4т — 5 |
Практическое использование выражений
Пример
3 мальчика ходят в театр. Стоимость билета и попкорна составляет 33 и 15 долларов соответственно. Сколько стоит на человека?
Стоимость билета и попкорна составляет 33 и 15 долларов соответственно. Сколько стоит на человека?
Решение
Скажем,
x = стоимость билета на человека
у = стоимость попкорна на человека
Общая стоимость фильма (билет + попкорн) на человека = x + y
Итого стоимость билета + попкорн на 3 мальчика = 3 (x + y)
= 3 (33 + 15)
= 3 (48)
= 144
Следовательно, общая стоимость билета в кино и попкорна для 3 мальчиков составляет 144 доллара.
УравнениеЕсли мы используем знак равенства между двумя выражениями, они образуют уравнение.
Уравнение удовлетворяет только определенному значению переменной.
Знак равенства означает, что LHS равно RHS, и значение переменной, которая делает их равными, является единственным решением этого уравнения.
Пример
3 + 2x = 13
5 мес. — 7 = 3
п / 6 = 18
Если вместо знака равенства стоит знак «больше» или «меньше», то это утверждение не является уравнением.
Некоторые примеров, которые не являются уравнением
23 + 6x> 8
6f — 3 <24
Решение уравненияЗначение переменной, которая удовлетворяет уравнению, является решением этого уравнения. Чтобы проверить, является ли конкретное значение решением или нет, мы должны проверить, что LHS должен быть равен RHS с этим значением переменной.
Метод проб и ошибок
Чтобы найти решение уравнения, мы используем метод проб и ошибок.
Пример
Найдите значение x в уравнении 25 — x = 15.
Решение
Здесь мы должны проверить некоторые значения, которые, по нашему мнению, могут быть решением, поместив значение переменной x и проверив, что LHS = RHS.
Возьмем x = 5
25-5 = 15
20 ≠ 15
Итак, x = 5 не является решением этого уравнения.
Возьмем x = 10
25–10 = 15
15 = 15
слева =
справа Следовательно, x = 10 является решением этого уравнения.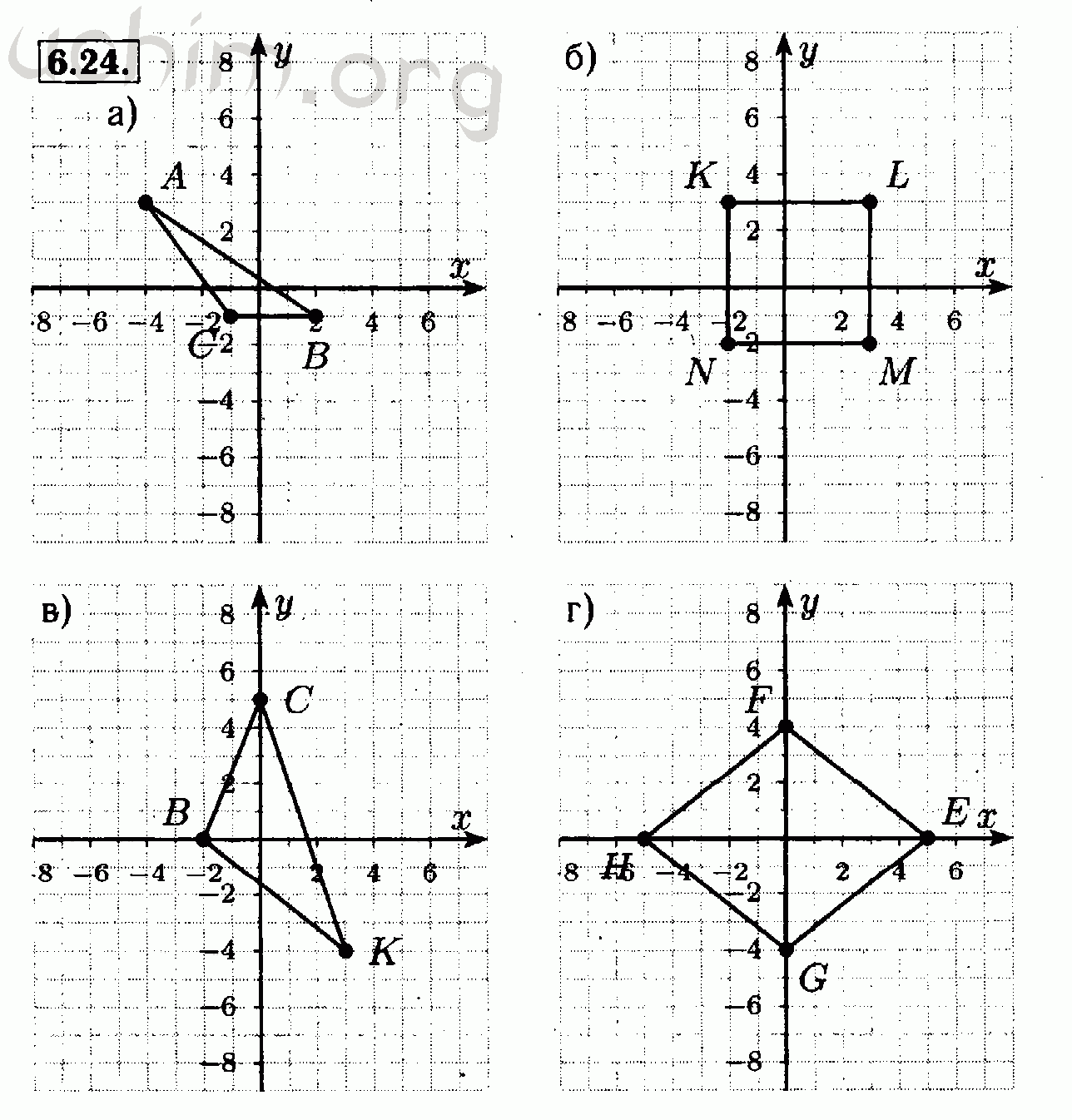
NCERT для математики класса 6 Глава 11
Страница № 226:
Вопрос 1:
Найдите правило, указывающее количество спичек, необходимое для изготовления следуя образцам спичек. Используйте переменную, чтобы написать правило.
(а) А узор из буквы Т как T
(б) А узор из буквы Z как Z
(с) А узор из буквы П как U
(г) А узор из буквы V как V
(e) A узор из буквы Е как E
(f) A узор из буквы S как S
(г) А узор из буквы А как A
Ответ:
(а)
из На рисунке видно, что для сделать T .Следовательно, шаблон равен 2 n .
(б)
из
На рисунке видно, что для
сделать Z . Следовательно, шаблон равен 3 n .
(в)
из На рисунке можно заметить, что для сделать U . Следовательно, шаблон равен 3 n .
(г)
из На рисунке видно, что для сделать V .Следовательно, шаблон равен 2 n .
(д)
из На рисунке видно, что для сделайте E . Следовательно, шаблон равен 5 n .
(ж)
из На рисунке видно, что для сделать S . Следовательно, шаблон равен 5 n .
(г)
из рисунок, можно заметить, что потребуется шесть спичек для сделайте A .Следовательно, шаблон равен 6 n .
Страница № 227:
Вопрос 2:
Мы уже знать правило построения букв L, C и F. Некоторые из буквы из некоторых букв из (а) Т, (б) Z, (в) U, (г) V, (e) E, (f) S, (g) R дают нам то же правило, что и L. эти? Почему это происходит?
Ответ:
Это
известно, что L требуется только две спички. Следовательно, шаблон
для L — 2 n . Среди всех букв, приведенных выше в вопросе 1,
только T и V — две буквы, для которых нужны две спички.
Следовательно, шаблон
для L — 2 n . Среди всех букв, приведенных выше в вопросе 1,
только T и V — две буквы, для которых нужны две спички.
Следовательно, (а) и (d)
Страница № 227:
Вопрос 3:
курсантов маршируют на параде. В ряду 5 курсантов. Какое правило что дает количество курсантов с учетом количества рядов? (Используйте n по количеству рядов.)
Ответ:
Пусть число рядов — n .
Количество курсантов в одном ряду = 5
Всего количество курсантов = количество курсантов в ряду × количество рядов
= 5 n
Страница № 227:
Вопрос 4:
Если есть
50 манго в коробке, как вы напишете общее количество
манго по количеству ящиков? (Используйте b для номера
коробок. )
)
Ответ:
Пусть количество ящиков должно быть б .
Количество манго в коробке = 50
Всего количество манго = количество манго в коробке × количество ящики
= 50 b
Страница № 227:
Вопрос 5:
The Учитель раздает каждому ученику по 5 карандашей.Вы можете сказать, сколько карандаши нужны, учитывая количество учеников? (Используйте s для количество учеников.)
Ответ:
Пусть количество учеников с .
карандаши выдано каждому студенту = 5
Всего количество карандашей
= Число карандашей, выданных каждому ученику × Количество учеников
= 5 с
Страница № 227:
Вопрос 6:
Птица
пролетает 1 километр за одну минуту. Можете ли вы выразить пройденное расстояние?
птицей по времени ее полета в минутах? (Используйте т для
время полета в минутах.)
Можете ли вы выразить пройденное расстояние?
птицей по времени ее полета в минутах? (Используйте т для
время полета в минутах.)
Ответ:
Пусть Время полета составит т минут.
Расстояние пройдена за минуту = 1 км
Расстояние пройдено за т минут = пройденное расстояние за одну минуту × Время полета
= 1 × т = т км
Страница № 227:
Вопрос 7:
Радха — это рисование точки Ранголи (красивый узор из линий, соединяющих точки с меловой порошок.У нее 9 точек подряд. Сколько точек будет на ее Ранголи есть для р рядов? Сколько будет точек, если рядов 8? Если рядов 10?
Ответ:
Количество точек в 1 ряду = 9
Количество ряды = r
Всего количество точек в r строк = количество строк × количество точек подряд
= 9 r
Количество точек в 8 рядах = 8 × 9 = 72
Количество точек в 10 рядах = 10 × 9 = 90
Страница № 227:
Вопрос 8:
Лила
Младшая сестра Радхи. Лила на 4 года младше Радхи.
Можете ли вы записать возраст Лилы через возраст Радхи? Взять
Возраст Радхи х лет.
Лила на 4 года младше Радхи.
Можете ли вы записать возраст Лилы через возраст Радхи? Взять
Возраст Радхи х лет.
Ответ:
Пусть Возраст Радхи — х лет.
Leela’s age = возраст Радхи — 4
= ( x — 4) лет
Страница № 227:
Вопрос 9:
Мать имеет сделал ладдус.Она дает ладду гостям и членам семьи; осталось еще 5 ладду. Если количество подаренных матерью ладдусов равно l , сколько ладду она сделала?
Ответ:
Количество ладдус отдан = л
Количество осталось ладду = 5
Всего количество ладду = количество отданных ладду + количество ладду
оставшиеся
= л + 5
Страница № 227:
Вопрос 10:
Апельсины
должны быть перенесены из больших ящиков в меньшие. Когда
большая коробка опорожняется, апельсины из нее заполняют две меньшие коробки и
еще 10 апельсинов остаются снаружи. Если количество апельсинов в небольшом
коробки принимаются размером x , сколько апельсинов в
коробка побольше?
Когда
большая коробка опорожняется, апельсины из нее заполняют две меньшие коробки и
еще 10 апельсинов остаются снаружи. Если количество апельсинов в небольшом
коробки принимаются размером x , сколько апельсинов в
коробка побольше?
Ответ:
Количество апельсины в одной маленькой коробке = x
Количество апельсины в двух маленьких коробках = 2 x
Количество осталось апельсинов = 10
Количество апельсины в большой коробке = количество апельсинов в двух маленьких коробках
+ Количество апельсинов осталось
= 2 х + 10
Страница № 227:
Вопрос 11:
(а) Посмотрите на следующий образец квадратов из спичек.Квадраты
не отдельные. Два соседних квадрата имеют общую спичку.
Наблюдайте за закономерностями и найдите правило, определяющее количество
спички по количеству квадратов. (Подсказка: если вы удалите
вертикальную палку на конце, у вас получится выкройка Cs.)
(Подсказка: если вы удалите
вертикальную палку на конце, у вас получится выкройка Cs.)
(b) Данный рисунок представляет собой узор из треугольников из спичек. найти общее правило, определяющее количество спичек с точки зрения количество треугольников.
Ответ:
(a) Может Обратите внимание, что в данном шаблоне спичек количество
спичек — 4, 7, 10 и 13, что на 1 больше, чем в три раза количество квадратов в выкройке.
Следовательно, шаблон равен 3 n + 1, где n — количество квадраты.
(b) Может Обратите внимание, что в данном шаблоне спичек количество
спички 3, 5, 7 и 9, что на 1 больше, чем вдвое количество треугольников в узоре.
Следовательно, шаблон равен 2 n + 1, где n — количество треугольники.
Страница № 230:
Вопрос 1:
Сторона
равностороннего треугольника показано l . Выразить
периметр равностороннего треугольника используя l .
Выразить
периметр равностороннего треугольника используя l .
Ответ:
Сторона равносторонний треугольник = л
Периметр = л + л + л = 3 л
Страница № 230:
Вопрос 2:
Сторона правильного шестиугольника (см. рисунок) обозначается l .Выразите периметр шестиугольника, используя l .
(Подсказка: A У правильного шестиугольника все шесть сторон равны по длине.)
Ответ:
Сторона правильный шестигранник = л
Периметр = 6 л
Страница № 230:
Вопрос 3:
Куб — это трехмерная фигура, показанная на данном рисунке. У него шесть граней, и все они одинаковые квадраты. Длина ребра куба равна l . Найдите формулу для общей длины ребер куба.
У него шесть граней, и все они одинаковые квадраты. Длина ребра куба равна l . Найдите формулу для общей длины ребер куба.
Ответ:
Длина лезвия = л
Количество ребер = 12
Общая длина кромок = Количество кромок × Длина одной кромки
= 12 л
Видео решение для алгебры (Страница: 230, Q.№: 3)
Решение NCERT для математики класса 6 — алгебра 230, вопрос 3
Страница № 231:
Вопрос 4:
The диаметр круга — это линия, соединяющая две точки на окружности. а также прошел через центр круга. (В соседнем цифра AB — диаметр окружности; C — его центр.) Выразите диаметр круга ( d ) через его радиус ( r ).
Ответ:
Диаметр = AB = AC + CB = r + r = 2 r
d = 2 r
Страница № 231:
Вопрос 5:
Найти сумму трех чисел 14, 27 и 13 можно двумя способами:
(a) Мы можем сначала сложить 14 и 27, чтобы получить 41, а затем добавить 13, чтобы получить общая сумма 54 или
(b) Мы можем сложить 27 и 13, чтобы получить 40, а затем добавить 14, чтобы получить сумму 54.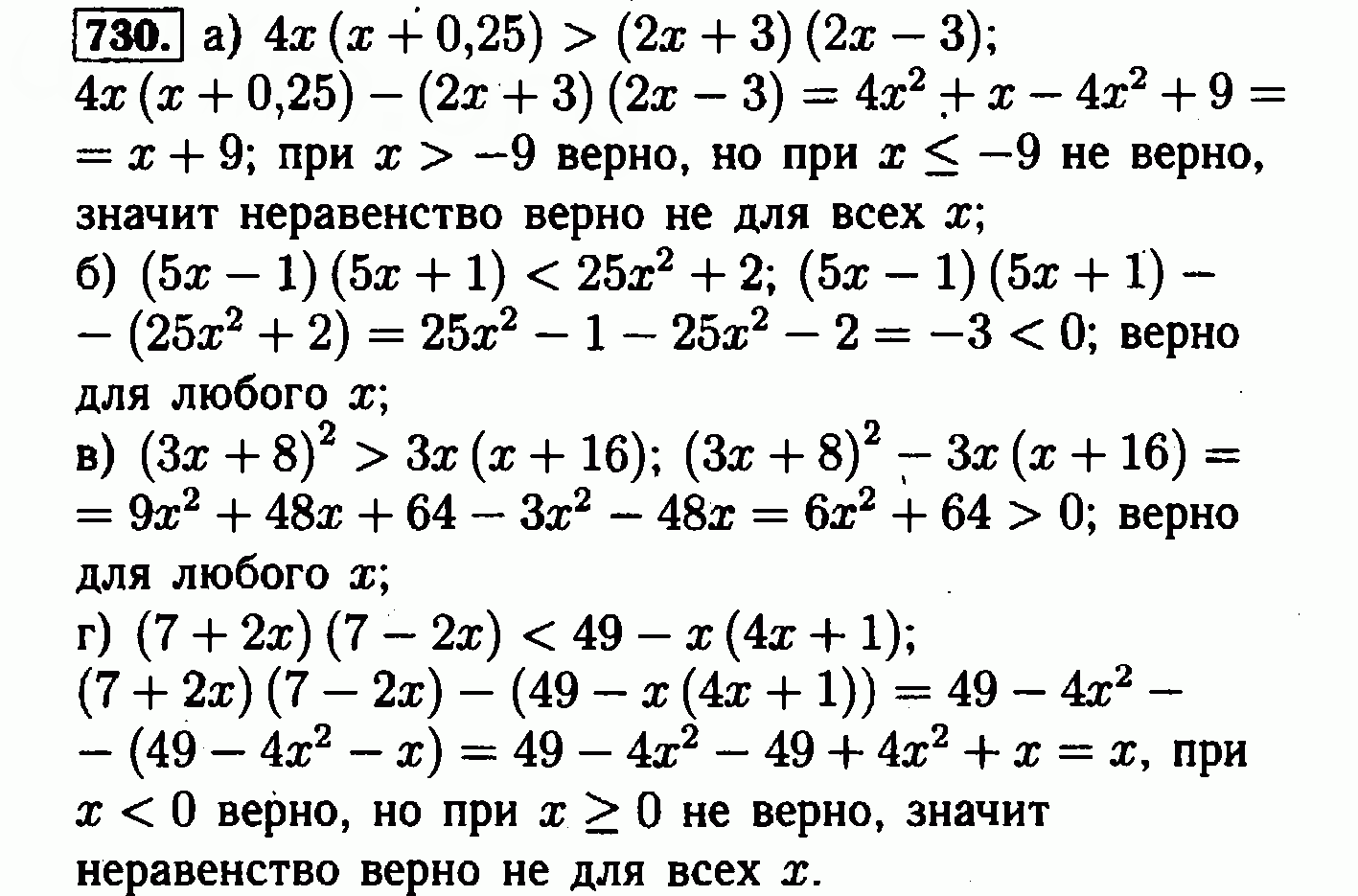 Таким образом, (14 + 27) + 13 = 14 + (27 + 13)
Таким образом, (14 + 27) + 13 = 14 + (27 + 13)
Это можно сделать для любых трех чисел. Это свойство известно как ассоциативность сложения чисел . Выразите это свойство которые мы уже изучили в главе о целых числах, в в общем случае, используя переменные a , b и c .
Ответ:
Для любого три целых числа a , b и c ,
( a + b ) + c = a + ( b + c )
Страница № 233:
Вопрос 1:
Макияж как много выражений с числами (без переменных), как можно из трех числа 5, 7 и 8.Каждый номер следует использовать не более одного раза. Используйте только сложение, вычитание и умножение.
(Подсказка: три возможных выражения: 5 + (8-7), 5 — (8 — 7), (5 × 8) + 7;
сделать
другие выражения. )
)
Ответ:
Многие выражения могут быть составлены с помощью трех чисел 5, 7 и 8.
Некоторые из это следующие.
5 × (8–7)
5 × (8 + 7)
(8 + 5) × 7
(8 — 5) × 7
(7 + 5) × 8
(7 — 5) × 8
Страница № 233:
Вопрос 2:
Какие из следующих выражений содержат только числа?
(а) y + 3 (б) (7 × 20) — 8 z
(в) 5 (21-7) + 7 × 2 (г) 5
(д) 3 x (е) 5-5 n
(г) (7 × 20) — (5 × 10) — 45 + п.
Ответ:
Это может быть заметил, что выражения в альтернативах (c) и (d) формируются используя только числа.
Страница № 233:
Вопрос 3:
Определить
операции (сложение, вычитание, деление, умножение) в
формировать следующие выражения и рассказывать, как выражения имеют
был сформирован.
(а) z + 1, z — 1, y + 17, y — 17 (б)
(в) 2 y + 17, 2 y -17 (г) 7 м , — 7 м + 3, — 7 м — 3
Ответ:
(а) Дополнение поскольку 1 добавляется к z .
Вычитание, поскольку 1 вычитается из z .
Сложение как 17 прибавляется к y .
Вычитание как 17 вычитается из y .
(б) Умножение поскольку y умножается на 17.
Деление y делится на 17.
Умножение как z умножается на 5.
(c) Умножение и дополнение
y умножается на 2, и к результату прибавляется 17.
Умножение и вычитание
y умножается на 2, и 17 вычитается из результата.
(d) Умножение поскольку м умножается на 7.
Умножение и сложение как m умножается на −7, и добавлено 3
к результату.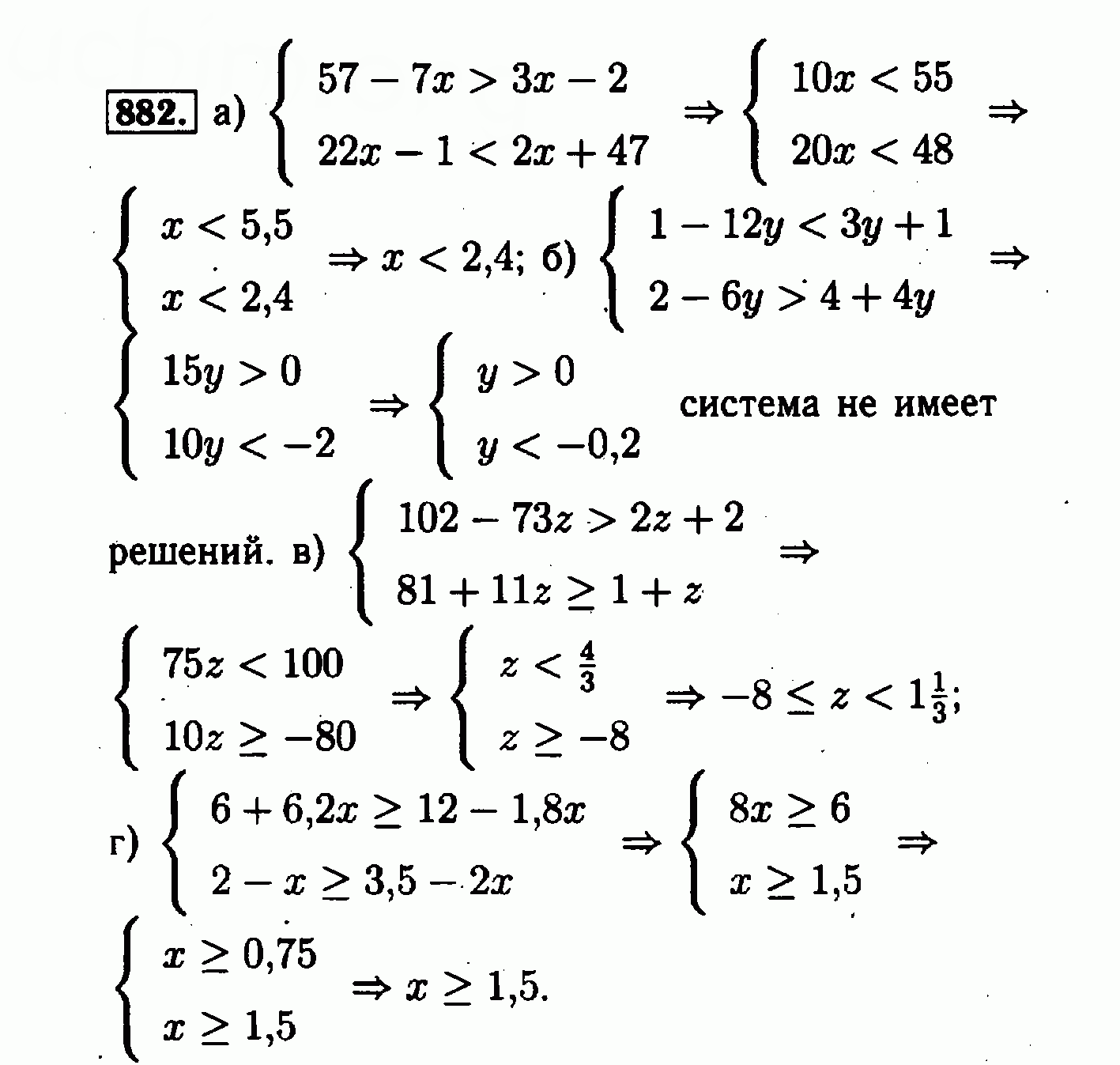
Умножение и вычитание, поскольку м умножается на −7, а 3 —
вычитается из результата.
Страница № 233:
Вопрос 4:
Приведите выражения для следующих случаев.
(a) 7 прибавлено к p (b) 7 вычтено из p
(c) p , умноженное на 7 (d) p , разделенное на 7
(e) 7 вычитается из — м (f) — p умножено на 5
(g) — p разделить на 5 (h) p умножить на — 5
Ответ:
(а) п + 7
(б) п — 7
(в) 7 п
(г)
(е) — м — 7
(ж) — 5 п
(г)
(ч) — 5 п
Страница № 234:
Вопрос 5:
Приведите выражения в следующих случаях.
(a) 11 добавлено к 2 м
б 11 вычтено из 2 м
(c) 5 умножить на y , к которому прибавляется 3
(г) 5 умножить на y , из которого вычтено 3
(д) y умножается на — 8
(ж) г. умножается на — 8, а затем к результату прибавляется 5
(г) y умножается на 5, и результат вычитается из 16
(в) y умножается на — 5, и результат прибавляется к 16
Ответ:
(а) 2 м + 11
(б) 2 м — 11
(в) 5 л + 3
г 5 л — 3
(е) — 8 y
(ж) — 8 y + 5
(г) 16 — 5 л
(ч) — 5 и + 16
Страница № 234:
Вопрос 6:
(a) Сформируйте выражения, используя t и 4. Используйте не более одного
числовая операция. Каждое выражение должно содержать t .
Используйте не более одного
числовая операция. Каждое выражение должно содержать t .
(b) Формируйте выражения, используя y , 2 и 7. Каждое выражение должно в нем есть y . Используйте только две числовые операции. Это должно быть другой.
Ответ:
(а) т + 4, т — 4, 4 т , , , 4 — т , 4 + т
(б) 2 л + 7, 2 y — 7, 7 y + 2,…
Страница № 235:
Вопрос 1:
Ответьте следующее:
(a) Примем, что нынешний возраст Сариты составляет y лет
(i) Какого возраста она будет через 5 лет?
(ii) Сколько ей было лет 3 года назад?
(iii) Дед Сариты в 6 раз старше ее.Сколько лет ее дедушке?
(iv) Бабушка младше дедушки на 2 года. Сколько лет бабушке?
(v) Возраст отца Сариты на 5 лет больше, чем в 3 раза старше Сариты. Сколько лет ее отцу?
Сколько лет ее отцу?
(b) Длина прямоугольного зала на 4 метра меньше трех ширины зала. Какая длина, если ширина b метров?
(c) Прямоугольная коробка имеет высоту х см. Его длина в 5 раз больше высоты, а ширина на 10 см меньше длины.Выразите длину и ширину коробки через высоту.
(d) Мина, Бина и Лина поднимаются по ступеням на вершину холма. Мина на шаге с , Бина на 8 шагов впереди, а Лина на 7 шагов позади. Где Бина и Мина? Общее количество ступенек на вершину холма в 10 раз меньше, чем Мина. Выразите общее количество шагов, используя с .
(e) Автобус едет со скоростью v км в час. Он идет от Даспура до Беспура.После того, как автобус проехал 5 часов, Беспур все еще находится в 20 км. Какое расстояние от Daspur до Beespur? Выразите это с помощью v .
Ответ:
(a) (i) Возраст Сариты через 5 лет = нынешний возраст Сариты + 5
= и + 5
(ii) 3 года назад, возраст Сариты = нынешний возраст Сариты — 3
= и — 3
(iii) возраст деда = 6 × нынешний возраст Сариты = 6 y
(iv) Возраст бабушки = нынешний возраст дедушки — 2 = 6 y — 2
(v) Возраст отца = 5 + 3 × нынешний возраст Сариты = 5 + 3 9 1024 y
(b) Длина = 3 × Ширина — 4
л = (3 b -4) метров
(c) Длина = 5 × Высота
л = 5 ч см
Ширина = 5 × Высота — 10
b = (5 ч -10) см
(d) Шаг, на котором находится Бина = (Шаг, на котором находится Мина) + 8
= с + 8
Шаг, на котором находится Лина = (Шаг, на котором находится Мина) — 7
= с — 7
Всего шагов = 4 × (Шаг, на котором находится Мина) — 10 = 4 9 1024 с — 10
(e) Скорость = v км / ч
Пройденное расстояние за 5 часов = 5 × v = 5 9 1024 v км
Общее расстояние между Даспуром и Беспуром = (5 v + 20) км
Видео решение для алгебры (Страница: 235, Q.
 №: 1)
№: 1)Решение NCERT для математики класса 6 — алгебра 235, вопрос 1
Страница № 236:
Вопрос 2:
Измените следующие операторы с использованием выражений в операторы в обычных язык.
(Например, Гивен Салим набирает r пробегов в матче по крикету, Налин забивает
( р + 15) работает.На обычном языке — Налин набирает на 15 пробежек больше чем Салим.)
(а) Примечание книга стоит рупий р. Книга стоит 3 рупий рупий.
(b) Тони кладет на стол q шариков. В его распоряжении 8 q шариков. коробка.
(c) Наши В классе n учеников. В школе обучается 20 n учеников.
(d) Джаггу z лет. Его дяде 4 z лет а его тете (4 z — 3) года.
(e) В
расположение точек — r рядов. Каждая строка содержит 5
точки.
Ответ:
(а) Книга стоит в три раза дороже ноутбука.
(b) Тони коробка содержит в 8 раз больше шариков на столе.
(c) Итого количество учеников в школе в 20 раз больше, чем в нашем классе.
г) дядя Джаггу в 4 раза старше, чем дядя Джаггу и Джаггу. тетя младше дяди на 3 года.
(e) общее количество точек в 5 раз превышает количество строк.
Страница № 236:
Вопрос 3:
(а) Учитывая возраст Мунну x лет, можете ли вы догадаться, что ( x — 2) может показывать?
(Подсказка: подумайте о младшем брате Манну.)
Угадаете, что может показать ( x + 4)? Что (3 x + 7) может шоу?
(б) Учитывая, что сегодня возраст Сары составляет и лет.Подумай о ней возраст в будущем или в прошлом.
Что укажет следующее выражение?
(c) Учитывая n учеников в классе, подобном футболу, что может 2 n шоу? Что может
шоу?
(Подсказка: подумайте о других играх, кроме футбола).
Ответ:
(a) ( x — 2) означает, что лицо, возраст которого составляет ( x — 2) лет, на 2 года младше Мунну.
( x + 4) означает, что лицо, чей возраст составляет ( x + 4) лет, на 4 года старше Мунну.
(3 x + 7) означает, что лицо, возраст которого (3 x + 7) лет, старше Мунну и на 7 лет старше трех времена эпохи Мунну.
(б) В будущее
Через n лет, возраст Сары будет ( y + n ) лет.
Прошлые
n лет назад, возраст Сары был ( y — n ) лет.
( y + 7) означает, что лицо, чей возраст ( y + 7) лет, на 7 лет старше Сары.
( y — 3) означает, что человек, возраст которого ( y — 3) года, младше Сары на 3 года.
( y +
)
означает, что лицо, возраст которого ( y +
)
лет, это лет старше Сары.
( y -) означает, что лицо, возраст которого ( y — ) лет, это лет младше Сары.
(c) 2 n может представлять количество студентов, которым нравится либо футбол или другая игра, например крикет, тогда как представляет количество студентов, которые любят крикет, из общего числа количество студентов, которым нравится футбол.
Стр. № 240:
Вопрос 1:
Государство которые из следующего являются уравнениями (с переменной).Объясните причину за ваш ответ. Обозначьте переменную из уравнений с помощью переменная.
(а) 17 = x + 7 (b) ( т -7)> 5
(в) (г) (7 × 3) — 19 = 8
(д) 5 × 4 — 8 = 2 x (f) x — 2 = 0
(г) 2 м <30 (в) 2 n + 1 = 11
(i) 7 = (11 × 5) — (12 × 4) (j) 7 = (11 × 2) + п.
(k) 20 = 5 y (l)
(м) z + 12> 24 (п) 20 — (10-5) = 3 × 5
(o) 7 — 9 · 1024 x 9 · 1025 = 5
Ответ:
(а) An уравнение с переменной x
(б) Ан неравенство
(c) Нет, это
числовое уравнение.
(d) Нет, это числовое уравнение.
(e) An уравнение с переменной x
(f) An уравнение с переменной x
(г) An неравенство
(h) An уравнение с переменной n
(i) Нет, это числовое уравнение.
(j) An уравнение с переменной p
(k) An уравнение с переменной y
(л) Ан неравенство
(м) Ан неравенство
(n) Нет, это числовое уравнение.
(o) An уравнение с переменной x
Страница № 241:
Вопрос 2:
Заполните записи в третьем столбце таблицы.
С. № | Уравнение | Значение переменной | Уравнение выполнено Да / Нет |
(а) | 10 y = 80 | y = 10 | – |
(б) | 10 y = 80 | y = 8 | – |
(в) | 10 y = 80 | y = 5 | – |
(г) | 4 л = 20 | л = 20 | – |
e | 4 л = 20 | л = 80 | – |
(ж) | 4 л = 20 | л = 5 | – |
(г) | b + 5 = 9 | б = 5 | – |
(в) | b + 5 = 9 | б = 9 | – |
(i) | b + 5 = 9 | б = 4 | – |
(j) | ч — 8 = 5 | ч = 13 | – |
(к) | ч — 8 = 5 | ч = 8 | – |
(л) | ч — 8 = 5 | ч = 0 | – |
(м) | п + 3 = 1 | п = 3 | – |
(п) | п + 3 = 1 | p = 1 | – |
(о) | п + 3 = 1 | п = 0 | – |
(п) | п + 3 = 1 | П = — 1 | – |
(кв) | п + 3 = 1 | П = — 2 | – |
Ответ:
(а) 10 y = 80
y = 10 не является решением данного уравнения, поскольку для y = 10,
10 y = 10 × 10 = 100, а не 80
(б) 10 y = 80
y = 8 является решением данного уравнения, потому что для y = 8,
10 y = 10 × 8 = 80 и, следовательно, уравнение имеет вид довольный.
(в) 10 y = 80
y = 5 не является решением данного уравнения, потому что для y = 5,
10 y = 10 × 5 = 50, а не 80
(г) 4 л = 20
l = 20 не является решением данного уравнения, поскольку для л = 20,
4 л = 4 × 20 = 80, а не 20
(д) 4 л = 20
l = 80 не является решением данного уравнения, поскольку для л = 80,
4 л = 4 × 80 = 320, а не 20
(ж) 4 л = 20
l = 5 является решением данного уравнения, потому что для l = 5,
4 l = 4 × 5 = 20 и, следовательно, уравнение удовлетворяется.
(г) б + 5 = 9
b = 5 не является решением данного уравнения, поскольку для b = 5,
b + 5 = 5 + 5 = 10, а не 9
(h) b + 5 = 9
b = 9 не является решением данного уравнения, потому что для b = 9,
b + 5 = 9 + 5 = 14, а не 9
(i) b + 5 = 9
b = 4 является решением данного уравнения, поскольку для b = 4,
b + 5 = 4 + 5 = 9 и, следовательно, уравнение удовлетворяется.
(к) ч — 8 = 5
h = 13 является решением данного уравнения, поскольку для h = 13,
ч — 8 = 13 — 8 = 5 и, следовательно, уравнение имеет вид довольный.
(к) ч — 8 = 5
h = 8 не является решением данного уравнения, потому что для h = 8,
ч — 8 = 8 — 8 = 0, а не 5
(л) ч — 8 = 5
h = 0 не является решением данного уравнения, потому что для h = 0,
ч — 8 = 0-8 = −8, а не 5
(м) п + 3 = 1
p = 3 не является решением данного уравнения, потому что для p = 3,
p + 3 = 3 + 3 = 6, а не 1
(п) п + 3 = 1
p = 1 не является решением данного уравнения, потому что для p = 1,
p + 3 = 1 + 3 = 4, а не 1
(o) p + 3 = 1
p = 0 не является решением данного уравнения, потому что для p = 0,
p + 3 = 0 + 3 = 3, а не 1
(п) п + 3 = 1
p = −1 не является решением данного уравнения потому что для p = −1,
p + 3 = −1 + 3 = 2, а не 1
(q) p + 3 = 1
p = −2 является решением данного уравнения, поскольку для p = −2,
p + 3 = — 2 + 3 = 1 и, следовательно, уравнение имеет вид довольный.
Страница № 241:
Вопрос 3:
Выбрать решение из значений, указанных в скобках рядом с каждым уравнение. Покажите, что другие значения не удовлетворяют уравнению.
(а) 5 9 10 24 м 9 10 25 = 60 (10, 5, 12, 15)
(б) н + 12 = 20 (12, 8, 20, 0)
(в) п — 5 = 5 (0, 10, 5 — 5)
(г) (7, 2, 10, 14)
e r — 4 = 0 (4, — 4, 8, 0)
(ж) x + 4 = 2 (- 2, 0, 2, 4)
Ответ:
(а) 5 9 10 24 м 9 10 25 = 60
м = 12 является решением данного уравнения, потому что для м = 12,
5 м = 5 × 12 = 60 и, следовательно, уравнение удовлетворяется.
м = 10 не является решением данного уравнения, потому что для м = 10,
5 м = 5 × 10 = 50, а не 60
м = 5 не является решением данного уравнения, потому что для м = 5,
5 м = 5 × 5 = 25, а не 60
м = 15 не является решением данного уравнения, потому что для м = 15,
5 м = 5 × 15 = 75, а не 60
(б) н + 12 = 20
n = 8 является решением данного уравнения, потому что для n = 8,
n + 12 = 8 + 12 = 20 и, следовательно, уравнение удовлетворяется.
n = 12 не является решением данного уравнения, поскольку для n = 12,
n + 12 = 12 + 12 = 24, а не 20
n = 20 не является решением данного уравнения, поскольку для n = 20,
n + 12 = 20 + 12 = 32, а не 20
n = 0 не является решением данного уравнения, поскольку для n = 0,
n + 12 = 0 + 12 = 12, а не 20
(в) п — 5 = 5
p = 10 является решением данного уравнения, поскольку для p = 10,
p — 5 = 10 — 5 = 5 и, следовательно, уравнение имеет вид довольный.
p = 0 не является решением данного уравнения, потому что для p = 0,
p -5 = 0-5 = −5, а не 5
p = 5 не является решением данного уравнения, поскольку для p = 5,
p — 5 = 5 — 5 = 0, а не 5
p = −5 не является решением данного уравнения, поскольку для p = −5,
p — 5 = — 5 — 5 = −10, а не 5
(г)
q = 14 является решением данного уравнения, потому что для q = 14,
и следовательно, уравнение удовлетворяется.
q = 7 не является решением данного уравнения, так как для q = 7,
, а не 7
q = 2 не является решением данного уравнения, потому что для q = 2,
, а не 7
q = 10 не является решением данного уравнения, поскольку для q = 10,
, а не 7
e r — 4 = 0
r = 4 является решением данного уравнения, потому что для r = 4,
r — 4 = 4 — 4 = 0 и, следовательно, уравнение имеет вид довольный.
r = −4 не является решением данного уравнения, поскольку для r = −4,
r — 4 = — 4 — 4 = −8, а не 0
r = 8 не является решением данного уравнения, потому что для r = 8,
r — 4 = 8 — 4 = 4, а не 0
r = 0 не является решением данного уравнения, потому что для r = 0,
r — 4 = 0 — 4 = −4, а не 0
(розетка) x + 4 = 2
x = −2 является решением данного уравнения, потому что для x = −2,
x + 4 = — 2 + 4 = 2 и, следовательно, уравнение имеет вид довольный.
x = 0 не является решением данного уравнения, потому что для x = 0,
x + 4 = 0 + 4 = 4, а не 2
x = 2 не является решением данного уравнения, потому что для x = 2,
x + 4 = 2 + 4 = 6, а не 2
x = 4 не является решением данного уравнения, потому что для x = 4,
x + 4 = 4 + 4 = 8, а не 2
Страница № 241:
Вопрос 4:
(а) Заполните таблицу и, осмотрев ее, найдите Решение уравнения м + 10 = 16.
м
1
2
3
4
5
6
7
8
9
10
…
м + 10
–
–
–
–
–
–
–
–
–
–
–
(b) Заполните таблицу и, осмотрев ее, найдите Решение уравнения 5 t = 35.
т
3
4
5
6
7
8
9
10
11
…
5 т
–
–
–
–
–
–
–
–
–
–
(c) Заполните таблицу и найдите решение уравнения z / 3 = 4 используя таблицу.
z
8
9
10
11
12
13
14
15
16
…
3
–
–
–
–
–
–
–
(d) Завершено таблицы и найти решение уравнения м — 7 = 3
м
5
6
7
8
9
10
11
12
13
…
м — 7
–
–
–
–
–
–
–
–
–
–
Ответ:
(a) Для м + 10 таблица может быть построена следующим образом.
м
м + 10
1
1 + 10 = 11
2
2 + 10 = 12
3
3 + 10 = 13
4
4 + 10 = 14
5
5 + 10 = 15
6
6 + 10 = 16
7
7 + 10 = 17
8
8 + 10 = 18
9
9 + 10 = 19
10
10 + 10 = 20
При осмотре можно найти, что 9 · 1024 м 9 · 1025 = 6 является решением уравнение выше, как для м = 6, м + 10 = 6 + 10 = 16
(б) Для 5 t , таблица может быть построена следующим образом.
т
5 т
3
5 × 3 = 15
4
5 × 4 = 20
5
5 × 5 = 25
6
5 × 6 = 30
7
5 × 7 = 35
8
5 × 8 = 40
9
5 × 9 = 45
10
5 × 10 = 50
11
5 × 11 = 55
При осмотре можно найти, что t = 7 является решением Вышеприведенное уравнение как для t = 7, 5 t = 5 × 7 = 35
(c) Для , таблица может быть построена следующим образом.
z
8
9
10
11
12
13
14
15
16
При осмотре можно найти, что z = 12 является решением приведенное выше уравнение как для z = 12, = 4
(d) Для м — 7 таблица может быть построена следующим образом.
м
м — 7
5
5-7 = — 2
6
6–7 = — 1
7
7-7 = 0
8
8–7 = 1
9
9–7 = 2
10
10–7 = 3
11
11–7 = 4
12
12–7 = 5
13
13–7 = 6
При осмотре можно найти, что 9 · 1024 м 9 · 1025 = 10 является решением уравнение выше, как для м = 10, м — 7 = 10 — 7 = 3
Страница № 242:
Вопрос 5:
Отгадайте следующие загадки, вы можете сами загадывать такие загадки.
Кто я?
(i) Обойти квадрат
Считаем каждый угол
Трижды и не более!
Прибавь мне счет
Чтобы получить ровно тридцать четыре!
(ii) На каждый день недели
Сделайте счет от меня
Если вы не ошиблись
Вы получите двадцать три!
(iii) Я особый номер
Убери у меня шестерку!
Вся крикетная команда
Вы все еще сможете исправить!
(iv) Скажи мне, кто я
Я дам хорошую подсказку!
Ты вернешь меня
Если вы выберете меня из двадцати двух!
Ответ:
(i) В квадрате четыре угла.
Трижды количество углов в квадрате будет 3 × 4 = 12
Когда этот результат, то есть 12, добавляется к числу, получается 34. Следовательно, число будет разницей между 34 и 12, т.е. 34 — 12 = 22
(ii) 23 было результатом, когда в воскресенье пересчитали старое число.
22 было результатом подсчета старого числа в субботу.
21 был результатом пересчета старого числа в пятницу.
20 — результат пересчета старого числа в четверг.
19 было результатом, когда в среду пересчитали старое число.
18 было результатом пересчета старого числа во вторник.
17 был результатом пересчета старого числа в понедельник.
Следовательно, число, взятое в начале = 17 — 1 = 16
(iii) В команде по крикету 11 игроков. Следовательно, число таково, что если вычесть из него 6, получится 11. Следовательно, число будет 11 + 6 = 17
(iv) Число таково, что если его вычесть из 22, результатом снова будет само число.Число 11, что снова дает 11, если вычесть из 22.
Видео решение для алгебры (Страница: 242, Q.No: 5)
Решение NCERT для математики класса 6 — алгебра 242, вопрос 5
Просмотреть решения NCERT для всех глав класса 6
CBSE NCERT Notes Class 6 Maths Algebra
Введение
Алгебра — это раздел математики, в котором используются буквы.Буквы позволяют нам писать формулы, правила, а также определять неизвестные величины. Таким образом, эти буквы могут обозначать переменные. Переменная означает что-то, что может меняться и может меняться. Значение переменной, которое может удовлетворять уравнению, называется решением уравнения. Например: если для образования буквы «L» требуются две спички, то мы получаем следующее правило:
(Буква «L». Как показано, из двух спичек получается одна буква «L»)
Количество необходимых спичек = 2 шт.
Здесь n — необходимое количество Ls. Таким образом, если один L использует две спички, то 2 L будут использовать 4 спички. Это получается по следующему правилу:
2n = 2 (2) = 4.
Здесь n — переменная, и мы можем поставить число в зависимости от того, сколько Ls нам нужно заработать.
Использование переменной можно понять, решив несколько вопросов.
Задача: Найдите правило, определяющее количество спичек, необходимое для изготовления следующих образцов спичек.Используйте переменную, чтобы написать правило. Шаблон письма как
(буква «U»)
Решение:
Количество спичек, используемых для изготовления одной спички U = 3
Количество необходимых спичек = 3n
Где n — необходимое количество Us.
Проблема: Лила — младшая сестра Радхи. Лила на 4 года младше Радхи. Можете ли вы записать возраст Лилы через возраст Радхи? Возьмем возраст Радхи х год.Лила и Радха
Решение:
Возраст Радхи = x год
Лил на 4 года младше Радхи. Следовательно, мы можем получить возраст Лилы, вычтя 4 года из возраста Радхи. Итак, получаем:
Возраст Лилы = ( x — 4) лет
Проблема: Апельсины нужно переливать из больших ящиков в меньшие. Когда большая коробка опорожняется, апельсины из нее заполняют две меньшие коробки, а 10 апельсинов остаются снаружи.Если принять количество апельсинов в маленькой коробке равным x , каково количество апельсинов в большей коробке?
Решение:
Количество апельсинов в 1 маленькой коробке = x
Количество апельсинов в 2 маленьких коробках = 2 x
Количество оставшихся апельсинов = 10
Следовательно, количество апельсинов в большей коробке = 2 x + 10
NCERT Solutions Class 6 Математика Глава 11 Алгебра
Решения NCERT Математика класса 6 Глава 11 Алгебра — Вот все решения NCERT для класса 6 математики Глава 11.Это решение содержит вопросы, ответы, изображения и пояснения к полной главе 11 под названием «Алгебра математики», которую преподают в классе 6. Если вы ученик 6 класса и изучает математику по учебнику NCERT, то вы должны познакомиться с главой 11 «Алгебра». После того, как вы изучили урок, вы должны искать ответы на его вопросы. Здесь вы можете получить полные решения NCERT для класса 6 по математике и главе 11 по алгебре в одном месте.
Решения NCERT Класс 6 Математика Глава 11 Алгебра
Здесь, на сайте AglaSem Schools , вы можете получить доступ к NCERT Book Solutions в бесплатном формате PDF по математике для класса 6, чтобы вы могли обращаться к ним по мере необходимости.NCERT Решения для вопросов после каждой единицы учебников NCERT, направленные на то, чтобы помочь студентам решать сложные вопросы.
Для лучшего понимания этой главы вам также следует ознакомиться с кратким содержанием главы 11 Алгебра, математика, класс 6.
| Класс | 6 |
| Тема | Математика |
| Книга | Математика |
| Номер главы | 11 |
| Название главы | Алгебра |
Решения NCERT Класс 6 Математика Глава 11 Алгебра
Класс 6, Математика, глава 11, Решения по алгебре приведены ниже в формате PDF.Вы можете просмотреть их в Интернете или загрузить файл PDF для использования в будущем.
Алгебра Загрузить
Решения NCERT для математики 6 класса Глава 11 АлгебраСчитаете ли вы, что NCERT Solutions Class 6 Maths Chapter 11 Algebra полезны? Если да, прокомментируйте ниже. Также, пожалуйста, поставьте лайк и поделитесь этим с друзьями!
NCERT Solutions Class 6 Maths Chapter 11 Algebra — Video
Вы также можете посмотреть видеорешения NCERT Class6 Maths, глава 11, алгебра здесь.
Если вам понравилось видео, подпишитесь на наш канал YouTube, чтобы получать больше таких интересных и полезных учебных ресурсов.
Скачать NCERT Solutions Class 6 Maths Chapter 11 Algebra в формате PDF
Вы также можете скачать здесь NCERT Solutions Class 6 Maths chapter 11 Algebra в формате PDF.
Кликните сюда чтобы загрузить NCERT Solutions for Class 6 Maths chapter 11 Algebra
Вопросы и ответы
Q.1: Найдите правило, которое дает количество спичек, необходимое для изготовления следующих образцов спичек. Используйте переменную, чтобы написать правило. (а) Образец буквы Т как T (б) Образец буквы Z как Z (c) Образец буквы U как U (d) Образец буквы V как V (e) Образец буквы E как E (f) Образец буквы S как S (g) Образец буквы А как A
Ответ: (е)
В.2: Мы уже знаем правило для образца букв L. C и F. Некоторые буквы из некоторых букв из (a) T, (b) Z, (c) U, (d) V, (e) E, (f) S, (g) R дайте нам то же правило, что и данное? Почему это происходит?
Ответ: Известно, что L требует только две спички. Следовательно, образец для L равен 2n. Среди всех букв, приведенных выше в вопросе 1, только T и V являются двумя буквами, для которых требуются две спички. Следовательно, (а) и (г)
В.3: Курсанты проходят парадом. В ряду 5 курсантов. Какое правило определяет количество курсантов с учетом количества рядов? (Используйте n для количества строк.)
Ответ: Пусть количество строк равно n. Количество курсантов в одном ряду 5 Общее количество курсантов = количество курсантов в ряду x количество рядов = 5n
Q.4: Если в коробке ТАК манго, как вы запишете общее количество манго через количество коробок? (Используйте b для количества ящиков.)
Ответ: Пусть количество ящиков будет b. Количество манго в коробке = 50 Общее количество манго = количество манго в коробке x количество коробок = 50 / б
Q.5: Учитель раздает каждому ученику по 5 карандашей. Вы можете сказать, сколько потребуется карандашей, учитывая количество учеников? (Используйте s для количества студентов.)
Ответ: Пусть количество учеников будет s. Карандаши выдаются каждому ученику = 5 Общее количество карандашей = Количество карандашей, выданных каждому ученику x Количество учеников = 5 шиллингов
Книга NCERT / CBSE по математике 6 класса
Вы можете бесплатно загрузить NCERT Book for Class 6 Maths в формате PDF.В противном случае вы также можете легко купить его в Интернете.
- Щелкните здесь, чтобы получить книгу NCERT по математике для 6 класса
- Нажмите здесь, чтобы купить NCERT Book for Class 6 Maths
Все решения NCERT, класс 6
Все решения NCERT
Вы также можете ознакомиться с решениями NCERT для других классов здесь. Щелкните номер класса ниже, чтобы перейти к соответствующим решениям NCERT класса 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.
Загрузите приложение NCERT Solutions для быстрого доступа к NCERT Solutions Class 6 Maths Chapter 11 Algebra.Это поможет вам оставаться в курсе актуальных учебных материалов, которые помогут вам стать лучше в классе!
предыдущий следующий
Чтобы получать оповещения об экзаменах и вакансиях в правительстве Индии в кратчайшие сроки, присоединяйтесь к нашему каналу Telegram.





 Какое общее количество учеников в этом классе?
Какое общее количество учеников в этом классе?  Каково отношение синих шариков к общему количеству шариков?
Каково отношение синих шариков к общему количеству шариков? 
