Распределительное свойство умножения дробей 6 класс: Применение распределительного свойства умножения 6 класс онлайн-подготовка на Ростелеком Лицей

Применение распределительного свойства умножения 6 класс онлайн-подготовка на Ростелеком Лицей

51. Применение распределительного свойства умножения.

Напомню, что распределительное свойство умножения относительно сложения и вычитания записывается так.

(a + b) · c = a · c + b · c = ac + bc;

(a — b) · c = a · c — b · c = ac — bc.

Распределительное свойство умножения относительно сложения и относительно вычитания позволяет решать примеры.

Пример 1. 35-13∙15=35∙15-13∙15=3∙155-1∙153=9-5=4.

Пример 2. Найдем значение произведения

2314∙7=2+314∙7=2∙7+314∙7=14+3*714=1512.

Чтобы умножить смешанное число на натуральное число, можно:

1. Умножить целую часть на это число.
2. Умножить дробную часть на это число.
3. Сложить полученные результаты.

Пример 3. Найдем значение выражения

538∙28+258∙28=538+258∙28=8∙28=2.

Используя распределительное свойство умножения, можно упрощать выражения вида:

58a+34a=58+34∙a=148а=134 а

34x-15x=34-15x=1520-420x=1120x.

Пример 4. Квартира состоит из двух комнат. Длина большей комнаты 5110, а ширина 4 м. Длина меньшей комнаты 4 м, а ширина 3110 м. На сколько площадь одной комнаты меньше площади другой?

Площадь первой комнаты

S=a∙b=5110∙4=5+110∙4=5∙4+110∙4=20+25=2025 м².

Площадь второй комнаты

S=a∙b=3110∙4=3+110∙4=3∙4+110∙4=12+25=1225 м².

Разница площадей 2025-1225=8 м².

Чтобы умножить смешанное число на смешанное число,

можно:

1. Перевести одно смешанное число в неправильную дробь.
2. Умножить целую часть второго множителя на неправильную дробь.
3. Умножить дробную часть второго множителя на неправильную дробь.
4. Сложить полученные результаты.

Пример 5. Найдем значение выражения

225∙412=225∙92=2∙92+25∙92=9+95=1045 .

Конспект урока по теме «Применение распределительного свойства умножения»

Тема урока: «Применение распределительного свойства

умножения». (Слайд № 1).

6 класс. Учитель математики ГОУ СОШ № 904 Курнаева О.В.

Тип урока: урок усвоения новых знаний

Цели урока:

— повторить распределительное свойство умножения относительно сложения и вычитания;

— показать применение распределительного свойства умножения при работе с обыкновенными дробями и смешанными числами;

— совершенствовать навыки рациональных вычислений;

— способствовать развитию логического мышления, умению формулировать и обосновывать суждения;

— воспитывать аккуратность, точность и внимательность при работе с обыкновенными дробями.

Оборудование:

ТСО: компьютер, принтер, проектор, СМАРТ-доска ;

карточки со смайликами у каждого учащегося.

Структура урока:

1. Организационный момент ( 2 мин.)

-Сегодняшний урок начнём с высказывания Л.Н, Толстого: «Человек подобен дроби: в знаменателе – то, что он о себе думает, в числителе – то, что он есть на самом деле. Чем больше знаменатель, тем меньше дробь». (Слайд № 2)

-Как вы понимаете эти слова? (Чем больше человек о себе воображает, тем меньше он что-то из себя представляет).

II. Актуализация знаний (10 мин.)

Устно найти значения выражений:

1). ∙ 5). ∙ 3

2). ∙ 6). ∙ ∙ ∙

3). 6 ∙ 7 7). ∙ ∙ 6 ∙

4). 2 ∙ 6 (Слайд № 3)

-Среди чисел, записанных внизу, найдите правильные ответы и из соответствующих букв составьте слово:

13 2 14 42 9 1 6 47

Р И К А Е П Г О Ф Н

-Проверим себя: (Слайд № 4)

9 2 47 14 1 6 13

П И Ф А Г О Р

ПИФАГОР – древнегреческий учёный, философ, живший в VI веке до н. э. Его открытия в области математики актуальны и в наше время.

— Какие свойства умножения вы применяли для решения примеров 6 и 7? (Переместительное и сочетательное).

— Какие ещё свойства умножения вызнаете? (Распределительное свойство умножения).

— Сформулируйте распределительное свойство умножения относительно сложения.

(Чтобы сумму умножить на число можно каждое слагаемое умножить на это число и сложить полученные произведения).

-Сформулируйте распределительное свойство умножения относительно вычитания.

(Чтобы разность умножить на число можно уменьшаемое умножить на это число, вычитаемое умножить на это число, затем из первого произведения вычесть второе).

3. Изучение нового материала (15 мин.)

-Сегодня на уроке мы выясним, в каких случаях удобно применять распределительное свойство умножения при работе с обыкновенными дробями и смешанными числами.

Помните, что всегда надо смотреть, как удобнее выполнять вычисления!

Рассмотрим четыре случая применения распределительного свойства умножения, поэтому разделимся на четыре команды.

Каждая команда должна догадаться, как применить распределительное свойство умножения для решения её примера.

1 команда: 2 команда:

( + ) ∙ 16 3 ∙ 7

3 команда: 4 команда:

( — ) ∙ 15 5 ∙ + 1 ∙ (Слайд № 5)

По одному ученику от группы выходят к доске и записывают решение с подробным объяснением. Остальные учащиеся записывают решения в тетрадях.

1). ( + ) ∙ 16 = ∙ 16 + ∙ 16 = 6 + 4 = 10

— Как сумму умножили на число?

(Каждое слагаемое умножили на число и сложили полученные произведения)

2). ( — ) ∙ 15 = ∙ 15 — ∙ 15 = 12 – 5 = 7

— Как разность умножили на число?

(Уменьшаемое умножили на число, вычитаемое умножили на

число, и из первого произведения вычли второе)

3). 3 ∙ 7 = (3 + ) ∙ 7 = 3 ∙ 7 + ∙ 7 = 21 + = 21

— В каком виде можно представить смешанное число? (

В виде суммы целой и дробной частей).

(Смешанное число представили в виде суммы целой и дробной частей и умножили сумму на число)

— Прочитайте правило умножения смешанного числа на натуральное число в учебнике на стр. 87.

-Запишем распределительное свойство умножения относительно сложения и вычитания с помощью букв:

(а + в) ∙с = а ∙ с + в ∙ с

(а – в) ∙ с = а ∙ с – в ∙ с (Слайд № 6)

4). 5 ∙ + 1 ∙ = ∙ (5 + 1) = ∙ 7 = 2

— Что представляет собой выражение?

(Сумма двух произведений).

— Что можно заметить?

(Одинаковые множители).

-Что можно сделать?

(Вынести общий множитель за скобки).

— Применение распределительного свойства умножения облегчает вычисления, делает их более красивыми, рациональными.

3. Физкультминутка (1 мин.

   )

Поднимает руки класс – это «раз».

Повернулась голова – это «два».

Руки вниз, вперёд смотри – это «три».

Руки в стороны пошире развернули на «четыре»,

С силой их к плечам прижать – это «пять».

Всем ребятам надо сесть – это «шесть».

(Повторить 3 раза).

3. Закрепление изученного материала (12 мин.)

Учебник:

№ 536 (а, б)

№ 537 (в, д, ж)

№ 538(д, е) (Слайд 7)

Решение на доске с подробным объяснением. Более подготовленные учащиеся решают самостоятельно. В случае, если решение правильное и получено раньше, чем на доске, учитель выставляет оценку.

№ 536

а) ( + ) ∙ 21 = ∙ 21 + ∙ 21 = 6 + 5 = 11;

б) ( — ) ∙ 12 = ∙ 12 — ∙ 12 = 7 — = 7 — 6 = .

№ 537

в) 3 ∙ 7 = 7 ∙ 3 + ∙ 3 = 21 + = 21;

д) 4 ∙ 4 = 4 ∙ 4 + ∙ 4 = 16 + 1 = 17;

ж) 10 ∙ 5 = 5 ∙ 10 + ∙ 10 = 50 + 4 = 54.

№ 538

д) 8 ∙ 4 + 8 ∙ 6 = 8( 4 + 6) = 8 ∙ 11 = 8 ∙ 11+ ∙ 11= = 88 + ∙5 = 93;

е) 6 ∙ 7 — 2 ∙ 6 = 6( 7 — 2) = 6 ∙ 5 =6 ∙ 5 + ∙ 5 =30 +3 = = 33.

3. Итоги урока (3 мин.)

— Что нового вы узнали сегодня на уроке?

-Сформулируйте распределительное свойство умножения относительно сложения и вычитания.

— Как умножить смешанное число на натуральное число?

3. Домашнее задание (1 мин)

П. 15

№ 549

№ 553

№ 562 (Слайд 8)

3. Рефлексия (1 мин.)

С каким настроением вы уходите с урока? Поднимите тот смайлик, который соответствует вашему настроению.

хорошее равнодушное плохое (Слайд 9)

Спасибо за урок! До свидания! (Слайд 10)

Распределительное свойство умножения | Математика

Распределительное свойство умножения — важное правило, полезное в устном счете и при раскрытии скобок.

Распределительное свойство умножения относительно сложения:

Чтобы умножить число на сумму двух чисел, можно это число умножить на каждое слагаемое и полученные результаты сложить.

С помощью букв распределительное свойство умножения относительно сложения записывают так:

   

либо так:

   

Распределительное свойство умножения относительно вычитания:

Чтобы умножить число на разность двух чисел, можно умножить это число на уменьшаемое и на вычитаемое, и из первого произведения вычесть второе.

С помощью букв распределительное свойство умножения относительно вычитания записывают так:

   

либо так:

   

Распределительное свойство умножения верно и для большего количества чисел. Например, для трех слагаемых распределительное свойство умножения относительно сложения имеет вид:

   

Распределительное свойство умножения упрощает устный счет.

Примеры:

   

   

Этот пример можно решить также с помощью распределительного свойства умножения относительно вычитания:

   

   

   

   

или

   

   

   

   

   

С помощью распределительного свойства умножения можно раскрывать скобки.

Примеры:

   

   

   

   

(Более подробно тема раскрытия скобок рассматривается после изучения отрицательных чисел).

Распределительное свойство умножения можно применить и в обратном порядке:

   

Говорят: «Общий множитель a выносим за скобки. В скобках остается b плюс c».

   

Говорят: «Общий множитель a выносим за скобки. В скобках остается b минус c».

Более подробно вынесение общего множителя за скобки изучают в курсе алгебры 7 класса.

Распределительное свойство сложения и умножения: формулы и примеры

Благодаря знанию распределительного свойства умножения и сложения, можно устно решить сложные, на первый взгляд, примеры. Изучается данное правило на уроках алгебры в 7 классе. Задания с использованием данного правила встречаются на ОГЭ и ЕГЭ по математике.

Распределительное свойство умножения

Для того, чтобы произвести умножение суммы некоторых чисел, можно умножить каждое слагаемое по отдельности и сложить полученные результаты.

Проще говоря, a × (в + с) = ав + ас или (в + с) ×а = ав + ас.

Также, для упрощения решения, данное правило действует и в обратном порядке: а×в + а×с = а × (в + с), то есть общий множитель выносится за скобки.

Используя распределительное свойство сложения, можно решить следующие примеры.

1. Пример 1: 3 × (10 + 11). Умножьте число 3 на каждое слагаемое: 3 × 10 + 3 × 11. Сложите: 30 + 33 = 63 и запишите полученный результат. Ответ: 63.
2. Пример 2: 28 × 7. Представьте число 28 как сумму двух чисел 20 и 8 и перемножьте на 7, вот так: (20 + 8) × 7. Выполните вычисления: 20 × 7 + 8 × 7 = 140 + 56 = 196. Ответ: 196.
3. Пример 3. Решите следующее задание: 9 × (20 – 1). Перемножьте на число 9 и уменьшаемое 20, и вычитаемое 1: 9 × 20 – 9 × 1. Вычислите полученные результаты: 180 – 9 = 171. Ответ: 171.

Это же правило действует не только на сумму, но и на разность двух и более выражений.

Распределительное свойство умножения относительно разности

Для того, чтобы выполнить умножение разности на число, следует умножить на него уменьшаемое, а затем вычитаемое и выполнить вычисление полученных результатов.

a × (в — с) = а×в — а×с или (в — с) × а = а×в — а×с.

Пример 1: 14 × (10 — 2). Используя распределительный закон, умножьте 14 на оба числа: 14× 10 -14 × 2. Найдите разность полученных значений: 140 – 28 = 112 и запишите полученный результат. Ответ: 112.

Пример 2: 8 × (1 + 20). Аналогично решается данное задание: 8 × 1 + 8 × 20 = 8 + 160 = 168. Ответ: 168.

Пример 3: 27× 3. Найдите значение выражения, пользуясь изученным свойством. Представьте 27 как разность двух чисел 30 и 3, вот так: 27 × 3 = (30 — 3) × 3 = 30 × 3- 3 × 3 = 90 – 9 = 81. Ответ: 81.

Применение свойства для более двух слагаемых

Распределительное свойство умножения применяется не только для двух слагаемых, а для абсолютно любого количества, в таком случае формула имеет данный вид:

а × (в + с+ d) = a×в +a×с+ a×d.

а × (в — с — d) = a×в — a×с — a×d.

Пример 1: 354×3. Представьте 354 как сумму трех чисел: 300, 50 и 3: (300 + 50 + 3) ×3= 300×3 + 50×3 + 3×3 = 900 + 150 + 9 =1059. Ответ: 1059.

Упростите несколько выражений, используя упомянутое ранее свойство.

Пример 2: 5 × (3х + 14у). Раскройте скобки, используя распределительный закон умножения: 5 × 3х + 5 × 14у = 15х + 70у. 15 х и 70у сложить нельзя, так как слагаемые не являются подобными и имеют различную буквенную часть. Ответ: 15х + 70у.

Пример 3: 12 × (4с – 5d). Учитывая правило, умножьте на 12 и 4с и 5d: 12 × 4с – 12 × 5d = 48с — 60d. Ответ: 48с — 60d.

Используя при решении примеров распределительное свойство сложения и умножения:

• с легкостью решаются сложные примеры, их решение можно свести к устному счету;
• заметно экономится время при решении сложных, на первый взгляд, задач;
• благодаря полученным знаниям, можно с легкостью упростить выражения.

Презентация»Сочетательное и распределительное свойство умножения»

библиотека
материалов

Содержание слайдов

Номер слайда 1

Сочетательное и распределительное свойства умножения. Тема урока

Номер слайда 2

Устный счётпредставьте в виде произведения сумму: 72+72+72 = 40+40+40+40+40 = Х+Х+Х+Х = y+y+y = (a+b)+ (a+b)+(a+b) =72  3 40  54 Х3у3(a+b)

Номер слайда 3

Как вы думаете , выражение 3(a+b) можно каким –то образом записать без скобок?Пока на этот вопрос мы ответить не можем. Для этого нам необходимо ввести свойства умножения

Номер слайда 4

Давайте повторим свойство, которое изучали на предыдущих уроках. ПЕРЕМЕСТИТЕЛЬНОЕa • b = b • a ОТ ПЕРЕСТАНОВКИ МНОЖИТЕЛЕЙ ПРОИЗВЕДЕНИЕ НЕ МЕНЯЕТСЯ

Номер слайда 5

Теперь познакомимся еще с двумя свойствамиstyle. colorfillcolorfill.typefill.on

Номер слайда 6

(a • b) • c = a b + a c. Сочетательное свойство умноженияstyle.colorfillcolorfill.typestyle.colorfillcolorfill.type

Номер слайда 7

Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего чисел. В тетрадь запишите: сочетательное свойство умножения:(a • b) • c = a b + a c

Номер слайда 8

Далее открываем учебник на стр. 117 и выполняем № 420 Работа по учебнику:style.colorfillcolorfill.typefill.on

Номер слайда 9

1) 2  328  5 =№ 420 Вычислите удобным способом: Дальше смотрим, какие числа нам удобней перемножить в первую очередь? (2  5) Применим сочетательное свойство  328 == 3280 Далее выполняем самостоятельно 2, 3, 4, 5, 6style. colorfillcolorfill.typeppt_xstyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.type

Номер слайда 10

23а + 37а =14  6у =Упростите выражение (устно)?60а84уу + 56у =48х  4а =192ха57у2р  11k  т =4t  8 =15d  r =22рkm32t15dr

Номер слайда 11

Далее выполняем № 422 Работа по учебнику:

Номер слайда 12

(a + b) • c = a c + b c. Распределительное свойство умножения. Чтобы число умножить на сумму двух чисел, можно это число умножить на каждое слагаемое и полученные произведения сложитьstyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.type

Номер слайда 13

(a — b) • c = a c — b c. Распределительное свойство умножения. Аналогично и для вычитания чиселпри условии, если: a  b или a = b ppt_xstyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.type

Номер слайда 14

выполняем № 426(применяя распределительное свойство)Работа по учебнику: Пример: 3(a + 7) = 3a + 21style. colorfillcolorfill.type

Номер слайда 15

§17, вопросы стр. 116 (устно)№ 421, № 423, № 427 (письменно)

Номер слайда 16

СПАСИБО ЗА ВНИМАНИЕ!

Дроби шестого класса Планы уроков, домашние задания, викторины

Дроби шестого класса Планы уроков, домашние задания, викторины

Шестой класс Fractions

• • Шестой класс
  • 24,532 Просмотры
  • 7 Избранное

  Разместите дроби, десятичные дроби и проценты в числовой строке

  Кайулани Айвори Акпан из средней школы Элиота Хайна

  Расположение: дроби, десятичные дроби и проценты (эквиваленты и значения)

  Цель: SWBAT поместить дроби, десятичные дроби и числа в числовую строку. SWBAT сравнивает и упорядочивает дроби, десятичные дроби и проценты.

• • Шестой класс
  • 12,944 Просмотры
  • 1 Любимый

• • Шестой класс
  • 11,311 Просмотры
  • 2 Избранное

  Сравнить и заказать десятичные дроби

  Кайулани Айвори Акпан из средней школы Элиота Хайна

  Расположение: дроби, десятичные дроби и проценты (эквиваленты и значения)

  Цель: SWBAT сравнить и упорядочить десятичные дроби. SWBAT сравнивает дроби и десятичные числа.

• • Шестой класс
  • 12,379 Просмотры
  • 1 Любимый

• • Шестой класс
  • 12,418 Просмотры
  • 2 Избранное

• • Шестой класс
  • 5,066 Просмотры
  • 2 Избранное

• com/lesson/443971/rational-numbers-on-the-number-line?grade=18&subject=1″>

  Большая идея: Числовая линия — полезный инструмент при заказе положительных и отрицательных рациональных чисел

  .

  Ресурсы (16)

  Размышления (1)

  Избранное (86)

• • Шестой класс
  • 6,443 Просмотры
  • 2 Избранное

• Смысл чисел с дробями

  Эми Шах

  Место нахождения: 6 класс по математике

  Описание: День 1 — SWBAT переименовывает эквивалентные дроби (включая графические изображения), 6-3A, 6-2A (a), 6-2B (a) День 2 — SWBAT переименовывает эквивалентные смешанные числа и…

• • Шестой класс
  • 4,255 Просмотры
  • 1 Любимый

• • Пятый класс
    Шестой класс, Седьмой класс еще 2. .., Шестой класс, Седьмой класс
  • 5,130 Просмотры

  Разделение дробей на дроби

  Рашеда Вебстер из Высшей школы технологий Маккинли

  Расположение: разделение на дроби

  Задача: Студенты рассмотрят и применит концепции дробей и деления, чтобы применить эти навыки для решения реальных математических задач, требующих деления на…

  • Пятый класс
    Шестой класс, Седьмой класс еще 2…, Шестой класс, Седьмой класс
• • Пятый класс
    Шестой класс, Седьмой класс, Восьмой класс еще 3 . .., Шестой класс, Седьмой класс, Восьмой класс
  • 8,096 Просмотры

  Дроби — задачи со словами (все операции)

  Уилл Остин из Roxbury Prep, кампус Mission Hill

  Расположение: 7.Дроби

  Задача: Учащиеся смогут выбрать правильную операцию для решения задач с дробными словами.

  • Пятый класс
    Шестой класс, Седьмой класс, Восьмой класс еще 3 …, Шестой класс, Седьмой класс, Восьмой класс
• • Пятый класс
    Шестой класс, Седьмой класс, Восьмой класс еще 3. .., Шестой класс, Седьмой класс, Восьмой класс
  • 4,100 Просмотры
  • Пятый класс
    Шестой класс, Седьмой класс, Восьмой класс еще 3 …, Шестой класс, Седьмой класс, Восьмой класс
• • Шестой класс
  • 1,744 Просмотры
  • 1 Любимый

• • Пятый класс
    Шестой класс, Седьмой класс, Восьмой класс еще 3. .., Шестой класс, Седьмой класс, Восьмой класс
  • 2,094 Просмотры

  Дроби — задачи на сложение и вычитание, день второй

  Уилл Остин из Roxbury Prep, кампус Mission Hill

  Расположение: 7.Дроби

  Задача: Учащиеся смогут решать задачи на сложение и вычитание дробных слов.

  • Пятый класс
    Шестой класс, Седьмой класс, Восьмой класс еще 3 …, Шестой класс, Седьмой класс, Восьмой класс

Что-то пошло не так.Смотрите подробности для получения дополнительной информации

Решения

NCERT для математики класса 7 Глава 2

Стр. № 31:

Ответ:

(i)

(ii)

(iii)

(iv)

(в)

(vi)

(vii)

Стр. № 31:

Вопрос 2:

Устроить следующие в порядке убывания:

(i) (ii)

Ответ:

(i)

Замена их на дроби, получаем

Поскольку 42> 24> 14,

(ii)

Изменив их на подобные дроби, получим

Как 49> 30> 14,

Стр. № 31:

Вопрос 3:

в «Магический квадрат», сумма чисел в каждой строке, в каждый столбик и по диагонали одинаковы.Это волшебство квадрат?

Ответ:

Вдоль первая строка, сумма =

Вдоль вторая строка, сумма =

Вдоль третья строка, сумма =

Вдоль первый столбец, сумма =

Вдоль второй столбец, сумма =

Вдоль третий столбец, сумма =

Вдоль первая диагональ, сумма =

Вдоль вторая диагональ, сумма =

Поскольку сумма чисел в каждой строке, в каждом столбце и вдоль диагонали такие же, это магический квадрат.

Стр. № 31:

Вопрос 4:

А прямоугольный лист бумаги см долго и см широкий.

Найди свой периметр.

Ответ:

Длина =

Ширина =

Периметр = 2 × (длина + ширина)

Стр. № 31:

Вопрос 5:

Найдите периметры (i) ΔABE (ii) прямоугольника BCDE на этом рисунке.Чей периметр больше?

Ответ:

(i) Периметр ΔABE = AB + BE + EA

(ii)

Периметр прямоугольника = 2 (длина + ширина)

Периметр ΔABE =

Изменив их на подобные дроби, получим

17720 = 177 × 320 × 3 = 53160476 = 47 × 106 × 10 = 47060

As 531> 470,

⇒ 17720> 476

Периметр (ΔABE)> Периметр (BCDE)

Стр. № 31:

Вопрос 6:

Салил хочет поместить картинку в рамку.Картина см широкий.

Подходит для Рамка для картины не может быть больше см широкий. Насколько нужно обрезать картинку?

Стр. № 32:

Вопрос 7:

Риту съела часть яблока, а оставшееся яблоко съел ее брат Сому. Сколько яблока съел Сому? У кого была большая доля? На сколько?

Ответ:

Часть яблока, съеденного Риту =

Часть яблока, съеденного Сому = 1 — Часть яблока, съеденного Риту

=

Следовательно, Сому съел часть яблока.

Поскольку 3> 2, Риту была большая доля.

Разница между 2 долями =

Следовательно, доля Риту больше, чем доля Сому на.

Видео решение для дробей и десятичных знаков (Страница: 32, Q. No .: 7)

Решение NCERT для математики класса 7 — дроби и десятичные дроби 32, вопрос 7

Стр. № 32:

Вопрос 8:

Майкл закончил раскрашивать картинку в час.Вайбхав закончил раскрашивать ту же картинку в час. Кто работал дольше? На какую долю он был длиннее?

Ответ:

Время занято автор Michael =

Время занято по Vaibhav =

Преобразование эти дроби на одинаковые, получаем

С 9> 7,

Вайбхав проработал дольше.

Разница знак равно знак равно знак равно

Стр. № 36:

Вопрос 1:

На каком из рисунков (a) — (d) показано:

(я) (ii) (iii) (iv)

(а)

(б)

(в)

(г)

Стр. № 36:

Вопрос 2:

Некоторые рисунки с (а) по (с) приведены ниже.Скажите, какие из них показывают:

(я) (ii) (iii)

(а)

(б)

(в)

Стр. № 36:

Ответ:

(i)

(ii)

(iii)

(iv)

(в)

(vi)

(vii)

(viii)

(ix)

(х)

Стр. № 37:

Вопрос 4:

Оттенок:

(я) из кружки в квадрате (a) (ii) из треугольники в рамке (б)

(iii) из квадраты в коробке (c)

Стр. № 37:

Вопрос 5:

Находка:

(а) из (i) 24 (ii) 46

(б) из (i) 18 (ii) 27

(с) из (i) 16 (ii) 36

(d) из (i) 20 (ii) 35

Ответ:

(а) (i)

(ii)

(б) (я)

(ii)

(c) (i)

(ii)

(г) (я)

(ii)

Стр. № 37:

Стр. № 37:

Стр. № 37:

Вопрос 8:

Видья и Пратап пошли на пикник.Мать дала им бутылку с водой, в которой было 5 литров воды. Видья выпила воду. Пратап выпил оставшуюся воду.

(i) Сколько воды выпила Видья?

(ii) Какую долю от общего количества воды выпил Пратап?

Ответ:

(i) Вода, потребляемая Видьей = 5 литров

(ii) Вода, потребляемая Пратапом =

Калькулятор долей

Ниже приведены несколько калькуляторов дробей, способных выполнять сложение, вычитание, умножение, деление, упрощение и преобразование дробей и десятичных знаков.Поля над сплошной черной линией представляют числитель, а поля ниже — знаменатель.

Калькулятор смешанных чисел

Калькулятор упрощенных дробей

Калькулятор десятичных дробей

Калькулятор дробей в десятичную

Калькулятор дробей большого числа

Используйте этот калькулятор, если числители или знаменатели являются очень большими целыми числами.

В математике дробь — это число, которое представляет собой часть целого.Он состоит из числителя и знаменателя. В числителе указано количество равных частей целого, а в знаменателе — общее количество частей, составляющих это целое. Например, в дроби

числитель равен 3, а знаменатель — 8. Более наглядный пример может включать пирог с 8 кусочками. 1 из этих 8 ломтиков будет составлять числитель дроби, а всего 8 ломтиков, которые составляют весь пирог, будут знаменателем. Если бы человек съел 3 ломтика, оставшаяся часть пирога была бы такой, как показано на изображении справа.Обратите внимание, что знаменатель дроби не может быть равен 0, так как это сделает дробь неопределенной. Дроби могут подвергаться множеству различных операций, некоторые из которых упомянуты ниже.

Дополнение:

В отличие от сложения и вычитания целых чисел, таких как 2 и 8, дроби требуют общего знаменателя для выполнения этих операций. Один из способов найти общий знаменатель заключается в умножении числителей и знаменателей всех участвующих дробей на произведение знаменателей каждой дроби.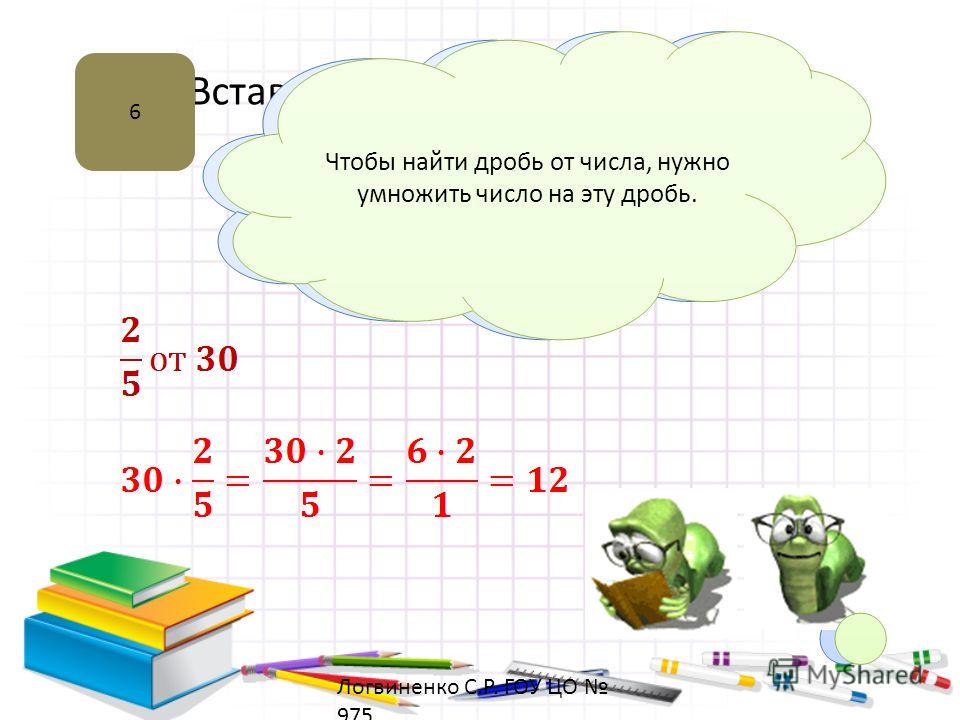 Умножение всех знаменателей гарантирует, что новый знаменатель обязательно будет кратным каждому отдельному знаменателю. Числители также необходимо умножить на соответствующие коэффициенты, чтобы сохранить значение дроби в целом. Это, пожалуй, самый простой способ убедиться, что дроби имеют общий знаменатель. Однако в большинстве случаев решения этих уравнений не будут представлены в упрощенной форме (предоставленный калькулятор вычисляет упрощение автоматически). Ниже приведен пример использования этого метода.

Этот процесс можно использовать для любого количества фракций. Просто умножьте числители и знаменатели каждой дроби в задаче на произведение знаменателей всех остальных дробей (не включая соответствующий знаменатель) в задаче.

Альтернативный метод поиска общего знаменателя состоит в том, чтобы определить наименьшее общее кратное (НОК) для знаменателей, а затем сложить или вычесть числители, как если бы это было целое число. Использование наименьшего общего кратного может быть более эффективным и, скорее всего, приведет к дроби в упрощенной форме. В приведенном выше примере знаменатели были 4, 6 и 2. Наименьшее общее кратное — это первое общее кратное из этих трех чисел.

Кратное 2: 2, 4, 6, 8 10, 12

Кратное 4: 4, 8, 12

Кратное 6: 6, 12

Первое кратное, которое они все разделяют, — 12, так что это наименьшее общее кратное. Чтобы выполнить задачу сложения (или вычитания), умножьте числители и знаменатели каждой дроби в задаче на любое значение, которое сделает знаменатели 12, а затем сложите числители.

Вычитание:

Вычитание фракции по сути то же самое, что и сложение дроби. Для выполнения операции требуется общий знаменатель. Обратитесь к разделу добавления, а также к уравнениям ниже для пояснения.

Умножение:

Умножение дробей довольно просто. В отличие от сложения и вычитания, нет необходимости вычислять общий знаменатель для умножения дробей. Просто числители и знаменатели каждой дроби умножаются, и результат образует новый числитель и знаменатель. По возможности решение следует упростить. Обратитесь к уравнениям ниже для пояснения.

Дивизион:

Процесс деления дробей аналогичен процессу умножения дробей. Чтобы разделить дроби, дробь в числителе умножается на величину, обратную дроби в знаменателе. Число , обратное , — это просто

. Когда a является дробью, это, по сути, включает замену числителя и знаменателя местами.Таким образом, величина, обратная дроби. Обратитесь к уравнениям ниже для пояснения.

Упрощение:

Часто проще работать с упрощенными дробями. Таким образом, фракционные растворы обычно выражаются в их упрощенных формах.

, например, более громоздкий, чем. Предоставленный калькулятор возвращает входные дроби как в неправильной, так и в смешанной форме чисел. В обоих случаях дроби представлены в их низшей форме путем деления числителя и знаменателя на их наибольший общий множитель.

Преобразование дробей в десятичные дроби:

Преобразование десятичных дробей в дроби выполняется просто. Однако необходимо понимать, что каждый десятичный разряд справа от десятичной точки представляет собой степень 10; первый десятичный разряд — 10 ¹ , второй — 10 ² , третий — 10 ³ и т. д. Просто определите, до какой степени 10 распространяется десятичная дробь, используйте эту степень 10 в качестве знаменателя, введите каждое число справа от десятичной точки в качестве числителя и упростите.Например, если посмотреть на число 0,1234, число 4 находится в четвертом десятичном разряде, что составляет 10 ⁴ или 10 000. В результате дробь составит

, что упрощается до, поскольку наибольший общий делитель числителя и знаменателя равен 2.

Точно так же дроби со знаменателями, которые являются степенями 10 (или могут быть преобразованы в степени 10), могут быть переведены в десятичную форму, используя те же принципы. Возьмем, к примеру, дробь

. Чтобы преобразовать эту дробь в десятичную, сначала преобразуйте ее в дробь.Зная, что первый десятичный разряд представляет 10 ^-1 , можно преобразовать в 0,5.