Номер 300 по математике 6 класс виленкин: Номер №300 — ГДЗ по Математике 6 класс: Виленкин Н.Я.

Содержание

Номер 300 — ГДЗ по Математике 6 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2020. Часть 2 (решебник)

Номер 300 — ГДЗ по Математике 6 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд 2020. Часть 2 (решебник) — GDZwow

Перейти к содержанию

Search for:

Авторы: Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И.

Издательство: Мнемозина

Тип: Учебник

Новая версия

ЧАСТЬ 1
Выберите номер упражнения

ЧАСТЬ 2
Выберите номер упражнения

Adblock
detector

Номер 300 — ГДЗ по Математике 5 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд.

Часть 2

Номер 300 — ГДЗ по Математике 5 класс Учебник Виленкин, Жохов, Чесноков, Шварцбурд. Часть 2 — ГДЗ РЕД

Перейти к содержанию

Search for:

Авторы: Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И.

Издательство: Мнемозина

Тип: Учебник

Новая версия

Часть 1

Выберите номер

Часть 2

Выберите номер

123456789101112131415161718192122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394959697989910010110210310410510610710810911011111211311411511611711811912012112212312412512612712812913013113213313413513613713813914014114214314414514614714814915015115215315415515615715815916016116216316416516616716816917017117217317417517617717817918018118218318418518618718818919019119219319419519619719819920020120220320420520620720820921021121221321421521621721821922022122222322422522622722822923023123223323423523623723823924024124224324424524624724824925025125225325425525625725825926026126226326426526626726826927027127227327427527627727827928028128228328428528628728828929029129229329429529629729829930030130230330430530630730830931031131231331431531631731831932032132232332432532632732832933033133233333433533633733833934034134234334434534634734834935035135235335435535635735835936036136236336436536636736836937037137237337437537637737837938038138238338438538638738838939039139239339439539639739839940040140240340440540640740840941041141241341441541641741841942042142242342442542642742842943043143243343443543643743843944044144244344444544644744845045145245345445545645745845946046146246346446546646746846947047147247347447547647747847948048148248348448548648748848949049149249349449549649749849950050150250350450550650750850951051151251351451551651751851952052152252352452552652752852953053153253353453553653753853954054154254354454554654754854955055155255355455555655755855956056156256356456556656756856957057157257357457557657757857958058158258358458558658758858959059159259359459559659759859960060160260360460560660760860961061161261361461561661761861962062162262362462562662762862963063163263363463563663763863964064164264364464564664764864965065165465565665765865966066166266366466566666766866967067167267367467567667767867968068168268368468568668768868969069169269369469569669769869970070170270370470570670770870971071171271371471571671771871972072172272372472572672772872973073173273373473573673773873974074174274374474574674774874975075175275375475575675775875976076176276376476576676776876977077177277377477577677777877978078178278378478578678778878979079179279379479579679779879980080180280380480580680780880981081181281381481581681781881982082182282382482582682782882983083183283383483583683783883984084184284384484584684784884985085185285385485585685785885986086186286386486586686786887087187287387487587687787887988088188288388488588688788888989089189289389489589689789889990090190290390490590690790890991091191291391491591691791891992092192292392492592692792892993093193293393493593693793893994094194294394494594694794894995095195295395495595695795895996096196296396496596696796896997097197297397497597697797897998098198298398498598698798898999099199299399499599699799899910001001100210031004100510061007100810091010101110121013101410151016101710181019102010211022102310241025102610271028102910301031103210331034103510361037103810391040104110421043104410451046104710481049105010511052105310541055105610571058105910601061106210631064106510661067106810691070107110721073107410751076107710781079108010811082108310841085108610871088108910901091109210931094109510961097109810991100110111021103110411051106110711081109111011111112111311141115111611171118111911201121112211231124112511261127112811291130113111321133113411351136113711381139114011411142114311441145114611471148114911501151115211531154115511561157115811591160116111621163116411651166116711681169117011711172117311741175117611771178117911801181118211831184118511861187118811891190119111921193119511961197119811991200120112021203120412051206120712081209121012111212121312141215121612171218121912201221122212231224122512261227122812291230123112321233123412351236123712381239124012411242124312441245124612471248124912501251125212531254125512561257125812591260126112621263126412651266126712681269127012711272127312741275127612771278127912801281128212831284128512861287128812891290129112921293129412951296129712981299130013011302130313041305130613071308130913101311131213131314131513161317131813191320132113221323132413251326132713281329133013311332133313341335133613371338133913401341134213431344134513461347134813491350135113521353135413551356135713581359136013611362136313641365136613671368136913701371137213731374137513761377137813791380138113821383138413851386138713881389139013911392139313941395139613971398139914001401140214031404140514061407140814091410141114121413141414151416141714181419142014211422142314241425142614271428142914301431143214331434143514361437143814391440144114421443144414451446144714481449145014511452145314541455145614571458145914601461146214631464146514661467146814691470147114721473147414751476147714781479148014811482148314841485148614871488148914901491149214931494149514961497149814991500150115021503150415051506150715081509151015111512151315141515151615171518151915201521152215231524152515261527152815291530153115321533153415351536153715381539154015411542154315441545154615471548154915501551155215531554155515561557155815591560156115621563156415651566156715681569157015711572157315741575157615771578157915801581158215831584158515861587158815891590159115921593159415951596159715981599160016011602160316041605160616071608160916101611161216131614161516161617161816191620162116221623162416251626162716281629163016311632163316341635163616371638163916401641164216431644164516461647164816491650165116521653165416551656165716581659166016611662166316641665166616671668166916701671167216731674167516761677167816791680168116821683168416851686168716881689169016911692169316941695169616971698169917001701170217031704170517061707170817091710171117121713171417151716171717181719172017211722172317241725172617271728172917301731173217331734173517361737173817391740174117421743174417451746174717481749175017511752175317541756175717581759176017611762176317641765176617671768176917701771177217731774177517761777177817791780178117821783178417851786178717881789179017911792179317941795179617971798179918001801180218031804180518061807180818091810181118121813181418151816181718181819182018211822182318241825182618271828182918301831183218331834183518361837183818391840184118421843184418451846184718481849

Старая версия

Выберите страницу

678911121314151617181920212324252627282930313235363738394041434445464748495051525354555657586061626364656768697071727375767778798081828384868788899091929495969798100101102103104105106107108109110111112113115116117118119120121122123124127128129130131134135136137138140141142143144145147148149150152153154155156157158159160161162163164165166167169170171172173175176177178179181182183184186187188189190192193194195196197198200201202203205206207208210211212213214215216217218219220221222223224225226227228229230231233234235236237238239240241242243245246247248249251252253254255256257258259261262263264265266267268269270271272273274260

Adblock
detector

учебник математики 5 класс виленкин? — Товары для хобби и отдыха в Москве

Алгебра: 1. Математика 5, 6 класс Виленкин 1979, 1993, — 700р/шт. 2. Алгебра и начала анализа 9-10 класс, Колмогоров 1981 — 500р. 3. Алгебра, Калнин 1963 — 500р. 4. Арифметика 5-6 кл., Шевченко 1967 — 400р. 5. Алгебра 6-8 класс, Барсуков 1968 — 600р. 6. Алгебра и матем. Анализ 10 класс, Виленкин 1992 — 1200р. 7. Курс высшей математики для техникумов, Зайцев 1963 — 250р. 8. Алгебра и элементарные функции часть 1,2 Кочетков 1973- 300р/ шт. 9. Факультативный курс по математике 7-8 классы, Никольская 1991 — 250р. 10. Алгебра 6,7,8,9 класс, Макарычев 1972- 1982г — от 300 до 800р ( от состояния). 11. Избранные главы теории аналитических функций, Маркушевич 1976 — 200р. 12. Алгебра и начала анализа 10 класс, Колмогоров 1978 — 500р. 13. Избранные вопросы математики 9 класс, Виленкин, Антипов 1979 — 700р. 14. Математика, справочные материалы, Гусев — 300р. 15. Алгебра и элементарные функции, Калнин 1964 — 250р. 16. Алгебра 8 класс для школ с углублённым изучением, Виленкин 1995 — 1000р. 17. Алгебра 7 классе, Алиев 1991 — 1000р.

18. Элементарная математика, Зайцев 1974 — 800р. 19. Элементы высшей математики для школьников, Фаддеев 1987 — 300р. 20. Алгебра и начала анализа часть 2, Каченовский, Колягин 1988 — 350р. Геометрия: 1. Тригонометрия 9-10 класс, Новосёлов 1965 — 500р. 2. Геометрия 7-9 Атанасян 1991- 150р, 1990 — 500р. 3. Геометрия 10 класс, Клопский 1977 — 150р. 4. Геометрии 9-10 класс 1, 2 часть, Киселев 1973 — 700 и 600р/ часть. 5. Геометрия 1 часть, Базылев 1974 — 400р. 6. Прямые и кривые, Васильев 2006 — 100р. 7. Геометрия 6-10 класс, Погорелов 1987 — 800р. 8. Геометрия, теория и ее использование для решения задач, Яковлев — 150р. 9. Тригонометрия, доп. Материал к 9-10 классу, 1971 -. 10. Геометрия 9-10, Клопский 1978 — 300р. 11. Геометрия 7 класс, Атанасян 1986 — 200р. 12. Геометрия 9 класс, Болтянский 1963 — 150р. 13. Геометрия 6-8 класс, Колмогоров 1982 — 1000р. 14. Геометрическое черчение 7 класс, Григорьева 2000г — 50р. 15. Дифференциальная геометрия ( лекции по геометрии, 4 семестр) Постников 1988 — 700р.

16. Геометрия 6,7,8 класс, Колмогоров 1973 — 300р/ шт. Задачники, Справочники: 1. Сборник задач по элементарной геометрии, Атанасян 1964 — 400р. 2. Справочник по элементарной математике, Бевз 1972 — 150р. 3. Сборник задач по математике, Матвеев, 1965 — 200р. 4. Брадис Четырехзначные математические таблицы, 1972г -50р. 5. Задачи на доказательство по алгебре, Баранова 1954 — 400р. 6. Сборник задач и упражнений по арифметике 5-6 класс, Пономарев 1967 — 500р. 7. Сборник задач по математике для поступающих в вузы, Дыбов 1982 — 250р. 8. Сборник задач по алгебре и элементарным функциям, Худобин 1969 — 500р. 9. Сборник задач по математике для поступающих в вузы, Сканави 2003 — 250р и 150р. 10. Факультативный курс математики 7-8 класс, Сикорский 1969 — 300р. 11. Задачи по элементарной математике, Лидский 1967 — 200р. 12. Сборник задач по тригонометрии 9-10 класс, Стратилатов 1965 — 200р. 13. Письменные контрольные работы по геометрии для 6-8 классов, Макуха 1970 — 350р. 14. Сборник задач по элементарной математике, Антонов 1961 — 200р.

15. Сборник вопросов и задач по математике для поступающих в техникумы, Кондратьева 1983 — 200р. 16. Сборник задач московских математических олимпиад, Зубелевич 1971 — 350р. 17. Сборник задач по элементарной математике повышенной трудности, Шахно 1967 — 800р. 18. Сборник вопросов и задач по математике, Соломоник 1970 — 150р. 19. Счётная линейка, Панов 1971 — 250р. 20. Измерительные работы на местности, Смычников 1953 — 800р. 21. Сборник задач по алгебре, геометрии и началам анализа, Петрушко 2007 — 200р. 22. Функции, задачи и решения, Кушнир 1996 — 1000р. 23. Самостоятельные и контрольные работы по алгебре, Муравин 1971 — 500р. 24. Сборник задач по алгебре и началам анализа 10-11 класс, Карп 1995 — 1000р. 25. Справочник по математике, Рывкин 1987 — 250р. 26. Пособие по математике для поступающих в техникумы и училища, Метельский 1973 — 500р. 27. Сборник задач по математике для поступающих в вузы, Егерев 1988 — 250р. 28. Заочные математические Олимпиады, Васильев 1986 — 500р. 29. Сборник задач по алгебре 6-8 класс, Ларичев 1968 — 100р.

30. Сборник задач по геометрии для 6-8 классов, Никитин 1970 — 350р. 31. Задания для внеклассной работы по математике, Василевский 1988 — 500р. 32. Экстремальные задачи, Беляева 1977 — 150р. 33. Справочник по математике для инженеров и учащихся втузов, Бронштейн 1986 — 350р. 34. Справочник по элементарной математике, Бевз 1872 — 150р. 35. Как строить графики, Шилов 1959 — 300р. 36. Системы линейных неравенств, Солодовников 1977 — 200р. 37. Самостоятельные работы на уроках алгебры, Леонтьева — 150р. 38. Задачи по математике для внеклассных занятий, Сивашинский 1968 — 300р. 39. Сборник упражнений по математике 4-5 класс, Пономарёв 1973 — 500р. 40. Сборник задач по алгебре и началам анализа для 9-10 классов, Ивлев 1978 — 500р. 41. Задачи письменного экзамена по математике за курс средней школы, Звавич 1994 — 300р. 42. Задачи повышенной трудности по алгебре и началам анализа, Ивлев 1990 — 100р. 43. Сборник задач по геометрии 9-10 класс, Стратилатов 1986 — 100р.

ГДЗ По Математике Номер 300 – Telegraph

>>> ПОДРОБНЕЕ ЖМИТЕ ЗДЕСЬ <<<

ГДЗ По Математике Номер 300

ГДЗ (готовое домашние задание из решебника) на Номер №300 по учебнику Математика . 6 класс : учебник для общеобразовательных учреждений / Н . Я . Виленкин, В . И . Жохов, А . С . Чесноков, С . И . Шварцбурд . — 30-е изд ., стер .

Размещенные на данной странице готовые домашние задания помогут освоить программу по математике 6 класса, разобрать те моменты, которые были не до конца поняты на уроке, и выполнить на отлично все упражнения .

ГДЗ по математике 6 класс Виленкин учебник . номер — 300 (305) . Авторы : Н .Я . Виленкин, В .И . Жохов, А .С . Чесноков, С .И . Шварцбурд .

Подробный решебник (ГДЗ ) по Математике за 6 (шестой) класс — готовый ответ глава 4 упражнение — 300 . Авторы: Герасимов В .Д ., Пирютко О .Н . Издательство: Образование и воспитание 2019 год . Тип: Учебник . Подробный решебник (ГДЗ ) по Математике за 6 (шестой) . .

Подробное решение задачи по математике № 300 . Задача по математике 6 класс № 300 . Заходи сюда, помощь в домашке + тесты

Готовые домашние задания по математике 6 класса под авторством Герасимов В . Д . и Пирютко О .Н . 2019-2020 . Школьники, который решил пару примеров с решебником, сможет сам решить пример на уроке . ГДЗ по математике — идеальный вариант сэкономить время с . .

ГДЗ учебник по математике 6 класс Виленкин . авторы: Н .Я . Виленкин, В .И . Жохов, А .С . Чесноков, С .И . Шварцбурд . ГДЗ — Готовые Домашние Задания .

Онлайн решебник и ГДЗ по математике для 6-го класса к учебнику 2019 года, автора Герасимова, с подробными ответами . ГДЗ (решебник) по математике 6 класс Герасимов . Авторы: Герасимов В . Д ., Пирютко О . Н ., Лобанов А . П .

Решение задания номер 300 . Открыть номер 300 с телефона . Нужен решебник к старой версии учебника? Тогда введите номер задания здесь

ГДЗ Герасимов, Пирютко за 5 класс по Математике часть 1 . Издатель: Образование и воспитание 2019 год . Белорусские ГДЗ и Решебник за 5 класс по Математике часть 1 поможет Вам найти верный ответ на самый сложный номер задания онлайн . 300 .

О сервисе Прессе Правообладателям Связаться с нами Авторам Рекламодателям . .
Решебник, готовые домашние задания (ГДЗ ) по математике для учащихся 6 класса, авторов Герасимов В . Д ., Пирютко О . Н . В 6 классе ты заканчиваешь изучать математику . Дальше — алгебра и геометрия . На протяжении учебного года ты получишь знания, которые используются . .

Задача №300 , ГДЗ по математике за 6 класс к учебнику Виленкина с подробным решением . Виленкин, Жохов, Чесноков . 2 .10 Приведение дробей к общему знаменателю . Номер №300 .

Описание задания 300 . В задании 300 вам нужно привести восемь пар дробей к наименьшему общему знаменателю . Правила нахождения наименьшего общего знаменателя дробей есть на странице 44 . Если вы хотите понять, как это правило применяется на конкретных примерах, то . .

Задание № 300 — Математика 6 класс (Виленкин, Жохов) Посмотрел видео? Пройди тест: Пройди тест Письменное решение Другие номера Приведение дробей к общему знаменателю В задании 300 вам нужно привести восемь пар дробей к наименьшему общему знаменателю .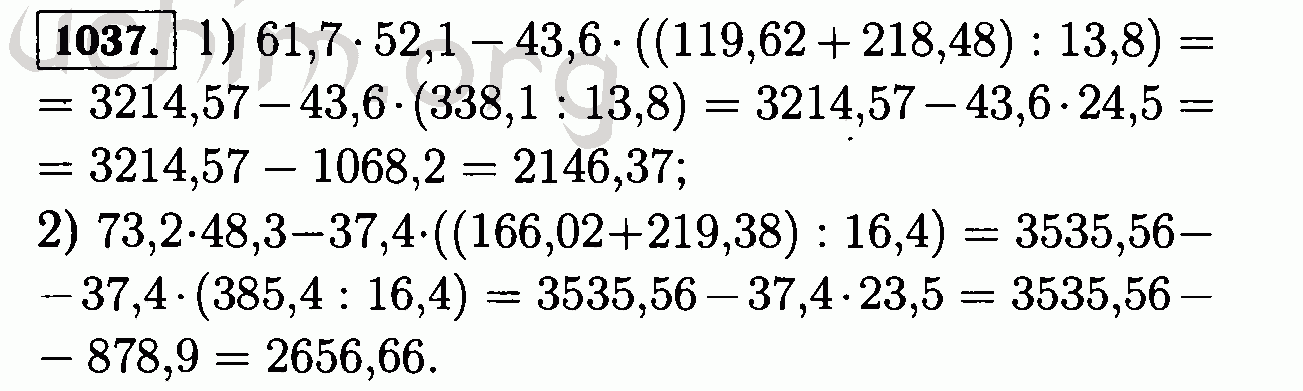

ГДЗ По Английскому Комарова 6 Класс Тетрадь
Решебник Учебник Пятый Класс
ГДЗ По Учебнику Комарова Ларионова
ГДЗ Русский 8 Разумовская 2014
Решебник ГДЗ Спотлайт
Решебник По Истории 5 Класс Кошелева
ГДЗ Математика Учебник 1 Часть Перспектива
Решебник Муравьева 5
ГДЗ Русский Язык 3 Класс Иванова Евдокимова
ГДЗ По Геометрии Лс Атанасян 7 Класса
ГДЗ По Чтению Рассказ
Решебник 5 Класса 3 Часть
ГДЗ По Математике 3 Тпо
ГДЗ По Истории 8 Класс Учебник Белоусов
ГДЗ По Английскому Страница 6
ГДЗ Азбука 1 Класс Школа России
ГДЗ Математический Тренажер 5 Класс Жохов Ответы
ГДЗ Литературное Чтение 2 Класс Стр 8
ГДЗ По Немецкому 3
Oxford Exam Support Workbook Решебник
ГДЗ По Математике Шестой Класс Зубарева
ГДЗ По Мат 5 Класс Бунимович Учебник
ГДЗ По Математике Шестой Класс Упражнение
ГДЗ По Математике 6 Класс Упр 58
ГДЗ По Английскому 7 Класс Никольский
ГДЗ По Английскому Языку 5 Класс Тест
Решебник По Английскому Языку 9 Класс Virginia
Учебник По Немецкому 5 Класс Горизонты ГДЗ
ГДЗ Математика 4 Класс Страница 57
ГДЗ По Алгебре 9 Класс Макарычев 34
ГДЗ По Нем Яз 11 Класс Бим
ГДЗ Языку 10 Класс Биболетова
ГДЗ По Русскаму Яз?Ку 7 Класс Ладыженская
ГДЗ По Истории Страница 13
ГДЗ Быкова Сборник Упражнений 2
ГДЗ 6 Кл Мордкович
ГДЗ 7 Класс Starlight Student S
Звездный Английский 4 Решебник
ГДЗ Русский Язык 8 Разумовская 2014
ГДЗ По Проверочным Математика 4 Класс
ГДЗ По Алгебре Седьмой Класс Баранов
Решебник По Английскому Языку Барашкова
ГДЗ Путина По Алгебре 8 Класс Мордкович
ГДЗ По Биологии 8 Класс Тпо
Рамзаева Русский Решебник
Петерсон Решебник 3 Класс 1часть
Математика 4 Класс Учебник Моро ГДЗ Решебник
ГДЗ По Алгебре 78 Класс Мерзляк
ГДЗ Критская 6 Класс Учебник
Решебник По Английскому Языку Учебник 9 Класс

ГДЗ По Ал 9 Класс Мерзляк

ГДЗ По Математике 6 Класс Номер 90

Гдз По Русскому Языку Т

Гдз По Русскому Языку 1 Кузнецова

ГДЗ По Геометрии 10 Класс Атанасян 2012

ГДЗ решебник по математике 6 класс Виленкин

Авторы: Виленкин Н.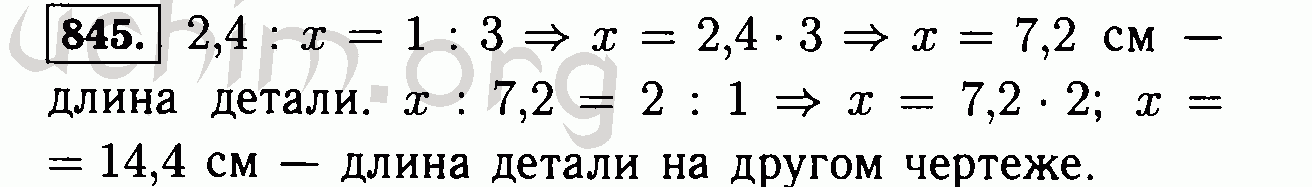 Я. Жохов В.И. Чесноков А.С. Шварцбурд С.И.
Издательство: М.: 2004-2008/2010, 2013-2015 ФГОС

Сборник готовых ответов содержит все самые доступные пояснения, помогающие ребенку получить правильные результаты решения заданий из учебника математики за 6 класс Виленкина Н.Я. 2013-2015 ФГОС.

Решебник поможет свободно оперировать сложными действиями с целыми и дробными числами десятыми, сотыми и тысячными долями, уверенно работать над несколькими способами получения правильного ответа, строить графики и углы, выполнять с ними разные действия и необходимые построения. А кажущиеся нерешаемыми сложные уравнения с несколькими неизвестными сдадутся ученику.

В учебном пособии авторов Виленкина Н.Я и др. к учебнику математики для 6 класса Виленкина Н.Я. (2004-2008/2010г.) все упражнения содержат самый тщательный разбор их решения. Дроби и рациональные числа больше не будут создавать трудности при решении задач, поскольку понятен сам ход работы с ними.

Такие термины, как делимость и пропорция, отношения и действия с отрицательными числовыми значениями, не будут пугающими и легко поддадутся успешной работе с ними.

Система координат так же раскроет свои тайны и ребенок самостоятельно сможет находить на плоскости нужные координаты.

Быстрый поиск

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376 377 378 379 380 381 382 383 384 385 386 387 388 389 390 391 392 393 394 395 396 397 398 399 400 401 402 403 404 405 406 407 408 409 410 411 412 413 414 415 416 417 418 419 420 421 422 423 424 425 426 427 428 429 430 431 432 433 434 435 436 437 438 439 440 441 442 443 444 445 446 447 448 449 450 451 452 453 454 455 456 457 458 459 460 461 462 463 464 465 466 467 468 469 470 471 472 473 474 475 476 477 478 479 480 481 482 483 484 485 486 487 488 489 490 491 492 493 494 495 496 497 498 499 500 501 502 503 504 505 506 507 508 509 510 511 512 513 514 515 516 517 518 519 520 521 522 523 524 525 526 527 528 529 530 531 532 533 534 535 536 537 538 539 540 541 542 543 544 545 546 547 548 549 550 551 552 553 554 555 556 557 558 559 560 561 562 563 564 565 566 567 568 569 570 571 572 573 574 575 576 577 578 579 580 581 582 583 584 585 586 587 588 589 590 591 592 593 594 595 596 597 598 599 600 601 602 603 604 605 606 607 608 609 610 611 612 613 614 615 616 617 618 619 620 621 622 623 624 625 626 627 628 629 630 631 632 633 634 635 636 637 638 639 640 641 642 643 644 645 646 647 648 649 650 651 652 653 654 655 656 657 658 659 660 661 662 663 664 665 666 667 668 669 670 671 672 673 674 675 676 677 678 679 680 681 682 683 684 685 686 687 688 689 690 691 692 693 694 695 696 697 698 699 700 701 702 703 704 705 706 707 708 709 710 711 712 713 714 715 716 717 718 719 720 721 722 723 724 725 726 727 728 729 730 731 732 733 734 735 736 737 738 739 740 741 742 743 744 745 746 747 748 749 750 751 752 753 754 755 756 757 758 759 760 761 762 763 764 765 766 767 768 769 770 771 772 773 774 775 776 777 778 779 780 781 782 783 784 785 786 787 788 789 790 791 792 793 794 795 796 797 798 799 800 801 802 803 804 805 806 807 808 809 810 811 812 813 814 815 816 817 818 819 820 821 822 823 824 825 826 827 828 829 830 831 832 833 834 835 836 837 838 839 840 841 842 843 844 845 846 847 848 849 850 851 852 853 854 855 856 857 858 859 860 861 862 863 864 865 866 867 868 869 870 871 872 873 874 875 876 877 878 879 880 881 882 883 884 885 886 887 888 889 890 891 892 893 894 895 896 897 898 899 900 901 902 903 904 905 906 907 908 909 910 911 912 913 914 915 916 917 918 919 920 921 922 923 924 925 926 927 928 929 930 931 932 933 934 935 936 937 938 939 940 941 942 943 944 945 946 947 948 949 950 951 952 953 954 955 956 957 958 959 960 961 962 963 964 965 966 967 968 969 970 971 972 973 974 975 976 977 978 979 980 981 982 983 984 985 986 987 988 989 990 991 992 993 994 995 996 997 998 999 1000 1001 1002 1003 1004 1005 1006 1007 1008 1009 1010 1011 1012 1013 1014 1015 1016 1017 1018 1019 1020 1021 1022 1023 1024 1025 1026 1027 1028 1029 1030 1031 1032 1033 1034 1035 1036 1037 1038 1039 1040 1041 1042 1043 1044 1045 1046 1047 1048 1049 1050 1051 1052 1053 1054 1055 1056 1057 1058 1059 1060 1061 1062 1063 1064 1065 1066 1067 1068 1069 1070 1071 1072 1073 1074 1075 1076 1077 1078 1079 1080 1081 1082 1083 1084 1085 1086 1087 1088 1089 1090 1091 1092 1093 1094 1095 1096 1097 1098 1099 1100 1101 1102 1103 1104 1105 1106 1107 1108 1109 1110 1111 1112 1113 1114 1115 1116 1117 1118 1119 1120 1121 1122 1123 1124 1125 1126 1127 1128 1129 1130 1131 1132 1133 1134 1135 1136 1137 1138 1139 1140 1141 1142 1143 1144 1145 1146 1147 1148 1149 1150 1151 1152 1153 1154 1155 1156 1157 1158 1159 1160 1161 1162 1163 1164 1165 1166 1167 1168 1169 1170 1171 1172 1173 1174 1175 1176 1177 1178 1179 1180 1181 1182 1183 1184 1185 1186 1187 1188 1189 1190 1191 1192 1193 1194 1195 1196 1197 1198 1199 1200 1201 1202 1203 1204 1205 1206 1207 1208 1209 1210 1211 1212 1213 1214 1215 1216 1217 1218 1219 1220 1221 1222 1223 1224 1225 1226 1227 1228 1229 1230 1231 1232 1233 1234 1235 1236 1237 1238 1239 1240 1241 1242 1243 1244 1245 1246 1247 1248 1249 1250 1251 1252 1253 1254 1255 1256 1257 1258 1259 1260 1261 1262 1263 1264 1265 1266 1267 1268 1269 1270 1271 1272 1273 1274 1275 1276 1277 1278 1279 1280 1281 1282 1283 1284 1285 1286 1287 1288 1289 1290 1291 1292 1293 1294 1295 1296 1297 1298 1299 1300 1301 1302 1303 1304 1305 1306 1307 1308 1309 1310 1311 1312 1313 1314 1315 1316 1317 1318 1319 1320 1321 1322 1323 1324 1325 1326 1327 1328 1329 1330 1331 1332 1333 1334 1335 1336 1337 1338 1339 1340 1341 1342 1343 1344 1345 1346 1347 1348 1349 1350 1351 1352 1353 1354 1355 1356 1357 1358 1359 1360 1361 1362 1363 1364 1365 1366 1367 1368 1369 1370 1371 1372 1373 1374 1375 1376 1377 1378 1379 1380 1381 1382 1383 1384 1385 1386 1387 1388 1389 1390 1391 1392 1393 1394 1395 1396 1397 1398 1399 1400 1401 1402 1403 1404 1405 1406 1407 1408 1409 1410 1411 1412 1413 1414 1415 1416 1417 1418 1419 1420 1421 1422 1423 1424 1425 1426 1427 1428 1429 1430 1431 1432 1433 1434 1435 1436 1437 1438 1439 1440 1441 1442 1443 1444 1445 1446 1447 1448 1449 1450 1451 1452 1453 1454 1455 1456 1457 1458 1459 1460 1461 1462 1463 1464 1465 1466 1467 1468 1469 1470 1471 1472 1473 1474 1475 1476 1477 1478 1479 1480 1481 1482 1483 1484 1485 1486 1487 1488 1489 1490 1491 1492 1493 1494 1495 1496 1497 1498 1499 1500 1501 1502 1503 1504 1505 1506 1507 1508 1509 1510 1511 1512 1513 1514 1515 1516 1517 1518 1519 1520 1521 1522 1523 1524 1525 1526 1527 1528 1529 1530 1531 1532 1533 1534 1535 1536 1537 1538 1539 1540 1541 1542 1543 1544 1545 1546 1547 1548 1549 1550 1551 1552 1553 1554 1555 1556 1557 1558 1559 1560 1561 1562 1563 1564 1565 1566 1567 1568 1569 1570 1571 1572 1573 1574 1575 1576 1577 1578 1579 1580 1581 1582 1583 1584 1585 1586 1587 1588 1589 1590 1591 1592 1593 1594 1595

Оцените решебник:

Загрузка. ..

6 класс — Common Core: математика для 6 класса

All Common Core: математические ресурсы для 6 класса

6 диагностических тестов 186 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 3 4 5 6 7 8 9 … 175 176 Следующая →

Common Core: Справка по математике для 6-го класса » 6 класс

Если кандидат А получает голоса за каждый голос, который получает кандидат Б. В конце выборов у кандидата Б есть голоса. Сколько голосов получил кандидат А?

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы решить эту задачу, нам нужно создать отношение с данной информацией. В нем говорится, что за каждый голос, отданный за кандидата А, кандидат Б получает голоса. Мы можем записать следующее соотношение.

Теперь подставьте данные числа.

Мы знаем, что кандидат Б получил голоса. Напишите новый коэффициент.

Теперь, используя исходное соотношение, создайте пропорцию и найдите количество голосов, полученных кандидатом А.

Крест умножить и решить.

Упрощение.

Разделите обе части уравнения на .

Решить.

Сообщить об ошибке

Если кандидат А получает голоса за каждый голос, который получает кандидат Б. В конце выборов кандидат Б имеет голоса. Сколько голосов получил кандидат А?

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы решить эту задачу, нам нужно создать отношение с данной информацией. В нем говорится, что за каждый голос, отданный за кандидата А, кандидат Б получил голоса. Мы можем записать следующее соотношение.

Теперь подставьте данные числа.

Мы знаем, что кандидат Б получил голоса. Напишите новый коэффициент.

Крест умножить и решить.

Упрощение.

Разделите обе части уравнения на .

Решить.

Сообщить об ошибке

Возможные ответы:

Правильный ответ:

Объяснение:

Теперь подставьте данные числа.

Мы знаем, что кандидат Б получил голоса. Напишите новый коэффициент.

Крест умножить и решить.

Упрощение.

Разделите обе части уравнения на .

Решить.

Сообщить об ошибке

Возможные ответы:

Правильный ответ:

Объяснение:

Теперь подставьте данные числа.

Мы знаем, что кандидат Б получил голоса. Напишите новый коэффициент.

Крест умножить и решить.

Упрощение.

Разделите обе части уравнения на .

Решить.

Сообщить об ошибке

Возможные ответы:

Правильный ответ:

Объяснение:

Теперь подставьте данные числа.

Уменьшить.

Мы знаем, что кандидат Б получил голоса. Напишите новый коэффициент.

Крест умножить и решить.

Упрощение.

Разделите обе части уравнения на .

Решить.

Сообщить об ошибке

Возможные ответы:

Правильный ответ:

Объяснение:

Теперь подставьте данные числа.

Мы знаем, что кандидат Б получил голоса. Напишите новый коэффициент.

Крест умножить и решить.

Упрощение.

Разделите обе части уравнения на .

Решить.

Сообщить об ошибке

Возможные ответы:

Правильный ответ:

Объяснение:

Теперь подставьте данные числа.

Мы знаем, что кандидат Б получил голоса. Напишите новый коэффициент.

Крест умножить и решить.

Упрощение.

Разделите обе части уравнения на .

Решить.

Сообщить об ошибке

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы решить эту задачу, нам нужно создать отношение с данной информацией. В нем говорится, что за каждый голос, отданный за кандидата А, кандидат Б получает голос. Мы можем записать следующее соотношение.

Теперь подставьте данные числа.

Мы знаем, что кандидат Б получил голоса. Напишите новый коэффициент.

Крест умножить и решить.

Упрости и реши.

Сообщить об ошибке

Возможные ответы:

Правильный ответ:

Объяснение:

Теперь подставьте данные числа.

Мы знаем, что кандидат Б получил голоса. Напишите новый коэффициент.

Крест умножить и решить.

Упрощение.

Разделите обе части уравнения на .

Решить.

Сообщить об ошибке

Если кандидат А получает голоса за каждый голос, полученный кандидатом Б. В конце выборов кандидат Б имеет голоса. Сколько голосов получил кандидат А?

Возможные ответы:

Правильный ответ:

Объяснение:

Теперь подставьте данные числа.

Мы знаем, что кандидат Б получил голоса. Напишите новый коэффициент.

Крест умножить и решить.

Упрощение.

Разделите обе части уравнения на .

Решить.

Сообщить об ошибке

← Предыдущая 1 2 3 4 5 6 7 8 9 … 175 176 Следующая →

186 практических тестов Вопрос дня Карточки Учитесь по концепции

6 класс / 6 класс Математика

Список поставок 6 класса
2022 Летнее чтение
6 класс ЭЛА
6 класс Математика
Обществоведение 6 класс
6 класс Наука
6 класс Мировые языки

Цель программы округа по математике состоит в том, чтобы дать учащимся опыт, который позволит им развить математическое мышление и приобрести основные математические понятия и навыки. В начальной учебной программе широко используются манипуляторы (конкретные объекты) для более глубокого понимания.
Учебная программа предназначена для развития у учащихся компетенций, необходимых для математического развития. По мере прохождения курсовой работы у них будут развиваться все более сложные способности решения задач, ряд математических «привычек ума» и набор высокоразвитых навыков математического мышления. Кроме того, учащиеся будут все больше и больше владеть устными и письменными математическими выражениями, поскольку они будут свободно говорить на языке математики и смогут устанавливать связи в математике.
Математика 6
Типы Оценки: Конец модульных тестов, викторины средней единицы и кумулятивные квартальные Учащиеся 6-го класса математики переходят от элементарного внимания к пониманию идеи единицы и общих черт между единицами к средней школе, сосредотачивающейся на соотношениях, о том, как числа связаны друг с другом и которыми можно манипулировать.
Основное внимание уделяется соотношениям и пропорциональным рассуждениям, а также основам алгебры с выражениями и уравнениями.
1. Коэффициенты и удельные ставки
  a. Представление и рассуждения о соотношениях
  b. Удельные ставки
  c. Проценты
2. Арифметические операции
  1. Деление дробей
  2. Многоразрядные десятичные операции
  3. Деление целых чисел и десятичных дробей
3. Рациональные числа
  1. Положительные и отрицательные числа в числовой строке
  2. Рациональные числа и координаты
  3. Абсолютное значение
4. Выражения и уравнения
5. Специальные обозначения
6. Расширение, факторинг и распространение
7. Выражение в алгебраической форме
8. Решение уравнений
9. Применение уравнений
10. Площадь, площадь поверхности и объем
11. Площадь треугольников и четырехугольников
12. Многоугольники на координатной плоскости
13. Том
14. Сетки и поверхность
15. Статистика
16. Суммирование распределений с учетом симметрии, среднего и среднего абсолютного отклонения.
17. Искаженные данные
18. Описание дистрибутивов
ТЕКСТ
- Заметки и раздаточные материалы, предоставленные учителем (основной)
- Курс математики 2 , Холт (главным образом справочник для домашнего использования)
ОЖИДАНИЯ ОТ РАБОТЫ
Приходить вовремя на занятия. Принесите необходимые материалы и будьте готовы (сделайте домашнюю работу и готовьтесь к любым оценкам). Будьте уважительны и слушайте, пока другие говорят. Поднимите руку, чтобы вас призвали. Уважайте принадлежности в классе и одноклассников. Поймите, что у всех учащихся разные стили обучения и они учатся с разной скоростью.

Математика 6 Расширенный
Types of Assessments: End of unit tests, mid-unit quizzes and cumulative quarterlies
Prerequisite: Math 5
Credit: 1
____________________________________________________________
DESCRIPTION
Students in 6th grade advanced mathematics are переход от элементарного внимания к пониманию идеи единицы и общих черт между единицами к средней школе, сосредоточенной на соотношениях, о том, как числа связаны друг с другом и которыми можно манипулировать. Учащиеся этого класса приглашаются на основании оценок, склада ума и рекомендации учителя. Основное внимание уделяется соотношениям и пропорциональным рассуждениям, а также основам алгебры с выражениями и уравнениями.
1. Соотношения и удельные ставки
2. Арифметические операции
  1. Деление дробей
  2. Многоразрядные десятичные операции
  3. Деление целых чисел и десятичных дробей
3. Рациональные числа
  1. Положительные и отрицательные числа на числовой прямой
  2. Рациональные числа и координаты
  3. Абсолютное значение
4. Выражения и уравнения
  1. Специальные обозначения
  2. Расширение, факторинг и распространение
  3. Выражение в алгебраической форме
  4. Решение уравнений
  5. Применение уравнений
5. Площадь, площадь поверхности и объем
  1. Площадь треугольников и четырехугольников
  2. Многоугольники на координатной плоскости
  3. Том
  4. Сетки и поверхность
6. Статистика
  1. Суммирование распределений с учетом симметрии, среднего и среднего абсолютного отклонения
  2. Искаженные данные
  3. Описание дистрибутивов
ТЕКСТ
- Примечания и раздаточные материалы, предоставленные учителем (основной)
- Курс математики 2 , Холт (главным образом справочник для домашнего использования)
ОЖИДАНИЯ ОТ РАБОТЫ
Приходить вовремя на занятия. Принесите необходимые материалы и будьте готовы. Будьте уважительны и слушайте, пока другие говорят. Поднимите руку, чтобы вас призвали. Уважайте принадлежности в классе и одноклассников. Поймите, что у всех учащихся разные стили обучения и они учатся с разной скоростью. Ожидается, что учащиеся будут обладать складом ума, демонстрирующим, что они могут работать выше уровня своего класса и добиваться успеха.

Подробное описание системы оценивания

Перенос баллов ЕГЭ производится после подсчета первичного результата, на основании утвержденной шкалы, он конвертируется в баллы за тест.
Играют важную роль при поступлении в вуз и фиксируются в справке о сдаче экзамена.

Тем, кто заканчивает 11 классов и готовится к поступлению в вуз, особенно интересно узнать, как переводится балл ЕГЭ.

Ежегодно эту процедуру проходят сотни тысяч студентов. Для получения аттестата достаточно сдать всего два предмета – математику и русский язык.

Остальные предметы – а всего их 14 – сдаются на добровольной основе в зависимости от выбранного вуза.

Для того, чтобы результаты отображались в аттестате, выпускнику необходимо набрать больше установленного минимума баллов.

Как оцениваются результаты экзамена

Результаты экзамена оцениваются комиссией и переводятся в 100-балльную систему.

Существует алгоритм преобразования этих сумм в более привычные оценки. Официально этот способ не применяется с 2009 года.

Но при желании вы можете ознакомиться со шкалой перевода отметок ЕГЭ.

Оценка результатов проводится в два этапа:

по количеству выполненных заданий студенту выставляется первичный балл. Он состоит из суммы по всем заданиям, выполненным правильно;
, то баллы по первичному ЕГЭ переводятся в баллы за тесты. Эта цифра фиксируется в аттестате ЕГЭ и играет важную роль для поступления в вуз. Ниже приведена таблица перевода для экзамена по математике.

Важно: весы разработаны с учетом сложности задач.

Актуальную информацию об экзамене всегда можно получить на портале http://ege.edu.ru/ru.

Какой минимальный балл

Для получения сертификата ЕГЭ учащемуся необходимо набрать больше установленного минимального балла по русскому языку и математике.

Определяется ежегодно для каждого отдельного субъекта. На самом деле минимальная оценка эквивалентна трем.

Этот результат свидетельствует о том, что учащийся удовлетворительно усвоил учебную программу.

Минимальный балл:

Определяет выдачу сертификата о сдаче экзамена.
Устанавливается по каждому предмету ежегодно после сдачи экзамена и до публикации результатов.

В конце 2016 года для получения аттестата необходимо было набрать не менее 36 тестовых баллов по русскому языку.

По математике этот предел равен 3, а по профильному уровню — 27.

Разница между первичными баллами и тестовыми баллами

При оценке результатов сдачи ЕГЭ в первую очередь выставляется первичная сумма. Затем эти баллы ЕГЭ 2017 переводятся в баллы за тесты.

Определяются по 100-бальной шкале. Этот балл будет в аттестате ЕГЭ, если он выше минимального.

При подсчете баллов алгоритм следующий:

За каждое правильно выполненное задание начисляется один или несколько баллов.
В конце подсчитывается сумма за всю работу.
Идет перевод первичных баллов ЕГЭ.

Что касается результатов тестов, то они рассчитываются по 100-балльной системе. Но количество первичных может отличаться для разных предметов.

Например, по математике можно получить 30 первичных баллов, а по иностранным языкам этот предел равен 80.

Оценка задания зависит от его сложности. По заданиям части Б за правильный ответ начисляется один первичный балл.

Для части С есть несколько вариантов: за задания 1 и 2 начисляется 2 первичных балла, правильный ответ на вопрос 3 и 4 сразу дает 3, а задания 5 и 6 добавят к результату ученика 4 балла.

Баллы ЕГЭ и 9 баллов0767

Хотя существует примерная шкала перевода баллов ЕГЭ в оценки, знакомая всем учащимся, с 2009 года эта система не применяется.

Отказ в переводе в оценки связан с тем, что сумма баллов не влияет на показатель в аттестате. Он фиксируется в отдельном сертификате.

В случае, если учащийся набрал меньше минимального результата по одному из обязательных предметов, ему не выдается ни аттестат, ни аттестат об окончании средней школы.

Если это предмет из тех, что сдаются на добровольной основе, то результат просто нигде не будет засчитан.

Если по результатам экзамена получена неудовлетворительная оценка, что делать? Все зависит от того, какой предмет.

Если количество набранных баллов ниже минимального по математике или русскому языку, вы можете пересдать экзамен в том же году в один из резервных дней.
При получении неудовлетворительной оценки сразу по обоим предметам пересдача возможна только на следующий год.
Если вам не удалось набрать достаточное количество баллов по факультативному предмету, вы можете пересдать экзамен только в следующем году. Неудовлетворительный результат не будет отражен ни в одном документе. На самом деле все будет выглядеть так, как будто выпускник вообще не сдавал этот экзамен.

В зависимости от предмета пересдача возможна либо в том же году в резервные дни, либо в следующем.

Таким образом, если школьник не сдал математику на базовом уровне, он может использовать резервные дни.

А если по результатам профильного уровня получен низкий балл, то пересдача будет возможна только через год.

Что делать, если выпускник не согласен с оценкой

Если выпускник уверен, что его работа заслуживает более высокой оценки, он имеет право подать апелляцию.

В такой ситуации работа будет повторно рассмотрена конфликтной комиссией.

Возможны два исхода. Когда оценка кажется низкой, учащемуся могут либо дать баллы, либо баллы снять.

Важно: по результатам ЕГЭ в 2010 году из всех поданных обращений удовлетворена третья часть.

Первые две части экзамена тестируются без участия человека. Не исключена возможность ошибок.

Причиной этого может быть неразборчивый почерк и подобные обстоятельства.

Если окажется, что оценка низкая, учащиеся подают апелляцию.

Что такое экзамен

Общий текст задания состоит из трех частей.

Часть А представляет собой тест. Из четырех предложенных ответов выпускник должен выбрать один правильный.
В части Б возможны следующие типы заданий: написание односложного ответа, выбор нескольких правильных вариантов или установление соответствия.
В части C учащегося просят дать развернутый ответ на вопрос.

В зависимости от типа задачи процесс проверки отличается. Первые две части проверяются автоматически. Ответы сканируются системой и оцениваются.

Этот процесс происходит без вмешательства человека. По завершении тестирования результаты отправляются в центр тестирования, расположенный в Москве.

Часть C оценивается двумя независимыми экспертами. Если результаты совпадают, эта сумма устанавливается.

Если после оценки обнаруживается небольшое расхождение, отображается средний результат.

При заметном несоответствии назначается третий специалист.

После завершения проверки все данные отправляются в единый центр тестирования. Там они обрабатываются и фиксируются в базе данных.

Оттуда их отправляют в школы, где сдавали экзамен.

Как результаты ЕГЭ влияют на поступление в вузы?

Чтобы подать заявление о приеме в университет, выпускникам необходимо сдать экзамен.

Всего можно поступить в 5 вузов, в каждом из них не более чем на три специальности.

Заявление составляется в письменной форме и вручается лично или направляется по почте.

При выборе второго варианта потребуется оформить заказное письмо с описанием вложения, а также уведомлением о получении.

Чтобы узнать, была ли одобрена заявка, необходимо зайти на официальный сайт вуза.

Когда прием документов завершен, там выкладывается список подающих заявление на зачисление. Там же показаны их результаты. сдача экзамена.

Регистрация проходит в два этапа.

При публикации первого списка абитуриентам отводится несколько дней на предоставление оригиналов своих документов (в большинстве случаев высылают копии).
Если срок подачи документов истек, а вакансии еще есть, составляется второй список.

Для поступления в вуз потребуется следующий пакет документов:

заявление о приеме;
заверенные копии удостоверения и документа, удостоверяющего личность;
бланк с перечнем набранных баллов по результатам ЕГЭ;
фотографий (их размер и количество устанавливаются правилами вуза).

У заявителя могут быть запрошены и другие документы. Для получения дополнительной информации, пожалуйста, свяжитесь с интересующим университетом.

Зачисление баллов ЕГЭ в 2017 году осуществляется по той же системе, что и в предыдущие годы.

Для сдачи экзамена необходимо набрать не менее минимального количества баллов, которое установлено по каждому предмету ежегодно.

Чтобы получить аттестат и справку с результатами ЕГЭ, нужно превысить этот лимит по обязательным предметам.

Как перевести первичные баллы в ЕГЭ 2015 по русскому языку

Многие выпускники спрашивают, сколько баллов нужно набрать на ЕГЭ по тому или иному предмету. Русский язык, как и математика, обычно вызывает наибольший интерес.

Минимальный балл

Следует отметить, что русский язык является обязательным предметом ЕГЭ. Успешное преодоление минимального уровня позволяет получить аттестат о среднем общем образовании. Оценка «2» выставляется за результат от 0 до 35 баллов. В этом случае экзамен считается проваленным. Зачет по обязательному предмету можно пересдать в специальные резервные дни (но это может быть только русский язык или математика — пересдача зачета по обоим предметам в течение одного года не допускается). Если дополнительный экзамен также был провален, студент имеет право на пересдачу только на следующий год. Таким образом, чтобы сдать ЕГЭ по русскому языку с первого раза, нужно набрать не менее 36 баллов.

Сколько баллов нужно тройкам, отличникам и отличникам?

Если по русскому языку в аттестате пятерка, можно не переживать за то, что по ЕГЭ могут снизить оценку. Результаты ЕГЭ долгое время не влияли на итоговые школьные оценки. Тем не менее существует шкала перевода результатов тестирования в обычную пятибалльную систему:

0–35 – два;
36–57 — три;
58–71 — четыре;
72 и выше — пять.

Таким образом, если ваш результат равен хотя бы 72 баллам, то считайте, что он соответствует отличному аттестату. Если вы наберете, например, 65 баллов, то есть получите четверку, это не отразится на оценке в аттестате. Результат будет указан только в специальной справке о сдаче экзамена.

Сколько баллов нужно, чтобы поступить в колледж?

Для большинства выпускников ЕГЭ не только основной экзамен, позволяющий получить аттестат о среднем образовании, но и вступительные испытания в высшее учебное заведение. Сложно сказать, сколько баллов по русскому языку нужно набрать, чтобы поступить в вуз. Все зависит от количества бюджетных мест, престижности учебного заведения, конкурса и т. д. Кроме того, сегодня при поступлении в вузы учитывается сумма баллов по всем вступительным испытаниям. Таким образом, их точное количество важно для любого направления, где для поступления необходим русский язык.

Трудно определить, хороша такая система или нет. С одной стороны, он обязывает одинаково интенсивно готовиться по всем предметам, с другой стороны, дает шанс, даже если баллы по основной дисциплине не равны 100. ЕГЭ (русский и иностранный язык и, литература и факультатив творческий вступительный тест), каждый из которых оценивался по 100-балльной шкале. Конечным результатом, на основании которого происходило зачисление, была сумма набранных баллов по каждому предмету.

Окончание школы и поступление в вуз сопровождается сдачей единого государственного экзамена. При его сдаче выпускники недоумевают, как первичный балл переводится в стопроцентную шкалу.

Перевод баллов ЕГЭ в оценки направлен на определение того, на какой показатель может рассчитывать будущий школьник.

Калькулятор ЕГЭ по предметам

Шкала перевода баллов ЕГЭ в оценки

В процессе обучения в школе дети получают оценки по пятибалльной шкале, а фактически даже по четырехбалльной, так как редко данный.

При сдаче экзаменов в девятом и одиннадцатом классах учащиеся сталкиваются с такими понятиями, как первичные баллы за задания, а также со стобалльной шкалой.

Базовая процедура проверки основана на компьютерном анализе и рецензировании. Тестовая часть подвергается автоматизированному расчету, оспорить данные проблематично. Но та часть, которую проверяют специалисты, может быть подвергнута дополнительному анализу.

Все баллы также конвертируются в оценки. Несмотря на то, что этот показатель не оказывает существенного влияния, многих учащихся интересует, какие оценки дают те или иные первичные предметы.

Математика

За последние несколько лет проводятся два вида экзаменов по математике:

базовый, который необходим для получения сертификата;
— Необходим для поступления в технические ВУЗы.

В первом случае максимально возможный первичный балл равен двадцати, для пятерки требуется семнадцать очков, для четверки — двенадцать, а для тройки — всего семь очков.

Что касается профиля, то отличную оценку получают те, кто набрал от тринадцати до тридцати баллов. Четверка ставится тем, кто получил баллы от десяти до двенадцати баллов, а тройка ставится из шести первичных баллов.

Русский язык

Максимальный первичный балл по русскому языку — тридцать девять, для получения пятерки допустимо потерять пять баллов. Четверка начинается с двадцати пяти очков, а тройка с пятнадцати. При наборе менее четырнадцати экзамен считается не сданным.

Иностранные языки

Высший первичный балл всех экзаменов — по иностранным языкам — семьдесят.

Чтобы получить отличную оценку, нужно набрать не менее пятидесяти девяти баллов.

Что касается четырех, то вполне достаточно сорока шести очков, а трех — двадцати девяти.

Если выпускник набрал меньше двадцати восьми, то экзамен не засчитывается.

География

Чтобы быть отличником по географии, нужно решать задачи на двадцать семь баллов, максимальная планка тридцать два. Четыре — от двадцати до двадцати шести, а для тройки достаточно всего двенадцати баллов.

Биология

За экзамен по биологии можно набрать сорок шесть баллов, причем нижняя планка для пятерки – тридцать семь баллов.

Тройка начинается с тринадцати, а четверка начинается с двадцати шести.

Тест, набравший менее двенадцати баллов, считается не пройденным.

Литература

При успешной сдаче литературы в рамках ЕГЭ можно получить до тридцати трех баллов, при пятерке от двадцати семи. Для четверки достаточно двадцати баллов, а для тройки – двенадцати.

Химия

По химии допускается набрать тридцать четыре балла, из них двадцати семи будет достаточно для отличной оценки. Четверка начинается с девятнадцати, а для тройки достаточно девяти очков.

Рассказ

За экзамен по истории начисляется 44 балла.

Отсутствие даже девяти баллов дает выпускнику отличную оценку.

Хорошим учеником по истории будет тот, кто решит тест на двадцать четыре балла. Удовлетворительная оценка начинается с тринадцати баллов.

Информатика

Самый низкий первичный балл за экзамен по информатике — двадцать два. Однако для того, чтобы получить пятерку, допустим недобор составляет всего четыре балла. Тройка начинается с пяти очков, а тройка начинается с двенадцати.

Социальные науки

Чтобы получить пятерку по общественным наукам, нужно набрать от тридцати четырех до тридцати пяти баллов. Хорошим ученикам будет достаточно двадцати пяти, а тем, кто удовлетворится удовлетворительной оценкой, будет достаточно и пятнадцати.

Подготовка к экзамену

Онлайн-сервис ГДЗ, на котором представлены решения разных авторов, в том числе Виленкина 6 класса по математике, имеет множество преимуществ перед использованием бумажных решений:

сервис бесплатный;
можно скачать учебники;
услуга доступна в любое время суток, в любой день недели;
Воспользоваться услугой можно из любого места, где есть доступ в Интернет;
сервис содержит решения, составленные высококвалифицированными специалистами, что исключает возможность получения недостоверной или некачественной информации.

Важными преимуществами онлайн-сервиса ГДЗ является возможность доступа с любого компьютерного устройства, независимо от установленной на устройстве операционной системы.

Широкий выбор книг с решениями, представленный на сайте, позволяет найти ответ практически на любой интересующий школьника вопрос. Так что теперь учиться стало легче.

Что означает первичный балл на ЕГЭ

Основные понятия:

Первичный — количество баллов, которое можно набрать за решенные задания; В зависимости от сложности заданиям присваивается определенное количество баллов.
Тест — баллы переводятся в систему сто баллов за решенные задания.

Данная система была придумана для упрощения подсчета результатов, так как поступление в вуз осуществляется по сумме баллов за несколько экзаменов, а максимальный первичный показатель по предметам разный.

Дело в том, что каждое задание в темах оценивается отдельно и есть специальный счетчик для распределения баллов.

Как перевести первичные баллы во вторичные

Для того, чтобы перевести первичные баллы в вторичные, необходимо использовать специальную шкалу, которая представлена на официальных сайтах ФИПИ, а также в ряде сторонних источников.

Произвести расчет самостоятельно проблематично, для этого нужно точно знать принцип пересчета.

В статье представлен калькулятор для перевода информации. Критерии, которые учитываются, основаны на результатах сданного экзамена.

Минимальные баллы за экзамен

Минимальные баллы утверждаются каждый год в качестве основы, необходимой для окончания школы и подачи заявления.

В соответствии с действующим законодательством для окончания школы с официальным документом об образовании необходимо сдать два предмета:

русский — двадцать четыре;
математика — двадцать семь.

Все остальные предметы принимаются при поступлении в университет. Это значит, что ученик имеет право ничего не выбирать, кроме русского языка и математики, и брать хоть все предметы со стола.

Что касается входных баллов при поступлении, то высшее учебное заведение самостоятельно определяет порог по каждому предмету, но этот параметр не может быть ниже установленного на государственном уровне.

Показатели выглядят так:

Русский язык, химия, биология и физика — тридцать шесть.
Математика — двадцать семь.
Информатика — сорок.
История и литература — тридцать два.
Иностранные языки – двадцать два.
Обществоведение — сорок два.
География — тридцать семь.

Этот список содержит второстепенные баллы, то есть баллы уже переведены в стобалльную систему. Важно учитывать тот факт, что тот или иной вуз вправе устанавливать завышенные требования к баллу, это не запрещено законом.

Максимальный балл на ЕГЭ

Максимальный балл на ЕГЭ по каждому из предметов — сто в средней системе.

Для определения максимально допустимого количества баллов по дисциплине необходимо обратиться либо к таблице перевода основных баллов в дополнительные, либо к кодификатору предметов, представленных в каждом среднем тестовом испытании.

Как набрать 100 баллов на ЕГЭ

Для набора максимального количества баллов ЕГЭ требуется не только хорошее понимание предмета, но и умение грамотно решать стандартные тестовые задания.

При подготовке следует руководствоваться следующим:

В течение нескольких лет ежедневно изучать материал по предметам, которые планируется сдавать после окончания учебы.
Решите множество заданий тестового типа, это поможет вам набить руку и повторить все темы не один раз.
При решении задач письменной части стоит обратиться к специалистам, которые помогут в разборе и подскажут правила оформления.
На самом экзамене ведите себя спокойно, если выпускник хорошо разбирается в теме, то проблем с решениями не будет.

Перевод баллов ЕГЭ в оценки — это формальность, позволяющая более привычно оценить результаты. Но расчет от первичного к вторичному — важный этап. высшие учебные заведения устанавливают планки и проходные нормативы по стобалльной шкале.

О бюджете 2018 года — еще одна проверка. В интернете много информации по этому вопросу, она есть на сайтах вузов и других официальных источниках. Чтобы помочь вам разобраться, мы собрали все данные в одной статье. перед вами пошаговая инструкция, которая поможет оценить ваши шансы на бесплатное обучение.

В России государство оплачивает около 50% мест в вузах

Шаг 1. Изучение количества свободных мест

Каждый государственный вуз обязан выделять места на бюджетной основе. Количество мест на бесплатном отделении зависит от популярности факультета и специальности. А получить бюджетное высшее образование можно не только в московских вузах. В некоторых местах количество свободных мест достигает 1,5-2 тысяч. Например, в Белгороде, Воронеже, Волгограде, Кирове, Ростове-на-Дону, Иркутске, Краснодаре, Челябинске и других городах России.

Шаг 2. Знакомство с терминами

Рассмотрим понятия, без которых сложно оценить свои шансы на поступление:

минимальный порог баллов ЕГЭ;
минимальное количество баллов для поступления;
проходной балл в вузах.

Что такое пороговая оценка?

Чтобы получить аттестат, нужно набрать определенное количество баллов по каждому предмету. Вот как это было в 2017 году:

Русский язык – 36 баллов;
математика – 27 баллов;
обществознание – 42 балла;
информатика – 40 баллов;
иностранный язык – 22 балла.

Например, вы выбрали для сдачи экзамена иностранный язык, тогда вам нужно набрать 36 баллов по русскому языку, 27 по математике и 22 по иностранному языку — всего 85 баллов. По идее, этого достаточно, чтобы подать документы в университет. Но на практике этого очень мало, чтобы поступить на бесплатное отделение.

Каков минимальный балл?

Каждый вуз устанавливает свое минимальное количество баллов ЕГЭ для поступления. Многие техникумы не готовы принимать тех, кто набрал менее 50 баллов по математике. Гуманитарные – выдвигают повышенные требования к языкам.

Что такое проходной балл

Проходной балл зависит от результатов ЕГЭ, с которыми абитуриенты были зачислены в прошлом году. Особенно важен результат последнего счастливчика, вошедшего в бюджет с минимальным количеством баллов.

Пример. Желающих поступить 200 человек, а бюджетных мест было 50. Ученик с наименьшим баллом. Например, со 150 баллами, а остальные имели более высокий балл.

Средний балл ЕГЭ в 2017 году составляет 68,2

Шаг 3. Выбор вуза по проходному баллу

Если вы можете рассчитать, какой балл вы получите по ЕГЭ, значит, пора выбирать правильный вуз. Кстати, пробные экзамены помогают хорошо оценить свои шансы.

Все вузы со свободными местами, их еще называют бюджетными высшими учебными заведениями, для удобства разделим на три категории:

самые популярные, или топовые;
средний;
непопулярный.

Обычно топовые вузы выдвигают повышенные требования, а остальные снижают планку для привлечения абитуриентов. Давайте посмотрим на проходные баллы вузов по всем трем категориям в 2017 году.

Если ваш средний балл выше 85: проходные баллы в популярных вузах

Заключение . Для поступления в топовые вузы средний балл ЕГЭ должен быть выше 80-85. Трудно попасть в число таких отличников, согласитесь? Если вы не уверены в хороших результатах, рассмотрите школы с менее строгими требованиями.

При среднем балле от 65 до 80: проходные баллы в общеобразовательные вузы

Заключение . При среднем балле ЕГЭ 65-80 в 2017 году можно было поступить в бюджетные и ведущие региональные вузы.

Если ваш средний балл 55-65 баллов: проходные баллы в непопулярные вузы

Заключение .Если вы набрали меньше 65 баллов, не паникуйте. Проходные баллы во многих региональных вузах ниже этой планки. И сегодня получить хорошее высшее образование можно не только в столицах.

Шаг 4. Оцените свои шансы по количеству баллов

280-300 баллов — лучшие вузы страны, любая специальность.

200-250 баллов — популярные вузы, специальности: языкознание, иностранный язык, право, экономика, менеджмент, здравоохранение, математика, физика.

200 баллов — общеобразовательные вузы, специальности: информатика и вычислительная техника, педагогика, химия и биотехнология, автоматика и управление, электротехника, энергетика. Или ведущие региональные вузы, по любой специальности.

150-200 баллов — общеобразовательные вузы, специальности: геология, экология, транспорт, сельское хозяйство и рыболовство. Или непопулярные вузы, любые специальности.

Меньше 150 баллов — непопулярные вузы, некоторые специальности.

Иногда даже с высоким баллом нельзя попасть в заветную двадцатку, а с низким, по счастливой случайности, можно поступить в желанный вуз. Главное, использовать все шансы и не забывать о запасных вариантах.

При сдаче Единого государственного экзамена (ЕГЭ) особое место занимает минимальный балл ЕГЭ. Это минимальный порог знаний в баллах ЕГЭ, при преодолении которого выдается сертификат ЕГЭ по обязательным предметам. Или другими словами, это балл ЕГЭ, соответствующий удовлетворительной отметке. В случае получения балла меньше минимального по предметам по выбору в аттестат ничего не заносится. Минимальный балл ЕГЭ по всем предметам устанавливается ежегодно после сдачи ЕГЭ и до объявления результатов.

Таблица минимальных баллов ЕГЭ 2018 по всем предметам

Вещь	Минимальный балл ЕГЭ
Русский язык	36
Математика (П)	27
Математика (Б)	27
Общественные науки	42
Физика	36
История	32
Биология	36
Химия	36
Английский язык	22
Информатика	40
Литература	32
География	37
немецкий	22
Французский	22
Испанский язык	22

Однако каждый вуз вправе устанавливать минимальный балл ЕГЭ выше рекомендованного Рособрнадзором. Разница может достигать 20-40 баллов и даже больше. Например, чтобы поступить в Санкт-Петербургский национальный исследовательский академический университет в 2018 году, вам потребуется набрать не менее 65 баллов по ЕГЭ по русскому языку и не менее 75 баллов по ЕГЭ по математике и физике. . При этом в вузах, подведомственных Министерству культуры РФ, минимальный балл ЕГЭ по одному предмету может различаться в зависимости от специальности и местонахождения вуза (региона): минимальный порог для вузов, расположенных в Москве, МО и ул. выше.

Шкала перевода баллов ЕГЭ 2018 по всем предметам

Для перевода первичных баллов в баллы зачетов необходима специальная таблица, разработанная Рособрнадзором (приложение № 2 к приказу Федеральной службы по надзору в сфере образования и науки от 26.04.2017 № 920-10). Он называется «Соответствие между первичными баллами и тестовыми баллами по всем учебным предметам по 100-балльной системе оценок.

Между тем, в любом правиле есть исключение, оно нашлось и здесь. Это экзамен по математике на базовом уровне. Результаты этого экзамена выражаются в первичных баллах и переводятся в пятибалльную систему подсчета очков.

Переводим баллы ЕГЭ в школьную оценку

Официально шкала перевода баллов по предметам ЕГЭ в пятибалльную оценку давно не используется (а именно с 2008 года). Однако многие все же хотят интерпретировать свой результат в более привычной «школьной» системе. Для этого можно воспользоваться таблицей ниже или онлайн-калькуляторами.

Вещь	«2» (сбой)	«3» (удовлетворительно)	«4» (хорошо)	«5» (отлично)
Русский язык	из 72	57-71	36-56	0-35
Математика	из 68	50-67	27-49	0-26
Общественные науки	из 70	58-69	42-57	0-41
Химия	из 73	56-72	36-55	0-35
География	из 67	51-66	37-50	0-36
Биология	из 72	55-71	36-54	0-35
Иностранные языки	из 84	59-83	22-58	0-21
Литература	из 67	52-66	32-54	0-31
История	из 68	50-67	32-49	0-31
Физика	из 68	53-67	36-52	0-35
Информатика	из 73	57-72	40-56	0-39

Можно ли пересдать ЕГЭ по обязательным предметам в 2018 году

Да, выпускники 2018 года могут пересдать ЕГЭ по обязательному предмету. Обязательны экзамены по русскому языку и математике. Но порядок проведения государственной итоговой аттестации в России не позволяет пересдавать экзамен для улучшения результата всем желающим.

Порядок строгий, и выглядит он так:

можно пересдать экзамен только по одному из двух обязательных предметов,
Пересдача экзамена возможна только при неудовлетворительной оценке.

Таким образом, если выпускник провалил оба обязательных экзамена: и по русскому языку, и по математике, пересдача в резервные даты в конце июня для него будет невозможна. При получении неудовлетворительных оценок по обоим обязательным предметам студент сможет пойти на пересдачу только в сентябре, когда пройдет осенняя волна пересдачи ЕГЭ.

Нахождение числа по заданному значению. Нахождение числа по его дроби, дробные выражения. Нахождение числа по его дроби

Решение задач из задачника Виленкина, Жохова, Чеснокова, Шварцбурда для 6 класса по математике на тему:

Глава I.

Обыкновенные дроби.
§ 3. Умножение и деление обыкновенных дробей:
18. Нахождение числа по его дроби

1 Мы очистили от снега 2/5 катка, что составляет 800 м2. Найдите площадь всего катка.
РЕШЕНИЕ

2 2400 га засеяно пшеницей. что составляет 0,8 всего поля. Найдите его площадь.
РЕШЕНИЕ

3 Повысив производительность труда на 7%, рабочий изготовил за тот же период на 98 деталей больше, чем было запланировано по плану. Сколько деталей должен был сделать рабочий по плану?
РЕШЕНИЕ

647 Девушка прошла 300 м, что составило 3/8 всей дистанции. Какова длина дистанции?
РЕШЕНИЕ

648 Свая возвышается над водой на 1,5 м, что составляет 3/16 длины всей сваи. Какова его длина
РЕШЕНИЕ

649 На элеватор отправлено 211,2 т зерна, что составляет 0,88 обмолоченного зерна за сутки. Сколько зерна было намолочено за день?
РЕШЕНИЕ

650 После замены двигателя средняя скорость самолета увеличилась на 18%, что составляет 68,4 км/ч. Какова была средняя скорость самолета с таким же двигателем?
РАСТВОР

651 Масса сушеной рыбы составляет 55% массы свежей рыбы. Сколько нужно взять свежего, чтобы получить 231 кг сушеного?
РАСТВОР

652 Вес винограда в первом ящике составляет 7/9 веса винограда во втором. Сколько килограммов винограда было в двух ящиках, если в первом было 21 кг винограда?
РЕШЕНИЕ

653 Продано 3/8 лыж, поступивших в магазин, после чего осталось 120 пар лыж. Сколько пар получил магазин?
РАСТВОР

654 При сушке картофель теряет 85,7% своей массы. Сколько нужно взять сырого картофеля, чтобы получить 71,5 тонны сушеного?
РЕШЕНИЕ

655 Банк купил несколько акций завода и через год продал их за 576,8 млн руб., получив 3% прибыли. Сколько банк потратил на покупку акций?
РЕШЕНИЕ

656 В первый день туристы прошли 5/24 намеченного маршрута, а во второй день — 0,8 от того, что они прошли в первый день. Какой длины запланированный путь, если во второй день туристы прошли 24 км?
РЕШЕНИЕ

657 Учащийся сначала прочитал 75 страниц, а затем еще несколько страниц. Их количество составило 40% от прочитанного впервые. Сколько страниц в книге, если прочитано 3/4 книги?
РЕШЕНИЕ

658 Велосипедист проехал сначала 12 1/4 км, а затем еще несколько километров, что составило 3/7 первого отрезка пути. После этого ему предстояло проехать 2/3 всего пути. Какова его длина
РЕШЕНИЕ

659 3/5 числа 12 составляет 1/4 неизвестного числа. Найдите это число.
РЕШЕНИЕ

660 35% от 128,1 составляет 49% от неизвестного числа. Найти
РЕШЕНИЕ

661 В киоске в первый день было продано 40% всех ноутбуков, во второй 53%, а в третий оставшиеся 847 ноутбуков. Сколько ноутбуков продал киоск за три дня?
РЕШЕНИЕ

662 В первый день овощная база отпустила 40% всего имеющегося картофеля, во второй день 60% остатка, в третий день оставшиеся 72 тонны. Сколько тонн картофеля было на базе?
РЕШЕНИЕ

663 Трое рабочих изготовили несколько деталей. Первый рабочий изготовил 0,3 всех деталей, второй 0,6 остатка, а третий оставшиеся 84 детали. Сколько всего деталей изготовили рабочие?
РЕШЕНИЕ

664 В первый день тракторная бригада вспахала 3/8 участка, во второй 2/5 оставшихся, в третий оставшиеся 216 га. Определить площадь участка.
РЕШЕНИЕ

665 Автомобиль преодолел 4/9 всего пути за первый час, 3/5 оставшегося пути за второй час и остаток пути за третий. Известно, что за третий час он прошел на 40 км меньше, чем за второй. Сколько километров проехал автомобиль за эти 3 часа?
РЕШЕНИЕ

666 Выполните расчеты. С помощью микрокалькулятора найдите число, 12,7% которого равняется 4,5212; число 8,52%, из которых равно 3,0246.
РАСТВОР

668 Сравнить без деления.
РЕШЕНИЕ

669 Во сколько раз меньше обратного: 1/5; 2/3; 1/6; 0,3?
РЕШЕНИЕ

670 Задумайте число, которое в 4 раза меньше обратного ему числа; 9 раз.
РЕШЕНИЕ

671 Устно разделите центральное число на обведенные числа.
РЕШЕНИЕ

672 Сколько квадратных плиток со стороной 20 см потребуется для укладки пола в комнате длиной 5,6 м и шириной 4,4 м. Решите задачу двумя способами.
РЕШЕНИЕ

673 Найдите правило размещения чисел в полукругах и вставьте пропущенные числа
РЕШЕНИЕ

675 За 3/5 часа велосипедист проехал 7 1/2 км. Сколько километров проедет велосипедист за 2 1/2 часа, если он будет двигаться с той же скоростью
РЕШЕНИЕ

676 За 1/3 часа пешеход прошел 1 1/2 км. Сколько километров пройдет пешеход за 2,5 часа, если он будет идти с той же скоростью?
РЕШЕНИЕ

678 Найдите значение выражения
РАСТВОР

679 Выполнить шаги 10,1 + 9,9 107,1: 3,5: 6,8 — 4,85; 12,3 + 7,7 187,2: 4,5: 6,4 — 3,4
РАСТВОР

680 7/12 керосина вылили из бочки. Сколько литров керосина было в бочке, если из нее вылилось 84 литра
РЕШЕНИЕ

681 Володя прочитал 234 страницы, что составляет 36% всей книги. Сколько страниц в этой книге?
РЕШЕНИЕ

682 Использование нового трактора для вспашки поля привело к экономии времени на 70% и заняло 42 часа. Сколько времени потребуется, чтобы выполнить эту работу на старом тракторе?
РЕШЕНИЕ

683 Столб, вкопанный в землю на 2/13 своей длины, возвышается над землей на 5 1/2 метра. Найдите длину столба.
РЕШЕНИЕ

684 Токарь, обточив на станке 145 деталей, перевыполнил план на 16%. Сколько деталей нужно было вырезать по плану?
РЕШЕНИЕ

685 Точка C делит отрезок AB на два отрезка AC и CB. Длина АС составляет 0,65 длины отрезка СВ. Найдите СВ и АВ, если АС = 3,9 см.
РЕШЕНИЕ

686 Лыжная дистанция разделена на три части. Длина первого участка составляет 0,48 длины всей дистанции, второго — 5/12 длины первого участка. Какова длина всего пути, если длина второго участка равна 5 км? Какова длина третьего?
РАСТВОР

687 Из полной бочки взяли 14,4 кг квашеной капусты и потом еще 5/12 от этого количества. После этого в бочке осталось 5/8 той квашеной капусты, которая была там ранее. Сколько килограммов капусты было в полной бочке?
РЕШЕНИЕ

688 Когда Костя прошел 0,3 всего пути от дома до школы, ему осталось пройти 150 м до середины пути. Сколько времени занимает путь от дома до школы?
РЕШЕНИЕ

689 Три группы школьников сажали деревья вдоль дороги. Первая группа посадила 35% всех доступных деревьев, вторая группа посадила 60% оставшихся деревьев, а третья группа посадила оставшиеся 104 дерева. Сколько всего деревьев было посажено?
РАСТВОР

690 В цеху имелись токарные, фрезерные и шлифовальные станки. Токарные станки составляли 5/11 всех этих станков. Количество шлифовальных станков составляет 2/5 от числа токарных станков. Сколько станков этих типов было в мастерской, если фрезерных станков на 8 меньше, чем токарных?
РАСТВОР

691 Выполните шаги (1,704: 0,8–1,73) 7,16–2,64; 227,36: (865,6 — 20,8 40,5) 8,38 + 1,12; (0,9464: (3,5 0,13) + 3,92) 0,18; 275,4: (22,74 + 9,66) (937,7 — 30,6 30,5).

В этом уроке мы рассмотрим виды задач на акции и проценты. Давайте научимся решать эти проблемы и выясним, с какими из них мы можем столкнуться в реальной жизни. Узнаем общий алгоритм решения подобных задач.

Мы не знаем, каким было число изначально, но знаем, сколько оно получилось, когда от него отняли определенную дробь. Нам нужно найти оригинал.

То есть мы не знаем , но знаем и .

Пример 4

Дедушка провел свою жизнь в деревне, которая составила 63 года. Сколько лет дедушке?

Мы не знаем исходного числа — возраст. Но мы знаем долю и сколько лет эта доля от возраста. Мы создаем равенство. Оно имеет вид уравнения с неизвестным. Выражаем и находим.

Ответ: 84 года.

Не очень реальная задача. Вряд ли дедушка выдаст такие сведения о годах своей жизни.

Но очень распространена следующая ситуация.

Пример 5

Скидка в магазине по карте 5%. Покупатель получил скидку 30 руб. Какова была цена покупки до скидки?

Мы не знаем исходный номер — стоимость покупки. Но мы знаем дробь (проценты, которые написаны на карточке) и сколько была скидка.

Мы составляем нашу стандартную линию. Выражаем неизвестное значение и находим его.

Ответ: 600 руб.

Пример 6

Чаще всего мы сталкиваемся с этой проблемой. Мы видим не размер скидки, а какая стоимость после применения скидки. И вопрос тот же: сколько бы мы заплатили без скидки?

Давайте снова 5% дисконтную карту. Мы показали карту на кассе и заплатили 1140 рублей. Какая цена без скидки?

Чтобы решить задачу за один шаг, немного переформулируем ее. Поскольку у нас есть скидка 5%, сколько мы платим за полную цену? 95%.

То есть мы не знаем начальную стоимость, но знаем, что 95% она составляет 1140 руб.

Применяем алгоритм. Получаем начальное значение.

3. Сайт «Математика Онлайн» ()

Домашнее задание

1. Математика. 6 класс / Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. — М.: Мнемозина, 2011. С. 104-105. п. 18. № 680; № 683; № 783 (а, б)

2. Математика. 6 класс / Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. — М.: Мнемозина, 2011. № 656.

3. В программу школьных спартакиад вошли прыжки в длину, высоту и бег. В соревнованиях по бегу приняли участие все участники соревнований, в соревнованиях по прыжкам в длину — 30% от всех участников, а в соревнованиях по прыжкам в высоту — остальные 34 студента. Найдите количество конкурентов.

Для использования предварительного просмотра презентаций создайте учетную запись Google (аккаунт) и войдите в нее: https://accounts.google.com

Подписи к слайдам:

«Считайте несчастливым тот день или тот час, в который вы не ничему новому не научился и ничего не прибавил к своему образованию» Я.А. Каменский

Нахождение числа по заданному значению его дроби Учитель математики Токарева И.А. МБОУ гимназия №1 Липецк

Прочтите дроби: Как их по другому назвать? Расположите эти дроби в порядке возрастания.

Найти из 40; 2. Сколько дециметров в полуметре? 3. Найдите часть наименьшего шестизначного числа. 4. Сколько часов в частях суток?

5. Сколько секунд в долях минуты? 6. Сколько минут в четверти часа? 7. В классе 30 учеников, некоторые из них хороши. Сколько хороших учеников в классе? 8. Сколько месяцев содержит

9. Длина провода 64 м. От него были отрезаны части. Сколько метров провода отрезали? (64 40 м) 10. Задумали число, равное 15. Какое число придумали? (15:3 5=25.)

Нахождение числа по заданному значению его дроби Прочитайте самостоятельно текст учебника, с. 91, вплоть до примера. Решите задачу 10 по-новому. 10. Они задумали число, равное 15. Какое число они задумали?

Найдите число, если: Какой вывод можно сделать? (Если дробь правильная, то число больше значения дроби, если дробь неправильная, то число меньше значения дроби.)

На тему: методические разработки, презентации и конспекты

Урок математики в 6 классе Тема Деление дробей. Решение задач на нахождение числа по заданному значению его дроби.

Урок математики в 6 классе Тема Деление дробей. Решение задач на нахождение числа по заданному значению…

Нахождение числа по его дроби. Нахождение дроби числа.

Презентация к уроку. Обобщить и систематизировать знания по темам нахождения числа по его дроби и нахождения дроби числа….

Презентация к уроку математики «Нахождение числа по заданному значению его дроби»

Презентация содержит цели и задачи урока, примеры заданий на нахождение числа по заданному значению его дроби. …

Класс: 6 Презентации к уроку0547

Назад вперед

Внимание! Предварительный просмотр слайдов предназначен только для информационных целей и может не отражать весь объем презентации. Если вас заинтересовала эта работа, пожалуйста, скачайте полную версию.

Назад вперед

Эпиграф к уроку:

«Тот, кто учится сам, успевает в семь раз больше, чем тот, кому все объясняют» (Артур Гитерманн, немецкий поэт)

Тип урока: урок изучения нового материала.

Методы: частичный поиск.

Формы: индивидуальная, коллективная, групповая, индивидуальная.

( Место — 1 занятие по теме)

Вид занятия: объяснительно-иллюстративный

Цель занятия: придумать новый способ решения задач дробями, закрепить умения и навыки решения проблем.

систематизировать решение задач по частям, вывести новый метод решения задач на нахождение числа по его части.

способствовать развитию интереса учащихся не только к содержанию, но и в процессе усвоения знаний, расширять кругозор учащихся. Развитие мышления учащихся, математической речи, мотивационной сферы личности, исследовательских способностей.

прививать учащимся чувство удовлетворения от возможности показать свои знания на уроке. Создать у учащихся положительную мотивацию к совершению умственных и практических действий. Воспитание ответственности, организованности, настойчивости в решении задач.

Оборудование: иллюстративный материал, презентация к занятию. Листы с заданием на размышление, учебник по математике Математика. 6 класс / Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. М.: Мнемозина, 2011.

План урока:

Организационное время.

Актуализация базовых знаний и их коррекция.

Изучение новых знаний.

Физкультминутка.

Первичное крепление.

Первичный тест понимания изучаемого.

Подведение итогов урока. Отражение.

Домашнее задание.

Оценки.

Во время занятий

1. Организационный момент.

( дидактическое задание. психологическое состояние учащихся

Здравствуйте, присаживайтесь. Сообщаем тему, задачи урока и практическую значимость темы.

Цель нашего урока — прийти придумали новый способ решения задач с дробями.

2. Актуализация базовых знаний и их коррекция

(Дидактическая задача — подготовка учащихся к работе на уроке. Обеспечение мотивации и принятия учащимися цели, учебно-познавательной деятельности, актуализация основных знаний и умений).

пятнадцать; ; 3 6; ; (2; ; 19; в)

Вопросы к классу:

Как умножить дробь на натуральное число?

Как найти произведение дробей?

Как найти произведение смешанного числа на число? (используя распределительное свойство умножения или переводя смешанное число в неправильную дробь)

Как умножать смешанные числа?

2) :2; в:; :; :; (; ; ; X)

Вопросы к классу:

Как разделить дробь на натуральное число?

Как разделить одну дробь на другую?

Как разделить смешанное число на смешанное число?

Столы на горке и опоры на столы слабой группы:

Повторить алгоритмы решения задач на нахождение числа по его части.

1) Очистили от снега каток, а это 800 м 2 . Найдите площадь всего катка.

(800:2 5 = 2000 м 2)

2) Винни-Пух собрал из ульев х кг меда, что составляет 30% от того количества, которое ему приснилось. Сколько мёда тебе приснилось, Винни-Пух? (x:30 100)

3) Удав дал обезьяне «v» бананов из того количества, которое он всегда давал. Сколько он всегда давал? (а)

Вопрос к классу:

Какое правило следует здесь запомнить?

(Чтобы найти число по его дробной части, можно эту часть разделить на числитель и умножить на знаменатель)

3. Изучение нового материала. «Открытие» новых знаний детьми.

(Дидактическая задача организовать и направить познавательную деятельность учащихся к цели)

Сегодня на уроке мы попробуем найти более простой способ решения задач на нахождение числа из его дроби. В этом нам помогут выученные правила умножения и деления дробей.

– Запишите правило в тетрадь (а = в: m n).

— Замените знак деления на черту дроби и попробуйте записать в виде одного действия с цифрой «а» и дробью.

N = = в = в:

— Перевести полученное правило на математический язык.

(Чтобы найти число по его части, можно разделить эту часть на дробь) Открытие. Повторите это правило про себя.

Теперь работайте в парах:

Вариант 1 сообщает правилу вариант 2, а вариант 2 — первому.

Чем это правило лучше предыдущего? (Проблема решается одним действием вместо

два)

4. Физическое воспитание.

(Задание снять стресс)

Найти все цвета радуги (каждый охотник хочет знать, где сидит фазан). Цветные квадраты развешены в разных местах по классу. Вы должны вращаться, чтобы найти правильный цвет. Затем упражнения для глаз.

Приложение 1.

5. Первичное крепление.

(Дидактическая задача — добиться от учащихся воспроизведения, осознания, первичного обобщения и систематизации новых знаний. Закрепление метода предстоящего ответа учащегося при очередном опросе)

Первичное закрепление происходит в форме фронтального работать и работать в парах.

(с комментарием вслух)

1) Найдите число, если оно равно 10.

2) Найдите число, если 1% равно 4.

письменно

(с комментариями и записью на доске и в тетрадях)

1) Маша прошла 500 м, это была вся дистанция. Какова длина дистанции? (500:=800м)

2) Масса вяленой рыбы составляет 55% массы свежей рыбы. Сколько свежей рыбы брать. Чтобы получить 231 кг вяленого мяса? (231:=420 кг)

3) Масса клубники в первом ящике равна массе клубники во втором ящике. Сколько кг клубники было в двух ящиках, если в первом было 24 кг клубники?

Работа в парах

(совместная работа) Составьте выражение для задач.

1) Прекрасным летним утром котенок по имени Гав съел x сосисок, которые составляли его ежедневный рацион. Сколько сосисок съедает котенок Гав в день? (x:=сосиски)

2) Незнайка прочитал 117 страниц, что составило 9% волшебной книги. Сколько страниц в волшебной книге? (117:=1300стр)

6. Первичная проверка понимания изучаемого

(в виде самостоятельной работы с проверкой на занятии).

( Дидактическое задание – контроль знаний и устранение пробелов по данной теме)

По одному человеку от каждого варианта вызвать, они будут молча работать над крыльями доски. Затем проверяем решение.

1 вариант

1) найти число, если оно равно 21. (49)

2) найти число, если 15% от него х. ()

3) найти число если 0,88 то 211,2. (240)

Вариант 2

1) найти число, если оно равно 24. (64)

2) найти число, если 20% от него равно х. (5x)

3) найти число если 0,25 то 6,25. (25)

Оцените себя: ни одной ошибки — «5»; 1 ошибка — «4»; у кого больше ошибок — делать работу над ошибками.

7. Подведение итогов урока.

( Дидактическая задача — проанализировать и оценить успешность достижения цели и наметить перспективы дальнейшей работы). Вы сегодня на уроке сделали открытие

придумали новый способ решения задач на дроби, а значит у них получилось в семь раз больше, чем если бы я сам вам все рассказал (посмотрите еще раз на эпиграф к нашему уроку)

Отражение.

(Дидактическая задача — мобилизация учащихся на рефлексию своего поведения, мотивации, способов деятельности, общения).

А теперь ребята продолжайте предложение: Сегодня на уроке я выучила… Сегодня на уроке мне понравилось… Сегодня на уроке повторила… Сегодня на уроке закрепила… Сегодня на уроке На уроке я дала себе оценку… Какие виды работ вызвали затруднения и требуют повторения. .. В каких знаниях я уверен… Помог ли урок продвинуться в знаниях, умениях, навыках по предмету… К над кем, над чем еще надо поработать…

Насколько эффективным сегодня был урок… улыбчивый человечек, если урок понравился и все получилось, и грустный человечек, если еще что-то не получается (у всех на партах картинки с человечками ).

6

. Домашнее задание

(Комментарий, дифференцирован) (Дидактическое задание — обеспечивающее понимание цели, содержания и способов выполнения домашнего задания).

стр. 104-105. п. 18. № 680; № 683; №783(а, б)

Дополнительное задание №656. (для сильных учащихся).

Для творческой группы — придумать задания на новую тему.

7. Оценки за урок.

Все хорошо работали, с аппетитом впитывали знания. Дети! Спасибо за урок.

В этом уроке мы рассмотрим виды заданий на акции и проценты. Давайте научимся решать эти проблемы и выясним, с какими из них мы можем столкнуться в реальной жизни. Узнаем общий алгоритм решения подобных задач.

То есть мы не знаем , но знаем и .

Пример 4

Дед провел свою жизнь в деревне, которая составила 63 года. Сколько лет дедушке?

Ответ: 84 года.

Не очень реальная задача. Вряд ли дедушка выдаст такие сведения о годах своей жизни.

Но очень распространена следующая ситуация.

Пример 5

Скидка в магазине по карте 5%. Покупатель получил скидку 30 руб. Какова была цена покупки до скидки?

Составляем нашу стандартную линейку. Выражаем неизвестное значение и находим его.

Ответ: 600 руб.

Пример 6

Давайте снова 5% дисконтную карту. Мы показали карту на кассе и заплатили 1140 рублей. Какая цена без скидки?

То есть мы не знаем начальную стоимость, но знаем, что 95% она составляет 1140 руб.

Применяем алгоритм. Получаем начальное значение.

3. Сайт «Математика Онлайн» ()

Домашнее задание

1. Математика. 6 класс / Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С. И. Шварцбурд. — М.: Мнемозина, 2011. С. 104-105. п. 18. № 680; № 683; № 783 (а, б)

2. Математика. 6 класс / Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. — М.: Мнемозина, 2011. № 656.

3. В программу школьных спартакиад вошли прыжки в длину, прыжки в высоту и бег. В соревнованиях по бегу приняли участие все участники соревнований, в соревнованиях по прыжкам в длину — 30% от всех участников, а в соревнованиях по прыжкам в высоту — остальные 34 студента. Найдите количество конкурентов.

Проценты. Нахождение процентов от заданного числа. Нахождение числа по его проценту

Урок математики.

Класс: 6

Тема: «Нахождение числа по его дроби».

Цели урока:

Образовательные:

Разработка:

Образовательные:

Тип урока: комбинированный урок.

Оборудование: экран , ПК, проектор, презентация, карточки, учебник.

План:

Организационное время

Контрольное домашнее задание.

Устный счет

Изучение нового материала

Тест

Итог урока

Домашнее задание

Рефлексия

Во время занятий

1. Организационный момент

–Привет, ребята! Сегодня у нас на уроке гости, давайте поприветствуем их и поздороваемся! Присаживайся. Я очень рад видеть вас сегодня. Меня зовут Татьяна Михайловна.

2. Проверка домашнего задания

— Скажи, пожалуйста, что тебе подарили дома?

(№ 635(д, ж), № 641)

— Посмотрите на него слайд, домашняя задача решена, сравните со своим решением

Итого — 156 тетрадей

Я- ? ноутбуки

II-? тетради — это из

Решение:

Пусть x тетрадей в 1 упаковке, затем x тетрадей в 2 упаковках

х = 156;

х = 156: ;

х = 156* ;

х = 84. (тет.) — в 1 уп.

Ответ: 84 тетради, 72 тетради.

— Молодец!

— Сегодня я хотел бы начать урок со следующего высказывания: «Считай неудачным день или час, когда ты не узнал ничего нового и ничего не прибавил к своему образованию». (Ж.-А. Камень небо)

— Эти слова будут девизом нашего урока. И этот день не будет несчастливым, ведь мы снова узнаем что-то новое, закрепим навыки нахождения дроби от числа, умножения и деления обыкновенных дробей, перевода % в десятичные и наоборот.

— Ребят, подскажите, с какого месяца началось?

(декабрь)

Какое время года декабрь?

(зима)

— А какой самый долгожданный праздник зимой?

(Новый год)

Мы всегда готовимся к этому дружному и веселому празднику, покупаем подарки, украшаем место, где живем и проводим много времени, наряжаем елку.

А сегодня на уроке я приглашаю вас принять участие в небольшом проекте «Наша елочка». Это будет не собственно проект, а подготовка к нему, ведь елка – часть новогоднего праздника.

2. Ментальный счет

Во-первых, я предлагаю вам зажечь гирлянду для нашей елки!

Запускаем «Новогодний ментальный счет»! перед вами новогодняя гирлянда, если вы правильно посчитаете или ответите, то ее огоньки станут разноцветными.

Следующее задание:

Как умножить две обыкновенные дроби?

Как делить на обыкновенную дробь?

Что такое обратные числа?

Ребята, как перевести % в число?

(% разделить на 100)

Как преобразовать число в процент?

(число умножить на 100)

И так следующее задание (Слайд)

0,65 65%

0,3 30%

48% 0,48

150% 1,5

А кто подскажет, как найти дробь числа?

(Чтобы найти дробь числа, нужно это число умножить на эту дробь)

от 36; 28

0,4 от 60; 24

1,2 от 0,5; 0,6

Следующее задание:

На елке 60 шаров. из которых красные. Сколько красных шаров?

(10)

Молодцы ребята, мы с Вали украсили нашу елку гирляндой.

Пояснения к новому материалу

Ребята. А чем украшать елку после гирлянды?

(звездочка)

И так следующее задание «Рождественская звезда»

Прочитайте пожалуйста задачу на слайде

« Очищена от снега ледовая арена 800 м 2 . Найдите площадь всего катка.

— Что известно в задаче?

(расчищено, а это 800 м 2 )

— А 800 м 2 это часть катка или весь каток?

(часть)

_ Что нужно найти в задаче?

(Площадь всей ледовой арены)

— Пусть х м 2 весь каток

Очистили от снега как найти дробь от числа?

(Вам нужно умножить это число на эту дробь)

ТЕХ. ИКС *

— мы знаем, что это такое?

(800)

— Составим уравнение

Х * = 800

В чем основное действие

(Умножение)

— назовите компоненты

(1 множитель, 2 множитель, произведение)

— что неизвестно?

(1 множитель)

— как его найти?

(1 множитель = произведение: x 2 множителя)

Х = 800:

Х = 800 *

Х = 1600 м 2

И так площадь всего катка 1600 м 2

Ребята, мы не знали самого числа в задаче, но знали что чему равно таковы его часть, т.е. по его дроби мы нашли само число.

Итак, давайте завершим Чтобы найти число по его дроби, вам нужно разделить это число на эту дробь.

Дети, все элементарно!

Объясняю популярно:

Не надо тут быть гением

И число данное нам

Начнем делить на дроби.

Итак, ребята, мы смогли украсить нашу елку новогодней звездой.

Физминутка

Звучит музыка, ребенок выходит и проводит физминутку

Вместе с вами мы считали и говорили о цифрах,

И вот мы вместе встали, потянулись костями.

На счет раз сожмем кулак, на счет два в локтях сожмем.

На счет три — прижать к плечам, на 4 — к небу

Ну прогнулись и улыбнулись друг другу

Не будем забывать о пятёрке — мы всегда будем добры.

На счет шесть прошу всех сесть.

Числа, я, и вы, друзья, вместе дружны 7-й.

4. Закрепление изученных знаний.

Ну вот, со всеми моими предыдущими заданиями вы справились, поэтому предлагаю перейти к следующему этапу украшения новогоднего шара на елку. — На этом этапе будем решать задачи на нахождение числа по его дроби и украшать елку новогодними игрушками.

Ребята посмотрите пожалуйста на доске на доске есть примеры которые мы должны решить

(по каждому примеру 1 ученик после решения ученик вешает шарики)

Найдите число если:

из этого числа 24 = 56

0,6 от этого числа равно 6 = 10

0,3 от этого числа равно 33 = 110

Ребята посмотрите пожалуйста на слайд

3) Ребята, у вас на столах лежат рабочие листы, с помощью которых мы сегодня решим не одну задачу. Итак, читаем внимательно условие задачи №1 и обращаем внимание на то, что мы знаем в задаче и что нужно найти.

Всего — ? км

Автомобиль — 30 км

Решение:

Ответ: 50 км

Всего — ? игры.

6 класс — 15 игр. — это

Другие классы — ? игры.

Решение:

Ответ: 30 игрушек

После решения двух задач 3 ученика решают тест за компьютером, а остальные продолжают решать задачи.

Самостоятельная работа

К)49; Л) 64; М) 56.

Г)90; Г) 10; Н) 20.

Б) 30; Г) 4; Г) 25.

Ответы:

Всего — ? дев.

6 класс — 3 гр. — это

Другие студенты — дев.

Решение:

1)3: = 11 (гир.) — всего

2) 11-3 = 8 (гир.) — прочие классы

Ответ: 8 гирлянд

Всего — ? окна

я — 30 окон — это

II-? окна

Решение:

30: 0,6 = 50 (окна) — всего в школе

50 — 30 = 20 (окна) — на 2 день

Ответ: 20 окон

Краткое содержание урока

– Наш урок подходит к концу, давайте подведем итоги.

Какие правила МЫ ПОВТОРЯЛИ НА СЕГОДНЯШНЕМ УРОКЕ?

О каком правиле мы сегодня говорим?

И так если посмотреть, то к новому году мы начали готовить елку, привезли и украсили ее, а помогла нам во всем этом наша любимая математика и наша тема «Нахождение, числа по его дробям»

В качестве домашнего задания , Я предлагаю вам задания, ПРЕДСТАВЛЕННЫЕ В ВАШИХ РАБОЧИХ ЛИСТАХ.

Домашнее задание.

3. Мама попросила сына полить 0,2 из всех клумб на даче. Сын быстро подсчитал и сказал, что мне не составит труда хорошо полить одну клумбу. Сколько клумб в стране?

4. Пять друзей купили конфеты и съели сразу три, это составило

В конце нашего урока мы должны выполнить самое приятное задание нарядить нашу зеленую красавицу разноцветных шаров! Эти шарики СМАЙЛИ у вас на столах, выберите тот, который подходит вашему настроению и, уходя, прикрепите его к нашей елочке!

Ребята, получившие подарки, могут сдать дневники на оценку.

БОЛЬШОЕ СПАСИБО ЗА УРОК! Желаю вам удачи в следующих уроках.

Красная карточка означает: «Я доволен уроком, урок был для меня полезен, я много, с пользой и хорошо занимался на уроке, понял все, что было сказано и сделано на уроке».

Карточка желтого цвета означает: «Урок был интересным, я принимал в нем активное участие, урок был для меня в определенной мере полезен, я ответил с места, мне удалось выполнить ряд заданий, я был достаточно комфортно на уроке».

Карточка синего цвета означает: «Я не получил большой пользы от урока, я не очень понял, о чем идет речь, мне это не очень нужно, я не буду делать домашнее задание, я не интересовался, не был готов к ответам на уроке».

РАБОЧИЙ ЛИСТ

Два дня школьники украшали окна в школе. В первый день асили 0,6 всех окон, что составило 30 окон. Сколько окон было украшено на второй день?

Домашнее задание.

1. Найдите значение количества, если:

а) 0,8 из них равны 576 г; б) 2/9 его равны 36 ф;

в) 24% равно 57,6 км; г) 2,3% от него равняется 2,07 рубля.

2. На подарок мальчику друзья собрали четверть стоимости велосипеда, что составило 120 руб. Сколько денег нужно детям, чтобы купить подарок?

Самоанализ.

Тема: Нахождение числа по его части ».

Цели урока:

Образовательные:

систематизировать знания учащихся о делении обыкновенных дробей;
отработать навыки выполнения действий с обыкновенными дробями;
способствуют формированию умения решать задачи на нахождение числа по его части, выраженной дробью, путем деления на дробь;
создать организационные условия для развития у учащихся умений анализировать и сравнивать;
создавать у учащихся положительную мотивацию к выполнению мыслительных и практических действий, способствовать развитию способности к сотрудничеству.

Разработка:

способствуют развитию логического мышления, памяти;

развивать умение анализировать ситуацию и оценивать результаты деятельности;

развивать самостоятельность и внимание.

Образовательные:

воспитание интереса к предмету на основе использования мультимедийных возможностей компьютера, а также интереса к традициям празднования Нового года.

воспитание аккуратности в оформлении работы.

Цели занятия направлены на получение знаний и умений:

Понимать учебную задачу, осуществлять решение учебной задачи как под руководством учителя, так и самостоятельно, контролировать свои действия в процессе ее выполнения, выявлять и исправлять ошибки, как чужие, так и свои, оценивать свои достижения.

Воспитывать любовь к математике, интерес к ней, уважение друг к другу, умение слушать, дисциплинированность, самостоятельность.

Ф формировать навыки деления и умножения обыкновенных дробей, правильно читать и писать выражения, содержащие обыкновенные дроби, формировать умение решать задачи по теме «Нахождение числа по его дроби».

Тип урока: изучение нового материала.

Оборудование: экран , ПК, проектор, презентация, рабочие листы.

Форм организация занятий:

Фронтальная

индивидуальная

Методы обучения :

визуальный

проблемно-поисковый

репродуктивный

Описание занятия

Тема занятия отражает в тематическом планировании и представляет собой 1 занятие из 5 по теме «Нахождение числа по его части» и базируется на содержании трех тем: «Взаимные числа », «Умножение дробей» и «Деление дробей». Я хотел, чтобы учащиеся на этом уроке увидели связь этой темы с ранее изученной и осознали (что особенно важно в математике), что все темы тесно взаимосвязаны, и их нельзя изучать изолированно друг от друга. В ходе урока дети применяют знания, полученные не только на этом уроке, но и на предыдущих уроках.

Структура урока 9 основных этапов

Организация времени

Проверка домашнего задания.

Счет

Изучение нового материала

Закрепление пройденного материала

Тест

Итог урока

Домашнее задание

Рефлексия

В начале урока орг. Момент позволил мне подготовиться к уроку. Разрешается давать положительный настрой на плодотворное сотрудничество.

На стадии мысленного счета цель заключалась в том, чтобы включить учащихся в работу, определить объем работы на уроке, поставить перед учащимися цель: создать игровую ситуацию о проекте «Наша новогодняя елка». Устная работа в игровой форме позволяла создать ситуацию успеха и отвечала психологическим особенностям возраста. Математический диктант способствовал формированию умения правильно читать выражения, содержащие обыкновенные дроби, а также самостоятельно выполнять действия, оценивать свои достижения.

На этапе изучение нового материала Детям было предложено прийти к выводу, что для нахождения числа по его дроби нужно это число разделить на эту дробь.

На стадии фиксации Изученный материал использовалась фронтальная и индивидуальная работа, формировались навыки деления и умножения обыкновенных дробей. Самопроверка (тест) способствовала формированию умения видеть свои ошибки, оценивать свои достижения.

Этап объяснения домашнего задания способствовал интересу учащихся. Задания ориентированы на практику и помогают убедить детей в том, что математика – наука, тесно связанная с жизнью.

Этап рефлексии явился логическим завершением урока и помог учащимся выразить свое отношение к уроку, а мне, как учителю, увидеть оценку своего урока.

Таким образом, цели, поставленные перед уроком, на мой взгляд, достигнуты.

«Нахождение числа по его дроби» — Учебник математики 6 класс (Виленкин)

Краткое описание:

Вы уже умеете находить дробь числа, и в этом разделе вы научитесь находить число из его дробь. Нужно быть очень внимательным, чтобы не запутаться, и решить все головоломки быстро и правильно.
Давайте быстро вспомним, как мы находим дробь числа: мы просто умножаем это число на дробь. Например, нужно найти 3/5 числа 15. Решаем 3/5 * 15 = 3*15 / 5 =3*3=9. Зачем нам нужно знать, как это сделать? Для того, чтобы суметь найти какую-то часть чего-то целого. Например, зная, какую часть книги вы прочитали и сколько в ней страниц, можно узнать, сколько страниц осталось прочитать. Помните, когда мы ищем дробь числа, у нас есть что-то целое и его часть, и нам нужно умножить это целое на часть, поэтому мы находим часть в количественном выражении и это число всегда будет меньше исходного количество.
В задачах, когда мы ищем число по его дроби, это число всегда должно быть больше, потому что, по сути, мы ищем что-то целое, зная только его часть. Например, вы прочитали 100 страниц книги, но это только ее третья часть. Сколько страниц в книге? Как мы найдем это число? Зная, что 100 страниц это треть, нам нужно 100*3 и тогда мы узнаем сколько страниц в книге — 100*3=300. А если попробовать решить через уравнение? Пусть х- общее количество страниц в книге, как узнать сколько мы прочитали, нужно х умножить на 1/3 и будет равно 100. Значит — х * 1/3 = 100. Решаем уравнение далее — х = 100:1/3, а мы уже узнали, что для того, чтобы число разделить на дробь, нужно умножить его на обратную. Получается х=100: 1/3 = 100 * 3/1 = 300. Понял? Итак, чтобы найти число, зная его дробную часть и его значение, нам нужно значение (натуральное число) разделить на дробь, то есть умножить на перевернутую дробь и это число всегда будет больше, чем данное нам в условие!
Если в задаче задана не дробь, а процент, что делать? Преобразование процентов в десятичные числа: 40%=0,40; 75% = 0,75 и решаем дальше по выученной схеме.

Весь каток.

Раствор. Обозначим площадь катка через х м 2 . По условию этой площади они равны 800 м 2 , т.е. х = 800.
Значит х = 800 := 800 = 2000. Площадь каток 2000 м2.

Чтобы найти число по значению его дроби, нужно разделить это значение на дробь.

Задача 2. Пшеницей засеяно 2400 га, что составляет 0,8 всего поля. Найдите площадь всего поля.

Раствор. Поскольку 2400:0,8 = 24000:8 = 3000, площадь всего поля составляет 3000 га.

Задание 3. Повысив производительность труда на 7%, рабочий за тот же период изготовил на 98 деталей больше, чем было запланировано по плану. Сколько деталей должен был сделать рабочий по плану?

Раствор. Так как 7% = 0,07, а 98:0,07 = 1400, рабочий по плану должен был изготовить 1400 деталей.

? Сформулируйте правило нахождения числа по его значению дробей . Расскажите, как найти число, зная значение его процента.

К 631. Девушка пробежала на лыжах 300 м, это была вся дистанция. Какова длина дистанции?

632. Свая возвышается над водой на 1,5 м, что составляет длину всей сваи. Какова длина всей стопки?

633. На элеватор отправлено 211,2 тонны зерна, что составляет 0,88 зерна за сутки. Сколько зерна было намолочено за день?

634. За рационализаторское предложение инженер получил сверх месячного оклада 68,4 руб. , что составляет 18% от этого оклада. Какова месячная зарплата инженера?

635. Масса вяленой рыбы составляет 55% массы свежей рыбы. Сколько нужно взять свежей рыбы, чтобы получить 231 кг вяленой рыбы?

636. Масса винограда в первом ящике равна массе винограда во втором ящике. Сколько килограммов винограда было в двух ящиках, если в первом ящике было 21 кг винограда?

637. Продал полученные магазином лыжи, после чего осталось 120 пар лыж. Сколько пар лыж получил магазин?

638. Картофель при сушке теряет 85,7% своей массы. Сколько взять сырого картофеля, чтобы получить 71,5 тонны сушеного?

639. Вкладчик Сбербанка внес определенную сумму на срочный вклад, а через год у него на сберкнижке было 576 рублей. 80 тыс. Какой была сумма вклада, если Сбербанк платит 3% годовых по срочным вкладам?

640. В первый день туристы проехали по намеченному маршруту, а во второй день — 0,8 от того, что они проехали в первый день. Какой длины запланированный путь, если во второй день туристы прошли 24 км?

641. Студент прочитал сначала 75 страниц, а потом еще несколько страниц. Их количество составило 40% от прочитанного впервые. Сколько страниц в книге, если общее количество прочитанных книг?

642. Велосипедист проехал сначала 12 км, а затем еще несколько километров, что составило первый отрезок пути. После этого ему пришлось ехать всю дорогу. Какова длина всего пути?

643. из числа 12 неизвестен номер. Найдите это число.

644. 35% 128D — это 49% неизвестного числа. Найдите это число.

645. В первый день в киоске было продано 40% всех ноутбуков, во второй день — 53% всех ноутбуков, в третий день — оставшиеся 847 ноутбуков. Сколько ноутбуков продал киоск за три дня?

646. Овощная база отпустила 40% всего имеющегося картофеля в первый день, 60% остатка во второй день и оставшиеся 72 тонны в третий день. Сколько тонн картофеля было на базе?

647. Трое рабочих изготовили ряд деталей. Первый рабочий изготовил 0,3 всех деталей, второй — 0,6 остатка, а третий — оставшиеся 84 детали. Сколько всего деталей изготовили рабочие?

648. В первый день тракторная бригада вспахала участок, во второй день остальные, а в третий день оставшиеся 216 га. Определить площадь участка.
649. Автомобиль прошел за первый час всего пути, за второй час оставшегося пути и за третий час оставшегося пути. Известно, что за третий час он прошел на 40 км меньше, чем за второй час. Сколько километров проехал автомобиль за эти 3 часа?

650. Вы можете найти число по заданному значению его процента с помощью микрокалькулятора. Например, чтобы найти число, 2,4% которого составляет 7,68, вы можете использовать следующую программу : Выполните вычисления. Найдите с помощью калькулятора:
а) число 12,7% от которого равно 4,5212;
б) число, 8,52% которого равны 3,0246.

P 651. Вычислите устно:

652. Не разделяя, сравните:

653. Во сколько раз меньше обратного:

654. Задумайте число, которое в 4 раза меньше обратного ему числа; 9 раз.

655. Устно разделите центральное число на число в кружках:

656. Сколько квадратных плиток со стороной 20 см потребуется для укладки пола в помещении длиной 5,6 м и площадью 4,4 м широкий. Решите задачу двумя способами.

M 657. Найдите правило размещения цифр полукругами и вставьте недостающие цифры (рис. 29).

658. Выполнение деления:

659. Велосипедист проехал 7 км за час. Сколько километров проедет велосипедист за 2 часа, если будет двигаться с той же скоростью?

660. За 4~ часа пешеход прошел 1 км. Сколько километров пройдет пешеход за 2 часа, если он будет идти с той же скоростью?

661. Уменьшить дробь:

663. Сделать следующее:

1) 10,14-9,9 107,1:3,5:6,8-4,8;
2) 12,34-7,7 187,2:4,5:6,4-3,4.

D 664. Керосин, который там был, вылили из бочки. Сколько литров керосина было в бочке, если из нее вылили 84 литра?

665. При покупке цветного телевизора в кредит было оплачено наличными 234 рубля, что составляет 36% от стоимости телевизора. Сколько стоит телевизор?

666. Рабочий получил путевку в санаторий со скидкой 70% и заплатил за нее 42 рубля. Сколько стоит путевка в санаторий?

667. Столб, вкопанный в землю на всю длину, возвышается над землей на 5 м. Найдите всю длину столба.

668. Токарь, обточив на станке 145 деталей, перевыполнил план на 16%. Сколько деталей нужно было вырезать по плану?

669. Точка C делит отрезок AB на два отрезка AC и CB. Длина отрезка АС составляет 0,65 длины отрезка СВ. Найдите длины отрезков СВ и АВ, если АС = 3,9 см.

670. Лыжная дистанция разделена на три участка. Длина первого участка равна 0,48 длины всей дистанции, длина второго участка равна длине Левого участка. Какова длина всего пути, если длина второго участка равна 5 км? Какова длина третьего участка?

671. Из полной бочки взяли 14,4 кг квашеной капусты и то такое количество. После этого в бочке осталась та квашеная капуста, которая была там раньше. Сколько килограммов квашеной капусты было в полной бочке?

672. Когда Костя прошел 0,3 пути от дома до школы, ему оставалось пройти 150 м до середины пути. Сколько времени занимает путь от дома Кости до школы?

673. Три группы школьников сажали деревья вдоль дороги. Первая группа посадила 35% всех доступных деревьев, вторая группа посадила 60% оставшихся деревьев, а третья группа посадила оставшиеся 104 дерева. Сколько деревьев было посажено?

674. В мастерской имелись токарные, фрезерные и шлифовальные станки. Токарные станки составляли все эти станки. Количество шлифовальных станков равнялось количеству токарных станков. Сколько станков этих типов было в мастерской, если фрезерных станков было на 8 меньше, чем токарных?

675. Сделайте следующее:

а) (1,704:0,8 -1,73) 7,16 -2,64;
б) 227,36: (865,6 — 20,8 40,5) 8,38 + 1,12;
в) (0,9464:(3,5 0,13) + 3,92) 0,18;
г) 275,4: (22,74 + 90,66) (937,7 — 30,6 30,5).

Н.Я.Виленкин, А.С. Чесноков, С.И. Шварцбурд, В.И. Жохов, Математика для 6 класса, Учебник для средней школы

Календарно-тематическое планирование по математике, задачи и ответы для школьника онлайн, курсы для учителя математики скачать

Содержание урока

конспект урока опорная рамка презентации урока ускоренные методы интерактивные технологии Практика заданий и упражнений самопроверка мастер-классы, тренинги, кейсы, квесты домашние задания вопросы для обсуждения риторические вопросы от учащихся иллюстрации

аудио, видеоклипы и мультимедиа фотографии, картинки графика, таблицы, схемы юмор, анекдоты, приколы, комиксы притчи, поговорки, кроссворды, цитаты Дополнения

рефераты статьи чипы для любознательных шпаргалки учебники основной и дополнительный словарь терминов прочее

Совершенствование учебников и уроков

исправление ошибок в учебнике обновление фрагмента в учебнике элементы новаторства на уроке замена устаревших знаний новыми Только для учителей

идеальные уроки календарь план на год руководство дискуссионные программы интегрированные уроки

В этом уроке мы рассмотрим виды заданий на акции и проценты. Давайте научимся решать эти проблемы и выясним, с какими из них мы можем столкнуться в реальной жизни. Изучите общий алгоритм решения подобных задач.

То есть мы не знаем , но знаем и .

Пример 4

Дед провел свою жизнь в деревне, которая составила 63 года. Сколько лет дедушке?

Ответ: 84 года.

Не очень реальная задача. Вряд ли дедушка выдаст такие сведения о годах своей жизни.

Но очень распространена следующая ситуация.

Пример 5

Скидка в магазине по карте 5%. Покупатель получил скидку 30 руб. Какова была цена покупки до скидки?

Мы составляем нашу стандартную линию. Выражаем неизвестное значение и находим его.

Ответ: 600 руб.

Пример 6

Давайте снова 5% дисконтную карту. Мы показали карту на кассе и заплатили 1140 рублей. Какая цена без скидки?

Чтобы решить задачу за один шаг, немного переформулируем ее. Поскольку у нас скидка 5%, сколько мы платим от полной цены? 95 %.

То есть мы не знаем начальную стоимость, но знаем, что 95% она составляет 1140 руб.

Применяем алгоритм. Получаем начальное значение.

3. Сайт «Математика Онлайн» ()

Домашнее задание

1. Математика. 6 класс / Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С. И. Шварцбурд. — М.: Мнемозина, 2011. С. 104-105. п. 18. № 680; № 683; № 783 (а, б)

2. Математика. 6 класс / Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. — М.: Мнемозина, 2011. № 656.

Интерес — одно из понятий прикладной математики, которые часто встречаются в повседневной жизни. Так, часто можно прочитать или услышать, что, например, в выборах приняли участие 56,3% избирателей, рейтинг победителя конкурса 74%, промышленное производство увеличилось на 3,2%, банк берет 8% годовых, молоко содержит 1,5% жира, ткань содержит 100% хлопка и т. д. Понятно, что понимание такой информации необходимо в современном обществе.

Один процент от любой величины — суммы денег, количества учеников в школе и т. д. — называется одной сотой. Процент обозначается знаком %, Таким образом,
1% равен 0,01, или \(\frac(1)(100)\) части значения

Вот несколько примеров:
— 1% от минимальной заработной платы 2300 рублей. (сентябрь 2007 г.) — это 2300/100 = 23 рубля;
— 1% населения России, равно примерно 145 млн человек (2007 г.), составляет 1,45 млн человек;
— 3%-ная концентрация раствора соли — это 3 г соли в 100 г раствора (напомним, что концентрация раствора — это та часть, которая составляет массу растворенного вещества от массы всего раствора).

Понятно, что вся рассматриваемая величина составляет 100 сотых, или 100% от самой себя. Поэтому, например, надпись на этикетке «хлопок 100%» означает, что ткань состоит из чистого хлопка, а 100% успеваемость означает, что в классе нет неуспевающих учеников.

Слово «процент» происходит от латинского pro centum, что означает «от ста» или «на 100». Эту фразу можно встретить в современной речи. Например, говорят: «Из каждых 100 участников лотереи 7 участников получили призы». Если это выражение понимать буквально, то это утверждение, конечно, неверно: ясно, что можно выбрать 100 человек, участвующих в лотерее и не получающих призов. На самом деле точное значение этого выражения состоит в том, что 7% участников лотереи получили призы, и именно такое понимание соответствует происхождению слова «процент»: 7% — это 7 из 100, 7 человек из 100. люди.

Знак «%» получил распространение в конце 17 века. В 1685 году в Париже вышла книга «Руководство по коммерческой арифметике» Матье де ла Порта. В одном месте речь шла о процентах, которые тогда обозначали «cto» (сокращение от cento). Однако наборщик принял это «c/o» за дробь и набрал «%». Так из-за опечатки этот знак и вошел в обиход.

Любой процент можно записать в виде десятичной дроби, выражающей часть количества.

Чтобы выразить процент в виде числа, разделите процент на 100. Например:

\(58\% = \frac(58)(100) = 0,58; \;\;\; 4,5\% = \frac(4,5)(100) = 0,045; \;\;\; 200\% = \frac(200)(100) = 2\)

Для обратного перехода, обратное действие. Таким образом, Чтобы выразить число в процентах, нужно умножить его на 100:

\(0,58 = (0,58 \cdot 100)\% = 58\%\) \(0,045 = (0,045 \ cdot 100)\%=4,5\%\)

В практической жизни полезно понимать соотношение между простейшими значениями процентов и соответствующими дробями: половина — 50%, четверть — 25%, три четверти — 75 %, пятая часть — 20 %, три пятых — 60 % и т. д.

Полезно также понимать разные формы выражения одного и того же изменения величины, сформулированные без процентов и с помощью процентов. Например, в сообщениях «МРОТ с февраля повышен на 50%» и «МРОТ с февраля повышен в 1,5 раза» означают одно и то же. Аналогично, увеличить в 2 раза — значит увеличить на 100%, увеличить в 3 раза увеличить на 200%, уменьшить в 2 раза — значит уменьшить на 50%.

Аналогично
— увеличить на 300% — значит увеличить в 4 раза,
— уменьшить на 80% — значит уменьшить в 5 раз.

Интересные задачи

Поскольку проценты могут быть выражены в виде дробей, задачи с процентами по существу аналогичны задачам с дробями. В простейших процентных задачах некоторое значение а принимается за 100 % («целое»), а его часть b выражается числом р %.

В зависимости от того, что неизвестно — а, б или р, различают три вида процентных задач. Эти задачи решаются так же, как и соответствующие дробные задачи, но перед их решением число p% выражается в виде дроби.

1. Нахождение процента от числа.
Чтобы найти \(\frac(p)(100) \) из a, умножьте a на \(\frac(p)(100) \):

\(b = a \cdot \frac(p)( 100) \)

Итак, чтобы найти p% числа, нужно это число умножить на дробь \(\frac(p)(100)\). Например, 20 % от 45 кг равно 45 0,2 = 9 кг, а 118 % от x равно 1,18x

2. Нахождение числа по его проценту.
Чтобы найти число по его части b, выраженной в виде дроби \(\frac(p)(100) , \; (p \neq 0) \), разделите b на \(\frac(p)(100) \):
\(a = b: \frac(p)(100) \)

Таким образом, чтобы найти число по его части, равной p% этого числа, надо эту часть разделить на \( \фрак(р)(100)\). Например, если 8% длины отрезка составляют 2,4 см, то длина всего отрезка равна 2,4:0,08 = 240:8 = 30 см.

3. Нахождение процента от двух чисел.
Чтобы найти, сколько процентов число b составляет от a \((a \neq 0) \), необходимо сначала выяснить, какая часть b составляет от a, а затем выразить эту часть в процентах:

\(p = \frac(b)(a)\cdot 100\%\) Итак, чтобы узнать, на сколько процентов первое число от второго, нужно первое число разделить на второе и умножьте результат на 100.
Например, 9 г соли в растворе 180 г это \(\frac(9\cdot 100)(180) = 5%\) раствор.

Частное двух чисел, выраженное в процентах, называется процентом этих чисел. Поэтому последнее правило называется правилом для нахождения процента двух чисел.

Легко видеть, что формулы

\(b = a \cdot \frac(p)(100), \;\; a = b: \frac(p)(100), \;\; p = \frac(b)(a) \cdot 100 \% \;\; (a,b,p \neq 0) \) взаимосвязаны, а именно, две последние формулы получаются из первой, если выразить значения а и р от него. Поэтому первая формула считается основной и называется формулой процентов. Формула процентов объединяет все три типа задач на дроби, и вы можете использовать ее, если хотите найти любое из неизвестных a, b и p.

Составные задачи на проценты решаются аналогично задачам на дроби.

Простой процентный рост

При несвоевременной оплате человеком квартплаты на него налагается штраф, который называется «штраф» (от латинского poena — наказание). Так, если пеня составляет 0,1% от суммы арендной платы за каждый день просрочки, то, например, за 19 дней просрочки сумма составит 1,9% от суммы арендной платы. Поэтому вместе, скажем, с 1000 р. арендной платы, человек должен будет заплатить штраф в размере 1000 0,019= 19 руб., а всего 1019 руб.

Понятно, что в разных городах и у разных людей квартплата, размер пени и время просрочки разные. Поэтому имеет смысл составить общую формулу ренты для неряшливых плательщиков, применимую во всех обстоятельствах.

Пусть S — месячная арендная плата, штраф — p% от арендной платы за каждый день просрочки, а n — количество дней просрочки. Сумму, которую лицо должно заплатить после n дней просрочки, обозначим S n .
Тогда за n дней просрочки штраф составит pn% от S, или \(\frac(pn)(100)S \), а в сумме придется заплатить \(S + \frac(pn)( 100)S = \left(1+ \frac(pn)(100) \right) S \)
Таким образом:
\(S_n = \left(1+ \frac(pn)(100) \right) S \)

Эта формула описывает множество конкретных ситуаций и имеет специальное название: формула для простого процентного роста.

Аналогичная формула получится, если некоторое значение уменьшится за заданный период времени на определенное количество процентов. Как и выше, легко проверить, что в этом случае
\(S_n = \left(1- \frac(pn)(100) \right) S \)

Эту формулу также называют простой процентной формулой роста, , хотя данное значение на самом деле уменьшается. Рост в этом случае «отрицательный».

Прирост сложных процентов

В российских банках по отдельным видам вкладов (так называемые срочные вклады, которые не могут быть приняты ранее, чем через срок, указанный в договоре, например, через год), очередная системная выплата доход: за первый год от внесенной суммы на счет доход составляет, например, 10% от нее. В конце года вкладчик может вывести из банка вложенные деньги и полученный доход — «проценты», как его обычно называют.

Если вкладчик этого не сделал, то проценты добавляются к первоначальному вкладу (капитализируются), и поэтому в конце следующего года банком начисляется 10% за новую, увеличенную сумму. Другими словами, при такой системе начисляются «проценты на проценты», или, как их обычно называют, сложных процентов.

Подсчитаем, сколько денег получит вкладчик через 3 года, если положит на срочный банковский счет 1000 рублей. и ни разу в течение трех лет не снимут деньги со счета.

10% от 1000 рублей составляют 0,1 1000 = 100 рублей, следовательно, через год на его счету будет
1000 + 100 = 1100(р.)

10% от новой суммы 1100 рублей. составляют 0,1 1100 = 110 руб., следовательно, через 2 года на его счету будет
1100 + 110 = 1210 (р.)

10% от новой суммы 1210 руб. составляют 0,1 1210 = 121 рубль, следовательно, через 3 года на его счету будет
1210 + 121 = 1331 (р. )

Нетрудно представить, сколько времени потребуется при таком прямом, «лобовом» расчет, чтобы найти сумму депозита через 20 лет. Между тем, расчет можно сделать гораздо проще.

А именно через год первоначальная сумма увеличится на 10%, то есть составит 110% от первоначальной суммы, или другими словами увеличится в 1,1 раза. В следующем году новая, уже увеличенная сумма также увеличится на те же 10%. Следовательно, через 2 года первоначальная сумма увеличится в 1,1 1,1 = 1,1 2 раза.

Еще через год эта сумма также увеличится в 1,1 раза, так что первоначальная сумма увеличится в 1,1 1,1 2 = 1,1 3 раза. При таком способе рассуждений получаем гораздо более простое решение нашей задачи: 1,1 3 1000 = 1,331 1000 — 1331(р.)

Теперь решим эту задачу в общем виде. Пусть банк начисляет доход в размере p% годовых, сумма депонирования равна S p., а сумма, которая будет на счете через n лет, равна S n p.

Значение p% от S равно \(\frac(p)(100)S \) r., и через год на счету будет сумма
\(S_1 = S+ \frac(p)(100) S = \left(1+ \frac(p)(100) \right)S \)
, то есть начальная сумма увеличится в \(1+ \frac(p)(100) \) раз.

За следующий год сумма S 1 увеличится на такую же сумму, и поэтому через два года на счете будет сумма 9n S \)

Эта формула называется формула роста сложных процентов , или просто формула сложных процентов.

Число, кратное двум. Наибольший общий делитель и наименьшее общее кратное

Наименьшее общее кратное двух чисел напрямую связано с наибольшим общим делителем этих чисел. Эта связь между НОД и НОК определяется следующей теоремой.

Теорема.

Наименьшее общее кратное двух целых положительных чисел a и b равно произведению чисел a и b на наибольший общий делитель чисел a и b, то есть НОК (a, b) = a b: gcd (a, b ).

Доказательство.

Пусть M — любое кратное чисел a и b. То есть M делится на a, и по определению делимости существует некоторое целое число k такое, что выполняется равенство M = a · k. Но M делится на b, тогда a · k делится на b.

Обозначим НОД (a, b) как d. Тогда мы можем записать равенства a = a 1 d и b = b 1 d, а a 1 = a: d и b 1 = b: d будут взаимно простыми числами. Поэтому полученное в предыдущем абзаце условие, что a k делится на b, можно переформулировать следующим образом: a 1 d k делится на b 1 d, а это, в силу свойств делимости, эквивалентно условию, что a 1 k делится на b 1 d. делится на b 1 .

Также необходимо записать два важных следствия рассматриваемой теоремы.

Общие кратные двух чисел равны кратным их наименьшему общему кратному.

Это действительно так, поскольку любое общее кратное M чисел a и b определяется равенством M = LCM (a, b) t для некоторого целого значения t.

Наименьшее общее кратное взаимно простых положительных чисел a и b равно их произведению.

Обоснование этого факта достаточно очевидно. Так как a и b взаимно просты, то НОД (a, b) = 1, следовательно, НОК (a, b) = a b: НОД (a, b) = a b: 1 = a b.

Наименьшее общее кратное трех или более чисел

Нахождение наименьшего общего кратного трех или более чисел можно свести к последовательному нахождению НОК двух чисел. Как это делается, показано в следующей теореме. A 1, a 2,…, a k совпадают с общими кратными m k-1 и a k, следовательно, совпадают с кратными m k. А так как наименьшим положительным кратным числа m k является само число m k, то наименьшим общим кратным чисел a 1, a 2,…, a k является m k.

Библиография.

Виленкин Н.Я. и другая математика. 6 класс: учебник для общеобразовательных учреждений.
Виноградов И.М. Основы теории чисел.
Михелович Ш.Х. Теория чисел.
Куликов Л.Я. и другие. Сборник задач по алгебре и теории чисел: учебник для студентов физико-математических факультетов. специальности педагогических институтов.

Общее кратное двух целых чисел — это целое число, которое без остатка делится на оба заданных числа.

Наименьшее общее кратное двух целых чисел — это наименьшее из всех целых чисел, которое делится без остатка на оба заданных числа.

Способ 1 … Найти НОК можно по очереди для каждого из заданных чисел, выписывая в порядке возрастания все числа, которые получаются при умножении их на 1, 2, 3, 4 и т.д. на.

Пример для чисел 6 и 9.
Умножаем число 6, последовательно, на 1, 2, 3, 4, 5.
Получаем: 6, 12, 18 , 24, 30
Умножаем число 9, последовательно, на 1, 2, 3, 4, 5.
Получаем: 9, 18 , 27, 36, 45
Как видите, НОК для чисел 6 и 9 будет 18.

Этот метод удобен, когда оба числа маленькие и их легко умножить на последовательность целых чисел. Однако бывают случаи, когда нужно найти НОК для двузначных или трехзначных чисел, а также когда исходных чисел три и даже больше.

Метод 2 … НОК можно найти, разложив исходные числа на простые множители.
После разложения необходимо вычеркнуть одинаковые числа из полученного ряда простых множителей. Остальные числа первого числа будут множителями для второго, а оставшиеся числа второго будут множителями для первого.

Пример для чисел 75 и 60.
Наименьшее общее кратное чисел 75 и 60 можно найти, не выписывая кратные этим числам подряд. Для этого разложим 75 и 60 на простые множители:
75 = 3 * 5 * 5, а
60 = 2 * 2 * 3 * 5 .
Как видите, множители 3 и 5 встречаются в обеих строках. Мысленно «вычеркиваем» их.
Выпишем остальные множители, входящие в разложение каждого из этих чисел. При расширении числа 75 у нас остается число 5, а при расширении числа 60 имеем 2*2
Итак, чтобы определить НОК для чисел 75 и 60, нам нужно перемножить оставшиеся числа из разложения 75 (это 5) на 60, а числа, оставшиеся от разложения числа 60 (это 2*2) умножаем на 75. То есть, для простоты понимания, мы говорим, что умножаем «накрест».
75 * 2 * 2 = 300
60 * 5 = 300
Вот как мы нашли НОК для чисел 60 и 75. Это число 300.

Пример … Определить НОК для чисел 12, 16, 24
В этом случае наши действия будут несколько сложнее. Но, сначала, как всегда, разложим все числа на простые множители
12 = 2 * 2 * 3
16 = 2 * 2 * 2 * 2
24 = 2 * 2 * 2 * 3
Чтобы правильно определить НОК, выбираем наименьшее из всех чисел (это число 12) и последовательно проходим его множители, вычеркивая их, если хотя бы в одном из других рядов чисел содержится такой же, еще не вычеркнутый множитель.

Шаг 1 . Мы видим, что 2*2 встречается во всех рядах чисел. Вычеркните их.
12 = 2 * 2 * 3
16 = 2 * 2 * 2 * 2
24 = 2 * 2 *2*3

Шаг 2. В простых делителях числа 12 остается только число 3. Но он присутствует в простых множителях числа 24. Вычеркнуть из обоих рядов число 3, при этом для числа 16 никаких действий не предполагается.
12 = 2 * 2 * 3
16 = 2 * 2 * 2 * 2
24 = 2 * 2 * 2 * 3

Как видите, при расширении числа 12 мы «зачеркнули» все числа. Это означает, что нахождение НОК завершено. Осталось только рассчитать его значение.
За число 12 берем остальные делители числа 16 (ближайшие по возрастанию)
12 * 2 * 2 = 48
Это НОК

Как видите, в данном случае найти LCM было несколько сложнее, но когда нужно найти его для трех и более чисел, этот способ позволяет сделать это быстрее. Однако оба метода нахождения LCM верны.

Рассмотрим три способа нахождения наименьшего общего кратного.

Разложение на множители

Первый способ — найти наименьшее общее кратное, разложив эти числа на простые множители.

Предположим, нам нужно найти НОК чисел: 99, 30 и 28. Для этого разложим каждое из этих чисел на простые множители:

Чтобы искомое число делилось на 99, 30 и 28, необходимо и достаточно, чтобы все простые множители этих делителей входили в Это. Для этого нужно возвести все простые множители этих чисел в максимально возможную степень и умножить их вместе:

2 2 3 2 5 7 11 = 13 860

Итак, НОК (99, 30, 28) = 13 860. Никакое другое число, меньшее 13 860, не делится ни на 99, ни на 30, ни на 28.

Чтобы найти наименьшее общее кратное этих чисел, вам нужно разложить их на простые множители, затем взять каждый простой множитель с наибольшим показателем степени, с которым он встречается, и перемножить эти множители вместе.

Поскольку взаимно простые числа не имеют общих простых делителей, их наименьшее общее кратное равно произведению этих чисел. Например, три числа: 20, 49 и 33 взаимно просты. Поэтому

НОК (20, 49, 33) = 20 49 33 = 32 340.

То же самое нужно делать при поиске наименьшего общего кратного различных простых чисел. Например, НОК (3, 7, 11) = 3 7 11 = 231,

Нахождение путем подбора

Второй способ — найти наименьшее общее кратное методом подбора.

Пример 1. Когда наибольшее из заданных чисел целиком делится на остальные заданные числа, то НОК этих чисел равен большему из них. Например, даны четыре числа: 60, 30, 10 и 6. Каждое из них делится на 60, поэтому:

НОК (60, 30, 10, 6) = 60

В противном случае используется следующая процедура для нахождения наименьшее общее кратное:

Определите наибольшее количество заданных чисел.
Далее находим числа, кратные наибольшему числу, умножая его на натуральные числа в порядке возрастания и проверяя, делятся ли остальные заданные числа на полученное произведение.

Пример 2. Даны три числа 24, 3 и 18. Определить наибольшее из них — это число 24. Далее найти числа, кратные 24, проверив, делится ли каждое из них на 18 и 3:

24 1 = 24 — делится на 3, но не делится на 18.

24 2 = 48 — делится на 3, но не делится на 18.

24 3 = 72 — делится на 3 и 18.

Итак НОК (24, 3, 18) = 72.

Нахождение путем последовательного нахождения НОК

Третий способ заключается в нахождении наименьшего общего кратного путем последовательного нахождения НОК.

НОК двух заданных чисел равен произведению этих чисел, деленному на их наибольший общий делитель.

Пример 1. Найдем НОК двух заданных чисел: 12 и 8. Определим их наибольший общий делитель: НОД (12, 8) = 4. Умножим эти числа:

Разделим произведение на их НОД:

Таким образом, НОК (12, 8) = 24.

Чтобы найти НОК трех или более чисел, используйте следующую процедуру:

Сначала найдите НОК любых двух из заданных чисел.
Затем НОК найденного наименьшего общего кратного и третьего заданного числа.
Затем LCM полученного наименьшего общего кратного и четвертого числа и т. д.
Таким образом, поиск LCM продолжается до тех пор, пока есть номера.

Пример 2. Найдем НОК трех заданных чисел: 12, 8 и 9. МОК чисел 12 и 8 мы уже нашли в предыдущем примере (это число 24). Осталось найти наименьшее общее кратное 24 и третьего заданного числа — 9. Определить их наибольший общий делитель: НОД (24, 9) = 3. Умножить НОК на число 9:

Делим произведение на их НОД :

Таким образом, НОК (12, 8, 9) = 72.

Тема «Множества» изучается в 5 классе общеобразовательной школы. Его цель — улучшить письменные и устные навыки математических вычислений. На этом занятии вводятся новые понятия — «кратные» и «делители», отрабатывается методика нахождения делителей и кратных натурального числа, умение находить НОК различными способами.

Эта тема очень важна. Знания о нем можно применить при решении примеров с дробями. Для этого нужно найти общий знаменатель, вычислив наименьшее общее кратное (НОК).

Кратным A является целое число, которое делится на A без остатка.

Каждое натуральное число имеет бесконечное число кратных ему. Сам он считается самым маленьким. Кратность не может быть меньше самого числа.

Нам нужно доказать, что 125 кратно 5. Для этого нужно разделить первое число на второе. Если 125 делится на 5 без остатка, то ответ положительный.

Этот метод применим для небольших количеств.

Существуют особые случаи при расчете LCM.

1. Если нужно найти общее кратное для 2-х чисел (например, 80 и 20), где одно из них (80) делится без остатка на другое (20), то это число (80) равно наименьшее кратное этих двух чисел.

НОК (80, 20) = 80.

2. Если два не имеют общего делителя, то можно сказать, что их НОК есть произведение этих двух чисел.

НОК (6, 7) = 42.

Давайте посмотрим на последний пример. 6 и 7 относительно 42 являются делителями. Они делят кратное без остатка.

В этом примере 6 и 7 являются парными делителями. Их произведение равно наибольшему кратному числу (42).

Число называется простым, если оно делится только само на себя или на 1 (3:1=3; 3:3=1). Остальные называются составными.

В другом примере нужно определить, является ли 9 делителем 42.

42: 9 = 4 (остаток 6)

Ответ: 9 не является делителем 42, потому что в ответе есть остаток.

Делитель отличается от кратного тем, что делитель — это число, на которое делятся натуральные числа, а само кратное делится на это число.

Наибольший общий делитель чисел a и b , умноженный на их наименьшее кратное, даст произведение самих чисел a и b .

А именно: НОД (а, б) х НОК (а, б) = а х б.

Обыкновенные кратные для более сложных чисел находятся следующим образом.

Например, найдем НОК для 168, 180, 3024.

Разложим эти числа на простые множители, запишем их в виде произведения степеней:

168 = 2³х3¹х7¹

2⁴х3³х5¹х7¹ = 15120

МОК (168, 180, 3024) = 15120.

Математические выражения и задачи требуют большого количества дополнительных знаний. NOC является одним из основных, особенно часто используется в Тема изучается в средней школе, при этом усвоить материал не представляет особой сложности, человеку, знакомому со степенями и таблицей умножения, не составит труда подобрать нужную нужные числа и найти результат.

Определение

Обыкновенное кратное — это число, которое можно полностью разделить на два числа одновременно (a и b). Чаще всего это число получается путем умножения исходных чисел а и b. Число должно делиться на оба числа сразу, без отклонений.

NOC — это сокращенное название, принятое для обозначения, составленное из первых букв.

Способы получения числа

Для нахождения НОК не всегда подходит метод умножения чисел, гораздо лучше он подходит для простых однозначных или двузначных чисел. принято делить по факторам, чем больше число, тем больше будет факторов.

Пример № 1

В качестве простейшего примера в школах обычно используются простые, однозначные или двузначные числа. Например, вам нужно решить следующую задачу, найти наименьшее общее кратное чисел 7 и 3, решение достаточно простое, достаточно их перемножить. В итоге есть число 21, меньшего числа просто нет.

Пример №2

Второй вариант задания намного сложнее. Учитывая числа 300 и 1260, поиск LCM обязателен. Для решения задачи предполагаются следующие действия:

Разложение первого и второго чисел на простейшие множители. 300 = 2 2 * 3 * 5 2; 1260 = 2 2 * 3 2 * 5 * 7. Первый этап пройден.

Второй этап предполагает работу с уже полученными данными. Каждое из полученных чисел должно участвовать в подсчете итогового результата. Для каждого фактора берется наибольшее количество вхождений из исходных чисел. НОК является итоговым числом, поэтому множители чисел должны повторяться в нем все до единицы, даже те, которые присутствуют в одном экземпляре. Оба исходных числа имеют в своем составе числа 2, 3 и 5, в разной степени, 7 только в одном случае.

Чтобы вычислить окончательный результат, нужно взять каждое число в наибольшей из степеней, представленных в уравнении. Остается только умножить и получить ответ, при правильном заполнении задание укладывается в два шага без объяснения причин:

1) 300 = 2 2 * 3 * 5 2 ; 1260 = 2 2 * 3 2 * 5 * 7.

2) НОК = 6300.

Вот и вся проблема, если попытаться вычислить нужное число умножением, то ответ точно будет неверным, так как 300*1260=378000.

Экспертиза:

6300/300 = 21 — верно;

6300/1260 = 5 — верно.

Правильность полученного результата определяют проверкой — делением НОК на оба исходных числа, если число в обоих случаях целое, то ответ правильный.

Что означает НОК в математике

Как известно, в математике нет ни одной бесполезной функции, эта не исключение. Чаще всего это число используется для приведения дробей к общему знаменателю. Чему обычно учат в 5-6 классах средней школы. Это также дополнительно общий делитель для всех кратных, если такие условия есть в задаче. Подобное выражение может найти кратное не только двум числам, но и гораздо большему числу — трем, пяти и так далее. Чем больше цифр — тем больше действий в задаче, но сложность от этого не увеличивается.

Например, зная числа 250, 600 и 1500, нужно найти их сумму НОК:

1) 250 = 25 * 10 = 5 2 * 5 * 2 = 5 3 * 2 — в этом примере описывается факторизация в Подробно, без отмены.

2) 600 = 60 * 10 = 3 * 2 3 * 5 2 ;

3) 1500 = 15 * 100 = 33 * 5 3 * 2 2 ;

Для составления выражения требуется указать все множители, в данном случае даны 2, 5, 3, — для всех этих чисел требуется определить максимальную степень.

Внимание: все множители необходимо довести до полного упрощения, по возможности расширив до уровня однозначных.

Экспертиза:

1) 3000/250 = 12 — верно;

2) 3000/600 = 5 — верно;

3) 3000/1500 = 2 — верно.

Этот метод не требует никаких ухищрений или гениальных способностей, все просто и понятно.

Другой способ

В математике многое связано, многое можно решить двумя и более способами, то же самое относится и к нахождению наименьшего общего кратного, НОК. Следующий метод можно использовать в случае простых двузначных и однозначных чисел. Составляется таблица, в которую по вертикали вносится множитель, по горизонтали множитель, а в пересекающихся ячейках столбца указывается произведение. Отразить таблицу можно с помощью линии, берется число и в строку записываются результаты умножения этого числа на целые числа, от 1 до бесконечности, иногда достаточно 3-5 точек, второе и последующие числа подвергается одному и тому же вычислительному процессу. Все происходит до тех пор, пока не будет найдено общее кратное.

Учитывая числа 30, 35, 42, нужно найти НОД, соединяющий все числа:

1) Кратные 30: 60, 90, 120, 150, 180, 210, 250 и т.д.

2) Кратные 35: 70, 105, 140, 175, 210, 245 и т.