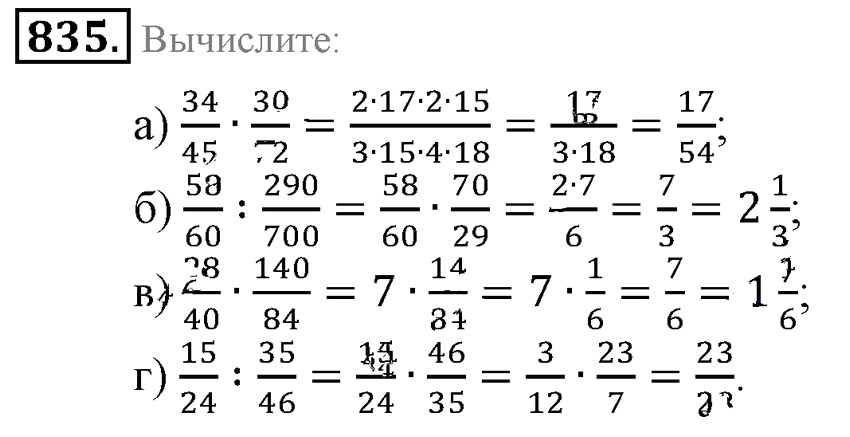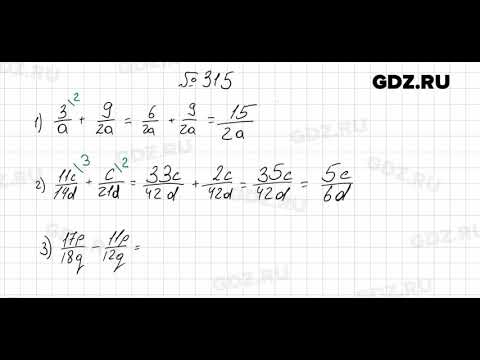Номер №393 — ГДЗ по Математике 6 класс: Виленкин Н.Я.
войтирегистрация
- Ответкин
- Решебники
- 6 класс
- Математика
- Виленкин
- Номер №393
НАЗАД К СОДЕРЖАНИЮ
2013г.ВыбранВыбрать ГДЗ (готовое домашние задание из решебника) на Номер №393 по учебнику Математика. 6 класс. Учебник для общеобразовательных учреждений / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 30-е издание. Мнемозина, 2013г.
2019г.ВыбранВыбрать
ГДЗ (готовое домашние задание из решебника) на Номер №393 по учебнику Математика. 6 класс. Учебник для общеобразовательных организаций / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С.
И. Шварцбурд. — 37-е издание в двух частях. Мнемозина, 2019г.
Условие 20132019г.
Cменить на 2013 г.
Cменить на 2019 г.
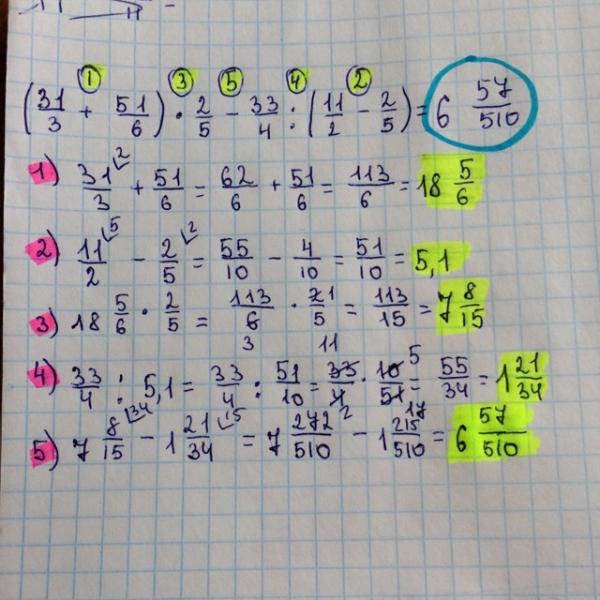
Три бригады вырастили горох на площади 72 19/20 га. Первая и вторая бригады вырастили горох на площади 44 3/4 га, а вторая и третья — на площади 52 9/20 га. Найдите площадь каждого участка.
На координатном луче отмечена точка А (m/n) (рис. 17). Отметьте на луче точки, координаты которых равны:
а) 1 + m/n; 6) 2 — m/n; в) 2 + m/n; г) 1 + 1 m/n.
Решение 1
Решение 1
Решение 2
Решение 2
Решение 3
Решение 3
ГДЗ по Математике 6 класс: Виленкин Н.Я.
Издатель: Виленкин Н.Я. Жохов В.И. Чесноков А.С. Шварцбурд С.
И. 2013/2019г.
ГДЗ по Математике 6 класс: Мерзляк А.Г.
Издатель: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. 2014г. / 2019г.
ГДЗ по Математике 6 класс: Никольский С.М.
Издатель: С.М. Никольский, М.К, Потапов, Н.Н. Решетников, А.В. Шевкин. 2015-2018
ГДЗ по Математике 6 класс: Зубарева, Мордкович
Издатель: И.И. Зубарева, А.Г. Мордкович. 2014-2019г.
ГДЗ по Математике 6 класс: Дорофеев Г.В.
Издатель: Г.В. Дорофеев, И.Ф. Шарыгин, С.Б. Суворова. 2016-2019г.
Сообщить об ошибке
Выберите тип ошибки:
Решено неверно
Опечатка
Плохое качество картинки
Опишите подробнее
в каком месте ошибка
Ваше сообщение отправлено
и скоро будет рассмотрено
ОК, СПАСИБО
[email protected]
© OTVETKIN.INFO
Классы
Предметы
Номер 393 — ГДЗ Математика 6 класс Дорофеев (решебник)
Номер 393 — ГДЗ Математика 6 класс Дорофеев (решебник) — GDZwowПерейти к содержанию
Search for:
Автор: Г.
В. Дорофеев, И.Ф. Шарыгин, С.Б. Суворова, Е.А. Бунимович
Издательство: Просвещение
Тип: Учебник
Номера упражнений
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394959697989910010110210310410510610710810911011111211311411511611711811912012112212312412512612712812913013113213313413513613713813914014114214314414514614714814915015115215315415515615715815916016116216316416516616716816917017117217317417517617717817918018118218318418518618718818919019119219319419519619719819920020120220320420520620720820921021121221321421521621721821922022122222322422522622722822923023123223323423523623723823924024124224324424524624724824925025125225325425525625725825926026126226326426526626726826927027127227327427527627727827928028128228328428528628728828929029129229329429529629729829930030130230330430530630730830931031131231331431531631731831932032132232332432532632732832933033133233333433533633733833934034134234334434534634734834935035135235335435535635735835936036136236336436536636736836937037137237337437537637737837938038138238338438538638738838939039139239339439539639739839940040140240340440540640740840941041141241341441541641741841942042142242342442542642742842943043143243343443543643743843944044144244344444544644744844945045145245345445545645745845946046146246346446546646746846947047147247347447547647747847948048148248348448548648748848949049149249349449549649749849950050150250350450550650750850951051151251351451551651751851952052152252352452552652752852953053153253353453553653753853954054154254354454554654754854955055155255355455555655755855956056156256356456556656756856957057157257357457557657757857958058158258358458558658758858959059159259359459559659759859960060160260360460560660760860961061161261361461561661761861962062162262362462562662762862963063163263363463563663763863964064164264364464564664764864965065165265365465565665765865966066166266366466566666766866967067167267367467567667767867968068168268368468568668768868969069169269369469569669769869970070170270370470570670770870971071171271371471571671771871972072172272372472572672772872973073173273373473573673773873974074174274374474574674774874975075175275375475575675775875976076176276376476576676776876977077177277377477577677777877978078178278378478578678778878979079179279379479579679779879980080180280380480580680780880981081181281381481581681781881982082182282382482582682782882983083183283383483583683783883984084184284384484584684784884985085185285385485585685785885986086186286386486586686786886987087187287387487587687787887988088188288388488588688788888989089189289389489589689789889990090190290390490590690790890991091191291391491591691791891992092192292392492592692792892993093193293393493593693793893994094194294394494594694794894995095195295395495595695795895996096196296396496596696796896997097197297397497597697797897998098198298398498598698798898999099199299399499599699799899910001001100210031004100510061007100810091010101110121013101410151016101710181019102010211022102310241025102610271028102910301031103210331034103510361037103810391040104110421043104410451046104710481049105010511052105310541055105610571058
Чему вы научились
Глава 1
123456789101112
Глава 2
1234567
Глава 3
123456789
Глава 4
1234567891011121314
Глава 5
1234567
Глава 6
123456789
Глава 7
12345678
Глава 8
1234567891011
Глава 9
123456789101112131415
Глава 10
123456789
Глава 11
12345678910111213141516
Глава 12
1234567891011
Adblockdetector
Делители числа 393 — Найти простые факторизации/множители числа 393 3, 131, 393.
Парные множители числа 393 равны (1, 393), (3, 131), а его простые множители равны 3 × 131.| 1. | Какие множители числа 393? |
| 2. | Коэффициенты 393 с помощью простой факторизации |
| 3. | Коэффициенты 393 в парах |
| 4. | Часто задаваемые вопросы о факторах 393 |
Что такое множители числа 393?
Множители 393 — это пары тех чисел, произведение которых дает 393. Эти множители являются либо простыми, либо составными числами.
Как найти делители числа 393?
Чтобы найти делители числа 393, нам нужно найти список чисел, на которые число 393 делится без остатка.
- 393/131 = 3; следовательно, 131 — это множитель 393, а 3 — тоже множитель 393.
- 393/393 = 1; следовательно, 393 является коэффициентом 393, а 1 также является коэффициентом 393.
Точно так же мы можем найти и другие факторы. Следовательно, множители числа 393 равны 1, 3, 131, 393.
☛ Также проверьте:
- Факторы 108 — Делители 108 равны 1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54, 108
- Коэффициенты 55 — Коэффициенты 55 равны 1, 5, 11, 55
- Множители 78 — Множители 78 равны 1, 2, 3, 6, 13, 26, 39., 78
- Множители 29 — Множители 29 равны 1, 29
- Факторы 6 — Делители 6 равны 1, 2, 3, 6
Коэффициенты 393 по простой факторизации
Число 393 составное, поэтому оно имеет простые делители. Теперь давайте научимся вычислять простые делители числа 393.
Первый шаг — разделить число 393 на наименьший простой множитель, здесь это 3.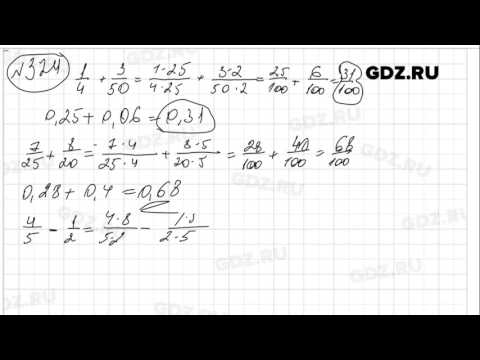
Продолжаем делить, пока не получится ненулевой остаток.
- 393 ÷ 3 = 131
Дальнейшее деление 131 на 3 дает ненулевой остаток. Итак, мы останавливаем процесс и продолжаем делить число 131 на следующий наименьший простой множитель. В конце концов мы останавливаемся, если следующего простого множителя не существует или когда мы не можем дальше делить.
Итак, разложение числа 393 на простые множители можно записать как 3 1 × 131 1 , где 3, 131 — простые числа.
Коэффициенты 393 в парах
Парные множители 393 — это пары чисел, которые при умножении дают произведение 393. Парные множители 393:
- 1 × 393 = (1, 393)
- 3 × 131 = (3, 131)
Отрицательные парные множители числа 393:
- -1 × -393 = (-1, -393)
- -3 × -131 = (-3, -131)
ПРИМЕЧАНИЕ: Если (a, b) является парным множителем числа, то (b, a) также является парным множителем этого числа.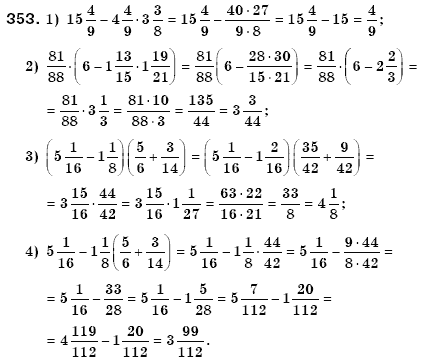
Коэффициенты 393 Решенные примеры
Пример 1: Сколько множителей существует для числа 393?
Решение:
Делители числа 393 равны 1, 3, 131, 393. Следовательно, число 393 имеет 4 делителя.
Пример 2. Найдите наименьшее общее кратное (НОК) и наибольший общий делитель (НОК) чисел 393 и 349.
Решение:
1 349,
Следовательно, наименьшее общее кратное (НОК) чисел 393 и 349 равно 137157, а наибольший общий делитель (НОК) чисел 393 и 349 равен 1.
Пример 3. Найдите, являются ли 3, 241 и 393 делителями 393.
Решение:
При делении 393 на 241 остается остаток. Следовательно, число 241 не является делителем 393. Все числа, кроме 241, являются делителями 393.
Пример 4. Найдите произведение всех простых множителей числа 39.3.
Решение:
Поскольку простые множители числа 393 равны 3 131. Следовательно, произведение простых множителей = 3 × 131 = 393,
перейти к слайдуперейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Забронировать бесплатный пробный урок
перейти к слайдуперейти к слайдуперейти к слайдуперейти к слайдуперейти к слайду
Часто задаваемые вопросы о множителях числа 393
Что такое множители числа 393?
Множители числа 393 равны 1, 3, 131, 393, а его отрицательные множители равны -1, -3, -131, -393.
Какова сумма множителей числа 393?
Делители числа 393 равны 1, 3, 131, 393, а сумма всех этих делителей равна 1 + 3 + 131 + 393 = 528
Каковы простые делители числа 393?
Простые делители числа 393 равны 3, 131.
Каков наибольший общий делитель чисел 393 и 92?
Делители числа 393 равны 1, 3, 131, 393, а числа 92 равны 1, 2, 4, 23, 46, 92. являются взаимно простыми.
Следовательно, наибольший общий делитель (НОД) чисел 393 и 92 равен 1.
Сколько делителей числа 393 также являются общими для делителей числа 377?
Так как множители числа 393 равны 1, 3, 131, 393, а делители числа 377 равны 1, 13, 29, 377. Следовательно, числа 393 и 377 имеют только один общий делитель, равный 1. Следовательно, числа 393 и 377 взаимно просты.
Math Progressions / Math Progressions
До разработки Common Core State Standards in Mathematics авторы Common Core подготовили серию документов, в которых описывалась конкретная тема или концепция для нескольких классов. Эти черновики документов о прогрессе обучения были основаны на исследованиях когнитивного развития детей и на логической структуре математики. Они легли в основу Единых базовых государственных стандартов по математике.
Совет школ большого города сотрудничает с Институтом математики и образования (IM&E) и Achieve для создания онлайн-модулей профессионального развития на основе этих учебных достижений.
Некоторые документы прогресса доступны ниже. Вы можете использовать следующую ссылку для доступа к полному набору документов прогрессии: http://commoncoretools.me/category/progressions/
Прогрессии:
К-5 Разработки Стандартов практики — Общие базовые государственные стандарты для математической практики в от детского сада до пятого класса (аннотировано).
6-8 Разработки Стандартов практики — Общие базовые государственные стандарты для математической практики в классы с шестого по восьмой (аннотированные).
K-5, Числа и операции в десятичной системе счисления — Эта прогрессия фокусируется на развитии числа и системы счисления с основанием десять.
Детский сад, счет и количество элементов; K-5, Операции и алгебраическое мышление . Эта прогрессия связана с ранним подсчетом и тем, «сколько в группе (количество элементов)». Последовательность иллюстрирует базовые операции, включая виды количественных отношений, которые они моделируют, и типы задач, которые можно решить.
3-5 Числа и операции – дроби — Эта прогрессия иллюстрирует концепцию дробей от третьего до пятого класса. Эта последовательность исследует концепцию дроби как числа, начинающегося с дробей на числовой прямой. Онлайн-модуль профессионального развития Fraction Progression основан на этой прогрессии.
K-5 Прогресс по геометрическим измерениям — Этот прогресс фокусируется на измерении при разработке концептуальной основы для соединения чисел и геометрии.
К-6 Прогресс по геометрии — Эта последовательность фокусируется на развитии геометрии от детского сада до шестого класса.