Математика 569 6 класс: Задача 569 — Виленкин Чесноков Математика 6 класс решебник

Ладыженская Т. А. 5 класс. Учебник №2, упр. 569, с. 74

569. Спишите. Подчеркните обстоятельства, выраженные именами существительными. Определите их падеж.

                        х                                                   П. п.
Наш   дом   находится  (где?  в  чём?)  в   узком  переулке,
                                                                    ^{–·–                 –·–·–·–·–·–·–}

                                                                              Р. п.
выбегающем  на  площадь.  (Откуда? от чего?) От площади
                                                                                                  ^{–·–·–·–·–·–·–·–}
       х
начинается  несколько улиц  и  шоссе¹. (Где? по чему?) По
                                                                                                                     ^–·–

                              Д. п.                         х
самой    широкой   улице   постоянно   ездят²   машины   со
                                       ^{–·–·–·–·–}

                                                                                  П. п.
строительными  материалами. (Где? на чём?) На этой улице
                                                                                              ^{–·–            –·–·–·–·–}

      х
строится несколько новых современных зданий³.

---

шоссе¹ — [шасэ] 2 слога.

ш — [ш] — согл., глух. парн. [ж], твёрд. непарн.
о — [а] — гласн., безуд.
с

   〉 [с] — согл., глух. парн. [з], твёрд. парн. [с’]
с
е — [э] — гласн., ударн.

5 б., 4 зв.

езд/[ят]² (езд- — корень, -ят — окончание, езд- — основа слова)

---

I Зданий³ — сущ.

II. Н. ф. — здание.

Пост. пр.: нариц., неодуш., ср. р., 2-го скл.;

Непост.: Р. п., мн. ч.

III. Несколько (чего?) зданий.
                                              ^{––––––––}

Ответы по русскому языку. 5 класс. Учебник. Часть 2. Ладыженская Т. А., Баранов М. Т., Тростенцова Л. А.

Ответы по русскому языку. 5 класс

4.7 / 5 ( 400 голосов )

569. Вычислите Результат проверьте умножениемa) 7.65 1.7. б) 3.848. 0,8 B) 0.414: 1.8 г) 84:

запиши числа.8 единиц 6-го разряда 7 единиц 4-го разряда 9 единиц 2-го разряда7 единиц 5-го разряда 5 единиц 1-го разряда4 единицы 6-го разряда 8 един … иц 5-го разряда 3 единицы 1-го разряда8 единиц 6-го разряда 4 единицы 5-го разряда 8 единиц 2-го разряда6 единиц 6-го разряда 5 единиц 5-го разряда 4 единицы 1-го разряда​

Найдите площадь и периметр фигуры, изображённой на рисунке (сторона клетки равна 5 мм). Нарисуйте прямоугольник, который имеет такие же площадь и пери … метр, как данная фигура.​

Найдите площадь и периметр фигуры, изображённой на рисунке (сторона клетки равна 5 мм). Нарисуйте прямоугольник, который имеет такие же площадь и пери … метр, как данная фигура.​

помогите в этом упражнении по алгебре, пожалуйста!!!!!

Метелик летів на луг, 10 бджіл летіло на луг ,а ще 5 ос летіли на луг і кожна оса їла пилок .Скільки комах летіло на луг.​

17. На базаре продаются рыбки, большие и маленькие. Сегодня три больших и одна маленькая стоят вместе столько же, сколько пять больших вчера. А две бо … льшие и одна маленькая сегодня стоят вместе столько же, сколько три больших и одна маленькая вчера. Можно ли по этим данным выяснить, что дороже одна большая и две маленьких сегодня, или пять маленьких вчера? 68, в классе учится меньше 50 школьников. За контрольную работу седьмая часть учеников получила пятёрки, третья — четверки, половина — тройки. Остальные работы были оценены как неудовлетворительные. Сколько было таких работ? P.S. Ребят можете ответить сразу на два, а можете на один

В птичком дворе находиться: гусей-3471,кур-5981,индюков-1679,уток-7398.завезли 2139 цисарки.Забили уток 2139,кур 3788,гусей 1843, индюков 782,цисарок … 1893.Сколько птиц до за воза,после завоза,после забоя.На сколько птиц меньше каждого вида после забоя?

Артемон подарил Мальвине букет из аленьких цветочков и чёрных роз. У каждой чёрной розы 4 пестика и 4 тычинки, а на стебле два листка. У каждого алень … кого цветочка 8 пестиков и 10 тычинок, а на стебле три листка. Листков в букете на 108 меньше, чем пестиков. Сколько Тычинок в букете?

B трёх мешках лежат сникерсы. В первом мешке на 6 кг сникерсов меньше, чем в двух других вместе. А во втором – на 10 кг меньше, чем в двух других вмес … те. Сколько орехов в третьем мешке, если каждый сникерс весит 50 г, а в каждом сникерсе 16 орехов?

Саше хочется купить семь разных книг. Книги стоят одинаково, а денег хватает только на три книги. Сколькими способами Саша может выбрать три книги из … семи?

Страница не найдена

Новости

7 июн

Единый государственный экзамен (ЕГЭ) по профильной математике в понедельник, 7 июня, будут сдавать около 393 тыс. человек. Об этом сообщили в пресс-службе Рособрнадзора.

5 июн

Министр здравоохранения России Михаил Мурашко рассказал, что двое детей, пострадавших в ходе стрельбы в казанской школе, продолжают оставаться в тяжёлом состоянии, но динамика лечения позитивная.

4 июн

Единый государственный экзамен по русскому языку прошёл в штатном режиме, без существенных сбоев и нарушений. Об этом заявили в пресс-службе Рособрнадзора.

4 июн

Сейчас многие школьники после 9-го класса идут в учреждения среднего специального образования, заявил министр просвещения России Сергей Кравцов. В интервью RT на полях ПМЭФ глава ведомства рассказал, как система образования приспособилась к условиям пандемии и сказалось ли это на уровне знаний учащихся. Кроме того, Кравцов отметил положительные стороны Единого госэкзамена и прокомментировал ход проверки учебников по истории, начатой после критики Владимира Путина одного из пособий.

4 июн

Сейчас многие школьники после 9-го класса идут в учреждения среднего специального образования, заявил министр просвещения России Сергей Кравцов. В интервью RT на полях ПМЭФ глава ведомства рассказал, как система образования приспособилась к условиям пандемии и сказалось ли это на уровне знаний учащихся. Кроме того, Кравцов отметил положительные стороны Единого госэкзамена и прокомментировал ход проверки учебников по истории, начатой после критики Владимира Путина одного из пособий.

4 июн

В России впервые состоится Национальная технологическая олимпиада для школьников. Она пройдёт в Год науки и технологий.

4 июн

В образовательных учреждениях необходимо ввести обязательное обучение правилам пожарной безопасности, заявил статс-секретарь замглавы МЧС России Алексей Серко.

Эхо Москвы в Перми — В России стартовала спецоперация «ЕГЭ»

16:48, 31 мая 2021

В каждом пункте сдачи ЕГЭ предприняты все меры антитеррористической и эпидемической безопасности.

_{Фото: gazeta-pedagogov.ru}

31 мая выпускники сдали предметы по выбору: географию, литературу и химию. В этом году ЕГЭ напишут 13 787 человек. Среди них не только выпускники текущего года, но и студенты среднего профессионального образования, выпускники прошлых лет. Как рассказала «Эху Перми» министр образования Пермского края Раиса Кассина, в регионе ежегодно растет количество участников ЕГЭ, набравших на экзаменах 100 баллов.

— У нас было много мультистобалльников в прошлом году. Ребята из Перми, Соликамска, Горнозаводского округа. В этом году мы занимались в основном в очном режиме. Я точно понимаю, что подготовиться мы успели. Хочу успокоить родителей и детей. Традиционно Пермский края сдает очень высоко ЕГЭ, причем по всем предметам. И общий балл, который ребята набирают, значительно больше, чем в среднем по России. У нас самый высокий показатель по географии, информатике, по литературе и математике профильной. По английскому языку высокие результаты.

Всего в Пермском крае в этом году организовано 104 пункта сдачи ЕГЭ. Из них 71 — на базе школ. Обязательно наличие металлодетектора на входе в здание, средств подавления сотовой связи и видеонаблюдения. ЕГЭ проходит с соблюдением всех мер безопасности, подчеркнула Раиса Кассина.

— Накануне экзамена пункт сдачи обрабатывается средствами дезинфекции. Все учителя и организаторы находятся в масках, дети — по желанию. Рассадка по десять человек. В обычное время в классе было по 15 выпускников. Санитайзеры установлены, и все противоэпидемические требования соблюдены. Сотрудники ЧОПов и Росгвардии стоят на входе. Каждый ребенок проверяется металлоискателем. Кроме того, Росгвардия курирует все образовательные учреждения, находится рядом с теми, где проходит ЕГЭ. Предприняты все меры. Ни один посторонний человек не сможет зайти в пункт сдачи ЕГЭ.

Родителям переживать за экзаменующихся детей придется на расстоянии. В аудиториях будут присутствовать общественные наблюдатели, в этом году их более 800 человек.

47803 рецепта салатов, супов и других блюд на все случаи на сайте «Еда»

Куриная грудка 4 штуки

Лук 2 штуки

Сладкий перец 3 штуки

Чеснок 3 зубчика

Помидоры 4 штуки

Овощной бульонный кубик 1 штука

Сыр 100 г

Смесь итальянских трав 1 столовая ложка

Вода ½ стакана

Сливки ½ стакана

Оливковое масло 2 столовые ложки

Мускатный орех щепотка

Соль по вкусу

Сливочное масло 1 столовая ложка

Молотый черный перец по вкусу

Factors of 569 — Найдите простое факторизацию / Factors of 569

Множители 569 — это список целых чисел, который мы можем разделить поровну на 569. Всего есть 2 множителя по 569, то есть 1 569, где 569 — самый большой множитель. Парные факторы 569 равны (1, 569), а его основные факторы — 569.

• Все множители 569: 1 и 569
• Отрицательные множители 569: -1 и -569
• Подводя итоги 569: 569
• Простая факторизация 569: 569 ¹
• Сумма множителей 569: 570

Какие множители перед числом 569?

Факторы 569 — это пары тех чисел, произведения которых дают 569.Эти множители могут быть простыми или составными числами.

Как найти множители 569?

Чтобы найти множители 569, нам нужно найти список чисел, которые делили бы 569 без остатка.

• 569/1 = 569; следовательно, 1 — это коэффициент 569.
• 569/569 = 1; следовательно, 569 — это коэффициент 569.

Следовательно, множители 569 равны 1 569.

☛ Также проверьте:

• Факторы 38 — Факторы 38: 1, 2, 19, 38
• Множители 9 — Множители 9 равны 1, 3, 9
• Факторы 81 — Факторы 81: 1, 3, 9, 27, 81
• Факторы 15 — Факторы 15 равны 1, 3, 5, 15
• Факторы 56 — Факторы 56: 1, 2, 4, 7, 8, 14, 28, 56

Коэффициент

из 569 по прайм-факторизации

Число 569 простое, поэтому его делителями являются только числа 1 и 569. Следовательно, у него есть только один простой множитель, то есть само число, то есть 569.

Итак, разложение на простые множители 569 можно записать как 569 ¹ , где 569 — простое число.

Факторы 569 в парах

Парные множители 569 — это пары чисел, которые при умножении дают произведение 569. Попарно множители 569 составляют:

Отрицательные парные множители 569:

ПРИМЕЧАНИЕ: Если (a, b) является парным множителем числа, то (b, a) также является парным множителем этого числа.

Факторы 569 решенных примеров

1. Пример 1: Сколько факторов у 569?

   Решение:

   Факторы 569 равны 1 569. Следовательно, 569 имеет 2 фактора.

2. Пример 2: Найдите наименьшее общее кратное (НОК) и наибольший общий делитель (НОД) 569 и 223.

   Решение:

   Факторы 569 — 1 569, а множители 223 — 1 223.

   Следовательно, наименьшее общее кратное (НОК) 569 и 223 равно 126887, а наибольшее общее делитель (НОД) 569 и 223 равно 1.

3. Пример 3. Найдите, если 1 и 232 делятся на 569.

   Решение:

   Когда мы делим 569 на 232, остается остаток. Следовательно, число 232 не делится на 569. Все числа, кроме 232, делятся на 569.

4. Пример 4: Найдите произведение всех множителей 569.

   Решение:

   Так как множители 569 равны 1, 569. Следовательно, произведение множителей = 1 × 569 = 569.

перейти к слайду перейти к слайду перейти к слайду

Готовы увидеть мир глазами математиков?

Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых занятиях и станьте экспертом во всем.

Забронируйте бесплатную пробную версию Класс

Часто задаваемые вопросы по факторам 569

Какие факторы у 569?

Факторы 569 — 1, 569, а отрицательные факторы — -1, -569.

Какова сумма множителей 569?

Все факторы 569 равны 1 569, поэтому сумма всех этих факторов составляет 1 + 569 = 570

.

Какие основные факторы у числа 569?

Простой множитель 569 равен 569.

Какой наибольший общий множитель у 569 и 193?

Множители 569 равны 1 569, а множители 193 равны 1 193. 569 и 193 имеют только один общий делитель, равный 1. Это означает, что 569 и 193 совпадают с простыми числами.

Следовательно, наибольший общий коэффициент (GCF) 569 и 193 равен 1.

Сколько факторов из 569 также являются факторами из 479?

Так как множители 569 равны 1 569, а множители 479 — 1 479. Следовательно, 569 и 479 имеют только один общий делитель, равный 1. Следовательно, 569 и 479 взаимно просты.

Что стало возможным при использовании вариационной теории обучения в преподавании математики?

В этом разделе мы сообщаем об эмпирических данных исследовательского проекта по преподаванию математики и естествознания, в котором учителя использовали теорию вариаций в качестве принципа проектирования (Kullberg 2016; Kullberg et al. 2016; Рунессон и Куллберг 2017). Мы проанализировали уроки, проведенные в 7-м классе (учащиеся 13 лет) до и после того, как учителя были вовлечены в учебную работу. В учебном исследовании (Cheng and Lo 2013; Marton 2015; Marton and Pang 2006; Lo 2012) команда учителей систематически планирует, разыгрывает, анализирует и пересматривает урок, чтобы помочь ученикам изучить предполагаемый объект обучения. Одно существенное различие между изучением урока (Lewis et al. 2009; Yoshida 1999) и учебным исследованием состоит в том, что учителя используют теорию вариаций (или другую теорию) в качестве инструмента для планирования и анализа уроков.В течение 1,5 лет двенадцать учителей средних школ в четырех командах работали вместе, по одному исследователю в каждой команде. Учителя были экспертами-предметниками, сертифицированными для преподавания математики в младших классах средней школы. Это были государственные школы с разнородными классами. Хотя для большинства учеников родным языком был шведский, во всех классах были ученики с другим этническим и языковым происхождением. Школы располагались в пригородах больших городов в четырех разных частях Швеции.Каждая команда провела три учебных исследования, по одному в семестр, по разным темам математики или естествознания. Для каждого учебного исследования учителя собирались примерно на семь встреч, на которых они заранее планировали исследование, составляли предварительные и последующие тесты, планировали и пересматривали три урока и, наконец, подводили итоги своих выводов. В каждом исследовании один урок был тщательно спланирован, реализован в одном классе одним из учителей в команде, проанализирован и отредактирован совместно и проведен в другом классе (второй урок) другим учителем.Второй урок в итеративном цикле был проанализирован и переработан, и, наконец, третий урок был спланирован и проведен в третьем классе. В процессе обучения учителя определили важнейшие аспекты познания учащимися объекта обучения. Команда совместно спланировала уроки и собрала информацию в результате предварительных и последующих тестов, чтобы проанализировать, как преподавание влияет на обучение их учеников (см. Guskey, 2002). Они использовали идеи теории вариаций для разработки уроков; например, они знали о некоторых моделях вариаций, например.ж., контраст и обобщение, а также идея выявления критических аспектов обучения учащихся. Наш исследовательский интерес к этому исследованию состоял в том, чтобы выяснить, повлияло ли вмешательство на индивидуально спланированное обучение учителей и каким образом. Мы предположили, что можно изучать аспекты того, чему учителя научились в процессе участия в теоретически ориентированном профессиональном учебном сообществе, путем анализа их обучения как «знания в действии» (Schön, 1983) или знания как предрасположенности к действию (Ryle, 1949). / 2002).Чтобы изучить изменения в педагогической практике, были собраны и проанализированы классные данные до и после вмешательства в учебное исследование. Один индивидуально спланированный и проведенный урок (Урок 1) по теме, выбранной учителем до вмешательства, и один урок (Урок 2) по той же теме два года спустя были записаны на видео. Мы выявили аналогичные различия в преподавании десяти из двенадцати учителей после вмешательства с точки зрения того, как содержание было обработано во время уроков (Kullberg et al.2016). Двое из двенадцати учителей были исключены из анализа: один из-за того, что она изменила тему, преподаваемую на двух уроках, а другой, потому что он преподавал два урока, следуя учебнику при выполнении лабораторных работ. Хотя в десяти проанализированных случаях учителя преподавали разные темы, в Уроке 2 они преподавали концепции по отношению к другим релевантным концепциям, тогда как в Уроке 1 преподавалось по одной концепции за раз. Мы дополнительно изучили примеры, использованные до и после вмешательства на микроуровне.В этой статье мы даем эмпирическую иллюстрацию и анализ преподавания одним учителем метода решения уравнений с одним неизвестным.

Различия в том, что стало возможным различать

Между Уроком 1 (L1) и Уроком 2 (L2) было общее сходство. Например, уроки были примерно одинаковой длины и преподавался один и тот же метод (отмены) решения уравнений с одним неизвестным. На обоих уроках ученики работали над созданием уравнений с одним неизвестным для сокурсника.Мы сосредоточились на сходствах и различиях в разыгрываемых пространствах примеров, чтобы исследовать на микроуровне влияние вмешательства на практику преподавания. Мы проанализировали примеры, представленные учителем во время обсуждения в классе, с использованием теории вариаций (Marton 2015). Наш анализ показывает, что разыгрываемый объект обучения и, следовательно, то, что стало возможным изучать на уроке, изменились. В L1 объект обучения в первую очередь включает в себя метод и процедуру решения путем нахождения ответов на уравнения с одним неизвестным.Когда тот же учитель преподавал L2 по той же теме после вмешательства, ответы на уравнения, использованные в уроке, были уже известны, и вместо этого целью обучения было понимание структуры уравнения : как можно создать уравнение и операции, использованные при его решении.

Учитель также сформулировал эти различия между уроками.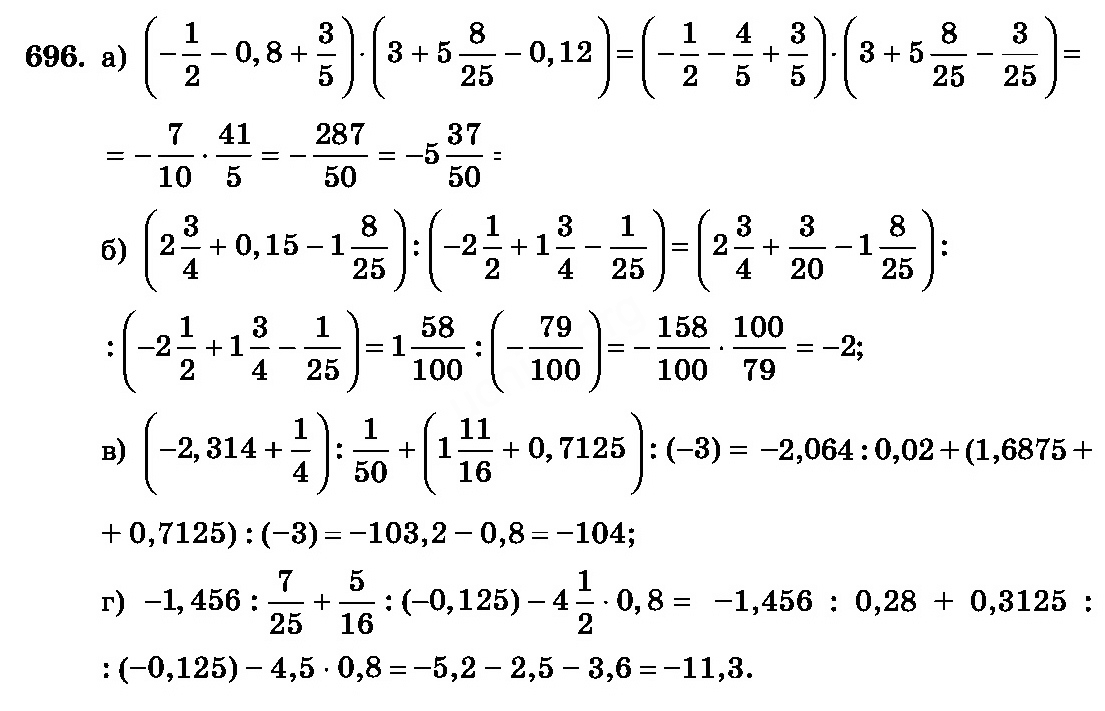 Что касается предполагаемого объекта обучения на L1, он сказал, что хочет, чтобы ученики были «более безопасными в методе (отмена),… но это больше, чем метод, который мне нужен…, они должны видеть, что он можно решить уравнение, увидеть его использование, что это хороший способ, что, так сказать, встает на свои места.После выступления он сказал о L2: «Я хочу сказать, что если вы понимаете, что такое уравнение и как оно структурировано, тогда вы можете их решать … вы можете научить их методу решения уравнения, не зная, что они действительно понимают. уравнение есть, потому что вы учите их методу, который дает результат, но вопрос в том, ли они имеют базовое понимание того, что такое уравнение ». Мы предполагаем, что в этом случае учитель изменил намеченные и реализованные объекты обучения, а также свое мнение о том, что студентам необходимо изучить, чтобы иметь возможность решать уравнения с одним неизвестным.В следующем анализе мы покажем, как использованные задания и примеры позволили учащимся различать различные аспекты (измерения вариации).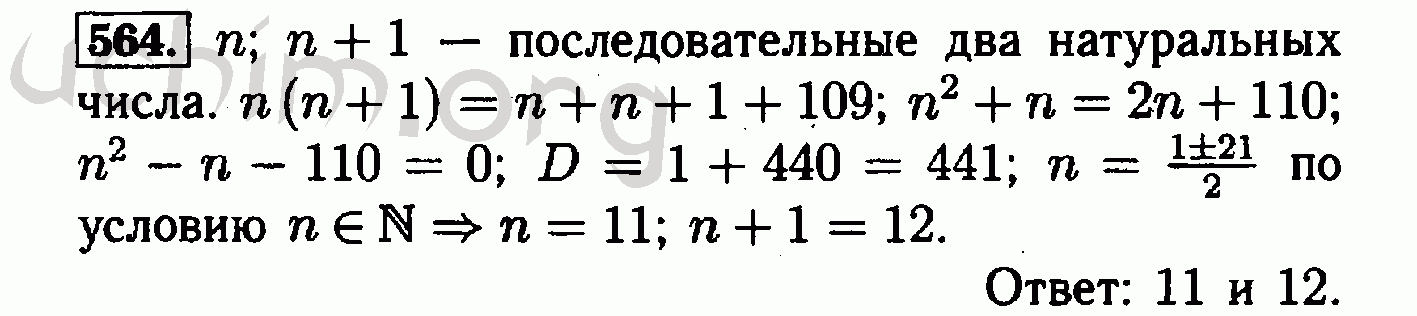

Урок 1

Наш анализ Урока 1 показывает, что разыгрываемый объект обучения и какие измерения вариации были открыты, в первую очередь, привели к процессу решения уравнения с одним неизвестным. Учитель вместе с учениками решил одно числовое уравнение с графическим изображением (Задание 2) и два уравнения, составленных из словесных задач (Задание 4), используя метод отмены.В следующем разделе анализируются задачи и то, какие аспекты являются вариативными / неизменными в установленных наборах примеров.

Решение уравнений с разными номерами

В Задаче 1 (см. Ниже) было решено и обсуждено несколько примеров уравнений с разными номерами по обе стороны от знака равенства, одно за другим, чтобы проиллюстрировать равенство. В двух первых примерах 12 является неизменным, но сторона, на которой находится двенадцать, варьируется, а также множители, которые умножаются, чтобы получить 12.Следовательно, в первых трех примерах уравнений учитель менял числа, порядок чисел и количество множителей по обе стороны от знака равенства, сохраняя неизменным знак равенства / равенства.

1. 1.

   3 × 4 = 12

2. 2.

   12 = 3 × 2 × 2

3. 3.

   12 × 2 = 3 × 2 × 2 × 2

4. 4.

   3 × 6 = 18 × 2 = 36 3 × 6 ≠ 18 × 2 = 36

За этим последовал один пример (см. Пример № 4), в котором учитель провел контраст между неправильным (3 × 6 = 18 × 2 = 36, «чтобы показать шаги в процессе вычисления»), ^{Сноска 1} и правильный способ (3 × 6 ≠ 18 × 2 = 36) использования знака равенства. В этом случае значение знака равенства изменилось по сравнению с предыдущими уравнениями, и был введен новый знак, обозначающий неравенство. Стало возможным различить, что, хотя и представлены по-разному, все части уравнения должны иметь одно и то же значение, чтобы знак равенства использовался правильно.

Решение уравнений с разными представлениями

Задача 2 представила два способа решения уравнения 3 x + 5 = 20 с методом сокращения.Учитель показал одно графическое изображение процесса решения, а также решил уравнение численно (рис. 1). Изначально на иконическом изображении была шкала с тремя коробками и пятью камнями с левой стороны и с двадцатью камнями с правой стороны.

Рис. 1

Вариация представления (числового и графического) процесса решения одного и того же уравнения (Задача 2). Примечание: пять камней по обе стороны шкалы были стерты в качестве первого шага в процессе решения.

В этой задаче представление менялось (иконическое / числовое), в то время как уравнение с одним неизвестным оставалось неизменным. Помимо возможности различить визуальное представление метода отмены, также стало возможным различить, что x может быть рядом объектов (камней).

Уравнения, которые вы не можете решить

В задаче 3 были обсуждены два уравнения, 3 x + 20 = 5 и 2 x + 3 = 3 x + 4, которые оказались неразрешимыми для положительных целые числа. Инвариантной особенностью этих примеров было то, что уравнения были неразрешимыми для положительных целых чисел, тогда как уравнения и числа в уравнениях менялись.Мы предполагаем, что из этих примеров и в отличие от уравнений в предыдущих задачах стало возможным определить, что некоторые уравнения с одним неизвестным не могут быть решены для положительных целых чисел.

Решение различных уравнений

В последней части урока, в Задании 4, два уравнения с одним неизвестным были составлены из словесных задач и решены одно за другим. Сравнение двух проблем не проводилось. Первая проблема касалась человека, покупающего вещи в магазине, ^{Footnote 2} , а вторая касалась отношения между возрастами трех сестер.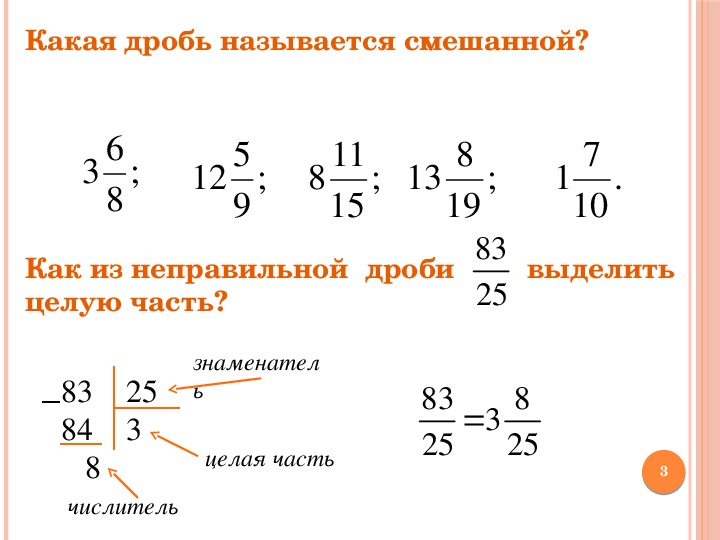 ^{Сноска 3} Два уравнения, x ÷ 3 + 495 = 1975 и 3 x + ( x + 5) + x = 40, различались в зависимости от контекста (цена, возраст), операции, используемые в уравнениях (сложение, деление) и числа в уравнениях. Для их решения использовался тот же метод (инвариант). Таким образом, стало возможным понять, что уравнения с одним неизвестным могут представлять разные ситуации и решать разные задачи.

Урок 2

Проведенный нами анализ Урока 2 показывает, что объект обучения акцентировал внимание на понимании уравнений , их структуры и того, как различные операции (сложение, вычитание, умножение и деление) влияют на уравнение.(В Уроке 1 операции использовались при решении уравнений с одним неизвестным, не обращая внимания на этот аспект.) Ответы на три уравнения, представленные во время урока, были уже известны с самого начала. В Задании 5 учитель использовал одно и то же уравнение (3 + 4 = 7), чтобы создать три разных уравнения с одним неизвестным (рис. 2). Сначала путем замены 3 на x было создано уравнение x + 4 = 7. Во втором уравнении x изменяется, когда 4 (в 3 + 4 = 7) было заменено на 2 × (3 + 2 x = 7).В третьем уравнении 3 + 4 = 7 остается отправной точкой, от которой снова изменяется x , когда 3 подставляется (с 6 x ÷ 4) в уравнение 6 x ÷ 4 + 4 = 7. Это был предоставлен студентам возможность увидеть создание уравнения с неизвестными числами и процесс решения этого уравнения одновременно. Поэтому в Уроке 2 основное внимание было сосредоточено не на поиске ответа, а на понимании того, что такое уравнение, путем изменения x и операций, используемых в процессе решения.В следующем разделе мы проиллюстрируем наш анализ, начиная с Задачи 1.

Рис. 2

Одно и то же уравнение используется для создания и решения трех разных уравнений с одним неизвестным в L2: иллюстрация белой доски (Задача 5)

Равенство, представленное различными операциями

Задача 1 раскрыла, аналогично L1, значение знака равенства / равенства путем варьирования равенства и неравенства. Однако в L2 больше наборов примеров иллюстрируют это, и числа, использованные в одном наборе примеров, остались неизменными (например,грамм. 6 × 4), варьируя различные операции и уравнения. В L2 первые два примера иллюстрировали неравенство по сравнению с L1, в котором равенство было отправной точкой. Итак, в L2 отправной точкой было противопоставление неправильного («показать шаги в процессе расчета») и правильного способа использования знака равенства.

1. 1.

   12 × 4 ≠ 48 ÷ 2 = 24

2. 2.

   6 × 4 ≠ 24 ÷ 2 = 12

3. 3.

   6 × 4 = 48 ÷ 2 = 24

4. 4.

   6 × 4 = 12 × 2 = 24

5. 5.

   6 + 2 = 8

6. 6.

   6 + 2 ≠ 8 ÷ 2 = 4

Стало возможным определить, что, хотя и представлены по-разному, все части уравнения должны иметь одинаковое значение, чтобы знак равенства использовался правильно.Следовательно, аналогичные измерения вариации были открыты в L2 (Задача 1) и в L1 (Задача 1).

Равенство, представленное различными операциями

Задача 2 касалась сложения и умножения и фокусировалась на представлении и различии между умножением на целые числа и умножением на x . Два примера, один с целыми числами и один с x , были сопоставлены, чтобы показать, как 3 + 3 + 3 + 3 = 4×3 не 43, тогда как x + x + x + x = 4 × x совпадает с 4 x . Следовательно, представление одного и того же числового значения менялось, сохраняя неизменными множитель (4) и x . Стало возможным различить, что при представлении множимого как x знак умножения можно опустить. Более того, можно было различить, что известное число можно было заменить на x .

Равенство, обрабатываемое различными операциями

Как операции изменяют или поддерживают равенство в уравнении, стало основной темой в Задачах 3 и 4, и мы предполагаем, что это было достигнуто путем систематического варьирования между примерами.В Задаче 3 (см. Ниже) четыре примера показывают, как умножение и деление с одним и тем же числом влияет на уравнение.

1. 1.

   5 × 3 ÷ 5 = 15 ÷ 5 = 3

2. 2.

   5 × 3 ÷ 3 = 15 ÷ 3 = 5

3. 3.

   6 × 4 ÷ 6 = 4

4. 4.

   6 x ÷ 6 = x

В первых двух примерах, 5 × 3 ÷ 5 = 15 ÷ 5 = 3 и 5 × 3 ÷ 3 = 15 ÷ 3 = 5, множители (5 и 3) остаются неизменными, меняется только делитель.В первом примере 5 разделили факторы, а во втором — 3. Это было дополнительно исследовано, когда один ученик попросил другой пример для проверки утверждения учителя: «Если у вас есть число (5), и вы умножаете это число на другое число (× 3), а затем делите на одно из чисел (например, ÷ 5) ) вы получите обратно другой номер (3) ».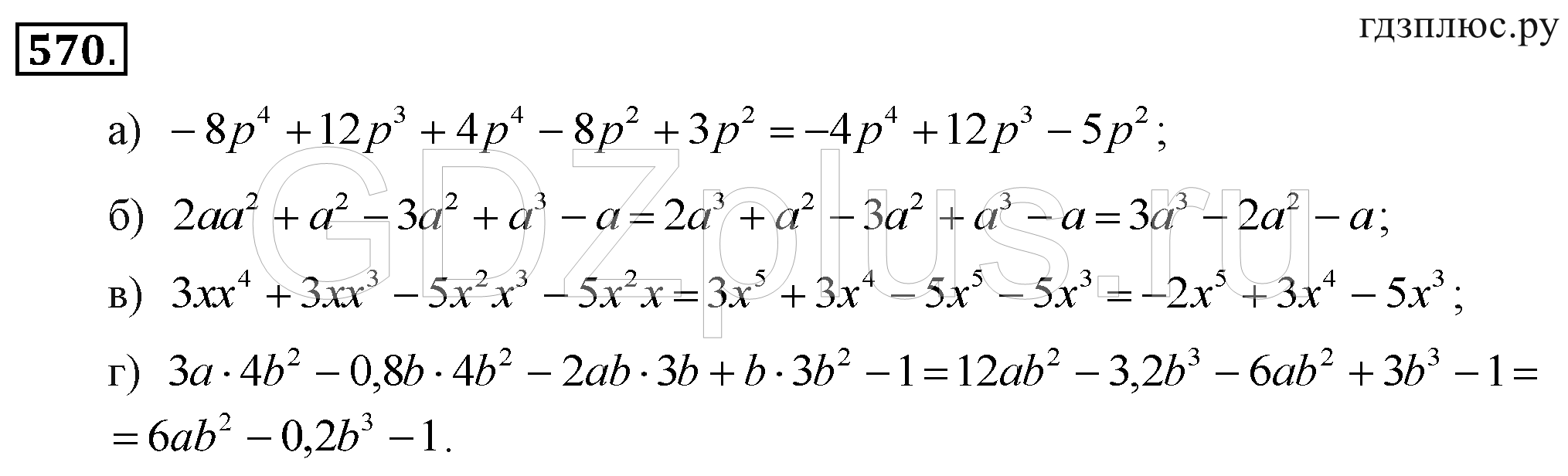 Итак, когда был приведен новый пример, на этот раз с совершенно другими числами, 6 × 4 ÷ 6 = 4, снова появилась возможность испытать умножение и деление с тем же числом (множитель / делитель).Последнее уравнение 6 x ÷ 6 = x аналогично 6 × 4 ÷ 6 = 4; в этом случае 4 используется вместо x в уравнении. Из приведенных примеров стало возможным понять, что умножение и деление на одно и то же число не меняет значения. Так же, как и в Задаче 2, стало возможным определить, что известное число можно заменить на x .

Свойства равенства

Как оперировать уравнением / равенством подробнее обсуждалось в Задаче 4 (см. Ниже).Однако в Задаче 4 это включало сложение, вычитание и умножение. Уравнение 3 + 4 = 7 оставалось неизменным в пяти примерах, тогда как операции в них менялись.

1. 1.

   3 + 4 = 7

2. 2.

   2 + 3 + 4 = 7 + 2

3. 3.

   2 + 3 + 4 –5 = 7 + 2 –5

4. 4.

   2 × 3 + 4 ≠ 7 × 2

5. 5.

   2 × 3 + 4 × 2 = 7 × 2

Было продемонстрировано, что равенство может поддерживаться, хотя уравнение оперируется, обращая внимание на аддитивное свойство равенства (a + c = b + c), свойство умножения равенства (a × c = b × c) и дистрибутивное свойство a × (b + c) = (a × b) + (a × c). Операции сложения и вычитания сравнивались с операциями умножения. При переходе от примера 2 + 3 + 4–5 = 7 + 2–5 к умножению 3 + 4 = 7 на 2 на 2 × 3 + 4 ≠ 7 × 2, стало возможным заметить распределительное свойство (2 × 3) + (4 × 2) = 7 × 2. Таким образом, стало возможным различить, что одна и та же операция должна выполняться по обе стороны от знака равенства, чтобы поддерживать равенство, и что при умножении оба сращения с каждой стороны необходимо обработать.Мы видим, что изменения между примерами немногочисленны и систематичны.

Создание и решение уравнений

В задаче 5 одно уравнение, 3 + 4 = 7, использовалось для создания и решения трех различных уравнений (см. Рис. 2 и ниже) с одним неизвестным. Как утверждалось ранее, три уравнения позволили студентам сосредоточиться на структуре уравнения и процессе его решения, а не на поиске ответа.

1. 1.

   х + 4 = 7

2. 2.

   3 + 2 х = 7

3. 3.

   6 x ÷ 4 + 4 = 7

Значение x могло изменяться, в то время как другие части уравнения и метод решения оставались неизменными.Стало возможным понять, как из одного и того же уравнения могут быть составлены разные уравнения с одним неизвестным.

Различные возможности обучения

Несмотря на то, что учитель преподавал одну и ту же тему на обоих уроках, мы предполагаем, что L1 и L2 сделали возможным различение разных измерений вариации (аспектов) и, следовательно, дали возможность изучать разные вещи. В L1 размерности вариации касались в основном: (1) значения знака равенства / равенства (=, ≠), (2) представления (пиктограммы, символики), (3) неразрешимых уравнений (решаемых, неразрешимых ), (4) контекст (камни, цена, возраст) в отношении решения уравнений с одним неизвестным. В L2 вместо этого рассматривались размеры вариации: (1) знак равенства / равенство (=, ≠), (2) представление уравнения / неизвестного (умножение на целое число, умножение на x ), (3) оперируя равенством (умножение, деление), (5) свойствами равенства (сложение, умножение) и (5) как можно составить уравнения (что x представляет собой разнообразное). Размеры вариации открылись в L1 и L2 соответственно, что позволило студентам испытать два совершенно разных объекта обучения.В L1 объектом обучения были, прежде всего, метод и процедура решения, тогда как в L2 это было понимание структуры уравнений. Формулировка учителем того, что он хотел, чтобы ученики изучали, подтверждает наш анализ того, что существует два разных объекта обучения.

Анализ показывает, что в L1 и L2 неизвестные x обрабатываются по-разному. В L1 неизвестное число в уравнении является отправной точкой и, следовательно, должно быть вычислено значение x .В L2 все наоборот. В Задаче 2 известное число (3) заменяется на x . Таким же образом в Задаче 3 число 4 в 6 × 4 ÷ 6 = 4 заменяется на x , чтобы получить 6 x ÷ 6 = x . В Задании 5 учитель создал три уравнения с одним неизвестным на основе уравнения 3 + 4 = 7. Мы предлагаем, чтобы, зная значение x в Задании 5 с самого начала и не вычисляя x , получилось. можно сосредоточиться на структуре уравнений в L2, а не в первую очередь на ответах.

Тем не менее, мы хотим отметить, что мы не можем делать выводы о том, действительно ли размеры вариаций (аспектов), представленные на уроках, были критическими для обучения учащихся. Это не изучалось и выходит за рамки данной статьи. Могут быть и другие аспекты, которые этим учащимся необходимо различить, чтобы освоить требуемые способности. Мы можем только сделать вывод, что эти два урока предлагали две совершенно разные возможности для обучения, поскольку были открыты разные измерения вариаций и, таким образом, стало возможным испытать их.

Планы уроков по летней безопасности Lovetoknow For Kids Рабочие листы 844×569 Вода и дети Повседневная математика

Mystique Hortense 13 мая 2021 г. Рабочий лист

Есть много возможностей научить вашего ребенка считать. У вас, вероятно, уже есть книги с числами и картинками, и вы можете все время считать вместе с ребенком. Существуют игры на счет и блоки с числами, настенные диаграммы и множество инструментов, которые помогут вам научить вашего ребенка основным принципам математики.Рабочие листы по математике могут помочь вам продолжить начальное обучение, чтобы познакомить вашего ребенка с основными принципами математики на том этапе его жизни, когда он хочет учиться и может быстро и легко усваивать новую информацию.

Для разных областей учебы дома доступны разные рабочие листы. Если вы знаете, что ваш ребенок будет изучать в течение года, вы уже можете найти рабочие листы для домашнего обучения по этой конкретной теме.

Есть много хороших рабочих тетрадей для детей детского сада.Однако с обычной рабочей тетрадью ребенок может выполнять каждое действие или рабочий лист только один раз. Хороший вариант — использовать рабочие листы для детского сада, которые можно распечатать. В основном это цифровые версии (например, электронные книги) рабочих листов, которые можно купить и загрузить на свой компьютер из Интернета или с компакт-дисков, а затем распечатать. Преимущество в том, что вы можете распечатать любой лист, который хотите. Если вам нужно еще раз разъяснить определенную концепцию, вы можете распечатать этот лист еще раз. Конечно, вам понадобится компьютер и принтер.

Эти листы помогают пользователям решать математические задачи. Решить эти проблемы стало намного проще с помощью математических листов.

Рабочие листы с прямым объектом

6 июня 2021 г.

Рабочие листы с фактами и мнениями

6 июня 2021 г.

Рабочие листы с рефлексивными местоимениями

6 июня 2021 г.

Хорошо составленные рабочие листы для детского сада могут быть интересны детям и могут быть очень полезны для закрепления основных понятий. Выполнение задания на листе может дать детям огромное чувство выполненного долга.

Систематический набор рабочих листов по математике поможет вам научить вашего ребенка основным принципам математики и поможет ему подготовиться к школе. Рабочие листы можно использовать как основу для подсчета и добавления игр и других действий. Обучая своего ребенка рабочим листам, он также может чувствовать себя более комфортно с рабочими листами, что поможет им, когда они попадут в детский сад или школу, где рабочие листы используются каждый день.

Фотографии рабочих листов по безопасности летом для детей

Оставьте свой ответ о планах уроков по безопасности летом Рабочие листы Lovetoknow для детей 844×569 Вода и дети, повседневная математика

10 лучших учителей в окрестностях Пало-Альто, Калифорния

Немного Квалификация репетитора

В настоящее время я работаю заместителем учителя в государственных школах Анн-Арбора в Анн-Арборе, штат Мичиган. Я обучаю учеников с K-12 классов. Имею степень магистра инженерных наук и 10 лет проработал разработчиком программного обеспечения.Я взял некоторое время в свободное от работы время, чтобы позаботиться о нуждах моих растущих детей. С годами я увлекся математикой, помогая своим детям на протяжении всех школьных лет. С последних 4 лет я заменял в государственных школах Анн-Арбора предалгебру и другие предметы по мере необходимости. Работая со своими учениками, моя цель — понять их слабые места и помочь им преодолеть их, чтобы они могли перейти к обучению. следующий уровень с уверенностью.

Рино С.

Я провожу практические занятия по обучению слуху при исполнении классической, эстрадной и джазовой музыки.Я закончил университетскую степень музыкального колледжа Беркли в Бостоне. У меня 38-летний педагогический стаж. Я профессионально выступаю на слух и на слух уже более 40 лет. У меня есть курсовая работа в колледже и непрерывное образование.

Рональд Х.

Я изучал китайский язык 7 лет и приобрел обширные знания китайского языка. Я работал со студентами по обмену, китайскими директорами из Шанхая и иностранными студентами в Геттисбургском колледже, моей школе. Я обучал многих своих друзей через уроки китайского языка и помог им добиться успеха с помощью объяснений и примеров.Я также уделяю большое внимание разговору на языке, так как это очень важно для беглости речи. Мне нравится распространять китайский язык среди других, и я чувствую, что мои знания помогут тем, кто хочет выучить этот язык.

Люк Г.

Мои оценки по Praxis I находятся в верхнем квартиле по каждому предметному тесту и почти идеальны по субтесту по математике. У меня также есть оценки Praxis II с> 90-м процентилем для каждого субтеста. У меня отличный результат по тесту на знание английской литературы и языкового содержания.

Эван К.

У меня более 20 лет опыта работы как учителем средней и старшей школы, так и репетитором, работающим со студентами над улучшением их учебных навыков, включая помощь в организации, методах и он-лайн ресурсах. Пожалуйста, смотрите мой профиль для получения дополнительной информации.

Шеннон Д.

Аутизм имеет широкий спектр. У меня был многолетний опыт работы со студентами на обоих концах спектра и повсюду между ними. Для меня совершенно естественно знать ученика, оценивать индивидуальные потребности и реализовывать соответствующую программу и проводить занятия.Жизненные навыки и соответствующие навыки социализации часто важнее любого предметного содержания.

Donna T.

У меня степень бакалавра в области управления бизнесом (управление проектами) и две степени MBA в области управления бизнесом; первый — в управлении проектами, второй — в управлении операциями. В настоящее время я являюсь адъюнкт-инструктором студентов MBA, которые преподают статистический анализ. Мой средний балл по программе бакалавриата составил 3,96 из 4,0, а в программах MBA средний балл составил 3,90 из 4,0.

Стефани А.

Образование и сертификация: у меня есть степень бакалавра искусств в области специального образования в колледже Сент-Роуз и степень магистра наук в области дошкольного образования, ясли и 1-6 классы в колледже Сент-Роуз. У меня есть постоянный сертификат учителя государственной школы, выданный Департаментом образования Университета штата Нью-Йорк, действующий с 01.09.96. Мои области сертификации следующие: специальное образование, ясли, детский сад и 1-6 классы, и у меня более 20 лет высокоэффективной работы учителем.

Elicia S.

См. Описание курса SAT Math, Reading and Writing.

Джек М.

Я выпускник Колумбийского университета и в настоящее время работаю внештатным писателем и редактором. У меня есть опыт работы со студентами, помогающий развить удовольствие от чтения. Я делаю это, работая над улучшением их навыков, используя их индивидуальные интересы для разработки планов уроков и выбора отрывков для чтения во время занятий.

Хлоя Л.

Другие просьбы таких учеников, как ты

У меня есть 9-летний пасынок, и я хотел бы выучить его английский в наступающем учебном году.

Jr U.

У меня есть старший ученик, которому нужна помощь с тригонометрией, и второкурсник, которому нужна помощь с физикой.

No related posts.