Открытый урок по математике 5 класс «Уравнение» | План-конспект урока (5 класс) по теме:
Тема урока: « Уравнение»
Цели урока: 1.Продолжить формировать умения и навыки решать уравнения, применяя знания при решении задач.
2. Развивать логическое мышление, познавательный интерес ,а также навыки контроля и самоконтроля.
3. Приучать школьников к эстетическому оформлению записи, умению выслушивать и умению общаться.
Тип урока: урок закрепления и совершенствования знаний.
Урок проводится по учебнику: Н .Я. Виленкин и др. «Математика 5» издательство «Мнемозина» , 2008;
Ход урока.
Организационный момент.
Постановка целей урока.
Прозвенел опять звонок
Начинается урок
Будем мы писать, считать, уравнения решать.
На уроке работай старательно , и успех тебя ждет обязательно.
Тема нашего урока « Уравнение ». Мы продолжим с вами отрабатывать навыки решения уравнений, задач, готовиться к контрольной работе.
3. Актуализация опорных знаний и устная работа.
Актуализация опорных знаний и устная работа.
1.Как найти неизвестное слагаемое?
2.Как найти неизвестное уменьшаемое?
3.Как найти неизвестное вычитаемое?
4. (Слайд № 2 ) Перед вами записаны уравнения, числа и буквы. Вам надо решить устно уравнения, среди чисел найти верный ответ и в черновик записать рядом стоящую букву.
а) х + 17 = 60; д) 59 + х = 59;
б) у – 51 =60; е) 88 – х = 78;
в) 60 = у + 51; ж) х – 0 = 82;
г) 62 = 100 – у; з) 0 + х = 24.
111; 10; 43; 9; 0; 82; 38; 77; 24.
о ц м л д ы о р !
(Слайд № 2) Молодцы! Кто правильно решил, тот получил слово — молодцы! Поднимите руки, у кого все решения верные . ( учитель фиксирует у себя результаты)
5. ( Слайд № ) Придумайте задачу которая решалась бы с помощью уравнения и решите ее. х + 15 =45.
6. ( Слайд № 4 ) Угадайте корень уравнения а) х + х = 42; б) 25 + у + у + у = 25
5. Математический диктант.
Математический диктант.
Запишите в тетрадях число, классная работа, мат. Диктант на листочках
Лес как вы знаете поглощает углекислый газ и выделяет кислород необходимый человеку. Лес еще работает как фильтр, очищая воздух от сажи и пыли. В таблице ( Слайд №5) приведены данные о количестве ( кг )выделяемого кислорода в год. Используя данные таблицы, выполните следующие задания.
1 гектар | Кол-во выделяемого кислорода в год ( кг ) |
Дубовый лес | 830 |
Березовый лес | 725 |
Осиновый лес | 575 |
Сосновый лес | 540 |
Еловый лес | 500 |
1.На сколько наибольшее число больше наименьшего числа ?
2.Найти сумму чисел которые оканчиваются цифрой 5.
3.Уменьшаемое – сосновый лес, разность – еловый лес. Найти вычитаемое.
Найти вычитаемое.
4.Первое слагаемое – еловый лес, сумма – березовый лес. Найти неизвестное слагаемое.
5.Вычитаемое – осиновый лес. Разность – сосновый лес. Найти уменьшаемое.
( Слайд №6) Проверь себя! (взаимопроверка)
1. 830 – 500 = 330; 2. 725 +575 = 1300; 3. 540 – х = 500, х = 40; 4.500 + х = 725, х = 225; 5. х – 575 = 540, х = 1115.
Поставьте оценку своему соседу по парте
( учитель фиксирует у себя результаты)
Выполнение упражнений.
( Слайд № 7) Найди ошибки и реши правильно.
Ученик решал уравнение ( х – 24 )+ 37 = 49, и получил вот такое решение
х – 24 =49 +37,
х – 24 =86,
х = 86 -24,
х =72.
Ребята посмотрели на его решение и дружно засмеялись. Чем же был вызван смех ребят?
Один ученик решает самостоятельно у доски, остальные решают в тетрадях любым способом который вам больше нравится. ( Сверяются решения)
х -24 = 49 -37.
х -24 =12,
х = 12 +24,
х = 36.
2. Работа с книгой. Решить самостоятельно уравнение
3. А сейчас разгадав ребус, вы ребята, узнаете чем мы будем заниматься далее.
( Слайд № 8) Ребус ( Задача )
Решим задачу № 377, уравнение составит у доски ( ученик), а решать полученное уравнение будем самостоятельно в тетрадях. Кто сможет решите двумя способами.
( наиболее подготовленные учащиеся решают двумя способами)
( х + 39 )- 43 =27,
х = 31.
Ответ: 31 литр.
Проверка знаний, умений, навыков.
Проведение самостоятельной работы с элементами теста в двух вариантах.
Вариант – 1.
1. Решите задачу с помощью уравнения.
Маша задумала число. Если его вычесть из числа 172, то получится 145. Какое число задумала Маша?
а) 27 б) 72 в) 37
2.Решить уравнение 44 + ( у – 85 ) = 105.
а) 145 б) 146 в) 164
3. Найдите значение выражения, предварительно упростив его.
( 256 – х ) – 156 , если х = 44
а) 65 б) 56 в) 44
Вариант –
Решите задачу с помощью уравнения.
Если из задуманного числа вычесть 137, то получится 153. Найти задуманное число.
а) 290 б) 300 в) 390
2.Решить уравнение 69 + ( 87 – х ) =103
а) 54 б) 35 в) 53
3. Найдите значение выражения, предварительно упростив его.
238 – ( 38 + х) , если х = 78
а) 200 б) 122 в) 72
( Слайд № 9) Проверь себя! ( Самопроверка) Проверив свою работу, поставьте себе оценку. ( учитель фиксирует у себя результаты)
Вариант – 1. Вариант – 2.
1. а 1. а
2. б 2. в
3. б 3. б
8. Итоги урока. Ребята, вот и подошел урок к концу. Что ж мы повторили на уроке? А что вам понравилось больше всего? Решение уравнений – важная тема, и мы на протяжении всей школьной жизни будем к ней постоянно возвращаться. А теперь выставим оценки.
А теперь выставим оценки.
Сдайте тетради, я ещё раз все у вас проверю.
9. Домашнее задание. Сегодня домашнее задание па карточкам. Решения выполнить в тетради.
В а р и а н т 1. С – 9. Решите уравнения а) 138 + х + 57 = 218 б) 248 – ( у + 123 ) =24 в) ( 24 – х ) + 37 = 49. Угадайте корень уравнения и сделайте проверку х + 3 = 9 – х. | В а р и а н т 2. С – 9. Решите уравнения а) 257 – х + 124 = 149 б) 165 – ( у + 112 ) = 37 в) 44 + ( а – 85 ) = 105 Угадайте корень уравнения и сделайте проверку 8 – у = у + 2. |
В а р и а н т 3. С – 9. Решите уравнения а) 175 + х – 37 = 108 б) 243 – ( у + 83 ) = 112 в) 69 + ( 87 – п ) = 103 Угадайте корень уравнения и сделайте проверку х + 7 = 11 – х. | В а р и а н т 4. С – 9. Решить уравнения а) ( х + 124 ) – 76 = 357 б) 375 – у + 218 = 123 в) ( т – 27 ) + 34 = 53. Угадайте корень уравнения и сделайте проверку 7 – у = у + 1. |
Решение уравнений (Слупко М.В.) 6 класс онлайн-подготовка на Ростелеком Лицей
Введение
Мы уже знаем, что уравнение – это равенство, в котором есть неизвестные (переменные). Пока мы будем говорить только об уравнениях с одной переменной. Рассмотрим уравнение: .
Подставим в уравнение вместо неизвестной . Получаем , неверное равенство.
Аналогичная ситуация возникнет, если подставим двойку: .
А вот если подставим тройку, то получим: , то есть верное равенство: .
Такие значения переменной, при которых уравнение превращается в верное равенство, называют корнями уравнения. То есть число является корнем данного уравнения.
А есть ли ещё у этого уравнения корни? Для того чтобы ответить на этот вопрос, надо научиться решать уравнения.
Решить уравнение – значит найти все его корни или доказать, что их нет (например, у уравнения нет корней, так как левая часть всегда равна нулю).
Как же найти этот корень (или корни)? Можно пробовать наугад подставлять разные числа и проверять, верное или неверное равенство получилось. Но этот метод больше напоминает поиск «иголки в стоге сена», так как чисел бесконечно много и все перебрать не получится. Значит, нужно научиться преобразовывать ту информацию, которая содержится в уравнении таким образом, чтобы найти его корни.
Начнем с уравнений, которые не вызывают у нас проблем при решении. С одной стороны уравнения переменная, с другой – число: .
Ответ: .
Ответ: .
В самом деле если подставлять вместо другие числа, то верного равенства не получишь.
Эквивалентные уравнения
Рассмотрим следующий пример: .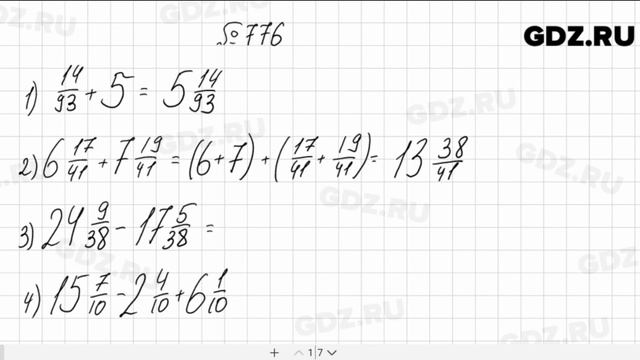
Уравнение – это информация о неизвестной переменной. Мы еще не знаем, чему равно , но знаем, что если умножить на и вычесть единицу, то получится . Но одну и ту же информацию можно сообщить разными, эквивалентными способами. Если после вычитания единицы будет , значит, до вычитания единицы было .Значит, эту же информацию можно записать и так: .
Мы еще не нашли корень этого уравнения, но знаем, что он такой же, как и у исходного уравнения. Такие уравнения, которые имеют одинаковые корни, называют эквивалентными.
Уравнение эквивалентно первому, но выглядит проще. Если умножить на , то получится . Но тогда если мы вспомним, что такое деление, то по определению получаем, что .
Это опять та же самая информация, но уже в явном виде. Корень этого уравнения .
Все уравнения были эквивалентны. Значит, является корнем и первого уравнения.
В самом деле подставим в первое уравнение вместо переменной. Получили верное равенство:
Ответ: .
Вот мы и получили идею метода решения уравнения. Нужно переписывать исходное уравнение в эквивалентном виде так, чтобы в итоге получилось простейшее уравнение, у которого в одной части переменная, а в другой число.
И остался последний вопрос. Что можно делать с уравнением, как его можно преобразовывать, чтобы новое уравнение было эквивалентно предыдущему?
Рис. 1. Иллюстрация к примеру
Если в двух вазах одинаковое количество яблок (пусть даже неизвестно, сколько точно), то если добавить в каждую по яблока, то количества в обеих снова будут одинаковы (рис. 1).
Такая же ситуация и с уравнением. Уравнение – это равенство двух количеств.
Если к обеим частям уравнения прибавить или от обеих частей отнять одно и то же число или переменную, то полученное уравнение будет эквивалентно исходному: .
Договоримся для краткости говорить, что уравнение не изменится (хотя внешне оно уже будет выглядеть иначе).
Эквивалентные преобразования.
 Перенос слагаемых
Перенос слагаемых
Пример 1. Добавить к обеим частям уравнения можно любое число. Но нужно выбрать такое, чтобы уравнение упростилось. Рассмотрим пример: .
Смотрим на ту часть, где находится переменная. Если там не будет слагаемого , то станет проще (получим в левой части переменную, а такие уравнения мы уже умеем решать). Если к числу прибавить противоположное, то в результате будет ноль. Для числа противоположным является . Добавим число к обеим частям уравнения.
Ответ: .
Пример 2.
Переменная входит в обе части уравнения. Мы же хотим, чтобы переменная была только в одной части (такие уравнения мы умеем решать). Добавим к обеим частям:
Ответ: .
Пример 3.
Добавим к обеим частям уравнения . Сравним исходное уравнение и полученное. В левой части исчезло, а в правой появилось противоположное число . Похоже, что число мы перенесли в правую часть, поменяв у него знак.
Любое слагаемое можно перенести из одной части уравнения в другую, поменяв знак на противоположный (это действие эквивалентно добавлению к обеим частям слагаемого, противоположного перенесённому).
Ответ: .
Пример 4.
Перенесем в правую часть, а – в левую. У обоих слагаемых при этом меняем знак на противоположный.
Ответ: .
Эквивалентные преобразования. Домножение и деление
Давайте снова обратимся к нашему опыту. Пусть в двух вазах одинаковое количество яблок. Увеличим количество яблок в каждой в два раза. Будет ли и теперь количество одинаковым? Конечно, будет. А если бы мы уменьшили количество яблок в каждой вазе в три раза? Опять количества остались бы равными.
Так же и с уравнением: если обе части уравнения умножить или поделить на одно и то же ненулевое число, то новое уравнение будет эквивалентно исходному (или мы говорим «не изменится»).
Примеры: . Поделим обе части уравнения на : .
Поделим обе части уравнения на : .
Ответ: 6.
Умножим обе части уравнения на : .
Ответ: .
Следующий пример: .
Разделим обе части уравнения на : .
Ответ: .
Решим еще несколько уравнений.
Пример 1.
Ответ: .
Пример 2.
Проверка: .
Ответ: .
Пример 3.
Ответ: .
Заключение
При решении уравнений наша цель – привести исходное уравнение к виду «неизвестная равна числу», в этом случае мы решили исходное уравнение.
Пример:
Для этого мы сначала собираем все слагаемые с неизвестной в одной части уравнения, а остальные – в другой:
Для решения уравнений мы используем следующие эквивалентные преобразования.
- Добавление или вычитание к обеим частям уравнения одного и того же выражения (или, по-другому, перенос слагаемых в другую часть уравнения с изменением его знака):
Или:
- Домножение или деление обеих частей уравнения на одно и то же ненулевое выражение:
1)
2)
Список рекомендованной литературы
- Математика 5 класс.



