Контрольная работа №5 по теме « Упрощение выражений»
Контрольная работа №5 по теме « Упрощение выражений»
Вариант 1.
1.Вычислите: а) 684 ∙ 397 – 584 ∙ 397; б) 23 + 32.
2. Решите уравнение: а) 7у – 15 = 41; б) х + 3х = 76. в)6∙х∙3 = 90
3. Упростите: а) 24а + 16 + 13а; б) х ∙ 5 ∙ 7;
4. Решите задачу с помощью уравнения: В книге напечатаны две сказки. Первая занимает в четыре раза больше страниц, чем вторая, а обе они занимают 30 страниц. Сколько страниц занимает каждая сказка?
5. Найдите значение выражения: 6х + 15 – 2х + 5 – х, если х = 5.
_____________________________________________________________________________________
Вариант 2.
1. 1.Вычислите: а) 394 ∙ 58 + 606 ∙ 58; б) 52 + 33.
2. Решите уравнение: а) 8х + 14 = 30; б) 5х – х = 68. в) у∙12∙6 =144
в) у∙12∙6 =144
3. Упростите: ) 37х + х + 13 + 22х; б) 50 ∙ х ∙ 12;
4. Решите задачу с помощью уравнения: В двух корзинах 98 яблок. В первой корзине яблок в шесть раз больше, чем во второй. Сколько яблок в каждой корзине?
5. Найдите значение выражения: 7х + 7 – 3х + 13 + х, если х = 3.
____________________________________________________________________________________
Вариант 3.
1. 1.Вычислите: а) 394 ∙ 583 + 417 ∙ 394; б) 42 + 23.
2. Решите уравнение: а) 6х + 12 = 240; б) 8х + х = 90. в) у∙7∙14 =98
3. Упростите: а) 16х + 19 + 23х; б) 60 ∙ х ∙ 5;
4. Решите задачу с помощью уравнения: За два дня в магазин привезли 1600 кг яблок. В первый день яблок привезли в четыре раза больше , чем во второй. Сколько яблок привезли в первый день и сколько во второй?
5. Найдите значение выражения: 5х + 7 + 2х + 5 – х, если х = 2.
Найдите значение выражения: 5х + 7 + 2х + 5 – х, если х = 2.
_____________________________________________________________________________________
Вариант 4.
1. 1.Вычислите: а) 635 ∙ 247 – 247 ∙ 535; б) 72 + 33.
2. Решите уравнение: а) 3х – 12 = 36; б) 9х – х = 240;. в) 5∙12∙с =120
3. Упростите: а) 9х + 16 + 3х; б) 90 ∙ х ∙ 4;
4. Решите задачу с помощью уравнения: Масса первой детали в 7 раз больше массы второй. Найдите массу каждой детали, если вместе они весят 56 кг.
5. Найдите значение выражения: 6х + 13 – 4х + 7 + х, если х = 3.
_____________________________________________________________________________________
Вариант 5.
1. 1.Вычислите: а) 392 ∙ 543 + 392 ∙ 457; б) 62 + 43.
2. Решите уравнение: а) 4х + 20 = 80; б) 9х + х = 90; в) 15∙х∙6 =720
3. Упростите: а) 8х + 25 + 4х; б) 6 ∙ х ∙ 30;
Упростите: а) 8х + 25 + 4х; б) 6 ∙ х ∙ 30;
4. Решите задачу с помощью уравнения: В первый вагон погрузили в 3 раза больше угля, чем во второй. Сколько тонн угля погрузили в каждый из этих вагонов, если всего погрузили 12 тонн угля?
5. Найдите значение выражения: 8х + 14 + 2х + 13 – х, если х = 2.
_____________________________________________________________________________________
Вариант 6.
1. 1.Вычислите: а) 947 ∙ 392 – 847 ∙ 392; б) 82 + 33.
2. Решите уравнение: а) 6х + 6 = 36; б) 6х – х = 60. в) 17∙3∙а =153
3. Упростите: а) 6х + 21 + 7х; б) 8 ∙ х ∙ 40;
4. Решите задачу с помощью уравнения: Первый кусок провода в 6 раз длиннее второго. Найдите длину каждого куска, если весь провод равен 420 метров.
5. Найдите значение выражения: 6х + 5 + 3х + 1 + х, если х = 8.
_____________________________________________________________________________
Вариант 7.
1. Вычислите: а) 398 ∙ 98 + 98 ∙ 602; б) 72 + 23.
2. Решите уравнение: а) 7х + 8 = 57; б) 8х + х = 720. в) у∙27∙3 =324
3. Упростите: а) 4х + 12 + 5х; б) 3 ∙ х ∙ 25;
4. Решите задачу с помощью уравнения: В первый день машина прошла расстояние в 3 раза больше, чем во второй. Сколько километров прошла автомашина в каждый из этих дней, если всего она прошла 360 километров?
5. Найдите значение выражения: 10х + 9 + 2х + 3 – х, если х = 4.
_____________________________________________________________________________
Вариант 8.
1. Вычислите: а) 249 ∙ 834 – 734 ∙ 249; б) 52 + 23.
2. Решите уравнение: а) 3х – 16 = 32; б) 9х – х = 720. в) 34∙х∙3 =510
в) 34∙х∙3 =510
3. Упростите: а) 6х + 19 + 2х; б) 8 ∙ х ∙ 5;
4. Решите задачу с помощью уравнения: Провод длиной 60 метров разрезали на два куска так, что длина одного из них оказалась в 5 раз больше другого. Найдите длину каждого куска.
5. Найдите значение выражения: 12х + 8 – 3х + 3 + х, если х = 2.
________________________________________________________________________
Вариант 9.
1. Вычислите: а) 692 ∙ 394 + 606 ∙ 692; б) 53 – 42.
2. Решите уравнение: а) 5х + 12 = 67; б) 11х + х = 60. в) у∙53∙2 =636
3. Упростите: а) 12х + 11 + 5х; б) 6 ∙ х ∙ 4;
4. Решите задачу с помощью уравнения: За день туристы прошли 15 км. После обеда они прошли в 4 раза больше, чем до обеда. Сколько километров прошли туристы после обеда и сколько до обеда?
5.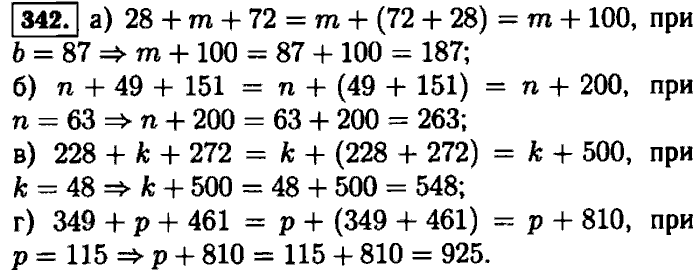 Найдите значение выражения: 17х + 9 – 7х + 3 – х, если х = 5.
Найдите значение выражения: 17х + 9 – 7х + 3 – х, если х = 5.
_____________________________________________________________________________________
Вариант 10.
1. Вычислите: а) 647 ∙ 99 – 547 ∙ 99 б) 52 – 23.
2. Решите уравнение: а) 3х – 7 = 65; б) 6х – х = 35. в) с∙12∙8 =960
3. Упростите: а) 7х + 12 + 4х; б) 2 ∙ х ∙ 3;
4. Решите задачу с помощью уравнения: В первый бидон налили в 5 раз больше масла, чем во второй. Сколько литров налили в каждый бидон, если всего было 30 литров масла?
5. Найдите значение выражения: 12х + 4 + 2х + х, если х = 5.
_____________________________________________________________________________
Вариант 11.
1. Вычислите: а) 394 ∙ 247 + 753 ∙ 394; б) 62 – 33.
2. Решите уравнение: а) 13х – 4 = 22; б) 12х – х = 33. в) 41∙6∙у =738
в) 41∙6∙у =738
3. Упростите: а) 6х + 11 + 3х; б) 6 ∙ х ∙ 8;
4. Решите задачу с помощью уравнения: Для оклейки комнаты и коридора купили 25 рулонов обоев. Сколько рулонов пойдёт на оклейку стен в комнате, сколько на оклейку стен в коридоре, если для оклейки стен комнаты требуется в 4 раза больше обоев, чем для коридора?
5. Найдите значение выражения: 6х + 3 – 2х + 10 + х, если х = 8.
_____________________________________________________________________________________
Вариант 12.
1. Вычислите: а) 647 ∙ 39 – 547 ∙ 39; б) 52 + 43.
2. Решите уравнение: а) 12х + 10 = 46; б) 14х + х = 45. в) 58∙4∙с =1160
3. Упростите: а) 2х + 3 + 6х; б) 3 ∙ х ∙ 8;
4. Решите задачу с помощью уравнения: Масса двух чемоданов 20 кг. Причём масса одного из них в 3 раза больше массы другого. Найдите массу каждого чемодана.
Найдите массу каждого чемодана.
5. Найдите значение выражения: 9х – 3х + 4 – х + 6, если х = 10
Решебник Контрольные и самостоятельные работы по математике к учебнику Н.Я. Виленкина, Попов М.А. 5 класс гдз
Задание не найдено
САМОСТОЯТЕЛЬНЫЕ РАБОТЫ
Самостоятельная работа № 1. Обозначение натуральных чисел
Вариант-1
Вариант-2
Самостоятельная работа № 4. Шкалы и координаты
Вариант-1
Вариант-2
Самостоятельная работа № 5. Меньше или больше
Вариант-1
Вариант-2
Самостоятельная работа № 6. Сложение натуральных чисел и его свойства
Вариант-1
Вариант-2
Самостоятельная работа № 7. Вычисления
Вариант-1
Вариант-2
Самостоятельная работа № 8. Числовые и буквенные выражения
Вариант-1
Вариант-2
Самостоятельная работа № 9. Буквенная запись свойств сложения и вычитания
Вариант-1
Вариант-2
Самостоятельная работа № 10. Уравнение
Уравнение
Вариант-1
Вариант-2
Самостоятельная работа № 11. Умножение натуральных чисел и его свойства
Вариант-1
Вариант-2
Самостоятельная работа № 12. Деление
Вариант-1
Вариант-2
Самостоятельная работа № 13. Деление с остатком
Вариант-1
Вариант-2
Самостоятельная работа № 14. Упрощение выражений
Вариант-1
Вариант-2
Самостоятельная работа № 15. Порядок выполнения действий
Вариант-1
Вариант-2
Самостоятельная работа № 16. Квадрат и куб числа
Вариант-1
Вариант-2
Самостоятельная работа № 17. Формулы
Вариант-1
Вариант-2
Самостоятельная работа № 18. Площадь. Формула площади прямоугольника
Вариант-1
Вариант-2
Самостоятельная работа № 19. Единицы измерения площадей
Вариант-1
Вариант-2
Самостоятельная работа № 20. Прямоугольный параллелепипед
Вариант-1
Вариант-2
Самостоятельная работа № 21. Объемы. Объем прямоугольного параллелепипеда
Вариант-1
Вариант-2
Самостоятельная работа № 22. Окружность и круг
Окружность и круг
Вариант-1
Вариант-2
Самостоятельная работа № 23. Доли. Обыкновенные дроби
Вариант-1
Вариант-2
Самостоятельная работа № 24. Сравнение дробей ….
Вариант-1
Вариант-2
Самостоятельная работа № 25. Правильные и неправильные дроби
Вариант-1
Вариант-2
Самостоятельная работа № 26. Сложение и вычитание дробей с одинаковыми знаменателями
Вариант-1
Вариант-2
Самостоятельная работа № 27. Деление и дроби
Вариант-1
Вариант-2
Самостоятельная работа № 28. Смешанные числа
Вариант-1
Вариант-2
Самостоятельная работа № 29. Сложение и вычитание смешанных чисел
Вариант-1
Вариант-2
Самостоятельная работа № 30. Десятичная запись дробных чисел
Вариант-1
Вариант-2
Самостоятельная работа № 31. Сравнение десятичных дробей
Вариант-1
Вариант-2
Самостоятельная работа № 32. Сложение и вычитание десятичных дробей
Вариант-1
Вариант-2
Самостоятельная работа № 33. Приближенные значения чисел. Округление чисел
Приближенные значения чисел. Округление чисел
Вариант-1
Вариант-2
Самостоятельная работа № 34. Умножение десятичных дробей на натуральные числа
Вариант-1
Вариант-2
Самостоятельная работа № 35. Деление десятичных дробей на натуральные числа
Вариант-1
Вариант-2
Самостоятельная работа № 36. Умножение десятичных дробей
Вариант-1
Вариант-2
Самостоятельная работа № 37. Деление на десятичную дробь
Вариант-1
Вариант-2
Самостоятельная работа № 38. Среднее арифметическое
Вариант-1
Вариант-2
Самостоятельная работа № 39. Микрокалькулятор
Вариант-1
Вариант-2
Самостоятельная работа № 40. Проценты
Вариант-1
Вариант-2
Самостоятельная работа № 41. Угол. Прямой и развернутый угол. Чертежный треугольник
Вариант-1
Вариант-2
Самостоятельная работа № 42. Измерение углов. Транспортир
Вариант-1
Вариант-2
Самостоятельная работа № 43. Круговые диаграммы
Круговые диаграммы
Вариант-1
Вариант-2
КОНТРОЛЬНЫЕ РАБОТЫ
Контрольная работа № 1. Обозначение натуральных чисел. Отрезок. Длина отрезка. Треугольник. Плоскость. Прямая. Луч. Шкалы и координаты. Меньше или больше
Вариант 1
Вариант 2
Вариант 3
Вариант 4
Контрольная работа № 2. Сложение натуральных чисел и его свойства. Вычитание
Вариант 1
Вариант 2
Вариант 3
Вариант 4
Контрольная работа № 3. Числовые и буквенные выражения. Буквенная запись свойств сложения и вычитания. Уравнение
Вариант 1
Вариант 2
Вариант 3
Вариант 4
Контрольная работа № 4. Умножение натуральных чисел и его свойства. Деление. Деление с остатком
Вариант 1
Вариант 2
Вариант 3
Вариант 4
Контрольная работа № 5. Упрощение выражений. Порядок выполнения действий. Квадрат и куб числа
Вариант 1
Вариант 2
Вариант 3
Вариант 4
Контрольная работа № 6. Формулы. Площадь. Формула площади прямоугольника. Единицы измерения площадей. Прямоугольный параллелепипед. Объемы. Объем прямоугольного параллелепипеда
Формула площади прямоугольника. Единицы измерения площадей. Прямоугольный параллелепипед. Объемы. Объем прямоугольного параллелепипеда
Вариант 1
Вариант 2
Вариант 3
Вариант 4
Контрольная работа № 7. Окружность и круг. Доли. Обыкновенные дроби. Сравнение дробей. Правильные и неправильные дроби
Вариант-4
Вариант 1
Вариант 2
Вариант 3
Контрольная работа № 8. Сложение и вычитание дробей с одинаковыми знаменателями. Деление и дроби. Смешанные числа. Сложение и вычитание смешанных чисел
Вариант 1
Вариант 2
Вариант 3
Вариант 4
Контрольная работа № 9, Десятичная запись дробных чисел. Сравнение десятичных дробей. Сложение и вычитание десятичных дробей. Приближенные значения чисел. Округление чисел
Вариант-1
Вариант-2
Вариант-3
Вариант-4
Контрольная работа № 10. Умножение десятичных дробей на натуральные числа. Деление десятичных дробей на натуральные числа
Вариант-1
Вариант-2
Вариант-3
Вариант-4
Контрольная работа № 11. Умножение десятичных дробей. Деление на десятичную дробь. Среднее арифметическое
Умножение десятичных дробей. Деление на десятичную дробь. Среднее арифметическое
Вариант-1
Вариант-2
Вариант-3
Вариант-4
Контрольная работа № 12. Микрокалькулятор. Проценты
Вариант-1
Вариант-2
Вариант-3
Вариант-4
Итоговая контрольная работа
Вариант-1
Вариант-2
Вариант-3
Вариант-4
Поурочные разработки по Математике 5 класс к УМК Н.Я. Виленкина
Примерное тематическое планирование учебного материала
Глава I. НАТУРАЛЬНЫЕ ЧИСЛА
§ 1. НАТУРАЛЬНЫЕ ЧИСЛА И ШКАЛЫ
Урок 1. Натуральные числа (вводный урок)
Урок 2. Натуральные числа
Урок 3. Натуральные числа
Урок 4. Отрезок. Длина отрезка. Треугольник
Урок 5. Отрезок. Длина отрезка. Треугольник
Урок 6. Отрезок. Длина отрезка. Треугольник
Урок 7. Плоскость. Прямая. Луч
Урок 8. Плоскость. Прямая. Луч
Урок 9. Шкалы и координаты
Урок 10. Шкалы и координаты
Урок 11. Шкалы и координаты
Урок 12. Меньше или больше
Меньше или больше
Урок 13. Меньше или больше
Урок 14. Меньше или больше
Урок 15. Контрольная работа по теме «Натуральные числа и шкалы»
§ 2. СЛОЖЕНИЕ И ВЫЧИТАНИЕ НАТУРАЛЬНЫХ ЧИСЕЛ
Урок 16. Сложение натуральных чисел и его свойства
Урок 17. Сложение натуральных чисел и его свойства
Урок 18. Сложение натуральных чисел и его свойства
Урок 19. Сложение натуральных чисел и его свойства
Урок 20. Сложение натуральных чисел и его свойства
Урок 21. Вычитание
Урок 22. Вычитание
Урок 23. Вычитание
Урок 24. Вычитание
Урок 25. Контрольная работа по теме «Сложение и вычитание натуральных чисел»
Урок 26. Числовые и буквенные выражения
Урок 27. Числовые и буквенные выражения
Урок 28. Числовые и буквенные выражения
Урок 29. Буквенная запись свойств сложения и вычитания
Урок 30. Буквенная запись свойств сложения и вычитания
Урок 31. Буквенная запись свойств сложения и вычитания
Урок 32. Уравнение
Уравнение
Урок 33. Уравнение
Урок 34. Уравнение
Урок 35. Уравнение
Урок 36. Контрольная работа по теме «Числовые и буквенные выражения. Уравнение»
§ 3. УМНОЖЕНИЕ И ДЕЛЕНИЕ НАТУРАЛЬНЫХ ЧИСЕЛ
Урок 37. Умножение натуральных чисел и его свойства
Урок 38. Умножение натуральных чисел и его свойства
Урок 39. Умножение натуральных чисел и его свойства
Урок 40. Умножение натуральных чисел и его свойства
Урок 41. Умножение натуральных чисел и его свойства
Урок 42. Деление
Урок 43. Деление
Урок 44. Деление
Урок 45. Деление
Урок 46. Деление
Урок 47. Деление
Урок 48. Деление
Урок 49. Деление с остатком
Урок 50. Деление с остатком
Урок 51. Деление с остатком
Урок 52. Контрольная работа по теме «Умножение и деление натуральных чисел»
Урок 53. Упрощение выражений
Урок 54. Упрощение выражений
Урок 55. Упрощение выражений
Урок 56. Упрощение выражений
Урок 57. Упрощение выражений
Упрощение выражений
Урок 58. Порядок выполнения действий
Урок 59. Порядок выполнения действий
Урок 60. Порядок выполнения действий
Урок 61. Квадрат и куб числа
Урок 62. Квадрат и куб числа
Урок 63. Контрольная работа по теме «Умножение и деление натуральных чисел»
§ 4. ПЛОЩАДИ И ОБЪЕМЫ
Урок 64. Формулы
Урок 65. Формулы
Урок 66. Площадь. Формула площади прямоугольника
Урок 67. Площадь
Урок 68. Единицы измерения площадей
Урок 69. Единицы измерения площадей
Урок 70. Единицы измерения площадей
Урок 71. Прямоугольный параллелепипед
Урок 72. Объемы. Объем прямоугольного параллелепипеда
Урок 73. Объемы. Объем прямоугольного параллелепипеда
Урок 74. Объемы. Объем прямоугольного параллелепипеда
Урок 75. Контрольная работа по теме «Площади и объемы»
Глава II. ДРОБНЫЕ ЧИСЛА
§ 5. ОБЫКНОВЕННЫЕ ДРОБИ
Урок 76. Окружность и круг
Урок 77. Окружность и круг
Урок 78. Доли. Обыкновенные дроби
Доли. Обыкновенные дроби
Урок 79. Обыкновенные дроби
Урок 80. Обыкновенные дроби
Урок 81. Обыкновенные дроби
Урок 82. Обыкновенные дроби
Урок 83. Сравнение дробей
Урок 84. Сравнение дробей
Урок 85. Сравнение дробей
Урок 86. Правильные и неправильные дроби
Урок 87. Правильные и неправильные дроби
Урок 88. Повторение. Подготовка к контрольной работе
Урок 89. Контрольная работа по темам «Обыкновенные дроби» и «Правильные и неправильные дроби»
Урок 90. Сложение и вычитание дробей с одинаковыми знаменателями
Урок 91. Сложение и вычитание дробей с одинаковыми знаменателями
Урок 92. Сложение и вычитание дробей с одинаковыми знаменателями
Урок 93. Деление и дроби
Урок 94. Деление и дроби
Урок 95. Смешанные числа
Урок 96. Смешанные числа
Урок 97. Сложение и вычитание смешанных чисел
Урок 98. Сложение и вычитание смешанных чисел
Урок 99. Сложение и вычитание смешанных чисел
Урок 100. Контрольная работа по темам «Смешанные числа» и «Сложение и вычитание смешанных чисел»
Контрольная работа по темам «Смешанные числа» и «Сложение и вычитание смешанных чисел»
§ 6. ДЕСЯТИЧНЫЕ ДРОБИ. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ
Урок 101. Десятичная запись дробных чисел
Урок 102. Десятичная запись дробных чисел
Урок 103. Сравнение десятичных дробей
Урок 104. Сравнение десятичных дробей
Урок 105. Сравнение десятичных дробей
Урок 106. Сложение и вычитание десятичных дробей
Урок 107. Сложение и вычитание десятичных дробей
Урок 108. Сложение и вычитание десятичных дробей
Урок 109. Сложение и вычитание десятичных дробей
Урок 110. Сложение и вычитание десятичных дробей
Урок 111. Приближенные значения чисел. Округление чисел
Урок 112. Приближенные значения чисел. Округление чисел
Урок 113. Контрольная работа по теме «Сложение и вычитание десятичных дробей. Округление чисел»
§ 7. УМНОЖЕНИЕ И ДЕЛЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ
Урок 114. Умножение десятичных дробей на натуральные числа
Урок 115. Умножение десятичных дробей на натуральные числа
Умножение десятичных дробей на натуральные числа
Урок 116. Умножение десятичных дробей на натуральные числа
Урок 117. Деление десятичных дробей на натуральные числа
Урок 118. Деление десятичных дробей на натуральные числа
Урок 119. Деление десятичных дробей на натуральные числа
Урок 120. Деление десятичных дробей на натуральные числа
Урок 121. Деление десятичных дробей на натуральные числа
Урок 122. Контрольная работа по теме «Умножение и деление десятичных дробей на натуральные числа»
Урок 123. Умножение десятичных дробей
Урок 124. Умножение десятичных дробей
Урок 125. Умножение десятичных дробей
Урок 126. Умножение десятичных дробей
Урок 127. Умножение десятичных дробей
Урок 128. Деление на десятичную дробь
Урок 129. Деление на десятичную дробь
Урок 130. Деление на десятичную дробь
Урок 131. Деление на десятичную дробь
Урок 132. Деление на десятичную дробь
Урок 133. Деление на десятичную дробь
Урок 134. Деление на десятичную дробь
Деление на десятичную дробь
Урок 135. Среднее арифметическое
Урок 136. Среднее арифметическое
Урок 137. Среднее арифметическое
Урок 138. Среднее арифметическое
Урок 139. Контрольная работа по теме «Умножение и деление десятичных дробей»
§ 8. ИНСТРУМЕНТЫ ДЛЯ ВЫЧИСЛЕНИЙ И ИЗМЕРЕНИЙ
Урок 140. Микрокалькулятор
Урок 141. Микрокалькулятор
Урок 142. Проценты
Урок 143. Проценты
Урок 144. Проценты
Урок 145. Проценты
Урок 146. Проценты
Урок 147. Контрольная работа по теме «Проценты»
Урок 148. Угол. Прямой и развернутый угол. Чертежный треугольник
Урок 149. Угол. Прямой и развернутый угол. Чертежный треугольник
Урок 150. Угол. Прямой и развернутый угол. Чертежный треугольник
Урок 151. Измерение углов. Транспортир
Урок 152. Измерение углов. Транспортир
Урок 153. Измерение углов. Транспортир
Урок 154. Круговые диаграммы
Урок 155. Круговые диаграммы
Урок 156. Контрольная работа по теме «Углы»
ПОВТОРЕНИЕ. РЕШЕНИЕ ЗАДАЧ
РЕШЕНИЕ ЗАДАЧ
Урок 157. Натуральные числа. Действия с натуральными числами
Урок 158. Натуральные числа. Действия с натуральными числами
Урок 159. Решение задач на встречное движение
Урок 160. Решение задач на движение
Урок 161. Решение задач на движение вдогонку
Урок 162. Обыкновенные дроби
Урок 163. Сложение и вычитание обыкновенных дробей
Урок 164. Десятичные дроби. Действия с десятичными дробями
Урок 165. Десятичные дроби. Действия с десятичными дробями
Урок 166. Десятичные дроби. Действия с десятичными дробями
Урок 167. Десятичные дроби. Решение задач
Урок 168. Проценты. Задачи на проценты
Урок 169. Решение задач
Урок 170. Решение задач
Урок 171. Самостоятельная работа
Урок 172. Итоговая контрольная работа
Урок 173. Работа над ошибками
Урок 174. Урок-игра «Брейн-ринг»
Урок 175. Урок-игра «Лабиринт»
Литература
Математика Попов — Дидактические материалы к уч.
 Виленкина 5 класс Контрольная работа №7. Окружность и круг. Доли. Обыкновенные дроби. Сравнение дробей. Правильные и неправильные дроби: — ГДЗ Решебники
Виленкина 5 класс Контрольная работа №7. Окружность и круг. Доли. Обыкновенные дроби. Сравнение дробей. Правильные и неправильные дроби: — ГДЗ РешебникиАвторы: Попов — Дидактические материалы к уч. Виленкина Год: 2017 год Издательство: Экзамен
На данной странице предствлены решения к учебнику по Математике для учеников 5 класса, Учебник издательства «Экзамен» 2017 года.
Популярные учебники
Английский язык Rainbow — Афанасьева 5 класс 2018
Авторы: Rainbow — Афанасьева, Михеева Год: 2018 Издательство: Дрофа
Биология Пасечник 5 класс 2018
Авторы: Пасечник, Суматохин, Калинина — рабочая тетрадь Год: 2018 Издательство: Просвещение
Информатика Босова — рабочая тетрадь 5 класс 2017
Авторы: Босова — рабочая тетрадь Год: 2017 Издательство: Бином
Русский язык Купалова 5 класс 2012
Авторы: Купалова, Еремеева, Лидман-Орлова
(Страница с 8 по 65).
 Самостоятельные работы.
Самостоятельные работы.Самостоятельная работа №1. Обозначение натуральных чисел:
Вариант №1 Вариант №2Самостоятельная работа №2. Отрезок. Длина отрезка. Треугольник:
Вариант №1 Вариант №2Самостоятельная работа №3. Плоскость. Прямая. Луч:
Вариант №1 Вариант №2Самостоятельная работа №4. Шкалы и координаты:
Вариант №1 Вариант №2Самостоятельная работа №5. Меньше или больше:
Вариант №1 Вариант №2Самостоятельная работа №6. Сложение натуральных чисел и его свойства:
Вариант №1 Вариант №2Самостоятельная работа №7. Вычитание:
Вариант №1 Вариант №2Самостоятельная работа №8. Числовые и буквенные выражения:
Вариант №1 Вариант №2Самостоятельная работа №9. Буквенная запись свойств сложения и вычитания:
Вариант №1 Вариант №2Самостоятельная работа №10. Уравнения:
Вариант №1 Вариант №2Самостоятельная работа №11. Умножение натуральных чисел и его свойства:
Вариант №1 Вариант №2Самостоятельная работа №12.
 Деление: Вариант №1
Вариант №2
Деление: Вариант №1
Вариант №2Самостоятельная работа №13. Деление с остатком:
Вариант №1 Вариант №2Самостоятельная работа №14. Упрощение выражений:
Вариант №1 Вариант №2Самостоятельная работа №15. Порядок выполнения действий:
Вариант №1 Вариант №2Самостоятельная работа №16. Квадрат и куб числа:
Вариант №1 Вариант №2Самостоятельная работа №17. Формулы:
Вариант №1 Вариант №2Самостоятельная работа №18. Площадь. Формула площади прямоугольника:
Вариант №1 Вариант №2Самостоятельная работа №19. Единицы измерения площадей:
Вариант №1 Вариант №2Самостоятельная работа №20. Прямоугольный параллелепипед:
Вариант №1 Вариант №2Самостоятельная работа №21. Объемы. Объем прямоугольного параллелепипеда:
Вариант №1 Вариант №2Самостоятельная работа №22. Окружность и круг:
Вариант №1 Вариант №2Самостоятельная работа №23. Доли. Обыкновенные дроби:
Вариант №1 Вариант №2Самостоятельная работа №24.
 Сравнение дробей: Вариант №1
Вариант №2
Сравнение дробей: Вариант №1
Вариант №2Самостоятельная работа №25. Правильные и неправильные дроби:
Вариант №1 Вариант №2Самостоятельная работа №26. Сложение и вычитание дробей с одинаковыми знаменателями:
Вариант №1 Вариант №2Самостоятельная работа №27. Деление и дроби:
Вариант №1 Вариант №2Самостоятельная работа №28. Смешанные числа:
Вариант №1 Вариант №2Самостоятельная работа №29. Сложение и вычитание смешанных чисел:
Вариант №1 Вариант №2Самостоятельная работа №30. Десятичная запись дробных чисел:
Вариант №1 Вариант №2Самостоятельная работа №31. Сравнение десятичных дробей:
Вариант №1 Вариант №2Самостоятельная работа №32. Сложение и вычитание десятичных дробей:
Вариант №1 Вариант №2Самостоятельная работа №33. Приближенные значения чисел. Округление чисел:
Вариант №1 Вариант №2Самостоятельная работа №34. Умножение десятичных дробей на натуральные числа:
Вариант №1 Вариант №2Самостоятельная работа №35.
 Деление десятичных дробей на натуральные числа: Вариант №1
Вариант №2
Деление десятичных дробей на натуральные числа: Вариант №1
Вариант №2Самостоятельная работа №36. Умножение десятичных дробей:
Вариант №1 Вариант №2Самостоятельная работа №37. Деление на десятичную дробь:
Вариант №1 Вариант №2Самостоятельная работа №38. Среднее арифметическое:
Вариант №1 Вариант №2Самостоятельная работа №39. Микрокалькулятор:
Вариант №1 Вариант №2Самостоятельная работа №40. Проценты:
Вариант №1 Вариант №2Самостоятельная работа №41. Угол. Прямой и развернутый угол. Чертежный треугольник:
Вариант №1 Вариант №2Самостоятельная работа №42. Измерение углов. Транспортир:
Вариант №1 Вариант №2Самостоятельная работа №43. Круговые диаграммы:
Вариант №1 Вариант №2Контрольные работы. (Страница с 66 по 103).
Контрольная работа №1. Обозначение натуральных чисел. Отрезок. Длина отрезка. Треугольник. Плоскость. Прямая. Луч. Шкалы и координаты:
Вариант №1 Вариант №2 Вариант №3 Вариант №4Контрольная работа №2.
 Сложение натуральных чисел и его свойства. Вычитание: Вариант №1
Вариант №2
Вариант №3
Вариант №4
Сложение натуральных чисел и его свойства. Вычитание: Вариант №1
Вариант №2
Вариант №3
Вариант №4Контрольная работа №3. Числовые и буквенные выражения. Буквенная запись свойств сложения и вычитания. Уравнение:
Вариант №1 Вариант №2 Вариант №3 Вариант №4Контрольная работа №4. Умножение натуральных чисел и его свойства. Деление. Деление с остатком:
Вариант №1 Вариант №2 Вариант №3 Вариант №4Контрольная работа №5. Упрощение выражений. Порядок выполнения действий. Квадрат и куб числа:
Вариант №1 Вариант №2 Вариант №3 Вариант №4Контрольная работа №6. Формулы. Площадь. Формула площади прямоугольника. Единицы измерения площадей. Прямоугольный параллелепипед. Объемы. Объем прямоугольного параллелепипеда:
Вариант №1 Вариант №2 Вариант №3 Вариант №4Контрольная работа №7. Окружность и круг. Доли. Обыкновенные дроби. Сравнение дробей. Правильные и неправильные дроби:
Вариант №1 Вариант №2 Вариант №3 Вариант №4Контрольная работа №8. Сложение и вычитание дробей с одинаковыми знаменателями.

Контрольная работа №9. Десятичная запись дробных чисел. Сравнение десятичных дробей. Сложение и вычитание десятичных дробей. Приближенные значения чисел. Округление чисел:
Вариант №1 Вариант №2 Вариант №3 Вариант №4Контрольная работа №10. Умножение десятичных дробей на натуральные числа. Деление десятичных дробей на натуральные числа:
Вариант №1 Вариант №2 Вариант №3 Вариант №4Контрольная работа №11. Умножение десятичных дробей. Деление на десятичную дробь. Среднее арифметическое:
Вариант №1 Вариант №2 Вариант №3 Вариант №4Контрольная работа №12. Микрокалькулятор. Проценты:
Вариант №1 Вариант №2 Вариант №3 Вариант №4Контрольная работа №13. Угол. Прямой и развернутый угол. Чертежный треугольник. Измерение углов. Транспортир. Круговые диаграммы:
Вариант №1 Вариант №2 Вариант №3 Вариант №4Контрольная работа №14. Итоговая контрольная работа:
Вариант №1 Вариант №2 Вариант №3 Вариант №4Задания на смекалку и логику:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30БЕСПЛАТНОЕ ГДЗ ЗА 1-11 КЛАСС
Чтобы у учеников не было стресса от больших нагрузок, страха получить плохую оценку, но при этом оставалось время на полноценный сон, дополнительные занятия, спорт, общение со сверстниками, стоит делать уроки вместе с ГДЗ. Готовые домашние задания – это возможность качественно подготовиться по разным предметам, не платя деньги репетиторам.
Готовые домашние задания – это возможность качественно подготовиться по разным предметам, не платя деньги репетиторам.
Если не хочется скачивать материалы, написанные «на коленке» студентами, а нужно работать с ГДЗ, над которыми трудились опытные преподаватели, умеющие понятно рассказывать теорию и грамотно оформлять практические задания, то надо заходить на Помогалку. Здесь можно без регистрации смотреть корректные решения номеров из учебников разных авторов по всем предметам и классам. Пусть школьная жизнь проходит без проблем!
Презентация к уроку Упрощение выражений 5 класс по ФГОС доклад, проект
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация на тему Презентация к уроку Упрощение выражений 5 класс по ФГОС, предмет презентации: Математика. Этот материал в формате pptx (PowerPoint) содержит 35 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
Этот материал в формате pptx (PowerPoint) содержит 35 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
Математику нельзя изучать наблюдая
3 + 4 = 7
2 х 2 =4
Сокращают выражения
Тема урока: «Сокращение выражений»
Доброго пути!
Вспомним свойства натуральных чисел
a + b =
(a + b) + c =
a — 0 =
a — (b + с) =
(а + b) — с =
а — а =
Продолжи буквенную запись
9) а * b =
10) (a * b) *c =
11) а * (b + c) =
12) а * (b — c) =
13) а : 1=
14) а : а =
15) 0 : а =
Продолжи буквенную запись
7) а + 0 =
Выполнив задание вы узнали кто автор известного мультфильма «Трое из Простоквашино»
Эдуард Успенский
Эдуард Успенский – автор многих детских произведений. Вам известны многие его герои — Чебурашка, крокодил Гена, Шапокляк, Хватайка, корова Мурка, Вера и Анфиса и другие.
Вам известны многие его герои — Чебурашка, крокодил Гена, Шапокляк, Хватайка, корова Мурка, Вера и Анфиса и другие.
Летом 1967 года Эдуард Успенский работал библиотекарем в пионерском лагере. Именно там он и начал сочинять историю про деревню Простоквашино и ее разношерстных обитателей.
Друзья приготовили чай и с нетерпением ждали нашего появления
Вам
посылка…
Решите уравнения и узнаете, что находится в этом ящике
х + 7 = 12
9 + у = 17
а – 11 =22
53 – в = 45
с * 13 = 39
64 : d = 32
m – 121 = 0
k * 246 = 246
550 : х =10
100 * р = 200
Что находится в ящике?
х + 7 = 12
9 + у = 17
а – 11 =22
53 – в = 45
с * 13 = 39
64 : d = 32
m – 121 = 0
k * 246 = 246
550 : х =10
100 * р = 200
МОЛОДЦЫ!!!
Задача.
Летом с друзьями мы ходили в трехдневный поход
Какой путь прошли в первый день, если во второй день прошли на 3 км меньше, чем в первый ,а в третий – на 6км больше, чем во второй?
За эти три дня Печкин, дядя Федор, Матроскин и Шарик прошли 18 км.
1 день —
2 день —
3 день —
Х км
на 3 км м.
на 6 км б.
18км
Какой путь прошли друзья в первый день?
1 день —
2 день —
3 день —
х км
(х — 3) км
(х — 3 + 6) км
+
х + (х — 3) + (х — 3 + 6)=18
Пусть в первый день друзья прошли Х км
х + (х — 3) + (х — 3 + 6)=18,
х + х — 3 + х — 3 + 6=18,
3х +6 — 3 — 3 =18,
3х +6 — (3 + 3) =18,
3х +0 =18,
3х =18,
х =18:3
х =6 км — мы прошли в 1 день
Спасибо, ребята, за урок!
Кот Матроскин завел корову, т. к. корова дает прибыль
к. корова дает прибыль
Задача.
За 10 дней Матроскин с Шариком надоили 130 л молока и сдали в магазин в 2 больших и в 5 маленьких бидонах.
Вот только хотелось бы знать сколько молока входит в маленький бидон, если он вмещает в 4 раза меньше чем большой.
Х
Большие —
Маленькие-
Пусть маленький бидон вмещает Х литров молока
2*4х + 5х = 130
Решим уравнение
2*4х + 5х = 130,
8х + 5х = 130,
13х = 130,
х = 130:13,
х= 10
литров молока вмещается в маленький бидон
ФИЗКУЛЬМИНУТКА
Спасибо вам, ребята
за помощь!
Нам вот еще домашнее задание
надо выполнить.
Помогите, пожалуйста!
Самостоятельная работа
Упростите выражение:
Проверьте себя:
63k
14x
43a
66d
20х +10
10t + 8
12у-4у+50=130
21х-4х-17=17
Пришла пора прощаться!
До свидания, ребята! Спасибо вам!
Понравился
тебе урок?
Поставь
оценку
№ 626 Разгадай чайнворд, помещенный на форзаце в конце учебника
Домашнее задание.
П.14, №614.
Придумайте задачу по уравнению:
т + 5т = 90
Используемые материалы
Картинки — Дизайн и графика WWW. OLIK.ru
OLIK.ru
Учебник математики 5 класс авт. Н. Я. Виленкин, задача №641
Скачать презентацию
Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.
Для правообладателей
Обратная связь
Email: Нажмите что бы посмотреть
Рабочая программа по математике, 5 класс, Виленкин, 5 часов
Муниципальное образовательное учреждение
средняя общеобразовательная школа № 53
г. Хабаровск
Согласовано Утверждаю:
на заседании МО Директор школы
Протокол № ________ _____________//
«_____»_____________2011 г. «_____»_____________2011 г.
Рабочая программа
поматематике
5 класс
I полугодие 5 ч
II полугодие 5 ч
175 ч в год
Составитель: Фещенко
Екатерина Владимировна
Составлена на основе
Программы образовательных учреждений.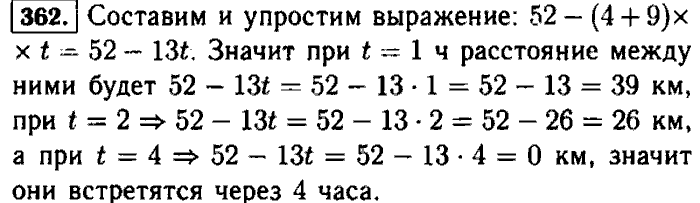 Математика. 5 — 6 классы.
Математика. 5 — 6 классы.
Сост. Бурмистрова Т.А. М.: Просвещение, 2009г.
2011 г.
Пояснительная записка
Рабочая программа составлена на основе нормативных документов:
Программы образовательных учреждений. Математика. 5 — 6 классы. Сост. Бурмистрова Т.А. М.: Просвещение, 2009г.
Федеральный компонент государственного образовательного стандарта начального общего, основного общего и среднего (полного) общего образования (Приказ МО РФ от 05.03.2004 №1089).
Примерной программы основного общего образования и авторской программы Н.Я. Виленкина. 2009г.
Федеральный базисный учебный план для среднего (полного) общего образования .
Программой отводится на изучение математики по 5 уроков в неделю, что составляет 175 часов в учебный год. Из них контрольных работ 14 часов, которые распределены по разделам следующим образом: «Натуральные числа и шкалы» 1 час, «Сложение и вычитание натуральных чисел» 2 часа, «Умножение и деление натуральных чисел» 2 часа, «Площади и объёмы» 1 час, «Обыкновенные дроби» 2 часа, «Сложение и вычитание десятичных дробей» 1 час, «Умножение и деление десятичных дробей» 2 часа, «Инструменты для вычислений и измерений» 2 часа и 1 час отведен на итоговую административную контрольную работу.
Данное планирование определяет достаточный объем учебного времени для повышения математических знаний учащихся в среднем звене школы, улучшения усвоения других учебных предметов.
Изучение математики на ступени основного общего образования направлено на достижение следующих целей:
• овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
• интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
• формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
• воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.
В задачи обучения математики входит:
развитие внимания, мышления учащихся, формирования у них умений логически мыслить, анализировать полученные знания, находить закономерности;
овладение школьными знаниями о понятиях, правилах, законах, фактах;
развитие представлений о полной картине мира, о взаимосвязи математики с другими предметами.
Содержание рабочей программы
Натуральные числа и шкалы.
Натуральные числа и их сравнение. Геометрические фигуры: отрезок, прямая, луч, треугольник. Измерение и построение отрезков. Координатный луч.
Сложение и вычитание натуральных чисел.
Сложение и вычитание натуральных чисел, свойства сложения. Решение текстовых задач. Числовое выражение. Буквенное выражение и его числовое значение. Решение линейных уравнений.
Умножение и деление натуральных чисел.
Умножение и деление натуральных чисел, свойства умножения. Квадрат и куб числа. Решение текстовых задач.
Площади и объёмы.
Вычисления по формулам. Прямоугольник. Площадь прямоугольника. Единицы площадей.
Обыкновенные дроби.
Окружность и круг. Обыкновенная дробь. Основные задачи на дроби. Сравнение обыкновенных дробей. Сложение и вычитание дробей с одинаковыми знаменателями.
Десятичные дроби. Сложение и вычитание десятичных дробей.
Десятичная дробь. Сравнение, округление, сложение и вычитание десятичных дробей. Решение текстовых задач.
Умножение и деление десятичных дробей.
Умножение и деление десятичных дробей. Среднее арифметическое нескольких чисел. Решение текстовых задач.
Инструменты для вычислений и измерений.
Начальные сведения о вычислениях на калькуляторе. Проценты. Основные задачи на проценты. Примеры таблиц и диаграмм. Угол, треугольник. Величина (градусная мера) угла. Единицы измерения углов. Измерение углов. Построение угла заданной величины.
Повторение. Решение задач.
Учебно-тематический план:
№ темы | Название темы | Количество часов |
1. | Натуральные числа и шкалы | 15 |
2. | Сложение и вычитание натуральных чисел | 21 |
3. | Умножение и деление натуральных чисел | 26 |
4. | Площади и объёмы | 15 |
5. | Обыкновенные дроби | 24 |
6. | Десятичные дроби. Сложение и вычитание десятичных дробей | 17 |
7. | Умножение и деление десятичных дробей | 22 |
8. | Инструменты для измерения | 24 |
9. | Повторение | 11 |
Итого: | 175 ч. | |
Требования к уровню подготовки обучающихся.
В результате изучения курса математики 5-го класса учащиеся должны уметь:
правильно употреблять термины, связанные с различными видами чисел и способами их записи: натуральное число, десятичная дробь, обыкновенная дробь, смешанное число;
переходить от одной формы записи чисел к другой; представлять десятичную дробь в виде обыкновенной и в простейших случаях обыкновенную в виде десятичной, проценты- в виде дроби и дробь — в виде процентов;
уметь выполнять устно арифметические действия: сложение и вычитание двузначных чисел и десятичных дробей , умножение однозначных чисел, сложение и вычитание дробей с одинаковыми знаменателями;
сравнивать натуральные числа, обыкновенные дроби с одинаковыми знаменателями, десятичные дроби; упорядочивать наборы чисел, понимать связь отношений «больше» и «меньше» с расположением точек на координатной прямой;
округлять целые числа и десятичные дроби; находить приближения чисел с недостатком и с избытком, выполнять оценку числовых выражений;
пользоваться основными единицами длины, массы, времени, площади, объёма, скорости; выражать более крупные единицы через более мелкие и наоборот;
решать текстовые задачи «на движение»; все виды задач на проценты;
составлять несложные буквенные выражения и формулы; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления;
решать простейшие линейные уравнения.
Поурочное тематическое планирование
(5 ч в неделю I полугодие, 5 ч в неделю II полугодие, всего 175 ч в год)
№ п/п | № раздела темы | Наименование разделов и тем | Кол-во часов | Дата | |||
Всего | Теоретические знания | Самостоятельные работы | Контрольные работы | ||||
ГлаваI. Натуральные числа. | |||||||
1. | Натуральные числа и шкалы. | 15 | |||||
1 | 1.1. | Инструктаж по ТБ. Обозначение натуральных чисел. | 1 | Понятие натурального ряда чисел. | |||
2 | 1.2. | Обозначение натуральных чисел. | 1 | Понятие многозначного числа. | 1 | ||
3 | 1.3. | Обозначение натуральных чисел | 1 | Классы цифр. | |||
4 | 1.4. | Отрезок. Длина отрезка. Треугольник | 1 | Понятие многоугольника. | |||
5 | 1.5. | Отрезок. Длина отрезка. Треугольник | 1 | Единицы длины. | |||
6 | 1.6. | Отрезок. Длина отрезка. Треугольник.Самостоятельная работа | 1 | Стороны и вершины многоугольника. | 1 | ||
7 | 1.7. | Плоскость. Прямая. Луч. | 1 | Понятие плоскости. | |||
8 | 1. | Плоскость. Прямая. Луч. Самостоятельная работа | 1 | Понятие дополнительных лучей. | 1 | ||
9 | 1.9. | Шкалы и координаты. | 1 | Понятие шкалы, делений шкалы. | |||
10 | 1.10. | Шкалы и координаты. Самостоятельная работа | 1 | Понятие координатного луча. | 1 | ||
11 | 1.11. | Шкалы и координаты. | 1 | Координаты точек. Единичный отрезок. | |||
12 | 1.12. | Меньше или больше. | 1 | Понятие двойного неравенства. | |||
13 | 1.13. | Меньше или больше. Самостоятельная работа | 1 | Сравнение чисел. | 1 | ||
14 | 1.14. | Меньше или больше. | 1 | Сравнение отрезков. | |||
15 | 1.15. | Контрольная работа № 1 по теме «Натуральные числа и шкалы». | 1 | 1 | |||
2. | Сложение и вычитание натуральных чисел | 21 | |||||
16 | 2.1. | Анализ контрольной работы. Сложение натуральных чисел и его свойства | 1 | Понятие слагаемых и их суммы. | |||
17 | 2.2. | Сложение натуральных чисел и его свойства. Самостоятельная работа | 1 | Свойства сложения: переместительное и сочетательное свойство. | 1 | ||
18 | 2.3. | Сложение натуральных чисел и его свойства. | 1 | Свойства сложения: переместительное и сочетательное свойство. | |||
19 | 2.4. | Сложение натуральных чисел и его свойства. Самостоятельная работа | 1 | Периметр треугольника. | 1 | ||
20 | 2.5. | Вычитание натуральных чисел. | 1 | Понятие уменьшаемого, вычитаемого и разности. | |||
21 | 2.6. | Вычитание натуральных чисел. Самостоятельная работа | 1 | Свойство вычитания суммы из числа. | 1 | ||
22 | 2.7. | Вычитание натуральных чисел. | 1 | Свойство вычитания числа из суммы. | |||
23 | 2. | Вычитание натуральных чисел. | 1 | Свойства вычитания. | |||
24 | 2.9. | Контрольная работа № 2 по теме: «Сложение и вычитание натуральных чисел». | 1 | 1 | |||
25 | 2.10. | Анализ контрольной работы. Числовые и буквенные выражения | 1 | Понятие числового выражения. | |||
26 | 2.11. | Числовые и буквенные выражения. Самостоятельная работа | 1 | Понятие буквенного выражения. | 1 | ||
27 | 2.12. | Числовые и буквенные выражения | 1 | Понятие значения выражения и буквы. | |||
28 | 2.13. | Буквенная запись свойств сложения и вычитания | 1 | Сочетательный и переместительный законы сложения. | |||
29 | 2.14. | Буквенная запись свойств сложения и вычитания. Самостоятельная работа | 1 | Свойство нуля при сложении и вычитании. | 1 | ||
30 | 2.15. | Буквенная запись свойств сложения и вычитания | 1 | Свойство вычитания суммы из числа. | |||
31 | 2.16. | Уравнение | 1 | Свойство вычитания числа из суммы. | |||
32 | 2.17. | Уравнение. Самостоятельная работа | 1 | Понятие уравнения и его корня. | 1 | ||
33 | 2.18. | Уравнение | 1 | Понятие уравнения и его корня. | |||
34 | 2.19. | Уравнение. | 1 | Неизвестное слагаемое, уменьшаемое и вычитаемое. | 1 | ||
35 | 2.20. | Уравнение. | 1 | Неизвестное слагаемое, уменьшаемое и вычитаемое. | |||
36 | 2.21. | Контрольная работа № 3 по теме: «Уравнение» | 1 | 1 | |||
3. | Умножение и деление натуральных чисел | 26 | |||||
37 | 3.1. | Анализ контрольной работы. Умножение натуральных чисел и его свойства | 1 | Понятие множителя и произведения. | |||
38 | 3.2. | Умножение натуральных чисел и его свойства. Самостоятельная работа | 1 | Переместительный и сочетательный законы умножения. | 1 | ||
39 | 3.3. | Умножение натуральных чисел и его свойства | 1 | Свойство нуля при умножении. | |||
40 | 3.4. | Умножение натуральных чисел. Самостоятельная работа | 1 | Свойство единицы при умножении. | 1 |
41 | 3.5. | Деление натуральных чисел | 1 | Понятие делимого, делителя и частного. | |||
42 | 3.6. | Деление натуральных чисел. Самостоятельная работа | 1 | Понятие неизвестного делителя и делимого. | 1 | ||
43 | 3.7. | Деление натуральных чисел | 1 | Понятие неизвестного множителя. | |||
44 | 3.8. | Деление натуральных чисел. Самостоятельная работа | 1 | Понятие неизвестного делителя, делимого и множителя. | 1 | ||
45 | 3.9. | Деление с остатком. | 1 | Понятие делимого, делителя, неполного частного и остатка. | |||
46 | 3.10. | Деление с остатком. Самостоятельная работа | 1 | Деление нацело и с остатком. | 1 | ||
47 | 3.11. | Деление с остатком. | 1 | Деление нацело и с остатком. | |||
48 | 3.12. | Деление с остатком. | 1 | Деление нацело и с остатком. | |||
49 | 3. | Контрольная работа № 4 по теме: «Умножение и деление натуральных чисел» | 1 | 1 | |||
50 | 3.14. | Анализ контрольной работы. Упрощение выражений | 1 | Распределительное свойство умножения относительно сложения. | |||
51 | 3.15. | Упрощение выражений. Самостоятельная работа | 1 | Распределительное свойство умножения относительно сложения. | 1 | ||
52 | 3.16. | Упрощение выражений. | 1 | Распределительное свойство умножения относительно вычитания. | |||
53 | 3.17. | Упрощение выражений. Самостоятельная работа | 1 | Сочетательное свойство умножения. | 1 | ||
54 | 3. | Порядок выполнения действий | 1 | Понятие действий первой и второй ступени. | |||
55 | 3.19. | Порядок выполнения действий. Самостоятельная работа | 1 | Порядок выполнения действий. | 1 | ||
56 | 3.20. | Порядок выполнения действий | 1 | Понятие программы вычисления. | |||
57 | 3.21. | Порядок выполнения действий. Самостоятельная работа | 1 | Понятие команд вычисления. | 1 | ||
58 | 3.22. | Степень числа. Квадрат и куб числа. | 1 | Понятие основания и показателя степени. | |||
59 | 3.23. | Степень числа. Квадрат и куб числа. | 1 | Понятие степени. | 1 | ||
60 | 3.24. | Степень числа. Квадрат и куб числа. | 1 | Квадрат и куб числа. | |||
61 | 3.25. | Степень числа. Квадрат и куб числа. | 1 | Порядок выполнения действий. | |||
62 | 3.26. | Контрольная работа № 5 по темам: «Упрощение выражений. Степень числа. Квадрат и куб числа» | 1 | 1 | |||
4. | Площади и объемы | 15 | |||||
63 | 4.1. | Анализ контрольной работы. Формулы | 1 | Понятие формулы. | |||
64 | 4.2. | Формулы. | 1 | Формула пути. | 1 | ||
65 | 4.3. | Площадь. Формула площади прямоугольника. | 1 | Понятие площади фигуры. | |||
66 | 4.4. | Площадь. Формула площади прямоугольника. Самостоятельная работа | 1 | Формула площади прямоугольника. | 1 | ||
67 | 4.5. | Площадь. Формула площади прямоугольника. | 1 | Формула площади квадрата. | |||
68 | 4.6. | Единицы измерения площадей | 1 | Понятие единиц измерения площадей. | |||
69 | 4.7. | Единицы измерения площадей. Самостоятельная работа | 1 | Понятие единиц измерения площадей. | 1 | ||
270 | 4.8. | Единицы измерения площадей | 1 | Понятие гектара и ара. |
71 | 4.9. | Прямоугольный параллелепипед | 1 | Понятие прямоугольного параллелепипеда. | |||
72 | 4.10. | Прямоугольный параллелепипед. Самостоятельная работа | 1 | Ребра, грани и вершины параллелепипеда. | 1 | ||
73 | 4.11. | Прямоугольный параллелепипед. | 1 | Понятие куба. Три измерения параллелепипеда — длина, ширина и высота. | |||
74 | 4.12. | Объемы. Объем прямоугольного параллелепипеда | 1 | Понятие объема. | |||
75 | 4.13. | Объемы. Объем прямоугольного параллелепипеда. Самостоятельная работа | 1 | Формула объема прямоугольного параллелепипеда. | 1 | ||
76 | 4.14. | Объемы. Объем прямоугольного параллелепипеда. | 1 | Формула объема куба. | |||
78 | 4.15. | Контрольная работа № 6 по теме: «Площади и объемы» | 1 | 1 | |||
ГЛАВАII.ДРОБНЫЕ ЧИСЛА. | |||||||
5. | Обыкновенные дроби | 25 | |||||
79 | 5.1. | Анализ контрольной работы. Окружность и круг | 1 | Понятие окружности и круга. | |||
80 | 5.2. | Окружность и круг. Самостоятельная работа | 1 | Понятие полуокружности и полукруга, радиуса и диаметра. | 1 | ||
81 | 5.3. | Доли. Обыкновенные дроби | 1 | Понятие доли. | |||
82 | 5.4. | Доли. Обыкновенные дроби. Самостоятельная работа | 1 | Понятие обыкновенной дроби. | 1 | ||
83 | 5.5. | Доли. Обыкновенные дроби. | 1 | Понятие числителя и знаменателя дроби. | |||
84 | 5.6. | Сравнение дробей | 1 | Понятие равных дробей. | |||
85 | 5. | Сравнение дробей. Самостоятельная работа | 1 | Сравнение дробей с одинаковыми знаменателями. | 1 | ||
86 | 5.8. | Правильные и неправильные дроби | 1 | Понятие правильной и неправильной дроби. | |||
87 | 5.9. | Правильные и неправильные дроби. Самостоятельная работа | 1 | Понятие правильной и неправильной дроби. | 1 | ||
88 | 5.10. | Правильные и неправильные дроби. | 1 | Сравнение дробей с единицей. | |||
89 | 5.11. | Контрольная работа № 7 по теме: «Обыкновенные дроби» | 1 | 1 | |||
90 | 5.12. | Анализ контрольной работы. | 1 | Правило сложения дробей с одинаковыми знаменателями. | |||
91 | 5.13. | Сложение и вычитание дробей с одинаковыми знаменателями. Самостоятельная работа | 1 | Правило вычитания дробей с одинаковыми знаменателями. | 1 | ||
92 | 5.14. | Сложение и вычитание дробей с одинаковыми знаменателями | 1 | Правила сложения и вычитания дробей с одинаковыми знаменателями. | |||
93 | 5.15. | Деление и дроби | 1 | Правило записи натурального числа в виде дроби. | |||
94 | 5.16. | Деление и дроби. Самостоятельная работа | 1 | Правило деления суммы на число. | 1 | ||
95 | 5.17. | Деление и дроби. | 1 | Правило деления суммы на число. | |||
96 | 5.18. | Смешанные числа | 1 | Понятие смешанного числа. | |||
97 | 5.19. | Смешанные числа. Самостоятельная работа | 1 | Правило выделения целой части из неправильной дроби. | 1 | ||
98 | 5.20. | Смешанные числа | 1 | Правило представления смешанного числа в виде неправильной дроби. | |||
99 | 5.21. | Сложение и вычитание смешанных чисел | 1 | Правило сложения смешанных чисел. |
100 | 5. | Сложение и вычитание смешанных чисел. Самостоятельная работа | 1 | Правило вычитания смешанных чисел. | 1 | ||
101 | 5.23. | Сложение и вычитание смешанных чисел. | 1 | Правила сложения и вычитания смешанных чисел. | |||
102 | 5.24. | Сложение и вычитание смешанных чисел. | 1 | Правила сложения и вычитания смешанных чисел. | |||
103 | 5.25. | Контрольная работа № 8 по темам: «Обыкновенные дроби» | 1 | 1 | |||
6. | Десятичные дроби. Сложение и вычитание десятичных дробей | 16 | |||||
104 | 6.1. | Анализ контрольной работы. Десятичная запись дробных чисел | 1 | Правило записи десятичной дроби. | |||
105 | 6.2. | Десятичная запись дробных чисел. Самостоятельная работа | 1 | Правило записи десятичной дроби. | 1 | ||
106 | 6.3. | Десятичная запись дробных чисел. | 1 | Правило записи десятичной дроби. | |||
107 | 6.4. | Сравнение десятичных дробей | 1 | Понятие равных десятичных дробей. | |||
108 | 6.5. | Сравнение десятичных дробей. Самостоятельная работа | 1 | Правило сравнения десятичных дробей. | 1 | ||
109 | 6.6. | Сравнение десятичных дробей | 1 | Правило сравнения десятичных дробей. | |||
110 | 6. | Сравнение десятичных дробей. Самостоятельная работа | 1 | Правило сравнения десятичных дробей. | 1 | ||
111 | 6.8. | Сложение и вычитание десятичных дробей | 1 | Правило сложения десятичных дробей. | |||
112 | 6.9. | Сложение и вычитание десятичных дробей. Самостоятельная работа | 1 | Правило вычитания десятичных дробей. | 1 | ||
113 | 6.10. | Сложение и вычитание десятичных дробей | 1 | Правила сложения и вычитания десятичных дробей. | |||
114 | 6.11. | Сложение и вычитание десятичных дробей. Самостоятельная работа | 1 | Правила сложения и вычитания десятичных дробей. | 1 | ||
115 | 6. | Приближенные значения чисел. Округление чисел | 1 | Понятие приближенного значения неизвестного с недостатком и с избытком. | |||
116 | 6.13. | Приближенные значения чисел. Округление чисел. Самостоятельная работа | 1 | Правило округления десятичных чисел. | 1 | ||
117 | 6.14. | Приближенные значения чисел. Округление чисел | 1 | Правило округления десятичных чисел. | |||
118 | 6.15. | Приближенные значения чисел. Округление чисел | 1 | Правило округления десятичных чисел. | |||
119 | 6.16. | Контрольная работа № 9 по теме: «Десятичные дроби. Сложение и вычитание десятичных дробей» | 1 | 1 | |||
7. | Умножение и деление десятичных дробей | 22 | |||||
120 | 7.1. | Анализ контрольной работы. Умножение десятичных дробей на натуральные числа | 1 | Правило умножения десятичной дроби на натуральное число. | |||
121 | 7.2. | Умножение десятичных дробей на натуральные числа. Самостоятельная работа. | 1 | Правило умножения десятичной дроби на 10, 100, 1000 и т.д. | 1 | ||
122 | 7.3. | Умножение десятичных дробей на натуральные числа | 1 | Правило умножения десятичной дроби на натуральное число. | |||
123 | 7.4. | Умножение десятичных дробей на натуральные числа. Самостоятельная работа. | 1 | Правило умножения десятичной дроби на натуральное число. | 1 |
124 | 7.5. | Деление десятичных дробей на натуральные числа | 1 | Правило деления десятичной дроби на натуральное число. | |||
125 | 7.6. | Деление десятичных дробей на натуральные числа. Самостоятельная работа. | 1 | Правило деления десятичной дроби на 10, 100, 1000 и т.д. | 1 | ||
126 | 7.7. | Деление десятичных дробей на натуральные числа | 1 | Правило деления десятичной дроби на натуральное число. | |||
127 | 7.8. | Деление десятичных дробей на натуральные числа | 1 | Правило деления десятичной дроби на натуральное число. | |||
128 | 7. | Контрольная работа № 10 по теме: «Умножение и деление десятичных дробей на натуральные числа» | 1 | 1 | |||
129 | 7.10. | Анализ контрольной работы. Умножение десятичных дробей | 1 | Правило умножения чисел на 0,1; 0,01; 0,001 и т.д. | |||
130 | 7.11. | Умножение десятичных дробей. Самостоятельная работа. | 1 | Правило умножения десятичных дробей. | 1 | ||
131 | 7.12. | Умножение десятичных дробей | 1 | Правило умножения десятичных дробей. | |||
132 | 7.13. | Умножение десятичных дробей. Самостоятельная работа. | 1 | Правило умножения десятичных дробей. | 1 | ||
133 | 7. | Деление на десятичную дробь | 1 | Правило деления чисел на десятичную дробь. | |||
134 | 7.15. | Деление на десятичную дробь. Самостоятельная работа. | 1 | Правило деления чисел на 0,1; 0,01; 0,001 и т.д. | 1 | ||
135 | 7.16. | Деление на десятичную дробь. | 1 | Правило деления чисел на десятичную дробь. | |||
136 | 7.17. | Деление на десятичную дробь. Самостоятельная работа. | 1 | Правило деления чисел на десятичную дробь. | 1 | ||
137 | 7.18. | Среднее арифметическое | 1 | Понятие среднего арифметического. | |||
138 | 7.19. | Среднее арифметическое. | 1 | Понятие средней скорости движения. | 1 | ||
139 | 7.20. | Среднее арифметическое | 1 | Правило поиска среднего арифметического нескольких чисел. | |||
140 | 7.21. | Среднее арифметическое | 1 | Правило поиска среднего арифметического нескольких чисел. | |||
141 | 7.22. | Контрольная работа № 11 по теме: «Умножение и деление десятичных дробей» | 1 | 1 | |||
8. | Инструменты для вычислений и измерений | 24 | |||||
142 | 8.1. | Анализ контрольной работы. Микрокалькулятор | 1 | Понятие микрокалькулятора. | |||
143 | 8.2. | Микрокалькулятор. Самостоятельная работа. | 1 | Вычисления на микрокалькуляторе. | 1 | ||
144 | 8.3. | Микрокалькулятор. | 1 | Вычисления на микрокалькуляторе. | |||
145 | 8.4. | Проценты | 1 | Понятие процента. | |||
146 | 8.5. | Проценты. Самостоятельная работа. | 1 | Правило перевода десятичной дроби в проценты. | 1 | ||
147 | 8.6. | Проценты. | 1 | Правило перевода процентов в десятичную дробь. | |||
148 | 8.7. | Проценты. Самостоятельная работа. | 1 | Правило перевода десятичной дроби в проценты. | 1 | ||
149 | 8.8. | Проценты. | 1 | Правило перевода процентов в десятичную дробь. | |||
150 | 8.9. | Проценты. | 1 | Правило перевода десятичной дроби в проценты. | |||
151 | 8.10. | Контрольная работа № 12 по теме: «Проценты» | 1 | 1 |
152 | 8.11. | Анализ контрольной работы. Угол. Прямой и развернутый угол. Чертежный треугольник | 1 | Понятие угла, его сторон и вершин. | |||
153 | 8.12. | Угол. Прямой и развернутый угол. Чертежный треугольник. Самостоятельная работа. | 1 | Понятие развернутого угла. | 1 | ||
154 | 8.13. | Угол. Прямой и развернутый угол. Чертежный треугольник. | 1 | Понятие чертежного треугольника. | |||
155 | 8.14. | Угол. Прямой и развернутый угол. Чертежный треугольник. Самостоятельная работа. | 1 | Понятие развернутого угла. | 1 | ||
156 | 8.15. | Измерение углов. Транспортир | 1 | Понятие транспортира, градуса. | |||
157 | 8.16. | Измерение углов. Транспортир. Самостоятельная работа. | 1 | Понятие прямого угла. | 1 | ||
158 | 8.17. | Измерение углов. Транспортир. | 1 | Понятие острого и тупого угла. | |||
159 | 8.19. | Измерение углов. Транспортир. Самостоятельная работа. | 1 | Понятие острого и тупого угла. | 1 | ||
160 | 8.20. | Круговые диаграммы | 1 | Понятие круговой диаграммы. | |||
161 | 8.21. | Круговые диаграммы. Самостоятельная работа. | 1 | Понятие круговой диаграммы. | 1 | ||
162 | 8.22. | Круговые диаграммы | 1 | Понятие круговой диаграммы. | |||
163 | 8.23. | Круговые диаграммы. | 1 | ||||
164 | 8.24. | Контрольная работа № 13 по теме: «Измерение углов. Транспортир» | 1 | 1 | |||
9. | Повторение. | 11 | |||||
165 | 9.1. | Анализ контрольной работы. Повторение. Сложение и вычитание десятичных дробей. | 1 | Правила сложения и вычитания десятичных дробей. | |||
166 | 9.2. | Повторение. Сложение и вычитание десятичных дробей. Самостоятельная работа. | 1 | 1 | |||
167 | 9.3. | Повторение. Умножение и деление десятичных дробей. | 1 | Правила умножения и деления десятичных дробей. | |||
168 | 9.4. | Повторение. Умножение и деление десятичных дробей. Самостоятельная работа. | 1 | 1 | |||
169 | 9.5. | Повторение. Проценты. | 1 | Умение составлять и решать пропорции. | |||
170 | 9.6. | Итоговая контрольная работа № 14. | 1 | 1 | |||
171 | 9.7. | Повторение. Уравнение. | 1 | Корень уравнения. | |||
172 | 9.8. | Повторение. Уравнение. Самостоятельная работа. | 1 | 1 | |||
173 | 9.9. | Повторение. Упрощение выражений. | |||||
174 | 9.10. | Повторение. Упрощение выражений. Самостоятельная работа. | 1 | ||||
175 | 9.11. | Итоговое занятие. | |||||
Итого: | 175 ч |
Литература и средства обучения:
1. Виленкин Н. Я., Жохов В. И., Чесноков А. С., Шварцбурд С. И. Математика 5. – М.: Мнемозина, 2009.
Виленкин Н. Я., Жохов В. И., Чесноков А. С., Шварцбурд С. И. Математика 5. – М.: Мнемозина, 2009.
Буланова Л. М., Дудницын Ю. П. Проверочные задания по математике для учащихся 5-8 и 10 классов. – М.: Просвещение, 2007.
2. Жохов В. И. Преподавание математики в 5-6классах. – М.: Мнемозина, 2005.
3. Жохов В. И., Митяева И. М. Математические диктанты для 5-9 классов. – М.: Просвещение, 2004.
4. Чесноков А. С., Нешков К. И. Дидактические материалы по математике, 5 класс. – М.: Просвещение, 2008.
5.Программы образовательных учреждений. Математика. 5 — 6 классы. Сост. Бурмистрова Т.А. М.: Просвещение, 2009г.
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/56298-rabochaja-programma-po-matematike-5-klass-vil
Математика как язык символов
Обучая своих студентов, изучающих предварительный математический анализ и математический анализ AP, я понял, что использование математических символов для создания алгебраических выражений и решения текстовых задач обычно представляет для них большую проблему. Они изо всех сил пытаются перевести словесную постановку задачи в символические математические выражения и уравнения.
Они изо всех сил пытаются перевести словесную постановку задачи в символические математические выражения и уравнения.
Допустим, учащиеся должны решить следующую задачу: «Найти площадь поверхности сферы в момент, когда скорость увеличения объема сферы в девять раз превышает скорость увеличения радиуса». 1 (На самом деле эта постановка задачи не очень хороша. В задаче упоминается «сфера», но речь идет не об одной сфере. Речь идет о семействе сфер, радиус которых меняется, каким образом или относительно какая переменная не объясняется.) Как видите, в этой задаче нет ни одного математического символа. Это всего лишь одно предложение, написанное на английском языке. Студенты должны уметь «перевести» его на математический язык с помощью формул и создать модель на основе заданных данных. Это очень сложная задача для моих учеников. Большинство из них готовы сдаться, даже не пытаясь.
Истоки этой борьбы восходят к арифметике и простой алгебре. Их нужно было научить писать алгебраические выражения и создавать математические модели текстовых задач. Эти навыки необходимы для их успеха в математике, физике и химии верхнего уровня. К сожалению, большинство из них если и обладают очень скромными навыками такого рода. Итак, моя цель при разработке этого раздела — помочь учителям и ученикам заполнить этот пробел.
Эти навыки необходимы для их успеха в математике, физике и химии верхнего уровня. К сожалению, большинство из них если и обладают очень скромными навыками такого рода. Итак, моя цель при разработке этого раздела — помочь учителям и ученикам заполнить этот пробел.
Боязнь математики похожа на боязнь говорить на иностранном языке. Некоторые слова на иностранном языке мы просто не знаем и поэтому мучаемся с переводом. Чтобы добиться успеха в математике, мы должны уметь «переводить» задачу с английского на математический язык. Частью этого является знание того, что означает каждое слово. Более глубокая трудность заключается в том, что перевод не может быть дословным. Он должен передавать общий смысл.
Возвращаясь к упомянутой выше задаче о связанных скоростях, студенты узнают, что словосочетание «скорость увеличения объема» переводится на математический язык очень просто: dV/dt . Анализируя задачу, учащиеся должны прийти к выводу, что объем меняется во времени. Им следует ввести переменную t (время) и подчеркнуть, что t была неуказанной переменной, вследствие неполноты задачи. Акт введения переменной t следует указать явно. Аналогичным образом, «скорость увеличения радиуса» составляет dr/dt .
Им следует ввести переменную t (время) и подчеркнуть, что t была неуказанной переменной, вследствие неполноты задачи. Акт введения переменной t следует указать явно. Аналогичным образом, «скорость увеличения радиуса» составляет dr/dt .
Для дальнейшего перевода нам потребуется составить алгебраическое выражение:
dV/dt = 9 dr/dt
Это выражение кажется изучающим алгебру сложным и «полностью греческим». Однако концепция, которую мы использовали при написании этого выражения, аналогична той, которую мы использовали бы для написания очень простого алгебраического выражения «число A в девять раз больше, чем число 9».0013 Б ».
А = 9 В
Таким образом, студентов следует обучать написанию алгебраических выражений как можно раньше.
Я преподаю в небольшой средней школе, куда дети должны подать заявление, чтобы поступить. Большая часть политики приема заключается в привлечении студентов с самым разным опытом. Поэтому студенческий состав очень разнообразен. У нас есть дети из элитных частных школ, а также дети из действительно неблагополучных городских средних школ. В результате навыки учащихся сильно различаются. Я должен соответствующим образом скорректировать свой стиль преподавания и подходить к своим ученикам индивидуально. В то время как некоторые из них проходят самые строгие курсы AP, многие из них борются с простыми математическими понятиями. Моя цель как учителя – удовлетворить потребности каждого ученика и дать каждому возможность добиться успеха.
Поэтому студенческий состав очень разнообразен. У нас есть дети из элитных частных школ, а также дети из действительно неблагополучных городских средних школ. В результате навыки учащихся сильно различаются. Я должен соответствующим образом скорректировать свой стиль преподавания и подходить к своим ученикам индивидуально. В то время как некоторые из них проходят самые строгие курсы AP, многие из них борются с простыми математическими понятиями. Моя цель как учителя – удовлетворить потребности каждого ученика и дать каждому возможность добиться успеха.
Англо-математический «словарь»
В первый день в школе я всегда говорю своим ученикам-математикам, что математика — это язык. И одна из его ключевых особенностей заключается в том, что он очень лаконичен. Компактность символьных выражений — важная особенность, которая позволяет нам эффективно работать с ними. Компромисс заключается в увеличении трудозатрат, необходимых для перевода символических выражений в вербальные. Цифры и буквы, а также некоторые специальные символы представляют «слова» этого удивительного языка. Когда мы соединяем «слова» с помощью знаков <, >, +, -, = и т. д., мы пишем предложения на математическом языке.
Цифры и буквы, а также некоторые специальные символы представляют «слова» этого удивительного языка. Когда мы соединяем «слова» с помощью знаков <, >, +, -, = и т. д., мы пишем предложения на математическом языке.
Большинство из них выглядят сбитыми с толку. Затем я прошу их перевести несколько случайных английских слов на испанский или французский. Делают это легко и с удовольствием. Следующее задание – перевести слова «сложить», «вычесть», «равно» на математический язык символов. Важно отметить, что существуют разные способы выражения на английском языке вещей, которые в конечном итоге будут иметь одинаковый символический смысл. Например, «сумма a и b », «возьмем a и прибавим к b » и « a плюс b » — все они приводят к выражению a + b . Это отправная точка их путешествия в удивительный мир математических символов. Мое утверждение о том, что математика является языком, становится для них ясным.
Теперь очередь моих учеников привести свои примеры. Они очень взволнованы. Мы создаем наш первый англо-математический «словарь». Вот как это может выглядеть:
Английский | Математика |
добавить | + |
вычесть | — |
умножить | × |
разделить | ÷ |
равно | = |
примерно равно | ≈ |
квадратный корень | √ |
больше или равно | ≥ |
меньше или равно | ≤ |
Мое любимое слово, к которому я всегда подхожу по-особому, это слово «ноль». Ноль означает «ничего».
Я обращаю особое внимание на 0, потому что учащиеся не чувствуют себя уверенно с этим числом, особенно когда они решают уравнения, и с обеих сторон уравнения ничего не остается. Они очень сбиты с толку и не могут решить задачу. «0» — очень важная и значимая цифра для математиков. Само открытие этой цифры дало нам возможность записывать числа с помощью таблицы разрядов. Это также важная концепция при написании алгебраических выражений. Я иногда говорю, что важность ничего не была важным математическим открытием.
Еще одна глава в этой беседе — верхние и нижние индексы. Надстрочные индексы — это маленькие символы, расположенные немного выше строки; нижние индексы находятся ниже обычной строки текста. Верхний или нижний индекс может быть числом, буквой или специальным математическим символом.
Традиционно учащиеся знают следующие надстрочные индексы:
градуса (45 градусов) | 45◦ |
процент | % |
число в квадрате (показатель степени) | x 2 |
Обычно используемый нижний индекс обозначает основные системы, такие как log 2 10 (логарифм по основанию 2 числа 10). В какой-то момент учащиеся также встречают нижние индексы, обозначающие термины в последовательности.
В какой-то момент учащиеся также встречают нижние индексы, обозначающие термины в последовательности.
Следующим логическим вопросом будет: «Можем ли мы, например, использовать другой символ для сложения? Зачем нужны символы? Почему бы нам просто не использовать слова для описания методов решения некоторых математических задач?» Кроме того, какова ценность соглашения о фиксированном символе для конкретной идеи, такой как объединение чисел путем сложения?
Алгебра — это обобщенная арифметика
Самое время вернуться в доисторические времена и кратко проследить путь человечества в его попытке разработать эффективный инструмент для описания вычислений и измерений.
«Современный способ записи цифр, простой и удобный, европейцы позаимствовали у арабов. В свою очередь арабы заимствовали эту систему у индийцев. Поэтому европейцы называют современные цифры «арабскими», а арабы — «индийскими цифрами». Интересно, что арабский и индийский варианты этих символов несколько отличаются от стандартных европейских. Английский ученый и путешественник Аделард познакомил европейцев с этой системой примерно в 1120 году. Подавляющее большинство стран приняло ее лишь к 1600 году». 2 Фибоначчи (Леонардо Пизанский) также следует упомянуть в этом развитии. Итак, человечеству потребовалось довольно много времени, чтобы хотя бы символизировать числа, которые мы используем для счета.
Английский ученый и путешественник Аделард познакомил европейцев с этой системой примерно в 1120 году. Подавляющее большинство стран приняло ее лишь к 1600 году». 2 Фибоначчи (Леонардо Пизанский) также следует упомянуть в этом развитии. Итак, человечеству потребовалось довольно много времени, чтобы хотя бы символизировать числа, которые мы используем для счета.
Следующая длинная цитата очень хорошо отражает идею моего отряда:
«Хотя то, что мы сейчас называем «алгебраическими задачами со словами», изучалось и решалось со времен Древнего Египта и Вавилонии, около 4000 лет назад, а может быть, и больше, символическая алгебра — это гораздо более позднее изобретение, пионером которого стал Франсуа Вите незадолго до 1600 г. и развивались в течение следующих 50 лет. (Использование x для неизвестного популяризировал Декарт.) Символическая алгебра, в свою очередь, была главным двигателем научной революции, в частности исчисления. Представьте себе науку без формул. Представьте, что вы пытаетесь даже говорить о производных, не говоря уже о их вычислении, без компактной записи для выражения разностного отношения.
Представьте, что вы пытаетесь даже говорить о производных, не говоря уже о их вычислении, без компактной записи для выражения разностного отношения.
Ударение в последнем предложении должно быть на «компактном». Подумайте о простом выражении, таком как 3 x +2. По сути, это рецепт для вычислений. Он неявно говорит: возьми число x , умножьте на 3 и прибавьте к результату 2. Однако он существенно короче! Составное выражение, такое как 4 y (3 x + 2) — 7, можно перевести как: взять число x , умножить его на 3 и прибавить к результату 2. Возьмите другое число y и умножьте его на 4. Умножьте первый результат на второй, а затем вычтите 7.
По мере усложнения выражений резко возрастает контраст между длиной полного набора вербальных инструкций, необходимых для перефразирования символического выражения, и краткостью самого выражения. Компактность символической формы вместе с компактным и элегантным набором правил (Правила арифметики) для преобразования (часто с целью упрощения) выражений позволяет практикующему специалисту составлять и манипулировать выражениями, чьи словесные переводы были бы неуправляемыми. Это сочетание краткости и формальности делает символическую алгебру мощным инструментом.
Это сочетание краткости и формальности делает символическую алгебру мощным инструментом.
Однако, как и в случае с другими темами математики, та же компактность, которая делает символическую запись мощной, также усложняет ее преподавание. Студенты, особенно студенты, которые могут прийти к алгебре, не уверенные в значениях числовых обозначений и с ограниченным пониманием операций, не сразу адаптируются к символическим алгебраическим обозначениям или реализуют возможности, которые они предлагают». 3
«Основная задача начинающих студентов-алгебраистов состоит в том, чтобы освоить работу с переменными и, в частности, с символическими выражениями — при их интерпретации, создании, манипулировании ими и использовании их для формулирования и решения уравнений, а также интерпретации решения». 4
Основная предпосылка этого модуля заключается в том, «что преподавание символической алгебры и ее использование при решении текстовых задач могут принести пользу с лингвистической точки зрения; что учащимся будет полезно увидеть, изучить, обсудить и проработать перевод на алгебру многих примеров словесно сформулированных ситуаций, включая работу по решению этих задач как с алгеброй, так и без нее, и сравнение алгебраического и арифметического решения этих задач. При этом они могут постепенно знакомиться с языком алгебраических обозначений, словарем и грамматикой полиномиальных выражений, а также с правилами перефразирования в рамках этого языка (т. е. с принципами преобразования выражений и уравнений). Более того, они могут практиковаться в переводе арифметики в алгебру и алгебры в арифметику. Убедившись в тесных связях между ними, они смогут понять изречение о том, что «алгебра — это обобщенная арифметика», а не думать о них как о далеких землях, разделенных безбрежным океаном, как это происходит со слишком многими американскими студентами (см. например, Ли и Уилер (1989))». 5
При этом они могут постепенно знакомиться с языком алгебраических обозначений, словарем и грамматикой полиномиальных выражений, а также с правилами перефразирования в рамках этого языка (т. е. с принципами преобразования выражений и уравнений). Более того, они могут практиковаться в переводе арифметики в алгебру и алгебры в арифметику. Убедившись в тесных связях между ними, они смогут понять изречение о том, что «алгебра — это обобщенная арифметика», а не думать о них как о далеких землях, разделенных безбрежным океаном, как это происходит со слишком многими американскими студентами (см. например, Ли и Уилер (1989))». 5
Чем раньше мы, учителя, приступим к этой работе, тем лучших результатов добьются ученики.
Набор прогрессивных задач
Для этого модуля я написал набор задач, которые развиваются от очень простых одноэтапных арифметических задач, подходящих для первоклассников и второклассников, до более сложных алгебраических задач, содержащих переменные.
Числовые и алгебраические выражения.
Задача I. Буханка хлеба стоит 2 доллара. Большая пицца стоит 20 долларов. Для каждого приведенного ниже вопроса напишите числовое выражение, которое дает ответ на вопрос. Затем вычислите значение каждого выражения.
- На сколько долларов буханка хлеба дешевле большой пиццы?
- Во сколько раз пицца дороже буханки хлеба?
- Сколько стоит пицца и буханка хлеба вместе?
- Сколько стоят две большие пиццы?
- Сколько стоят пять буханок хлеба?
- Сколько стоят вместе две большие пиццы и пять буханок хлеба?
- На сколько долларов две большие пиццы дороже пяти буханок хлеба?
- Во сколько раз две большие пиццы дороже, чем пять буханок хлеба?
Задачи I 1) от до I 5) — одношаговые задачи на сложение/вычитание и умножение/деление. Здесь важно, чтобы учащиеся сначала записали выражение, а не просто вычислили ответ. Например, в Задача I 3) выражение должно выглядеть так:
Цена пиццы и хлеба вместе: 20 долларов + 2 доллара = 22 доллара. Важно требовать, чтобы учащиеся выражали окончательный ответ в правильных единицах, и они должны знать единицы измерения, связанные с каждым числом, которое они используют. Все члены уравнения сложения должны относиться к одной и той же единице.
Важно требовать, чтобы учащиеся выражали окончательный ответ в правильных единицах, и они должны знать единицы измерения, связанные с каждым числом, которое они используют. Все члены уравнения сложения должны относиться к одной и той же единице.
Задачи 6) от до 8) — задачи из трех шагов. Например, выражение для Задача I 6) :
Цена двух больших пицц и пяти буханок хлеба в долларах = 2 (20) + 5 (2) = 50.
Учащиеся должны заметить, что все эти выражения содержат только числа и символы арифметических операций. Такие выражения называются числовыми выражениями .
Следующим шагом будет дать учащимся ту же задачу, но заменить числовые значения цен буквами.
Задача II. Буханка хлеба х долларов. Большая пицца стоит и долларов. Для каждого приведенного ниже вопроса напишите алгебраическое выражение, которое дает ответ на вопрос.
- На сколько долларов буханка хлеба дешевле большой пиццы?
- Во сколько раз пицца дороже буханки хлеба?
- Сколько стоит пицца и буханка хлеба вместе?
- Сколько стоят две большие пиццы?
- Сколько стоят пять буханок хлеба?
- Сколько стоят вместе две большие пиццы и пять буханок хлеба?
- На сколько долларов две большие пиццы дороже пяти буханок хлеба?
- Во сколько раз две большие пиццы дороже, чем пять буханок хлеба?
Например, решение задачи II 1) :
Буханка хлеба на y-x долларов дешевле, чем большая пицца.
Здесь важно научить детей тому, что эту задачу можно сформулировать по-другому. Мы можем спросить: насколько в долларах большая пицца дороже буханки хлеба? Учащиеся должны заметить, что решение задачи остается точно таким же.
Задача II 7) сложнее. Студенты должны усвоить, что термин для более дорогого продукта всегда является первым термином в выражении.
Две большие пиццы дороже пяти буханок хлеба. 2 y -5 x представляет собой разницу в цене. Опять же, дети должны иметь возможность изменить задачу, заменив «дороже» на «дешевле». Таким образом, проблема будет заключаться в следующем: насколько пять буханок хлеба дешевле двух больших пицц в долларах?
Как и в Задача II 1) , решение не изменится.
Учащиеся должны ответить на вопрос: В чем разница между Задача I и Задача II ? Им следует указать, что выражения в Задача II содержат не только цифры и символы арифметических действий, но и буквы, обозначающие числа, то есть переменные. Такие выражения называются алгебраическими выражениями .
Такие выражения называются алгебраическими выражениями .
Задача III . Напишите алгебраическое выражение, а затем найдите его значение, зная значение каждой переменной.
- Трехкратное количество разницы между a и b . Найдите значение, если a = 5 и b =4.
- Частное 25 от суммы чисел x и y . Найдите значение, если x = 3 и y = 2.
- Утроить число a и добавить его к b . Найдите значение, если a = 6 и b = 10.
- Разница 72 и удвоенная c . Найдите значение, если c = 20.
Задача III перекликается с Задача II , но на этот раз реальных сценариев нет. Студенты должны «перевести» каждое алгебраическое выражение с английского языка, используя математические символы, а затем оценить их. Решение на Задача III 3) может выглядеть так:
3 а + б
3(6) + 10 = 18+10 = 28
Важно, чтобы наборы задач включали разные сценарии, например Проблемы IV и V ниже. Дети могут представить себя в этой реальной жизненной ситуации, что делает для них более актуальной всю идею решения текстовых задач. Эти две проблемы также дают возможность учителю подчеркнуть, что математика также является языком науки. Физика учит, что для нахождения расстояния надо скорость умножить на время. Если мы заменим каждое слово в этом правиле буквами, мы сможем описать его на математическом языке. «Равенство, которое представляет собой правило вычисления значения некоторой переменной, называется формула ». 6
Дети могут представить себя в этой реальной жизненной ситуации, что делает для них более актуальной всю идею решения текстовых задач. Эти две проблемы также дают возможность учителю подчеркнуть, что математика также является языком науки. Физика учит, что для нахождения расстояния надо скорость умножить на время. Если мы заменим каждое слово в этом правиле буквами, мы сможем описать его на математическом языке. «Равенство, которое представляет собой правило вычисления значения некоторой переменной, называется формула ». 6
Задача IV . Автомобиль и велосипед стартуют в одной точке, но движутся в противоположных направлениях. Скорость автомобиля 60 км/ч. Скорость велосипеда 10 км/ч. Для каждого приведенного ниже вопроса напишите числовое выражение, которое дает ответ на вопрос. Затем вычислите значение каждого выражения.
- Какое расстояние будет между автомобилем и велосипедом через час после начала движения?
- С какой скоростью они удаляются друг от друга?
- Какое расстояние будет между автомобилем и велосипедом через два часа после начала движения?
- Какое расстояние проехал автомобиль за два часа?
- Какое расстояние проехал велосипед за два часа?
- Насколько больше расстояние, пройденное автомобилем, чем расстояние, пройденное велосипедом за 2 часа?
- Во сколько раз расстояние, пройденное автомобилем, больше, чем расстояние, пройденное велосипедом за 2 часа?
Задача V . Автомобиль и велосипед стартуют в одной точке, но движутся в противоположных направлениях. Скорость автомобиля х миль/ч. Скорость велосипеда х миль/ч. Для каждого приведенного ниже вопроса напишите алгебраическое выражение, которое дает ответ на вопрос.
Автомобиль и велосипед стартуют в одной точке, но движутся в противоположных направлениях. Скорость автомобиля х миль/ч. Скорость велосипеда х миль/ч. Для каждого приведенного ниже вопроса напишите алгебраическое выражение, которое дает ответ на вопрос.
- Какое расстояние будет между автомобилем и велосипедом через час после начала движения?
- С какой скоростью они удаляются друг от друга?
- Какое расстояние будет между автомобилем и велосипедом через два часа после начала движения?
- Какое расстояние проехал автомобиль за два часа?
- Какое расстояние проехал велосипед за два часа?
- Насколько больше расстояние, пройденное автомобилем, чем расстояние, пройденное велосипедом за 2 часа?
- Во сколько раз расстояние, пройденное автомобилем, больше, чем расстояние, пройденное велосипедом за 2 часа?
Числовое и алгебраическое выражение, записанное цифрами, буквами и символами арифметических операций, представляет собой «перевод» реальных событий из жизни с английского на математический язык. Как вы видели, несколько различных сценариев могут быть описаны с использованием одних и тех же математических моделей. По этой причине математика используется в строительстве, сельском хозяйстве, медицине, технике и многих других областях человеческой жизни. Следующие две задачи подчеркивают эту важную особенность математики.
Как вы видели, несколько различных сценариев могут быть описаны с использованием одних и тех же математических моделей. По этой причине математика используется в строительстве, сельском хозяйстве, медицине, технике и многих других областях человеческой жизни. Следующие две задачи подчеркивают эту важную особенность математики.
Проблема VI. Автомобиль проезжает расстояние 180 км за 2 часа, а грузовик преодолевает то же расстояние за 3 часа. Когда встретятся легковой и грузовой автомобиль, если расстояние между ними 300 км и они начинают двигаться навстречу друг другу?
Задача VII. Первая бригада трактористов вспахивает 180 акров за 2 дня. Вторая бригада может выполнить ту же работу за 3 дня. Сколько дней понадобится, чтобы вспахать 300 акров, если две бригады работают вместе?
Для решения задач VI и VII учащиеся должны составить и найти значение одного и того же алгебраического выражения:
300÷(180÷2+180÷3)
Эти две задачи подчеркнут идею о том, что абсолютно разные жизненные ситуации можно описать одним и тем же математическим языком. Это единственное числовое выражение является математической моделью обеих этих реальных жизненных ситуаций. Обратите внимание, однако, что в задаче VI единицами измерения являются часы, а в задаче VII — дни.
Это единственное числовое выражение является математической моделью обеих этих реальных жизненных ситуаций. Обратите внимание, однако, что в задаче VI единицами измерения являются часы, а в задаче VII — дни.
Обратный перевод.
Чрезвычайно важно, чтобы учащиеся могли делать обратный «перевод». Они должны понимать, какую реальную жизненную ситуацию описывает данная математическая модель.
Задача VIII. Посмотрите на таблицу ниже. Объясните, как вы это понимаете.
Дано | Математическая модель | Перевод |
В миске есть a апельсинов и b бананов. | а + б = 30 | Всего фруктов 30. |
а = 2 б | Апельсинов в два раза больше, чем бананов. | |
а = б + 10 | Апельсинов на 10 больше, чем бананов. |
В качестве примера учащиеся должны упомянуть, что в первом столбце есть некоторые данные. Второй столбец предоставляет нам математические модели, основанные на данных и некоторой новой информации. Третий столбец дает нам представление о том, как алгебраические выражения во втором столбце должны быть «переведены» на английский язык.
Задача IX. Создавайте сценарии, которые можно описать следующими числовыми выражениями:
- 2 × 94+17.
- 25 ÷(18÷6+18÷9).
Этот тип задач важен для развития навыков математического моделирования. Сценарии будут разными. Студенты могут бороться с этими проблемами. Я планирую провести обсуждение такого рода проблем в классе и приведу несколько примеров, прежде чем попросить своих учеников создать свои собственные сценарии для выражений. После этого я попрошу добровольцев поделиться своими сценариями со всем классом.
Связанные курсы.
Задачи этого раздела предназначены для изучающих математику. Чтобы преуспеть в этой теме, они должны легко «переводить» текстовые задачи с английского на математический «язык», уверенно чувствовать себя в построении и вычислении алгебраических выражений и работе с формулами. Это высший уровень математики, доступный для школьников. Что касается этой темы, мои студенты всегда упоминают, что это помогает им понять, почему они тратят так много времени на оттачивание навыков алгебраических выражений. «Вся математика» теперь имеет для них смысл.
Чтобы преуспеть в этой теме, они должны легко «переводить» текстовые задачи с английского на математический «язык», уверенно чувствовать себя в построении и вычислении алгебраических выражений и работе с формулами. Это высший уровень математики, доступный для школьников. Что касается этой темы, мои студенты всегда упоминают, что это помогает им понять, почему они тратят так много времени на оттачивание навыков алгебраических выражений. «Вся математика» теперь имеет для них смысл.
В качестве примера рассмотрим относительно простую задачу:
Задача X. «Точка движется по окружности радиусом 6 дюймов, закон ее движения
Ɵ = t 3 -6 t 2 +9 t , (10)
, где t (время) измеряется в секундах, а Ɵ (угол против часовой стрелки, который радиус точки образует с осью x) в радианах. Найти а) угловую скорость ω когда t = 4 секунды. Решение. (а) Из (10) получаем
(а) Из (10) получаем
ω = dƟ/dt = 3 t 2 -12 t +9. (11)
Следовательно, …угловая скорость при t =4 секунды равна
ω 1 = 3×4 2 -12×4+9=9 радиан в секунду». 7
Не учитывать вопрос вычисления производной; студенты должны быть в состоянии оценить выражение (11). Эта задача — хороший пример, подчеркивающий важность обучения алгебраическим выражениям в средней и старшей школе.
Следующая задача более строгая.
Задача XI. «Точка движется по прямой так, что пройденное расстояние (имеется в виду расстояние от положения, когда t = 0) изменяется пропорционально кубу времени. Если точка находится в 3 футах от начальной точки через 2 секунды, каковы будут ее расстояние от начальной точки и скорость через 6 секунд?
Раствор. Общий закон движения, сформулированный в виде уравнения, становится
s=k × t 3 , (3)
, где k — некоторая константа, а s — пройденное расстояние. Более того, по гипотезе s =3, когда t =2.
Более того, по гипотезе s =3, когда t =2.
Следовательно, (3) дает 3 = k × 8, так что k = 3/8 фут/сек 3 . Таким образом, точный закон движения равен
.S = (3 ̸8) × t 3 (4)
Таким образом, требуемое расстояние от начальной точки по истечении 6 секунд будет равно
S 1 = 3/8× 6 3 = 81 фут.
Что касается скорости, то из (4)
dS/dt =9/8× t 2 ,
Так что, в соответствии с пояснениями к этой статье, желаемая скорость по истечении 6 секунд будет
В 1 =9/8 × 6 2 =40 ½ фута в секунду». 8
Примечание : На самом деле вам не нужно вычислять k. Если расстояние от начала пропорционально t 3 , то, поскольку 6 = 3×2, точка будет на расстоянии 3 3 x 3 = 81 фут.
Как видите, на самом первом этапе учащиеся должны «перевести» первое предложение задачи с английского на математический язык. Связь между расстоянием и временем должна быть выражена в виде формулы. Если этот навык не был развит, они сразу же провалят задачу. Эта проблема ясно иллюстрирует важность обучения студентов тому, как переводить текстовые задачи в математические модели, начиная с самого раннего возраста.
Связь между расстоянием и временем должна быть выражена в виде формулы. Если этот навык не был развит, они сразу же провалят задачу. Эта проблема ясно иллюстрирует важность обучения студентов тому, как переводить текстовые задачи в математические модели, начиная с самого раннего возраста.
В этом разделе я хотел бы обсудить, как я планирую использовать задачи, подобные упомянутым выше, чтобы помочь моим ученикам улучшить свои навыки перевода и решения.
Урок 1.
Цель: Учащиеся будут практиковаться в написании числовых и алгебраических выражений для преобразования текстовых задач в математические модели.
Задачи в модуле составлены таким образом, чтобы постепенно повышать строгость, начиная с Задачи I , которая относительно проста. Таким образом, Задача I может быть приведена в классе в качестве примера. Я планирую организовать групповое обсуждение и помочь учащимся записать числовые выражения. Студенты должны найти значение каждого выражения без использования калькулятора.
Задача II основана на Задача I . Учащиеся должны выполнить его самостоятельно, используя идеи, изложенные в задаче I . Учащиеся могут по очереди написать ответ на каждое утверждение на доске, чтобы проверить решения.
Я решу, какие еще задачи использовать для работы в классе, и дам аналогичные для домашнего задания. Однако я не планирую делать больше пяти или семи за первый урок. Я также считаю, что должно быть несколько уроков с одной и той же целью.
Урок 2.
Цель: Учащиеся будут практиковаться в интерпретации каждой математической модели с точки зрения заданных сценариев.
Этот тип задач традиционно сложен. Студенты испытывают трудности с «расшифровкой» математических моделей. пожалуй начну с Задача VIII. В начале третий столбец «Перевод» должен быть пустым. Преподаватель поможет учащимся проанализировать математические модели для каждого сценария и заполнить графу. Учащиеся могут работать над другими задачами самостоятельно в парах или группах, после чего проводится групповое обсуждение.
Опять же, в зависимости от целей, навыков учащихся и сроков обучения, я буду корректировать конкретные классные и домашние задания.
Урок 3.
Цель: учащиеся решат задачи на связанные ставки.
Тема сложная. Мой подход будет заключаться в том, чтобы начать с Проблема X , постепенно прогрессируя со строгостью. Учащиеся могут работать над задачами X и XI самостоятельно или в группах с последующим обсуждением всей группой. Особо обращу внимание на юниты. Это поможет учащимся понять проблему физически.
Примечание : Вопрос о единицах в задаче X еще сложнее, чем в XI. «3», «12» и «9» имеют разные единицы измерения.
Набор задач
Задача I. Фунт клубники стоит x долларов. Фунт вишен равен y долларов. Напишите алгебраическое выражение для каждой фразы или вопроса ниже.
- Цена за 2 фунта клубники.
- Цена за 3 фунта вишни.
- На сколько денег фунт вишни дороже фунта клубники?
- Во сколько раз фунт вишни дороже фунта клубники?
- Цена 1 фунта клубники и 1 фунта вишни вместе.

- Цена за 2 фунта вишни и 3 фунта клубники.
- На сколько денег 2 фунта вишни дороже, чем 3 фунта клубники?
- Во сколько раз 2 фунта вишни дороже 3 фунтов клубники?
Чтобы найти значения алгебраических выражений, мы должны знать значение каждой переменной. Если мы знаем цену 1 фунта клубники и вишни, мы можем найти значение каждого выражения в Задача II .
Задача II . Пусть в задаче I 1 фунт клубники равен 2 долларам, а 1 фунт вишни равен 6 долларам.
Теперь найдите значение каждого выражения, которое вы создали для Задача I .
Задача III. Напишите числовое выражение для каждой фразы и найдите его значение:
- Произведение числа 100 и суммы чисел 8 и 7.
- Произведение разности чисел 57 и 42 и числа 1000.
- Частное суммы чисел 32 и 24 на число 7.
- Частное числа 81 на разность чисел 77 и 68.
Задача IV. Напишите алгебраическое выражение для каждой фразы:
Напишите алгебраическое выражение для каждой фразы:
- Произведение числа x и суммы чисел y и z .
- Произведение разности чисел a и b и числа c .
- Частное суммы чисел t и w и номер q .
- Частное числа f и разности чисел g и h .
Задача V. Напишите числовое выражение для каждой фразы и найдите ее значение:
- Сумма произведения чисел 15 и 2 и частного числа 42 на 6.
- Разность частного числа 270 на 3 и произведения чисел 25 и 3.
- Сумма произведения чисел 17 и 3 и произведения чисел 4 и 13.
- Разность частного числа 45 на 3 и частного числа 64 на 32.
Задача VI. Автомобиль и автобус начали свой путь из одной точки в противоположных направлениях. Скорость автомобиля 60 км/ч. Скорость автобуса 50 км/ч. Для каждого приведенного ниже вопроса напишите числовое выражение, которое дает ответ на вопрос. Затем вычислите значение каждого выражения.
Затем вычислите значение каждого выражения.
- Какое расстояние между автомобилем и автобусом через час?
- С какой скоростью они удаляются друг от друга?
- Какое расстояние будет между автомобилем и автобусом через 2 часа?
- Какое расстояние проехал автомобиль за два часа?
- Какое расстояние проехал автобус за два часа?
- Насколько больше расстояние, пройденное автомобилем, чем расстояние, пройденное автобусом за 2 часа?
- Во сколько раз расстояние, пройденное автомобилем, больше, чем расстояние, пройденное автобусом за 2 часа?
Задача VII. Автомобиль и автобус отправились в путь из одной точки в противоположных направлениях. Скорость автомобиля х км/ч. Скорость автобуса y миль/ч. Машина едет быстрее автобуса. Для каждого приведенного ниже вопроса напишите алгебраическое выражение, которое дает ответ на вопрос.
- Какое расстояние между автомобилем и автобусом через час?
- С какой скоростью они удаляются друг от друга?
- Какое расстояние будет между автомобилем и автобусом через 2 часа?
- Какое расстояние проехал автомобиль за два часа?
- Какое расстояние проехал автобус за два часа?
- Насколько больше расстояние, пройденное автомобилем, чем расстояние, пройденное автобусом за 2 часа?
- Во сколько раз расстояние, пройденное автомобилем, больше, чем расстояние, пройденное автобусом за 2 часа?
- Что означают выражения x-y и 2 x -3 y ?
Задача VIII. Цена одного тюльпана х долларов, роза дороже на и долларов. Напишите алгебраическое выражение для каждой фразы:
Цена одного тюльпана х долларов, роза дороже на и долларов. Напишите алгебраическое выражение для каждой фразы:
- Стоимость букета из 5 тюльпанов и 4 роз — 25 долларов.
- Три розы на 10 долларов дороже, чем пять тюльпанов.
- Цена семи тюльпанов меньше 20 долларов.
- Цена семи роз более 20 долларов.
- Что означают выражения 7 x +3( x + y ) и 12 ( x + y ) – 8 x означает?
Примечание : я попрошу своих учеников упростить эти выражения и указать, что означают упрощенные выражения, и имеет ли это смысл в контексте задачи; то есть ясно ли, что упрощенные выражения должны иметь те же значения, что и исходные?
Задача IX. Фунт яблок равен м долларов; фунт груш на 4 доллара дороже. Напишите алгебраическое выражение для каждой фразы:
- Цена 2 фунта. яблок и 3 фунта. груш составляет 17 долларов.

- Цена 7 фунтов. груш на 30 долларов больше, чем цена 5 фунтов. яблок.
- Цена 2 фунта. груш меньше 12 долларов.
- Цена 4 фунта. яблок стоит более 3 долларов.
- Что означают выражения 3 м +2( м +4) и 4( м +4)-3 м ?
Задача X. Объясните следующие математические модели, связанные с данными:
Дано | Математическая модель |
В ресторане есть a стульев и b столов. | 1) а =4 б 2) a = b +30 |
Задача XI. Интерпретируйте каждую математическую модель применительно к заданным сценариям.
Сценарий | Математическая модель |
В стаде a коров и b лошадей. | 1) a + b =30 2) а =3 б 3) a = b +15 4) а-б =17 5) а :5= б |
Путешественник прошел миль и проплыл на веслах б миль. | |
Человек заплатил a долларов за яблоки и b долларов за апельсины. | |
В классе a девочек и b мальчиков. |
Примечание : Студенты должны интерпретировать все пять математических моделей для каждого сценария.
Задача XII. Создайте сценарии, которые можно описать следующими математическими моделями.
- 100 – 3×15.
- 48÷ (10÷2+24÷8).
Проблемы со связанными ставками.
Список проблем связанных ставок и их решения предлагает KhanAcademy (см. Ресурсы). Здесь преподаватели и учащиеся могут найти все основные типы задач, возникающих в тесте AP Calculus AB. Веб-репетитор проведет вас через весь процесс решения проблем.
Проблемы со связанными ставками
https://www.khanacademy.org/math/ap-calculus-ab/derivative-applications-ab/related-rates-ab/e/related-rates
Внедрение стандартов обучения математике в государственных школах Вирджинии
Четвертый класс
Расчет и оценка
4. 4 Студент будет
4 Студент будет
e) составлять и решать одношаговые и многошаговые практические задачи на сложение, вычитание и умножение, а также одношаговые практические задачи на деление целых чисел.
Пятый класс
Паттерны, функции и алгебра
5.19 Учащийся будет
а) исследовать и описать понятие переменной;
б) написать уравнение, представляющее данное математическое отношение, используя переменную;
c) использовать выражение с переменной для представления заданного словесного выражения, включающего одну операцию; и
г) создать проблемную ситуацию на основе заданного уравнения, используя одну переменную и одну операцию.
Шестой класс
Паттерны, функции и алгебра
6.14 Учащийся будет
а) представляют практическую ситуацию с линейным неравенством по одной переменной; и
b) решить одношаговые линейные неравенства с одной переменной, включающие сложение или вычитание, и представить решение на числовой прямой.
Седьмой класс
Паттерны, функции и алгебра
7.11 Учащийся будет оценивать алгебраические выражения для заданных значений замены переменных.
Восьмой класс
Паттерны, функции и алгебра
8.14 Учащийся будет
а) вычислить алгебраическое выражение для заданных замещающих значений переменных; и
б) упростить алгебраические выражения с одной переменной.
Выражения и операции
A.1 Учащийся будет
а) представляет словесные количественные ситуации алгебраически; и
б) вычислить алгебраические выражения для заданных замещающих значений переменных.
Выше я перечислил соответствующие стандарты. Как видите, начиная с четвертого класса учащиеся должны уметь переводить практическую ситуацию в математическую модель, предполагающую запись числового или алгебраического выражения и его оценку. Они также должны быть компетентны в написании и решении уравнений для представления заданной математической зависимости. Таким образом, учителя начальных и средних классов смогут использовать задачи из моего модуля на своих уроках. После того, как учащиеся освоят содержание моего модуля, они будут лучше подготовлены к математике и физике верхнего уровня, где им придется переводить текстовые задачи в математические модели с использованием математического языка. В моем классе это устройство поможет мне исправить моих учеников, которые планируют сдавать AP Calculus в будущем.
Таким образом, учителя начальных и средних классов смогут использовать задачи из моего модуля на своих уроках. После того, как учащиеся освоят содержание моего модуля, они будут лучше подготовлены к математике и физике верхнего уровня, где им придется переводить текстовые задачи в математические модели с использованием математического языка. В моем классе это устройство поможет мне исправить моих учеников, которые планируют сдавать AP Calculus в будущем.
Башмакова Изабелла, Галина Смирнова Возникновение и развитие алгебры. Кембридж: Издательство Кембриджского университета, 2000.
Блюман, Алан . Демистификация математических словесных задач. Нью-Йорк: McGrawHill, авторское право 2005 г.
Форд, Уолтер Бертон. Первый курс дифференциального и интегрального исчисления. Нью-Йорк: Henry Holt And Company, авторское право 1928 г.
Лам, Лэй Йонг, Тянь Се Анг . Мимолетные шаги: прослеживание концепции арифметики и алгебры в Древнем Китае. Сингапур: World Scientific, авторское право 2004 г.
Сингапур: World Scientific, авторское право 2004 г.
Ма, Уильям. 5 шагов к 5 AP Calculus AB 2017. Нью-Йорк: McGrawHill, 2016 .
Роджер Хоу, От арифметики к алгебре. Пекин: Математический бюллетень, 2010.
Виленкин Наум. Математика 5 класс. Москва: Мнемозина, 1997 .
Зубарева Ирина, Мордкович Александр, Математика 5 класс. Москва: Мнемозина, 2004.
Зубарева Ирина, Мордкович Александр, Математика 6 класс. Москва: Мнемозина, 2004.
- Уильям Ма, 5 шагов к 5 AP Исчисление AB 2017 , 178.
- Наум Виленкин, Математика 5 класс , 44 (перевод с русского мною).
- Роджер Хоу, От арифметики к алгебре , 1.
- Роджер Хоу, От арифметики к алгебре , 2.

- Роджер Хоу, От арифметики к алгебре , 2.
- Зубарева Ирина, Мордкович Александр, Математика 6 класс , 62 (перевод с русского мною).
- Уолтер Бертон Форд, Первый курс дифференциального и интегрального исчисления , 107.
- Уолтер Бертон Форд, Первый курс дифференциального и интегрального исчисления , 105.
8 Квантовая космология | Квантовая гравитация
Фильтр поиска панели навигации Oxford AcademicQuantum Gravity (3-е изд.)Математическая и статистическая физикаКнигиЖурналы Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации Oxford AcademicQuantum Gravity (3-е изд.)Математическая и статистическая физикаКнигиЖурналы Термин поиска на микросайте
Расширенный поиск
Иконка Цитировать Цитировать
Разрешения
- Делиться
- Твиттер
- Еще
Cite
Kiefer, Claus,
‘8 Квантовая космология’
,
Квантовая гравитация
, 3 -е изд.
, Международная серия монографий по физике
(
Оксфорд,
2012;
онлайн Edn,
Oxford Academic
, 24 мая 2012
), HTTPS://doi. org/10.1093/acprof:oso/9780199585205.003.0008,
, по состоянию на 3 октября 2022 г.
Выберите формат Выберите format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)
Закрыть
Фильтр поиска панели навигации Oxford AcademicQuantum Gravity (3-е изд.)Математическая и статистическая физикаКнигиЖурналы Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации
Oxford AcademicQuantum Gravity (3-е изд. )Математическая и статистическая физикаКнигиЖурналы
Термин поиска на микросайте
)Математическая и статистическая физикаКнигиЖурналы
Термин поиска на микросайте
Advanced Search
Abstract
В этой главе рассматривается второе важное приложение квантовой гравитации — квантовая космология. Центральное понятие минисуперпространства вводится и применяется к квантованию вселенной Фридмана. Неоднородности учитываются в пертурбативном смысле. Центральную роль в этой главе играет обсуждение граничных условий, особенно предложения Хартла и Хокинга об отсутствии границ и условия туннелирования Виленкина и других; два предложения сравниваются в деталях. Глава также содержит разделы, посвященные петлевой квантовой космологии и предотвращению сингулярностей.
Ключевые слова: Квантовая космология, минисуперпространство, возмущения, граничные условия, предложение об отсутствии границ, предложение о туннелировании, петлевая квантовая космология, предотвращение сингулярности
Предмет
Математическая и статистическая физика
В настоящее время у вас нет доступа к этой главе.
Войти
Получить помощь с доступом
Получить помощь с доступом
Доступ для учреждений
Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:
Доступ на основе IP
Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.
Войдите через свое учреждение
Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.
- Нажмите Войти через свое учреждение.
- Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
- Находясь на сайте учреждения, используйте учетные данные, предоставленные вашим учреждением. Не используйте личную учетную запись Oxford Academic.
- После успешного входа вы вернетесь в Oxford Academic.
Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.
Войти с помощью читательского билета
Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.
Члены общества
Доступ члена общества к журналу достигается одним из следующих способов:
Войти через сайт сообщества
Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:
Если вы видите «Войти через сайт сообщества» на панели входа в журнале:
- Щелкните Войти через сайт сообщества.
- При посещении сайта общества используйте учетные данные, предоставленные этим обществом. Не используйте личную учетную запись Oxford Academic.
- После успешного входа вы вернетесь в Oxford Academic.
Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.
Вход через личный кабинет
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. Смотри ниже.
Личный кабинет
Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.
Просмотр учетных записей, вошедших в систему
Щелкните значок учетной записи в правом верхнем углу, чтобы:
- Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью.
- Просмотр институциональных учетных записей, предоставляющих доступ.
Выполнен вход, но нет доступа к содержимому
Oxford Academic предлагает широкий ассортимент продукции. Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ. Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю.
Ведение счетов организаций
Для библиотекарей и администраторов ваша личная учетная запись также предоставляет доступ к управлению институциональной учетной записью. Здесь вы найдете параметры для просмотра и активации подписок, управления институциональными настройками и параметрами доступа, доступа к статистике использования и т. д.
д.
Покупка
Наши книги можно приобрести по подписке или приобрести в библиотеках и учреждениях.
Информация о покупке
Термодинамика многих черных дыр
1. Обзор
Термодинамика черных дыр — обширная тема, охватывающая как классический, так и квантовый аспекты гравитации. Термодинамические заряды черной дыры, такие как энтропия и температура, хотя и являются квантовыми по своей природе, связаны с классическими атрибутами, такими как площадь горизонта и гравитация на поверхности [1–4]. Действительно, именно рассмотрение классической реакции черной дыры на падающее вещество привело Бардина, Картера и Хокинга к установлению связи между вариациями черной дыры и Первым законом термодинамики в их основополагающей статье [5].
В последнее время наше понимание термодинамики черных дыр и интерпретации различных параметров также улучшилось. Первый закон термодинамики в гравитационных системах получил более полное понимание как расширенный термодинамический закон за счет включения давления под видом вариаций энергии вакуума [6–10], а также более полного понимания природы « M » для черная дыра возникла как энтальпия системы [7] (см. обзор [11]).
обзор [11]).
Эти попытки понять Первый закон в основном рассматривали одиночные, изолированные черные дыры, как в семействе решений Керра-Ньюмана. Однако существуют более сложные, а потому и более интересные системы с несколькими черными дырами, для которых известны точные решения. Таким образом, такие геометрические формы поддаются термодинамическому анализу. Например, решение Исраэля-Хана [12] представляет собой асимптотически плоскую геометрию, состоящую из двух черных дыр, разделенных «стойкой» — коническим дефектом с угловым избытком, — соответствующим космической струне с отрицательным натяжением. В более общем смысле можно пожертвовать глобальной асимптотической плоскостностью, чтобы устранить нефизический дефект отрицательного натяжения, пропустив через пространство-время космическую струну с положительным натяжением [13–15]. При этом сохраняется локальная асимптотическая плоскостность вдали от ядра. Обобщая далее, ускоряющая черная дыра , закодированная в С-метрике [16, 17], состоит из черной дыры с торчащей космической струной [18] (или дисбалансом между антиподальными струнами), обеспечивающей ускоряющую силу. В этом случае не только теряется асимптотическая плоскостность вблизи уходящей в пространственную бесконечность струны, но и формируется некомпактный горизонт ускорения . Такие системы вызывают вопрос: как определить термодинамику для геометрии, которая не является ни асимптотически плоской, ни изолированной черной дырой, ни (в случае решения Израиля-Хана) стабильной?
В этом случае не только теряется асимптотическая плоскостность вблизи уходящей в пространственную бесконечность струны, но и формируется некомпактный горизонт ускорения . Такие системы вызывают вопрос: как определить термодинамику для геометрии, которая не является ни асимптотически плоской, ни изолированной черной дырой, ни (в случае решения Израиля-Хана) стабильной?
Ранние термодинамические исследования черных дыр с коническими дефектами были сосредоточены на фиксированном дефиците, пронизывающем горизонт [13, 19–22], или дефиците «вариации» во время захвата космической струны [23]. Однако термодинамические последствия действительно изменяющегося дефицита не были изучены до недавнего времени. В частности, ускоряющаяся асимптотически локально анти-де Ситтеровская черная дыра обеспечила контекст, в котором поддерживается превосходный вычислительный контроль. Это связано как со способностью ускорять черную дыру без образования горизонта ускорения, так и с наличием голографического словаря [24]. Отсюда был выведен полностью общий первый закон [25, 26], учитывающий изменение натяжения струны μ:
Отсюда был выведен полностью общий первый закон [25, 26], учитывающий изменение натяжения струны μ:
δM=TδS-λδμ+⋯. (1.1)
Это натяжение идет в паре с сопряженным термодинамическим потенциалом λ, названным термодинамической длиной струны [26]. Позднее эти результаты были обобщены на ускоряющиеся черные дыры, несущие вращательный и калибровочный заряд U (1) [27, 28]. Интересно, что выражение для термодинамического натяжения совпадает с выражением для гравитационного натяжения черных струн Калуцы-Клейна [29–31] — установки без конических дефектов.
Возникло также некоторое понимание происхождения термодинамической длины. Рассмотрев систему из двух черных дыр, соединенных распоркой, Кртоуш и Зельников [32] нашли термодинамическую длину, соответствующую мировому объему распорки, оцененному в некоторый фиксированный момент времени. С тех пор это было подтверждено для аналогично связанных черных дыр Керра-Ньюмена [33].
Следует ожидать, что если гравитационные решения действительно представляют первый закон термодинамики в классическом пределе, то можно найти общие черты, независимо от числа задействованных черных дыр. Мы демонстрируем это здесь, вычисляя вариации множества коллинеарных черных дыр, соединенных струнами, которые могут ускоряться внешними струнами, образуя горизонт ускорения. Мы позволяем всем параметрам в решении варьироваться и тем самым доказываем общий Первый закон 9.0003
Мы демонстрируем это здесь, вычисляя вариации множества коллинеарных черных дыр, соединенных струнами, которые могут ускоряться внешними струнами, образуя горизонт ускорения. Мы позволяем всем параметрам в решении варьироваться и тем самым доказываем общий Первый закон 9.0003
Δm = ∑itiΔsi-∑JλJΔμj, (1,2)
, где температура T I и энтропии S I
. Серкиз19 2-х гол1119. Дж и натяжение мк Дж струн. Мы обосновываем величины, фигурирующие в (1.2), и рассматриваем их следствия в ряде поучительных случаев, включая систему тройных черных дыр и С-метрическую геометрию. Ключевой особенностью нашего результата является то, что система ведет себя как композит; отдельные черные дыры термодинамически не изолированы, но каждая из них взаимодействует с другой, вариация одной из которых влияет на все остальные. Отметим также, что Первый закон (1.2) дополнительно поддерживает понятие M как энтальпии [7], даже несмотря на то, что здесь нет космологической постоянной. Энергетический импульс конического дефицита, или космической струны, принимает форму космологической постоянной мирового листа: струна имеет натяжение, равное по величине и противоположное по знаку плотности ее энергии. Таким образом, член «−δμ J » в (1.2) на самом деле является членом «+δ p J » или членом давления для космической струны. Что Первый закон содержит λ δp , а не pδλ указывает на то, что M действительно представляет собой энтальпию, а не внутреннюю энергию, как предполагалось ранее.
Энергетический импульс конического дефицита, или космической струны, принимает форму космологической постоянной мирового листа: струна имеет натяжение, равное по величине и противоположное по знаку плотности ее энергии. Таким образом, член «−δμ J » в (1.2) на самом деле является членом «+δ p J » или членом давления для космической струны. Что Первый закон содержит λ δp , а не pδλ указывает на то, что M действительно представляет собой энтальпию, а не внутреннюю энергию, как предполагалось ранее.
План статьи следующий: В разделе 2 мы рассматриваем конструкцию массивов черных дыр и горизонтов ускорения в калибровке Вейля [34]. В разделе 3 мы формулируем первый закон для таких систем, обосновывая соответствующие заряды и потенциалы. Раздел 4 обсуждает следствия результата с помощью некоторых поучительных примеров и содержит новую массовую формулу Христодулу-Руффини [35] для C-метрики.
2. Четырехмерная метрика Вейля: массивы черных дыр
В этом разделе мы кратко рассмотрим решения для множественных черных дыр, которые мы будем анализировать. Мы будем в основном следовать изложению [36] с небольшими изменениями в обозначениях. Основным новым результатом этого раздела является обсуждение определения масштаба ускорения массива ускоряющихся черных дыр в (2.31). Черные дыры выровнены вдоль оси и статичны в том смысле, что обладают времяподобной изометрией Киллинга в области между горизонтами черной дыры и ускорения. Хотя решение типа Исраэля-Хана для двух вращающихся черных дыр известно аналитически [37, 38], точные решения для трех или более черных дыр Керра остаются неуловимыми 1 . Чтобы сделать исследование термодинамики системы доступным, мы обходим здесь любое обсуждение вращения. Можно ожидать, что вращательные заряды могут быть включены очевидным образом, как только будет записано соответствующее семейство геометрий.
Мы будем в основном следовать изложению [36] с небольшими изменениями в обозначениях. Основным новым результатом этого раздела является обсуждение определения масштаба ускорения массива ускоряющихся черных дыр в (2.31). Черные дыры выровнены вдоль оси и статичны в том смысле, что обладают времяподобной изометрией Киллинга в области между горизонтами черной дыры и ускорения. Хотя решение типа Исраэля-Хана для двух вращающихся черных дыр известно аналитически [37, 38], точные решения для трех или более черных дыр Керра остаются неуловимыми 1 . Чтобы сделать исследование термодинамики системы доступным, мы обходим здесь любое обсуждение вращения. Можно ожидать, что вращательные заряды могут быть включены очевидным образом, как только будет записано соответствующее семейство геометрий.
При временной и осевой симметрии метрика может быть записана в блочно-диагональной (Вейлевской) форме с метрическими функциями γ, ν и α, зависящими только от поперечных координат r и z :
ds2=e2γdt2-e2 (ν-γ)(dr2+dz2)-α2e-2γdϕ2. (2.1)
(2.1)
Уравнения Эйнштейна: ] (2.3)
Δν+(∇γ)2=-8πGe2(ν-γ)Tϕϕ (2.4)
∂±2αα+2(∂±γ)2-2∂±ν∂±αα=8πG[Trr -Tzz±2iTrz] (2.5)
где Tab — тензор энергии-импульса любого объемного вещества, Δ — двумерный лапласиан (∂r2+∂z2=∂+∂-), где ∂ ± = ∂ r ∓ i∂ z производные по комплексным координатам ( г ± из )/2.
В отсутствие материи или космологической постоянной они имеют очень элегантное решение: просто фиксируют оставшуюся в метрике (2.1) конформную калибровочную свободу, полагая α ≡ r / K , что согласуется с ( 2.2). Заметим, что здесь мы вводим параметр K , чтобы сохранить 2π-периодичность координаты ϕ; это станет актуальным, когда мы будем обсуждать конические источники. При α ∝ r уравнение (2.3) превращается в цилиндрическое уравнение Лапласа для γ в вакууме с решением
γ=-2G∫S(r′)d3r′|r-r′| (2. 6)
6)
для источника с плотностью энергии S ( r ). Обратите внимание, что метрическая составляющая γ есть не что иное, как ньютоновский источник осевой симметрии. В свою очередь, ν определяется из γ с помощью (2.5). Поскольку уравнение для γ является линейным, его решения можно накладывать друг на друга; нелинейность гравитации Эйнштейна проявляется в решении ν. Обратите внимание, что, поскольку регулярность оси r требует ν(0, z ) = −log K , в общем случае будут конические особенности при наложении регулярных решений для γ. Их можно интерпретировать как струны или распорки, поддерживающие статические источники в равновесии.
2.1. Решение Шварцшильда.
z ∈ [− m, m ], что даетγS=-12∫-mmdz′[r2+(z-z′)2]1/2=12logR—Z-R+-Z+, (2.7)
, где
Z±=z∓m , R±2=r2+Z±2. (2.8)
Интегрирование (2.5) дает тогда
νS=12logE+-2R+R-, (2. 9)
9)
, где
E+-=R+R-+Z+Z-+r2. (2.10)
Хотя это и не похоже на знакомую черную дыру Шварцшильда, простое преобразование
z=(ρ-m)cosθ , r2=ρ(ρ-2m)sin2θ (2.11)
фактически возвращает метрику к своей стандартной сферической форме, с 2 м = 2 GM S представляет собой радиус Шварцшильда.
2.2. Пространство Риндлера
Интересно, что формально можно ввести горизонт ускорения, добавив полубесконечный линейный источник (SILM) [40], где z > z 0 :
γR=-12∫z0∞dz′[r2+(z-z′)2]1/2→12ln R0-Z0ℓγ, (2.12)
where Z 0 = ( з − z 0 ), R0=r2+Z02, а бесконечный интеграл регулируется масштабом ℓ γ . Решение для ν дает метрику Риндлера в координатах Вейля:
ds2=(R0-Z0)ℓγdt2-ℓγ2R0[dr2+dz2]-ℓγr2(R0-Z0)dϕ2. (2.13)
(2.13)
Поскольку пространство-время Риндлера — это просто плоское пространство-время, наблюдаемое ускоряющимся наблюдателем, мы можем преобразовать (2.12) в пространство-время Минковского (в цилиндрических полярах) посредством преобразования =ρℓγζ2-τ2z-z0=τ2+ρ2-ζ22ℓγ. (2.14)
Происхождение Минковского соответствует z = z 0 , r = 0, (т. е. начало SILM), как и ожидалось. Начало системы Вейля соответствует ζ=2ℓγz0, что дает естественный выбор калибровки для системы Вейля. Обратите внимание, что значения z 0 и ℓ γ независимы с точки зрения решения уравнений Эйнштейна, первое является калибровочным выбором — началом координаты z — а последнее потому, что одно и то же Горизонт Риндлера может применяться к наблюдателям с разными ускорениями A = 1/л γ (см. рис. 1). Интерпретируя начало системы Вейля как местонахождение ускоряющегося наблюдателя, тем самым фиксируя датчик, получаем z 0 = 1/2 A от ζ = 1/ A .
Рисунок 1 . Мировые линии Риндлера наблюдателей с разными ускорениями, но с одним и тем же горизонтом.
2.3. Много черных дыр
Теперь мы можем рассмотреть наложение решений для γ, чтобы построить решения с несколькими черными дырами, как описано в [36]. Мы кратко рассмотрим эти решения, используя немного отличающиеся от [36] обозначения, более подходящие для нашего рассуждения. Каждая черная дыра представлена стержнем длиной 2 м I , I = 1.. N , а ускорение представлено SILM, как описано выше. Мы отметим, что стержень заканчивается на Z I , где I = 1 .. N и Z 1 < Z 2 1 < Z 2 1 < Z 2 . черных дыр, n = 2 N +1, и SILM начинается с z n , если у нас есть массив (неускоряющихся) черных дыр, то n = 2 N четно. Такое расположение показано на рис. 2.
Такое расположение показано на рис. 2.
Рисунок 2 . Схема источника для системы с несколькими черными дырами из раздела 2.3. В неускоряющем случае точка z n , представляющая начало SILM (толстая красная стрелка), и сам SILM отсутствуют; его соседняя строка (штриховая черная) вместо этого простирается до z → ∞.
Естественным обобщением предыдущих обозначений является
Zi=z-zi,Ri2=r2+Zi2,Xi=Ri-Zi,Eij=RiRj+ZiZj+r2. (2.15)
Решение для γ представляет собой просто суперпозицию общих потенциалов из (2.7), где ν затем получается квадратурой:
γ=12∑i=1n(-1)i+1logXiℓγ,ν=14∑ i,j=1n(-1)i+j+1logEijℓν2+Onγ. (2.16)
Здесь ℓ являются константами интегрирования, которые сокращаются, только если n четно, а O n действует как «переключатель» для дополнительных членов, когда n нечетно:
On=n-2⌊n2⌋={1n нечетное0n четное. (2.17)
(2.17)
При переходе к термодинамике системы нам понадобится предел этих функций при приближении к оси, r → 0. Поэтому мы завершим этот пункт, найдя поведение (2.16) как r → 0, и обсуждаем конические дефициты на оси. Отметив, что R i → | Z и | при r → 0 мы видим, что
Xi~|Zi|-Zi+r22|Zi|={2|Zi|z
, следовательно,
γ~12∑i=1p(-1)i+1logr22|Zi|ℓγ +∑i=p+1n(-1)i+1log2|Zi|ℓγ : z∈(zp,zp+1 ) (2.19)
, где P = 0, если Z < Z 1 оставляя только вторую сумму и, наоборот, первую сумму для Z > Z > .
Далее,
Eij~{2ZiZjz Следовательно, если мы подойдем к оси на ITH Черная дыра, для которого Z ∈ ( Z 2 I −1 , Z 2 I ), 13II-14 ~ 14139393.139.139.139.139.139.139.139.139.139.139.139. -1)i+j+1log(2ZiZjℓν2) +14∑i,j=2In(-1)i+j+1log(2ZiZjℓν2) +12∑i=12I-1∑j=2In(-1)i+j +1log(r2(zi-zj)22|ZiZj|ℓν2)+Onγ. (2.21)
13II-14 ~ 14139393.139.139.139.139.139.139.139.139.139.139.139. -1)i+j+1log(2ZiZjℓν2) +14∑i,j=2In(-1)i+j+1log(2ZiZjℓν2) +12∑i=12I-1∑j=2In(-1)i+j +1log(r2(zi-zj)22|ZiZj|ℓν2)+Onγ. (2.21)
Вдали от черных дыр, записывая ν0=12log(2ℓνℓγ), имеем:
ν(0,z)=Onν0z Notice that z j − z i +1 < z j − z i < z j + 1 − z i , thus ν(0, z ) < ν 0 for the first string tension, and (for accelerating black holes) ν N < ν 0 . Теперь мы можем идентифицировать коническую структуру на оси. Ось будет иметь конический дефект, если длина окружности окружностей собственного радиуса Δ r вокруг него не являются 2πΔ r . δ=2πlimr→0[1-e-ν(0,z)K], (2.23) , что связано с натяжением космической струны через δ = 8π Gμ . Уравнение (2.22) определяет, как изменяется угол дефицита при перемещении между черными дырами. Напряжение между 9.1348 Ith и ( I +1) th черная дыра µI=14(1-e-Onν0K∏i=12I∏j=2I+1n(zj-zi)(-1)i+j ). (2.24) Последняя черная дыра имеет μ N как дефицит для z > z 2 N , μN -e-ν0K∏i=1N(zn-z2i-1)(zn-z2i))n=2N+1, (2.25) и для падающего натяжения z < z 1 , имеют μ0=14(1-e-Onν0K). Теперь мы видим интерпретацию K . Для массива неускоряющихся черных дыр через систему проходит окружающее напряжение, так как дефицит вне массива ) имеют такой же конический дефицит µ0=µN=14(1-1K). (2.27) Уравнение (2.22) показывает, что e ν(0, z ) < 1 между черными дырами. Следовательно, если бы мы не вставляли параметр K , вместо этого сохраняя 2π-периодичность ϕ для z < z 1 и z > z 2 N , превышение δ < 0, соответствующее отрицательному натяжению «космической стойки», как в [32]. Хотя такие системы можно рассматривать [20, 32, 33], мы предпочитаем сохранять физические источники. Поэтому мы берем K достаточно большим, чтобы все конические особенности были дефектами и в принципе соответствовали физическим космическим струнам [14, 15]. Обратите внимание, однако, что если K > 1, существует окружающий конический дефицит в пространстве-времени, независимо от того, есть ли ускорение. Для массива ускоряющихся черных дыр мы следуем соглашению [27, 41] о том, что K измеряет дефицит окружающей среды, т. е. µ0+µN=12(1-1K). (2.28) Это, в свою очередь, позволяет нам определить 12(1+Вн). (2.29) , таким образом, мы имеем µ0=14(1-2(1+Vn)K) , µN=12(1-2Vn(1+Vn)K). (2.30) Обратите внимание, однако, что выбор K не уникален; этот (2.30) соответствует той же нормализации, что и стандартная C-метрика, однако, если рассматривать метрику как расщепленную космическую струну, то альтернативным естественным выбором может быть нормализация «начального» дефицита. То есть мы могли бы выбрать µ0=14(1-1K), и в этом случае µN=14(1-VnK). Наконец, у нас остается шкала длины ℓ γ , которая (только) присутствует в ускоряющемся массиве. Этот параметр представляет чистую шкалу ускорения пространства-времени. Мы ожидаем, что при малых ускорениях (больших z n ) это должно асимптомировать значение Риндлера ℓ γ ~ 2 z n . ℓγ=Mµ0-µN=Vn+1Vn-1∑1N(-1)kzk, 2.31) , где M = ∑ m I / K — полная масса системы (см. раздел 3.1). Мы видим, что ℓ γ имеет требуемый большой предел z n и четкую физическую интерпретацию в тесной аналогии со своим чистым родственником Риндлера из раздела 2.2. Теперь выведем первый закон для коллинеарных черных дыр с переменным положительным натяжением струн и возможным горизонтом ускорения, решения для которого были представлены в разделе 2.3. Сначала нам нужно получить эти соответствующие термодинамические параметры. Для энтропии данной черной дыры мы вычисляем площадь соответствующего горизонта SI=limr→0π2K∫z2I-1z2Ireν-2γdz=πmIKlimr→0reν-2γ. Для температуры применяются стандартные методы, что дает TI=limr→012πe2γreν=mI2KSI. (3.2) Предел re ν−2γ при приближении к оси дается формулами (2.19), (2.21), и, используя (2.29), получаем: log(reν-2γ)→ log2+Onlog(ℓγeν02) +∑i=12I-1∑j=2In(-1)i+j+1log|zj-zi|. (3.3) Самой сложной термодинамической величиной для определения является общая масса. Частично это связано с тем, что внешние струны, простирающиеся до бесконечности, препятствуют глобальной асимптотической плоскостности и, таким образом, делают массу АДМ [42] плохо определенной. Еще больше усложняет дело наличие некомпактного горизонта разгона. Была предпринята некоторая попытка [21] переопределить массу АДМ при наличии конического дефекта путем вычисления массы относительно конического пространства Минковского, а не чистого Минковского, как в обычной конструкции. Однако такая конструкция дает нежелательные результаты. Хотя трудно найти полезное понятие массы АДМ, существование изометрии ∂ t означает, что в распоряжении остается конструкция Комара [43]. Сосредоточившись сначала на неускоряющемся случае, Коста и Перри [20] рассчитали массу АДМ для системы коллинеарных черных дыр без внешних струн (μ 0 = μ N = 0). Можно вычислить асимптотическое поведение подходящую радиальную координату и просто считайте массу. Как обсуждалось выше, когда у нас есть окружающий конический дефицит, масса ADM не определена, но вместо этого мы можем считать массу Комара как M=∑I=1NmI/K. При наличии горизонта ускорения ситуация требует дополнительных пояснений. Берем к = ∂ t как наше векторное поле Киллинга, генерирующее сдвиги времени. Нормализация k подразумевается выбором (2.31) ℓ γ ; см. обсуждение в конце раздела 2. Ковектор, связанный с k , равен k ♭ = e 2γ dt . Взяв внешнюю производную и двойственную по Ходжем, мы находим ⋆dk♭=rKe2γ[(∂re2γ)dz-(∂ze2γ)dr]∧dϕ. (3.5) Причинная структура пространства-времени теперь значительно сложнее, чем в неускоряющем случае, но по-прежнему существует четко определенная пространственная бесконечность [44]. Для вычисления полной массы можно было бы, в принципе, проинтегрировать эту форму по двугранной поверхности. Тем не менее, более поучительно использовать закон Гаусса, чтобы переписать граничный интеграл как сумму интегралов по каждому горизонту черной дыры и объемного интегрирования: 18π∫∞⋆dk♭=18π∑I=1N∫HI⋆dk♭+Mbulk. Количество в левой части – это общая масса 3 M . Из (2.19) и (2.21) имеем соответствующее поведение подынтегральной функции в правой части (3.6) вблизи горизонта I th HI, ∂re2γ~r2|z2I+1z2I|, e -2γ~4|z2I+1z2I|r2, (3.7) , упрощая подынтегральную функцию: limr→0[⋆dk♭]z∈(z2I,z2I+1)=2Kdz∧dϕ+…. (3.8) Отсюда заключаем, что интеграл по HI, который мы интерпретируем как массу отдельной черной дыры в массиве, равен MI≡18π∫HI⋆dk♭=mIK. (3.9) Наконец, заметим, что объемный интеграл M объем обращается в нуль и что сами струны не вносят вклада в вышеприведенное вычисление. Делается вывод, что общая масса Комаров напрямую связана с длинами стержней компактных горизонтов. Такой же результат для массы одиночной ускоряющейся черной дыры был предложен в [28], хотя и с уклончивым отношением к нормировке k . Теперь мы покажем, как вывести уравнение (1.2), первый закон термодинамики для множества коллинеарных черных дыр. Рассмотрим вариант массива. Решение (2.16) описывает связанную систему; любое изменение одной черной дыры повлияет на все остальные. Поэтому мы не ожидаем отдельных Первых Законов для каждой черной дыры. Вместо этого имеет смысл рассмотреть изменение общей массы M=∑I=1NmIK, (3.10) , так как это функция состояния всей системы. Действительно, это философия Первого Закона, полученная в [32]. Таким образом, чтобы вывести первый закон, мы должны вычислить δM=∑I=1N1KδmI-mIδKK2. (3.11) Начнем с вычисления изменения энтропий для отдельных черных дыр: ∑I=1NTIδSI=12∑I=1Nδ(mIK)+SΣ+OnM2(δℓγℓγ+δν0), заменил ℓν=e2ν0ℓγ/2, и где SΣ=∑I=1NmI2K∑i=12I-1∑j=2I2N(-1)i+j+1δ(zj-zi)zj-zi +On∑I=1NmI2K ∑i=12I-1(-1)iδ(zn-zi)zn-zi . Здесь содержится часть того, что нам нужно для Первого Закона, но сумма довольно запутанная! Теперь обратимся к космическим струнам. Запишем термодинамические длины струн как λI=-eνILI, а затем изменим натяжения в (2.24), (2.25) и (2.26), чтобы получить вклад в Первый закон от натяжений: -∑I =0NλIδµI=∑I=0NLIδK4K2+On∑I=0NLI4Kδν0+µΣ, (3.14) , где µΣ=∑I=1N-1LI4K∑i=12I∑j=2I+12N(-1)i+j+ 1δ(zj-zi)zj-zi +On∑I=1NLI4K∑i=12I(-1)iδ(zn-zi)zn-zi. (3.15) Соединяя эти два выражения вместе, мы имеем: ∑I=1NTIδSI-∑I=0NλIδμI =δM2+SΣ+µΣ+∑I=0NLIδK4K2+On4K∑I=0N(LI+2mI)δν0 +2mIδSI-ℓγℓγℓγℓγℓγℓγℓγℓγℓγℓγℓγℓγℓγℓγℓγℓγℓγℓγℓ (3.16) Сначала разберемся с суммами S Σ и µ Σ в этих выражениях. Наблюдая, что M I = ( Z 2 I — Z 2 I –1). Обобщение [32] Для термодинамической длины струн между горизонтами AS L I = Z 2 I +1 — Z 29199 2199 2 19 2 9 2 9 2 299 2 9 2 2 99 2 2 2 I +1 — 2 I +1 — . из L 0 и L N – см. далее) дает сумму напряжений как μΣ=∑k=22N-1 ∑i=12[k2]∑j=2[k2]+ 12N(-1)i+j+k4Kzkδ(zj-zi)zj-zi +On4K∑k=12N-1 ∑i=12[k2](-1)i+k+1zkδ(zn-zi)zn-zi +LN4K∑i=12N(-1)iδ(zn-zi)zn-zi. (3.18) Теперь мы видим, что многие члены в S Σ сокращаются членами в μ Σ , оставляя только k = 1, 2 N из суммы энтропии и промежуточные i, j членов от каждого, когда 2[k+12] отличается от 2[k2]+1: SΣ+µΣ=∑j=22N(-1)j+14Kz1δ(zj-z1)zj-z1+∑i=12N- 1(-1)i+14Kz2Nδ(z2N-zi)z2N-zi+∑k=22N-1[∑j=k+12N(-1)j+k4Kzkδ(zj-zk)zj-zk+∑i=1k-1 (-1)i+k+14Kzkδ(zi-zk)zi-zk]+On4K(∑i=12N-1[(-1)i(LN+z2N)-zi]δ(zn-zi)zn-zi +LNδ(zn-z2N)zn-z2N)=∑j=22N∑i=1j-1(-1)i+j+14K(δzj-δzi)+On4K∑k=12N(-1)k(LN+ z2N-zk)δ(zn-zk)zn-zk. Теперь нам нужно идентифицировать L N (и L 0 ). Мы пишем LN = ZC-Z2N, L0 = Z1-ZC (3,20) в соответствии с выражениями для L I , где Z C 808 AR C 9 9 9 9 9 9 9 8. что из SILM в γ, будет определено. Следовательно, мы можем сократить эту комбинацию до SΣ+μΣ=∑I=1NδmI2K +On4K∑k=12N(-1)k(δ(zn-zk)+(zc-zn)δ(zn-zk)zn-zk ) =∑I=1NδmI2K(1-On)+On4K(zc-zn)∑k=12N(-1)kδ(zn-zk)zn-zk = ∑I=1NδmI2K(1-On)-On4K(zc- zn)δVnVn. (3.21) Упростив S Σ +μ Σ , мы теперь обратимся к остальной части предполагаемого Первого закона (3.16). Заметим, что сумму термодинамических длин можно связать с суммой масс: ∑I=0NLI=∑I=1N-1(z2I+1-z2I)+LN+L0=-2∑I=1NmI . Следовательно, ∑i = 1ntiΔsi-∑’sλIΔμi = Δm2+∑i = 0nliΔK4k2+∑i = 1nΔmi2k+on4k [∑i = 1n2miΔℓγ-енти = 1n2k+on4k [∑i = 1n2miΔℓγ-γ- , где mtot=∑ImI — это сокращение для суммы масштабов длины отдельных стержней. Таким образом, мы получили первый закон (1.2) для общего массива черных дыр, если отождествить zc=zn+2mtotδℓγ/ℓγ-2δmtotδVn/Vn=zn-4VnmtotVn2-1, черная дыра. Для неускоряющейся черной дыры первый закон выполняется автоматически, и мы полагаем1348 z 2 N )/2. Получив эти выражения, интересно исследовать некоторые образцы массивов ускоряющихся и неускоряющихся черных дыр, чтобы понять взаимозависимость энтропии черных дыр и увидеть, как струны вклад в термодинамическую систему, а также перекрестную проверку известных результатов. Начнем с рассмотрения неускоряющихся черных дыр. Это включает в себя случай Шварцшильда как базовую перекрестную проверку наших результатов и систему двух черных дыр, которая уже рассматривалась в литературе [20, 32, 33]. Как обсуждалось в разделе 2, решение Шварцшильда (с аксиальным коническим дефектом) имеет n = 2, N = 1 и 2 м . Условно мы устанавливаем центр стержня в начало координат так, что z 2 = − z 1 = м . Из (3.1) и (3.2) находим, что энтропия и температура равны S = 4π м 2 / K и T = 1/8π м соответственно, как и ожидалось. Для космической струны, пронизывающей горизонт, имеем µ0=µ1=14(1-1K), а λ 0 = λ 1 = м в согласии с [26]. Первый закон для системы двух черных дыр с K = 1 исследовался в [32]. K≥D2-(m2-m1)2D2-(m1+m2)2 (4.1) где D — расстояние между центрами двух стержней, мы находим результаты, согласующиеся с их выводами : Первый закон выполняется с термодинамической длиной дефекта, соединяющего черные дыры, заданной объемом струны на мировом листе в единицу времени. Термодинамические длины полубесконечных струн теперь равны λ0=λ2=z4-z12=D2+m1+m22 (4.2) , т. е. система реагирует на среднюю массу и расстояние между черными дырами. Заметим, что λ1=-(z3-z2)eν1 также имеет фактор разделения, который важен для согласованности при изменении чистого конического дефицита системы. Мы обсудим это более подробно ниже для трех черных дыр. The three black hole system has rods on the intervals ( z 1 , z 2 ), ( z 3 , z 4 ), and ( z 5 , z 6 ) (см. Легко видеть, что µ 1 < µ 0 . Этого и следовало ожидать: чтобы сохранить равновесие, к внешним черным дырам необходимо приложить дополнительную силу, чтобы уравновесить их притяжение к средней. Рисунок 3 . Схема источника для трех (неускоряющихся) черных дыр. Для термодинамических длин имеем: λ0=(z6-z1)/2=(z0+m0)=λ3,λ1=-(z0-m0-m)(z02-m02)(z02-(m0+ m)2)z02(z02-(m0-m)2)=λ2. (4.4) Таким образом, термодинамическая длина окружающего дефицита, т. е. сумма двух строк 1 и 4, представляет собой расстояние от северного полюса самой верхней черной дыры до южного полюса самой нижней черной дыры. Длина, связанная с промежуточными струнами, равна минус расстояния между горизонтами соседних черных дыр (см. рис. 4). Рисунок 4 . Изменение напряжений и термодинамических длин системы трех черных дыр: (слева) для равных масс в зависимости от расстояния между черными дырами и (справа) для фиксированного расстояния между черными дырами, но с различной массой внешней черной дыры. Слева напряжение устанавливается путем принятия минимального значения, соответствующего нулевому напряжению между черными дырами при минимальном расстоянии друг от друга, z мин = 3, что дает окружающее напряжение 41/324. Мы обнаружили интересное явление, когда термодинамическая длина внешних струн положительна, а длина внутренних струн отрицательна. Это озадачивает с точки зрения отдельных черных дыр. Однако если рассматривать систему как составную, то это имеет смысл: если мы изменим общее напряжение, мы должны учитывать вклад как внутренних, так и внешних космических струн. Тогда отрицательный вклад внутренних длин противодействует положительному вкладу внешних длин. В явном виде сначала настройте три черные дыры так, чтобы не было дефицита между центральной и внешней черными дырами. то есть K принимает значение K0=z02(z02-(m0-m)2)(z02-m02)(z02-(m0+m)2). (4.5) Мы теперь «добавляем» космическую строку в систему, увеличив K до K 0 + K 1 , так, что δ Они m = K14K0 (K0 + K0 + K0 + K0 + K0 + K0 + K0 + K0 + K0 + K01 (K0 + K0 + K1 (K0 + K0 + K11 (K0 + K0 + K11 (K0 + K0 + K11 (K0 + K0 + K1 (K0 + K11). Обратите внимание, что натяжение объемлющей космической струны во всем пространстве-времени увеличивается от µ 0 = (1 − 1/ K 0 )/4 до µ 0 + δμ 0 . Однако в области между черными дырами, изначально не имевшей дефицита, теперь наблюдается космическая струна с натяжением K 0 δμ 0 , т. е. несколько большее натяжение, чем увеличение натяжения окружающей струны. Теперь посмотрим на общее изменение энергии: ∑I=03λIδμI=λ0δμ0+λ1δμ1+λ2δμ2+λ3δμ3 +K1) =(4m0+2m)K14K0(K0+K1). (4,7) Это общая длина струны, захваченной черными дырами, умноженная на натяжение. Таким образом, мы заключаем, что термодинамические длины действительно ведут себя согласованно, комбинируясь таким образом, что общее изменение напряжения оказывает заметное влияние на общую термодинамику системы. Обращаясь к энтропиям, можно увидеть, что S2/m2>S1/m02. Однако картина немного тоньше, чем это ожидалось широкими мазками; центральная черная дыра имеет однородное напряжение, μ 1 , проходящее через нее, поэтому наивно можно было бы ожидать, что энтропия может отслеживаться на 4πm2(1-4μ1), но на самом деле энтропия выше этого значения. Для внешних черных дыр мы могли бы ожидать, что энтропия будет отслеживаться по среднему напряжению между полюсами, но опять же, оно выше. Действительно, энтропия выше даже энтропии Шварцшильда для диапазона значений разделения z 0 (см. Рисунок 5 . Энтропия внешних (слева) и средних (справа) черных дыр для равных масс в зависимости от расстояния между черными дырами. Все черные дыры имеют единичную массу с окружающим напряжением 41/324. Натяжение задается путем взятия минимального значения, согласующегося с отсутствием распорки между черными дырами при минимальном расстоянии друг от друга, здесь z мин = 3. Точно так же мы можем проследить, что происходит с энтропией одной черной дыры, как в результате изменения массы остальных. Например, удерживая центральную черную дыру на единицу массы и удерживая две другие черные дыры на заданном расстоянии, мы можем увидеть, как энтропия центральной черной дыры Центр=4πK(1-m2/z02)(1+m/z0+1/z0)2(1-m/z0+1/z0)2 (4.8) изменяется при изменении массы внешней черные дыры. Масса внешней дыры m 0 может колебаться от нуля до z 0 − 1, однако в этой точке горизонты сливаются и для поддержания неотрицательного напряжения между черными дырами мы должны были бы иметь максимальный дефицит 2π. K=Kc≡z02(z02-(mmax-1)2)(z02-mmax2)(z02-(mmax+1)2). (4.9) На рис. 6 показано изменение энтропии центральной черной дыры для расстояния z 0 = 10 и диапазона масс до м max = 8,8. Это очень близко к пределу слияния, что дает большое внешнее натяжение μ 0 ~ 0,244, поэтому угол дефицита δ / (2π) ~ 0,977. Как и прежде, энтропия нормируется энтропией одиночной черной дыры в пространстве-времени с дефицитом окружающей среды ( S K = 4π/ K ), а также у черной дыры с космической струной натяжения μ 1 , проходящей через ( S μ = 4π(1 9 12 − 4 )). Рисунок 6 . Энтропии внешней (слева) и центральной (справа) черных дыр как функция массы m 0 внешних черных дыр. Теперь мы видим более тонкое поведение. Первоначально на высоте м = 0 пространство-время точно такое же, как у одиночной черной дыры единичной массы, пронизанной космической струной натяжения . Когда мы включаем массу черной дыры в точке z 0 , μ 1 уменьшается, и это приводит к увеличению энтропии, но это сверх того, что мы ожидали бы просто от падения μ 1 . Прежде всего это следует из зависимости m в (4.8). Однако по мере дальнейшего увеличения массы, в то время как функция S 2 / S K продолжает расти, отношение S 2 / Для малого R , Δ R ~ E ν (0, Z ) −γ (0, Z ) , а окружность RE –γ (0 8848 re –γ (0, 8848 re –γ (0,. ) / K , поэтому угол дефицита δ равен
Для малого R , Δ R ~ E ν (0, Z ) −γ (0, Z ) , а окружность RE –γ (0 8848 re –γ (0, 8848 re –γ (0,. ) / K , поэтому угол дефицита δ равен (2,26)
(2,26)
 Интерпретируя ускорение как общую массу составной системы черной дыры, деленную на общую силу, измеренную дифференциальным дефицитом, мы приходим к
Интерпретируя ускорение как общую массу составной системы черной дыры, деленную на общую силу, измеренную дифференциальным дефицитом, мы приходим к 3. Термодинамика массива черных дыр
3.1. Получение термодинамических параметров
 (3.1)
(3.1) В частности, можно было бы заключить, что масса C-метрики обращается в нуль. Это озадачивает с точки зрения отсутствия плавного перехода к неускоряющейся черной дыре. Это также противоречит интуиции, полученной от медленно ускоряющейся черной дыры в AdS, для которой масса (с соответствующим образом нормализованной временной координатой) равна М АдС = м / К . Можно быть уверенным в расчете AdS благодаря голографическому соответствию.
В частности, можно было бы заключить, что масса C-метрики обращается в нуль. Это озадачивает с точки зрения отсутствия плавного перехода к неускоряющейся черной дыре. Это также противоречит интуиции, полученной от медленно ускоряющейся черной дыры в AdS, для которой масса (с соответствующим образом нормализованной временной координатой) равна М АдС = м / К . Можно быть уверенным в расчете AdS благодаря голографическому соответствию.
 (3.6)
(3.6) Мы также наблюдаем явное сходство с голографически рассчитанной массой медленно ускоряющейся черной дыры в AdS [27].
Мы также наблюдаем явное сходство с голографически рассчитанной массой медленно ускоряющейся черной дыры в AdS [27]. 3.2. Первый закон термодинамики
 (3.13)
(3.13) =12N∑i=12[k+12]-1∑j=2[k+12]2N(-1)i+j+k+14Kzkδ(zj-zi)zj-zi +On4K∑k=12N∑i =12[k+12]-1(-1)i+kzkδ(zn-zi)zn-zi (3.17)
=12N∑i=12[k+12]-1∑j=2[k+12]2N(-1)i+j+k+14Kzkδ(zj-zi)zj-zi +On4K∑k=12N∑i =12[k+12]-1(-1)i+kzkδ(zn-zi)zn-zi (3.17) (3,19)
(3,19) (3.22)
(3.22) 4. Изучение пространства-времени с несколькими черными дырами

4.1. Неускоряющиеся массивы
4.1.1. Шварцшильда со струной
4.1.2. Две черные дыры
 Это значение K означает, что струны не уходят в бесконечность, а вместо этого черные дыры удерживаются на расстоянии распоркой с отрицательным натяжением. Тем не менее, для больших K ,
Это значение K означает, что струны не уходят в бесконечность, а вместо этого черные дыры удерживаются на расстоянии распоркой с отрицательным натяжением. Тем не менее, для больших K , 4.1.3. Three Black Holes
 рис. 3). Мы заинтересованы в изучении того, как расположение источников влияет на энтропию и напряжение и как возмущение одной черной дыры влияет на другие. Следовательно, мы рассматриваем установку, в которой две внешние черные дыры имеют одинаковую массу и расстояние от средней черной дыры, центр которой находится вокруг начала координат: z 6 − z 5 = z 2 − z 1 = 2 m 0 , and z 6 = − z 1 = z 0 , z 4 = − z 3 = м . Тогда энтропии и напряжения примут вид: z0-m0+m)2µ0=14(1-1K)µ1=14(1-z02(z02-(m0-m)2)(z02-m02)(z02-(m0+m)2)K)=µ2 . (4.3)
рис. 3). Мы заинтересованы в изучении того, как расположение источников влияет на энтропию и напряжение и как возмущение одной черной дыры влияет на другие. Следовательно, мы рассматриваем установку, в которой две внешние черные дыры имеют одинаковую массу и расстояние от средней черной дыры, центр которой находится вокруг начала координат: z 6 − z 5 = z 2 − z 1 = 2 m 0 , and z 6 = − z 1 = z 0 , z 4 = − z 3 = м . Тогда энтропии и напряжения примут вид: z0-m0+m)2µ0=14(1-1K)µ1=14(1-z02(z02-(m0-m)2)(z02-m02)(z02-(m0+m)2)K)=µ2 . (4.3)
 Справа расстояние равно z 0 = 10, а масса внешней черной дыры изменяется от нуля до 8,8, что очень близко к пределу максимального напряжения слияния, μ 0 ~ 0,244.
Справа расстояние равно z 0 = 10, а масса внешней черной дыры изменяется от нуля до 8,8, что очень близко к пределу максимального напряжения слияния, μ 0 ~ 0,244. =K14(K0+K1)=K0δµ0. (4.6)
=K14(K0+K1)=K0δµ0. (4.6) По сути, это говорит о том, что внутренняя черная дыра имеет более высокую энтропию в единицах своей массы (в квадрате), чем внешние. Мы понимаем это по влиянию конического дефицита: энтропия в целом уменьшается при наличии конического дефицита, поскольку часть горизонта «вырезается», оставляя форму мяча для регби, а не футбольного мяча. Можно было бы ожидать, что энтропия средней черной дыры будет относительно выше, поскольку дефицит, протекающий через эту черную дыру, меньше, чем дефицит, исходящий от внешних полюсов внешних черных дыр.
По сути, это говорит о том, что внутренняя черная дыра имеет более высокую энтропию в единицах своей массы (в квадрате), чем внешние. Мы понимаем это по влиянию конического дефицита: энтропия в целом уменьшается при наличии конического дефицита, поскольку часть горизонта «вырезается», оставляя форму мяча для регби, а не футбольного мяча. Можно было бы ожидать, что энтропия средней черной дыры будет относительно выше, поскольку дефицит, протекающий через эту черную дыру, меньше, чем дефицит, исходящий от внешних полюсов внешних черных дыр. рис. 5).
рис. 5). Вместо этого мы выбираем максимальную массу m max и устанавливаем K так, чтобы при максимальной массе не было дефицита между черными дырами:
Вместо этого мы выбираем максимальную массу m max и устанавливаем K так, чтобы при максимальной массе не было дефицита между черными дырами: Масса центральной черной дыры зафиксирована на уровне 1, а внешние черные дыры имеют такую же массу 9.1348 м 0 .
Масса центральной черной дыры зафиксирована на уровне 1, а внешние черные дыры имеют такую же массу 9.1348 м 0 . Внешние черные дыры расположены очень близко (в радиусе Шварцшильда) от центральной черной дыры, поэтому геометрия там сильно искажена.
Внешние черные дыры расположены очень близко (в радиусе Шварцшильда) от центральной черной дыры, поэтому геометрия там сильно искажена.
4.2. Accelerating Arrays
Теперь давайте рассмотрим ускоряющие массивы черных дыр типа, изображенного на рисунке 2. Основное отличие от неускоряющего массива состоит в том, что мы выбрали параметр K для представления напряжения окружающей среды, так что асимптотическое напряжение в принципе зависит от расположения концов стержней. Выражения для энтропии, температуры, напряжения и термодинамической длины легко выводятся из (3.1) и (3.2), хотя и не особенно информативны. Однако мы можем интуитивно понять общее поведение, изменяя массы и положения черных дыр.
Во-первых, обратите внимание, что μ 0 > μ N . Мы ожидаем этого, потому что, поскольку черные дыры ускоряются, должен существовать дисбаланс между натяжением струны, идущей из бесконечности, и натяжением струны, выходящей за горизонт ускорения. Затем, когда мы увеличим массу первой черной дыры m 1 , первое натяжение μ 1 упадет, так как больше силы натяжения струны будет использоваться для ускорения увеличенной массы. Будет ли последующее натяжение струн увеличиваться или уменьшаться, зависит от масс отдельных черных дыр: вторая черная дыра будет притягиваться к первой (и третьей, если она есть), что обеспечивает дополнительную силу притяжения сверх силы космической струны. Как правило, если черные дыры хорошо разделены относительно их размера, натяжение струн будет каскадно уменьшаться по величине по мере движения вдоль массива, но для больших черных дыр это не обязательно (см. Случай с двумя черными дырами ниже). .
Затем, когда мы увеличим массу первой черной дыры m 1 , первое натяжение μ 1 упадет, так как больше силы натяжения струны будет использоваться для ускорения увеличенной массы. Будет ли последующее натяжение струн увеличиваться или уменьшаться, зависит от масс отдельных черных дыр: вторая черная дыра будет притягиваться к первой (и третьей, если она есть), что обеспечивает дополнительную силу притяжения сверх силы космической струны. Как правило, если черные дыры хорошо разделены относительно их размера, натяжение струн будет каскадно уменьшаться по величине по мере движения вдоль массива, но для больших черных дыр это не обязательно (см. Случай с двумя черными дырами ниже). .
4.2.1. C-метрика
Стоит кратко проверить результаты C-метрики, впервые предложенные в [28] (см. также [45]). C-метрика имеет один горизонт и SILM, поэтому мы имеем n = 3 и N = 1. Метрика в форме Вейля равна
dz2] -r2ℓγx2x1x3dϕ2k2, (4. 10)
10)
, где z 0 = ( z 1 + z 2 )/2-это Центр Black Hape Shod, и Black Hare Shide1348 В 3 = ( z 3 − z 1 )/( z 2 − z). Здесь ℓ γ = 2( z 3 − z 0 ) показано как величина, обратная ускорению маленькой черной дыры в Приложении A, где мы также отмечаем преобразование между этой метрикой и более привычные сферические координаты.
Обращаясь к термодинамике, мы вычисляем z c как
zc=z3-(z3-z2)(z3-z1)(z3-z0)=(z3z0-z1z2)(z3-z0). (4.11)
При этом энтропийная и термодинамическая длины равны m(z3-z1)(z3-z2)→m(1+2мА)(1-2мА)λ1=eν1(z2-zc)=m(z3-z2)(z3-z1)→m(1-2мА) (1+2мА) (4.12)
в соответствии с параметрами, предложенными в [28].
Также несложно записать формулу типа Христодулу-Руффини [35] для C-метрики. Следуя [41], определим величину ∆, характеризующую среднее напряжение, выходящее из горизонта черной дыры, и величину C , характеризующий перепад напряжения:
Следуя [41], определим величину ∆, характеризующую среднее напряжение, выходящее из горизонта черной дыры, и величину C , характеризующий перепад напряжения:
Δ=1-2(μ0+μ1)=1K, C=μ0-μ1Δ=z2-z14ℓγ→мА. (4.13)
Тогда получается, что
M2=∆S4π(1-4C2). (4.14)
Увеличение ускорения черной дыры при сохранении постоянного дефицита окружающей среды приводит к удалению энергии из черной дыры. Этот результат не так тревожен, как может показаться на первый взгляд, поскольку энергия может быть потеряна как через горизонт ускорения, так и в виде гравитационного излучения в будущей бесконечности [46].
Электромагнитный заряд Q и вращательный заряд J напрямую вписываются в вышеприведенную историю. По аналогии с асимптотически AdS случаем [41] следует ожидать, что формула Христодулу-Руффини примет вид
M2=∆S4π[(1+πQ2∆S)2+(2πJ∆S)2-4C2]. (4.15)
Из заряженной, вращающейся (асимптотически плоской) C-метрики, записанной в координатах типа Бойера-Линдквиста, можно явно вычислить сохраняющиеся заряды, используя интегралы типа Комара. Это было сделано в [28]. Тогда оказывается, что (4.15) выполняется, только если временной вектор Киллинга нормализован, как это было в [28] (где выбор нормализации был сделан, чтобы обеспечить выполнение первого закона и соотношений Смарра). Поскольку величины Q , J , S , Δ и C не зависят от выбора нормировки, можно интерпретировать (4.15) как свидетельство того, что масса, предложенная в [28], является правильной.
Это было сделано в [28]. Тогда оказывается, что (4.15) выполняется, только если временной вектор Киллинга нормализован, как это было в [28] (где выбор нормализации был сделан, чтобы обеспечить выполнение первого закона и соотношений Смарра). Поскольку величины Q , J , S , Δ и C не зависят от выбора нормировки, можно интерпретировать (4.15) как свидетельство того, что масса, предложенная в [28], является правильной.
4.2.2. Две ускоряющиеся черные дыры
В качестве менее тривиального примера приведем результаты для системы двух ускоряющихся черных дыр, впервые исследованной в [36]. Имеем
ℓγ=2z5 -(z42-z32+z22-z12)z5-(z4-z3+z2-z1)(z1z3+z2z4)(z4-z3+z2-z1)z5+z1z3-z2z4 ~2( z5-zcom)+O(z5-1), (4.16)
где zcom=z42-z32+z22-z122(z4-z3+z2-z1) — центр масс пары черных дыр (эта формула обобщается на любое количество ускоряющихся черных дыр).
Размещение двух черных дыр на ± z b зафиксирует калибр, и мы сможем увидеть, как натяжение струны и энтропия черной дыры реагируют на изменения массы черной дыры и расстояния до горизонта (без ограничения общности мы можем оставить z b фиксированными в качестве выбора масштаба). Написание
Написание
S0=(m1+m2)(m1+m2+2zb)(m1m2-zb2+z52)2(z5+zb+m1)(z5-zb-m2)(z5(m2+m1)+zb(m2- m1)), (4.17)
энтропии равны
S1=4πm12KS0(2zb+m1-m2)(z5+zb-m1),S2=4πm22KS0(2zb+m2-m1)(z5-zb+m2). (4.18)
Мы можем быстро увидеть, что если m 1 = m 2 , энтропия первой черной дыры всегда будет меньше энтропии второй, что можно было бы ожидать как средний дефицит через первую черную дыру больше, чем через вторую. Однако, нормируя энтропии относительно их эталона SK=4πmI2/K, мы можем видеть, что мультипликативные множители в (4.18) показывают, что оба первоначально уменьшаются как m 2 increases from zero before turning, although S 2 / S K shows a sharper decrease and eventually drops below S 1 / S K . Опять же, такое поведение легко увидеть из соотношений в (4. 18). На рис. 7 показано это поведение при изменении м I .
18). На рис. 7 показано это поведение при изменении м I .
Рисунок 7 . Изменение энтропии и термодинамических длин в зависимости от массы в двух ускоряющихся черных дырах. Выходное напряжение фиксируется на уровне μ 0 = 1/8, а смещение каждого стержня от начала координат на z b = 5. Одна масса зафиксирована на единице, а другая масса изменяется от нуля до 4. Верхние графики показывают как изменяются энтропии, нормированные на 4πmI2/K, а нижний график показывает термодинамическую длину. Обратите внимание, что K изменяется так же, как m I , чтобы сохранить μ 0 фиксированным.
Чтобы сравнить влияние изменения массы черных дыр и их разделения, мы сначала фиксируем исходящее напряжение на уровне z → −∞, так что мы сравниваем одну и ту же коническую асимптотику. На рис. 7 показано влияние изменения массы внутренней и внешней черной дыры соответственно на энтропию и термодинамическую длину. В каждом случае мы фиксируем одну из масс на единицу и варьируем другую. В обоих случаях изменение массы черной дыры ближе к горизонту ускорения ( м 2 ) вызывает «перекрестное» поведение.
В каждом случае мы фиксируем одну из масс на единицу и варьируем другую. В обоих случаях изменение массы черной дыры ближе к горизонту ускорения ( м 2 ) вызывает «перекрестное» поведение.
На рис. 8 показано, как на энтропию, длину (и натяжение) влияет раздвигание черных дыр. Как и раньше, исходящее напряжение фиксируется на уровне 1/8, а массы обеих черных дыр фиксируются на уровне м 1 = м 2 = 1; горизонт ускорения находится на z 5 = 12. Нормированная энтропия черной дыры ближе к горизонту ускорения увеличивается по мере того, как черные дыры раздвигаются, тогда как энтропия другой черной дыры резко уменьшается. Мы можем получить приблизительное представление об этом, взглянув на натяжение струн; напряжение между второй черной дырой и горизонтом ускорения резко падает при большом расстоянии, а это означает, что дефицит отсекает меньшую часть углового направления, что увеличивает энтропию. Напряжение между черными дырами, мк 1 , напротив, увеличивается, что приводит к ожиданию уменьшения первой энтропии. Хотя эти утверждения в целом верны, обратите внимание, что мы уже нормализовали фактор K из энтропии, указывая на то, что эффект этой геометрии усиливается. Как и ожидалось, термодинамические длины демонстрируют масштабирование с увеличением расстояния, при этом промежуточная длина λ 1 отрицательна и уменьшается, чтобы компенсировать увеличение λ 0 .
Хотя эти утверждения в целом верны, обратите внимание, что мы уже нормализовали фактор K из энтропии, указывая на то, что эффект этой геометрии усиливается. Как и ожидалось, термодинамические длины демонстрируют масштабирование с увеличением расстояния, при этом промежуточная длина λ 1 отрицательна и уменьшается, чтобы компенсировать увеличение λ 0 .
Рисунок 8 . Изменение термодинамических параметров для двойной ускоряющейся черной дыры, где две черные дыры имеют одинаковую массу m 1 = m 2 = 1 и расстояние между ними 2 z b разнообразен. Горизонт ускорения зафиксирован на z 5 = 12.
5. Выводы
Подводя итог: мы доказали первый закон термодинамики для составной системы черных дыр, как ускоряющихся, так и изолированных. Мы допустили изменение натяжения космических струн вдоль оси, необходимое для поддержания равновесной конфигурации. Как и в ранее разработанной термодинамике ускоряющейся черной дыры AdS, эти струны имеют соответствующий потенциал, термодинамическую длину, которая имеет прямую спецификацию в терминах координаты Вейля, параметризующей ось симметрии массива черных дыр.
Как и в ранее разработанной термодинамике ускоряющейся черной дыры AdS, эти струны имеют соответствующий потенциал, термодинамическую длину, которая имеет прямую спецификацию в терминах координаты Вейля, параметризующей ось симметрии массива черных дыр.
Мы представили ряд ускоряющихся и неускоряющихся систем черных дыр, чтобы проиллюстрировать различные аспекты термодинамических параметров. Суть в том, что черные дыры образуют полностью сложную термодинамическую систему — изменение одной черной дыры влияет на все остальные. Мы также видим, как напряжения и длины в составной системе сливаются таким образом, что общая картина становится интуитивно понятной, в то время как вклад отдельных черных дыр может быть менее прозрачен.
Наши выводы о том, что термодинамические длины между компактными горизонтами связаны с правильным расстоянием вдоль оси, согласуются с предыдущими результатами [32, 33]. Однако в нашей конструкции есть также полубесконечные струны, для которых это собственное расстояние было бы бесконечным, но это не то, чего мы ожидали бы с точки зрения термодинамики. Термодинамическая длина представляет собой вклад в энтальпию от натяжения (отрицательного давления) космической струны внутри черной дыры, поэтому она должна быть конечной. Мы учитываем это с помощью процесса перенормировки, z c , аналогично перенормировке метрических коэффициентов.
Термодинамическая длина представляет собой вклад в энтальпию от натяжения (отрицательного давления) космической струны внутри черной дыры, поэтому она должна быть конечной. Мы учитываем это с помощью процесса перенормировки, z c , аналогично перенормировке метрических коэффициентов.
На самом деле, результат для λ, полученный в [32], может быть понят в терминах формализма ковариантного фазового пространства [47], так же как энтропия и температура черной дыры интерпретировались Вальдом [48] и Айером и Вальдом. [49]. В этой конструкции идея состоит в том, что на оболочке вариации действия состоят исключительно из граничных данных. Приняв эту вариацию за действие некоторого векторного поля Киллинга, соответствующего переносу времени, можно найти величину, которая обращается в нуль при интегрировании по срезу Коши. Взяв вариацию этой величины и разбив интеграл на граничные части по закону Гаусса, можно получить Первый закон. Вклад от бесконечности дает изменение массы, а вклад на горизонте дает TδS . При наличии струн необходимо также учитывать вклад новой поверхности: «трубки», в которую заключена струна 4 . Именно этот вклад дает λ δμ . С этой точки зрения термодинамические длины, рассчитанные в [27, 28] для AdS C-метрики, можно рассматривать как перенормированные мировые объемы (в единицу времени) бесконечных струн собственной длины. Смысл перенормировки внешних струн в асимптотически плоском случае менее ясен и его было бы интересно понять.
При наличии струн необходимо также учитывать вклад новой поверхности: «трубки», в которую заключена струна 4 . Именно этот вклад дает λ δμ . С этой точки зрения термодинамические длины, рассчитанные в [27, 28] для AdS C-метрики, можно рассматривать как перенормированные мировые объемы (в единицу времени) бесконечных струн собственной длины. Смысл перенормировки внешних струн в асимптотически плоском случае менее ясен и его было бы интересно понять.
Остаются открытыми вопросы относительно учета электрического заряда. Явные решения теории Эйнштейна-Максвелла, описывающие две электрически заряженные черные дыры, соединенные конической сингулярностью без внешних струн, известны и исследованы термодинамически [32, 33]. Следовательно, можно действовать, как в разделе 3, добавляя к системе внешние полубесконечные струны и определяя необходимые модификации полученных термодинамических длин. Однако, поскольку зарядка черных дыр разрушает свойство линейности, присутствующее в (2. 3), в настоящее время неизвестно, как построить массивы, содержащие произвольное число заряженных объектов.
3), в настоящее время неизвестно, как построить массивы, содержащие произвольное число заряженных объектов.
Хотя система многих черных дыр нестабильна, тем не менее интересно, что она также проявляет ощутимые термодинамические свойства, что еще раз подтверждает включение космических струн в термодинамическую картину.
Заявление о доступности данных
Первоначальные материалы, представленные в исследовании, включены в статью/дополнительный материал, дальнейшие запросы можно направлять соответствующему автору/авторам.
Вклад авторов
Все перечисленные авторы внесли существенный, непосредственный и интеллектуальный вклад в работу и одобрили ее для публикации.
Финансирование
Эта работа была частично поддержана STFC (консолидированный грант ST/P000371/1—RG, DTG—AS) и Институтом теоретической физики «Периметр» (RG). Исследования в Институте периметра поддерживаются правительством Канады через Министерство инноваций, науки и экономического развития Канады и провинцией Онтарио через Министерство исследований, инноваций и науки.
Конфликт интересов
Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов. 9Подобные идеи были применены к термодинамическим исследованиям черных дыр, обладающих струнами Мизнера [50, 51].
Ссылки
1. Бекенштейн Д.Д. Черные дыры и энтропия. Phys Rev D . (1973) 7:2333. doi: 10.1103/PhysRevD.7.2333
CrossRef Full Text
2. Bekenstein JD. Обобщенный второй закон термодинамики в физике черных дыр. Phys Rev D . (1974) 9:3292. doi: 10.1103/PhysRevD.9.3292
CrossRef Full Text
3. Хокинг С.В. Создание частиц черными дырами. Коммунальная математика, физика . (1975) 43:199–220. doi: 10.1007/BF02345020
Полный текст CrossRef | Google Scholar
4. Гиббонс Г.В., Хокинг С.В. Интегралы действия и статистические суммы в квантовой гравитации. Phys Rev D . (1977) 15:2752. doi: 10.1103/PhysRevD.15.2752
doi: 10.1103/PhysRevD.15.2752
CrossRef Full Text
5. Bardeen JM, Carter B, Hawking SW. Четыре закона механики черных дыр. Коммуна Математика Физика . (1973) 31:161–70. doi: 10.1007/BF01645742
Полный текст CrossRef | Google Scholar
6. Тейтельбойм К. Космологическая постоянная как термодинамический параметр черной дыры. Физика . (1985) 159B: 293–7. doi: 10.1016/0370-2693(85)
-4CrossRef Full Text | Google Scholar
7. Кастор Д., Рэй С., Трашен Дж. Энтальпия и механика черных дыр AdS. Класс Квант Грав . (2009) 26:195011. дои: 10.1088/0264-9381/26/19/195011
Полнотекстовая перекрестная ссылка | Google Scholar
8. Долан Б.П. Космологическая постоянная и уравнение состояния черной дыры. Класс Квант Грав . (2011) 28:125020. doi: 10.1088/0264-9381/28/12/125020
CrossRef Full Text | Google Scholar
9. Долан Б.П. Давление и объем в первом законе термодинамики черной дыры. Класс Квант Грав . (2001) 28:235017. doi: 10.1088/0264-9381/28/23/235017
(2001) 28:235017. doi: 10.1088/0264-9381/28/23/235017
CrossRef Full Text | Академия Google
10. Кубизняк Д., Манн Р.Б. P-V критичность заряженных черных дыр AdS. JHEP . (2012) 1207:033. doi: 10.1007/JHEP07(2012)033
Полный текст CrossRef | Google Scholar
11. Кубизняк Д., Манн Р.Б., Тео М. Химия черных дыр: термодинамика с лямбда. Класс Квант Грав . (2017) 34:063001. doi: 10.1088/1361-6382/aa5c69
Полный текст CrossRef | Google Scholar
12. Исраэль В., Хан К.А. Коллинеарные частицы и бонди-диполи в общей теории относительности. Нуово Сим . (1964) 33:331–44. doi: 10.1007/BF02750196
Полный текст CrossRef | Google Scholar
13. Арьял М., Форд Л., Виленкин А. Космические струны и черные дыры. Phys Rev D . (1986) 34:2263. doi: 10.1103/PhysRevD.34.2263
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
14. Ачукарро А., Грегори Р., Куйкен К. Волосы Хиггса Абеляна для черных дыр. Phys Rev D . (1995) 52:5729–42. doi: 10.1103/PhysRevD.52.5729
Phys Rev D . (1995) 52:5729–42. doi: 10.1103/PhysRevD.52.5729
Реферат PubMed | Полный текст перекрестной ссылки | Google Scholar
15. Грегори Р., Кубизняк Д., Уиллс Д. Вращающиеся волосы черной дыры. JHEP . (2013) 6:023. doi: 10.1007/JHEP06(2013)023
Полный текст CrossRef | Google Scholar
16. Кинерсли В., Уокер М. Равномерно ускоряющаяся заряженная масса в общей теории относительности. Phys Rev D . (1970) 2:1359. doi: 10.1103/PhysRevD.2.1359
Полный текст CrossRef | Google Scholar
17. Плебански Дж. Ф., Демьянски М. Вращающаяся, заряженная и равномерно ускоряющаяся масса в общей теории относительности. Энн Физ . (1976) 98:98–127. doi: 10.1016/0003-4916(76)-2
CrossRef Full Text | Google Scholar
18. Грегори Р., Хиндмарш М. Гладкие метрики для привязки строк. Phys Rev D . (1995) 52:5598–605. doi: 10.1103/PhysRevD.52.5598
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
19. Мартинес Э.А., Йорк Дж.В. мл. Термодинамика черных дыр и космических струн. Phys Rev D . (1990) 42:3580–3. doi: 10.1103/PhysRevD.42.3580
Мартинес Э.А., Йорк Дж.В. мл. Термодинамика черных дыр и космических струн. Phys Rev D . (1990) 42:3580–3. doi: 10.1103/PhysRevD.42.3580
Реферат PubMed | Полный текст перекрестной ссылки | Google Scholar
20. Коста М.С., Перри М.Дж. Взаимодействующие черные дыры. Нукл Физ В . (2000) 591:469–87. doi: 10.1016/S0550-3213(00)00577-0
Полный текст CrossRef | Google Scholar
21. Датта К., Рэй С., Трашен Дж. Увеличение массы и механика ускоренных черных дыр. Класс Квант Грав . (2006) 23:335–52. doi: 10.1088/0264-9381/23/2/005
CrossRef Full Text | Академия Google
22. Herdeiro C, Kleihaus B, Kunz J, Radu E. О законе площадей Бекенштейна-Хокинга для черных объектов с коническими особенностями. Phys Rev D . (2010) 81:064013. doi: 10.1103/PhysRevD.81.064013
Полный текст CrossRef | Google Scholar
23. Бонжур Ф., Эмпаран Р., Грегори Р. Вихри и экстремальные черные дыры: вопрос о выбросе потока. Phys Rev D . (1999) 59:084022. doi: 10.1103/PhysRevD.59.084022
(1999) 59:084022. doi: 10.1103/PhysRevD.59.084022
Полный текст CrossRef | Академия Google
24. Пападимитриу И., Скендерис К. Термодинамика асимптотически локально AdS-пространств-времен. JHEP . (2005) 8:4. doi: 10.1088/1126-6708/2005/08/004
CrossRef Full Text
25. Appels M, Gregory R, Kubizňák D. Термодинамика ускоряющихся черных дыр. Phys Rev Letter . (2016) 117:131303. doi: 10.1103/PhysRevLett.117.131303
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
26. Аппельс М., Грегори Р., Кубизняк Д. Термодинамика черных дыр с коническими дефектами. JHEP . (2017) 1705:116. doi: 10.1007/JHEP05(2017)116
Полный текст CrossRef | Google Scholar
27. Анабалон А., Аппельс М., Грегори Р., Кубизняк Д., Манн Р.Б., Овгюн А. Голографическая термодинамика ускоряющихся черных дыр. Phys Rev D . (2018) 98:104038. doi: 10.1103/PhysRevD.98.104038
Полный текст CrossRef | Google Scholar
28. Анабалон А., Грей Ф., Грегори Р., Кубизняк Д., Манн Р.Б. Термодинамика заряженных, вращающихся и ускоряющихся черных дыр. JHEP . (2019) 4:096. doi: 10.1007/JHEP04(2019)096
Анабалон А., Грей Ф., Грегори Р., Кубизняк Д., Манн Р.Б. Термодинамика заряженных, вращающихся и ускоряющихся черных дыр. JHEP . (2019) 4:096. doi: 10.1007/JHEP04(2019)096
Полный текст CrossRef | Google Scholar
29. Трашен Дж. Х., Фокс Д. Возмущения напряженности пространства-времени черной браны. Класс Квант Грав . (2004) 21: 289–306. doi: 10.1088/0264-9381/21/1/021
CrossRef Full Text | Google Scholar
30. Harmark T, Obers NA. Общее определение гравитационного напряжения. JHEP . (2004) 405:043. doi: 10.1088/1126-6708/2004/05/043
CrossRef Full Text | Академия Google
31. Кастор Д., Трашен Дж. Угловое напряжение черных дыр. Phys Rev D . (2012) 86:081501. doi: 10.1103/PhysRevD.86.081501
Полный текст CrossRef | Google Scholar
32. Кртоуш П., Зельников А. Термодинамика двух черных дыр. JHEP . (2020) 02:164. doi: 10.1007/JHEP02(2020)164
Полный текст CrossRef | Google Scholar
33. Рамирес-Вальдес С.Дж., Гарсия-Компеан Х., Манко В.С. Термодинамика двух выровненных черных дыр Керра. Phys Rev D . (2020) 102:024084. doi: 10.1103/PhysRevD.102.024084
Рамирес-Вальдес С.Дж., Гарсия-Компеан Х., Манко В.С. Термодинамика двух выровненных черных дыр Керра. Phys Rev D . (2020) 102:024084. doi: 10.1103/PhysRevD.102.024084
Полный текст CrossRef | Google Scholar
34. Weyl H. Zur Теория гравитации. Энн Физ . (1917) 359: 117–45. doi: 10.1002/andp.1
Полный текст CrossRef | Google Scholar
35. Christodoulou D, Ruffini R. Обратимые преобразования заряженной черной дыры. Phys Rev D . (1971) 4:3552. doi: 10.1103/PhysRevD.4.3552
Полный текст CrossRef | Академия Google
36. Даукер Х.Ф., Тамбьяхпиллаи С.Н. Множество ускоряющихся черных дыр. Класс Квант Грав . (2003) 20:127–36. doi: 10.1088/0264-9381/20/1/310
CrossRef Full Text | Google Scholar
37. Мунгия С. Неравные бинарные конфигурации взаимодействующих черных дыр Керра. Phys Letter B . (2018) 786: 466–71. doi: 10.1016/j.physletb.2018.10.037
CrossRef Полный текст | Google Scholar
38. Манько В.С., Руиз Э. Метрика для двух произвольных источников Керра. Phys Lett B . (2019) 794: 36–40. doi: 10.1016/j.physletb.2019.05.027
Манько В.С., Руиз Э. Метрика для двух произвольных источников Керра. Phys Lett B . (2019) 794: 36–40. doi: 10.1016/j.physletb.2019.05.027
CrossRef Полный текст | Google Scholar
39. Манько В.С., Руиз Э., Манько О.В. Возможно ли равновесие выровненных керровских черных дыр? Phys Rev Letter . (2000) 85:5504. doi: 10.1103/PhysRevLett.85.5504
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
40. Эмпаран Р., Реалл Х.С. Обобщенные решения Вейля. Phys Rev D . (2002) 65:084025. doi: 10.1103/PhysRevD.65.084025
Полнотекстовая перекрестная ссылка | Google Scholar
41. Грегори Р., Скоинс А. Ускорение химии черных дыр. Phys Letter B . (2019) 796: 191–5. doi: 10.1016/j.physletb.2019.06.071
CrossRef Полный текст | Google Scholar
42. Арновитт Р., Дезер С., Миснер С. Динамическая структура и определение энергии в общей теории относительности. Физика, версия . (1959) 116:1322–30. doi: 10.1103/PhysRev.116.1322
doi: 10.1103/PhysRev.116.1322
Полный текст CrossRef | Google Scholar
43. Комар А. Положительно определенная плотность энергии и глобальные последствия для общей теории относительности. физ. версия . (1963) 129:1873-6. doi: 10.1103/PhysRev.129.1873
Полный текст CrossRef | Google Scholar
44. Гриффитс Дж. Б., Кртоуш П., Подольский Дж. Интерпретация C-метрики. Класс Квант Грав . (2006) 23:6745–66. doi: 10.1088/0264-9381/23/23/008
CrossRef Full Text | Google Scholar
45. Болл А., Миллер Н. Ускорение термодинамики черной дыры с помощью времени разгона. [arXiv:2008.03682 [hep-th]] .
Академия Google
46. Подольский Дж., Ортаджио М., Кртоус П. Излучение ускоренных черных дыр во Вселенной анти-де Ситтера. Phys Rev D . (2003) 68:124004. doi: 10.1103/PhysRevD.68.124004
Полный текст CrossRef | Google Scholar
47. Харлоу Д., Ву Дж. Ковариантное фазовое пространство с границами. JHEP . (2020) 10:146. doi: 10.1007/JHEP10(2020)146
(2020) 10:146. doi: 10.1007/JHEP10(2020)146
Полный текст CrossRef | Google Scholar
48. Вальд Р.М. Энтропия черной дыры — это заряд Нётер. Phys.Rev D . (1993) 48:R3427–31. doi: 10.1103/PhysRevD.48.R3427
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
49. Айер В., Уолд Р.М. Некоторые свойства нётеровского заряда и предположение о динамической энтропии чёрной дыры. Phys Rev D . (1994) 50:846–64. doi: 10.1103/PhysRevD.50.846
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
50. Бордо А.Б., Грей Ф., Хеннигар Р., Кубизняк Д. Гравитационные заряды Мизнера и переменная сила струн. Класс Квант Грав . (2019) 36:1
. doi: 10.1088/1361-6382/ab3d4d
Полный текст CrossRef | Google Scholar
51. Бордо А.Б., Грей Ф., Хеннигар Р., Кубизняк Д. Первый закон вращения NUT. Phys Letter B . (2019) 798:134972. doi: 10.1016/j.physletb.2019.134972
CrossRef Полный текст | Google Scholar
52. Хонг К., Тео Э. Новая форма метрики C. Класс Квант Грав . (2003) 20:3269. дои: 10.1088/0264-9381/20/14/321
Хонг К., Тео Э. Новая форма метрики C. Класс Квант Грав . (2003) 20:3269. дои: 10.1088/0264-9381/20/14/321
Полнотекстовая перекрестная ссылка | Google Scholar
Приложение A
Системы координат для C-метрики
Мы собираем формулы преобразования между стандартной C-метрикой (выраженной в форме Хонга-Тео [52]) и формой Вейля раздела 2. C- metric in Weyl form is
ds2=X1X3ℓγX2dt2-ℓγE12E234R1R2R3E13(V3+12)2[dr2+dz2] -r2ℓγX2X1X3dϕ2K2, (A1)
where ℓ γ = z 3 − z 0 = г 3 − ( z 1 + z 2 )/2 — это z -расстояние до центра стержня черной дыры.
Теперь пусть м = ( z 2 − z 1 )/2 и A = 1/л γ . Определить
r=r-sinθf(r-)g(θ)(1+Ar-cosθ)2,z-z0=r-(Ar-+cosθ)(1-m/r-+mAcosθ)(1+ Ar-cosθ)2, (A2)
, где
f(R)=(1-A2r-2)(1-2mr-), g(θ)=(1+2mAcosθ). (А3)
(А3)
Тогда метрика Вейля (4.1) переходит в C-метрику в координатах Хонга-Тео [52], а не в стандартных координатах Кинерсли-Уокера, рассмотренных в [36]:
ds2=1(1+Ar¯cosθ) 2[f¯(r¯)dt2−dr¯2f¯(r¯) −r¯2(dθ2g¯(θ)−g¯(θ)sin2θdϕ2)]. (A4)
Здесь мы видим прямую интерпретацию ℓ γ как масштаба длины ускорения; для малых m , A = 1/ℓ γ соответствует величине четырехкратного ускорения черной дыры [44].
цикл квантовой гравитации | Космический блог Стэна
Физика
СтенБлог
В своих предыдущих блогах я кратко описал, как человеческий мозг воспринимает и моделирует пространство (Ой, еще кое-что), как Эйнштейн и другие физики отвергают пространство как иллюзию (Относительность и пространство), как теория относительности имеет дело с концепцией пространства (Итак, что ТАКОЕ пространство?), как должна была бы выглядеть теория квантовой гравитации (Квантовая гравитация, о боже!), и попутно почему идея бесконечности физически не реальна (Реальна ли бесконечность?) и почему пространство не есть ничто (думая ни о чем). Я даже обсуждал, как важно «мыслить визуально» при попытке смоделировать вселенную, например «струны» и «петли», используемые физиками в качестве аналога пространства (мыслить визуально)
Я даже обсуждал, как важно «мыслить визуально» при попытке смоделировать вселенную, например «струны» и «петли», используемые физиками в качестве аналога пространства (мыслить визуально)
И все же эти блоги не исчерпывают ни самого представления о космосе, ни проводимых исследований, направленных на то, чтобы докопаться до сути нашего опыта с ним.
В этом эссе, основанном на докладе, который я сделал в Астрономическом обществе Бельмонта 5 октября 2017 года, я попытаюсь осветить некоторые из этих других идей и подходов, которые, по общему мнению, станут частью будущей теории квантовой гравитации.
Что такое квантовая гравитация?
Основная идея состоит в том, что две великие физические теории, квантовая механика и общая теория относительности, несовместимы друг с другом и на самом деле не имеют дело с одними и теми же составляющими мира: пространством (временем) и материей. Квантовая гравитация — это гипотетическая теория, которая объединяет эти две великие идеи в единый язык, раскрывая ответы на некоторые из самых глубоких вопросов, которые мы можем задать о физическом мире. Это действительно Святой Грааль физики.
Это действительно Святой Грааль физики.
Зачем вообще нужна квантовая гравитация?
Квантовая механика — это теория, описывающая материю и поля, встроенные в ранее существовавшее пространство-время, которая не оказывает физического воздействия на эти поля, кроме предоставления координат для описания их положения во времени и пространстве. Говорят, что это теория, зависящая от фона. Общая теория относительности — это только теория пространства (времени) и вообще не описывает сущность материи. Он описывает, как материя влияет на геометрию пространства-времени и как пространство-время влияет на движение материи, но делает это в чисто «классических» терминах. Самое главное, общая теория относительности говорит, что никакого ранее существовавшего пространства-времени вообще не существовало. Она называется фононезависимой теорией. Квантовая гравитация — всеобъемлющая независимая от фона теория, которая объясняет квантовую природу материи, а также квантовую природу пространства-времени в масштабах, где эти эффекты важны, называемых шкалой Планка, где наименьшая единица пространства составляет 10^-33 см, а наименьшая единица времени составляет 10^-43 секунды.
Нам нужна квантовая гравитация, потому что расчеты в квантовой механике страдают от «бесконечностей», возникающих из-за того, что КМ предполагает, что пространство (время) бесконечно делится на более мелкие единицы длины. Когда физические процессы и напряженности поля суммируются на все меньших и меньших длинах для построения предсказания, бесконечно малые единицы приводят к бесконечно большим вкладам, которые «взрывают» расчеты, если только не используется какой-либо математический метод, называемый «перенормировкой». Но гравитационное поле, описываемое общей теорией относительности, нельзя перенормировать, чтобы устранить его бесконечности. Только путем установления нижнего предела «отсечки» пространства (времени), как это делает квантовая гравитация, эта проблема устраняется, и все вычисления становятся конечными.
Нам нужна квантовая гравитация, потому что черные дыры не обладают бесконечной энтропией. Площадь поверхности черной дыры, называемая ее горизонтом событий, связана с ее энтропией, которая является мерой количества информации, содержащейся внутри горизонта. Один бит информации закодирован на горизонте как площадь, равная 2 планковским длинам в квадрате. В соответствии с голографическим принципом поверхность черной дыры, ее двумерная поверхность, кодирует всю информацию, находящуюся в охватываемом трехмерном объеме, так что это означает, что пространство-время внутри черной дыры должно быть квантовано и не может быть быть бесконечно делимой, иначе голографический принцип был бы недействителен, и горизонт черной дыры должен был бы кодировать бесконечное количество информации и иметь бесконечную энтропию.
Один бит информации закодирован на горизонте как площадь, равная 2 планковским длинам в квадрате. В соответствии с голографическим принципом поверхность черной дыры, ее двумерная поверхность, кодирует всю информацию, находящуюся в охватываемом трехмерном объеме, так что это означает, что пространство-время внутри черной дыры должно быть квантовано и не может быть быть бесконечно делимой, иначе голографический принцип был бы недействителен, и горизонт черной дыры должен был бы кодировать бесконечное количество информации и иметь бесконечную энтропию.
Нам также нужна квантовая гравитация, потому что считается, что любая фундаментальная теория нашего физического мира должна быть независимой от фона, как показывает общая теория относительности, что пространство-время. Это означает, что квантовая механика в настоящее время является неполной теорией, потому что она все еще требует каркаса из ранее существовавшего пространства-времени и не «создает» этот каркас изнутри себя, как это делает общая теория относительности.
Итак, какова общая картина?
Исторически Ньютон дал нам пространство и время как вечно абсолютные и фиксированные предпосылки нашего мира, которые были определены раз и навсегда еще до того, как мы начали описывать силы и движение. Вторая крупная школа мысли того времени была развита Готфридом Лейбницем. Он сказал, что время и пространство не имеют значения сами по себе, а только как свойства, определяемые отношениями между телами. Относительность Эйнштейна и ее экспериментальное подтверждение доказали, что абсолютное пространство и время Ньютона полностью ложны, и заменили их принципом относительности Лейбница. Эйнштейн даже неоднократно говорил, что пространство — это воображаемая конструкция, которую мы принимаем как должное почти мифическим образом. Пространство не имеет самостоятельного существования, кроме своего возникновения из отношений между физическими телами. Эта связь настолько тесна, что в общей теории относительности материальные тела определяют саму геометрию пространства-времени как динамическое решение его знаменитого релятивистского уравнения гравитации.
Как возникает ощущение космоса?
В общей теории относительности единственное, что имеет значение, — это события на мировой линии частицы, также называемые ее историей. Эти события кодируют отношения между телами и создаются пересечениями других мировых линий от других частиц. Эта сеть фундаментальных мировых линий содержит всю информацию, необходимую для описания глобальной геометрии этой сети событий и мировых линий. Только геометрия этих мировых линий имеет значение для физических явлений во Вселенной.
Голова в виде каркаса на этой иллюстрации является аналогом мирского, соединяющегося вместе для создания геометрии. Черная «пустота» не содержит геометрической или размерной информации, и любые точки в ней не взаимодействуют ни с одной мировой линией, составляющей сеть. Вот почему «пространство» — это миф, и единственное, что определяет структуру нашего 4-мерного пространства-времени, — это мирское.
Общая теория относительности описывает, как геометрия этих мировых линий создает четырехмерное пространство-время. Эти мировые линии представляют частицы материи, и общая теория относительности описывает, как эти частицы материи создают кривизну мировых линий среди всей системы частиц и тем самым создают пространство и время. «Пустые» математические точки между мировыми линиями не имеют физического смысла, потому что они не связаны с событиями ни на одной из физических мировых линий, поэтому Эйнштейн сказал, что фоновое пространство, в которое, кажется, встроены мировые линии, на самом деле не существует! Когда мы смотрим в «пространство», мы смотрим вдоль мировых линий световых лучей. Мы не смотрим через уже существующее пространство. Это означает, что мы не видим «вещи в пространстве», мы видим процессы во времени на протяжении истории частицы!
Эти мировые линии представляют частицы материи, и общая теория относительности описывает, как эти частицы материи создают кривизну мировых линий среди всей системы частиц и тем самым создают пространство и время. «Пустые» математические точки между мировыми линиями не имеют физического смысла, потому что они не связаны с событиями ни на одной из физических мировых линий, поэтому Эйнштейн сказал, что фоновое пространство, в которое, кажется, встроены мировые линии, на самом деле не существует! Когда мы смотрим в «пространство», мы смотрим вдоль мировых линий световых лучей. Мы не смотрим через уже существующее пространство. Это означает, что мы не видим «вещи в пространстве», мы видим процессы во времени на протяжении истории частицы!
Сегодня работают над двумя основными теориями квантовой гравитации.
Теория струн утверждает, что частицы — это одномерные петли «чего-то», которые определены в 10-мерном пространстве-времени, из которых 4 измерения — это Большие, которые мы видим вокруг себя. Остальные компактны и своей геометрической симметрией определяют свойства самих частиц. Это подход к квантовой гравитации, который имеет несколько проблем.
Остальные компактны и своей геометрической симметрией определяют свойства самих частиц. Это подход к квантовой гравитации, который имеет несколько проблем.
Эта фигура представляет собой воображаемое изображение «струны».
Сначала предполагается, что пространство-время уже существует для перемещения струн. Это теория, зависящая от фона, в том же духе, что и ньютоновская теория абсолютного пространства и времени. Во-вторых, теория струн — это всего лишь теория материи и ее квантовых свойств на планковских масштабах, но на самом деле масштаб струны зависит от одного параметра, называемого натяжением струны. Если натяжение невелико, то эти «петли» струны в тысячи раз больше масштаба Планка, и нет никаких ограничений на то, каким должно быть фактическое значение натяжения. Это регулируемый параметр.
Этот рисунок представляет собой творческое изображение «петли».
Петля Квантовая гравитация — это чисто теория пространства-времени, которая не рассматривает вопрос, охватываемый квантовой механикой. Это независимая от фона теория, способная точно вычислить ответы на многие проблемы теории гравитации, в отличие от теории струн, которая должна подкрадываться к ответам, суммируя бесконечное число альтернативных возможностей. LQG приходит к ответу «2.0» за один шаг как к точному ответу, в то время как, например, теория струн должна суммировать последовательность 1 + 1/2 + 1/4 + 1/8 + 1/16 +…. Чтобы добраться до 2.000.
Это независимая от фона теория, способная точно вычислить ответы на многие проблемы теории гравитации, в отличие от теории струн, которая должна подкрадываться к ответам, суммируя бесконечное число альтернативных возможностей. LQG приходит к ответу «2.0» за один шаг как к точному ответу, в то время как, например, теория струн должна суммировать последовательность 1 + 1/2 + 1/4 + 1/8 + 1/16 +…. Чтобы добраться до 2.000.
LQG работает с элементарными компонентами пространства-времени, называемыми узлами и ребрами, для создания вращающихся сетей и вращающейся пены. Подобно силовым линиям магнитного поля, которые переносят магнитный поток, эти ребра действуют как силовые линии в пространстве и несут квантованные площади, равные 1 планковской длине в квадрате. Суммируя количество узлов в области спиновой сети, каждый узел несет квантовую единицу пространственного объема. Эти узлы связаны друг с другом сетью пересекающихся линий, называемой спиновой сетью, которая для очень больших сетей начинает выглядеть как снимок пространства, увиденный в определенный момент. Преобразование одной сети в другую называется спиновой пеной и является предшественником четырехмерного пространства-времени. В самих узлах и ребрах нет физического смысла, так же как нет физического смысла в одномерных петлях, составляющих строки в теории струн. . Это чисто математические конструкции.
Преобразование одной сети в другую называется спиновой пеной и является предшественником четырехмерного пространства-времени. В самих узлах и ребрах нет физического смысла, так же как нет физического смысла в одномерных петлях, составляющих строки в теории струн. . Это чисто математические конструкции.
На данный момент лучшая идея состоит в том, что LQG формирует основу для теории струн. Теория струн рассматривает пространство-время и материю гораздо выше планковского масштаба, и именно здесь проявляются свойства частиц материи. LQG создает фон пространства-времени, через который движутся струны. Однако есть большая проблема. LQG предсказывает, что космологическая постоянная должна быть отрицательной и малой, что и наблюдается астрономически, в то время как теория струн утверждает, что космологическая постоянная велика и положительна. Кроме того, хотя LQG может реконструировать большое 4-мерное пространство-время, в котором мы живем, похоже, в нем нет места для дополнительных 6 измерений, требуемых теорией струн для создания свойств наблюдаемых нами частиц. Одна из возможностей заключается в том, что эти дополнительные измерения вовсе не похожи на пространство, а просто являются инструментами «бухгалтерского учета», которыми должны пользоваться физики и которые в конечном итоге в будущем будут заменены полностью четырехмерной теорией струн.
Одна из возможностей заключается в том, что эти дополнительные измерения вовсе не похожи на пространство, а просто являются инструментами «бухгалтерского учета», которыми должны пользоваться физики и которые в конечном итоге в будущем будут заменены полностью четырехмерной теорией струн.
Другим подходом, все еще находящимся в зачаточном состоянии, является теория причинных множеств. Как и LQG, это независимая от фона теория пространства-времени. Он начинается с набора точек, которые связаны друг с другом только одним руководящим принципом, что пары точек упорядочены причинно-следственными связями. Это определяет, как эти точки упорядочены во времени, но это единственный организующий принцип для точек в наборе. Исследователи обнаружили, что такие наборы создают из себя физические концепции расстояния и времени и ведут к релятивистскому пространству-времени. Каузальные множества и узлы в спиновых сетях LQG могут быть связаны друг с другом.
Другое захватывающее открытие, связанное с тем, как элементы квантового пространства-времени создают пространство-время, связано с голографическим принципом, связанным с квантовой запутанностью.
Голографический принцип утверждает, что вся информация и отношения, обнаруженные в трехмерном объеме, «закодированы» на двумерном поверхностном экране, который окружает этот объем. Это означает, что отношения между поверхностными элементами отражаются на поведении внутренней физики. Недавно было обнаружено, что если вы используете квантовую запутанность для соединения двух точек на поверхности, соответствующие точки внутри становятся связанными вместе как физическое целое. Если вы отключите запутанность на поверхности, внутренние точки станут несвязанными, а внутреннее пространство растворится в несвязанных точках. Величина запутанности может быть напрямую связана с тем, насколько физически близки точки, и вот как единая геометрия пространства-времени внутри трехмерного «объема» может возникнуть из несвязанных точек, связанных друг с другом квантовой запутанностью.
Дополнительная литература:
Изучение квантового пространства [Моя книга на Amazon. com]
com]
Квантовая запутанность и квантовое пространство-время [Марк Рамсдонк]
Принцип независимости от фона [Ли Смолин] 900
Причинные множества: самоорганизующаяся вселенная [Scientific American]
Черная дырапетля квантовая гравитацияквантовая гравитацияотносительностькосмостеория струн
Астрономия, Физика
Стенблог
За пределами Большого взрыва
Написано Стеном Оденвальдом Copyright (C) 1987, Kalmbach Publishing. Перепечатано с разрешения
Где-то между 15 и 20 миллиардами лет назад возникла Вселенная. С самого начала человеческого сознания мы пытались понять, как и почему произошло это событие, и в результате этих усилий возникло множество идей. Древняя египетская легенда описывает, как Осирис Хепера создал вселенную из темного, безбрежного океана под названием Ню, и что Осирис Хепера создал себя из этого океана, произнеся свое собственное имя. Человеческая изобретательность не остановилась за 5000 лет, прошедшие с тех пор, как эти идеи были популярны. Современная теория Большого взрыва утверждает, что наша Вселенная возникла из более ранней фазы, в миллиарды раз более горячей, чем ядро нашего Солнца, и в триллионы раз более плотной, чем ядро атома. Чтобы подробно описать такие экстремальные физические условия, мы должны сначала иметь четкое представление о природе материи и фундаментальных сил. При высоких температурах, которые, вероятно, сопровождали Большой взрыв, все известные нам формы материи превратились в их основные составляющие. Силы гравитации и электромагнетизма вместе с сильными и слабыми ядерными взаимодействиями были основными средствами, с помощью которых взаимодействовали элементарные частицы материи.
Человеческая изобретательность не остановилась за 5000 лет, прошедшие с тех пор, как эти идеи были популярны. Современная теория Большого взрыва утверждает, что наша Вселенная возникла из более ранней фазы, в миллиарды раз более горячей, чем ядро нашего Солнца, и в триллионы раз более плотной, чем ядро атома. Чтобы подробно описать такие экстремальные физические условия, мы должны сначала иметь четкое представление о природе материи и фундаментальных сил. При высоких температурах, которые, вероятно, сопровождали Большой взрыв, все известные нам формы материи превратились в их основные составляющие. Силы гравитации и электромагнетизма вместе с сильными и слабыми ядерными взаимодействиями были основными средствами, с помощью которых взаимодействовали элементарные частицы материи.
Нигде обратная связь между космологией и физикой элементарных частиц не видна так ясно, как в изучении ранней истории Вселенной. В октябре 1985 года на гигантском ускорителе в Фермилабе впервые произошло столкновение протонов и антипротонов при энергиях 1,6 триллиона электрон-вольт, что примерно в 1600 раз превышает массу покоя протона. Это было уникальное событие, потому что на одну долю секунды на крошечной планете в ничем не примечательной галактике впервые за по крайней мере 15 миллиардов лет открылось маленькое окно в Событие Сотворения.
Это было уникальное событие, потому что на одну долю секунды на крошечной планете в ничем не примечательной галактике впервые за по крайней мере 15 миллиардов лет открылось маленькое окно в Событие Сотворения.
ГРАНИЦЫ ДОСТОВЕРНОСТИ
Стремление физиков к единой, всеобъемлющей теории, способной описать четыре силы природы, в качестве побочного продукта привело к некоторым неожиданным проблескам События Сотворения. Хотя до завершения такой теории, возможно, еще несколько десятилетий, общепризнано, что такая теория будет описывать настолько экстремальные физические условия, что вполне возможно, что мы никогда не сможем исследовать их из первых рук, даже с помощью ускорителей частиц, которые разрабатываются в настоящее время. разработан сегодня. Например, сверхпроводящий суперколлайдер, который должен быть построен к началу XIX в.90-е будут стоить 6 миллиардов долларов и позволят физикам сталкивать частицы с энергиями 40 триллионов электрон-вольт (40 000 ГэВ), что соответствует условиям, преобладающим через 10 секунд после Большого взрыва. Ожидаемый непредвиденный доход от такого ускорителя огромен и поможет ответить на многие насущные вопросы, которые сейчас преследуют теоретическое сообщество, но можем ли мы позволить себе инвестировать, возможно, значительно большие суммы денег в создание машин, способных исследовать мир квантовой гравитации при 10 ГэВ? Ожидается, что при этих энергиях станет непосредственно наблюдаемым полное объединение сил природы. Как любопытно, что определенные ответы на такие вопросы, как «Каково было Сотворение?» и «Имеют ли электроны и кварки внутреннюю структуру?», так неразрывно переплетены. Наша способность находить ответы на эти два вопроса, среди прочих, кажется, не ограничена каким-то метафизическим запретом, а ресурсами, которые наша цивилизация может позволить себе выделить для поиска ответов. К счастью, ситуация не столь безрадостна, ведь «машина» уже «построена», и все возможные эксперименты, которые мы только можем себе представить, уже проведены!
Ожидаемый непредвиденный доход от такого ускорителя огромен и поможет ответить на многие насущные вопросы, которые сейчас преследуют теоретическое сообщество, но можем ли мы позволить себе инвестировать, возможно, значительно большие суммы денег в создание машин, способных исследовать мир квантовой гравитации при 10 ГэВ? Ожидается, что при этих энергиях станет непосредственно наблюдаемым полное объединение сил природы. Как любопытно, что определенные ответы на такие вопросы, как «Каково было Сотворение?» и «Имеют ли электроны и кварки внутреннюю структуру?», так неразрывно переплетены. Наша способность находить ответы на эти два вопроса, среди прочих, кажется, не ограничена каким-то метафизическим запретом, а ресурсами, которые наша цивилизация может позволить себе выделить для поиска ответов. К счастью, ситуация не столь безрадостна, ведь «машина» уже «построена», и все возможные эксперименты, которые мы только можем себе представить, уже проведены!
ЧТО МЫ ДУМАЕМ, ЧТО ЗНАЕМ
Мы живем внутри крупнейшего из когда-либо созданных ускорителей частиц – Вселенной. За десять миллиардов лет до рождения Солнца был проведен эксперимент Природы по физике высоких энергий, и теперь экспериментальные данные можно исследовать, изучая свойства и содержание самой Вселенной. Сбор фундаментальных фактов, характеризующих нашу Вселенную, уникален тем, что он получен из самых разных источников. Частичный список этих «метафактов» выглядит так:
За десять миллиардов лет до рождения Солнца был проведен эксперимент Природы по физике высоких энергий, и теперь экспериментальные данные можно исследовать, изучая свойства и содержание самой Вселенной. Сбор фундаментальных фактов, характеризующих нашу Вселенную, уникален тем, что он получен из самых разных источников. Частичный список этих «метафактов» выглядит так:
1) Мы здесь, следовательно, некоторые регионы Вселенной благоприятны для создания сложных молекул и живых разумных организмов.
2) Наша Вселенная имеет 4 больших измерения, и все они увеличиваются в размерах по мере расширения Вселенной во времени и пространстве.
3) В Природе действуют 4 разные силы.
4) Доминирует только материя; галактик из антиматерии не существует, и эта материя состоит из 6 кварков и 6 типов лептонов.
Задача, стоящая перед физиком и астрономом, состоит в том, чтобы создать единую теорию, согласующуюся с этими метафактами, которую затем можно будет использовать для получения вторичных характеристик нашей Вселенной, таких как фоновое излучение 2,7 К, распространенность первичных элементов и формирование галактики. Взаимодействие между изучением макрокосма и микрокосма стало настолько интенсивным, что астрономы помогли физикам установить ограничения на число лептонных семейств — разрешено не более 4, иначе предсказанное космологическое изобилие гелия будет серьезно расходиться с тем, что наблюдается. . Физики, с другой стороны, используют астрономические верхние пределы текущего значения космологической постоянной, чтобы ограничить свои теории объединения.
Взаимодействие между изучением макрокосма и микрокосма стало настолько интенсивным, что астрономы помогли физикам установить ограничения на число лептонных семейств — разрешено не более 4, иначе предсказанное космологическое изобилие гелия будет серьезно расходиться с тем, что наблюдается. . Физики, с другой стороны, используют астрономические верхние пределы текущего значения космологической постоянной, чтобы ограничить свои теории объединения.
Расширение стандартной модели Большого взрыва под названием «Инфляционная Вселенная» (см. «Распад ложного вакуума») было создано физиком Массачусетского технологического института Аланом Гутом в 1981 году. Эта теория объединила теорию Великого объединения с космологией и, если она верна, позволяет астрономам проследить история Вселенной восходит к 10 секундам после Большого Взрыва, когда сильное, слабое и электромагнитное взаимодействия были объединены в единую «электроядерную» силу. В течение 4 лет, прошедших с тех пор, как была предложена модель инфляционной Вселенной, появились другие теоретические разработки, которые могут помочь нам исследовать события, происходящие на еще более ранней стадии, возможно, даже после самого События Сотворения. Десять лет назад теоретики открыли новый класс теорий, названных Суперсимметричными Теориями Великого Объединения (SUSY GUT). Эти теории, среди которых есть несколько конкурирующих типов, продемонстрировали большие надежды, обеспечив физиков единой структурой для описания не только электроядерной силы, но и гравитации, в дополнение к частицам, на которые они действуют (см. 1984). К сожалению, по мере более тщательного изучения SUSY GUT вскоре обнаружилось, что даже самые многообещающие кандидаты для Единой теории поля страдают некоторыми фундаментальными недостатками. Например:
Десять лет назад теоретики открыли новый класс теорий, названных Суперсимметричными Теориями Великого Объединения (SUSY GUT). Эти теории, среди которых есть несколько конкурирующих типов, продемонстрировали большие надежды, обеспечив физиков единой структурой для описания не только электроядерной силы, но и гравитации, в дополнение к частицам, на которые они действуют (см. 1984). К сожалению, по мере более тщательного изучения SUSY GUT вскоре обнаружилось, что даже самые многообещающие кандидаты для Единой теории поля страдают некоторыми фундаментальными недостатками. Например:
1) Было предсказано недостаточно основных полей для размещения известных частиц.
2) Левосторонняя и правосторонняя симметрия была предписана так, что слабую силу, нарушающую эту симметрию, приходилось прикладывать «вручную».
3) Имеются аномалии, включающие нарушение сохранения энергии и заряда.
4) Космологическая постоянная в 10 раз больше, чем предполагают нынешние верхние пределы.
В последние годы были предприняты значительные усилия по расширению и изменению постулатов SUSY GUT, чтобы избежать этих проблем. Один из способов заключался в том, чтобы подвергнуть сомнению легитимность самой основной предпосылки теорий поля, разработанных до сих пор. Наиболее активное направление теоретических исследований за последние 25 лет связано с изучением так называемых «точечных групп симметрии». Например, шестиугольник, повернутый на 60 градусов вокруг точки в его центре, неотличим от шестиугольника, повернутого на 120, 180, 240, 300 и 360 градусов. Эти 6 операций вращения образуют математическую группу, так что сложение или вычитание любых двух операций всегда приводит к операции вращения, которая уже является членом группы (180 = 120 + 60 и т. д.). Теории Великого объединения электроядерного взаимодействия основаны на группах точечной симметрии, названных SU(3), SU(2) и U(1), которые представляют собой аналогичные «вращения» в более сложном математическом пространстве. В контексте весомой материи группы точечной симметрии также являются математическим утверждением того, что мы считаем структурой фундаментальных частиц материи, а именно, что частицы имеют точечную форму и вообще не имеют физического размера. Но что, если это не так? Лучшее, что может предложить экспериментальная физика, это то, что электрон, принадлежащий к семейству 6 известных лептонов, ведет себя как точечная частица на масштабах до 10 см, но это все равно огромное расстояние по сравнению с гравитационным масштабом Планка в 10 см. где ожидается полное объединение с гравитацией.
В контексте весомой материи группы точечной симметрии также являются математическим утверждением того, что мы считаем структурой фундаментальных частиц материи, а именно, что частицы имеют точечную форму и вообще не имеют физического размера. Но что, если это не так? Лучшее, что может предложить экспериментальная физика, это то, что электрон, принадлежащий к семейству 6 известных лептонов, ведет себя как точечная частица на масштабах до 10 см, но это все равно огромное расстояние по сравнению с гравитационным масштабом Планка в 10 см. где ожидается полное объединение с гравитацией.
Предполагая, что элементарные частицы имеют внутреннюю структуру, Майкл Грин из Колледжа Королевы Марии и Джон Шварц из Калифорнийского технологического института сделали ряд замечательных открытий, о которых было объявлено в журнале NATURE в апреле 1985 года. Они предположили, что если заменить точечную частицу вибрирующей «струны», движущейся через 10-мерное пространство-время, казалось, что многие проблемы, преследующие SUSY кишка, исчезли чудесным образом. Более того, из всех возможных теорий «суперструн» было только две (называемые SO(32) и E8 x E8′), которые: 1) соответствовали как принципам относительности, так и принципам квантовой механики,2) допускали асимметрия между левыми и правыми отростками и, 3) Были свободны от аномалий. В обеих версиях также было достаточно места для 496 различных типов полей; достаточно, чтобы вместить все известные элементарные частицы, а затем и некоторые! Теории суперструн также имеют очень мало настраиваемых параметров, и с их помощью можно выполнять определенные вычисления квантовой гравитации, которые дают конечные ответы вместо бесконечных. Несмотря на свои теоретические успехи, теории суперструн страдают от трудности, заключающейся в том, что самые легкие частицы суперструн будут полностью безмассовыми, в то время как следующее более массивное поколение будет иметь массу 10 ГэВ. Непонятно даже, как эти сверхмассивные струнные частицы связаны с известными частицами, практически безмассовыми по сравнению с ними (протон имеет массу 1 ГэВ!).
Более того, из всех возможных теорий «суперструн» было только две (называемые SO(32) и E8 x E8′), которые: 1) соответствовали как принципам относительности, так и принципам квантовой механики,2) допускали асимметрия между левыми и правыми отростками и, 3) Были свободны от аномалий. В обеих версиях также было достаточно места для 496 различных типов полей; достаточно, чтобы вместить все известные элементарные частицы, а затем и некоторые! Теории суперструн также имеют очень мало настраиваемых параметров, и с их помощью можно выполнять определенные вычисления квантовой гравитации, которые дают конечные ответы вместо бесконечных. Несмотря на свои теоретические успехи, теории суперструн страдают от трудности, заключающейся в том, что самые легкие частицы суперструн будут полностью безмассовыми, в то время как следующее более массивное поколение будет иметь массу 10 ГэВ. Непонятно даже, как эти сверхмассивные струнные частицы связаны с известными частицами, практически безмассовыми по сравнению с ними (протон имеет массу 1 ГэВ!). Также неизвестно, будет ли 496 различных частиц охватят весь диапазон масс от 0 до 10 ГэВ. Возможно, что они могут сгруппироваться в две семьи с массами, сгруппированными вокруг этих двух крайних точек. В последнем случае у физиков-экспериментаторов может буквально закончиться количество новых частиц для открытия, пока не будут построены ускорители, достаточно мощные для создания сверхмассивных частиц.
Также неизвестно, будет ли 496 различных частиц охватят весь диапазон масс от 0 до 10 ГэВ. Возможно, что они могут сгруппироваться в две семьи с массами, сгруппированными вокруг этих двух крайних точек. В последнем случае у физиков-экспериментаторов может буквально закончиться количество новых частиц для открытия, пока не будут построены ускорители, достаточно мощные для создания сверхмассивных частиц.
Привлекательной чертой модели SO(32), которая представляет частицы как открытые струны, является то, что гравитация должна быть включена с самого начала, чтобы сделать теорию внутренне непротиворечивой и способной давать конечные предсказания. Это также теория, которая сводится к обычным точечным теориям поля при энергиях ниже 10 ГэВ. Комплементарная теория, E8 x E8′, является единственной другой теорией суперструн, которая, по-видимому, работает так же, как SO(32), и рассматривает частицы так, как если бы они были замкнутыми струнами без оголенных концов. Эта модель считается наиболее перспективной для описания реальных физических частиц. Он также включает гравитацию, но, в отличие от SO(32), E8 x E8′, по-видимому, сводится при низкой энергии к группам симметрии, связанным с сильными, слабыми и электромагнитными взаимодействиями, а именно, SU(3), SU(2) и У(1).
Он также включает гравитацию, но, в отличие от SO(32), E8 x E8′, по-видимому, сводится при низкой энергии к группам симметрии, связанным с сильными, слабыми и электромагнитными взаимодействиями, а именно, SU(3), SU(2) и У(1).
Если Е8 х Е8′ суждено стать «окончательной единой теорией поля», нас ждут дополнительные сюрпризы. Каждая группа, E8 и E8′, может быть математически сведена к произведениям групп, которые представляют сильное, слабое и электромагнитное взаимодействия; ВП(3) х ВП(2) х В(1). Если группа Е8 соответствует известным частицам, что представляет собой Е8′? С точки зрения математических свойств, одни только соображения симметрии, по-видимому, требуют, чтобы группа E8′ была зеркальным отображением группы E8. Если E8 содержит группы SU(3), SU(2) и U(1), то E8′ содержит SU(3)’, SU(2)’ и U(1)’. Штрихованные поля в E8′ будут иметь те же свойства, что и поля, которые мы приписываем сильным, слабым и электромагнитным взаимодействиям. Поля частиц E8′ могут соответствовать совершенно другому виду материи, чьи свойства так же отличаются от материи и антиматерии, как обычная материя отличается от антиматерии! «Теневая материя», как ее назвали Эдвард Колб, Дэвид Секель и Майкл Тернер из Фермилаб, может на самом деле сосуществовать с нашей материей — возможно, из-за недостающей массы, необходимой для закрытия Вселенной. Теневая материя обнаруживается только благодаря ее гравитационному влиянию и совершенно невидима, потому что электромагнитная сила теневого мира (теневой свет) не взаимодействует ни с одной из частиц в обычном мире.
Теневая материя обнаруживается только благодаря ее гравитационному влиянию и совершенно невидима, потому что электромагнитная сила теневого мира (теневой свет) не взаимодействует ни с одной из частиц в обычном мире.
ЗА ПРОСТРАНСТВОМ И ВРЕМЕНЕМ
Поиски математического описания физического мира, объединяющего очевидные различия между известными частицами и силами, привели физиков к замечательному выводу, что Вселенная населяет не только 4 измерения пространства и время, но гораздо большую арену, размерность которой может быть огромной (см. «Есть ли пространство больше трех измерений?»). И теории суперструн, и SUSY GUT согласны с тем, что наш физический мир должен иметь больше, чем 4 измерения, о которых мы привыкли думать. Замечательной особенностью теории суперструн является то, что из всех возможных размерностей пространства-времени только 10-мерное ( 9пространственные измерения и 1 временное измерение) приведет ли теория к вычислительно конечной и внутренне непротиворечивой модели физического мира, которая с самого начала включает слабое взаимодействие и где все неприятные аномалии точно компенсируются. Предполагается, что в таком 10-мерном мире 6 измерений теперь свернуты или «уплотнены» в крошечные сферы, которые сопровождают 4 координаты каждой точки пространства-времени. Как могло бы выглядеть описание ранней Вселенной с этой новой точки зрения? Считается, что шесть внутренних измерений имеют размер порядка 10 см.
Предполагается, что в таком 10-мерном мире 6 измерений теперь свернуты или «уплотнены» в крошечные сферы, которые сопровождают 4 координаты каждой точки пространства-времени. Как могло бы выглядеть описание ранней Вселенной с этой новой точки зрения? Считается, что шесть внутренних измерений имеют размер порядка 10 см.
По мере того, как мы следим за историей Вселенной в прошлое, 3 больших измерения пространства быстро сокращаются, пока в конце концов не станут всего 10 см в размере. Это произошло во времена Планковской эры, через 10 секунд после Сотворения. Внешний вид Вселенной в этих условиях почти невообразим. Сегодня, когда мы смотрим на самые далекие квазары, мы видим их на расстоянии миллиардов световых лет. В эпоху Планка материя, составляющая эти отдаленные системы, находилась всего в 10 см от материи, из которой состоит ваше собственное тело!
Что было такого особенного в этой эпохе, что только 4 из 10 измерений были выделены, чтобы вырасти до их огромных нынешних размеров?. Почему не 3 (2 пробела + 1 время) или 5 (4 пробела + 1 время)? Физики до сих пор не смогли найти объяснение этой фундаментальной загадке нашего пленума, с другой стороны, возможно, что если бы разбивка пространства-времени по измерениям была иной, чем «4 + 6», физические законы, которыми мы являемся продукты, были бы совершенно негостеприимны для жизни, какой мы ее знаем. 9-13 грамм каждый. Эти частицы в конечном итоге распались на знакомые нам кварки и лептоны, как только Вселенная по мере расширения стала холоднее. Кроме того, на эти частицы могла действовать только одна «сверхсила»; сила, характер которой содержал все индивидуальные атрибуты, которые мы теперь связываем с гравитацией, электромагнетизмом и сильными и слабыми ядерными взаимодействиями. Поскольку частицы, несущие «сверхсилу», имели массы, сходные с массами сосуществовавших тогда сверхмассивных частиц, различие между носителями силы и частицами, на которые они действуют, вероятно, полностью исчезло, и мир стал полностью суперсимметричным.
Почему не 3 (2 пробела + 1 время) или 5 (4 пробела + 1 время)? Физики до сих пор не смогли найти объяснение этой фундаментальной загадке нашего пленума, с другой стороны, возможно, что если бы разбивка пространства-времени по измерениям была иной, чем «4 + 6», физические законы, которыми мы являемся продукты, были бы совершенно негостеприимны для жизни, какой мы ее знаем. 9-13 грамм каждый. Эти частицы в конечном итоге распались на знакомые нам кварки и лептоны, как только Вселенная по мере расширения стала холоднее. Кроме того, на эти частицы могла действовать только одна «сверхсила»; сила, характер которой содержал все индивидуальные атрибуты, которые мы теперь связываем с гравитацией, электромагнетизмом и сильными и слабыми ядерными взаимодействиями. Поскольку частицы, несущие «сверхсилу», имели массы, сходные с массами сосуществовавших тогда сверхмассивных частиц, различие между носителями силы и частицами, на которые они действуют, вероятно, полностью исчезло, и мир стал полностью суперсимметричным.
Чтобы выйти за пределы эры Планка, может потребоваться радикальное изменение нашего привычного образа мышления о времени и пространстве. В уравнениях и теориях современной физики можно найти лишь проблески правильного способа осмысления этого многомерного ландшафта. После эры Планка все 10 измерений (и, возможно, другие) становятся равными, по крайней мере, с точки зрения их физического размера. Сверхмассивные частицы Суперструн начинают приобретать больше характеристик флуктуаций в геометрии пространства-времени, чем в качестве различимых ингредиентов изначального космологического «супа». Не было единой уникальной геометрии пространства-времени, вместо этого существовало постоянно меняющееся квантовое взаимодействие между пространствами-временями с неограниченным диапазоном геометрии. Подобно звуковым волнам, которые комбинируются друг с другом, создавая интерференцию и усиление, пространство-время, появившееся в эпоху Планка, считается результатом суперпозиции бесконечного числа альтернативных геометрий пространства-времени, которые, сложенные вместе, создали пространство-время, которое теперь мы являемся частью. 9-36 секунд после Большого Взрыва, вполне возможно, что в самые ранние моменты Вселенная родилась из тьмы, а не в ослепляющей вспышке света. Все, что существовало в этой тьме до появления света, было пустым пространством, из которого позднее возникло наше 10-мерное пространство-время. Конечно, в этих условиях непонятно, как нам дальше думать о самом времени.
9-36 секунд после Большого Взрыва, вполне возможно, что в самые ранние моменты Вселенная родилась из тьмы, а не в ослепляющей вспышке света. Все, что существовало в этой тьме до появления света, было пустым пространством, из которого позднее возникло наше 10-мерное пространство-время. Конечно, в этих условиях непонятно, как нам дальше думать о самом времени.
С точки зрения доступных сегодня теорий вполне может быть, что конкретное измерение, которое мы называем Временем, имело определенную нулевую точку, так что мы даже не можем логически говорить о том, что произошло до существования времени. Понятие «до» основано на презумпции упорядоченности во времени. Путешественник, стоящий на северном полюсе, никогда не сможет переместиться на землю на 1 милю севернее севера! Тем не менее, по укоренившейся привычке, мы говорим о времени до зарождения Вселенной, когда времени не существовало, и спрашиваем: «Что было до Большого взрыва?». Список физиков, исследующих это «состояние», сильно вырос за последние 15 лет. Число физиков во всем мире, которые публикуют исследования по этой теме, составляет немногим более 200 человек на 5-миллиардное население мира!
Число физиков во всем мире, которые публикуют исследования по этой теме, составляет немногим более 200 человек на 5-миллиардное население мира!
КВАНТОВАЯ КОСМОЛОГИЯ
В начале 1970-х годов Ю. Зельдович и А. Старобинский из СССР вместе с Эдвардом Трайоном из Хантер-колледжа предположили, что Вселенная возникла в результате флуктуации в вакууме. Эта флуктуация вакуума «убежала» сама с собой, создав все известные частицы из пустого пространства в «момент» безвременья. Чтобы понять, что это значит, необходимо применить фундаментальный факт релятивистской квантовой физики, открытый во второй половине XIX в.20-е годы. Флуктуации вакуума являются прямым следствием принципа неопределенности Гейзенберга, который ограничивает то, насколько хорошо мы можем одновременно знать импульс и местоположение частицы (или ее полную энергию и время жизни). То, что мы называем пустым пространством или физическим вакуумом, — такая же ньютоновская фикция, как абсолютное пространство и время. Известно, что пустое пространство не является бесплодной сценой, на которой материя играет свою роль. Известно, что пустое пространство заполнено «виртуальными частицами», которые спонтанно появляются и исчезают за пределами возможности прямого физического измерения. По этим частицам-призракам можно с поразительной точностью предсказать множество очень тонких явлений. В зависимости от общей энергии массы покоя виртуальных частиц, созданных флуктуациями вакуума, они могут прожить определенное время жизни, прежде чем принцип неопределенности Гейзенберга потребует, чтобы они снова исчезли в небытии вакуумного состояния. В таком квантовом мире менее массивные виртуальные частицы могут жить дольше, чем более массивные. Эдвард Тайрон предположил, что Вселенная — это всего лишь особенно долгоживущие вакуумные флуктуации, отличающиеся лишь по величине от тех, которые незаметно происходят повсюду вокруг нас. Причина, по которой вселенная живет так долго, несмотря на ее огромную массу, заключается в том, что положительная энергия, скрытая во всей материи во вселенной, уравновешивается отрицательной потенциальной энергией гравитационного поля вселенной.
Известно, что пустое пространство не является бесплодной сценой, на которой материя играет свою роль. Известно, что пустое пространство заполнено «виртуальными частицами», которые спонтанно появляются и исчезают за пределами возможности прямого физического измерения. По этим частицам-призракам можно с поразительной точностью предсказать множество очень тонких явлений. В зависимости от общей энергии массы покоя виртуальных частиц, созданных флуктуациями вакуума, они могут прожить определенное время жизни, прежде чем принцип неопределенности Гейзенберга потребует, чтобы они снова исчезли в небытии вакуумного состояния. В таком квантовом мире менее массивные виртуальные частицы могут жить дольше, чем более массивные. Эдвард Тайрон предположил, что Вселенная — это всего лишь особенно долгоживущие вакуумные флуктуации, отличающиеся лишь по величине от тех, которые незаметно происходят повсюду вокруг нас. Причина, по которой вселенная живет так долго, несмотря на ее огромную массу, заключается в том, что положительная энергия, скрытая во всей материи во вселенной, уравновешивается отрицательной потенциальной энергией гравитационного поля вселенной. Таким образом, полная энергия Вселенной точно равна нулю, а ее максимальное время жизни в качестве «квантовой флуктуации» может быть огромным и даже бесконечным! По словам Трайона, «Вселенная — это просто одна из тех вещей, которые происходят время от времени».
Таким образом, полная энергия Вселенной точно равна нулю, а ее максимальное время жизни в качестве «квантовой флуктуации» может быть огромным и даже бесконечным! По словам Трайона, «Вселенная — это просто одна из тех вещей, которые происходят время от времени».
Это предложение Трайона было воспринято астрономами с некоторым скептицизмом и даже удивлением и не получило дальнейшего развития. Это была судьба, которая также постигла работу Теодора Калуцы и Оскара Кляйна по пятимерной общей теории относительности в 1920-х годах, которая была возрождена только в конце 1970-х годов как мощное лекарство от болезней, преследующих теорию суперсимметрии.
В 1978 г. Р. Браут, П. Энглерт, Э. Гунциг и П. Шпиндель из Брюссельского университета предположили, что флуктуация, приведшая к созданию нашей Вселенной, началась в пустом плоском четырехмерном пространстве-времени. . Флуктуации в пространстве начались слабо, создав, возможно, единственную пару сверхмассивных частиц материя-антиматерия с массами 10^19ГэВ. Существование этой «первой пары» стимулировало создание из вакуума большего количества пар частица-античастица, которые стимулировали появление еще других и так далее. Пространство сильно искривилось и взорвалось, извергнув все суперчастицы, которые позже распались на знакомые лептоны, кварки и фотоны.
Существование этой «первой пары» стимулировало создание из вакуума большего количества пар частица-античастица, которые стимулировали появление еще других и так далее. Пространство сильно искривилось и взорвалось, извергнув все суперчастицы, которые позже распались на знакомые лептоны, кварки и фотоны.
Хайнц Пейджелс и Дэвид Аткатц из Рокфеллеровского университета в 1981 году предположили, что пусковым агентом, стоящим за Событием Сотворения, было явление туннелирования вакуума из состояния с более высокой энергией в состояние с более низкой энергией. В отличие от модели Браута-Энглера-Гунзига-Шпинделя, которая исходила из плоского пространства-времени, Пейджелс и Аткатц использовали дополнительный подход, согласно которому изначальное ничто, из которого возникла Вселенная, было пространственно замкнутым, компактным пустым пространством, другими словами, оно имело геометрическую форму. как двумерная поверхность сферы. но размерность его поверхности была намного выше 2. Опять же, это пространство содержало неважно что-всегда. Характеристики (пока еще неизвестные) процесса туннелирования определяли, возможно, случайным образом, как размерность пространства-времени будет «кристаллизоваться» в комбинацию 6+4, которая представляет полноту нашей вселенной.
Характеристики (пока еще неизвестные) процесса туннелирования определяли, возможно, случайным образом, как размерность пространства-времени будет «кристаллизоваться» в комбинацию 6+4, которая представляет полноту нашей вселенной.
Алекс Виленкин из Университета Тафтса в 1983 году предположил, что наше пространство-время было создано из «ничто», настолько полного, что даже его размерность не определена. В 1984 году Стивен Хокингс из Кембриджа и Джеймс Хартл из Калифорнийского университета в Сан-Франциско пришли к аналогичному выводу, проведя серию квантово-механических расчетов. Они описали геометрическое состояние Вселенной в терминах волновой функции, определяющей вероятность того, что пространство-время будет иметь одну из бесконечного числа возможных геометрий. Основная проблема с обычной теорией Большого взрыва заключалась в том, что Вселенная возникла из состояния, в котором пространство и время исчезли, а плотность Вселенной стала бесконечной; состояние, называемое Сингулярностью. Хокингс и Хартл смогли показать, что эта сингулярность Большого взрыва представляет собой особый вид геометрии, которая размывается в пространстве-времени из-за квантовой неопределенности. Вселенная, казалось, возникла из несингулярного состояния «небытия», похожего на неопределенное состояние, предложенное Виленкиным. Физик Фрэнк Вильчик лучше всего выражает эту замечательную ситуацию, говоря: «Причина того, что существует Нечто, а не Ничто, заключается в том, что Ничто неустойчиво».
Хокингс и Хартл смогли показать, что эта сингулярность Большого взрыва представляет собой особый вид геометрии, которая размывается в пространстве-времени из-за квантовой неопределенности. Вселенная, казалось, возникла из несингулярного состояния «небытия», похожего на неопределенное состояние, предложенное Виленкиным. Физик Фрэнк Вильчик лучше всего выражает эту замечательную ситуацию, говоря: «Причина того, что существует Нечто, а не Ничто, заключается в том, что Ничто неустойчиво».
СОВЕРШЕННАЯ СИММЕТРИЯ
Теории, подобные теориям SUSY GUTS и Superstrings, кажется, предполагают, что всего через несколько мгновений после Творения законы физики и содержание мира находились в высокосимметричном состоянии; одна сверхсила и, возможно, один вид суперчастицы. Единственным, что нарушало совершенную симметрию этой эпохи, было определенное направление и характер измерения, называемого Временем. До Творения изначальная симметрия могла быть настолько совершенной, что, как предположил Виленкин, размерность пространства сама по себе была неопределенной. Описать это состояние — сложная задача семантики и математики, потому что математический акт определения его размерности подразумевал бы выбор одной возможности из всех других и, таким образом, нарушение идеальной симметрии этого состояния. Предположительно, тогда не было ни частиц материи, ни даже фотонов света, потому что эти частицы родились из вакуумных флуктуаций в ткани пространства-времени, сопровождавших создание Вселенной. В таком мире ничего не происходит, потому что все «происшествия» происходят в системе отсчета времени и пространства. Присутствие единственной частицы в этом ничто мгновенно нарушило бы совершенную симметрию этой эпохи, потому что тогда была бы излюбленная точка в пространстве, отличная от всех других; точка, занятая частицей. Это ничто тоже не эволюционировало, потому что эволюция — это процесс, упорядоченный во времени. Введение времени в качестве предпочтительной координаты также нарушило бы симметрию. Казалось бы, состояние «Транс-Творения» не поддается общепринятому описанию, потому что любые слова, которые мы можем выбрать для его описания, изначально пронизаны концептуальным багажом времени и пространства.
Описать это состояние — сложная задача семантики и математики, потому что математический акт определения его размерности подразумевал бы выбор одной возможности из всех других и, таким образом, нарушение идеальной симметрии этого состояния. Предположительно, тогда не было ни частиц материи, ни даже фотонов света, потому что эти частицы родились из вакуумных флуктуаций в ткани пространства-времени, сопровождавших создание Вселенной. В таком мире ничего не происходит, потому что все «происшествия» происходят в системе отсчета времени и пространства. Присутствие единственной частицы в этом ничто мгновенно нарушило бы совершенную симметрию этой эпохи, потому что тогда была бы излюбленная точка в пространстве, отличная от всех других; точка, занятая частицей. Это ничто тоже не эволюционировало, потому что эволюция — это процесс, упорядоченный во времени. Введение времени в качестве предпочтительной координаты также нарушило бы симметрию. Казалось бы, состояние «Транс-Творения» не поддается общепринятому описанию, потому что любые слова, которые мы можем выбрать для его описания, изначально пронизаны концептуальным багажом времени и пространства. Хайнц Пейгельс размышляет об этой «самой ранней» стадии, говоря: «Ничто «до» сотворения вселенной — это самая полная пустота, которую мы можем себе представить. Не существовало ни пространства, ни времени, ни материи. Это мир без места, без длительности и вечности…»
Хайнц Пейгельс размышляет об этой «самой ранней» стадии, говоря: «Ничто «до» сотворения вселенной — это самая полная пустота, которую мы можем себе представить. Не существовало ни пространства, ни времени, ни материи. Это мир без места, без длительности и вечности…»
Изучение научной литературы за последние 20 лет позволяет предположить, что мы, возможно, быстро приближаемся к главному перекрестку в физике. Кажется, что одна дорога ведет к единой теории объединения, которая настолько уникальна среди всех остальных, что является единственной, которая согласуется со всеми известными нам основными законами. Он внутренне непротиворечив; удовлетворяет принципам относительности и квантовой механики и не требует никакой внешней информации для описания содержащихся в ней частиц и сил. Прототипом этого может быть теория суперструн с ее единственным регулируемым параметром, а именно натяжением струны. Другая дорога намного мрачнее. Может также оказаться, что мы создадим несколько теоретических систем, которые вроде бы все объясняют, но имеют в себе трудноуловимые изъяны. 19ГэВ.
19ГэВ.
Мне очень трудно устоять перед аналогией между нашим нынешним положением и положением греческих геометров. В течение 2000 лет основные постулаты евлиевой геометрии и следствия этой логической системы оставались неизменными. Это стало закрытой книгой, и лишь несколько человек в мире пытались найти исключения из нее, такие как опровержения постулата о параллельности. Наконец, в 19 веке была открыта неевклидова геометрия, и в геометрии произошел ренессанс. Не находятся ли физики на пороге такого же великого возраста, оказавшись в затруднении из-за того, что не могут изобрести новые способы осмысления старых проблем? Египетская космология основывалась на мотивах, которые люди той эпохи могли видеть в окружающем их мире; вода, небо, земля, биологическая репродукция. Сегодня мы все еще используем мотивы, которые находим в природе, чтобы объяснить происхождение вселенной; геометрия пространства, виртуальные частицы и флуктуации вакуума. Можно, вероятно, ожидать, что в последующие века наши потомки найдут еще другие мотивы, а от них и космологии моды, которые будут удовлетворять требованиям того будущего века, возможно, с гораздо большей точностью и эффективностью, чем наши сегодня. Возможно, в те будущие века ученые будут удивляться изобретательности современных физиков и астрономов и тому, как всего за 300 лет нам удалось создать собственную причудливую теорию, как это сделали египтяне до нас.
Возможно, в те будущие века ученые будут удивляться изобретательности современных физиков и астрономов и тому, как всего за 300 лет нам удалось создать собственную причудливую теорию, как это сделали египтяне до нас.
Тем временем физики и астрономы делают все возможное, чтобы создать космологию, которая удовлетворит интеллектуальные потребности нашего века. Сегодня, размышляя о происхождении Вселенной, мы обнаруживаем, что смотрим на темную, пустую пустоту, мало чем отличающуюся от той, которую могли вообразить наши египетские предшественники. Эта пустота — состояние изысканного совершенства и симметрии, которое, кажется, не поддается описанию в любых лингвистических терминах, которые мы можем вообразить. С помощью наших теорий мы запускаем математические исследовательские путешествия и наблюдаем, как пустота дрожит от квантовых возможностей невообразимых вселенных.
Большой взрывтеория великого объединенияинфляционная космологияпетлевая квантовая гравитацияпланковская эраквантовая гравитацияотносительностьпространствопространство-времятеория струнАстрономия, физика
СтенБлог
Распад ложного вакуума
Автор Стен Оденвальд. Авторское право (C) 1983 Kalmbach Publishing. Перепечатано с разрешения
В недавно разработанной Стивеном Вайнбергом и Абдусом Саламом теории, объединяющей электромагнитное и слабое взаимодействия, вакуум не пуст. Эта своеобразная ситуация возникает из-за существования поля нового типа, называемого полем Хиггса. Поле Хиггса имеет важное физическое следствие, поскольку его взаимодействие с частицами W, W и Z (носителями слабого взаимодействия) заставляет их набирать массу при энергиях ниже 100 миллиардов электрон-вольт (100 Гэв). Выше этой энергии они совершенно безмассовы, как и фотон, и именно эта характеристика делает слабые и электромагнитные взаимодействия такими похожими при высоких энергиях.
На несколько более абстрактном уровне рассмотрим рисунки 1 и 2, представляющие среднюю энергию вакуумного состояния. Если бы Вселенная была основана на вакуумном состоянии, показанном на рис. 1, предсказано, что симметрия между электромагнитным и слабым взаимодействиями была бы совершенно очевидной. Все частицы, передающие силы, были бы безмассовыми и вели бы себя одинаково. Соответствующие силы были бы неразличимы. Так было бы, если бы Вселенная имела среднюю температуру 1 триллион градусов, так что существующие частицы сталкивались бы при энергиях 100 Гэв. На рисунке 2, представляющем энергию вакуумного состояния для энергий столкновения ниже 100 ГэВ, вакуумное состояние теперь содержит поле Хиггса, а симметрия между силами внезапно теряется или «нарушается». Хотя при низкой энергии поведение сил асимметрично, фундаментальные законы, управляющие электромагнитными и слабыми взаимодействиями, по своей сути остаются симметричными. Это очень замечательное и глубокое предсказание, поскольку оно подразумевает, что определенные симметрии в Природе могут быть скрыты от нас, но, тем не менее, существуют.
1, предсказано, что симметрия между электромагнитным и слабым взаимодействиями была бы совершенно очевидной. Все частицы, передающие силы, были бы безмассовыми и вели бы себя одинаково. Соответствующие силы были бы неразличимы. Так было бы, если бы Вселенная имела среднюю температуру 1 триллион градусов, так что существующие частицы сталкивались бы при энергиях 100 Гэв. На рисунке 2, представляющем энергию вакуумного состояния для энергий столкновения ниже 100 ГэВ, вакуумное состояние теперь содержит поле Хиггса, а симметрия между силами внезапно теряется или «нарушается». Хотя при низкой энергии поведение сил асимметрично, фундаментальные законы, управляющие электромагнитными и слабыми взаимодействиями, по своей сути остаются симметричными. Это очень замечательное и глубокое предсказание, поскольку оно подразумевает, что определенные симметрии в Природе могут быть скрыты от нас, но, тем не менее, существуют.
За последние 10 лет физики разработали еще более мощные теории, пытающиеся объединить не только электромагнитное и слабое взаимодействие, но и сильное ядерное взаимодействие. Они называются Теориями Великого Объединения (ТВО), а известная упрощенная теория была разработана Говардом Джорджи, Хелен Куинн и Стивеном Вайнбергом и называется SU(5) (произносится как «ess you Five»). Эта теория предсказывает, что ядерные и «электрослабые» силы в конечном итоге будут иметь одинаковую силу, но только тогда, когда частицы сталкиваются при энергиях выше 1 тысячи триллионов ГэВ, что соответствует невообразимой температуре в 10 тысяч триллионов триллионов градусов! SU(5) требует ровно 24 частиц для передачи сил, из которых 8 безмассовых глюонов ядерного взаимодействия, 3 безмассовых промежуточных векторных бозона слабого взаимодействия и один безмассовый фотон электромагнитного взаимодействия составляют 12. Остальные 12 представляют собой полностью новый класс частиц, называемых лептокварковыми бозонами, которые обладают замечательным свойством превращать кварки в электроны. Таким образом, SU(5) предсказывает существование «сверхслабого» взаимодействия; новая пятая сила во Вселенной! В настоящее время это взаимодействие в 10 тысяч триллионов триллионов раз слабее слабого взаимодействия, но тем не менее в 100 миллионов раз сильнее гравитации.
Они называются Теориями Великого Объединения (ТВО), а известная упрощенная теория была разработана Говардом Джорджи, Хелен Куинн и Стивеном Вайнбергом и называется SU(5) (произносится как «ess you Five»). Эта теория предсказывает, что ядерные и «электрослабые» силы в конечном итоге будут иметь одинаковую силу, но только тогда, когда частицы сталкиваются при энергиях выше 1 тысячи триллионов ГэВ, что соответствует невообразимой температуре в 10 тысяч триллионов триллионов градусов! SU(5) требует ровно 24 частиц для передачи сил, из которых 8 безмассовых глюонов ядерного взаимодействия, 3 безмассовых промежуточных векторных бозона слабого взаимодействия и один безмассовый фотон электромагнитного взаимодействия составляют 12. Остальные 12 представляют собой полностью новый класс частиц, называемых лептокварковыми бозонами, которые обладают замечательным свойством превращать кварки в электроны. Таким образом, SU(5) предсказывает существование «сверхслабого» взаимодействия; новая пятая сила во Вселенной! В настоящее время это взаимодействие в 10 тысяч триллионов триллионов раз слабее слабого взаимодействия, но тем не менее в 100 миллионов раз сильнее гравитации. 29Приблизительно через 32 года вся материя катастрофически распалась на электроны, нейтрино и фотоны. Эра Материи с ее живыми организмами, звездами и галактиками была бы сметена навсегда, представив лишь мимолетный эпизод в истории вселенной. В дополнение к распаду протона, SU(5) предсказывает, что при энергетической характеристике перехода ТВО мы увидим влияние нового семейства частиц, называемых сверхмассивными бозонами Хиггса, массы которых, как ожидается, составят примерно 1 тысячу триллионов ГэВ! Эти частицы взаимодействуют с 12 лептокварками и делают их массивными точно так же, как бозоны Хиггса при 100 ГэВ сделали тяжелыми частицы W, W и Z. Вооружившись этими знаниями, давайте рассмотрим некоторые из замечательных космологических следствий этих захватывающих теорий. 9-37 секунд после Создания. Протоны и нейтроны, с которыми мы знакомы сегодня, еще не сформировались, поскольку составляющие их кварки взаимодействовали слишком слабо, чтобы позволить им связываться вместе в «пакеты», такие как нейтроны и протоны.
29Приблизительно через 32 года вся материя катастрофически распалась на электроны, нейтрино и фотоны. Эра Материи с ее живыми организмами, звездами и галактиками была бы сметена навсегда, представив лишь мимолетный эпизод в истории вселенной. В дополнение к распаду протона, SU(5) предсказывает, что при энергетической характеристике перехода ТВО мы увидим влияние нового семейства частиц, называемых сверхмассивными бозонами Хиггса, массы которых, как ожидается, составят примерно 1 тысячу триллионов ГэВ! Эти частицы взаимодействуют с 12 лептокварками и делают их массивными точно так же, как бозоны Хиггса при 100 ГэВ сделали тяжелыми частицы W, W и Z. Вооружившись этими знаниями, давайте рассмотрим некоторые из замечательных космологических следствий этих захватывающих теорий. 9-37 секунд после Создания. Протоны и нейтроны, с которыми мы знакомы сегодня, еще не сформировались, поскольку составляющие их кварки взаимодействовали слишком слабо, чтобы позволить им связываться вместе в «пакеты», такие как нейтроны и протоны. Остальные составляющие материи, электроны, мюоны и тау-лептоны, также не имели массы и перемещались по существу со скоростью света; Они были буквально новой формой излучения, во многом похожей на современный свет! Двенадцать сверхмассивных лептокварков, а также сверхмассивные бозоны Хиггса существовали бок о бок со своими античастицами. Каждая пара частица-античастица, которая была уничтожена, была уравновешена воскрешением новой пары где-то еще во Вселенной. В этот период частицы, которые передавали сильное, слабое и электромагнитное взаимодействия, были совершенно безмассовыми, так что эти силы уже нельзя было различить. Жителю той эпохи не пришлось бы теоретизировать о существовании симметрии между сильными, слабыми и электромагнитными взаимодействиями, эту симметрию можно было бы непосредственно наблюдать, и, кроме того, существовало бы меньше типов частиц, за которыми жители могли бы следить. Тогда Вселенная была бы намного проще!
Остальные составляющие материи, электроны, мюоны и тау-лептоны, также не имели массы и перемещались по существу со скоростью света; Они были буквально новой формой излучения, во многом похожей на современный свет! Двенадцать сверхмассивных лептокварков, а также сверхмассивные бозоны Хиггса существовали бок о бок со своими античастицами. Каждая пара частица-античастица, которая была уничтожена, была уравновешена воскрешением новой пары где-то еще во Вселенной. В этот период частицы, которые передавали сильное, слабое и электромагнитное взаимодействия, были совершенно безмассовыми, так что эти силы уже нельзя было различить. Жителю той эпохи не пришлось бы теоретизировать о существовании симметрии между сильными, слабыми и электромагнитными взаимодействиями, эту симметрию можно было бы непосредственно наблюдать, и, кроме того, существовало бы меньше типов частиц, за которыми жители могли бы следить. Тогда Вселенная была бы намного проще!
Поскольку Вселенная продолжала расширяться, температура продолжала стремительно падать. 15 и 100 ГэВ, когда силы Природы внезапно стали различимы, все еще исследуется, но недавно различные группы теоретиков, работающих над этой проблемой, предложили некоторые дразнящие описания. . Согласно исследованиям Алана Гута, Стивена Вайнберга и Фрэнка Уилчика между 1979 и 1981, когда произошел переход ТВО, это произошло так же, как образование пузырьков пара в котле с кипящей водой. В этой аналогии внутренняя часть пузырей представляет собой состояние вакуума в новой фазе, где силы различимы, встроенные в старую симметричную фазу, где ядерные, слабые и электромагнитные силы неразличимы. Внутри этих пузырей энергия вакуума относится к типу, показанному на рисунке 2, а снаружи она представлена на рисунке 1. Поскольку мы живем в новой фазе с ее четырьмя различимыми силами, это состояние было названо «истинным» состоянием вакуума. В состоянии ложного вакуума силы остаются неразличимыми, что, конечно же, не та ситуация, в которой мы находимся сегодня!
15 и 100 ГэВ, когда силы Природы внезапно стали различимы, все еще исследуется, но недавно различные группы теоретиков, работающих над этой проблемой, предложили некоторые дразнящие описания. . Согласно исследованиям Алана Гута, Стивена Вайнберга и Фрэнка Уилчика между 1979 и 1981, когда произошел переход ТВО, это произошло так же, как образование пузырьков пара в котле с кипящей водой. В этой аналогии внутренняя часть пузырей представляет собой состояние вакуума в новой фазе, где силы различимы, встроенные в старую симметричную фазу, где ядерные, слабые и электромагнитные силы неразличимы. Внутри этих пузырей энергия вакуума относится к типу, показанному на рисунке 2, а снаружи она представлена на рисунке 1. Поскольку мы живем в новой фазе с ее четырьмя различимыми силами, это состояние было названо «истинным» состоянием вакуума. В состоянии ложного вакуума силы остаются неразличимыми, что, конечно же, не та ситуация, в которой мы находимся сегодня!
Космическая инфляция
Захватывающее предсказание модели Гута состоит в том, что Вселенная, возможно, прошла по крайней мере один период в своей истории, когда расширение было гораздо более быстрым, чем предсказывает «стандартная» модель Большого взрыва. Причина этого в том, что сам вакуум также вносит свой вклад в энергетическое содержание Вселенной точно так же, как материя и излучение, однако вклад в противоположном смысле. Хотя гравитация является силой притяжения, космический вакуум создает силу отталкивания. Как показано на рисунках 1 и 2, минимальное энергетическое состояние ложного вакуума в точке «А» до перехода ТВО имеет более высокую энергию, чем состояние истинного вакуума в точке «В» после перехода. Эта разница энергий и вносит свой вклад в энергию вакуума. В течение переходного периода ТВО положительное давление за счет энергии вакуума было бы намного больше, чем сдерживающее давление, создаваемое гравитационным влиянием вещества и излучения. Вселенная раздулась бы с огромной скоростью, инфляция была вызвана давлением вакуума! В этой картине Вселенной космологическая постоянная Эйнштейна приобретает совершенно новое значение, поскольку теперь она представляет собой определенное физическое понятие; Это просто мера разницы энергий между истинным и ложным состояниями вакуума («В» и «А» на рисунках 1 и 2) в определенный момент истории Вселенной.
Причина этого в том, что сам вакуум также вносит свой вклад в энергетическое содержание Вселенной точно так же, как материя и излучение, однако вклад в противоположном смысле. Хотя гравитация является силой притяжения, космический вакуум создает силу отталкивания. Как показано на рисунках 1 и 2, минимальное энергетическое состояние ложного вакуума в точке «А» до перехода ТВО имеет более высокую энергию, чем состояние истинного вакуума в точке «В» после перехода. Эта разница энергий и вносит свой вклад в энергию вакуума. В течение переходного периода ТВО положительное давление за счет энергии вакуума было бы намного больше, чем сдерживающее давление, создаваемое гравитационным влиянием вещества и излучения. Вселенная раздулась бы с огромной скоростью, инфляция была вызвана давлением вакуума! В этой картине Вселенной космологическая постоянная Эйнштейна приобретает совершенно новое значение, поскольку теперь она представляет собой определенное физическое понятие; Это просто мера разницы энергий между истинным и ложным состояниями вакуума («В» и «А» на рисунках 1 и 2) в определенный момент истории Вселенной. Это также говорит нам о том, что, как и в модели де Ситтера, Вселенная, в которой вакуум вносит свой вклад, должна расширяться во времени экспоненциально, а не линейно, как предсказывает модель Большого взрыва. Сценарий Гута для расширения Вселенной обычно называют «инфляционной Вселенной» из-за быстроты расширения и представляет собой фазу, которая закончится только после того, как истинный вакуум вытеснит ложный вакуум старой, симметричной фазы.
Это также говорит нам о том, что, как и в модели де Ситтера, Вселенная, в которой вакуум вносит свой вклад, должна расширяться во времени экспоненциально, а не линейно, как предсказывает модель Большого взрыва. Сценарий Гута для расширения Вселенной обычно называют «инфляционной Вселенной» из-за быстроты расширения и представляет собой фазу, которая закончится только после того, как истинный вакуум вытеснит ложный вакуум старой, симметричной фазы.
Основная проблема оригинальной модели Гута заключалась в том, что инфляционная фаза длилась очень долго, потому что состояние ложного вакуума очень стабильно. Вселенная оказывается в ловушке тупика состояния ложного вакуума, и экспоненциальное расширение никогда не прекращается. Это было бы чем-то похоже на воду, отказывающуюся замерзать, даже если ее температура упала значительно ниже 0 градусов по Цельсию. Недавние модификации исходной модели «инфляционной Вселенной» привели к тому, что сейчас называется «новой» моделью инфляционной Вселенной. В этой модели Вселенной удается выйти из состояния ложного вакуума и за короткое время эволюционирует в привычное состояние истинного вакуума. 9-24 секунды, за это время Вселенная претерпела бы 10 миллиардов удвоений своего размера! Это число, которое действительно за гранью понимания. Для сравнения: чтобы раздуть атом водорода до размеров всей видимой Вселенной, требуется всего 120 удвоений! Согласно инфляционной модели, пузырьки истинно вакуумной фазы расширялись со скоростью света. Многие из них должны были столкнуться, когда Вселенная была очень молода, чтобы видимая Вселенная сегодня казалась такой однородной. Единственный пузырь не стал бы достаточно большим, чтобы охватить всю нашу видимую вселенную в это время; Радиус около 15-20 миллиардов световых лет. С другой стороны, новая инфляционная модель утверждает, что даже пузыри увеличивались в размерах экспоненциально, как и их разделение. Сами пузыри выросли до огромных размеров, намного превышающих размер нашей наблюдаемой Вселенной.
В этой модели Вселенной удается выйти из состояния ложного вакуума и за короткое время эволюционирует в привычное состояние истинного вакуума. 9-24 секунды, за это время Вселенная претерпела бы 10 миллиардов удвоений своего размера! Это число, которое действительно за гранью понимания. Для сравнения: чтобы раздуть атом водорода до размеров всей видимой Вселенной, требуется всего 120 удвоений! Согласно инфляционной модели, пузырьки истинно вакуумной фазы расширялись со скоростью света. Многие из них должны были столкнуться, когда Вселенная была очень молода, чтобы видимая Вселенная сегодня казалась такой однородной. Единственный пузырь не стал бы достаточно большим, чтобы охватить всю нашу видимую вселенную в это время; Радиус около 15-20 миллиардов световых лет. С другой стороны, новая инфляционная модель утверждает, что даже пузыри увеличивались в размерах экспоненциально, как и их разделение. Сами пузыри выросли до огромных размеров, намного превышающих размер нашей наблюдаемой Вселенной. 3000 см. Мы не должны слишком беспокоиться о том, что эти пузыри расширяются во много раз со скоростью света, поскольку их границы не представляют собой физическую сущность. Нет ни электронов, ни кварков, движущихся на расширяющейся ударной волне. Вместо этого расширяется нематериальный вакуум пространства. Скорость расширения пузырьков не ограничивается никаким физическим пределом скорости, например скоростью света.
3000 см. Мы не должны слишком беспокоиться о том, что эти пузыри расширяются во много раз со скоростью света, поскольку их границы не представляют собой физическую сущность. Нет ни электронов, ни кварков, движущихся на расширяющейся ударной волне. Вместо этого расширяется нематериальный вакуум пространства. Скорость расширения пузырьков не ограничивается никаким физическим пределом скорости, например скоростью света.
GUM в GUT
Потенциальная проблема для космологий, которые имеют фазовые переходы в эпоху GUT, заключается в том, что любопытный зоопарк объектов мог бы быть порожден, если бы происходили частые слияния пузырей, как того требует инфляционная модель Гута. Во-первых, каждый пузырек истинно вакуумной фазы содержит свое поле Хиггса, имеющее уникальную ориентацию в пространстве. Кажется вероятным, что ни у каких двух пузырей не будет полей Хиггса, ориентированных совершенно одинаково, так что при слиянии пузырей образуются узлы. Согласно Герхарду т’Хофту и Александру Полякову, эти узлы в поле Хиггса — это магнитные монополи, первоначально предложенные 40 лет назад Полем Дираком, и их должно быть примерно столько же, сколько было слияний пузырей в переходный период. 16 ГэВ) их должно быть в 1 триллион триллионов раз меньше, чем фотонов. на космическом фоне 3К. Расчеты, основанные на старой инфляционной модели, предполагают, что этих GUM (монополей Великого объединения) могло быть в 100 триллионов раз больше, чем верхний предел! Такая Вселенная определенно была бы «закрытой» и, более того, прошла бы всю свою историю между расширением и повторным коллапсом в течение нескольких тысяч лет. Новая модель инфляционной вселенной решает эту проблему перепроизводства «GUM», поскольку мы живем только внутри одного из этих пузырей, которые теперь почти бесконечно больше, чем наша видимая Вселенная. Поскольку столкновения пузырей больше не требуются для гомогенизации материи и излучения во Вселенной, в нашей видимой Вселенной будет существовать очень мало монополей, если они вообще будут.
16 ГэВ) их должно быть в 1 триллион триллионов раз меньше, чем фотонов. на космическом фоне 3К. Расчеты, основанные на старой инфляционной модели, предполагают, что этих GUM (монополей Великого объединения) могло быть в 100 триллионов раз больше, чем верхний предел! Такая Вселенная определенно была бы «закрытой» и, более того, прошла бы всю свою историю между расширением и повторным коллапсом в течение нескольких тысяч лет. Новая модель инфляционной вселенной решает эту проблему перепроизводства «GUM», поскольку мы живем только внутри одного из этих пузырей, которые теперь почти бесконечно больше, чем наша видимая Вселенная. Поскольку столкновения пузырей больше не требуются для гомогенизации материи и излучения во Вселенной, в нашей видимой Вселенной будет существовать очень мало монополей, если они вообще будут.
Горизонты
Продолжительный период инфляции оказал бы важное влияние на излучение космического огненного шара. Одной из давних проблем современной космологии является то, что все направления на небе имеют одинаковую температуру с точностью до поразительной 1 части на 10 000. Если учесть, что регионы, разделенные на небе всего на несколько градусов, только недавно сообщались друг с другом, трудно понять, как регионы, расположенные дальше друг от друга, могут быть настолько похожи по температуре. Излучение из одной из этих областей, движущееся со скоростью света, еще не преодолело промежуточное расстояние до другой, хотя излучение могло начать свой путь с момента возникновения Вселенной. Этот «коммуникационный разрыв» помешает этим регионам сгладить разницу температур.
Если учесть, что регионы, разделенные на небе всего на несколько градусов, только недавно сообщались друг с другом, трудно понять, как регионы, расположенные дальше друг от друга, могут быть настолько похожи по температуре. Излучение из одной из этих областей, движущееся со скоростью света, еще не преодолело промежуточное расстояние до другой, хотя излучение могло начать свой путь с момента возникновения Вселенной. Этот «коммуникационный разрыв» помешает этим регионам сгладить разницу температур.
В стандартной модели Большого взрыва, когда мы оглядываемся на более ранние эпохи из настоящего времени, расстояния между частицами уменьшаются медленнее, чем сужаются их горизонты. Соседние регионы космоса в настоящее время разъединяются, поэтому разность температур может развиваться свободно. В конце концов, когда мы оглядываемся назад, в очень древние времена, горизонты настолько малы, что каждая существующая частица буквально заполняет весь объем своей собственной наблюдаемой вселенной. 86) имел почти идентичные свойства, такие как температура. Любое отклонение от этой ситуации в то время вылилось бы в значительные перепады температур в отдаленных частях неба в настоящее время. К сожалению, какой-то организации пришлось бы устанавливать эти точно настроенные начальные условия, нарушая причинно-следственную связь. Противоречие состоит в том, что никакая сила не может действовать, передавая свое влияние быстрее скорости света. В инфляционных моделях это противоречие устраняется, поскольку расстояние между широко разбросанными точками в пространстве становится почти бесконечно малым по сравнению с размером горизонта, когда мы оглядываемся назад на эпоху инфляции. Поскольку эти точки теперь находятся в пределах световых горизонтов друг друга, любая разница температур была бы немедленно устранена, поскольку более горячие области теперь находились бы в радиационном контакте с более холодными. Благодаря этой экспоненциально растущей фазе де Ситтера в ранней истории Вселенной у нас теперь есть средство для решения проблемы горизонта.
86) имел почти идентичные свойства, такие как температура. Любое отклонение от этой ситуации в то время вылилось бы в значительные перепады температур в отдаленных частях неба в настоящее время. К сожалению, какой-то организации пришлось бы устанавливать эти точно настроенные начальные условия, нарушая причинно-следственную связь. Противоречие состоит в том, что никакая сила не может действовать, передавая свое влияние быстрее скорости света. В инфляционных моделях это противоречие устраняется, поскольку расстояние между широко разбросанными точками в пространстве становится почти бесконечно малым по сравнению с размером горизонта, когда мы оглядываемся назад на эпоху инфляции. Поскольку эти точки теперь находятся в пределах световых горизонтов друг друга, любая разница температур была бы немедленно устранена, поскольку более горячие области теперь находились бы в радиационном контакте с более холодными. Благодаря этой экспоненциально растущей фазе де Ситтера в ранней истории Вселенной у нас теперь есть средство для решения проблемы горизонта. 32 лет из-за распада протона.
32 лет из-за распада протона.
Несмотря на очевидные успехи, даже новая инфляционная модель Вселенной не лишена недостатков. Хотя кажется, что она дает объяснение нескольким космологическим загадкам, она не дает убедительного способа создания галактик. Те флуктуации плотности материи, которые переживают инфляционный период, настолько плотны, что в конце концов коллапсируют в черные дыры размером с галактику! Ни точный способ перехода к обычному хаббелевскому расширению, ни продолжительность инфляционного периода точно не определены.
Если бы инфляционные космологии могли удовлетворительно ответить на каждый из этих вопросов, мы могли бы иметь, как предложил Дж. Ричард Готт III, самую замечательную модель вселенной, в которой почти бесконечное число «пузырьковых вселенных», каждая из которых имеет почти бесконечное число размер, сосуществовать в одном и том же 4-мерном пространстве-времени; все эти пузырьковые вселенные возникли в один и тот же момент творения. Это менее проблематично, чем можно было бы подозревать, поскольку, если наша Вселенная на самом деле бесконечна, как предполагают имеющиеся данные, то она также была бесконечной даже в момент своего рождения! Можно даже предположить, что Вселенная «просачивается» с постоянно возникающими новыми пузырьковыми вселенными. Вся наша видимая Вселенная, вплоть до самого далекого квазара, была бы всего лишь одним бесконечно малым пятном внутри одной из этих пузырьковых областей. Есть ли в этих других вселенных галактики, звезды, планеты и живые существа, статистически подобные тем, что есть в нашей вселенной? Мы можем никогда не узнать. Эти другие вселенные, порожденные тем же пароксизмом Творения, что и наша собственная, навсегда находятся за пределами нашего внимания, но, очевидно, не в нашем воображении!
Вся наша видимая Вселенная, вплоть до самого далекого квазара, была бы всего лишь одним бесконечно малым пятном внутри одной из этих пузырьковых областей. Есть ли в этих других вселенных галактики, звезды, планеты и живые существа, статистически подобные тем, что есть в нашей вселенной? Мы можем никогда не узнать. Эти другие вселенные, порожденные тем же пароксизмом Творения, что и наша собственная, навсегда находятся за пределами нашего внимания, но, очевидно, не в нашем воображении!
После начала…
Наконец, что можно сказать о периоде до Великого объединения? Можно предположить, что при более высоких температурах, чем в эпоху ТВО, даже сверхмассивные бозоны Хиггса и лептокварка становятся безмассовыми, и в конце концов мы приходим ко времени, когда гравитационное взаимодействие объединяется со слабыми, электромагнитными и сильными взаимодействиями. Тем не менее, наши поиски понимания происхождения Вселенной остаются незавершенными, поскольку гравитацию еще предстоит привести в единство с остальными силами на теоретической основе. Этот последний шаг обещает быть не только самым трудным на долгом пути к объединению, но и, по-видимому, несет в себе величайшие надежды на то, что он прольет свет на некоторые из самых глубоких тайн физического мира. Даже сейчас несколько теоретиков по всему миру усердно работают над теорией под названием «Супергравитация», которая объединяет носители взаимодействия (фотоны, глюоны, гравитоны и бозоны слабого взаимодействия) с частицами, на которые они воздействуют (кварками, электронами и т. д.). Теория супергравитации также предсказывает существование новых частиц, называемых фотино и гравитино. Есть даже предположение, что фотино могут заполнять всю Вселенную и объяснять невидимую «недостающую» материю, необходимую для придания Вселенной критической массы, необходимой для того, чтобы она стала точно евклидовой. С другой стороны, гравитино не позволяют вычислениям, включающим обмен гравитонами, давать бесконечные ответы для задач, ответы на которые, как известно, совершенно конечны.
Этот последний шаг обещает быть не только самым трудным на долгом пути к объединению, но и, по-видимому, несет в себе величайшие надежды на то, что он прольет свет на некоторые из самых глубоких тайн физического мира. Даже сейчас несколько теоретиков по всему миру усердно работают над теорией под названием «Супергравитация», которая объединяет носители взаимодействия (фотоны, глюоны, гравитоны и бозоны слабого взаимодействия) с частицами, на которые они воздействуют (кварками, электронами и т. д.). Теория супергравитации также предсказывает существование новых частиц, называемых фотино и гравитино. Есть даже предположение, что фотино могут заполнять всю Вселенную и объяснять невидимую «недостающую» материю, необходимую для придания Вселенной критической массы, необходимой для того, чтобы она стала точно евклидовой. С другой стороны, гравитино не позволяют вычислениям, включающим обмен гравитонами, давать бесконечные ответы для задач, ответы на которые, как известно, совершенно конечны. До сих пор эти расчеты не учитывали влияния гравитино.
До сих пор эти расчеты не учитывали влияния гравитино.
Возможно, в течение следующего десятилетия будет выработано больше деталей последнего этапа Объединения, и тогда можно будет рассказать всю историю рождения нашей вселенной. Это действительно захватывающее время в истории человечества. Будут ли будущие поколения вечно завидовать нашему счастью, стать свидетелями раскрытия первой всеобъемлющей теории Существования при нашей жизни?
Большой взрывобщая теория относительностигравитацияпетлевая квантовая гравитацияквантовая гравитациятеория струнсуперсимметрияАстрономия, Физика
Стенблог
Имеет ли пространство более трех измерений?
Написано Стеном Оденвальдом
Copyright (C) 1984 Kalmbach Publishing. Перепечатано с разрешения
Интуитивное представление о том, что Вселенная имеет три измерения, кажется неопровержимым фактом. В конце концов, мы можем двигаться только вверх или вниз, влево или вправо, внутрь или наружу. Но все ли эти три измерения нам нужны для описания природы? Что, если есть больше измерений? Обязательно ли они повлияют на нас? А если нет, то как мы могли о них узнать? Некоторые физики и математики, изучающие происхождение Вселенной, думают, что у них есть некоторые ответы на эти вопросы. Они утверждают, что Вселенная имеет гораздо больше, чем три, четыре или пять измерений. Они считают, что их одиннадцать! Но давайте отступим на мгновение. Откуда мы знаем, что наша Вселенная состоит только из трех пространственных измерений? Давайте взглянем на некоторые «доказательства».
Но все ли эти три измерения нам нужны для описания природы? Что, если есть больше измерений? Обязательно ли они повлияют на нас? А если нет, то как мы могли о них узнать? Некоторые физики и математики, изучающие происхождение Вселенной, думают, что у них есть некоторые ответы на эти вопросы. Они утверждают, что Вселенная имеет гораздо больше, чем три, четыре или пять измерений. Они считают, что их одиннадцать! Но давайте отступим на мгновение. Откуда мы знаем, что наша Вселенная состоит только из трех пространственных измерений? Давайте взглянем на некоторые «доказательства».
На двумерном листе бумаги можно нарисовать бесконечное количество полигонов. Но когда вы попробуете тот же трюк в трех измерениях, вы столкнетесь с проблемой. Правильных многогранников всего пять и только пять. Правильный многогранник определяется как объемная фигура, грани которой представляют собой одинаковые многоугольники — треугольники, квадраты и пятиугольники — и которая построена так, что на каждом ребре встречаются только две грани. Если бы вы перешли от одной грани к другой, вы бы пересекли только одно ребро. Короткие пути внутри многогранника, которые могут привести вас от одной грани к другой, запрещены. Давным-давно математик Леонард Эйлер показал важное соотношение между количеством граней (F), ребер (E) и углов (C) для каждого правильного многогранника: C – E + F = 2. Например, куб имеет 6 граней, 12 ребер и 8 углов, а у додекаэдра 12 граней, 30 ребер и 20 углов. Прогоните эти числа через уравнение Эйлера, и результат всегда будет равен двум, как и в случае с оставшимися тремя многогранниками. Только пять твердых тел удовлетворяют этому соотношению — ни больше, ни меньше.
Если бы вы перешли от одной грани к другой, вы бы пересекли только одно ребро. Короткие пути внутри многогранника, которые могут привести вас от одной грани к другой, запрещены. Давным-давно математик Леонард Эйлер показал важное соотношение между количеством граней (F), ребер (E) и углов (C) для каждого правильного многогранника: C – E + F = 2. Например, куб имеет 6 граней, 12 ребер и 8 углов, а у додекаэдра 12 граней, 30 ребер и 20 углов. Прогоните эти числа через уравнение Эйлера, и результат всегда будет равен двум, как и в случае с оставшимися тремя многогранниками. Только пять твердых тел удовлетворяют этому соотношению — ни больше, ни меньше.
Не ограничиваясь только тремя измерениями, математики обобщили отношение Эйлера к многомерным пространствам и, как и следовало ожидать, получили интересные результаты. Например, в мире с четырьмя пространственными измерениями мы можем построить только шесть правильных тел. Один из них — «гиперкуб» — объемная фигура в четырехмерном пространстве, ограниченная восемью кубами, подобно тому как куб ограничен шестью квадратными гранями. Что произойдет, если мы добавим в пространство еще одно измерение? Даже самый амбициозный геометр, живущий в пятимерном мире, смог бы собрать только три правильных тела. Это означает, что два известных нам правильных тела — икосаэдр и додекаэдр — не имеют партнеров в пятимерной вселенной.
Что произойдет, если мы добавим в пространство еще одно измерение? Даже самый амбициозный геометр, живущий в пятимерном мире, смог бы собрать только три правильных тела. Это означает, что два известных нам правильных тела — икосаэдр и додекаэдр — не имеют партнеров в пятимерной вселенной.
Для тех из вас, кто успешно освоил визуализацию гиперкуба, попробуйте представить, как выглядит «ультракуб». Это пятимерный аналог куба, но на этот раз он ограничен одним гиперкубом на каждой из своих 10 граней! В конце концов, если бы наш привычный мир не был трехмерным, геометры не нашли бы всего пять правильных многогранников после 2500 лет поисков. Они нашли бы шесть (с четырьмя пространственными измерениями) или, возможно, только три (если бы мы жили в пятимерной вселенной). Вместо этого мы знаем только о пяти правильных твердых телах. А это говорит о том, что мы живем во Вселенной, имеющей не более трех пространственных измерений.
Хорошо, давайте предположим, что наша Вселенная на самом деле состоит из четырех пространственных измерений. Что случается? Поскольку теория относительности говорит нам, что мы также должны рассматривать время как измерение, теперь у нас есть пространство-время, состоящее из пяти измерений. Следствием пятимерного пространства-времени является то, что гравитация может действовать так, как мы этого не хотим.
Что случается? Поскольку теория относительности говорит нам, что мы также должны рассматривать время как измерение, теперь у нас есть пространство-время, состоящее из пяти измерений. Следствием пятимерного пространства-времени является то, что гравитация может действовать так, как мы этого не хотим.
Согласно лучшим доступным измерениям гравитация подчиняется закону обратных квадратов; то есть гравитационное притяжение между двумя объектами быстро уменьшается с увеличением расстояния. Например, если мы удвоим расстояние между двумя объектами, сила тяжести между ними станет на 1/4 меньше; если мы утроим расстояние, сила станет 1/9как сильный и так далее. Пятимерная теория гравитации вводит дополнительные математические термины, определяющие поведение гравитации. Эти члены могут принимать различные значения, в том числе нулевое. Однако если бы они были равны нулю, это было бы то же самое, что сказать, что гравитации требуется только три пространственных измерения и одно временное измерение, чтобы «дать ей жизнь». Тот факт, что космический корабль «Вояджер» смог пересечь миллиарды миль космоса за несколько лет и прибыть в космос в течение нескольких секунд от предсказанного времени, является прекрасной демонстрацией того, что нам не нужны дополнительные пространственные измерения для описания движений в гравитационном поле Солнца.
Тот факт, что космический корабль «Вояджер» смог пересечь миллиарды миль космоса за несколько лет и прибыть в космос в течение нескольких секунд от предсказанного времени, является прекрасной демонстрацией того, что нам не нужны дополнительные пространственные измерения для описания движений в гравитационном поле Солнца.
Из приведенных выше геометрических и физических аргументов мы можем заключить (что неудивительно), что пространство трехмерно — в масштабах от повседневных объектов до, по крайней мере, Солнечной системы. Если бы это было не так, то геометры нашли бы более пяти правильных многогранников и гравитация действовала бы совсем иначе, чем сейчас — «Вояджер» не прибыл бы вовремя. Итак, мы определили, что нашим физическим законам требуется не более трех пространственных измерений, чтобы описать, как устроена Вселенная. Или они? Возможно, есть какая-то другая арена в физическом мире, где многомерное пространство было бы преимуществом, а не недостатком?
Начиная с 1920-х годов физики пробовали многочисленные подходы к объединению основных природных взаимодействий: гравитации, электромагнетизма, сильных и слабых взаимодействий в атомных ядрах. К сожалению, вскоре физики поняли, что общей теории относительности в четырехмерном пространстве-времени не хватает математических «ручек», на которые можно было бы навесить рамки для трех других сил. Между 1921 и 1927 годами Теодор Калуца и Оскар Кляйн разработали первую многообещающую теорию, сочетающую гравитацию и электромагнетизм. Они сделали это, расширив общую теорию относительности до пяти измерений. Для большинства из нас общая теория относительности достаточно загадочна в обычном четырехмерном пространстве-времени. Какие чудеса могут ожидать нас в этой расширенной вселенной?
К сожалению, вскоре физики поняли, что общей теории относительности в четырехмерном пространстве-времени не хватает математических «ручек», на которые можно было бы навесить рамки для трех других сил. Между 1921 и 1927 годами Теодор Калуца и Оскар Кляйн разработали первую многообещающую теорию, сочетающую гравитацию и электромагнетизм. Они сделали это, расширив общую теорию относительности до пяти измерений. Для большинства из нас общая теория относительности достаточно загадочна в обычном четырехмерном пространстве-времени. Какие чудеса могут ожидать нас в этой расширенной вселенной?
Общая теория относительности в пяти измерениях дала теоретикам возможность манипулировать пятью дополнительными величинами помимо 10, необходимых для адекватного определения гравитационного поля. Калуца и Клейн заметили, что четыре из пяти дополнительных величин можно отождествить с четырьмя компонентами, необходимыми для определения электромагнитного поля. На самом деле, к радости Калуцы и Кляйна, эти четыре величины подчинялись тем же типам уравнений, что и уравнения, выведенные Максвеллом в конце 1800-х годов для электромагнитного излучения. Хотя это было многообещающее начало, этот подход так и не прижился и вскоре был наплыв теоретических работ по квантовой теории электромагнитных сил. Только в 19 в. началась работа над теорией супергравитации.75, что метод Калуцы и Клейна вызвал новый интерес. Его время наконец пришло.
Хотя это было многообещающее начало, этот подход так и не прижился и вскоре был наплыв теоретических работ по квантовой теории электромагнитных сил. Только в 19 в. началась работа над теорией супергравитации.75, что метод Калуцы и Клейна вызвал новый интерес. Его время наконец пришло.
Что надеются получить теоретики, расширяя общую теорию относительности за пределы обычных четырех измерений пространства-времени? Возможно, изучая общую теорию относительности в многомерной формулировке, мы сможем объяснить некоторые константы, необходимые для описания сил природы. Например, почему протон в 1836 раз массивнее электрона? Почему существует только шесть типов кварков и лептонов? Почему нейтрино безмассовые? Возможно, такая теория сможет дать нам новые правила для расчета масс элементарных частиц и способов их влияния друг на друга. Эти многомерные теории относительности могут также рассказать нам кое-что о количестве и свойствах таинственного нового семейства частиц — бозонов Хиггса, существование которых предсказывается различными схемами космического объединения. (См. «Распад ложного вакуума», АСТРОНОМИЯ, 19 ноября.83.)
(См. «Распад ложного вакуума», АСТРОНОМИЯ, 19 ноября.83.)
Эти ожидания — не просто несбыточные мечты физиков — они на самом деле, кажется, развиваются как естественные следствия некоторых типов теорий, изученных за последние несколько лет. В 1979 году Джон Тейлор из Королевского колледжа в Лондоне обнаружил, что некоторые формализмы высших измерений могут дать предсказания для максимальной массы бозона Хиггса (примерно в 76 раз больше, чем у протона). предсказывают существование этих частиц — они не могут предоставить конкретных подробностей об их физических характеристиках. Но теоретики могут определить некоторые из этих деталей, используя расширенные теории общей теории относительности. Экспериментально нам известны шесть лептонов: электрон, мюон, тауон и три связанных с ними нейтрино. Однако самое замечательное предсказание этих расширенных схем относительности состоит в том, что число лептонов, способных существовать во Вселенной, связано с числом измерений пространства-времени. Например, в шестимерном пространстве-времени может существовать только один лептон — предположительно электрон. В 10-мерном пространстве-времени может существовать четыре лептона, но этого недостаточно, чтобы разместить шесть наблюдаемых нами. В 12-мерном пространстве-времени мы можем учесть все шесть известных лептонов, но мы также приобретаем два дополнительных лептона, которые еще не обнаружены. Ясно, что на фундаментальном уровне мы бы многого добились, если бы смогли немного увеличить количество измерений в наших теориях.
Например, в шестимерном пространстве-времени может существовать только один лептон — предположительно электрон. В 10-мерном пространстве-времени может существовать четыре лептона, но этого недостаточно, чтобы разместить шесть наблюдаемых нами. В 12-мерном пространстве-времени мы можем учесть все шесть известных лептонов, но мы также приобретаем два дополнительных лептона, которые еще не обнаружены. Ясно, что на фундаментальном уровне мы бы многого добились, если бы смогли немного увеличить количество измерений в наших теориях.
Сколько дополнительных измерений нам нужно рассмотреть, чтобы объяснить элементарные частицы и силы, о которых мы знаем сегодня? Очевидно, нам требуется по крайней мере одно дополнительное пространственное измерение для каждого отдельного «заряда», который характеризует, как каждая сила взаимодействует с материей. Для электромагнитной силы нам нужны два электрических заряда: положительный и отрицательный. Для сильного взаимодействия, которое связывает кварки вместе, образуя, среди прочего, протоны и нейтроны, нам нужны три «цветовых» заряда — красный, синий и зеленый. Наконец, нам нужны два «слабых» заряда, чтобы объяснить слабое ядерное взаимодействие. если мы добавим пространственное измерение для каждого из этих зарядов, мы получим в общей сложности семь дополнительных измерений. Должным образом расширенная общая теория относительности, которую мы ищем, — это теория с 11-мерным пространством-временем, по крайней мере. Подумайте об этом — одно только пространство должно иметь по крайней мере 10 измерений, чтобы вместить все поля, известные сегодня.
Наконец, нам нужны два «слабых» заряда, чтобы объяснить слабое ядерное взаимодействие. если мы добавим пространственное измерение для каждого из этих зарядов, мы получим в общей сложности семь дополнительных измерений. Должным образом расширенная общая теория относительности, которую мы ищем, — это теория с 11-мерным пространством-временем, по крайней мере. Подумайте об этом — одно только пространство должно иметь по крайней мере 10 измерений, чтобы вместить все поля, известные сегодня.
Конечно, эти дополнительные измерения не обязательно должны быть похожи на те, о которых мы уже знаем. В контексте современной единой теории поля эти дополнительные измерения в некотором смысле являются внутренними для самих частиц — «личной тайной», доступной только частицам и полям, которые на них воздействуют! Эти измерения не наблюдаемы физически в том же смысле, что и три пространственных измерения, которые мы переживаем; они стоят по отношению к обычным трем измерениям пространства так же, как пространство стоит по отношению ко времени.
Сегодняшний настоящий ренессанс в поиске единства между силами и частицами, составляющими космос, причем некоторые методы отличаются от тех, которые мы обсуждали, эти новые подходы приводят нас к удивительно схожим выводам. Похоже, что четырехмерное пространство-время просто недостаточно сложно для того, чтобы физика могла так действовать.
Мы знаем, что частицы, называемые бозонами, передают силы природы. Мы также знаем, что эти силы действуют на частицы, называемые фермионами. Члены семейства фермионов носят знакомые имена электрон, мюон, нейтрино и кварк; бозоны — это менее известные гравитонные, фотонные, глюонные и промежуточные векторные бозоны. Теории великого объединения развивались с 1975 теперь показывают, что эти частицы являются «ароматами» более абстрактного семейства суперчастиц — точно так же, как мюон — это другой тип электрона. Это выражение нового вида космической симметрии, получившей название суперсимметрии, потому что она всеобъемлюща. Сюда входят не только бозоны, переносящие взаимодействие, но и частицы, на которые действуют эти силы. Существует также соответствующая сила, помогающая природе поддерживать суперсимметрию во время различных взаимодействий. Это называется супергравитацией. Теория суперсимметрии вводит два новых типа фундаментальных частиц — гравитино и фотино. Гравитино обладает замечательным свойством математически смягчать силу различных видов взаимодействий, связанных с обменом гравитонами. Фотоно, двоюродный брат фотона, может помочь объяснить «недостающую массу» во Вселенной.
Существует также соответствующая сила, помогающая природе поддерживать суперсимметрию во время различных взаимодействий. Это называется супергравитацией. Теория суперсимметрии вводит два новых типа фундаментальных частиц — гравитино и фотино. Гравитино обладает замечательным свойством математически смягчать силу различных видов взаимодействий, связанных с обменом гравитонами. Фотоно, двоюродный брат фотона, может помочь объяснить «недостающую массу» во Вселенной.
Теория суперсимметрии на самом деле представляет собой комплекс из восьми различных теорий, наложенных друг на друга, как ступеньки лестницы. Чем выше ступень, тем больше ее дополнение разрешенных состояний частиц фермионов и бозонов. Кажется, самой «вместительной» из всех теорий является SO(8) (произносится как «эсс-о-восемь»), которая может содержать 99 различных типов бозонов и 64 различных типа фермионов. Но SO(8) превосходит своего подчиненного, SO(7), только на одно дополнительное измерение и одно дополнительное состояние частицы. Поскольку SO(8) идентичен SO(7) во всех его существенных чертах, вместо этого мы обсудим SO(7). Однако мы знаем гораздо больше, чем 162 типа частиц, которые может вместить SO(7), и многие из предсказанных типов никогда не наблюдались (например, безмассовое гравитино). SO(7) требует семь внутренних измерений в дополнение к четырем, которые мы знаем, — времени и трем «повседневным» пространственным измерениям. Если SO(7) вообще отражает реальность, то наша Вселенная должна иметь как минимум 11 измерений! К сожалению, В. Нам в Европейском центре ядерных исследований в Женеве, Швейцария, продемонстрировал, что теории суперсимметрии для пространства-времени с более чем 11 измерениями теоретически невозможны. SO(7), очевидно, имеет максимально возможное количество пространственных измерений, но в нем все еще недостаточно места для размещения всех известных типов частиц.
Поскольку SO(8) идентичен SO(7) во всех его существенных чертах, вместо этого мы обсудим SO(7). Однако мы знаем гораздо больше, чем 162 типа частиц, которые может вместить SO(7), и многие из предсказанных типов никогда не наблюдались (например, безмассовое гравитино). SO(7) требует семь внутренних измерений в дополнение к четырем, которые мы знаем, — времени и трем «повседневным» пространственным измерениям. Если SO(7) вообще отражает реальность, то наша Вселенная должна иметь как минимум 11 измерений! К сожалению, В. Нам в Европейском центре ядерных исследований в Женеве, Швейцария, продемонстрировал, что теории суперсимметрии для пространства-времени с более чем 11 измерениями теоретически невозможны. SO(7), очевидно, имеет максимально возможное количество пространственных измерений, но в нем все еще недостаточно места для размещения всех известных типов частиц.
Неясно, к чему ведут эти различные направления исследований. Возможно, нигде. Безусловно, существует множество исторических прецедентов для идей, от которых позже отказались, поскольку они оказались концептуальными тупиками. Но что, если они окажутся правильными на каком-то уровне? Начала ли наша Вселенная свою жизнь как некий 11-мерный «объект», который затем кристаллизовался в наш четырехмерный космос?
Но что, если они окажутся правильными на каком-то уровне? Начала ли наша Вселенная свою жизнь как некий 11-мерный «объект», который затем кристаллизовался в наш четырехмерный космос?
Хотя эти внутренние измерения могут не иметь большого отношения к реальному миру в настоящее время, возможно, так было не всегда. Э. Креммер и Дж. Шерк из I’Ecole Normale Superieure в Париже показали, что точно так же, как Вселенная претерпевала фазовые переходы в своей ранней истории, когда силы природы стали различимы, Вселенная могла также пройти через фазовый переход, когда менсиональность измененный. Предположительно материя имеет что-то вроде четырех внешних измерений (с которыми мы сталкиваемся каждый день) и что-то вроде семи внутренних измерений. К счастью для нас, эти семь дополнительных измерений не распространяются на большую четырехмерную реальность, в которой мы живем. Если бы они это сделали, простая прогулка по парку могла бы превратиться в настоящую полосу препятствий, усеянную червоточинами в космосе и кто знает чем еще! 9-31 сантиметр к настоящему времени. Пятое измерение Вселенной почти исчезло и составляет 20 степеней 10 — 100 миллиардов миллиардов раз — меньше, чем размер протона. Хотя Вселенная кажется четырехмерной в пространстве-времени, такое восприятие случайно из-за нашего большого размера по сравнению с масштабами других измерений. Большинство из нас думают, что измерение простирается до бесконечности, но это еще не все. Например, если нашей Вселенной действительно суждено вновь схлопнуться в далеком будущем, то трехмерное пространство, которое мы знаем сегодня, на самом деле ограничено само по себе — оно в конечном итоге будет обладать максимальным, конечным размером. Так уж получилось, что физические размеры человека вынуждают нас рассматривать эти три пространственных измерения как бесконечно большие.
Пятое измерение Вселенной почти исчезло и составляет 20 степеней 10 — 100 миллиардов миллиардов раз — меньше, чем размер протона. Хотя Вселенная кажется четырехмерной в пространстве-времени, такое восприятие случайно из-за нашего большого размера по сравнению с масштабами других измерений. Большинство из нас думают, что измерение простирается до бесконечности, но это еще не все. Например, если нашей Вселенной действительно суждено вновь схлопнуться в далеком будущем, то трехмерное пространство, которое мы знаем сегодня, на самом деле ограничено само по себе — оно в конечном итоге будет обладать максимальным, конечным размером. Так уж получилось, что физические размеры человека вынуждают нас рассматривать эти три пространственных измерения как бесконечно большие.
Нетрудно смириться с мыслью, что пятое (или шестое, или одиннадцатое) измерение может быть меньше атомного ядра — в самом деле, мы, вероятно, можем быть благодарны за то, что это так.
размерностьобщая теория относительностигравитацияпетлевая квантовая гравитацияквантовая гравитацияпространствотеория струнастрономия, физика
Стенблог
Космический фактор выдумки Эйнштейна
Автор Стен Оденвальд
Copyright (C) 1991. Sky Publishing Corporation. Перепечатано с разрешения. См. выпуск за апрель 1991 г.
Черные дыры… кварки… темная материя. Кажется, что космос становится немного страннее каждый год. До недавнего времени астрономическая вселенная, известная людям, была населена планетами, звездами, галактиками и рассеянными туманностями из пыли и газа. Теоретики говорят нам, что он также может быть населен такими объектами, как суперструны, темная материя и массивные нейтрино — объектами, которые еще предстоит открыть, если они вообще существуют!
Как бы странно ни звучали эти новые компоненты, вам не нужно быть ученым-ракетчиком, чтобы оценить самый загадочный ингредиент из всех. Именно чернильная чернота самого космоса приковывает наше внимание, когда мы смотрим на ночное небо; не редкие точки света, которые сигнализируют о наличии широко рассеянного вещества.
В течение последних нескольких десятилетий физики и астрономы начали осознавать, что понятие пустого пространства содержит больше тонкостей, чем когда-либо прежде. Пространство — это не просто пассивный сосуд, который должен быть заполнен материей и излучением, но самостоятельная динамическая физическая сущность.
Одна глава в истории нашей новой концепции пространства начинается со знаменитой теоретической ошибки, допущенной почти 75 лет назад, которая теперь, кажется, обрела собственную жизнь.
В 1917 году Альберт Эйнштейн попытался использовать свою недавно разработанную общую теорию относительности для описания формы и эволюции Вселенной. В то время господствовало представление о том, что Вселенная статична и неизменна. Эйнштейн полностью ожидал, что общая теория относительности поддержит эту точку зрения, но, как ни удивительно, этого не произошло. Неумолимая сила гравитации, притягивающая каждую частицу материи, требовала, чтобы Вселенная рухнула под собственным весом.
Его решением этой дилеммы было добавление нового термина «антигравитация» к своим исходным уравнениям. Это позволило его математической вселенной казаться такой же постоянной и неизменной, как реальная. Этот термин, обычно записываемый как заглавная греческая лямбда, называется «космологической постоянной». Оно имеет точно такое же значение повсюду во Вселенной, тщательно подобранное, чтобы компенсировать тенденцию к гравитационному коллапсу в каждой точке пространства.
Простой мысленный эксперимент может помочь проиллюстрировать природу лямбды. Возьмите кубический метр пространства и удалите из него всю материю и излучение. Большинство из нас согласится, что это идеальный вакуум. Но, подобно призраку в ночи, космологическая постоянная все еще была бы здесь. Итак, пустое пространство на самом деле вовсе не пусто — Лямбда придает ему своеобразную «скрытую энергию». Другими словами, даже Ничто есть Нечто!
Выдуманное решение Эйнштейна оставалось неоспоримым до 1922 года, когда русский математик Александр Фридман начал создавать убедительные космологические модели, основанные на уравнениях Эйнштейна, но без дополнительных величин. Вскоре после этого теоретики, внимательно изучавшие модель Эйнштейна, обнаружили, что, подобно карандашу, балансирующему на острие, она неустойчива к коллапсу или расширению. Позже в том же десятилетии астроном Маунт-Вильсон Эдвин П. Хаббл обнаружил прямое наблюдательное свидетельство того, что Вселенная не статична, а расширяется.
Вскоре после этого теоретики, внимательно изучавшие модель Эйнштейна, обнаружили, что, подобно карандашу, балансирующему на острие, она неустойчива к коллапсу или расширению. Позже в том же десятилетии астроном Маунт-Вильсон Эдвин П. Хаббл обнаружил прямое наблюдательное свидетельство того, что Вселенная не статична, а расширяется.
Все это упоминание о том, что мотивация введения космологической постоянной казалась надуманной. Признав свою ошибку, Эйнштейн отказался от лямбды в 1932 году. Сначала казалось, что это положило конец спорам о ее существовании. Тем не менее, десятилетия спустя, несмотря на опровержение великого физика, Лямбда продолжает появляться в дискуссиях космологов о происхождении, эволюции и судьбе Вселенной.
ТЕОРИЯ СООТВЕТСТВУЕТ НАБЛЮДЕНИЯМ
Стандартная модель Фридмана «Большого взрыва» без космологической постоянной предсказывает, что возраст Вселенной t0 и скорость ее расширения (представленная параметром Хаббла H0) связаны уравнением t0 = 2/3H0. Некоторые астрономы предпочитают значение H0 около 50 километров в секунду на мегапарсек (один мегапарсек равен 3,26 миллиона световых лет). Но вес данных наблюдений, похоже, склоняет чашу весов к значению, близкому к 100. В модели Фридмана это означает, что космосу может быть не более 7 миллиардов лет. Тем не менее возраст некоторых шаровых скоплений нашей галактики оценивается независимыми методами от 12 до 18 миллиардов лет!
Некоторые астрономы предпочитают значение H0 около 50 километров в секунду на мегапарсек (один мегапарсек равен 3,26 миллиона световых лет). Но вес данных наблюдений, похоже, склоняет чашу весов к значению, близкому к 100. В модели Фридмана это означает, что космосу может быть не более 7 миллиардов лет. Тем не менее возраст некоторых шаровых скоплений нашей галактики оценивается независимыми методами от 12 до 18 миллиардов лет!
В том, что называется космологией Эйнштейна-ДеСиттера, лямбда-член помогает разрешить это несоответствие. Теперь большое значение параметра Хаббла можно частично объяснить «космическим отталкиванием». Это изменяет отношение между t0 и H0, так что для данного размера Вселенная старше, чем предсказывает модель Фридмана.
В одной формулировке уравнения Эйнштейна лямбда выражается в единицах плотности материи. Это означает, что мы можем спросить, как космологическая постоянная, если она вообще существует, соотносится с плотностью Вселенной в формах звезд и галактик.
До сих пор тщательный анализ доступных астрономических данных дал только верхние пределы величины лямбда. Они варьируются в значительном диапазоне — примерно от 10 процентов плотности обычного вещества до плотности в несколько раз больше этой.
Космологическая постоянная также может наложить свой отпечаток на свойства гравитационных линз и слабых галактик. Одной из замечательных особенностей общей теории относительности Эйнштейна является ее предсказание того, что пространство и время деформируются или «искажаются» вблизи массивного тела, такого как планета, звезда или даже галактика. Пути световых лучей, проходящих через такие области искривленного «пространства-времени», меняются. На космологической арене близлежащие галактики могут отклонять и искажать изображения более далеких галактик позади них. Иногда изображения этих далеких галактик могут выглядеть как несколько изображений, окружающих близлежащую «линзирующую» галактику.
В Киотском университете М. Фукугита и его коллеги предсказали, что будет обнаружено больше слабых галактик и гравитационных линз, чем во Вселенной Фридмана, если лямбда более чем в несколько раз превышает плотность материи. Эдвин Тернер, астрофизик из Принстонского университета, также проанализировал существующие скудные данные о гравитационных линзах и обнаружил, что их количество столь же велико, как и ожидалось, для лямбда, меньше чем в несколько раз превышающей плотность вещества. Судя по наилучшей астрономической разведке, лямбда, вероятно, не больше, чем наблюдаемая средняя плотность материи во Вселенной. Если на то пошло, нет убедительных доказательств того, что лямбда не точно равна нулю. Так почему бы просто не отбросить это как ненужное осложнение? Потому что космологическая постоянная больше не является, строго говоря, конструкцией теоретической космологии.
Эдвин Тернер, астрофизик из Принстонского университета, также проанализировал существующие скудные данные о гравитационных линзах и обнаружил, что их количество столь же велико, как и ожидалось, для лямбда, меньше чем в несколько раз превышающей плотность вещества. Судя по наилучшей астрономической разведке, лямбда, вероятно, не больше, чем наблюдаемая средняя плотность материи во Вселенной. Если на то пошло, нет убедительных доказательств того, что лямбда не точно равна нулю. Так почему бы просто не отбросить это как ненужное осложнение? Потому что космологическая постоянная больше не является, строго говоря, конструкцией теоретической космологии.
НИЧЕГО И ВСЕ
Чтобы понять, как возникла наша Вселенная и как эволюционировали ее различные составляющие, мы должны глубоко изучить фундаментальные составляющие материи и силы, определяющие ее взаимодействие. Это означает, что вопросы, которые нам придется задать, будут иметь больше общего с физикой, чем с астрономией. Вскоре после Большого взрыва Вселенная была при такой высокой температуре и плотности, что важны были только детали состава материи (кварки, электроны и т. д.) и то, как они взаимодействуют через четыре фундаментальные силы природы. Они представляли собой самые сложные из существующих скоплений материи задолго до того, как на сцену вышли атомы, планеты, звезды и галактики.
Вскоре после Большого взрыва Вселенная была при такой высокой температуре и плотности, что важны были только детали состава материи (кварки, электроны и т. д.) и то, как они взаимодействуют через четыре фундаментальные силы природы. Они представляли собой самые сложные из существующих скоплений материи задолго до того, как на сцену вышли атомы, планеты, звезды и галактики.
Вот уже два десятилетия физики пытаются объединить силы и частицы, из которых состоит наш мир, чтобы найти общее математическое описание, охватывающее их все. Некоторые думают, что такая Теория Всего находится в пределах досягаемости. Это объясняет не только известные формы материи, но и фундаментальные взаимодействия между ними: гравитацию, электромагнетизм, сильные и слабые ядерные взаимодействия.
Эти теории объединения известны под разными названиями: теория великого объединения, теория суперсимметрии и теория суперструн. Их основное утверждение состоит в том, что Природа действует в соответствии с небольшим набором простых правил, называемых симметриями.
Концепция симметрии так же стара, как древняя греческая цивилизация, чье искусство и архитектура являются шедеврами простоты и баланса. Геометрам давно известно, что простой куб можно повернуть на 90 градусов без изменения его внешнего вида. В двух измерениях равнобедренные треугольники выглядят одинаково, если их повернуть на 120 градусов. Это примеры геометрической концепции вращательной симметрии.
Существуют параллели с геометрической симметрией в способах выражения различных физических явлений и качеств материи. Например, хорошо известный принцип сохранения энергии является следствием того факта, что когда некоторые совокупности материи и энергии исследуются в разное время, каждая из них имеет в точности одинаковую полную энергию, так же как куб выглядит одинаково, когда он вращается в пространстве на заданную величину. Симметрия при «сдвиге во времени» так же тесно связана с законом сохранения энергии, как и симметрия куба при повороте на 90 градусов.
Среди прочего, симметрии Природы определяют силу и диапазон природных сил и свойства частиц, на которые они воздействуют. Хотя симметрии Природы скрыты в сегодняшнем холодном мире, они проявляются при очень высоких температурах и могут быть изучены в современных ускорителях частиц.
Хотя симметрии Природы скрыты в сегодняшнем холодном мире, они проявляются при очень высоких температурах и могут быть изучены в современных ускорителях частиц.
Настоящая цель теории объединения на самом деле двояка: не только раскрыть и описать основные симметрии мира, но и найти физические механизмы для их «нарушения» при низкой энергии. Ведь мы живем в сложном мире, наполненном разнообразием частиц и сил, а не в пресном мире с одним видом силы и одним видом частицы!
Теоретики, работающие над этой проблемой, часто вынуждены добавлять в свои уравнения члены, представляющие совершенно новые области в Природе. Понятие поля было изобретено математиками, чтобы показать, как конкретная величина может изменяться от точки к точке пространства. Физики с 18 века приняли эту идею для количественного описания того, как такие силы, как гравитация и магнетизм, изменяются на разных расстояниях от тела.
Взаимодействие этих полей с кварками, электронами и другими частицами приводит к нарушению симметрии. Эти поля обычно сильно отличаются от тех, о которых мы уже знаем. Например, столь востребованное поле бозона Хиггса было введено Шелдоном Глэшоу, Абдусом Саламом и Стивеном Вайнбергом в их объединенной теории электромагнитных и слабых ядерных взаимодействий.
Эти поля обычно сильно отличаются от тех, о которых мы уже знаем. Например, столь востребованное поле бозона Хиггса было введено Шелдоном Глэшоу, Абдусом Саламом и Стивеном Вайнбергом в их объединенной теории электромагнитных и слабых ядерных взаимодействий.
До их работы слабое взаимодействие, вызывающее распад определенных частиц, и электромагнитное взаимодействие, ответственное за притяжение между заряженными частицами и движение стрелки компаса, считались разными силами в природе. Объединив свои математические описания в общий язык, они показали, что это различие вовсе не принципиально для сил! Новое поле в природе, называемое полем Хиггса, заставляет эти две силы действовать по-разному при низкой температуре. Но при температурах выше 1000 триллионов градусов слабое и электромагнитное взаимодействия становятся практически идентичными в том, как они воздействуют на материю. Соответствующие частицы, называемые бозоном Хиггса, не только вызывают нарушение симметрии между электромагнитными и слабыми взаимодействиями при низкой температуре, но и ответственны за придание свойства массы таким частицам, как электроны и кварки!
Однако есть цена, которую приходится платить за введение новых полей в математический аппарат. Они не только нарушают симметрию, но и могут придать вакуумному состоянию огромную скрытую энергию, которая, как ни странно, ведет себя точно так же, как лямбда в космологических моделях.
Они не только нарушают симметрию, но и могут придать вакуумному состоянию огромную скрытую энергию, которая, как ни странно, ведет себя точно так же, как лямбда в космологических моделях.
Неловкость от необходимости воскрешать устаревшую величину Лямбда усугубляется, когда для предсказания ее значения используются теории объединения. Вместо того, чтобы быть в лучшем случае исчезающе малым компонентом Вселенной, предсказанные значения в некоторых случаях в 10 раз превышают даже самые щедрые астрономические верхние пределы!
Неприятным фактом жизни физиков является то, что лучшие кандидаты в Теорию Всего всегда должны быть доработаны, чтобы избавиться от их нежелательных космологических последствий. Без надлежащей настройки эти кандидаты могут давать правильные предсказания в микроскопическом мире физики элементарных частиц, но предсказывать вселенную, которая в своих самых больших масштабах сильно отличается от той, в которой мы живем.
Подобно вестнику из глубин времени, малость – или отсутствие – космологической постоянной сегодня говорит нам кое-что важное о том, как создать правильную Теорию Всего. Это указатель того, как симметрия природы нарушается при низкой энергии, и надоедливое напоминание о том, что наше понимание физического мира все еще неполно в каком-то фундаментальном смысле.
Это указатель того, как симметрия природы нарушается при низкой энергии, и надоедливое напоминание о том, что наше понимание физического мира все еще неполно в каком-то фундаментальном смысле.
ВЕРОЯТНАЯ ИСТОРИЯ
Большинство физиков ожидают, что Теория всего будет описывать гравитацию так же, как мы сейчас описываем материю, сильные, слабые и электромагнитные взаимодействия — на языке квантовой механики. В конце концов, гравитация — это просто еще одна сила в Природе. До сих пор это оказалось неуловимым, отчасти из-за явной сложности уравнений общей теории относительности. Ученые со времен Эйнштейна описывали гравитацию (а также пространство и время) в чисто геометрических терминах. Таким образом, мы говорим о гравитации как о «кривизне пространства-времени».
Для достижения полного объединения диалекты квантовой материи и геометрического пространства должны быть объединены в единый язык. Материя представляется довольно точно описанной на языке квантовой механики. Кварки и электроны обмениваются переносящими взаимодействие частицами, такими как фотоны и глюоны, и тем самым ощущают электромагнитное и сильное ядерное взаимодействие. Но гравитация описывается общей теорией относительности Эйнштейна как чисто геометрическое явление. Эти геометрические идеи кривизны и размерности пространства не имеют ничего общего с квантовой механикой.
Кварки и электроны обмениваются переносящими взаимодействие частицами, такими как фотоны и глюоны, и тем самым ощущают электромагнитное и сильное ядерное взаимодействие. Но гравитация описывается общей теорией относительности Эйнштейна как чисто геометрическое явление. Эти геометрические идеи кривизны и размерности пространства не имеют ничего общего с квантовой механикой.
Чтобы объединить эти две великие основы физики, необходимо найти общий язык. К этому новому языку нужно привыкнуть. В ней различие между материей и пространством растворяется и полностью теряется; материя становится геометрическим явлением, и в то же время пространство становится экзотической формой материи.
Начиная с работы по квантовой теории гравитации Джона Уилера и Брайса ДеВитта в 1960-х годах и продолжая так называемой теорией суперструн Джона Шварца и Майкла Грина в 19В 80-х годах появляется примитивная версия такого «квантово-геометрического» языка. Неудивительно, что она заимствует многие идеи из обычной квантовой механики.
Основная концепция квантовой механики заключается в том, что каждая система элементарных частиц определяется математической величиной, называемой волновой функцией. Эту функцию можно использовать, например, для предсказания вероятности обнаружения электрона в определенном месте и в определенное время внутри атома. Волновая функция представляет собой не одну величину, а сумму бесконечного числа факторов или «состояний», каждое из которых представляет собой возможный результат измерения. Одновременно можно наблюдать только одно из этих состояний.
По прямой аналогии, в квантовой гравитации геометрия пространства-времени, плоская или искривленная, является лишь одной из бесконечного разнообразия геометрических форм пространства-времени, а значит, и Вселенной. Все эти возможности описываются как отдельные состояния волновой функции Вселенной.
Но что определяет вероятность того, что Вселенная будет иметь именно ту геометрию, которую мы сейчас наблюдаем, из бесконечного множества других? В квантовой механике вероятность того, что электрон находится где-то внутри атома, определяется внешним электрическим полем, действующим на него. Это поле обычно создается протонами в атомном ядре. Может ли существовать какое-то таинственное поле «вне» нашей Вселенной, определяющее ее вероятность?
Это поле обычно создается протонами в атомном ядре. Может ли существовать какое-то таинственное поле «вне» нашей Вселенной, определяющее ее вероятность?
По словам теоретика из Кембриджского университета Стивена Хокинга, это неверный взгляд на проблему. В отличие от электрона, на который действуют протоны, наша Вселенная полностью автономна. Он не требует никаких внешних условий или полей, чтобы помочь определить его вероятность. Вероятность того, что наша Вселенная выглядит именно так, зависит только от силы полей внутри нее.
Среди этих внутренних полей могут быть и такие, которые мы еще не открыли. Может ли космологическая постоянная быть в нашей Вселенной отпечатком нового «скрытого» поля в Природе? Это новое поле может повлиять на вероятность существования нашей Вселенной так же, как котелок с супом может содержать неизвестные ингредиенты, хотя мы все еще можем точно определить массу котла.
Ряд математических соображений привел Хокинга к выводу, что чем слабее становится скрытое поле, тем меньше будет наблюдаемое нами значение космологической постоянной и тем более вероятной будет текущая геометрия Вселенной.
Это, в свою очередь, означает, что если бы лямбда была достаточно большой, чтобы ее могли измерить астрономы, наша Вселенная была бы маловероятной. С философской точки зрения это может не беспокоить тех, кто считает наш космос абсолютно уникальным, но в мире, который, казалось бы, управляется вероятностью, возможна и противоположная точка зрения. На самом деле может существовать бесконечное количество вселенных, но только в меньшинстве из них есть правильное сочетание физических законов и физических условий, напоминающее нашу питающую жизнь вселенную.
Хокинг продолжил свою линию рассуждений, предположив, что если в так называемой планковской шкале от 10 до степени -33 сантиметра космос можно представить как шипучий ландшафт или «пространственно-временную пену», то, возможно, может существовать естественный механизм для устранения космологической постоянной навсегда.
Одним из любопытных моментов объединения скорости света и постоянной тяготения Ньютона из общей теории относительности с постоянной Планка из квантовой механики является то, что их можно заставить определять уникальные значения длины, времени и энергии. Физики считают, что на этих планковских шкалах, представленных 10 в степени -33 сантиметра и 10 в степени -43 секунды, общая теория относительности и квантовая механика сливаются вместе, чтобы стать единой всеобъемлющей теорией физического мира: Теорией всего. . Энергия, связанная с этим объединением, равна 10 в степени 19.миллиардов электрон-вольт, почти невообразимо много по меркам современной технологии.
Физики считают, что на этих планковских шкалах, представленных 10 в степени -33 сантиметра и 10 в степени -43 секунды, общая теория относительности и квантовая механика сливаются вместе, чтобы стать единой всеобъемлющей теорией физического мира: Теорией всего. . Энергия, связанная с этим объединением, равна 10 в степени 19.миллиардов электрон-вольт, почти невообразимо много по меркам современной технологии.
Сама Вселенная вскоре после Большого Взрыва тоже должна была пройти через такие масштабы пространства, времени и энергии в первые мгновения своего существования. Космологи называют этот период Эрой Планка. Это знаменует собой самые ранние времена, когда физики могут исследовать физическое состояние Вселенной, не имея полной Теории Всего, которой они могли бы руководствоваться.
КРОВОТЫ
Физик из Гарвардского университета Сидней Коулман недавно довел эту мысль до возможного вывода. Вместо какого-то таинственного нового поля в Природе, возможно, в наших теориях появляется термин Лямбда, потому что мы используем неправильную исходную модель для геометрии пространства в масштабе Планка.
Предыдущие размышления о структуре пространства-времени предполагали, что оно в некотором смысле ведет себя как гладкий резиновый лист. Под действием материи и энергии пространство-время может деформироваться в различные формы, каждая из которых представляет собой возможное геометрическое состояние Вселенной. Почти все кандидаты в Теорию Всего встраивают свои поля и симметрии в такую гладкую геометрическую арену.
Но что, если бы пространство-время было намного сложнее? Одна из возможностей состоит в том, что существуют «червоточины», заполняющие пространство-время сетью туннелей. Ткань пространства-времени может иметь больше общего с кусочком швейцарского сыра, чем с гладким резиновым листом.
Согласно Коулману, добавление червоточин в пространство-время означает, что, подобно ряби от множества камней, брошенных в пруд, одно геометрическое состояние Вселенной может мешать другому. Наиболее вероятные состояния (или самые большие волны) выиграют. Математика предполагает, что интерференция квантовых червоточин в планковском масштабе делает существование вселенных с космологическими константами, отличными от нуля, крайне маловероятным.
Насколько большими должны быть червоточины, чтобы иметь такие драматические последствия? Удивительно, но расчеты показывают, что маленькое красиво. Червоточины размером с собаку и планету были бы очень редки. Вселенные, содержащие даже несколько из них, существовали бы с исчезающе малой вероятностью. Но червоточины размером менее 10 в степени -33 сантиметра могут быть повсюду. Объем размером с кубик сахара может быть кишит бесчисленными триллионами их то появляющихся, то исчезающих!
Коулман предполагает, что действие этих ранее игнорировавшихся мини-червоточин на геометрическую ткань вселенной приводит к тому, что лямбда почти равна нулю. Подобно квантовым «Pac Men», они поглощают всю скрытую энергию пространства-времени, которая иначе предстала бы перед нами в виде измеримой космологической постоянной!
Добавление червоточин к описанию пространства-времени допускает возможность того, что наша Вселенная не возникла отчужденной и независимой, а находилась под влиянием того, как уже развивались другие пространства-времени — призрачные математические вселенные, с которыми мы никогда не сможем общаться напрямую.
У наиболее вероятной из этих вселенных лямбда близка к нулю, и именно эти состояния превосходят всех остальных претендентов. В причудливой форме квантовой демократии наша Вселенная, возможно, была вынуждена следовать за большинством, эволюционируя в состояние высокой вероятности, которое мы сейчас наблюдаем, без обнаруживаемой космологической постоянной.
ЭПИЛОГ
Червоточины? Волновые функции? Скрытые поля? Ответ на вопрос о малости или отсутствии космологической постоянной, похоже, уходит в самые дальние уголки абстрактного мышления быстрее, чем большинство из нас может его догнать.
Какими бы гениальными ни казались эти новые идеи, последние страницы этой необычной истории, вероятно, еще не написаны, тем более что мы не можем напрямую проверить ни одну из этих идей. Это дань уважения гению Эйнштейна, что даже его «самая большая ошибка», допущенная в начале этого века, до сих пор досаждает физикам и астрономам, когда мы готовимся вступить в 21 век. Кто бы мог подумать, что то, чего может даже не существовать, приведет к таким огромным проблемам!
Кто бы мог подумать, что то, чего может даже не существовать, приведет к таким огромным проблемам!
Астрономия, Физика
Стенблог
Пространство-время: Последний рубеж
Автор Стен Оденвальд. Авторские права (C) Sky Publishing Corporation, 1995 г. См. выпуск за февраль 1996 г.
НОЧНОЕ НЕБО, если подумать, является одним из самых странных зрелищ, которые только можно себе представить. Точечные звезды, которые бросаются в глаза, почти поглощены черной пустотой космоса — сущностью глубиной в миллиарды световых лет, с которой мы здесь, на Земле, не имеем прямого опыта.
Что такое пустое пространство на самом деле? Сначала вопрос кажется глупым. Ничего страшного! Но взгляните еще раз в свете того, что знает и подозревает современная физика, и вы увидите, что природа пространства становится одной из самых важных «спящих» проблем, растущих за последние 50 лет. «Природа не терпит пустоты», — провозгласил Аристотель более 2300 лет назад. Сегодня физики открывают для себя, что это так, а древние греки и представить себе не могли.
«Природа не терпит пустоты», — провозгласил Аристотель более 2300 лет назад. Сегодня физики открывают для себя, что это так, а древние греки и представить себе не могли.
Правда, космос состоит в основном из вакуума. Однако сам вакуум оказывается вовсе не пустым. Это гораздо сложнее, чем может предположить большинство людей. «Но ведь, — спросите вы, — если вы возьмете контейнер и удалите из него все — каждый атом, каждый фотон — ничего не останется?» Отнюдь не. С 19Физики 20-х годов осознали, что в микроскопическом масштабе сам вакуум полон активности. Более того, эта сеть активности может простираться вплоть до самой структуры пространства-времени. Тонкая структура вакуума может в конечном итоге дать ключи к некоторым из самых глубоких вопросов, стоящих перед физикой — от того, почему элементарные частицы обладают такими свойствами, до причины Большого взрыва и вероятности существования других вселенных за пределами нашей.
ВЕЩИ, КОТОРЫЕ ВЗРЫВАЮТСЯ В ТЕМНОТЕ
Современное состояние физики — наше самое глубокое современное понимание мира — воплощено в так называемой Стандартной модели, в которой вся материя и силы объясняются поразительно малым количеством типов частиц (см. Sky & Telescope – декабрь 1987 г., стр. 582). Шесть кварков и шесть лептонов составляют все возможные формы материи. На практике всего два кварка (верхний и нижний) и один лептон (электрон) объясняют все в мире, за исключением нескольких дуновений экзотики, известных только физикам высоких энергий. На 12 частиц материи (и 12 соответствующих им частиц антиматерии или античастиц) действуют «частицы-посланники», несущие все известные силы. Фотон является посредником электромагнитной силы, включая все известные химические и структурные силы вокруг нас на Земле. Члены семейства глюонов несут сильное взаимодействие, которое связывает нейтроны и протоны вместе в атомных ядрах. W’, W- и Zo опосредуют слабое ядерное взаимодействие, а еще не открытый гравитон, как полагают, несет силу гравитации.
Sky & Telescope – декабрь 1987 г., стр. 582). Шесть кварков и шесть лептонов составляют все возможные формы материи. На практике всего два кварка (верхний и нижний) и один лептон (электрон) объясняют все в мире, за исключением нескольких дуновений экзотики, известных только физикам высоких энергий. На 12 частиц материи (и 12 соответствующих им частиц антиматерии или античастиц) действуют «частицы-посланники», несущие все известные силы. Фотон является посредником электромагнитной силы, включая все известные химические и структурные силы вокруг нас на Земле. Члены семейства глюонов несут сильное взаимодействие, которое связывает нейтроны и протоны вместе в атомных ядрах. W’, W- и Zo опосредуют слабое ядерное взаимодействие, а еще не открытый гравитон, как полагают, несет силу гравитации.
Каждое возможное событие с участием 12 частиц материи можно полностью объяснить как обмен частицами-посланниками. Во время некоторых из этих событий, например, когда электроны ускоряются в антенне радиопередатчика, передающие частицы (в данном случае фотоны) материализуются и путешествуют в пространстве. Однако в других случаях мессенджеры остаются почти полностью скрытыми внутри взаимодействующей системы. Когда посланники существуют в этой скрытой форме, их называют «виртуальными частицами». Виртуальные частицы могут казаться призрачными и нереальными по повседневным меркам. Но они настоящие. Более того, они не ограничиваются своей ролью опосредования взаимодействий. Виртуальные частицы также могут появляться и исчезать из пустого пространства сами по себе.
Однако в других случаях мессенджеры остаются почти полностью скрытыми внутри взаимодействующей системы. Когда посланники существуют в этой скрытой форме, их называют «виртуальными частицами». Виртуальные частицы могут казаться призрачными и нереальными по повседневным меркам. Но они настоящие. Более того, они не ограничиваются своей ролью опосредования взаимодействий. Виртуальные частицы также могут появляться и исчезать из пустого пространства сами по себе.
Квантовая механика, свод правил Стандартной модели, утверждает в качестве основополагающего принципа, что для измерения энергии или массы частицы с заданной степенью точности требуется определенное время. Чем короче время наблюдения, тем более неопределенным является измерение. Если время очень короткое, неопределенность становится больше, чем вся масса частицы, и вы не можете сказать, есть ли частица вообще. Чем легче частица, тем больше время ее неопределенности. В случае электрон-позитронной пары временная шкала неопределенности составляет около 10^-21″ секунд.
В более коротких масштабах времени виртуальные электроны и позитроны могут появляться и исчезать из небытия, как горошины в игре в ракушки. Это как если бы вы не могли сказать, что частица не существует, если взглянуть очень кратко, то в каком-то смысле она существует. Это не просто теоретизирование. В 1958 году настольный эксперимент продемонстрировал «эффект Казимира», измеряя силу, вызванную появлением и исчезновением виртуальных частиц в полном вакууме за счет притяжения, которое они вызывали между двумя параллельными металлическими пластинами. Если бы вакуум был действительно пуст, пластины не должны были бы притягиваться, но непрекращающийся танец виртуальных частиц в пространстве между ними производит заметный эффект.
Каждая частица — как материя, так и посланник — кажется, отображает виртуальную форму, каждая из которых кипит в большем или меньшем изобилии в том, что физики называют «физическим вакуумом». Более того, когда дело доходит до воздействия на обычный мир, виртуальные частицы могут делать гораздо больше, чем просто опосредовать силы. Некоторые на самом деле могут придавать материи свойство, которое мы называем массой. Электрон — простейшая из материальных частиц. Наши знания о физическом мире основаны на твердом понимании его свойств. Тем не менее, несмотря на его изобилие в схемах вокруг нас, электрон таит в себе загадку. Тот факт, что он имеет массу, не может быть объяснен в Стандартной модели, по крайней мере, в тех ее частях, которые были подтверждены экспериментально. Более 30 лет назад физик элементарных частиц Питер Хиггс предположил, что существование массы связано с новым компонентом природы, который теперь называется полем Хиггса. ».
Некоторые на самом деле могут придавать материи свойство, которое мы называем массой. Электрон — простейшая из материальных частиц. Наши знания о физическом мире основаны на твердом понимании его свойств. Тем не менее, несмотря на его изобилие в схемах вокруг нас, электрон таит в себе загадку. Тот факт, что он имеет массу, не может быть объяснен в Стандартной модели, по крайней мере, в тех ее частях, которые были подтверждены экспериментально. Более 30 лет назад физик элементарных частиц Питер Хиггс предположил, что существование массы связано с новым компонентом природы, который теперь называется полем Хиггса. ».
Поле Хиггса еще предстоит открыть, но многие физики ожидают, что оно будет существовать повсюду в физическом вакууме, гарантируя, что благодаря взаимодействию с электронами и другими частицами они будут проявлять массу. Даже сейчас ускорители частиц в ЦЕРН в Швейцарии и в Фермилабе под Чикаго напрягают свои максимальные возможности, чтобы заставить всего один «бозон Хиггса», предполагаемую частицу-посланника для этого поля, вырваться из вакуума и оставить заметный след. Успех обеспечил бы триумфальное завершение Стандартной модели.
Успех обеспечил бы триумфальное завершение Стандартной модели.
Таким образом, чтобы ответить на наш вопрос о том, действительно ли контейнер с пустым пространством пуст, лучшее, что можно сделать, это удалить нормальные физические частицы, которые природа позволяет нам видеть и которыми можно манипулировать. Виртуальные частицы никогда не могут быть выселены. И вдобавок может существовать вездесущее поле Хиггса.
КВАНТОВАЯ ГРАВИТАЦИЯ
На протяжении большей части этого столетия физики изо всех сил пытались включить гравитацию в схему сил, которые передаются виртуальными частицами-посредниками. Иными словами, общая теория относительности, которая показывает, что сила гравитации является искривлением пространства-времени, должна быть интегрирована с квантовой механикой, которая показывает, что силы представляют собой обмен виртуальными частицами. Исходя из предположения, что такой союз возможен, физики назвали частицей-посланником гравитации гравитон. -33 сантиметра — квантовая природа гравитации становится важной.
-33 сантиметра — квантовая природа гравитации становится важной.
Предположим, вы могли бы волшебным образом посмотреть в микроскоп, увеличивающий атомное ядро до размера примерно 10 световых лет в поперечнике. При таком увеличении самые маленькие гравитоны, то есть самые энергичные и массивные, имели бы размер около миллиметра. Здесь мы могли бы увидеть странный мир, в котором само пространство-время определялось гравитонами, пересекающимися и петляющими друг вокруг друга. В том же духе Роджер Пенроуз предположил, что гравитационное поле и пространство-время состоят из еще более примитивных математических сущностей, называемых твисторами, и что «в конечном итоге концепция [пространства-времени], возможно, будет исключена из основы физической теории. вообще». В сущности, пространство и время выносятся за скобки как менее чем фундаментальные части физического мира.
С этой точки зрения только взаимодействия между твисторами или, возможно, гравитонами определяют, когда и где пространство-время есть, а где нет. Есть ли в физическом вакууме пробелы, пустоты истинного и абсолютного ничего, где не существует самих пространства и времени?
Есть ли в физическом вакууме пробелы, пустоты истинного и абсолютного ничего, где не существует самих пространства и времени?
Другой взгляд на структуру пространства-времени предлагает «теория суперструн». Теории струн утверждают, что фундаментальные объекты природы представляют собой скорее одномерные линии, чем точки; измеряемые нами «элементарные» частицы — лишь колебания этих струн. Однако кажется, что теория суперструн работает только в том случае, если пространство-время имеет не четыре измерения (три пространственных и одно временное), а 10 измерений. Это вряд ли похоже на мир, в котором мы живем. Чтобы скрыть дополнительные шесть измерений, математики сворачивают их в концептуальные уголки, которые носят такие загадочные названия, как «многообразия Калаби-Яу» и «орбифолдное пространство». В недавнем учебнике по этому предмету делается задумчивое замечание: «Если идея о струнах верна, мы никогда не сможем увидеть больше, чем проблеск реальности во всей ее полноте».
Совсем недавно теоретики Карло Ровелли (Университет Питтсбурга) и Ли Смолин (Университет штата Пенсильвания) завершили анализ модели квантовой гравитации, разработанной Абхаем Аштекаром в Сиракузском университете в 1985 году. В отличие от теории струн, работа Аштекара применима только к гравитации. Однако он утверждает, что на планковском масштабе пространство-время растворяется в сети «петлей», которые скреплены узлами. Пространство-время чем-то похоже на кольчугу, которую носили рыцари прошлого, напоминает ткань, сотканную в четырех измерениях из этих крошечных одномерных петель и узлов энергии.
В отличие от теории струн, работа Аштекара применима только к гравитации. Однако он утверждает, что на планковском масштабе пространство-время растворяется в сети «петлей», которые скреплены узлами. Пространство-время чем-то похоже на кольчугу, которую носили рыцари прошлого, напоминает ткань, сотканную в четырех измерениях из этих крошечных одномерных петель и узлов энергии.
Таков ли мир на самом фундаментальном уровне, или математики оторвались от реальности? Теория суперструн уже более десяти лет привлекает физиков тем, что намекает на сверхобъединение всех четырех фундаментальных сил природы. Но по-прежнему крайне трудно забросить якоря из этих облачных замков в реальный мир наблюдений и экспериментов. Знаменитое замечание о том, что теория суперструн — это «часть физики 21-го века, случайно попавшая в 20-й век», отражает как волнение, так и разочарование рабочих, застрявших с инструментами 20-го века.
Удивительно, но теория струн, зацикленное пространство-время Аштекара и твисторы не являются полностью независимыми взглядами на пространство-время. В 1986 году теоретики обнаружили, что суперструны имеют некоторые общие черты с твисторами. Между двумя очень разными независимыми теориями была обнаружена глубокая связь. Словно две бригады проходчиков, стартовавших с противоположных сторон горы, они встретились посредине — возможно, это признак того, что они имеют дело с одной настоящей горой, а не с отдельными горами в их собственном воображении. А в 1995 Ровелли и Смолин также обнаружили, что их гравитонные петли очень тесно связаны как с твисторами, так и с суперструнами, хотя и не идентичны во всех отношениях.
В 1986 году теоретики обнаружили, что суперструны имеют некоторые общие черты с твисторами. Между двумя очень разными независимыми теориями была обнаружена глубокая связь. Словно две бригады проходчиков, стартовавших с противоположных сторон горы, они встретились посредине — возможно, это признак того, что они имеют дело с одной настоящей горой, а не с отдельными горами в их собственном воображении. А в 1995 Ровелли и Смолин также обнаружили, что их гравитонные петли очень тесно связаны как с твисторами, так и с суперструнами, хотя и не идентичны во всех отношениях.
КОСМИЧЕСКАЯ СВЯЗЬ
Пространство-время может быть странным и в других отношениях. Теоретик Джон А. Уилер (Институт перспективных исследований) уже давно утверждает, что на планковском масштабе пространство-время имеет сложную форму, меняющуюся от мгновения к мгновению. Уилер назвал свою картину «пространственно-временной пеной» — морем квантовых черных дыр и червоточин, появляющихся и исчезающих в масштабе времени около 10^-43″ секунд. Это планковское время, время, за которое свет пересекает планковскую длину. Короче время, как и пространство, по-видимому, не может существовать — или, по крайней мере, наши повседневные представления о них перестают быть действительными. 9-5 грамм) в таком маленьком объеме, что его собственная гравитация на поверхности давала бы ему скорость убегания, превышающую скорость света. Другими словами, это крошечная черная дыра. Но черная дыра — это не обычный объект, находящийся в пространстве-времени наподобие частицы; это структура самого искаженного, запутанного пространства-времени. Хотя последствия таких явлений непонятны, разумно предположить, что эти виртуальные частицы резко искажают все пространство-время на планковском масштабе.
Это планковское время, время, за которое свет пересекает планковскую длину. Короче время, как и пространство, по-видимому, не может существовать — или, по крайней мере, наши повседневные представления о них перестают быть действительными. 9-5 грамм) в таком маленьком объеме, что его собственная гравитация на поверхности давала бы ему скорость убегания, превышающую скорость света. Другими словами, это крошечная черная дыра. Но черная дыра — это не обычный объект, находящийся в пространстве-времени наподобие частицы; это структура самого искаженного, запутанного пространства-времени. Хотя последствия таких явлений непонятны, разумно предположить, что эти виртуальные частицы резко искажают все пространство-время на планковском масштабе.
Если мы примем это рассуждение за чистую монету и рассмотрим эксперименты десятилетней давности, доказывающие, что феномен виртуальных частиц в вакууме реален, трудно поверить, что пространство-время является гладким на планковском масштабе или ниже. Пространство должно быть разбито и квантовано. Вопрос только в том, как. Первоначальная идея Уилера о пространственно-временной пене особенно эффективна, потому что, согласно недавним предложениям Сиднея Коулмана (Гарвард) и Стивена Хокинга (Кембриджский университет), ее червоточины не только соединяют различные точки очень близко друг к другу в нашем пространстве-времени, но и соединяют наши пространство-время к другим вселенным, которые для нас существуют только как призрачные вероятности. Эти связи с другими вселенными вызывают так называемую космологическую постоянную — раздражающее вторжение в уравнения космологии со времен Эйнштейна (см. Sky & Telescope — 19 апреля).91, стр. 362) — аккуратно исчезнуть в нашей собственной вселенной.
Пространство должно быть разбито и квантовано. Вопрос только в том, как. Первоначальная идея Уилера о пространственно-временной пене особенно эффективна, потому что, согласно недавним предложениям Сиднея Коулмана (Гарвард) и Стивена Хокинга (Кембриджский университет), ее червоточины не только соединяют различные точки очень близко друг к другу в нашем пространстве-времени, но и соединяют наши пространство-время к другим вселенным, которые для нас существуют только как призрачные вероятности. Эти связи с другими вселенными вызывают так называемую космологическую постоянную — раздражающее вторжение в уравнения космологии со времен Эйнштейна (см. Sky & Telescope — 19 апреля).91, стр. 362) — аккуратно исчезнуть в нашей собственной вселенной.
Пена пространства-времени также считается питательной средой для детских вселенных. В нескольких теориях, объясняющих причину Большого взрыва и то, что было до него, Большой взрыв может отпочковаться от ранее существовавшего пространства-времени, полностью отделиться, оставаясь микроскопическим, и раздуться вместе с материей, чтобы стать новыми собственными вселенными, полностью несвязанными. «непересекающиеся») от их пространственно-временного происхождения. Этот процесс, предложенный Аланом Гутом (MIT) и другими, дает представление о том, что многие считают еще одним ключевым вопросом физики 21-го века: был ли наш Большой взрыв уникальным? Или это было просто рутинным побочным эффектом естественных процессов, постоянно происходящих в каком-то большем внешнем мире? (см. Небо и Телескоп — 19 сентября105 эрг на кубический сантиметр. Это в 10 миллиардов миллиардов раз больше массы всех галактик в наблюдаемой Вселенной, упакованной в каждый кубический сантиметр! К счастью, Мать-Природа, похоже, изобрела средства, позволяющие точно компенсировать это явление с точностью до 120 знаков после запятой. Проблема в том, что мы понятия не имеем, как это сделать.
«непересекающиеся») от их пространственно-временного происхождения. Этот процесс, предложенный Аланом Гутом (MIT) и другими, дает представление о том, что многие считают еще одним ключевым вопросом физики 21-го века: был ли наш Большой взрыв уникальным? Или это было просто рутинным побочным эффектом естественных процессов, постоянно происходящих в каком-то большем внешнем мире? (см. Небо и Телескоп — 19 сентября105 эрг на кубический сантиметр. Это в 10 миллиардов миллиардов раз больше массы всех галактик в наблюдаемой Вселенной, упакованной в каждый кубический сантиметр! К счастью, Мать-Природа, похоже, изобрела средства, позволяющие точно компенсировать это явление с точностью до 120 знаков после запятой. Проблема в том, что мы понятия не имеем, как это сделать.
Ужасно думать, что в 16 дюймах, отделяющих эту страницу от ваших глаз, новые большие взрывы, возможно, порождаются из нашего тихого пространства-времени каждое мгновение. По сравнению с этим кажется довольно скучным, что фотоны, с помощью которых вы видите эту страницу, могут играть в классики, чтобы избежать пробелов, где пространство-время не существует.
ПРОВЕРКА НА РЕАЛЬНОСТЬ
Некоторые физики начали категорически отвергать эти фантастические идеи. Например, в 1993 году Мэтт Виссер (Вашингтонский университет) изучал математические свойства квантовых червоточин и обнаружил, что после образования они становятся стабильными: они вообще не могут пениться. Кадзуо Гороку (Технологический институт Фукуока, Япония) также обнаружил, что квантовые червоточины становятся стабильными, даже если учитывать их взаимодействие с другими полями. То, что Уилер назвал пространственно-временной пеной, может быть чем-то совершенно другим.
Среди нерешенных проблем, стоящих перед теоретиками, — природа времени, которое было признано неразрывно связанным с пространством с тех пор, как Эйнштейн постулировал постоянную скорость света. В общей теории относительности не всегда очевидно, как определить, что мы подразумеваем под временем, особенно на шкале Планка, где время, кажется, теряет свое обычное значение. Центральное место в любой квантовой теории занимает понятие измерения, но что это означает для физики на планковском масштабе, который устанавливает окончательный предел возможности измерения? Как можно проверить любую из этих идей о пространстве-времени, в настоящее время неизвестно. Некоторые физики считают, что это делает эти идеи вообще не настоящими научными исследованиями. И стоит помнить, что математика иногда может вводить понятия, которые являются лишь средством для достижения цели и не имеют самостоятельной реальности.
Некоторые физики считают, что это делает эти идеи вообще не настоящими научными исследованиями. И стоит помнить, что математика иногда может вводить понятия, которые являются лишь средством для достижения цели и не имеют самостоятельной реальности.
В абстрактном мире математических символов не всегда ясно, что реально, а что нет. Например, когда мы выполняем длинное деление на бумаге, чтобы разделить 54 162 на 2 и получить 27 081, мы генерируем промежуточные числа 14, 16 и 2, которые затем просто отбрасываем. Являются ли виртуальные частицы, компактные 6-мерные многообразия и твисторы просто нефизическими средствами достижения цели — простыми артефактами того, как мы, люди, занимаемся математикой? Физикам, занимающимся элементарными частицами, часто приходится иметь дело с «призрачными полями», которые представляют собой просто временные леса, используемые для расчетов, и которые исчезают, когда расчеты завершены. Нефизические устройства, такие как отрицательная вероятность и тахионные частицы со скоростью, превышающей скорость света, неохотно допускаются до тех пор, пока они исчезают до того, как будут получены окончательные ответы. Недавние работы показывают, что даже в теории суперструн можно построить непротиворечивые модели полностью в обычном четырехмерном пространстве-времени, не прибегая к более высоким измерениям.
Недавние работы показывают, что даже в теории суперструн можно построить непротиворечивые модели полностью в обычном четырехмерном пространстве-времени, не прибегая к более высоким измерениям.
ТОРТ АНГЕЛСКАЯ ЕДА
Итак, что мы должны думать о великой темной пустоте, в которую мы смотрим ночью? Все улики указывают на то, что пространство-время является своего рода слоеным пирогом, заполненным явлениями субмикроскопического масштаба. Самый верхний слой содержит кварки и электроны, составляющие обычную материю, разбросанные тут и там, как изюм в глазури. Эти изюминки можно убрать, чтобы часть пространства казалась пустой. Сама глазурь состоит из виртуальных частиц, в первую очередь несущих электромагнитные, слабые и сильные взаимодействия, заполняющих вакуум непрекращающейся активностью, которую невозможно отключить. Их квантовые приходы и уходы могут полностью заполнить пространство-время, так что ни одна точка не будет потеряна. Этот слой пирога «пустого пространства» кажется довольно хорошо установленным лабораторным экспериментом.
Под этим слоем находится область предполагаемого поля Хиггса. С этой точки зрения, независимо от того, куда деваются «изюм» электрона и кварка, рядом всегда есть частица поля Хиггса, воздействующая на них и придающая им массу. Ниже слоя Хиггса могут существовать другие слои, представляющие поля, которые нам еще предстоит открыть. Но в конце концов мы приходим к низшему слою — гравитационному полю. Это поле больше там, где в слоях над ним присутствует масса, но нет места, где оно полностью отсутствует. Этот слой напоминает вавилонскую Великую черепаху, которая несла вселенную на своей спине. Без него все остальные слои выше исчезли бы в небытие. 9-33 см, пространство-время должно кардинально изменить свою структуру. Это может быть мир, в котором общепринятые представления о размерности, времени и пространстве необходимо переопределить и, возможно, полностью исключить.
Тщеславие об уникальности нашей вселенной может исчезнуть, когда большие взрывы станут рассматриваться как заурядные события в каком-то гораздо большем внешнем мире, а физические константы будут приписаны причинам в пространстве-времени, навсегда выходящим за рамки человеческого опыта.
В физическом вакууме много жуткого. Эта жуткость может быть больше связана с тем, как работает наш мозг, чем с каким-то объективным аспектом природы. Эйнштейн подчеркивал: «Пространство и время — это не условия, в которых мы живем, а способы, которыми мы мыслим». Наше понимание пространства остается в зачаточном состоянии. С Аристотелем, улыбающимся нам на протяжении веков, мы теперь видим пустоту как нечто большее, чем вакансия. Пройдет много десятилетий, если не столетий, прежде чем будет сформировано ее полное понимание. А пока наслаждайтесь ночным видом!
ДОПОЛНИТЕЛЬНОЕ ЧТЕНИЕ
Дэвис, Пол. Новая физика. Кембридж: Издательство Кембриджского университета, 1989.
Маллов, Юджин. «Самовоспроизводящаяся Вселенная». Sky & Telescope, сентябрь 1988 г., стр. 253.
Мэтьюз, Роберт. «Нет ничего лучше вакуума». New Scientist, 25 февраля 1995 г., стр. 30.
Pagels, Heinz. «Идеальная симметрия». Нью-Йорк: Саймон и Шустер, 1985.
Исследования мозга, Физика
StenBlog 2 комментария
После написания тринадцати эссе о космосе я совершенно забыл завершить всю дискуссию некоторыми мыслями об общей картине! Если вы перейдете по ссылкам в этом эссе, вы попадете на эссе, где я объяснил идею более подробно!
Почему я начал эти эссе с такого большого количества рассуждений об исследованиях мозга? В конце концов, именно мозг пытается создать представление о том, что вы видите, основываясь на том, что ему говорят органы чувств. Сумасшествие заключается в том, что то, что мозг делает с сенсорной информацией, довольно странно, когда вы следуете за стимулами на всем пути к сознанию. На самом деле, если вы посмотрите на все синаптические связи в мозге, только небольшое их количество имеет какое-либо отношение к сенсорным входам. Это как если бы вы буквально выдернули мозг из тела, и он вряд ли понял бы, что ему нужна сенсорная информация, чтобы оставаться счастливым. Он проводит большую часть своего времени, «принимая» себя.
Это как если бы вы буквально выдернули мозг из тела, и он вряд ли понял бы, что ему нужна сенсорная информация, чтобы оставаться счастливым. Он проводит большую часть своего времени, «принимая» себя.
Сама идея пространства на самом деле кажется средством представления мира мозгу, чтобы помочь ему разобраться в правилах, необходимых ему для выживания и воспроизводства. Наиболее важным правилом является причинно-следственная связь или «Если произойдет А, то последует Б». Это также формирует хардкорную основу логики и математических рассуждений!
Но с научной точки зрения мы знаем, что пространство и время — это не просто какая-то иллюзия, потому что объективно они кажутся очень твердой валютой, посредством которой Вселенная представляет нам сенсорные стимулы. То, как мы размещаем себя в пространстве и времени, само по себе является интересным вопросом. Мы можем использовать нашу логику и наблюдения, чтобы выработать множество правил, которыми руководствуется Вселенная и которые включают свободные параметры времени и пространства. Но когда мы глубоко погружаемся в то, как работает наш мозг и взаимодействует с миром за пределами наших синапсов, мы сталкиваемся с чем-то удивительным.
Но когда мы глубоко погружаемся в то, как работает наш мозг и взаимодействует с миром за пределами наших синапсов, мы сталкиваемся с чем-то удивительным.
Мозг должен отслеживать, что находится внутри тела, называемое Атманом, и что находится вне тела. Если он не может сделать это безошибочно, он не может отслеживать, какие факторы контролируют его выживание, а какие связаны исключительно с его внутренним миром мыслей, чувств и воображаемых сценариев. Это не может быть просто особенностью человеческого мозга, но должно быть и то, что есть у многих других существ на каком-то рудиментарном уровне, чтобы они тоже могли функционировать во внешнем мире с его многочисленными опасностями. В нашем случае эта особенность мозга присутствует как реальная физическая область в коре головного мозга. Когда он активен и стимулируется, у нас появляется ясное и отчетливое восприятие нашего тела и его отношения к пространству. Мы можем использовать это, чтобы управлять своими мышцами, правильно ориентироваться в пространстве, ходить и выполнять многие другие навыки, требующие острого восприятия этого внешнего мира. Удивительно, но когда вы устраняете активность в этой области с помощью наркотиков или медитации, вы больше не можете локализовать себя в пространстве, и это приводит к ощущению, что ваше тело «едино» с миром, ваше Я исчезло, а в других случаях вы испытайте полное отделение Я от тела, которое вы испытываете как путешествие вне тела.
Удивительно, но когда вы устраняете активность в этой области с помощью наркотиков или медитации, вы больше не можете локализовать себя в пространстве, и это приводит к ощущению, что ваше тело «едино» с миром, ваше Я исчезло, а в других случаях вы испытайте полное отделение Я от тела, которое вы испытываете как путешествие вне тела.
Какое отношение это имеет к космосу в реальном мире? Что ж, за миллионы лет эволюции мы выработали множество правил о пространстве и о том, как действовать в нем, но затем Эйнштейн дал нам теорию относительности, которая показала, что пространство и время гораздо более пластичны, чем любые из правил, которые мы усвоили в течение жизни. тысячелетия. Но именно правила и концепции относительности составляют наш внешний мир, а не приблизительные идеи «здравого смысла», которые мы все носим с собой. Наши внутренние правила, касающиеся пространства и времени, никогда не были предназначены для того, чтобы дать нам точное внутреннее представление о движении со скоростью, близкой к скорости света, или о функционировании в областях внешнего мира, близких к большим массам, искажающим пространство.
Но теперь, когда у нас есть научный способ придумать еще больше правил, касающихся пространства и времени, мы обнаруживаем, что наши собственные логические рассуждения хотят нарисовать еще большую картину происходящего и с удовольствием делают это, не слишком беспокоясь об этом. многое с фактическими (сенсорными) данными. По другим причинам мы развили чувство артистизма, красоты и эстетики, которое применительно к математике и физике привело нас в область унификации наших правил относительно внешнего мира, так что их становится все меньше и меньше. Эта страсть к упрощению и унификации привела ко многим открытиям о внешнем мире, которые чудесным образом могут быть подтверждены как действительные объективные факты этого мира.
На этом пути к упрощению физики даже основы пространства и времени становятся игроками в декорациях, а не отчужденными партнерами на сцене. Это то, с чем мы боремся сегодня в физике. Если вы сделаете пространство и время игроками в пьесе, сама сцена исчезнет и должна быть каким-то образом воссоздана посредством действий самих актеров. Именно на это и надеется сделать квантовая гравитация, независимо от того, называете ли вы математику Петлей, Квантовой Гравитацией или Струной. Теория. Это также приводит к одной из самых сложных концепций во всей физике… и философии.
Именно на это и надеется сделать квантовая гравитация, независимо от того, называете ли вы математику Петлей, Квантовой Гравитацией или Струной. Теория. Это также приводит к одной из самых сложных концепций во всей физике… и философии.
Что нам делать с ингредиентами, которые вместе создают наше ощущение пространства и времени? Являются ли эти ингредиенты сами по себе вне пространства и времени, подобно тому как части кольчужного жилета сильно отличаются от жилета, который они создают благодаря своим связям? И что представляет собой арена, на которой эти части соединяются вместе, создавая пространство и время?
Именно на эти вопросы я потратил всю свою взрослую жизнь, пытаясь осмыслить их и поделиться ими с людьми, не являющимися учеными, и они ведут прямо к концепции эмерджентных структур. новые объекты, не имеющие никакого сходства с ингредиентами, такие как эволюция, возникающая из химии, или разум, возникающий из элементарных синаптических разрядов. По-видимому, время и пространство могут возникнуть из ингредиентов еще более примитивных, которые могут не иметь ничего общего ни со временем, ни с пространством!
Согласитесь, из этих идей можно составить интересные истории у костра!
Вернитесь сюда в понедельник, 26 декабря, чтобы узнать о начале новой серии блогов на разные темы!
Мозговая петля квантовая гравитациямоделивосприятиеотносительностьтеория струнАстрономия, физика
StenBlog 12 комментариев
Итак, вот большая проблема.
Сейчас у физиков есть подробная математическая модель того, как работают фундаментальные силы в природе: электромагнетизм, сильные и слабые ядерные взаимодействия. К этому добавляется подробный список фундаментальных частиц в природе, таких как электрон, кварки, фотоны, нейтрино и другие. Названная Стандартной моделью, она была тщательно проверена и оказалась удивительно точным способом описания почти всего, что мы видим в физическом мире. Это объясняет, почему одни частицы имеют массу, а другие нет. Он точно описывает, как силы генерируются частицами и передаются в пространстве. Экспериментаторы на Большом адронном коллайдере ЦЕРН буквально рвут на себе волосы, чтобы найти ошибки или недостатки в Стандартной модели, которые противоречат расчетным предсказаниям, но пока не смогли ничего обнаружить. Они называют это поиском Новой Физики.
Наряду с этой точной моделью физических сил и частиц в нашей Вселенной у нас есть общая теория относительности и ее описание гравитационных полей и пространства-времени. ОТО не дает объяснения тому, как это поле генерируется материей и энергией. Он также не дает описания квантовой структуры материи и сил в Стандартной модели. ОТО и Стандартная модель говорят на двух очень разных языках и описывают две совершенно разные физические области. В течение десятилетий физики пытались найти способ объединить эти две великие теории, и результаты были многообещающими, но не поддающимися проверке. Это описание гравитационных полей, основанное на тех же принципах, что и Стандартная модель, стало называться квантовой гравитацией.
ОТО не дает объяснения тому, как это поле генерируется материей и энергией. Он также не дает описания квантовой структуры материи и сил в Стандартной модели. ОТО и Стандартная модель говорят на двух очень разных языках и описывают две совершенно разные физические области. В течение десятилетий физики пытались найти способ объединить эти две великие теории, и результаты были многообещающими, но не поддающимися проверке. Это описание гравитационных полей, основанное на тех же принципах, что и Стандартная модель, стало называться квантовой гравитацией.
Все многие идеи, которые были предложены для квантовой гравитации, глубоко математические и очень слабо касаются нашего экспериментального мира. Возможно, вы пытались читать книги на эту тему, написанные практикующими, но, как и я, вы будете разочарованы математикой и языком, который это сообщество разработало за эти годы для описания своих открытий.
Проблема, с которой столкнулась Квантовая Гравитация, заключается в том, что гравитационные поля, кажется, отображают свои квантовые свойства только на так называемой шкале Планка 10^-33 сантиметра и 10^-43 секунды. 19ГэВ или 10 миллиардов миллиардов ГэВ, что в 1000 триллионов раз превышает энергию, которую могут достичь современные ускорители частиц.
19ГэВ или 10 миллиардов миллиардов ГэВ, что в 1000 триллионов раз превышает энергию, которую могут достичь современные ускорители частиц.
Нет известных технологий, которые могли бы достичь масштабов, позволяющих измерить эти эффекты для проверки этих теорий. Даже само понятие измерения рушится! Это происходит потому, что те самые частицы (фотоны), которые вы пытаетесь использовать для изучения физики в масштабе Планка , несут столько энергии, что превращаются в квантовые черные дыры и не могут рассказать вам, что они видели или обнаружили!
Один из подходов к QG называется петлевой квантовой гравитацией. Как и теория относительности, она предполагает, что гравитационное поле — это все, что существует, и что пространство и время становятся зернистыми или «квантуются» на шкале Планка. Пространство и время, которые мы знаем и можем воспринимать в целом, состоят из отдельных частей , которые объединяются в огромном количестве, образуя вид почти непрерывного и гладкого гравитационного поля.
Проблема в том, что вы не можете визуализировать то, что происходит в этом масштабе, потому что в математике это представлено не самородками пространства и времени, а более абстрактными математическими объектами, называемыми петлями и спиновыми сетями. Исполнение художника выше — это именно то, что нужно.
Итак, здесь, что касается диаграмм Фейнмана, у нас есть математическая картина, представляющая процесс, но картина символическая, а не фотографическая. Однако самая большая проблема заключается в том, что, хотя работает квантовая теория гравитации, Петлевая квантовая гравитация не включает ни одну из частиц Стандартной модели. Она представляет собой квантовую теорию гравитационного поля (вселенная пространства и времени) без материи!
Другими словами, это описание торта, а не глазури.
Второй подход — это теория струн. Эта теория предполагает, что уже существует какое-то фоновое пространство и время, через которое движется другая математическая конструкция, называемая струной. Струны, образующие замкнутые петли, могут вибрировать, и каждый образец колебаний представляет собой отдельный тип фундаментальной частицы. Чтобы теория струн работала, струны должны существовать в 10 измерениях, и большинство из них свернуты в замкнутые геометрические шары, называемые пространствами Калаби-Яу. Каждое из этих пространств имеет свою собственную геометрию, внутри которой вибрируют струны. Это означает, что могут быть миллионы различных «решений» уравнений теории струн: каждое из них представляет собой отдельную вселенную со своим особым типом подпространства Калаби-Яу, которое приводит к определенному набору фундаментальных частиц и взаимодействий. Проблема в том, что теория струн нарушает общую теорию относительности, требуя фонового пространства!
Струны, образующие замкнутые петли, могут вибрировать, и каждый образец колебаний представляет собой отдельный тип фундаментальной частицы. Чтобы теория струн работала, струны должны существовать в 10 измерениях, и большинство из них свернуты в замкнутые геометрические шары, называемые пространствами Калаби-Яу. Каждое из этих пространств имеет свою собственную геометрию, внутри которой вибрируют струны. Это означает, что могут быть миллионы различных «решений» уравнений теории струн: каждое из них представляет собой отдельную вселенную со своим особым типом подпространства Калаби-Яу, которое приводит к определенному набору фундаментальных частиц и взаимодействий. Проблема в том, что теория струн нарушает общую теорию относительности, требуя фонового пространства!
Другими словами, он описывает глазурь, а не торт!
Одно из решений, предложенных физиком Ли Смолином, заключается в том, что петлевая квантовая гравитация является основой для создания струн в теории струн. Если бы вы посмотрели на одну из этих нитей при большом увеличении, ее поверхность, похожая на макароны, превратилась бы в пучок петель, связанных вместе, возможно, как средневековые кольчужные доспехи. Проблема в том, что Петлевая Квантовая Гравитация не требует гравитационного поля с более чем четырьмя измерениями (тремя пространственными и одним временным), в то время как для струн требуется десять или даже одиннадцать. Что-то по-прежнему не так, и прямо сейчас никто толком не знает, как это исправить. Не имея фактических достоверных данных, мы даже не знаем, ближе ли какая-либо из этих теорий к реальности!
Если бы вы посмотрели на одну из этих нитей при большом увеличении, ее поверхность, похожая на макароны, превратилась бы в пучок петель, связанных вместе, возможно, как средневековые кольчужные доспехи. Проблема в том, что Петлевая Квантовая Гравитация не требует гравитационного поля с более чем четырьмя измерениями (тремя пространственными и одним временным), в то время как для струн требуется десять или даже одиннадцать. Что-то по-прежнему не так, и прямо сейчас никто толком не знает, как это исправить. Не имея фактических достоверных данных, мы даже не знаем, ближе ли какая-либо из этих теорий к реальности!
Это гибридное решение пытается найти аспекты торта, которые можно интерпретировать как частицы глазури!
Эта работа все еще продолжается, но есть несколько вещей, которые мы узнали о природе самого пространства. В нашем масштабе это выглядит как непрерывное гравитационное поле, пересекаемое мировыми линиями атомов, звезд и галактик. Вот как это выглядит даже в атомном масштабе, потому что теперь вы можете добавить мировые линии бесчисленных «виртуальных частиц», которые составляют различные силы в Стандартной модели. Но когда мы приближаемся к шкале Планка, пространство и пространство-время перестают быть гладкими, как лист бумаги, и начинают распадаться на нечто другое, что, как мы думаем, раскрывает зернистую природу гравитации как поля, состоящего из бесчисленных жужжащих гравитонов.
Но когда мы приближаемся к шкале Планка, пространство и пространство-время перестают быть гладкими, как лист бумаги, и начинают распадаться на нечто другое, что, как мы думаем, раскрывает зернистую природу гравитации как поля, состоящего из бесчисленных жужжащих гравитонов.
Но как «выглядят» эти фрагментарные элементы пространства и времени, сказать невозможно. Все, что у нас есть, — это математические инструменты для их описания, и, как и наши попытки описать электрон, они ведут к миру чистой абстракции, который нельзя наблюдать напрямую.
Если вы хотите узнать немного больше о природе космоса, прочитайте мою короткую брошюру «Изучение квантового пространства », доступную на amazon.com. В нем описывается удивительная история наших знаний о космосе, начиная с древнегреческих идей «здравого смысла» и заканчивая выдающимися положениями современной квантовой теории.
Вернитесь сюда в четверг, 22 декабря, чтобы увидеть последний блог из этой серии!
петля квантовая гравитацияматематикаШкала Планкаотносительностьпространствопространствовремятеория струнУпрощение работы: 5 лучших практик
Упрощение работы, также называемое упрощением работы, является вмешательством в структуру работы. В этой статье мы подробно рассмотрим упрощение работы, дадим определение и перечислим ряд лучших практик, как это сделать хорошо.
В этой статье мы подробно рассмотрим упрощение работы, дадим определение и перечислим ряд лучших практик, как это сделать хорошо.
Содержание
Что такое упрощение работы? Определение
Упрощение работы: краткая история
5 методов упрощения работы
Что такое упрощение работы? Определение
Работа или упрощение работы – это процесс удаления задач из существующих ролей, чтобы сделать их более сфокусированными. Цель упрощения работы заключается в разработке усовершенствованных методов работы, которые максимизируют производительность при минимальных затратах и затратах.
Рассмотрим пример работы упрощение в работе.
Эми работает в приемной
быстрорастущая компания. Ее роль — заниматься администрированием, заботиться об офисе
дела и принимать гостей. Эми любила свою работу. Однако, когда компания выросла
с 50 до 150 человек за два года, она начала
ее административные задачи и начали проявлять симптомы эмоционального выгорания. Над этими двумя
года, обязанности Эми остались прежними, но группа людей, которых она
пришлось позаботиться, увеличилось на 300%!
Над этими двумя
года, обязанности Эми остались прежними, но группа людей, которых она
пришлось позаботиться, увеличилось на 300%!
Затем ее менеджер усадил ее и спросил какие части роли она любила больше всего. Эми любила работу по дому и получать гостей, но административные задачи стали для нее непосильными. Затем компания принято решение о создании дополнительной функции офис-менеджера, которая будет заниматься к этим административным задачам. Обязанности Эми были сведены к другим два вида деятельности.
Упрощение работы: краткая история
Упрощение работы было популяризировано Фредерик Тейлор. Он выступал за то, чтобы сложные работы были разбиты на простые компоненты. Это небольшие задачи, которые относительно легко освоить и выполнять. Преимущество в том, что требуется низкий уровень квалификации, это дешевле для организации, и меньше ошибок из-за специализации.
В подходе Тейлора рабочие становятся
специалистов в своей конкретной области. Впервые этот подход был реализован
Генри Форд, который смог производить автомобили серийно по гораздо более низкой цене, чем любой другой. своего конкурса.
своего конкурса.
Еще одним преимуществом для работодателя является то, что сотрудников легче заменить, поскольку они являются узкоспециализированными, а их навыки легко учиться. Таким образом, сотрудники являются заменимыми винтиками в производстве. машина. Этот подход был назван инженерным подходом, т. выход (производительность) был основным критерием для принятия этих решений.
В связи с ростом автоматизации и повышение осведомленности об условиях труда для сотрудников, упрощение труда упал с популярности. Вместо инженерного подхода мотивационный подход отстаивался. Этот подход был направлен на то, чтобы сделать рабочие места мотивирующими к работайте над собой, особенно для работников умственного труда.
Несмотря на снижение популярности,
упрощение рабочих мест остается одним из четырех ключевых способов проектирования рабочих мест. В
Кроме того, можно привести аргумент в пользу повторного введения упрощения труда в качестве
технику упрощения ролей в возрасте, когда сложная работа может привести к стрессу и
проблемы со здоровьем.
Упрощение работы — это один из четырех методов планирования работы, которые являются ключевой частью организационного развития, наряду с расширением, обогащением работы и ротацией работы.
5-этапная техника упрощения работы
Подход к упрощению работы имеет пять шаги и не отличается от любого процесса редизайна работы. Работа или роль сначала анализируются, а затем оптимизируются на основе ряда критериев. Шаги для упрощение работы заключается в следующем.
- Выбор задания или изучаемая деятельность . Хорошей отправной точкой является деятельность, требующая много времени или неэффективная. Желательно, чтобы это была деятельность с которыми вы знакомы, в противном случае вам следует взять интервью у людей, которые ознакомиться с заданием, чтобы лучше понять человека, выполняющего его. Это помогает понять деятельность.
- Сбор данных и
информация о выбранной работе . Здесь
приоритетом является получение всех фактов и перечисление каждого отдельного шага, связанного с
делать работу.

- Все подвергать сомнению выполнение задания . На этом этапе вы идете через все шаги и факты и анализировать все, спрашивая «почему, где, когда, кто и как». Затем вы изучаете альтернативные процедуры и обстоятельства.
- Разработка возможных улучшения . Здесь вы можете использовать четыре критерия для все разные задачи. Это устранение, объединение, перестановка и упрощение. Цель состоит в том, чтобы сделать работу проще, безопаснее или эффективнее. На этом этапе вы должны иметь в виду, что вы можете использовать инструменты, в том числе физические инструменты, цифровые технологии и автоматизация. После этого запишите результаты и создайте предложен новый метод.
- Оценка результатов и
имплантация усовершенствованного метода . Здесь вы можете
протестируйте свой новый прототип, оптимизируйте и настройте его на основе первоначальных результатов и
внедрить усовершенствованный метод. Это может включать некоторое управление заинтересованными сторонами или
убедить вышестоящего.

Хотя вышеупомянутый подход был опубликованный еще в 1950-х годах, он очень похож на сегодняшний дизайн мыслительный процесс. Вы пытаетесь понять работу и обстоятельства (подчеркните), определить проблему, проанализировать процесс, прототипы решений и результаты испытаний.
Это краткое руководство по упрощению работы. Подводя итог: цель упрощения работы — разработать методы работы, которые максимизируют производительность при минимальных затратах. Таким образом, это очень целенаправленный подход. Тем не менее, есть и другие факторы, которые необходимо учитывать, в том числе то, насколько мотивирующей будет работа и подходит ли новая упрощенная работа сотруднику на этой работе. Если бы Эми любила административные задачи, она не была бы счастлива отказаться от них, демонстрируя важность применения человеческого подхода к упрощению работы.
Защитите свою карьеру в области HR на будущее, постоянно расширяя свой набор навыков с помощью новейших и наиболее актуальных навыков HR.


 Самостоятельная работа
Самостоятельная работа 8.
8.

 8.
8.
 Самостоятельная работа
Самостоятельная работа

 13.
13. 18.
18. Самостоятельная работа
Самостоятельная работа Самостоятельная работа
Самостоятельная работа