Конспект урока математики в 5 классе по теме «Распределительный закон»
5 класс
МАТЕМАТИКА
Урок №25
Тема: Распределительный закон.
Тип: урок изучения нового материала.
Цель: познакомить учащихся с распределительным законом умножения; научить
применять распределительный закон при решении задач; практиковать
выполнение вычислений значения выражений, содержащих многозначные
числа, применяя распределительный закон умножения; развивать логическое
мышление учащихся; воспитывать умения слушать, понимать и анализировать.
Автор разработки: Попов Дмитрий Сергеевич.
ХОД УРОКА
I. Организационный момент
На доске написан эпиграф урока:
«Математика уступает свои крепости лишь сильным и смелым» А.П. Конфорович
— Добрый день! Я рад приветствовать вас на уроке математики. Прочитайте эпиграф урока.
— Считаете ли вы себя достаточно сильными и смелыми для математики?
— Я считаю, что вы сможете покорить сегодня ещё одну «крепость математики».
II. Анализ самостоятельной работы
Учитель оглашает ученикам оценки за самостоятельную работу, раздаёт тетради, для ознакомления с допущенными ошибками.
III. Постановка темы и целей урока
— Когда-то один из философов сказал: «Математики – очень ленивые люди». Я считаю, что согласиться с этим трудно, но вы уже знаете, что в математике есть закон, которые могут значительно сократить время вычисления выражений. Сегодня на уроке мы познакомимся с новым закон – распределительным, и тема нашего урока будет называться так «Распределительный закон».
IV. Изучение нового материала
Распределительный закон звучит так: чтобы число умножить на сумму двух чисел, надо это число умножить на каждое слагаемое и полученные произведения сложить.
Распределительный закон можно записать в виде равенства, которое верно для любых чисел а, b и c: а ⋅ (b+c) = a⋅ b + a⋅ c
Давайте это проверим.
Вычислим и сравним значения выражений 3 ∙ (4 + 6) и 3 ∙ 4 + 3 ∙ 6.
3 ∙ (4 + 6) = 3 ∙ 10 = 30
3 ∙ 4 + 3 ∙ 6 = 12 + 18 = 30
30 = 30
Оба выражения имеют одинаковое значение, поэтому можно сделать вывод, что распределительный закон справедлив.
Кроме того, если b больше или равно с (b≥c), то верно равенство: a⋅ (b−c)=a⋅ b−a⋅ c
Переход от произведений числа и суммы и числа, и разности соответственно к сумме произведений и разности произведений называют раскрытием скобок.
а ∙ (b + c) = a ∙ b + a ∙ с
а ∙ (b – c) = a ∙ b – a ∙ с
Переход от суммы произведений к произведению числа и суммы и от разности произведений к произведению числа и разности соответственно называют вынесением общего множителя за скобки.
a ∙ b + a ∙ с = а ∙ (b + c)
a ∙ b – a ∙ с = а ∙ (b – c)
Вынесение общего множителя за скобки позволяет упрощать вычисления.
V. Решение упражнений
№107 – 110; №112 — №113 – выполнение у доски.
VI. Закрепление изученного материала
Проводится самостоятельная работа по № 114 на отдельных листочках:
I вариант – решает примеры из I столблика;
II вариант – решает примеры из II столблика;
VI. Рефлексия
– Ребята, как вы можете оценить свою работу на уроке по 10-балльной шкале?
– Поставьте себе на полях оценку по 10-балльной шкале.
– Кто, по вашему мнению, активнее всех работал на уроке?
VII. Подведение итогов урока
Учитель выставляет оценки, тем самым подводя итоги урока.
VII. Анонс домашнего задания
Прочитать §1.8
Решить №111 и №116.
Разработка урока математики 5 класс «Распределительный закон»
Автор: Трушина Н.В.
МБОУ «Краснопоймовская СОШ»
Разработка урока по математике 5 класс на тему: «Распределительный закон умножения»
Учитель: Трушина Н.
В.
Класс: 5 класс
Продолжительность: 45 минут
Цели урока:
Образовательные: Установление новой важной связи между сложением и умножением чисел при изучении темы «Распределительное свойство умножения относительно сложения и вычитания».
Развивающие: Развитие стремления открывать и исследовать новое, способности находить и выражать оригинальные идеи, умения анализировать результаты своей деятельности, выявлять места и причины затруднений, умения ставить цели урока и подводить итог.
Воспитательные: Развитие интереса к предмету, создание условий для формирования чувства взаимопонимания, толерантности, взаимовыручки, самоконтроля.
Познавательные: владеют общим приемом решения заданий.
Коммуникативные: договариваются о совместной деятельности, приходят к общему решению, в том числе в ситуации столкновения интересов.
План урока:
Организационный момент (1 мин)
Актуализация знаний и умений (устный счет – 10 мин)
Формирование умений и навыков (25 мин)
Физкультминутка (4 мин)
Итоги урока (3 мин)
Постановка домашнего задания (2 мин)
Организационный момент.
Мотивация к учебной деятельности-1 мин
Мотивировать обучающихся к учебной деятельности на уроке, определить содержательные рамки урока. Учитель обеспечивает мотивацию, создает условия для возникновения у обучающихся внутренней потребности включения в учебную деятельность.
Я сегодня хочу начать урок с таких слов, которые будут сегодня девизом нашего урока: «Считайте несчастным тот день и тот час, в который ты не усвоил ничего нового, ничего не прибавил к своему образованию».
Я. А. Коменский
2. Актуализация знаний – 10 мин
Устный счет:
25+65+75
5*12*4
34+17+83
76*5*2
27+123+16+234
25*8*4
Формирование умений и навыков – 25 мин
Организовать коммуникативное взаимодействие для построения нового способа действий, зафиксировать новый способ действий в знаковой, вербальной форме.
Организуется работа в группах по четыре человека. Каждая группа получает задачу, которую необходимо решить различными способами (Подсчитаем двумя способами число квадратов, изображенных на рисунке:
Перейдем к обсуждению проделанной нами работы и ее результатов.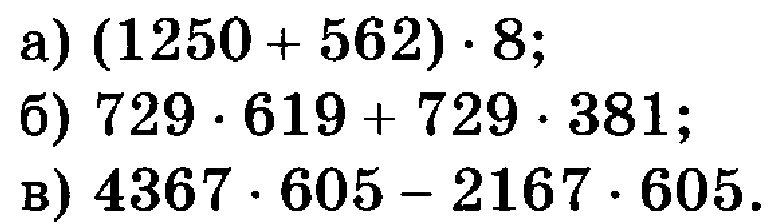
Сколько разных способов рассмотрели?
Обсудим 1 способ решения данной задачи:
В каждом ряду расположено 3 синих и 5 красных квадратов, а всего в каждом ряду (3+5) квадратов. В четырех же рядах всего 4*(3+5) квадратов.
Сравним полученные выражения при 2 способе решения задачи:
Синие квадраты расположены в четырех рядах по 3 квадрата в каждом, т.е. синих квадратов 4*3. Красных квадратов 4*5, а всего 4*3+4*5 квадратов
Что в них общего?
Сравните ответы – результаты задачи при решении первым и вторым способом. В таких случаях говорят, что числовое значение первого выражения равно числовому значению второго выражения. Какой вывод можно сделать из этого факта?
Одно и то же число квадратов подсчитано двумя способами, поэтому 4*(3+5)=4*3+4*5
Верно!
Запишите соответствующие равенства к задаче. Давайте составим буквенное выражение для задачи, для этого разные числа заменим разными буквами.
Сколько различных букв нам необходимо для записи буквенного выражения? Что можно записать при помощи буквенного выражения?
а*(в + с) =а*в + а*с
Так, наверное, у нас тоже получился какой – то закон? Как его прочитать? Попробуйте перевести его с математического языка на русский.
Чтобы число умножить на сумму двух чисел, можно это число умножить на каждое слагаемое и полученные произведения сложить.
Это свойство назвали распределительным свойством умножения относительно сложения.
Отметим, что распределительный закон верен не только для двух, но и для любого числа слагаемых. Например, верно равенство: 9*(3+4+5+6) =9*3+9*4+9*5+9*6.
Как вы думаете, почему его назвали распределительным?
Ребята устанавливают закономерности; делают выводы; формулируют правило (эталон), фиксируют преодоление возникшего затруднения; перерабатывают информацию.
Переход от произведений, а * (в + с) и, а * (в – с) соответственно к сумме, а * в – а * с называют раскрытием скобок.
Переход от суммы, а * в + а * с к произведению, а * (в + с) и от разности, а * в – а * с к произведению, а * (в – с) называют вынесением общего множителя за скобки.
Физкультминутка – 4 мин
Решение заданий из учебника:
№ 108 (1, 2 столбик)
№ 111
№ 113 (а, б)
Итоги урока – 3 мин
Организовать рефлексию и самооценку обучающихся
Постановка домашнего задания – 2 мин
Обсудить и записать домашнее задание.
П. 1.8 № 108 (3 столбик)
№ 109
№ 113 (б, г)
Спасибо всем за урок!
Ребята воспринимают информацию, записывают в дневник домашнее задание.
Что такое распределительная собственность? Определение, Пример формулы, Факты
Распределение собственности Определение
«Раздать» означает разделить что-то или дать долю или часть чего-то.
Так что же означает распределительная собственность в математике?
Распределительный закон умножения по отношению к основным арифметическим действиям, таким как сложение и вычитание, известен как распределительное свойство.
Рекомендуемые рабочие листы:
Что такое распределительная собственность?
В соответствии с этим свойством умножение суммы двух или более слагаемых на число даст тот же результат, что и умножение каждого слагаемого по отдельности на число с последующим сложением произведений.
Другими словами, согласно дистрибутивному свойству, выражение вида A (B $+$ C) может быть решено как A (B $+$ C) $=$ AB $+$ AC.
Это свойство применимо и к вычитанию.
A (B $–$ C) $=$ AB $–$ AC
Это указывает на то, что операнд A является общим для двух других операндов.
Давайте посмотрим на формулу распределительной собственности:
Где A, B и C — любые действительные числа.
Вот пример того, как результат не меняется при обычном решении и при решении с использованием распределительного свойства:
Это свойство помогает упростить сложные задачи. Вы можете использовать это свойство умножения, чтобы переписать выражение, распределив или разбив множитель на сумму или разность двух чисел.
Распределительное свойство умножения на сложение
Когда нам нужно умножить число на сумму двух чисел, мы используем это свойство умножения вместо сложения. Давайте поймем, как лучше использовать распределительное свойство на примере:
Пример: Решите выражение: $6$ $(20 + 5)$, используя распределительное свойство умножения над сложением.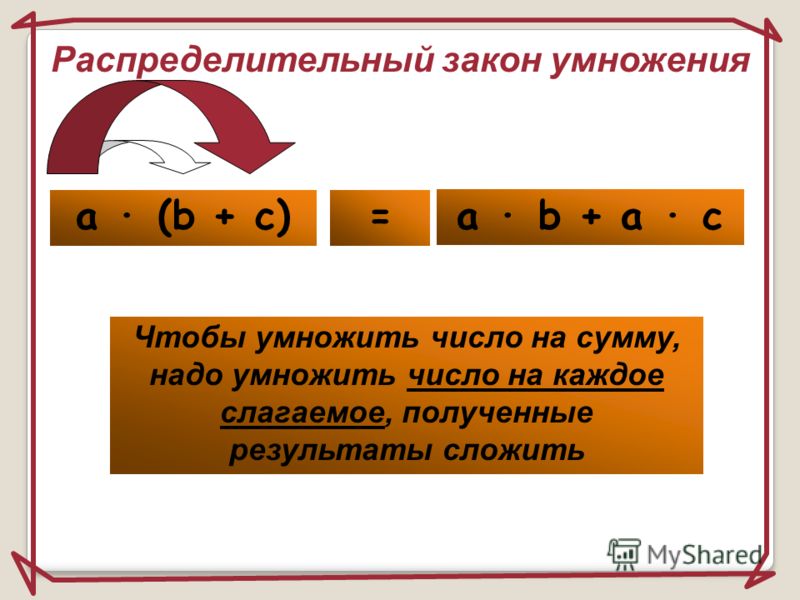
Воспользуемся этим свойством для вычисления выражения $6$ $(20 + 5)$, число 6 распределено между двумя слагаемыми. Проще говоря, мы умножаем каждое слагаемое на 6, после чего можно складывать произведения.
$6 20 + 6 5 = 120 + 30 = 150$
Возьмем другой пример:
Пример: Решите выражение $2$ $(2 + 4)$, используя распределительный закон умножения над сложением.
Решение: $2 (2 + 4) = 2 2 + 2 4 = 4 + 8 = 12$
Если мы попытаемся решить это выражение с помощью правила PEMDAS, нам придется сложить числа в скобках и затем умножьте сумму на число за скобками. Отсюда следует:
$2 (2 + 4)$ $= 2 \times 6 =$ $12$
Таким образом, мы получаем один и тот же результат независимо от используемого метода.
Распределительное свойство умножения над вычитанием
Распределительное свойство умножения над вычитанием эквивалентно распределительному свойству умножения над сложением, за исключением операций сложения и вычитания.
A(B − C) и AB − AC эквивалентны выражениям.
Рассмотрим приведенные ниже примеры распределительной собственности.
Пример: Решите выражение $6 (20 – 5)$, используя распределительное свойство умножения над вычитанием.
Решение : Использование распределительного свойства умножения над вычитанием
Пример : Решите выражение 2 (4 – 3), используя распределительный закон умножения на вычитание.
Решение : $2 (4 – 3) = 2 4 – 2 3 = 8 – 6 = 2$
Опять же, если мы попытаемся решить выражение с порядком операций или PEMDAS, нам придется вычесть числа в скобках , затем умножьте разницу на число за скобками, что означает:
$2 (4 – 3) = 2 1 = 2$
Распределительное свойство вычитания доказано, поскольку оба метода дают одинаковый результат.
Забавные факты
Несмотря на то, что деление является обратным умножению, закон распределения верен только в случае деления, когда делимое распределяется или разбивается на частичные дивиденды, которые полностью делятся на делитель.
Например, используя распределительный закон для 1326
132, можно разбить его на 60 + 60 + 12 долларов, что упрощает деление.
Мы не можем разбить 132 6 как $(50 + 50 + 32) 6$.
Кроме того, мы не можем разорвать делитель: $132(4+2)$ даст неверный результат.
Заключение
Мы поняли, как свойство дистрибутивности можно использовать для упрощения сложных уравнений и задач. Откройте для себя новый способ изучения математики с помощью SplashLearn,
предлагает интерактивную платформу для детей, где каждая концепция превращается в игровую сессию. С интересными таблицами, увлекательными викторинами и простыми для понимания темами измените то, как ваш ребенок понимает математику!
Решенные примеры
Пример 1. Решите $(5 + 7 + 3) 4$ .
Решение : Используя распределительное свойство умножения над сложением,
A (B $+$ C) = AB $+$ AC
$(5 + 7 + 3) 4 = 5 4 + 7 4 + 3 4 = 20 + 28 + 12 = 60$
Или,
$(5 + 7 + 3) 4 = 15 4 = 60$
Пример 2: Решите следующее уравнение распределения $−2 (−$x$ − 7)$ .
Решение : Использование распределительного свойства,
A (B $–$ C) $=$ AB $–$ AC
$−2 (−$x$ − 7) = (−2)(− $x$) − (−2)(7) = 2$x$ − (−14) = 2$x$ + 14$
Пример 3. Какое свойство делает уравнение $3 (4 − 9) = 3 4 − 3 9$ показать?
Решение : Приведенное выше уравнение показывает распределительное свойство умножения над вычитанием.
Практические задачи
1
Выражение $7 ($x$ + 6)$ равно
x $+ 42$
$7$x $+ 13$
$7$x $+ 42$
5 7 90 x $+ 6$
Правильный ответ: $7$x $+ 42$
Используя распределительное свойство умножения над сложением,
A (B $+$ C) $=$ AB $+$ AC
$7 ($x $+ 6) = 7($x$) + 7(6) = 7$x $+ 42$
2
Выражение $3 (7$x $– 8)$ равно
$13$x
$7 $x$ – 24$
$21$x$ – 24$
$21$x$ – 8$
Правильный ответ: $21$x$ – 24$
Используя распределительное свойство умножения над вычитанием,
A (B $–$ C) $ =$ AB $–$ AC
$3 (7$x $– 8) = 3 (7$x$) – 3 (8) = 21$x$ — 24$
3
Выражение m $(3$ n $– 9)$ равно
$3$mn $– 9$n
$3$mn $– 9$
$3$mn $– 9$m
$3$mn$+9$m
Правильный ответ составляет: $3$mn $– 9$m
Используя распределительное свойство умножения над вычитанием,
A (B $–$ C) $=$ AB $–$ AC
m $(3$n $– 9)$ $=$ m $(3$n$) –$ m $(9) = 3$ млн $– 9 млн $
4
Урожайность банановой фермы составляет 355 десятков бананов.
Сколько бананов было собрано?4260
3550
2130
426
Правильный ответ: 4260
Общее количество собранных бананов определяется выражением $355 x 12$.
Дюжина или 12 могут быть распределены как 10 и 2.
Общее количество собранных бананов $= 355 \times (10 + 2)$
Используя распределительное свойство умножения над сложением,
A (B $+$ C) $=$ AB $+$ AC
$= 355 \times 10 + 355 \times 2$
$= 3550 + 710 = 4260$
Всего на ферме было собрано 4260 бананов.
Часто задаваемые вопросы
Применяется ли раздел имущества также и к разделу?
Свойство распределения применимо к делению так же, как и к умножению. Однако понятие «разбивка» или «распределение» может быть применено к делению только путем деления числителя на более мелкие суммы, которые точно делятся на делитель.
Например, чтобы решить $\frac{125}{5}$, мы можем разделить числитель (125) как: (50 + 50 + 25), поэтому: $\frac{125}{5}$ = $\ frac{50}{5}$ + $\frac{50}{5}$ + $\frac{25}{5}$ = 10 + 10 + 5 = 25.
Каково правило для распределительного свойства ?
Согласно распределительному свойству, умножение суммы двух или более слагаемых на число дает тот же результат, что и при умножении каждого слагаемого на число по отдельности и сложении произведений.
Как распределительная собственность может помочь в решении сложных вопросов?
Распределяющее свойство распределяет сложные выражения в более простые термины и, таким образом, упрощает решение задач, особенно с несколькими факторами.
Можно ли убрать скобки после распространения?
Да, при применении распределительного свойства внешний множитель умножается на каждое слагаемое в скобках. Это позволяет избавиться от скобок.
Распределительное свойство умножения – определение, формула, примеры
Согласно распределительному свойству умножения, когда мы умножаем число на сумму двух или более слагаемых, мы получаем результат, равный результату, который получается при умножении каждого слагаемого в отдельности на число.
Распределительное свойство умножения распространяется на сумму и разность еще двух чисел.
| 1. | Что такое распределительное свойство умножения? |
| 2. | Распределительное свойство формулы умножения |
| 3. | Распределительное свойство умножения на сложение |
| 4. | Распределительное свойство умножения над вычитанием |
| 5. | Часто задаваемые вопросы о распределительном свойстве умножения |
Что такое распределительное свойство умножения?
Распределительное свойство умножения, справедливое для сложения и вычитания, помогает распределить заданное число на операцию, чтобы легко решить данное уравнение. Простыми словами, когда число умножается на сумму двух чисел, то произведение такое же, как произведение, которое мы получаем, когда число распределяется на два числа внутри скобок и умножается на каждое из них в отдельности.
Давайте разберемся в этом на примере. Когда мы получаем выражение вроде 6(3 + 5), мы используем порядок операций, сначала раскрывая скобки, а затем умножая результат на другое число следующим образом: 6(3 + 5) = 6 (8) = 6 × 8 = 48,
Однако, когда мы применяем распределительное свойство умножения к тому же выражению 6(3 + 5), мы распределяем число 6 на 3, а затем на 5 следующим образом: (6 × 3) + (6 × 5) = 48. Мы получаем одинаковый результат обоими методами. Теперь вопрос в том, почему мы используем свойство дистрибутивности, если мы получаем один и тот же результат обоими методами. Ответ заключается в том, что распределительное свойство используется для решения выражений, в которых вместо чисел используются переменные. Поскольку разные переменные нельзя складывать или вычитать, в этом случае помогает распределительное свойство.
Распределительное свойство формулы умножения
Формула распределительного свойства умножения: a(b + c) = ab + ac. Эта формула объясняет, что мы получаем один и тот же продукт в обеих частях уравнения, даже если мы умножаем «а» на сумму «b» и «с» в левой части или когда мы распределяем «а» на «b», а затем «c» справа.
Обратите внимание на следующую формулу распределительного свойства умножения. Следует отметить, что это свойство применимо к сложению и вычитанию.
Распределительное свойство умножения на сложение
Распределительное свойство умножения над сложением гласит, что умножение суммы двух или более слагаемых на число дает тот же результат, что и умножение каждого слагаемого по отдельности на число и последующее сложение произведений вместе. Это свойство умножения над сложением используется, когда нам нужно умножить число на сумму. Например, решим выражение 7(9+ 3). Если решить его в обычном порядке действий, то мы сначала решим скобки, а затем умножим число на полученный результат. 7(9 + 3) = 7(12) = 84
Однако, в соответствии с распределительным свойством умножения над сложением, мы умножаем 7 на каждое слагаемое. Это называется распределить число 7 на 9 и 3, а затем мы добавляем каждый продукт. Итак, найдем произведение распределенного числа: 7 × 9 и 7 × 3.
Это дает нам: 7(9) + 7(3) = 63 + 21 = 84. Это показывает, что мы получаем одно и то же произведение.
Обратите внимание на следующее уравнение, которое показывает обычный метод в левой части и распределительное свойство умножения над сложением в правой части. Применяя распределительное свойство, мы распределяем число 7 на 9 и 3, затем умножаем соответствующие числа на 7 и складываем результаты. В каждом случае результат одинаков.
7(9 + 3) = 7(9) + 7(3)
7(12) = 63 + 21
84 = 84
Распределительное свойство умножения на вычитание
Распределительное свойство умножения над вычитанием гласит, что умножение числа на разность двух других чисел равно разности произведений распределенного числа. Формула распределительного свойства умножения над вычитанием: a(b — c) = ab — ac. Например, решим: 9(20 — 10).
Используя обычный порядок действий, находим разность чисел, указанных в скобках, а затем умножаем результат на 9.
9(20 -10) = 9(10) = 90
Теперь давайте воспользуемся распределительным свойством умножения над вычитанием, чтобы решить 9(20 — 10).
Мы умножаем 9 на каждое значение внутри скобки, а затем находим разницу произведений.
Итак, перемножим: 9 × 20 и 9 × 10. Получим: 9(20) — 9(10) = 180 — 90 = 90. Результат такой же, как и выше.
Обратите внимание на следующее уравнение, в котором обычный метод показан в левой части, а распределительное свойство умножения применяется в правой части. Применяя распределительное свойство умножения над вычитанием, мы распределяем число 9до 20 и 10, затем умножаем соответствующие числа на 9 и вычитаем произведения. В обоих случаях мы получаем один и тот же ответ.
9(20 — 10) = 9(20) — 9(10)
9(10) = 180 — 90
90 = 90 умножение.
- Формула распределительной собственности
- Ассоциативное свойство умножения
- Умножение
Часто задаваемые вопросы о распределительном свойстве умножения
Что такое распределительное свойство умножения в математике?
Согласно распределительному свойству умножения, когда мы умножаем число на сумму двух или более слагаемых, мы получаем результат, равный результату, который получается при умножении каждого слагаемого в отдельности на число.
Распределительное свойство умножения распространяется на сумму и разность еще двух чисел. Он используется для простого решения выражений путем распределения числа на числа, указанные в скобках. Например, если мы применим свойство дистрибутивности для решения выражения: 3(2 + 4), мы решим его следующим образом: 3(2 + 4) = (3 × 2) + (3 × 4) = 6 + 12 = 18,
Что такое распределительное свойство формулы умножения?
Распределительное свойство формулы умножения применяется к сложению и вычитанию и выражается как:
- a(b+c) = ab + bc
- а(б-в) = аб-бк
Как решить распределительное свойство умножения на сложение?
Распределительное свойство умножения над сложением используется, когда мы умножаем значение на сумму двух или более чисел. Например, решим выражение: 5(5 + 9). Это выражение можно решить, умножив 5 на оба слагаемых. Итак, 5(5) + 5(9) = 25 + 45 = 70.
Как решить распределительное свойство умножения над вычитанием?
Распределительное свойство умножения по сравнению с вычитанием применяется, когда мы умножаем значение на разность двух чисел.