Гдз по математики 5 класс сферы
Скачать гдз по математики 5 класс сферы EPUB
Все это становится поводом для использования специально разработанного ГДЗ к учебнику Математики 5 класс Е.А. Бунимович, Г.В. Дорофеев, С.Б. Суворова. УМК «Сферы». Решебник подготовлен перворазрядными специалистами в данной области, с учетом требований ФГОС и включает в себя несколько разделов, соответствующих книге по прохождению настоящего курса. Он для успешного написания заданий доступен онлайн и содержит все ответы на интересующие вопросы. Пользоваться им очень удобно посредством современных гаджетов — ноутбука, планшета и даже смартфона.
Бесплатный решебник (ГДЗ) к учебнику по математике за 5 класс, авторы: Е.А. Бунимович, Г.В. Дорофеев, С.Б. Суворова. ГДЗ к задачнику по математике за 5 класс Е.А.
Бунимович можно смотреть здесь. Данное пособие содержит решебник (ГДЗ) Арифметика. Геометрия. по Математике за 5 класс. Автора: Е.А. Бунимович, Г.В. Дорофеев, С.
авторы: Е.А. Бунимович, Г.В. Дорофеев, С.Б. Суворова. ГДЗ БОТ содержит верные ответы с несколькими вариантами решения по Математике за 5 класс, автор издания: Е.А. Бунимович, Г.В.
Дорофеев, С.Б. Суворова. Арифметика. Геометрия. ГДЗ: готовые решения по математике за 5 класс Бунимович, Дорофеев, онлайн ответы на Еуроки. Серия: Сферы. Решебник: Еуроки ГДЗ. Стремящиеся получить углубленные знания по дисциплине пятиклассники регулярно изучают учебник и представленные на его задания ответы по математике для 5 класса (авторов Бунимовича Е. А. и Кузнецовой Л. В.). Такая подготовка по заранее составленному плану всегда приносит высокие результаты.
Сборник применяется школьниками не только для того, чтобы переписать верное решение, но и для того, чтобы глубже и полнее понять, изучить даже самый сложный материал.
Применение решебника по математике за 5 класс Бунимовича.
5класс. ГДЗ по математике за 5 класс учебник Бунимовича. Ответы и решения из онлайн решебника. Бунимович, Дорофеев (учебник). Просвещение, 1глава. Линии. (Задачи с 1 по 54). §1. Разнообразный мир линий. 1 2 3 4 5 6 7 8 9 10 11 12 Ответы на домашнее задание к тетради-тренажеру по математике за 5 класс автора Бунимович. Решебник к тетради-тренажеру по математике за 5 класс авторов Бунимович Е.А., Кузнецовой Л.В., Суворовой С.Б.
года издания. Сборник содержит более страниц уже готовых заданий разного типа и уровня сложности. В упражнениях тетради уже произведена работа с линиями, натуральными числами и действиями с ними, углами, многоугольниками, делимостью чисел, дробями. Также выполнены расчеты с многогранниками, заполнены таблицы и диаграммы.
Всего в пособии 11 глав, охватывающих заданий по алгебре и геометрии. Быстрый поиск. ГДЗ Математика 5 класс Сферы. авторы: Е.А. Бунимович, Г.В. Дорофеев, С.Б.
Суворова. Увлекательные направления ждут обывателей школьных парт на пятом году обучения. Мало того, что в повседневном расписании появиться много новых названий, так еще и старые заиграют совершенно другими красками. Гдз по математике для 5 класса Бунимовича идентичен своему оригиналу, и представляет собой, сборник грамотно построенных, а главное верно выполненных уравнений.
Онлайн решебник на протяжении всей учебной карьеры станет незаменимым товарищем и поможет решить не один десяток сложных упражнений.
txt, fb2, djvu, txtПохожее:
Урок 26. окружность и круг. сфера и шар — Математика — 5 класс
Математика
5 класс
Урок №26
Окружность и круг. Сфера и шар
Сфера и шар
Переченьрассматриваемыхвопросов:
— понятия «окружность», «круг», «сфера», «шар» и их элементы;
— изображение окружности на плоскости, сферы в пространстве.
Тезаурус
Окружность – это плоская замкнутая кривая, все точки которой находятся на одинаковом расстоянии от некоторой точки – её центра.
Круг – плоская геометрическая фигура, являющаяся местом точек, расположенных на одинаковом расстоянии от некоторой точки (центра).
Центр окружности – это точка, равноудалённая от точек окружности.
Радиус окружности – это отрезок, соединяющий какую-нибудь точку этой окружности с её центром.
Хорда окружности – это отрезок, соединяющий какие-нибудь две точки окружности.
Диаметр окружности – это хорда, проходящая через центр окружности.
Шар – это геометрическое тело, совокупность всех точек пространства, находящихся от центра на расстоянии, не больше заданного.
Сфера – это замкнутая поверхность, геометрическое место точек в пространстве, равноудалённых от данной точки, которую называют центром сферы.
Обязательная литература
Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений.// С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.
Дополнительная литература
1. Чулков П. В. Математика: тематические тесты. 5 класс.// П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы.// И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.
Теоретический материал для самостоятельного изучения
Ещё в глубокой древности люди изобрели колесо, придумали гончарный круг, сделали украшения в виде колец, то есть создали предметы, в основе которых лежит окружность или круг. В современных устройствах эти геометрические фигуры тоже встречаются очень часто. Сегодня мы поговорим не только о том, как они используются в наше время, но и выясним их отличие друг от друга.
Итак, что же такое окружность?
Окружность – это замкнутая плоская кривая, которая состоит из всех точек на плоскости, равноудалённых от заданной точки.
Построим окружность. Для этого поставим точку О. Возьмём циркуль и выставим с помощью линейки отрезок длиной 3 см. Поставим иголку циркуля в точку О и начертим окружность, вращая ножку циркуля с грифелем вокруг этой точки. Грифель описывает замкнутую линию, которую называют окружностью. Часть плоскости, которая лежит внутри окружности, вместе с самой окружностью, называют кругом, то есть окружность есть граница круга.
При построении окружности расстояние между ножками циркуля не меняется. Поэтому все точки окружности равно удалены от точки О. Точку O называют центром и окружности, и круга. Отметим на окружности любую точку – например, точку L. Построим отрезок, соединяющий точку L с центром окружности – точкой О.
Отрезок ОL называют радиусом окружности.
Отметим на окружности любые две точки. Например, C и D. Построим отрезок, соединяющий точки C и D.
Отрезок CD называют хордой окружности. Некоторые хорды окружности проходят через её центр.
Концы диаметра делят окружность на две равные части. Длина диаметра окружности равна двум радиусам. Две точки делят окружность на две части, называемые дугами. Например, CD. Обычно рассматривается одна из дуг окружности, определяемая по смыслу задачи.
Окружность разбивает плоскость на две части – внутреннюю область и внешнюю.
Давайте представим себе яблоко и воздушный шарик.
Чем они отличаются друг от друга?
Они оба имеют форму шара. Однако воздушный шарик полый внутри. Для таких предметов в математике есть название – сфера. А яблоко, с точки зрения математиков, – это шар.
Шар–это геометрическое тело, совокупность всех точек пространства, находящихся от центра на расстоянии, не больше заданного.
Отрезок, соединяющий точку поверхности шара с его центром, называется радиусом шара.
Отрезок, соединяющий две точки поверхности шара и проходящий через центр шара, называют диаметром шара.
Поверхность шара называется сферой.
Сфера – это замкнутая поверхность, геометрическое место точек в пространстве, равноудалённых от данной точки, которую называют центром сферы.
Окружность и круг являются плоскими фигурами, то есть такими, которые располагаются в пределах одной плоскости. Такие фигуры – это не что иное, как рисунки на листе бумаги. Рассмотренные на уроке сфера и шар относятся к пространственным телам. Между сферой, шаром, окружностью и кругом есть взаимосвязь. Сфера и шар образуются вращением вокруг оси окружности и круга соответственно.
Легенда о циркуле
В жизни для построений мы используем различные инструменты. Так, для того чтобы нарисовать окружность, необходим циркуль. Но как появился циркуль? Обратимся к мифам Древней Греции.
В далёкие времена в Афинах жил юноша, которого звали Талос. Он с детства был очень талантлив. В 12 лет он изобрёл гончарный круг для изготовления посуды. Также он придумал первую пилу, обратив в живой природе внимание на то, что скелет рыбы напоминает острые зубья. И наконец, Талос изобрёл устройство для построения окружностей, так называемый циркуль – инструмент в виде двух одинаковых стержней, соединённых шарниром. Так гласит легенда, а как было на самом деле, история умалчивает: известно лишь то, что на древних памятниках искусства фигуры и орнаменты из окружностей, умело выполненные древними мастерами, почти идеальны.
И наконец, Талос изобрёл устройство для построения окружностей, так называемый циркуль – инструмент в виде двух одинаковых стержней, соединённых шарниром. Так гласит легенда, а как было на самом деле, история умалчивает: известно лишь то, что на древних памятниках искусства фигуры и орнаменты из окружностей, умело выполненные древними мастерами, почти идеальны.
Тренировочные задания
№ 1. Подпишите соответствующие элементы окружности.
Вспомним определения радиуса (это отрезок, соединяющий какую-нибудь точку этой окружности с её центром), хорды (это отрезок, соединяющий какие-нибудь две точки окружности), диаметра (это хорда, проходящая через центр окружности) и ценрта окружности (это точка, равноудалённая от точек окружности).
Правильный ответ:
BO – радиус;
ВА – диаметр;
DE – хорда;
О – центр окружности.
№ 2. Выберите правильный ответ.
Рассмотрим отрезок АК, длина которого равна 8см. Построено две окружности: первая – с центром в точке A, а вторая – с центром в точке К. Их радиусы, соответственно, равны 4 см и 6 см. Сколько общих точек имеют окружности?
Их радиусы, соответственно, равны 4 см и 6 см. Сколько общих точек имеют окружности?
Решение: чтобы ответить на вопрос, изобразим отрезок и окружности.
Ответ: общих точек будет две. Они будут лежать на пересечении двух окружностей.
конспект математика 5 класс тема окружность и круг. Сфера и шар
Урок по математике для 5 класса
Тема: «Окружность и круг. Сфера и шар»
Цель: повторить понятия окружности и круга, сферы и шара, радиуса, хорды и диаметра; развивать логическое мышление, внимание, творческие и познавательные способности, воображение, умение анализировать, делать выводы; развивать трудолюбие, дисциплинированность, уважение к одноклассникам; формировать интерес к математике.
Тип урока: комбинированный
Оборудование: карточки с самостоятельной работой
Ход урока
Организационный этап
Проверка домашнего задания
Так как домашнее задание было творческого характера, то на данном этапе урока следует только проверить его наличие и собрать тетради.
Актуализация опорных знаний
Фронтальный опрос:
С какими понятиями познакомились на прошлом уроке?
Чем отличается окружность от круга?
Чем отличается сфера от шара?
Чем отличается окружность от сферы?
Чем отличается круг от шара?
Чем отличается хорда от диаметра?
Как с помощью радиуса можно выразить диаметр?
С целью проверки усвоения основных понятий провести самостоятельную работу по теории (приложение 1).
Окружность – это множество точек плоскости, равноудаленных от центра.
АО – радиусhello_html_m7c7afb.png
МВ – диаметр
КС – хорда
Диаметр равен двум радиусам
Две точки делят окружность на две части, называемые дугами.
Круг – часть плоскости, состоящая из всех точек окружности и всех точек, лежащих внутри окружности.
Все точки пространства, удаленные от центра на одно и то же расстояние, образуют сферу.
Шаром называют часть пространства, состоящую из всех точек сферы и всех точек, находящихся внутри сферы.
Отработка навыков
№ 402, 404, 407 устно.
№ 408
АВ=2 см
hello_html_55d33257.png
Физкультминутка (игра “истинно — ложно”)
Если высказыванье, верно, то учащиеся встают со своих мест и хлопают в ладоши.
Делить на нуль нельзя.
32 = 6
1см=100мм
131=13
13*1=13
Прямая имеет начало.
Луч это отрезок.
Хорда это прямая.
Диаметр равен двум радиусам.
Мячик это круг.
№ 412 (устно): а) вне окружности; б) внутри окружности.
№ 413
hello_html_m49263a76.png
№ 414 устно
№ 417
hello_html_m7bc427ed.png
Для тех, кто справится раньше, дополнительное задание № 418
hello_html_m5ac3e82d.png
Итог урока
Давайте вспомним, что сегодня на уроке мы повторили: диаметр, радиус, хорда, круг, окружность, шар, сфера.
Домашнее задание
№ 411 б,
№415
hello_html_5be96890.png
Приложение 1
Окружность – это множество ______________________________________________
________________________________________________________________________________
АО – ________________hello_html_m7c7afb. png
png
МВ – ________________
КС – ________________
Диаметр равен двум ______________
Две точки делят окружность на две части, называемые___________________________
Круг – часть плоскости,____________________________________________________ __________________________________________________________________________
Все точки пространства, удаленные от центра на одно и то же расстояние, образуют _____________________________________________________________
Шаром называют________________________________________________________
_________________________________________________________________________________
Окружность – это множество ______________________________________________
________________________________________________________________________________
АО – ________________hello_html_m7c7afb.png
МВ – ________________
КС – ________________
Диаметр равен двум ______________
Две точки делят окружность на две части, называемые___________________________
Круг – часть плоскости,____________________________________________________ __________________________________________________________________________
Все точки пространства, удаленные от центра на одно и то же расстояние, образуют _____________________________________________________________
Шаром называют________________________________________________________
________________________________________________________________________________
Окружность – это множество ______________________________________________
________________________________________________________________________________
АО – ________________hello_html_m7c7afb. png
png
МВ – ________________
КС – ________________
Диаметр равен двум ______________
Две точки делят окружность на две части, называемые___________________________
Круг – часть плоскости,____________________________________________________ __________________________________________________________________________
Все точки пространства, удаленные от центра на одно и то же расстояние, образуют _____________________________________________________________
Шаром называют________________________________________________________
20 самых необычных приложений для Android / Программное обеспечение
Каждый из нас использует возможности своего смартфона по-разному: это зависит от вида деятельности, круга решаемых задач, интересов и прочих факторов. Одни по старинке довольствуются только телефонными возможностями устройства, другие совмещают голосовую коммуникацию с общением в социальных сетях, веб-серфингом и играми, третьи вовсю применяют гаджеты для съемок фото и видео, навигации, осуществления банковских операций, чтения книг. Немало находится и тех, кто использует смартфон или планшет в деловой деятельности: для работы с электронной корреспонденцией и документами, оперативной связи с коллегами и партнерами, развития бизнеса. Сфера применения мобильной техники огромна, однако немногие догадываются о существовании в магазине приложений Google Play продуктов, позволяющих взглянуть на привычные устройства с совершенно иной стороны и полностью раскрыть заложенный в них потенциал. Заинтересовались? Тогда переходим к иллюстрированному обзору двадцати самых необычных приложений для Android!
Немало находится и тех, кто использует смартфон или планшет в деловой деятельности: для работы с электронной корреспонденцией и документами, оперативной связи с коллегами и партнерами, развития бизнеса. Сфера применения мобильной техники огромна, однако немногие догадываются о существовании в магазине приложений Google Play продуктов, позволяющих взглянуть на привычные устройства с совершенно иной стороны и полностью раскрыть заложенный в них потенциал. Заинтересовались? Тогда переходим к иллюстрированному обзору двадцати самых необычных приложений для Android!
Открывает наш ТОП-20 пара приложений, имеющих одинаковое название Smart Tools и доступных для скачивания по этой и этой ссылкам в Google Play. С их помощью не составит труда превратить смартфон в «швейцарский армейский нож» и использовать его в качестве шумомера, дальномера, виброметра, металлодетектора, прибора для измерения освещенности, термометра, радара для измерения скорости движущихся объектов, уровня, лупы, метронома, камертона, кардиографа и десятка других полезных в хозяйстве инструментов. Для полноценной работы обеих программ необходима поддержка в мобильном устройстве целого вороха датчиков: освещенности, приближения, акселерометра/гироскопа, магнитометра (цифрового компаса), барометра и других. На точность производимых Smart Tools измерений, конечно, рассчитывать не стоит, однако в некоторых случаях такой набор программных помощников может сослужить добрую службу. Например, он может пригодиться для поиска на скорую руку скрытой проводки в стене или выравнивания стиральной машины по горизонтальной плоскости.
Для полноценной работы обеих программ необходима поддержка в мобильном устройстве целого вороха датчиков: освещенности, приближения, акселерометра/гироскопа, магнитометра (цифрового компаса), барометра и других. На точность производимых Smart Tools измерений, конечно, рассчитывать не стоит, однако в некоторых случаях такой набор программных помощников может сослужить добрую службу. Например, он может пригодиться для поиска на скорую руку скрытой проводки в стене или выравнивания стиральной машины по горизонтальной плоскости.
Раз уж речь зашла об измерительных инструментах, то отличным дополнением к упомянутым выше приложениям может стать Planimeter — инструмент для определения расстояния, площади, периметра, углов на местности с использованием Google Maps и встроенного в смартфон GPS/ГЛОНАСС-приемника. Такая программа может найти применение в различных областях: полевых и сельскохозяйственных работах, планировании, строительстве, в путешествии и для развлечения. Также она может быть полезна для агентов по продаже недвижимости. Для вычисления периметра или площади любого объекта (к примеру, земельного участка) достаточно выставить на карте начальную точку, включить трекинг маршрута и затем обойти объект вокруг. Planimeter автоматически произведет все расчеты и выдаст результат измерений. Аналогичным образом можно измерять расстояние между двумя точками на карте и углы между линиями.
Для вычисления периметра или площади любого объекта (к примеру, земельного участка) достаточно выставить на карте начальную точку, включить трекинг маршрута и затем обойти объект вокруг. Planimeter автоматически произведет все расчеты и выдаст результат измерений. Аналогичным образом можно измерять расстояние между двумя точками на карте и углы между линиями.
Более прогрессивна в плане измерений программа Radioactivity Counter, позволяющая на полном серьезе применять смартфон в качестве… простейшего дозиметра радиации! Для мониторинга радиационной обстановки используется светочувствительная матрица камеры мобильника, объектив которой нужно предварительно закрыть темной пленкой – например, от дискеты или рентгеновского снимка. После этого потребуется произвести калибровку приложения по приведенной на сайте разработчиков инструкции, и можно приступать к измерению радиационного фона. При ссылке также представлены различные научно-исследовательские материалы, результаты экспериментов с использованием профессионального оборудования и демонстрационные видеоролики, подтверждающие практическую ценность и работоспособность Radioactivity Counter.
Школьников старших классов и студентов технических вузов обязательно порадует приложение PhotoMath для решения математических задач с помощью камеры смартфона и технологии оптического распознавания тестов Optical Character Recognition (OCR). Принцип работы с программой прост, как все гениальное: достаточно навести камеру на математическую задачу, и PhotoMath сразу же выдаст ответ и приведет подробное пошаговое решение. Возможности приложения позволяют распознавать не только печатный, но и рукописный текст, а также вносить правки в отсканированные формулы и уравнения. Справедливости ради отметим, что такой мобильный помощник может пригодиться не только учащимся, но и родителям – для проверки правильности выполнения детьми домашний заданий.
Обзор был бы неполным без упоминания Im2Calories — экспериментального приложения компании Google, позволяющего определять калорийность еды по фото. По словам разработчиков, задействованные в программе технологии искусственного интеллекта и машинного обучения позволяют ей с высокой точностью определять тип продукта, входящие в его состав ингредиенты и размер порции, а затем на основе полученной информации делать вывод о количестве содержащихся в блюде калорий. При этом совершенно не обязательно, чтобы снимок был высокого разрешения, — достаточно даже фото из Instagram. К сожалению, пока неизвестно, когда именно состоится полноценный релиз Im2Calories. Как только приложение увидит свет, мы обязательно расскажем о нем подробнее.
При этом совершенно не обязательно, чтобы снимок был высокого разрешения, — достаточно даже фото из Instagram. К сожалению, пока неизвестно, когда именно состоится полноценный релиз Im2Calories. Как только приложение увидит свет, мы обязательно расскажем о нем подробнее.
Еще одно заслуживающие внимание творение команды Google – приложение PhotoScan для создания цифровых копий памятных и дорогих сердцу бумажных фотографий. По заверениям создателей программы, она не просто делает снимок изображения, а переносит его на цифровой носитель с высоким качеством. Используя технологии искусственного интеллекта, PhotoScan самостоятельно определяет границы, выравнивает изображение, меняет его ориентацию, убирает ненужные блики. В результате сканирования получаются копии правильной прямоугольной формы с исправленной перспективой, которые можно сохранить в памяти смартфона или в облачном сервисе Google Photos.
Не отстают и отечественные организации, в том числе государственные. Одной из них является Федеральная служба по регулированию алкогольного рынка (Росалкогольрегулирование), создавшая актуальное для любителей «принять на грудь» приложение «АнтиКонтрафакт Алко», которое предназначено для определения подлинности алкогольной продукции. Посредством камеры телефона программа считывает акцизную марку (либо штрихкод на чеке), производит сверку с Единой государственной автоматизированной информационной системой (ЕГАИС) и демонстрирует на экране результаты проверки. О найденном нарушении можно сразу сообщить в Росалкогольрегулирование и оповестить ведомство о нелегальной точке продажи алкоголя. Также в приложении есть карта магазинов, обладающих лицензией на торговлю алкоголем. В свете широко обсуждаемых в СМИ случаев массового отравления населения метиловым спиртом и контрафактной алкогольной продукцией списывать со счетов «АнтиКонтрафакт Алко» определенно не стоит.
Посредством камеры телефона программа считывает акцизную марку (либо штрихкод на чеке), производит сверку с Единой государственной автоматизированной информационной системой (ЕГАИС) и демонстрирует на экране результаты проверки. О найденном нарушении можно сразу сообщить в Росалкогольрегулирование и оповестить ведомство о нелегальной точке продажи алкоголя. Также в приложении есть карта магазинов, обладающих лицензией на торговлю алкоголем. В свете широко обсуждаемых в СМИ случаев массового отравления населения метиловым спиртом и контрафактной алкогольной продукцией списывать со счетов «АнтиКонтрафакт Алко» определенно не стоит.
Для автомобилистов в нашей подборке представлены сразу три программы: «Автоускорение», Car Alarm и «МетеоМойка». Первая позволяет превратить смартфон в прибор для измерения времени разгона машины до 100 км/ч, вторая — в простейшую сигнализацию для защиты от угона, повреждения или эвакуации машины, третья — в помощника, подсказывающего наиболее удачный день для мойки автомобиля и автоматически выстраивающего маршрут до ближайшей автомойки. Принципиальное отличие приложения «Автоускорение» от конкурентов — использование информации от двух датчиков: GPS-приёмника и акселерометра. Они же задействованы и в Car Alarm, контролирующей местоположение транспортного средства и в случае тревоги уведомляющей владельца звонком или SMS-сообщением. Особенность «МетеоМойки» — система анализа метеорологических данных и оценки прогноза погоды на несколько дней вперед. Именно она определяет наиболее подходящее время для мытья транспорта.
Принципиальное отличие приложения «Автоускорение» от конкурентов — использование информации от двух датчиков: GPS-приёмника и акселерометра. Они же задействованы и в Car Alarm, контролирующей местоположение транспортного средства и в случае тревоги уведомляющей владельца звонком или SMS-сообщением. Особенность «МетеоМойки» — система анализа метеорологических данных и оценки прогноза погоды на несколько дней вперед. Именно она определяет наиболее подходящее время для мытья транспорта.
Хорошим дополнением к набору упомянутых программ для автолюбителей является приложение Nexar — AI Dashcam, которое превращает смартфон в продвинутый видеорегистратор, умеющий одновременно записывать видео с фронтальной и тыловой камер, на лету анализировать дорожную обстановку и информировать водителя о возникающих опасностях.
Не менее интересен Ink Hunter — программный продукт для виртуальной примерки татуировок перед посещением тату-салона. Благодаря поддержке технологий дополненной реальности (Augmented Reality, AR) приложение позволяет воочию увидеть, как будет смотреться на теле та или иная татуировка в различных ракурсах. В программе предусмотрен набор эскизов тату на любой вкус, имеется возможность загрузки пользовательских изображений.
Благодаря поддержке технологий дополненной реальности (Augmented Reality, AR) приложение позволяет воочию увидеть, как будет смотреться на теле та или иная татуировка в различных ракурсах. В программе предусмотрен набор эскизов тату на любой вкус, имеется возможность загрузки пользовательских изображений.
Увлекающимся музыкой может пригодиться приложение для настройки струнных инструментов GuitarTuna. Программа автоматически распознает звук с микрофона телефона и контролирует процесс настройки. Поддерживаются два режима работы («профессиональный» и «для новичков»), имеется встроенный метроном и набор игр для разучивания аккордов и песен на гитаре. С помощью GuitarTuna даже начинающим музыкантам не составит труда наладить правильное звучание струн электрической и акустической гитары, мандолины, укулеле, скрипки, виолончели, банджо, балалайки и многих других струнных инструментов.
Тем, чья профессия связана с программированием, мы можем смело порекомендовать интегрированную среду разработки AIDE, позволяющую создавать приложения непосредственно на мобильном устройстве. В качестве средств разработки могут быть использованы Java, C/C++, HTML5, CSS и JavaScript. Для удобства работы в AIDE предусмотрены продвинутый редактор с функциями автоподстановки кода и поиска ошибок, компилятор, отладчик, файловый менеджер c поддержкой протокола SSH и подробнейшая справочная документация. Также заявлена совместимость со средами разработки Eclipse, Android Studio и системой управления версиями Git.
В качестве средств разработки могут быть использованы Java, C/C++, HTML5, CSS и JavaScript. Для удобства работы в AIDE предусмотрены продвинутый редактор с функциями автоподстановки кода и поиска ошибок, компилятор, отладчик, файловый менеджер c поддержкой протокола SSH и подробнейшая справочная документация. Также заявлена совместимость со средами разработки Eclipse, Android Studio и системой управления версиями Git.
С установленным приложением Chemist смартфон под управлением Android может сгодиться и для проведения химических опытов. Программа позволяет оперировать более чем двумястами реагентами, разливать химические вещества по стаканам и пробиркам, изучать химические реакции и проводить различные эксперименты без риска для здоровья — все это в интерактивном режиме и с отрисовкой в трехмерной графике. Также в виртуальной лаборатории можно нагревать химикаты с помощью горелки и даже положить кусочек цезия в воду, вызвав тем самым взрыв. По каждой химической реакции предоставляется подробное описание происходящих процессов. После завершения работы с Chemist пользователь может создать лабораторный отчет с описанием всех процедур. Готовый документ можно сохранить в памяти мобильного устройства или отправить другим людям.
После завершения работы с Chemist пользователь может создать лабораторный отчет с описанием всех процедур. Готовый документ можно сохранить в памяти мобильного устройства или отправить другим людям.
Немало в Google Play представлено приложений, позволяющих превратить Android-гаджет в беспроводную мышь, клавиатуру или трекпад для компьютера и различных мультимедийных устройств. К числу таких необычных решений относится программа Wi-Fi Mouse, использующая для передачи управляющих команд сетевое соединение. Ее отличительные особенности: поддержка голосового ввода и мультитач-жестов для трекпада, а также наличие встроенных средств дистанционного управления играми, веб-браузерами, презентациями Power Point и медиаплеерами, такими как Windows Media Player, VLC, Winamp и многими другими. Wi-Fi Mouse поддерживает взаимодействие с устройствами под управлением операционных систем Windows, macOS и Linux. Перед началом работы с приложением необходимо установить на компьютер дополнительный софт Mouse server, скачать который можно с сайта разработчиков.
Благодаря приложению ABBYY FineScanner смартфон на базе Android может справиться с ролью карманного сканера для документов и книг. Созданный российским разработчиком продукт позволяет создавать PDF- или JPG-файлы из любых печатных документов (счетов, свидетельств, договоров, персональных документов). В программу встроена технология OCR, которая распознает тексты на 193 языках и с сохранением форматирования выгружает результаты в 12 популярных форматов, в том числе DOCX, XLSX, PPTX, PDF. Готовые документы можно перенести в любое из восьми облачных хранилищ, распечатать, отправить по e-mail, открыть в другом приложении для работы с PDF. Для сканирования книжных и журнальных изданий в ABBYY FineScanner предусмотрена функция BookScan, которая автоматически разделяет сфотографированный разворот книги на две страницы, выпрямляет изгибы строк, удаляет дефекты и делает сканерную копию, которую можно распознать и получить редактируемый файл.
Системным IT-администраторам стоит занести в закладки приложение с говорящим названием Web Monitor, предназначенное для мониторинга и диагностики серверов в сетях TCP/IP. Программа периодически, с заданным интервалом времени, отправляет запросы выставленным в настройках площадкам, фиксирует поступающие от них ответы и формирует подробную статистику работы сетевых узлов. При использовании такого мобильного инструмента не составит труда узнать, функционирует ли сервер, не «завис» ли он и когда был недоступен, а также проанализировать качество и загруженность канала связи. По сути, Web Monitor представляет собой усовершенствованный вариант диагностической утилиты Ping, входящей в поставку всех современных операционных систем и предназначенной для проверки соединений в сетях на основе TCP/IP.
Программа периодически, с заданным интервалом времени, отправляет запросы выставленным в настройках площадкам, фиксирует поступающие от них ответы и формирует подробную статистику работы сетевых узлов. При использовании такого мобильного инструмента не составит труда узнать, функционирует ли сервер, не «завис» ли он и когда был недоступен, а также проанализировать качество и загруженность канала связи. По сути, Web Monitor представляет собой усовершенствованный вариант диагностической утилиты Ping, входящей в поставку всех современных операционных систем и предназначенной для проверки соединений в сетях на основе TCP/IP.
Более совершенным и технологически продвинутым аналогом Web Monitor является Pulseway — программный комплекс для всестороннего мониторинга рабочих станций и серверов под управлением платформ Windows, macOS и Linux, а также виртуальных сред Microsoft Hyper-V, VMware и XenServer, систем управления базами данных MS SQL Server, серверов IIS, Exchange, Active Directory и других сервисов корпоративного уровня. С его помощью можно в дистанционном режиме контролировать работу устройств и выполняемых задач, просматривать снимки экранов, анализировать производительность оборудования, получать сведения о статусе сервисов и служб, а также возникающих ошибках и сбоях в работе систем. Pulseway позволяет отправлять команды удаленным машинам: перезагружать их, приостанавливать работу процессов, рассылать сообщения авторизованным пользователям и выполнять прочие операции, с полным списком которых можно ознакомиться на сайте продукта pulseway.com. Сбор необходимых сведений и управление компьютерами осуществляется посредством специальных программных клиентов, устанавливаемых на рабочих станциях и серверах.
С его помощью можно в дистанционном режиме контролировать работу устройств и выполняемых задач, просматривать снимки экранов, анализировать производительность оборудования, получать сведения о статусе сервисов и служб, а также возникающих ошибках и сбоях в работе систем. Pulseway позволяет отправлять команды удаленным машинам: перезагружать их, приостанавливать работу процессов, рассылать сообщения авторизованным пользователям и выполнять прочие операции, с полным списком которых можно ознакомиться на сайте продукта pulseway.com. Сбор необходимых сведений и управление компьютерами осуществляется посредством специальных программных клиентов, устанавливаемых на рабочих станциях и серверах.
Ну а замыкает нашу подборку мобильный инструмент WiFi Analyzer, позволяющий использовать смартфон в качестве сетевого сканера. Программа сканирует эфир на предмет сигналов Wi-Fi, определяет уровень сигнала каждой из обнаруженных сетей, а также их характеристики (SSID, канал, метод шифрования, MAC-адрес маршрутизатора и прочее) и на основе собранной информации вырисовывает наглядные графики, отражающие чёткую картину беспроводных сетей. WiFi Analyzer поддерживает работу с различными частотными диапазонами и может быть использована для определения оптимальных настроек и местоположения Wi-Fi-устройств в целях улучшения качества приема сигнала и правильного построения беспроводных локальных сетей в организации. Добрую службу приложение может сослужить при проведении аудита безопасности сети и устранении неисправностей сетевого оборудования.
WiFi Analyzer поддерживает работу с различными частотными диапазонами и может быть использована для определения оптимальных настроек и местоположения Wi-Fi-устройств в целях улучшения качества приема сигнала и правильного построения беспроводных локальных сетей в организации. Добрую службу приложение может сослужить при проведении аудита безопасности сети и устранении неисправностей сетевого оборудования.
Таков наш топ-20 программных продуктов для Android, которые позволяют значительно расширить спектр практического применения мобильных устройств. Сразу скажем, что составленный нами список нельзя отнести к разряду исчерпывающих: в Google Play свыше 2,6 млн приложений (по данным ресурса AppBrain), и выбрать из них самые интересные — непростая задача. Именно по этой причине мы призываем читателей 3DNews поделиться своими заслуживающими внимания широкой аудитории находками в данной области. Оставляйте комментарии, ссылки, краткие описания и названия продуктов, обзор которых мы постараемся сделать в следующих выпусках мобильного дайджеста.
Если Вы заметили ошибку — выделите ее мышью и нажмите CTRL+ENTER.
Определение объема и площади поверхности
Результаты обучения
- Найдите объем и площадь поверхности сферы
Сфера — это баскетбольный мяч, похожий на трехмерный круг. Как и в случае с кругом, размер сферы определяется ее радиусом, который представляет собой расстояние от центра сферы до любой точки на ее поверхности. Формулы для объема и площади поверхности сферы приведены ниже.
Показать, откуда взялись эти формулы, как мы это сделали для прямоугольного твердого тела, выходит за рамки этого курса. Мы аппроксимируем [латекс] \ pi [/ latex] с помощью [latex] 3.14 [/ latex].
Объем и площадь поверхности
Для шара радиусом [латекс] r \ text {:} [/ latex]
пример
Сфера имеет радиус [латекс] 6 [/ латекс] дюймов. Найдите его 1. объем и 2. площадь поверхности.
Решение
Шаг 1 одинаков для обоих 1. и 2., так что покажем только один раз.
и 2., так что покажем только один раз.
| Шаг 1. Прочтите проблему. Нарисуйте фигуру и подпишите это с данной информацией. |
| 1. | |
| Шаг 2. Определите то, что вы ищете. | объем сферы |
| Шаг 3. Имя. Выберите переменную для ее представления. | let [латекс] V [/ latex] = объем |
| Шаг 4.{3} [/ латекс] [латекс] V \ около 904,32 \ text {кубические дюймы} [/ латекс] | |
| Шаг 6. Проверка: Еще раз проверьте свои математические данные на калькуляторе. | |
| Шаг 7. Ответьте на вопрос. | Объем [латекс] составляет приблизительно 904,32 [/ латекс] кубических дюймов. |
[латекс] S \ приблизительно 452,16 [/ латекс]
пример
Глобус Земли имеет форму шара радиусом [латекс] 14 [/ латекс] сантиметров.Найдите его 1. объем и 2. площадь поверхности. Округлите ответ до ближайшей сотой.
Показать решениеРешение
| Шаг 1. Прочтите проблему. Нарисуйте фигуру дать информацию и обозначить ее. |
| 1. | |
| Шаг 2. Определите то, что вы ищете. | объем сферы |
| Шаг 3.{3} [/ латекс] | |
| Шаг 5. Решить. | [латекс] V \ около 11 488,21 [/ латекс] |
| Шаг 6. Чек: Мы предоставляем вам проверить ваши расчеты. | |
| Шаг 7. Ответьте на вопрос. | Объем [латекс] составляет приблизительно 11 488,21 [/ латекс] кубических дюймов. |
| 2. | |
| Шаг 2. Определите то, что вы ищете.{2} [/ латекс] | |
| Шаг 5. Решить. | [латекс] S \ приблизительно 2461,76 [/ латекс] |
Шаг 6. Чек: Мы предоставляем вам проверить ваши расчеты. | |
| Шаг 7. Ответьте на вопрос. | Площадь поверхности [латекс] составляет приблизительно 2461,76 [/ латекс] квадратных дюймов. |
% PDF-1.4
%
1098 0 объект
>
endobj
xref
1098 240
0000000016 00000 н.
0000006539 00000 н.
0000006628 00000 н.
0000006877 00000 н.
0000009019 00000 н.
0000009068 00000 н.
0000009118 00000 п.
0000009168 00000 п.
0000009218 00000 п.
0000009268 00000 н.
0000009318 00000 п.
0000009368 00000 н.
0000009423 00000 н.
0000009473 00000 н.
0000009523 00000 п.
0000009573 00000 п.
0000009624 00000 н.
0000009675 00000 н.
0000009726 00000 н.
0000009777 00000 н.
0000009827 00000 н.
0000009877 00000 н.
0000009927 00000 н.
0000009983 00000 н.
0000010033 00000 п.
0000010376 00000 п.
0000011002 00000 п.
0000011380 00000 п.
0000011671 00000 п.
0000011985 00000 п.
0000012062 00000 н.
0000012141 00000 п.
0000012190 00000 п. 0000012240 00000 п.
0000012290 00000 н.
0000012340 00000 п.
0000012389 00000 п.
0000012440 00000 п.
0000012490 00000 п.
0000012540 00000 п.
0000028656 00000 п.
0000028734 00000 п.
0000029223 00000 п.
0000029582 00000 п.
0000041071 00000 п.
0000049930 00000 н.
0000050006 00000 п.
0000050275 00000 п.
0000050586 00000 п.
0000051008 00000 п.
0000051364 00000 п.
0000052148 00000 п.
0000052511 00000 п.
0000052620 00000 п.
0000052659 00000 п.
0000053271 00000 п.
0000053334 00000 п.
0000053395 00000 п.
0000053508 00000 п.
0000053801 00000 п.
0000054466 00000 п.
0000054846 00000 п.
0000055025 00000 п.
0000055542 00000 п.
0000055932 00000 п.
0000056593 00000 п.
0000057291 00000 п.
0000069842 00000 п.
0000082885 00000 п.
0000096254 00000 п.
0000096484 00000 н.
0000096865 00000 п.
0000096919 00000 п.
0000105449 00000 н.
0000106230 00000 н.
0000106494 00000 н.
0000106757 00000 н.
0000118345 00000 н.
0000118436 00000 н.
0000118507 00000 н.
0000121200 00000 н.
0000012240 00000 п.
0000012290 00000 н.
0000012340 00000 п.
0000012389 00000 п.
0000012440 00000 п.
0000012490 00000 п.
0000012540 00000 п.
0000028656 00000 п.
0000028734 00000 п.
0000029223 00000 п.
0000029582 00000 п.
0000041071 00000 п.
0000049930 00000 н.
0000050006 00000 п.
0000050275 00000 п.
0000050586 00000 п.
0000051008 00000 п.
0000051364 00000 п.
0000052148 00000 п.
0000052511 00000 п.
0000052620 00000 п.
0000052659 00000 п.
0000053271 00000 п.
0000053334 00000 п.
0000053395 00000 п.
0000053508 00000 п.
0000053801 00000 п.
0000054466 00000 п.
0000054846 00000 п.
0000055025 00000 п.
0000055542 00000 п.
0000055932 00000 п.
0000056593 00000 п.
0000057291 00000 п.
0000069842 00000 п.
0000082885 00000 п.
0000096254 00000 п.
0000096484 00000 н.
0000096865 00000 п.
0000096919 00000 п.
0000105449 00000 н.
0000106230 00000 н.
0000106494 00000 н.
0000106757 00000 н.
0000118345 00000 н.
0000118436 00000 н.
0000118507 00000 н.
0000121200 00000 н. 0000121940 00000 н.
0000127889 00000 н.
0000138634 00000 п.
0000144490 00000 н.
0000147311 00000 п.
0000147495 00000 н.
0000149020 00000 н.
0000149976 00000 н.
0000153059 00000 н.
0000154992 00000 н.
0000157016 00000 н.
0000162643 00000 н.
0000165320 00000 н.
0000169423 00000 н.
0000169522 00000 н.
0000169822 00000 н.
0000170336 00000 н.
0000170408 00000 п.
0000170495 00000 н.
0000170600 00000 н.
0000170740 00000 н.
0000170818 00000 н.
0000170890 00000 н.
0000171004 00000 н.
0000171094 00000 н.
0000171184 00000 н.
0000171345 00000 н.
0000171459 00000 н.
0000171579 00000 н.
0000171699 00000 н.
0000171910 00000 н.
0000172515 00000 н.
0000173025 00000 н.
0000173547 00000 н.
0000174156 00000 н.
0000174297 00000 н.
0000174486 00000 н.
0000174721 00000 н.
0000175003 00000 н.
0000176845 00000 н.
0000177130 00000 н.
0000177236 00000 н.
0000178354 00000 н.
0000178608 00000 н.
0000178949 00000 н.
0000179005 00000 н.
0000179425 00000 н.
0000179653 00000 н.
0000121940 00000 н.
0000127889 00000 н.
0000138634 00000 п.
0000144490 00000 н.
0000147311 00000 п.
0000147495 00000 н.
0000149020 00000 н.
0000149976 00000 н.
0000153059 00000 н.
0000154992 00000 н.
0000157016 00000 н.
0000162643 00000 н.
0000165320 00000 н.
0000169423 00000 н.
0000169522 00000 н.
0000169822 00000 н.
0000170336 00000 н.
0000170408 00000 п.
0000170495 00000 н.
0000170600 00000 н.
0000170740 00000 н.
0000170818 00000 н.
0000170890 00000 н.
0000171004 00000 н.
0000171094 00000 н.
0000171184 00000 н.
0000171345 00000 н.
0000171459 00000 н.
0000171579 00000 н.
0000171699 00000 н.
0000171910 00000 н.
0000172515 00000 н.
0000173025 00000 н.
0000173547 00000 н.
0000174156 00000 н.
0000174297 00000 н.
0000174486 00000 н.
0000174721 00000 н.
0000175003 00000 н.
0000176845 00000 н.
0000177130 00000 н.
0000177236 00000 н.
0000178354 00000 н.
0000178608 00000 н.
0000178949 00000 н.
0000179005 00000 н.
0000179425 00000 н.
0000179653 00000 н. 0000179943 00000 н.
0000180008 00000 н.
0000180400 00000 н.
0000180599 00000 н.
0000180894 00000 н.
0000225717 00000 н.
0000225758 00000 н.
0000267155 00000 н.
0000267196 00000 н.
0000267351 00000 п.
0000267789 00000 н.
0000267942 00000 н.
0000285512 00000 н.
0000287293 00000 н.
0000292035 00000 н.
0000297644 00000 н.
0000303760 00000 н.
0000309111 00000 п.
0000309455 00000 н.
0000309608 00000 н.
0000309954 00000 н.
0000310107 00000 н.
0000310414 00000 п.
0000310567 00000 п.
0000310857 00000 п.
0000311010 00000 н.
0000311290 00000 н.
0000311443 00000 н.
0000311766 00000 н.
0000311919 00000 п.
0000312242 00000 н.
0000312395 00000 н.
0000318389 00000 н.
0000324441 00000 н.
0000330464 00000 н.
0000336483 00000 н.
0000342415 00000 н.
0000348346 00000 п.
0000354305 00000 н.
0000360260 00000 н.
0000366228 00000 н.
0000372182 00000 н.
0000378123 00000 н.
0000384069 00000 н.
00003
0000179943 00000 н.
0000180008 00000 н.
0000180400 00000 н.
0000180599 00000 н.
0000180894 00000 н.
0000225717 00000 н.
0000225758 00000 н.
0000267155 00000 н.
0000267196 00000 н.
0000267351 00000 п.
0000267789 00000 н.
0000267942 00000 н.
0000285512 00000 н.
0000287293 00000 н.
0000292035 00000 н.
0000297644 00000 н.
0000303760 00000 н.
0000309111 00000 п.
0000309455 00000 н.
0000309608 00000 н.
0000309954 00000 н.
0000310107 00000 н.
0000310414 00000 п.
0000310567 00000 п.
0000310857 00000 п.
0000311010 00000 н.
0000311290 00000 н.
0000311443 00000 н.
0000311766 00000 н.
0000311919 00000 п.
0000312242 00000 н.
0000312395 00000 н.
0000318389 00000 н.
0000324441 00000 н.
0000330464 00000 н.
0000336483 00000 н.
0000342415 00000 н.
0000348346 00000 п.
0000354305 00000 н.
0000360260 00000 н.
0000366228 00000 н.
0000372182 00000 н.
0000378123 00000 н.
0000384069 00000 н.
00003
00000 н.
0000395960 00000 н.
0000402003 00000 н.
0000407967 00000 н. 0000425541 00000 п.
0000431540 00000 н.
0000437539 00000 н.
0000443560 00000 н.
0000449597 00000 н.
0000455563 00000 н.
0000461553 00000 н.
0000467517 00000 н.
0000473459 00000 н.
0000475232 00000 н.
0000477973 00000 п.
0000478681 00000 н.
0000478834 00000 н.
0000479578 00000 н.
0000479731 00000 н.
0000480158 00000 н.
0000480311 00000 п.
0000480675 00000 н.
0000480932 00000 н.
0000481264 00000 н.
0000481478 00000 н.
0000481683 00000 н.
0000481983 00000 н.
0000482247 00000 н.
0000482504 00000 н.
0000482879 00000 н.
0000484653 00000 н.
0000489589 00000 н.
0000492194 00000 н.
0000494277 00000 н.
0000494502 00000 н.
0000494714 00000 н.
0000494966 00000 н.
0000496030 00000 н.
0000496380 00000 н.
0000498035 00000 н.
0000498900 00000 н.
0000499912 00000 н.
0000500106 00000 н.
0000500278 00000 н.
0000500487 00000 н.
0000500690 00000 н.
0000501702 00000 н.
0000501887 00000 н.
0000502062 00000 н.
0000502232 00000 н.
0000502429 00000 н.
0000503413 00000 н.
0000425541 00000 п.
0000431540 00000 н.
0000437539 00000 н.
0000443560 00000 н.
0000449597 00000 н.
0000455563 00000 н.
0000461553 00000 н.
0000467517 00000 н.
0000473459 00000 н.
0000475232 00000 н.
0000477973 00000 п.
0000478681 00000 н.
0000478834 00000 н.
0000479578 00000 н.
0000479731 00000 н.
0000480158 00000 н.
0000480311 00000 п.
0000480675 00000 н.
0000480932 00000 н.
0000481264 00000 н.
0000481478 00000 н.
0000481683 00000 н.
0000481983 00000 н.
0000482247 00000 н.
0000482504 00000 н.
0000482879 00000 н.
0000484653 00000 н.
0000489589 00000 н.
0000492194 00000 н.
0000494277 00000 н.
0000494502 00000 н.
0000494714 00000 н.
0000494966 00000 н.
0000496030 00000 н.
0000496380 00000 н.
0000498035 00000 н.
0000498900 00000 н.
0000499912 00000 н.
0000500106 00000 н.
0000500278 00000 н.
0000500487 00000 н.
0000500690 00000 н.
0000501702 00000 н.
0000501887 00000 н.
0000502062 00000 н.
0000502232 00000 н.
0000502429 00000 н.
0000503413 00000 н. A` \ 0p3oqyq ~
A` \ 0p3oqyq ~
Иллюстративная математика 8 класс, Раздел 5.20 — Учителя
Распределите студентов по группам по 2 человека. Показать для всеобщего обозрения:
Сфера плотно входит в цилиндр, так что ее окружность касается изогнутой поверхности цилиндра, а верх и низ касаются оснований цилиндра.
Развернуть изображение
Спросите: «На предыдущем уроке мы думали о полусферах в цилиндрах. Вот сфера в цилиндре. Что больше: объем цилиндра или объем шара? Как вы думаете, тот, что побольше, в два раза больше, более чем в два раза или меньше чем в два раза? » затем дайте студентам 1 минуту спокойного времени на размышления.Предложите студентам поделиться своими ответами и держите их так, чтобы их ответы были видны всем на протяжении урока, чтобы на них можно было ссылаться во время обобщения урока.
Покажите видео и попросите учащихся записать все, что они замечают или удивляются во время просмотра. Попросите студентов поделиться тем, что они заметили и задались вопросом. Запишите и покажите их ответы для всеобщего обозрения. Если учащиеся не упомянули об этом, обязательно поднимите эти вопросы:
Запишите и покажите их ответы для всеобщего обозрения. Если учащиеся не упомянули об этом, обязательно поднимите эти вопросы:
- Уведомление:
- Сфера помещается внутри цилиндра.
- Сфера заполнена.
- Вокруг сферы внутри цилиндра есть пространство.
- Требуется объем одного конуса, чтобы заполнить оставшееся пространство в цилиндре.
- Чудо:
- Имеют ли сфера и цилиндр одинаковый радиус?
- У конуса и цилиндра одинаковый радиус?
- Конус и цилиндр имеют одинаковую высоту?
Скажите учащимся, что сфера внутри цилиндра, показанная на видео, такая же, как на изображении, показанном ранее.Спросите студентов: «Это дает нам какие-либо ответы на список чудес?» (Да, это говорит нам о том, что сфера и цилиндр имеют одинаковый радиус.)
Скажите ученикам, что конус и цилиндр имеют одинаковую высоту и одинаковую площадь основания. Спросите студентов:
- «Дает ли это нам еще ответы на список чудес?» (Да, конус и цилиндр имеют одинаковую высоту и радиус.
 )
) - «Что это означает для объема конуса и объема цилиндра на видео?» (Объем конуса равен \ (\ frac13 \) объему цилиндра.)
Покажите видео еще раз и попросите учащихся подумать о том, как мы можем вычислить объем сферы, если мы знаем радиус конуса или цилиндра. Дайте студентам 1 минуту спокойного размышления, а затем время для обсуждения с партнером. Дайте студентам время поработать над задачей, а затем обсудите их в классе.
Видео Объем цилиндра, сферы и конуса доступно на https://player.vimeo.com/video/304138133.
Репрезентация: усвоить понимание. Продемонстрируйте и побудите учащихся использовать цветовое кодирование и аннотации, чтобы выделить связи между представлениями в задаче. Например, попросите учащихся обозначить цветом радиусы и высоту каждого рисунка и при вычислении объема.
Поддерживает специальные возможности для: визуально-пространственной обработки
Представляющий: MLR7 Compare and Connect. Используйте эту процедуру, чтобы сравнить и сопоставить различные способы, которыми учащиеся вычисляли объем сферы.Попросите учащихся подумать, что общего и чем отличается каждый используемый метод. Обратите внимание студентов на различные вычисления (например, \ (2 (250/3) \ pi \) или \ (250 \ pi− (250/3) \ pi = (500/3) \ pi \)), которые приравнивают к объему сферы и как эти вычисления связаны с объемом конуса и цилиндра. В этом обсуждении подчеркните, что язык, используемый, чтобы помочь учащимся понять стратегии, используемые для расчета объема сферы. Эти обмены улучшают использование учащимися математического языка и объемное мышление.
Принцип (ы) дизайна: Максимальное повышение мета-осведомленности; Поддержка смысла
Оценка: 8 — Геометрия 2
Особенности специального образования
Рекомендации по специальному образованию, написанные учителями специального образования штата Индиана, предназначены для повышения вовлеченности и поддержки роста учащихся в рамках специального образования. Это не исчерпывающий список стратегий, но эта поддержка поможет вам сделать обучение математике более доступным для учащихся.Педагоги должны адаптировать стратегии к потребностям ваших учеников и убедиться, что вы создаете возможности для всех учеников, чтобы они могли взаимодействовать с строгим содержанием.
Это не исчерпывающий список стратегий, но эта поддержка поможет вам сделать обучение математике более доступным для учащихся.Педагоги должны адаптировать стратегии к потребностям ваших учеников и убедиться, что вы создаете возможности для всех учеников, чтобы они могли взаимодействовать с строгим содержанием.
| Универсальные стратегии для математиков, испытывающих трудности | |
|---|---|
Стратегии | Примеры |
Вовлечение в стратегии исполнительного функционирования |
|
Примерные примеры |
|
Поощряйте и моделируйте математическую беседу |
|
Проверить понимание при использовании «математических правил»; объясните почему |
|
Обучение математике — ключевые слова |
|
Используйте сокращения, чтобы помочь учащимся запомнить шаги / процессы |
|
Использование общественных дисплеев для поддержки детского творчества и вычислительного мышления на трехмерных поверхностях
большая сфера и 77% понравилось показывать свои проекты всем остальным.
Тем не менее, не всем ученикам нравился этот последний, «публичный» аспект работы
— повторный опрос родителей по электронной почте показал
следующее объяснение от родителей младшего ученика: «Просмотр работы
отображается не важно. Она была взволнована, пока не увидела
, как ее по сравнению с другими учениками ». Это говорит о том, что презентация
в общественных местах требует большей подготовки и внимательности
в управлении ожиданиями учащихся, особенно когда учащиеся имеют широкий диапазон возрастов и способностей
.При изучении
изменений в их достижениях перед тестированием по предметам оценки по математике,
геометрии и использованию языка программирования MoS, было отмечено небольшое увеличение на
в целом в обеих группах и в группе 2 студентов (
секунд). день) добился большего. Это несколько ожидаемо, поскольку
им дали на час больше компьютерного времени с использованием
MoS.
При изучении конкретных достижений студентов перед тестированием по
тех вопросов, которые касались геометрии, студенты получили дополнительные
успехов на своих предварительных знаниях плоской геометрии, однако
набрали меньше баллов по вопросам, которые были направлены на проверку их знаний
сферической геометрии (рисунок 5.) Студенты явно имели некоторые базовые знания о плоской геометрии
до начала семинара, и
эти знания, вероятно, были подкреплены и уточнены во время обучения на семинаре
, о чем свидетельствуют их ответы после тестирования.
Тем не менее, ученики все еще были сбиты с толку относительно представления
в виде линии и треугольника при отображении на сферической поверхности.
Рис. 5. Процент правильных ответов на пять вопросов по геометрии
учащихся, прошедших предварительный и последующий опрос (N = 21)
Что делать с этими результатами? Во-первых, на основе этого первого семинара
, на котором была протестирована ранняя версия программного обеспечения MoS в общественном научном центре
, мы воодушевлены тем, что студенты могут создать
проектов для общественности за несколько часов при поддержке. Тем не менее, в этот короткий день в
Тем не менее, в этот короткий день в
ученики все еще строили свою интуицию о
навигации по трехмерной поверхности, а некоторые оставались в недоумении относительно
неевклидовых идей (например, треугольник может иметь более одного прямого угла
). Этот результат не обескураживает нас, так как 3D-геометрия
является сложной темой в математике. Мы ожидаем, что многодневный семинар
с более длительными периодами позволит детям пройти
еще дальше в изучении сферической геометрии.Наши планы состоят в том, чтобы
продолжить совершенствовать язык программирования MoS и функциональность
, а также добавить семинары, чтобы
можно было расширить до класса с несколькими занятиями, чтобы лучше поддержать интерес детей
к обучению программированию, сферической геометрии и
вычислительное мышление. Кроме того, мы планируем использовать заблуждение детей
относительно неплоских поверхностей как возможность обучения для дальнейшего обсуждения
, а также создать более качественные оценки для измерения
знаний и отношения, полученных на семинаре.
В среднесрочной и долгосрочной перспективе мы планируем создать
документальных материалов, доступных через сам веб-сайт, что позволит провести более
расширенных (или, возможно, продвинутых) исследований такого рода, что
будет трудно представить вкратце. музейная мастерская.
Действительно, одной из мотивирующих особенностей этого проекта является то, что
он объединяет интенсивный музейный опыт (такой как наша мастерская
) с более неторопливой долгосрочной работой дома или в классе
.Возможно, домашние проекты
сами по себе могут послужить поводом для повторного посещения музея в более позднее время
, чтобы опробовать усовершенствованный дизайн сферы, созданный в течение более длительного периода.
Наконец, следует отметить, что проект MoS сам по себе является первым шагом
в том, что мы считаем новым и интересным. Для экземпляра
проект представляет собой начальный шаг, позволяющий детям
создавать программы на неплоской (в данном случае сферической) поверхности
; можно было представить распространение этой идеи на другие интересные математические поверхности
, такие как цилиндры, конусы или гиперболоиды.
Еще одним важным направлением является то, что дети теперь могут писать
и показывать результаты своей программы в больших общественных местах; можно представить себе
в этом ключе, будущие начинания, в которых программы будут отображаться (например) на стенах зданий или на большой игровой площадке
мест. Точно так же настраиваемые интерфейсы типа MoS могут быть
, предназначенными для личных окружающих учебных пространств, таких как базовая планировка
спальни ребенка или школьного класса.Таким образом,
детей в конечном итоге смогут писать программы, которые могут отображать
рисунков на стенах, потолке или поверхностях неподвижных объектов в конкретной комнате
. Нам неизвестно о существующих приложениях, которые могут это сделать. Хотя MoS, как уже отмечалось, является лишь начальным шагом в
таких направлениях, мы полагаем, что он предполагает обещание гораздо более расширенной и повсеместной культуры программирования, доступной
детям в будущем.
5. БЛАГОДАРНОСТИ
Работа, описанная в этой статье, была частично поддержана Национальным научным фондом
в рамках гранта DRL1114388. Майкл
Макферрин разработал оригинальное математическое программное обеспечение MoS;
Антраниг Басман и Мишель Редик запрограммировали текущую систему
. Сара Элович, Риса Вулфсон и Элизабет Хагер —
Барнард совместно проводили семинар, а Майя Вернер-Авидон вела оценку
.Спасибо также технической группе CTI в Зале науки Лоуренса
. Также благодарим Франсиско Саласа из планетария Fiske
и Национальную администрацию океанических и атмосферных исследований
(Боулдер, Колорадо) за их поддержку.
6. ССЫЛКИ
[1] Абельсон, Х. и ДиСесса, А. 1980. Геометрия черепахи.
Кембридж, Массачусетс: MIT Press.
[2] Basman, A .; Redick, M .; и Айзенберг, М. 2012. Математика в сфере
: к общественному контролю над публичными дисплеями.
(рукопись в стадии подготовки. )
)
[3] Клементс Д. Х. и Сарама Дж. 2009. Обучение и преподавание
Ранняя математика: подход, основанный на траекториях обучения. Тейлор и
Фрэнсис. Клементс Д. Х. и Баттиста М. Т. (1989) Изучение
геометрических концепций в среде с логотипом. Журнал
Исследования в области математического образования, 20, стр. 450-467.
[4] Хайн, Г. 1998. Обучение в музее. Рутледж.
[5] Хасауна, А.A. 2009. Оценка программирования логотипа
среди иорданских учеников седьмого класса через черепаху
geometry, International Journal of Mathematical Education
in Science and Technology, 40: 5, 619-639
[6] Papert, S.1980. Mindstorms. NY: Basic Books
IDC 2012 SHORT PAPERS 12-15 июня, Бремен, Германия
251
Как найти центр, радиус и уравнение сферы — Криста Кинг Математика
Как найти центр и радиус из уравнение сферы
Пример
Найдите центр и радиус сферы.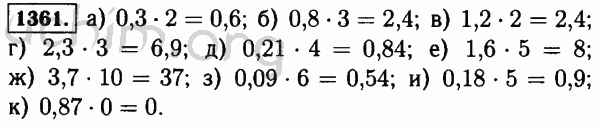 2 ???
2 ???
Для этого нам нужно заполнить квадрат по каждой переменной. Помните, что процесс заполнения квадрата требует от нас использования коэффициента при члене первой степени. Для ??? х ??? это ??? 2x ??? так что коэффициент ??? 2 ???; для тебя??? это ??? — 2г ??? значит коэффициент ??? — 2 ???; для ??? z ??? это ??? — 6z ??? так что коэффициент ??? — 6 ???. Завершение квадрата говорит нам, что мы разделим каждый из этих коэффициентов на «2», а затем возьмем полученный результат и возведем его в квадрат.2 = 25 ???
??? r = 5 ???
Подводя итог нашим выводам, можно сказать, что сфера имеет центр ??? (- 1,1,3) ??? и радиус ??? r = 5 ???.
Сферическая геометрия: изучение мира с помощью математики
Сферическая геометрия: изучение мира с помощью математики Сферический
Геометрия:
Изучение мира с помощью математики
Птолемей :
Изображение любезно предоставлено
Альмагест эфемериды
Калькулятор
Карен Франко
kffranco (at) interchange (точка) ubc (точка) ca
Студент № 46347985
MATH 308, раздел 102
Заключительный проект
15 декабря 2002 г.
Содержание:
Я. Введение
II. Основы сферической геометрии
III. Большие круги
IV. Сферические треугольники
Повесть о двух городах: межконтинентальное применение решения
Сферические треугольники
V. Вывод
Каталожные номера
I. Введение
Капитан Кук, математик? Малоизвестный факт, что капитан Джеймс Кук,
первооткрыватель Австралии, Новой Зеландии, Папуа-Новой Гвинеи, Гавайев, Таити и др.
острова в Тихом океане, получил образование как штурмана, так и математика.На самом деле математика и исследования имеют долгую историю, восходящую к
времена греческих и финикийских моряков.
В современном мире математика обычно рассматривается как «сидячая» наука —
предмет, проблемы которого часто решаются, сидя в классе или
office, а приложения часто связаны с теорией, финансами или бизнесом. Тем не мение,
в дни исследований, когда было обнаружено, что мир действительно
круглый, а не плоский, сферическая геометрия была неотъемлемой частью при отображении
мир, в навигации по семи морям и в использовании положения звезд для
наметить курсы с одного континента на другой.
Тем не мение,
в дни исследований, когда было обнаружено, что мир действительно
круглый, а не плоский, сферическая геометрия была неотъемлемой частью при отображении
мир, в навигации по семи морям и в использовании положения звезд для
наметить курсы с одного континента на другой.
Сферическая геометрия определяется как «исследование фигур на
поверхность сферы »(MathWorld), и является трехмерной, сферической
аналог евклидовой или планарной геометрии. На сфере две линии могут быть
параллельны и все еще пересекаются друг с другом не один раз, а дважды , сумма
углы треугольника больше 180, а кратчайшее расстояние между
две точки на сфере находятся по периметру большого круга, который не
обязательно прямая линия на плоской карте.Поскольку форма Земли примерно
аппроксимированные сферой, эти свойства сферической геометрии помогли исследователям
в построении карты земного шара и астрономов в построении курса планет и
звезды. Сегодняшнее применение этих же свойств включает планирование
полеты, круизы и спутниковые орбиты по всему миру.
II. Основы сферической геометрии
Сфера определяется как замкнутая поверхность в 3D, образованная набором точек равного
расстояние R от центра сферы, O .Радиус сферы
это расстояние от центра сферы до поверхности сферы, поэтому на основе
по приведенному выше определению радиус сферы = R .
Произвольная прямая (не лежащая в сфере) и сфера в трех мерное пространство может либо (а) вообще не пересекаться; (б) пересекаются в одном точка на сфере, когда линия касательная к сфере в точке точка пересечения; или (c) пересекаются ровно в двух точках, когда прямая проходит через сферу.В данном конкретном случае, если линия проходит через центр сферы и пересекает поверхность сферы в двух точках, точки пересечения образуют антиподов сферы. В Северный и Южный полюса (как магнитный, так и географический полюса) являются примерами антиподы на земном шаре.
Рисунок 1: Линия, проходящая через центр сферы; точки пересечения антиподов (PostScript файл)
III. Большие круги
Большие круги
Подобно линиям и сферам, произвольная прямая плоскость и сфера в трех
размерное пространство не может иметь (а) пересечения; (б) одна точка пересечения,
когда плоскость касательна к сфере в этой точке; или (c)
бесконечное количество точек пересечения, когда плоскость пересекает
сфере и образует круг пересечения.
Рисунок 2: Примером меридианов долготы большие круги (анимированный PostScript)
Большие круги определяются как те круги пересечения, которые имеют общие
тот же радиус R и тот же центр O , что и сфера, которую она пересекает.Как следует из их названия, большие круги — это самые большие круги
пересечение можно получить, пропустив прямую плоскость через сферу. На
земной шар, линия или меридиан долготы образует половину большого круга, идущего
от полюса к полюсу и с центром в центре Земли. Другой
Пример большого круга на земном шаре — экватор, находящийся на нулевой широте.
Другой
Пример большого круга на земном шаре — экватор, находящийся на нулевой широте.
Рисунок 3: Параллели широты являются примерами маленькие кружочки (анимированный PostScript)
Представьте себе линию от Северного до Южного полюса, проходящую через центр Глобус.Круги пересечения, образованные земным шаром и плоскостью перпендикулярно этой воображаемой линии образуют линии земного шара или параллели широта. Каждый из этих кругов пересечения, за исключением Экватор, в которой плоскость находится в средней точке линии от полюса к полюсу, называются малыми кругами именно потому, что их радиус измеряется меньше радиуса Земли R .
Навигаторы часто использовали большие круги, чтобы найти наиболее эффективный маршрут к
их пункты назначения.Оказывается, кратчайший путь между двумя точками на
сфера проходит по траектории большого круга, то есть по дуге большого круга. Вы когда-нибудь задумывались, почему самолет летит из Ванкувера на Филиппины?
следует по маршруту, пролегающему над Японией и Кореей, а не по прямому
линия над Тихим океаном? Или почему рейс из Нью-Йорка в Европу должен
путешествовать по Приморью и почти достигать Гренландии вместо того, чтобы идти прямым путем
над Атлантическим океаном? Точная причина логики принятия отличных
круговые пути для путешествий по миру объясняются и доказываются в следующих
раздел.
Вы когда-нибудь задумывались, почему самолет летит из Ванкувера на Филиппины?
следует по маршруту, пролегающему над Японией и Кореей, а не по прямому
линия над Тихим океаном? Или почему рейс из Нью-Йорка в Европу должен
путешествовать по Приморью и почти достигать Гренландии вместо того, чтобы идти прямым путем
над Атлантическим океаном? Точная причина логики принятия отличных
круговые пути для путешествий по миру объясняются и доказываются в следующих
раздел.
IV. Сферические треугольники
Когда дуги трех больших окружностей пересекаются на поверхности сферы,
Линии ограничивают область, известную как сферический треугольник . Углы
между большими кругами измеряются путем вычисления угла между плоскостями
на которых лежат сами большие круги. Как это возможно? Сферический
угол, образованный двумя пересекающимися дугами больших окружностей, равен углу
между касательными линиями, образованными, когда плоскости большого круга касаются круга
в их общей точке (антипод сферы, поскольку два больших круга
пересекаются друг с другом по линии, проходящей через центр сферы).
Вы когда-нибудь слышали о треугольнике, сумма углов которого больше 180? В На рисунке ниже два меридиана долготы разделены углом 90 и обе линии долготы падают перпендикулярно экватору (единственная большая круг широты). Каждый угол в этом сферическом треугольнике равен 90, а сумма всех трех составляет 270.
Рис. 4: В этом треугольнике сумма трех углов превышает 180 (и равна 270)
Сферы имеют положительную кривизну (поверхность изгибается наружу от центра), следовательно, сумма трех углов треугольника превышает 180.В самолете с при нулевой кривизне сумма углов треугольников равна точно 180.
Как и их углы, измеряются длины сторон сферического треугольника.
в градусах или радианах. В частности, длина стороны сферического
треугольник равен измерению его противоположного угла. В географии угол
между двумя меридианами долготы равняется тому же числу градусов, что и дуга
отрезанные этими линиями долготы на любом круге широты. Итак, в приведенном выше
На рисунке каждая из сторон имеет размер 90, поскольку каждый из их противоположных углов
меры 90.
Итак, в приведенном выше
На рисунке каждая из сторон имеет размер 90, поскольку каждый из их противоположных углов
меры 90.
Возможно, наиболее полезное применение сферических треугольников и больших окружностей
вычисление кратчайшего маршрута между двумя точками земного шара. Этот
приложение часто упоминается как решение сферических треугольников и широко использует хорошо известный закон косинусов для треугольников на плоскости: c 2 = a 2 + b 2 — 2ab cos C .Учитывая две стороны сферического
треугольник и угол между этими сторонами, решение для сферической
треугольник дает длину третьей стороны.
Рисунок 5: Решение
сфера
- Сферический треугольник abc образован пересечениями больших окружностей с плоскостями пересекаются в точках OA, OBQ и OCP.
- Самолет PQA частично
состоит из двух касательных: AQ, касательная к c и AP касательная к b ,
и будем называть нашу касательную плоскость.

- Следовательно, OAQ и OAP являются прямыми углами, а PAQ равен углу A противоположной стороны a .
Рисунок 6: Сеть тетраэдр, используемый для решения сферического треугольника (анимированный PostScript)
- Извлечение
окруженный плоскостями тетраэдр и положив его на плоскость в виде сетки, мы
исследуем 4 составных треугольника:
- Треугольники OAQ и OAP
прямоугольные треугольники, поэтому, используя теорему Пифагора:
- PO 2 = AO 2 + ПА 2
- QO 2 = AO 2 + QA 2
- Два других
треугольники, QAP и QOP являются общими плоскими треугольниками, поэтому использование закона косинуса
для плоских треугольников мы видим, что
- PQ 2 = PO 2 + QO 2 — 2 POQO cos a
- PQ 2 = PA 2 + QA 2 -2 PAQA cos A
- Вычитание двух
уравнения выше друг от друга, получаем:
- (PO 2 — PA 2 ) + (QO 2 — QA 2 ) — (2 POQO cos a — 2 PAQA cos А) = (PQ 2 — PQ 2 )
- (ПО 2 — ПА 2 ) + (QO 2 — QA 2 ) — 2 POQO cos a + 2 PAQA cos A = 0
- Замена AO2 на
(PO2 — PA2) и (QO2 — QA2):
- 2 АО 2 + 2 PAQA cos A = 2 POQO cos a
- Деление на оба
сторон по 2 POQO:
- cos a = (AO / PO) (AO / QO) + (PA / PO) (QA / QO) cos A
- Но мы знаем, что
(AO / PO) = cos POA, (AO / QO) = cos QOA, (PA / PO) = sin POA и (QA / QO) = sin
QOA
- cos a = cos POA cos QOA + sin POA sin QOA cos A
- Наконец, подставив
сторона, противоположная сферическому углу, b для угла POA и c для угла QOA:
- cos a = cos b cos c + sin b sin c cos A
- Треугольники OAQ и OAP
прямоугольные треугольники, поэтому, используя теорему Пифагора:
Следовательно, формула для третья сторона, a , сферического треугольника с двумя сторонами, b и c , а их угол при включении A равен
cos a = cos b cos c + sin b sin c cos A
История двух городов: межконтинентальное применение решения
Сферические треугольники
Рисунок 7: Изображения
любезно предоставлено Maps. com
com
Представьте, что вам нужно было найти лучший маршрут из Нью-Йорка в Лондон. Нью-Йорк географически расположен вдоль большого круга 74 0 ‘западной долготы и примерно 40 42 ‘широты к северу от экватора, что составляет 90-40 42 ‘= 49 18’ к югу от Северного полюса. Лондон, напротив, расположен вдоль большого круга долготы 0 5 ‘з.д. примерно на 51 32’ к северу от экватора, что составляет 90 — 51 32 ‘= 38 28’ к югу от Северного полюса.Стороны b и c задаются длиной дуг от Северный полюс до Нью-Йорка и Лондона соответственно, поэтому b = 49 18 ‘и c = 38 28 ‘. Угол A определяется разностью меридианов долготы для два города: A = 74 0 ‘W — 0 5’ W = 73 55 ‘.
Применение решения cos a = cos b cos c + sin b sin c cos A , получаем следующий расчет:
cos a = cos 49 18 ‘ cos 38 28 ‘ + грех 49 18 ‘ sin 38 28 ‘ cos 73 55 ‘
cos a = (0.6521 0,7830) + (0,7581 0,6221 0,2770)
cos a = 0,6412
a = 50,1186 или 50 7 ‘
Это означает, что великий расстояние по кругу между Нью-Йорком и Лондоном составляет примерно 50 7 футов. В милях, учитывая, что один градус большого круга составляет примерно 69 миль (110,4 километров), это расстояние составляет примерно 50,1151 x 69 миль = 3458 миль (5533,0934 км).
В.Вывод
Геометрия происходит от греческих слов geometria и .
geometrein , что означает «измерение земли». С другой стороны, география
получил свое значение от греческих слов geographia и geographein что означает «описывать или писать о земле». Можно было ожидать слов так
похожи по смыслу, чтобы быть похожими и по концепции. Однако два поля
были отдельными и отличными друг от друга до времен Древней Греции, когда Птолемей
(астроном, математик и географ) использовал геометрию в рассуждениях
подробнее о Земле и ее форме:
«В географии надо созерцать протяженность всей земли, а также ее форму и положение под небом, чтобы можно было правильно определить, какие особенности и пропорции той части, с которой имеешь дело… Это великое и изысканное достижение математики, чтобы показать все эти вещи человеческому разуму … «
Интересно, что это было
также Птолемей, а не Христофор Колумб, открывший, что Земля
сферический, а не плоский, и изложил свое обоснование в Альмагесте 1300
лет до того, как Колумб совершил кругосветное плавание:
«Если бы земля была плоской с востока на запад звезды взойдут для жителей Запада так же быстро, как и для восточные, что неверно.Кроме того, если бы земля была плоской с севера на юг и наоборот, звезды, которые всегда были видны любому, продолжали быть таким, куда бы он ни пошел, что неверно. Но для человеческого зрения это кажется плоским потому что он такой обширный ».
Подобно геометрии и географии, миры сферической геометрии (используются в география) и плоская геометрия (обычно преподается на большинстве курсов геометрии). тесно связаны, но в то же время очень разные.
Любой, кто закончил среднюю школу по геометрии (или в некоторой степени, элементарная геометрия) знает, что в евклидовой или планарной геометрии два параллельных линии никогда не пересекаются, сумма трех углов треугольника в сумме дает 180, и Самый короткий путь из одной точки в другую — прямая. в мир сферической геометрии, две параллельные линии на больших кругах пересекаются дважды сумма трех углов треугольника на поверхности сферы превышает 180 из-за положительной кривизны и кратчайший путь от одной точки до другой — не прямая линия на карте, а линия, которая следует за малой дугой большой круг.Карты позволяют передавать сферический вид планарное изображение, проецируя топологии и местоположения Земли на выровнять поверхность методами Молота, Меркатора или цилиндрической формы. Последовательный и стандартное представление, минимизирующее проективные искажения, еще предстоит учредил.
Открытие сферической геометрии не только изменило историю и лицо математики и геометрии Евклида, но также изменили взгляды людей и наметил мир.Используя эти новые знания, исследователи и астрономы использовали круговой путь звезд, чтобы перемещаться по земле, открывать новые земли и разум о космосе.
Ссылки:
Borowski, E.J. и Борвейн, J.M. Справочник по математике Коллинза. 1989: Коллинз. Лондон и Глазго.
Кассельман, доктор В. Пособие по математической иллюстрации. [MATH 308 текст]
Хогбен, Ланселот. Математика для миллиона. 1951: W.W. Нортон и Компания, Inc. Нью-Йорк.
Хогбен, Ланселот. Наука для гражданина. 1950: W.W. Нортон и Company, Inc. Нью-Йорк.
Maps.com — учись и играй. Навыки карты: большие круги. [Maps.com веб-страница]
Музей моряков, ул. Музей моряков — Ньюпорт-Ньюс, Вирджиния. [фоновое изображение для Интернета страница, историческая справка]
Оссерман, Роберт. Поэзия Вселенной: математическое исследование Космос. 1995: Якорные книги, Doubleday. Нью-Йорк.
Полкинг, Джон К. Геометрия сферы 1. [базовый информация о сферах]
WhatIs? Com. Широта и долгота: определение WhatIs. [что широта и долгота?]
Wolfram Research, Inc. MathWorld: Мир математики Эрика Вайсштейна. [MathWorld Web страница]
УСТРАНЕНИЕ НЕПОЛАДОК:
Для запуска любого из файлы PostScript, вам понадобится бесплатный интерпретатор PostScript, установленный на вашем компьютер: GhostView и GhostScript — самые популярные ед.Щелкните по ссылкам, чтобы получить их.
Для latitude.ps и longitude.ps, убедитесь, что у вас есть ps3d.inc в том же каталоге, что и эти файлы (см. файл KarenFrancoProject.zip, если он отсутствует).
.

 )
)
