Что такое угол? Определение, виды, как обозначают, примеры
Определение угла
Угол — это простая геометрическая фигура. Определение угла напрямую связано с понятием луча.
Луч — прямая линия, у которой есть начало, но нет конца, и продолжается она только в одну сторону.
Если нам дана прямая a на плоскости, и на ней есть некоторая точка O — выходит, что прямая разделена точкой на две части, каждая из которых является лучом с началом в точке O.
Луч можно обозначить одной строчной буквой латинского алфавита или двумя прописными. Например, вот так:
Угол — часть плоскости между двумя линиями, исходящими из одной точки. Каждая сторона угла является лучом, а вершина — общим началом сторон.
Что такое вершина и стороны угла
В математике существует специальный символ для обозначения угла, вот он: ∠.
Если стороны угла названы малыми латинскими буквами, то их записывают после символа. Например, так: ∠ab или ∠ba.
Если стороны угла названы большими буквами, то обозначение угла будет состоять из символа и трех букв, при этом вершина всегда записывается в центре. При сторонах угла OA и OB название угла запишем так: ∠AOB и ∠BOA. Также можно назвать угол одной большой буквой, которая указывает на его вершину, например: ∠O.
Иногда встречается обозначение в виде цифр — так тоже можно.
Для наглядности — все способы обозначения углов:
Так как угол делит плоскость на две части, одна будет внутренней областью угла, а другая — внешней областью угла. Вот так:
Единица измерения углов — градусы.
Символ для обозначения градуса угла: °.
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Виды углов
Есть разные типы углов и у каждого своё название:
- острый
- прямой
- тупой
- развернутый
- выпуклый
- полный
Различать виды углов в геометрии важно. Определять можно на глаз или с помощью линейки.
Прямой угол — это угол, стороны которого перпендикулярны друг другу. Прямой угол всегда равен 90°.
Если два смежных угла равны между собой, то каждый из них является прямым. Для удобства прямой угол обозначается уголком. Вот так:
На картинке изображены два прямых угла ∠AOC и ∠COB. Общая сторона OC перпендикулярна прямой AB, а точка O — основание перпендикуляра.
Острый угол — это угол, который меньше прямого угла, то есть < 90°.
Развернутый угол — это открытый угол, который образован двумя лучами и равен сумме двух прямых углов. Развернутый угол равен 180°. Как выглядит развернутый угол, показано на первой картинке.
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Неразвернутый угол — это любой угол, который не является развернутым, то есть не равен 180°.
Тупой угол — это угол, который больше прямого угла, но меньше развернутого:
90° < тупой угол < 180°.
Выпуклый угол — это угол, который больше развернутого угла, но меньше полного:
180° < выпуклый угол < 360°.
Полный угол — это угол, обе стороны которого совпадают с одним лучом.
Он равен сумме четырех прямых углов, то есть = 360°.
Прилежащие углы — это пара углов с общей вершиной и стороной, другие стороны при этом лежат по разные стороны от общей стороны.
На картинке мы видим два прилежащих угла ∠AOB и ∠BOC, общую вершину O и общую сторону OB.
Можно сформулировать определение по-другому: если из вершины любого угла провести луч, разделяющий угол на два, то образованные углы будут прилежащими.
Чтобы найти угол, который разделен лучом, нужно сложить полученные углы: ∠AOB = ∠AOC + ∠COB. Из этого можно выделить следующие верные разности:
- ∠AOC = ∠AOB − ∠COB,
- ∠COB = ∠AOB − ∠AOC.
Запоминаем!
Угол называется прямым, если он равен 90°, острым, если он меньше 90°, тупым, если он больше 90°, но меньше 180°. Развернутый угол равен 180°.
Онлайн-школа Skysmart приглашает детей и подростков на курсы по математике — за интересными задачами, новыми прикладными знаниями и хорошими оценками!
Сравнение углов
Для сравнения углов можно использовать самый простой способ из программы 4 класса — метод наложения.
Для этого нужно совместить две вершины и сторону одного угла со стороной другого. Если стороны заданных углов совпадут, значит углы равные. Если нет, то угол, который лежит внутри другого, будет меньшим. Здесь два наглядных примера с равными и неравными углами:
При этом развернутые углы всегда являются равными.
Совмещение углов ∠𝐴𝐵𝐶 и ∠𝑀𝑁𝐾 происходит следующим образом:
- Вершину 𝐵 одного угла совмещаем с вершиной 𝑁 другого угла.
- Сторону 𝐵𝐴 одного угла накладываем на сторону 𝑁𝑀 другого угла так, чтобы стороны 𝐵𝐶 и 𝑁𝐾 располагались в одном направлении.
Если совпадут и другие стороны, то углы равны: ∠𝐴𝐵𝐶 = ∠𝑀𝑁𝐾.
Если нет, то один угол — меньше другого: ∠𝐴𝐵𝐶<∠𝑀𝑁𝐾.
Сравнить углы можно также, измерив их величины. Для этого понадобится специальный инструмент для построения и измерения углов — транспортир.
Вот как он выглядит:
Как правильно измерять углы
Измерение углов похоже на измерение отрезков: нужно сравнить их с углом, принятым за единицу измерения. В геометрии обычно за единицу измерения принимают
Градусная мера угла — положительное число, которое показывает, сколько раз градус и его части укладываются в данном углу.
Есть еще две возможные меры угла: минуты и секунды. Они позволяют выполнять более точные расчеты, особенно, когда величина не является целым обозначением градуса.
Минута — 1/60 часть градуса. Обозначается ´.
Секунда — 1/60 часть минуты. Обозначается ´´.
Градус состоит из 3600 секунд, то есть: 1° = 60´ = 3600´´.
Как происходит измерение угла: сначала измеряют стороны угла, а после — его внутреннюю область. Всегда нужно считать количество уложенных углов, так как они предопределяют меру измеряемого угла.
Когда луч делит угол на два или более углов, градусная мера всего угла равна сумме градусных мер этих углов.
На рисунке изображен угол АОВ, он состоит из углов АОС, СОD и DОВ. Можно записать так: ∠AOB = ∠AOC + ∠COD + ∠DOB = 45° + 30° + 60° = 135 °.
Равные углы имеют равную градусную меру.
Обозначение углов на чертеже
Чертеж помогает решать задачки по геометрии в разы быстрее. Чтобы наглядно изображать углы и прочие фигуры, придумали даже отдельное направление — геометрический чертеж.
Задачи с углами могут быть разными, и не всегда есть возможность правильно изобразить и отметить угол. Вот что важно запомнить при обозначении лучей и углов:
- Равные углы обозначают одинаковым количеством дуг.
- Неравные углы обозначают разным количеством дуг, чтобы они отличались между собой.
На чертеже отмечены три неравных угла:
Для обозначения на чертеже более трех углов используем разные виды дуг: волнистые, зубчатые.
Обозначать углы можно разными цветами. Главное, чтобы было просто и броско. При этом не обязательно отмечать все-все углы — достаточно только тех, которые нам нужны для решения задачки.
Угол. Обозначение углов
Представим себе такую историю.
– Саша, а ты знаешь, что листья на ветке растения всегда располагаются в строгом порядке? – спросил Паша.
– Что значит в строгом порядке? – удивился Саша. – Как числа в натуральном ряду что ли?
– Нет, Саша, листья на ветке растения отстоят друг от друга на определённый угол по или против часовой стрелки – продолжил Паша. – Величина этого угла разная для разных растений.
– Ого! – удивился Саша. – И ведь правда, а я даже и не замечал такого раньше! Но ведь угол – это геометрическое понятие. Зачем растениям углы?
– Такое расположение позволяет листьям растений наиболее эффективно получать влагу и солнечный свет.
– Паша, а ты знаешь, как в математике строят углы? – решил спросить Саша.
– Да, – ответил Паша, – если мы на листе бумаги из одной точки проведём два луча, то получим фигуру, которая называется углом.
– А углы в математике тоже имеют свои названия? – спросил Саша.
– Да, но об этом лучше спросить у Электроши – сказал Паша.
– Ребята, прежде чем я вам расскажу об углах и их обозначениях, давайте немного разомнёмся и выполним устные задания, – предложил Электроша.
– Давайте сверимся! Посмотрите, что у вас должно было получиться!
– Ну а теперь поговорим об углах, – продолжил
Электроша. – Давайте проведём на листе бумаги два луча ВА и ВС с общим началом
в точке В.
Запомните! Фигуру, образованную двумя лучами, имеющими общее начало, называют углом.
– Значит, угол – это два луча с общим началом? – спросил Саша.
– Всё верно! – подтвердил Электроша.
Лучи называют сторонами угла, а их общее начало – вершиной угла.
Так, например, в угле, который мы с вами построили, лучи ВА и ВС – это стороны угла, а точка В – его вершина.
– Визуально углы делят на «внешний»
и «внутренний». Мы же чаще будем работать именно с внутренними углами.– А как обозначают углы? – спросил Паша.
– Для обозначения углов используют следующий символ: . Тогда наш угол можно обозначить так: ∠АВС или ∠СВА. Обратите внимание: называть угол можно с любого края, но не с вершины. Буква, которая соответствует вершине угла, должна всегда находиться в середине названия.
Также этот же угол можно обозначить и короче,
одной заглавной латинской буквой, указывающей его вершину.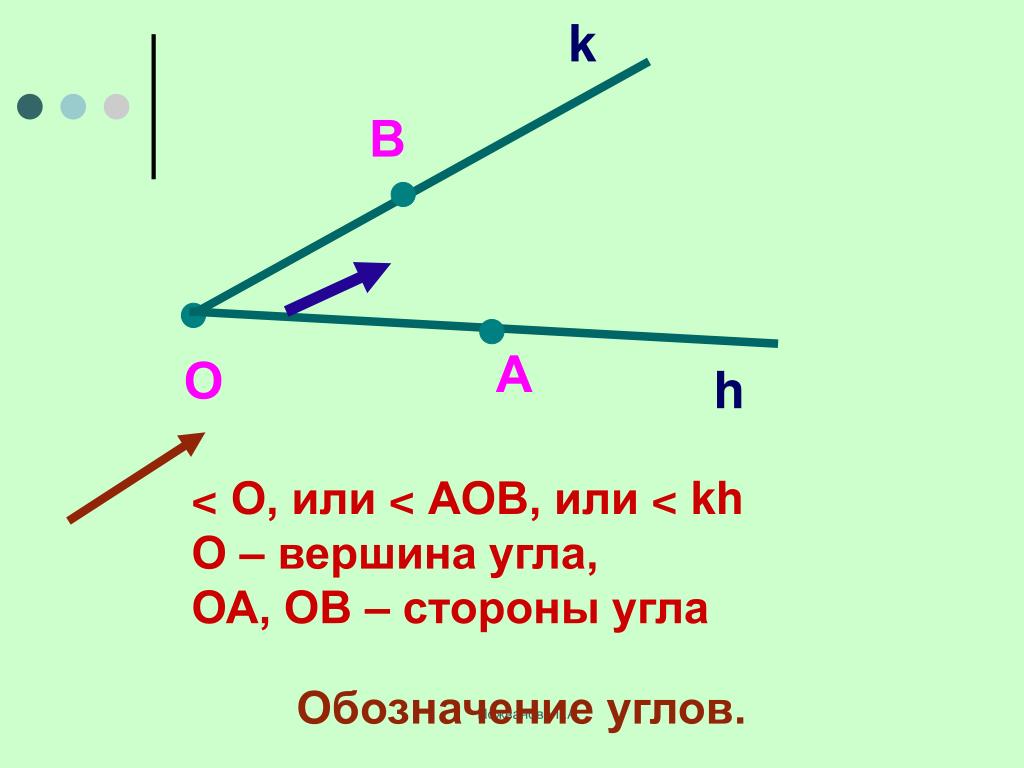
Тогда наш угол можно
обозначить так: угол В.
– Посмотрите, я построил три различных угла – продолжил Электроша. – Может, вы сможете их назвать? – спросил он у ребят.
– Первый угол можно обозначить, как ∠PQR – начал Саша, – второй ∠EFT, а третий – ∠KOZ.
– Ещё эти углы можно обозначить так, – продолжил Паша, –
– Молодцы! – похвалил ребят Электроша. – А теперь посмотрите на следующие углы. Попробуйте сосчитать и назвать все углы на рисунке.
– Угол AOB, – начал Паша, – угол BOC и угол AOC.
– Всё верно! – сказал Электроша. – На нашем рисунке изображены три угла.
– А как же угол О? – спросил Саша.
– Ни один из трёх углов на рисунке нельзя обозначить только одной буквой. У них одна и та же вершина – точка О, но сами углы разные.
– Два угла могут иметь одну общую сторону, –
продолжил Электроша. – На нашем рисунке углы AOB и BOC имеют общую сторону ОB.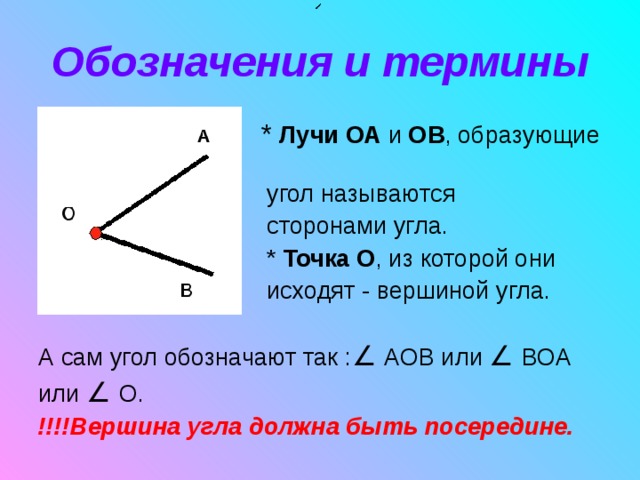
Также в этом случае говорят, что луч ОB проходит между сторонами угла АОC и делит его на два угла: АОB и BОC.
– А теперь давайте проведём небольшой эксперимент. Возьмём лист бумаги, отметим на нём точки M, О, N таким образом, как показано на рисунке. Перегнём лист так, чтобы его две соседние стороны совместились. Затем по линии сгиба проведём луч, например, ОP. Обратите внимание, мы получили два угла: угол MОP и угол NОP, которые совпадают.
Запомните! Два угла называют равными, если они совпадают при наложении.
– То есть углы MОP и NОP равны? – решили спросить ребята.
– Да! – ответил Электроша. – Угол MОP равен углу NОP, а записывают это так: . На рисунке равные углы, как правило, отмечают равным количеством дужек.
– Луч ОP имеет своё название. Такой луч называют биссектрисой угла.
Запомните! Биссектриса делит угол на два равных угла.
– А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько заданий.
Задание первое: отметьте в тетради точку О и проведите через неё две прямые. На прямых отметьте точки А, B, C и D по разные стороны от точки О. Сколько всего углов у вас получилось? Назовите их.
Решение: на рисунке получилось шесть углов: угол АОB, угол BОC, угол CОD, угол DОА, угол АОC и угол BОD.
Следующее задание: на рисунке угол АОC равен углу BОD. Есть ли ещё на рисунке равные углы? Если есть, то назовите их.
Решение: угол АОC состоит из двух углов: угла АОB и угла BОC. Аналогично и угол BОD состоит из углов BОC и CОD. Видим, что угол BОC общий угол углов АОC и BОD. Значит, углы АОB и CОD равны тоже.
– Ребята, вы отлично справляетесь с заданиями! – с радостью сказал Электроша. – А значит, вы обязательно справитесь с моей непростой задачей.
Итак, масса 4 персиков и 3 яблок вместе 425 г.
А 3 персика и 4 яблока (вместе) имеют общую массу 345 г. Все персики имеют
одинаковую массу. Яблоки тоже весят одинаково. Какова общая масса одного
персика и одного яблока (вместе)?
Решение: так как по условию задачи 4 персика и 3 яблока вместе весят 425 г, а также 3 персика и 4 яблока вместе весят 345 г, то можем узнать, сколько будут весить 7 персиков и 7 яблок вместе, то есть к 425 прибавим 345, получим 770 г. А теперь можем найти вес одного персика и одного яблока вместе: 770 разделим на 7 и получим 110 г.
Ответ: 110 грамм общая масса одного персика и одного яблока.
Углов
Углы используются в повседневной жизни. Инженеры и архитекторы используют углы для конструкций, дорог, зданий и спортивных сооружений. Спортсмены используют углы, чтобы повысить их производительность. Плотники используют углы, чтобы сделать стулья, столы и диваны. Художники используют свои знания ракурсов для набросков портретов и картины.
Если две прямые встречаются (или пересекаются) в одной точке, то образуется угол .
Точка пересечения линий называется 9.0004 вершина .
Ниже показан угол.
Линии AB и AC пересекаются в точке A , образуя угол. Точка A является вершиной угла, и линии, которые встречаются, образуя угол, называются плечами угла .
Именование углов
Размер угла
Величина поворота от одного плеча угла к другому называется размер угла .
Величина угла измеряется в градусах ; и используемый символ
представлять степень.
В полном обороте (или круге) 360.
Примечание:
градуса определяется таким образом, что угол одного полного оборота (или окружность) составляет 360 градусов.
Измерение углов
Транспортир используется для измерения углов. В этом разделе мы будем рассмотреть использование транспортира, который имеет форму полукруга и два шкалы отмечены от 0 до 180.
Две шкалы облегчают нам измерение
углы смотрят в разные стороны.
Чтобы измерить угол ABC , поместите транспортир на
угла так, чтобы центр транспортира находился прямо над углом
вершина, В; а базовая линия транспортира проходит по плечу, BA ,
угла.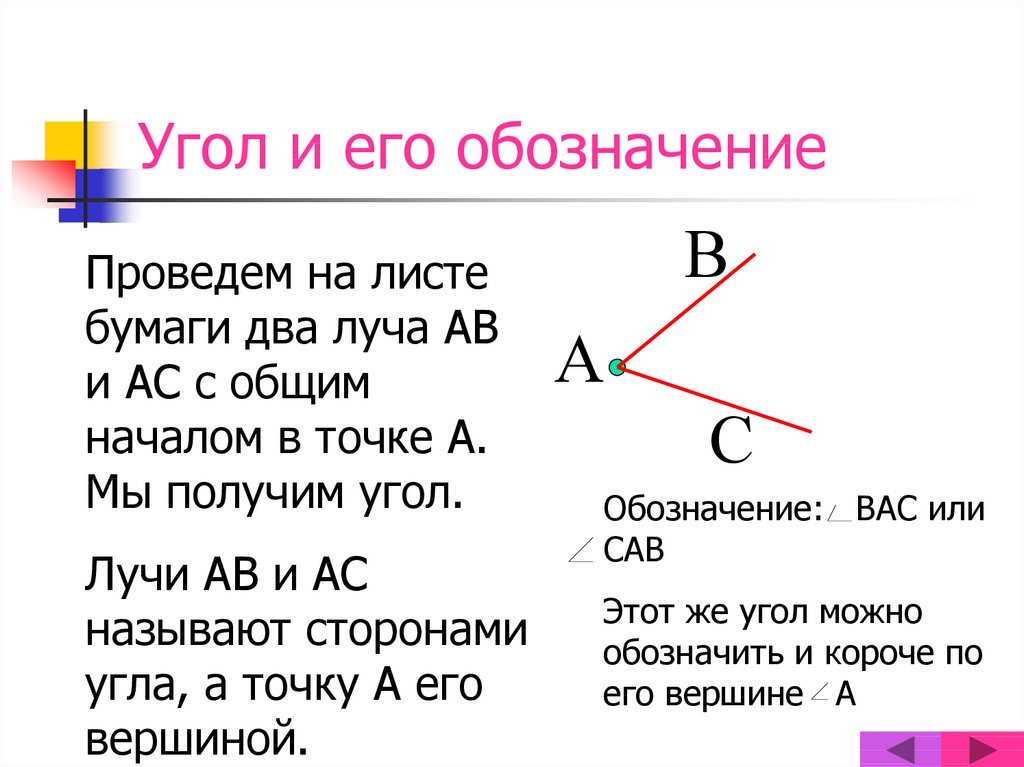
Внутренней шкалой измеряем угол ABC , так как плечо AB проходит через ноль внутренней шкалы . Следующий внутренней шкалы вокруг транспортира, мы находим, что другое плечо, до н.э. , проходит через внутреннюю шкалу в точке 60. Итак, размер угла ABC равен 60 градусов. Запишем это так:
Чтобы измерить размер угла PQR , поместите транспортир на
угла так, чтобы центр транспортира находился прямо над углом
вершина, Q ; а базовая линия транспортира проходит по плечу PQ ,
угла.
Используем внешнюю шкалу для измерения угла PQR , так как плечо PQ проходит через ноль внешней шкалы .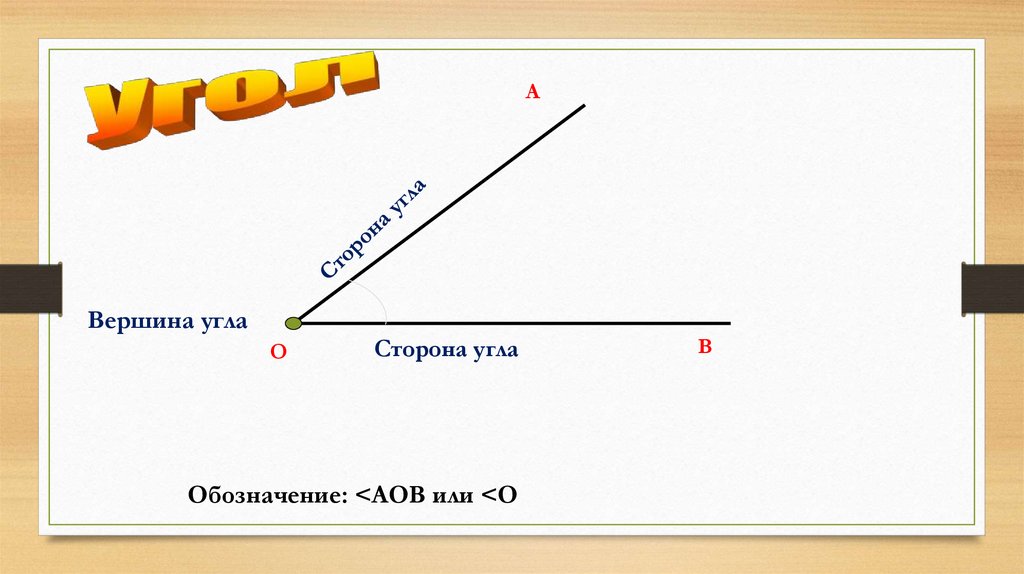
Следующий
внешней шкалы вокруг транспортира, мы находим, что другой рычаг, QR ,
проходит через внешнюю шкалу под углом 120. Таким образом, размер угла PQR равен
120 градусов. Запишем это так:
Типы уголков
Углы классифицируются по размеру.
Острый угол больше 0 и меньше 90.
A прямой угол ровно равен 90.
Обратите внимание, что прямой угол отмечен на схеме маленьким квадратом.
Тупой угол больше 90 и меньше 180.
Прямой угол ровно равен 180.
Угол рефлекса больше 180 и меньше 360.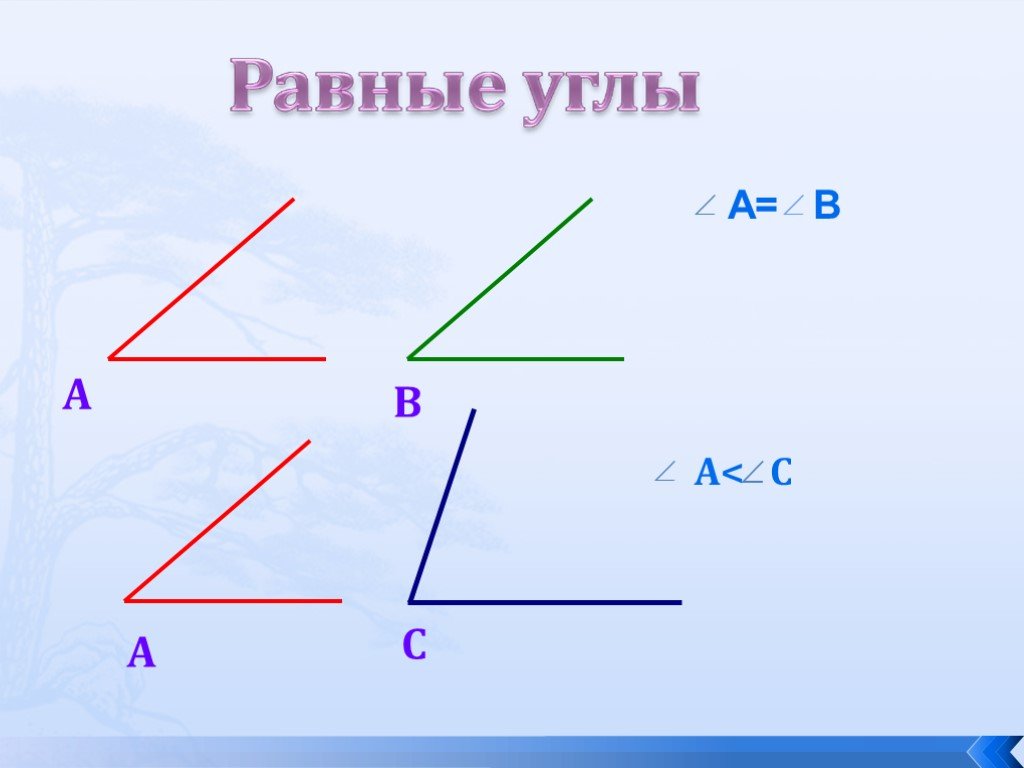
Перигон (или оборот ) — это угол, который точно равен
360.
Измерение углов отражения
Напомним, что:
Транспортир можно использовать для измерения величины острого угла (между 0 и 90) и тупой угол (от 90 до 180).
Теперь мы будем использовать транспортир для измерения угла рефлекса PQR .
Чтобы измерить угол рефлекса PQR , вытяните рычаг PQ до A , чтобы сформировать угол PQA , который представляет собой прямой угол. Затем измерьте размер угол AQR и добавить 180.
Основные термины
точка, угол, вершина, плечи угла, величина угла, градусы, транспортир, внутренний шкала, внешняя шкала, острый угол, прямой угол, тупой угол, прямая угол, угол отражения, перигон, оборот
Введение в углы | SkillsYouNeed
После того, как вы усвоили идею точек, линий и плоскостей, следующее, что нужно рассмотреть, это то, что происходит, когда две линии или лучи встречаются в точке, создавая угол между ними.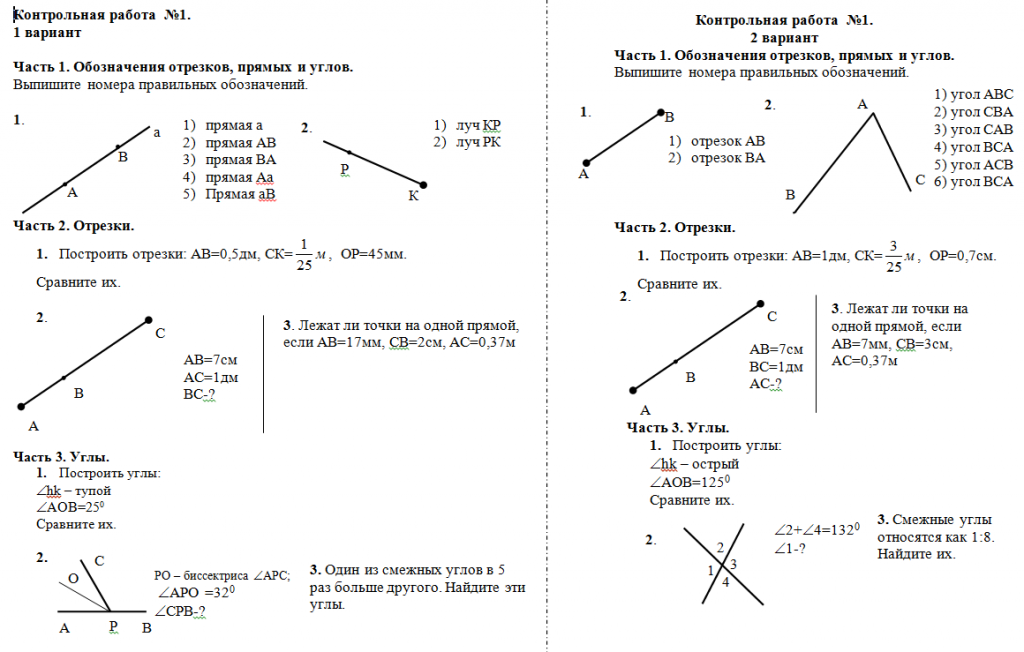
Углы используются в геометрии для описания таких фигур, как многоугольники и многогранники, а также для объяснения поведения линий, поэтому полезно ознакомиться с некоторыми терминами и с тем, как мы измеряем и описываем углы.
Что такое угол?
Углы образуются между двумя лучами, исходящими из одной точки:
Углы обычно рисуются в виде дуги (части круга), как указано выше.
Свойства углов
Углы измеряются в градусах , что является мерой окружности или вращения.
Полный оборот, при котором вы возвращаетесь лицом в том же направлении, составляет 360°. Таким образом, полукруг равен 180°, а четверть окружности или прямой угол равен 90°.
Два или более угла на прямой в сумме дают 180°. На приведенной выше диаграмме круг слева разделен на три сектора, углы зеленого и белого секторов равны 9.0°, что в сумме дает 180°.
На рисунке справа видно, что углы a и b также составляют в сумме 180°.
Когда вы смотрите на диаграмму таким образом, это легко увидеть, но на практике это также удивительно легко забыть.
Обозначение различных углов
Угол меньше 90° называется острым , а угол больше 90°, но меньше 180° тупым .
Угол, равный 180°, называется прямым . Углы больше 180° называются рефлекс углы.
На циферблате часов можно демонстрировать разные ракурсы. Часовая стрелка часов движется по кругу по мере прохождения времени в течение дня. Угол поворота выделен зеленым цветом.
Противоположные углы: пересекающиеся прямые
При пересечении двух прямых противоположные углы равны. В этом случае не только а и а совпадают, но, конечно же, а и b в сумме дают 180°:
Пересечения с параллельными линиями: особый случай
Наша страница Введение в геометрию знакомит с концепцией параллельных линий: линий, которые всегда идут бок о бок и никогда не пересекаются, как железнодорожные пути.
Углы вокруг любых прямых, пересекающих параллельные прямые, также обладают некоторыми интересными свойствами.
Если две параллельные прямые (А и В) пересекает третья прямая (С), то угол, под которым пересекаются пересекающиеся прямые, будет одинаковым для обеих параллельных прямых.
Говорят, что два угла a и два угла b равны соотв.
Вы также сразу увидите, что a и b в сумме дают 180°, так как они лежат на прямой.
Угол с, который, как вы поняли из предыдущего раздела, идентичен углу а, называется альтернативным с а.
Z и F Углы
c и a называются z-углами , потому что, если вы проследите линию от вершины c до низа a, она образует форму буквы z (обозначена красным на диаграмме выше). ).
а и а считаются F-образные углы , поскольку линия образует форму F от основания верхнего угла a вниз и вокруг основания нижнего угла a (зеленый цвет на схеме)
Измерение углов
A транспортир обычно используется для измерения углов.
Транспортиры обычно имеют круглую или полукруглую форму и сделаны из прозрачного пластика, поэтому их можно накладывать на фигуры, нарисованные на листе бумаги, что позволяет измерить угол.
В этом примере показано, как использовать транспортир для измерения трех углов треугольника, но тот же метод применим и к другим фигурам или любым углам, которые вы хотите измерить.
- Совместите центральную отметку на основании транспортира с вершиной , или точкой пересечения линий. Треугольник имеет три вершины, по одной на каждый измеряемый угол.
- Большинство транспортиров имеют двунаправленную шкалу, что означает, что вы можете выполнять измерения в любом направлении. Убедитесь, что вы используете правильный масштаб — вы сможете легко определить, больше или меньше ваш угол 90 °, и, следовательно, используйте правильный масштаб. Если вы не уверены, вернитесь к нашему разделу, посвященному именованию углов.
В этом примере зафиксированы углы A=90° B=45° и C=45°.
Многоугольники часто определяются своими внутренними углами, а сумма внутренних углов зависит от количества сторон. Например, сумма внутренних углов треугольника всегда равна 180°. Подробнее об этом читайте на нашей странице Polygons .
Градусы или радианы?
Когда нам нужно измерить или описать угол, мы обычно используем «градусы» в качестве единицы измерения. Однако очень редко можно встретить углы, упомянутые в 9.0217 радиан .
Радиан — это международная стандартная единица измерения углов (СИ), которая используется во многих областях науки и математики.
Выше мы сказали, что полный оборот углов через дугу окружности равен 360°. Оно также равно 2π радианам, где π (пи) — специальное число, равное (приблизительно) 3,142 (подробнее о π см. на нашей странице Special Numbers and Concepts ).
Один радиан равен 360/2π = 57,3°. Мы также используем пи, когда нам нужно вычислить площадь или окружность круга, или объем сферы (подробнее об этом читайте на нашей странице 9).